正方形专练二

合集下载

长方形、正方形的周长与面积专项练习

长方形、正方形的周长与面积专项练习
1、一个正方形鱼塘，边长15米，这个鱼塘的周长是多少米？面积是多少？
2、一个正方形鱼塘，绕着走一圈，走了36米，这个鱼塘有多大？
3、给一块长方形的桌布四周缝上花边，花边的长度是36分米，桌布长1米，这块桌布有多大？
4、有一块长方形西瓜地，长50米，宽30米，平均每平方米可收西瓜35千克，这块瓜地共可收西瓜多少千克？
5、同学们办的墙报，长 18 分米、宽 12 分米。

墙报的面积是多少平方分米？在墙报四周贴一条花边，花边的总长是多少米？
6、小红每天坚持锻炼身体，她绕着小区里的正方形荷花池跑步，跑二圈正好是240米，这个正方形荷花池的面积是多少？
7、一台压路机，每分钟行驶50米，压路的宽度是6米。

压路机行驶8分钟，能压多大的路面？
8、一个长方形广场，长30米，宽20米。

小明绕着广场走5圈，他走了多远？这个广场的面积是多少？
9、一间长方形的办公室，长10米，宽8米。

要铺上边长4分米的地砖，需要多少块地砖才能铺满？
10、一个长方形的游泳池，长12米，宽9米。

要铺上周长24分米的正方形地砖，需要多少块地砖才能铺满？
11、一个长方形的商场，长24米，宽18米。

要铺上面积36平方分米的正方形地砖，需要多少块地砖才能铺满？。

部编版三年级下册数学面积应用题专项练习卷二(附答案)

部编版三年级下册数学面积应用题专项练习卷
二（附答案）
1、一张床长9米，宽20分米，它的面积是多少?
2、一块边长为800米的正方形实验田,如果每公顷收稻谷约8吨。

这块实验田可收稻谷约多少吨?
3、莉莉家的客厅宽4m,长比宽的2倍少1m.
(1)莉莉家的客厅的面积是多少?
(2)这种瓷砖的边长是2dm，如果莉莉家用这种瓷砖铺客厅的话，至少需要多少块?
4、一块长方形地与一块正方形地的周长相等,长方形地长30m，宽是10m,正方形地的面积是多少平方米?
5、小明沿着长200米的长方形操场跑了一圈，共跑了600
米。

这个操场的面积是多少？
6、用篱笆围成一个长方形的养鸡场，一边利用18长的墙壁，篱笆共长40米,求养鸡场的面积。

7、把一张长12分米、宽10分米的长方形铁皮剪成一个面积最大的正方形，这张正方形铁皮的面积是多少平方分米?
8、将一块长3米、宽2米的长方形布,剪去一个面积最大的正方形，剩下部分的面积是多少平方米?
9、幼儿园要粉刷走廊的一面墙作为展示墙，这面墙长22米、高3米，墙上有4扇边长为20分米的正方形窗户。

这面墙要粉刷的面积是多少平方米?
10、如果是一块菜地，长是33米，宽是27米，菜地中间留了宽1米的路，把菜地平均分成四块，每块的面积是多少?
答案
1.1800平方分米或18平方米
2.512吨
3.28平方米700块
4.400平方米
5.2000平方米
6.198平方米
7.100平方分米
8.2平方米
9.50平方米
10.208平方米。

长方体正方体专项练习题

长方体正方体专项练习题长方体正方体单元练题（应用题）1.一个长方体的长是10厘米，宽是8厘米，高是2厘米，这个长方体的棱长之和是多少厘米表面积是多少体积是多少２.一根长96厘米的铁丝围成一个正方体，这个正方体的棱长是多少厘米表面积体积4、用一根铁丝刚好焊成一个棱长8厘米的正方体框架，如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架，它的高应该是多少厘米6.一个长4分米、宽3分米、高2分米的长方体，它占地面积最大是多少平方分米最小是多少表面积是多少平方米7.用72分米长的铁丝做一个正方体的框架，然后在外面贴上一层纸，至少需要多少平方分米的纸8、一个长17厘米，高20厘米，宽15厘米的长方体饼干盒，如果在它的侧面贴上一圈商标纸，这张商标纸至少需要多少平方厘米9.一个长方体通风管，长4米，宽和高都是20厘米（横截面是边长20厘米的正方形）。

做100根这样的通风管，至少需要铁皮多少平方米10、要做一种管口是正方形，周长40厘米的通气管子10根，管子长2米，至少需要铁皮多少平方米11.一个无盖的铁桶，底面是周长16分米的正方形，高是5分米，做20个这样的铁桶至少需铁皮几何平方分米12、一个长方体泅水池，长20米，宽15米，深2米，现要将它的每一个面先抹上水泥，再贴上边长4分米瓷砖，需求这样的瓷砖几何块13.一种长方体铁皮烟囱，底面是边长3分米的正方形，高4米，制这样一节烟囱至少要用铁皮多少平方米14、一个正方体木块，若把它切成3个完全相等的长方体后，表面积增加了80平方厘米，这个正方本木块原来的表面积是多少平方厘米15、三个同样大的正方体拼成一个长方体后，表面积减少了144平方厘米，这个长方体的表面积是多少16、一间长米,宽3米,高米的房间。

它的四面墙的下部刷了米高的浅绿色油漆(开门处1m²不刷),如果1m²浅绿色油漆造价10元,一共要用多少钱17、一个长方体的宽和高相等，都是8分米，如果将长去掉2分米，这个长方体就变成了正方体。

18.22 平面直角坐标系中的正方形(专项练习)-2020-2021学年八年级数学下册(人教版)

专题18.22 平面直角坐标系中的正方形（专项练习）一、填空题1．（2019·广东红岭中学八年级期中）如图，在平面直角坐标系中，正方形ABCD 的边长为2，点A 的坐标为(1,1)．若直线y x b =+与正方形有两个公共点，则b 的取值范围是____________．2．（2020·山东九年级）如图，在平面直角坐标系中，将边长为1的正方形OABC 绕O 点顺时针旋转45︒后得到正方形111OA B C ，依此方式，绕O 点连续旋转2021次得到正方形202120212021OA B C ，则点2021A 的坐标为_______．3．（2020·河北八年级期末）正方形111A B C O ，正方形2221A B C C ，正方形3332A B C C ，按如图所示的方式放置在平面直角坐标系中，若点1A 、2A 、3A 和1C 、2C 、3C …分别在直线1y x =+和x 轴上，则点2020B 的坐标是__________．4．（2019·北京人大附中八年级期中）如图，在平面直角坐标系xOy 中，正方形ABCD 的顶点D 在y 轴上，且(3,0),(2,)A B b -，则直线CD 的解析式是_____________．5．（2019·丹东市第七中学九年级月考）如图，平面直角坐标系中正方形OABC ，点A 的坐标为(1，2)，则点C 的坐标 __6．（2021·湖北八年级期末）如图，将正方形OABC 放在平面直角坐标系中，O 是原点，A的坐标为(，则点B 的坐标为______．7．（2020·宁波市第十五中学八年级期末）如图，平面直角坐标系中有一正方形OABC ，点C 的坐标为()2,1--点B 坐标为________．8．（2019·河南八年级期末）如图在平面直角坐标系中，A (4,0)，B (0,2)，以AB 为边作正方形ABCD ，则点C 的坐标为___________.9．（2020·甘肃八年级期末）如图：在平面直角坐标系中，直线:1l y x =-与x 轴交于点1A ，如图所示依次作正方形111A B C O 、正方形2221A B C C 、…、正方形1n n n n A B C C -，使得点1A 、2A 、3A 、．．．在直线l 上，点1C 、2C 、3C 、…在y 轴正半轴上，则点2018B 的坐标是__________．10．（2020·湖北九年级期末）如图，在平面直角坐标系中，将边长为1的正方形OABC 绕点O 逆时针旋转45°后得到正方形111OA B C ，继续旋转至2020次得到正方形202020202020OA B C ，那点2020B 的坐标是__________．11．（2021·沭阳县修远中学八年级月考）如图，在平面直角坐标系xOy 中，一次函数24y x =-的图象经过正方形OABC 的顶点A 和C ，则正方形OABC 的面积为____．二、解答题12．（2016·浙江八年级月考）如图，平面直角坐标系中有一正方形OABC ，点C 的坐标为（﹣4，﹣2），（1）求点A 的坐标.（2）线段BO 的长度.13．（2019·北京八年级期中）如图，在平面直角坐标系xOy 中，正方形ABCD 的顶点D 在y 轴上，且A （-3，0），B （2，b ），求正方形ABCD 的面积．14．（2018·青岛超银中学九年级单元测试）在平面直角坐标系中，正方形OABC 的点()2,0A ，()0,0O ，()0,2C ，现将此正方形绕O 逆时针旋转45，得到正方形111OA B C ，求正方形111OA B C 各顶点的坐标．15．（2019·四川八年级期中）如图所示，在平面直角坐标系中，正方形OABC 的点A 、C分别在x 轴和y 轴的正半轴上，点()6,6B 在第一象限，AP 平分CAB ∠交OB 于P .（1）求OPA ∠的度数和OP 的长；（2）点P 不动，将正方形OABC 绕点O 逆时针旋转至图2的位置，60COP ∠=︒，AP 交OB 于点F ，连接CF .求证：OF CF PF +=；（3）如图3，在（2）的条件下，正方形的边AB 交x 轴于点D 、OE 平分BAD ∠，M 、N 是OB 、OE 上的动点，求BN MN +的最小值，请在图中画出示意图并简述理由. 16．（2019·天津中考模拟）在平面直角坐标系中，O 为原点，点A （﹣6，0）、点C （0，6），若正方形OABC 绕点O 顺时针旋转，得正方形OA′B′C′，记旋转角为α：（1）如图①，当α＝45°时，求BC 与A′B′的交点D 的坐标；（2）如图①，当α＝60°时，求点B′的坐标；（3）若P 为线段BC′的中点，求AP 长的取值范围（直接写出结果即可）．17．（2020·广东九年级）在平面直角坐标系中，O 为坐标原点，点A （0，1），点C （1，0），正方形AOCD 的两条对角线的交点为B ，延长BD 至点G ，使DG BD =．延长BC 至点E ，使CE BC =，以BG ，BE 为邻边做正方形BEFG ．（①）如图①，求OD 的长及AB BG的值；（①）如图①，正方形AOCD 固定，将正方形BEFG 绕点B 逆时针旋转，得正方形BE F G '''，记旋转角为α（0°＜α＜360°），连接AG '．①旋转过程中，当BAG ∠'=90°时，求α的大小；①在旋转过程中，求AF'的长取最大值时，点F'的坐标及此时α的大小（直接写出结果即可）．18．（2020·四川八年级期末）如图，将正方形ABCD放置在平面直角坐标系中的第一象限，点A，点B分别在y轴，x轴正半轴上，AB所在的直线方程为443y x=-+．（1）求点C和点D的坐标；（2）连接BD，将线段BD绕点B顺时针方向旋转至BE的位置，交线段CD于点F若DE DF=，求直线CE的解析式．19．（2021·广东八年级期末）如图所示，在平面直角坐标系中，已知一次函数112y x=+的图象与x轴，y轴分别交于A，B两点，以AB为边在第二象限内作正方形ABCD．（1）求正方形ABCD的面积；（2）求点C，D的坐标；（3）在x轴上是否存在点M，使MDB∆的周长最小？若存在，请求出点M的坐标；若不存在，请说明理由．20．（2019·福建八年级期末）如果P 是正方形ABCD 内的一点，且满足①APB＋①DPC＝180°，那么称点P 是正方形 ABCD 的“对补点”.（1）如图1，正方形ABCD 的对角线AC ，BD 交于点M ，求证：点M 是正方形ABCD 的对补点；（2）如图2，在平面直角坐标系中，正方形ABCD 的顶点A （1，1），C （3，3）.除对角线交点外，请再写出一个该正方形的对补点的坐标，并证明.21．（2020·天津九年级月考）已知正方形OABC 在平面直角坐标系中，点A ，C 分别在x 轴，y 轴的正半轴上，等腰直角三角形OEF 的直角顶点O 在原点，E ，F 分别在OA ，OC 上，且4OA =，2OE =．将OEF 绕点O 逆时针旋转，得OEF 点E ，F 旋转后的对应点为1E ，1F ．（①）①如图①，求11E F 的长；①如图①，连接1CF ，1AE ，求证11OAE OCF △≌△；（①）将OEF 绕点O 逆时针旋转一周，当11OE CF ∥时，求点1E 的坐标（直接写出结果即可）．22．如图，在平面直角坐标系中，直角梯形ABCO 的边OC 落在x 轴的正半轴上，且AB ①OC ，BC OC ⊥，AB =4，BC =6，OC =8．正方形ODEF 的两边分别落在坐标轴上，且它的面积等于直角梯形ABCO 面积．将正方形ODEF 沿x 轴的正半轴平行移动，设它与直角梯形ABCO 的重叠部分面积为S ．（1）分析与计算：求正方形ODEF 的边长；（2）操作与求解：①正方形ODEF 平行移动过程中，通过操作、观察，试判断S （S ＞0）的变化情况是； A ．逐渐增大B ．逐渐减少C ．先增大后减少D ．先减少后增大①当正方形ODEF 顶点O 移动到点C 时，求S 的值；（3）探究与归纳：设正方形ODEF 的顶点O 向右移动的距离为x ，求重叠部分面积S 与x 的函数关系式．23．（2020·北京四中九年级）在ABC 中，点D 在AB 边上（不与点B 重合），DE BC ⊥，垂足为点E ，如果以DE 为对角线的正方形上的所有点都在ABC 的内部或边上，则称该正方形为ABC 的内正方形．（1）如图，在ABC 中，4AB =，30B ∠=︒，点D 是AB 的中点，画出ABC 的内正方形，直接写出此时内正方形的面积；（2）在平面直角坐标系xOy 中，点(,2)A t ，(0,0)B ，3,02C t ⎛⎫ ⎪⎝⎭． ①若2t =，求ABC 的内正方形的顶点E 的横坐标的取值范围；①若对于任意的点D ，ABC 的内正方形总是存在，直接写出t 的取值范围．24．（2020·四川师范大学附属中学九年级月考）如图，在平面直角坐标系中，直线12:43l y x =-+分别交x 、y 轴于B 、A 两点，将AOB 沿直线29:22l y x =-折叠，使点B 落在点C 处．（1）求点C 的坐标．（2）若点D 沿射线BA 运动，连接OD ，当CDB △与CDO 面积相等时，求直线OD 的解析式．（3）在（2）的条件下，当点D 在第一象限时，沿x 轴平移直线OD ，分别交x ，y 轴于点E ，F ，在平面直角坐标系中，是否存在点(),3M m ）和点P ，使四边形EFMP 为正方形？若存在，求出点P 的坐标；若不存在，说明理由．25．（2020·湖北江夏一中八年级期中）如图1，在平面直角坐标系中，(,)A a b ，(,0)B c 是x轴正半轴上一点，30ABO ∠=︒|2|a -互为相反数．（1）求c 的值；（2）如图2，AC AB ⊥交x 轴于C ，以AC 为边的正方形ACDE 的对角线AD 交x 轴于F ．①求证：2BE OC =；①记22BF OF m -=，2OC n =，求m n的值． 26．（2019·辽宁七年级期末）在平面直角坐标系xOy 中，如图正方形ABCD 的顶点A ，B 坐标分别为()1,0A -，()3,0B ，点E ，F 坐标分别为(),0E m ，()3,0F m ，且12m -<≤，以EF 为边作正方形EFGH .设正方形EFGH 与正方形ABCD 重叠部分面积为S .（1）①当点F 与点B 重合时，m 的值为______；①当点F 与点A 重合时，m 的值为______. （2）请用含m 的式子表示S ，并直接写出m 的取值范围.27．（2019·北京八年级期末）在平面直角坐标系xOy 中，正方形ABCD 的两个顶点的坐标分别为(2,0)A -，4()2,D -，顶点B 在x 轴的正半轴上．(1)写出点,B C 的坐标；(2)直线55y x =+与x 轴交于点E ，与y 轴交于点F ．求EFC ∆的面积．28．（2019·河北九年级）如图，在平面直角坐标系中，点()()2,1,6,1B C ，四边形ABCD 是正方形，作直线()0y kx k =>与正方形AB CD 、边所在直线相交于E F 、（1）若直线()0y kx k =>经过点A ，求k 的值；（2）若直线()0y kx k =>平分正方形ABCD 的面积，求E 的坐标；（3）若AEF ∆的外心在其内部，直接写出k 的取值范围．29．（2020·天津南开翔宇学校九年级月考）在平面直角坐标系中，O 为原点，点(6,0)A -，点(0,6)C .若正方形OABC 绕点O 顺时针旋转，得正方形'''OA B C ，记旋转角为α.（①）如图①，当45α=︒时，求BC 与''A B 的交点D 的坐标；（①）如图①，当60α=︒时，求点'B 的坐标；（①）若P 为线段'BC 的中点，求AP 长的取值范围（直接写出结果即可)．参考答案1．﹣2＜b ＜2【解析】【分析】当直线y =x +b 过D 或B 时，求得b ，即可得到结论．【详解】①正方形ABCD 的边长为2，点A 的坐标为（1，1），①D （1，3），B （3，1）．当直线y =x +b 经过点D 时，3=1+b ，此时b =2．当直线y =x +b 经过点B 时，1=3+b ，此时b =﹣2．所以，直线y =x +b 与正方形有两个公共点，则b 的取值范围是﹣2＜b ＜2．故答案为﹣2＜b ＜2．【点拨】本题考查了一次函数图象上点的坐标特征，正方形的性质，关键是掌握待定系数法正确求出函数的解析式．2．22⎛⎫-- ⎪ ⎪⎝⎭【分析】探究规律，利用规律解决问题即可．【详解】如图，①四边形OABC 是正方形，且OA=1，①A （0，1），①将正方形OABC 绕点O 逆时针旋转45°后得到正方形OA 1B 1C 1，①A 1），A 2（1，0），A 3，），…，发现是8次一循环，所以2021÷8=252……5，①点A 2021的坐标为（2-，2-）．故答案为（2-，2-）．【点拨】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角．也考查了坐标与图形的变化、规律型：点的坐标等知识，解题的关键是学会从特殊到一般的探究规律的方法，属于中考常考题型．3．20202019201921,2()B ﹣ 【分析】根据直线解析式先求出OA 1=1，再求出第一个正方形的边长为2，第三个正方形的边长为22，得出规律，即可求出第n 个正方形的边长，从而求得点B n 的坐标，即可求得点B 2020的坐标．【详解】解：①直线y=x+1，当x=0时，y=1，当y=0时，x=-1，①OA 1=1，①B 1（1，1），①OA 1=1，OA=1，①①OAA 1=45°，①①A 2A 1B 1=45°，①A 2B 1=A 1B 1=1，①A 2C 1=2=21，①B 2（3，2）同理得：A 3C 2=4=22，…，①B 3（7，4）；B 4（24-1，24-1），即B （15，8），①B n （2n -1，2n -1），①B （22020-1，22019）故答案为（22020-1，22019）．【点拨】本题考查了一次函数图象上点的坐标特征以及正方形的性质；通过求出第一个正方形、第二个正方形和第三个正方形的边长得出规律是解题的关键．4．355y x =-+ 【分析】根据A(-3，0)，B (2，b)，得到OA=3，OE=2，易证得≅≅Rt AOD Rt BEA Rt DFC ，得到DF=AO=3，OD=AE=CF=5，即可求得点C 、D 的坐标，从而求得直线CD 的解析式．【详解】作CF①y 轴于F ，BE①x 轴于E ，①A(-3，0)，B (2，b)，①OA=3，OE=2，①AE= OA+OE =5，①四边形ABCD 是正方形，①AB=AD=CD ，①BAD=①ADC=90︒，①①1+①DAO=90︒，①2+①DAO=90︒，①2+①CDF=90︒，①3+①CDF=90︒，①①1=①2=①3，①≅≅Rt AOD Rt BEA Rt DFC ，①DF=AO=3，OD=AE=CF=5，①OF= OD - DF=2，①点C 的坐标为(5，2)，点D 的坐标为(0，5)，设直线CD 的解析式为5y kx =+，把点C 的坐标为(5，2)代入得：255k =+，解得：35k =-，①直线CD 的解析式为355y x =-+，故答案为：355y x =-+．【点拨】本题考查了正方形的性质、坐标与图形的性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线构造全等三角形解决问题，属于中考常考题型．5．(-2，1)【分析】过点A 作AD①x 轴于D ，过点C 作CE①x 轴于E ，根据同角的余角相等求出①OAD=①COE ，再利用“角角边”证明①AOD 和①OCE 全等，根据全等三角形对应边相等可得OE=AD ，CE=OD ，然后根据点C 在第二象限写出坐标即可．【详解】如图，过点A 作AD①x 轴于D ，过点C 作CE①x 轴于E ，①四边形OABC 是正方形，①OA=OC ，①AOC=90°，①①COE+①AOD=90°，又①①OAD+①AOD=90°，①①OAD=①COE ，在①AOD 和①OCE 中，90OAD COE ADO OEC OA OC ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩①OE=AD=2，CE=OD=1，①点C 在第二象限，①点C 的坐标为（-2，1）．故答案为（-2，1）．【点拨】本题考查了全等三角形的判定与性质，正方形的性质，坐标与图形性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．6．(1-+【分析】过点A作AE①x轴，垂足为点E，过点B作BF①y轴，垂足为点F，交EA的延长线于点D，证明①AOE①①BAD，得到BF，DE的长度，后将线段的长度转化为点的坐标即可．【详解】过点A作AE①x轴，垂足为点E，过点B作BF①y轴，垂足为点F，交EA的延长线于点D，①四边形ABCO是正方形，①OA＝AB，①OAB＝90°，①①DBA+①BAD＝90°，①BAD+①EAEO＝90°，①①DBA＝①EAO，在①DBA和①EAO中，①DBA=①AEO,①D=①EAB=OA，①①BDA①①AEO，①BD＝AE，AD＝OE，①A（1），①OE＝AD＝DF=1，BD＝1，+1，①点B坐标为（1+1），故答案为：(1+．【点拨】本题考查了正方形的性质，一线三直角全等模型，线段与坐标的关系，根据图形的特点，熟练构造模型证明三角形全等是解题的关键．7．()3,1-【分析】过点A 作AD y ⊥轴于D ，过点C 作CE x ⊥轴，过点B 作BF CE ⊥交CE 的延长线于F ．先证明AOD COE BCF ∆∆∆≌≌，得到1AD CE BF ===，2OD OE CF ===，根据点的坐标定义即可求解．【详解】解：如图，过点A 作AD y ⊥轴于D ，过点C 作CE x ⊥轴，过点B 作BF CE ⊥交CE 的延长线于F ．()2,1C --，2OE ∴=，1CE =．四边形OABC 是正方形，OA OC BC ∴==．易求AOD COE BCF ∠=∠=∠．又90ODA OEC F ∠=∠=∠=︒①AOD COE BCF ∆∆∆≌≌，1AD CE BF ∴===，2OD OE CF ===，∴点A 的坐标为()1,2-，211EF =-=，点B 到y 轴的距离为123+=，∴点B 的坐标为()3,1-．故答案为：()3,1-【点拨】本题考查了平面直角坐标系点的坐标，全等三角形的判定与性质，根据题意，添加辅助线构造全等三角形是解题关键．8．(2,6)或(−2,−2)【解析】【分析】当点C 在AB 上方时，过点C 作CE①y 轴于点E ，易证①AOB①①BEC （AAS ），根据全等三角形的性质可得BE=AO=4，EC=OB=2，从而得到点C 的坐标为（2,6），同理可得当点C 在AB 下方时，点C 的坐标为：（-2,-2）.【详解】解：如图所示，当点C 在AB 上方时，过点C 作CE①y 轴于点E ，①A (4,0)，B (0,2)，四边形ABCD 为正方形，①①BEC=①AOB=90°，BC=AB ，①①BCE+①EBC=90°，①OBA+①EBC=90°，①①BCE=①OBA ，①①AOB①①BEC （AAS ），①BE=AO=4，EC=OB=2，①OE=OB+BE=6，①此时点C 的坐标为：（2,6），同理可得当点C 在AB 下方时，点C 的坐标为：（-2,-2），综上所述，点C 的坐标为：(2,6)或(−2,−2)故答案为：(2,6)或(−2,−2).【点拨】本题主要考查坐标与图形以及三角形全等的判定和性质，注意分情况讨论，不要漏解. 9．（22017，22018-1）【分析】根据一次函数图象上点的坐标特征和正方形的性质找出A 1、B 1、A 2、B 2、A 3、B 3的坐标，从而求出B n ，从而求出结论．【详解】解：将y=0代入1y x =-中，得x=1①A 1（1，0），①OA 1= A 1B 1=1，即点B 1（1，1）=（21-1，21-1）；将y=1代入1y x =-中，得x=2①A 2（2，1），①A 2 C 1= A 2B 2=2，即点B 2的坐标为（2，1＋2）=（2，3）=（22-1，22-1）；将y=3代入1y x =-中，得x=4①A 2（4，3），①A 3C 2= A 3B 3=2，即点B 3的坐标为（4，1＋2＋4）=（4，7）=（23-1，23-1）； ①点B n 的坐标是（2n -1，2n -1）．①点2018B 的坐标是（22018-1，22018-1）=（22017，22018-1）．故答案为：（22017，22018-1）．【点拨】此题考查一次函数图象上点的坐标特征以及规律型坐标的变化，根据点的坐标的变化找出变化规律“点B n 的坐标是（2n -1，2n -1）（n 为正整数）”是解题的关键．10．（-1，-1）【分析】连接OB ，根据图形可知，点B 在以点O 为圆心、、OB 为半径的圆上运用，将正方形OABC绕点O 逆时针依次旋转45°，可得点B 的对应点坐标，根据图形及对应点的坐标发现是8次一个循环，进而得出结论．【详解】解：如图，①四边形OABC 是正方形，且OA=1，①B （1,1），连接OB ，由勾股定理可得OB = ，由旋转的性质得：1232OB OB OB OB ===== 将正方形OABC 绕点O 逆时针依次旋转45°，得：11245AOB BOB B OB ∠=∠=∠==︒，①(10B ，()21,1B -，()3B ，41(1)B --，，…，可发现8次一循环， ①202082524÷=，①点2020B 的坐标为(11)--，, 故答案为(11)--，．【点拨】本题考查了几何图形的规律探究，根据计算得出“8次一个循环”是解题的关键． 11．325【分析】过点C 作CD x ⊥轴于点D ，过点A 作AE y ⊥轴于点E ，由正方形的性质就可以得出CDO AEO ∆≅∆，就可以得出CD AE =，OD OE =，由一次函数24y x =-的图象经过正方形OABC 的顶点A 和C ，设点(,24)C a a -，就可以得出(24,)A a a --代入解析式就可以求出a 的值，由正方形的面积等于2OC 就可以求出结论．【详解】解：过点C 作CD x ⊥轴于点D ，过点A 作AE y ⊥轴于点E ，90CDO AEO ∴∠=∠=︒．四边形OABC 是正方形，90AOC ∴∠=︒，OC OA =．90DOE ∠=︒，AOC DOE ∴∠=∠，AOC AOD DOE AOD ∴∠-∠=∠-∠，COD AOE ∴∠=∠．在CDO ∆和AEO ∆中，CDO AEO COD AOE OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩，()CDO AEO AAS ∴∆≅∆CD AE ∴=，OD OE =．一次函数24y x =-的图象经过正方形OABC 的顶点A 和C ，设点(,24)C a a -， OD a ∴=，24CD a =-，OE a ∴=，24AE a =-，(24,)A a a ∴--，2(24)4a a ∴-=--，125a ∴=． 125OD ∴=，45CD =，在Rt CDO ∆中，由勾股定理，得2222212432555OC OD CD ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭． 2OABC S CO =正方形，325OABC S ∴=正方形．故答案为：325．【点拨】本题考查了正方形的性质及面积公式的运用，垂直的性质的运用，勾股定理的运用，全等三角形的判定及性质的运用，一次函数图象上点的坐标的特征的运用，构造K 字形全等，得出AC 两点坐标关系是解题的关键．12．（1）A(-2,4)；（2）【解析】试题分析：（1）过点A 作AE①y 轴，垂足为E ，过点C 作CD①y 轴，垂足为D,易证①AEO①①ODC ，即可求得A 点的坐标；（2）过点B 作BF①CD 交DC 的延长线于点F ，易证①BFC①①ODC ，即可求得点B 的坐标，由勾股定理求得正方形的边长，即可求得正方形的对角线OB 的长.试题解析：（1）过点A 作AE①y 轴，垂足为E ，过点C 作CD①y 轴，垂足为D,易证①AEO ≅①ODC,得A(-2,4)；（2）同理可证①BFC ≅①ODC ，得B(-6,2)，得.13．34【分析】过点B 作BM①x 轴于点M ，通过证明AOD BMA ≅，可得,AO MB DO AM ==，即可得出AO 、DO 的值，根据勾股定理求出AD 的值，即可求出正方形的面积．【详解】过点B 作BM①x 轴于点M①四边形ABCD 是正方形,90AD AB DAB ︒∴=∠=90OAD BAM ︒∴∠+∠=90BAM ABM ︒∠+∠=OAD ABM ∴∠=∠在①AOD 和①BMA 中AOD AMBOAD ABM AD AB∠=∠⎧⎪∠=∠⎨⎪=⎩AOD BMA ∴≅,AO MB DO AM ∴==(3,0),(2,)A B b -3,2AO OM ∴==3,325MB AM AO OM ∴==+=+=5DO ∴=22292534AD AO DO =+=+=234ABCD S AD ∴==正方形．【点拨】本题考查了正方形的面积问题，掌握正方形的性质、全等三角形的性质以及判定定理、勾股定理是解题的关键．14．1A ，(1B ，(1C ，()0,0O ．【分析】作A 1D①x 轴于D ，C 1E①x 轴于E ，如图，根据正方形的性质得，①BOA=①BOC=45°，再根据旋转的性质得点B 1在y 轴上，OB 1，①A 1OD=45°，①B 1OC 1=45°，OA 1=OA=OC 1=2，则可判断①A 1OD 和①EOC 1都是等腰直角三角形，于是可根据等腰直角三角形的性质得到A 1D=OD=2OA 1，C 1E=OE=2OC 1，然后根据各象限点的坐标特征和y 轴上点的坐标特征写出正方形OA 1B 1C 1各顶点的坐标．【详解】解：作1A D x ⊥轴于D ，1C E x ⊥轴于E ，如图，①正方形OABC 的点()2,0A ，()0,0O ，()0,2C ，①OB =45BOA BOC ∠=∠=，①正方形OABC 绕O 逆时针旋转45，得到正方形111OA B C ，①点1B 在y 轴上，1OB OB ==，145A OD ∠=，1145B OC ∠=，112OA OA OC ===，①1A OD 和1EOC 都是等腰直角三角形，①112A D OD OA ===112C E OE ===，①1A ，(1B ，(1C ，()0,0O ．【点拨】本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．15．（1）∠OP A=67.5°；OP ＝6；（2）详见解析；（3）【分析】（1）先求出①3=①2=①BAC=45°，进而得出①CAP=22.5°，即可得出OP=OA ，即可得出结论；（2）先求出①P=15°，进而判断出①FOG 是等边三角形，再判断出①COF①①POG ，即可得出结论，（3）先作出点B 关于OE 的对称点B'，得出BN+MN=B'M ，然后根据垂线段最短的性质可确定M 点坐标，即可计算出结论．【详解】解：（1）如图1，①AC ，OB 是正方形OABC 的对角线，①OA ＝AB ，①2＝①3＝①BAC ＝45°，①AP 是①BAC 的角平分线，①①1＝12①BAC ＝22.5°， ①①OAP ＝①3+①1＝67.5°，在①OAP 中，①OP A ＝180°﹣①2﹣①OAP ＝67.5°，①①OAP ＝①OP A ，①OA ＝OP ，①B （6，6），①AB ＝6，①OA ＝AB ＝6，①OP ＝6；（2）如图2，①四边形OABC 是正方形，①OA ＝OC ，①AOC ＝90°，①①COP ＝60°，①①AOP ＝150°，由（1）知，OP ＝OA①①P ＝15°，由（1）知，①POG ＝45°，①①AGO ＝①P +①POG ＝60°，①OB 是正方形的对角线，①①BOC ＝45°，①①COP ＝60°，①POG ＝45°，①①BOG ＝①COP ＝60°，①①OFG 是等边三角形，①OF ＝FG ＝OG ，在①COF 和①POG 中，45OF OGCOF POG OC OP=⎧⎪∠=∠=︒⎨⎪=⎩，①①COF ①①POG ，①PG ＝CF ，①CF +OF ＝PG +FG ＝PF ；（3）如图3，过点B 作BQ ①OE 于Q ，延长BQ 交x 轴于B '，①OE 是①DOB 的平分线，①BQ ＝B 'Q ，①点B '与点B 关于OE 对称，连接B 'M '交OE 于N '，①BN '+M 'N '＝B 'N '+M 'N '＝B 'M '，过点B '作B 'M ①OB 于M ，交OE 于N ，此时，BN +MN 最小，①OB 是边长为6的正方形的对角线，①OB ＝由作图知，OB '＝OB ＝，由（2）易知，①BOD ＝30°，在Rt①B 'OM 中，B 'M ＝12OB '＝3，即：BN +MN 的最小值为【点拨】此题是四边形综合题，主要考查了正方形的性质，等腰三角形的判定和性质，全等三角形的判定和性质，轴对称性质，角平分线的性质，灵活运用所学知识进行推理证明是解题关键．16．（1）(6-；（2）3,3+；（3）3323AP +.【分析】（1）当α＝45°时，延长OA′经过点B ，在Rt①BA′D 中，①OBC ＝45°，A′B ＝6，可求得BD 的长，进而求得CD 的长，即可得出点D 的坐标；（2）过点C′作x 轴垂线MN ，交x 轴于点M ，过点B′作MN 的垂线，垂足为N ，证明①OMC′①①C′NB′，可得C′N＝OM＝，B′N＝C′M＝3，即可得出点B′的坐标；（3）连接OB，AC相交于点K，则K是OB的中点，因为P为线段BC′的中点，所以PK＝12OC′＝3，即点P在以K为圆心，3为半径的圆上运动，即可得出AP长的取值范围．【详解】解：（1）①A（﹣6，0）、C（0，6），O（0，0），①四边形OABC是边长为6的正方形，当α＝45°时，如图①，延长OA′经过点B，①OB＝OA′＝OA＝6，①OBC＝45°，①A′B＝6，①BD＝（6）12=-，①CD＝6﹣（12-=6，①BC与A′B′的交点D的坐标为（6-6）；（2）如图①，过点C′作x轴垂线MN，交x轴于点M，过点B′作MN的垂线，垂足为N，①①OC′B′＝90°，①①OC′M＝90°﹣①B′C′N＝①C′B′N，①OC′＝B′C′，①OMC′＝①C′NB′＝90°，①①OMC′①①C′NB′（AAS），当α＝60°时，①①A′OC′＝90°，OC′＝6，①①C′OM＝30°，①C′N＝OM＝，B′N＝C′M＝3，①点B′的坐标为(3,3+；（3）如图①，连接OB，AC相交于点K，则K是OB的中点，①P为线段BC′的中点，①PK＝12OC′＝3，①P在以K为圆心，3为半径的圆上运动，①AK＝①AP最大值为3，AP的最小值为3，①AP长的取值范围为3323AP+.【点拨】本题考查正方形性质，全等三角形判定与性质，三角形中位线定理．（3）问解题的关键是利用中位线定理得出点P的轨迹．17．（①，12AB BG =；（①）①α=30°，α=150°，①F '），α=315°．【分析】（①）根据正方形的性质以及勾股定理即可解决问题；（①）①因为①BAG ′=90°，BG ′=2AB ，可知sin①AG ′B ='AB BG =12，推出①AG ′B =30°，推出旋转角α=30°，据对称性可知，当①ABG ″=60°时，①BAG ″=90°，也满足条件，此时旋转角α=150°；①当α=315°时，A 、B 、F ′在一条直线上时，AF ′的长最大．【详解】解：（①）如图①中，①A （0，1），①OA =1．①四边形OADC 是正方形，①①OAD =90°，AD =OA =1，①OD =AC ，①AB =BC =BD =BO =2． ①BD =DG ，①BG ，①AB BG=12．（①）①如图①中，①①BAG ′=90°，BG ′=2AB ，①sin①AG ′B ='AB BG =12， ①①AG ′B =30°，①①ABG ′=60°，①①DBG ′=30°，①旋转角α=30°，根据对称性可知，当①ABG ″=60°时，①BAG ″=90°，也满足条件，此时旋转角α=150°．综上所述：旋转角α=30°或150°时，①BAG ′=90°． ①如图3中，连接OF ．①四边形BE ′F ′G ′，①BF ′=2，①当α=315°时，A 、B 、F ′在一条直线上时，AF ′的长最大，最大值为2+2，此时α=315°，F ′（1122+-，）．【点拨】本题考查的是正方形的性质、旋转变换的性质以及锐角三角函数的定义，掌握正方形的四条边相等、四个角相等，旋转变换的性质是解题的关键，注意特殊角的三角函数值的应用． 18．（1）点C 的坐标为(7,3)，点D 的坐标为(4,7)；（2）直线CE 的解析式为746y x =-．【分析】（1）先求出点A 、B 的坐标，从而可得3,4OB OA ==，再根据正方形的性质、直角三角形的性质可得,AB BC OAB HBC =∠=∠，然后根据三角形全等的判定定理与性质可得3, 4CH BO BH AO ====，从而可得7OH =，由此即可得出点C 的坐标，同样的方法可求出点D 的坐标；（2）设旋转角DBE ∠的大小为x ，先根据正方形的性质、等腰三角形的性质、三角形的外角性质求出30x =︒，再根据直角三角形的性质、平行四边形的判定与性质可得//BD CE ，然后利用待定系数法求出直线BD 的解析式，从而可得直线CE 的解析式中的一次项系数，最后将点C 的坐标代入即可得．【详解】（1）AB 所在的直线方程为443y x =-+，当0x =时，4y =，即()0,4A ，当0y =时，4403x -+=，解得3x =，即(3,0)B ， 3,4OB OA ∴==，如图，过点C 作⊥CH x 轴，垂足为H ，四边形ABCD 是正方形，90,ABC AB BC ∴∠=︒=，90OAB OBA OBA HBC ∴∠+∠=∠+∠=︒， OAB HBC ∴∠=∠，在OAB 和HBC 中，90OAB HBC AOB BHC AB BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，()OAB AAS HBC ∴≅，3, 4CH BO BH AO ∴====，347OH OB BH ∴=+=+=，∴点C 的坐标为(7,3)，同理可得：点D 的坐标为(4,7)；（2）设旋转角DBE ∠的大小为x ，四边形ABCD 是正方形，45BDC ∴∠=︒，AC BD =，AC BD ⊥， DFE ∠是BDF 的一个外角，45DFE DBE BDC x ∴∠=∠+∠=+︒， DE DF =，45DEF DFE x ∴∠=∠=+︒，由旋转的性质得：BD BE =，45BDE BED x ∴∠=∠=+︒，4545EDF BDE BDC x x ∴∠=∠-∠=+︒-︒=，在EDF 中，由三角形的内角和定理得：180EDF DEF DFE ∠+∠+∠=︒，即()245180x x ++︒=︒，解得30x =︒，如图，过点E 作EM BD ⊥于点M ，连接AC ，交BD 于点N ，则1122CN AC BD ==，在Rt BEM 中，30EBM x ∠==︒，1122EM BE BD ∴==， EM CN ∴=，,E AC BD M BD ⊥⊥，//EM CN ∴，∴四边形EMNC 是平行四边形，//BD CE ∴，设直线BD 的解析式为y kx b =+，将()3,0B 和()4,7D 代入得：3047k b k b +=⎧⎨+=⎩，解得721k b =⎧⎨=-⎩，则直线BD 的解析式为721y x =-，//BD CE ，∴设直线CE 的解析式为7y x m =+，将点()7,3C 代入得：493m +=，解得46m =-，故直线CE 的解析式为746y x =-．【点拨】本题考查了正方形的性质、三角形全等的判定定理与性质、等腰三角形的性质、利用待定系数法求一次函数的解析式等知识点，较难的是题（2），利用平行四边形的判定与性质得出//BD CE 是解题关键．19．（1）5；（2）()1,3C -，()3,2D -；（3）存在，()1,0M - 【分析】（1）在直角三角形AOB 中，由OA 与OB 的长，利用勾股定理求出AB 的长即可；（2）过C 作y 轴垂线，过D 作x 轴垂线，分别交于点E ，F ，可得三角形CBE 与三角形ADF 与三角形AOB 全等，利用全等三角形对应边相等，确定出C 与D 坐标即可；（3）作出B 关于x 轴的对称点B′，连接B′D ，与x 轴交于点M ，连接BD ，BM ，此时①MDB 周长最小，求出此时M 的坐标即可．【详解】（1）对于直线112y x =+，令0x =，得到1y =；令0y =，得到2x =， ①()2,0A -，()0,1B ，在Rt AOB ∆中，2OA =，1OB =，根据勾股定理得：AB == 所以正方形ABCD 面积为5.（2）作CE y ⊥轴，DF x ⊥轴，可得90CEB AFD AOB ∠=∠=∠=︒， ①正方形ABCD ，①BC AB AD ==，90DAB ABC ∠=∠=︒， ①90DAF BAO ∠+∠=︒，90ABO CBE ∠+∠=︒，①90DAF ADF ∠∠=+︒，90BAO ABO ∠+∠=︒， ①BAO ADF CBE ∠=∠=∠， ①BCE DAF ABO ∆∆∆≌≌，①2BE DF OA ===，1CE AF OB ===，①213OE OB BE =+=+=，213OF OA AF =+=+=， ①()1,3C -，()3,2D -；（3）找出B 关于x 轴的对称点B ′，连接B D '，与x 轴交于点M ，此时BMD ∆周长最小， ①()0,1B ， ①()0,1B '-设直线B D '的解析式为y kx b =+，把B ′与D 坐标代入得：132b k b =-⎧⎨-+=⎩，解得：11k b =-⎧⎨=-⎩，即直线B D '的解析式为1y x =--，令0y =，得到1x =-，即()1,0M -．【点拨】此题属于一次函数综合题，涉及的知识有：待定系数法确定一次函数解析式，正方形的性质，全等三角形的判定与性质，一次函数与坐标轴的交点，勾股定理，熟练掌握定理及性质是解本题的关键．20．（1）证明见解析；（2）对补点如：N（52，52）．证明见解析【解析】试题分析：(1)根据正方形的对角线互相垂直,得到①DMC＝①AMB＝90°,从而得到点M是正方形ABCD的对补点.(2) 在直线y＝x（1＜x＜3）或直线y＝－x＋4（1＜x＜3）上除（2，2）外的任意点均可,通过证明①DCN①①BCN,得到①CND＝①CNB,利用邻补角的性质即可得出结论.试题解析：（1）①四边形ABCD是正方形，① AC①BD．① ①DMC＝①AMB＝90°.即①DMC＋①AMB＝180°．① 点M是正方形ABCD的对补点．（2）对补点如：N（52，52）．说明：在直线y＝x（1＜x＜3）或直线y＝－x＋4（1＜x＜3）上除（2，2）外的任意点均可.证明（方法一）：连接AC ，BD由（1）得此时对角线的交点为（2，2）．设直线AC的解析式为：y＝kx＋b，把点A（1，1），C（3，3）分别代入，可求得直线AC的解析式为：y＝x．则点N（52，52）是直线AC上除对角线交点外的一点，且在正方形ABCD内.连接AC，DN，BN，① 四边形ABCD是正方形，① DC＝BC，①DCN＝①BCN．又① CN＝CN，① ①DCN①①BCN．① ①CND＝①CNB．① ①CNB＋①ANB＝180°，① ①CND＋①ANB＝180°．① 点N是正方形ABCD的对补点．证明（方法二）：连接AC ，BD，由（1）得此时对角线的交点为（2，2）．设点N是线段AC上的一点（端点A，C及对角线交点除外），连接AC，DN，BN，① 四边形ABCD是正方形，① DC＝BC，①DCN＝①BCN．又① CN＝CN，① ①DCN①①BCN．① ①CND＝①CNB．① ①CNB＋①ANB＝180°，① ①CND＋①ANB＝180°．① 点N是正方形ABCD除对角线交点外的对补点．设直线AC的解析式为：y＝kx＋b，把点A（1，1），C（3，3）分别代入，可求得直线AC的解析式为：y＝x．在1＜x ＜3范围内，任取一点均为该正方形的对补点，如N （52，52）．21．（①）①11=E F ①见解析；（①）点1E 的坐标为(或(1,．【分析】（1）①根据勾股定理求出EF 的长，11E F 的长；根据SAS 定理证明11OAE OCF △≌△即可；（2）由于①OEF 是等腰Rt①，若OE①CF ，那么CF 必与OF 垂直；在旋转过程中，E 、F 的轨迹是以O 为圆心，OE （或OF ）长为半径的圆，若CF①OF ，那么CF 必为①O 的切线，且切点为F ；可过C 作①O 的切线，那么这两个切点都符合F 点的要求，因此对应的E 点也有两个；在Rt①OFC 中，OF=2，OC=OA=4，可证得①FCO=30°，即①EOC=30°，已知了OE 的长，通过解直角三角形，不难得到E 点的坐标，由此得解．【详解】解：（①）①①等腰直角三角形OEF 的直角顶点O 在原点，2OE =， ①90EOF ∠=︒，2OF OE ==．在Rt OEF 中，由勾股定理，得EF =．①11OE F △是由OEF 绕点O 逆时针旋转得到的，①11=E F①①四边形OABC 为正方形， ①OA OC =，①将OEF 绕点O 逆时针旋转，得11OE F △， ①11AOE COF ∠=∠，又OEF 是等腰直角三角形， ①11OE F △是等腰直角三角形， ①11OE OF =， ①11OAE OCF △≌△．（①）如图，①OE①OF ，①过点F 与OE 平行的直线有且只有一条，并与OF 垂直，当三角板OEF 绕O 点逆时针旋转一周时，则点F 在以O 为圆心，以OF 为半径的圆上． ①过点F 与OF 垂直的直线必是圆O 的切线．又点C 是圆O 外一点，过点C 与圆O 相切的直线有且只有2条，不妨设为CF 1和CF 2，此时，E 点分别在E 1点和E 2点，满足CF 1①OE 1，CF 2①OE 2．当切点F 1在第二象限时，点E 1在第一象限． cos①COF 1=112OF OC =， ①①COF 1=60°，①①AOE 1=60°． ①点E 1的横坐标为：x E1=2cos60°=1，点E 1的纵坐标为：y E1①点E 1的坐标为(1；当切点F 2在第一象限时，点E 2在第四象限．同理可求：点E 2的坐标为(1，)．综上所述，三角板OEF 绕O 点逆时针旋转一周，存在两个位置，使得OE①CF ，此时点E 的坐标为E 1(1或E 2(1，．【点拨】本题考查了图形的旋转变化、全等三角形的判定和性质、切线的判定、解直角三角形、以及分类讨论的数学思想．能够联系圆的相关知识来解答（3）题是此题的一个难点． 22．（1）①ODEF 1S =(48)6362ABCO S =+⨯=，设正方形的边长为x ，①236x =，6x =或6x =-（舍去）．。

人教版五年级下册数学正方体长方体应用题专练

人教版五年级下册数学正方体长方体应用题专练1、把一个长10米，宽6米，深2米的水池注满水，然后把两块同样长2米，宽1.5米，高2米的长方体石块放入水池中，溢出的水的体积是多少立方米？2、把棱长分别为6厘米和8厘米的两个正方体铁块熔铸成一个长方体，已知这个长方体的长是13厘米，宽是7厘米，求它的高是多少厘米？3、有一块棱长是80厘米的正方体的铁块，现在要把它溶铸成一个横截面积是20平方厘米的长方体，这个长方体的长是多少厘米？4、有一块棱长为4厘米的正方体铜块，要将它融化后铸成长2厘米，宽4厘米的长方体，铸成后长方体铜块的高是多少厘米？（不计损耗）5、1立方米水重1吨，一个长方体水池能蓄水960吨，已知水池长20米，宽12米，深多少米？6、一个正方体玻璃容器，从里面量棱长为2分米，向容器内倒入5.5升的水，再把一个苹果浸没在水中，这时量得容器内的水深15是厘米，这个苹果的体积是多少立方分米？7、一个长方体容器里面装有水，一块棱长24厘米的正方体铁块浸没在水中。

现将铁块取出，水面下降18厘米；如果将一个长18厘米，宽16厘米，高12厘米的长方体铁块浸入水中：水面将上升多少厘米?8、一个长方体的药水箱里装了60升的药水，已知药水箱里面长5分米，宽3分米，它的深是多少分米？9、一块钢材长2米，横截面是边长为4厘米的正方形，如果把它锻造成横截面是25平方厘米的长方体钢材，长多少厘米？10、在有一个长是50厘米，宽是10厘米，高是10厘米的全封闭的容器，里面装有8厘米高的水。

如果将这个容器竖放，水面的高度是多少厘米？11、一个棱长为3分米的正方体水槽内装有一部分水，往水槽中投入一个铅锤，此时有部分水溢出，将铅锤从水槽中取出，量得水面高2.4分米，铅锤的体积是多少立方分米？12、在一个长40厘米，宽20厘米的的玻璃缸中，放入一个棱长10厘米的正方体铁块，这是水深12厘米（铁块浸没在水中，水末溢出），如果把这个铁块从缸中取出，缸中的水深会变为多少厘米？13、一个正方体玻璃容器棱长2dm，向容器中到入5L水，再把一块石头放入水中。

正方形的性质专项练习30题(有答案)ok

正方形的性质专项练习30题（有答案）1．如图，在正方形ABCD中，AB=4，F为DC的中点，E为BC上一点，且EC=BC．求△AEF的面积．2．如图所示，在正方形ABCD中，点E、F分别是AD、BC的中点．求证：四边形BFDE是平行四边形．3．如图，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F，求证：EF+AC=AB．4．如图，在正方形ABCD中，E为对角线AC上一点，连接EB、ED；①求证：△BEC≌△DEC；②延长BE交AD于点F，若∠DEB=130°，求∠AFE的度数．5．如图，在正方形ABCD中，E是CD边的中点，AC与BE相交于点F，连接DF．（1）求证：∠1=∠2；（2）连接AE，试判断AE与DF的位置关系，并证明你的结论．6．如图，E、F分别是正方形ABCD中BC和CD边上的点，且AB=4，CE=BC，F为CD的中点，连接AF、AE，问△AEF是什么三角形？请说明理由．7．如图，点E、F在正方形ABCD的边BC、CD上，且BE=CF，试判断AE、BF的关系，并说明理由．8．如图，正方形ABCD中，E为对角线BD上一点，且∠AEC=132°，求∠DAE的度数．9．如图，在正方形ABCD中，AE=AB，∠AEB=75°．求证：（1）△BEF是等腰三角形；（2）点E在线段AD的垂直平分线上．10．如图，E是正方形ABCD外的一点，连接AE、BE、DE，且∠EBA=∠ADE，点F在DE上，连接AF，BE=DF．（1）求证：△ADF≌△ABE；（2）小明还发现线段DE、BE、AE之间满足等量关系：DE﹣BE=AE．请你说明理由．11．如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．（1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；（2）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P 运动到什么位置时，△ADQ 恰为等腰三角形．12．如图，延长正方形ABCD的边BC到E，使CE=CB，连接AE交CD于F，连接BF．△BEF和△ABF是否是等腰三角形，说明理由．13．如图，正方形ABCD中，M是BC上任意一点（点M与B、C不重合），DE⊥AM于E，BF⊥AM于F，在图中找出一对全等三角形，并加以证明．14．如图，E是正方形ABCD中AD边的中点，延长BA到点F，使AF=AE，判断BE与DF之间有何关系？并说明理由．15．已知，如图，正方形ABCD的面积为100，菱形PQCB的面积为80，求阴影部分的面积．16．如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG．求证：BE=DG．17．如图，点P是正方形ABCD边AB上一点（不与点A，B重合），连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE，DF．（1）求证：∠ADP=∠EPB；（2）求∠CBE的度数．18．在△ABC中，∠C=90°，四边形ABDE，AGFC都是正方形，如图，求证：BG=EC．19．如图，在正方形ABCD中，E为CD边上一点，F为BC延长线上一点，CE=CF．求证：BE=DF．20．如图，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=AB，那么DF，BE在数量上有什么关系，并说明理由．21．如图，E为正方形ABCD的对角线AC上一点，过点E作EF⊥BC于F，EG⊥AB于G，连接FG．（1）若AE=AB，求∠CDE的度数．（2）FG与DE相等吗？为什么？22．如图，在正方形ABCD中，E为线段CD上一点，且DE=3CE，M、N分别是AD、AE的中点，点F在CD的延长线上，且∠DMF=∠DAE．（1）求cos∠DAE的值；（2）求证：四边形MNEF是等腰梯形．23．如图，正方形ABCD内一点P，使得PA：PB：PC=1：2：3，请利用旋转知识，证明∠APB=135°．（提示：将△ABP绕点B顺时针旋转90°至△BCP′，连接PP′）．24．如图，E为正方形ABCD外一点，且△ADE为等边三角形，试求∠CEB的度数．25．如图，正方形ABCD中，G是CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE，连接BG并延长交DE于H．（1）求证：∠BGC=∠DEC．（2）若正方形ABCD的边长为1，试问当点G运动到什么位置时，BH垂直平分DE？26．点E是正方形ABCD外一点，点F在DE上，且AF=AE=，∠EAF=90°，FB=3．（1）求证：△AFD≌△AEB；（2）求∠DEB的度数；（3）求正方形ABCD的面积．27．如图，已知点E为正方形ABCD的边BC上一点，连接AE，过点D作DG⊥AE，垂足为G，延长DG交AB 于点F．求证：AF=BE．28．如图，在正方形ABCD中，E为AB边上的一点，连接DE，过A作AF⊥DE于F，过C作CG⊥DE于G．已知AF=1，CG=2，求正方形的边长．29．如图，正方形ABCD中，E是AD上一点（E与A、D不重合）．连接CE，将△CED绕点D顺时针旋转90°，得到△AFD．（1）猜想CE和AF之间的关系，并进行证明．（2）连接EF，若∠ECD=30°，求∠AFE的度数．30．如图，正方形ABCD的边长为1，G是CD边上的一个动点（G不与C、D重合），以CG为一边向正方形ABCD 外作正方形GCEF，连接DE、BG，并延长BG交DE于点H．（l）求证：①△BCG≌△DCE；②BH⊥DE．（2）当点G运动到何处时，四边形DGEF是平行四边形，并加以证明．（3）当点G运动到何处时，BH垂直平分DE？请说明理由．参考答案：1．由题意知正方形ABCD的边长为4，则EC=1，BE=3，CF=DF=2，由勾股定理，得，AE2=AB2+BE2=42+32=25，AF2=AD2+DF2=42+22=20，EF2=EC2+CF2=12+22=5，∴AF2+EF2=AE2，由勾股定理的逆定理知△AEF是以AE为斜边的直角三角形．∴S△AEF=AF•EF=××==5．2．∵四边形ABCD是正方形，∴AD=BC，AD∥BC，即DE∥BF，∵点E、F是AD、BC的中点，∴DE=AD，BF=BC，∴DE=BF，又DE∥BF∴四边形BFDE是平行四边形3．如图，过F作FM⊥AB于点M，∵AC⊥BD于点E，∴AE=AC，∠ABD=∠CBD=45°，∵AF平分∠BAC，∴EF=MF．又∵AF=AF，∴Rt△AMF≌Rt△AEF，∴AE=AM，∵∠MFB=∠ABF=45°，∴MF=MB，∴MB=EF，∴EF+AC=MB+AE=MB+AM=AB．4．（1）证明：∵四边形ABCD是正方形，∴CD=CB，∠DCA=∠BCA，∵CE=CE，∴△BEC≌△DEC．（2）解：∵∠DEB=130°，∵△BEC≌△DEC，∵∠DAB=90°，∴∠DAC=∠BAC=45°，∴∠AFE=180°﹣65°﹣45°=70°．答：∠AFE的度数是70°．5．（1）证明：∵四边形ABCD是正方形，∴AD=AB，∠DAF=∠BAF=45°，在△ADF与△ABF 中，，∴△ADF≌△ABF（SAS），∴∠1=∠2；（2）如图：AE⊥DF．设AE与DF相交于点H，∵四边形ABCD是正方形，E是DC的中点，∴△ADE≌△BCE（SAS），∴∠3=∠4，又∵∠1=∠2（已证），∴∠1+∠3=∠2+∠4=90°，∴∠AHD=90°，∴AE⊥DF．6．∵AB=4，CE=BC，∴EC=1，BE=3，∵F为CD的中点，∴DF=FC=2，∴EF==，AF==，AE==．∴AE2=EF2+AF2．∴△AEF是直角三角形．7．AE=BF且AE⊥BF．理由：∵四边形ABCD是正方形，∴AB=BC=CD，∠ABC=∠BCD=90°．∴△ABE≌△BCF（SAS）∴AE=BF，∠BAE=∠CBF．∵∠ABE=90°∴∠BAE+∠AEB=90°∴∠CBF+∠AEB=90°∴∠BGE=90°∴AE⊥BF．∴AE=BF且AE⊥BF．8．在正方形ABCD中，AB=CB，∠ABE=∠CBE=∠ADB=45°，在△ABE和△CBE 中，，∴△ABE≌△CBE（SAS），∴∠AEB=∠CEB，∵∠AEC=132°，∴∠AEB=×132°=66°，∴∠DAE=∠AEB﹣∠ADB=66°﹣45°=21°．9．（1）∵AE=AB，∴∠ABE=∠AEB=75°，∴∠FBE=∠ABE﹣∠ABD=75°﹣45°=30°，在△BEF中，∠BFE=180°﹣∠FBE﹣∠AEB=180°﹣30°﹣75°=75°，∴∠BFE=∠AEB，∴BF=BE，即△BEF是等腰三角形；（2）连接DE，在△ABE中，∠BAE=180°﹣∠ABE﹣∠AEB=180°﹣75°﹣75°=30°，∴∠DAE=∠DAB﹣∠BAE=90°﹣30°=60°，∵正方形ABCD中，AD=AB，又∵AB=AE，∴AE=AD，∴△ADE是等边三角形．∴AE=DE，∴点E在线段AD的垂直平分线上．10．（1）∵四边形正ABCD是正方形，∴AB=AD，，∴△ADF≌△ABE；（2）理由如下：由（1）有△ADF≌△ABE，∴AF=AE，∠3=∠4，在正方形ABCD中，∠BAD=90°，∴∠BAF+∠3=90°，∴∠BAF+∠4=90°，∴∠EAF=90°，∴△EAF是等腰直角三角形，∴EF2=AE2+AF2，∴EF2=2AE2，∴EF=AE，即DE﹣DF=AE，∴DE﹣BE=AE．11．（1）证明：在正方形ABCD中，无论点P运动到AB上何处时，都有AD=AB，∠DAQ=∠BAQ=45°，在△ADQ和△ABQ 中，，∴△ADQ≌△ABQ（SAS）；（2）若△ADQ是等腰三角形，则有①如图1，AQ=DQ时，点Q为正方形ABCD的中心，点B、P重合；②如图2，AQ=AD时，根据等边对等角有∠ADQ=∠AQD，∵正方形ABCD的边长为4，∴AC==4，∴CQ=AC﹣AQ=4﹣4，∵AD∥BC，∴∠CPQ=∠ADQ，∴∠CQP=∠CPQ，∴CP=CQ=4﹣4，此时点P在距离点B：4﹣（4﹣4）=8﹣4；③如图3，AD=DQ时，点C、P、Q三点重合；综上所述，当点P运动到①点B的位置；②在BC上，且到点B的距离为8﹣4处；③运动到点C的位置时，△ADQ恰为等腰三角形12．△BEF和△ABF是等腰三角形，理由：∵四边形ABCD是正方形，∴AB∥CD，∵CE=CB，DC⊥BE，∴BF=EF，∴△BEF是等腰三角形，∵FC∥AB，∴=又∵BC=EC，∴EF=AF，∴△ABF是等腰三角形13．△ADE≌△BAF．证明：∵DE⊥AM于E，BF⊥AM，∠AFB=∠AED=90°．又∵∠BAF+∠EAD=90°，在直角△ABF中，∠BAF+∠ABF=90°．∴∠ABF=∠EAD．∴在△ADE与△BAF中：∴△ADE≌△BAF．14．BE=DF且BE⊥DF．理由如下：∵四边形ABCD为正方形，∴∠FAD=∠EAB=90°，AD=AB，而AF=AE，∴把△AFD绕点A顺时针旋转90°后得到△AEB；延长BE交DF于G，如图，∵把△AFD绕点A顺时针旋转90°后得到△AEB，∴BE=DF，∠ABE=∠ADF，∵∠AEB=∠DEG，∠BAE=90°∴∠ABE+∠AEB=∠ADF+∠DEG=90°，∴∠DGE=90°，即BE⊥DF，∴BE=DF且BE⊥DF．15．∵正方形ABCD的面积是100，∴AB=BC=BP=PQ=QC=10，又∵S菱形BPQC=PQ×EC=10×EC=80，∴EC=8，在Rt△QEC中，EQ==6；∴PE=PQ﹣EQ=4，∴S阴影=S正方形ABCD﹣S梯形PBCE=100﹣×（10+4）×8=100﹣56=44．16．∵四边形ABCD和四边形ECGF都是正方形，∴在△BCE和△DCG中，，∴△BCE≌△DCG（SAS），∴BE=DG．17．1）证明：∵四边形ABCD为正方形，∴∠A=90°，∴∠ADP+∠DPA=90°，又∵线段PD绕点P顺时针方向旋转90°得到线段PE，∴∠DPE=90°，∴∠DPA+∠EPB=90°，∴∠ADP=∠EPB；（2）过E点作EG⊥AB于G，如图，∵线段PD绕点P顺时针方向旋转90°得到线段PE，∴PD=PE，而∠ADP=∠EPB，又∵∠A=∠G=90°，∴Rt△PAD≌Rt△EPG，∴AP=EG，AD=PG，而AD=AB，∴AP+PB=PB+BG，∴AP=BG，∴BG=EG，∴△EBG为等腰直角三角形，∴∠EBG=45°，∴∠CBE=45°．18．∵四边形ABDE，AGFC都是正方形，∴∠EAC=∠BAG，在△EAC和△BAG中，，∴△EAC≌△BAG（SAS），∴BG=CE．19．∵四边形ABCD是正方形，∴BC=DC，∠BCD=∠DCF=90°，在△BCE和△DCF中，∵，∴△BCE≌△DCF（SAS），∴BE=DF20．DF=BE．理由如下：在正方形ABCD中，AB=AD，∠BAD=90°，∴∠DAF=180°﹣90°=90°，∴∠BAD=∠DAF，∵E是AD的中点，∴AE=AD=AB，∵AF=AB，∴AE=AF，∵在△ABE和△ADF中，，∴△ABE≌△ADF（SAS），∴DF=BE．21．（1）由题意得，AE=AB=AD，∠DAE=45°，故可得∠ADE=∠AED=67.5°，故∠CDE=∠ADC﹣∠ADE=90°﹣∠ADE=22.5°；（2）FG和DE相等．理由如下：由题意得，EN=EG，EM=EF=ND，（角平分线上的点到角的两边距离相等），在Rt△GEF和Rt△END 中，，故△GEF≌△END（HL），故可得出FG=DE．22．（1）在正方形ABCD中，设DC=4a，∵DE=3CE，∴DE=3a，∴在Rt△ADE中，AE=5a，∴cos∠DAE==；（2）∵M、N分别是AD、AE的中点，∴MN∥DE且MN=DE，∴∠AMN=90°．在△AMN和△MDF中，有∠AMN=∠MDF=90°，AM=MD，∠DAE=∠DMF，∴△AMN≌△MDF，∴MF=AN，又AN=NE，∴MF=NE，又MN∥EF且MN≠EF，∴四边形MNEF是等腰梯形．23．如图，画出旋转后的图形，并连接PP′．设PA=x，PB=2x，PC=3x，∵将△APB绕B点顺时针旋转90°，得△BP′C，∴△BP′C≌△APB，∠APB=∠BP′C，∴△BP′P为等腰直角三角形，∴∠BP′P=45°，∵PB=BP′=2x，∴PP′==2 x，∵PC=3x，CP′=PA=x，∴PC2=PP′2+CP′2，∴∠PP′C=90°，∴∠APB=∠BP′C=∠BP′P+∠PP′C=45°+90°=135°．24．∵四边形ABCD为正方形，∴AB=AD=CD，∠CDA=∠DAB=90°，又∵△ADE为等边三角形，∴AE=AD=DE，∠EDA=∠EAD=∠AED=60°，∴AB=AE=CD=CE，∠EDC=∠EAB=150°，∴△ABE和△DCE都为全等的等腰三角形，（4分）∴∠AEB=∠DEC==15°，（6分）∴∠CEB=60°﹣15°﹣15°=30°．25．（1）证明：∵四边形ABCD、GCEF都是正方形，∴BC=DC，∠BCG=∠DCE=90°，GC=EC∴△BCG≌△DCE∴∠BGC=∠DEC（2）连接BD如果BH垂直平分DE，则有BD=BE∵BC=CD=1，∴BD=（8分）∴CE=BE﹣BC=﹣1∴CG=CE=﹣1即当CG=﹣1时，BH垂直平分DE．26．1）证明：∵四边形ABCD是正方形，∴AB=AD，∠DAB=90°，又∵∠EAF=90°，∴∠EAB=∠DAF，在△AFD与△AEB中，∵，∴△AFD≌△AEB（SAS）；（2）解：∵AF=AE=，∠EAF=90°，∴∠AFE=∠AEF=45°，∵∠AFE+∠DFA=180°，∴∠DFA=135°，∵△AFD≌△AEB，∴∠AEB=∠DFA=135°，∴∠DEB=∠AEB﹣∠AEF=135°﹣45°=90°；（3）在Rt△AEF中，EF===2，在Rt△BEF中，BE===，∵△AFD≌△AEB，∴DF=BE=，连接BD，设正方形ABCD的边长为x，则在Rt△ABD 中，BD=x，在Rt△BED中，BE2+DE2=BD2，即（）2+（2+）2=（x）2，∴x2=7+2，∴正方形ABCD的面积为（7+2）．27．∵正方形ABCD，∴AD=AB，∠CDA=∠DAB=∠B=90°，∵DG⊥AE，∴∠DGA=90°，∴∠ADG+∠DAG=90°，∵∠ADG+∠EAB=90°，∴∠ADG=∠EAB，∵AD=AB，∠DAF=∠B=90°，∴△ADF≌△BAE，∴AF=BE．28．∵ABCD是正方形，∴AD=DC，∠ADC=90°，∴∠CDG+∠FDA=90°，∵AF⊥DE，CG⊥DE，∴∠AFD=∠CGD=90°，∴∠FAD+∠FDA=90°，∴∠FAD=∠CDG，∴△ADF≌△DCG，∴FD=CG=2，∴AD==．故正方形的边长为．29．（1）CE=AF，且CE⊥AF（1分）证明：如图，∵△AFD是由△CED绕点D顺时针旋转90°而得到的．∴△ADF≌△CDE，∴CE=AF，∠1=∠2，DE=DF．（3分）延长CE交AF于点G．∵四边形ABCD是正方形，∠CDA=90°．又∠3=∠4，∠2+∠4+∠EGA=∠1+∠3+∠CDE=180°∴∠EGA=∠CDE=90°即CE⊥AF；（5分）（2）∵∠1=30°，∠2=30°又∠ADF=90°，∴∠AFD=60°（7分）∵DE=DF，∴∠EFD=45°（9分）∴∠AFE=∠AFD﹣∠EFD=15°30．1）证明：①∵四边形ABCD和四边形CEFG是正方形，∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，在△BCG和△DCE中，，∴△BCG≌△DCE（SAS），②∵△BCG≌△DCE，∴∠CBG=∠CDE，又∠CBG+∠BGC=90°，∴∠CDE+∠DGH=90°，∴∠DHG=90°，∴BH⊥DE；（2）解：当G是CD的中点，即CG=CD时，四边形DGEF是平行四边形．理由：连接DF、GE，∵G是CD的中点，∴CG=GD，∵四边形ABCD和四边形CEFG是正方形，∴DG∥EF，CG=EF，∴DG=EF，∴四边形DGEF是平行四边形．∴当G是CD的中点，即CG=CD时，四边形DGEF 是平行四边形．（3）解：当CG=﹣1时，BH垂直平分DE，理由：连接BD，∵四边形ABCD和四边形CEFG是正方形，∴∠A=90°，AB=AD=BC=1，∴BD==，∵CG=﹣1，∴BE=BC+CE=，∴BD=BE，∵BH⊥DE，∴DH=EH，∴BH垂直平分DE，∴当CG=﹣1时，BH垂直平分DE．。

长方形正方形周长专题练习

长方形和正方形的周长专题练习（一）一、判断1、长方形和正方形的周长，都是四条边长度的和。

………………………… （）2、长方形的长是7米，宽是3米，周长是20米。

………………………… （）3、一个正方形的边长是6厘米，它的周长是24米。

………………………… （） 4．两个相同的三角形能够拼成一个正方形。

……………………………………………（） 5．正方形是特殊的长方形。

………………………………………………………………（）二、填空2、一个正方形的边长是8厘米，它的周长是（）厘米，一个长方形的长26分米，宽9分米周长是（）厘米。

3、一个正方形的游泳池，围着这个游泳池走一圈要走160米，这个游泳池的边长是（）米。

4、一个长方形长9厘米，宽比长少3厘米，它的周长是( ) 三、应用题1、一个正方形林场，边长是8千米，李明每小时步行4千米。

他绕林场一周需要多少小时？2、把12张正方形书法作品贴在一起，每张书法作品边长是4厘米，做一个“书法园地”，园地四周贴上花边，怎样设计才能使花边最短？3、①图形的周长是 6 cm ②图形的周长是4、用一根长28厘米的铁丝围成一个正方形。

它的边长是多少？5、一个长方形纸长25米宽16米，从这张纸上剪下一个最大的正方形，正方形的周长是多少？剩下的图形周长是多少？6、一个正方形的草地，边长是100米，绕着草地的四周走2圈，要走多少米？7、一个正方形和一个长方形的周长相等，正方形边长是10厘米，长方形的长是12厘米，长方形的宽是多少米？8、一块长方形菜地，长18米，宽9米，一面靠墙，其它三面墙围上竹篱笆。

竹篱笆长多少米？9、用一根铁丝围成一个长为26厘米，宽为16厘米的长方形还多2厘米，将它围成一个边长为20厘米的正方形还多多少厘米？10、长方形的长16分米，宽6分米，如果长增加15分米，周长变成多少分米？11、一根铁丝围成一个长10厘米，宽8厘米的长方形，周长是多少？同一根铁丝能围成边长是多少厘米的正方形？12、把两个完全相同的长方形拼在一起，长方形长4厘米，宽2厘米。

五年级数学下册期末-长方体和正方体的表面积《解决问题》专项练习二(人教版,含答案)

14．一个房间长6米，宽4米，高3米，如果在房间四壁贴墙纸，除去门窗7平方米，每平方米墙纸12元，共要多少元的墙纸？
15．光华街口装了一个新的长方体铁皮邮箱，长50厘米，宽40厘米，高60 厘米，做这个邮箱至少需要多少平方厘米的铁皮？
16．一个正方体盒子，棱长为0.3cm，这个正方体的表面积是多少？
29．学校要粉刷多媒体教室，经测量多媒体教室的长是9米，宽是7米，高是3米，门窗面积是12.6平方米．求需要粉刷的面积是多少平方米？
30．一间大会议室长20m、宽15m、高4m，门窗和黑板的面积是20m2。装修时给会议室的四壁和天花板进行粉刷（扣除门窗和黑板的面积），要粉刷多少平方米？
参考答案
1．
解析：
20．用一根铁丝刚好焊成一个棱长10cm的正方体框架，如果把它改成一个长12cm，宽7cm的长方体框架。
(1)长方体框架的高是多少厘米？
(2)如果用彩纸把这个长方体和正方体框架包起来，哪个用的彩纸多？多多少？
21．一块长30厘米，宽25厘米的长方形铁皮，从四个角各切掉一个边长是5厘米的正方形，然后做成盒子。盒子的表积是多少？
4．
解析：
粉刷的面积：
15×8＋15×3×2＋8×3×2－30.5
＝72.5（平方米）
答：粉刷的面积是72.5平方米。
点评：
本题考查了长方体表面积，完整的长方体表面积＝（长×宽＋长×高＋宽×高）×2。
3．
解析：
10×8×2＋6×8×2
＝160＋96
＝256（平方分米）
答：这张商标纸的面积至少有256平方分米。
点评：
本题考查了长方体表面积，完整的长方体表面积＝（长×宽＋长×高＋宽×高）×2。
10．一间教室长9米，宽7米，高3米.要粉刷教室的屋顶和底面墙壁(除去门窗和黑板的面积29.6平方米)，粉刷面积是多少平方米？如果平均每平方米用0.2千克涂料，至少需要多少千克涂料？

正方形的性质与判定专题练习

正方形专题训练（含答案)一．选择题（共11小题）1．如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1，）,则点C的坐标为（）2．）如图，点E在正方形ABCD的对角线AC上，且EC=2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为(）A．a2B．a2C．a2D．a23．如图，F是正方形ABCD的边CD上的一个动点，BF 的垂直平分线交对角线AC于点E，连接BE，FE，则∠EBF 的度数是（）A．45°B．50°C．60°D．不确定4．平行四边形、矩形、菱形、正方形都具有的是（）A．对角线互相平分B．对角线互相垂直C ．对角线相等D．对角线互相垂直且相等5．正方形的一条对角线长为4,则这个正方形的面积是（)6．（2014•福州）如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（）A．45°B．55°C．60°D．75°7．顺次连接菱形各边的中点所形成的四边形是（）A．等腰梯形B．矩形C．菱形D．正方形8．下列说法中，正确的是（）A．相等的角一定是对顶角B．四个角都相等的四边形一定是正方形C．平行四边形的对角线互相平分D．矩形的对角线一定垂直9．已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中,选两个作为补充条件后，使得四边形ABCD是正方形,现有下列四种选法，其中错误的是（）A．选①②B．选②③C．选①③D．选②④10．如图，在正方形ABCD中，CE=MN，∠MCE=35°，那么∠ANM等于（）A．45°B．50°C．55°D．60°11．如图,菱形ABCD中,∠B=60°，AB=5，则以AC为边长的正方形ACEF的面积为（）A．9B．16 C．20 D．25二．填空题(共5小题）12．如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEB=_________度．13．如图，已知P是正方形ABCD对角线BD上一点，且BP=BC，则∠ACP度数是_________度．14．如图，四边形ABCD为正方形，△ADE为等边三角形．AC为正方形ABCD的对角线，则∠EAC=_________度．A．8B．4C．8D．1615．已知：如图，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的正方形ACEF的周长为_________．16．如图所示，正方形ABCD 的周长为16cm，顺次连接正方形ABCD各边的中点,得到四边形EFGH,则四边形EFGH的周长等于_________cm,四边形EFGH的面积等于_________cm．三．解答题（共6小题）17．如图，正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为点G．求证：AE=BF．18．如图，在正方形ABCD中，P是对角线AC上的一点,连接BP、DP，延长BC到E,使PB=PE．求证：∠PDC=∠PEC．19．如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G．（1）求证：AE=CF；（2）若∠ABE=55°，求∠EGC的大小．20．在平面内正方形ABCD与正方形CEFH如图放置，连DE，BH，两线交于M．求证：（1）BH=DE．（2）BH⊥DE．21．已知：如图，▱ABCD中，O是CD的中点，连接AO 并延长,交BC的延长线于点E．(1）求证：△AOD≌△EOC；（2）连接AC，DE,当∠B=∠AEB=_________°时，四边形ACED是正方形？请说明理由．22．（2014•随州）已知：如图,在矩形ABCD中，M、N 分别是边AD、BC的中点,E、F分别是线段BM、CM的中点．（1）求证：△ABM≌△DCM；（2）填空：当AB：AD=_________时，四边形MENF 是正方形．一．选择题（共11小题）1．（2014•南充）如图，将正方形OABC 放在平面直角坐标系中，O 是原点，A 的坐标为（1，)，则点C 的坐标为( ）A ．（﹣，1） B ． (﹣1，） C ． (，1) D ．（﹣，﹣1）考点：全等三角形的判定与性质；坐标与图形性质；正方形的性质．专题：几何图形问题．分析：过点A 作AD ⊥x 轴于D ，过点C 作CE ⊥x 轴于E ，根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD 和△OCE 全等，根据全等三角形对应边相等可得OE=AD ，CE=OD ，然后根据点C 在第二象限写出坐标即可．解答：解：如图，过点A 作AD ⊥x 轴于D ，过点C 作CE ⊥x 轴于E ，∵四边形OABC 是正方形， ∴OA=OC ，∠AOC=90°, ∴∠COE+∠AOD=90°，又∵∠OAD+∠AOD=90°， ∴∠OAD=∠COE, 在△AOD 和△OCE 中，，∴△AOD ≌△OCE （AAS)， ∴OE=AD=，CE=OD=1，∵点C 在第二象限, ∴点C 的坐标为（﹣,1）．故选:A ．点评：本题考查了全等三角形的判定与性质，正方形的性质，坐标与图形性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．2．（2014•山西)如图，点E 在正方形ABCD 的对角线AC 上，且EC=2AE ，直角三角形FEG 的两直角边EF 、EG 分别交BC 、DC 于点M 、N ．若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为（）A ． a 2B ． a 2C ． a 2D ． a 2考点：全等三角形的判定与性质；正方形的性质．专题：几何图形问题．分析：作EP ⊥BC 于点P ，EQ ⊥CD 于点Q ，△EPM ≌△EQN,利用四边形EMCN 的面积等于正方形MCQE 的面积求解．解答：解：作EP ⊥BC 于点P,EQ ⊥CD 于点Q ，∵四边形ABCD是正方形，∴∠BCD=90°，又∵∠EPM=∠EQN=90°，∴∠PEQ=90°,∴∠PEM+∠MEQ=90°，∵三角形FEG是直角三角形，∴∠NEF=∠NEQ+∠MEQ=90°,∴∠PEM=∠NEQ,∵AC是∠BCD的角平分线，∠EPC=∠EQC=90°，∴EP=EN，四边形MCQE是正方形，在△EPM和△EQN中，，∴△EPM≌△EQN(ASA）∴S△EQN=S△EPM,∴四边形EMCN的面积等于正方形MCQE的面积, ∵正方形ABCD的边长为a，∴AC=a，∵EC=2AE，∴EC=a，∴EP=PC=a，∴正方形MCQE的面积=a ×a=a2，∴四边形EMCN的面积=a2,故选：D．点评:本题主要考查了正方形的性质及全等三角形的判定及性质，解题的关键是作出辅助线,证出△EPM≌△EQN．3．（2014•台州）如图，F是正方形ABCD的边CD上的一个动点，BF的垂直平分线交对角线AC于点E，连接BE，FE，则∠EBF的度数是(）A．45°B．50°C．60°D．不确定考点:全等三角形的判定与性质；正方形的性质．专题：几何图形问题．分析:过E作HI∥BC，分别交AB、CD于点H、I，证明Rt△BHE≌Rt△EIF，可得∠IEF+∠HEB=90°，再根据BE=EF即可解题．解答:解：如图所示，过E作HI∥BC，分别交AB、CD于点H、I，则∠BHE=∠EIF=90°,∵E是BF的垂直平分线EM上的点，∴EF=EB，∵E是∠BCD角平分线上一点，∴E到BC和CD的距离相等，即BH=EI，Rt△BHE和Rt△EIF中，，∴Rt△BHE≌Rt△EIF（HL），∴∠HBE=∠IEF ， ∵∠HBE+∠HEB=90°， ∴∠IEF+∠HEB=90°， ∴∠BEF=90°， ∵BE=EF ，∴∠EBF=∠EFB=45°．故选：A ．点评：本题考查了正方形角平分线和对角线重合的性质,考查了直角三角形全等的判定，全等三角形对应角相等的性质．4．（2014•郴州）平行四边形、矩形、菱形、正方形都具有的是( ) A ．对角线互相平分 B ．对角线互相垂直 C ．对角线相等 D ．对角线互相垂直且相等考点：正方形的性质;平行四边形的性质；菱形的性质；矩形的性质．专题：证明题．分析: 本题主要依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断．解答：解：A 、对角线相等是平行四边形、矩形、菱形、正方形都具有的性质;B 、对角线互相垂直是菱形、正方形具有的性质；C 、对角线相等是矩形和正方形具有的性质；D 、对角线互相垂直且相等是正方形具有的性质．故选:A ．点评：本题主要考查平行四边形、矩形、菱形、正方形的性质定理．5．（2014•来宾）正方形的一条对角线长为4，则这个正方形的面积是（）A ． 8B ． 4C ． 8D ． 16考点：正方形的性质．分析：根据正方形的面积等于对角线乘积的一半列式计算即可得解．解答：解:∵正方形的一条对角线长为4, ∴这个正方形的面积=×4×4=8．故选:A ．点评：本题考查了正方形的性质，熟记利用对角线求面积的方法是解题的关键．6．（2014•福州）如图,在正方形ABCD 的外侧,作等边三角形ADE ，AC 、BE 相交于点F ，则∠BFC 为（）A ． 45°B ． 55°C ． 60°D ．75°考点: 正方形的性质；等腰三角形的性质;等边三角形的性质．分析: 根据正方形的性质及全等三角形的性质求出∠ABE=15°，∠BAC=45°,再求∠BFC ．解答：解：∵四边形ABCD 是正方形， ∴AB=AD又∵△ADE 是等边三角形， ∴AE=AD=DE,∠DAE=60° ∴AD=AE∴∠ABE=∠AEB ，∠BAE=90°+60°=150° ∴∠ABE=（180°﹣150°）÷2=15° 又∵∠BAC=45° ∴∠BFC=45°+15°=60°故选:C ．点评：本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°．7．（2014•来宾）顺次连接菱形各边的中点所形成的四边形是（） A ．等腰梯形 B ．矩形 C ．菱形D ．正方形考点:正方形的判定；三角形中位线定理；菱形的性质．分析：根据三角形的中位线定理以及菱形的性质即可证得．解答：解：∵E ，F 是中点， ∴EH ∥BD ，同理，EF ∥AC,GH ∥AC ，FG ∥BD ， ∴EH ∥FG ,EF ∥GH ，则四边形EFGH 是平行四边形．又∵AC ⊥BD ， ∴EF ⊥EH ，∴平行四边形EFGH 是矩形．故选：B ．点评：本题主要考查了矩形的判定定理，正确理解菱形的性质以及三角形的中位线定理是解题的关键．8．（2014•湘西州）下列说法中，正确的是（） A ．相等的角一定是对顶角B ．四个角都相等的四边形一定是正方形C ．平行四边形的对角线互相平分D ．矩形的对角线一定垂直考点：正方形的判定;对顶角、邻补角;平行四边形的性质;矩形的性质．分析：根据对顶角的定义,正方形的判定，平行四边形的性质，矩形的性质对各选项分析判断利用排除法求解．解答：解：A 、相等的角一定是对顶角错误，例如,角平分线分成的两个角相等，但不是对顶角,故本选项错误；B 、四个角都相等的四边形一定是矩形，不一定是正方形,故本选项错误；C 、平行四边形的对角线互相平分正确，故本选项正确；D 、矩形的对角线一定相等，但不一定垂直,故本选项错误．故选：C ．点评：本题考查了正方形的判定，平行四边形的性质，矩形的性质,对顶角的定义，熟记各性质与判定方法是解题的关键．9．（2014•株洲）已知四边形ABCD 是平行四边形，再从①AB=BC ，②∠ABC=90°，③AC=BD,④AC ⊥BD 四个条件中,选两个作为补充条件后，使得四边形ABCD 是正方形，现有下列四种选法，其中错误的是（ ) A ．选①② B ．选②③ C ．选①③ D ．选②④考点：正方形的判定；平行四边形的性质．分析:要判定是正方形，则需能判定它既是菱形又是矩形．解答: 解:A 、由①得有一组邻边相等的平行四边形是菱形，由②得有一个角是直角的平行四边形是矩形，所以平行四边形ABCD 是正方形，正确，故本选项不符合题意；B 、由②得有一个角是直角的平行四边形是矩形，由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD 是正方形，错误，故本选项符合题意；C 、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形，所以平行四边形ABCD 是正方形，正确，故本选项不符合题意； D 、由②得有一个角是直角的平行四边形是矩形，由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ABCD 是正方形，正确，故本选项不符合题意．故选：B ．点评：本题考查了正方形的判定方法：①先判定四边形是矩形，再判定这个矩形有一组邻边相等;②先判定四边形是菱形，再判定这个矩形有一个角为直角．③还可以先判定四边形是平行四边形，再用1或2进行判定．10．（2014•红桥区三模）如图，在正方形ABCD 中,CE=MN ，∠MCE=35°，那么∠ANM 等于（）A ． 45°B ．50° C ．55° D ．60°考点：全等三角形的判定与性质；正方形的性质．分析: 过B 作BF ∥MN 交AD 于F,则∠AFB=∠ANM ，根据正方形的性质得出∠A=∠EBC=90°,AB=BC,AD ∥BC,推出四边形BFNM 是平行四边形，得出BF=MN=CE ，证Rt △ABF ≌Rt △BCE,推出∠AFB=∠ECB 即可．解答：解：过B 作BF ∥MN 交AD 于F ，则∠AFB=∠ANM ， ∵四边形ABCD 是正方形，∴∠A=∠EBC=90°，AB=BC,AD ∥BC ， ∴FN ∥BM,BE ∥MN ，∴四边形BFNM 是平行四边形， ∴BF=MN ， ∵CE=MN ， ∴CE=BF,在Rt △ABF 和Rt △BCE 中∴Rt △ABF ≌Rt △BCE （HL ）, ∴∠AFB=∠ECB=35°， ∴∠ANM=∠AFB=55°，故选C ．点评：本题考查了平行四边形的性质和判定，全等三角形的性质和判定，正方形的性质的应用，主要考查学生的推理能力．11．(2014•四会市一模）如图，菱形ABCD 中,∠B=60°，AB=5,则以AC 为边长的正方形ACEF 的面积为( ）A ． 9B ． 16C ． 20D ． 25考点:菱形的性质；正方形的性质．分析：据已知可求得△ABC 是等边三角形，从而得到AC=AB,从而求出正方形ACEF 的边长,进而可求出其面积．解答：解：∵B=60°,AB=BC ， ∴△ABC 是等边三角形，∴AC=AB=5，∴正方形ACEF 的边长为5， ∴正方形ACEF 的面积为25，故选D ．点评：本题考查菱形与正方形的性质，属于基础题，对于此类题意含有60°角的题目一般要考虑等边三角形的应用．二．填空题(共5小题）12．（2009•江西模拟）如图,在正方形ABCD 的外侧,作等边三角形ADE ，则∠AEB= 15 度．考点:正方形的性质;等边三角形的性质．分析: 由等边三角形的性质可得∠DAE=60°，进而可得∠BAE=150°，又因为AB=AE ，结合等腰三角形的性质，易得∠AEB 的大小．解答: 解：△ADE 是等边三角形;故∠DAE=60°， ∠BAE=90°+60°=150°，又有AB=AE,故∠AEB=30°÷2=15°；故答案为15°．点评: 主要考查了正方形基本性质：①两组对边分别平行;四条边都相等；相邻边互相垂直；②四个角都是90°;③对角线互相垂直；对角线相等且互相平分；每条对角线平分一组对角．13．(2008•佛山）如图,已知P 是正方形ABCD 对角线BD 上一点，且BP=BC,则∠ACP 度数是 22.5 度．考点：正方形的性质．专题:计算题．分析：根据正方形的性质可得到∠DBC=∠BCA=45°又知BP=BC,从而可求得∠BCP 的度数,从而就可求得∠ACP 的度数．解答：解：∵ABCD 是正方形， ∴∠DBC=∠BCA=45°，∵BP=BC ，∴∠BCP=∠BPC=（180°﹣45°）=67。

长方形正方形的面积专项练习30题(有答案)ok

长方形正方形的面积专项练习30题（有答案）1．一块正方形果园，边长是80米，这块果园占地面积是多少平方米？如果每棵果树占地4平方米，果园中一共有多少棵果树？2．一块长方形菜地，长是9米，宽是6米．这块菜地一共收青菜972千克．平均每平方米收青菜多少千克？3．一块长方形的萝卜地，长17米，宽12米．在这块地里一共收萝卜3080千克，平均每平方米收多少千克？4．一个边长为8.4厘米的正方形铁皮，从中挖去一块面积为40.5平方厘米的铁皮，剩下的铁皮面积是多少？？5．小明家新房的面积是120平方米，用边长为0.6平方米的正方形瓷砖铺地，300块够吗？6．一块长方形草坪的面积是4800平方米，它的宽是60米，它的长是多少米？（用方程解答）7．一个长方形运动场的面积是960平方米，这个运动场的宽是24米，长是多少米？（列方程解）8．一块长方形玻璃，长是宽的2倍，周长是54分米，这个长方形的面积是多少？9．王婆婆的菜园，长48米，宽32米，这个菜园的周长是多少米？如果每平方米大约收菜20千克，这个菜园大约可收多少千克的菜？10．已知长方形的面积是1000平方厘米，宽是8厘米，求周长．11．有一游泳池，长50米，宽25米，它的周长和面积各是多少？12．一块长方形土地，长75米，宽45米．王大伯要在四周围上篱笆，一共需要多长的篱笆？这块地的面积有多大？13．一块正方形菜地，边长是16米，如果四周用篱笆围起来，篱笆长多少米？这块菜地占地面积是多少平方米？14．一个正方形的边长是1.2米，这个正方形的周长和面积分别是多少？15．一个正方形水池，周长1200米，这个水池占地多少公顷？16．一个正方形的周长是37.2分米，这个正方形的面积是多少？17．一个长方形的苗圃，长40米、宽18米，按每平方米育树苗5棵计算．这个苗圃一概可以育多少棵树苗？18．一间教室长8m，宽6m，高3m，要给教室地面铺上地板砖，已知地板砖长宽均为40cm，共需要多少块地板砖？19．一面长方形的墙壁需要重新粉刷，它的长是10米、宽是8米，如果按每平方米涂料2元钱，粉刷完这面墙壁要付多少钱？20．一间客厅是6m，宽是4m，若要用边长是40cm的正方形方砖铺地，至少需要多少块？如果每块地砖5元，铺满这个客厅要多少元？21．一块正方形菜地边长540分米，这块菜地的面积是多少平方分米？合多少平方米？22．一辆洒水车，每分钟前进220米，洒水的宽度是6米．洒水车行驶2分钟，能给多大的地面洒水？23．中山公园里的一块草坪长280m、宽250m，它的面积是多少平方米？合多少公顷？24．一个长方形的面积与边长为16厘米的正方形面积相等，这个长方形的宽是8厘米，长是多少厘米？（列方程解决）25．一个正方形，边长增加5米，面积增加125平方米，求原来这个正方形面积是多少平方米？26．一个正方形周长是156cm，面积是多少平方厘米？27．一块菜地长24米，宽16米，用其中的地面种白菜，白菜的种植面积是多少平方分米？28．一面镜子长12分米，宽5分米．它的面积是多少平方分米？这种镜子的价格是每平方分米2元，买这面镜子要多少元？29．一块长方形花圃的宽7米，面积248平方米，扩建后长不变，宽增加到21米，求扩建后的面积是多少平方米？30．一个正方形边长9厘米把它分成四个相等大小的小正方形请问小正方形的面积是多少？参考答案：1．（1）80×80=6400（平方米），（2）6400÷4=1800（棵）；答：这块果园占地面积是6400平方米，果园中一共有1800棵果树．2．972÷（9×6）=972÷54=18（千克）；答：平均每平方米收青菜18千克．3．3080÷（17×12）=3080÷204=15（千克）．答：平均每平方米收15千克．4．8.4×8.4﹣40.5=70.56﹣40.5=30.06（平方厘米）；答：剩下的铁皮面积是30.06平方厘米．5．0.6×0.6×300=0.36×300=108（平方米），108＜120，答：300块不够6．解：设它的长是x米，根据题意得60x=4800，60x÷60=4800÷60，x=80．答：它的长是80米．7．解：设长方形的长是x米，根据题意可得方程：24x=960，24x÷24=960÷24，x=40．答：长是40米8．长和宽的和的总份数：1+2=3，长与宽的和：54÷2=27（分米），则长为：27÷3×2=18（分米），宽为：27÷3×1=9（分米），长方形的面积：18×9=162（平方分米）．答：这个长方形的面积是162平方分米9．（48+32）×2=80×2=160（米），48×32=1536（平方米），1536×20=30720（千克），答：这个菜地的周长是160米，可以收30720千克的菜10．1000÷8=125（厘米），所以长方形的周长是：（125+8）×2=133×2=266（厘米），答：这个长方形的周长是266厘米11．（50+25）×2=75×2=150（米）；50×25=1250（平方米）．答：这个长方形的游泳池的周长是150米，面积是1250平方米12．（75+45）×2=120×2=240（米），75×45=3375（平方米），答：篱笆长是240米，菜地面积是3375平方米13．周长：16×4=84（米），面积：16×16=256（平方米），答：篱笆长84米，这块菜地占地面积是256平方米14．1.2×4=4.8（米），1.2×1.2=1.44（平方米），答：这个正方形的周长是4.8米，面积是1.44平方米15．1200÷4=300（米），300×300=90000（平方米）=9公顷，答：这个水池占地9公顷16．37.2÷4=9.3（分米），9.3×9.3=86.49（平方分米）．答：这个正方形的面积是86.49平方分米．17．苗圃的面积为：40×18=720（平方米），720×5=3600（棵），答：这个苗圃一共可以育苗3600棵18．40厘米=0.4米；8×6÷（0.4×0.4）=48÷0.16=300（块），答：共需要300块19．10×8×2=80×2=160（元）．答：粉刷完这面墙壁要付160元20．40厘米=0.4米，6×4÷（0.4×0.4）=24÷0.16=150（块）；150×5=750（元）；答：至少需要150块，铺满这个客厅要750元21．1平方米=100平方分米，540×540=291600（平方分米），291600平方分米=2916平方米；答：这块菜地的面积是291600平方分米，合2916平方米22．220×2×6=440×6=2640（平方米）；答：能给2640平方米的地面洒水．24．设长方形的长为x厘米，8x=16×16，x=，x=32，答：长是32厘米．25．根据题干分析可得：原来正方形的边长为：（125﹣5×5）÷2÷5=（125﹣25）÷10=100÷10=10（米），则原来正方形的面积为：10×10=100（平方米），答：原正方形的面积为100平方米26．156÷4=39（厘米），39×39=1521（平方厘米），答：正方形的面积是1521平方厘米27．24×16=384（平方米）=38400（平方分米）；答：白菜的种植面积是384平方分米28．12×5=60（平方分米）；2×60=120（元）；答：它的面积是60平方分米，买这面镜子要多120元29．248÷7×21=×21=744（平方米）；答：扩建后的面积是744平方米平方米．30．9×9÷4=81÷4=20.25（平方厘米）；答：小正方形的面积是20.25平方厘米．。

矩形、菱形、正方形(解答题)专练(详细答案)

9.4 矩形、菱形、正方形（解答题）1．如图，在平行四边形ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．2．如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD 的延长线于点F，求证：DF=BE．3．如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．4．已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF．5．如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．6．如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP=FP=6，EF=6，∠BAD=60°，且AB＞6．（1）求∠EPF的大小；（2）若AP=10，求AE+AF的值；（3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值．7．如图，在△ABC中，∠ACB=90°，D，E分别为AC，AB的中点，BF∥CE交DE 的延长线于点F．（1）求证：四边形ECBF是平行四边形；（2）当∠A=30°时，求证：四边形ECBF是菱形．8．如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，AC与BD相交于点O，连接CD（1）求∠AOD的度数；（2）求证：四边形ABCD是菱形．9．如图，△ABC≌△ABD，点E在边AB上，CE∥BD，连接DE．求证：（1）∠CEB=∠CBE；（2）四边形BCED是菱形．10．如图，在Rt△ABC中，∠B=90°，点E是AC的中点，AC=2AB，∠BAC的平分线AD交BC于点D，作AF∥BC，连接DE并延长交AF于点F，连接FC．求证：四边形ADCF是菱形．11．如图，在四边形ABCF中，∠ACB=90°，点E是AB边的中点，点F恰是点E 关于AC所在直线的对称点．（1）证明：四边形CFAE为菱形；（2）连接EF交AC于点O，若BC=10，求线段OF的长．12．如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于长为半径画弧，两弧交于一点P，连接AP并延长交BC于点E，连接EF．（1）四边形ABEF是；（选填矩形、菱形、正方形、无法确定）（直接填写结果）（2）AE，BF相交于点O，若四边形ABEF的周长为40，BF=10，则AE的长为，∠ABC=°．（直接填写结果）13．如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）若AB=，∠DCF=30°，求四边形AECF的面积．（结果保留根号）14．如图，已知BD是矩形ABCD的对角线．（1）用直尺和圆规作线段BD的垂直平分线，分别交AD、BC于E、F（保留作图痕迹，不写作法和证明）．（2）连结BE，DF，问四边形BEDF是什么四边形？请说明理由．15．如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．（1）求证：四边形AECF是平行四边形；（2）若AB=6，AC=10，求四边形AECF的面积．16．如图，矩形ABCD中，延长AB至E，延长CD至F，BE=DF，连接EF，与BC、AD分别相交于P、Q两点．（1）求证：CP=AQ；（2）若BP=1，PQ=2，∠AEF=45°，求矩形ABCD的面积．17．如图，矩形ABCD的对角线AC，BD相交于点O，若AB=AO，求∠ABD的度数．18．已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．19．如图，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM．（1）当AN平分∠MAB时，求DM的长；（2）连接BN，当DM=1时，求△ABN的面积；（3）当射线BN交线段CD于点F时，求DF的最大值．20．如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．21．如图，将平行四边形ABCD的边AB延长到点E，使BE=AB，连接DE，交边BC于点F．（1）求证：△BEF≌△CDF；（2）连接BD、CE，若∠BFD=2∠A，求证：四边形BECD是矩形．22．阅读下面材料：在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？小敏在思考问题是，有如下思路：连接AC．结合小敏的思路作答（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由；参考小敏思考问题方法解决一下问题：（2）如图2，在（1）的条件下，若连接AC，BD．①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．23．如图，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H．（1）求证：△PHC≌△CFP；（2）证明四边形PEDH和四边形PFBG都是矩形，并直接写出它们面积之间的关系．24．已知，如图，正方形ABCD中，E为BC边上一点，F为BA延长线上一点，且CE=AF．连接DE、DF．求证：DE=DF．25．如图，在正方形ABCD中，点E（与点B、C不重合）是BC边上一点，将线段EA绕点E顺时针旋转90°到EF，过点F作BC的垂线交BC的延长线于点G，连接CF．（1）求证：△ABE≌△EGF；=2S△ECF，求BE．（2）若AB=2，S△ABE26．已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ 于点P．（1）求证：AP=BQ；（2）在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．27．在平面直角坐标系中，点O为原点，点A的坐标为（﹣6，0）．如图1，正方形OBCD的顶点B在x轴的负半轴上，点C在第二象限．现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG．（1）如图2，若α=60°，OE=OA，求直线EF的函数表达式．（2）若α为锐角，tanα=，当AE取得最小值时，求正方形OEFG的面积．（3）当正方形OEFG的顶点F落在y轴上时，直线AE与直线FG相交于点P，△OEP的其中两边之比能否为：1？若能，求点P的坐标；若不能，试说明理由28．如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF=CA，连接AF，∠ACF的平分线分别交AF，AB，BD于点E，N，M，连接EO．（1）已知EO=，求正方形ABCD的边长；（2）猜想线段EM与CN的数量关系并加以证明．29．如图，四边形ABCD是正方形，点E是BC的中点，∠AEF=90°，EF交正方形外角的平分线CF于F．求证：AE=EF．30．如图，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连结CE、DF．求证：CE=DF．答案与解析1．（2016•安顺）如图，在平行四边形ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．（1）求证：△ABE≌△CDF；（2）当四边形AECF为菱形时，求出该菱形的面积．【分析】第（1）问要证明三角形全等，由平行四边形的性质，很容易用SAS证全等．第（2）要求菱形的面积，在第（1）问的基础上很快知道△ABE为等边三角形．这样菱形的高就可求了，用面积公式可求得．【解答】（1）证明：∵在▱ABCD中，AB=CD，∴BC=AD，∠ABC=∠CDA．又∵BE=EC=BC，AF=DF=AD，∴BE=DF．∴△ABE≌△CDF．（2）解：∵四边形AECF为菱形，∴AE=EC．又∵点E是边BC的中点，∴BE=EC，即BE=AE．又BC=2AB=4，∴AB=BC=BE，∴AB=BE=AE，即△ABE为等边三角形，▱ABCD的BC边上的高为2×sin60°=，∴菱形AECF的面积为2．【点评】考查了全等三角形，四边形的知识以及逻辑推理能力．（1）用SAS证全等；（2）若四边形AECF为菱形，则AE=EC=BE=AB，所以△ABE为等边三角形．2．（2016•广安）如图，四边形ABCD是菱形，CE⊥AB交AB的延长线于点E，CF⊥AD交AD的延长线于点F，求证：DF=BE．【分析】连接AC，根据菱形的性质可得AC平分∠DAE，CD=BC，再根据角平分线的性质可得CE=FC，然后利用HL证明Rt△CDF≌Rt△CBE，即可得出DF=BE．【解答】证明：连接AC，∵四边形ABCD是菱形，∴AC平分∠DAE，CD=BC，∵CE⊥AB，CF⊥AD，∴CE=FC，∠CFD=∠CEB=90°．在Rt△CDF与Rt△CBE中，，∴Rt△CDF≌Rt△CBE（HL），∴DF=BE．【点评】此题考查了菱形的性质，角平分线的性质，关键是掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；角平分线的性质：角的平分线上的点到角的两边的距离相等．同时考查了全等三角形的判定与性质．3．（2016•荆州）如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△A′C′D′的位置，若平移开始后点D′未到达点B时，A′C′交CD于E，D′C′交CB于点F，连接EF，当四边形EDD′F为菱形时，试探究△A′DE的形状，并判断△A′DE与△EFC′是否全等？请说明理由．【分析】当四边形EDD′F为菱形时，△A′DE是等腰三角形，△A′DE≌△EFC′．先证明CD=DA=DB，得到∠DAC=∠DCA，由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状．由EF∥AB推出∠CEF=∠EA′D，∠EFC=∠A′D′C=∠A′DE，再根据A′D=DE=EF即可证明．【解答】解：当四边形EDD′F为菱形时，△A′DE是等腰三角形，△A′DE≌△EFC′．理由：∵△BCA是直角三角形，∠ACB=90°，AD=DB，∴CD=DA=DB，∴∠DAC=∠DCA，∵A′C′∥AC，∴∠DA′E=∠A，∠DEA′=∠DCA，∴∠DA′E=∠DEA′，∴DA′=DE，∴△A′DE是等腰三角形．∵四边形DEFD′是菱形，∴EF=DE=DA′，EF∥DD′，∴∠C′EF=∠DA′E，∠EFC′=∠C′D′A′，∵CD∥C′D′，∴∠A′DE=∠A′D′C′=∠EFC′，在△A′DE和△EFC′中，，∴△A′DE≌△EFC′．【点评】本题考查平移、菱形的性质、全等三角形的判定和性质、直角三角形斜边中线定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．4．（2016•淮安）已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF．【分析】由菱形的性质得出AD=CD，由中点的定义证出DE=DF，由SAS证明△ADE ≌△CDF即可．【解答】证明：∵四边形ABCD是菱形，∴AD=CD，∵点E、F分别为边CD、AD的中点，∴AD=2DF，CD=2DE，∴DE=DF，在△ADE和△CDF中，，∴△ADE≌△CDF（SAS）．【点评】此题主要考查了全等三角形的判定、菱形的性质；熟练掌握菱形的性质，证明三角形全等是解决问题的关键．5．（2016•苏州）如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D 作对角线BD的垂线交BA的延长线于点E．（1）证明：四边形ACDE是平行四边形；（2）若AC=8，BD=6，求△ADE的周长．【分析】（1）根据平行四边形的判定证明即可；（2）利用平行四边形的性质得出平行四边形的周长即可．【解答】（1）证明：∵四边形ABCD是菱形，∴AB∥CD，AC⊥BD，∴AE∥CD，∠AOB=90°，∵DE⊥BD，即∠EDB=90°，∴∠AOB=∠EDB，∴DE∥AC，∴四边形ACDE是平行四边形；（2）解：∵四边形ABCD是菱形，AC=8，BD=6，∴AO=4，DO=3，AD=CD=5，∵四边形ACDE是平行四边形，∴AE=CD=5，DE=AC=8，∴△ADE的周长为AD+AE+DE=5+5+8=18．【点评】此题考查平行四边形的性质和判定问题，关键是根据平行四边形的判定解答即可．6．（2016•枣庄）如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP=FP=6，EF=6，∠BAD=60°，且AB＞6．（1）求∠EPF的大小；（2）若AP=10，求AE+AF的值；（3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值．【分析】（1）根据锐角三角函数求出∠FPG，最后求出∠EPF．（2）先判断出Rt△PME≌Rt△PNF，再根据锐角三角函数求解即可，（3）根据运动情况及菱形的性质判断求出AP最大和最小值．【解答】解：（1）过点P作PG⊥EF于点G，如图1所示．∵PE=PF=6，EF=6，∴FG=EG=3，∠FPG=∠EPG=∠EPF．在Rt△FPG中，sin∠FPG===，∴∠FPG=60°，∴∠EPF=120°．（2）过点P作PM⊥AB于点M，作PN⊥AD于点N，如图2所示．∵AC为菱形ABCD的对角线，∴∠DAC=∠BAC，AM=AN，PM=PN．在Rt△PME和Rt△PNF中，PM=PN，PE=PF，∴Rt△PME≌Rt△PNF，∴ME=NF．又AP=10，∠PAM=∠DAB=30°，∴AM=AN=APcos30°=10×=5，∴AE+AF=（AM+ME）+（AN﹣NF）=AM+AN=10．（3）如图，当△EFP的三个顶点分别在AB，AD，AC上运动，点P在P′，P之间运动，∴P′O=PO=3，AO=9，∴AP的最大值为12，AP的最小值为6，【点评】此题是菱形的性质题，主要考查了菱形的性质，锐角三角函数，特殊角的三角函数，解本题的关键是作出辅助线．7．（2016•三明）如图，在△ABC中，∠ACB=90°，D，E分别为AC，AB的中点，BF∥CE交DE的延长线于点F．（1）求证：四边形ECBF是平行四边形；（2）当∠A=30°时，求证：四边形ECBF是菱形．【分析】（1）利用平行四边形的判定证明即可；（2）利用菱形的判定证明即可．【解答】证明：（1）∵D，E分别为边AC，AB的中点，∴DE∥BC，即EF∥BC．又∵BF∥CE，∴四边形ECBF是平行四边形．（2）∵∠ACB=90°，∠A=30°，E为AB的中点，∴CB=AB，CE=AB．∴CB=CE．又由（1）知，四边形ECBF是平行四边形，∴四边形ECBF是菱形．【点评】此题主要考查了平行四边形的判定以及菱形的判定与性质，利用平行四边形的判定以及菱形的判定是解题关键．8．（2016•抚顺）如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，AC与BD相交于点O，连接CD（1）求∠AOD的度数；（2）求证：四边形ABCD是菱形．【分析】（1）首先根据角平分线的性质得到∠DAC=∠BAC，∠ABD=∠DBC，然后根据平行线的性质得到∠DAB+∠CBA=180°，从而得到∠BAC+∠ABD=（∠DAB+∠ABC）=×180°=90°，得到答案∠AOD=90°；（2）根据平行线的性质得出∠ADB=∠DBC，∠DAC=∠BCA，根据角平分线定义得出∠DAC=∠BAC，∠ABD=∠DBC，求出∠BAC=∠ACB，∠ABD=∠ADB，根据等腰三角形的判定得出AB=BC=AD，根据平行四边形的判定得出四边形ABCD是平行四边形，即可得出答案．【解答】解：（1）∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC=∠BAC，∠ABD=∠DBC，∵AE∥BF，∴∠DAB+∠CBA，=180°，∴∠BAC+∠ABD=（∠DAB+∠ABC）=×180°=90°，∴∠AOD=90°；（2）证明：∵AE∥BF，∴∠ADB=∠DBC，∠DAC=∠BCA，∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC=∠BAC，∠ABD=∠DBC，∴∠BAC=∠ACB，∠ABD=∠ADB，∴AB=BC，AB=AD∴AD=BC，∵AD∥BC，∴四边形ABCD是平行四边形，∵AD=AB，∴四边形ABCD是菱形．【点评】本题考查了等腰三角形的性质，平行四边形的判定，菱形的判定的应用，能得出四边形ABCD是平行四边形是解此题的关键．9．（2016•沈阳）如图，△ABC≌△ABD，点E在边AB上，CE∥BD，连接DE．求证：（1）∠CEB=∠CBE；（2）四边形BCED是菱形．【分析】（1）欲证明∠CEB=∠CBE，只要证明∠CEB=∠ABD，∠CBE=∠ABD即可．（2）先证明四边形CEDB是平行四边形，再根据BC=BD即可判定．【解答】证明；（1）∵△ABC≌△ABD，∴∠ABC=∠ABD，∵CE∥BD，∴∠CEB=∠DBE，∴∠CEB=∠CBE．（2））∵△ABC≌△ABD，∴BC=BD，∵∠CEB=∠CBE，∴CE=CB，∵CE∥BD，∴四边形CEDB是平行四边形，∵BC=BD，∴四边形CEDB是菱形．【点评】本题考查全等三角形的性质、菱形的判定、平行四边形的判定等知识，熟练掌握全等三角形的性质是解题的关键，记住平行四边形、菱形的判定方法，属于中考常考题型．10．（2016•聊城）如图，在Rt△ABC中，∠B=90°，点E是AC的中点，AC=2AB，∠BAC的平分线AD交BC于点D，作AF∥BC，连接DE并延长交AF于点F，连接FC．求证：四边形ADCF是菱形．【分析】先证明△AEF≌△CED，推出四边形ADCF是平行四边形，再证明△AED ≌△ABD，推出DF⊥AC，由此即可证明．【解答】证明：∵AF∥CD，∴∠AFE=∠CDE，在△AFE和△CDE中，，∴△AEF≌△CED．∵AF∥CD，∴四边形ADCF是平行四边形．由题意知，AE=AB，∠EAD=∠BAD，AD=AD，∴△AED≌△ABD．∴∠AED=∠B=90°，即DF⊥AC．∴四边形ADCF是菱形．【点评】本题考查菱形的判定、全等三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是灵活运用这些知识解决问题，属于基础题，中考常考题型．11．（2016•德阳）如图，在四边形ABCF中，∠ACB=90°，点E是AB边的中点，点F恰是点E关于AC所在直线的对称点．（1）证明：四边形CFAE为菱形；（2）连接EF交AC于点O，若BC=10，求线段OF的长．【分析】（1）根据直角三角形的性质得到CE=AB=EA，根据轴对称的性质得到AE=AF，CE=CF，得到CE=EA=AF=CF，根据菱形的判定定理证明结论；（2）根据菱形的性质得到OA=OC，OE=OF，根据三角形中位线定理求出OE，得到答案．【解答】（1）证明：∵∠ACB=90°，点E是AB边的中点，∴CE=AB=EA，∵点F是点E关于AC所在直线的对称点，∴AE=AF，CE=CF，∴CE=EA=AF=CF，∴四边形CFAE为菱形；（2）解：∵四边形CFAE为菱形；∴OA=OC，OE=OF，∴OE=BC=5，∴OF=5．【点评】本题考查的是菱形的判定和性质、轴对称的性质，掌握四条边相等的四边形是菱形、菱形的对角线垂直且互相平分是解题的关键．12．（2016•梅州）如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于长为半径画弧，两弧交于一点P，连接AP并延长交BC于点E，连接EF．（1）四边形ABEF是菱形；（选填矩形、菱形、正方形、无法确定）（直接填写结果）（2）AE，BF相交于点O，若四边形ABEF的周长为40，BF=10，则AE的长为10，∠ABC=120°．（直接填写结果）【分析】（1）先证明△AEB≌△AEF，推出∠EAB=∠EAF，由AD∥BC，推出∠EAF=∠AEB=∠EAB，得到BE=AB=AF，由此即可证明．（2）根据菱形的性质首先证明△AOB是含有30°的直角三角形，由此即可解决问题．【解答】解：（1）在△AEB和△AEF中，，∴△AEB≌△AEF，∴∠EAB=∠EAF，∵AD∥BC，∴∠EAF=∠AEB=∠EAB，∴BE=AB=AF．∵AF∥BE，∴四边形ABEF是平行四边形∵AB=AF，∴四边形ABEF是菱形．故答案为菱形．（2）∵四边形ABEF是菱形，∴AE⊥BF，BO=OF=5，∠ABO=∠EBO，∵AB=10，∴AB=2BO，∵∠AOB=90°∴∠BA0=30°，∠ABO=60°，∴AO=BO=5，∠ABC=2∠ABO=120°．故答案为，120．【点评】本题考查菱形的判定和性质、平行四边形的性质、作图﹣基本作图等知识，解题的关键是全等三角形的证明，想到利用特殊三角形解决问题，属于中考常考题型．13．（2016•贺州）如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）若AB=，∠DCF=30°，求四边形AECF的面积．（结果保留根号）【分析】（1）由过AC的中点O作EF⊥AC，根据线段垂直平分线的性质，可得AF=CF，AE=CE，OA=OC，然后由四边形ABCD是矩形，易证得△AOF≌△COE，则可得AF=CE，继而证得结论；（2）由四边形ABCD是矩形，易求得CD的长，然后利用三角函数求得CF的长，继而求得答案．【解答】（1）证明：∵O是AC的中点，且EF⊥AC，∴AF=CF，AE=CE，OA=OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFO=∠CEO，在△AOF和△COE中，，∴△AOF≌△COE（AAS），∴AF=CE，∴AF=CF=CE=AE，∴四边形AECF是菱形；（2）解：∵四边形ABCD是矩形，∴CD=AB=，在Rt△CDF中，cos∠DCF=，∠DCF=30°，∴CF==2，∵四边形AECF是菱形，∴CE=CF=2，∴四边形AECF是的面积为：EC•AB=2．【点评】此题考查了矩形的性质、菱形的判定与性质以及三角函数等知识．注意证得△AOF≌△COE是关键．14．（2016•衢州）如图，已知BD是矩形ABCD的对角线．（1）用直尺和圆规作线段BD的垂直平分线，分别交AD、BC于E、F（保留作图痕迹，不写作法和证明）．（2）连结BE，DF，问四边形BEDF是什么四边形？请说明理由．【分析】（1）分别以B、D为圆心，比BD的一半长为半径画弧，交于两点，确定出垂直平分线即可；（2）连接BE，DF，四边形BEDF为菱形，理由为：由EF垂直平分BD，得到BE=DE，∠DEF=∠BEF，再由AD与BC平行，得到一对内错角相等，等量代换及等角对等边得到BE=BF，再由BF=DF，等量代换得到四条边相等，即可得证．【解答】解：（1）如图所示，EF为所求直线；（2）四边形BEDF为菱形，理由为：证明：∵EF垂直平分BD，∴BE=DE，∠DEF=∠BEF，∵AD∥BC，∴∠DEF=∠BFE，∴∠BEF=∠BFE，∴BE=BF，∵BF=DF，∴BE=ED=DF=BF，∴四边形BEDF为菱形．【点评】此题考查了矩形的性质，菱形的判定，以及作图﹣基本作图，熟练掌握性质及判定是解本题的关键．15．（2016•扬州）如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．（1）求证：四边形AECF是平行四边形；（2）若AB=6，AC=10，求四边形AECF的面积．【分析】（1）首先由矩形的性质和折叠的性质证得AB=CD，AD∥BC，∠ANF=90°，∠CME=90°，易得AN=CM，可得△ANF≌△CME（ASA），由平行四边形的判定定理可得结论；（2）由AB=6，AC=10，可得BC=8，设CE=x，则EM=8﹣x，CM=10﹣6=4，在Rt △CEM中，利用勾股定理可解得x，由平行四边形的面积公式可得结果．【解答】（1）证明：∵折叠，∴AM=AB，CN=CD，∠FNC=∠D=90°，∠AME=∠B=90°，∴∠ANF=90°，∠CME=90°，∵四边形ABCD为矩形，∴AB=CD，AD∥BC，∴AM=CN，∴AM﹣MN=CN﹣MN，即AN=CM，在△ANF和△CME中，，∴△ANF≌△CME（ASA），∴AF=CE，又∵AF∥CE，∴四边形AECF是平行四边形；（2）解：∵AB=6，AC=10，∴BC=8，设CE=x，则EM=8﹣x，CM=10﹣6=4，在Rt△CEM中，（8﹣x）2+42=x2，解得：x=5，∴四边形AECF的面积的面积为：EC•AB=5×6=30．【点评】本题主要考查了折叠的性质、矩形的性质、平行四边形的判定定理和勾股定理等，综合运用各定理是解答此题的关键．16．（2016•遵义）如图，矩形ABCD中，延长AB至E，延长CD至F，BE=DF，连接EF，与BC、AD分别相交于P、Q两点．（1）求证：CP=AQ；（2）若BP=1，PQ=2，∠AEF=45°，求矩形ABCD的面积．【分析】（1）由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°，AB=CD，AD=BC，AB∥CD，AD∥BC，证出∠E=∠F，AE=CF，由ASA证明△CFP≌△AEQ，即可得出结论；（2）证明△BEP、△AEQ是等腰直角三角形，得出BE=BP=1，AQ=AE，求出PE=BP=，得出EQ=PE+PQ=3，由等腰直角三角形的性质和勾股定理得出AQ=AE=3，求出AB=AE﹣BE=2，DQ=BP=1，得出AD=AQ+DQ=4，即可求出矩形ABCD 的面积．【解答】（1）证明：∵四边形ABCD是矩形，∴∠A=∠ABC=∠C=∠ADC=90°，AB=CD，AD=BC，AB∥CD，AD∥BC，∴∠E=∠F，∵BE=DF，∴AE=CF，在△CFP和△AEQ中，，∴△CFP≌△AEQ（ASA），∴CP=AQ；（2）解：∵AD∥BC，∴∠PBE=∠A=90°，∵∠AEF=45°，∴△BEP、△AEQ是等腰直角三角形，∴BE=BP=1，AQ=AE，∴PE=BP=，∴EQ=PE+PQ=+2=3，∴AQ=AE=3，∴AB=AE﹣BE=2，∵CP=AQ，AD=BC，∴DQ=BP=1，∴AD=AQ+DQ=3+1=4，∴矩形ABCD的面积=AB•AD=2×4=8．【点评】本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识；熟练掌握矩形的性质，证明三角形全等是解决问题的关键．17．（2016•广州）如图，矩形ABCD的对角线AC，BD相交于点O，若AB=AO，求∠ABD的度数．【分析】首先证明OA=OB，再证明△ABO是等边三角形即可解决问题．【解答】解：∵四边形ABCD是矩形，∴OA=OC，OB=OD，AC=BD，∴AO=OB，∵AB=AO，∴AB=AO=BO，∴△ABO是等边三角形，∴∠ABD=60°．【点评】本题考查矩形的性质、等边三角形的判定和性质等知识，熟练掌握矩形的性质是解题的关键，属于基础题，中考常考题型．18．（2016•岳阳）已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．【分析】由四边形ABCD为矩形，得到四个角为直角，再由EF与FD垂直，利用平角定义得到一对角互余，利用同角的余角相等得到一对角相等，利用ASA得到三角形BEF与三角形CFD全等，利用全等三角形对应边相等即可得证．【解答】证明：∵四边形ABCD是矩形，∴∠B=∠C=90°，∵EF⊥DF，∴∠EFD=90°，∴∠EFB+∠CFD=90°，∵∠EFB+∠BEF=90°，∴∠BEF=∠CFD，在△BEF和△CFD中，，∴△BEF≌△CFD（ASA），∴BF=CD．【点评】此题考查了矩形的性质，以及全等三角形的判定与性质，熟练掌握矩形的性质是解本题的关键．19．（2016•福州）如图，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM．（1）当AN平分∠MAB时，求DM的长；（2）连接BN，当DM=1时，求△ABN的面积；（3）当射线BN交线段CD于点F时，求DF的最大值．【分析】（1）由折叠性质得∠MAN=∠DAM，证出∠DAM=∠MAN=∠NAB，由三角函数得出DM=AD•tan∠DAM=即可；（2）延长MN交AB延长线于点Q，由矩形的性质得出∠DMA=∠MAQ，由折叠性质得出∠DMA=∠AMQ，AN=AD=3，MN=MD=1，得出∠MAQ=∠AMQ，证出MQ=AQ，设NQ=x，则AQ=MQ=1+x，证出∠ANQ=90°，在Rt△ANQ中，由勾股定理得出方程，解方程求出NQ=4，AQ=5，即可求出△ABN的面积；（3）过点A作AH⊥BF于点H，证明△ABH∽△BFC，得出对应边成比例=，得出当点N、H重合（即AH=AN）时，AH最大，BH最小，CF最小，DF最大，此时点M、F重合，B、N、M三点共线，由折叠性质得：AD=AH，由AAS证明△ABH≌△BFC，得出CF=BH，由勾股定理求出BH，得出CF，即可得出结果．【解答】解：（1）由折叠性质得：△ANM≌△ADM，∴∠MAN=∠DAM，∵AN平分∠MAB，∠MAN=∠NAB，∴∠DAM=∠MAN=∠NAB，∵四边形ABCD是矩形，∴∠DAB=90°，∴∠DAM=30°，∴DM=AD•tan∠DAM=3×tan30°=3×=；（2）延长MN交AB延长线于点Q，如图1所示：∵四边形ABCD是矩形，∴AB∥DC，∴∠DMA=∠MAQ，由折叠性质得：△ANM≌△ADM，∴∠DMA=∠AMQ，AN=AD=3，MN=MD=1，∴∠MAQ=∠AMQ，∴MQ=AQ，设NQ=x，则AQ=MQ=1+x，∵∠ANM=90°，∴∠ANQ=90°，在Rt△ANQ中，由勾股定理得：AQ2=AN2+NQ2，∴（x+1）2=32+x2，解得：x=4，∴NQ=4，AQ=5，∵AB=4，AQ=5，=S△NAQ=×AN•NQ=××3×4=；∴S△NAB（3）过点A作AH⊥BF于点H，如图2所示：∵四边形ABCD是矩形，∴AB∥DC，∴∠HBA=∠BFC，∵∠AHB=∠BCF=90°，∴△ABH∽△BFC，∴=，∵AH≤AN=3，AB=4，∴当点N、H重合（即AH=AN）时，AH最大，BH最小，CF最小，DF最大，此时点M、F重合，B、N、M三点共线，如图3所示：由折叠性质得：AD=AH，∵AD=BC，∴AH=BC，在△ABH和△BFC中，，∴△ABH≌△BFC（AAS），∴CF=BH，由勾股定理得：BH===，∴CF=，∴DF的最大值=DC﹣CF=4﹣．【点评】本题考查了矩形的性质、折叠的性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识；本题综合性强，难度较大，熟练掌握矩形和折叠的性质，证明三角形相似和三角形全等是解决问题的关键．20．（2016•吉林）如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．【分析】根据菱形的性质得出AC⊥BD，再根据平行四边形的判定定理得四边形AODE为平行四边形，由矩形的判定定理得出四边形AODE是矩形．【解答】证明：∵四边形ABCD为菱形，∴AC⊥BD，∴∠AOD=90°，∵DE∥AC，AE∥BD，∴四边形AODE为平行四边形，∴四边形AODE是矩形．【点评】本题考查了矩形的判定以及菱形的性质，还考查了平行四边形的判定，掌握平行四边形的判定方法是解题的关键．21．（2016•南通）如图，将▱ABCD的边AB延长到点E，使BE=AB，连接DE，交边BC于点F．（1）求证：△BEF≌△CDF；（2）连接BD、CE，若∠BFD=2∠A，求证：四边形BECD是矩形．【分析】（1）先根据平行四边形的性质得出AB=CD，AB∥CD，再由BE=AB得出BE=CD，根据平行线的性质得出∠BEF=∠CDF，∠EBF=∠DCF，进而可得出结论；（2）根据平行四边形的性质可得AB∥CD，AB=CD，∠A=∠DCB，再由AB=BE，可得CD=EB，进而可判定四边形BECD是平行四边形，然后再证明BC=DE即可得到四边形BECD是矩形【解答】（1）证明：∵四边形ABCD是平行四边形，∵AB=CD，AB∥CD．∵BE=AB，∴BE=CD．∵AB∥CD，∴∠BEF=∠CDF，∠EBF=∠DCF，在△BEF与△CDF中，∵，∴△BEF≌△CDF（ASA）；（2）证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∠A=∠DCB，∵AB=BE，∴CD=EB，∴四边形BECD是平行四边形，∴BF=CF，EF=DF，∵∠BFD=2∠A，∴∠BFD=2∠DCF，∴∠DCF=∠FDC，∴DF=CF，∴DE=BC，∴四边形BECD是矩形．【点评】此题主要考查的值矩形的判定及平行四边形的性质，关键是掌握平行四边形的对边相等；对角相等；对角线互相平分．22．（2016•兰州）阅读下面材料：在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？小敏在思考问题是，有如下思路：连接AC．结合小敏的思路作答（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由；参考小敏思考问题方法解决一下问题：（2）如图2，在（1）的条件下，若连接AC，BD．①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．【分析】（1）如图2，连接AC，根据三角形中位线的性质得到EF∥AC，EF=AC，然后根据平行四边形判定定理即可得到结论；（2）由（1）知，四边形EFGH是平行四边形，且FG=BD，HG=AC，于是得到当AC=BD时，FG=HG，即可得到结论；（3）根据平行线的性质得到GH⊥BD，GH⊥GF，于是得到∠HGF=90°，根据矩形的判定定理即可得到结论．【解答】解：（1）是平行四边形，证明：如图2，连接AC，∵E是AB的中点，F是BC的中点，∴EF∥AC，EF=AC，同理HG∥AC，HG=AC，综上可得：EF∥HG，EF=HG，故四边形EFGH是平行四边形；（2）AC=BD．理由如下：由（1）知，四边形EFGH是平行四边形，且FG=BD，HG=AC，∴当AC=BD时，FG=HG，∴平行四边形EFGH是菱形，（3）当AC⊥BD时，四边形EFGH为矩形；理由如下：同（2）得：四边形EFGH是平行四边形，∵AC⊥BD，GH∥AC，∴GH⊥BD，∴GH⊥GF，∴∠HGF=90°，∴四边形EFGH为矩形．【点评】此题主要考查了中点四边形，关键是掌握三角形中位线定理，三角形的中位线平行于第三边且等于第三边的一半．23．（2016•台州）如图，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H．（1）求证：△PHC≌△CFP；（2）证明四边形PEDH和四边形PFBG都是矩形，并直接写出它们面积之间的关系．【分析】（1）由矩形的性质得出对边平行，再根据平行线的性质得出相等的角，结合全等三角形的判定定理AAS即可得出△PHC≌△CFP；（2）由矩形的性质找出∠D=∠B=90°，再结合对边互相平行即可证出四边形PEDH 和四边形PFBG都是矩形，通过角的正切值，在直角三角形中表示出直角边的关系，利用矩形的面积公式即可得出两矩形面积相等．【解答】证明：（1）∵四边形ABCD为矩形，∴AB∥CD，AD∥BC．∵PF∥AB，∴PF∥CD，∴∠CPF=∠PCH．。

第九章立体几何专练2—基本立体图形(提升练)-2022届高三数学一轮复习

第九章立体几何专练2—基本立体图形（提升练）一、单选题1．将一半圆沿半径剪成两个扇形，其中一个扇形的圆心角为3π，以这两个扇形为侧面围成一高一低两个圆锥（不计接缝处的损耗），则高圆锥与低圆锥的高之比为( ) A ．2:1B ．70:8C ．4:1D ．32:702．如图所示的扇形是某个圆锥的侧面展开图，已知扇形所在圆的半径5R =，扇形弧长4l π=，则该圆锥的表面积为( )A ．2πB ．(425)π+C ．(35)π+D ．85π+3．斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”，它的画法是：以斐波那契数：1，1，2，3，5，⋯为边的正方形拼成长方形（斐波那契数列由1和1开始，之后的数就是由之前的两数相加而得出），然后在每个正方形中画一个圆心角为90︒的圆弧，这些圆弧所连起来的弧线就是斐波那契螺旋线．自然界存在很多斐波拉契螺旋线的图案，例如向日葵、鹦鹉螺等，如图为该螺旋线的前一部分，如果用接下来的一段圆弧所对应的扇形做圆锥的侧面，则该圆锥的高为( )A ．215B ．415C ．515D ．6154．碌碡是我国古代人民发明的一种把米、麦、豆等粮食加工成粉末的器具，如图，近似圆柱形碌碡的轴固定在经过圆盘圆心且垂直于圆盘的木桩上，当人或动物推动木柄时，碌碡在圆盘上滚动．若人或动物推动木柄绕圆盘转动一周，碌碡恰好滚动了3圈，则该圆柱形碌碡的底面圆的半径与其高之比为( )A ．1:2B ．1:3C ．1:4D ．2:35．如图，圆柱1OO 的轴截面11ABB A 是正方形，D ，E 分别是1AA 和1BB 的中点，C 是弧AB 的中点，则经过C 、D 、E 的平面与圆柱1OO 侧面相交所得到的曲线的离心率是( )A ．1B ．22C ．2D ．626．一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为1h 、2h 、3h ，则123::(h h h = ) A ．2:3:3B ．23:1:1C ．3:2:2D ．3:6:67．在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑A BCD -中，AB ⊥平面BCD ，且BD CD ⊥，AB BD CD ==，点P 在棱AC 上运动，设CP 的长度为x ，若PBD ∆的面积为()f x ，则()f x 的图象大致为( )A ．B ．C ．D ．8．如图几何体为一个圆柱和圆锥的组合体，圆锥的底面和圆柱的一个底面重合，圆锥的顶点为P ，圆柱的上、下底面的圆心分别为1O ，2O ，若该几何体有半径为1的外接球，且球心为O ，则不正确的是( )A ．如果圆锥的体积为圆柱体积的16，则圆锥的体积为8πB ．12122O O PO +=C ．如果112PO O O =，则O 与1O 重合D ．如果112:1:3PO O O =，则圆柱的体积为96125π二、多选题9．一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R 相等，下列结论正确的是( )A ．圆柱的侧面积为22R πB ．圆锥的侧面积为22R πC ．圆柱的侧面积与球面面积相等D．圆锥的表面积最小10．已知圆锥的顶点为S1，A，B是底面圆周上两个动点，下列说法正确的是()A．圆锥的侧面积是B．SA与底面所成的角是6πC．SAB∆D11．已知正三棱台的上底面边长为2，下底面边长为4，侧棱长为2，则下列说法正确的是( )A．棱台的侧面积为BCD12．已知圆锥的顶点为P，母线长为2A，B为底面圆周上两个动点，则下列说法正确的是()A．圆锥的高为1B．三角形PABC．三角形PAB内切圆半径的最大值为2D．圆锥外接球的体积为32 3π三、填空题13．如图，四边形ABCD为梯形，//AD BC，90ABC∠=︒，图中阴影部分绕AB旋转一周所形成的几何体的体积为．14．已知圆锥的顶点为S，底面圆周上的两点A、B满足SAB∆为等边三角形，且面积为43，又知SA与圆锥底面所成的角为45︒，则圆锥的表面积为．15．已知圆柱的底面圆半径为1，高为2，AB为上底面圆的一条直径，C是下底面圆周上的一个动点，则ABC的面积的取值范围为．16．“牟和方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体，它是由两个相同的圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体（如图1)．如图2所示的“四脚帐篷”类似于“牟和方盖”的一部分，其中APC与BPD 为相互垂直且全等的半圆面，它们的圆心为O，半径为1．用平行于底面ABCD的平面α去截“四脚帐篷”所得的截面图形为；当平面α经过OP的中点时，截面图形的面积为．四、解答题17．将半径为33α的扇形，用剩下的扇形铁皮制成一个圆锥形的容器，该圆锥的高记为h，体积为V．（1）求体积V有关h的函数解析式．（2）求当扇形的圆心角α多大时，容器的体积V最大．18．如图所示，有一块矩形铁皮ABCD ，4AB =，剪下一个半圆面作圆锥的侧面，余下的铁皮内剪下一个与其相切的圆面，恰好作为圆锥的底面．试求：（1）矩形铁皮AD 的长度；（2）做成的圆锥体的体积．第九章立体几何专练2—基本立体图形（提升练）答案1．解：不妨设半圆的半径为1，用圆心角为3π的扇形围成的圆锥的底面周长为133ππ⨯=，设其底面圆的半径为r ，则23r ππ=，解得16r =，则该圆锥的高21351()6h =-，用圆心角为23π的扇形围成的圆锥的底面周长为22133ππ⨯=，设其底面圆的半径为R ，则223R ππ=，解得13R =，则该圆锥的高21221()3H =-，3567022=．故选：B ．2．解：圆锥的侧面展开图中，扇形所在圆的半径R ，扇形弧长4l π=，所以扇形的面积为142S π==扇形；设扇形的底面圆半径为r ，则24r ππ=，解得2r =，所以底面圆的面积为224S ππ=⨯=底面圆；所以该圆锥的表面积为4(4S ππ=+=+．故选：B ．3．解：由斐波那契数的规律知，从第三项起，每一个数都是前面两个数之和，所以接下来的圆弧对应的圆面半径是358+=，对应的弧长是12844l ππ=⨯⨯=，设圆锥底面半径为r ，则24r ππ=，解得2r =，所以圆锥的高为h == 故选：A ．4．解：由题意，人推动木柄绕圆盘转动1周，碌碡恰好滚动了3圈，因为圆的周长为2c r π=，所以圆盘与碌碡的半径之比为3:1，所以圆柱形碌碡的高与其底面圆的直径之比约为3:2，所以该圆柱形碌碡的底面圆的半径与其高之比为1:3．故选：B ．5．解：设轴截面的正方形的边长为2，设1C 是弧11B A 的中点，且与C 关于圆柱的中心对称，由题意可知，截面曲线为椭圆，椭圆的短轴长为2，长轴1C C =，所以长半轴长a =1b =，故半焦距为1c ==，所以椭圆的离心率为c e a ==．故选：B ．6．解：设四棱锥为A BCFE -，三棱锥为A DEF -，则三棱锥A DEF -为正四面体，四棱锥A BCFE -为正四棱锥，显然23h h =．设AB a =，正方形BCFE 的中心为M ，正三角形DEF 的中心为N ，连接AM ，AN ，CM ，DN ，则22CM a =，233323DN a a =⨯=， 2222AM AC CM a ∴=-=，2263AN AD DN a =-=，即122h AM a ==，2363h h AN a ===， 123266::::3:2:2233h h h ∴==．故选：C ．7．解：作PQ BC ⊥于点Q ，作QR BD ⊥于点R ，连接到PR ，由已知可得//PQ AB ，//QR CD ，且AB ⊥平面BCD ，所以PQ ⊥平面BCD ，又BD ⊂平面BCD ，所以PQ BD ⊥，又QR BD ⊥，PQQR Q =，PQ ，QR ⊂平面PQR ，所以BD ⊥平面PQR ，又PR ⊂平面PQR ，所以BD PR ⊥，设1AB BD CD ===，则3AC =，则13x PQ =，所以3xPQ =，又313QR BQ x BC -==，解得33xQR -=，所以22233()()2233333x x PR x x -=+=-+，故23()22336f x x x =-+，其函数图像是关于直线32x =对称的图像且开口上，故选项B ，C ，D 错误．故选：A ．8．解：由O 为外接球的球心，得PO AO CO DO ===；对于A ，21121121136O B PO V V O B O O ππ⋅⋅==⋅⋅圆锥圆柱，所以11212PO O O =，又12122O O PO +=，所以112PO =，121O O =，所以112OO =，所以2113144O B =-=，所以211113133428V O B PO πππ=⋅⋅=⨯⨯=锥，选项A 正确；对于B ，由于BO DO =，则O 为12O O 中点，如图所示：因为111PO PO O O R =+==，21OO OO =，所以121PO OO +=，所以111212122PO O O PO OO O O PO +++=+=，选项B 正确；对于C ：若O 与1O 重合，则2PO OO =，所以2OC OD OO OP =>≠与题设矛盾，选项C 不正确；对于D ，由112:1:3PO O O =，12122O O PO +=，可得125PO =，1265O O =，所以1121325OO O O ==，又有1OB =，则145O B =，所以221124696()55125V O B O O πππ=⋅⋅=⋅⋅=，所以选项D 正确．故选：C ．9．解：对于A ，圆柱的底面直径和高都与一个球的直径2R 相等，∴圆柱的侧面积为2224S R R R ππ=⨯=，故A 错误；对于B ，圆锥的底面直径和高都与一个球的直径2R 相等，∴圆锥的侧面积为222(2)5S R R R R ππ=+，故B 错误；对于C ，圆柱的侧面积为2224S R R R ππ=⨯=，球面面积为24S R π=球，∴圆柱的侧面积与球面面积相等，故C 正确；对于D ，圆柱的表面积为222226S R R R R πππ=⨯+=圆柱，圆锥的表面积为()2222(2)51S R R R R R πππ=+=圆锥，球的表面积为24S R π=球，∴圆锥的表面积最小，故D 正确．故选：CD ．10．解：因为圆锥的顶点为S 31，设圆锥的底面圆心为O ，则1SO =，底面半径3r =，所以母线长132l =+=，故圆锥的侧面积是23rl ππ=，故选项A 正确；因为A ，B 是底面圆周上两个动点，则SA 为圆锥的一条母线，又SO ⊥底面圆，则SAO ∠即为SA 与底面所成的角，在Rt SAO ∆中，13tan 33SO SAO r ∠===，所以SA 与底面所成的角是6π，故选项B 正确；设ASB α∠=，则0120α︒︒，且2SA SB ==，所以SAB ∆的面积为212sin 2S α=⨯⨯，所以当90α=︒，时，SAB ∆的面积最大为2，故选项C 错误；设圆锥内接圆柱的底面半径为(03)x x <<，高为h ，则有13x h h -=，可得13xh =-，则圆柱的侧面积为221233x x S x x ππ⎛⎫⎛⎫=-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭侧，由二次函数的性质可知，当32x =时，S 侧有最大值为23()3322[]223ππ⨯-+=，故选项D 正确．故选：ABD ．11．解：由题意作右图正三棱台111ABC A B C -，在平面11ABB A 中由点1A 向AB 作垂线，垂足为D ，取线段BC 的中点E ，连接AE ，在平面1AEA 中由点1A 向AE 作垂线，垂足为F ，连接DF ，在等腰梯形11ABB A 中，4AB =，112B A =，12AA =，则(42)21AD =-÷=，221213A D =-=故棱台的侧面积为13(24)3932⨯+⨯=，故A 正确，易知1A F 为棱台的高，在Rt ADF ∆中，3tan 63DF AD π=⋅=，2123133AF =+=，在Rt △1A DF 中，22112633A F A D DF =-=≠，故B 错误，棱台的侧棱与底面所成角为1A AE ∠，112333cos 23AF A AE AA ∠===，故C 正确，棱台的侧面与底面所成锐二面角为1A DE ∠，11313cos 33DF A DE A D ∠===，故D 错误，故选：AC ．12．解：圆锥的顶点为P ，母线长为2，底面半径为3，如图所示：所以圆锥的高为222(3)1h -，所以选项A 正确；由于A 和B 为底面圆周上两个动点，由于满足PA PB =，所以PAB ∆为等腰三角形，由轴截面为等腰三角形PAC ，且顶角为2260120APC APO ∠=∠=⨯︒=︒，当等腰三角形PAB 的顶角为90︒时，PAB ∆的面积取得最大值为： 122sin9022PAB S ∆=⨯⨯⨯︒=，所以选项B 错误；设PAB ∆内切圆的半径为r ，由题意知当PAB ∆的面积取得最大值时r 取得最大值，由等积法知，1(2222)22r ++=，解得22r =-，所以PAB ∆内切圆半径的最大值为22-，选项C 正确；由题意知，圆锥外接球的半径是轴截面PAC ∆外接圆的半径，由正弦定理得2324sin120R ==︒，解得2R =，所以圆锥外接球的体积为3432233V ππ=⨯=外接球，选项D 正确．故选：ACD ．13．解：由题意可知，所求旋转体是一个圆台，从上面挖去一个半球，圆台的上底面面积14S π=，下底面面积216S π=，所以圆台的体积为()14416163283V πππππ=⨯+⨯+⨯=圆台，又半球的体积为314162233V ππ=⨯⨯⨯=半球，故旋转体的体积为16682833V V πππ-=-=圆台半球．故答案为：683π． 14．解：如图所示，设圆锥母线长为l ，由SAB ∆为等边三角形，且面积为43，得23434l ⋅=，解得4l =；设圆锥底面半径为r ，由SA 与圆锥底面所成的角为45︒，得4cos4522r =⨯︒=；所以圆锥的表面积为：()()2222422821S rl r πππππ=+=⋅⋅+⋅=+圆锥表．故答案为：8(21)π+．15．解：如图1，上底面圆心记为O ，下底面圆心记为O '，连结OC ，过点C 作CM AB ⊥，垂足为点M ，则12ABC S AB CM ∆=⨯⨯，根据题意，AB 为定值2，所以ABC S ∆的大小随着CM 的长短变化而变化，如图2所示，当点M 与点O 重合时，22125CM OC ==+= 此时ABC S ∆取得最大值为12552⨯如图3所示，当点M 与点B 重合，CM 取最小值2，此时ABC S ∆取得最小值为12222⨯⨯=．综上所述，ABC S ∆的取值范围为5]．故答案为：5]．16．解：由题意，图2所示的“四脚帐篷”类似于“牟和方盖”的一部分，因为底面ABCD 为正方形，由平行截面的性质可知，用平行于底面ABCD 的平面α去截“四脚帐篷”所得的截面图形A B C D ''''为正方形，当平面α经过OP 的中点时，因为1OP =，则12OO '=，OO O B '''⊥，又1OB '=，所以3O B ''= 故3322A B ''==，所以截面图形A B C D ''''的面积为233()22=．故答案为：正方形；32．17．解：（1）将半径为33α的扇形，用剩下的扇形铁皮制成一个圆锥形的容器，该圆锥的高记为h ，体积为V ．设圆锥底面圆的半径为r ，则22227r R h h -=- 223111()(27)9333V h r h h h h h ππππ=⨯⨯⨯=⨯⨯-⨯=-+．∴体积V 有关h 的函数解析式为31()93V h h h ππ=-+．⋯（4分）（2）31()9,(0)3V h h h h ππ=-+>，2()9V h h ππ'=-，⋯（6分）令()0V h '>，03h <<．令()0V h '<，3h >．∴当(0,3)x ∈，()V h 递增，当(3,)x ∈+∞，()V h 递减．当3h =，[()]max V h V =（3）⋯（8分）．222r h R +=，∴32r = (2)2R r παπ-=，∴626α-=⋯（10分） ∴当626α-时，该圆锥的体积最大．⋯（12分） 18．解：如图所示，取半圆的圆心记作O 点，圆面的圆心记作O '，作O E AD '⊥交AD 于点E ，设圆锥底面半径为22ABr ==，圆锥母线长为4l AB ==，则：6OO l r '=+=，2EO r '==；（1）在Rt △OO E '中，由勾股定理可得：226242EO =-∴4422642AD DO OE EA =++=+=+（2）由（1）可得：圆锥的母线长4l =，底面半径2r =，则圆锥的高为：2223h l r =-=； ∴圆锥的体积为：283133V r h ππ==圆锥．。

小学奥数4-5-2 长方体与正方体(二).专项练习及答案解析

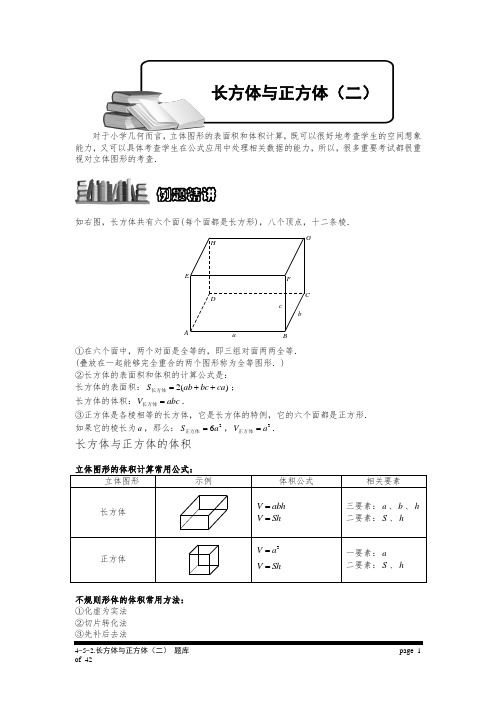
对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．cba HGFEDCBA①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是：长方体的表面积：2()S ab bc ca =++长方体；长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．长方体与正方体的体积不规则形体的体积常用方法： ①化虚为实法 ②切片转化法例题精讲长方体与正方体（二）④实际操作法⑤画图建模法【例1】一个长方体的棱长之和是28厘米，而长方体的长宽高的长度各不相同，并且都是整厘米数，则长方体的体积等于立方厘米。

【考点】长方体与正方体【难度】2星【题型】填空【关键词】希望杯， 6年级，第16题，6分【解析】由题意知长、宽、高的和为2847÷=，又根据题意长、宽、高各不相同，且是整数，所以只能是1、2、4，所以体积为8立方厘米【答案】8【例2】将几个大小相同的正方体木块放成一堆，从正面看到的视图是图（a），从左向右看到的视图是图（b），从上向下看到的视图是图（c），则这堆木块最多共有___________块。

【考点】长方体与正方体【难度】2星【题型】填空【关键词】希望杯，4年级，初赛，8题【解析】对于图c来说，每个小方块都摞了2层，最多有6块。

【答案】6【例3】一根长方体木料，体积是0.078立方米．已知这根木料长1.3米．宽为3分米，高该是多少分米?孙健同学把高错算为3分米．这样，这根木料的体积要比0.078立方米多多少?【考点】长方体与正方体【难度】2星【题型】解答【关键词】小数报，决赛【解析】0.078(1.30.3)0.2÷⨯=(米)．0.2米=2分米．⨯⨯-=(立方米)．1.30.30.30.0780.039所以这根木料的高是2分米；算错后，这根木料的体积比0.078立方米多0.039立方米．【答案】0.039【例4】如图，两个同样的铁环连在一起长28厘米，每个铁环长16厘米。

正方形的判定专项练习30题(有答案)ok

正方形的判定专项练习30题(有答案)ok1.已知平行四边形ABCD中，对角线AC、BD交于点O，E是DB延长线上一点，且△___是等边三角形。

1) 证明ABCD是菱形。

2) 如果∠AEB=2∠EAB，证明ABCD是正方形。

2.在△ABC中，CE、CF分别是内角和外角平分线，过点A 作CE、CF的垂线，垂足分别为E、F。

1) 证明AECF是矩形。

2) 什么条件下AECF是正方形？3.在△ABC中，D、E分别为边AB、AC的中点，将△ADE绕点D旋转180°至△BDF。

1) 证明BCEF是平行四边形。

2) 添加什么条件可以使BFEC成为一种特殊的平行四边形？4.在矩形ABCD中，AF、BE、CE、DF分别是四个角的角平分线，E、M、F、N是其交点，证明EMFN是正方形。

5.在△ABC中，∠ACB=90°，D为AB中点，四边形BCED 为平行四边形，DE、AC相交于点F。

1) 证明F为AC中点。

2) 确定四边形ADCE的形状并说明理由。

3) 什么条件下ADCE是正方形？6.证明对角线相等的菱形是正方形。

7.在△ACD中，∠D=90°，∠D的平分线交AC于点E，EF⊥AD交AD于点F，EG⊥DC交DC于点G，证明EFDG 是正方形。

8.已知：如图，点M是矩形ABCD的边AD的中点，点P是BC边上的一动点，PE⊥CM，PF⊥___，垂足分别为E、F。

Ⅰ）当四边形PEMF为矩形时，矩形ABCD的长与宽满足什么条件？请说明理由。

Ⅱ）在（Ⅰ）中当点P运动到什么位置时，矩形PEMF变为正方形？为什么？9.如图，D是△___的边BC的中点，DE⊥AC，___⊥AB，垂足分别是E、F，且BF=CE。

1）求证：△BFD≌△CED。

2）当∠A=90°时，求证：四边形AFDE是正方形。

10.如图，四边形ABCD是矩形，E是BD上的一点，∠BAE=∠BCE，∠AED=∠CED，点G是BC、AE延长线的交点，AG与CD相交于点F。

【精品】小学奥数4-5-2 长方体与正方体(二).专项练习

对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．cba HGFEDCBA①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是：长方体的表面积：2()S ab bc ca =++长方体；长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．长方体与正方体的体积不规则形体的体积常用方法： ①化虚为实法例题精讲长方体与正方体（二）②切片转化法③先补后去法④实际操作法⑤画图建模法【例1】一个长方体的棱长之和是28厘米，而长方体的长宽高的长度各不相同，并且都是整厘米数，则长方体的体积等于立方厘米。

【例2】将几个大小相同的正方体木块放成一堆，从正面看到的视图是图（a），从左向右看到的视图是图（b），从上向下看到的视图是图（c），则这堆木块最多共有___________块。

【例3】一根长方体木料，体积是0.078立方米．已知这根木料长1.3米．宽为3分米，高该是多少分米?孙健同学把高错算为3分米．这样，这根木料的体积要比0.078立方米多多少?【例4】如图，两个同样的铁环连在一起长28厘米，每个铁环长16厘米。

8个这样的铁环依此连在一起长厘米。

【例5】某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条(如图所示)在三个方向上的加固．所用尼龙编织条分别为365厘米，405厘米，485厘米．若每个尼龙加固时接头重叠都是5厘米．问这个长方体包装箱的体积是多少立方米?高长【例6】某工人用木板钉成一个长方体邮件包装箱，并用三根长度分别为235厘米、445厘米、515厘米的尼龙带进行加固（如下图），若每根尼龙带加固时截头重叠都是5厘米，那么这个长方体包装箱的体积是立方米。

2023-2024年小学数学四年级上册知识梳理真题讲练专题二 (人教版含解析)

专题02 公顷和平方千米知识点一：公顷和平方千米一、我们学过的面积单位有：平方厘米、平方分米、平方米、公顷、平方千米。

1、边长是100米的正方形的面积是1公顷。

1公顷=10000平方米2、边长是1000米的正方形的面积是1平方千米1平方千米=1000000平方米=100公顷3、正方形周长=边长×4 面积=边长×边长4、长方形周长=（长+宽）×2 面积=长×宽二、单位换算（大化小乘进率，小化大除进率）1、平方厘米和平方分米之间的进率是100 1平方分米=100平方厘米2、平方分米和平方米之间的进率是100 1平方米=100平方分米3、公顷和平方米之间的进率是10000 1公顷=10000平方米4、平方千米和公顷之间的进率是100 1平方千米=100公顷5、平方千米和平方米之间的进率是1000000 1平方千米=1000000平方米真题讲练：一、选择题1．（2021·广东广州·四年级期末）以下表达正确的是（）。

A．3平方千米＝3000平方米B．3000平方米＝3公顷C．300公顷＝3平方千米【答案】C【分析】根据面积单位之间的进率进行换算，然后选择正确的一项即可，1平方千米＝1000000平方米＝100公顷，1公顷＝10000平方米，依此换算。

【详解】A．3×1000000＝3000000，3平方千米＝3000000平方米，因此此项表达错误；B．3×10000＝30000，3公顷＝30000平方米，因此此项表达错误；C．300÷100＝3，因此300公顷＝3平方千米；因此此项表达正确；故答案为：C【点睛】此题考查的是面积单位之间的换算，熟记面积单位之间的进率是解答本题的关键。

2．（2021·广东广州·四年级期末）某中学运动场地的总面积约2（）。

A．平方米B．公顷C．平方千米【答案】B【分析】根据生活经验以及对面积单位和数据大小的认识，可知计量某中学运动场地的总面积用“公顷”作单位。

长方形正方形的面积专项练习30题(有答案)ok

长方形正方形的面积专项练习30题(有答案)ok1.一块边长为80米的正方形果园，面积为6400平方米。

如果每棵果树占地4平方米，那么果园中一共有1600棵果树。

2.一块长为9米，宽为6米的长方形菜地，面积为54平方米。

如果一共收青菜972千克，那么平均每平方米收青菜18千克。

3.一块长为17米，宽为12米的长方形萝卜地，面积为204平方米。

如果一共收萝卜3080千克，那么平均每平方米收萝卜15.1千克。

4.一个边长为8.4厘米的正方形铁皮，从中挖去一块面积为40.5平方厘米的铁皮，剩下的铁皮面积为56.7平方厘米。

5.XXX家新房的面积是120平方米，用边长为0.6米的正方形瓷砖铺地，需要300块瓷砖。

6.一块宽为60米的长方形草坪面积为4800平方米，那么它的长为80米。

7.一个宽为24米的长方形运动场面积为960平方米，那么它的长为40米。

8.一块长为宽2倍的长方形玻璃，周长为54厘米，那么它的长为36厘米，面积为648平方厘米。

9.XXX的菜园长48米，宽32米，周长为160米。

如果每平方米大约收菜20千克，那么这个菜园大约可收千克的菜。

10.已知长为8厘米的长方形面积为1000平方厘米，那么它的周长为42厘米。

11.一个长50米，宽25米的游泳池面积为1250平方米，周长为150米。

12.一块长为75米，宽为45米的长方形土地面积为3375平方米。

XXX要在四周围上篱笆，一共需要240米的篱笆。

13.一个边长为16米的正方形菜地，面积为256平方米。

如果四周用篱笆围起来，篱笆长64米。

14.一个边长为1.2米的正方形，周长为4.8米，面积为1.44平方米。

15.一个周长为1200米的正方形水池面积为平方米，占地3公顷。

16.一个周长为37.2厘米的正方形面积为138.24平方厘米。

17.一个长为40米，宽为18米的长方形苗圃面积为720平方米，可以育3600棵树苗。

18.一间长为8米，宽为6米，高为3米的教室，需要600块地板砖。

初二正方形数学练习题

初二正方形数学练习题1. 计算正方形的周长和面积。

2. 已知一个正方形的边长为6cm，求其周长和面积。

3. 如果一个正方形的面积为49平方厘米，求其边长。

4. 一个正方形的周长为20cm，求其面积。

5. 一个正方形的面积是25平方米，求其边长。

6. 如果一个正方形的边长是x厘米，求其周长和面积的表达式。

解答：1. 正方形的周长公式为：周长 = 4 * 边长；面积公式为：面积 = 边长 * 边长。

2. 已知边长为6cm的正方形，周长 = 4 * 6 = 24cm，面积 = 6 * 6 =36平方厘米。

3. 设正方形边长为x厘米，根据面积公式得出方程：x * x = 49。

解这个方程可以得到x = 7厘米，所以边长为7厘米。

4. 已知周长为20cm的正方形，根据周长公式得出方程：4 * x = 20。

解这个方程可以得到x = 5cm，所以边长为5cm。

根据面积公式计算面积：面积 = 5 * 5 = 25平方厘米。

5. 已知面积为25平方厘米的正方形，设边长为x厘米，根据面积公式得出方程：x * x = 25。

解这个方程可以得到x = 5厘米，所以边长为5厘米。

6. 若正方形的边长为x厘米，则周长 = 4 * x，面积 = x * x。

通过以上解答，我们可以发现正方形的周长和面积可以通过简单的计算公式得到。

同时，根据已知条件，我们可以解方程来求解未知的边长或面积大小。

这些练习题有助于我们巩固对正方形的周长和面积概念的理解，并且加强了我们对代数方程的解决能力。

希望以上练习题能够帮助你更加熟练地运用正方形的周长和面积公式，并提升解代数方程的能力。

加油！。

2024年中考数学二轮复习模块专练—正方形(含答案)

2024年中考数学二轮复习模块专练—正方形（含答案）一、正方形的性质1．正方形具有平行四边形、矩形、菱形的所有性质；2.边的性质：对边平行，四条边相等；3.角的性质：四个角都是直角；4.对角线的性质：对角线垂直平分且相等，每条对角线平分一组对角；两条对角线把正方形分成4个全等的等腰直角三角形；5.对称性：是轴对称图形，有4条对称轴；是中心对称图形，对称中心也叫正方形的中心；二、正方形的判定1.在矩形的基础上判定（1）有一组邻边相等的矩形是正方形；（2）对角线垂直的矩形是正方形；2.在菱形的基础上判定（1）有一个角是直角的菱形是正方形；（2）对角线相等的菱形是正方形；三、中点四边形1.连接任意四边形各边中点得到的四边形是平行四边形；2.连接矩形各边中点得到的四边形是菱形；3.连接菱形各边中点得到的四边形是矩形；《义务教育数学课程标准》2022年版，学业质量要求：试卷第2页，共12页1.理解正方形的概念；2.理解矩形、菱形、正方形之间的包含关系；3.掌握正方形的性质和判定；【例1】（2023·四川攀枝花·统考中考真题）1．如图，已知正方形ABCD 的边长为3，点P 是对角线BD 上的一点，PF AD ⊥于点F ，PE AB ⊥于点E ，连接PC ，当:1:2PE PF =时，则PC =（）AB ．2CD ．52【变1】（2023·福建·统考中考真题）2．如图，正方形四个顶点分别位于两个反比例函数3y x =和n y x=的图象的四个分支上，则实数n 的值为（）A ．3-B ．13-C ．13D ．3【例1】（2022·四川攀枝花·统考中考真题）3．如图，以ABC 的三边为边在BC 上方分别作等边ACD 、ABE 、BCF △．且点A 在BCF △内部．给出以下结论：①四边形ADFE 是平行四边形；②当150BAC ∠=︒时，四边形ADFE 是矩形；③当AB AC =时，四边形ADFE 是菱形；④当AB AC =，且150BAC ∠=︒时，四边形ADFE 是正方形．其中正确结论有（填上所有正确结论的序号）．【变1】（2022·辽宁阜新·统考中考真题）4．已知，四边形ABCD 是正方形，DEF 绕点D 旋转（DE AB <），90EDF ∠=︒，DE DF =，连接AE ，CF ．试卷第4页，共12页(1)如图1，求证：ADE V ≌CDF ；(2)直线AE 与CF 相交于点G ．①如图2，BM AG ⊥于点M ，⊥BN CF 于点N ，求证：四边形BMGN 是正方形；②如图3，连接BG ，若4AB =，2DE =，直接写出在DEF 旋转的过程中，线段BG长度的最小值．【例1】（2022·广西玉林·统考中考真题）5．若顺次连接四边形ABCD 各边的中点所得的四边形是正方形，则四边形ABCD 的两条对角线,AC BD 一定是()A ．互相平分B ．互相垂直C ．互相平分且相等D ．互相垂直且相等【变1】（2023·山东临沂·统考一模）6．四边形ABCD 的对角线AC ，BD 交点O ，点M ，N ，P ，Q 分别为边AB ，BC ，CD ，DA 的中点．有下列四个推断，①对于任意四边形ABCD ，四边形MNPQ 可能不是平行四边形；②若AC BD =，则四边形MNPQ 一定是菱形；③若AC BD ⊥，则四边形MNPQ 一定是矩形；④若四边形ABCD 是菱形，则四边形MNPQ 也是菱形．所有正确推断的序号是．一、选择题（2023·重庆·统考中考真题）7．如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，连接AE ，AF ，EF ，45EAF ∠=︒．若BAE α∠=，则FEC ∠一定等于（）A ．2αB ．902α︒-C ．45α︒-D ．90α︒-（2022·江苏泰州·统考中考真题）8．如图，正方形ABCD 的边长为2，E 为与点D 不重合的动点，以DE 一边作正方形DEFG .设DE =d 1，点F 、G 与点C 的距离分别为d 2，d 3，则d 1＋d 2＋d 3的最小值为()试卷第6页，共12页AB ．2C．D ．4（2022·内蒙古包头·中考真题）9．如图，在矩形ABCD 中，AD AB >，点E ，F 分别在,AD BC 边上，EF AB ∥,AE AB =，AF 与BE 相交于点O ，连接OC ，若2BF CF =，则OC 与EF 之间的数量关系正确的是（）A．2OC =B2EF =C．2OC D ．OC EF =（2022·浙江绍兴·统考中考真题）10．如图，在平行四边形ABCD 中，22AD AB ==，60ABC ∠=︒，E ，F 是对角线BD 上的动点，且BE DF =，M ，N 分别是边AD ，边BC 上的动点．下列四种说法：①存在无数个平行四边形MENF ；②存在无数个矩形MENF ；③存在无数个菱形MENF ；④存在无数个正方形MENF ．其中正确的个数是（）A ．1B ．2C ．3D ．4二、填空题（2023·湖南怀化·统考中考真题）11．如图，点P 是正方形ABCD 的对角线AC 上的一点，PE AD ⊥于点E ，3PE =．则点P 到直线AB 的距离为．（2023·四川宜宾·统考中考真题）12．如图，M 是正方形ABCD 边CD 的中点，P 是正方形内一点，连接BP ，线段BP 以B 为中心逆时针旋转90︒得到线段BQ ，连接MQ ．若4AB =，1MP =，则MQ 的最小值为．（2022·辽宁·统考中考真题）13．如图，在正方形ABCD 中，对角线AC ，BD 相交于点O ，点E 是OD 的中点，连接CE 并延长交AD 于点G ，将线段CE 绕点C 逆时针旋转90°得到CF ，连接EF ，点H 为EF 的中点．连接OH ，则GE OH 的值为．（2023·浙江衢州·统考中考真题）14．如图，点A 、B 在x 轴上，分别以OA ，AB 为边，在x 轴上方作正方形OACD ，ABEF ．反比例函数()0k y k x=>的图象分别交边CD ，BE 于点P ，Q ．作PM x ⊥轴于点M ，QN y ⊥试卷第8页，共12页轴于点N ．若2OA AB =，Q 为BE 的中点，且阴影部分面积等于6，则k 的值为．三、解答题（2022·湖南邵阳·统考中考真题）15．如图，在菱形ABCD 中，对角线AC ，BD 相交于点O ，点E ，F 在对角线BD 上，且BE DF =，OE OA =．求证：四边形AECF是正方形．（2023·湖北十堰·统考中考真题）16．如图，ABCD Y 的对角线,AC BD 交于点O ，分别以点,B C 为圆心，11,22AC BD 长为半径画弧，两弧交于点P ，连接,BP CP．(1)试判断四边形BPCO 的形状，并说明理由；(2)请说明当ABCD Y 的对角线满足什么条件时，四边形BPCO 是正方形？（2022·江苏镇江·统考中考真题）17．已知，点E 、F 、G 、H 分别在正方形ABCD 的边AB 、BC 、CD 、AD 上．(1)如图1，当四边形EFGH 是正方形时，求证：AE AH AB +=；(2)如图2，已知AE AH =，CF CG =，当AE 、CF 的大小有_________关系时，四边形EFGH 是矩形；(3)如图3，AE DG =，EG 、FH 相交于点O ，:4:5OE OF =，已知正方形ABCD 的边长为16，FH 长为20，当OEH △的面积取最大值时，判断四边形EFGH 是怎样的四边形？证明你的结论．（2022·贵州黔东南·统考中考真题）18．阅读材料：小明喜欢探究数学问题，一天杨老师给他这样一个几何问题：如图，ABC 和BDE △都是等边三角形，点A 在DE 上．求证：以AE 、AD 、AC 为边的三角形是钝角三角形．(1)【探究发现】小明通过探究发现：连接DC ，根据已知条件，可以证明DC AE =，120ADC ∠=︒，从而得出ADC △为钝角三角形，故以AE 、AD 、AC 为边的三角形是钝角三角形．请你根据小明的思路，写出完整的证明过程．(2)【拓展迁移】如图，四边形ABCD 和四边形BGFE 都是正方形，点A 在EG 上．试卷第10页，共12页①试猜想：以AE 、AG 、AC 为边的三角形的形状，并说明理由．②若2210AE AG +=，试求出正方形ABCD 的面积．（2022·四川乐山·统考中考真题）19．华师版八年级下册数学教材第121页习题19.3第2小题及参考答案．2．如图，在正方形ABCD 中，CE DF ⊥．求证：CE DF =．证明：设CE 与DF 交于点O ，∵四边形ABCD 是正方形，∴90B DCF ∠=∠=︒，BC CD =．∴90BCE DCE ∠+∠=︒．∵CE DF ⊥，∴90COD ∠=︒．∴90CDF DCE ∠+∠=︒．∴CDF BCE ∠=∠．∴CBE DFC ≌△△．∴CE DF =．某数学兴趣小组在完成了以上解答后，决定对该问题进一步探究(1)【问题探究】如图，在正方形ABCD 中，点E 、F 、G 、H 分别在线段AB 、BC 、CD 、DA 上，且EG FH ⊥．试猜想EG FH 的值，并证明你的猜想．(2)【知识迁移】如图，在矩形ABCD 中，AB m =，BC n =，点E 、F 、G 、H 分别在线段AB 、BC 、CD 、DA 上，且EG FH ⊥．则EG FH=______．(3)【拓展应用】如图，在四边形ABCD 中，90DAB ∠=︒，60ABC ∠=︒，AB BC =，点E 、F 分别在线段AB 、AD 上，且CE BF ⊥．求CE BF 的值．（2023·辽宁丹东·统考一模）20．已知正方形ABCD 和等腰直角三角形AEF ，90EAF ∠=︒，连接BD ，BE ，BF ，DE ，点G ，H ，I 分别为线段BD ，BF ，DE 的中点，连接GH ，G I ，HI ．试卷第12页，共12页(1)如图1，当点B ，A ，F 在一条直线上时，请直接写出线段GH 与G I 的关系；(2)如图2，将AEF △绕点A 顺时针旋转()090αα︒<<︒，判断线段GH 与G I 的关系，并说明理由；(3)在（2）的条件下，若4AB =，3AE =，ADE V ，ABF △，GHI 的面积分别为1S ，2S ，S ．①请直接写出1S 与2S 大小关系；②直接写出124S S S +-的值．（2023·山东日照·统考中考真题）21．在平面直角坐标系xOy 内，抛物线()2520y ax ax a =-++>交y 轴于点C ，过点C作x 轴的平行线交该抛物线于点D．(1)求点C ，D 的坐标；(2)当13a =时，如图1，该抛物线与x 轴交于A ，B 两点（点A 在点B 的左侧），点P 为直线AD 上方抛物线上一点，将直线PD 沿直线AD 翻折，交x 轴于点(4,0)M ，求点P 的坐标；(3)坐标平面内有两点()1,1,5,1E a F a a ⎛⎫++ ⎪⎝⎭，以线段EF 为边向上作正方形EFGH ．①若1a =，求正方形EFGH 的边与抛物线的所有交点坐标；②当正方形EFGH 的边与该抛物线有且仅有两个交点，且这两个交点到x 轴的距离之差为52时，求a 的值．参考答案：1．C【分析】先证四边形AEPF 是矩形，可得PE AF =，90PFD ∠=︒，由等腰直角三角形的性质可得PF DF =，可求AF ，DF 的长，由勾股定理可求AP 的长，由“SAS ”可证ABP CBP △≌△，可得AP PC ==【详解】解：如图：连接AP ，四边形ABCD 是正方形，3AB AD ∴==，45ADB ∠=︒，PF AD ⊥ ，PE AB ⊥，90BAD ∠=︒，∴四边形AEPF 是矩形，PE AF ∴=，90PFD ∠=︒，PFD ∴ 是等腰直角三角形，PF DF ∴=，:1:2PE PF = ，:1:2AF DF ∴=，1AF ∴=，2DF PF ==，AP ∴=答案第2页，共37页AB BC = ，45ABD CBD ∠=∠=︒，BP BP =，(SAS)ABP CBP ∴△≌△，AP PC ∴==故选：C ．【点睛】本题考查了正方形的性质，全等三角形的判定和性质，矩形的性质，勾股定理等知识，灵活运用这些性质解决问题是解题的关键．2．A【分析】如图所示，点B 在3y x=上，证明AOC OBD ≌，根据k 的几何意义即可求解．【详解】解：如图所示，连接正方形的对角线，过点,A B 分别作x 轴的垂线，垂足分别为,C D ，点B 在3y x =上，∵OB OA =，90AOB BDO ACO ∠=∠=∠=︒，∴90CAO AOC BOD ∠=︒-∠=∠．∴AOC OBD ≌．∴32AOC OBD S S == n =．∵A 点在第二象限，∴3n =-．故选：A ．【点睛】本题考查了正方形的性质，反比例函数的k 的几何意义，熟练掌握以上知识是解题的关键．3．①②③④【分析】对于结论①，由等边三角形的性质可得，(SAS)EFB ACB ≌△△，则EF AC AD ==；同理，由CDF CAB ≌△△，得DF AB AE ==，由AE DF =，AD EF =即可得出四边形ADFE 是平行四边形；对于结论②，当150BAC ∠=︒时，36090EAD BAE BAC CAD ∠=︒-∠-∠-∠=︒，结合结论①，可知结论②正确；对于结论③，当AB AC =时，AE AD =，结合结论①，可知结论③正确；对于结论④，综合②③的结论知：当AB AC =，且150BAC ∠=︒时，四边形AEFD 既是菱形，又是矩形，故结论④正确．【详解】解析：①ABE 、CBF V 是等边三角形，BE AB ∴=，BF CB =，60FB EBA C =∠=︒∠，60EBF ABC ABF ∴∠=∠=︒-∠，(SAS)EFB ACB ∴≌△△，EF AC AD \==，同理由CDF CAB ≌△△，得DF AB AE ==，由AE DF =，AD EF =即可得出四边形ADFE 是平行四边形，故结论①正确；②当150BAC ∠=︒时，360360601506090EAD BAE BAC CAD ∠=︒-∠-∠-∠=︒-︒-︒-︒=︒，由①知四边形AEFD 是平行四边形，∴平行四边形ADFE 是矩形，故结论②正确；③由①知AB AE =，AC AD =，四边形AEFD 是平行四边形，∴当AB AC =时，AE AD =，∴平行四边形AEFD 是菱形，故结论③正确；答案第4页，共37页④综合②③的结论知：当AB AC =，且150BAC ∠=︒时，四边形AEFD 既是菱形，又是矩形，∴四边形AEFD 是正方形，故结论④正确．故答案为：①②③④．【点睛】本题主要考查了平行四边形、菱形、矩形、正方形的判定方法，熟练掌握以上图形的判定方法是解题的关键．4．(1)见解析(2)①见解析②【分析】()1根据SAS 证明三角形全等即可；()2①根据邻边相等的矩形是正方形证明即可；②作DH AG ⊥交AG 于点H ，作BM AG ⊥于点M ，证明BMG △是等腰直角三角形，求出BM 的最小值，可得结论．【详解】（1）证明：四边形ABCD 是正方形，AD DC ∴=，90ADC ∠=︒．DE DF = ，90EDF ∠=︒．ADC EDF ∴∠=∠，ADE CDF \Ð=Ð，在ADE V 和CDF 中，DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩ADE ∴V ≌()SAS CDF △；（2）①证明：如图2中，设AG 与CD 相交于点P ．90ADP ∠=︒ ，90DAP DPA ∴∠+∠=︒．ADE ≌CDF ，DAE DCF ∴∠=∠．DPA GPC ∠∠= ，90DAE DPA GPC GCP ∠∠∠∠∴+=+=︒．90PGN ∠∴=︒，BM AG ⊥ ，BN GN ⊥，∴四边形BMGN 是矩形，90MBN ∴∠=︒．四边形ABCD 是正方形，AB BC ∴=，90ABC MBN ∠∠==︒．ABM CBN ∴∠=∠．又90AMB BNC ∠∠==︒ ，AMB ∴ ≌CNB ．MB NB ∴=．∴矩形BMGN 是正方形；答案第6页，共37页②解：作DH AG ⊥交AG 于点H ，作BM AG ⊥于点M，∵90,90,DHA AMB ADH DAH BAM AD AB∠=∠=︒∠=︒-∠=∠=∴AMB ≌DHA ．BM AH ∴=．222AH AD DH =- ，4=AD ，DH ∴最大时，AH 最小，2DH DE ==最大值．BM AH ∴==最小值最小值．由()2①可知，BGM是等腰直角三角形，BG ∴==最小值【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题．5．D【分析】由题意作出图形，然后根据正方形的判定定理可进行排除选项．【详解】解：如图所示，点E 、F 、G 、H 分别是四边形ABCD 边AD 、DC 、BC 、AB 的中点，∴11////,////,,22EF AC GH EH BD FG EF GH AC EH FG BD ====，∴四边形EFGH 是平行四边形，对于A 选项：对角线互相平分，四边形EFGH 仍是平行四边形，故不符合题意；对于B 选项：对角线互相垂直，则有EF EH ⊥，可推出四边形EFGH 是矩形，故不符合题意；对于C 选项：对角线互相平分且相等，则有EF EH =，可推出四边形EFGH 是菱形，故不符合题意；对于D 选项：对角线互相垂直且相等，则有EF EH ⊥，EF EH =，可推出四边形EFGH 是正方形，故符合题意；故选D ．【点睛】本题主要考查三角形中位线及正方形、菱形、矩形、平行四边形的判定，熟练掌握三角形中位线及正方形、菱形、矩形、平行四边形的判定是解题的关键．6．②③【分析】根据四边形的性质及中位线的性质推导即可．【详解】解：点M ，N ，P ，Q 分别为边AB ，BC ，CD ，DA 的中点，MN AC ∴∥且12MN AC =，PQ AC ∥且12PQ AC =，MN PQ ∴∥且MN PQ =，MNPQ∴是平行四边形，故①错误；点M，N，P，Q分别为边AB，BC，CD，DA的中点，∴12MN AC=，12PN BD=，AC BD=，MN PN∴=，MNPQ是平行四边形，∴四边形MNPQ是菱形，故②正确；点M，N，P，Q分别为边AB，BC，CD，DA的中点，MN AC∴∥，MQ BD∥，AC BD⊥，MN MQ∴⊥，90QMN∴∠=︒，MNPQ是平行四边形，∴MNPQ是矩形，故③正确；若要四边形MNPQ是菱形，需满足AC BD=,当四边形ABCD是菱形，AC不一定等于BD，故④错误；综上，正确的有：②③，故答案为：②③．答案第8页，共37页【点睛】本题考查了中位线定理，菱形的判定和性质，矩形的判定和性质，平行四边形的判定和性质，熟练掌握知识点是解题的关键．7．A【分析】利用三角形逆时针旋转90︒后，再证明三角形全等，最后根据性质和三角形内角和定理即可求解．【详解】将ADF 绕点A 逆时针旋转90︒至ABH，∵四边形ABCD 是正方形，∴AB AD =，90ABC D BAD C ∠=∠=∠=∠=︒，由旋转性质可知：DAF BAH ∠=∠，90D ABH ∠=∠=︒，AF AH =，∴180ABH ABC ∠+∠=︒，∴点H B C ，，三点共线，∵BAE α∠=，45EAF ∠=︒，90BAD HAF ∠=∠=︒，∴45DAF BAH α∠=∠=︒-，45EAF EAH ∠=∠=︒，∵90AHB BAH ∠+∠=︒，∴45AHB α∠=︒+，在AEF 和AEH 中AF AH FAE HAE AE AE =⎧⎪∠=∠⎨⎪=⎩，答案第10页，共37页∴45AHE AFE α∠=∠=︒+，∴45AHE AFD AFE α∠=∠=∠=︒+，∴902DFE AFD AFE α∠=∠+∠=︒+，∵90DFE FEC C FEC ∠=∠+∠=∠+︒，∴2FEC α∠=，故选：A ．【点睛】此题考查了正方形的性质，全等三角形的判定和性质，旋转的性质，解题的关键是能正确作出旋转，再证明三角形全等，熟练利用性质求出角度．8．C【分析】连接CF 、CG 、AE ，证()ADE CDG SAS ∆≅∆可得AE CG =，当A 、E 、F 、C 四点共线时，即得最小值；【详解】解：如图，连接CF 、CG 、AE，∵90ADC EDG ∠=∠=︒∴ADE CDG∠=∠在ADE ∆和CDG ∆中，∵AD CD ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩=∴AE CG++=++∴DE CF CG EF CF AE++=时，最小，当EF CF AE ACAC===∴d1＋d2＋d3的最小值为，故选：C．【点睛】本题主要考查正方形的性质、三角形的全等证明，正确构造全等三角形是解本题的关键．9．A==，【分析】过点O作OM⊥BC于点M，先证明四边形ABFE是正方形，得出MF CF OM再利用勾股定理得出OC=，即可得出答案．【详解】过点O作OM⊥BC于点M，90∴∠=︒，OMC四边形ABCD是矩形，∴∠=∠=︒，90ABC BADEF AB∥∴∠AEF=180°-∠BAD=90°，∴∠=∠=∠=︒，ABC BAD AEF90∴四边形ABFE是矩形，答案第12页，共37页又∵AB =AE ，∴四边形ABFE 是正方形，45,AFB OB OF ∴∠=︒=，EF =BF ，12MF BF OM ∴==，2BF CF = ，MF CF OM ∴==，EF =2CF ，由勾股定理得OC ===，2OC ∴=，故选：A ．【点睛】本题考查了矩形的性质，正方形的判定和性质，平行线的性质，勾股定理，熟练掌握知识点是解题的关键．10．C【分析】根据题意作出合适的辅助线，然后逐一分析即可．【详解】如图，连接AC 、与BD 交于点O ，连接ME ，MF ，NF ，EN ，MN ，∵四边形ABCD 是平行四边形∴OA =OC ，OB =OD∵BE =DF∴OE =OF∵点E 、F 时BD 上的点，∴只要M，N过点O，那么四边形MENF就是平行四边形∴存在无数个平行四边形MENF，故①正确；只要MN=EF，MN过点O，则四边形MENF是矩形，∵点E、F是BD上的动点，∴存在无数个矩形MENF，故②正确；只要MN⊥EF，MN过点O，则四边形MENF是菱形；∵点E、F是BD上的动点，∴存在无数个菱形MENF，故③正确；只要MN=EF，MN⊥EF，MN过点O，则四边形MENF是正方形，而符合要求的正方形只有一个，故④错误；故选：C【点睛】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定、解答本题的关键时明确题意，作出合适的辅助线．11．3⊥于Q，证明四边形四边形AEPQ是正方形，即可求解．【分析】过点P作PQ AB⊥于Q，【详解】解：如图所示，过点P作PQ AB答案第14页，共37页∵点P 是正方形ABCD 的对角线AC 上的一点，PE AD ⊥于点E∴四边形AEPQ 是矩形，45EAP ∠=︒∴AEP △是等腰直角三角形，∴AE EP=∴四边形AEPQ 是正方形，∴3PQ EP ==，即点P 到直线AB 的距离为3故答案为：3．【点睛】本题考查了正方形的性质与判定，点到直线的距离，熟练掌握正方形的性质与判定是解题的关键．12．1【分析】连接BM ，将BM 以B 中心，逆时针旋转90︒，M 点的对应点为E ，由P 的运动轨迹是以M 为圆心，1为半径的半圆，可得：Q 的运动轨迹是以E 为圆心，1为半径的半圆，再根据“圆外一定点到圆上任一点的距离，在圆心、定点、动点，三点共线时定点与动点之间的距离最短”，所以当M 、Q 、E 三点共线时，MQ的值最小，可求ME ==，从而可求解．【详解】解，如图，连接BM ，将BM 以B 中心，逆时针旋转90︒，M 点的对应点为E， P 的运动轨迹是以M 为圆心，1为半径的半圆，∴Q 的运动轨迹是以E 为圆心，1为半径的半圆，如图，当M 、Q 、E 三点共线时，MQ 的值最小，四边形ABCD 是正方形，4CD AB BC ∴===，90C ∠=︒，M 是CM 的中点，2CM ∴=，BM ∴==由旋转得：BM BE =，ME ∴==MQ ME EQ∴=-1=，∴MQ的值最小为1．故答案：1．【点睛】本题考查了正方形的性质，旋转的性质，勾股定理，动点产生的线段最小值问题，掌握相关的性质，根据题意找出动点的运动轨迹是解题的关键．13【分析】以O 为原点，平行于AB 的直线为x 轴，建立直角坐标系，过E 作EM ⊥CD 于M ，过F 作FN ⊥DC ，交DC 延长线于N ，设正方形ABCD 的边长为2，从而求出E 的坐标，然后根据待定系数法求出直线CE 的解析式，即可求出G 的坐标，从而可求出GE ，根据旋转的性质可求出F 的坐标，进而求出H 的坐标，则可求OH ，最后代入计算即可得出答案．【详解】解：以O 为原点，平行于AB 的直线为x 轴，建立直角坐标系，过E 作EM ⊥CD答案第16页，共37页于M ，过F 作FN ⊥DC ，交DC 延长线于N，如图：设正方形ABCD 的边长为2，则C （1，1），D （﹣1，1），∵E 为OE 中点，∴E （12-，12），设直线CE 解析式为y ＝kx +b ，把C （1，1），E （12-，12）代入得：11122k b k b +=⎧⎪⎨-+=⎪⎩，解得1323k b ⎧=⎪⎪⎨⎪=⎪⎩，∴直线CE 解析式为1233y x =+，在1233y x =+中，令x ＝﹣1得y ＝13，∴G （﹣1，13），∴GE∵将线段CE 绕点C 逆时针旋转90°得到CF ，∴CE ＝CF ，∠ECF ＝90°，∴∠MCE ＝90°﹣∠NCF ＝∠NFC ，∵∠EMC ＝∠CNF ＝90°，∴△EMC ≌△CNF （AAS ），∴ME ＝CN ，CM ＝NF ，∵E （12-，12），C （1，1），∴ME ＝CN ＝12，CM ＝NF ＝32，∴F （32，12-），∵H 是EF 中点，∴H （12，0），∴OH ＝12，∴GE OH ＝612＝3．故答案为：3．【点睛】本题考查了正方形的性质，旋转的性质，两点间距离公式等知识，以O 为原点，平行于AB 的直线为x 轴，建立直角坐标系是解题的关键．14．24【分析】设4OA a =，则2AB a =，从而可得()4,0A a 、()6,0B a ，由正方形的性质可得()4,4C a a ，由QN y ⊥轴，点P 在CD 上，可得,44k P a a ⎛⎫ ⎪⎝⎭，由于Q 为BE 的中点，BE x ⊥轴，可得1==2BQ AB a ，则()6,Q a a ，由于点Q 在反比例函数()0k y k x =>的图象上可得26k a =，根据阴影部分为矩形，且长为4k a，宽为a ，面积为6，从而可得124=6ak a ⨯⨯，即可求解．【详解】解：设4OA a =，∵2OA AB =，∴2AB a =，∴==6OB AB OA a +，∴()6,0B a ，答案第18页，共37页在正方形ABEF 中，2AB BE a ==，∵Q 为BE 的中点，∴=12=BQ AB a ，∴()6,Q a a ，∵Q 在反比例函数()0k y k x =>的图象上，∴2=6=6k a a a ⨯，∵四边形OACD 是正方形，∴()6,6C a a ，∵P 在CD 上，∴P 点纵坐标为4a ，∵P 点在反比例函数()0k y k x =>的图象上，∴P 点横坐标为=4k x a，∴,44k P a a ⎛⎫ ⎪⎝⎭，∵===90HMO HNO NOM ∠∠∠︒，∴四边形OMHN 是矩形，∴=4k NH a，MH a =，∴64OMHN k S NH MH a a =⨯=⨯= ，∴24k =，故答案为：24．【点睛】本题考查反比例函数图象的性质及正方形的性质及矩形的面积公式，读懂题意，灵活运用所学知识是解题的关键．15．证明过程见解析【分析】菱形的两条对角线相互垂直且平分，再根据两条对角线相互垂直平分且相等的四边形是正方形即可证明四边形AECF 是正方形．【详解】证明：∵四边形ABCD 是菱形∴OA =OC ，OB =OD 且AC ⊥BD ，又∵BE =DF∴OB -BE =OD -DF即OE =OF∵OE =OA∴OA =OC =OE =OF 且AC =EF又∵AC ⊥EF∴四边形DEBF 是正方形．【点睛】此题考查了菱形的性质和正方形的判定，解题的关键是掌握上述知识．16．(1)平行四边形，见解析(2)AC BD =且AC BD⊥【分析】（1）根据平行四边形的性质，得到11,22BP AC OC CP BD OB ====，根据两组对边分别相等的四边形是平行四边形判定即可．（2）根据对角线相等、平分且垂直的四边形是正方形判定即可．【详解】（1）四边形BPCO 是平行四边形．理由如下：∵ABCD Y 的对角线,AC BD 交于点O ，∴,AO OC BO OD ==，∵以点,B C 为圆心，11,22AC BD 长为半径画弧，两弧交于点P ，答案第20页，共37页∴11,22BP AC OC CP BD OB ====∴四边形BPCO 是平行四边形．（2）∵对角线相等、平分且垂直的四边形是正方形，∴AC BD =且AC BD ⊥时，四边形BPCO 是正方形．【点睛】本题考查了平行四边形的判定和性质，正方形的判定和性质，熟练掌握判定和性质是解题的关键．17．(1)见解析(2)AE CF=(3)平行四边形，证明见解析【分析】（1）利用平行四边形的性质证得BEF AHE ∠=∠，根据角角边证明AEH BFE △≌△．（2）当AE CF =，证得AEH FCG △≌△，EBF △是等腰直角三角形，∠HEF =∠EFG =90°，即可证得四边形EFGH 是矩形．（3）利用正方形的性质证得AEGD 为平行四边形，过点H 作HM BC ⊥，垂足为点M ，交EG 于点N ，由平行线分线段成比例，设4OE x =，5OF x =，HN h =，则可表示出HN ，从而把△OEH 的面积用x 的代数式表示出来，根据二次函数求出最大值，则可得OE =OG ，OF =OH ，即可证得平行四边形．【详解】（1）∵四边形ABCD 为正方形，∴90A B ∠=∠=︒，∴90AEH AHE ∠+∠=°．∵四边形EFGH 为正方形，∴EH EF =，90HEF ∠=︒，∴90AEH BEF ∠+∠=︒，∴BEF AHE ∠=∠．在AEH △和BFE △中，∵90A B ∠=∠=︒，AHE BEF ∠=∠，EH FE =，∴AEH BFE △≌△．∴AH BE =．∴AE AH AE BE AB +=+=；（2）AE CF =；证明如下：∵四边形ABCD 为正方形，∴90A B ∠=∠=︒，AB =BC =AD =CD ，∵AE =AH ，CF =CG ，AE =CF ，∴AH =CG ，∴AEH FCG △≌△，∴EH =FG ．∵AE =CF ，∴AB －AE =BC －CF ，即BE =BF ，∴EBF △是等腰直角三角形，∴∠BEF =∠BFE =45°，∵AE =AH ，CF =CG ，∴∠AEH =∠CFG =45°，∴∠HEF =∠EFG =90°，∴EH ∥FG ，答案第22页，共37页∴四边形EFGH 是矩形．（3）∵四边形ABCD 为正方形，∴AB CD ∥．∵AE DG =，AE DG ∥，∴四边形AEGD 为平行四边形．∴AD EG ∥．∴EG BC ∥．过点H 作HM BC ⊥，垂足为点M ，交EG 于点N ，∴HN HO HM HF=．∵:4:5OE OF =，设4OE x =，5OF x =，HN h =，则2051620h x -=，∴()44h x =-．∴21144(4)8(2)3222S OE HN x x x =⋅⋅=⋅⋅-=--+．∴当2x =时，OEH △的面积最大，∴1482OE x EG OG ====，15102OF x HF OH ====，∴四边形EFGH是平行四边形．【点睛】此题考查了正方形的性质，矩形的判定和平行四边形的性质与判定，平行线分线段成比例定理，全等三角形的判定与性质，等腰三角形的性质，二次函数的最值，有一定的综合性，解题的关键是熟悉这些知识并灵活运用．18．(1)钝角三角形；证明见详解(2)①直角三角形；证明见详解；②S 四边形ABCD =5【分析】（1）根据等边三角形性质得出，BE =BD ，AB =CB ，∠EBD =∠ABC =60°，再证△EBA ≌△DBC （SAS ）∠AEB =∠CDB =60°，AE =CD ，求出∠ADC =∠ADB +∠BDC =120°，可得△ADC 为钝角三角形即可；（2）①以AE 、AG 、AC 为边的三角形是直角三角形，连结CG ，根据正方形性质，得出∠EBG =∠ABC ，EB =GB ，AB =CB ，∠BEA =∠BGE =45°，再证△EBA ≌△GBC （SAS ）得出AE =CG ，∠BEA =∠BGC =45°，可证△AGC 为直角三角形即可；②连结BD ，根据勾股定理求出AC=，然后利用正方形的面积公式求解即可．【详解】（1）证明：∵△ABC 与△EBD 均为等边三角形，∴BE =BD ，AB =CB ，∠EBD =∠ABC =60°，∴∠EBA +∠ABD =∠ABD +∠DBC ，∴∠EBA =∠DBC ，在△EBA 和△DBC 中，EB DB EBA DBC AB CB =⎧⎪∠=∠⎨⎪=⎩，∴△EBA ≌△DBC （SAS ），∴∠AEB =∠CDB =60°，AE =CD ，∴∠ADC =∠ADB +∠BDC =120°，答案第24页，共37页∴△ADC 为钝角三角形，∴以AE 、AD 、AC为边的三角形是钝角三角形．（2）证明：①以AE 、AG 、AC 为边的三角形是直角三角形．连结CG ，∵四边形ABCD 和四边形BGFE 都是正方形，∴∠EBG =∠ABC ，EB =GB ，AB =CB ，∵EG 为正方形的对角线，∴∠BEA =∠BGE =45°，∴∠EBA +∠ABG =∠ABG +∠GBC =90°，∴∠EBA =∠GBC ，在△EBA 和△GBC 中，G EB B EBA GBC AB CB =⎧⎪∠=∠⎨⎪=⎩，∴△EBA ≌△GBC （SAS ），∴AE =CG ，∠BEA =∠BGC =45°，∴∠AGC =∠AGB +∠BGC =45°+45°=90°，∴△AGC 为直角三角形，∴以AE 、AG 、AC 为边的三角形是直角三角形；②连结BD ，∵△AGC 为直角三角形，2210AE AG +=，由（2）可知，AE =CG ，∴AC 2210AG CG +=，∴四边形ABCD 为正方形，∴AC =BD 10，∴S 四边形ABCD =211522AC BD AC ⋅==．【点睛】本题考查等边三角形的性质，三角形全等判定与性质，正方形的性质，勾股定理，掌握等边三角形的性质，三角形全等判定与性质，正方形的性质，勾股定理是解题关键．19．(1)1；证明见解析(2)n m 32【分析】（1）过点A 作AM ∥HF 交BC 于点M ，作AN ∥EG 交CD 的延长线于点N ，利用答案第26页，共37页正方形ABCD ，AB ＝AD ，∠ABM ＝∠BAD ＝∠ADN ＝90°求证△ABM ≌△ADN 即可．（2）过点A 作AM ∥HF 交BC 于点M ，作AN ∥EC 交CD 的延长线于点N ，利用在矩形ABCD 中，BC ＝AD ，∠ABM ＝∠BAD ＝∠ADN ＝90°，求证△ABM ∽△ADN ．再根据其对应边成比例，将已知数值代入即可．（3）先证ABC ∆是等边三角形，设AB BC AC a ===，过点CN AB ⊥，垂足为N ，交BF 于点M ，则12AN BN a ==，在Rt BCN ∆中，利用勾股定理求得CN 的长，然后证NCE ABF ∆∆∽，利用相似三角形的对应边对应成比例即可求解．【详解】（1）1EG FH=，理由为：过点A 作AM ∥HF 交BC 于点M ，作AN ∥EG 交CD 的延长线于点N ，∵四边形ABCD 是正方形，∴AB ∥CD ，AD ∥BC ，∴四边形AMFH 是平行四边形，四边形AEGN是平行四边形，∴AM ＝HF ，AN ＝EG ，在正方形ABCD 中，AB ＝AD ，∠ABM ＝∠BAD ＝∠ADN ＝90°∵EG ⊥FH ，∴∠NAM ＝90°，∴∠BAM ＝∠DAN ，在△ABM 和△ADN 中，∠BAM ＝∠DAN ，AB ＝AD ，∠ABM ＝∠ADN∴△ABM ≌△ADN∴AM ＝AN ，即EG ＝FH ，∴1EG FH=；（2）解：过点A 作AM ∥HF 交BC 于点M ，作AN ∥EC 交CD 的延长线于点N ，∵四边形ABCD 是矩形，∴AB ∥CD ，AD ∥BC ，∴四边形AMFH 是平行四边形，四边形AEGN 是平行四边形，∴AM ＝HF ，AN ＝EG ，在矩形ABCD 中，BC ＝AD ，∠ABM ＝∠BAD ＝∠ADN ＝90°，∵EG ⊥FH ，∴∠NAM ＝90°，∴∠BAM ＝∠DAN ．∴△ABM ∽△ADN ，∴AM AB AN AD=，∵AB m =，BC AD n ==，AM ＝HF ，AN ＝EG ，∴HF m EG n =，∴EG n FH m=；故答案为：nm （3）解：∵60ABC ∠=︒，AB BC =，∴ABC ∆是等边三角形，答案第28页，共37页∴设AB BC AC a ===，过点CN AB ⊥，垂足为N ，交BF 于点M ，则12AN BN a ==，在Rt BCN ∆中，2CN a ===，∵CN AB ⊥，CE BF ⊥，∴90ABF BMN ∠+∠=︒，90ECN CMF ∠+∠=︒，又∵CMF BMN ∠=∠，∴ABF ECN ∠=∠，∵CN AB ⊥，90DAB ∠=︒，∴90DAB CNE ∠=∠=︒，∴NCE ABF ∆∆∽，∴CE CN BF AB =，即2CE BF a ==．【点睛】此题主要考查学生对相似三角形的判定与性质，全等三角形的判定与性质，勾股定理等知识点的理解和掌握，综合性较强，难度较大，是一道难题．20．(1)GH GI =且GH GI⊥(2)GH GI =且GH GI ⊥，理由见详解(3)①12S S =，②258【分析】（1）连接DF ，延长BE 交DF 于P ，可证BAE DAF ≌ ，结合三角形中位线即可求解；（2）连接DF 交BE 于Q ，AD 与BE 交于M ，可证BAE DAF ≌ ，结合三角形中位线即可求解；（3）①过F 作FO BA ⊥，交BA 的延长线于O ，过E 作EN AD ⊥，可证FAO EAN ≌ ，即可求解；②可求218S BE =，由12EAF ABD BFED S S S S S +=-- 四边形即可求解．【详解】（1）解：GH GI =且GH GI ⊥，如图，连接DF ，延长BE 交DF 于P，四边形ABCD 是正方形，AB AD ∴=，90BAC ∠=︒，BAE DAF ∴∠=∠，AEF 是等腰直角三角形，AE AF ∴=，在BAE 和DAF △中AB AD BAE DAF AE AF =⎧⎪∠=∠⎨⎪=⎩，BAE DAF ∴≌ (SAS )，BE DF ∴=，ABE ADF ∠=∠，点G ，H ，I 分别为线段BD ，BF ，DE 的中点，答案第30页，共37页12GI BE ∴=，GI BE ∥，12GH DF =，GH DF ∥，GI GH ∴=；90ABE BEA ∠+∠=︒ ，BEA DEP ∠=∠，90ABE DEP ∴∠+∠=︒，90ADF DEP ∴∠+∠=︒，BE DF ∴⊥，BE GH ∴⊥，GI GH ∴⊥；故GH GI =且GH GI ⊥．（2）解：GH GI =且GH GI ⊥，如图，连接DF 交BE 于Q ，AD 与BE 交于M，由（1）得：，AE AF =，90BAM EAF ∠=∠=︒，BAM DAE EAF DAE∴∠+∠=∠+∠BAE DAF∴∠=∠在BAE 和DAF △中AB AD BAE DAF AE AF =⎧⎪∠=∠⎨⎪=⎩，BAE DAF ∴≌ (SAS )，BE DF ∴=，ABE ADF ∠=∠，点G ，H ，I 分别为线段BD ，BF ，DE 的中点，12GI BE ∴=，GI BE ∥，12GH DF =，GH DF ∥，GI GH ∴=；90ABM BMA ∠+∠=︒ ，BMA DMQ ∠=∠，90ABM DMQ ∴∠+∠=︒，90ADF DMQ ∴∠+∠=︒，BE DF ∴⊥，BE GH ∴⊥，GI GH ∴⊥；故GH GI =且GH GI ⊥．（3）解：①12S S =，如图，过F 作FO BA ⊥，交BA 的延长线于O ，过E 作EN AD ⊥，90ANE OAF ∴∠=∠=︒，90FAO OAE ∴∠+∠=︒，90EAN OAE ∠+∠=︒，FAO EAN ∴∠=∠，。

正方形专练二

长方形、正方形的周长与面积专项练习

部编版三年级下册数学面积应用题专项练习卷二(附答案)

长方体正方体专项练习题

18.22 平面直角坐标系中的正方形(专项练习)-2020-2021学年八年级数学下册(人教版)

人教版五年级下册数学 正方体长方体 应用题专练

正方形的性质专项练习30题(有答案)ok

长方形 正方形周长专题练习

五年级数学下册期末-长方体和正方体的表面积《解决问题》专项练习二(人教版,含答案)

正方形的性质与判定专题练习

长方形正方形的面积专项练习30题(有答案)ok

矩形、菱形、正方形(解答题)专练(详细答案)

第九章 立体几何专练2—基本立体图形(提升练)-2022届高三数学一轮复习

小学奥数4-5-2 长方体与正方体(二).专项练习及答案解析

正方形的判定专项练习30题(有答案)ok

【精品】小学奥数4-5-2 长方体与正方体(二).专项练习

2023-2024年小学数学四年级上册知识梳理真题讲练 专题二 (人教版含解析)

长方形正方形的面积专项练习30题(有答案)ok

初二正方形数学练习题

2024年中考数学二轮复习模块专练—正方形(含答案)

人教版五年级下册数学正方体长方体应用题专练

长方形正方形周长专题练习

第九章立体几何专练2—基本立体图形(提升练)-2022届高三数学一轮复习

2023-2024年小学数学四年级上册知识梳理真题讲练专题二 (人教版含解析)