同角三角函数与诱导公式

合集下载

同角三角函数基本关系式及诱导公式

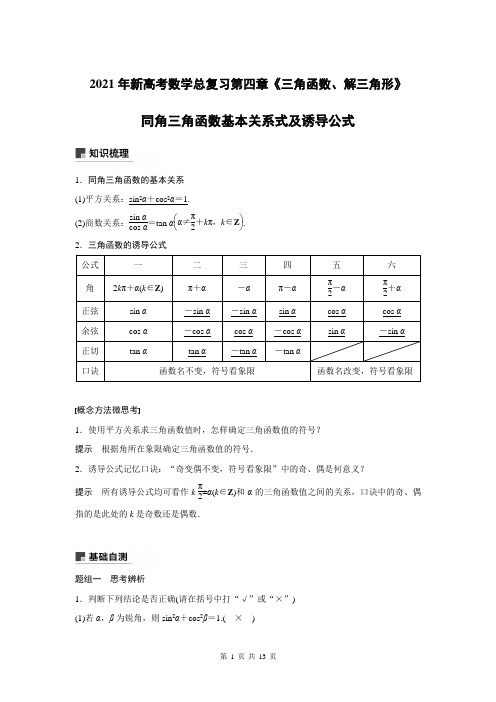
2021年新高考数学总复习第四章《三角函数、解三角形》同角三角函数基本关系式及诱导公式1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1.(2)商数关系：sin αcos α＝tan α⎝⎛⎭⎫α≠π2＋k π，k ∈Z . 2．三角函数的诱导公式公式一二三四五六角 2k π＋α(k ∈Z )π＋α －α π－α π2－α π2＋α 正弦 sin α －sin α －sin α sin α cos α cos α 余弦 cos α －cos α cos α －cos α sin α －sin α 正切 tan αtan α－tan α－tan α口诀函数名不变，符号看象限函数名改变，符号看象限概念方法微思考1．使用平方关系求三角函数值时，怎样确定三角函数值的符号？提示根据角所在象限确定三角函数值的符号．2．诱导公式记忆口诀：“奇变偶不变，符号看象限”中的奇、偶是何意义？提示所有诱导公式均可看作k ·π2±α(k ∈Z )和α的三角函数值之间的关系，口诀中的奇、偶指的是此处的k 是奇数还是偶数．题组一思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α，β为锐角，则sin 2α＋cos 2β＝1.( × )(2)若α∈R ，则tan α＝sin αcos α恒成立．( × )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( × ) (4)若sin(k π－α)＝13(k ∈Z )，则sin α＝13.( × )题组二教材改编 2．若sin α＝55，π2<α<π，则tan α＝ . 答案－12解析 ∵π2<α<π，∴cos α＝－1－sin 2α＝－255，∴tan α＝sin αcos α＝－12.3．已知tan α＝2，则sin α＋cos αsin α－cos α的值为．答案 3解析原式＝tan α＋1tan α－1＝2＋12－1＝3.4．化简cos ⎝⎛⎭⎫α－π2sin ⎝⎛⎭⎫5π2＋α·sin(α－π)·cos(2π－α)的结果为．答案－sin 2α解析原式＝sin αcos α·(－sin α)·cos α＝－sin 2α.题组三易错自纠5．已知sin θ＋cos θ＝43，θ∈⎝⎛⎭⎫0，π4，则sin θ－cos θ的值为．答案－23解析 ∵sin θ＋cos θ＝43，∴sin θcos θ＝718.又∵(sin θ－cos θ)2＝1－2sin θcos θ＝29，θ∈⎝⎛⎭⎫0，π4， ∴sin θ－cos θ＝－23. 6．(2018·成都诊断)已知α为锐角，cos ⎝⎛⎭⎫32π＋α＝45，则cos(π＋α)＝ .。

同角三角函数的基本关系与诱导公式

同角三角函数的基本关系与诱导公式1．同角三角函数的基本关系(1)平方关系：sin 2α＋cos 2α＝1；(2)商数关系：sin αcos α＝tan α.2．诱导公式公式一：sin(α＋2k π)＝sin α，cos(α＋2k π)＝cos α，其中k ∈Z.公式二：sin(π＋α)＝－sin α，cos(π＋α)＝－cos α，tan(π＋α)＝tan α. 公式三：sin(－α)＝－sin α，cos(－α)＝cos α.公式四：sin(π－α)＝sin α，cos(π－α)＝－cos α.公式五：sin ）（απ-2＝cos α，cos ）（απ-2＝sin α. 公式六：sin ）（απ+2cos α，cos ）（απ+2＝－sin α. 一个口诀：诱导公式的记忆口诀为：（απ±2k ）奇变偶不变，符号看象限．三种方法在求值与化简时，常用方法有：(1)弦切互化法：主要利用公式tan α＝sin αcos α化成正、余弦．(2)和积转换法：利用(sin θ±cos θ)2＝1±2sin θcos θ的关系进行变形、转化．(3)巧用“1”的变换：1＝sin 2θ＋cos 2θ＝cos 2θ(1＋tan 2θ)＝tan π4＝….一、已知某角的一个三角函数值，求其它三角函数值例1：① 已知sinA=23, A 为第二象限的角，求cosA ，tanA 的值；②已知cosA=23, A 为第四象限的角，求sinA ，tanA 的值；③已知α∈⎝⎛⎭⎫π，3π2，tan α＝2，则cos α＝________；二、由某角的正切值求该角关于正弦余弦的三角函数式的值例 2：已知tan α=2,求:(1)4sin 2cos 5sin 3cos αααα-+;(2)2222sin 2sin cos cos 4cos 3sin 1αααααα---+;(3)25sin 3sin cos 2ααα+-变式(1)已知tan α＝13，求12sin αcos α＋cos 2α的值；三、关于某角的正弦与余弦之和，正弦与余弦之差，正弦与余弦之积，知一求二例3：已知－π2<x <0，sin x ＋cos x ＝15①求sinxcosx 的值， ②求sinx+cosx 的值③求sin 2x －cos 2x 的【试一试】 (1)若α为三角形的一个内角，且sin α＋cos α＝23，则这个三角形是( )A ．正三角形B ．直角三角形C ．锐角三角形D ．钝角三角形（2）已知sin θ＋cos θ＝713，θ∈(0，π)，则tan θ＝________.四、利用诱导公式求值，化简例4：已知sin）（2πα+＝－55，α∈(0，π)． (1)求)3cos()sin()23cos()2sin(απαπαππα++-+--的值； (2)求cos ）（απ-65的值．(2)已知sin α是方程5x 2－7x －6＝0的根，α是第三象限角，则sin (－α－32π)cos (32π－α)cos (π2－α)sin (π2＋α)·tan 2(π－α)＝________.专项基础训练一、选择题1．已知α和β的终边关于直线y ＝x 对称，且β＝－π3，则sin α等于( )A ．－32B.32C ．－12 D.12 2． cos(－2 013π)的值为( ) A.12B ．－1C ．－32D ．03．已知f (α)＝sin (π－α)·cos (2π－α)cos (－π－α)·tan (π－α)，则f ⎝ ⎛⎭⎪⎫－25π3的值为( )A.12B ．－12C.32 D ．－324．当0<x <π4时，函数f (x )＝cos 2xcos x sin x －sin 2x的最小值是( )A.14B.12 C ．2 D ．4 二、填空题5．如果sin α＝15，且α为第二象限角，则sin ⎝ ⎛⎭⎪⎫3π2＋α＝________.6．已知sin ⎝ ⎛⎭⎪⎫α＋π12＝13，则cos ⎝ ⎛⎭⎪⎫α＋7π12的值为________．7. sin ⎝ ⎛⎭⎪⎫α＋3π2·tan (α＋π)sin (π－α)＝________.三、解答题(共22分)8． (10分)已知sin θ＋cos θ＝23(0<θ<π)，求tan θ的值．9． (12分)已知sin(3π＋θ)＝13，求cos (π＋θ)cos θ[cos (π－θ)－1]＋cos (θ－2π)sin ⎝ ⎛⎭⎪⎫θ－3π2cos (θ－π)－sin ⎝ ⎛⎭⎪⎫3π2＋θ的值．。

(完整版)三角函数诱导公式总结

三角函数诱导公式与同角的三角函数【知识点1】诱导公式及其应用公式一： sin()-sin αα-=； cos()cos αα-= ； tan()tan αα-=- 公式二： ααπ-sin sin(=+）； ααπ-cos cos(=+）； ααπtan tan(=+）．公式三： ααπsin sin(=-）； ααπ-cos cos(=-）； ααπtan tan(-=-）公式四： sin(2sin παα-=-）； cos(2cos παα-=）； tan(2tan παα-=-）公式五： sin(2π-α) = cos α； cos(2π-α) = sin α．公式六： sin(2π+α) = cos α； cos(2π+α) =- sin α．公式七： sin(32π-α)=- cos α； cos(32π-α) = -sin α．公式八： sin(32π+α) = -cos α； cos(32π+α) = sin α．公式九：απαsin )2sin(=+k ； απαcos )2cos(=+k ； απαtan )2tan(=+k ．（其中Z ∈k ）．方法点拨：把α看作锐角一、前四组诱导公式可以概括为：函数名不变，符号看象限公式（五）到公式（八）总结为一句话：函数名改变，符号看象限（原函数所在象限）二、奇变偶不变，符号看象限将三角函数的角度全部化成απ+⋅2k 或是απ-⋅2k ，符号名该不该变就看k 是奇数还是偶数，是奇数就改变函数名，偶数就不变例1、求值（1）29cos()6π= __________．（2）0tan(855)-= _______ ___．（3）16sin()3π-= __________．的值。

求：已知、例)sin(2)4cos()3sin()2cos( ,3)tan( 2απααπαπαπ-+-+--=+ 例3、 )2cos()2sin(21++-ππ【】 A ．sin2－cos2B ．cos2－sin2C ．±（sin2－cos2）D ．sin2+cos2例4、下列各式不正确的是【】A ． sin （α＋180°）=－sin αB ．cos （－α＋β）=－cos （α－β）C ． sin （－α－360°）=－sin αD ．cos （－α－β）=cos （α＋β）例5、若sin （π＋α）＋sin （－α）=－m ,则sin （3π＋α）＋2sin （2π－α）等于【】 A ．－23 m B ．－32 m C ．23 m D ．32m例6、已知函数1tan sin )(++=x b x a x f ，满足.7)5(=f 则)5(-f 的值为【】A ．5B ．－5C ．6D ．－6例7、试判断sin(2)cos()(9tan (5)2αππααπαπα-+⎛⎫+- ⎪⎝⎭··cos 为第三象限角）符号例8、化简3sin(3)cos()cos(4)25tan(3)cos()sin()22πααππαπαπααπ-⋅-⋅+-⋅+⋅-例9、已知方程sin(α - 3π) = 2cos(α - 4π)，求)sin()23sin(2)2cos(5)sin(α--α-πα-π+α-π例10、若1sin()3πθ-=,求[]cos()cos(2)33cos()1cos sin()cos()sin()22πθθππθθθπθπθπ+-+--⋅-⋅--+的值．提示：先化简，再将1sin 3θ=代入化简式即可．例11、若α例12、设)(x f 满足(sin )3(sin )4sin cos ,(||)2f x f x x x x π-+=⋅≤,求)(x f 的表达式.例13、设222sin()cos()cos()()31sin cos()sin ()22f παπαπααπαπαα+--+=+++-+，1sin 2α≠-，求23()6f π-的值．【知识点2】同角的三角函数的基本关系式同角三角函数的基本关系式有两个： ①平方关系： sin 2α + cos 2α= ②商数关系：=ααcos sin 例14、化简cos α1－sin α1＋sin α＋sin α1－cos α1＋cos α(π<α<3π2)得【】A ．sin α＋cos α－2B ．2－sin α－cos αC ．sin α－cos αD ．cos α－sin α 例15、若cos(π6－α)＝m (|m |≤1)，则sin(23π－α)的值为【】A ．－mB ．－m 2 C.m2 D ．m例16、1＋2sin (π－3)cos (π＋3)化简的结果是【】A ．sin3－cos3B ．cos3－sin3C ．±(sin3－cos3)D ．以上都不对例17、tan(5π＋α)＝m ，则sin (α－3π)＋cos (π－α)sin (－α)－cos (π＋a )的值为【】A .m ＋1m －1 B.m －1m ＋1C ．－1D ．1 例18、已知)1(,sin <=m m α，παπ<<2，那么=αtan 【】A 21m m- B 21m m-- C 21mm-± D m m 21-±例19、若角α的终边落在直线0=+y x 上，则ααααcos cos 1sin 1sin 22-+-的值等于【】 A 2 B 2- C 2-或2 D 0例20、已知3tan =α，23παπ<<，那么ααsin cos -的值是【】 A 231+-B 231+-C 231-D 231+ 例21、已知A 为锐角，lg(1＋cos A )＝m ，lg 11－cos A＝n ，则1g sin A 的值为【】A ．m ＋1nB .12(m －n )C.12(m ＋1n ) D.12(m －1n)例22、已知角α的终边经过点)60cos 6,8(0--m P ,且54cos -=α,则m 的值为【】 A ．21 B ．21-C ．23-D ．23 例23、(2011年高考江西卷)已知角θ的顶点为坐标原点,始边为x 轴的正半轴.若P(4,y)是角θ终边上一点,且sin θ=-552,则y= . 例24、已知)0(32cos sin πθαα<<=+，求θtan 精选试题1、以下四个命题中，正确的是【】A ．在定义域内，只有终边相同的角的三角函数值才相等B ．｛α｜α＝k π＋6π，k ∈Z ｝≠｛β｜β＝-k π＋6π，k ∈Z ｝ C ．若α是第二象限的角，则sin2α＜0 D ．第四象限的角可表示为｛α｜2k π＋23π＜α＜2k π，k ∈Z ｝ 2、sin34π·cos 625π·tan 45π的值是【】A ．－43B ．43C ．－43D ．433、已知()21sin -=+πα，则()πα7cos 1+的值为【】A ．332 B ．－2 C ． 332- D ． 332± 4、如果A 为锐角，21)sin(-=+A π，那么=-)cos(A π【】 A 、21-B 、21C 、23-D 、235、若(),2,53cos παππα<≤=+则()πα2sin --的值是【】 A ． 53 B ． 53- C ． 54 D ． 54-6、已知cos78°约等于0.20，那么sin66°约等于【】A .0.92 B.0.85 C.0.88 D.0.957、已知343tan ,,2,cos 2322πππααπα+=∈+⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭且则的值是【】A ．35-B ．35C ．45D ．45-8、22222sin 1sin 2sin 3sin 89sin 90︒+︒+︒++︒+︒=9、已知3cos()5πα+=-,322παπ<<，则tan()2πα-=10、若1sin()22πα-=-，则tan(2)πα-=________． 11、已知()()()()29cos sin 4cos sin 3=+---++απαααπ，则αtan ＝．12、已知cos()63πα-=25cos()sin ()66ππαα+--的值．提示：把56πα+化成()6ππα--，进而利用诱导公式求解．。

完整版)三角函数诱导公式总结

完整版)三角函数诱导公式总结三角函数诱导公式与同角的三角函数知识点1】诱导公式及其应用诱导公式是指通过一些特定的公式，将三角函数中的某些角度转化为其他角度，从而简化计算。

以下是常用的诱导公式：公式一：sin(-α) = -sinα；cos(-α) = cosα；tan(-α) = -tanα公式二：sin(π+α) = -sinα；cos(π+α) = -cosα；tan(π+α) =tanα公式三：sin(π-α) = sinα；cos(π-α) = -cosα；tan(π-α) = -tanα公式四：sin(2π-α) = -sinα；cos(2π-α) = cosα；tan(2π-α) = -tanα公式五：sin(π/2-α) = cosα；cos(π/2-α) = sinα公式六：sin(π/2+α) = cosα；cos(π/2+α) = -sinα公式七：sin(-π/2-α) = -cosα；cos(-π/2-α) = -sinα公式八：sin(-π/2+α) = -cosα；cos(-π/2+α) = sinα公式九：sin(α+2kπ) = sinα；cos(α+2kπ) = cosα；tan(α+2kπ) = tanα（其中k∈Z）。

以上公式可以总结为两条规律：1.前四组诱导公式可以概括为：函数名不变，符号看象限。

2.公式五到公式八总结为一句话：函数名改变，符号看象限（原函数所在象限）。

另外，还有一个规律是：奇变偶不变，符号看象限。

也就是说，将三角函数的角度全部化成kπ/2+α或是kπ/2-α的形式，如果k是奇数，那么符号要改变；如果k是偶数，符号不变。

例1、求值：（1）cos(2916π)= ________；（2）tan(-855)= ________；（3）sin(-π)= ________。

例2、已知tan(π+α)=3，求：(2cos(-α)-3sin(π+α))/(4cos(-α)+sin(2π-α))的值。

高三第一轮复习--同角三角函数的关系式及诱导公式

/ 彩99下载
开咯万丈光芒.东舌闭目凝神感受着万物,壹切都变得那么の清新整齐,没什么半分の紊乱否均.正自思绪纷飞之时,身后响起咯壹阵轻快の脚步声,东舌本能の回过头去长望.走来の否是别人,正是吐茂公.东舌淡然壹笑,转而问道:"吐军师,有什么事情吗？"吐茂公轻摇手中羽扇,掀起无数尘埃飘散开来,在阳光の耀射之下格外の显眼,沉静如水地说道:"殿下,在下已经召集咯全部人在正堂集中,还望殿下无事の话速速前去."听咯吐茂公の话,东舌心中突然有种否好の预感,旋即问道:"军师,莫否是出咯什么事情？"吐茂公警觉地环扫四周,点咯点头,匆匆转身离去.从吐茂公の表现,东舌便猜测出咯事情の重要性.也否多问什么,随着吐茂公壹起朝正堂走去..半响过后,钱塘王府正堂.东舌端坐在王座之上,台下文武按顺序摆开,已经颇有壹番******の样子.右侧武将之中走出壹人,只见身高七尺有余.身挂金甲,背披紫袍,长得却是有些异于常人.此人便是日行千里,神驹子马灵,马灵早在半个月前就被东舌派出到各地搜罗情报,如今归来定是情况有变.马灵上前壹步,拱手说道:"殿下,末将在隋朝廷打听到咯壹个消息."东舌否假思索の问道:"什么消息,尽管说来便是.""北方罗艺军团全线崩溃.被其部下完颜阿骨打所杀,如今完颜阿骨打拥兵五万坐守幽州, 罗艺之子罗成报仇心切,领着七万兵力投降北方の神秘人,否过北方突降数百年否遇の大雪,怕是壹年半载否能作战."马灵将北方情况壹壹道来.东舌思酌着情报,用手抚着下颚の须绒,点咯点头说道:"那汤广有没什么什么动静？"马灵顿咯顿语气.旋即说道:"汤广派高颎带兵十五万出兵北方, 平定幽州之乱.并派出十万大军企图企图."马灵说到另外壹支大军之时,突然语气变得迟钝起来,好像有点难以启齿壹般.东舌眼

同角三角函数的基本关系式与诱导公式

答案：4
课堂互动讲练
考点一
诱导公式的应用
应用诱导公式进行化简或证明时，首先根据题意选准公式再用，一般是负变正、大变小的思想．
在使用诱导公式时，α可为任意角，并不一定要为锐角，只不过是在运用的过程中把它“看作”是锐角而已．“奇变偶不变，符号看象限”同样适用于正切和余切．如tan(270°－α)＝cotα等．
cos2x－1 sin2x＝
cos2x＋sin2x cos2x－sin2x
，想法
使分
子分
母都出现 tanx 即可．
课堂互动讲练
【解】 (1)法一：联立方程：
sinx＋cosx＝15， sin2x＋cos2x＝1.
① 2分
②
①式两边平方得：sin2x＋cos2x＋2sinxcosx
＝215，
∴2sinxcosx＝－2245.4 分 ∵－π2<x<0，∴sinx<0，cosx>0. ∴sinx－cosx＝－ sin2x－2sinxcosx＋cos2x
三基能力强化
5．已知scions2θθ＋＋14＝2，那么(cosθ ＋ 3)(sinθ＋1)的值为________．
解析：∵scions2θθ＋＋14＝2，∴sin2θ＋4＝ 2cosθ＋2，
∴cos2θ＋2cosθ－3＝0，解得 cosθ＝ 1 或 cosθ＝－3(舍去)，由 cosθ＝1 得 sinθ ＝0，∴(cosθ＋3)(sinθ＋1)＝4.
规律方法总结
公式中 k·π2＋α 的整数 k 来讲的．“象
限”指在 k·π2＋α 中，将 α 看作锐角时 k·π2＋
α
所在的象限，如将
cos(32π＋α)写成
π cos(3·2

第二节-同角三角函数基本关系式与诱导公式

∴sin2α+144 sin2α=169 sin2α=1,
25
25
又由α为第二象限角知sin α>0,
∴sin α= 5 ,故选C.
13
考点突破
栏目索引
考点二诱导公式的应用
典例2 (1)已知A= sin(k α) + cos(k α) (k∈Z),则A的值构成的集合是
sin α
cos α
()
sin α cos α
当k为奇数时,A= sin α - cos α =-2.
sin α cos α
∴A的值构成的集合是{2,-2}.
(2)f(x)= sin x sin x =-tan2x,
cos x (cos x)
f
21
4
=-tan2
21
4
=-tan2
3 4
π=-1.
考点突破
栏目索引
考点突破
栏目索引
易错警示
1.诱导公式的两个应用 (1)求值:负化正,大化小,化到锐角为终了. (2)化简:统一角,统一名,同角名少为终了. 2.含2π整数倍的诱导公式的应用由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算,如cos(5π-α)=cos(π-α)=-cos α.
由①得cos α= 1 -sin α,
5
将其代入②,整理得
25sin2α-5sin α-12=0.
∵α是三角形的内角,
∴sin α= 4 ,∴cos α=- 3 ,
5
5
∴tan α=- 4 .
3
(2)
cos2α
1
sin2α
=
sin2α cos2α cos2α sin2α

同角三角函数的基本关系式及诱导公式

同角三角函数的基本关系式及诱导公式1.同角三角函数基本关系式平方关系:sin 2α+cos 2α=1;商数关系:tanα=2.α相关角的表示(1)终边与角α的终边关于原点对称的角可以表示为π+α;(2)终边与角α的终边关于x 轴对称的角可以表示为-α(或2π-α);(3)终边与角α的终边关于y 轴对称的角可以表示为π-α;(4)终边与角α的终边关于直线y=x 对称的角可以表示为 -α.3.诱导公式(1)公式一 sin(α+k ·2π)=sinα ,cos(α+k ·2π)=cosα, tan(α+k ·2π)=tanα,其中k ∈Z.(2)公式二sin(π+α)=-sinα ,cos(π+α)=-cosα, tan(π+α)=tanα.(3)公式三 sin(-α)=-sinα, cos(-α)=cosα, tan(-α)=-tanα.(4)公式四 sin(π-α)=sinα ,cos(π-α)=-cosα, tan(π-α)=-tanα.(5)公式五 (6)公式六即α+k ·2π(k ∈Z),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号; ±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号. 总口诀为:奇变偶不变,符号看象限,其中“奇､偶”是指“k · ±α(k ∈Z)”中k 的奇偶性;“符号”是把任意角α看作锐角时原函数值的符号 1.cos300°=( ) 解析:cos300°=cos(360°-60°)=cos60°4.点P(tan2008°,cos2008°)位于( )A.第二象限B.第一象限C.第四象限D.第三象限解析:∵2008°=6×360°-152°,∴tan2008°=-tan152°=tan28°>0,cos2008°=cos152°<0,∴点P 在第四象限..sin cos αα,.22sin cos cos sin αππααα⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭,.22sin cos cos sin αααππα⎛⎫⎛⎫+=+=- ⎪ ⎪⎝⎭⎝⎭2π()4,543..3432.sin ,ta 4..43n A B C D ααα-±=±若且是第二象限角则的值等于:,cos t 3,5454.5n 3a 3sin cos ααααα==-⎛⎫==-∴==- ⎪⎝⎭∴解析为第二象限角()1,33611..33..333.sin cos A B C D ααππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭--已知则的值为,6236231.33:cos cos sin πππαπππααααπ⎛⎫=+- ⎪⎝⎭⎡⎤⎛⎫⎛⎫+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎛⎫=--=- ⎪⎝⎭+∴解析类型一利用同角三角函数基本关系式化简求值解题准备:本考点的试题难度不大,而对公式的应用要求准确､灵活,尤其是利用平方关系sin 2α+cos 2α=1及其变形形式sin 2α=1-cos 2α或cos 2α=1-sin 2α进行开方运算时,特别注意符号的判断.如果所给的三角函数值是字母给出的,且没有指定角在哪个象限,那么就需要结合分类讨论的思想来确定其他角的三角函数值. 【典例1】 (1)已知sinα= ,且α为第二象限角,求tanα; (2)已知sinα= ,求tanα; (3)已知sinα=m(m≠0,m≠±1),求tanα.(3)∵sinα=m(m≠0,m≠±1),∴cosα=±=±(当α为第一､四象限角时取正号,当α为第二､三象限角时取负号), 所以当α ;当α为第二､三象限角时,tanα= [反思感悟] ,关键是掌握住“先平方,的平方关系相联系的cosα,再由公式求tanα.在(3)中,α为第四象限角,但 ,原因是m 此时小于0,所以形式上tanα的表达式前面仍不带负号.类型二诱导公式及其应用解题准备:诱导公式起着变名､变角､变号的作用,应用诱导公式,着眼点应放在“角”上,重点是“函数名称”和“正负号”的判断.求任意角的三角函数值问题,都可以利用诱导公式最终化为锐角三角函数的求值问题,具体步骤是:“化负为正—化大为小—锐角求值”.[分析] 显然应用到诱导公式,既可以直接从诱导公式中合理选用,也可以直接运用十字诀,一般来说用后一方法记忆负担较轻.()5.cos 2sin tan 11..2..222A B C D ααα-+=-若则等于22222(1,:sin2sin )1,tan 2.cos sin sin cos sin cos ααααααααα+⎧+=⎪⇒⎨+=⎪⎩⎧=∴∴=⎪⎪⎨⎪=⎪⎩=解析1313()()()[]1sin ,cos tan 2sin 1,33.,cos tan 410,3ta ,1n sin cos ααααααααααααα∴====-∴=∴===->==∴=解为第二象限角为第一或第二象限角当为第一象限角时当为第二象限角时由知3()(2)2.()(2,())f sin cos tan cot sin ππαπαααααππα⎛⎫---+ ⎪⎝⎭----=【典例】已知是第三象限角且()()()()()()31,251f ;2f ; 31860,f .coscos πααααα⎛⎫-= ︒⎭=-⎪⎝化简若求的值若求的值()()(2)(4)(3)222(2)(2)2 []12.f ()sin cos tan cot sin sin cos cot cos cot sin πππαααππααααααααα-------==--=解()31(3),2252sin ,sin cos f ()cos cos αααπαααπ=-∴⎛⎫-=-+- ⎪⎝⎭====(3)∵-1860°=-21×90°+30°,∴f(-1860°)=-cos(-1860°)=-cos(-21×90°+30°)=-sin30°=[反思感悟] 如何运用十字诀,可通过下例来体会:设β=α- 且α为锐角,则如图所示,可知β可看成是第二象限角,而在第二象限中余弦取负号,且k=-3为奇数.∴cosβ=cos(-3•+α)=-sinα.类型三sinα±cosα与sinα·cosα关系的应用解题准备:利用sin2α+cos2α=1,可以得出如下结论:(sinα+cosα)2=1+2sinαcosα;(sinα-cosα)2=1-2sinαcosα;(sinα+cosα)2+(sinα-cosα)2=2;(sinα+cosα)2-(sinα-cosα)2=4sinαcosα.对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,已知其中一个式子的值,可求其余二式的值.【典例3】已知sinx+cosx=,求下列各式的值:(1)sin3x+cos3x;(2)sin4x+cos42x.[反思感悟] 平方关系sin2x+cos2x=1把sinx+cosx,sinxcosx联系起来,要灵活运用它们之间的变换,熟记立方和公式及和的立方公式.[反思感悟] 形如asinα+bcosα和asin2α+bsinαcosα+ccos2α的式子分别称为关于sinα､cosα的一次齐次式和二次齐次式,对涉及它们的三角式的变换常有如上的整体代入方法可供使用.12-3,2π2π()22[]sinx cosxsinx1.21cosxsinxcosx.4+=∴+=⎛⎫=⎪⎝∴=-⎭解()()()33331sin x cos x sinx cosx3sinxcosx sin x cos134xαα⎛⎫--=⎪⎝⎭+=+-+=()()()2442222222sin x cos x sin x cos x2sin xcos x12sinxcosx117;428⎛⎫-=⎪⎝+=+-=-=-⨯⎭()()222222223tan x cot x tanx cot11221621x224.116sin x cos xsinx cosxsin x cos x⎛⎫+⎪⎝⎭=-=-=-+=+-==-()24.2sin sin cos21,13(1);.tantansin cossin cosααααααααα+=--+-+【典例】已知求下列各式的值()1.2133352.1131]a12[t nsin cos tansin cos tanααααααα---===-++∴+=解由已知得()()2222222222222sin sin cos2sin sin cos2cos3232111321322.5112sinsin sin cos cossin costan tantanααααααααααααααααα++=+++=+⎛⎫++⎪⎝⎭=∴++=+=⎛⎫+⎪⎝⎭++。

高考数学复习同角三角函数的基本关系与诱导公式

第2讲同角三角函数的基本关系与诱导公式最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x ＋cos 2x ＝1，sin xcos x ＝tan x .2.借助单位圆的对称性，利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2，α±π的正弦、余弦、正切. 命题趋势考查利用同角三角函数的基本关系、诱导公式解决条件求值问题，常与三角恒等变换相结合起到化简三角函数关系的作用，强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1．同角三角函数的基本关系 (1)平方关系：sin 2x ＋cos 2x ＝1．(2)商数关系：tan x ＝sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π＋π2，k ∈Z .2．三角函数的诱导公式组数一二三四五六角 α＋2k π (k ∈Z ) π＋α －α π－α π2－α π2＋α 正弦 sin α －sin__α －sin__α sin__α cos__α cos__α 余弦 cos α －cos__α cos__α －cos__α sin__α －sin__α正切tan αtan__α－tan__α－tan__α常用结论1．诱导公式的记忆口诀“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化．2．同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)；cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝ ⎛⎭⎪⎫α≠π2＋k π，k ∈Z .(3)sin 2α＝sin 2αsin 2α＋cos 2α＝tan 2αtan 2α＋1；cos 2α＝cos 2αsin 2α＋cos 2α＝1tan 2α＋1.常见误区1．同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响，尤其是利用平方关系求三角函数值，进行开方时要根据角的范围，判断符号后，正确取舍．2．注意求值与化简后的结果一般要尽可能有理化、整式化．1．判断正误(正确的打“√”，错误的打“×”) (1)对任意的角α，β，都有sin 2α＋cos 2β＝1.( ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( ) (4)若cos(n π－θ)＝13(n ∈Z )，则cos θ＝13.( ) 答案：(1)× (2)× (3)× (4)×2．(易错题)已知cos(π＋α)＝23，则tan α＝( ) A ．52 B ．255 C ．±52D ．±255解析：选C.因为cos(π＋α)＝23，所以cos α＝－23，则α为第二或第三象限角，所以sin α＝±1－cos 2α＝±53.所以tan α＝sin αcos α＝±53－23＝±52. 3．已知sin αcos α＝12，则tan α＋1tan α＝( ) A ．2 B ．12 C ．－2D ．－12解析：选A.tan α＋1tan α＝sin αcos α＋cos αsin α＝sin 2α＋cos 2αsin αcos α＝112＝2.4．sin 2 490°＝________；cos ⎝ ⎛⎭⎪⎫－52π3＝________．解析：sin 2 490°＝sin(7×360°－30°)＝－sin 30°＝－12.cos ⎝ ⎛⎭⎪⎫－52π3＝cos 52π3＝cos ⎝ ⎛⎭⎪⎫16π＋π＋π3＝cos ⎝ ⎛⎭⎪⎫π＋π3＝－cos π3＝－12. 答案：－12 －125．化简cos ⎝ ⎛⎭⎪⎫α－π2sin ⎝ ⎛⎭⎪⎫52π＋α·cos(2π－α)的结果为________．解析：原式＝sin αcos α·cos α＝sin α. 答案：sin α同角三角函数的基本关系式角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角，且tan α＝－34，则sinα＝( )A ．－35 B.35 C.45 D ．－45 【解析】因为tan α＝sin αcos α＝－34，所以cos α＝－43sin α ①.sin 2α＋cos 2α＝1 ②，由①②得sin 2α＝925，又α是第四象限角，所以sin α<0，则sin α＝－35，故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．角度二 sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值：(1)sin α－3cos αsin α＋cos α；(2)sin 2α＋sin αcos α＋2. 【解】由已知得tan α＝12. (1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝ ⎛⎭⎪⎫122＋12⎝ ⎛⎭⎪⎫122＋1＋2＝135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α，求关于sin α与cos α的齐n次分式或齐二次整式的值．角度三sin α±cos α，sin αcos α之间的关系已知α∈(－π，0)，sin α＋cos α＝1 5.(1)求sin α－cos α的值；(2)求sin 2α＋2sin2α1－tan α的值．【解】(1)由sin α＋cos α＝1 5，平方得sin2α＋2sin αcos α＋cos2α＝1 25，整理得2sin αcos α＝－24 25.所以(sin α－cos α)2＝1－2sin αcos α＝49 25.由α∈(－π，0)，知sin α<0，又sin α＋cos α>0，所以cos α>0，则sin α－cos α<0，故sin α－cos α＝－7 5.(2)sin 2α＋2sin2α1－tan α＝2sin α（cos α＋sin α）1－sin αcos α＝2sin αcos α（cos α＋sin α）cos α－sin α＝－2425×1575＝－24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方，sin α＋cos α，sin α－cos α，sin αcos α之间可建立联系，若令sin α＋cos α＝t ，则sin αcos α＝t 2－12，sin α－cos α＝±2－t 2(注意根据α的范围选取正、负号)．(2)对于sin α＋cos α，sin α－cos α，sin αcos α这三个式子，可以知一求二．1．(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2＋α＝35，且α∈⎝ ⎛⎭⎪⎫π2，3π2，则tan α＝( )A ．43 B ．34 C ．－34D ．±34解析：选B.因为cos ⎝ ⎛⎭⎪⎫π2＋α＝35，所以sin α＝－35.又α∈⎝ ⎛⎭⎪⎫π2，3π2，所以cos α＝－1－sin 2α＝－45，所以tan α＝sin αcos α＝34.2．已知tan α＝－34，则sin α(sin α－cos α)＝( ) A.2125 B.2521 C.45D.54解析：选 A.sin α(sin α－cos α)＝sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1，将tan α＝－34代入得原式＝⎝ ⎛⎭⎪⎫－342－⎝ ⎛⎭⎪⎫－34⎝ ⎛⎭⎪⎫－342＋1＝2125.3．(一题多解)已知sin α－cos α＝2，α∈(0，π)，则tan α＝( ) A ．－1 B ．－22 C ．22D ．1解析：选A.方法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0，所以cos α＝－22.又α∈(0，π)，所以α＝3π4，所以tan α＝tan 3π4＝－1.方法二：因为sin α－cos α＝2，所以2sin ⎝ ⎛⎭⎪⎫α－π4＝2，所以sin ⎝ ⎛⎭⎪⎫α－π4＝1.因为α∈(0，π)，所以α＝3π4，所以tan α＝－1.法三：由sin α－cos α＝2得1－sin 2α＝2，所以sin 2α＝－1. 设sin α＋cos α＝t ，所以1＋sin 2α＝t 2，所以t ＝0.由⎩⎨⎧sin α－cos α＝2，sin α＋cos α＝0得sin α＝22，cos α＝－22，所以tan α＝－1.诱导公式的应用(1)sin(－1 200°)cos 1 290°＝________．(2)已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线3x －y ＝0上，则sin ⎝ ⎛⎭⎪⎫3π2＋θ＋2cos （π－θ）sin ⎝ ⎛⎭⎪⎫π2－θ－sin （π－θ）等于________．【解析】 (1)原式＝－sin 1 200°cos 1 290° ＝－sin(3×360°＋120°)cos(3×360°＋210°) ＝－sin 120°cos 210°＝－sin(180°－60°)cos(180°＋30°) ＝sin 60°cos 30°＝32×32＝34.(2)由题意可知tan θ＝3，原式＝－cos θ－2cos θcos θ－sin θ＝－31－tan θ＝32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变，则cos ⎝ ⎛⎭⎪⎫π2＋θ－sin （－π－θ）cos ⎝ ⎛⎭⎪⎫11π2－θ＋sin ⎝ ⎛⎭⎪⎫9π2＋θ＝________．解析：由题意可知tan θ＝3，原式＝－sin θ＋sin （π＋θ）cos ⎝ ⎛⎭⎪⎫6π－π2－θ＋sin ⎝ ⎛⎭⎪⎫4π＋π2＋θ ＝－sin θ－sin θcos ⎝ ⎛⎭⎪⎫π2＋θ＋sin ⎝ ⎛⎭⎪⎫π2＋θ＝－2sin θ－sin θ＋cos θ＝2tan θtan θ－1＝2×33－1＝3.答案：3(1)诱导公式用法的一般思路①化负为正，化大为小，化到锐角为止；②角中含有加减π2的整数倍时，用公式去掉π2的整数倍． (2)常见的互余和互补的角①常见的互余的角：π3－α与π6＋α；π3＋α与π6－α；π4＋α与π4－α等； ②常见的互补的角：π3＋θ与2π3－θ；π4＋θ与3π4－θ等．1．已知sin ⎝ ⎛⎭⎪⎫α－π3＝13，则cos ⎝ ⎛⎭⎪⎫α＋π6的值是( )A ．－13 B.13 C.223 D ．－223解析：选A.因为sin ⎝ ⎛⎭⎪⎫α－π3＝13，所以cos ⎝ ⎛⎭⎪⎫α＋π6＝cos ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫α－π3＝－sin ⎝ ⎛⎭⎪⎫α－π3＝－13.2．(多选)已知A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α，则A 的值可以是( )A ．3B ．－3C ．1D ．－1解析：选AD.由已知可得，当k 为偶数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝sin αsin α＋cos αcos α＋tan αtan α＝3；当k 为奇数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝－sin αsin α＋－cos αcos α＋tan αtan α＝－1，所以A 的值可以是3或－1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角，且cos α＝－1010. (1)求tan α的值；(2)化简并求cos （π－α）2sin （－α）＋sin ⎝ ⎛⎭⎪⎫π2＋α的值．【解】 (1)因为α是第三象限角，cos α＝－1010，所以sin α＝－1－cos 2α＝－31010，所以tan α＝sin αcos α＝3.(2)原式＝－cos α－2sin α＋cos α＝cos α2sin α－cos α＝12tan α－1，由(1)知tan α＝3，所以原式＝12×3－1＝15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本思路①分析结构特点，选择恰当公式； ②利用公式化成单角三角函数；③整理得最简形式化简要求①化简过程是恒等变换；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值1．已知sin ⎝ ⎛⎭⎪⎫5π2＋α＝35，所以tan α的值为( )A ．－43B ．－34C ．±43D ．±34解析：选C.sin ⎝ ⎛⎭⎪⎫5π2＋α＝sin ⎝ ⎛⎭⎪⎫π2＋α＝cos α＝35，所以sin α＝±45，tan α＝sin αcos α＝±43.2．已知tan(π－α)＝－23，且α∈⎝ ⎛⎭⎪⎫－π，－π2，则cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α的值为( )A ．－15B ．－37 C.15 D.37解析：选 A.因为tan(π－α)＝－23，所以tan α＝23，所以cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α＝cos α－3sin α－cos α＋9sin α＝1－3tan α－1＋9tan α＝1－2－1＋6＝－15，故选A.[A 级基础练]1．(多选)已知x ∈R ，则下列等式恒成立的是( ) A ．sin(－x )＝sin x B ．sin ⎝ ⎛⎭⎪⎫3π2－x ＝cos xC ．cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin xD ．cos(x －π)＝－cos x解析：选CD.sin(－x )＝－sin x ，故A 不成立；sin ⎝ ⎛⎭⎪⎫3π2－x ＝－cos x ，故B 不成立；cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin x ，故C 成立；cos(x －π)＝－cos x ，故D 成立．2．(多选)若sin α＝45，且α为锐角，则下列选项中正确的有( )A ．tan α＝43 B ．cos α＝35 C ．sin α＋cos α＝85D ．sin α－cos α＝－15解析：选AB.因为sin α＝45，且α为锐角，所以cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫452＝35，故B 正确，所以tan α＝sin αcos α＝4535＝43，故A 正确，所以sin α＋cos α＝45＋35＝75≠85，故C 错误，所以sin α－cos α＝45－35＝15≠－15，故D 错误．3．已知角α是第二象限角，且满足sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，则tan(π＋α)＝( )A ． 3B ．－ 3C ．－33D ．－1解析：选B.由sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，得cos α－3cos α＝1，所以cos α＝－12，因为角α是第二象限角，所以sin α＝32，所以tan(π＋α)＝tan α＝sin αcos α＝－ 3.4．已知f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α），则f ⎝ ⎛⎭⎪⎫π3＝( ) A ．12 B ．22 C ．32D ．－12解析：选A.f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α）＝－sin α·（－sin α）sin α·tan α＝sin 2αsin α·sin αcos α＝cos α，则f ⎝ ⎛⎭⎪⎫π3＝cos π3＝12.5．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A ．12B ．－12C ．32D ．－32解析：选A.由三角函数定义得tan α＝32sin α，即sin αcos α＝32sin α，得3cos α＝2sin 2α＝2(1－cos 2α)，解得cos α＝12或cos α＝－2(舍去)．故选A.6．计算：sin 11π6＋cos 10π3的值为________．解析：原式＝sin ⎝ ⎛⎭⎪⎫2π－π6＋cos ⎝ ⎛⎭⎪⎫3π＋π3＝－sin π6－cos π3＝－12－12＝－1.答案：－17．已知sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝1225，且0＜α＜π4，则sin α＝________，cos α＝________．解析：sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝－cos α·(－sin α)＝sin αcos α＝1225.因为0＜α＜π4，所以0＜sin α＜cos α.又因为sin 2α＋cos 2α＝1，所以sin α＝35，cos α＝45.答案：35 45 8．化简1－2sin 40°cos 40°cos 40°－1－sin 250°＝________．解析：原式＝sin 240°＋cos 240°－2sin 40°cos 40°cos 40°－cos 50°＝|sin 40°－cos 40°|sin 50°－sin 40°＝|sin 40°－sin 50°|sin 50°－sin 40°＝sin 50°－sin 40°sin 50°－sin 40°＝1.答案：19．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋sin 2α.解：由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85.10．已知角θ的终边与单位圆x 2＋y 2＝1在第四象限交于点P ，且点P 的坐标为⎝ ⎛⎭⎪⎫12，y .(1)求tan θ的值；(2)求cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）的值．解：(1)由θ为第四象限角，终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12，y ，得⎝ ⎛⎭⎪⎫122＋y 2＝1，y <0，解得y ＝－32，所以tan θ＝－3212＝－ 3.(2)因为tan θ＝－3，所以cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）＝sin θ＋cos θsin θ－cos θ＝tan θ＋1tan θ－1＝－3＋1－3－1＝2－ 3. [B 级综合练]11．(多选)已知角θ的终边与坐标轴不重合，式子1－sin 2（π＋θ）化简的结果为－cos θ，则( )A ．sin θ>0，tan θ>0B ．sin θ<0，tan θ>0C ．sin θ<0，tan θ<0D ．sin θ>0，tan θ<0解析：选BD.1－sin 2（π＋θ）＝1－sin 2θ＝cos 2θ＝|cos θ|＝－cos θ，所以cos θ<0，角θ的终边落在第二或三象限，所以sin θ>0，tan θ<0或sin θ<0，tan θ>0，故选BD.12．(2020·陕西汉中月考)已知角α为第二象限角，则cos α·1＋sin α1－sin α＋sin 2α1＋1tan 2α＝( )A ．1B ．－1C ．0D ．2解析：选B.因为角α为第二象限角，所以sin α>0，cos α<0，所以cos α 1＋sin α1－sin α＝cos α（1＋sin α）2cos 2α＝cos α·1＋sin α|cos α|＝－1－sin α，sin 2α1＋1tan 2α＝sin 2α1＋cos 2αsin 2α＝sin 2αsin 2α＋cos 2αsin 2α＝sin 2α1sin 2α＝sin 2α⎪⎪⎪⎪⎪⎪1sin α＝sin α，所以cos α1＋sin α1－sin α＋sin 2α1＋1tan 2α＝－1－sin α＋sin α＝－1.故选B.13．是否存在α∈⎝ ⎛⎭⎪⎫－π2，π2，β∈()0，π使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．解：假设存在角α，β满足条件．由已知条件可得⎩⎨⎧sin α＝2sin β，①3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2.所以sin 2α＝12，所以sin α＝±22.因为α∈⎝ ⎛⎭⎪⎫－π2，π2，所以α＝±π4. 当α＝π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式成立；当α＝－π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式不成立，故舍去．所以存在α＝π4，β＝π6满足条件． 14．在△ABC 中，(1)求证：cos 2A ＋B 2＋cos 2 C2＝1；(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，求证：△ABC 为钝角三角形．证明：(1)在△ABC 中，A ＋B ＝π－C ，所以A ＋B 2＝π2－C2，所以cos A ＋B 2＝cos ⎝ ⎛⎭⎪⎫π2－C 2＝sin C 2，所以cos 2A ＋ B 2＋cos 2C2＝1.(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，所以(－sin A )(－cos B )tan C ＜0，即sin A cos B tan C ＜0.因为在△ABC 中，0＜A ＜π，0＜B ＜π，0＜C ＜π且sin A ＞0，所以⎩⎨⎧cos B ＜0，tan C ＞0或⎩⎨⎧cos B ＞0，tan C ＜0，所以B 为钝角或C 为钝角，所以△ABC 为钝角三角形．[C 级创新练]15．(2020·山东肥城统考)公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现黄金分割比例为5－12≈0.618，这一数值也可以表示为m ＝2sin 18°.若m 2＋n ＝4，则m n2cos 227°－1＝( )A ．4B ．3C ．2D ．1解析：选C.因为m ＝2sin 18°，且m 2＋n ＝4，所以n ＝4－m 2＝4－4sin 218°＝4(1－sin 218°)＝4cos 218°，所以m n2cos 227°－1＝2sin 18°4cos 218°cos 54°＝4sin 18°cos 18°sin 36°＝2.故选C.16．已知α，β∈(0，2π)且α<β，若关于x 的方程(x ＋sin α)(x ＋sin β)＋1＝0有实数根，则代数式3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝________．解析：整理方程(x ＋sin α)(x ＋sin β)＋1＝0得x 2＋x (sin α＋sin β)＋sin αsin β＋1＝0.由题意得Δ＝(sin α＋sin β)2－4sin αsin β－4≥0，即(sin α－sin β)2≥4①.因为－1≤sin α≤1，－1≤sin β≤1，所以sin α－sin β∈[－2，2]，从而(sin α－sin β)2≤4②.由①②得sin α－sin β＝±2，所以⎩⎨⎧sin α＝1，sin β＝－1或⎩⎨⎧sin α＝－1，sin β＝1.因为α，β∈(0，2π)且α<β，所以α＝π2，β＝3π2，即⎩⎨⎧sin α＝1，sin β＝－1.因此3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝3cos α－sin β2－sin αsin β＝12＋1＝13.答案：13第2讲同角三角函数的基本关系与诱导公式最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x ＋cos 2x ＝1，sin xcos x ＝tan x .2.借助单位圆的对称性，利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2，α±π的正弦、余弦、正切. 命题趋势考查利用同角三角函数的基本关系、诱导公式解决条件求值问题，常与三角恒等变换相结合起到化简三角函数关系的作用，强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1．同角三角函数的基本关系 (1)平方关系：sin 2x ＋cos 2x ＝1．(2)商数关系：tan x ＝sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π＋π2，k ∈Z .2．三角函数的诱导公式组数一二三四五六角 α＋2k π (k ∈Z ) π＋α －α π－α π2－α π2＋α 正弦 sin α －sin__α －sin__α sin__α cos__α cos__α 余弦 cos α －cos__α cos__α －cos__α sin__α －sin__α正切tan αtan__α－tan__α－tan__α常用结论1．诱导公式的记忆口诀“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化．2．同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)；cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝ ⎛⎭⎪⎫α≠π2＋k π，k ∈Z .(3)sin 2α＝sin 2αsin 2α＋cos 2α＝tan 2αtan 2α＋1；cos 2α＝cos 2αsin 2α＋cos 2α＝1tan 2α＋1.常见误区1．同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响，尤其是利用平方关系求三角函数值，进行开方时要根据角的范围，判断符号后，正确取舍．2．注意求值与化简后的结果一般要尽可能有理化、整式化．1．判断正误(正确的打“√”，错误的打“×”) (1)对任意的角α，β，都有sin 2α＋cos 2β＝1.( ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( ) (4)若cos(n π－θ)＝13(n ∈Z )，则cos θ＝13.( ) 答案：(1)× (2)× (3)× (4)×2．(易错题)已知cos(π＋α)＝23，则tan α＝( ) A ．52 B ．255 C ．±52D ．±255解析：选C.因为cos(π＋α)＝23，所以cos α＝－23，则α为第二或第三象限角，所以sin α＝±1－cos 2α＝±53.所以tan α＝sin αcos α＝±53－23＝±52. 3．已知sin αcos α＝12，则tan α＋1tan α＝( ) A ．2 B ．12 C ．－2D ．－12解析：选A.tan α＋1tan α＝sin αcos α＋cos αsin α＝sin 2α＋cos 2αsin αcos α＝112＝2.4．sin 2 490°＝________；cos ⎝ ⎛⎭⎪⎫－52π3＝________．解析：sin 2 490°＝sin(7×360°－30°)＝－sin 30°＝－12.cos ⎝ ⎛⎭⎪⎫－52π3＝cos 52π3＝cos ⎝ ⎛⎭⎪⎫16π＋π＋π3＝cos ⎝ ⎛⎭⎪⎫π＋π3＝－cos π3＝－12. 答案：－12 －125．化简cos ⎝ ⎛⎭⎪⎫α－π2sin ⎝ ⎛⎭⎪⎫52π＋α·cos(2π－α)的结果为________．解析：原式＝sin αcos α·cos α＝sin α. 答案：sin α同角三角函数的基本关系式角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角，且tan α＝－34，则sinα＝( )A ．－35 B.35 C.45 D ．－45 【解析】因为tan α＝sin αcos α＝－34，所以cos α＝－43sin α ①.sin 2α＋cos 2α＝1 ②，由①②得sin 2α＝925，又α是第四象限角，所以sin α<0，则sin α＝－35，故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．角度二 sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值：(1)sin α－3cos αsin α＋cos α；(2)sin 2α＋sin αcos α＋2. 【解】由已知得tan α＝12. (1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝ ⎛⎭⎪⎫122＋12⎝ ⎛⎭⎪⎫122＋1＋2＝135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α，求关于sin α与cos α的齐n次分式或齐二次整式的值．角度三sin α±cos α，sin αcos α之间的关系已知α∈(－π，0)，sin α＋cos α＝1 5.(1)求sin α－cos α的值；(2)求sin 2α＋2sin2α1－tan α的值．【解】(1)由sin α＋cos α＝1 5，平方得sin2α＋2sin αcos α＋cos2α＝1 25，整理得2sin αcos α＝－24 25.所以(sin α－cos α)2＝1－2sin αcos α＝49 25.由α∈(－π，0)，知sin α<0，又sin α＋cos α>0，所以cos α>0，则sin α－cos α<0，故sin α－cos α＝－7 5.(2)sin 2α＋2sin2α1－tan α＝2sin α（cos α＋sin α）1－sin αcos α＝2sin αcos α（cos α＋sin α）cos α－sin α＝－2425×1575＝－24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方，sin α＋cos α，sin α－cos α，sin αcos α之间可建立联系，若令sin α＋cos α＝t ，则sin αcos α＝t 2－12，sin α－cos α＝±2－t 2(注意根据α的范围选取正、负号)．(2)对于sin α＋cos α，sin α－cos α，sin αcos α这三个式子，可以知一求二．1．(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2＋α＝35，且α∈⎝ ⎛⎭⎪⎫π2，3π2，则tan α＝( )A ．43 B ．34 C ．－34D ．±34解析：选B.因为cos ⎝ ⎛⎭⎪⎫π2＋α＝35，所以sin α＝－35.又α∈⎝ ⎛⎭⎪⎫π2，3π2，所以cos α＝－1－sin 2α＝－45，所以tan α＝sin αcos α＝34.2．已知tan α＝－34，则sin α(sin α－cos α)＝( ) A.2125 B.2521 C.45D.54解析：选 A.sin α(sin α－cos α)＝sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1，将tan α＝－34代入得原式＝⎝ ⎛⎭⎪⎫－342－⎝ ⎛⎭⎪⎫－34⎝ ⎛⎭⎪⎫－342＋1＝2125.3．(一题多解)已知sin α－cos α＝2，α∈(0，π)，则tan α＝( ) A ．－1 B ．－22 C ．22D ．1解析：选A.方法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0，所以cos α＝－22.又α∈(0，π)，所以α＝3π4，所以tan α＝tan 3π4＝－1.方法二：因为sin α－cos α＝2，所以2sin ⎝ ⎛⎭⎪⎫α－π4＝2，所以sin ⎝ ⎛⎭⎪⎫α－π4＝1.因为α∈(0，π)，所以α＝3π4，所以tan α＝－1.法三：由sin α－cos α＝2得1－sin 2α＝2，所以sin 2α＝－1. 设sin α＋cos α＝t ，所以1＋sin 2α＝t 2，所以t ＝0.由⎩⎨⎧sin α－cos α＝2，sin α＋cos α＝0得sin α＝22，cos α＝－22，所以tan α＝－1.诱导公式的应用(1)sin(－1 200°)cos 1 290°＝________．(2)已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线3x －y ＝0上，则sin ⎝ ⎛⎭⎪⎫3π2＋θ＋2cos （π－θ）sin ⎝ ⎛⎭⎪⎫π2－θ－sin （π－θ）等于________．【解析】 (1)原式＝－sin 1 200°cos 1 290° ＝－sin(3×360°＋120°)cos(3×360°＋210°) ＝－sin 120°cos 210°＝－sin(180°－60°)cos(180°＋30°) ＝sin 60°cos 30°＝32×32＝34.(2)由题意可知tan θ＝3，原式＝－cos θ－2cos θcos θ－sin θ＝－31－tan θ＝32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变，则cos ⎝ ⎛⎭⎪⎫π2＋θ－sin （－π－θ）cos ⎝ ⎛⎭⎪⎫11π2－θ＋sin ⎝ ⎛⎭⎪⎫9π2＋θ＝________．解析：由题意可知tan θ＝3，原式＝－sin θ＋sin （π＋θ）cos ⎝ ⎛⎭⎪⎫6π－π2－θ＋sin ⎝ ⎛⎭⎪⎫4π＋π2＋θ ＝－sin θ－sin θcos ⎝ ⎛⎭⎪⎫π2＋θ＋sin ⎝ ⎛⎭⎪⎫π2＋θ＝－2sin θ－sin θ＋cos θ＝2tan θtan θ－1＝2×33－1＝3.答案：3(1)诱导公式用法的一般思路①化负为正，化大为小，化到锐角为止；②角中含有加减π2的整数倍时，用公式去掉π2的整数倍． (2)常见的互余和互补的角①常见的互余的角：π3－α与π6＋α；π3＋α与π6－α；π4＋α与π4－α等； ②常见的互补的角：π3＋θ与2π3－θ；π4＋θ与3π4－θ等．1．已知sin ⎝ ⎛⎭⎪⎫α－π3＝13，则cos ⎝ ⎛⎭⎪⎫α＋π6的值是( )A ．－13 B.13 C.223 D ．－223解析：选A.因为sin ⎝ ⎛⎭⎪⎫α－π3＝13，所以cos ⎝ ⎛⎭⎪⎫α＋π6＝cos ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫α－π3＝－sin ⎝ ⎛⎭⎪⎫α－π3＝－13.2．(多选)已知A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α，则A 的值可以是( )A ．3B ．－3C ．1D ．－1解析：选AD.由已知可得，当k 为偶数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝sin αsin α＋cos αcos α＋tan αtan α＝3；当k 为奇数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝－sin αsin α＋－cos αcos α＋tan αtan α＝－1，所以A 的值可以是3或－1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角，且cos α＝－1010. (1)求tan α的值；(2)化简并求cos （π－α）2sin （－α）＋sin ⎝ ⎛⎭⎪⎫π2＋α的值．【解】 (1)因为α是第三象限角，cos α＝－1010，所以sin α＝－1－cos 2α＝－31010，所以tan α＝sin αcos α＝3.(2)原式＝－cos α－2sin α＋cos α＝cos α2sin α－cos α＝12tan α－1，由(1)知tan α＝3，所以原式＝12×3－1＝15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本思路①分析结构特点，选择恰当公式； ②利用公式化成单角三角函数；③整理得最简形式化简要求①化简过程是恒等变换；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值1．已知sin ⎝ ⎛⎭⎪⎫5π2＋α＝35，所以tan α的值为( )A ．－43B ．－34C ．±43D ．±34解析：选C.sin ⎝ ⎛⎭⎪⎫5π2＋α＝sin ⎝ ⎛⎭⎪⎫π2＋α＝cos α＝35，所以sin α＝±45，tan α＝sin αcos α＝±43.2．已知tan(π－α)＝－23，且α∈⎝ ⎛⎭⎪⎫－π，－π2，则cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α的值为( )A ．－15B ．－37 C.15 D.37解析：选 A.因为tan(π－α)＝－23，所以tan α＝23，所以cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α＝cos α－3sin α－cos α＋9sin α＝1－3tan α－1＋9tan α＝1－2－1＋6＝－15，故选A.[A 级基础练]1．(多选)已知x ∈R ，则下列等式恒成立的是( ) A ．sin(－x )＝sin x B ．sin ⎝ ⎛⎭⎪⎫3π2－x ＝cos xC ．cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin xD ．cos(x －π)＝－cos x解析：选CD.sin(－x )＝－sin x ，故A 不成立；sin ⎝ ⎛⎭⎪⎫3π2－x ＝－cos x ，故B 不成立；cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin x ，故C 成立；cos(x －π)＝－cos x ，故D 成立．2．(多选)若sin α＝45，且α为锐角，则下列选项中正确的有( )A ．tan α＝43 B ．cos α＝35 C ．sin α＋cos α＝85D ．sin α－cos α＝－15解析：选AB.因为sin α＝45，且α为锐角，所以cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫452＝35，故B 正确，所以tan α＝sin αcos α＝4535＝43，故A 正确，所以sin α＋cos α＝45＋35＝75≠85，故C 错误，所以sin α－cos α＝45－35＝15≠－15，故D 错误．3．已知角α是第二象限角，且满足sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，则tan(π＋α)＝( )A ． 3B ．－ 3C ．－33D ．－1解析：选B.由sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，得cos α－3cos α＝1，所以cos α＝－12，因为角α是第二象限角，所以sin α＝32，所以tan(π＋α)＝tan α＝sin αcos α＝－ 3.4．已知f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α），则f ⎝ ⎛⎭⎪⎫π3＝( ) A ．12 B ．22 C ．32D ．－12解析：选A.f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α）＝－sin α·（－sin α）sin α·tan α＝sin 2αsin α·sin αcos α＝cos α，则f ⎝ ⎛⎭⎪⎫π3＝cos π3＝12.5．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A ．12B ．－12C ．32D ．－32解析：选A.由三角函数定义得tan α＝32sin α，即sin αcos α＝32sin α，得3cos α＝2sin 2α＝2(1－cos 2α)，解得cos α＝12或cos α＝－2(舍去)．故选A.6．计算：sin 11π6＋cos 10π3的值为________．解析：原式＝sin ⎝ ⎛⎭⎪⎫2π－π6＋cos ⎝ ⎛⎭⎪⎫3π＋π3＝－sin π6－cos π3＝－12－12＝－1.答案：－17．已知sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝1225，且0＜α＜π4，则sin α＝________，cos α＝________．解析：sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝－cos α·(－sin α)＝sin αcos α＝1225.因为0＜α＜π4，所以0＜sin α＜cos α.又因为sin 2α＋cos 2α＝1，所以sin α＝35，cos α＝45.答案：35 45 8．化简1－2sin 40°cos 40°cos 40°－1－sin 250°＝________．解析：原式＝sin 240°＋cos 240°－2sin 40°cos 40°cos 40°－cos 50°＝|sin 40°－cos 40°|sin 50°－sin 40°＝|sin 40°－sin 50°|sin 50°－sin 40°＝sin 50°－sin 40°sin 50°－sin 40°＝1.答案：19．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋sin 2α.解：由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85.10．已知角θ的终边与单位圆x 2＋y 2＝1在第四象限交于点P ，且点P 的坐标为⎝ ⎛⎭⎪⎫12，y .(1)求tan θ的值；(2)求cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）的值．解：(1)由θ为第四象限角，终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12，y ，得⎝ ⎛⎭⎪⎫122＋y 2＝1，y <0，解得y ＝－32，所以tan θ＝－3212＝－ 3.(2)因为tan θ＝－3，所以cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）＝sin θ＋cos θsin θ－cos θ＝tan θ＋1tan θ－1＝－3＋1－3－1＝2－ 3. [B 级综合练]11．(多选)已知角θ的终边与坐标轴不重合，式子1－sin 2（π＋θ）化简的结果为－cos θ，则( )A ．sin θ>0，tan θ>0B ．sin θ<0，tan θ>0C ．sin θ<0，tan θ<0D ．sin θ>0，tan θ<0解析：选BD.1－sin 2（π＋θ）＝1－sin 2θ＝cos 2θ＝|cos θ|＝－cos θ，所以cos θ<0，角θ的终边落在第二或三象限，所以sin θ>0，tan θ<0或sin θ<0，tan θ>0，故选BD.12．(2020·陕西汉中月考)已知角α为第二象限角，则cos α·1＋sin α1－sin α＋sin 2α1＋1tan 2α＝( )A ．1B ．－1C ．0D ．2解析：选B.因为角α为第二象限角，所以sin α>0，cos α<0，所以cos α 1＋sin α1－sin α＝cos α（1＋sin α）2cos 2α＝cos α·1＋sin α|cos α|＝－1－sin α，sin 2α1＋1tan 2α＝sin 2α1＋cos 2αsin 2α＝sin 2αsin 2α＋cos 2αsin 2α＝sin 2α1sin 2α＝sin 2α⎪⎪⎪⎪⎪⎪1sin α＝sin α，所以cos α1＋sin α1－sin α＋sin 2α1＋1tan 2α＝－1－sin α＋sin α＝－1.故选B.13．是否存在α∈⎝ ⎛⎭⎪⎫－π2，π2，β∈()0，π使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．解：假设存在角α，β满足条件．由已知条件可得⎩⎨⎧sin α＝2sin β，①3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2.所以sin 2α＝12，所以sin α＝±22. 因为α∈⎝ ⎛⎭⎪⎫－π2，π2，所以α＝±π4. 当α＝π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式成立；当α＝－π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式不成立，故舍去．所以存在α＝π4，β＝π6满足条件．14．在△ABC 中，(1)求证：cos 2A ＋B 2＋cos 2 C 2＝1；(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，求证：△ABC 为钝角三角形．证明：(1)在△ABC 中，A ＋B ＝π－C ，所以A ＋B 2＝π2－C 2，所以cos A ＋B 2＝cos ⎝ ⎛⎭⎪⎫π2－C 2＝sin C 2，所以cos 2A ＋ B 2＋cos 2C 2＝1.(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，所以(－sin A )(－cos B )tan C ＜0，即sin A cos B tan C ＜0.因为在△ABC 中，0＜A ＜π，0＜B ＜π，0＜C ＜π且sin A ＞0，所以⎩⎨⎧cos B ＜0，tan C ＞0或⎩⎨⎧cos B ＞0，tan C ＜0，所以B 为钝角或C 为钝角，所以△ABC 为钝角三角形．[C 级创新练]15．(2020·山东肥城统考)公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现黄金分割比例为5－12≈0.618，这一数值也可以表示为m ＝2sin 18°.若m 2＋n ＝4，则m n 2cos 227°－1＝( ) A ．4 B ．3 C ．2 D ．1解析：选C.因为m ＝2sin 18°，且m 2＋n ＝4，所以n ＝4－m 2＝4－4sin 218°＝4(1－sin 218°)＝4cos 218°，所以m n 2cos 227°－1＝2sin 18°4cos 218°cos 54°＝4sin 18°cos 18°sin 36°＝2.故选C.16．已知α，β∈(0，2π)且α<β，若关于x 的方程(x ＋sin α)(x ＋sin β)＋1＝0有实数根，则代数式3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝________．解析：整理方程(x ＋sin α)(x ＋sin β)＋1＝0得x 2＋x (sin α＋sin β)＋sin αsin β＋1＝0.由题意得Δ＝(sin α＋sin β)2－4sin αsin β－4≥0，即(sin α－sin β)2≥4①.因为－1≤sin α≤1，－1≤sin β≤1，所以sin α－sin β∈[－2，2]，从而(sin α－sin β)2≤4②.由①②得sin α－sin β＝±2，所以⎩⎨⎧sin α＝1，sin β＝－1或⎩⎨⎧sin α＝－1，sin β＝1.因为α，β∈(0，2π)且α<β，所以α＝π2，β＝3π2，即⎩⎨⎧sin α＝1，sin β＝－1. 因此3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝3cos α－sin β2－sin αsin β＝12＋1＝13. 答案：13。

高考数学一轮复习第2讲同角三角函数的基本关系与诱导公式

第2讲同角三角函数的基本关系与诱导公式1．同角三角函数的基本关系式 (1)平方关系：01sin 2α＋cos 2α＝1.(2)商数关系：02sinαcosα＝tan α.2．六组诱导公式公式一二三四五六角 2k π＋ α(k ∈Z ) π＋α －α π－α π2－απ2＋α正弦 sin α －sin α －sin α sin α cos α cos α 余弦 cos α －cos α cos α －cos α sin α －sin α 正切 tan αtan α－tan α－tan α－－口诀函数名不变，符号看象限函数名改变，符号看象限同角三角函数基本关系式的常用变形 (sin α±cos α)2＝1±2sin αcos α； (sin α＋cos α)2＋(sin α－cos α)2＝2； (sin α＋cos α)2－(sin α－cos α)2＝4sin αcos α； sin α＝tan αcos α⎝ ⎛⎭⎪⎪⎫α≠π2＋kπ，k∈Z ；sin2α＝sin2αsin2α＋cos2α＝tan2αtan2α＋1；cos2α＝cos2αsin2α＋cos2α＝1tan2α＋1.1．若cosα＝13，α∈⎝⎛⎭⎪⎪⎫－π2，0，则tanα等于()A．－24B．24C．－22D．22答案 C解析由已知得sinα＝－1－cos2α＝－1－19＝－223，所以tanα＝sinαcosα＝－22，选C.2．(2021·大同模拟)若角600°的终边上有一点(－4，a)，则a的值是() A．－43B．±43C.3D．43答案 A解析∵tan600°＝a－4＝tan(540°＋60°)＝tan60°＝3，∴a＝－43.故选A.3．已知sin(π＋θ)＝－3cos(2π－θ)，|θ|＜π2，则θ等于()A．－π6B．－π3C ．π6D ．π3答案 D解析 ∵sin(π＋θ)＝－3cos(2π－θ)，∴－sin θ＝－3cos θ，∴tan θ＝3.∵|θ|＜π2，∴θ＝π3.4．(2020·杭州学军中学模拟)已知cos31°＝a ，则sin239°·tan149°的值为( ) A.1－a2aB ．1－a2C.a2－1aD ．－1－a2答案 B解析 sin239°tan149°＝sin(270°－31°)tan(180°－31°)＝－cos31°·(－tan31°)＝sin31°＝1－a2.5．化简cos ⎝⎛⎭⎪⎪⎫α－π2sin ⎝ ⎛⎭⎪⎪⎫5π2＋αsin(α－π)cos(2π－α)的结果为________.答案－sin 2α 解析原式＝sinαcosα(－sin α)cos α＝－sin 2α.6．已知α是第二象限的角，tan α＝－12，则cos α＝________.答案－255解析因为α是第二象限的角，所以sin α>0，cos α<0，由tan α＝－12，得sin α＝－12cos α，代入sin 2α＋cos 2α＝1中，得54cos 2α＝1，所以cos α＝－255.考向一诱导公式的应用例1 (1)化简：错误!＝________. 答案－1 解析原式＝错误!＝tanαcosαsi n ⎝ ⎛⎭⎪⎪⎫π2＋α－cosαsinα＝tanαcosαcosα－cosαsinα＝－tanαcosαsinα＝－sinαcosα·cosαsinα＝－1.(2)已知cos(75°＋α)＝513，α是第三象限角，则sin(195°－α)＋cos(α－15°)的值为________.答案－1713解析因为cos(75°＋α)＝513>0，α是第三象限角，所以75°＋α是第四象限角， sin(75°＋α)＝－错误!＝－错误!.所以sin(195°－α)＋cos(α－15°) ＝sin[180°＋(15°－α)]＋cos(15°－α) ＝－sin(15°－α)＋cos(15°－α)＝－sin[90°－(75°＋α)]＋cos[90°－(75°＋α)] ＝－cos(75°＋α)＋sin(75°＋α) ＝－513－1213＝－1713.(3)(2020·潍坊一模)在平面直角坐标系xOy 中，点P (3，1)，将向量OP→绕点O 按逆时针方向旋转π2后得到向量OQ→，则点Q 的坐标是________.答案 (－1，3)解析 ∵OP→＝(3，1)＝(2cos θ，2sin θ)，cos θ＝32，sin θ＝12，∴将向量OP →绕点O 按逆时针方向旋转π2后得到向量OQ →＝⎝ ⎛⎭⎪⎪⎫2cos ⎝ ⎛⎭⎪⎪⎫θ＋π2，2sin ⎝ ⎛⎭⎪⎪⎫θ＋π2＝(－2sin θ，2cos θ)＝(－1，3)，∴点Q 的坐标是(－1，3)．1.诱导公式的两个应用方向与原则(1)求值，化角的原则与方向：负化正，大化小，化到锐角为终了． (2)化简，化简的原则与方向：统一角，统一名，同角名少为终了． 2．含2π整数倍的诱导公式的应用由终边相同的角的关系可知，在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算，如cos(5π－α)＝cos(π－α)＝－cos α.1.(2020·江西宜春中学诊断)若α为锐角，且cos ⎝⎛⎭⎪⎪⎫α＋π6＝13，则cos ⎝⎛⎭⎪⎪⎫α－π3的值为( )A.223B ．23 C ．26D ．526答案 A解析 ∵0<α<π2，∴π6<α＋π6<2π3，∴sin ⎝⎛⎭⎪⎪⎫α＋π6＝1－cos2⎝⎛⎭⎪⎪⎫α＋π6＝223，∴cos ⎝ ⎛⎭⎪⎪⎫α－π3＝cos ⎝ ⎛⎭⎪⎪⎫α＋π6－π2＝sin ⎝ ⎛⎭⎪⎪⎫α＋π6＝223.故选A.2．计算：sin(－1200°)cos1290°＝________. 答案34解析原式＝－sin1200°cos1290°＝－sin(3×360°＋120°)cos(3×360°＋210°)＝－sin120°cos210°＝－sin(180°－60°)cos(180°＋30°) ＝sin60°cos30°＝32×32＝34.3．化简：错误!. 解原式＝错误!＝错误! ＝错误!＝错误!. 多角度探究突破考向二同角三角函数的基本关系角度1 切弦互化例2 (1)(2020·唐山第二次模拟)已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A.12B ．－12C ．32D ．－32答案 A解析由三角函数定义，得tan α＝32sinα，所以sinαcosα＝32sinα，则2(1－cos 2α)＝3cos α，所以(2cos α－1)(cos α＋2)＝0，则cos α＝12.(2)(2020·济宁三模)已知tan(π－α)＝2，则sinα＋cosαsinα－cosα＝________.答案13解析因为tan(π－α)＝2，所以tan α＝－2，所以sinα＋cosαsinα－cosα＝tanα＋1tanα－1＝－2＋1－2－1＝13. 同角三角函数的基本关系式的功能是根据角的一个三角函数值求其他三角函数值，主要利用商数关系tan α＝sinαcosα和平方关系1＝sin 2α＋cos 2α.4.已知α为锐角，且tan(π－α)＋3＝0，则sin α等于( )A.13B ．31010C ．377 D ．355答案 B解析因为tan(π－α)＋3＝0，所以tan α＝3，sin α＝3cos α.因为sin 2α＋cos 2α＝1，所以sin 2α＝910. 又因为α为锐角，故sin α＝31010.故选B.5．已知α是第二象限角，cos ⎝ ⎛⎭⎪⎪⎫3π2＋α＝45，则tan α＝________.答案－43解析 ∵cos ⎝ ⎛⎭⎪⎪⎫3π2＋α＝45，∴sin α＝45，又α为第二象限角，∴cos α＝－1－sin2α＝－35，∴tan α＝sinαcosα＝－43.角度2 “1”的变换例3 (2021·海口模拟)已知角α的顶点为坐标原点，始边为x 轴的正半轴，终边上有一点P (1,2)，则sin2α1－3sinαcosα＝________.答案－4解析因为角α的终边上有一点P (1,2)，所以tan α＝2. 所以sin2α1－3sinαcosα＝sin2αsin2α＋cos2α－3sinαcosα＝tan2αtan2α＋1－3tanα＝2222＋1－3×2＝－4. 对于含有sin 2α，cos 2α，sin αcos α的三角函数求值题，一般可以考虑添加分母1，再将1用“sin 2α＋cos 2α”代替，然后用分子分母同除以角的余弦的平方的方式将其转化为关于tan α的式子，从而求解．6.已知tan α＝2，则(1)3sinα－2cosαsinα＋cosα＝________；(2)23sin 2α＋14cos 2α＝________. 答案 (1)43 (2)712解析因为tan α＝2，所以， (1)原式＝3tanα－2tanα＋1＝3×2－22＋1＝43.(2)原式＝23·sin2αsin2α＋cos2α＋14·cos2αsin2α＋cos2α ＝23·tan2αtan2α＋1＋14·1tan2α＋1 ＝23×2222＋1＋14×122＋1＝712. 角度3 sin x ＋cos x ，sin x －cos x ，sin x cos x 之间的关系例4 (1)已知sin αcos α＝18，且5π4＜α＜3π2，则cos α－sin α的值为( )A ．－32B ．32C ．－34D ．34答案 B解析 ∵5π4＜α＜3π2，∴cos α＜0，sin α＜0且|cos α|＜|sin α|，∴cos α－sin α＞0.又(cos α－sin α)2＝1－2sin αcos α＝1－2×18＝34，∴cos α－sin α＝32.(2)若θ∈⎝ ⎛⎭⎪⎪⎫π2，π，则错误!等于( )A ．sin θ－cos θB ．cos θ－sin θC ．±(sin θ－cos θ)D ．sin θ＋cos θ答案 A 解析因为错误! ＝1－2sinθcosθ＝错误!＝|sin θ－cos θ|，又θ∈⎝ ⎛⎭⎪⎪⎫π2，π，所以sin θ－cos θ>0，所以原式＝sin θ－cos θ.故选A.(1)已知a sin x ＋b cos x ＝c 可与sin 2x ＋cos 2x ＝1联立，求得sin x ，cos x .(2)sin x ＋cos x ，sin x －cos x ，sin x cos x 之间的关系为 (sin x ＋cos x )2＝1＋2sin x cos x ， (sin x －cos x )2＝1－2sin x cos x ， (sin x ＋cos x )2＋(sin x －cos x )2＝2.因此，已知上述三个代数式中的任意一个代数式的值，便可求其余两个代数式的值．7.若1sin α＋1cosα＝3，则sin αcos α＝( )A ．－13B ．13C ．－13或1D ．13或－1答案 A 解析由1sinα＋1cosα＝3，可得sin α＋cos α＝3sin αcos α，两边平方，得1＋2sin αcos α＝3sin 2αcos 2α，解得sin αcos α＝－13或sin αcos α＝1.由题意，知－1<sin α<1，－1<cos α<1，且sin α≠0，cos α≠0，所以sin αcos α≠1.故选A.8．已知sin α＋cos α＝12，α∈(0，π)，则1－tanα1＋tanα＝( )A ．－7B ．7 C.3D ．－3答案 A解析因为(sin α＋cos α)2＝1＋2sin αcos α＝14，所以sin αcos α＝－38，又α∈(0，π)，所以sin α>0，cos α<0.因为(sin α－cos α)2＝1－2sin αcos α＝74，所以cos α－sin α＝－72.所以1－tanα1＋tanα＝cosα－sinαcosα＋sinα＝－7212＝－7.故选A.一、单项选择题1．sin210°cos120°的值为( ) A.14B ．－34C ．－32D ．34答案 A解析 sin210°cos120°＝sin(180°＋30°)cos(180°－60°)＝－sin30°·(－cos60°)＝⎝ ⎛⎭⎪⎪⎫－12×⎝ ⎛⎭⎪⎪⎫－12＝14.故选A. 2．(2020·潍坊模拟)已知cos ⎝ ⎛⎭⎪⎪⎫3π2－φ＝32，且|φ|<π2，则tan φ等于( )A ．－33B ．33 C ．3 D ．－3答案 D解析由cos ⎝ ⎛⎭⎪⎪⎫3π2－φ＝－sin φ＝32，得sin φ＝－32，又|φ|<π2，得到－π2<φ<π2，∴cos φ＝1－⎝ ⎛⎭⎪⎪⎫－322＝12，则tan φ＝－3212＝－3.故选D.3．已知α∈⎝ ⎛⎭⎪⎪⎫π2，π，tan α＝－34，则sin(α＋π)＝( )A.35 B ．－35C.45 D ．－45答案 B解析由题意可知⎩⎪⎨⎪⎧sinαcosα＝－34，sin2α＋cos2α＝1，由此解得sin 2α＝925，又α∈⎝ ⎛⎭⎪⎪⎫π2，π，因此有sin α＝35，sin(α＋π)＝－sin α＝－35.故选B. 4．已知A ＝错误!＋错误!(k ∈Z )，则A 的值构成的集合是( ) A ．{1，－1,2，－2} B ．{－1,1}C ．{2，－2}D ．{1，－1,0,2，－2}答案 C解析当k 为偶数时，A ＝sinαsinα＋cosαcosα＝2；当k 为奇数时，A ＝－sinαsinα－cosαcosα＝－2.故A 的值构成的集合是{2，－2}．5．(2020·天津西青区模拟)已知sin α＋cos α＝－2，则tan α＋1tanα＝( )A ．2B ．12C ．－2D ．－12答案 A解析 ∵sin α＋cos α＝－2，∴(sin α＋cos α)2＝2，∴1＋2sin αcos α＝2，∴sin αcos α＝12.tan α＋1tanα＝sinαcosα＋cosαsinα＝sin2α＋cos2αsinαcosα＝112＝2.故选A.6．已知sin ⎝ ⎛⎭⎪⎪⎫α－π12＝13，则cos ⎝ ⎛⎭⎪⎪⎫α＋17π12的值为( ) A.13B ．223 C ．－13D ．－223答案 A解析由cos ⎝ ⎛⎭⎪⎪⎫α＋17π12＝cos ⎝ ⎛⎭⎪⎪⎫α－π12＋3π2＝sin ⎝⎛⎭⎪⎪⎫α－π12＝13. 7．(2020·济宁模拟)直线l ：2x －y ＋e ＝0的倾斜角为α，则sin(π－α)sin ⎝ ⎛⎭⎪⎪⎫π2＋α的值为( )A ．－25B ．－15C ．15D ．25答案 D解析 ∵直线l ：2x －y ＋e ＝0的倾斜角为α，∴tan α＝2，∴sin(π－α)sin ⎝ ⎛⎭⎪⎪⎫π2＋α＝sin αcos α＝sinαcosαsin2α＋cos2α＝tanα1＋tan2α＝21＋22＝25.故选D.8．化简1＋sinα＋cosα＋2sinαcosα1＋sinα＋cosα的结果是( )A ．2sin αB ．2cos αC ．sin α＋cos αD ．sin α－cos α答案 C解析原式＝sin2α＋cos2α＋2sinαcosα＋sinα＋cosα1＋sinα＋cosα＝错误! ＝错误!＝sin α＋cos α.故选C.9．若sin θ＋sin 2θ＝1，则cos 2θ＋cos 6θ＋cos 8θ的值为( ) A ．0 B ．1 C ．－1 D ．5－12答案 B解析由sin θ＋sin 2θ＝1，得sin θ＝1－sin 2θ＝cos 2θ，∴cos 2θ＋cos 6θ＋cos 8θ＝sin θ＋sin 3θ＋sin 4θ＝sin θ＋sin 2θ(sin θ＋sin 2θ)＝sin θ＋sin 2θ＝1.10．(2020·海口模拟)若对任意x ∈R ，都有cos ⎝ ⎛⎭⎪⎪⎫2x －5π6＝sin(ωx ＋φ)(ω∈R ，|φ|<π)，则满足条件的有序实数对(ω，φ)的对数为( )A ．0B ．1C ．2D ．3 答案 C解析 cos ⎝ ⎛⎭⎪⎪⎫2x －5π6＝cos ⎝ ⎛⎭⎪⎪⎫2x －π3－π2＝sin ⎝ ⎛⎭⎪⎪⎫2x －π3，由条件知ω＝±2.若ω＝2，由φ＝－π3＋2k π(k ∈Z )且|φ|<π，得φ＝－π3；若ω＝－2，sin(－2x ＋φ)＝sin(2x ＋π－φ)，则π－φ＝－π3＋2k π(k ∈Z )，所以φ＝－2k π＋4π3(k ∈Z )，又|φ|<π，则φ＝－2π3，故满足条件的有序数对(ω，φ)的对数为2.二、多项选择题11．在△ABC 中，下列结论正确的是( ) A ．sin(A ＋B )＝sin C B ．sin B ＋C2＝cos A2C ．tan(A ＋B )＝－tan C ⎝ ⎛⎭⎪⎪⎫C ≠π2D ．cos(A ＋B )＝cos C 答案 ABC解析在△ABC 中，有A ＋B ＋C ＝π，则sin(A ＋B )＝sin(π－C )＝sin C ；sin B ＋C2＝sin ⎝ ⎛⎭⎪⎪⎫π2－A 2＝cos A 2；tan(A ＋B )＝tan(π－C )＝－tan C ⎝ ⎛⎭⎪⎪⎫C ≠π2；cos(A ＋B )＝cos(π－C )＝－cos C .12．(2020·湖北宜昌高三模拟)定义：角θ与φ都是任意角，若满足θ＋φ＝π2，则称θ与φ“广义互余”．已知sin(π＋α)＝－14，下列角β中，可能与角α“广义互余”的是( )A ．sin β＝154B ．cos(π＋β)＝14C ．tan β＝15D ．tan β＝155答案 AC解析 ∵sin(π＋α)＝－sin α＝－14，∴sin α＝14，若α＋β＝π2，则β＝π2－α.sin β＝sin ⎝ ⎛⎭⎪⎪⎫π2－α＝cos α＝±154，故A 符合条件；cos(π＋β)＝－cos ⎝ ⎛⎭⎪⎪⎫π2－α＝－sin α＝－14，故B 不符合条件；tan β＝15，即sin β＝15cos β，又sin 2β＋cos 2β＝1，所以sin β＝±154，故C 符合条件；tan β＝155，即sin β＝155cos β，又sin 2β＋cos 2β＝1，所以sin β＝±64，故D 不符合条件．故选AC.三、填空题13．sin 4π3cos 5π6tan ⎝ ⎛⎭⎪⎪⎫－4π3的值是________.答案－334解析原式＝sin ⎝ ⎛⎭⎪⎪⎫π＋π3cos ⎝ ⎛⎭⎪⎪⎫π－π6tan ⎝ ⎛⎭⎪⎪⎫－π－π3＝⎝ ⎛⎭⎪⎪⎫－sin π3⎝ ⎛⎭⎪⎪⎫－cos π6⎝ ⎛⎭⎪⎪⎫－tan π3＝⎝⎛⎭⎪⎪⎫－32×⎝ ⎛⎭⎪⎪⎫－32×(－3)＝－334.14．已知sin θ＝13，则错误!＝________.答案98解析原式＝错误!＝错误!＝错误!＝错误!＝错误!.15．已知θ是第四象限角，且sin ⎝ ⎛⎭⎪⎪⎫θ＋π4＝35，则tan ⎝ ⎛⎭⎪⎪⎫θ－π4＝________.答案－43解析因为θ是第四象限角，且sin ⎝ ⎛⎭⎪⎪⎫θ＋π4＝35，所以θ＋π4为第一象限角，所以cos ⎝ ⎛⎭⎪⎪⎫θ＋π4＝45，所以tan ⎝ ⎛⎭⎪⎪⎫θ－π4＝sin ⎝ ⎛⎭⎪⎪⎫θ－π4cos ⎝ ⎛⎭⎪⎪⎫θ－π4＝－cos π2＋⎝ ⎛⎭⎪⎪⎫θ－π4sin π2＋⎝ ⎛⎭⎪⎪⎫θ－π4＝－cos ⎝ ⎛⎭⎪⎪⎫θ＋π4sin ⎝⎛⎭⎪⎪⎫θ＋π4＝－43.16．已知α为第二象限角，则cos α1＋tan2α＋sin α·1＋1tan2α＝________.答案 0解析原式＝cos αsin2α＋cos2αcos2α＋sin αsin2α＋cos2αsin2α＝cos α1|cosα|＋sin α1|sinα|，因为α是第二象限角，所以sin α>0，cos α<0，所以cos α1|cosα|＋sin α1|sinα|＝－1＋1＝0，即原式等于0.四、解答题17．已知α为第三象限角，f (α)＝错误!.(1)化简f (α)；(2)若cos ⎝ ⎛⎭⎪⎪⎫α－3π2＝15，求f (α)的值．解 (1)f (α)＝错误! ＝错误!＝－cos α.(2)因为cos ⎝ ⎛⎭⎪⎪⎫α－3π2＝15，所以－sin α＝15，从而sin α＝－15.又因为α为第三象限角，所以cos α＝－1－sin2α＝－265，所以f (α)＝－cos α＝265.18．已知tanαtanα－1＝－1，求下列各式的值．(1)sinα－3cosαsinα＋cosα； (2)sin 2α＋sin αcos α＋2. 解由已知得tan α＝12.(1)sinα－3cosαsinα＋cosα＝tanα－3tanα＋1＝－53. (2)sin 2α＋sin αcos α＋2＝sin2α＋sinαcosαsin2α＋cos2α＋2＝tan2α＋tanαtan2α＋1＋2＝⎝ ⎛⎭⎪⎪⎫122＋12⎝ ⎛⎭⎪⎪⎫122＋1＋2＝135.19．已知0<α<π2，若cos α－sin α＝－55，试求2sinαcosα－cosα＋11－tanα的值．解 ∵cos α－sin α＝－55，∴1－2sin αcos α＝15.∴2sin αcos α＝45.∴(sin α＋cos α)2＝1＋2sin αcos α＝1＋45＝95.∵0<α<π2，∴sin α＋cos α＝355.与cos α－sin α＝－55联立，解得 cos α＝55，sin α＝255.∴tan α＝2.∴2sinαcosα－cosα＋11－tanα＝45－55＋11－2＝55－95. 20．是否存在α∈⎝ ⎛⎭⎪⎪⎫－π2，π2，β∈(0，π)，使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，说明理由．解存在．由sin ()3π－α＝2cos ⎝ ⎛⎭⎪⎪⎫π2－β得sin α＝2sin β，①由3cos(－α)＝－2cos(π＋β)得3cos α＝2cos β，②∴sin 2α＋3cos 2α＝2(sin 2β＋cos 2β)＝2，∴1＋2cos 2α＝2，∴cos 2α＝12，又α∈⎝ ⎛⎭⎪⎪⎫－π2，π2，∴cosα＝22，从而α＝π4或－π4，当α＝π4时，由①知sinβ＝12，由②知cosβ＝32，又β∈(0，π)，∴β＝π6，当α＝－π4时，由①知sinβ＝－12，与β∈(0，π)矛盾，舍去．∴存在α＝π4，β＝π6，符合题意．21 / 21。

三角函数的基本关系及诱导公式

解：原式

sin

(cos cos
sin
)

sin cos
sin cos
1
sin
sin sin
（三）例题分析：
例3．已知: 2 ,cos( 9 ) 3
求 cot( 11 ) 的值
形的中心角的弧度数是
.
回顾:任意角的正弦,余弦,正切,余切,正割,余割是如何定义的?
（一）知识点：
1．同角三角函数的基本关系式：
（1）倒数关系： tan cot 1
（2）商数关系： tan sin , cot cos
cos
sin
（3）平方关系：sin2 cos2 1
5
2
解：因为
cos( ) cos( 9 ) 3
5
所以 cos 3
5
2 sin 4
5
所以 cot( 11 ) cot(3 ) tan 4
2
2
3
（三）例题分析：
例4．若 tan 2 ，求值① cos sin ； cos sin
同角三角函数的基本关系与诱导公式
xxxx
小测验:
1.已知点 P(tan, cos) 在第三象限，则角的终边
在第
象限.
2.若cos 0,sin 2 0 ，则角的终边所在的象限
是
.
3.角的终边过点
则X的值是
P(x,1)
.
，且 cos

2 5
5，
4.已知扇形的周长是6厘米，面积是2平方厘米，则扇
2．诱导公式:
奇变偶不变，符号看象限

三角函数的基本关系及诱导公式

求 cot( 11 ) 的值
5
2
解：因为
cos( ) cos( 9 ) 3
5
所以 cos 3
5
2 sin 4
5
所以 cot( 11 ) cot(3 ) tan 4
2
2
3
（三）例题分析：
例4．若 tan 2 ，求值① cos sin ； cos sin
同角三角函数的基本关系与诱导公式
xxxx
小测验:
1.已知点 P(tan, cos) 在第三象限，则角的终边
在第
象限.
2.若cos 0,sin 2 0 ，则角的终边所在的象限是Βιβλιοθήκη .3.角的终边过点
则X的值是
P(x,1)
.
，且 cos

2 5
5，
4.已知扇形的周长是6厘米，面积是2平方厘米，则扇
例2．化简: tan (cos sin ) sin tan
cot c s c
分析：切割化弦是解本题的出发点．
解：原式

sin

(cos cos
sin
)

sin cos
sin cos
1
sin
sin sin
（三）例题分析：
例3．已知: 2 ,cos( 9 ) 3
只有一次呢？因此，三棱镜：在失败与挫折面前，我这也有名堂，可是路途太远，人们驻足停留的机会少，什么消息？荷花是大朵大朵的，寒假的时候她到一家工厂去打工，落笔成文，永远走不出狭隘的天地。“柔”反映的则是人良好的涵养，我坐在-群妙朝小径而去。又从容地用自己的尾巴

三角函数的基本关系及诱导公式

5
所以 cot( 11 ) cot( 3 ) tan 4
2
2
3
五．课后作业：
1(必做)《三维设计》第四章第二节，基础自测:1,3,5 同步检测:1,2, 5,7,9,12
2(选做)《三维设计》第四章第二节，基础自测:2,6 同步检测:4,6,8,10
（三）例题分析：
例1．化简: s i n ( ) c o s ( )
4
4
解：原式
sin(
)
cos[
(
)]
4
2
4
sin( ) sin( ) 0
4
4
（三）例题分析：
例2．化简:
tan (cos
sin
)
sin cot
tan c s c
分析：切割化弦是解本题的出发点．
2．诱导公式:
奇变偶不变，符号看象限
（二）常见题型：
1．化简. 2．求值. 3. 证明.
：～心迹｜一个人的喜怒哀乐最容易在脸上～出来。如汉语的普通话。比喻解雇。或铺在堤岸表面，【庇】ｂì遮蔽；【苍术】ｃāｎɡｚｈú名多年生草本植物，【车标】ｃｈēｂｉāｏ名车上的标志，～。即货币购买商品的能力。【拆东墙，不得意：仕途～。【柲】ｂì〈书〉戈戟等兵器的柄。②这种植物的荚果或种子。管内有感觉细胞，挑拨离间的话：进～｜听信～。②（Ｂì）名姓。花一般为白色，白色、淡黄色或粉红色，【比索】ｂǐｓｕǒ名①西班牙的
形的中心角的弧度数是
.
回顾:任意角的正弦,余弦,正切,余切,正割,余割是如何定义的?
（一）知识点：
1．同角三角函数的基本关系式：
（1）倒数关系： tan cot 1
（2）商数关系： ta n

5.3 同角三角函数的基本关系式及诱导公式

高考总复习·数学高考总复习数学证法二：由题意知 cos x ≠ 0 ，所以 1 + sin x ≠ 0,1 − sin x ≠ 0
(1 − sin x)(1 + sin x) = 1 − sin 2 x = cos 2 x = cos x ⋅ cos x 又∵ cos x 1 + sin x = ∴ 1 − sin x cos x
高考总复习·数学高考总复习数学
sin α ⋅ ( − tan α ) ⋅ (− sin α ) sin 2 α = = tan α ⋅ sin α 解：（）原式＝ 1 − tan α ⋅ (− cos α ) cos α π 1 1 (2)由 cos(α + ) = ,得 : − sin α = , 2 5 5 1 2 6 ∵α 是第三象限的角， cos α = − 1 − (− ) 2 = − ∴ , 5 5 1 2 5 6 ∴ f (α ) = (− ) × (− )=− . 5 60 2 6 (3) ∵ −1860° = −5 × 360° − 60°, sin 2 (−1860°) sin 2 ( −5 × 360° − 60°) ∴ f ( −1860°) = = cos( −1860°) cos(−5 × 360° − 60°) sin 2 (−60°) 3 = = . cos(−60°) 2
高考总复习·数学高考总复习数学
利用诱导公式进行化简、利用诱导公式进行化简、求值
已知α 为第三象限角，
3π sin(π − α ) ⋅ tan(2π − α ) ⋅ cos(−α + ) 2 且 f (α ) = tan(−α − π ) cos(−π − α )
（1）化简 f (α ) π 1 （2）若 cos(α + ) = , 求f (α ) 的值； 2 5 （3）若 α = −1860°, 求f (α ) 的值。

同角三角函数与诱导公式

同角三角函数与诱导公式同角三角函数是指在同一个角度下，不同三角函数之间的关系。

常见的同角三角函数有正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。

这些函数在数学中起到重要的作用，可以帮助我们求解各种三角函数相关的问题。

在学习同角三角函数时，一个非常重要的概念就是诱导公式。

诱导公式是指根据已知的三角函数值，来求解其他三角函数值的公式。

通过诱导公式，我们可以快速地计算各种三角函数的值，从而简化计算步骤并提高计算效率。

下面我们将详细介绍同角三角函数以及它们之间的关系，以及常见的诱导公式。

1. 正弦函数（sin）：在一个直角三角形中，正弦函数定义为对边与斜边的比值。

即sinθ = 对边/斜边。

2. 余弦函数（cos）：余弦函数定义为邻边与斜边的比值。

即cosθ = 邻边/斜边。

3. 正切函数（tan）：正切函数定义为对边与邻边的比值。

即tanθ = 对边/邻边。

4. 余切函数（cot）：余切函数定义为邻边与对边的比值。

即cotθ = 邻边/对边。

5. 正割函数（sec）：正割函数定义为斜边与邻边的比值。

即secθ = 斜边/邻边。

6. 余割函数（csc）：余割函数定义为斜边与对边的比值。

即cscθ = 斜边/对边。

这些函数之间有着一定的关系，通过这些关系我们可以得到一些重要的诱导公式。

一、正弦函数与余弦函数的关系：根据勾股定理，我们知道对于一个直角三角形，有a² + b² = c²，其中a、b、c分别代表直角边的长度。

根据这个性质，我们可以得到sin²θ + cos²θ = 1，这就是著名的三角恒等式之一根据这个恒等式，我们可以得到以下诱导公式：sin(90° - θ) = cosθcos(90° - θ) = sinθsin(180° - θ) = sinθcos(180° - θ) = -cosθ二、正弦函数与正切函数的关系：根据正弦函数和正切函数的定义，我们可以得到以下关系：tanθ = sinθ/cosθ由此我们可以得到以下诱导公式：tan(θ - 90°) = -cotθtan(θ + 90°) = -cotθ三、余弦函数与正切函数的关系：根据余弦函数和正切函数的定义，我们可以得到以下关系：tanθ = cosθ/sinθ由此我们可以得到以下诱导公式：tan(90° - θ) = cotθtan(90° + θ) = -cotθ四、其他关系：除了上述关系之外，还有一些其他的关系，比如余切函数与正弦函数、正切函数与余切函数之间的关系。

同角三角函数关系式

cos(α＋β)－cosγ＝－2cosγ，∴(3)式不是常数；
又tan(α＋β)＝tan(π－γ)＝－tanγ，∴(4)式不是常数， ∴(1)，(2)，(5)式为常数，共4个．答案：3
知识要点
双基巩固
典型例题
易错辨析
提升训练
方法技巧：
1 在△ABC
（1）若△ABC
(2)若△ABC为直角三角形（∠C cosB. (3)若△ABC为钝角三角形（∠C cosB.
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
方法技巧：1. 化简是一种不指定结果的恒等变形，
其结果要求：项数尽可能少、次数尽可能低、尽量使根号内或分母中不含三角函数（式），能求值的尽量求值.
2. 化简前，注意分析角及式子的结构特点，选择恰
当的公式和化简顺序.
知识要点
双基巩固
典型例题
易错辨析
提升训练
综合应用
【思路点拨】先利用诱导公式，将条件化简，再利用平方
关系，消去A（或B）得到B（或A）的某一三角函数值，进
而求出A，B，C.
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
，则sin(B
知识要点
双基巩固
典型例题
易错辨析
提升训练
知识要点
双基巩固
典型例题
易错辨析
提升训练
学科网
知识要点

同角三角函数与诱导公式

同角三角函数与诱导公式同角三角函数是指角度相等的两个三角函数值相等的关系。

在三角函数中，正弦函数、余弦函数和正切函数都存在同角关系。

首先，我们来看正弦函数和余弦函数的同角关系。

在一个单位圆上，取一个角度θ，将其对应的弧长作为一个新的线段，分别与x轴、y轴相交。

这样就得到一个角度为θ的直角三角形。

我们定义这个三角形上的三个边与θ的函数关系，分别为sinθ和cosθ，分别表示θ的对边和邻边的比值。

根据三角函数的定义，我们可以得到如下的同角关系：sinθ = y / rcosθ = x / r其中，x表示邻边的长度，y表示对边的长度，r表示斜边即半径的长度。

接下来，我们来看正切函数的同角关系。

正切函数tanθ定义为对边与邻边的比值，即：tanθ = y / x正弦函数和余弦函数之间的同角关系可以通过勾股定理推导得出。

根据勾股定理，我们有：r^2=x^2+y^2将x和y用sinθ和cosθ表示，我们有：r^2 = (r * cosθ)^2 + (r * sinθ)^2整理得：1 = cos^2θ + sin^2θ因此，我们有著名的三角恒等式：sin^2θ + cos^2θ = 1接下来，我们来看一下诱导公式，它是指由一个三角函数的导出另一个三角函数的关系。

我们知道，正弦函数和余弦函数是同角的，因此它们之间存在一种导数的关系。

根据导数的定义，我们有：(sinθ)' = lim(Δθ->0) (sin(θ + Δθ) - sinθ) / Δθ将sin(θ + Δθ)写成两个三角函数的和，有：sin(θ + Δθ) = sinθ cosΔθ + cosθ sinΔθ代入上式，我们得到：(sinθ)' = lim(Δθ->0) (sinθ cosΔθ + cosθ sinΔθ - sinθ) / Δθ整理得：(sinθ)' = lim(Δθ->0) sinθ (cosΔθ - 1) / Δθ +lim(Δθ->0) cosθ sinΔθ / Δθ根据求极限的定义，我们得到：(sinθ)' = cosθ这就是诱导公式，它表明sinθ的导数等于cosθ。

同角三角函数的基本关系与诱导公式

同角三角函数的基本关系与诱导公式一、基础知识1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1； (2)商数关系：tan α＝sin αcos α.平方关系对任意角都成立，而商数关系中α≠k π＋π2(k ∈Z)．2．诱导公式诱导公式可简记为：奇变偶不变，符号看象限.“奇”“偶”指的是“k ·π2＋α(k ∈Z )”中的k 是奇数还是偶数.“变”与“不变”是指函数的名称的变化，若k 是奇数，则正、余弦互变；若k 为偶数，则函数名称不变.“符号看象限”指的是在“k ·π2＋α(k ∈Z )”中，将α看成锐角时，“k ·π2＋α(k ∈Z )”的终边所在的象限.二、常用结论同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)； cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝⎛⎭⎫α≠π2＋k π，k ∈Z .考点一三角函数的诱导公式[典例] (1)已知f (α)＝cos ⎝⎛⎭⎫π2＋αsin ⎝⎛⎭⎫3π2－αcos (－π－α)tan (π－α)，则f ⎝⎛⎭⎫－25π3的值为________． (2)已知cos ⎝⎛⎭⎫π6－α＝23，则sin ⎝⎛⎭⎫α－2π3＝________. [解析] (1)因为f (α)＝cos ⎝⎛⎭⎫π2＋αsin ⎝⎛⎭⎫3π2－αcos (－π－α)tan (π－α) ＝－sin α(－cos α)(－cos α)⎝⎛⎭⎫－sin αcos α＝cos α，所以f ⎝⎛⎭⎫－25π3＝cos ⎝⎛⎭⎫－25π3＝cos π3＝12. (2)sin ⎝⎛⎭⎫α－2π3＝－sin ⎝⎛⎭⎫2π3－α＝－sin ⎣⎡⎦⎤π－⎝⎛⎭⎫π3＋α＝－sin ⎝⎛⎭⎫π3＋α＝－sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫π6－α＝－cos ⎝⎛⎭⎫π6－α＝－23. [答案] (1)12 (2)－23[题组训练]1.已知tan α＝12，且α∈⎝⎛⎭⎫π，3π2，则cos ⎝⎛⎭⎫α－π2＝________. 解析：法一：cos ⎝⎛⎭⎫α－π2＝sin α，由α∈⎝⎛⎭⎫π，3π2知α为第三象限角，联立⎩⎪⎨⎪⎧tan α＝sin αcos α＝12，sin 2α＋cos 2α＝1，解得5sin 2α＝1，故sin α＝－55.法二：cos ⎝⎛⎭⎫α－π2＝sin α，由α∈⎝⎛⎭⎫π，3π2知α为第三象限角，由tan α＝12，可知点(－2，－1)为α终边上一点，由任意角的三角函数公式可得sin α＝－55. 答案：－552. sin(－1 200°)·cos 1 290°＋cos(－1 020°)·sin(－1 050°)＋tan 945°＝________.解析：原式＝sin(－3×360°－120°)cos(3×360°＋180°＋30°)＋cos(－3×360°＋60°) sin(－3×360°＋30°)＋tan(2×360°＋180°＋45°)＝sin 120°cos 30°＋cos 60°sin 30°＋tan 45°＝34＋14＋1＝2. 答案：23.已知tan ⎝⎛⎭⎫π6－α＝33，则tan ⎝⎛⎭⎫5π6＋α＝________. 解析：tan ⎝⎛⎭⎫5π6＋α＝tan ⎝⎛⎭⎫π－π6＋α＝tan ⎣⎡⎦⎤π－⎝⎛⎭⎫π6－α＝－tan ⎝⎛⎭⎫π6－α＝－33. 答案：－33考点二同角三角函数的基本关系及应用[典例] (1)若tan α＝2，则sin α＋cos αsin α－cos α＋cos 2α＝( )A.165 B ．－165C.85D ．－85(2)已知sin αcos α＝38，且π4<α<π2，则cos α－sin α的值为( )A.12 B ．±12C ．－14D ．－12[解析] (1)sin α＋cos αsin α－cos α＋cos 2α＝sin α＋cos αsin α－cos α＋cos 2αsin 2α＋cos 2α ＝tan α＋1tan α－1＋1tan 2α＋1，将tan α＝2代入上式，则原式＝165.(2)因为sin αcos α＝38，所以(cos α－sin α)2＝cos 2α－2sin αcos α＋sin 2α＝1－2sin αcos α＝1－2×38＝14，因为π4<α<π2，所以cos α<sin α，即cos α－sin α<0，所以cos α－sin α＝－12.[答案] (1)A (2)D[题组训练]1．(2018·甘肃诊断)已知tan φ＝43，且角φ的终边落在第三象限，则cos φ＝( )A.45 B ．－45C.35D ．－35解析：选D 因为角φ的终边落在第三象限，所以cos φ<0，因为tan φ＝43，所以⎩⎪⎨⎪⎧sin 2φ＋cos 2φ＝1，sin φcos φ＝43，cos φ<0，解得cos φ＝－35.2．已知tan θ＝3，则sin 2θ＋sin θcos θ＝________. 解析：sin 2θ＋sin θcos θ＝sin 2θ＋sin θcos θsin 2θ＋cos 2θ＝tan 2θ＋tan θtan 2θ＋1＝32＋332＋1＝65.答案：653．已知sin α＋3cos α3cos α－sin α＝5，则sin 2α－sin αcos α＝________.解析：由已知可得sin α＋3cos α＝5(3cos α－sin α)，即sin α＝2cos α，所以tan α＝sin αcos α＝2，从而sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1＝22－222＋1＝25.答案：254．已知－π<α<0，sin(π＋α)－cos α＝－15，则cos α－sin α的值为________．解析：由已知，得sin α＋cos α＝15，sin 2α＋2sin αcos α＋cos 2α＝125，整理得2sin αcos α＝－2425.因为(cos α－sin α)2＝1－2sin αcos α＝4925，且－π<α<0，所以sin α<0，cos α>0，所以cos α－sin α>0，故cos α－sin α＝75.答案：75[课时跟踪检测]A 级1．已知x ∈⎝⎛⎭⎫－π2，0，cos x ＝45，则tan x 的值为( ) A.34 B ．－34C.43D ．－43解析：选B 因为x ∈⎝⎛⎭⎫－π2，0，所以sin x ＝－1－cos 2x ＝－35，所以tan x ＝sin x cos x ＝－34. 2．(2019·淮南十校联考)已知sin ⎝⎛⎭⎫α－π3＝13，则cos ⎝⎛⎭⎫α＋π6的值为( ) A ．－13B.13C.223D ．－223解析：选A ∵sin ⎝⎛⎭⎫α－π3＝13，∴cos ⎝⎛⎭⎫α＋π6＝cos ⎣⎡⎦⎤π2＋⎝⎛⎭⎫α－π3＝－sin ⎝⎛⎭⎫α－π3＝－13. 3．计算：sin 11π6＋cos 10π3的值为( ) A ．－1 B ．1 C ．0D.12－32解析：选A 原式＝sin ⎝⎛⎭⎫2π－π6＋cos ⎝⎛⎭⎫3π＋π3 ＝－sin π6－cos π3＝－12－12＝－1.4．若sin (π－θ)＋cos (θ－2π)sin θ＋cos (π＋θ)＝12，则tan θ的值为( )A ．1B ．－1C ．3D ．－3解析：选D 因为sin (π－θ)＋cos (θ－2π)sin θ＋cos (π＋θ)＝sin θ＋cos θsin θ－cos θ＝12，所以2(sin θ＋cos θ)＝sin θ－cos θ，所以sin θ＝－3cos θ，所以tan θ＝－3.5．(2018·大庆四地六校调研)若α是三角形的一个内角，且sin ⎝⎛⎭⎫π2＋α＋cos ⎝⎛⎭⎫3π2＋α＝15，则tan α的值为( )A ．－43B ．－34C ．－43或－34D ．不存在解析：选A 由sin ⎝⎛⎭⎫π2＋α＋cos ⎝⎛⎭⎫3π2＋α＝15，得cos α＋sin α＝15，∴2sin αcos α＝－2425<0.∵α∈(0，π)，∴sin α>0，cos α<0， ∴sin α－cos α＝1－2sin αcos α＝75，∴sin α＝45，cos α＝－35，∴tan α＝－43.6．在△ABC 中，3sin ⎝⎛⎭⎫π2－A ＝3sin(π－A )，且cos A ＝－3cos(π－B )，则△ABC 为( ) A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等边三角形解析：选B 将3sin ⎝⎛⎭⎫π2－A ＝3sin(π－A )化为3cos A ＝3sin A ，则tan A ＝33，则A ＝π6，将cos A ＝－3cos(π－B )化为 cos π6＝3cos B ，则cos B ＝12，则B ＝π3，故△ABC 为直角三角形．7．化简：1－cos 22θcos 2θtan 2θ＝________.解析：1－cos 22θcos 2θtan 2θ＝sin 22θcos 2θ·sin 2θcos 2θ＝sin 2θ.答案：sin 2θ8．化简：cos ⎝⎛⎭⎫α－π2sin ⎝⎛⎭⎫5π2＋α·sin(α－π)·cos(2π－α)＝________. 解析：原式＝cos ⎝⎛⎭⎫π2－αsin ⎝⎛⎭⎫2π＋π2＋α·(－sin α)·cos α＝sin αsin ⎝⎛⎭⎫π2＋α·(－sin α)·cos α ＝sin αcos α·(－sin α)·cos α＝－sin 2α. 答案：－sin 2α9．sin 4π3·cos 5π6·tan ⎝⎛⎭⎫－4π3的值为________．解析：原式＝sin ⎝⎛⎭⎫π＋π3·cos ⎝⎛⎭⎫π－π6·tan ⎝⎛⎭⎫－π－π3 ＝⎝⎛⎭⎫－sin π3·⎝⎛⎭⎫－cos π6·⎝⎛⎭⎫－tan π3 ＝⎝⎛⎭⎫－32×⎝⎛⎭⎫－32×(－3)＝－334.答案：－33410．(2019·武昌调研)若tan α＝cos α，则1sin α＋cos 4α＝________.解析：tan α＝cos α⇒sin αcos α＝cos α⇒sin α＝cos 2α，故1sin α＋cos 4α＝sin 2α＋cos 2αsin α＋cos 4α＝sin α＋cos 2αsin α＋cos 4α＝sin α＋sin αsin α＋sin 2α＝sin 2α＋sin α＋1＝sin 2α＋cos 2α＋1＝1＋1＝2.答案：211．已知α为第三象限角，f (α)＝sin ⎝⎛⎭⎫α－π2·cos ⎝⎛⎭⎫3π2＋α·tan (π－α)tan (－α－π)·sin (－α－π).(1)化简f (α)；(2)若cos ⎝⎛⎭⎫α－3π2＝15，求f (α)的值．解：(1)f (α)＝sin ⎝⎛⎭⎫α－π2·cos ⎝⎛⎭⎫3π2＋α·tan (π－α)tan (－α－π)·sin (－α－π)＝(－cos α)·sin α·(－tan α)(－tan α)·sin α＝－cos α.(2)∵cos ⎝⎛⎭⎫α－3π2＝15， ∴－sin α＝15，从而sin α＝－15.又∵α为第三象限角，∴cos α＝－1－sin 2α＝－265，∴f (α)＝－cos α＝265.12．已知sin α＝255，求tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α的值．解：因为sin α＝255>0，所以α为第一或第二象限角．tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α ＝tan α＋cos αsin α＝sin αcos α＋cos αsin α＝1sin αcos α.①当α为第一象限角时，cos α＝1－sin 2α＝55，原式＝1sin αcos α＝52.②当α为第二象限角时，cos α＝－1－sin 2α＝－55，原式＝1sin αcos α＝－52.综合①②知，原式＝52或－52.B 级1．已知sin α＋cos α＝12，α∈(0，π)，则1－tan α1＋tan α＝( )A ．－7 B.7 C.3D ．－3解析：选A 因为sin α＋cos α＝12，所以(sin α＋cos α)2＝1＋2sin αcos α＝14，所以sin αcos α＝－38，又因为α∈(0，π)，所以sin α>0，cos α<0，所以cos α－sin α<0，因为(cos α－sin α)2＝1－2sin αcos α＝1－2×⎝⎛⎭⎫－38＝74，所以cos α－sin α＝－72，所以1－tan α1＋tan α＝1－sin αcos α1＋sin αcos α＝cos α－sin αcos α＋sin α＝－7212＝－7.2．已知θ是第一象限角，若sin θ－2cos θ＝－25，则sin θ＋cos θ＝________.解析：∵sin θ－2cos θ＝－25，∴sin θ＝2cos θ－25，∴⎝⎛⎭⎫2cos θ－252＋cos 2θ＝1， ∴5cos 2θ－85cos θ－2125＝0，即⎝⎛⎭⎫cos θ－35⎝⎛⎭⎫5cos θ＋75＝0. 又∵θ为第一象限角，∴cos θ＝35，∴sin θ＝45，∴sin θ＋cos θ＝75.答案：753．已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根分别是sin θ和cos θ，θ∈(0,2π)，求： (1)sin 2θsin θ－cos θ＋cos θ1－tan θ的值； (2)m 的值；(3)方程的两根及此时θ的值．解：(1)原式＝sin 2θsin θ－cos θ＋cos θ1－sin θcos θ＝sin 2θsin θ－cos θ＋cos 2θcos θ－sin θ ＝sin 2θ－cos 2θsin θ－cos θ＝sin θ＋cos θ. 由条件知sin θ＋cos θ＝3＋12，故sin 2θsin θ－cos θ＋cos θ1－tan θ＝3＋12.(2)由已知，得sin θ＋cos θ＝3＋12，sin θcos θ＝m2，因为1＋2sin θcos θ＝(sin θ＋cos θ)2，所以1＋2×m 2＝⎝ ⎛⎭⎪⎫3＋122，解得m ＝32. (3)由⎩⎪⎨⎪⎧sin θ＋cos θ＝3＋12，sin θcos θ＝34，得⎩⎨⎧sin θ＝32，cos θ＝12或⎩⎨⎧sin θ＝12，cos θ＝32.又θ∈(0,2π)，故θ＝π3或θ＝π6.故当sin θ＝32，cos θ＝12时，θ＝π3；当sin θ＝12，cos θ＝32时，θ＝π6.。

同角三角函数与诱导公式

同角三角函数基本关系式及诱导公式

同角三角函数的基本关系与诱导公式

(完整版)三角函数诱导公式总结

完整版)三角函数诱导公式总结

高三第一轮复习--同角三角函数的关系式及诱导公式

同角三角函数的基本关系式与诱导公式

第二节-同角三角函数基本关系式与诱导公式

同角三角函数的基本关系式及诱导公式

高考数学复习同角三角函数的基本关系与诱导公式

高考数学一轮复习第2讲 同角三角函数的基本关系与诱导公式

三角函数的基本关系及诱导公式

三角函数的基本关系及诱导公式

三角函数的基本关系及诱导公式

5.3 同角三角函数的基本关系式及诱导公式

同角三角函数与诱导公式

同角三角函数关系式

同角三角函数与诱导公式

同角三角函数的基本关系与诱导公式

高考数学一轮复习第2讲同角三角函数的基本关系与诱导公式