八年级(上)第一章《平行线》单元测试(三)
题目:《平行线》单元测试题(含答案)

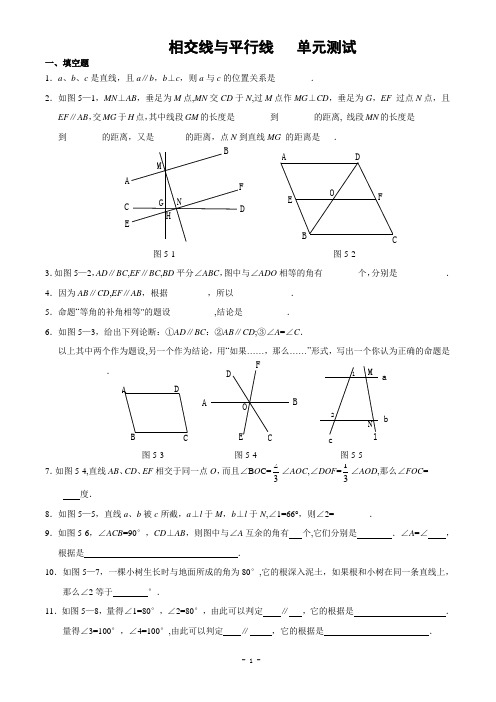
题目:《平行线》单元测试题(含答案)平行线单元测试题(含答案)第一部分:选择题(每小题2分,共20分)1. 下列选项中,哪个是平行线的性质?- A. 两条平行线之间的距离恒定- B. 两条平行线不会相交- C. 两条平行线的斜率相等- D. 两条平行线的夹角为90度2. 已知两条直线L和M是平行线,且L与M之间的距离为5cm。
如果将直线L向上平移2cm,那么L和M之间的距离将变为多少?- A. 3cm- B. 5cm- C. 7cm- D. 10cm3. 在平面直角坐标系中,过点(2,3)和(5,7)的直线与x轴的交点为:- A. (2,0)- B. (3,0)- C. (5,0)- D. (7,0)4. 两条平行线的斜率分别为2和-3,那么这两条直线的夹角为:- A. 30度- B. 45度- C. 60度- D. 90度5. 在平面直角坐标系中,过点(-3,4)和(5,-2)的直线的斜率为:- A. -2- B. -1/2- C. -1- D. 26. 在某个平面上,直线L的斜率为3,直线M的斜率为1/3。
如果L与M相互垂直,那么L和M的斜率乘积为多少?- A. -1- B. 0- C. 1- D. 37. 已知直线L的斜率为2,且它在平面上与y轴相交于点(0,4),那么直线L的方程式为:- A. y = 2x + 4- B. y = 2x - 4- C. y = 4x + 2- D. y = -4x + 28. 两条平行线L和M的斜率分别为1/2和2/3,它们之间的夹角为:- A. 20度- B. 30度- C. 40度- D. 50度9. 已知直线L和M是平行线,且直线L的斜率为2。
如果直线L过点(3,5),那么直线M的方程式为:- A. y = 2x - 7- B. y = 2x + 7- C. y = -2x - 1- D. y = -2x + 110. 若两条平行线的斜率分别为a和2a,且a不等于0,那么这两条直线的夹角为:- A. 30度- B. 45度- C. 60度- D. 90度第二部分:简答题(每小题5分,共20分)1. 简述平行线的性质。
八年级物理上册第一章第三节《运动的快慢》单元测试题新人教版 (1143)

八年级物理上册第一章《运动的快慢》测试卷
学校:__________ 姓名:__________ 班级:__________ 考号:__________
题号 一
二
三
四 总分
得分
评卷人 得分
一、选择题
1.(2 分)汽车在平直公路上匀速行驶,在如图所示的四个图象中,能正确表示汽车速度与 时间关系的图象是............................................................................................................. ( )
29.s=100m+50m=150m
t=vs=155m0/ms =30s
30.解:t=t1+t2=vs11+vs22=7144k8mkm/h+110408kkmm/h=3.48h ⑵v=st=239.64k8mh =8.05km/h
23.(3 分)甲、乙、丙三辆小车同时、同地向同一方向运动,它们运动的图像如图所示,由 图像可知:运动速度相同的小车是 和 ;经过 5s,跑在最前面的小车是 。
评卷人 得分
三、实验探究
24.(5 分)(6 分)“频闪摄影”是研究物体运动时常用的一种实验方法。
(1)物体在 BD 间的平均速度为 (2)相邻两段时间内的路程差为
D 评卷人
得分
二、填空题
11.60 360 12.6;21.6 13.(3 分)小于(1 分);小于(2 分)
14.510 850
15.3.81×108
16.是 1513.38
17.60.0020s/t0.9
18.7
19.快慢 20 12
(完整版)《相交线与平行线》单元测试卷含答案

第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1.如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D.对顶角2.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD的度数为()A.40°B.35°C.50°D.45°1 2 33.如图,AB∥EC,下列说法不正确的是()A. ∠B=∠ECDB. ∠A=∠ECDC. ∠B+∠ECB=180°D. ∠A+∠B+∠ACB=180°4.如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整的图案,最终所有图案消失,则对小方块进行的操作为()A.向右平移1格再向下B.向右平移3格再向下C.向右平移2格再向下D.以上答案均可5.如图所示,3块相同的三角尺拼成一个图形,图中有很多对平行线,其中不能由下面的根据得出两直线平行的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.平行于同一直线的两直线平行D.垂直于同一直线的两直线平行6.如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是()A.40°B.70°C.80°D.140°7.同一平面内的四条互不重合的直线满足a⊥b,b⊥c,c⊥d,则下列各选项中关系能成立的是()A.a∥dB.a⊥cC.a⊥dD.b⊥d8.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120 °B.130°C.140°D.150°9.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为()A.30°B.60°C.80°D.120°10.如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是()6 8 9 10二、填空题(每题3分,共21分)11.如图所示,某地一条小河的两岸都是直的,小明和小亮分别在河的两岸,他们拉紧了一根细绳,当测出∠1和∠2满足关系________时,河岸的两边才是平行的.12.同一个平面内的三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=________.13.在测量跳远成绩时,从落地点到起跳线所拉的皮尺应当与起跳线________.14.如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A'B'C'的位置时,B'C=3 cm,则三角形ABC平移的距离为cm.11 14 1515.如图是我们常用的折叠式小刀,刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是度.16.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=°.17.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是第1个图案经过平移而得,那么第2015个图案中有白色六边形地面砖块.三、解答题(22~24题每题9分,其余每题8分,共59分)18.如图,在一条公路l的两侧有A,B两个村庄.(1)现在镇政府为民服务,沿公路开通公共汽车,同时修建A,B两个村庄到公路的道路,要使两个村庄村民乘车最为方便,请你设计道路路线,在图中画出(标明①),并标出公共汽车停靠点的位置,说出你这样设计的理由;(2)为方便两村物流互通,A,B两村计划合资修建一条由A村到达B村的道路,要使两个村庄物流、通行最为方便,请你设计道路路线,在图中画出(标明②),说出你这样设计的理由.19.如图所示,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.20.如图,CD⊥AB,EF⊥AB,∠E=∠EMC,说明:CD是∠ACB的平分线.21.如图,已知点A,O,B在同一直线上,OC是从点O出发的任意一条射线,OD是∠AOC的平分线,OE是∠COB的平分线,试确定OD和OE的位置关系,并说明理由.22.如图,∠E=∠3,∠1=∠2,试说明:∠4+∠BAP =180°.23.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时,入射光线与平面镜的夹角等于反射光线与平面镜的夹角(∠1=∠2,∠3=∠4).请说明为什么进入潜望镜的光线和离开潜望镜的光线是平行的.24.如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①②③④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(1)当动点P落在第①部分时,如图①,试说明:∠APB=∠PAC+∠PBD;(2)当动点P落在第②部分时,如图②,∠APB=∠PAC+∠PBD是否成立?若不成立,请说明理由.参考答案一、1.【答案】B 2.【答案】C3.【答案】B解:根据两直线平行,同位角相等,得出A正确;根据两直线平行,同旁内角互补,得出C正确;根据两直线平行,内错角相等,得出∠A=∠ACE,而∠ACE+∠B+∠ACB=180°,则∠A+∠B+∠ACB=180°.得出D正确.故选B.4.【答案】C5.【答案】C6.【答案】B7.【答案】C8.【答案】C9.【答案】A10.【答案】B二、11.【答案】∠1=∠212.【答案】4解:a=3,b=1.13.【答案】垂直14.【答案】215.【答案】9016.【答案】14017.【答案】8062三、18.解:(1)画图如图,P,Q即为公共汽车停靠点的位置垂线段最短;(2)画图如图,两点之间,线段最短.19.解:因为AB∥CD,所以∠ECD=∠A=37°,又因为DE⊥AE,所以∠CED=90°,所以∠D=180°-90°-37°=53°.20.解:因为CD⊥AB,EF⊥AB,所以CD∥EF(垂直于同一直线的两直线平行).相等),又因为∠E=∠EMC,所以∠BCD=∠ACD(等量代换).所以CD是∠ACB的平分线(角平分线定义).21.解:OD和OE互相垂直,即OD⊥OE.理由如下:因为点A,O,B在同一直线上,所以∠AOB=180°.又因为OD是∠AOC的平分线,OE是∠COB的平分线,所以∠DOC=∠AOC,∠COE=∠COB.所以∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB=×180°=90°,所以OD⊥OE.22.解:因为∠ENM=∠3(对顶角相等),∠E=∠3(已知),所以∠ENM=∠E(等量代换),所以AE∥HM(内错角相等,两直线平行).所以∠EAM=∠AMH(两直线平行,内错角相等).又因为∠1=∠2,所以∠EAM+∠1=∠AMH+∠2(等式性质),即∠BAM=∠AMC.所以AB∥CD(内错角相等,两直线平行).所以∠AMD+∠BAP=180°(两直线平行,同旁内角互补).因为∠4=∠AMD(对顶角相等),所以∠4+∠BAP=180°(等量代换).23.解:根据题意,作出如图所示的几何图形,已知:AB∥CD,∠1=∠2,∠3=∠4.试说明:EF∥GH.说明过程:因为AB∥CD(已知),所以∠2=∠3(两直线平行,内错角相等).又因为∠1=∠2,∠3=∠4,所以∠1=∠2=∠3=∠4.因为∠5=180°-(∠1+∠2),∠6=180°-(∠3+∠4),所以∠5=∠6,所以EF∥GH(内错角相等,两直线平行).即进入潜望镜的光线和离开潜望镜的光线是平行的.24.解:(1)如图①:过点P作MP∥AC,则MP∥BD,因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,①②(2)不成立.理由如下:如图②,过点P作MP∥AC,则MP∥BD, 因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,即:360°-∠APB=∠PAC+∠PBD.所以∠APB=∠PAC+∠PBD不成立.。
浙教版八年级上册数学第1章单元测试卷

浙教版八年级上册数学第1章单元测试卷第一章测试卷一、选择题(每题3分,共30分)1.如图,∠ACD = 120°,∠B = 20°,则∠A的度数是(。
)。
A。
120° B。
90° C。
100° D。
30°2.下列各组数分别是三根小木棒的长度,将它们首尾相连能摆成三角形的是()。
A。
3 cm,4 cm,8 cm B。
4 cm,4 cm,8 cm C。
5 cm,6 cm,8 cm D。
5 cm,5 cm,12 cm3.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A'O'B' = ∠AOB的依据是()。
A。
SSS B。
SAS C。
ASA D。
AAS4.如图,△ABC ≌△A'B'C',则∠C的度数是(。
)。
A。
56° B。
51° C。
107° D。
73°5.如图,在△ABC中,边AB的垂直平分线交BC于点D,连结AD。
若AB = 7,BC = 8,AC = 5,则△ADC的周长为()。
A。
12 B。
13 C。
15 D。
166.下列命题是假命题的是()。
A。
如果a∥b,b∥c,那么a∥cB。
锐角三角形中最大的角一定大于或等于60°C。
两条直线被第三条直线所截,内错角相等D。
同角或等角的补角相等7.如图,点B,E在线段FC上,且CE = BF,AB = DE,增加以下条件能判定△ABC ≌△DEF的是()。
A。
∠A = ∠D B。
∠C = ∠F C。
BC = EF D。
AC = DF8.在△ABC中,∠C = 90°,点O为△ABC三条角平分线的交点,OD ⊥ BC于D,OE ⊥ AC于E,OF ⊥ AB于F,且AB = 10cm,BC = 8cm,AC = 6cm,则点O到三边AB,AC,BC的距离分别为()。
A。
2 cm,2 cm,2 cm B。
(必考题)初中数学八年级数学上册第七单元《平行线的证明》测试卷(答案解析)(3)

一、选择题1.下列命题中,为真命题的是( )A .13是13的算术平方根B .三角形的一个外角大于任何一个内角C .13是最简二次根式 D .两条直线被第三条直线所截,内错角相等 2.小明和小亮在研究一道数学题,如图EF AB ⊥,CD AB ⊥,垂足分别为E 、D ,G 在AC 上.小明说:“如果CDG BFE ∠=∠,则能得到AGD ACB ∠=∠”;小亮说:“连接FG ,如果//FG AB ,则能得到GFC ADG ∠=∠”.则下列判断正确的是( )A .小明说法正确,小亮说法错误B .小明说法正确,小亮说法正确C .小明说法错误,小亮说法正确D .小明说法错误,小亮说法错误 3.下列命题中,属于假命题的是( )A .相等的角是对顶角B .三角形的内角和等于180°C .两直线平行,同位角相等D .两点之间,线段最短4.下列命题是真命题的个数为( ) ①两条直线被第三条直线所截,内错角相等.②三角形的内角和是180°.③在同一平面内平行于同一条直线的两条直线平行.④相等的角是对顶角.⑤两点之间,线段最短.A .2B .3C .4D .5 5.如图,ABC 中,将A ∠沿DE 翻折,若30A ∠=︒,25BDA '∠=︒,则CEA '∠多少度( )A .60°B .75°C .85°D .90°6.下列命题中真命题有( )①周长相等的两个三角形是全等三角形;②一组数据中,出现次数最多的数据为这组数据的众数;③同位角相等;④方差可以刻画数据的波动程度,方差越大,波动越小;方差越小,波动越大. A .1个 B .2个 C .3个 D .4个7.在下列条件中:①A C B ∠=∠-∠,②::2:3:5A B C ∠∠∠=,③90A B ∠=︒-∠,④90B C ∠-∠=︒中,能确定ABC 是直角三角形的条件有( )A .1个B .2个C .3个D .4个8.如图,下列条件中,不能判断直线a ∥b 的是( )A .∠1=∠3B .∠2=∠3C .∠4=∠5D .∠2+∠4=180° 9.如图,直线a ∥b ,点B 在a 上,且AB ⊥BC ,若∠1=35°,那么∠2等于( )A .45°B .50°C .55°D .60°10.已知下列命题(1)等边三角形的三个内角都相等;(2)平行四边形相邻的两个角都相等;(3)线段垂直平分线上的点到这条线段两个端点距离相等;(4)底角相等的两个等腰三角形全等.其中原命题和逆命题均为真命题的有( )A .1个B .2个C .3个D .4个11.如图,//AB EF ,C 点在EF 上,EAC ECA ∠=∠,BC 平分DCF ∠,且AC BC ⊥.下列结论:①AC 平分DCE ∠;②//AE CD ;③190B ∠+∠=︒;④BDC 21∠=∠.其中结论正确的个数有( )A .1个B .2个C .3个D .4个12.如图,//AB CD ,BE 交CD 于点F ,48B ∠=︒,20E ∠=︒,则D ∠的度数为( ).A .28B .20C .48D .68二、填空题13.命题“如果两个三角形全等,那么这两个三角形的周长相等”的逆命题是_______命题(填“真”或“假”).14.如图,AB ,CD 相交于点E ,ACE AEC ∠=∠,BDE BED ∠=∠,过A 作AF BD ⊥,垂足为F .求证:AC AF ⊥.证明:∵ACE AEC ∠=∠,BDE BED ∠=∠又AEC BED ∠=∠(________________)∴ACE BDE ∠=∠∴//AC DB (________________________)∴CAF AFD ∠=∠(________________________)∵AF DB ⊥∴90AFD ∠=︒(________________________)∴90CAF =︒∠∴AC AF ⊥15.如图,25AOB ∠=︒,点M ,N 分别是边OA ,OB 上的定点,点P ,Q 分别是边OB ,OA 上的动点,记MPQ α∠=,PQN β∠=,当MP PQ QN ++的值最小时,βα-的大小=__________(度).16.如图,在△ABC 中,点O 是△ABC 内一点,且点O 到△ABC 三边的距离相等,若∠A =70°,则∠BOC =________.17.如图,在ABC 中,AD 是BC 边上的高,且ACB BAD ∠=∠,AE 平分CAD ∠,交BC 于点E ,过点E 作EF AC ,分别交AB 、AD 于点F 、G .则下列结论:①90BAC ∠=︒;②AEF BEF ∠=∠;③BAE BEA ∠=∠;④2B AEF ∠=∠,其中正确的有_____.18.把“同角的补角相等”改成“如果···那么···”的形式_________________.19.如图,AB CD ,一副三角尺按如图所示放置,∠AEG =20度,则 HFD ∠为 ______________度.20.在四边形ABCD 中,ADC ∠与BCD ∠的角平分线交于点E ,115DEC ∠=︒,过点B 作//BF AD 交CE 于点F ,2CE BF =,54CBF BCE ∠=∠,连接BE ,254BCE S ∆=,则CE =___.三、解答题21.推理填空:如图,AD BC ⊥于D ,EG BC ⊥于G ,1E ∠=∠,可得AD 平分BAC ∠. 理由如下:∵AD BC ⊥于D ,EG BC ⊥于G ,(已知)∴90ADC EGC ∠=∠=︒,(____________________)∴//AD EG ,(____________________)∴1∠=__________,(____________________)3E ∠=∠,(____________________)又∵1E ∠=∠,(____________________)∴3∠=___________,(____________________)∴AD 平分BAC ∠.(____________________)22.如图,在ABC 中,P 是ABC ∠,ACB ∠的角平分线的交点.(1)若80A ∠=︒,求BPC ∠的度数;(2)有位同学在解答(1)后得出1902BPC A ∠=︒+∠的规律,你认为正确吗?请说明理由.23.填空:(将下面的推理过程及依据补充完整)如图,已知:CD 平分ACB ∠,//AC DE ,//CD EF ,求证:EF 平分DEB ∠.证明:∵CD 平分ACB ∠(已知),DCA DCE ∴∠=∠(角平分线的定义),//AC DE (已知),DCA ∴∠=____(两直线平行,内错角相等)DCA CDE ∴∠==∠(等量代换),//CD EF (已知),∴_____CDE =∠(_________);DCE BEF ∠=∠(__________),∴__________=__________(等量代换),EF ∴平分DEB ∠(______________).24.如图,BAE ∠,CBF ∠,ACD ∠是ABC 的三个外角.求BAE CBF ACD ∠+∠+∠的度数.(要求:写出求解过程,不能直接用外角和公式)25.如图,在四边形ABCD 中,E 、F 分别是CD 、AB 延长线上的点,连接EF ,分别交AD 、BC 于点G 、H .若12∠=∠,A C ∠=∠,试判断AB 与CD 的位置关系,并说明理由.补全解答过程.猜想:AB 与CD 的位置关系是 ① .证明:∵12∠=∠(已知),1AGH ∠=∠(②),∴2AGH ∠=∠(③).∴ ④ (同位角相等,两直线平行).∴ADE C ∠=∠(⑤),∵A C ∠=∠(已知),∴ ⑥ (等量代换).∴ ⑦ (⑧).26.如图已知12B C ∠=∠∠=∠,,求证://AB CD .证明:∵12∠=∠(已知),且14∠=∠(__________),∴24∠∠=(__________).∴//BF _____(__________). ∴∠____3=∠(__________).又∵B C ∠=∠(已知),∴_____________(等量代换).∴//AB CD (__________).【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】根据算术平方根、三角形外角定理、最简二次根式定义、平行线性质逐项判断即可求解.【详解】解:1313的算术平方根”,判断正确,符合题意;B. “三角形的一个外角大于任何一个内角”,应为“三角形的一个外角大于和它不相邻的任意一个内角”,判断错误,不合题意;13”,不是最简二次根式,判断错误,不合题意;D. “两条直线被第三条直线所截,内错角相等”,两条直线不一定平行,判断错误,不合题意.故选:A【点睛】本题考查了命题、算术平方根、三角形外角定理、最简二次根式定义、平行线性质等知识,熟练掌握相关知识是解题的关键,注意:题设成立,结论一定成立的命题是真命题;题设成立,结论不一定成立的命题是假命题.2.A解析:A【分析】由EF⊥AB,CD⊥AB,知CD∥EF,然后根据平行线的性质与判定即可得出答案.【详解】解:∵EF⊥AB,CD⊥AB,∴CD∥EF,若∠CDG=∠BFE,∵∠BCD=∠BFE,∴∠BCD=∠CDG,∴DG∥BC,∴∠AGD=∠ACB,故小明说法正确;∵FG∥AB,∴∠B=∠GFC,故得不到∠GFC=∠ADG,故小亮说法错误,故选:A.【点睛】本题考查了平行线的判定与性质,属于基础题,关键是掌握平行线的性质与判定.3.A解析:A【分析】利用对顶角、三角形内角和、平行线的性质等分别判断后即可确定正确的选项.【详解】解:A、相等的角不一定是对顶角,原命题是假命题;B、三角形三个内角的和等于180°,是真命题;C、两直线平行,同位角相等,是真命题;D、两点之间,线段最短,是真命题;故选:A.【点睛】本题考查了命题与定理的知识,解题的关键是了解对顶角、平行线的性质和三角形内角和,难度不大.4.B解析:B【分析】首先判断所给命题的真假,再选出正确的选项.【详解】解:∵两条直线被第三条直线所截,两直线平行,内错角相等,∴①错误;∵三角形的内角和是180°,∴②正确;∵在同一平面内平行于同一条直线的两条直线平行,∴③正确;∵相等的角可以是对顶角,也可以是内错角、同位角等等,∴④错误;∵连接两点的所有连线中,线段最短,∴⑤正确;∴真命题为②③⑤,故选B .【点睛】本题考查命题的真假判断,根据所学知识判断一个命题条件成立的情况下,结论是否一定成立来判断命题是真命题还是假命题是解题关键.5.C解析:C【分析】根据折叠前后对应角相等可得ADE A DE '∠=∠,AED A ED '∠=∠,再运用平角的定义和三角形内角和定理依次求得ADE ∠、AED ∠,再次运用平角的定义即可求得CEA '∠.【详解】解:∵将A ∠沿DE 翻折,∴ADE A DE '∠=∠,AED A ED '∠=∠,∵D 是线段AB 上的点,25BDA '∠=︒,∴180ADE A D B E DA '∠+∠-'∠=︒,即251280ADE ︒=∠-︒,解得102.5ADE ∠=︒,∵30A ∠=︒,180A AED ADE ∠+∠+∠=︒,∴180180102.53047.5AED ADE A ∠=︒-∠-∠=︒-︒-︒=︒,∴18018047.547.585CEA AED A ED ''∠=︒-∠-∠=︒-︒-︒=︒.故选:C .【点睛】本题考查折叠的性质,三角形内角和定理,平角的定义.理解折叠前后对应角相等是解题关键.6.A解析:A【分析】根据题意对四个命题作出判断即可求解.【详解】解:①周长相等的两个三角形是全等三角形,是假命题;②一组数据中,出现次数最多的数据为这组数据的众数,是真命题;③同位角相等,是假命题;④方差可以刻画数据的波动程度,方差越大,波动越小;方差越小,波动越大,是假命题.真命题有1个.故选:A【点睛】本题考查全等三角形的判定,众数,方差等知识,熟知相关知识是解题关键.7.C解析:C【分析】根据直角三角形的判定方法对各个选项进行分析,从而得到答案.【详解】①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形;②因为∠A:∠B:∠C=2:3:5,设∠A=2x,则2x+3x+5x=180,x=18°,∠C=18°×5=90°,所以△ABC是直角三角形;③因为∠A=90°﹣∠B,所以∠A+∠B=90°,则∠C=180°﹣90°=90°,所以△ABC是直角三角形;④因为∠B﹣∠C=90°,则∠B=90°+∠C,所以三角形为钝角三角形.所以能确定△ABC是直角三角形的有①②③.故选:C.【点睛】本题考查了三角形的内角和定理:三角形的内角和为180°;理解三角形内若有一个内角为90°,则△ABC是直角三角形.8.B解析:B【分析】根据平行线的判定定理逐项判断即可.【详解】A、当∠1=∠3时,a∥b,内错角相等,两直线平行,故正确;B、∠2与∠3不是同位角,也不是内错角,无法判断,故错误;C、当∠4=∠5时,a∥b,同位角相等,两直线平行,故正确;D、当∠2+∠4=180°时,a∥b,同旁内角互补,两直线平行,故正确.故选:B.【点睛】本题考查了平行线的判定,熟记判定定理是解题的关键.9.C解析:C【分析】先根据直线平行的性质得到∠BAC=∠1=35°,再由三角形内角和定理求出55BCA ∠=︒,再根据对顶角的性质即可得到答案.【详解】解:∵直线a ∥b ,∴∠BAC=∠1=35°(两直线平行,内错角相等),又∵AB ⊥BC ,∴∠ABC=90°,∴180903555BCA ∠=︒-︒-︒=︒ (三角形内角和定理),∴255BCA ∠=∠=︒(对顶角相等),故选:C .【点睛】本题主要考查了直线平行的性质、三角形内角和定理、对顶角的性质,掌握对顶角相等以及两直线平行内错角相等是解题的关键.10.B解析:B【分析】根据逆命题的概念分别写出各个命题的逆命题,根据等边三角形的判定和直线定理、平行四边形的判定和性质定理、线段垂直平分线的判定和性质、全等三角形的判定和性质定理判断即可.【详解】解:(1)等边三角形的三个内角都相等,是真命题,逆命题为:三个角相等的三角形是等边三角形,是真命题;(2)平行四边形相邻的两个角互补,但不一定相等,本说法是假命题,逆命题为:相邻的两个角都相等的四边形是平行四边形,是真命题;(3)线段垂直平分线上的点到这条线段两个端点距离相等,是真命题,逆命题为:到线段两个端点距离相等的点在线段垂直平分线上,是真命题;(4)底角相等的两个等腰三角形不一定全等,本说法是假命题,逆命题为:两个全等的等腰三角形的底角相等,是真命题;故选:B .【点睛】本题考查的是命题的真假判断、逆命题的概念,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.11.D解析:D【分析】根据平行线的性质及角度的计算,等腰三角形的性质即可进行一一求解判断.【详解】根据//AB EF , BC 平分DCF ∠,且AC BC ⊥可得∠1+∠BCD=90°,∠BCD=12∠DCF , 又∠DCF+∠ECD=180°,∴∠1=12∠ECD ,故AC 平分DCE ∠,①正确; ∵AC 平分DCE ∠,∴∠1=∠ECA,∵EAC ECA ∠=∠∴EAC ∠=∠1,∴//AE CD ,②正确;∵EF ∥AB ,∴∠FCB=∠B ,∴∠B=∠DCB ,∵∠1+∠DCB=90°,∴190B ∠+∠=︒,③正确;∵EF ∥AB ,∴∠ECA=∠CAD ,∵∠1=∠ECA∴∠1=∠CAD∵∠CDB 是△ACD 的一个外角,∴∠CAD=∠1+∠CAD=2∠1,④正确;故选D【点睛】此题主要考查平行线的角度计算,解题的关键是根据图像的特点进行求解.12.A解析:A【分析】由//AB CD 和48B ∠=︒,可得到CFB ∠;再由对顶角相等和三角形内角和性质,从而完成求解.【详解】∵//AB CD∴180********CFB B ∠=-∠=-=∴132EFD CFB ∠=∠=∴1801801322028D EFD E ∠=-∠-∠=--=故选:A .【点睛】本题考察了平行线和三角形内角和的知识;求解的关键是熟练掌握三角形内角和、平行线的性质,从而完成求解.二、填空题13.假;【分析】将原命题的条件与结论对换位置即可得到逆命题然后判断真假【详解】如果两个三角形全等那么这两个三角形的周长相等的逆命题是如果两个三角形的周长相等那么这两个三角形全等根据周长相等无法判定三角形 解析:假;【分析】将原命题的条件与结论对换位置,即可得到逆命题,然后判断真假.【详解】“如果两个三角形全等,那么这两个三角形的周长相等”的逆命题是“如果两个三角形的周长相等,那么这两个三角形全等”,根据周长相等,无法判定三角形全等,故该逆命题是假命题,故答案为:假.【点睛】本题考查逆命题与命题的判断,掌握原命题与逆命题的关系是解题的关键.14.对顶角相等;内错角相等两直线平行;两直线平行内错角相等;垂直定义【分析】依据对顶角相等推出利用平行线的判定定理内错角相等两直线平行利用平行线的性质得由垂直再根据同旁内角互补即可【详解】证明:∵又(对 解析:对顶角相等;内错角相等,两直线平行;两直线平行,内错角相等;垂直定义【分析】依据对顶角相等推出ACE BDE ∠=∠,利用平行线的判定定理内错角相等两直线平行//AC DB ,利用平行线的性质得CAF AFD ∠=∠,由垂直90AFD ∠=︒,再根据同旁内角互补90CAF =︒∠即可.【详解】证明:∵ACE AEC ∠=∠,BDE BED ∠=∠,又AEC BED ∠=∠(对顶角相等),∴ACE BDE ∠=∠,∴//AC DB (内错角相等,两直线平行),∴CAF AFD ∠=∠(两直线平行,内错角相等),∵AF DB ⊥,∴90AFD ∠=︒(垂直定义),∴90CAF =︒∠,∴AC AF ⊥.故答案为:对顶角相等;内错角相等,两直线平行;两直线平行,内错角相等;垂直定义.【点睛】本题主要考查了平行线的判定和性质,对顶角性质,等式的性质,垂直定义,掌握平行线的判定和性质,对顶角性质,等式的性质,垂直定义,解题时注意:两直线平行,同旁内角互补是解题关键.15.50【分析】作M 关于OB 的对称点N 关于OA 的对称点连接交OB 于点P 交OA 于点Q 连接MPQN 可知此时最小此时再根据三角形外角的性质和平角的定义即可得出结论【详解】作M 关于OB 的对称点N 关于OA 的对称点 解析:50【分析】作M 关于OB 的对称点M ',N 关于OA 的对称点N ',连接M N '',交OB 于点P ,交OA于点Q ,连接MP ,QN ,可知此时MP PQ QN ++最小,此时OPM OPM NPQ OQP AQN AQN ''∠=∠=∠∠=∠=∠,,再根据三角形外角的性质和平角的定义即可得出结论.【详解】作M 关于OB 的对称点M ',N 关于OA 的对称点N ',连接M N '',交OB 于点P ,交OA 于点Q ,连接MP ,QN ,如图所示.根据两点之间,线段最短,可知此时MP PQ QN++最小,即MP PQ QN M N ''++=, ∴OPM OPM NPQ OQP AQN AQN ''∠=∠=∠∠=∠=∠,,∵MPQ PQN αβ∠=∠=,, ∴11(180)(180)22QPN OQP αβ∠=︒-∠=︒-,, ∵QPN AOB OQP ∠=∠+∠,25AOB ∠=︒, ∴11(180)25(180)22αβ︒-=︒+︒- , ∴50βα-=︒ . 故答案为:50.【点睛】本题考查轴对称-最短问题、三角形内角和,三角形外角的性质等知识,灵活运用所学知识解决问题是解题的关键,综合性较强.16.125°【分析】求出O 为△ABC 的三条角平分线的交点求出∠OBC=∠ABC ∠OCB=∠ACB 根据三角形内角和定理求出∠ABC+∠ACB 求出∠OBC+∠OCB 再根据三角形内角和定理求出∠BOC 的度数即解析:125°【分析】求出O 为△ABC 的三条角平分线的交点,求出∠OBC=12∠ABC ,∠OCB=12∠ACB ,根据三角形内角和定理求出∠ABC+∠ACB,求出∠OBC+∠OCB,再根据三角形内角和定理求出∠BOC的度数即可;【详解】∵在△ ABC中,点O是△ABC内的一点,且点O到△ ABC三边距离相等,∴ O为△ABC的三条角平分线的交点,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∵∠A=70°,∴∠ABC+∠ACB=180°-∠A=110°,∴∠OBC+∠OCB=55°,∴∠BOC=180°-∠OBC-∠OCB=125°,故答案为:125°.【点睛】本题考查了角平分线的有关计算,三角形内角和定理的应用,能正确掌握与角平分线有关的三角形内角和问题是解题的关键;17.①③④【分析】利用高线和同角的余角相等三角形内角和定理即可证明①再利用等量代换即可得到③④均是正确的②缺少条件无法证明【详解】由已知可知∠ADC=∠ADB=90°∵∠ACB=∠BAD∴90°-∠AC解析:①③④【分析】利用高线和同角的余角相等,三角形内角和定理即可证明①,再利用等量代换即可得到③④均是正确的,②缺少条件无法证明.【详解】由已知可知∠ADC=∠ADB=90°,∵∠ACB=∠BAD∴90°-∠ACB=90°-∠BAD,即∠CAD=∠B,∵三角形ABC的内角和=∠ACB+∠B+∠BAD+∠CAD=180°,∴∠CAB=90°,①正确,∵AE平分∠CAD,EF∥AC,∴∠CAE=∠EAD=∠AEF,∠C=∠FEB=∠BAD,②错误,∵∠BAE=∠BAD+∠DAE,∠BEA=∠BEF+∠AEF,∴∠BAE=∠BEA,③正确,∵∠B=∠DAC=2∠CAE=2∠AEF,④正确,故答案为:①③④.【点睛】本题考查了三角形的综合性质,高线的性质,平行线的性质,综合性强,难度较大,利用角平分线和平行线的性质得到相等的角,再利用等量代换推导角之间的关系是解题的关键.18.如果两个角是同一个角的补角那么这两个角相等【分析】把命题的题设写在如果的后面把命题的结论写在那么的后面即可【详解】解:命题同角的补角相等改成如果…那么…的形式为:如果两个角是同一个角的补角那么这两个解析:如果两个角是同一个角的补角,那么这两个角相等【分析】把命题的题设写在如果的后面,把命题的结论写在那么的后面即可.【详解】解:命题“同角的补角相等”改成“如果…,那么…”的形式为:如果两个角是同一个角的补角,那么这两个角相等.故答案为:如果两个角是同一个角的补角,那么这两个角相等.【点睛】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.19.35【解析】分析:过点G作AB平行线交EF于P根据平行线的性质求出∠EGP求出∠PGF根据平行线的性质平角的概念计算即可详解:过点G作AB平行线交EF于P由题意易知AB∥GP∥CD∴∠EGP=∠AE解析:35【解析】分析:过点G作AB平行线交EF于P,根据平行线的性质求出∠EGP,求出∠PGF,根据平行线的性质、平角的概念计算即可.详解:过点G作AB平行线交EF于P,由题意易知,AB∥GP∥CD,∴∠EGP=∠AEG=20°,∴∠PGF=70°,∴∠GFC=∠PGF=70°,∴∠HFD=180°-∠GFC-∠GFP-∠EFH=35°.故答案为35°.点睛:本题考查的是平行线的性质、三角形内角和定理的应用,掌握两直线平行、内错角相等是解题的关键.20.5【分析】设∠BCE=4x∠CBF=5x设∠ADE=∠EDC=y构建方程组求出xy证明∠CFB=90°再利用三角形的面积公式构建方程即可解决问题【详解】解:∵∴可以假设∠BCE=4x则∠CBF=5x解析:5【分析】设∠BCE=4x ,∠CBF=5x ,设∠ADE=∠EDC=y ,构建方程组求出x ,y ,证明∠CFB=90°,再利用三角形的面积公式构建方程即可解决问题.【详解】解:∵54CBF BCE ∠=∠, ∴可以假设∠BCE=4x ,则∠CBF=5x ,∵DE 平分∠ADC ,CE 平分∠DCB ,∴∠ADE=∠EDC ,∠ECD=∠ECB=4x ,设∠ADE=∠EDC=y ,∵AD ∥BF ,∴∠A+∠ABF=180°,∴∠ADC+∠DCB+∠CBF=180°,∴2y+13x=180°①,∵∠DEC=115°,∴∠EDC+∠ECD=65°,即y+4x=65° ②,联立①②解得x=10°,y=25°,∴∠BCF=40°,∠CBF=50°,∴∠CFB=90°,∴BF ⊥EC ,∴CE=2BF ,设BF=m ,则CE=2m ,12524∆=⨯⨯=BCE S EC BF , ∴125224⨯⨯=m m , 解得52m =(负值舍去), ∴CE=2m =5,故答案为5.【点睛】 本题考查了角平分线的性质,平行线的性质,三角形内角和定理,二元一次方程组等知识,解题的关键是学会利用参数构建方程或方程组组解决问题.三、解答题21.垂直的定义;同位角相等,两直线平行;∠2;两直线平行,内错角相等;两直线平行,同位角相等;已知;∠2;等量代换;角平分线的定义.【分析】根据证明的前后联系填写理由或结论即可.【详解】解:∵AD ⊥BC 于D ,EG ⊥BC 于G ,(已知)∴∠ADC =∠EGC =90°,(垂直的定义)∴AD ∥EG ,(同位角相等,两直线平行)∴∠1=∠2,(两直线平行,内错角相等)∠E =∠3,(两直线平行,同位角相等)又∵∠E =∠1(已知)∴∠3=∠2(等量代换)∴AD 平分∠BAC (角平分线的定义).故答案为:垂直的定义;同位角相等,两直线平行;∠2;两直线平行,内错角相等;两直线平行,同位角相等;已知;∠2;等量代换;角平分线的定义.【点睛】本题考查平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角,明确每步说理的原因是正确答题的关键.22.(1)130°;(2)正确,理由见解析.【分析】(1) 在△ABC 内,由三角形内角和定理可求得∠ABC+∠ACB ,再利用角平分线的定义可求得∠PBC+∠PCB ,在△PBC 中由三角形内角和可求得∠BPC ;(2) 由(1) 的过程可证明其正确.【详解】解:(1)80A ∠=︒,得到∠ABC+∠ACB=100° ,BP ,CP 分别平分ABC ∠,ACB ∠,1()502PBC PCB ABC ACB ∴∠+∠=∠+∠=︒, 18050130BPC ∴∠=︒-︒=︒.(2)我认为正确.理由如下:BP ,CP 分别平分ABC ∠,ACB ∠, 1()2PBC PCB ABC ACB ∴∠+∠=∠+∠, 180ABC ACB A ∠+∠=︒-∠()111809022PBC PCB A A ∴∠+∠=︒-∠=︒-∠, 11180909022BPC A A ⎛⎫∴∠=︒-︒-∠=︒+∠ ⎪⎝⎭. 【点睛】本题主要考查与角平分线有关的三角形内角和问题,掌握三角形内角和为180°是解题的关键,注意整体思想的应用.23.∠CDE ;∠DEF ;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF ;∠FEB ;角平分线的定义.【分析】根据平行线的性质和平行线的判定及等量代换等来完成解答即可.【详解】解:证明:∵CD 平分∠ACB (已知),∴∠DCA=∠DCE (角平分线的定义),∵AC ∥DE (已知),∴∠DCA=∠CDE (两直线平行,内错角相等),∴∠DCE=∠CDE ( 等量代换),∵CD ∥EF ( 已知 ),∴∠DEF=∠CDE (两直线平行,内错角相等),∠DCE=∠FEB (两直线平行,同位角相等),∴∠DEF=∠FEB (等量代换),∴EF 平分∠DEB ( 角平分线的定义 ).故答案为:∠CDE ;∠DEF ;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF ;∠FEB ;角平分线的定义.【点睛】本题考查了平行线的性质和平行线的判定在几何证明中的应用,明确相关性质及定理是解题的关键.24.360BAE CBF ACD ∠+∠+∠=︒【分析】利用邻补角的定义以及三角形内角和定理,计算即可求解.【详解】解:∵1180BAE ∠+∠=︒,2180CBF ︒∠+∠=,3180ACD ︒∠+∠=,∴1231803540BAE CBF ACD ∠+∠+∠+∠+∠+∠=︒⨯=︒,又∵123180∠+∠+∠=︒,∴540(123)540180360BAE CBF ACD ︒︒︒︒∠+∠+∠=-∠+∠+∠=-=.【点睛】本题考查了邻补角的定义以及三角形内角和定理,正确的识别图形是解题的关键. 25.①//AB CD ;②对顶角相等;③等量代换;④//AD BC ;⑤两直线平行,同位角相等;⑥ADE ∠A =∠;⑦//AB CD ;⑧内错角相等,两直线平行【分析】先根据同位角相等,两直线平行,判定AD ∥BC ,进而得到∠ADE=∠C ,再根据内错角相等,两直线平行,即可得到AB ∥CD .【详解】猜想:AB 与CD 的位置关系是AB ∥CD .证明:∵∠1=∠2(已知)∠1=∠AGH (对顶角相等)∴∠2=∠AGH (等量代换)∴AD ∥BC (同位角相等,两直线平行)∴∠ADE=∠C (两直线平行,同位角相等)∵∠A=∠C (已知)∴∠ADE=∠A (等量代换)∴AB ∥CD (内错角相等,两直线平行)故答案为:①//AB CD ;②对顶角相等;③等量代换;④//AD BC ;⑤两直线平行,同位角相等;⑥ADE ∠A =∠;⑦//AB CD ;⑧内错角相等,两直线平行.【点睛】本题主要考查了平行线的判定与性质,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系;平行线的性质是由平行关系来寻找角的数量关系.26.见解析【分析】根据平行线的判定和性质解答.【详解】解:证明:∵∠1=∠2(已知),且∠1=∠4(对顶角相等),∴∠2=∠4(等量代换),∴BF ∥EC (同位角相等,两直线平行),∴∠C=∠3(两直线平行,同位角相等).又∵∠B=∠C (已知),∴∠3=∠B (等量代换),∴AB ∥CD (内错角相等,两直线平行).【点睛】本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.。
青岛版八年级数学上册单元测试《第1章 全等三角形》(解析版)

第1章全等三角形一、选择题(共4小题)1.如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF 的长为()A.2B.3 C.D.2.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()A.4个B.3个C.2个D.1个3.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有()A.1个B.2个C.3个D.4个4.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是()A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE二、填空题(共5小题)5.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为.6.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .7.如图,正方形ABCD的对角线相交于点O,△OEF是正三角形,且AE=BF,则∠AOE= .8.如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是.9.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是.(请写出正确结论的序号).三、解答题(共21小题)10.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.11.如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.(1)求证:DE=AB.(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求的长.12.如图,∠1=∠2,∠3=∠4,求证:AC=AD.13.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.14.如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD.(2)若AB=CF,∠B=30°,求∠D的度数.15.已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:(1)∠AEC=∠BED;(2)AC=BD.16.如图,在△ABC中,AB=AC,点E,F分别是边AB,AC的中点,点D在边BC上.若DE=DF,AD=2,BC=6,求四边形AEDF的周长.17.已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.18.如图,四边形ABCD、BEFG均为正方形,连接AG、CE.(1)求证:AG=CE;(2)求证:AG⊥CE.19.如图,在▱ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.(1)求证:AE=AF;(2)求∠EAF的度数.20.如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.(1)求证:∠ABC=∠EDC;(2)求证:△ABC≌△EDC.21.如图1,在△ABC中,∠ACB=90°,∠BAC=60°,点E是∠BAC角平分线上一点,过点E作AE 的垂线,过点A作AB的垂线,两垂线交于点D,连接DB,点F是BD的中点,DH⊥AC,垂足为H,连接EF,HF.(1)如图1,若点H是AC的中点,AC=2,求AB,BD的长;(2)如图1,求证:HF=EF;(3)如图2,连接CF,CE.猜想:△CEF是否是等边三角形?若是,请证明;若不是,说明理由.22.如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)AB∥DE.23.已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.24.如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE 相交于点E,求证:AD=CE.25.如图,在▱ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.26.如图,在▱ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.27.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.28.如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.(1)求证:AE=DF;(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.29.如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.30.如图,点B,C是线段AD的三等分点,以BC为直径作⊙O,点P是圆上异于B,C的任意一点,连接PA,PB,PC,PD.(1)当PB=PC时,求tan∠APB的值;(2)当P是上异于B,C的任意一点时,求tan∠APB•tan∠DPC的值.第1章全等三角形参考答案与试题解析一、选择题(共4小题)1.如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF 的长为()A.2B.3 C.D.【考点】全等三角形的判定与性质;勾股定理;正方形的性质.【专题】压轴题.【分析】首先延长FD到G,使DG=BE,利用正方形的性质得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性质易得△GCF≌△ECF,利用勾股定理可得AE=3,设AF=x,利用GF=EF,解得x,利用勾股定理可得CF.【解答】解:如图,延长FD到G,使DG=BE;连接CG、EF;∵四边形ABCD为正方形,在△BCE与△DCG中,,∴△BCE≌△DCG(SAS),∴CG=CE,∠DCG=∠BCE,∴∠GCF=45°,在△GCF与△ECF中,,∴△GCF≌△ECF(SAS),∴GF=EF,∵CE=3,CB=6,∴BE===3,∴AE=3,设AF=x,则DF=6﹣x,GF=3+(6﹣x)=9﹣x,∴EF==,∴(9﹣x)2=9+x2,∴x=4,即AF=4,∴GF=5,∴DF=2,∴CF===2,故选:A.【点评】本题主要考查了全等三角形的判定及性质,勾股定理等,构建全等三角形,利用方程思想是解答此题的关键.2.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()A.4个B.3个C.2个D.1个【考点】全等三角形的判定与性质;角平分线的性质;相似三角形的判定与性质.【分析】根据等腰三角形的性质三线合一得到BD=CD,AD⊥BC,故②③正确;通过△CDE≌△DBF,得到DE=DF,CE=BF,故①④正确.【解答】解:∵BF∥AC,∴∠C=∠CBF,∵BC平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,∴AB=AC,∵AD是△ABC的角平分线,∴BD=CD,AD⊥BC,故②③正确,在△CDE与△DBF中,,∴△CDE≌△DBF,∴DE=DF,CE=BF,故①正确;∵AE=2BF,∴AC=3BF,故④正确.故选A.【点评】本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质,掌握等腰三角形的性质三线合一是解题的关键.3.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有()A.1个B.2个C.3个D.4个【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】压轴题.【分析】由等边三角形的性质得出AB=DB,∠ABD=∠CBE=60°,BE=BC,得出∠ABE=∠DBC,由SAS即可证出△ABE≌△DBC;由△ABE≌△DBC,得出∠BAE=∠BDC,根据三角形外角的性质得出∠DMA=60°;由ASA证明△ABP≌△DBQ,得出对应边相等BP=BQ,即可得出△BPQ为等边三角形;证明P、B、Q、M四点共圆,由圆周角定理得出∠BMP=∠BMQ,即MB平分∠AMC.【解答】解:∵△ABD、△BCE为等边三角形,∴AB=DB,∠ABD=∠CBE=60°,BE=BC,∴∠ABE=∠DBC,∠PBQ=60°,在△ABE和△DBC中,,∴△ABE≌△DBC(SAS),∴①正确;∵△ABE≌△DBC,∴∠BAE=∠BDC,∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,∴②正确;在△ABP和△DBQ中,,∴△ABP≌△DBQ(ASA),∴BP=BQ,∴△BPQ为等边三角形,∴③正确;∵∠DMA=60°,∴∠AMC=120°,∴∠AMC+∠PBQ=180°,∴P、B、Q、M四点共圆,∵BP=BQ,∴,∴∠BMP=∠BMQ,即MB平分∠AMC;∴④正确;综上所述:正确的结论有4个;故选:D.【点评】本题考查了等边三角形的性质与判定、全等三角形的判定与性质、四点共圆、圆周角定理;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.4.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是()A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE【考点】全等三角形的判定与性质.【分析】利用全等三角形的判定与性质进而得出当∠D=∠B时,△ADF≌△CBE.【解答】解:当∠D=∠B时,在△ADF和△CBE中∵,∴△ADF≌△CBE(SAS),故选:B.【点评】此题主要考查了全等三角形的判定与性质,正确掌握全等三角形的判定方法是解题关键.二、填空题(共5小题)5.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为30°.【考点】全等三角形的判定与性质;等腰三角形的性质;正方形的性质.【分析】由正方形和等边三角形的性质得出∠ADE=∠BCE=150°,AD=DE=BC=CE,得出∠DEA=∠CEB=15°,即可得出∠AEB的度数.【解答】解:∵四边形ABCD是正方形,∴∠BCD=∠ADC=90°,AD=BC=DC,∵△CDE是等边三角形,∴∠EDC=∠ECD=∠DEC=60°,DE=DC=CE,∴∠ADE=∠BCE=90°+60°=150°,AD=DE=BC=CE,∴∠DEA=∠CEB=×(180°﹣150°)=15°,∴∠AEB=60°﹣15°﹣15°=30°;故答案为:30°.【点评】本题考查了正方形的性质、等边三角形的性质、等腰三角形的判定与性质、三角形内角和定理;熟练掌握正方形和等边三角形的性质,并能进行推理计算是解决问题的关键.6.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= 3 .【考点】全等三角形的判定与性质.【分析】由已知条件易证△ABE≌△ACD,再根据全等三角形的性质得出结论.【解答】解:△ABE和△ACD中,,∴△ABE≌△ACD(AAS),∴AD=AE=2,AC=AB=5,∴CE=BD=AB﹣AD=3,故答案为3.【点评】本题主要考查了全等三角形的性质和判定,熟记定理是解题的关键.7.如图,正方形ABCD的对角线相交于点O,△OEF是正三角形,且AE=BF,则∠AOE= 15°.【考点】全等三角形的判定与性质;等边三角形的性质;正方形的性质.【分析】根据正方形、等边三角形的性质,可得AO=BO,OE=OF,根据SSS可得△AOE≌△BOF,根据全等三角形的性质,可得对应角相等,根据角的和差,可得答案.【解答】解:∵四边形ABCD是正方形,∴OA=OB,∠AOB=90°.∵△OEF是正三角形,∴OE=OF,∠EOF=60°.在△AOE和△BOF中,,∴△AOE≌△BOF(SSS),∴∠AOE=∠BOF,∴∠AOE=(∠AOB﹣∠EOF)÷2=(90°﹣60°)÷2=15°,故答案为15°.【点评】本题考查了全等三角形的性质与判定,正方形、等边三角形的性质,利用SSS证明三角形全等得出∠AOE=∠BOF是解题的关键.8.如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是.【考点】全等三角形的判定与性质;勾股定理;圆心角、弧、弦的关系;圆周角定理.【专题】压轴题.【分析】将△ACD绕点C逆时针旋转120°得△CBE,根据旋转的性质得出∠E=∠CAD=30°,BE=AD=5,AC=CE,求出A、B、E三点共线,解直角三角形求出即可;过C作CE⊥AB于E,CF⊥AD于F,得出∠E=∠CFD=∠CFA=90°,推出=,求出∠BAC=∠DAC,BC=CD,求出CE=CF,根据圆内接四边形性质求出∠D=∠CBE,证△CBE≌△CDF,推出BE=DF,证△AEC≌△AFC,推出AE=AF,设BE=DF=x,得出5=x+3+x,求出x,解直角三角形求出即可.【解答】解:解法一、∵A、B、C、D四点共圆,∠BAD=60°,∴∠BCD=180°﹣60°=120°,∵∠BAD=60°,AC平分∠BAD,∴∠CAD=∠CAB=30°,如图1,将△ACD绕点C逆时针旋转120°得△CBE,则∠E=∠CAD=30°,BE=AD=5,AC=CE,∴∠ABC+∠EBC=(180°﹣CAB+∠ACB)+(180°﹣∠E﹣∠BCE)=180°,∴A、B、E三点共线,过C作CM⊥AE于M,∵AC=CE,∴AM=EM=×(5+3)=4,在Rt△AMC中,AC===;解法二、过C作CE⊥AB于E,CF⊥AD于F,则∠E=∠CFD=∠CFA=90°,∵点C为弧BD的中点,∴=,∴∠BAC=∠DAC,BC=CD,∵CE⊥AB,CF⊥AD,∴CE=CF,∵A、B、C、D四点共圆,∴∠D=∠CBE,在△CBE和△CDF中∴△CBE≌△CDF,∴BE=DF,在△AEC和△AFC中∴△AEC≌△AFC,∴AE=AF,设BE=DF=x,∵AB=3,AD=5,∴AE=AF=x+3,∴5=x+3+x,解得:x=1,即AE=4,∴AC==,故答案为:.【点评】本题考查了圆心角、弧、弦之间的关系,圆内接四边形性质,解直角三角形,全等三角形的性质和判定的应用,能正确作出辅助线是解此题的关键,综合性比较强,难度适中.9.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).【考点】全等三角形的判定与性质;等边三角形的性质;平行四边形的判定;正方形的判定.【专题】压轴题.【分析】由三角形ABE与三角形BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到三角形EBF与三角形DFC全等,利用全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形,若AB=AC,∠BAC=120°,只能得到AEFD为菱形,不能为正方形,即可得到正确的选项.【解答】解:∵△ABE、△BCF为等边三角形,∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,即∠CBA=∠FBE,在△ABC和△EBF中,,∴△ABC≌△EBF(SAS),∴EF=AC,又∵△ADC为等边三角形,∴CD=AD=AC,∴EF=AD=DC,同理可得△ABC≌△DFC,∴DF=AB=AE=DF,∴四边形AEFD是平行四边形,选项②正确;∴∠FEA=∠ADF,∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,在△FEB和△CDF中,.∴△FEB≌△CDF(SAS),选项①正确;若AB=AC,∠BAC=120°,则有AE=AD,∠EAD=120°,此时AEFD为菱形,选项③错误,故答案为:①②.【点评】此题考查了全等三角形的判定与性质,等边三角形的性质,平行四边形的判定,以及正方形的判定,熟练掌握全等三角形的判定与性质是解本题的关键.三、解答题(共21小题)10.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.【考点】全等三角形的判定与性质.【专题】证明题.【分析】根据BE=CF,求出BC=EF,根据AAS推出△ABC≌△DEF,根据全等三角形的性质推出即可.【解答】证明:∵BE=CF(已知),∴BE+EC=EC+CF,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(AAS),∴AC=DF(全等三角形对应边相等).【点评】本题考查了全等三角形的性质和判定的应用,解此题的关键是推出△ABC≌△DEF,注意:全等三角形的对应边相等.11.如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.(1)求证:DE=AB.(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求的长.【考点】全等三角形的判定与性质;含30度角的直角三角形;矩形的性质;弧长的计算.【分析】(1)由矩形的性质得出∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,得出∠EAD=∠AFB,由AAS 证明△ADE≌△FAB,得出对应边相等即可;(2)连接DF,先证明△DCF≌△ABF,得出DF=AF,再证明△ADF是等边三角形,得出∠DAE=60°,∠ADE=30°,由AE=BF=1,根据三角函数得出DE,由弧长公式即可求出的长.【解答】(1)证明:∵四边形ABCD是矩形,∴∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,∴∠EAD=∠AFB,∵DE⊥AF,∴∠AED=90°,在△ADE和△FAB中,,∴△ADE≌△FAB(AAS),∴DE=AB;(2)解:连接DF,如图所示:在△DCF和△ABF中,,∴△DCF≌△ABF(SAS),∴DF=AF,∵AF=AD,∴DF=AF=AD,∴△ADF是等边三角形,∴∠DAE=60°,∵DE⊥AF,∴∠AED=90°,∴∠ADE=30°,∵△ADE≌△FAB,∴AE=BF=1,∴DE=AE=,∴的长==.【点评】本题考查了矩形的性质、全等三角形的判定与性质、等边三角形的判定与性质、三角函数以及弧长公式;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.12.如图,∠1=∠2,∠3=∠4,求证:AC=AD.【考点】全等三角形的判定与性质.【专题】证明题.【分析】先证出∠ABC=∠ABD,再由ASA证明△ABC≌△ABD,得出对应边相等即可.【解答】证明:∵∠3=∠4,∴∠ABC=∠ABD,在△ABC和△ABD中,,∴△ABC≌△ABD(ASA),∴AC=AD.【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.13.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.【考点】全等三角形的判定与性质.【专题】证明题.【分析】先证出∠ACB=∠DCE,再由SAS证明△ABC≌△DEC,得出对应角相等即可.【解答】证明:∵∠ACD=∠BCE,∴∠ACB=∠DCE,在△ABC和△DEC中,,∴△ABC≌△DEC(SAS),∴∠A=∠D.【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.14.如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD.(2)若AB=CF,∠B=30°,求∠D的度数.【考点】全等三角形的判定与性质.【分析】(1)易证得△ABE≌△CDF,即可得AB=CD;(2)易证得△ABE≌△CDF,即可得AB=CD,又由AB=CF,∠B=30°,即可证得△ABE是等腰三角形,解答即可.【解答】证明:(1)∵AB∥CD,∴∠B=∠C,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AB=CD;(2)∵△ABE≌△CDF,∴AB=CD,BE=CF,∵AB=CF,∠B=30°,∴AB=BE,∴△ABE是等腰三角形,∴∠D=.【点评】此题考查全等三角形问题,关键是根据AAS证明三角形全等,再利用全等三角形的性质解答.15.已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:(1)∠AEC=∠BED;(2)AC=BD.【考点】全等三角形的判定与性质.【专题】证明题.【分析】(1)根据CE=DE得出∠ECD=∠EDC,再利用平行线的性质进行证明即可;(2)根据SAS证明△AEC与△BED全等,再利用全等三角形的性质证明即可.【解答】证明:(1)∵AB∥CD,∴∠AEC=∠ECD,∠BED=∠EDC,∵CE=DE,∴∠ECD=∠EDC,∴∠AEC=∠BED;(2)∵E是AB的中点,∴AE=BE,在△AEC和△BED中,,∴△AEC≌△BED(SAS),∴AC=BD.【点评】本题主要考查了全等三角形的判定以及全等三角形的性质,关键是根据SAS证明全等.16.如图,在△ABC中,AB=AC,点E,F分别是边AB,AC的中点,点D在边BC上.若DE=DF,AD=2,BC=6,求四边形AEDF的周长.【考点】全等三角形的判定与性质;等腰三角形的性质;勾股定理.【分析】先由SSS证明△ADE≌△ADF,得出∠DAE=∠DAF,即AD平分∠BAC,再由等腰三角形的三线合一性质得出BD=CD=BC=3,AD⊥BC,根据勾股定理求出AB,由直角三角形斜边上的中线性质得出DE=AB,DF=AC,证出AE=AF=DE=DF,即可求出结果.【解答】解:∵点E,F分别是边AB,AC的中点,∴AE=BE=AB,AF=CF=AC,∵AB=AC,∴AE=AF,在△ADE和△ADF中,,∴△ADE≌△ADF(SSS),∴∠DAE=∠DAF,即AD平分∠BAC,∴BD=CD=BC=3,AD⊥BC,∴∠ADB=∠ADC=90°,∴AB===,∵在Rt△ABD和Rt△ACD中,E,F分别是边AB,AC的中点,∴DE=AB,DF=AC,∴AE=AF=DE=DF,∴四边形AEDF的周长=4AE=2AB=2.【点评】本题考查了全等三角形的判定与性质、等腰三角形的性质、勾股定理、直角三角形斜边上的中线性质;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.17.已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.【考点】全等三角形的判定与性质;矩形的性质.【专题】证明题.【分析】由矩形的性质得出∠A=∠D=90°,AB=DC,再证出AF=DE,由SAS证明△ABF≌△DCE,得出对应边相等即可.【解答】证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,AB=DC,∵AE=DF,∴AF=DE,在△ABF和△DCE中,,∴△ABF≌△DCE(SAS),∴BF=CE.【点评】本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.18.如图,四边形ABCD、BEFG均为正方形,连接AG、CE.(1)求证:AG=CE;(2)求证:AG⊥CE.【考点】全等三角形的判定与性质;正方形的性质.【专题】证明题.【分析】(1)由正方形的性质得出AB=CB,∠ABC=∠GBE=90°,BG=BE,得出∠ABG=∠CBE,由SAS 证明△ABG≌△CBE,得出对应边相等即可;(2)由△ABG≌△CBE,得出对应角相等∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.【解答】(1)证明:∵四边形ABCD、BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE,在△ABG和△CBE中,,∴△ABG≌△CBE(SAS),∴AG=CE;(2)证明:如图所示:∵△ABG≌△CBE,∴∠BAG=∠BCE,∵∠ABC=90°,∴∠BAG+∠AMB=90°,∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.【点评】本题考查了正方形的性质、全等三角形的判定与性质、垂线的证法;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.19.如图,在▱ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.(1)求证:AE=AF;(2)求∠EAF的度数.【考点】全等三角形的判定与性质;等边三角形的性质;平行四边形的性质.【专题】证明题.【分析】(1)由平行四边形的性质得出∠BAD=∠BCD=120°,∠ABC=∠ADC,AB=CD,BC=AD,由等边三角形的性质得出BE=BC,DF=CD,∠EBC=∠CDF=60°,证出∠ABE=∠FDA,AB=DF,BE=AD,根据SAS 证明△ABE≌△FDA,得出对应边相等即可;(2)由全等三角形的性质得出∠AEB=∠FAD,求出∠AEB+∠BAE=60°,得出∠FAD+∠BAE=60°,即可得出∠EAF的度数.【解答】(1)证明:∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=120°,∠ABC=∠ADC,AB=CD,BC=AD,∵△BCE和△CDF都是正三角形,∴BE=BC,DF=CD,∠EBC=∠CDF=60°,∴∠ABE=∠FDA,AB=DF,BE=AD,在△ABE和△FDA中,,∴△ABE≌△FDA(SAS),∴AE=AF;(2)解:∵△ABE≌△FDA,∴∠AEB=∠FAD,∵∠ABE=60°+60°=120°,∴∠AEB+∠BAE=60°,∴∠FAD+∠BAE=60°,∴∠EAF=120°﹣60°=60°.【点评】本题考查了平行四边形的性质、等边三角形的性质、全等三角形的判定与性质;熟练掌握平行四边形和等边三角形的性质,证明三角形全等是解决问题的关键.20.如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.(1)求证:∠ABC=∠EDC;(2)求证:△ABC≌△EDC.【考点】全等三角形的判定与性质.【专题】证明题.【分析】(1)根据四边形的内角和等于360°求出∠B+∠ADC=180°,再根据邻补角的和等于180°可得∠CDE+∠ADE=180°,从而求出∠B=∠CDE;(2)根据“边角边”证明即可.【解答】(1)证明:在四边形ABCD中,∵∠BAD=∠BCD=90°,∴90°+∠B+90°+∠ADC=360°,∴∠B+∠ADC=180°,又∵∠CDE+∠ADC=180°,∴∠ABC=∠CDE,(2)连接AC,由(1)证得∠ABC=∠CDE,在△ABC和△EDC中,,∴△ABC≌△EDC(SAS).【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,根据四边形的内角和定理以及邻补角的定义,利用同角的补角相等求出夹角相等是证明三角形全等的关键,也是本题的难点.21.如图1,在△ABC中,∠ACB=90°,∠BAC=60°,点E是∠BAC角平分线上一点,过点E作AE 的垂线,过点A作AB的垂线,两垂线交于点D,连接DB,点F是BD的中点,DH⊥AC,垂足为H,连接EF,HF.(1)如图1,若点H是AC的中点,AC=2,求AB,BD的长;(2)如图1,求证:HF=EF;(3)如图2,连接CF,CE.猜想:△CEF是否是等边三角形?若是,请证明;若不是,说明理由.【考点】全等三角形的判定与性质;等边三角形的判定与性质;三角形中位线定理.【专题】压轴题.【分析】(1)根据直角三角形的性质和三角函数即可得到结果;(2)如图1,连接AF,证出△DAE≌△ADH,△DHF≌△AEF,即可得到结果;(3)如图2,取AB的中点M,连接CM,FM,在R△ADE中,AD=2AE,根据三角形的中位线的性质得t到AD=2FM,于是得到FM=AE,由∠CAE=∠CAB=30°∠CMF=∠AMF﹣AMC=30°,证得△ACE≌△MCF,问题即可得证.【解答】解:(1)∵∠ACB=90°,∠BAC=60°,∴∠ABC=30°,∴AB=2AC=2×2=4,∵AD⊥AB,∠CAB=60°,∴∠DAC=30°,∵AH=AC=,∴AD==2,∴BD==2;(2)如图1,连接AF,∵AE是∠BAC角平分线,∴∠HAE=30°,∴∠ADE=∠DAH=30°,在△DAE与△ADH中,,∴△DAE≌△ADH,∴DH=AE,∵点F是BD的中点,∴DF=AF,∵∠EAF=∠EAB﹣∠FAB=30°﹣∠FAB∠FDH=∠FDA﹣∠HDA=∠FDA﹣60°=(90°﹣∠FBA)﹣60°=30°﹣∠FBA,∴∠EAF=∠FDH,在△DHF与△AEF中,,∴△DHF≌△AEF,∴HF=EF;(3)如图2,取AB的中点M,连接CM,FM,∵F、M分别是BD、AB的中点,∴FM∥AD,即FM⊥AB.在R△ADE中,AD=2AE,t∵DF=BF,AM=BM,∴AD=2FM,∴FM=AE,∵∠ABC=30°,∴AC=CM=AB=AM,∵∠CAE=∠CAB=30°∠CMF=∠AMF﹣∠AMC=30°,在△ACE与△MCF中,,∴△ACE≌△MCF,∴CE=CF,∠ACE=∠MCF,∵∠ACM=60°,∴∠ECF=60°,∴△CEF是等边三角形.【点评】本题考查了全等三角形的判定和性质,直角三角形的性质,等边三角形的判定,正确的作出辅助线构造全等三角形是解题的关键.22.如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)AB∥DE.【考点】全等三角形的判定与性质;平行线的判定.【专题】证明题.【分析】(1)由SAS容易证明△ABC≌△DEF;(2)由△ABC≌△DEF,得出对应角相等∠B=∠DEF,即可得出结论.【解答】证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE=90°,在△ABC和△DEF中,,∴△ABC≌△DEF(SAS);(2)∵△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE.【点评】本题考查了全等三角形的判定与性质、平行线的判定;熟练掌握全等三角形的判定与性质,证明三角形全等是解决问题的关键.23.已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题.【分析】作DG∥BC交AC于G,先证明△DFG≌△EFC,得出GD=CE,再证明△ADG是等边三角形,得出AD=GD,即可得出结论.【解答】证明:作DG∥BC交AC于G,如图所示:则∠DGF=∠ECF,在△DFG和△EFC中,,∴△DFG≌△EFC(AAS),∴GD=CE,∵△ABC是等边三角形,∴∠A=∠B=∠ACB=60°,∵DG∥BC,∴∠ADG=∠B,∠AGD=∠ACB,∴∠A=∠ADG=∠AGD,∴△ADG是等边三角形,∴AD=GD,∴AD=CE.【点评】本题考查了全等三角形的判定与性质、等边三角形的判定与性质;熟练掌握等边三角形的判定与性质,并能进行推理论证是解决问题的关键.24.如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE 相交于点E,求证:AD=CE.【考点】全等三角形的判定与性质.【专题】证明题.【分析】根据平行线的性质得出∠EAC=∠ACB,再利用ASA证出△ABD≌△CAE,从而得出AD=CE.【解答】证明:∵AE∥BD,∴∠EAC=∠ACB,∵AB=AC,∴∠B=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,,∴△ABD≌△CAE,∴AD=CE.【点评】此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质、平行线的性质,关键是利用ASA证出△ABD≌△CAE.25.如图,在▱ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.【考点】全等三角形的判定与性质;平行四边形的性质.【专题】证明题.【分析】先根据平行四边形的性质得到∠B=∠D,AB=CD,再利用垂直的定义得∠AEB=∠GFD=90°,于是可根据“ASA”判定△AEB≌△GFD,根据全等的性质得AB=DC,所以有DG=DC.【解答】证明:∵四边形ABCD为平行四边形,∴∠B=∠D,AB=CD,∵AE⊥BC,FG⊥CD,∴∠AEB=∠GFD=90°,在△AEB和△GFD中,,∴△AEB≌△GFD,∴AB=DG,∴DG=DC.【点评】本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了平行四边形的性质.26.如图,在▱ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.【考点】全等三角形的判定与性质;平行四边形的性质.【专题】证明题.【分析】根据平行四边形的性质,证明AB=CD,AB∥CD,进而证明∠BAC=∠DCF,根据ASA即可证明△ABE≌△CDF,根据全等三角形的对应边相等即可证明.【解答】证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF,∴△ABE和△CDF中,,∴△ABE≌△CDF,∴BE=DF.【点评】本题考查的是利用平行四边形的性质结合三角形全等来解决有关线段相等的证明.27.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.【考点】全等三角形的判定与性质.【专题】计算题.【分析】AC与BD垂直,理由为:利用SSS得到三角形ABD与三角形CBD全等,利用全等三角形对应角相等得到BD为角平分线,利用三线合一性质即可得证.【解答】解:AC⊥BD,理由为:在△ABD和△CBD中,,∴△ABD≌△CBD(SSS),∴∠ABO=∠CBO,∵AB=CB,∴BD⊥AC.【点评】此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.28.如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.(1)求证:AE=DF;(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.【考点】全等三角形的判定与性质;菱形的判定.【专题】证明题.【分析】(1)利用AAS推出△ADE≌△DAF,再根据全等三角形的对应边相等得出AE=DF;(2)先根据已知中的两组平行线,可证四边形DEFA是▱,再利用AD是角平分线,结合AE∥DF,易证∠DAF=∠FDA,利用等角对等边,可得AE=DF,从而可证▱AEDF实菱形.【解答】证明:(1)∵DE∥AC,∠ADE=∠DAF,同理∠DAE=∠FDA,∵AD=DA,∴△ADE≌△DAF,∴AE=DF;(2)若AD平分∠BAC,四边形AEDF是菱形,∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∴∠DAF=∠FDA.∴AF=DF.∴平行四边形AEDF为菱形.【点评】考查了全等三角形的判定方法及菱形的判定的掌握情况.29.如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.【考点】全等三角形的判定与性质;平行线的性质;等腰三角形的判定与性质.【分析】(1)当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.首先根据OC是∠AOB的平分线,CD∥OB,判断出∠DOC=∠DC0,所以OD=CD=DM+CM;然后根据E是线段OC的中点,CD∥OB,推得CM=ON,即可判断出OD=DM+ON,据此解答即可.(2)当点M在线段CD延长线上时,线段OD、ON、DM之间的数量关系是:OD=ON﹣DM.由(1),可得OD=DC=CM﹣DM,再根据CM=ON,推得OD=ON﹣DM即可.【解答】解:(1)当点M在线段CD上时,线段OD、ON、DM之间的数量关系是:OD=DM+ON.证明:如图1,,∵OC是∠AOB的平分线,∴∠DOC=∠C0B,又∵CD∥OB,∴∠DCO=∠C0B,∴∠DOC=∠DC0,∴OD=CD=DM+CM,∵E是线段OC的中点,∴CE=OE,∵CD∥OB,。
(word)苏教版八年级数学上册《全等三角形》单元测试题4有答案

学大教育第1章全等三角形检测题〔本检测题总分值:100分,时间:90分钟〕一、选择题〔每题3分,共30分〕要测量河两岸相对的两点错误!未找到引用源。
的距离,先在错误!未找到引用源。
的垂线错误!未找到引用源。
上取两点错误!未找到引用源。
,使错误!未找到引用源。
,再作出错误!未找到引用源。
的垂线错误!未找到引用源。
,使错误!未找到引用源。
在一条直线上〔如下列图〕,可以说明△错误!未找到引用源。
≌△错误!未找到引用源。
,得错误!未找到引用源。
,因此测得错误!未找到引用源。
的长就是错误!未找到引用源。
的长,判定△错误!第1题图未找到引用源。
≌△错误!未找到引用源。
最恰当的理由是〔〕A.边角边B.角边角C.边边边D.边边角2.如下列图,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走第2题图2 021m停下,那么这个微型机器人停在〔〕A.点A处B.点B处C.点C 处D.点E处3.如图,ABCDADBCAC与BD交于点AEBD于点ECFBD于点,,那么图中全等的三角形有( ) 对对对对4.以下命题中正确的选项是〔〕全等三角形的高相等全等三角形的中线相等全等三角形的角平分线相等全等三角形对应角的平分线相等如下列图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,那么以下结论不一定成立的是〔〕A.△ACE≌△BCDB. △BGC≌△AFCC.△DCG≌△ECFD. △ADB≌△CEA如下列图,错误!未找到引用源。
分别表示△ABC的三边长,那么下第3题图面与△错误!未找到引用源。
一定全等的三角形是〔〕第5题图第6题图7.:如下列图,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,1第7题图学大教育AC⊥CD,那么不正确的结论是〔〕A.∠A与∠D互为余角 B .∠A=∠2C.△ABC≌△CED D .∠1=∠2如下列图,两条笔直的公路错误!未找到引用源。
(常考题)人教版初中数学八年级数学上册第一单元《三角形》测试卷(答案解析)(3)

一、选择题1.下列长度的三条线段可以组成三角形的是( )A .1,2,4B .5,6,11C .3,3,3D .4,8,12 2.如图,ABC 中,BC 边上的高是( )A .AEB .ADC .CD D .CF 3.如图,AD 是ABC 的外角CAE ∠的平分线,35B ∠=︒,60=︒∠DAC ,则ACD∠的度数为( )A .25︒B .85︒C .60︒D .95︒4.如图,在ABC 中,B C ∠=∠,D 为BC 边上的一点,点E 在AC 边上,ADE AED ∠=∠,若10CDE ∠=︒,则BAD ∠的度数为( )A .20°B .15°C .10°D .30°5.如图,1∠等于( )A .40B .50C .60D .70 6.若多边形的边数由3增加到n (n 为大于3的正整数),则其外角和的度数( ) A .不变 B .减少 C .增加 D .不能确定 7.做一个三角形的木架,以下四组木棒中,符合条件的是( )A .4cm, 5cm,9cmB .4cm, 5cm, 6cmC .5cm,12cm,6cmD .4cm,2cm,2cm 8.正十边形每个外角等于( )A .36°B .72°C .108°D .150° 9.将下列长度的三根木棒首尾顺次连接,不能组成三角形的是( ) A .4、5、6B .3、4、5C .2、3、4D .1、2、3 10.下列长度的三条线段,能组成三角形的是( ) A .3,5,6 B .3,2,1 C .2,2,4 D .3,6,10 11.如图,在七边形ABCDEFG 中,AB ,ED 的延长线交于点O .若1,2,3,4∠∠∠∠的外角和于210°,则BOD ∠的度数为( )A .30°B .35°C .40°D .45°12.如图,105DBA ∠=︒,125ECA ∠=︒,则A ∠的度数是( )A .75°B .60°C .55°D .50°二、填空题13.如图1,△ABC 中,有一块直角三角板PMN 放置在△ABC 上(P 点在△ABC 内),使三角板PMN 的两条直角边PM 、PN 恰好分别经过点B 和点C .若∠A =52°,则∠1+∠2=__________;14.如图,已知ABC 中,90,50ACB B D ︒︒∠=∠=,为AB 上一点,将BCD △沿CD 折叠后,点B 落在点E 处,且//CE AB ,则ACD ∠的度数是___________.15.如图,飞机P 在目标A 的正上方,飞行员测得目标B 的俯角为30°,那么APB ∠的度数为______°.16.如图,在ABC 中,80B ∠=︒,BAC ∠和BCD ∠的平分线交于点E ,则E ∠的度数是______.17.ABC 中,,AB AC 边上的高,CE BD 相交于点F ,,ABC ACB ∠∠的角平分线交于点G ,若=125CGB ∠︒,则CFB ∠=______.18.如图,已知AE 是ABC 的边BC 上的中线,若8AB cm =,ACE △的周长比AEB △的周长多2cm ,则AC =______cm .19.如图,AD 、AE 分别是ABC 的高和角平分线,且76B ∠=︒,36C ∠=︒,则DAE ∠的度数为_________.20.如图,在ABC ∆中,BD 平分ABC ∠,AE BD ⊥.若30ABC ∠=︒,50C ∠=︒,则CAE ∠的度数为_______︒.三、解答题21.如图,BP 平分ABC ∠,交CD 于点F ,DP 平分ADC ∠交AB 于点E ,AB 与CD 相交于点G ,42A ∠=︒.(1)若60ADC ∠=︒,求AEP ∠的度数;(2)若38C ∠=︒,求P ∠的度数.22.如图,所有小正方形的边长都为1个单位,A 、B 、C 均在格点上.(1)过点A 画线段BC 的垂线,垂足为E ;(2)过点A 画线段AB 的垂线,交线段CB 的延长线于点F ;(3)线段BE 的长度是点 到直线 的距离;(4)线段AE 、BF 、AF 的大小关系是 .(用“<”连接)23.如果一个多边形的内角和是它的外角和的4倍,求这个多边形的对角线总数. 24.如图,已知直线//AB CD ,直线EF 分别交直线AB ,CD 于点E ,F ,BEF ∠的平分线与DFE ∠的平分线相交于一点P .试说明:90P ∠=︒.25.(1)已知△ABC 中,∠B=5∠A ,∠C-∠B=15°,求∠A ,∠B ,∠C 的度数. (2)在△ABC 中,∠A=50°,BD ,CE 为高,直线BD ,CE 交于点H ,求∠BHC 的度数. 26.如图,在ABC 中,40B ∠=,80C ∠=.(1)求BAC ∠的度数;(2)AE 平分BAC ∠交BC 于E ,AD BC ⊥于D ,求EAD ∠的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【详解】解:A 、1+2<4,不能构成三角形;B 、5+6=11,不能构成三角形;C 、3+3>3,能构成三角形;D 、8+4=12,不能构成三角形.故选:C .【点睛】本题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于最大的数.2.B解析:B【分析】根据从三角形顶点向对边作垂线,顶点和垂足之间的线段叫做三角形的高,确定出答案即可.【详解】由图可知,过点A 作BC 的垂线段AD ,则ABC 中,BC 边上的高是AD .故选:B【点睛】本题主要考查了三角形的高的定义,熟记概念是解题的关键.3.D解析:D【分析】根据角平分线的定义可得∠DAC =∠DAE ,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠D ,然后利用三角形的内角和定理列式计算即可得解.【详解】解:∵AD 是∠CAE 的平分线,60=︒∠DAC ,∴∠DAC =∠DAE =60°,又∵35B ∠=︒由三角形的外角性质得,∠D =∠DAE−∠B =60°−35°=25°,∴在△ACD 中,∠ACD =180°−∠DAC -∠D =180°−60°−25°=95°.故选:D .【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和定理,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.4.A解析:A【分析】先根据三角形外角的性质得出∠ADC=∠B+∠BAD ,∠AED=∠C+∠EDC ,再根据∠B=∠C ,∠ADE=∠AED 即可得出结论.【详解】解:∵∠ADC 是△ABD 的外角,∴∠ADC=∠B+∠BAD ,∴∠ADE=∠ADC-∠CDE=∠B+∠BAD-∠CDE∵∠AED 是△CDE 的外角,∴∠AED=∠C+∠EDC ,∵∠ADE=∠AED ,∴∠B+∠BAD-∠CDE=∠C+∠EDC ,∵∠B=∠C ,∴∠BAD=2∠EDC ,∵10CDE ∠=︒∴∠BAD=20°;故选:A【点睛】本题考查的是三角形外角的性质,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.5.D解析:D【分析】根据三角形外角的性质直接可得出答案.【详解】解:由三角形外角的性质,得160=130∠+︒︒11306070∴∠=︒-︒=︒故选D .【点睛】本题考查了三角形外角的性质,比较简单.6.A解析:A【分析】利用多边形的外角和特征即可解决问题.【详解】解:因为多边形外角和固定为360°,所以外角和的度数是不变的.故选:A .【点睛】此题考查多边形内角与外角的性质,容易受误导,注意多边形外角和等于360°. 7.B解析:B【分析】三角形的任意两边的和大于第三边,根据三角形的三边关系就可以求解.【详解】解:根据三角形的三边关系,知:A中,4+5=9,排除;B中,4+5>6,满足;C中,5+6<12,排除;D中,2+2=4,排除.故选:B.【点睛】本题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.8.A解析:A【分析】根据正十边形的外角和等于360︒,每一个外角等于多边形的外角和除以边数,即可得解.【详解】︒÷=︒,3601036∴正五边形的每个外角等于36︒,故选:A.【点睛】本题考查了正多边形的外角和、边数、外角度数之间的关系,熟记正多边形以上三者之间的关系是解题的关键.9.D解析:D【分析】根据三角形三边关系定理:三角形两边之和大于第三边进行分析即可.【详解】D、4+5>6,能组成三角形,故此选项错误;B、3+4>5,能组成三角形,故此选项错误;A、2+3>4,能组成三角形,故此选项错误;D、1+2=3,不能组成三角形,故此选项正确;故选:D.【点睛】此题主要考查了三角形的三边关系定理,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.10.A解析:A【分析】根据三角形三边长关系,逐一判断选项,即可得到答案.【详解】A. ∵3+5>6,∴长度为3,5,6的三条线段能组成三角形,故该选项符合题意,B. ∵1+2=3,∴长度为3,2,1的三条线段不能组成三角形,故该选项不符合题意,C. ∵2+2=4,∴长度为2,2,4的三条线段不能组成三角形,故该选项不符合题意,D. ∵3+6<10,∴长度为3,6,10的三条线段不能组成三角形,故该选项不符合题意, 故选A【点睛】本题主要考查三角形三边长的关系,掌握三角形任意两边之和大于第三边,是解题的关键.11.A解析:A【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和,由五边形内角和可求得五边形OAGFE 的内角和,即可求得∠BOD .【详解】解:∵∠1、∠2、∠3、∠4的外角的角度和为210°,∴∠1+∠2+∠3+∠4+210°=4×180°,∴∠1+∠2+∠3+∠4=510°,∵五边形OAGFE 内角和=(5-2)×180°=540°,∴∠1+∠2+∠3+∠4+∠BOD=540°,∴∠BOD=540°-510°=30°.故选:A.【点睛】本题主要考查多边形的内角和,利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键.12.D解析:D【分析】根据邻补角的定义可求得ABC ∠和ACB ∠,再根据三角形内角和为180°即可求出A ∠.【详解】解:105DBA ∠=︒,125ECA ∠=︒,18010575ABC ∴∠=︒-︒=︒,18012555ACB ∠=︒-︒=︒.180755550A ∴∠=︒-︒-︒=︒.故选D .【点睛】 本题考查了邻补角和三角形内角和定理,识记三角形内角和为180°是解题的关键.二、填空题13.38°【分析】根据三角形内角和定理易求∠ABC +∠ACB 的度数已知∠P =90°根据三角形内角和定理易求∠PBC +∠PCB 的度数进而得到∠1+∠2的度数【详解】∵∠A =52°∴∠ABC +∠ACB =18解析:38°【分析】根据三角形内角和定理易求∠ABC +∠ACB 的度数.已知∠P =90°,根据三角形内角和定理易求∠PBC +∠PCB 的度数,进而得到∠1+∠2的度数.【详解】∵∠A =52°,∴∠ABC +∠ACB =180°−52°=128°,∵∠P =90°,∴∠PBC +∠PCB =90°,∴∠ABP +∠ACP =128°−90°=38°,即∠1+∠2=38°.故答案为:38°.【点睛】本题考查的是三角形内角和定理以及直角三角形的性质等知识,注意运用整体法计算,解决问题的关键是求出∠ABC +∠ACB ,∠PBC +∠PCB 的度数.14.25°【分析】先求出∠A 的度数再根据折叠的性质可得∠E 的度数根据平行线的性质求出∠ADE 的度数进而即可求解【详解】∵∴∠A=40°∵沿折叠后点B 落在点E 处∴∠E=∠B=50°∵∴∠ADE=∠E=50解析:25°【分析】先求出∠A 的度数,再根据折叠的性质可得∠E 的度数,根据平行线的性质求出∠ADE 的度数,进而即可求解.【详解】∵90,50ACB B ︒︒∠=∠=, ∴∠A=40°,∵BCD △沿CD 折叠后,点B 落在点E 处,∴∠E=∠B=50°,∵//CE AB ,∴∠ADE=∠E=50°,∴∠BDC=∠EDC=(180°-50°)÷2=65°,∴∠ACD=∠BDC-∠A=65°-40°=25°,故答案是:25°.【点睛】本题主要考查折叠的性质,三角形外角的性质,平行线的性质,直角三角形的性质,掌握平行线的性质以及三角形外角的性质,是解题的关键.15.60【分析】先由题意得到∠A=∠B=根据直角三角形两锐角互余求得结果【详解】∵飞机P在目标A的正上方飞行员测得目标B的俯角为30°∴∠A=∠CPB=∵CP∥AB∴∠B=∠CPB=∴=-∠B=故答案为解析:60【分析】先由题意得到∠A=90︒,∠B=30,根据直角三角形两锐角互余求得结果.【详解】∵飞机P在目标A的正上方,飞行员测得目标B的俯角为30°,∴∠A=90︒,∠CPB=30,∵CP∥AB,∴∠B=∠CPB=30,∴APB∠=90︒-∠B=60︒,故答案为:60.【点睛】此题考查直角三角形两锐角互余的性质,理解飞行员测得目标B的俯角为30°得到∠B=30是解题的关键.16.40°【分析】根据角平分线的性质可得∠EAC=∠BAC∠ECD=∠BCD最后根据三角形外角的性质解答即可【详解】解:∵∠BAC的平分线与∠BCD的平分线交于点E∴∠EAC=∠BAC∠ECD=∠BCD解析:40°【分析】根据角平分线的性质可得∠EAC=12∠BAC,∠ECD=12∠BCD,最后根据三角形外角的性质解答即可.【详解】解:∵∠BAC的平分线与∠BCD的平分线交于点E,∴∠EAC=12∠BAC,∠ECD=12∠BCD,∵∠BCD-∠BAC=∠B=80°,∴∠ECD-∠EAC=12(∠BCD-∠BAC )=40°, ∵E ∠是△ACE 的外角∴∠E=∠ECD-∠EAC=40°.故答案为40°.【点睛】本题主要考查了三角形内角和定理、角平分线的定义以及三角形的外角的性质等知识点,灵活利用三角形外角的性质是解答本题的关键.17.110°【分析】根据三角形的内角和定理求出∠GBC +∠GCB 根据角平分线的定义求出∠ABC +∠ACB 从而求出∠A 根据三角形高的定义可得∠AEC=∠FDC=90°然后根据三角形的内角和定理求出∠ACE解析:110°【分析】根据三角形的内角和定理求出∠GBC +∠GCB ,根据角平分线的定义求出∠ABC +∠ACB ,从而求出∠A ,根据三角形高的定义可得∠AEC=∠FDC=90°,然后根据三角形的内角和定理求出∠ACE ,最后利用三角形外角的性质即可求出结论.【详解】解:∵=125CGB ∠︒∴∠GBC +∠GCB=180°-∠CGB=55°∵,ABC ACB ∠∠的角平分线交于点G ,∴∠ABC=2∠GBC ,∠ACB=2∠GCB∴∠ABC +∠ACB=2∠GBC +2∠GCB=2(∠GBC +∠GCB )=110°∴∠A=180°-(∠ABC +∠ACB )=70°∵,AB AC 边上的高,CE BD 相交于点F ,∴∠AEC=∠FDC=90°,∴∠ACE=180°-∠AEC -∠A=20°∴CFB ∠=∠FDC +∠ACE=110°故答案为:110°.【点睛】此题考查的是三角形内角和定理、三角形外角的性质、三角形的高和角平分线,掌握三角形内角和定理、三角形外角的性质、三角形的高的定义和角平分线的定义是解题关键. 18.10【分析】依据AE 是△ABC 的边BC 上的中线可得CE=BE 再根据AE=AE △ACE 的周长比△AEB 的周长多2cm 即可得到AC 的长【详解】解:∵AE 是△ABC 的边BC 上的中线∴CE=BE 又∵AE=A解析:10【分析】依据AE 是△ABC 的边BC 上的中线,可得CE=BE ,再根据AE=AE ,△ACE 的周长比△AEB 的周长多2cm ,即可得到AC 的长.【详解】解:∵AE 是△ABC 的边BC 上的中线,∴CE=BE ,又∵AE=AE ,△ACE 的周长比△AEB 的周长多2cm ,∴AC-AB=2cm ,即AC-8=2cm ,∴AC=10cm ,故答案为:10;【点睛】本题考查了三角形的角平分线、中线和高,求出两个三角形的周长的差等于两边的差是解题的关键.19.20°【分析】根据高线的定义以及角平分线的定义分别得出∠BAD=14°∠CAD=54°进而得出∠DAE 的度数进而得出答案【详解】∵ADAE 分别是△ABC 的高和角平分线且∠B=76°∠C=36°∴∠B解析:20°【分析】根据高线的定义以及角平分线的定义分别得出∠BAD=14°,∠CAD=54°,进而得出∠DAE 的度数,进而得出答案.【详解】∵AD ,AE 分别是△ABC 的高和角平分线,且∠B=76°,∠C=36°,∴∠BAC=180763668︒-︒-︒=︒,∠BAD=9076︒-︒=14°,∠CAD=9036︒-︒=54°,∴∠BAE=12∠BAC=12×68°=34°, ∴∠DAE=34°-14°=20°.故答案为:20°.【点睛】 本题主要考查了高线以及角平分线的性质,得出∠BAD 和∠CAD 的度数是解题关键. 20.25【分析】依据角平分线的定义即可得到∠DBC 的度数再根据三角形外角的性质即可得到∠CAE 的度数【详解】解:∵∠ABC=30°BD 平分∠ABC ∴∠DBC=∠ABC=×30°=15°又∵AE ⊥BD ∴∠解析:25【分析】依据角平分线的定义即可得到∠DBC 的度数,再根据三角形外角的性质,即可得到∠CAE 的度数.【详解】解:∵∠ABC=30°,BD 平分∠ABC ,∴∠DBC=12∠ABC=12×30°=15°, 又∵AE ⊥BD ,∴∠BEA=90°-15°=75°,∵∠AEB 是△ACE 的外角,∴∠CAE=∠AEB-∠C=75°-50°=25°,故答案为:25.【点睛】本题考查了三角形内角和定理,解决问题的关键是掌握三角形外角的性质.三角形的一个外角等于和它不相邻的两个内角的和.三、解答题21.(1)72︒;(2)40︒.【分析】(1)根据角平分线的定义可得∠ADP=12ADC ∠ ,然后利用三角形外角的性质即可得解;(2)根据角平分线的定义可得∠ADP=∠PDF ,∠CBP=∠PBA ,再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP ,∠C+∠CBP=∠P+∠PDF ,所以∠A+∠C=2∠P ,即可得解.【详解】解:(1)∵DP 平分∠ADC ,∴∠ADP=∠PDF=12ADC ∠, ∵60ADC ∠=︒,∴30ADP ∠=︒,∴304272AEP ADP A ∠=∠+∠=︒+︒=︒;(2)∵BP 平分∠ABC ,DP 平分∠ADC ,∴∠ADP=∠PDF ,∠CBP=∠PBA ,∵∠A+∠ADP=∠P+∠ABP ,∠C+∠CBP=∠P+∠PDF ,∴∠A+∠C=2∠P ,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°. 【点睛】本题考查了三角形的内角和定理及三角形外角的性质,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.22.(1)见解析;(2)见解析;(3)B ,AE ;(4)AE <AF <BF【分析】(1)根据垂线的做法画出图象;(2)根据垂线的做法画出图象;(3)根据点到直线距离的定义填空;(4)利用直角三角形的斜边和直角边的大小关系,得出结果.【详解】(1)如图所示;(2)如图所示;(3) ∵BE AE⊥,∴线段BE的长度是点B到直线AE的距离,故答案是:B,AE;(4)∵AE是直角三角形AEF的直角边,AF是直角三角形AEF的斜边,∴AE AF<,∵BF是直角三角形ABF的斜边,AF是直角三角形ABF的直角边,∴AF BF<,∴AE AF BF<<,故答案是:AE AF BF<<.【点睛】本题考查作垂线和直角三角形的性质,解题的关键是掌握作垂线的方法和直角三角形的直角边和斜边的大小关系.23.35条【分析】一个多边形的内角和等于外角和的4倍而任何多边形的外角和是360°,因而多边形的内角和等于1440°.n边形的内角和可以表示成(n-2)•180°,设这个正多边形的边数是n,就得到方程,从而求出边数,即可求出答案.【详解】解:设这是一个n边形,依题意得:(n-2).180°=4×360°,解得n=10故这个多边形的总条数为()10103352⨯-=(条)答:对角线的总数为35条.【点睛】本题主要考查多边形内角与外角的知识点,此题比较简单,只要结合多边形的内角和公式寻求等量关系,构建方程求解即可.24.证明见解析【分析】由AB∥CD,可知∠BEF与∠DFE互补,由角平分线的性质可得∠PEF+∠PFE=90°,由三角形内角和定理可得出结论.【详解】∵AB∥CD,∴∠BEF+∠DFE=180°.又∵∠BEF的平分线与∠DFE的平分线相交于点P,∴∠PEF=12∠BEF,∠PFE=12∠DFE,∴∠PEF+∠PFE=12(∠BEF+∠DFE)=90°.∵∠PEF+∠PFE+∠P=180°,∴∠P=90°.【点睛】本题主要考查了平行线的性质、角平分线的定义、三角形内角和等知识,解题时注意:两直线平行,同旁内角互补.25.(1)∠A=15°,∠B=75°,∠C =90°;(2)130°【分析】(1)将∠C用∠A表示,然后利用三角形内角和即可求解∠A,然后在依次求出∠B,∠C 即可;(2)根据题意作出示意图,然后根据四边形内角和即可求出∠DHE,根据对顶角相等即可求解∠BHC.【详解】(1)∵∠C-∠B=15°,即∠C =15°+∠B又∵∠B=5∠A∴∠C =15°+5∠A∵∠A+∠B+∠C=180°∴∠A+5∠A +15°+5∠A =180°解得∠A=15°∴∠B=75°,∠C =90°∴∠A=15°,∠B=75°,∠C =90°(2)根据题意作出下图,∵BD AC ⊥,CE AB ⊥∴∠BDA =90°,∠CEA=90°∵在四边形AEHD 中,∠A+∠HDA+∠HEA+∠DHE =360°∴∠DHE=360°-∠A-∠HAD-∠HEA=360°-50°-90°-90°=130°∴∠BHC=∠DHE=130°∴∠BHC =130°.【点睛】本题考查了三角形的内角和和四边形内角和,重点是熟记多边形内角和公式. 26.(1)60BAC ∠=;(2)20EAD ∠=【分析】(1)根据三角形的内角和定理求解即可;(2)根据垂直定义和三角形内角和定理求得∠DAC=10°,再根据角平分线的定义求得∠CAE=30°,两角作差即可求解.【详解】解:(1)∵180B BAC C ∠+∠+∠=,40B ∠=,80C ∠=,∴180408060BAC ∠=--=;(2)∵AD BC ⊥,∴90ADC ∠=,∵180,80DAC ADC C C ∠=-∠-∠∠=,∴180908010DAC ∠=--=,∵AE 平分BAC ∠, ∴1302BAE CAE BAC ∠=∠=∠=, ∵EAD CAE DAC ∠=∠-∠,∴20EAD ∠=.【点睛】本题考查了三角形的内角和定理、角平分线的定义、垂直定义,熟练掌握角平分线的定义和三角形的内角和定理是解答的关键.。
相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题(每题2分,共20分)1. 下列说法中,正确的是:A. 经过直线外一点,有且只有一条直线与已知直线平行B. 经过直线外一点,有且只有一条直线与已知直线相交C. 经过直线外一点,可以画无数条直线与已知直线平行D. 经过直线外一点,可以画无数条直线与已知直线相交2. 如果两直线相交,那么它们相交所成的角是:A. 锐角B. 直角C. 钝角D. 任意角3. 两条直线被第三条直线所截,如果同侧的内错角相等,那么这两条直线:A. 平行B. 相交C. 垂直D. 无法判断4. 平行线的性质中,下列说法不正确的是:A. 平行线之间的距离处处相等B. 平行线永不相交C. 两条平行线可以确定一个平面D. 平行线之间的夹角是锐角5. 对于两条平行线,下列说法正确的是:A. 它们之间的距离在任何地方都是相同的B. 它们可以相交C. 它们之间的夹角可以是任意角D. 它们可以确定一个平面二、填空题(每题2分,共10分)6. 如果两条直线相交成直角,则称这两条直线互相______。
7. 两条直线相交,如果其中一个角是锐角,则其他三个角分别是______。
8. 平行线之间的距离是指______。
9. 两条直线相交所成的角中,最大的角是______。
10. 如果两条直线被第三条直线所截,那么内错角相等的条件是这两条直线______。
三、判断题(每题1分,共10分)11. 两条直线相交所成的角都是锐角。
()12. 平行线在任何地方的距离都是相等的。
()13. 两条直线相交,形成的对顶角相等。
()14. 两条平行线之间的夹角是直角。
()15. 如果两条直线被第三条直线所截,同位角相等,则这两条直线平行。
()四、简答题(每题5分,共20分)16. 解释什么是“同位角”、“内错角”和“同旁内角”,并说明它们在判断两条直线是否平行时的作用。
17. 描述如何使用直角三角板来检验两条直线是否平行。
18. 给出两条直线相交的几何图形,并说明如何确定它们相交所成的角的大小。
第1章平行线单元测试(解析版)

第1章平行线单元测试一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022•东阳市校级开学)图中,∠1和∠2是同位角的是()A.B.C.D.【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,由此即可判断.【解答】解:A、∠1和∠2不是同位角,故A不符合题意;B、∠1和∠2不是同位角,故B不符合题意;C、∠1和∠2不是同位角,故C不符合题意;D、∠1和∠2是同位角,故D符合题意.故选:D.2.(2022春•西湖区校级期中)下列运动属于平移的是()A.冷水加热过程中小气泡上升成为大气泡B.投篮时的篮球运动C.小华乘手扶电梯从一楼到二楼D.随风飘动的树叶在空中的运动【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动.平移后图形的位置改变,形状、大小、方向不变;旋转:在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转.这个定点叫做旋转中心,转动的角度叫做旋转角.旋转前后图形的位置和方向改变,形状、大小不变.【解答】解:小华乘手扶电梯从一楼到二楼属于平移,其余选项属于旋转.故选:C.3.(2022春•嵊州市期末)如图,a∥b,若∠1=56°,则∠2的度数是()A.56°B.124°C.134°D.144°【分析】先根据平行线的性质求出∠3,再根据邻补角的性质求出∠2即可.【解答】解:如图,∵a∥b,∠1=56°,∴∠1=∠3=56°,∵∠2+∠3=180°,∴∠2=124°.故选:B.4.(2022春•萧山区期中)如图,图中给出了过直线外一点作已知直线的平行线的方法,其依据的是()A.同平行于一条直线的两直线平行B.同旁内角互补,两直线平行C.内错角相等,两直线平行D.同位角相等,两直线平行【分析】应用平行线的判定方法进行判断即可得出答案.【解答】解:根据题意可得,在三角板平移的过程中,由同位角相等,可得两直线平行.故选:D.5.(2022秋•瑞安市校级月考)如图,AC∥DF,将一个含30°角的直角三角板如图放置,使得点E恰巧落在直线DF上,若∠ABE=72°,则∠PEF的度数为()A.12°B.15°C.18°D.20°【分析】利用平行线的性质即可得出答案.【解答】解:∵AC∥DF,∴∠ABE=∠BEF=72°,∴∠PEF=72°﹣60°=12°.故选:A.6.(2022春•临平区月考)如图,已知直线l1∥l2,直线l与l1,l2分别相交于点A,B,把一块含30°角的直角三角尺按如图位置摆放,若∠1=130°,则∠ABD的度数为()A.15°B.20°C.25°D.30°【分析】先由对顶角求出∠EAB,再根据两直线平行同旁内角互补求出∠ABC,进而求出∠ABD.【解答】解:如图:∠EAB=∠1=130°(对顶角相等),∵l1∥l2,∴∠EAB+∠ABC=180°(两直线平行,同旁内角互补).∴∠ABC=180°﹣130°=50°.∴∠ABD=∠ABC﹣∠CBD=50°﹣30°=20°.故选:B.7.(2022春•仙桃月考)如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠A B.∠1=∠2C.∠D=∠DCE D.∠D+∠ACD=180°【分析】根据平行线的判定分别进行分析可得答案.【解答】解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;故选:B.8.(2021春•北仑区期中)如图,不能判断l1∥l2的条件是()A.∠1=∠3B.∠2+∠4=180°C.∠4=∠5D.∠2=∠3【分析】根据题意,结合图形对选项一一分析,排除错误答案.【解答】解:A、∠1=∠3正确,内错角相等两直线平行;B、∠2+∠4=180°正确,同旁内角互补两直线平行;C、∠4=∠5正确,同位角相等两直线平行;D、∠2=∠3错误,它们不是同位角、内错角、同旁内角,故不能推断两直线平行.故选:D.9.(2019春•杭州期中)若将一副三角板按如图所示的方式放置,则下列结论正确的是()A.∠1=∠2B.如果∠2=30°,则有AC∥DEC.如果∠2=45°,则有∠4=∠D D.如果∠2=50°,则有BC∥AE【分析】根据平行线的判定和性质一一判断即可【解答】解:∵∠CAB=∠DAE=90°,∴∠1=∠3,故A错误.∵∠2=30°,∴∠1=∠3=60°∴∠CAE=90°+60°=150°,∴∠E+∠CAE=180°,∴AC∥DE,故B正确,∵∠2=45°,∴∠1=∠2=∠3=45°,∵∠E+∠3=∠B+∠4,∴∠4=30°,∵∠D=60°,∴∠4≠∠D,故C错误,∵∠2=50°,∴∠3=40°,∴∠B≠∠3,∴BC不平行AE,故D错误.故选:B.10.(2022春•绍兴期末)如图,已知直线AB∥CD,直线EF分别交直线AB、CD于E、F,EM平分∠AEF交CD 于M,G是射线MD上一动点(不与M、F重合).EH平分∠FEG交CD于点H,设∠MEH=α,∠EGF=β,现有下列四个式子:①2α=β;②2α﹣β=180°;③α﹣β=30°;④2α+β=180°.其中正确的是()A.①②B.①④C.①③④D.②③④【分析】根据平行线的性质和三角形的内角和求解.【解答】解:当点G在点F右侧时,如图示:∵EH平分∠FEG,EM平分∠AEF,∴∠MEF=∠AEF,∠FEH=∠FEG,∵AB∥CD,∴∠BEG=∠EGF=β.∴∠MEH=α=∠MEF+∠FEH=(∠AEF+∠FEG)=(180°﹣∠BEG)=(180°﹣β),∴2α+β=180°,故④是正确的;当点G在M和F之间时,如图:∵EH平分∠FEG,EM平分∠AEF,∴∠MEF=∠AEF,∠FEH=∠FEG,∵AB∥CD,∴∠BEG=∠EGF=β.∴∠MEH=α=∠MEF﹣∠FEH=∠AEF﹣∠FEG=(180°﹣∠BEF)﹣(180°﹣β﹣∠BEF)=β,∴2α=β,故①是正确的.故选:B.二、填空题(本大题共6小题,每小题4分,共24分)请把答案直接填写在横线上11.(2022•东阳市校级开学)如图所示,图中用数字标出的角中,∠2的内错角是∠6.【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,由此即可判断.【解答】解:图中用数字标出的角中,∠2的内错角是∠6.故答案为:∠6.12.(2022春•温州期中)一直角三角板的直角顶点恰好放在直尺的边缘线上(如图所示),若∠2=50°,则∠1=40度.【分析】根据平行线的性质求解即可.【解答】解:如图,∵直尺的对边平行,∠2=50°,∴∠4=∠2=50°,∴∠3=90°﹣∠4=40°,∵直尺的对边平行,∴∠1=∠3=40°,故答案为:40.13.(2022•舟山二模)将一副含30°角和45°角的直角三角板按如图共顶点摆放,若AB∥CD,则∠CAE=30°.【分析】根据平行线的性质求解即可.【解答】解:∵∠C=60°,AB∥CD,∴∠BAC=∠C=60°,∵∠BAE=90°,∴∠CAE=∠BAE﹣∠BAC=30°,故答案为:30°.14.(2022春•杭州期中)如图,在△ABC中,∠ABC+∠ACB=α,按图进行翻折,使MD∥NG∥BC,ME∥FG,则∠NFE的度数是2α﹣180°.【分析】利用平行线的性质以及翻折的性质求解即可.【解答】解:∵MD∥NG∥BC,∴∠M=∠MEF,∠N=∠NFE,∵ME∥FG,∴∠MEF=∠GFC,由翻折可知,∠ABC=∠M,∠GFC=∠NFG,∠N=∠C,∵∠NFE+∠GFC+∠NFG=180°,∠ABC+∠ACB=α,∴∠NFE=2α﹣180°.故答案为:2α﹣180°.15.(2018春•杭州期中)下列说法:①两点之间的距离是两点间的线段的长度;②过一点有且只有一条直线与已知直线平行;③两点之间的所有连线中,线段最短;④若a⊥b,c⊥b,则a与c的关系是平行;⑤只有一个公共点的两条直线叫做相交直线;其中正确的是①③⑤.【分析】根据平行线的定义及平行公理和两点间的距离定义进行判断.【解答】解:两点之间的距离是两点间的线段的长度,①正确;过直线外一点有且只有一条直线与已知直线平行,②错误;两点之间的所有连线中,线段最短,③正确;在同一平面内,垂直于同一直线的两条直线平行,④错误;只有一个公共点的两条直线叫做相交直线,⑤正确;故答案为:①③⑤.16.(2022春•孝南区期中)如图是一块长方形ABCD的场地,长AB=a米,宽AD=b米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为(ab﹣a﹣2b+2)米2.【分析】根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.【解答】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(a﹣2)米,宽为(b﹣1)米.所以草坪的面积应该是长×宽=(a﹣2)(b﹣1)=ab﹣a﹣2b+2(米2).故答案为(ab﹣a﹣2b+2).三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)17.(2022春•恩施市期末)补全证明过程,并在()内填写推理的依据.已知:如图,直线a,b,c被直线d,e所截,∠1=∠2,∠4+∠5=180°,求证:∠6=∠7.证明:∵∠1=∠2,∠2=∠3(对顶角相等),∴∠1=∠3,∴c∥a(同位角相等,两直线平行),∵∠4+∠5=180°,∴c∥b(同旁内角互补,两直线平行).∴a∥b(平行于同一直线的两条直线互相平行).∴∠6=∠7(两直线平行,内错角相等).【分析】由已知得∠1=∠3,证出a∥c,由∠4+∠5=180°,证出b∥c(同旁内角互补,两直线平行),则a∥b,由平行线的性质即可得出结论.【解答】解:∵∠1=∠2,∠2=∠3(对顶角相等),∴∠1=∠3,∴a∥c(同位角相等,两直线平行),∵∠4+∠5=180°,∴c∥b(同旁内角互补,两直线平行),∴a∥b(平行于同一直线的两条直线互相平行),∴∠6=∠7(两直线平行,内错角相等),故答案为:对顶角相等;同位角相等,两直线平行;c;同旁内角互补,两直线平行;平行于同一条直线的两条直线互相平行;两直线平行,内错角相等.18.(2022春•象山县期中)如图,在直角三角形ABC中,∠ABC=90°,将△ABC沿射线BC方向平移,得到△DEF,A,B,C的对应点分别是D,E,F,AD∥BF.(1)请说明∠DAC=∠F.(2)若BC=6cm,当AD=2EC时,则AD=4cm.【分析】(1)先根据平移的性质得到AC∥DF,再利用平行线的性质得到∠ACB=∠F,由AD∥BF得到∠ACB =∠DAC,然后利用等量代换得到结论;(2)根据平移的性质得到AD=BE=CF,设AD=x,则CE=x,BE=CF=x,则利用BC=6得到x+x=6,然后解方程即可.【解答】解:(1)∵△ABC沿射线BC方向平移,得到△DEF,∴AC∥DF,∴∠ACB=∠F,∵AD∥BF,∴∠ACB=∠DAC,∴∠DAC=∠F;(2)∵△ABC沿射线BC方向平移,得到△DEF,∴AD=BE=CF,设AD=x,则CE=x,BE=CF=x,∵BC=6,∴x+x=6,解得x=4,即AD的长为4cm.故答案为:4cm.19.(2009秋•杭州期末)按要求完成作图,并回答问题;如图在△ABC中:(1)过点A画BC的垂线,垂足为E;(2)画∠ABC的平分线,交AC于F;(3)过E画AB的平行线,交AC于点G;(4)过点C画AB所在的直线的垂线段,垂足为H.【分析】(1)借用量角器,测出∠AEC=90°即可;(2)利用角平分线的作法作出∠ABC的平分线;(3)利用平行线的性质:同位角相等,作图;(4)借用量角器,测出∠AHC=90°即可.【解答】解:(1)作法利用量角器测得∠AEC=90°,AE即为所求;(2)作法:①以点B为圆心,以任意长为半径画弧,两弧交∠ABC两边于点M,N.②分别以点M,N为圆心,以大于MN的长度为半径画弧,两弧交于点P③作射线BP,则射线BP为角ABC的角平分线;④射线BP交AC于点F;(3)作法:用量角器测得∠ABC=∠GEC,EG即为所求;(4)作法:利用量角器测得∠BHC=90°,CH即为所求.20.(2018春•金华期中)如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.(1)请指出与∠1是同旁内角的有哪些角?请指出与∠2是内错角的有哪些角?(2)若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.【分析】(1)根据同旁内角、内错角的定义(两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角;处于两条直线之间,处于第三条直线两侧的两个角叫内错角)逐个判断即可.(2)根据平行线的性质解答即可.【解答】解:(1)与∠1是同旁内角的有∠AOE,∠MOE,∠ADE;与∠2是内错角的有∠MOE,∠AOE;(2)∵AB∥CD,∴∠BOE=∠1=115°,∵∠BOM=145°,∴∠MOE=∠BOM﹣∠BOE=145°﹣115°=30°,∴往上弯了30°.21.(2022春•鹿城区校级期中)如图,已知AD∥BC,点E在AB的延长线上,连结DE交BC于点F,且∠C=∠A.(1)请说明∠E=∠CDE的理由;(2)若∠1=75°,∠E=30°,求∠A的度数.【分析】(1)由平行线的性质可得∠A=∠CBE,从而可得∠C=∠CBE,即有CD∥AB,即可求证;(2)由对顶角可得∠BFE=∠1=75°,再由三角形的内角和定理求得∠CBE=75°,即可求∠A.【解答】解:(1)∵AD∥BC,∴∠A=∠CBE,∵∠C=∠A,∴∠C=∠CBE,∴CD∥AB,∴∠E=∠CDE;(2)∵∠1=75°,∴∠BFE=∠1=75°,∵∠E=30°,∴∠CBE=180°﹣∠BFE﹣∠E=75°,∵AD∥BC,∴∠A=∠CBE=75°.22.(2022春•富阳区期中)如图,已知直线CB∥OA,∠C=∠OAB=100°,点E、F在线段BC上,满足∠FOB =∠FBO=α,OE平分∠COF.(1)OC与AB是否平行?请说明理由.(2)用含有α的代数式表示∠COE的度数;(3)若左右平移线段AB,是否存在∠OEC=∠OBA的可能?若存在,求出此时α的值;若不存在,请说明理由.【分析】(1)由平行线的性质,通过等量代换证明∠COA+∠OAB=180°,即可证明OC∥AB;(2)先求出∠CFO=2α,推出∠COF=180°﹣2α﹣100°=80°﹣2α,再利用角平分线的定义求解即可;(3)因为∠COE=∠EOF=40°﹣α,∠FOB=∠FBO=α,推出∠EOB=40°,可得∠ABO=∠CEO=∠EOB+∠FBO=40°+α,根据∠ABC=80°,构建方程解决问题即可.【解答】解:(1)OC∥AB,理由如下:∵BC∥OA,∴∠COA+∠C=180°,∵∠C=∠OAB,∴∠COA+∠OAB=180°,∴OC∥AB;(2)∵∠CFO=∠FOB+∠FBO,∠FOB=∠FBO=α,∴∠CFO=2α,∴∠COF=180°﹣2α﹣100°=80°﹣2α,∵OE平分∠COF,∴∠COE=∠COF=40°﹣α;(3)存在∠OEC=∠OBA,理由如下:∵∠COE=∠EOF=40°﹣α,∠FOB=∠FBO=α,∴∠EOB=40°,∵∠CEO=∠ABO,∴∠ABO=∠CEO=∠EOB+∠FBO=40°+α,∵AB∥OC,∴∠C+∠ABC=180°,∵∠C=100°,∴∠ABC=80°,∴40°+α+α=80°,∴α=20°.23.(2022春•杭州期中)(1)问题发现:如图①,直线AB∥CD,连接BE,CE,可以发现∠B+∠C=∠BEC.请把下面的证明过程补充完整:证明:过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法),∴EF∥DC(平行于同一直线的两直线平行).∴∠C=∠CEF.(两直线平行,内错角相等).∵EF∥AB,∴∠B=∠BEF(同理).∴∠B+∠C=∠BEF+∠CEF(等量代换).即∠B+∠C=∠BEC.(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,说明:∠B+∠C=360°﹣∠BEC.(3)解决问题:如图③,AB∥DC,E、F、G是AB与CD之间的点,找出∠1,∠2,∠3,∠4,∠5之间的数量关系,并说明理由.【分析】(1)过点E作EF∥AB,根据平行线的性质及角的和差求解即可;(2)过点E作EF∥AB,根据平行线的性质及角的和差求解即可;(3)过点F作FM∥AB,根据(1)求解即可.【解答】(1)证明:如图①,过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法),∴EF∥DC(平行于同一直线的两直线平行),∴∠C=∠CEF(两直线平行,内错角相等),∵EF∥AB,∴∠B=∠BEF(同理),∴∠B+∠C=∠BEF+∠CEF(等量代换),即∠B+∠C=∠BEC,故答案为:平行于同一直线的两直线平行;两直线平行,内错角相等;∠BEF+∠CEF;(2)解:如图②,过点E作EF∥AB,∵AB∥CD,EF∥AB,∴EF∥CD,∴∠C+∠CEF=180°,∠B+∠BEF=180°,∴∠B+∠C+∠AEC=360°,∴∠B+∠C=360°﹣(∠BEF+∠CEF),即∠B+∠C=360°﹣∠BEC;(3)解:∠1+∠3+∠5=∠2+∠4,理由如下:如图,过点F作FM∥AB,则AB∥FM∥CD,由(1)得,∠1+∠3+∠5=∠2+∠4.。
苏科版八年级上《第1章全等三角形》单元测试(3)含答案解析

《第1章 全等三角形》一、选择题1.如图,OA=OB ,OC=OD ,∠O=50°,∠D=35°,则∠AEC 等于( )A .60°B .50°C .45°D .30°2.如图,小强利用全等三角形的知识测量池塘两端M 、N 的距离,如果△PQO ≌△NMO ,则只需测出其长度的线段是( )A .POB .PQC .MOD .MQ3.已知△A 1B 1C 1,△A 2B 2C 2的周长相等,现有两个判断:①若A 1B 1=A 2B 2,A 1C 1=A 2C 2,则△A 1B 1C 1≌△A 2B 2C 2;②若∠A 1=∠A 2,∠B 1=∠B 2,则△A 1B 1C 1≌△A 2B 2C 2,对于上述的两个判断,下列说法正确的是( )A .①正确,②错误B .①错误,②正确C .①,②都错误D .①,②都正确4.如图,已知点A 、D 、C 、F 在同一条直线上,AB=DE ,BC=EF ,要使△ABC ≌△DEF ,还需要添加一个条件是( )A .∠BCA=∠FB .∠B=∠EC .BC ∥EFD .∠A=∠EDF5.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个6.如图,△ABD与△ACE均为正三角形,且AB<AC,则BE与CD之间的大小关系是()A.BE=CD B.BE>CDC.BE<CD D.大小关系不确定7.如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE 交AB于点E.某同学分析图形后得出以下结论:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE;上述结论一定正确的是()A.①②③B.②③④C.①③⑤D.①③④8.如图所示,已知△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,AE与BD与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC,FG,其中正确结论的个数是()①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.A.1个B.2个C.3个D.4个二、填空题9.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是.10.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED等于.11.如图,已知点C是∠AOB平分线上的点,点P、P′分别在OA、OB上,如果要得到OP=OP′,需要添加以下条件中的某一个即可:①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.请你写出所有可能的结果的序号:.12.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是.(将你认为正确的结论的序号都填上)13.如图:在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB于E,若四边形ABCD的面积为16,则DE的长为.14.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是.15.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC 交CD的延长线于点F,若EF=5cm,则AE= cm.16.如图,小明为了测量河的宽度,他站在河边的点C,头顶为点D,面向河对岸,压低帽檐使目光正好落在河对岸的岸边点A,然后他姿势不变,在原地方转了180°,正好看见了他所在的岸上的一块石头点B,他测出BC=30m,你能猜出河有多宽吗?说说理由.答:m.17.如图,高速公路上有A、B两点相距25km,C、D为两村庄.已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离相等,则AE的长是km.18.已知三角形的两边长分别为5和7,则第三边上的中线长x的取值范围是.三、解答题19.如图,把大小为4×4的正方形方格图形分别分割成两个全等图形,例如图①,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.20.已知:AD∥BC,AD=CB,AE=CF,请问∠B=∠D吗?为什么?21.如图,已知:CD⊥AB于D,BE⊥AC于E,且BD=CE,BE交CD于点O.求证:AO平分∠BAC.22.如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),在E移动过程中BE和DE是否相等?若相等,请写出证明过程;若不相等,请说明理由.23.如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,AF∥DC,连接AC,CF.求证:CA是∠DCF的平分线.24.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连接DC.(1)请找出图2中与△ABE全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC⊥BE.25.如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l,边EF与边AC重合,且EF=FP.(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.《第1章全等三角形》参考答案与试题解析一、选择题1.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于()A.60° B.50° C.45° D.30°【考点】全等三角形的判定与性质;多边形内角与外角.【分析】首先由已知可求得∠OAD的度数,通过三角形全等及四边形的知识求出∠AEB的度数,然后其邻补角就可求出了.【解答】解:∵在△AOD中,∠O=50°,∠D=35°,∴∠OAD=180°﹣50°﹣35°=95°,∵在△AOD与△BOC中,OA=OB,OC=OD,∠O=∠O,∴△AOD≌△BOC,故∠OBC=∠OAD=95°,在四边形OBEA中,∠AEB=360°﹣∠OBC﹣∠OAD﹣∠O,=360°﹣95°﹣95°﹣50°,=120°,又∵∠AEB+∠AEC=180°,∴∠AEC=180°﹣120°=60°.故选:A.【点评】本题考查了全等三角形的判定及性质;解题过程中用到了三角形、四边形的内角和的知识,要根据题目的要求及已知条件的位置综合运用这些知识.2.如图,小强利用全等三角形的知识测量池塘两端M 、N 的距离,如果△PQO ≌△NMO ,则只需测出其长度的线段是( )A .POB .PQC .MOD .MQ【考点】全等三角形的应用.【分析】利用全等三角形对应边相等可知要想求得MN 的长,只需求得其对应边PQ 的长,据此可以得到答案.【解答】解:要想利用△PQO ≌△NMO 求得MN 的长,只需求得线段PQ 的长,故选:B .【点评】本题考查了全等三角形的应用,解题的关键是如何将实际问题与数学知识有机的结合在一起.3.已知△A 1B 1C 1,△A 2B 2C 2的周长相等,现有两个判断:①若A 1B 1=A 2B 2,A 1C 1=A 2C 2,则△A 1B 1C 1≌△A 2B 2C 2;②若∠A 1=∠A 2,∠B 1=∠B 2,则△A 1B 1C 1≌△A 2B 2C 2,对于上述的两个判断,下列说法正确的是( )A .①正确,②错误B .①错误,②正确C .①,②都错误D .①,②都正确【考点】全等三角形的判定.【专题】压轴题.【分析】根据SSS 即可推出△A 1B 1C 1≌△A 2B 2C 2,判断①正确;根据“两角法”推知两个三角形相似,然后结合两个三角形的周长相等推出两三角形全等,即可判断②.【解答】解:∵△A 1B 1C 1,△A 2B 2C 2的周长相等,A 1B 1=A 2B 2,A 1C 1=A 2C 2,∴B 1C 1=B 2C 2,∴△A 1B 1C 1≌△A 2B 2C 2(SSS ),∴①正确;∵∠A 1=∠A 2,∠B 1=∠B 2,∴△A 1B 1C 1∽△A 2B 2C 2∵△A 1B 1C 1,△A 2B 2C 2的周长相等,∴△A 1B 1C 1≌△A 2B 2C 2∴②正确;故选:D .【点评】本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,而AAA 和SSA 不能判断两三角形全等.4.如图,已知点A 、D 、C 、F 在同一条直线上,AB=DE ,BC=EF ,要使△ABC ≌△DEF ,还需要添加一个条件是( )A .∠BCA=∠FB .∠B=∠EC .BC ∥EFD .∠A=∠EDF【考点】全等三角形的判定.【分析】全等三角形的判定方法SAS 是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE ,BC=EF ,其两边的夹角是∠B 和∠E ,只要求出∠B=∠E 即可.【解答】解:A 、根据AB=DE ,BC=EF 和∠BCA=∠F 不能推出△ABC ≌△DEF ,故本选项错误;B 、∵在△ABC 和△DEF 中,∴△ABC ≌△DEF (SAS ),故本选项正确;C 、∵BC ∥EF ,∴∠F=∠BCA ,根据AB=DE ,BC=EF 和∠F=∠BCA 不能推出△ABC ≌△DEF ,故本选项错误;D 、根据AB=DE ,BC=EF 和∠A=∠EDF 不能推出△ABC ≌△DEF ,故本选项错误.故选B .【点评】本题考查了对平行线的性质和全等三角形的判定的应用,注意:有两边对应相等,且这两边的夹角相等的两三角形才全等,题目比较典型,但是一道比较容易出错的题目.5.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个【考点】全等三角形的判定.【分析】∠1=∠2,∠BAC=∠EAD,AC=AD,根据三角形全等的判定方法,可加一角或已知角的另一边.【解答】解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD,加①AB=AE,就可以用SAS判定△ABC≌△AED;加③∠C=∠D,就可以用ASA判定△ABC≌△AED;加④∠B=∠E,就可以用AAS判定△ABC≌△AED;加②BC=ED只是具备SSA,不能判定三角形全等.其中能使△ABC≌△AED的条件有:①③④故选:B.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.做题时要根据已知条件在图形上的位置,结合判定方法,进行添加.6.如图,△ABD与△ACE均为正三角形,且AB<AC,则BE与CD之间的大小关系是()A.BE=CD B.BE>CDC.BE<CD D.大小关系不确定【考点】全等三角形的判定与性质;等边三角形的性质.【分析】由全等三角形的判定可证明△BAE≌△DAC,从而得出BE=CD.【解答】解:∵△ABD与△ACE均为正三角形∴BA=DA,AE=AC,∠BAD=∠CAE=60°∴∠BAE=∠DAC∴△BAE≌△DAC∴BE=CD故选A.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.7.如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE 交AB于点E.某同学分析图形后得出以下结论:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE;上述结论一定正确的是()A.①②③B.②③④C.①③⑤D.①③④【考点】全等三角形的判定;等腰三角形的性质.【分析】根据等腰三角形的性质及角平分线定义可得有关角之间的相等关系.运用三角形全等的判定方法AAS或ASA判定全等的三角形.【解答】解:∵AB=AC,∴∠ABC=∠ACB.∵BD平分∠ABC,CE平分∠ACB,∴∠ABD=∠CBD=∠ACE=∠BCE.∴①△BCD≌△CBE (ASA);③△BDA≌△CEA (ASA);④△BOE≌△COD (AAS或ASA).故选D.【点评】此题考查等腰三角形的性质和全等三角形的判定,难度不大.8.如图所示,已知△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,AE与BD与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC,FG,其中正确结论的个数是()①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.A.1个B.2个C.3个D.4个【考点】全等三角形的判定与性质;等边三角形的性质;平行线分线段成比例.【专题】几何综合题;压轴题.【分析】根据题意,结合图形,对选项一一求证,判定正确选项.【解答】解:(1)△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,∴AC=BC,EC=DC,∠ACB=∠DCE=60°,∴∠ACE=∠BCD=120°,在△BCD和△ACE中∵,∴△BCD≌△ACE∴AE=BD,故结论①正确;(2)∵△BCD≌△ECA,∴∠GAC=∠FBC,又∵∠ACG=∠BCF=60°,AC=BC∴△ACG≌△BCF,∴AG=BF,故结论②正确;(3)∠DCE=∠ABC=60°,∴DC∥AB,∴,∵∠ACB=∠DEC=60°,∴DE∥AC,∴ =,∴,∴FG∥BE,故结论③正确;(4)过C作CN⊥AE于N,CZ⊥BD于Z,则∠CNE=∠CZD=90°,∵△ACE≌△BCD,∴∠CDZ=∠CEN,在△CDZ和△CEN中∵,∴△CDZ≌△CEN,∴CZ=CN,∵CN⊥AE,CZ⊥BD,∴∠BOC=∠EOC,故结论④正确.综上所述,四个结论均正确,故本题选D.【点评】本题综合考查了全等、圆、相似、特殊三角形等重要几何知识点,有一定难度,需要学生将相关知识点融会贯通,综合运用.二、填空题9.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是利用三角形的稳定性.【考点】三角形的稳定性.【分析】三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.【解答】解:这样做的道理是利用三角形的稳定性.【点评】本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.10.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED等于70°.【考点】全等三角形的判定与性质.【分析】在△BCO中利用外角和定理求得∠DBE的度数,然后证明△ADO≌△BCO,求得∠D的度数,在△BED中利用内角和定理求解.【解答】解:∠DBE=∠O+∠C=60°+25°=85°,∵在△ADO和△BCO,,∴△ADO≌△BCO,∴∠D=∠C=25°,∴∠BED=180°﹣∠D﹣∠DBE=180°﹣25°﹣85°=70°.故答案是:70°.【点评】本题考查全等三角形的判定与性质,以及三角形的外角的性质以及三角形内角和定理,正确证明△ADO≌△BCO是关键.11.如图,已知点C是∠AOB平分线上的点,点P、P′分别在OA、OB上,如果要得到OP=OP′,需要添加以下条件中的某一个即可:①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.请你写出所有可能的结果的序号:①②④.【考点】全等三角形的判定与性质.【分析】要得到OP=OP′就要证明两三角形全等,现有的条件为有一对角相等,一条公共边,缺少角,于是答案可得.【解答】解:①OCP=∠OCP′,符合ASA,可得二三角形全等,从而得到OP=OP′;②∠OPC=∠OP′C;符合AAS,可得二三角形全等,从而得到OP=OP′;④PP′⊥OC,符合ASA,可得二三角形全等,从而得到OP=OP′;③中给的条件是边边角,全等三角形判定中没有这个定理.故填①②④.【点评】本题考查了全等三角形的判定与性质;转化为添加条件使三角形全等是正确解答本题的关键.12.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN ≌△ABM;④CD=DN.其中正确的结论是①②③.(将你认为正确的结论的序号都填上)【考点】全等三角形的判定与性质.【分析】此题考查的是全等三角形的判定和性质的应用,只要先找出图中的全等三角形就可判断题中结论是否正确.【解答】解:∵∠E=∠F=90°,∠B=∠C,AE=AF,∴△ABE≌△ACF,∴AC=AB,BE=CF,即结论②正确;∵AC=AB,∠B=∠C,∠CAN=∠BAM,∴ACN≌△ABM,即结论③正确;∵∠BAE=∠CAF,∵∠1=∠BAE﹣∠BAC,∠2=∠CAF﹣∠BAC,∴∠1=∠2,即结论①正确;∴△AEM≌△AFN,∴AM=AN,∴CM=BN,∴△CDM≌△BDN,∴CD=BD,∴题中正确的结论应该是①②③.故答案为:①②③.【点评】此题考查了三角形全等的判定和性质;对图中的全等三角形作出正确判断是正确解答本题的关键.13.如图:在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB于E,若四边形ABCD的面积为16,则DE的长为 4 .【考点】全等三角形的判定与性质;三角形的面积.【专题】计算题.【分析】可过点C作CF⊥DE,得出Rt△ADE≌Rt△DCF,得出线段之间的关系,进而将四边形的面积转化为矩形BCFE的面积与2个△CDF的面积,通过线段之间的转化,即可得出结论.【解答】解:过点C作CF⊥DE交DE于F,∵AD=CD,∠ADE=90°﹣∠CDF=∠DCF,∠AED=∠DFC=90°,∴△ADE≌△DCF(AAS),∴DE=CF=BE,又四边形ABCD的面积为16,即S矩形BCFE +2S△CDF=16,即BE•EF+2×CF•DF=16,BE•DE=BE•BE=16,解得DE=4.故此题答案为4.【点评】本题主要考查了全等三角形的判定及性质以及三角形、矩形面积的计算,能够熟练掌握.14.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是 1 .【考点】全等三角形的判定与性质.【专题】几何图形问题.【分析】根据AD⊥BC,CE⊥AB,得出∠ADB=∠AEH=90°,再根据∠BAD=∠BCE,利用AAS得到△HEA ≌△BEC,由全等三角形的对应边相等得到AE=EC,由HC=EC﹣EH代入计算即可.【解答】解:∵AD⊥BC,CE⊥AB,∴∠ADB=∠AEH=90°,∵∠AHE=∠CHD,∴∠BAD=∠BCE,∵在△HEA和△BEC中,,∴△HEA≌△BEC(AAS),∴AE=EC=4,则CH=EC﹣EH=AE﹣EH=4﹣3=1.故答案为:1.【点评】此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质,解题的关键是找出图中的全等三角形,并进行证明.15.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC 交CD的延长线于点F,若EF=5cm,则AE= 3 cm.【考点】全等三角形的判定与性质.【分析】根据直角三角形的两锐角互余的性质求出∠ECF=∠B,然后利用“角边角”证明△ABC和△FCE全等,根据全等三角形对应边相等可得AC=EF,再根据AE=AC﹣CE,代入数据计算即可得解.【解答】解:∵∠ACB=90°,∴∠ECF+∠BCD=90°,∵CD⊥AB,∴∠BCD+∠B=90°,∴∠ECF=∠B(等角的余角相等),在△FCE和△ABC中,,∴△ABC≌△FEC(ASA),∴AC=EF,∵AE=AC﹣CE,BC=2cm,EF=5cm,∴AE=5﹣2=3cm.故答案为:3.【点评】本题考查了全等三角形的判定与性质,根据直角三角形的性质证明得到∠ECF=∠B是解题的关键.16.如图,小明为了测量河的宽度,他站在河边的点C,头顶为点D,面向河对岸,压低帽檐使目光正好落在河对岸的岸边点A,然后他姿势不变,在原地方转了180°,正好看见了他所在的岸上的一块石头点B,他测出BC=30m,你能猜出河有多宽吗?说说理由.答:30 m.【考点】全等三角形的应用.【专题】应用题.【分析】要转化为数学问题,须仔细读题,找出有用的已知条件,其中∠BDC=∠ADC是不易被发现的.【解答】解:由题意知∠BCD=∠ACD=90°,CD=CD,∠BDC=∠ADC,∴△BCD≌△ACD,∴AC=BC=30m.故答案为:30.【点评】解决本题的关键是条件∠BDC=∠ADC的找出,做题时要认真读题,理解题意,这是正确解题的保证.17.如图,高速公路上有A、B两点相距25km,C、D为两村庄.已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离相等,则AE的长是15 km.【考点】全等三角形的应用.【分析】根据题意设出AE的长为x,再由勾股定理列出方程求解即可.【解答】解:设AE=x,则BE=25﹣x,由勾股定理得:在Rt△ADE中,DE2=AD2+AE2=102+x2,在Rt△BCE中,CE2=BC2+BE2=152+(25﹣x)2,由题意可知:DE=CE,所以:102+x2=152+(25﹣x)2,解得:x=15km.所以,E应建在距A点15km处.故答案为:15【点评】本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.18.已知三角形的两边长分别为5和7,则第三边上的中线长x的取值范围是1<x<6 .【考点】三角形三边关系;全等三角形的判定与性质.【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,即可求解.【解答】解:如图所示,AB=5,AC=7,设BC=2a,AD=x,延长AD至E,使AD=DE,在△BDE与△CDA中,∵AD=DE,BD=CD,∠ADC=∠BDE,∴△BDE≌△CDA,∴AE=2x,BE=AC=7,在△ABE中,BE﹣AB<AE<AB+BE,即7﹣5<2x<7+5,∴1<x<6.故答案为:1<x<6.【点评】有关三角形的中线问题,通常要倍数延长三角形的中线,把三角形的一边变换到与另一边和中线的两倍组成三角形,再根据三角形三边关系定理列出不等式,然后解不等式即可.三、解答题19.(春•大丰市期末)如图,把大小为4×4的正方形方格图形分别分割成两个全等图形,例如图①,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形分割成两个全等图形.【考点】作图—应用与设计作图.【专题】网格型.【分析】利用正方形的对称轴和中心结合正方形的面积即可解决问题.【解答】解:如图所示:【点评】本题一方面考查了学生的动手操作能力,另一方面考查了学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程.20.已知:AD∥BC,AD=CB,AE=CF,请问∠B=∠D吗?为什么?【考点】全等三角形的判定与性质.【分析】由平行线的性质可得∠A=∠C,已知AD=BC,根据等式的性质得AF=CE,从而可根据SAS判定△DAF≌△BCE,根据全等三角形的对应角相等即可求证.【解答】解:∠B=∠D.原因如下:∵AD∥BC,∴∠A=∠C.∵AE=CF,∴AF=CE.∵AD=BC,∴△DAF≌△BCE.∴∠B=∠D.【点评】此题主要考查学生对全等三角形的判定方法及全等三角形的性质的理解及运用.21.如图,已知:CD⊥AB于D,BE⊥AC于E,且BD=CE,BE交CD于点O.求证:AO平分∠BAC.【考点】全等三角形的判定与性质.【专题】证明题.【分析】首先证得△BOD≌△COE,得到:BD=CE,然后证明Rt△AOD≌Rt△AOE,从而证得.【解答】证明:∵OD⊥AB,OE⊥AC∴∠BDO=∠CEO=90°,又∵∠BOD=∠COE,BD=CE,∴△BOD≌△COE∴OD=OE又由已知条件得△AOD和△AOE都是Rt△,且OD=OE,OA=OA,∴Rt△AOD≌Rt△AOE.∴∠DAO=∠EAO,即AO平分∠BAC.【点评】本题主要考查了三角形全等的判定,可以通过全等三角形的对应边相等,对应角相等.22.如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),在E移动过程中BE和DE是否相等?若相等,请写出证明过程;若不相等,请说明理由.【考点】全等三角形的判定与性质.【专题】动点型.【分析】要证BE=DE,先证△ADC≌△ABC,再证△ADE≌△ABE即可.【解答】解:相等.证明如下:在△ABC和△ADC中,AB=AD,AC=AC(公共边)BC=DC,∴△ABC≌△ADC(SSS),∴∠DAE=∠BAE,在△ADE和△ABE中,AB=AD,∠DAE=∠BAE,AE=AE,∴△ADE≌△ABE(SAS),∴BE=DE.【点评】本题重点考查了三角形全等的判定定理,利用全等得出结论证明三角形全等是常用的方法.23.如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,AF∥DC,连接AC,CF.求证:CA是∠DCF的平分线.【考点】全等三角形的判定与性质.【专题】证明题.【分析】先证△ABF≌△CBF,得出AF=FC,利用等腰三角形的性质可知∠3=∠4,再利用平行线的性质可证出∠4=∠5,等量代换,可得:∠3=∠5.那么AC就是∠DCF的平分线.【解答】证明:∵BF是∠ABC的平分线,∴∠1=∠2,又AB=BC,BF=BF,∴△ABF≌△CBF(SAS),∴FA=FC,∴∠3=∠4,又AF∥DC,∴∠4=∠5,∴∠3=∠5,∴CA是∠DCF的平分线.【点评】本题考查了角平分线的性质、判定,全等三角形的判定和性质;找着并利用△ABF≌△CBF 是正确解答题目的关键.24.(•泰安)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连接DC.(1)请找出图2中与△ABE全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC⊥BE.【考点】全等三角形的判定与性质.【专题】几何综合题.【分析】根据等腰直角三角形的性质利用SAS判定△ABE≌△ACD;因为全等三角形的对应角相等,所以∠ACD=∠ABE=45°,已知∠ACB=45°,所以可得到∠BCD=∠ACB+∠ACD=90°,即DC⊥BE.【解答】(1)解:图2中△ACD≌△ABE.证明:∵△ABC与△AED均为等腰直角三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=90°.∴∠BAC+∠CAE=∠EAD+∠CAE.即∠BAE=∠CAD.∵在△ABE与△ACD中,∴△ABE≌△ACD(SAS);(2)证明:由(1)△ABE≌△ACD,则∠ACD=∠ABE=45°.又∵∠ACB=45°,∴∠BCD=∠ACB+∠ACD=90°.∴DC⊥BE.【点评】此题主要考查学生对等腰三角形的性质及全等三角形的判定方法的理解及运用.25.(•河北)如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l,边EF与边AC重合,且EF=FP.(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.【考点】全等三角形的判定与性质;平移的性质.【专题】探究型.【分析】(1)根据图形就可以猜想出结论.(2)要证BQ=AP,可以转化为证明Rt△BCQ≌Rt△ACP;要证明BQ⊥AP,可以证明∠QMA=90°,只要证出∠1=∠2,∠3=∠4,∠1+∠3=90°即可证出.(3)类比(2)的证明就可以得到,结论仍成立.【解答】解:(1)AB=AP;AB⊥AP;(2)BQ=AP;BQ⊥AP.证明:①由已知,得EF=FP,EF⊥FP,∴∠EPF=45°.又∵AC⊥BC,∴∠CQP=∠CPQ=45°.∴CQ=CP.∵在Rt△BCQ和Rt△ACP中,BC=AC,∠BCQ=∠ACP=90°,CQ=CP,∴△BCQ≌△ACP(SAS),∴BQ=AP.②如图,延长BQ交AP于点M.∵Rt△BCQ≌Rt△ACP,∴∠1=∠2.∵在Rt△BCQ中,∠1+∠3=90°,又∠3=∠4,∴∠2+∠4=∠1+∠3=90°.∴∠QMA=90°.∴BQ⊥AP;(3)成立.证明:①如图,∵∠EPF=45°,∴∠CPQ=45°.又∵AC⊥BC,∴∠CQP=∠CPQ=45°.∴CQ=CP.∵在Rt△BCQ和Rt△ACP中,BC=AC,CQ=CP,∠BCQ=∠ACP=90°,∴Rt△BCQ≌Rt△ACP.∴BQ=AP.②如图③,延长QB交AP于点N,则∠PBN=∠CBQ.∵Rt△BCQ≌Rt△ACP,∴∠BQC=∠APC.∵在Rt△BCQ中,∠BQC+∠CBQ=90°,又∵∠CBQ=∠PBN,∴∠APC+∠PBN=90°.∴∠PNB=90°.∴QB⊥AP.【点评】证明两个线段相等可以转化为证明三角形全等的问题.证明垂直的问题可以转化为证明两直线所形成的角是直角来解决.。
八年级上册数学单元测试题ANM 第1章 平行线

二、填空题
16.如图,为实现城市建设大发展.杭州市先后对文一路、文二路、学院路、教工路进行了改造、假设有一路段(呈直线),从西头测得公路的走向是北偏东72°,如果东、西两头同时开工,在东头应按的走向进行施工,才能使公路准确对接.
解析:南偏西72°
17.如图,已知AB∥CD,BE平分∠ABC,∠CDE =150°,则∠C =.
答案:D
8.在同一平面内,作已知直线 的平行线,且到 的距离为7 cm,这样的平行线最多可以作()
A.1条B.2条C.3条D.无数条
答案:B
9.如图所示,把直线 沿箭头方向平移2.5 cm,得直线 ,则这两条直线之间的距离是()
A.等于2.5 cmB.小于2.5 cmC.大于2.5 cmD.以上都不对
A.AC∥DEB.AC∥EFC.CD∥EFD.以上都不是
答案:C
3.如图,在Rt△ABC中,∠ACB = 90°,DE过点C且平行于AB.若∠BCE = 35°,则∠A等于()
A.35°B.45°C.55°D.65°
答案:C
4.如图,AB∥CD,AC⊥BC于点C,图中与∠CAB互余的角有()
A.1个B.2个C.3个D.4个
解析:∠l=∠2,理由略
37.如图,已知AB∥CD,∠1 = 53°,∠2 = 67°,试求∠3的度数.
解析:60°
38.如图,BD平分∠ABC,且∠1 =∠D,请判断AD与BC的位置关系,并说明理由.
八年级上册数学单元测试题
第1章平行线
一、选择题
1.如图,直线 、 被直线 所截,现给出下列四个条件:(1)∠l =∠5;(2)∠1 =∠7;(3)∠2 +∠3 =180°;(4)∠4 =∠7.其中能判定a∥b的条件的序号是()
《相交线与平行线》的单元测试题(含答案)
相交线与平行线 单元测试一、填空题1.a 、b 、c 是直线,且a ∥b ,b ⊥c ,则a 与c 的位置关系是________.2.如图5—1,MN ⊥AB ,垂足为M 点,MN 交CD 于N ,过M 点作MG ⊥CD ,垂足为G ,EF 过点N 点,且EF ∥AB ,交MG 于H 点,其中线段GM 的长度是________到________的距离, 线段MN 的长度是________到________的距离,又是_______的距离,点N 到直线MG 的距离是___.3.如图5—2,AD ∥BC ,EF ∥BC ,BD 平分∠ABC ,图中与∠ADO 相等的角有_______ 个,分别是___________. 4.因为AB ∥CD ,EF ∥AB ,根据_________,所以_____________. 5.命题“等角的补角相等"的题设__________,结论是__________. 6.如图5—3,给出下列论断:①AD ∥BC :②AB ∥CD ;③∠A =∠C .以上其中两个作为题设,另一个作为结论,用“如果……,那么……”形式,写出一个你认为正确的命题是___________.7.如图5-4,直线AB 、CD 、EF 相交于同一点O ,而且∠B O C=23∠AOC ,∠DOF =13∠AOD ,那么∠FOC =_____ _ 度.8.如图5—5,直线a 、b 被c 所截,a ⊥l 于M ,b ⊥l 于N ,∠1=66°,则∠2=________.9.如图5-6,∠ACB =90°,CD ⊥AB ,则图中与∠A 互余的角有 个,它们分别是 .∠A =∠ ,根据是 .10.如图5—7,一棵小树生长时与地面所成的角为80°,它的根深入泥土,如果根和小树在同一条直线上,那么∠2等于 °.11.如图5—8,量得∠1=80°,∠2=80°,由此可以判定 ∥ ,它的根据是 .量得∠3=100°,∠4=100°,由此可以判定 ∥ ,它的根据是 .G H NMFEDC BAFEODCBA 图5-1 图5-2DCBAFEO DCBAclNMb a21图5-3 图5-4 图5-512.猜谜语:(打本章两个几何名称)剩下十分钱: ;斗牛 . 13.a 、b 、c 是直线,且a ∥b , b ∥c , 则a ___c ; a 、b 、c 是直线,且a ⊥b , b ⊥c , 则a ___c ;14. 如图5—9,直线AD 、BC 交于O 点,∠+∠=︒AOB COD 110,则∠COD 的度数为 .15. 如图5-10,直线AB 与CD 交于O 点,∠-∠=︒3180,则∠2= .16. 如图5—11,直线AB 、EF 相交于O 点,CD AB ⊥于O 点,∠=︒'EOD 12819,则∠∠BOF AOF,的度数分别为 .二、选择题17.若a ⊥b ,c ⊥d 则a 与c 的关系是( )A .平行B .垂直C .相交D .以上都不对 18.如图5-12,∠ADE 和∠CED 是( )A .同位角B .内错角C .同旁内角D .互为补角 19.如图5—13,l l 1211052140//,,∠=∠=,则∠=α( ) A . 55B . 60C . 65D . 7020.如图5-14,能与∠α构成同旁内角的角有( ) A . 5个 B .4个 C . 3个 D . 2个21.如图5—15,已知AB CD //,∠α等于( ) A .75B . 80C . 85D . 95AB 120°α25°CDBMCA N P D22.如图5—16,AB CD MP AB MN ////,,平分∠∠=∠=AMD A D ,,4030,则∠NMP 等于( ) A . 10B . 15C . 5D . 75.23.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30,那么这两个角是( ) A . 42138、B . 都是10C . 42138、或4210、D . 以上都不对24.如图5—17,a ∥b ,∠1与∠2互余,∠3=1150,则∠4等于( )A .1150B . 1550C . 1350D .125025.如图5—18,∠1=150, ∠AOC =900,点B 、O 、D 在同一直线上,则∠2的度数为( )A .750B .150C .1050D . 1650图5-13 d第(18)题4321cba 第(20)题DCBAO第(19)题DCBA21图5-17 图5-18 图5-19图5-15 图5-1626.如图5—19,能表示点到直线(或线段)距离的线段有( )A . 2条B .3条C .4条D .5条 27.下列语句错误的是( )A .连接两点的线段的长度叫做两点间的距离B .两条直线平行,同旁内角互补C .若两个角有公共顶点且有一条公共边,和等于平角, 则这两个角为邻补角D .平移变换中,各组对应点连成两线段平行且相等 28.如图5—20,如果AB ∥CD ,那么图中相等的内错角是( )A .∠1与∠5,∠2与∠6;B .∠3与∠7,∠4与∠8;C .∠5与∠1,∠4与∠8;D .∠2与∠6,∠7与∠329.下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )A .①、②是正确的命题B .②、③是正确命题C .①、③是正确命题D .以上结论皆错30.下列与垂直相交的洗法:①平面内,垂直于同一条直线的两条直线互相平行;②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;③平行内, 一条直线不可能与两条相交直线都垂直,其中说法错误个数有( )A .3个B .2个C .1个D .0个 三、解答题31.如图5—21,过P 点,画出OA 、OB 的垂线.2.32.如图5-22,过P 点,画出AB 、CD 的垂线.3. B C DBA33.如图5-23,是一条河,C 河边AB 外一点:(1)过点C 要修一条与河平行的绿化带,请作出正确的示意图.(2)现欲用水管从河边AB ,将水引到C 处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)87654321D CB A 图5-20 图5-21图5-22图5-2334.如图5—24,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?NMFE DCBA35.如图5-25,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.36.如图5—26,已知:CE =DF ,AC =BD ,∠1=∠2.求证:∠A =∠B .B37.如图5-27,已知:AB //CD ,AB =CD ,求证:AC 与BD 互相平分.C38.如图5—27,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .图5-24图5-26图5-262 ABECFDHG 139.如图5—28,已知:在∆ABC 中,∠=︒C 90,AC =BC ,BD 平分∠CBA ,DE AB ⊥于E ,求证:AD +DE =BE .40.如图5—29,已知:AB //CD ,求证:∠B +∠D +∠BED =360︒(至少用三种方法)EABCD图5-27 图5-28图5-29参考答案一、填空题 1.互相垂直2.点M ,直线CD 点M,直线EF 平行线AB 、EF 间 线段GN 的长度 3.4个 ∠EOB 、 ∠DOF 、∠ABD 、∠CBD4.两条直线都与第三条直线平行,这两条直线也互相平行 CD ∥EF 5.两个角是相等两角的补角 这两个角相等6.如果一个四边形的两组对边平行,那么它的对角相等;或若一个四边形的一组对边平行,一组对角相等,那么它的另一组对边也互相平行 7.156 8.114°9.两;∠ACD 和∠B;∠BCD ;同角的余角相等 10.10°11.AB ∥CD;同位角相等,两直线平行;EF ∥GH ;内错角相等,两直线平行 12.余角;对顶角 13.∥;∥14.55︒(点拨: ∠=∠∴∠=∠=︒AOB COD AOB COD 55)15.50︒(点拨: ∠+∠=︒∠-∠=︒⎧⎨⎩311803180,∴∠=︒∠=︒⎧⎨⎩1503130,又︒=∠∴∠=∠50221 )16. 3819'︒;14141'︒(点拨:9138909112890'︒=︒-'︒=∠-∠=∠∴︒=∠AOD EOD AOE AOD ,9138'︒=∠=∠∴AOE BOF ,又 ∠+∠=︒BOF AOF 180,141419138180'︒='︒-︒=∠∴AOF )二、选择题 17.C 18.B 19.C 20.A 21.C 22.C 23.D 24.B 25.C 26.D 27.C 28.D 29.A 30.D三、解答题 31.如图5—12.32.如图5—233.略.34.(1)CD∥AB因为CD⊥MN,AB⊥MN,所以CDN=∠ABM=90°所以CD∥AB(2)平行因为∠CDN=∠ABN=90°,∠FDC=EBA所以∠FDN=∠EBN所以FD∥EB35.(1)平行因为∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义)所以∠1=∠CDB所以AE∥FC(同位角相等两直线平行)(2)平行,因为AE∥CF,所以∠C=∠CBE(两直线平行,内错角相等)又∠A=∠C 所以∠A=∠CBE所以AF∥BC(两直线平行,内错角相等)(3)平分因为DA平分∠BDF,所以∠FDA=∠ADB因为AE∥CF,AD∥BC所以∠FDA=∠A=∠CBE,∠ADB=∠CBD所以∠EBC=∠CBD36.证明:答图5-1∠=∠∴∠=∠=∴+=+==∠=∠=∴≅∴∠=∠⎧⎨⎪⎩⎪12(已知)(等角的补角相等)(已知)即在和中,(已知)(已证)(已证)()(全等三角形的对应角相等)ECB FDA AC BD AC CD BD CDAD BCADF BCE DF CE FDA ECB AD BC ADF BCE SAS A B ∆∆∆∆37. 证明: AB CD //(已知)∴∠=∠∠=∠∠=∠=∠=∠∴≅∴==⎧⎨⎪⎩⎪BAO DCO ABO CDO ABO CDO BAO DCO AB CD ABO CDO ABO CDO ASA AO CO BO DO ,(两直线平行,内错角相等)在和中(已证)(已知)(已证)(),(全等三角形对应边相等)∆∆∆∆即AC 与BD 互相平分. 38. 证明: ∠=∠12(已知)∠=∠∴∠=∠∴∴∠=∠12AHB AHB AF ED D AFC (对顶角相等)(等量代换)(同位角相等,两直线平行)(两直线平行,同位角相等)//又 ∠=∠A D (已知)∴∠=∠∴∴∠=∠A AFC AB CD B C (等量代换)(内错角相等,两直线平行)(两直线平行,内错角相等)//39. 证明: BD CBA 平分(已知)∠∴∠=∠⊥∴∠=︒∠=︒EBD CBD DE AB DEB C (角平分线的定义)(已知)(垂直的定义)(已知)9090∴∠=∠DEB C (等量代换) 在∆∆DEB DCB 和中∠=∠∠=∠=∴≅⎧⎨⎪⎩⎪DEB C EBD CBD DB DB DEB DCB AAS (已证)(已证)(公共边)()∆∆∴==+==∴+=DE DC BE BC AD DC AC BC AD DE BE ,(全等三角形的对应边相等)(已知)(等量代换)40. 证明:(1)连结BD ,如图5—3AB CD ABD CDB BED ABD CDB BED ABE CDE BED //(已知)(两直线平行,同旁内角互补)(三角形内角和为)即∴∠+∠=︒∠+∠+∠=︒︒∴∠+∠+∠+∠+∠=︒∠+∠+∠=︒1801218018012360360(2)延长DE 交AB 延长线于F ,如图5—4AB CD F D ABE FEB F BED FBE F ABE CDE BED//(已知)(两直线平行,同旁内角互补),(三角形一个外角等于和它不相邻的两个内角的和)∴∠+∠=︒∠=∠+∠∠=∠+∠∴∠+∠+∠180=∠+∠+∠+∠+∠FEB F CDE FBE F=︒+︒=︒180180360(3)过点E 作EF//AB ,如图5—5- 11 -AB CD //∴AB EF CD ////(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)∴∠+∠=︒∠+∠=︒∴∠+∠+∠+∠=︒+︒=︒∴∠+∠+∠=︒B BEF D DEF B BEF D DEF B D BED 180180180180360360(两直线平行,同旁内角互补)。
平行线单元测试2

第1章 平行线 单元测试一、选择题(每题3分,共30分)1、若1∠与2∠是两条平行线上的同位角,那么1∠与2∠的关系是 ( )A. 相等B. 互补C. 相等或互补D. 不能确定2、如图,图中1∠与2∠是内错角的是 ( )a. b. c. d. A. a.和b. B. b.和c. C. c.和d. D. b.和d.3、如图,CD 平分A C B ∠,DE AC ,且1=35∠︒,则2∠= 度 ( )A. 35︒B. 70︒C. 110︒D. 不能确定4、如图,AD BC ,那么下列结论中错误的是 ( )A. 1=D ∠∠B. 1=B ∠∠C. 180A B ∠+∠=︒D. 180D B C D ∠+∠=︒5、如图,与1∠是同旁内角的角有几个 ( )A. 0个B.1个C. 2个D. 3个6、已知两条平行直线被第三条直线所截,那么下列说法中不正确的是 ( )A. 它们所构成的同位角相等B. 它们所构成的内错角相等C. 两平行线之间的距离并非处处相等D. 它们所构成的同旁内角互补7、在满足“三线八角”的情况下,同位角、内错角、同旁内角的对数分别为( )A. 4,2,2B. 2,4,2C. 2,2,4D. 都有可能8、如图,在长方形ABCD 中AB=3cm ,BC=2cm ,则AB 与CD 之间的距离为 ( )A. 2 cmB. 3 cmC. 5 cmD. 不能确定9、如图,直线a , b 被直线c 所截,在下列条件中,不能判断a b 的一组条件是( )A. 34∠=∠B. 35180∠+∠=︒C. 35∠=∠D. 32∠=∠10、如图,若直线a b ,则1∠= 度 ( )A. 50︒B. 100︒C. 不能确定D. 130︒二、填空题(每题6分,共30分) 1、平行线的判定: 相等,两直线平行;相等,两直线平行;互补,两直线平行。
2、如图,两条直线被第三条直线所截,构成8个角中,像 和 这样的一对角叫做同位角;像 和 这样的一对角叫做内错角;像37∠∠和这样的一对角叫做 。
八年级数学上册《第一章 全等三角形》单元测试卷及答案

八年级数学上册《第一章全等三角形》单元测试卷及答案一.选择题(共8小题,满分32分)1.如图所示,△ABC≌△AEF,在下列结论中,不正确的是()A.∠EAB=∠FAC B.BC=EFC.∠BAC=∠CAF D.CA平分∠BCF2.如图所示,在△ABC中,按下列步骤作图:第一步:在AB、AC上分别截取AD、AE,使AD=AE;第二步:分别以点D和点E为圆心、适当长(大于DE的一半)为半径作圆弧,两弧交于点F;第三步:作射线AF交BC于点M;第四步:过点M作MN⊥AB于点N.下列结论一定成立的是()A.CM=MN B.AC=AN C.∠CAM=∠BAM D.∠CMA=∠NMA3.如图,在3×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是()A.∠1=∠2 B.∠2=2∠1 C.∠2=90°+∠1 D.∠1+∠2=180°4.如图,点E、F在BC上,BE=FC,∠B=∠C.添加下列条件不能使得△ABF≌△DCE的是()A.AB=DC B.∠A=∠D C.AF=DE D.∠AFB=∠DEC5.如图,AD是△ABC的高,AD=BD,DE=DC,∠BAC=65°,则∠ABE的度数是()A.20°B.25°C.30°D.35°6.如图,要测量河两岸相对的两点A,B之间的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长,则上述操作,判定△EDC≌△ABC的理由是()A.SSS B.ASA C.AAS D.SAS7.如图,Rt△ABC中,∠C=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是()A.B.C.D.8.如图,已知∠AOB与∠EO'F,分别以O,O'为圆心,以同样长为半径画弧,分别交OA,OB于点A',B',交O'E,O'F于点E',F'.以B'为圆心,以E'F'长为半径画弧,交弧A'B'于点H.下列结论不正确的是()A.∠AOB=2∠EO'F B.∠AOB>∠EO'FC.∠HOB=∠EO'F D.∠AOH=∠AOB﹣∠EO'F二.填空题(共8小题,满分32分)9.如图所示的图案是由全等的图形拼成的,其中AD=0.5,BC=1,则AF=.10.如图所示是用直尺画平行线的方法,画图原理是.11.下列语句:①作∠AOB=3∠α;②以点O为圆心作弧;③以点A为圆心,线段a的长为半径作弧;④作∠ABC,使∠ABC=∠α+∠β.其中错误的为.(填序号即可)12.如图,AC=DB,AO=DO,CD=200m,则A,B两点间的距离为m.13.如图,已知∠C=∠D,再添加一个条件能判定△ABC≌△BAD.14.∠AOB=50°,以O为圆心,任意长为半径画弧,交OA,OB于M,N;分别以M,N为圆心,大于的长为半径画弧,两弧交于P;作射线OP.则∠AOP=°.15.如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′,BE,CD交于点F.若∠BAC=40°,则∠BFC的度数为.16.如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠BAC的度数为.三.解答题(共6小题,满分56分)17.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.18.如图,在四边形ABCD中,AB=CB,AD=CD,连接BD,试说明△ABD≌△CBD.19.如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿着堤岸走到电线杆B旁,接着再往前走相同的距离,达到C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点,量得CD的距离是35米.你知道在点A处小明与游艇的距离吗?请说出他这样做的理由.20.如图,已知Rt△ABC和射线CM,∠A=90°,∠ACB=65°,请用尺规作图法,在CM上作一点P,使得∠CBP=25°.(保留作图痕迹,不写作法)21.如图,点F、G分别在正五边形ABCDE的边BC、CD上,连结AF、BG相交于H,△ABF≌△BCG.(1)求∠ABC的度数;(2)求∠AHG的度数.22.已知:如图,DB⊥AB,DC⊥AC,∠1=∠2.求证:AD平分∠BAC.参考答案与试题解析一.选择题(共8小题,满分32分)1.解:∵△ABC≌△AEF,∴BC=EF,AC=AF,∠B=∠E,∠BAC=∠EAF,∠BCA=∠F,故B正确,不符合题意;C错误,符合题意;∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,即∠EAB=∠FAC,故A正确,不符合题意;∵AC=AF,∴∠ACF=∠F,∴∠BCA=∠ACF,∴CA平分∠BCF,故D正确,不符合题意;故选:C.2.解:由题意可知,AM平分∠CAB,∵∠C不一定等于90°,∴CM≥MN,因此A选项不符合题意;∵∠C不一定等于90°,∴AC不一定等于AN,因此B选项不符合题意;∵AM平分∠CAB,∴∠CAM=∠BAM,因此C选项符合题意;∵∠C不一定等于90°,∴∠CMA不一定等于∠NMA,因此D选项不符合题意.故选:C.3.解:如图,在△ABC与△EDF中,,∴△ABC≌△EDF(SAS),∴∠1=∠ABC.∵∠ABC+∠2=180°,∴∠1+∠2=180°.故选:D.4.解:∵BE=CF,∴BF=CE,若AB=DC,∠B=∠C,由“SAS”可证△ABF≌△DCE;若∠A=∠D,∠B=∠C,由“AAS”可证△ABF≌△DCE;若AF=DE,∠B=∠C,不能证明△ABF≌△DCE;若∠AFB=∠DEC,∠B=∠C,由“ASA”可证△ABF≌△DCE;故选:C.5.解:∵AD是△ABC的高,∴∠ADB=∠ADC=90°,在△BDE和△ADC中,,∴△BDE≌△ADC(SAS),∴∠DAC=∠DBE,∵∠DAC=∠BAC﹣∠BAD=65°﹣45°=20°,∴∠DBE=20°,∴∠ABE=∠ABD﹣∠DBE=25°,故选:B.6.解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,所以用到的是两角及这两角的夹边对应相等即ASA这一方法.故选:B.7.解:A.由作法知AD=AC,∴△ACD是等腰三角形,故选项A不符合题意;B.由作法知所作图形是线段BC的垂直平分线,∴不能推出△ACD和△ABD是等腰三角形,故选项B符合题意;C由作法知,所作图形是线段AB的垂直平分线,∴DA=DB,∴△ABD是等腰三角形,故选项C不符合题意;D.∠C=90°,∠B=30°,∠BAC=60°,由作法知AD是∠BAC的平分线,∴∠BAD=30°=∠B,∴DB=DA,∴△ABD是等腰三角形,故选项D不符合题意;故选B.8.解:由作图可知,∠EO′F=∠HOB′,∠AOB>∠EO′F,∠AOH=∠AOB﹣∠EO′F,故选项B,C,D正确,故选:A.二.填空题(共8小题,满分32分)9.解:由题可知,图中有8个全等的梯形,所以AF=4AD+4BC=4×0.5+4×1=6,故答案为:6.10.解:由作图得到∠1=∠BAC,则根据同位角相等,两直线平行可判断a∥b.故答案为:同位角相等,两直线平行.11.解:作∠AOB=3∠α,所以①正确;以点O为圆心,线段a的长为半径作弧,所以②错误;以点A为圆心,线段a的长为半径作弧,所以③正确;作∠ABC,使∠ABC=∠α+∠β,所以④正确.故答案为:②.12.解:∵AC=DB,AO=DO,∴BO=CO,在△AOB和△DOC中,,∴△AOB≌△DOC(SAS),∴AB=DC,∵CD=200m,∴AB=200m,即A,B两点间的距离是200m,故答案为:200.13.解:∵∠C=∠D,AB=AB根据AAS判定△ABC≌△BAD,可以添加∠DAB=∠CBA或者∠DBA=∠CAB;故答案为:∠DAB=∠CBA(答案不唯一).14.解:由基本作图可知,OP是∠AOB的平分线,∴∠AOP=∠AOB=×50°=25°,故答案为:25.15.解:延长C′D交AB′于H.∵△AEB≌△AEB′,∴∠ABE=∠AB′E,∵C′H∥EB′,∴∠AHC′=∠AB′E,∴∠ABE=∠AHC′,∵△ADC≌△ADC′,∴∠C′=∠ACD,∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,∴∠BFC=∠AHC′+∠C′+∠DAC,∵∠DAC=∠DAC′=∠CAB′=40°,∴∠C′AH=120°,∴∠C′+∠AHC′=60°,∴∠BFC=60°+40°=100°,故答案为:100°.16.解:∵AD=AE,∴∠ADC=∠AEB,在△ACD和△ABE中,,∴△ACD≌△ABE(SAS),∴AC=AB,∠CAD=∠BAE=60°,∴∠B=∠C,∵∠C=∠1﹣∠CAD=110°﹣60°=50°,∴∠B=50°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣50°=80°,故答案为:80°.三.解答题(共6小题,满分56分)17.解:如图所示,(答案不唯一)18.证明:在△ABD和△CBD中,,∴△ABD≌△CBD(SSS).19.解:在A点处小明与游艇的距离为35米,理由:在△ABS与△CBD中,,∴△ABS≌△CBD(ASA),∴AS=CD,∵CD=35米,∴AS=CD=35米,答:在A点处小明与游艇的距离为35米,20.解:如图,点P为所作.21.解:(1)∵正五边形的内角和为:(5﹣2)×180°=540°,∴∠ABC=×540°=108°;(2)∵△ABF≌△BCG,∴∠BAF=∠CBG,∵∠BAF+∠ABH=∠AHG,∴∠CBH+∠ABH=∠AHG=∠ABC=×540°=108°,∴∠AHG=108°.22.证明:∵DB⊥AB,DC⊥AC,∴∠ABD=∠ACD=90°.∵∠1=∠2,∴DB=DC,∵AD=AD,在Rt△ABD和Rt△ACD中,,∴Rt△ABD≌Rt△ACD(HL).∴∠BAD=∠CAD,∴AD平分∠BAC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级(上)第一章《平行线》单元测试(三)
一、填空题:
1.如图1,若12//,145l l ∠=︒,则2∠=________; l 2
l 1
2
1
b
a
d c
3
2
1b
a d
c 3
4
2
1
图1 图2 图3
2.如图2,已知直线//,//,1115a b c d ∠=︒,则2∠=________,3∠=________;
D
C
B
A
O
αD C E
B A
21
124︒
78︒
D
C
E
B
A
图4 图5 图6 3.如图3,182,298,380∠=︒∠=︒∠=︒,则4∠的度数为________;
4.如图4,//,AD BC AC 与B D 相交于O ,则图中相等的角有________对;
D
C
F E
B A
647
5
4
3
2
1
图7 图8 图9
5.如图5,已知//,1100,2120AB CD ∠=︒∠=︒,则α∠=________;
6.如图6,D AE 是一条直线,//D E B C ,则B A C ∠=________;
7.如图7,//,//AB CD AD BC ,则图中与A ∠相等的角有________个;
8.如图8,标有角号的7个角中共有________对内错角,________对同位角,________对同旁内角;
9.如图9,(1)∵______A ∠=(已知), ∴//A C E D (________________) (2)∵2______∠=(已知), ∴//A C E D (________________) (3)∵______180A ∠+=︒(已知), ∴//A B F D (________________) (4)∵//______AB (已知),
∴2180AED ∠+∠=︒(________________) (5)∵//______AC (已知),
∴1C ∠=∠(________________) 二、选择题:
10.下列命题正确的是( )
A.内错角相等;
B. 三条直线相交 ,必产生同位角、内错角、同旁内角;
C.相等的角是对顶角;
D.同位角相等,两直线平行;
11.两平行直线被第三条直线所截,同位角的平分线( ) A.互相重合;B.互相平行;C.互相垂直;D.相交;
12.如图10,已知1,2B C ∠=∠∠=∠,则下列结论不成立的是( ) A.//A D B C ;B.B C ∠=∠;C.2180B ∠+∠=︒;D.//A B C D ;
D C
B
A
2
1E
D
B
A
图10 图11
13.如图11,若//A B C D ,则,,A E D ∠∠∠之间的关系是( ) A.180A E D ∠+∠+∠=︒;B 180A E D ∠-∠+∠=︒; C. 180A E D ∠+∠-∠=︒;D. 270A E D ∠+∠+∠=︒; 三、解答题:
14.如图,C D 平分,//,80ACB DE BC AED ∠∠=︒,求E D C ∠的度数;
E
D
C
B
A
15.如图,已知//,65,AB CD B CM ∠=︒平分,90BCE MCN ∠∠=︒,求D C N ∠的度数;
E
D
C
B
A M
N
16.如图,//,70,20,130CD AB DCB CBF EFB ∠=︒∠=︒∠=︒,问直线E F 与A B 有怎样的位置关系,为什么?
F
E
D
C
B
A
17.如图,//,AB CD HP 平分D H F ∠,若80AG H ∠=︒,求D H P ∠的度数;
F
E
D
C
B
A
G
H P
18.根据下列证明过程填空:
如图,,,,BD AC EF AC D F ⊥⊥分别为垂足,且14∠=∠,求证:A D G C ∠=∠; 证明:∵,BD AC EF AC ⊥⊥(________) ∴2390∠=∠=︒,
∴//B D E F (________)
∴4______∠=(________________)
∵14∠=∠(________________)
∴1______∠=(________________) ∴//D G B C (________________) ∴A D G C ∠=∠(________________)
19.阅读下面的证明过程,指出其错误:
已知A B C ∆,求证:180A B C ∠+∠+∠=︒; 证明:过A 作//D E B C ,且使1C ∠=∠, ∵//D E B C (画图)
∴2B ∠=∠(两直线平行,内错角相等) ∵1C ∠=∠(画图)
∴3213180B C ∠+∠+∠=∠+∠+∠=︒, 即180BAC B C ∠+∠+∠=︒;
20.已知:如图,,CB AB CE ⊥平分,BCD DE ∠平分,1290CDA ∠∠+∠=︒, 求证:D A AB ⊥;
E
D
C
B A 2
1。
