03第3章_平面结构的运动分析
第三章平面机构的运动分析

第三章平⾯机构的运动分析第三章平⾯机构的运动分析§3-1 研究机构运动分析的⽬的和⽅法1、运动分析:已知各构件尺⼨和原动件的运动规律→从动件各点或构件的(⾓)位移、(⾓)速度、(⾓)加速度。
2、⽬的:判断运动参数是否满⾜设计要求?为后继设计提供原始参数3.⽅法:图解法:形象直观、概念清晰。
精度不⾼?(速度瞬⼼法,相对运动图解法)解析法:⾼的精度。
⼯作量⼤?实验法: §3-2速度瞬⼼法及其在机构速度分析上的应⽤1、速度瞬⼼:两构件作平⾯相对运动时,在任意瞬间总能找到这样的点:两构件的相对运动可以认为是绕该点的转动。
深⼊理解速度瞬⼼:1)两构件上相对速度为零的重合点,即同速点; 2)瞬时具有瞬时性(时刻不同,位置不同);3)两构件的速度瞬⼼位于⽆穷远,表明两构件的⾓速度相同或仅作相对移动;4)相对速度瞬⼼:两构件都是运动的;绝对速度瞬⼼:两构件之⼀是静⽌的(绝对速度为零的点;并⾮接触点的变化速度);2、机构中瞬⼼的数⽬年K :2)1(-=n n K n —— 构件数(包括机架) 3、瞬⼼位置的确定1)直接观察法(定义法,由于直接形成运动副的两构件);2=N P 23设:1k V 3、13)曲柄滑块机构4)直动平底从动件凸轮机构62)14(4=-?=N K5)图⽰机构,已知M点的速度,⽤速度瞬⼼法求出所有的瞬⼼,并求出V C,V D,i12。
解:直接观察:P12、P23、P34;P14=(n_-n).×V M ; P13= P12P23. ×P14P34P24= P12P14×C·P24P34 ; ω1= V M/ P14M ; V B= P14B·ω1ω2=V B/ P12P24 ; V C= P24C·ω2ω1/ω2=( V M/ P14M)/( V B/ P12P24); V D= P24D·ω2速度瞬⼼法⼩结:1)速度瞬⼼法仅⽤于求解速度问题,不能⽤于求解加速度问题。
第三章平面机构运动简图

F=3n-2PL-PH =3 3-23-1
=2 ×
F=3n-2PL-PH =3 2-2 2- 1
=1 √
3.虚约束:
在特殊的几何条件下,有些约束所起的限制作用是重复
的,这种不起独立限制作用的约束称为虚约束。
例如:图示凸轮机构中的两个移动副(C、C′)所起的 限制作用是一样的,即其中一个是起重复约束作用。
F>0, 原动件数<F,相对运动不确定
原动件数>F,机构破坏
机构(运动链)具有确定相对运动的条件为:
原动件数 =自由度数且大于零(F>0)
三、几种特殊情况的处理
1.复合铰链 由两个以上构件在一处产生的转动副
2 1
3
处理:m 个构件同时在一处以转动副相联,它必然构 成( m-1)个转动副。
例: 试计算图示平面直线的机构自由度。
2
A
B
1
3
D 4 C
第三节平面机构具有确定相对运动的条件
一、机构的自由度及其计算
1.机构自由度概念:机构中各构件相对于机架 所能具有的独立运动的数目。 2.计算机构自由度
设n个活动构件,PL个低副,PH个高副 n个活动构件具有3n个独立运动 由于1个平面低副引入2个约束, 减少2个自由度。PL个低副 将减少2PL个自由度;由于1个平面高副引入1个约束, 减 少1个自由度。PH个高副将减少PH个自由度。因此,机构自 由度为:
F=3n-2PL-PH=3× 7-2×14 - 0
= -7 ×
F=3n-2PL-PH=3× 7-2×10 - 0
=1 √
平面直线机构
F
2.局部自由度
局部自由度:不影响整个机构运动的、局部的独立运动
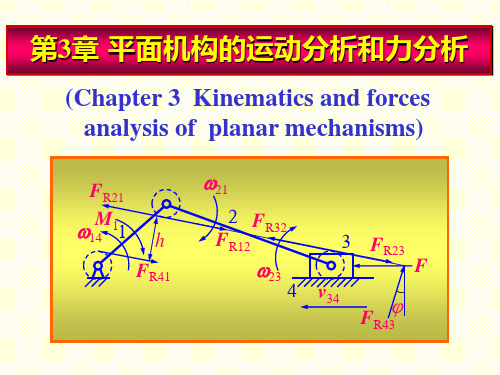
机械原理-第3章 平面机构的运动分析和力分析
a
大小:2w1×vB2B1=2w1vB2B1sin90°=2w1vB2B1; k B 2 B1 方向:将vB2B1的方向沿w1转过90°。
vB1B2 1
2 B
(B1B2)
vB1B2 1
2 B
(B1B2)
ω1
a
k B 2 B1
ω1
a
k B 2 B1
(3)注意事项
B (B1B2)
1
2
vB1 = vB2,aB1 = aB2,
目的: 了解现有机构的运动性能,为受力 分析奠定基础。 方法:1)瞬心法(求速度和角速度); 2)矢量方程图解法; 3)解析法(上机计算)。
3.1
速度瞬心
(Instant center of velocity )
3.1.1 速度瞬心
两个互作平行平面运动的构件 定义:
上绝对速度相等、相对速度为
零的瞬时重合点称为这两个构 件的速度瞬心, 简称瞬心。瞬 心用符号Pij表示。
图(b) 2
(B1B2B3)
扩大刚体(扩大构件3),看B点。
B 1 A
b2
C
vB3 = vB2 + vB3B2
方向:⊥BD ⊥AB 大小: ? lAB w1 ∥CD ?
3
w1
D
4
p
选 v ,找 p 点 。
v
v B 3 pb3 μv ω3 (逆 ) l BD l BD
b3
(b)
例4:已知机构位臵、尺寸,w1为常数,求w2、a2。
C B
n t n t aC aC a B aCB aCB
2
1
E
方向:C→D ⊥CD B→A C→B ⊥CB 大小:lCD w32 ? lABw12 lCB w22 ?
3平面机构的运动分析

VP 24 P12 P24 2 P14 P24 4
解得:
3
4
ω4
P14
ω4 P P24 12 4 2 P P24 14
VP24
P24
2
P12
ω2
1
例2 图示凸轮机构,设已知各构件的尺寸及凸轮的角速度ω2, 试求从动件 3 的移动速度V。 解: 1取长度比例尺μL作机构图 2求P23如图所示。 3 求V
水平
B→A
a
t A CB
ε1 ω1
aCB
C 3
⊥AB
C→B
⊥CB
p
n aB
aC
c
实际加速度( m / s 2) a 图示加速度( mm)
p c
b
a B
aB
aCB
aCB
b
aCB 2 lCB
ac
ac pc a
c
n aCB
注意:图示矢量 bc 与 aCB 下标字母顺序相反
V3 lP14 P13 1
P13 1、2、3 1、4、3 P24
1
P12∞ P34∞ VP13 P34∞ ∞ P12
P12∞ P13 4 P34∞
例5 求出图示机构的全部瞬心,假设各部尺寸和ω1为已知, 求滑块的速度V3及杆件2的角速度。 解:1 求全部瞬心 P13 1、2、3 P24 2、3、4 2、1、4 1、4、3 2 求滑块3的速度 P24 P24是绝对瞬心 3 求杆件2的角速度
P23∞ P12 P23∞ P23∞
P24 2
A B
P23 3 P34 4
C
1
P12
P13∞
P14∞ 14∞ P
第三章第三章平面机构的运动分析平面机构的运动分析

若既有滚动又有滑 动, 则瞬心在高副接 触点处的公法线上。
三、机构中瞬心位置的确定 (续) ◆ 不直接相联两构件的瞬心位置确定
三心定理:三个彼此作平面平行运动的构 件的三个瞬心必位于同一直线上。 例题:试确定平面四杆机构在图示位置 时的全部瞬心的位置。 解: 机构瞬心数目为: K=6 瞬心P13、P24用 于三心定理来求 P24 P12 P23 2 3 4 P34 P13
e
n n' ①由极点p1向外放射的矢量代表构件相应点的绝对加速 度;
b' 注意:速度影像和加速度影像 只适用于构件。
②连接两绝对加速度矢量矢端的矢量代表构件上相应两 点间的相对加速度,其指向与加速度的下角标相反; ③也存在加速度影像原理。
三、两构件重合点间的速度和加速度的关系
已知图示机构尺寸和原动件1的运动。求重合点C的运动。 1. 依据原理 构件2的运动可以认为是随同构件1的牵连运动和构件2 相对于构件1的相对运动的合成。 2、依据原理列矢量方程式 vc2c1 B 2 C1、C2、C3 C 大小: ? √ ? 方向:⊥ CD ⊥AC ∥AB
vC 2 = vC 1 + vC 2C 1
ω1
1
ac1 4
3 大小: √ ? √ D vc1 √ ? C→D ⊥CD √ 方向:
n k r aC2 = aC3D +atC3D = aC1 +aC2C1 +aC2C1
√ ∥AB
A
a
k C 2 C1
= 2ω1vC 2C1
科氏加速度方向是将vC2C1沿 牵连角速度ω1转过90o的方向。
(1) 速度解题步骤:
★求VC ①由运动合成原理列矢量方程式
v C = v B + v CB
3 平面机构运动分析

vE = μv pe
(方向:p→e )
F
vF = μv pf
(方向:p→f )
E
ω1
B
1
A
ω2
2x
vB
(a)
3
C
vC x
4
p f
(b) 图3-1 曲柄滑块机构
c eb
2. 确定构件的加速度和角加速度
根据相对运动的合成原理得加速度方程为:
方向:
aC = anB + atB + anCB + atCB x-x B→A ⊥AB C→B ⊥BC
§3-2 用图解法作机构的运动分析
问 §3-2-1 用矢量方程图解法作机构的运动分析
题
1: 矢
1、同一构件上两点间的速度和加速度求解法
量
方
图3-1(a )所示为曲柄滑块
程 图
机构,比例尺为μl 。
解所 法必
已知曲柄 1 的角速度ω1和
作须 机的
角加速度1,求图示位置时
构几 的个
连杆 2 的角速度ω2、角加速
1
1
C
vB3B2
3
ω3
3
D
例3-1有结构尺寸,1= 60,1=10rad/s, =100。
4
(a)
图3-2 曲柄导杆机构
1. 速度分析
vB3
方向: ⊥BD 大小: ?
vB1 (B2,
(vB2) ω1
1
B3,
B
B4)
2
A 1
= vB2 + vB3 B2
⊥AB
∥BC
( 3-3 )
ω1 lAB
? vB3 =μv pb3 (方向:p→b3 )
第三章 平面机构的运动分析

1. 矢量方程图解法的基本原理和作法
在用矢量方程图解法对机构进行速度和加速度分析
时,首先是根据相对运动原理,建立点与点之间的 速度和加速度矢量方程,然后用作图法求解矢量方 程,按比例绘出机构的速度多边形和加速度多边形, 求得未知的运动参数。
第三章 平面机构的运动分析
第三章 平面机构的运动分析
两构件以平面高副相联接时,当两构件作 纯滚动,接触点相对速度为零,
该接触点M即为瞬心P12;
第三章 平面机构的运动分析
若高副元素间既作相对滚动,又作相对滑 动,由于相对速度v12存在,并且其方向沿 切线方向,
瞬心P12必位于过接触点的公法线(切线的垂线) n---n上,具体在法线的哪一点,须根据其它 条件再作具体分析确定。
B
A
第三章 平面机构的运动分析
速度分析
①
②
通过分析,了解从动件的速度变化
为加速度分析作准备。
规律是否满足工作要求。如牛头刨床; 加速度分析 ① 确定各构件及其上某些点的加速度; ② ③ 了解机构加速度的变化规律; 为机构的力分析打基础。 ●图解法 ●解析法
速度瞬心法
矢量方程图解法
机构运动分析的方法
第三章 平面机构的运动分析
第一节 机构运动分析的任务、目的及方法
机构的运动分析:就是对机构的位移、速度和 加速度进行分析
位移、轨位形),绘制 机构位置图。 ② 确定构件的运动空间,判断是否发生 干涉。 ③ 确定构件行程, 找出极限位置。 ④ 确定点的轨迹(连杆曲线)。
设有矢量方程: D= A + B + C 因每一个矢量具有大小和方向两个参数,根据 已知条件的不同,上述方程有以下四种情况: D= A + B + C 大小:? √ √ √ 方向:? √ √ √
第三章平面机构的运动分析

P24
K = N(N-1)/ 2
3
2 ∞
= 4(4-1)/ 2
=6
2、求出全部瞬心 P34
∞ P34
P13
1
P12
2
1
P23
3
P14
4
3、求出3的速度
∵P13为构件1、3等速重合点
v 3 v P13 1 p14 p13 l
P34∞
VP13
2
P24
P34∞
P13
1
P12
a
实际加速度 图示尺寸
m / s2 mm
, 作矢量多边形。
c´
p b
n
由加速度多边形得:
aC a pc m / s 2
t 2 aCB l BC
a nc l BC
同样,如果还需求出该构件上E 点的加速度 aE,则
c´ p
acbt
n t aE aB aEB aEB
速度分析 ① 位移、轨迹分析
加速度分析
通过分析,了解从动件
①
②
确定各构件及其上某些点的加
速度; 了解机构加速度的变化规律;
的速度变化规律是否满足工
作要求。如牛头刨床; ② 为加速度分析作准备。
③
为机构的力分析打基础。
3. 机构运动分析的方法
速度瞬心法 ● 图解法 矢量方程图解法 ● 解析法
第三章 平面机构的运动分析
基本要求: 本章重点: 的应用;
明确机构运动分析的目的
和方法;
速度瞬心的概念和“三心定理” 应用相对运动图解法原理求二
级机构构件上任意点和构件的运 动参数。
理解速度瞬心(绝对瞬心
第3章 平面连杆机构的运动分析

1 2 1 P12 2 n
P12
滚滑高副,瞬心在过接触点公法线上某处。
第二节 用速度瞬心法进行机构的速度分析
2)两构件之间没有用运动副连接时的瞬心位置
三心定理:作平面运动的三个构件有三个瞬 心,三个瞬心位于一条直线上。
n
2
C
3 VC2 VC3 P23 B 1 P13
ω2
A
1 P12
二、用瞬心法进行机构的速度分析
已知机构尺寸和主动件角速度ω1,求ω2和ω3
P24
1、利用Vp12求ω2
ω2
V P12
V p12 = ω1 L p12 p14
2 P23 3 P43
P12
= ω 2 L p12 p 24
LP 14 P 12 ω2 = ω1 LP 24 P 12
P13
ω1
P14
1 4
3、引入加速度比例尺 μa ,把加速度向量转化为长度向量。
实际加速度( m/s 2 ) µa = 图 中的长度( mm)
4、列速度和加速度矢量方程,进行矢量加法或减法的图解运算
第三节 用相对运动图解法对机构进行运动分析
二、相对运动图解法
例 1
E 2 B C 大小
V= VB + VCB C
ω2 ω3
1
P
2
第二节 用速度瞬心法进行机构的速度分析
一、瞬心的基本概念
瞬心的意义:
A1(A2)
VA2A1
绝对速度相等的重合点
B1(B2)
VB2B1
VP1 = VP2 相对速度为零的重合点 VP1P2 = 0 绝对瞬心、相对瞬心
1
P
2
第二节 用速度瞬心法进行机构的速度分析
第3章 平面机构的运动分析

Δbce 与 ΔBCE 的对应边相互
垂直,故两者相似,且字母顺 序方向也一致。图形 bce 称 为构件图形 BCE 的速度影像 (velocity image of link)。
F
借助速度影像在已知某构 件两点速度时求该构件上 第三点的速度就很方便。 如求F点速度。
注意:速度影像原理只适用于 构件,而不适用于整个机构。
方向: 大小: √ √ 垂直BE ? √ √ 垂直CE ?
左图即为机构的速度多边形 (velocity of vector polygon of mechanism)或速度图。
p 点称为速度多边形的极点,
即(绝对)速度为零的点。 由极点向外与图中任一点所作的带箭头的矢量 线代表机构中构件上相应点的绝对速度。而连接两 绝对速度矢量端的矢量线代表构件上相应两点间的 相对速度。如 pb 表示 vb ; bc 代表 v CB ,方向 由B指向C。
瞬心也可定义为两构件上瞬时相对速度为零或 瞬时绝对速度相等的重合点。 以Pij表示构件i、j的瞬心。
绝对瞬心(absolute instantaneous centre of velocity)
绝对速度为零的瞬心。即
vP 0 vP 0
相对瞬心(relative instantaneous centre of velocity) 绝对速度不为零的瞬心。即
第3章 平面机构的运动分析
基本要求:
1、了解对平面机构进行运动分析的任务及目的 和常用的方法; 2、掌握平面机构瞬心的概念及瞬心求法和利用 瞬心对平面机构进行速度分析; 3、掌握利用矢量方程图解法作机构的速度及加 速度分析; 4、了解用解析法对机构进行运动分析。
主要内容:
1、速度瞬心概念与机构瞬心位置求解;
第03章 平面机构的运动分析

例题分析
实际尺寸 1、取长度比例尺l m / mm , 作机构运动简图。 图示尺寸 2、速度分析
a)列出速度矢量方程式
vC vB vCB
方向:∥xx
⊥AB ⊥CB
大小: ?
√
?
实际速度 m / s b)根据矢量方程式,取速度比例尺v , 图示尺寸 mm 作矢量多边形。
、α υ χ
大小: ?
√
?
√
?
α υ C、 χ υ α
C
极点
χ
构件BCE的速度影像
a)
(vE )vB vEB vC vEC
方向: ? ⊥AB ⊥BE √ ⊥CE
vE v pe m / s
大小: ?
√
?
√
?
3、加速度分析 a)根据运动合成原理,列
出加速度矢量方程式:
aC aB aCB aB aCB aCB
'
n
' '
同样,如果还需求出该构件上E点的加速度 aE,则:
α ω α υ 、 χ
C C
υ α
χ
构件BCE的加速度影像
a)
n t n t ( aE ) aB aEB aEB aC aEC aEC 极点
aC a p' c' m / s2
c'
方向: √ E→B ⊥BE
大小: √ ω2 lBE ?
aC 2 aC 1 aC 2 C 1 aC 2 C 1
方向: ? 大小: ?
√ √
k
k
r
√ √
∥AB ?
r n t
k
大小:a aC 2 aC 1 aC 2 C 1 aC 2C 1w1C 3 D aC 3 D 2 av
3平面机构的运动分析

瞬心的数目 K=N(N-1)/2 ( - )
N—构件数(含机架) 构件数(含机架) 构件数
瞬心的位置
1)转动副 ) 转动副的瞬心就在转动副中心 转动副中心. 转动副的瞬心就在转动副中心.
P12 1 2 P∞
1 A VB 2 VA
2)移动副 移动副 移动副的瞬心在垂直于导路方向的无穷远处 垂直于导路方向的无穷远处. 移动副的瞬心在垂直于导路方向的无穷远处. n 滚动副 3)平面高副 3)平面高副 滚滑副 1 纯滚动副 P 2 2 滚滑副 1ω 12
V1p13 = V3P13 = V3
V3 =lP14 P13 ω1 =l
P13 1,2,3 , , 1,4,3 , , P24
ω1
P12∞ P13 4 P34∞
求出图示机构的全部瞬心,假设各部尺寸和ω 为已知, 例5 求出图示机构的全部瞬心,假设各部尺寸和 1为已知, 求滑块的速度V 及杆件2的角速度 的角速度. 求滑块的速度 3及杆件 的角速度. 1,2,3 2,3,4 , , , , 解:1 求全部瞬心 P13 P24 2,1,4 , , 1,4,3 , , 2 求滑块 的速度 求滑块3的速度 P24 P24是绝对瞬心 3 求杆件 的角速度 求杆件2的角速度
V12
B
P∞
n
瞬心位置小结 转动副的瞬心就在转动副中心. 转动副的瞬心就在转动副中心. 转动副中心 移动副的瞬心在垂直于导路方向的无穷远处. 移动副的瞬心在垂直于导路方向的无穷远处. 垂直于导路方向的无穷远处 纯滚动副的瞬心就在其接触点上 纯滚动副的瞬心就在其接触点上 接触点 滚滑副的瞬心在其过接触点所作的公法线上 滚滑副的瞬心在其过接触点所作的公法线上 过接触点所作的公法线
运动分析的内容: 运动分析的内容:
03第3章平面结构的运动分析

已知:构件2的角速度ω2 和长度 比例尺μl
求:从动件3 的速度V3;
解:由直接观察法可得P12,由三 心定理可得P13和P23如图所示。 由瞬心的概念可知:
vvP23 2P12 P23l
瞬心法小结
1)瞬心法 仅适用于求解速度问题,不可用于加速度分析。
2)瞬心法 适用于构件数较少的机构的速度分析。 (多构件导致瞬心数量过多,分析复杂。)
(1)复数矢量法 (2)矩阵法
位置方程:是速度分析和加速度分析的基础 所用数学工具 :矢量、复数、矩阵
重点:矢量方程图法和复数矢量法
3.2 用速度瞬心法作机构速度分析
1. 速度瞬心及其位置的确定
瞬心是瞬时等速重合点。 瞬时,是指瞬心的位置随时间而变; 等速,是指在瞬心这一点,两构件的 绝对速度相等(包括大小和方向)、 相对速度为零; 重合点,是指瞬心既在构件1上,也 在构件2上,是两构件的重合点。
机构运动分析还为机械系统的动力学分析提供速度和加 速度数据。
3 .机构运动分析的方法:
图解法 解析法
速度瞬心法 矢量方程图解法 复数矢量法 矩阵法
1. 图解法:形象、直观 ,精度也能满足实际问题的要求, 但不高 ; (1)对于速度分析,有瞬心法。 (2)矢量方程图解法(相对运动图解法)。
2. 解析法: 效率高,速度快 ,精度高; 便于对机构进行深入的研究。
三心定理:作平面运动的三个构件,共有三个瞬心,它 们位于同一 条直线上。
KN(NI)323
2
2
2. 用瞬心法作机构的速度分析
1. 铰链四杆机构
已知:各杆长及1 ,1。求:2 ,3 。 V E
KN(NI)436
2
2
P14、P12、P23、P34位于铰链中心 用三心定理确定P13、P24
机械原理课件第三章平面机构的运动分析

目录
• 引言 • 平面机构的运动分析基础 • 平面机构的运动特性分析 • 平面机构的力分析 • 平面机构的运动误差分析 • 平面机构运动分析的应用实例
01 引言
平面机构运动分析的目的和任务
01
02
目的:平面机构运动分 任务 析的主要目的是确定机 构中各构件在任意时刻 的位置、速度和加速度, 为机构的优化设计、性 能评估及控制系统设计 提供依据。
平面机构的运动速度分析
总结词
描述平面机构中各构件的运动速度。
详细描述
运动速度是反映机构动态特性的重要参数。通过分析各构件的运动速度,可以了 解机构的动态性能,如传动的平稳性、振动和冲击等。常用的速度分析方法包括 瞬时速度法和平均速度法。
平面机构的运动加速度分析
总结词
描述平面机构中各构件的运动加速度。
详细描述
运动加速度是反映机构动态特性的另一个重要参数。通过分析各构件的运动加速度,可以了解机构的 动态性能,如振动、冲击和稳定性等。常用的加速度分析方法包括瞬时加速度法和平均加速度法。
04 平面机构的力分析
平面机构的力平衡分析
静力学平衡分析
通过计算机构各构件所受的力, 判断机构在静止状态下是否平衡 。
动态力的影响
研究动态力对机构运动的影响,如振 动、冲击等。
05 平面机构的运动误差分析
平面机构的运动误差概念
运动误差
机构实际运动与理论运动 的偏差量。
静态误差
机构在静止状态下产生的 误差。
动态误差
机构在运动状态下产生的 误差。
平面机构的运动误差计算方法
解析法
基于数学模型和公式计算误差。
实验法
通过实验测量机构的实际运动数 据,与理论数据进行比较。
第三章平面结构的运动分析

第一节 引言
• 三、与理论力学的区别 • 点--刚体 • 用运动副联结的构件(刚体) •
第二节 速度分析的瞬心法
• 一、引言 • 图解法的一种,概念清楚,后面用到, 有时很简单。 • 二、瞬心的定义 • 两构件运动速度相同的点 • 相对瞬心---两构件均在运动。 • 相对瞬心---有一个构件静止
• 运动分析图解法 • 瞬心法(确定、应用、特点) • 相对运动图解法 • 解析法 • 两者的关系
• 一、基本原理 • 运动的合成 • 点的绝对运动=坐标系的运动+相对于 坐标系的运动 • 即∶ VB VA VBA
• 二、不含哥氏加速度的机构运动分析 • 哥氏加速度----动系--转动坐标系
第三节 运动分析的矢量方程图解法
• 动点相对与动系有相对运动 • -----移动副,转动系统 • 用例子说明 • -----矢量方程 • 影象法---同一构件上已知两点的速 度(加速度)求第三点的速度(加速度)用影 象法,-----图形的大小成比例,转向相同
第三节 运动分析的矢量方程图解法 • 2、矩阵法 • 列成矩阵方程 • 3、杆组法 • ( 略) • 三、运动线图 • 定义∶以某一输入参数为自变量(一般 为主动件的转角),描述机构上某点运动 特性的曲线叫运动线图。
第三节 运动分析的矢量方程图解法 • 如∶速度线图 • 加速度线图 • 等等
本章 总结
• 2)不直接构成运动副的两构件 • 三心定理∶三个构件,三个瞬心,它 们必然在一条直线上。
• 五、应用
第二节 速度分析的瞬心法
• 四连杆机构 • 凸轮机构 • 齿轮机构
第二节:速度瞬心法
• 六、特点 • 简明 • 速度分析,机构不能太复杂,有时瞬 心在纸面外。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.机构运动分析的目的:分析现有机构工作性能,检验新 机构运动分析的目的:分析现有机构工作性能, 目的 机构。 机构。 通过轨迹分析 确定构件运动所需空间 通过轨迹分析,确定构件运动所需空间,判断运动是否 轨迹分析 确定构件运动所需空间, 干涉。 干涉。 通过速度分析 确定构件的速度是否合乎要求,为加速 通过速度分析,确定构件的速度是否合乎要求, 速度分析 确定构件的速度是否合乎要求 度分析和受力分析提供必要的数据。 度分析和受力分析提供必要的数据。 通过加速度分析 确定构件的加速度是否合乎要求 通过加速度分析,确定构件的加速度是否合乎要求,为 加速度分析 确定构件的加速度是否合乎要求, 惯性力的计算提供加速度数据。 惯性力的计算提供加速度数据。 因此,运动分析把机构分析和机构综合问题联系起来, 因此,运动分析把机构分析和机构综合问题联系起来, 优化设计, 力分析的基础 便于机构的优化设计 同时也是力分析的基础。 便于机构的优化设计,同时也是力分析的基础。
P12
1
转动副
1 2
移动副
2
P
→∞ 12
n
A
1
2
n
平面高副
纯滚动: 纯滚动:A点 滚动+滑动: ---n 滚动+滑动:n---n 线
(2)三心定理法-------用于不直接相连构件。 三心定理法-------用于不直接相连构件。 用于不直接相连构件 三心定理:作平面运动的三个构件,共有三个瞬心, 三心定理:作平面运动的三个构件,共有三个瞬心,它 条直线上。 们位于同一 条直线上。
例: 用瞬心法求ω1/ ω3 找出齿轮1和齿轮3 找出齿轮1和齿轮3 相对瞬心P 的相对瞬心 13和它 们的绝对瞬心 16 、 们的绝对瞬心P 绝对瞬心 P36。 P13 P16
P23
P12
ω 1 P36 P13 = ω 3 P16 P13
P36
3.3 用矢量方程图解法作机构的运动分析
矢量方程图解法的基本原理及作图法 1、基本原理 —— 相对运动原理 B A
同一构件上两点间的运动关系
B(B1B2) 1
2
两构件重合点间的运动方程
v B = v A + v BA
v B 2 = v B1 + v B 2 B1
a B 2 = a B1 + a
r B 2 B1
a B = a A + a BA
n t = a A + a BA + a BA
+a
k B 2 B1
k a B 2 B1 = 2ω 1 × v B 2 B1
2. 解析法 效率高,速度快 ,精度高; 解析法: 效率高, 精度高; 便于对机构进行深入的研究。 便于对机构进行深入的研究。 (1)复数矢量法 (2)矩阵法 位置方程: 位置方程:是速度分析和加速度分析的基础 矢量、复数、 所用数学工具 :矢量、复数、矩阵 重点:矢量方程图法和 重点:矢量方程图法和复数矢量法
P12 A2(A1) VA2A1 B2(B1) VB2B1 ω21
瞬心的种类
1. 2. 绝对瞬心:构成瞬心的两个构件之一固定不动, 绝对瞬心:构成瞬心的两个构件之一固定不动,瞬心点 的绝对速度为零 。 相对瞬心:构成瞬心的两个构件均处于运动中, 相对瞬心:构成瞬心的两个构件均处于运动中,瞬心点 的绝对速度相等、 的绝对速度相等、相对速度为零 。 由此可知,绝对瞬心是相对瞬心的一种特殊情况 由此可知,绝对瞬心是相对瞬心的一种特殊情况。
C
v E = v B + v EB = v C + v EC
? ⊥EB ?
1 A
·
E G3 D
大小 方向
⊥EC
ϕ1
4
v E = µ v • pe
对应边互相垂直 Δbce ∽ΔBCE 且字母顺 序一致,Δbce称为 序一致,Δbce称为 速度影像。 ΔBCE 的速度影像。
b e f vCB c
vB vE vC g P
第三章 平面机构的运动分析
1.机构运动分析的任务、 1.机构运动分析的任务、目的及方法 机构运动分析的任务 2.用速度瞬心法作机构的速度分析 2.用速度瞬心法作机构的速度分析 3.用矢量方程图解法作机构的速度及加速度 3.用矢量方程图解法作机构的速度及加速度 分析 4.用解析法作机构的运动分析 4.用解析法作机构的运动分析
C
v B = ω 1 l AB
v C = v B + v CB
大小 方向 ? ? ⊥CD ⊥AB ⊥BC
ω1
1
B
·
2 E
3
A ϕ1
4
D
按比例尺µ 取基点p,按比例尺µv m/s)/mm作速度图 (m/s)/mm作速度图
b
v C = µ v • pc v CB = µ v • bc
ω
2
VCB
c
VB p VC
3.2 用速度瞬心法作机构速度分析
1. 速度瞬心及其位置的确定 瞬心是瞬时等速重合点。 瞬心是瞬时等速重合点。 瞬时等速重合点 瞬时,是指瞬心的位置随时间而变; 瞬时,是指瞬心的位置随时间而变; 等速,是指在瞬心这一点, 等速,是指在瞬心这一点,两构件的 绝对速度相等(包括大小和方向)、 绝对速度相等(包括大小和方向)、 相对速度为零; 相对速度为零; 重合点,是指瞬心既在构件1 重合点,是指瞬心既在构件1上,也 在构件2 在构件2上,是两构件的重合点。 是两构件的重合点。 速度瞬心具有瞬时性,不同时刻其位置可能不同。 速度瞬心具有瞬时性,不同时刻其位置可能不同。 1 2
V P12 = ω 1 • P14 P12 = ω 2 • P24 P12
P24ω2 P23 C NhomakorabeaB P13 A 1
P14
2
P12
E
VE
D
3
P34
ω1 4
ω2 P P P P = 14 12 ⇒ ω 2 = ω1 14 12 ω1 P24 P P24 P 12 12
V E = ω 2 • P24 E
1. 铰链四杆机构 已知:各杆长及ω 已知:各杆长及ω1 ,ϕ1。求:ω2 ,ω3 。/ ω3为机构中原动机1和 ω1 V E 为机构中原动机1 从动件3 从动件3的瞬时角速度之比 N (N − I ) 4 × 3 K = = =6 ,称为机构的传动比或传递 2 2 函数。 函数。 P24 P14、P12、P23、P34位于铰链中心 用三心定理确定P 用三心定理确定P13、P24 P14、P24、P34是绝对瞬心 P12、P23、P13是相对瞬心
v = vP 23 = ω2 P P23 µl 12
瞬心法小结
仅适用于求解速度问题 不可用于加速度分析。 速度问题, 1)瞬心法 仅适用于求解速度问题,不可用于加速度分析。 适用于构件数较少的机构的速度分析 机构的速度分析。 2)瞬心法 适用于构件数较少的机构的速度分析。 (多构件导致瞬心数量过多,分析复杂。) 多构件导致瞬心数量过多,分析复杂。) 属于图解法,每次只分析一个位置, 3)瞬心法 属于图解法,每次只分析一个位置,对于机构整 个运动循环的速度分析,工作量很大。 个运动循环的速度分析,工作量很大。 的速度分析 其不足之处,由后续的矢量方程图解法和解析法来弥补。 其不足之处,由后续的矢量方程图解法和解析法来弥补。
凸轮机构 2. 凸轮机构
已知:构件2的角速度ω 已知:构件2的角速度ω2 和长度 比例尺μ 比例尺μl 求:从动件3 的速度V3; 从动件3 的速度V 解:由直接观察法可得P12,由三 由直接观察法可得P 心定理可得P 如图所示。 心定理可得P13和P23如图所示。 由瞬心的概念可知: 由瞬心的概念可知:
机构中瞬心的数目
设机构中有N 设机构中有N个(包括机架)构件,每两个进行组合, 包括机架)构件,每两个进行组合, 则该机构中总的瞬心数目为:K= N(N-1) / 2 。 N(N则该机构中总的瞬心数目为
速度瞬心的位置 (1)直接观察法(定义法)-------用于直接成副的两构件。 直接观察法(定义法)-------用于直接成副的两构件。 用于直接成副的两构件
ω2
1. 铰链四杆机构 已知:各杆长及ω 已知:各杆长及ω1 ,ϕ1。求:ω2 ,ω3 。 V E
N (N − I ) 4 × 3 =6 K = = 2 2
P14、P12、P23、P34位于铰链中心 用三心定理确定P 用三心定理确定P13、P24 P14、P24、P34是绝对瞬心 P12、P23、P13是相对瞬心 便于确定不直接成副的瞬 ——瞬心多边形 心——瞬心多边形 P13
N (N − I ) 3× 2 K = = =3 2 2
2. 用瞬心法作机构的速度分析 1. 铰链四杆机构 已知:各杆长及ω 已知:各杆长及ω1 ,ϕ1。求:ω2 ,ω3 。 V E
N (N − I ) 4 × 3 K = = =6 2 2
P14、P12、P23、P34位于铰链中心 用三心定理确定P13、P24 用三心定理确定P P14、P24、P34是绝对瞬心 P12、P23、P13是相对瞬心
v = CB l BC
ω
3
v = C l CD
方向判定: 方向判定:采用矢量平移法 判定
已知:机构的位置,各构件的长度及原动件角速度ω 已知:机构的位置,各构件的长度及原动件角速度ω1。 求:vC,vE,aC, aE, ω 2, ω 3, α 2, α 3 1、绘制机构运动简图 F 2、速度分析 B 2 ω1
1 4 2 3
P24
ω2 P23 C
B A 1
P14
2
P12
E
VE
ω3
3
ω1 4
D
P34
顶点——构件(编号) 顶点——构件(编号) ——构件 瞬心——任意两个顶点连线; ——任意两个顶点连线 实线, 瞬心——任意两个顶点连线;成副瞬心 — 实线,不成副瞬 ——虚线 心——虚线 任何构成三角形的三条边所代表的三个瞬心位于同一直线上
