20、21、22课后答案

合集下载

胡裕树-《现代汉语》课后习题答案

语音学作业第一节语音概说1.什么是语音？语音同自然界的声音有什么不同？答案：语音是语言的物质外壳，是指人类用发音器官发出来的有一定意义目的的，用来进行社会交际的声音。

区别：语音具有社会性质，自然界的其他声音没有。

2.什么是音高、音强、音长、音色？它们在现代汉语语音里有什么作用？答案：音高是指声音的高低，决定于发声体振动的频率。

音强是指声音的强弱，决定于发声体的振幅。

音长是指声音的长短，决定于发音体振动持续的时间长短。

音色是指声音放入个性和特色，决定于声波振动的形式。

它们在现代汉语中的作用是：音高决定音调，音强决定轻声。

3.隔壁有几个熟人在说话，热部门为什么能说话者是张三还是李四？答案：是由于每个人的音色不同。

4.写出下列图中发音器官各部分的名称(图略)1.上唇2.下唇3.上齿4.下齿5.齿龈6.硬腭7.软腭8.小舌9.舌尖10.舌面11.舌根12.鼻腔13.口腔14.咽头15.会厌16.食道17.气管18.声带19.喉头5.学习和研究语音为什么要理解语音的社会性质？答案：因为语音的社会性质是语音的根本属性，是语音区别于自然案界声音的根本原因。

否认或忽略语音的社会性质就难以说明许多语音现象，也无法合理的语音上的各种问题。

6.试谈汉语拼音方案在学习现代汉语语音以及其他方面的作用。

由于汉字字形不能准确表音，学习汉字就需要一套注音工具。

人们学习现代汉语语音、学习普通话也需要记音工具来记录普通话语音，拼注普通话读物，这两方面都需要运用汉语拼音方案。

此外，汉语拼音方案还可作为我国少数民族创造和改革文字的共同基础；用于译写我国人名地名，转写外国人名、地名和部分科技术语；用于电报、旗语、工业产品代号、盲字及聋哑人“汉语手指字母”以及编制音序检字等。

汉语拼音方案在汉字和拉丁字母间起到桥梁作用，我们现在将汉字输入电脑多用拼音输入法，母语使用拉丁字母的学生学习汉语时借助汉语拼音方案也有利于掌握普通话语音。

7.学习英语常常利用国际音标，学习现代汉语语音有时也用国际音标，这两处所说的国际音标是同一种记音符号吗？为什么英语里所用的国际音标同现代汉语的语音部分出现的不完全一样？是同一种记音符号。

答案之书(解答之书) - 电子版精选答案

1 别太赶了。 2 别想了。 3 不。 4 不然呢？ 5 不要抱期望。 6 要求不要太高。 7 这是必然的，不要抗拒。 8 不要浪费精力。 9 不要浪费你的时间了。 10 不要做得过火了。 11 不用担心。 12 车到山前必有路。 13 答案就在你身边。 14 大胆一点。 15 大方一点。 16 等等。 17 放轻松点，慢慢来。 18 管它呢。 19 毫无疑问。 20 好运将会降临。 21 忽略了一件显而易见的事。 22 换个角度想想。 23 会付出代价。 24 会感到庆幸。 25 会很不顺利。 26 会很顺利。 27 会后悔的。 28 会失去自我。 29 会特别顺利。 30 继续前进。 31 结果可能让人惊讶。 32 绝对不。 33 肯定的。 34 没错。
69 想得美。 70 想想有没有机会。 71 休息一下就好了。 72 学会妥协。 73 眼光长远一点。 74 要变通。 75 要有点耐心。 76 要知足。 77 要抓住问题的关键。 78 一定会有好结果的。 79 一笑了之。 80 以后再说。 81 用尽一切办法去努力。 82 有。 83 有可能。 84 仔细想想再说。 85 再等等看。 86 障碍重重。 87 这辈子都不可能。 88 这不可取。 89 这不切实际。 90 这不值得努力。 91 这会影响你的形象。 92 这件事会很麻烦。 93 这件事你说了不算。 94 这没什么意义。 95 这取决于你的行动。 96 这是肯定的。 97 没法保证。 98 无法预测。 99 这是在浪费金钱。 100 没什么好结果。 101 值得奋斗。 102 这种事情不要告诉别人。
35 木已成舟。 36 你必须解决一些相关的问题。 37 不会后悔的。 38 不会失望的。 39 得真正地努力一下。 40 还有别的选择。 41 你将取得成功。 42 你说了算。 43 你心里已经有答案了。 44 需要合作。 45 需要冒险。 46 要主动。 47 你在开玩笑吗？ 48 你做什么都没用。 49 奇迹即将降临。 50 千万别信。 51 千万不能失败。 52 全力以赴。 53 认清现实吧。 54 三思而后行。 55 尚待时日。 56 省点力气吧。 57 时机未到。 58 听听别人怎么说。 59 听听专家的意见。 60 万一错过，就没这个机会了。 61 为什么不呢？ 62 问问你的亲人。 63 问问自己，为什么要这么干。 64 先做点别的。 65 现在还说不清。 66 现在你可以。 67 相信你的直觉。 68 相信你最初的想法。

统计学(第五版)课后答案

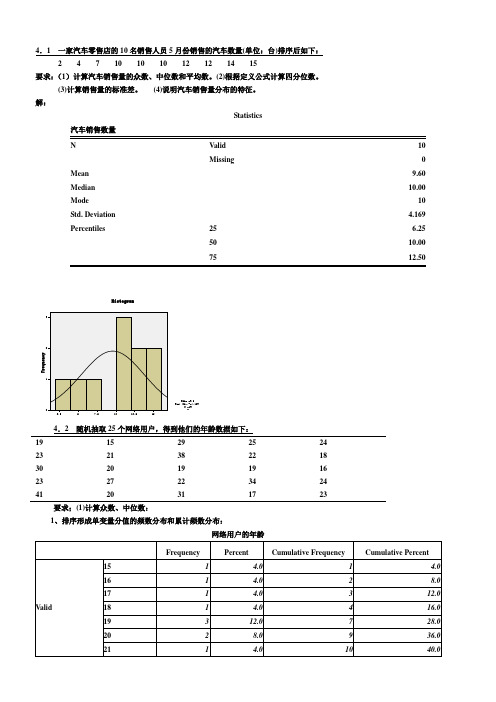
4．1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位：台)排序后如下：2 4 7 10 10 10 12 12 14 15要求：（1）计算汽车销售量的众数、中位数和平均数。

(2)根据定义公式计算四分位数。

(3)计算销售量的标准差。

(4)说明汽车销售量分布的特征。

解：Statistics汽车销售数量N Valid 10Missing 0 Mean 9.60 Median 10.00 Mode 10 Std. Deviation 4.169 Percentiles 25 6.2550 10.0075 12.504．2 随机抽取25个网络用户，得到他们的年龄数据如下：19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求；(1)计算众数、中位数：1、排序形成单变量分值的频数分布和累计频数分布：网络用户的年龄从频数看出，众数Mo 有两个：19、23；从累计频数看，中位数Me=23。

(2)根据定义公式计算四分位数。

Q1位置=25/4=6.25，因此Q1=19，Q3位置=3×25/4=18.75，因此Q3=27，或者，由于25 和27都只有一个，因此Q3也可等于25+0.75×2=26.5。

(3)计算平均数和标准差； Mean=24.00；Std. Deviation=6.652 (4)计算偏态系数和峰态系数： Skewness=1.080；Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析：分布，均值=24、标准差=6.652、呈右偏分布。

如需看清楚分布形态，需要进行分组。

为分组情况下的直方图：为分组情况下的概率密度曲线：分组：1、确定组数：()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K=+=+=+=，取k=62、确定组距：组距＝( 最大值 - 最小值)÷ 组数=（41-15）÷6=4.3，取53、分组频数表网络用户的年龄(Binned)分组后的均值与方差：分组后的直方图：4．6 在某地区抽取120家企业，按利润额进行分组，结果如下：要求：(1)计算120家企业利润额的平均数和标准差。

机械制造基础第三版课后答案.doc

机械制造基础第三版课后答案【篇一：机械制造基础习题集和答案】txt> 机械工程材料一．名词解释题强度：是指金属材料抵抗塑形变形和断裂的能力。

塑形：金属材料在外力作用下发生塑性变形而不破坏的能力。

硬度：金属材料抵抗其他更硬物体压入表面的能力。

韧性：金属材料在断裂前吸收变形能量的能力。

合金：由两种或两种以上的金属元素，或金属元素与非金属元素组成的具有金属特性的物质。

同素异构性：同一金属在不同温度下具有不同晶格类型的现象。

调质处理：指淬火及高温回火的热处理工艺。

淬硬性：钢淬火时的硬化能力。

回火稳定性：钢在回火时抵抗硬度下降的能力。

二．判断正误1、细化晶粒虽能提高金属的强度，但增大了金属的脆性。

（╳）2、结构钢的淬透性，随钢中碳含量的增大而增大。

（╳）3、普通低合金结构钢不能通过热化处理进行强化。

（√）4、置换固溶体必是无限固溶体。

（╳）5、单晶体必有各向异性。

（√）6、普通钢和优质钢是按其强度等级来区分的。

（╳）7、过热钢经再结晶退火后能显著细化晶粒。

（╳）8、奥氏体耐热钢也就是奥氏体不锈钢。

（╳）9、马氏体的晶体结构和铁素体的相同。

（√）10、弹簧钢的最终热处理应是淬火+低温回火。

（╳）11、凡单相固溶体均能进行形变强化。

（√）12、陶瓷组织中的气相能起到一定的强化作用。

（╳）13、高速钢淬火后经回火可进一步提高其硬度。

（√）14、马氏体的强度和硬度总是大于珠光体的。

（╳）15、纯铁在室温下的晶体结构为面心立方晶格。

（╳）16、马氏体的硬度主要取决于淬火时的冷却速度。

（╳）17、所谓白口铸铁是指碳全部以石墨形式存在的铸铁。

（╳）18、白口铸铁铁水凝固时不会发生共析转变。

（╳）19、铸件可用再结晶退火细化晶粒。

（√）20、冷热加工所形成的纤维组织都能使金属出现各向异性。

（√）21、奥氏体的塑性比铁素体的高。

（√）22、白口铸铁在室温下的相组成都为铁素体和渗碳体。

（√）23、过共析钢的平衡组织中没有铁素体相。

药物化学课后习题及答案

绪论一、选择题1．药物他莫昔芬作用的靶点为（）A 钙离B 雌激素受体C 5－羟色胺受体D β1－受体E 胰岛受体2．下述说法不属于商品名的特征的是（）A 简易顺口B 商品名右上标以○RC 高雅D 不庸俗E 暗示药品药物的作用3．后缀词干cillin是药物（）的A 青霉素B 头孢霉素C 咪唑类抗生素D 洛昔类抗炎药E 地平类钙拮抗剂4．下述化学官能团优先次序第一的是（）A 异丁基B 烯丙基C 苄基D 三甲胺基E 甲氨基5．下述药物作用靶点是在醇活中心的是（）A 甲氧苄啶B 普萘洛尔C 硝苯地平D 氮甲E 吗啡6．第一个被发现的抗生素是（）A 苯唑西林钠B 头孢克洛C 青霉素D 头孢噻肟E 头孢他啶二、问答题1.为什么说抗生素的发现是个划时代的成就？2.简述药物的分类。

3.简述前药和前药的原理。

4.何为先导化合物？答案一、选择题1．B 2.E 3.A 4.A 5.A 6.C二、问答题答案1. 答：抗生素的医用价值是不可估量的，尤其是把这种全新的发现逐渐发展成为一种能够大规模生产的产品，能具有实用价值并开拓出抗生素类药物一套完善的系统研究生产方法（比如说利用发酵工程大规模生产抗生素），确实是一个划时代的成就。

2. 答：可以分为天然药物、伴合成药物、合成药物以及基因工程药物四大类，其中，天然药物有可以分为植物药、抗生素和生化药物。

3．答：前药又称为前体药物，将一个药物分子经结构修饰后，使其在体外活性较小或无活性，进入体内后经酶或非酶作用，释放出原药物分发挥作用，这种结构修饰后的药物称作前体药物，简称前药。

4. 答：先导化合物简称先导物，是通过各种途径和手段得到的具有某种生物活性和化学结构的化合物，用于进一步的结构改造和修饰，是现代新药研究的出发点。

第二章中枢神经系统药物一、选择题A型题（五个备选答案中有一个为正确答案）1．异戊巴比妥不具有下列那些性质( )Ａ．弱酸性Ｂ．溶于乙醚、乙醇Ｃ．水解后仍有活性Ｄ．钠盐溶液易水解Ｅ．加入过量的硝酸银试液，可生成银盐沉淀2．盐酸吗啡加热的重排产物主要是( )Ａ．双吗啡Ｂ．可待因Ｃ．苯吗喃Ｄ．阿朴吗啡Ｅ．Ｎ－氧化吗啡3．结构上没有含氮杂环的镇痛药是( )Ａ．盐酸吗啡Ｂ．枸橼酸芬太尼Ｃ．二氢埃托啡Ｄ．盐酸美沙酮Ｅ．盐酸普鲁卡因4．盐酸氟西汀属于哪一类抗抑郁药( )Ａ．去甲肾上腺素重摄取抗抑郁剂Ｂ．但胺氧化酶抑制剂Ｃ．阿片受体抑制剂Ｄ．５－羟色胺再摄取抑制剂Ｅ．５－羟色胺受体抑制剂5．(-)-Morphine分子结构中B/C环，C/D环，C/E环的构型为( ) A．B/C环呈顺式，C/D环呈反式，C/E环呈反式B．B/C环呈，C/D环呈反式，C/E环呈顺式C．B/C环呈顺式, C/D环呈反式，C/E呈顺式D．B/C环呈顺式, C/D环呈反式，C/E环呈顺式E．B/C环呈反式, C/D环呈顺式，C/E环呈顺式6．Morphine Hydrochloride 注射剂放置过久颜色变深,发生了以下哪种反应( ) A．水解反应B．氧化反应C．还原反应D．水解和氧化反应E．重排反应7．中国药典规定, Morphine Hydrochloride 水溶液加碳酸氢钠和碘试液, 加乙醚振摇后, 醚层不得显红色, 水层不得显绿色, 这是检查以下何种杂质( )A．双吗啡B．氢吗啡酮C．羟吗啡酮D．啊朴吗啡E．氢可酮8．按化学结构分类，Pethadone属于( )A．生物碱类B．吗啡喃类C．苯吗啡类D．哌啶类E．苯基丙胺类(氨基酮类) 9．按化学结构分类，Methadone属于( )A．生物碱类B．哌啶类C．苯基丙胺类D．吗啡喃类E．苯吗啡类B型题（每题只有一个正确答案，每个答案可被选择一次或一次以上，也可以不被选用。

数据挖掘原理与实践蒋盛益答案

数据挖掘原理与实践蒋盛益答案习题参考答案第 1 章绪论1.1 数据挖掘处理的对象有哪些？请从实际生活中举出至少三种。

答：数据挖掘处理的对象是某一专业领域中积累的数据，对象既可以来自社会科学,又可以来自自然科学产生的数据,还可以是卫星观测得到的数据。

数据形式和结构也各不相同, 可以是传统的关系数据库,可以是面向对象的高级数据库系统,也可以是面向特殊应用的数据库,如空间数据库、时序数据库、文本数据库和多媒体数据库等,还可以是 Web 数据信息。

实际生活的例子：①电信行业中利用数据挖掘技术进行客户行为分析，包含客户通话记录、通话时间、所开通的服务等，据此进行客户群体划分以及客户流失性分析。

②天文领域中利用决策树等数据挖掘方法对上百万天体数据进行分类与分析，帮助天文学家发现其他未知星体。

③制造业中应用数据挖掘技术进行零部件故障诊断、资源优化、生产过程分析等。

④市场业中应用数据挖掘技术进行市场定位、消费者分析、辅助制定市场营销策略等。

1.2 给出一个例子，说明数据挖掘对商务的成功是至关重要的。

该商务需要什么样的数据挖掘功能？它们能够由数据查询处理或简单的统计分析来实现吗？答：例如，数据挖掘在电子商务中的客户关系管理起到了非常重要的作用。

随着各个电子商务网站的建立，企业纷纷地从“产品导向”转向“客户导向”，如何在保持现有的客户同时吸引更多的客户、如何在客户群中发现潜在价值，一直都是电子商务企业重要任务。

但是，传统的数据分析处理，如数据查询处理或简单的统计分析，只能在数据库中进行一些简单的数据查询和更新以及一些简单的数据计算操作，却无法从现有的大量数据中挖掘潜在的价值。

而数据挖掘技术却能使用如聚类、关联分析、决策树和神经网络等多种方法，对数据库中庞大的数据进行挖掘分析，然后可以进行客户细分而提供个性化服务、可以利用挖掘到的历史流失客户的特征来防止客户流失、可以进行产品捆绑推荐等，从而使电子商务更好地进行客户关系管理，提高客户的忠诚度和满意度。

数字电路与数字电子技术课后答案第四章(供参考)

+BC + AC
(4) F=ΠM(5,7,13,15)
= BD
F= +
(5) F=ΠM(1,3,9,10,11,14,15)
= AC+ D
F = ( + )(B+ )
(6) F=∑m (0,2,4,9,11,14,15, 16,17,19,23,25,29,31)
F= + + BCD+ B E+AB E+ACDE+A +A E
= A⊙B⊙C
(6) = ⊙ ⊙
证:
左=
= [(A⊕B)+ ] (A⊙B)+C]
= (A⊙B) +[(A⊕B)C]
= +AB + BC+A C
右= ( ⊙ )⊙
= [( ⊙ ) + ]
= [( +AB) + ]
= +AB +
= +AB +(A⊕B)C
= +AB + BC+A C
9.证明
(1)如果a + b = c，则a + c = b，反之亦成立
(2)F在输入组合为1,3,5,7时使F=1
15.变化如下函数成另一种标准形式
(1) F=∑m (1,3,7)
(2) F=∑m (0,2,6,11,13,14)
(3) F=ΠM(0,3,6,7)
(4) F=ΠM(0,1,2,3,4,6,12)
解:
(1)F=ΠM(0,2,4,5,6)
(2)F=ΠM(1,3,4,5,7,8,9,10,12,15)
(3)F=∑m (1,2,4,5)

新概念英语第三册：课后多项选择题Lesson20-21答案解析

【导语】新概念系列教材的经典早已家喻户晓。

其⽂章的短⼩精悍，语句的幽默诙谐，语法的全⾯⽽系统，历来被公认为是适合绝⼤多数朋友学习英语的资料之⼀。

你或许还没有加⼊到学习中来，但是任何时候的学习都不会晚。

快来学习吧！为您整理了以下内容，仅供参考。

希望对您的学习有帮助！如果您想要了解更多相关内容，欢迎关注！【篇⼀】Lesson20答案解析 1. C正确 2. B正确 3. make another forced landing…迫降 4. C正确　序数词和不定式搭配连⽤ 5. A正确　not till not until 6. C正确 7. D正确　pormised: 有什么的可能，有发⽣的迹象——好 8. A正确 9. no further: 修饰距离 no longer: 修饰时间或长度 no more: 修饰某物 I can walk no further. He no longer lives here. I can eat no more. 10.D正确　The ship rode the waves. hold water: 论点，观点站得住脚，说得通 11.A正确 12.immense: 修饰⾯积⼤得难以测量【篇⼆】Lesson 21 Daniel Mendoza1 Richard Humphries offered to train Mendoza because ______ . a.he wanted to learn the techniques that Mendoza had introduced to boxing b.for one so young, Mendoza had displayed an unusual grasp of the game c.he had attended the boxing match which led to Mendoza's early fame d.he was anxious to establish himself as a superior boxer to Mendoza 2 At the match between Humphries and Mendoza at Stilton ______ . a.Mendoza lost a great deal of money to the public b.after an hour's fighting Humphries became champion of England c.Mendoza lost twice to Humphries d.the argument between the two men was settled in favour of Humphries 3 Apart from the money he earned at matches, Mendoza ______ . a.earned a lot from the Academy which he founded after becoming Champion c.greatly supplemented his income by teaching the art of boxing d.was given enormous sums by Lord Byron Structure 结构 4 In those days, ______ ‘prizefighters’ because they fought with bare fists for prize money. (11. 2-3) a.they called boxers b.boxers called c.boxers being called d.they were called boxers 5 A prizefighter could suffer a serious injury or ______ during a … (11. 4-5) a.even be killed b.be even killed c.even killed d.was even killed 6 Mendoza ______ boxing into a sport. (11. 8-9) a.was much changed by b.did a great deal to change c.changed a great deal of d.much changed 7 He was so extravagant that he ______ people money. (1. 20) a.always owed to b.always owed c.owed always d.was always owing to Vocabulary 词汇 8 One of the most ______ in boxing history was …(11. 6-7) a.vivid personalities6 b.famous people c.painted images d.imaginative characters 9 ---- after a boxing match at the ______ young age of fourteen. (1. 11) a.marvellously b.singly c.exceptionally 10 Mendoza's ______ to fame was noted7 by Richard Humphries. (11. 11-12) a.rise b.rose c.raise d.claim 11 Humphries soon became ______ Mendoza's success. (11. 13-14) a.jealous of b.disinterested8 in c.revolted by d.changed by 12 Mendoza finally ______ Humphries and became Champion of England. (11. 17-18) a.conquered b.gained c.won d.beat【篇三】Lesson21答案解析　1...b... 2...d... 3...c... apart from: 除什么之外还有 4...a... 5...a... 6...b... 7...b... owe money to people 8...b... personality:个性=character image:偶像 9...c... exceptionally->unusually: 不同寻常的 marvellously=wonderfully:奇妙的，奇异的 singly: 单独的 unequally:独⼀⽆⼆的 an exceptionally beautiful girl 10...a... 名词形式，名词所有格，rise:vi.&n. 11...a... 12...d... conquer:征服 gain:赢得，获得 win: 赢得(⽐赛)。

《管理运筹学》茹少峰课后答案

y 10
� 10000
x 12 � x 11 � 2000 � x 10 � y 10 � y 11 � 10000
y 10 � 2000 � x 10
y 11
�
x 11
�
2000
�x �y
10
10
y 12
�
x 12
�
x 11
� 2000
�x �y �y
10
10
11
�
x 11
�
2000
�
x 10
�
y 10
若每个月仅在1号进货1次且要求年底时商品存量达到3000件在以上条件下建立该问题的线性规划模型使公司获得最大利润注不考虑库存费用表29进货和销售价格月份进货价格元件销售价格元件12为每月购进的货物109010011951001298115解1110ixi121110iyi为每月销售的货物
1�用图解法求解两个变量线性规划问题的最优解和最优值。
�1 �
解�由题意知�A= � 1
1
1�
�2�
2
4
� �
=�
p 1,
p
2,
p
3
�
��
b= � 6 �
c=�3�1�3�
�1� B 1 =� p 1 , p 2 �� B 1 � ≠0� B 1 是基� x 1 � x 2 是基变量� x 3 是非基变量�令
� x1 �
��
� x2 �
x 3 =0�得 x 1 =-2� x 2 =4
号进货 1 次�且要求年底时商品存量达到 3000 件�在以上条件下�建立该问题的线性
规划模型�使公司获得最大利润��注�不考虑库存费用�

信息论与编码技术第五章课后习题答案

码，并求出其编码效率。
解：
信源符号概率编码
码字码长
X1
3/8 0
0
1
X2
1/6 1
0
10 2
X3
1/8
1
11 2
X4
1/8 2
0
20 2
X5
1/8
1
21 2
X6
1/12
2
22 2
H(X)=-((3/8)*log(3/8)+(1/6)*log(1/6)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/12)*log(1/12))
=2.3852 （三进制单位/信源符号）
H3(X)= H(X)/ 1.5850=2.3852/1.5850= 1.5049（三进制单位/信源符号）
L ＝(3/8)*1+ (1/6)*2+ (1/8)*2+ (1/8)*2+ (1/8)*2+ (1/12)*2＝1.625（码符号/信源符号）
η= H3(X)/ L =1.5049/1.625= 92.61 ％
5.8 已知符号集合 {x1, x2 , x3,"} 为无限离散消息集合，它们出现的概率分别为 p(x1) = 1/ 2 ， p(x2 ) = 1/ 4 ， p(x3 ) = 1/ 8 ， p(xi ) = 1/ 2i ，……。
(1) 用香农编码方法写出各个符号消息的码字。 (2) 计算码字的平均信息传输速率。
L =4*（1/4）*1=1（码符号/信源符号）
Rt= H(X)/(t* L )=1/(1*10*10-2)=10(比特/秒)

金融企业会计课后习题答案(1)-立信会计出版社-刘学华-主编

金融企业会计课后习题答案(1)-立信会计出版社-刘学华-主编<金融企业会计>章后练习题部分答案第二章存款业务的核算习题一（1）借：库存现金100000贷：吸收存款—单位活期存款—红星商店 100000（2）借：吸收存款—单位活期存款—A 25000贷：库存现金25000（3）借：吸收存款—单位活期存款—B 500000贷：吸收存款—单位定期存款—B 500000（4）借：利息支出—单位活期存款利息支出户2000贷：应付利息—单位活期存款应付利息户 2000借：应付利息—单位活期存款应付利息户2000贷：吸收存款—单位活期存款—某单位2000（5）借：吸收存款—单位定期存款—C 200000应付利息—单位定期存款应付利息户3500贷：吸收存款—单位活期存款—C 203500（6）借：库存现金5000贷：吸收存款—个人活期存款—王某5000（7）借：库存现金40000贷：吸收存款—个人定期存款—李某40000（8）借：吸收存款—个人活期存款—张某300000贷：吸收存款—个人定期存款—张某300000（9）1月20日借：库存现金50000贷：吸收存款—个人定期存款—整存整取刘某 500006月18日借：吸收存款—个人定期存款—整存整取刘某 50000应付利息—个人定期存款应付利息户496.67贷：库存现金50471.84应交税费—代扣代缴个人存款利息所得税 24.83应付利息=50000×0.2%/30×（12+28+31+30+31+17）=486.67应交税费=486.67×5%=24.83（10）借：吸收存款—个人定期存款—马某30000应付利息—个人定期存款应付利息户 594 （=30000×1.98%）贷：吸收存款—个人活期存款—马某30000库存现金564.3应交税费—代扣代缴个人存款利息所得税 29.7 （=594×5%）习题二(1)计算过程及结果如下表2-2亚运村支行分户账户名：A公司月利率：0.6‰单位：元20××年摘要借方贷方借/贷余额日数积数月日6 21开户54000贷5400316200024转存4700.2贷58700.26352201.2 3转支 5200 贷53500.2105350027 1现收845贷61950.20 01转支 6000 贷55950.26335701.2 16转存623贷62180.21593270331转支4813.4贷57366.87401567.68 7 现收6785贷64151.812769821.61 9 转支5685.1贷58466.715877000.59 3 转存800贷66466.79598200.31 2 转支10645.9贷55820.89502387.22 0 止息贷55820.82 1 利息入账109.33贷55930.13至结息日累计会计92日数至结息日累计计息积数5466 585（2）9月20日的计算利息数为：计算利息数=至结息日累计计息积数×日利率=5466585×0.6‰÷30=109.33(元)9月21日编制“利息清单”，办理利息转账，并结出新的存款余额。

高等数学课后习题及参考答案(第四章)

高等数学课后习题及参考答案（第四章）习题4-11. 求下列不定积分:(1)⎰dx x 21;解 C x C x dx x dx x +-=++-==+--⎰⎰112111222.(2)⎰dx x x ; 解 C x x C x dx x dx x x +=++==+⎰⎰212323521231. (3)⎰dx x1;解C x C x dx xdx x+=++-==+--⎰⎰21211112121. (4)⎰dx x x 32; 解 C x x C x dx x dx x x+=++==+⎰⎰3313737321031371. (5)⎰dx xx 21;解C x x C x dx xdx xx +⋅-=++-==+--⎰⎰12312511125252. (6)dx x m n ⎰; 解C x m n m C x mn dx x dx x mn m m nm nmn++=++==++⎰⎰111.(7)⎰dx x 35;解 C x dx x dx x +==⎰⎰4334555.(8)⎰+-dx x x )23(2;解 C x x x dx dx x dx x dx x x ++-=+-=+-⎰⎰⎰⎰2233123)23(2322.(9)⎰ghdh 2(g 是常数);解C ghC h gdh hgghdh +=+⋅==⎰⎰-22212122121. (10)⎰-dx x 2)2(;解 C x x x dx dx x dx x dx x x dx x ++-=+-=+-=-⎰⎰⎰⎰⎰423144)44()2(23222.(11)⎰+dx x 22)1(;解 C x x x dx dx x dx x dx x x dx x +++=++=++=+⎰⎰⎰⎰⎰3524242232512)12()1(.(12)dx x x ⎰-+)1)(1(3;解 ⎰⎰⎰⎰⎰⎰-+-=-+-=-+dx dx x dx x dx x dx x x x dx x x 23212323)1()1)(1(C x x x x +-+-=25233523231.(13)⎰-dx xx 2)1(;解C x x x dx x x xdx xx x dx xx ++-=+-=+-=-⎰⎰⎰-2523212321212252342)2(21)1(. (14)⎰+++dx x x x 1133224; 解C x x dx x x dx x x x ++=++=+++⎰⎰arctan )113(1133322224.(15)⎰+dx x x 221;解⎰⎰⎰+-=+-=+-+=+C x x dx xdx xx dx x x arctan )111(111122222.(16)⎰+dx xe x )32(;解 C x e dx xdx e dx x e x x x ++=+=+⎰⎰⎰||ln 32132)32(.(17)⎰--+dx xx )1213(22;解 ⎰⎰⎰+-=--+=--+C x x dx xdx x dx xx arcsin 2arctan 3112113)1213(2222.(18)dx xe e x x⎰--)1(;解 C x edx xe dx xe e xxx x+-=-=-⎰⎰--21212)()1(.(19)⎰dx e x x 3;解 C e C e e dx e dx e xx x xxx++=+==⎰⎰13ln 3)3ln()3()3(3.(20)⎰⋅-⋅dx xxx 32532; 解 C x C x dx dx x xx xxx+--=+-=-=⋅-⋅⎰⎰)32(3ln 2ln 5232ln )32(52])32(52[32532. (21)⎰-dx x x x )tan (sec sec ;解 ⎰⎰+-=-=-C x x dx x x x dx x x x sec tan )tan sec (sec )tan (sec sec 2.(22)⎰dx x2cos 2;解 C x x dx x dx x dx x ++=+=+=⎰⎰⎰)sin (21)cos 1(212cos 12cos 2.(23)⎰+dx x 2cos 11;解 ⎰⎰+==+C x dx xdx x tan 21cos 212cos 112.(24)⎰-dx xx xsin cos 2cos ;解 ⎰⎰⎰+-=+=--=-C x x dx x x dx xx xx dx x x x cos sin )sin (cos sin cos sin cos sin cos 2cos 22.(25)⎰dx x x x22sin cos 2cos ;解 ⎰⎰⎰+--=-=-=C x x dx xx dx x x x x dx x x x tan cot )cos 1sin 1(sin cos sin cos sin cos 2cos 22222222.(26)⎰-dx x x x)11(2;解 ⎰⎪⎭⎫ ⎝⎛-dx x x x 211⎰++=-=--C x x dx x x 41474543474)(.2. 一曲线通过点(e 2, 3), 且在任一点处的切线的斜率等于该点横坐标的倒数, 求该曲线的方程.解设该曲线的方程为y =f (x ), 则由题意得xx f y 1)(='=',所以 C x dx xy +==⎰||ln 1.又因为曲线通过点(e 2, 3), 所以有=3-2=1 3=f (e 2)=ln|e 2|C =2C ,C =3-2=1. 于是所求曲线的方程为 y =ln|x | 1.3. 一物体由静止开始运动, 经t 秒后的速度是3t 2(m/s ), 问 (1)在3秒后物体离开出发点的距离是多少？ (2)物体走完360m 需要多少时间？解设位移函数为s =s (t ), 则s '=v =3 t 2, C t dt t s +==⎰323. 因为当t =0时, s =0, 所以C =0. 因此位移函数为s =t 3. (1)在3秒后物体离开出发点的距离是s =s (3)=33=27.(2)由t 3=360, 得物体走完360m 所需的时间11.73603≈=t s. 4. 证明函数x e 221, e x sh x 和e x ch x 都是x x e xsh ch -的原函数.证明 x x xx x x x x x e ee e e e e e x x e 222sh ch ==--+=----. 因为x x e e 22)21(=', 所以x e 221是x x e xsh ch -的原函数.因为(e x sh x )'=e x sh x e x ch x =e x (sh x ch x )x xx x x x e e e e e e 2)22(=++-=--, 所以e x sh x 是xx e xsh ch -的原函数.因为(e x ch x )'=e x ch x e x sh x =e x (ch x sh x )x xx x x x e e e e e e 2)22(=-++=--, 所以e xch x 是xx e x sh ch -的原函数.习题4-21. 在下列各式等号右端的空白处填入适当的系数, 使等式成立(例如: )74(41+=x d dx :(1) dx = d (ax );解dx = a 1d (ax ).(2) dx = d (7x -3);解dx = 71d (7x -3).(3) xdx = d (x 2); 解xdx = 21 d (x 2).(4) x d x = d (5x 2);解x d x = 101d (5x 2).(5))1( 2x d xdx -=;解 )1( 212x d xdx --=.(6)x 3dx = d (3x 4-2);解x 3dx = 121d (3x 4-2).(7)e 2x dx = d (e 2x ); 解e 2x dx = 21 d (e 2x ).(8))1( 22x x ed dxe --+=;解 )1( 2 22x xe d dx e --+-=.(9))23(cos 23sin x d xdx =;解 )23(cos 32 23sin x d xdx -=.(10)|)|ln 5( x d xdx=; 解 |)|ln 5( 51x d x dx =. (11)|)|ln 53( x d xdx-=; 解|)|ln 53( 51x d x dx --=. (12))3(arctan 912x d x dx=+; 解 )3(arctan 31912x d x dx =+. (13))arctan 1( 12x d xdx -=-;解)arctan 1( )1( 12x d xdx --=-.(14))1( 122x d x xdx -=-.解)1( )1( 122x d x xdx --=-.2. 求下列不定积分(其中a , b , ω, ϕ均为常数): (1)⎰dt e t 5; 解 C e x d e dt e xx t +==⎰⎰55551551. (2)⎰-dx x 3)23(; 解 C x x d x dx x +--=---=-⎰⎰433)23(81)23()23(21)23(. (3)⎰-dx x 211; 解C x x d x dx x +--=---=-⎰⎰|21|ln 21)21(21121211.(4)⎰-332xdx ;解C x C x x d x xdx+--=+-⋅-=---=-⎰⎰-3232313)32(21)32(2331)32()32(3132. (5)⎰-dx e ax bx)(sin ;解C be ax ab x d e b ax d ax a dx e ax b xb xbx+--=-=-⎰⎰⎰cos 1)()(sin 1)(sin .(6)⎰dt tt sin ;解⎰⎰+-==C t t d t dt tt cos 2sin 2sin .(7)⎰⋅xdx x 210sec tan ;解 ⎰⋅xdx x 210sec tan C x x xd +==⎰1110tan 111tan tan . (8)⎰xx x dxln ln ln ;解C x x d x x d x x x x x dx +===⎰⎰⎰|ln ln |ln ln ln ln ln 1ln ln ln ln 1ln ln ln .(9)⎰+⋅+dx xx x 2211tan ;解 ⎰+⋅+dx x x x 2211tan 2222211cos 1sin 11tan x d x x x d x +++=++=⎰⎰C x x d x ++-=++-=⎰|1cos |ln 1cos 1cos 1222.(10)⎰xx dxcos sin ;解 C x x d xdx x x x x dx +===⎰⎰⎰|tan |ln tan tan 1tan sec cos sin 2. (11)⎰-+dx e e xx 1;解 ⎰-+dx e e xx 1C e de edx e e x x xx x +=+=+=⎰⎰arctan 11122.(12)⎰-dx xe x 2; 解 .21)(212222C e x d e dx xe x x x +-=--=---⎰⎰ (13)⎰⋅dx x x )cos(2;解 C x x d x dx x x +==⋅⎰⎰)sin(21)()cos(21)cos(2222. (14)⎰-dx xx 232;解C x C x x d x dx x x+--=+--=---=-⎰⎰-2212221223231)32(31)32()32(6132.(15)⎰-dx xx 4313; 解⎰⎰+--=---=-C x x d x dx x x |1|ln 43)1(11431344443.(16)⎰++dt t t ))sin((cos 2ϕωϕω; 解 C t t d t dt t t ++-=++-=++⎰⎰)(cos 31)cos()(cos 1)sin()(cos 322ϕωωϕωϕωωϕωϕω. (17)⎰dx x x3cos sin ; 解 C x C x x xd dx xx +=+=-=--⎰⎰2233sec 21cos 21cos cos cos sin . (18)⎰-+dx x x xx 3cos sin cos sin ; 解 )sin cos (cos sin 1cos sin cos sin 33x x d x x dx x x x x +--=-+⎰⎰ C x x x x d x x +-=--=⎰-3231)cos (sin 23)cos (sin )cos (sin .(19)⎰--dx xx 2491;解dx xx dx xdx xx ⎰⎰⎰---=--22249491491)49(49181)32()32(1121222x d x x d x --+-=⎰⎰C x x +-+=2494132arcsin 21.(20)⎰+dx xx 239; 解 C x x x d xx d x x dx x x ++-=+-=+=+⎰⎰⎰)]9ln(9[21)()991(21)(9219222222223. (21)⎰-dx x 1212;解⎰⎰⎰+--=+-=-dx x x dx x x dx x )121121(21)12)(12(11212 ⎰⎰++---=)12(121221)12(121221x d x x d x C x x C x x ++-=++--=|1212|ln 221|12|ln 221|12|ln 221.(22)⎰-+dx x x )2)(1(1;解C x x C x x dx x x dx x x ++-=++--=+--=-+⎰⎰|12|ln 31|1|ln |2|(ln 31)1121(31)2)(1(1.(23)⎰xdx 3cos ;解 C x x x d x x d x xdx +-=-==⎰⎰⎰3223sin 31sin sin )sin 1(sin cos cos .(24)⎰+dt t )(cos 2ϕω; 解 C t t dt t dt t +++=++=+⎰⎰)(2sin 4121)](2cos 1[21)(cos 2ϕωωϕωϕω. (25)⎰xdx x 3cos 2sin ; 解 ⎰xdx x 3cos 2sin C x x dx x x ++-=-=⎰cos 215cos 101)sin 5(sin 21. (26)⎰dx xx 2cos cos ;解 C x x dx x x dx x x ++=+=⎰⎰21sin 23sin 31)21cos 23(cos 212cos cos .(27)⎰xdx x 7sin 5sin ; 解 C x x dx x x xdx x ++-=--=⎰⎰2sin 4112sin 241)2cos 12(cos 217sin 5sin . (28)⎰xdx x sec tan 3;解 x d x xdx x x xdx x sec tan tan sec tan sec tan 223⎰⎰⎰=⋅=C x x x d x +-=-=⎰sec sec 31sec )1(sec 32.(29)⎰-dx xx2arccos 2110;解C x d x d dx xx xxx+-=-=-=-⎰⎰⎰10ln 210)arccos 2(1021arccos 10110arccos 2arccos 2arccos 22arccos 2.(30)⎰+dx x x x )1(arctan ;解C x x d x x d x xdx x x x +==+=+⎰⎰⎰2)(arctan arctan arctan 2)1(arctan 2)1(arctan .(31)⎰-221)(arcsin xx dx;解C xx d x x x dx+-==-⎰⎰arcsin 1arcsin )(arcsin 11)(arcsin 222.(32)⎰+dx x x x 2)ln (ln 1; 解C xx x x d x x dx x x x+-==+⎰⎰ln 1)ln ()ln (1)ln (ln 122. (33)⎰dx xx xsin cos tan ln ;解⎰⎰⎰=⋅=x d x x xdx x x dx x x x tan tan tan ln sec tan tan ln sin cos tan ln 2C x x d x +==⎰2)tan (ln 21tan ln tan ln .(34)⎰-dx x a x 222(a >0);解⎰⎰⎰⎰-===-dt t a dt t a tdt a t a t a t a x dx xa x 22cos 1sin cos cos sin sin 22222222令, C x a xa x a C t a t a +--=+-=222222arcsin 22sin 421. (35)⎰-12x x dx ;解C x C t dt tdt t t t tx x x dx +=+==⋅⋅=-⎰⎰⎰1arccos tan sec tan sec 1sec 12令.或C x x d x dx xx x x dx +=--=-=-⎰⎰⎰1arccos 111111112222.(36)⎰+32)1(x dx ;解C t tdt t d t tx x dx +==+=+⎰⎰⎰sin cos tan )1(tan 1tan )1(3232令C x x ++=12.(37)⎰-dx xx 92; 解⎰⎰⎰=-=-tdt t d tt t x dx x x 222tan 3)sec 3(sec 39sec 9sec 39令 C x x C t t dt t+--=+-=-=⎰3arccos 393tan 3)1cos 1(322.(38)⎰+xdx 21;解C x x C t t dt t tdt t t x xdx ++-=++-=+-=+=+⎰⎰⎰)21ln(2)1ln()111(11221令.(39)⎰-+211x dx ;解⎰⎰⎰⎰-=+-=+=-+dt tdt t tdt t tx x dx)2sec211()cos 111(cos cos 11sin 1122令 C xxx C t t t C t t +-+-=++-=+-=211arcsin cos 1sin 2tan . (40)⎰-+21x x dx .解⎰⎰⎰+-++=⋅+=-+dt tt tt t t tdt t t tx x x dx cos sin sin cos sin cos 21cos cos sin 1sin 12令C t t t t t d t t dt +++=+++=⎰⎰|cos sin |ln 2121)cos (sin cos sin 12121 C x x x ++-+=|1|ln 21arcsin 212.习题4-3求下列不定积分: 1. ⎰xdx x sin ; 解C x x x xdx x x x xd xdx x ++-=+-=-=⎰⎰⎰sin cos cos cos cos sin .2. ⎰xdx ln ;解 C x x x dx x x x xd x x xdx +-=-=-=⎰⎰⎰ln ln ln ln ln . 3. ⎰xdx arcsin ;解 ⎰⎰-=x xd x x xdx arcsin arcsin arcsin ⎰--=dx xx x x 21arcsinC x x x +-+=21arcsin . 4. ⎰-dx xe x ;解 ⎰⎰⎰----+-=-=dx e xe xde dx xe x x x x C x e C e xe x x x ++-=+--=---)1(. 5. ⎰xdx x ln 2; 解 ⎰⎰⎰-==x d x x x xdx xdx x ln 31ln 31ln 31ln 3332 C x x x dx x x x +-=-=⎰332391ln 3131ln 31.6. ⎰-xdx e x cos ; 解因为⎰⎰⎰⎰------+=-==xdx e x e xde x e x d e xdx e x x x x x x sin sin sin sin sin cos ⎰⎰-----+-=-=x x x x x xde x e x e x d e x e cos cos sin cos sin⎰-----=xdx e x e x e x x x cos cos sin ,所以 C x x e C x e x e xdx e x x x x +-=+-=----⎰)cos (sin 21)cos sin (21cos .7. ⎰-dx xe x 2sin 2;解因为⎰⎰⎰-----==x x x x de xx e x d e dx x e 22222cos 22cos 22cos 22sin⎰⎰----+=+=2sin 82cos 22cos 42cos 22222xd e x e dx x e x e x x x x⎰----+=x x x de xx e x e 2222sin 82sin 82cos 2⎰---++=dx xe x e x e x x x 2sin 162sin 82cos 2222,所以 C xx e dx x e x x ++-=--⎰)2sin 42(cos 1722sin 22.8. ⎰dx xx 2cos ;解 C xx x dx x x x x xd dx x x ++=-==⎰⎰⎰2cos 42sin 22sin 22sin 22sin 22cos .9. ⎰xdx x arctan 2; 解 ⎰⎰⎰+⋅-==dx x x x x xdx xdx x 233321131arctan 31arctan 31arctan ⎰⎰+--=+-=2232223)111(61arctan 31161arctan 31dx xx x dx x x x x C x x x x +++-=)1ln(6161arctan 31223.10. ⎰xdx x 2tan解 ⎰⎰⎰⎰⎰+-=-=-=x xd x xdx xdx x dx x x xdx x tan 21sec )1(sec tan 2222C x x x x xdx x x x +++-=-+-=⎰|cos |ln tan 21tan tan 2122.11. ⎰xdx x cos 2;解 ⎰⎰⎰⎰+=⋅-==x xd x x xdx x x x x d x xdx x cos 2sin 2sin sin sin cos 2222C x x x x x xdx x x x x +-+=-+=⎰sin 2cos 2sin cos 2cos 2sin 22. 12. ⎰-dt te t 2;解 ⎰⎰⎰----+-=-=dt e te tde dt te t t tt 2222212121 C t e C e te t t t ++-=+--=---)21(214121222.13. ⎰xdx 2ln ;解 ⎰⎰⎰-=⋅⋅-=xdx x x dx xx x x x xdx ln 2ln 1ln 2ln ln 222C x x x x x dx x x x x x x ++-=⋅+-=⎰2ln 2ln 12ln 2ln 22.14. ⎰xdx x x cos sin ; 解 ⎰⎰⎰⎰+-=-==xdx x x x xd xdx x xdx x x 2cos 412cos 412cos 412sin 21cos sin C x x x ++-=2sin 812cos 41.15. ⎰dx xx 2cos 22; 解 ⎰⎰⎰⎰-+=+=+=xdx x x x x x d x x dx x x dx x x sin sin 2161sin 2161)cos 1(212cos 2323222⎰⎰-++=++=xdx x x x x x x xd x x x cos cos sin 2161cos sin 21612323C x x x x x x +-++=sin cos sin 216123.16. ⎰-dx x x )1ln(; 解 ⎰⎰⎰-⋅--=-=-dx x x x x dx x dx x x 1121)1ln(21)1ln(21)1ln(222 ⎰-⋅++--=dx x x x x )111(21)1ln(212C x x x x x +-----=)1ln(212141)1ln(2122.17. ⎰-xdx x 2sin )1(2;解 ⎰⎰⎰⋅+--=--=-xdx x x x x d x xdx x 22cos 212cos )1(212cos )1(212sin )1(222 ⎰+--=x xd x x 2sin 212cos )1(212⎰-+--=xdx x x x x 2sin 212sin 212cos )1(212C x x x x x +++--=2cos 412sin 212cos )1(212.18. ⎰dx x x 23ln ;解⎰⎰⎰⎰+-=+-=-=xdx xx x x d x x x x xd dx x x22333323ln 13ln 1ln 1ln 11ln ln⎰⎰+--=--=x d xx x x x x xd x x 22323ln 13ln 3ln 11ln 3ln 1⎰⎰---=+--=x xd x x x x dx x x x x x x 1ln 6ln 3ln 1ln 16ln 3ln 123223⎰+---=dx xx x x x x x 22316ln 6ln 3ln 1C x x x x x x x +----=6ln 6ln 3ln 123.19. ⎰dx e x3;解 ⎰⎰⎰==t t xde t dt e t t x dx e223333令⎰⎰-=-=t t t t tde e t dt te e t 636322 ⎰+-=dt e te e t t t t 6632 C e te e t t t t ++-=6632 C x x ex ++-=)22(33323.20. ⎰xdx ln cos ; 解因为⎰⎰⋅⋅+=dx xx x x x xdx 1ln sin ln cos ln cosdx xx x x x x x xdx x x 1ln cos ln sin ln cos ln sin ln cos ⋅⋅-+=+=⎰⎰⎰-+=xdx x x x x ln cos ln sin ln cos , 所以 C x x xxdx ++=⎰)ln sin ln (cos 2ln cos .21. ⎰dx x 2)(arcsin ;解 ⎰⎰-⋅⋅-=dx xx x x x dx x 22211arcsin 2)(arcsin )(arcsin⎰-+=221arcsin 2)(arcsin x xd x x ⎰--+=dx x x x x 2arcsin 12)(arcsin 22 C x x x x x +--+=2arcsin 12)(arcsin 22. 22. ⎰xdx e x 2sin . 解 ⎰⎰⎰-=-=xdx e e dx x e xdx e xx x x 2cos 2121)2cos 1(21sin 2, 而 dx x e x e xde xdx e x x x x ⎰⎰⎰+==2sin 22cos 2cos 2cos⎰⎰-+=+=xdx e x e x e de x x e x x x x x 2cos 42sin 22cos 2sin 22cos ,C x x e xdx e x x ++=⎰)2sin 22(cos 512cos ,所以 C x x e e xdx e x x x ++-=⎰)2sin 22(cos 10121sin 2.习题4-4求下列不定积分:1. dx x x ⎰+33;解 dx x x x x dx x x dx x x ⎰⎰⎰+-+-+=+-+=+327)93)(3(327273233 ⎰⎰+-+-=dx x dx x x 3127)93(2 C x x x x ++-+-=|3|ln 279233123.2. ⎰-++dx x x x 103322;解 C x x x x d x x dx x x x +-+=-+-+=-++⎰⎰|103|ln )103(1031103322222.3. ⎰--+dx xx x x 3458; 解 ⎰⎰⎰--++++=--+dx xx x x dx x x dx x x x x 3223458)1(8 ⎰⎰⎰--+-+++=dx x dx x dx x x x x 13148213123C x x x x x x +--+-+++=|1|ln 3|1|ln 4||ln 8213123.4. ⎰+dx x 133;解 ⎰⎰⎰+-⋅++--⋅-+=+-+-++=+dx x x x x x x dx x x x x dx x )11231122111()1211(132223⎰⎰-+-++-+--+=)21()23()21(123)1(1121|1|ln 2222x d x x x d x x xC x x x x +-++-+=312arctan31|1|ln2. 5. ⎰+++)3)(2)(1(x x x xdx;解dx x x x x x x xdx )331124(21)3)(2)(1(+-+-+=+++⎰⎰C x x x ++-+-+=|)1|ln |3|ln 3|2|(ln 21.6. ⎰-++dx x x x )1()1(122;解 ⎰⎰+--⋅++⋅=-++dx x x x dx x x x ])1(111211121[)1()1(1222 C x x x +++-+-=11|1|ln 21|1|ln 21C x x +++-=11|1|ln 212.7. dx x x )1(12+⎰; 解 C xx dx x x x dx x x ++-=+-=+⎰⎰)1ln(21||ln )11()1(1222.8. ⎰++))(1(22x x x dx;解⎰⎰+⋅-++⋅-=++dx x x x x x x x dx )112111211())(1(222⎰++-+-=dx x x x x 1121|1|ln 21||ln 2⎰⎰+-+-+-=dx x dx x x x x 11211241|1|ln 21||ln 22C x x x x +-+-+-=arctan 21)1ln(41|1|ln 21||ln 2.9. ⎰+++)1)(1(22x x x dx; 解dx x xx x x x x x dx )111()1)(1(2222⎰⎰+-+++=+++)1ln(21112111221222+-++++++=⎰⎰x dx x x x x x ⎰++++-++=dx x x x x x 1121)1ln(21|1|ln 21222C x x x x ++++-++=312arctan 33)1ln(21|1|ln 2122. 10. ⎰+dx x 114;解dx x x x x dx x ⎰⎰+-++=+)12)(12(111224⎰⎰+-+-++++=dx x x x dx x x x 12214212214222⎰⎰+----++++=dx x x x dx x x x 1222)22(21421222)22(214222 )1212(41]12)12(12)12([82222222⎰⎰⎰⎰+-+++++-+--++++=x x dxx x dx x x x x d x x x x d C x x x x x x +-++++-++=)12arctan(42)12arctan(42|1212|ln 8222. 11. ⎰++--dx x x x 222)1(2; 解 ⎰⎰⎰++-++-=++--dx x x dx x x x dx x x x 11)1(1)1(2222222 ⎰⎰⎰++-++-+++=dx x x dx x x dx x x x 11)1(123)1(122122222 ⎰⎰++-++-++⋅-=dx x x dx x x x x 11)1(12311212222, 因为)312arctan(32)312()312(11321122+=+++=++⎰⎰x x d x dx x x , 而⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1由递推公式 ⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx ,得⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1312arctan 323211231)1121()23(212222+⋅++++⋅=++++++=⎰x x x x x x dx x x x , 所以 ⎰++--dx x x x 222)1(2C x x x x x x x ++-+-+++-++⋅-=312arctan 32312arctan 3211221112122C x x x x ++-+++-=312arctan34112.12. ⎰+x dx2sin 3;解⎰⎰⎰+=-=+x d x dx x x dx tan 3tan 41cos 41sin 3222C x x d x +=+=⎰3tan 2arctan321tan )23(tan 14122.13.⎰+dx x cos 31;解 ⎰⎰⎰+=+=+)2sec 1(2cos )2(2cos 121cos 31222x x x d x dx dx x ⎰+=+=C x x x d 22tanarctan 212tan 22tan 2. 或⎰⎰+⋅++=+du u u u xu dx x221212312tancos 31令 C xC u du u +=+=+=⎰22tan arctan212arctan21)2(122. 14.⎰+dx x sin 21;解 ⎰⎰⎰+=+=+)2cot 2(csc 2sin )2(2cos 2sin 22sin 2122x x x x d x x dx dx x⎰⎰+++-=++-=222)23()212(cot )212(cot 12cot 2cot )2(cot x x d x x x dC x ++-=312cot 2arctan 32. 或⎰⎰+⋅++=+du u u u xu dx x221212212tansin 21令 ⎰⎰++=++=du u du u u 222)23()21(111C xC u ++=++=312tan 2arctan 32312arctan 32. 15.⎰++x x dxcos sin 1;解 ⎰⎰⎰+=+=+=++C x x xd x x dx x x dx |2tan |ln 2tan1)2(tan )2tan 1(2cos 21cos sin 12. 或⎰⎰+⋅+-+++=++du u u u u ux u xx dx2222121112112tancos sin 1令C xC u du u ++=++=+=⎰|12tan |ln |1|ln 11. 16.⎰+-5cos sin 2x x dx; 解⎰⎰⎰++=+⋅++--+=+-du u u du u u u u ux u x x dx2231125111412tan5cos sin 222222令C xC u du u ++=++=++=⎰512tan 3arctan 51513arctan 51)35()31(13122. 或⎰⎰+⋅++--+=+-du uu uu u x u x x dx2222125111412tan5cos sin 2令⎰⎰++=++=du u du u u 222)35()31(1312231C xC u ++=++=512tan 3arctan 51513arctan 51. 17.⎰++dx x 3111;解⎰⎰⎰++-=⋅+=+=++du uu du uu ux dx x )111(33111111233令 C x x x C u u u +++++-+=+++-=)11ln(313)1(23|1|ln 332333322.18.⎰++dx x x 11)(3;解C x x x dx x x dx x x ++-=+-=++⎰⎰232233221]1)[(11)(.19.⎰++-+dx x x 1111;解⎰⎰⎰++-=⋅+-=+++-+du u u udu u u u x dx x x )122(221111111令 C u u u +++-=|)1|ln 2221(22C x x x +++++-+=)11ln(414)1(. 20.⎰+4xx dx ;解⎰⎰⋅+=+du uu u u x xx dx 324441令C u u u du uu +++-=++-=⎰|1|ln 442)111(42 C x x x +++-=)1ln(4244.21.⎰+-xdxx x 11;解令u x x=+-11, 则2211u u x +-=, du u u dx 22)1(4+-=,⎰⎰⎰++-=+-⋅-+⋅=+-du uu du u u u u u x dx x x )1111(2)1(41111222222 C u u u +++-=arctan 2|11|ln C xxxx x x ++-+++-+--=11arctan2|1111|ln . 22.⎰-+342)1()1(x x dx .解令u x x =-+311, 则1133-+=u u x , 232)1(6--=u udx , 代入得C x x C u du x x dx +-+-=+-=-=-+⎰⎰334211232323)1()1(.总习题四求下列不定积分(其中a , b 为常数):1. ⎰--x x e e dx;解 C e e de e dx e e e e dxx x xx x xxx ++-=---=-⎰⎰⎰-|11|ln 2111122.2. dx x x ⎰-3)1(; 解C x x dx x dx x dx x x+-⋅+-=----=-⎰⎰⎰2323)1(12111)1(1)1(1)1(. 3. ⎰-dx xa x 662(a >0);解 C ax a x a x d x a dx x a x +-+=-=-⎰⎰||ln 61)()()(1313333332323662.4. ⎰++dx x x xsin cos 1;解 C x x x x d x x dx x x x ++=++=++⎰⎰|sin |ln )sin (sin 1sin cos 1.5. ⎰dx xxln ln ; 解 C x x x dx x x x x x x xd dx x x +-⋅=⋅⋅-⋅==⎰⎰⎰ln ln ln ln 1ln 1ln ln ln ln ln ln ln ln ln .6.⎰+dx x xx 4sin 1cos sin ; 解 C x x d x x d xx dx x x x +=+=+=+⎰⎰⎰222244sin arctan 21)(sin )(sin 1121sin sin 1sin sin 1cos sin . 7. ⎰xdx 4tan ; 解 xxd x x d xx xdx tan sin tan tan cos sin tan 22244⎰⎰⎰==⎰⎰++-=+=x d x x x d x x tan )1tan 11(tan tan 1tan tan 2224c x x x c x x x ++-=++-=tan tan 31tan arctan tan tan 3133.8. ⎰xdx x x 3sin 2sin sin ; 解 ⎰⎰--=xdx x x xdx x x 3sin )cos 3(cos 213sin 2sin sin ⎰⎰+-=xdx x xdx x 3sin cos 213sin 3cos 21 ⎰⎰++=dx x x x xd )2sin 4(sin 41)3(cos 3cos 61 C x x x +--=2cos 814cos 1613cos 1212. 9.⎰+)4(6x x dx;解 C x x dx x x x x x dx++-=+-=+⎰⎰)4ln(241||ln 41)41(41)4(6656.10.)0(>-+⎰a dx xa xa ; 解⎰⎰⎰⎰-+-=-+=-+dx xa xdx x a a du x a x a dx x a x a 2222221C x a a xa +--=22arcsin .11.⎰+)1(x x dx ;解C x x C x x x d x x x dx +++=+++=+=+⎰⎰)1ln(2))(1ln(2)(112)1(22.12. ⎰xdx x 2cos ; 解 ⎰⎰⎰+=+=x xd x dx x x x xdx x 2sin 4141)2cos (21cos 22 C x x x x xdx x x x +++=-+=⎰2cos 812sin 41412sin 412sin 414122.13. ⎰bxdx e ax cos ; 解因为dx bx e a b bx e a bxde a bxdx e ax axax ax ⎰⎰⎰+==sin cos 1cos 1cos dx bx e ab bx e a b bx e a de bx a b bx e a ax ax ax axax ⎰⎰-+=+=cos sin cos 1sin cos 12222,所以 C bx e ab bx e a b a a bxdx e axax ax+++=⎰)sin cos 1(cos 2222C bx b bx a e ba ax +++=)sin cos (122.14.⎰+xedx 1;解⎰⎰⎰⎰+--=-=-=++du u u du u u d u u e edx xx)1111(112)1ln(11122令.c e e c u u x x +++-+=++-=1111ln |11|ln .15.⎰-122x xdx ;解C t tdt tdt t t t tx x x dx+==⋅⋅=-⎰⎰⎰sin cos tan sec tan sec 1sec 1222令C xx +-=12.16.⎰-2/522)(x a dx;解⎰⎰⋅=-tdt a t a ta x x a dx cos )cos (1sin )(52/522令⎰⎰+==t d t adt ta tan )1(tan1cos 112444C t at a++=tan 1tan 31434C xa x ax a x a+-+-⋅=224322341)(31.17.⎰+241xxdx;解tdt t t tx x xdx 2424secsec tan 1tan 1⋅⋅=+⎰⎰令⎰⎰==t d t tdt t tsin sin cos sin cos 4243 C t tt d t t ++-=-=⎰sin 1sin 31sin )sin 1sin 1(324 C xx x x ++++-=233213)1(.18.⎰dx x x sin ;解⎰⎰⎰=⋅=tdt t tdt t t t x dx x x sin 22sin sin 2令⎰⎰⋅+-=-=tdt t t t t d t 2cos 2cos 2cos 222⎰⎰-+-=+-=tdt t t t t t td t t sin 4sin 4cos 2sin 4cos 222 C t t t t t +++-=cos 4sin 4cos 22C x x x x x +++-=cos 4sin 4cos 2. 19. ⎰+dx x )1ln(2;解 ⎰⎰+⋅-+=+dx xx x x x dx x 22212)1ln()1ln(⎰+--+=dx x x x )111(2)1ln(22C x x x x ++-+=arctan 22)1ln(2. 20.⎰dx x x32cos sin ;解 x d x xx x d x x dx x xtan )1tan tan (tan tan cos sin cos sin 2232⎰⎰⎰+-== C x x ++-=)1ln(tan 21tan 2122.21. ⎰dx x arctan ;解 x d xx x x dx x ⎰⎰+⋅-=11arctan arctan x d xx x ⎰+⋅--=)111(arctan C x x x x ++-=arctan arctan C x x x +-+=arctan )1(. 22.dx xx⎰+sin cos 1;解C x x x d x dx x x xdx x x +-===+⎰⎰⎰|2cot 2csc |ln 222csc 22cos2sin 22cos2sin cos 1. 23.⎰+dx x x 283)1(;解 C x x x dx x dx x x +++⋅=+=+⎰⎰]arctan 1[2141)1(141)1(484428283. 提示: 已知递推公式⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx . 24. ⎰++dx x x x 234811; 解 ⎰⎰⎰++=++=++dt t t t t x dx x x x dx x x x 234123412322444884811令 ⎰⎰+++-=+++-=dt t t dt t t t )11241(41)23231(412 C t t t ++++-=|1|ln 41|2|ln 41C x x x ++++=21ln 414444.25.⎰-416x dx;解⎰⎰⎰++-=+-=-dx x x dx x x x dx)4141(81)4)(4(11622224C xx x ++-+=)2arctan 21|22|ln 41(81C x x x ++-+=2arctan 161|22|ln 321. 26.dx x x⎰+sin 1sin ;解 ⎰⎰⎰-=--=+dx xxx dx x x x dx x x 222cos sin sin sin 1)sin 1(sin sin 1sinC x x x dx x x x++-=+-=⎰tan sec )cos 11cos sin (22.27. dx xxx ⎰++cos 1sin ;解⎰⎰⎰⎰+=+=++dx x xdx x x dx x x x dx x x x 2cossin 212cos 212cos 2sin cos 1sin 222 ⎰⎰+=dx xx xd 2tan 2tanC xx dx x dx x x x +=+-=⎰⎰2tan 2tan 2tan 2tan .28. ⎰-dx x x x x e x23sin cos sin cos ;解 ⎰⎰⎰⋅⋅-⋅⋅=-xdx x e xdx e x dx xx x x ex x xsec tan cos cos sin cos sin sin 23sin⎰⎰-=x d e x d xe x x sec sin sin sin ⎰⎰+⋅-=x x x xde e x xde sin sin sin sec sec⎰⎰⋅⋅+⋅--=xdx e x e x dx e xe x x x x cos sec sec sin sin sin sin C e x xe x x +⋅-=sin sin sec .29.⎰+dx x x x x)(33;解dt t t dt t t t t t t x dx x x x x)111(66)()(52362633+-=⋅+=+⎰⎰⎰令C x x C t t ++=++=66)1(ln 1ln6. 30.⎰+2)1(x e dx;解⎰⎰⎰---=-⋅=++dt t t t dt t tt e e dxx x )1111(1111)1(222令 C tt t ++--=1ln )1ln(C ee x xx ++++-=11)1ln(.31. ⎰+-+dx e e e e x x xx 1243;解)()(1111222243x xx x x x xx x x x x e ed e e dx e e e e dx e e e e ------+=+-+=+-+⎰⎰⎰C e e x x +-=-)arctan( C x +=)sh 2arctan(. 32.⎰+dx e xe xx 2)1(;解⎰⎰⎰+-=++=+11)1()1()1(22x x x x xe xd e d e x dx e xe⎰⎰+++-=+++-=x x x x x x de e e e x dx e e x )1(11111⎰+-++-=x xxxde e ee x )111(1 C e e e xx x x ++-++-=)1ln(ln 1C e e xe x x x++-+=)1ln(1.33. ⎰++dx x x )1(ln 22;解 dx x x x x x x dx x x ])1([ln )1(ln )1(ln 222222'++⋅-++=++⎰⎰ ⎰+⋅++-++=dx xx x x x x x 22221)1ln(2)1(ln⎰+++-++=22221)1ln(2)1(ln x d x x x x x⎰'++⋅+++++-++=dx x x x x x x x x x ])1[ln(12)1ln(12)1(ln 222222 ⎰++++-++=dx x x x x x x 2)1ln(12)1(ln 2222 C x x x x x x x +++++-++=2)1ln(12)1(ln 2222.34.⎰+dx x x2/32)1(ln ;解因为⎰⎰⎰++=+==⋅=+C xx C t tdt tdt t t x dx x 2232/321sin cos sec sec 1tan )1(1令,所以⎰⎰⎰⋅+-+=+=+dx x x xx x x x x xd dx x x111ln )1(ln )1(ln 2222/32 C x x x x x +++-+=)1ln(1ln 22.35. ⎰-xdx x arcsin 12;解⎰⎰⎰+=⋅=-dt t t t tdt t t x xdx x )2cos (21cos sin arcsin 122令⎰⎰-+=+=tdt t t t t t t 2sin 412sin 41412sin 414122C t t t t +++=2cos 812sin 41412122241arcsin 121)(arcsin 41C x x x x x +--+=.36.⎰-dx xx x 231arccos ;解⎰⎰⎰--=-⋅=-2222231arccos 1arccos 1arccos x xd x dx x x x x dx x x x⎰'⋅-+--=dx x x x x x x )arccos (1arccos 12222 ⎰-⋅-⋅-+--=dx xx x x x x x x )11arccos 2(1arccos 122222⎰⎰-⋅-+--=dx x xdx x x x x x 2222arccos 12arccos 1⎰-----=32322)1(arccos 3231arccos 1x xd x x x x⎰-------=dx x x x x x x x )1(32arccos )1(3231arccos 1232322。

数据挖掘作业答案

数据挖掘作业答案数据挖掘作业题⽬+答案华理计算机专业选修课第⼆章：假定⽤于分析的数据包含属性age。

数据元组中age值如下（按递增序）：13 ，15 ，16 ，16 ，19 ，20 ，20，21 ，22 ，22，25 ，25 ，25 ，25 ，30 ，33 ，33 ，35 ，35 ，35，35，36，40，45，46，52，70.分别⽤按箱平均值和边界值平滑对以上数据进⾏平滑，箱的深度为3.使⽤最⼩-最⼤规范化，将age值35转换到[0.0,1.0]区间使⽤z-Score规范化转换age值35 ，其中age的标准差为12.94年。

使⽤⼩数定标规范化转换age值35。

画⼀个宽度为10的等宽直斱图。

该数据的均值是什么？中位数是什么？该数据的众数是什么？讨论数据的峰（即双峰，三峰等）数据的中列数是什么？（粗略地）找出数据的第⼀个四分位数（Q1 ）和第三个四分位数（Q3 ）给出数据的五数概括画出数据的盒图第三章假定数据仓库包含三个维：time doctor和patient ；两个度量：count和charge；其中charge是医⽣对病⼈⼀次诊治的收费。

画出该数据仓库的星型模式图。

由基本⽅体[day, doctor, patient]开始，为列出2004年每位医⽣的收费总数，应当执⾏哪些OLAP操作。

如果每维有4层（包括all ），该⽴⽅体包含多少⽅体（包括基本⽅体和顶点⽅体）？第五章数据库有4个事务。

设min_sup=60%,min_conf=80%TID Itmes_boughtT100 {K,A,D,B}T200 {D,A,C,E,B}T300 {C,A,B,E}T400 {B,A,D}分别使⽤Apriori和FP-增长算法找出频繁项集。

列出所有的强关联规则（带⽀持度s和置信度c ），它们不下⾯的元规则匹配，其中，X是代表顼客的变量，itmei是表⽰项的变量（例如：A、B等）下⾯的相依表会中了超级市场的事务数据。

生物医学研究的统计学方法-课后习题答案

思考与练习参考答案第1章绪论一、选择题1. 研究中的基本单位是指( D)。

A．样本 B. 全部对象C．影响因素D. 个体E. 总体2. 从总体中抽取样本的目的是（ B ）。

A．研究样本统计量 B. 由样本统计量推断总体参数C．研究典型案例 D. 研究总体统计量Ｅ. 计算统计指标3. 参数是指（ B ）。

A．参与个体数 B. 描述总体特征的统计指标C．描述样本特征的统计指标 D. 样本的总和 E. 参与变量数4. 下列资料属名义变量的是（E）。

A．白细胞计数B．住院天数C．门急诊就诊人数D．患者的病情分级 E. ABO血型5．关于随机误差下列不正确的是（C）。

A．受测量精密度限制B．无方向性 C. 也称为偏倚Ｄ．不可避免 E. 增加样本含量可降低其大小二、名称解释（答案略）1. 变量与随机变量2. 同质与变异3. 总体与样本4. 参数与统计量5. 误差6. 随机事件7. 频率与概率三、思考题1. 生物统计学与其他统计学有什么区别和联系？答：统计学可细分为数理统计学、经济统计学、生物统计学、卫生统计学、医学统计学等，都是关于数据的学问，是从数据中提取信息、知识的一门科学与艺术。

而生物统计学是统计学原理与方法应用于生物学、医学的一门科学，与医学统计学和卫生统计学很相似，其不同之处在于医学统计学侧重于介绍医学研究中的统计学原理与方法，而卫生统计学更侧重于介绍社会、人群健康研究中的统计学原理与方法。

2. 某年级甲班、乙班各有男生50人。

从两个班各抽取10人测量身高，并求其平均身高。

如果甲班的平均身高大于乙班，能否推论甲班所有同学的平均身高大于乙班？为什么？答：不能。

因为，从甲、乙两班分别抽取的10人，测量其身高，得到的分别是甲、乙两班的一个样本。

样本的平均身高只是甲、乙两班所有同学平均身高的一个点估计值。

即使是按随机化原则进行抽样，由于存在抽样误差，样本均数与总体均数一般很难恰好相等。

因此，不能仅凭两个样本均数高低就作出两总体均数熟高熟低的判断，而应通过统计分析，进行统计推断，才能作出判断。

组合数学引论课后答案部分

组合数学引论课后答案习题一1.1任何一组人中都有两个人，它们在该组内认识的人数相等。

1.2任取11个整数，求证其中至少有两个数，它们的差是10的倍数1.3任取n+1个整数，求证其中至少有两个数，它们的差是n的倍数1.4在1.1节例4中证明存在连续的一些天，棋手恰好下了k盘棋(k=1,2,…，21).问是否可能存在连续的一些天，棋手恰好下了22盘棋1.5将1.1节例5推广成从1,2，…，2n中任选n+1个数的问题1.6从1,2,…,200中任取100个整数，其中之一小于16，那么必有两个数，一个能被另一个整除1.7从1,2,…,200中取100个整数，使得其中任意两个数之间互相不能整除1.8任意给定52个数，它们之中有两个数，其和或差是100的倍数1.9在坐标平面上任意给定13个整点（即两个坐标均为整数的点），则必有一个以它们中的三个点为顶点的三角形，其重心也是整点。

1.10上题中若改成9个整点，问是否有相同的结论？试证明你的结论1.11证明：一个有理数的十进制数展开式自某一位后必是循环的。

1.12 证明：对任意的整数N ，存在着N 的一个倍数，使得它仅有数字0和7组成。

（例如，N=3,我们有3259=777⨯;N=4,有41952=7700⨯;N=5,有514=70⨯;……）1.13(1) 在一边长为1的等边三角形中任取5个点，则其中必有两个点，该两点的距离至多为12；(2) 在一边长为1的等边三角形中任取10个点，则其中必有两个点，该两点的距离至多为13；(3) 确定n m ，使得在一边长为1的等边三角形中任取n m 个点，则其中必有两个点，该两点的距离至多为1n ；1.14 一位学生有37天时间准备考试，根据以往的经验，她知道至多只需要60个小时的复习时间，她决定每天至少复习1小时，证明：无论她的复习计划怎样，在此期间都存在一些天，她正好复习了13个小时。

1.15 从1,2,…,2n 中任选n+1个整数，则其中必有两个数，它们的最大公约数为1出的数属于同一个鸽巢，即它们的最大公约数为11.16 针对1.1节的例6，当m,n 不是互素的两个整数时，举例说明例中的结论不一定成立习题二2.1证明：在一个至少有2人的小组中，总存在两个人，他们在组内所认识的人数相同。

三年级下册语文课时练20、21、22、页课后练习答案大全

三年级下册语文课时练20、21、22、页课后练习答案大全一、选(xuǎn)择(zé)正(zhèng)确(què)的(de)读(dú)音(yīn)画(huà)上(shàng)。

引雷针“_____”二、根(gēn)据(jù)大(dà)写(xiě)字(zì)母(mǔ)写(xiě)出(chū)小(xiǎo)写(xiě)字(zì)母(mǔ)。

N T R Q B A “_____”三、读(dú)一(yì)读(dú)，连(lián)一(yì)连(lián)。

半眼官钱相让张霜降四、写(xiě)出(chū)四(sì)个(gè)描(miáo)写(xiě)春(chūn)天(tiān)的(de)词(cí)语(yǔ)。

___________ ___________ ___________ ___________五、读(dú)一(yì)读(dú)，做(zuò)一(yí)做(zuò)。

祖国多么广大大兴安岭，雪花还在飞舞。

长江两岸，柳枝已经发芽。

海南岛上，到处盛开着鲜花。

我们的祖国多么广大。

1.我们的祖国，多么_____ ________。

2.读一读，连一连。

大兴安岭长江两岸海南岛上鲜花盛开雪花飞舞柳枝发芽参考答案：一、yīn léi zhèn二、n t r q b a三、an：半眼官钱ang：相让张霜降四、示例：春回大地万物复苏百花齐放百鸟争鸣五、1.广大2.大兴安岭—雪花飞舞长江两岸—柳枝发芽海南岛上—鲜花盛开。

水力学第三版课后答案

水力学第三版课后答案水力学第三版课后答案【篇一：[工程流体力学(水力学)]__禹华谦1-10章习题解答】．20℃的水2.5m3，当温度升至80℃时，其体积增加多少？[解] 温度变化前后质量守恒，即?1v1??2v2又20℃时，水的密度?1?998.23kg/m380℃时，水的密度?2?971.83kg/m3 ?v2??1v1?2.567m93 ?2则增加的体积为?v?v2?v1?0.0679m31-2．当空气温度从0℃增加至20℃时，运动粘度?增加15%，重度?减少10%，问此时动力粘度?增加多少（百分数）？[解] ??????(1?0.15)?原(1?0.1)?原?1.035?原?原?1.035?原????原1.035?原??原??0.035 ?原?原此时动力粘度?增加了3.5%1-3．有一矩形断面的宽渠道，其水流速度分布为u?0.002?g(hy?0.5y2)/?，式中?、?分别为水的密度和动力粘度，h 为水深。

试求h?0.5m时渠底（y=0）处的切应力。

[解] ?du?0.002?g(h?y)/? dydu?0.002?g(h?y) dy????当h=0.5m，y=0时??0.002?1000?9.807(0.5?0)?9.807pa[解] 木块重量沿斜坡分力f与切力t平衡时，等速下滑mgsin??t??adu dy??mgsin?5?9.8?sin22.62?u1a0.4?0.45??0.001??0.1047pa?s1-5．已知液体中流速沿y方向分布如图示三种情况，试根据牛顿内摩擦定律???绘出切应力沿y方向的分布图。

[解]du，定性dy第二章流体静力学2-1．一密闭盛水容器如图所示，u形测压计液面高于容器内液面h=1.5m，求容器液面的相对压强。

[解] ?p0?pa??gh?pe?p0?pa??gh?1000?9.807?1.5?14.7kpa2-2．密闭水箱，压力表测得压强为4900pa。

(完整版)数据挖掘概念课后习题答案

其它可用来数据光滑的方法包括别的分箱光滑方法，如中位数光滑和箱边界光滑。作为选择，等宽箱可被用来执行任何分箱方式，其中每个箱中的数据范围均是常量。除了分箱方法外，可以使用回归技术拟合成函数来光滑数据，如通过线性或多线性回归。分类技术也能被用来对概念分层，这是通过将低级概念上卷到高级概念来光滑数据。
�数据延边分析描述和模型化随时间变化的对象的规律或趋势，尽管这可能包括时间相关数据的特征化、区分、关联和相关分析、分类、或预测，这种分析的明确特征包括时间序列数据分析、序列或周期模式匹配、和基于相似性的数据分析
1.9列举并描述说明数据挖掘任务的五种原语。
五种原语是：
�任务相关数据：这种原语指明给定挖掘所处理的数据。它包括指明数据库、数据库表、或数据仓库，其中包括包含关系数据、选择关系数据的条件、用于探索的关系数据的属性或维、关于修复的数据排序和分组。
�关联是指发现关联规则，这些规则表示一起频繁发生在给定数据集的特征值的条件。例如，一个数据挖掘系统可能发现的关联规则为：
major(X,“computingscience”)⇒owns(X,“personalcomputer”)[support=12%,confidence=98%]
其中，X是一个表示学生的变量。这个规则指出正在学习的学生，12%（支持度）主修计算机科学并且拥有一台个人计算机。这个组一个学生拥有一台个人电脑的概率是98%（置信度，或确定度）。
�分类与预测不同，因为前者的作用是构造一系列能描述和区分数据类型或概念的模型（或功能），而后者是建立一个模型去预测缺失的或无效的、并且通常是数字的数据值。它们的相似性是他们都是预测的工具：分类被用作预测目标数据的类的标签，而预测典型的应用是预测缺失的数字型数据的值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课后答案
20课
课中思考题
你怎样评价康有为的“移花接木”法?
康有为在研究和宣传维新改革理论时，把西学中的有关政治学说与儒家经史相结合，即“移花接木”。

这一方面使维新理论的传播减少了很多阻力，同时也说明了康有为变法理论的保守性和局限性。

【解析与探究】
请结合时代背景，对“西学中源”说在不同时期的不同内涵进行分析评价。

①材料一是“开眼看世界”时期的看法，它对西学的认识还停留在技术层面上，林昌彝提出“西学中源”说是为了解西方技术提供合理的理由。

材料二是“体用之争”时期的看法，它对西学的认识已经提高到学习运用的阶段上，奕的反驳是为了给洋务派大规模运用西学技术提供依据，这种说法是以“中学为体，西学为用”的论调为基础的，并不主张改变“中学”的核心内容如政治制度、纲
常伦理等。

材料三是“维新思潮”时期的看法，它对西学的认识已经深入到制度层面。

严复的批判则是对“中体”说的彻底颠覆，要求直接去掉“中学”的遮盖，全面系统学习西学的深层理论。

②不同时期的不同看法，实际上反映了近代中国对西学了解的不断深入，以及社会思潮和现实需要的不断发展。

就各阶段而言，这些主张都有一定进步性，对当时的西学传播起到了积极作用，对“西学中源”说不管是支持还是批评，都为西学的传播提供了有利条件。

而各种不足与缺陷，则属于时代的局限，不能绝对片面地看待。

自我测评
1.概述鸦片战争后中国人学习西方、寻求变革的思想历程。

第一阶段是以林则徐、魏源为代表的先进知识分子积极翻译、介绍西方的地理、法律等知识，开始了学习西方的第一步;第二阶段是洋务派大规模地运用和采纳西学，他们所开展的洋务运动以及与顽固派的争论，将西学的传播推进到新的阶段;第三阶段是以康有为、梁启超为代表的维新派，他们在吸取、借鉴和批判前人的基础上，主张从制度上学习和借鉴西方，要求变法革新，并通过著述、翻译、办报等活动，极大地解放了时人的思想。

20课
简述维新思潮的主要内容及其历史影响。

维新代表
人物
重要活动代表论著影响
康有为开办学堂、研究维新
理论、撰写书籍《惭学伪经
考》
《孔子改制
考》
为维新变法提供
了合乎传
统文化价值的理
论依据
梁启超宣传民权思想和君主
立宪《使法通
议》
维新派的宣传家
谭嗣同抨击纲常礼教，批判专
制君权、
宗法等级制度，倡导男
女平等《仁学》批判纲常礼教最
为激烈
严复翻译西方知识书籍《天演论》系统介绍西方近
代文化的第一人
21
课中思考题
请思考政治、经济等诸种解放与思想解放的关系。

新文化运动是近代中国的一次伟大的思想解放运动，它发生在辛亥革命推翻了帝制并建立了资产阶级共和国、民族资本主义获得一定发展的大背景下，也是思想文化领域的近代化运动。

中国近代化历程在经济、政治、文化领域全面启动并逐步深入，这说明政治、经济与思想、三大领域的发展和变动是互相影响、互相促进的。

阅读与思考
白话文、新体诗改革有何历史影响?
首先是文学革命，它为新文化、新思想的传播与普及提供了文化载体，进一步促进了新文化运动的发展;其次，它们不仅从文学体裁，更从主旨内容等方面推动人们改变传统的思维方式和思想观念，为新民主主义革命的酝酿和发动做了文化思想方面的准备;最后，新文化运动的干将们在文学革命中所体现出的、与传统相决裂的勇气和对新文化的信心，号召了更多的先进知识分子加入到新文化运动中来。

解析与探究
反动势力和守旧派文人为何如此仇视新文化运动?请从中探究这场思想斗争的性质和意义。

①原因:新文化运动触及了旧文化中最根本和最核心的内容即纲常礼教，从而使旧文化没有任何栖身之地，这是新文化运动遭到仇视的最根本原因。

除此之外，还有新文化运动损害了反动势力和守旧派文人既得利益等因素。

②性质:是旧文化与资产阶级新文化之间的斗争。

③意义:对于破除专制旧文化和传统礼教起到了极为重要的作用，极大地启发了社会各界追求进步和真理的思想，并为马克思主义的传播和五四运动的兴起奠定了基础o
自我测试
概括说明新文化运动的主要内容及历史影响。

提示:①主要内容:提倡科学，反对愚昧;提倡民主，反对专制;提倡新文学，反对旧文学;提倡新道德，反对旧道德。

②历史影响:略
22
【课中思考题】
请思考:新三民主义与旧三民主义有何异同?
提示t①相同之处:旧三民主义所提出的基本纲领，新三民主义基本上都继承了，因为旧三民主义是新三民主义的基础。

②不同之处:新三民主义突出了反对帝国主义的内容，而旧三民主义主要强调反对满清统治，具有狭隘性;新三民主义强调普遍的、平等的民权，而旧三民主义只提出“国民一律平等”的空洞口号;新三民主义以“平均地权，节制资本”为两大原则，具体提出了农民的土地问题和工人生活问题，与“扶助农工”政策紧密相连;旧三民主义只空洞地提出“平均地权”。

【解析与探究】
请思考，上述内容反映了新旧民主主义革命的哪些区别?为什么有这些区别?
旧民主主义革命的目标不包括材料中提出的彻底实现人民权利、八小时工作制、彻底的土地革命纲领、实现社会主义和共产主义。

因为新民主主义革命是中国共产党领导的，代表工人阶级和广大人民群众的根本利益，在阶级属性上与国民党或领导旧民主主义革命的其他政治力量有根本的不同。

中国共产党以实现共产主义为党奋斗的最终目标。

【自我测评】
概述三民主义的基本内容及其历史影响。

三民主义是指民族主义、民权主义、民生主义。

其中民族主义是反对民族压迫，反对满洲贵族对中国的专制统治；民权主义是推翻君主专制政体，建立资产阶级民主共和国，国民一律平等；民生主义以解决土地为中心的财富重新分配问题，平均地权。

新三民主义是三民主义在20世纪20年代新的历史条件下的继续和发展，其主要内容是：民族主义是对外反对帝国主义，谋求中华民族与世界其他民族的独立和平等，对内反对民族压迫，中国境内各民族一律平等，强调各民族的平等和自由；民权主义是赋予一切反对帝国主义和封建军阀的个人与团体一切自由和权利；民生主义是平均地权，节制资本，实行“耕者有其田”，改善农民和工人的生活状况。

历史影响：三民主义是资产阶级民主思想的核心，既具有鲜明的资产阶级民主革命的时代内容，又具有浓厚的爱国主义的民族特色，并迅速成为当时中国先进政治思想的主流和近代中国人民进行反帝反封建及救亡图存革命斗争的纲领。

新三民主义促成了国共第一次合作。

掀起国民革命运动高潮。