数电 1-2 数制码制
数字电路不挂科-1-数制与码制

(2)补码计算。 (−13) 补 +(−10) 补 = (−13 − 10) 补 即 110011 + 110110 = 101001 。(注意符号位参与运算,舍去进位)
(3)将其转化为原码:补码再求补码即得原码。 结果对应的原码为:110111 ,转化为十十进制数即为−23 。
数字电路 不挂科 1.数制与码制 2.常用用的编码
数字电路 不挂科 1.数制与码制 2.常用用的编码 1.原码、反码、补码
例例题1-4 用用二二进制补码运算求出 −13 − 10 。
解析1-4
(1)确定位数。从十十进制结果−23 看出其数值23处于16和32之间,所以尾数部分需要5 位二二进制数来表示。
−13 (原码)101101 (补码)110011 −10 (原码)101010 (补码)110110
数制与码制
数字电路 不挂科 第一讲
常用的编码 小小节2 BCD码
小小节3 格雷雷码
数字电路 不挂科 1.数制与码制 2.常用用的编码 3.格雷雷码
格雷码
格雷雷码不不是BCD 码,其位数⻓长度没有限制。 在一一组二二进制代码中,两个相邻代码对应位置上不不同码值的数目目称为码距。 格雷雷码的特征就是相邻两个格雷雷码码距为 1 ,所以在代码转换过程中不不会因为物理理器器件变化速度 的不不同产生生过渡“噪声”;且除最高高位外,其余各位具有镜像对称的特点。
二进制与N进制的相互转换
二二进制与八八进制互相转换:每一一位八八进制与三位二二进制数对应。 二二进制与十十六进制互相转换:每一一位十十六进制数与四位二二进制数对应。
数字电路 不挂科 1.数制与码制 1.数制间的转换 2.二二进制与N进制的相互转换
例例题1-1 将二二进制数 (1001.1101)2 化为相应的八八进制数。 解析1-1 每3位二二进制数与1位八八进制数对应。从小小数点开始,分别向高高位和低位每三位划分一一组,写出对应的八八进制数。最
1-2计算机的数制与编码
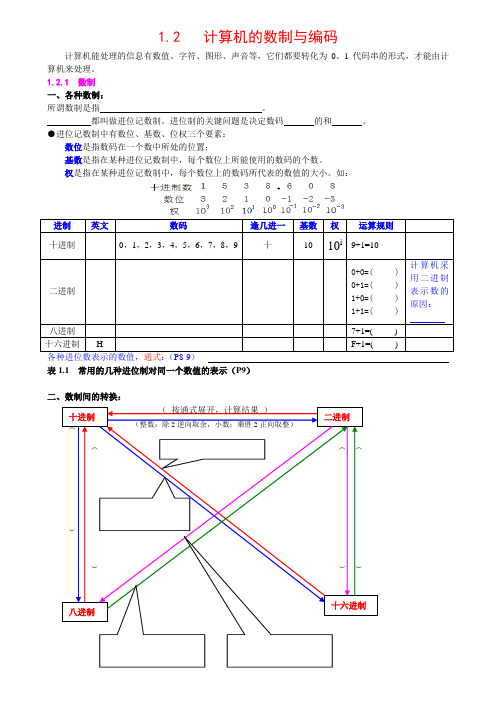
1.2 计算机的数制与编码计算机能处理的信息有数值、字符、图形、声音等,它们都要转化为0、1代码串的形式,才能由计算机来处理。
1.2.1 数制 一、各种数制:所谓数制是指 。
都叫做进位记数制。
进位制的关键问题是决定数码 的和 。
●进位记数制中有数位、基数、位权三个要素: 数位是指数码在一个数中所处的位置;基数是指在某种进位记数制中,每个数位上所能使用的数码的个数。
权是指在某种进位记数制中,每个数位上的数码所代表的数值的大小。
如:表1.1 常用的几种进位制对同一个数值的表示(P9)二、数制间的转换:例:(重点:十进制与二进制的互相转换)●各种进制转十进制●十进制转各种进制●二进制转八进制、八进制转二进制与二进制转十六进制、十六进制转二进制练习:P39:20、21、22、23、24、25、26、27、28、29(写在课本上)如何检查?(计算器!)1.2.2 ASCII码●通称为字符。
字符没有数值意义。
为了便于计算机的应用推广,这些字符必须用统一的规定编码方式来表示。
目前在国际上广泛采用“”表示、和作为使用的等。
●ASCII码的英文全称:,中文。
●ASCII码用位0、1代码串来编码一个符号,每个符号占的存储空间,字节最高位(左)为,作奇偶校验用。
(注:1字节= 位,一个字符的ASCII码占位,余下位用作)●ASCII码给出了个数码,个英文字母,个通用符号,个动作控制符的编码标准。
◆例:查表P308(1)字母“A”的ASCCII的二进制表示为:,十六进制表示为:,十进制表示为:(2)将字符“2”的ASCII码当成数值,转换为十进制数得到50,数字字符“5”的ASCII码转换为十进制数应得到●ASCII码的比较:(详见附录1:P308)空格(space)的ASCCII码是32‘0’~‘9’的ASCCII码是48~57‘A’~‘Z’的ASCCII码是65~90‘a’~‘z’的ASCCII码是97~1221.2.3 汉字编码1.国标码GB 2312-80《》1级汉字个,按顺序排列、2级汉字个,按排列,汉字有6763个,常用符号、字母、图形符号等682个,共计7445个。
数字电路基础_D01-02数制与二进制编码

1.2数制与二进制编码1.2.1数制数制是构成多位数码中每一位的方法和由低位向高位的进位规则,它也是人们在日常生活和科学研究中采用的计数方法。
如十进制是人们常用的进位计数制,十二进制是日常钟表的计时制。
在计算机和数字通信设备中广泛使用二进制、八进制和十六进制计数制。
1.十进制在十进制中,每一位有0、l 、2、3、4、5、6、7、8、9十个数码,超过9的数应―逢十进一‖,即用多位数表示,这种方法称为位置计数法。
例如,十进制数328.25可写成:(328.25)l0=3×102十2 X101十8×100十2×10-1十5×10-2上式各数位的乘数即102,101,100,10-1,l0-2称为各相应数位的―权‖,与―位权‖相乘的数称为系数。
因此,任意一个十进制数均可按权展开为∑--==110)10()(n m i i i k S (1-2-1)其中,K i 是第i 位的系数,它可以是0—9这十个数码中的任何一个,整数部分为n 位,小数部分为m 位。
式中使用的下脚注10表示括号中的数为十进制数,有时也可用D(decimal)代替。
若用N 取代上式中的10,即可得到任意进制(N 进制)的按权展开式为∑--==110)()(n m i i i N k N (1-2-2) 式中,(N)i 称为第i 位的权值。
2.二进制在数字系统中,广泛地采用二进制计数制。
主要原因是二进制的每一位数只有两种可能取值,即―0‖或―1‖,可以用具有两个不同稳定状态的电子开关来表示,使数据的存储和传送用简单而可靠的方式进行。
二进制数的特点是:(1)每位二进制数只有两个数码0或1;(2)二进制数的计数规则是―逢二进一‖,与十进制数一样,采用位置计数法表示。
二进制各位的―权‖是基数2的幂。
一个任意二进制数(S)2的按权展开式为(S)2=K n-1 2 n-1十K n-2 2 n-2十··十K 1 2 1十K 0 2 0十K -1 2 -1十…十K -m 2 –m (1-2-3)式中,K i 、n 、m 的定义与十进制相同,只是K i 的取值为0或1,二进制有时用B(Binary)表示。
数字电路01 数制和码制

逢十六进一
十进制: D ki 10i N进制: D kiNi (基数N、权Ni)
ki :是第 i 位的系数,可以是 0~N-1 中的任何一个
小数部分:i 为负数
二进制
D Ki 2i
K (0,1)
(101.11)2 1 22+0 21+1 20+1 2-1+1 2-2 (5.75)10
0.8125
2 1.6250
整数部分= 1 =k1
0.6250
2 1.2500
整数部分= 1 =k2
故
(0.8125 )10 (0.1101 )2
0.2500
2 0.5000
整数部分= 0 =k3
0.5000
2 1.000
整数部分= 1 =k4
三、二-十六转换
例:将(01011110.10110010)2化为十六进制
八进制
D Ki8i
K (0,7)
(12.4)8 181+2 80+4 8-1 (10.5)10
十六进制
D Ki16i
K (0, F)
(2A.7F)16 2 161+10 160+7 16-1+1516-2 (42.4960937)10
不同进制数的对照表
十进制数 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15
同理
例:
kn 2n1 kn1 2n2 k1 2(kn 2n2 kn12n3 k2 ) k1
∟ 2 173余数=1=k0 ∟ 2 86 余数=0=k1 ∟ 2 43 余数=1=k2 ∟ 2 21 余数=1=k3 ∟ 2 10 余数=0=k4 ∟ 2 5余数=1=k5 ∟ 2 2余数=0=k6
数字电路-数制与编码

数码的个 数和计数 规律是进 位计数制 的两个决 定因素
一、 十进制数的表示 数码个数10: ⒈ 数码个数 :
0,1,2,3,4,5,6,7,8,9
计数规律: 计数规律
逢十进 1,借一当10
2.基与基数 2.基与基数
用来表示数的数码的集合称为基 用来表示数的数码的集合称为基(0—9), ) 称为基数 十进制为10)。 称为基数(十进制为 。 基数 十进制为 集合的大小
lg α j≥i lg β
取满足不等式的最小整数
)16 ,已知精度为±(0.1)410
例: (0.3021)10→(
解: α=10,β=16,i=4
lg10 j≥ 4 = 3.32 取 j=4 lg16
⑵按题意要求
例: (0.3021)10→( 解:
)2 ,要求精度 0.1% ∴取 j=10
1 1 0.1% = ≥ 10 1000 2
X ;0 ≤ X < 2n [ X ]补= 2n +1 + X ;-2n ≤ X < 0
例 2:
(321.4)8 = ( )10 =3×82+2×81+1×80 +4×8-1 =(209.5)10 192 16 1 0.5
基数乘除法( 10 → R )
分整数部分和小数部分分别转换。 ⒈整数的转换——基数除法 规则:除基取余, 规则:除基取余,商零为止 例1:(25) 10 = ( ) 2
例:已知 X1=1100 X2=1010 求 Y1= X1- X2 ; Y2= X2- X1
01100 +10101 100001 + 1 00010 01010 +10011 11101
数制及编码

∴(0.3125)10 =(0.0101)2
说明:有时可能无法得到0的结果,这时应
根据转换精度的要求适当取一定位数。
2024/2/21
7
2. 二进制与八进制、十六进制之间的转换
(1)二进制与八进制之间的转换 三位二进制数对应一位八进制数。
(6574)8 =(110,101,111,100)2 =(110101111100)2
12
(1)8421码
选取0000~1001表示十进制数0~9。 按自然顺序的二进制数表示所对应的十进制数字。 是有权码,从高位到低位的权依次为8、4、2、1,
故称为8421码。 1010~1111等六种状态是不用的,称为禁用码。
例:
(1985)10 =(0001 1001 1000 0101)8421BCD
(101011100101)2 =(101,011,100,101)2 =(5345)8
2024/2/21
8
(2)二进制与十六进制之间的转换 四位二进制数对应一位十六进制数。
例如: (9A7E)16 =(1001 1010 0111 1110)2
=(1001101001111110)2
(10111010110)2 =(0101 1101 0110)2
2024/2/21
19
表1-5 美国标准信息交换码(ASCII码)
2024/2/21
20
b2
2∣27 …………余1
b3
2∣13 …………余1
b4
2∣6 …………余0
b5
2∣3 …………余1
b6
2∣1 …………余1
b7
0
2024∴/2/21(217)10 =(11011001)2
数电知识点总结(整理版)

数电复习知识点第一章1、了解任意进制数的一般表达式、2-8-10-16 进制数之间的相互转换;2、了解码制相关的基本概念和常用二进制编码(8421BCD格雷码等);第三章1 、掌握与、或、非逻辑运算和常用组合逻辑运算(与非、或非、与或非、异或、同或)及其逻辑符号;2 、掌握逻辑问题的描述、逻辑函数及其表达方式、真值表的建立;3、掌握逻辑代数的基本定律、基本公式、基本规则(对偶、反演等);4、掌握逻辑函数的常用化简法(代数法和卡诺图法);5、掌握最小项的定义以及逻辑函数的最小项表达式;掌握无关项的表示方法和化简原则;6、掌握逻辑表达式的转换方法(与或式、与非-与非式、与或非式的转换);第四章1、了解包括M0爭内的半导体元件的开关特性;2、掌握TTL门电路和M0S1电路的逻辑关系的简单分析;3、了解拉电流负载、灌电流负载的概念、噪声容限的概念;4、掌握0D门、0C门及其逻辑符号、使用方法;5、掌握三态门及其逻辑符号、使用方法;6、掌握CMOS专输门及其逻辑符号、使用方法;7、了解正逻辑与负逻辑的定义及其对应关系;8、掌握TTL与CMOS1电路的输入特性(输入端接高阻、接低阻、悬空等);第五章1 、掌握组合逻辑电路的分析与设计方法;2、掌握产生竞争与冒险的原因、检查方法及常用消除方法;3、掌握常用的组合逻辑集成器件(编码器、译码器、数据选择器);4、掌握用集成译码器实现逻辑函数的方法;5、掌握用2n 选一数据选择器实现n 或者n+1 个变量的逻辑函数的方法;1、掌握各种触发器(RS D、JK、T、T')的功能、特性方程及其常用表达方式(状态转换表、状态转换图、波形图等);2、了解各种RS触发器的约束条件;3、掌握异步清零端Rd和异步置位端Sd的用法;2、了解不同功能触发器之间的相互转换;第七章1 、了解时序逻辑电路的特点和分类;2、掌握时序逻辑电路的描述方法(状态转移表、状态转移图、波形图、驱动方程、状态方程、输出方程);3、掌握同步时序逻辑电路的分析与设计方法,掌握原始状态转移图的化简;4、了解异步时序逻辑电路的简单分析;5、掌握移位寄存器、计数器的功能、工作原理和实际应用等;6、掌握集成计数器实现任意进制计数器的方法;7、掌握用移位寄存器、计数器以及其他组合逻辑器件构成循环序列发生器的原理;第八章1、掌握门电路和分立元件构成的施密特触发器、单稳态触发器、多谐振荡器的电路组成及工作原理,掌握相关参数的计算方法;2、掌握用555电路构成施密特触发器、单稳态触发器、多谐振荡器的方法以及工作参数的计算或者改变方法;第九章1、了解ROM和RAM的基本概念;2、了解存储器容量的表示方法和扩展方法,了解存储容量与地址线、数据线的关系。
数电知识点总结

数电知识点总结数字电子技术(简称数电)是电子信息类专业的一门重要基础课程,它主要研究数字信号的传输、处理和存储。
下面为大家总结一些关键的数电知识点。
一、数制与码制数制是指用一组固定的数字和一套统一的规则来表示数的方法。
常见的数制有十进制、二进制、八进制和十六进制。
十进制是我们日常生活中最常用的数制,它由 0、1、2、3、4、5、6、7、8、9 这十个数字组成,遵循“逢十进一”的原则。
二进制则只有 0 和 1 两个数字,其运算规则简单,是数字电路中最常用的数制,遵循“逢二进一”。
八进制由0、1、2、3、4、5、6、7 这八个数字组成,“逢八进一”。
十六进制由 0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F 这十六个数字和字母组成,“逢十六进一”。
码制是指用不同的代码来表示不同的信息。
常见的码制有BCD 码、格雷码等。
BCD 码用四位二进制数来表示一位十进制数,有 8421 BCD 码、5421 BCD 码等。
格雷码的特点是相邻两个编码之间只有一位发生变化,这在数字电路中可以减少错误的产生。
二、逻辑代数基础逻辑代数是数字电路分析和设计的数学工具。
基本逻辑运算包括与、或、非三种。
与运算表示只有当所有输入都为 1 时,输出才为 1;或运算表示只要有一个输入为 1,输出就为 1;非运算则是输入为 1 时输出为 0,输入为 0 时输出为 1。
逻辑代数的基本定律有交换律、结合律、分配律、反演律和吸收律等。
这些定律在逻辑函数的化简和变换中经常用到。
逻辑函数的表示方法有真值表、逻辑表达式、逻辑图、卡诺图等。
真值表是将输入变量的所有可能取值组合及其对应的输出值列成的表格;逻辑表达式是用逻辑运算符将输入变量连接起来表示输出的式子;逻辑图是用逻辑门符号表示逻辑函数的电路图;卡诺图则是用于化简逻辑函数的一种图形工具。
三、门电路门电路是实现基本逻辑运算的电子电路。
常见的门电路有与门、或门、非门、与非门、或非门、异或门和同或门等。
数字电子技术基础第一章-数制和码制

05
结束语
本章总结
01 02
数制和码制的概念理解
通过本章的学习,我们深入理解了数制和码制的概念,掌握了二进制、 八进制、十进制和十六进制等数制的表示方法和转换规则,同时了解了 不同码制的特性和应用场景。
数制转换的实际操作
通过实例和实践操作,我们学会了如何进行不同数制之间的转换,包括 二进制、八进制、十进制和十六进制之间的转换,以及补码表示法等。
03
码制的优缺点分析
对比分析了二进制、八进制、十进制和十六进制等不同码制的优缺点,
理解了不同码制在计算机科学和技术中的重要性和应用范围。
下章预告
数字逻辑基础
在下一章中,我们将学习数字逻辑基础,了解逻辑门电路 的基本概念和原理,掌握逻辑代数的基本运算和逻辑函数 的表示方法。
逻辑门电路及其应用
进一步了解不同类型逻辑门电路的特性和工作原理,如与 门、或门、非门等,并探讨其在计算机硬件系统中的应用 和实践。
二进制转十进制
总结词
将二进制数转换为十进制数需要采用乘权求和法,即将二进制数的每一位乘以对应的权 值(2的幂次方),然后求和得到十进制数。
详细描述
将二进制数转换为十进制数的过程称为"乘权求和法"。具体步骤如下
二进制转十进制
2. 将得到的积相加,即为该 二进制数的十进制表示。
0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 0 + 4 + 0 +1=5
例如,将二进制数1010转换 为十进制数的计算过程如下
因此,二进制数1010等于十 进制数5。
八进制转十进制
总结词
将八进制数转换为十进制数需要采用乘权求 和法,即将八进制数的每一位乘以对应的权 值(8的幂次方),然后求和得到十进制数 。
数字电子技术-数制与编码-

000 0 0
000 1 1
001 2 0
8
100 8
0
9
100 9
1
10 101 A 0
(0010
1111
1011.1110
10103)2
001 1
3
11 101 B 1
=(2FB.EA)16
4 010 4 12 110 C
0
0
5 010 5 13 110 D 例 1 - 9 : ( 4B E5 .9 7D )16 = ( 0 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 . 10101 0 1 1 1 1 1 0 11) 2
7
• 84由21B于CD是代码,代码本身不是数,没有大小之分; • 必须4位一组,最高位、最低位的0不可去掉;
10n
0.0 1
0.1 1
10
10 0
10
3
104 105 106 107
108 109 1010
2n 0.2 0.5 1 2 4 8 16 32 64 128 25 512 1024
5
6
请熟练记住上表中二进制的权,在数制转换时非常有用。
最小的10位二进制数(1000000000)2=(29)10=(512)
四位二进制代码
一位十进制数字
22
(1)8421BCD码
• 选取0000⁓1001表示十进制数0⁓9。
10进制数 0 1
• 按自然顺序的二进制数表示所对应的十进制数字。
2
• 是有权码,从高位到低位的权依次为8、4、2、1, 3
故称为8421码。
4
数字电路的数制与码制

2020年7月13日星期一
第一章 数制与码制
22
2. 二进制、八进制、十六进制间转换 特点:三种进制的基数都是2的正整数幂。 方法:直接转换。
例1:(101011.1)2 = ( ? )8 = ( ? )16 解:(101011.1)2 = (101011.100)2 = (53.4)8
(101011.1)2 = (00101011.1000)2 = (2B.8)16
2020年7月13日星期一
第一章 数制与码制
23
Байду номын сангаас
第二节 码制(编码的制式)
一、二进制码
n位码元
2n个对象
1. 自然二进制码
2. 格雷码 :码间距为1的一种代码。
例1: 0011和 0010 码间距为1
例2: 0011和 1111 码间距为2 循环码:格雷码的一种,特点为首尾代码也只有
一位对应码元不同。
接收方
0000 0000
0
0001
0
0011
偶校验检错结果
0错 0 “对”
2020年7月13日星期一
第一章 数制与码制
26
二、二—十进制(BCD)码(Binary Coded Decimal Codes)
1. 引入BCD码的原因: 习惯用十进制,而数字系统只处理二进制
2. 分类 (1)有权码:有固定位权 8421BCD、5421BCD、2421BCD、631-1BCD (2)无权码:无固定位权
2020年7月13日星期一
第一章 数制与码制
33
(2)减法运算 例1:( 0110 )8421BCD - ( 0001 )8421BCD = ( ? )8421BCD
数制和码制

单元1 数制和码制
《数字电子技术》
单元1 数制和码制
《数字电子技术》
单元1 数制和码制
二、数据集与数据分析
《数字电子技术》
4. 规范性分析——建立在预测性分析的结果之上,用来规范需要执行的行动。其注 重的不仅是哪项操作最佳,还包括了其原因。换言之,规范性分析提供了经得起质 询的结果,因为它们嵌入了情境理解的元素。因此,这种分析常常用来建立优势或 者降低风险。如:
(1)存储在一个文本文件中的推文 (2)一个文件夹中的图像文件 (3)存储在一个CSⅤ格式文件中的从数据库中提取出来的行数据 (4)存储在一个XML文件中的历史气象观测数据 例如:XML数据、关系型数据和图像数据就是三种不同数据格式的数据集。
单元1 数制和码制
《数字电子技术》
二、数据集与数据分析
数据分析:通过处理数据,从数据中发现一些深层知识、模式、关系或是趋 势的过程。数据分析的总体目标是做出更好的决策。
单元1 数制和码制
《数字电子技术》
感谢聆听!
单元1 数制和码制
二、数制转换
2、十 —二进制数转换
(2)其次讨论小数的转换
《数字电子技术》
若(S)10是一个十进制的小数,对应的二进制小数为
则:
将上式两边同乘以2得到:
将小数(S)10 乘以2所得乘积的整数部分即为 k-1 。
同理,将乘积的小数部分再乘以2又可得到:
在数字电路中经常使用的计数进制除了十进制以外还经 常使用二进制、八进制和十六进制。
单元1 数制和码制
《数字电子技术》
1、十进制
十进制数有0~9十个数码,以10为基数。计数时,“逢十进 一,借一当十”。数码在不同的位置代表的实际大小不同。
数电课件第一章 数制和码制

数字电路的特点
以逻辑代数为数学基础,适合工作在存储、控制、 决策等系统中
系统可靠性高、精度高 集成度高、体积小、功耗低
数字电路的应用
计算机系统:主板、内存、硬盘、显卡…… 消费类电子产品:手机、电子表、MP3\4……
方法:将二进制数按权展开后相加,即得到 等值的十进制数。 例:
(1011.01)
3
2
2 1 0 -1
1 2 + 0 2 +1 2 + 1 2 + 0 2
+1 2
-2
=( 11 . 25 ) 10
简便算法:将为1的那些位的位权直接相加即可。
二、十-二转换
整数部分: 除二取余法
如:十进制基数是10,二进制基数是2
位权:数制中每位数字所对应的权重;
位权的大小=基数i,i是数字的位序,
数字的大小=数码乘上该位的权重 例如:十进制数243.15: 3的位权是100 4的位权是101 1的权重为10-1……
按权展开式:将数码写成加权和的形式
例如:243.15= 2×102+4×101+3×100 +1×10-1+5×10-2 十进制数的通用形式:
二进制补码运算原理
引例:将表从10点调到5点
法一:往回拨5格,10-5=5 法二:往前拨7格,超过12以 后产生进位,舍弃进位, 则10+7-12=5 可见: 1、10-5可以在舍弃进位的 条件下,用10+7代替。 2、而7是-5对12的补码
数字电子技术基础-第一章-数制和码制

②格雷码
自然二进制码
先将格雷码的最高位直接抄下,做为二进制 数的最高位,然后将二进制数的最高位与格雷码 的次高位异或,得到二进制数的次高位,再将二 进制数的次高位与格雷码的下一位异或,得二进 制数的下一位,如此一直进行下去,直到最后。
奇偶校验码
组成
信 息 码 : 需要传送的信息本身。
1 位校验位:取值为 0 或 1,以使整个代码 中“1”的个数为奇数或偶数。
二、数字电路的特点
研究对象 输出信号与输入信号之间的逻辑关系
分析工具 逻辑代数
信 号 只有高电平和低电平两个取值
电子器件 工作状态
导通(开)、截止(关)
主要优点
便于高度集成化、工作可靠性高、 抗干扰能力强和保密性好等
1.1 数制和码制
主要要求:
掌握十进制数和二进制数的表示及其相互转换。 了解八进制和十六进制。 理解 BCD 码的含义,掌握 8421BCD 码, 了解其他常用 BCD 码。
(10011111011.111011)2 = ( ? )16
0100111111001111.111111001110 0
补 04 F B
E 补C 0
(10011111011.111011)2= (4FB.EC)16
十六进制→二进制 :
每位十六进制数用四位二进
制数代替,再按原顺序排列。
(3BE5.97D)16 = (11101111100101.100101111101)2
0000
0000
0011
1
0001 0001
0001
0001
0100
2
0010 0010
0010
0010
0101
【数电】(一)数制和码制

【数电】(⼀)数制和码制⼀、数制常⽤的数制有⼆进制(Binary)、⼗进制(Decimal)、⼗六进制(Hexdecimal)和⼋进制(Octal)。
感觉⼋进制不常⽤啊。
1.1 ⼗进制→⼆进制 (64.03)10=(?)2整数部分:64/2=32——余032/2=16——余016/2 = 8——余08/2 = 4——余04/2 = 2——余02/2 = 1——余01/2 = 0——余1从下往上为整数部分⼆进制结果1000000⼩数部分:0.03x2=0.06——整数部分00.06x2=0.12——00.12x2=0.24——00.24x2=0.48——00.48x2=0.96——00.96x2=1.92——10.92x2=1.84——10.84x2=1.68——10.68x2=1.36——10.36x2=0.72——0从上到下为⼩数部分0.0000011110(精确到了⼩数点后10位有效数字)因此(64.03)10=(1000000.0000011110)21.2 ⼆进制→⼗进制 (101.011)2=(?)10 =22+0x21+20+0x2-1+2-2+2-3 =5.375⼆、编码与码制2.1 原码、反码和补码在数字电路中,⼗进制数字⼀般⽤⼆进制来表⽰,原因就是逻辑电路的输出⾼低电平刚好可以表⽰⼆进制数的1和0。
在⼆进制数前增加⼀位符号位即可区分数字的正负,正数符号位为0,负数符号位为1,这种形式称之为原码。
正数的原码、反码和补码都是⾃⼰。
负数的反、补码规则如下:原码:1 1001(⼆进制增加符号位后的形式)反码:1 0110(符号位对应取反)补码:1 0111(反码+1) //“+1”这⼀操作使得正负相加刚好溢出正数+对应负数的补码=0 !2.2 常⽤编码8421码、余3码、2421码、5211码和余3循环码都属于⼗进制代码。
8421码(BCD码):BCD码的每⼀位上的1都代表⼀个固定的⼗进制数,分别为8、4、2、1,将其代表的数值相加就是8421码对应的⼗进制数,属于恒权代码。
《数字电子技术基础》第六版_第01章_数制和码制

例:
0.8125 2 整数部分= 1 =k 1 1.6250 0.6250 2 整数部分= 1 =k 2 1.2500 0.2500 2 整数部分= 0 =k 3 0.5000 0.5000 2 整数部分= 1 =k 4 1.000
第
章
数制和码制
数字电子技术基础
第六版
1.4二进制数运算
1.4.2 反码、补码和补码运算
二进制数的正、负号也是用0/1表示的。 在定点运算中,最高位为符号位(0为正,1为负) 如 +89 = (0 1011001) -89 = (1 1011001)
第
章
数制和码制
数字电子技术基础
第六版
二进制数的补码: • 最高位为符号位(0为正,1为负) • 正数的补码和它的原码相同 • 负数的补码 = 数值位逐位求反(反码) + 1
第
章
数制和码制
数字电子技术基础
第六版
1.3不同数制间的转换
一、二-十转换
例:
D Ki 2
i
K (0,1)
3 2 1 0 - 1 -2 (1011.01) 1 2 + 0 2 + 1 2 + 1 2 + 0 2 + 1 2 2
=( 11.25)10
第
章
数制和码制
数字电子技术基础
第六版
二、十-二转换
n n 1 n2 1 0 整数部分: ( S )10 kn 2 kn1 2 kn2 2 k1 2 k0 2
2( k n 2 n1 k n1 2 n2 k1 ) k0 同理 k n 2 n1 k n1 2 n 2 k1 2( k n 2 n 2 k n1 2 n3 k 2 ) k1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i
例:( 1001 ) 2 = 1 × 2 3 + 0 × 2 2 + 0 × 21 + 1 × 20 = ( 9 ) D 例:( 1101.01 ) 2
= 1 × 2 3 + 1 × 2 2 + 0 × 21 + 1 × 2 0 + 0 × 2 1 + 1 × 2 2
= ( 13.25 ) 10
28
21
三、八进制
以八为基数的计数体制
特 点
八进制计数码: 八进制计数码:0,1, 2, 3, 4, 5, 6, 7
遵循逢八进一 逢八进一的规律 遵循逢八进一的规律 如 7 + 1 = 10 表示方法: 表示方法: (12.4)8 或 (12.4)O )
(N) = ) Oຫໍສະໝຸດ ∑K ×8ii
1 × 81 + 2 × 8 0 + 4 × 8 1 = ( 10.5) D (12.4)O =
25
个数码的不同进制表示。 表1.2.1为0~15个数码的不同进制表示。 为 ~ 个数码的不同进制表示 表1.2.1 D 0 1 2 3 4 5 6 7 B 0000 0001 0010 0011 0100 0101 0110 0111 O 00 01 02 03 04 05 06 07 H 0 1 2 3 4 5 6 7 D 8 9 10 11 12 13 14 15 B 1000 1001 1010 1011 1100 1101 1110 1111 O 10 11 12 13 14 15 16 17 H 8 9 A B C D E F
(d)锯齿冲
12
注意
研究模拟信号时, 研究模拟信号时,我们注重电路 输入、输出信号间的大小、相位关系。 输入、输出信号间的大小、相位关系。 相应的电子电路就是模拟电路, 相应的电子电路就是模拟电路,包括 交直流放大器、滤波器、信号发生器 交直流放大器、滤波器、 等。 在模拟电路中,晶体管一般工作在 在模拟电路中,晶体管一般工作在 放大状态。 放大状态。
二、二进制
以二为基数的计数体制
特 点
表示数的两个数码: 表示数的两个数码: 0, 1 遵循逢二进一的规律 遵循逢二进一的规律 逢二进一
(N) = ∑Ki × 2i 如 1 + 1 = 10 (读作 壹零 读作 壹零) B
(110.01) B = 1× 2 + 1× 2 + 0 × 2 + 0 × 2 + 1× 2
10
二、数字信号和模拟信号 电 子 电 路 中 的 信 号 数字信号 和 果
11
模拟信号 枻 信号
模拟信号(包括正弦波信号和脉冲信号) 模拟信号(包括正弦波信号和脉冲信号) 脉冲信号如方波、矩形波、尖脉冲锯齿波、 脉冲信号如方波、矩形波、尖脉冲锯齿波、梯形 波等。 波等。
(a)正弦波
(b)矩形波(方波) (c)尖脉冲 矩形波(方波) 几种模拟信号的波形
同理, 同理,若将任意进制数转换为十进 制数,只需将数(N)R写成按权R 制数,只需将数( ) 写成按权 将数 展开的多项式表示式, 展开的多项式表示式,并按十进制 规则进行运算, 规则进行运算, 便可求得相应的 十进制数( ) 十进制数(N)10。
(N) = ) R
∑K ×R
i
2
i
例:( 145 ) 8 = 1× 8 + 4 × 8 + 5 × 8
9
§ 1.1 概述
一、数字量和模拟量 自 然 模拟量 在时间上和数值上都是连 续变化的物理量。 续变化的物理量。 界 中 例如:温度、压力、 例如:温度、压力、速度 的 物 在时间上和数值上都是离 理 量 散变化的物理量, 散变化的物理量,而且每 数字量 次增减变化都是某个最小 例如:人数、 量的整数倍 。例如:人数、 物件
26
1.3 数制转换
二进制 十进制 二进制 十六进制 八进制 十六进制 十进制 二进制 十六进制 二进制 二进制 十进制
27
十进制的转换( 十转换): 一、二进制→十进制的转换(二—十转换): 十转换 转换方法:按权 或多项式 或多项式)展开相加 转换方法:按权(或多项式 展开相加
(N) = ∑Ki × 2 B
23
(N) = ∑Ki ×16 H
1 0
i
(2A.7F)H = 2 × 16 + 10 × 16 + 7 × 16 + 15 × 16 = ( 42.4960937) D
1
2
24
(N) = ) R
∑K ×R
i
i
一个数码的进制表示,可用下标, 一个数码的进制表示,可用下标,如(N)2表示 ) 二进制; 二进制; (N)10表示十进制; (N)8表示八进制, ) 表示十进制; ) 表示八进制, (N)16表示十六进制 ) 有时也用字母做下标, 有时也用字母做下标,如(N)B表示二进制,B- ) 表示二进制, - ;(N) Binary;( )D表示十进制,D-Decimal;( )O表 ;(N) 表示十进制, - ;( ;( 示八进制, - ;(N) 表示十六进制, - 示八进制,O-Octal;( )H 表示十六进制,H- ;( Hexadecimal; ;
6
学习重点:
1、在具体的数字电路与分析和设计方法之 间,以分析和设计方法为主。 以分析和设计方法为主。 以分析和设计方法为主 2、在具体的设计步骤和所依据的概念和原 理之间,以概念和原理为主。 以概念和原理为主。 以概念和原理为主 3、在集成电路的内部工作原理和外部特性 之间,以外部特性为主。 以外部特性为主。 以外部特性为主
2
1 0
i1
i2
等式两边分别除以2得 等式两边分别除以 得
i1
= (ki 2 +ki12 +… +k2 2 +k12 ) … 0 i2 i3 = 2(ki 2 +ki12 +… +k22 ) +k1 …
1
2.电子技术的发展←→电子器件的改进与创新 1904年发明电真空器件(电子管)——电子管时代。 1904
电子管(真空管) 电子管(真空管)
2
1948年发明半导体器件——晶体管时代。 1948
晶体管图片
3
20世纪60 60年代制造出集成电路——集成电路时代。 20 60
4
2.电子技术的发展←→电子器件的改进与创新 1904年发明电真空器件(电子管)——电子管时代。 1904 1948年发明半导体器件——晶体管时代。 1948 20世纪60 60年代制造出集成电路——集成电路时代。 20 60 3.电子技术的分类 3.电子技术的分类 电子技术:研究电信号的产生、传送、接收和 处理。 模拟电子技术 数字电子技术
1
0
= ( 101 ) D
29
二进制数的转换( 二转换) 二转换 二、十进制数→二进制数的转换(十—二转换) 然后依次用2除所得的商,余数依次是 然后依次用 除所得的商,余数依次是K1、 除所得的商 K2、…… 、Kn 。转换结果为( K n、Kn-1 … K0 ) 转换结果为( 、 2。 小数部分乘以2, ◆小数部分乘以 ,积的整数部分是二进制 数的K 然后依次用2乘所得的积的小数部分 乘所得的积的小数部分, 数的 -1 ,然后依次用 乘所得的积的小数部分, 整数部分依次是K 整数部分依次是 -2、K-3、…… K-m 。转换结果 为( K -1K-2 … K-m )2 。
22
四、十六进制: 以十六为基数的计数体制 十六进制: 十六进制计数码: 十六进制计数码:
特 点
0,1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15) 遵循逢十六进一 逢十六进一的规律 遵循逢十六进一的规律 如 F + 1 = 10 表示方法: 表示方法: (2A.FF)H 或 (2A.FF)16 )
数字电子技术基础
阎石主编(第五版) 阎石主编(第五版) 信息科学与工程学院基础部
电子技术的发展与应用
1. 电子技术的应用 科学研究中,先进的仪器设备; 传统的机械行业,先进的数控机床、自动化生 产线; 通信、广播、电视、雷达、医疗设备、新型武 器、交通、电力、航空、宇航等领域; 日常生活的家用电器; 电子计算机及信息技术。
30
◆整数部分除以2,余数是二进制数的K0 整数部分除以 ,余数是二进制数的
,
(a)十进制的整数部分(N)10转换为二进制 十进制的整数部分( ) 十进制的整数部分
(N)10 = k i 2 + k i 1 2 )
i i 1
+ …… + k 2 2 + k1 2 + k0 2
1 0
2
1
0
2
商
= 2(ki 2 +ki12 +… +k2 2 +k12 ) +k0 …
2 1 0
1
2
= (6.25 ) 10 = (110.01) B
20
用电路的两个状态---开关来表示 用电路的两个状态 开关来表示 二进制数,易于物理实现; 二进制数,易于物理实现;操作 简单,运算方便;可靠性高, 简单,运算方便;可靠性高,抗 干扰能力强;逻辑设计方便。 干扰能力强;逻辑设计方便。 位数较多,不好读、不易记, 位数较多,不好读、不易记,使 用不便。 用不便。
n 1
9
数
0 的
n
1 m的
数
数
数 数
18
m
数
(N)D = ∑Ki ×10
i
若在数字电路中采用十进制, 若在数字电路中采用十进制,必须 要有十个电路状态与十个计数码相对应。 要有十个电路状态与十个计数码相对应。 这样将在技术上带来许多困难, 这样将在技术上带来许多困难,而且很 不经济。 不经济。
