数字电子技术 数制与码制答案共35页
《数字电子技术》部分习题解答

《数字电子技术》部分习题解答第1 章数字逻辑基础1.3 将下列十进制数转换成等值的二进制数、八进制数、十六进制数。
要求二进制数保留小数点后4位有效数字。
(1)(19)D ;(2)(37.656)D ;(3)(0.3569)D解:(19)D=(10011)B=(23)O=(13)H(37.656)D=(100101.1010)B=(45.5176)O=(25.A7E)H(0.3569)D=(0.01011)B=(0.266)O=(0.5B)H1.4 将下列八进制数转换成等值的二进制数。
(1)(137)O ;(2)(36.452)O ;(3)(0.1436)O解:(137)O=(1 011 111)B(36.452)O=(11110. 10010101)B(0.1436)O=(0.001 100 011 11)B1.5 将下列十六进制数转换成等值的二进制数。
(1)(1E7.2C)H ;(2)(36A.45D)H ;(3)(0.B4F6)H解:(1E7.2C)H=(1 1110 0111.0010 11)B(36A.45D)H=(11 0110 1010. 0100 0101 1101)B(0.B4F6)H=(0.1011 0100 1111 011)B1.6 求下列BCD码代表的十进制数。
(1)(1000011000110101.10010111)8421BCD ;(2)(1011011011000101.10010111)余3 BCD ;(3)(1110110101000011.11011011)2421BCD;(4)(1010101110001011.10010011)5421BCD ;解:(1000 0110 0011 0101.1001 0111)8421BCD=(8635.97)D(1011 0110 1100 0101.1001 0111)余3 BCD =(839.24)D(1110 1101 0100 0011.1101 1011)2421BCD=(8743.75)D(1010 1011 1000 1011.1001 0011)5421BCD=(7858.63)D1.7 试完成下列代码转换。
数字电子技术 (佘新平 著) 华中科技大学出版社 课后答案

第一章数制与编码1.1 自测练习1.1.1、模拟量数字量1.1.2、(b)1.1.3、(c)1.1.4、(a)是数字量,(b)(c)(d)是模拟量1.2 自测练习1.2.1. 21.2.2. 比特bit1.2.3. 101.2.4. 二进制1.2.5. 十进制1.2.6. (a)1.2.7. (b)1.2.8. (c)1.2.9. (b)1.2.10. (b)1.2.11. (b)1.2.12. (a)1.2.13. (c)1.2.14. (c)1.2.15. (c)1.2.16. 1001001 1.2.17. 111.2.18. 110010 1.2.19. 1101 1.2.20. 8进制1.2.21. (a)1.2.22. 0,1,2,3,4,5,6,71.2.23. 十六进制1.2.24. 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 1.2.25. (b)1.3 自测练习1.3.1. 1221.3.2. 675.521.3.3. 011111110.011.3.4. 521.3.5. 1BD.A81.3.6. 1110101111.11101.3.7. 38551.3.8. 28.3751.3.9. 100010.111.3.10. 135.6251.3.11. 570.11.3.12. 120.51.3.13. 2659.A1.4 自测练习1.4.1. BCD Binary coded decimal 二—十进制码1.4.2. (a)1.4.3. (b)1.4.4. 8421BCD码,4221BCD码,5421BCD 1.4.5. (a)1.4.6. 011001111001.10001.4.7. 111111101.4.8. 101010001.4.9. 111111011.4.10. 61.051.4.11. 01011001.01110101 1.4.12. 余3码1.4.13. XS31.4.14. XS31.4.15. 1000.10111.4.16. 1001100000111.4.17. 521.4.18. 110101.4.19. 0101111.4.20. (b)1.4.21. ASCII1.4.22. (a)1.4.23. ASCII American Standard Code for Information Interchange美国信息交换标准码EBCDIC Extended Binary Coded Decimal Interchange Code 扩展二-十进制交换吗1.4.24. 10010111.4.25. ASCII1.4.26. (b)1.4.27. (b)1.4.28. 110111011.4.29. -1111.4.30. +231.4.31. -231.4.32. -861.5 自测练习1.5.1 略1.5.2 110111011.5.3 010001011.5.4 11100110 补码形式1.5.5 011111011.5.6 10001000 补码形式1.5.7 11100010 补码形式习题1.1 (a)(d)是数字量,(b)(c)是模拟量,用数字表时(e)是数字量,用模拟表时(e)是模拟量1.2 (a)7, (b)31, (c)127, (d)511, (e)40951.3 (a),(b),(c)(d)522104108×+×+320410910×+×+×26108108×+×+321102105100×+×+×+21+1.4 (a), (b), (c)(d)3212121×+×+984+12+12+×××4311212121×+×+×+212×64212+12+12+12+1××××1212+×2220110327.15310210710110510..=×+×+×+×+×3210-1-221011.0112+02+12+12+02+12=××××××210-18437.448+38+78+48=××××10-1-2163A.1C316+A16+116+C16=××××,,,1.6 (a)11110, (b)100110,(c)110010, (d)10111.7 (a)1001010110000, (b)10010111111.8 110102 = 2610, 1011.0112 = 11.37510,57.6438 = 71.81835937510,76.EB16 = 118. 91796875101.9 1101010010012 = 65118 = D4916,0.100112 = 0.468 = 0.9816,1011111.011012 = 137.328 = 5F.68161.10 168 = 1410,1728 = 12210,61.538 = 49.671875,126.748 = 86.9375101.11 2A16 = 4210 = 1010102 = 528,B2F16 = 286310 = 1011001011112 = 54578,D3.E16= 211.87510 = 11010011.11102 = 323.78,1C3.F916 = 451.9726562510 =111000011.111110012 = 703.76281.12 (a)E, (b)2E, (c)1B3, (d)3491.13 (a)22, (b)110, (c)1053, (d)20631.14 (a)4094, (b)1386, (c)492821.15 (a)23, (b)440, (c)27771.16 198610 = 111110000102 = 00011001100001108421BCD,67.31110 = 1000011.010012 =01100111.0011000100018421BCD, 1.183410 = 1.0010112 = 0001.00011000001101008421BCD ,0.904710 = 0.1110012 = 0000.10010000010001118421BCD1.17 1310 = 000100118421BCD = 01000110XS3 = 1011Gray, 6.2510 = 0110.001001018421BCD =1001.01011000 XS3 = 0101.01Gray,0.12510 = 0000.0001001001018421BCD =0.010*********XS3 = 0.001 Gray1.18 101102 = 11101 Gray,0101102 = 011101 Gray1.19 110110112 = 0010000110018421BCD,45610 = 0100010101108421BCD,1748=0010011101008421BCD,2DA16 = 0111001100008421BCD,101100112421BCD = 010*********BCD,11000011XS3 = 100100008421BCD1.20 0.0000原= 0.0000反= 0.0000补,0.1001原= 0.1001反= 0.1001补,11001原= 10110反= 10111补1.21 010100原= 010100补,101011原= 110101补,110010原= 101110补,100001原= 111111补1.22 1310 = 00001101补,11010 = 01101110补,-2510 = 11100111补,-90 =10100110补1.23 01110000补= 11210,00011111补= 3110,11011001补= -3910,11001000补= -56101.24 1000011 1000001 1010101 1010100 1001001 1001111 1001110 0100001 0100000 1001000 1101001 1100111 1101000 0100000 1010110 1101111 1101100 1110100 1100001 1100111 11001011.25 0100010 1011000 0100000 0111101 0100000 0110010 0110101 0101111 1011001 01000101.26 BEN SMITH1.27 00000110 100001101.28 01110110 10001110第二章逻辑门2.1 自测练习2.1.1. (b)2.1.2. 162.1.3. 32, 6 2.1.4. 与2.1.5. (d)2.1.6. 162.1.7. 32, 6 2.1.8. 或2.1.9. 非2.1.10. 12.2 自测练习2.2.1. FAB=.2.2.2. (b)2.2.3. 高2.2.4. 322.2.5. 16,52.2.6. 12.2.7. 串联2.2.8. (d)2.2.9. 不相同2.2.10. 高2.2.11. 相同2.2.12. (a)2.2.13. (c)2.2.14. 奇2.3 自测练习2.3.1. OC,上拉电阻2.3.2. 0,1,高阻2.3.3. (b)2.3.4. (c)2.3.5. ,FAB=. 高阻2.3.6. 不能2.4 自测练习2.4.1. TTL,CMOS2.4.2. Transisitor Transistor Logic2.4.3. Complementary Metal Oxide Semicoductor2.4.4. 高级肖特基TTL,低功耗和高级低功耗肖特基TTL 2.4.5. 高,强,小2.4.6. (c)2.4.7. (b)2.4.8. (c)2.4.9. 大2.4.10. 强2.4.11. (a)2.4.12. (a)2.4.13. (b)2.4.14. 高级肖特基TTL2.4.15. (c)习题2.1 与,或,与2.2 与门,或门,与门2.3 (a)F=A+B, F=AB (b)F=A+B+C, F=ABC (c)F=A+B+C+D, F=ABCD 2.4 (a)0 (b)1 (c)0 (d)02.5 (a)0 (b)0 (c)1 (d)02.6 (a)1 (b)1 (c)1 (d)12.7 (a)4 (b)8 (c)16 (d)322.8 (a)3 (b)4 (c)5 (d)6ABCF0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 11111112.9 (a)(b)ABCDF1110 1 1 1 0 1 0 0 00 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 00 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 111111112.10 YABAC=+ 2.11ABCY0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 11111112.122.13F1 = A(B+C), F2=A+BCA B C F1 F2 0 0 0 0 0 0 0 1 0 0 0 1 0 00 0 1 1 0 1 1 0 1 1 1 1 0 0 0 1 1 1 0 1 1 111112.142.15 (a)0 (b)1 (c)1 (d)02.16 (a)1 (b)0 (c)0 (d)12.17 (a)0 (b)02.182.19 CDEF.2.20 CY ABDF.2.21 102.22 402.23 当TTL反相器的输出为3V,输出是高电平,红灯亮。
数字电子技术参考答案

数字电子技术试卷(1)参考答案一.填空1. 1111011,7B2. 8613. 与,或,非 4. 0,1,高阻5. 真值表,逻辑图,逻辑表达式,卡诺图,波形图(时序图) 6. 波形的整形 7. 20伏8. 并行A/D ,串并行A/D ,逐次比较A/D ,双积分A/D (写出三种) 二.判断题1.× 2.√ 3.× 4.√ 5.√三.化简逻辑函数1.D B A Y +=-2.--+=D B A Y四.C B A Y ⊕⊕=, C B A AB C )(1++=,全加器,Y 为和,1C 为进位。
五.AQ Q Qn +=-+1,A Q n =+1六.采用D 触发器,-=122Q Q D ,--=231Q Q D ,1230Q Q Q D -+=电路图略。
将非工作状态101,110,111带入方程得次态,101→001,110→101→001, 111→001,电路可以自启动。
七.f =65Hz数字电子技术(2)参考答案 一.填空题(16)1. 100011.110,23.C 2. 0,13. 当前输入,原状态4. 0,1,高阻;任何时候,只能有1个三态门被选通。
5. 有两个稳态,在触发信号作用下状态可相互转变,有记忆功能 6. 延时 7. 5.5v 8. 13二.判断题(10)1.√ 2.× 3.×4.√ 5.√三.化简题(14)1. B Y =2. -++=D A C B Y 四.(15)CD A B A Y --+= 五.(15)--+=B A Qn 11, Q B Q A Qn ---++=21六.(15)驱动方程:1,121=⊕=-K Q X J ,1,212=⊕=K Q X J逻辑功能:X=0时,同步三进制计数器;X =1时,同步三进制减法计数器。
该电路为同步三进制可逆计数器,并且能自启动。
七.(15)数字电子答案3 一.填空题(16)1. 1010110,100001102. 7 3. 16,64. 状态转换表,状态转换图,特性方程5. 06. 256×4bit 7. 5.275伏8. 转换精度,转换速度二.回答问题(10)1. 不正确。
数字电子技术课后习题答案(全部)

第一章数制与编码1.1自测练习1.1.1、模拟量数字量1.1.2、(b)1.1.3、(c)1.1.4、(a)是数字量,(b)(c)(d)是模拟量1.2 自测练习1.2.1. 21.2.2.比特bit1.2.3.101.2.4.二进制1.2.5.十进制1.2.6.(a)1.2.7.(b)1.2.8.(c)1.2.9.(b)1.2.10.(b)1.2.11.(b)1.2.12.(a)1.2.13.(c)1.2.14.(c)1.2.15.(c)1.2.16.10010011.2.17.111.2.18.1100101.2.19.11011.2.20.8进制1.2.21.(a)1.2.22.0,1,2,3,4,5,6,71.2.23.十六进制1.2.24.0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 1.2.25.(b)1.3自测练习1.3.1.1221.3.2.675.521.3.3.011111110.011.3.4.521.3.5.1BD.A81.3.6.1110101111.11101.3.7.38551.3.8.28.3751.3.9.100010.111.3.10.135.6251.3.11.570.11.3.12.120.51.3.13.2659.A1.4自测练习1.4.1.BCD Binary coded decimal 二—十进制码1.4.2.(a)1.4.3.(b)1.4.4.8421BCD码,4221BCD码,5421BCD1.4.5.(a)1.4.6.011001111001.10001.4.7.111111101.4.8.101010001.4.9.111111011.4.10.61.051.4.11.01011001.011101011.4.12.余3码1.4.13.XS31.4.14.XS31.4.15.1000.10111.4.16.1001100000111.4.17.521.4.18.110101.4.19.0101111.4.20.(b)1.4.21.ASCII1.4.22.(a)1.4.23.ASCII American Standard Code for Information Interchange美国信息交换标准码EBCDIC Extended Binary Coded Decimal Interchange Code 扩展二-十进制交换吗1.4.24.10010111.4.25.ASCII1.4.26.(b)1.4.27.(b)1.4.28.110111011.4.29.-1131.4.30.+231.4.31.-231.4.32.-861.5 自测练习 1.5.1 略1.5.2 11011101 1.5.3 010001011.5.4 11100110 补码形式 1.5.5 011111011.5.6 10001000 补码形式 1.5.7 11100010 补码形式习题1.1 (a )(d )是数字量,(b )(c )是模拟量,用数字表时(e )是数字量,用模拟表时(e )是模拟量 1.2 (a )7, (b )31, (c )127, (d )511, (e )40951.3 (a )22104108⨯+⨯+, (b )26108108⨯+⨯+,(c )321102105100⨯+⨯+⨯+(d )322104109105⨯+⨯+⨯+ 1.4 (a )212121⨯+⨯+, (b )4311212121⨯+⨯+⨯+, (c )64212+12+12+12+1⨯⨯⨯⨯(d )9843212+12+12+12+12⨯⨯⨯⨯⨯ 1.5 2201210327.15310210710110510--=⨯+⨯+⨯+⨯+⨯,3210-1-221011.0112+02+12+12+02+12=⨯⨯⨯⨯⨯⨯,210-18437.448+38+78+48=⨯⨯⨯⨯, 10-1-2163A.1C 316+A 16+116+C 16=⨯⨯⨯⨯1.6 (a )11110, (b )100110,(c )110010, (d )1011 1.7 (a )1001010110000, (b )10010111111.8 110102 = 2610, 1011.0112 = 11.37510, 57.6438 = 71.81835937510, 76.EB 16= 118.91796875101.9 1101010010012 = 65118 = D4916,0.100112 = 0.468 = 0.9816,1011111.011012 = 137.328 = 5F.68161.10 168 = 1410,1728 = 12210,61.538 = 49.671875, 126.748 = 86.9375101.11 2A 16 = 4210 = 1010102 = 528, B2F 16 = 286310 = 1011001011112 = 54578, D3.E 16= 211.87510 = 11010011.11102 = 323.78, 1C3.F916 = 451.9726562510 = 111000011.111110012 = 703.76281.12 (a )E, (b )2E, (c )1B3, (d )349 1.13 (a )22, (b )110, (c )1053, (d )2063 1.14 (a )4094, (b )1386, (c )49282 1.15(a )23, (b )440, (c )27771.16 198610 = 111110000102 = 00011001100001108421BCD , 67.31110 = 1000011.010012 =01100111.0011000100018421BCD , 1.183410 = 1.0010112 = 0001.00011000001101008421BCD ,0.904710 = 0.1110012 = 0000.10010000010001118421BCD1.17 1310 = 000100118421BCD = 01000110XS3 = 1011Gray, 6.2510 = 0110.001001018421BCD=1001.01011000 XS3 = 0101.01Gray,0.12510= 0000.0001001001018421BCD= 0011.010*********XS3 = 0.001 Gray1.18 101102 = 11101 Gray,0101102 = 011101 Gray1.19 110110112 = 0010000110018421BCD,45610 = 0100010101108421BCD,1748=0010011101008421BCD,2DA16 = 0111001100008421BCD,101100112421BCD = 010*********BCD, 11000011XS3 = 100100008421BCD1.20 0.0000原= 0.0000反= 0.0000补,0.1001原= 0.1001反= 0.1001补,11001原= 10110反= 10111补1.21 010100原= 010100补,101011原= 110101补,110010原= 101110补,100001原=111111补1.22 1310 = 00001101补,11010 = 01101110补,-2510 = 11100111补,-90 =10100110补1.23 01110000补= 11210,00011111补= 3110,11011001补= -3910,11001000补= -56101.24 1000011 1000001 1010101 1010100 1001001 1001111 1001110 0100001 01000001001000 1101001 1100111 1101000 0100000 1010110 1101111 1101100 1110100 1100001 1100111 11001011.25 0100010 1011000 0100000 0111101 0100000 0110010 0110101 0101111 101100101000101.26 BEN SMITH1.27 00000110 100001101.28 01110110 10001110第二章逻辑门1.1 自测练习2.1.1. (b)2.1.2. 162.1.3. 32, 62.1.4. 与2.1.5. (b)2.1.6. 162.1.7. 32, 62.1.8. 或2.1.9. 非2.1.10. 12.2 自测练习=⋅2.2.1. F A B2.2.2. (b)2.2.3. 高2.2.4. 322.2.5. 16,52.2.6. 12.2.7. 串联2.2.8. (b)2.2.9. 不相同2.2.10. 高2.2.11. 相同2.2.12. (a)2.2.13. (c)2.2.14. 奇2.3 自测练习2.3.1. OC,上拉电阻2.3.2. 0,1,高阻2.3.3. (b)2.3.4. (c)2.3.5. F A B=⋅, 高阻2.3.6. 不能2.4 自测练习1.29 TTL,CMOS1.30 Transisitor Transistor Logic1.31 Complementary Metal Oxide Semicoductor1.32 高级肖特基TTL,低功耗和高级低功耗肖特基TTL1.33 高,强,小1.34 (c)1.35 (b)1.36 (c)1.37 大1.38 强1.39 (a)1.40 (a)1.41 (b)1.42 高级肖特基TTL1.43 (c)习题2.1 与,或,与2.2 与门,或门,与门2.3 (a)F=A+B, F=AB (b)F=A+B+C, F=ABC (c)F=A+B+C+D, F=ABCD2.4 (a )0 (b )1 (c )0 (d )0 2.5 (a )0 (b )0 (c )1 (d )0 2.6 (a )1 (b )1 (c )1 (d )1 2.7 (a )4 (b )8 (c )16 (d )32 2.8 (a )3 (b )4 (c )5 (d )62.9 (a )(b ) A B C D F 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 11112.10 Y AB AC =+2.11A B C Y 0 0 0 0 0 0 1 0 011A B C F 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 11110 1 1 11 0 0 01 0 1 11 1 0 01 1 1 12.122.13F1 = A(B+C), F2=A+BCA B C F1F20 0 0 0 00 0 1 0 00 1 0 0 00 1 1 0 11 0 1 1 11 0 0 0 11 1 0 1 11 1 1 1 12.142.15 (a)0 (b)1 (c)1 (d)02.16 (a)1 (b)0 (c)0 (d)12.17 (a)0 (b)02.182.19 Y AB BC DE F=⋅⋅⋅2.20 Y AB CD EF=⋅⋅2.21 102.22 402.23 当TTL反相器的输出为3V,输出是高电平,红灯亮。
阎石《数字电子技术基础》(第5版)(课后习题 数制和码制)【圣才出品】

1.3 将下列二进制小数转换为等值的十进制数。
(1)(0.1001)2
;(2)(0.0111)2
;(3)(0.101101)2
(0.001111)2 。
解:(1) (0.1001)2 1 21 0 22 0 23 1 24 0.5625 (2) (0.0111)2 0 21 1 22 1 23 1 24 0.4375
3/8
圣才电子书
十万种考研考证电子书、题库视频学习平
台
1.9 将下列十进制数转换为等值的二进制数和十六进制数。要求二进制数保留小数点
以后 4 位有效数字。
Байду номын сангаас
(1)(25.7)10 ; (2)(188.875)10 ; (3)(107.39)10 ; (4)
(174.06)10 。
2/8
圣才电子书
十万种考研考证电子书、题库视频学习平
台
。
解:(1)
8C 16
1000
1100 2
(2) 3D.
BE 16
0011 1101.1011 1110 2
(3)
8F
.FF
16
1000
1111. 1111
1111 2
(4) 10.
00 16
0001
0000.0000
(4) (255)10 (11111111)2 (FF )16
1.8 将下列十进制数转换为等值的二进制数和十六进制数。要求二进制数保留小数点 以后 8 位有效数字。
(1)(0.519)10 ; (2)(0.251)10 ; (3)(0.0376)10 ; (4) (0.5128)10 。
解:(1) (0.519)10 (0.10000100)2 (0.84)16 (2) (0.251)10 (0.01000000)2 (0.40)16 (3) (0.0376)10 (0.00001001)2 (0.09)16 (4) (0.5128)10 (0.10000011)2 (0.83)16
数字电子技术课后习题答案(全部)

第一章数制与编码1.1自测练习1.1.1、模拟量数字量1.1.2、(b)1.1.3、(c)1.1.4、(a)是数字量,(b)(c)(d)是模拟量1.2 自测练习1.2.1. 21.2.2.比特bit1.2.3.101.2.4.二进制1.2.5.十进制1.2.6.(a)1.2.7.(b)1.2.8.(c)1.2.9.(b)1.2.10.(b)1.2.11.(b)1.2.12.(a)1.2.13.(c)1.2.14.(c)1.2.15.(c)1.2.16.11.2.17.111.2.18.1.2.19.11011.2.20.8进制1.2.21.(a)1.2.22.0,1,2,3,4,5,6,71.2.23.十六进制1.2.24.0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 1.2.25.(b)1.3自测练习1.3.1.1221.3.2.675.521.3.3.011111110.011.3.4.521.3.5.1BD.A81.3.6.1111.11101.3.7.38551.3.8.28.3751.3.9.100010.111.3.10.135.6251.3.11.570.11.3.12.120.51.3.13.2659.A1.4自测练习1.4.1.BCD Binaryl二—十进制码1.4.2.(a)1.4.3.(b)1.4.4.8421BCD码,4221BCD码,5421BCD1.4.5.(a)1.4.6.011001111001.10001.4.7.111111101.4.8.101010001.4.9.111111011.4.10.61.051.4.11.01011001.011101011.4.12.余3码1.4.13.XS31.4.14.XS31.4.15.1000.10111.4.16.1001100000111.4.17.521.4.18.110101.4.19.0101111.4.20.(b)1.4.21.ASCII1.4.22.(a)1.4.23.ASCII h ange美准码EBCDICExtende d BinaryCoded Decimal Interch ange Code 扩展二-十进制 1.4.24.10010111.4.25.ASCII1.4.26.(b)1.4.27.(b)1.4.28.110111011.4.29.-1131.4.30.+231.4.31.-231.4.32.-861.5 自测练习 1.5.1 略 1.5.2 11011101 1.5.3 01000101 1.5.4 11100110 补码形式 1.5.5 01111101 1.5.6 10001000 补码形式 1.5.7 11100010 补码形式 习题1.1 (a )(d )是数字量,(b )(c )是模拟量,用数字表时(e )是数字量,用模拟表时(e )是模拟量1.2 (a )7, (b )31, (c )127, (d )511, (e )40951.3 (a )22104108⨯+⨯+, (b )26108108⨯+⨯+,(c )321102105100⨯+⨯+⨯+(d )322104109105⨯+⨯+⨯+1.4 (a )212121⨯+⨯+, (b )4311212121⨯+⨯+⨯+, (c )64212+12+12+12+1⨯⨯⨯⨯(d )9843212+12+12+12+12⨯⨯⨯⨯⨯ 1.5 2201210327.15310210710110510--=⨯+⨯+⨯+⨯+⨯,3210-1-221011.0112+02+12+12+02+12=⨯⨯⨯⨯⨯⨯, 210-18437.448+38+78+48=⨯⨯⨯⨯, 10-1-2163A.1C 316+A 16+116+C 16=⨯⨯⨯⨯1.6 (a )11110, (b ) ,(c ) , (d )1011 1.7 (a ) 0, (b ) 1111 1.8 110102 = 2610, 1011.0112 = 11.37510, 57.6438 = 71.81835937510, 76.EB 16 = 118.7510 1.9 1101010010012 = 65118 = D4916,0.100112 = 0.468 = 0.9816,1011111.011012 =137.328 = 5F.68161.10 168 = 1410,1728 = 12210,61.538 = 49.671875, 126.748 = 86.937510 1.11 2A 16 = 4210 = 2 = 528, B2F 16 = 286310 = 2 = 54578,D3.E 16 = 211.87510 = 11.11102 = 323.78, 1C3.F916 = 451 2510 = 011.111110012 = 703.76281.12 (a )E, (b )2E, (c )1B3, (d )349 1.13 (a )22, (b )110, (c )1053, (d )2063 1.14 (a )4094, (b )1386, (c )49282 1.15 (a )23, (b )440, (c )2777 1.16 198610 = = 00011001100001108421BCD , 67.31110 = 1.010012 = 01100111.0011000100018421BC D ,1.183410 = 1.0010112 = 0001.00011000001101008421BCD , 0.904710 = 0.1110012 = 0000.10010000010001118421BCD1.17 1310 = 000100118421B CD = 01000110XS3 = 1011Gra y, 6.2510 = 0110.001001018421B CD = 1001.01011000XS3 = 0101.01Gray,0.12510= 0000.000100100101 = 0011.010001101000X S3 = 0.001 Gray8421BCD1.18 101102= 11101 Gray,0101102 = 011101 Gray1.19 110110112 = 0010000110018421BCD,45610 = 0100010101108421BCD,1748=0010011101008421BCD,2DA16 = 0111001100008421BCD,101100112421B CD = 010100118421B CD,11000011XS3 = 100100008421B CD1.20 0.0000原= 0.0000反= 0.0000补,0.1001原= 0.1001反= 0.1001补,11001原=10110反=10111补1.21 010100原= 010100补,101011原= 110101补,110010原= 101110补,100001原=111111补1.22 1310 = 00001101补,11010 = 01101110补,-2510 = 11100111补,-90 = 10100110补1.23 01110000补= 11210,00011111补= 3110,11011001补= -3910,11001000补= -56101.24 100001110000011010101101010010010011001111 1001110010000101000001001000 1101001 1100111 1101000 0100000 1010110 1101111 1101100 1110100 1100001 1100111 11001011.25 010001010110000100000011110101000000110010 01101010101111101100101000101.26 BEN SMITH1.27 00000110 100001101.28 01110110 10001110第二章逻辑门1.1 自测练习2.1.1. (b)2.1.2. 162.1.3. 32, 62.1.4. 与2.1.5. (b)2.1.6. 162.1.7. 32, 62.1.8. 或2.1.9. 非2.1.10. 12.2 自测练习2.2.1. F A B=⋅2.2.2. (b)2.2.3. 高2.2.4. 322.2.5. 16,52.2.6. 12.2.7. 串联2.2.8. (b)2.2.9. 不相同2.2.10. 高2.2.11. 相同2.2.12. (a)2.2.13. (c)2.2.14. 奇2.3 自测练习2.3.1. OC,上拉电阻2.3.2. 0,1,高阻2.3.3. (b)2.3.4. (c)2.3.5. F A B=⋅, 高阻2.3.6. 不能2.4 自测练习1.29 TTL,CMOS1.30 Transis itor Transis tor Logic1.31 Complem entary Metal Oxide Semicod uctor1.32 高级肖特基TT L, 高级 肖特基T TL1.33 高,强,小1.34 (c)1.35 (b)1.36 (c)1.37 大1.38 强1.39 (a)1.40 (a)1.41 (b)1.42 高级肖特基TT L1.43 (c)习题2.1 与,或,与2.2 与门,或门,与门2.3 (a)F=A+B, F=AB (b)F=A+B+C, F=ABC (c)F=A+B+C+D, F=ABCD2.4 (a )0 (b )1 (c )0 (d )0 2.5 (a )0 (b )0 (c )1 (d )0 2.6 (a )1 (b )1 (c )1 (d )1 2.7 (a )4 (b )8 (c )16 (d )32 2.8 (a )3 (b )4 (c )5 (d )6 2.9 (a )(b ) A B C D F 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 11112.10 Y AB AC =+2.11A B C Y 0 0 0 0 0 0 1 0 011A B C F 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 11110 1 1 11 0 0 01 0 1 11 1 0 01 1 1 12.122.13F1 = A(B+C), F2=A+BCA B C F1F20 0 0 0 00 0 1 0 00 1 0 0 00 1 1 0 11 0 1 1 11 0 0 0 11 1 0 1 11 1 1 1 12.142.15 (a)0 (b)1 (c)1 (d)02.16 (a)1 (b)0 (c)0 (d)12.17 (a)0 (b)02.18=⋅⋅⋅2.19 Y AB BC DE F=⋅⋅2.20 Y AB CD EF2.21 102.22 402.23 当TTL反相器的输出为3V,输出是高电 ,红灯亮。
数字电子技术基础习题答案完整版

数字电子技术基础习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字电子技术基础答案第1章自测题 填空题 1.2. 43. n 24. 逻辑代数 卡诺图5.)(D C B A F )(D C B A F +='6.))((C B D C B A F7. 代数法 卡诺图8. 1 判断题1. √2.√3. × 选择题A F =1⊙B AB F 2 B A F +=3C L =AB C B A BC Y 习题1.1 当000012 A A A ,7A 到3A 有1个不为0时,就可以被十进制8整除 1.2 (a)AC BC AB F ++=1 (b )B A AB F +=2(c)C B A S ⊕⊕= AC BC AB C 0 略(1) )(B A D C F )(1 ))((1B A D C F ++=' (2) )(B A B A F )(2 ))((2B A B A F ++=' (3) E D C B A F 3 DE C AB F ='3(4) )()(4D A B A C E A F )())()((4D A C AB E A F +++='C B A F ⊕⊕=(1) B A C B C A L (2) D B C B D C A L (3) AD L (4) E ABCD L (5) 0 L C B A BC A C AB ABC C B A L ),,((1) ABD D A C F 1 (2) BC AB AC F 2(3) C A B A B A F 3 (有多个答案) (4) C B D C AB C A CD F +++=4 (5) C B A ABD C B A D B A F 5 (6) 16 F (1) AD D C B B A F 1 (2) B A AC F 2(3) D A D B C B F 3 (4) B C F 4 (1) C A B F 1 (2) B C F 2(3) D A B C F 3 (4) C B A D B D C F 4 C A B A D F(1) D B A D C A D C B F 1(多种答案) (2) C B BCD D C D B F 2 (3) C B C A D C F 3 (4) A B F 4 (5) BD D B F 5 (6) C B D A D C A F 6(多种答案) (7) C A D B F 7(多种答案) (8) BC D B F 8(多种答案) (9) B D C F 9 略第2章自测题 判断题1. √2. √3. ×4. √5. √6. √7. ×8. √9. × 10√ 选择题1.A B 2.C D 3.A 4.B 5.B 6.A B D 7.C 8.A C D 9.A C D 习题解:ABC Y =1 解:(a)mA 234.0503.012=-=-=C CES CC BS R U V I β∴三极管处于放大状态,)V (711.05012=⨯⨯-=-=C B CC O R I V u β。
数字电子技术习题答案

(1)Y = (A + B)(A + B)C + BC
ww w. kh
Y = ABC + ABC + B + C
答 案
Y = A + B + C = ABC
课 后
网
co
m
4.用卡诺图化简法将下列函数化为 最简与或形式。
(2)Y = AB+ AC + BC
课
后
答
案
(4)Y(A,B,C,D) = ∑(m0 ,m1,m2 ,m3,m4 ,m6 ,m8 ,m9 ,m10 ,m11,m14 )
01
11
10
Байду номын сангаас
m
5.将下列函数化为最简与或函数式。
Y = C D( A ⊕ B) + ABC + AC D
约束条件AB+CD=0 (2)Y(A,B,C,D)=Σ (m3,m5,m6,m7,m10),给定约束条件为 m0+m1+m2+m4+m8=0 (3)Y(A,B,C,D)=Σ (m2,m3,m7,m8,m11,m14) 给定约束条件为: m0+m5+m10+m15=0。
da 课 后 答 案 网 ww w. kh w. co m
答案:
课
后
答
= A B C + A B C + A B C + ABC Y2
案
网
ww
(b) Y 1 = AB + BC + AC
w. kh
da
(a)Y = ABC + BC
w.
co
m
《数字电子技术(第二版)》课后习题参考答案
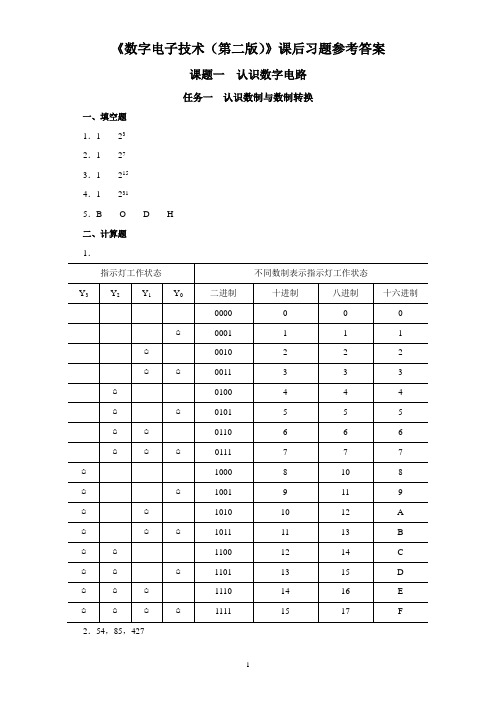
《数字电子技术(第二版)》课后习题参考答案课题一认识数字电路任务一认识数制与数制转换一、填空题1.1 232.1 273.1 2154.1 2315.B O D H二、计算题1.2.54,85,4273.0101,1100,1 1000,11 01114.17O,37O,66 O5.110B,010 111B,001 101 110B6.0FH,36H,0AE63H7.0001 0110B,0010 1010B,1111 1100 0000B任务二学习二进制数算术运算一、计算题(给出的二进制均是无符号数)1.(1)1 0000 (2)1 0000 10012.(1)10 1010 (2)1010 11113.(1)1 0100 (2)110 00004.(1)101 (2)11二、写出下列带符号位二进制数(原码)所表示的十进制数(1)+110 (2)-15 (3)-42 (4)+127 (5)+111(6)-63 (7)+0 (8)+32 767 (9)-32 768三、问答题1.(1)答:左移,移动3位,应作乘以8运算。
(2)答:左移,移动4位,应作乘以16运算。
(3)答:右移,移动7位,应作除以128运算。
(4)答:右移,移动3位,应作除以8运算。
2.答:4位二进制无符号数的最大值是15。
3.答:8位二进制无符号数、有符号数的最大值分别是255和+127。
4.答:16位二进制有符号数的最大值是+32 767。
任务三学习二进制代码一、填空题1.二进制数2.43.8,4,2,1二、判断题1.×2.× 3.√ 4.× 5.× 6.×三、计算题1.36,55,892.[0011 0010]8421,[0101 0010 0111]8421,[0001 0011 0110 1001]8421任务四认识基本逻辑关系并测试逻辑门一、填空题1.与或非2.13.04.1 05.Y=AB6.Y=A+B7.Y=A8.Y=AB9.Y=A+B10.Y=A B=AB+AB二、选择题1.D 2.A 3.B,C 4.A,D三、判断题1.× 2.× 3.× 4.√四、问答题1.答:Y1=ABCD2.答:Y2=A+B+C+D五绘图题1.2.3.4.任务五测试TTL集成门电路1.答:TTL集成门电路电源电压范围为4.75~5.25V之间,额定电压为5V。
数字电子技术-数制与编码-

000 0 0
000 1 1
001 2 0
8
100 8
0
9
100 9
1
10 101 A 0
(0010
1111
1011.1110
10103)2
001 1
3
11 101 B 1
=(2FB.EA)16
4 010 4 12 110 C
0
0
5 010 5 13 110 D 例 1 - 9 : ( 4B E5 .9 7D )16 = ( 0 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 . 10101 0 1 1 1 1 1 0 11) 2
7
• 84由21B于CD是代码,代码本身不是数,没有大小之分; • 必须4位一组,最高位、最低位的0不可去掉;
10n
0.0 1
0.1 1
10
10 0
10
3
104 105 106 107
108 109 1010
2n 0.2 0.5 1 2 4 8 16 32 64 128 25 512 1024
5
6
请熟练记住上表中二进制的权,在数制转换时非常有用。
最小的10位二进制数(1000000000)2=(29)10=(512)
四位二进制代码
一位十进制数字
22
(1)8421BCD码
• 选取0000⁓1001表示十进制数0⁓9。
10进制数 0 1
• 按自然顺序的二进制数表示所对应的十进制数字。
2
• 是有权码,从高位到低位的权依次为8、4、2、1, 3
故称为8421码。
4
《数字电子技术(第二版)习题册》答案

《数字电⼦技术(第⼆版)习题册》答案数字电⼦技术(第⼆版)》习题册部分参考答案课题⼀认识数字电路任务⼀认识数制与数制转换⼀、填空题1.时间数值1 02.1 8 153.1 128 2554.75.96.16⼆、选择题1.C 2.B 3.C 4.B 5.C 6.A 7.D三、判断题1.V2. V3. X4.X5.V6.X7.V 8.V 9.X四、问答题1.答:数字电路中的信号为⾼电平或低电平两种状态,它正好与⼆进制的 1 和0 相对应,因此,采⽤⼆进制更加⽅便和实⽤。
2.答:⼗六进制具有数据读写⽅便,与⼆进制相互转换简单,较直观地表⽰位状态等优点。
五、计算题1. (1)7 (2)15 (3)31 (4)2132. (1)[1010]2 (2)[1 0000]23)[100 0000 0000]2 (4)[100 0000 0110]23. (1)[650]8 (4)[3153]84. (1)[010 111]2 (2)[001 101 110]23)[010 000 000]2 (4)[001 110 101 101]25. (1)0FH (2)1FH3)36H (4)0AE63H6. (1)0001 0110 B (2)0010 1010 1110 B3)1011 1000 1111 1100B (4)0011 1111 1101 0101B 任务⼆学习⼆进制数算术运算⼀、填空题1.加减乘除2. 0+0=0 0+1=1 1+0=1 1+1=103.0-0=0 1-0=1 1-1=0 10-1=14.0X0=0 0X1=0 1X0=0 1X1=15.1 06.最⾼正负原码7.字节 8.半字节 9.字⼆、选择题1.C 2.B 3.C 4.B 5.B 6.B 7.C3.x4. V四、问答题1.答:将⼆进制数 001 1移位⾄ 0110,是向左移动⼀位,应做乘2运算。
2.答:将⼆进制数 1010 0000 移位⾄ 0001 0100,是向右移动三位,应做除以 8运算。
数字电子技术课后习题答案

ABACBC
BC
A
00 01 11 10
00
1
0
1
11
0
1
0
Y ABC
❖ 3.13某医院有一、二、三、四号病室4间,每室设有 呼叫按钮,同时在护士值班室内对应的装有一号、 二号、三号、四号4个指示灯。
❖ 现要求当一号病室的按钮按下时,无论其它病室的 按钮是否按下,只有一号灯亮。当一号病室的按钮 没有按下而二号病室的按钮按下时,无论三、四号 病室的按钮是否按下,只有二号灯亮。当一、二号 病室的按钮都未按下而三号病室的按钮按下时,无 论四号病室的按钮是否按下,只有三号灯亮。只有 在一、二、三号病室的按钮均未按下四号病室的按 钮时,四号灯才亮。试用优先编码器74148和门电路 设计满足上述控制要求的逻辑电路,给出控制四个 指示灯状态的高、低电平信号。
HP RI/BIN
I0
0/ Z1 0 10 ≥1
I1
1/ Z1 1 11
I2
2/ Z1 2 12 18
YS
I3
3/ Z1 3 13
I4
4/ Z1 4 14
YEX
I5
5/ Z1 5 15
I6
6/ Z1 6 16
I7
7/ Z1 7 17
Y0
V18
Y1
ST
E N
Y2
(b)
74148
(a)引脚图;(b)逻辑符号
A
00 01 11 10
00
0
0
1
11
1
0
1
Y AB BC AC
由于存在AC 项,不存在相切的圈,故无冒险。
❖ 4.1在用或非门组成的基本RS触发器中,已知 输入SD 、RD的波形图如下,试画出输出Q, Q
数字电子技术基础课后习题及答案

第1章习题与参考答案【题1-1】将以下十进制数转换为二进制数、八进制数、十六进制数。
〔1〕25;〔2〕43;〔3〕56;〔4〕78解:〔1〕25=〔11001〕2=〔31〕8=〔19〕16〔2〕43=〔101011〕2=〔53〕8=〔2B〕16〔3〕56=〔111000〕2=〔70〕8=〔38〕16〔4〕〔1001110〕2、〔116〕8、〔4E〕16【题1-2】将以下二进制数转换为十进制数。
〔1〕10110001;〔2〕10101010;〔3〕11110001;〔4〕10001000解:〔1〕10110001=177〔2〕10101010=170〔3〕11110001=241〔4〕10001000=136【题1-3】将以下十六进制数转换为十进制数。
〔1〕FF;〔2〕3FF;〔3〕AB;〔4〕13FF解:〔1〕〔FF〕16=255〔2〕〔3FF〕16=1023〔3〕〔AB〕16=171〔4〕〔13FF〕16=5119【题1-4】将以下十六进制数转换为二进制数。
〔1〕11;〔2〕9C;〔3〕B1;〔4〕AF解:〔1〕〔11〕16=〔00010001〕2〔2〕〔9C〕16=〔10011100〕2〔3〕〔B1〕16=〔1011 0001〕2〔4〕〔AF〕16=〔10101111〕2【题1-5】将以下二进制数转换为十进制数。
〔1〕1110.01;〔2〕1010.11;〔3〕1100.101;〔4〕1001.0101解:〔1〕〔1110.01〕2=14.25〔2〕〔1010.11〕2=10.75〔3〕〔1001.0101〕2=9.3125【题1-6】将以下十进制数转换为二进制数。
〔1〕20.7;〔2〕10.2;〔3〕5.8;〔4〕101.71解:〔1〕20.7=〔10100.1011〕2〔2〕10.2=〔1010.0011〕2〔3〕5.8=〔101.1100〕2〔4〕101.71=〔1100101.1011〕2【题1-7】写出以下二进制数的反码与补码〔最高位为符号位〕。
《数字电子技术》习题及答案

第1章 数制和码制 一、填空题1.数制转换:(011010)2 =( )10 =( )8 =( )16。
2.数制转换:(35)10 =( )2 =( )8 =( )16。
3.数制转换:(251)8 =( )2 =( )16 =( )10。
4.数制转换:(4B )16 =( )2 =( )8 =( )10。
5.数制转换:(69)10 =( )2 =( )16 =( )8。
6.将二进制数转换为等值的八进制和十六进制数 (10011011001)2 =( )8 =( )16。
7.将二进制数转换为等值的八进制和十六进制数 (1001010.011001)2 =( )8 =( )16。
一、填空题答案: 1.26、32、1A ; 2.100011、43、 23; 3.10101001、A9、169; 4.1001011、113、75; 5.1000101、45、105; 6.2331、4D9; 7.112.31、4A.64。
第2章 逻辑代数基础 一、填空题1.逻辑函数Y AB A B ''=+,将其变换为与非-与非形式为 。
2.逻辑函数Y A B AB C ''=+,将其变换为与非-与非形式为 。
3. 将逻辑函数AC BC AB Y ++=化为与非-与非的形式,为 。
4.逻辑函数Y A A BC '''=+,化简后的最简表达式为 。
5.逻辑函数Y A B A B ''=++,化简后的最简表达式为 。
6.逻辑函数()()Y A BC AB ''''=+,化简后的最简表达式为 。
7. 逻辑函数Y AB AB A B ''=++,化简后的最简表达式为 。
一、填空题答案1.()()()Y AB A B '''''= ; 2.()()()Y A B AB C '''''=; 3. ()()()()Y AB BC AC ''''=; 4. Y A '=; 5.1Y =; 6.1Y =; 7.Y A B =+。
数字电子技术基础课后答案全解

【 3-5】用卡诺图化简下列带有约束条件的逻辑函数
(1) P1 A, B, C, D
m(3,6,8,9,11,12)
(0,1,2,13,14,15) AC BD BCD (或ACD)
d
(2) P2(A,B,C,D)= m(0,2,3,4,5,6,11,12)
(8,9,10,13,14,15) BC BC D
有” 1”
4、摩根定理表示为: A B = A B ; A B = A B 。
5、函数表达式 Y= AB C D ,则其对偶式为 Y = ( A B)C D 。
6、根据反演规则,若 Y= AB C D C ,则 Y ( AB C D) C 。
7、指出下列各式中哪些是四变量 A B C D 的最小项和最大项。在最小项后的(
(1) F1 = ABC AB 1
(2) F2 = ABCD ABD ACD AD
(3) F3 AC ABC ACD CD A CD
(4) F4 A B C ( A B C ) ( A B C ) A BC
【 3-3】 用卡诺图化简下列各式
(1) F1 BC AB ABC AB C
(3) F3 AC AC BC BC AB AC BC
第 3 页 /共 46 页
CMOS
A F1
10k
(a)
TTL
A
B
F2
100
(b)
CMOS
A
B
F3
51
(c)
TTL
A
B
F4
100k
CMOS
A
B
F5
10k
(d)
解: (a) F1 A (b)
(e) 图 4.4
数字电子技术习题答案

习题答案第一章数制和码制1.数字信号和模拟信号各有什么特点?答:模拟信号——量值的大小随时间变化是连续的。
数字信号——量值的大小随时间变化是离散的、突变的(存在一个最小数量单位△)。
2.在数字系统中为什么要采用二进制?它有何优点?答:简单、状态数少,可以用二极管、三极管的开关状态来对应二进制的两个数。
3.二进制:0、1;四进制:0、1、2、3;八进制:0、1、2、3、4、5、6、7;十六进制:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
4.(30.25)10=( 11110.01)2=( 1E.4)16。
(3AB6)16=( 0011101010110110)2=(35266)8。
(136.27)10=( 10001000.0100)2=( 88.4)16。
5. B E6.ABCD7.(432.B7)16=( 010*********. 10110111)2=(2062. 556)8。
8.二进制数的1和0代表一个事物的两种不同逻辑状态。
9.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
这种表示法称为原码。
10.正数的反码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
11.正数的补码与原码相同,负数的补码即为它的反码在最低位加1形成。
12.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
正数的反码、补码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
负数的补码即为它的反码在最低位加1形成。
补码再补是原码。
13.A:(+1011)2的反码、补码与原码均相同:01011;B: (-1101)2的原码为11101,反码为10010,补码为10011.14.A: (111011)2 的符号位为1,该数为负数,反码为100100,补码为100101. B: (001010)2的符号位为0,该数为正,故反码、补码与原码均相同:001010.15.两个用补码表示的二进制数相加时,和的符号位是将两个加数的符号位和来自最高有效数字位的进位相加,舍弃产生的进位得到的结果就是和的符号。
《数字电子技术》课后习题答案

第1单元能力训练检测题(共100分,120分钟)一、填空题:(每空0.5分,共20分)1、由二值变量所构成的因果关系称为逻辑关系。
能够反映和处理逻辑关系的数学工具称为逻辑代数。
2、在正逻辑的约定下,“1”表示高电平,“0”表示低电平。
3、数字电路中,输入信号和输出信号之间的关系是逻辑关系,所以数字电路也称为逻辑电路。
在逻辑关系中,最基本的关系是与逻辑、或逻辑和非逻辑。
4、用来表示各种计数制数码个数的数称为基数,同一数码在不同数位所代表的权不同。
十进制计数各位的基数是10,位权是10的幂。
5、8421 BCD码和2421码是有权码;余3码和格雷码是无权码。
6、进位计数制是表示数值大小的各种方法的统称。
一般都是按照进位方式来实现计数的,简称为数制。
任意进制数转换为十进制数时,均采用按位权展开求和的方法。
7、十进制整数转换成二进制时采用除2取余法;十进制小数转换成二进制时采用乘2取整法。
8、十进制数转换为八进制和十六进制时,应先转换成二进制,然后再根据转换的二进数,按照三个数码一组转换成八进制;按四个数码一组转换成十六进制。
9、逻辑代数的基本定律有交换律、结合律、分配律、反演律和非非律。
10、最简与或表达式是指在表达式中与项中的变量最少,且或项也最少。
13、卡诺图是将代表最小项的小方格按相邻原则排列而构成的方块图。
卡诺图的画图规则:任意两个几何位置相邻的最小项之间,只允许一位变量的取值不同。
14、在化简的过程中,约束项可以根据需要看作1或0。
二、判断正误题(每小题1分,共10分)1、奇偶校验码是最基本的检错码,用来使用PCM方法传送讯号时避免出错。
(对)2、异或函数与同或函数在逻辑上互为反函数。
(对)3、8421BCD码、2421BCD码和余3码都属于有权码。
(错)4、二进制计数中各位的基是2,不同数位的权是2的幂。
(对)3、每个最小项都是各变量相“与”构成的,即n个变量的最小项含有n个因子。
(对)4、因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。
(完整word版)高等职业教育数字电子技术课后习题答案(人民邮电出版社)

(完整word版)高等职业教育数字电子技术课后习题答案(人民邮电出版社)第1单元能力训练检测题(共100分,120分钟)一、填空题:(每空0.5分,共20分)1、由二值变量所构成的因果关系称为逻辑关系。
能够反映和处理逻辑关系的数学工具称为逻辑代数。
2、在正逻辑的约定下,“1”表示高电平,“0”表示低电平。
3、数字电路中,输入信号和输出信号之间的关系是逻辑关系,所以数字电路也称为逻辑电路。
在逻辑关系中,最基本的关系是与逻辑、或逻辑和非逻辑。
4、用来表示各种计数制数码个数的数称为基数,同一数码在不同数位所代表的权不同。
十进制计数各位的基数是10,位权是10的幂。
5、8421 BCD码和2421码是有权码;余3码和格雷码是无权码。
6、进位计数制是表示数值大小的各种方法的统称。
一般都是按照进位方式来实现计数的,简称为数制。
任意进制数转换为十进制数时,均采用按位权展开求和的方法。
7、十进制整数转换成二进制时采用除2取余法;十进制小数转换成二进制时采用乘2取整法。
8、十进制数转换为八进制和十六进制时,应先转换成二进制,然后再根据转换的二进数,按照三个数码一组转换成八进制;按四个数码一组转换成十六进制。
9、逻辑代数的基本定律有交换律、结合律、分配律、反演律和非非律。
10、最简与或表达式是指在表达式中与项中的变量最少,且或项也最少。
13、卡诺图是将代表最小项的小方格按相邻原则排列而构成的方块图。
卡诺图的画图规则:任意两个几何位置相邻的最小项之间,只允许一位变量的取值不同。
14、在化简的过程中,约束项可以根据需要看作1或0。
二、判断正误题(每小题1分,共10分)1、奇偶校验码是最基本的检错码,用来使用PCM方法传送讯号时避免出错。
(对)2、异或函数与同或函数在逻辑上互为反函数。
(对)3、8421BCD码、2421BCD码和余3码都属于有权码。
(错)4、二进制计数中各位的基是2,不同数位的权是2的幂。
(对)3、每个最小项都是各变量相“与”构成的,即n个变量的最小项含有n个因子。
