Z3 SYMMETRY AND W3 ALGEBRA IN LATTICE VERTEX OPERATOR ALGEBRAS
亚铁磁材料的磁化曲线 英语

亚铁磁材料的磁化曲线英语英文回答:Ferrimagnetic Materials and Their Magnetization Curves.Ferrimagnetic materials are a type of magnetic material that exhibit a spontaneous magnetic moment, but the magnetic moments of their constituent atoms are not aligned in the same direction. This results in a net magnetic moment that is weaker than that of ferromagnetic materials. Ferrimagnetic materials are commonly used in permanent magnets and magnetic recording devices.The magnetization curve of a ferrimagnetic material is a graph of the material's magnetization as a function of the applied magnetic field. The magnetization curve for a ferrimagnetic material typically has a sigmoidal shape, with a sharp increase in magnetization at low magnetic fields, followed by a gradual increase in magnetization at higher magnetic fields.The initial sharp increase in magnetization is due to the alignment of the magnetic moments of the ferrimagnetic material's constituent atoms with the applied magnetic field. As the magnetic field is increased, the magnetic moments of the atoms become more and more aligned, resulting in an increase in the net magnetization of the material.At high magnetic fields, the magnetization of the ferrimagnetic material reaches a saturation value. This is because all of the magnetic moments of the atoms are aligned with the applied magnetic field, and there is no further increase in magnetization.中文回答:亚铁磁材料及其磁化曲线。
ABSTRACT Progressive Simplicial Complexes

Progressive Simplicial Complexes Jovan Popovi´c Hugues HoppeCarnegie Mellon University Microsoft ResearchABSTRACTIn this paper,we introduce the progressive simplicial complex(PSC) representation,a new format for storing and transmitting triangu-lated geometric models.Like the earlier progressive mesh(PM) representation,it captures a given model as a coarse base model together with a sequence of refinement transformations that pro-gressively recover detail.The PSC representation makes use of a more general refinement transformation,allowing the given model to be an arbitrary triangulation(e.g.any dimension,non-orientable, non-manifold,non-regular),and the base model to always consist of a single vertex.Indeed,the sequence of refinement transforma-tions encodes both the geometry and the topology of the model in a unified multiresolution framework.The PSC representation retains the advantages of PM’s.It defines a continuous sequence of approx-imating models for runtime level-of-detail control,allows smooth transitions between any pair of models in the sequence,supports progressive transmission,and offers a space-efficient representa-tion.Moreover,by allowing changes to topology,the PSC sequence of approximations achieves betterfidelity than the corresponding PM sequence.We develop an optimization algorithm for constructing PSC representations for graphics surface models,and demonstrate the framework on models that are both geometrically and topologically complex.CR Categories:I.3.5[Computer Graphics]:Computational Geometry and Object Modeling-surfaces and object representations.Additional Keywords:model simplification,level-of-detail representa-tions,multiresolution,progressive transmission,geometry compression.1INTRODUCTIONModeling and3D scanning systems commonly give rise to triangle meshes of high complexity.Such meshes are notoriously difficult to render,store,and transmit.One approach to speed up rendering is to replace a complex mesh by a set of level-of-detail(LOD) approximations;a detailed mesh is used when the object is close to the viewer,and coarser approximations are substituted as the object recedes[6,8].These LOD approximations can be precomputed Work performed while at Microsoft Research.Email:jovan@,hhoppe@Web:/jovan/Web:/hoppe/automatically using mesh simplification methods(e.g.[2,10,14,20,21,22,24,27]).For efficient storage and transmission,meshcompression schemes[7,26]have also been developed.The recently introduced progressive mesh(PM)representa-tion[13]provides a unified solution to these problems.In PM form,an arbitrary mesh M is stored as a coarse base mesh M0together witha sequence of n detail records that indicate how to incrementally re-fine M0into M n=M(see Figure7).Each detail record encodes theinformation associated with a vertex split,an elementary transfor-mation that adds one vertex to the mesh.In addition to defininga continuous sequence of approximations M0M n,the PM rep-resentation supports smooth visual transitions(geomorphs),allowsprogressive transmission,and makes an effective mesh compressionscheme.The PM representation has two restrictions,however.First,it canonly represent meshes:triangulations that correspond to orientable12-dimensional manifolds.Triangulated2models that cannot be rep-resented include1-d manifolds(open and closed curves),higherdimensional polyhedra(e.g.triangulated volumes),non-orientablesurfaces(e.g.M¨o bius strips),non-manifolds(e.g.two cubes joinedalong an edge),and non-regular models(i.e.models of mixed di-mensionality).Second,the expressiveness of the PM vertex splittransformations constrains all meshes M0M n to have the same topological type.Therefore,when M is topologically complex,the simplified base mesh M0may still have numerous triangles(Fig-ure7).In contrast,a number of existing simplification methods allowtopological changes as the model is simplified(Section6).Ourwork is inspired by vertex unification schemes[21,22],whichmerge vertices of the model based on geometric proximity,therebyallowing genus modification and component merging.In this paper,we introduce the progressive simplicial complex(PSC)representation,a generalization of the PM representation thatpermits topological changes.The key element of our approach isthe introduction of a more general refinement transformation,thegeneralized vertex split,that encodes changes to both the geometryand topology of the model.The PSC representation expresses anarbitrary triangulated model M(e.g.any dimension,non-orientable,non-manifold,non-regular)as the result of successive refinementsapplied to a base model M1that always consists of a single vertex (Figure8).Thus both geometric and topological complexity are recovered progressively.Moreover,the PSC representation retains the advantages of PM’s,including continuous LOD,geomorphs, progressive transmission,and model compression.In addition,we develop an optimization algorithm for construct-ing a PSC representation from a given model,as described in Sec-tion4.1The particular parametrization of vertex splits in[13]assumes that mesh triangles are consistently oriented.2Throughout this paper,we use the words“triangulated”and“triangula-tion”in the general dimension-independent sense.Figure 1:Illustration of a simplicial complex K and some of its subsets.2BACKGROUND2.1Concepts from algebraic topologyTo precisely define both triangulated models and their PSC repre-sentations,we find it useful to introduce some elegant abstractions from algebraic topology (e.g.[15,25]).The geometry of a triangulated model is denoted as a tuple (K V )where the abstract simplicial complex K is a combinatorial structure specifying the adjacency of vertices,edges,triangles,etc.,and V is a set of vertex positions specifying the shape of the model in 3.More precisely,an abstract simplicial complex K consists of a set of vertices 1m together with a set of non-empty subsets of the vertices,called the simplices of K ,such that any set consisting of exactly one vertex is a simplex in K ,and every non-empty subset of a simplex in K is also a simplex in K .A simplex containing exactly d +1vertices has dimension d and is called a d -simplex.As illustrated pictorially in Figure 1,the faces of a simplex s ,denoted s ,is the set of non-empty subsets of s .The star of s ,denoted star(s ),is the set of simplices of which s is a face.The children of a d -simplex s are the (d 1)-simplices of s ,and its parents are the (d +1)-simplices of star(s ).A simplex with exactly one parent is said to be a boundary simplex ,and one with no parents a principal simplex .The dimension of K is the maximum dimension of its simplices;K is said to be regular if all its principal simplices have the same dimension.To form a triangulation from K ,identify its vertices 1m with the standard basis vectors 1m ofm.For each simplex s ,let the open simplex smdenote the interior of the convex hull of its vertices:s =m:jmj =1j=1jjsThe topological realization K is defined as K =K =s K s .The geometric realization of K is the image V (K )where V :m 3is the linear map that sends the j -th standard basis vector jm to j 3.Only a restricted set of vertex positions V =1m lead to an embedding of V (K )3,that is,prevent self-intersections.The geometric realization V (K )is often called a simplicial complex or polyhedron ;it is formed by an arbitrary union of points,segments,triangles,tetrahedra,etc.Note that there generally exist many triangulations (K V )for a given polyhedron.(Some of the vertices V may lie in the polyhedron’s interior.)Two sets are said to be homeomorphic (denoted =)if there ex-ists a continuous one-to-one mapping between them.Equivalently,they are said to have the same topological type .The topological realization K is a d-dimensional manifold without boundary if for each vertex j ,star(j )=d .It is a d-dimensional manifold if each star(v )is homeomorphic to either d or d +,where d +=d:10.Two simplices s 1and s 2are d-adjacent if they have a common d -dimensional face.Two d -adjacent (d +1)-simplices s 1and s 2are manifold-adjacent if star(s 1s 2)=d +1.Figure 2:Illustration of the edge collapse transformation and its inverse,the vertex split.Transitive closure of 0-adjacency partitions K into connected com-ponents .Similarly,transitive closure of manifold-adjacency parti-tions K into manifold components .2.2Review of progressive meshesIn the PM representation [13],a mesh with appearance attributes is represented as a tuple M =(K V D S ),where the abstract simpli-cial complex K is restricted to define an orientable 2-dimensional manifold,the vertex positions V =1m determine its ge-ometric realization V (K )in3,D is the set of discrete material attributes d f associated with 2-simplices f K ,and S is the set of scalar attributes s (v f )(e.g.normals,texture coordinates)associated with corners (vertex-face tuples)of K .An initial mesh M =M n is simplified into a coarser base mesh M 0by applying a sequence of n successive edge collapse transforma-tions:(M =M n )ecol n 1ecol 1M 1ecol 0M 0As shown in Figure 2,each ecol unifies the two vertices of an edgea b ,thereby removing one or two triangles.The position of the resulting unified vertex can be arbitrary.Because the edge collapse transformation has an inverse,called the vertex split transformation (Figure 2),the process can be reversed,so that an arbitrary mesh M may be represented as a simple mesh M 0together with a sequence of n vsplit records:M 0vsplit 0M 1vsplit 1vsplit n 1(M n =M )The tuple (M 0vsplit 0vsplit n 1)forms a progressive mesh (PM)representation of M .The PM representation thus captures a continuous sequence of approximations M 0M n that can be quickly traversed for interac-tive level-of-detail control.Moreover,there exists a correspondence between the vertices of any two meshes M c and M f (0c f n )within this sequence,allowing for the construction of smooth vi-sual transitions (geomorphs)between them.A sequence of such geomorphs can be precomputed for smooth runtime LOD.In addi-tion,PM’s support progressive transmission,since the base mesh M 0can be quickly transmitted first,followed the vsplit sequence.Finally,the vsplit records can be encoded concisely,making the PM representation an effective scheme for mesh compression.Topological constraints Because the definitions of ecol and vsplit are such that they preserve the topological type of the mesh (i.e.all K i are homeomorphic),there is a constraint on the min-imum complexity that K 0may achieve.For instance,it is known that the minimal number of vertices for a closed genus g mesh (ori-entable 2-manifold)is (7+(48g +1)12)2if g =2(10if g =2)[16].Also,the presence of boundary components may further constrain the complexity of K 0.Most importantly,K may consist of a number of components,and each is required to appear in the base mesh.For example,the meshes in Figure 7each have 117components.As evident from the figure,the geometry of PM meshes may deteriorate severely as they approach topological lower bound.M 1;100;(1)M 10;511;(7)M 50;4656;(12)M 200;1552277;(28)M 500;3968690;(58)M 2000;14253219;(108)M 5000;029010;(176)M n =34794;0068776;(207)Figure 3:Example of a PSC representation.The image captions indicate the number of principal 012-simplices respectively and the number of connected components (in parenthesis).3PSC REPRESENTATION 3.1Triangulated modelsThe first step towards generalizing PM’s is to let the PSC repre-sentation encode more general triangulated models,instead of just meshes.We denote a triangulated model as a tuple M =(K V D A ).The abstract simplicial complex K is not restricted to 2-manifolds,but may in fact be arbitrary.To represent K in memory,we encode the incidence graph of the simplices using the following linked structures (in C++notation):struct Simplex int dim;//0=vertex,1=edge,2=triangle,...int id;Simplex*children[MAXDIM+1];//[0..dim]List<Simplex*>parents;;To render the model,we draw only the principal simplices ofK ,denoted (K )(i.e.vertices not adjacent to edges,edges not adjacent to triangles,etc.).The discrete attributes D associate amaterial identifier d s with each simplex s(K ).For the sake of simplicity,we avoid explicitly storing surface normals at “corners”(using a set S )as done in [13].Instead we let the material identifier d s contain a smoothing group field [28],and let a normal discontinuity (crease )form between any pair of adjacent triangles with different smoothing groups.Previous vertex unification schemes [21,22]render principal simplices of dimension 0and 1(denoted 01(K ))as points and lines respectively with fixed,device-dependent screen widths.To better approximate the model,we instead define a set A that associates an area a s A with each simplex s 01(K ).We think of a 0-simplex s 00(K )as approximating a sphere with area a s 0,and a 1-simplex s 1=j k 1(K )as approximating a cylinder (with axis (j k ))of area a s 1.To render a simplex s 01(K ),we determine the radius r model of the corresponding sphere or cylinder in modeling space,and project the length r model to obtain the radius r screen in screen pixels.Depending on r screen ,we render the simplex as a polygonal sphere or cylinder with radius r model ,a 2D point or line with thickness 2r screen ,or do not render it at all.This choice based on r screen can be adjusted to mitigate the overhead of introducing polygonal representations of spheres and cylinders.As an example,Figure 3shows an initial model M of 68,776triangles.One of its approximations M 500is a triangulated model with 3968690principal 012-simplices respectively.3.2Level-of-detail sequenceAs in progressive meshes,from a given triangulated model M =M n ,we define a sequence of approximations M i :M 1op 1M 2op 2M n1op n 1M nHere each model M i has exactly i vertices.The simplification op-erator M ivunify iM i +1is the vertex unification transformation,whichmerges two vertices (Section 3.3),and its inverse M igvspl iM i +1is the generalized vertex split transformation (Section 3.4).Thetuple (M 1gvspl 1gvspl n 1)forms a progressive simplicial complex (PSC)representation of M .To construct a PSC representation,we first determine a sequence of vunify transformations simplifying M down to a single vertex,as described in Section 4.After reversing these transformations,we renumber the simplices in the order that they are created,so thateach gvspl i (a i)splits the vertex a i K i into two vertices a i i +1K i +1.As vertices may have different positions in the different models,we denote the position of j in M i as i j .To better approximate a surface model M at lower complexity levels,we initially associate with each (principal)2-simplex s an area a s equal to its triangle area in M .Then,as the model is simplified,wekeep constant the sum of areas a s associated with principal simplices within each manifold component.When2-simplices are eventually reduced to principal1-simplices and0-simplices,their associated areas will provide good estimates of the original component areas.3.3Vertex unification transformationThe transformation vunify(a i b i midp i):M i M i+1takes an arbitrary pair of vertices a i b i K i+1(simplex a i b i need not be present in K i+1)and merges them into a single vertex a i K i. Model M i is created from M i+1by updating each member of the tuple(K V D A)as follows:K:References to b i in all simplices of K are replaced by refer-ences to a i.More precisely,each simplex s in star(b i)K i+1is replaced by simplex(s b i)a i,which we call the ancestor simplex of s.If this ancestor simplex already exists,s is deleted.V:Vertex b is deleted.For simplicity,the position of the re-maining(unified)vertex is set to either the midpoint or is left unchanged.That is,i a=(i+1a+i+1b)2if the boolean parameter midp i is true,or i a=i+1a otherwise.D:Materials are carried through as expected.So,if after the vertex unification an ancestor simplex(s b i)a i K i is a new principal simplex,it receives its material from s K i+1if s is a principal simplex,or else from the single parent s a i K i+1 of s.A:To maintain the initial areas of manifold components,the areasa s of deleted principal simplices are redistributed to manifold-adjacent neighbors.More concretely,the area of each princi-pal d-simplex s deleted during the K update is distributed toa manifold-adjacent d-simplex not in star(a ib i).If no suchneighbor exists and the ancestor of s is a principal simplex,the area a s is distributed to that ancestor simplex.Otherwise,the manifold component(star(a i b i))of s is being squashed be-tween two other manifold components,and a s is discarded. 3.4Generalized vertex split transformation Constructing the PSC representation involves recording the infor-mation necessary to perform the inverse of each vunify i.This inverse is the generalized vertex split gvspl i,which splits a0-simplex a i to introduce an additional0-simplex b i.(As mentioned previously, renumbering of simplices implies b i i+1,so index b i need not be stored explicitly.)Each gvspl i record has the formgvspl i(a i C K i midp i()i C D i C A i)and constructs model M i+1from M i by updating the tuple (K V D A)as follows:K:As illustrated in Figure4,any simplex adjacent to a i in K i can be the vunify result of one of four configurations in K i+1.To construct K i+1,we therefore replace each ancestor simplex s star(a i)in K i by either(1)s,(2)(s a i)i+1,(3)s and(s a i)i+1,or(4)s,(s a i)i+1and s i+1.The choice is determined by a split code associated with s.Thesesplit codes are stored as a code string C Ki ,in which the simplicesstar(a i)are sortedfirst in order of increasing dimension,and then in order of increasing simplex id,as shown in Figure5. V:The new vertex is assigned position i+1i+1=i ai+()i.Theother vertex is given position i+1ai =i ai()i if the boolean pa-rameter midp i is true;otherwise its position remains unchanged.D:The string C Di is used to assign materials d s for each newprincipal simplex.Simplices in C Di ,as well as in C Aibelow,are sorted by simplex dimension and simplex id as in C Ki. A:During reconstruction,we are only interested in the areas a s fors01(K).The string C Ai tracks changes in these areas.Figure4:Effects of split codes on simplices of various dimensions.code string:41422312{}Figure5:Example of split code encoding.3.5PropertiesLevels of detail A graphics application can efficiently transitionbetween models M1M n at runtime by performing a sequence ofvunify or gvspl transformations.Our current research prototype wasnot designed for efficiency;it attains simplification rates of about6000vunify/sec and refinement rates of about5000gvspl/sec.Weexpect that a careful redesign using more efficient data structureswould significantly improve these rates.Geomorphs As in the PM representation,there exists a corre-spondence between the vertices of the models M1M n.Given acoarser model M c and afiner model M f,1c f n,each vertexj K f corresponds to a unique ancestor vertex f c(j)K cfound by recursively traversing the ancestor simplex relations:f c(j)=j j cf c(a j1)j cThis correspondence allows the creation of a smooth visual transi-tion(geomorph)M G()such that M G(1)equals M f and M G(0)looksidentical to M c.The geomorph is defined as the modelM G()=(K f V G()D f A G())in which each vertex position is interpolated between its originalposition in V f and the position of its ancestor in V c:Gj()=()fj+(1)c f c(j)However,we must account for the special rendering of principalsimplices of dimension0and1(Section3.1).For each simplexs01(K f),we interpolate its area usinga G s()=()a f s+(1)a c swhere a c s=0if s01(K c).In addition,we render each simplexs01(K c)01(K f)using area a G s()=(1)a c s.The resultinggeomorph is visually smooth even as principal simplices are intro-duced,removed,or change dimension.The accompanying video demonstrates a sequence of such geomorphs.Progressive transmission As with PM’s,the PSC representa-tion can be progressively transmitted by first sending M 1,followed by the gvspl records.Unlike the base mesh of the PM,M 1always consists of a single vertex,and can therefore be sent in a fixed-size record.The rendering of lower-dimensional simplices as spheres and cylinders helps to quickly convey the overall shape of the model in the early stages of transmission.Model compression Although PSC gvspl are more general than PM vsplit transformations,they offer a surprisingly concise representation of M .Table 1lists the average number of bits re-quired to encode each field of the gvspl records.Using arithmetic coding [30],the vertex id field a i requires log 2i bits,and the boolean parameter midp i requires 0.6–0.9bits for our models.The ()i delta vector is quantized to 16bitsper coordinate (48bits per),and stored as a variable-length field [7,13],requiring about 31bits on average.At first glance,each split code in the code string C K i seems to have 4possible outcomes (except for the split code for 0-simplex a i which has only 2possible outcomes).However,there exist constraints between these split codes.For example,in Figure 5,the code 1for 1-simplex id 1implies that 2-simplex id 1also has code 1.This in turn implies that 1-simplex id 2cannot have code 2.Similarly,code 2for 1-simplex id 3implies a code 2for 2-simplex id 2,which in turn implies that 1-simplex id 4cannot have code 1.These constraints,illustrated in the “scoreboard”of Figure 6,can be summarized using the following two rules:(1)If a simplex has split code c12,all of its parents havesplit code c .(2)If a simplex has split code 3,none of its parents have splitcode 4.As we encode split codes in C K i left to right,we apply these two rules (and their contrapositives)transitively to constrain the possible outcomes for split codes yet to be ing arithmetic coding with uniform outcome probabilities,these constraints reduce the code string length in Figure 6from 15bits to 102bits.In our models,the constraints reduce the code string from 30bits to 14bits on average.The code string is further reduced using a non-uniform probability model.We create an array T [0dim ][015]of encoding tables,indexed by simplex dimension (0..dim)and by the set of possible (constrained)split codes (a 4-bit mask).For each simplex s ,we encode its split code c using the probability distribution found in T [s dim ][s codes mask ].For 2-dimensional models,only 10of the 48tables are non-trivial,and each table contains at most 4probabilities,so the total size of the probability model is small.These encoding tables reduce the code strings to approximately 8bits as shown in Table 1.By comparison,the PM representation requires approximately 5bits for the same information,but of course it disallows topological changes.To provide more intuition for the efficiency of the PSC repre-sentation,we note that capturing the connectivity of an average 2-manifold simplicial complex (n vertices,3n edges,and 2n trian-gles)requires ni =1(log 2i +8)n (log 2n +7)bits with PSC encoding,versus n (12log 2n +95)bits with a traditional one-way incidence graph representation.For improved compression,it would be best to use a hybrid PM +PSC representation,in which the more concise PM vertex split encoding is used when the local neighborhood is an orientableFigure 6:Constraints on the split codes for the simplices in the example of Figure 5.Table 1:Compression results and construction times.Object#verts Space required (bits/n )Trad.Con.n K V D Arepr.time a i C K i midp i (v )i C D i C Ai bits/n hrs.drumset 34,79412.28.20.928.1 4.10.453.9146.1 4.3destroyer 83,79913.38.30.723.1 2.10.347.8154.114.1chandelier 36,62712.47.60.828.6 3.40.853.6143.6 3.6schooner 119,73413.48.60.727.2 2.5 1.353.7148.722.2sandal 4,6289.28.00.733.4 1.50.052.8123.20.4castle 15,08211.0 1.20.630.70.0-43.5-0.5cessna 6,7959.67.60.632.2 2.50.152.6132.10.5harley 28,84711.97.90.930.5 1.40.453.0135.7 3.52-dimensional manifold (this occurs on average 93%of the time in our examples).To compress C D i ,we predict the material for each new principalsimplex sstar(a i )star(b i )K i +1by constructing an ordered set D s of materials found in star(a i )K i .To improve the coding model,the first materials in D s are those of principal simplices in star(s )K i where s is the ancestor of s ;the remainingmaterials in star(a i )K i are appended to D s .The entry in C D i associated with s is the index of its material in D s ,encoded arithmetically.If the material of s is not present in D s ,it is specified explicitly as a global index in D .We encode C A i by specifying the area a s for each new principalsimplex s 01(star(a i )star(b i ))K i +1.To account for this redistribution of area,we identify the principal simplex from which s receives its area by specifying its index in 01(star(a i ))K i .The column labeled in Table 1sums the bits of each field of the gvspl records.Multiplying by the number n of vertices in M gives the total number of bits for the PSC representation of the model (e.g.500KB for the destroyer).By way of compari-son,the next column shows the number of bits per vertex required in a traditional “IndexedFaceSet”representation,with quantization of 16bits per coordinate and arithmetic coding of face materials (3n 16+2n 3log 2n +materials).4PSC CONSTRUCTIONIn this section,we describe a scheme for iteratively choosing pairs of vertices to unify,in order to construct a PSC representation.Our algorithm,a generalization of [13],is time-intensive,seeking high quality approximations.It should be emphasized that many quality metrics are possible.For instance,the quadric error metric recently introduced by Garland and Heckbert [9]provides a different trade-off of execution speed and visual quality.As in [13,20],we first compute a cost E for each candidate vunify transformation,and enter the candidates into a priority queueordered by ascending cost.Then,in each iteration i =n 11,we perform the vunify at the front of the queue and update the costs of affected candidates.4.1Forming set of candidate vertex pairs In principle,we could enter all possible pairs of vertices from M into the priority queue,but this would be prohibitively expensive since simplification would then require at least O(n2log n)time.Instead, we would like to consider only a smaller set of candidate vertex pairs.Naturally,should include the1-simplices of K.Additional pairs should also be included in to allow distinct connected com-ponents of M to merge and to facilitate topological changes.We considered several schemes for forming these additional pairs,in-cluding binning,octrees,and k-closest neighbor graphs,but opted for the Delaunay triangulation because of its adaptability on models containing components at different scales.We compute the Delaunay triangulation of the vertices of M, represented as a3-dimensional simplicial complex K DT.We define the initial set to contain both the1-simplices of K and the subset of1-simplices of K DT that connect vertices in different connected components of K.During the simplification process,we apply each vertex unification performed on M to as well in order to keep consistent the set of candidate pairs.For models in3,star(a i)has constant size in the average case,and the overall simplification algorithm requires O(n log n) time.(In the worst case,it could require O(n2log n)time.)4.2Selecting vertex unifications fromFor each candidate vertex pair(a b),the associated vunify(a b):M i M i+1is assigned the costE=E dist+E disc+E area+E foldAs in[13],thefirst term is E dist=E dist(M i)E dist(M i+1),where E dist(M)measures the geometric accuracy of the approximate model M.Conceptually,E dist(M)approximates the continuous integralMd2(M)where d(M)is the Euclidean distance of the point to the closest point on M.We discretize this integral by defining E dist(M)as the sum of squared distances to M from a dense set of points X sampled from the original model M.We sample X from the set of principal simplices in K—a strategy that generalizes to arbitrary triangulated models.In[13],E disc(M)measures the geometric accuracy of disconti-nuity curves formed by a set of sharp edges in the mesh.For the PSC representation,we generalize the concept of sharp edges to that of sharp simplices in K—a simplex is sharp either if it is a boundary simplex or if two of its parents are principal simplices with different material identifiers.The energy E disc is defined as the sum of squared distances from a set X disc of points sampled from sharp simplices to the discontinuity components from which they were sampled.Minimization of E disc therefore preserves the geom-etry of material boundaries,normal discontinuities(creases),and triangulation boundaries(including boundary curves of a surface and endpoints of a curve).We have found it useful to introduce a term E area that penalizes surface stretching(a more sophisticated version of the regularizing E spring term of[13]).Let A i+1N be the sum of triangle areas in the neighborhood star(a i)star(b i)K i+1,and A i N the sum of triangle areas in star(a i)K i.The mean squared displacement over the neighborhood N due to the change in area can be approx-imated as disp2=12(A i+1NA iN)2.We let E area=X N disp2,where X N is the number of points X projecting in the neighborhood. To prevent model self-intersections,the last term E fold penalizes surface folding.We compute the rotation of each oriented triangle in the neighborhood due to the vertex unification(as in[10,20]).If any rotation exceeds a threshold angle value,we set E fold to a large constant.Unlike[13],we do not optimize over the vertex position i a, but simply evaluate E for i a i+1a i+1b(i+1a+i+1b)2and choose the best one.This speeds up the optimization,improves model compression,and allows us to introduce non-quadratic energy terms like E area.5RESULTSTable1gives quantitative results for the examples in thefigures and in the video.Simplification times for our prototype are measured on an SGI Indigo2Extreme(150MHz R4400).Although these times may appear prohibitive,PSC construction is an off-line task that only needs to be performed once per model.Figure9highlights some of the benefits of the PSC representa-tion.The pearls in the chandelier model are initially disconnected tetrahedra;these tetrahedra merge and collapse into1-d curves in lower-complexity approximations.Similarly,the numerous polyg-onal ropes in the schooner model are simplified into curves which can be rendered as line segments.The straps of the sandal model initially have some thickness;the top and bottom sides of these straps merge in the simplification.Also note the disappearance of the holes on the sandal straps.The castle example demonstrates that the original model need not be a mesh;here M is a1-dimensional non-manifold obtained by extracting edges from an image.6RELATED WORKThere are numerous schemes for representing and simplifying tri-angulations in computer graphics.A common special case is that of subdivided2-manifolds(meshes).Garland and Heckbert[12] provide a recent survey of mesh simplification techniques.Several methods simplify a given model through a sequence of edge col-lapse transformations[10,13,14,20].With the exception of[20], these methods constrain edge collapses to preserve the topological type of the model(e.g.disallow the collapse of a tetrahedron into a triangle).Our work is closely related to several schemes that generalize the notion of edge collapse to that of vertex unification,whereby separate connected components of the model are allowed to merge and triangles may be collapsed into lower dimensional simplices. Rossignac and Borrel[21]overlay a uniform cubical lattice on the object,and merge together vertices that lie in the same cubes. Schaufler and St¨u rzlinger[22]develop a similar scheme in which vertices are merged using a hierarchical clustering algorithm.Lue-bke[18]introduces a scheme for locally adapting the complexity of a scene at runtime using a clustering octree.In these schemes, the approximating models correspond to simplicial complexes that would result from a set of vunify transformations(Section3.3).Our approach differs in that we order the vunify in a carefully optimized sequence.More importantly,we define not only a simplification process,but also a new representation for the model using an en-coding of gvspl=vunify1transformations.Recent,independent work by Schmalstieg and Schaufler[23]de-velops a similar strategy of encoding a model using a sequence of vertex split transformations.Their scheme differs in that it tracks only triangles,and therefore requires regular,2-dimensional trian-gulations.Hence,it does not allow lower-dimensional simplices in the model approximations,and does not generalize to higher dimensions.Some simplification schemes make use of an intermediate vol-umetric representation to allow topological changes to the model. He et al.[11]convert a mesh into a binary inside/outside function discretized on a three-dimensional grid,low-passfilter this function,。
郑州大学硕士论文模板

学校代码 10459学号或申请号密级硕士学位论文论文题目作者姓名:张三导师姓名:李四教授学科门类:工科专业名称:培养院系:大电气、大物工完成时间:20xx年4月A thesissubmitted toZhengzhouUniversityfor the degree ofMasterThesis TitleBySan ZhangSupervisor: Prof. Si LiMajor NameInstitute NameApril20xx学位论文原创性声明本人郑重声明:所呈交的学位论文,是本人在导师的指导下,独立进行研究所取得的成果。
除文中已经注明引用的内容外,本论文不包含任何其他个人或集体已经发表或撰写过的科研成果。
对本文的研究作出重要贡献的个人和集体,均已在文中以明确方式标明。
本声明的法律责任由本人承担。
学位论文作者:日期:年月日学位论文使用授权声明本人在导师指导下完成的论文及相关的职务作品,知识产权归属郑州大学。
根据郑州大学有关保留、使用学位论文的规定,同意学校保留或向国家有关部门或机构送交论文的复印件和电子版,允许论文被查阅和借阅;本人授权郑州大学可以将本学位论文的全部或部分编入有关数据库进行检索,可以采用影印、缩印或者其他复制手段保存论文和汇编本学位论文。
本人离校后发表、使用学位论文或与该学位论文直接相关的学术论文或成果时,第一署名单位仍然为郑州大学。
保密论文在解密后应遵守此规定。
学位论文作者:日期:年月日摘要随着我国工业技术水平的快速发展与进步,对材料的质量的要求也越来越高。
在各个行业领域中,材料和器件中表面和亚表面的完整性会影响和决定系统和仪器设备的工作效率以及运行寿命。
此外,随着中国工业的高速发展,空气及水源污染问题也变得日益严峻。
环境污染导致了某些疾病的高发,皮肤病即是受环境因素诱导的典型疾病之一。
近年来,中国居民的皮肤病发病率逐年上升,且新增病例呈年轻化趋势。
因此实现对材料表面裂纹和皮肤表面病变的无损检测尤为重要。
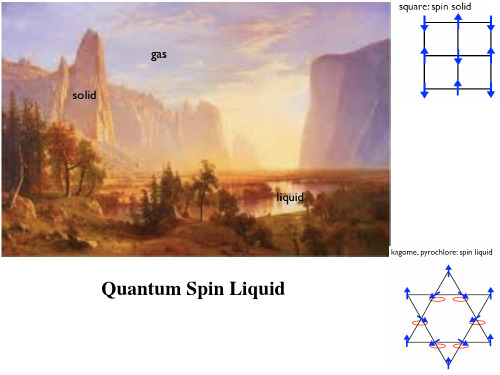
几何阻挫磁体简介000
PM
阻挫磁体的判据: f
CW
TF
5
S0 / kB lnW
特征:基态存在很大的简并度 传统反铁磁体:
f
CW
TF
~1
Square Lattice:
Td ~ 2CW Td ~ 0.75CW
Triangular Lattice:
•多重简并基态
Triangular Lattice
三角晶格:6重简并 2重简并(FM) Kagome Lattice
→AFM+Spin
Liquid
→AFM
例2:ZnCr2O4
AFM → Quasispin Glass
问题1:几何阻挫磁体是否存在亚铁磁体?
First experimental realization of spin Ladder with FM Legs
问题2:几何阻挫自旋玻璃与传统自旋玻璃区别?
PRL,106, 247202 (2011
1.ACr2O4 (A=Zn,Cd,Hg) 几何阻挫磁体(Tetragonal Lattice)
•Cr3+ 占据四面体顶角
•Cr3+ 自旋占据t2g轨道, 只有自旋—晶格耦合
Cd
Cr
c
b
a
•强磁场诱导磁相变
强磁场调制“自旋—晶格”耦合
Orthorhombic(Fddd)
量子临界行为
磁场诱导量子相变
?
?
Magnetic Field-induced quantum phase transition: 概念:Noncollinear spin structure ———— Collinear spin Structure (First Order Transition) Example: Pyrochlore Lttice
The decay $rho^{0}to pi^{+}+pi^{-}+gamma$ and the coupling constant g$_{rhosigmagamma}$

a rXiv:n ucl-t h /441v28Ma y2The decay ρ0→π++π−+γand the coupling constant g ρσγA.Gokalp ∗and O.Yilmaz †Physics Department,Middle East Technical University,06531Ankara,Turkey(February 8,2008)Abstract The experimental branching ratio for the radiative decay ρ0→π++π−+γis used to estimate the coupling constant g ρσγfor a set of values of σ-meson parameters M σand Γσ.Our results are quite different than the values of this constant used in the literature.PACS numbers:12.20.Ds,13.40.HqTypeset using REVT E XThe radiative decay processρ0→π++π−+γhas been studied employing different approaches[1,5].There are two mechanisms that can contribute to this radiative decay: thefirst one is the internal bremsstrahlung where one of the charged pions from the decay ρ0→π++π−emits a photon,and the second one is the structural radiation which is caused by the internal transformation of theρ-meson quark structure.Since the bremsstrahlung is well described by quantum electrodynamics,different methods have been used to estimate the contribution of the structural radiation.Singer[1]calculated the amplitude for this decay by considering only the bremsstrahlung mechanism since the decayρ0→π++π−is the main decay mode ofρ0-meson.He also used the universality of the coupling of theρ-meson to pions and nucleons to determine the coupling constant gρππfrom the knowledge of the coupling constant gρter,Renard [3]studied this decay among other vector meson decays into2π+γfinal states in a gauge invariant way with current algebra,hard-pion and Ward-identities techniques.He,moreover, established the correspondence between these current algebra results and the structure of the amplitude calculated in the single particle approximation for the intermediate states.In corresponding Feynman diagrams the structural radiation proceeds through the intermediate states asρ0→S+γwhere the meson S subsequently decays into aπ+π−pair.He concluded that the leading term is the pion bremsstrahlung and that the largest contribution to the structural radiation amplitude results from the scalarσ-meson intermediate state.He used the rough estimate gρσγ≃1for the coupling constant gρσγwhich was obtained with the spin independence assumption in the quark model.The coupling constant gρππwas determined using the then available experimental decay rate ofρ-meson and also current algebra results as3.2≤gρππ≤4.9.On the other hand,the coupling constant gσππwas deduced from the assumed decay rateΓ≃100MeV for theσ-meson as gσππ=3.4with Mσ=400MeV. Furthermore,he observed that theσ-contribution modifies the shape of the photon spectrum for high momenta differently depending on the mass of theσ-meson.We like to note, however,that the nature of theσ-meson as a¯q q state in the naive quark model and therefore the estimation of the coupling constant gρσγin the quark model have been a subject ofcontroversy.Indeed,Jaffe[6,7]lately argued within the framework of lattice QCD calculation of pseudoscalar meson scattering amplitudes that the light scalar mesons are¯q2q2states rather than¯q q states.Recently,on the other hand,the coupling constant gρσγhas become an important input for the studies ofρ0-meson photoproduction on nucleons.The presently available data[8] on the photoproduction ofρ0-meson on proton targets near threshold can be described at low momentum transfers by a simple one-meson exchange model[9].Friman and Soyeur [9]showed that in this picture theρ0-meson photoproduction cross section on protons is given mainly byσ-exchange.They calculated theγσρ-vertex assuming Vector Dominance of the electromagnetic current,and their result when derived using an effective Lagrangian for theγσρ-vertex gives the value gρσγ≃2.71for this coupling ter,Titov et al.[10]in their study of the structure of theφ-meson photoproduction amplitude based on one-meson exchange and Pomeron-exchange mechanisms used the coupling constant gφσγwhich they calculated from the above value of gρσγinvoking unitary symmetry arguments as gφσγ≃0.047.They concluded that the data at low energies near threshold can accommodate either the second Pomeron or the scalar mesons exchange,and the differences between these competing mechanisms have profound effects on the cross sections and the polarization observables.It,therefore,appears of much interest to study the coupling constant gρσγthat plays an important role in scalar meson exchange mechanism from a different perspective other than Vector Meson Dominance as well.For this purpose we calculate the branching ratio for the radiative decayρ0→π++π−+γ,and using the experimental value0.0099±0.0016for this branching ratio[11],we estimate the coupling constant gρσγ.Our calculation is based on the Feynman diagrams shown in Fig.1.Thefirst two terms in thisfigure are not gauge invariant and they are supplemented by the direct term shown in Fig.1(c)to establish gauge invariance.Guided by Renard’s[3]current algebra results,we assume that the structural radiation amplitude is dominated byσ-meson intermediate state which is depicted in Fig. 1(d).We describe theρσγ-vertex by the effective LagrangianL int.ρσγ=e4πMρMρ)2 3/2.(3)The experimental value of the widthΓ=151MeV[11]then yields the value g2ρππ2gσππMσ π· πσ.(4) The decay width of theσ-meson that follows from this effective Lagrangian is given asΓσ≡Γ(σ→ππ)=g2σππ8 1−(2Mπ2iΓσ,whereΓσisgiven by Eq.(5).Since the experimental candidate forσ-meson f0(400-1200)has a width (600-1000)MeV[11],we obtain a set of values for the coupling constant gρσγby considering the ranges Mσ=400-1200MeV,Γσ=600-1000MeV for the parameters of theσ-meson.In terms of the invariant amplitude M(Eγ,E1),the differential decay probability for an unpolarizedρ0-meson at rest is given bydΓ(2π)31Γ= Eγ,max.Eγ,min.dEγ E1,max.E1,min.dE1dΓ[−2E2γMρ+3EγM2ρ−M3ρ2(2EγMρ−M2ρ)±Eγfunction ofβin Fig.5.This ratio is defined byΓβRβ=,Γtot.= Eγ,max.50dEγdΓdEγ≃constant.(10)ΓσM3σFurthermore,the values of the coupling constant gρσγresulting from our estimation are in general quite different than the values of this constant usually adopted for the one-meson exchange mechanism calculations existing in the literature.For example,Titov et al.[10] uses the value gρσγ=2.71which they obtain from Friman and Soyeur’s[9]analysis ofρ-meson photoproduction using Vector Meson Dominance.It is interesting to note that in their study of pion dynamics in Quantum Hadrodynamics II,which is a renormalizable model constructed using local gauge invariance based on SU(2)group,that has the sameLagrangian densities for the vertices we use,Serot and Walecka[14]come to the conclusion that in order to be consistent with the experimental result that s-waveπN-scattering length is anomalously small,in their tree-level calculation they have to choose gσππ=12.Since they use Mσ=520MeV this impliesΓσ≃1700MeV.If we use these values in our analysis,we then obtain gρσγ=11.91.Soyeur[12],on the other hand,uses quite arbitrarly the values Mσ=500 MeV,Γσ=250MeV,which in our calculation results in the coupling constant gρσγ=6.08.We like to note,however,that these values forσ-meson parameters are not consistent with the experimental data onσ-meson[11].Our analysis and estimation of the coupling constant gρσγusing the experimental value of the branching ratio of the radiative decayρ0→π++π−+γgive quite different values for this coupling constant than used in the literature.Furthermore,since we obtain this coupling constant as a function ofσ-meson parameters,it will be of interest to study the dependence of the observables of the reactions,such as for example the photoproduction of vector mesons on nucleonsγ+N→N+V where V is the neutral vector meson, analyzed using one-meson exchange mechanism on these parameters.AcknowledgmentsWe thank Prof.Dr.M.P.Rekalo for suggesting this problem to us and for his guidance during the course of our work.We also wish to thank Prof.Dr.T.M.Aliev for helpful discussions.REFERENCES[1]P.Singer,Phys.Rev.130(1963)2441;161(1967)1694.[2]V.N.Baier and V.A.Khoze,Sov.Phys.JETP21(1965)1145.[3]S.M.Renard,Nuovo Cim.62A(1969)475.[4]K.Huber and H.Neufeld,Phys.Lett.B357(1995)221.[5]E.Marko,S.Hirenzaki,E.Oset and H.Toki,Phys.Lett.B470(1999)20.[6]R.L.Jaffe,hep-ph/0001123.[7]M.Alford and R.L.Jaffe,hep-lat/0001023.[8]Aachen-Berlin-Bonn-Hamburg-Heidelberg-Munchen Collaboration,Phys.Rev.175(1968)1669.[9]B.Friman and M.Soyeur,Nucl.Phys.A600(1996)477.[10]A.I.Titov,T.-S.H.Lee,H.Toki and O.Streltrova,Phys.Rev.C60(1999)035205.[11]Review of Particle Physics,Eur.Phys.J.C3(1998)1.[12]M.Soyeur,nucl-th/0003047.[13]S.I.Dolinsky,et al,Phys.Rep.202(1991)99.[14]B.D.Serot and J.D.Walecka,in Advances in Nuclear Physics,edited by J.W.Negeleand E.Vogt,Vol.16(1986).TABLESTABLE I.The calculated coupling constant gρσγfor differentσ-meson parametersΓσ(MeV)gρσγ500 6.97-6.00±1.58 8008.45±1.77600 6.16-6.68±1.85 80010.49±2.07800 5.18-9.11±2.64 90015.29±2.84900 4.85-10.65±3.14 90017.78±3.23Figure Captions:Figure1:Diagrams for the decayρ0→π++π−+γFigure2:The photon spectra for the decay width ofρ0→π++π−+γ.The contributions of different terms are indicated.Figure3:The pion energy spectra for the decay width ofρ0→π++π−+γ.The contri-butions of different terms are indicated.Figure4:The decay width ofρ0→π++π−+γas a function of minimum detected photon energy.Figure5:The ratio Rβ=Γβ。
The Optimal Isodual Lattice Quantizer in Three Dimensions

x · x dx
(1)
lattice has the largest packing radius and the smallest covering radius. The m.c.c. lattice, denoted here by M3 , has Gram matrix √ −1 −1 1+ 2 √ √ 1 −1 1+ 2 1− 2 2 √ √ −1 1− 2 1+ 2 determinant 1, packing radius
(3)
where α, β , h are any real numbers satisfying 0 ≤ 2h ≤ α ≤ β , αβ − h2 = 1. In the indecomposable case the nonzero conorms are: p01 = αβ 2α(1 − β ) α(2 − β ) , p02 = , p03 = , γ γ βγ 2β (1 − α) 2(1 − α)(1 − β ) β (2 − α) , p13 = , p23 = , αγ γ γ (4)
The Optimal Isodual Lattice Quantizer in Three Dimensions
J. H. Conway Mathematics Department Princeton University Princeton, NJ 08544 N. J. A. Sloane AT&T Shannon Labs 180 Park Avenue Florham Park, NJ 07932-0971 Email: conway@, njas@ Jan 02 2006. Abstract The mean-centered cuboidal (or m.c.c.) lattice is known to be the optimal packing and covering among all isodual three-dimensional lattices. In this note we show that it is also the best quantizer. It thus joins the isodual lattices Z, A2 and (presumably) D4 , E8 and the Leech lattice in being simultaneously optimal with respect to all three criteria. Keywords: quantizing, self-dual lattice, isodual lattice, f.c.c. lattice, b.c.c. lattice, m.c.c. lattice AMS 2000 Classification: 52C07 (11H55, 94A29)
Superfluidity in a Three-flavor Fermi Gas with SU(3) Symmetry

arXiv:cond-mat/0604580v4 [cond-mat.other] 9 Sep 2006
I.
INTRODUCTION
The superfluidity in strongly interacting atomic Fermi gas and the associated BCS-Bose Einstein condensation(BEC) crossover phenomena[1, 2, 3] have been observed in experiments[4, 5, 6, 7] via the method of Feshbach resonance. The experimental study of superfluidity in atomic Fermi gas may be important for us to understand the solid-state phenomena such as hightemperature superconductivity, and may give some clue to search for the ground state of the dense quark matter and nuclear matter. In the past years, most theoretical and experimental studies concentrated on the two-flavor systems such as a 6 Li gas with the two lowest hyperfine states (In this paper, we use the
离散数学中英文名词对照表

离散数学中英⽂名词对照表离散数学中英⽂名词对照表外⽂中⽂AAbel category Abel 范畴Abel group (commutative group) Abel 群(交换群)Abel semigroup Abel 半群accessibility relation 可达关系action 作⽤addition principle 加法原理adequate set of connectives 联结词的功能完备(全)集adjacent 相邻(邻接)adjacent matrix 邻接矩阵adjugate 伴随adjunction 接合affine plane 仿射平⾯algebraic closed field 代数闭域algebraic element 代数元素algebraic extension 代数扩域(代数扩张)almost equivalent ⼏乎相等的alternating group 三次交代群annihilator 零化⼦antecedent 前件anti symmetry 反对称性anti-isomorphism 反同构arboricity 荫度arc set 弧集arity 元数arrangement problem 布置问题associate 相伴元associative algebra 结合代数associator 结合⼦asymmetric 不对称的(⾮对称的)atom 原⼦atomic formula 原⼦公式augmenting digeon hole principle 加强的鸽⼦笼原理augmenting path 可增路automorphism ⾃同构automorphism group of graph 图的⾃同构群auxiliary symbol 辅助符号axiom of choice 选择公理axiom of equality 相等公理axiom of extensionality 外延公式axiom of infinity ⽆穷公理axiom of pairs 配对公理axiom of regularity 正则公理axiom of replacement for the formula Ф关于公式Ф的替换公式axiom of the empty set 空集存在公理axiom of union 并集公理Bbalanced imcomplete block design 平衡不完全区组设计barber paradox 理发师悖论base 基Bell number Bell 数Bernoulli number Bernoulli 数Berry paradox Berry 悖论bijective 双射bi-mdule 双模binary relation ⼆元关系binary symmetric channel ⼆进制对称信道binomial coefficient ⼆项式系数binomial theorem ⼆项式定理binomial transform ⼆项式变换bipartite graph ⼆分图block 块block 块图(区组)block code 分组码block design 区组设计Bondy theorem Bondy 定理Boole algebra Boole 代数Boole function Boole 函数Boole homomorophism Boole 同态Boole lattice Boole 格bound occurrence 约束出现bound variable 约束变量bounded lattice 有界格bridge 桥Bruijn theorem Bruijn 定理Burali-Forti paradox Burali-Forti 悖论Burnside lemma Burnside 引理Ccage 笼canonical epimorphism 标准满态射Cantor conjecture Cantor 猜想Cantor diagonal method Cantor 对⾓线法Cantor paradox Cantor 悖论cardinal number 基数Cartesion product of graph 图的笛卡⼉积Catalan number Catalan 数category 范畴Cayley graph Cayley 图Cayley theorem Cayley 定理center 中⼼characteristic function 特征函数characteristic of ring 环的特征characteristic polynomial 特征多项式check digits 校验位Chinese postman problem 中国邮递员问题chromatic number ⾊数chromatic polynomial ⾊多项式circuit 回路circulant graph 循环图circumference 周长class 类classical completeness 古典完全的classical consistent 古典相容的clique 团clique number 团数closed term 闭项closure 闭包closure of graph 图的闭包code 码code element 码元code length 码长code rate 码率code word 码字coefficient 系数coimage 上象co-kernal 上核coloring 着⾊coloring problem 着⾊问题combination number 组合数combination with repetation 可重组合common factor 公因⼦commutative diagram 交换图commutative ring 交换环commutative seimgroup 交换半群complement 补图(⼦图的余) complement element 补元complemented lattice 有补格complete bipartite graph 完全⼆分图complete graph 完全图complete k-partite graph 完全k-分图complete lattice 完全格composite 复合composite operation 复合运算composition (molecular proposition) 复合(分⼦)命题composition of graph (lexicographic product)图的合成(字典积)concatenation (juxtaposition) 邻接运算concatenation graph 连通图congruence relation 同余关系conjunctive normal form 正则合取范式connected component 连通分⽀connective 连接的connectivity 连通度consequence 推论(后承)consistent (non-contradiction) 相容性(⽆⽭盾性)continuum 连续统contraction of graph 图的收缩contradiction ⽭盾式(永假式)contravariant functor 反变函⼦coproduct 上积corank 余秩correct error 纠正错误corresponding universal map 对应的通⽤映射countably infinite set 可列⽆限集(可列集)covariant functor (共变)函⼦covering 覆盖covering number 覆盖数Coxeter graph Coxeter 图crossing number of graph 图的叉数cuset 陪集cotree 余树cut edge 割边cut vertex 割点cycle 圈cycle basis 圈基cycle matrix 圈矩阵cycle rank 圈秩cycle space 圈空间cycle vector 圈向量cyclic group 循环群cyclic index 循环(轮转)指标cyclic monoid 循环单元半群cyclic permutation 圆圈排列cyclic semigroup 循环半群DDe Morgan law De Morgan 律decision procedure 判决过程decoding table 译码表deduction theorem 演绎定理degree 次数,次(度)degree sequence 次(度)序列derivation algebra 微分代数Descartes product Descartes 积designated truth value 特指真值detect errer 检验错误deterministic 确定的diagonal functor 对⾓线函⼦diameter 直径digraph 有向图dilemma ⼆难推理direct consequence 直接推论(直接后承)direct limit 正向极限direct sum 直和directed by inclution 被包含关系定向discrete Fourier transform 离散 Fourier 变换disjunctive normal form 正则析取范式disjunctive syllogism 选⾔三段论distance 距离distance transitive graph 距离传递图distinguished element 特异元distributive lattice 分配格divisibility 整除division subring ⼦除环divison ring 除环divisor (factor) 因⼦domain 定义域Driac condition Dirac 条件dual category 对偶范畴dual form 对偶式dual graph 对偶图dual principle 对偶原则(对偶原理) dual statement 对偶命题dummy variable 哑变量(哑变元)Eeccentricity 离⼼率edge chromatic number 边⾊数edge coloring 边着⾊edge connectivity 边连通度edge covering 边覆盖edge covering number 边覆盖数edge cut 边割集edge set 边集edge-independence number 边独⽴数eigenvalue of graph 图的特征值elementary divisor ideal 初等因⼦理想elementary product 初等积elementary sum 初等和empty graph 空图empty relation 空关系empty set 空集endomorphism ⾃同态endpoint 端点enumeration function 计数函数epimorphism 满态射equipotent 等势equivalent category 等价范畴equivalent class 等价类equivalent matrix 等价矩阵equivalent object 等价对象equivalent relation 等价关系error function 错误函数error pattern 错误模式Euclid algorithm 欧⼏⾥德算法Euclid domain 欧⽒整环Euler characteristic Euler 特征Euler function Euler 函数Euler graph Euler 图Euler number Euler 数Euler polyhedron formula Euler 多⾯体公式Euler tour Euler 闭迹Euler trail Euler 迹existential generalization 存在推⼴规则existential quantifier 存在量词existential specification 存在特指规则extended Fibonacci number ⼴义 Fibonacci 数extended Lucas number ⼴义Lucas 数extension 扩充(扩张)extension field 扩域extension graph 扩图exterior algebra 外代数Fface ⾯factor 因⼦factorable 可因⼦化的factorization 因⼦分解faithful (full) functor 忠实(完满)函⼦Ferrers graph Ferrers 图Fibonacci number Fibonacci 数field 域filter 滤⼦finite extension 有限扩域finite field (Galois field ) 有限域(Galois 域)finite dimensional associative division algebra有限维结合可除代数finite set 有限(穷)集finitely generated module 有限⽣成模first order theory with equality 带符号的⼀阶系统five-color theorem 五⾊定理five-time-repetition 五倍重复码fixed point 不动点forest 森林forgetful functor 忘却函⼦four-color theorem(conjecture) 四⾊定理(猜想)F-reduced product F-归纳积free element ⾃由元free monoid ⾃由单元半群free occurrence ⾃由出现free R-module ⾃由R-模free variable ⾃由变元free-?-algebra ⾃由?代数function scheme 映射格式GGalileo paradox Galileo 悖论Gauss coefficient Gauss 系数GBN (G?del-Bernays-von Neumann system)GBN系统generalized petersen graph ⼴义 petersen 图generating function ⽣成函数generating procedure ⽣成过程generator ⽣成⼦(⽣成元)generator matrix ⽣成矩阵genus 亏格girth (腰)围长G?del completeness theorem G?del 完全性定理golden section number 黄⾦分割数(黄⾦分割率)graceful graph 优美图graceful tree conjecture 优美树猜想graph 图graph of first class for edge coloring 第⼀类边⾊图graph of second class for edge coloring 第⼆类边⾊图graph rank 图秩graph sequence 图序列greatest common factor 最⼤公因⼦greatest element 最⼤元(素)Grelling paradox Grelling 悖论Gr?tzsch graph Gr?tzsch 图group 群group code 群码group of graph 图的群HHajós conjecture Hajós 猜想Hamilton cycle Hamilton 圈Hamilton graph Hamilton 图Hamilton path Hamilton 路Harary graph Harary 图Hasse graph Hasse 图Heawood graph Heawood 图Herschel graph Herschel 图hom functor hom 函⼦homemorphism 图的同胚homomorphism 同态(同态映射)homomorphism of graph 图的同态hyperoctahedron 超⼋⾯体图hypothelical syllogism 假⾔三段论hypothese (premise) 假设(前提)Iideal 理想identity 单位元identity natural transformation 恒等⾃然变换imbedding 嵌⼊immediate predcessor 直接先⾏immediate successor 直接后继incident 关联incident axiom 关联公理incident matrix 关联矩阵inclusion and exclusion principle 包含与排斥原理inclusion relation 包含关系indegree ⼊次(⼊度)independent 独⽴的independent number 独⽴数independent set 独⽴集independent transcendental element 独⽴超越元素index 指数individual variable 个体变元induced subgraph 导出⼦图infinite extension ⽆限扩域infinite group ⽆限群infinite set ⽆限(穷)集initial endpoint 始端initial object 初始对象injection 单射injection functor 单射函⼦injective (one to one mapping) 单射(内射)inner face 内⾯inner neighbour set 内(⼊)邻集integral domain 整环integral subdomain ⼦整环internal direct sum 内直和intersection 交集intersection of graph 图的交intersection operation 交运算interval 区间invariant factor 不变因⼦invariant factor ideal 不变因⼦理想inverse limit 逆向极限inverse morphism 逆态射inverse natural transformation 逆⾃然变换inverse operation 逆运算inverse relation 逆关系inversion 反演isomorphic category 同构范畴isomorphism 同构态射isomorphism of graph 图的同构join of graph 图的联JJordan algebra Jordan 代数Jordan product (anti-commutator) Jordan乘积(反交换⼦)Jordan sieve formula Jordan 筛法公式j-skew j-斜元juxtaposition 邻接乘法Kk-chromatic graph k-⾊图k-connected graph k-连通图k-critical graph k-⾊临界图k-edge chromatic graph k-边⾊图k-edge-connected graph k-边连通图k-edge-critical graph k-边临界图kernel 核Kirkman schoolgirl problem Kirkman ⼥⽣问题Kuratowski theorem Kuratowski 定理Llabeled graph 有标号图Lah number Lah 数Latin rectangle Latin 矩形Latin square Latin ⽅lattice 格lattice homomorphism 格同态law 规律leader cuset 陪集头least element 最⼩元least upper bound 上确界(最⼩上界)left (right) identity 左(右)单位元left (right) invertible element 左(右)可逆元left (right) module 左(右)模left (right) zero 左(右)零元left (right) zero divisor 左(右)零因⼦left adjoint functor 左伴随函⼦left cancellable 左可消的left coset 左陪集length 长度Lie algebra Lie 代数line- group 图的线群logically equivanlent 逻辑等价logically implies 逻辑蕴涵logically valid 逻辑有效的(普效的)loop 环Lucas number Lucas 数Mmagic 幻⽅many valued proposition logic 多值命题逻辑matching 匹配mathematical structure 数学结构matrix representation 矩阵表⽰maximal element 极⼤元maximal ideal 极⼤理想maximal outerplanar graph 极⼤外平⾯图maximal planar graph 极⼤平⾯图maximum matching 最⼤匹配maxterm 极⼤项(基本析取式)maxterm normal form(conjunctive normal form) 极⼤项范式(合取范式)McGee graph McGee 图meet 交Menger theorem Menger 定理Meredith graph Meredith 图message word 信息字mini term 极⼩项minimal κ-connected graph 极⼩κ-连通图minimal polynomial 极⼩多项式Minimanoff paradox Minimanoff 悖论minimum distance 最⼩距离Minkowski sum Minkowski 和minterm (fundamental conjunctive form) 极⼩项(基本合取式)minterm normal form(disjunctive normal form)极⼩项范式(析取范式)M?bius function M?bius 函数M?bius ladder M?bius 梯M?bius transform (inversion) M?bius 变换(反演)modal logic 模态逻辑model 模型module homomorphism 模同态(R-同态)modus ponens 分离规则modus tollens 否定后件式module isomorphism 模同构monic morphism 单同态monoid 单元半群monomorphism 单态射morphism (arrow) 态射(箭)M?bius function M?bius 函数M?bius ladder M?bius 梯M?bius transform (inversion) M?bius 变换(反演)multigraph 多重图multinomial coefficient 多项式系数multinomial expansion theorem 多项式展开定理multiple-error-correcting code 纠多错码multiplication principle 乘法原理mutually orthogonal Latin square 相互正交拉丁⽅Nn-ary operation n-元运算n-ary product n-元积natural deduction system ⾃然推理系统natural isomorphism ⾃然同构natural transformation ⾃然变换neighbour set 邻集next state 下⼀个状态next state transition function 状态转移函数non-associative algebra ⾮结合代数non-standard logic ⾮标准逻辑Norlund formula Norlund 公式normal form 正规形normal model 标准模型normal subgroup (invariant subgroup) 正规⼦群(不变⼦群)n-relation n-元关系null object 零对象nullary operation 零元运算Oobject 对象orbit 轨道order 阶order ideal 阶理想Ore condition Ore 条件orientation 定向orthogonal Latin square 正交拉丁⽅orthogonal layout 正交表outarc 出弧outdegree 出次(出度)outer face 外⾯outer neighbour 外(出)邻集outerneighbour set 出(外)邻集outerplanar graph 外平⾯图Ppancycle graph 泛圈图parallelism 平⾏parallelism class 平⾏类parity-check code 奇偶校验码parity-check equation 奇偶校验⽅程parity-check machine 奇偶校验器parity-check matrix 奇偶校验矩阵partial function 偏函数partial ordering (partial relation) 偏序关系partial order relation 偏序关系partial order set (poset) 偏序集partition 划分,分划,分拆partition number of integer 整数的分拆数partition number of set 集合的划分数Pascal formula Pascal 公式path 路perfect code 完全码perfect t-error-correcting code 完全纠-错码perfect graph 完美图permutation 排列(置换)permutation group 置换群permutation with repetation 可重排列Petersen graph Petersen 图p-graph p-图Pierce arrow Pierce 箭pigeonhole principle 鸽⼦笼原理planar graph (可)平⾯图plane graph 平⾯图Pólya theorem Pólya 定理polynomail 多项式polynomial code 多项式码polynomial representation 多项式表⽰法polynomial ring 多项式环possible world 可能世界power functor 幂函⼦power of graph 图的幂power set 幂集predicate 谓词prenex normal form 前束范式pre-ordered set 拟序集primary cycle module 准素循环模prime field 素域prime to each other 互素primitive connective 初始联结词primitive element 本原元primitive polynomial 本原多项式principal ideal 主理想principal ideal domain 主理想整环principal of duality 对偶原理principal of redundancy 冗余性原则product 积product category 积范畴product-sum form 积和式proof (deduction) 证明(演绎)proper coloring 正常着⾊proper factor 真正因⼦proper filter 真滤⼦proper subgroup 真⼦群properly inclusive relation 真包含关系proposition 命题propositional constant 命题常量propositional formula(well-formed formula,wff)命题形式(合式公式)propositional function 命题函数propositional variable 命题变量pullback 拉回(回拖) pushout 推出Qquantification theory 量词理论quantifier 量词quasi order relation 拟序关系quaternion 四元数quotient (difference) algebra 商(差)代数quotient algebra 商代数quotient field (field of fraction) 商域(分式域)quotient group 商群quotient module 商模quotient ring (difference ring , residue ring) 商环(差环,同余类环)quotient set 商集RRamsey graph Ramsey 图Ramsey number Ramsey 数Ramsey theorem Ramsey 定理range 值域rank 秩reconstruction conjecture 重构猜想redundant digits 冗余位reflexive ⾃反的regular graph 正则图regular representation 正则表⽰relation matrix 关系矩阵replacement theorem 替换定理representation 表⽰representation functor 可表⽰函⼦restricted proposition form 受限命题形式restriction 限制retraction 收缩Richard paradox Richard 悖论right adjoint functor 右伴随函⼦right cancellable 右可消的right factor 右因⼦right zero divison 右零因⼦ring 环ring of endomorphism ⾃同态环ring with unity element 有单元的环R-linear independence R-线性⽆关root field 根域rule of inference 推理规则Russell paradox Russell 悖论Ssatisfiable 可满⾜的saturated 饱和的scope 辖域section 截⼝self-complement graph ⾃补图semantical completeness 语义完全的(弱完全的)semantical consistent 语义相容semigroup 半群separable element 可分元separable extension 可分扩域sequent ⽮列式sequential 序列的Sheffer stroke Sheffer 竖(谢弗竖)simple algebraic extension 单代数扩域simple extension 单扩域simple graph 简单图simple proposition (atomic proposition) 简单(原⼦)命题simple transcental extension 单超越扩域simplication 简化规则slope 斜率small category ⼩范畴smallest element 最⼩元(素)Socrates argument Socrates 论断(苏格拉底论断)soundness (validity) theorem 可靠性(有效性)定理spanning subgraph ⽣成⼦图spanning tree ⽣成树spectra of graph 图的谱spetral radius 谱半径splitting field 分裂域standard model 标准模型standard monomil 标准单项式Steiner triple Steiner 三元系⼤集Stirling number Stirling 数Stirling transform Stirling 变换subalgebra ⼦代数subcategory ⼦范畴subdirect product ⼦直积subdivison of graph 图的细分subfield ⼦域subformula ⼦公式subdivision of graph 图的细分subgraph ⼦图subgroup ⼦群sub-module ⼦模subrelation ⼦关系subring ⼦环sub-semigroup ⼦半群subset ⼦集substitution theorem 代⼊定理substraction 差集substraction operation 差运算succedent 后件surjection (surjective) 满射switching-network 开关⽹络Sylvester formula Sylvester公式symmetric 对称的symmetric difference 对称差symmetric graph 对称图symmetric group 对称群syndrome 校验⼦syntactical completeness 语法完全的(强完全的)Syntactical consistent 语法相容system ?3 , ?n , ??0 , ??系统?3 , ?n , ??0 , ??system L 公理系统 Lsystem ?公理系统?system L1 公理系统 L1system L2 公理系统 L2system L3 公理系统 L3system L4 公理系统 L4system L5 公理系统 L5system L6 公理系统 L6system ?n 公理系统?nsystem of modal prepositional logic 模态命题逻辑系统system Pm 系统 Pmsystem S1 公理系统 S1system T (system M) 公理系统 T(系统M)Ttautology 重⾔式(永真公式)technique of truth table 真值表技术term 项terminal endpoint 终端terminal object 终结对象t-error-correcing BCH code 纠 t -错BCH码theorem (provable formal) 定理(可证公式)thickess 厚度timed sequence 时间序列torsion 扭元torsion module 扭模total chromatic number 全⾊数total chromatic number conjecture 全⾊数猜想total coloring 全着⾊total graph 全图total matrix ring 全⽅阵环total order set 全序集total permutation 全排列total relation 全关系tournament 竞赛图trace (trail) 迹tranformation group 变换群transcendental element 超越元素transitive 传递的tranverse design 横截设计traveling saleman problem 旅⾏商问题tree 树triple system 三元系triple-repetition code 三倍重复码trivial graph 平凡图trivial subgroup 平凡⼦群true in an interpretation 解释真truth table 真值表truth value function 真值函数Turán graph Turán 图Turán theorem Turán 定理Tutte graph Tutte 图Tutte theorem Tutte 定理Tutte-coxeter graph Tutte-coxeter 图UUlam conjecture Ulam 猜想ultrafilter 超滤⼦ultrapower 超幂ultraproduct 超积unary operation ⼀元运算unary relation ⼀元关系underlying graph 基础图undesignated truth value ⾮特指值undirected graph ⽆向图union 并(并集)union of graph 图的并union operation 并运算unique factorization 唯⼀分解unique factorization domain (Gauss domain) 唯⼀分解整域unique k-colorable graph 唯⼀k着⾊unit ideal 单位理想unity element 单元universal 全集universal algebra 泛代数(Ω代数)universal closure 全称闭包universal construction 通⽤结构universal enveloping algebra 通⽤包络代数universal generalization 全称推⼴规则universal quantifier 全称量词universal specification 全称特指规则universal upper bound 泛上界unlabeled graph ⽆标号图untorsion ⽆扭模upper (lower) bound 上(下)界useful equivalent 常⽤等值式useless code 废码字Vvalence 价valuation 赋值Vandermonde formula Vandermonde 公式variery 簇Venn graph Venn 图vertex cover 点覆盖vertex set 点割集vertex transitive graph 点传递图Vizing theorem Vizing 定理Wwalk 通道weakly antisymmetric 弱反对称的weight 重(权)weighted form for Burnside lemma 带权形式的Burnside引理well-formed formula (wff) 合式公式(wff) word 字Zzero divison 零因⼦zero element (universal lower bound) 零元(泛下界)ZFC (Zermelo-Fraenkel-Cohen) system ZFC系统form)normal(Skolemformnormalprenex-存在正则前束范式(Skolem 正则范式)3-value proposition logic 三值命题逻辑。
Differential Scanning Calorimetry Determination of Gelatinization Rates in Different Starches due

Differential Scanning Calorimetry Determination of Gelatinization Rates in Different Starches due toMicrowave HeatingMatrid Ndife, G ¨ul ¨um ¸Sumnu* and Levent BayındırlıM. Ndife: The Ohio State University, Food Science and Technology Department, Columbus, OH 43210(U.S.A.)G. ¸Sumnu, L. Bayındırlı: Middle East Technical University, Food Engineering Department, 06531 Ankara,(Turkey)(Received December 5, 1997; accepted April 28, 1998)Wheat, corn and rice starch dispersions having water–starch ratios of 1.0:1.0, 1.5:1.0 and 2.0:1.0 (w/w) were heated in a microwave oven for 15 to 30 s and the degree of gelatinization was determined by differential scanning calorimetry. During 15 to 25 s of microwave heating, corn starch gelatinization rates were significantly lower and slower than wheat and rice starch rates. Beyond 25 s of heating no significant difference in the degree of gelatinization was detected. Microwave heating was nonuniform and produced chalky regions that were significantly less gelatinized than normally pasted regions. The chalky regions were due to the low water content. The quantitative quadratic model developed to depict the relation between water content and the rate of gelatinization during microwave heating of corn, rice and wheat starches showed a good fit with the experimental data.©1998 Academic PressKeywords: gelatinization; microwave heating; starchIntroductionStudies relating to starch gelatinization during micro-wave heating are limited and focus on the comparison of starch granule swelling patterns between microwave-and convection-heated starch suspensions or starch-based products (1–3). Starch-granule swelling patterns in potatoes heated by microwave and convection heating were noted to be different (3). The stages of starch granule swelling during microwave heating were found to be the same as that of convection heating (2).Comparative studies on the behavior and properties of different starches during microwave heating are lim-ited. The objective of this study is to compare the gelatinization rates of different types of starches (wheat, corn and rice) during microwave heating.Materials and MethodsMaterialsWheat starch (Midsol 50, Midwest Grain Products, Inc.,Atchinson, KS), corn starch (Amaizo, American Maize Products Company, NJ) and rice starch (Remy NeutralDr, A&B Ingredients, NJ) were studied. The original water content of these starches was 100 g/kg.Measurement of dielectric propertiesThe dielectric loss factor of starch suspensions (1:2starch–water ratio) was determined in triplicate using a dielectric probe and a network analyzer at 2450 MHz (Model HP 85070, Hewlett Packard, Santa Rosa, CA).The dielectric probe was calibrated by using air, short circuit and water at 25°C before dielectric measure-ments were done. Dielectric loss factor data were taken*To whom correspondence should be addressed.Fig. 1 Gelatinization of different starches with a starch–water ratio of 1:2. ᭜: wheat a ; ᭹: corn b ; ᭝: rice a ; ––: model. Starches with different letters (a,b,c etc.) are significantly different (P ²0.05). Values are means of three determinationsArticle No. fs980397Lebensm.-Wiss. u.-Technol., 31, 484–488 (1998)0023-6438/98/050484+05 $30.00/0©1998 Academic Presschalky region (2). This hypothesis is supported by other studies which report that as the water content decreases, higher temperatures are required for gelat-inization to occur and reach completion (6–8). In this study we observed that as the water concentration increased, the chalky region disappeared. The observa-tions are due to the greater potential of the granules to undergo phase transitions to higher water levels. Figure 8shows that the degree of gelatinization in chalky regions is lower than that in pasted regions, this may be a consequence of limited water content. Differences in the temperature profiles of starches at various water levels were also observed (Fig. 9). These differences in the temperature profiles are reflective of the difference in the dielectric and thermal properties of the starches.ConclusionsIt is advisable to use rice and wheat starch in microwave-baked products where poor starch gelat-inization resulting from a short baking time needs to be avoided. Microwave heating of starches in limited water systems, 1:1 starch–water ratio, resulted in nonuniform heating and the development of chalky and gel regions which are significantly different in the extent to which they are gelatinized. Chalky regions may be a consequence of limited water content. Quadratic equations with high regression coefficients were developed to show the rate of gelatinization in microwave-heated wheat, rice and corn starches hydrated at 1:1, 1:1.5, 1:2 starch–water ratios.AcknowledgementsResearch support was provided by state and federal funds appropriated to the Ohio Agricultural Research and Development Center and The Ohio State Uni-versity. Support for this research was also provided by NATO A-2 Fellowship of The Scientific and Technical Research Council of Turkey (TUBITAK). References1G OEBEL, N.K., G RIDER, J., D A VIS, E.A. AND G ORDON, J. The effects of microwave energy and convection heating on wheat starch granule transformations. Food Microstructure, 3, 73–82 (1984)2Z YLEMA, B.J., G RIDER, J.A. AND D A VIS, E.A. Model wheat starch systems heated by microwave irradiation and conduction with equalized heating times. Cereal Chemistry, 62, 447–453 (1984)3H UANG, J., H ESS, W.M., W EBER, D.J., P URCELL, A.E. AND H UBER, C.S. Scanning electron microscopy: tissue charac-teristics and starch granule variations of potatoes after microwave and conductive heating. Food Structure, 9, 113–122 (1990)4B UFFLER, C. Microwave Cooking and Processing: Engi-neering Fundamentals for the Food Scientists. New York: Avi Book (1993)5SAS. SAS User’s Guide. Raleigh, NC: SAS Institute Inc, pp. 94–100 (1988)6B URT, D.J. AND R USSELL, P.L. Gelatinization of low water content wheat starch–water mixtures. Starch/St¨a rke, 35, 354–360 (1983)7C HUNGCHAROEN, A. AND L UND, D.B. Influence of solutes and water on rice starch gelatinization. Cereal Chemistry, 64, 240–243 (1987)8D ONA V AN, J.W. Phase transitions of the starch–water system. Biopolymers, 18, 263–275 (1979)lwt/vol. 31 (1998) No. 5。
Phys LettersB.286,118

(3)
ቤተ መጻሕፍቲ ባይዱ
(4)
C
C'
where v[C, C'] is the number of right-handed minus the number of left-handed intersections of C and C'. (A right-handed intersection occurs when, if we move along the positive direction of C, C' crosses from right to left. ) Thus, the commutator gives a representation of the intersection form for Wilson loops. For closed curves C and C', v [ C, C' ] is a topological invariant and if either C or C' is contractible, u [ C, C' ] must vanish. Therefore, there is a nontrivial commutator only for homologically nontrivial curves. If%, fJj,j= 1..... g, are a canonical set of closed curves on Y.g generating its first homology group then v[a;, aj] = u[[3;, [3j] =0, v[ct;, [3j] =d;j. Upon imposition of the constraint (2) the integrals of A over the one-cycles a;, ~i are the only remaining degrees of freedom and, modulo the remaining symmetry under large gauge transformations, they form the reduced phase space [ 2 ]. It is the property (4), that the symplectic structure gives the intersection form for loops on E g, which we shall discover on the lattice as a consequence of lattice gauge invariance and locality. We work in continuum time and a square spatial lattice with spacing I. We begin by fixing some notation. The forward and backward shift operators are S ; f ( x ) = f (x + [), $7 ~f(x) = f ( x - {), respectively, and forward and backward difference operators are d i f ( x ) = f ( x + f) - f ( x ) , d;= S i - 1, a j ( x ) = f ( x ) - f ( x - [), a; = 1 - s7 ~= s7 ~d;. Summation by parts on a lattice takes the form (neglecting surface terms ) Y x f ( x ) d;g (x) = - Yx a;f(x) g (x) by virtue of the lattice Leibniz rule d;(fg) = f d ; g + d J S;g=fd;g+ S; (aorg) (no sum on i). The components A,(x) of the gauge field are realvalued functions on the links specified by the pair [x, [], Ao is a function on lattice sites, the magnetic field B (x) = d iA2(x) - d z A l (X) is a function on plaquettes where x labels the plaquette with corners x, x + L x + T + 2, x + 2 , and the electric field Fo;=e]i- de4o is a function on links. A gauge invariant, local, nondegenerate Chern-Simons term was found in ref. [ 11 ] :
材料科学相关英文术语

仪器分析方法:差热分析:Differential thermal analysis,简称DTA差示扫描量热法:Differential scanning calorimetry,简称DSC热重法:Thermogravimetry,简称TGCharacterization, property, crystalline, inorganic, nanoscale, emphasis, solids, periodic, crystal, bonding, structure, diffraction, classical, quantum models, electronic, applications, semiconductors, chemical, structure-property relationships, synthesis methods, optical, electronic, junction, nanomaterials, real space lattices, reciprocal lattice and diffraction, diffraction/phase diagrams, band theory(能带理论), photonic, amorphous, synthetic biomaterials, infrared, conducting, polymers, solar cells, plasmonics, dielectrics, classifications, natural, artificial, ceramics, alloy, ferroelectrics, superconductors, magnetic, optical, microelectronic, surface engineering, superalloys, structural, composites, composition, biological, measure, characterize, remake, experimentalist, theoretician, materials by design, characterization techniques, crystallography, X-ray/electron scattering, microscopy, spectroscopy, scanning probes, electrical, magnetic, materials modeling, advanced, experimental, optimization, integration, certification, manufacturing, initiative, acceleration, liquid, resistance, planes, chains, diode(二极管), transistors(晶体管), zeolites(沸石), catalysis, separation, purification, hexagon(六边形), pentagon(五边形), spherical, fullerene(富勒烯), allotrope(同素异形体), graphene, dimethyl(二甲基), size-dependent property, solution, discrete(分裂的,不连续的), bandgap(能带隙), periodicity, quartz, formation, kinetics, favorable kinetics, periodic, array, atom, ion, molecules, lattice, symmetry(对称性), Bravais lattices, orientation, vector(矢量), constant(常数), zincblende, miller indices, crystallography, planes, directions, row, d-spacing, individual, set of, equivalent, axis, intercept(截距), specify, lattice directions, quasicrystals(准晶体), diagonal(对角线), interpenetrate(互相渗透), hexagonal close packed(hcp, 密方六排结构), crystallography晶体学, integer 整数, inverse intercept 截距的倒数, axes 轴的复数, reciprocal倒数, equivalent, symmetry 对称性, perpendicular 垂直的, parallelepiped 平行六面体, translational invariance 平移不变性, point symmetry 点对称, aperiodic 非周期性的(quasi-periodic), binary 二元的, ternary 三元的, intermetallic 金属间的, geology地质学, spectroscopy光谱学, pyrite黄铁矿, galena 方铅矿, coordination number(CN, 配位数), surface plasmon resonance(SPR, 表面等离子共振), quantum dots 量子点, coprecipitation 共沉淀, high-temperature decomposition 高温分解法, micro-emulsion 微乳液法, gel-sol 溶胶凝胶法, sonochemistry 超声化学法, laser pyrolysis 激光分解法, biotinylated 生物素化, real-time 实时, longitudinal relaxation 纵向弛豫, transverse relaxation 横向弛豫, superparamagnetic 超顺磁性, boundary effects 边界效应, intergration by parts 分步积分, curie temperature 居里温度, ferromagnetic 铁磁性, aperiodic 非周期性的, stereograms 立体图, pyrite 黄铁矿, galena 方铅矿, cosine 余弦, sine 正弦, tangent 正切, stoichiometry 化学计量学, thermochemistry 热化学, enthalpy 焓, electron spin 电子旋转, Pauli exclusion principle保利不相容原理, electron affinity 电子亲和性, electronegativity 电负性, energetics动力学, covalent bonding 共价键, molecular geometry 分子几何学, bonding theories 键合理论, chemical kinetics 化学动力学, classical thermodynamics 经典热力学, entropy 熵, Gibbs free energy 吉布斯自由能, crystal field theory, 晶体场理论, mineralogy 矿物学, metallurgy 冶金学, array 排列, hollow 空隙, stack 堆垛, repulsion 排斥力, coordination number 配位数, packing efficiency 致密度, density 晶体密度, tetrahedrons 四面体, pentagons 五角形, constituent 构成的/成分, spatial dimensions 三维空间, arbitrary 随意的, planar 平面的, enantiomorphic 对映体, parallelepiped 平行六面体, coplanar 共面的,perpendicular 垂直的, adjacent 邻近的, interplanar spacing 平面间距, parallel 平行的, fractional 分数的, ionization energy 电离能, cation 阳离子, anion 阴离子, electrostatic 静电的, covalency 共价, intermolecular force 分子力, dipole-dipole force 偶极作用, rock salt 岩盐, alkali 碱halide 卤化物, hydride 氢键, octahedra 八面体, polyhedral 多面体的, arsenide 砷化物, fluorite 萤石, calcium 钙, hole 空隙, antifluorite 反萤石, wurtzite 纤维锌矿, van der Waals attraction 范德瓦尔斯力, rutile(TiO2) 金红石, spinel 尖晶石, perovskite 钙钛矿, Ilmenite 钛铁矿, radii(radius的名词复数), Lanthanide contraction 镧系收缩, proportional 比例的, interlocking 联锁的, valence 原子价, brittle 易碎的, silica 硅石,二氧化硅, large coefficient of expansion 扩散系数, Band model 能带模型, silicates 硅酸盐, polymorphic 多晶形的, quartz 石英, ionization energy 离子能, electron affinity 电子亲和势, lattice energy 晶格能, magnitudes 数级, permittivity 介电常数, permittivity of vacuum 真空介电常数, equation 方程式, polarizable 可极化的, molten state 熔融状态, solubility 溶解度, solvent 溶剂, polar solvent 极性溶剂,句子:1.Materials Chemistry is the foundation for the field of Nanoscience and technology.材料化学是纳米科学技术领域的基石。
IMPAC INFRAROT THERMOMETER IS 310与IGA 310系列产品介绍说明书

Small, stationary infrared thermometer using 2-wire technique for non-contact temperature measurement of metallic surfaces, graphite or ceramics between 300 °C and 2500 °C IS 310 • IGA 310Typical Applications:• preheating • annealing • tempering • welding • forging • hardening • sintering • melting • soldering • brazing • rolling• Very small housing dimensions for easy installation, suited for use in confined spaces• 2-wire technique for current supply and temperature measurement at the same time• Internal digital signal processing for high accuracy• High quality optics for detection of small measuring objects• Built-in LED targeting light for easyalignment to the measuring objectThe IS 310 and IGA 310 are stationary pyrometers for non-contact temperature measurement of metallic surfaces, graphite, ceramics, etc.The very small housing dimen-sions enable the integration of the pyrometer in compact production machines, the2-wire technique ensures very easy electrical connection, and the solid and robust design of the instrument guaran-tees reliability, even in rough industrial environments.The pyrometers are equipped with a connector for electrical installation, this offers theoption to use connection cables up to 30 m.For optimal match 3 different focusable optics with smallspot sizes are available.Temperature Range:IS 310 IGA 310650...1800 °C (MB 18) 800...2300 °C (MB 23)1150...2500 °C (MB 25) 300...1300 °C (MB 13L) 500...1500 °C (MB 15)Spectral Ranges:IS 310IGA 3100.8 ... 1.1 µm 1.45 ... 1.8 µm Detector:IS 310IGA 310Si photo diode InGaAs photo diodeOutput: 4 to 20 mA, load independent current, linear temperature output Max load:500 Ω at 24 V power supply, max. 200 Ω at 18 V max. 800 Ω at 30 V Emissivity ε:0.2 to 1; adjustable Response Time t 90:10 msMeas.uncertainty:(at ε=1, T amb .=23 °C)Up to 1500 °C: 0.8% of measured value + 1 °CAbove 1500 °C: 1% of measured value + 1 °CRepeatability:0.3% of measured value (at ε=1, T amb .=23 °C)Power supply:24 V DC ± 25% stabilized, ripple < 50 mV5 to 30 V DC for LED targeting light (I ≤ 30 mA)Sighting:LED targeting light Ambient temperature:0 to 70 °C Storagetemperature:-20 to 70 °CRelative humidity:No condensing conditions Housing:Stainless steel Protection class:IP65 (DIN 40 050)Mounting position:AnyWeight:275 gConnection cable: 2 m - 30 m length, connection via connectorCE label:According to EU directives about electromagnetic immunityNote: The calibration / adjustment of this pyrometer is carried out in accordance withVDI/VDE 3511, Part 4.4. See /calibration for more information.All dimensions in mm*) Aperture D depending on instrument type, see next pageThe pyrometers are equipped ex works with one of the following optics. These optics are fixed to a certain distance, i.e. at these distances each optic achieves its smallest spot size in relation to the measuring distance. The spot size will change in any other distance (shorter or longer). Please note that the measuring object must be at least as big as the spot size.The following table shows the size of the spots (spot size M in mm) at a given measuring distance a. Values between the stated data can be calculated by inter-polation. The spot size for measuring distance 0 is equivalent to the aperture diameter D of the optics, this value is used e.g. to calculate measuring distances in intermediate distances.Typea : M *)a [mm]M [mm]a 1 [mm]M 1 [mm]a 2 [mm]M 2 [mm]D [mm]IS 310MB 18140 : 1250 1.860011.6100023 5.2MB 23 + 25250 : 119.720MB 18150 : 16004100010.1200026MB 23 + 25300 : 12 6.820MB 18155 : 114009200015.1300025MB 23 + 25310 : 1 4.58.716IGA 310MB 13L + MB 15125 : 1250260017.41000359135 : 1600 4.5100013.5200036155 : 114009200016.8300030OpticsLED targeting lightConnection cable with connector*) a : M; distance ratio (90% intensity), M: spot size, a: measuring distance, D: aperture (effective lens diameter)I S 310I G A 310MB 18a = 250 mm MB 23+25MB 18a = 600 mm MB 23+25a = 250 mm a = 600 mm I S 310I S 310MB 18a = 1400 mm MB 23+25a = 1400 mm250 mm1.81600 mm421400 mm94.5250 mm2600 mm 4.51400 mm9*********************©2014 LumaSense Technologies. All rights reserved.LumaSense Technologies, Inc., reserves the right to change the information in this publication at any time.Americas and Australia Sales & Service Santa Clara, CAPh: +1 800 631 0176Fax: +1 408 727 1677Europe, Middle East, Africa Sales & ServiceFrankfurt, Germany Ph: +49 69 97373 0Fax: +49 69 97373 167IndiaSales & Support Center Mumbai, IndiaPh: +91 22 67419203Fax: +91 22 67419201ChinaSales & Support Center Shanghai, ChinaPh:+86133****7766Fax: +86 21 5877 2383LumaSense TechnologiesAwakening Your 6th SenseIS310_IGA310 Datasheet-EN - Rev. 02/27/2014Optics 650 to 1800 ºC (MB 18)800 to 2300 ºC (MB 23)1100 to 2500 ºC(MB 25)a = 250 mm 3 902 210 3 902 250 3 902 310a = 600 mm 3 902 220 3 902 260 3 902 320a = 1400 mm3 902 2303 902 2703 902 330Ordering note: A connection cable is not included in scope of delivery and needs to be ordered separately.Scope of delivery: Instrument, works certificate, and user manual.AccessoriesPower supplies NG DC / NG2DAirpurge unit90° mirrorwith air purge unitOptics 300 to 1300 ºC (MB 13L)500 to 1500 ºC (MB 15)a = 250 mm 3 902 050 3 902 110a = 600 mm 3 902 060 3 902 120a = 1400 mm3 902 0703 902 1303 821 610Connection cable IS / IGA 310, 2 m 3 821 620Connection cable IS / IGA 310, 5 m 3 821 630Connection cable IS / IGA 310, 10 m 3 821 640Connection cable IS / IGA 310, 15 m 3 821 650Connection cable IS / IGA 310, 20 m 3 821 660Connection cable IS / IGA 310, 25 m 3 821 670Connection cable IS / IGA 310, 30 m 3 834 210Adjustable mounting support for water cooling jacket3 843 460SCA 300, scanning attachment with quartz glass window; 24 V AC/DC3 834 230Adjustable mounting support, stainless steel 3 835 180Air purge unit, stainless steel3 835 24090°-mirror3 837 480Water cooling jacket for Series 310 & 320, stain-less steel, with integrated air purge unit 3 835 290Air purge unit for scanning attachment 3 890 610Galvanic separator for measuring output (carrier rail mounting housing)3 863 010Converter (4 - 20 mA to 0 - 20 mA)3 846 170Mounting tube3 852 290Power supply, NG DC, 100 to 240 V AC, 50 to 60 Hz ⇒ 24 V DC, 1 A3 852 280Power supply, 230 V AC, 500 mA, ⇒ 24 V DC, for C/Z-carrier rail mounting3 890 640DA 4000-N: LED-display, 2-wire power supply, 230 V AC3 891 210DA 4000-N: LED-display, 2-wire power supply, 115 V AC3 890 650DA 4000: like DA 4000-N with 2 limit contacts, 230 V AC3 891 220DA 4000: like DA 4000-N with 2 limit contacts, 115 V AC3 890 520DA 6000: LED display, RS232, 2-wire power supply, maximum value storage, analog output3 890 530DA 6000 with RS4853 890 150DA 6000-T, digital display, RS 232, measures the time to cool from 800 ºC to 500 ºC (for welding processes)LED digital displayMounting supportscanning attachmentWater cooling jacket with air purge unit。
The dimension of a variety

a r X i v :mat h /62493v2[mat h.LO]27M ay206THE DIMENSION OF A VARIETY EWA GRACZY ´NSKA AND DIETMAR SCHWEIGERT Abstract.The results of this paper were presented during the Workshop AAA71and CYA21in B¸e dlewo,Poland on February 11,2006.Derived varieties were invented by P.Cohn in [4].Derived varieties of a given type were invented by the authors in [10].In the paper we deal with derived variety V σof a given variety,by a fixed hypersubstitution σ.We introduce the notion of the dimension of a variety as the cardinality κof the set of all proper derived varieties of V included in V .We examine dimensions of some varieties in the lattice of all varieties of a given type τ.Dimensions of varieties of lattices and all subvarieties of regular bands are determined.Keywords :derived algebras,derived varieties,the dimension of a variety.AMS Mathematical Subject Classification 2000:Primary:08B99,08A40.Secondary:08B05,08B15.1.Notations By τwe denote a fixed type τ:I →N ,where I is an index set and N is the set of all natural numbers.We use the definition of an n -ary term of type τfrom [4,p.6].T (τ)denotes the set of all term symbols of type τ.For a given variety V of type τ,two terms p and q of type τare called equivalent (in V )if the identity p ≈q holds in V .Definition 1.1.For a given type τ,F denotes the set of all funda-mental operations F ={f i :i ∈I }of type τ,i.e.τ(i )is the arity of the operation symbol f i ,for i ∈I .Let σ=(t i :i ∈I )be a fixed choice of terms of type τwith τ(t i )=τ(f i ),for every i ∈I .Recall from [10](cf.[4,p.13]),that for a given σ,the extension of σto the mapσ(f i (p 0,...,p n −1))=σ(f i )(σ(p n −1))is called a hypersubstitution of type τ.12EWA GRACZY´NSKA AND DIETMAR SCHWEIGERT In the sequel,we shall useσinstead ofTHE DIMENSION OF A VARIETY3 Note,that our definition of afluid variety does not coincide with that of[16].2.The DimensionDefinition2.1.If V is a variety of typeτ,then the dimension of V is the cardinalityκof the set of all proper derived varieties Vσof V included in V,forσ∈H(τ).We write then thatκ=dim(V).From the definitions above it follows that the trivial variety T of a given type is of dimension0.Theorem2.1.Minimal varieties are of dimension0.Fluid varieties are of dimension0.Later on we shall use the well-known conjugate property of[3](cf. [9,p.35]and[11])and quote as:Theorem2.2.Let A be an algebra andσbe a hypersubstitution of typeτ.Then an identity p≈q of typeτis satisfied in the derived algebra Aσif and only if the derived identityσ(p)≈σ(q)holds in A. From the theorem above,it immediately follows:Theorem2.3.Let V be a variety and two hypersubstitutionsσ1and σ2of typeτbe given.Ifσ1(f i)≈σ2(f i),is an identity of V for everyi∈I,then the derived varieties Vσ1and Vσ2are equal.Proof.The proof follows by induction on the complexity of terms of typeτ.2In the proof we use the relation∼V on sets of hypersubstitutions which was introduced by J.P l onka in[14]and used in[3]to determine the notion of V-equivalent hypersubstitutions in order to simplify the procedure of checking whether an identity is satisfied in a variety V as a hyperidentity.Theorem2.4.Assume that in a variety V(of afinite type)there is only afinite number of non-equivalent n-ary terms,for every n∈N. Then V is of afinite dimension.Proof.The proof follows from the fact that under the assumption,in V there are onlyfinitely many non-equivalent fundamental operations and non-equivalent hypersubstitutions of typeτ.Therefore there are onlyfinitely many derived varieties of V and dim(V)isfinite.24EWA GRACZY´NSKA AND DIETMAR SCHWEIGERT3.Dimensions of varieties of latticesWe present some examples in lattice varieties as an answer to a problem posed by Brian Davey(La Trobe University,Australia)during the Conference on Universal Algebra and Lattice Theory(July2005) at Szeged University(Hungary).Let L=(L,∨,∧)be a lattice.A variety Lσderived from a variety L of lattices must not be a variety of lattices.This follows from the fact,that there are only four non-equivalent binary terms in lattices,namely x,y,x∨y and x∧y.Given a hyper-substitutionσof type(2,2).Ifσis trivial,then the derived algebra Lσis L itself.If one takesσgenerated byσ(∨)=∧andσ(∧)=∨,then Lσis the dual lattice L d=(L,∧,∨).Otherwise the derived algebra Lσis not a lattice at all,as some lattice axioms will be failed,unless L is trivial(i.e.one-element lattice).We got immediately:Example3.1.Let V be a nontrivial variety of lattices.Then a derived variety Vσis the dual variety of lattices V d or a variety which is not a variety of lattices.Example3.2.The variety L of all lattices in type(2,2)isfluid and not solid.The variety L isfluid as it is selfdual,i.e.L=L d.It is not solid,as the commutativity laws for∨and∧are not satisfied as hyperidentities in lattices,for example.Theorem3.1.Every variety of lattices isfluid.Proof.Let V be a variety of lattices.Consider the dual variety of V,i.e.the variety V d of all dual lattices of V.Then there are only two possibilities:(i)V d⊆V and consequently V=V dor(ii)V and V d are incomparable in the lattice of all varieties of lat-tices.Therefore we conclude,that either V is selfdual or V and V d are incomparable.In consequence V isfluid and dim(V)=0.24.Dimensions of subvarieties of regular bandsIn this section we concentrate on the lattice of all subvarieties of regular bands,described in[6]–[7]and[8].THE DIMENSION OF A VARIETY5 Definition4.1.Bands is the variety B of algebras of type(2),de-fined by:associativity and idempotency(i.e.a band is an idempotent semigroup).Following[5,p.11],let us note,that the variety of bands has only six non-equivalent binary terms,therefore only six hypersubstitutions of type(2)in the variety of bands should be checked,namely:σ1−σ6 defined as follows:σ1(xy)=x,σ2(xy)=y,σ3(xy)=xy,σ4(x,y)=yx,σ5(xy)=xyx andσ6(xy)=yxy to be considered in order to determine all derived varieties of a given subvariety of regular bands.Recall Proposition3.1.5(i)from[4,p.11,77]:Definition4.2.A variety V of type(2)is called hyperassociative if the associativity law is satisfied in V as a hyperidentity.Proposition4.1.A variety of bands is hyperassociative if and only if it is contained in the variety RegB of regular bands.The propositions above may be considered as a motivation of our interest in the lattice of all subvarieties of the variety of regular bands. In order to determine the dimension of all subvarieties of RegB,we shall use the following two theorems of[11]:Theorem4.1.The variety of B all bands constitutes a notfluid and not solid variety of type(2).Theorem4.2.A variety V of bands isfluid if and only if it is minimal. Remark4.1.Note,that a nontrivial variety V is of dimension0if and only if it isfluid.Definition4.3.An identity e of the form p≈q is called leftmost (rightmost)if and only if it has the samefirst(last)variable on each side.One which meets both of these conditions is called outermost. First we express three technical lemmas:Lemma4.1.LetΣbe a set of identities of typeτwhich are leftmost (or rightmost).Then the set E(Σ)consists only of leftmost(rightmost) identities.Proof.The proof follows from the observation that all rules of infer-ence(1)–(5)preserves the property of being the leftmost(or rightmost) identity.Therefore the closure of the set of left(right)most identities consists of left(right)most identities.2From[6]–[7]and[8]it follows that every subvariety of the variety B of all bands is defined by one additional identity added to two axioms of bands(i.e.associativity and idempotency).6EWA GRACZY´NSKA AND DIETMAR SCHWEIGERTLemma4.2.Assume that V and W are varieties of bands,W is de-fined by a single identity p≈q,i.e.W=Mod(p≈q)(in the varieties of bands).Then:Vσ⊆W,for a givenσ∈H(τ),if and only if the derived identityσ(p)≈σ(q)is satisfied in V,i.e. V|=σ(p)≈σ(q).Proof.Vσ=HSP(σ(V))⊆W if and only ifσ(V)|=p≈q.By theorem2.2we conclude that Aσ|=p≈q,for every algebra Aσ∈σ(V),if and only if A|=σ(p)≈σ(q),for every algebra A∈V,i.e. V|=σ(p)≈σ(q).2A simple generalization of the above lemma is the following:Lemma 4.3.Assume that V and W are varieties of typeτ,W is defined by a setΣof identities of typeτ,i.e.W=Mod(Σ).Then:Vσ⊆W,for a givenσ∈H(τ),if and only if the derived identityσ(p)≈σ(q)is satisfied in V,i.e.V|=σ(p)≈σ(q),for every identity p≈q∈Σ.Proof.The proof is similar as that of lemma4.2,where p≈q is any identity of the given axiomaticΣ.2The next three propositions show some regularities in the dimensions of all subvarieties of regular bands described in[7,p.244]and[8]:Definition4.4.The variety of RB in the variety B of bands is defined by the identity:y≈yxy.It is called the variety of rectangular bands.The fact that the variety RB is solid was proved in[5,p.96].We expressed the situation of theorems above on the diagram,which describes the bottom part of the lattice of all identities of bands,see [10]and[12,p.244]Proposition3.1.5of[4]:THE DIMENSION OF A VARIETY 7p s ss ssss szxyz =zyxzs sszxyz =zxzyzs s V 5V 6V 4V 2xy =y yx =y V 1V 3x =ySL RBRegBNBLZ RZ T Theorem 4.3.The variety RB is of dimension 2.Proof .The variety of RB of rectangular bands has only two sub-varieties,namely the variety LZ defined by the identities:yx ≈y (called the variety of left-zero semigroups)and the variety RZ defined by xy ≈y (called the variety of right-zero semigroups),respectively.Both of them are derived varieties of RB by the first and the second pro-jection,respectively.To prove that,let (A )σ1∈σ1(RB ),for A ∈RB .Then the identity yx ≈y is satisfied in A σ1,as:σ1(yx )≈y ≈y ≈σ1(y )is satisfied in A and consequently in (RB )σ1.Similarly for σ2.We con-clude that dim (RB )=2.2Theorem 4.4.The varieties V 1and V 2of bands defined by the identi-ties:(1)zxy ≈zyx and (2)yxz ≈xyz ,respectively,are mutually derived by σ4.Moreover,dim (V 1)=dim (V 2)=1.Proof .Note,that the varieties V 1and V 2has only two proper subvari-eties,namely:the variety of left (right)zero-semigroups (respectively)and the variety SL of semilattices.The variety of semilattices,defined (in the variety of bands)by the commutativity law:xy ≈yx is not a derived variety of V 1,nether of V 2.This follows from the fact,that if the variety SL of semilattices would be a derived variety of V 1,then8EWA GRACZY´NSKA AND DIETMAR SCHWEIGERTSL=(V1)σ5or SL=(V1)σ6.This is impossible,via theorem1.3,asthe derived identity of xy≈yx by the hypersubstitionsσ5(orσ6),i.e.σ5(xy)≈σ5(yx)(orσ6(xy)≈σ6(yx))is of the form xyx≈yxy is nei-ther leftmost nor rightmost and therefore,by lemma4.1is not satisfied in V1as every identity satisfied in V1is leftmost.Similarly for V2.The proof follows from the fact that the only proper derived variety of V1 included in V1is the variety LZ of left zero semigroups.Similarly,one can show that the only proper derived subvariety of V2by the second projectionσ2is the variety RZ of right zero semigroups.Finally we conclude that dim(V1)=dim(V2)=1.2Definition4.5.Varieties of dimension1will be called prefluid. Theorem4.5.The varieties V3and V4of bands defined by the identi-ties:(3)yx≈yxy and(4)xy≈yxy,respectively,are mutually derived byσ4.Moreover,dim(V3)=dim(V4)=1. Proof.The variety(V3)σ1is the variety LZ of bands defined byyx≈y.We obtain that:(V3)σ1is different as V3,therefore(V3)σ1isproper and(V3)σ1⊆V3.Note,that the derived variety(V3)σ2is properand is the variety RZ of right-zero semigroups but is not included in V3.Similarly as in the previous theorem we conclude,that the variety SL of semilattices is not a derived variety of V3,as all the identities of V3are leftmost.In order to exclude that,the variety V1defined by the identity(1)zxy≈zyx is the derived variety of V3byσ5consider the derived identityσ5(zxy)≈σ5(zyx)of(1)byσ5,i.e.the identity zxyxz≈zyxyz.If this identity would be satisfied in V3,then the identity zxyz≈zyxz would be satisfied in V3,which is not true due to the results of[6]–[8].Dually,the derived variety of V3byσ6is not the variety V1.Therefore we conclude,that dim(V3)=1.Similarly one can prove that dim(V4)=1.2Theorem4.6.The varieties V5and V6of bands defined by the identi-ties:(5)zxy≈zxzy and(6)yxz≈yzxz,respectively,are mutually derived byσ4.Moreover,dim(V5)=dim(V6)=3.Proof.The proof that(V5)σ1((V5)σ2is the variety LZ(RZ)of left(right)zero semigroups follows from the proof of previous observations. Obviously:σ4(V5)=V6,as the derived identityσ4(yxz)≈σ4(yzxz) of(6)byσ4gives rise to the identity(5)zxy≈zxzy and vice versa. Therefore V6and V5are mutually derived byσ4.We will show that the derived variety of V5by the hypersubstitutionσ5is the variety V3,THE DIMENSION OF A VARIETY9 i.e.σ5(V5)=V3.To show this consider the derived identity of(3)by σ5,i.e.the identityσ5(yx)≈σ5(yxy).This gives rise to the identity yxy≈yxyxy,which is obviously satisfied in V5.Moreover,note that the derived identity of(1)byσ5,i.e.σ5(zxy)≈σ5(zyx)gives rise to the identity zxyxz≈zyxyz,which can not be satisfied in V5,as otherwise the identity zxyz≈zyxz would be satisfied in V3,which is impossible by the results of[6]–[8]and it has been shown already in the proof of theorem4.5.Similarly one can show,that the derived variety of V5byσ6is the variety V4.We conclude that dim(V5)=3.Similarly, dim(V6)=3.2Definition4.6.The variety NB of normal bands is defined by the identity:(7)zxyz≈zyxz.Theorem4.7.dim(NB)=4.Proof.For solidity of the variety NB confront[5,p.96].It follows, that all derived varieties of the variety of NB are included in the variety of NB.Similarly as before we show that(NB)σ1is the variety LZ of left-zero semigroups and(NB)σ2is the variety RZ of right-zero semigroups.Both of them are proper subvarieties of NB.It is obviousthat(NB)σ3=(NB)σ4=NB.We show only that(NB)σ5=V1,asthe derived indentity of(1)zxy≈zyx byσ5,i.e.σ5(zxy)≈σ5(zyx) gives rise to the identity zxyxz≈zyxyz satisfied in NB.In order to exclude that the variety LZ of left zero semigroups,defined by the identity yx≈y equals to(NB)σ5,notice that the derived identity of yx≈y byσ5is the identity yxy≈y,which is not satisfied in NB,as the variety of NB is defined by the set of regular identities(cf.[13]), which has only regular consequences.Similarly(NB)σ6=V2,as the derived identity of(2)yxz≈xyz byσ6,i.e.σ6(yxz)≈σ6(xyz)gives rise to the identity zxyxz≈zyxyz satisfied in NB and we conclude that dim(NB)=4.2Theorem4.8.dim(RegB)=4.Proof.For solidity of the variety RegB confront[5,p.96].Two de-rived subvarieties of RegB are LZ and RZ,byσ1andσ2,respectively. The derived varieties of RegB viaσ3andσ4are equal to RegB.We show that(RegB)σ5=V3.To prove that,consider the derived identity of the identity(3)yx≈yxy byσ5,i.e.the identityσ5(yx)≈σ5(yxy) which gives rise to the identity yxy≈yxyxy which is satisfied in RegB. In order to show that the derived variety of RegB byσ5is not equal to the variety V1,note that the derived identity of(1)zxy≈zyx10EWA GRACZY ´NSKA AND DIETMAR SCHWEIGERTby σ5,i.e.the identity σ5(zxy )≈σ5(zyx )gives rise to the identity zxyxz ≈zyxyz which is not satisfied in RegB ,as it was shown in the proof of theorem 4.6that this identity is not satisfied in V 5,which is a subvariety of RegB .Similarly,one can show,that the derived variety of RegB by σ6is the variety V 4.This finishes the proof that dim (RegB )=4.2We expressed the situation of theorems above on the diagram:p ss s s s s s ss sss s 3311114000240Acknowledgement .The first author expresses her thanks to the referee for his valuable comments.References[1]G.Birkhoff,On the structure of abstract algebras ,J.Proc.Cambridge Phil.Soc.31,1935,433–454.[2]P.M.Cohn,Universal Algebra ,Reidel,1981Dordreht.[3]K.Denecke,J.Koppitz,M-solid varieties of algebras ,Advances in Mathemat-ics,Vol.10,Springer,2006.[4]K.Denecke,S.L.Wismath,Hyperidentities and Clones ,Gordon &Breach,2000.ISBN 90-5699-235-X.ISSN 1041-5394.[5]T.Evans,The lattice of semigroups varieties ,Semigroup Forum 2,1971,1–43.[6]Ch.F.Fennemore,All varieties of bands ,Ph.D.dissertation,Pensylvania StateUniversity,1969.[7]Ch.F.Fennemore,All varieties of bands I ,Mathematische Nachrichten,48,1971,237-252.[8]J.A.Gerhard,The lattice of equational classes of idempotent semigroups ,J.of Algebra,15,1970,195–224.THE DIMENSION OF A VARIETY11 [9]E.Graczy´n ska,Universal algebra via tree operads,Opole2000.ISSN1429-6063.ISBN83-88492-75-6.[10]E.Graczy´n ska and D.Schweigert,Hyperidentities of a given type,AlgebraUniversalis27,1990,305–318.[11]E.Graczy´n ska and D.Schweigert,Derived andfluid varieties,in print.[12]G.Gr¨a tzer,Universal Algebra.2nd ed.,Springer,New York1979.[13]J.P l onka,On equational classes of abstract algebras defined by regular equa-tions,Fund.Math.64,1969,241–247.[14]J.P l onka,Proper and inner hypersubstitutions of varieties,Proceedings ofthe International Conference Sommer School on General Algebra and Ordered Sets,Olomouc1994,106–116.[15]D.Schweigert,Hyperidentities,in:I.G.Rosenberg and G.Sabidussi,Algebrasand Orders,1993Kluwer Academic Publishers,405–506.ISBN0-7923-2143-X.[16]D.Schweigert,On derived varieties,Discussiones Mathematicae Algebra andStochastic Methods18,1998,17–26.Opole University of Technology,Institute of Mathematicsul.Luboszycka3,45-036Opole,PolandE-mail address:egracz@po.opole.pl http://www.egracz.po.opole.pl/ Technische Universit¨a t Kaiserslautern,F achbereich Mathematik Postfach3049,67653Kaiserslautern,Germany。
Discovering Similar Multidimensional Trajectories

Discovering Similar Multidimensional TrajectoriesMichail VlachosUC Riverside mvlachos@George KolliosBoston Universitygkollios@Dimitrios GunopulosUC Riversidedg@AbstractWe investigate techniques for analysis and retrieval of object trajectories in a two or three dimensional space. Such kind of data usually contain a great amount of noise, that makes all previously used metrics fail.Therefore,here we formalize non-metric similarity functions based on the Longest Common Subsequence(LCSS),which are very ro-bust to noise and furthermore provide an intuitive notion of similarity between trajectories by giving more weight to the similar portions of the sequences.Stretching of sequences in time is allowed,as well as global translating of the se-quences in space.Efficient approximate algorithms that compute these similarity measures are also provided.We compare these new methods to the widely used Euclidean and Time Warping distance functions(for real and synthetic data)and show the superiority of our approach,especially under the strong presence of noise.We prove a weaker ver-sion of the triangle inequality and employ it in an indexing structure to answer nearest neighbor queries.Finally,we present experimental results that validate the accuracy and efficiency of our approach.1IntroductionIn this paper we investigate the problem of discovering similar trajectories of moving objects.The trajectory of a moving object is typically modeled as a sequence of con-secutive locations in a multidimensional(generally two or three dimensional)Euclidean space.Such data types arise in many applications where the location of a given object is measured repeatedly over time.Examples include features extracted from video clips,animal mobility experiments, sign language recognition,mobile phone usage,multiple at-tribute response curves in drug therapy,and so on.Moreover,the recent advances in mobile computing, sensor and GPS technology have made it possible to collect large amounts of spatiotemporal data and there is increas-ing interest to perform data analysis tasks over this data [4].For example,in mobile computing,users equipped with mobile devices move in space and register their location at different time instants via wireless links to spatiotemporal databases.In environmental information systems,tracking animals and weather conditions is very common and large datasets can be created by storing locations of observed ob-jects over time.Data analysis in such data include deter-mining andfinding objects that moved in a similar way or followed a certain motion pattern.An appropriate and ef-ficient model for defining the similarity for trajectory data will be very important for the quality of the data analysis tasks.1.1Robust distance metrics for trajectoriesIn general these trajectories will be obtained during a tracking procedure,with the aid of various sensors.Here also lies the main obstacle of such data;they may contain a significant amount of outliers or in other words incorrect data measurements(unlike for example,stock data which contain no errors whatsoever).Figure1.Examples of2D trajectories.Two in-stances of video-tracked time-series data representingthe word’athens’.Start&ending contain many out-liers.Athens 1Athens 2Boston 1Boston 2DTWLCSSFigure 2.Hierarchical clustering of 2D series (displayed as 1D for clariry).Left :The presence of many outliers in the beginning and the end of the sequences leads to incorrect clustering.DTW is not robust under noisy conditions.Right :The focusing on the common parts achieves the correct clustering.Our objective is the automatic classification of trajec-tories using Nearest Neighbor Classification.It has been shown that the one nearest neighbor rule has asymptotic er-ror rate that is at most twice the Bayes error rate[12].So,the problem is:given a database of trajectories and a query (not already in the database),we want to find the trajectory that is closest to .We need to define the following:1.A realistic distance function,2.An efficient indexing scheme.Previous approaches to model the similarity between time-series include the use of the Euclidean and the Dy-namic Time Warping (DTW)distance,which however are relatively sensitive to noise.Distance functions that are ro-bust to extremely noisy data will typically violate the trian-gular inequality.These functions achieve this by not consid-ering the most dissimilar parts of the objects.However,they are useful,because they represent an accurate model of the human perception,since when comparing any kind of data (images,trajectories etc),we mostly focus on the portions that are similar and we are willing to pay less attention to regions of great dissimilarity.For this kind of data we need distance functions that can address the following issues:Different Sampling Rates or different speeds.The time-series that we obtain,are not guaranteed to be the outcome of sampling at fixed time intervals.The sensors collecting the data may fail for some period of time,leading to inconsistent sampling rates.Moreover,two time series moving at exactly the similar way,but one moving at twice the speed of the other will result (most probably)to a very large Euclidean distance.Similar motions in different space regions .Objectscan move similarly,but differ in the space they move.This can easily be observed in sign language recogni-tion,if the camera is centered at different positions.If we work in Euclidean space,usually subtracting the average value of the time-series,will move the similar series closer.Outliers.Might be introduced due to anomaly in the sensor collecting the data or can be attributed to hu-man ’failure’(e.g.jerky movement during a track-ing process).In this case the Euclidean distance will completely fail and result to very large distance,even though this difference may be found in only a few points.Different lengths.Euclidean distance deals with time-series of equal length.In the case of different lengths we have to decide whether to truncate the longer series,or pad with zeros the shorter etc.In general its use gets complicated and the distance notion more vague.Efficiency.It has to be adequately expressive but suf-ficiently simple,so as to allow efficient computation of the similarity.To cope with these challenges we use the Longest Com-mon Subsequence (LCSS)model.The LCSS is a varia-tion of the edit distance.The basic idea is to match two sequences by allowing them to stretch,without rearranging the sequence of the elements but allowing some elements to be unmatched .The advantages of the LCSS method are twofold:1)Some elements may be unmatched,where in Eu-clidean and DTW all elements must be matched,even the outliers.2)The LCSS model allows a more efficient approximatecomputation,as will be shown later(whereas in DTW you need to compute some costly Norm).Infigure2we can see the clustering produced by the distance.The sequences represent data collected through a video tracking process.Originally they represent 2d series,but only one dimension is depicted here for clar-ity.The fails to distinguish the two classes of words, due to the great amount of outliers,especially in the begin-ning and in the end of the ing the Euclidean distance we obtain even worse results.The produces the most intuitive clustering as shown in the samefigure. Generally,the Euclidean distance is very sensitive to small variations in the time axis,while the major drawback of the is that it has to pair all elements of the sequences.Therefore,we use the model to define similarity measures for trajectories.Nevertheless,a simple extension of this model into2or more dimensions is not sufficient, because(for example)this model cannot deal with paral-lel movements.Therefore,we extend it in order to address similar problems.So,in our similarity model we consider a set of translations in2or more dimensions and wefind the translation that yields the optimal solution to the problem.The rest of the paper is organized as follows.In section2 we formalize the new similarity functions by extending the model.Section3demonstrates efficient algorithms to compute these functions and section4elaborates on the indexing structure.Section5provides the experimental validation of the accuracy and efficiency of the proposed approach and section6presents the related work.Finally, section7concludes the paper.2Similarity MeasuresIn this section we define similarity models that match the user perception of similar trajectories.First we give some useful definitions and then we proceed by presenting the similarity functions based on the appropriate models.We assume that objects are points that move on the-plane and time is discrete.Let and be two trajectories of moving objects with size and respectively,whereand.For a trajectory,let be the sequence.Definition1Given an integer and a real number,we define the as follows:A Ba and andThe constant controls how far in time we can go in order to match a given point from one trajectory to a point in another trajectory.The constant is the matching threshold(see figure3).Thefirst similarity function is based on the and the idea is to allow time stretching.Then,objects that are close in space at different time instants can be matched if the time instants are also close.Definition2We define the similarity function between two trajectories and,given and,as follows:Definition3Given,and the family of translations,we define the similarity function between two trajectories and,as follows:So the similarity functions and range from to. Therefore we can define the distance function between two trajectories as follows:Definition4Given,and two trajectories and we define the following distance functions:andNote that and are symmetric.is equal to and the transformation that we use in is translation which preserves the symmetric prop-erty.By allowing translations,we can detect similarities be-tween movements that are parallel in space,but not iden-tical.In addition,the model allows stretching and displacement in time,so we can detect similarities in move-ments that happen with different speeds,or at different times.Infigure4we show an example where a trajectory matches another trajectory after a translation is applied. Note that the value of parameters and are also important since they give the distance of the trajectories in space.This can be useful information when we analyze trajectory data.XFigure4.Translation of trajectory.The similarity function is a significant improvement over the,because:i)now we can detect parallel move-ments,ii)the use of normalization does not guarantee that we will get the best match between two u-ally,because of the significant amount of noise,the average value and/or the standard deviation of the time-series,that are being used in the normalization process,can be distorted leading to improper translations.3Efficient Algorithms to Compute the Simi-larity3.1Computing the similarity functionTo compute the similarity functions we have to run a computation for the two sequences.Thecan be computed by a dynamic programming algorithm in time.However we only allow matchings when the difference in the indices is at most,and this allows the use of a faster algorithm.The following lemma has been shown in[5],[11].Lemma1Given two trajectories and,with and,we canfind the in time.If is small,the dynamic programming algorithm is very efficient.However,for some applications may need to be large.For that case,we can speed-up the above computa-tion using random sampling.Given two trajectories and ,we compute two subsets and by sampling each trajectory.Then we use the dynamic programming algo-rithm to compute the on and.We can show that,with high probability,the result of the algorithm over the samples,is a good approximation of the actual value. We describe this technique in detail in[35].3.2Computing the similarity functionWe now consider the more complex similarity function .Here,given two sequences,and constants, we have tofind the translation that maximizes the length of the longest common subsequence of()over all possible translations.Let the length of trajectories and be and re-spectively.Let us also assume that the translationis the translation that,when applied to,gives a longest common subsequence,and it is also the translation that maximizes the length of the longest common subsequence.The key observation is that,although there is an infinite number of translations that we can apply to,each transla-tion results to a longest common subsequence between and,and there is afinite set of possible longest common subsequences.In this section we show that we can efficiently enumerate afinite set of translations,such that this set provably includes a translation that maximizes the length of the longest common subsequence of and .To give a bound on the number of transformations that we have to consider,we look at the projections of the two trajectories on the two axes separately.We define theprojection of a trajectoryto be the sequence of the valueson the -coordinate:.A one di-mensional translation is a function that adds a con-stant to all the elements of a 1-dimensional sequence:.Take the projections of and ,and respec-tively.We can show the following lemma:Lemma 2Given trajectories ,if ,then the length of the longest common subsequence of the one dimensional sequences and,is at least :.Also,.Now,consider and .A translation by ,applied to can be thought of as a linear transformation of the form .Such a transformation will allowto be matched to all for which ,and.It is instructive to view this as a stabbing problem:Con-sider the vertical line segments,where (Figure 5).Bx,i By,i+2Bx,i+3Bx,i+4Bx,i+5Ax,iAx,i+1Ax,i+2fc1(x) = x + c1fc2(x) = x + c2Ax axisBx axisFigure 5.An example of two translations.These line segments are on a two dimensional plane,where on the axis we put elements ofand on the axis we put elements of .For every pair of elementsin and that are within positions from eachother (and therefore can be matched by the algo-rithm if their values are within ),we create a vertical line segment that is centered at the point and extends above and below this point.Since each element in can be matched with at most elements in ,the total number of such line segments is .A translation in one dimension is a function of the form .Therefore,in the plane we de-scribed above,is a line of slope 1.After translatingby ,an element of can be matched to an el-ement of if and only if the line intersects the line segment .Therefore each line of slope 1defines a set of possi-ble matchings between the elements of sequences and.The number of intersected line segments is actually an upper bound on the length of the longest common sub-sequence because the ordering of the elements is ignored.However,two different translations can result to different longest common subsequences only if the respective lines intersect a different set of line segments.For example,the translations and in figure 5intersect different sets of line segments and result to longest common subsequences of different length.The following lemma gives a bound on the number of possible different longest common subsequences by bound-ing the number of possible different sets of line segments that are intersected by lines of slope 1.Lemma 3Given two one dimensional sequences ,,there are lines of slope 1that intersect different sets of line segments.Proof:Let be a line of slope 1.If we move this line slightly to the left or to the right,it still in-tersects the same number of line segments,unless we cross an endpoint of a line segment.In this case,the set of inter-sected line segments increases or decreases by one.There are endpoints.A line of slope 1that sweeps all the endpoints will therefore intersect at most different sets of line segments during the sweep.In addition,we can enumerate the trans-lations that produce different sets of potential matchings byfinding the lines of slope 1that pass through the endpoints.Each such translation corresponds to a line .This set of translations gives all possible matchings for a longest common subsequence of .By applying the same process on we can also find a set of translations that give all matchings of.To find the longest common subsequence of the se-quences we have to consider only thetwo dimensional translations that are created by taking the Cartesian product of the translations on and the trans-lations on .Since running the LCSS algorithm takeswe have shown the following theorem:Theorem 1Given two trajectories and,withand ,we can compute theintime.3.3An Efficient Approximate AlgorithmTheorem 1gives an exact algorithm for computing ,but this algorithm runs in cubic time.In this section we present a much more efficient approximate algorithm.The key in our technique is that we can bound the difference be-tween the sets of line segments that different lines of slope 1intersect,based on how far apart the lines are.Consider again the one dimensional projections. Lets us consider the translations that result to different sets of intersected line segments.Each translation is a line of the form.Let us sort these trans-lations by.For a given translation,let be the set of line segments it intersects.The following lemma shows that neighbor translations in this order intersect similar sets of line segments.Lemma4Let be the different translations for sequences and,where.Then the symmetric difference.We can now prove our main theorem:Theorem2Given two trajectories and,with and,and a constant,we canfind an ap-proximation of the similaritysuch that intime.Proof:Let.We consider the projections of and into the and axes.There exists a translation on only such that is a superset of the matches in the optimal of and.In addition,by the previous lemma,there are translations()that have at most different matchings from the optimal. Therefore,if we use the translations,fortime if we runpairs of translations in the plane.Since there is one that is away from the optimal in each dimension,there is one that is away from the optimal in2dimensions.Setting-th quantiles for each set,pairs of translations.4.Return the highest result.4Indexing Trajectories for Similarity Re-trievalIn this section we show how to use the hierarchical tree of a clustering algorithm in order to efficiently answer near-est neighbor queries in a dataset of trajectories.The distance function is not a metric because it does not obey the triangle inequality.Indeed,it is easy to con-struct examples where we have trajectories and, where.This makes the use of traditional indexing techniques diffi-cult.We can however prove a weaker version of the triangle inequality,which can help us avoid examining a large por-tion of the database objects.First we define:Clearly,or in terms of distance:In order to provide a lower bound we have to maximize the expression.Therefore,for every node of the tree along with the medoid we have to keep the trajectory that maximizes this expression.If the length of the query is smaller than the shortest length of the trajec-tories we are currently considering we use that,otherwise we use the minimum and maximum lengths to obtain an approximate result.4.2Searching the Index tree for Nearest Trajec-toriesWe assume that we search an index tree that contains tra-jectories with minimum length and maximum length .For simplicity we discuss the algorithm for the1-Nearest Neighbor query,where given a query trajectory we try tofind the trajectory in the set that is the most sim-ilar to.The search procedure takes as input a nodein the tree,the query and the distance to the closest tra-jectory found so far.For each of the children,we check if the child is a trajectory or a cluster.In case that it is a trajectory,we just compare its distance to with the current nearest trajectory.If it is a cluster,we check the length of the query and we choose the appropriate value for .Then we compute a lower bound to the distance of the query with any trajectory in the cluster and we compare the result with the distance of the current near-est neighbor.We need to examine this cluster only if is smaller than.In our scheme we use an approximate algorithm to compute the.Consequently,the value offrom the bound we compute for.Note that we don’t need to worry about the other terms since they have a negative sign and the approximation algorithm always underestimates the .5Experimental EvaluationWe implemented the proposed approximation and index-ing techniques as they are described in the previous sec-tions and here we present experimental results evaluating our techniques.We describe the datasets and then we con-tinue by presenting the results.The purpose of our experi-ments is twofold:first,to evaluate the efficiency and accu-racy of the approximation algorithm presented in section3 and second to evaluate the indexing technique that we dis-cussed in the previous section.Our experiments were run on a PC AMD Athlon at1GHz with1GB RAM and60 GB hard disk.5.1Time and Accuracy ExperimentsHere we present the results of some experiments using the approximation algorithm to compute the similarity func-tion.Our dataset here comes from marine mammals’satellite tracking data.It consists of sequences of geo-graphic locations of various marine animals(dolphins,sea lions,whales,etc)tracked over different periods of time, that range from one to three months(SEALS dataset).The length of the trajectories is close to.Examples have been shown infigure1.In table1we show the computed similarity between a pair of sequences in the SEALS dataset.We run the exact and the approximate algorithm for different values of and and we report here some indicative results.is the num-ber of times the approximate algorithm invokes the procedure(that is,the number of translations that we try).As we can see,for and we get very good results.We got similar results for synthetic datasets.Also, in table1we report the running times to compute the simi-larity measure between two trajectories of the same dataset. The approximation algorithm uses again from to differ-ent runs.The running time of the approximation algorithm is much faster even for.As can be observed from the experimental results,the running times of the approximation algorithm is not pro-portional to the number of runs().This is achieved by reusing the results of previous translations and terminat-ing early the execution of the current translation,if it is not going to yield a better result.The main conclusion of the above experiments is that the approximation algorithm can provide a very tractable time vs accuracy trade-off for computing the similarity between two trajectories,when the similarity is defined using the model.5.2Classification using the Approximation Algo-rithmWe compare the clustering performance of our method to the widely used Euclidean and DTW distance functions. Specifically:cover.htmlSimilarityApproximate for K tries Exact9494250.250.3160.18460.2530.00140.0022 0.50.5710.4100.5100.00140.0022 0.250.3870.1960.3060.00180.00281 0.50.6120.4880.5630.00180.00280 0.250.4080.2500.3570.001910.0031 0.50.6530.4400.5840.001930.0031 Table1.Similarity values and running times between two sequences from our SEALS dataset.1.The Euclidean distance is only defined for sequencesof the same length(and the length of our sequences vary considerably).We tried to offer the best possible comparison between every pair of sequences,by slid-ing the shorter of the two trajectories across the longer one and recording their minimum distance.2.For DTW we modified the original algorithm in orderto match both x and y coordinates.In both DTW and Euclidean we normalized the data before computing the distances.Our method does not need any normal-ization,since it computes the necessary translations.3.For LCSS we used a randomized version with andwithout sampling,and for various values of.The time and the correct clusterings represent the average values of15runs of the experiment.This is necessary due to the randomized nature of our approach.5.2.1Determining the values for&The values we used for and are clearly dependent on the application and the dataset.For most datasets we had at our disposal we discovered that setting to more than of the trajectories length did not yield significant improvement.Furthermore,after some point the similarity stabilizes to a certain value.The determination of is appli-cation dependent.In our experiments we used a value equal to the smallest standard deviation between the two trajec-tories that were examined at any time,which yielded good and intuitive results.Nevertheless,when we use the index the value of has to be the same for all pairs of trajectories.5.2.2Experiment1-Video tracking data.The2D time series obtained represent the X and Y position of a human tracking feature(e.g.tip offinger).In conjuc-tion with a”spelling program”the user can”write”various words[19].We used3recordings of5different words.The data correspond to the following words:’athens’,’berlin’,’london’,’boston’,’paris’.The average length of the series is around1100points.The shortest one is834points and the longest one1719points.To determine the efficiency of each method we per-formed hierarchical clustering after computing thepairwise distances for all three distance functions.We eval-uate the total time required by each method,as well as the quality of the clustering,based on our knowledge of whichword each trajectory actually represents.We take all possi-ble pairs of words(in this case pairs)and use the clustering algorithm to partition them into two classes.While at the lower levels of the dendrogram the clustering is subjective,the top level should provide an accurate divi-sion into two classes.We clustered using single,complete and average linkage.Since the best results for every dis-tance function are produced using the complete linkage,we report only the results for this approach(table2).The same experiment is conducted with the rest of the datasets.Exper-iments have been conducted for different sample sizes and values of(as a percentage of the original series length).The results with the Euclidean distance have many clas-sification errors and the DTW has some errors,too.For the LCSS the only real variations in the clustering are for sam-ple sizes.Still the average incorrect clusterings for these cases were constantly less than one().For 15%sampling or more,there were no errors.5.2.3Experiment2-Australian Sign LanguageDataset(ASL).The dataset consists of various parameters(such as the X,Y, Z hand position,azimuth etc)tracked while different writ-ers sign one the95words of the ASL.These series are rel-atively short(50-100points).We used only the X and Y parameters and collected5recordings of the following10 words:’Norway’,’cold’,’crazy’,’eat’,’forget’,’happy’,’innocent’,’later’,’lose’,’spend’.This is the experiment conducted also in[25](but there only one dimension was used).Examples of this dataset can be seen infigure6.Correct Clusterings(out of10)Complete Linkage Euclidean34.96DTW237.6412.7338.04116.17328.85145.06565.203113.583266.753728.277Distance Time(sec)CorrectClusterings(out of45)ASL with noiseEuclidean 2.271520Figure 7.ASL data :Time required to compute the pairwise distances of the 45combinations(same for ASL and ASL withnoise)Figure 8.Noisy ASL data :The correct clusterings of the LCSS method using complete linkage.Figure 9.Performance for increasing number of Near-est Neighbors.Figure 10.The pruning power increases along with the database size.jectories.We executed a set of -Nearest Neighbor (K-NN)queries for ,,,and and we plot the fraction of the dataset that has to be examined in order to guarantee that we have found the best match for the K-NN query.Note that in this fraction we included the medoids that we check during the search since they are also part of the dataset.In figure 9we show some results for -Nearest Neigh-bor queries.We used datasets with ,and clusters.As we can see the results indicate that the algorithm has good performance even for queries with large K.We also per-formed similar experiments where we varied the number of clusters in the datasets.As the number of clusters increased the performance of the algorithm improved considerably.This behavior is expected and it is similar to the behavior of recent proposed index structures for high dimensional data [9,6,21].On the other hand if the dataset has no clusters,the performance of the algorithm degrades,since the major-ity of the trajectories have almost the same distance to the query.This behavior follows again the same pattern of high dimensional indexing methods [6,36].The last experiment evaluates the index performance,over sets of trajectories with increasing cardinality.We in-dexed from to trajectories.The pruning power of the inequality is evident in figure 10.As the size of the database increases,we can avoid examining a larger frac-tion of the database.6Related WorkThe simplest approach to define the similarity between two sequences is to map each sequence into a vector and then use a p-norm distance to define the similarity measure.The p-norm distance between two n-dimensional vectors and is defined as。
洛伦兹球面中的Ⅲ型洛伦兹等参超曲面的开题报告

洛伦兹球面中的Ⅲ型洛伦兹等参超曲面的开题报告
1. 研究目的:
本文的主要研究目的是探究用洛伦兹度量所定义的球面上的Ⅲ型洛伦兹等参超曲面的特性和性质,揭示其在几何学中的应用和作用,为进一步的研究提供参考和基础。
2. 研究方法:
本文主要采用数学分析和几何计算的方法来研究Ⅲ型洛伦兹等参超曲面在洛伦兹球面中的性质和特性。
具体包括对该等参超曲面的定义、参数化表示、切空间与切向量、曲率性质等的探讨和分析。
3. 研究内容:
(1)Ⅲ型洛伦兹等参超曲面的定义及参数化表示:讨论Ⅲ型洛伦兹等参超曲面
的定义和参数化表示方法,包括其在洛伦兹球面中的表示和坐标系的选取。
(2)切空间与切向量:探讨该等参超曲面在众多切向量中的切空间和切向量,
并对其正交性和变换特性进行讨论和分析。
(3)曲率特性:对该等参超曲面的曲率性质进行了详细的研究和讨论,包括各
种曲率的定义、特性及其与变量的关系等。
(4)应用展望:对Ⅲ型洛伦兹等参超曲面在几何学中的应用前景进行展望和分析,包括其在流形理论、微分几何、物理学等领域的应用价值和意义。
4. 研究意义:
Ⅲ型洛伦兹等参超曲面是几何学中的重要分支之一,其具有很高的应用价值和理论意义。
本文的研究旨在揭示这一等参超曲面的特性和性质,为它在理论和实践中的
应用提供理论基础和参考依据,对推动几何学的发展以及应用研究的深入开展都具有
重要意义。
三维磁敏感成像联合三维动脉自旋标记技术对急性期轻度创伤性脑损伤患者的应用价值

三维磁敏感成像联合三维动脉自旋标记技术对急性期轻度创伤性脑损伤患者的应用价值李晖;张惠英【期刊名称】《河北联合大学学报(医学版)》【年(卷),期】2018(020)006【摘要】①目的探讨三维磁敏感成像(3D SWAN)与三维动脉自旋标记技术(3D ASL)联合应用对急性期轻度创伤性脑损伤(mTBI)患者的应用价值.②方法选取符合入选标准及排除标准的54例急性期mTBI患者,于伤后72小时内进行MR常规序列、3D SWAN及3D ASL序列的一站式扫描.③结果对于出血性病变,MR常规序列检出23处,3D SWAN检出73处,二者比较差异具有统计学意义(P<0.05);对于非出血性病变,MR常规序列检出43处,3D ASL检出92处,包括局部低灌注区81处,局部高灌注区11处,差异具有统计学意义(P<0.05);3D SWAN与3D ASL的阳性患者检出率均明显高于MR常规序列,差异具有统计学意义(P<0.05).④结论 3D SWAN及3D ASL序列对评估急性期mTBI患者的出血性病变及非出血性病变有重要的应用价值,3D SWAN序列及3D ASL序列对水肿病变显示不足,需要MR常规序列的补充.应尽早联合应用三种序列,以全面评估急性期mTBI患者的脑损伤情况,从而为临床早期诊断mTBI及采取相应的治疗措施提供影像学依据.【总页数】8页(P459-465,470)【作者】李晖;张惠英【作者单位】华北理工大学河北唐山063000;华北理工大学附属医院河北唐山063000【正文语种】中文【中图分类】R651【相关文献】1.三维伪连续动脉自旋标记技术用于遗忘型轻度认知功能障碍患者随访 [J], 刘颖;曾祥柱;王筝;张海峰;王华丽;袁慧书2.三维磁敏感成像联合三维动脉自旋标记技术对急性期轻度创伤性脑损伤患者的应用价值 [J], 李晖;张惠英;;3.磁共振血管成像联合三维动脉自旋标记技术检查在缺血性脑血管疾病患者诊断中的应用 [J], 刘佩4.磁共振血管成像联合三维动脉自旋标记技术在短暂性脑缺血发作诊断中的应用价值 [J], 侯梦5.经阴道三维超声SonoAVCTM技术联合女性基础激素测定在大龄不孕患者卵巢储备功能评估中的应用价值 [J], 罗伟花;曾渝航;尤爱娟;林德嫦因版权原因,仅展示原文概要,查看原文内容请购买。
姜泰勒扭曲和轨道序诱导的二维铁磁性

姜泰勒扭曲和轨道序诱导的二维铁磁性
张俊廷;吴宗铄;沈小凡
【期刊名称】《物理学报》
【年(卷),期】2024(73)1
【摘要】随着体系维度的降低,材料内部的量子限制效应和电子关联作用会相应地增强,往往可以衍生一些新奇的物理特性.在钙钛矿材料中,姜泰勒扭曲和轨道序通常会引起丰富的电子关联行为.本文通过第一性原理计算、对称性分析和蒙特卡罗模拟等方法,对比研究了钙钛矿氟化物KCuF_(3)及其单层结构,揭示了钙钛矿二维化引起的晶格动力学、结构、电子及磁性质等方面的变化.结果表明,KCuF_(3)块体中出现的协作姜泰勒扭曲和面内交错轨道序可以维持到单层极限,导致单层为二维铁磁绝缘体.与块体相不同的是,在单层中姜泰勒扭曲模式作为原型相的软模出现,且单层的绝缘性不依赖于姜泰勒扭曲的出现,而是与电子关联效应的增强有关.本文为研究二维钙钛矿材料以及设计基于钙钛矿的二维铁磁体提供了指导和借鉴.
【总页数】11页(P285-295)
【作者】张俊廷;吴宗铄;沈小凡
【作者单位】中国矿业大学材料与物理学院;南京大学物理学院
【正文语种】中文
【中图分类】G63
【相关文献】
1.二价铜的配位几何在姜-泰勒扭曲效应下的一个结构证明(英文)
2.反重力电诱导自组装构造二维亚微米有序结构
3.被孤独扭曲的心灵--论彼得·泰勒的"老处女的故事"
4.5d过渡金属原子掺杂六方氮化铝单层的磁性及自旋轨道耦合效应:可能存在的二维长程磁有序
5.第VII族单核羰基配合物的稳定种态-第一部分:分子轨道、结构和姜一泰勒效应
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
W3 ALGEBRA AND LATTICE VERTEX OPERATOR ALGEBRAS
245
246
DONG/LAM/TANABE/YAMADA/YOKOYAMA
subalgebra M in VL , which is of the form L 1 ,0 ⊗ L 2 7 ,0 ⊕ L 10 1 1 , 2 2 ⊗L 7 3 , 10 2
and is invariant under τ . The representation theory of M was stuБайду номын сангаасied in [21] and [24]. We are interested in the subalgebra M τ of fixed points of τ in M . Its Virasoro element is ω = ω 1 + ω 2 . The central charge of ω is 1/2+7/10 = 6/5. We find an element J of weight 3 in M τ such that the component operators L(n) = ωn+1 and J (n) = Jn+2 satisfy the same commutation relations as in [3, (2.1), (2.2)] for W3 . Thus the vertex operator subalgebra W generated by ω and J is a W3 algebra with central charge 6/5. We construct 20 irreducible M τ -modules. 8 of them are inside irreducible untwisted M -modules, while 6 of them are inside irreducible τ -twisted M modules and the remaining 6 are inside irreducible τ 2 -twisted M -modules. There are exactly two inequivalent irreducible τ i -twisted M -modules MT (τ i ) and WT (τ i ), i = 1, 2. We investigate the irreducible τ i -twisted VL -modules constructed in [7] and obtain MT (τ i ) and WT (τ i ) inside them. We classify the irreducible modules for W by determining the Zhu algebra A(W ) (cf. [36]). The method used here is similar to that in [35], where the Zhu algebra of a W3 algebra with central charge −2 is studied. We can define a map of the polynomial algebra C[x, y ] with two variables x, y to A(W ) by x → [ω ] and y → [J ], which is a surjective algebra homomorphism. Thus it is sufficient to determine its kernel I . The key point is the existence of a singular vector v for the W3 algebra W of weight 12. A positive definite invariant Hermitian form on VL implies that v is in fact 0. Thus [v] = 0. Moreover, [J (−1)v] = [J (−2)v] = [J (−1)2 v] = 0. Hence the corresponding polynomials in C[x, y ] must be contained in the ideal I . It turns out that I is generated by those four polynomials and the classification of irreducible W -modules is established by Zhu’s theory ([36]). That is, there are exactly 20 inequivalent irreducible W -modules. The calculation of explicit form of the singular vector v and the calculation of the ideal I were done by a computer algebra system Risa/Asir. By the classification of irreducible W -modules and a positive definite invariant Hermitian form, we can show that M τ = W . The eigenvalues of the action of weight preserving operators L(0) = ω1 and J (0) = J2 on the top levels of those 20 irreducible M τ -modules coincide with the values n m n m of [14, (1.2), (5.6)] with p = 5. Hence our M τ and w ∆ n m n m is an algebra denoted by [Z3 ] in [14]. We prove that W is C2 -cofinite and rational by using the singular vector v of weight 12 and the irreducible modules for W . In the course of the proof we use a result about a general vertex operator algebra V. It says that if V
1. Introduction The vertex operator algebras associated with positive definite even lattices afford a large family of known examples of vertex operator algebras. An isometry of the lattice induces an automorphism of the lattice vertex operator algebra. The subalgebra of fixed points of an automorphism is the so-called orbifold vertex operator algebra. In this paper we deal with the √ √ case where the lattice L = 2A2 is 2 times an ordinary root lattice of type A2 and the isometry τ is an element of the Weyl group of order 3. We use this algebra to study the W3 algebra of central charge 6/5. In fact, by using both coset construction and orbifold theory we construct the W3 algebra of central charge 6/5 inside VL and classify its irreducible modules. We also prove that the W3 algebra is rational and compute the characters of the irreducible modules. √ The vertex operator algebra VL associated with L = 2A2 contains three mutually orthogonal conformal vectors ω 1 , ω 2 , ω 3 with central charge c = 1/2, 7/10, or 4/5 respectively [10]. The subalgebra Vir(ω i ) generated by ω i is the Virasoro vertex operator algebra L(c, 0), which is the irreducible unitary highest weight module for the Virasoro algebra with central charge c and highest weight 0. The structure of VL as a module for Vir(ω 1 ) ⊗ Vir(ω 2 ) ⊗ Vir(ω 3 ) was discussed in [23]. Among other things it was shown that VL contains a subalgebra of the form L(4/5, 0) ⊕ L(4/5, 3). Such a vertex operator algebra is called a 3-state Potts model. This subalgebra is contained in the subalgebra (VL )τ of fixed points of τ . There is another
