北京市各区2018届九年级上期末试卷分类汇编:图形变换
2018-2020年北京中考数学复习各地区模拟试题分类——图形的变化
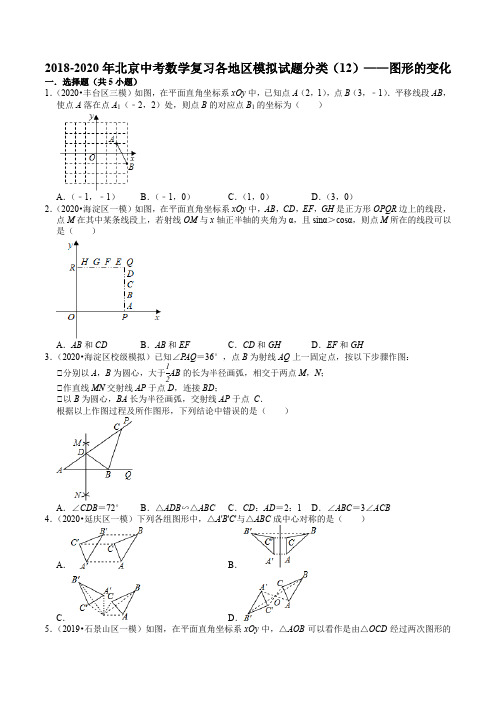
2018-2020年北京中考数学复习各地区模拟试题分类(12)——图形的变化一.选择题(共5小题)1.(2020•丰台区三模)如图,在平面直角坐标系xOy中,已知点A(2,1),点B(3,﹣1).平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为()A.(﹣1,﹣1)B.(﹣1,0)C.(1,0)D.(3,0)2.(2020•海淀区一模)如图,在平面直角坐标系xOy中,AB,CD,EF,GH是正方形OPQR边上的线段,点M在其中某条线段上,若射线OM与x轴正半轴的夹角为α,且sinα>cosα,则点M所在的线段可以是()A.AB和CD B.AB和EF C.CD和GH D.EF和GH3.(2020•海淀区校级模拟)已知∠P AQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于12AB的长为半径画弧,相交于两点M,N;①作直线MN交射线AP于点D,连接BD;①以B为圆心,BA长为半径画弧,交射线AP于点C.根据以上作图过程及所作图形,下列结论中错误的是()A.∠CDB=72°B.△ADB∽△ABC C.CD:AD=2:1D.∠ABC=3∠ACB 4.(2020•延庆区一模)下列各组图形中,△A'B'C'与△ABC成中心对称的是()A.B.C.D.5.(2019•石景山区一模)如图,在平面直角坐标系xOy中,△AOB可以看作是由△OCD经过两次图形的变化(平移、轴对称、旋转)得到的,这个变化过程不可能是( )A .先平移,再轴对称B .先轴对称,再旋转C .先旋转,再平移D .先轴对称,再平移二.填空题(共13小题)6.(2020•海淀区校级模拟)如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点,AE ⊥EF .有下列结论:①∠BAE =30°;①射线FE 是∠AFC 的角平分线;①AE 2=AD •AF ;①AF =AB +CF .其中正确结论为是 .(填写所有正确结论的序号)7.(2020•海淀区校级模拟)如图,已知∠MON =120°,点A ,B 分别在OM ,ON 上,且OA =OB =a ,将射线OM 绕点O 逆时针旋转得到OM ′,旋转角为α(0°<α<120°且a ≠60°),作点A 关于直线OM ′的对称点C ,画直线BC 交于OM ′与点D ,连接AC ,AD .有下列结论:①∠BDO +∠ACD =90°;①∠ACB 的大小不会随着α的变化而变化;①当α=30°时,四边形OADC 为菱形;①△ACD 面积的最大值为√3a 2.其中正确的是 .(把你认为正确结论的序号都填上)8.(2020•丰台区模拟)如图,在正方形ABCD 中,对角线AC ,BD 相交于点O ,E 是OB 的中点,连接AE并延长交BC 于点F .若△BEF 的面积为1,则△AED 的面积为 .9.(2020•丰台区模拟)如图,在①ABCD 中,点E 在DA 的延长线上,且AE =13AD ,连接CE 交BD 于点F ,则EE EE 的值是 .10.(2020•昌平区模拟)为了测量校园水平地面上一棵不可攀爬的树的高度,小文同学做了如下的探索:根据物理学中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在合适的位置,刚好能在镜子里看到树梢顶点,此时小文与平面镜的水平距离为2.0米,树的底部与平面镜的水平距离为8.0米,若小文的眼睛与地面的距离为1.6米,则树的高度约为 米(注:反射角等于入射角).11.(2020•西城区校级模拟)太阳能光伏发电是一种清洁、安全、便利、高效的新兴能源,因而逐渐被推广使用.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB 的长度相同,支撑角钢EF 长为290√33cm ,AB 的倾斜角为30°,BE =CA =50cm ,支撑角钢CD ,EF 与底座地基台面接触点分别为D ,F ,CD 垂直于地面,FE ⊥AB 于点E .两个底座地基高度相同(即点D ,F 到地面的垂直距离相同),均为 30cm ,点A 到地面的垂直距离为50cm ,则支撑角钢CD 的长度是 cm ,AB 的长度是 cm .12.(2019•海淀区二模)如图,在△ABC 中,P ,Q 分别为AB ,AC 的中点.若S △APQ =1,则S四边形PBCQ= .13.(2019•丰台区一模)如图,将△ABC 沿BC 所在的直线平移得到△DEF ,如果AB =7,GC =2,DF =5,那么GE = .14.(2019•怀柔区一模)如图,在△ABC 中,DE ∥AB ,DE 分别与AC ,BC 交于D ,E 两点.若△ABC 与△DEC 的周长比为3:2,AC =6,则DC = .15.(2019•海淀区一模)如图,在矩形ABCD中,E是边CD的延长线上一点,连接BE交边AD于点F,若AB=4,BC=6,DE=2,则AF的长为.16.(2019•海淀区校级三模)如图,在平面直角坐标系xOy中,点A的坐标为A(3,0),等腰直角三角形ABC的边AB在x轴的正半轴上,∠ABC=90°,点B在点A的右侧,点C在第一象限,将△ABC绕点A逆时针旋转75°,如果点C的对应点E恰好落在y轴的正半轴上,那么边AB的长为.17.(2019•怀柔区模拟)如图所示,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE =1:3,则S△BDE:S四边形DECA的值为.18.(2019•海淀区校级模拟)如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(﹣2,3),嘴唇C的坐标为(﹣1,1),若把此“QQ”笑脸向右平移3个单位长度后,则与右眼B对应的点的坐标是.三.解答题(共24小题)19.(2020•怀柔区模拟)在等腰直角三角形ABC中,∠ACB=90°,P是BC上的一动点(不与B,C重合),射线AP绕点A顺时针旋转45°,得到射线AQ,过点C作CE垂直AB,交AB与点D,交射线AQ于点E,连接PE.(1)依题意补全图形;(2)求∠APE的度数;(3)用等式表示线段PE,DE,AC三条线段之间的数量关系,并证明.20.(2020•石景山区二模)在△ABC中,AB=AC,D是边BC上的一点(不与点B重合),边BC上点E在点D的右边且∠DAE=12∠BAC,点D关于直线AE的对称点为F,连接CF.(1)如图1,①依题意补全图1;①求证:CF=BD.(2)如图2,∠BAC=90°,用等式表示线段DE,CE,CF之间的数量关系,并证明.21.(2020•门头沟区一模)在△ABC中,∠ACB=90°,∠CAB=30°,点D在AB上,连接CD,并将CD 绕点D逆时针旋转60°得到DE,连接AE.(1)如图1,当点D为AB中点时,直接写出DE与AE长度之间的数量关系;(2)如图2,当点D在线段AB上时,①根据题意补全图2;①猜想DE与AE长度之间的数量关系,并证明.22.(2020•东城区校级模拟)如图1,在△ABC中,∠ACB=90°,AC=BC,点D是射线CB上一点,连接AD,过D作DE⊥AD交射线AB于点E,以A为旋转中心,将线段AD绕点A逆时针旋转90°得线段AF,过点F作FG⊥AF交AC的延长线于点G,连接EG.(1)如图1,点D在CB上.①依题意补全图1;①猜想DE、EG、FG之间的数量关系并证明;(2)如图2,点D在CB的延长线上.请直接写出DE、EG、FG之间的数量关系为.23.(2020•东城区模拟)如图,△ABC中,AB=AC,∠BAC<60°,将线段AB绕点A逆时针旋转60°得到点D,点E与点D关于直线BC对称,连接CD,CE,DE.(1)依题意补全图形;(2)判断△CDE的形状,并证明;(3)请问在直线CE上是否存在点P,使得P A﹣PB=CD成立?若存在,请用文字描述出点P的准确位置,并画图证明;若不存在,请说明理由.24.(2020•朝阳区校级模拟)已知等边△ABC,点D为BC上一点,连接AD.(1)若点E是AC上一点,且CE=BD,连接BE,BE与AD的交点为点P,在图(1)中根据题意补全图形,直接写出∠APE的大小;(2)将AD绕点A逆时针旋转120°,得到AF,连接BF交AC于点Q,在图(2)中根据题意补全图形,用等式表示线段AQ和CD的数量关系,并证明.25.(2019•海淀区校级模拟)在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段P A绕点P顺时针旋转2α得到线段PQ.(1)若α=60°且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,请补全图形,并写出∠CDB的度数;(2)在图2中,点P不与点B,M重合,线段CQ的延长线于射线BM交于点D,猜想∠CDB的大小(用含α的代数式表示),并加以证明;(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=QD,请直接写出α的范围.26.(2019•东城区二模)如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.(1)求证:BD=CE;(2)延长ED交BC于点F,求证:F为BC的中点;(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.27.(2019•顺义区二模)已知:在△ABC中,∠BAC=90°,AB=AC.(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.①求证:∠AED=∠CED;①用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD 的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.28.(2018•昌平区二模)如图,在△ABC中,AB=AC>BC,BD是AC边上的高,点C关于直线BD的对称点为点E,连接BE.(1)①依题意补全图形;①若∠BAC=α,求∠DBE的大小(用含α的式子表示);(2)若DE=2AE,点F是BE中点,连接AF,BD=4,求AF的长.29.(2018•门头沟区一模)如图,在△ABC中,AB=AC,∠A=2α,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.(1)∠EDB=°(用含α的式子表示)(2)作射线DM与边AB交于点M,射线DM绕点D顺时针旋转180°﹣2α,与AC边交于点N.①根据条件补全图形;①写出DM与DN的数量关系并证明;①用等式表示线段BM、CN与BC之间的数量关系,(用含α的锐角三角函数表示)并写出解题思路.30.(2018•丰台区一模)如图,Rt△ABC中,∠ACB=90°,CA=CB,过点C在△ABC外作射线CE,且∠BCE=α,点B关于CE的对称点为点D,连接AD,BD,CD,其中AD,BD分别交射线CE于点M,N.(1)依题意补全图形;(2)当α=30°时,直接写出∠CMA的度数;(3)当0°<α<45°时,用等式表示线段AM,CN之间的数量关系,并证明.31.(2018•房山区一模)如图,已知Rt△ABC中,∠C=90°,∠BAC=30°,点D为边BC上的点,连接AD,∠BAD=α,点D关于AB的对称点为E,点E关于AC的对称点为G,线段EG交AB于点F,连接AE,DE,DG,AG.(1)依题意补全图形;(2)求∠AGE的度数(用含α的式子表示);(3)用等式表示线段EG与EF,AF之间的数量关系,并说明理由.32.(2018•朝阳区模拟)在平面直角坐标系xOy中,△ABC的顶点分别为A(1,1),B(2,4),C(4,2).(1)画出△ABC关于原点O对称的△A1B1C1;(2)点C关于x轴的对称点C2的坐标为;(3)点C2向左平移m个单位后,落在△A1B1C1内部,写出一个满足条件的m的值:.33.(2020•丰台区三模)如图,在△ABC中,∠BAC=30°,AB=AC,将线段AC绕点A逆时针旋转α°(0<α<180),得到线段AD,连接BD,交AC于点P.(1)当α=90°时,①依题意补全图形;①求证:PD=2PB;(2)写出一个α的值,使得PD=√3PB成立,并证明.34.(2020•顺义区二模)已知:如图,AB是①O的直径,△ABC内接于①O.点D在①O上,AD平分∠CAB 交BC于点E,DF是①O的切线,交AC的延长线于点F.(1)求证:DF⊥AF;(2)若①O的半径是5,AD=8,求DF的长.35.(2020•平谷区一模)△ABC中,AB=BC,∠ABC=90°,将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.作射线BD,点C关于射线BD的对称点为点E.连接AE,CE.(1)依题意补全图形;(2)若α=20°,直接写出∠AEC的度数;(3)写出一个α的值,使AE=√2时,线段CE的长为√3−1,并证明.36.(2020•海淀区校级模拟)如图,在△ABP中,∠ABP=60°,90°<∠APB<120°,过点A的直线l 垂直于线段BP所在的直线.设点B,P关于直线l的对称点分别为点B′,P′(1)在图中画出△ABP关于直线l对称的三角形△AB′P′.(2)若∠BAP=α,求∠AP′B的度数.(用α表示)(3)若点P′关于直线AB′的对称点为M,连接AM,PM.请写出P A、PM之间的数量关系和位置关系,并证明你的结论.37.(2020•昌平区模拟)如图,在梯形ABCD中,AB∥DC,AD=BC=5,AB=10,CD=4,连接并延长BD到E,使DE=BD,作EF⊥AB,交BA的延长线于点F.(1)求tan∠ABD的值;(2)求AF的长.38.(2019•门头沟区二模)如图,在等边三角形ABC中,点D为BC边上的一点,点D关于直线AB的对称点为点E,连接AD、DE,在AD上取点F,使得∠EFD=60°,射线EF与AC交于点G.(1)设∠BAD=α,求∠AGE的度数(用含α的代数式表示);(2)用等式表示线段CG与BD之间的数量关系,并证明.39.(2019•平谷区二模)在等边三角形ABC外侧作射线AP,∠BAP=α,点B关于射线AP的对称点为点D,连接CD交AP于点E.(1)依据题意补全图形;(2)当α=20°时,∠ADC=°;∠AEC=°;(3)连接BE,求证:∠AEC=∠BEC;(4)当0°<α<60°时,用等式表示线段AE,CD,DE之间的数量关系,并证明.40.(2019•石景山区二模)如图在△ABC中,∠ACB=90°,AC=BC,E为外角∠BCD平分线上一动点(不与点C重合),点E关于直线BC的对称点为F,连接BE,连接AF并延长交直线BE于点G.(1)求证:AF=BE;(2)用等式表示线段FG,EG与CE的数量关系,并证明.41.(2019•朝阳区一模)如图,在Rt△ABC中,∠A=90°,AB=AC,将线段BC绕点B逆时针旋转α°(0<α<180),得到线段BD,且AD∥BC.(1)依题意补全图形;(2)求满足条件的α的值;(3)若AB=2,求AD的长.42.(2019•通州区一模)如图,在等边△ABC中,点D是线段BC上一点.作射线AD,点B关于射线AD 的对称点为E.连接CE并延长,交射线AD于点F.(1)设∠BAF=α,用α表示∠BCF的度数;(2)用等式表示线段AF、CF、EF之间的数量关系,并证明.2018-2020年北京中考数学复习各地区模拟试题分类(12)——图形的变化参考答案与试题解析一.选择题(共5小题)1.【解答】解:如图,B1(﹣1,0),故选:B.2.【解答】解:如图,当点M在线段AB上时,连接OM.∵sinα=EEEE,cosα=EEEE,OP>PM,∴xinα<cosα,同法可证,点M在CD上时,sinα<cosα,如图,当点M在EF上时,作MJ⊥OP于J.∵sinα=EEEE,cosα=EEEE,OJ<MJ,∴sinα>cosα,同法可证,点M在GH上时,sinα>cosα,故选:D.3.【解答】解:由作图可知,MN垂直平分AB,AB=BC,∵MN垂直平分AB,∴DA=DB,∴∠A=∠DBA,∵∠P AQ=36°,∴∠CDB=∠A+∠DBA=72°,故A正确;∵AB=BC,∴∠A=∠ACB,又∵∠A=∠A,∴△ADB ∽△ABC ,故B 正确;∵∠A =∠ACB =36°,∴∠ABC =180°﹣∠A ﹣∠ACB =108°,∴∠ABC =3∠ACB ,故D 正确;∵∠ABD =36°,∠ABC =108°,∴∠CBD =∠ABC ﹣∠ABD =72°,∴∠CBD =∠CDB =72°,∴CD =BC ,∵∠A =∠ACB =36°,∴AB =BC ,∴CD =AB ,∵AD +DB >AB ,AD =DB ,∴2AD >AB ,∴2AD >CD ,故C 错误.故选:C .4.【解答】解:A 、是平移变换图形,故本选项错误;B 、是轴对称图形,故本选项错误;C 、是旋转变换图形,故本选项错误;D 、是中心对称图形,故本选项正确.故选:D .5.【解答】解:将△ABO 沿y 轴向左翻折,再沿y 轴向下平移3个单位长度得到△OCD ,或先沿y 轴向下平移3个单位长度,再沿y 轴向左翻折得到△OCD ,或先将△ABO 沿x 轴向下翻折,再旋转得出△OCD 故选:C .二.填空题(共13小题)6.【解答】解:∵在正方形ABCD 中,E 是BC 的中点,∴AB =BC ,BE =12AB ,∴tan A =EE EE =12,∵tan30°=√33,∴∠BAE ≠30°,故①错误;∵∠B =∠C =90°,AE ⊥EF ,∴∠BAE +∠BEA =90°,∠BEA +∠CEF =90°,∴∠BAE =∠CEF ,∴△ABE ∽△ECF ,∵AB =2BE =2CE ,∴EC =2CF ,设CF =a ,则EC =BE =2a ,AB =4a ,∴AE =2√5a ,EF =√5a ,tan ∠CFE =2,∴tan ∠AFE =EE EE =2, ∴∠AFE =∠CFE ,即射线FE 是∠AFC 的角平分线,故①正确;∵四边形ABCD 是正方形,∴∠B =∠C =90°,AB =BC =CD ,∵AE ⊥EF ,∴∠AEF =∠B =90°,∴∠BAE +∠AEB =90°,∠AEB +FEC =90°,∴∠BAE =∠CEF ,∴△BAE ∽△CEF ,∴EE EE =EE EE ,∵BE =CE ,∴EE EE=EE EE , ∵∠B =∠AEF =90°, ∴△ABE ∽△AEF , ∴EE EE =EE EE ,∴AE 2=AD •AF ;故①正确;作EG ⊥AF 于点G ,∵FE 平分∠AFC ,∠C =90°,∴EG =EC ,∴EG =EB ,∵∠B =∠AGE =90°,在Rt △ABE 和Rt △AGE 中{EE =EE EE =EE , ∴Rt △ABE ≌Rt △AGE (HL ),∴AB =AG ,又∵CF =GF ,AF =AG +GF ,∴AF =AB +CF ,故①正确,由上可得,①①①正确,故答案为:①①①.7.【解答】解:①∵A 、C 关于直线OM '对称,∴OM '是AC 的垂直平分线,∴CD =AD ,∠BDO +∠ACD =90°.故①正确;①连接OC ,由①知:OM '是AC 的垂直平分线,∴OC =OA ,∴OA =OB =OC ,以O 为圆心,以OA 为半径作①O ,交AO 的延长线于E ,连接BE ,则A 、B 、C 都在①O 上, ∵∠MON =120°,∴∠BOE =60°,∵OB =OE ,∴△OBE 是等边三角形,∴∠E =60°,∵A 、C 、B 、E 四点共圆,∴∠ACD =∠E =60°,∴∠ACB =120°是定值,故①正确;①当α=30°时,即∠AOD =∠COD =30°,∴∠AOC =60°,∴△AOC 是等边三角形,∴∠OAC =60°,OC =OA =AC ,由①得:CD =AD ,∴∠CAD =∠ACD =∠CDA =60°,∴△ACD 是等边三角形,∴AC =AD =CD ,∴OC =OA =AD =CD ,∴四边形OADC 为菱形;故①正确;①∵CD =AD ,∠ACD =60°,∴△ACD 是等边三角形,当AC 最大时,△ACD 的面积最大,∵AC 是①O 的弦,当AC 为直径时最大,此时AC =2a ,S △ACD =√34×(2a )2=√3a 2;故①正确,所以本题结论正确的有:①①①①故答案为:①①①①.8.【解答】解:∵四边形ABCD 是正方形,∴OB =OD ,AD ∥BC ,∴△BEF ∽△DEA ,∴EE EE=EE EE , ∵E 是OB 的中点, ∴EE EE =13, ∴EE EE =13, ∴E △EEE E △EEE =EE EE =13, ∵△BEF 的面积为1,∴△AEB 的面积为3,∵EE EE =13, ∴E △EEEE △EEE =13, ∴△AED 的面积为9,故答案为:9.9.【解答】解:∵四边形ABCD 是平行四边形,∴AD ∥BC .AD =BC ,设AD =3a ,则AE =a ,∵DE ∥BC ,∴△EDF ∽△CBF ,∴EE EE =EE EE =4E 3E =43 故答案为43.10.【解答】解:根据题意得:△CED ∽△AEB ,∴EE EE =EE EE ,∵DE =2.0米,BE =8.0米,CD =1.6米, ∴AB =EE ⋅EE EE =1.6×82=6.4(米), 则树的高度约为6.4米,故答案为:6.411.【解答】解:过A 作AG ⊥CD 于G ,则∠CAG =30°,在Rt △ACG 中,CG =AC sin30°=50×12=25,∵GD =50﹣30=20,∴CD =CG +GD =25+20=45,即支撑角钢CD 的长度是45cm .连接FD 并延长与BA 的延长线交于H ,则∠H =30°,在Rt △CDH 中,CH =2CD =90,∴AH =CH ﹣AC =90﹣50=40,∵在Rt △EFH 中,EH =EE EEE30°=290√33√33=290, ∴AE =EH ﹣AH =290﹣40=250,∴AB =AE +BE =250+50=300,即AB 的长度是300cm .故答案为45,300.12.【解答】解:∵P ,Q 分别为AB ,AC 的中点,∴PQ ∥BC ,PQ =12BC , ∴△APQ ∽△ABC ,∴E △EEEE △EEE =(12)2=14, ∵S △APQ =1,∴S △ABC =4,∴S 四边形PBCQ =S △ABC ﹣S △APQ =3,故答案为3.13.【解答】解:∵△DEF 由△ABC 平移而成,∴AB =DE =7,BE =CF ,AC ∥DF ,∴△EGC ∽△EDF .∴EEEE =EEEE .∵AB =7,GC =2,DF =5,∴EE 7=25. ∴GE =145.故答案是:145.14.【解答】解:∵ED ∥AB ,∴△CDE ∽△CAB ,∴EE EE =△EEE 的周长△EEE 的周长=23, ∵AC =6,∴CD =4,故答案为4.15.【解答】解:∵四边形ABCD 是矩形,∴BC =AD =6,AB ∥CE ,设AF =x ,则DF =6﹣x ,∵AB ∥DE ,∴△ABF ∽△DEF ,∴EE EE =EE EE ,∴42=E 6−E , ∴x =4,∴AF =4.故答案为416.【解答】解:∵A (3,0),∴OA =3,∵∠BAC =45°,∠CAE =75°,∴∠EAO =180°﹣75°﹣45°=60°,∵∠AOB =90°,∴∠ABO =30°,∴AB =2OA =6,∴AC =AE =6,∵AB =BC ,∴AB =6•cos45°=3√2.故答案为3√2.17.【解答】解:∵S △BDE :S △CDE =1:3,∴BE :EC =1:3,∵DE ∥AC ,∴△BED ∽△BCA ,∴S △BDE :S △BCA =(EE EE )2=1:16,∴S △BDE :S 四边形DECA =1:15,故答案为:1:15.18.【解答】解:如图,根据左眼A 的坐标是(﹣2,3),建立直角坐标系,∵右眼B 的坐标为(0,3),∴向右平移3个单位后,右眼的坐标为(3,3).故答案为:(3,3)三.解答题(共24小题)19.【解答】解:(1)补全图形,如图,(2)∵△ABC 是等腰直角三角形,∴∠BAC =45°,∵∠EAP =45°,∴∠EAD =∠CAP ,又∵∠EDA =∠ACP =90°,∴△ADE ∽△ACP ,∴EE EE =EE EE ,由旋转知,∠P AE =∠CAD =45°,∴△APE ∽△ACD ,∴∠APE =∠ACD ,∵AC =BC ,∠ACB =90°,∴∠CAD =45°,∵CE ⊥AB ,∴∠ADC =90°,∴∠ACD =45°,∴∠EP A =45°;(3)2PE 2=2DE 2+AC 2.证明:由(2)可知,∠P AE =∠EP A =45°,∴∠AEP =90°,AE =PE ,∴AP =√2PE ,∴△AEP 是等腰直角三角形,在Rt △APC 中,根据勾股定理得,AP 2=PC 2+AC 2 由(2)知,∠ADC =90°,∠BAC =45°,∴AC =√2AD ,由(2)知,△ADE ∽△ACP ,∴EE EE =EE EE =√2,∴EE =√2EE ,∴(√2EE )2=(√2EE )2+EE 2,即2PE 2=2DE 2+AC 2.20.【解答】解:(1)①依题意补全图形,如图1;①证明:连接AF ,如图1,∵∠3=12EEEE ,∴∠3=∠1+∠2.∵点F与点D关于直线AE对称,∴AF=AD,∠F AE=∠3=∠1+∠2.∴∠4=∠F AE﹣∠2=(∠1+∠2)﹣∠2=∠1.又∵AC=AB,∴△ACF≌△ABD(SAS),∴CF=BD;(2)线段DE,CE,CF之间的数量关系是DE2=CE2+CF2.证明:连接F A,FE,如图2,∵AB=AC,∠BAC=90°,∴∠1=∠2=45°,由(1)①,可得FE=DE,∠3=∠2=45°,∴∠FCE=90°,在Rt△FCE中,由勾股定理,得FE2=CE2+CF2,∴DE2=CE2+CF2.21.【解答】解:(1)结论:DE=AE.理由:如图1中,∵∠ACB=90°,∠BAC=30°,∴AB=2BC,∠B=60°,∵AD=DB,∴CD=AD=DB,∴△CDB是等边三角形,∴∠CDB=60°,∵DC=DE,∠CDE=60°,∴∠ADE=180°﹣∠ED﹣∠CDB=60°,∵DA=DC,DC=DE,∴AD=DE,∴△ADE是等边三角形,∴DE=AE.(2)①图形如图2所示:①如图2﹣1中,结论:DE=AE.理由:取AB的中点F,连接CE,CF,EF.∵∠ACB=90°,AF=BF,∴CF=AF=BF,∵∠B=60°,∴△BCF是等边三角形,∵DC=DE,∠CDE=60°,∴△ECD是等边三角形,∴∠1+∠2=∠2+∠3=60°,CE=CD,CF=CB,∴∠1=∠3,∴△ECF≌△DCB(SAS),∴∠5=∠B=60°,∵∠6=60°,∴∠4=∠5=60°,∵EF=EF,F A=FC,∴△EF A≌△EFC(SAS),∴AE=EC,∵EC=ED,∴AE=ED.22.【解答】解:(1)①补全图形如图1所示,①FG=EG+DE,理由:过点A作AH⊥AB交FG于H,∴∠BAH=90°,由旋转知,AD=AF,∠DAF=90°=∠BAH,∴∠DAE=∠F AH,∵DE⊥AD,FG⊥AF,∴∠ADE=∠AFH=90°,∴△ADE≌△AFH(ASA),∴DE=FH,AE=AH,∵在△ABC中,∠ACB=90°,AC=BC,∴∠CAB=45°,∵∠BAH=90°,∴∠HAG=45°=∠CAB,∵AG=AG,∴△AGE≌△AGH(SAS),∴EG=HG,∴FG=HG+FH=EG+DE;(2)如图2,过点A作AH⊥AB交GF的延长线于H,同(1)的方法得,△ADE≌△AFH(ASA),∴DE=FH,AE=AH,同(1)的方法得,△AGE≌△AGH(SAS),∴EG=HG,∴EG=FG+FH=FG+DE,故答案为:EG=FG+DE.23.【解答】解:(1)补全图形如图1.(2)△CDE为等边三角形,证明如下:延长BC与DE交于F,∵AB=AC,∴∠ABC=∠ACB,①∵线段AB绕点A逆时针旋转60°得到点D,∴AD=AB=AC,∠BAD=60°,∴∠ACD=∠ADC,①∵四边形ABCD中,∠BAD+∠ABC+∠BCD+∠CDA=360°.∴∠ABC+∠ACB+∠ACD+∠ADC=300°,①∴由①①①,得∠ACB+∠ACD=150°,即∠BCD=150°,∴∠DCF=180°﹣∠BCD=30°,∵点E与点D关于直线BC对称,∴∠ECF=∠DCF=30°,DC=CE,∴∠DCE=60°.∴△DCE是等边三角形;(3)存在,作AG⊥BC于G,直线EC与AG的交点即为点P,证明:延长AG与DC交于点Q,连接QB,BD,由(2)可知,∠PCD=180°﹣∠DCE=120°,∠PCQ=∠DCE=60°,∠PCG=∠FCE=30°,∴∠CPG=90°﹣∠PCG=60°,∴∠PQC=∠CPQ=∠PCQ=60°,∴△PCQ为等边三角形,∴PC=CQ,∠APC=120°﹣∠PCD,①∵AG⊥BC,AC=AB,∴AG垂直平分BC,∴PB=PC=QB=QC,∴四边形PBQC 是菱形,∴PB =QC ,∠PBQ =∠PCQ =60°,①∵QB =QC ,∴∠QBC =∠QCB ,∴∠ABQ =∠ACQ ,∵AB =AD ,∠BAD =60°,∴△ABD 为等边三角形,∴∠ABD =60°=∠PCQ ,∴∠ABQ ﹣∠ABD =∠ACQ ﹣∠PCQ ,∴∠DBQ =∠ACP ,①∴由①①①得△ACP ≌△DBQ (AAS ),∴AP =DQ .∵CQ =PB ,∴AP =DQ =DC +CQ =DC +PB .即P A ﹣PB =CD 成立.24.【解答】(1)补全图形图1, 证明:在△ABD 和△BEC 中,{EE =EEEEEE =EE =60°EE =EE∴△ABD ≌△BEC (SAS )∴∠BAD =∠CBE .∵∠APE 是△ABP 的一个外角,∴∠APE =∠BAD +∠ABP =∠CBE +∠ABP =∠ABC =60°;(2)补全图形图2,EE =12EE ,证明:在△ABD 和△BEC 中,{EE =EEEEEE =EE =60°EE =EE∴△ABD ≌△BEC (SAS )∴∠BAD =∠CBE ,∵∠APE 是△ABP 的一个外角,∴∠APE =∠BAD +∠ABP =∠CBE +∠ABP =∠ABC =60°.∵AF 是由AD 绕点A 逆时针旋转120°得到,∴AF =AD ,∠DAF =120°.∵∠APE =60°,∴∠APE +∠DAF =180°.∴AF ∥BE ,∴∠1=∠F ,∵△ABD ≌△BEC ,∴AD =BE .∴AF =BE .在△AQF 和△EQB 中,{∠1=∠EEEEE =EEEE EE =EE△AQF ≌△EQB (AAS ),∴AQ =QE ,∴EE =12EE ,∵AE =AC ﹣CE ,CD =BC ﹣BD ,且AC =BC ,CE =BD .∴AE =CD ,∴EE=12 EE.25.【解答】解:(1)∵BA=BC,∠BAC=60°,M是AC的中点,∴BM⊥AC,AM=MC,∵将线段P A绕点P顺时针旋转2α得到线段PQ,∴AM=MQ,∠AMQ=120°,∴CM=MQ,∠CMQ=60°,∴△CMQ是等边三角形,∴∠ACQ=60°,∴∠CDB=30°;(2)如图2,连接PC,AD,∵AB=BC,M是AC的中点,∴BM⊥AC,即BD为AC的垂直平分线,∴AD=CD,AP=PC,PD=PD,在△APD与△CPD中,∵{EE=EE EE=EE EE=EE,∴△APD≌△CPD(SSS),∴∠ADB=∠CDB,∠P AD=∠PCD,又∵PQ=P A,∴PQ=PC,∠ADC=2∠1,∠4=∠PCQ=∠P AD,∴∠P AD+∠PQD=∠4+∠PQD=180°,∴∠APQ+∠ADC=360°﹣(∠P AD+∠PQD)=180°,∴∠ADC=180°﹣∠APQ=180°﹣2α,∴2∠CDB=180°﹣2α,∴∠CDB=90°﹣α;(3)∵∠CDB=90°﹣α,且PQ=QD,∴∠P AD=∠PCQ=∠PQC=2∠CDB=180°﹣2α,∵点P不与点B,M重合,∴∠BAD>∠P AD>∠MAD,∵点P在线段BM上运动,∠P AD最大为2α,∠P AD最小等于α,∴2α>180°﹣2α>α,∴45°<α<60°.26.【解答】证明:(1)∵将线段AD绕点A逆时针旋转60°得到线段AE,∴AD=AE,∠DAE=60°∴△ADE是等边三角形∵△ABC为等边三角形∴AB=AC,∠BAC=∠DAE=60°∴∠DAB=∠CAE,且AB=AC,AD=AE∴△ADB≌△AEC(SAS)∴BD=CE(2)如图,过点C作CG∥BP,交EF的延长线于点G,∵∠ADB=90°,∠ADE=60°∴∠BDG=30°∵CG∥BP∴∠G=∠BDG=30°,∵△ADB≌△AEC∴BD=CE,∠ADB=∠AEC=90°∴∠GEC=∠AEC﹣∠AED=30°∴∠G=∠GEC=30°∴GC=CE,∴CG=BD,且∠BDG=∠G,∠BFD=∠GFC∴△BFD≌△CFG(AAS)∴BF=FC∴点F是BC中点(3)如图,连接AF,∵△ABC是等边三角形,BF=FC∴AF⊥BC∴∠AFC=90°∴∠AFC=∠AEC=90°∴点A,点F,点C,点E四点在以AC为直径的圆上,∴EF最大为直径,即最大值为127.【解答】证明:(1)①∵将线段AC绕点A逆时针旋转60°得到AD,∴AC=AD,∠DAC=60°∴∠BAD=∠BAC+∠CAD=150°,且AB=AC=AD∴∠3=∠5=15°∵∠BAC=90°,AB=AC,AE平分∠BAC∴∠1=∠2=45°,∠ABC=∠ACB=45°又∵AE=AE,∴△ABE≌△ACE(SAS)∴∠3=∠4=15°∴∠6=∠7=30°∴∠DEC=∠6+∠7=60°∵∠AED=∠3+∠1=60°∴∠AED=∠CED①BD=2CE+AE理由如下:过点A作AH⊥BD于点H,∵∠EBC=∠ECB∴BE=CE,∵∠AED=60°,AH⊥BD∴AE=2EH∵AB=AD,AH⊥BD∴BD=2BH=2(BE+EH)=2BE+AE=2EC+AE(2)补全图形如图,2CE﹣AE=BD理由如下:如图2,以A为顶点,AE为一边作∠EAF=60°,AF交DB延长线于点F.∵∠BAC=90°,AB=AC,AE平分∠BAC∴∠BAE=∠CAE=45°,∠ABC=∠ACB=45°.∵将线段AC绕点A逆时针旋转60°得到AD,∴AC=AD,∠DAC=60°∴∠DAE=∠DAC﹣∠CAE=15°,AB=AD∴∠ABD=∠ADB,∠BAD=30°∴∠ABD=∠ADB=75°∴∠AED=∠ADB﹣∠DAE=60°∵∠EAF=60°又∵∠EAF=60°,∴∠F=60°∴△AEF是等边三角形.∴AE=AF=EF.∵AC=AD,∠CAE=∠DAF=45°,AE=AF,∴△CAE≌△DAF(SAS).∴CE=DF.∵AB=AC,∠BAE=∠CAE=45°,AE=AE,∴△BAE≌△CAE(SAS).∴BE=CE.∴BE=CE.∵DF+BE﹣EF=BD,∴2CE﹣AE=BD28.【解答】(1)解:①如图.①∵AB=AC,∠BAC=α,∴∠ABC=∠ACB=90°−12 E.∵点C关于直线BD的对称点为点E,BD是AC边上的高.∴BD⊥CE,CD=DE.∴BE=BC.∴∠BEC=∠ACB=90°−12 E.∴∠DBE=12 E;(2)作FG⊥AC于G,∵BD⊥CE,∴FG∥BD∵点F是BE中点,∴EG=DG.∴EE=12 EE,∵DE=2AE,∴AE=EG=DG,设AE=EG=DG=x,则CD=DE=2x,AC=5x,∴AB=AC=5x.∴BD=4x.∵BD=4,∴x=1,∴AG=2.∵EE=12EE=2,∴AF=2√2.29.【解答】解:(1)∵AB=AC,∴∠B=∠C=12(180°﹣∠A)=90°﹣α,而DE⊥AB,∴∠DEB=90°,∴∠EDB=90°﹣∠B=90°﹣(90°﹣α)=α;故答案为α;(2)①如图,连接AD,①DM =DN .理由如下:∵AB =AC ,BD =DC∴DA 平分∠BAC ,∵DE ⊥AB 于点E ,DF ⊥AC 于点F ,∴DE =DF ,∠MED =∠NFD =90°,∵∠A =2α∴∠EDF =180°﹣2α,∵∠MDN =180°﹣2α,∴∠MDE =∠NDF ,在△MDE 和△NDF 中{∠EEE =∠EEEEE =EE EEEE =EEEE,∴△MDE ≌△NDF ,∴DM =DN ;①数量关系:BM +CN =BC •sinα.证明思路为:先由△MDE ≌△NDF 可得EM =FN ,再证明△BDE ≌△CDF 得BE =CF ,所以BM +CN =BE +EM +CF ﹣FN =2BE ,接着在Rt △BDE 可得BE =BD sinα,从而有BM +CN =BC •sinα.30.【解答】解:(1)如图.(2)∵∠1=∠2=30°,∠4=90°,∴∠ACD =150°,∵CA =CB =CD ,∴∠3=∠CAD =15°,∴∠5=∠2+∠3=45°,即∠AMC =45°.(3)结论:AM =√2CN .理由:作AG ⊥EC 于G .∵点B 、D 关于CE 对称,∴CE 是BD 的垂直平分线,∴CB =CD ,∴∠1=∠2=α,∵CA =CB ,∴CA =CD ,∴∠3=∠CAD ,∵∠4=90°,∴∠3=12(180°﹣∠ACD )=12(180°﹣90°﹣α﹣α)=45°﹣α,∴∠5=∠2+∠3=α+45°﹣α=45°,∵∠4=90°,CE 是BD 的垂直平分线,∴∠1+∠7=90°,∠1+∠6=90°,∴∠1=∠6,∵AG ⊥EC ,∴∠G =∠8=90°,在△BCN 和△CAG 中,{∠8=∠EE7=E6EE =EE,∴△BCN ≌△CAG ,∴CN =BG ,∵Rt △AGM 中,∠G =90°,∠5=45°,∴AM =√2AG ,∴AM =√2CN .31.【解答】解:(1)如图如图所示:(2)由轴对称性可知,AB 为ED 的垂直平分线,AC 为EG 的垂直平分线. ∴AE =AG =AD ,∴∠AEG =∠AGE ,∠BAE =∠BAD =α,∴∠EAC =∠BAC +∠BAE =30°+α,∴∠EAG =2∠EAC =60°+2α,∴∠AGE =12(180°−EEEE )=60°﹣α,或:∠AGE =∠AEG =90°﹣∠EAC =90°﹣(∠BAC +∠EAB )=90°﹣(30°+α)=60°﹣α.(3)结论:EG =2EF +AF .法1:设AC 交EG 于点H .∵∠BAC=30°,∠AHF=90°,∴FH=12 EE,∴EH=EF+FH=EF+12 EE,又∵点E,G关于AC对称,∴EG=2EH,∴EG=2(EF+12EE)=2EF+AF,法2:在FG上截取NG=EF,连接AN.又∵AE=AG,∴∠AEG=∠AGE∴△AEF≌△AGN∴AF=AN∵∠EAF=α,∠AEG=60°﹣α∴∠AFN=60°,∴△AFN为等边三角形,∴AF=FN,∴EG=EF+FN+NG=2EF+AF.32.【解答】解:(1)如图所示:△A1B1C1,即为所求;(2)点C2的坐标为:(4,﹣2).故答案为:(4,﹣2);(3)答案不唯一.如:6.33.【解答】解:(1)当α=90°时,①如图即为补全的图形;①证明:∵∠BAC=30°,AB=AC,根据题意可知:AC=AD,∴AD =AB ,∴∠ABD =∠ADB ,∵∠CAD =90°,∴∠DAB =120°,∴∠ABD =∠D =∠BAC =30°,∴AP =BP ,在Rt △APD 中,∠ADB =30°,∴PD =2AP ,∴PD =2PB ;(2)当α=60(或120°)时,PD =√3PB 成立,情况1,如图所示:当α=60°时,过点D 作DF ⊥AC 于点F ,过点B 作BE ⊥AC 于点E ,∴DF ∥BE ,∴△DFP ∽△BEP ,∴EE EE =EE EE ,在Rt △ABE 中,∠BAC =30°,∴AC =AB =2BE ,在Rt △ADF 中,∠CAD =60°,∴AD =2√33DF , ∵AD =AC =AB ,∴2BE =2√33DE ,∴√3BE =DF ,∴PD =√3PB .情况2,如图所示:当α=120°时,过点D 作DF ⊥AC 于点F ,过点B 作BE ⊥AC 于点E ,∴DF ∥BE ,∴△DFP ∽△BEP ,∴EE EE =EE EE ,在Rt △ABE 中,∠BAC =30°,∴AC =AB =2BE ,在Rt △ADF 中,∠F AD =60°,∴AD =2√33DF , ∵AD =AC =AB ,∴2BE =2√33DE , ∴√3BE =DF ,∴PD =√3PB .34.【解答】(1)证明:连接OD .∵DF 是①O 的切线,∴OD ⊥DF ,∴∠ODF =90°.∵AD 平分∠CAB ,∴∠CAD =∠DAB .又∵OA =OD ,∴∠DAB =∠ADO .∴∠CAD =∠ADO .∴AF ∥OD .∴∠F +∠ODF =180°.∴∠F =180°﹣∠ODF =90°.∴DF ⊥AF .(2)解:连接DB .∵AB 是直径,①O 的半径是5,AD =8,∴∠ADB =90°,AB =10.∴BD =6.∵∠F =∠ADB =90°,∠F AD =∠DAB ,∴△F AD ∽△DAB .∴EE EE =EE EE .∴EE =EE ⋅EE EE =8×610=245. 35.【解答】解:(1)如图1,(2)∠AEC=135°,证明:连接AC、BE,如图2,由题意,BC=BE=BA,∴∠BCE=∠BEC,∠BAE=∠BEA,∵∠BCE+∠BEC+∠BAE+∠BEA+∠ABC=360°∵∠ABC=90°,∴2(∠BEC+∠BEA)=270°,∴∠BEC+∠BEA=135°,即∠AEC=135°,(3)α=30°,证明:过A作AG⊥CE于G,∵∠AEC=135°,∴∠AEG=45°,∵AE=√2,∴AG=GE=1,当α=30°时,则∠ABD=75°,∵∠ABC=90°,∴∠CBF=15°,∴∠EBC=30°,∵BC=BE,∴∠BCG=75°,∵∠BCA=45°,∴∠ACG=30°,∴EE=√3,∴EE=√3−1.36.【解答】解:(1)图形如图1所示:(2)解:如图1中,设直线l交PP′于C,∵P′,P关于直线l对称,过点A的直线l垂直于线段BP所在的直线,∴AC⊥PP′,CP=CP′,∴AP=AP′,∴∠APP′=∠AP′B,又∵在△ABP中,∠B=60°,∠BAP=α,∴∠AP′B=∠APP′=∠B+∠BAP=60°+α.(3)如图2中,结论:P A=PM,P A与PM所成锐角为60°.理由:设直线l交PP′于C,AB交MP′于D.∵B,B′关于直线l对称∴AC⊥BB′,CB=CB′,∴AB=AB′,∵∠B=60°,∴∠B=∠B′=60°,在△AP′B′中∠2=∠B′+∠3=60°+∠3,又∵∠2=60°+α,∴∠3=α,∵P′,M关于AB′对称,∴AB′⊥P′M,DP′=DM,∴AP′=AM,∴∠4=∠3=α,∵∠5=α,∴∠4=∠5,∴∠P AM=∠P AB′+∠4=∠P AB′+∠5=∠BAB′,∵AB =AB ′,∠B =60°,∴△BAB ′为等边三角形,∴∠BAB ′=∠P AM =60°,又∵由(2)得AP =AP ′,AP ′=AM ,∴AP =AM∴△P AM 为等边三角形∴P A =PM ,∠APM =60°,即P A =PM ,P A 与PM 所成角为60°.37.【解答】解:(1)作DM ⊥AB 于点M ,CN ⊥AB 于点N .(如图) ∵AB ∥DC ,DM ⊥AB ,CN ⊥AB ,∴∠DMN =∠CNM =∠MDC =90°,∴四边形MNCD 是矩形,∵CD =4,∴MN =CD =4,∵在梯形ABCD 中,AB ∥DC ,AD =BC =5,∴∠DAB =∠CBA ,DM =CN ,∴△ADM ≌△BCN ,又∵AB =10,∴AM =BN =12(AB ﹣MN )=12×(10﹣4)=3,∴MB =BN +MN =7.(2分)∵在Rt △AMD 中,∠AMD =90°,AD =5,AM =3,∴DM =√EE −EE =4,∴tan ∠ABD =EE EE =47.(3分)(2)∵EF ⊥AB ,∴∠F =90°,∵∠DMN =90°,∴∠F =∠DMN ,∴DM ∥EF ,∴△BDM ∽△BEF ,∵DE =BD ,∴EE EE =EE EE =12, ∴BF =2BM =14.(4分)∴AF =BF ﹣AB =14﹣10=4.(5分)38.【解答】解:(1)∵△ABC 是等边三角形,∴∠BAC =60°,∵∠BAD =α,∴∠F AG =60°﹣α,∵∠AFG =∠EFD =60°,∴∠AGE =180°﹣60°﹣(60°﹣α)=60°+α;(2)CG =2BD ,理由是:如图,连接BE ,过B 作BP ∥EG ,交AC 于P ,则∠BPC =∠EGP ,∵点D关于直线AB的对称点为点E,∴∠ABE=∠ABD=60°,∵∠C=60°,∴∠EBD+∠C=180°,∴EB∥GP,∴四边形EBPG是平行四边形,∴BE=PG,∵∠DFG+∠C=120°+60°=180°,∴∠FGC+∠FDC=180°,∴∠ADB=∠EGP=∠BPC,∵AB=BC,∠ABD=∠C=60°,∴△ABD≌△BCP(AAS),∴BD=PC=BE=PG,∴CG=2BD.39.【解答】解:(1)如图,补全图形:(2)连接AD,∵三角形ABC为等边三角形,∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°,由对称可知,AD=AB,∴AD=AC,∵∠BAP=α=20°,∴∠DAB=40°,∴∠DAC=40°+60°=100°,∴∠ADC=∠ACD=180°−100°2=40°,∠AEC=∠ADC+∠DAE=40°+20°=60°,故答案为40,60;(3)由对称可知,∠BAE=∠DAE=α,∵AD=AB=AC,∴∠ADC =180°−(60°+2E )2=60°−E , ∠AEC =60°,∵∠ACB =60°,∠ACD =∠ADC =60°﹣α,∴∠BCE =α,∵∠ABC =60°,∠ABE =∠ADC =60°﹣α,∴∠BEC =60°,∴∠AEC =∠BEC ;(4)当0°<α<60°时,CD =2DE +AE ,证明:在CD 上截取BG =BE ,∵∠BEC =60°,∴△BGE 是等边三角形,∴∠BGC =∠AED =120°,∵∠BCE =∠DAE =α,∴△BCG ≌△DAE (AAS ),∴AE =CG ,∵EG =BE =DE ,∴CD =2DE +CG ,即CD =2DE +AE .40.【解答】解:(1)如图,连接CF .∵,∠ACB =90°,CE 平分∠BCD ,∴∠BCE =45°,∵点E 、F 关于直线BC 对称,∴CE =CF ,∠FCB =∠BCE =45°,∴∠FCA =45°,在△FCA 与△ECB 中,{EE =EE EEEE =EEEE EE =EE∴△FCA ≌△ECB (SAS ),∴AF =BE ;(2)FG ,EG 与CE 的数量关系:GE 2+GF 2=2CE 2, 证明:∵△FCA ≌△ECB ,∴∠AFC =∠BEC ,∵∠AFC +∠CFG =180°,∴∠CFG +∠CEG =180°,∴∠ECF +∠EGF =180°,∵∠ECF =45°+45°=90°,∴∠EGF =90°,连接EF ,∴GE 2+GF 2=EF 2,∵CE =CF ,∴CE 2+CF 2=2CE 2=EF 2,∴GE 2+GF 2=2CE 2.41.【解答】解:(1)满足条件的点D和D′如图所示.(2)作AF⊥BC于F,DE⊥BC于E.则四边形AFED是矩形.∴AF=DE,∠DEB=90°,∵AB=AC,∠BAC=90°,AF⊥BC,∴BF=CF,∴AF=12 BC,∵BC=BD,AF=DE,∴DE=12 BD,∴∠DBE=30°,∴∠D′BC=120°+30°=150°,∴满足条件的α的值为30°或150°.(3)由题意AB=AC=2,∴BC=2√2,∴AF=BF=DE=√2,∴BE=√3DE=√6,∴AD=√6−√2,AD′=2√6−(√6−√2)=√6+√2.42.【解答】解:(1)连接AE.∵点B关于射线AD的对称点为E,∴AE=AB,∠BAF=∠EAF=α,∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ACB=60°,∴∠EAC=60°﹣2α,AE=AC,∴∠EEE=12[180°﹣(60°﹣2α)]=60°+α,∴∠BCF=∠ACE﹣∠ACB=60°+α﹣60°=α.(2)结论:AF =EF +CF .证明:如图,作∠FCG =60°交AD 于点G ,连接BF .∵∠BAF =∠BCF =α,∠ADB =∠CDF ,∴∠ABC =∠AFC =60°,∴△FCG 是等边三角形,∴GF =FC ,∵△ABC 是等边三角形,∴BC =AC ,∠ACB =60°,∴∠ACG =∠BCF =α,在△ACG 和△BCF 中,{EE =EE EEEE =EEEE EE =EE ,∴△ACG ≌△BCF .∴AG =BF ,∵点B 关于射线AD 的对称点为E ,∴BF =EF ,∴AF ﹣AG =GF ,∴AF =EF +CF .。
北京市海淀区九级(上)数学期末试卷

海淀区 2018-2018 学年九年级第一学期期末数学试卷(分数: 120 分时间: 120 分钟)一、选择题(此题共32 分,每题 4 分)下边各题均有四个选项,此中只有一个..是切合题意的.1.的值是()A.3B.- 3C.D.62.如图,将一张矩形纸片沿对角线剪开获得两个直角三角形纸片,将这两个直角三角形纸片经过图形变换组成以下四个图形,这四个图形中是中心对称图形的是 ( ).....矩形纸片A B C D3.如图,在△中,点、分别为边、上的点,且∥,若,,,则的长为()A.3B.6 C.9 D.124.二次函数的图象如下图,将其绕坐标原点O 旋转,则旋转后的抛物线的解读式为( )A .B .C. D .5.在平面直角坐标系中,以点为圆心, 4为半径的圆与y 轴所在直线的地点关系是 ()A .相离B.相切C.订交D.没法确立6.若对于的方程没有实数根,则的取值范围是A .B. C .D.7.如图,是⊙的切线,为切点,的延伸线交⊙于点,连结,若,,则等于 ( C. D.8.如图, Rt △ ABC 中, AC=BC =2 ,正方形CDEF 的极点 D 、F分别在 AC、 BC 边上,C、 D 两点不重合,设CD 的长度为 x,△ ABC 与正方形 CDEF 重叠部分的面积为y,则下列图象中能表示 y 与 x 之间的函数关系的是()yyy y22241111A B C D二、填空题(此题共16 分,每题 4 分)9.比较大小:(填“>”、“ =”或“ <”).10.如图,是⊙ O 上的点,若,则___________度.11.已知点 P( - 1,m)在二次函数的图象上,则m 的值为;平移此二次函数的图象,使点P 与坐标原点重合,则平移后的函数图象所对应的解读式为. 12.在△中,分别是边上的点,是边的等分点,,.如图1,若,,则∠+∠+∠++∠度;如图2,若,,则∠+∠+∠++∠(用含,的式子表示) .BP1P2P3F P n-1C E A图 2三、解答题(此题共30 分,每题 5 分)13.计算:.14.解方程:.15.如图,在△和△中,,为线段上一点,且.求证:.16.已知抛物线经过(0,- 1),(3,2)两点.求它的解读式及极点坐标.17.如图,在四边形ABCD 中,∥且,E是BC上一点,且.求证:.18.若对于的方程有实数根.(1)求的取值范围;(2)当获得最大整数值时,求此时方程的根.四、解答题(此题共20 分,每题 5 分)19.如图,用长为20M 的篱笆恰巧围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为M ,面积为平方 M .(注:的近似值取3)( 1)求出与的函数关系式,并写出自变量的取值范围;( 2)当半径为什么值时,扇形花坛的面积最大,并求面积的最大值.20.如图, AB 为O 的直径,射线AP 交O 于 C 点,∠ PCO 的均分线交O 于 D 点,过点 D作交AP于E点.( 1)求证: DE 为O 的切线;( 2)若,,求直径的长.21.已知二次函数.( 1)若点与在此二次函数的图象上,则(填“ >”、“ =”或“<”);( 2)如图,此二次函数的图象经过点,正方形ABCD 的极点C、 D 在 x 轴上,A、 B 恰幸亏二次函数的图象上,求图中暗影部分的面积之和.22.晓东在解一元二次方程时,发现有这样一种解法:如:解方程.解:原方程可变形,得.,,.直接开平方并整理,得.我们称晓东这类解法为“均匀数法”.( 1)下边是晓东用“均匀数法”解方程时写的解题过程.解:原方程可变形,得.,.直接开平方并整理,得¤.上述过程中的“”,“” ,“☆”,“¤”表示的数分别为_____,_____,_____, _____.(2)请用“均匀数法”解方程:.五、解答题(此题共22 分,第 23、 24 小题各 7 分,第 25 小题 8 分)23.已知抛物线().(1)求抛物线与轴的交点坐标;(2)若抛物线与轴的两个交点之间的距离为2,求的值;(3)若一次函数的图象与抛物线一直只有一个公共点,求一次函数的解读式.24.已知四边形ABCD 和四边形 CEFG 都是正方形,且AB>CE.( 1)如图 1,连结 BG、 DE.求证: BG=DE ;( 2)如图2,假如正方形ABCD 的边长为,将正方形CEFG 绕着点 C 旋转到某一地点时恰巧使得 C G//BD,BG=BD .①求的度数;②请直接写出正方形CEFG 的边长的值 .图 1图 225.如图 1,已知二次函数的图象与x轴交于A、B两点(B在A的左边),极点为C,点 D (1, m)在此二次函数图象的对称轴上,过点 D 作 y 轴的垂线,交对称轴右边的抛物线于 E 点.( 1)求此二次函数的解读式和点 C 的坐标;( 2)当点 D 的坐标为( 1, 1)时,连结BD、.求证:均分;( 3)点 G 在抛物线的对称轴上且位于第一象限,若以A、 C、 G 为极点的三角形与以G、D 、E 为极点的三角形相像,求点 E 的横坐标.图1备用图1备用图2海淀区九年级第一学期期末练习数学试卷答案及评分参照:1.,,, .2.,.3.,.32412345678A CB DC B B A1649<1013011 0,(2)12(2 )30,51354.5145.145 1552=3△△451650-1322341 - 25 175123△△.45 1851.12 212.34 ,52051951lM....2.3 2..5 205P 1:ECOD.21D,F 3.CDPCO A BO..1....DE O.2(2)O F..,.3,ODEF...4 Rt AOF...52151<.220 - 4m = - 43ABCDyOD=OC.Bn 2nn >0B..4 B24.=2 4=8522.5(1)42- 1- 7 .22..3.452223 24725823.71...x 1 00 .22..3...4 3..6.724.71...1..22BE.1BG=DE ...,.3,A D..4G,.BFC.E5.7 25.81 D 1 m1 C1-422D 1 1 DE y E 1 DE xyED EB O A xED E =C图 1A3,0B-1,0BD =BD=DE343ACG G D EGDEACGGA3,0C1-4,G1 1AG=AC=图 211/12AC=2 AG.GD=2 DE DE =2 GD .t >1.D G DE=t1-GD =() =.i.2GD =2 DE= 2(t- 1)..()5图 3 ii.3DE =2GDt - 1=2()..()6.DG DE=t - 1GD=1-()= -.i.4GD =2 DE= 2 t - 1 .图 4.()7=2 GDt- 1=2..()8E.图 512/12。
2017-2018北京初三(上)期末数学各区试题汇-图形变换

●知识模块3:图形变换1.(东城18期末6)△DEF 和△ABC 是位似图形,点O 是位似中心,点D ,E ,F 分别是OA ,OB ,OC 的中点,若△DEF 的面积是2,则△ABC 的面积是( ) A .2 B .4 C .6 D .8 2.(海淀18期末4)如图,将△ABC 绕点A 逆时针旋转100°,得到△ADE .若点D 在线段BC 的延长线上,则B ∠的大小为( )A .30°B .40°C .50°D .60°3(海淀18期末6)6.如图,在平面直角坐标系xOy 中,点A 从(3,4)出发,绕点O 顺时针旋转一周,则点A不.经过( ) A .点MB .点NC .点PD .点Q4.(昌平18期末6)如图,将ΔABC 绕点C 顺时针旋转,点B 的对应点为点E ,点A 的对应点为点D ,当点E 恰好落在边AC 上时,连接AD ,若∠ACB=30°,则∠DAC 的度数是( ) A .60° B .65°C .70°D .75°5.(门头沟18期末10)已知线段5AB cm =,将线段AB 以点A 为旋转中心,逆时针旋转90°得到线段'AB ,则点B 、点'B 的距离为__________. 6.(朝阳18期末10)如图,把△ABC 绕着点A 顺时针方向旋转,得到△A B 'C ',点C 恰好在B 'C '上,旋转角为α,则∠C '的度数为 (用含α的式子表示). 7.(昌平18期末10)如图,在平面直角坐标系xOy 中,点A ,点B 的坐标分别为(0,2),(1-,0),将线段AB 沿x 轴的正方向平移,若点B 的对应点的坐标为'B (2,0),则点A 的对应点'A 的坐标为 .ED C BAC'EB C D A8.(昌平18期末14)如图,在直角三角形ABC中,∠C=90°,BC=6,AC=8,点D是AC边上一点,将△BCD沿BD折叠,使点C 落在AB边的E点,那么AE的长度是.9.(昌平18期末15)如图,在平面直角坐标系xOy中,△CDE 可以看作是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△CDE的过程:_________________________________________________________________________________________.10.(朝阳18期末14)如图,在平面直角坐标系中,△COD 可以看作是△AOB经过若干次图形的变化(平移、轴对称、旋转、位似)得到的,写出一种由△AOB得到△COD的过程:_________________________________________________________________________.11.(石景山18期末15)如图,在平面直角坐标系xOy中,△ABC 经过若干次图形的变化(平移、轴对称、旋转)得到△DEF,写出一种由△ABC得到△DEF的过程:________________ __________________________________________________.12.(平谷18期末15)如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:____________________________________________________________________________.13.(门头沟18期末15)如图,在平面直角坐标系xOy中,图形L2可以看作是由图形L1经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由图形L1得到图形L2的过程________________________________________________________________________________.14.(燕山18期末18)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).(1)在图1中画出△ABC关于y轴对称的△A1B1C1,直接写出点C的对应点C1的坐标.(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可).直接写出点C的对应点C2的坐标.15.(朝阳18期末19)如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1).(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A′B′C;(2)在(1)中的条件下,①点A经过的路径的长为(结果保留π);②写出点B′的坐标为.16.(东城18期末22)如图,在Rt△ABC中,∠A=90°,∠C=30°.将△ABC绕点B顺时针旋转60°得到△A BC'', 其中点A', C'分别是点A,C的对应点.(1)作出△A BC''(要求尺规作图,不写作法,保留作图痕迹);(2)连接AA',求∠C A A''的度数.AA'17.(西城18期末20)在△ABC 中,AB=AC=2,45BAC ∠=︒.将△ABC 绕点A 逆时针旋转α度(0<α<180)得到△ADE ,B ,C 两点的对应点分别为点D ,E ,BD ,CE 所在直线交于点F .(1)当△ABC 旋转到图1位置时,∠CAD = (用α的代数式表示),BFC ∠的度数为 ︒;(2)当α=45时,在图2中画出△ADE ,并求此时点A 到直线BE 的距离.。
北京市西城区九级第一学期期末数学试题(含答案)

北京市西城区2018— 2018学年度第一学期期末试卷九年级数学 2018.1一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.二次函数()257y x =-+的最小值是 A .7- B .7 C .5-D .52.如图,在Rt △ABC 中,∠C =90°,AC =3,BC =4,则cos A 的值为A .35B .53C .45D .343.如图,⊙C 与∠AOB 的两边分别相切,其中OA 边与⊙C 相切于点P .若∠AOB =90°,OP =6,则OC 的长为A .12B .C ..4.将二次函数265y x x =-+用配方法化成2()y x h k =-+的形式,下列结果中正确的是 A .2(6)5y x =-+ B .2(3)5y x =-+C .2(3)4y x =--D .2(3)9y x =+-5.若一个扇形的半径是18cm ,且它的弧长是12π cm ,则此扇形的圆心角等于 A .30° B .60° C .90°D .120°6.如图,在平面直角坐标系xOy 中,点A 的坐标为(1-,2),AB ⊥x 轴于点B .以原点O 为位似中心,将△OAB 放大为 原来的2倍,得到△OA 1B 1,且点A 1在第二象限,则点A 1 的坐标为 A .(2-,4)B .(12-,1)C .(2,4-)D .(2,4)7.如图,一艘海轮位于灯塔P 的南偏东37°方向,距离灯塔40 海里的A 处,它沿正北方向航行一段时间后, 到达位于灯塔P 的正东方向上的B 处.这时,B 处与 灯塔P 的距离BP 的长可以表示为 A .40海里B .40tan37°海里C .40cos37°海里D .40sin37°海里8.如图,A ,B ,C 三点在已知的圆上,在△ABC 中, ∠ABC =70°,∠ACB =30°,D 是 的中点, 连接DB ,DC ,则∠DBC 的度数为 A .30° B .45° C .50°D .70°9.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x 元后,每星期售出商品的总销售额为y 元,则y 与x 的关系式为A .60(30020)y x =+B .(60)(30020)y x x =-+ C.300(6020)y x =- D .(60)(30020)y x x =--10.二次函数228y x x m =-+满足以下条件:当21x -<<-时,它的图象位于x 轴的下方;当67x <<时,它的图象位于x 轴的上方,则m 的值为 A .8 B .10- C .42-D .24-二、填空题(本题共18分,每小题3分) 11.若34a b =,则a bb+的值为. 12.点A (3-,1y ),B (2,2y )在抛物线25y x x =-上,则1y 2y .(填“>”,“<”或“=”)13.△ABC 的三边长分别为5,12,13,与它相似的△DEF 的最小边长为15,则△DEF 的周长为.14.如图,线段AB 和射线AC 交于点A ,∠A =30°,AB =20.点D 在射线AC 上,且∠ADB 是钝角,写出一个满足条件 的AD 的长度值:AD =.15.程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?” 【注释】1步=5尺. 译文:“当秋千静止时,秋千上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,已知这个人身高是5尺.美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”如图,假设秋千的绳索长始终保持直线状态,OA 是秋千的静止状态,A 是踏板,CD 是地面,点B 是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知AC =1尺,CD =EB =10尺,人的身高BD =5尺.设绳索长OA =OB =x 尺,则可列方程为. BAC16.阅读下面材料:在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:小敏的作法如下:老师认为小敏的作法正确.请回答:连接OA ,OB 后,可证∠OAP =∠OBP =90°,其依据是;由此可证明直线P A ,PB 都是⊙O 的切线,其依据是.三、解答题(本题共72分,第17﹣26题,每小题5分,第27题7分,第28题7分,第29题8分)解答应写出文字说明,演算步骤或证明过程.17.计算:24cos30tan60sin 45︒⋅︒-︒.18.如图,△ABC 中,AB =12,BC =15,AD ⊥BC 于点D ,∠BAD 求tan C 的值.19.已知抛物线223y x x =-++与x 轴交于A ,B 两点,点A 在点B 的左侧.(1)求A ,B 两点的坐标和此抛物线的对称轴;(2)设此抛物线的顶点为C ,点D 与点C 关于x 轴对称,求四边形ACBD 的面积.20.如图,四边形ABCD 中,AD ∥BC ,∠A =∠BDC .(2)若AB =12,AD =8,CD =15,求DB 的长.21.某小区有一块长21M ,宽8M 的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x M 的人行通道.如果这两块绿地的面积之和为60平方M ,人行通道的宽度应是多少M ?22.已知抛物线1C :2124y x x k =-+与x 轴只有一个公共点.(1)求k 的值;(2)怎样平移抛物线1C 就可以得到抛物线2C :222(1)4y x k =+-?请写出具体的平移方法;(3)若点A (1,t )和点B (m ,n )都在抛物线2C :222(1)4y x k =+-上,且n t <,直接写出m 的取值范围.23.如图,AB 是⊙O 的一条弦,且AB =C ,E 分别在⊙O 上,且OC ⊥AB 于点D ,∠E =30°,连接OA . (1)求OA 的长;(2)若AF 是⊙O 的另一条弦,且点O 到AF 的距离为直接写出∠BAF 的度数.24.奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B 处测得最高塔塔顶A 的仰角为45°,然后向最高塔的塔基直行90M 到达C 处,再次测得最高塔塔顶A 的仰角为58°.请帮助他们计算出最高塔的高度AD 约为多少M .(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)25.如图,△ABC 内接于⊙O ,AB 是⊙O 的直径.PC 是⊙O 的切线,C 为切点,PD ⊥AB 于点D ,交AC 于点E .(1)求证:∠PCE =∠PEC ; (2)若AB =10,ED =3,sin A =3,求PC 的长.26.阅读下面材料:如图1,在平面直角坐标系xOy 中,直线1y ax b =+双曲线2ky x=交于A (1,3)和B (3-,1-)两点. 观察图象可知:①当3x =-或1时,12y y =; ②当30x -<<或1x >时,12y y >,即通过观察函 数的图象,可以得到不等式kax b x+>的解集. 有这样一个问题:求不等式32440x x x +-->的解集.某同学根据学习以上知识的经验,对求不等式32440x x x +-->的解集进行了探究. 下面是他的探究过程,请将(2)、(3)、(4)补充完整: (1)将不等式按条件进行转化 当0x =时,原不等式不成立;当0x >时,原不等式可以转化为2441x x x +->; 当0x <时,原不等式可以转化为2441x x x+-<;(2)构造函数,画出图象设2341y x x =+-,44y x=中分别画出这两个函数的图象.双曲线44y x=如图2所示,请在此坐标系中 画出抛物线.....2341y x x =+-;(不用列表)(3)确定两个函数图象公共点的横坐标观察所画两个函数的图象,猜想并通过代入函数解读式验证可知:满足34y y =的所有x 的值为;(4)借助图象,写出解集结合(1)的讨论结果,观察两个函数的图象可知:不等式32440x x x +-->的解集为.27.如图,在平面直角坐标系xOy 中,二次函数212y x bx c =-++的图象经过点A (1,0),且当0x =和5x =时所对应的函数值相等.一次函数3y x =-+与二次函数212y x bx c =-++的图象分别交于B ,C 两点,点B 在第一象限.(1)求二次函数21y x bx c =-++的表达式;(2(328.在△ABC 中,∠ACB =90°,AC =BC = 4,M 为AB 的中点.D 是射线BC 上一个动点,连接AD ,将线段AD 绕点A 逆时针旋转90°得到线段AE ,连接ED ,N 为ED 的中点,连接AN ,MN .(1)如图1,当BD =2时,AN =_______,NM 与AB 的位置关系是____________; (2)当4<BD <8时,①依题意补全图2;②判断(1)中NM 与AB 的位置关系是否发生变化,并证明你的结论;(3)连接ME ,在点D 运动的过程中,当BD 的长为何值时,ME 的长最小?最小值是多少?请直接写出结果.图1 图2 备用图29.在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P 称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.图1 图2 图3(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线;(2)当⊙O的半径为1时,如图3,①第一象限内的一条入射光线平行于x轴,且自⊙O的外部照射在其上点P处,此光线经⊙O反射后,反射光线与y轴平行,则反射光线与切线l的夹角为__________°;,0)出发的入射光线,在⊙O内不断地反射.若第1个反射点P1在②自点A(1第二象限,且第12个反射点P12与点A重合,则第1个反射点P1的坐标为______________;(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.图4北京市西城区2018— 2018学年度第一学期期末试卷九年级数学参考答案及评分标准2018.1一、选择题(本题共30分,每小题3分)三、解答题(本题共72分,第17﹣26题,每小题5分,第27题7分,第28题7分,第29题8分)17.解:原式=24………………………………………………………3分=162-=112.…………………………………………………………………………5分18.解:∵AD⊥BC于点D,∴∠ADB=∠ADC=90°.∵在Rt△ABD中,AB=12,∠BAD=30°,∴BD=12AB=6,…………………………………1分AD=AB·cos∠BAD =12·cos30°=2分∵BC=15,∴CD= BC-BD=15-6=9.………………………………………………………3分∴在Rt△ADC中,tan C=ADCD……………………………………………………4分=9=3.………………………………………5分19.解:(1)令0=y ,则2230x x -++=.解得 11-=x ,32=x .………………………………………………………1分 ∵点A 在点B 的左侧,∴A (1-,0),B (3,0).…………………………………………………2分 对称轴为直线1=x .…………………………………………………………3分 (2)∵当1x =时,4=y ,∴顶点C 的坐标为(1,4).…………………………………………………4分∵点C ,D 关于x 轴对称,∴点D 的坐标为(1,4-).∵AB =4,∴=ACB DCB ACBD S S S ∆∆+四边形1442162=⨯⨯⨯=.………………………………5分20.(1)证明:∵AD ∥BC ,∴∠ADB=∠DBC .……………………1分 ∵∠A =∠BDC ,∴△ABD ∽△DCB .……………………3分(2)解:∵△ABD ∽△DCB ,∴AB ADDC DB=.…………………………………………………………4分 ∵AB =12,AD =8,CD =15, ∴12815DB=. ∴DB =10.………………………………………………………………5分21.解:根据题意,得 (213)(82)60x x --=.…………………………………………2分整理得 211180x x -+=.解得 12x =,29x =.…………………………………………………………3分 ∵9x =不符合题意,舍去,∴2x =.……………………………………………………………………………4分答:人行通道的宽度是2M .……………………………………………………5分 22.解:(1)∵抛物线1C :2124y x x k =-+与x 轴有且只有一个公共点,∴方程2240x x k -+=有两个相等的实数根.∴2(4)420k ∆=--⨯=.……………………………………………………1分 解得 2k =.…………………………………………………………………2分(2)∵抛物线1C :21242y x x =-+22(1)x =-,顶点坐标为(1,0),抛物线2C :222(1)8y x =+-的顶点坐标为(-1,-8), ………………3分∴将抛物线1C 向左平移2个单位长度,再向下平移8个单位长度就可以得到抛物线2C .…………………………………………………………………4分(3)31m -<<.……………………………………………………………………5分 23.解:(1)∵OC ⊥AB 于点D ,∴AD =DB , ……………………………………1分∠ADO =90°.∵AB =∴AD =∵∠AOD =2∠E ,∠E =30°,∴∠AOD =60°.………………………………………………………………2分∵在Rt △AOD 中,, ∴OA =︒=∠60sin 32sin AOD AD =4.………………………………………………3分 (2)∠BAF =75°或15°.……………………………………………………………5分24.解:(1)∵在Rt △ADB 中,∠ADB =90°,∠B =45°,∴∠BAD =90°—∠B =45°. ∴∠BAD =∠B .∴AD =DB .……………………………1分 设AD =x ,∵在Rt △ADC 中,tan ∠ACD =ADDC,∠ACD =58°, ∴DC =tan 58x.………………………………………………………………3分∵DB = DC + CB =AD ,CB =90,∴tan 58x+90=x .……………………………………………………………4分将tan58°≈1.60代入方程,解得x ≈240.…………………………………………………………………5分答:最高塔的高度AD 约为240M .25.(1)证明:连接OC ,如图1.∵ PC 是⊙O 的切线,C 为切点,∴OC ⊥PC .……………………………1分∴∠PCO =∠1+∠2=90°.∵PD ⊥AB 于点D ,∴∠EDA =90°.∴∠A +∠3=90°.∵OA =OC ,∴∠A =∠1.∴∠2=∠3.∵∠3=∠4,∴∠2=∠4.即∠PCE =∠PEC .…………………………………………………………2分(2)解:作PF ⊥EC 于点F ,如图2.∵AB 是⊙O 的直径,∴∠ACB =90°.∵在Rt △ABC 中,AB =10,3sin 5A =, ∴BC =AB ·sin A =6.∴AC =22BC AB -=8.………………………………………………………3分∵在Rt △AED 中,ED =32, ∴AE =sin ED A =52. ∴EC=AC -AE =112. ∵∠2=∠4,∴PE=PC .∵PF ⊥EC 于点F ,∴FC=124分 ∠PFC =90°.图1 图2∴∠2+∠5=90°.∵∠A +∠2=∠1+∠2=90°.∴∠A =∠5.∴sin ∠5 =35. ∴在Rt △PFC 中,PC =sin 5FC ∠=1255.……………………………………5分26.解:(2)抛物线如图所示; ……………………1分(3)x =4-,1-或1; ……………………3分(4)41x -<<-或1x >.……………………5分27.解:(1)∵二次函数212y x bx c =-++, 当0x =和5x =时所对应的函数值相等, ∴二次函数212y x bx c =-++的图象的对称 轴是直线52x =. ∵二次函数212y x bx c =-++的图象经过点A (1,0), ∴10,25.2b c b ⎧=-++⎪⎪⎨⎪=⎪⎩……………………………………………………………1分 解得 2,5.2c b =-⎧⎪⎨=⎪⎩∴二次函数的表达式为215222y x x =-+-.………………………………2分 (2)过点B 作BD ⊥x 轴于点D ,如图1.∵一次函数3y x =-+与二次函数212y x bx c =-++的图象分别交于B ,C 两点, ∴2153222x x x -+=-+-. 解得 12x =,25x =.………………3分∴交点坐标为(2,1),(5,2-).∵点B 在第一象限,∴点B 的坐标为(2,1).∴点D 的坐标为(2,0).在Rt △ABD 中,AD =1,BD =1,∴AB 2.…………………………………………………4分(3)结论:四边形ABCN 的形状是矩形.………………………………………5分证明:设一次函数3y x =-+的图象与x 轴交于点E ,连接MB ,MN ,如图2.∵点B 绕点M 旋转∴M 是线段BN 的中点.∴MB = MN .∵M 是线段AC 的中点,∴MA = MC.∴四边形ABCN 是平行四边形.……∵一次函数3y x =-+ 当0y =时,3x =.∴点E 的坐标为(3,0).∴DE =1= DB .∴在Rt △BDE 中,∠DBE =∠DEB =45°.同理∠DAB =∠DBA =45°.∴∠ABE =∠DBA +∠DBE =90°.∴四边形ABCN 是矩形.……………………………………………7分28.解:(1 …………………………2分(2)①补全图形如图所示; ………………3分②结论:(1)中NM 与AB 的位置关系不变.证明:∵∠ACB =90°,AC =BC ,∴∠CAB =∠B =45°.∴∠CAN +∠NAM =45°.∵AD 绕点A 逆时针旋转90°得到线段AE ,∴AD =AE ,∠DAE =90°.∵N 为ED 的中点,∴∠DAN =12∠DAE =45°, AN ⊥DE . ∴∠CAN +∠DAC =45°,∠AND =90°.∴∠NAM =∠DAC .………………………………………………4分在Rt △AND 中,AN AD =cos ∠DAN在Rt △ACB 中,AC AB =cos ∠CAB∵M 为AB 的中点, ∴AB =2AM. ∴22AC AC AB AM ==∴AM AC . ∴AN AD =AM AC. ∴△ANM ∽△ADC .∴∠AMN =∠ACD .∵点D 在线段BC 的延长线上, ∴∠ACD =180°-∠ACB =90°.∴∠AMN =90°. ∴NM ⊥AB .………………………………………………………5分(3)当BD 的长为 6 时,7分29.解:(1)所得图形,如图1所示.……………………1分(2)①45°; ………………………………………3分②(,12)或(12-); ……………5分 (3)①如图2,直线OQ 与⊙M 相切于点Q ,点Q 在第一象限,连接MQ ,过点Q 作QH ⊥x 轴于点H .∵直线OQ 与⊙M 相切于点Q ,∴MQ ⊥OQ .∴∠MQO =90°.∵MO =2,MQ =1, ∴在Rt △MQO 中,sin ∠MOQ=21=MO MQ . ∴∠MOQ =30°.M Q∴OQ =OM ﹒cos ∠MOQ =3.∵QH ⊥x 轴,∴∠QHO =90°.∵∠QOH =90°-∠MOQ =60°,∴在Rt △QOH 中,QH = OQ ﹒sin ∠QOH =23.…………………………6分 ②如图3,当反射光线PN 与坐标轴平行时,连接MP 并延长交x 轴于点D ,过点P 作PE ⊥OD 于点E ,过点O 作OF ⊥PD 于点F .∵直线l 是⊙M 的切线,∴MD ⊥l .∴∠1+∠OPD =∠2+∠NPD =90°.∵∠1=∠2,∴∠OPD =∠NPD .∵PN ∥x 轴,∴∠NPD =∠PDO .∴∠OPD =∠PDO .∴OP =OD .∵OF ⊥PD ,∴∠MFO =90°,PF =FD .∵cos OMF ∠=MFMOMO MD =,设PF =FD =x ,而MO =2,MP =1, ∴12212x x +=+.解得x =∵0x >,∴34x -+=.∵PE ⊥OD ,∴∠PED =90°=∠MOD .∴PE ∥MO .∴∠EPD =∠OMF .∴cos ∠EPD = cos ∠OMF . ∴MO MFPD PE=. ∴PD MO MFPE ⋅= =122xx +⋅(1)x x =+=158-.…………………………………………………………7分. 可知,当反射点P 从②中的位置开始,在⊙M 上沿逆时针方向运动,到与①中的点Q 重合之前,都满足反射光线与坐标轴无公共点,所以反射点P 的纵坐标的取值范围是15382P y <.………………………………8分。
2018-2019年北京中考数学真题分类解析【04】图形的变换(原卷版)

1.(2003年北京市4分)如果圆柱的底面半径为4cm ,底面为5cm ,那么它的侧面积等于【 】A. 220cm πB. 240cm πC. 20cm 2D. 40cm 22. (2004年北京市4分)如果圆锥的底面半径为3cm ,母线长为4cm ,那么它的侧面积等于【 】(A )24πcm 2 (B )12πcm 2 (C )12cm 2 (D )6πcm 23. (2006年北京市课标4分)将如图所示的圆心角为90的扇形纸片AOB 围成圆锥形纸帽,使扇形的两条半径OA 与OB 重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是【 】4. (2007年北京市4分)下图所示是一个三棱柱纸盒,在下面四个图中,只有一个是这个纸盒的展开图,那么这个展开图是【 】5. (2008年北京市4分)已知O 为圆锥的顶点,M 为圆锥底面上一点,点P 在OM 上.一只蜗牛从P 点出发,绕圆锥侧面爬行,回到P 点时所爬过的最短路线的痕迹如左图所示.若沿OM 将圆锥侧面剪开并展开,所得侧面展开图是【 】6. (2009年北京市4分)若下图是某几何体的三视图,则这个几何体是【】A.圆柱B.正方体C.球D.圆锥7. (2019年北京市4分)美术课上,老师要求同学们将下图所示的白纸只沿虚线裁开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下列四个示意图中,只有一个....符合上述要求,那么这个示意图是【】8. (2019年北京市4分)下图是某个几何体的三视图,该几何体是【】A.长方体 B.正方体 C.圆柱 D.三棱柱9.(2019年北京市3分)下图是几何体的三视图,该几何体是【】A.圆锥 B.圆柱 C.正三棱柱 D.正三棱锥1.(2006年北京市大纲4分)如图,圆锥的底面半径为2cm ,母线长为4cm ,那么它的侧面积等于 ▲ cm 2。
2.(2007年北京市4分)下图是对称中心为点O 的正六边形。
如果用一个含30°角的直角三角板的角,借助点O (使角的顶点落在点O 处),把这个正六边形的面积n 等分,那么n 的所有可能的值是 ▲ 。
北京市各区2018届九年级上期末数学试卷按考点分类汇编:尺规作图(含答案)
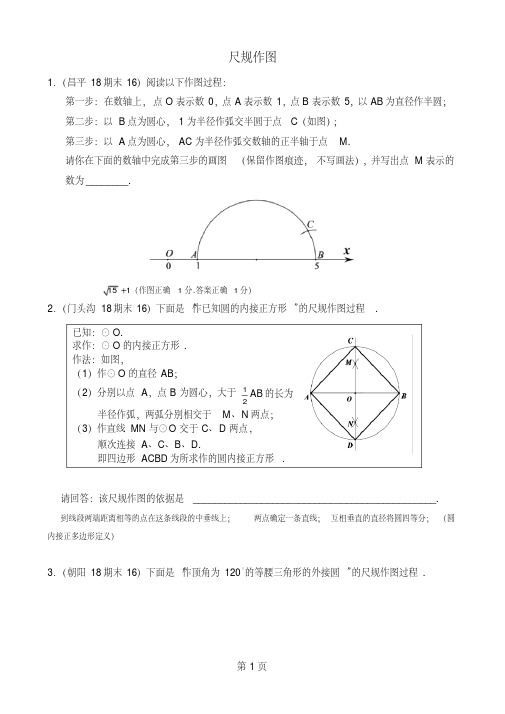
尺规作图1.(昌平18期末16)阅读以下作图过程:第一步:在数轴上,点O 表示数0,点A 表示数1,点B 表示数5,以AB 为直径作半圆;第二步:以B 点为圆心,1为半径作弧交半圆于点C (如图);第三步:以A 点为圆心,AC 为半径作弧交数轴的正半轴于点M.请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M 表示的数为________.151(作图正确1分.答案正确1分)2.(门头沟18期末16)下面是“作已知圆的内接正方形”的尺规作图过程.请回答:该尺规作图的依据是______________________________________________.到线段两端距离相等的点在这条线段的中垂线上;两点确定一条直线;互相垂直的直径将圆四等分;(圆内接正多边形定义)3.(朝阳18期末16)下面是“作顶角为120°的等腰三角形的外接圆”的尺规作图过程.已知:⊙O.求作:⊙O 的内接正方形. 作法:如图,(1)作⊙O 的直径AB ;(2)分别以点A ,点B 为圆心,大于12AB 的长为半径作弧,两弧分别相交于M 、N 两点;(3)作直线MN 与⊙O 交于C 、D 两点,顺次连接A 、C 、B 、D.即四边形ACBD 为所求作的圆内接正方形.请回答:该尺规作图的依据是_____________________________________________.4.(石景山18期末16)石景山区八角北路有一块三角形空地(如图1)准备绿化,拟从点A 出发,将△ABC 分成面积相等的三个三角形,栽种三种不同的花草.下面是小美的设计(如图2).请回答,CAC C AC ABC SSS 2211成立的理由是:①;②.16.①两条直线被一组平行线所截,所得的对应线段成比例;②等底同高的三角形面积相等5.(燕山18期末16)16.在数学课上,老师提出利用尺规作图完成下面问题:作法:(1)作射线BM ;(2)在射线BM 上顺次截取BB 1=B 1B 2=B 2B 3;(3)连接B 3C ,分别过B 1、B 2作B 1C 1∥B 2C 2∥B 3C ,交BC 于点C 1、C 2;(4)连接AC 1、AC 2.则CAC C AC ABC S S S2211.已知:△ABC ,AB =AC ,∠A =120°.求作:△ABC 的外接圆. 作法:(1)分别以点B 和点C 为圆心,AB 的长为半径作弧,两弧的一个交点为O ;(2)连接BO ;(3)以O 为圆心,BO 为半径作⊙O.⊙O 即为所求作的圆.已知:∠ ACB 是△ ABC 的一个内角.求作:∠ APB= ∠ ACB .小路的作法如下:如图,P①作线段AB 的垂直平分线m ;②作线段BC 的垂直平分线n ,与直线m 交于点O ;On③以点O 为圆心,OA 为半径作△ ABC 的外接圆; A B④在弧ACB 上取一点P ,连结AP ,BP .m所以∠ APB= ∠ ACB .老师说:“小路的作法正确.”请回答:(1)点O 为△ABC 外接圆圆心(即OA=OB=OC)的依据是;(2)∠APB= ∠ACB 的依据是.16.(1)线段垂直平分线上的点与这条线段两个端点的距离相等;(2)同弧所对的圆周角相等.6.(怀柔18期末16)阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:小明的作法如下:已知:△OAB.求作:⊙O ,使⊙O 与△OAB 的边AB 相切.请回答:这样做的依据是.16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.7.(丰台18期末16、密云18期末16)下面是“过圆外一点作圆的切线”的尺规作图过程.请回答以下问题:(1)连接OA ,OB ,可证∠OAP =∠OBP = 90°,理由是;(2)直线PA ,PB 是⊙O 的切线,依据是.16.直径所对的圆周角是直角;经过半径的外端,并且垂直于这条半径的直线是圆的切线.8.(大兴18期末16)下面是“作出所在的圆”的尺规作图过程.已知:⊙O 和⊙O 外一点P .求作:过点P 的⊙O 的切线.作法:如图,(1)连接OP ;(2)分别以点O 和点P 为圆心,大于12OP 的长为半径作弧,两弧相交于M ,N 两点;(3)作直线MN ,交OP 于点C ;(4)以点C 为圆心,CO 的长为半径作圆,交⊙O 于A ,B 两点;(5)作直线P A ,PB .直线P A ,PB 即为所求作⊙O 的切线.如图,①取线段OB 的中点M ;以M 为圆心,MO 为半径作⊙M ,与边AB 交于点C ;②以O 为圆心,OC 为半径作⊙O ;所以,⊙O 就是所求作的圆.已知:.求作:所在的圆.作法:如图,(1)在上任取三个点D,C,E;(2)连接DC,EC;(3)分别作DC和EC的垂直平分线,两垂直平分线的交点为点O.(4)以O为圆心,OC长为半径作圆,所以⊙O即为所求作的所在的圆..请回答:该尺规作图的依据是.16. 不在同一直线上的三个点确定一个圆;圆是到定点的距离等于定长的点的集合;线段垂直平分线上的点到线段两个端点的距离相等.9.(通州18期末16)16. 阅读下面材料:在数学课上,老师提出如下问题:尺规作图:作已知角的角平分线.已知:如图,已知BAC.求作:BAC的角平分线AP.小霞的作法如下:(1)如图,在平面内任取一点O;(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;(3)连接DE,过点O作射线OP垂直线段DE,交⊙O于点P;(4)连接AP.所以射线AP为所求.老师说:“小霞的作法正确.”请回答:小霞的作图依据是.10.(海淀18期末16、平谷18期末16)下面是“作一个30°角”的尺规作图过程.已知:平面内一点A.求作:∠A,使得∠A30°.作法:如图,(1)作射线AB;(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.∠DAB即为所求的角.请回答:该尺规作图的依据是.16.三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,一条弧所对的圆周角是它所对圆心角的一半;或:直径所对的圆周角为直角,三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,直角三角形两个锐角互余;或:直径所对的圆周角为直角,1sin2A,A为锐角,30A.11.(昌平18期末21)尺规作图:如图,AC为⊙O的直径.(1)求作:⊙O的内接正方形ABCD.(要求:不写作法,保留作图痕迹);(2)当直径AC=4时,求这个正方形的边长.21.(1)如图所示,,,,,,,, 2分(2)解:∵直径AC =4,∴OA =OB=2.,,,,,,,,,3分∵正方形ABCD为⊙O的内接正方形,∴∠AOB=90°,,,,,,,,,,4分∴2222AB OA OB,,,,,,,, 5分.。
北京市西城区九级(上)数学期末试卷

北京市西城区2018-2018 学年度第一学期期末试卷九年级数学考1.本试卷共 7 页,共五道大题,25 道小题,满分120 分。
考试时间120 分钟。
2.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效。
生须3.在答题卡上,选择题、作图题用 2B 铅笔作答,其余试卷用黑色笔迹署名笔作知答。
一、选择题(此题共32 分,每题 4 分)下边各题均有四个选项,此中只有一个..是切合题意的.1.抛物线的极点坐标是A.B.C. D .2.如图,⊙ O 是△ ABC 的外接圆,若,则∠ ACB 的度数是A.40°B. 50°C. 60°D. 80°3.若两个圆的半径分别为 2 和 1,圆心距为3,则这两个圆的地点关系是A.内含B.内切C.订交 D .外切4.以下图形中,既是轴对称图形又是中心对称图形的是A B C D5.在 Rt △ ABC 中,∠ C= 90°,若 BC=1, AC= 2,则 sinA 的值为A.B.C.D.26.如图,抛物线的对称轴为直线.以下结论中,正确的选项是A. a<0B.当时,y随x的增大而增大C.-1D .当时,y的最小值是7.如图,在平面直角坐标系xOy 中,△ ABC 极点的横、纵坐标都是整数.若将△ABC 以某点为旋转中心,顺时针旋转90°获得△ DEF ,则旋转中心的坐标是A.B.C.D.8.若抛物线(m是常数)与直线有两个交点,且这两个交点分别在抛物线对称轴的双侧,则的取值范围是A.B.C.D.二、填空题(此题共16 分,每题 4 分)9.如图,△A BC 中,点 D, E 分别在 AB, AC 边上, DE∥ BC,若,,,则BC的长是.10.把抛物线向右平移1个单位,再向下平移 3 个单位,获得抛物线.11.如图,在△ABC 中,∠ ACB= 90°,∠ ABC = 30°,BC =2.将△ ABC 绕点 C 逆时针旋转角后获得△A′B′C,当点 A 的对应点 A' 落在 AB 边上时,旋转角的度数是度,暗影部分的面积为.xOy 中,过点作AB⊥x轴于点12 .在平面直角坐标系B.半径为的⊙ A 与 AB 交于点 C,过 B 点作⊙ A 的切线BD,切点为 D ,连结 DC 并延伸交 x 轴于点 E.( 1)当时,EB的长等于;( 2)点 E 的坐标为(用含r的代数式表示).三、解答题(此题共30 分,每题 5 分)13.计算:.14.已知:二次函数的图象经过点.(1)求二次函数的解读式;(2)求二次函数的图象与 x 轴的交点坐标;( 3)将( 1)中求得的函数解读式用配方法化成的形式.15.如图,在梯形ABCD 中, AB∥ DC,∠ A= 90°,点P 在 AD 边上,且.若 AB=6, DC = 4, PD= 2,求 PB 的长.16.列方程或方程组解应用题:“美化城市,改良人民居住环境”是城市建设的一项重要内容.某市最近几年来,通过植草、栽树、修筑公园等举措,使城区绿地面积不停增添,2018 年末该市城区绿地总面积约为75 公顷,截止到2018 年末,该市城区绿地总面积约为108 公顷,求从2018 年末至 2018 年末该市城区绿地总面积的年均匀增添率.17.如图,为了估量某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥ BD ,∠ ACB = 45°,∠ADB = 30°,并且点B,C, D 在同一条直线上.若测得CD=30M ,求河宽AB(结果精准到1M ,取,取).18.如图, AB 是⊙ O 的弦, OC⊥ AB 于点 C,连结 OA, AB= 12,.(1)求 OC 的长;(2)点 E, F 在⊙ O 上, EF∥ AB.若 EF= 16,直接写出 EFO 与 AB 之间的距离.CA B四、解答题(此题共20 分,每题 5 分)19.设二次函数的图象为 C .二次函数的图象与 C11对于 y 轴对称.( 1)求二次函数的解读式;( 2)当≤ 0 时,直接写出的取值范围;( 3)设二次函数图象的顶点为点 A,与 y 轴的交点为点B,一次函数( k, m 为常数, k≠ 0)的图象经过 A, B 两点,当时,直接写出x 的取值范围.20.如图,在矩形ABCD 中, E 是 CD 边上随意一点(不与点C,D 重合),作AF ⊥AE 交 CB 的延伸线于点F .(1)求证:△ ADE ∽△ ABF ;(2)连结 EF , M 为 EF 的中点, AB = 4, AD =2,设 DE=x,①求点 M 到 FC 的距离(用含x 的代数式表示);②连结 BM ,设,求y与x之间的函数关系式,并直接写出BM 的长度的最小值.21.如图, AB 是⊙ O 的直径,点C 在⊙ O 上,连结 BC, AC,作 OD∥ BC 与过点 A 的切线交于点 D ,连结 DC 并延伸交 AB 的延伸线于点 E.( 1)求证: DE 是⊙ O 的切线;( 2)若,求的值.22.阅读下边资料:定义:与圆的全部切线和割线都有公共点的几何图形叫做这个圆的关系图形........问题:⊙ O 的半径为 1,画一个⊙O 的关系图形.在解决这个问题时,小明以O 为原点成立平面直角坐标系xOy 进行研究,他发现能画出好多⊙ O 的关系图形,比如:⊙ O 自己和图 1 中的△ ABC(它们都是关闭的图形),以(及图 2 中以 O 为圆心的DmE (它是非关闭的图形),它们都是⊙ O 的关系图形.而图 2 中以P, Q 为端点的一条曲线就不是⊙ O的关系图形.参照小明的发现,解决问题:( 1)在以下几何图形中,⊙ O 的关系图形是(填序号);① ⊙O 的外切正多边形② ⊙O 的内接正多边形③ ⊙O 的一个半径大于 1 的齐心圆( 2)若图形G 是⊙ O 的关系图形,而且它是关闭的,则图形G 的周长的最小值是____ ;(DmE( 3)在图 2 中,当⊙ O 的关系图形 的弧长最小时,经过D ,E 两点的直线为 y=__ ;( 4 )请你在备用图中画出一个⊙O 的关系图形,所绘图形的长度 l 小于( 2)中图形G 的周长的最小值,并写出l 的值(直接画出图形,不写作法).五、解答题(此题共22分,第 23题 7分,第 24题 7分,第 25题 8分)23. 已知:二次函数( m 为常数).( 1)若这个二次函数的图象与x 轴只有一个公共点 A ,且 A 点在 x 轴的正半轴上.①求 m 的值;②四边形 AOBC 是正方形,且点B 在 y 轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰巧经过B , C两点,求平移后的图象对应的函数解读式;( 2)当 0≤ ≤2 时 ,求函数的最小值(用含m 的代数式表示).24. 已知:△ ABC ,△ DEF 都是等边三角形, M 是 BC 与 EF 的中点,连结AD , BE.( 1)如图 1,当 EF 与 BC 在同一条直线上时,直接写出AD 与 BE 的数目关系和地点关系;( 2)△ ABC 固定不动,将图 1 中的△ DEF 绕点 M 顺时针旋转( ≤ ≤ )角,如图 2 所示,判断( 1)中的结论能否仍旧成立,若成立,请加以证明;若不可立, 说明原因;( 3 )△ ABC 固定不动,将图1 中的△ DEF 绕点 M 旋转 ( ≤ ≤ )角,作DH ⊥ B C 于点 H .设 BH =x ,线段 AB ,BE ,ED , DA 所围成的图形面积为 S .当A B = 6, DE = 2 时,求 S 对于 x 的函数关系式,并写出相应的x 的取值范围.25.已知:二次函数的图象与x 轴交于点A, B( A 点在 B 点的左侧),与y 轴交于点C,△ ABC 的面积为 12.( 1)①填空:二次函数图象的对称轴为;②求二次函数的解读式;( 2)点 D 的坐标为(- 2, 1),点 P 在二次函数图象上,∠ADP 为锐角,且,求点 P 的横坐标;( 3)点 E 在 x 轴的正半轴上,,点O与点对于EC所在直线对称.作⊥于点 N,交 EC 于点 M.若 EM·EC= 32,求点 E 的坐标.北京市西城区 2018-2018 学年度第一学期期末九年级数学试卷参照答案及评分标准一、选择题(此题共 32 分,每题 4 分)题号 1 2 3 4 5 6 7 8 答案ABDBADCA二、填空题(此题共16 分,每题4 分)题号 9101112答案60,阅卷说明:第 11 题、第 12 题每空 2 分.三、解答题(此题共 30 分,每题5 分)13.解:.....................................................................................4 分. ................................................................................................................5 分14.解:( 1)∵ 二次函数的图象经过点A(2, 5),∴. ..........................................................................................1 分∴.∴ 二次函数的解读式为. ...................................................2 分( 2)令,则有.解得,.∴ 二次函数的图象与x 轴的交点坐标为和. ..........................4 分( 3). .............................................................................................. 5 分15.解:∵ 在梯形 ABCD 中, AB ∥ CD ,∠ A=90 °,∴ ∠ D=90°. ∴ .∵ , ∴∠ BPC=90°, .∴∠ DCP=∠ APB . ................................................ 2 分 ∴.在 Rt △ PCD 中, CD =2, PD=4,∴.在 Rt △ PBA 中, AB =6,∴.∴.∴. ...............................................................................................................4分∴. ...................................................................................5分16.解:设从 2018 年末至 2018 年末该市城区绿地总面积的年均匀增添率是x. ..........1分依题意,得. ......................................................................................2分整理,得. ...........................................................................................3分.解得 x=0.2=20% , x =-(舍去). ......................................................................4分12答:从 2018 年末至 2018 年末该市城区绿地总面积的年均匀增添率是20%. .........5分17 .解:设河宽 AB 为 xM . ..................................................................................................1分∵AB⊥BC ,∴∠ ABC =90°.∵在 Rt △ ABC 中,∠ AC B=45°,∴ AB = BC = x. ................................... 2 分∵在 Rt △ ABD 中,∠ ADB =30°,∴ BD=. ....................... 3 分∴.∴. ...................................................................................................... 4 分解得41.答:河宽 AB 约为 41M . ................................................................................................. 5 分18 .解:( 1)∵AB 是⊙ O 的弦, OC⊥ AB 于 C,AB =12 ,∴............................................ 1 分∵在 Rt△ AOC 中,∠ ACO=90°,,O∴. ....................................................... 2 分C∴. ............................... 3 分A B ( 2) 2 或 14. .......................................................................................................... 5 分四、解答题(此题共20 分,每题 5 分)19 .解:( 1 )二次函数图象的极点对于y 轴的对称点坐标为,····································1 分∴ 所求的二次函数的解读式为,················2 分即.(2)≤ ≤ 3.········································4 分(3).·········································5 分20 .( 1)证明:∵在矩形 ABCD 中,∠ DAB =∠ ABC =∠ C =∠ D =90 °.∴.∵ AF⊥ AE,∴ ∠EAF =.∴.∴ ∠DAE =∠ BAF.∴ △ADE ∽△ ABF .······························2 分(2)解:①如图,取 FC 的中点 H,连结 MH .∵M 为 EF 的中点,∴ MH∥DC ,.∵在矩形 ABCD 中,∠ C =90 °,∴ MH⊥ FC,即 MH 是点 M 到 FC 的距离.∵DE=x,DC =AB=4.∴EC=,∴.即点 M 到 FC 的距离为MH..................................................... 3分②∵△ ADE∽△ ABF ,∴.∴.∴,FC=,FH = CH=.∴.∵,∴在 Rt△ MHB 中,.∴(), .......................................................... 4 分当时, BM 长的最小值是. ....................................................... 5 分21.( 1)证明:如图,连结OC .∵AD 是过点 A 的切线, AB 是⊙ O 的直径,∴ AD⊥AB,∴ ∠ DAB =90 °.∵OD ∥ BC,∴ ∠ DOC =∠ OCB,∠ AOD =∠ ABC .∵OC =OB ,∴ ∠ OCB =∠ABC .∴ ∠ DOC =∠AOD.在△ COD 和△ AOD 中,OC = OA,∠DOC=∠ AOD,OD=OD ,∴ △ COD ≌△ AOD . ............................................................................................... 1 分∴ ∠ OCD= ∠DAB = 90°.∴ OC⊥DE 于点 C.∵ OC 是⊙ O 的半径,∴ DE 是⊙ O 的切线. .............................................................................................. 2 分( 2)解:由,可设,则. .. .........................................3 分∴.∴在 Rt△DAE 中,.∴.∵在 Rt△OCE 中,.∴,∴.∴在 Rt△AOD 中,. .. ..............................................4 分∴. .. ...............................................................5 分22.解:( 1)①③;.........2 分( 2); ............. 3 分( 3); ....4 分( 4 )答案不独一,所绘图形是非关闭的,长度l 知足≤ l <.比如:在图 1 中 l,在图 2 中 l........ 5分图1图2阅卷说明:在(1)中,只填写一个结果得1分,有错误结果不得分;在(4)中绘图正确且图形长度都正确得 1 分,不然得 0 分.五、解答题(此题共22 分,第23题 7分,第 24 题 7分,第 25题 8分)23.解:( 1)①∵ 二次函数的图象与 x 轴只有一个公共点A,∴. ....................................................................1 分整理,得.解得,,.又点 A 在 x 轴的正半轴上,∴.∴ m=4. ............................................................................................................ 2 分②由①得点 A 的坐标为.∵四边形 AOBC 是正方形,点 B 在 y 轴的负半轴上,∴点B的坐标为,点 C 的坐标为. ...................................... 3 分设平移后的图象对应的函数解读式为(b, c 为常数 ).∴解得∴平移后的图象对应的函数解读式为. .................................... 4 分(2)函数的图象是极点为,且张口向上的抛物线.分三种状况:(ⅰ )当,即时,函数在0≤≤ 2内y随x的增大而增大,此时函数的最小值为;(ⅱ )当 0≤≤ 2,即 0≤≤4 时,函数的最小值为;(ⅲ )当,即时,函数在0≤≤ 2 内 y 随 x 的增大而减小,此时函数的最小值为.综上,当时,函数的最小值为;当时,函数的最小值为;当时,函数的最小值为................. 7 分24.( 1),. ......................................................................................... 2 分( 2)证明:连结DM ,AM.在等边三角形ABC 中, M 为 BC 的中点,∴,,.∴.同理,,.∴,.··3分∴ △ADM ∽△ BEM.分∴. (4)延伸 BE 交 AM 于点 G,交 AD 于点 K.∴,.∴.5 分∴. ............................................................................................( 3)解: (ⅰ) 当△ DEF 绕点 M 顺时针旋转(≤ ≤)角时,∵ △ADM ∽△ BEM,∴.∴∴.∴( 3≤≤)......................................................... 6分(ⅱ ) 当△ DEF 绕点 M 逆时针旋转(≤≤) 角时,可证△ ADM ∽△ BEM,∴.∴.∴.∴(≤ ≤3).综上,(≤ ≤). ........................................................7 分25.解:( 1)①该二次函数图象的对称轴为直线; ...............................................1 分②∵当 x=0 时, y=-4,∴点C的坐标为.∵=12,∴ AB=6.又∵点 A , B 对于直线对称,∴ A 点和 B 点的坐标分别为,.∴.解得.∴ 所求二次函数的解读式为. ......................................2 分( 2)如图,作 DF ⊥ x 轴于点 F .分两种状况:(ⅰ )当点 P 在直线 AD 的下方时,如下图.由( 1)得点 A,点 D,∴DF =1 ,AF =2 .在 Rt△ ADF 中,,得.延伸 DF 与抛物线交于点P1,则 P1点为所求.∴点 P1的坐标为. ....................................................................... 3 分( ⅱ)当点 P 在直线 AD 的上方时,延伸P1A 至点 G 使得 AG =AP 1,连结 DG ,作 GH ⊥ x 轴于点 H ,如下图.可证△GHA≌△.∴HA = AF ,GH = P1F ,GA = P1A.又∵,,∴ 点的坐标是.在△ ADP 1中,, DP1=5,,∴.∴.∴DA⊥.∴.∴.∴.设 DG 与抛物线的交点为 P2,则 P2点为所求.作DK ⊥GH 于点 K ,作 P2S∥ GK 交 DK 于点 S.设 P2点的坐标为,则,.由,,,得.整理,得.解得.∵ P2点在第二象限,∴ P2点的横坐标为(舍正).综上, P 点的横坐标为- 2 或........................................................... 5分( 3)如图,连结O,交CE于T.连结 C .∵点 O 与点对于EC所在直线对称,∴ O⊥CE,CE,∠C E.∴C⊥ E.∵ON⊥ E,∴C∥N.∴ C E.∴. ......................................................................................................... 6 分∴.∵在 Rt△ETO 中,,,在 Rt△中,,,∴.∴.同理.∴.∵,∴.∵点 E 在 x 轴的正半轴上,∴ E 点的坐标为) . ................................................................................ 8 分。
北京市各区2018届九年级上期末数学试卷分类汇编:几何综合(数学试卷 新课标人教版)

几何综合1.(昌平18期末27)已知,△ABC 中,∠ACB =90°,AC =BC ,点D 为BC 边上的一点.(1)以点C 为旋转中心,将△ACD 逆时针旋转90°,得到△BCE ,请你画出旋转后的图形;(2)延长AD 交BE 于点F ,求证:AF ⊥BE ;(3)若,BF=1,连接CF ,则CF 的长度为 .27.(1)补全图形…………………… 2分(2)证明:∵ΔCBE 由ΔCAD 旋转得到,∴ΔCBE ≌ΔCAD ,……………… 3分∴∠CBE =∠CAD ,∠BCE =∠ACD =90°,……………4分∴∠CBE +∠E =∠CAD +∠E ,∴∠BCE =∠AFE =90°,∴AF ⊥BE .……………………………………5分(37分2.(朝阳18期末25)△ACB 中,∠C =90°,以点A 为中心,分别将线段AB ,AC 逆时针旋转60°得到线段AD ,AE ,连接DE ,延长DE 交CB 于点F .(1)如图1,若∠B =30°,∠CFE 的度数为 ;(2)如图2,当30°<∠B <60°时,①依题意补全图2;②猜想CF 与AC 的数量关系,并加以证明.图1 图23.(西城18期末27)如图1,在Rt△AOB中,∠AOB=90°,∠OAB=30°,点C在线段OB 上,OC=2BC,AO边上的一点D满足∠OCD=30°.将△OCD绕点O逆时针旋转α度(90°<α<180°)得到△OC D'',C,D两点的对应点分别为点C',D',连接AC',BD',取AC'的中点M,连接OM.(1)如图2,当C D''∥AB时,α=°,此时OM 和BD'之间的位置关系为;(2)画图探究线段OM和BD'之间的位置关系和数量关系,并加以证明.4.(丰台18期末27)如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角两边与BA,DA交于点M,N,与BA,DA延长线交于点E,F,连接AC.(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.图1 图227.解:(1)证明:∵AB=AD ,BC=CD ,AC=AC ,∴△ABC ≌△ADC . …1分∴∠BAC =∠DAC =45°,可证∠FAC =∠EAC =135°. ……2分又∵∠FCA =∠ECA ,∴△ACF ≌△ACE . ∴AE =AF . ……3分其他方法相应给分.(2)过点C 作CG ⊥AB 于点G ,求得AC =2.……4分∵∠FAC =∠EAC =135°,∴∠ACF +∠F =45°.又∵∠ACF +∠ACE =45°,∴∠F =∠ACE .∴△ACF ∽△AEC. ……5分 ∴ACAF AE AC =,即AF AE AC ⋅=2. ……6分 ∴2=⋅AFAE . ……7分5.(怀柔18期末27)在等腰△ABC 中,AB =AC ,将线段BA 绕点B 顺时针旋转到BD ,使BD ⊥AC 于H ,连结AD 并延长交BC 的延长线于点P .(1)依题意补全图形;(2)若∠BAC =2α,求∠BDA 的大小(用含α的式子表示);(3)小明作了点D 关于直线BC 的对称点点E ,从而用等式表示线段DP 与BC 之间的数量关系.请你用小明的思路补全图形并证明线段DP 与BC 之间的数量关系.27.解:(1)如图……………………………………………1分(2) ∵∠BAC =2α,∠AHB =90°∴∠ABH =90°-2α …………………………………………………………………………… 2分∵BA =BD∴∠BDA =45°+α………………………………………………………………………………3分(3)补全图形,如图………………4分证明过程如下:∵D 关于BC 的对称点为E ,且DE 交BP 于G∴DE ⊥BP ,DG =GE ,∠DBP =∠EBP ,BD =BE ;…………………………………………5分∵AB=AC ,∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH =90°-2α∠DBP =90°-α-(90°-2α)=α∴∠DBP =∠EBP =α∴∠BDE =2α∵AB =BD∴△ABC ≌△BDE ………………………………………………………………………………6分∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DPDE =2, ∴DP BC =2, ∴BC =2DP .………………………………………………………………………………7分6.(平谷18期末27)如图,在Rt △ABC 中,∠BAC =90°,AB=AC .在平面内任取一点D ,连结AD (AD <AB ),将线段AD 绕点A 逆时针旋转90°得到线段AE ,连结DE ,CE ,BD .(1)请根据题意补全图1;(2)猜测BD 和CE 的数量关系并证明;(3)作射线BD ,CE 交于点P ,把△ADE 绕点A 旋转,当∠EAC =90°,AB =2,AD =1时,补全图形,直接写出PB 的长.27.解:(1)如图 (1)B 图1 B 备用图(2)BD 和CE 的数量是:BD =CE ; (2)∵∠DAB +∠BAE =∠CAE +∠BAE =90°,∴∠DAB=∠CAE . (3)∵AD=AE ,AB=AC ,∴△ABD ≌△ACE .∴BD =CE . (4)(3)PB (7)7.(密云18期末27)如图,已知Rt ABC ∆中,90ACB ∠=︒,AC=BC ,D 是线段AB 上的一点(不与A 、B 重合). 过点B 作BE ⊥CD ,垂足为E.将线段CE 绕点C 顺时针旋转90︒,得到线段CF ,连结EF.设BCE ∠度数为α.(1)①补全图形; ②试用含α的代数式表示CDA ∠.(2)若2EF AB = ,求α的大小. (3)直接写出线段AB 、BE 、CF 之间的数量关系.27.(1)①补全图形.……………………………..1分②45α︒+ ……………………………..3分(2)在FCE ∆和ACB ∆中,45CFE CAB ∠=∠=︒ ,90FCE ACB ∠=∠=︒∴ FCE ∆∽ ACB ∆∴CF EF AC AB =EF AB =∴CF AC = ………………………………..5分 连结FA.90,ECB 90FCA ACE ACE ∠=︒-∠∠=︒-∠∴ECB FCA ∠=∠=α在Rt CFA ∆中,90CFA ∠=︒,cos FCA ∠= ∴30FCA ∠=︒即30α=︒. ………………………………6分(3)22222AB CF BE =+ …………………………………………8分8.(石景山18期末27)在正方形ABCD中,点P在射线AC上,作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP.(1)当点P在线段AC上时,如图1.①依题意补全图1;②若EQ=BP,则∠PBE的度数为,并证明;(2)当点P在线段AC的延长线上时,如图2.若EQ=BP,正方形ABCD的边长为1,请写出求BE长的思路.(可以不写出计算结果)27.(本小题满分7分)(1)解:①正确作图………………………1分②45°………………………2分连接PD,PE易证△CPD≌△CPB∴DP=BP,∠CDP=∠CBP∵P、Q关于直线CD对称∴EQ=EP∵EQ=BP∴DP=EP∴∠C D P=∠D E P………………………………………………3分∵∠CEP+∠DEP=180°∴∠CEP+∠CBP=180°∵∠BCD=90°∴∠BPE=90°∵BP=EP∴∠PBE=45°.…………………………………………………………4分(2)解:连接PD,PE易证△CPD≌△CPB∴DP=BP,∠1=∠2∵P、Q关于直线CD对称,∴EQ=EP,∠3=∠4∵EQ=BP,∴DP=EP∴∠3=∠1,∴∠3=∠2∴∠5=∠BCE=90°∵BP=EP,∴∠PEB=45°∴∠3=∠4=22.5°,在△BCE中,已知∠4=22.5°,BC=1,可求BE长.……………7分9.(东城18期末27)如图1,在△ABC中,∠ACB=90°,AC=2,BC=B为圆心,'⊥,使点P'落在直线BC的P为B上的动点,连接PC,作P C PC'=BP ,AP'.上方,且满足:P C PC(1)求∠BAC的度数,并证明△AP C'∽△BPC;(2)若点P在AB上时,①在图2中画出△AP’C;②连接BP',求BP'的长;图1 图2(3)点P在运动过程中,BP'是否有最大值或最小值?若有,请直接写出BP'取得最大值或最小值时∠PBC的度数;若没有,请说明理由.备用图10.(顺义18期末27)综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB= ;(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.27.(1)AB ;……………………….2分(2)解:过点E 作横线的垂线,交l 1,l 2于点M ,N ,……………………………..….3分∴∠DME =∠EDF = 90°,∵∠DEF =90°,∴∠2+∠3=90°,∵∠1+∠3=90°,∴∠1=∠2,∴△DME ∽△ENF ,………….…….4分 ∴DM ME DE EN NF EF==, ∵EF =2DE , ∴12DM ME DE EN NF EF ===, ∵ME =2,EN =3,∴NF =4,DM =1.5,根据勾股定理得DE =2.5,EF =5,DF =……………………….5分 (3)EG=2.5.…………………………………………………………..…….7分11.(门头沟18期末27)如图1有两条长度相等的相交线段AB 、CD ,它们相交的锐角中有一个角为60°,为了探究AD 、CB 与CD (或AB )之间的关系,小亮进行了如下尝试:(1)在其他条件不变的情况下使得AD BC ∥,如图2,将线段AB 沿AD 方向平移AD 的长度,得到线段DE ,然后联结BE ,进而利用所学知识得到AD 、CB 与CD (或AB )之间的关系:____________________;(直接写出结果)(2)根据小亮的经验,请对图27-1的情况(AD 与CB 不平行)进行尝试,写出AD 、CB 与CD (或AB )之间的关系,并进行证明;图1 图2(3)综合(1)、(2)的证明结果,请写出完整的结论: __________________________.27.(本小题满分7分)(1) AD CB AB += ……………………………………………1分(2)补全图形正确 ………………………………………2分结论:AD CB AB +>………………………………………3分理由:如图:将线段AB 沿AD 方向平移AD 的长度,得到线段DE ,联结BE 、CE ,且可得AB DE ∥且AB DE =∴四边形A 、B 、E 、D 是平行四边形………………………4分∴AD BE =∵AB CD =∴DE CD =∵AB DE ∥,60AOD ∠=︒∴DCE △是等边三角形……………………………………5分∴CE AB =由于AD 与CB 不平行,所以C 、B 、E 构成三角形∴BE CB CE +>……………………………………………6分∴AD CB AB +>(3)AD CB AB +≥ …………………………………………7分12.(通州18期末24)如图1,在矩形ABCD 中,点E 为AD 边中点,点F 为BC 边中点;点G ,H 为AB 边三等分点,I ,J 为CD 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形GKLH 的面积与图3中四边形KPOL 的面积相等吗?(1)小瑞的探究过程如下在图2中,小瑞发现, ABCD G KLH S S _______=;在图3中,小瑞对四边形KPOL 面积的探究如下. 请你将小瑞的思路填写完整: 设a S DEP =△,b S AKG =△∵AF EC ∥∴DAK DEP ∽△△,且相似比为2:1,得到a S DAK 4=△∵BI GD ∥∴ABM AGK ∽△△,且相似比为3:1,得到b S ABM 9=△又∵ABCD DAG S b a S 614=+=△,ABCD ABF S a b S 419=+=△ ∴a b b a S ABCD 436624+=+=∴b a ____=,b S ABCD _____=,b S KPOL _____=∴ABCD KPO L S S _____=,则G KLH KPO L S S ____(填写“>”,“<”或“=”)(2)小瑞又按照图4的方式连接矩形ABCD 对边上的点.则ABCD ANML S S _____=.13.(海淀18期末28)在△ABC 中,∠A =90°,AB =AC .(1)如图1,△ABC 的角平分线BD ,CE 交于点Q ,请判断“QB =”是否正确:_______(填“是”或“否”);(2)点P 是△ABC 所在平面内的一点,连接P A ,PB ,且PB =A .①如图2,点P 在△ABC 内,∠ABP =30°,求∠P AB 的大小;②如图3,点P 在△ABC 外,连接PC ,设∠APC =α,∠BPC =β,用等式表示α,β之间的数量关系,并证明你的结论.图1 图2图3 28.解:(1)否. ………………1分(2)① 作PD ⊥AB 于D ,则∠PDB =∠PDA =90°,∵ ∠ABP =30°,∴ 12PD BP =. ………………2分∵ PB =,∴ 2PD PA =.∴ sin 2PD PAB PA ∠==. 由∠P AB 是锐角,得∠P AB =45°. ………………3分 另证:作点P 关于直线AB 的对称点'P ,连接',',B P P A P P ,则',',','P B A P B A P A B P A B B PB P A P A P∠=∠∠=∠==. ∵∠ABP =30°,∴'60P BP ∠=︒.∴△'P BP 是等边三角形.∴'P P BP =.∵PB =,∴'P P =. ………………2分 ∴222''P P PA P A =+.∴'90PAP ∠=︒.∴45PAB ∠=︒. ………………3分② 45αβ+=︒,证明如下: ………………4分作AD ⊥AP ,并取AD =AP ,连接DC ,DP .∴ ∠DAP =90°.∵ ∠BAC =90°,∴ ∠BAC +∠CAP =∠DAP +∠CAP ,即 ∠BAP =∠CAD .∵ AB =AC ,AD =AP ,∴ △BAP ≌△CAD .∴ ∠1=∠2,PB =CD . ………………5分∵ ∠DAP =90°,AD =AP ,∴ PD =,∠ADP =∠APD =45°.∵ PB =,∴ PD =PB =CD .∴ ∠DCP =∠DPC .∵ ∠APC =α,∠BPC =β, ∴ 45DPC α∠=+︒,12αβ∠=∠=-. ∴ 31802902DPC α∠=︒-∠=︒-. ∴ 139045ADP αβ∠=∠+∠=︒--=︒. ∴ 45αβ+=︒. ………………7分。
北京初三(上)期末数学各区试题汇图形变换

●知识模块3:图形变换1.(东城18期末6)△DEF 和△ABC 是位似图形,点O 是位似中心,点D,E,F 分别是OA ,O B,OC 的中点,若△D EF的面积是2,则△AB C的面积是( ) A.2 B .4 ﻩC.6 D.8 2.(海淀18期末4)如图,将△ABC 绕点A 逆时针旋转100°,得到△ADE .若点D 在线段BC 的延长线上,则B ∠的大小为( )A .30° ﻩﻩﻩB.40° C .50°ﻩ ﻩD.60°3(海淀18期末6)6.如图,在平面直角坐标系xO y中,点A 从(3,4)出发,绕点O顺时针旋转一周,则点A 不.经过( )A.点M B .点N C.点P ﻩD .点Q4.(昌平18期末6)如图,将ΔAB C绕点C顺时针旋转,点B 的对应点为点E ,点A 的对应点为点D ,当点E恰好落在边AC 上时,连接AD ,若∠ACB=30°,则∠DAC 的度数是( )A .60° ﻩB.65°C.70° ﻩD.75°5.(门头沟18期末10)已知线段5AB cm =,将线段AB 以点A 为旋转中心,逆时针旋转90°得到线段'AB ,则点B 、点'B 的距离为__________. 6.(朝阳18期末10)如图,把△AB C绕着点A顺时针方向旋转,得到△A B 'C ',点C恰好在B 'C '上,旋转角为α,则∠C '的度数为 (用含α的式子表示). 7.(昌平18期末10)如图,在平面直角坐标系xO y中,点A ,点B 的坐标分别为(0,2),(1-,0),将线段AB 沿x 轴的正方向平移,若点B 的对应点的坐标为'B (2,0),则点A 的对应点'A 的坐标为 . ﻬED C BAC'B'CEB C DAxy–1–2–3–4–5–6123456–1–2–3–4–512345PQN M AO8.(昌平18期末14)如图,在直角三角形ABC 中,∠C =90°,BC =6,AC =8,点D 是AC 边上一点,将△BCD 沿BD 折叠,使点C落在AB边的E 点,那么AE 的长度是 .9.(昌平18期末15)如图,在平面直角坐标系xOy 中,△CDE 可以看作是△A OB 经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△A OB得到△CDE 的过程:_________________________________________________________________________________________.10.(朝阳18期末14) 如图,在平面直角坐标系中,△C OD 可以看作是△A OB 经过若干次图形的变化(平移、轴对称、旋转、位似)得到的,写出一种由△AOB 得到△C OD 的过程:_________________________________________________________________________. 11.(石景山18期末15)如图,在平面直角坐标系x Oy 中,△ABC 经过若干次图形的变化(平移、轴对称、旋转)得到△DEF ,写出一种由△AB C得到△DEF 的过程:________________ __________________________________________________.12.(平谷18期末15)如图,在平面直角坐标系xO y中,△DEF 可以看作是△ABC 经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC 得到△DEF 的过程:____________________________________________________________________________.yxD CBA7654321-7-6-5-3-2-19765432-48O 1xy FE DC BA 123-1-2-3-4-3-2-1321Oy45613.(门头沟18期末15)如图,在平面直角坐标系xOy中,图形L2可以看作是由图形L1经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由图形L1得到图形L2的过程________________________________________________________________________________.14.(燕山18期末18)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).(1)在图1中画出△ABC关于y轴对称的△A1B1C1,直接写出点C的对应点C1的坐标.(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可).直接写出点C的对应点C2的坐标.15.(朝阳18期末19)如图,在平面直角坐标系xOy中,点A(3,3),点B(4,0),点C(0,﹣1).(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A′B′C;(2)在(1)中的条件下,①点A经过的路径的长为(结果保留π);②写出点B′的坐标为.16.(东城18期末22)如图,在Rt△ABC中,∠A=90°,∠C=30°.将△ABC绕点B顺时针旋转60°得到△A BC'', 其中点A', C'分别是点A,C的对应点.ﻩ(1)作出△A BC''(要求尺规作图,不写作法,保留作图痕迹);ﻩ(2)连接AA',求∠C A A''的度数.ﻬ17.(西城18期末20)在△ABC中,AB=AC=2,45BAC∠=︒.将△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,B,C两点的对应点分别为点D,E,BD,CE所在直线交于点F.(1)当△ABC旋转到图1位置时,∠CAD= (用α的代数式表示),BFC∠的度数为︒;AA'xy-1-11BCAO1(2)当 =45时,在图2中画出△ADE,并求此时点A到直线BE的距离.图1 图2。
北京市西城区2018届九年级上期末考试数学试题有答案(精)

北京市西城区2017-2018学年度第一学期期末试卷九年级数学 2018.1一、选择题(本题共16分,每小题2分)1. 如图,在Rt △ABC 中,∠ACB =90°,如果AC =3,AB =5,那么sin B 等于( ).A .35B . 45C . 34D . 432.点1(1,)A y ,2(3,)B y 是反比例函数6y x=-图象上的两点,那么1y ,2y 的大小关系是( ). A .12y y > B .12y y = C .12y y < D .不能确定3.抛物线2(4)5y x =--的顶点坐标和开口方向分别是( ).A .(4,5)-,开口向上B .(4,5)-,开口向下C .(4,5)--,开口向上D .(4,5)--,开口向下4.圆心角为60︒,且半径为12的扇形的面积等于( ).A .48πB .24πC .4πD .2π5.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,如果∠ACD =34°,那么∠BAD等于( ).A .34°B .46°C .56°D .66°6.如果函数24y x x m =+-的图象与x 轴有公共点,那么m 的取值范围是( ). A .m ≤4 B .<4m C . m ≥4- D .>4m -7.如图,点P 在△ABC 的边AC 上,如果添加一个条件后可以得到△ABP ∽△ACB ,那么以下添加的条件中,不.正确的是( ). A .∠ABP =∠C B .∠APB =∠ABCC .2AB AP AC =⋅D .AB AC BP CB= 8.如图,抛物线32++=bx ax y (a ≠0)的对称轴为直线1x =,如果关于x 的方程082=-+bx ax (a ≠0)的一个根为4,那么该方程的另一个根为( ).A .4-B .2-C .1D . 3二、填空题(本题共16分,每小题2分)9. 抛物线23y x =+与y 轴的交点坐标为 .10. 如图,在△ABC 中,D ,E 两点分别在AB ,AC 边上,DE ∥BC ,如果3=AD ,AC =10,那么EC = .xOy 中,第一象限内的点(,)P x y与点(2,2)A 在同一个反比例函数的图象上,PC ⊥y 轴于点C ,PD ⊥x 轴于点D ,那么矩形ODPC 的面积等于 .15.如图,抛物线2 (0)y ax bx c a =++≠与y 轴交于点C ,与x 轴交于A ,B 两点,其中点B 的坐标为(4,0)B ,抛物线的对称轴交x 轴于点D ,CE ∥AB ,并与抛物线的对称轴交于点E .现有下列结论:①0a >;②0b >;③420a b c ++<;④4AD CE +=.其中所有正确结论的序号是 .16. 如图,⊙O 的半径为3,A ,P 两点在⊙O 上,点B 在⊙O 内,4tan 3APB ∠=,AB AP ⊥.如果OB ⊥OP ,那么OB 的长为 .三、解答题(本题共68分,第17-20题每小题5分,第21、22题每小题6分,第23、24题每小题5分,第25、26题每小题6分,第27、28题每小题7分)17.计算:22sin30cos 45tan60︒+︒-︒.18.如图,AB ∥CD ,AC 与BD 的交点为E ,∠ABE=∠ACB .(1)求证:△ABE ∽△ACB ;(2)如果AB=6,AE=4,求AC ,CD 的长.19.在平面直角坐标系xOy 中,抛物线1C :22y x x =-+.(1(2)将抛物线1212回答:抛物线2C 与x 轴的两交点之间的距离是抛物线1C 与x 轴的两交点之间距离的多少倍.20.在△ABC 中,AB=AC=2,45BAC ∠=︒.将△ABC 绕点A 逆时针旋转α度(0<α<180)得到△ADE ,B ,C 两点的对应点分别为点D ,E ,BD ,CE 所在直线交于点F .(1)当△ABC 旋转到图1位置时,∠CAD = (用α的代数式表示),BFC ∠的度数为 ︒;(2)当α=45时,在图2中画出△ADE ,并求此时点A 到直线BE 的距离.21.运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h (m )与它的飞行时间t (s )满足二次函数关系,t 与h 的几组对应值如下表所示.t (s )0 0.5 h (m )0 8.75 1)求h 与t 之间的函数关系式(不要求写(2)求小球飞行3 s 时的高度;(3)问:小球的飞行高度能否达到22 m ?请说明理由.22.如图,在平面直角坐标系xOy 中,双曲线k y x=(k ≠0)与直线12y x =的交点为(,1)A a -,(2,)B b 两点,双曲线上一点P 的横坐标为1,直线P A ,PB 与x 轴的交点分别为点M ,N ,连接AN .(1)直接写出a ,k 的值;(2)求证:PM=PN ,PM PN ⊥.23.如图,线段BC 长为13,以C 为顶点,CB 为一边的α∠满足5cos 13α=.锐角△ABC 的顶点A 落在α∠的另一边l 上,且 满足4sin 5A =.求△ABC 的高BD 及AB 边的长,并结合你的 计算过程画出高BD 及AB 边.(图中提供的单位长度供补全图形使用)24.如图,AB 是半圆的直径,过圆心O 作AB 的垂线,与弦AC交于点D ,点E 在OD 上,=DCE B ∠∠.(1)求证:CE 是半圆的切线;(2)若CD=10,2tan 3B =,求半圆的半径.25.已知抛物线G :221y x ax a =-+-(a 为常数).(1)当3a =时,用配方法求抛物线G 的顶点坐标;(2)若记抛物线G 的顶点坐标为(,)P p q . ①分别用含a 的代数式表示p ,q ;②请在①的基础上继续用含p 的代数式表示q ;③由①②可得,顶点P 的位置会随着a 的取值变化而变化,但点P 总落在 的图象上.A .一次函数B .反比例函数C .二次函数(3)小明想进一步对(2)中的问题进行如下改编:将(2)中的抛物线G 改为抛物线H :22y x ax N =-+(a 为常数),其中N 为含a 的代数式,从而使这个新抛物线H 满足:无论a 取何值,它的顶点总落在某个一次函数的图象上.请按照小明的改编思路,写出一个符合以上要求的新抛物线H 的函数表达式:(用含a 的代数式表示),它的顶点所在的一次函数图象的表达式y kx b =+(k ,b为常数,k ≠0)中,k= ,b= .26.在平面直角坐标系xOy 中,抛物线M :2 (0)y ax bx c a =++≠经过(1,0)A -,且顶点坐标为(0,1)B .(1)求抛物线M 的函数表达式;(2)设(,0)F t 为x 轴正半轴...上一点,将抛物线M 绕点F 旋转180°得到抛物线1M . ①抛物线1M 的顶点1B 的坐标为 ;②当抛物线1M 与线段AB 有公共点时,结合函数的图象,求t 的取值范围.27.如图1,在Rt △AOB 中,∠AOB =90°,∠OAB =30°,点C 在线段OB 上,OC =2BC ,AO 边上的一点D满足∠OCD =30°.将△OCD 绕点O 逆时针旋转α度(90°<α<180°)得到△OC D '',C ,D 两点的对应点分别为点C ',D ',连接AC ',BD ',取AC '的中点M ,连接OM .(1)如图2,当C D ''∥AB 时,α= °,此时OM 和BD '之间的位置关系为 ;(2)画图探究线段OM 和BD '之间的位置关系和数量关系,并加以证明.28.在平面直角坐标系xOy 中,A ,B 两点的坐标分别为(2,2)A ,(2,2)B -.对于给定的线段AB 及点P ,Q ,给出如下定义:若点Q 关于AB 所在直线的对称点Q '落在△ABP 的内部(不含边界),则称点Q 是点P 关于线段AB 的内称点.(1)已知点(4,1)P -.①在1(1,1)Q -,2(1,1)Q 两点中,是点P 关于线段AB 的内称点的是____________;②若点M 在直线1y x =-上,且点M 是点P 关于线段AB 的内称点,求点M 的横坐标M x 的取值范围;(2)已知点(3,3)C ,⊙C 的半径为r ,点(4,0)D ,若点E 是点D 关于线段AB 的内称点,且满足直线DE与⊙C 相切,求半径r 的取值范围.。
北京市各区2018届九年级上期末数学试卷分类汇编:尺规作图

尺规作图1.(昌平18期末16)阅读以下作图过程:第一步:在数轴上,点O表示数0,点A表示数1,点B表示数5,以AB为直径作半圆;第二步:以B点为圆心,1为半径作弧交半圆于点C(如图);第三步:以A点为圆心,AC为半径作弧交数轴的正半轴于点M.请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M表示的数为________.2.(门头沟18期末16)下面是“作已知圆的内接正方形”的尺规作图过程.请回答:该尺规作图的依据是______________________________________________.到线段两端距离相等的点在这条线段的中垂线上;两点确定一条直线;互相垂直的直径将圆四等分;(圆内接正多边形定义)3.(朝阳18期末16)下面是“作顶角为120°的等腰三角形的外接圆”的尺规作图过程.请回答:该尺规作图的依据是_____________________________________________.4.(石景山18期末16)石景山区八角北路有一块三角形空地(如图1)准备绿化,拟从点A出发,将△ABC分成面积相等的三个三角形,栽种三种不同的花草.下面是小美的设计(如图2).请回答,CACCACABCSSS2211∆∆∆==成立的理由是:①;②.16.①两条直线被一组平行线所截,所得的对应线段成比例;②等底同高的三角形面积相等5.(燕山18期末16)16.在数学课上,老师提出利用尺规作图完成下面问题:作法:(1)作射线BM;(2)在射线BM上顺次截取BB1=B1B2=B2B3;(3)连接B3C,分别过B1、B2作B1C1∥B2C2∥B3C,交BC于点C1、C2;(4)连接AC1、AC2.则CACCACABCSSS2211∆∆∆==.已知:∠ ACB 是△ ABC 的一个内角. 求作:∠ APB= ∠ ACB .小路的作法如下:n④在弧 ACB 上取一点 P ,连结 AP ,BP . m所以∠ APB= ∠ ACB .老师说:“小路的作法正确.”请回答:(1)点 O 为△ ABC 外接圆圆心(即 OA=OB=OC )的依据是;(2)∠ APB= ∠ ACB 的依据是.16. (1)线段垂直平分线上的点与这条线段两个端点的距离相等;(2)同弧所对的圆周角相等.6.(怀柔18期末16)阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:小明的作法如下:请回答:这样做的依据是 .16.圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线.7.(丰台18期末16、密云18期末16)下面是“过圆外一点作圆的切线”的尺规作图过程.请回答以下问题:(1)连接OA ,OB ,可证∠OAP =∠OBP = 90°,理由是 ; (2)直线P A ,PB 是⊙O 的切线,依据是 .16.直径所对的圆周角是直角;经过半径的外端,并且垂直于这条半径的直线是圆的切线.8.(大兴18期末16)下面是“作出所在的圆”的尺规作图过程.已知:⊙O 和⊙O 外一点P .求作:过点P 的⊙O 的切线. 作法:如图, (1)连接OP ;(2)分别以点O 和点P 为圆心,大于 12OP 的长为 半径作弧,两弧相交于M ,N 两点; (3)作直线MN ,交OP 于点C ;(4)以点C 为圆心,CO 的长为半径作圆,交⊙O 于A ,B 两点; (5)作直线P A ,PB .直线P A ,PB 即为所求作⊙O 的切线.如图,①取线段OB 的中点M ;以M 为圆心,MO 为 半径作⊙M ,与边AB 交于点C ; ②以O 为圆心,OC 为半径作⊙O ; 所以,⊙O 就是所求作的圆.请回答:该尺规作图的依据是 .16. 不在同一直线上的三个点确定一个圆;圆是到定点的距离等于定长的点的集合;线段垂直平分线上的点到线段两个端点的距离相等.9.(通州18期末16)16. 阅读下面材料:在数学课上,老师提出如下问题: 小霞的作法如下:尺规作图:作已知角的角平分线.已知:如图,已知BAC ∠.求作: BAC ∠的角平分线AP .已知:.求作:所在的圆. 作法:如图,(1)在上任取三个点D ,C ,E ;(2)连接DC ,EC ;(3)分别作DC 和EC 的垂直平分线,两垂直平分线的交点为点O. (4)以 O 为圆心,OC 长为半径作圆,所以⊙O 即为所求作的所在的圆..老师说:“小霞的作法正确.”请回答:小霞的作图依据是.10.(海淀18期末16、平谷18期末16)下面是“作一个30°角”的尺规作图过程.,作射线AD.请回答:该尺规作图的依据是.16.三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,一条弧所对的圆周角是它所对圆心角的一半;或:直径所对的圆周角为直角,三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,直角三角形两个锐角互余;或:直径所对的圆周角为直角,1sin2A=,A∠为锐角,30A∠=︒.(1)如图,在平面内任取一点O;(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;(3)连接DE,过点O作射线OP垂直线段DE,交⊙O于点P;(4)连接AP.所以射线AP为所求.11.(昌平18期末21)尺规作图:如图,AC为⊙O的直径.(1)求作:⊙O的内接正方形ABCD.(要求:不写作法,保留作图痕迹);(2)当直径AC=4时,求这个正方形的边长.21.(1)如图所示…………………… 2分(2)解:∵直径AC =4,∴OA =OB=2.………………………3分∵正方形ABCD为⊙O的内接正方形,∴∠AOB=90°,………………………4分∴AB== 5分.。
2017-2018北京市各区初三数学期末考试分类汇编-提升题,推荐文档

lD CNM B 2018.1 北京市各区期末考试数学试题提升题部分2018.1 石景ft区7.如图,将函数y =1 (x - 2)23+ 1 的图象沿y 轴向上平移得到新函数图象,其中原函数图象上的两点A(1, m) 、B(4, n) 平移后对应新函数图象上的点分别为点A' 、B' .若阴影部分的面积为6,则新函数的表达式为(A)y =1 (x - 2)2 + 23(C)y=1(x-2)2-13(B)y =1 (x - 2)2 + 33(D)y =1 (x - 2)2 - 33第7 题8.如图,点M 为□ABCD 的边AB 上一动点,过点M作直线l 垂直于AB,且直线l 与□ABCD 的另一边交于点N.当点M 从A→B 匀速运动时,设点M 的运动时间为t,△AMN 的面积为S,能大致反A映S 与t 函数关系的图象是第8 题(A)(B)(C)(D)27.在正方形ABCD 中,点P 在射线AC 上,作点P 关于直线CD 的对称点Q,作射线BQ交射线DC 于点E,连接BP.(1)当点P 在线段AC 上时,如图1.①依题意补全图1;②若EQ=BP,则∠PBE 的度数为,并证明;(2)当点P 在线段AC 的延长线上时,如图2.若EQ=BP,正方形ABCD 的边长为1,请写出求BE 长的思路.(可以不写出计算结果)23图1 图228.在平面直角坐标系xOy 中,点P 的坐标为(x1, y1) ,点Q 的坐标为(x2 , y2 ),且x1≠x2,y1≠y2,若PQ 为某个等腰三角形的腰,且该等腰三角形的底边与x 轴平行,则称该等腰三角形为点P,Q 的“相关等腰三角形”.下图为点P,Q 的“相关等腰三角形” 的示意图.(1)已知点A 的坐标为(0,1) ,点B 的坐标为(- 3,0) ,则点A,B 的“相关等腰三角形”的顶角为°;(2)若点C 的坐标为(0, 3) ,点D 在直线y = 4 上,且C,D 的“相关等腰三角形”为等边三角形,求直线CD 的表达式;(3)⊙O 的半径为,点N 在双曲线y =-3x上.若在⊙O 上存在一点M,使得点M、N 的“相关等腰三角形”为直角三角形,直接写出点N 的横坐标x N的取值范围.2018 门头沟区27.如图27-1 有两条长度相等的相交线段AB、CD,它们相交的锐角中有一个角为60°,为了探究AD、CB 与CD(或AB)之间的关系,小亮进行了如下尝试:(1)在其他条件不变的情况下使得AD∥BC ,如图27-2,将线段AB 沿AD 方向平移AD 的长度,得到线段DE,然后联结BE,进而利用所学知识得到AD、CB 与CD(或AB)之间的关系:;(直接写出结果)(2)根据小亮的经验,请对图27-1 的情况(AD 与CB 不平行)进行尝试,写出AD、CB 与CD(或AB)之间的关系,并进行证明;图27-1 图27-2(3)综合(1)、(2)的证明结果,请写出完整的结论: .28.以点P 为端点竖直向下的一条射线PN ,以它为对称轴向左右对称摆动形成了射线PN1 ,PN2 ,我们规定:∠N1PN2 为点P 的“摇摆角”,射线PN 摇摆扫过的区域叫作点P的“摇摆区域”(含PN1 ,PN2 ).在平面直角坐标系xOy 中,点P(2 , 3) .(1)当点P 的摇摆角为60︒时,请判断O(0 , 0) 、A(1 , 2) 、B(2 , 1) 、C(2 +P的摇摆区域内的点是(填写字母即可);, 0) 属于点(2)如果过点D(1 , 0) ,点E(5 , 0) 的线段完全在点P 的摇摆区域内,那么点P 的摇摆角至少为°;(3)⊙W 的圆心坐标为(a , 0) ,半径为1 ,如果⊙W 上的所有点都在点P 的摇摆角为60︒时的摇摆区域内,求a 的取值范围.备用图352018 丰台区27. 如图,∠BAD=90°,AB=AD ,CB=CD ,一个以点 C 为顶点的 45°角绕点 C 旋转,角的两边与 BA ,DA 交于点 M ,N ,与 BA ,DA 的延长线交于点 E ,F ,连接 AC .(1) 在∠FCE 旋转的过程中,当∠FCA =∠ECA 时,如图 1,求证:AE =AF ; (2) 在∠FCE 旋转的过程中,当∠FCA ≠∠ECA 时,如图 2,如果∠B=30°,CB=2,用等式表示线段 AE ,AF 之间的数量关系,并证明.FEA MNBCD图 128. 对于平面直角坐标系 xOy 中的点 P 和⊙C ,给出如下定义:如果⊙C 的半径为 r ,⊙C外一点 P 到⊙C 的切线长小于或等于 2r ,那么点 P 叫做⊙C 的“离心点”.(1) 当⊙O 的半径为 1 时,①在点 P ( 1 , 3 ),P (0,-2),P (,0)中,⊙O 的“离心点”是12 22 3;②点 P (m ,n )在直线 y = -x + 3 上,且点 P 是⊙O 的“离心点”,求点 P 横坐标 m 的取值范围;(2)⊙C 的圆心 C 在 y 轴上,半径为 2,直线 y = - 1x + 1 与 x 轴、y 轴分别交于点2 A ,B . 如果线段 AB 上的所有点都是⊙C 的“离心点”,请直接写出圆心 C 纵坐标的取值范围.EF AMN B图 2C D2018 顺义区27.综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB= ;(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF 的长;(3)在(2)的条件下,若橫格纸上过点E 的横线与DF 相交于点G,直接写出EG 的长.A D BE28. 在平面直角坐标系 xOy 中,抛物线 y =(1) 求 b 的值;1x 29+ bx 经过点 A (-3,4).(2) 过点 A 作 x 轴的平行线交抛物线于另一点 B ,在直线 AB 上任取一点 P ,作点 A 关于直线 OP 的对称点 C ;①当点 C 恰巧落在 x 轴时,求直线 OP 的表达式; ②连结 BC ,求 BC 的最小值.2018 密云区27. 如图,已知 Rt ∆ABC 中, ∠ACB = 90︒ ,AC=BC ,D 是线段 AB 上的一点(不与 A 、B重合). 过点 B 作 BE ⊥CD ,垂足为 E.将线段 CE 绕点 C 顺时针旋转90︒ ,得到线段CF ,连结 EF.设∠BCE 度数为. (1) ①补全图形.②试用含的代数式表示∠CDA .CEF3 (2) 若=,求的大小.AB2(3) 直接写出线段 AB 、BE 、CF 之间的数量关系.y54321-5 -4 -3 -2 -1O 1 2-13 4 5 x-2-3-4-5y54321-5 -4 -3 -2 -1O 1 2-13 4 5 x-2-3-4-528.已知在平面直角坐标系xOy 中的点P 和图形G,给出如下的定义:若在图形G 上存在一点Q ,使得P、Q 之间的距离等于1,则称P 为图形G 的关联点.(1)当 O 的半径为 1 时,1①点P1(2, 0) , P2(1, 3) , P3(0, 3) 中, O 的关联点有.②直线经过(0,1)点,且与y 轴垂直,点 P 在直线上.若 P 是 O 的关联点,求点 P 的横坐标x 的取值范围.(2)已知正方形 ABCD 的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径r 的取值范围.备用图备用图2018 大兴区27.已知:如图,AB 为半圆O 的直径,C 是半圆O 上一点,过点C 作AB 的平行线交⊙O于点E,连接AC、BC、AE,EB. 过点C 作CG⊥AB 于点G,交 EB 于点H.(1)求证:∠BCG=∠E BG;(2)若sin ∠CAB= ,求EC的值.5 GB28.一般地,我们把半径为 1 的圆叫做单位圆,在平面直角坐标系xOy中,设单位圆的圆心与坐标原点 O 重合,则单位圆与x轴的交点分别为(1,0),(-1,0),与y轴的交点分别为(0,1),(0,-1).在平面直角坐标系xOy 中,设锐角的顶点与坐标原点 O 重合,的一边与x 轴的正半轴重合,另一边与单位圆交于点P (x1 , y1 ) ,且点 P 在第一象限.(1)x1=_ (用含的式子表示);y1= _ (用含的式子表示) ;(2)将射线OP 绕坐标原点O 按逆时针方向旋转90︒后与单位圆交于点Q(x2 , y2 ) .5①判断y1与x2数量关系, 并证明;y1 y2的取值范围是:_ . ②“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
北京市西城区2018届九年级数学上学期期末考试试题

北京市西城区2018届九年级数学上学期期末考试试题一、选择题(本题共16分,每小题2分)1. 如图,在Rt △ABC 中,∠ACB =90°,如果AC =3,AB =5,那么sin B 等于( ).A.35B. 45C. 34D. 432.点1(1,)A y ,2(3,)B y 是反比例函数6y x =-图象上的两点,那么1y ,2y 的大小关系是().A.12y y >B.12y y =C.12y y <D.不能确定3.抛物线2(4)5y x =--的顶点坐标和开口方向分别是( ).A.(4,5)-,开口向上B.(4,5)-,开口向下C.(4,5)--,开口向上D.(4,5)--,开口向下4.圆心角为60︒,且半径为12的扇形的面积等于( ).A.48πB.24πC.4πD.2π5.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,如果∠ACD =34°,那么∠BAD等于( ).A .34°B .46°C .56°D .66°6.如果函数24y x x m =+-的图象与x 轴有公共点,那么m 的取值范围是( ).A.m ≤4B.<4mC. m ≥4-D.>4m -7.如图,点P 在△ABC 的边AC 上,如果添加一个条件后可以得到△ABP ∽△ACB ,那么以下添加的条件中,不.正确的是( ).A .∠ABP =∠CB .∠APB =∠ABCC .2AB AP AC =⋅D .ABACBP CB =8.如图,抛物线32++=bx ax y (a ≠0)的对称轴为直线1x =,如果关于x 的方程082=-+bx ax (a ≠0)的一个根为4,那么该方程的另一个根为( ).A .4-B .2-C .1D . 3二、填空题(本题共16分,每小题2分)9. 抛物线23y x =+与y 轴的交点坐标为 .10. 如图,在△ABC 中,D ,E 两点分别在AB ,AC 边上,DE ∥BC ,如果23=DB AD ,AC =10,那么EC = .11. 如图,在平面直角坐标系xOy 中,第一象限内的点(,)P x y与点(2,2)A 在同一个反比例函数的图象上,PC ⊥y 轴于点C ,PD ⊥x 轴于点D ,那么矩形ODPC 的面积等于 .12.如图,直线1y kx n =+(k ≠0)与抛物22y ax bx c =++(a ≠0)分别交于(1,0)A -,(2,3)B -两点,那么当12y y >时,x 的取值范围是 .13. 如图,⊙O 的半径等于4,如果弦AB 所对的圆心角等于120︒,那么圆心O 到弦AB 的距离等于 .14.2017年9月热播的专题片《辉煌中国——圆梦工程》展示的中国桥、中国路等超级工程展现了中国现代化进程中的伟大成就,大家纷纷点赞“厉害了,我的国!”片中提到我国已成为拥有斜拉桥最多的国家,世界前十座斜拉桥中,中国占七座,其中苏通长江大桥(如图1所示)主桥的主跨长度在世界斜拉桥中排在前列.在图2的主桥示意图中,两座索塔及索塔两侧的斜拉索对称分布,大桥主跨BD 的中点为E ,最长的斜拉索CE 长577 m ,记CE 与大桥主梁所夹的锐角CED ∠为α,那么用CE 的长和α的三角函数表示主跨BD 长的表达式应为BD = (m) .315.如图,抛物线2(0)y ax bx c a =++≠与y 轴交于点C ,与x 轴交于A ,B 两点,其中点B 的坐标为(4,0)B ,抛物线的对称轴交 x 轴于点D ,CE ∥AB ,并与抛物线的对称轴交于点E .现有下列结论:①0a >;②0b >;③420a b c ++<;④4AD CE +=.其中所有正确结论的序号是 .16. 如图,⊙O 的半径为3,A ,P 两点在⊙O 上,点B 在⊙O内,4tan 3APB ∠=,AB AP ⊥.如果OB ⊥OP ,那么OB 的长为 .三、解答题(本题共68分,第17-20题每小题5分,第21、22题每小题6分,第23、24题每小题5分,第25、26题每小题6分,第27、28题每小题7分)17.计算:22sin30cos 45tan60︒+︒-︒.18.如图,AB ∥CD ,AC 与BD 的交点为E ,∠ABE=∠ACB .(1)求证:△ABE ∽△ACB ;(2)如果AB=6,AE=4,求AC ,CD 的长.19.在平面直角坐标系xOy 中,抛物线1C :22y x x =-+.(1)补全表格:(2)将抛物线1C 向上平移3个单位得到抛物线2C ,请画出抛物线1C ,2C ,并直接回答:抛物线2C 与x 轴的两交点之间的距离是抛物线1C 与x 轴的两交点之间距离的多少倍.20.在△ABC 中,AB=AC=2,45BAC ∠=︒.将△ABC 绕点A 逆时针旋转α度(0<α<180)得到△ADE ,B ,C 两点的对应点分别为点D ,E ,BD ,CE 所在直线交于点F .(1)当△ABC 旋转到图1位置时,∠CAD = (用α的代数式表示),BFC ∠的 度数为 ︒;(2)当α=45时,在图2中画出△ADE ,并求此时点A 到直线BE 的距离.21.运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h (m )与它的飞行时间t (s )满足二次函数关系,t 与h 的几组对应值如下表所示.5(1)求h 与t 之间的函数关系式(不要求写t 的取值范围);(2)求小球飞行3 s 时的高度;(3)问:小球的飞行高度能否达到22 m ?请说明理由.22.如图,在平面直角坐标系xOy 中,双曲线k y x=(k ≠0)与直线12y x =的交点为(,1)A a -,(2,)B b 两点,双曲线上一点P 的横坐标为1,直线PA ,PB 与x 轴的交点分别为点M ,N ,连接AN .(1)直接写出a ,k 的值;(2)求证:PM=PN ,PM PN ⊥.23.如图,线段BC 长为13,以C 为顶点,CB 为一边的α∠满足5cos 13α=.锐角△ABC 的顶点A 落在α∠的另一边l 上,且 满足4sin 5A =.求△ABC 的高BD 及AB 边的长,并结合你的 计算过程画出高BD 及AB 边.(图中提供的单位长度供补全图形使用)24.如图,AB 是半圆的直径,过圆心O 作AB 的垂线,与弦AC 的延长线交于点D ,点E 在OD 上,=DCE B ∠∠.(1)求证:CE是半圆的切线;(2)若CD=10,2tan 3B =,求半圆的半径.25.已知抛物线G:221y x ax a =-+-(a 为常数).(1)当3a =时,用配方法求抛物线G 的顶点坐标;(2)若记抛物线G 的顶点坐标为(,)P p q .①分别用含a 的代数式表示p ,q ;②请在①的基础上继续用含p 的代数式表示q ;③由①②可得,顶点P 的位置会随着a 的取值变化而变化,但点P 总落在 的图象上.A .一次函数B .反比例函数C .二次函数(3)小明想进一步对(2)中的问题进行如下改编:将(2)中的抛物线G 改为抛物线H :22y x ax N =-+(a 为常数),其中N 为含a 的代数式,从而使这个新抛物线H 满足:无论a 取何值,它的顶点总落在某个一次函数的图象上.请按照小明的改编思路,写出一个符合以上要求的新抛物线H 的函数表达式: (用含a 的代数式表示),它的顶点所在的一次函数图象的表达式y kx b=+(k ,b 为常数,k ≠0)中,k= ,b= .26.在平面直角坐标系xOy 中,抛物线M :2(0)y ax bx c a =++≠经过(1,0)A -,且顶点坐标为(0,1)B .(1)求抛物线M 的函数表达式;(2)设(,0)F t 为x 轴正半轴...上一点,将抛物线M 绕点F 旋转180°得到抛物线1M . ①抛物线1M 的顶点1B 的坐标为 ;②当抛物线1M 与线段AB 有公共点时,结合函数的图象,求t 的取值范围.727.如图1,在Rt △AOB 中,∠AOB =90°,∠OAB =30°,点C 在线段OB 上,OC =2BC ,AO 边上的一点D 满足∠OCD =30°.将△OCD 绕点O 逆时针旋转α度(90°<α<180°)得到△OC D '',C ,D 两点的对应点分别为点C ',D ',连接AC ',BD ',取AC '的中点M ,连接OM .(1)如图2,当C D ''∥AB 时,α= °,此时OM 和BD '之间的位置关系为 ;(2)画图探究线段OM 和BD '之间的位置关系和数量关系,并加以证明.28.在平面直角坐标系xOy 中,A ,B 两点的坐标分别为(2,2)A ,(2,2)B -.对于给定的线段AB 及点P ,Q ,给出如下定义:若点Q 关于AB 所在直线的对称点Q '落在△ABP 的内部(不含边界),则称点Q 是点P 关于线段AB 的内称点.(1)已知点(4,1)P -.①在1(1,1)Q -,2(1,1)Q 两点中,是点P 关于线段AB 的内称点的是____________;②若点M 在直线1y x =-上,且点M 是点P 关于线段AB 的内称点,求点M 的横坐标M x 的取值范围;(2)已知点(3,3)C ,⊙C 的半径为r ,点(4,0)D ,若点E 是点D 关于线段AB 的内称点,且满足直线DE 与⊙C 相切,求半径r 的取值范围.91113。
2018年北京市初三数学二模分类汇编-第7讲:图形变换
第7讲图形变换【2018·昌平二模】1.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种花纹,构成种类繁多的优美图案.下列表示我国古代窗棂样式结构图案中,是中心对称图形但不是轴对称图形的是()A.B.C.D.【答案】D【2018·朝阳二模】2.中国传统扇文化有着深厚的底蕴,下列扇面图形既是轴对称图形又是中心对称图形的是【答案】C【2018·丰台二模】3.为丰富国民精神文化生活,提升文化素养,全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方,更是成为人们休闲的好去处. 下列图书馆标志的图形中不.是.轴对称图形的是(A)(B)(C)(D)【答案】B【2018·石景山二模】4.下列是一组logo设计的图片,其中不是..中心对称图形的是(A)(B)(C)(D)【答案】A【2018·东城二模】5. 如图,在平面直角坐标系xOy 中,点A ,P 分别在x 轴、 y 轴上,30APO ∠=︒ . 先将线段PA 沿y 轴翻折得到线段PB ,再将线段PA 绕点P 顺时针旋转30°得到线段PC ,连接BC . 若点【2018·丰台二模】6.如图,在平面直角坐标系xOy 中,正方形OABC 的边长为1,点D ,E 分别在OA ,OC 上,OD = CE ,△OCD 可以看作是△CBE 经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△CBE 得到△OCD 的过程:.【答案】将△CBE 绕点C 逆时针旋转90°,再向下平移1个单位得到△OCD (答案不唯一);【2018·石景山二模】7.如图,在平面直角坐标系xOy 中,点A 、B 的坐标分别为(-4,1)、(-1,3),在经过两次变化(平移、轴对称、旋转)得到对应点A ''、B ''的坐标分别为(1,0)、(3,-3),则由线段AB 得到线段A B ''的过程是: ,由线段A B ''得到线段A B ''''【答案】向右平移4个单位长度;绕原点顺时针旋转90︒.【2018·朝阳二模】8.如图,在平面直角坐标系xOy中,四边形OABC是正方形,点C(0,4),D是OA中点,将△CDO以C为旋转中心逆时针旋转90°后,再将得到的三角形平移,使点C与点O重合,写出此时点D的对应点的坐标:.【答案】(4,2)【2018·房山二模】9. 如图,在正方形网格中,线段A′B′可以看作是线段AB经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段AB得到线段A′B′的过程: .【答案】如:将线段AB绕点B逆时针旋转90°,再向左平移2个单位长度;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市各区2018届九年级上期末试卷分类汇编:图形变换
图形变换
1.(东城18期末6)△DEF和△ABC是位似图形,点O是位似
中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积
是2,则△ABC的面积是()
A.2B.4
C.6D.8
D
2.(海淀18期末4)如图,将△ABC绕点A逆时针旋转100°,
得到△ADE.若点D在线段BC的延长线上,则B
∠的大小为
()
A.30°B.40°
C.50°D.60°
B
3(海淀18期末6)6.如图,在平面直角坐标系xOy中,
点A从(3,4)出发,绕点O顺时针旋转一周,则点A
不.经过()
A.点M B.点N
C.点P D.点Q
C
4.(昌平18期末6)如图,将ΔABC绕点C顺时针旋转,点B
的对应点为点E,点A的对应点为点D,当点E恰好落在边
AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是()
A.60°B.65°
C.70°D.75°
D
5.(门头沟18期末10)已知线段5
AB cm
=,将线段AB以点A为旋转中心,逆时针旋转90°得到线段'
AB,则点B、点'B的距离为__________.
6.(朝阳18期末10)如图,把△ABC绕着点A顺时针方向旋转,
得到△A B 'C ',点C恰好在B 'C '上,旋转角为α,则∠C '的
度数为(用含α的式子表示).
7.(昌平18期末10)如图,在平面直角坐标系xOy中,点A,
,0),将线段AB沿x 点B的坐标分别为(0,2),(1
轴的正方向平移,若点B的对应点的坐标为'B(2,0),则点A的对应点'A的坐标为.
(3,2)
8.(昌平18期末14)如图,在直角三角形ABC中,∠C=90°,BC=6,AC=8,点D是AC边上一点,将△BCD沿BD折叠,使点C落在AB边的E点,那么AE的长度是.4
9.(昌平18期末15)如图,在平面直角坐标系xOy中,△CDE 可以看作是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△CDE的过程:
___________________________________________
______________________________________________.
将△AOB绕点O顺时针旋转90°,再沿x轴向右平移一个单位(答
案不唯一)
10.(朝阳18期末14)如图,在平面直角坐标系中,△COD可以看作是△AOB经过若干次图形的变化(平
移、轴对称、旋转、位似)得到的,写出一种由△AOB
得到△COD的过程:
_____________________________
____________________________________________.
11.(石景山18期末15)如图,在平面直角坐标系xOy中,△ABC经过若干次图形的变化(平移、轴对称、旋转)得到△DEF,写出一种由△ABC得到△DEF的过程:________________
__________________________________________________.
15.先以点C为中心顺时针旋转90º,再以y轴为对称轴翻折(答案不唯一)
12.(平谷18期末15)如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:_______________________________
_____________________________________________.
15.答案不唯一,如:△ABC绕点O逆时针旋转90°
13.(门头沟18期末15)如图,在平面直角坐标系xOy中,图形L2可以看作是由图形L1经过若干次图形的变化(平移、旋转、轴对称)得到
的,写出一种由图形L1得到图形L2的过程
__________________________________
______________________________________________.
答案不唯一
例:先将以点B为旋转中心顺时针旋转90°,在向左平移7个单位长度
14.(燕山18期末18)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立
平面直角坐标系后,△ABC 的顶点均在格点上,点B 的坐标为(1,0).
(1)在图1中画出△ABC 关于y 轴对称的△A 1B 1C 1,直接写出点C 的对应点C 1的坐标.
(2)在图2中,以点O 为位似中心,将△ABC 放大,使放大后的△A 2B 2C 2与△ABC 的对应边的比为2:1(画出一种即可).直接写出点C 的对应点C 2的坐标.
18.(1)画出△ABC 关于y 轴对称的△A 1B 1C 1…………..1′
点C 1的坐标(-3,1).…………………….……………….2′
(2)放大后的△A 2B 2C 2(画出一种即可)…………..4′. C 2的坐标( ).…………………………………..5′
15.(朝阳18期末19)如图,在平面直角坐标系xOy 中,点
A (3,3),点
B (4,0),点
C (0,﹣1).
(1)以点C 为中心,把△ABC 逆时针旋转90°,画出旋
转后的图形△A′B′C ;
(2)在(1)中的条件下,
①点A 经过的路径的长为
(结果保留
π); ②写出点B′的坐标为 .
16.(东城18期末22)如图,在Rt △ABC 中,∠A =90°,∠C=30°.将△ABC 绕点B 顺时针
旋转60°得到△A BC '', 其中点A ', C '分别是点A ,C 的对应点.
(1)作出△A BC ''(要求尺规作图,不写作法,保留作图痕迹);
(2)连接AA ',求∠C A A ''的度数.
17.(西城18期末20)在△ABC 中,AB=AC=2,45BAC ∠=︒.将△ABC 绕点A 逆时针旋转
α度(0<α<180)得到△ADE ,B ,C 两点的对应点分别为点D ,E ,BD ,CE 所在直线交于点F .
(1)当△ABC 旋转到图1位置时,∠CAD = (用α的代数式表示),BFC ∠的度数为 ;
(2)当α=45时,在图2中画出△ADE ,并求此时点A 到直线BE 的距离.。
