初二数学周清测试题
数学周清试卷八年级下册

1. 已知方程x² - 5x + 6 = 0 的两个根分别为 x₁和 x₂,则 x₁ + x₂等于()A. 2B. 5C. 6D. 12. 若a² = 4,b² = 9,则 |a| + |b| 等于()A. 5B. 6C. 7D. 83. 在直角坐标系中,点 P(2,3)关于 x 轴的对称点坐标为()A.(2,-3)B.(-2,3)C.(-2,-3)D.(2,-3)4. 已知 a、b、c 成等差数列,且 a + b + c = 12,则 b 的值为()A. 4B. 6C. 8D. 105. 在△ABC中,∠A = 30°,∠B = 45°,则∠C 的度数为()A. 45°B. 60°C. 75°D. 90°6. 已知一次函数 y = kx + b 的图象经过点(2,3),则该函数的斜率 k 等于()A. 1B. 2C. 3D. 47. 已知二次函数y = ax² + bx + c 的图象开口向上,且 a > 0,则该函数的顶点坐标为()A.(-b/2a,c - b²/4a)B.(b/2a,c - b²/4a)C.(-b/2a,c + b²/4a)D.(b/2a,c + b²/4a)8. 若 a、b、c 成等比数列,且 a = 2,b = 4,则 c 的值为()A. 8B. 6C. 3D. 19. 在等腰三角形 ABC 中,底边 BC 的长度为 4,腰 AB = AC = 6,则三角形 ABC 的面积为()A. 12B. 18C. 24D. 3010. 若x² - 2x + 1 = 0,则 x 的值为()A. 1B. 2C. 3D. 411. 若m² - 3m + 2 = 0,则 m 的值为________。
12. 已知 a、b、c 成等差数列,且 a + b + c = 12,则 b 的值为________。
八年级上册数学周清试卷

一、选择题(每题4分,共20分)1. 下列各数中,绝对值最小的是()A. -2B. -1.5C. 0D. 12. 如果a < b,那么下列不等式中正确的是()A. a + 2 < b + 2B. a - 2 > b - 2C. a + 2 > b + 2D. a - 2 < b - 23. 已知一次函数y = kx + b的图象经过点(1,3),则下列说法正确的是()A. k > 0,b > 0B. k < 0,b < 0C. k > 0,b < 0D. k < 0,b > 04. 在等腰三角形ABC中,AB = AC,且∠BAC = 60°,那么∠ABC的度数是()A. 30°B. 45°C. 60°D. 90°5. 一个长方形的长是8cm,宽是5cm,它的周长是()A. 18cmB. 26cmC. 30cmD. 40cm二、填空题(每题5分,共25分)6. 若|a| = 5,则a的值为______。
7. 若∠A = 45°,∠B = 90°,则∠C = ______。
8. 一个圆的半径为r,则它的周长为______。
9. 已知一次函数y = 2x - 3,当x = 2时,y的值为______。
10. 在直角三角形中,若直角边分别为3cm和4cm,则斜边的长度为______。
三、解答题(每题10分,共30分)11. (10分)已知a、b是方程x^2 - 4x + 3 = 0的两个实数根,求a + b的值。
12. (10分)已知一次函数y = kx + b的图象经过点(2,-1)和(-2,5),求该一次函数的解析式。
13. (10分)在△ABC中,AB = AC,∠BAC = 80°,求∠ABC的度数。
四、应用题(15分)14. (15分)某商店销售一种商品,已知每件商品的进价为80元,售价为100元。
周清题3

八年级数学第二次周清姓名 班级一、选择题.1、下列判断两个三角形全等的条件中,正确的是 ( ) A 、一条边对应相等 B 、两条边对应相等 C 、三个角对应相等 D 、三条边对应相等2、如图,在①AB =AE ;②AD =AE ;③∠B =∠C ;④BD =CE 四个条件中,能证明△ABD 与△ACE 全等的条件序号是 ( )A 、①②③B 、②③④C 、①②④D 、①③④3、如图,在△ABC 中,AB =AC ,D 、E 两点在BC 上,且有AD =AE ,BD =CE ,若∠BAD =30°,∠DAE =50°,则∠BAC 的度数为 ( )A 、130°B 、120°C 、110°D 、100°4、下列画图语句表述正确的是 ( ) A 、延长线段AB 至点C ,使AB =BC B 、以点O 为圆心作弧C 、以点O 为圆心,以AC 的长为半径画弧D 、在射线OA 上截取CB =a ,BC =b ,则有OC =a+b 二、填空题5、如图,AB =AC ,BE =CD ,要使△ABE ≌△ACD 的依据是“SSS ”,则还需添加的条件 ____6、如图,AB =ED ,AC =EC ,C 是BD 的中点,若∠A =36°,则∠E =7、如图,已知AB =AC ,EB =EC ,AE 的延长线交BC 于D ,则图中全等的三角形共有 对。
8、在平面直角坐标系中有两点A (4,0)、B (0,2),如果点C在坐标平面内,当点C 的坐标为 时,由点B 、O 、C 组成的三角形与△AOB 全等。
三、解答题.9、已知:如图,AB=EF ,BC=FD ,AD=EC ,求证:∠B=∠F .10、如图,已知AB=AC ,AD=AE ,BD=CE ,你能运用上面条件证明出几对三角形全等?•选一对进行证明11、 已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF.求证:AC ∥DF .12、已知:如图,AD=BC ,AB=DC ,求证:∠A=∠C .BCDEBCDEB CDEAB CDEABCDE AAA。
八年级数学上册周清题卷

班级: 数学周清题 姓名:(提示:本卷共分三个板块,九、十班学生做第一、三两个板块题目,其他学生做第一、二两个板块题目)板块一:一、填空题(每空2.5分共55分)1、正数有_____个立方根, 0有___ 个立方根,负数有____个立方根,2、如果a 3=3,那么a=______. 那么a=_______3、 立方根等于它本身的数是 ,平方根等于本身的数是 .4、(1)立方根是-8的数是__; (2)833-的立方根是________ (3)________的立方根是1.0-. (4)65-是________的立方根. (5)-216的立方根的绝对值是_ _5、若642=x ,则3x =____.6、327-= ; 37-的相反数是 ;7、-8的立方根与4的平方根之和是________.8、若a 与b 互为相反数,则它们的立方根的和是________.9、一个数的平方根与立方根相等,则这个数是 .10、3512=_____ ; 36427--=_____;0196.0-=______ ;33a - = ______。
二、选择题:(每题3分共12分)11、下面哪个估算误差过大A ≈3.6B ≈3.2C 5.3D 4.112、下列式子中正确的是A 、1 0 ∠ 11B 、10 m ∠ 12C 、12 ∠ 13D 、13 ∠ 1413、下列式子成立的是( ) A. 3223< B. 35->- C. π<39 D. 42.12>14的值应在( )A.3.9~4.0之间 B.4.0~4.1之间C.4.1~4.2之间 D.4.2~4.3之间板块二:15、计算 (8分) (1)3833+ (2) 9114-16、(31在哪两个整数之间( )A 、1与2B 、2与3C 、3与4D 、4与517、(12分)比较大小:; 310 0.1 (填“>”或“<”)18、(4分)已知a 、b 是两个连续的整数,且a b,求a+b 的值19、(6分)若2x+19的立方根是3,求3x+4的平方根。
八年级下册周清数学试卷

一、选择题(每题3分,共30分)1. 若a > b,那么下列不等式中一定成立的是()A. a + 2 > b + 2B. a - 2 < b - 2C. 2a > 2bD. 2a < 2b2. 下列各数中,有理数是()A. √3B. πC. 0.1010010001...D. 3/43. 若一个三角形的三边长分别为3,4,5,那么这个三角形是()A. 等腰三角形B. 直角三角形C. 等边三角形D. 不规则三角形4. 下列关于二次函数y = ax^2 + bx + c(a≠0)的说法正确的是()A. 当a > 0时,函数开口向上B. 当a < 0时,函数开口向下C. 当a = 0时,函数开口向上D. 当a = 0时,函数开口向下5. 若直角三角形的两条直角边分别为3cm和4cm,那么斜边的长度是()A. 5cmB. 7cmC. 8cmD. 9cm6. 下列各图中,面积最大的图形是()A.B.C.D.7. 下列关于反比例函数y = k/x(k≠0)的说法正确的是()A. 当k > 0时,函数图象在第一、三象限B. 当k < 0时,函数图象在第一、三象限C. 当k > 0时,函数图象在第二、四象限D. 当k < 0时,函数图象在第二、四象限8. 下列关于一次函数y = kx + b(k≠0)的说法正确的是()A. 当k > 0时,函数图象在第一、三象限B. 当k < 0时,函数图象在第一、三象限C. 当b > 0时,函数图象在第一、二象限D. 当b < 0时,函数图象在第一、二象限9. 下列各数中,无理数是()A. √4B. √9C. √16D. √2510. 若一个正方形的对角线长为10cm,那么这个正方形的面积是()A. 50cm^2B. 100cm^2C. 150cm^2D. 200cm^2二、填空题(每题5分,共25分)11. 若a < b < c,那么a - c的值是()12. 若一个长方形的周长是24cm,长是8cm,那么这个长方形的面积是()13. 若一个平行四边形的对角线互相平分,那么这个平行四边形是()14. 若一个梯形的上底是5cm,下底是10cm,高是4cm,那么这个梯形的面积是()15. 若一个圆的半径是3cm,那么这个圆的周长是()三、解答题(每题10分,共40分)16. 已知一元二次方程x^2 - 5x + 6 = 0,求该方程的解。
数学周周清考试卷(一次函数)
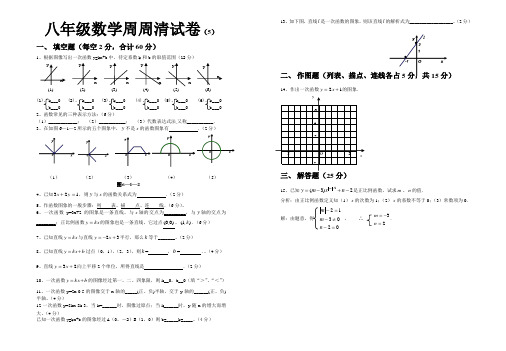
图6—1—2八年级数学周周清试卷(5)一、填空题(每空2分,合计60分)1、根据图像写出一次函数y=kx+b中,待定系数k和b的取值范围(12分)(1)、k___0 (2)、 k___0 (3)、k___0 (4)、k___0 (5)、k___0 (6)、k___0b___0 b___0 b___0 b___0 b___0 b___02、函数常见的三种表示方法:(6分)(1)____________;(2)___________;(3)代数表达式法,又称___________.3、在如图6—1—2所示的五个图象中,y不是x的函数图象有.(2分)(1)(2)(3)(4)(5)4、已知123=+yx,则y与x的函数关系式为.(2分)5、作函数图象的一般步骤:列表、描点、连线.(6分)。
6、一次函数y=3x+2的图象是一条直线,与x轴的交点为_________,与y轴的交点为________;正比例函数kxy=的图象也是一条直线,它过点)0,0(,),1(k.(6分)7、已知直线kxy=与直线32+-=xy平行,那么k等于_______。
(2分)8、已知直线bkxy+=过点(0,1),(2,3),则k= ,b= .。
(4分)9、直线23+=xy向上平移2个单位,所得直线是.(2分)10、一次函数bkxy+=的图像经过第一、二、四象限,则k__0,b__0(填“>”、“<”)11、一次函数y=2x-0.5的图像交于x轴的_____(正、负)半轴,交于y轴的______(正、负)半轴。
(4分)12一次函数y=5kx-5k-3,当k=______时,图像过原点;当k______时,y随x的增大而增大。
(4分)已知一次函数y=kx+b的图象经过A(0,-2)B(1,0)则b=_____k=____。
(4分)13、如下图,直线l是一次函数的图象,则该直线l的解析式为__________________。
(2分)●●二、作图题(列表、描点、连线各占5分,共15分)14、作出一次函数12+=xy的图象.三、解答题(25分)15、已知2)3(2-+-=-nxmy m是正比例函数,试求m、n的值.分析:由正比例函数定义知(1)x的次数为1;(2)x的系数不等于0;(3)常数项为0.解:由题意,得2312=-≠-=-nmm,∴23=-=nm.。
2024八年级数学上册第十二章整式的乘除周周清检测内容:12

检测内容:12.3-12.5得分________ 卷后分________ 评价________一、选择题(每小题4分,共32分)1.(广元中考)下列运算中正确的是( D )A .(a 2)3=a 5B .(2x +1)(2x -1)=2x 2-1C .a 8÷a 2=a 4D .(a -3)2=a 2-6a +92.(百色中考)因式分解x -4x 3的最终结果是( C )A .x (1-2x )2B .x (2x -1)(2x +1)C .x (1-2x )(2x +1)D .x (1-4x 2)3.(河南期中)计算(2a 3b 2)2÷ab 2的结果为( D )A .2a 2B .2a 5b 2C .4a 4b 2D .4a 5b 24.(河南期中)已知x 2-8x +a 可以写成一个因式的平方,则a 可为( C )A .4B .8C .16D .-165.若(3x 2y -2xy 2)÷M =xy ,则代数式M 为( B )A .3x +2yB .3x -2yC .6xyD .x -y6.(邓州市期中)多项式①4x 2-x ;②(x -1)2-4(x -1);③1-x 2;④-4x 2-1+4x ,分解因式后,结果中含有相同因式的是( D )A .①和②B .③和④C .①和④D .②和③7.(邓州市期中)用四个全等的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4.若用a ,b 分别表示长方形的长和宽(a >b ),则下列关系中不正确的是( D )A.a +b =12B .a -b =2C .ab =35D .a 2+b 2=848.对于随意整数n ,多项式(4n +5)2-9都能( C )A .被6整除B .被7整除C .被8整除D .被6或8整除二、填空题(每小题4分,共24分)9.计算:(9x -4y )(9x +4y )=__81x 2-16y 2__;(-2x +12 y )2=__4x 2-2xy +14y 2__. 10.4xy ·(__3xy 2-5x 2y +2xy __)=12x 2y 3-20x 3y 2+8x 2y 2.11.(汝阳县期末)已知|m-n|=1,m+n=5,则m2-n2=__±5__.12.若a+b=-1,则3a2+6ab+3b2-5的值为__-2__.13.分解因式:(1)(遂宁中考)3a2-3b2=__3(a+b)(a-b)__;(2)(本溪中考)2a2-8ab+8b2=__2(a-2b)2__.14.如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为m,则这个长方形的周长为__(8m+12)__.三、解答题(共44分)15.(6分)计算:(1)(-4a2b3c)3÷(-2a3b2c)2;解:原式=-64a6b9c3÷4a6b4c2=-16b5c(2)[(2xy-3)(2xy+3)+(xy+3)2]÷xy.解:原式=(4x2y2-9+x2y2+6xy+9)÷xy=5xy+616.(6分)化简:(1)(x+2)(x-2)-(x-2)2;解:原式=x2-4-(x2-4x+4)=4x-8(2)(2a-1)2(1+2a)2(4a2+1)2.解:原式=(4a2-1)2(4a2+1)2=256a8-32a4+117.(12分)把下列多项式分解因式:(1)x2(y-4)-(y-4);解:原式=(y-4)(x+1)(x-1)(2)-4m3+16m2-16m;解:原式=-4m(m-2)2(3)x4-81y4;解:原式=(x2+9y2)(x+3y)(x-3y)(4)(a2+4b2)2-16a2b2.解:原式=(a+2b)2(a-2b)218.(8分) (上蔡县期中)(1)已知a2+b2=17,ab=4,求a+b的值;(2)已知a-b=5,(a+b)2=49,求a2+b2的值.解:(1)∵a2+b2=17,ab=4,∴(a+b)2=a2+b2+2ab=17+2×4=25.∴a+b=±25=±5(2)∵a-b=5,∴(a-b)2=a2+b2-2ab=25①.又∵(a+b)2=a2+b2+2ab=49②,由①②得a2+b2=3719.(12分)问题:已知多项式x4+mx3+nx-16含有因式(x-1)和(x-2),求m,n的值.解:设x4+mx3+nx-16=A(x-1)(x-2)(其中A为整式),∴取x=1,得1+m+n-16=0,①取x=2,得16+8m+2n-16=0,②由①②解得m=-5,n=20.依据以上阅读材料解决下列问题:(1)若多项式3x3+ax2-2含有因式(x-1),求实数a的值;(2)若多项式2x2+mxy+ny2-4x+2y含有因式(x+y-2),求实数m,n的值;(3)假如一个多项式与某非负数的差含有某个一次因式,则称这个非负数是这个多项式除以该一次因式的余数.恳求出多项式x2 020+2x1 010+3除以一次因式(x+1)的余数.解:(1)设3x3+ax2-2=M(x-1)(其中M为整式),∴取x=1,得3+a-2=0,解得a =-1(2)设2x2+mxy+ny2-4x+2y=N(x+y-2)(其中N为整式),∴取x=0,y=2,得4n+4=0①,取x=1,y=1,得2+m+n-4+2=0②,由①②得m=1,n=-1(3)设这个非负数为a,另一因式为Q,∴可得到关系式为x2 020+2x1 010+3-a=Q(x+1).取x=-1,得1+2+3-a=0,解得a=6.故x2 020+2x1 010+3除以一次因式(x+1)的余数为6。
2024八年级数学上册第一章勾股定理周周清检测内容1

检测内容:1.1-1.3得分________卷后分________评价________一、选择题(每小题5分,共30分)1.(开封期末)下列各组数据是三角形的三边长,能构成直角三角形的是( D )A.2,3,4 B.4,5,6C.32,42,52D.6,8,102.如图,在Rt△ABC中,∠ACB=90°.若AB=15 cm,则正方形ADEC和正方形BCFG 的面积和为( C )A.150 cm2B.200 cm2C.225 cm2D.无法计算第2题图第4题图第5题图3.始终角三角形的周长为24,斜边长与始终角边长之比为5∶4,则这个直角三角形的面积是( B )A.20 B.24 C.28 D.304.如图,在某次海上编队演习中,两艘航母护卫舰从同一港口O同时动身,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时的速度航行,离开港口1.5小时后它们分别到达相距30海里的A,B两点,则二号舰航行的方向是( C )A.南偏东30°B.北偏东30°C.南偏东60°D.南偏西60°5.如图,一个工人拿了一个2.5 m长的梯子,底端A放在距离墙根C点0.7 m处,另一头B点靠墙.假如梯子的顶部下滑0.4 m,则梯子的底部向外滑了( D ) A.0.4 m B.0.6 m C.0.7 m D.0.8 m6.(辉县市期末)如图①是我国古代闻名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是( D )图①图②A.72 B.52 C.80 D.76二、填空题(每小题5分,共25分)7.如图,起重机吊运物体,∠ABC =90°.若BC =12 m ,AC =13 m ,则AB =__5__m. 8.已知一组勾股数中有一个数是2mn (m ,n 都是正整数,且m >n ≥2),尝试写出其他两个数(均用含m ,n 的代数式表示,只要写出一组):__m 2-n 2,m 2+n 2(答案不唯一)__.9.小东拿着一根长竹竿进一个宽为4 m 的长方形城门,他先横着拿进不去,又竖起来拿,结果竿比城门高0.5 m ,当他把竿斜着时,两端刚好顶着城门的对角,则竿长__16.25__m.10.如图,在△ABC 中,AB =AC =5,BC =6.M 为BC 的中点,过点M 作MN ⊥AC 于点N ,则MN =__125__.11.如图,长方体的底面边长分别为2 cm 和4 cm ,高为5 cm.若一只蚂蚁从P 点起先经过4个侧面爬行一圈到达Q 点,则蚂蚁爬行的最短路径长为__13__cm.三、解答题(共45分)12.(10分)如图,在△ABC 中,CD ⊥AB 于点D ,AC =4,BC =3,DB =95. (1)求CD ,AD 的长;(2)试推断△ABC 的形态,并说明理由.解:(1)因为CD ⊥AB ,所以CD 2+DB 2=BC 2,即CD 2+(95 )2=32,所以CD =125.因为AD 2+CD 2=AC 2,即AD 2+(125 )2=42,所以AD =165 (2)因为AB =AD +DB =165 +95=5,所以AB 2=AC 2+BC 2,所以△ABC 为直角三角形13.(10分)如图,在△ABC 中,AB =AC, BC =20 cm ,D 是腰AB 上一点,且CD =16 cm ,BD =12 cm.求:(1)∠BDC 的度数;(2)△ABC 的周长.解:(1)因为BD 2+CD 2=122+162=202=BC 2,所以∠BDC =90°(2)设AD =x cm ,则AB =AC =(x +12) cm.因为∠BDC =90°,所以∠ADC =90°,所以AD 2+CD 2=AC 2,即x 2+162=(x +12)2,解得x =143 ,∴AB =AC =1623cm ,所以△ABC 的周长为1623 +1623 +20=5313(cm) 14.(12分)强大的台风使得山坡上的一棵树甲从A 点处拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部C 处,已知AB =4 m ,BC =13 m ,两棵树的水平距离为12 m ,求这棵树原来的高度.解:过点C 作CD ⊥AB 的延长线于点D ,则CD =12 m .由勾股定理得BD 2+CD 2=BC 2,即BD 2+122=132,所以BD =5,所以AD =AB +BD =4+5=9 m.在Rt △ACD 中,AC 2=CD 2+AD 2=122+92,所以AC =15,所以AC +AB =15+4=19(m),所以这棵树原来的高度是19 m15.(13分)台风是一种自然灾难,它以台风中心为圆心在四周上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB 由A 行驶向B ,已知点C 为一海港,且点C 与直线AB 上的两点A ,B 的距离分别为AC =300 km ,BC =400 km ,AB =500 km ,以台风中心为圆心四周250 km 以内为受影响区域.(1)求∠ACB 的度数;(2)海港C 受台风影响吗?为什么?(3)若台风的速度为20千米/小时,当台风运动到点E 处时,海港C 刚好受到影响,当台风运动到点F 时,海港C 刚好不受影响,即CE =CF =250 km ,则台风影响该海港持续的时间有多长?解:(1)因为AC 2+BC 2=3002+4002=5002=AB 2,所以△ABC 是直角三角形,∠ACB =90° (2)海港C 受台风影响,理由:过点C 作CD ⊥AB 于点D .因为S △ABC =12 AC ×BC =12CD ×AB .所以CD =240(km)<250 km ,所以海港C 受台风影响(3)在Rt △CDE 中,由勾股定理得ED 2+CD 2=CE 2,即ED 2+2402=2502,所以ED =70,所以EF =140 km ,则140÷20=7(小时).答:台风影响该海港持续的时间有7小时。
八年级数学周清试卷

一、选择题(每题3分,共30分)1. 下列各数中,绝对值最小的是()A. -3B. 2C. 0D. -52. 如果a > 0,b < 0,那么下列不等式中正确的是()A. a > bB. a < bC. -a > -bD. -a < -b3. 下列函数中,图象是一条直线的是()A. y = x^2B. y = 2x + 3C. y = √xD. y = x^34. 在直角三角形ABC中,∠C = 90°,AC = 3cm,BC = 4cm,那么AB的长度是()A. 5cmB. 6cmC. 7cmD. 8cm5. 下列关于圆的命题中,正确的是()A. 所有半径相等的圆都是同心圆B. 所有直径相等的圆都是同心圆C. 所有圆心在一条直线上的圆都是同心圆D. 所有圆周长相等的圆都是同心圆6. 如果一个正方形的对角线长度为6cm,那么这个正方形的边长是()A. 3cmB. 4cmC. 5cmD. 6cm7. 下列各式中,正确的是()A. (a + b)^2 = a^2 + b^2B. (a - b)^2 = a^2 - b^2C. (a + b)^2 = a^2 + 2ab + b^2D. (a - b)^2 = a^2 - 2ab + b^28. 下列各数中,是负数的是()A. -√9B. -√4C. -√16D. -√259. 如果x^2 = 25,那么x的值是()A. 5B. -5C. 5 或 -5D. 无法确定10. 下列关于二次函数的图象的说法中,正确的是()A. 二次函数的图象一定是抛物线B. 二次函数的图象开口方向一定向上C. 二次函数的图象开口方向一定向下D. 二次函数的图象一定经过原点二、填空题(每题5分,共25分)11. 有理数a的相反数是______。
12. 在直角三角形中,如果一个角的正弦值是0.5,那么这个角的度数是______。
13. 如果一个圆的半径是r,那么这个圆的周长是______。
八年级数学第1周周清测试题(解析卷)

八年级数学周周清测试题参考答案与试题解析一.选择题(共10小题)1.下列从左边到右边的变形,是因式分解的是()A.4a2﹣4a+1=4a(a﹣1)+1B.2+1=o+1)C.(x+2)(x﹣2)=x2﹣4D.x2﹣4=(x+2)(x﹣2)【分析】把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式,据此逐项判断即可.【解答】解:4a2﹣4a+1=4a(a﹣1)+1中等号右边不是积的形式,则A不符合题意;x2+1=x(x+1)中1不是整式,则B不符合题意;(x+2)(x﹣2)=x2﹣4是乘法运算,则C不符合题意;x2﹣4=(x+2)(x﹣2)符合因式分解的定义,则D符合题意;故选:D.2.多项式2x2﹣13x+b中,有一个因式为(x﹣5),则b的值为()A.﹣15B.﹣3C.15D.3【分析】设另一个因式为(2x+m),根据因式分解的意义计算(x﹣5)(2x+m)后即可求得答案.【解答】解:设另一个因式为(2x+m),则(x﹣5)(2x+m)=2x2﹣13x+b,整理得:2x2+(m﹣10)x﹣5m=2x2﹣13x+b,则m﹣10=﹣13,b=﹣5m,那么m=﹣3,b=15,故选:C.3.分解因式:x2﹣x=()A.x(x﹣1)B.(x+1)(x﹣1)C.2x D.x(x+1)【分析】用提公因式法分解因式即可.【解答】解:x2﹣x=x(x﹣1).故选:A.4.把多项式﹣7ab﹣14abx+49aby分解因式,提公因式﹣7ab后,另一个因式是()A.1+2x﹣7y B.1﹣2x﹣7y C.﹣1+2x+2y D.﹣1﹣2x+7y【分析】﹣7ab﹣14abx+49aby的公因式为﹣7ab,提取公因式后化简即可.【解答】解:﹣7ab﹣14abx+49aby=﹣7ab(1+2x﹣7y).故选:A.5.下列多项式中不能用公式法分解因式的是()A.2++14B.2ab+a2+b2C.﹣a2+25D.﹣4﹣b2【分析】根据完全平方公式和平方差公式逐项进行分析判断即可.【解答】解:A.2++14=(+12)2,能用完全平方公式进行因式分解,不符合题意;B.2ab+a2+b2=(a+b)2,能用完全平方公式进行因式分解,不符合题意;C.﹣a2+25=(5+a)(5﹣a),能用平方差公式进行因式分解,不符合题意;D.﹣4﹣b2=﹣(4+b2),不能用公式法分解,符合题意;故选:D.6.已知9x2+mxy+16y2能运用完全平方公式因式分解,则m的值为()A.12B.±12C.24D.±24【分析】这里首末两项是3x和4y个数的平方,那么中间一项为加上或减去3x和4y乘积的2倍,进而得出答案.【解答】解:∵(3x±4y)2=9x2±24xy+16y2,∴在9x2+mxy+16y2中,m=±24.故选:D.7.小明做了如下四个因式分解题,你认为小明做得对但不完整的一题是()A.x2y﹣xy2=xy(x﹣y)B.m2﹣2mn+n2=(m﹣n)2C.a3﹣a=a(a2﹣1)D.﹣x2+y2=(y+x)(y﹣x)【分析】原式各项分解得到结果,即可做出判断.【解答】解:A、x2y﹣xy2=xy(x﹣y),正确;B、m2﹣2mn+n2=(m﹣n)2,正确;C、a3﹣a=a(a2﹣1)=a(a+1)(a﹣1),错误;D、﹣x2+y2=(y+x)(y﹣x),正确,故选:C.8.若k为任意整数,则(2k+3)2﹣(2k﹣2)2的值总能()A.被2整除B.被3整除C.被5整除D.被7整除【分析】利用平方差公式分解因式后可得结论.【解答】解:(2k+3)2﹣(2k﹣2)2=[(2k+3)+(2k﹣2)][(2k+3)﹣(2k﹣2)]=(2k+3+2k﹣2)(2k+3﹣2k+2)=5(4k+1),∴(2k+3)2﹣(2k﹣2)2的值总能被5整除.故选:C.9.若a+b=3,a﹣b=7,则a2﹣b2的值为()A.﹣21B.21C.﹣10D.10【分析】利用平方差公式分解因式,进而将已知代入求出即可.【解答】解:∵a+b=3,a﹣b=7,∴a2﹣b2=(a+b)(a﹣b)=3×7=21.故选:B.10.已知m+n=8,则2+22+(1﹣m)(1﹣n)的值为()A.32B.25C.10D.64【分析】对所求的式子进行变形处理,得到含(m+n)的式子,再代入m+n=8即可.【解答】解:∵2+22+(1﹣m)(1﹣n)=2+22+1﹣(m+n)+mn,=2+2+2B2+1﹣(m+n)=(rp22+1﹣(m+n)∵m+n=8,所以原式=32+1﹣8=25.故选:B.二.填空题(共4小题)11.将多项式6a2b﹣3ab2+12a2b2分解因式时,应提取的公因式是3ab.【分析】公因式的确定,一看系数:若各项系数都是整数,应提取各项系数的最大公因数;二看字母:公因式的字母是各项相同的字母;三看字母的指数:各相同字母的指数取指数最低的.【解答】解:对多项式6a2b﹣3ab2+12a2b2分解因式时,应提取的公因式是3ab,故答案为:3ab.12.根据如图所示的拼图过程,写出一个多项式的因式分解:x2+2x+4x+8=(x+4)(x+2).【分析】利用两种方法表示出这个图形的面积,列出等式即可.【解答】解:四张长方形或正方形纸片拼成一个大长方形,面积可以表示为:x2+2x+4x+8=x2+6x+8=(x+4)(x+2).故答案为:x2+2x+4x+8=(x+4)(x+2).13.分解因式:ab2﹣a2=a(b2﹣a).【分析】先找出多项式的公因式是a,再分解因式即可.【解答】解:ab2﹣a2=a(b2﹣a).故答案为:a(b2﹣a).14.分解因式:29a2−43a+2=29(a﹣3)2.【分析】先提取公因式29,再对余下的多项式利用完全平方公式继续分解.【解答】解:29a2−43a+2=29(a2﹣6a+9)=29(a﹣3)2.故答案为:29(a﹣3)2.三.解答题15.把下面各式因式分解:(1)6ax﹣12ay+18az;(2)﹣15m3n2+20m2n﹣5mn;(3)3a(x﹣y)﹣3b(x﹣y);【解答】解:(1)6ax﹣12ay+18az=6a(x﹣2y+3z);(2)﹣15m3n2+20m2n﹣5mn=﹣5mn(3m2n﹣4m+1);(3)3a(x﹣y)﹣3b(x﹣y)=3(x﹣y)(a﹣b);16.把下面各式因式分解:(1)9x2﹣16.(3)x2(m﹣2)+y2(2﹣m).(3)x2(x﹣2)﹣16(x﹣2);【解答】解:(1)9x2﹣16=(3x+4)(3x﹣4).(2)x2(m﹣2)+y2(2﹣m)=(m﹣2)(x2﹣y2)=(m﹣2)(x+y)(x﹣y).(3)x2(x﹣2)﹣16(x﹣2)=(x﹣2)(x2﹣16)=(x﹣2)(x﹣4)(x+4);17.把下面各式因式分解:(1)3a2﹣6ab+3b2;(2)(m﹣n)2﹣6(n﹣m)+9.(3)9(2x﹣1)2﹣6(2x﹣1)+1.【解答】解:(1)3a2﹣6ab+3b2=3(a2﹣2ab+b2)=3(a﹣b)2;(2)(m﹣n)2﹣6(n﹣m)+9=(m﹣n)2+6(m﹣n)+9=[(m﹣n)+3]2=(m﹣n+3)2.(3)9(2x﹣1)2﹣6(2x﹣1)+1=[3(2x﹣1)﹣1]2=(6x﹣4)2=4(3x﹣2)2.18.利用因式分解的方法简算(1)2022﹣542+256×352(2)89×18−25×0.125(3)1022+102×196+982【解答】解:(1)2022﹣542+256×352=(202+54)(202﹣54)+256×352=256×148+256×352=256×(148+352)=256×500=128000;(2)89×18−25×0.125=89×18−25×18=(89−25)×18=64×18=8;(3)1022+102×196+982=1022+2×102×98+982=(102+98)2=2002=40000.19.先分解因式,然后计算;(1)已知x﹣y=1,求12x2﹣xy+12y2;(2)﹣9x2+12xy﹣4y2,其中x=43,y=−12;(3)(r2)2−(K2)2,其中a=−18,b=2.【解答】解:(1)∵x﹣y=1,∴12x2﹣xy+12y2=12(x﹣y)2=12×12=12;(2)∵x=43,y=−12,∴﹣9x2+12xy﹣4y2=﹣(9x2﹣12xy+4y2)=﹣(3x﹣2y)2=﹣[3×43−2×(−12)]2=﹣25;(3)∵a=−18,b=2,∴(r2)2−(K2)2,=(r2+K2)(r2K2)=ab=−18×2=−14.。
八年级数学周清3

八年级数学周清题(共50分)
姓名: 班级:
一、填空(每题4分,共12分)
1、在 ABCD 中,若AB=4cm,∠A=60°,则CD= ,∠C= 。
2.矩形ABCD 中,若AB=5,对角线AC=13,则矩形的面积为 。
3.菱形的周长为32cm ,两邻角的比是1:2,则菱形较短的对角线的长为 。
二、选择(每题4分,共12分)
4.如图, ABCD 中,EF ∥AB ,GH ∥BC ,则图中的平行四边形共有( )个 A .4 B.5 C.8 D.9
5.如图,把一张长方形纸片如图折一下,重全部分是( )图形
A
.矩形 B.正方形 C.菱形 D.等腰梯形 6.某班同学要在广场上布置一个矩形的花坛,计划用“牡丹”摆成两条对角线, 如果一条对角线用了38盆“牡丹”,则需从花房再运来“牡丹”( )盆。
A .38 B .37 C .39 D .38或39. 三、解答
7.已知:如图,菱形ABCD 中,AC=16,BD=12。
求AB 边上的高DE 的长。
(8分)
8.如图:矩形ABCD 的对角线交于点O ,OF ⊥AD 于F ,OF=2cm,AE 垂直平分OB ,求:AC 的长。
(9分)
9.如图:正方形ABCD 中,E 是BC 边上的中点,EF ⊥AE , CF 平分∠BCD 的外角。
求证:AE=EF 。
(9分)
A F
E
H
G
D C
B
4题 5题
A
E
B C
D
F
A
E
O
D
A
C
B
F
D
C
E B
A。
八年级数学周清题(7)

八年级数学周清题(七) 班级 姓名 一、填空题(每小题3分,共9分) 1、如图2,在菱形ABCD 中,对角线AC=4,∠BAD=120°,则菱形ABCD 的周长为( )A .20B .18C .16D .152、如图,矩形ABCD 的两条对角线相交于点O ,602AOB AB ∠==°,,则矩形的对角线AC 的长是( )A .2B .4C .23D .433、如图所示,正方形ABCD 的面积为12,ABE △是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD PE +的和最小,则这个最小值为( ) A .23 B .26 C .3 D .6 二、填空题(每小题3分,共21分)1.化简)0(||2<<--y x x y x 的结果是( )2、当3-=x 时,二次根7522++x x m 式的值为5,则m 等于( )3、如图,矩形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点E 、F ,23AB BC ==,,则图中阴影部分的面积为 . A .1 B .34 C .23D .24、如图,P 是菱形ABCD 对角线BD 上一点,PE ⊥AB 于点E ,PE=4cm ,则点P 到BC的距离是_____cm.5、斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .6、已知a ,b ,c 为三角形的三边,则222)()()(a c b a c b c b a -++--+-+= 。
7、 一长方形的一边长为cm 3,面积为212cm ,那么它的一条对角线长是 . 三、计算(每小题5分,共10分)1.3)154276485(÷+- 2.0)13(27132--+-四、解答题(每小题5分,共10分)1、已知:如图,在矩形ABCD 中,AF =BE 。
求证:DE =CF2、两个完全相同的矩形纸片ABCD 、BFDE 如图放置,BF AB =。
八年级数学上册 周周清9(检测内容 15.2.3-15.3)(新版)新人教版-(新版)新人教版初中八

得分________ 卷后分________ 评价________一、选择题(每小题4分,共32分)1.下列方程不是分式方程的是( B )A .1x +x =1B .x 3+3x 4=25C .21+x -11+x =2D .5x =7x -72.(2019·某某)某种计算机完成一次基本运算的时间约为1纳秒(ns),已知1纳秒=0.000 000 001秒,该计算机完成15次基本运算,所用时间用科学记数法表示为( C )×10-9秒 B .15×10-9秒×10-8秒 D .15×10-8秒3.在数(-12)-2,(-2)-2,(-12)-1,(-2)-1中,最大的数是( A ) A .(-12 )-2 B .(-2)-2 C .(-12 )-1 D .(-2)-1 4.解分式方程x 3+x -22+x=1时,去分母后可得( C ) A .x (2+x )-2(3+x )=1B .x (2+x )-2=2+xC .x (2+x )-2(3+x )=(2+x )(3+x )D .x -2(3+x )=3+x5.(2019·株洲)关于x 的分式方程2x -5x -3=0的解为( B ) A .-3 B .-2 C .2 D .36.(某某中考)已知关于x 的分式方程m -2x +1=1的解是负数,则m 的取值X 围是( D ) A .m ≤3 B .m ≤3且m ≠2C .m <3D .m <3且m ≠27.如果m +n =1,那么代数式(3m +n m 2-mn +1m )·(m 2-n 2)的值为( D )A .-4B .-1C .1D .48.(2019·某某)世界文化遗产“三孔”景区已经完成5G 基站布设,“,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G 网络的峰值速率为每秒传输x 兆数据,依题意,可列方程是( A )A .500x -50010x =45B .50010x -500x=45 C .5 000x -500x =45 D .500x -5 000x=45 二、填空题(每小题4分,共24分)9.将代数式2-1x -3y 2化为只含有正整数指数幂的形式:__y 22x __. 10.(2×10-6)×(3.2×103)=__6.4×10-3__.11.(2019·某某)分式方程5y -2=3y 的解为y =__-3__. 12.(2019·某某)甲、乙两地相距1 000 km ,如果乘高铁列车从甲地到乙地比乘特快列车少用3 h ,,设特快列车的平均速度为x km/h ,根据题意可列方程为__1 000x -1 000x=3__. 13.(某某中考)某商店第一次用600元购进2B 铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的54倍,购进数量比第一次少了30支.则该商店第一次购进的铅笔每支的进价是__4__元.14.(达州中考)若关于x 的分式方程xx -3+3a 3-x =2a 无解,则a 的值为__1或12__. 三、解答题(共44分)15.(6分)计算下列各式:(1)(-14)-1+(-2)2×2 0200-(13)-2; 解:原式=-9(2)(a 3b -1)-2·(a -3b 2)2. 解:原式=a -6b 2·a -6b 4=a -12b 6=b 6a 1216.(6分)解下列方程:(1)(某某中考)x -3x -2+1=32-x; 解:去分母,得x -3+x -2=-3,整理,得2x =2,解得x ,x =1是原方程的解(2)(2019·某某)x x -1-3(x -1)(x +2)=1. 解:去分母,得x 2+2x -3=(x -1)(x +2),解得x =1,经检验x =1不是原分式方程的解.∴原方程无解17.(10分)先阅读下面的材料,然后解答问题.通过计算,发现:方程x +1x =2+12的解为x 1=2,x 2=12; 方程x +1x =3+13的解为x 1=3,x 2=13; 方程x +1x =4+14的解为x 1=4,x 2=14;… (1)观察猜想:关于x 的方程x +1x =n +1n 的解是__x 1=n ,x 2=1n__; (2)实践运用:对于关于x 的方程x -1x =m -1m的解,小明观察得“x 1=m ”是该方程的一个解,请你猜想该方程的另一个解,并用方程的解的概念对该解进行验证;(3)拓展延伸:请利用上面的规律,求关于x 的方程x +1x -3=a +1a -3的解. 解:(1)x 1=n ,x 2=1n(2)另一个解是 x 2=-1m,验证略 (3)x +1x -3=a +1a -3,可得x -3+1x -3=a -3+1a -3, 类比(1)可得:x 1=a ,x 2=1a -3+3=3a -8a -318.(10分)(2019·某某)甲、乙两同学的家与某科技馆的距离均为4 000 m .甲、乙两人同时从家出发去科技馆,甲同学先步行800 m ,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5 min.求乙到达科技馆时,甲离科技馆还有多远.解:设甲步行的速度为x 米/分,则乙骑自行车的速度为4x 米/分,公交车的速度是8x米/分钟,根据题意得4 0004x +2.5=800x +4 000-8008x, 解得x ,x =80是原分式方程的解.所以2.5×8×80=1 600(m),答:乙到达科技馆时,甲离科技馆还有1 600 m19.(12分)(某某中考)为落实“美丽某某”的工作部署,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的32倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.(1)甲、乙两工程队每天能改造道路的长度分别是多少米?(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1 200米,改造总费用不超过145万元,至少安排甲队工作多少天?解:(1)设乙工程队每天能改造道路的长度为x 米,则甲工程队每天能改造道路的长度为32x 米,根据题意得360x -36032x =3,解得x ,x =40是原分式方程的解,且符合题意, ∴32x =32×40=60. 答:乙工程队每天能改造道路的长度为40米,甲工程队每天能改造道路的长度为60米(2)设安排甲队工作m 天,则安排乙队工作1 200-60m 40天,根据题意,得7m +5×1 200-60m 40≤145,解得m ≥10.答:至少安排甲队工作10天。
初二周周清数学试卷答案

一、选择题(每题3分,共30分)1. 若a,b是实数,且a + b = 0,则a与b互为()A. 相等B. 相邻C. 倒数D. 相反数答案:D解析:根据实数的性质,若a + b = 0,则a与b互为相反数。
2. 下列方程中,解为正数的是()A. x + 1 = 0B. x - 1 = 0C. x^2 - 1 = 0D. x^2 + 1 = 0答案:C解析:解方程x^2 - 1 = 0,得到x = ±1,其中正数解为1。
3. 下列图形中,既是轴对称图形又是中心对称图形的是()A. 等腰三角形B. 等边三角形C. 矩形D. 圆答案:D解析:矩形和圆既是轴对称图形又是中心对称图形。
4. 若a,b,c成等差数列,则()A. a + b + c = 0B. a^2 + b^2 + c^2 = 3abcC. a^2 + b^2 + c^2 = 2ab + 2bc + 2acD. a^2 + b^2 + c^2 = (a + b + c)^2答案:C解析:由等差数列的性质可知,a + b + c = 3a,代入C选项得到a^2 + b^2 + c^2 = 2ab + 2bc + 2ac。
5. 若一个数的平方等于它本身,则这个数是()A. 0B. 1C. -1D. 0或1答案:D解析:0的平方等于0,1的平方等于1,-1的平方等于1,因此这个数是0或1。
二、填空题(每题5分,共20分)6. 若x^2 - 4x + 3 = 0,则x的值为______。
答案:x = 1或x = 3解析:将方程因式分解得到(x - 1)(x - 3) = 0,解得x = 1或x = 3。
7. 若a,b,c成等比数列,则b^2 =______。
答案:b^2 = ac解析:由等比数列的性质可知,b^2 = ac。
8. 若a,b,c成等差数列,则a^2 + b^2 + c^2 =______。
答案:a^2 + b^2 + c^2 = (a + b + c)^2解析:由等差数列的性质可知,a^2 + b^2 + c^2 = (a + b + c)^2。
八年级数学下册周清试题3试题

卜人入州八九几市潮王学校周清试题3一、选择题〔每一小题2分,一共20分〕1.二次根式1a -中,字母a 的取值范围是〔〕 A .1a <B .a≤1 C.a≥1D.1a > 2.以下根式中属最简二次根式的是〔〕 A .21a +B .12C .8D .273.化简40的结果是〔〕A .10B .210C .45D .204.以下根式中能与3合并的二次根式为〔〕A .32B .24C .12D .185.以下计算正确的选项是〔〕A .235+=B .236=·C .84=D .2(3)3-=-6.以下各数中,与23的积为有理数的是〔〕A .32+B .32-C .32+-D .37.假设2121m m m --+=,那么m 的取值范围是〔〕A .1m >B .1m <C .1m ≥D .1m ≤8.计算112753483⎛⎫+- ⎪ ⎪⎝⎭的结果是〔〕A .6B .43C .236+D .129.估计132202⨯+的运算结果应在〔〕A .6到7之间B .7到8之间C .8到9之间D .9到10之间10.右图是一个正方体的展开图,这个正方体各对面的式子之积是相等的,那么x 为〔〕A .3B .23C .26D .26二、填空题〔每一小题2分,一共10分〕11.函数1x y x =-中,自变量x 的取值范围是_____________. 12.实数a ,b 在数轴上的位置如下列图,那么化简|a -b|-2a 的结果是.13.y=2x -+2x -+5,那么x y =________.14.假设最简二次根式7a b +与36b a b +-是同类二次根式,那么a =______,b =______. 15.假设y x 2-+823-+y x =0,那么(x +y )x =________. 三、解答题19.〔10分〕阅读下面问题:12)12)(12()12(1211-=-+-⨯=+;23)23)(23(23231-=-+-=+;25)25)(25(25251-=-+-=+,……。
周清试卷

八年级数学周清试题2015/3/15一、填空题(每空4分,共36分)1.已知:如图,AB=AC,FD⊥BC于D,DE⊥AB于E,若∠AFD=145°,则∠EDF =.(第1题图) (第5题图) (第6题图)2.在直角三角形中,如果一个锐角为30°,而斜边与较小直角边的和为12,那么斜边长为.3.等腰直角三角形中,若斜边为16,则直角边的长为.4.“直角三角形两条直角边的平方和等于斜边的平方”的逆定理是.5.如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC=. 6.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若DB=10cm,则AC=.7.在△ABC中,AB=AC,∠A=58°,AB的垂直平分线交AC于N,则∠NBC = . 8.正三角形的边长为a,则它的面积为.9.命题“线段垂直平分线上的点到这条线段两个端点的距离相等”的条是,结论是.10.(2011•怀化)如图,在△ABC中,AB=AC,∠BAC的角平分线交BC边于点D,AB=5cm,BC=6cm,则AD=.11.等腰三角形一腰上的高与另一腰的夹角为300,腰长为6,则其底边上的高是。
12.(2011•衡阳)如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为.13.(2013•泰安)如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是.第10题 第12题 第13题 第14题14.(2005•绵阳)如图,在△ABC 中,BC=5cm ,BP 、CP 分别是∠ABC 和∠ACB 的角平分线,且PD ∥AB ,PE ∥AC ,则△PDE 的周长是 cm .二、解答题15.已知:如图,点D 是△ABC 内一点,AB =AC ,∠1=∠2.求证:AD 平分∠BAC .16.已知:如图,△ABC 和△CDE 都是等边三角形,点D 在BC 边上.求证:AD =BE .17.求证:等腰三角形两腰上的中线的交点到底边两个端点的距离相等.18.如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.(1)求AB的长;(2)求△ABC的面积;(3)求CD的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
初二数学周清测试题
一、选择题(本大题共8个小题,每小题4分,满分32 分) 1.下列不等式中,是一元一次不等式的是( )
A .012>-x
B .21<-
C .123-≤-y x
D .532>+y 2.不等式54≤-x 的解集是 ( )
A .45-≤x
B .45-≥x
C .54-≤x
D .5
4
-≥x
3. A .121->x B .
32
3
-≥+x C .11-≥+x D .42>-x 4.不等式2x-5<5-2x 的正整数解有( ) A.1个 B.2个 C.3个 D.4个
5.要使代数式2
9
x +的值为非负数,则x 的取值范围应是( )
A.x ≥0
B.x ≤0
C.x>-2
D.x ≥-2
6.下列各式从左到右的变形错误的是( )
(A)2
2)()(y x x y -=- (B ))(b a b a +-=--
(C)3
3)()(a b b a --=- (D))(n m n m +-=+- 7.分解因式x x x 16842
3-+-的结果是( )
(A))1684(2+--x x x (B))1684(2
-+-x x x
(C))42(42-+-x x (D))42(42
+--x x x 8.下列各式是完全平方式的是( )
(A)2242y xy x ++ (B)2
21025b ab a ++ (C)2
2q pq p ++ (D)22412n mn m +
-
二、填空题:(每空4 分,共32分)
9、用适当的不等式表示下列关系:n 的值不超过15_____________; 10、写出不等式3x -10≤0所有的正整数解是:x =_______。
11、分解因式=-+a ab ab 322
________.
12、已知2264y kxy x +-是完全平方式,则k=________.
13. 当a_______时(a-2)x>2(a-2)的解集为x>2.
14.若a<0,则不等式组,
x a x a
>⎧⎨<-⎩的解集是_______.
15.x 的
1
2
与5的差不小于3,用不等式表示为________. 16.当x_______时,式子3x-5的值大于5x+3的值. 三、解答题:(共36分)
17.解不等式
11237x x
--≤ (6分) 18、解不等式组: ⎩
⎨⎧<-<-x x x 332312(6分) 并把解集表示在数轴上.
18.分解因式:(1)3x 3y –12xy (4分) (2) 3ax 2+6axy+3ay 2 (4分)
19. 已知013642
2=++-+b a b a ,求a + b 的值(6分)
20. 某童装厂,现有甲种布料38米,乙种布料26米,现计划用这两种布料生产L 、M 两种型号的童装共50套.已知做一套L 型号的童装需用甲种布料0.5米,乙种布料1米,做一套M 型号的童装需用甲种布料0.9米,乙种布料0.2米。
(1)设生产L 型号的童装套数为x (套),写出x 应满足的不等式组;(2)有哪几种符合题意的生产方案?请你帮助设计。
(10分)。
