精讲精练13 2017—2019年高考真题精讲精练
2017年新课标全国卷古诗鉴赏题——精讲精练,各个击破!

晚归山居 刘沧 寥落霜空木叶稀,初行郊野思依依。 深秋频忆故乡事,日暮独寻荒径归。 山影暗随云水动,钟声潜入远烟微。 娟娟唯有西林月,不惜清光照竹扉。 8.这首诗的颈联与王维《山居秋暝》的颔联“明月松间照,清泉 石上流”相比,在写景角度上有何相同点?在意境上有何区别? 请简要分析。(5分) ①在写景角度上,二者都从视觉、听觉的角度描写了景物。(1 分)刘诗颈联从视觉角度描写“山影”,从听觉角度表现“钟 声”。王诗颔联从视觉角度描写“明月”,从视觉、听觉角度描 写“清泉”。(1分)②在意境上,刘诗颈联描写了山影投映溪 水,随波暗涌,古寺钟声悠长,又随远烟逝去,意境幽暗空寂。 (2分)而王诗颔联描写了一场秋雨后,只见皎洁的月光透过松 枝星星点点洒落下来,又闻泉水淙淙流泻于山石之间,意境幽清 明净。(1分)
表达了诗人凄凉孤寂、思乡的感情。(2分) “鸿雁”是书信的代称,“不闻鸿雁信”表达思乡而不得消息的苦 恼;“鹧鸪”叫声常有凄切思念之意,它的啼叫也勾起词人的故 旧之思; “落花”含有悲情的意思,借“落花”进一步表达出词人内心的凄 凉和孤寂。(4分,每个意象分析1分。)
春 尽 韩偓 惜春连日醉昏昏,醒后衣裳见酒痕。 细水浮花归别涧,断云含雨入孤村。 人闲易有芳时恨,地迥难招自古魂。 惭愧流莺相厚意,清晨犹为到西园。 【注】①韩偓官至翰林学士承旨,但后遭排挤,被贬淮州,后因避难投靠节度使 王审知。当时朱全忠弑帝,建立梁期,王审知接受梁的封号,韩偓离开王审 知定居于闽南泉州。诗作于此时。②招魂,语出《楚辞•招魂》,原指祈祷死 者复生的一种宗教仪式,这里只是一般地用作招致魂魄。 9.这首诗的后两联表达了作者什么样的情感?请简要分析。( 6分)
①伤春惜春之情。“芳时恨”表现了作者的心惜春之情。 ②年华迟暮,有志难骋的沉痛:芳时春尽,人生老去,诗人却只能“闲”置一隅, 其苦闷沉痛可知。 ③孤身独处,苦无知音的寂寞:诗人地处偏僻,非但亲朋息迹,古人魂魄也难招 致,唯有“流莺相厚”,更见其寂寞之感。
高考必考语法精讲精练专题十二:非谓语动词(含解析)
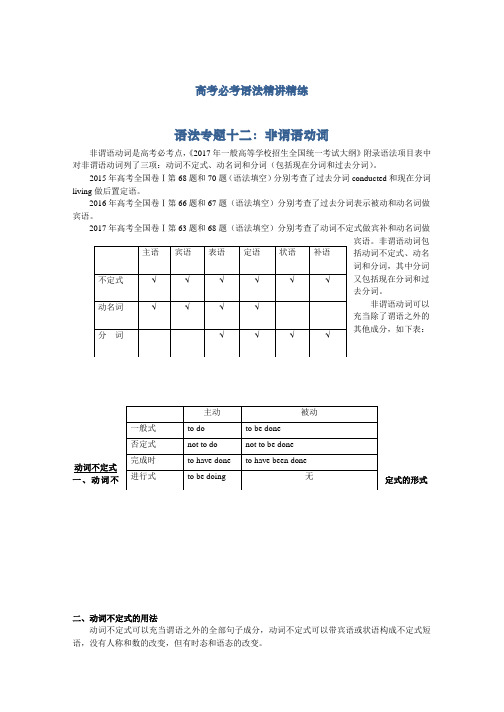
高考必考语法精讲精练语法专题十二:非谓语动词非谓语动词是高考必考点,《2017年一般高等学校招生全国统一考试大纲》附录语法项目表中对非谓语动词列了三项:动词不定式、动名词和分词(包括现在分词和过去分词)。
动词不定式一、动词不定式的形式二、动词不定式的用法动词不定式可以充当谓语之外的全部句子成分,动词不定式可以带宾语或状语构成不定式短语,没有人称和数的改变,但有时态和语态的改变。
1.作主语(1)动词不定式作主语,一般表示详细的某次动作,谓语动词用单数形式。
例如:①To see is to believe.②To master English is of great importance.(2)不定式或不定式短语作主语时,常用it作形式主语,构成“It is + adj+for sb.+to do”结构,或It is +adj+for sth +to be done。
例如:①It is impossible for him to give up smoking.②It is not easy to find your way in the mountain.③It is difficult for the problem to be solved.④It is impossible for my question to be answered in his absence.2.作宾语(1)动词不定式作宾语时,常跟在某些及物动词后面,常见的有:agree,dare,decide,expect,help,hope,learn,manage,offer,pretend,promise,refuse,want, intend, fail, wish, choose等。
例如:①I mean to go there at once.②We must learn to tell friends from enemies.(2)不定式短语作宾语时,假如还带有宾语补足语,往往把不定式短语放在宾补之后,而用it 作形式宾语。
精讲精练15 2017—2019年高考真题精讲精练

高考真题精讲精练:训练步骤:1、先花十八分钟做完这三篇阅读理解。
2、再仔细阅读做题思维过程及试题分析和阅读技巧点拨。
3、然后翻译的文章要仔细研读并做到精通文章原意而且最好是能脱口而出。
2017阅读全国卷一阅读下列短文,从每题所给的A、B、C和D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
APacific Science Center Guide◆Visit Pacific Science Center’sStoreDon’t forget to stop by Pacific Science Center’s Store while you are here to pick up a wonderful science activity or remember your visit. The store is located (位于) upstairs in Building 3 right next to the Laster Dome.◆HungryOur exhibits will feed your mind but what about your body? Our café offers a complete menu of lunch and snack options, in addition to seasonal specials. The café is located upstairs in Building 1 and is open daily until one hour before Pacific Science Center closes.◆Rental InformationLockers are available to store any belongings during your visit. The lockers are located in Building 1 near the Information Desk and in Building 3. Pushchairs and wheelchairs are available to rent at the Information Desk and Denny Way entrance. ID required.◆S upport Pacific Science CenterSince 1962 Pacific Science Center has been inspiring a passion (热情) for discovery and lifelong learning in science, math and technology. Today Pacific Science Center serves more than 1.3 million people a year and beings inquiry-based science education to classrooms and community events all over Washington State. It’s an amazing accomplishment and one we can not achieve without generous support from individuals, corporations, and other social organizations. visit to find various ways you can support Pacific Science Center.21. Where can you buy a souvenir at Pacific Science Center?A. In Building 1.B. In Building 3.C. At the last Dome.D. At the Denny Way entrance.22. What does PacificScience Center do for schools?A. Train Science teachers.B. Disncie science books.C. Inspire scientific research.D. Take science to the classroom.23. What is the purpose of the last part of the text?A. To encourage donations.B. To advertise coming events.C. To introduce special exhibits.D. To tell about the Center’s history.BI work with Volunteers for Wildlife, a rescue and education organization at Bailey Arboretum in Locust Valley. Trying to help injured, displaced or sick creatures can be heartbreaking; survival is never certain. However, when it works, it is simply beautiful.I got a rescue call from a woman in Muttontown. She had found a young owl (猫头鹰) on the ground. When I arrived, I saw a 2-to 3-week-old owl. It had already been placed in a carrier for safety.I examined the chick (雏鸟) and it seemed fine. If I could locate the nest, I might have been able to put it back, but no luck. My next work was to construct a nest and anchor it in a tree.The homeowner was very helpful. A wire basket was found. I put some pine branches into the basket to make this nest safe and comfortable. I placed the chick in the nest, and it quickly calmed down.Now all that was needed were the parents, but they were absent. I gave the homeowner a recording of the hunger screams of owl chicks. These advertise the presence of chicks to adults; they might also encourage our chick to start calling as well. I gave the owner as much information as possible and headed home to see what news the night might bring.A nervous night to be sure, but sometimes the spirits of nature smile on us all! The homeowner called to say that the parents had responded to the recordings. I drove over and saw the chick in the nest looking healthy and active. And it was accompanied in the nest by the greatest sight of all --- LUNCH! The parents had done their duty and would probably continue to do so.24. What is unavoidable in the author’s rescue work according to paragraph 1?A. Efforts made in vain.B. Getting injured in his work.C. Feeling uncertain about his future.D. Creatures forced out of their homes.25. Why was the author called to Muttontown?A. To rescue a woman.B. To take care of a woman.C. To look at a baby owl.D. To cure a young owl.26. What made the chick calm down?A. A new nest.B. Some food.C. A recording.D. Its parents.27. How would the author feel about the outcome of the event?A. It’s unexpected.B.It’s beautiful.C.It’s humorous.D.It’s discouraging.CSome of the world’s most famous musicians recently gathered in Paris and New Orleans to celebrate the first annual International Jazz Day. UNESCO (United Nations Educational, Scientific and Cultural Organization) recently set April 30 as a day to raise awareness of jazz music, its significance, and its potential as a unifying (联合) voice across cultures.Despite the celebrations, though, in the U.S. the jazz audience continues to shrink and grow older, and the music has failed to connect with younger generations.It’s Jason Moran’s job to help change that. As the Kennedy Center’s artistic adviser for jazz, Moran hopes to widen the audience for jazz, make the music more accessible, and preserve its history and culture.“Jazz seems like it’s not really a part of the American appetite,” Moran tells National Public Radio’s reporter Neal Conan. “What I’m hoping to accomplish is that my generation and younger start to reconsider and understand that jazz is not black and write anymore. It’s actually color, and it’s actually digital.”Moran says one of the problems with jazz today is that the entertainment aspect of the music has been lost. “The music can’t be presented today the way it was in 1908 or 1958. It has to continue to move, because the way the world works is not the same,” says Moran.Last year, Moran worked on a project that arranged Fats Waller’s music for a dance party, “Just to kind of put it back in the mind that Waller is dance music as much as it is concert music,” says Moran. “For me, it’s the recontextualization. In music, where does the emotion (情感) lie? Are we, as humans, gaining any insight (感悟) on how to talk about ourselves and how something as abstract as a Charlie Parker record gets us into a dialogue about our emotions and our thoughts? Sometimes we lose sight that the music has a wider context,” says Moran, “so I want to continue those dialogues. Those are the things I want to foster.”28.Why did UNESCO set April 30 as International Jazz Day?A.To remember the birth of jazz.B.To protect cultural diversity.C.To encourage people to study music.D.To recognize the value of jazz.29.What does the underlined word “that” in paragraph 3 refer to?A.Jazz becoming more accessible.B.The production of jazz growing faster.C.Jazz being less popular with the young.D.The jazz audience becoming larger.30.What can we infer about Moran’s opinion on jazz?A.It will disappear gradually.B.It remains black and white.C.It should keep up with the times.D.It changes every 50 years.31.Which of the following can be the best title for the text?A.Exploring the Future of Jazz.B.The Rise and Fall of Jazz.C.The Story of a Jazz Musician.D.Celebrating the Jazz Day.下面我们来看看A篇文章的思维过程解析和解题技巧点拨:往往A篇都是信息查找题,因此可以直接做题以节约时间提高做题效率。
2017-2019年高考真题数学(理)分项汇编_专题12 数列

专题12数列1.【2019年高考全国I 卷理数】记n S 为等差数列{}n a 的前n 项和.已知4505S a ==,,则 A .25n a n =-B .310n a n =-C .228n S n n =-D .2122n S n n =- 【答案】A【解析】由题知,41514430245d S a a a d ⎧=+⨯⨯=⎪⎨⎪=+=⎩,解得132a d =-⎧⎨=⎩,∴25n a n =-,24n S n n =-,故选A . 【名师点睛】本题主要考查等差数列通项公式与前n 项和公式,渗透方程思想与数学计算等素养.利用等差数列通项公式与前n 项公式即可列出关于首项与公差的方程,解出首项与公差,再适当计算即可做了判断.2.【2019年高考全国III 卷理数】已知各项均为正数的等比数列{}n a 的前4项和为15,且53134a a a =+,则3a = A .16 B .8C .4D .2【答案】C【解析】设正数的等比数列{a n }的公比为q ,则231111421111534a a q a q a q a q a q a ⎧+++=⎨=+⎩, 解得11,2a q =⎧⎨=⎩,2314a a q ∴==,故选C .【名师点睛】本题利用方程思想求解数列的基本量,熟练应用公式是解题的关键.3.【2019年高考浙江卷】设a ,b ∈R ,数列{a n }满足a 1=a ,a n +1=a n 2+b ,n *∈N ,则A .当101,102b a => B .当101,104b a => C .当102,10b a =-> D .当104,10b a =->【答案】A【解析】①当b =0时,取a =0,则0,n a n *=∈N .故B 项不正确. 故本题正确答案为A.【名师点睛】遇到此类问题,不少考生会一筹莫展.利用函数方程思想,通过研究函数的不动点,进一步讨论a 的可能取值,利用“排除法”求解.4.【2018年高考全国I 卷理数】设n S 为等差数列{}n a 的前n 项和,若3243S S S =+,12a =,则5a = A .12- B .10- C .10D .12【答案】B【解析】设等差数列的公差为d ,根据题中的条件可得3243332224222d d d ⨯⨯⎛⎫⨯+⋅=⨯++⨯+⋅ ⎪⎝⎭, 整理解得3d =-,所以51421210a a d =+=-=-,故选B .【名师点睛】该题考查的是有关等差数列的求和公式和通项公式的应用,在解题的过程中,需要利用题中的条件,结合等差数列的求和公式,得到公差d 的值,之后利用等差数列的通项公式得到5a 与1a d ,的关系,从而求得结果.5.【2018年高考浙江卷】已知1234,,,a a a a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则 A .1324,a a a a << B .1324,a a a a >< C .1324,a a a a <>D .1324,a a a a >>【答案】B【解析】令()ln 1,f x x x =--则()11f x x'=-,令()0,f x '=得1x =,所以当1x >时,()0f x '>,当01x <<时,()0f x '<,因此()()10,ln 1f x f x x ≥=∴≥+.若公比0q >,则()1234123123ln a a a a a a a a a a +++>++>++,不合题意; 若公比1q ≤-,则()()212341110,a a a a a q q +++=++≤但()()212311ln ln 1ln 0a a a a q q a ⎡⎤++=++>>⎣⎦,即()12341230l n a a a a a a a +++≤<++,不合题意;因此()210,0,1q q -<<∈,22113224,0a a q a a a q a ∴>=<=<,故选B.【名师点睛】构造函数对不等式进行放缩,进而限制参数取值范围,是一个有效方法.如()2ln 1,e 1,e 10.x x x x x x x ≥+≥+≥+≥6.【2017年高考全国I 卷理数】记n S 为等差数列{}n a 的前n 项和.若4524a a +=,648S =,则{}n a 的公差为 A .1 B .2 C .4D .8【答案】C【解析】设公差为d ,45111342724a a a d a d a d +=+++=+=,611656615482S a d a d ⨯=+=+=,联立112724,61548a d a d +=⎧⎨+=⎩解得4d =,故选C . 【秒杀解】因为166346()3()482a a S a a +==+=,即3416a a +=, 则4534()()24168a a a a +-+=-=,即5328a a d -==,解得4d =,故选C .【名师点睛】求解等差数列基本量问题时,要多多使用等差数列的性质,如{}n a 为等差数列,若m n p q +=+,则m n p q a a a a +=+.7.【2017年高考全国I 卷理数】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N :N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A .440 B .330C .220D .110【答案】A【解析】由题意得,数列如下:11,1,2,1,2,4,1,2,4,,2k-则该数列的前(1)122k k k ++++=项和为11(1)1(12)(122)222k k k k S k -++⎛⎫=+++++++=-- ⎪⎝⎭,要使(1)1002k k +>,有14k ≥,此时122k k ++<,所以2k +是第1k +组等比数列1,2,,2k 的部分和,设1212221t t k -+=+++=-,所以2314t k =-≥,则5t ≥,此时52329k =-=, 所以对应满足条件的最小整数293054402N ⨯=+=,故选A. 【名师点睛】本题非常巧妙地将实际问题和数列融合在一起,首先需要读懂题目所表达的具体含义,以及观察所给定数列的特征,进而判断出该数列的通项和求和.另外,本题的难点在于数列里面套数列,第一个数列的和又作为下一个数列的通项,而且最后几项并不能放在一个数列中,需要进行判断. 8.【2017年高考全国II 卷理数】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯 A .1盏 B .3盏 C .5盏D .9盏【答案】B【解析】设塔的顶层共有灯x 盏,则各层的灯数构成一个首项为x ,公比为2的等比数列,结合等比数列的求和公式有7(12)38112x -=-,解得3x =,即塔的顶层共有灯3盏,故选B . 【名师点睛】用数列知识解相关的实际问题,关键是列出相关信息,合理建立数学模型——数列模型,判断是等差数列还是等比数列模型;求解时要明确目标,即搞清是求和、求通项、还是解递推关系问题,所求结论对应的是解方程问题、解不等式问题、还是最值问题,然后将经过数学推理与计算得出的结果放回到实际问题中,进行检验,最终得出结论.9.【2017年高考全国III 卷理数】等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .24- B .3- C .3D .8【答案】A【解析】设等差数列{}n a 的公差为d ,由a 2,a 3,a 6成等比数列可得2326a a a =,即()()()212115d d d +=++,整理可得220d d +=,又公差不为0,则2d =-,故{}n a 前6项的和为()()()6166166166122422S a d ⨯-⨯-=+=⨯+⨯-=-.故选A . 【名师点睛】(1)等差数列的通项公式及前n 项和公式共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了用方程的思想解决问题.(2)数列的通项公式和前n 项和公式在解题中起到变量代换作用,而a 1和d 是等差数列的两个基本量,用它们表示已知和未知是常用方法.10.【2017年高考浙江卷】已知等差数列{a n }的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6>2S 5”的 A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【解析】由46511210212(510)S S S a d a d d +-=+-+=,可知当0d >时,有46520S S S +->,即4652S S S +>,反之,若4652S S S +>,则0d >,所以“d >0”是“S 4 + S 6>2S 5”的充要条件,选C .【名师点睛】本题考查等差数列的前n 项和公式,通过套入公式与简单运算,可知4652S S S d +-=,结合充分必要性的判断,若p q ⇒,则p 是q 的充分条件,若p q ⇐,则p 是q 的必要条件,该题“0d >”⇔“46520S S S +->”,故互为充要条件.11.【2019年高考全国I 卷理数】记S n 为等比数列{a n }的前n 项和.若214613a a a ==,,则S 5=___________.【答案】1213【解析】设等比数列的公比为q ,由已知21461,3a a a ==,所以32511(),33q q =又0q ≠, 所以3,q =所以55151(13)(1)12131133a q S q --===--. 【名师点睛】准确计算,是解答此类问题的基本要求.本题由于涉及幂的乘方运算、繁分式的计算,部分考生易出现运算错误.12.【2019年高考全国III 卷理数】记S n 为等差数列{a n }的前n 项和,12103a a a =≠,,则105S S =___________. 【答案】4【解析】设等差数列{a n }的公差为d ,因213a a =,所以113a d a +=,即12a d =,所以105S S =11111091010024542552a d a a a d⨯+==⨯+. 【名师点睛】本题主要考查等差数列的性质、基本量的计算.渗透了数学运算素养.使用转化思想得出答案.13.【2019年高考北京卷理数】设等差数列{a n }的前n 项和为S n ,若a 2=−3,S 5=−10,则a 5=__________,S n 的最小值为___________. 【答案】 0,10-. 【解析】等差数列{}n a 中,53510S a ==-,得32,a =-又23a =-,所以公差321d a a =-=,5320a a d =+=,由等差数列{}n a 的性质得5n ≤时,0n a ≤,6n ≥时,n a 大于0,所以n S 的最小值为4S 或5S ,即为10-. 【名师点睛】本题考查等差数列的通项公式、求和公式、等差数列的性质,难度不大,注重重要知识、基础知识、基本运算能力的考查.14.【2019年高考江苏卷】已知数列*{}()n a n ∈N 是等差数列,n S 是其前n 项和.若25890,27a a a S +==,则8S 的值是___________. 【答案】16【解析】由题意可得:()()()25811191470989272a a a a d a d a d S a d ⎧+=++++=⎪⎨⨯=+=⎪⎩, 解得:152a d =-⎧⎨=⎩,则8187840282162S a d ⨯=+=-+⨯=. 【名师点睛】等差数列、等比数列的基本计算问题,是高考必考内容,解题过程中要注意应用函数方程思想,灵活应用通项公式、求和公式等,构建方程(组),如本题,从已知出发,构建1a d ,的方程组.15.【2018年高考全国I 卷理数】记n S 为数列{}n a 的前n 项和,若21n n S a =+,则6S =___________.【答案】63-【解析】根据21n n S a =+,可得1121n n S a ++=+,两式相减得1122n n n a a a ++=-,即12n n a a +=,当1n =时,11121S a a ==+,解得11a =-,所以数列{}n a 是以−1为首项,以2为公比的等比数列,所以()66126312S --==--,故答案是63-.【名师点睛】该题考查的是有关数列的求和问题,在求解的过程中,需要先利用题中的条件,类比着往后写一个式子,之后两式相减,得到相邻两项之间的关系,从而确定出该数列是等比数列,之后令1n =,求得数列的首项,最后应用等比数列的求和公式求解即可,只要明确对既有项又有和的式子的变形方向即可得结果.16.【2018年高考北京卷理数】设{}n a 是等差数列,且a 1=3,a 2+a 5=36,则{}n a 的通项公式为___________.【答案】63n a n =-【解析】设等差数列的公差为d ,()133343663616 3.n a d d d a n n =∴+++=∴=∴=+-=-,,, 【名师点睛】先根据条件列出关于公差的方程,求出公差后,代入等差数列通项公式即可.在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为首项与公差(公比)问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.17.【2018年高考江苏卷】已知集合*{|21,}A x x n n ==-∈N ,*{|2,}nB x x n ==∈N .将AB 的所有元素从小到大依次排列构成一个数列{}n a .记n S 为数列{}n a 的前n 项和,则使得112n n S a +>成立的n 的最小值为___________. 【答案】27【解析】所有的正奇数和()2n n *∈N 按照从小到大的顺序排列构成{}n a ,在数列|{}n a 中,25前面有16个正奇数,即5621382,2a a ==.当n =1时,1211224S a =<=,不符合题意;当n =2时,2331236S a =<=,不符合题意;当n =3时,3461248S a =<=,不符合题意;当n =4时,4510<12=60S a =,不符合题意;……;当n =26时,()2752621221(141)441625032121=2516S a ⨯-⨯+=+=+=<-,不符合题意;当n =27时,()8527221222(143)21484+62=546>12=5420S a ⨯-⨯+=+=-,符合题意.故使得+1>12n n S a 成立的n 的最小值为27.【名师点睛】本题主要考查等差数列、等比数列的前n 项和,考查考生的运算求解能力,考查的核心素养是数学运算.18.【2017年高考全国II 卷理数】等差数列{}n a 的前n 项和为n S ,33a =,410S =,则11nk kS ==∑___________. 【答案】21nn + 【解析】设等差数列的首项为1a ,公差为d ,由题意有1123434102a d a d +=⎧⎪⎨⨯+=⎪⎩,解得111a d =⎧⎨=⎩, 数列的前n 项和()()()111111222n n n n n n n S na d n --+=+=⨯+⨯=, 裂项可得12112()(1)1k S k k k k ==-++, 所以1111111122[(1)()()]2(1)223111nk knSn n n n ==-+-++-=-=+++∑. 【名师点睛】等差数列的通项公式及前n 项和公式,共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了用方程的思想解决问题.数列的通项公式和前n 项和公式在解题中起到变量代换作用,而a 1和d 是等差数列的两个基本量,用它们表示已知和未知是常用得方法.使用裂项法求和时,要注意正、负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点.19.【2017年高考全国III 卷理数】设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3,则a 4 =___________.【答案】8-【解析】设等比数列{}n a 的公比为q ,很明显1q ≠-,结合等比数列的通项公式和题意可得方程组:1212131(1)1(1)3a a a q a a a q +=+=-⎧⎨-=-=-⎩①②,由②①可得:2q =-,代入①可得11a =,由等比数列的通项公式可得3418a a q ==-.【名师点睛】等比数列基本量的求解是等比数列中的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前n 项和公式时,应该要分类讨论,有时还应善于运用整体代换思想简化运算过程.20.【2017年高考江苏卷】等比数列{}n a 的各项均为实数,其前n 项和为n S ,已知3676344S S ==,,则8a =___________.【答案】32【解析】当1q =时,显然不符合题意;当1q ≠时,3161(1)714(1)6314a q q a q q⎧-=⎪-⎪⎨-⎪=⎪-⎩,解得1142a q ⎧=⎪⎨⎪=⎩,则7812324a =⨯=. 【名师点睛】在解决等差、等比数列的运算问题时,有两个处理思路:①利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;②利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质成立的前提条件,有时需要进行适当变形.在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.21.【2017年高考北京卷理数】若等差数列{}n a 和等比数列{}n b 满足11–1a b ==,448a b ==,则22a b =___________. 【答案】1【解析】设等差数列的公差和等比数列的公比分别为d 和q ,则3138d q -+=-=,求得2,3q d =-=,那么221312a b -+==. 【名师点睛】等差、等比数列各有五个基本量,两组基本公式,而这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化为解关于基本量的方程(组)问题,因此可以说数列中的绝大部分运算题可看作方程应用题,所以用方程思想解决数列问题是一种行之有效的方法. 22.【2019年高考全国II 卷理数】已知数列{a n }和{b n }满足a 1=1,b 1=0,1434n n n a a b +-=+,1434n n n b b a +-=-.(1)证明:{a n +b n }是等比数列,{a n –b n }是等差数列;(2)求{a n }和{b n }的通项公式. 【答案】(1)见解析;(2)1122n n a n =+-,1122n nb n =-+. 【解析】(1)由题设得114()2()n n n n a b a b +++=+,即111()2n n n n a b a b +++=+. 又因为a 1+b 1=l ,所以{}n n a b +是首项为1,公比为12的等比数列. 由题设得114()4()8n n n n a b a b ++-=-+,即112n n n n a b a b ++-=-+. 又因为a 1–b 1=l ,所以{}n n a b -是首项为1,公差为2的等差数列. (2)由(1)知,112n n n a b -+=,21n n a b n -=-. 所以111[()()]222n n n n n n a a b a b n =++-=+-, 111[()()]222n n n n n n b a b a b n =+--=-+.【名师点睛】本题考查了数列的相关性质,主要考查了等差数列以及等比数列的相关证明,证明数列是等差数列或者等比数列一定要结合等差数列或者等比数列的定义,考查推理能力,考查化归与转化思想,是中档题.23.【2019年高考北京卷理数】已知数列{a n },从中选取第i 1项、第i 2项、…、第i m 项(i 1<i 2<…<i m ),若12m i i i a a a <<⋅⋅⋅<,则称新数列12m i i i a a a ⋅⋅⋅,,,为{a n }的长度为m 的递增子列.规定:数列{a n }的任意一项都是{a n }的长度为1的递增子列.(1)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;(2)已知数列{a n }的长度为p 的递增子列的末项的最小值为0m a ,长度为q 的递增子列的末项的最小值为0n a .若p <q ,求证:0m a <0n a ;(3)设无穷数列{a n }的各项均为正整数,且任意两项均不相等.若{a n }的长度为s 的递增子列末项的最小值为2s –1,且长度为s 末项为2s –1的递增子列恰有2s -1个(s =1,2,…),求数列{a n }的通项公式. 【答案】(1) 1,3,5,6(答案不唯一);(2)见解析;(3)见解析. 【解析】(1)1,3,5,6.(答案不唯一)(2)设长度为q 末项为0n a 的一个递增子列为1210,,,,q r r r n a a a a -.由p <q ,得10p q r r n a a a -≤<.因为{}n a 的长度为p 的递增子列末项的最小值为0m a , 又12,,,p r r r a a a 是{}n a 的长度为p 的递增子列,所以0p m r a a ≤. 所以00m n a a <·(3)由题设知,所有正奇数都是{}n a 中的项.先证明:若2m 是{}n a 中的项,则2m 必排在2m −1之前(m 为正整数). 假设2m 排在2m −1之后. 设121,,,,21m p p p a a a m --是数列{}n a 的长度为m 末项为2m −1的递增子列,则121,,,,21,2m p p p a a a m m --是数列{}n a 的长度为m +1末项为2m 的递增子列.与已知矛盾.再证明:所有正偶数都是{}n a 中的项.假设存在正偶数不是{}n a 中的项,设不在{}n a 中的最小的正偶数为2m .因为2k 排在2k −1之前(k =1,2,…,m −1),所以2k 和21k -不可能在{}n a 的同一个递增子列中. 又{}n a 中不超过2m +1的数为1,2,…,2m −2,2m −1,2m +1,所以{}n a 的长度为m +1且末项为2m +1的递增子列个数至多为1(1)22221122m m m --⨯⨯⨯⨯⨯⨯=<个.与已知矛盾.最后证明:2m 排在2m −3之后(m ≥2为整数).假设存在2m (m ≥2),使得2m 排在2m −3之前,则{}n a 的长度为m +1且末项为2m +l 的递增子列的个数小于2m.与已知矛盾.综上,数列{}n a 只可能为2,1,4,3,…,2m −3,2m ,2m −1,…. 经验证,数列2,1,4,3,…,2m −3,2m ,2m −1,…符合条件.所以1,1,n n n a n n +⎧=⎨-⎩为奇数,为偶数.【名师点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.24.【2019年高考天津卷理数】设{}n a 是等差数列,{}n b 是等比数列.已知1122334,622,24a b b a b a ===-=+,.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足111,22,2,1,,k k n kk c n c b n +=⎧<<=⎨=⎩其中*k ∈N . (i )求数列(){}221n n a c -的通项公式; (ii )求()2*1ni ii a c n =∈∑N .【答案】(1)31n a n =+;32nn b =⨯(2)(i )()221941n n n a c -=⨯-(ii )()()2*211*12725212nn n i i i a c n n n --=∈=⨯+⨯--∈∑N N【解析】(1)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q .依题意得2662,6124,q d q d =+⎧⎨=+⎩解得3,2,d q =⎧⎨=⎩故14(1)331,6232n nn n a n n b -=+-⨯=+=⨯=⨯.所以,{}n a 的通项公式为{}31,n n a n b =+的通项公式为32n n b =⨯.(2)(i )()()()()22211321321941n n n n n n n a c a b -=-=⨯+⨯-=⨯-. 所以,数列(){}221n n a c -的通项公式为()221941n n n a c -=⨯-. (ii )()()22221111211n n niini iiiiii i i i a c a a c a a c====⎡⎤=+-=+⎣⎦-∑∑∑∑()()12212439412n n n ni i =⎛⎫- ⎪=⨯+⨯+⨯- ⎪⎝⎭∑()()2114143252914n n n n ---=⨯+⨯+⨯--()211*2725212n n n n --=⨯+⨯--∈N .【名师点睛】本小题主要考查等差数列、等比数列的通项公式及其前n 项和公式等基础知识.考查化归与转化思想和数列求和的基本方法以及运算求解能力.25.【2019年高考江苏卷】定义首项为1且公比为正数的等比数列为“M -数列”.(1)已知等比数列{a n }()n *∈N 满足:245132,440a a a a a a =-+=,求证:数列{a n }为“M -数列”;(2)已知数列{b n }()n *∈N 满足:111221,n n n b S b b +==-,其中S n 为数列{b n }的前n 项和. ①求数列{b n }的通项公式;②设m 为正整数,若存在“M -数列”{c n }()n *∈N ,对任意正整数k ,当k ≤m 时,都有1k k k c b c +剟成立,求m 的最大值.【答案】(1)见解析;(2)①b n =n ()*n ∈N ;②5.【解析】解:(1)设等比数列{a n }的公比为q ,所以a 1≠0,q ≠0.由245321440a a a a a a =⎧⎨-+=⎩,得244112111440a q a q a q a q a ⎧=⎨-+=⎩,解得112a q =⎧⎨=⎩.因此数列{}n a 为“M—数列”. (2)①因为1122n n n S b b +=-,所以0n b ≠. 由1111,b S b ==,得212211b =-,则22b =. 由1122n n n S b b +=-,得112()n n n n n b b S b b ++=-, 当2n ≥时,由1n n n b S S -=-,得()()111122n n n nn n n n n b b b b b b b b b +-+-=---,整理得112n n n b b b +-+=.所以数列{b n }是首项和公差均为1的等差数列.因此,数列{b n }的通项公式为b n =n ()*n ∈N .②由①知,b k =k ,*k ∈N .因为数列{c n }为“M–数列”,设公比为q ,所以c 1=1,q >0. 因为c k ≤b k ≤c k +1,所以1k k q k q -≤≤,其中k =1,2,3,…,m .当k =1时,有q ≥1; 当k =2,3,…,m 时,有ln ln ln 1k kq k k ≤≤-. 设f (x )=ln (1)x x x >,则21ln ()xf 'x x-=. 令()0f 'x =,得x =e.列表如下:因为ln 2ln8ln 9ln 32663=<=,所以max ln 3()(3)3f k f ==.取q =k =1,2,3,4,5时,ln ln kq k…,即k k q ≤, 经检验知1k q k -≤也成立.因此所求m 的最大值不小于5.若m ≥6,分别取k =3,6,得3≤q 3,且q 5≤6,从而q 15≥243,且q 15≤216,所以q 不存在.因此所求m 的最大值小于6. 综上,所求m 的最大值为5.【名师点睛】本题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力.26.【2019年高考浙江卷】设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每个12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式;(2)记,n c n *=∈N证明:12+.n c c c n *++<∈N【答案】(1)()21n a n =-,()1n b n n =+;(2)证明见解析. 【解析】(1)设数列{}n a 的公差为d ,由题意得11124,333a d a d a d +=+=+,解得10,2a d ==.从而*22,n a n n =-∈N . 所以2*n S n n n =-∈N ,,由12,,n n n n n n S b S b S b +++++成等比数列得()()()212n n n n n n S b S b S b +++=++.解得()2121n n n n b S S S d++=-. 所以2*,n b n n n =+∈N .(2)*n c n ===∈N . 我们用数学归纳法证明.(i )当n =1时,c 1=0<2,不等式成立;(ii )假设()*n k k =∈N时不等式成立,即12k c c c +++<.那么,当1n k =+时,121k k c c c c +++++<<<==.即当1n k =+时不等式也成立. 根据(i )和(ii),不等式12n c c c +++<对任意*n ∈N 成立.【名师点睛】本题主要考查等差数列、等比数列、数列求和、数学归纳法等基础知识,同时考查运算求解能力和综合应用能力.27.【2018年高考全国II 卷理数】记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-.(1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.【答案】(1)a n =2n –9;(2)S n =n 2–8n ,最小值为–16. 【解析】(1)设{a n }的公差为d ,由题意得3a 1+3d =–15. 由a 1=–7得d =2.所以{a n }的通项公式为a n =2n –9. (2)由(1)得S n =n 2–8n =(n –4)2–16. 所以当n =4时,S n 取得最小值,最小值为–16.【名师点睛】数列是特殊的函数,研究数列最值问题,可利用函数性质,但要注意其定义域为正整数集这一限制条件.(1)根据等差数列前n 项和公式,求出公差,再代入等差数列通项公式得结果;(2)根据等差数列前n 项和公式得n S 关于n 的二次函数关系式,根据二次函数对称轴以及自变量为正整数求函数最值.28.【2018年高考全国III 卷理数】等比数列{}n a 中,15314a a a ==,.(1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .【答案】(1)1(2)n n a -=-或12n n a -=;(2)6m =. 【解析】(1)设{}n a 的公比为q ,由题设得1n n a q -=.由已知得424q q =,解得0q =(舍去),2q =-或2q =.故1(2)n n a -=-或12n n a -=.(2)若1(2)n n a -=-,则1(2)3n n S --=.由63m S =得(2)188m-=-,此方程没有正整数解.若12n n a -=,则21n n S =-.由63m S =得264m=,解得6m =.综上,6m =.【名师点睛】本题主要考查等比数列的通项公式和前n 项和公式,属于基础题.29.【2018年高考浙江卷】已知等比数列{a n }的公比q >1,且a 3+a 4+a 5=28,a 4+2是a 3,a 5的等差中项.数列{b n }满足b 1=1,数列{(b n +1−b n )a n }的前n 项和为2n 2+n .(1)求q 的值;(2)求数列{b n }的通项公式.【答案】(1)2q =;(2)2115(43)()2n n b n -=-+⋅.【解析】本题主要考查等差数列、等比数列、数列求和等基础知识,同时考查运算求解能力和综合应用能力.(1)由42a +是35,a a 的等差中项得35424a a a +=+, 所以34543428a a a a ++=+=, 解得48a =.由3520a a +=得18()20q q+=, 因为1q >,所以2q =.(2)设1()n n n n c b b a +=-,数列{}n c 前n 项和为n S .由11,1,, 2.n nn S n c S S n -=⎧=⎨-≥⎩解得41n c n =-.由(1)可知12n n a -=,所以111(41)()2n n n b b n -+-=-⋅,故211(45)(),22n n n b b n n ---=-⋅≥,11123221()()()()n n n n n b b b b b b b b b b ----=-+-++-+-23111(45)()(49)()73222n n n n --=-⋅+-⋅++⋅+.设221113711()(45)(),2222n n T n n -=+⋅+⋅++-⋅≥,2211111137()(49)()(45)()22222n n n T n n --=⋅+⋅++-⋅+-⋅ 所以22111111344()4()(45)()22222n n n T n --=+⋅+⋅++⋅--⋅,因此2114(43)(),22n n T n n -=-+⋅≥,又11b =,所以2115(43)()2n n b n -=-+⋅.【名师点睛】用错位相减法求和应注意的问题:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“”与“”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.30.【2018年高考江苏卷】设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项为1b ,公比为q 的等比数列.(1)设110,1,2a b q ===,若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围;(2)若*110,,a b m q =>∈∈N ,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,,1n m =+均成立,并求d 的取值范围(用1,,b m q 表示). 【答案】(1)75[,]32;(2)见解析.【解析】本小题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力.满分16分. (1)由条件知:112(,)n n n a n d b -=-=. 因为1||n n a b b -≤对n =1,2,3,4均成立, 即1 12|()1|n n d ---≤对n =1,2,3,4均成立, 即1≤1,1≤d ≤3,3≤2d ≤5,7≤3d ≤9,得7532d ≤≤. 因此,d 的取值范围为75[,]32.(2)由条件知:111(1),n n n a b n d b b q -=+-=.若存在d ,使得1||n n a b b -≤(n =2,3,···,m +1)成立,即1111 |1|2,3,,(1())n b n d b q b n m -+--≤=+,即当2,3,,1n m =+时,d 满足1111211n n q q b d b n n ---≤≤--.因为q ∈,则112n m q q -<≤≤,从而11201n q b n --≤-,1101n q b n ->-,对2,3,,1n m =+均成立.因此,取d =0时,1||n n a b b -≤对2,3,,1n m =+均成立.下面讨论数列12{}1n q n ---的最大值和数列1{}1n q n --的最小值(2,3,,1n m =+). ①当2n m ≤≤时,111 2222111()()()n n n n n n n n q q nq q nq n q q q n n n n n n -------+--+-==---, 当112mq <≤时,有2n m q q ≤≤,从而1() 20n n n n q q q ---+>.因此,当21n m ≤≤+时,数列12{}1n q n ---单调递增,故数列12{}1n q n ---的最大值为2m q m-. ②设()()21x f x x =-,当x >0时,ln 21(0(n )l 22)x f x x '=--<, 所以()f x 单调递减,从而()f x <f (0)=1.当2n m ≤≤时,111112111()()()nn n q q n n f q n n n n --=≤-=<-, 因此,当21n m ≤≤+时,数列1{}1n q n --单调递减,故数列1{}1n q n --的最小值为mq m. 因此,d 的取值范围为11(2)[,]m mb q b q m m-.31.【2018年高考天津卷理数】设{}n a 是等比数列,公比大于0,其前n 项和为()n S n *∈N ,{}n b 是等差数列. 已知11a =,322a a =+,435a b b =+,5462a b b =+. (1)求{}n a 和{}n b 的通项公式;(2)设数列{}n S 的前n 项和为()n T n *∈N ,(i )求n T ;(ii )证明221()22()(1)(2)2n nk k k k T b b n k k n +*+=+=-∈+++∑N . 【答案】(1)12n n a -=,n b n =;(2)(i )122n n T n +=--;(ii )见解析.【解析】本小题主要考查等差数列的通项公式,等比数列的通项公式及其前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.满分13分.(1)设等比数列{}n a 的公比为q.由1321,2,a a a ==+可得220q q --=.因为0q >,可得2q =,故12n n a -=.设等差数列{}n b 的公差为d ,由435a b b =+,可得13 4.b d +=由5462a b b =+, 可得131316,b d +=从而11,1,b d ==故.n b n =所以,数列{}n a 的通项公式为12n n a -=,数列{}n b 的通项公式为.n b n =(2)(i )由(1),有122112nn n S -==--,故 1112(12)(21)22212n nnkkn n k k T n n n +==⨯-=-=-=-=---∑∑.(ii )证明:因为11212()(222)222(1)(2)(1)(2)(1)(2)21k k k k k k+k T +b b k k k k k k k k k k k k ++++--++⋅===-++++++++,所以,324321221()2222222()()()2(1)(2)3243212n n n nk k k k T b b k k n n n ++++=+=-+-++-=-+++++∑. 【名师点睛】本题主要考查数列通项公式的求解,数列求和的方法,数列中的指数裂项方法等知识,意在考查学生的转化能力和计算求解能力.32.【2017年高考天津卷理数】已知{}n a 为等差数列,前n 项和为()n S n *∈N ,{}n b 是首项为2的等比数列,且公比大于0,2312b b +=,3412b a a =-,11411S b =. (1)求{}n a 和{}n b 的通项公式;(2)求数列221{}n n a b -的前n 项和()n *∈N .【答案】(1)32n a n =-,2nn b =;(2)1328433n n +-⨯+. 【解析】(1)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q .由已知2312b b +=,得21()12b q q +=,而12b =,所以260q q +-=. 又因为0q >,解得2q =.所以,2nn b =.由3412b a a =-,可得138d a -=①. 由114=11S b ,可得1516a d +=②,联立①②,解得11a =,3d =,由此可得32n a n =-.所以,数列{}n a 的通项公式为32n a n =-,数列{}n b 的通项公式为2nn b =.(2)设数列221{}n n a b -的前n 项和为n T ,由262n a n =-,12124n n b --=⨯,有221(31)4nn n a b n -=-⨯,故23245484(31)4n n T n =⨯+⨯+⨯++-⨯,23414245484(34)4(31)4n n n T n n +=⨯+⨯+⨯++-⨯+-⨯,上述两式相减,得23112(14)324343434(31)44(314n nn n T n n +⨯--=⨯+⨯+⨯++⨯--⨯=----111)4(32)48n n n ++⨯=--⨯-,得1328433n n n T +-=⨯+. 所以,数列221{}n n a b -的前n 项和为1328433n n +-⨯+. 【名师点睛】利用等差数列和等比数列通项公式及前n 项和公式列方程组求数列的首项和公差或公比,进而写出通项公式及前n 项和公式,这是等差数列、等比数列的基本要求,数列求和的方法有倒序相加法、错位相减法、裂项相消法和分组求和法等,本题考查的是错位相减法求和. 33.【2017年高考山东卷理数】已知{x n }是各项均为正数的等比数列,且x 1+x 2=3,x 3-x 2=2.(1)求数列{x n }的通项公式;(2)如图,在平面直角坐标系xOy 中,依次连接点P 1(x 1, 1),P 2(x 2, 2),…,P n+1(x n+1, n +1)得到折线P 1 P 2…P n+1,求由该折线与直线y =0,11n x x x x +==,所围成的区域的面积n T .【答案】(1)12n n x -=;(2)(21)21.2n n n T -⨯+=【解析】(1)设数列{}n x 的公比为q ,由已知0q >.由题意得1121132x x q x q x q +=⎧⎨-=⎩,所以23520q q --=,因为0q >,所以12,1q x ==,因此数列{}n x 的通项公式为12.n n x -=(2)过123,,,P P P …,1n P +向x 轴作垂线,垂足分别为123,,,Q Q Q …,1n Q +,由(1)得111222.n n n n n x x --+-=-=记梯形11n n n n P P Q Q ++的面积为n b . 由题意12(1)2(21)22n n n n n b n --++=⨯=+⨯, 所以123n T b b b =+++…+n b=101325272-⨯+⨯+⨯+…+32(21)2(21)2n n n n ---⨯++⨯①,又0122325272n T =⨯+⨯+⨯+…+21(21)2(21)2n n n n ---⨯++⨯②,①-②得121132(222)(21)2n n n T n ----=⨯++++-+⨯=1132(12)(21)2.212n n n ---+-+⨯- 所以(21)21.2n n n T -⨯+=【名师点睛】本题主要考查等比数列的通项公式及求和公式、数列求和的错位相减法.此类题目是数列问题中的常见题型.本题覆盖面广,对考生的计算能力要求较高.解答本题,布列方程组,确定通项公式是基础,准确计算求和是关键,易错点是在“错位”之后求和时,弄错等比数列的项数.本题将数列与解析几何结合起来,适当增大了难度,能较好地考查考生的数形结合思想、逻辑思维能力及基本计算能力等. 34.【2017年高考江苏卷】对于给定的正整数k ,若数列{}n a 满足:1111n k n k nnnk n ka aa a aa --+-++-++++++++2n ka =对任意正整数()n n k >总成立,则称数列{}n a 是“()P k 数列”.(1)证明:等差数列{}n a 是“(3)P 数列”;(2)若数列{}n a 既是“(2)P 数列”,又是“(3)P 数列”,证明:{}n a 是等差数列.【答案】(1)见解析;(2)见解析.【解析】(1)因为{}n a 是等差数列,设其公差为d ,则1(1)n a a n d =+-, 从而,当4n ≥时,n k n k a a a -++=+11(1)(1)n k d a n k d --+++-122(1)2n a n d a =+-=,1,2,3,k =所以6n n n n n n n a a a a a a a ---+++++=321123+++, 因此等差数列{}n a 是“(3)P 数列”.(2)数列{}n a 既是“(2)P 数列”,又是“(3)P 数列”, 因此,当3n ≥时,n n n n n a a a a a --+++++=21124,① 当4n ≥时,n n n n n n n a a a a a a a ---++++++++=3211236.② 由①知,n n n a a a ---+=-32141()n n a a ++,③n n n a a a ++++=-23141()n n a a -+,④将③④代入②,得n n n a a a -++=112,其中4n ≥, 所以345,,,a a a 是等差数列,设其公差为d'.在①中,取4n =,则235644a a a a a +++=,所以23a a d'=-, 在①中,取3n =,则124534a a a a a +++=,所以132a a d'=-, 所以数列{}n a 是等差数列.【名师点睛】(1)利用等差数列性质得n k n k n a a a -++=2,即得n n n n n a a a a a ---+++++32112++n n a a +=36,再根据定义即可判断;(2)先根据定义得21n n n n n a a a a a --+++++=124,n n n n n a a a a a ---++++++32112n n a a ++=36,再将条件集中消元:n n n a a a ---+=-32141()n n a a ++,n n n a a a ++++=-23141()n n a a -+,即得n n n a a a -++=112,最后验证起始项也满足即可. 35.【2017年高考北京卷理数】设{}n a 和{}n b 是两个等差数列,记1122max{,,,}n n n c b a n b a n b a n =--⋅⋅⋅-(1,2,3,)n =⋅⋅⋅,其中12max{,,,}s x x x ⋅⋅⋅表示12,,,s x x x ⋅⋅⋅这s个数中最大的数.(1)若n a n =,21n b n =-,求123,,c c c 的值,并证明{}n c 是等差数列; (2)证明:或者对任意正数M ,存在正整数m ,当n m ≥时,nc M n>;或者存在正整数m ,使得12,,,m m m c c c ++⋅⋅⋅是等差数列.【答案】(1)详见解析;(2)详见解析. 【解析】(1)111110,c b a =-=-=21122max{2,2}max{121,322}1c b a b a =--=-⨯-⨯=-,3112233max{3,3,3}max{131,332,533}2c b a b a b a =---=-⨯-⨯-⨯=-.当3n ≥时,1111()()()()20k k k k k k k k b na b na b b n a a n ++++---=---=-<, 所以k k b na -关于*k ∈N 单调递减. 所以112211max{,,,}1n n n c b a n b a n b a n b a n n =---=-=-.所以对任意1,1n n c n ≥=-,于是11n n c c +-=-, 所以{}n c 是等差数列.(2)设数列{}n a 和{}n b 的公差分别为12,d d ,则12111121(1)[(1)]()(1)k k b na b k d a k d n b a n d nd k -=+--+-=-+--.所以1121211121(1)(),,n b a n n d nd d nd c b a n d nd -+-->⎧=⎨-≤⎩当时,当时,①当10d >时,取正整数21d m d >,则当n m ≥时,12nd d >,因此11n c b a n =-. 此时,12,,,m m m c c c ++是等差数列.②当10d =时,对任意1n ≥,1121121(1)max{,0}(1)(max{,0}).n c b a n n d b a n d a =-+-=-+--此时,123,,,,,n c c c c 是等差数列.③当10d <时, 当21d n d >时,有12nd d <. 所以1121121112(1)()()n c b a n n d nd b d n d d a d n n n-+---==-+-++ 111212()||.n d d a d b d ≥-+-+--对任意正数M ,取正整数12112211||max{,}M b d a d d d m d d +-+-->-,故当n m ≥时,nc M n>. 【名师点睛】近几年北京卷理科压轴题一直为新信息题,本题考查学生对新定义的理解能力和使用能力,本题属于偏难问题,反映出学生对新的信息的理解和接受能力,本题考查数列的有关知识及归纳法证明,即考查了数列(分段形函数)求值,又考查了归纳法证明和对数据的分析研究,考查了学生的分析问题能力和逻辑推理能力,本题属于拔高难题,特别是第二问难度较大,适合选拔优秀学生. 36.【2017年高考浙江卷】已知数列{x n }满足:x 1=1,x n =x n +1+ln(1+x n +1)(n *∈N ).证明:当n *∈N 时, (1)0<x n +1<x n ;(2)2x n +1−x n ≤12n n x x +; (3)112n -≤x n ≤212n -.【答案】(1)见解析;(2)见解析;(3)见解析. 【解析】(1)用数学归纳法证明:0n x >. 当n =1时,x 1=1>0. 假设n =k 时,x k >0,那么n =k +1时,若10k x +≤,则110ln(1)0k k k x x x ++<=++≤,矛盾,故10k x +>.。
高考英语(精讲精练精析)专题 人物故事人物传记类试题(含解析)

定额市鞍钢阳光实验学校专题18人物故事、人物传记类阅读预测三题目设置灵活多样,通常以细节理解题为主,推理判断题为辅,【考点定位】2017考纲解读和近几年考点分布人物传记主要向读者介绍科学家、文学家、思想家、政治家、企业家和影视、体育明星等杰出人物在各自领域所取得的重大成就,尤其注重介绍这些杰出人物如何克服身体残缺、自然环境和社会环境所造成的各种困难。
为人类做出巨大贡献,也为自己的事业谱写精彩篇章。
这些杰出人物不仅推动了社会的进步,而且他们对事业的追求、对人民的厚爱成为时代最重要的精神财富。
通过阅读人物的小传记或摘录该人物一些典型事件,如人生的起伏、克服困难取得成功等,考生可以得到激励或受到启发,同时也可以了解这些人物所生活的社会文化背景。
1.熟悉人物介绍文特点人物传记是高考英语阅读理解题重要题材,它主要向读者介绍科学家、文学家、思想家、政治家和企业家等杰出人物在各行各业所取得的重大成就,并特别着重介绍这些杰出人物如何克服自身身体残缺或自然环境和社会环境所造成的各种困难,用强烈的事业心和责任感、用汗水和泪水、用鲜血和青春为人类做出巨大贡献,为生命谱写精彩乐章。
当然这些杰出人物留给社会的不仅仅是和平发展和经济效益,更重要的是,他们对事业的追求和对人民的厚爱成为我们这个时代最重要的精神财富。
(1)人物时段介绍判断题这种试题往往以What is the article mainly about? What life part of the hero is mentioned in the text? 为设问方式考查对人物时段介绍的判断。
因为人物传记往往介绍杰出人物一生学习、工作和生活情况,因此这种试题往往以The life of the hero.或The whole life of the hero is mentioned in our text.为答案。
这种试题也可转换形式,以How old is the hero now? How old was the hero when he died? How many years did he live?为设问方式。
精讲精练17 2017—2019年高考真题精讲精练

高考真题精讲精练:训练步骤:1、先花十八分钟做完这三篇阅读理解。
2、再仔细阅读做题思维过程及试题分析和阅读技巧点拨。
3、然后翻译的文章要仔细研读并做到精通文章原意而且最好是能脱口而出。
2017阅读全国卷二阅读下列短文,从每题所给的A、B、C和D四个选项中,选出最佳答案。
AIn the coming months, we are bringing together artists form all over the globe, to enjoy speaking Shakespeare’s plays in their own language, in our Globe, within the architecture Shakespeare wrote for. Please come and join us.National Theatre of China Beijing | ChineseThis great occasion (盛会) will be the National Theatre of China’s first visit to the UK. The company’s productions show the new face of 21st century Chinese theatre. This production of Shakespeare’s Richard III will be directed by the National’s Associate Director, Wang Xiaoying.Date & Time: Saturday 28 April, 2.30 pm & Sunday 29 April, 1.30 pm & 6.30 pmMarjanishvili Theatre Tbilisi | GeorgianOne of the most famous theatres in Georgia, the Marjanishvili, founded in 1928, appears regularly at theatre festivals all over the world. This new production of it is helmed(指导)by the company’s Artistic Director Levan Tsuladze.Date & Time: Friday 18 May, 2.30 pm & Saturday 19 May, 7.30 pmDeafinitely Theatre London | British Sign Language(BSL)By translating the rich and humorous text of Love’s Labour’s Lost into the physical language of BSL, Deafinitely Theatre creates a new interpretation of Shakespeare’s comedy and aims to build a bridge between deaf and hearing worlds by performing to both groups as one audience.Date & Time: Tuesday 22 May, 2.30 pm & Wednesday 23 May, 7.30 pmHabima National Theatre Tel Aviv | HebrewThe Habima is the centre of Hebrew-language theatre worldwide, Founded in Moscow after the 1905 revolution, the company eventually settled in Tel Aviv in the late 1920s. Since 1958, they have been recognised as the national theatre of Israel. This production of Shakespeare’s The Merchant of Venice marks their first visit to the UK.Date & Time: Monday 28 May, 7.30 & Tuesday 29 May, 7.30 pm21. Which play will be performed by the National Theatre of China?A.Richard Ⅲ.B.Lover’s Labour’s LostC.As You Like ItD.The Merchant of V enice22. What is special about Deafinitely Theatre?A. It has two groups of actorsB. It is the leading theatre in LondonC.It performs plays in BSLD. It is good at producing comedies23. When can you see a play in Hebrew?A. On Saturday 28 April.B. On Sunday 29 AprilC. On Tuesday 22 May.D. On Tuesday 29 MayBI first met Paul Newman in 1968, when George Roy Hill, the director of Butch Cassidy and the Sundance Kid, introduced us in New York City. When the studio didn’t want me for the film ---it wanted somebody as well-known as Paul --- he stood up for me. I don’t know how many people would have done that; they would have listened to their agents or the studio powers.The friendship that grew out of the experience of making that film and The Sting four years later had its root in the fact that although there was an age difference, we both came from a tradition of theater and live TV. We were respectful of craft(技艺)and focused on digging into the characters we were going to play. Both of us had the qualities and virtues that are typical of American actors: humorous, aggressive, and making fun of each other --- but always with an underlying affection. Those were also at the core(核心)of our relationship off the screen.We shared the belief that if you’re fortunate enough to have success, you should put something back - he with his Newman’s Own food and his Hole in the Wall camps for kids who are seriously ill, and me with Sundance and the institute and the festival. Paul and I didn’t see each other all that regularly, but sharing that brought us together. We supported each other financially and by showing up at events.I last saw him a few months ago. He’d been in and out of the hospital. He and I both knew what the deal was,and we didn’t talk about it. Ours was a relationship that didn’t need a lot of words.24. Why was the studio unwilling to give the role to author at first?A. Paul Newman wanted it.B. The studio powers didn’t like his agent.C. He wasn’t famous enough.D. The director recommended someone else.25. Why did Paul and the author have a lasting friendship?A. They were of the same age.B. They worked in the same theater.C. They were both good actors.D. They had similar characteristics.26. What does the underlined word “that” in paragraph 3 refer to?A. Their belief.B. Their care for children.C. Their success.D. Their support for each other.27. What is the author’s purpose in writing the test?A. To show his love of films.B. To remember a friend.C. To introduce a new movie.D. To share his acting experience.CTerrafugia Inc. said Monday that its new flying car has completed its first flight, bringing the company closer to its goal of selling the flying car within the next year. The vehicle-named the Transition –has two seats, four wheels and wings that fold up so it can be driven like a car. The Transition, which flew at 1,400 feet for eight minutes last month, can reach around 70 miles per hour on the road and 115 in the air. It flies using a 23-gallon tank of gas and bums 5 gallons per hour in the air. On the ground, it gets 35 miles per gallon.Around 100 people have already put down a $10,000 deposit to get a Transition when they go on sale, and those numbers will likely rise after Terrafugia introduces the Transition to the public later this week at the New York Auto Show. But don’t expect it to show up in too many driveways. It’s expected to cost $279,000. And it won’t help if you’re stuck in traffic. The car needs a runway.Inventors have been trying to make flying cars since the 1930s, according to Robert Mann, an airline industry expert. But Mann thinks Terrafugia has come closer than anyone to making the flying car a reality. The government has already permitted the company to use special materials to make it easier for the vehicle to fly. The Transition is now going through crash tests to make sure it meets federal safety standards.Mann said Terrafugia was helped by the Federal Aviation Administration’s decision five years ago to create a separate set of standards for light sport aircraft, which are lower than those pilots of larger planesTerrafugia says an owner would need to pass a test and complete 20 hours of flying time to be able to fly the Transition, a requirement pilots would find relatively easy to meet.28. What is the first paragraph mainly about?A. The basic data of the Transition.B. The advantages of flying cars.C. The potential market for flying cars. C. The designers of the Transition.29. Why is the Transition unlikely to show up in too many driveways?A. It causes traffic jams.B. It is difficult to operate.C. It is very expensive.D. It bums too much fuel.30. What is the government’s attitude to the development of the flying car?A. CautiousB. Favorable.C. Ambiguous.D. Disapproving.31. What is the best title for the text?A. Flying Car at Auto ShowB. The Transition’s First FlightC. Pilots’ Dream Coming TrueD. Flying Car Closer to Reality先来看A篇阅读理解的思维过程解析和技巧点拨:这类信息题直接做题以提高做题效率,缩短你做题时间。
精讲精练08 2017—2019年高考真题精讲精练

高考真题精讲精练:训练步骤:1、先花十二分钟做完这两篇阅读理解和七选五。
2、再仔细阅读做题思维过程及试题分析和阅读技巧点拨。
3、然后翻译的文章要仔细研读并做到精通文章原意而且最好是能脱口而出。
2019年全国卷三阅读理解DMonkeys seem to have a way with numbers.A team of researchers trained three Rhesus monkeys to associate 26 clearly different symbols consisting of numbers and selective letters with 0-25 drops of water or juice as a reward. The researchers then tested how the monkeys combined --- or added --- the symbols to get the reward.Here’s how Harvard Medical School scientist Margaret Livingstone, who led the team, described the experiment: In their cages the monkeys were provided with touch screens. On one part of the screen, a symbol would appear, and on the other side two symbols inside a circle were shown. For example, the number 7 would flash on one side of the screen and the other end would have 9 and 8. If the monkeys touched the left side of the screen they would be rewarded with seven drops of water or juice; if they went for the circle, they would be rewarded with the sum of the numbers --- 17 in this example.After running hundreds of tests, the researchers noted that the monkeys would go for the higher values more than half the time, indicating that they were performing a calculation, not just memorizing the value of each combination.When the team examined the results of the experiment more closely, they noticed that the monkeys tended to underestimate(低估)a sum compared with a single symbol when the two were close in value ---sometimes choosing, for example, a 13 over the sum of 8 and 6. The underestimation was systematic: When adding two numbers, the monkeys always paid attention to the larger of the two, and then added only a fraction(小部分)of the smaller number to it.“This indicates that there is a certain way quantity is represented in their brains,” Dr. Livingstone says. “But in this experiment what they’re doing is paying more attention to the big number than the little one.”32. What did the researchers do to the monkeys before testing them?A. They fed them.B. They named them.C. They trained them.D. They measured them.33. How did the monkeys get their reward in the experiment?A. By drawing a circle.B. By touching a screen.C. By watching videos.D. By mixing two drinks.34. What did Livingstone's team find about the monkeys?A. They could perform basic addition.B. They could understand simple words.C. They could memorize numbers easily.D. They could hold their attention for long.35. In which section of a newspaper may this text appear?A. Entertainment.B. Health.C. Education.D. Science.根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。
三年高考2017 2019高考数学真题分项汇编专题13不等式推理与证明理含解析

专题13不等式、推理与证明1.【2019年高考全国I卷理数】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长15?5?1(度之比是≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最225?1.若某人满足上述两个黄金分割比例,美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是2且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是175 cm B.A.165 cm190 cmD.185 cm .C B【答案.【解析】方法一:如下图所依题意可知AACB C>10腿长105 c得,C64.8A AAC64.810169.8A>169.89.所②头顶至脖子下端长度26 cAB<26,即AB?42.07BC?,5?12.<68.07+BCAC=AB,AC110.15?CD?,1?52<68.07+110.15=178.22CDAC+,<178.22AD.所以169.89<AD<178.22.综上,故B.2626?x5?1??yx,得 cm cm,肚脐至腿根的长为,则方法二:设人体脖子下端至肚脐的长为xy?1052x?42.07cm,y?5.15cm.又其腿长为105cm,头顶至脖子下端的长度为26cm,所以其身高约为42.07+5.15+105+26=178.22,接近175cm.故选B.【名师点睛】本题考查类比归纳与合情推理,渗透了逻辑推理和数学运算素养.采取类比法,利用转化思想解题.2.【2019年高考全国II卷理数】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测L点器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日2L MM,地月距离的轨道运行.,月球质量为点是平衡点,位于地月连线的延长线上.设地球质量为212L rrR满足方律,程:引运动定律和万有力定顿距为,到点月球的离为,根据牛2345MMM????3?3r?1213)rR??(???3??的值很小,,因此在近似计算中.设,由于2322(R?r)rR?)(1?R.r的近似值为则MM22RR AB..MM211M3M22RR. D C .33MM311D 【答案】r???R?r,得【解析】由RMMM112??(R?r)因为,223R?r)r(RMMM?112)(1???,所以22222??R(1?RR)543???M313??23???23??]?[(1??)即,22??)(1M(1??)1M3?2?,解得3M1M3?2R?r?.R所以3M1【名师点睛】由于本题题干较长,所以,易错点之一就是能否静心读题,正确理解题意;易错点之二是复杂式子的变形出错.ab,则> 2019年高考全国II卷理数】若3.【ab ba<3)>0 3A.ln(B?.33abab││>│C.D.│?>0 C【答案】1?2,a?b0)?b ln(a?ba?ba3?3?39?错,【解析】取B,知;因为,满足,知A,错,排除A a?1b,??22?a1??b3ba?xy?取排除D,B,满足;因为幂函数是增函数,,排除错,知,D a?b33,故选C.,所以b?a【名师点睛】本题主要考查对数函数性质、指数函数性质、幂函数性质及绝对值意义,渗透了逻辑推理和运算能力素养,利用特殊值排除即可判断.y1?|x|?x+yyyx满足的最大值为≥?1【2019年高考北京卷理数】若,,则3,且4. 1 A.?7 B.7 DC.5 .C 【答案】y??1?,.作出可行域如图阴影部分所示【解析】由题意?y?1?x?1y??x3?z?z?3x?y,y,设??x3l:y?z?12,?z C时,.取最大值经过点5.当直线故选0注,?,根据“画?移解”等步骤可得解.题目难度不大【名师点睛】本题是简单线性规划问题的基本题型.基本技能的考查重了基础知识?年高考北京卷理数】在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮20195.【E51kmmEm,天狼星=26.72lg,其中星等为).已知太阳的星等是的星的亮度为(?=1,度满足?kk12E221.45?,则太阳与天狼星的亮度的比值为的星等是10.1. B 10.1 .A 10. C 10D .–10.1 lg10.1A【答案】E51lg m??mm??1.45,m??26.7, ,令【解析】两颗星的星等与亮度满足12122E2.EE22??10.1111010.1,?26.7)(?1.45???m?m?lg?. 12E55E22故选:A.【名师点睛】本题以天文学问题为背景,考查考生的数学应用意识?信息处理能力?阅读理解能力以及指数对数运算.x?y?2?0,??x?y?2?0,?x,y z??4x?y?的最大值,则目标函数满足约束条件年高考天津卷理数】设变量6.【2019…1,?x??…1,y??为.3 BA.26.D .C5D【答案】 .【解析】已知不等式组表示的平面区域如图中的阴影部分yz?y?4x轴上的截距,目标函数的几何意义是直线在A.处取得最大值故目标函数在点0,?2?x?y?1,1)(?A,得由,?1?x??5?1(?4??1)??z. 所以max C. 故选分界线是实线还是虚线,线性规划问题,【名师点睛】首先明确可行域对应的是封闭区域还是开放区域,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值或范围.即:一画,二移,三求.1??1||x2R x?05xx??”是“年高考天津卷理数】设,则“”的.7【2019 .充分而不必要条件A .必要而不充分条件B .充要条件C .既不充分也不必要条件D B【答案】11??x50?x?推不出【解析】化简不等式,可知,11?x?5x?0?,由能推出1?x|?1|20xx??5”是“”的必要不充分条件,故“B.故选.【名师点睛】本题考查充分必要条件,解题关键是化简不等式,由集合的关系来判断条件0?y?4x?3??y,x y?2z?3x03x??4?y?,则年高考浙江卷】若实数8.【2019满足约束条件的最大值是?0?x?y?1?B..A 1D. 10 . 12C C【答案【解析】画出满足约束条件的可行域如图中阴影部分所示。
(2017-2019)高考语文真题分类汇编专题13 图文转换(教师版)

专题13:图文转换【2019年高考】一、【2019年高考天津卷】某初中校就“喜欢的榜样类型”对本校学生进行了调查,请根据下图的统计结果,就今后的榜样教育向学校提两条建议。
要求:不能出现数字。
(4分)(改编自2019年4月11日《中国教育报》)【答案】①鼓励学生以父母、师长、同学等“身边人”为榜样②多宣传英模劳模等杰出人物的事迹③对崇拜影视明星的学生要正面引导④关注榜样缺失的学生群体【解析】本题考查图文转换的能力。
解答此类题目,首先要认真审题,观察图表,弄清坐标代表的含义,注意各项之间的横向、纵向的比较。
建议要根据图表的信息提出。
本题是某初中校就喜欢的榜样类型进行的调查,要求根据调查给出建议。
根据图表信息,有45%的学生以父母、师长、同学为榜样,据此可建议“鼓励学生以父母、师长、同学等‘身边人’为榜样”;有30%多的学生以英模、劳模为榜样,有25%的学生以科学家为榜样,有不到15%的学生以政商界精英为榜样,据此可建议“多宣传英模、劳模等杰出人物的事迹”;有不到40%的人以影视明星为榜样,据此可建议“对崇拜明星的学生要正面引导”;有近15%的学生没有榜样,据此可建议“关注榜样缺失的学生群体”。
二、【2019年高考江苏卷】阅读下图,对VR(即“虚拟现实”)技术的解说不正确...的是一项是(3分)A.VR技术能提供三个维度的体验:知觉体验、行为体验和精神体验。
B.现有的VR技术在精神体验上发展较快,而在知觉体验上发展较慢。
C.VR技术的未方向是知觉体验、行为体验和精神体验的均衡发展。
D.期许的VR体验将极大提高行为体验的自由度和精神体验的满意度。
【答案】B【解析】本题考查语言表达简明、连贯、准确的能力。
这是一道图文转换题,解答本题的关键是认真读图,首先要从整体上把握图形代表含义,然后根据文字说明,运用恰当的语言进行表述。
整个图形分两部分,内部直线勾画的不规则三角形代表“现有的VR体验”,外面虚线勾勒的等腰三角形代表的是“期许的VR 体验”,由此可知C、D两项表述正确;内部直线勾画的不规则三角形又分为三部分,分别代表“沉浸的知觉体验”“自如的行为体验”“梦幻般的精神体验”,由此可知A项表述正确;由图可知,现有的三种体验发展并不均衡,并没有体现出发展速度,所以B项表述没有依据。
备战2017高考英语(精讲+精练+精析)专题14 交际用语试题(含解析)

专题14 交际用语【2017年高考命题预测】【考点定位】2017考纲解读和近几年考点分布【考点pk】名师考点透析英语交际型试题主要考查考生对英语知识的理解和应用能力,考查考生对中西方文化差异的掌握情况及对英语的使用和驾驭能力。
在高考英语试题中,交际用语的考查点相对集中。
主要考查社会交往中的一些日常交际用语。
考查的方式以应答为主,提问为辅;以跨文化交际中差异明显的交际项目为重点考查对象。
命题方式有以下几种。
考点1 习惯应答类3.常见的祝愿和祝贺用语有:Good luck!/Best wishes to you./Have a nice time./Wish you a pleasant journey./Congratulations!/Merry Christmas!/Happy birthday to you.而应答用语有:Thank you./The same to you./You too.4.接受请求和邀请的应答用语有:With pleasure./I’d be happy(glad)to./Yes,help yourself./No problem./Good idea/Sounds good/Why not?拒绝请求和邀请的应答用语有:Sorry,but…/I’d rather you…/Thank you,but…/No way!/Forget it。
5.其他场景习惯应答用语考生也应注意。
问候的应答用语有:How do you do./Fine,thank you.介绍的应答用语有:Very glad(pleased)to see you.接电话的习惯用语有:This is Li Ming speaking.道别的习惯用语有:Bye./So long./See you later.服务人员的应答用语有:Yes,Sir./Yes,Madame./Take your time.考点2 破交际定势类汉语和英语在交际文化方面有许多共同之处,但也存在诸多差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考真题精讲精练:训练步骤:1、先花十八分钟做完这三篇阅读理解。
2、再仔细阅读做题思维过程及试题分析和阅读技巧点拨。
3、然后翻译的文章要仔细研读并做到精通文章原意而且最好是能脱口而出。
2018阅读全国卷三阅读下列短文,从每题所给的A、B、C和D四个选项中,选出最佳选项。
AWelcome to Holker Hall & GardensVisitor InformationHow to Get to HolkerBy Car: Follow brown signs an A590 from JB6, M6. Approximale travel times: Windermere - 20 minutes, Kendal - 25 minutes, Lancaster - 45 minutes, Manchester - 1 hour 30 minutes.By Rail: The nearest station is Cark-in-Cartmel with trains to Carnforth, Lancaster Preston for connections to major cities & airports.Opening TimesSunday-Friday (closed on Saturday)11:00 am-4:00pm, 30 March-2nd November.Admission ChargesSpecial EventsProducers: Market 13th AprilJoin us to taste a variety of fresh local food and drinks. Meet the producers and get some excellent recipe ideas.Holker Garden Festival 30th MayThe event celebrate its 22nd anniversary with a great show of the very best of gardening, making it one of themost popular events in gardening.National Garden Day 28th AugustHolker once again opens its gardens in aid of the disadvantaged. For just a small donation you can take a tour with our garden guide.Winter Market 8th NovemberThis is an event for all the family. Wander among a variety of shops selling gifts while enjoying a live music show and nice street entertainment.21. How long does it probably take a tourist to drive to Holker from Manchester?A. 20 minutes.B. 25 minutes.C. 45 minutes.D. 90 minutes.22. How much should a member of a tour group pay to visit to Hall & Cardens?A. £12.00.B. £9.00.C. £8.0D. £5.5023. Which event will you go to if you want to see a live music show?A. Producers’ Market.B. Holker Garden Festival.C. National Garden Day.D. Winter Market.BCities usually have a good reason for being where they are, like a nearby port or river. People settle in these places because they are easy to get to and naturally suited to communications and trade. New York City, for example, is near a large harbour at the mouth of the Hudson River. Over 300 years its population grew gradually from 800 people to 8 million. But not all cities develop slowly over a long period of time. Boom towns grow from nothing almost overnight. In 1896, Dawson, Canada, was unmapped wilderness (荒野). But gold was discovered there in 1897, and two years later, it was one of the largest cities in the West, with a population of 30,000.Dawson did not have any of the natural conveniences of cities like London or Paris. People went there for gold. They travelled over snow-covered mountains and sailed hundreds of miles up icy rivers. The path to Dawson was covered with thirty feet of wet snow that could fall without warming. An avalanche (雪崩) once closed the path, killing 63 people. For many who made it to Dawson, however, the rewards were worth the difficult trip. Of the first 20,000 people who dug for gold, 4,000 got rich. About 100 of these stayed rich men for the rest of their lives.But no matter how rich they were, Dawson was never comfortable. Necessities like food and wood were very expensive. But soon, the gold that Dawson depended on had all been found. The city was crowded withdisappointed people with no interest in settling down, and when they heard there were new gold discoveries in Alaska, they left Dawson City as quickly as they had come. Today, people still come and go --- to see where the Canadian gold rush happened. Tourism is now the chief industry of Dawson City --- its present population is 762.24. What attracted the early settlers to New York City?A. Its business culture.B. Its small population.C. Its geographical position.D. Its favourable climate.25. What do we know about those who first dug for gold in Dawson?A. Two-thirds of them stayed there.B. One out of five people got rich.C. Almost everyone gave up.D. Half of them died.26. What was the main reason for many people to leave Dawson?A. They found the city too crowded.B. They wanted to try their luck elsewhere.C. They were unable to stand the winter.D. They were short of food.27. What is the text mainly about?A. The rise and fall of a city.B. The gold rush in Canada.C. Journeys into the wilderness.D. Tourism in Dawson.CWhile famous foreign architects are invited to lead the designs of landmark buildings in China such as the new CCTV tower and the National Center for the Performing Arts, many excellent Chinese architects are making great efforts to take the center stage.Their efforts have been proven fruitful. Wang Shu, a 49-year-old Chinese architect, won the 2012 Pritzker Architecture Prize --- which is often referred to as the Nobel Prize in architecture --- on February 28. He is the first Chinese citizen to win this award.Wang serves as head of the Architecture Department at the China Academy of Art (CAA). His office is located at the Xiangshan campus (校园) of the university in Hangzhou, Zhejiang Province. Many buildings on the campus are his original creations.The style of the campus is quite different from that of most Chinese universities. Many visitors were amazed by the complex architectural space and abundant building types. The curves (曲线) of the buildings perfectlymatch the rise and fall of hills, forming a unique view.Wang collected more than 7 million abandoned bricks of different ages. He asked the workers to use traditional techniques to make the bricks into walls, roofs and corridors. This creation attracted a lot of attention thanks to its mixture of modern and traditional Chinese elements (元素).Wang’s works show a deep understanding of modern architecture and a good knowledge of traditions. Through such a balance, he had created a new type of Chinese architecture, said Tadao Ando, the winner of the 1995 Pritzker Prize.Wang believes traditions should not be sealed in glass boxes at museums. “That is only evidence that traditions once existed,” he said.“Many Chinese people have a misunderstanding of traditions. They think tradition means old things from the past. In fact, tradition also refers to the things that have been developing and that are still being created,” he said.“Today, many Chinese people are learning Western styles and theories rather than focusing on Chinese traditions. Many people tend to talk about traditions without knowing what they really are,” said Wang.The study of traditions should be combined with practice. Otherwise, the recreation of traditions would be artificial and empty, he said.28. Wang’s winning of the prize means that Chinese architects are ___________.A. following the latest world trendB. getting international recognitionC. working harder than ever beforeD. relying on foreign architects29. What impressed visitors to the CAA Xiangshan campus most?A. Its hilly environment.B. Its large size.C. Its unique style.D. Its diverse functions.30. What made Wang’s architectural design a success?A. The mixture of different shapes.B. The balance of East and West.C. The use of popular techniques.D. The harmony of old and new.31. What should we do about Chinese traditions according to Wang?A. Spread them to the world.B. Preserve them at museums.C. Teach them in universities.D. Recreate them in practice.现在来看A篇文章的解题思路和技巧点拨:像这样的信息查找题根本不用看文章内容,利用审关键词——》文中定位——》比对定选十二字方针原则来做题,这样可以节约做题时间,提高做题效率。
