电路7章1syl
合集下载
《电子第七章》课件
ωt
iBIBQ ibIBQ Ibm sin t
iCIC QicIC QIcm sin t
ωt
u C E U CE u Q ce U CE U Q ce sm itn
ωt
2. 放大电路的非线性失真
作为放大电路,应使输出电压尽可能大,但受
到三极管的非线性特性的限制,当信号过大或
静态工作点不合适,输出波形将会发生失真。
静态工作点过高会引起饱和失真,静态工 作点过低会导致截止失真。
iC 交流负载线
ic
iC/mA
ib
交流负载线
0
t0
0
t iC
交流负载线 ic
ib
uCE uCE
Q 直流负载线
Uces
uCE/V
UCEQ
ICQR'L 最大不失真输出波形
失真输出波形
0
t0
0
t
uCE uCE
4. 三种基本组态放大电路的分析
用微变等效电路对三种基本放大电路进行分析
ib ube
ic
ib
ic
ib
uce ube rbe
uce
弄清楚等效的概念: 1、对谁等效。2、怎么等效。
c b
e
等效
bc e
2、放大电路的微变等效电路
ui
Rb
RC RL uo
交流通道 将交流通道中的三极管用微变等效电路代替
UCEQ12236V
280Ω
+12V 3kΩ β=50
直流通路
二、静态工作点的估算法分析 +VCC
RC ICQ
ICQ=βIBQ
ui=0时 ui Rb
IBQ VBB
T IEQ=IBQ+ICQ
电工基础电子讲义大连

11
R
例a
已知:US=2V, R=1Ω
IR US
UR
b
U
问: 当U分别为 3V 和 1V 时,IR=?
解: (1) 假定电路中物理量的正方向如图所示; (2) 列电路方程:
U U R US UR U US
IR
UR R
U
US R
11/17/2019
12
R a
IR US UR
(3) 数值计算
I5
电位升
或:
电位降
+ U _ 11/17/2019
3
R3
I4R4 I5R5 U3 U4 I3R3 0
41
基尔霍夫电压定律也适合开路。
例 +
US _ R I
a
Uab US U ab I R
电压降 电压降
b
11/17/2019
42
关于独立方程式的讨论
问题的提出:在用基尔霍夫电流定律或电压定 律列方程时,究竟可以列出多少个独立的方程?
R ui const
11/17/2019
20
欧姆定律
I
I
I
U
R
U
RU
R
U IR U IR U IR
注意:用欧姆定律列方程时,一定要在图中标 明正方向。
11/17/2019
21
广义欧姆定律
(支路中含有电压时的欧姆定律)
R
I
+ US _
a
U ab IR US
Uab
b
I U ab US R
11/17/2019
34
2、短路
RO
《电路第七章》课件

诺顿定理
总结词
诺顿定理是电路分析中的另一个重要定 理,它与戴维南定理类似,可以将一个 有源二端网络等效为一个电流源和一个 电阻并联的形式。
VS
详细描述
诺顿定理的应用与戴维南定理类似,它也 可以简化复杂电路的分析过程。通过将有 源二端网络等效为简单的等效电路,我们 可以更容易地计算出电路中的电流和电压 。与戴维南定理不同的是,诺顿定理将网 络等效为一个电流源和电阻的形式,适用 于分析和计算动态响应和瞬态电流的情况 。
电路的作用与分类
总结词
电路的作用是实现电能的传输和转换,根据不同的分类标准,电路可分为多种类 型。
详细描述
电路的主要作用是实现电能的传输和转换,即将电能转换为其他形式的能量,如 机械能、光能等。根据不同的分类标准,电路可分为交流电路和直流电路、开路 和闭路、串联和并联等类型。
电路的基本物理量
总结词
叠加定理
总结词
叠加定理是线性电路的一个重要性质,它表明在多个独立电 源共同作用下,电路中某支路的电流或电压等于各个独立电 源单独作用于该支路产生的电流或电压的代数和。
详细描述
叠加定理是线性电路分析中常用的一个定理,它简化了多个 电源作用下的电路分析过程。通过应用叠加定理,我们可以 分别计算各个独立电源对电路的影响,然后将结果相加得到 最终结果。
电感元件
电流滞后电压90度相位, 相量模型为复数,虚部为 感抗。
电容元件
电压滞后电流90度相位, 相量模型为复数,虚部为 容抗。
复杂交流电路的分析与计算
串联电路
复杂电路的分析方法
各元件电流相同,总电压等于各元件 电压之和。
利用基尔霍夫定律和相量法进行电路 的分析与计算。
并联电路
电路理论课本讲解7

Chp7 正弦稳态电路分析
本章主要内容 正弦量的相量 正弦稳态电路的相量分析法 正弦稳态电路的功率 谐振
7.1 正弦量的基本概念
正弦量:随时间按正弦或余弦规律变化的电压或电流。
u
+ u 0
Um
t
u Um cos(t )
瞬时值表达式 一、正弦量的三要素
Um
波形图
u值正、负号的意义?
o
1
7.3 基尔霍夫定律的相量形式
1. KCL的相量形式
i
k
0
ik 2Ik cos(t k )
i
k
2I k cos(t k )
Re[ 2I k e jt ]
Re[{ ( 2I k )}e jt ] 0 I k 0
或 2. KVL的相量形式 同理可得
例3. 下面各种电流的表示式正确么?
(1)i 4 cos(t 60 ) A 4 60 A 5e j 30 A 5 2 cos(t 30 ) A (2) I
(3)i 845 A (4) I 10 30 A
二、正弦量运算与相量运算的对应关系
1 2
同频正弦量和、差的相量等于其相量的和、差 2. 微分性质
设 i 2I cos(t )
则
di d jt ] Re[ d ( 2 Ie jt )] Re[ 2 Ie dt dt dt
Re[ 2 jIe jt ]
正弦量微分的相量等于原正弦量的相量乘以 j
一、正弦量的三要素
u Um cos(t )
Um
Um
u (t )
i
0
本章主要内容 正弦量的相量 正弦稳态电路的相量分析法 正弦稳态电路的功率 谐振
7.1 正弦量的基本概念
正弦量:随时间按正弦或余弦规律变化的电压或电流。
u
+ u 0
Um
t
u Um cos(t )
瞬时值表达式 一、正弦量的三要素
Um
波形图
u值正、负号的意义?
o
1
7.3 基尔霍夫定律的相量形式
1. KCL的相量形式
i
k
0
ik 2Ik cos(t k )
i
k
2I k cos(t k )
Re[ 2I k e jt ]
Re[{ ( 2I k )}e jt ] 0 I k 0
或 2. KVL的相量形式 同理可得
例3. 下面各种电流的表示式正确么?
(1)i 4 cos(t 60 ) A 4 60 A 5e j 30 A 5 2 cos(t 30 ) A (2) I
(3)i 845 A (4) I 10 30 A
二、正弦量运算与相量运算的对应关系
1 2
同频正弦量和、差的相量等于其相量的和、差 2. 微分性质
设 i 2I cos(t )
则
di d jt ] Re[ d ( 2 Ie jt )] Re[ 2 Ie dt dt dt
Re[ 2 jIe jt ]
正弦量微分的相量等于原正弦量的相量乘以 j
一、正弦量的三要素
u Um cos(t )
Um
Um
u (t )
i
0
网络设备基础知识
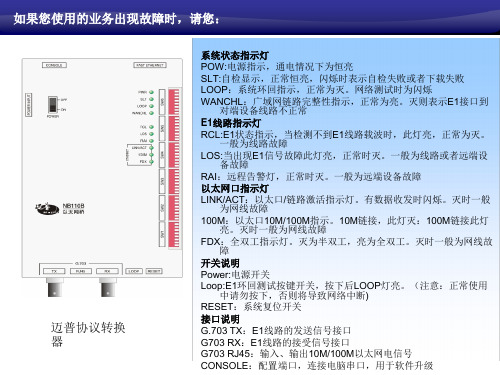
故障现象:网络速率慢,丢包严重,设备指示灯正常 故障判断与分析:网络丢包,有可能是局域网内有病毒,某些电脑占用大量带宽 故障处理:将主线连接笔记本电脑,测试网络带宽是否达到预期值,使用ping命令测试网络丢包情况。 主线无故障后,使用排除法线将全部电脑网线拔除,然后分别将一部分电脑连接到交换机,测试无 问题后,再连接一部分。直到找到故障电脑。 拨码图见设备下方说明,此文档不另描述
初灵M10故障案例
故障现象:网络中断,RL、RS、RF灯灭 故障判断与分析:RL、RS、RF灯分别为远端电口连接指示、速率指示、全/半双工指示,均灭则表示 远端电口无连接 故障处理:通知远端检查电口连接,远端检测后,故障排除 故障现象:网络中断,FL灯灭 故障判断与分析:FL灯灭说明设备没有收到光信号 故障处理:检查尾纤完好性,重新拔查尾纤,联系对端检查对端设备及尾纤,检查无问题后,测试光纤 连接是否正常,如发现光纤中断,从最近基站测试到机房光纤是否正常,一段一段排查,找出光纤 中断的地点,然后通知抢修队,对中断处进行重新连接,连接完成后测试衰减值是否在正常范围内 ,故障排除。 故障现象:网络速率慢,TL等亮,TS、TF灯灭 故障判断与分析:TL灯亮,说明数据有发送,TS、TF灯灭说明本端电口处于10M半双工工作状态。导 致发送数据慢,达不到预期值 故障处理:检查双绞线,使用测线仪测试发现双绞线制作正确,1~8芯都连接正常。检查电口所连接设 备的端口,发现为端口配置错误,重新配置为自适应后,故障排除
•
网络故障处理步骤
(2)设备的软件故障是指系统及配置上的故障,它可以分为以下几类。 • 系统错误。网络设备是硬件和软件的结合体,软件的错误和我们常见的windows错误一样,在条件 合适时,会导致设备丢包、错包和指示灯不规律闪亮。此类故障通过重新启动设备可以排除。 • 外部因素。由于病毒等情况的存在,有可能某台主机想所连接的端口发送大量数据包,致使数据包 来不急转发,进而导致缓冲区溢出产生丢包现象。还有一种就是广播风暴,它不仅会占用大量的网 络带宽,而且还将占用大量的CPU处理时间。网络如果长时间被大量的广播数据包所占用,正常的 点对点通信就无法进行,网络速度就会边慢或者瘫痪。一块网卡或者端口发生故障都有可能引起广 播风暴。 网络设备的故障多种多样,不同的故障有不同的表现形式。故障分析时需要通过各种现象灵活运用排除 法和替换法找出故障所在,并及时排除 • 排除法。当我们面对故障现象分析问题时,无意中就已经学会使用排除法来确定发生故障的方向了 。这种方法时指依据所观察到的故障现象,尽可能全面的列举出所有可能发生的故障,然后逐个分 析、排除。在排除时要遵循由简到繁的原则,提高效率。 • 替换法。替换法时我们最常用的方法了,也时在维修电脑种使用频率较高的方法。替换法是指使用 正常的设备部件或者设备来替换可能有故障的设备,从而找出故障点的方法。
初灵M10故障案例
故障现象:网络中断,RL、RS、RF灯灭 故障判断与分析:RL、RS、RF灯分别为远端电口连接指示、速率指示、全/半双工指示,均灭则表示 远端电口无连接 故障处理:通知远端检查电口连接,远端检测后,故障排除 故障现象:网络中断,FL灯灭 故障判断与分析:FL灯灭说明设备没有收到光信号 故障处理:检查尾纤完好性,重新拔查尾纤,联系对端检查对端设备及尾纤,检查无问题后,测试光纤 连接是否正常,如发现光纤中断,从最近基站测试到机房光纤是否正常,一段一段排查,找出光纤 中断的地点,然后通知抢修队,对中断处进行重新连接,连接完成后测试衰减值是否在正常范围内 ,故障排除。 故障现象:网络速率慢,TL等亮,TS、TF灯灭 故障判断与分析:TL灯亮,说明数据有发送,TS、TF灯灭说明本端电口处于10M半双工工作状态。导 致发送数据慢,达不到预期值 故障处理:检查双绞线,使用测线仪测试发现双绞线制作正确,1~8芯都连接正常。检查电口所连接设 备的端口,发现为端口配置错误,重新配置为自适应后,故障排除
•
网络故障处理步骤
(2)设备的软件故障是指系统及配置上的故障,它可以分为以下几类。 • 系统错误。网络设备是硬件和软件的结合体,软件的错误和我们常见的windows错误一样,在条件 合适时,会导致设备丢包、错包和指示灯不规律闪亮。此类故障通过重新启动设备可以排除。 • 外部因素。由于病毒等情况的存在,有可能某台主机想所连接的端口发送大量数据包,致使数据包 来不急转发,进而导致缓冲区溢出产生丢包现象。还有一种就是广播风暴,它不仅会占用大量的网 络带宽,而且还将占用大量的CPU处理时间。网络如果长时间被大量的广播数据包所占用,正常的 点对点通信就无法进行,网络速度就会边慢或者瘫痪。一块网卡或者端口发生故障都有可能引起广 播风暴。 网络设备的故障多种多样,不同的故障有不同的表现形式。故障分析时需要通过各种现象灵活运用排除 法和替换法找出故障所在,并及时排除 • 排除法。当我们面对故障现象分析问题时,无意中就已经学会使用排除法来确定发生故障的方向了 。这种方法时指依据所观察到的故障现象,尽可能全面的列举出所有可能发生的故障,然后逐个分 析、排除。在排除时要遵循由简到繁的原则,提高效率。 • 替换法。替换法时我们最常用的方法了,也时在维修电脑种使用频率较高的方法。替换法是指使用 正常的设备部件或者设备来替换可能有故障的设备,从而找出故障点的方法。
电路基础之第7章(new)

若非正弦周期电流流过某一电阻R,其平均 功率为
P
I R
2 2 2 2 I 0 R I1 R I 2 R I k R 2
即可用非正弦电流有效值的平方乘电阻R求 得。
在非正弦周期电流电路中有时也用到视 在功率,定义为
S UI
功率因数定义为
P S
f (t )dt
0
T
f (t ) cos ktdt
0
T
f (t ) sin ktdt
0
T
两式的系数有如下关系
以上两式的无穷 三角级数称为周期函 数的傅立叶级数,后 一式中A0称为的直流 分量,它是非正弦周 期函数一周期内的平 均值。 Akm sin( kt k ) Akm称为次谐波分量的 称为f(t)的k次谐波分量。 振幅, k 称为k次谐波分量的初相角。
A0 a0 a A cos km k k bk Akm sin k 2 2 A a b km k k bk k arctan ak
k2
特别地,当k=1时, A1m sin( t 1 ) 称为f(t) 的基波分量,其周期或频率与f(t)相同。 k2 的各项统称为高次谐波。高次谐波的频 率是基波的整数倍。 将周期函数f(t)分解为直流分量、基波 分量和一系列不同频率的各次谐波分量之 和,称为谐波分析。
C (1)
C (1)
jC
C (k )
(3)应用叠加定理,将步骤(2)所计算的 结果化为瞬时值表达式后进行相加,最终求 得电路的响应。这里要注意:因为不同谐波 分量的角频率不同,其对应的相量直接相加 是没有意义的。
7.4 非正弦周期量的有效值、 平均值和平均功率
7.4.1 非正弦周期量的有效值
dianlu7

0+等效电路 1 4
+
+
10V -
2A uL
-
uL(0+)= -2×4=-8V
小结 求初始值的步骤:
1.由换路前电路(稳定状态)求uC(0-)和iL(0-)。 2.由换路定律得 uC(0+) 和 iL(0+)。 3.画0+等效电路。
(1)换路后的电路;
(2)电容(电感)用电压源(电流源)替代。
S
i1
5F + 2
i2
-uC
3 6 i3
等效电路 5F + i1
t >0
-uC 4
解 这是一个求一阶RC 零输入响应问题,有
t
uC U 0e RC
U0 24V RC 5 4 20s
S
i1
5F + 2
i2
-uC
3 6 i3
5F + i1 -uC 4
t
uC 24e 20 V t 0
第七章 一阶电路和二阶电路 的时域分析
7-1 动态电路的方程及其初始条件
7-7 一阶电路和二阶电路的阶跃响应
7-2 一阶电路的零输入响应
7-8 一阶电路和二阶电路的冲激响应
7-3 一阶电路的零状态响应
*7-9 卷积积分
7-4 一阶电路的全响应
*7-10 状态方程
7-5 二阶电路的零输入响应
*7-11 动态电路时域分析中的几个问题
动态
任意激励(本章主要研 究直流激励)
换路发生后的整个过程 微分方程的通解
3.电路的初始条件
初始条件为 t = 0+时,u 、i 及其(n-1)阶导数的 值(此时方程为n阶),用来确定解答中的积分常数
电工学课件第七章
(2)若启动时改为Y接法,求 Ist Y
解: (1)Ist =7 IN =720=140A
(2) I lY 1
I l
3
7.4
Ist Y = Ist /3=140/3=47A
#
电工学课件第七章
§ 9.5 三相异步电动机的选择 一、三相异步机铭牌与技术数据
1. 型号 Y 132M-4
异步电动机
磁极数(极对数 p=2)
三相定子绕组:产生旋转磁场
定子绕组 (三相)
定子
转子:在旋转磁场作用下,产 生感应电动势或电流。
U
V’
W’
线绕式 鼠笼式
W
转子
V U’
鼠笼转子
电工学课件第七章
机座
7.1.2 异步电动机的工作原理-----旋转磁场的产生 异步机中,旋转磁场代替了旋转磁极
(•)电流出
V’
n U
1
W’
W
V
U’
()电流入
7.1 三相异步电动机的结构及工作原理
电动机的分类 交流电动机
电动机
异步机 同步机
鼠笼式 绕线式
直流电动机 他励、异励、串励、复励
鼠笼式异步交流电动机授课内容: 基本结构、工作原理、 机械特性、控制方法
电工学课件第七章
U
定子 三相异步机的结构
V’
W’
转子 W
V U’
电工学课件第七章
7.1.1 三相异步机的结构
所以降压起动适合于空载或轻载起动的场合
正常 运行
UP Z A
C
X
YB
A
UP' Z X
CY
起动
B 7.4U P 来自1 3 UP1
解: (1)Ist =7 IN =720=140A
(2) I lY 1
I l
3
7.4
Ist Y = Ist /3=140/3=47A
#
电工学课件第七章
§ 9.5 三相异步电动机的选择 一、三相异步机铭牌与技术数据
1. 型号 Y 132M-4
异步电动机
磁极数(极对数 p=2)
三相定子绕组:产生旋转磁场
定子绕组 (三相)
定子
转子:在旋转磁场作用下,产 生感应电动势或电流。
U
V’
W’
线绕式 鼠笼式
W
转子
V U’
鼠笼转子
电工学课件第七章
机座
7.1.2 异步电动机的工作原理-----旋转磁场的产生 异步机中,旋转磁场代替了旋转磁极
(•)电流出
V’
n U
1
W’
W
V
U’
()电流入
7.1 三相异步电动机的结构及工作原理
电动机的分类 交流电动机
电动机
异步机 同步机
鼠笼式 绕线式
直流电动机 他励、异励、串励、复励
鼠笼式异步交流电动机授课内容: 基本结构、工作原理、 机械特性、控制方法
电工学课件第七章
U
定子 三相异步机的结构
V’
W’
转子 W
V U’
电工学课件第七章
7.1.1 三相异步机的结构
所以降压起动适合于空载或轻载起动的场合
正常 运行
UP Z A
C
X
YB
A
UP' Z X
CY
起动
B 7.4U P 来自1 3 UP1
第七章--正弦交流电路

φ=(ωt+φi1)-(ωt+φi2)=φi1-φi2 可见,相位差=初相位之差。
若 φ>0,φi1>φi2,i1超前i2; φ=0,φi1=φi2,i1与i2同相位; φ<0,φi1<φi2,i1滞后i2;
i1 i2
i2 i1
φi2 φi1
i1超前i2
φi2 φi1
i1滞后i2
7.2 周期交流电量的有效值
UR RIR
瞬时功率: p iRuR 2U R IR sin2 (t )
URIR[1 cos 2(t )]
平均功率
P 1 T
T URiRdt UI I 2R
0
P
it
u.
IR
.
.
UR
. IR R
UR
2)电感元件
时域表达式 iL 2IL sin ωt
uL
L
diL dt
iL UL
交流电路:电压或电流是时间的周期性函数,一周期内平均值为零. 正弦交流电路:电压或电流是时间的正弦函数.
1)正弦交流电流描述 (电流参考方向如图所示)
瞬时值 i
瞬时表达式 i=Imsin(ωt+i)
电流波形图
iR
i
瞬时表达式需规定参考方向!
Im
t
2)正弦交流电的三要素
瞬时表达式 i=Imsin(ωt+i)
IR
UL U sin θ 100 0.8 80V ,
UR UL cos θ 80 0.6 48V
XC
UR IC
48 3
16Ω
.
U
.
IC θ
R UR 48 12Ω IR 4
XL
UL IL
80 5
16Ω
电路8章1syl

判断准则: 互感电压的正极性端与产生该互感电压的
线圈电流的流入端为同名端,则互感电压极性 为正。
耦合电感的电路符号
a+
i 1
M
i2 + c
u1
L* 1
* L2
u2
b-
-d
图8-1(a)
VCR中互感电压取+
a+ i1
M
i
2 +c
u1
L*1 L2
u2
b-
*
-d
图8-1(b)
VCR中互感电压取-
或:互感电压的正极性端与产生该互感电压的 线圈电流的流入端为同名端。
a-
i 1
M
i
2 -c
u1
L* 1
L2
u2
b+
* +d
u1
uL1
uM1
L1
di1 dt
-
M
di2 dt
u2
uL2
uM
2
L2
di2 dt
M di1 dt
电路模型也可以用受 控源的形式表示:
则可去掉M和同名端 标记,但受控源的方向 与同名端有关。
a- i1
u
L 1
1 M di2
b + dt
i2
L 2 M di1 dt
联接方式:串联,并联和三端联接
去耦等效: 耦合电感用无耦合的等效电路去等效。
8-2-1 耦合电感的串联
顺串:异名端相接。反串:同名端相接
* L1 M * L2
i + u1 - + u2 -
+u顺串
L1 * M * L2
i + u1 - + u2 -
线圈电流的流入端为同名端,则互感电压极性 为正。
耦合电感的电路符号
a+
i 1
M
i2 + c
u1
L* 1
* L2
u2
b-
-d
图8-1(a)
VCR中互感电压取+
a+ i1
M
i
2 +c
u1
L*1 L2
u2
b-
*
-d
图8-1(b)
VCR中互感电压取-
或:互感电压的正极性端与产生该互感电压的 线圈电流的流入端为同名端。
a-
i 1
M
i
2 -c
u1
L* 1
L2
u2
b+
* +d
u1
uL1
uM1
L1
di1 dt
-
M
di2 dt
u2
uL2
uM
2
L2
di2 dt
M di1 dt
电路模型也可以用受 控源的形式表示:
则可去掉M和同名端 标记,但受控源的方向 与同名端有关。
a- i1
u
L 1
1 M di2
b + dt
i2
L 2 M di1 dt
联接方式:串联,并联和三端联接
去耦等效: 耦合电感用无耦合的等效电路去等效。
8-2-1 耦合电感的串联
顺串:异名端相接。反串:同名端相接
* L1 M * L2
i + u1 - + u2 -
+u顺串
L1 * M * L2
i + u1 - + u2 -
电工学第七章

R 10k
R 10k
C 0.01u R3 A R2 RP R1 DZ VZ= 6V vO
vP +
C 0.01u
–
vN
VRP
幅度较小时, AV 3
V o
幅度增大到稳压管击穿时,
RP和R1的电流、 R2的压降不变
AV
V o
V N 负反馈系数 F V
o
稳幅时 VN VP 1 Vom 3
VN VRp VZ Vom VR p
VN RP R1
例1:试用相位平衡条件判断下图电路能否产生自 激振荡 +UCC
正反馈
RB1 C1 RB2 - RE CE
L
-
C
-
注意:用瞬时极性法判断反馈的极性时, 耦合电容、旁路电容两端的极性相同, 属于选频网络的电容,其两端的极性相反。
频率响应
VCC M vo Rb1
(+) (+)
VCC Rb1
(-) (+) b
M (-) L c
C
(+) b
L c (-) T e
C
(+)
T e
(-)
Rb2 C1
C1
Ce
Rb2
Re
Re
反馈 反馈
满足相位平衡条件 满足相位平衡条件
首端
三点式LC并联电路
L1 中间端 L2 尾端 C
仍然由LC并联谐振电路构成选频网络
一般有 R L 则
Z L 1 R j(L ) C
1 LC
C
当 0 谐振时
1 LC
时, 电路谐振。 0
为谐振频率
R 10k
C 0.01u R3 A R2 RP R1 DZ VZ= 6V vO
vP +
C 0.01u
–
vN
VRP
幅度较小时, AV 3
V o
幅度增大到稳压管击穿时,
RP和R1的电流、 R2的压降不变
AV
V o
V N 负反馈系数 F V
o
稳幅时 VN VP 1 Vom 3
VN VRp VZ Vom VR p
VN RP R1
例1:试用相位平衡条件判断下图电路能否产生自 激振荡 +UCC
正反馈
RB1 C1 RB2 - RE CE
L
-
C
-
注意:用瞬时极性法判断反馈的极性时, 耦合电容、旁路电容两端的极性相同, 属于选频网络的电容,其两端的极性相反。
频率响应
VCC M vo Rb1
(+) (+)
VCC Rb1
(-) (+) b
M (-) L c
C
(+) b
L c (-) T e
C
(+)
T e
(-)
Rb2 C1
C1
Ce
Rb2
Re
Re
反馈 反馈
满足相位平衡条件 满足相位平衡条件
首端
三点式LC并联电路
L1 中间端 L2 尾端 C
仍然由LC并联谐振电路构成选频网络
一般有 R L 则
Z L 1 R j(L ) C
1 LC
C
当 0 谐振时
1 LC
时, 电路谐振。 0
为谐振频率
讲义第七章(1).ppt

电路初始值的确定 ➢ 根据换路定则,iC (0) uL (0) 时,有:
由电路的uC(0-) 和iL(0-) 确定uC(0+)和iL(0+) 时刻的值 电路中其他电流和电压在 t=0+ 时刻的值通过 0+ 等效电路求得
独立初始条件: uC(0+)和iL(0+)
- 无跳变
非独立初始条件: uL(0+) 、iC(0+)、uR(0+) 、iR(0+)
在 t = 0+的等效电路
令τ= L/R,称τ为RL电路的时间常数
时间常数τ
➢电阻Req的值为戴维南等效电路中的等效电阻值
时间常数的几何意义
➢τ的大小反映了电路过渡过程(如电容充、放电)时间的长短, 即:τ大,过渡过程时间长;τ小 ,过渡过程时间短
下表给出了电容电压在τ=τ,2τ,3τ,……时刻的值
即有 uC (0 ) uC (0 ) ; iL (0 ) iL (0 ) ; 过渡过程:当电路状态发生改变后(或换路后)需要经历一
个变化过程才能达到新的稳定状态,这个变化过程称为电路 的过渡过程
分析动态电路的过渡过程的方法
根据KCL、KVL和电感、电容的VCR关系建立描述电路 的方程,方程是以时间为自变量的线性常微分方程
求初始值的具体步骤
➢ 由换路前 t=0-时刻的电路(一般为稳定状态) 求uC (0-) 或 iL (0-)
➢ 由连续性得uC (0+) 和iL (0+)
画 t=0+ 时刻的等效电路: 电容用电压源替代,电感用电流源替代
(取 0+ 时刻值,方向与电容电压、电感电流方向相同)
➢ 由 0+ 时的等效电路求所需其他各变量的 0+ 值
由电路的uC(0-) 和iL(0-) 确定uC(0+)和iL(0+) 时刻的值 电路中其他电流和电压在 t=0+ 时刻的值通过 0+ 等效电路求得
独立初始条件: uC(0+)和iL(0+)
- 无跳变
非独立初始条件: uL(0+) 、iC(0+)、uR(0+) 、iR(0+)
在 t = 0+的等效电路
令τ= L/R,称τ为RL电路的时间常数
时间常数τ
➢电阻Req的值为戴维南等效电路中的等效电阻值
时间常数的几何意义
➢τ的大小反映了电路过渡过程(如电容充、放电)时间的长短, 即:τ大,过渡过程时间长;τ小 ,过渡过程时间短
下表给出了电容电压在τ=τ,2τ,3τ,……时刻的值
即有 uC (0 ) uC (0 ) ; iL (0 ) iL (0 ) ; 过渡过程:当电路状态发生改变后(或换路后)需要经历一
个变化过程才能达到新的稳定状态,这个变化过程称为电路 的过渡过程
分析动态电路的过渡过程的方法
根据KCL、KVL和电感、电容的VCR关系建立描述电路 的方程,方程是以时间为自变量的线性常微分方程
求初始值的具体步骤
➢ 由换路前 t=0-时刻的电路(一般为稳定状态) 求uC (0-) 或 iL (0-)
➢ 由连续性得uC (0+) 和iL (0+)
画 t=0+ 时刻的等效电路: 电容用电压源替代,电感用电流源替代
(取 0+ 时刻值,方向与电容电压、电感电流方向相同)
➢ 由 0+ 时的等效电路求所需其他各变量的 0+ 值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i2 ( t ) I 2m cos(t 2 )
电流i1(t)与i2(t)间的相位差为
(t 1 ) (t 2 ) 1 2
上式表明两个同频率正弦量在任意时刻 的相位差均等于它们初相之差,与时间t 无关。 相位差反映出两个正弦量在时间上的 超前和滞后关系:
j
极坐标形式: A =a a1=acos a2=asin
a a1 a2
2 2
a2
j a
复数的复 平面表示
arctg
a2 a1
a1
+1
0
正弦量的相量表示
分析正弦稳态的有效方法是相量法 (Phasor method),相量法的基础是用 相量(向量)或复数来表示正弦量的 振幅和初相。注意:其频率不变。 j f ( t ) F cos(t )
2 2
T
0
T /2
[1 cos 2t]d t
A 2
0.5 A
可得半波整流波形的有效值是振幅值 的0.5倍。
由此可见: (1)正弦量的有效值只与振幅值有关, 与角频率和初相无关; (2)非正弦周期量的有效值没有上述关 系,需要单独计算。
当然,还有平均值的定义。即:一 个周期内取其平均。
相量图的另一个好处是可以用向量和 复数的运算法则求同频率正弦电压或 电流之和。平行四边形法则。
1。试求下列正弦量的振幅相量和有效值 相量
(1) (2) i1 (t ) 5 cos tA i2 (t ) 10 cos(t / 2)A
2。试写出下列相量所代表的正弦量。已 知 314rad / s
Im 2
0.707 I m
结果表明,振幅为Im的正弦电流与 数值为I=0.707Im的直流电流,在一个周 期内,对电阻R提供相同的能量。也就 是说正弦电压电流的有效值为振幅值的 0.707倍,或者说正弦电压电流的振幅 是其有效值的 2 倍 正弦电压u(t)=Umcos(t+)的有效值为
U 1 T 1 T
560 A I1m
i2 ( t ) 10 sin( 314t 60 ) 10 cos(314t 30 ) 10150 A 10 cos(314t 150 ) I 2m
相量图如图所示。
从相量图容易看 出各正弦电压电 流的相位关系: i2(t)超前于 i1(t) 90°。
( 180) ( 45 ) 135
u(t)与i2(t)的相位差为
( 180) 60 240
习惯上将相位差的范围控制在 -180°到 +180°之间。 如:我们不说电压u(t)与电流i2(t) 的相位差为-240 ,而说电压u(t) 与电流i2(t)的相位差为(360240)=120, 即:u(t)超前于i2(t) 120 。
解:角频率 函数表达式为
2 T
2 100 10
3
20 rad/s
u(t ) U m cos(t ) 10 cos( 20t 10cos(62.8 t 30 ) V
6
)
波形如右图。
例2 试求正弦量 f (t ) 10 sin(100 t ) 6 的振幅Fm 、初相与频率f 。
正弦稳态分析的重要性在于:(1) 正 弦信号是最基本的信号,它容易产生 、加工和传输;(2) 很多实际电路都 工作于正弦稳态。例如电力系统的大 多数电路。(3) 用相量法分析正弦稳 态十分有效。(4) 已知电路的正弦稳 态响应,可以得到任意波形信号激励 下的响应。 分析正弦稳态的有效方法——相量法。
m
Re[Fme
j
e
jt
]
Fm sin
相量图
F e j F Fm m m
Fm
称为:f (t)的振幅相量
0
+1 Fm cos
有效值相量 正弦量有效值与复值的关系:
Fm 2F
正弦量 f (t) 的有效值相量
Fe j F F
f ( t ) Fm cos(t ) Fm Fm f (t ) 2 F cos(t ) F F
正弦量与其相量的对应关系:
正弦量f(t)是以角速度ω沿反时针方向旋 e j t 在实轴投影。即: 转的旋转相量 Fm
e jt ] f ( t ) Re[Fm
1 Fm
j
f(t)
t2 t
e j t Fm
t2
可见,一个按正弦规律变化的电压和电 流,可以用一个相量(复常数)来表示。 已知正弦量的时间表达式,可得相应的 相量。反过来,已知电压电流相量,也 就知道正弦电压电流的振幅和初相,再 加上角频率,就能写出正弦电压电流的 时间表达式(两者存在一一对应关系)。 即
e jt ] Re[ 2 I e jt ] Re[ I km k
e ]0 代入KCL中得: i (t ) Re[ I
j t k 1 n k k 1 n km
n
n
e ]0 i (t ) Re[ 2 I
通过周期电流信号i(t)时,电阻吸收的 功率p(t)= i2(t)R是时间的函数,在一 个周期T内获得的能量为
W
0
T
i
2
( t ) Rdt
当直流电流I或者电流i(t)通过同一电阻 R时,假设它们在一个周期的时间内获 得相同的能量,即
W I RT
2
0
T
i ( t ) Rdt
2
由此解得
u(t ) U m cos( t u ) U m U m u i (t ) I m cos( t i ) I m I m i
或:
u(t) U m cos(ω t φu ) 2U cos (ωt φu ) U Uφu i(t) I m cos (ω t φi ) 2 I cos (ωt φi ) I Iφi
10 A (1) I 2 (2) U 4 j 4V
7-3 正弦稳态电路的相量模型
7-3-1 基尔霍夫定律的相量形式
KCL:
k 1
ik ( t )
n
0
电路中全部电流都具有同一频率ω,则 可用振幅相量或有效值相量表示: ik (t ) 2 I k cos(t k )
例3 已知正弦电压u(t)和电流i1(t), i2(t)的表达式为 u(t ) 311cos( t 180 ) V
i1 ( t ) 5 cos( t 45 ) A
i 2 ( t ) 10 cos( t 60 ) A
试求: u(t)与i1(t)和i2(t)的相位差。 解: u(t)与i1(t)的相位差为
T 0
u (t )d t
2
T 0
U m cos ( t )d t 0.707U m
2 2
对于半波整流 波形,其表达 式 :
h( t ) A sinωt (0 t T / 2)
H 1 T A
0
2
T
h ( t )d t 1 2
2
1 T
0
T /2
A sin td t
解:将正弦量表达式化为基本形式:
f ( t ) 10 sin(100 t 10 cos(100 t
6
) 10 sin(100 t
5 6
) )
5 6
2
) 10 cos(100 t
3
所以 Fm =10, = /3rad, =100rad/s, f =/2=50Hz
练习1: 已知正弦电压 u 40 sin( 314t / 4)V
(1)试求振幅、周期、频率、角频率和初 相; (2)画出其波形图。
7-1-2
正弦量间的相位差
正弦稳态电路中,各电压电流都是 频率相同的正弦量,常常需要将这些正 弦量的相位进行比较。两个正弦电压电 流相位之差,称为相位差 。如两个同 频率的正弦电流 i1 ( t ) I1m cos(t 1 )
练习2 已知两个正弦电压
u1 U1m cos(1000t 60 )V
u2 U 2 m sin( 1000t 150 )V
试求这两个正弦电压的相位差。
7-1-3 正弦量的有效值
将直流电流I和正弦电流i(t)通过电 阻R时的功率和能量作一比较,导出正 弦电压电流的有效值。
电阻R通过直流电流I时,吸收的功率 P=I2R , 在 时 间 T 内 获 得 的 能 量 为 W=PT=I2RT .
当=1-2>0时,表明i1(t)超前i2(t),
超前的角度为 。 当=1-2<0时,表明i1(t)滞后i2(t), 滞后的角度为||。
当=1-2 =0时, i1(t)与i2(t)同相。 当=1-2 =时, i1(t)与i2(t)反相。 当=1-2 =/2时, i1(t)与i2(t)正交
(a) 电流i1超前于电流i2, (b) 电流i1滞后于电流i2
(c) 同相 (d) 正交 (e) 反相 注意:角频率不同的两个正弦间的相 位差为
(t ) (1t 1 ) ( 2t 2 ) (1 2 )t (1 2 )
是时间t的函数,不再等于初相之差。
练习2 已知两个正弦电压
u1 U1m cos(1000t 60 )V
u2 U 2 m sin( 来自000t 150 )V
当t=0时,u1(0)=5V,u2(0)=8V,试求这两个 正弦电压的振幅、有效值。
电流i1(t)与i2(t)间的相位差为
(t 1 ) (t 2 ) 1 2
上式表明两个同频率正弦量在任意时刻 的相位差均等于它们初相之差,与时间t 无关。 相位差反映出两个正弦量在时间上的 超前和滞后关系:
j
极坐标形式: A =a a1=acos a2=asin
a a1 a2
2 2
a2
j a
复数的复 平面表示
arctg
a2 a1
a1
+1
0
正弦量的相量表示
分析正弦稳态的有效方法是相量法 (Phasor method),相量法的基础是用 相量(向量)或复数来表示正弦量的 振幅和初相。注意:其频率不变。 j f ( t ) F cos(t )
2 2
T
0
T /2
[1 cos 2t]d t
A 2
0.5 A
可得半波整流波形的有效值是振幅值 的0.5倍。
由此可见: (1)正弦量的有效值只与振幅值有关, 与角频率和初相无关; (2)非正弦周期量的有效值没有上述关 系,需要单独计算。
当然,还有平均值的定义。即:一 个周期内取其平均。
相量图的另一个好处是可以用向量和 复数的运算法则求同频率正弦电压或 电流之和。平行四边形法则。
1。试求下列正弦量的振幅相量和有效值 相量
(1) (2) i1 (t ) 5 cos tA i2 (t ) 10 cos(t / 2)A
2。试写出下列相量所代表的正弦量。已 知 314rad / s
Im 2
0.707 I m
结果表明,振幅为Im的正弦电流与 数值为I=0.707Im的直流电流,在一个周 期内,对电阻R提供相同的能量。也就 是说正弦电压电流的有效值为振幅值的 0.707倍,或者说正弦电压电流的振幅 是其有效值的 2 倍 正弦电压u(t)=Umcos(t+)的有效值为
U 1 T 1 T
560 A I1m
i2 ( t ) 10 sin( 314t 60 ) 10 cos(314t 30 ) 10150 A 10 cos(314t 150 ) I 2m
相量图如图所示。
从相量图容易看 出各正弦电压电 流的相位关系: i2(t)超前于 i1(t) 90°。
( 180) ( 45 ) 135
u(t)与i2(t)的相位差为
( 180) 60 240
习惯上将相位差的范围控制在 -180°到 +180°之间。 如:我们不说电压u(t)与电流i2(t) 的相位差为-240 ,而说电压u(t) 与电流i2(t)的相位差为(360240)=120, 即:u(t)超前于i2(t) 120 。
解:角频率 函数表达式为
2 T
2 100 10
3
20 rad/s
u(t ) U m cos(t ) 10 cos( 20t 10cos(62.8 t 30 ) V
6
)
波形如右图。
例2 试求正弦量 f (t ) 10 sin(100 t ) 6 的振幅Fm 、初相与频率f 。
正弦稳态分析的重要性在于:(1) 正 弦信号是最基本的信号,它容易产生 、加工和传输;(2) 很多实际电路都 工作于正弦稳态。例如电力系统的大 多数电路。(3) 用相量法分析正弦稳 态十分有效。(4) 已知电路的正弦稳 态响应,可以得到任意波形信号激励 下的响应。 分析正弦稳态的有效方法——相量法。
m
Re[Fme
j
e
jt
]
Fm sin
相量图
F e j F Fm m m
Fm
称为:f (t)的振幅相量
0
+1 Fm cos
有效值相量 正弦量有效值与复值的关系:
Fm 2F
正弦量 f (t) 的有效值相量
Fe j F F
f ( t ) Fm cos(t ) Fm Fm f (t ) 2 F cos(t ) F F
正弦量与其相量的对应关系:
正弦量f(t)是以角速度ω沿反时针方向旋 e j t 在实轴投影。即: 转的旋转相量 Fm
e jt ] f ( t ) Re[Fm
1 Fm
j
f(t)
t2 t
e j t Fm
t2
可见,一个按正弦规律变化的电压和电 流,可以用一个相量(复常数)来表示。 已知正弦量的时间表达式,可得相应的 相量。反过来,已知电压电流相量,也 就知道正弦电压电流的振幅和初相,再 加上角频率,就能写出正弦电压电流的 时间表达式(两者存在一一对应关系)。 即
e jt ] Re[ 2 I e jt ] Re[ I km k
e ]0 代入KCL中得: i (t ) Re[ I
j t k 1 n k k 1 n km
n
n
e ]0 i (t ) Re[ 2 I
通过周期电流信号i(t)时,电阻吸收的 功率p(t)= i2(t)R是时间的函数,在一 个周期T内获得的能量为
W
0
T
i
2
( t ) Rdt
当直流电流I或者电流i(t)通过同一电阻 R时,假设它们在一个周期的时间内获 得相同的能量,即
W I RT
2
0
T
i ( t ) Rdt
2
由此解得
u(t ) U m cos( t u ) U m U m u i (t ) I m cos( t i ) I m I m i
或:
u(t) U m cos(ω t φu ) 2U cos (ωt φu ) U Uφu i(t) I m cos (ω t φi ) 2 I cos (ωt φi ) I Iφi
10 A (1) I 2 (2) U 4 j 4V
7-3 正弦稳态电路的相量模型
7-3-1 基尔霍夫定律的相量形式
KCL:
k 1
ik ( t )
n
0
电路中全部电流都具有同一频率ω,则 可用振幅相量或有效值相量表示: ik (t ) 2 I k cos(t k )
例3 已知正弦电压u(t)和电流i1(t), i2(t)的表达式为 u(t ) 311cos( t 180 ) V
i1 ( t ) 5 cos( t 45 ) A
i 2 ( t ) 10 cos( t 60 ) A
试求: u(t)与i1(t)和i2(t)的相位差。 解: u(t)与i1(t)的相位差为
T 0
u (t )d t
2
T 0
U m cos ( t )d t 0.707U m
2 2
对于半波整流 波形,其表达 式 :
h( t ) A sinωt (0 t T / 2)
H 1 T A
0
2
T
h ( t )d t 1 2
2
1 T
0
T /2
A sin td t
解:将正弦量表达式化为基本形式:
f ( t ) 10 sin(100 t 10 cos(100 t
6
) 10 sin(100 t
5 6
) )
5 6
2
) 10 cos(100 t
3
所以 Fm =10, = /3rad, =100rad/s, f =/2=50Hz
练习1: 已知正弦电压 u 40 sin( 314t / 4)V
(1)试求振幅、周期、频率、角频率和初 相; (2)画出其波形图。
7-1-2
正弦量间的相位差
正弦稳态电路中,各电压电流都是 频率相同的正弦量,常常需要将这些正 弦量的相位进行比较。两个正弦电压电 流相位之差,称为相位差 。如两个同 频率的正弦电流 i1 ( t ) I1m cos(t 1 )
练习2 已知两个正弦电压
u1 U1m cos(1000t 60 )V
u2 U 2 m sin( 1000t 150 )V
试求这两个正弦电压的相位差。
7-1-3 正弦量的有效值
将直流电流I和正弦电流i(t)通过电 阻R时的功率和能量作一比较,导出正 弦电压电流的有效值。
电阻R通过直流电流I时,吸收的功率 P=I2R , 在 时 间 T 内 获 得 的 能 量 为 W=PT=I2RT .
当=1-2>0时,表明i1(t)超前i2(t),
超前的角度为 。 当=1-2<0时,表明i1(t)滞后i2(t), 滞后的角度为||。
当=1-2 =0时, i1(t)与i2(t)同相。 当=1-2 =时, i1(t)与i2(t)反相。 当=1-2 =/2时, i1(t)与i2(t)正交
(a) 电流i1超前于电流i2, (b) 电流i1滞后于电流i2
(c) 同相 (d) 正交 (e) 反相 注意:角频率不同的两个正弦间的相 位差为
(t ) (1t 1 ) ( 2t 2 ) (1 2 )t (1 2 )
是时间t的函数,不再等于初相之差。
练习2 已知两个正弦电压
u1 U1m cos(1000t 60 )V
u2 U 2 m sin( 来自000t 150 )V
当t=0时,u1(0)=5V,u2(0)=8V,试求这两个 正弦电压的振幅、有效值。
