高一数学复习八
高一数学第8章知识点梳理

高一数学第8章知识点梳理在高一的数学课程中,第8章是一个重要的章节,主要涵盖了向量的基本概念、向量的运算、向量的线性运算、向量共线与平行、向量的数量积以及向量的应用等内容。
本文将对这些知识点进行梳理并进行简要讲解。
1. 向量的基本概念向量是有大小和方向的量,常用有向线段表示。
向量的大小表示为向量的模或向量的长度。
同时,向量还有起点和终点之分,通常用起点和终点的坐标表示向量。
向量的表示方法有坐标表示法和字母表示法。
2. 向量的运算向量的运算主要包括加法和减法。
向量的加法满足交换律和结合律。
向量的减法可以等效为向量的加法。
3. 向量的线性运算向量的线性运算包括数乘和倍乘。
数乘是指将向量的大小进行相乘,同时保持方向不变。
倍乘是指将两个向量进行数乘后相加。
4. 向量共线与平行向量的共线性可以通过数乘判断,如果两个向量的数乘为0,则说明两个向量共线;如果两个向量的数乘不为0,则说明两个向量不共线。
向量的平行性可以通过向量的坐标表示进行判断,如果两个向量的坐标比例相等,则说明两个向量平行。
5. 向量的数量积向量的数量积又称点积,是指两个向量与它们之间夹角的余弦值相乘所得的一个标量。
向量的数量积具有交换律和分配律。
向量的数量积可以用来求解夹角的余弦值、向量的投影以及判断两个向量的夹角大小。
6. 向量的应用向量的应用非常广泛,可以用来表示物理量,如力或速度。
同时,向量的数量积还可以用来求解平面几何问题,如判断平面上的点是否在一条直线上。
本章的知识点比较抽象,需要同学们进行大量的练习除了理解外,还要进行运用。
因此,建议同学们在学习时要多做一些相关的习题巩固所学知识。
同时,也要注意数学语言的表达,避免使用过于简单和模糊的词汇。
总之,高一数学第8章的知识点对于同学们的数学学习和理解具有重要的意义。
通过学习本章的知识,同学们不仅可以提高数学分析和问题解决的能力,还可以为后续的学习打下坚实的基础。
因此,在学习过程中,同学们要保持积极的态度,勤奋学习,善于总结和归纳,提高数学思维的灵活性和应用能力。
高考数学一轮复习 第八章 立体几何 第5讲 简单几何体的再认识(表面积与体积)教学案 理
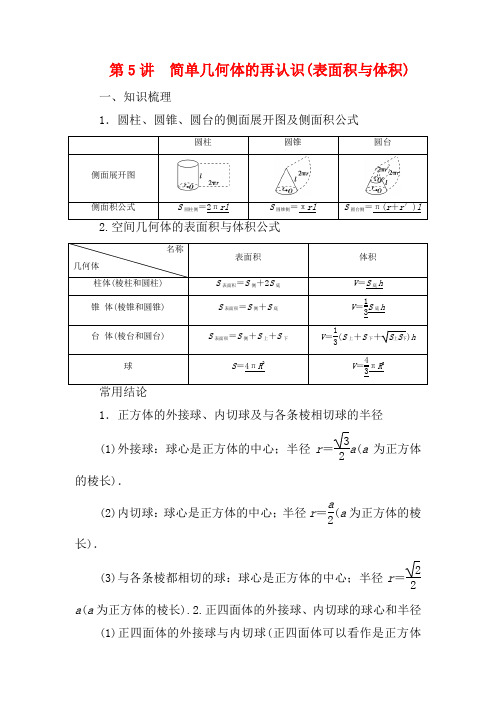
第5讲 简单几何体的再认识(表面积与体积)一、知识梳理1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrl S 圆锥侧=πrlS 圆台侧=π(r +r ′)l名称几何体表面积体积柱体(棱柱和圆柱) S 表面积=S 侧+2S 底 V =S 底h 锥 体(棱锥和圆锥) S 表面积=S 侧+S 底 V =13S 底h台 体(棱台和圆台)S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h球S =4πR 2V =43πR 31.正方体的外接球、内切球及与各条棱相切球的半径 (1)外接球:球心是正方体的中心;半径r =32a (a 为正方体的棱长).(2)内切球:球心是正方体的中心;半径r =a2(a 为正方体的棱长).(3)与各条棱都相切的球:球心是正方体的中心;半径r =22a (a 为正方体的棱长).2.正四面体的外接球、内切球的球心和半径(1)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分).(2)外接球:球心是正四面体的中心;半径r =64a (a 为正四面体的棱长).(3)内切球:球心是正四面体的中心;半径r =612a (a 为正四面体的棱长).二、教材衍化1.已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为________.解析:S 表=πr 2+πrl =πr 2+πr ·2r =3πr 2=12π, 所以r 2=4,所以r =2. 答案:2 cm 2.如图,将一个长方体用过相邻三条棱的中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体体积的比为________.解析:设长方体的相邻三条棱长分别为a ,b ,c ,它截出棱锥的体积V 1=13×12×12a ×12b ×12c =148abc ,剩下的几何体的体积V 2=abc -148abc =4748abc ,所以V 1∶V 2=1∶47.答案:1∶47 一、思考辨析判断正误(正确的打“√”,错误的打“×”) (1)多面体的表面积等于各个面的面积之和.( ) (2)锥体的体积等于底面积与高之积.( )(3)球的体积之比等于半径比的平方.( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差.( )(5)长方体既有外接球又有内切球.( )答案:(1)√(2)×(3)×(4)√(5)×二、易错纠偏常见误区|K(1)不能把三视图正确还原为几何体而错解表面积或体积;(2)考虑不周忽视分类讨论;(3)几何体的截面性质理解有误;(4)混淆球的表面积公式和体积公式.1.已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则该四棱锥的体积为________m3.解析:根据三视图可知该四棱锥的底面是底边长为2 m,高为1 m的平行四边形,四棱锥的高为 3 m.故该四棱锥的体积V=1 3×2×1×3=2(m3).答案:22.将一个相邻边长分别为4π,8π的矩形卷成一个圆柱,则这个圆柱的表面积是________.解析:当底面周长为4π时,底面圆的半径为2,两个底面的面积之和是8π;当底面周长为8π时,底面圆的半径为4,两个底面的面积之和为32π.无论哪种方式,侧面积都是矩形的面积32π2,故所求的表面积是32π2+8π或32π2+32π.答案:32π2+8π或32π2+32π3.已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为________.解析:因为过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为22,底面圆的直径为22,所以该圆柱的表面积为2×π×(2)2+22π×22=12π.答案:12π4.一个球的表面积是16π,那么这个球的体积为________. 解析:设球的半径为R ,则由4πR 2=16π,解得R =2,所以这个球的体积为43πR 3=323π.答案:323π空间几何体的表面积(师生共研)(1)(2020·河南周口模拟)如图,在三棱柱ABC A 1B 1C 1中,AA 1⊥底面ABC ,AB ⊥BC ,AA 1=AC =2,直线A 1C 与侧面AA 1B 1B 所成的角为30°,则该三棱柱的侧面积为( )A .4+4 2B .4+43C .12D .8+42(2)(2020·四川泸州一诊)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( )A .(5+2)πB .(4+2)πC .(5+22)πD .(3+2)π【解析】 (1)连接A 1B .因为AA 1⊥底面ABC ,则AA 1⊥BC ,又AB ⊥BC ,AA 1∩AB =A ,所以BC ⊥平面AA 1B 1B ,所以直线A 1C 与侧面AA 1B 1B 所成的角为∠CA 1B=30°.又AA 1=AC =2,所以A 1C =22,BC = 2.又AB ⊥BC ,则AB =2,则该三棱柱的侧面积为22×2+2×2=4+42,故选A.(2)因为在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2,所以将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB =1,高为BC -AD =2-1=1的圆锥,所以该几何体的表面积S =π×12+2π×1×2+π×1×12+12=(5+2)π.故选A.【答案】 (1)A (2)A空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)旋转体的表面积问题注意其侧面展开图的应用. 1.在如图所示的斜截圆柱中,已知圆柱底面的直径为40 cm ,母线长最短50 cm ,最长80 cm ,则斜截圆柱的侧面面积S =________cm 2.解析:将题图所示的相同的两个几何体对接为圆柱,则圆柱的侧面展开图为矩形.由题意得所求侧面展开图的面积S=12×(50+80)×(π×40)=2 600π(cm2).答案:2 600π2.已知一几何体的三视图如图所示,它的主视图与左视图相同,则该几何体的表面积为________.解析:由三视图知,该几何体是一个正四棱柱与半球的组合体,且正四棱柱的高为2,底面对角线长为4,球的半径为2,所以该正四棱柱的底面正方形的边长为22,该几何体的表面积S=1 2×4π×22+π×22+22×2×4=12π+16.答案:12π+16空间几何体的体积(多维探究)角度一直接利用公式求体积(2020·山东省实验中学模拟)我国古代《九章算术》里,记载了一个“商功”的例子:今有刍童,下广二丈,袤三丈,上广三丈,袤四丈,高三丈.问积几何?其意思是:今有上下底面皆为长方形的草垛(如图所示),下底宽2丈,长3丈,上底宽3丈,长4丈,高3丈.问它的体积是多少?该书提供的算法是:上底长的2倍与下底长的和与上底宽相乘,同样下底长的2倍与上底长的和与下底宽相乘,将两次运算结果相加,再乘以高,最后除以6.则这个问题中的刍童的体积为( )A.13.25立方丈B.26.5立方丈C.53立方丈D.106立方丈【解析】 由题意知,刍童的体积为[(4×2+3)×3+(3×2+4)×2]×3÷6=26.5(立方丈),故选B.【答案】 B角度二 割补法求体积《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何?刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1),那么该刍甍的体积为( )A .4B .5C .6D .12【解析】 如图所示,由三视图可还原得到几何体ABCDEF ,过E ,F 分别作垂直于底面的截面EGH 和FMN ,可将原几何体切割成三棱柱EHG FNM ,四棱锥E ADHG 和四棱锥F MBCN ,易知三棱柱的体积为12×3×1×2=3,两个四棱锥的体积相同,都为13×1×3×1=1,则原几何体的体积为3+1+1=5.故选B.【答案】 B角度三 等体积法求体积(2020·贵州部分重点中学联考)如图,在直四棱柱ABCD A 1B 1C 1D 1中,底面ABCD 是平行四边形,点E 是棱BB 1的中点,点F 是棱CC 1上靠近C 1的三等分点,且三棱锥A 1AEF 的体积为2,则四棱柱ABCD A 1B 1C 1D 1的体积为( )A .12B .8C .20D .18【解析】 设点F 到平面ABB 1A 1的距离为h ,由题意得V A 1AEF=V F A 1AE .又V F A 1AE =13S △A 1AE ·h =13×⎝ ⎛⎭⎪⎫12AA 1·AB ·h =16(AA 1·AB )·h =16S 四边形ABB 1A 1·h =16V ABCD A 1B 1C 1D 1,所以V ABCD A 1B 1C 1D 1=6V A 1AEF =6×2=12.所以四棱柱ABCD A 1B 1C 1D 1的体积为12.故选A.【答案】 A(1)处理体积问题的思路①“转”:指的是转换底面与高,将原来不易求面积的底面转换为易求面积的底面,或将原来不易看出的高转换为易看出并易求解长度的高;②“拆”:指的是将一个不规则的几何体拆成几个简单的几何体,便于计算;③“拼”:指的是将小几何体嵌入一个大几何体中,如将一个三棱锥复原成一个三棱柱,将一个三棱柱复原成一个四棱柱,这些都是拼补的方法.(2)求空间几何体的体积的常用方法①公式法:对于规则几何体的体积问题,可以直接利用公式进行求解;②割补法:把不规则的图形分割成规则的图形,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积;③等体积法:一个几何体无论怎样转化,其体积总是不变的.如果一个几何体的底面面积和高较难求解时,我们可以采用等体积法进行求解.等体积法也称等积转化或等积变形,它是通过选择合适的底面来求几何体体积的一种方法,多用来解决有关锥体的体积,特别是三棱锥的体积.1.(2020·江西上饶二模)已知下图为某几何体的三视图,则其体积为( )A .π+23B .π+13C .π+43D .π+34解析:选C.几何体为半圆柱与四棱锥的组合体(如图),半圆柱的底面半径为1,高为2,四棱锥的底面为边长为2的正方形,高为1,故几何体的体积V =12×π×12×2+13×22×1=π+43.故选C.2.(2019·高考全国卷Ⅲ)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD A 1B 1C 1D 1挖去四棱锥O EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,AB =BC =6 cm ,AA 1=4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗,制作该模型所需原料的质量为________g.解析:由题易得长方体ABCD A 1B 1C 1D 1的体积为6×6×4=144(cm 3),四边形EFGH 为平行四边形,如图所示,连接GE ,HF ,易知四边形EFGH 的面积为矩形BCC 1B 1面积的一半,即12×6×4=12(cm 2),所以V四棱锥O EFGH =13×3×12=12(cm 3),所以该模型的体积为144-12=132(cm 3),所以制作该模型所需原料的质量为132×0.9=118.8(g).答案:118.8球与空间几何体的接、切问题(多维探究) 角度一 外接球(1)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .3π4C.π2D .π4(2)已知三棱锥S ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S ABC的体积为9,则球O 的表面积为________.【解析】 (1)设圆柱的底面圆半径为r ,则r 2=12-⎝ ⎛⎭⎪⎫122=34,所以,圆柱的体积V =34π×1=3π4,故选B.(2)设球O 的半径为R ,因为SC 为球O 的直径,所以点O 为SC 的中点,连接AO ,OB ,因为SA =AC ,SB =BC ,所以AO ⊥SC ,BO ⊥SC ,因为平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,所以AO ⊥平面SCB ,所以V S ABC =V A SBC =13×S △SBC ×AO =13×(12×SC ×OB )×AO ,即9=13×(12×2R ×R )×R ,解得R =3,所以球O 的表面积为S =4πR2=4π×32=36π.【答案】 (1)B (2)36π角度二 内切球(1)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,表面积为S 1,球O 的体积为V 2,表面积为S 2,则V 1V 2的值是__________,S 1S 2=________. (2)已知棱长为a 的正四面体,则此正四面体的表面积S 1与其内切球的表面积S 2的比值为________.【解析】 (1)设圆柱内切球的半径为R ,则由题设可得圆柱O 1O 2的底面圆的半径为R ,高为2R ,所以V 1V 2=πR 2·2R 43πR 3=32.S 1S 2=2πR ·2R +2πR 24πR 2=32. (2)正四面体的表面积为S 1=4×34×a 2=3a 2,其内切球半径r 为正四面体高的14,即r =14×63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2πa 26=63π. 【答案】 (1)32 32 (2)63π解决与球有关的切、接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:1.(2020·四川成都一诊)如图,在矩形ABCD 中,EF ∥AD ,GH ∥BC ,BC =2,AF =FG =BG =1.现分别沿EF ,GH 将矩形折叠使得AD 与BC 重合,则折叠后的几何体的外接球的表面积为( )A .24πB .6π C.163π D .83π 解析:选C.由题意可知,折叠后的几何体是底面为等边三角形的三棱柱,底面等边三角形外接圆的半径为23× 12-⎝ ⎛⎭⎪⎫122=33.因为三棱柱的高为BC =2,所以其外接球的球心与底面外接圆圆心的距离为1,则三棱柱外接球的半径为R =⎝ ⎛⎭⎪⎪⎫332+12=233,所以三棱柱外接球的表面积S =4πR 2=16π3.故选C.2.(2020·黑龙江哈尔滨师范大学附属中学模拟)在底面是边长为2的正方形的四棱锥P ABCD 中,点P 在底面的射影H 为正方形ABCD 的中心,异面直线PB 与AD 所成角的正切值为2.若四棱锥P ABCD 的内切球半径为r ,外接球的半径为R ,则r R=( ) A.23B .25 C.12D .13解析:选B.如图,取E ,F 分别为AB ,CD 的中点,连接EF ,PE ,PF .由题意知,P ABCD 为正四棱锥,底面边长为2.因为BC ∥AD ,所以∠PBC 即为异面直线PB 与AD 所成的角.因为∠PBC 的正切值为2,所以四棱锥的斜高为2,所以△PEF 为等边三角形,则正四棱锥P ABCD 的内切球的半径r 即为△PEF 的内切圆的半径,为33. 设O 为正四棱锥外接球的球心,连接OA ,AH .由题可得AH =2,PH = 3.在Rt △OHA 中,R 2=(2)2+(3-R )2,解得R =536, 所以r R =25. 确定球心位置的三种方法决定球的几何要素是球心的位置和球的半径,在球与其他几何体的结合问题中,通过位置关系的分析,找出球心所在的位置是解题的关键,不妨称这个方法为球心位置分析法.方法一 由球的定义确定球心若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体外接球的球心.(1)长方体或正方体的外接球的球心是其体对角线的中点;(2)正三棱柱的外接球的球心是上、下底面中心连线的中点;(3)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点;(4)正棱锥的外接球球心在其高上,具体位置可通过建立直角三角形运用勾股定理计算得到;(5)若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( )A.16π B.20πC.24πD.32π【解析】已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,可求得底面边长为2,故球的直径为22+22+42=26,则半径为6,故球的表面积为24π,故选C.【答案】C方法二构造长方体或正方体确定球心(1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥,可将三棱锥补形成长方体或正方体;(2)同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥,可将三棱锥补形成长方体或正方体;(3)若已知棱锥含有线面垂直关系,则可将棱锥补形成长方体或正方体;(4)若三棱锥的三个侧面两两垂直,则可将三棱锥补形成长方体或正方体.如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为( )A. 2 B.6 2C.112D.52【解析】易知四面体A′EFD的三条侧棱A′E,A′F,A′D 两两垂直,且A′E=1,A′F=1,A′D=2,把四面体A′EFD补成从顶点A′出发的三条棱长分别为1,1,2的一个长方体,则长方体的外接球即为四面体A′EFD的外接球,球的半径为r=1 212+12+22=62.故选B.【答案】B方法三由性质确定球心利用球心O与截面圆圆心O′的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质,确定球心.正三棱锥ABCD内接于球O,且底面边长为3,侧棱长为2,则球O的表面积为________.【解析】如图,M为底面△BCD的中心,易知AM⊥MD,DM=1,AM= 3.在Rt△DOM中,OD2=OM2+MD2,即OD2=(3-OD)2+1,解得OD=23 3,故球O的表面积为4π×⎝⎛⎭⎪⎪⎫2332=163π.【答案】163π[基础题组练]1.圆柱的底面积为S ,侧面展开图是一个正方形,那么圆柱的侧面积是( )A .4πSB .2πSC .πSD .233πS 解析:选A.由πr 2=S 得圆柱的底面半径是S π,故侧面展开图的边长为2π·S π=2πS ,所以圆柱的侧面积是4πS ,故选A. 2.已知圆锥的高为3,底面半径长为4,若一球的表面积与此圆锥的侧面积相等,则该球的半径长为( ) A .5B .5C .9D .3解析:选B.因为圆锥的底面半径R =4,高h =3,所以圆锥的母线l =5,所以圆锥的侧面积S =πRl =20π.设球的半径为r ,则4πr 2=20π,所以r =5,故选B.3.(2020·安徽黄山一模)如图所示为某几何体的三视图,则几何体的体积为( )A.12B .1 C.32D .3 解析:选B.由主视图可得如图的四棱锥P ABCD ,其中平面ABCD ⊥平面PCD .由主视图和俯视图可知AD =1,CD =2,P 到平面ABCD 的距离为32. 所以四棱锥P ABCD 的体积为V =13×S 长方形ABCD ×h =13×1×2×32=1.故选B.4.(2020·河南郑州三模)某几何体的三视图如图所示,则该几何体的体积为( )A.5π3B .4π3 C.π3D .2π3 解析:选D.几何体是半个圆柱挖去半个圆锥所形成的,如图,由题意可知几何体的体积为:12×12·π×2-13×12×12·π×2=2π3.故选D. 5.(2020·广东茂名一模)在长方体ABCD A 1B 1C 1D 1中,四边形ABCD 是边长为2的正方形,D 1B 与DC 所成的角是60°,则长方体的外接球的表面积是( )A .16πB .8πC .4πD .42π解析:选A.如图,在长方体ABCD A 1B 1C 1D 1中,因为DC ∥AB ,所以相交直线D 1B 与AB 所成的角是异面直线D 1B 与DC 所成的角.连接AD 1,由AB ⊥平面ADD 1A 1,得AB ⊥AD 1,所以在Rt △ABD 1中,∠ABD 1就是D 1B 与DC 所成的角,即∠ABD 1=60°,又AB =2,AB =BD 1cos 60°,所以BD 1=AB cos 60°=4,设长方体ABCD A 1B 1C 1D 1外接球的半径为R ,则由长方体的体对角线就是长方体外接球的直径得4R 2=D 1B 2=16,则R =2,所以长方体外接球的表面积是4πR 2=16π.故选A.6.一个四棱锥的侧棱长都相等,底面是正方形,其主视图如图所示,则该四棱锥的侧面积是________.解析:因为四棱锥的侧棱长都相等,底面是正方形,所以该四棱锥为正四棱锥,如图,由题意知底面正方形的边长为2,正四棱锥的高为2, 取正方形的中心O ,AD 的中点E ,连接PO ,OE ,PE ,可知PO 为正四棱锥的高,△PEO 为直角三角形,则正四棱锥的斜高PE =22+12= 5.所以该四棱锥的侧面积S =4×12×2×5=4 5. 答案:457.已知圆锥SO ,过SO 的中点P 作平行于圆锥底面的截面,以截面为上底面作圆柱PO ,圆柱的下底面落在圆锥的底面上(如图),则圆柱PO 的体积与圆锥SO 的体积的比值为________.解析:设圆锥SO 的底面半径为r ,高为h ,则圆柱PO 的底面半径是r 2,高为h 2, 所以V 圆锥SO =13πr 2h ,V 圆柱PO =π⎝ ⎛⎭⎪⎫r 22·h 2=πr 2h 8,所以V 圆柱PO V 圆锥SO =38. 答案:388.已知正三棱锥的高为1,底面边长为23,内有一个球与四个面都相切,则棱锥的内切球的半径为________.解析:如图,过点P 作PD ⊥平面ABC 于点D ,连接AD 并延长交BC 于点E ,连接PE ,因为△ABC 是正三角形,所以AE 是BC 边上的高和中线,D 为△ABC 的中心.因为AB =BC =23,所以S △ABC =33,DE =1,PE = 2.所以S 表=3×12×23×2+33=36+3 3. 因为PD =1,所以三棱锥的体积V =13×33×1= 3. 设球的半径为r ,以球心O 为顶点,三棱锥的四个面为底面,把正三棱锥分割为四个小棱锥,则r =3336+33=2-1. 答案:2-19.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置,P 为所在线段的中点,Q 为顶点,求在几何体表面上,从P 点到Q 点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12(2πa )·(2a )=2πa 2, S 圆柱侧=(2πa )·(2a )=4πa 2,S 圆柱底=πa 2,所以S 表=2πa 2+4πa 2+πa 2=(2+5)πa 2.(2)沿P 点与Q 点所在母线剪开圆柱侧面,如图.则PQ =AP 2+AQ 2=a 2+(πa )2=a 1+π2,所以从P 点到Q 点在侧面上的最短路径的长为a 1+π2.10.如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1)证明:平面AEC ⊥平面BED ;(2)若∠ABC =120°,AE ⊥EC ,三棱锥E ACD 的体积为63,求该三棱锥的侧面积.解:(1)证明:因为四边形ABCD 为菱形,所以AC ⊥BD . 因为BE ⊥平面ABCD ,所以AC ⊥BE .故AC ⊥平面BED .又AC 平面AEC , 所以平面AEC ⊥平面BED .(2)设AB =x ,在菱形ABCD 中,由∠ABC =120°,可得AG =GC=32x ,GB =GD =x 2.因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =32x .由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =22x .由已知得,三棱锥E ACD 的体积V 三棱锥E ACD =13×12·AC ·GD ·BE=624x 3=63,故x =2.从而可得AE =EC =ED = 6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5. 故三棱锥E ACD 的侧面积为3+2 5.[综合题组练])1.如图,以棱长为1的正方体的顶点A 为球心,以2为半径作一个球面,则该正方体的表面被球面所截得的所有弧长之和为( )A.3π4 B .2π C.3π2D .9π4解析:选C.正方体的表面被该球面所截得的弧长是相等的三部分,如图,上底面被球面截得的弧长是以A 1为圆心,1为半径的圆周长的14,所以所有弧长之和为3×2π4=3π2.故选C.2.(2020·江西萍乡一模)如图,网格纸上小正方形的边长为1,粗线画的是某几何体的三视图,则该几何体的体积为( )A.236 B .72C.76D .4解析:选A.由三视图可得,该几何体是如图所示的三棱柱ABB 1DCC 1,挖去一个三棱锥E FCG 所形成的,故所求几何体的体积为12×(2×2)×2-13×⎝ ⎛⎭⎪⎫12×1×1×1=236. 故选A.3.(2020·福建厦门外国语学校模拟)已知等腰直角三角形ABC 中,∠ACB =90°,斜边AB =2,点D 是斜边AB 上一点(不同于点A ,B ).沿线段CD 折起形成一个三棱锥A CDB ,则三棱锥A CDB 体积的最大值是( )A .1B .12C.13D .16解析:选D.设AD =x ,将△ACD 折起使得平面ACD ⊥平面BCD .在△ACD 中,由面积公式得12CD ·h 1=12AD ·1(h 1为点A 到直线CD 的距离),则h 1=x1+(x -1)2.由题易知h 1为点A 到平面BCD 的距离,故三棱锥A CDB 体积为V =13S △BCD ·h 1=13×⎝ ⎛⎭⎪⎫12BD ·1·h 1=16·2x -x 2x 2-2x +2,x ∈(0,2).令t =x 2-2x +2,则t ∈[1,2),故V =16·2-t 2t =16·⎝ ⎛⎭⎪⎫2t -t .由于2t -t 是减函数,故当t =1时,V取得最大值为16×(2-1)=16.故选D.4.设A ,B ,C ,D 是同一个半径为4的球的球面上的四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为( )A .12 3B .183C .24 3D .543解析:选B.如图,E 是AC 的中点,M 是△ABC 的重心,O 为球心,连接BE ,OM ,OD ,BO .因为S △ABC =34AB 2=93,所以AB =6,BM =23BE=23AB 2-AE 2=2 3.易知OM ⊥平面ABC ,所以在Rt △OBM 中,OM =OB 2-BM 2=2,所以当D ,O ,M 三点共线且DM =OD +OM 时,三棱锥D ABC 的体积取得最大值,且最大值V max =13S △ABC ×(4+OM )=13×93×6=18 3.故选B. 5.如图所示,已知三棱柱ABC A 1B 1C 1的所有棱长均为1,且AA 1⊥底面ABC ,则三棱锥B 1ABC 1的体积为________.解析:三棱锥B 1ABC 1的体积等于三棱锥A B 1BC 1的体积,三棱锥A B 1BC 1的高为32,底面积为12,故其体积为13×12×32=312.答案:3126.已知半球O 的半径r =2,正三棱柱ABC A 1B 1C 1内接于半球O ,其中底面ABC 在半球O 的大圆面内,点A 1,B 1,C 1在半球O 的球面上.若正三棱柱ABC A 1B 1C 1的侧面积为63,则其侧棱的长是________.解析:依题意O 是正三角形ABC 的中心,设AB =a ,分析计算易得0<a <23,AO =33a ,在Rt △AOA 1中,A ′O =r =2,则AA 1=r 2-AO 2=4-a 23,所以正三棱柱ABC A 1B 1C 1的侧面积S =3a ·AA 1=3a4-a 23=3-a 43+4a 2=63,整理得a 4-12a 2+36=0,解得a 2=6,即a =6,此时侧棱AA 1= 2.答案:27.如图,正方体ABCD A 1B 1C 1D 1的棱长为1,P 为BC 边的中点,Q 为线段CC 1上的动点,过点A ,P ,Q 的平面截正方体所得的截面为S ,当CQ =1时,S 的面积为________.解析:当CQ =1时,Q 与C 1重合.如图,取A 1D 1,AD 的中点分别为F ,G .连接AF ,AP ,PC 1,C 1F ,PG ,D 1G ,AC 1,PF .因为F 为A 1D 1的中点,P 为BC 的中点,G 为AD 的中点, 所以AF =FC 1=AP =PC 1=52,PG 綊CD ,AF 綊D 1G .由题意易知CD 綊C 1D 1,所以PG 綊C 1D 1,所以四边形C 1D 1GP 为平行四边形, 所以PC 1綊D 1G ,所以PC 1綊AF , 所以A ,P ,C 1,F 四点共面, 所以四边形APC 1F 为菱形.因为AC 1=3,PF =2,过点A ,P ,Q 的平面截正方体所得的截面S 为菱形APC 1F ,所以其面积为12AC 1·PF =12×3×2=62.答案:628.已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为515,则该圆锥的侧面积为________.解析:如图所示,设S 在底面的射影为S ′,连接AS ′,SS ′.△SAB 的面积为12·SA ·SB ·sin ∠ASB =12·SA 2·1-cos 2∠ASB =1516·SA 2=515,所以SA 2=80,SA =4 5.因为SA 与底面所成的角为45°,所以∠SAS ′=45°,AS ′=SA ·cos 45°=45×22=210.所以底面周长l =2π·AS ′=410π,所以圆锥的侧面积为12×45×410π=402π.答案:402π。
高考数学总复习考点知识专题讲解8 排列与组合

高考数学总复习考点知识专题讲解专题8 排列与组合知识点一排列的定义一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.知识点二排列相同的条件两个排列相同的充要条件:(1)两个排列的元素完全相同.(2)元素的排列顺序也相同.【例1】判断下列问题是否为排列问题:(1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同);(2)选2个小组分别去植树和种菜;(3)选2个小组去种菜;(4)选10人组成一个学习小组;(5)选3个人分别担任班长、学习委员、生活委员;(6)某班40名学生在假期相互打电话.知识点三 排列数的定义从n 个不同元素中取出m (m ≤n )个元素的所有不同排列的个数,叫做从n 个不同元素中取出m 个元素的排列数,用符号A m n 表示. 知识点四 排列数公式及全排列 1.排列数公式的两种形式(1)A m n =n (n -1)(n -2)…(n -m +1),其中m ,n ∈N *,并且m ≤n .(2)A m n =n !(n -m )!. 2.全排列:把n 个不同的元素全部取出的一个排列,叫做n 个元素的一个全排列,全排列数为A n n =n !(叫做n 的阶乘).规定:0!=1. 【例2】(2023•泰州期末)678910⨯⨯⨯⨯可以表示为()A .410AB .510AC .410CD .510C【例3】(2023•莱州市开学)已知18934x x A A -=,则x 等于() A .6B .13C .6或13D .12【例4】(2023•浑南区期末)12320222232022232022M A A A A =++++,20232023N A =,则M 与N 的大小关系是()A .M N =B .M N >C .M N <D .M N …知识点五“相邻”与“不相邻”问题相邻问题捆绑法,不相邻问题插空法.【例5】3名男生,4名女生,这7个人站成一排在下列情况下,各有多少种不同的站法? (1)男、女各站在一起;(2)男生必须排在一起;(3)男生不能排在一起;(4)男生互不相邻,且女生也互不相邻.【例6】(2023•香坊区期末)加工某种产品需要5道工序,分别为A,B,C,D,E,其中工序A,B必须相邻,工序C,D不能相邻,那么有()种加工方法.A.24B.32C.48D.64【例7】(2023•沈阳模拟)甲、乙、丙、丁、戊、己6人站成一排拍合照,要求甲必须站在中间两个位置之一,且乙、丙2人相邻,则不同的排队方法共有() A.24种B.48种C.72种D.96种知识点六定序问题用除法对于定序问题,可采用“除阶乘法”解决.即用不限制的排列数除以顺序一定元素的全排列数.【例8】7人站成一排.(1)甲必须在乙的前面(不一定相邻),则有多少种不同的排列方法?(2)甲、乙、丙三人自左向右的顺序不变(不一定相邻),则有多少不同的排列方法?知识点七特殊元素的“在”与“不在”问题分析法对于“在”与“不在”问题,可采用“特殊元素优先考虑,特殊位置优先安排”的原则解决.【例9】(2023•卧龙区月考)甲乙丙丁戊5名同学站成一排参加文艺汇演,若甲不站在两端、丙和丁相邻的不同排列方式有() A .24种B .36种C .48种D .144种【例10】(2023•宜宾月考)“四书”“五经”是我国9部经典名著《大学》《论语》《中庸》《孟子》《周易》《尚书》《诗经》《礼记》《春秋》的合称.为弘扬中国传统文化,某校计划在读书节活动期间举办“四书”“五经”知识讲座,每部名著安排1次讲座,若要求《大学》《论语》相邻,但都不与《周易》相邻,则排法种数为() A .622622A A A B .6262A A C .622672A A A D .622662A A A【例11】(2023•武强县期中)用数字0,1,2,3,4,5组成没有重复数字的四位数. (1)可组成多少个不同的四位数? (2)可组成多少个不同的偶数?【例12】从包括甲、乙两名同学在内的7名同学中选出5名同学排成一列,求解下列问题.(1)甲不在首位的排法有多少种?(2)甲既不在首位也不在末位的排法有多少种? (3)甲与乙既不在首位也不在末位的排法有多少种? (4)甲不在首位,同时乙不在末位的排法有多少种?同步训练(一)1.(2023•宿迁期末)下列各式中,不等于n !的是()A .n n AB .1n n A -C .1n n nA +D .11n n nA --2.(2023•宿迁月考)(1998)(1999)(2021)(2022)(n n n n n N ----∈,2022)n >可表示为()A .241998n A -B .251998n A -C .242022n A -D .252022n A -3.(2023•河南模拟)从3,5,7,11这四个质数中,每次取出两个不同的数分别为a ,b ,共可得到lga lgb -的不同值的个数是()A .6B .8C .12D .164.(2023•揭阳期末)已知甲、乙两个家庭排成一列测核酸,甲家庭是一对夫妻带1个小孩,乙家庭是一对夫妻带2个小孩.现要求2位父亲位于队伍的两端,3个小孩要排在一起,则不同的排队方式的种数为()A.288B.144C.72D.365.(2023•海淀区校级期末)某晚会有三个唱歌节目,两个舞蹈节目,要求舞蹈节目不能相邻,有()种排法?A.72B.36C.24D.126.(20123•会宁县期中)用0,1,2,3,4五个数字:(1)可组成多少个五位数;(2)可组成多少个无重复数字的五位数;(3)可组成多少个无重复数字的且是3的倍数的三位数;(4)可组成多少个无重复数字的五位奇数.7.三个女生和五个男生排成一排.(1)如果女生必须全排在一起,可有多少种不同的排法?(2)如果女生必须全分开,可有多少种不同的排法?(3)如果两端都不能排女生,可有多少种不同的排法?(4)如果两端不能都排女生,可有多少种不同的排法?知识点八组合及组合数的定义1.组合一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合.2.组合数从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号C m n表示.知识点九排列与组合的关系【例13】(1)某铁路线上有4个车站,则这条铁路线上共需准备多少种车票?(2)把5本不同的书分给5个学生,每人一本;(3)从7本不同的书中取出5本给某个学生.【例14】一个口袋内装有大小相同的7个白球和1个黑球.(1)从口袋内取出3个球,共有多少种取法?(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?知识点十组合数公式规定:C 0n =1.知识点十一 组合数的性质 性质1:C mn =C n -mn .性质2:C m n +1=C m n +C m -1n .【例15】(2023•朝阳区期末)已知2188m m C C -=,则m 等于() A .1B .3C .1或3D .1或4【例16】(2023•吉水县期末)计算33334562015C C C C ++++的值为()A .42015CB .32015C C .420161C -D .520151C -【例17】(2023•崂山区期末)对于伯努利数()n B n N ∈,有定义:001,(2)nk n n k k B B C B n ===∑….则()A .216B =B .4130B =C .6142B =D .230n B +=【例18】(2023•沙坪坝区模拟)某项活动安排了4个节目,每位观众都有6张相同的票,活动结束后将票全部投给喜欢的节目,一位观众最喜欢节目A,准备给该节目至少投3张,剩下的票则随机投给其余的节目,但必须要A节目的得票数是最多的,则4个节目获得该观众的票数情况有()种A.150B.72C.20D.17【例19】(2023•东湖区期末)某校举行科技文化艺术节活动,学生会准备安排6名同学到两个不同社团开展活动,要求每个社团至少安排两人,其中A,B两人不能分在同一个社团,则不同的安排方案数是()A.56B.28C.24D.12知识点十二分组、分配问题(1)分组问题属于“组合”问题,常见的分组问题有三种:①完全均匀分组,每组的元素个数均相等,均匀分成n组,最后必须除以n!;②部分均匀分组,应注意不要重复,有n组均匀,最后必须除以n!;③完全非均匀分组,这种分组不考虑重复现象.(2)分配问题属于“排列”问题,分配问题可以按要求逐个分配,也可以分组后再分配.1 平均分组【例20】(1)6本不同的书,分给甲、乙、丙三人,每人两本,有多少种方法?(2)6本不同的书,分为三份,每份两本,有多少种方法?2 不平均分组【例21】(1)6本不同的书,分为三份,一份一本,一份两本,一份三本,有多少种方法?(2)6本不同的书,分给甲、乙、丙三人,一人一本,一人两本,一人三本,有多少种不同的方法?3 分配问题【例22】6本不同的书,分给甲、乙、丙三人,每人至少一本,有多少种不同的方法?【例23】(2022秋•浑南区期末)将6本不同的书分给甲、乙、丙、丁4个人,每人至少一本的不同分法共有种.(用数字作答)【例24】(2022秋•浑南区期末)某市聘请6名农业专家安排到三个乡镇作指导,每个乡镇至少一人,则安排方案的种数是()A.495B.540C.630D.720【例25】(2023•云南模拟)中国空间站()ChinaSpaceStation的主体结构包括天和核心舱、问天实验舱和梦天实验舱.2022年10月31日15:37分,我国将“梦天实验舱”成功送上太空,完成了最后一个关键部分的发射,“梦天实验舱”也和“天和核心舱”按照计划成功对接,成为“T”字形架构,我国成功将中国空间站建设完毕.2023年,中国空间站将正式进入运营阶段.假设中国空间站要安排甲、乙等5名航天员进舱开展实验,其中“天和核心舱”安排2人,“问天实验舱”安排2人,“梦天实验舱”安排1人.若甲、乙两人不能同时在一个舱内做实验,则不同的安排方案共有()A.9种B.24种C.26种D.30种知识点十三相同元素分配问题之隔板法隔板法:如果将放有小球的盒子紧挨着成一行放置,便可看作排成一行的小球的空隙中插入了若干隔板,相邻两块隔板形成一个“盒”,每一种插入隔板的方法对应着小球放入盒子的一种方法,此法称之为隔板法,隔板法专门解决相同元素的分配问题.将n个相同的元素分给m个不同的对象(n≥m),有C m-1n-1种方法,可描述为(n-1)个空中插入(m -1)块板.【例26】6个相同的小球放入4个编号为1,2,3,4的盒子,求下列方法的种数.(1)每个盒子都不空;(2)恰有一个空盒子;(3)恰有两个空盒子.【例27】(2023•浦东新区期末)10个相同的小球放到6个不同的盒子里,每个盒子里至少放一个小球,则不同的放法有种.【例28】(2023•海淀区期末)没有一个冬天不可逾越,没有一个春天不会来临.某街道疫情防控小组选派7名工作人员到A ,B ,C 三个小区进行调研活动,每个小区至少去1人,恰有两个小区所派人数相同,则不同的安排方式共有() A .1176B .2352C .1722D .1302【例29】(2023•多选•玄武区期末)甲、乙、丙、丁、戊共5位志愿者被安排到A ,B ,C ,D 四所山区学校参加支教活动,要求每所学校至少安排一位志愿者,且每位志愿者只能到一所学校支教,则下列结论正确的是() A .不同的安排方法共有240种 B .甲志愿者被安排到A 学校的概率是14C .若A 学校安排两名志愿者,则不同的安排方法共有120种D .在甲志愿者被安排到A 学校支教的前提下,A 学校有两名志愿者的概率是25【例30】(2023•多选•营口期末)某校的高一和高二年级各10个班级,从中选出五个班级参加活动,下列结论正确的是()A .高二六班一定参加的选法有420C 种B .高一年级恰有2个班级的选法有231010C C 种C .高一年级最多有2个班级的选法为52012C 种D .高一年级最多有2个班级的选法为231451*********C C C C C ++种【例31】(2023•福建模拟)近年来,“剧本杀”门店遍地开花.放假伊始,7名同学相约前往某“剧本杀”门店体验沉浸式角色扮演型剧本游戏,目前店中仅有可供4人组局的剧本,其中A ,B 角色各1人,C 角色2人.已知这7名同学中有4名男生,3名女生,现决定让店主从他们7人中选出4人参加游戏,其余3人观看,要求选出的4人中至少有1名女生,并且A ,B 角色不可同时为女生.则店主共有348种选择方式.【例32】(2023•和平区校级模拟)我们常常运用对同一个量算两次的方法来证明组合恒等式,如:从装有编号为1,2,3,⋯,1n +的1n +个球的口袋中取出m 个球(0m n <…,m ,)n N ∈,共有1m n C +种取法.在1m n C +种取法中,不取1号球有m n C 种取法;取1号球有1m n C -种取法.所以11m m m n n n C C C -++=.试运用此方法,写出如下等式的结果:323232323142241n n n n n C C C C C C C C ----+⋅+⋅++⋅+=.同步训练(二)8.(多选)下列问题是组合问题的有()A .10个朋友聚会,每两人握手一次,一共握手多少次B .平面上有2 021个不同的点,它们中任意三点不共线,连接任意两点可以构成多少条线段C .集合{a 1,a 2,a 3,…,a n }中含有三个元素的子集有多少个D .从高三(19)班的54名学生中选出2名学生分别参加校庆晚会的独唱、独舞节目,有多少种选法9.(2023•宣城期中)关于排列组合数,下列结论错误的是() A .m n m n n C C -=B .11m m m n n n C C C -+=+C .11m m n n A mA --=D .11m m mn n n A mA A -++=10.(2023•多选•朝阳区期末)关于排列组合数,下列结论正确的是() A .m n m n n C C -=B .11m m m n n n C C C -+=+C .11m m n n A mA --=D .!()!mn n A n m =-11.课外活动小组共13人,其中男生8人,女生5人,并且男、女生各有一名队长,现从中选5人主持某项活动,依下列条件各有多少种选法? (1)至少有一名队长当选;(2)至多有两名女生当选;(3)既要有队长,又要有女生当选.12.将4个编号为1,2,3,4的小球放入4个编号为1,2,3,4的盒子中.(1)有多少种放法?(2)每盒至多1个球,有多少种放法?(3)恰好有1个空盒,有多少种放法?(4)每个盒内放1个球,并且恰好有1个球的编号与盒子的编号相同,有多少种放法?(5)把4个不同的小球换成4个相同的小球,恰有一个空盒,有多少种放法?13.(多选)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数可能为()A.1 B.2 C.3 D.414.已知10件不同产品中有4件是次品,现对它们进行一一测试,直至找出所有4件次品为止.(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品,则这样的不同测试方法数是多少?(2)若恰在第5次测试后,就找出了所有的4件次品,则这样的不同测试方法数是多少?15.现有8名青年,其中有5名能胜任英语翻译工作,有4名能胜任德语翻译工作(其中有1名青年两项工作都能胜任).现在要从中挑选5名青年承担一项任务,其中3名从事英语翻译工作,2名从事德语翻译工作,则有多少种不同的选法?16.空间中有10个点,其中有5个点在同一个平面内,其余点无三点共线,无四点共面,则以这些点为顶点,共可构成四面体的个数为()A.205 B.110 C.204 D.20017.4名优秀学生全部保送到3所学校去,每所学校至少去1名,则不同的保送方案有______种.18.甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是________.(用数字作答)19.(2023•长沙期末)6名志愿者分配到3个社区参加服务工作,每名志愿者只分配到一个社区,每个社区至少分配一名志愿者且人数各不相同,不同的分配方案共有() A .540种B .360种C .180种D .120种20.(2023•多选•罗湖区期末)在10件产品中,有7件合格品,3件不合格品,从这10件产品中任意抽出3件,则下列结论正确的有()A .抽出的3件产品中恰好有1件是不合格品的抽法有1237C C 种 B .抽出的3件产品中至少有1件是不合格品的抽法有1239C C 种 C .抽出的3件产品中至少有1件是不合格品的抽法有1221337373C C C C C ++种D .抽出的3件产品中至少有1件是不合格品的抽法有33107C C -种。
【导与练】(新课标)2019届高三数学一轮复习 第8篇 抛物线学案 理

第五十四课时 抛物线课前预习案1.掌握抛物线的定义、几何图形、标准方程及简单性质;会求抛物线的标准方程,能运用抛物线的定义、标准方程处理一些简单的实际问题。
2.熟练掌握抛物线的范围、对称性、顶点等简单几何性质,并能运用性质解决相关问题.3.能解决直线与抛物线的相交问题.1.平面内与一个定点F 和一条定直线l 的距离 的点的轨迹叫做抛物线,点F 叫做抛物线的 ,直线l 叫做抛物线的 ,定点F 定直线l 上。
3.根据抛物线的定义,可知22(0)y px p =>上一点11(,)M x y 到焦点 的距离为 。
4. 抛物线22(0)y px p =>的焦点弦(过焦点的弦)为AB ,若1122(,),(,)A x y B x y ,则有如下结论:(1)|AB |= ;(2)12y y = ;12x x = 。
5. 在抛物线22(0)y px p =>中,通过焦点而垂直于x 轴的直线与抛物线两交点的坐标分别为 ,连结这两点的线段叫做 ,它的长为 。
1. 根据下列条件,写出抛物线的标准方程:(1)焦点是F (0,-3);(2)准线方程 是x = 14; (3)焦点到准线的距离是2。
2. 过点A (4,-2)的抛物线的标准方程为( )A .2y x =或28x y =-B .2y x =或28y x =C .28y x =-D . 28x y =- 3. 抛物线214x y a=的焦点坐标为( ) A .1(,0)a - B .(,0)a - C .1(,0)aD . (,0)a 4. 抛物线214y x =上点P 的纵坐标是4,则其焦点F 到点P 的距离为( ) A .3 B .4 C .5 D . 65.点M 与点F (4,0)的距离比它到直线l :x +5=0的距离小1,求点M 的轨迹方程.课堂探究案考点1求抛物线的标准方程【典例1】 根据下列条件求抛物线的标准方程(1)抛物线的焦点是双曲线22169144x y -=的左顶点;(2)过点P (2,-4);(3)抛物线的焦点在x 轴上,直线3y =-与抛物线交于点A ,||5AF =.【变式1】【2018陕西】如图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.考点2 抛物线定义的应用【典例2】已知抛物线22y x =的焦点是F ,点P 是抛物线上的动点,点A (3,2),求|PA |+|PF |的最小值,并求出取最小值时点P 的坐标.【变式2】(1) 在22y x = 上有一点P ,它到A (2,10)的距离与它到焦点F 的距离之和最小,则P 的坐标为( )A .(-2,8)B .(2,8)C .(2,8)--D .( 2,-8)(2)已知抛物线24y x =,点P 是抛物线上的动点,又有点A (6,3),|PA |+|PF |的最小值是__________.考点3 抛物线几何性质的应用【典例3】已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点0(2,)M y .若点M 到该抛物线焦点的距离为3,则||OM =( )A 、、、4 D 、【变式3】已知A 、B 是抛物线22(0)y px p =>上两点,O 为坐标原点,若|OA|=|OB|,且AOB ∆的垂心恰是此抛物线的焦点,则直线AB 的方程是( )A.x=3pB.x=pC.x=52p D.x=32p1.已知点P 是抛物线22y x =上的一个动点,则点P 到点(0,2)的距离与P 到该抛物线准线的距离之和的最小值为( )A .2B .3CD .922. 过抛物线焦点F 的直线与抛物线相交于A ,B 两点,若A ,B 在抛物线准线上的射影分别是A 1,B 1,则11A FB ∠为( )A .45°B .60°C .90°D .120°3.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为 .课后拓展案组全员必做题1.(2019年四川(理))抛物线24y x =的焦点到双曲线2213y x -=的渐近线的距离是( )A .12B .1 D 2.(2018辽宁理3)已知F 是抛物线2y x =的焦点,A ,B 是该抛物线上的两点,3AF BF +=,则线段AB的中点到y 轴的距离为( ). A .34 B .1 C .54 D .743.已知直线1:4360l x y -+=和直线2:1l x =-,抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值是( ) A.2 B.3 C.115 D.37164.(2019年课标Ⅰ(文8))O 为坐标原点,F 为抛物线2:C y =的焦点,P 为C 上一点,若||PF =,则POF ∆的面积为( )A .2B .C .D .4组提高选做题 1.(2018山东文)抛物线)0(21:21>=p x py C 的焦点与双曲线222:13x C y -=的右焦点的连线交1C 于第一象限的点M,若1C 在点M 处的切线平行于2C 的一条渐近线,则p =( )A .163B .83C .332D .334 2.(2019年普通高等学校招生统一考试新课标Ⅱ卷数学(理)设抛物线2:2(0)C y px p =>的焦点为F ,点M 在C 上,5MF =,若以MF 为直径的圆过点)2,0(,则C 的方程为( )A .24y x =或28y x =B .22y x =或28y x =C .24y x =或216y x =D .22y x =或216y x =参考答案1.(1)212x y =-;(2)2y x =-;(3)24x y =,24x y =-,24y x =,24y x =-.2.A3.D4.C5. 216y x =【典例1】(1)212y x =-;(2)28y x =或2x y =-;(3)x y 22±=或x y 182±=【变式1】【典例2】最小值为72;(2,2)P . 【变式2】(1)B ;(2)7.【典例3】B【变式3】C1.A2.C3. 28y x =组全员必做题1.B2.C3.A4.C组提高选做题1.D2.C。
高一数学重点知识点(实用8篇)

高一数学重点知识点(实用8篇)高一数学重点知识点第1篇一、集合有关概念1、集合的含义:某些指定的对象集在一起就成为一个集合,其中每一个对象叫元素。
2、集合的中元素的三个特性:元素的确定性;元素的互异性;元素的无序性说明:(1)对于一个给定的集合,集合中的元素是确定的,任何一个对象或者是或者不是这个给定的集合的元素。
(2)任何一个给定的集合中,任何两个元素都是不同的对象,相同的对象归入一个集合时,仅算一个元素。
(3)集合中的元素是平等的,没有先后顺序,因此判定两个集合是否一样,仅需比较它们的元素是否一样,不需考查排列顺序是否一样。
(4)集合元素的三个特性使集合本身具有了确定性和整体性。
3、集合的表示:{…}如{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}集合的表示方法:列举法与描述法。
二、集合间的基本关系“包含”关系—子集注意:有两种可能(1)A是B的一部分,;(2)A与B是同一集合。
反之:集合A不包含于集合B,或集合B不包含集合A,记作AB或BA “相等”关系(5≥5,且5≤5,则5=5)实例:设A={x|x2-1=0}B={-1,1}“元素相同”结论:对于两个集合A与B,如果集合A的任何一个元素都是集合B 的元素,同时,集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,即:A=B①任何一个集合是它本身的子集。
AíA②真子集:如果AíB,且A1B那就说集合A是集合B的真子集,记作AB(或BA)③如果AíB,BíC,那么AíC④如果AíB同时BíA那么A=B不含任何元素的集合叫做空集,记为Φ规定:空集是任何集合的子集,空集是任何非空集合的真子集。
三、集合的运算交集的定义:一般地,由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.记作A∩B(读作”A交B”),即A∩B={x|x∈A,且x∈B}.2、并集的定义:一般地,由所有属于集合A或属于集合B的元素所组成的集合,叫做A,B的'并集。
高一数学讲义 第八章 空间直线与平面

高一数学讲义 第八章 空间直线与平面8.1平面及其基本性质几何里的平面与直线一样,是无限延伸的,我们不能把一个无限延伸的平面在纸上表现出来,通常用平面的一部分表示平面.例如,我们常用平行四边形表示平面(图8-1).但我们要把它想象成无限延展的.通常我们用一个希腊字母如:αβγ、、…来表示平面,也可以用表示平面的平行四边形的对角顶点的字母来表示,如平面AC .DCBAβα图81平面的基本性质公理l 如果一条直线上有两个点在同一个平面上,那么这条直线上所有的点都在这个平面上(即直线在平面上).公理2 如果两个平面存在一个公共点,那么它们所有公共点的集合是一条直线.公理3 不在同一直线上的三点确定一个平面(即经过不在同一直线上三点有且仅有一个平面). 在上述公理的基础上,可以得到以下三个推论: 推论1 一条直线和直线外一点确定一个平面.证明:如图8-2,在直线l 上任取两个点A B 、,则A B C 、、是不在同一直线上的三点,由公理3可知,经过此三点的平面有且仅有1个,设为平面α,则A B ∈、平面α,又A B 、在直线l 上,由公理1可知直线l 在平面α上.即经过直线l 和直线外一点的平面有且仅有一个.图82推论2 两条相交直线确定一个平面. 推论3 两条平行直线确定一个平面.例1.如图8-3,在正方体1111ABCD A B C D -中,点E F 、分别是棱1AA 、1CC 的中点.试画出过点1D E F 、、三点的截面.B 1C 1D 1A 1EHF GDCB A 图83解:连1D F 并延长1D F 与DC 的延长线交于点H ,联结1D E 并延长与DA 的延长线交于点G ,联结GH 与AB BC 、两条棱交于点B ,联结BE BF 、,则1BED F 就是过点1D E F 、、三点的截面.例2.如图8-4,在正方体1111ABCD A B C D -中,E F 、分别为1CC 和1AA 上的中点,画出平面1BED F 与平面ABCD 的交线.PF C E A DB A 1B 1D 1C 1图84解:在平面11AA D D 内,延长1D F ,1D F 与DA 不平行,因此1D F 与DA 必相交于一点,设为P ,则1P FD P DA ∈∈,. 又1FD ⊂平面1BED F ,AD ⊂平面ABCD 内,P ∴∈平面1BED F P ∈,平面ABCD .又B 为平面ABCD 与平面1BED F 的公共点,∴联结PB PB ,即为平面1BFD F 与平面ABCD 的交线.例3.已知E F G H 、、、分别是空间四边形ABCD (四条线段首尾相接,且联结点不在同一平面内,所组成的空间图形叫空间四边形).各边AB AD CB CD 、、、上的点,且直线EF 和HG 交于点P ,如图8-5,求证:点B D P 、、在同一条直线上.G DPF ECBA图85证明:如图直线EF 直线HG P =.P ∴∈直线EF .而EF ⊂平面ABD , P ∴∈平面ABD .同理,P ∈平面CBD ,即点P 是平面ABD 和平面CBD 的公共点.显然,点B D 、也是平面ABD 和平面CBD 的公共点,由公理2知,点B D P 、、都在平面ABD 和平面CBD 的交线上,即点B D P 、、在同一条直线上. 基础练习1.用符号语言表示下列语句(1)点A 在平面α内,但在平面β外;(2)直线a 经过平面α外一点M ;(3)直线a 在平面α内,又在平面β内,即平面α和β相交于直线a . 2.已知a b c 、、空间三条直线,且a b ∥与a b 、都相交,求证直线a b c 、、在同一个平面上. 3.怎样用两根细绳检查一张桌子的四条腿的下端是否在一个平面内?4.如图8-6所示,ABC △与111A B C △不在同一个平面内,如果三直线1AA 、1BB 、1CC 两两相交,证明:三直线111AA BB CC 、、交于一点.PC 1B 1A 1C BA图865.已知ABC △在平面α外,它的三边所在的直线分别交平面α于P Q R ,,三点,证明P Q R ,,三点在同一条直线上.6.画水平放置的正五边形的直观图. 8.2空间直线与直线之间的位置关系公理4 平行于同一条直线的两条直线平行(即平行线的传递性). 例1.如图8-7所示,设E F G H ,,,分别是空间四边形ABCD 的边AB BC CD DA ,,,上的点,且AE AH CF CGAB AD CB CDλμ====,,求证:F GH EDCBA图87(1)当λμ=时,四边形EFGH 是平行四边形; (2)当λμ≠时,四边形EFGH 是梯形. 证明:联结BD , 在ABD △中,AE AHAB ADλ==,EH BD ∴,∥且EH BD λ=. 在CBD △中,CF CGCB CDμ==,FG BD ∴,∥且FG BD μ=. EH FG ∴∥,∴顶点E F G H ,,,在由EH 和FG 确定的平面内. (1)当λμ=时,EH FG =,故四边形EFGH 为平行四边形; (2)当λμ≠时,EH FG ≠,故四边形EFGH 是梯形.等角定理 如果两条相交直线与另两条相交直线分别平行,那么这两组相交直线所成的锐角(或直角)相等.证明:当两组平行直线在同一平面内,即为初中几何中的等角定理. 当它们不在同一平面时,如图8-8所示.a 1O 1B 1A 1BA Oba 图88设直线a b 、相交于点O ,直线11a b 、相交于点1O ,且11a a b b ,∥∥,在直线a b 、上分别任取点A B 、(异于点O ),在直线11a b 、上分别任取点11A B 、(异于点1O ),使得11OA O A =,11OB O B =,111AOB AO B ∠∠,分别是a b 、,与11a b 、所成的角. 1111OA O A OA O A =,∥ ∴四边形11OO A A 为平行四边形. 1111OO AA OO AA ∴=,∥.同理1111OO BB OO BB =,∥.1111BB AA BB AA ∴=,∥.四边形11BB A A 为平行四边形. 11AB A B ∴=,因此111AOB AO B △△≌. 111AOB AO B ∴∠=∠.在平面中两条直线的位置关系可以根据交点个数来判断:当两条直线仅有1个交点时.它们是相交的;当没有交点时它们是平行的.但在空间中两条直线没有交点却未必是平行的,如图8-9直线a 在平面α上,直线b 与平面α交于点P ,且P 不在直线b 上,那么直线a 与直线b 即不平行也不相交.此时直线a 与直线b 不能在同一平面内,我们称直线a 、b 是异面直线.baP图89在空间任取一点Q 过Q 分别作a b 、的平行线11a b 、,我们把11a b 、所成的锐角或直角称为异面直线a b 、所成的角.当所成的角为90︒时称异面直线a b 、相互垂直.此外,我们把和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线.两条异面直线的公垂线在这两条异面直线间的线段长度,叫做两条异面直线的距离.例2.如图8-10,在正方体1111ABCD A B C D -中,判断下列直线之间的位置父系,并求出它们所成角的大小.A 2D 2B 2C 2D 1C 1B 1A 1D CBA图810(1)AC 与1BC ;(2)1B D 与1BC . 解:(1)AC 与1BC 是异面直线. 11AA CC ∥且11AA CC =,∴四边形11AA C C 为平行四边形,即11AC AC ∥.11AC B ∴∠为所求AC 与1BC 所成的角.易知11A C B △为等边三角形,即11π3AC B ∠=(2)1B C 与1BC 是异面直线如图8-10:在原正方体下方补一个相同大小的正方体11112222A B C D A B C D -中121B C BC ∥,12DB C ∴∠为所求1B D 与1BC 所成的角.设正方体的棱长为a ,在12DB C △中,112212π2DB B C DC DB C ==∴∠=,,,. 例3.空间四边形ABCD中,2AB BD AD BC CD =====,32AC =,延长BC 到E ,使BC CE =,取BD 中点F ,求异面直线AF 与DE 的距离和他们所成的角.F ED BA图811解:(1)2AB AD BD === ∴三角形ABD 为等边三角形 F 为BD 中点,AF BD ∴⊥,即AF FD ⊥90BC CD CE BDE DF DE ===∴∠=︒∴⊥, DF 长即为异面直线AF DE ,的距离,又112DF BD ==,AF ∴与DE 的距离为1.(2)联结CF F C ,,分别是BD ,BF 的中点, FC ∴平行且等于12DE ,AFC ∴∠即为异面直线AF 与DE 所成的角. 在等边三角形ABD中,AF == 在直角三角形BDE中,12CF DE ==. 三角形AFC 中,由余弦定理得2221cos 22AF FC AC AFC AF FC +-∠==⨯⨯.60AFC ∴∠=︒,即异面直线AF 与DF 成60︒角. 基础练习 1.从止方体的12条棱和12条面对角线中选出n 条,使得其中任意两条线段所在的直线都是异面直线,则n 的最大值为__________.2.如图8-12,已知三棱锥S ABC -中,90ABC ∠=︒,侧棱SA ⊥底面ABC ,点A 在棱SB 和SC 上的射影分别是点E F 、,求证:EF SC ⊥.SGF E CBA 图8123.已知a b 、是两条异面直线,直线a 上的两点A B 、的距离为6.直线b 上的两点C D 、的距离为8,AC BD 、的中点分别为M N 、且5MN =,见图8-13.求异面直线a b 、所成的角.图813bMNO aDCBA4.已知四面体S ABC -的所有棱长均为a .求: (1)异面直线SC 、AB 的公垂线段EF 及EF 的长; (2)异面直线EF 和SA 所成的角.5.如图8-14,等腰直角三角形ABC中,90A BC DA AC DA AB ∠=︒=⊥⊥,,,若1DA =,且E 为DA 的中点.求异面直线BE 与CD 所成角的余弦值.图814FE D CBA6.如图8-15,在正三角形ABC 中,D E F ,,分别为各边的中点,G H I J ,,,分别为AF AD BE DE ,,,的中点.将ABC △沿DE EF DF ,,折成三棱锥以后,求GH 与IJ 所成角的度数.I JH GFEDCB A 图8157.长方体1111ABCD A B C D -中,143AB AA AD ===,,则异面直线1A D 与11B D 间的距离为__________.8.空间两条异面直线a b 、所成角α,过空间一定点O 与a b ,所成角都是θ的直线l 有多少条? 8.3空间直线与平面空间中直线l 与平面α的位置关系,按照它们交点的个数分成以下三种情况:若直线l 与平面α没有公共点,那么称直线l 与平面α平行,记作l α∥;若直线l 与平面α仅有一个公共点,那么直线l 与平面α是相交的;若直线l 与平面α有1个以上的公共点,由公理1可知直线l 在平面α上.我们将直线与平面平行和相交统称为直线在平面外.直线和平面平行的判定定理 如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.直线和平面平行的性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行. 例1.已知:ABCD 是平行四边形,点P 是平面ABCD 外一点,M 是PC 的中点,在DM 上任取一点G ,过G 和AP 作平面交平面BDM 于GH .求征:AP GH ∥. 证明:如图8-16.联结AC 交BD 于O ,联结MO ,G HPOMD CBA图816ABCD 是平行四边形O ∴是AC 中点,又M 是PC 中点, AP OM ∴∥,又OM ⊂面BM DPA ∴∥平面BM D (线面平行判定定理)又PA ⊂平面PAHG ,且面PAHG 平面BMD GH =, PA GH ∴∥(线面平行的性质定理)例2.正方体1111ABCD A B C D -中,E G 、分别是BC 、11C D 的中点如图8-17.求证:EG ∥平面11BB D D .D C 1A 1C图817证明:取BD 的中点F ,联结FF 、1D F .E 为BC 的中点,EF ∴为BCD △的中位线,则EF DC ∥,且12EF CD =.G 为11C D 的中点,1D G CD ∴∥且112D G CD =,1EF D G ∴∥且1EF D G =, ∴四边形1EFD G 为平行四边形,∴1D F EG ∥,而1D F ⊂平面11BDD B ,EG ⊄平面11BDD B , ∴EG ∥平面11BDD B .直线l 与平面α相交,且与平面内所有直线都垂直,称直线l 垂直于平面α,记作l α⊥.直线l 称为平面α的垂线,l 与平向α的交点称为垂足.直线和平面垂直判定定理 如果直线l 与平面α内两条相交直线a b 、都垂直,那么直线与平面垂直. 证明:设直线a b O =,直线c 为平面α上任意一条直线 (1)当直线l 与直线c 都经过点O 时在直线l 上点O 的两侧分别取点P Q 、使得OP OQ =,在平面α上作一条直线,使它与a b c 、、分别交于点A B C 、、联结PA PB PC QA QB QC 、、、、、(见图8-18). acb αO QB A P图818OA 垂直平分PQ ,PQ QA ∴=. 同理PB QB =. PA QA PB QB AB AB ===,,, PAB QAB PC QC ∴∴=,△△≌.PQ c ∴⊥,即l c ⊥.(2)若直线l 与直线c 不都经过点O ,则过O 引l 与直线c 的平行线1l 与直线1c ,由(1)可知11l c ⊥.由等角定理可知l c ⊥.综上所述,l α⊥.直线和平面垂直性质定理 如果两条直线同垂直于一个平面,那么这两条直线平行.过空间一点P 有且仅有一条直线l 和一个平面α垂直,反之过一点P 有且仅有一个平面α与直线l 垂直,垂足Q 称为点P 在平面α上的射影,线段PQ 的大小称为点P 到平面α的距离.若一条直线与一个平面平行,则这条直线上任意一点到平面的距离,叫做这条直线到平面的距离. 若一条直线与一个平面α相交且不垂直,称直线l 与平面α斜交,直线l 为平面α的斜线,交点称为斜足.平面的斜线与其在平面上的射影所成的角称为直线与平面所成的角.最小角定理 斜线和平面所成的角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角. 例3.已知:一条直线l 和一个平面α平行.求证:直线l 上各点到平面α的距离相等. 证明:过直线l 上任意两点A B ,分别引平面α的垂线AA ,′BB ′,垂足分别为A B ,′′(见图8-19).βαB'A'B A图819AA BB αα⊥⊥,′′ AA BB ∴∥′′设经过直线AA ′和BB ′的平面为A B ββα=,′′l l A B α∴∴,∥∥′′AA BB ∴′′是平行四边形 AA BB ∴=′′即直线l 上各点到平面的距离相等例4.如图8-20,已知正方形ABCD 的边长为4,E F ,分别是边AB AD ,的中点,GC 垂直于ABCD 所在的平面,且2GC =,求点B 到平面EFG 的距离.OSGH F E DCBA图820证明:联结DB AC ,,设DB AC O = E F ,分别为AB AD ,中点DB EF ∴∥;又DB ⊄平面EFG , BD ∴∥平面EFG .∴点B 到平面EFG 的距离就是DB 到平面EFG 的距离. ∴即点O 到平面X O 的距离.设EF AC H =,在平面CHG 中,作OS GH ⊥ DB AC ⊥,又EF BD ∥ EF AC ∴⊥又GC ⊥面ABCD ,GC EF ∴⊥ EF ∴⊥面CHG EF OS ∴⊥,又OS GH ⊥ OS ∴⊥面EFG ∴OS 即为O 点到平面EFG 的距离,即为所求 直角三角形HSO 与直角三角形HGC 相似 SO HOGC GH∴=,又124GC HO AC GH =====,2SO ∴= ∴B 到平面EFG的距离为11. 例5.相交成60︒的两条直线AB AC ,和平面α所成的角分别为30︒和45︒,求这两条斜线在平面α内的射影所成的角.解:如图8-21,作平面AO ⊥平面A ,垂足为O ,O CBA图821则30ABO ∠=︒,45ACO ∠=︒,设AO h =,则2AB h =,AC =,BO =,CO h =, 在三角形ABC 中,根据余弦定理有22222(2))cos606BC h h h =+-⨯⨯︒=-.同理,在三角形BOC 中,令BOC θ∠=,则有22222)cos 4cos BC h h h θθ=+-⨯⨯=-.222264cos h h θ∴-=-.cos θ∴=,θ∴=. 三垂线定理 在平面内的一条直线,如果和平面的一条斜线的射影垂直,那么它也和这条斜线垂直.如图8-22,直线PM 为平面α的斜线,M 为斜足,Q 为P 在平面α内的射影,a 为平面α内一条直线,且a MQ ⊥.求证:a PM ⊥.图822ab a PQM证明:过点M 作的a 平行线b ,则b MQ b PQ ⊥⊥, 即b ⊥平面PMQ ,MQ ⊆平面PMQ 所以b PM a b ⊥,∥,即a PM ⊥.类似地,我们也可以证明:三垂线的逆定理 在平面内的一条直线,如果和平面的一条斜线垂直,那么它也和这条斜线的射影垂直. 基础练习1.如果三个平面αβγ、、两两相交于三条交线a b c 、、,讨论三条交线的位置关系,并证明你的结论. 2.在正方体1111ABCD A B C D -中,P 为棱AB 上一点,过点P 在空间作直线l ,使l 与平面ABCD 和平面11ABC D 均成30︒角,求这样的直线条数3.已知空间四边形ABCD P Q ,、分别是ABC △和BCD △的重心,求证:PQ ∥平面ACD .4.在棱长为a 正方体1111ABCD A B C D -中, (1)求证:11B D CD ⊥; (2)求证:1B D ⊥平面1ACD ; (3)求点D 到平面1ACD 的距离.5.正方体1111ABCD A B C D -中,求1B D 与平面11ABC D 所成角的大小.6.正方体ABCD A B C D -′′′′的棱长为a ,则异面直线CD ′与BD 间的距离等于__________. 7.正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE BD 、上各取一点P Q 、.且AP DQ =.求证:PQ ∥面BCE .8.如图8-23,已知AOB ∠在平面M 上,P 为平面外一点,满足POA ∠POB =∠θ=(θ为锐角),点P 在平面上的射影为Q .P OQFE AM 图823(1)求证点Q 在AOB ∠的平分线OT 上;(2)讨论POA ∠、POQ ∠、QOA ∠之间的关系.9.若直线l 与平面α成角π3,直线a 在平面α内,且和直线l 异面,则l 与a 所成角的取值范围是多少? 10.如图8-24,AB 为平面α的斜线,B 为斜足,AH 垂直平面α于H 点,BC 为平面α内的直线,,,ABH HBC ABC θαβ∠=∠=∠=,求证:cos cos cos βαθ=⋅. αθβH D CB Aα图82411.如图8-25,平面α内有一半圆,直径AB ,过A 作SA ⊥平面α,在半圆上任取一点M .连SM 、SB ,且N 、H 分别是A 在SM 、SB 上的射影.N MBA HSα图825(1)求证:NH SB ⊥;(2)这个图形中有多少个线面垂直关系? (3)这个图形中有多少个直角三角形? (4)这个图形中有多少对相互垂直的直线?12.如图8-26,在正方体1111ABCD A B C D -中,EF 为异面直线1A D 与AC 的公垂线,求证:1EF BD ∥.FE D CBAD 1C 1B 1A 1图82613.如图8-27所示,90BAC ∠=︒.在平面α内,PA 是α的斜线,60PAB PAC ∠=∠=︒.求PA 与平面α所成的角.B αA CMO NP图8278.4空间平面与平面的位置关系空间两个平面根据交点的个数可以分为:若两个平面没有交点则称两个平面互相平行;若两个平面有交点则称两个平面是相交的.平行于同一平面的两个平面互相平行,分别在两个平行平面上的直线是异面或平行的.两个平面平行的判定定理 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.推论 如果一个平面内的两条相交直线,分别平行于另一个平面内的两条相交直线,那么这两个平面平行.两个平面平行的性质定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 例1.平行四边形ABCD 和平行四边形ABEF 不在同一平面内,M ,N 分别为对角线AC ,BF 上的点,且AM ACFN FB=.求证:MN ∥平面BEC .证明:如图8-28,在平行四边形ABCD 中,过M 作MP BC ∥交BC 于P ,联结PN .FP MNEDCBA图828AM AP AC AB =,又AM AC FN BF =,即AM FNAC BF=. ,AP FN PN AF BE AB BF∴=∴∥∥. 又MP BC ∥,∴平面MPN ∥平面CBE . 又MN ⊂平面MPN , MN ∴∥平面BEC .例2.如图8-29所示,平面α平面β,点A C α∈、,点B D β∈、,AB a =是α、β的公垂线,CD 是斜线.若AC BD b ==,CD c =,M 、N 分别是AB 和CD 的中点.图829(1)求证:MN β∥;(2)求MN 的长. 证明:(1)联结AD ,设P 是AD的中点,分别联结PM 、PN . M 是AB 的中点,PM BD ∴∥.又,PM ββ⊂∴∥. 同理N 是CD 的中点,PN AC ∴∥. AC α⊂,PN α∴∥.,,PN PM P αβ=∥PMN β∴∥. MN ⊂平面PMN ,MN β∴∥. (2)分别联结MC MD 、.1,,2AC BD b AM BM a ====又AB 是αβ、的公垂线,90CAM DBM ∴∠=∠=︒,Rt Rt ACM BDM ∴≌△△,CM DM ∴=,DMC ∴△是等腰三角形. 又N 是CD 的中点,MN CD ∴⊥.在Rt CMN △中,MN =一般地,当两个平面相交时,它们的交线l 将各平面分割为两个半平面,由两个半平面αβ、及其交线l 组成的空间图形叫做二面角(dihedral angle ),记作l αβ--.交线l 称之为二面角的棱,两个半平面αβ、叫做二面角的面.如果αβ、上分别有点P Q 、,那么二面角l αβ--也可以记作P l Q --.为了刻画二面角的大小,我们在棱l 上任取一点O ,在面αβ、上分别作棱l 的垂线OM 、ON ,则[](0,π)MON θ∠=∈称为二面角l αβ--的平面角.若π2α=,则称平面αβ⊥. 两个平面垂直的判定定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直. 两个平面垂直的性质定理 如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.例3.如图8-30,在空间四边形SABC 中,SA ⊥平面ABC ,AB BC ⊥,DE 在平面SAC 内,DE 垂直平分SC ,且分别交AC ,SC 于D ,E ,又SA AB =,SB BC =,求以BD 为棱,以BDE 和BDC 为面的二面角的大小.E DCBAS图830解:SB SC =,且E 为SC 的中点,BE SC ∴⊥. 又DE 垂直平分SC ,SC ∴⊥面,BDE SC BD ∴⊥. 又BD ⊥平面SAC ,,,BD DE BD DC ∴⊥⊥EDC ∴∠即为E BD C --的平面角.设SA a =,则,,AB a SB ==SA ⊥面ABC ,BC AB ⊥.,SB BC SC ∴⊥∴为等腰直角三角形SBC的斜边,又BC =,2,,cos ,30SC a AC SCA SCA ∴==∠=∴∠=︒. DE SC ⊥,∴在直角三角形EDC 中,60EDC ∠=︒,即为所求.例4.已知:如图8-31所示,平行四边形ABCD中,AB =AD BD ==,沿BD 将其折成一个二面角A BD C --,若折后AB CD ⊥.63223DCBA图831(1)求二面角A BD C --的大小;(2)求折后点C C 到平面ABD 的距离.解:(1)在平行四边形ABCD中AB =AD BD ==.222AB AD BD ∴=+ ,AD BD BC BD ∴⊥⊥. 作AH ⊥平面BDC ,联结DH (见图8-32).HEDCB A图832AD BD ⊥,由三垂线定理逆定理得DH BD ⊥, ∴ADH ∠是二面角A BD C --的平面角.联结BH,AB DC ⊥,由三垂线定理逆定理, 得BH DC ⊥,设垂足为E ,在直角三角形ABC中,2BD BC BE DC ⋅===,DE ∴ 三角形DHB 与三角形DBE 相似,DH DEDB BE∴=,即DE BD DH BE ⋅=在直角三角形ADH中,1cos 2DH ADH AD ∠===,π3ADH ∴∠=. 即二面角--A BD C 的大小为π3. (2)由对称性,C 到平面ABD 的距离等于A 到平面ABD 的距离. AH ⊥平面BCD ,∴点A 到平面BCD 的距离即是线段AH 的长, 直角三角形ADH中,sin 3AH AD ADH =⋅∠==, ∴点C 到平面ABD 的距离为3. 例5.如图8-33,已知A B 、在平面α上,点C 是平面外一点,且在平面α上的射影为D ,且A B D、、三点不共线,二面角C AB D --的大小为θ,求证:cos DABCABS S θ=.αM DCBA图833证明:过点D 作DM 垂直AB ,垂足为M ,联结CM . 因为,CD AB αα⊥⊆,所以CD AB ⊥,又AB DM ⊥,因此AB ⊥平面CDM ,即AB CM ⊥. 所以CMD ∠为二面角--C AB D 的平面角. 在直角三角形CDM △中有cos cos ABDCBDS DM CMD CM S θ=∠==. 例6.如图8-34,已知两异面直线,a b 所成的角为θ,它们的公垂线段AA ′的长度为d .在直线,a b 上分别取点,E F ,设,A E m AF n ==′,求EF .A'βnb a m F G A图834解:设经过b 且与AA ′垂直的平面为α,经过a 和AA ′的平面为β,c αβ=;则c a ∥,因而b ,c 所成角为θ,且AA c ⊥′;又,AA b AA a ⊥∴⊥′′, 根据两个平面垂直的判定定理,βα⊥. 在平面β内作EG c ⊥,则EG AA =′. 并且根据两个平面垂直的性质定理,EG α⊥ 联结FG ,则EG FG ⊥.在直角三角形EFG 中,222EF EG FG =+AG m =,三角形AFG 中,2222cos FG m n mn θ=+-;又22ED d =,22222cos EF d m n mn θ∴=++-,因此EF =1.已知平面αβ∥,AB ,CD 为夹在,αβ间的异面线段,E 、F 分别为AB CD 、的中点. 求证:,EF EF αβ∥∥.2.如果αβ∥,AB 和AC 是夹在平面α与β之间的两条线段,AB AC ⊥,且2AB =,直线AB 与平面α所成的角为30︒,求线段AC 长的取值范围.3.如图8-35,已知正方体1111ABCD A B C D -中,E F 、分别为1AB AA 、的中点.求平面1CEB 与平面11D FB 所成二面角的平面角的正弦值.CB E AF D 1C 1B 1A 1图8354.如图8-36,点A 在锐二面角MN αβ--的棱MN 上,在面α内引射线AP ,使AP 与MN 所成的角PAM ∠为45︒,与面β所成的角大小为30︒,求二面角MN αβ--的大小.NM APβα图8365.正方形ABCD 边长为4,点E 是边CD 上的一点,将AED △沿AE 折起到1AED 的位置时,有平面1ACD ⊥平面ABCE ,并且11BD CD ⊥.(1)判断并证明E 点的具体位置; (2)求点D ′到平面ABCE 的距离.6.在正三角形ABC 中,E F P 、、分别是AB AC BC 、、边上的点,满足12AE EB CF FA CP PB ===∶∶∶∶,如图8-37.将AEF △沿EF 折起到1A EF △的位置,使二面角1A EF B --成直二面角,联结1A B 、1A P ,如图8-38.A BP FEC图837CEF P BA 图838(1)求证:1A E ⊥平面BEP ;(2)求直线1A E 与平面1A BP 所成角的大小;(3)求二面角1B A P F --的大小(用反三角函数表示).7.如图8-39,将边长为a 的正三角形ABC 以它的高AD 为折痕折成一个二面角C AD C --′.C'DCB A图839(1)指出这个二面角的面、棱、平面角; (2)若二面角C AD C --′是直二面角,求C C ′的长; (3)求AC ′与平面C CD ′所成的角; (4)若二面角C AD C --′的平面角为120︒,求二面角A C C D --′的平面角的正切值. 8.在棱长为a 的正方体中.求异面直线BD 和1B C 之间的距离.9.设由一点S 发出三条射线,,,,SA SB SC ASB BSC ASC αβθαβθ∠=∠=∠=、、、、均为锐角,且cos cos cos θβθ⋅=.求证:平面ASB ⊥平面BSC .10.如图8-40,矩形ABCD ,PD ⊥平面ABCD ,若2PB =,PB 与平面PCD 所成的角为45︒,PB 与平面ABD 成30︒角,求:PF EDCBA图840(1)CD 的长;(2)求PB 与CD 所在的角;(3)求二面角C PB D --的余弦值. 11.如图8-41,线段PQ 分别交两个平行平面αβ、于A B 、两点,线段PD 分别交αβ、于C D 、两点,线段QF 分别交αβ、于F E 、两点,若9PA =,12AB =,12BQ =,ACF △的面积为72.求BDE △的面积.βαAB Q ED CPF图84112.如图8-42,已知正方形ABCD .E F 、分别是AB CD 、的中点.将ADE △沿DE 折起,如图8-43所示,记二面角A DE C --的大小为θ(0πθ<<).FEDCBA图842F EDCBA 图843(1)证明BF ∥平面ADE ;(2)若ACD △为正三角形,试判断点A 在平面BCDE 内的射影G 是否在直线EF 上,证明你的结论,并求角θ的余弦值.13.在矩形ABCD 中,已知1,AB BC a ==,PA ⊥平面ABCD ,且1PA =. (1)在BC 边上是否存在点Q ,使得PQ QD ⊥,说明理由;(2)若BC 边上有且仅有一个点Q ,使PQ QD ⊥,求AD 与平面PDQ 所成角的弦值; (3)在(2)的条件下,求出平面PQD 与平面PAB 所成角的大小.14.两个平行平面α和β将四面体ABCD 截成三部分.已知中间一部分的体积小于两端中任一部分的体积,点A 和B 到平面α的距离分别为30和20.而点A 和C 到平面β的距离分别为20和16,两个截面中有一个是梯形,点D 到平面α的距离小于24.求平面α和β截四面体所得的截面面积之比. 8.5空间向量及其坐标表示我们把具有大小和方向的量叫做向量.同向且大小相等的两个向量是同一个向量或相等的向量,大小相等方向相反的两个向量是互为负向量,大小为0的向量称为零向量.对空间任意两个向量a b 、.作OA a OC AB b ===,,则O A B 、、三点共面,见图8-44.因此,空间任意两个向量都可以用在同一平面内的两条有向线段表示.与平面向量运算一样,我们可以定义空间向量的加法、减法与数乘运算如下:a图844OB OA AB a b =+=+; CA OA OC a b =-=-;0000a a a λλλλλλ⎧>⎪⎪>⎨⎪<⎪⎩方向相同,大小,,方向相同,大小,为为- 与平面向量类似,在空间两个向量的方向相同或相反,则称他们为共线向量或平行向量,共线向量所在直线平行或重合.类似我们可以验证空间向量的加法与数乘运算满足如下规律: (1)加法交换律:a b b a +=+(2)加法结合律:()()a b c a b c ++=++ (3)数乘分配律:()a b a b λλλ+=+类似地,可以定义两个向量的夹角和向量的数量积:cos a b a b θ⋅=,其中θ为两个向量的夹角,[]0πa b θ∈,,、表示向量a b 、的大小 当π2θ=时称两个向量垂直记作a b ⊥. 与平向向量类似有下列性质成立: (1)0a b a b ⊥⇔⋅=. (2)2a a a =⋅. (3)()()ab a b λλ⋅=⋅.(4)a b b a ⋅=⋅. (5)()()()a b c a b a c ⋅+=⋅+⋅.例1.A B C D 、、、为空间不共面的四点,以A B C D 、、、四点为顶点的线段围成一个空间四面体,若AC BD BC BD ==,,求证AB CD ⊥.图845DBA解:BC AC AB BD AD AB =-=-,, BC BD =, 22BC BD ∴=.2()()BC BC BC AC AB AC AB =⋅=-⋅- 222AC AC AB AB =-⋅+.同理2222BD AD AD AB AB AD AC =-⋅+=,, AD AB AC AB ∴⋅=⋅即()AD AC AB -⋅=0.即CD AB ⋅=0,AB CD ∴⊥.通常我们将可以平移到同一个平面的向量,叫做共面向量.对空间任意两个向量,它们总是共面的,但空间任意三个向量就不一定是共面向量.如上例中a b c 、、中任意两个共面,但a b c 、、却不共面.下面讨论三个向量共面的条件.已知a b 、为不共线的向量,而a b c 、、三个向量共面,则表示可以将它们平移到同一个平面上.由平面向量唯一分解定理.存在实数()λμ,满足c a b λμ=+.反之,若存在实数对()λμ,满足c a b λμ=+,对空间任意一点O 作111OA a OB b OA a A B b λμ====,,,,则1111OB OA A B a b c λμ=+=+=即c 可以平移到O A B 、、三点所在平面上,因此a b c 、、共面.由此可得a b c 、、共面的充要条件是:存在实数对()λμ,满足c a b λμ=+.例2.求证:任意三点不共线的四点A B C D 、、、共面的充要条件是:对空间任意点O 有:OD xOA yOB zOC =++(其中1x y z ++=).证明:A B C D 、、、共面的充要条件是存在实数对()λμ,满足AD AB AC λμ=+(见图8-46).图846()()OD OA AD OB OA OC OA μμ∴-==-+-, (1)OD OA OB OC λμλμ∴=--++.令1x λμ=--,y z λμ==,,则OD xOA yOB zOC =++(其中1x y z ++=).定理 如果三个向量a b c 、、不共面,那么对于空间任意向量P ,存在唯一的实数对()x y z ,,满足:P xa yb zc =++证明:如图8-47,过空间任意点O 作OA a OB b OC c OP P ====,,,, 图847P过点P 作1PP OC ,∥交平面OAB 于点1P ;则11P OP OP PP ==+. 11PP OC PP zc z ∴=∈R ,,∥. 在平面AOB 中存在z ,y ∈R ,满足1OP xOA yOB =+, 因此有11P OP OP PP xOA yOB zOC ==+=++. 若存在111()()x y z x y z ≠,,,,也满足:111P x a y b z c =++, 则有111P xa yb zc x a y b z c =++=++. 111()()x y z x y z ≠,,,,,不妨设1x x ≠,1111y y z za b c x x x x --∴=+--.a b c ∴、、共面,矛盾.由此定理可知,如果三个向量a b c 、、,那么所有空间向量均可以由a b c 、、唯一表示,此时我们称(a b c 、、)为空间向量的一个基底,a b c 、、都叫做基本向量.如果空间的一个基底的三个基向量互相垂直,且大小为1,则称这个基底为单位正交基底,常用(i j k 、、)表示.在空间选定一点O 和一个单位正交基底(i j k 、、),以O 点为坐标原点,分别以i j k 、、的方向为正方向建立三条数轴:x 轴、y 轴、z 轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系O xyz -,那么对于任意向量P ,存在唯一的实数对(x y z ,,)满足:P OP xi y j zk ==++,简记为()P x y z =,,,此时称点P 的坐标为()x y z ,,,见图8-48.图848若111()OA a x y z ==,,,222()OB b x y z ==,,,则 121212()a b x x y y z z +=+++,,,121212()BA OA OB a b x x y y z z =-=-=---,,,111()a x y z λλλλ=,,.例3.在直三棱柱111A B C ABC -中,π2BAC ∠=,11AB AC AA ===.已知G 与E 分别为11A B 和1CC 的中点,D 与F 分别为线段AC 和AB 上的动点(不包括端点).若GD EF ⊥,求线段DF 的长度的取值范围解:建立直角坐标系,以A 为坐标原点,AB 为x 轴,AC 为y 轴,1AA 为z 轴,则112211(00)(01)0101(00)(01)22F t t E G D t t ⎛⎫⎛⎫<<<< ⎪ ⎪⎝⎭⎝⎭,,,,,,,,,,,.所以12111122EF t GD t ⎛⎫⎛⎫=--=-- ⎪ ⎪⎝⎭⎝⎭,,,,,.因为GD EF ⊥,所以1221t t +=,由此推出2102t <<.又12(0)DF t t =-,,,21DF t =1DF <.例4.已知四边形ABCD 和ABEF 是两个正方形,它们所在的平面互相垂直,M AC ∈,N BF ∈,且AM FN =,见图8-49.求证:不论M 在AC 上何处,直线MN 不可能同时垂直AC 和BF .MNFEDCBA图849证明:设BA a BE b BC c BN t BF ====⋅,,,, 则()(1)()BN t a b AM t c a =⋅+=--, 于是()(1)()(1)MN BN BM t a b t c a a tb t c ⎡⎤⎡⎤=-=+---+=--⎣⎦⎣⎦, 假设MN 同时垂直AC 和BF ,则00.MN AC MN BF ⎧⋅=⎪⎨⋅=⎪⎩,由题设,知00a b b c ⋅=⋅=,, 由2(1)()(1)MN AC tb t c c a t c ⎡⎤⋅=--⋅-=-⋅⎣⎦,得10t -=即1t =.由2(1)()0MN BF tb t c a b t b ⎡⎤⋅=--⋅+=⋅=⎣⎦得0t =,矛盾!所以,MN 不可能同时垂直AC 和BF .基础练习1.如图8-50,OA a OB b OC c ===,,,M N P 、、分别为AB 、BC 、CA 的中点,试用a b c 、、表示下列向量:OM MN AN ,,.图8502.已知空间三点(202)A -,,,(212)B -,,,(303)C -,,.设a AB b AC ==,,是否存在实数k ,使向量ka b +与2ka b -互相垂直,若存在,求k 的值;若不存在,说明理由.。
高一数学第8章知识点总结

高一数学第8章知识点总结第一节一次函数1. 概念:一次函数是指函数的表达式中最高次数为1的函数,通常的表达式形式为y=ax+b,其中a和b为常数,a称为斜率,b 称为截距。
2. 斜率的性质:- 斜率为正数时,函数呈现上升趋势;- 斜率为负数时,函数呈现下降趋势;- 斜率为0时,函数为水平线;- 斜率的绝对值越大,函数的变化越剧烈。
3. 截距的性质:- 当x=0时,函数的截距为b,表示函数与y轴的交点;- 函数在平面直角坐标系中与x轴的交点为(-b/a, 0)。
第二节二次函数1. 概念:二次函数是指函数的表达式中最高次数为2的函数,通常的表达式形式为y=ax^2+bx+c,其中a、b、c为常数,a称为二次项系数,b称为一次项系数,c称为常数项。
2. 抛物线的性质:- 当a>0时,抛物线开口向上,称为正向抛物线,最低点为顶点;- 当a<0时,抛物线开口向下,称为负向抛物线,最高点为顶点;- 顶点的横坐标为-x轴的对称轴,纵坐标为函数的最值。
3. 零点的计算:- 函数的零点即为使函数取值为0的x的值;- 可通过因式分解、配方法、根的公式等方法计算二次函数的零点。
第三节幂函数1. 概念:幂函数是指形式为y=ax^m的函数,其中a和m是常数,m称为指数。
2. 幂函数的性质:- 当m>0时,函数呈现上升趋势;- 当m<0时,函数呈现下降趋势;- 当m为偶数时,函数图像关于y轴对称;- 当m为奇数时,函数图像关于原点对称。
3. 特殊幂函数:- 当m=1时,得到一次函数;- 当m=0时,得到常函数y=a;- 当m为负整数时,得到反比例函数。
第四节对数函数1. 概念:对数函数是指形式为y=logₐ(x)的函数,其中a为底数,x为真数。
2. 对数函数的性质:- 对数函数与指数函数是互逆的;- 对数函数的定义域为正实数集,值域为实数集;- 对数函数的图像在y轴左侧趋近于负无穷,右侧趋近于正无穷。
高一数学总复习题

高一数学总复习题# 高一数学总复习题## 一、函数与方程1. 函数的基本概念- 定义域与值域- 函数的单调性与奇偶性2. 一次函数与二次函数- 一次函数的图像与性质- 二次函数的图像与性质3. 指数函数与对数函数- 指数函数的定义与性质- 对数函数的定义与性质4. 方程的解法- 一元一次方程- 一元二次方程- 无理方程与分式方程## 二、不等式1. 不等式的基本性质- 不等式的基本运算规则- 不等式的性质2. 一元一次不等式的解法- 线性不等式的解集表示3. 一元二次不等式的解法- 判别式的应用- 一元二次不等式的解集4. 不等式组的解法- 线性不等式组的解集## 三、数列1. 数列的基本概念- 等差数列与等比数列的定义 - 数列的通项公式2. 等差数列的性质- 等差数列的求和公式3. 等比数列的性质- 等比数列的求和公式4. 数列的极限- 数列极限的概念## 四、三角函数1. 三角函数的定义- 正弦、余弦、正切的定义2. 三角函数的基本性质- 周期性、奇偶性3. 三角函数的图像- 正弦、余弦函数的图像4. 三角恒等变换- 基本的三角恒等式## 五、平面解析几何1. 直线的方程- 斜截式、点斜式、一般式2. 圆的方程- 圆的标准方程3. 直线与圆的位置关系- 切线、相切、相交4. 椭圆、双曲线、抛物线- 标准方程与性质## 六、立体几何1. 空间直线与平面的位置关系 - 平行、垂直2. 空间几何体的体积与表面积 - 长方体、圆柱、圆锥、球3. 向量在立体几何中的应用- 向量法解决立体几何问题## 七、概率与统计初步1. 概率的基本概念- 事件、概率的定义2. 概率的计算方法- 古典概型、条件概率3. 统计初步- 数据的收集与处理- 描述性统计## 八、综合应用题1. 函数与方程的综合应用- 函数的图像与方程的解2. 不等式与数列的综合应用- 不等式求解与数列求和3. 三角函数与解析几何的综合应用- 三角函数在解析几何中的应用4. 立体几何与向量的综合应用- 向量法解决立体几何问题通过上述复习题,可以全面地回顾高一数学的各个知识点,为进一步的学习打下坚实的基础。
8高一数学第八讲期中复习总结

知识要点总结 一、集合1、含义与表示:(1)集合中元素的特征:确定性,互异性,无序性 (2)集合的表示法:列举法,描述法,图示法2、集合间的关系:子集:对任意x A ∈,都有 x B ∈,则称A 是B 的子集。
记作A B ⊆真子集:若A 是B 的子集,且在B 中至少存在一个元素不属于A ,则A 是B 的真子集,记作A B ≠⊂集合相等:若:A B B A ⊆⊆且,则A B =3、元素与集合的关系:属于:∈;不属于:∉;空集:φ4、集合的运算:交集:定义:由集合A 和集合B 中的公共元素组成的集合叫交集,记为A B 性质:,A A A A A B B A A B A A B B A B A B A ⋂=⋂∅=∅⋂=⋂⋂⊆⋂⊆⊆⇔⋂=,,,, 并集:定义:由属于集合A 或属于集合B 的元素组成的集合叫并集,记为A B 性质:A A A A A A B B A A B A A B B A B A B B ⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃=,,,,, 补集:定义:在全集U 中,由所有不属于集合A 的元素组成的集合叫补集,记为U C A5、集合12{,,,}n a a a 的子集个数共有2n 个;真子集有21n -个;非空子集有21n-个;6、常用数集:自然数集:N 正整数集:*N 整数集:Z 有理数集:Q 实数集:R二、函数1、映射定义:设A 、B 是两个非空的集合,如果按某一个确定的对应关系,使对于集合A 中的任意一个元素x , 在集合B 中都有唯一确定的元素y 与之对应,那么就称对应f :A →B 为从集合A 到集合B 的一个映射。
3、函数的单调性定义:对于定义域为D 的函数f (x ),若任意的x 1, x 2∈D ,且x 1 < x 2高一数学讲义(64期)第八讲 期中复习传统定义:如果在某变化中有两个变量x ,y ,并且对于x 在 某个范围内的每一个确定的值,按照某个对应关系f , y 都有唯一确定的值和它对应。
数学高一第八章知识点总结

数学高一第八章知识点总结第八章的内容主要包括函数的概念、函数的图象、函数的性质、函数的运算、一次函数及其应用、二次函数及其应用、幂函数及其应用、指数函数及其应用、对数函数及其应用等。
一、函数的概念1. 函数的定义: 如果对于每一个x,都有且只有一个y与之对应,那么y是x的一个函数。
2. 自变量与因变量: 函数中,自变量是x,因变量是y。
3. 定义域和值域: 函数的所有自变量的取值范围称为定义域,函数的所有因变量的取值范围称为值域。
4. 基本初等函数: 常数函数、一次函数、二次函数、幂函数、指数函数、对数函数等。
二、函数的图象1. 函数的图象: 函数的图象是由函数的各对应自变量和因变量组成的点的集合。
2. 基本初等函数的图象: 常数函数的图象是一条水平线;一次函数的图象是一条直线;二次函数的图象是抛物线;幂函数的图象是抛物线的一部分;指数函数的图象是一条不经过原点的曲线;对数函数的图象是挨着y轴的一段曲线。
三、函数的性质1. 奇函数和偶函数: 如果对于所有x∈定义域,都有f(-x)=-f(x),那么函数f(x)是奇函数;如果对于所有x∈定义域,都有f(-x)=f(x),那么函数f(x)是偶函数。
2. 周期函数: 如果存在一个正数T,使得对于所有x∈定义域,都有f(x+T)=f(x),那么函数f(x)是周期函数。
3. 单调性: 如果对于任意的x1<x2,都有f(x1)<f(x2),那么函数f(x)是单调递增的;如果对于任意的x1<x2,都有f(x1)>f(x2),那么函数f(x)是单调递减的。
4. 奇偶性与周期性: 一次函数是一次函数是奇函数或者偶函数,二次函数是偶函数;幂函数是奇函数或者偶函数;指数函数是奇函数;对数函数是奇函数;正弦函数是奇函数,余弦函数是偶函数;正切函数、余切函数、正割函数、余割函数是周期函数。
四、函数的运算1. 函数加减法: (f+g)(x)=f(x)+g(x),(f-g)(x)=f(x)-g(x)。
高一数学1到8章知识点

高一数学1到8章知识点第一章:集合的基本概念集合是数学中最基本的概念之一,它是由一些确定的对象组成的整体。
数学中常用的符号表示集合,例如大写字母A、B、C等表示集合,而小写字母a、b、c等表示集合中的元素。
集合的基本操作包括并集、交集、差集和补集。
并集是指将两个集合的所有元素合并在一起,交集是指两个集合中共同的元素,差集是一个集合中减去另一个集合中相同的元素所得到的集合,补集是指在某个集合中不属于另一个集合中的元素的集合。
第二章:整式与分式的基本概念整式是指只包含代数变量和常数的运算式,其中包括常数项、一次项、二次项等。
分式是指两个整式之间的比值,其中包括真分式和假分式。
在整式的运算中,我们需要掌握加法、减法、乘法和除法的运算规则。
在分式的运算中,我们需要掌握分式加法、减法、乘法和除法的运算规则。
第三章:一元一次方程与不等式一元一次方程是指只含有一个未知数的一次方程,解一元一次方程的方法有等式两边加、减、乘、除同一个数等法则。
一元一次不等式是指只含有一个未知数的一次不等式,解一元一次不等式的方法有图解法和代入法。
第四章:平面直角坐标系与二次函数平面直角坐标系是由横轴和纵轴组成的,用于表示点的位置。
在平面直角坐标系中,我们可以通过坐标表示一个点的位置。
二次函数是指函数的表达式为a*x^2+b*x+c的函数,其中a、b、c为常数且a不等于0。
我们可以通过平移、翻折和缩放的方式来研究二次函数的图像和性质。
第五章:三角函数三角函数是指以角为自变量的函数,其中包括正弦函数、余弦函数和正切函数。
三角函数在几何学和物理学中有着广泛的应用。
在三角函数的运算中,我们需要掌握角度与弧度的互相转换,以及基本角的各种性质和计算方法。
第六章:平面向量与解析几何平面向量是指有大小和方向的量,常用箭头表示。
在平面上,我们可以通过向量的运算,例如加法、减法、数量积和向量积等,来研究和解决问题。
解析几何是指将几何问题转化为代数问题进行研究的方法。
高一数学第八章知识点总结

高一数学第八章知识点总结高一数学第八章知识点总结本章主要介绍了函数的定义域、值域、定义域和值域的对应关系、函数的极值、函数的单调性、函数的图像、函数的基本性质以及函数的应用等内容。
下面是本章的知识点总结:1. 函数的定义域和值域的对应关系定义域是指函数的输入范围,值域是指函数的输出范围。
函数的定义域和值域的对应关系为:定义域对应值域,值域对应定义域。
即当函数的定义域越界时,其值域也越界,当函数的定义域不界时,其值域也不界。
2. 函数的极值函数的极值是指函数在某个区间内出现的最大或最小值。
函数的极值可以通过函数的对称轴和导数来求解。
3. 函数的单调性函数的单调性是指函数在自变量不变时,对数函数的值随着自变量的增加而单调增加,指数函数的值随着自变量的增加而单调减少。
函数的单调性可以通过函数的导数来判断。
4. 函数的图像函数的图像是指函数在某一点取值时的取值范围的图像。
函数的图像可以通过对数函数和指数函数的图像进行描述。
5. 函数的基本性质函数的基本性质是指函数的一些基本特征,包括函数的定义域、值域、定义域和值域的对应关系、函数的极值、函数的单调性、函数的图像等。
6. 函数的应用函数在数学中有着广泛的应用,包括代数、几何、三角函数、指数函数、对数函数、三角函数、概率统计等。
函数的应用可以通过函数的求解、函数的图像、函数的性质来展开。
拓展:除了上述知识点外,函数还有一些重要的性质,包括函数的连续性、函数的可导性、函数的递推性等,这些性质对于理解和应用函数都非常重要。
此外,函数的应用也不仅仅局限于上述内容,函数在物理、工程、经济、生物等领域都有广泛的应用。
高一数学第八章 立体几何初步

第八章《立体几何初步》一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知圆锥的轴截面是一个边长为2的等边三角形,则该圆锥的体积为() A.33B.πC.D.2π2.如图,等腰梯形A B C D ''''是水平放置的一个平面图形的直观图,其中4A B ''=,2C D ''=,则原图形ABCD 的面积是()A.6B.B.C.D.3.若直线l ∥平面α,直线a ⊂α,则()A.l ∥a B.l 与a 异面C.l 与a 相交D.l 与a 没有公共点4.已知直线l⊥平面α,直线//m 平面β,则“//αβ”是“l m ⊥”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既非充分也非必要条件5.已知正四面体ABCD ,M 为AB 中点,则直线CM 与直线BD 所成角的余弦值为()A.23B.6C.D.421216.设α,β,γ是互不重合的平面,m ,n 是互不重合的直线,给出四个命题:①若//m α,//n α,则//m n ②若m γ⊥,n γ⊥,则//m n ③若//m α,n α⊥,则m n ⊥④若//m n ,//n α,则//m α其中正确命题的个数是()A.1B.2C.3D.47.已知三棱锥-P ABC 的底面ABC 是边长为1的等边三角形,PA ⊥平面ABC 且PA =ABC 的中心沿表面爬至点P ,则其爬过的路程最小值为()A.6B.433C.393D.38.如图,直三棱柱111ABC A B C -中,1,,AB BC AA AB P ⊥=为棱11A B 的中点,Q 为线段1AC 上的动点.以下结论中正确的是()A.存在点Q ,使BQ AC ∥B.不存在点Q ,使11BQ B C ⊥C.对任意点Q ,都有1BQ AB ⊥ D.存在点Q ,使BQ 平面1PCC 二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列说法中正确的是()A.若直线l 与平面α不平行,则l 与α相交B.直线l 在平面α外,则直线l 上不可能有两个点在平面α内C.如果直线l 上有两个点到平面α的距离相等,则直线l 与平面α平行D.如果,a b 是异面直线,,A B a ∈,,C D b ∈,则,AC BD ,是异面直线10.如图圆台12O O ,在轴截面ABCD 中,122AB AD BC CD ====,下面说法正确的是()A.线段AC =B.该圆台的表面积为11πC.该圆台的体积为D.沿着该圆台的表面,从点C 到AD 中点的最短距离为511.如图所示,正四棱台1111ABCD A B C D -中,111226AB A B AA ===,点P 在四边形ABCD 内,点E 是AD 上靠近点A 的三等分点,则下列说法正确的是()A.1AA ⊥平面1A BDB.该正四棱台的高为322C.若1362A P =,则动点P 的轨迹长度是5πD.过点E 的平面α与平面1D AC 平行,则平面α截该正四棱台所得截面多边形的面积为三、填空题:本题共3小题,每小题5分,共15分.12.已知空间中两个角α,β,且角α与角β的两边分别平行,若105α=︒,则β=______.13.一个直角梯形上底、下底分别为3cm 和4cm ,将此直角梯形以垂宜于底的腰为轴旋转周形成一个圆台,此圆台外接球的半径为5cm ,则这个圆台的高为_________.14.根据祖暅原理,界于两个平行平面之间的两个几何体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个几何体的体积相等.如图1所示,一个容器是半径为R R 的圆柱内嵌一个底面半径和高均为R 的圆锥,这两个容器的容积相等.若将这两容器置于同一平面,注入等体积的水,则其水面高度也相同.如图2,一个圆柱形容器的底面半径为4cm ,高为10cm ,里面注入高为1cm 的水,将一个半径为4cm 的实心球缓慢放入容器内,当球沉到容器底端时,水面的高度为______cm . 1.26≈)四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.如图,在四棱锥P ABCD -中,PD ⊥平面ABCD ,底面ABCD 为正方形,E ,F 分别是AB ,PB 的中点.(1)求证://EF 平面PAD ;(2)求证:EFCD ⊥.16.如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 是正方形,2PA AB ==,点M 是棱PC 的中点.(1)求证:平面BDM ⊥平面ABCD ;(2)求三棱锥P BDM -的体积.17.如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,PA AB ⊥,点E 是PB 的中点.(1)求证:PD ∥平面EAC ;(2)若2PC AD ==,1==PA AB ,3APC π∠=,求点P 到平面AEC 的距离.18.如图,在四棱锥P ABCD -中,底面ABCD 是菱形,平面PAD ⊥平面PCD ,PAD是边长为2的正三角形,PC =,E 是PC 中点,过点A ,B ,E 的平面与PD 交于点F .(1)求证://AB EF ;(2)求证:AF AB ⊥;(3)求二面角F PC A --的正切值.19.球面几何在研究球体定位等问题有重要的基础作用.球面上的线是弯曲的,不存在直线,连接球面上任意两点有无数条曲线,它们长短不一,其中这两点在球面上的最短路径的长度称为两点间的球面距离.(1)纬度是指某点与地球球心的连线和地球赤道面所成的线面角,赤道为0︒纬线,赤道以北叫做北纬.如图1,将地球看作球体,假设地球半径为R ,球心为O ,北纬30︒的纬线所形成的圆设为圆O ',且A B ''是圆O '的直径,球面被经过球心O 和点A ',B '的平面截得的圆设为圆O ,求圆O 中劣弧 A B ''的长度,并判断其是否是A ',B '两点间的球面距离(只需判断、无需证明).(2)如图2,点A ,B 在球心为1O 的球面上,且AB 不是球的直径,试问A ,B 两点间的球面距离所在的圆弧 AB 是否与球心1O 共面?若是,写出证明过程,并求出当14O A =,1π4AO B ∠=时,A ,B 两点间球面距离所在的圆弧 AB 与球心1O 所形成的扇形1AO B 的面积;若不是,请说明理由.。
高一数学第八章知识点总结

高一数学第八章知识点总结数学是一门让人爱恨交织的学科,有的人喜欢它的逻辑性和严谨性,有的人则觉得它难以理解和运用。
然而,对于高一学生来说,数学是必修的科目之一,而其中的第八章则是本学期最重要的内容之一。
在本文中,我们将对高一数学第八章的知识点进行一个总结和回顾。
第一节:平面直角坐标系平面直角坐标系是我们研究平面几何学和代数学的基础。
它由两个互相垂直的坐标轴组成,通常分别称为x轴和y轴。
我们可以用有序数对(x, y)来表示平面上的一个点,其中x代表该点在x轴上的位置,y代表该点在y轴上的位置。
通过平面直角坐标系,我们可以方便地描述和计算平面上的点、线和图形。
第二节:平面直角坐标系中的直线与曲线在平面直角坐标系中,直线是一种简单的图形,可以由方程y = kx+ b来描述,其中k是直线的斜率,b是直线在y轴上的截距。
通过斜率和截距,我们可以方便地画出一条直线,并计算直线上的点。
曲线则是一个更加复杂的图形,它可以通过方程或者函数来描述。
曲线在平面直角坐标系中有不同的形状和性质,如抛物线、椭圆、双曲线等。
通过分析曲线的方程和性质,我们可以了解曲线的形状、对称性、焦点等重要信息。
第三节:平面直角坐标系中的距离、斜率与中点公式在平面直角坐标系中,我们可以使用距离公式来计算两个点之间的距离。
假设有两个点A(x₁, y₁)和B(x₂, y₂),它们之间的距离d可以通过以下公式进行计算:d = √((x₂-x₁)² + (y₂-y₁)²)。
这个距离公式在解决平面几何问题时是非常有用的。
斜率是直线的一个重要属性,它可以帮助我们了解直线的倾斜程度。
斜率可以通过两个点的坐标来计算,公式为k = (y₂-y₁) / (x₂-x₁)。
斜率可以用来判断两条直线的关系,如平行、垂直等。
中点公式是另一个在平面几何中常用的工具,它可以帮助我们计算两个点的中点坐标。
假设有两个点A(x₁, y₁)和B(x₂, y₂),它们的中点坐标M可以通过以下公式进行计算:M = ((x₁+x₂)/2, (y₁+y₂)/2)。
数学高一第八单元知识点

数学高一第八单元知识点数学作为一门理科学科,对于高中生来说是一个必修课程。
它的学习既需要理解各种概念和原理,又要掌握一定的计算方法和技巧。
在高一的数学课程中,第八单元是重要的一个部分,下面将对该单元的知识点进行详细介绍。
一、线性方程组与矩阵1. 线性方程组的概念和性质:线性方程组的解集、线性方程组的可解性。
2. 二元一次方程组的解法:代入法、消元法。
3. 三元一次方程组的解法:代入法、消元法、克拉默法则。
4. 矩阵的概念和运算:矩阵的行列式、矩阵的加法和数乘、矩阵的乘法。
5. 矩阵方程及其解法:齐次线性方程组的矩阵表示、非齐次线性方程组的矩阵表示,矩阵方程的解法。
二、二次函数1. 二次函数的概念和性质:二次函数的定义、二次函数的图像、二次函数的值域、二次函数的最值。
2. 二次函数的变形:平移、伸缩、翻折。
3. 二次函数的解析式和图像的关系:二次函数的标准形式、顶点式、描点法。
4. 二次函数与相关问题:二次函数与一次函数的关系、二次函数与直线的位置关系、二次函数与求解问题。
三、三角函数1. 角度制与弧度制:角度与弧度的换算、弧度的性质与运算。
2. 任意角的三角比:正弦函数、余弦函数、正切函数及其定义域、值域、图像。
3. 三角函数的性质与公式:同角三角函数的性质、和差化积公式、倍角公式、半角公式等。
四、指数和对数函数1. 指数函数的概念和性质:指数函数的定义、指数函数的性质与运算规律、指数函数的图像与性质。
2. 对数函数的概念和性质:对数函数的定义、对数函数的性质与运算规律、对数函数的图像与性质。
3. 指数方程与对数方程的解法:指数方程与对数方程的性质、指数方程与对数方程的求解方法。
五、概率统计1. 随机事件与概率:随机事件的概念、样本空间、事件的概率。
2. 概率的运算:事件的相等、互斥、对立与对立事件的概率、事件的和与积的概率。
3. 条件概率与事件的独立性:条件概率的概念与计算、事件的独立性判定。
高一数学-八充分条件与必要条件 精品

§1.8.1 充分条件与必要条件教学目标1.理解推断符号“⇒”的含义;2.理解掌握充分条件、必要条件的意义及应用;3.培养学生的逻辑推理能力。
教学重点充分条件、必要条件的判断教学难点理解充分条件、必要条件的判断方法教具准备投影片共2张教学过程(I)复习回顾命题(1)为假;命题(2)、(3)、(4)为真。
引入:本节将在判断“若 p则q”命题的真假的基础上,研究p是q成立的充分条件还是必要条件问题。
(II)讲授新课1.推断符号“⇒”的含义:上述命题(2)、(3)、(4)为真,是由p经过推理可以得出q,即如果p成立,那么q一定成立,此时可记作“p⇒q”。
(若p则q,或“p蕴涵q”)又例如命题(1)为假,是由p经过推理得不出q,即即使p成立,推不出q成立,此时可记作“p⇏q”。
问题2:用推断符号“⇒”写出上述命题。
⇒(1)a>b⇏ac>bc; (2)a>b⇒a+c>b+c;(3)x≥0⇒x2≥0;(4)两三角形全等⇒两三角形面积相等。
2.充分条件与必要条件(1)定义(板书)说明:由上述定义中,“p⇒q”即如果具备了条件p,就足以保证q成立,所以p是q的充分条件,这点容易理解。
但同时说q是p的必要条件是为什么呢?应注意条件和结论是相对而言的。
由“p⇒q”等价命题是“┐q⇒┐p”,即若q不成立,则p就不成立,故q就是p 成立的必要条件了。
但还必须注意,q成立时,p可能成立,也可能不成立,即q成立不保证p一定成立。
问题3:回答上述问题(2)、(3)、(4)中的条件关系。
⇒(2)中:“a>b”是“a+c>b+c”的充分条件;“a+c>b+c”是“a>c”的必要条件。
(3)中:“x ≥0”是“x 2≥0”的充分条件;“x 2≥0”是“x ≥0”的必要条件。
(4)中:“两三角形全等”是“两三角形面积相等”的充分条件。
“两三角形面积相等”是“两三角形全等”的必要条件。
数学高一第八章知识点归纳

数学高一第八章知识点归纳高一数学第八章知识点归纳数学是一门理性与逻辑的科学,而高中数学则是对于初中数学知识的巩固与拓展。
在高一数学的学习过程中,第八章《三角函数》是一门重要的数学分支。
本章主要涉及三角函数的定义、性质与应用等内容,深入理解这些知识点对于高中数学的后续学习以及数学思维的培养具有重要意义。
本文将对高一数学第八章的知识点进行归纳总结,以帮助同学们更好地理解和掌握这一章节的内容。
1. 弧度制与角度制在三角函数的学习中,我们需要掌握并灵活运用弧度制与角度制。
弧度制是以圆半径等于1的圆的弧长为单位,角度制则是以度数为单位。
两者之间的转换关系是:1弧度=180°/π。
2. 常用角的正弦、余弦与正切正弦、余弦和正切是三角函数的基本概念。
以一个锐角Θ为例,定义正弦为对边与斜边的比值,余弦为邻边与斜边的比值,正切为对边与邻边的比值。
其中,对边是指一个角的对称边,邻边是指一个角的相邻边,斜边是指一个角的斜边。
3. 三角函数的正负对于任意一个角Θ,根据它所在的象限不同,三角函数的值会有正负变化。
四个象限都有变号的三角函数分别为正弦、余弦、正切。
例如:在第一象限内,正弦、余弦、正切均为正值;在第二象限内,正弦为正值,余弦和正切均为负值;以此类推。
4. 三角函数的周期性所有三角函数都具有周期性,即在某一个固定的角度范围内,三角函数的值会不断重复。
以正弦函数为例,它的周期为2π,即在0到2π的范围内,正弦函数的值会不断重复。
5. 三角函数的图像与性质通过绘制正弦、余弦以及正切函数的图像,可以帮助我们更好地理解它们的性质。
正弦函数的图像是一条连续且周期为2π的曲线,其最大值为1,最小值为-1;余弦函数的图像也是一条连续且周期为2π的曲线,最大值为1,最小值同样为-1;正切函数的图像是一系列由直线组成的曲线,它有无穷多个零点。
6. 三角函数之间的基本关系正弦、余弦、正切等三角函数之间有一系列的基本关系。
数学高一第八章知识点

数学高一第八章知识点高一的数学学习中,第八章是一个重要的章节,主要介绍了几个重要的知识点,包括函数、二次函数和函数的图像等。
下面是对这些知识点的详细介绍。
1. 函数函数是数学中的一个重要概念,简单来说,函数是指两个变量之间的依赖关系。
通常用f(x)来表示函数,其中x是自变量,f(x)是函数值或因变量。
函数可以用不同的表达形式表示,比如显式函数、隐式函数、参数方程等。
函数的定义域和值域是函数的两个重要概念,分别表示自变量和因变量的取值范围。
2. 二次函数二次函数是一类特殊的函数,表达式一般为f(x) = ax^2+bx+c,其中a、b和c是常数且a不等于0。
二次函数的图像呈现抛物线的形状,其开口方向取决于a的正负。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
通过分析二次函数的系数,可以确定其图像的特征,如顶点、对称轴、零点等。
3. 函数的图像图像是研究函数性质的重要工具之一。
函数的图像可以通过绘制函数的坐标点来得到,也可以通过变换函数的基本图像得到。
常见的函数图像有直线、抛物线、三角函数等。
绘制函数图像时,可以确定函数的特征点,如零点、最值点、拐点等,从而更好地理解函数的性质。
4. 函数的性质函数的性质是指函数在数学上的一些重要特点。
常见的函数性质有奇偶性、单调性、周期性等。
奇偶性指函数的对称性,即f(x) = f(-x)时函数为偶函数,f(x) = -f(-x)时函数为奇函数。
单调性指函数的增减趋势,可以通过导数的正负来判断函数的单调性。
周期性指函数的图像在横坐标上有重复的规律。
5. 函数的应用函数在实际生活和各个学科中都有广泛的应用。
在物理学中,函数可以用来描述物体的运动规律;在经济学中,函数可以用来描述供求关系;在工程学中,函数可以用来描述信号的变化规律。
函数的应用涉及到数学与现实世界的联系,帮助我们更好地理解和解决实际问题。
以上是数学高一第八章的知识点介绍,通过学习这些知识点,我们可以更好地理解和应用数学,在解决实际问题中发挥作用。
高一数学第八章知识点总结

高一数学第八章知识点总结第八章是高一数学的重要章节,主要涉及到函数与导数的相关知识。
下面将对该章节的知识点进行总结。
一、函数的概念和性质函数是一种特殊的关系,它将一个自变量的值与一个因变量的值相对应。
函数可以用图像、表格、公式等形式表示。
函数的定义域、值域、分段函数、奇偶性等都是函数的重要性质。
二、函数的基本类型1. 一次函数:y = kx + b,k为斜率,b为截距。
一次函数的图像是一条直线,斜率决定了直线的倾斜程度,截距决定了直线与y轴的交点。
2. 二次函数:y = ax² + bx + c,a≠0。
二次函数的图像是一条抛物线,开口方向由二次项系数a的正负确定。
3. 反比例函数:y = k/x,k≠0。
反比例函数的图像是一个双曲线,通过原点,随着x的增大,y的值逐渐减小或增大。
4. 幂函数:y = x^a,a为常数。
幂函数的图像形状多种多样,a的正负和大小决定了图像的特征。
三、函数的图像与性质1. 函数的图像可以通过函数的定义域、值域、单调性、最值等性质来确定。
2. 函数的单调性可以分为增函数和减函数,增函数表示随着自变量的增加,函数值也随之增加;减函数表示随着自变量的增加,函数值却减小。
3. 函数的最值表示在定义域范围内的最大值和最小值。
四、导数的概念与性质导数是函数的一个重要属性,表示函数在某一点的变化率。
导数的定义是函数在该点的极限值。
导数可以用于求函数图像的切线方程、函数的单调区间、函数的极值等。
五、导数的计算法则1. 基本导数法则:常数函数的导数为0,幂函数的导数为该幂次的系数乘以幂次减1。
2. 和、差、积的导数法则:和、差、积的导数等于各个函数的导数之和、差、积。
3. 商的导数法则:商的导数等于分子的导数乘以分母减去分母的导数乘以分子,再除以分母的平方。
六、导数的应用1. 函数的极值问题:通过求函数的导数,可以确定函数的极值点及极值。
2. 函数的单调性:通过求函数的导数,可以确定函数的单调递增或单调递减区间。
高一数学 第八讲 基本不等式

第八讲 基本不等式1.∀a ,b ∈R ,有a 2+b 2≥2ab ,当且仅当a =b 时,等号成立.特别地,如果a >0,b >0,我们用分别代替上式中的a ,b 2a bab+,当且仅当a =b 时等号成立.通常称此不等式为基本不等式,其中,2a b+叫做正数a ,b 的算术平均数,叫做正数a ,b 的几何平均数.2.基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.3.基本不等式与最大(小)值 口诀:和定积最大,积定和最小两个正数的和为常数时,它们的积有最大值;两个正数的积为常数时,它们的和有最小值. (1)已知x ,y 都是正数,如果和x +y 等于定值S ,那么当x =y 时,积xy 有最大值14S 2.(2)已知x ,y 都是正数,如果积xy 等于定值P ,那么当x =y 时,和x +y 有最小值4.基本不等式在解决实际问题中有广泛的应用,是解决最大(小)值问题的有力工具. 5.(0,0)2a baba b +>>. 6.能灵活应用基本不等式解决一些证明、比较大小问题.7.进一步熟练掌握基本不等式,能够通过拼凑、变形等利用基本不等式求最值. 8.能够利用基本不等式解决实际问题.考点一:用基本不等式证明不等式例2.若0a >,0b >,求证:11()()4a b a b++.【解析】证明:左式11b a a b=+++ 224b a +⨯==右式. ∴11()()4a b a b++.考点二:利用基本不等式直接求最值例3.已知x ,(0,)y ∈+∞,1x y +=,则xy 的最大值为( )A .1B .12 C .13D .14【答案】D【解析】因为x ,(0,)y ∈+∞,1x y +=, 所以21()24x y xy +=,当且仅当12x y ==时取等号, 故选D .考点三:与基本不等式有关的比较大小问题例1.已知a ,b R +∈,证1()2M a b =+,N =,2abP a b=+,则M ,N ,P 之间的大小关系是 .【答案】P N M 【解析】a ,b R +∈,∴11()222M a b ab N =+⨯= 222ab ab P N a b ab=+故答案为P N M考点四:基本不等式的应用例4.若a ,b R ∈,且0ab >,则下列不等式中,恒成立的是( ) A .222a b ab +> B .2a b ab + C .2b aa b+ D .112a bab+【答案】C【解析】A .2()0a b -,222a b ab ∴+,当且仅当a b =时等号成立,因此不正确. B .取a ,0b <时,2a b ab +不成立.C .0ab >,∴ab,0b a >,∴22b a b a a b a b +=,当且仅当a b =时取等号,正确.D .取a ,0b <时,112a b ab+不成立.故选C .1.已知0x >,0y >,若1x y +=,则1xy的最小值为( ) A .4B .14C .2D .12【答案】A【解析】因为0x >,0y >,1x y +=, 所以21()24x y xy +=,当且仅当12x y ==时取等号, 则14xy,即最小值为4. 故选A . 2.若0x <,则4x x+的最大值为( ) A .8- B .6- C .4- D .2-【答案】C【解析】因为0x <,则0x ->, 则44[()()]2()4x x x x x +=--+---=-, 当且仅当4x x-=-,即2x =-时取等号,此时取得最大值4-.故选C .3.已知x ,y 为正实数,且21x y +=,则21x y+的最小值为( ) A .4 B .7 C .9 D .11【答案】C【解析】x ,0y >且21x y +=,∴2121222()(2)5529x y x x y x y x y y x y +=++=+++=, 当且仅当22x y y x =,即11,33x y ==时,等号成立. ∴21x y+的最小值为9. 故选C .4.已知x ,y 为正实数,且4xy =,则4x y +的最小值是( ) A .4 B .8 C .16 D .32【答案】B 【解析】0x >,0y >4248x y xy ∴+=,当且仅当4x y =且4xy =,即4x =,1y =时取等号,4x y ∴+的最小值为8.故选B .5.设0a >,0b >,41a b +=,则11a b+的最小值为( )A .7B .9C .32D 3【答案】B【解析】0a >,0b >,41a b +=,111144()(4)()552549b a b a b a b a b a b a ∴+=++=+++=+=, 当且仅当4b a a b =,即126a b ==时取等号, ∴11a b+的最小值为9. 故选B .6.已知0x >,0y >,且191x y+=,则xy 的最小值为( ) A .100 B .81 C .36 D .9【答案】C 【解析】0x >,0y >,且191x y+=, 由基本不等式可得912xy ,当且仅当1912x y ==即2x =,18y =时取等号, 解可得36xy ,即xy 的最小值36. 故选C .7.已知3x >,13y x x =+-,则y 的最小值为( ) A .2 B .3 C .4 D .5【答案】D【解析】因为113333y x x x x =+=-++--,又因为3x >,所以30x ->, 所以5y ,当且仅当4x =时,等号成立, 故选D .8.设正数a ,b 满足21a b +=,21a b+的最小值为 . 【答案】9【解析】正数a ,b 满足21a b +=,∴212(2)22225529a b a b b a b a b a b a b a +++=+=+++=, 当且仅当22b aa b=且21a b +=,即13a b ==时取等号, 故答案为:9.9.(1)已知0x ≠,求1y x x=+的范围. (2)已知102x <<,求(12)y x x =-的最大值. 【解析】(1)根据题意,1y x x=+,(0)x ≠ 当0x >时,有1122y x x x x=+⨯⨯=,当且仅当1x =时等号成立, 当0x <时,有11[()]2y x x x x=+=--+--,当且仅当1x =-时等号成立, 故y 的取值范围为(-∞,2][2-,)+∞; (2)根据题意,102x <<,则0x >且120x -> 22(12)12121(12)()2228x x x x y x x ⨯-+-=-=⨯=,1(0)2x <<当且仅当14x =时等号成立, 即(12)y x x =-的最大值为18,1.若0a >,0b >,且240a b +-=,则ab 的最大值是( ) A .12B .1C .2D .4【答案】C【解析】0a >,0b >,且240a b +-=,4222a b ab ∴=+,即2ab ,即24ab ,2ab ∴,当且仅当22a b ==时取“= “,ab ∴的最大值是2,故选C .2.函数11(0)y x x x=++>的最小值为( ) A .1 B .2 C .3 D .4【答案】C 【解析】0x >,111213y x x x x ∴=+++=,当且仅当1x x=,即1x =时,等号成立, 11(0)y x x x∴=++>的最小值为3. 故选C .3.已知0x >,0y >,且4x y +=,则xy 最大值为( ) A .1 B .2 C .3 D .4【答案】D 【解析】0x >,0y >,且4x y +=,由基本不等式可得,2()42x y xy +=, 当且仅当2x y ==时,等号成立, 故xy 最大值为4. 故选D .4.已知m ,0n >,4m n mn +=,则m n +的最小值为( ) A .72B .7C .8D .9【答案】D【解析】4m n mn +=,∴411n m+=. 0m >,0n >,4144()()()5()529m n m m n m n n m n m n ∴+=++=+++,(当且仅当4m nn m=取等号).故m n +的最小值为9. 故选D .5.已知0t >,则函数222t t y t -+=的最小值为( )A .2-B .12C .3D .2【答案】C【解析】0t >,则函数22222212213t t y t t t t t-+==+--=,当且仅当1t =时取等号.∴函数222t t y t-+=的最小值为3.故选C .6.已知0x >,则23x x+的最小值为( )A .3B .C .D .【答案】D【解析】因为0x >, 所以2232326x x x x+=,当且仅当23x x=即x故选D .7.已知正数a 、b 满足1a b +=( )A .最小值12B .最小值2C .最大值12D .最大值2【答案】C【解析】因为正数a 、b 满足1a b +=,122a b ab+=,当且仅当a b =12, 故选C . 8.函数16(2)2y x x x =+>-+取最小值时x 的值为 【答案】2 【解析】1616222162622y x x x x =+=++--=++, 当且仅当24x +=即2x =时等号成立, 故答案为:2.9.已知正数x ,y 满足1x y +=. (Ⅰ)求xy 的最大值; (Ⅱ)求12x y+的最小值. 【解析】(Ⅰ)21()24x y xy +=,当且仅当12x y ==时,等号成立;(Ⅱ)122()223323x y x y y x y x x y x y x y x y+++=+=+++=+,当且仅当2y xx y=,即1x =,2y =时,等号成立; 10.求函数1(3)3y x x x =+>-的最小值. 【解析】因为3x >, 所以30x ->, 所以11332(3)3533y x x x x =+-+-+=--, 当且仅当133x x -=-即4x =时取等号,此时取得最小值5.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学复习八
(必修四第二章)
考试范围:xxx;考试时间:100分钟;命题人:xxx
1.已知下面四个命题:①;②;③;
④.其中正确的个数为()
A.1个B.2个C.3个D.4个
2.下列向量组中,能作为表示它们所在平面内所有向量的基底的是().
A.e1=(0,0),e2=(1,-2)B.e1=(-1,2),e2=(5,7)
C.e1=(3,5),e2=(6,10)
D.e1=(2,-3),e2=
3.已知=4,=8,与的夹角为120°,则=()
A.B.C.D.
4.化简得()
A.B.C.D.
5.已知向量,,则()
A.(3,7)B.(3,9)C.(5,7)D.(5,9)6.平面向量,,若,则等于
A.B.C.D.
7.已知向量,,,若为实数,,则
C.1 D.2
A.B.
8.已知等边的边长为1,则
A.B.C.D.
9.若向量,则( )
A.(1,1) B.(-1,-1)C.(3,7) D.(-3,-7)
10.在边长为的正三角形中,设,,若,则的值为()
A.
B.
C.
D.
已知向量与的夹角为且,;则
已知平面向量,满足,,则与的夹角为已知为单位向量,,则
已知,若,则的值为
已知单位向量,满足。
)求;
求的值。
已知是一个平面内的三个向量,其中=)||=,∥,求及·.
||=,且+2与3-垂直,求与的夹角
17.已知,
(1)求与的夹角;(2)求。
18.(本小题满分12分)已知,
(I)若,且∥(),求x的值;
(II)若,求实数的取值范围.
19.(本小题满分12分)已知向量.令
,
(1)求的最小正周期;
(2)当时,求的最小值以及取得最小值时的值.
20.向量,,已知,且有函数. (1)求函数的周期;
(2)已知锐角的三个内角分别为,若有,边
,,求的长及的面积.。
