人教A版高中必修二试题湖南省新田一中高中课时作业:1.3.2球的体积和表面积(无答案).docx
人教A版高中必修二试题1-3-2球的体积和表面积

高中数学学习材料金戈铁骑整理制作第1章 1.3.2一、选择题1.两个球的体积之比为8∶27,则它的表面积之比为( ) A .2∶3 B .4∶9 C .1∶2D .1∶3[答案] B[解析] 由体积比知半径之比为2∶3, ∴面积之比为4∶9,故选B.2.两个球的体积之和是12π,大圆周长之和是6π,则两球半径之差是( ) A .1 B .2 C .3D.32[答案] A[解析] 设两球半径为r 2,r 1,r 2>r 1,则 4π3(r 32+r 31)=12π,2π(r 2+r 1)=6π 解得r 1=1,r 2=2,∴r 2-r 1=1,故选A.3.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( ) A .16π B .20π C .24π D .32π [答案] C[解析] 设正四棱柱底面边长为a ,则S 底=a 2, ∴V =S 底·h =4a 2=16,∴a =2.又正四棱柱内接于球,设球半径为R ,则(2R )2=22+22+42=24,∴R =6,∴球的表面积为4πR 2=24π.4. 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )A.40003cm 3B.80003cm 3C .2000cm 3D .4000cm 3[答案] B[解析] 由俯视图知此几何体的底面为一个边长为20的正方形,结合正视图、侧视图知,此几何体为四棱锥,高为20,所以其体积为13×20×20×20=80003cm 3,故选B.5.两个半径为1的铁球,熔化成一个大球,这个大球的半径为( ) A .2 B. 2 C.32D.1234 [答案] C[解析] 设大球半径为r ,则43πr 3=2×4π3,∴r =32,故选C.6.若一个圆锥的底面半径和一个半球的半径相等,体积也相等,则它们的高度之比为( )A .2∶1B .2∶3C .2∶πD .2∶5[答案] A[解析] 13πr 2h =43πr 3×12∴h =2r ,故选A.7.湖面上漂着一个球,湖面结冰后将球取出,冰面上留下了一个面直径为24,深为8的空穴,则球的半径为( )A .8B .12C .13D .8 2[答案] C[解析] 122+(R -8)2=R 2,∴R =13.故选C.8.( 已知正方体的外接球的体积为323π,则该正方体的表面积为( )A.433B.163C.643D .32[答案] D[解析] 设球半径为R ,内接正方体棱长为a ,则4π3R 3=32π3,∴R =2,又3a 2=(2R )2,∴a 2=163,∴V 正方体=6a 2=32.9.在△ABC 中,AB =2,BC =1.5,∠ABC =120°,若将△ABC 绕直线BC 旋转一周,则所形成的旋转体的体积是( )A.92πB.72πC.52πD.32π [答案] D[解析] 本题是旋转问题....,考查锥体的体积公式和空间想像能力.如图所示,该旋转体的体积为圆锥CD 与圆锥BD 体积之差.在△ABD 中,AB =2,∠ABD =60°, ∴BD =1,AD =3,∴V =V 1-V 2=13×π×(3)2×(1+1.5)-13×π×(3)2×1=3π2.10.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12π [答案] D[解析] 本题是三视图还原为几何体的正投影问题.....,考查识图能力,空间想像能力.由题设可知,该几何体是圆柱的上面有一个球,圆柱的底面半径为1,高为3,球的半径为1,∴该几何体的表面积为2π×1×3+2π×12+4π×12=12π. 二、填空题11.已知某球体的体积与其表面积的数值相等,则此球体的半径为________. [答案] 3[解析] 43πR 3=4πR 2 ∴R =3.12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1、2、3,则此球的表面积为________.[答案] 14π[解析] 球的直径d =12+22+32=14, r =d2,S =4πr 2=14π. 13.一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为3,底面周长为3,则这个球的体积为______.[答案]4π3[解析] 如图所示的正六棱柱内接于球,则球心O 在体对角线AD ′上,∵正六边形周长为3, ∴其边长为12,∴AD =1,又DD ′=3,∴AD ′=AD 2+DD ′2=2, ∴球的体积V =4π3·⎝⎛⎭⎫AD ′23=4π3. 14. 已知四棱锥P -ABCD 的三视图如图所示,则四棱锥P -ABCD 的体积为________,其外接球的表面积为________.[答案] 236π[解析] 由俯视图知,四棱锥底面为边长为1的正方形,由正视图与侧视图知,该四棱锥的高为2,故其体积V =13×12×2=23,其外接球的直径为2R =12+12+22=6,∴表面积为4πR 2=4π×⎝⎛⎭⎫622=6π. 三、解答题*15.在球心同侧有相距9cm 的两个平行截面,它们的面积分别为49πcm 2和400πcm 2.求球的表面积.[解析] 如图为球的过球心的截面,由球的截面性质知,AO 1∥BO 2,且O 1、O 2分别为两截面圆的圆心,则OO 1⊥AO 1,OO 2⊥BO 2,设球的半径为R .∵π·O 2B 2=49π,∴O 2B =7cm , 同理πO 1A 2=400π,∴O 1A =20cm. 设OO 1=x cm ,则OO 2=(x +9)cm. 在Rt △OO 1A 中,R 2=x 2+202, 在Rt △OO 2B 中,R 2=(x +9)2+72, ∴x 2+202=72+(x +9)2,解得x =15, ∴R 2=x 2+202=252,∴R =25cm. ∴S 球=4πR 2=2 500πcm.∴球的表面积为2 500πcm 2.16.一个长方体的全面积为11,十二条棱长度之和为24.求长方体外接球的表面积. [解析] 设长方体长、高、宽分别为x 、y 、z ,则由已知条件知 ⎩⎪⎨⎪⎧xy +yz +zx =1124(x +y +z )=24,即⎩⎪⎨⎪⎧2xy +2yz +2xz =11 ①x +y +z =6 ②将②式两边平方与①式两边分别相减得,x 2+y 2+z 2=25, ∴长方体体对角线长为x 2+y 2+z 2=5, ∴外接球半径r =52,面积为4πr 2=25π.17.体积相等的正方体、球、等边圆柱的全面积分别是S 1、S 2、S 3,试比较它们的大小. [解析] 设正方体的棱长为a ,球的半径为R ,等边圆柱的底面半径为r ,则S 1=6a 2,S 2=4πR 2,S 3=6πr 2.由题意知,43πR 3=a 3=πr 2·2r ,∴R =334πa ,r =312πa ,∴S 2=4π⎝ ⎛⎭⎪⎫334πa 2=4π·3916π2a 2=336πa 2,S 3=6π⎝ ⎛⎭⎪⎫312πa 2=6π·314π2a 2=354πa 2,∴S 2<S 3.又6a 2>332πa 2=354πa 2,即S 1>S 3. ∴S 1、S 2、S 3的大小关系是S 2<S 3<S 1.18.一试管的上部为圆柱形,底部为与圆柱底面半径相同的半球形.圆柱形部分的高为h cm ,半径为r cm.试管的容量为108π cm 3,半球部分容量为全试管容量的16.(1)求r 和h ;(2)若将试管垂直放置,并注水至水面离管口4 cm 处,求水的体积. [解析] (1)∵半球部分容量为全试管容量的16,∴半球部分与圆柱体部分容量比为15,即15=43πr 3×12πr 2×h∴h =103r ,43πr 3×12=108π×16∴r =3(cm),h =10(cm). (2)V =43πr 3×12+πr 2×(h -4)=43π×33×12+π×32×6=72π(cm 3).。
人教A版全能练习必修2第一章第三节1.3.2球的体积和表面积 答案和解析

人教A 版全能练习必修2第一章第三节1.3.2球的体积和表面积学校:___________姓名:___________班级:___________考号:___________一、单选题1倍,那么体积扩大到原来的( )A .2倍B .C 倍 D2.若一个球的体积为,则它的表面积为( )A .9πB .10πC .11πD .12π 3.一个正方体的表面积与一个球的表面积相等,那么它们的体积的比值是( )A .6B .2C .2D .64.一个平面载一球得到直径为6cm 的圆面,球心到这个圆面的距离为4cm ,则球的体积为( )A .3100cm 3πB .3208cm 3πC .3500cm 3πD 3 5.已知长方体的长、宽、高分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对 6.如果两个球的体积之比为8:27,那么这两个球的表面积之比为( ) A .8﹕27 B .2﹕13 C .4﹕9 D .2﹕9 7.把3个半径为R 的铁球熔成一个底面半径为R 的圆柱,则圆柱的高为( ) A .R B .2R C .3R D .4R8.用与球心距离为1的平面去截面面积为π,则球的体积为A .323πB .83πC .D .3 9.如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为( )A .5003πcm 3 B .8663πcm 3 C .13723πcm 3 D .10003πcm 3 10.已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为( ) A .36π B .64π C .144π D .256π11.设A B C D ,,,是同一个半径为4的球的球面上四点,ABC 为等边三角形且其面积为D ABC -体积的最大值为A .B .C .D .二、填空题12.某几何体的三视图如图所示, 则其表面积为 .13. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为____.14.盛有水的圆柱形容器的内壁底面半径为5cm ,两个直径为5cm 的玻璃小球都浸没于水中,若取出这两个小球,则水面将下降______cm.15.已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若3AB =,4AC =,AB AC ⊥,112AA =,则球的表面积为______.三、解答题16.如图所示,半径为R的半圆内(其中30∠=)的阴影部分以直径AB所在直BAC︒线为轴,旋转一周得到一个几何体,求该几何体的表面积及体积.17.已知球的两平行截面的面积分别为5π和8π,它们之间的距离为1,且位于球心的同一侧,求这个球的表面积.AB=,18.由已知过球面上A,B,C三点的截面到球心的距离等于球半径的一半,且18 AC=,求球的表面积和体积.24BC=,30参考答案1.B【解析】【分析】根据球的体积公式,分别求得原来球的体积和变大后的球的体积,即可求解,得到答案.【详解】设球的半径为R ,则体积为3143V R π=,,体积为3324)33V R π==,则21V V =21V =, 故选B【点睛】本题主要考查了球的体积的计算与应用,其中解答中熟记球的体积公式,准确运算是解答的关键,着重考查了运算与求解能力,属于基础题.2.D【分析】利用球的体积公式,求得球的半径R =,再由球的表面积公式,即可求解.【详解】设球的半径为R ,可得343R π=,解得R = 所以球的表面积为2412S R ππ==.故选D【点睛】本题主要考查了球的表面积和体积公式的应用,其中解答中熟记球的表面积和体积公式,准确计算是解答的关键,着重考查了运算与求解能力,属于基础题.3.A【分析】设正方体的边长为a ,球的半径为R ,根据表面积相等,求得a R =,再由体积公式,即可求解.【详解】设正方体的边长为a ,球的半径为R ,则2264a R π=,解得a R =,又由333344363V a V R ππ⎛⎫==⨯= ⎪ ⎪⎝⎭正方体球. 故选A【点睛】本题主要考查了正方体和球的体积公式的应用,其中解答根据两几何体的表面积相等,求得正方体的棱长和球的半径的关系是解答的关键,着重考查了运算与求解能力,属于基础题. 4.C【解析】【分析】根据球的性质知,球的半径5R ==,再利用球的体积公式,即可求解,得到答案.【详解】设球的半径为R,根据球的性质知,球的半径5(cm)R ==, 又由球的体积公式,可得3345005(cm )33V ππ=⨯=球. 故选C【点睛】本题主要考查了球的截面性质,以及球的体积的计算,其中解答中根据球的截面的性质,求得球的半径是解答的关键,着重考查了运算与求解能力,属于基础题.5.B【分析】根据长方体的对角线长等于其外接球的直径,求得2252R =,再由球的表面积公式,即可求解.【详解】设球的半径为R,根据长方体的对角线长等于其外接球的直径,可得2R =解得2252R =,所以球的表面积为22544502S R πππ==⨯=球.【点睛】本题主要考查了长方体的外接球的性质,以及球的表面积的计算,其中解答中熟练应用长方体的对角线长等于其外接球的直径,求得球的半径是解答的关键,着重考查了运算与求解能力,属于基础题.6.C【分析】设两个球的半径分别为12,R R ,则12827V V =,解得1223R R =,再利用球的表面积公式,即可求解.【详解】 由题意,设两个球的半径分别为12,R R ,则3113224834273R V V R ππ==,解得1223R R =, 所以22111222224449S R R S R R ππ===, 故选C.【点睛】本题主要考查了球的表面积和体积公式的应用,其中解答中熟记球的表面积和体积公式,准确运算是解得关键,着重考查了运算与求解能力,属于基础题.7.D【分析】由球的体积公式,可求出3个半径为R 的铁球的总体积,进而根据熔化过程中体积不变,代入圆柱体积公式可求出圆柱的高.【详解】3个半径为R 的铁球总体积V=3×43πR 3=4πR 3 由铸成一个底面半径为R 的圆柱时总体积不变故V=πR 2H=4πR 3解得H=4R故选D .本题考查的知识点是球的体积,圆柱的体积,解答的关键是理解据熔化过程中体积不变. 8.D【解析】截面半径1r =,所以R ==,所以体积3433V R π==,故选D . 9.A【解析】作出该球轴截面的图像如下图所示,依题意2BE =,4AE CE ==,设DE x =,故2AD x =+,因为222AD AE DE =+,解得3x =,故该球的半径5AD =,所以3450033V R ππ==.【学科网考点定位】本题考查球体的体积公式,考查学生的空间想象能力.10.C【详解】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时2311136326O ABC C AOB V V R R R --==⨯⨯==,故6R =,则球O 的表面积为24144S R ππ==,故选C .考点:外接球表面积和椎体的体积.11.B【详解】分析:作图,D 为MO 与球的交点,点M 为三角形ABC 的中心,判断出当DM ⊥平面ABC时,三棱锥D ABC -体积最大,然后进行计算可得.详解:如图所示,点M 为三角形ABC 的中心,E 为AC 中点,当DM ⊥平面ABC 时,三棱锥D ABC -体积最大此时,OD OB R 4===2ABC S AB == AB 6∴=,点M 为三角形ABC 的中心2BM 3BE ∴==Rt OMB ∴中,有OM 2==DM OD OM 426∴=+=+=()max 163D ABC V -∴=⨯=故选B.点睛:本题主要考查三棱锥的外接球,考查了勾股定理,三角形的面积公式和三棱锥的体积公式,判断出当DM ⊥平面ABC 时,三棱锥D ABC -体积最大很关键,由M 为三角形ABC 的重心,计算得到2BM 3BE ==OM ,进而得到结果,属于较难题型.12. 【解析】综合三视图可知,,立体图是一个半径r=1的半个球体.其表面积 =13.92π 【解析】设正方体边长为a ,则226183a a =⇒= ,外接球直径为34427923,πππ3382R V R ====⨯=. 【考点】 球【名师点睛】求多面体的外接球的面积和体积问题常用方法有(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心,本题就是第三种方法.14.53【解析】【分析】由两个小球的直径为5cm ,则半径为52cm ,得到两个小球的体积的和为3125()3cm π,再由圆柱的体积公式,列出方程,即可求解.【详解】设取出小球后,容器中水面下降h cm ,由两个小球的直径为5cm ,则半径为52cm ,所以两个小球的体积为33451252()323cm ππ⎡⎤⎛⎫⨯⨯=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦, 则212553h ππ=⨯⨯,解得53h cm , 即若取出这两个小球,则水面将下降53cm . 故答案为53【点睛】本题主要考查了球的体积公式,以及圆柱的体积公式的应用,其中解答熟记球的体积公式和圆柱的体积公式,准确计算是解答的关键,着重考查了运算与求解能力,属于基础题. 15.169π【解析】【分析】把直三棱柱111ABC A B C -的补成一个长方体,则直三棱柱111ABC A B C -的外接球和长方体的外接球是同一个球,由长方体的对角线长等于球的直径,求得球的半径,再利用球的表面积公式,即可求解.【详解】由题意,直三棱柱111ABC A B C -的底面ABC ∆为直角三角形,可把直三棱柱111ABC A B C -的补成一个长方体,则直三棱柱111ABC A B C -的外接球和长方体的外接球是同一个球,又由长方体的对角线长等于球的直径,且13,4,12AB AC AA ===,即213R ===,即132R =, 所以球的表面积为221344()1692S R πππ==⨯=. 故答案为:169π【点睛】 本题主要考查了直三棱柱与球的组合体问题,以及球的表面积的计算,其中解答中根据组合体的结构特征,求得球的半径是解答的关键,着重考查了运算与求解能力,属于基础题.16235,6R R π 【分析】根据旋转体的定义,得到该平面图形旋转后是一个球挖去两个同底的圆锥,利用球和圆锥的表面积和体积公式,准确计算,即可求解.【详解】如图所示,过C 作1CO AB ⊥于1O ,在半圆中可得90BCA ︒∠=,又30BAC ︒∠=,2AB R =,∴AC =,BC R =,12CO R =,∴12322AO S R R ππ=⨯=圆锥侧,1222BO S R R R π=⨯⨯=圆锥侧,∴112++AO BO S S S S R ==球几何体表圆锥侧圆锥侧,2R . 又343V R =π球,1221111134AO V AO CO R AO ππ=⋅⋅⋅=⋅圆锥,12211111CO 34BO V BO BO R ππ=⋅⋅=⋅圆锥, ∴()1135+6AO BO V V V V R π=-=球几何体圆锥圆锥.【点睛】本题主要考查了旋转体的概念,以及球的表面积与体积和圆锥的表面积公式的应用,其中解答中根据旋转体的定义确定出几何体的结构特征,准确利用公式计算是解答的关键,着重考查了空间想象能力,以及运算与求解能力,属于基础题.17.36π【解析】【分析】设以1r 为半径的截面面积为5π,以2r 为半径的截面面积为8π,且121O O =,设球的半径为R ,2OO x =,根据球的截面性质,求得1x =,进而得到3R =,利用球的表面积公式,即可求解.【详解】如图所示,设以1r 为半径的截面面积为5π,以2r 为半径的截面面积为8π,且121O O =, 设球的半径为R ,2OO x =,根据球的截面性质,可得2222r R x =-且()22228r R x πππ=-=,2221(1)r R x =-+且2221(1)5r R x πππ⎡⎤=-+=⎣⎦,于是()2222[(1)]85R x R x ππππ---+=-, 即2222213R x R x x --+++=,整理得22x =,解得1x =, 又∵()228R x ππ-=,∴218R -=,即29R =,解得3R =,∴球的表面积2244336S R πππ==⨯=.【点睛】本题主要考查了球的截面性质的应用,以及球的表面积的计算,其中解答中熟练应用球的截面性质,求得球的半径是解答的关键,着重考查了运算与求解能力,属于基础题.18.1200,π【分析】由题意得ABC ∆是直角三角形,且90B ︒∠=,得到斜边AC 为截面圆O '的直径,再利用球的截面的性质,求得球的半径R =【详解】由题意,知18AB =,24BC =,30AC =,可得222AC AB BC =+,所以ABC ∆是直角三角形,且90B ︒∠=,又球心O 在截面ABC 上的正投影O '为截面圆的圆心,也是Rt ABC ∆的外接圆的圆心, ∴斜边AC 为截面圆O '的直径.设球的半径为R ,截面圆的半径为r ,在Rt CO O '∆中,由题设知1sin 2OO O CO OC ''∠==,所以30O CO '︒∠=,又由cos302r R ︒==,即R =,又230r AC ==,∴15r =,∴R =∴球的表面积22441200S R πππ==⨯=,球的体积334433V R ππ==⨯=. 【点睛】本题主要考查了球的截面性质的应用,以及球的表面积与体积的计算,其中解答中熟练应用球的截面性质,求得球的半径是解答的关键,着重考查了空间想象能力,以及运算与求解能力,属于基础题.。
人教新课标版数学高一-人教A必修二习题 1.3.2球的体积和表面积

(本栏目内容,在学生用书中以独立形式分册装订!)一、选择题(每小题5分,共20分)1.两个球的半径之比为2∶3,那么这两个球的表面积之比为( )A .2∶3B .4∶9 C.2∶ 3 D .8∶27解析: 设两球的半径分别为r 1,r 2,表面积分别为S 1,S 2,则S 1S 2=4πr 214πr 22=r 21r 22=49.故选B. 答案: B2.(2015·德阳市中江县龙台中学高二(上)期中)设长方体的长、宽、高分别为2a 、a 、a ,其顶点都在一个球面上,则该球的表面积为( )A .3πa 2B .6πa 2C .12πa 2D .24πa 2解析: 根据题意球的半径R 满足(2R )2=6a 2,所以S 球=4πR 2=6πa 2,故选B.答案: B3.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12π解析: 由几何体的三视图可知此几何体是圆柱体与球体的组合体,其表面积S =4πR 2+2πr 2+2πr ·h ,代入数据得S =4π+2π+2π×3=12π.故选D.答案: D4.(2015·唐山市玉田县林南仓中学高二(上)期中)若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为S1、S2,则S1∶S2等于()A.1∶1 B.2∶1C.3∶2 D.4∶1解析:由题意可得圆柱的底面直径和高都与球的直径相等,设球的半径为1,则S1=6π,S2=4π.所以S1∶S2=3∶2,故选C.答案: C二、填空题(每小题5分,共15分)5.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为2,则此球的体积为________.解析:利用截面圆的性质先求得球的半径长.如图,设截面圆的圆心为O′,M为截面圆上任一点,则OO′=2,O′M=1,∴OM=(2)2+1=3,即球的半径为3,∴V=4π(3)3=43π.3答案:43π6.(2015·吕梁学院附中高二(上)月考)若各顶点都在一个球面上的长方体的高为4,底面边长都为2,则这个球的表面积是________.解析:长方体的体对角线长为22+22+42=26,球的直径是2R=26,所以R=6,所以这个球的表面积S=4π(6)2=24π.答案:24π7.(2015·河源市高二(上)期中)湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下了一个直径为6 cm,深为1 cm的空穴,则该球半径是________ cm,表面积是________cm2.解析:设球心为O,OC是与冰面垂直的一条球半径,冰面截球得到的小圆圆心为D,AB为小圆D的一条直径,设球的半径为R,则OD=R-1,则(R-1)2+32=R2,解之得R=5 cm,所以该球表面积为S=4πR2=4π×52=100π(cm2).答案:5100π三、解答题(每小题10分,共20分)8.如果一个几何体的正视图与侧视图都是全等的长方形,边长分别是4 cm与2 cm,如图所示,俯视图是一个边长为4 cm的正方形.求该几何体的外接球的体积.解析:由题意可知,该几何体是长方体,底面是正方形,边长是4,高是2.由长方体与球的性质可得,长方体的体对角线是球的直径,记长方体的体对角线为d,球的半径是r,d=16+16+4=36=6(cm),所以球的半径为r=3 cm.因此球的体积V=4πr3=43×27π=36π(cm3),3所以外接球的体积是36π cm3.9.(2015·大同一中高二(上)月考)如图所示(单位:cm)四边形ABCD是直角梯形,求图中阴影部分绕AB 旋转一周所成几何体的表面积和体积.解析: 12S 球=12×4π×22=8π(cm 2), S 圆台侧=π(2+5)(5-2)2+42=35π(cm 2), S 圆台下底=π×52=25π(cm 2),即该几何体的表面积为8π+35π+25π=68π(cm 2).又V 圆台=π3×(22+2×5+52)×4=52π(cm 3), V 半球=12×4π3×23=16π3(cm 3). 所以该几何体的体积为V 圆台-V 半球=52π-16π3=140π3(cm 3).。
2016秋数学人教A版必修2练习:1.3.2 球的体积和表面积 含解析
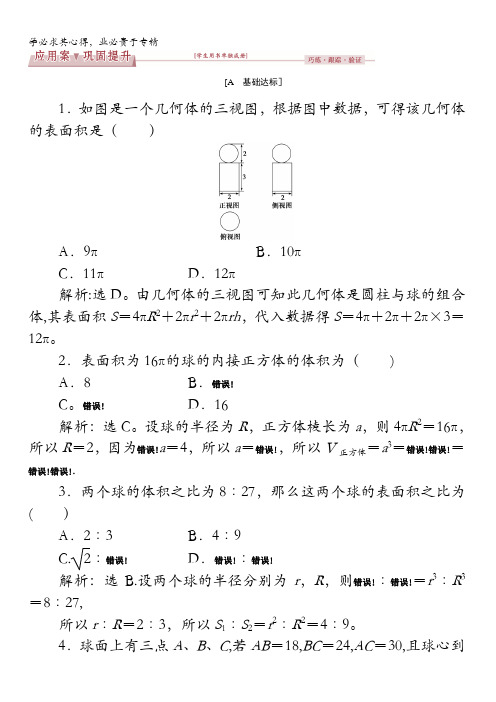
[A基础达标]1.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A.9πB.10πC.11πD.12π解析:选D。
由几何体的三视图可知此几何体是圆柱与球的组合体,其表面积S=4πR2+2πr2+2πrh,代入数据得S=4π+2π+2π×3=12π。
2.表面积为16π的球的内接正方体的体积为()A.8 B.错误!C。
错误!D.16解析:选C。
设球的半径为R,正方体棱长为a,则4πR2=16π,所以R=2,因为错误!a=4,所以a=错误!,所以V正方体=a3=错误!错误!=错误!错误!.3.两个球的体积之比为8∶27,那么这两个球的表面积之比为( )A.2∶3 B.4∶9C.2∶错误!D.错误!∶错误!解析:选B.设两个球的半径分别为r,R,则错误!∶错误!=r3∶R3=8∶27,所以r∶R=2∶3,所以S1∶S2=r2∶R2=4∶9。
4.球面上有三点A、B、C,若AB=18,BC=24,AC=30,且球心到△ABC所在平面的距离等于球半径的一半,则这个球的表面积为()A。
错误!πB.300πC.1 200πD.1 600π解析:选C。
设球的半径为R,由题意得,错误!R=15,所以R =10错误!,即S球=4πR2=1 200π.5.若等边圆柱(轴截面是正方形)、球、正方体的体积相等,则它们的表面积的大小关系是()A.S球<S圆柱<S正方体 B.S正方体<S球<S圆柱C.S圆柱<S球<S正方体 D.S球<S正方体<S圆柱解析:选A.设等边圆柱底面圆半径为r,球半径为R,正方体棱长为a,则πr2·2r=错误!πR3=a3,错误!错误!=错误!,错误!错误!=2π,S圆柱=6πr2,S球=4πR2,S正方体=6a2,错误!=错误!=错误!·错误!错误!=错误!<1,错误!=错误!=错误!·错误!错误!=错误!>1.故选A。
6.已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面得到圆M,若圆M的面积为3π,则球O的表面积等于________.解析:设球的半径为R,圆M的半径为r,则πr2=3π,即r2=3.由题意得R2-错误!错误!=3,所以R2=4,所以4πR2=16π。
人教A版高一必修二_132球的体积和表面积数学试题(有答案)

人教A版高一必修二 1.3.2球的体积和表面积数学试题一、单选题1. 如果三个球的半径之比是1︰2︰3,那么最大球的表面积是其余两个球的表面积之和的()A.倍B.倍C.2倍D.3倍2. 若两球的体积之和是12π,经过两球球心的截面圆周长之和为6π,则两球的半径之差为( )A.1B.2C.3D.43. 一个正方体表面积与一个球表面积相等,那么它们的体积比是()A. B. C. D.4. 球的表面积与它的内接正方体的表面积之比是()A. B. C. D.5. 正方体内切球与外接球体积之比为()A.1∶B.1∶3C.1∶3D.1∶9参考答案与试题解析人教A 版高一必修二 1.3.2球的体积和表面积数学试题一、单选题 1.【答案】 B【考点】球的表面积和体积 【解析】设小球半径为1,则大球的表面积S 加=36π,S 加+S 加=20π,36π20π=95故答案为B .【解答】 此题暂无解答 2.【答案】 A【考点】球的表面积和体积旋转体(圆柱、圆锥、圆台) 球内接多面体 【解析】设两球的半径分别为R 、f (R >r ),则由题意得{4π3R 3+4π3,3=12π,2πR +2π=6π,解得{R =2y =1,故R −r =1 【解答】 此题暂无解答 3. 【答案】 A【考点】球的表面积和体积 【解析】设正方体的棱长为a ,球的半径为R, 由6a 2=4πR 2得a R =√2π3,故V1V 2=a 343πR 2=3π4√2π3)3=√6π6故答案为A . 【解答】此题暂无解答 4.【答案】 C【考点】由三视图求体积 二次函数的应用函数的最值及其几何意义【解析】试题分析:设正方体棱长为a.因为,球的直径是其内接正方体的对角线,所以,2r=√3a,球的表面积与它的内接正方体的表面积之比是:4πr26a2=π(√3a)26a2=π2,故选C.【解答】此题暂无解答5.【答案】C【考点】球的表面积和体积【解析】设正方体的棱长为a,则它的内切球的半径为12a,它的外接球的半径为√32a,故所求体积之比为1:3√3故答案为C.【解答】此题暂无解答。
人教新课标版数学高一-必修2训练 1.3.2球的体积和表面积

数学·必修2(人教A 版)1.3 空间几何体的表面积与体积1.3.2 球的体积和表面积基础达标1.若球的大圆周长是C ,则这个球的表面积是( )A.C 24πB.C 22πC.C 2πD .2πC 2 解析:由2πR =C ,得R =C 2π,∴S 球=4πR 2=C 2π. 答案:C2.两个球的表面积之差为48π,它们的大圆周长之和为12π,这两个球的半径之差为( )A .4B .3C .2D .1解析:由4πR 2-4πr 2=48π,2πR +2πr =12π,得R -r =2.3.正方体的内切球和外接球的半径之比为( ) A.3∶1 B.3∶2 C .2∶ 3 D.3∶3解析:内切球与外接球的半径之比为正方体棱长与体对角线长之比,即为3∶3.答案:D4.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.8π3B.82π3 C .82π D.32π3解析:截面面积为π,则该小圆的半径为1,设球的半径为R ,则R 2=12+12=2,∴R =2,V =43πR 3=82π3. 答案:B5.球的半径扩大为原来的2倍,它的体积扩大为原来的________ 倍.解析:设球原来半径为R ,则扩大后半径为2R ,V 球原=43πR 3,V 球扩=43π(2R )3=8V 球原.6.将一钢球放入底面半径为3 cm的圆柱形玻璃容器中,水面升高4 cm,则钢球的半径是________.解析:圆柱形玻璃容器中水面升高4 cm,则钢球的体积为V=π×32×4=36π,即有43πR3=36π,∴R=3.答案:3 cm巩固提升7.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1、2、3,则此球的表面积为________.答案:14π8.球面上有四个点P,A,B,C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.解析:PA,PB,PC两两互相垂直,将三棱锥补成一个以P为顶点的正方体,且PA=PB=PC=a,∴正方体的对角线长就是球的直径,∴2R=3a,R=32a,∴这个球的表面积为S 球=4πR 2=4π⎝ ⎛⎭⎪⎫32a 2=3πa 2.9.把直径分别为6 cm,8 cm,10 cm 的三个铜球熔制成一个较大的铜球,再把球削成一个棱长最长的正方体,求此正方体的体积.解析:设熔制后的大铜球半径为r ,则43π(33+43+53)=43πr 3,∴r =6 cm.据题意:此正方体为球的内接正方体,球的直径即为正方体对角线的长,故正方体的棱长a =2r 3=123=4 3 cm. ∴V 正方体=a 3=(43)3=192 3 cm 3.10.如图所示,一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R ,正四棱台的上、下底面边长分别为2.5R 和3R ,斜高为0.6R .(1)求这个容器盖子的表面积(用R 表示,焊接处对面积的影响忽略不计);解析:由题意,知S正四棱台=4×12×(2.5R+3R)×0.6R+(2.5R)2+(3R)2=21.85R2,S球=4πR2,所以这个盖子的表面积为S表=(21.85+4π)R2,(2)若R=2 cm,为盖子涂色时所用的涂料每0.4 kg可以涂1 m2,计算为100个这样的盖子涂色用涂料多少千克(精确到0.1 kg).解析:取R=2,π=3.14,得S表=137.64(cm2).100个这样的盖子共需涂料约为(137.64×100)÷10 000×0.4≈0.6 kg.。
人教A版高一数学必修二 1-3-2 球的表面积与体积 检测

1.3.2 球的体积和表面积时间:30分钟,总分:70分 班级: 姓名:一、选择题 (共6小题,每题5分,共30分)1.把球的表面积扩大到原来的2倍,那么体积扩大到原来的 ( )A.2倍B.2倍C.倍D.倍2.将棱长为2的正方体削成一个体积最大的球,则这个球的体积为 ( ) A.π B. C.π D.4π 3、一个几何体的三视图如图所示,其中府视图与侧视图均为半径是1的圆,则这个几何体的体积是( )A .3πB .23πC .πD .43π 4.若长方体的一个顶点上三条棱长分别是1、2、2,且它的八个顶点都在同一球面上,则这个球的表面积是( )A .6πB .9πC .3πD .12π5、平面α截球O 的球面所得圆的半径为1,球心O 到平面α,则球O 的表面积为( )A .B .12πC .8πD .4π 6、设长方体的长、宽、高分别为2a 、a 、a ,其顶点都在一个球面上,则该球的表面积为( )A .3πa 2B .6πa 2C .12πa 2D .24πa 2二、填空题 (共4小题,每题5分,共20分)7、圆柱形容器的内壁底半径是10 cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm,则这个铁球的表面积为________ cm2.8.球内切于正方体的六个面,正方体的棱长为a,则球的表面积为________.9、已知H是球O的直径AB上一点,:1:2AH HB=,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为________.10、如图,球O的半径为5,一个内接圆台的两底面半径分别为3和4(球心O在圆台的两底面之间),则圆台的体积为.三、解答题(共2小题,每题10分,共20分)11、某街心花园有许多钢球(钢的密度为7.9 g/cm3),每个钢球重145 kg,并且外径等于50 cm,试根据以上数据,判断钢球是空心的还是实心的.如果是空心的,请你计算出它的内径(π取3.14,结果精确到1 cm,2.243≈11.24098).12、如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成.已知半球的直径是6 cm,圆柱筒高为2 cm.(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?(2)要在2500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?。
2019-2020学年人教A版必修二 1.3.2 球的体积和表面积 课时作业

课时作业(六)1.若球的大圆面积扩大为原来的2倍,球的体积扩大为原来的( ) A .8倍 B .4倍 C .22倍 D .2倍答案 C解析 根据球的体积公式知,体积比为半径比的立方.2.设长方体的长、宽、高分别为2a ,a ,a ,其顶点都在一个球面上,则该球的表面积为( ) A .3πa 2 B .6πa 2 C .12πa 2 D .24πa 2答案 B解析 由题可知,长方体的长、宽、高分别为2a ,a ,a ,其顶点在同一个球面上,所以球的直径等于长方体的体对角线的长,故2R =4a 2+a 2+a 2,解得R =62a ,所以球的表面积S =4πR 2=6πa 2,故选B.3.两个球的表面积之差为48π,它们的大圆周长之和为12π,这两个球的半径之差为( ) A .4 B .3 C .2 D .1答案 C解析 ⎩⎪⎨⎪⎧4πR 2-4πr 2=48π,2πR +2πr =12π⇒R -r =2.4.某几何体的三视图如图所示,它的体积为( )A.72πB.48πC.30πD.24π答案 C解析首先通过观察三视图判断出几何体的直观图,然后按照体积公式进行计算.此组合体由半个球体与一个圆锥组成,其体积V=12×4 3π×33+13π×32×52-32=30π,故选C.5.正四面体内切球与外接球的体积的比为()A.1∶3 B.1∶9C.1∶27 D.1∶81(注:正四面体是特殊的三棱锥,它的每个面都是正三角形.) 答案 C解析内切球半径是高的14,外接球半径是高的34,所以半径之比为1∶3,故体积之比为1∶27.6.64个直径都为a4的球,记它们的体积之和为V甲,表面积之和为S 甲;一个直径为a的球,记其体积为V乙,表面积为S乙,则() A.V甲>V乙且S甲>S乙B.V甲<V乙且S甲<S乙C.V甲=V乙且S甲>S乙D.V甲=V乙且S甲=S乙答案 C解析 V 甲=64×4π3×(a 4×12)3=16πa 3, S 甲=64×4π×(a 4×12)2=4πa 2, V 乙=43π×(a ×12)3=16πa 3, S 乙=4π×(a ×12)2=πa 2, ∴V 甲=V 乙,S 甲>S 乙,选C.7.一个球的表面积是144π cm 2,它的体积是________ cm 3. 答案 288π8.半径为R 的球的外切圆柱的表面积是________. 答案 6πR 29.将一个半径为R 的木球削成尽可能大的正方体,则此正方体的体积为________. 答案 893R 3解析 该正方体与球内接,球的直径为正方体的体对角线. 10.体积为8的一个正方体,其全面积与球O 的表面积相等,则球O 的体积等于________. 答案86ππ解析 设球的半径为R ,依题设有6(38)2=4πR 2,则R 2=6π,球的体积为43πR 3=43π⎝ ⎛⎭⎪⎫6π32=86ππ.11.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为________厘米.答案 12解析 πr 2h =43πR 3,R =364×27=12.12.正四棱锥S -ABCD 的底面边长和各侧棱长都为2,点S 、A 、B 、C 、D 都在同一个球面上,则该球的体积为________. 答案 43π解析 球内接正四棱锥各棱长为2,则该球半径为1(连接正方体六个面的中心所得八面体就是两个棱长都相等的正四棱锥重合底面所得),所以球的体积为V =43π.13.如图,半球内有一个内接正方体,正方体的一个面在半球的底面圆内,若正方体棱长为6,求球的表面积和体积.解析 作轴截面如图所示,CC ′=6,AC =2·6=23,设球的半径为R ,则R 2=OC 2+CC ′2=(6)2+(3)2=9. ∴R =3,∴S 球=4πR 2=36π,V 球=43πR 3=36π.14.已知正三棱锥的高为1,底面边长为26,其内有一个球和该三棱锥的四个面都相切.求: (1)棱锥的全面积; (2)球的半径R.解析 (1)如图所示,正三棱锥A -BCD.由题可知AE =1,CD =26,EF =13×32×CD = 2.∴侧面的高AF =AE 2+EF 2= 3.∴S 全=3×26×3×12+26×32×26×12 =92+6 3.(2)由题可得1-R 3=R2,∴R =6-2.1.下图是一个正方体的展开图,将其折叠起来,变成正方体后的图形是( )答案 B解析 ∵在这个正方体的展开图中,与有圆的面相邻的三个面中都有一条直线,当变成正方体后,这三条直线应互相平行,∴选B. 2.已知三个球的半径R 1,R 2,R 3满足R 1+2R 2=3R 3,则它们的表面积S 1,S 2,S 3,满足的等量关系是( ) A .S 1+2S 2=3S 3 B .S 1+4S 2=9S 3 C.S 1+2S 2=3S 3 D.S 1+S 2=S 3答案 C解析 S 1=4πR 12,S 1=2πR 1,同理:S 2=2πR 2,S 3=2πR 3,即R 1=S 12π,R 2=S 22π,R 3=S 32π,由R 1+2R 2=3R 3,得S 1+2S 2=3S 3.3.体积相等的球、正四面体和正方体,它们表面积间的大小关系是( )A .S 球<S 正四面体<S 正方体B .S 球<S 正方体<S 正四面体C .S 正四面体<S 球<S 正方体D .S 正方体<S 球<S 正四面体答案 B解析 通过球、正四面体和正方体体积相等,找到球的半径、正四面体和正方体的棱长之间的等量关系,从而进一步计算表面积. 4.如图,由三个正方体木块粘合成的模型,它们的棱长分别为1 m ,2 m ,4 m ,要在表面上涂刷油漆,若大正方体的下底面不涂油漆,则模型涂油漆的总面积是________ m 2. 答案 1005.一个倒立的圆锥形容器,它的轴截面是正三角形,在这个容器内注入水并且放入一个半径为r 的铁球,这时水面恰好和球面相切,问将球从圆锥内取出后,圆锥内水面的高是多少?解析 设球未取出时高PC =h ,球取出后水面高PH =x.如图所示:∵AC =3r ,PC =3r ,∴以AB 为底面直径的圆锥容积为V 圆锥=13πAC 2·PC =13π(3r)2·3r=3πr 3,V 球=43πr 3.球取出后水面下降到EF ,水的体积为V 水=13πEH 2·PH =13π(PH·tan30°)2·PH =19πx 3.而V 水=V 圆锥-V 球,即19πx 3=3πr 3-43πr 3, ∴x =315r.故球取出后水面的高为315r.1.(2015·陕西)一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .2π+4D .3π+4答案 D解析 由所给三视图可知,该几何体是圆柱从底面圆直径处垂直切了一半,故该几何体的表面积为12×2π×1×2+2×12×π×12+2×2=3π+4,故选D.2.(2015·新课标全国Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18 B.17 C.16 D.15答案 D解析 如图,不妨设正方体的棱长为1,则截去部分三棱锥A -A 1B 1D 1,其体积为16,又正方体的体积为1,则剩余部分的体积为56,故所求比值为15.故选D.3. 某四棱台的三视图如右图所示,则该四棱台的体积是( )A .4 B.143 C.163 D .6答案 B解析 由四棱台的三视图可知,台体上底面积S 1=1×1=1,下底面积S 2=2×2=4,高h =2,代入台体的体积公式V =13(S 1+S 1S 2+S 2)h =13×(1+1×4+4)×2=143.4.将正方体(如图所示)截去两个三棱锥,得到如图所示的几何体,则该几何体的左视图为( )答案 B解析 左视图中能够看到线段AD 1,画为实线,看不到线段B 1C ,画为虚线,而且AD 1与B 1C 不平行,投影为相交线,所以选择B. 5.若一个几何体的三视图如图所示,则此几何体的体积为( )A.112 B .5 C.92 D .4答案 D解析 由三视图可知,所求几何体是一个底面为六边形,高为1的直棱柱,因此只需求出底面面积即可.由俯视图和主视图可知,底面面积为1×2+2×12×2×2=4,所以该几何体的体积为4×1=4.故应选D.6.右图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图.其中真命题的个数是()A.3 B.2C.1 D.0答案 A解析把底面是等腰直角三角形的直三棱柱的一个侧面放在水平面上,当这个直三棱柱的底面三角形的直角边等于放在水平面上的侧面的宽度就可以使得这个三棱柱的正视图和俯视图符合要求,故命题①是真命题;把一个正四棱柱的一个侧面放置在水平面上即可满足要求,故命题②是真命题;只要把圆柱侧面的一条母线放置在水平面即符合要求,故命题③是真命题.7.如图,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为()A.18 3 B.12 3C.9 3 D.6 3答案 C解析该几何体为一个斜棱柱,其直观图如图所示,由题知该几何体的底面是边长为3的正方形,高为3,故V=3×3×3=9 3.8.若某几何体的三视图如图所示,则这个几何体的直观图可以是()答案 B解析 从俯视图看,B 和D 符合,从正视图看B 符合,而从侧视图看B 也是符合的.9.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32B .16+16 2C .48D .16+32 2答案 B解析 该空间几何体是底面边长为4、高为2的正四棱锥,这个四棱锥的斜高为22,故其表面积是4×4+4×12×4×22=16+16 2. 10.如图是某几何体的三视图,则该几何体的体积为( )A .9π+42B .36π+18 C.92π+12D.92π+18答案 D解析 这个空间几何体上半部分是一个半径为32的球,下半部分是一个底面正方形边长为3、高为2的正四棱柱,故其体积为4π3×(32)3+3×3×2=9π2+18.11.某几何体的三视图如图所示,则它的体积是( )A .8-2π3 B .8-π3 C .8-2π D.2π3答案 A解析 圆锥的底面半径为1,高为2,该几何体体积为正方体体积减去圆锥体积,即V =22×2-13×π×12×2=8-23π,正确选项为A. 12.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )答案 D解析 被截去的四棱锥的三条可见侧棱中有两条为长方体的面对角线,它们在右侧面上的投影与右侧面(长方形)的两条边重合,另一条为体对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图,只有选项D 符合.13.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于( ) A. 3 B .2 C .2 3 D .6答案 D解析 由正视图可知此三棱柱是一个底面边长为2的正三角形、侧棱为1的直三棱柱,则此三棱柱的侧面积为2×1×3=6.14.若几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________cm 3.答案 24解析 根据三视图、几何体是一个三棱柱削去一个三棱锥,体积V =12×3×4×5-13×12×4×3×3=24 cm 3. 15.某几何体的三视图如图所示,则该几何体的体积是________.答案 16π-16解析 由三视图可知该几何体是一个底面半径为2,高为4的圆柱中间挖去一个底面边长为2,高为4的正四棱柱后剩下的部分,所以其体积为π×22×4-22×4=16π-16.16.如下图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则几何体体积为________.答案2 317.一个几何体的三视图如图所示,则该几何体的体积为________.答案12+π解析由三视图可知该组合体的上方是一个高为1,底面直径为2的圆柱,下方是一个长、宽、高分别为4、3、1的长方体,如图所示,它的体积V=1×π+4×3×1=12+π.1.一个几何体的三视图如图,该几何体的表面积为()A.280 B.292C .360D .372答案 C解析 该几何体的直观图如图,则所求表面积为S 表=2×(2×8+8×10+2×10)+2×(8×6+8×2)=360,故选C.2.若某空间几何体的三视图如图所示,则该几何体的体积是( )A.13B.23 C .1 D .2答案 C解析 空间几何体的直观图为平放的直三棱柱,且直三棱柱底面为直角三角形,两直角边边长分别为1和2,侧棱长为2,直接利用公式可知V =2×12×1×2=1.3.一个空间几何体的三视图如图所示,则该几何体的表面积为( )A .48B .32+817C .48+817D .80答案 C4.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )答案 D5.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是________cm 3.答案 144解析 该空间几何体的上部分是底面长为4,高为2的正四棱柱,体积为16×2=32;下部分是上底面边长为4,下底面边长为8,高为3的正四棱台,体积为13×(16+4×8+64)×3=112.故该空间几何体的体积为144.6.一个几何体的三视图如图所示,则这个几何体的体积为________.答案 103解析 由三视图可知本题的几何体是:下面是一个正四棱柱,上面是一个正四棱锥.于是可以得到体积是1×2+13×2×2×1=103. 7.圆柱形容器内部盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm. 答案 4解析 设球的半径为r cm ,则底面圆的半径为r cm ,从而有8πr 2+3×43πr 3=6r·πr 2,由此解得r =4.。
湖南省新田一中高中数学 1.3.2 球的体积和表面积课时作业(无答案) 新人教A版必修2

基础达标1.一个三棱锥的三条侧棱两两互相垂直且长分别为3,4,5,则它的外接球的表面积是( ).A .202πB .252πC .50πD .200π2.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V ,求其直径d的一个近似公式d ≈ 3169V .人们还用过一些类似的近似公式.根据π=3.141 59…判断,下列近似公式中最精确的一个是 ( ).A .d ≈ 3169V B .d ≈ 32V C .d ≈ 3300157V D .d ≈ 32111V 3.已知一个表面积为24的正方体,设有一个与每条棱都相切的球,则此球的体积为( ).A.4π3 B .43π C.246π3 D.82π34.已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB =6,BC =23,则棱锥O -ABCD 的体积为________.5.若一个底面边长为32,侧棱长为6的正六棱柱的所有顶点都在一个球面上,则此球的体积为________.6.直三棱柱ABC A 1B 1C 1的各顶点都在同一球面上.若AB =AC =AA 1=2,∠BAC =120°,则此球的表面积等于________.7.若圆锥与球的体积相等,且圆锥底面半径与球的直径相等,求圆锥侧面积与球面面积之比.能力提升8.如图,在等腰梯形ABCD 中,AB =2DC =2,∠DAB=60°,E 为AB 的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B 重合于点P ,则三棱锥P DCE 的外接球的体积为( ). A.43π27 B.6π2 C.6π8 D.6π249.球与圆台的上、下底面及侧面都相切,且球面面积与圆台的侧面积之比为3∶4,则球的体积与圆台的体积之比为________.10.在棱长为2R 的正方体容器内装满水,先把半径为R 的球放入水中,然后再放入一球,使它淹没在水中,且使溢出的水最多,问这个球的半径应是多少?并计算放入这两个球后溢出的水量与容器容量之比.。
人教新课标版数学高一人教A必修2试题 1.3.2球的体积和表面积

第一章 1.3 1.3.2基础巩固一、选择题1.如果三个球的半径之比是123,那么最大球的表面积是其余两个球的表面积之和的( )A .59倍B .95倍C .2倍D .3倍[答案] B[解析] 设小球半径为1,则大球的表面积S 大=36π,S 小+S 中=20π,36π20π=95.2.若两球的体积之和是12π,经过两球球心的截面圆周长之和为6π,则两球的半径之差为( ) A .1 B .2 C .3 D .4 [答案] A[解析] 设两球的半径分别为R 、r (R >r ),则由题意得⎩⎪⎨⎪⎧4π3R 3+4π3r 3=12π,2πR +2πr =6π.解得⎩⎪⎨⎪⎧R =2,r =1.故R-r =1.3.一个正方体表面积与一个球表面积相等,那么它们的体积比是( ) A .6π6 B .π2C .2π2D .3π2π[答案] A [解析] 由6a 2=4πR 2得a R=2π3,∴V 1V 2=a 343πR 3=34π⎝⎛⎭⎫2π33=6π6.4.已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是( ) A .65B .5 4C .4 3D .32[答案] D[解析] 设球的半径为R ,则圆柱的高h =2R ,底面的半径也为R ,∴S 柱S 球=2πR 2+4πR 24πR 2=32.5.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12π[答案] D[解析] 本题是三视图还原为几何体的正投影问题.....,考查识图能力,空间想像能力.由题设可知,该几何体是圆柱的上面有一个球,圆柱的底面半径为1,高为3,球的半径为1,∴该几何体的表面积为2π×1×3+2π×12+4π×12=12π.6.64个直径都为a4的球,记它们的体积之和为V 甲,表面积之和为S 甲;一个直径为a 的球,记其体积为V 乙,表面积为S 乙,则( )A .V 甲>V 乙且S 甲>S 乙B .V 甲<V 乙且S 甲<S 乙C .V 甲=V 乙且S 甲>S 乙D .V 甲=V 乙且S 甲=S 乙 [答案] C[解析] 计算得V 甲=16πa 3,S 甲=4πa 2,V 乙=16πa 3,S 乙=πa 2,∴V 甲=V 乙,且S 甲>S 乙.二、填空题7.某几何体的三视图如图所示,则其表面积为________.[答案] 3π[分析] 由三视图可知该几何体为半个球,利用球的表面积公式求解即可.[解析] 由三视图,易知原几何体是个半球,其半径为1,S =π×12+12×4×π×12=3π.8.已知棱长为2的正方体的体积与球O 的体积相等,则球O 的半径为________.[答案] 36π[解析] 设球O 的半径为r ,则43πr 3=23,解得r =36π. 三、解答题9.体积相等的正方体、球、等边圆柱(轴截面为正方形)的全面积分别是S 1、S 2、S 3,试比较它们的大小.[解析] 设正方体的棱长为a ,球的半径为R ,等边圆柱的底面半径为r ,则S 1=6a 2,S 2=4πR 2,S 3=6πr 2.由题意知,43πR 3=a 3=πr 2·2r ,∴R =334πa ,r =312πa ,∴S 2=4π⎝ ⎛⎭⎪⎫334πa 2=4π·3916π2a 2=336πa 2, S 3=6π⎝ ⎛⎭⎪⎫312πa 2=6π·314π2a 2=354πa 2, ∴S 2<S 3.又6a 2>332πa 2=354πa 2,即S 1>S 3. ∴S 1、S 2、S 3的大小关系是S 2<S 3<S 1.10.如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成.已知半球的直径是6 cm ,圆柱筒高为2 cm.(1)这种“浮球”的体积是多少cm 3(结果精确到0.1)?(2)要在2500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?[解析] (1)因为半球的直径是6 cm ,可得半径R =3 cm , 所以两个半球的体积之和为 V 球=43πR 3=43π·27=36π(cm 3).又圆柱筒的体积为V 圆柱=πR 2·h =π×9×2=18π(cm 3). 所以这种“浮球”的体积是:V =V 球+V 圆柱=36π+18π=54π≈169.6(cm 3). (2)根据题意,上下两个半球的表面积是 S 球表=4πR 2=4×π×9=36π(cm 2), 又“浮球”的圆柱筒的侧面积为: S 圆柱侧=2πRh =2×π×3×2=12π(cm 2), 所以1个“浮球”的表面积为 S =36π+12π104=48104π(m 2).因此,2500个这样的“浮球”表面积的和为2500S =2500×48104π=12π(m 2).因为每平方米需要涂胶100克,所以共需要胶的质量为:100×12π=1200π(克).能力提升一、选择题1.(2015·广东深圳一模)用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是( )[答案] B[解析]选项D为主视图或者侧视图,俯视图中显然应有一个被遮挡的圆,所以内圆是虚线,故选B.2.已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是()A.4B.3C.2D.5[答案] B[解析]BD=5,AC=22,CD=OD-OC=R2-BD2-R2-AC2=R2-5-R2-8=1.解得R=3.3.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为323π,那么这个正三棱柱的体积是()A.96 3 B.16 3C.24 3 D.48 3[答案] D[解析]由题意可知正三棱柱的高等于球的直径,从棱柱中间截得球的大圆内切于正三角形,正三角形与棱柱底的三角形全等,设三角形边长为a,球半径为r,由V球=43×πr3=32π3解r=2.S△=12a2sin60°=12a·r×3,得a=23r=43,所以V柱=S△·2r=48 3.4.(2015·河北衡水中学下学期二调考试)已知某几何体的三视图如图所示,其中正视图、侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为()A .2π3+12B .4π3+16C .2π6+16D .2π3+12[答案] C[解析] 由已知的三视图可知原几何体的上方是三棱锥,下方是半球,∴V =13×(12×1×1)×1+[43π(22)3]×12=16+2π6,故选C . 二、填空题5.(2015·甘肃武威铁路中学专题训练)一个半径为2的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为________.[答案] 16π[解析] 该几何体是从一个球体中挖去14个球体后剩余的部分,所以该几何体的表面积为34×(4π×22)+2×π×222=16π. 6.若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为________. [答案] 31 2[解析] V 柱=πR 2×2R =2πR 3,V 锥=13πR 2×2R =2π3R 3,V 球=43πR 3.V 柱V 锥V 球=31 2.三、解答题7.某街心花园有许多钢球(钢的密度为7.9 g /cm 3),每个钢球重145 kg ,并且外径等于50 cm ,试根据以上数据,判断钢球是空心的还是实心的.如果是空心的,请你计算出它的内径(π取3.14,结果精确到1 cm,2.243≈11.24098).[解析] 由于外径为50 cm 的钢球的质量为7.9×43π×(502)3≈516792(g),街心花园中钢球的质量为145 000 g ,而145 000<516 792, 所以钢球是空心的.设球的内径为2x cm ,那么球的质量为 7.9×[43π×(502)3-43πx 3]=145 000.解得x 3≈11 240.98, ∴x ≈22.4,2x ≈45(cm).即钢球是空心的,其内径约为45 cm.8.已知正四面体的棱长为a ,求它外接球的体积及内切球的半径.[解析] 如图,设SO 1是正四面体S -ABC 的高,则外接球的球心O 在SO 1上.设外接球半径为R .∵正四面体的棱长为a ,O 1为正△ABC 中心, ∴AO 1=23×32a =33a ,SO 1=SA 2-AO 21=a 2-13a 2=63a ,在Rt △OO 1A 中,R 2=AO 21+OO 21=AO 21+(SO 1-R )2,即R2=(33a)2+(63a-R)2,解得R=64a,∴所求外接球体积V球=43πR3=68πa3.∴OO1即为内切球的半径,OO1=63a-64a=612a,∴内切球的半径为612a.。
2019-2020学年高中数学人教A版必修2作业:1.3.2 球的体积和表面积

1.3.225分)已知两个球的半径之比为:3.:.:C.:3 D.:1解析:设两球的半径分别为r1,r2,表面积分别为S1,S2,∵r1:r2=:3,∴S1:S2=4πr21:4πr22=r21:r22=:9.故选A.答案:A2.[2019·安徽省合肥市检测]平面α截球O所得截面圆的半径为1,球心O到平面α的距离为2,则此球的体积为()解析:由题意知,球的半径R=336π,故球的体积为43πR3=43π·36π=48,则长方体的高为48÷6÷4=2,故长方体的表面积为2×(6×4+4×2+6×2)=88.答案:C二、填空题(每小题5分,共15分)6.已知三棱锥P-ABC中,P A⊥底面ABC,P A=3,底面ABC是::比.解析:设三个球的半径分别为R1,R2,R3,∵三个球的表面积之比为::9,∴4πR21:4πR22:4πR23=::9,即R21:R22:R23=::9,∴R1:R2:R3=::3,∴V1:V2:V3=43πR31:43πR32:43πR33=R31:R32:R33=::27.10.已知球心O到过球面上三点A,B的截面的距离等于球半径的一半,且AB=BC=3 cm,求球的体积.B,C三点的截面为圆,的中心,r ,R 及圆柱的高的一半构成直角三角形.∴r =12-⎝ ⎛⎭⎪⎫122=32. ∴圆柱的体积为V =πr 2h =34π×1=3π4. 故选B. 答案:B12.长方体的共顶点的三个侧面面积分别为3、5、15,则它1:R 2:R =:2:1:S 2:S 21:R 22:R =::3.即这三个球的表面积之比为::3.14.一个高为16的圆锥内接于一个体积为972π的球,在圆锥内又有一个内切球.求:作出轴截面,则等腰三角形πR3=972π,。
人教A版高中数学必修二课时训练:1.3.2球的表面积和体积
人教A 版数学必修二第一章 空间几何体1.3 空间几何体的表面积与体积1.3.2 球的表面积与体积 课时训练一、选择题1.已知实心铁球的半径为R ,将铁球熔成一个底面半径为R 、高为h 的圆柱,则h R =( ) A .32 B .43 C .54 D .22.半球内有一个内接正方体,则这个半球的体积与正方体的体积之比为( )A :6B :2C .:2πD .5:12π3.已知点,,,A B C D 均在球O 上,3AB BC AC ===,若三棱锥D ABC -体积的最大值为4,则球O 的体积为A .323πB .16πC .32πD .163π 4.已知正三棱柱111ABC A B C -的顶点都在球O 的球面上,2AB =,14AA =,则球O 的表面积为( ) A .323π B .32π C .64π D .643π 5.四棱锥P -ABCD 的五个顶点都在一个球面上,该四棱锥的三视图如图所示,E ,F 分别是棱AB ,CD的中点,直线EF 被球面所截得的线段长为( )A .9πB .3πC .D .12π6.如图,ABCD -A 1B 1C 1D 1是棱长为1的正方体,S -ABCD 是高为1的正四棱锥,若点S ,A 1,B 1,C 1,D 1在同一个球面上,则该球的体积为( )A .2516πB .4916πC .8116πD .243128π 7.已知底面边长为1的正四棱柱的各顶点均在同一个球面上,则该球的体积为( ) A .323π B .4π C .2π D .43π 8.若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为、,则:=( ). A .1:1 B .2:1 C .3:2 D .4:19.已知圆锥的底面半径为3,母线长为5,球O 与圆锥的底面和侧面均相切,设球O 的体积为1V ,圆锥的体积为2V ,则12V V =( ) A .18 B .38 C .14 D .82710.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,若该几何体的表面积是174π,则它的体积是( )A .76πB .78πC .283πD .π 11.若三棱锥P ﹣ABC 的底面边长与侧棱长都是3,则它的内切球的表面积为( )A .32πB .272π CD .23π12.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑,已知鳖臑P ABC -的三视图如图所示,则该几何体的外接球的表面积为( )A .41πB .16πC .25πD .64π二、填空题 13.已知一个铜质的实心圆锥的底面半径为6,高为3,现将它熔化后铸成一个铜球(不计损耗),则该铜球的半径是__________.14.四面体A BCD -中,AB ⊥底面BCD ,AB BD =1CB CD ==,则四面体A BCD -的外接球的表面积为______15.正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上.若163P ABCD V -=,则球O 的体积是______. 16.我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”,现有一“阳马”如图所示,PA ⊥平面ABCD ,4PA =,AB =1AD =,则该“阳马”外接球的表面积为________.三、解答题17.如图,某甜品创作一种冰淇淋,其上半部分呈半球形,下半部分呈圆锥形,现把半径为10cm 的圆形蛋皮等分成5个扇形,用一个扇形蛋皮固成圆锥的侧面(蛋皮厚度忽略不计).(1)这种蛋筒的表面积;(2)若要制作500个这样的蛋筒,需要多少升冰淇淋?(精确到0.1L )18.在长方体1111ABCD A B C D -中,2AB BC ==,过1A ,1C ,B 三点的平面截去长方体的一个角后,得到如图所示的几何体111ABCD A C D -,这个几何体的体积为403.(1)求棱1AA 的长;(2)求经过1A ,1C ,B ,D 四点的球的表面积和体积.19.有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点,若正方体的棱长为a ,求这三个球的表面积.20.一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R,正四棱台的上、下底面边长分别为2.5R和3R,斜高为0.6R(1)求这个容器盖子的表面积(用R表示,焊接处对面积的影响忽略不记);(2)若R=2cm,为盖子涂色时所用的涂料每0.4kg可以涂1m2,计算100个这样的盖子约需涂料多少kg (精确到0.1kg)1.3.2 球的表面积与体积 课时训练参考答案1—12 BBADDCDCBAAA13.314.4π15.323π 16.20π17.解:(1)由题意可知圆锥的母线10l =,所以21=205S rl l πππ==侧 并且2r =,所以2=28S r ππ=半球,所以=+=20+8=28S S S πππ表侧半球(2)由(1)知圆锥的高度为h =2311141657.83233V r h r πππ=+⋅=+≈ 所以3150050057.82890029.0V V cm L ==⨯=≈18.(1)设AA 1=x ,依题意可得4011 2222332x x =⨯⋅-⨯⨯⨯⋅ ,解得x=4,故棱AA 1的长为4,(2)依题意可知,经过A 1,C 1,B ,D 四点的球就是长方体ABCD -A 1B 1C 1D 1的外接球,这个球的直径就是长方体的体对角线,∴球的直径2R R =∴=,所以所求球的表面积为4πR 2=24π,体积为34 3R π=.19.(1)正方体的内切球球心是正方体的中心,切点是六个面(正方形)的中心,经过四个切点及球心作截面,如图(1),所以有2r 1=a ,r 1=a 2,所以S 1=4π21r =πa 2.(2)球与正方体各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,如图(2),所以有2r 2a ,r 2=2a ,所以S 2=4π22r =2πa 2.(3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图(3),所以有2r3a,r3,所以S3=4π23r=3πa2.20.(1)∴球的半径为R∴球的表面积为4πR2又∴四棱台的上、下底面边长分别为2.5R和3R,则四棱台的上、下底面积分别为6.25R2和9R2又由正四棱台的斜高为0.6R则四棱台的侧面积为412⨯⨯(2.5R+3R)×0.6R=6.6R2∴容器盖子的表面积S=(21.85+4π)R2(2)由(1)得S=(21.85+4π)R2R=2cm时,S=(87.4+16π)cm2100个这样的盖子约需涂料为(87.4+16π)×100÷10000×0.4kg≈0.6kg。
高中数学人教A版必修2一课三测:1.3.2 球的体积和表面积
1.3.2 球的体积和表面积填一填球的体积和表面积公式(1)体积公式:V =43πR 3.(2)表面积公式:4πR 2.判一判1.2.球的表面积是关于球半径的一个函数.(√) 3.球的表面积等于球的体积的6倍.(×) 4.决定球的大小的因素是球的半径.(√)5.球面被经过球心的平面截得的圆的半径等于球的半径.(√)6.球的体积V 与球的表面积S 的关系为V =R3S .(√)7.正方体的外接球的半径等于它的体对角线.(×)8.球的半径扩大到原来的2倍,则它的表面积增大到原来的2倍.(×)想一想1.提示:(1)由三视图计算球或球与其他几何体的组合体的表面积与体积,最重要的是还原组合体,并弄清组合体的结构特征和三视图中数据的含义,根据球与球的组合体的结构特征及数据计算其表面积或体积.此时要特别注意球的三种视图都是直径相同的圆.(2)计算球与球的组合体的表面积与体积时要恰当地分割与拼接,避免重叠和交叉等. 2.求解球的截面问题的方法归纳.提示:设球的截面圆上一点A ,球心为O ,截面圆心为O 1,则△AO 1O 是以O 1为直角顶点的直角三角形,解答球的截面问题时,常用该直角三角形求解,并常用过球心和截面圆心的轴截面进行求解.3.求球的表面积与体积的一个关键和两个结论.提示:关键:把握住球的表面积公式S 球=4πR 2,球的体积公式V 球=43πR 3是计算球的表面积和体积的关键,半径与球心是确定球的条件.把握住公式,球的体积与表面积计算的相关题目也就迎刃而解了.两个结论:①两个球的表面积之比等于这两个球的半径比的平方;②两个球的体积之比等于这两个球的半径比的立方.4.常见的与球有关的切接问题有哪些? 提示:(1)正方体的内切球.球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为r 1=a2,过在一个平面上的四个切点作截面如图①.(2)球与正方体的各条棱相切.球与正方体的各条棱相切于各棱的中点,过球心作正方体的对角面有r 2=22a ,如图②. (3)长方体的外接球.长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径,若长方体过同一顶点的三条棱长为a ,b ,c ,则过球心作长方体的对角面有球的半径为r 3=12a 2+b 2+c 2,如图③.(4)正方体的外接球.正方体棱长a 与外接球半径R 的关系为2R =3a . (5)正四面体的外接球.正四面体的棱长a 与外接球半径R 的关系为:2R =62a .思考感悟:练一练1.半径为3的球的体积是( )A .9πB .81πC .27πD .36π 答案:D2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的( ) A .2倍 B .22倍C.2倍D.32倍 答案:B3.如果三个球的半径之比是1:2:3,那么最大球的表面积是其余两个球的表面积之和的________倍.答案:954.若火星的半径与地球的半径之比是1:2,则地球表面积与火星表面积之比是________,体积之比是________.答案:4:1 8:1知识点一球的体积和表面积1.若一个球的体积为32π3,则该球的表面积为________.解析:设该球的半径为R ,则43πR 3=32π3,解得R =2,所以该球的表面积S =4πR 2=16π.答案:16π2.(1)已知球的表面积为64π,求它的体积;(2)已知球的体积为5003π,求它的表面积.解析:(1)设球的半径为R ,则4πR 2=64π,解得R =4,所以球的体积V =43πR 3=43π·43=2563π.(2)设球的半径为R ,则43πR 3=5003π,解得R =5,22知识点二 球的截面问题3.是( )A.100π3 cm 3B.208π3 cm 3C.500π3 cm 3D.41613π3cm 3解析:根据球的截面的性质,得球的半径R =32+42=5(cm),所以V 球=43πR 3=500π3(cm 3).答案:C4.一个球内有相距9 cm 的两个平行截面,它们的面积分别为49π cm 2和400π cm 2,求球的表面积.解析:当截面在球心的同侧时,如图1所示为球的轴截面,由球的截面性质知AO 1∥BO 2,且O 1,O 2为两截面圆的圆心,则OO 1⊥AO 1,OO 2⊥BO 2.设球的半径为R ,∵πO 2B 2=49π,∴O 2B =7 cm. 同理,得O 1A =20 cm.设OO 1=x cm ,则OO 2=(x +9)cm. 在Rt △O 1OA 中,R 2=x 2+202,① 在Rt △OO 2B 中,R 2=72+(x +9)2,② 联立①②可得x =15,R =25. ∴S 球=4πR 2=2 500π(cm 2), 故球的表面积为2 500 π(cm 2).当截面在球心的两侧时,如图2所示为球的轴截面,由球的截面性质知,O 1A ∥O 2B ,且O 1,O 2分别为两截面圆的圆心,则OO 1⊥O 1A ,OO 2⊥O 2B .设球的半径为R ,∵π·O 2B 2=49π,∴O 2B =7 cm. ∵π·O 1A 2=400π,∴O 1A =20 cm. 设O 1O =x cm ,则OO 2=(9-x ) cm. 在Rt △OO 1A 中,R 2=x 2+400. 在Rt △OO 2B 中,R 2=(9-x )2+49.∴x 2+400=(9-x )2+49,解得x =-15,不合题意,舍去. 2).知识点三 球的切、接问题5.. 解析:设球的半径为r .正方体的内切球的球心是正方体的中心,切点是六个面(正方形)的中心,所以有2r =a ,r =a2,所以球的表面积S =4πr 2=πa 2.答案:πa 26.正四棱锥的顶点都在同一球面上,若该棱锥的高为6,底面边长为4,则该球的表面积为( )A.443πB.4849πC.814π D .16π解析:如图,正四棱锥P -ABCD 中,PE 为四棱锥的高,根据球的相关知识可知,四棱锥的外接球的球心O 必在正四棱锥的高线PE 所在的直线上,因为底面边长为4,所以AE =22,设球半径为R ,在Rt △AEO 中, AE 2+OE 2=AO 2,即(22)2+(6-R )2=R 2,解得R =113,则S =4πR 2=4π⎝⎛⎭⎫1132=4849π,故选B. 答案:综合知识 球的体积和表面积7.已知一个三棱锥的所有棱长均为2,求该三棱锥的内切球的体积.解析:如图,AE ⊥平面BCD ,设O 为正四面体A -BCD 内切球的球心, 则OE 为内切球的半径,设OA =OB =R , 又正四面体A -BCD 的棱长为2,在等边△BCD 中,BE =63,所以AE =2-69=233.由OB 2=OE 2+BE 2,得R 2=⎝⎛⎭⎫233-R 2+23,解得R =32,所以OE =AE -R =36,即内切球的半径是36,所以内切球的体积为43π×⎝⎛⎭⎫363=354π.8.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r =1,l =3,试求该组合体的表面积和体积.解析:该组合体的表面积S =4πr 2+2πrl =4π×12+2π×1×3=10π,该组合体的体积V =43πr 3+πr 2l =43π×13+π×12×3=13π3.基础达标一、选择题1.若一个球的直径为2,则此球的表面积为( )A .2πB .16πC .8πD .4π解析:因为R =d2=1,所以球的表面积S =4πR 2=4π.答案:D2.若将气球的半径扩大到原来的2倍,则它的体积扩大到原来的( ) A .2倍 B .4倍 C .8倍 D .16倍解析:设气球原来的半径为r ,体积为V ,则V =43πr 3.当气球的半径扩大到原来的2倍后,其体积变为43π(2r )3=8×43πr 3.答案:C3.一个几何体的三视图如图所示,则此几何体的表面积S =( )A .32+πB .32+2πC .28+2πD .28+π解析:由三视图可知此几何体的上半部分为半个球,下半部分是一个长方体,故其表面积S =4π×12+4×2×3+2×2+2×2-π=32+π.答案:A4.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积S 1和球的表面积S 2之比为( )A .4:3B .3:1C .3:2D .9:4解析:画出轴截面如图所示,设球的半径为r .则OD =r ,PO =2r ,∠PDO =90°,∴∠CPB=30°,又∠PCB =90°,∴CB =33PC =3r ,PB =23r ,圆锥的侧面面积S 1=6πr 2,球的表面积S 2=4πr 2,∴S 1:S 2=3:2. 答案:C5.已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是( )A .4B .3C .2D .5解析:BD =5,AC =22, CD =OD -OC=R 2-BD 2-R 2-AC 2 =R 2-5-R 2-8=1. 解得R =3. 答案:B6.长方体ABCD -A 1B 1C 1D 1的八个顶点落在球O 的表面上,已知AB =3,AD =4,BB 1=5,那么球O 的表面积为( )A .25πB .200πC .100πD .50π解析:由长方体的体对角线为外接球的直径, 设球半径为r ,则2r =9+16+25=52,则r =522,4πr 2=4×⎝⎛⎭⎫5222π=50π.答案:D7.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的半径是( )A. 3 cm B .2 cm C .3 cm D .4 cm解析:设球的半径为r , 则V 水=8πr 2,V 球=4πr 3, 加入小球后,液面高度为6r , 所以πr 2·6r =8πr 2+4πr 3,解得r =4.故选D. 答案:D 二、填空题8.若一个球的体积为43π,则它的表面积为________.解析:设球的半径为R ,则43πR 3=43π,解得R =3,则表面积S =4π×(3)2=12π.答案:12π9.过球一条半径的中点,作一垂直于这个半径的截面,截面面积为48π cm 2,则球的表面积为________cm 2.解析:易知截面为一圆面,如图所示,圆O 是球的过已知半径的大圆,AB 是截面圆的直径,作OC 垂直AB 于点C ,连接OA .由截面面积为48π cm 2,可得AC =4 3 cm.设OA =R ,则OC =12R ,所以R 2-⎝⎛⎭⎫12R 2=(43)2,解得R =8 cm.故球的表面积S =4πR 2=256π(cm 2). 答案:256π10.如图为某几何体的三视图,则该几何体的体积为________.解析:由三视图可知该几何体是一个组合体,上半部分是半径为1的球的14,其体积V 1=14×43π×13=π3;下半部分是底面半径为1,高为1的圆柱,其体积V 2=π×12×1=π.所以该几何体的体积V =V 1+V 2=43π.答案:43π11.底面为正方形,顶点在底面的投影为底面中心的棱锥P -ABCD 的五个顶点在同一球面上,若该棱锥的底面边长为4,侧棱长为26,则这个球的表面积为________.解析:正四棱锥P -ABCD 外接球的球心在它的高PO 1上,记为O ,OP =OA =R ,PO 1=4,OO 1=4-R ,或OO 1=R -4(此时O 在PO 1的延长线上). 在Rt △AO 1O 中,R 2=8+(R -4)2得R =3, 所以球的表面积S =36π. 答案:36π12.已知P A ,PB ,PC 两两垂直且P A =2,PB =3,PC =2,则过P ,A ,B ,C 四点的球的体积为________.解析:以PB ,P A ,PC 为长方体的长、宽、高作长方体,则长方体的对角线长为P A 2+PB 2+PC 2=3,即球半径为32,V 球=43πR 3=92π.答案:92π三、解答题13.如图所示(单位:cm)四边形ABCD 是直角梯形,求图中阴影部分绕AB 旋转一周所成几何体的表面积和体积.解析:12S 球=12×4π×22=8π(cm 2),S 圆台侧=π(2+5)(5-2)2+42=35π(cm 2), S 圆台下底=π×52=25π(cm 2),即该几何体的表面积为8π+35π+25π=68π(cm 2).又V 圆台=π3×(22+2×5+52)×4=52π(cm 3),V 半球=12×4π3×23=16π3(cm 3).所以该几何体的体积为V 圆台-V 半球=52π-16π3=140π3(cm 3).14.某街心花园有许多钢球(钢的密度为7.9 g/cm 3),每个钢球重145 kg ,并且外径等于50 cm ,试根据以上数据,判断钢球是空心的还是实心的.如果是空心的,请你计算出它的内径(π取3.14,结果精确到1 cm,2.243≈11.240 98).解析:由于外径为50 cm 的钢球的质量为7.9 ×43π×⎝⎛⎭⎫5023≈516 792(g), 街心花园中钢球的质量为145 000 g , 而145 000<516 792, 所以钢球是空心的. 设球的内径为2x cm ,那么球的质量为7.9×⎣⎡⎦⎤43π×⎝⎛⎭⎫5023-43πx 3=145 000. 解得x 3≈11 240.98,所以x ≈22.4,2x ≈45(cm).能力提升15.r 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.解析:作出轴截面,如图所示,当球在容器内时,水的深度为3r ,水面半径BC 的长为3r ,则容器内水的体积为V =V 圆锥-V 球=13π(3r )2·3r -43πr 3=53πr 3,将球取出后,设容器中水的深度为h ,则水面圆的半径为33h ,从而容器内水的体积为V ′=13π⎝⎛⎭⎫33h 2h =19πh 3,由V =V ′,得h =315r .16.已知球心到过球面上三点A ,B ,C 的截面的距离等于球的半径的一半,且AC =BC =6,AB =4,求球的表面积和体积.解析:如图,设球心为O ,球的半径为R ,作OO 1垂直平面ABC 于点O 1,由于OA =OB =OC =R , 则O 1是△ABC 的外心, 即O 1A =O 1B =O 1C .设M 是AB 的中点,连接CM , 由于AC =BC ,则O 1在CM 上. 设O 1M =x ,易知O 1M ⊥AB ,则O 1A =22+x 2,O 1C =CM -O 1M =42-x . 又O 1A =O 1C ,所以22+x 2=42-x ,解得x =724,则O 1A =O 1B =O 1C =924.在Rt △OO 1A 中,O 1O =R2,∠OO 1A =90°,OA =R .由勾股定理得⎝⎛⎭⎫R 22+⎝⎛⎭⎫9242=R 2,解得R =362. 由S 球=4πR 2=54π,V 球=43πR 3=276π.由Ruize收集整理。
人教新课标版数学高一-人教A版必修2 课时提升 1.3.2 球的体积和表面积1

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(六)球的体积和表面积(25分钟60分)一、选择题(每小题5分,共25分)1.将棱长为2的正方体削成一个体积最大的球,则这个球的体积为( )A.πB.C.πD.4π【解析】选B.根据题意知,此球为正方体的内切球,所以球的直径等于正方体的棱长,故r=1,所以V=πr3=π.2.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面积和球的表面积之比为( )A.4∶3B.3∶1C.3∶2D.9∶4【解析】选C.作圆锥的轴截面,如图,设球半径为R,则圆锥的高h=3R,圆锥底面半径r=R,则l==2R,所以【延伸探究】本题条件不变,求圆锥的体积与表面积之比.【解析】设球的半径为R,则圆锥的高为h=3R,圆锥底面半径r=R,3.(2015·济宁高一检测)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A.9πB.10πC.11πD.12π【解题指南】由三视图可知该几何体上部是一个球,下部是一个圆柱,从而可求其表面积.【解析】选D.该几何体的上部是一个球,其表面积为4π×12=4π;下部是一个圆柱,其表面积是2π×1×3+2π×12=8π,故该几何体的表面积为12π.4.(2015·上饶高二检测)空间几何体的外接球,理解为能将几何体包围,几何体的顶点和弧面在此球上,且球的半径要最小.若如图是一个几何体的三视图,则该几何体的外接球的表面积为( )A. B. C. D.【解析】选A.该几何体是一个圆柱和一个正方体的组合体,作出其外接球的轴截面如图所示:则R2=x2+1=(2-x)2+,解得:x=,R2=x2+1=,故该几何体的外接球的表面积S=4πR2=π.【补偿训练】已知某球的大圆周长为c,则这个球的表面积是( ) A. B. C. D.2πc2【解析】选C.设球的半径为r,则2πr=c,所以r=,所以球的表面积为S=4πr2=4π·=.5.(2014·陕西高考)已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A. B.4π C.2π D.【解题指南】根据截面圆半径,球心到截面圆的距离,球半径构成直角三角形,满足勾股定理,求出球的半径,代入球的体积公式求解. 【解析】选D.由正四棱柱的各顶点均在同一个球面上,可设正四棱柱的上底成截面圆的半径为R 1,则+=1,可得=;又侧棱长为,所以球心到上底成截面圆的距离d=;由截面圆半径,球心到截面圆的距离,球半径构成直角三角形,根据勾股定理得球半径R===1,代入球的体积公式得球的体积为.【补偿训练】(2014·济南高一检测)正四棱锥(顶点在底面的投影为底面中心)P-ABCD的五个顶点在同一个球面上,若其底面边长为4,侧棱长为2,则此球的表面积为( )A.18πB.36πC.72πD.9π【解析】选B.设球的半径为r,正方形ABCD的对角线的交点为M,则球心在直线PM上,MC=AC=2,由勾股定理,得PM===4,再由射影定理,得PC2=PM×2r,即24=4×2r,所以r=3,所以此球的表面积为4πr2=36π.二、填空题(每小题5分,共15分)6.将一钢球放入底面半径为3cm的圆柱形玻璃容器中,水面升高4cm,则钢球的半径是________.【解析】设钢球的半径为r cm,则πr3=π×32×4,所以r=3.答案:3cm7.用过球心的平面将一个球分成两个半球,则一个半球的表面积与原来整球的表面积之比为________.【解析】设球的半径为r,则半球的表面积为S半=×4πr2+πr2=3πr2,整球的表面积为S=4πr2,所以半球的表面积与原来整球的表面积之比为3∶4.答案:3∶48.(2015·广州高一检测)已知高与底面直径之比为2∶1的圆柱内接于球,且圆柱的体积为500π,则球的体积为________.【解析】设圆柱的底面半径为r,则高为4r,由题意知πr2·4r=500π,则r=5,设球的半径为R,则R2=r2+4r2=125,所以R=5,故V球=π×(5)3=答案:三、解答题(每小题10分,共20分)9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.【解析】两半球的表面积为S1=4πr2=4π,圆柱的侧面积为S2=2πr l=2π×1×3=6π,故该组合体表面积为4π+6π=10π,两半球的体积为V1=πr3=π,圆柱的体积为V2=πr2·l=π×12×3=3π,故该几何体的体积为V1+V2=π+3π=π.10.有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点,若正方体的棱长为a,求这三个球的表面积.【解析】(1)正方体的内切球球心是正方体的中心,切点是六个面(正方形)的中心,经过四个切点及球心作截面,如图(1),所以有2r1=a,r1=,所以S 1=4π=πa2.(2)球与正方体各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,如图(2),所以有2r 2=a,r2=a,所以S2=4π=2πa2.(3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图(3),所以有2r 3=a,r3=a,所以S 3=4π=3πa2.(20分钟40分)一、选择题(每小题5分,共10分)1.若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为S1,S2,则S1∶S2= ( )A.1∶1B.2∶1C.3∶2D.4∶1【解析】选C.由圆柱的底面直径和高都与球的直径相等,可设球的半径为1,所以圆柱的表面积为S1=6π,球的表面积为S2=4π,所以圆柱的表面积与球的表面积之比为S1∶S2=3∶2.【补偿训练】(2014·定西高一检测)已知两个球的表面积之比为1∶16,则这两个球的半径之比为( )A.1∶16B.1∶48C.1∶32D.1∶4【解析】选D.设大球与小球两个球的半径分别为R,r,所以两个球的表面积分别为S1=4πR2,S2=4πr2.因为两个球的表面积之比为1∶16,所以==,所以=.2.(2014·湖南高考)一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A.1B.2C.3D.4【解题提示】先由三视图画出直观图,判断这个几何体是底面是边长为6,8,10的直角三角形,高为12的水平放置的直三棱柱,底面的内切圆的半径就是得到的最大球的半径.【解析】选B.由三视图画出直观图如图,判断这个几何体是底面边长为6,8,10的直角三角形,高为12的水平放置的直三棱柱,直角三角形的内切圆的半径为r==2,这就是得到的最大球的半径.二、填空题(每小题5分,共10分)3.(2015·上海高二检测)已知底面边长为1,高为2的正六棱柱的顶点都在一个球面上,则该球的表面积为________.【解析】因为正六棱柱的底面边长为1,高为2,所以正六棱柱体对角线的长为=2.又因为正六棱柱的顶点在同一球面上,所以正六棱柱体对角线恰好是球的一条直径,得球半径R=,根据球的表面积公式,得此球的表面积为S=4πR2=8π.答案:8π4.一个长方体的各顶点均在同一球的球面上,且同一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为________.【解析】球的直径d==,r=,S=4πr2=14π.答案:14π【延伸探究】一个长方体的各顶点均在同一球的球面上,且一个顶点上的三个侧面的面积为,,,则此球的表面积为________. 【解析】如图为过长方体的一条体对角线的截面.设长方体有公共顶点的三条侧棱的长分别为x,y,z,则由已知有:解得所以球的半径R=AB==.所以外接球的表面积S球=4πR2=9π.答案:9π三、解答题(每小题10分,共20分)5.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.【解析】由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.根据切线性质知,当球在容器内时,水深为3r,水面的半径为r,则容器内水的体积为V=V圆锥-V球=π·(r)2·3r-πr3=πr3,而将球取出后,设容器内水的深度为h,则水面圆的半径为h,从而容器内水的体积是V′=π··h=πh3,由V=V′,得h=r,即容器中水的深度为r.6.体积相等的正方体、球、等边圆柱(轴截面为正方形的圆柱)的表面积分别是S1,S2,S3,试比较它们的大小.【解题指南】根据三种几何体的体积相等,用正方体的棱长表示球的半径和等边圆柱的底面半径,进而表示出三种几何体的表面积,比较其大小.【解析】设正方体的棱长为a,球的半径为R,等边圆柱的底面半径为r,则S1=6a2,S2=4πR2,S3=6πr2.由题意知,πR3=a3=πr2·2r,所以R=a,r=a,所以S2=4π(a)2=4π·a2=a2,打印版S 3=6π(a)2=6π·a2=a2,所以S2<S3.又6a2>3a2=a2,即S1>S3.所以S1,S2,S3的大小关系是S2<S3<S1.关闭Word文档返回原板块高中数学。
人教A版高中必修二试题1.3.2课时练.docx

§1.3.2球的体积和表面积(课时练)一、选择题1、已知正方体的外接球的体积是332π,那么正方体的棱长等于( ) 22、A 332、B 324、C 334、D 2、设D C B A 、、、是球面上的四个点,且在同一平面内,3====DA CD BC AB ,球心到该平面的距离是球的半径的一半,则球的体积是( ) π68、A π664、B π224、C π272、D 3、三个球的半径之比为1∶2∶3,那么最大球的表面,积是其余两个球的表面积之和的( )A.1倍B.2倍C.59倍D.47倍 4、表面积为32的正八面体的各个顶点都在同一个球面上,则此球的体积为( ) A.32π B.3π C.32π D.322π 5、两个半径为1的铁球,熔化成一个大球,则大球的表面积为( )A.6πB.8πC.π344D.π3286、将若干毫升水倒入底面半径为2 cm 的圆柱形器皿中,量得水面的高度为6 cm ;若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是( )A .6 3 cmB .6 cmC .2318 cmD .3312 cm7.已知高与底面直径之比为2∶1的圆柱内接于球,且圆柱的体积为500π,则球的体积为( )A.5003πB.25003πC.25005π3D.125003π 8.用一平面去截体积为43π的球,所得截面的面积为π,则球心到截面的距离为( ) A .2 B. 3 C. 2 D .1二、填空题9、若与球心距离为4的平面截球所得的截面圆的面积是9π,则球的表面积是____________.10、若三个球的表面积之比为1:2:3,则它们的体积之比是_______________.11、一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为___________.12、一个球与正四面体的六条棱都相切,若正四面体的棱长为a ,则这个球的体积为_____________.13、一个店面半径为R 的圆柱形两杯中装入适量的水,若放入一个半径为r 的实心铁球,水面恰好升高r ,则=r R :_____________.三、解答题 14.长方体的共顶点的三个侧面面积分别为3,5,15,试求它的外接球的表面积.*15、有一个轴截面为正三角形的圆锥容器,内放一个半径为R 的内切球,然后将容器注满水,现把球从容器中取出,水不损耗,且取出球后水面与圆锥底面平行形成一圆台体,问容器中水的高度为多少?提示:圆锥的母线长等于内切球半径R 的32倍,可以算出体积之比,从而借助三角形相似可以求出水的高度.。
人教新课标版数学高一-必修2课时作业 1.3.2球的体积和表面积

1.3.2球的体积和表面积【课时目标】1.了解球的体积和表面积公式.2.会用球的体积和表面积公式解决实际问题.3.培养学生的空间想象能力和思维能力.1.球的表面积设球的半径为R,则球的表面积S=________,即球的表面积等于它的大圆面积的________倍.2.球的体积设球的半径为R,则球的体积V=________.一、选择题1.一个正方体与一个球表面积相等,那么它们的体积比是()A.6π6B.π2C.2π2D.3ππ2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的() A.2倍B.22倍C.2倍D.32倍3.正方体的内切球和外接球的体积之比为()A.1∶ 3 B.1∶3C.1∶3 3 D.1∶94.若三个球的表面积之比为1∶2∶3,则它们的体积之比为()A.1∶2∶3 B.1∶2∶ 3C.1∶22∶3 3 D.1∶4∶75.长方体的一个顶点上的三条棱长分别为3,4,5,且它的8个顶点都在同一个球面上,则这个球的表面积为()A.25πB.50πC.125πD.以上都不对6.一个圆锥与一个球的体积相等,圆锥的底面半径是球半径的3倍,圆锥的高与球半径之比为()A.4∶9 B.9∶4C.4∶27 D.27∶4二、填空题7.毛泽东在《送瘟神》中写到:“坐地日行八万里”.又知地球的体积大约是火星的8倍,则火星的大圆周长约________万里.8.将一钢球放入底面半径为3 cm的圆柱形玻璃容器中,水面升高4 cm,则钢球的半径是________.9.(1)表面积相等的正方体和球中,体积较大的几何体是________;(2)体积相等的正方体和球中,表面积较小的几何体是________.三、解答题10.如图所示,一个圆锥形的空杯子上放着一个直径为8 cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?11.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.能力提升12.已知棱长都相等的正三棱锥内接于一个球,某学生画出了四个过球心的平面截球与三棱锥所得的图形,如图所示,则()A.以上四个图形都是正确的B.只有(2)(4)是正确的C.只有(4)是错误的D.只有(1)(2)是正确的13.有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.1.利用球的半径、球心到截面圆的距离、截面圆的半径可构成直角三角形,进行相关计算.2.解决球与其他几何体的切接问题,通常作截面,将球与几何体的各量体现在平面图形中,再进行相关计算.3.解答组合体问题要注意知识的横向联系,善于把立体几何问题转化为平面几何问题,运用方程思想与函数思想解决,融计算、推理、想象于一体.1.3.2 球的体积和表面积 答案知识梳理1.4πR 2 4 2.43πR 3 作业设计1.A [先由面积相等得到棱长a 和半径r 的关系a =6π3r ,再由体积公式求得体积比为6π6.] 2.B [由面积扩大的倍数可知半径扩大为原来的2倍,则体积扩大到原来的22倍.]3.C [关键要清楚正方体内切球的直径等于棱长a ,外接球的直径等于3a .]4.C [由表面积之比得到半径之比为r 1∶r 2∶r 3=1∶2∶3,从而得体积之比为V 1∶V 2∶V 3=1∶22∶33.]5.B [外接球的直径2R =长方体的体对角线=a 2+b 2+c 2(a 、b 、c 分别是长、宽、高).]6.A [设球半径为r ,圆锥的高为h ,则13π(3r)2h =43πr 3,可得h ∶r =4∶9.] 7.4解析 地球和火星的体积比可知地球半径为火星半径的2倍,日行8万里指地球大圆的周长,即2πR地球=8,故R 地球=4π(万里),所以火星的半径为2π万里,其大圆的周长为4万里.8.3 cm 解析 设球的半径为r ,则36π=43πr 3,可得r =3 cm . 9.(1)球 (2)球解析 设正方体的棱长为a ,球的半径为r .(1)当6a 2=4πr 2时,V 球=43πr 3=6πa 3>a 3=V 正方体; (2)当a 3=43πr 3时,S 球=4πr 2=63π6a 2<6a 2=S 正方体. 10.解 要使冰淇淋融化后不会溢出杯子,则必须V 圆锥≥V 半球,V 半球=12×43πr 3=12×43π×43, V 圆锥=13Sh =13πr 2h =13π×42×h . 依题意:13π×42×h ≥12×43π×43,解得h ≥8. 即当圆锥形杯子杯口直径为8 cm ,高大于或等于8 cm 时,冰淇淋融化后不会溢出杯子. 又因为S 圆锥侧=πrl =πr h 2+r 2,当圆锥高取最小值8时,S 圆锥侧最小,所以高为8 cm 时,制造的杯子最省材料.11.解 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.根据切线性质知,当球在容器内时,水深为3r ,水面的半径为3r ,则容器内水的体积为V =V 圆锥-V 球=13π·(3r)2·3r -43πr 3=53πr 3,而将球取出后,设容器内水的深度为h ,则水面圆的半径为33h ,从而容器内水的体积是V ′=13π·(33h)2·h =19πh 3,由V =V ′,得h =315r . 即容器中水的深度为315r .12.C[正四面体的任何一个面都不能外接于球的大圆(过球心的截面圆).]13.解设正方体的棱长为a.如图所示.①正方体的内切球球心是正方体的中心,切点是正方体六个面的中心,经过四个切点及球心作截面,所以有2r1=a,r1=a2,所以S1=4πr21=πa2.②球与正方体的各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,2r2=2a,r2=22a,所以S2=4πr22=2πa2.③正方体的各个顶点在球面上,过球心作正方体的对角面得截面,所以有2r3=3a,r3=32a,所以S3=4πr23=3πa2.综上可得S1∶S2∶S3=1∶2∶3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础达标
1.一个三棱锥的三条侧棱两两互相垂直且长分别为3,4,5,则它的外接球的
表面积是 ( ).
A .202π
B .252π
C .50π
D .200π
2.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,
九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的
体积V ,求其直径d 的一个近似公式d ≈ 3169V .人们还用过一些类似的近似
公式.根据π=3.141 59…判断,下列近似公式中最精确的一个是 ( ).
A .d ≈ 3169
V B .d ≈ 32V C .d ≈ 3300157V D .d ≈ 32111V
3.已知一个表面积为24的正方体,设有一个与每条棱都相切的球,则此球的体
积为 ( ).
A.4π3 B .43π C.246π3 D.82π3
4.已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB =6,BC =23,
则棱锥O -ABCD 的体积为________.
5.若一个底面边长为32,侧棱长为6的正六棱柱的所有顶点都在一个球面上,
则此球的体积为________.
6.直三棱柱ABC -A 1B 1C 1的各顶点都在同一球面上.若AB =AC =AA 1=2,∠BAC
=120°,则此球的表面积等于________.
7.若圆锥与球的体积相等,且圆锥底面半径与球的直径相等,求圆锥侧面积与
球面面积之比.
能力提升
8.如图,在等腰梯形ABCD 中,AB =2DC =2,
∠DAB =60°,E 为AB 的中点,将△ADE
与△BEC 分别沿ED 、EC 向上折起,使A 、
B 重合于点P ,则三棱锥P -DCE 的外接球的
体积为 ( ). A.43π27 B.6π2 C.6π8 D.6π24
9.球与圆台的上、下底面及侧面都相切,且球面面积与圆台的侧面积之比为
3∶4,则球的体积与圆台的体积之比为________.
10.在棱长为2R 的正方体容器内装满水,先把半径为R 的球放入水中,然后再
放入一球,使它淹没在水中,且使溢出的水最多,问这个球的半径应是多少?并计算放入这两个球后溢出的水量与容器容量之比.。
