文件中国矿业大学周圣武概率论与数理统计5第五章 大数定律与中心极限定理.ppt
概率论与数理统计第五章 大数定律及中心极限定理

在100次炮击中炮弹命中的总颗数
100
X = ∑ Xk k =1
相互独立地服从同一分布,
E(Xk)=2, D(Xk)=1.52 (k=1,2,…,100)
随机变量
∑ 1
100 × 1.5
100 k =1
(
X
k
−
2)
=
1 15
(
X
−
200)
2. 伯努利定理 事件发生的频率依概率收敛于事件的概率
3. 辛钦定理 (随机变量序列独立同分布且数学期望存在)
n个随机变量的算术平均值以概率收敛于算术 平均值的数学期望。
给出了“频率稳定性”的严格数学解释. 提供了通过试验来确定事件概率的方法. 是数理统计中参数估计的重要理论依据之一.
§5.2 中心极限定理
望 E( Xk ) = µ (k = 1,2,"),则对于任意ε > 0,有
∑ lim
n→∞
P {|
1 n
n k =1
Xk
−
µ
|<
ε
}
=
1
说明
伯努利大数定理是辛钦定理的特殊情
况。n个随机变量的算术平均值以概率收敛于算
术平均值的数学期望。
三 小结
1、切比雪夫(Chebyshev)定理的特殊情况 算术平均值依概率收敛于数学期望
= 1 − P { V − 100 ≤ 0.387 } (10 12 ) 20
∫ 0.387
≈ 1−
1
e − t 2 dt
−∞ 2π
= 1 −Φ (0.387) = 0.348
所以 P{V > 105} ≈ 0.348
概率论与数理统计 第5章 大数定律和中心极限定理

5.1 大 数 定 律 作为上述定理得特殊情况,可以得到如下重要定 理: 定理 5.3 (伯努利大数定律)设 nA 是 n 重伯努利试 验中事件 A 发生的次数, p 是事件 A 在每次试验中 发生的概率,则对于任意正数,有
nA P nA 即 (5.4) p ( n ) limP p 1 n n n
第五章 大数定律和中心极限定理 【吸烟率调查问题】 某卫生组织为确定某城市成年男子的吸烟率p,将 被调查的成年男子中吸烟的频率作为p的估计,现在 要保证有 90% 以上的把握,使得调查对象吸烟者的
频率与该城市成年男子的吸烟率p之间的差异不大于
5%,问至少要调查多少对象?
5.1
大 数定 律
对某个随机变量 X进行大量的重复观测,所得到 的大批观测数据的算术平均值也具有稳定性,由于 这类稳定性都是在对随机变量进行大量重复试验的 条件下呈现出来的,历史上把这种试验次数很大时 出现的规律统称为大数定律.
即对于任意正数,有
1 n limP X i 1 n n i 1
1 n P X (n ) 也即 (5.3) i n i 1 n n 1 1 1 证:因为 E ( X i ) E ( X i ) n n n i 1 n i 1 1 n 1 D( X i ) 2 n i 1 n
nA p 实际上几乎是必定要发生的,即对于给 n
用事件发生的频率来近似地代替事件发生的概率.
5.1 大 数 定 律 上 述 契 比 谢 夫 大 数 定 律 中 要 求 随 机 变 量 X1 , X2 , … , Xn , … 的方差存在,实际上,在高等概率
论中已经证明了在不要求D(Xi)(i = 1,2,…)存在
概率论与数理统计 第二版 第五章 大数定律及中心极限定理

解 设Xi表示 “装运的第i箱的重量”(单位:千克), n为所n求箱数,则X1, X2,
, X n相互独立同分布, n箱的总重量 T n =X1+X2+ +X n = Xi ,且 E(Xi)=50,
D(Xi)=25, 由林德伯格-列维中心极限定理知
n
i 1
n
P{Tn
5000}=P{
n i 1
Xi
5000
}=P
i
1
Xi 50n
5n
5000
50n
=P
i 1
5n
Xi 5
50n
1000
10n
n
n
( 1000 10n) >
0.977=(2) ,
解得 n < 98.0199 ,
n
所以每辆汽车最多装 98 箱 .
第五章 大数定律及中心极限定理 §5.2 中心极限定理
μ
|
ε}
1,
1 n
lim
n
P{|
n
i 1
Xi
μ|
ε}
0
.
第五章 大数定律及中心极限定理 §5.1 大数定律
例1 (P149例1)设随机变量X1 , X2 , , X n , 相互独立同服从参
数为 2的指数分布, 则当n∞时, Yn =
1 n
n
i 1
X
2 i
依概率收敛于
____
.
解 因为随机变量 X1 , X2 , , X n 相互独立同分布, 所以
定理1 (伯努利大数定律) 设随机变量序列 X1 , X2 , , X n ,
中国矿业大学周圣武概率论与数理统计5第五章-大数定律与中心极限定理PPT课件

可知,当 n时,有
1 n
ni1
Xi
P E(X1)a
因此我们可取 n 次测量值 x1,x2, ,xn的算术平均值
5
请注意 :
Xn依概率收敛于a,意味着对任意给定的0,
当n充分大时,事件Xna的概率很大,接近于 1; 并不排除事件Xna的发生,而只是说他发生的
可能性很小 . 依概率收敛比中 高的 等普 数通 学意义下
弱些,它具有定 某性 种 . 不确
6
命题 (切比雪夫Chebyshev不等式)
设随机变量X 的数学期望 E (X )和 方 差 D ( X ) 2
n
其部分和 X i 在什么条件下以正态分布为极限 i1
分布。
3
第一节 大数定律
第五章
一、 切比雪夫Chebyshev不等式 二、几个常见的大数定律
4
定义1 设随机变量序列 X1,X2, ,Xn,如果存
在常数 a ,使得对于任意 0 有:
ln i m P{X |na|}1
则称 X n 依概率收敛于a ,记为 Xn Pa.
存在,则对任意 0, 不等式
P{|XE(X)|}D(X 2 )
或 P{|XE(X)|}1D (X 2)成立,
则称此式为切比雪夫不等式。
证明 设 X 为连续性(离散型类似),其密度为 f ( x )
7
则 P {|XE (X)|} f(x)dx |xE (X)|
|xE(X)|[xE 2(X)]2 f(x)dx
又由于各次试验相互独立,所以
X1,X2, ,Xn独立同分布, 则由辛钦大数定律可得
lim P{n| Ap|}1
n n
17
例3 如何测量某一未知的物理量a ,使得误差较小?
第五章 大数定律与中心极限定理 《概率论》PPT课件

概率论与数理统计
§5.2 中心极限定理
2)中 心极限 定理表明,若 随 机 变 量 序 列
X 1 , X 2 , , X n 独立同分布,且它们的数学期
望及方差存在,则当n充分大时,其和的分布,
n
即 X k 都近似服从正态分布. (注意:不一定是 k 1
标准正态分布)
3)中心定理还表明:无论每一个随机变量 X k ,
概率论与数理统计
§5.1 大数定律
定理1(Chebyshev切比雪夫大数定律)
假设{ Xn}是两两不相关的随机
变量序列,EXn , DXn , n 1,2, 存在,
其方差一致有界,即 D(Xi) ≤L,
i=1,2, …, 则对任意的ε>0,
lim P{|
n
1 n
n i1
Xi
1 n
n i1
E(Xi ) | } 1.
概率论与数理统计
§5.2 中心极限定理
现在我们就来研究独立随机变量之和所 特有的规律性问题.
在概率论中,习惯于把和的分布 收敛于正态分布这一类定理都叫做中心 极限定理.
下面给出的独立同分布随机变量序 列的中心极限定理, 也称列维——林德 伯格(Levy-Lindberg)定理.
概率论与数理统计
§5.2 中心极限定理
大量的随机现象平均结果的稳定性
大量抛掷硬币 正面出现频率
生产过程中的 字母使用频率 废品率
概率论与数理统计
§5.1 大数定律
一、大数定律
阐明大量的随机现象平均结果的稳定性的一系
列定理统称为大数定律。
定义1 如果对于任意 0, 当n趋向无穷时,事件
" Xn X " 的概率收敛到1,即
概率论与数理统计第5章-大数定律与中心极限定理

又设函数 g ( x , y ) 在点 (a , b ) 连续,
P 则 g( X n , Yn ) g(a , b ).
证明
因为 g( x , y ) 在 (a , b) 连续,
0, 0,
g( x , y ) g(a , b) ,
g ( x, y) g (a, b) ,
因此0 P{ g( X n , Yn ) g(a, b) }
n 0, P X n a P Yn b 2 2
P 则 g( X n , Yn ) g(a , b).
[证毕]
定理5.1(贝努里大数定律) 设nA是n重贝努里试验中事件A发生的 次数, p是事件A在一次试验中发生的概率, 则对于任意的 0, 有
P P 注 : 若X n X , Yn Y , 则 P P (1) X n Yn X Y ;(2) X n Yn X Y;
Xn P X (3) X nYn XY ;(4) Yn Y
P
依概率收敛序列的性质
P P 设 Xn a , Yn b, (a , b为常数)
第五章 大数定律与中心极限定理
5.1 大数定律 5.2 中心极限定理
“概率是频率的稳定值”。前面已经提到,当随机 试验的次数无限增大时,频率总在其概率附近摆动, 逼近某一定值。大数定理就是从理论上说明这一结果。 正态分布是概率论中的一个重要分布,它有着非常广 泛的应用。 中心极限定理阐明,原本不是正态分布的一般随机 变量总和的分布,在一定条件下可以渐近服从正态分 布。这两类定理是概率统计中的基本理论,在概率统 计中具有重要地位。
大数定律的客观背景 大量的随机现象中平均结果的稳定性
概率论与数理统计:大数定律与中心极限定理ppt课件

123456 7 14916 25 36 91 2 E x ,E x 6 2 6 6 91 49 182 147 35 2 2 D x E x (E x) 6 4 12 12 D x 35 2 7 1: 2 P (|x |1 ) 12 3 2 D x 35 35 1 7 2: 2 P (|x |2 ) 4 12 48 3 2
X ,X , ,X 1 2 n 相互独立, nA X k
n k 1
1n pq 记Y Xk , E ( Y ) p , D ( Y ) n n n n k1 n
由 Chebyshev 不等式, = 0.01n ,故
0 . 1875 n P |X 0 . 75 n | 0 . 01 n 1 2 ( 0 . 01 n )
令
0 .1875 n 1 0 .90 2 (0 .01 n )
解得 n 18750
若 E(X ) = , D(X ) = 2, 类似于正态分布的3 原理,由 Chebyshev 不等式可估计 1 P |X | 3 0 . 1111 9 1 P |X | 2 0 . 25 4 由 Chebyshev 不等式,可看出 D (X) 反映了 X 偏离 E(X ) 的程度. 固定 , 较小者,
实际精确计算:
X 1 P 0 . 01 P 940 X 1060 6 6000
1 5 C 6 6
k 1059 k 6000 k 941
6000 k
0 . 959036
用Poisson 分布近似计算:
5.1
大数定律
理学大数定律及中心极限定理PPT课件
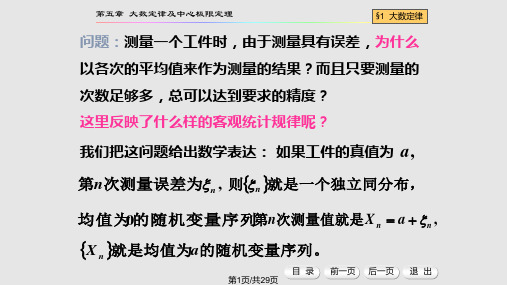
k 1
其中 X 1 ,, X n 相互独立且都服从于两点分布,且
EX k p,DX k pq
n
X k n
由定理1有结论成立。
lim P{ k1
n
n
x}
1
x t2
e 2 dt
2
第14页/共29页 目 录 前一页 后一页 退 出
第五章 大数定律及中心极限定理
推论:
lim
P{
n
np
n
npq
P{X r} 0.999
目 录 前一页 后一页 退 出 第16页/共29页
第五章 大数定律及中心极限定理
而 P{X r}
P{a n b}
( b np ) ( a np )
npq
npq
( r 200 0.6 ) ( 200 0.6 )
200 0.6 0.4
200 0.6 0.4
设不超过的界限为,则应有:
P
X 6000
-
1 6
0.99
由德莫佛-拉普拉斯定理 目 录 前一页 后一页 退 出 第20页/共29页
第五章 大数定律及中心极限定理
P
X 6000
-
1 6
n 6000, p 1 / 6.
lim
P{
n
np
x}
( x)
n
npq
P
X 6000 1/ 6
6000
EX k , DX k 存在,令:
n
n
Yn ( Xk EXk ) /
k 1
k 1
n
DXk ,
k 1
若对任意 x R1 有
1 x t2
lim
n
P{Yn
概率论与数理统计教案 第5章 大数定律与中心极限定理

第5章大数定律与中心极限定理
教学要求
1.理解切比雪夫不等式及其含义. 会用切比雪夫不等式估计概率和证明大数定律.
2.了解依概率收敛的概念.
3.理解大数定律的意义,掌握切比雪夫大数定理、辛钦大数定理、伯努利大数定理成立的条件和结论.
4.理解中心极限定理的实质,掌握独立同分布和棣莫佛-拉普拉斯中心极限定理的条件和结论,并会利用这两个定理近似计算有关事件的概率,了解李雅普诺夫中心极限定理成立的条件和结论.
教学重点
切比雪夫不等式与切比雪夫大数定理,独立同分布和棣莫佛-拉普拉斯中心极限定理.教学难点
用切比雪夫不等式与,独立同分布和棣莫佛-拉普拉斯中心极限定理估计概率.
课时安排
本章安排2课时.
教学内容和要点
一、大数定律
1.切比雪夫不等式
2.大数定理
二、中心极限定理
1.独立同分布中心极限定理
2.棣莫佛-拉普拉斯中心极限定理
3.李雅普诺夫中心极限定理
主要概念
依概率收敛。
概率论与数理统计第五章ppt课件

完整编辑ppt
8
定理1 (切贝谢夫定理)设1,2,...,是相互独立的随机 变量序列,各有数学期望E1,E2,...及方差D1,D2,... 并且对于所有i=1,2,...Di M,M与i无关,则任给0
limP n
1 n
n i1
i
1 n
n i1
Ei
1
此 定 理 表 明 n 个 独 立 随 机 变 量 的 平 均 值 n 1i n 1 i 依 概 率 收 敛 于 其 数 学 期 望 n 1i n1Ei
E
E (x E 2 )2 (x )d x E (x E 2 )2 (x )d x
(xE)2 2
(x)dx
D 2
完整编辑ppt
3
例 1设 是 掷 一 颗 骰 子 所 出 现 的 点 数 , 若 给 定 = 1, 2, 实 际 计 算 P(|-E|),并 验 证 切 贝 谢 夫 不 等 式 成 立 。
完整编辑ppt
23
例7 每颗炮弹命中飞机的概率为0.01,求500发炮弹 中命中5发的概率。
解 : 5 0 0 发 炮 弹 中 命 中 飞 机 的 数 目 服 从 二 项 分 布
n=500 p=0.01
np 5
npq 2.225
(1)直接计算
P ( 5 ) C 5 5 0 00 .0 1 5 0 .0 9 4 9 5=0.17635
第五章 大数定律与中心极限定理
§1 切贝谢夫不等式
研究随机变量的离差与方差的关系。
切贝谢夫不等式: 设 随 机 变 量 有 期 望 值 E 与 方 差 D 。 对 任 给 >0,有 P(|E|)D 2 P(|E|)1D 2
证 : 若 是 离 散 型 随 机 变 量 ,
概率论与数理统计第五章大数定律与中心极限定理

第五章 大数定律与中心极限定理第一节 大数定律在第一章中我们已经指出,人们经过长期实践认识到,虽然个别随机事件在某次试验中可能发生也可能不发生,但是在大量重复试验中却呈现明显的规律性,即随着试验次数的增大,一个随机事件发生的频率在某一固定值附近摆动.这就是所谓的频率具有稳定性.同时,人们通过实践发现大量测量值的算术平均值也具有稳定性.而这些稳定性如何从理论上给以证明就是本节介绍的大数定律所要回答的问题.在引入大数定律之前,我们先证一个重要的不等式——契比雪夫(Chebyshev )不等式. 设随机变量X 存在有限方差D (X ),则有对任意ε>0,P {|X -E (X )|≥ε}≤2)(εX D . (5.1)证 如果X 是连续型随机变量,设X 的概率密度为f (x ),则有P {|X -E (X )|≥ε}=⎰⎰≥-≥--≤εεε)(22)()()()(X E x X E x x x f X E x x x f d d ≤[].)()()(1222⎰+∞∞-=-εεX D x x f X E x d 请读者自己证明X 是离散型随机变量的情况.契比雪夫不等式也可表示成P {|X -E (X )|<ε}≥1-2)(εX D . (5.2)这个不等式给出了在随机变量X 的分布未知的情况下事件{|X -E (X )|<ε}的概率的下限估计,例如,在契比雪夫不等式中,令ε=3)(X D ,4)(X D 分别可得到P {|X -E (X )|<3)(X D }≥0.8889,P {|X -E (X )|<4)(X D }≥0.9375.例5.1 设X 是掷一颗骰子所出现的点数,若给定ε=1,2,实际计算P {|X -E (X )|≥ε},并验证契比雪夫不等式成立.解 因为X 的概率函数是P {X =k }=1/6(k =1,2,…,6),所以E (X )=7/2, D (X )=35/12,P {|X -7/2|≥1=P {X =1}+P {X =2}+P {X =5}+P {X =6}=2/3;P {|X -7/2|}≥2}=P {X =1}+P {X =6}=1/3.ε=1:2)(εX D =35/12>2/3, ε=2:2)(εX D =1/4×35/12=35/48>1/3.可见契比雪夫不等式成立.例5.2 设电站供电网有10000盏电灯,夜晚每一盏灯开灯的概率都是0.7,而假定开、关时间彼此独立,估计夜晚同时开着的灯数在6800与7200之间的概率.解 设X 表示在夜晚同时开着的灯的数目,它服从参数为n =10000,p =0.7的二项分布.若要准确计算,应该用贝努里公式:P {6800<X <7200}=∑=-⨯⨯7199680110000100003.07.0k k k k C .如果用契比雪夫不等式估计: E (X )=np =10000×0.7=7000,D (X )=npq =10000×0.7×0.3=2100,P {6800<X <7200}=P {|X -7000|<200}≥1-22002100≈0.95. 可见,虽然有10000盏灯,但是只要有供应7200盏灯的电力就能够以相当大的概率保证够用.事实上,契比雪夫不等式的估计只说明概率大于0.95,后面将具体求出这个概率约为0.99999.契比雪夫不等式在理论上具有重大意义,但估计的精确度不高.契比雪夫不等式作为一个理论工具,在大数定律证明中,可使证明非常简洁.定义5.1 设Y 1,Y 2,…,Y n ,…是一个随机变量序列,a 是一个常数,若对于任意正数ε有{}1lim =<-∞→εa YP n n ,则称序列Y 1,Y 2,…,Y n ,…依概率收敛于a ,记为Y n P a .定理5.1(契比雪夫(Chebyshev )大数定律) 设X 1,X 2,…是相互独立的随机变量序列,各有数学期望E (X1),E (X2),…及方差D (X 1),D (X 2),…,并且对于所有i =1,2,…都有D (X i )<l ,其中l 是与i 无关的常数,则对任给ε>0,有1)(1111lim =⎭⎬⎫⎩⎨⎧<-∑∑==∞→εn i n i i i n X E n X n P . (5.3) 证因X 1,X 2,…相互独立,所以n l nl n X D n X n D n i i n i i =⋅<=⎪⎭⎫ ⎝⎛∑∑==21211)(11. 又因,)(1111∑∑===⎪⎭⎫ ⎝⎛ni i n i i X E n X n E 由(5.2)式,对于任意ε>0,有2111)(11εεn l X E n X n P n i i n i i -≥⎭⎬⎫⎩⎨⎧<-∑∑==, 但是任何事件的概率都不超过1,即1)(111112≤⎭⎬⎫⎩⎨⎧<-≤-∑∑==εεni i n i i X E n X n P n l,因此1)(1111lim =⎭⎬⎫⎩⎨⎧<-∑∑==∞→εn i n i i i n X E n X n P . 契比雪夫大数定律说明:在定理的条件下,当n 充分大时,n 个独立随机变量的平均数这个随机变量的离散程度是很小的.这意味,经过算术平均以后得到的随机变量n Xn i i∑=1将比较密的聚集在它的数学期望n X E ni i ∑=1)(的附近,它与数学期望之差依概率收敛到0.定理5.2(契比雪夫大数定律的特殊情况) 设随机变量X 1,X 2,…,X n ,…相互独立,且具有相同的数学期望和方差:E (X k )=μ,D (X k )=σ2(k =1,2,…).作前n 个随机变量的算术平均∑==nk k n X n Y 11则对于任意正数ε有 {}1lim =<-∞→εμn n Y P . (5.4)定理5.3(贝努里(Bernoulli )大数定律) 设n A 是n 次独立重复试验中事件A 发生的次数.p 是事件A 在每次试验中发生的概率,则对于任意正数ε>0,有1lim =⎭⎬⎫⎩⎨⎧<-∞→εp n n P A n , (5.5) 或 0lim =⎭⎬⎫⎩⎨⎧≥-∞→εp n n P A n . 证 引入随机变量X k =⎩⎨⎧=,,2,1,1,0 k ,A k ,A k 发生次试验中若在第不发生次试验中若在第,显然 n A =∑=n k k X1.由于X k 只依赖于第k 次试验,而各次试验是独立的.于是X 1,X 2,…,是相互独立的;又由于X k 服从(0-1)分布,故有E (X k )=p , D (X k )=p (1-p ), k =1,2,….由定理5.2有111lim n i n k P X p n ε→∞=⎧⎫-<=⎨⎬⎩⎭∑, 即 1lim =⎭⎬⎫⎩⎨⎧<-∞→εp n n P A n .贝努里大数定律告诉我们,事件A 发生的频率nn A 依概率收敛于事件A 发生的概率p ,因此,本定律从理论上证明了大量重复独立试验中,事件A 发生的频率具有稳定性,正因为这种稳定性,概率的概念才有实际意义.贝努里大数定律还提供了通过试验来确定事件的概率的方法,即既然频率nn A 与概率p 有较大偏差的可能性很小,于是我们就可以通过做试验确定某事件发生的频率,并把它作为相应概率的估计.因此,在实际应用中,如果试验的次数很大时,就可以用事件发生的频率代替事件发生的概率.定理5.2中要求随机变量X k (k =1,2,…,n )的方差存在.但在随机变量服从同一分布的场合,并不需要这一要求,我们有以下定理.定理5.4(辛钦(Khinchin )大数定律)设随机变量X 1,X 2,…,X n ,…相互独立,服从同一分布,且具有数学期望E (X k )=μ (k =1,2,…),则对于任意正数ε,有111lim n i n k P X n με→∞=⎧⎫-<=⎨⎬⎩⎭∑. (5.6) 显然,贝努里大数定律是辛钦大数定律的特殊情况,辛钦大数定律在实际中应用很广泛. 这一定律使算术平均值的法则有了理论根据.如要测定某一物理量a ,在不变的条件下重复测量n 次,得观测值X 1,X 2,…,X n ,求得实测值的算术平均值∑=ni i X n 11,根据此定理,当n 足够大时,取∑=ni i X n 11作为a 的近似值,可以认为所发生的误差是很小的,所以实用上往往用某物体的某一指标值的一系列实测值的算术平均值来作为该指标值的近似值.第二节 中心极限定理在客观实际中有许多随机变量,它们是由大量相互独立的偶然因素的综合影响所形成的,而每一个因素在总的影响中所起的作用是很小的,但总起来,却对总和有显著影响,这种随机变量往往近似地服从正态分布,这种现象就是中心极限定理的客观背景.概率论中有关论证独立随机变量的和的极限分布是正态分布的一系列定理称为中心极限定理(Central limit theorem),现介绍几个常用的中心极限定理.定理5.5(独立同分布的中心极限定理) 设随机变量X 1,X 2,…,X n ,…相互独立,服从同一分布,且具有数学期望和方差E (X k )=μ,D (X k )=σ2≠0(k =1,2,…).则随机变量σμn n X X D X E X Y n k k n k k n k k n k k n -=⎪⎭⎫ ⎝⎛-=∑∑∑∑====1111)( 的分布函数F n (x )对于任意x 满足⎰∑∞--=∞→∞→=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤-=x t n k k n n n t x n n X P x F .21lim )(lim 212d e πσμ (5.7) 从定理5.5的结论可知,当n 充分大时,近似地有Y n =21σμn n Xn k k -∑=~N (0,1).或者说,当n 充分大时,近似地有 ().,~21σμn n N Xn k k ∑= (5.8) 如果用X 1,X 2,…,X n 表示相互独立的各随机因素.假定它们都服从相同的分布(不论服从什么分布),且都有有限的期望与方差(每个因素的影响有一定限度).则(5.8)式说明,作为总和∑=n k k X1这个随机变量,当n 充分大时,便近似地服从正态分布.例5.3 一个螺丝钉重量是一个随机变量,期望值是1两,标准差是0.1两.求一盒(100个)同型号螺丝钉的重量超过10.2斤的概率.解 设一盒重量为X ,盒中第i 个螺丝钉的重量为X i (i =1,2,…,100).X 1,X 2,…,X 100相互独立,E (X i )=1,)(i X D =0.1,则有X =∑=1001i i X,且E (X )=100·E (X i )=100(两),)(i X D =1(两).根据定理5.5,有P {X >102}=}2100{111001021100≤--=⎭⎬⎫⎩⎨⎧->-X P X P ≈1-Φ(2)=1-0.977250=0.022750.例5.4 对敌人的防御地进行100次轰炸,每次轰炸命中目标的炸弹数目是一个随机变量,其期望值是2,方差是1.69.求在100次轰炸中有180颗到220颗炸弹命中目标的概率. 解令第i 次轰炸命中目标的炸弹数为X i ,100次轰炸中命中目标炸弹数X =∑=1001i i X,应用定理5.5,X 渐近服从正态分布,期望值为200,方差为169,标准差为13.所以P {180≤X ≤220}=P {|X -200|≤20}=⎭⎬⎫⎩⎨⎧≤-132013200X P ≈2Φ(1.54)-1=0.87644.定理5.6(李雅普诺夫(Liapunov )定理) 设随机变量X 1,X 2,…相互独立,它们具有数学期望和方差:E (X k )=μk , D (X k )=σk 2≠0 (k =1,2,…).记∑==n k k n B 122σ,若存在正数δ,使得当n →∞时, {}∑=++→-n k k k nX E B 12201δδμ, 则随机变量Z n =n nk k nk k n k k n k n k k k B X X D X E X∑∑∑∑∑=====-=-11111)()(μ的分布函数F n (x )对于任意x ,满足⎰∑∑∞--==∞←∞→=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤-=x t n n k k n k k n n n t x B X P x F d e π211221lim )(lim μ. (5.9) 这个定理说明,随机变量Z n =n n k kn k k B X ∑∑==-11μ当n 很大时,近似地服从正态分布N (0,1).因此,当n 很大时,∑∑==+=nk k n n n k k Z B X11μ 近似地服从正态分布⎪⎭⎫ ⎝⎛∑=21,n n k k B N μ.这表明无论随机变量X k (k =1,2,…)具有怎样的分布,只要满足定理条件,则它们的和∑=n k k X1当n 很大时,就近似地服从正态分布.而在许多实际问题中,所考虑的随机变量往往可以表示为多个独立的随机变量之和,因而它们常常近似服从正态分布.这就是为什么正态随机变量在概率论与数理统计中占有重要地位的主要原因.在数理统计中我们将看到,中心极限定理是大样本统计推断的理论基础.下面介绍另一个中心极限定理.定理5.7 设随机变量X 服从参数为n ,p (0<p <1)的二项分布,则(1) (拉普拉斯(Laplace)定理) 局部极限定理:当n →∞时P {X =k }≈⎪⎪⎭⎫ ⎝⎛-=--npq np k npq npq npq np k ϕ1212)(2e π, (5.10)其中p +q =1,k =0,1,2,…,n ,2221)(x x -=e πϕ. (2) (德莫佛-拉普拉斯(De MoivreLaplace)定理) 积分极限定理:对于任意的x ,恒有 ⎰∞--∞→=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤--x t n t x p np np X P d e π2221)1(lim . (5.11) 这个定理表明,二项分布以正态分布为极限.当n 充分大时,我们可以利用上两式来计算二项分布的概率.例5.5 10部机器独立工作,每部停机的概率为0.2,求3部机器同时停机的概率. 解 10部机器中同时停机的数目X 服从二项分布,n =10,p =0.2,np =2,npq ≈1.265.(1) 直接计算:P {X =3}=310C ×0.23×0.87≈0.2013; (2) 若用局部极限定理近似计算:P {X =3}=)79.0(265.11265.123265.111ϕϕϕ=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-npq np k npq =0.2308. (2)的计算结果与(1)相差较大,这是由于n 不够大.例5.6 应用定理5.7计算§5.1中例5.2的概率.解 np =7000,npq ≈45.83.P {6800<X <7200}=P {|X -7000|<200}=1)36.4(236.483.457000-=⎭⎬⎫⎩⎨⎧<-ΦX P =0.99999.例5.7 产品为废品的概率为p =0.005,求10000件产品中废品数不大于70的概率. 解 10000件产品中的废品数X 服从二项分布,n =10000,p =0.005,np =50,npq ≈7.053.P {X ≤70}=)84.2(053.75070ΦΦ=⎪⎭⎫ ⎝⎛- =0.9977. 正态分布和泊松分布虽然都是二项分布的极限分布,但后者以n →∞,同时p →0,np →λ为条件,而前者则只要求n →∞这一条件.一般说来,对于n 很大,p (或q )很小的二项分布(n p ≤5)用正态分布来近似计算不如用泊松分布计算精确.例5.8 每颗炮弹命中飞机的概率为0.01,求500发炮弹中命中5发的概率.解 500发炮弹中命中飞机的炮弹数目X 服从二项分布,n =500,p =0.01,np =5,npq ≈2.2.下面用三种方法计算并加以比较:(1) 用二项分布公式计算:P {X =5}=5500C ×0.015×0.99495=0.17635.(2) 用泊松公式计算,直接查表可得:np =λ=5,k =5,P 5(5)≈0.175467.(3) 用拉普拉斯局部极限定理计算:P {X =5}=⎪⎪⎭⎫ ⎝⎛-npq np npq 51ϕ≈0.1793. 可见后者不如前者精确.小 结本章介绍了契比雪夫不等式、四个大数定律和三个中心极限定理.契比雪夫不等式给出了随机变量X 的分布未知,只知道E (X )和D (X )的情况下,对事件{|X -E (X )|≤ε}概率的下限估计.人们在长期实践中认识到频率具有稳定性,即当试验次数增大时,频率稳定在一个数的附近.这一事实显示了可以用一个数来表征事件发生的可能性的大小.这使人们认识到概率是客观存在的,进而由频率的三条性质的启发和抽象给出了概率的定义,因而频率的稳定性是概率定义的客观基础.贝努里大数定律则以严密的数学形式论证了频率的稳定性.中心极限定理表明,在相当一般的条件下,当独立随机变量的个数增加时,其和的分布趋于正态分布.这一事实阐明了正态分布的重要性.中心极限定理也揭示了为什么在实际应用中会经常遇到正态分布,也就是揭示了产生正态分布变量的源泉.另一方面,它提供了独立同分布随机变量之和∑=n k k X1(其中X k 的方差存在)的近似分布,只要和式中加项的个数充分大,就可以不必考虑和式中的随机变量服从什么分布,都可以用正态分布来近似,这在应用上是有效和重要的.中心极限定理的内容包含极限,因而称它为极限定理是很自然的.又由于它在统计中的重要性,称它为中心极限定理,这是Polya 在1920年取的名字.本章要求读者理解大数定律和中心极限定理的概率意义,并要求会使用中心极限定理估算有关事件的概率.重要术语及主题契比雪夫不等式 依概率收敛契比雪夫大数定律及特殊情况 贝努里大数定律辛钦大数定律 独立同分布中心极限定律李雅普诺夫中心极限定理 德莫佛拉普拉斯中心极限定理.习 题 五1. 一颗骰子连续掷4次,点数总和记为X .估计P {10<X <18}.2. 假设一条生产线生产的产品合格率是0.8.要使一批产品的合格率达到在76%与84%之间的概率不小于90%,问这批产品至少要生产多少件?3. 某车间有同型号机床200部,每部机床开动的概率为0.7,假定各机床开动与否互不影响,开动时每部机床消耗电能15个单位.问至少供应多少单位电能才可以95%的概率保证不致因供电不足而影响生产.4. 一加法器同时收到20个噪声电压V k (k =1,2,…,20),设它们是相互独立的随机变量,且都在区间(0,10)上服从均匀分布.记V =∑=201k k V,求P {V >105}的近似值.5. 有一批建筑房屋用的木柱,其中80%的长度不小于3m.现从这批木柱中随机地取出100根,问其中至少有30根短于3m 的概率是多少?6. 某药厂断言,该厂生产的某种药品对于医治一种疑难的血液病的治愈率为0.8.医院检验员任意抽查100个服用此药品的病人,如果其中多于75人治愈,就接受这一断言,否则就拒绝这一断言.(1) 若实际上此药品对这种疾病的治愈率是0.8,问接受这一断言的概率是多少?(2) 若实际上此药品对这种疾病的治愈率是0.7,问接受这一断言的概率是多少?7. 用Laplace 中心极限定理近似计算从一批废品率为0.05的产品中,任取1000件,其中有20件废品的概率.8. 设有30个电子器件.它们的使用寿命T 1,…,T 30服从参数λ=0.1[单位:(小时)-1]的指数分布,其使用情况是第一个损坏第二个立即使用,以此类推.令T 为30个器件使用的总计时间,求T 超过350小时的概率.9. 上题中的电子器件若每件为a 元,那么在年计划中一年至少需多少元才能以95%的概率保证够用(假定一年有306个工作日,每个工作日为8小时).10. 对于一个学生而言,来参加家长会的家长人数是一个随机变量,设一个学生无家长、1名家长、2名家长来参加会议的概率分别为0.05,0.8,0.15.若学校共有400名学生,设各学生参加会议的家长数相与独立,且服从同一分布.(1) 求参加会议的家长数X 超过450的概率?(2) 求有1名家长来参加会议的学生数不多于340的概率.11. 设男孩出生率为0.515,求在10000个新生婴儿中女孩不少于男孩的概率?12. 设有1000个人独立行动,每个人能够按时进入掩蔽体的概率为0.9.以95%概率估计,在一次行动中:(1)至少有多少个人能够进入?(2)至多有多少人能够进入?13. 在一定保险公司里有10000人参加保险,每人每年付12元保险费,在一年内一个人死亡的概率为0.006,死亡者其家属可向保险公司领得1000元赔偿费.求:(1) 保险公司没有利润的概率为多大;(2) 保险公司一年的利润不少于60000元的概率为多大?14. 设随机变量X 和Y 的数学期望都是2,方差分别为1和4,而相关系数为0.5试根据契比雪夫不等式给出P {|X -Y |≥6}的估计. (2001研考)15. 某保险公司多年统计资料表明,在索赔户中,被盗索赔户占20%,以X 表示在随机抽查的100个索赔户中,因被盗向保险公司索赔的户数.(1) 写出X 的概率分布;(2) 利用中心极限定理,求被盗索赔户不少于14户且不多于30户的概率近似值.(1988研考)16. 一生产线生产的产品成箱包装,每箱的重量是随机的.假设每箱平均重50千克,标准差为h5千克,若用最大载重量为5吨的汽车承运,试利用中心极限定理说明每辆车最多可以装多少箱,才能保障不超载的概率大于0.977. (2001研考)资料仅供参考!!!资料仅供参考!!!h。
概率论与数理统计第5章

i 1
22
例1 设有30个电子元件,它们的寿命均服从参数为 0.1的指数分布(单位:小时),每个元件工作相互 独立,求他们的寿命之和超过350小时的概率.
解 设Ti为第i个元件的寿命, i 1,2,,30,T为寿命之和
显 然T1 ,T2 ,,T30相 互 独 立
30
且 Ti ~ E(0.1), i 1,2,.30 T Ti
且EX i , DXi 2 0,则x R,有
n
lim
P
i 1
Xi
n
x
x
n
n
1
t2
e 2 dt ( x)
2
莱 维n 中心 极 限 定 理表 明
记量 即Y的Yn n分当~•i布1NnX 函(ni 0数,1n,)收随敛机则于n变YX标量准ni为~序正 • Ni列 态 n1(inXn分1iX,的 布ni 的的标2标)分准准布化化函随随数. 机 机 变变 量
1
t2
e 2 dt ( x)
n np(1 p) 2
n
证明 由于 X n ~ B(n, p) 则X n X k , k 1
其中 X1, X2 ,, Xn 是相互独立的、服从同一
(0-1) 分布的随机变量, 分布律为
P{ Xk i} pi (1 p)1i , i 0, 1.
30
分nll设布ii其 (mm0X,随-P中Pn1则机)Xin分对X变k11n,nX1布任X量Xni 2n的意k,Xpn, n随x服,,X机从xn有x变是参量相数x,x互分n,1独布21p(立e律0et2的2为t2d2 dtp、t服1()从 x的) 同二一项
20
服从均匀分布。记 V Vk 求P{V>105}的近似值 k 1
概率论与数理统计(经管类)复习要点 第5章 大数定律及中心极限定理

第五章 大数定律及中心极限定理1. 概率统计是研究随机变量统计规律性的数学学科,而随机变量的规律只有在对大量随机现象的考察中才能显现出来。
研究大量随机现象的统计规律,常常采用极限定理的形式去刻画,由此导致对极限定理进行研究,极限定理的内容非常广泛,比如大数定律、中心极限定理。
大数定律的客观背景:大量随机试验中,事件发生的频率稳定于某一常数,测量值的算术平均值具有稳定性。
2. 切比雪夫不等式方差描述随机变量的概率分布对期望的分散程度。
D (X )=E (X 2)-[ E (X )] 22017.10填解:设X 服从参数n=1000,p=0.5的二项分布,E (X )=500,D (X )=250 P {400<X <600}=P {丨X -500丨<100}≥1-2501002=3940 3. 贝努力大数定律设 m 是n 次独立重复试验中事件A 发生的次数,p 是事件A 在每次试验中发生的概率,则对于任意正数ε>0 ,有贝努里大数定律表明,当重复试验次数n 充分大时,事件A 发生的频率nm与事件A 的概率p 有较大偏差的概率很小。
——概率是频率的稳定值设电站供电网有10000盏灯,夜晚每一盏灯开灯的概率都是0.7,而假定所有电灯开或关是彼此独立的。
试用切比雪夫不等式估计夜晚同时开着的灯数在6800-7200的概率。
解:设X 表示在夜晚同时开着的电灯的数目,它服从参数n=10000,p=0.7的二项分布,于是有 E (X )=np=10000×0.7=7000 D (X )=npq=10000×0.7×0.3=2100 P {6800<X <7200}=P {丨X -7000丨<200} ≥1-21002002≈0.95 可见,虽然有10000盏灯,但是只要有供应7000盏灯的电力就足够以相当大的概率保证够用。
事件发生的频率可以代替事件的概率。
概率论与数理统计第五章_大数定律和中心极限定理精品教案

第五章 大数定律和中心极限定理本章介绍概率论中最基本也是最重要的两类定理:大数定律和中心极限定理,它们都是使用极限方法研究大量随机现象统计规律性的。
概括讲来,阐明大量重复试验的平均结果具有稳定性的定律称为大数定律;论证随机变量(试验结果)之和渐进服从某一分布的定理称为中心极限定理.5.1 大数定律在第一章我们曾指出,当试验次数很大时,随机事件发生的频率将与其概率非常接近。
本节将从理论上讨论这个问题。
为此,先介绍一个重要的不等式—切比雪夫(Chebyshev)不等式:若随机变量X 的数学期望E (X )和方差D (X )都存在,则对于任意0ε>,都有{}2()()D X P X E X εε-≤≥, (5.1)证明 仅证X 是连续型随机变量的情况.设()f x 是X 的概率密度,则{}22|()||()|222[()]|()|()d ()d 1()[()]()d x E X x E X x E X P X E X f x x f x x D X x E X f x x εεεεεε--+∞-∞--=-=⎰⎰⎰.≥≥≥≤≤ 若取3()D X ε=,由切比雪夫不等式可知{}()()3()0.119()D X P X E X D X D X -≈≥≤. 也就是说,X 落在区间(()3()()3()E X D X E X D X --以外的可能性很小,而落在此区间中的概率很大。
当D (X )较小时,X 的取值便集中在E (X )附近。
D (X )越小,X 的取值越集中在E (X )附近,这正是方差的意义所在。
显然,切比雪夫不等式可以表示成如下的等价形式:{}2()|()|1D X P X E X εε-<≥-. (5.2)当D (X )已知时,(5.2)式给出了X 与E (X )的偏差小于ε的概率的估计值.例1 设某供电网有10000盏电灯,夜晚每盏灯开灯的概率均为0.7,假定灯的开、关是相互独立的,使用切比雪夫不等式估计夜晚同时开灯的盏数在6800至7200之间的概率.解 令X 表示在夜晚同时开灯的盏数,则X 服从n =10000,p =0.7的二项分布,这时()7000E X np ==,()2100D X npq ==,由切比雪夫不等式可得22100{68007200}{|7000|200}10.95200P X P X <<=-<-≈.≥ 可见,虽然有10000盏灯,但是只要供应7200盏灯的电力就能够以相当大的概率保证够用.事实上,这个概率的近似值表明,在10000盏灯中,开着的灯数在6800到7200的概率大于0.95,而由二项概率公式算出此概率的精确值为0.99999.由此可知,切比雪夫不等式虽可用来估计概率,但精度不够高.1866年,俄国数学家切比雪夫证明了一个相当普遍的结论−−大量观察结果的平均值具有稳定性,这就是切比雪夫大数定律.定理1 切比雪夫大数定律 设随机变量12,,,,n X X X L L 相互独立,每一随机变量都有数学期望12(),(),,(),n E X E X E X L L 和有限的方差1()D X ,2()D X ,L ,()n D X ,L ,并且它们有公共上界c ,即(),1,2,k D X c k ≤=L ,则对任意ε >0,皆有1111lim ()1n nk k n k k P X E X n n ε→∞==⎧⎫-<=⎨⎬⎩⎭∑∑. (5.3)证 因12,,,,n X X X L L 相互独立,所以2211111()n nk k k k c D X D X nc n n n n ==⎛⎫== ⎪⎝⎭∑∑≤. 又因 1111()()n n k k k k E X E X n n ===∑∑,由切比雪夫不等式可得 2211111111()11n n n k k k k k k c P X E X D X n n n n εεε===⎧⎫⎛⎫≥-<--⎨⎬ ⎪⎝⎭⎩⎭∑∑∑≥≥, 所以1111lim ()1n nk k n k k P X E X n n ε→∞==⎧⎫-<=⎨⎬⎩⎭∑∑. 切比雪夫大数定律表明,相互独立的随机变量的算术平均值11n n i i X X n ==∑与其数学期望的差,在n 充分大时以概率1是一个无穷小量.这意味着在n 充分大时,n X 的值将比较紧密地聚集在它的数学期望()n E X 附近.由切比雪夫大数定律可以得到如下推论:推论1 设随机变量12,,,,n X X X L L 独立同分布,并且有数学期望μ及方差2σ,则对任意正数ε,都有11lim 1n i n k P X n με→∞=⎧⎫-<=⎨⎬⎩⎭∑. (5.4) 推论1是我们利用重复观测值的算术平均来近似真实值的理论依据.例如,要测量某一物理量a ,进行n 次重复测量,得到n 个测量值12,,,n X X X L ,显然可以视它们为n 个独立同分布的随机变量,并且有数学期望a .由大数定律可知,当n 充分大时,n 次测量的平均值可作为a 的近似值,即121(....)n a X X X n ≈+++ (5.5) 且当n 充分大时,近似计算的误差很小.定理2 贝努里大数定律 设n μ是n 重贝努里试验中事件A 出现的次数,p 是事件A 在每次试验中出现的概率,则对任意0ε>,都有lim 1n n P p n με→∞⎧⎫-<=⎨⎬⎩⎭. (5.6) 证 设i X 是第i 次试验中事件A 发生的次数,则i X 服从参数为p 的0-1分布,(),()i i E X p D X pq ==,其中1,1,2,3,,q p i n =-=L .又12,,,n X X X L 相互独立,且1nn i i X μ==∑,从而有1111(),n n n i i i i E E X E X p n n n μ==⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭∑∑ 21111()n n n i i i i pq D D X D X n n n n μ==⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭∑∑. 由切比雪夫不等式得221n n pq P p D n n n μμεεε⎧⎫⎛⎫-=⎨⎬ ⎪⎝⎭⎩⎭≥≤, 因此lim 0n n P p n με→∞⎧⎫-=⎨⎬⎩⎭≥, 亦即lim 1n n P p n με→∞⎧⎫-<=⎨⎬⎩⎭. 历史上,贝努里大数定律是概率论中极限定理方面的第一个重要结论。
中国矿业大学周圣武概率论与数理统计116页PPT

1
1/4 27/64 27/64 9/64 1/64
2
2/4
3
3/4
袋中白 球数m p
1
1/4
2
2/4
3
3/4
抽到白球数x x=0 x=1 x=2 x=3 27/64 27/64 9/64 1/64 8/64 24/64 24/64 8/64
袋中白 球数m p
1
1/4
2
2/4
3
3/4
抽到白球数x x=0 x=1 x=2 x=3 27/64 27/64 9/64 1/64 8/64 24/64 24/64 8/64 1/64 9/64 27/64 27/64
Ak
1 n
n i1
Xik
P k
证 X1,X2, ,Xn 独立、 同分布
X1k,X2 k, ,Xn k 独立、 同分布
E (X i k ) E (X k ) k , i 1 ,2 , ,n
辛钦大数定律
Ak
1 n
n i1
Xik
Pk
矩估计的基本思想:令
Akk k1,2,
⑴若X为连续型随机变量,设概率密度为
3 12
1, 1, 1, 3, 2, 1, 3, 2, 2, 1, 2, 2, 3, 1, 1, 2
试求θ的矩估计值。
解
n 16,
A1x11611
27
4
1 E ( X ) 1 2 3 ( 1 2 ) 3 3
令 A1 1,
3 3 7
4
θ的矩估计值为 ˆ 5 12
称为θ的矩估计量。
例1 设总体X 的概率密度为
(1)x, 0x1 其中 1
f(x)
0,
中国矿业大学周圣武概率论与数理统计PPT文档116页

36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
谢谢!
116
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人,、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
《概率论与数理统计》第五章作业解答

∞ ∞ 1∑ 1 ∑ 1 1 n D( Xi ) = 2 D(Xi ) ≤ 2 · = n n n 4 4n i=1 i=1
由切比雪夫不等式,对于任给的 ϵ > 0, 有 1∑ 1∑ Xi − E (Xi )| < ϵ} ≥ 1 − P {| n n
∞ ∞ i=1 i=1 ∞ ∞ 1 n2
2 习题解答
3
5、某射手每次射击的命中率为 p=0.8,现射击 100 发子弹,各次射击互不影响,求命中次数在 72 与 88 之间的概率, 解:设 Y 为命中次数, E (Y ) = np = 100 × 0.8 = 80, D(Y ) = np(1 − p) = 16 80 − 72 80 − 88 P {72 < Y < 88} = Φ( √ ) − Φ( √ ) = Φ(2) − Φ(−2) = 2Φ(2) − 1 = 0.9544. 40 40
2
习题解答
1、进行 600 次伯努利试验,事件 A 在每次试验中发生的概率为 p = 2 ,设 Y 表示 600 次试验中事 5 件 A 发生的总次数,利用切比雪夫不等式估计概率 P{216<Y<264}. 解: E (Y ) = np = 600 × 1 2 = 240 5
2 习题解答 2 3 × = 144 5 5
2
D(Y ) = np(1 − p) = 600 × 切比雪夫不等式:P {|X − E (X )| < ϵ} ≥ 1 −
D (X ) ϵ2
P {216 < Y < 264} = P {|Y − 240| < 24} ≥ 1 −
144 3 = 2 24 4
2、若随机变量 X1 , X2 , ..., X100 相互独立且都服从区间(0,6)上的均匀分布. 设 Y = 利用切比雪夫不等式估计概率 P{260<Y<340}. 解: E (Xi ) = 3, D(Xi ) = 3, E (Y ) = 300, D(Y ) = 300 P {260 < Y < 340} = P {|Y − 300| < 40} ≥ 1 − 300 13 = 2 40 16
概率论与数理统计 第5章大数定律及中心极限定理习题及答案

第 5 章 大数定律与中心极限定理一、填空题:1.设随机变量μξ=)(E ,方差2σξ=)(D ,则由切比雪夫不等式有≤≥-}|{|σμξ3P 91 . 2.设nξξξ,,, 21是n 个相互独立同分布的随机变量,),,,(,)(,)(n i D E i i 218===ξμξ对于∑==ni in1ξξ,写出所满足的切彼雪夫不等式 228εεξεμξn D P =≤≥-)(}|{| ,并估计≥<-}|{|4μξP n 211- . 3. 设随机变量129,,,X X X 相互独立且同分布, 而且有1i EX =,1(1,2,,9)i DX i == , 令91i i X X ==∑, 则对任意给定的0ε>, 由切比雪夫不等式直接可得{}≥<-ε9X P 291ε-. 解:切比雪夫不等式指出:如果随机变量X 满足:()E X μ=与2()D X σ=都存在, 则对任意给定的0ε>, 有22{||}P X σμεε-≥≤, 或者22{||}1.P X σμεε-<≥-由于随机变量129,,,X X X 相互独立且同分布, 而且有 1,1(1,2,9),i i EX DX i === 所以999111()()19,i i i i i E X E X E X μ===⎛⎫===== ⎪⎝⎭∑∑∑9992111()()19.i i i i i D X D X D X σ===⎛⎫===== ⎪⎝⎭∑∑∑4. 设随机变量X 满足:2(),()E X D X μσ==, 则由切比雪夫不等式, 有{||4}P X μσ-≥ 116≤. 解:切比雪夫不等式为:设随机变量X 满足2(),()E X D X μσ==, 则对任意的0ε>, 有22{||}.P X σμεε-≥≤由此得 221{||4}.(4)16P X σμσσ-≥≤=5、设随机变量2σξμξξ==)(,)(,D E ,则≥<-}|{|σμξ2P 43.6、设n ξξξ,,, 21为相互独立的随机变量序列,且),,( 21=i i ξ服从参数为λ的泊松分布,则≤-∑=∞→}{lim x n n P ni in λλξ1⎰∞--xt dt e22 .7、设n η表示n 次独立重复试验中事件A 出现的次数,p 是事件A 在每次试验中出现的概率,则≈≤<}{b a P n η⎰-----)1()1(2221p np np b p np np a t dt e π.8. 设随机变量n ξ, 服从二项分布(,)B n p , 其中01,1,2,p n <<= , 那么, 对于任 一实数x , 有lim {|||}n n P np x ξ→+∞-<= 0 .9. 设12,,,n X X X 为随机变量序列,a 为常数, 则{}n X 依概率收敛于a 是指 {}=<->∀+∞>-εεa X P n n lim ,0 1 ,或{}=≥->∀+∞>-εεa X P n n lim ,0 0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
优选
6
命题 (切比雪夫Chebyshev不等式)
设随机变量X 的数学期望 E(X ) 和方差D(X) 2
存在,则对任意 0 , 不等式
P{|
X
E(X
) |
}
D(X )
2
或
P{| X
E(X
)
|
}
1
D( X
2
)
成立,
则称此式为切比雪夫不等式。
证明 设 X 为连续性(离散型类似),其密度为 f (x)
由切比雪夫不等式
P{ X EX
2100}
1
D( X ) (2100)2
1 ( 700 )2 1 1 8
2100
99
即每毫升白细胞数在5200-9400之间的概率不小于8/9。
优选
11
大数定律的客观背景
大量抛掷硬币 正面出现频率
生产过程中的 废品率
字母使用频率
大量的随机现象中平均结果的稳定性
设nA是n重贝努里试验中事件A发生的次数, P是事件A发生的概率,则对任给的ε> 0,有
lim P{| nA p | } 1 或
n
n
即 nA P p . n
lim P{| nA p | } 0
n
n
证明 引入随机变量
Xi
1, 0,
第i次试验中A发生,
第i次试验中A不发生,i
1,2,
优选
16
显然 nA X1 X 2 X n 且 E(X)i p , D(Xk) p(1 p),k 1,2, n
中心极限定理:对于随机变量序列 X1, X 2, , X n
n
其部分和 X i 在什么条件下以正态分布为极限 i1
分布。
优选
3
第一节 大数定律
第五章
一、 切比雪夫Chebyshev不等式 二、几个常见的大数定律
优选
4
定义1 设随机变量序列 X1, X 2, , X n ,如果存
在常数 a ,使得对于任意 0 有:
n
E(Xi)
i 1 优选
1 n
n i1
13
D(1 n
n i1
Xi)
1 n2
n
D(Xi )
i1
1 n2
n
2
i1
2
n
由切比雪夫不等式得:
1
P{|
1 n
n k 1
Xk
|
} 1
2 n 2
所以
lim P{|
n
1 n
n i1
Xi
|
} 1
注:当n充分大时,
1 n
n i 1
Xi
差不多不再是随机的了,
9
若
优选
9
例1 一电网有1万盏路灯,晚上每盏灯开的概率为0.7.
求同时开的灯数在6800至7200之间的概率至少为多少?
解 设X 为同时开的灯数。X ~ b(104,0.7)
由二项分布 E(X ) np 7000 D(X ) npq 2100
7200
P{6800 X 7200}
C
k 104
其取值接近于其数学期望的概率接近于1.
优选
14
定理2(辛钦定律)
设随机变量序列X1 , X2 , … 独立同分布,
且具有相同的数学期望 E(Xi ) ,i 1,2,
则
lim P{|
n
1 n
n i1
Xi
|
} 1
辛钦
辛钦大数定律中,随机变量的方差可以不存在,只要 独立同分布就可以了。
优选
15
定理3(伯努利大数定律)
0.7
k
0.310k
k 6800
用切比雪夫不等式
P{6800 X 7200}
P{6800 7000 X 7000 7200 7000}
P{
X
7000
200}
1
优选
2100 2002
0.95
200
10
例2 已知正常男性成人血液中,每一毫升白细胞数 平均是7300,均方差是700, 利用切比雪夫不等式
lim
n
P{|
X
n
a
|
}
1
则称 X n 依概率收敛于a ,记为 X n Pa .
优选
5
请注意 :
X n依概率收敛于a,意味着对任意给定的 0,
当n充分大时,事件 X n a 的概率很大,接近于1; 并不排除事件 X n a 的发生,而只是说他发生的
可能性很小. 依概率收敛比高等数学中的普通意义下的收敛
D(
X
2
)
.
优选
8
P{|
X
E(X
)
|
} 1
D( X
2
)
可见D(X) 越小,事件 {| X | }的概率越接近1。
X 的值密集在其数学期望附近的概率越大。
例如:对未知分布X,取 3 , 2 ,
P{|
X
|
2} 1 2
/2 2
3 4
0.75
P{| X | 3} 1 2 / 3 2 8 0.89
可知,当 n 时,有
1
n
n i1
Xi
P E( X1)
a
因此我们可取 n 次测量值 x1, x2, , xn 的算术平均值
作为a
得近似值,即
a
1n n优i选1
xi ,当n充分大时误差很小。
优选
12
几个常见的大数定律
定理1(切比雪夫大数定律)
设 X1 , X2 , … 是一列相互独立的随机变量序列,
它们都有相同的数学期望 E(Xi ) 和方差D(X)i 2
则
1
n
n i1
Xi
P
.
即对任意的ε> 0,
lim
n
P{|
1 n
n i1
Xi
|
}
1
证明
E(1 n
n i1
Xi)
1 n
第五章 大数定律与中心极限定理
一、大数定律 二、中心极限定理
优选
1
本章是关于随机变量序列的极限理论。
目的是从理论上对第一章中提出的“频率的 稳定性”给出严格的数学证明。
大数定律:对于随机变量序列 X1, X 2, , X n
描述其平均值
1 n
n i1
Xi
在什么条件下以什么形
式呈现出稳定性。
优选
2
估计每毫升白细胞数在 5200~9400 之间的概率 .
解 设每毫升白细胞数为X
依题意,EX =7300,DX =7002 所求为
P{5200 X 9400}
P{5200 7300 X 7300 9400 7300}
P{2100 X EX 2100} P{ X EX 2100}
又由于各次试验相互独立,所以
X1, X2,
, X n 独立同分布, 则由辛钦大数定律可得
lim P{| nA p | } 1
n
n
优选
17
例3 如何测量某一未知的物理量a ,使得误差较小?
解 在相同的条件下测量n 次,其结果为
X1, X 2, , X n,它们可看成是相互独立、相同分布的
随机变量,并且有数学期望为a . 于是由辛钦大数定律
优选
7
则 P{| X E(X ) | } f (x)dx |xE( X )|
|xE
(
X
)|[Biblioteka xE(2
X
)]2
f (x)dx
[x
E( X )]2
2
1
1
2
[x
E(
X
)]2
f
(x)dx
D(X )
2
注:Chebyshev不等式对随机变量在以 E(X )为中心
的一个ε邻域外取值的概率给出了一个上界
