D、用十字相乘法把二次三项式分解因式
因式分解之十字相乘法

因式分解之十字相乘法利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
(1)二次项系数为1的十字相乘法:如果二次三项式2++x px q 中的常数项q 能分解成两个因式a 、b 的积,且一次项系数p 恰好是+a b ,那么2++x px q 可以进行如下分解因式,即()()()22++=+++=++x px q x a b x ab x a x b ,用十字交叉线来表示:x+ax +b【要点诠释】①在对2x bx c ++分解因式时,要先从常数项c 的正、负入手,若0c >,则p q 、同号(若0c <,则p q 、异号),然后依据一次项系数b 的正负再确定p q 、的符号;②若2x bx c ++中的b c 、为整数时,要先将c 分解成两个整数的积(要考虑到分解的各种可能),然后看这两个整数之和能否等于b ,直到凑对为止。
(2)二次项系数不为1的十字相乘法:在二次三项式2ax bx c ++(a ≠0)中,如果二次项系数a 可以分解成两个因数之积,即12a a a =,常数项c 可以分解成两个因数之积,即12c c c =,把1212a a c c ,,,排列如下:按斜线交叉相乘、再相加,得到1221a c a c +,若它正好等于二次三项式2ax bx c ++的一次项系数b ,即1221a c a c b +=,那么二次三项式就可以分解为两个因式11a x c +与22a x c +之积,即()()21122ax bx c a x c a x c ++=++.【要点诠释】①分解思路为“看两端,凑中间”;②二次项系数a 一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上。
基础强化练习【例1】因式分解:(1)21124x x ++=;(2)21024x x ++=;(3)2224x x --=;(4)2524x x +-=;(5)22524x x ++=;(6)21424x x ++=;(7)21024x x +-=;(8)22324x x --=.【例2】将下列各式因式分解:(1)2109x x ++(2)2212x xy y --(3)2310x x --(4)2243n mn m --(5)22712x y xy -+(6)2412n n x x --(7)2(2)6(2)27x y x y +++-(8)42536x x --(9)()()222812a a a a +-++(8)22483m mn n ++(9)22627x y xy +-(10)2215x x --(11)22443(2)2m mn n m n -+--+(12)632827x x -+(13)()()2222483482x x x x x x x ++++++(14)20322--x x (15)222064xy y x -++(16)256x x -++(17)22(1)7(1)3x x ++++(18)22()5()3x y x y -+--(19)()()421336a b a b +-++(20)()()21623122x y x y +-+-(21)2222(6)4(6)5x x x x ----(22)(1)(2)(3)(6)20x x x x +---+(23)22(1)(2)12x x x x ++++-(24)22(6)(8)24x x x x +-+--(25)()()2243123515x x x x +++++【例3】用十字相乘法解方程:(1)22730x x -+=(2)26750x x --=(3)22530x x --=(4)221570x x ++=(5)23840a a -+=(6)25760x x +-=(7)2611100y y --=(8)2250x -+=(9)2252x x -=-【例4】已知二次三项式218x ax +-能在有理数范围内分解因式,求整数a 的可能值,并分解因式。
高中十字相乘法

高中十字相乘法
十字相乘法是因式分解中12种方法之一,另外十一种分别都是:1分组分解法,2.拆添项法,3.配方法,4.因式定理(公式法),5.换元法,6.主元法,7.特殊值法,8.待定系数法,9.双十字相乘法,10.二次多项式,11.提公因式法。
十字相乘法能用于二次三项式(一元二次式)的分解因式(不一定是在整数范围内)。
对于像ax²+bx+c=(a₁x+c₁)(a₂x+c₂)这样的整式来说,这个方法的关键是把二次项系数a分解成两个因数a₁,a₂的积,把常数项c分解成两个因数c₁,c₂的积,并使a₁c₂+a₂c₁正好等于一次项的系数b。
那么可以直接写成结
果:ax²+bx+c=(a₁x+c₁)(a₂x+c₂)。
在运用这种方法分解因式时,要注意观察,尝试,并体会,它的实质是二项式乘法的逆过程。
用十字相乘法把二次三项式分解因式

因式分解补充方法:十字相乘法一、 知识归纳和例子讲解:(1) 对于某些首项系数是1的二次三项式2x Px q ++ 【2()x a b x ab +++】的因式分解:有22()()()x Px q x a b x ab x a x b ++=+++=++.(掌握这种方法的关键是确定适合条件的两个数,即把常数项分解成两个数的积,且其和等于一..................次项系数,.....通常要借助画十字交叉线的办法来确定,故称十字相乘法。
) 如对于二次三项式232x x ++,其中3p =,2q =,能找到两个数1、2,使12,12,p q +=⎧⎨⨯=⎩故有232(1)(2)x x x x ++=++. 例1:因式分解(1) x 2 + 10x + 9 ; 解:1 1 (x + 1) 1 9 (x + 9) 1×9=9;1×9+1×1=10∴x 2 + 10x + 9=(x + 1)(x + 9)说明:用十字相乖法分解二次三项式2x Px q ++,式中的p 、q 通常是整数,要找的a 、b 两数也通常是在整数中去找.由于把p 拆成两个整数之和可以有无数种情形,而把q 分解成两个整数之积只有有限几种可能,故应先把q 分解成两个整数之积,然后检验哪两个整数之和得p . 练习题(因式分解):(1)=+-652x x ___ __ __ ____. (2)=++652x x ___ __ __ _____ (3)=--652x x ___ __ __ ____ (4)=-+652x x ___ __ __ ____(2) 对于二次三项ax bx c 2++【()a a x a c a c x c c 122122112+++】(a 、b 、c 都是整数,且a ≠0)的因式分解:一般地,∵()()a x c a x c 1122++=()a a x a c a c x c c 122122112+++,∴()a a x a c a c x c c 122122112+++=()()a x c a x c 1122++.例2分解因式:(1)2273x x -+; (2)2675x x --(1)解:∴2273x x -+= (3)(21)x x --(2)解:(2)2675x x -- 所有可能的十字形式:∴2675(21)(35)x x x x --=+- 口诀:(分两头,凑中间) 练习题(因式分解):(1)2x 2+7x +3=___ __ __ ____ (2)3x 2-5x +2=___ __ __ ____ (3)2x 2+5x -7=___ __ __ ____ (4)5x 2-3x -2=___ __ __ ____二、练一练、做一做:1、把下列各式分解因式:(1)8722--ab b a (2)2243n mn m --(3)42627x x -- (4)(a +b)2+5(a +b)-36 2、将下列各式因式分解(1)x x x 21423-- (2)111024-+x x3、将下列各式因式分解(1)20322--x x ; (2)2x 2+5x +2;(3))3x 2+7x -6 ; (4)2x 2-5xy +2y 24、用因式分解法列下列方程:(1)x 2 + 2x -3 = 0 (2)2x 2-7x + 6 = 0(3)x(x -2) = 3 (4) (2x -3)2 + 3(2x -3) + 2 = 0.。
十字相乘法因式分解

4a b 4a 2b
2 2
四项三一分
x 2 xy y z
2 2
2
1.
2 (a+b)
+a+b
2. a2-4b2-a-2b.
3. y 4y 4 9 x
2
2
2 2 4.xy–xz–y +2yz–z
2 2 2 5.a –b –c –2bc–2a+1
2 2 1、已知:x +y +4x-6y+13=0,
2
x 6x 16
2
x 8x 2
提示:当二次项系数为-1时 出负号再因式分解 。 ,先提
分组分解法
四项二二分
要发现式中隐含的条件,通过交换项的 位置,添、去括号等一些变换达到因式分解 的目的。 例1:因式分解 ab–ac+bd–cd 。 解:原式 = (ab – ac) + (bd – cd) = a (b – c ) + d (b – c ) = (a + d ) (b – c )
求xy的值。
2 2 2、已知:a +b -6a-8b+25=0,
求xy的值。
2 2
x -x 6
2 2
x 7 x 12
小结:
x 3x 10
当常数项为正数时,拆分成的两个有理数一 定同号,符号与一次项系数相同; 当常数项为负数时,拆分成的两个有理数异 号,绝对值大的数与一次项系数同号
例2 分解因式: x 6 x 16
2
解: x 6 x 16
应用条件:
1.二次三项式 2.一个平方项 3.一次项系数为两数的和, 常数项为两数的积。
十字相乘法口诀是什么乘法公式技巧

十字相乘法口诀是什么乘法公式技巧十字相乘法口诀十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数具体步骤:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数原理:运用了乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。
十字相乘法能把二次三项式分解因式(不一定在整数范围内)。
对于形如ax²+bx+c=(a1x+c1)(a2x+c2)的整式计算步骤:⑴把二次项系数a分解成两个因数a1,a2的积a1·a2⑵把常数项c分解成两个因数c1,c2的积c1·c2⑶使a1c2+a2c1正好等于一次项的系数b⑷结果:ax²+bx+c=(a1x+c1)(a2x+c2)实质:二项式乘法的逆过程。
当首项系数不是1时,需注意各项系数的符号。
基本式子:x²+(p+q)x+pq=(x+p)(x+q)。
十字相乘顺口溜竖分常数交叉验,横写因式不能乱。
步骤注释①竖分二次项与常数项②交叉相乘,积相加③检验确定,横写因式十字相乘法对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
【十字相乘法的方法】十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。
【十字相乘法的用处】(1)用十字相乘法来分解因式。
(2)用十字相乘法来解一元二次方程。
因式分解的一般步骤(1) 如果多项式的各项有公因式时,应先提取公因式;(2) 如果多项式的各项没有公因式,则考虑是否能用公式法来分解;(3) 对于二次三项式的因式分解,可考虑用十字相乘法分解;(4) 对于多于三项的多项式,一般应考虑使用分组分解法进行。
在进行因式分解时,要结合题目的形式和特点来选择确定采用哪种方法。
以上这四种方法是彼此有联系的,并不是一种类型的多项式就只能用一种方法来分解因式,要学会具体问题具体分析。
十字相乘法因式分解(经典全面)

十字相乘法分解因式(1)对于二次项系数为1方法的特征是“拆常数项,凑一次项”当常数项为正数时,把它分解为两个同号因数的积,因式的符号与一次项系数的符号相同;当常数项为负数时,把它分解为两个异号因数的积,其中绝对值较大的因数的符号与一次项系数的符号相同.(2)对于二次项系数不是1的二次三项式它的特征是“拆两头,凑中间”当二次项系数为负数时,先提出负号,使二次项系数为正数,然后再看常数项;常数项为正数时,应分解为两同号因数,它们的符号与一次项系数的符号相同;常数项为负数时,应将它分解为两异号因数,使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同注意:用十字相乘法分解因式,还要注意避免以下两种错误出现:一是没有认真地验证交叉相乘的两个积的和是否等于一次项系数;二是由十字相乘写出的因式漏写字母.例5、分解因式:652++x x分析:将6分成两个数相乘,且这两个数的和要等于5。
由于6=2×3=(-2)×(-3)=1×6=(-1)×(-6),从中可以发现只有2×3的分解适合,即2+3=5。
1 2解:652++x x =32)32(2⨯+++x x 1 3 =)3)(2(++x x 1×2+1×3=5用此方法进行分解的关键:将常数项分解成两个因数的积,且这两个因数的代数和要等于一次项的系数。
例1、分解因式:672+-x x解:原式=)6)(1()]6()1[(2--+-+-+x x 1 -1=)6)(1(--x x 1 -6(-1)+(-6)= -7练习1、分解因式(1)24142++x x (2)36152+-a a (3)542-+x x练习2、分解因式(1)22-+x x (2)1522--y y (3)24102--x x(二)二次项系数不为1的二次三项式—— c bx ax ++2条件:(1)21a a a = 1a 1c (2)21c c c = 2a 2c(3)1221c a c a b += 1221c a c a b +=分解结果:c bx ax ++2=))((2211c x a c x a ++例2、分解因式:101132+-x x分析: 1 -2(-6)+(-5)= -11解:101132+-x x =)53)(2(--x x练习3、分解因式:(1)6752-+x x (2)2732+-x x(3)317102+-x x (4)101162++-y y(三)多字母的二次多项式例3、分解因式:221288b ab a --分析:将b 看成常数,把原多项式看成关于a 的二次三项式,利用十字相乘法进行分解。
如何利用十字相乘法分解因式

数学篇学思导引所谓的“十字相乘法”就是借助画十字交叉线分解系数,从而把二次三项式ax 2+bx +c 分解因式的方法.十字相乘法在因式分解中经常用到,它可以解答很多公式法、配方法等不能解答的问题.在运用十字相乘法分解因式时需要拆分常数项或二次项系数,并逐一核验对角线乘积的和是否等于一次项系数,若相等,则拆分成功,否则拆分不成功,需要舍弃,最后将拆分后的项按照乘积的形式书写出来,即可完成因式分解.一、二次项系数为“1”时,拆常数项,凑一次项对于二次三项式x 2+bx +c ,当二次项系数为1时,采用十字相乘法分解因式通常是“拆常数项,凑一次项”.即将常数项c 拆分成两个因数c 1和c 2,使这两个因数c 1和c 2的乘积结果刚好是常数项c ,同时c 1和c 2的和刚好是一次项系数b .如图1所示:只要能满足c =c 1c 2,b =c 1+c 2,则x 2+bx +c =x 2+(c 1+c 2)x +c 1c 2=(x +c 1)(x +c 2).图1例1分解因式y 2-8y +15.分析:此二项式的二次项系数为“1”,直接拆分常数项15即可.常数项15=1×15=-1×图2解:y 2-8y +15=(y -3)(y -5).例2分解因式x 2-2x -15.分析:此题可直接拆分常数项-15,因为常数项是负数,所以拆分的因数中需要安排一个负号,这就需要核验一次项系数后确定.-15=-1×15=1×(-15)=-3×5=3×(-5),-1×15和1×(-15)的情形很容易看出不符合要求,另外两种情形如图3、图4所示;拆分为图3核验结果为1×5+1×(-3)=2,不等于一次项系数-2,舍弃;图4验核结果为1×(-5)+1×3=-2,等于一次项系数-2,核验正确.图3图4解:x 2-2x -15=(x +3)(x -5).评注:从以上的解题过程可以发现:当常数项为正数时,把它分解为两个同号因数的积,每个因数的符号与一次项系数的符号相同;当常数项为负数时,把它分解为两个异号因数的积,其中绝对值较大的因数的符号与一次项系数的符号相同.二、二次项系数不为“1”时,拆两头,凑中间如何利用十字相乘法分解因式盐城市初级中学陈爱荣数学篇学思导引“拆两头,凑中间”,即分别把二次项系数a 和常数项c 各自拆分成两个因数a 1和a 2、c 1和c 2,使a 1和a 2的乘积结果等于二次项系数a ,c 1和c 2的乘积结果等于常数项c ,并使a 1c 2+a 2c 1正好等于一次项系数b ,如图5所示,则ax 2+bx +c =a 1a 2x 2+(a 1c 2+a 2c 1)x +c 1c 2=(a 1x +c 1)(a 2x +c 2),a x1c 1a x 2c 2a x 1a 22c 1c 2(a +1c a c x 221)图5例3分解因式5x 2+7x -6.分析:此题中二次项系数不为“1”,需要拆分二次项系数和常数项系数,即5=1×5,-6=-1×6=1×(-6)=-2×3=2×(-3),如下图6-1至6-8所示,然后逐一核对对角线乘积和与一次项系数是否一致,由表1可知,图6-6的分解符合题意.图6-1图6-2图6-3图6-4图6-5图6-6图6-7图6-8表1十字相乘法数据核验表序号12345678图示6-16-26-36-46-56-66-76-8数据验核1×6+5×(-1)=11×(-6)+5×1=-11×1+5×(-6)=-291×(-1)+5×6=291×3+5×(-2)=-71×(-3)+5×2=71×2+5×(-3)=-131×(-2)+5×3=13取舍情况舍弃,×舍弃,×舍弃,×舍弃,×舍弃,×正确,√舍弃,×舍弃,×解:5x 2+7x -6=(5x -3)(x +2).例4分解因式9+5x -4x 2.分析:此题二次项系数为负数,如果提取负号则可以转化为二次项系数为正数的情形,即9+5x -4x 2=-(4x 2-5x -9).然后求解出4x 2-5x -9的因式分解结果即可.二次项系数可拆分为4=1×4=2×2,常数项可拆分为-9=-1×9=1×(-9)=-3×3,如下图7-1至7-9所示,然后逐一核对对角线乘积和转化后的一次项系数(-5)是否一致.由表2可知,图7-2的分解符合题意.图7-1图7-2图7-3图7-4图7-5图7-6图7-7图7-8图7-9表2十字相乘法数据核验表(转化后)序号123456789图示7-17-27-37-47-57-67-77-87-9数据验核1×9+4×(-1)=51×(-9)+4×1=-51×1+4×(-9)=-351×(-1)+4×9=351×3+4×(-3)=-91×(-3)+4×3=92×9+2×(-1)=162×(-9)+2×1=-162×(-3)+2×3=0取舍情况舍弃,×正确,√舍弃,×舍弃,×舍弃,×舍弃,×舍弃,×舍弃,×舍弃,×解:9+5x -4x 2=-(4x 2-5x -9)=-(x +1)(4x -9).评注:当二次项系数和常数项系数有多种拆分情况时,同学们需要逐一核验拆分后对角线乘积的和是否与一次项系数一致,然后舍弃所有不符合的情况,保留正确的拆分情况.此外,如果二次项系数是负数,则应先将负号提到括号外面,使二次项系数为正数,然后再进行因式分解.27。
十字相乘法因式分解(经典全面)

十字相乘法分解因式(1)对于二次项系数为1方法的特征是“拆常数项,凑一次项”当常数项为正数时,把它分解为两个同号因数的积,因式的符号与一次项系数的符号相同;当常数项为负数时,把它分解为两个异号因数的积,其中绝对值较大的因数的符号与一次项系数的符号相同.(2)对于二次项系数不是1的二次三项式它的特征是“拆两头,凑中间”当二次项系数为负数时,先提出负号,使二次项系数为正数,然后再看常数项;常数项为正数时,应分解为两同号因数,它们的符号与一次项系数的符号相同;常数项为负数时,应将它分解为两异号因数,使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同注意:用十字相乘法分解因式,还要注意避免以下两种错误出现:一是没有认真地验证交叉相乘的两个积的和是否等于一次项系数;二是由十字相乘写出的因式漏写字母.例5、分解因式:652++x x分析:将6分成两个数相乘,且这两个数的和要等于5。
由于6=2×3=(-2)×(-3)=1×6=(-1)×(-6),从中可以发现只有2×3的分解适合,即2+3=5。
1 2解:652++x x =32)32(2⨯+++x x 1 3 =)3)(2(++x x 1×2+1×3=5用此方法进行分解的关键:将常数项分解成两个因数的积,且这两个因数的代数和要等于一次项的系数。
例1、分解因式:672+-x x解:原式=)6)(1()]6()1[(2--+-+-+x x 1 -1=)6)(1(--x x 1 -6(-1)+(-6)= -7练习1、分解因式(1)24142++x x (2)36152+-a a (3)542-+x x练习2、分解因式(1)22-+x x (2)1522--y y (3)24102--x x(二)二次项系数不为1的二次三项式—— c bx ax ++2条件:(1)21a a a = 1a 1c(2)21c c c = 2a 2c(3)1221c a c a b += 1221c a c a b +=分解结果:c bx ax ++2=))((2211c x a c x a ++例2、分解因式:101132+-x x分析: 1 -2(-6)+(-5)= -11解:101132+-x x =)53)(2(--x x练习3、分解因式:(1)6752-+x x (2)2732+-x x(3)317102+-x x (4)101162++-y y(三)多字母的二次多项式例3、分解因式:221288b ab a --分析:将b 看成常数,把原多项式看成关于a 的二次三项式,利用十字相乘法进行分解。
十字相乘法只能对二次三项式进行因式分解吗?

(x 2 y 3)(2x 11y 1)
22y2 35y 3 (2y 3)(11y 1) . 再利用十字相乘法对关于 x 的二次三项式进行分解,于是:
2x2 7xy 22 y2 5x 35y 3 2x2 (5 7 y)x (22 y2 35y 3) 2x2 (5 7 y)x (2 y 3)(11y 1)
这就是推广后的十字相乘法,其原理已经不局限于多项式的系数,更不局限于二次多项 式,它适合于任意的一个多项式,当然,前提是要拆得出来.看下面的几个例子.
例 1 将多项式 f (x) 2x3 2x2 x 1
把 2x3 看成 A ,将 2x2 x 看成 B ,将 1 看成C ,进行十字相乘:
x
1
对于某些二元二次六项式 ax2 +bxy+cy2 dx ey f ,也可以用十字相乘法分解因式.
例 3 分解因式: 2x2 7xy 22y2 5x 35y 3 . 将上式按 x 降幂排列,并把 y 当作常数,于是上式可变形为:
2x2 (5 7y)x (22y2 35y 3) , 可以看作是关于 x 的二次三项式. 对于常数项而言,它是关于 y 的二次三项式,也可以用十字相乘法,分解为:
a1
c1
a2
c2
a1a2 a c1c2 c a1c2 a2c1 b
在运用这种方法分解因式时,要注意观察、尝试,并体会它实质是二项式乘法的逆过程. 当首项系数不是 1 时,往往需要多次试验,务必注意各项系数的符号.
初中数学教材中,仅介绍了以下特殊形式:
x2 +( p q)x+pq (x+p)(x+q)
2x2
1
对角线的乘积之和等于 2x2 x ,所以 f (x) (x 1)(2x2 1) .
十字相乘法的解法步骤

十字相乘法的解法步骤十字相乘法是一种常用的因式分解方法,主要用于分解二次三项式。
本文将介绍十字相乘法的解法步骤,帮助读者掌握这种方法。
引言十字相乘法是一种因式分解的方法,主要用于分解二次三项式(也就是具有形式 ax^2+bx+c 的多项式),它能够将多项式分解成两个一次因式的乘积。
下面将介绍十字相乘法的解法步骤。
步骤一:将多项式写成标准形式将多项式写成标准形式,也就是将常数项写在二次项和一次项的中间,使得多项式具有形式 ax^2+bx+c。
如果多项式不是这个形式,可以通过移项和化简的方式将其转化为标准形式。
步骤二:找到两个数的乘积等于常数项,且它们的和等于一次项的系数找到两个数的乘积等于常数项 c,且它们的和等于一次项的系数b。
这两个数通常被称为“十字相乘法因子”。
可以通过因数分解或者试除法来找到这两个因子。
步骤三:将多项式分解成两个一次因式的乘积将多项式分解成两个一次因式的乘积,通常可以将多项式写成以下形式:(ax+m)(ax+n),其中 m 和 n 是两个十字相乘法因子。
展开这个式子可以得到:(ax+m)(ax+n) = a^2x^2 + (m+n)ax + mn比较这个式子和原多项式,可以得到:a^2 = am+n = bmn = c根据第一个等式,可以知道 a 等于 1 或者 -1。
如果 a 等于 1,那么多项式已经是一个一次因式的平方,可以直接写成完全平方式的形式。
如果 a 等于 -1,那么多项式可以写成以下形式:-x^2+bx-c,可以将其分解成两个一次因式的乘积:-(x-m)(x-n)。
步骤四:验证分解是否正确将得到的两个一次因式相乘,看看是否能够得到原来的多项式。
如果乘积等于原来的多项式,那么分解是正确的。
结语以上就是十字相乘法的解法步骤,通过这些步骤,可以轻松地将二次三项式分解成两个一次因式的乘积。
(完整版)十字相乘法因式分解

当q>0时,q分解的因数a、b( 当q<0时, q分解的因数a、b(
) 同号 ) 异号
观察:p与a、b符号关
系
x2 14x 45 (x 5)(x 9)
x2 29x 138 (x 23)(x 6)
小结: 当q>0时,q分解的因数a、b(
) 同号
且(a、b符号)与p符号相同
x2 7x 60 (x 12)(x 5) x2 14x 72 (x 4)(x 18)
当q<0时, q分解的因数a、b(
) 异号
(其中绝对值较大的因数符号)与p符号相同
练习:在 横线上 填 、 符号
__ __ x2 4x 3 =(x + 3)(x + 1)
_-_ __ x2 2x 3 =(x
3)(x + 1)
_-_ _-_ y2 9y 20 =(y
4)(y 5)
_-_ __ t2 10t 56 =(t
4)(t +14)
当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)与p符号相同
试将 x2 6x 16 分解因式
x2 6x 16
x2 6x 16
x 8x 2
提示:当二次项系数为 -1 时 , 先提出负号再因式分解 。
十字相乘法②
试因式分解6x2+7x+2。
这里就要用到十字相乘法(适用于二次三项式)。
既然是二次式,就可以写成(ax+b)(cx+d)的形式。 (ax+b)(cx+d)=acx2+(ad+bc)x+bd
十字相乘法和分式

十字相乘法及分组分解法要点一、十字相乘法利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.对于二次三项式2x bx c ++,若存在pq cp q b=⎧⎨+=⎩ ,则()()2x bx c x p x q ++=++要点诠释:(1)在对2x bx c ++分解因式时,要先从常数项c 的正、负入手,若0c >,则p q 、同号(若0c <,则p q 、异号),然后依据一次项系数b 的正负再确定p q 、的符号 (2)若2x bx c ++中的b c 、为整数时,要先将c 分解成两个整数的积(要考虑到分解的各种可能),然后看这两个整数之和能否等于b ,直到凑对为止. 要点二、首项系数不为1的十字相乘法在二次三项式2ax bx c ++(a ≠0)中,如果二次项系数a 可以分解成两个因数之积,即12a a a =,常数项c 可以分解成两个因数之积,即12c c c =,把1212a a c c ,,,排列如下:按斜线交叉相乘,再相加,得到1221a c a c +,若它正好等于二次三项式2ax bx c ++的一次项系数b ,即1221a c a c b +=,那么二次三项式就可以分解为两个因式11a x c +与22a x c +之积,即()()21122ax bx c a x c a x c ++=++.要点诠释:(1)分解思路为“看两端,凑中间”(2)二次项系数a 一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.要点三、分组分解法对于一个多项式的整体,若不能直接运用提公因式法和公式法进行因式分解时,可考虑分步处理的方法,即把这个多项式分成几组,先对各组分别分解因式,然后再对整体作因式分解——分组分解法.即先对题目进行分组,然后再分解因式.要点诠释:分组分解法分解因式常用的思路有: 方法分类分组方法特点分组分解法四项二项、二项 ①按字母分组②按系数分组 ③符合公式的两项分组 三项、一项先完全平方公式后平方差公式 五项三项、二项 各组之间有公因式 六项三项、三项二项、二项、二项 各组之间有公因式 三项、二项、一项可化为二次三项式要点四:添、拆项法把多项式的某一项拆开或填补上互为相反数的两项(或几项),使原式适合于提公因式法、公式法或分组分解法进行分解.要注意,必须在与原多项式相等的原则下进行变形.添、拆项法分解因式需要一定的技巧性,在仔细观察题目后可先尝试进行添、拆项,在反复尝试中熟练掌握技巧和方法. 【典型例题】 类型一、十字相乘法1、将下列各式分解因式: (1); (2)21016x x -+; (3)2310x x --举一反三:【变式1】分解因式:(1)1072++x x ; (2)822--x x ; (3)2718x x --+【变式2】因式分解:m 2n ﹣5mn+6n.2、将下列各式分解因式: (1)22355x x +-; (2)25166x x ++(3)22616x xy y --; (4).举一反三:【变式】将下列各式分解因式:(1)10722+-xy y x ; (2)()()342++-+b a b a .3、将下列各式分解因式: (1); (2)举一反三:【变式】分解因式:(1)2314x x +-;(2)2344x x --+;(3)2631105x x +-;类型二、分组分解法4、先阅读下列材料,然后回答后面问题:将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.能分组分解的多项式通常有四项或六项,一般的分组分解有四种形式,即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等.如“2+2”分法: ax+ay+bx+by=(ax+ay )+(bx+by ) =a (x+y )+b (x+y ) =(x+y )(a+b ) 如“3+1”分法:2xy+y 2﹣1+x 2=x 2+2xy+y 2﹣1=(x+y )2﹣1 =(x+y+1)(x+y ﹣1)请你仿照以上方法,探索并解决下列问题: (1)分解因式:x 2﹣y 2﹣x ﹣y ;(2)分解因式:45am 2﹣20ax 2+20axy ﹣5ay 2;(3)分解因式:4a 2+4a ﹣4a 2b ﹣b ﹣4ab+1.举一反三:【变式】分解因式:22244a b ab c +--【巩固练习】 一.选择题1. 将21016a a ++因式分解,结果是( ) A.()()28a a -+ B.()()28a a +- C.()()28a a ++ D.()()28a a --2.(2014•保定二模)下列因式分解正确的是( ) A . x 2﹣7x+12=x (x ﹣7)+12B . x 2﹣7x+12=(x ﹣3)(x+4)C . x 2﹣7x+12=(x ﹣3)(x ﹣4) D . x 2﹣7x+12=(x+3)(x+4)3. 如果()()2x px q x a x b -+=++,那么p 等于( )A.abB.a b +C.ab -D.a b --4. 若()()236123x kx x x +-=-+,则k 的值为( ) A.-9 B.15 C.-15 D.95. 如果,则b 为 ( )A .5B .-6C .-5D .6 6.把2222a b c bc --+进行分组,其结果正确的是( ) A. 222()(2)a c b bc --- B. 222()2a b c bc --+ C. 222()(2)a b c bc --- D. 222(2)a b bc c --+ 二.填空题7. 若()()21336m m m a m b -+=++,则a b -= .8. 因式分解22a b ac bc -++___________. 9.因式分解:4a 2+4a ﹣15= .10. 因式分解:ax bx cx ay by cy +++++=_______________; 11. 因式分解()2064x x -+= . 12.分解因式:321a a a +--=________.三.解答题 13.分解因式:(1)268x x -+; (2)21024x x +-;(3)215238a a -+; (4)22568x xy y -++;(5)225533a b a b --+.分式的概念和性质要点一、分式的概念一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子AB叫做分式.其中A 叫做分子,B 叫做分母.要点诠释:(1)分式的形式和分数类似,但它们是有区别的.分数是整式,不是分式,分式是两个整式相除的商式.分式的分母中含有字母;分数的分子、分母中都不含字母.(2)分式与分数是相互联系的:由于分式中的字母可以表示不同的数,所以分式比分数更具有一般性;分数是分式中字母取特定值后的特殊情况.(3)分母中的“字母”是表示不同数的“字母”,但π表示圆周率,是一个常数,不是字母,如aπ是整式而不能当作分式. (4)分母中含有字母是分式的一个重要标志,判断一个代数式是否是分式不能先化简,如2x y x是分式,与xy 有区别,xy 是整式,即只看形式,不能看化简的结果.要点二、分式有意义,无意义或等于零的条件 1.分式有意义的条件:分母不等于零.2.分式无意义的条件:分母等于零.3.分式的值为零的条件:分子等于零且分母不等于零. 要点诠释:(1)分式有无意义与分母有关但与分子无关,分式要明确其是否有意义,就必须分析、讨论分母中所含字母不能取哪些值,以避免分母的值为零.(2)本章中如果没有特殊说明,所遇到的分式都是有意义的,也就是说分式中分母的值不等于零.(3)必须在分式有意义的前提下,才能讨论分式的值. 要点三、分式的基本性质分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,这个性质叫做分式的基本性质,用式子表示是:A A M A A MB B M B B M⨯÷==⨯÷,(其中M 是不等于零的整式). 要点诠释:(1)基本性质中的A 、B 、M 表示的是整式.其中B ≠0是已知条件中隐含着的条件,一般在解题过程中不另强调;M ≠0是在解题过程中另外附加的条件,在运用分式的基本性质时,必须重点强调M ≠0这个前提条件.(2)在应用分式的基本性质进行分式变形时,虽然分式的值不变,但分式中字母的取值范围有可能发生变化.例如:,在变形后,字母x 的取值范围变大了.要点四、分式的变号法则对于分式中的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变;改变其中任何一个或三个,分式成为原分式的相反数.要点诠释:根据分式的基本性质有b b a a -=-,b b a a-=-.根据有理数除法的符号法则有b b b a a a -==--.分式a b 与ab-互为相反数.分式的符号法则在以后关于分式的运算中起着重要的作用. 要点五、分式的约分,最简分式与分数的约分类似,利用分式的基本性质,约去分子和分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.如果一个分式的分子与分母没有相同的因式(1除外),那么这个分式叫做最简分式.要点诠释:(1)约分的实质是将一个分式化成最简分式,即约分后,分式的分子与分母再没有公因式.(2)约分的关键是确定分式的分子与分母的公因式.分子、分母的公因式是分子、分母的系数的最大公约数与相同因式最低次幂的积;当分式的分子、分母中含有多项式时,要先将其分解因式,使之转化为分子与分母是不能再分解的因式积的形式,然后再进行约分.要点六、分式的通分与分数的通分类似,利用分式的基本性质,使分式的分子和分母同乘适当的整式,不改变分式的值,把分母不同的分式化成相同分母的分式,这样的分式变形叫做分式的通分.要点诠释:(1)通分的关键是确定各分式的最简公分母:一般取各分母所有因式的最高次幂的积作为公分母.(2)如果各分母都是单项式,那么最简公分母就是各系数的最小公倍数与相同字母的最高次幂的乘积;如果各分母都是多项式,就要先把它们分解因式,然后再找最简公分母.(3)约分和通分恰好是相反的两种变形,约分是对一个分式而言,而通分则是针对多个分式而言. 【典型例题】 类型一、分式的概念1、下列式子中,哪些是整式?哪些是分式?2a ,3x ,1m m +,23x +,5π,2a a ,23-.类型二、分式有意义,分式值为02、下列各式中,m 取何值时,分式有意义? (1)2m m +;(2)1||2m -;(3)239mm --.举一反三:【变式1】在什么情况下,下列分式没有意义?(1)3(7)x x x +;(2)21x x +;(3)222x x ++.【变式2】当x 为何值时,下列各式的值为0.(1)2132x x +-;(2)221x x x +-;(3)224x x +-.类型三、分式的基本性质3、不改变分式的值,将下列分式的分子、分母中的系数化为整数.(1)0.20.020.5x y x y+-; (2)11341123x yx y +-.举一反三:【变式1】如果把分式yx x232-中的y x ,都扩大3倍,那么分式的值( )A 扩大3倍B 不变C 缩小3倍D 扩大2倍【变式2】填写下列等式中未知的分子或分母.(1)22?x y x y x y +-=-; (2)()()?()()()b a c b a c a b b c a c--=----.4、 不改变分式的值,使下列分式的分子和分母不含“-”号. (1)2a b -;(2)45x y --;(3)3m n -;(4)23bc--.类型四、分式的约分、通分5、 将下列各式约分:(1)23412ax x ;(2)243153n n x y x y +-;(3)211a a --;(4)321620m m m m -+-.举一反三: 【变式】通分:(1)4b ac ,22a b c ;(2)22x x +,211x -.(3)232a b 与2a b ab c -;(4)12x +,244x x -,22x -.【巩固练习】 一.选择题1.在代数式22221323252,,,,,,33423x x xy x x x x π+-+中,分式共有( ). A.2个 B.3个C.4个D.5个2.使分式5+x x值为0的x 值是( ) A .0 B .5 C .-5D .x ≠-53. 下列判断错误..的是( ) A .当23x ≠时,分式231-+x x 有意义 B .当a b ≠时,分式22aba b-有意义 C .当21-=x 时,分式214x x+值为0 D .当x y ≠时,分式22x y y x --有意义4.x 为任何实数时,下列分式中一定有意义的是( )A .21x x+B .211x x -- C .11x x -+ D .211x x -+ 5.如果把分式yx yx ++2中的x 和y 都扩大10倍,那么分式的值( ) A .扩大10倍 B .缩小10倍 C .是原来的32D .不变6.下列各式中,正确的是( )A .a m ab m b+=+ B .0a ba b+=+ C .1111ab b ac c +-=-- D .221x y x y x y-=-+二.填空题7.当x =______时,分式632-x x无意义. 8.若分式67x--的值为正数,则x 满足______. 9.(1)112()x xx --=- (2).y x xy x22353)(= 10.(1)22)(1yx y x -=+ (2)⋅-=--24)(21y y x11.分式2214a b 与36xab c的最简公分母是_________. 12. 化简分式:(1)3()x yy x -=-_____;(2)22996x x x -=-+_____. 三.解答题13.当x 为何值时,下列分式有意义?(1)12x x +-;(2)1041x x -+;(3)211x x -+;(4)2211x x ---.14.已知分式,y ay b-+当y =-3时无意义,当y =2时分式的值为0, 求当y =-7时分式的值.15.不改变分式的值,使分子、分母中次数最高的项的系数都化为正数.(1)22x x y --(2)2ba a-- (3)2211x x x x---+(4)2231m m m ---。
十字相乘法非常非常好用详解
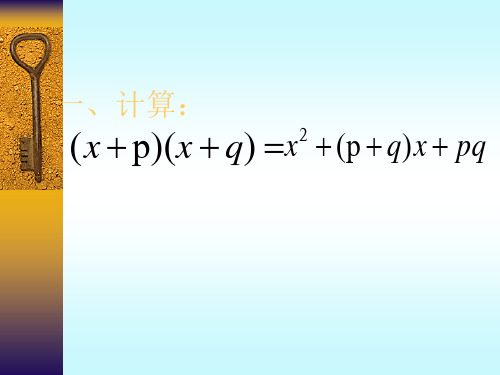
把下列各式分解因式
1. x2-11x-12 2. x2+4x-12 3. x2-x-12 4. x2-5x-14 5. y2-11y+24
例2、把 y4-7y2-18 分 解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
例7、把 (x+1)(x+2)(x+3)(x+4)-3分解 因式
拓展创新
把下列各式分解因式 1、x2-4xy+4y2-6x+12y+8
2、(x2+2x)(x2+2x-11)+11 3、x n+1+3xn+2xn-1 4、(x+1)(x+3)(x+5)(x+7)+16
x
7
x 1
②交叉相乘,和相加 ③检验确定,横写因式
顺口溜:
x7x 6x
பைடு நூலகம்
竖分常数交叉乘, 横写因式不能乱。
试一试:
(顺口溜:竖分常数交叉乘,横写因式不能乱。)
x2 8x 15 (x 5)(x 3) 小结:
用十字相乘法把形如
x
5
x
3
x2 ax b
二次三项式分解因式使
a p q,b pq
(3x) (5x) 8x
x2-5x+6 X2+5x-6 x2-5x-6 X2+5x+6
人教版数学八年级 5、用十字相乘法把二次三项式分解因式

5、用十字相乘法把二次三项式分解因式【知识精读】对于首项系数是1的二次三项式的十字相乘法,重点是运用公式()()x a b x ab x a x b 2+++=++()进行因式分解。
掌握这种方法的关键是确定适合条件的两个数,即把常数项分解成两个数的积,且其和等于一次项系数。
对于二次三项ax bx c 2++(a 、b 、c 都是整数,且a ≠0)来说,如果存在四个整数a c a c 1122,,,满足a a a c c c 1212==,,并且a c a c b 1221+=,那么二次三项式ax bx c 2++即()a a x a c a c x c c 122122112+++可以分解为()()a x c a x c 1122++。
这里要确定四个常数a c a c 1122,,,,分析和尝试都要比首项系数是1的类型复杂,因此一般要借助画十字交叉线的办法来确定。
下面我们一起来学习用十字相乘法因式分解。
【分类解析】1. 在方程、不等式中的应用例1. 已知:x x 211240-+>,求x 的取值范围。
分析:本题为二次不等式,可以应用因式分解化二次为一次,即可求解。
解:Θx x 211240-+> ()()∴-->∴->->⎧⎨⎩-<-<⎧⎨⎩∴><x x x x x x x x 3803080308083或或例2. 如果x x mx mx 43222-+--能分解成两个整数系数的二次因式的积,试求m 的值,并把这个多项式分解因式。
分析:应当把x 4分成x x 22⋅,而对于常数项-2,可能分解成()-⨯12,或者分解成()-⨯21,由此分为两种情况进行讨论。
解:(1)设原式分解为()()x ax x bx 2212+-++,其中a 、b 为整数,去括号,得:()()x a b x x a b x 43222++++-- 将它与原式的各项系数进行对比,得:a b m a b m +=-=-=-1122,,解得:a b m =-==101,,此时,原式()()=+--x x x 2221(2)设原式分解为()()x cx x dx 2221+-++,其中c 、d 为整数,去括号,得:()()x c d x x c d x 43222++-+-- 将它与原式的各项系数进行对比,得:c d m c d m +=-=--=-1122,,解得:c d m ==-=-011,,此时,原式()()=--+x x x 22212. 在几何学中的应用例. 已知:长方形的长、宽为x 、y ,周长为16cm ,且满足 x y x xy y --+-+=22220,求长方形的面积。
十字相乘法

“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解二次三 项式。 例1、把 x2+6x-7分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
2
步骤:
x
x
x 6 x 7 ( x 7)(x 1) ①竖分二次项与常数项
7
②交叉相乘,和相加 ③检验确定,横写因式
1
顺口溜: 竖分常数交叉验, 横写因式ቤተ መጻሕፍቲ ባይዱ能乱。
x 7x 6x
试一试:
(顺口溜:竖分常数交叉验,横写因式不能乱。)
小结:
2
x x
x 8x 15 ( x 5)(x 3)
2
用十字相乘法把形如
x px q
二次三项式分解因式使
5 3
q ab, p a b
x
x
a b
(3x) (5x) 8x∴x2+px+q=(x+a)(x+b)
2 x -5x+6 2 x -5x-6 2 X +5x-6
2 X +5x+6
十字相乘法的 要领是: “头尾分解, 交叉相乘,
求和凑中,
观察试验”。
注意: 当常数项是正数时,分解的 两个数必同号,即都为正或都为 负,交叉相乘之和得一次项系数。 当常数项是负数时,分解的两个 数必为异号,交叉相乘之和仍得 一次项系数。因此因式分解时, 不但要注意首尾分解,而且需十 分注意一次项的系数,才能保证 因式分解的正确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D 、用十字相乘法把二次三项式分解因式
【知识精读】
对于首项系数是1的二次三项式的十字相乘法,重点是运用公式
()()x a b x ab x a x b 2
+++=++()进行因式分解。
掌握这种方法的关键是确
定适合条件的两个数,即把常数项分解成两个数的积,且其和等于一次项系数。
()a a x a c a c x c c 122122112+++可以分解为()()a x c a x c 1122++。
这里要确定四个常数a c a c 1122,,,,分析和尝试都要比首项系数是1的类型复杂,因此一般要借助画十字交叉线的办法来确定。
下面我们一起来学习用十字相乘法因式分解。
【分类解析】
1. 在方程、不等式中的应用
例.已知:x x 2
11240-+>,求x 的取值范围。
2. 在几何学中的应用
例. 已知:长方形的长、宽为x 、y ,周长为16cm ,且满足
x y x xy y --+-+=22220,求长方形的面积。
分析:要求长方形的面积,需借助题目中的条件求出长方形的长和宽。
3、中考点拨
1.把2
2224954y y x y x --分解因式的结果是________________。
2. 因式分解:6752
x x --=_______________
5、题型展示
例. 若x y mx y 2256-++-能分解为两个一次因式的积,则m 的值为( ) A. 1
B. -1
C. ±1
D. 2
解:()()x y mx y x y x y mx y 225656-++-=+-++- -6可分解成()-⨯23或()-⨯32,因此,存在两种情况:
(1)x +y -2 (2)x +y -3
x-y 3 x-y 2
由(1)可得:m =1,由(1)可得:m =-1 故选择C 。
说明:对二元二次多项式分解因式时,要先观察其二次项能否分解成两个一次式乘积,再通过待定系数法确定其系数,这是一种常用的方法。
例2. 已知:a 、b 、c 为互不相等的数,且满足()()()a c b a c b -=--2
4。
求证:a b b c -=-
证明:()()() a c b a c b -=--2
4
()()()()()()∴----=∴-+-+-+=∴+-++=∴+-=∴+-=∴-=-a c b a c b a ac c bc ac ab b a c b a c b a c b a c b a b b c
2
2222
2
2
40
244440
4402020
例3. 若x x x a 32
57+++有一因式x +1。
求a ,并将原式因式分解。
解: x x x a 32
57+++有一因式x +1
∴当x +=10,即x =-1时,x x x a 3
2
570+++= ∴=a 3
()()()()()
()()()()()
x x x x x x x x x x x x x x x x x x x x x 3232222
2
573
4433
1413114311313+++=+++++=+++++=+++=+++=++
说明:由条件知,x =-1时多项式的值为零,代入求得a ,再利用原式有一个因式是x +1,分解时尽量出现x +1,从而分解彻底。
【实战模拟】 1. 分解因式:
(1)a b ab 2
2
1639++ (2)15742122x x y y n n n n +-++
(3)(
)
()x x x x 2
2
2322372+-++
2. 分解因式:3529422x xy y x y +-++-
5. 已知:x y x y +=+=05312..,,求312922x xy y ++的值。
