机床主轴结构优化设计

合集下载

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计目前，数控机床主轴结构主要包括主轴箱、主轴、轴承和冷却系统等部分。

针对这些部分的改进设计将有助于提高数控机床的性能和使用效果。

下面将从主轴箱结构、主轴结构和轴承结构三个方面进行详细的改进设计讨论。

一、主轴箱结构的改进设计主轴箱结构是数控机床主轴的重要组成部分，其设计对主轴的稳定性、刚性和传动精度等方面有着重要影响。

在当前主轴箱结构中，存在一些问题，如难以满足高速、高功率主轴的需求，容易产生振动和噪音等。

为了解决这些问题，需要对主轴箱结构进行改进设计。

可以采用卧式主轴箱结构替代立式主轴箱结构。

卧式主轴箱结构相对于立式主轴箱结构具有更好的刚性和稳定性，可以有效降低振动和噪音，提高主轴的加工精度和稳定性。

卧式主轴箱结构也更适合于高速、高功率主轴的设计和加工。

可以采用分体式主轴箱结构。

分体式主轴箱结构将主轴箱分为上下两部分，通过精密调整螺母来调整主轴箱的上下间隙，从而使主轴箱具有更好的密封性和刚性。

这种结构不仅可以有效防止主轴箱内部润滑油渗漏，还可以提高主轴箱的动态刚性和热稳定性，有利于主轴的高速、高精度加工。

可以采用陶瓷复合材料制造主轴箱。

陶瓷复合材料具有良好的耐磨性、耐热性和耐腐蚀性，通过采用陶瓷复合材料制造主轴箱，可以有效提高主轴箱的使用寿命和可靠性。

陶瓷复合材料还具有较低的热膨胀系数和较高的热导率，有利于主轴箱的热稳定性和散热性能。

可以采用空气动力主轴结构替代机械传动主轴结构。

空气动力主轴结构采用气体压力来传递动力，不需要传统的机械传动部件，可以实现零摩擦、零磨损的运转。

空气动力主轴结构的传动效率高、温升小、运转平稳性好，有利于提高主轴的加工精度和稳定性。

可以采用磁悬浮主轴结构。

磁悬浮主轴结构通过磁场来支撑和传递动力，不需要机械轴承，可以实现无接触、无摩擦的运转。

磁悬浮主轴结构具有较高的刚性和稳定性，可以有效降低振动和噪音，提高主轴的加工精度和寿命。

可以采用弹性变形主轴结构。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计数控机床作为现代制造业中的重要设备，其主轴结构的设计对于机床性能和加工质量具有非常重要的影响。

随着制造技术的不断发展，传统的数控机床主轴结构已经不能满足现代制造业对高精度、高效率、高稳定性的需求。

对数控机床主轴结构进行改进设计已成为当今的研究热点之一。

一、数控机床主轴结构的基本形式数控机床主轴结构是由主轴箱、主轴和主轴驱动系统组成的，其中主轴箱起到支撑和导向主轴的作用，主轴承载加工刀具和承受切削负载，主轴驱动系统则负责驱动主轴旋转。

传统的数控机床主轴结构通常采用滚动轴承或滑动轴承支撑主轴，由电机通过皮带传动或直接连接方式驱动主轴旋转。

由于滚动轴承和滑动轴承在高速、高负载工况下易产生磨损和热变形，从而影响机床的加工精度和稳定性。

二、数控机床主轴结构的改进设计方向针对传统数控机床主轴结构存在的问题，现代研究者提出了一系列的改进设计方案，主要包括以下几个方向：采用高速轴承技术、使用直接驱动技术、应用新材料和新工艺等。

这些改进设计方案旨在提高数控机床主轴的转速、承载能力和稳定性，从而提高机床的加工精度和效率。

1. 采用高速轴承技术传统数控机床主轴结构采用的滚动轴承或滑动轴承在高速工况下容易出现磨损和热变形，限制了主轴的转速和稳定性。

而采用高速轴承技术可以有效地提高主轴的转速和承载能力，同时减小主轴的振动和磨损，从而改善机床的加工精度和稳定性。

目前，国内外一些制造商已经开始使用陶瓷轴承和陶瓷滚珠轴承等高速轴承技术来改善数控机床主轴结构。

2. 使用直接驱动技术传统数控机床主轴结构通常采用电机通过皮带传动或直接连接方式来驱动主轴旋转，然而这种方式存在传动效率低、振动大、维护成本高等问题。

使用直接驱动技术成为了现代数控机床主轴结构改进的重要方向。

直接驱动技术通过在主轴内部集成电机，利用电磁力直接驱动主轴旋转，不仅可以减小机床的占地面积，提高传动效率，还可以减小振动和噪音，从而提高机床的加工精度和稳定性。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计数控机床主轴是数控机床的关键部件，其性能直接影响机床加工精度和加工效率。

随着数控技术的不断发展，对数控机床主轴结构的要求也越来越高。

为了满足市场对数控机床加工精度的需求，需要对数控机床主轴结构进行改进设计，以提高其性能和可靠性。

一、数控机床主轴结构存在的问题1. 结构复杂：传统的数控机床主轴结构通常采用多个轴承和润滑系统，结构复杂，加工成本高。

2. 刚性不足：部分数控机床主轴刚性不足，加工时容易产生振动和变形，影响加工精度。

3. 温升大：部分数控机床主轴在高速加工时容易产生较大的温升，影响机床稳定性和使用寿命。

4. 维护困难：传统数控机床主轴结构维护和保养较为繁琐，需要定期更换润滑油和轴承。

以上问题严重影响了数控机床的加工精度和稳定性，需要通过改进设计来解决。

二、改进设计方案针对数控机床主轴结构存在的问题，可以采取以下几点改进设计方案：1. 优化结构：采用轴向预紧轴承和径向预紧轴承的组合方式，降低轴承数量，简化结构，减小主轴体积和重量。

2. 提高刚性：采用高强度材料和优化设计，提高数控机床主轴的刚性，减小振动和变形，提高加工精度。

3. 降低温升：采用先进的冷却系统和材料，减小高速加工时的温升，提高机床稳定性和使用寿命。

4. 简化维护：采用自动润滑系统和可拆卸设计，简化维护和保养，减小维护成本和时间。

上述改进设计方案可以有效解决传统数控机床主轴结构存在的问题，提高数控机床的加工精度和稳定性，提升竞争力。

三、改进设计实施过程改进设计实施过程中，需要参考市场需求和技术发展趋势，充分调研国内外同类产品的主轴结构和性能，进行方案比较和优化设计。

1. 方案比较：对不同的数控机床主轴结构方案进行技术比较和性能测试，寻找最适合产品需求的方案。

2. 优化设计：在方案确定后，对数控机床主轴结构进行进一步的优化设计，满足产品性能指标和质量要求。

3. 样机制造：根据优化设计方案制作数控机床主轴样机，进行性能测试和验证，验证设计方案的可行性和有效性。

基于matlab的机床主轴结构优化设计

基于matlab的机床主轴结构优化设计机床主轴是机床的核心部件，其结构设计的好坏直接影响到机床的加工精度和效率。

因此，对机床主轴的结构优化设计具有重要的意义。

本文将介绍基于matlab的机床主轴结构优化设计方法。

一、机床主轴结构分析机床主轴结构一般由主轴箱、主轴轴承、主轴轴颈、主轴电机等组成。

其中，主轴箱是主轴的支撑结构，主轴轴承是主轴的支撑部件，主轴轴颈是主轴的转动部件，主轴电机是主轴的驱动部件。

主轴箱的结构设计应考虑刚度、强度和稳定性等因素，主轴轴承的选型应考虑承载能力、转速和寿命等因素，主轴轴颈的设计应考虑转速、径向载荷和刚度等因素，主轴电机的选型应考虑功率、转速和效率等因素。

二、机床主轴结构优化设计方法1.建立机床主轴有限元模型建立机床主轴有限元模型是机床主轴结构优化设计的基础。

有限元模型应包括主轴箱、主轴轴承、主轴轴颈和主轴电机等部件。

有限元模型应考虑主轴的静态和动态特性，包括主轴的刚度、强度、自然频率和振动模态等。

2.确定机床主轴结构优化目标机床主轴结构优化目标应包括主轴的刚度、强度、自然频率和振动模态等。

优化目标应根据机床主轴的工作条件和加工要求确定。

3.确定机床主轴结构优化设计变量机床主轴结构优化设计变量应包括主轴箱、主轴轴承、主轴轴颈和主轴电机等部件的尺寸、材料和结构参数等。

设计变量应根据机床主轴的工作条件和加工要求确定。

4.建立机床主轴结构优化设计模型机床主轴结构优化设计模型应包括有限元模型、优化目标和设计变量等。

优化模型应考虑主轴的静态和动态特性，包括主轴的刚度、强度、自然频率和振动模态等。

5.进行机床主轴结构优化设计机床主轴结构优化设计应采用优化算法进行求解。

常用的优化算法包括遗传算法、粒子群算法、模拟退火算法等。

优化算法应根据机床主轴的工作条件和加工要求选择。

6.验证机床主轴结构优化设计结果机床主轴结构优化设计结果应进行验证。

验证方法包括有限元分析、试验验证等。

验证结果应与优化设计目标相符合。

机床主轴结构优化设计

% 机床主轴结构优化设计% 1-约束非线性优化函数fmincon的调用参数赋值% 设计变量的初始值（x(1）：主轴跨度l、x(2）：主轴外径D、x(3）：悬臂长度a）x0=[500;100;120]; % 单位：mm% 设计变量的下界与上界Lb=[300;60;90];Ub=[650;140;150];% 调用多维约束优化函数% 没有线性不等式约束，参数A,b定义为空矩阵符号“[]”% 没有线性等式约束，参数Aeq,beq定义为空矩阵符号“[]”[x_opt,f_opt,exitflag,output]=fmincon('jczzjg_f',x0,[],[],[],[],Lb,Ub,'jczzjg_g')% 检验螺栓联接优化设计结果的约束函数值g=jczzjg_g(x_opt)% 2-机床主轴质量的目标函数(jczzjq_f)function f=jczzjg_f(x);d=30; % 主轴内径（mm）rho=7.8e-3; % 钢材密度（g/mm^3）f=pi*rho*(x(1)+x(3))*(x(2)^2-d^2)/4;% 3-机床主轴悬臂端挠度的非线性约束函数(jczzjg_g)function [g,Ceq]=jczzjg_g(x);F=1.5e4; % 主轴悬臂端载荷（N）d=30; % 主轴内径（mm）y0=0.05; % 主轴悬臂端许用挠度（mm）E=2.1e5; % 钢材弹性模量（MPa）J=pi*(x(2)^4-d^4)/64; % 主轴惯性矩（mm^4）% 非线性不等式约束（the nonlinear inequality constraints）g=F*x(3)^2*(x(1)+x(3))/(3*E*J)-y0; % 主轴悬臂端约束函数% 非线性等式约束（the nonlinear equality constraints）Ceq=[];计算结果：Optimization terminated: first-order optimality measure lessthan options.TolFun and maximum constraint violation is lessthan options.TolCon.Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlin ineqnonlin1 13x_opt =300.000074.889890.0000f_opt =1.1249e+004exitflag =1 % 返回值exitflag>0表示计算收敛output =iterations: 10 % iterations是优化过程中迭代次数funcCount: 51 % funcCount是代入函数值的次数stepsize: 1 % 1algorithm是优化所采用的算法（中等规模，拟牛顿SQP）algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'firstorderopt: 7.5880e-007 % 一阶优化精度cgiterations: []message: [1x144 char]g =-3.4694e-017。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计
数控机床主轴结构是数控机床的关键部件之一，其性能直接影响到机床的加工精度和
加工效率。

针对传统数控机床主轴结构存在的问题，如转动精度低、刚性不够、加工效率
低等，需要进行改进设计。

可以采用高精度轴承来提高主轴的转动精度。

传统的数控机床主轴常采用普通轴承，
其转动精度受到轴承自身的限制。

而高精度轴承具有更好的精度和刚度，能够大幅度提高
主轴的转动精度。

可以考虑采用陶瓷轴承、磁悬浮轴承或者超精密轴承等高精度轴承来替
代传统的普通轴承。

可以采用优化的主轴结构来提高主轴的刚性。

传统的数控机床主轴结构多为采用进给
轴和回转轴串联的结构，刚性较差。

改进设计可以考虑采用进给轴和回转轴并联的结构，
或者采用短连接结构，提高主轴的刚性。

可以增加主轴的直径，提高主轴的刚性和承载能力。

可以采用高速主轴设计来提高机床的加工效率。

传统数控机床主轴转速较低，加工效
率有限。

改进设计可以采用电主轴、液压主轴或者电液混合主轴等高速主轴设计，提高主
轴的转速和加工效率。

还可以采用主轴冷却系统来控制主轴的温度，提高主轴的稳定性和
使用寿命。

为了提高数控机床的稳定性和可靠性，可以采用主轴预紧力调节装置。

通过对主轴预
紧力的调节，可以减小运动中的轴向游隙，提高传动精度和位置精度。

通过对数控机床主轴结构进行改进设计，可以提高主轴的转动精度、刚性和加工效率，进而提高机床的加工精度和加工效率。

这对于满足现代制造业对高精度和高效率加工的需
求具有重要意义。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计1. 引言1.1 研究背景数控机床主轴作为整个机床中的核心部件，在加工精度、效率和稳定性等方面起着至关重要的作用。

随着制造业的不断发展和技术的进步，对数控机床主轴结构的要求也越来越高。

目前市场上常见的数控机床主轴结构存在着一些问题，比如轴承摩擦力大、振动噪音大、稳定性差等，影响了机床加工质量和效率。

对数控机床主轴结构进行改进设计具有重要意义。

在当前工业生产中，高精度、高效率、高速度是制造企业追求的目标。

而数控机床主轴结构作为影响机床性能的关键部件之一，需要不断进行创新和改进，以适应不断变化的市场需求。

深入研究主轴结构的改进设计，优化结构材料和加工工艺，对提升数控机床的加工精度和效率具有重要意义。

【2000字】1.2 研究目的研究目的是为了通过对数控机床主轴结构进行改进设计，提高机床的加工精度和工作效率。

当前市场上存在着许多数控机床主轴结构设计较为传统，存在一定的问题，例如在高速高效加工过程中容易产生振动和噪音，影响加工精度和表面质量。

本研究旨在通过优化设计改进数控机床主轴结构，提高其稳定性和刚性，减少振动和噪音，从而提高加工质量和效率。

通过结合结构材料优化和加工工艺改进，探索出一种更加先进和可靠的数控机床主轴结构设计方案，并分析其在技术和经济方面的可行性，为数控机床行业的进一步发展提供参考和指导。

2. 正文2.1 数控机床主轴结构现状数控机床主轴结构是数控机床的核心部件之一，主要负责转动切削工具进行加工。

目前的数控机床主轴结构主要分为直线主轴和滚珠主轴两种类型。

直线主轴结构简单，操作方便，适用于对工件精度要求不高的加工，但主轴刚度较低，容易产生振动。

滚珠主轴结构采用滚珠轴承支撑，具有较高的刚度和承载能力，适用于高精度加工，但制造成本较高。

当前数控机床主轴结构在设计上存在一些问题，如主轴转速范围窄、刚度不足、温升较大等。

这些问题制约了数控机床的加工效率和加工质量。

为了解决这些问题，可以采取改进设计方案。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计随着制造业的发展和技术的进步，数控机床在工业生产中扮演着越来越重要的角色。

数控机床主轴作为数控机床的核心部件之一，其性能和结构对机床的加工精度和效率具有重要影响。

为了提高数控机床主轴的加工精度和稳定性，需要对其结构进行改进设计。

本文将从数控机床主轴的结构特点、存在问题以及改进设计方面进行探讨，以期为数控机床主轴结构的改进设计提供一些参考意见。

一、数控机床主轴的结构特点数控机床主轴是数控机床的核心部件，其主要功能是带动刀具进行切削加工。

数控机床主轴的结构特点主要包括以下几个方面：1.高速高精度数控机床主轴需要具备高速高精度的特点，以满足不同加工要求的需求。

在高速高精度的要求下，主轴需要具备较强的刚性和稳定性。

2.刚性要求高数控机床主轴在工作时需要承受较大的切削力和转矩，因此需要具备较高的刚性。

良好的刚性能够有效地抵抗切削力和振动，保证加工精度和表面质量。

3.稳定性要求高数控机床主轴在高速旋转时需要保持稳定，避免产生振动和不稳定的现象。

稳定的主轴运转能够保证加工的精度和表面质量。

尽管数控机床主轴具有高速高精度、高刚性高稳定性的特点，但在实际应用中还是存在一些问题：1.噪音大部分数控机床主轴在高速旋转时会产生较大的噪音，给工人的工作环境带来一定的影响。

2.振动大部分数控机床主轴在高速旋转时会产生较大的振动，导致加工精度和表面质量下降。

3.散热不好部分数控机床主轴在长时间高速运转时会产生较大的热量，散热效果不佳，导致主轴温度过高，影响主轴的使用寿命和稳定性。

三、改进设计方案针对数控机床主轴存在的以上问题，可以从以下几个方面进行改进设计：1.采用新材料可以采用新型复合材料或者金属材料来替代传统的主轴材料，以提高主轴的强度和刚性，减少噪音和振动。

2.结构优化可以对数控机床主轴的结构进行优化设计，增加降噪材料和减振装置，以减少噪音和振动；采用新的轴承结构和支撑方式，提高主轴的稳定性和寿命。

4-主轴结构参数优化设计

d )
4
64
4
a
g1( X ) y0
64 Fx 3 ( x 1 x 3 )
2
3 E ( x 2 d )
4 4
0

应当指出，由于对机床主轴有较高的刚度要求，当满足刚度要求的情况下，其强度应该有相当的富裕。因此，不需要再提出主轴强度条件的约束条件。 2、设计变量的边界条件三个设计变量的边界约束条件为
机床主轴力学模型
x1 l X x2 D x3 a

一、设计变量和目标函数与主轴重量设计方案有关设计变量包括主轴的外径 D 、孔径 d 、两支承跨度 l 和外伸段长度 a。由于机床主轴的孔径d 主要取决于待加工棒料的直径，不能作为设计变量处理。
0

解：1、建立优化设计的数学模型
f ( X ) 0 . 785398163
T
( x 1 x 3 )( x 2 d )
2 2
T
X x 1 , x 2 , x 3 l , D , a
g 1 ( X ) 1 97 . 00872722

x 3 ( x1 x 3 )

可见，这是一个3维有5个不等式约束的非线性优化设计问题。

2、优化方法与结果采用内点惩罚函数法求解，初始惩罚因子 r (1 ) 2 ，惩罚因子递减系数 e 0 . 2 ，收敛精度 10 。按照题目给定的设计变量边界条件，取可行域内的初始点 X 480 ,100 ,120 ，经过17次迭代计算，得到最优解 T * * * * T X x 1 , x 2 , x 3 300 . 036 , 75 . 244 , 90 . 001

基于matlab的机床主轴结构优化设计

基于matlab的机床主轴结构优化设计基于MATLAB的机床主轴结构优化设计引言：机床主轴是数控机床的核心部件之一，其结构设计的优劣直接影响到机床的加工精度和工作效率。

为了提高机床主轴的性能，优化设计成为一种重要的研究方向。

本文基于MATLAB，探讨机床主轴结构的优化设计，旨在提高机床的加工效率和精度。

1. 优化设计的背景机床主轴是机床加工的关键部件，其结构设计直接影响加工质量和效率。

传统的机床主轴结构存在着重量大、刚性差等问题，需要进行优化设计以满足现代制造的需求。

2. 优化设计的目标优化设计的目标是提高机床主轴的刚性和动态特性，降低振动和噪声，提高加工精度和效率。

3. 优化设计的方法基于MATLAB的优化设计方法可以通过建立数学模型，进行参数优化，得到最佳的主轴结构设计。

4. 参数优化通过调整主轴的结构参数，如直径、长度等，可以改善主轴的刚性和动态特性。

利用MATLAB的优化工具箱，可以进行参数优化，得到最佳的主轴结构设计。

5. 结构优化主轴的结构优化可以通过改变材料、几何形状等方式来提高主轴的性能。

利用MATLAB的有限元分析工具，可以对主轴进行结构优化，提高其刚性和动态特性。

6. 优化结果分析通过对优化结果的分析，可以评估主轴的性能是否达到设计要求。

MATLAB提供了丰富的数据处理和可视化工具，可以对优化结果进行分析和展示。

7. 实验验证为了验证优化设计的效果，可以进行实验测试。

利用MATLAB的数据处理工具，可以对实验数据进行分析和比较，验证优化设计的有效性。

8. 结果讨论通过分析优化结果和实验数据，可以得出结论：基于MATLAB的机床主轴结构优化设计能够有效提高机床的加工精度和效率。

9. 总结和展望本文基于MATLAB，探讨了机床主轴结构的优化设计方法和实验验证，取得了一定的研究成果。

但是仍然有一些问题需要进一步研究，如如何进一步提高主轴的刚性和动态特性等。

结论：基于MATLAB的机床主轴结构优化设计方法可以提高机床的加工精度和效率。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计数控机床是现代机械加工领域不可或缺的设备，而主轴则是数控机床中最重要的部件之一，它负责驱动加工刀具完成不同形状的切削加工。

随着机械加工技术的不断发展，数控机床主轴的结构也在不断地改进和优化，以适应不同的加工要求和提高加工效率。

一、优化轴承结构轴承是数控机床主轴中的重要部件，它直接影响到主轴的精度、耐磨性和寿命等。

因此，目前主要的改进设计方向是优化轴承结构，采用更先进的轴承材料和结构设计，提高轴承的承载能力和稳定性，从而大幅提高数控机床主轴的精度和耐用性。

另外，采用一些特殊的轴承形式，如角接触轴承和圆锥滚子轴承，可以在提高主轴负载能力的同时，保持其高精度。

二、提高转速范围数控机床主轴的转速范围是评估其性能的一个重要指标，因为转速范围越广，就能满足更多不同的加工要求。

因此，当前的改进设计方向是提高主轴的转速范围，通过优化主轴结构，例如采用更轻的材料和更坚固的轴承等，以及改善冷却系统等方式，来实现更高的转速范围。

特别是在高速加工领域，对于提高主轴转速范围的要求更为迫切。

三、减小主轴摩擦阻力主轴的摩擦阻力会影响主轴的加工精度和效率，而减小主轴的摩擦阻力是改进设计的一个重要方向。

例如，采用滚动轴承结构，可以大大减小主轴的摩擦阻力，从而提高加工效率和精度。

另外，在主轴的设计中还可以采用更平滑的表面处理和优异的润滑系统，也可以减小主轴的摩擦阻力。

四、提高主轴刚性主轴的刚性对于加工的精度和质量都有直接的影响，因此提高主轴的刚性是改进设计的一个重要方向。

目前主要的方法是采用更优质的材料和结构设计，增加主轴的横向和纵向刚性。

此外，对于超精密加工要求，还可以采用主轴的自动补偿技术，通过实时调整主轴位置和速度来改善加工精度和表面光洁度。

机床主轴结构优化设计

主轴刚度是一个重要性能指标，其外伸端的挠度y不得超过规定值，据此建立性能约束
g(x)=y-
在外力F给定的情况下，y是设计变量x的函数，其值按下式计算
y=
式中，I=
则 g(x)=
此外，通常还应考虑主轴内最大应力不得超过许用应力。由于机床主轴对刚度要求比较高，当满足要求时，强度尚有相当富裕，因此应力约束条件可不考虑。边界约束条件为设计变量的取值范围，即
四、优化方法的选择
该实例中，设计变量数n=3，约束函数个数m=5，且有一个约束函数是非线性的，故属于非线性多变量约束优化问题。可以选择MATLAB中的fmincon()函数。因为fmincon函数是实现多变量约束优化，解决非线性多变量约束问题的一种优化方法。当然也可以选择遗传算法ga()。
五、程序及编译结果
lower upper ineqlin ineqnonlin
1 1
3
x =
300.0000
74.8898
90.0000
f =
11.2494
exitflag =
1
output =
iterations: 11
funcCount: 44
lssteplength: 1
stepsize: 4.8867e-007
f =
11.2497
exitflag =
1
output =
problemtype: 'nonlinearconstr'
rngstate: [1x1 struct]
generations: 4
funccount: 5180
message: [1x140 char]
maxconstraint: 0

机床主轴结构的优化课件

感谢您的观看
软件三
软件介绍：Altair OptiStruct是一款专业的结构优化软件，基于有限元方法进行结构分析和优化设计。它广泛应用于汽车、航空航天、机械等领域，为产品设计提供全面的性能分析和优化建议。
Altair OptiStruct具有强大的建模功能和高效的优化算法，可以快速建立复杂的三维模型并进行精细的网格划分。同时，它拥有丰富的材料库和约束条件设置功能，可以根据实际工况模拟各种复杂的物理场。通过后处理功能，用户可以直观地查看分析结果并进行优化设计。此外，它还提供了多种优化策略和算法，如拓扑优化、形状优化、尺寸优化等，可以帮助用户快速找到最优设计方案。
CHAPTER 02
机床主轴结构优化设计
优化设计理论与方法
传统优化设计方法
包括数学规划法、拉格朗日乘子法、罚函数法等，用于求解约束条件下目标函数的最优解。
智能优化设计方法
如遗传算法、粒子群算法、蚁群算法等，利用生物或自然界的规律进行优化搜索。
多目标优化设计方法
处理多个相互冲突的目标函数，寻求整体最优解。
CHAPTER 04
机床主轴结构优化软件介绍及使用教程
软件一：ANSYS有限元分析软件
软件介绍：ANSYS是一款全球领先的有限元分析软件，广泛应用于机械、电子、土木等领域。它能够进行结构、流体、电磁等多种物理场的模拟，为产品设计提供全面的性能分析和优化建议。
ANSYS有限元分析软件具有强大的建模功能和灵活的网格划分工具，可以快速建立复杂的三维模型并进行精细的网格划分。同时，它拥有丰富的材料库和边界条件设置功能，可以根据实际工况模拟各种复杂的物理场。通过后处理功能，用户可以直观地查看分析结果并进行优化设计。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计全文共四篇示例，供读者参考第一篇示例：数控机床主轴结构的改进设计一、引言数控机床主轴是数控机床的核心部件，直接关系到整个机床的加工精度和效率，因此对数控机床主轴的结构和设计要求是非常高的。

由于市场对数控机床主轴的要求越来越高，对主轴结构进行改进设计是十分必要的。

本文将从数控机床主轴的现状和存在的问题出发，结合最新的技术趋势，提出了一种改进设计方案，以期能够提高数控机床主轴的加工精度和效率，满足市场需求。

二、数控机床主轴的现状和存在的问题在现代工业生产中，数控机床已经成为主要的加工设备之一，而数控机床的主轴作为数控机床的核心部件，在加工过程中的稳定性、刚性和精度要求都非常高。

然而传统的数控机床主轴结构存在一些问题，如主轴转速和扭矩范围受限制、刚性不足、加工精度低、寿命短等。

这些问题制约了数控机床的进一步发展和应用。

三、改进设计方案针对数控机床主轴存在的问题，我们提出了以下改进设计方案：1. 采用新材料：选用高强度耐磨材料对主轴进行加工，提高主轴的表面硬度和耐磨性，延长主轴的使用寿命。

2. 引入新技术：采用先进的液压技术和动态平衡技术对主轴进行设计，提高主轴的稳定性和刚性，使主轴在高速转动时仍能保持高精度。

3. 结构优化：通过有限元分析和模拟优化设计，对主轴结构进行优化，提高主轴的刚性和稳定性。

4. 集成传感器：在主轴上集成多功能传感器，实时监测主轴的运行状态和工况参数，使主轴能够实现自动调节和自动保护。

5. 联网智能化：将主轴与数控系统实现数据共享和远程监控，实现主轴的智能化管理，提高加工效率和质量。

通过以上的改进设计方案，我们可以获得以下优势：1. 提高加工精度：采用新材料和新技术对主轴进行改进设计，能够有效提高主轴的加工精度，保证加工零件的质量。

2. 提高加工效率：结构优化和智能化管理使主轴能够在高速转动时保持高精度，提高加工效率。

3. 增加使用寿命：改进设计方案能够延长主轴的使用寿命，降低了主轴的维护成本。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计随着数控技术的发展和应用越来越广泛，数控机床在工业生产中发挥着越来越重要的作用。

而数控机床主轴作为数控机床的重要组成部分，其性能对整个数控机床的加工精度、加工效率和加工质量起着至关重要的作用。

对数控机床主轴结构的改进设计显得尤为重要，本文将对数控机床主轴结构的改进设计进行探讨。

一、数控机床主轴结构的基本原理数控机床主轴通常由主轴轴承、主轴箱、主轴驱动装置、主轴附件等组成。

主轴轴承是数控机床主轴的核心部件，支撑着主轴的转动，并承受着主轴上的加工负荷和转速。

主轴箱是主轴的固定部件，起到支撑、定位和密封的作用。

主轴驱动装置是主轴转动的动力源，通常采用电机驱动。

主轴附件包括主轴夹持装置、主轴冷却装置、主轴调速装置等，用于保证主轴工作时的稳定性和可靠性。

传统数控机床主轴结构存在一些问题，如主轴刚性不足、转速范围窄、热变形大、寿命短等。

这些问题在高速、高精度、高效率的数控加工中尤为突出，制约了数控机床的发展和应用。

急需对数控机床主轴结构进行改进设计，提高其刚性、稳定性和可靠性，以满足现代制造业对高精度、高效率加工的需求。

1. 提高主轴刚性主轴刚性是影响数控机床加工精度和表面质量的重要因素。

为了提高主轴刚性，可以采用镶钢套的轴承座设计，增加主轴箱的壁厚和加强结构连接，采用预紧式轴承和高刚性的轴承支撑结构等。

这些设计可以有效提高主轴的刚性和稳定性，提高加工精度和表面质量。

2. 扩大主轴转速范围在某些特定的加工工艺中，对主轴的转速范围要求较大。

为了满足这一需求，可以采用变频调速的主轴驱动装置，同时配合合理的主轴箱结构设计和高速、高精度的主轴轴承，以实现主轴转速范围的扩大。

3. 降低主轴热变形主轴在加工过程中会受到热变形的影响，导致加工精度下降。

为了降低主轴热变形，可以设计主轴冷却装置，通过主轴中的冷却液循环冷却，有效降低主轴的温升，减小热变形，提高加工精度。

4. 提高主轴寿命主轴在长时间高速运转下容易产生磨损和疲劳，降低主轴的使用寿命。

关于数控机床主轴结构的改进设计

关于数控机床主轴结构的改进设计数控机床主轴结构一直是数控机床的重要组成部分，直接影响着机床的加工精度、稳定性和效率。

随着数控技术的不断发展，对数控机床主轴的要求也越来越高，因此需要不断进行改进设计，以满足市场的需求。

本文将对数控机床主轴结构的改进设计进行探讨。

目前，传统的数控机床主轴结构一般由主轴箱、主轴和主轴轴承组成。

主轴箱是主轴的支撑和固定部分，主要由主轴箱体、电动机和传动装置组成；主轴是机床上用以支撑和带动切削工具进行切削加工的重要部件，其精度、稳定性和可靠性直接影响着机床的加工质量和效率；主轴轴承则是主轴的重要支撑组件，承受着主轴的径向和轴向负荷，其性能直接决定了主轴的转速、精度和寿命。

传统的数控机床主轴结构存在一些问题，首先是刚性不足。

由于主轴箱的设计和加工精度、主轴的材料和热处理工艺以及主轴轴承的选型和安装精度等因素的限制，传统的数控机床主轴在高速、超精密加工及重负荷加工等方面存在刚性不足的问题。

其次是转速范围有限。

传统的主轴箱结构和主轴轴承类型限制了主轴的转速范围，不能满足高速加工的需求。

主轴结构复杂、部件繁多、装配和调试难度大、维护成本高等也是影响机床主轴使用的因素。

针对传统数控机床主轴结构存在的问题，可以进行如下改进设计：2.1 刚性改进提高主轴箱的刚性，采用更高强度和更刚性的材料，优化结构设计，改进加工精度和技术工艺，以提高主轴箱的刚性，保证主轴的稳定性和可靠性。

可以采用更大直径的主轴，提高主轴的强度和刚性，以满足高速、超精密和重负荷加工的需求。

2.2 转速范围扩大采用新型的主轴箱结构和主轴轴承，优化传动装置，改进冷却系统等，以提高主轴的转速范围和稳定性。

可以采用自冷式主轴箱、高速主轴轴承、高速电动主轴等技术手段，使主轴的转速范围达到数十万转每分钟，以满足高速加工的需求。

2.3 结构简化简化主轴结构，减少主轴箱部件和主轴轴承数量，统一标准化部件，优化结构布局，减少装配和调试难度，降低维护成本。

机床主轴结构优化设计(温正方)

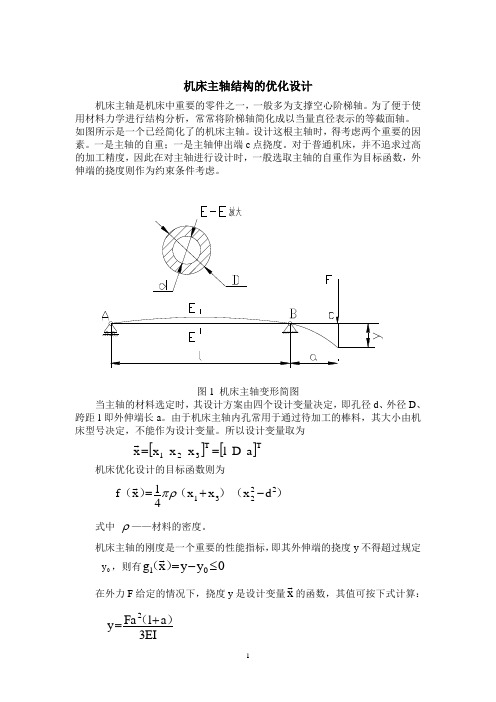
机床主轴结构的优化设计机床主轴是机床中重要的零件之一，一般多为支撑空心阶梯轴。

为了便于使用材料力学进行结构分析，常常将阶梯轴简化成以当量直径表示的等截面轴。

如图所示是一个已经简化了的机床主轴。

设计这根主轴时，得考虑两个重要的因素。

一是主轴的自重；一是主轴伸出端c 点挠度。

对于普通机床，并不追求过高的加工精度，因此在对主轴进行设计时，一般选取主轴的自重作为目标函数，外伸端的挠度则作为约束条件考虑。

图1 机床主轴变形简图当主轴的材料选定时，其设计方案由四个设计变量决定，即孔径d 、外径D 、跨距l 即外伸端长a 。

由于机床主轴内孔常用于通过待加工的棒料，其大小由机床型号决定，不能作为设计变量。

所以设计变量取为[][]T T 321a D l x x x x ==机床优化设计的目标函数则为））（（）（22231d x x x 41x f -+=πρ 式中 ρ——材料的密度。

机床主轴的刚度是一个重要的性能指标，即其外伸端的挠度y 不得超过规定0y ，则有0y y x g 01≤-=）（在外力F 给定的情况下，挠度y 是设计变量x的函数，其值可按下式计算：EI3a l Fa y 2）（+=式中）（44d -D 64I π= 则0y d x E 3x x Fx 64x g 044231231≤--+=）（）（）（π 此外，通常还应考虑主轴内最大应力不得超过许用应力。

由于机床主轴对刚度要求比较高，当刚度满足要求时，强度尚有相当富裕，因此应力条件约束可以不考虑。

另外，根据设计变量的取值范围有max min l l l ≤≤max min D D D ≤≤max min a a a ≤≤综上所述，可将主轴设计的数学模型表示如下：221321min f x x x x d 4πρ+-（）=（）（）（g ） s.t.2313104422min 132max 4min 252max 6min 373max 64Fx x x g x y 03E x d g x l x 0g x x -l 0g x D x 0g x x -D 0g x a -x 0g x x -a 0π+=-≤-≤≤≤≤≤≤（）（）（）（）=-（）=（）=-（）=（）=（）=在这里做如下假定：取主轴材料选45钢，查得ρ=7.85g/cm3，E=206Gpa ，主轴内径d=300mm ，F=15000N ，许用挠度y 0=0.05mm ，设计变量的初值为x 1=480mm ，x 2=100mm ，x 3=120mm ，上下限为150x 90140x 60650x 300321≤≤≤≤≤≤，，。