云南省泸西县中枢镇2018中考数学复习第四章三角形讲义
2018年云南中考数学一轮复习课件-第4章第3节 等腰三角形与直角三角形

第4页
2018中考数学复习课件
ห้องสมุดไป่ตู้
第5页
2018中考数学复习课件
1.(人教八下 P34 习题 17.2 第 1 题改编)下列各组线段中,不能 构成直角三角形的是( B ) A.a=8,b=15,c=17 B.a=10,b=24, c= 25 C.a=4,b=5,c= 41 D.a=5,b=12,c=13
第8页
2018中考数学复习课件
4 .( 北师八下 P31 例 3 改编)如图,AB ∥CD,∠CAB 与 ∠ACD 的平分线相交于 H 点,点 E 为 AC 的中点,若 EH =2 ,则 AC=4.
第9页
2018中考数学复习课件
5.(人教八上 P83 第 14 题改编) 如图,点 M,N 是△ABC 的边 BC 上的两点,且 BM =MN=NC=AM=AN,则∠BAN=90.
第17页
2018中考数学复习课件
【名师提醒】在等腰三角形中, 要注意分情况讨论: 1. 当已知等腰三角形的一个内角时 ,通常需要按这个角是顶角或 底角两种情况进行讨论, 此时要注意等腰三角形的底角一定是锐角, 即在等腰三角形中 ,钝角只能是顶角. 2. 当已知等腰三角形的两边时, 要按照其中一条边是腰或者底边 两种情况进行讨论 ,此时要注意使用三角形的三边关系进行验证,底 边长一定小于腰长的 2 倍 ,否则不能构成三角形.
(4)当∠A 为顶角时,如错解,则∠BAC=90°综上,∠BAC 的度数为 90°或 75°或 15°.
第16页
2018中考数学复习课件
2.(2017·淄博 )在边长为 4 的等边三角形 ABC 中,D 为 BC 边 上的任意一点 , 过点 D 分别作 DE⊥ AB, DF⊥ AC, 垂足分别 为 E ,F, 则 DE+ DF= __2 3__.,易错点:未进行分类讨论 而出现错解或漏解 ⇨ 【错因分析】 题目中并没有指明 BC 是等腰△ABC 的底或 腰.当 BC 为底时, 可求得∠BAC= 90° ;当 BC 为腰时, 还 应对 ∠B 的大小进行讨论.
2018年云南中考数学一轮复习课件-第4章第1节 角、相交线和平行线

第7页
2018中考数学复习课件
(2)邻补角 举例:∠ 2 与∠3,∠ 3 与 ∠ 4 , ∠4 与∠ 1, ∠1 与 ∠2 性质:邻补角之和等于 180°
第8页
2018中考数学复习课件
2.三线八角(如图 2)
(1)同位角:∠ 1 与∠5,∠ 2 与∠6,∠ 3 与∠7,∠ 4 与__∠ 8__; (2)内错角:∠ 2 与∠8,∠ 3 与__∠ 5__; (3)同旁内角:∠2 与∠ 5, ∠3 与__∠8__.
第14页
2018中考数学复习课件
1.(北师七下 P58 复习题第 1 题改编)下列结论中正确的是( A.一个角的补角大于这个角 B.两直线被第三条直线所截 ,同位角相等 C.余角和补角与角的位置有关 D.在同一平面内,若 a⊥l,b⊥l,则 a∥ b
D
)
第15页
2018中考数学复习课件
2. (人教七下 P9 第 10 题改编 )若直线 a∥b∥c, a 与 b 之间的 距离为 7 cm,b 与 c 之间的距离为 3 cm,则 a 与 c 之间的 距离为( D ) A. 4 cm B.10 cm C. 3 cm D.4 cm 或 10 cm
2018中考数学复习课件
第四章 三角形 第一节 角、相交线和平行线 【云南考情分析】 云南近五年主要考查角的计算,角的平分线 的定义,余角、补角的性质,平行线的性质和判定.出题简单, 常以选择题或填空题出现,常结合三角形内角和及外角一起考 查.
第1页
2018中考数学复习课件
知识点 1:直线、线段 1.两个基本事实: (1)过两点__有且只有__一条直线(两点确定 一条直线);(2)两点之间 __线段 __最短. ,点 C 把线段 AB 分成相等的两 1 条线段 AC 和 BC, 则点 C 叫做线段 AB 的中点. 即有 AC= BC= AB. 2 2.线段的中点:如图
云南中考数学第一部分教材知识梳理第四章第三节等腰三角形与直角三角形课件

故选A.
拓展题1图
类型二 直角三角形的相关计算 例2(’14 宿迁)如图,在Rt△ABC中,∠ACB= 90°,AD平分∠BAC与BC相交于点D,若BD=4, CD=2,则AB的长是_________.
例2题图
【解析】如解图,过点D作DE⊥AB,∵∠ACB
= 90° , AD 平 分 ∠ BAC , ∴ DE = CD = 2 , 在
类型一 等腰三角形的相关计算 例1 如图,在△ABC中,AB=AC,AD⊥BC于点D, 若AB=6,CD=4,则△ABC的周长是______.
例1题图
【解析】在△ABC中,∵AB=AC, AD⊥BC,∴BD=CD= 1 BC,
2
∴ BC = 2CD = 8 , AC = AB = 6 ,
∴△ABC的周长是6+6+8= 20 .
是50°.故选A.
解法二:由题意知三角形的一个内角为50°,则底角 = 1(180°-50°)=65°.故选B.
2
上述解法出现错误的原因是
_未__对__等__腰__三__角__形__的__底__角__和___顶__角__分__类__讨__论__,应改为 _当__5_0_°__角__为__顶__角__时__,__它__的__底__角__为___1_(_1_8_0_°__-__5_0_°__)_=___
判定
(1)三边都相等的三角形是等边三角形 (2)三个角都相等的三角形是等边三角 形 (3)有一个角是④___6_0_°___的等腰三角 形是等边三角形
面积 S= 1 ah 3 a(2 h= 3 a)
2
4
2
考点二 直角三角形的性质及判定
性质
(1)两锐角之和等于⑤__9_0_°_ (2)斜边上的中线等于斜边的⑥_一__半____ (3)30°角所对的直角边等于斜边的⑦ __一__半___ (4)勾股定理:若直角三角形的两直角边分 别为a,b,斜边为c,则有a2+b2=c2 (5)在直角三角形中,如果一条直角边等于 斜边的一半,那么这条直角边所对的锐角等 于⑧3_0_°___
云南省泸西县中枢镇2018中考数学复习第1_8章(打包8套)

1.二元一次方程
定义:含有个未知数,并且含有未知数的项的次数都是的整式方程。
一般形式: ax+by=c,有无数组解。
2.二元一次方程组的解法
⑴代入消元法:多适用于方程组中有一个未知数的系数是或的情形。
⑵:多适用于方程组的两个方程中相同未知数的系数或互为的情形。
【考点3】一次方程(组)的应用
如果 =a,那么x叫做a的平方根;正数a的正的平方根叫做a的算术平方根,记作 , 0的算术平方根为0.如果 =a,那么x叫做a的立方根,记作
2.最简二次根式
满足下列条件的二次根式,叫做最简二次根式:
(1)被开方式的因数是整数,因式是整式。
(2)被开方式中不含能开的尽方的因数或因式
3.运算法则: =(a≥0)
1.列方程组解应用题的一般步骤:
⑴审:即审清题意,分清题中的已知量、未知量;
⑵设:即设关键未知数;
⑶列:即找出适当等量关系,列出方程(组);
⑷解:即解方程(组);
⑸验:即检验所解答案是否正确或是否符合题意;
⑹答:即规范作答,注意单位名称。
2.列一元一次方程常见的应用题类型及关系式
⑴利润率问题:利润=售价-进价;利润率= ×100﹪
倒数:非零实数a的倒数是,互为倒数的两个数的积等于。
数轴:规定了的直线叫数轴。
绝对值: 即正数的绝对值等于它,零的绝对值等于零,负数的绝对值等于它的。
【考点2】近似数,有效数字和科学记数法
(1)近似数:对一个实际数所取得近似值,要注意精确度,如0.13456,精确到百分位是,精确到千分位是。
(2)有效数字:对于 一个近似数,从边第一个不是0的数字起,到止,都是这个近似数的有效数字。
2018年中考数学总复习第四章基本图形(一)第19讲特殊三角形第1课时等腰三角形讲解篇
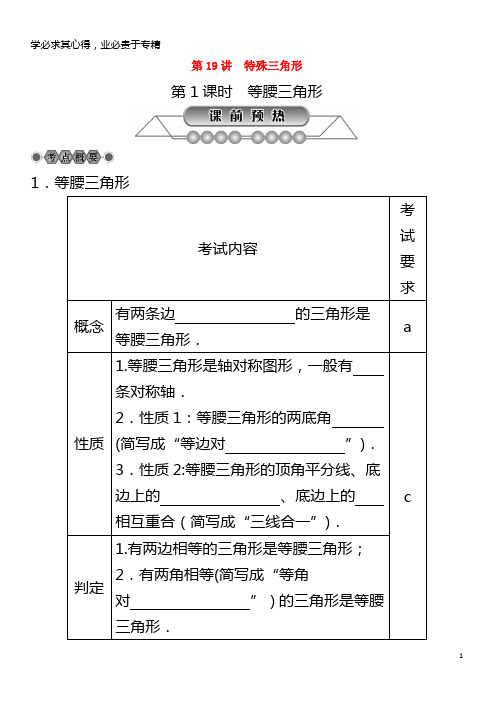
第19讲特殊三角形第1课时等腰三角形1.等腰三角形考试内容考试要求概念有两条边的三角形是等腰三角形.a性质1.等腰三角形是轴对称图形,一般有条对称轴.2.性质1:等腰三角形的两底角(简写成“等边对”).3.性质2:等腰三角形的顶角平分线、底边上的、底边上的相互重合(简写成“三线合一”).c判定1.有两边相等的三角形是等腰三角形;2.有两角相等(简写成“等角对”)的三角形是等腰三角形.2。
等边三角形考试内容考试要求概念有条边相等的三角形叫做等边三角形.a性质1.具有一般等腰三角形的所有性质;2.等边三角形的三个角都相等,并且每个角都于;3.等边三角形是轴对称图形,共有条对称轴.c判定1.三条边相等的三角形是等边三角形;2.三个角都的三角形是等边三角形;3.有一个角是的等腰三角形是等边三角形.拓展S等边△ABC=错误!ah=错误!a2,h=错误!a,其中a为边长,h为高.考试内容考试要求基本方法求等腰三角形腰上的高,在所给条件不确定的条件下,应按顶角为锐角和钝角两种情况来考虑:(1)当顶角为锐角时,腰上的高在三角形内部;(2)当顶角为钝角时,腰上的高在三角形外部.c1.(2017·台州)如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()A.AE=EC B.AE=BE C.∠EBC=∠BAC D.∠EBC=∠ABE2.(2017·丽水)等腰三角形的一个内角为100°,则顶角的度数是____________________.3.(2015·义乌)由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是____________________cm。
云南省泸西县中枢镇2018中考数学复习第四章三角形讲义

第2题图321F E D CBA第四章 三角形第一节 角、相交线与平行线考点1角及其平分线考点2 同一平面内两直线的位置关考点3 垂线性质及垂直平分线的性质 1、 垂线的性质(1) 平面内经过一点有且只有一条直线垂直于已知直线;(2) 直线外一点与直线上各点连接的所有线段中,垂线段最短;点到直线的距离:从直线外一点向已知直线作垂线,这一点和垂足之间的线段的长度叫做点到直线的距离。
2、 垂直平分线(1) 性质:线段垂直平分线上的点到该线段两端点的距离相等。
(2) 逆定理:和线段的两端点的距离相等的点在该线段的垂直平分线上。
考点4 平行线与平行公理1、 在同一平面内,不相交的两条直线叫做平行线。
2、 经过直线外一点,有且只有一条直线与这条直线平行。
3、 平行线的性质定理与判定定理。
习题精编1、从3时到6时,钟表的时针旋转角的度数是( ) A .30° B .60° C .90° D .120°2、如图,AB ∥CD ,EF ⊥CD 于F ,已知∠2=30°,则∠1是( )A .20B .60C .30D .45第3题图D C B A 第6题图ED C B A 第7题图D C B A第8题图21b a第9题图E D C B A3、如图,C 、D 是线段AB 上两点,若CD=5cm ,DB=8cm ,且D 是AC 的中点,则AC 的长等于( )A .3cmB .6cmC .8cmD .11cm4、已知∠α=72°,则∠α的余角是 _____________________。
5、在命题“同位角相等,两直线平行”中,题设是:___________________________________。
6、如图,AB ∥CD ,AC ⊥BC,垂足为C ,若∠A=40°,则∠BCD=______________。
7、在Rt △ABC 中,∠C=90°,若BC=10,AD 平分∠BAC 交BC 于点D ,且BD ∶CD=3∶2,则点D 到线段AB 的距离为___________。
云南省泸西县中枢镇2019中考数学复习第四章三角形讲义

第四章三角形第一节角、相交线与平行线两直线相交[fg T对顶角相等五雄(垂线段最短T点到直线的距离垂线(过一点有且只歹一条克线与己知克线垂直/同位角两条直线被第三条直线所截内错角I同芳内角平行线-平行公理及性质傑麹鞋儡勰考点3 垂线性质及垂直平分线的性质1、垂线的性质(1)平面内经过一点有且只有一条直线垂直于已知直线;(2)直线外一点与直线上各点连接的所有线段中,垂线段最短;点到直线的距离:从直线外一点向已知直线作垂线,这一点和垂足之间的线段的长度叫做点到直线的距离。
2、垂直平分线(1)性质:线段垂直平分线上的点到该线段两端点的距离相等。
(2)逆定理:和线段的两端点的距离相等的点在该线段的垂直平分线上。
考点4 平行线与平行公理1、在同一平面内,不相交的两条直线叫做平行线。
2、经过直线外一点,有且只有一条直线与这条直线平行。
3、平行线的性质定理与判定定理。
习题精编1、从3时到6时,钟表的时针旋转角的度数是()A. 30° B . 60° C . 90° D . 120 °2、如图,AB// CD EF±CD于F,已知/ 2=30°,则/ 1 是(A. 20 B . 60 C . 30 D 453、如图,C D是线段AB上两点,若CD=5cm DB=8cm且D是AC的中点,贝U AC的长等于()A. 3cm B . 6cm C . 8cm D . 11cm4、已知/ a =72°,则/ a的余角是__________________________ 。
5、 ___________________________________________________________________________________ 在命题“同位角相等,两直线平行”中,题设是:____________________________________________ <6、如图,AB// CD ACL BC,垂足为C,若/ A=40°,则/ BCD=___________________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21F B A 第四章 三角形
第一节 角、相交线与平行线
考点1角及其平分线
考点2 同一平面内两直线的位置关
考点3 垂线性质及垂直平分线的性质 1、 垂线的性质
(1) 平面内经过一点有且只有一条直线垂直于已知直线;
(2) 直线外一点与直线上各点连接的所有线段中,垂线段最短;
点到直线的距离:从直线外一点向已知直线作垂线,这一点和垂足之间的线段的长度叫做点到直线的距离。
2、 垂直平分线
(1) 性质:线段垂直平分线上的点到该线段两端点的距离相等。
(2) 逆定理:和线段的两端点的距离相等的点在该线段的垂直平分线上。
考点4 平行线与平行公理
1、 在同一平面内,不相交的两条直线叫做平行线。
2、 经过直线外一点,有且只有一条直线与这条直线平行。
3、 平行线的性质定理与判定定理。
习题精编
1、从3时到6时,钟表的时针旋转角的度数是( ) A .30° B .60° C .90° D .120°
2、如图,AB ∥CD ,EF ⊥CD 于F ,已知∠2=30°,则∠1是( ) A .20 B .60 C .30 D .45
第3题图D C B
A 第7题图
D C B A
第8题图21b a
第9题图E D C B A
3、如图,C 、D 是线段AB 上两点,若CD=5cm ,DB=8cm ,且D 是AC 的中点,则AC 的长等于( )
A .3cm
B .6cm
C .8cm
D .11cm
4、已知∠α=72°,则∠α的余角是 _____________________。
5、在命题“同位角相等,两直线平行”中,题设是:___________________________________。
6、如图,AB ∥CD ,AC ⊥BC,垂足为C ,若∠A=40°,则∠BCD=______________。
7、在Rt △ABC 中,∠C=90°,若BC=10,AD 平分∠BAC 交BC 于点D ,且BD ∶CD=3∶2,则点D 到线段AB 的距离为___________。
8、如图,直线a 、b 被第三条直线c 所截,并且a ∥b ,若∠1=65°,则∠2=____________ 9、如图,B 、A 、E 三点在同一条直线上,请你添加一个条件,使AD ∥BC ,你所添加的条件是______________________(不允许添加任何辅助线)。
第二节 三角形及其性质
考点1 三角形的分类(按边分、按角分) 1、 按边分
2、 按角分
3、 按角、边综合分类
考点2 一般三角形的性质
1、三角形的三边关系及内角和定理
(1)三角形的两边这和大于第三边,两边之差小于第三边。
(2)三角形的内角和等于180°。
(3)在同一直角三角形中,大边对大角,小边对小角。
2、三角形内外角的关系
(1)三角形的任一个外角等于与它不相邻的两相个内角之和。
(2)三角形的任一个外角大于任何一个和它不相邻的内角。
(3)三角形的“四线”
三角形的“四心”
(4)
考点3 特殊三角形的性质及判定
对称轴。
)内外心重合;
,则以
为边的三角形是直角三角形。
等于
第三节全等三角形
考点1 全等三角形的性质
性质1、全等三角形的对应边相等,对应角相等。
性质2、全等三角形的对应线段(角平分线、中线、高、中位线)相等,对应周长相等,对应面积相等。
考点2 三角形全等的判定
第1题图
D C
B A 第2题图
P
O D C
B
A
三角形全等的证明思路:
考点3 直角三角形全等的性质及判定
(1) 性质:和一般三角形全等的性质相同。
(2) 判定:HL 公理;斜边和直角边对应相等的两个直角三角形全等。
考点4 全等三角形的应用
全等三角形的应用主要有:证明线段、角相等;求线段的长度、角的度数、三角形面积;测量不可直接测量的距离等。
习题精编:
1、如图,在中,E 是AD 的中点,请添加适当条件后,构造出一对全等的三角形,
并说明理由。
2、如图,OP 平分∠AOD ,且OA=OB
(1) 写出图中三对你认为全等的三角形(注:不添加任何辅助线);
(2) 从(10)中任选一个结论进行证明。
第3题图
F E
D C
B
A
第4题图
P E
D C
B A
3、如图,点B、D、C、F在一条直线上,且BC=FD,AB=EF。
(1)请你添加一个条件(不再清加辅助线),使△ABC≌△EFD,你添加的条件是;
(2)添加了条件后,证明△ABC≌△EFD。
4、已知:如图,点P为平行四边形ABCD中CD边的延长线上的一点,连接BP,交AD于点E。
探究:当PD与CD有什么数量关系时,△ABE≌△DPE,画出图形并证明△ABE≌△DPE。
第四节解直角三角形
,正弦;余弦
=;正切
考点3 解直角三角形的类型和解法
c =
B=90°-A,a = c
b =
c (
=
A, ∠B=90°
b = ,由,
求∠A,∠B=90
考点4 直角三角形边角关系的应用
i==
P B
北
东
习题精编
1、如图,小明家住的楼房高度AB=10米,到对面较高楼房的距离BD=20米,当阳光刚好从两楼房的顶部射入时,测得光线与水平线的夹角为40°,根据以上条件,小明便知楼房CD 的高。
请你写出计算过程(结果精确到0.1米,参考数据:sin400.77,tan40°≈0.84)
3、 如图,小岛A 在港口P 的南偏西45°方向,距离港口70海里外甲船从A 出发,乙船从
港口P 出发沿AP 方向以每小时20海里的速度驶向港口P ;乙船从港口P 出发沿着南偏东60°方向,以每小时15海里的速度驶离港口,若两船同时出发。
(1) 甲船出发x 小时,与港口P 的距离是多少海里(用含x 的式子表示)? (2) 几小时后两船与港口P 的距离相等?
(3) 当乙船在甲船的正方向时,船体发生了故障不能继续航行,此时,乙船向甲船
发出求救信号,问甲船以现有航速赶去救援,需几小时能到达出事地点(不考虑其它影响航速的因素)?(最后结果精确到0.1)(参考数据:
1.41
≈1.73)。
