通用版201X年中考数学总复习第五章基本图形一第18讲三角形与全等三角形练本课件
(通用版)2019年中考数学总复习 第五章 基本图形(一)第18讲 三角形与全等三角形(讲本)课件

题组训练
2.(2018·黄石)如图,△ ABC 中,AD 是 BC 边上的高,AE,
BF 分别是∠BAC,∠ABC 的平分线,∠BAC=50°,∠ABC
=60°,则∠EAD+∠ACD=( A )
A.75°
B.80°
C.85°
D.90°
26
3.如图,已知在 Rt△ ABC 中,∠C=90°,AC=BC,AB =6,点 P 是 Rt△ ABC 的重心,则点 P 到 AB 所在直线的距
(1)求证:△ ABC≌△DEF; (2)若∠A=55°,∠B=88°,求∠F 的度数.
34
证明:(1)∵AC=AD+DC,DF=DC+CF,且 AD=CF,
AB=DE ∴AC = DF , 在 △ ABC 和 △DEF 中 , BC=EF ,
AC=DF
∴△ABC≌△DEF(SSS); (2)由(1)可知,∠F=∠ACB,∵∠A=55°,∠B=88°,
38
Hale Waihona Puke 4.(2018·北京)用一组 a,b,c 的值说明命题“若 a<b,则
ac<bc”是错误的,这组值可以是 a= 1 ,b= 2 ,c = -1 .
39
5.(2018·永州)一副透明的三角板,如图叠放,直角三角板
的斜边 AB,CE 相交于点 D,则∠BDC= 75° .
40
中考失分点 21:忽视三角形的三边关系 1.现有 3 cm,4 cm,7 cm,9 cm 长的四根木棒,任取其中三根
2018绵阳如图在abc中ac3bc4若acbc边上的中线bead垂直相交于精选ppt24解析利用三角形中线定义得到bd2ae可判定点o为abc的重心所以ao2odob2oe由勾股定理得bo精选ppt25思路方法对于三角形中求线段长度的问题
2021年中考数学复习第18讲 三角形与全等三角形(教学课件)

考点精讲
对对应应训训练练
6.(2020·玉林)下列命题中,其逆命题是真命题的是( B ) A.对顶角相等 B.两直线平行,同位角相等 C.全等三角形的对应角相等 D.正方形的四个角都相等
考考点点精精讲讲
对应训练
考 点 五 全等三角形的性质和判定
1.全等三角形的性质 (1)全等三角形的对应边⑪_相__等_,对应角⑫相__等__ (2)全等三角形的周长⑬相__等__,面积⑭_相__等_ (3)全等三角形对应的中线、高线、角平分线、中位线都相等
A.8 B.2 2 C.16 D.4
3.在△ABC中,若一个内角等于另外两个内角的差,则( D ) A.必有一个内角等于30° B.必有一个内角等于45° C.必有一个内角等于60° D.必有一个内角等于90°
4.能说明命题“关于x的方程x2-4x+m=0一定有实数根”是 假命题的反例为( D )
解:∵在 Rt△ABC 中,AD 是△ABC 的中线, AD=8,∴BD=AD=CD=8,∵BE 是△ABC 的角平分线,∴∠ABE=∠DBE,∵AD⊥BE, ∴∠ANB=∠DNB=90°,∵BN=BN,∴△ ABN≌△DBN(ASA),∴AB=BD,∴AB=8
=12 BC,∴∠C=30°,∴AC= 3 AB=8 3 .
重点题型
题题组组训训练练
6.如图,在△ABC中,AD是BC边上的中线,E是AB边上一 点,过点C作CF∥AB交ED的延长线于点F. (1)求证:△BDE≌△CDF; (2)当AD⊥BC,AE=1,CF=2时,求AC的长.
(1) 证 明 : ∵CF∥AB , ∴ ∠ B = ∠FCD , ∠ BED = ∠F , ∵ AD 是 BC 边 上 的 中 线 , ∴ BD = CD , ∴△BDE≌△CDF(AAS); (2) 解 : ∵△BDE≌△CDF , ∴ BE = CF = 2 , ∴ AB = AE + BE=1+2=3,∵AD⊥BC,BD=CD,∴AC=AB=3.
++2025年中考数学一轮总复习++第18课时 三角形的相关概念与性质+++课件

小于第三边.
任
意两边之和
任意两边
之差
(3)三角形的内(外)角和定理
定
理
三角形三个内角的和等于
推
论
(1)三角形的外角等于
(2)三角形的外角大于任何一个 (3)直角三角形的两个锐角
2∠C=∠1+∠2
2∠C=∠2-∠1
2. 掌握分类的方法,不论是三角形的分
类,还是相关概念,比如:由于三角形
的高不一定在三角形内部,所以三角形
中涉及高的题目可能需要分类讨论.3. 了解三角形的五心中的三心(重心、
内心、外心),知道这三心的基本性质.
考点一 三角形的三边关系例1 (1)从长度为2,4,6,8的四条
AC=13,BC=10,则四边形EBFC的
面积为 ;
60
(5)如图5,在△ABC中,∠ABC,
∠ACB的平分线交于点O,∠ACB的外
角平分线所在直线与∠ABC的平分线相
交于点D,与∠ABC的外角平分线相交
于点E,则下列结论一定正确的是
.(填序号) ①∠BOC=90°+ ∠A;②∠D= ∠A;③∠E=∠A;④∠E+∠DCF=90°+∠ABD.
①
②④
1. 如图,AD,BE,CF依次是△ABC
的高、中线和角平分线,则下列表达式
中错误的是( C )
A. S△BAE=S△BCE
B. ∠ADC=90°
C. ∠CAD=∠CBE
D. ∠ACB=2∠ACF
C
2. (2024·南开)如图,在Rt△ABC中,
∠ABC=90°,BD平分∠ABC交AC于
点D,点E为BC边上靠近点C的三等分
点,且AB=BE,若阴影部分面积为4,
中考数学总复习 第5章 第18讲 三角形与全等三角形考点集训

中考数学总复习第5章第18讲三角形与全等三角形考点集训一、选择题1.(2014·毕节)下列叙述正确的是( C )A.方差越大,说明数据就越稳定B.在不等式两边同乘或同除以一个不为0的数时,不等号的方向不变C.不在同一直线上的三点确定一个圆D.两边及其一边的对角对应相等的两个三角形全等2.(2014·云南)如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC 的度数是( A )A.85°B.80°C.75°D.70°,第2题图) ,第3题图)3.(2014·益阳)如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( A )A.AE=CF B.BE=FDC.BF=DE D.∠1=∠24.(2012·嘉兴)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( A) A.40° B.60° C.80° D.90°5.(2014·遂宁)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE =2,AB=4,则AC长是( A )A.3 B.4 C.6 D.56.(2014·泰州)如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( D ) A.1,2,3 B.1,1, 2C.1,1, 3 D.1,2, 3二、填空题7.(2014·绥化)如图,AC,BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是__AB=CD__.(填出一个即可),第7题图) ,第9题图) 8.已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b ⊥c ;②如果b ∥a ,c ∥a ,那么b ∥c ;③如果b ⊥a ,c ⊥a ,那么b ⊥c ;④如果b ⊥a ,c ⊥a ,那么b ∥c .其中为真命题的是__①②④__.(填写所有真命题的序号)9.如图,三角形纸片ABC 中,∠A =65°,∠B =75°,将纸片的一角折叠,使点C 落在△ABC 内,若∠1=20°,则∠2的度数为__60°__.10.如图,△ABC 中,AB =AC =13 cm ,AB 的垂直平分线交AB 于D ,交AC 于E ,若△EBC 的周长为21 cm ,则BC =__8__cm.,第10题图) ,第12题图)11.在△ABC 中,若AB =BC ≠AC ,则与△ABC 只有一条公共边,且与△ABC 全等的三角形一共有__7__个.12.(2014·绵阳)如图,在正方形ABCD 中,E ,F 分别是边BC ,CD 上的点,∠EAF =45°,△ECF 的周长为4,则正方形ABCD 的边长为__2__.三、解答题13.(2014·云南)如图,在△ABC 和△ABD 中,AC 与BD 相交于点E ,AD =BC ,∠DAB =∠CBA,求证:AC =BD.在△ADB 和△BCA 中,⎩⎪⎨⎪⎧AD =BC ,∠DAB =∠CBA ,AB =BA ,∴△ADB ≌△BCA (SAS ),∴AC =BD14.(2014·台湾)如图,四边形ABCD 中,E 点在AD 上,其中∠BAE=∠BCE=∠ACD=90°,且BC =CE.请说明为何△ABC 与△DEC 全等的理由.∵∠BCE =∠ACD =90°,∴∠3+∠4=∠4+∠5,∴∠3=∠5,在△ACD 中,∠ACD =90°,∴∠2+∠D =90°,∵∠BAE =∠1+∠2=90°,∴∠1=∠D ,在△ABC 和△DEC 中,⎩⎪⎨⎪⎧∠1=∠D ,∠3=∠5,BC =CE ,∴△ABC ≌△DEC (AAS )15.(2014·内江)如图,点M ,N 分别是正五边形ABCDE 的边BC ,CD 上的点,且BM =CN ,AM 交BN 于点P.(1)求证:△ABM≌△BCN;(2)求∠APN 的度数.(1)∵正五边形ABCDE ,∴AB =BC ,∠ABM =∠C.∵在△ABM 和△BCN 中,⎩⎪⎨⎪⎧AB =BC ,∠ABM =∠C ,BM =CN ,∴△ABM ≌△BCN (SAS ) (2)∵△ABM≌△BCN ,∴∠BAM =∠CBN ,∴∠APN =∠BAM +∠ABP =∠CBN +∠ABP =∠ABC =(5-2)×180°5=108°16.(2014·德州)问题背景:如图1:在四边形ABCD 中,AB =AD ,∠BAD =120°,∠B =∠ADC=90°,E ,F 分别是BC ,CD 上的点,且∠EAF=60°.探究图中线段BE ,EF ,FD 之间的数量关系.小王同学探究此问题的方法是延长FD 到点G ,使DG =BE.连结AG ,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是__EF =BE +DF __;探索延伸:如图2,若在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E ,F 分别是BC ,CD 上的点,且∠EAF =12∠BAD ,上述结论是否仍然成立?并说明理由; 实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30°的A 处,舰艇乙在指挥中心南偏东70°的B 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E ,F 处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.问题背景:EF =BE +DF ;探索延伸:EF =BE +DF 仍然成立.证明如下:延长FD 到G ,使DG =BE ,连结AG ,∵∠B +∠ADC =180°,∠ADC +∠ADG =180°,∴∠B =∠ADG ,在△ABE和△ADG 中,⎩⎪⎨⎪⎧DG =BE ,∠B =∠ADG ,AB =AD ,∴△ABE ≌△ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠EAF =12∠BAD ,∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD -∠EAF =∠EAF ,∴∠EAF =∠GAF ,在△AEF 和△AGF 中,⎩⎪⎨⎪⎧AE =AG ,∠EAF =∠GAF ,AF =AF ,∴△AEF ≌△AGF (SAS ),∴EF =FG ,∵FG =DG +DF ,∴EF =BE +DF ;实际应用:如图,连结EF ,延长AE ,BF 相交于点C ,∵∠AOB =30°+90°+(90°-70°)=140°,∠EOF =70°,∴∠EAF =12∠AOB ,又∵OA =OB ,∠OAC +∠OBC =(90°-30°)+(70°+50°)=180°,∴符合探索延伸中的条件,∴结论EF =AE +BF 成立,即EF =1.5×(60+80)=210,即此时两舰艇之间的距离是210海里。
中考数学 考点聚焦 第5章 图形的性质(一)第18讲 三角形与全等三角形1

3.(2016·新疆)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE ,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( D)
A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF
4.(2016·河南)如图,在△ABC中,∠ACB=90°,AC=8,AB=10 ,DE垂直平分AC交AB于点E,则DE的长为( D)
错解 证明:在△AEB和△AEC中,∵AE=AE,EB=EC,∠1=∠2 ,∴△AEB≌△AEC(SSA),∴∠BAE=∠CAE.
先看一个事实,如图,将等腰△ABC的底边BC延长线上的任一点和顶 点A相连,所得的△DAB和△DAC无疑是不全等的,由此可知,有两边及 其一边的对角对应相等的两个三角形(简称“边边角”)不一定全等.因此 ,在判定三角形全等时,一定要留心“边边角”,别上当哟.
1.证明三角形全等的三种基本思路 (1)有两边对应相等时,找夹角相等或第三边对应相等; (2)有一边和一角对应相等时,找另一角相等或夹等角的另一边相等; (3)有两个角对应相等时,找一对边对应相等.另外,在寻求全等条件时 ,要善于挖掘图形中公共边、公共角、对顶角等隐含条件. 2.证明几何题的四种思考方法 (1)顺推分析:从已知条件出发,运用相应的定理,分别或联合几个已知 条件加以发展,一步一步地去靠近欲证目标; (2)逆推分析:从欲证结论入手,分析达到欲证的可能途径,逐步沟通它 与已知条件的联系,从而找到证明方法; (3)顺推分析与逆推分析相结合; (4)联想分析:对于一道与证明过的题目有类似之处的新题目,分析它们 之间的相同点与不同点,尝试把对前一道题的思考转用于现在的题目中, 从而找到它的解法.
③连接 P2P3,∵(3+0)÷2=1.5,(0+4)÷2=2,∴E(1.5,2), ∵1.5×2-9265=-2215,2×2-7225=2258,∴P3(-2251,2285).
中考数学总复习 第五单元 三角形 第18课时 三角形课件

2021/12/9
第十八页,共二十一页。
高频考向探究
3.[2018·东城一模] 如图 18-7,在△ ABC 中,∠BAC=90°,AD⊥
证明:∵∠BAC=90°,∴∠FBA+∠AFB=90°.
BC 于点 D,BF 平分∠ABC 交 AD 于点 E,交 AC 于点 F.求
∵AD⊥BC,∴∠DBE+∠DEB=90°.
(2)三角形的一个外角大于任何一个和它③ 不相邻(xiānɡ
的内角.
(3)直角三角形的两个锐角④ 互余
(4)三角形的外角和为⑤ 360°
.
.
2021/12/9
第六页,共二十一页。
课前双基巩固
对点演练(yǎn liàn)
[答案(dáàn)] C
题组一 必会题
1.如图 18-1,在△ ABC 中,D,E 分别是边 AB,AC 的中点,已知
证:AE=AF.
∵BE 平分∠ABC,∴∠DBE=∠FBA.
∴∠AFB=∠DEB.
∵∠DEB=∠FEA,∴∠AFB=∠FEA.
图 18-7
∴AE=AF.
2021/12/9
第十九页,共二十一页。
高频考向探究
4.[2017·西城一模] 如图 18-8,在△ ABC 中,BC 的垂直平分线
证明:∵DE 垂直平分 BC,
况考虑不全面.
6.根据下面每组给出的三条线段长度,判断能围成三角形的组
号是
(1)2,4,4
.
(2)2,7,5
(3)3,3,3
7.等腰三角形有一个内角是 40°,则这个等腰三角形底角的度
数是
.
2021/12/9
第十一页,共二十一页。
高频考向探究
中考数学基础过关复习第五章三角形全等三角形

2021/12/9
第三十四页,共三十六页。
解 : 由 前 面 的 已 知 条 件 不 能 证 明 △ABC≌△DEF. 需要再添加条件①或条件③.
证明:∵BF=CE,∴EF=BC. 添加条件①时,∵EF=BC,∠ABC=∠DEF,AB= DE,∴△ABC≌△DEF(SAS); 添加条件③时,∵AC∥DF,∴∠ACB=∠DFE, 又∵EF=BC,∠ABC=∠DEF, ∴△ABC≌△DEF(ASA); 添加条件②AC=DF 时,此时是 SSA 不能证明全等.
第三十二页,共三十六页。
9.如图,点 F,B,E,C 在同一直线上,并且 BF =CE,∠ABC=∠DEF.能否由上面的已知条件证明 △ABC≌△DEF?
2021/12/9
第三十三页,共三十六页。
如果能,请给出证明;如果不能,请从下列三个条件 中选择一个合适的条件,添加到已知条件中,使 △ABC≌△DEF,并给出证明.提供的三个条件是: ①AB=DE;②AC=DF;③AC∥DF.
求证:AE=CE. 证明(zhèngmíng):∵FC∥AB,∴∠A=∠ECF.
在△ADE和△CFE中,
∠A= ∠ECF ∠AED= ∠CEF
DE=FE
∴△ADE≌△CFE(AAS),
∴AE=CE
2021/12/9
第十五页,共三十六页。
3.如图,点C是AE的中点(zhōnɡ diǎn),∠A=∠ECD,
A.AC∥DF C.AC=DF
2021/12/9
B.∠A=∠D D.∠ACB=∠F
第二十三页,共三十六页。
2.如图,点 E 是矩形 ABCD 的边 AD 延长线上的
一点,且 AD=DE,连接 BE 交 CD 于点 O,连接 AO,
中考数学 专题18 全等形与全等三角形(知识点串讲)(原卷版)
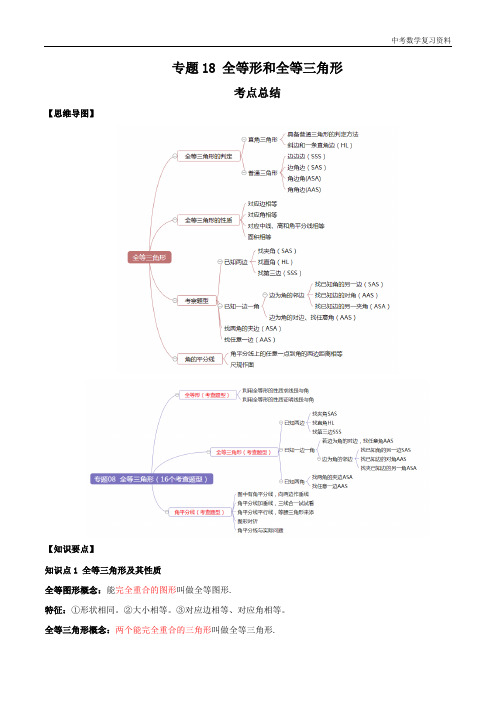
专题18 全等形和全等三角形考点总结【思维导图】【知识要点】知识点1 全等三角形及其性质全等图形概念:能完全重合的图形叫做全等图形.特征:①形状相同。
②大小相等。
③对应边相等、对应角相等。
全等三角形概念:两个能完全重合的三角形叫做全等三角形.小结:把两个全等三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.表示方法:全等用符号“≌”,读作“全等于”。
书写三角形全等时,要注意对应顶点字母要写在对应位置上。
全等变换定义:只改变图形的位置,而不改变图形的形状和大小的变换。
变换方式(常见):平移、翻折、旋转。
全等三角形的性质:对应边相等,对应角相等。
1.(2017·四川中考模拟)已知四边形ABCD 各边长如图所示,且四边形OPEF ≌四边形ABCD .则PE 的长为( )A .3B .5C .6D .102.(2019·福建中考模拟)如图,若,则点应是图中的( )MNP MEQ △≌△QA .点B .点C .点D .点ABCD3.(2018·广西中考模拟)下列说法中不正确的是( )A .全等三角形的周长相等 B .全等三角形的面积相等C .全等三角形能重合D .全等三角形一定是等边三角形考查题型一 利用全等三角形性质求线段与角1.(2019·武冈市第七中学中考模拟)如图,三角形纸片ABC ,AB =10cm ,BC =7cm ,AC =6cm ,沿过点B 的直线折叠这个三角形,使顶点C 落在AB 边上的点E 处,折痕为BD ,则△AED 的周长为( )A .9cmB .13cmC .16cmD .10cm2.(2017·江苏南京溧水孔镇中学中考模拟)如图,△ABC ≌△DEF ,点A 与D ,B 与E 分别是对应顶点,且测得BC=5cm ,BF=7cm ,则EC 长为()A .1cmB .2cmC .3cmD .4cm3.(2016·广东中考模拟)如图,△ACB ≌△,∠ACA′=30°,则∠BCB′的度数为( )A CB ''A .20°B .30°C .35°D .40°4.(2019·沂源县中庄中学初一月考)如图,点B ,C ,D 在同一条直线上,∠B=∠D=90°,△ABC ≌△CDE,AB=6,BC=8,CE=10.(1)求△ABC 的周长;(2)求△ACE 的面积.考查题型二 利用全等三角形性质证明线段、角相等1.(2019·湖北黄石十四中初二期中)如图,点E 在AB 上,△ABC ≌△DEC ,求证:CE 平分∠BED .2.(2018·颍上县第五中学初二期中)若△ABC ≌△DCB ,求证:∠ABE=∠DCE.知识点2:全等三角形的判定(重点)一般三角形直角三角形判定边角边(SAS )、角边角(ASA )角角边(AAS )、边边边(SSS )具备一般三角形的判定方法斜边和一条直角边对应相等(HL )性质对应边相等,对应角相等对应中线相等,对应高相等,对应角平分线相等注:① 判定两个三角形全等必须有一组边对应相等;② 全等三角形周长、面积相等.证题的思路(重点):考查题型三 已知一边一角(若边为角的对边,找任意角AAS )1.(2018·四川中考模拟)如图,AB=AE ,∠1=∠2,∠C=∠D .求证:AC=AD .2.(2014·北京中考模拟)已知:如图,E是AC上一点,AB=CE,AB∥CD,∠ACB =∠D.求证:BC =ED.3.(2018·四川中考模拟)已知,如图,E、F分别为□ABCD的边BC、AD上的点,且∠1=∠2,.求证:AE=CF.4.(2016·福建中考模拟)如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.考查题型四已知一边一角(边为角的邻边(找已知角的另一边SAS))1.(2016·四川中考真题)如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.2.(2018·云南中考模拟)如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:∠C=∠D.3.(2019·辽宁中考真题)如图,点,在上,,,,求证:E F BC BE CF =AB DC =B C ∠=∠.AF DE =考查题型五 已知一边一角(边为角的邻边(找已知边的对角AAS ))1.(2013·浙江中考真题)如图,△ABC 与△DCB 中,AC 与BD 交于点E ,且∠A=∠D ,AB=DC .(1)求证:△ABE ≌DCE ;(2)当∠AEB=50°,求∠EBC 的度数。
