物理化学第一章.jsp
合集下载
物理化学课件第一章 热力学第一定律
Joule(焦耳)和 Mayer(迈耶尔)自1840年 起,历经20多年,用各种实验求证热和功的转 换关系,得到的结果是一致的。
即: 1 cal = 4.1840 J
这就是著名的热功当量, 为能量守恒原理提供了科学 的实验证明。 现在,国际单位制中已不 用cal,热功当量这个词将逐 渐被废除。
能量守恒定律 到1850年,科学界公认能量守恒定律是自 然界的普遍规律之一。能量守恒与转化定律可 表述为: 自然界的一切物质都具有能量,能量有各 种不同形式,能够从一种形式转化为另一种形
式,但在转化过程中,能量的总值不变。
1.热力学能
系统总能量通常有三部分组成:
(1)系统整体运动的动能
(2)系统在外力场中的位能 (3)热力学能,也称为内能U 体系宏观静止,无外立场存在,则体系总能量=内能 热力学能是指系统内部能量的总和,包括分子 运动的平动能、分子内的转动能、振动能、电子能、
核能以及各种粒子之间的相互作用位能等。
2.热和功
热(heat)系统与环境之间因温差而传递的能量 称为热,用符号Q 表示。 Q的取号: 系统吸热,Q>0 系统放热,Q<0
热的本质是分子无规则运动强度的一种体现 计算热一定要与系统与环境之间发生热交换 的过程联系在一起,系统内部的能量交换不可能
是热。
功(work)系统与环境之间传递的除热以外的
机械平衡(mechanical equilibrium) 系统各部的压力都相等,边界不再移动。 相平衡(phase equilibrium) 多相共存时,各相的组成和数量不随时间而改变
化学平衡(chemical equilibrium ) 反应系统中各物的数量不再随时间而改变
§1.3
热力学第一定律
物理化学第一章

中系统的温度等于环境温度,即T1 = T2 =Tsu。
定压过程:若过程的始态、终态的压力相等,且过程 中系统的压力恒定等于环境的压力,即p1=p2=psu。 定容过程:系统的状态变化过程中体积的量值保持恒 定,V1=V2。 绝热过程:系统状态变化过程中,与环境间的能量传 递仅可能有功的形式,而无热的形式,即Q = 0。
量传递也有能量传递。
环境 有质量传递
有能量传递
27
1.1.1 系统和环境
封闭系统:系统与环境之间通过界面只有能量传递,
而无物质的质量传递。
环境 无质量传递
有能量传递
28
1.1.1 系统和环境
隔离系统:系统与环境之间既无物质的质量传递亦 无能量传递。
环境 无质量传递
无能量传递
29
1.1.2 系统的宏观性质
V f T , p
系统的状态函数之间的定量关系式,称为状态方 程。
37
1.1.6 系统状态的变化过程
过程:在一定条件下,系统由始态变化到终态的经 过。 系统状态的变化过程分为单纯 p、V、T变化过程,
相变化过程,化学变化过程。
几种主要的单纯 p、V、T变化过程
定温过程:若过程的始态、终态的温度相等,且过程
几种主要的单纯 p、V、T变化过程
对抗恒定外压过程:系统在体积膨胀的过程中所对
抗的环境的压力 psu=常数。
自由膨胀过程(向真空膨胀过程):psu=0
循环过程:系统由始态经一连串单一过程又回复到
始态的连续过程。
状态2
状态1
20
已知组成系统的理想气体n =1mol ,T=300K,
V=24.78dm3,p =100kPa,试计算摩尔气体常量R?
物理化学专业-上册主要内容.jsp

+
RT
ln
xB
=
µ
∇ B
+
RT
ln
xB
非理想溶液:
µB
=
µ
* B
+
RT
ln aB
渗透系数 Φ = ln aA,x = 1 + lnγ A,x (溶剂)
ln xA
ln xA
20
5 依数性计算
− ln xA
=
− ln(1− xB ) =
xB
=
nB n
≈
nB nA
=
∆p p*A
=
ΠVA,m RT
=
∆vap H m, A RTb*2
1 平衡常数
化学平衡
标准 平衡 常数
∏ ∏ ∏ K
o p
=
B
pB po
ν B
K
o c
=
B
cB co
ν B
K
o f
=
B
fB po
ν B
经验 平衡 常数
∏ K p =
p νB B
B
∏ K x =
x νB B
B
∏ Ka =
a νB B
B
∏ Kc =
c νB B
B
Kp
=
K
o p
)Z
(
∂t ∂k
)Z
(
∂k ∂y
)Z
复合函数 微分法
∂Z ∂x
t
=
∂Z ∂x
y
+
∂Z ∂y
x
∂y ∂x
t
( ∂U ∂T
)p
=
( ∂U ∂T
物理化学第一章课后习题解答

1.12 CO2 气体在 40℃时的摩尔体积为 0.381dm3 .mol-1 。设 CO2 为范德华气体,试 求其压力,并比较与实验值 5066.3kPa 的相对误差。
解: ,Vm =0.381× 10-3 m3 .mol-1 ,T=313.15K CO2 的范德华常数 a=364× 10-3 /Pa.m3 .mol-2 , b =42.67× 10-6 m3 .mol-1 代入方程得: P=5187.674KPa 相对误差=(5187.674-5066.3)/ 5066.3=2.4% 1.13 今有 0℃, 40530kPa 的 N2 气体,分别用理想气体状态方程及范德华方程计算 其摩尔体积.实验值为 70.3cm.mol-1 。 解:T=273.15K ,p=40530kPa N2 的范德华常数 a=140.8× 10-3 /Pa.m3 .mol-2 , b =39.13× 10-6 m3 .mol-1 =0.05603 m3 .mol-1
第一章
习题解答
1.1 物质的体膨胀系数α V 与等温压缩率κ T 的定义如下:
试导出理想气体的
、
与压力、温度的关系
解:对于理想气体: PV=nRT , V= nRT/P
求偏导:
1.2 气柜储存有 121.6kPa, 27℃的氯乙烯 (C2 H3 Cl) 气体 300m3 , 若以每小时 90kg 的流量输往使用车间,试问储存的气体能用多少小时? 解:将氯乙烯(Mw=62.5g/mol)看成理想气体: PV=nRT , n= PV/RT n=121600300/8.314300.13 (mol)=14618.6mol m=14618.662.5/1000(kg)=913.66 kg t=972.138/90(hr)=10.15hr 1.3 0℃,101.325kPa 的条件常称为气体的标准状况,试求甲烷在标准状况下的密 度? 解:将甲烷(Mw=16g/mol)看成理想气体: PV=nRT , PV =mRT/ M w 甲烷在标准状况下的密度为=m/V= PMw/RT =101.32516/8.314273.15(kg/m3 ) =0.714 kg/m3 1.4 一抽成真空的球形容器,质量为 25.0000g。充以 4 ℃水之后,总质量为 125.0000g。 若改充以 25℃, 13.33kPa 的某碳氢化合物气体, 则总质量为 25.0163g。 -3 试估算该气体的摩尔质量。水的密度按 1 g.cm 计算。 解:球形容器的体积为 V=(125-25)g/1 g.cm-3 =100 cm3 将某碳氢化合物看成理想气体:PV=nRT , PV =mRT/ M w Mw= mRT/ PV=(25.0163-25.0000)8.314300.15/(1333010010-6 ) Mw =30.51(g的空气。为进行实验时确保安全,采用同样温度 的纯氮进行置换,步骤如下:向釜内通氮直到 4 倍于空气的压力,尔后将釜内混 合气体排出直至恢复常压,重复三次。求釜内最后排气至恢复常压时其中气体含 氧的摩尔分数。设空气中氧、氮摩尔分数之比为 1:4。 解: 根据题意未通氮之前 : ,操作 n 次后, , 操作 1 次后, ,重复三次, ,V,T 一定, 故
物理化学第一章 多媒体版 (葛华才 袁高清 彭程 着) 高等教育出版社

M mix =
∑ mA / ∑ nB = ∑ nA M A / ∑ nB = ∑ yA M A
A B A B A
其中:
m=
∑ mA , n= ∑ nB , yA =nA / ∑ nB
A B B
PDF 文件使用 "pdfFactory Pro" 试用版本创建 Ì
g {Vm,c} 图1.1.1 CO2 定温p-Vm,c 图
b
a
ቤተ መጻሕፍቲ ባይዱ
定压段的压力为该温度下的蒸气压(即该温度下使蒸气液化 所需压力)。 温度升高,如T2,p-V 线上定压水平段缩短,到温度Tc缩为 一点c,此点即为临界状态(critical state)。临界状态是气液 不可分的状态。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
1869年安德鲁斯(Andrews)作了一系列实验测定,系统 地研究了CO2 在各种温度下的p、V 关系。
T1 T2 Tc {p} c l b 图1.1.1 a g {Vm,c} 图 T3 T1< T2< Tc< T3 Tc=30.98℃
CO2 恒温p-Vm,c
图中,每条曲线称为 p-V 恒温线,c点所处状态称为临界状态。
1.1.2 实际气体的液化与临界现象
1 mol 实际气体的性质: f( p, Vm, T ) = 0 pVT关系复杂 常用作图法描述: 固定1个变量,作另两变量间的曲线 一般: 恒T,作 p ~Vm 曲线,称恒温线图 理想气体: 实际气体: T 定,pVm=RT=常数,p - Vm 双曲线 p - Vm关系如何?
R-摩尔气体常数
PDF 文件使用 "pdfFactory Pro" 试用版本创建 Ì
物理化学第一章热力学第一定律

→→确定系统的状态,其他的性质。 独立变量:被选来确定系统状态的独立变化
的性质。
11
若对于一定量的纯物质单相系统,已知系统的独 立性质为 x 与 y ,则系统任一其它性质 X 是这两个 变量的函数,即:
X = f (x, y)
例对物质的量为n的某纯物质、单相系统,其状 态可由T,p来确定,其它性质,如V,即是T,p的 函数。V=f (T, p)
14
还需掌握的一个数学公式(以后推导其他公 式要用到)
z = f(x ,y )
dz
=
( ∂z ∂x
)y dx
+
(
∂z ∂y
)x dy
如理想气体: V = nRT 即:V = f ( p,T) p
15
4.过程与途径 定义
系统从一个状态变到另一个状态,称为过程。 前一个状态称为始态,后一个状态称为末态。 实现这一过程的具体步骤称为途径。 过程与途径这两个概念常常不严格区别。
循环过程 (始态=末态, ∮dZ=0)
17
5.热力学平衡态(自学) 定义
在一定条件下,系统中各个相的宏观性质不随时间 变化;且如系统已与环境达到平衡,则将系统与环境 隔离,系统性质仍不改变的状态。
系统若处于平衡态,则系统满足:
①内部有单一的温度,即热平衡; ②内部有单一的压力,即力平衡; ③内部各相组成不变,即相间扩散平衡; ④内部各组分的物质的量不变,即化学平衡。
21
特点: (1)热力学能的绝对值无法确定 (2)热力学能是状态函数 (3)热力学能是广度性质
22
热力学第一定律的文字表述(自学)
在化学热力学中,研究的体系大多为宏观上静 止且无特殊外电场存在,故EK=EP=0,E=U
的性质。
11
若对于一定量的纯物质单相系统,已知系统的独 立性质为 x 与 y ,则系统任一其它性质 X 是这两个 变量的函数,即:
X = f (x, y)
例对物质的量为n的某纯物质、单相系统,其状 态可由T,p来确定,其它性质,如V,即是T,p的 函数。V=f (T, p)
14
还需掌握的一个数学公式(以后推导其他公 式要用到)
z = f(x ,y )
dz
=
( ∂z ∂x
)y dx
+
(
∂z ∂y
)x dy
如理想气体: V = nRT 即:V = f ( p,T) p
15
4.过程与途径 定义
系统从一个状态变到另一个状态,称为过程。 前一个状态称为始态,后一个状态称为末态。 实现这一过程的具体步骤称为途径。 过程与途径这两个概念常常不严格区别。
循环过程 (始态=末态, ∮dZ=0)
17
5.热力学平衡态(自学) 定义
在一定条件下,系统中各个相的宏观性质不随时间 变化;且如系统已与环境达到平衡,则将系统与环境 隔离,系统性质仍不改变的状态。
系统若处于平衡态,则系统满足:
①内部有单一的温度,即热平衡; ②内部有单一的压力,即力平衡; ③内部各相组成不变,即相间扩散平衡; ④内部各组分的物质的量不变,即化学平衡。
21
特点: (1)热力学能的绝对值无法确定 (2)热力学能是状态函数 (3)热力学能是广度性质
22
热力学第一定律的文字表述(自学)
在化学热力学中,研究的体系大多为宏观上静 止且无特殊外电场存在,故EK=EP=0,E=U
物理化学第一章1【精选】
2019/9/27
上一内容 下一内容 回主目录
返回
热力学的重要意义
在设计新的反应路线或试制新的化学产品时,变 化的方向和限度问题,显然是十分重要的。只有确 知存在反应的可能性的前提下,再去考虑反应的 速率问题,否则将徒劳无功:
如在19世纪末进行了从石墨制造金刚石的尝 试,所有的实验都以失败告终。以后通过热力学 计算知道,只有当压力超过大气压15000倍时, 石墨才有可能转变成金刚石。现在已经成功地实 现了这个转变过程。
1. 系统(System)与环境(Surroundings)
系统: 在科学研究时必须先 确定研究对象,把一部分物质与 其余分开,这种分离可以是实际 的,也可以是想象的。这种被划 定的研究对象称为系统,亦称为 体系。
环境: 与系统密切相关、有 相互作用或影响所能及的部分称 为环境。
2019/9/27
上一内容 下一内容 回主目录
上一内容 下一内容 回主目录
返回
4
热力学的方法特点:
(3)在热力学研究中无时间概念
即不管(反应)变化速率。 例如根据热力学计算,金刚石可自发地变成石墨
,但这个过程需用多少时间?发生变化的根本原因和 机理?热力学中无法知道。
这些特点既是热力学方法的优点,也是它的局 限性。
上一内容 下一内容 回主目录
物理化学电子教案
△U = Q + W
上一内容 下一内容 回主目录
返回
热力学的基本内容
热力学:研究不同形式能量转化的科学
化学热力学与物理中的热力学不同,本课程主要讲与化学变化相 关的热力学(Chemical Thermodynamics)
1. 第一定律:能量守恒,解决过程的能量衡算问题 (功、热、热力学能等) 2. 第二定律:过程进行的方向判据 3. 第三定律:解决物质熵的计算
物理化学第1章 热力学第一定律

物理化学
第1章 热力学第一定律
1.1 理想气体
一、理想气体状态方程
1.理想气体状态方程
pV nRT
pVm RT
R 8.314 J mol K
1 1
2.理想气体状态方程的其他形式 基本形式 导出形式
pV nRT
m pV RT M
pM RT
pV
V
M
RT
3.理想气体状态方程的应用
B
理想混合气体的总压等于各组分单独存在于混合气
体的T、V时产生的压力总和。
nRT 总压 p V
分压
nB RT pB V
nB RT n V B pB yB = nRT n p V
n nB
B
pB yB p
nB pB yB nB p
B
【例1-2】在一个2.80dm3的容器中,有0.174g的
具有加和性。如T、p、ρ等。
⑶两者的关系:广度性质的摩尔量是强度性质,
如摩尔体积Vm等。
2.状态函数的特征 ⑴系统的状态确定之后,它的每一状态函数都具 有单一的确定数值。这些数值只决定于系统现在
所处的状态而与状态的历史无关。
⑵当系统的状态发生变化时,状态函数也发生变
化,其改变值只与系统的始态和终态有关,而与
p( H 2 ) y( H 2 ) p总 =0.6427 108.9=70.00 kPa
p( N2 ) p总 p( H2 ) 38.89 kPa
四、阿马格分体积定律
由A、B、C组成的理想气体混合物
nRT (nA nB nC ) RT V p p
VA VB VC
六、可逆过程和不可逆过程
第1章 热力学第一定律
1.1 理想气体
一、理想气体状态方程
1.理想气体状态方程
pV nRT
pVm RT
R 8.314 J mol K
1 1
2.理想气体状态方程的其他形式 基本形式 导出形式
pV nRT
m pV RT M
pM RT
pV
V
M
RT
3.理想气体状态方程的应用
B
理想混合气体的总压等于各组分单独存在于混合气
体的T、V时产生的压力总和。
nRT 总压 p V
分压
nB RT pB V
nB RT n V B pB yB = nRT n p V
n nB
B
pB yB p
nB pB yB nB p
B
【例1-2】在一个2.80dm3的容器中,有0.174g的
具有加和性。如T、p、ρ等。
⑶两者的关系:广度性质的摩尔量是强度性质,
如摩尔体积Vm等。
2.状态函数的特征 ⑴系统的状态确定之后,它的每一状态函数都具 有单一的确定数值。这些数值只决定于系统现在
所处的状态而与状态的历史无关。
⑵当系统的状态发生变化时,状态函数也发生变
化,其改变值只与系统的始态和终态有关,而与
p( H 2 ) y( H 2 ) p总 =0.6427 108.9=70.00 kPa
p( N2 ) p总 p( H2 ) 38.89 kPa
四、阿马格分体积定律
由A、B、C组成的理想气体混合物
nRT (nA nB nC ) RT V p p
VA VB VC
六、可逆过程和不可逆过程
物理化学-第一章1

Z=Z(x,y) ( , )
∂Z ∂Z dZ = ( ) Y dX + ( ) X dY ∂X ∂Y
∆Z1 = ∆Z2
Ⅰ
Ⅱ B
V
过程与途径
体系状态所发生的一切变化成为过程。
按物质变化类型分类: 单纯PVT变化(单纯状态变化) 相变 化学变化
按条 件分 类
等温过程:初、终态温度相同且等于环境温度的过程 等压过程:初态压力、终态压力与环境压力都相同的过 程 等容过程:系统体积不变的过程 绝热过程:系统与环境间不存在热量传递,只有功传递 的过程 循环过程:初态与终态是同一状态的过程 恒外压过程:P外=常数 真空自由膨胀过程:P外=0 可逆过程:?如何实现
内能
通常体系的总能量由下述三部分组成:
E = U+T+V
• E: 体系所含的全部能量,即总能量. • T: 体系具有的宏观动能, 如: T=1/2·mV2. • V: 体系所具有的势能, 如重力势能等. • U: 体系的内能,指体系内部能量的总和,含粒子的平动 能、转动能、振动能、核运动能量、电子运动能量和分子 间相互作用势能等。 在化学热力学中,通常是不考虑系统整体运动的动能 以及系统在外场中的势能,而只需考虑系统的内部的能量 即内能。
内能的性质
什么是状态函数? 什么是状态函数?如果内能 是状态函数会怎样? 是状态函数会怎样?如果不 是会怎样? 是会怎样?
状态2 状态2
A △UA B
状态1 状态1 △UB
内能的特征:
⑴ U是状态函数; ∆U = U2-U1 ⑵ U是系统的广度性质,与系统所含物质的量成正比; ⑶ U绝对值未知,只能求出它的变化值。 ⑷ 系统进行单纯PVT变化时, U = f(T,V)
思考:T、p、V 是状态函数吗?
∂Z ∂Z dZ = ( ) Y dX + ( ) X dY ∂X ∂Y
∆Z1 = ∆Z2
Ⅰ
Ⅱ B
V
过程与途径
体系状态所发生的一切变化成为过程。
按物质变化类型分类: 单纯PVT变化(单纯状态变化) 相变 化学变化
按条 件分 类
等温过程:初、终态温度相同且等于环境温度的过程 等压过程:初态压力、终态压力与环境压力都相同的过 程 等容过程:系统体积不变的过程 绝热过程:系统与环境间不存在热量传递,只有功传递 的过程 循环过程:初态与终态是同一状态的过程 恒外压过程:P外=常数 真空自由膨胀过程:P外=0 可逆过程:?如何实现
内能
通常体系的总能量由下述三部分组成:
E = U+T+V
• E: 体系所含的全部能量,即总能量. • T: 体系具有的宏观动能, 如: T=1/2·mV2. • V: 体系所具有的势能, 如重力势能等. • U: 体系的内能,指体系内部能量的总和,含粒子的平动 能、转动能、振动能、核运动能量、电子运动能量和分子 间相互作用势能等。 在化学热力学中,通常是不考虑系统整体运动的动能 以及系统在外场中的势能,而只需考虑系统的内部的能量 即内能。
内能的性质
什么是状态函数? 什么是状态函数?如果内能 是状态函数会怎样? 是状态函数会怎样?如果不 是会怎样? 是会怎样?
状态2 状态2
A △UA B
状态1 状态1 △UB
内能的特征:
⑴ U是状态函数; ∆U = U2-U1 ⑵ U是系统的广度性质,与系统所含物质的量成正比; ⑶ U绝对值未知,只能求出它的变化值。 ⑷ 系统进行单纯PVT变化时, U = f(T,V)
思考:T、p、V 是状态函数吗?
物理化学第一章热力学第一定律(材料版)
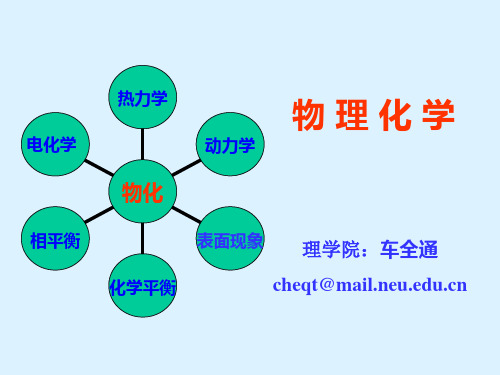
也可用U = Q - W表示,两种表达式完全等效,只是W的取 号不同。用该式表示的W的取号为:环境对系统作功,W<0 ;系 统对环境作功, W>0 。
热 力 学 能 (内 能)
热力学能(内能):系统内部能量的总和,包括分子运动的 平动能、分子内的转动能、振动能、电子能、核能以及各种粒 子之间的相互作用位能等。
• H. Helmholtz(1821-1894, 德国): 通过动物热的研究途径, 发现了 能量守恒定律.
• 柯尔丁(?-?, 丹麦): 发现或接近发现能量守恒和转换定律. • 威廉.汤姆生(即凯尔文勋爵,1824-?,英国):
1848年创立了绝对温标(-273oC=0K); 1851年提出热力学第二定律; 1852年发现汤姆生-焦尔效应; 1853年在焦耳协助下, 对热力学第一定律作了完整表述.
热力学能是状态函数,用符号U表示,它的绝对值无法测 定,只能求出它的变化值ΔU。
内能可表示为n, T, V的函数,即 U = U(n,T,V)。若为封闭系统, n一定,则: U = U (T,V),对于一个微小的变化过程,内能的增量可 用全微分dU表示。
dU = (U / T) V dT + (U / V) T dV or dU = (U / T) p dT + (U / p) T dp
(2) 恒压过程:p1=p2=pex 过程中压力恒定。恒压变化:p1 = p2 (3) 恒容过程:V1 = V2 过程中体积恒定。
状态2
(4) 绝热过程:Q = 0 系统与环境之间没有热的交换。 状态1 循环过程
(5) 循环过程:系统从始态出发,经一系列步骤又回到始态的过程。
(6) 自由膨胀过程:气体膨胀所克服的外压力为零。
热 力 学 能 (内 能)
热力学能(内能):系统内部能量的总和,包括分子运动的 平动能、分子内的转动能、振动能、电子能、核能以及各种粒 子之间的相互作用位能等。
• H. Helmholtz(1821-1894, 德国): 通过动物热的研究途径, 发现了 能量守恒定律.
• 柯尔丁(?-?, 丹麦): 发现或接近发现能量守恒和转换定律. • 威廉.汤姆生(即凯尔文勋爵,1824-?,英国):
1848年创立了绝对温标(-273oC=0K); 1851年提出热力学第二定律; 1852年发现汤姆生-焦尔效应; 1853年在焦耳协助下, 对热力学第一定律作了完整表述.
热力学能是状态函数,用符号U表示,它的绝对值无法测 定,只能求出它的变化值ΔU。
内能可表示为n, T, V的函数,即 U = U(n,T,V)。若为封闭系统, n一定,则: U = U (T,V),对于一个微小的变化过程,内能的增量可 用全微分dU表示。
dU = (U / T) V dT + (U / V) T dV or dU = (U / T) p dT + (U / p) T dp
(2) 恒压过程:p1=p2=pex 过程中压力恒定。恒压变化:p1 = p2 (3) 恒容过程:V1 = V2 过程中体积恒定。
状态2
(4) 绝热过程:Q = 0 系统与环境之间没有热的交换。 状态1 循环过程
(5) 循环过程:系统从始态出发,经一系列步骤又回到始态的过程。
(6) 自由膨胀过程:气体膨胀所克服的外压力为零。
第一课物理化学第一章(1)

四. 状态函数与状态方程
1. 状态函数 (1)定义:
体系状态的性质,即描述体系状态的宏观物理 量。(如T、P、V、 、、U、S、H和G等 )
(2) 状态函数的特点 a. 状态函数是状态的单值函数: ---- 状态定,状态函数的数值也确定;
b. 体系的始末态定,状态函数的变化值 也确定;
c. 体系恢复原态,状态函数也恢复原数值;
第三节.热力学第一定律
一. 热力学第一定律 二. 内能 三. 热力学第一定律的数学表达式
第三节.热力学第一定律
一. 热力学第一定律的文字描述
1. 自然界的一切物质都具有能量,能量 有各种不同形式,能够从一种形式转化 为另一种形式,但在转化过程中,能量 的总值不变。
2. 第一类永动机是不可能制成的。
(1).自由膨胀(free expansion)
( pe 0, dT 0) W pedV 0
(2). 等外压一次膨胀
( p2 pe p1 )
W
V2 V1
pedV
pe (V2
V1)
p2 (V2
V1 )
p1
( p1 ,V1 )
p2
( p2,V2 )
p2
结论:体系经历无限多次等外压膨
V1
V2 胀从1变化到2,再由无限多次等外
压压缩变回到1后,体系恢复原状的
同时,环境也恢复原状,而不留下
任何的痕迹,该过程为可逆过程。
∴上述的无限多次等外压膨胀与压缩过程 也称为理想气体的等温可逆膨胀和等温可 逆压缩过程。
V1
V2
V1 V3
V2
V1
V2
结论:上述的无限多次等外压膨胀与压缩过 程也称为理想气体的等温可逆膨胀和等温可 逆压缩过程。而等温一次膨胀、等温一次压 缩、等温二次膨胀、等温二次压缩与等温自 由膨胀均为热力学不可逆过程。
物理化学第一章

III.相变化过程(phase transformation) 如气化(vaporization)、液化(liquefaction)、凝固(freeze)、 熔化(fusion)、升华(sublimation)、凝华(condensation)、晶型 转化(crystal form transition)等
(理想气体定温可逆过程)
【例1-2】 求过程体积功。10molN2由300K、1.0MPa定温可逆膨 胀到1.0kPa。 解: WV psu (V )dV p(V )dV V1 V1 V2 nRT dV V1 V p2 nRT ln p1 1103 MPa 1 1 10mol 8.3145 J .mol .k 300 K ln 1.0MPa 172.3kJ
surrounding
system
interface
Fig.1-1 system and surrounding
I.
系统(system)与环境(surrounding)的关系:物质交换(matter exchange)、能量交换(energy exchange)。
+E
matter exchange system energy exchange
1.2.3 体积功(volume work)的计算
I. 基本方法:
WV psu (V)dV
WV psu (V)dV
V1 V2
II. 几何解释:psu~V坐标系中,-W为 psu~V曲线与V轴围 成的曲边梯形的面积。
{psu} Psu=f(V)
V1
V2 {v}
Fig.1.2-1 体积功几何解释
III. 体积功的计算
(V)dv psu (V)dv 0 a) 定容过程: WV V psu V
物理化学 01章_热力学第一定律及其应用
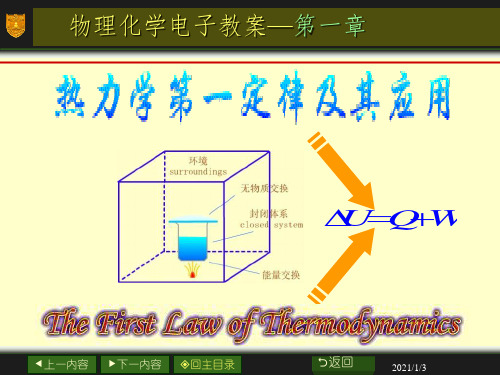
功可分为膨胀功和非膨胀功两大类。W的取号:
环境对体系作功,W>0;体系对环境作功,W<0 。
Q和W都不是状态函数,其数值与变化途径有关。
上一内容 下一内容 回主目录
返回
2021/1/3
1.2 热力学第一定律
•热功当量 •能量守恒定律 •热力学能 •第一定律的文字表述 •第一定律的数学表达式
上一内容 下一内容 回主目录
返回
2021/1/3
热功当量
焦耳(Joule)和迈耶(Mayer)自1840年起,历经 20多年,用各种实验求证热和功的转换关系, 得到的结果是一致的。
即: 1 cal = 4.1840 J
这就是著名的热功当量,为能量守恒原理 提供了科学的实验证明。
上一内容 下一内容 回主目录
返回
2021/1/3
热力学的方法和局限性
热力学方法 •研究对象是大数量分子的集合体,研究 宏观性质,所得结论具有统计意义。
•只考虑变化前后的净结果,不考虑物质 的微观结构和反应机理。
•能判断变化能否发生以及进行到什么程 度,但不考虑变化所需要的时间。
局限性 不知道反应的机理、速率和微观性
状态函数的特性可描述为:异途同归,值变 相等;周而复始,数值还原。
状态函数在数学上具有全微分的性质。
上一内容 下一内容 回主目录
返回
2021/1/3
状态方程
体系状态函数之间的定量关系式称为状态方 程(state equation )。
对于一定量的单组分均匀体系,状态函数 T,p,V 之间有一定量的联系。经验证明,只有两个 是独立的,它们的函数关系可表示为:
•体系与环境 •体系的分类 •体系的性质 •热力学平衡态 •状态函数 •状态方程 •热和功
物理化学-第一章热力学第一定律-new

4. QP = H
即:等压过程,体系的H和转换的热能 在数值上是相等的;体系吸收的热全部 用来改变体系的焓。
§1.6
热
容 (heat capacity)
1、热容( C ) 定义:物质的温度升高1K所需的热 dQ C= dT
´= 无相变,无化学变化,且 W
0
若物质的量为1mol,则为摩尔热容Cm
nRT/V dV V
W可逆= -nRT㏑(V2/V1 )=-nRT ㏑(P1/P2 ) 注意:只有等温可逆过程,W才可以用 上式计算,此时的W为体系对环境 做的最大功。
例2:2molH2,起始体积为15×10-3m3 若在恒定温度298.2K时,经下列过程 膨胀至终态体积为50×10-3m3下,试 计算各过程的W (1)自由膨胀; (2) 反抗恒外压100KPa; (3) 可逆膨胀过程。
研究物质的内部结构,及物质的结构与性 能之间的关系。
二、物理化学与其他学科的联系 1、是化学和药学的理论基础。 2、渗入到生命科学的各个领域 3、医检与物理化学的关系(仪器分析) 电位滴定 电泳分析
电解质分析仪 血液分析仪
三、物理化学学习方法: 1,抓三基:基本概念、基本理论、基本计算 2,掌握公式的使用条件及物理意义。 3,注意章节之间的联系,善于回顾。
3、等压热容Cp:
H= Qp
dQP dH = CP = dT dT
T2 T2 ∫ C QP =∫ CP dT = T nCPm dT=n· Pm(T2-T1) T1 1
QP = H =n· Pm(T2-T1) C 应用:等压过程,W’=0时,体系的简变 过程的H和交换热Q的计算。 适用于体系任意简变过程 H的计算;
4,重视习题。
第一章
物理化学第一章热力学第一定律

常用的热量单位是卡(cal):
热力学所采用的热功当量为:
1
2
3
4
5
01
等压过程和焓
02
若体系经历一等压过程,且不作有用功,由热力学第一定律:
03
U=Q+W=Q-∫p外dV
04
等压过程: p外=p2=p1
05
U=Q-p1or2(V2-V1)
06
对上式进行改写:
07
(U2-U1)=Q-(p2V2-p1V1)
理想气体的微观模型: 满足以下两个条件的体系为理想气体.
. 分子之间没有作用力, 分子间不存在作用势能;
. 分子的体积可以忽略不计, 可视为数学上的点.
热力学定义: 满足理想气体状态方程的体系. 方程为:
pV = nRT
式中n为体系所含物质的量,R为气体常数: R=8.314 J/mol.K.
08
(U2+p2V2)-(U1+p1V1)=Qp (1)
第二节 焓 (enthalpy)
上式的左边全是状态函数,而右边为过程量Q,对于等压过程,式中括号中的量总是一起出现,故可定义: H≡U+pV (2) H称为焓(enthalpy)。 因为H是状态函数的组合,所以H必为状态函数。 把H代入(1)式,可得: H=Qp (3) 上式物理含义是: 无有用功的等压过程热效应等于体系的焓变。
第一节 热力学第一定律
1
热力学第一定律(first law of thermodynamics)
2
自然界的能量既不能创生,也不会消灭.
3
热力学第一定律即为: 能量守恒原理.
4
更广泛地可定义为: 物质不灭定律.
5
第一定律可表述为: 第一类永动机不可能
物理化学第一章第一部分

体系能量的组成
体系与环境能量传递的形式
U
W Q
U Q W dU Q W
体系能量转化遵循的定律
§1.4 体积功
一.体积功 1.定义式 2.理想气体几种等外压变化过程的体积功 a. 自由膨胀 b. 一次等外压膨胀 c. 多次等外压膨胀 d. 无限次等外压膨胀(等温可逆膨胀) 二.可逆过程与不可逆过程 1.什么是可逆过程 2.可逆过程的特点 三.可逆相变的体积功 四.化学变化的体积功
注意:
(1)不论是膨胀还是压缩,体积功都以 -pe· dV 来表示。所采用的都是外压力pe; (2)只有-pe· dV这个量才是体积功,pe· V 或Vdp都不是体积功。Leabharlann . 四种等温膨胀过程体系对环境做的功
设在定温下,一定量理想气体在活塞筒 中克服外压pe,经4种不同途径,体积从V1 膨胀到V2。求体系对环境所作的功。 (1).自由膨胀(free expansion)
态和终态,而与变化的途径无关;
3.是体系的广度性质,与体系内所含物质
的数量成正比,具有加和性。
二、 热和功 (heat and work)
功和热是系统与环境之间进行能量交换的
两种不同的形式。
热(heat): 体系与环境之间因温度差而传递的能 量称为热,用符号Q 表示。 Q的取号: 体系吸热,Q>0; 体系放热,Q<0 。
3. 状态函数的特点
d. 状态函数在数学上具有全微分的性质, 可以用全微分的关系来处理,其微分 量冠以“d”,如,dV, dp……
dV 0
e. 状态函数的集合(和、差、商和积)也 是状态函数;
3. 状态函数的特点
f. 同一体系各个状态性质相互关联; 某一状态性质的改变将引起一个或多个状 态性质的改变;所以只需确定体系的几个 状态性质,便能确定体系的状态。 如:纯物质单相: 纯物质单相的密闭体系: 多组分单相:
体系与环境能量传递的形式
U
W Q
U Q W dU Q W
体系能量转化遵循的定律
§1.4 体积功
一.体积功 1.定义式 2.理想气体几种等外压变化过程的体积功 a. 自由膨胀 b. 一次等外压膨胀 c. 多次等外压膨胀 d. 无限次等外压膨胀(等温可逆膨胀) 二.可逆过程与不可逆过程 1.什么是可逆过程 2.可逆过程的特点 三.可逆相变的体积功 四.化学变化的体积功
注意:
(1)不论是膨胀还是压缩,体积功都以 -pe· dV 来表示。所采用的都是外压力pe; (2)只有-pe· dV这个量才是体积功,pe· V 或Vdp都不是体积功。Leabharlann . 四种等温膨胀过程体系对环境做的功
设在定温下,一定量理想气体在活塞筒 中克服外压pe,经4种不同途径,体积从V1 膨胀到V2。求体系对环境所作的功。 (1).自由膨胀(free expansion)
态和终态,而与变化的途径无关;
3.是体系的广度性质,与体系内所含物质
的数量成正比,具有加和性。
二、 热和功 (heat and work)
功和热是系统与环境之间进行能量交换的
两种不同的形式。
热(heat): 体系与环境之间因温度差而传递的能 量称为热,用符号Q 表示。 Q的取号: 体系吸热,Q>0; 体系放热,Q<0 。
3. 状态函数的特点
d. 状态函数在数学上具有全微分的性质, 可以用全微分的关系来处理,其微分 量冠以“d”,如,dV, dp……
dV 0
e. 状态函数的集合(和、差、商和积)也 是状态函数;
3. 状态函数的特点
f. 同一体系各个状态性质相互关联; 某一状态性质的改变将引起一个或多个状 态性质的改变;所以只需确定体系的几个 状态性质,便能确定体系的状态。 如:纯物质单相: 纯物质单相的密闭体系: 多组分单相:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Vm= V/n
两个容量性质之比为体系的强度性质, = m / V。
2/14/2019
状态函数的特性?
(1)状态一定时, 所有状态函数均具有确定的数值;
(2)体系状态变化时,状态函数的改变值只取决于变 化的始终态,与变化的途径无关。
异途同归,值变相等;
★★体系经历循环过程后(始、终态相同),各状态函 数的变化值? 周而复始,数值还原。
2/14/2019
(2)Q、W 既为能量交换形式,其数值自然有正, 负 之分。 规定: 体系吸热,Q > 0;体系放热, Q < 0;
环境对体系做功,W > 0;体系对环境做功,W < 0。
2/14/2019
2.热力学第一定律
热力学第一定律可以表述为:自然界的一切物
质都具有能量,能量有各种形式,并且可以从一种
第一章 化学热力学基础
环境 surroundings 无物质交换 封闭系统 Closed system
△U = Q + W
有能量交换
2/14/2019
§1.1 热力学能量守恒原理
1.基本概念
2.热力学第一定律
2/14/2019
1.基本概念
Ⅰ:体系与环境: 划分出来作为研究对象的部分—体系(system) 体系之外而又与之有关的部分—环境(surroundings) 讨论:
(1)体系的确定以解决问题的方便为前提。
(2)对同一问题,选择体系不同,所得结论亦不相同。
2/14/2019
“体系”与“环境”之间应有一定的 “边界”,这个
边界可以是真实的物理界面(如图2,3),可以是虚
构的界面(如图 1中的虚线)。
2/14/2019
体系
交换物质
交换能量
环境
体系类型 敞开体系
物质的传递 有
O
Ⅳ:热和功
热和功是热力学过程中的两种能量交换形式。
热 (heat) Q:体系与环境间因温差引起的能量交换 功 (work) W:除 Q 以外的其它能量交换形式 讨论: (1)Q 和 W 不是状态函数,Q 和 W 均为过程 量; Q、W 值与变化途径有关。在确定的状态下,是不 存在热和功的。 Q和W的微小变化用符号δ 而不能用d 表示。
2/14/2019
状态函数的分类及其特征:
(1)广度性质:其数值与体系中物质的量成正比,这种 性质有加和性。如 m、 V、C、U、S、G、H 等; (2)强度性质:其数值取决于体系自身的特点,与体系 中物质的数量无关,不具有加和性,如 T、p、ρ等。 指定了物质量的广度性质即成为强度性质,如摩尔体积
2/14/2019
状态1 U1
①Q1 W1
②Q2 W2 ③Q3 W3
状态2 U2
Q1 ≠ Q2 ≠ Q3,W1 ≠ W2 ≠ W3
△U =U2-U1=Q1 +W1= Q2 +W2= Q3 + W3 △U = Q + W (1-1)
dU =δQ + δW
2/14/2019
热力学第一定律的数学表达式
△U = Q + W dU =δQ + δW
根据过程中物理量的变化情况,又可分为以下过程: ①定温过程(Isothermal process) : T1=T2= Te ②定压过程(Isobaric process) : p 1=p 2= pe ③定容过程(Isochoric process) : V1=V2
④绝热过程(adiabatic process) : Q=0
2/14/2019
Hale Waihona Puke (3) 体系的状态函数在数学上为连续函数,其微小变 化可写成全微分,并可积分。 如,理想气体的p、V、T之间可写成下列函数关系 式:V=V(T,p)
V V dV = ( ) P dT + ( ) T dP T P
(4)对纯物质单相密闭系统,状态函数 p、 V、T 之 间有一定量的联系。经验证明,只需两个状态性质(如 T、p)就可确定其状态。
⑤循环过程:始态与终态相同
2/14/2019
如:一定量理想气体由始态A(300K ,100kPa)变到 终态Z(450K,150kPa)。
途径a; 途径b; 途径c b2, c1 为恒温线
C p c1
c2 Z a A b2 b1 V B
体系始、终态相同,所有状态函数的改变值均相同。
2/14/2019
Joule(焦耳)和 Mayer(迈耶尔)自1840年起,历 经40年、四百多次测定实验,求证热和功的转换关系。 由重物质量和下降的距离得出 叶片所做的机械功,由水和量热 器的质量、比热容、升高的温度 即: 1 cal = 4.1840 J 算出得到的热量。实验结果证明, 消耗的机械功跟产生的热量总是 这就是著名的热功当量, 成正比的,这个比值叫热功当量。 为能量守恒原理提供了科学 的实验证明。
2/14/2019
Ⅱ:状态与状态函数 状态 (state ):体系所有宏观性质的综合表现。 体系的性质—用于确定体系状态的各种宏观物理量。 如 V、 T 、 p、U、H、 G、 S、 F 等。 当体系的状态确定后,各宏观性质具有确定的值。 状态函数(state furction):描述体系状态的各种宏观性质。
2/14/2019
Ⅲ:过程与途径
体系状态发生的变化—过程 (process) 变化的具体步骤或方式—途径 (path)
常见的热力学过程有以下三类:
(1)简单状态变化过程:无相变,无化学变化,简 单 p 、 V、T 变化。 (2)相变过程:体系物态发生变化。
(3)化学变化过程: 化学反应。
2/14/2019
形式转化为另一种形式,在转化过程中,能量的总
量不变。热力学能、热和功之间可以相互转化,但 总的能量不变。
也可以表述为:第一类永动机是不可能制成的。
热力学第一定律是人类经验的总结,事实证明违 背该定律的实验都将以失败告终。
2/14/2019
永动机的设想图
2/14/2019
不需要外界提供能量,却能不断地对外做功。
能量的传递 有
封闭体系
2/14/2019
无
无
有
无
孤立体系
H2O(g) H2O(l)
体系 H2O(l) H2O(l)+ H2O(g)
物质交换 有 无 无
能量交换 有 有 无
体系类型
敞开体系 open system 电炉丝
封闭体系closed system
孤立体系 isolated system
H2O(l)+H2O(g) + 电炉丝+ 电 源等
