物理化学第一章知识点
物理化学上热力学第一定律知识框架图总结
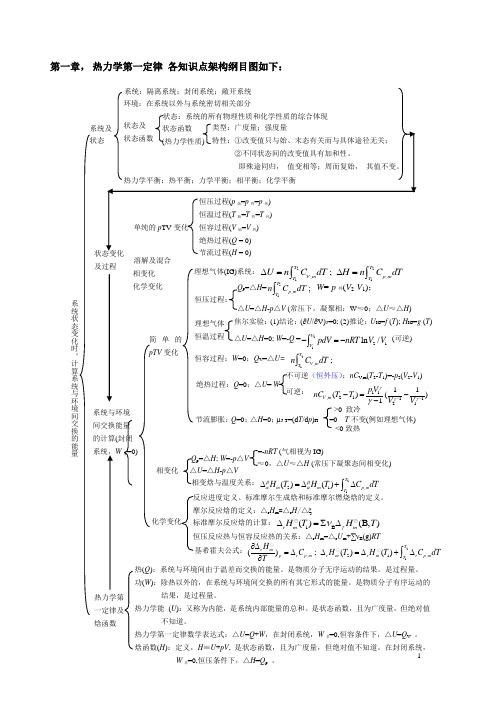
1第一章, 热力学第一定律 各知识点架构纲目图如下:及过程 溶解及混合 化学变化 相变化 热(Q ):系统与环境间由于温差而交换的能量。
是物质分子无序运动的结果。
是过程量。
功(W ):除热以外的,在系统与环境间交换的所有其它形式的能量。
是物质分子有序运动的结果,是过程量。
热力学能 (U ):又称为内能,是系统内部能量的总和。
是状态函数,且为广度量,但绝对值不知道。
热力学第一定律数学表达式:△U =Q +W ,在封闭系统,W 非=0,恒容条件下,△U =Q V 。
焓函数(H ):定义,H ≡U +pV , 是状态函数,且为广度量,但绝对值不知道。
在封闭系统,W 非=0,恒压条件下,△H =Q p 。
热力学第一定律及 焓函数系统与环境间交换能量 的计算(封闭 系统,W 非=0)简单的pTV 变化 理想气体(IG)系统:2211,,;T TV m p mT T U n C dT H n C dT ∆=∆=⎰⎰ 理想气体 恒温过程 焦尔实验:(1)结论:(∂U /∂V)T =0; (2)推论:U IG =f (T ); H IG =g (T ) △U =△H =0; W =-Q =2121ln /VVpdV nRT V V -=-⎰ (可逆)恒容过程:W =0;Q V =△U= 21,;TV mT n C dT ⎰绝热过程:Q =0;△U = W 不可逆(恒外压):nC V ,m (T 2-T 1)=-p 2(V 2-V 1) 可逆: 11,21112111()()1V m p V nC T T V V γγγγ---=-- Q p =△H =21,;T p m T n C dT ⎰W =-p 外(V 2-V 1); △U =△H -p △V (常压下,凝聚相:W ≈0;△U ≈△H )恒压过程: 节流膨胀:Q =0;△H =0;μJ-T =(d T /d p )H =0 T 不变(例如理想气体) <0致热 >0 致冷 相变化 △U =△H -p △VQ p =△H ; W =-p △V≈0,△U ≈△H (常压下凝聚态间相变化)=-nRT (气相视为IG) 相变焓与温度关系:2121,()()Tm m p mT H T H T C dT ββαα∆=∆+∆⎰化学变化 摩尔反应焓的定义:△r H m =△r H /△ξ 恒压反应热与恒容反应热的关系:△r H m =△r U m +∑νB (g)RT标准摩尔反应焓的计算:1B ()(B,)r m f mH T H T ν∆=∑∆反应进度定义、标准摩尔生成焓和标准摩尔燃烧焓的定义。
【化学】中考浙教版科学九年级上册物理化学知识点梳理

中考浙教版科学九年级上册物理化学知识点梳理第一章基础知识分析第1节物质的变化1、物理变化与化学变化:区别:变化后有无新物质生成。
联系:物质发生化学变化的同时一定伴随着物理变化,但发生物理变化时一定不发生化学变化。
2、探究物质变化的基本方法:观察和实验。
3、物质变化的证据:颜色、气味或味道的改变、状态的改变、沉淀生成、气体产生等。
4、硫酸铜晶体:蓝色晶体。
加热时失去结晶水而变成白色粉末,该粉末遇水又变成兰色晶体。
CuSO4·5H2O====== CuSO4+5H2O ; CuSO4+5H2O===== CuSO4·5H2O5、物质变化规律的应用:(1)硫酸铜溶液检验蛋白质的存在,使其产生沉淀;(2)白色硫酸铜粉末检验水分的存在,遇水变蓝色。
第2节酸1、电离:一些物质在水溶液或融化状态下电离成自由移动离子的过程。
2、酸:一些物质电离时,其阳离子全部是氢离子的化合物。
HCI ==== H+ + CI — H2SO4 ====2 H++ SO42— HNO3===== H++ NO3—3、常见的酸:盐酸 HCI 硫酸H2SO4硝酸HNO3碳酸H2CO3磷酸H3PO4醋酸CH3COOH4、检验物质酸碱性和测定溶液的酸碱度:(1)检验物质酸碱性:酸碱指示剂(2)测定溶液的酸碱度:PH试纸。
一、酸的通性1、酸使指示剂变色;2、酸 + 碱 ===== 盐 + 水3HCl+ Al(OH)3 ==== AlCl3+3H2O (用胃舒平治疗胃酸过多)H2SO4 +2 NaOH==== Na2SO4 + H2O1、酸 + 某些盐 ===== 新盐 + 新酸2HCl + CaCO3====CaCl2 + H2O + CO2↑(实验室制取CO2)HCl + AgNO3 ==== AgCl ↓ + HNO3 (用AgNO3溶液和稀硝酸检验盐酸)H2SO4 + BaCl2 ==== BaSO4 ↓ + 2HCl (用BaCI2溶液和稀硝酸检验硫酸)2、酸 + 金属氧化物 ==== 盐 + 水6HCl+ Fe2O3 ====2 FeCl3 +3 H2O (用稀盐酸清除铁锈,铁锈溶解,形成黄色溶液)H2SO4 + CuO ==== CuSO4 + H2O (氧化铜黑色粉末溶解,形成蓝色溶液)3、酸 + 某些金属 ==== 盐 + 氢气Fe + 2HCl ==== FeCl2 + H2↑Zn + H2SO4==== ZnSO4 + H2↑(实验室用于制H2)二、酸的个性1、盐酸HCl:盐酸是HCl气体的水溶液,具有挥发性,挥发出的HCl气体在瓶口遇水蒸汽形成盐酸的小液滴而出现白雾。
大学物理化学知识点归纳

第一章气体的pvT关系一、理想气体状态方程pV=(m/M)RT=nRT (1.1)或pVm=p(V/n)=RT (1.2)式中p、V、T及n的单位分别为P a 、m3、K及mol。
Vm=V/n称为气体的摩尔体积,其单位为m3·mol。
R=8.314510J·mol-1·K-1称为摩尔气体常数。
此式适用于理想,近似于地适用于低压下的真实气体。
二、理想气体混合物1.理想气体混合物的状态方程(1.3)pV=nRT=(∑BBn)RTpV=mRT/Mmix (1.4)式中Mmix为混合物的摩尔质量,其可表示为Mmix def ∑BBy M B(1.5)Mmix=m/n=∑BBm/∑BBn(1.6)式中MB为混合物中某一种组分B 的摩尔质量。
以上两式既适用于各种混合气体,也适用于液态或固态等均匀相混合系统平均摩尔质量的计算。
2.道尔顿定律p B =nBRT/V=yBp(1.7)P=∑BB p(1.8)理想气体混合物中某一种组分B 的分压等于该组分单独存在于混合气体的温度T及总体积V的条件下所具有的压力。
而混合气体的总压即等于各组分单独存在于混合气体的温度、体积条件下产生压力的总和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
3.阿马加定律VB*=nBRT/p=yBV (1.9)V=∑VB* (1.10)VB*表示理想气体混合物中物质B的分体积,等于纯气体B在混合物的温度及总压条件下所占有的体积。
理想气体混合物的体积具有加和性,在相同温度、压力下,混合后的总体积等于混合前各组分的体积之和。
以上两式适用于理想气体混合系统,也近似适用于低压混合系统。
三、临界参数每种液体都存在有一个特殊的温度,在该温度以上,无论加多大压力,都不可能使气体液化,我们把这个温度称为临界温度,以Tc或tc表示。
我们将临界温度Tc时的饱和蒸气压称为临界压力,以pc表示。
在临界温度和临界压力下,物质的摩尔体积称为临界摩尔体积,以Vm,c表示。
物理化学的知识点总结

物理化学的知识点总结一、热力学1. 热力学基本概念热力学是研究能量转化和传递规律的科学。
热力学的基本概念包括系统、环境、热、功、内能、焓、熵等。
2. 热力学第一定律热力学第一定律描述了能量守恒的原理,即能量可以从一个系统转移到另一个系统,但总能量量不变。
3. 热力学第二定律热力学第二定律描述了能量转化的方向性,熵的增加是自然界中不可逆过程的一个重要特征。
4. 热力学第三定律热力学第三定律表明在绝对零度下熵接近零。
此定律是热力学的一个基本原理,也说明了热力学的某些现象在低温下会呈现出独特的特性。
5. 热力学函数热力学函数是描述系统状态和性质的函数,包括内能、焓、自由能、吉布斯自由能等。
二、化学热力学1. 热力学平衡和热力学过程热力学平衡是指系统各个部分之间没有宏观可观察的能量传输,热力学过程是系统状态发生变化的过程。
2. 能量转化和热力学函数能量转化是热力学过程中的一个重要概念,热力学函数则是描述系统各种状态和性质的函数。
3. 热力学理想气体理想气体是热力学研究中的一个重要模型,它通过状态方程和理想气体定律来描述气体的性质和行为。
4. 热力学方程热力学方程是描述系统热力学性质和行为的方程,包括焓-熵图、温度-熵图、压力-体积图等。
5. 反应焓和反应熵反应焓和反应熵是化学热力学研究中的重要参数,可以用来描述化学反应的热力学过程。
三、物质平衡和相平衡1. 物质平衡物质平衡是研究物质在化学反应和物理过程中的转化和分配规律的一个重要概念。
2. 相平衡相平衡是研究不同相之间的平衡状态和转化规律的一个重要概念,包括固相、液相、气相以及其之间的平衡状态。
3. 物质平衡和相平衡的研究方法物质平衡和相平衡的研究方法包括热力学分析、相平衡曲线的绘制和分析、相平衡图的绘制等。
四、电化学1. 电解质和电解电解质是能在水溶液中发生电离的化合物,电解是将电能转化为化学能或反之的过程。
2. 电化学反应和电势电化学反应是在电化学过程中发生的化学反应,电势是描述电化学系统状态的一个重要参数。
《大学物理化学》知识点总结

第一章 理想气体1、理想气体:在任何温度、压力下都遵循PV=nRT 状态方程的气体。
2、分压力:混合气体中某一组分的压力。
在混合气体中,各种组分的气体分子分别占有相同的体积(即容器的总空间)和具有相同的温度。
混合气体的总压力是各种分子对器壁产生撞击的共同作用的结果。
每一种组分所产生的压力叫分压力,它可看作在该温度下各组分分子单独存在于容器中时所产生的压力B P 。
P y P B B =,其中∑=BBB B n n y 。
分压定律:∑=BB P P道尔顿定律:混合气体的总压力等于与混合气体温度、体积相同条件下各组分单独存在时所产生的压力的总和。
∑=BB V RT n P )/(3、压缩因子ZZ=)(/)(理实m m V V 4、范德华状态方程 RT b V V ap m m=-+))((2 nRT nb V Van p =-+))((225、临界状态(临界状态任何物质的表面张力都等于0)临界点C ——蒸气与液体两者合二为一,不可区分,气液界面消失; 临界参数:(1)临界温度c T ——气体能够液化的最高温度。
高于这个温度,无论如何加压 气体都不可能液化;(2)临界压力c p ——气体在临界温度下液化的最低压力; (3)临界体积c V ——临界温度和临界压力下的摩尔体积。
6、饱和蒸气压:一定条件下,能与液体平衡共存的它的蒸气的压力。
取决于状态,主要取决于温度,温度越高,饱和蒸气压越高。
7、沸点:蒸气压等于外压时的温度。
8、对应状态原理——处在相同对比状态的气体具有相似的物理性质。
对比参数:表示不同气体离开各自临界状态的倍数 (1)对比温度c r T T T /= (2)对比摩尔体积c r V V V /= (3)对比压力c r p p p /= 9、rr r c r r r c c c T Vp Z T V p RT V p Z =⋅=10、压缩因子图:先查出临界参数,再求出对比参数r T 和r p ,从图中找出对应的Z 。
物理化学知识点总结(热力学第一定律)

热力学第一定律一、基本概念1.系统与环境敞开系统:与环境既有能量交换又有物质交换的系统。
封闭系统:与环境只有能量交换而无物质交换的系统。
(经典热力学主要研究的系统)孤立系统:不能以任何方式与环境发生相互作用的系统。
2.状态函数:用于宏观描述热力学系统的宏观参量,例如物质的量n、温度T、压强p、体积V等。
根据状态函数的特点,我们把状态函数分成:广度性质和强度性质两大类。
广度性质:广度性质的值与系统中所含物质的量成正比,如体积、质量、熵、热容等,这种性质的函数具有加和性,是数学函数中的一次函数,即物质的量扩大a倍,则相应的广度函数便扩大a倍。
强度性质:强度性质的值只与系统自身的特点有关,与物质的量无关,如温度,压力,密度,摩尔体积等。
注:状态函数仅取决于系统所处的平衡状态,而与此状态的历史过程无关,一旦系统的状态确定,其所有的状态函数便都有唯一确定的值。
二、热力学第一定律热力学第一定律的数学表达式:对于一个微小的变化状态为:dU=公式说明:dU表示微小过程的内能变化,而δQ和δW则分别为微小过程的热和功。
它们之所以采用不同的符号,是为了区别dU是全微分,而δQ和δW不是微分。
或者说dU与过程无关而δQ和δW却与过程有关。
这里的W既包括体积功也包括非体积功。
以上两个式子便是热力学第一定律的数学表达式。
它们只能适用在非敞开系统,因为敞开系统与环境可以交换物质,物质的进出和外出必然会伴随着能量的增减,我们说热和功是能量的两种传递形式,显然这种说法对于敞开系统没有意义。
三、体积功的计算1.如果系统与环境之间有界面,系统的体积变化时,便克服外力做功。
将一定量的气体装入一个带有理想活塞的容器中,活塞上部施加外压。
当气体膨胀微小体积为dV时,活塞便向上移动微小距离dl,此微小过程中气体克服外力所做的功等于作用在活塞上推力F与活塞上移距离dl的乘积因为我们假设活塞没有质量和摩擦,所以此活塞实际上只代表系统与环境之间可以自由移动的界面。
物理化学第一章知识点解析

G 等叫热力学系统的宏观性质( 或简称热力学性质)。
宏观性质分为两类:强度性质——与系统中所含物质的量无关, 无
加和性( 如p、T 等) ;广度性质——与系统中所含物质的量有关, 有加 和性( 如V、U、H⋯ 等) , 而
另 一 一 种 种 广 广 度 度 性 性 质 质=强 度 性 质,如
Vm
=
V n
,
= m V
3.系统的状态和状态函数
系统的状态是指系统所处的样子。热力学中采用系统的宏观性质 来描述系统的状态, 所以系统的宏观性质也称为系统的状态函数。
( i) 对于一定量的组成不变的均相流体系统, 系统的任意一个宏观性 质是另外两个独立的宏观性质的函数。这一结论是由实验结果得到的,
p2 = psu , 此过程叫定压过程。而定压变化, 仅有p1 = p2, 过程中压力可不恒定。 ( iii ) 定容过程
系统状态变化过程中体积保持恒定, V1 = V2 , 此为定容过程。 ( iv) 绝热过程
系统状态变化过程中, 与环境间的能量传递仅可能有功的形式, 而无热的形式, 即Q = 0 , 叫绝热过程。 ( v) 循环过程
(II)封闭系统——系统与环境之间通过界面只有能量的传递, 而无 物质的质量传递。因此封闭系统中物质的质量是守恒的。
(III)隔离系统——系统与环境之间既无物质的质量传递亦无能量 的传递。因此隔离系统中物质的质量是守恒的, 能量也是守恒的。
2.系统的宏观性质
热力学系统是大量分子、原子、离子等微观粒子组成的宏观集合
过程——在一定环境条件下, 系统由始态变化到终态的经过。 途径——系统由始态变化到终态所经历的过程的总和。
物理化学知识点归纳

焓是状态函数,是广度性质,具有能量单位,本身没有物理意义,在等压下没有非体积 功的热效应等于焓的改变量。
等容热容: CV
= δ QV dT
=
⎛ ⎜⎝
∂U ∂T
⎞ ⎟⎠ V
等压热容: Cp
=
δ Qp dT
=
⎛ ⎜⎝
∂H ∂T
⎞ ⎟⎠ p
对于理想气体: Cp − CV = nR
3. 理想气体各基本过程中W 、 Q 、 ∆U 、 ∆H 的计算
Helmholtz 自由能判据:等温等容条件下不做非膨胀功 dA ≤ 0
Gibbs 自由能判据:等温等压条件下不做非膨胀功 dG ≤ 0
5. 热力学函数的基本关系式
组成恒定(无相变、无化学变化),不做非体积功的封闭系统的热力学基本方程
热力学基本方程
全微分与系数的关系
Maxwell 关系
dU = TdS − pdV
dT
∫ T2 T1
CV
dT
∫ T2 T1
CV
dT
∫ T2 T1
CV
dT
∆H
0
0
∫ T2 T1
C
pdT
∫ T2 T1
C
pdT
∫ T2 T1
C
pdT
∫ T2 T1
C
pdT
3
乐山师范学院 化学与生命科学学院
4. 焦耳-汤姆逊系数
µ
=
⎛ ⎜ ⎝
∂T ∂p
⎞ ⎟ ⎠H
=
−1 Cp
⎛ ∂H
⎜ ⎝
∂p
⎞ ⎟ ⎠T
z ' = vaπ d 2n
当其他分子也动时,一个分子在单位时间内与其他分子相碰撞的次数: z ' = 2vaπ d 2n
物理化学知识点总结

第一章 热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律热力学第一定律:ΔU =Q +W 。
焦耳实验:ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式1、体积功的计算 δW = -p e d V恒外压过程:W = -p e ΔV可逆过程:1221ln ln p p nRT V V nRT W ==2、热效应、焓等容热:Q V =ΔU (封闭系统不作其他功) 等压热:Q p =ΔH (封闭系统不作其他功) 焓的定义:H =U +pV ; d H =d U +d(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂=定压热容与定容热容的关系:nR C C =-V p 热容与温度的关系:C p =a +bT +c’T 2 四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p e d V 等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V 可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程:Q =0 ; 利用C V (T 2-T 1)=-p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化:ΔH =Q =n Δ_H ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、热化学物质的标准态;热化学方程式;盖斯定律;标准摩尔生成焓。
摩尔反应热的求算:)298,()298(B H H m f B m r θθν∆=∆∑反应热与温度的关系—基尔霍夫定律:)(])([,p B C T H m p BB m r ∑=∂∆∂ν。
大学课程《物理化学》各章节知识点汇总

第一定律的数学表达式
U Q W
对微小变化: dU Q W
等容热效应
dU Q W W pdV 0
dU QV
CV
QV
dT
U T
V
U QV ,
U nB
S ,V ,n j B
H nB
S, p,nj B
F nB
T ,V ,n j B
B
G nB
T , p,n j B
n B
S ,V ,n j B
F f (T ,V , n1, n2 )
H f (S, p, n1, n2 )
组成可变系统的热力学基本关系式:
dU TdS pdV BdnB
Q和W都不是状态函数,其数值与变化途径有关。
§1-4 可逆过程和体积功
一、体积功
因系统的体积变化而引起的系统与环境之间交换的功称
为体积功。 pe
W Fedl ( pe A)dl
ped ( Al) pedV
A
dl
pi
二、功与过程
功不是状态函数,其数值与过程有关。系统由同一始态 经不同的过程变化到同一终态,则体统对环境或环境对 体系所作的功不同。
p2 dp
压缩
p1
p1
p2 , V2
p1, V1
p2
V1
V2
W
V1 V2
pedV
( p V1
V2
i
dp)dV
V1 V2
pi dV
三、可逆过程
某系统经一系列的过程后,如果系统回到初始状态叫做 系统的复原;环境在经历一些的变化后,如果既没有功 的得失也没有热的得失就叫做环境的复原。
厦门大学 物理化学 (上) 各章 知识点 总结

第1章第零定律与物态方程一、基本要点公式及其适用条件1.系统的状态和状态函数及其性质系统的状态—就是系统物理性质和化学性质的综合表现,它采用系统的宏观性质来描述系统的状态,系统的宏观性质,也称为系统的"状态函数"。
系统的宏观性质(状态函数)—就是由大量(摩尔级)的分子、原子、离子等微观粒子组成的宏观集合体所表现出的集团行为,简称"热力学性质"或“热力学函数”如p、V、T、U、H、S、A、G 等。
Z=f(x,y)表示一定量、组成不变的均相系统,其任意宏观性质(Z)是另两个独立宏观性质(x,y)的函数。
状态函数Z具有五个数学特征:(1),状态函数改变量只决定于始终态,与变化过程途径无关。
(2),状态函数循环积分为零,这是判断Z是否状态函数的准则之一。
(3),系Z的全微分表达式(4),系Z的Euler 规则,即微分次序不影响微分结果。
(5),系Z、x、y满足循环式,亦称循环规则。
2.热力学第零定律即热平衡定律:当两个物态A和B分别与第三个物体C处于热平衡,则A和B之间也必定彼此处于热平衡。
T =t+273.15,T是理想气体绝对温标,以"K"为单位。
t是理想气体摄氏温标,以"℃"为单位。
绝对温标与摄氏温标在每一度大小是一样的,只是绝对温标的零度取在摄氏温标的-273.15℃处,可以看出,有了绝对温标的概念后,只需确定一个固定参考点(pV)0p=0,依国际计量大会决定,这个参考点选取在纯水三相点,并人为规定其温度正好等于273.16K。
3.理想气态方程及其衍生式为:;式中p、V、T、n单位分别为Pa、m3、K、mol;R=8.314J〃mol-1〃K-1,V m为气体摩尔体积,单位为m3〃mol-1,ρ 为密度单位kg〃m-3,M 为分子量。
此式适用于理想气或近似地适用于低压气。
4.理想混合气基本公式(1)平均摩尔质量;式中M B和y B分别为混合气中任一组份B 的摩尔质量与摩尔分数。
物理化学复习知识点

物理化学复习总结第一章气体的PVT关系 (4)1.1理想气体状态方程 (4)1.2理想气体分压、分体积定律 (4)1.2.1理想气体分压定律: (4)1.2.2理想气体分体积定律: (4)1.3饱和蒸汽压 (4)第二章热力学第一定律 (5)2.1.基本概念 (5)2.1.1系统和环境 (5)2.1.4过程与途径 (5)2.1.5相及相变化 (6)2.1.6热和功 (6)2.2体积功的计算(可逆过程) (6)2.3热力学第一定律及热力学能 (7)2.3.1热力学能U (7)2.3.2热一律 (7)2.4恒容热、恒压热及焓 (8)2.4.1恒容过程热: (8)2.4.2恒压过程热及焓: (8)2.5热容及热的计算 (9)2.5.1热容定义 (9)2.5.2分别利用恒容、恒压摩尔热容计算反应热公式: (9)2.5.3热容与温度的关系 (9)2.6热力学第一定律的应用 (9)2.6.1理想气体的热力学能及焓只是温度的函数 (9)2.6.2热一律对简单状态参量变化过程的应用(计算题) (10)2.6.3热一律的另一应用——相变化过程热一律的计算 (10)2.6.4热一律的应用Ⅲ——热化学 (10)第三章热力学第二定律 (12)3.1自发过程的共同特征及热二律的表述 (12)3.1.1自发过程的共同特征: (12)3.1.2热二律的表述 (13)3.2卡诺热机及热机效率 (13)3.3熵增加原理及热二律的数学表达式 (13)3.3.1熵的提出 (13)3.3.2熵的定义及热二律的数学表达式 (14)3.3.3熵增加原理 (14)3.4熵变的计算 (15)3.4.1 单纯p、V、T 变化过程ΔS的计算 (15)3.4.2理想气体的混合过程 (16)3.4.3定T 定p下相变化过程 (17)3.4.4热力学第三定律及化学反应熵变的计算 (17)3.5亥姆霍茨函数和吉布斯函数 (18)3.5.1 亥姆霍茨(Helmholtz)函数及其判据 (18)3.5.2 吉布斯(Gibbs)函数及其判据 (18)3.5.3引入A、G的意义 (19)3.5.4定温过程ΔA、ΔG 的计算 (19)3.6热力学函数的重要关系式 (20)3.6.1定义式 (20)3.6.2热力学基本方程(4个) (20)3.6.3对应系数方程(8个) (20)3.6.4麦克斯韦方程(4个) (20)3.6.5其它关系 (20)3.7克拉贝龙(Clapeyron)方程 (21)3.7.1克拉贝龙(Clapeyron)方程 (21)3.7.2克拉贝龙方程的应用 (21)3.8热力学能的本质及熵的统计意义 (22)3.8.1热力学能的本质 (22)3.8.2熵的统计意义 (22)3.8.3熵增加原理的限制 (22)第四章多组分系统热力学及相平衡 (23)4.1 理解偏摩尔量和化学势的概念 (23)4.1.1偏摩尔量 (23)4.1.2化学势的概念,解并掌握化学势判据及其应用 (26)4.2理解并掌握Clapeyron公式和 Clausius-Clapeyron方程,并能进行有关计算 (27)4.2.1克拉贝龙(Clapeyron)方程(含克-克方程) (27)4.3理解理想液体混合物和理想稀溶液中各组分化学势的表达式 (29)4.3.1理想液态混合物中各组分化学势等温式 (29)4.3.2理想稀溶液中各组分的化学势等温式 (29)4.4理解并掌握形成理想液体混合物过程热力学函数变的计算方法 (32)4.5掌握Raoult定律、Henry定律等相平衡规律的简单计算(如蒸汽压下降、凝固点降低等) (33)4.5.1拉乌尔定律 (33)4.5.2亨利定律 (34)4.5.3两个定律的对比 (34)4.6理解相律的意义:掌握单组分体系和二组分体系典型相图的特点 (34)4.6.1相率 (34)4.6.2单组分(纯物质)系统的相平衡 (35)4.6.3纯组分系统的相图 (35)4.6.4二组分体系典型相图 (35)第五章化学平衡 (37)5.1明了热力学标准平衡常数的定义,会用热力学数据计算标准平衡常数 (37)5.1.1平衡常数的热力学推导 (37)5.1.2平衡常数的计算 (37)5.2理解并掌握Van’t Hoff等温方程及等压方程的含义及其应用,能够分析和计算各种因素对化学反应平衡组成的影响(如系统的温度、浓度、压力和惰性气体等) (38)5.2.1、等温方程式 (38)5.2.2 化学反应等压方程式 (40)第六章电化学 (41)6.1 法拉第定律 (41)6.2离子的平均活度和平均活度系数 (41)6.3离子强度及强电解质溶液的离子互吸理论 (42)6.4可逆电池热力学 (42)6.5可逆电极的类型 (43)6.6电极电势的Nernst方程 (44)6.7浓差电池 (44)6.8电池电动势和电极电势的应用 (45)6.9电极极化 (46)第七章界面现象 (47)7.1比表面吉布斯函数和表面张力 (47)7.2界面现象热力学 (48)7.3弯曲界面的附加压力 (48)7.4拉普拉斯(Laplace)方程 (49)7.5分散度对物质性质的影响 (49)7.6润湿 (51)第八章化学动力学 (52)8.1反应速率、速率常数等基本概念 (52)8.2简单级数反应方程及其特征 (53)8.2.1一级反应 (53)8.2.2二级反应 (53)8.2.3零级反应 (54)8.2.4 n级反应 (54)8.3几种典型的复合反应 (56)8.3.1对峙反应(可逆反应) (56)8.3.2连串反应 (56)8.3.3平行反应 (57)8.4复合反应速率方程的求法 (58)8.4.1平衡态近似法 (58)8.4.2稳定态近似法 (59)8.5 阿累尼乌斯(Arrhenius)方程 (60)第一章气体的PVT关系1.1理想气体状态方程PV=nRT,其中P的单位是Pa,V的单位是m3,n的单位是mol,T的单位是K,摩尔气体常数R=8.315J·mol-1·K-1。
物理化学上册分章知识点归纳08

将实验可测偏微商来代替那些不易直接测定的偏微商。 将实验可测偏微商来代替那些不易直接测定的偏微商。
上一内容 下一内容 回主目录
2011-10-8
Maxwell关系式的应用2
由:
dU = TdS − pdV
即: Cv.m/ T=(∂S / ∂ T)v
物理化学课程的学习方法
( ) d ln y A d ln ( ) = ⇒ = 2 2 dx Rx dT RT d ln p ∆ v ap H 克-克方程,饱和蒸汽压与温度的关系 克方程, = dT RT 2
d ln K ∆ r H = 2 dT RT
范特霍夫等压方程, 范特霍夫等压方程,平衡常数与温度的关系
W =∫
上一内容
W = ∆U = nCV ,m (T2 − T1 )
V2
V1
K K P2V2 − PV1 1−γ 2 1 − γ dV = [V ]1 = γ −1 γ −1 V
回主目录
2011-10-8
下一内容
本章内容框架
△U = Q + W
Q
ⅰ~显热,用热容 ⅱ~相变热 ⅲ~溶解热 ⅳ~化学反应热
回主目录
2011-10-8
上一内容
下一内容
回主目录
2011-10-8
逸度与逸度因子
1.逸度及逸度因子 1.逸度及逸度因子
~ / pθ ) ϕ B = ~B / p B p µ B ( pg ) = µ B ( g ) + RT ln( pB
θ
2.路易斯 2.路易斯——兰德尔逸度规则 路易斯 兰德尔逸度规则
B t /℃ ℃ B
(3)
(4)
物理化学知识点总结[物理化学知识点归纳]
![物理化学知识点总结[物理化学知识点归纳]](https://img.taocdn.com/s3/m/ea35e0ce227916888586d7c1.png)
物理化学知识点总结[物理化学知识点归纳]热力学第一定律...............................................................................(1)第二章热力学第二定律. (3)第三章化学势 (7)第四章化学平衡 (10)第五章多相平衡 (12)第六章统计热力学基础 (14)第七章电化学 (16)第八章表面现象与分散系统 (20)第九章化学动力学基本原理 (24)第十章复合反应动力学 (27)物理化学知识点归纳根据印永嘉物理化学简明教程第四版编写,红色的公式要求重点掌握,蓝色的公式掌握。
第一章热力学第一定律本章讨论能量的转换和守恒,其目的主要解决变化过程的热量,求功的目的也是为了求热。
1. 热力学第一定律热力学第一定律的本质是能量守恒定律,对于封闭系统,其数学表达式为∆U =Q +W 微小过程变化:d U =δQ +δW只作体积功:d U =δQ −p e d V 理想气体的内能只是温度的函数。
2. 体积功的计算:δW V =−p 外d VW V =−∫p 外d VV 1V 2外压为0(向真空膨胀,向真空蒸发):W V =0;恒容过程:W V =0恒外压过程:W V =−p 外(V 2−V 1) 恒压过程:W V =−p (V 2−V 1) 可逆过程:W V =−∫V 2V 1p d V (主要计算理想气体等温可逆、绝热可逆过程的功)3. 焓和热容由于大多数化学反应是在等压下进行的,为了方便,定义一个新的函数焓:H =U +pV焓是状态函数,是广度性质,具有能量,本身没有物理意义,在等压下没有非体积功的热效应等于焓的改变量。
等容热容:C V = δQ V⎛∂U ⎛=⎛⎛ d T ⎛∂T ⎛V等压热容:C p =δQ p⎛∂H ⎛=⎛⎛ d T ⎛∂T ⎛p对于理想气体:C p −C V =nR4. 理想气体各基本过程中W 、Q 、∆U 、∆H 的计算5. 焦耳-汤姆逊系数µ=⎛⎛∂T ⎛1⎛∂H ⎛=−⎛⎛⎛,用于判断气体节流膨胀时的温度变化。
物理化学知识点总结

物理化学每章总结 第1章 热力学第一定律及应用1.系统、环境及性质热力学中把研究的对象(物质和空间)称为系统,与系统密切相关的其余物质和空间称为环境。
根据系统与环境之间是否有能量交换和物质交换系统分为三类:孤立系统、封闭系统和敞开系统。
2.热力学平衡态系统的各种宏观性质不随时间而变化,则称该系统处于热力学平衡态。
必须同时包括四个平衡:力平衡、热平衡、相平衡、化学平衡。
3.热与功 (1) 热与功的定义热的定义:由于系统与环境间温度差的存在而引起的能量传递形式。
以Q 表示,Q>0 表示环境向系统传热。
功的定义:由于系统与环境之间压力差的存在或其它机、电的存在引起的能量传递形式。
以W 表示。
W>0 表示环境对系统做功。
(2) 体积功与非体积功功有多种形式,通常涉及到是体积功,是系统体积变化时的功,其定义为:V p Wd δe -=式中pe 表示环境的压力。
对于等外压过程 )(12e V V p W --=对于可逆过程,因ep p =,p 为系统的压力,则有Vp W V V d 21⎰-=体积功以外的其它功,如电功、表面功等叫非体积功,以W ′表示。
4.热力学能热力学能以符号U 表示,是系统的状态函数。
若系统由状态1变化到状态2,则过程的热力学增量为 12U U U -=∆对于一定量的系统,热力学能是任意两个独立变量的状态函数,即),(V T f U =则其全微分为VV U T T U U TV d d d ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=对一定量的理想气体,则有 0=⎪⎭⎫⎝⎛∂∂TV U 或 U =f (T )即一定量纯态理想气体的热力学能只是温度的单值函数。
5.热力学第一定律及数学表达式 (1) 热力学第一定律的经典描述① 能量可以从一种形式转变为另一种形式,但在转化和传递过程中数量不变 ② “不供给能量而可连续不断做功的机器称为第一类永动机,第一类永动机是不可能存在的。
(2) 数学表达式对于封闭系统,热力学第一定律的数学表达式为W Q U δδd += 或 W Q U +=∆即封闭系统的热力学能的改变量等于过程中环境传给系统的热和功的总和。
物理化学知识点(全)
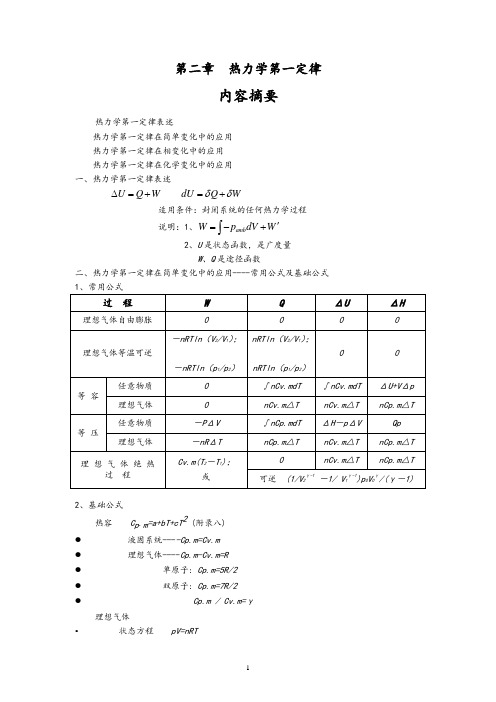
第二章热力学第一定律内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用 热力学第一定律在相变化中的应用 热力学第一定律在化学变化中的应用 一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件:封闭系统的任何热力学过程 说明:1、amb W p dV W '=-+⎰2、U 是状态函数,是广度量W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式 过 程WQΔUΔH理想气体自由膨胀理想气体等温可逆-nRTln (V 2/V 1); -nRTln (p 1/p 2) nRTln (V 2/V 1);nRTln (p 1/p 2)0 0等 容任意物质0 ∫nCv.mdT ∫nCv.mdT ΔU+V Δp 理想气体 0 nCv.m △T nCv.m △T nCp.m △T 等 压任意物质-P ΔV ∫nCp.mdT ΔH -p ΔV Qp 理想气体-nR ΔT nCp.m △TnCv.m △T nCp.m △T 理 想 气 体 绝 热过 程 Cv.m(T 2-T 1);或nCv.m △TnCp.m △T可逆 (1/V 2γ-1-1/ V 1γ-1)p 0V 0γ/(γ-1)2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程 恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T =• 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程1、 可逆相变化 Q p =n Δ相变H m W = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m - p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = -Δ蒸发H m (T)Δ凝固H m (T) = -Δ熔化H m (T) Δ凝华H m (T) = -Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT 解题要点: 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。
物理化学考研知识点

第一章 绪 论(Introduction )高分子化合物(High Molecular Compound ):所谓高分子化合物,系指那些由众多原子或原子团主要以共价键结合而成的相对分子量在一万以上的化合物。
合成高分子:一般是由许多结构相同的、简单的化学结构,通过共价键重复连接而成的相对分子质量很大的化合物。
生物高分子:一般倾向于是对化学结构组成多样、排列顺序严格的、相对分子质量很高的具有生物活性的高分子化合物。
单体(monomer ):能够形成聚合物中结构单元的小分子化合物称为单体。
聚合物(high polymer or polymer ):由相同的化学结构多次重复通过共价键或配位键连接而成的高分子化合物,称聚合物。
单体单元(monomer unit ):由苯乙烯单体反应得到的聚苯乙稀,其结构单元的原子种类、个数都与单体相同,仅电子结构发生变化,故这类聚合物的结构单元又称为单体单元。
结构单元(structure unit ):聚氯乙稀这样的聚合物,括号内的化学结构称为结构单元。
即组成高分子的、重复连接的、来源于单体的化学结构单元称“结构单元”。
重复单元(repeating unit ):聚氯乙稀分子链可以看作结构单元多次重复构成,因此括号内的化学结构也可称为重复单元或链节(chain element )。
聚合度(degree of polymerigation ):重复单元的数目n ,表征聚合物分子量大小的一个物理参数。
数均分子量:各种不同分子的分子量的总合除以分子数总合得到的平均值。
其中:分子量为Mi 的大分子,相应的分子分数为Ni 。
重均分子量:不同分子分子量与分子重量乘积的总和除以整个分子重量得到的平均值。
其中:分子量为Mi 的大分子重量为Wi =NiMi粘均分子量:用聚合物稀溶液的特性粘度测定的分子量。
一般情况下,0.5<α<0.9若 α=1 则 M η = Mw (均一聚合物,α=1 )Z 均分子量:用超速离心法测定的分子量。
物理化学重要知识点总结及其考点说明

第一章气体的pvT关系⑴波义尔定律:当n、T一定时,PV=常数⑵盖-吕萨克定律:当n、P一定时,V/T=常数⑶阿伏伽德罗定律:当T、P一定时,V/n=常数●⑷理想气体状态方程:PV=(m/M)RT= nRT或者或PVm=p(V/n)=RTR=8.314mol-1·K-1称为摩尔气体常数;T为华氏温度⑸摩尔分数:X B=n B/n总●⑹道尔顿定律:P B=P总X B;P总=P分⑺实际气体状态方程:PV=znRT(z为压缩因子)●⑻理想气体特征:①分子间无相互作用力②分子本身不占有体积第二章热力学第一定律热力学第一定律(能量守恒定律)●⑴系统:①隔离系统:无能量、无物质交换②★封闭系统:有能量、无物质交换(热力学基础;热力学研究对象)③敞开系统:有能量、有物质交换●⑵状态函数:P、V、T、U、H、G、A、S (P、T、C p, m、C V,m 为强度量,其他均为广度量) 状态函数特征:①有可微分性,能计算②只与始末状态有关●途径函数:Q、W●⑶热:系统从环境中吸热(Q>0);系统对环境做功(W<0)●⑷热力学能:△U=Q+W(封闭系统);U只是温度T的函数;只与首末有关非体积功的计算①气体向真空膨胀时体积功所的计算W=0②恒外压过程体积功W=-p(V2-V1)=-p△V③对于理想气体恒压变温过程W=-p△V=-nR△T④可逆过程体积功W=-p(v2-v1)●⑤理想气体恒温可逆过程体积功 W=-p(v2-v1)或者W=-nRTln(V1/V2)或者W=nRTln(p2/ p1)⑥理想气体绝热可逆过程体积功W=-p(v2-v1)=(-)γ= C p, m /C V,m(双原子气体为1.4)T2/T1=(V1/V2) 的γ-1次方;T2/T1=(P1/P2)的(γ-1)/γ次方;P2/P1=(V1/V2)的γ次方●⑦恒温膨胀可逆功最大,系统对环境作最大功;恒温可逆压缩,环境对系统做最小功⑧可逆相变体积功W=-pdV恒热容、恒压热,焓⑴焓定义:H=U + PV⑵焓变:△H=△U+△(pV)式中△(pV)为p V乘积的增量,只有在恒压下△(pV)=p(V2-V1)在数值上等于体积功。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体的pVT关系
一、理想气体状态方程
pV=nRT (R=8.314472Pa·m3·mol·K-1)
根据V m=V/n,n=n/M可得
pV m=RT
pV m=(m/M)RT
根据ρ=m/V和理想气态方程可以求出气体的ρ、V、T、n、M、ρ各种性质。
ρ=pM/RT、M=ρRT/p=RTM/Pv、m=Pvm/RT、n=Pv/RT
二、理想气体模型
(一)、分子间作用力:两个分子间的相互吸引势能与距离r的6次方成反比,相互排
除势能与距离r的12次方成反比。
E=E吸引+E排斥=-A/r6+B/r12
(二)、理想气体的微观上的两个特征
1、分子间无相互作用力。
2、分子本身不占体积。
(三)、在任何温度和压力下均符合理想气体模型或服从
理想气体状态方程的气体称为理想气体
图一:兰纳德-琼斯势能曲线示意图
(四)、摩尔气体常数
当压力趋于零的极限条件下,各种气体pVT均服从pV m=RT的定量关系,R是一个对各种气体都适用的常数。
R=8.314472Pa·m3·mol·K-1
三、真实气体状态方程
(一)、范德华方程
(p+a/V2m)(V m-b)=RT
将V m=V/n带入可得(p+n2a/V2)(V-nb)=nRT
a只与气体的种类有关,与温度条件无关。
(a/V m2)又称为内压力说明了分子间相互吸引力对压力的影响反比于分子间距离r的6次方。
一般分子间作用力越大,a越大。
a的单位是Pa·m6·mol-2
b应该与气体的温度有关。
b是体积修正项,表示每摩尔真实气体分子本身占有体积儿时分子自由活动空间减少的数值。
b的单位是m3·mol-1。
范德华认为真实气体由于分子间的相互作用力会导致气体的压强比理想气体小即p=(p理+a/V2m),体积在考虑了分子本身占有的体积b之后自由活动空间应该是(V m-b)。
范德华方程是一种被简化了的真实气体的数学模型,在任何温度、压力条件下均符合范德华方程的气体叫范德华气体
(二)、维里方程
pV m=RT(1+Bp2+Cp3+Dp4+……)
维里方程是纯经验方程,当压力p→0,摩尔体积V m→0时,维里方程还原为理想气态方程。
在计算精度不高时,只用到维里方程的第二项。
四、临界参数
每种液体都存在一个特殊的温度,在该温度以上,无论加多大压力,都不能使气体液化。
这个温度称为临界温度。
临界温度T c时的饱和蒸汽压称为临界压力,用p c表示。
临界压力是临界温度下使气体液化所需要的最低压力。
在临界温度和临界压力下,物质的摩尔体积称为临界摩尔体积,用V m,c表示。
物质处于临界温度、临界压力下的状态称为临界状态。
此时气、液两相的摩尔体积及其他性质完全相同,相界面消失。
五、对应状态原理及普遍化压缩因子
(一)、压缩因子
Z=pV/nRT=pV m/RT。
