模电第五章放大电路的频率响应
《模拟电子技术》课件第5章放大电路的频率响应
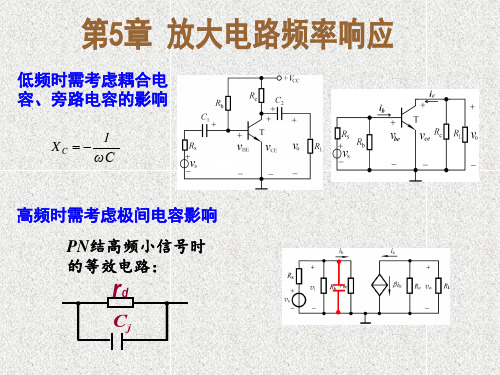
中频增益或通 带源电压增益
f
H
1 2πRC
上限频率
②高频响应和上限频率
共射放大电路
A VSH A VSM 1
1 j( f
/
fH )
RC低通电路
A VH
1
1 j( f
/
fH )
频率响应曲线变化趋势相同
幅频响应
20l g|A VSH | 20l g|A VSM |
20lg
1
1 ( f / fH )2
最大误差 -3dB
1 fH 2 πRC
fH称转折频率,上限截止 频率(上限频率),AVH(s) 的极点频率。
10
2. 低频特性
---- RC高通电路
RC高通电路
RC电路的电压增益:
AVH
Vo Vi
R
R
1
j ωC
1
1 1
j 2 πfR C
令
fL
1 2 πR
C
AVH
Vo Vi
1
1 j(fL /
f)
gmV b'e rce—c-e间的动态电阻(约100kΩ)
Cbe --发射结电容
互导
gm
iC vBE
VCE
iC vBE
VCE
2.混合等效电路中各元件的讨论: 简化模型 rce RL 略去rce
rbc
1 jω Cbc
略 去rbc
混合型高频小信号模型
晶体管的混合Π型等效电路
3.混合型等效电路的获得 低频时,混合模型与H参数模型等价
β0
1 ( f / fβ )2
的相频响应 arctg f
fβ fβ ——共发射极截止频率
模电第5章

低通电路: 二. 低通电路:频率响应
f<<fH时放大 倍数约为1 倍数约为
fH
1 Uo 1 jω C = Au = = 1 1 + jωRC Ui R+ jω C
1 1 = 令f H = ,则Au 2 πRC 1+ j f fH
1 Au = 1 + ( f fH )2 = arctan( f f ) H
fL
= 1 , = 45 0; f = f L : Au 2 f f
f << f L : A << 1, u ≈
fL fL Au 也下降10倍;当 f 趋于0时, u 趋于0,趋于90 0 。 A
,表明 f 每下降10倍,
画出特性曲线如图, 称为下限截止频率。 画出特性曲线如图, fL称为下限截止频率。
' 高频段: 的影响, 开路。 高频段:考虑 Cπ 的影响,C 开路。 '
'
一. 中频电压放大倍数
Uo Ausm = Us U i U b'e U o = U U Us i b'e
带负载时: 带负载时: Ausm = 空载时: 空载时:
rb'e Ri [ g m ( Rc ∥ RL )] Rs + Ri rbe
5.2 晶体管的高频等效电路
5.2.1 混合π模型:形状像Π,参数量纲各不相同 混合π模型:形状像Π
完整的混合π模型 一. 完整的混合 模型 结构:由体电阻、结电阻、结电容组成。 结构:由体电阻、结电阻、结电容组成。
因面积大 而阻值小
因多子浓 度高而阻 值小
rbb’:基区体电阻 rb’e’:发射结电阻 Cπ:发射结电容 re:发射区体电阻 rb’c’:集电结电阻 C:集电结电容 rc:集电区体电阻
模拟电路第五章 放大电路的频率响应

5.2.1 晶体管的混合π模型
结构:由体电阻、结电阻、结电容组成。
阻值小, 可忽略
阻值小, 可忽略
整理ppt
rbb’:基区体电阻 rb’e’:发射结电阻 Cπ:发射结电容 re:发射区体电阻 rb’c’:集电结电阻 Cμ:集电结电容 rc:集电区体电阻
④ Cπ的求法。
整理ppt
5.3 场效应管的高频等效电路
可与晶体管高频等效电流类比,简化、单向化变换。
单向化变换
忽略d-s间等效电容
很大,可忽略其电流
C g ' sC g s (1gm RL ' )C gd
极间电容 数值/pF
Cgs
Cgd
1~10 1~10 整理ppt
Cds 0.1~1
5.4 单管放大电路的频率响应 5.4.1 单管共射放大电路的频率响应
放大电路对信号频率适应程度,即信号频率对放大倍数的影响。 在使用一个放大电路时应了解其信号频率的适用范围,在设计放 大电路时,应满足信号频率的范围要求。
整理ppt
5.1.2 频率响应基本概念
一、RC高通电路频率响应
Au U Uoi 1RR1jjRRCC jC
令fL
1 2πRC
则Au
jf 1j
f
第五章 放大电路的频率响应
5.1 频率响应概述 5.2 晶体管的高频等效模型 5.3 场效应管的高频等效模型 5.4 单管放大电路的频率响应 5.5 多级放大电路的频率响应
5.1 频率响应概述
5.1.1 必要性
由于放大电路中耦合电容、旁路电容、半导体器件极间电容的存 在,当输入信号频率过低或过高时,放大倍数变小,并且产生超 前或滞后相移,即,放大倍数是频率的函数。
模拟电子技术_ ( 放大电路的频率响应)_

频率响应的基本概念1.绪论2.晶体二极管及应用电路3.晶体三极管及基本放大电路4.场效应管及基本放大电路5.放大电路的频率响应(4学时)6.负反馈放大电路7.双极型模拟集成电路8.双般型模拟集成电路的分析与应用 9.MOS 模拟集成电路(自学) 10.直流稳压电源电路课程主要内容1/68主讲:刘颖第五章放大电路的频率响应问题:1.什么是电路的频率响应?2.工程上如何绘制频率响应曲线?3. 三极管的高频模型与低频模型(h参数模型)有何不同?4.耦合电容、旁路电容、三极管结电容对电路频率特性有怎样的影响?第五章放大电路的频率响应5.1 频率响应的基本概念5.2 晶体三极管的高频模型5.3 频率响应的分析方法5.4 单管共射放大电路的频率响应5.5 共集、共基放大电路的频率响应5.6 多级放大电路的频响5.1 频率响应的基本概念CE 组态基本放大电路5.1.1. 放大电路频率响应概念 概念:放大电路增益随着频率变化而变化的特性称为频率响应特性,可表示为 其中:()()()j U U A j A j f f feϕ=()()U A j f f ϕ称为增益的幅频特性 称为增益的相频特性4/685/68 -180° -90° -270°A U|A U (j f )|fφ(f )f中频段:A U =常数 低频段高频段A U 下降中频段:相位差 φ =常数 低频段高频段φ 改变增益幅度|A U (j f )∣与频率f 的关系称为幅频特性。
增益相位φ(j f )与频率f 的关系称为称为相频特性。
幅频特性曲线相频特性曲线说明:放大电路的频率响应特性是增益幅频特性和相频特性统称。
幅度频率失真:幅频特性偏离中频值的现象相位频率失真:相频特性偏离中频值的现象♦ 中频增益: 中间频率段的增益♦ 频率失真f L f h 0.707A UA UA (j f )f幅频特性曲线-180° -90° -270°φ(f )f相频特性曲线5.1.2. 放大电路的带宽放大电路的带宽:也称通频带、有效带宽,带宽BW=f h -f L上限截止频f h 、下限截止频f L 定义:增益下降到中频增益的0.707倍(即3dB 处)所对应的频率。
第5章 放大电路的频率响应1PPT课件

Au 2,45
2
Au f ,90
f L
下限截止频率
5-1-6
三、低通电路
1
AuUo Ui
jC
R 1
1
1 jRC
jC
τ RC
H
1 RC
fH
1
2RC
—上限截止频率
Au
1
1 jH
1 1 j f fH
5-1-7
A u
1
1 j f
f
H
A u
1 1 ( f )2
fH
arctanf
fL
5-1-8
>>>>>幅频特性 >>>>>相频特性
fL
1 j f
fL
5-1-4
jf
Au
1
1 L
1
1
f L
f
L
1 j f
j
jf
f
L
A u
f f
L
1 ( f )2 f
L
>>>>>幅频特性
90 arctan f
fL
>>>>>相频特性
5-1-5
A u
f fL
f f
L
1 ( f )2 f
L
Au 1,0
90 arctan f
f L
频率特性:
f fL f fL
通常rb’c 、 rce开路, 折合
到电路中以后忽略,得到简化的 等效模型。
二、晶体管简化等效模型:
混合 模型的主要参数:
rbb 可以从手册中查出。
rb'e
模拟电子技术基础课课件-5放大电路的频率响应

在低频段,随着信号频率逐渐降低,耦合电容、旁路 电容等的容抗增大,使动态信号损失,放大能力下降。
在高频段,随着信号频率逐渐升高,晶体管极间电容和 分布电容、寄生电容等杂散电容的容抗减小,使动态信号 损失,放大能力下降。
§5.2 晶体管的高频等效电路
一、混合π模型
一、混合π模型
1. 模型的建立:由结构而建立,形状像Π,参数量纲各不相同。
90o arctan
f
fL
使输出电压幅值下降到 70.7%,相位为±45º的信 号频率为截止频率。
二、高通电路和低通电路
2. 低通电路:信号频率越低,输出电压越接近输入电压。
. I
Uo滞后Ui,当 f 时;
. Ui
Uo 0,Uo滞后Ui 90。
.
Uo
1
A
UO
Ui
jC 1
R
1
1 j RC
相频特性,用三段直线取代曲线;以10fL和0.1fL为两个拐点。
20 lg
Au
20lg
f fL
20lg
1
f fL
2
2、低通
Au
1
2
1
f fH
arctan
f fH
2
20lg Au 20lg
1
f fH
四、放大电路中的频率参数
结电容
高通 电路
低通 电路
下限频率
fbw fH fL 上限频率
1、高通
2
f
f
20 lg Au
20lg 20lg fL
1
fL
在电路的近似分析中,为简单起见,常将波特图的曲线折线 化,称为近似的波特图。
近似的波特图:对于高通电路,在对数幅频特性中,以截止频率fL为拐点,有两段直线近
模拟电子技术基础--第5章--放大电路的频率响应

等效变换后电流不变
X C 'µ
ɺ X Cµ U b'e = ≈ ' ɺ I Cµ 1 + g m RL
' ' Cµ ≈ (1 + g m RL )Cµ
k −1 ⋅ Cµ 同理可得,C ≈ k
'' µ
晶体管简化的高频等效电路
' 为什么不考虑 Cµ'?
如何得到模型中的参数?
' ' C π = C π + Cµ
≈
I EQ UT
=?
低中频时 C
b ′c
和 C
b ′e
视为开路
rbe = rbb′ + rb′e
又因为
所以
gm =
ɺ V b ′e = ɺ g mVb′e β
rb′e
ɺ I b rb ′e ɺ = βI b
IE = VT
UT rbe = rb + (1 + β ) re = rb + (1 + β ) IE
3. 晶体管的频率参数
共基截 止频率 共射截 止频率
ɺ β=
特征 频率
集电结电容
β0
1+ j
f fβ
ɺ f β 、fα、f T、Cob (C µ )。 使 β = 1时的频率为f T f T ≈ fα ≈ β 0 f β 1 fβ = 2 π rb'e ( C π + Cµ )
手册 查得 通过以上分析得出的结论: 通过以上分析得出的结论: 低频段和高频段放大倍数的表达式; ① 低频段和高频段放大倍数的表达式; 截止频率与时间常数的关系; ② 截止频率与时间常数的关系; 波特图及其折线画法; ③ 波特图及其折线画法; 的求法。 ④ Cπ的求法。
第5章 放大电路的频率响应(091110修简版)

令
则
对数幅频特性和相频特性表达式为: 对数幅频特性和相频特性表达式为 20lg| |=20lg| |–20lg
四、波特图
综上所述, 综上所述,电路全频段的电压放大倍 数表达式为: 数表达式为:
当fL《f《fH时,fL/f和f/fH均趋于零, 均趋于零, 《 故 接近f ;当f 接近 L时,f《fH ,故 《 接近f 接近 H时,f 》fL,故 若电路在低频段有f 若电路在低频段有 L1~fLN个
所在回路是低 通回路, 通回路,在阶跃信 号作用时, 号作用时, 上的 电压 将按指数 规律上升,其起始值 规律上升 其起始值 为0,终了值为 , , 回路时间常数为RCπ' , 因而: 因而:
图5.7.3 图5.4.1 所示电路输入回路的阶跃响应
上升到0.1UI ,可以求出 上升到 所需的时间为0.1 而上升到0.9UI所需的时间为 所需的时间为 RCπ' ,而上升到 而上升到 2.3 RCπ' 。所以 。
则
将
用其幅值与相角表, 用其幅值与相角表,得:
二、低通电路
将
用幅值及相角表示, 用幅值及相角表示,得:
图5.1.2低通电路及其频率响应 低通电路及其频率响应
5.1.3 波特图
在对数坐标中反映频率特性曲线 对数坐标中反映频率特性曲线
高通: 高通:
低通: 低通:
波特图小结: 波特图小结
1、电路的截止频 、 率决定于电容 所在回路的时 间常数τ。 间常数 。 2、当信号频率等 、 于 fL 或 fH 时 ,
第五章 放大电路的频率特性
5.1 频率响应概述
5.1.1 研究放大电路频率响应的必要性
放大电路的放大倍数是信号频率的函数, 放大电路的放大倍数是信号频率的函数,我们称 之为频率响应 频率特性; 频率响应或 之为频率响应或频率特性; 在设计电路时,必须先了解信号的频率范围, 在设计电路时,必须先了解信号的频率范围,以 便使所设计的电路具有适应于该信号频率范围的 通频带; 通频带; 在使用电路前,应查阅手册、资料、 在使用电路前,应查阅手册、资料、或实测其通 频带,以便确定电路是否适用。 频带,以便确定电路是否适用。
模拟电路第05章 放大电路的频率响应图

图5.1.1 高通电路及频率响应
返回
图5.1.2 低频电路及其频率响应
返回
图5.1.3 高通电路与低通电路的波特图
返回
5.2 晶体管的高频等效模型
• 图5.2.1 晶体管结构示意图及混合π模型 • 图5.2.2 混合π模型的简化 • 图5.2.3 的分析 • 图5.2.4 的波特图
返回
C1
RS +
VS -
VCC
大 RB
RC
C2 + RL VO -
b rbb b’cBiblioteka RS+ VS
-
e
rbe gmvbe
RL Vo
e
中频增益:
Am
VO VS
Vbe VS
VO Vbe
rbe
gm Vbe RL
RS rbb rbe
Vbe
RS
rbe rbb
rbe
gm RL
O RL rbe O RL
5、查手册得:rbb、cbc、fT (已知条件);
6、
e
结电容:cbe
gm
2 fT
cbc
Miller 定理
I1
Z
Z in + V1 ~ -
Ii I +
ri AV1 -
I2
单向化
Z in
+
+ I1
V2 -
V1 ~ -
Z1
Ii II +
ri AV1 -
I2
+ Z2 V2
-
加 V1 产生 V2 :
Z1 IIV 1 I
返回
图5.6.1 未加频率补偿的集成运放的频率响应
模电基础第5章 频率响应

第5章 频率响应
5–1 频率响应的概念 5–2 单级共射放大器的高频响应 5–3 共集电路的高频响应 5–4 共基电路的高频响应 5–5 差分放大器的频率响应 5–6 场效应管放大器的高频响应 5–7 放大器的低频响应 5–8 多级放大器的频率响应 5–9 建立时间tr与上限频率fH的关系 5–10 举例及计算机仿真
b rbb′
b′
Cb′e
Rs
Cb′e
rb′e
.
Us
. gmUb′e
第5章 频率响应
R′L c +
rce
RC
RL
. Uo
-
e
(b)
图5–6 (a)电路;(b)等效电路(设RB1‖RB2>>Rs)
AuI
0.707 AuI
(5–4)
BW fH fL fH
(5–5)
GH 20lg Au ( jfH ) 20lg AuI 3dB
(5–6)
GL 20lg Au ( jfL ) 20lg AuI 3dB
G BW AuI BW AuI fH
(5–7)
第5章 频率响应
5–2单级共射放大器的高频响应
第5章 频率响应
三、不失真条件––理想频率响应 综上所述,若放大器对所有不同频率分量信号的 放大倍数相同,延迟时间也相同,那么就不可能产生 频率失真,故不产生频率失真的条件为
Au ( j ) Au ( j ) /_ ( j ) _ Au ( j ) K (常数) ( j ) td (td也为常数)
第5章 频率响应
|Au(jω)| 0.7 07A| uI|
|AuI|
L 半功率点
半功率点 H
理想幅频特性 实际幅频特性
模电 第五章 放大电路的频率响应

图5.3.1场效应管的高频等效模型(a)
一般情况下 rgs和 rds比外接电阻大得多,可认为是开路
Cgd可进行等效变化,使电路单向化
第五章
Cgd等效变化
g-s之间的等效电容为
C gs (1 K )C gd ) C gs ( K g m RL
0 3dB 20
高通特性:
20dB/十倍频
40
图 5.1.3(a)
幅频特性
1 A u 1 当 f < fL (低频), A u
当 f ≥ fL(高频),
的值愈小, 且频率愈低,A u
最大误差为 3 dB, 发生在 f = fL处
低频信号不能通过。
第五章
对数相频特性
f 相角: 90 arctan( ) fL
f
O
f 0.1f
fT
对数相频特性
f arctan f
0 45º 90º
10 f
f
的波特图 图 5.2.4
第五章
几个频率的分析 1.共射截止频率 f
1 0 )时的频率。 值下降到 0.707 0 (即 2
当 f = f 时,
1 0 0.707 0 2
0
f 1 T f
2
1;
得:
fT 0 f
第五章
3.共基截止频率 f
值下降为低频 0 时 的 0.707 时的频率。
0
f 1 j f
第五章
f 与 f 、 fT 之间关系:
因为
1
,
第五章 放大电路的频率响应

电子与通信工程系
电子学教研室
Electronics Staff Room of Dept. Electronic and Communication
第五章——放大电路的频率响应
二. 频率响应的基本概念
主讲人:何玉钧
放大电路的频率响应:指的是在输入正弦信号情况下, 放大电路的频率响应:指的是在输入正弦信号情况下,输出随频率连 续变化的稳态响应。 续变化的稳态响应。
2
当 << fH时 20lg Au ≈ 0dB, ≈ 0 f , ; 当 = fH时 20lg Au ≈ 3dB, ≈ 45o; , f ≈ 20lg f , 当 >> fH时 20lg Au f , fH 表 f每 升 倍 增 下 20dB; 明 上 10 , 益 降
电子与通信工程系
电子学教研室
电子与通信工程系 电子学教研室
Electronics Staff Room of Dept. Electronic and Communication
第五章——放大电路的频率响应
3. 波特图
主讲人:何玉钧
在研究放大电路的频率响应时,输入信号( 在研究放大电路的频率响应时 输入信号(即加在放大电路输入端的 输入信号 测试信号)的频率范围常常设置在几赫到上百兆赫,甚至更宽; 测试信号)的频率范围常常设置在几赫到上百兆赫,甚至更宽;而放大 电路的放大倍数可从几倍到上百万倍; 电路的放大倍数可从几倍到上百万倍;为了在同一坐标系中表示如此宽 的变化范围,在画频率特性曲线时常采用对数坐标,称为波特图 波特图。 的变化范围,在画频率特性曲线时常采用对数坐标,称为波特图。 波特图由对数幅频特性和对数相频特性两部分组成。它们的横轴采 波特图由对数幅频特性和对数相频特性两部分组成。 表示,单位为分贝; 幅频特性的纵轴采用20lg A 表示,单位为分贝;相频 用对数刻度 lgf ,幅频特性的纵轴采用 u 表示。 特性的纵轴仍用 表示。
第5章 放大电路的频率响应

ϕ = arctg( y / x)
Z1 ⋅ Z2 = Z1 ⋅ Z2 ⋅ e
Z1 i(ϕ1−ϕ2 ) Z1 = ⋅e Z2 Z2
arctan ∞ = 90
i(ϕ1 +ϕ2 )
4
5.1.2. 频率响应的基本概念
(1)高通电路:信号频率越高,输出电压越接近输入电压。 高通电路:信号频率越高,输出电压越接近输入电压。 . ɺ ɺ U o 超前 U i . I
2
2
fT =0 令 20 lg β 0 − 20 lg 1 + f β
求得 f T ≈ β 0 f β
β α= 1+ β
fα = (1 + β0 ) fβ ≈ fT
特征频率
共基放大电路截止频率高,频带宽。 共基放大电路截止频率高,频带宽。
17
5.4.1 单管共射放大电路的频率响应
2
放大倍数随频率变化曲线——幅频特性曲线 幅频特性曲线 放大倍数随频率变化曲线
Au Aum 0.707Aum
低 频 段
通频带: 通频带: fbw=fH – fL
频 通频带 频 频率 频率
3
fL
通频带 放大
频率
fH
f
Z = x + iy
Z = x +y
2 2
arctan 0 = 0
o o o
arctan1 = 45
µ
'' Cµ可以忽略。 可以忽略。
简化的混合π 简化的混合π模型
14
三、混合π模型的主要参数 混合π
Cµ
'
ɺ ɺ = (1 − K )C µ ≈ (1 + K )C µ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+ ui -
C1
O
f / Hz
(a)
图5-1 放大电路全电容等效电路与放大特性曲线 (a) 电路图; (b) 特性曲线
表5.1 高、低频信号对各种电容的影响(场效管对应类似)
二、 线性失真的分类 线性失真有两种形式:频率失真和相位失真。
下面从频域说明线性失真产生的原因。一个周期信号经傅
里叶级数展开后,可以分解为基波、一次谐波、二次谐波等多 次谐波。假设输入波形 Ui(t) 仅由基波、二次谐波、三次谐波构 成, 它们之间的振幅比例为 10∶6∶3,如图4-2(a)所示。该 输入波形经过线性放大电路后,由于放大电路对不同频率信号 的不同放大倍数,使得这些信号之间的比例发生了变化, 变成 了10∶3∶1.5,这三者累加后所得的输出信号 Uo(t)如图4-2(b) 所 示。 对比Ui(t), 可见两者波形发生了很大的变化,这就是线性失
为了能在同一坐标系中表示如此宽的频率范围,由 H.W.Bode 首先提出了基于对数坐标的频率特性曲线的作图法, 称之为
波特图法。
波特图由对数幅频特性与对数相频特性两部分组成, 其 横坐标采用对数刻度lgf, 幅频特性的纵坐标采用20lg|Au|,单位 为分贝(dB);相频特性的纵坐标采用 φ, 单位为角度。这样 一方面扩展了表示的范围,另一方面也将增益表达式由乘除运 算变成了加减运算。
真的第一种形式,即频率失真。
Ui (t )
放大器
Uo (t)
Ui (t ) 0
Uo (t) 0
t
t
基波 10 0 t 10 0
基波
t
二次谐波 6 0 t 3 0
二次谐波 t
三次谐波 3 0 t 1 .5 0
三次谐波 t
图 5-2 幅度失真示意图 (a) 输入电压;(b) 输出电压
(a)
(b)
线性失真的第二种形式如图5-3所示。设输入信号Ui(t)由基 波和二次谐波组成,如图(a)所示, 经过线性电路后, 基波与 二次谐波振幅之间的比例没有变化, 但是它们之间的时间对应 关系变了,叠加合成后同样引起输出波形不同于输入波形, 这 种线性失真称之为相位失真。
1 Uo 1 j C Au Ui R 1 1 jRC j C
回路的时间常数为τ=RC, 令ωH=1/τ, 则
图5.1.2 低频电路及其频率响应
H 1 1 fH 2 2 2RC
代入上式可得
Au
1 j H
1
1 f 1 j fH
1 1 ( f / fH )
Ui (t) 基波
Uo (t) 基波 二次谐波
O 二次谐波 (a)
t
O
t
图5-3 相位失真示意图 (a) 输入电压; (b) 输出电压
(b)
5.1.3 一、 低通电路
频率响应问题的分析方法
为了便于理解有关频率响应的基本要领, 首先不妨以无源 单级 RC 低通滤波电路为例进行分析。如下图所示 RC 低通滤波 电路,增益为 :
rb 'e rb 'e Ri ' U s .U i . .U s rbe rbe Rs Ri
高频等效电路
R rb 'e //(rbb ' Rs // Rb ) U U ' U U o o b 'e s A ush U U ' U U
利用波特图法分析低通电路的对数频率特性为 :
f 20 lg | Au | 20 lg 1 f H
2
f arct an fH
由上面分析可得:当f<<fH时,20 lg|Au|≈0 dB, φ≈0°;
当f=fH时, 20lg | Au | 20lg 2 3dB , φ≈-45°;
高通电路
低通电路
5.2 晶体管的高频等效模型
5.2.1 晶体管的混合π模型
集电结 电容 发射结 电容
一、完整的混合π模型
晶体管结构示意图
混合π模型
图5.2.1 晶体管结构示意图及混合π模型
b +
rbb
+
b
c +
U i
-
U be
-
rbe
g mU be
rce U o
-
e
晶体管中频小信号模型
当 f>>fH 时, 20 lg|Au|≈-20lg(f/fH), 表明 f 每上升十倍,增益下降
20 dB, 即对数幅频特性在此区间可等效为斜率为(-20dB/十
倍频)的直线。在电路的近似分析中,为简化分析起见,常
常将波特图中的曲线近似折线化,称近似波特图。
图5.1.3 高通电路与低通电路的波特图
' R R //( r r ) R // r , R 输入电阻: i b bb ' b 'e b be L Rc // RL
中频电压放大倍数为 :
A usm
U U U rb 'e Ri ' o o b 'e U i ( g m RL ) U U U U rbe Rs Ri s b 'e i s
二、 低频电压放大倍数:极间电容视为开路,考虑旁路电容影响
低频等效电路 图5.4.3 单管共射放大电路的低频等效电路
输出回路的 等效电路
' U U U Ri rb 'e RL 低频电压放 o o o A ' ( g m Rc ) 大倍数为 : usl U 1 Uo U s R Rs Ri rbe s R c L jC2
因此,实际应用中,放大电路的增益是信号频率的函数, 这种频率函数关系称之为频率响应,有时也可称之为频率特性。 研究放大电路增益的幅度与频率的特性关系,称为放大器的幅 频特性;放大电路增益的相位与频率的特性关系,称为放大器
的相频特性。
5.1.2 频率响应线性失真问题
一、 什么是频率响应线性失真
在放大电路中,由于耦合电容的存在,对信号构成了高通电 路, 即对频率足够高的信号而言, 电容相当于短路,信号几乎 可以无损失地通过; 而当信号频率低到一定程度时,电容带来 的容抗影响不可忽略,信号将在其上产生压降, 从而改变增益 大小及相移。与耦合电容相反的是,由于半导体三极管极间电容 的存在, 对信号构成了低通电路,对低频信号相当于开路,对 电路不产生影响,而对高频信号则进行分流, 导致增益改变及 相移变化。增益改变及相移变化均会带来失真问题,而这种失真 的产生主要是来自于同一电路对不同频率信号的不同放大倍数和 不同相移的影响, 并没有产生新的频率分量,故属于线性失真。
同样,对于跨接于g、d之间的电容Cgd,也可用miller定理 作等效变换,将其折合到输入回路和输出回路,即电路的单向 化变换。这样g、s间的等效电容和d、s间的等效电容分别为
|)C C C gs (1 | K gd
' gs
K 1 ' Cds Cds C gd K ' K g m RL
Ri rb 'e j ( Rc RL )C 1 ' ( g m RL ) Ausm fL Rs Ri rbe 1 j ( Rc RL )C 1 jf 1
下限频率:
fL
2 ( Rc RL )C
三、 高频电压放大倍数:旁路电容视为短路,考虑极间电容影响
fT 0 f
特征频率
f ( 1 0)f fT
的共基截止频率: 同理可求
其截止频率远高于共射放 大电路的截止频率,因此 共基放大电路可做为宽频 放大电路。
的波特图 图5.2.4
5.3场效应管的高频等效模型
图5.3.1 场效应管高频等效模型 (a) 高频等效模型;(b) 简化模型
上限频率:
Ri rb 'e ' ( g m RL ) Rs Ri rbe
1 fH ' 2RC R ( Rs // Rb rbb ' ) // rb 'e
表5.1结合图4 - 1(a)放大电路考虑耦合电容C1、C2, 旁路电容Ce与晶体管极间 电容Cbe , Cbc的等效电路, 对放大电路的高频与低频特性作了一个定性对比 分析,可有效帮助读者理解高、低频信号对各种电容的影响。
+UCC Rb Cb c Rc V1 Cb e Re Ce C2 RL + uo - (b) Au
由于C ds′容值较小,容抗1/ωC较大,一般视为开路而忽略, 因 此场效应管的高频简化模型如图5.3.1 (b)所示。
5.4 单管放大电路的频率响应
5.4.1 单管共射放大器的频率响应(中频段、低频段、高频段)
图5.4.1 单管共射放大电路及其等效电路
一、 中频电压放大倍数:极间电容视为开路,耦合(旁路)电容 视为短路。 中频等效电路为:
0
' |)C C C (1 K
g m 0 / rb 'e I EQ / U T g U ,K 0 I c m b 'e
1 j
f f
2
f 20 lg | | 20 lg 0 20 lg 1 f f 的共射截止频率 arct an , f 为 f
之差,称为通频带 fBW 。
图5.1.1 高通电路及其频率响应 (a) 高通电路; (b) 频率响应 即 fBW=fH-fL
三、 波特图
在研究放大电路的频率响应时,输入信号常设置在几十到 几百兆赫兹的频率范围内,甚至更宽,如目前CMOS工艺放大
电路已经设计到了几十吉赫兹,而放大电路的增益范围也很宽。
