单元三 组合体习题答案
【苏教版】四年级上册数学第三单元考点集训卷_含答案

第三单元考点集训考点一:从不同方向观察同一物体
一、他们分别看到的是什么形状?请连一连。
考点二:观察由几个正方体摆成的组合体
二、看一看,按要求填序号。
1.从上面看是的有( )。
2.从前面看是的有( )。
3.从上面看是的有( )。
4.从右面看是的有( )。
考点三:观察由几个正方体摆成的立体图形
三、摆一摆,连一连。
四、下面的立体图形从前面、右面和上面看到的形状分别是什么?画一画。
五、从三个不同的方向看到的立体图形的形状如下。
这个立体图形是由( )个正方体组成的,请你摆出这个立体图形。
第三单元考点集训一、
二、1.①⑦ 2.②④⑥ 3.③⑧⑨
4.⑤⑦⑧⑨
三、略
四、
五、5。
2020国开大学机械制图单元测试答案(模块三)

模块三:单元测试答案一、根据下图所示组合体,回答如下问题。
题目1正确获得25.00分中的25.00分标记题目题干该组合体可分解为()较简单的几何形体。
选择一项或多项:A. 肋板B. 前面带孔的空心圆柱,且空心圆柱上面不通C. 竖立圆管D. 凸台E. 四孔底板反馈太棒了,您答对了!The correct answers are: 四孔底板, 竖立圆管, 肋板题目2标记题目题干该组合体的组成体间的组成形式有()。
选择一项或多项:A. 相切叠加B. 相交叠加式C. 堆砌叠加式D. 截切式E. 支承板相交反馈太棒了,您答对了!The correct answers are: 堆砌叠加式, 相交叠加式, 截切式标记题目信息文本二、根据下图所示组合体,回答如下问题。
题目3正确获得25.00分中的25.00分标记题目题干该组合体可分解为()较简单的几何形体。
选择一项或多项:A. 凸台B. 肋板C. 卧式半圆管D. 左右双孔底板E. 半拱形带孔立板反馈太棒了,您答对了!The correct answers are: 左右双孔底板, 卧式半圆管, 半拱形带孔立板题目4正确获得25.00分中的25.00分标记题目题干该组合体的组成形式错误说法有()。
选择一项或多项:A. 堆砌叠加式B. 相交叠加式C. 支承板相交D. 相切叠加E. 截切式反馈太棒了,您答对了!The correct answers are: 相切叠加, 支承板相交。
第五章组合体习题集答案PPT课件
讲师:XXXXXX XX年XX月XX日
P20-7
P20-8
P21-1
P21-2
P21-3
P21-4
由物体的主俯视图补画左视图 P22-1
由物体的主俯视图补画左视图 P22-2
由物体的主俯视图补画左视图 P22-3
由物体的主俯视图补画左视图 P22-4
由物体的主俯视图补画左视图 P22-5
由物体的主俯视图补画左视图 P22-6
三视图的形成及投影特性 补画组合体视图中所缺的图线 P19-1
三视图的形成及投影特性 补画组合体视图中所缺的图线 P19-2
三视图的形成及投影特性 补画组合体视图中所缺的图线 P19-3
三视图的形成及投影特性 补画组合体视图中所缺的图线 P19-4
三视图的形成及投影特性 补画组合体视图中所缺的图线 P19-5
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
结束语
感谢聆听
不足之处请大家批评指导
补画视图中所缺线 P23-5
补画视图中所缺线 P23-6
补画视图中所缺线 P23-7
补画视图中所缺线 P23-8
补画视图中所缺线 P23-9
读懂两视图后,补画第三视图 P25-1
读懂两视图后,补画第三视图 P25-2
读懂两视图后,补画第三视图 P25-3
读懂两视图后,补画第三视图 P25-4
立体几何中的组合体问题专题(有答案)

立体几何中的组合体问题专题(有答案)例1.正方体与球问题:正方体的棱长为1.求球的半径:⑴若正方体的八个顶点都在球面上,⑵若球内切于正方体;⑶12条棱组成一个正方体,一充气球在正方体内,求球的最大半径.例2.正四面体与球问题:正四面体的棱长为1.求球的半径:⑴若正四面体的四个顶点都在球面上,⑵若球内切于正四面体;⑶6条棱组成一个正四面体,一充气球在正四面体内,求球的最大半径.例3.四球问题:四个球的半径都为1.⑴桌面放两两相切的3个球,这3个球上面放一个球,求这个球的最高点离桌面的距离;⑵求与上述4个球都相切的小球的半径.例4.圆锥、圆柱与球⑴底面半径为1cm高为10cm的圆柱内,可以放几个半径为0.5cm的小球?⑵圆锥底面半径为3,高为4,一个球内切于圆锥,求球的半径;⑶圆锥底面半径为3,高为4,两个半径相同的球两两相切,放在圆锥底面上,且内切于圆锥,求这两个球的半径;⑷圆锥底面半径为3,高为4,三个半径相同的球两两相切,放在圆锥底面上,且内切于圆锥,求这两个球的半径;⑸圆锥底面半径为3,内接于一个半径为4的球,求圆锥的高.例5.圆锥与正四棱柱⑴圆锥底面半径为3,高为4,正四棱柱的高为3,且内接于圆锥,求正四棱柱的底面边长;⑵圆锥底面半径为3,高为4,正四棱柱的高为x,且内接于圆锥,求正四棱柱的体积.练习一、补(补成长方体或正方体)1. 一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为A 、3πB 、4πC 、33πD 、6π2. 在正三棱锥ABC S -中,M 、N 分别是棱SC 、BC 的中点,且AM MN ⊥,若侧棱32=SA ,则正三棱锥ABC S -外接球的表面积是( ) A .π12 B .π32 C .π36 D .π483. 点P 在直径为6的球面上,过P 作两两互相垂直的三条弦(两端点均在球面上的线段),若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是 A .6B .435C .2215D .210554. 一个正方体的体积是8,则这个正方体的内切球的表面积是( )A .8πB .6πC .4πD .π 5. 设正方体的棱长为233,则它的外接球的表面积为( )A .π38B .2πC .4πD .π346. 已知三棱锥S ABC -的三条侧棱两两垂直,且2,4SA SB SC ===,则该三棱锥的外接球的半径为 A .3 B .6 C .36 D .97. 已知长方体1111ABCD A B C D -的外接球的表面积为16,则该长方体的表面积的最大值为A .32B .36C .48D .648. 长方体1111ABCD A B C D -的各个顶点都在表面积为16π的球O 的球面上,其中1::2:1:3AB AD AA =,则四棱锥O ABCD -的体积为A .263 B . 63C .23D .3 9.【山东省潍坊一中2013届高三12月月考测试数学文】四棱锥P ABCD 的三视图如右图所示,四棱锥P ABCD 的五个顶点都在一个球面上,E 、F 分别是棱AB 、CD 的中点,直线EF 被球面所截得的线段长为22,则该球表面积为A .12B .24C .36D .4810. (河南省豫东、豫北十所名校2013届高三阶段性测试四)已知四面体ABCD 中,AB =AD =6,AC =4,CD =213,AB 丄平面ACD ,则四面体 ABCD 外接球的表面积为A . π36B . π88C . π92D . π12811. 正方体1111ABCD A B C D -的棱长为6,一个球与正方体的棱长都相切,则这个球的半径是____________.12. 三棱锥A -BCD 中,侧棱AB 、AC 、AD 两两垂直,ΔABC ,ΔACD , ΔADB 的面积分别为,222,则三棱锥A -BCD 的外接球的体积为. ______13. 四面体ABCD 中,共顶点A 的三条棱两两相互垂直,且其长分别为361、、,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
组合体三视图练习题

组合体三视图练习题一、选择题(每题2分,共20分)1. 组合体三视图包括主视图、左视图和哪个视图?A. 俯视图B. 仰视图C. 侧视图D. 底视图2. 在组合体三视图中,主视图通常表示物体的哪个面?A. 正面B. 侧面C. 顶面D. 底面3. 以下哪个不是三视图的画法规则?A. 长对正B. 高平齐C. 宽相等D. 角度一致4. 组合体三视图中,如果一个视图上的线条与另一个视图上的线条不相交,这些线条表示的是?A. 同一条线B. 不同的线C. 相互平行的线D. 相互垂直的线5. 在组合体三视图中,如果一个物体的俯视图和左视图的尺寸相同,那么这个物体可能是?A. 立方体B. 圆柱体C. 圆锥体D. 球体6. 组合体三视图中,若主视图和俯视图的尺寸不同,但左视图与主视图尺寸相同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体7. 在组合体三视图中,若主视图和左视图的尺寸相同,但俯视图的尺寸不同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体8. 组合体三视图中,若主视图和左视图的尺寸不同,但俯视图与主视图尺寸相同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体9. 在组合体三视图中,若俯视图和左视图的尺寸相同,但主视图的尺寸不同,该物体可能是?A. 长方体B. 正方体C. 圆柱体D. 圆锥体10. 组合体三视图中,若俯视图是一个圆形,左视图和主视图是两个相同的矩形,该物体可能是?A. 长方体B. 圆柱体C. 圆锥体D. 球体二、填空题(每题2分,共20分)11. 组合体三视图中,______视图通常用来表示物体的顶面或底面。
12. 在组合体三视图中,______视图通常用来表示物体的侧面。
13. 组合体三视图中,______视图通常用来表示物体的正面。
14. 组合体三视图的画法规则包括______、______和______。
15. 如果一个物体的三视图都是圆形,那么这个物体可能是______。
画组合体三视图习题解答
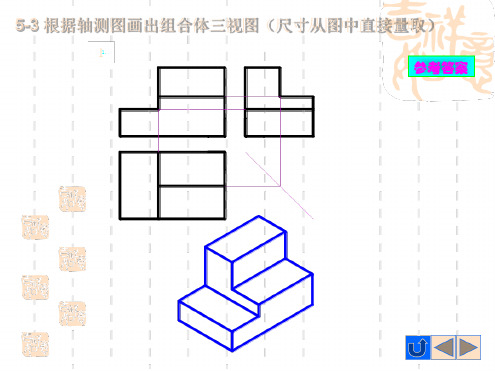
1.
CD是 正平 线 A面是 正垂 面 B面是 正平 面
2.
参考答案
A面是 正平 面
B面在C面之 下方
DE是 正平
线
3.
参考答案
A面是 侧平 面 B面是 正垂 面 B面在A面之 右方
4.
参考答案
AB是一般位置直 线 P面是 正垂 面 Q面是 水平 面
5.
参考答案
AB是 正平 线 P面是 水平 面 Q面是 正垂 面
1画出组合体三视图参考答案55参考答案右方参考答案水平参考答案56补画视图中所缺图线答案方法答案方法答案方法答案方法
5-3 根据轴测图画出组合体三视图(尺寸从图中直接量取)
11. 参考答案
2.ห้องสมุดไป่ตู้
2 参考答案
5-4 根据轴测图上所注尺寸,用1:1画出组合体三视图 1
参考答案
2
参考答案
5-5 标出指定的图线和线框在其他视图上的投影,并填空
6.
参考答案
A面是 正垂 面 B面在C面之 前方 DE 是 侧垂 线
5-6 补画视图中所缺图线
1
2
3
答案
方法
4.
答案
方法
5
答案
方法
6.
答案
方法
2021-2022学年六年级数学下册典型例题系列之第三单元:组合立体图形的表面积专项练习(解析版)

2021-2022学年六年级数学下册典型例题系列之第三单元:组合立体图形的表面积专项练习(解析版)1.有一个工具箱下半部分为正方体,上半部分为圆柱体一半(下图),如果把工具箱的表面涂上油漆(包括底面),求涂油漆部分的面积。
【解析】可以将两个半圆拼成一个完整的圆,涂色部分包括正方体5个面、圆柱侧面积的一半、以及圆柱一个底面积,据此列式解答即可。
20²×5+3.14×20×20÷2+3.14×(20÷2)²=2000+628+3.14×100=2000+628+314=2942(平方厘米)答:涂油漆部分的面积是2942平方厘米。
2.计算下面组合图形的表面积。
(单位:cm)【解析】6×6×6+3.14×6×5,=216+94.2,=310.2(平方厘米)答:它的表面积是30.2平方厘米。
3.求下面图形的表面积和体积。
(单位:cm)【解析】表面积=大正方体的表面积+圆柱的侧面积,10×10×6+3.14×4×6=600+75.36=675.36(cm2);4.下图是一个灯笼图片,阿姨做这个灯笼至少需要多大的彩纸?【解析】用外圆柱侧面积+内圆柱侧面积+上下两个圆环面积即可。
4÷2=2(分米),2÷2=1(分米)3.14×4×5+3.14×2×5+3.14×(22-12)×2=62.8+31.4+3.14×3×2=62.8+31.4+18.84=113.04(平方分米)答:做这个灯笼至少需要113.04平方分米的彩纸。
5.有三个圆柱,一个堆在一个上面,底层圆柱最大,上层最小,它们的直径分别是4分米、 3分米、2分米,高都是2分米,这样的立体图形的表面积是多少?【解析】由图可知:这个立体图形的表面积等于最下面大圆柱的表面积加上上面两个小圆柱的侧面积。
画组合体三视图)习题解答

俯视图的绘制
选择合适的观察高度
俯视图应选择一个与主视图和左视图平行的观察高度,以便展示组合体的顶部形 状。
反映组合体的长度和宽度
俯视图应清晰表达组合体的长度和宽度,特别是对于具有水平结构特征的部分。
三视图的对应关系
投影一致性
在左视图上。在左视图中,应将组合体的各个组成部分表示清楚,并注
意投影的对应关Leabharlann 。03俯视图俯视图是反映组合体的水平面形状的视图,通常将组合体的水平投影绘
制在俯视图上。在俯视图中,应将组合体的各个组成部分表示清楚,并
注意投影的对应关系。
02 组合体的三视图绘制
主视图的选择
确定观察方向
选择一个能反映组合体主要形状特征的方向作为主视图的观察方 向。
习题二解析
复杂组合练习
习题二涉及更复杂的组合体,包括多个基础几何体的叠加、切割和组合。通过练习,学生可以提高对复杂组合体的空间想象 能力和绘图技能。
习题三解析
装配关系练习
习题三注重表现组合体之间的装配关系,例如螺栓、轴承等连接方式。通过练习,学生可以加深对组 合体内部结构和装配关系的理解。
习题四解析
在绘制叠加型组合体的主视图时,应先画出最底层的几何体,然后依次 画出上层叠加的几何体,特别注意处理好各几何体之间的前后关系。
在绘制左视图和俯视图时,应依据主视图,逐层画出各几何体的轮廓线, 并注意各几何体的投影变化。
切割型组合体的绘制
切割型组合体是由一个基本几何体经过 多次切割、钻孔等操作形成的。在绘制 其三视图时,应先画出完整的基本几何 体,再依据切割、钻孔等操作逐一画出
在绘制综合型组合体的主视图时,应先确定 各基本几何体的位置和形状,然后依据“长 对正、高平齐、宽相等”的原则,从整体到 局部进行绘制。
组合体三视图练习题

组合体三视图练习题一、基础题1. 根据给定的物体,绘制其主视图、俯视图和左视图。
2. 给出物体的主视图,补全其俯视图和左视图。
3. 根据物体的俯视图,绘制其主视图和左视图。
二、进阶题6. 给出两个物体的组合体,绘制其三视图。
9. 根据给定的组合体三视图,推导出其实物图。
10. 给出组合体的主视图和俯视图,绘制其左视图。
三、提高题12. 给出组合体的三视图,求出其体积。
15. 给出组合体的三视图,绘制其局部视图。
四、综合题17. 给出组合体的三视图,求出其表面积。
20. 给出组合体的三视图,绘制其展开图。
五、创新题21. 设计一个组合体,绘制其三视图,并说明其功能。
25. 给出组合体的三视图,尝试用不同的材料进行制作。
六、空间想象题26. 根据描述,想象组合体的形状,并绘制其三视图。
27. 给出组合体的空间位置关系,绘制其三视图。
28. 从不同角度观察组合体,绘制其三视图。
30. 根据给定的物体轮廓,绘制其可能的三视图。
七、实际应用题31. 根据建筑图纸,绘制某一层楼的三视图。
32. 分析机械零件的三视图,确定其加工步骤。
33. 给出家具的三视图,说明其组装方法。
34. 根据电子设备的三视图,指出其主要功能区域。
35. 绘制一个简单桥梁的三视图,并标注关键尺寸。
八、纠错题37. 给出组合体的三视图,其中有误,请指出并更正。
九、拓展题41. 给出组合体的三视图,尝试添加一个新部分,并重新绘制三视图。
44. 给出组合体的三视图,设计一个与之配套的零件,并绘制其三视图。
十、挑战题46. 给出多个组合体的三视图,要求将它们组合成一个更大的组合体,并绘制三视图。
48. 给出组合体的三视图,要求在不改变功能的前提下,减少其材料用量。
50. 设计一个组合体,使其三视图在某个特定角度下呈现出特定的图案或文字。
答案一、基础题1. 答案略。
2. 答案略。
4. 答案略。
5. 答案略。
二、进阶题6. 答案略。
7. 答案略。
组合体 大连理工大学机械制图习题集答案
形体分析法画组合体视图的方法和步骤看组合体视图的方法和步骤标注组合体尺寸的方法组合体的构形设计组合体的视图线面分析法恢复原形法组合体的视图组合体由基本几何形体(棱柱、圆柱、棱锥、圆锥、圆球、圆环等)组合构成的立体。
视图机件向多面投影体系的各投影面做正投影所得的图形。
六个基本视图组合体的三视图六个基本视图主视图由前向后投射所得的视图俯视图由上向下投射所得的视图左视图由左向右投射所得的视图右视图由右向左投射所得的视图仰视图由下向上投射所得的视图后视图由后向前投射所得的视图六个基本视图的形成组合体的三视图组合体的三视图一般是指:主视图、俯视图、左视图。
三视图的投影规律——三等规律:主、俯视图——长对正;主、左视图——高平齐;俯、左视图——宽相等。
应用“三等规律”的要点:1. 机件的整体和局部都要符合“三等规律”。
示例2. 在俯、左视图上,远离主视图的一侧是机件的前面,靠近主视图的一侧是机件的后面。
示例3. 要特别注意宽度方向尺寸在俯、左视图上的不同方位。
示例“三等规律”是画图、看图的基本投影规律。
绘图时,应通过绘图工具或绘图软件的功能来保证“三等规律”的实现。
通过绘图工具实现“三等规律”形体分析法形体分析法假想把组合体分解为若干个基本几何形体(简称形体),并确定各形体之间的组合形式和相对位置的方法。
形体间的组合形式形体间的相对位置和邻接表面关系形体分析法应用举例形体组合的基本形式叠加、挖切形体组合形式举例形体间的相对位置形体叠加、挖切组合后,形体之间可能处于上下、左右、前后或对称、同轴等相对位置。
形体间的相对位置和邻接表面关系形体间邻接表面关系:共面、相切或相交1.共面当两形体邻接表面共面时,在共面处不应有邻接表面的分界线。
2.相切当两形体邻接表面相切时,相切处是光滑过渡。
相切处是光滑过渡,切线的投影规定不画。
注意:在某个视图上,当切线处存在回转面的转向线时,应画出该转向线的投影。
3. 相交两形体邻接表面相交时,邻接表面之间产生交线。
工程制图组合体答案(教师版)

1.根据轴测图及尺寸,画出组合体的三视图。
26 – 1
返回 答案
(1)
2.根据轴测图及尺寸,画出组合体的三视图。
26 – 2
返回 答案
(2)
典型较复杂相贯体2620答案作图过程返回2720答案作图过程返回2820答案作图过程返回2920答案作图过程返回3020答案作图过程返回3120答案作图过程返回3221答案作图过程返回3321答案作图过程返回3421答案作图过程返回3521110答案作图过程返回3621111答案作图过程返回3721112答案作图过程返回3822113答案作图过程返回3922114答案作图过程返回4022115答案作图过程返回4122116答案作图过程返回4223答案返回4323答案返回4423答案返回4523答案返回4623答案返回4723答案返回4824答案返回答案
返回 作图过程 答案
21 – 1(9)
返回 作图过程 答案
21 – 1(10)
返回 作图过程 答案
21 – 1(11)
返回 作图过程 答案
21 – 1(12)
返回 作图过程 答案
22 – 1(13)
返回 作图过程 答案
22 – 1(14)
返回 作图过程 答案
22 – 1(15)
返回 答案 作图过程
24-3(2)
返回
25-(1)
25-(2)
25-(3)
返回
25-(4)
26- 1
26- 2
返回
17 – 1(1)
返回 作图过程 答案
17 – 1(2)
返回 作图过程 答案
17 – 1(3)
返回 作图过程 答案
17 – 1(4)
返回 作图过程 答案
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元三组合体习题答案3-1参照立体示意图,补画三视图中漏画的图线。
1.
2.
3.
4.
3-2观察物体的三视图,在立体示意图中找出相对应的形体,并填写对应的序号。
1. 2. 3. 4.
5. 6. 7. 8.
9. 10. 11. 12.
1. (12 )
2. (3 )
3. ( 4)
4. ( 7)
5. ( 5)
6. (9 )
7. (11 )
8. (10 )
9. ( 8) 10. ( 6) 11. ( 1) 12. (2 )
3-3已知两视图,参考立体图补画所缺视图。
1. 2.
3. 4.
5. 6.
3-4. 根据立体示意图,辨认其相应的两视图,把序号填在括号中,并补画第三视图:1.(2) 2.(3) 1. 2.
3.(6)
4.(4) 3. 4.
5.(1)
6.(5) 5. 6.
7.(10)8.(7)7. 8.
9.(9) 10.(8) 9. 10.
3-5
已知组合体立体图,进行形体分析,并绘制组合体的三视图。
1. 2.
3. 4.
5. 6.
7. 8.
3-7已知组合体立体图,进行形体分析,并绘制组合体的三视图。
1. 2.
3. 4.
5. 6.
3-10选择与三视图对应的组合体编号填入括号中。
1. (5)
2. (4)
3. (3)
3-11选择与主视图对应的俯视图及组合体的编号填入表格内。
主视图俯视图组合体
1 c E
2 e H
3 a G
4 h F
5 d D
6 b B
7 g C
8 f A
3-12按给出的组合体补画视图。
画俯视图与左视图(半圆板厚5mm,凸出部分向前伸出3mm)。
3-13补画左视图。
1.
2.
3-14根据立体示意图找出三视图,并在括号内填写相应的编号。
1
(11 )2
(4 )
3
(9 )
4
(2 )5
(5 )
6
(8 )
7
(7 )8
(3 )
9
(10 )
10 11 12
( 6)(12 )( 1)
3-15根据给出的俯视图,构思不同的组合体,画出它们的主左视图,至少构思三个组合体。
(答案填在表格中)
俯视图1
构思组合体实体图主视图左视图
俯视图2
构思组合体实体图主视图左视图
俯视图3
构思组合体实体图主视图左视图1. 2. 3.
5. 6.
7. 8.。
