三角函数及反三角函数

合集下载

三角函数与反三角函数

在三角函数的前面加上arc ，表示它们的反函数f–1 (x)。

即由一个三角函数值得出当时的角度。

1. 正弦函数sin x，反正弦函数arcsin xsinx arcsinxy = sin x，x∈R，y∈[–1，1]，周期为2π，函数图像以x = (π/2) + kπ 为对称轴y = arcsin x，x∈[–1，1]，y∈[–π/2，π/2]sin x = 0 ←→ arcsin x = 0sin x = 1/2 ←→ arcsin x = π/6sin x = √2/2 ←→ arcsin x = π/4sin x = 1 ←→ arcsin x = π/22. 余弦函数cos x，反余弦函数arccos xcosx arecosxy = cos x，x∈R，y∈[–1，1]，周期为2π，函数图像以x = kπ 为对称轴y = arccos x，x∈[–1，1]，y∈[0，π]cos x = 0 ←→ arccos x = π/2cos x = 1/2 ←→ arccos x = π/3cos x = √2/2 ←→ arccos x = π/4cos x = 1 ←→ arccos x = 03. 反正弦函数arcsin x，反余弦函数arccos xarcsinx arccosxy = arcsin x 与y = arccos x 自变量的取值范围都是x∈[–1，1] y = arcsin x 与y = arccos x 的图像关于直线y = π/4 对称，相交与点(√2/2 ，π/4)4. 正切函数tan x，余切函数cot xtanx cotxy = tan x，x∈( (–π/2) + kπ，(π/2) + kπ )，y∈R，周期为π，当x → ± (π/2) + kπ 时，函数的极限是无穷大∞y = cot x = 1 / tan x，x∈( 0，kπ )，y∈R，周期为π，当x → kπ 时，函数的极限是无穷大∞y = tan x 与y = cot x 的图像关于x = (π/4) + kπ/2 对称在单个周期内（第一个），y = tan x 与y = cot x 的图像相交与点（π/4 ，1）。

高等数学课件：三角函数反三角函数

y 10
-2
5
0
-5
-10
2
4
2
x 6
(5) 正割函数 secx
y 6
4
2
-4 -2 0
-2
x 24 68
-4
-6
(6) 余割函数 cscx
y
6
4
2
-2 0
x
2
4
6
8
-2
-4
-6
5. 反三角函数(常用的四个)
(1) 反正弦函数 Arcsin x 主值 arcsinx [ , ]
22
(2) 反余弦函数 Arccos x
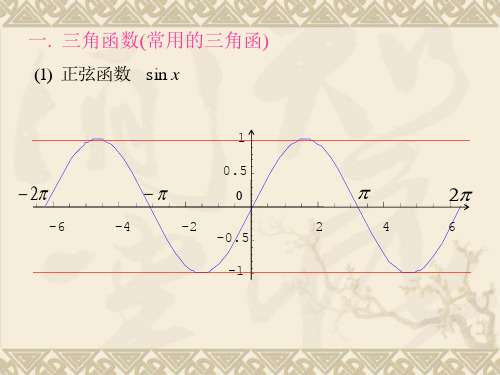
一. 三角函数(常用的三角函)
(1) 正弦函数 sin x
2
-6
1
0.5
0
-4
-2
-0.5
-1
2
2
4
6
(2) 余弦函数 cos x
1
3
2
2
0.5
2
-6
-4
-2
0
2
-0.5
-1
3
2
4
6
(3) 正切函数 tan x
3
2
-4
y 6
4
2
2
2
-2 0
2
-2
-4
-6
3 2
x 4
Back
(4) 余切函数 cot x
2
( 2 ) 双曲余弦 ch x = e x ex ( 偶函数 ) 2
( 3 ) 双曲正切
th
x
=
sh ch
x x
=
ex ex
ex ex
( 奇函数 )

三角函数与反三角函数的关系公式

三角函数与反三角函数的关系公式
三角函数与反三角函数的关系公式：sin(A+B)=sinAcosB+cosAsinBsin(A-B)。

反三角函数是一种基本初等函数。

它是反正弦arcsinx，反余弦arccosx，反正切arctanx，反余切arccotx，反正割arcsecx，反余割arccscx这些函数的统称，各自表示其反正弦、反余弦、反正切、反余切，反正割，反余割为x的角。

三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

也可以等价地用与单位圆有关的各种线段的长度来定义。

三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。

在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

(完整word)三角函数及反三角函数

二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝———-—1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α三角函数的和差化积公式三角函数的积化和差公式α＋βα－βsinα＋sinβ＝2sin—－－·cos—－-2 2α＋βα－βsinα－sinβ＝2cos—－－·sin-－—22α＋βα－βcosα＋cosβ＝2cos-－－·cos—－—22α＋βα－βcosα－cosβ＝－2sin—－－·sin—－—22sinα·cosβ=（1/2)［sin(α+β)+sin(α-β）］cosα·sinβ=（1/2)[sin(α+β）—sin(α—β）]cosα·cosβ=(1/2)［cos(α+β)+cos（α—β）］sinα·sinβ=-（1/2）［cos（α+β）—cos(α—β）]化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式）函数变换360k+αsinαcosαtanαcotαsecαcscαcosαsinαcotαtanαcscαsecα90°—α90°+αcosα-sinα—cotα—tanα—cscαsecα180°—sinα-cosα—tanα-cotα—secαcscαα—sinα-cosαtanαcotα-secα—cscα180°+α270°--cosα—sinαcotαtanα-cscα—secαα270°+—cosαsinα-cotα-tanαcscα-secαα360°--sinαcosα-tanα-cotαsecα-cscαα﹣α—sinαcosα-tanα—cotαsecα-cscα反三角函数三角函数的反函数，是多值函数。

三角函数-反三角函数公式大全

三角函数-反三角函数公式大全tan （π＋α）= tanα cot （π＋α）= cotα 公式三：任意角α与 -α的三角函数值之间的关系： sin （-α）= -sinα cos （-α）= cosα tan （-α）= -tanα cot （-α）= -cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinα cos （π-α）= -cosα tan （π-α）= -tanα cot （π-α）= -cotα 公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六：2π±α及23π±α与α的三角函数值之间的关系：sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A正切函数sin tan cos x x x =；余切函数cos cot sin xx x =；正割函数1sec cos x x =；余割函数1csc sin x x= 三角函数奇偶、周期性sin x ，tan x ，cot x 奇函数；cos x 偶函数；sin x，cos x 周期2π；sin()t ωϕ+ 周期2πω；tan x ，cot x 周期π常用三角函数公式：22cos sin 1x x += 22cos sin cos2x x x -=2s i n c o ssx x x = 21cos 22sin x x -= 21c o s 22c o sx x +=22211tan sec cos x x x+== 22211cotcsc sin x x x +==1sin sin [cos()cos()]2x y x y x y =-+-- 1c o sc o s[c o s ()c o s ()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数：a r c s i na r c c o s 2x x π+=a r c t a na r c c o t2x x π+=arcsin x：定义域[1,1]-，值域[,]22ππ-；arccos x ：定义域[1,1]-，值域[0,]π；arctan x：定义域(,)-∞+∞，值域(,)22ππ-；arccot x ：定义域(,)-∞+∞，值域(0,)π式中n为任意整数.arc sin x = arc cos x = arc tan x = arc cot x =。

三角函数与三角函数的反函数

三角函数与三角函数的反函数三角函数是数学中的一个重要概念，它与角度和三角比例息息相关。

而与三角函数密切相关的还有三角函数的反函数。

本文将对三角函数及其反函数进行详细的介绍和分析。

一、三角函数的定义及性质在直角三角形中，我们定义了几个特殊的角，如正弦、余弦和正切。

这些角度的比例被称为三角函数，其定义如下：1. 正弦函数（sin）：在直角三角形中，正弦函数是指对边与斜边之比，记作sinθ。

2. 余弦函数（cos）：在直角三角形中，余弦函数是指邻边与斜边之比，记作cosθ。

3. 正切函数（tan）：在直角三角形中，正切函数是指对边与邻边之比，记作tanθ。

这些函数在特定角度下有一些基本性质：1. 周期性：正弦、余弦和正切函数都具有周期性，周期为360°或2π弧度。

2. 奇偶性：正弦函数为奇函数，即sin(-θ)=-sin(θ)；余弦函数为偶函数，即cos(-θ)=cos(θ)；正切函数也为奇函数，即tan(-θ)=-tan(θ)。

3. 范围：正弦和余弦函数的值范围在-1到1之间，而正切函数的值范围为负无穷到正无穷。

二、三角函数的反函数与三角函数对应的是三角函数的反函数。

反函数是一种将函数的输出值映射回其输入值的过程。

对于三角函数而言，反函数也被称为反三角函数。

常用的反三角函数有反正弦、反余弦和反正切。

1. 反正弦函数（arcsin）：反正弦函数是正弦函数的反函数。

记为y=arcsin(x)或sin^(-1)(x)，其中-π/2 ≤ y ≤ π/2，-1 ≤ x ≤ 1。

它表示的是对应于特定值x的角度y，即sin(y)=x。

2. 反余弦函数（arccos）：反余弦函数是余弦函数的反函数。

记为y=arccos(x)或cos^(-1)(x)，其中0 ≤ y ≤ π，-1 ≤x ≤ 1。

它表示的是对应于特定值x的角度y，即cos(y)=x。

3. 反正切函数（arctan）：反正切函数是正切函数的反函数。

三角函数的反函数与反三角函数

三角函数的反函数与反三角函数在数学中，三角函数是一类广泛应用于几何学、物理学、信号处理等领域的函数。

它们能够描述角度与边长之间的关系，包括正弦、余弦、正切、余切、正割和余割六个基本三角函数。

然而，在实际问题中，我们有时需要求解与已知三角函数值相对应的角度，或者需要求解角度对应的三角函数值。

这就引出了三角函数的反函数与反三角函数的概念。

一、三角函数的反函数所谓三角函数的反函数，即是指正弦、余弦、正切函数的反函数。

这些反函数分别记作arcsin(x)、arccos(x)和arctan(x)，其中x属于函数的定义域。

1. 反正弦函数（arcsin）反正弦函数是指对应于给定比值的弧度值或角度值。

正弦函数的定义域为[-1, 1]，因此反正弦函数的定义域为[-1, 1]，值域为[-π/2, π/2]。

反正弦函数的图像关于y=x对称。

2. 反余弦函数（arccos）反余弦函数是指对应于给定比值的弧度值或角度值。

余弦函数的定义域也为[-1, 1]，因此反余弦函数的定义域为[-1, 1]，值域为[0, π]。

反余弦函数的图像关于y=x对称。

3. 反正切函数（arctan）反正切函数是指对应于给定比值的弧度值或角度值。

正切函数的定义域为全体实数，值域为(-π/2, π/2)。

反正切函数的定义域为全体实数，值域为(-π/2, π/2)。

反正切函数的图像关于y=x对称。

二、反三角函数反三角函数是指对应于给定比值的角度值。

反正弦函数、反余弦函数和反正切函数统称为反三角函数。

1. 反正弦函数（arcsin）反正弦函数的定义域为[-1, 1]，值域为[-π/2, π/2]。

它表示对应于给定正弦值的角度值，通常用于解决求解角度的问题。

2. 反余弦函数（arccos）反余弦函数的定义域为[-1, 1]，值域为[0, π]。

它表示对应于给定余弦值的角度值，常用于几何问题和解三角形问题中。

3. 反正切函数（arctan）反正切函数的定义域为全体实数，值域为(-π/2, π/2)。

三角函数的反函数与反三角函数

三角函数的反函数与反三角函数三角函数是数学中常见的一类函数，包括正弦函数、余弦函数和正切函数等。

在三角函数中，存在着一种特殊的函数关系，即反函数与反三角函数。

本文将就三角函数的反函数和反三角函数进行详细讨论。

一、三角函数的反函数首先，我们先了解一下什么是函数的反函数。

在数学中，如果函数f(x)的定义域为D，值域为R，且对于任意的x∈D和y∈R，满足f(x)=y当且仅当f^(-1)(y)=x，则称函数f^(-1)(y)为函数f(x)的反函数。

反函数是指从函数的输出得到输入的一种映射关系。

对于三角函数来说，由于其周期性和多值性，存在着不同的反函数。

以正弦函数sin(x)为例，其反函数通常称为反正弦函数或arcsin(x)，记作y=arcsin(x)。

其定义域为[-1, 1]，值域为[-π/2, π/2]。

通过反正弦函数，我们可以求得给定值的角度，即sin(x)=y，则x=arcsin(y)。

同样地，余弦函数cos(x)的反函数为反余弦函数或arccos(x)，正切函数tan(x)的反函数为反正切函数或arctan(x)，以此类推。

二、反三角函数与三角函数的反函数不同，反三角函数是指将给定的三角函数值作为输入，求解相应的角度值。

反三角函数可以帮助我们解决三角函数方程以及在实际问题中的应用。

常见的反三角函数包括反正弦函数、反余弦函数和反正切函数等。

以反正弦函数arcsin(x)为例，其定义域为[-1, 1]，值域为[-π/2, π/2]。

通过反正弦函数，我们可以求得给定值的角度，即arcsin(x)=y，则x=sin(y)。

类似地，反余弦函数arccos(x)的定义域为[-1, 1]，值域为[0, π]，反正切函数arctan(x)的定义域为R，值域为(-π/2, π/2)。

三、三角函数的性质与应用除了反函数和反三角函数的定义和性质，我们还需要了解三角函数的一些基本性质和应用。

1. 周期性：正弦函数和余弦函数的周期都是2π，即sin(x+2π)=sin(x)和cos(x+2π)=cos(x)；而正切函数的周期是π，即tan(x+π)=tan(x)。

三角函数及反三角函数

tanα－tanβtan（α－β）＝——————1＋tanα ·tanβ半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝—————1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α三角函数的和差化积公式三角函数的积化和差公式α＋βα－βsinα＋sinβ＝2sin—－－·cos—－—2 2α＋βα－βsinα－sinβ＝2cos—－－·sin—－—2 2α＋βα－βcosα＋cosβ＝2cos—－－·cos—－—2 2α＋βα－βcosα－cosβ＝－2sin—－－·sin—－—2 2sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]化asinα ±bcosα为一个角的一个三角函数的形式（辅助角的三角函数的公式）函数变换360k+αsinαcosαtanαcotαsecαcscα90°-αcosαsinαcotαtanαcscαsecα90°+αcosα-sinα-cotα-tanα-cscαsecα180°-αsinα-cosα-tanα-cotα-secαcscα180°+α-sinα-cosαtanαcotα-secα-cscα270°-α-cosα-sinαcotαtanα-cscα-secα270°+α-cosαsinα-cotα-tanαcscα-secα360°-α-sinαcosα-tanα-cotαsecα-cscα﹣α-sinαcosα-tanα-cotαsecα-cscα反三角函数三角函数的，是多值函数。

(完整版)三角函数_反三角函数公式大全

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tan(A-B) =tanAtanB -1tanB tanA +tanAtanB1tanBtanA +-cot(A+B) = cot(A-B) =cotA cotB 1-cotAcotB +cotAcotB 1cotAcotB -+倍角公式tan2A =Sin2A=2SinA•CosA Atan 12tanA2-Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(+a)·tan(-a)3π3π半角公式sin()= cos()= tan()= cot()=2A 2cos 1A -2A 2cos 1A +2A A A cos 1cos 1+-2Atan()==A A cos 1cos 1-+2A A A sin cos 1-AAcos 1sin +和差化积 sina+sinb=2sincos sina-sinb=2cos sin 2b a +2b a -2b a +2ba -cosa+cosb = 2coscos cosa-cosb = -2sin sin 2b a +2b a -2b a +2ba -tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = -[cos(a+b)-cos(a-b)] cosacosb = [cos(a+b)+cos(a-b)]2121sinacosb = [sin(a+b)+sin(a-b)] cosasinb = [sin(a+b)-sin(a-b)]2121诱导公式s in(-a) = -sina c os(-a) = cosa sin(-a) = cosa cos(-a) = sina2π2πsin(+a) = cosa cos(+a) = -sina sin(π-a) = sina cos(π-a) = -cosa2π2πsin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin 万能公式sina=cosa= tana=2)2(tan 12tan2a a +22)2(tan 1)2(tan 1aa+-2)2(tan 12tan2aa-其它公式a•sina+b•cosa=×sin(a+c) [其中tanc=])b (a 22+ab a•sin(a)-b•cos(a) = ×cos(a-c) [其中tan(c)=])b (a 22+ba 1+sin(a) =(sin+cos )22a 2a 1-sin(a) = (sin-cos )22a 2a 其他非重点三角函数csc(a) =sec(a) =a sin 1acos 1公式一：设α为任意角，终边相同的角的同一三角函数的值相等： sin （2kπ＋α）= sinα cos （2kπ＋α）= cosα tan （2kπ＋α）= tanα cot （2kπ＋α）= cotα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin （π＋α）= -sinα cos （π＋α）= -cosαtan （π＋α）= tanα cot （π＋α）= cotα 公式三：任意角α与 -α的三角函数值之间的关系： sin （-α）= -sinα cos （-α）= cosα tan （-α）= -tanα cot （-α）= -cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinα cos （π-α）= -cosα tan （π-α）= -tanα cot （π-α）= -cotα 公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六：±α及±α与α的三角函数值之间的关系： 2π23πsin （+α）= cosα cos （+α）= -sinα2π2πtan （+α）= -cotα cot （+α）= -tanα2π2πsin （-α）= cosα cos （-α）= sinα tan （-α）= cotα cot （-α）=2π2π2π2πtanα sin （+α）= -cosα cos （+α）= sinα 23π23πtan （+α）= -cotα cot （+α）= -tanα 23π23πsin （-α）= -cosα cos （-α）= -sinα 23π23πtan （-α）= cotα cot （-α）= tanα 23π23π(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =×sin)cos(222ϕθ⋅++AB B A )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A 正切函数；余切函数；sin tan cos x x x =cos cot sin xx x=正割函数；余割函数1sec cos x x =1csc sin x x=三角函数奇偶、周期性，，奇函数；偶函数； sin x tan x cot x cos x ，周期；周期；，周期sin x cos x 2πsin()t ωϕ+2πωtan x cot x π常用三角函数公式：22cos sin 1x x +=22cos sin cos 2x x x -=2sin cos sin 2x x x = 21cos 22sin x x -=21cos 22cos x x += 22211tan sec cos x x x +==22211cot csc sin x x x+== 1sin sin [cos()cos()]2x y x y x y =-+--1cos cos [cos()cos()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数：arcsin arccos 2x x π+=arctan arccot 2x x π+=：定义域，值域；：定义域，值域；arcsin x [1,1]-[,22ππ-arccos x [1,1]-[0,]π：定义域，值域；：定义域，值域arctan x (,)-∞+∞(,)22ππ-arc cot x (,)-∞+∞(0,)πe i r b e i n g a re go o式中n 为任意整数.arc sin x =arc cos x =arc tan x =arc cot x =。

三角函数与反三角函数

三角函数与反三角函数三角函数是数学中一个重要的概念，它们在解决几何问题、物理问题以及工程问题等方面起着不可替代的作用。

与之相对应的，反三角函数是解三角函数方程时经常使用的工具。

本文将介绍三角函数和反三角函数的定义、性质以及它们在实际问题中的应用。

一、三角函数的定义与性质三角函数是利用一个角的弧度或角度值，计算该角对应三角比值的函数。

常见的三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)等。

1. 正弦函数正弦函数sin(x)的定义是：在单位圆上，角x所对应点的纵坐标值。

正弦函数的性质有：- 周期性：sin(x)的周期是2π，即sin(x + 2π) = sin(x)。

- 奇偶性：正弦函数是奇函数，即sin(-x) = -sin(x)。

2. 余弦函数余弦函数cos(x)的定义是：在单位圆上，角x所对应点的横坐标值。

余弦函数的性质有：- 周期性：cos(x)的周期是2π，即cos(x + 2π) = cos(x)。

- 偶性：余弦函数是偶函数，即cos(-x) = cos(x)。

3. 正切函数正切函数tan(x)的定义是：在单位圆上，角x所对应点的纵坐标值与横坐标值的比值。

正切函数的性质有：- 周期性：tan(x)的周期是π，即tan(x + π) = tan(x)。

- 奇偶性：正切函数是奇函数，即tan(-x) = -tan(x)。

除了这三个常见的三角函数，还有诸如余割函数csc(x)、正割函数sec(x)和余切函数cot(x)等函数，它们的性质可以通过正弦函数和余弦函数的倒数关系得到。

二、反三角函数的定义与性质反三角函数是三角函数的反函数。

在实际问题中，我们经常需要求解三角函数方程，即已知三角函数的值，求解相应角的值。

此时就需要用到反三角函数。

常见的反三角函数包括反正弦函数arcsin(x)、反余弦函数arccos(x)、反正切函数arctan(x)等。

1. 反正弦函数反正弦函数arcsin(x)的定义是：满足sin(y) = x的角y，其中y的取值范围是[-π/2, π/2]。

三角函数及反三角函数公式大全

三角函数是数学中的一种基本函数，它可以描述角度与直角三角形的边长之间的关系。

而反三角函数则是三角函数的逆运算，它可以用来求解角度或直角三角形的边长。

在数学和物理等领域中，三角函数和反三角函数广泛应用，包括圆的运动、波的传播、信号处理等。

本文将介绍三角函数及反三角函数的定义、性质和公式，希望能够对读者有所帮助。

一、三角函数的定义与性质1. 正弦函数（sin）正弦函数可以用来描述直角三角形中某个角的正弦值，定义为对边与斜边的比值。

正弦函数的性质包括周期性、奇偶性、界值等，它在数学和物理中有着重要的应用。

2. 余弦函数（cos）余弦函数是描述直角三角形中某个角的余弦值的函数，定义为邻边与斜边的比值。

余弦函数也具有周期性、奇偶性、界值等性质，它与正弦函数有着密切的关系。

3. 正切函数（tan）正切函数可以用来描述直角三角形中某个角的正切值，定义为对边与邻边的比值。

正切函数的性质包括周期性、奇偶性、界值等，它在数学和工程中有着广泛的应用。

4. 余切函数（cot）余切函数是描述直角三角形中某个角的余切值的函数，定义为邻边与对边的比值。

余切函数也具有周期性、奇偶性、界值等性质，它与正切函数有着密切的关系。

5. 正割函数（sec）正割函数可以用来描述直角三角形中某个角的正割值，定义为斜边与邻边的比值。

正割函数的性质包括周期性、奇偶性、界值等，它在数学和物理中有着重要的应用。

6. 余割函数（csc）余割函数是描述直角三角形中某个角的余割值的函数，定义为斜边与对边的比值。

余割函数也具有周期性、奇偶性、界值等性质，它与正割函数有着密切的关系。

二、反三角函数的定义与性质1. 反正弦函数（arcsin）反正弦函数是正弦函数的逆运算，可以用来求解某个数值的角度。

反正弦函数的定义域和值域、奇偶性、单调性等性质是求解问题时需要考虑的重要因素。

2. 反余弦函数（arccos）反余弦函数是余弦函数的逆运算，可以用来求解某个数值的角度。

三角函数公式及反三角函数公式整理版_

三角函数公式表
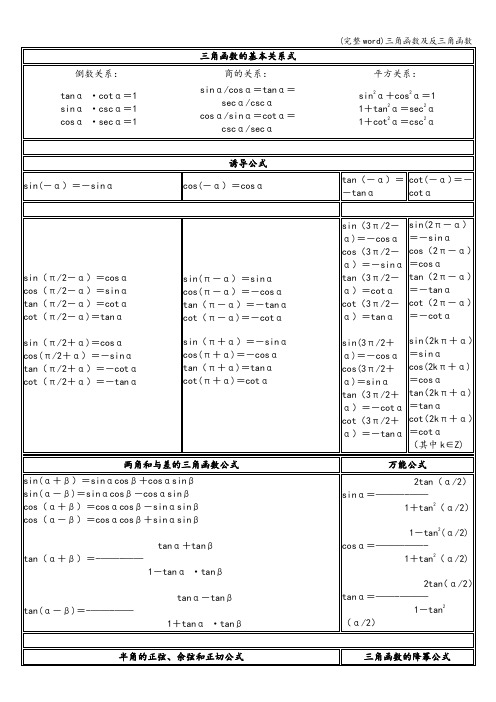
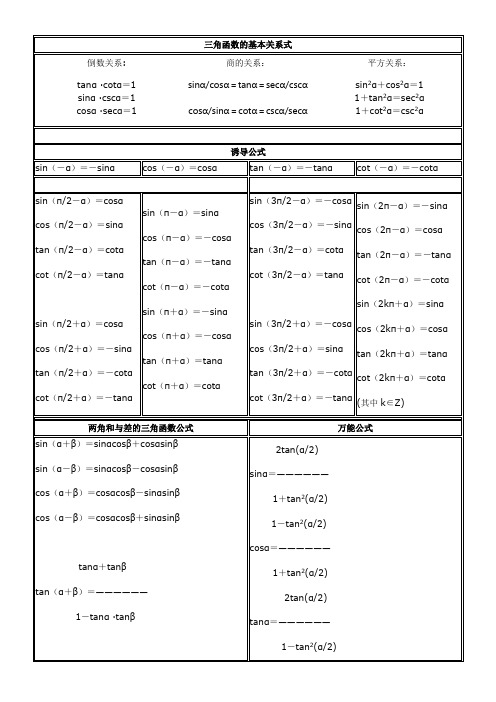
同角三角函数的基本关系式倒数关系: tanα ·cotα＝1 sinα ·cscα＝1 cosα ·secα＝1 商的关系：平方关系： sin2α＋cos2α＝1 1＋tan2α＝sec2α 1＋cot2α＝csc2α
sin sec tan con csc con csc cot sin sec
sinsinsin2coscos2sintan2cotcot2tansin2coscos2sintan2cotcot2tan两角和与差的三角函数公式sinsincoscostan1tan半角的正弦余弦和正切公式coscossinsincoscostantancotcotsinsincoscostantancotcottantansin32coscos32sintan32cotcot32tansin32coscos32sintan32cotcot32tan万能公式cotcotsin2sincos2costan2tancot2cotsin2ksincos2kcostan2ktancot2kcot其中kzsinsinsincoscoscoscoscoscoscossinsincossinsinsintantantantantantantan1tan22tan1tan2sin2221tan1tan22cos22tan21tantan2三角函数的降幂公式二倍角的正弦余弦和正切公式sin22cos22tan1tan三角函数的和差化积公式三倍角的正弦余弦和正切公式sin33cos33tan13tan三角函数的积化和差公式121212sin2sincoscossin2222cos112sin2tan233sin4cos4sin3costan32tan3sinsincoscossinsincoscos2sin2cos2cos2sincossincossin22222222sincossinsincossinsinsincoscossincos12coscoscos化asinbcos为一个角的一个三角函数的形式辅助角的三角函数的公式三角函数的反函数是多值函数

三角函数的反函数与反三角函数计算

三角函数的反函数与反三角函数计算在数学中，三角函数是非常重要的一类函数，包括正弦函数、余弦函数、正切函数等。

而三角函数的反函数与反三角函数计算则是在解决各种三角函数相关问题时不可或缺的工具。

本文将详细介绍三角函数的反函数和反三角函数的概念，以及如何进行计算。

一、三角函数的反函数三角函数的反函数是指，通过将三角函数的值作为输入，计算出与之对应的角度。

以正弦函数为例，正常情况下我们通过给定一个角度，计算出其对应的正弦值。

而反函数则是给定一个正弦值，计算出其对应的角度。

以正弦函数sin(x)为例，其反函数记为arcsin(x)或者sin^(-1)(x)。

表示为sin^(-1)(x)=y，其中x为正弦函数的值，y表示对应的角度。

当x∈[-1,1]时，arcsin(x)存在唯一的解。

二、反三角函数的计算反三角函数包括反正弦函数（arcsin），反余弦函数（arccos），反正切函数（arctan）等。

它们的定义和使用方法如下：1. 反正弦函数（arcsin）：反正弦函数arcsin(x)的定义域为[-1,1]，值域为[-π/2,π/2]。

我们可以通过输入正弦函数的值，来计算对应的角度。

例如，如果要计算sin^(-1)(0.5)，即要求正弦函数为0.5时，对应的角度。

我们可以使用计算器或查表得到结果，arcsin(0.5)≈π/6，即30°。

2. 反余弦函数（arccos）：反余弦函数arccos(x)的定义域为[-1,1]，值域为[0,π]。

与反正弦函数类似，我们可以通过输入余弦函数的值，计算对应的角度。

例如，要计算cos^(-1)(0.5)，即要求余弦函数为0.5时，对应的角度。

可以得到arccos(0.5)≈π/3，即60°。

3. 反正切函数（arctan）：反正切函数arctan(x)的定义域为实数集，值域为[-π/2,π/2]。

我们可以通过输入正切函数的值，计算对应的角度。

例如，要计算tan^(-1)(1)，即要求正切函数为1时，对应的角度。

三角函数与反三角函数的关系公式

三角函数与反三角函数的关系公式
三角函数是一类常用函数，它具有几何意义和代数意义，它们可以用来描述物理运动和数学模型的变化。

三角函数可以用来表示图形，它们也可以用来表示数学概念和算法。

反三角函数被定义为将三角函数的值反转的函数，它们具有与三角函数相似的性质。

三角函数和反三角函数之间的关系可以用一个公式来描述：
三角函数与反三角函数的关系公式是：
y=arcsin(sin x)；
y=arccos(cos x)；
y=arctan(tan x)；
这三种关系公式表明，反三角函数和三角函数之间有一种对应关系。

因此，可以通过将三角函数的值反转来计算反三角函数的值。

例如，如果知道sin x=0.5，则可以计算出arcsin(sin x)=arcsin(0.5)=30°。

反三角函数可以用来计算特定的角度，例如计算一个角度的正弦值、余弦值和正切值。

此外，反三角函数还可以用来解决特定的数学问题，如对称性问题，三角形问题，平面几何问题等。

总之，三角函数与反三角函数之间有一种特定的关系公式，即
y=arcsin(sin x)；y=arccos(cos x)；y=arctan(tan x)；。

该公式可以用来计算特定角度的三角函数的值，以及解决一些涉及三角函数的数学问题。