练习二十九试题 (打印)

合集下载

部编人教版语文1年级下册-练习试卷试题【课时练习】(二十九)

语文园地四测评一、将下列字的音节补充完整。

____éi ____uǐ眉腿____iǎo ____uǐ脚嘴二、选择加点字的正确读音，画“√”。

脖．子( ) ( )bō bó手臂．( ) ( )bì pī嘴．巴( ) ( )zuǐ zhuǐ鼻．子( ) ( )bībí三、我来选择。

1．下列词语中“子”读轻声的是( )。

A．胆子B．子女2．下列词语中没有轻声读音的是( )。

A．爸爸B．老爸3．写“我”时，右上方的点要( )。

A．先写B．后写四、先连一连，再按照笔顺规则写一写。

先写点后写点点在正上方点在右上方点在左上方书我五、将古诗补充完整。

寻隐者不遇( )下问童子，言师( )药去。

( )在此山中，( )深不知处。

六、读儿歌，回答问题。

妞妞赶牛妞妞赶牛河边走，牛牛要吃河边柳，妞妞护柳扭牛走，牛牛扭头顶妞妞，妞妞拗不过牛牛，低头捡石头，吓得牛牛扭头走。

1．妞妞扭牛走是因为( )。

A．牛牛要吃河边柳B．牛牛太贪玩了2．牛牛吓得扭头走是因为( )。

A．妞妞捡石头B．妞妞使劲扭参考答案一、m t j z二、bóbìzuǐbí三、1.A 2.B 3.B四、五、松采只云六、1.A 2.A10 端午粽课时测评方案一、将下列字的音节补充完整。

____uān ____ù端据____iàn ____òu念肉二、选择加点字的正确读音，画“√”。

粽．子zònɡzhònɡ中间．jiān jiàn总．会zǒnɡzhǒnɡ带．来dāi dài三、看拼音，写汉字。

wǔ dòu m ǐ zhēn1．中用红与白做的饭香。

yè fēn2．请把这些子成两份。

四、填上合适的词语。

( )的箬竹叶 ( )的枣( )的糯米( )的粽子五、照样子，写句子。

例：一到端午节，外婆总会煮好一锅粽子，盼着我们回去。

人教版九年级数学下册第二十九章综合测试卷及答案

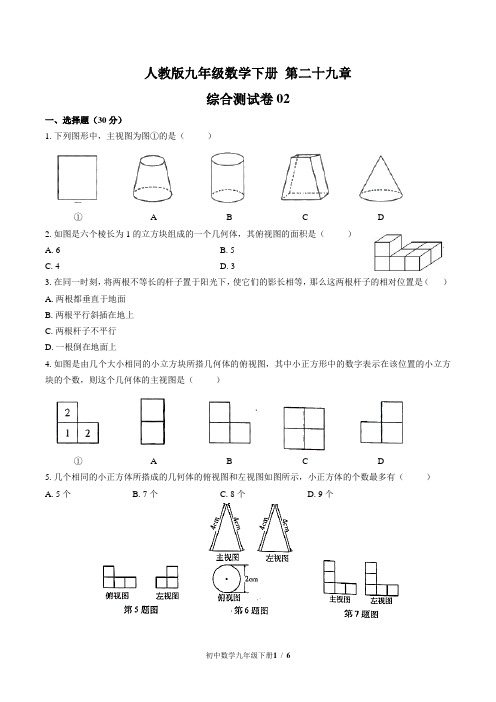
人教版九年级数学下册第二十九章综合测试卷02一、选择题（30分）1.下列图形中，主视图为图①的是（）① A B C D2.如图是六个棱长为1的立方块组成的一个几何体，其俯视图的面积是（）A.6B.5C.4D.33.在同一时刻，将两根不等长的杆子置于阳光下，使它们的影长相等，那么这两根杆子的相对位置是（）A.两根都垂直于地面B.两根平行斜插在地上C.两根杆子不平行D.一根倒在地面上4.如图是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是（）① A B C D5.几个相同的小正方体所搭成的几何体的俯视图和左视图如图所示，小正方体的个数最多有（）A.5个B.7个C.8个D.9个6.一个几何体的三视图如图所示，这个几何体的侧面积为（） A .22π cmB .24π cmC .28π cmD .216π cm7.某几何体由若干个大小相同的小正方体搭成，其主视图与左视图如图所示，则搭成这个几何体的小正方体最少有（） A .4个B .5个C .6个D .7个8.小颗同学到学校领来n 盒粉笔，整齐地擦在讲桌上，其三视图如图所示，则a 的值是（） A .6B .7C .8D .99.如图是某几何体的三视图，根据图中数据，求得该几何体的体积为（） A .60πB .70πC .90πD .160π10.如图是由8个相同的小立方块搭成的几何体，它的三个视图都是22⨯的正方形，若拿掉若干个小立方块后（几何体不倒掉），其三个视图仍都为22⨯的正方形，则最多能拿掉小立方块的个数为（） A .1B .2C .3D .4二、填空题（24分）11.已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积为________.12.如图所示，正方形ABCD 的边长为3 cm ，以直线AB 为轴，将正方形旋转一周，所得几何体的主视图的面积是________.13.几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是________.14.如图是由一些小立方块所搭几何体的三视图，若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个大正方体，至少还需要________个小立方块15.如图是由棱长为1的正方体搭成的积木三视图，则图中棱长为1的正方体的个数是________.15题图第16题图第17题图第18题图16.如图，正三棱柱的底面周长为9，截去一个底面周长为3的正三棱柱，所得几何体的俯视图的周长是________.17.看图，小军小珠之间的距离为2.7 m.他们在同一盏路灯下的是长分别为1.5 m，1.3 m，已知小军、小珠的身高分别为1.8 m，1.5 m，则路灯的高约为________m.（精确到1 m）18.一个由16个完全相同的小立方块搭成的几何体，其最下面一层摆放了9个小立方块，它的主视图和左视图如图所示，那么这个几何体的搭法共有几________种.三、解答题（4+6+8+8+10+10=46分）19.分别将下列四个物体与其相应的俯视图连起来.CD20.如图，小华、小军、小丽同时站在路灯下，其中小军和小丽的影子分别是AB，.（1）请你在图中画出路灯灯泡所在的位置（用点P表示）.（2）画出小华此时在路灯下的影子（用线段EF表示）.21.如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图. （1）小立方体的个数不可能是_________.（填字母） A .6B .7C .8D .9（2）说明你的理由.22.如图是一个由若干个同样大小的正方体所搭成的几何体的俯视图，小正方形中的数字表示在该位置的正方体的个数.（1）请你画出它的主视图和左视图.（2）如果每个正方体的楼长均为2厘米，那么该几何体的表面积是多少？23.根据如图所示的视图（单位：mm ），求该物体的体积.24.如图，AB 和DE 是直立在地面上的两根立柱， 5 m AB =，某一时刻，AB 在阳光下的投影 4 m BC =. （1）请你在图中画出此时DE 在阳光下的投影.（2）在测量AB 的投影长时，同时测出DE 在阳光下的投影长为6 m ，请你计算DE 的长.第二十九章综合测试答案一、 1.【答案】B 2.【答案】B 3.【答案】C 4.【答案】C 5.【答案】B 6.【答案】B 7.【答案】B 8.【答案】B 9.【答案】B 10.【答案】B 二、11.【答案】20π 12.【答案】218 cm 13.【答案】5 14.【答案】54 15.【答案】6 16.【答案】8 17.【答案】3 18.【答案】10 三、19.【答案】解：①—d ②—b ③—a ④—c 21.【答案】解：（1）D（2）根据左视图可以推测1d e ==，a ，b ，c 中至少有一个为2.当a ，b ，c 中一个为2时，小立方体的个数为112116++++=；当a ，b ，c 中两个为2时，小立方体的个数为112217++++=；当a ，b ，c 三个都为2时，小立方体的个数为112228++++=.所以小立方体的个数可能为6，7，8.22.解：（1）如图所示.（2）438152⨯=（平方厘米）.故该几何体的表面积是152平方厘米.23.【答案】解：由三视图知：该几何体是两个圆柱叠放在一起，上面圆柱的底面直径为8，高为4，下面圆柱的底面直径为16，高为16，故体积为()223π (162)16π(82)4 1 088πmm ÷⨯+÷⨯=.24.【答案】解：（1）作法：连接AC ，过点D 作DF AC ∥，交直线BE 于点F ，则EF 就是DE 的投影。

ISPN考试模拟试题(二十九)

ISPN考试模拟试题（三十）Practice Test Questions88. The nurse hears a client calling out for help, hurries down the hallway to the client’s room and finds the client lying on the floor. The nurse performs an assessment, assists the client back to bed, notifies the health care provider of the incident, and completes an incident report. Which statement should the nurse document on the incident report?1. The client fell out of bed.2. The client climbed over the side rails.3. The client was found lying on the floor.4. The client became restless and tried to get out of bed.89. A client is brought to the emergency department by emergency medical services (EMS) after being hit by a car. The name of the client is unknown, and the client has sustained a severe head injury and multiple fractures and is unconscious. An emergency craniotomy is required. Regarding informed consent for the surgical procedure, which is the best action?1. Obtain a court order for the surgical procedure.2. Ask the EMS team to sign the informed consent.3. Transport the victim to the operating room for surgery.4. Call the police to identify the client and locate the family.90. The nurse has just assisted a client back to bed after a fall. The nurse and health care provider have assessed the client and have determined that the client is not injured. After completing the incident report, the nurse should implement which action next?1. Reassess the client.2. Conduct a staff meeting to describe the fall.3. Document in the nurse’s notes that an incident report was completed.4. Contact the nursing supervisor to update information regarding the fall. 88. 3Rationale:The incident report should contain the client’s name, age, and diagnosis. The report should contain a factual description of the incident, any injuries experienced by those involved, and the outcome of the situation. The correct option is the only one that describes the facts as observed by the nurse. Options 1, 2, and 4 are interpretations of the situation and are not factual information as observed by the nurse.Test-Taking Strategy: Focus on the subject, documentation ofevents, and read the information in the question to select when documenting, and avoid including interpretations. This will direct you to the correctoption.Client Needs: Safe and Effective Care Environment89. 3Rationale: In general, there are two situations in which informed consent ofan adult client is not needed. One is when an emergency is present and delaying treatment for the purpose of obtaining informed consent would result in injury or death to the client. The second is when the client waives the right to give informed consent. Option 1 will delay emergency treatment, and option 2 is inappropriate. Although option 4 may be pursued, it is not the best action.Test-Taking Strategy: Note the strategic word best. Recalling that when an emergency is present and a delay in treatment for the purpose of obtaining informed consent could result in injury or death will direct you tothe correct option.Client Needs: Safe and Effective Care Environment90. 1Rationale: After a client’s fall, the nurse must frequently reassess the client because potential complications do not always appearimmediately after that fall. The client’s fall should be treated as private information and shared on a “need to know” basis. Communication regarding the event should involve only the individuals participating in the client’s care. An incident report is aproblem-solving document; however, its completion is not documented in the nurse’s notes. If the nursing supervisor has been made aware of the incident, the supervisor will contact the nurse if status update is necessary.Test-Taking Strategy: Focus on the data in the question and thestrategic word next. Using the steps of the nursing process will direct you to the correct option. Remember that assessment is the first step.。

数学九年级下第二十九章整理与复习练习题

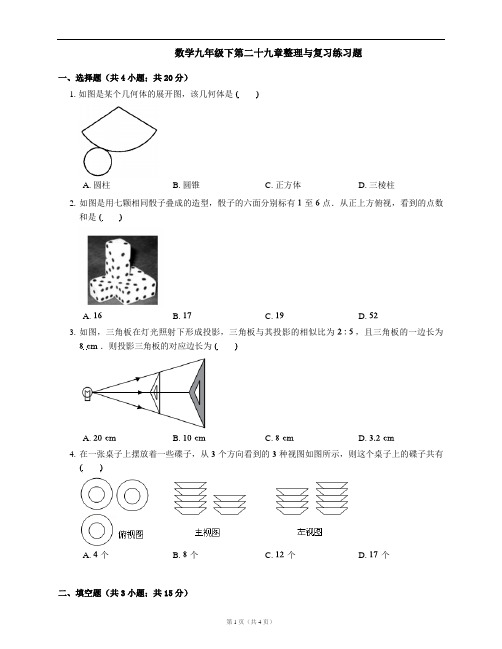
数学九年级下第二十九章整理与复习练习题一、选择题（共4小题；共20分）1. 如图是某个几何体的展开图，该几何体是A. 圆柱B. 圆锥C. 正方体D. 三棱柱2. 如图是用七颗相同骰子叠成的造型，骰子的六面分别标有至点．从正上方俯视，看到的点数和是A. B. C. D.3. 如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为，且三角板的一边长为．则投影三角板的对应边长为A. B.4. 在一张桌子上摆放着一些碟子，从个方向看到的种视图如图所示，则这个桌子上的碟子共有A. 个B. 个C. 个D. 个二、填空题（共3小题；共15分）5. 一圆锥的母线长为，底面半径为，则该圆锥的侧面积为．6. 将一面积为的正方形硬纸片作为侧面围成一个圆柱，则这个圆柱的底面周长为．7. 如图为某几何体的展开图，该几何体的名称是．三、解答题（共3小题；共39分）8. 如图，路灯，的高度都为，路灯柱之间的距离为．身高的小明在线段上行走．试探究：小明在两个路灯下的影子长之和是否为定值?若为定值，则求出此定值；若不为定值，请说明理由．9. 根据下列主视图和俯视图，将对应的物体用线连起来．10. 根据下列几何体的三视图，画出它们的展开图．（1）（2）答案第一部分1. B2. B3. A 【解析】设投影三角尺的对应边长为，三角尺与投影三角尺相似，，解得．4. C 【解析】易得三摞碟子数从左往右分别为，，，则这个桌子上共有个碟子．第二部分5.【解析】圆锥的侧面积．6.7. 圆柱第三部分8. 为定值，值为．9. （）-（C），（）-（D），（）-（B），（）-（A）．10. （1）从左至右分别是：三棱柱的展开图（2）圆柱的展开图。

第二十九期党课试题答案

第二十九期试题答案一、填空题（34分，每空1分）1、长期共存互相监督肝胆相照荣辱与共2、全心全意为人民服务实现共产主义3、中国先进生产力的发展要求、中国先进文化的前进方向、中国最广大人民的根本利益4、马克思列宁主义毛泽东思想邓小平理论“三个代表”重要思想5、党的领导、人民当家作主、依法治国6、立党为公、执政为民7、政治思想组织8、自觉性、统一性、强制性和严肃性9、党章10、坚持社会主义道路坚持人民民主专政坚持中国共产党的领导坚持马克思列宁主义毛泽东思想11、立党之本、执政之基、力量之源12、党风问题、党同人民群众联系问题二、单项选择（8分）1、A2、 A3、B4、A5、C6、A7、A8、B三、多项选择题（8分）1、ABD2、ABCD3、ABCD4、ABEFG5、ABCD6、ABCD7、ABD 8、ABC四、名词解释（25分）1、（共4分）入党誓词：我志愿加入中国共产党，拥护党的纲领，遵守党的章程，履行党员义务，（1分）执行党的决定，严守党的纪律，保守党的秘密（1分），对党忠诚，积极工作（1分），为共产主义奋斗终身，随时准备为党和人民牺牲一切，永不叛党（1分）。

2、（共5分中国共产党中是国工人阶级的先锋队（1分），同时也是中国人民和中华民族的先锋队，是中国特色社会主义事业的领导核心，（1分）代表中国先进生产力的发展要求，（1分）代表中国先进文化的发展方向，（1分）代表中国最广大人民的根本利益。

（1分）3、（共4分）年满十八岁的中国工人、农民、军人、知识分子和其他社会阶层的先进分子，（1分）承认党的纲领和章程，（1分）愿意参加党的一个组织并在其中积极工作、执行党的决议和按期缴纳党费的，（1分）可以申请加入中国共产党。

（1分）4、（共3分）实现推进现代化建设（1分）、完成祖国统一（1分）、维护世界和平与促进共同发展（1分）5、（共3分）科学发展观是同马克思列宁主义、毛泽东思想、邓小平理论和“三个代表”重要思想既一脉相承又与时俱进的科学理念，（1分）是国我经济社会发展的重要指导方针，（1分）是发展中国特色社会主义必须坚持和贯彻的重大战略思想。

人教版九年级数学下册第二十九章达标测试卷含答案

人教版九年级数学下册第二十九章达标测试卷一、选择题(每题2分，共20分)1．一个矩形木框在太阳光的照射下，在地面上的投影不可能是()2．下列关于投影与视图的说法正确的是()A．平行投影中的光线是聚成一点的B．线段的正投影还是线段C．三视图都是大小相同的圆的几何体是球D．正三棱柱的俯视图是正三角形3．中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯，如图，甲木构件带有榫头，乙木构件带有卯，两个构件可完全咬合，则乙木构件的俯视图是()4.如图，树AB在路灯O的照射下形成投影AC，若树高AB＝2 m，树影AC＝3 m，树与路灯的水平距离AP＝4.5 m，则路灯的高度OP是()A．3 m B．4 m C．5 m D．6 m5．一个几何体的三视图如图所示，则这个几何体是()6．如图，在房檐E处安有一台监视器，房子前有一面落地的广告牌，那么监视器的盲区是()A．△ACE B．△ADF C．△ABD D．四边形BCED7．如图，太阳光线与地面成60°的角，照射在放置在地面上的一个皮球上，皮球在地面上的投影长是20 3，则皮球的直径是()A．15 B．8 3 C．10 3 D．30(第7题)(第9题)(第10题)8.在平面直角坐标系中，点P(2，4)是一个光源，木杆AB两端的坐标分别是(1，2)，(4，1)，则木杆AB在x轴上的投影A′B′的长是()A．4 B.143 C.92D．59．如图，将由6个棱长为1的小正方体组成的几何体在桌面上顺时针旋转90°后，左视图的面积为()A．3 B．4 C．5 D．610．如图是某风车的示意图，其大小、形状相同的四个叶片均匀分布，点M在旋转中心O的正下方．某一时刻，太阳光恰好垂直照射叶片OA，OB，叶片影子为线段CD，测得MC＝8.5米，CD＝13米，此时垂直于地面的标杆EF与它的影子FG的长度之比为23(其中点M，C，D，F，G在同一直线上)，则OM的长为()A．10米B．13米C.13米D．20米二、填空题(每题3分，共18分)11．广场上，一个大型字母宣传牌垂直于地面放置，其投影如图所示，则该投影属于____________．(填“平行投影”或“中心投影”)(第11题)(第13题) (第14题)12.在①长方体、②球、③圆锥、④圆柱、⑤正方体、⑥三棱柱这六种几何体中，其主视图、左视图、俯视图可以完全相同的是__________(填序号)．13．一个几何体的主视图和俯视图如图所示，若这个几何体最多由m个小正方体组成，最少由n个小正方体组成，则m＋n＝________．14．公元前6世纪，古希腊学者泰勒斯用图①的方法巧测金字塔的高度．如图②，小明仿照这个方法，测量圆锥形小山包的高度，已知圆锥底面周长为62.8 m．先在小山包旁边立起一根木棒，当木棒影子的长度等于木棒高度时，测得AB的长为23 m(直线AB过圆锥底面圆的圆心)，则圆锥形小山包的高度约为________m(π取3.14)．15．如图是一个三棱柱的三视图，在△EFG中，EF＝6 cm，EG＝10 cm，∠EGF ＝30°，则AB的长为________cm.(第15题) (第16题)16.在同一时刻两根垂直于水平地面的木杆在太阳光下的影子如图所示，其中木杆AB＝2.5 m，它的影子BC＝2 m，木杆PQ的影子有一部分落在了墙上(MN)，PM＝1.6 m，MN＝1 m，则木杆PQ的长度为________．三、解答题(17题6分，18～21题每题8分，22，23题每题10分，24，25题每题12分，共82分)17．(6分)把下图中的几何体与它们对应的三视图用线连接起来．18.(8分)如图所示的图形是一个水平放置的直三棱柱被斜着截去一部分后形成的，请画出它的主视图、左视图和俯视图．19．(8分)一个几何体的三视图如图所示．(1)写出这个几何体的名称；(2)求这个几何体侧面展开图的圆心角；(3)求这个几何体的全面积．20.(8分)如图是某时刻的太阳光线，光线与水平面的夹角为45°.小星身高1.6米．(1)若小星正站在水平地面上的点A处，则他的影长为多少米？(2)若小星来到一个倾斜角为30°的坡面底端B处，则他在坡面上前进多少米时，他的影子恰好都落在坡面上？21．(8分)学校食堂厨房的桌子上整齐地摆放着若干个相同规格的菜碟，每一摞菜碟的高度与菜碟的个数的关系如表所示．菜碟的个数菜碟的高度(单位：cm)1 323＋1.833＋3.643＋5.4……(1)把x个菜碟放成一摞时，这一摞菜碟的高度为________(用含x的式子表示)；(2)如图所示，是几摞菜碟的三视图，厨师想把它们整齐地叠成一摞，求叠成一摞后的高度．22．(10分)如图，两栋居民楼之间的距离CD＝45 m，楼AC和BD均为11层，每层楼高为3 m．上午某时刻，太阳光线GB与水平面的夹角为30°，此刻楼BD的影子会遮挡到楼AC的第几层？(参考数据：3≈1.7，2≈1.4)23．(10分)如图所示，有4张除了正面图案不同，其余都相同的卡片，将这4张卡片背面朝上洗匀．(1)若小李从中抽一张卡片，求抽到的卡片上所示的立体图形的主视图为矩形的概率；(2)若小李先从中随机抽出一张后放回并洗匀，小张再随机抽出一张，请用列表法或画树状图法求两人抽到的卡片上所示的立体图形的主视图都是矩形的概率．24．(12分)按要求完成下列问题．(1)如图①，它是由6个同样大小的正方体摆成的几何体．将正方体①移走后，新几何体的三视图与原几何体的三视图相比，哪一个视图没有发生改变？(2)如图②，请你借助虚线网格(甲)画出该几何体的俯视图．(3)如图③，它是由几个小正方形组成的俯视图，小正方形上的数字表示该位置上的正方体的个数，请你借助虚线网格(乙)画出该几何体的主视图．(4)如图④，它是由8个大小相同的正方体组成的几何体的主视图和俯视图，请你借助虚线网格(丙)画出该几何体的左视图．25．(12分)如图①是一个直四棱柱，如图②是它的三视图，其俯视图是等腰梯形．(1)根据图②中给出的数据，可得俯视图(等腰梯形)的高为________，腰长为________；(2)主视图和左视图中a＝________，b＝________，c＝________，d＝________；(3)请你根据图①②和问题(1)中的结果，计算这个直四棱柱的侧面积．(结果可保留根号)答案一、1.B 2.C 3.C 4.C 5.D 6.C7.D8.B9.B10．A点拨：如图，过点O作OP∥BD，交MG于P，过P作PN⊥BD于N，则OB＝PN.∵AC∥BD∥EG，∴AC∥OP∥BD∥EG，∴OAOB＝CPPD，∠EGF＝∠OPM，∴tan∠EGF＝tan∠OPM.∵OA＝OB，∴CP＝PD＝12CD＝6.5米，∴MP＝CM＋CP＝8.5＋6.5＝15(米)，∴EFFG＝OMMP＝23，∴OM＝23×15＝10(米)．二、11.中心投影12.②⑤13.1614.3315．5点拨：如图，过点E作EH⊥FG交FG于点H.∵EH⊥FG，∠EGF＝30°，EG＝10 cm，∴EH＝12×EG＝12×10＝5(cm)，由题中三视图可得，AB＝EH＝5 cm，故答案为5.16．3 m点拨：如图，过点N作ND⊥PQ于点D，则易知四边形DPMN是矩形．∴DN＝PM，PD＝MN.由题知，BCAB＝DNQD，∵AB＝2.5 m，BC＝2 m，DN＝PM＝1.6 m，∴QD＝AB·DNBC＝2.5×1.62＝2(m)，∴PQ＝QD＋DP＝QD＋NM＝2＋1＝3(m)．三、17.解：如图所示．18．解：如图所示．19．解：(1)该几何体为圆锥．(2)由题图上数据知圆锥的底面圆的直径为4，母线长为6，设这个几何体的侧面展开图的圆心角为n°，则π×4＝nπ×6 180，所以n＝120，所以这个几何体侧面展开图的圆心角为120°.(3)该几何体的全面积为S侧＋S底＝π×42×6＋π×⎝⎛⎭⎪⎫422＝16π.20．解：(1)如图，由题意得AD＝1.6米，∠DCA＝45°，AD⊥CA，∴AC＝AD＝1.6米．答：他的影长为1.6米．(2)如图，由题意得EF＝1.6米．∵∠FBG＝30°，FG⊥BG，∴设FG ＝x 米，则BF ＝2x 米，∴BG ＝3x 米， ∴EG ＝EF ＋FG ＝(x ＋1.6)米，在Rt △EBG 中，∠EBG ＝45°，∴BG ＝EG ，∴3x ＝1.6＋x ，解得x ＝45(3＋1)， ∴BF ＝2x ＝2×45(3＋1)＝85(3＋1)(米)．答：他在坡面上前进85(3＋1)米时，他的影子恰好都落在坡面上． 21．解：(1)(1.8x ＋1.2)cm(2)由题中三视图可知，共有7＋4＋3＝14(个)菜碟，所以叠成一摞后的高度是1.8×14＋1.2＝26.4(cm)．22．解：设太阳光线GB 交AC 于点F ，过F 作FH ⊥BD 于点H ，如图．由题意知，AC ＝BD ＝3×11＝33(m)，易知四边形FCDH 是矩形，∠BFH ＝30°，∴FH ＝CD ＝45 m ，在Rt △BFH 中，tan ∠BFH ＝BH FH ＝BH 45＝33，∴BH ＝45×33＝15 3≈25.5(m)， ∴FC ＝HD ＝BD －BH ≈33－25.5＝7.5(m)． ∵7.5÷3＝2.5，∴在2层的上面，即第3层， ∴此刻楼BD 的影子会遮挡到楼AC 的第3层．23．解：(1)∵球的主视图为圆，长方体的主视图是矩形，圆锥的主视图为等腰三角形，圆柱的主视图为矩形，每张卡片被抽到是等可能的，∴小李从中抽一张卡片，抽到的卡片上所示的立体图形的主视图为矩形的概率为 24＝12.(2)列表可得，小张小李A B C DA (A，A) (A，B) (A，C) (A，D)B (B，A) (B，B) (B，C) (B，D)C (C，A) (C，B) (C，C) (C，D)D (D，A) (D，B) (D，C) (D，D)由表可知，共有16种等可能的结果，其中两人抽到的卡片上所示的立体图形的主视图都是矩形的结果有4种，所以两人抽到的卡片上所示的立体图形的主视图都是矩形的概率为416，即14.24．解：(1)将正方体①移走后，新几何体的三视图与原几何体的三视图相比，左视图没有发生改变．(2)如图甲所示．(3)如图乙所示．(4)如图丙所示．25．解：(1)6；4 3(2)2 3；3 3；2 3；6(3)这个直四棱柱的侧面积为3 3×20＋7 3×20＋2×4 3×20＝60 3＋1403＋160 3＝360 3.11。

报关员考试第六类第二十九章商品归类习题

第⼆⼗九章有机化学品⼀、本章商品范围概述除少数品⽇条⽂另有规定的以外,本章仅包括单独的⼰有化学定义的化合物。

但应注意,不是所有的单独的已有化学定义的化合物均归⼊第⼆⼗九章,也不是所有的⾮单独的已有化学定义的化合物便不归⼊本章。

本章分成13个分章,共有42个品⽬O其品⽬结构按商品分⼦结构从简单到复杂排列。

即(1)短(第⼀分章);(2)含氧基化合物(第⼆分章~第⼋分章);(3)含氮基化合物(第九分章);(4)有机-元机化合物、杂环化合物、核酸、磺眈胶(第⼗分章);(5)从动植物料提取的初始物质(第⼗⼀分章~第⼗⼆分章);(6)其他有机物(第⼗三分章)。

⼆、本章归类注意点 1.第⼆⼗九章注释⼀(⼀)规定归⼊本章的产品必须是"单独的已有化学定义的有机化合物,不论是否含有杂质"。

对于"单独的已有化学定义的化合物",在第⼆⼗⼋章中重点放在"化学计量⽐"上,⽽在第⼆⼗九章则放在其结构上,即应为"已知化学结构且在⽣产(包括纯化)过程中未故意加⼊其他物质的化学化合物"。

2.杂质的主要类型及是否可视为本章所允许的杂质,原则与第⼆⼗⼋章所述⼀样。

三、商品归类练习题及解析 1.维⽣素B2药丸2.维⽣素C和维⽣素E的混合物原药3.纯净丙三醇(俗称⽢油) 4.500毫升瓶装化学纯级⼄酸⼄醋 5.福尔马林 6.头拖拉皖(先锋霉素类抗菌素原药) 7.奎宁碱 8.尼龙-66盐 9.磺胶略院(磺胶类原药,通式为NH2-C6H4-S02NHR) 10.作饲料添加剂⽤的化学纯氨基酸(⾮零售包装) 11.作饲料添加剂⽤的天然维⽣素D浓缩物和天然维⽣素A浓缩物的混合物(⾮零售包装、未配定剂量) 12.氢化可的松(未配定剂量,⾮零售包装) 答案及解析 1.[3004.5000]维⽣素B2是从酿酒及发酵残余物以及⽜肝中提取,但常通过合成制得,为橙黄⾊结晶体。

三视图练习题（含答案）

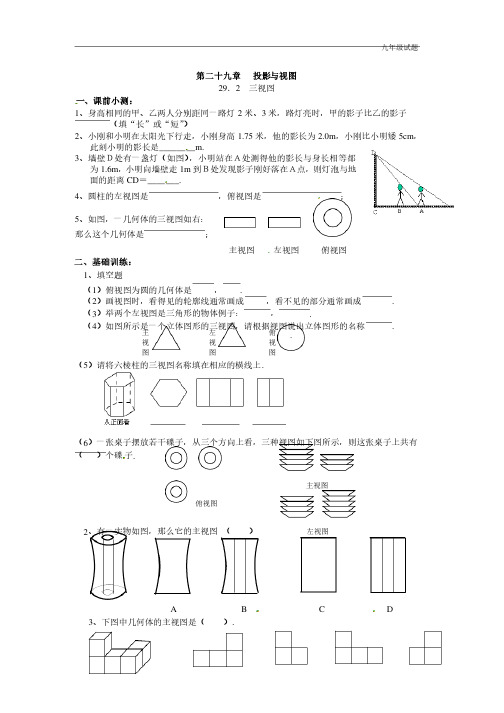
第二十九章投影与视图29．2 三视图一、课前小测：1、身高相同的甲、乙两人分别距同一路灯2米、3米，路灯亮时，甲的影子比乙的影子（填“长”或“短”）2、小刚和小明在太阳光下行走，小刚身高1.75米，他的影长为2.0m ，小刚比小明矮5cm ，此刻小明的影长是________m.3、墙壁Ｄ处有一盏灯（如图），小明站在Ａ处测得他的影长与身长相等都为1.6m ，小明向墙壁走1m 到Ｂ处发现影子刚好落在Ａ点，到Ｂ处发现影子刚好落在Ａ点，则灯泡与地则灯泡与地面的距离CD ＝_______.4、圆柱的左视图是，俯视图是；5、如图，一几何体的三视图如右：那么这个几何体是；主视图左视图俯视图二、基础训练：1、填空题（1）俯视图为圆的几何体是，.（2）画视图时，看得见的轮廓线通常画成，看不见的部分通常画成. （3）举两个左视图是三角形的物体例子：，.（4）如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称.（5）请将六棱柱的三视图名称填在相应的横线上.（6）一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有（）个碟子.2、有一实物如图，那么它的主视图（）AB C D 3、下图中几何体的主视图是（）. 俯视图主视图左视图主视图左视图俯视图俯视图主（正）视图左视图(A) (B) (C ) (D)4、若干桶方便面摆放在桌子上，实物图片左边所给的是它的三视图，则这一堆方便面共有（有（）（A ）5桶（B ） 6桶（C ）9桶（D ）12桶5、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图，若图中“2”在正方体的前面，则这个正方体的后面是方体的前面，则这个正方体的后面是 ( ) ( )A ．OB O B．． 6C 6 C．快．快．快D D D．乐．乐．乐三、综合训练：1．小明从正面观察下图所示的两个物体，看到的是（．小明从正面观察下图所示的两个物体，看到的是（）2、右图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数是（的小立方块的个数是（）A 5个B 6个C 7个D 8个3、如果用□表示1个立方体，用表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是（）4、下面是空心圆柱在指定方向上的视图，正确的是…（、下面是空心圆柱在指定方向上的视图，正确的是…（）B AC D正面 A B C D (A) (B) (C) (D)5、画出下面实物的三视图：实物的三视图：第二十九章投影与视图29．2 三视图三视图参考答案：考答案：课前小测：课前小测：1、短、短2、35723、15644、矩形，圆、矩形，圆5、空心圆柱、空心圆柱二、基础训练：二、基础训练：1、(1)球，圆柱体；（2）实线，虚线；（3）圆锥，正四棱锥，倒放的正三棱柱等；（4）圆锥；（5）俯视图，正视图，左视图；（6）12.2、A ；3、C4、B5、B三、综合训练：三、综合训练：1、C2、D3、B ；4、A ；5、题图：图：主视图左视图俯视图。

人教版-数学-九年级下册--第二十九章 29.1～29.3 综合训练(含答案)

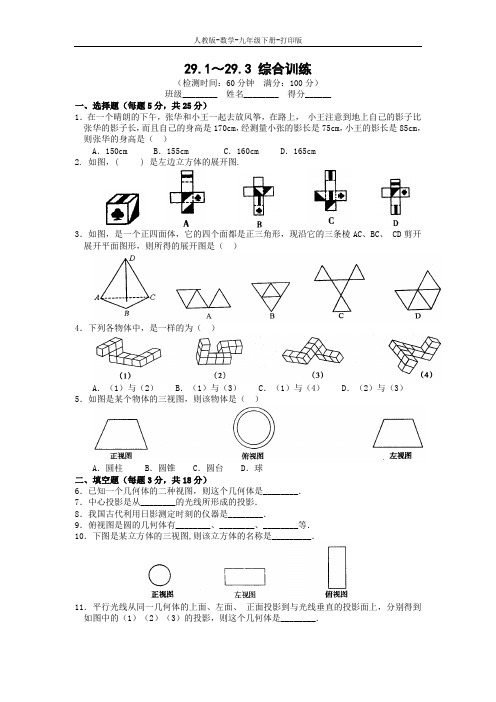
29.1～29.3 综合训练（检测时间：60分钟满分：100分）班级________ 姓名________ 得分______一、选择题（每题5分，共25分）1．在一个晴朗的下午，张华和小王一起去放风筝，在路上，•小王注意到地上自己的影子比张华的影子长，而且自己的身高是170cm，经测量小张的影长是75cm，小王的影长是85cm，则张华的身高是（）A．150cm B．155cm C．160cm D．165cm2. 如图，( ) 是左边立方体的展开图.3．如图，是一个正四面体，它的四个面都是正三角形，现沿它的三条棱AC、BC、•CD剪开展开平面图形，则所得的展开图是（）4．下列各物体中，是一样的为（）A．（1）与（2） B．（1）与（3） C．（1）与（4） D．（2）与（3）5．如图是某个物体的三视图，则该物体是（）A．圆柱 B．圆锥 C．圆台 D．球二、填空题（每题3分，共18分）6．已知一个几何体的二种视图，则这个几何体是________．7．中心投影是从________的光线所形成的投影．8．我国古代利用日影测定时刻的仪器是________．9．俯视图是圆的几何体有________、________、________等．10．下图是某立方体的三视图,则该立方体的名称是_________．11．平行光线从同一几何体的上面、左面、•正面投影到与光线垂直的投影面上，分别得到如图中的（1）（2）（3）的投影，则这个几何体是________．三、解答题（57分）12．（9分）小明和他的同桌李华在太阳下行走，李华身高1.60m，他的影长2.0m，小明比他高5cm，此时小明的影长为多少米？13．（8分）小明吃早饭后进行植树，他先后栽了一棵樟树和一棵柳树，如图，•请你猜一猜他先栽的一棵是什么树？请说明你的理由．14．（10分）连线，根据下列主视图和俯视图（如图），用线连结对应的物体．15．（10分）（作图题）根据要求画出图中立体图形的视图．16．（10分）如图（2）是图（1）的主视图和俯视图，在视图上确定点A、B、C•的位置并画出左视图．17．（10分）如图是由几个小立方体所搭几何体的左视图，小正方形中的数学表示在该位置上的小立方块的个数，请你画出相应几何体的主视图和俯视图．答案:1．A 2．B 3．B 4．B 5．C6．不能确定7．一点发出8．日晷9．圆柱 •圆锥圆台10．圆柱体11．圆锥12．由于太阳光是平行光线，并且小华身高与影长的比等于小明身高与影长的比，设小明影长为x，则1.60 1.600.05 2x+=，∴x=2.0625（m）13．•先栽的一棵是樟树，因为太阳光是东起西落，故树的影子是由西向东，而在上午，影子由西→西北→北移动，且影子的大小是由大至小，故先栽的一棵是樟树．15．如答图16．•点略，左视图如答图17．如答图，（此题还有其它多种画法，满足题意即可）。

数学八下全品学练考华师版课时作业29

数学八下全品学练考华师版课时作业291、14．将△ABC的三个顶点坐标的横坐标都乘以-1，并保持纵坐标不变，则所得图形与原图形的关系是（）[单选题] *A．关于x轴对称B．关于y轴对称(正确答案)C．关于原点对称D．将原图形沿x轴的负方向平移了1个单位2、14．在防治新型冠状病毒的例行体温检查中，检查人员将高出37℃的部分记作正数，将低于37℃的部分记作负数，体温正好是37℃时记作“0”。

记录一被测人员在一周内的体温测量结果分别为+1，-3，-5，+1，-6，+2，-4，那么，该被测者这一周中测量体温的平均值是（??）[单选题] *A．1℃B．31℃C．8℃(正确答案)D．69℃3、x+2=3的解为（）[单选题] *A. x=1(正确答案)B. x=2C. x=3D. x=44、两个有理数相加，如果和小于每一个加数，那么[单选题] *A.这两个加数同为负数(正确答案)B.这两个加数同为正数C.这两个加数中有一个负数，一个正数D.这两个加数中有一个为零5、23、在直角坐标平面内有点A，B，C，D，那么四边形ABCD的面积等于（）[单选题]A. 1B. 2C. 4(正确答案)D. 2.56、已知a+b=3,则代数式(a+b)(a-b)+6b的值是(? ????) [单选题] *A. -3B. 3C. -9D. 9(正确答案)7、已知2x=8,2y=4,则2x+y=（）[单选题] *A 、32(正确答案)B、33C、16D、48、7. 3位同学准备去学校饭堂吃午饭，学校饭堂有2个，则不同的去法共有( )种．[单选题] *A. 2＋3=5种B.2×3=6种C.3×3=9种D.2×2×2=8种(正确答案)9、20．已知集合A={x|x2(x的平方)－2 023x＋2 022<0}，B={x|x<a}，若A?B，则实数a的取值范围是___. [单选题] *A a≥2022(正确答案)B a>2022C a<2022D a≥110、f（x）=-2x+5在x=1处的函数值为（）[单选题] *A、-3B、-4C、5D、3(正确答案)11、5．将△ABC的三个顶点的横坐标乘以－1，纵坐标不变，则所得图形与原图的关系是( ) [单选题] *A．关于x轴对称B．关于y轴对称(正确答案)C．关于原点对称D．将原图向x轴的负方向平移了1个单位长度12、32、在、、、、、3.14这六个数中, 无理数的个数有（）[单选题] *A) 1 个;B) 2 个; (正确答案)C) 3 个;D) 4 个.13、已知二次函数f（x）=2x2-x+2，那么f（1）的值为（）。

河北省保定市高阳中学2014届高三下学期周练(二十九)数学试题

河北省保定市高阳中学2014届高三下学期周练（二十九）数学试题１．设集合{}R x x x A ∈≥-=,31, ⎭⎬⎫⎩⎨⎧∈≥+=R x x x x B ,03, 则A∩B= ．２．在等比数列{}n a 中，32,317483－=-=+a a a a ，公比q 是整数，则10a = ．３．已知0<2a<1,若A=1+a 2, B=a-11, 则A 与B 的大小关系是．４．在数列{}n a 中，已知51=a ，当2≥n 时，5511+=--n n n a a a ，那么=50a ．５．正数,x y 满足21x y +=，则yx 11+的最小值为 __．６．已知数列{}n a，)n a n +=∈N ，且数列{}n a 的前n 项和为9n s =，那么n 的值为__________．７．已知函数86)(2++-=k kx kx x f 的定义域是R ，则实数k 的取值范围是 _ ．８．等差数列的前15项的和为-5，前45项的和为30，则前30项的和为________．９．已知两个等差数列{},{}n n a b 的前n 项的和分别为,n n S T ，且723n n S n T n +==+，则 55a b ＝_ ． 10．若{}n a 是等差数列，首项10,a >200320040a a +>，200320040a a ⋅<，则使前n 项和0n S >成立的最大正整数n 是．11．．若正数a 、b 满足ab=a+b+3, 则ab 的取值范围是．12．设a ≥0，≥0，且1222=+b a ，则21b a +的最大值为____ __． 13．不等式(0x -≥的解集是．14．若不等式)1(122->-x m x 对满足2≤m 的所有m 都成立，则x 的取值范围．答案1． ),4[)3,(+∞--∞2．—1283． A <B4．101.5． 3+__6． 997． [0,1]8． 59． 651210．400611．[9,)+∞12． 423 13．{|3x x ≥或1}x =-14．（712-,312+）。

人教版数学九年级下册第二十九章基础过关测试卷(解析版)

人教版数学九年级下册第二十九章基础过关测试卷一、选择题1．（2019湖北天门中考，2）如图所示的正六棱柱的主视图是( ) 2．（2019广西贺州中考，4）如图是某几何体的三视图，则该几何体是( )A．长方体B．正方体C．三棱柱D．圆柱3．如图所示，投影线的方向如箭头所示，它的正投影是( )4．（2019江苏镇江中考，14）一个物体如图所示，它的俯视图是( )5．六个大小相同的正方体搭成的几何体如图所示，其主视图是( )6．在同一时刻，两根长度不等的木杆置于阳光下，但它们的影长相等，则它们的相对位置是( )A．两根木杆都垂直于地面B．两根木杆平行地斜插在地面上C．两根木杆不平行D．一根木杆倒在地上7．如图，小明夜晚从路灯下的A处走到B处，在这一过程中，他在路上的影子( )A．逐渐变长B．逐渐变短C．长度不变D．先变短后变长8．（2019山东滨州中考，4）如图所示，一个几何体由5个大小相同、棱长为1的小正方体搭成，下列说法正确的是( )A．主视图的面积为4 B．左视图的面积为4C．俯视图的面积为3 D．三种视图的面积都是49．如图是一个由若干个小正方体组成的几何体的三视图，则该几何体最多可由几个小正方体组合而成？( )A．6个B．9个C．11个D．13个10.如图是某几何体的三视图，则该几何体的体积是( )A.318B．3108C．354D．3216二、填空题11.太阳光透过一个矩形玻璃窗户，照射在地面上，影子的形状可能是________.（说出一种形状即可）12.在如图所示的几何体中，其三视图中有矩形的是____．（写出所有正确答案的序号）13.如图所示是6个棱长为1的立方体组成的几何体，其俯视图的面积是____.14.一天小明和爸爸在阳光下的操场上散步，小明测得在同一时刻他和爸爸的影子长度分别是2.1 m和2m，已知小明爸爸的身高是1.8 m，去年两人一样高，则小明今年长高了____cm.15.如图，已知路灯离地面的高度AB为4.8 m，身高为1.6 m的小明垂直站立在D处的影长为2m，那么此时小明离AB的距离BD为____m．16.如图，一电线杆AB的高度为10米，当太阳光线与地面的夹角为60°时，其影长AC为____米．17.如图是一个长方体的主视图、左视图与俯视图（单位：cm），根据图中数据，计算这个长方体的体积是____.18.如果一个圆锥的主视图是等边三角形，俯视图是面积为4πcm²的圆（有圆心），那么这个圆锥的高是____.三、解答题19.画出如图所示几何体的三视图．20.如图所示，太阳光线AC和A'C'是平行的，同一时刻两个建筑物在太阳下的影子一样长，那么这两个建筑物是否一样高？请说明理由．21.一个几何体的三视图如图所示（单位：cm），根据图示的数据计算该几何体的侧面积和体积．22.如图所示，小欣站在灯光下，投在地面上的影长AB= 2.4 m，蹲下来，则影长AC= 1.05 m，已知小欣的身高AD= 1.6 m，蹲下时的高度等于站立高度的一半，求灯离地面的高度PH.23.学校厨房的桌子上整齐地摆放着若干相同规格的碟子，一摞碟子的个数与累积高度的关系如下表：(1)当一摞碟子有x个时，请写出此时的累积高度（用含x的式子表示）；(2)桌子上有一些碟子，其三视图如图所示，厨房师傅想把这些碟子全部叠成一摞，求叠成一摞后的累积高度．第二十九章基础过关测试卷1．B题图所示的正六棱柱的主视图是矩形，看见的两条棱用实线表示．故选B．2．B 三个视图为全等的正方形，则该几何体是正方体，故选B．3．A该几何体的正投影为矩形，看得见的棱用实线表示，故选A．4．D该几何体可看成两部分，下面的长方体的俯视图是矩形，上方的长方体的俯视图也是矩形，看得见的棱用实线表示．故选D.5．C从正面看有三列，从左起第一列有一个正方形，第二列有两个正方形，第三列有一个正方形，C符合题意．故选C.6．C在同一时刻，两根木杆置于阳光下，它们的影长相等，那么这两根木杆的顶部到地面的垂直距离相等，又因为木杆的长度不等，所以两根木杆不平行，故选C．7．A当他从A处走到B处时，光线与地面的夹角越来越小，小明在地面上的影子越来越长，故选A．8．A观察该几何体可知，主视图有四个小正方形，面积为4；左视图有3个小正方形，面积为3；俯视图有四个小正方形，面积为4，A正确.故选A.9．C由三视图知该几何体由3层小正方体组成，最下面一层有6个小正方体，中间一层最多有4个小正方体，最上面一层有1个小正方体，故最多有6+4+1= 11个小正方体，故选C．10．B由三视图可得，该几何体是正六棱柱，其底面正六边形的边长为6，高是2，所以该几何体的体积=6×43×6²×2= 1083，故选B．11．答案：矩形（或正方形或平行四边形）解析：矩形玻璃窗户在阳光下的投影形状的对边应该是相等的，所以影子的形状可能是矩形或正方形或平行四边形．12．答案：①②解析：长方体的主视图、左视图、俯视图都是矩形；圆柱的主视图是矩形，左视图是矩形，俯视图是圆；圆锥的主视图、左视图是等腰三角形，俯视图是带有圆心的圆．13.答案：5解析：由题中几何体知俯视图由5个正方形组成，故其俯视图的面积为5．14.答案：9解析：设小明今年的身高是x m，由题意得21.28.1=x，解得x= 1.89．1.89-1.8=0.09(m)，0.09 m=9 cm，故小明今年长高了9 cm.15．答案：4解析：易知DE∥AB，∴△CDE∽△CBA，∴ABDECBCD=，即8.46.12=CB∴CB=6 m．∴BD=BC-CD=6-2=4(m).16.答案：3310解析：在Rt△ABC中，∠ACB= 60°，∵AB=10米，tan 60°= 310==ACACAB，∴AC=3310米．17．答案：24 cm³解析：由该几何体的主视图及左视图都是矩形，俯视图也是一个矩形，可知这个几何体是一个长方体，故该几何体的体积为3×2×4= 24 cm³.18．答案：23cm解析：设圆锥的底面圆的半径为r cm，则πr²= 4π，解得r=2，因为圆锥的主视图是等边三角形，所以圆锥的母线长为4 cm，所以该圆锥的高=2422 =23cm.19.解析：该几何体的三视图如图所示．20．解析：这两个建筑物一样高．理由：∵AB⊥BC，A'B'⊥B'C'．∴∠ABC=∠A'B'C'= 90°．∵AC∥A'C'，∴∠ACB= ∠A'C'B'．在△ABC和△A'B'C'中，．∴△ABC≌△A'B'C'(ASA)，∴AB=A’B’.故这两个建筑物一样高，21.解析：根据三视图可得该几何体是一个三棱柱，其侧面积为3×4×6=72(cm²).体积为21×4×4sin 60°×6= 243( cm³)．22.解析：∵M是AD的中点，∴AM=MD.∵AD∥PH，∴△ADB∽△HPB，△AMC∽△HPC．∴AB: HB=AD: PH，AC: AM=HC: PH，即2.4:(2.4+AH)= 1.6: PH，1.05: 0.8=(1.05+HA):PH，解得PH= 7.2 m．故灯离地面的高度PH为7.2 m．23．解析：(1)由题表可知，每增加一个碟子累积高度增加1.5 cm，当一摞碟子有x个时，累积高度为2+1.5(x-1)=(1.5x+0.5) cm．(2)由题图可知，共有3摞，左前一摞有4个碟子，左后一摞有5个碟子，右边一摞有3个碟子，共有3+4+5= 12个碟子，叠成一摞后的累积高度为1.5×12+0.5=18.5(cm)．。

2022年精品解析冀教版九年级数学下册第二十九章直线与圆的位置关系课时练习试卷(含答案解析)

九年级数学下册第二十九章直线与圆的位置关系课时练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，一把宽为2cm的刻度尺（单位：cm），放在一个圆形茶杯的杯口上，刻度尺的一边与杯口外沿相切，另一边与杯口外沿两个交点处的读数恰好是2和10，茶杯的杯口外沿半径为（）A．10cm B．8cm C．6cm D．5cm2、如图，AB是⊙O的直径，点M在BA的延长线上，MA＝AO，MD与⊙O相切于点D，BC⊥AB交MD的延长线于点C，若⊙O的半径为2，则BC的长是（）A ．4B ．C ．D ．33、如图，BE 是⊙O 的直径，点A 和点D 是⊙O 上的两点，过点A 作O 的切线交BE 延长线于点C ，若∠ADE =36°，则∠C 的度数是（）A ．18°B ．28°C ．36°D ．45°4、矩形ABCD 中，AB ＝8，BC ＝4，点P 在边AB 上，且AP ＝3，如果⊙P 是以点P 为圆心，PD 为半径的圆，那么下列判断正确的是（）A ．点B 、C 均在⊙P 内B ．点B 在⊙P 上、点C 在⊙P 内 C ．点B 、C 均在⊙P 外D ．点B 在⊙P 上、点C 在⊙P 外5、如图，面积为18的正方形ABCD 内接于⊙O ，则⊙O 的半径为（）A ．32 BC ．3D ．6、下列四个命题中，真命题是（）A ．相等的圆心角所对的两条弦相等B ．三角形的内心是到三角形三边距离相等的点C ．平分弦的直径一定垂直于这条弦D ．等弧就是长度相等的弧7、下面四个结论正确的是（）A ．度数相等的弧是等弧B ．三点确定一个圆C ．在同圆或等圆中，圆心角是圆周角的2倍D ．三角形的外心到三角形的三个顶点的距离相等8、在Rt ABC 中，90C ∠=︒，3AC =cm ，4BC =cm ．以C 为圆心，r 为半径的C 与直线AB 相切．则r 的取值正确的是（）A ．2cmB ．2.4cmC ．3cmD ．3.5cm9、如图，P 为正六边形ABCDEF 边上一动点，点P 从点D 出发，沿六边形的边以1cm/s 的速度按逆时针方向运动，运动到点C 停止．设点P 的运动时间为()s x ，以点P 、C 、D 为顶点的三角形的面积是()2cm y ，则下列图像能大致反映y 与x 的函数关系的是（）A ．B ．C ．D ．10、已知O 是正六边形ABCDEF 的外接圆，正六边形ABCDEF 扇形OAC 围成一个圆锥的侧面，则该圆锥的底面圆的半径为（）A．1 B．13C．23D．43第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在△ABC中，AB＝AC BC＝2，以点A为圆心作圆弧，与BC相切于点D，且分别交边AB，AC于点EF，则扇形AEF的面积为 _____．（结果保留π）2、如图，在矩形ABCD中，F是边AD上的点，经过A，B，F三点的O与CD相切于点E．若6AB=，2FD=，则O的半径是__________．3、如图，点A，B，C均在66⨯的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C 三点外还能经过的格点数为_________．4、如图，在ABC 中，90ACB ∠=︒，BE 平分ABC ∠，CF 平分ACB ∠，CF ，BE 交于点P ，4AC =cm ，3BC =cm ，5AB =cm ，则CPB △的面积为_______cm 2．5、⊙O 的半径为3cm ，如果圆心O 到直线l 的距离为d ，且d =5cm ，那么⊙O 和直线l 的位置关系是____________．三、解答题（5小题，每小题10分，共计50分）1、如图，点E 是ABC 的内心，AE 的延长线交BC 于点F ，交ABC 的外接圆O 点D ．过D 作直线DM BC ∥．(1)求证：DM 是O 的切线；(2)求证：DE BD =；(3)若DE =8BC =，求O 的半径．2、如图，已知AB是O的直径，点C在O上，点E在O外．(1)动手操作：作ACB∠的角平分线CD，与圆交于点D（要求：尺规作图，不写作法，保留作图痕迹）∠=∠，求证：AE是O的切线．(2)综合运用，在你所作的图中．若EAC ADC3、如图，⊙O是ABC的外接圆，∠ABC=45°，OC∥AD，AD交BC的延长线于D，AB交OC于E．(1)求证：AD是⊙O的切线；(2)若AE=CE=2，求⊙O的半径和线段BC的长．4、苏科版教材八年级下册第94页第19题，小明在学过圆之后，对该题进行重新探究，请你和他一起完成问题探究．【问题探究】小明把原问题转化为动点问题，如图1，在边长为6cm的正方形ABCD中，点E从点A 出发，沿边AD向点D运动，同时，点F从点B出发，沿边BA向点A运动，它们的运动速度都是2cm/s，当点E运动到点D时，两点同时停止运动，连接CF、BE交于点M，设点E，F运动时问为t 秒．(1)【问题提出】如图1，点E ，F 分别在方形ABCD 中的边AD 、AB 上，且BE CF =，连接BE 、CF 交于点M ，求证：BE CF ⊥．请你先帮小明加以证明．(2)如图1，在点E 、F 的运动过程中，点M 也随之运动，请直接写出点M 的运动路径长 cm ．(3)如图2，连接CE ，在点E 、F 的运动过程中．①试说明点D 在△CME 的外接圆O 上； ②若①中的O 与正方形的各边共有6个交点，请直接写出t 的取值范围．5、如图，在Rt ABC △中，90ACB ∠=︒，BO 平分ABC ∠，交AC 于点O ，以点O 为圆心，OC 长为半径画O ．(1)求证：AB 是O 的切线；(2)若3AO =，1tan 3OBC ∠=，求O 的半径．-参考答案-一、单选题1、D【解析】【分析】作OD ⊥AB 于C ，OC 的延长线交圆于D ，其中点O 为圆心，OA OB ，为半径，2CD =cm ，8AB =cm ；设茶杯的杯口外沿半径为r ，在Rt AOC △中，由勾股定理知r =【详解】解：作OD ⊥AB 于C ，OC 的延长线交圆于D ，其中点O 为圆心，OA OB ，为半径，由题意可知2CD =cm ，8AB =cm ；∵⊥OD AB∴AC =BC =4cm ，设茶杯的杯口外沿半径为r则在Rt AOC △中，由勾股定理知r =解得=5r故选D ．【点睛】本题考查了垂径定理，切线的性质，勾股定理的应用．解题的关键在于将已知线段长度转化到一个直角三角形中求解计算．2、B【解析】【分析】连接OD，求出BC是⊙O的切线，根据切线长定理得出CD＝BC，根据切线的性质求出∠ODM＝90°，根据勾股定理求出MD，再根据勾股定理求出BC即可．【详解】解：连接OD，∵MD切⊙O于D，∴∠ODM＝90°，∵⊙O的半径为2，MA＝AO，AB是⊙O的直径，∴MO＝2+2＝4，MB＝4+2＝6，OD＝2，由勾股定理得：MD∵BC⊥AB，∴BC切⊙O于B，∵DC切⊙O于D，∴CD＝BC，设CD＝CB＝x，在Rt△MBC中，由勾股定理得：MC2＝MB2+BC2，即（x）2＝62+x2，解得：x＝即BC＝故选：B．【点睛】本题考查了切线的性质和判定，圆周角定理，勾股定理等知识点，能综合运用定理进行推理是解此题的关键．3、A【解析】【分析】连接OA，DE，利用切线的性质和角之间的关系解答即可．【详解】解：连接OA，DE，如图，∵AC是O的切线，OA是O的半径，∴OA⊥AC∴∠OAC=90°∠ADE=36°∴∠AOE=2∠ADE=72°∴∠C=90°-∠AOE=90°-72°=18°故选：A.本题考查了圆周角定理，切线的性质，能求出∠OAC和∠AOC是解题的关键．4、D【解析】【分析】如图所示，连接DP，CP，先求出BP的长，然后利用勾股定理求出PD的长，再比较PC与PD的大小，PB与PD的大小即可得到答案．【详解】解：如图所示，连接DP，CP，∵四边形ABCD是矩形，∴∠A=∠B=90°，∵AP=3，AB=8，∴BP=AB-AP=5，∵5PD==，∴PB=PD，>=，∴PC PB PD∴点C在圆P外，点B在圆P上，故选D．本题主要考查了点与圆的位置关系，勾股定理，矩形的性质，熟知用点到圆心的距离与半径的关系去判断点与圆的位置关系是解题的关键．5、C【解析】【分析】连接OA 、OB ，则OAB 为等腰直角三角形，由正方形面积为18，可求边长为2=18AB ，进而通过勾股定理，可得半径为3．【详解】解：如图，连接OA ，OB ，则OA =OB ，∵四边形ABCD 是正方形，∴90AOB ∠=︒，∴OAB 是等腰直角三角形，∵正方形ABCD 的面积是18，∴2=18AB ，∴222+18OA OB AB ==，即：2218OA =∴3OA =故选C ．【点睛】本题考查了正多边形和圆、正方形的性质等知识，构造等腰直角三角形是解题的关键．6、B【解析】【分析】利用圆的有关性质及定理、三角形的内心的性质、垂径定理等知识分别判断后即可确定正确的选项．【详解】解：A、同圆或等圆中，相等的圆心角所对的两条弦相等，则原命题是假命题，故本选项不符合题意；B、三角形的内心是到三角形三边距离相等的点，是真命题，故本选项符合题意；C、平分弦（不是直径）的直径一定垂直于这条弦，则原命题是假命题，故本选项不符合题意；D、等弧是能够完全重合的弧，长度相等的弧不一定是等弧，则原命题是假命题，故本选项不符合题意；故选：B【点睛】本题主要考查了命题与定理的知识，解题的关键是了解圆的有关性质及定理、三角形的内心的性质、垂径定理等知识，难度不大．7、D【解析】【分析】根据圆的有关概念、确定圆的条件、圆周角定理及三角形的外心的性质解得即可．【详解】解：A、在同圆或等圆中，能完全重合的弧才是等弧，故错误；B、不在同一直线上的三点确定一个圆，故错误；C、在同圆或等圆中，同弧或等弧所对的圆心角是圆周角的2倍，故错误；D、三角形的外心到三角形的三个顶点的距离相等，故正确；故选D．【点睛】本题考查了圆的有关的概念，属于基础知识，必须掌握．8、B【解析】【分析】如图所示，过C作CD⊥AB，交AB于点D，在直角三角形ABC中，由AC与BC的长，利用勾股定理求出AB的长，利用面积法求出CD的长，即为所求的r．【详解】解：如图所示，过C作CD⊥AB，交AB于点D，在Rt△ABC中，AC=3cm，BC=4cm，根据勾股定理得：AB（cm），∵S△ABC=12BC•AC=12AB•CD，∴12×3×4=12×10×CD，解得：CD=2.4，则r=2.4（cm）．故选：B ．【点睛】此题考查了切线的性质，勾股定理，以及三角形面积求法，熟练掌握切线的性质是解本题的关键．9、A【解析】【分析】设正六边形ABCDEF 的边长为1，当P 在DE 上时，过P 作PH CD ⊥于,H 而120,,CDP PD x 求解此时的函数解析式，当P 在EF 上时，延长,CD FE 交于点,M 过P 作PQ CD ⊥于,Q 并求解此时的函数解析式，当P 在AF 上时，连接,,AC CF 并求解此时的函数解析式，由正六边形的对称性可得：P 在AB 上的图象与P 在EF 上的图象是对称的，P 在BC 上的图象与P 在DE 上的图象是对称的，从而可得答案.【详解】解：设正六边形ABCDEF 的边长为1，当P 在DE 上时，过P 作PH CD ⊥于,H 而120,,CDP PD x60,PDH 3sin 60,2PH PD x11331,2224y CD PH x x 当P 在EF 上时，延长,CD FE 交于点,M 过P 作PQ CD ⊥于,Q同理：120,CDE FED60,EDM DEM则DEM△为等边三角形，60,1,, EMD EM ED PM PE EM PE ED x3sin60,2PQ PM x11331,2224y CD PQ x x当P在AF上时，连接,,AC CF由正六边形的性质可得：120,,ABC BAF AFE BA BC118012030,1203090,2BAC CAF由正六边形的对称性可得：160,2AFC AFE而1,AFtan603,AC AF11313,222y CD AC由正六边形的对称性可得：P在AB上的图象与P在EF上的图象是对称的，P在BC上的图象与P在DE上的图象是对称的，所以符合题意的是A，故选A【点睛】本题考查的是动点问题的函数图象，锐角三角函数的应用，正多边形的性质，清晰的分类讨论是解本题的关键.10、C【解析】【分析】根据边心距求得外接圆的半径为2，根据圆锥的底面圆周长等于扇形的弧长，计算圆锥的半径即可．【详解】如图,过点O作OG⊥AF，垂足为G，∵正六边形ABCDEF∴∠AOG=30°，OG∴OA=2AG，∴2243-=，GA GA解得GA=1，∴OA=2，设圆锥的半径为r ，根据题意，得2πr =1202180π⨯⨯，解得r =23，故选C ．【点睛】本题考查了扇形的弧长公式，圆锥的侧面积，熟练掌握弧长公式，圆锥的侧面积公式是解题的关键．二、填空题1、4π##14π 【解析】【分析】先判断出△ABC 是等腰直角三角形，从而连接AD ，可得出AD =1，直接代入扇形的面积公式进行运算即可．【详解】解：∵AB =AC BC =2，∴AB 2+AC 2=BC 2，∴△ABC 是等腰直角三角形，∴∠BAC =90°，连接AD ，则AD =12BC =1，则S 扇形AEF =29013604ππ⨯=．故答案为：4π．【点睛】本题考查了扇形的面积计算、勾股定理的逆定理及等腰直角三角形的性质，直角三角形斜边上的中线等于斜边的一半，难度一般，解答本题的关键是得出AD的长度及∠BAC的度数．2、134##134【解析】【分析】连接EO，并延长交圆于点G，在Rt△DEF中求出EF的值，再证明△DEF∽△FGE，然后根据相似三角形的性质即可求解．【详解】解：连接EO，并延长交圆于点G，∵四边形ABCD是矩形，∴CD=6AB ，∠D=90°，∵O与CD相切于点E，∴OE⊥CD，再结合矩形的性质可得：∴DE=CE=3．∵2FD=，∴EF∵O与CD相切于点E，∴∠GED=90°．∵GE是直径，∴∠GFE=90°，∴∠DEF+∠GEF=90°，∠EGF+∠GEF=90°，∴∠DEF=∠EGF．∵∠D=∠∠GFE=90°，∴△DEF∽△FGE，∴DF EFEF GE=，，∴GE=132，∴O的半径是134，故答案为；134．【点睛】本题考查了矩形的性质，勾股定理，切线的性质，以及相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解答本题的关键．3、5【解析】【分析】根据圆的确定方法做出过A ，B ，C 三点的外接圆，从而得出答案．【详解】如图，分别作AB 、BC 的中垂线，两直线的交点为O ，以O 为圆心、OA 为半径作圆，则⊙O 即为过A ，B ，C 三点的外接圆，由图可知，⊙O 还经过点D 、E 、F 、G 、H 这5个格点，故答案为5．【点睛】此题考查了确定圆的方法，三角形的外接圆，解题的关键是根据题意确定三角形ABC 外接圆的圆心． 4、1.5【解析】【分析】根据BE 平分ABC ∠，CF 平分ACB ∠，CF ，BE 交于点P ，得出点P 是ABC ∆的内心，并画出ABC ∆的内切圆，再根据切线长定理列出方程组，求出BCP ∆的边BC 上的高，进而求出其面积．【详解】解：BE 平分ABC ∠，CF 平分ACB ∠，CF ，BE 交于点P ，∴点P 是ABC ∆的内心．如图，画出ABC ∆的内切圆，与BC 、AC 、AB 分别相切于点G 、M 、N ，且连接PG ，设CG x =，BG y =，AF z =，得方程组：354x y y z z x +=⎧⎪+=⎨⎪+=⎩解得：123x y z =⎧⎪=⎨⎪=⎩， 1PG x ∴==，CPB ∴∆的面积21131 1.5()22BC PG cm =⨯⨯=⨯⨯=．故答案为：1.5．【点睛】此题主要考查三角形内切圆的应用，解题的关键是熟知三角形内切圆的性质，根据其性质列出方程组求解．5、相离【解析】【分析】根据直线和圆的位置关系的判定方法判断即可．【详解】解：∵⊙O 的半径为3cm ，圆心O 到直线l 的距离为d ＝5cm ，∴d ＞r ，∴直线l 与⊙O 的位置关系是相离，故答案为：相离．【点睛】本题考查了直线和圆的位置关系的应用，注意：已知⊙O的半径为r，如果圆心O到直线l的距离是d，当d＞r时，直线和圆相离，当d＝r时，直线和圆相切，当d＜r时，直线和圆相交．三、解答题1、 (1)见解析(2)见解析(3)⊙O的半径为5．【解析】【分析】（1）连接OD交BC于H，根据圆周角定理和切线的判定即可证明；（2）连接BD，由点E是△ABC的内心，得到∠ABE=∠CBE，∠DBC=∠BAD，推出∠BED=∠DBE，根据等角对等边得到BD=DE；（3）根据垂径定理和勾股定理即可求出结果．(1)证明：连接OD交BC于H，如图，∵点E是△ABC的内心，∴AD平分∠BAC，即∠BAD=∠CAD，∴BD CD=，∴OD⊥BC，BH=CH，∵DM∥BC，∴OD⊥DM，∴DM是⊙O的切线；(2)证明：∵点E是△ABC的内心，∴∠ABE=∠CBE，∵BD CD=，∴∠DBC=∠BAD，∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE，即∠BED=∠DBE，∴BD=DE；(3)解：设⊙O的半径为r，连接OD，OB，如图，由（1）得OD⊥BC，BH=CH，∵BC=8，∴BH=CH=4，∵DE BD=DE，∴BD在Rt△BHD中，BD2=BH2+HD2，∴（2=42+HD2，解得：HD=2，在Rt△BHO中，r2=BH2+（r-2）2，解得：r=5．∴⊙O的半径为5．【点睛】本题考查了三角形的内心，切线的判定与性质，三角形的外接圆与外心，圆周角定理，垂径定理，解决本题的关键是综合运用以上知识．2、 (1)作图见解析(2)证明见解析【解析】【分析】（1）如图，以点C为圆心BC为半径画弧交AC于点M；以B、M为圆心，大于1BM为半径画弧，交点2为N，连接CN交O于点D即可．∠=∠，（2）连接AD，9090，，，EAC ADC∠=∠∠=︒∠+∠=︒ADC ABC ACB ABC BACBAE∠=︒，AB为直径，进而可得AE是O的切线．，，90EAC ABC EAC BAC90∠=∠∠+∠=︒(1)解：如图，以点C为圆心BC为半径画弧交AC于点M；以B、M为圆心，大于1BM为半径画弧，交点2为N，连接CN交O于点D．(2)解：连接AD，如图∵AC AC AB=，为直径∴9090，，ADC ABC ACB ABC BAC∠=∠∠=︒∠+∠=︒∠=∠∵EAC ADC∴90EAC ABC EAC BAC ∠=∠∠+∠=︒，∴90BAE ∠=︒又∵AB 为直径∴AE 是O 的切线．【点睛】本题考查了角平分线的画法，圆周角，切线的判定等知识．解题的关键在于对知识的灵活熟练的运用．3、 (1)见解析(2)4 【解析】【分析】（1）连接OA ．由AD OC ∥及圆周角定理求出∠OAD =90°，即可得到结论；（2）设⊙O 的半径为R ，在Rt △OAE 中，勾股定理求出R ，延长CO 交⊙O 于F ，连接AF ，证明△CEB ∽△AEF ，得到AE AF CE BC=，由此求出⊙O 的半径和线段BC 的长． (1)证明：连接OA ．∵AD OC ∥，∴∠AOC +∠OAD =180°，∵∠AOC =2∠ABC =2×45°=90°，∴∠OAD =90°，∴OA ⊥AD ，∵OA 是半径，∴AD 是⊙O 的切线．(2)解：设⊙O 的半径为R ，则OA =R ，OE =R -2．在Rt △OAE 中，222AO OE AE +=，∴222(2)R R +-=，解得14R =或22R =-（不合题意，舍去），延长CO 交⊙O 于F ，连接AF ，∵∠AEF =∠CEB ，∠B =∠AFE ，∴△CEB ∽△AEF ， ∴AE AF CE BC=， ∵CF 是直径，∴CF =8，∠CAF =90°，又∵∠F =∠ABC =45°，∴∠F =∠ACF =45°，∴AF =BC=∴BC ．．【点睛】此题考查了证明直线是圆的切线，勾股定理，相似三角形的判定及性质，直径所对的圆周角是直角的性质，等腰直角三角形的性质，正确作出辅助线解题是解题的关键．4、 (1)见解析 (2)32π (3)①见解析；②304t <<【解析】【分析】（1）根据正方形的性质以及动点的路程相等，证明BAE CBF ≌△△，根据同角的余角相等，即可证明90MBC ∠=︒，即BE CF ⊥；（2）当t ＝0时，点M 与点B 重合，当3t =时，M 点随之停止，求得运动轨迹为14圆，根据弧长公式进行计算即可；（3）①根据（2）可得△CME 的外接圆的圆心O 是斜边CE 的中点，继而判断点D 、C 、M 、E 在同一个圆（O ）上；②当O 与AB 相切时，O 与正方形的各边共有5个交点，如图5则有6个交点，所以“当O 与AB 相切时”是临界情况．如图4，当O 与AB 相切（切点为G ），连接OG ，并延长GO 交CD 于点H ，在Rt △CHO 中求得半径R ,进而勾股定理求得3t 4=，即可求得当304t <<时，O 与正方形的各边共有6个交点． (1)四边形ABCD是正方形，AB BC∴=，BAE CBF∠=∠又,E F的运动速度都是2cm/s，2AE BF t∴==BAE CBF∴≌BCF ABE∴∠=∠90ABE EBC ABC∠+∠=∠=︒90BCF EBC∴∠+∠=︒90MBC∴∠=︒即BE CF⊥(2)∵90CMB∠=．∴点M在以CB为直径的圆上，如图1，当t＝0时，点M与点B重合；如图2，当t＝3时，点M为正方形对角线的交点．点M的运动路径为14圆，其路径长13642ππ⨯=．故答案为：3 2π(3)①如图3．由前面结论可知：90CME∠=∴△CME的外接圆的圆心O是斜边CE的中点，则12OM OC OE CE ===在Rt △CDE 中，90D ∠=，O 是CE 的中点． ∴12OD CE =，∴OM OC OE OD ===∴点D 、C 、M 、E 在同一个圆（O ）上，即点D 在△CME 的外接圆O 上；． ②304t <<．如图4，当O 与AB 相切时，O 与正方形的各边共有5个交点，如图5则有6个交点，所以“当O 与AB 相切时”是临界情况．如图4，当O 与AB 相切（切点为G ），连接OG ，并延长GO 交CD 于点H ．∵AB 与O 相切，∴OG AB ⊥，又∵AB CD ∥，∴OH CD ⊥，132CH DC ∴== 设O 的半径为R ．由题意得：在Rt △CHO 中，2223(6)R R +-=，解得154R =∴159,22CE DE === ∴32AE =，即3t 4= ∴如图5，当304t <<时，O 与正方形的各边共有6个交点．【点睛】本题考查了求弧长，切线的性质，直径所对的圆周角是直角，三角形的外心，正方形的性质，全等三角形的性质与判定，分类讨论是解题的关键．5、 (1)见解析(2)2.4．【解析】【分析】（1）过O 作OD ⊥AB 交AB 于点D ，先根据角平分线的性质求出DO =CO ，再根据切线的判定定理即可得出答案；（2）设圆O 的半径为r ，即OC =r ，由1tan 3OBC ∠=得BC =3r ，由勾股定理求得AD ，AB =3r +222(3(3)(3)r r r =++求解即可．(1)如图所示：过O 作OD ⊥AB 交AB 于点D ．∵OC ⊥BC ，且BO 平分∠ABC ，∴OD =OC ，∵OC 是圆O 的半径∴AB 与圆O 相切．(2)设圆O 的半径为r ，即OC =r ， ∵1tan 3OBC ∠= ∴13OC r BC BC == ∴=3BC r∵OC ⊥BC ，且OC 是圆O 的半径∴BC 是圆O 的切线，又AB 是圆O 的切线，∴BD =BC =3r在Rt OAD ∆中，3OD r AO ==，∴AD =∴3AB r =在Rt ABC ∆中，222AB BC AC =+∴222(3(3)(3)r r r =++整理得，253360r r +-=解得，1 2.4r =，23r =-（不合题意，舍去）∴O 的半径为2.4【点睛】此题主要考查了复杂作图以及切线的判定等知识，正确把握切线的判定定理是解题关键．。

九年级数学(下)第二十九章《投影与视图》全章测试题含答案

九年级数学（下）第二十九章《投影与视图》全章测试题一、选择题1．平行投影中的光线是( )A．平行的B．聚成一点的C．不平行的D．向四面八方发散2．正方形在太阳光下的投影不可能是( )A．正方形B．一条线段C．矩形D．三角形3．如图1，将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆洞，最后将正方形纸片展开，得到的图案是( )4．由一些完全相同的小立方块搭成的几何体的三视图如图所示，那么搭成这个几何体所用的小立方块的个数是( )第4题图A．8 B．7 C．6 D．5 5．如图是某几何体的三视图及相关数据，则判断正确的是( )第5题图A．a＞c B．b＞cC．4a2＋b2＝c2D．a2＋b2＝c26．若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是( )A．2 B．3C．4 D．5二、填空题7．一个圆柱的俯视图是______，左视图是______．8．如果某物体的三视图如图所示，那么该物体的形状是______．第8题图9．一空间几何体的三视图如图所示，则这个几何体的表面积是______cm2．第9题图10．如图，水平放置的长方体的底面是边长为2和4的矩形，它的左视图的面积为6，则长方体的体积等于______．三、解答题11．楼房、旗杆在路灯下的影子如图所示．试确定路灯灯炮的位置，再作出小树在路灯下的影子．(不写作法，保留作图痕迹)12．画出图中的九块小立方块搭成几何体的主视图、左视图和俯视图．13．如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示该位置小立方块的个数，请画出这个几何体的主视图和左视图．14．如图是一个几何体的主视图和俯视图，求该几何体的体积( 取3.14)．15．拿一张长为a，宽为b的纸，作一圆柱的侧面，用不同的方法作成两种圆柱，画出图形并求这两种圆柱的表面积．答案与提示第二十九章投影与视图全章测试1．A ． 2．D ． 3．A ． 4．A ． 5．D ． 6．B ． 7．圆；矩形． 8．三棱柱． 9．48π． 10．24． 11．如图：12．如图：13．如图：14．体积为π×102×32＋30×25×40≈40 048(cm 3)．15．第一种：高为a ，表面积为;π221b ab S +=第二种：高为b ，表面积为⋅+=π222a ab S。

精品解析2022年人教版九年级数学下册第二十九章-投影与视图章节测评试题(含答案及详细解析)

人教版九年级数学下册第二十九章-投影与视图章节测评考试时间：90分钟；命题人：教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，一个水晶球摆件，它是由一个长方体和一个球体组成的几何体，则其主视图是（）A．B．C．D．2、下列立体图形中，从上面看到的形状图是三角形的是( )A．B．C．D．3、如图所示的几何体，从上面看到的形状图是（）A．B．C．D．4、如图，是空心圆柱体，其主视图是下列图中的（）A．B．C．D．5、如图，这个几何体是将一个正方体中间挖出一个圆柱体后的剩余部分，该几何体的主视图是（）A．B．C．D．6、一个由若干个相同的小正方体组成的几何体的主视图和俯视图如图所示，则小正方体的最少个数为（）A．6 B．7 C．8 D．97、图1、图2均是正方体，图3是由一些大小相同的正方体搭成的几何体从正面看和左面看得到的形状图，小敏同学经过研究得到如下结论：（1）若将图1中正方体的表面沿某些棱剪开，展成一个平面图形，需要剪开7条棱；（2）用一个平面从不同方向去截图1中的正方体，得到的截面可能是三角形、四边形、五边形或六边形；（3）用一个平面去截图1中的正方体得到图2，截面三角形ABC中∠ABC＝45°；（4）如图3，要搭成该几何体的正方体的个数最少是a，最多是b，则a＋b＝19其中正确结论的个数有（）A．1个B．2个C．3个D．4个8、下面的三视图所对应的几何体是（）A．B．C． D．9、下面左侧几何体的主视图是（）A．B．C．D．10、如图是由5个相同的小立方块搭成的几何体，则从左面看这个几何体的形状图是（）A．B．C．D．第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、由一些大小相同的小正方体搭成的几何体从正面和从左面看到的图形如图所示，则搭成该几何体的小正方体的个数最少是____2、一个圆柱体的三视图如图所示，根据图中数据计算圆柱的体积为___________．（答案含）3、一个几何体是由一些大小相同的校正方体摆成的，从正面看与从上面看得到的形状如图所示，则组成这个几何体的校正方体最多有_________个4、由若干个相同的小正方体搭成的几何体的三视图相同，如图所示．至少再加_____个小正方体，该几何体可成为一个正方体．5、将7个棱长为1的小立方体摆成如图所示几何体，该几何体的俯视图的面积为_____．三、解答题（5小题，每小题10分，共计50分）1、（1）一个几何体由一些大小相同的小正方体搭成，如图是从上面看这个几何体的形状图，小正方形中的数字表示在该位置的小正方体的个数，请在网格中画出从正面和左面看到的几何体的形状图．（2）用小立方块搭一几何体，使它从正面看，从左面看，从上面看得到的图形如图所示．请在从上面看到的图形的小正方形中填人相应的数字，使得小正方形中的数字表示在该位置的小立方块的个数．其中，图1填人的数字表示最多组成该几何体的小立方块的个数，图2填入的数字表示最少组成该几何体的小立方块的个数．2、如图，路灯下一墙墩(用线段AB表示)的影子是BC，小明(用线段DE表示)的影子是EF，在M处有一棵小树，它的影子是MN．（1）画出路灯的位置(用点P表示)；（2）在图中画出表示小树的线段．3、从正面、左面、上面观察如图所示的几何体，分别画出你所看到的几何体的形状图．4、如图，一个正方体由27个大小相同的小立方块搭成，现从中取走若干个小立方块，得到一个新的几何体．若新几何体与原正方体的表面积相等，问最多可以取走几个小立方块．5、如图是由5个同样大小的小正方体搭成的几何体，请在下面方格纸中分别画出这个几何体从正面看、从左面看、从上面看的形状图．---------参考答案-----------一、单选题1、D【分析】根据从正面看得到的图形是主视图，可得答案．【详解】解：从正面看下边是一个矩形，矩形的上边是一个圆，故选：D．【点睛】本题考查了简单组合体的三视图，掌握从正面看得到的图形是主视图是解决此题关键．2、C【分析】根据三视图的性质得出主视图的形状进而得出答案．【详解】解：正方体从上面看到的形状图是正方形，故A项不符合题意；圆柱从上面看到的形状图是圆，故B项不符合题意；圆锥从上面看到的形状图是带圆心的圆，故D项不符合题意．三棱柱从上面看到的形状图是三角形，故C项符合题意；故选：C．【点睛】本题题主要考查了简单几何体的三视图，熟悉主视图性质是解题关键．3、B【分析】找出从几何体的上面看所得到的视图即可．【详解】解：从上面看到的形状图是，故选：B【点睛】此题主要考查了简单几何体的视图，注意培养学生的思考能力和对几何体三种视图的空间想象能力是解题的关键．4、C【分析】从正面观察空心圆柱体，能够看见的部分用实线表示，不能看见的部分用虚线表示，即可得到主视图.【详解】主视图是在几何体正面面观察物体得到的图形．能够看见的部分用实线表示，不能看见的部分用虚线表示．本题圆柱体的主视图整体是个矩形，中间包含两条竖直的虚线．故选：C【点睛】本题主要考查三视图, 主视图是在物体正面从前向后观察物体得到的图形；俯视图是在水平面内从上向下观察物体得到的图形；左视图是在几何体左侧面观察物体得到的图形．5、A【分析】根据主视图的概念求解即可．【详解】解：由题意可得，该几何体的主视图是：．故选：A．【点睛】此题考查了几何体的主视图，解题的关键是熟练掌握几何体主视图的概念．6、B【分析】根据几何体的三视图特点解答即可．【详解】解：根据俯视图，最底层有4个小正方体，由主视图知，第二层最少有2个小正方体，第三层最少有1个小正方体，∴该几何体最少有4+2+1=7个小正方体组成，故选：B．【点睛】本题考查几何体的三视图，掌握三视图的特点是解答的关键．7、B【分析】根据正方体的棱的条数以及展开后平面之间应有棱连着可判断（1）；正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形可判断（2）（3）；作出相应的俯视图，标出搭成该几何体的小正方体的个数最多（少）时的数字即可．为【详解】解：（1）若将图1中正方体的表面沿某些棱剪开，展成一个平面图形，需要剪开7条棱；正确，因为正方体有6个表面，12条棱，要展成一个平面图形必须5条棱连接，所以至少要剪开12﹣5＝7条棱．（2）用一个平面从不同方向去截图1中的正方体，得到的截面可能是三角形、四边形、五边形或六边形；正确，因为用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形．（3）用一个平面去截图1中的正方体得到图2，截面三角形ABC中∠ABC＝45°；错误，因为△ABC是等边三角形，所以∠ABC＝60°．8、C【分析】根据“俯视打地基、主视疯狂盖、左视拆违章”得出组成该几何体的小正方体分布情况，继而得出答案．【详解】解：根据三视图知，组成该几何体的小正方体分布情况如下：与之相对应的C选项，故选：C．【点睛】本题考查由三视图判断几何体，关键是由主视图和左视图、俯视图可判断确定几何体的具体形状．9、A【分析】找出从几何体的正面看所得到的图形即可．【详解】解：从几何体的正面看，是一行两个并列的矩形．故选：A．【点睛】本题主要考查了几何体的三视图，准确分析判断是解题的关键．10、D【分析】观察图形可知，从左面看到的图形是2列，分别有2，1个正方形，据此即可判断．【详解】解：从左面看这个几何体的形状图如图所示：故选D．【点睛】此题考查了从不同方向观察物体和几何体和画简单图形的三视图的方法，是基础题型．二、填空题1、4【解析】【分析】由主视图可知几何体有两列，两层；由左视图可知几何体有两排，两层，所以第一列最少1个正方体，第二列有最少有3个正方体，由此可解．【详解】解：由主视图，左视图画出几何体，如图：故答案为：4．【点睛】本题意在考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．2、24【解析】【分析】根据主视图确定出圆柱体的底面直径与高，根据圆柱体的体积公式列式计算即可．【详解】解：由图知，圆柱体的底面直径为4，高为6，∴V圆柱=πr2h=π×22×6=24π．故答案为24π．【点睛】本题考查了立体图形的三视图和学生的空间想象能力，圆柱体的体积公式．根据主视图确定出圆柱体的底面直径与高是解题的关键．3、6【解析】【分析】易得这个几何体共有2层，由主视图和俯视图可得第一层最多正方体的个数为3块，第二层最多正方体的个数为3块，相加即可．【详解】解：组成这个几何体的小正方块最多有3+3=6块．故答案为：6．【点睛】本题考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．4、4【解析】【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，依此可得有几个小正方体，再用8减去小正方体的个数即可求解．【详解】解：根据三视图可得第一层有3个正方体，第二层有1个正方体，共有4个小正方体，8﹣4＝4（个）．故至少再加4个小正方体，该几何体可成为一个正方体．故答案为：4．【点睛】本题主要考查三视图，能够根据三视图想象出立体图是解题的关键．5、4【解析】【分析】据从上面看得到的图形是俯视图，直接观察，可得答案．【详解】解：从上面看，底层是两个小正方形，上层是两个小正方形，如图所示，所以该几何体的俯视图的面积为4．故答案为：4．【点睛】本题考查了简单组合体的三视图，从上面看得到的图形是俯视图是解题关键．三、解答题1、（1）见解析；（2）见解析【分析】（1）根据俯视图中小正方体的个数结合主视图，主视图是从前面向后看得到的图形，从正面看分左中右三列，左边列有2个正方形，中间列有3个正方形，右边列有4个正方形画出图形，根据俯视图中小正方体的个数结合左视图，左视图是从左边向右看得到的图形，从左边看分左中右三列，左边列1个正方形，中间列4个正方形，右边列2个正方形画出图形即可；（2）根据俯视图的图形两行三列，中间列一行，从正面看分左中右三例，左边列3个正方形，中间列1个正方形，右边列2个正方形，从左面看，分两行，前行后行，前行2个正方形，后行3个正方形，左列前行可以是1个正方体或2个正方体，左列后行3个正方体，中间列只有前行1个正方体，右边列前行2个正方体，右边列后行可以1个或2个正方体，最多10个正方体如图1，最少8个正方体如图2在俯视图中标出个数即可．【详解】解：（1）从正面看分左中右三列，左边列有2个正方形，中间列有3个正方形，右边列有4个正方形，如图从左边看分左中右三列，左边列1个正方形，中间列4个正方形，右边列2个正方形，如图所示：（2）从正面看分左中右三例，左边列3个正方形，中间列1个正方形，右边列2个正方形，从左面看，分两行，前行后行，前行2个正方形，后行3个正方形，左列前行可以是1个正方体或两个正方体，，左列后行3个正方体，中间列只有前行1个正方体，右边列前行2个正方体，后列可以1个或2个正方体，最多10个正方体如图1，最少8个正方体如图2．根据题意，填图如下：【点睛】本题考查根据俯视图画主视图与左视图，根据主视图与左视图确定组成图形的正方体的个数，从立体图形到平面图形的转化三视图，由平面图形三视图到立体图形还原几何体空间想象能力，本题难度较大，培养空间想象力，掌握相关知识是解题关键．2、（1）见解析；（2）见解析．【分析】（1）连接CA并延长与FD的延长线交于点P，点P即路灯的位置；（2）连接PN，作MG垂直于MN与PN交于点G，线段GM即为表示小树的线段．【详解】解：（1）如图，连接CA并延长与FD的延长线交于点P，点P是路灯的位置．（2）如图，连接PN，作MG垂直于MN与PN交于点G，线段MG表示小树．【点睛】此题考查了中心投影，解题的关键是熟练掌握中心投影的性质．3、见解析【分析】根据三视图的画法，直接画出主视图、左视图和俯视图即可．【详解】解：如图所示：【点睛】本题考查三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．本题画几何体的三视图时应注意小正方形的数目及位置．4、最多可以取走16个小立方块．【分析】根据表面积不变，只需留11个，分别是正中心的3个和四角上各2个．【详解】解：若新几何体与原正方体的表面积相等，最多可以取走16个小正方体，只需留11个，分别是正中心的3个和四角上各2个，如图所示：答：最多可以取走16个小立方块．【点睛】本题主要考查了几何体的表面积，熟知几何体表面积的定义以及正方体的表面积公式是解答本题的关键．5、见解析【分析】根据图形及三视图的定义作图即可．【详解】解：三视图如下所示：【点睛】此题主要考查了作三视图，根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形是解题关键．。

七年级数学上册1.2.4 绝对值-求一个数的绝对值选择题专项练习二十九(人教版,含解析)

2021-2022学年度人教版七年级数学上册练习1.2.4 绝对值-求一个数的绝对值一、选择题1．实数﹣3的绝对值是（）A ．3B ．﹣3C ．0D 2．下列各组数中，互为相反数的是（）A ．|3|-与3B ．|3|-与-3C ．|3|--与-3D ．|3|-与+3 3．在7-，0，()243-----，，，43，9100+，0.27-中，负数有( ) A ．1个 B ．2个 C ．3个 D ．4个4．）A ．3BC ．D ．5．|﹣2013|的值是（）A ．12013B ．12013-C ．2013D ．﹣20136．－2 的绝对值是（）A ．－B ．±2C ．2D ．－27．|-6|的相反数是（）A ．6B ．-6C ．16D ．-16 8．3--的值为A ．3B ．－3C ．D ．－ 9．52-的绝对值是（）A ．52 B ．25 C ．25- D ．52- 10．-8的绝对值是（）A ．8B ．-8C ．1D ．18- 11．有四包真空小包装火腿，每包以标准克数（450克）为基准，超过的克数记作正数，不足的克数记作负数，以下数据是记录结果，其中表示实际克数最接近标准克数的是（）A ．+4B ．+3C ．﹣2D ．﹣112．3的相反数的绝对值是（）A ．13- B ．13 C ．-3 D ．313．绝对值不大于3的整数的个数是（）A ．4B ．5C ．6D ．714．下列结果为2的是（）A ．﹣（+2）B ．12 C ．|﹣2| D ．﹣|﹣2|15．下列各式正确的是( )A ．︱－5︱=－5B ．－︱－3︱=3C ．－︱+7︱=-7D ．+︱－8︱=－816．(2017四川泸州第1题)7-的绝对值为（）A ．7B ．7-C ．17 D ．17- 17．下列正确的是（）A2=± B 4= C ．4.3 4.5<< D ．11=18．绝对值等于其本身的数有（）A ．1个B ．2个C ．0个D ．无数个19．如图，若数轴上A 、B 两点所对应的有理数分别为a 、b ，则a 、b 两数的绝对值大小关系为（）A ．︱a ︱大B ．︱b ︱大C ．︱a ︱＝︱b ︱D ．无法确定 20．16-的绝对值为（）A ．6B ．16- C ．16 D ．﹣621．1||2020-的相反数是（）A．2020 B．2020-C．12020D．12020-22．一个正有理数在增大时，它的绝对值（）．A．在减小B．不变C．在增大D．不一定变23．9的绝对值是（）A．9 B．-9 C．1/9 D．-1/9243的绝对值是( )A 3 B．3C 3 D 3 25．下列说法中正确的是（）．A．一个数的绝对值一定大于这个数的相反数B．若|a|=-a，则a≤0C．绝对值等于3的数是-3D．绝对值不大于2的数是±2，±1，0参考答案一、选择题1．A解析：试题分析：根据负数的绝对值是它的相反数，可得﹣3的绝对值是3，故A 正确. 故选A ．考点：绝对值2．B解析：把各数化简后根据相反数的定义判断即可.详解：A. ∵|3|-=3，∴ |3|-与3不是互为相反数；B. ∵|3|-=3，∴|3|-与-3是互为相反数；C. ∵|3|--=-3，∴ |3|--与-3不是互为相反数；D. ∵|3|-=3，∴ |3|-与+3不是互为相反数；故选B.点睛：本题考查了绝对值的定义，以及相反数的定义，解答本题的关键是熟练掌握相反数的定义，符号不同且绝对值相等的两个数互为相反数，0的相反数是0.3．D解析：先化简题目中的数据，即可得到负数的个数．详解：∵()22--=，44--=-，∴7-，4--，3-，0.27-，都是负数，共4个，故选：D ．点睛：本题考查了正数和负数、相反数、绝对值，正确化简各数是解题的关键．4．B解析：利用绝对值的性质求解即可.详解：解：∵=故选B.点睛：本题主要考察绝对值的性质，正数的绝对值是它本身，负数的绝对值是它的相反数，零的绝对值是零.5．C解析：根据数轴上某个数与原点的距离叫做这个数的绝对值的定义，在数轴上，点﹣2013到原点的距离是2013，所以|﹣2013|=2013，故选C．6．C解析：试题分析：正数的绝对值等于它本身，负数的绝对值等于它的相反数，零的绝对值为零.考点：求绝对值.7．B解析：先计算|-6|，再求其相反数即可．详解：因为|-6|＝8，所以|-6|的相反数是－6．故选：B．点睛：考查了去绝对值符号和求一个数的相反数，解题关键是理解绝对值和相反数概念．8．B解析：试题分析：负数的绝对值等于其相反数，33-=，所以33--=-；故答案选B. 考点：绝对值.9．A解析：根据绝对值的性质进行选择即可．详解：解：55=22﹣，故选：A ．点睛：本题考查了绝对值，掌握绝对值的性质是解题的关键．10．A解析：根据正数的绝对值等于它本身；负数的绝对值等于它的相反数；0的绝对值等于0，可得答案．详解：﹣8的绝对值是8．故选：A ．点睛：本题考查了绝对值，正数的绝对值等于它本身；负数的绝对值等于它的相反数；0的绝对值等于0.11．D解析：实际克数最接近标准克数的是绝对值最小的那个数．详解：解：A 、+4的绝对值是4；B 、+3的绝对值是3；C、-2的绝对值是2；D、-1的绝对值是1．D选项的绝对值最小．故选：D．点睛：本题主要考查正负数的绝对值的大小比较．12．D解析：根据相反数和绝对值的定义求解．详解：解：3的相反数是-3；-3的绝对值是3∴3的相反数的绝对值是3故选：D．点睛：本题考查相反数和绝对值的概念，认真审题掌握和理解相关概念是解题关键．13．D解析：试题分析：绝对值不大于3的整数即为绝对值分别等于3、2、1、0的整数．解：不大于3的整数绝对值有0，1，2，3．因为互为相反数的两个数的绝对值相等，所以绝对值不大于3的整数是0，±1，±2，±3；故选D．考点：绝对值．14．C解析：根据绝对值的性质和相反数的性质逐一计算可得．详解：A、﹣（+2）＝﹣2，此选项不符合题意；B、1≠2，此选项不符合题意；2C、|﹣2|＝2，此选项符合题意；D、﹣|﹣2|＝﹣2，此选项不符合题意；故选C．点睛：本题主要考查绝对值和相反数，解题的关键是熟练掌握绝对值和相反数的性质．15．C-=，∴A错误；解析：A选项，∵55--=-，∴B错误；B选项，∵33C选项，∵77，∴C正确；+-=，∴D错误.D选项，∵88故选C.16．A解析：根据绝对值的性质可得-7的绝对值为7，故选A.点睛：此题考查了绝对值的性质，要求掌握绝对值的性质及其定义，并能熟练运用到实际运算当中．绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．17．C解析：根据绝对值和平方根的性质逐一判断即可得．详解：解：A2=，此选项错误；B2，此选项错误；C、4.3 4.5，此选项正确；D、|11，此选项错误.故选C.点睛：本题主要考查绝对值与平方根，解题的关键是掌握绝对值和平方根的性质，熟记绝对值的非负性.18．D解析：根据正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0进行判断．详解：有理数的绝对值等于其本身的数是正数和0，所以有无数个.故选D.点睛：此题考查绝对值，解题关键在于掌握其定义.19．A解析：根据图形可得点A到原点的距离>点B到原点的距离，即可判断a、b两数的绝对值大小关系．详解：由图形可得：点A到原点的距离>点B到原点的距离∴|a|>|b|故选A．点睛：此题考查绝对值、数轴，解题关键在于利用绝对值与数轴的结合运用判断即可.20．C解析：直接根据绝对值的意义求解．详解：解：|16|＝16，故选：C．点睛：本题考查了绝对值：当a＞0时，|a|=a；当a=0，|a|=0；当a＜0时，|a|=-a．21．D解析：11||20202020-=，即可得出其相反数．详解：解：11 ||20202020 -=所以它的相反数为1 2020 -故答案为：D．点睛：本题考查绝对值与相反数，属于基础题型．22．C解析：根据绝对值的性质，即可完成求解．详解：∵正有理数的绝对值=正有理数∴正有理数在增大时，它的绝对值在增大故选：C．点睛：本题考查了有理数绝对值的知识；求解的关键是熟练掌握有理数绝对值的性质，从而完成求解．23．A解析：根据绝对值的性质解答即可．详解：|-9|=9．故选A．点睛：本题考查了绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．24．B解析：根据绝对值定义进行计算可得答案.详解：5-3=故选B.点睛：本题主要考查绝对值定义.25．B解析：试题分析：0的绝对值是0,0的相反数也是0，因此A选项一个数的绝对值一定大于这个数的相反数说法错误；根据正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0，所以若|a|=-a，则a≤0，故B说法正确；C选项绝对值等于3的数有两个，是±3，因此C说法错误；D选项应是绝对值不大于2的整数是±2，±1，0，故D说法错误．因此本题选B．考点：对绝对值的理解．。

29六年级数学训练

数学试卷
六年级数学训练二十九
班级姓名学号
列方程解应用题。

1. 水果超市运来2500千克苹果，比运来的梨的2倍少250千克，水果店运
来梨多少千克？
2. 一组相互啮合的齿轮，大齿轮有48个齿，小齿轮有16个齿，如果大齿轮
转15周，小齿轮转多少周？
3. 某小学有教师50人，其中男教师人数是女教师的1
4。

这个小学男、女教师各有多少人？
4. 某玩具厂要生产1200件玩具，每天生产80件，已经生产了3天，余下的
如果每天生产96件，还要多少天完成任务？
5. 一辆汽车从甲地到乙地，前3小时行了156千米，照这样的速度，从甲地
到乙地共需8小时，甲乙两地相距多少千米？
6. 学校食堂用方砖铺地，如果用面积为9dm2的方砖，需要48块。

如果改用
面积为16dm2的方砖，需要多少块？。

人教版九年级数学下册第二十九章-投影与视图综合测评试题(含解析)

人教版九年级数学下册第二十九章-投影与视图综合测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图所示的领奖台是由三个长方体组合而成的几何体，则这个几何体的左视图是（）A．B．C．D．2、如图是由6个大小相同的小正方体组成的几何体，它的左视图是（）A．B．C．D．3、如图是由几个大小相同的小正方体搭成的几何体，若去掉1号小正方体，则下列说法正确的是（）A．左视图和俯视图不变B．主视图和左视图不变C．主视图和俯视图不变D．都不变4、下列立体图形的主视图是（）A．B．C．D．5、一个几何体从不同方向看到的图形如图所示，这个几何体是( )A．球B．圆柱C．圆锥D．立方体6、如图，图形从三个方向看形状一样的是（）A．B．C．D．7、下列几何体中，俯视图为三角形的是（）A．B．C．D．8、如图，几何体的左视图是（）A．B．C．D．9、如图为某几何体的三视图，则该几何体是（）A．圆锥B．圆柱C．三棱柱D．四棱柱10、四个相同的小正方体组成的立体图形如图所示，它的主视图为（）A．B．C．D．第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、一个圆柱形橡皮泥，底面积是212cm．高是5cm．如果用这个橡皮泥的一半，把它捏成高为5cm的圆锥，则这个圆锥的底面积是______2cm2、如图所示是从不同的方向观察一个圆柱体得到的形状图，由图中数据计算此圆柱体的侧面积为________（结果保留）．从正面看从左面看从上面看3、阳光下，同学们整齐地站在操场上做课间操，小勇和小宁站在同一列，小勇的影子正好落到后面一个同学身上，而小宁的影子却没有落到后面一个同学身上，据此判断他们的队列方向是______（填“背向太阳”或“面向太阳”），小宁比小勇_______（填“高”、“矮”、或“一样高”）．4、一个立体图形，从正面看到的形状是，从左面看到的形状图是．搭这样的立体图形，最少需要________个小正方体，最多可以有________个正方体．5、如图，是一个由若干个小正方体搭成的几何体的主视图与视图，设搭这样的几何体最多需要m块小立方块，最少需要n块小立方块，则m+n=_____．三、解答题（5小题，每小题10分，共计50分）1、画出几何体的三种视图．2、如图，是由若干个完全相同的棱长为1的小正方体组成的一个几何体．（1）请画出这个几何体的三视图；（2）该几何体的表面积（含下底面）为；（3）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和左视图不变，那么最多可以再添加个小正方体．3、下列几何体是用相同的正方体搭成的，画出从三个不同方向看到的图形4、（1）如图1所示，快下降到地面的某伞兵在灯光下的影子为AB．试确定灯源P的位置，并画出竖立在地面上木桩的影子EF．（保留作图痕迹，不要求写作法）（2）画出图2实物的三视图．5、如图是由大小相同的小正方体组合成的简单几何体．（1）在下面的网格中画出该几何体从正面看和从左面看的形状图．（2）每个正方体棱长为1cm，那么搭成这个几何体的表面积是cm2．---------参考答案-----------一、单选题1、C【分析】左视图是从左边看得到的视图，结合选项即可得出答案．【详解】解：A是俯视图，B、D不是该几何体的三视图，C是左视图．故选：C．【点睛】本题考查了简单组合体的三视图，属于基础题，从正面看到的图是主视图，从上面看到的图形是俯视图，从左面看到的图形是左视图，能看到的线画实线，被遮挡的线画虚线．2、D【分析】细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定则可．【详解】解：从物体左面看，是左边2个正方形，右边1个正方形．故选：D.．【点睛】本题考查了三视图的知识，左视图是从物体左面看所得到的图形，解答时学生易将三种视图混淆而错误的选其它选项．3、A【分析】根据从正面看得到的图形是主视图，从左边看得到的图形是左视图，从上边看得到的图形是俯视图，再从看到的小正方形的个数与排列方式两个方面逐一分析可得答案．【详解】解：若去掉1号小正方体，主视图一定变化，主视图中最右边的一列由两个小正方形变为一个，从上面看过去，看到的小正方形的个数与排列方式不变，所以俯视图不变，从左边看过去，看到的小正方形的个数与排列方式不变；所以左视图不变，所以A符合题意，B，C，D不符合题意；故选：A．【点睛】本题考查的是由小正方体堆砌而成的图形的三视图，掌握“三视图的含义”是解本题的关键.4、A【分析】主视图是从正面所看到的图形，根据定义和立体图形即可得出选项．【详解】解：主视图是从正面所看到的图形，是：故选：A【点睛】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．5、B【分析】根据各个几何体的三视图，依次判别即可；【详解】解：A、球的三视图均为圆形；B、圆柱的三视图与题图相符；C、圆锥的主视图和左视图为等腰三角形；D、立方体的三视图均为四边形．故选：B．【点睛】本题考查了由三视图判断几何体，熟悉相关性质是解题的关键．6、C【分析】根据从上面看得到的图形是俯视图，从正面看得到的图形是主视图，从左边看得到的图形是左视图，可得答案．【详解】解：A．从上面看是一个圆，从正面和从左边看是一个矩形，故本选项不合题意；B．从上面看是一个有圆心的圆，从正面和从左边看是一个等腰三角形，故本选项不合题意；C．从三个方向看形状一样，都是圆形，故本选项符合题意；D．从上面看是一个正方形，从正面和从左边看是一个长方形形，故本选项不合题意．故选：C．【点睛】本题考查了简单几何体的三视图，从上面看到的图形是俯视图，从正面看到的图形是主视图，从左面看到的图形是左视图．7、（4）如图3，要搭成该几何体的正方体的个数最少是a，最多是b，则a+b＝错误，应该是a＝6，b ＝11，a+b＝17．故选：B．【点睛】此题主要考查了正方体的展开图的性质，截正方体以及简单组合体的三视图等知识，根据展开图的性质得出一个平面图形必须5条棱连接是解题关键．19．D【分析】从正面、上面和左面三个不同的方向看一个物体，并描绘出所看到的三个图形，即几何体的三视图．【详解】从上方朝下看只有D选项为三角形．故选：D．【点睛】本题考查了简单几何体的三视图，三视图是从正面、左面、上面以平行视线观察物体所得的图形．从视图反过来考虑几何体时，它有多种可能性．例如，正方体的主视图是一个正方形，但主视图是正方形的几何体有很多，如三棱柱、长方体、圆柱等．因此在学习时应结合实物，亲自变换角度去观察，才能提高空间想象能力．8、C【分析】找到从左面看所得到的图形，比较即可．【详解】解：观察可知，从物体的左边看是一个竖长横短的长方形，由于右边有一条横向棱被遮挡看不见，画为虚线，如图所示的几何体的左视图是：．故选C．【点睛】本题考查了三视图的知识，左视图是从物体的左面看得到的视图．9、C【分析】根据三视图判断该几何体即可．【详解】解：根据该几何体的主视图与左视图均是矩形，主视图中还有一条棱，俯视图是三角形可以判断该几何体为三棱柱．故选：C．【点睛】本题考查三视图，解题的关键是理解三视图的定义，属于中考常考题型．10、A【分析】根据几何体的三视图解答即可．【详解】根据立体图形得到：主视图为：，左视图为：，俯视图为：，故选：A【点睛】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．二、填空题1、18【解析】【分析】首先求出圆柱体积，根据题意得出圆柱体积的一半即为圆锥的体积，根据圆锥体积计算公式列出方程，即可求出圆锥的底面积．【详解】Ｖ圆柱＝Sh =212560cm ，这个橡皮泥的一半体积为：2160302V cm ，把它捏成高为5cm的圆锥，则圆锥的高为5cm，故1303Sh，即15=303S，解得=18S（cm2），故填：18．【点睛】本题考查了圆柱的体积和圆锥的体积计算公式，解题关键是理解题意，熟练掌握圆柱体积和圆锥体积计算公式．2、6π【解析】【分析】根据主视图确定出圆柱体的底面直径与高，然后根据圆柱体的侧面积公式列式计算即可得解．【详解】解：由图可知，圆柱体的底面直径为2，高为3，所以，侧面积236ππ=⋅⨯=．故答案为：6π．【点睛】本题考查了立体图形的三视图和学生的空间想象能力，圆柱体的侧面积公式，解题的关键是根据主视图判断出圆柱体的底面直径与高．3、面向太阳矮【解析】【分析】根据小勇的影子正好落到后面一个同学身上可得他们的队列方向是面向太阳，根据同时同地，身高与影长成正比可得答案．【详解】∵小勇的影子正好落到后面一个同学身上，∴他们的队列方向是面向太阳，∵小宁的影子却没有落到后面一个同学身上，∴小勇的影子比小宁的影子长，∴小宁比小勇矮．故答案为：面向太阳，矮【点睛】本题考查平行投影，熟练掌握同时同地，身高与影长成正比是解题关键．4、 6 10【解析】【分析】根据题中所给的正面的形状和左面的形状即可得．【详解】解：根据题中所给的正面的形状和左面的形状可知，最少需要6个，将小正方体横着摆5个，再在任意一个小正方体的后面放一个小正方体；最多需要10个，将小正方体横着摆5个，再在每一个小正方体的后面放一个小正方体；故答案为：6，10．【点睛】本题考查了三视图，解题的关键是根据三视图得出立体图形．5、15【解析】【分析】易得这个几何体共有3层，由俯视图可得第一层正方体的个数为4，由主视图可得第二层最少为2块，最多的正方体的个数为3块，第三层只有一块，相加即可．【详解】解：有两种可能；有主视图可得：这个几何体共有3层，由俯视图可得：第一层正方体的个数为4，由主视图可得第二层最少为2块，最多的正方体的个数为3块，第三层只有一块，故：最多m为3+4+1=8个小立方块，最少n为个2+4+1=7小立方块．m+n=15，故答案为：15【点睛】此题主要考查了由三视图判断几何体，关键是掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就很容易得到答案．三、解答题1、见详解【分析】从正面看从左往右3列正方形的个数依次为1，3，2；从左面看从左往右3列正方形的个数依次为3，1；从上面看从左往右3列正方形的个数依次为1，2，1．依此画出图形．【详解】解：如图所示：【点睛】本题考查了三视图的画法；得到从各个方向看得到的每列正方形的个数是解决本题的关键．2、（1）见解析；（2）28；（3）2【分析】（1）从正面看得到从左往右3列正方形的个数依次为1，3，2；从左面看得到从左往右2列正方形的个数依次为3，1；从上面看得到从左往右3列正方形的个数依次为1，2，1，依此画出图形即可；（2）有顺序的计算上下面，左右面，前后面的表面积之和即可；（3）根据保持这个几何体的主视图和左视图不变，可知添加小正方体是1列和3列各加1个，依此即可求解．【详解】（1）如图所示：（2）（4×2+6×2+4×2）×（1×1）＝（8+12+8）×1＝28故答案为：28（3）由分析可知，最多可以再添加2个小正方体，如图，故答案为：2【点睛】此题考查了作图−三视图，用到的知识点为：计算几何体的表面积应有顺序的分为相对的面进行计算不易出差错；三视图分为主视图、左视图、俯视图，分别是从物体正面、左面和上面看，所得到的图形．3、见解析【分析】从正面看：共有3列，从左往右分别有3，2，1个小正方形；从左面看：共有2列，从左往右分别有3，1个小正方形；从上面看：共分3列，从左往右分别有2，1，1个小正方形．据此可画出图形．【详解】解：如图所示：【点睛】本题考查画三视图的知识；用到的知识点为：主视图，左视图，俯视图分别是从物体的正面，左面，上面看得到的图形．4、（1）见解析；（2）见解析【分析】BD AC，两射线交于点P即可求得P的位置，过P和木桩的顶（1）如图，分别以,A B为端点作射线,端，以P为端点做射线，与底面交于点F，木桩底部为E点，连接EF，则EF即为竖立在地面上木桩的影子；（2）根据三视图的作法要求画三视图即可，主视图为等边三角形，左视图为矩形，俯视图为矩形，中间有一条实线【详解】（1）如图所示，P为灯源，EF为竖立在地面上木桩的影子，（2）如图所示，【点睛】本题考查了中心投影，三视图，掌握中心投影与三视图的作图方法是解题的关键．5、（1）图见解析；（2）38．【分析】（1）由已知条件可知，从正面看的视图有3列，每列小正方数形数目分别为3，1，2，据此可画出图形；从左面看的视图有3列，每列小正方形数目分别为3，2，1；（2）根据三视图的面积和被挡住的面积即可计算总面积；【详解】解:（1）如图所示：（2）搭成这个几何体的表面积是：6×2+6×2+6×2+2=38 cm2．【点睛】本题考查从不同方向看几何体，几何体的表面积等知识．解题的关键是熟练掌握基本知识，属于中考常考题型．。