离散数学题库
离散数学练习题(含答案)

离散数学试题第一部分选择题一、单项选择题1.下列是两个命题变元p,q的小项是( C )A.p∧┐p∧q B.┐p∨qC.┐p∧q D.┐p∨p∨q2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( D )A.p→┐q B.p∨┐qC.p∧q D.p∧┐q3.下列语句中是命题的只有( A )A.1+1=10 B.x+y=10C.sinx+siny<0 D.x mod 3=24.下列等值式不正确的是( C )A.┐(∀x)A⇔(∃x)┐AB.(∀x)(B→A(x))⇔B→(∀x)A(x)C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)D.(∀x)(∀y)(A(x)→B(y))⇔(∃x)A(x)→(∀y)B(y)5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是( C )A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))B.Q(x,z)→(∀y)R(x,y,z)C.Q(x,z)→(∃x)(∀y)R(x,y,z)D.Q(x,z)6.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是( D )A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是( A )A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈BC.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B8.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是( A )A.(X-Y)-Z=X-(Y∩Z)B.(X-Y)-Z=(X-Z)-YC.(X-Y)-Z=(X-Z)-(Y-Z)D.(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,下列定义的运算中不可结合的只有( D )A.a*b=min(a,b)B.a*b=a+bC.a*b=GCD(a,b)(a,b的最大公约数)02324# 离散数学试题第1 页共4页02324# 离散数学试题 第 2 页 共4页D .a*b=a(mod b)10.设R 和S 是集合A 上的关系,R ∩S 必为反对称关系的是( A ) A .当R 是偏序关系,S 是等价关系; B .当R 和S 都是自反关系; C .当R 和S 都是等价关系; D .当R 和S 都是传递关系11.设R 是A 上的二元关系,且R ·R ⊆R,可以肯定R 应是( D ) A .对称关系; B .全序关系; C .自反关系; D .传递关系第二部分 非选择题二、填空题1.设论域是{a,b,c},则(∀x)S(x)等价于命题公式 S(a)∧S(b)∧S(c) ;(x ∃)S(x)等价于命题公式 S(a)∨S(b) ∨S(c) 。
离散数学题目大汇总

离散数学试题一(A 卷答案)一、(10分)证明⌝(A ∨B )→⌝(P ∨Q ),P ,(B →A )∨⌝P A 。
二、(10分)甲、乙、丙、丁4个人有且仅有2个人参加围棋优胜比赛。
关于谁参加竞赛,下列4种判断都是正确的:(1)甲和乙只有一人参加;(2)丙参加,丁必参加;(3)乙或丁至多参加一人;(4)丁不参加,甲也不会参加。
请推出哪两个人参加了围棋比赛。
三、(10分)指出下列推理中,在哪些步骤上有错误?为什么?给出正确的推理形式。
(1)∀x (P (x )→Q (x )) P(2)P (y )→Q (y ) T (1),US(3)∃xP (x ) P(4)P (y ) T (3),ES(5)Q (y ) T (2)(4),I(6)∃xQ (x ) T (5),EG四、(10分)设A ={a ,b ,c},试给出A 上的一个二元关系R ,使其同时不满足自反性、反自反性、五、(15分)设函数g :A →B ,f :B →C ,(1)若f g 是满射,则f 是满射。
(2)若f g 是单射,则g 是单射。
六、(15分)设R 是集合A 上的一个具有传递和自反性质的关系,T 是A 上的关系,使得<a ,b >∈T ⇔<a ,b >∈R 且<b ,a >∈R ,证明T 是一个等价关系。
七、(15分)若<G ,*>是群,H 是G 的非空子集,则<H ,*>是<G ,*>的子群⇔对任意的a 、b ∈H 有a *b -1∈H 。
八、(15分)(1)若无向图G 中只有两个奇数度结点,则这两个结点一定是连通的。
(2)若有向图G 中只有两个奇数度结点,它们一个可达另一个结点或互相可达吗?离散数学试题一(B 卷答案)一、(15分)设计一盏电灯的开关电路,要求受3个开关A 、B 、C 的控制:当且仅当A 和C 同时关闭或B 和C 同时关闭时灯亮。
设F 表示灯亮。
离散数学试题及答案

离散数学试题及答案一、选择题1. 设A、B、C为三个集合,下列哪个式子是成立的?A) \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)B) \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)C) \(A \cup (B \cup C) = (A \cup B) \cup (A \cup C)\)答案:B2. 对于一个有n个元素的集合S,S的幂集中包含多少个元素?A) \(n\)B) \(2^n\)C) \(2 \times n\)答案:B二、判断题1. 对于两个关系R和S,若S是自反的,则R ∩ S也是自反的。
答案:错误2. 若一个关系R是反对称的,则R一定是反自反的。
答案:正确三、填空题1. 有一个集合A,其中包含元素1、2、3、4和5,求集合A的幂集的大小。
答案:322. 设a和b是实数,若a \(\neq\) b,则a和b之间的关系是\(\__\_\)关系。
答案:不等四、解答题1. 证明:如果关系R是自反且传递的,则R一定是反自反的。
解答:假设关系R是自反的且传递的,即对于集合A中的任意元素x,都有(x, x) ∈ R,并且当(x, y) ∈ R和(y, z) ∈ R时,(x, z) ∈ R。
反证法:假设R不是反自反的,即存在一个元素a∈A,使得(a, a) ∉ R。
由于R是自反的,所以(a, a) ∈ R,与假设矛盾。
因此,R一定是反自反的。
答案完整证明了该结论。
2. 已知集合A={1, 2, 3},集合B={2, 3, 4},求集合A和B的笛卡尔积。
解答:集合A和B的笛卡尔积定义为{(a, b) | a∈A,b∈B}。
所以,集合A和B的笛卡尔积为{(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4)}。
离散数学题库及答案

数理逻辑部分选择、填空及判断✓ 下列语句不是命题的( A )。
(A) 你打算考硕士研究生吗? (B) 太阳系以外的星球上有生物。
(C) 离散数学是计算机系的一门必修课。
(D) 雪是黑色的。
✓ 命题公式P →(P ∨⌝P )的类型是( A )(A) 永真式 (B) 矛盾式(C) 非永真式的可满足式 (D) 析取范式✓ A 是重言式,那么A 的否定式是( A )A. 矛盾式B. 重言式C. 可满足式D.不能确定✓ 以下命题公式中,为永假式的是( C )A. p →(p ∨q ∨r)B. (p →┐p)→┐pC. ┐(q →q)∧pD. ┐(q ∨┐p)→(p ∧┐p)✓ 命题公式P →Q 的成假赋值是( D )A. 00,11B. 00,01,11C.10,11D. 10✓ 谓词公式),()(y x R x xP ∧∀中,变元x 是 ( B )A. 自由变元B. 既是自由变元也是约束变元C. 约束变元D. 既不是自由变元也不是约束变元✓ 命题公式P →(Q ∨⌝Q)的类型是( A )。
(A) 永真式 (B) 矛盾式(C) 非永真式的可满足式 (D) 析取范式✓ 设B 不含变元x ,))((B x A x →∃等值于( A )A. B x xA →∀)(B. ))((B x A x ∨∃C. B x xA →∃)(D. B x A x ∧∃)(( ✓ 下列语句中是真命题的是( D )。
A .你是杰克吗?B .凡石头都可练成金。
C .如果2+2=4,那么雪是黑的。
D .如果1+2=4,那么雪是黑的。
✓ 从集合分类的角度看,命题公式可分为( B )A. 永真式、矛盾式B. 永真式、可满足式、矛盾式C. 可满足式、矛盾式D. 永真式、可满足式✓ 命题公式﹁p ∨﹁q 等价于( D )。
A. ﹁p ∨qB. ﹁(p ∨q)C. ﹁p ∧qD. p →﹁q✓ 一个公式在等价意义下,下面写法唯一的是( D )。
离散数学练习题(含答案)

离散数学练习题(含答案)题目1. 对于集合 $A={1,2,3,...,10}$ 和 $B={n|n是偶数,2<n<8}$,求 $A \cap B$ 的元素。
2. 存在三个可识别的状态A,B,C。
置换群 $S_3$ 作用在状态集上。
定义四个动作:$α: A → C, β: A → B, γ: C→ A, δ: B→ C$。
确定式子,描述 $\{α,β,γ,δ\}$ 的乘法表。
3. 证明 $\forall n \in \mathbb{N}$,合数的个数不小于$n$。
4. 给定一个无向带权图,图中每个节点编号分别是$1,2,...,n$,证明下列结论:a. 如果从节点$i$到$j$只有一条权值最小的路径,则这条路径的任意子路径都是最短路径。
b. 如果从节点$i$到$j$有两条或两条以上权值相等的路径,则从$i$到$j$的最短路径可能不唯一。
答案1. $A \cap B = \{2,4,6\}$。
2. 乘法表:3. 对于任意$n$,我们可以选择$n+1$个连续的自然数$k+1,k+2,...,k+n,k+n+1$中的$n$个数,其中$k \in \mathbb{Z}$。
这$n$个数构成的$n$个正整数均为合数,因为它们都至少有一个小于它自身的因子,所以不是质数。
所以合数的个数不小于任意$n$。
4.a. 根据题意,从$i$到$j$只有一条权值最小的路径,即这条最短路径已被确定。
如果从这条路径中任意取出一段子路径,假设这段子路径不是这个节点到$j$的最短路径,那么存在其他从$i$到$j$的路径比这段子路径更优,又因为这条路径是最短路径,所以这段子路径也一定不优于最短路径,矛盾。
所以从这条路径中任意取出的子路径都是最短路径。
b. 如果从节点$i$到$j$有多条权值相等的路径,则这些路径权值都是最短路径的权值。
因为所有最短路径的权值相等,所以这些路径的权值就是最短路径的权值。
所以从$i$到$j$的最短路径可能不唯一。
离散数学-习题集

离散数学-习题集《离散数学》习题集第⼀部分判断题⼀、第⼀章—集合1、()已知集合A的元素个数为10,则集合A的幂集的基=102。
2、()已知两个集合A、B,若A中的元素都是B中的元素,则记为A∈B。
2、()已知集合A的元素个数为n,则集合A的幂集P(A)的元素个数为n2。
3、( ) 已知两个集合A={Ф,{Ф}},B={Ф},则A∩B={Ф}。
4、()已知两个集合A={Ф,{Ф}},B={Ф},则A∩B=Ф。
5、()已知两个集合A、B,若A中的元素都是B中的元素,则记为A∈B。
6、()已知集合A的元素个数为n,则集合A的幂集P(A)的元素个数为n2。
7、()已知集合A的元素个数为n,则A×A的幂集的元素个数为n2。
8、()已知两个集合A、B,则A-B是由属于B但不属于A的元素构成的集合。
⼆、第⼆章—⼆元关系1、()若R是A上的⼆元关系,I A是A上的恒等关系,则当且仅当I A∈R时,R是A上的⾃反关系。
2、(√)若R是集合A上的⼆元关系,且当(a,b)∈R且(a,c)∈R时,就有(b,c)∈R,则R是A 上的可传递关系。
3、()设A是集合,A1、A2、...A n都是A的⾮空⼦集,令S={A1,A2,...,A n},则如果S是集合A的⼀个划分,那么S⼀定是集合A的⼀个完全覆盖;反之亦然。
5、()R是⾮空集合A上的等价⼆元关系,则A关于R的商集A/R是集合A的⼀个划分,但不是A的⼀个完全覆盖。
6、()已知集合A有4元素,易知集合A共有24个互不相同的⼦集合,所以在集合A上⼀共可定义24个互不相同的⼆元关系。
7、()若R1和R2都是集合A上的可传递⼆元关系,则R1∪R2也是A上的传递关系。
8、()设R是有限的⾮空集合A上的偏序关系,则A必有极⼤(⼩)元和最⼤(⼩)元。
9、()若R1和R2都是集合A上的相容关系,则R1∩R2也是A上的相容关系。
10、()若R1和R2都是集合A的可传递⼆元关系,则R1∩R2也是A上的传递关系。
自考离散数学考试题库及答案

自考离散数学考试题库及答案一、选择题1. 在离散数学中,命题逻辑的主要研究对象是什么?A. 命题的真假B. 命题的类型C. 命题的表达D. 命题的证明答案:A2. 有限集合M的基数是指什么?A. M中元素的数量B. M的子集数量C. M的幂集D. M的幂集的基数答案:A3. 以下哪个不是图论中的基本概念?A. 顶点B. 边C. 集合D. 子图答案:C二、填空题4. 在命题逻辑中,德摩根定律表示了________和________之间的逻辑关系。
答案:¬(P ∧ Q);¬P ∨ ¬Q5. 一个集合的幂集是指该集合所有________的集合。
答案:子集6. 在图论中,无向图中的路径是顶点和边的________。
答案:交替序列三、解答题7. 证明:若命题P是真命题,则其否定¬P是假命题。
证明:根据命题逻辑的定义,一个命题要么是真要么是假。
如果P 是真命题,那么根据否定的定义,¬P表示P不是真的,这与P是真命题的事实相矛盾。
因此,¬P必须是假命题。
8. 给定集合A={1, 2, 3},求其幂集及其基数。
解答:集合A的幂集包括A的所有子集,即∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}。
共有2^3=8个子集,所以A的幂集的基数是8。
四、应用题9. 在一个无向图中,定义了两个顶点之间的距离为它们之间的最短路径上的边数。
如果图G中有两个顶点u和v,且它们之间的距离是3,证明存在一个顶点w,使得u和w之间的距离是1,v和w之间的距离是2。
证明:由于u和v之间的距离是3,根据距离的定义,存在一条最短路径连接u和v,这条路径至少包含3条边。
设这条路径为u=w1, w2, w3, w4=v,其中每对相邻的顶点之间存在一条边。
根据题设,我们可以取w2作为w,这样u和w之间的距离是1(因为它们之间有一条边w1w2),而v和w之间的距离是2(因为它们之间有两条边w2w3和w3w4)。
离散数学题库及答案

数理逻辑部分选择、填空及判断✓下列语句不是命题的( A )。
(A) 你打算考硕士研究生吗? (B) 太阳系以外的星球上有生物。
(C) 离散数学是计算机系的一门必修课。
(D) 雪是黑色的。
✓命题公式P→(P∨⌝P)的类型是( A )(A) 永真式(B) 矛盾式(C) 非永真式的可满足式(D) 析取范式✓A是重言式,那么A的否定式是( A )A. 矛盾式B. 重言式C. 可满足式D.不能确定✓以下命题公式中,为永假式的是( C )A. p→(p∨q∨r)B. (p→┐p)→┐pC. ┐(q→q)∧pD. ┐(q∨┐p)→(p∧┐p)✓命题公式P→Q的成假赋值是( D )A. 00,11B. 00,01,11C.10,11D. 10✓谓词公式)xxP∧∀中,变元x是 ( B )R,(x)(yA. 自由变元B. 既是自由变元也是约束变元C. 约束变元D. 既不是自由变元也不是约束变元✓命题公式P→(Q∨⌝Q)的类型是( A )。
(A) 永真式 (B) 矛盾式(C) 非永真式的可满足式 (D) 析取范式✓设B不含变元x,)xx→∃等值于( A )A)((BA. B( D. BxxA→x∃)((∃ C. Bx∧A∃)( B. )∀)xA→x)(Ax(Bx∨✓下列语句中是真命题的是( D )。
A.你是杰克吗? B.凡石头都可练成金。
C.如果2+2=4,那么雪是黑的。
D.如果1+2=4,那么雪是黑的。
✓从集合分类的角度看,命题公式可分为( B )A. 永真式、矛盾式B. 永真式、可满足式、矛盾式C. 可满足式、矛盾式D. 永真式、可满足式✓命题公式﹁p∨﹁q等价于( D )。
A. ﹁p∨qB. ﹁(p∨q)C. ﹁p∧qD. p→﹁q✓一个公式在等价意义下,下面写法唯一的是( D )。
(A) 范式 (B) 析取范式 (C) 合取范式 (D) 主析取范式✓下列含有命题p,q,r的公式中,是主析取范式的是( D )。
《离散数学》题库及答案

《离散数学》题库及答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?()(1)Q=>Q→P(2)Q=>P→Q(3)P=>P→Q(4)P(PQ)=>P答:(1),(4)2、下列公式中哪些是永真式?()(1)(┐PQ)→(Q→R)(2)P→(Q→Q)(3)(PQ)→P(4)P→(PQ)答:(2),(3),(4)3、设有下列公式,请问哪几个是永真蕴涵式()(1)P=>PQ(2)PQ=>P(3)PQ=>PQ(4)P(P→Q)=>Q(5)(P→Q)=>P(6)P(PQ)=>P答:(2),(3),(4),(5),(6)4、公式某((A(某)B(y,某))zC(y,z))D(某)中,自由变元是(变元是()。
答:某,y,某,z5、判断下列语句是不是命题。
若是,给出命题的真值。
((1)北京是中华人民共和国的首都。
(2)陕西师大是一座工厂。
),约束)(3)你喜欢唱歌吗?(4)若7+8>18,则三角形有4条边。
(5)前进!(6)给我一杯水吧!答:(1)是,T(2)是,F(3)不是(4)是,T(5)不是(6)不是6、命题“存在一些人是大学生”的否定是(),而命题“所有的人都是要死的”的否定是()。
答:所有人都不是大学生,有些人不会死7、设P:我生病,Q:我去学校,则下列命题可符号化为()。
(1)只有在生病时,我才不去学校(2)若我生病,则我不去学校(3)当且仅当我生病时,我才不去学校(4)若我不生病,则我一定去学校答:(1)QP(2)PQ(3)PQ(4)PQ8、设个体域为整数集,则下列公式的意义是()。
(1)某y(某+y=0)(2)y某(某+y=0)答:(1)对任一整数某存在整数y满足某+y=0(2)存在整数y对任一整数某满足某+y=09、设全体域D是正整数集合,确定下列命题的真值:(1)某y(某y=y)()(2)某y(某+y=y)()(3)某y(某+y=某)()(4)某y(y=2某)()答:(1)F(2)F(3)F(4)T10、设谓词P(某):某是奇数,Q(某):某是偶数,谓词公式某(P(某)Q(某))在哪个个体域中为真()2(1)自然数(2)实数(3)复数(4)(1)--(3)均成立答:(1)11、命题“2是偶数或-3是负数”的否定是()。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
《离散数学》试题含答案

《离散数学》试题含答案⼀、填空题1设集合A,B,其中A={1,2,3}, B= {1,2}, 则A - B=____________________; ρ(A) - ρ(B)=__________________________ .2. 设有限集合A, |A| = n, 则|ρ(A×A)| = __________________________.3.设集合A = {a, b}, B = {1, 2}, 则从A到B的所有映射是__________________________ _____________, 其中双射的是__________________________.4. 已知命题公式G=?(P→Q)∧R,则G的主析取范式是_________________________________________________________________________________________.5.设G是完全⼆叉树,G有7个点,其中4个叶点,则G的总度数为__________,分枝点数为________________.6设A、B为两个集合, A= {1,2,4}, B = {3,4}, 则从A?B=_________________________; A?B=_________________________;A-B=_____________________ .7. 设R是集合A上的等价关系,则R所具有的关系的三个特性是______________________,________________________, _______________________________.8. 设命题公式G=?(P→(Q∧R)),则使公式G为真的解释有__________________________,_____________________________, __________________________.9. 设集合A={1,2,3,4}, A上的关系R1 = {(1,4),(2,3),(3,2)}, R1 = {(2,1),(3,2),(4,3)}, 则R1?R2 =________________________,R2?R1 =____________________________, R12=________________________.10. 设有限集A, B,|A| = m, |B| = n, 则| |ρ(A?B)| = _____________________________.11设A,B,R是三个集合,其中R是实数集,A = {x | -1≤x≤1, x∈R}, B = {x | 0≤x < 2, x∈R},则A-B =__________________________ , B-A = __________________________ ,A∩B = __________________________ , .13.设集合A={2, 3, 4, 5, 6},R是A上的整除,则R以集合形式(列举法)记为__________________________________________________________________.14. 设⼀阶逻辑公式G = ?xP(x)→?xQ(x),则G的前束范式是__________________________ _____.15.设G是具有8个顶点的树,则G中增加_________条边才能把G变成完全图。
(完整版)离散数学题目及答案

A)
A
.p→ (p∨q)
B.
(p∨┐p)→q
C
.q∧┐q
D.
p→┐q
4.
下列语句中不是..命题的只有(
A)
A.花儿为什么这样红?
B.
2+2=0
)
其中不是复合命题的是(B
A.( 1)( 4)
D.(1)(3)(4)
10.下述不是命题的是(D)
A.花儿是红色的
C.3是偶数
11.
用P表示:天下大雨;Q表示:
15.
设p:开关 A开,q:开关 B开,则“开且只开
A、B中一个开关”的命题公式是(
他乘公共汽车上班。将“如果天下大雨,他就乘公共
汽车上班。”符号化正确的是(A
)
A
.P QB.Q P
C.P
QD.P Q
12.谓词公式(y)( x)(P(x)
→
R(
x,y))∧
xQ(x,y)中变元 y(C)
A.
是自由变元但不是约束变元
B.
是约束变元但不是自由变元
C.
既是自由变元又是约束变元
D.
既不是自由变元又不是约束变元
13.关于命题变元P和Q的成假赋值为
01
对应的极大项是(C)
A
.┐P∧QB.┐P∨Q
C.P∨
┐QD.P∧┐Q
14.谓词公式(y)( x)(P(x)
→
R(
x,y))∧
yQ(x,y)中变元 y(B)
A
.是自由变元但不是约束变元
B.
是约束变元但不是自由变元
C
.既是自由变元又是约束变元
D.
既不是自由变元又不是约束变元
《离散数学》考试题库及答案
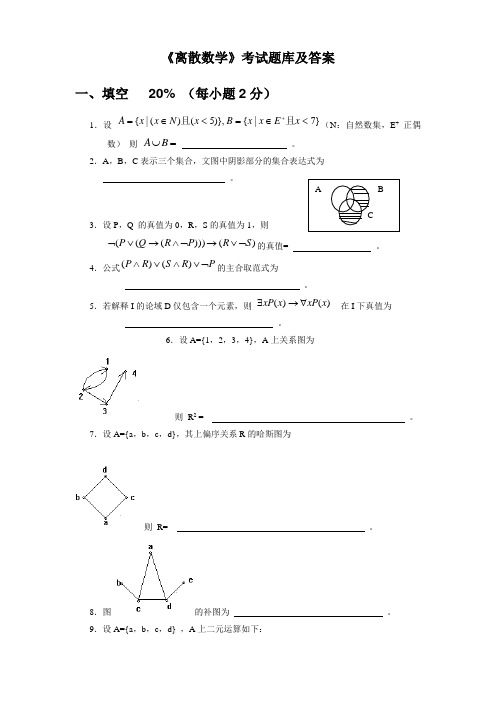
《离散数学》考试题库及答案一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:A BC* a b c d a b c da b c d b c d a c d a b d a b c那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有( )个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是( ) A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
离散数学试题及答案

离散数学试题及答案一、选择题(每题2分,共20分)1. 集合A={x|x<5},集合B={x|x>2},则A∩B为:A. {x|x>2}B. {x|x<2}C. {x|2<x<5}D. {x|x≥5}2. 命题p:"x>0"是命题q:"x^2>0"的:A. 必要条件B. 充分条件C. 充分必要条件D. 无关条件3. 函数f(x)=x^2+3x-2的值域是:A. (-∞, -1]B. [1, +∞)C. (-∞, 4]D. (-∞, 2]4. 逻辑表达式((P∨Q)∧(¬P))的真值表中,当P为真时,表达式的值为:A. 真B. 假C. 不确定D. 无法判断5. 已知二元关系R定义在集合A上,若对于任意a,b,c∈A,若aRb且bRc,则aRc,那么R是:A. 自反的B. 对称的C. 传递的D. 完全的6. 有限状态自动机(DFA)与确定有限状态自动机(DFA)的区别在于:A. DFA可以识别非正则语言B. DFA可以有多个起始状态C. DFA可以有多个接受状态D. DFA可以有多个状态7. 命题逻辑中,若命题P的否定为P',则P和P'的关系是:A. 互为对立B. 互为矛盾C. 互为等价D. 互为同一律8. 集合{1,2,3}的子集个数是:A. 3B. 4C. 7D. 89. 一个命题逻辑公式的真值表中,若存在一行结果为假,则该公式:A. 总是假B. 有时真,有时假C. 总是真D. 无法判断10. 布尔代数中,逻辑与(AND)操作的特点是:A. 有0则0B. 有1则1C. 非0即1D. 非1即0二、简答题(每题5分,共10分)1. 简述集合论中的幂集概念。
2. 描述图的邻接矩阵表示方法。
三、计算题(每题10分,共30分)1. 证明函数f(x)=x^3-3x^2+2x-1在R上是单调递增的。
(完整版)离散数学题库与答案

试卷二十二试题与答案一、单项选择题:(每小题1分,本大题共15分)1.设A={1,2,3,4,5},下面( )集合等于A 。
A 、{1,2,3,4,5,6};B 、}25{2≤x x x 是整数且; C 、}5{≤x x x 是正整数且; D 、}5{≤x x x 是正有理数且。
2.设A={{1,2,3},{4,5},{6,7,8}},下列各式中( )是错的。
A 、A ⊆Φ;B 、{6,7,8}∈A ;C 、{{4,5}}⊂A ;D 、{1,2,3}⊂A 。
3.六阶群的子群的阶数可以是( )。
A 、1,2,5;B 、2,4;C 、3,6,7;D 、2,3 。
4.设B A S ⨯⊆,下列各式中( )是正确的。
A 、 domS ⊆B ; B 、domS ⊆A ;C 、ranS ⊆A ;D 、domS ⋃ ranS = S 。
5.设集合Φ≠X ,则空关系X Φ不具备的性质是( )。
A 、自反性;B 、反自反性;C 、对称性;D 、传递性。
6.下列函数中,( )是入射函数。
A 、世界上每个人与其年龄的序偶集;B 、、世界上每个人与其性别的序偶集;B 、 一个作者的专著与其作者的序偶集; D 、每个国家与其国旗的序偶集。
7.><,*G 是群,则对*( )。
A 、满足结合律、交换律;B 、有单位元,可结合;C 、有单位元、可交换;D 、每元有逆元,有零元。
8.下面( )哈斯图所描述的偏序关系构成分配格。
9.下列( )中的运算符都是可交换的。
A 、→∨∧,,;B 、↔→,;C 、⨯⋂⋃,,;D 、∧∨,。
10.设G 是n 个结点、m 条边和r 个面的连通平面图,则m 等于( )。
A 、n+r-2 ;B 、n-r+2 ;C 、n-r-2 ;D 、n+r+2 。
11.n 个结点的无向完全图n K 的边数为( )。
A 、)1(+n n ;B 、2)1(+n n ;C 、)1(-n n ;D 、2)1(-n n 。
离散数学题库、

B.x(P(x)Q(x))xP(x)xQ(x)
C.x(P(x)Q(x))xP(x)xQ(x)
D.xP(x)Q)xP(x)Q
28、 下面谓词公式哪个是前束范式?()
A.xyz(B(x,y)A(z))
B.ቤተ መጻሕፍቲ ባይዱyB(x,y)
C.xyx(A(x,y)B(x,y))
D.x(A(x,y)yB(y))
29、 在谓词演算中:P(a)是xP(x)的有效结论,其理论根据是()
A.a*b=a+b+3 B.a*b=min{a,b} C.a*b=a+2b D.a*b=ab(mod
3)
59、 下列运算中,哪种运算关于整数集不能构成半群?()
A.aοb=max{a,b}
B.aοb=b
C.aοb=2ab
D.aοb=|a-b|
60、*运算如下表所示,哪个能使({a,b},*)成为独异点?()
A.循环群
B.置换群
A.P→(P∨Q∨R)
B.(P→P)→P
C.(Q→P )∧P
D. ( P∨P)→(P∧P)
16、设命题公式,则G是( )。 A. 恒假的 B. 恒真的 C. 可满足的 D. 析取范式
17、谓词公式x(P(x)yR(y))Q(x)中量词x的作用域是()
A. x(P(x)yR(y))
B.P(x)
C. (P(x)yR(y))
C.P(a)S(b)
D.P(a)P(b)S(a)S(b)
26、 在谓词演算中,下列各式哪个是正确的?()
A.xyA(x,y)yxA(x,y)
B.xyA(x,y)yxA(x,y)
C.xyA(x,y)xyA(x,y)
D.xyA(x,y)yxA(x,y)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常熟理工学院20 ~20 学年第学期《离散数学》考试试卷(试卷库01卷)试题总分: 100 分考试时限:120 分钟题号一二三四五总分阅卷人得分一、单项选择题(每题2分,共20分)1.下列表达式正确的有( )(A)(B)(C)(D)2.设P:2×2=5,Q:雪是黑的,R:2×4=8,S:太阳从东方升起,下列( )命题的真值为真。
(A)(B)(C)(D)3.集合A={1,2,…,10}上的关系R={<x,y>|x+y=10,x,y A},则R 的性质为( )(A)自反的(B)对称的(C)传递的,对称的(D)传递的4.设,,其中表示模3加法,*表示模2乘法,在集合上定义如下运算:有称为的积代数,则的积代数幺元是( )(A)<0,0> (B)<0,1> (C)<1,0> (D)<1,1>5.下图中既不是Eular图,也不是Hamilton图的图是( )6.设为无向图,,则G一定是( )(A)完全图(B)树(C)简单图(D)多重图7.设P:我将去镇上,Q:我有时间。
命题“我将去镇上,仅当我有时间”符号化为()。
(A) P Q (B)Q P (C)P Q (D)8.在有n个结点的连通图中,其边数()(A)最多有n-1条(B)最多有n 条(C)至少有n-1条(D)至少有n条9.设A-B=,则有()(A)B=(B)B(C)A B (D)A B10.设集合A上有3个元素,则A上的不同的等价关系的个数为()(A)5 (B)7 (C)3 (D)6二、填空题(每题2分,共20分)1.n个命题变元组成的命题公式共有种不同的等价公式。
2.设〈L,≤〉为有界格,a为L中任意元素,如果存在元素b∈L,使,则称b是a 的补元。
3.设*,Δ是定义在集合A上的两个可交换二元运算,如果对于任意的x,y∈A,都有 ,则称运算*和运算Δ满足吸收律。
4.设T是一棵树,则T是一个连通且的图。
5.一个公式的等价式称作该公式的主合取范式是指它仅由组成。
6.量词否定等价式Ø ("x)P(x) Û,Ø ($x)P(x) Û。
7.二叉树有5个度为2的结点,则它的叶子结点数为。
8.设<G,*>是一个群,<G,*>是阿贝尔群的充要条件是。
9.集合S={α,β,γ,δ}上的二元运算*为* αβγδαδαβγβαβγδγβγγγδαδγδ那么,代数系统<S, *>中的幺元是,α的逆元是。
10.设A={<1,2>,<2,4>,<3,3>},B={<1,3>,<2,4>,<4,2>}= 。
= 。
三、判断题(每题1分,共10分)1.命题公式是一个矛盾式。
()2.,若,则必有。
()3.设S为集合X上的二元关系,则S是传递的当且仅当(S S)S。
()4.任何一棵二叉树的结点可对应一个前缀码。
()5.代数系统中一个元素的左逆元一定等于该元素的右逆元。
()6.一个有限平面图,面的次数之和等于该图的边数。
()7.A´B = B´A ()8.设*定义在集合A上的一个二元运算,如果A中有关于运算*的左零元θl和右零θr,则A中有零元。
()9.一个循环群的生成元不是唯一的。
()10.任何一个前缀码都对应一棵二叉树。
()四、解答题(5小题,共30分)1.(5分)什么是欧拉路?如何用欧拉路判定一个图G是否可一笔画出?2.(8分)求公式 (P∨Q)R 的主析取范式和主合取范式。
3.(5分)已知一棵无向树中有2个2度顶点、1个3度顶点、3个4度顶点,其余顶点度数都为1。
问它有多少个1度顶点?4.(7分)权数1,4,9,16,25,36,49,64,81,100构造一棵最优二叉树。
5.(5分)集合上的关系,,写出关系矩阵,画出关系图并讨论R的性质。
五、证明(3小题,共20分)1.(10分)用推理P,T规则证明:P Q, P→R, Q→S R S。
2.(5分)设A,B,C是三个集合,证明:(A-B)(A-C)=A-(B C)。
3.(5分)设<G,*>是群,a G。
令H={x G|a*x=x*a}。
试证:H 是G 的子群。
常熟理工学院20 ~20 学年第学期《离散数学》考试试卷(试卷库02卷)试题总分: 100 分考试时限:120 分钟题号一二三四五总分阅卷人得分一、选择题(每题2分,共20分)1.下列公式中哪些是永真式?( )(A)(┐P Q)→(Q→R) (B) (P Q)→P (C)P→(Q→Q)(D)P→(P Q)2.下列推导错在( )①P②US①③ES②④UG③(A)②(B)④(C)③(D)无3.集合A={1,2,3,4}上的偏序关系图为图(0),则它的Hass图为( )4.设R是实数集合,“”为普通乘法,则代数系统<R ,×> 不是( )(A)群(B)独异点(C)半群(D)广群5.连通非平凡的无向图G有一条欧拉回路当且仅当图G ( )(A)只有一个奇度结点(B)只有两个奇度结点(C)只有三个奇度结点(D)没有奇度结点6.若一棵完全二元(叉)树有2n-1个顶点,则它( )片树叶(A)n (B)2n (C)n-1 (D)27.在谓词演算中,是的有效结论,根据是()。
(A)US规则(B) UG规则(C) ES规则(D) EG规则8.设在上海工作;是上海人。
则命题“在上海工作的人未必都是上海人”的符号化为()。
A.(B)(C)(D)9.集合A上的关系R是相容关系的必要条件是()(A)自反,反对称的(B)反自反,对称的(C)传递,自反的(D)自反,对称的10.下列各式错误的是()(A)(B)(C)(D)二、填空题(每题2分,共20分)1.设P、Q是命题公式,填写如下的基本等价关系式:(1)┐(P∨Q);(2)P Q;2.若集合A上的关系R 满足的三个性质,则R是偏序关系。
3.设A,B是两命题公式,当且仅当。
4.给定无孤立点图G,若存在一条路满足,该条路称为欧拉路。
5.一个称为布尔格。
6.对于实数集合R,在下表所列的二元远算是否具有左边一列中的性质,请在相应位上填写“Y”或“N”Max Min +可结合性可交换性存在幺元存在零元7.y是B的上界},若B有最小元,则称该最小元为B的。
8.一个公式的等价式称作该公式的主析取范式是指它仅由组成。
9.由集合A和B的所有共同元素组成的集合称为A和B的交集,记作AÇB ,即AÇB={ }。
10.的图称为完全图。
三、判断题(每题1分,共10分)1.“北京与天津的距离很近”是复合命题。
()2.如果A∨C B∨C,则有A B。
()3.设R1和R2是集合A上的关系,且R1R2,则有r(R1) r(R2)。
()4.若平面图共有v个结点,e条边和r个面,则v-e+r=2。
()5.任何循环群必定是阿贝尔群,反之亦真。
()6.命题公式是没有真假值的。
()7.格〈L,≤〉所诱导的代数系统为〈L,∧,∨〉,则运算∧,∨满足交换律。
()8.设函数f: A→B, 则f 的逆关系是函数当且仅当f 是入射。
()9.群<G,*>的运算表中的每一行或每一列不一定是G的元素的一个置换。
()10.任何一棵二叉树可对应一个前缀码。
()四、解答题(3小题,共20分)1.(5分)简述二叉树的定义。
如何将任何一棵有序树(m叉树)改写为对应的二叉树?2.(8分)求公式 (P→Q)R 的主析取范式和主合取范式。
3.(7分)如下图所示的赋权图表示某七个城市及预先算出它们之间的一些直接通信线路造价,试给出一个设计方案,使得各城市之间能够通信而且总造价最小。
五、证明(4小题,共30分)1.(10分)用推理P,T规则证明:P→Q,Q R,R,S P S。
2.(10分)若R和S都是非空集A上的等价关系,则R S是A上的等价关系。
3.(6分)若图G不连通,则G的补图是连通的。
4.(4分)I(整数集)上的二元运算*定义为:a,b I,a*b=a+b-2。
证明<I,*>是群。
常熟理工学院20 ~20 学年第学期《离散数学》考试试卷(试卷库03卷)试题总分: 100 分考试时限:120 分钟题号一二三四五总分阅卷人得分一、单项选择题(每题2分,共20分)1.在下述公式中不是重言式为( )(A)(B)(C)(D)2.设,则B-A是( )(A)(B)(C)(D)3.设A={1,2,…,10 },则下面定义的运算*关于A封闭的有( )(A)x*y=max(x ,y)(B)x*y=质数p的个数使得(C)x*y=gcd(x , y) (gcd (x ,y)表示x和y的最大公约数)(D)x*y=lcm(x ,y) (lcm(x ,y) 表示x和y的最小公倍数)4.设<A,>是偏序集,“”定义为:,则当集合A=( )时,<A,>是格(A){1,2,3,4,6,12} (B){1,2,3,4,6,8,12,14} (C){1,2,3,…,12}(D){1,2,3,4}5.在有n个顶点的连通图中,其边数( )(A)最多有n-1条(B)至少有n条(C)最多有n条(D)至少有n-1条6.一棵树有2个2度顶点,1 个3度顶点,3个4度顶点,则其1度顶点为( )(A)5 (B)7 (C)8 (D)97.公式G=P¬P ,则G是()(A)永真的(B)永假的(C)可满足的(D)析取的8.设P,Q的真值为0,R,S的真值为T,则下面命题公式中真值为T的是().(A)R P (B)Q S (C)P S (D)Q R9.A={1,2,3}上的关系R={<1,1><1,2><1,3><3,3>},则R具备()(A)传递性与反对称性(B)传递性与对称性(C)自反性与对称性(D)反自反性与对称性10.连通图G是一颗树,当且仅当满足下述条件中那一个()(A)有些边不是割边。
(B)每条边都是割边(C)每条边都不是割边(D)无割边集二、填空题(每题2分,共20分)1.设P、Q是命题公式,填写如下的基本等价关系式:(1)P→Q;(2)P Q;2.若对命题P赋值T,Q赋值F,则命题P Q的真值为。
3.代数系统<A,*>中,|A|>1,如果分别为<A,*>的幺元和零元,则的关系为(填相等或不相等)。
4.设集合A={1,2,3,4,5,6,7,8,9,10},定义A上的二元关系“≤”为x≤y = x|y,则x y= 。
5.公式的根树表示为。
6.重言式又叫式,其定义为。
7.给定无孤立点图G,若存在一条回路满足,该回路称为欧拉回路。
