天体运动高三一轮复习
高考物理一轮复习专题4.4万有引力定律与天体运动(精讲)(解析版)

专题万有引力定律与天体运动1.掌握万有引力定律的内容,并可以用万有引力定律求解有关问题。
2.理解第一宇宙速的意义。
3.认识第二宇宙速度和第三宇宙速度。
知识点一开普勒行星运动定律的应用定律内容图示或公式开普勒第一全部行星绕太阳运动的轨道都是椭圆,太定律 (轨道定律 )阳处在椭圆的一个焦点上开普勒第二对随意一个行星来说,它与太阳的连线在定律 (面积定律 )相等的时间内扫过的面积相等开普勒第三全部行星的轨道的半长轴的三次方跟它a3T2= k,k 是一个与行星没关的常量定律 (周期定律 )的公转周期的二次方的比值都相等知识点二万有引力定律的理解及应用1.内容(1)自然界中任何两个物体都互相吸引。
(2)引力的方向在它们的连线上。
(3)引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r 的二次方成反比。
2.表达式m1m2F=G r 2,此中G 为引力常量,G= 6.67 ×10-11 N ·m2/kg 2,由卡文迪许扭秤实验测定。
3.合用条件(1)两个质点之间的互相作用。
(2)对证量散布平均的球体,r 为两球心间的距离。
知识点三、宇宙速度1.三个宇宙速度第一宇宙速度1v = 7.9 km/s ,是人造卫星在地面邻近绕地球做匀速圆周运动的(环绕速度 ) 速度第二宇宙速度(离开速度 ) v 2= 11.2 km/s ,是物体摆脱地球引力约束的最小发射速度第三宇宙速度(逃逸速度 )v 3= 16.7 km/s ,是物体摆脱太阳引力约束的最小发射速度2.第一宇宙速度的理解:人造卫星的最大环绕速度,也是人造卫星的最小发射速度。
3.第一宇宙速度的计算方法Mmv 2GM (1) 由 G R 2=m R 得 v =R.v 2(2) 由 mg = m R 得 v = gR.知识点四、经典时空观和相对论时空观1.经典时空观(1)在经典力学中,物体的质量是不随运动状态而改变的。
(2)在经典力学中,同一物理过程发生的位移和对应时间的丈量结果在不一样的参照系中是相同的。
高考物理一轮复习课件:天体运动

1 1
2
(2)只有在两极,mg=G
1 1
2
,其他地方mg<G
,但
1 1
2
相差不大,在忽略地球自转的情况下,认为mg=G
.
(3)重力在两极、赤道,两个力的方向相同(都是指向圆
心),其他地方二者方向不同,略有偏差.万有引力的方
向指向地心,重力的方向竖直向下.
1.地球赤道上的重力加速度为g,物体在赤道上的向心加速度约为a,若使赤道上的物
(4)发 ≥16.7 km/s,卫星将挣脱太阳引力的束缚,飞到太阳系以外的空间.
1、美国国家科学基金会宣布,天文学家发现一颗迄今为止与地球最类似的行星,该行
星绕太阳系外的红矮星Gliese581做匀速圆周运动.这颗行星距离地球约20光年,公转
周期约为37天,它的半径大约是地球的1.9倍,表面重力加速度与地球相近.下列说法
它的运行周期最短。
2、第二宇宙速度:v=11.2km/s
如果7.9 km/s<发 <11.2 km/s,卫星绕地球运动的轨迹为椭圆.当飞行器的速度大于或者是等于
11.2km/h时,他就会克服地球的引力,永远离开地球。此时他就跟地球一个级别,开始围绕着太阳做
圆周运动。
(3)11.2 km/s≤发 <16.7 km/s,卫星绕太阳做椭圆运动.
C.从P到Q阶段,速率逐渐变小
D.从M到N阶段,万有引力对它先做负功后做正功
CD)
(3)牛顿在思考万有引力定律时就曾想,把物体从高山上水平抛出速度一次比一次大,
落点一次比一次远.如果速度足够大,物体就不再落回地面,它将绕地球运动,成为人
造地球卫星.如图所示是牛顿设想的一颗卫星,它沿椭圆轨道运动.下列说法正确的是
天体运动中的三大模型(课件)--2025年高考物理一轮复习(新教材新高考)

由
=
=
=
=
2. 当在近代轨道时(即h=0): 由 =
=
∝
=
=
=
∝
3
∝
∝
=
地
(即黄金代换式)
越
高
越
慢
2025
知识固本
知识点2.地球静止轨道卫星的6个“一定”
B.下一次的“木星冲日”时间在2026年
C.木星运行的加速度比地球的大
D.木星运行的周期比地球的大
提示:
AB. 当再一次出现“木星冲日”,即地球再次运动到太阳和木星的连线上,解题
思路与第4题D相同;
CD. 对于天体的卫星,轨道半径越大,只有T在变大,w、a、v、机械能等均变小。
2025
考向洞察
1.(多选)有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,
A.每颗星球的角速度都在逐渐变小
B.两颗星球的距离在逐渐变大
由 =
12
=m1ω2r1=m2ω2r2,解得
2
C.两颗星球的轨道半径之比保持不变
D.每颗星球的加速度都在变小
由
2
,可知,周期变小,角速度变大。故A错误
=
(1+2)
,可知w变大,距离L逐渐变小
3
12
1
2
2
2 =m1ω r1=m2ω r2,解得
D.下一次“火星冲日”将出现在2023年12月8日之前
(完整word)高三一轮专题复习:天体运动知识点归类解析,推荐文档

天体运动知识点归类解析【问题一】行星运动简史 1、两种学说(1)地心说:地球是宇宙的中心,而且是静止不动的,太阳、月亮以及其他行星都绕地球运动。
支持者托勒密。
(2).日心说:太阳是宇宙的中心,而且是静止不动的,地球和其他行星都绕太阳运动。
(3).两种学说的局限性都把天体的运动看的很神圣,认为天体的运动必然是最完美,最和谐的圆周运动,而和丹麦天文学家第谷的观测数据不符。
2、开普勒三大定律开普勒1596年出版《宇宙的神秘》一书受到第谷的赏识,应邀到布拉格附近的天文台做研究工作。
1600年,到布拉格成为第谷的助手。
次年第谷去世,开普勒成为第谷事业的继承人。
第谷去世后开普勒用很长时间对第谷遗留下来的观测资料进行了整理与分析他在分析火星的公转时发现,无论用哥白尼还是托勒密或是第谷的计算方法得到的结果都与第谷的观测数据不吻合。
他坚信观测的结果,于是他想到火星可能不是按照人们认为的匀速圆周运动他改用不同现状的几何曲线来表示火星的运动轨迹,终于发现了火星绕太阳沿椭圆轨道运行的事实。
并将老师第谷的数据结果归纳出三条著名定律。
第一定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
第二定律:对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等。
如图某行星沿椭圆轨道运行,远日点离太阳的距离为a ,近日点离太阳的距离为b ,过远日点时行星的速率为a v ,过近日点时的速率为b v由开普勒第二定律,太阳和行星的连线在相等的时间内扫过相等的面积,取足够短的时间t ∆,则有:t bv t av b a ∆=∆2121①所以bav v a b = ② ②式得出一个推论:行星运动的速率与它距离成反比,也就是我们熟知的近日点快远日点慢的结论。
②式也当之无愧的作为第二定律的数学表达式。
第三定律:所有行星的轨道半长轴的三次方跟它的公转周期平方的比值都相等。
用a 表示半长轴,T 表示周期,第三定律的数学表达式为k T a =23,k 与中心天体的质量有关即k 是中心天体质量的函数)(23M k T a =①。
2024高考物理一轮复习--天体运动专题--卫星运行参量的分析、近地、同步卫星与赤道上物体的比较

卫星运行参量的分析、近地、同步卫星与赤道上物体的比较一、卫星运行参量与轨道半径的关系1.天体(卫星)运行问题分析将天体或卫星的运动看成匀速圆周运动,其所需向心力由万有引力提供. 2.物理量随轨道半径变化的规律G Mmr 2= ⎩⎪⎨⎪⎧ma →a =GM r 2→a ∝1r2m v 2r →v =GM r →v ∝1r mω2r →ω=GM r 3→ω∝1r3m 4π2T 2r →T =4π2r3GM→T ∝r 3即r 越大,v 、ω、a 越小,T 越大.(越高越慢)3.公式中r 指轨道半径,是卫星到中心天体球心的距离,R 通常指中心天体的半径,有r =R +h .4.同一中心天体,各行星v 、ω、a 、T 等物理量只与r 有关;不同中心天体,各行星v 、ω、a 、T 等物理量与中心天体质量M 和r 有关.5.所有轨道平面一定通过地球的球心。
如右上图6.同步卫星的六个“一定”二、宇宙速度1.第一宇宙速度的推导 方法一:由G Mm R 2=m v 12R,得v 1=GMR = 6.67×10-11×5.98×10246.4×106m/s≈7.9×103 m/s.方法二:由mg =m v 12R得v 1=gR =9.8×6.4×106 m/s≈7.9×103 m/s.第一宇宙速度是发射人造卫星的最小速度,也是人造卫星的最大环绕速度,此时它的运行周期最短,T min =2πRg=2π 6.4×1069.8s≈5 075 s≈85 min. 2.宇宙速度与运动轨迹的关系(1)v 发=7.9 km/s 时,卫星绕地球表面做匀速圆周运动. (2)7.9 km/s<v 发<11.2 km/s ,卫星绕地球运动的轨迹为椭圆. (3)11.2 km/s≤v 发<16.7 km/s ,卫星绕太阳运动的轨迹为椭圆.(4)v 发≥16.7 km/s ,卫星将挣脱太阳引力的束缚,飞到太阳系以外的空间.三、近地卫星、同步卫星及赤道上物体的运行问题1.如图所示,a 为近地卫星,半径为r 1;b 为地球同步卫星,半径为r 2;c 为赤道上随地球自转的物体,半径为r 3。
高考物理一轮复习 天体运动题型归纳

天体运动题型归纳李仕才题型一:天体的自转【例题1】一物体静置在平均密度为ρ的球形天体表面的赤道上。
已知万有引力常量为G ,若由于天体自转使物体对天体表面压力怡好为零,则天体自转周期为( ) A .124π3G ρ⎛⎫ ⎪⎝⎭B .1234πG ρ⎛⎫ ⎪⎝⎭C .12πG ρ⎛⎫ ⎪⎝⎭D .123πG ρ⎛⎫ ⎪⎝⎭解析:在赤道上22R m mg RMm Gω+=① 根据题目天体表面压力怡好为零而重力等于压力则①式变为22R m RMmGω=②又 T πω2= ③ 334R M ρπ= ④②③④得:23GTπρ= ④即21)3(ρπG T =选D练习1、已知一质量为m 的物体静止在北极与赤道对地面的压力差为ΔN,假设地球是质量分布均匀的球体,半径为R 。
则地球的自转周期为( )A. 2T =2T =R N m T ∆=π2 D.N m RT ∆=π22、假设地球可视为质量均匀分布的球体,已知地球表面的重力加速度在两极的大小为g 0,在赤道的大小为g ;地球自转的周期为T ,引力常数为G ,则地球的密度为: A.0203g g g GT π- B. 0203g g gGT π- C. 23GT π D.23g g GTπρ=题型二:近地问题+绕行问题【例题1】若宇航员在月球表面附近高h 处以初速度0v 水平抛出一个小球,测出小球的水平射程为L 。
已知月球半径为R ,引力常量为G 。
则下列说法正确的是A .月球表面的重力加速度g 月=hv 2L2B .月球的质量m 月=hR 2v 20GL2C .月球的第一宇宙速度v =v 0L2h D .月球的平均密度ρ=3hv 22πGL 2R解析 根据平抛运动规律,L =v 0t ,h =12g 月t 2,联立解得g 月=2hv 20L 2;由mg 月=G mm 月R 2,解得m 月=2hR 2v 20GT 2;由mg 月=m v 2R ,解得v =v 0L 2hR ;月球的平均密度ρ=m 月43πR 3=3hv 22πGL 2R。
届高考物理一轮复习专题天体运动

专题八—天体运动 知识点总结一 开普勒三定律的理解和应用1.行星绕太阳的运动通常按圆轨道处理.2.开普勒行星运动定律也适用于其他天体,例如月球、卫星绕地球的运动.3.开普勒第三定律a 3T2=k 中,k 值只与中心天体的质量有关,不同的中心天体k 值不同.但该定律只能用在同一中心天体的两星体之间. 二 万有引力定律的理解 1.万有引力与重力的关系地球对物体的万有引力F 表现为两个效果:一是重力mg ,二是提供物体随地球自转的向心力F 向.(1)在赤道上:G MmR 2=mg 1+m ω2R .(2)在两极上:G MmR2=mg 0.(3)在一般位置:万有引力G MmR2等于重力mg 与向心力F 向的矢量和.越靠近南、北两极,g 值越大,由于物体随地球自转所需的向心力较小,常认为万有引力近似等于重力,即GMmR2=mg .2.星球上空的重力加速度g ′星球上空距离星体中心r =R +h 处的重力加速度为g ′,mg ′=GmM (R +h )2,得g ′=GM (R +h )2.所以g g ′=(R +h )2R 2. 3.万有引力的“两点理解”和“两个推论”(1)两点理解①两物体相互作用的万有引力是一对作用力和反作用力.②地球上的物体(两极除外)受到的重力只是万有引力的一个分力. (2)两个推论①推论1:在匀质球壳的空腔内任意位置处,质点受到球壳的万有引力的合力为零,即∑F 引=0.②推论2:在匀质球体内部距离球心r 处的质点(m )受到的万有引力等于球体内半径为r 的同心球体(M ′)对其的万有引力,即F =G M ′mr2.三 天体质量和密度的估算 天体质量和密度常用的估算方法使用方法已知量 利用公式 表达式 备注质量的计算利用运行天体r 、T G Mm r 2=mr 4π2T 2 M =4π2r 3GT 2只能得到中心天体的质量r 、vG Mm r 2=m v 2r M =rv 2Gv 、TG Mm r 2=m v 2r G Mm r 2=mr 4π2T2 M =v 3T 2πG利用天体表面重力加速度 g 、Rmg =GMm R 2M =gR 2G密度利用运r 、T 、R G Mm r 2=mr 4π2T 2 ρ=3πr 3GT 2R3 利用近地的计算行天体M =ρ·43πR 3当r =R 时 ρ=3πGT2卫星只需测出其运行周期利用天体表面重力加速度g 、Rmg =GMm R2M =ρ·43πR 3ρ=3g4πGR卫星运行参量 相关方程 结论线速度v G Mm r 2=m v 2r ⇒v = GM r r 越大,v 、ω、a 越小,T 越大角速度ωG Mmr2=m ω2r ⇒ω= GM r 3周期TG Mm r 2=m ⎝ ⎛⎭⎪⎫2πT 2r ⇒T =2π r 3GM向心加速度aG Mm r 2=ma ⇒a =GM r2 五 1.解决同步卫星问题的“四点”注意(1)基本关系:要抓住G Mm r 2=ma =m v 2r =mr ω2=m 4π2T2r .(2)重要手段:构建物理模型,绘制草图辅助分析. (3)物理规律:①不快不慢:具有特定的运行线速度、角速度和周期.②不高不低:具有特定的位置高度和轨道半径.③不偏不倚:同步卫星的运行轨道平面必须处于地球赤道平面上,只能静止在赤道上方的特定的点上.(4)重要条件:①地球的公转周期为1年,其自转周期为1天(24小时),地球半径约为6.4×103 km,地球表面重力加速度g约为9.8 m/s2.②月球的公转周期约27.3天,在一般估算中常取27天.③人造地球卫星的运行半径最小为r=6.4×103km,运行周期最小为T=84.8 min,运行速度最大为v=7.9 km/s.2.两个向心加速度卫星绕地球运行的向心加速度物体随地球自转的向心加速度产生原因由万有引力产生由万有引力的一个分力(另一分力为重力)产生方向指向地心垂直且指向地轴大小a=GMr2(地面附近a近似等于g)a=rω2,r为地面上某点到地轴的距离,ω为地球自转的角速度特点随卫星到地心的距离的增大而减小从赤道到两极逐渐减小3.两种周期(1)自转周期是天体绕自身某轴线转动一周所需的时间,取决于天体自身转动的快慢.(2)公转周期是运行天体绕中心天体做圆周运动一周所需的时间,T=2πr3GM,取决于中心天体的质量和运行天体到中心天体的距离.六卫星变轨问题1.变轨原理及过程(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.如图所示.(2)在A点(近地点)点火加速,由于速度变大,万有引力不足以提供卫星在轨道Ⅰ上做圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ.(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ.2.变轨过程各物理量分析(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在轨道Ⅱ上过A点和B点时速率分别为v A、v B.在A点加速,则v A>v1,在B点加速,则v3>v B,又因v1>v3,故有v A>v1>v3>v B.(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同,同理,经过B点加速度也相同.(3)周期:设卫星在Ⅰ、Ⅱ、Ⅲ轨道上的运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律r3T2=k可知T1<T2<T3.(4)机械能:在一个确定的圆(椭圆)轨道上机械能守恒.若卫星在Ⅰ、Ⅱ、Ⅲ轨道的机械能分别为E1、E2、E3,则E1<E2<E3.七 双星模型 1.双星模型(1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示.(2)特点:①各自所需的向心力由彼此间的万有引力提供,即Gm 1m 2L 2=m 1ω12r 1,Gm 1m 2L2=m 2ω22r 2 ②两颗星的周期及角速度都相同,即T 1=T 2,ω1=ω2③两颗星的半径与它们之间的距离关系为:r 1+r 2=L④两颗星到圆心的距离r 1、r 2与星体质量成反比,即m 1m 2=r 2r 1.⑤双星的运动周期T =2πL 3G (m 1+m 2)⑥双星的总质量M 八 天体的追及相遇问题 1.相距最近两卫星的运转方向相同,且位于和中心连线的半径上同侧时,两卫星相距最近,从运动关系上,两卫星运动关系应满足(ωA -ωB )t =2n π(n =1,2,3,…). 2.相距最远当两卫星位于和中心连线的半径上两侧时,两卫星相距最远,从运动关系上,两卫星运动关系应满足(ωA -ωB )t ′=(2n -1)π(n =1,2,3…). 1+m 2=4π2L 3T 2G专题练习一、选择题1.1970年成功发射的“东方红一号”是我国第一颗人造地球卫星,该 卫星至今仍沿椭圆轨道绕地球运动.如图所示,设卫星在近地点、远地点的速度分别为v 1、v 2,近地点到地心的距离为r ,地球质量为M ,引力常量为G 。
高考物理一轮复习 第5章 天体运动 第20课时 天体运动
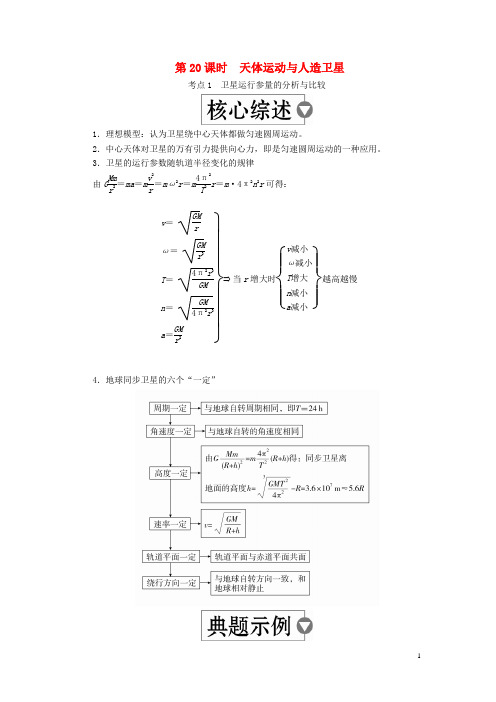
第20课时 天体运动与人造卫星考点1 卫星运行参量的分析与比较1.理想模型:认为卫星绕中心天体都做匀速圆周运动。
2.中心天体对卫星的万有引力提供向心力,即是匀速圆周运动的一种应用。
3.卫星的运行参数随轨道半径变化的规律由G Mm r 2=ma=m v 2r =mω2r =m 4π2T2r =m ·4π2n 2r 可得:⎭⎪⎪⎬⎪⎪⎫v =GM rω= GM r 3T = 4π2r3GM n =GM 4π2r3a =GMr2⇒当r 增大时⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫v 减小ω减小T 增大n 减小a 减小越高越慢4.地球同步卫星的六个“一定”[例1] (2015·北京高考)假设地球和火星都绕太阳做匀速圆周运动,已知地球到太阳的距离小于火星到太阳的距离,那么( )A .地球的公转周期大于火星的公转周期B .地球公转的线速度小于火星公转的线速度C .地球公转的加速度小于火星公转的加速度D .地球公转的角速度大于火星公转的角速度 解析 由T =2πr 3GM,得T 地<T 火,A 错误;由v =GM r 得v 地>v 火,B 错误;由a =GM r2得a 地>a 火,C 错误;由ω=GMr 3得ω地>ω火,D 正确。
答案 D(1)一个模型天体(包括卫星)的运动可简化为质点的匀速圆周运动模型。
(2)两条思路思路一:万有引力提供向心力G Mm r 2=m v 2r =mω2r =m 4π2T2r =ma 思路二:在中心天体表面,万有引力等于重力mg =GMmR2(g 为天体表面处的重力加速度)(3)a 、v 、ω、T 均与卫星(或行星)的质量无关,只由轨道半径和中心天体质量共同决定,所有参量的比较,最终归结到半径的比较。
有a 、b 、c 、d 四颗地球卫星,a 还未发射,在地球赤道上随地球一起转动,b 在地面附近近地轨道上正常运动,c 是地球同步卫星,d 是高空探测卫星,各卫星排列位置如图所示,则下列说法中正确的是( )A .a 的向心加速度等于重力加速度gB .c 在4 h 内转过的圆心角是π6C .在相同时间内b 转过的弧长最长D .d 的运行周期可能是23 h 答案 C解析 地球赤道上静止的物体随地球自转的向心加速度小于重力加速度,A 错误;同步卫星c 在4 h 内转过的圆心角φ=π3,B 错误;相同时间内转过的弧长s =vt 由线速度v决定,卫星b 的线速度最大,因此相同时间内b 转过的弧长最长,C 正确;d 的轨道比同步卫星c 的轨道高,其运行周期比c 的大,故其运行周期一定大于24 h ,D 错误。
天体运动-高三一轮复习 讲义版

天体运动【知识框架】【知识点一】行星运动规律第一定律:所有行星绕太阳运动的轨道都是椭圆,太阳位于椭圆的一个焦点上第二定律:太阳与任何一个行星的连线(矢径)在相等的时间内扫过的面积相等,即:S1=S2第三定律:行星绕太阳运行轨道半长轴r 的立方与其公转周期T 的平方成正比,即:k Tr =23其中k 是与中心天体有关的常数【例】某行星绕太阳运行的椭圆轨道如图所示,F 1和F 2是椭 圆 轨道的两个焦点,行星在A 点的速率比在B 点的大,则太阳是位于( )A F2 B AC F 1D B【例】设行星绕恒星的运动轨道是圆,则其运行周期T 的平方与其运动轨道半径R 的三次方之比为常数,即R 3/T 2=k ,那么k 的大小( )A 只与行星质量有关B 只与恒星质量有关C 与恒星及行星的质量均有关D 与恒星的质量及行星的速率有关【知识点二】万有引力定律及其应用 1、万有引力定律:2rmGM F =,由牛顿总结而得 注:式中,G 为引力常量,由卡文迪许扭秤实验测出。
r 为两质点距离,若是两个均匀球体,则r 是两球心的距离。
2、应用万有引力定律分析天体运动 地面上的物体与地球一起运动:G F =万,即mg m2=RGM ,得2g GM R =(黄金代换式) 绕地球做圆周运动的物体g m '==向万F F 即g m 2mr mr r mv r m 2222'=⎪⎭⎫ ⎝⎛===T GM πω 归纳变轨卫星:↓↓↓↓↓↑↑↑F E T ,,,,,,,g a v r ω 3、两种特殊卫星近地卫星(第一宇宙速度) 得R g v =同步卫星 相对地面静止,运动轨迹在赤道正上空4、宇宙速度理解第一宇宙速度:最小发射速度,最大环绕速度第二宇宙速度:发射速度大于第二宇宙速度,将脱离地球束缚,绕太阳运动变成“人造行星” 第三宇宙速度:发射速度大小第三宇宙速度,将脱离太阳束缚,跑到其他星系中题型一:万有引力定律公式的理解 【例】对于太阳与行星间引力的表述2rmGM F =式,下面说法中正确的是( ) A 公式中G 为引力常量,它是牛顿规定的 B r 为太阳半径C 太阳与行星受到的引力总是大小相等的、方向相反,是一对平衡力D 太阳与行星受到的引力总是大小相等的、方向相反,是一对作用力与反作用力【例】关于万有引力定律,下列说法正确的是( ) A 牛顿提出了万有引力定律,并测定了引力常量的数值 B 万有引力定律只适用于天体之间C 万有引力的发现,揭示了自然界一种基本相互作用的规律D 地球绕太阳在椭圆轨道上运行,在近日点和远日点受到太阳的万有引力大小是相同的【例】关于万有引力定律及其表达式221rm m G F =的理解,下列说法中正确的是( ) A 万有引力定律对质量大的物体适用,对质量小的物体不适用 B 公式中的是引力常量,说明它在数值上等于质量为1kg 的两个质点相距1m 时的相互作用力C 当物体间的距离r 趋于零时,万有引力趋于无穷大D 两个物体间的引力总是大小相等、方向相反的,是一对平衡力【例】 如图所示,有人设想要“打穿地球”从中国建立一条通过地心的光滑隧道直达巴西。
专题10 天体运动-2023届高考物理一轮复习热点题型专练(解析版)

专题10天体运动目录题型一开普勒定律的应用 (1)题型二万有引力定律的理解 (3)类型1万有引力定律的理解和简单计算 (3)类型2不同天体表面引力的比较与计算 (4)类型3重力和万有引力的关系 (5)类型4地球表面与地表下某处重力加速度的比较与计算 (7)题型三天体质量和密度的计算 (8)类型1利用“重力加速度法”计算天体质量和密度 (8)类型2利用“环绕法”计算天体质量和密度 (9)类型3利用椭圆轨道求质量与密度 (11)题型四卫星运行参量的分析 (13)类型1卫星运行参量与轨道半径的关系 (13)类型2同步卫星、近地卫星及赤道上物体的比较 (15)类型3宇宙速度 (17)题型五卫星的变轨和对接问题 (19)类型1卫星变轨问题中各物理量的比较 (19)类型2卫星的对接问题 (22)题型六天体的“追及”问题 (23)题型七星球稳定自转的临界问题 (25)题型八双星或多星模型 (26)类型1双星问题 (27)类型2三星问题 (29)类型4四星问题 (31)题型一开普勒定律的应用【解题指导】1.行星绕太阳运动的轨道通常按圆轨道处理.2.由开普勒第二定律可得12Δl1r1=12Δl2r2,12v1·Δt·r1=12v2·Δt·r2,解得v1v2=r2r1,即行星在两个位置的速度之比与到太阳的距离成反比,近日点速度最大,远日点速度最小.3.开普勒第三定律a3T2=k中,k值只与中心天体的质量有关,不同的中心天体k值不同,且该定律只能用在同一中心天体的两星体之间.【例1】(2022·山东潍坊市模拟)中国首个火星探测器“天问一号”,已于2021年2月10日成功环绕火星运动。
若火星和地球可认为在同一平面内绕太阳同方向做圆周运动,运行过程中火星与地球最近时相距R0、最远时相距5R0,则两者从相距最近到相距最远需经过的最短时间约为()A.365天B.400天C.670天D.800天【答案】B【解析】设火星轨道半径为R1,公转周期为T1,地球轨道半径为R2,公转周期为T2,依题意有R1-R2=R0,R1+R2=5R0,解得R1=3R0,R2=2R0,根据开普勒第三定律有R31T21=R32T22,解得T1=278年,设从相距最近到相距最远需经过的最短时间为t,有ω2t-ω1t=π,ω=2πT,代入数据可得t=405天,故选项B正确。
2023届高三物理一轮复习最新试题汇编:天体运动

2023届高三物理一轮复习最新试题汇编:天体运动物理考试注意事项:1、填写答题卡的内容用2B 铅笔填写2、提前 xx 分钟收取答题卡第Ⅰ卷 客观题第Ⅰ卷的注释(共9题;共18分)1.(2分)如图所示,2021年2月我国“天问一号”火星探测器先由地火转移轨道1进入火星停泊轨道2,进行相关探测后进入较低的轨道3开展科学探测,则探测器( )A .在轨道2与轨道3同一近火点的加速度相等B .在轨道2上近火点的机械能比远火点的机械能小C .在轨道1上的运行速度不超过地球的第一宇宙速度D .在轨道2上近火点加速可进入轨道32.(2分)中国目前在轨运行的人造地球卫星数量已超400颗,居世界第二位。
假设这些卫星均可视为绕地球做匀速圆周运动,仅知道它们的轨道半径。
关于这些卫星,下列哪个物理量的大小关系不能进行比较( ) A .加速度B .线速度C .周期D .动能3.(2分)神舟十四号载人飞船于2022年6月5日成功发射升空,航天员陈冬、刘洋、蔡旭哲进驻中国空间站天和核心舱。
若认为天和核心舱绕地球近似做匀速圆周运动,周期约90分钟,下列说法正确的是( ) A .航天员在核心舱内不受地球引力作用B .天和核心舱距离地面的高度小于地球同步卫星距离地面的高度C .天和核心舱在圆周轨道上匀速飞行时的速度大于第一宇宙速度D .神舟十四号载人飞船与天和核心舱对接时,若以地面为参考系,则神舟十四号是静止不动4.(2分)2021年5月15日,我国首次火星探测任务“天问一号”探测器在火星乌托邦平原南部预选着陆区着陆。
“天问一号”到达火星时,经过多次变轨进入环火圆轨道Ⅰ,图为变轨示意图,P 为椭圆轨道Ⅰ近火点,Q 为椭圆轨道Ⅰ的远火点,设“天问一号”的质量保持不变,则下列说法正确的是( )A .“天问一号”在轨道Ⅰ上的线速度一定比在轨道Ⅰ上线速度小B .“天问一号”在轨道Ⅰ上的加速度一定比在轨道Ⅰ上加速度小C .“天问一号”在轨道Ⅰ上的机械能一定比在轨道Ⅰ上机械能小D .“天问一号”在轨道Ⅰ上的运行周期一定比在轨道Ⅰ上运行周期大5.(2分)2021年6月17日,神舟十二号载人飞船采用自主快速交会对接模式成功对接于天和核心舱前向端口,与此前已对接的天舟二号货运飞船一起构成三舱组合体。
1高三一轮复习——天体运动 基础版

A B C D 地球 卫星高三一轮复习——万有引力定律(一)一、基本概念1、开普勒三大定律(1)开普勒第一定律:所有行星绕太阳运行的轨道都是_______,太阳处在所有椭圆的_______上.(2)开普勒第二定律:对于每一个行星,太阳和行星的连线在相等的时间内扫过的_______相等.由此可得:v 近日点____v 远日点(<、>、=)(3)开普勒第三定律:所有行星的半长轴的_____次方跟公转周期的______的比值都相等。
即_____________.2、牛顿万有引力定律:_______________(写公式)。
注意:万有引力常数G 是由____________测定。
例1.(2018年石景山期末)由万有引力定律可知,两个物体的质量分别为m 1和m 2,其间距为r 时,它们之间万有引力的大小为122m m F Gr =,式中G 为引力常量。
在国际单位制中,G 的单位是( ) A .N ·m 2/kg 2 B .kg 2/ (N ·m 2) C .N ·m 2/kg D .N ·kg 2/m 2练习1、(2017年东城一模)已知两个质点相距为r 时,它们之间的万有引力大小为F 。
若只将它们之间的距离变为2r ,则它们之间的万有引力大小为 ( )A .41F B .21F C .2F D . 4F 例2.(2019年西城一模)如图所示,一颗卫星绕地球做椭圆运动,运动周期为T ,图中虚线为卫星的运行轨迹,A 、B 、C 、D 是轨迹上的四个位置,其中A 距离地球最近,C 距离地球最远。
B 和D 点是弧线ABC 和ADC 的中点,下列说法正确的是( )A .卫星在C 点的速度最大B .卫星在C 点的加速度最大C .卫星从A 经D 到C 点的运动时间为T/2D .卫星从B 经A 到D 点的运动时间为T/2 练习2.(2018年西城一模)2016年9月15日,我国发射了空间实验室“天宫二号”。
天体运动高三一轮复习

图648级高三物理一轮复习学案 —— 预习案§ 万有引力定律与天体运动(第一课时)编制:谢秀杰 解华【考纲要求】 万有引力定律及其应用(Ⅱ级要求) 环绕速度 (Ⅱ级要求)第二、第三宇宙速度 (Ⅰ级要求) 【知识梳理】1、 请你复述开普勒三定律的内容。
2、 请你复述万有引力定律内容,规律的适用条件 表达式: 。
3、模型:正常运行情况下的天体运动可看成是 ,其向心力由 提供。
①由22Mm v G m r r =可得v = ②由r m rMm G 22ω=可得ω= .③由r T m r Mm G222⎪⎭⎫⎝⎛=π可得:T = .④由向ma r Mm G =2可得:_____=向a 4、根据万有引力定律,在地球表面,对于质量为m 的物体有:G M 地mR 2地= ,得黄金代换: 。
5、同步卫星的特点:【预习检测】1、火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知( ) A 、太阳位于木星运行轨道的中心B 、火星和木星绕太阳运行速度的大小始终相等C 、火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方D 、相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积2、对万有引力定律的表达式F =Gm 1m 2r 2,下列说法正确的是 ( ) A .公式中G 为常量,没有单位,是人为规定的 B .r 趋向于零时,万有引力趋近于无穷大C .两物体之间的万有引力总是大小相等,与m 1、m 2是否相等无关D .两个物体间的万有引力总是大小相等,方向相反的,是一对平衡力3、 2010年10月1日我国成功发射“嫦娥二号”绕月卫星,绕月运行高度为100公里.2007年10月24日发射的“嫦娥一号”绕月运行高度为200公里,如图6所示.“嫦娥二号”卫星与“嫦娥一号”卫星绕月运行相比,下列判断正确的是 ( )A .周期小,线速度大B .周期大,加速度小C .线速度大,加速度小D .角速度大,线速度大4、设太阳质量为M ,某行星绕太阳公转周期为T ,轨道可视为r 的圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
48 级高三物理一轮复习学案——预习案§ 6.1万有引力定律与天体运动(第一课时)编制:谢秀杰解华【考纲要求】万有引力定律及其应用(Ⅱ级要求)环绕速度(Ⅱ级要求)第二、第三宇宙速度(Ⅰ级要求)【知识梳理】1、请你复述开普勒三定律的内容。
2、请你复述万有引力定律内容,规律的适用条件表达式:。
3、模型:正常运行情况下的天体运动可看成是,其向心力由提供。
①由 G Mmm v2可得 v②由 GMmm2 r 可得.r 2r r 2③由 G Mmm22.④由 GMmr 可得:T ma向可得: a向_____ r 2T r 2M地 m万有引力定律,在地球表面,对于质量为m 的物体有: G 2=,得黄金代换:。
R地5、同步卫星的特点:【预习检测】1、火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知()A、太阳位于木星运行轨道的中心B、火星和木星绕太阳运行速度的大小始终相等C、火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方D、相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积2、对万有引力定律的表达式 F = G m1m2() r2,下列说法正确的是A .公式中 G 为常量,没有单位,是人为规定的B . r 趋向于零时,万有引力趋近于无穷大C.两物体之间的万有引力总是大小相等,与m1、m2是否相等无关D.两个物体间的万有引力总是大小相等,方向相反的,是一对平衡力3、 2010 年 10 月 1 日我国成功发射“嫦娥二号”绕月卫星,绕月运行高度为100 公里 .2007 年 10 月 24 日发射的“嫦娥一号”绕月运行高度为200 公里,如图 6 所示.“嫦娥二号”卫星与“嫦娥一号”卫星绕月运行相比,下列判断正确的是()A .周期小,线速度大B.周期大,加速度小C.线速度大,加速度小D.角速度大,线速度大图64、设太阳质量为M,某行星绕太阳公转周期为T,轨道可视为 r 的圆。
已知万有引力常量为G,则描述该行星运动的上述物理量满足( )4 2 r 3 4 2r 2 4 2r 2 4 r 3A.GM B .GM C .GM D .GMT2T 2T 3T 2【典型例题】一、万有引力定律的应用例 1、如图所示,三颗质量均为m的地球同步卫星等间隔分布在半径为r 的圆轨道上,设地球质量为半径为 R。
下列说法正确的是()A.地球对一颗卫星的引力大小为GMm(r R) 2B.一颗卫星对地球的引力大小为GMmr 2C.两颗卫星之间的引力大小为Gm23r 2D.三颗卫星对地球引力的合力大小为3GMmr2二、稳定圆轨道上的环绕模型例 2、人造卫星以地心为圆心,作匀速圆周运动,下列说法正确的是:()A 、半径越大,环绕速度越小,周期越大B、半径越大,环绕速度越大,周期越小C、卫星的向心加速度与它的质量有关D、卫星的向心加速度与卫星的质量、半径均无关例 3、两颗人造地球卫星质量之比m1∶ m2=1 ∶ 2,轨道半径之比R1∶ R2=3∶ 1,下列正确的是()A. 周期之比 T1∶ T2=3∶ 1B. 线速度之比 v1∶ v2=3∶ 1C.向心力之比 F1∶ F2=1∶ 9D.向心加速度之比a1∶ a2=1∶ 9三、天体质量和密度的计算例 4、“嫦娥一号”是我国首次发射的探月卫星,它在距月球表面高度为200 km 的圆形轨道上运行,运行周期为127 分钟。
已知引力常量G=6.67×10– 1122,月球的半径为 1.74 ×103km 。
利用以N?m/kg上数据估算月球的质量约为()A.8.1 ×10 10 kg B.7.4 ×10 13 kgC.5.4×1019kg D.7.4×1022kg四、三种环绕模型——同步卫星、近地卫星、赤道上随地球自转的物体例 5、如图所示,地球赤道上的山丘e,近地资源卫星p 和同步通信卫星q 均在赤道平面上绕地心做匀速圆周运动.设e、 p、 q 的圆周运动周期分别为T1、 T2、T3,线速率分别为v1、v2、v3,角速度分别为ω1、ω2、ω3,向心加速度分别为a1、a2、a3,则()A.T >T>TB.v <v <v2C. ω>ω>ω3D. a <a <a212313121348 级高三物理一轮复习学案——课堂案§6.1万有引力定律与天体运动编制:谢秀杰解华【变式训练】类 1、如图所示,在火星与木星轨道之间有一小行星带。
假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动。
下列说法正确的是()A.太阳对各小行星的引力相同B.各小行星绕太阳运动的周期均小于一年C.小行星带内侧小行星的向心加速度值大于外侧小行星的向心加速度值D.小行星带内个小行星圆周运动的线速度值大于地球公转的线速度值类 2、一行星绕恒星作圆周运动。
由天文观测可得,其运动周期为T ,速度为v,引力常量为G,则()A .恒星的质量为v3TB .行星的质量为4 2v3 2 G GT 2C.行星运动的轨道半径为vT 2 v 2D .行星运动的加速度为T类 3、天文学家新发现了太阳系外的一颗行星,这颗行星的体积是地球的 4.7 倍,质量是地球的 25 倍.已知某一近地卫星绕地球运动的周期约为 1.4 小时,引力常量 G=6.67× 10-11N ·m2/kg 2,由此估算该行星的平均密度约为()A . 1.8× 103 kg/m3B. 5.6 ×103 kg/m3C. 1.1× 104kg/m3D. 2.9 ×104kg/m3类 4、如图 4 所示,同步卫星与地心的距离为r,运行速率为 v1,向心加速度为a1;地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则下列比值正确的是()A.a1=rB.a1R2 a2R=()a2rC.v1= rD.v1=Rv2R v2r【自主检测】图 4 1、关于环绕地球卫星的运动,下列说法正确的是A.分别沿圆轨道和椭圆轨道运行的两颗卫星,不可能具有相同的周期B.沿椭圆轨道运行的一颗卫星,在轨道不同位置可能具有相同的速率C.在赤道上空运行的两颗地球同步卫星,它们的轨道半径有可能不同D.沿不同轨道经过北京上空的两颗卫星,它们的轨道平面一定会重合2、我国发射的“天宫一号”和“神州八号”在对接前,“天宫一号”的运行轨道高度为350km, “神州八号”的运行轨道高度为343km. 它们的运行轨道均视为圆周,则( )A.“天宫一号”比“神州八号”速度大B.“天宫一号”比“神州八号”周期长C.“天宫一号”比“神州八号”角速度大D.“天宫一号”比“神州八号”加速度大3、2011 年 8 月,“嫦娥二号”成功进入了绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家,如图所示,该拉格朗日点位于太阳与地球连线的延长线上,一飞行器位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的()拉格朗日点A .线速度大于地球的线速度地球B .向心加速度大于地球的向心加速度C.向心力仅由太阳的引力提供太阳D .向心力仅由地球的引力提供4、一物体静置在平均密度为ρ的球形天体表面的赤道上,已知万有引力常量为G,若由于天体自转使物体对天体表面压力恰好为零,则天体自转周期为()A.4πB.33πD.π3Gρ4πGρC.GρGρ5、 2011 年 11 月 3 日,“神州八号”飞船与“天宫一号”目标飞行器成功实施了首次交会对接。
任务完成后“天宫一号”经变轨升到更高的轨道,等待与“神州九号”交会对接。
变轨前和变轨完成后“天宫一号”的运行轨道均可视为圆轨道,对应的轨道半径分别为R1、 R2,线速度大小分别为v1 v2。
则v1等于()v2R13B.R2R22R2A.R1C. D.R23R2R116、一人造地球卫星绕地球做匀速圆周运动,加入该卫星变轨后仍做匀速圆周运动,动能减小为原来的1,不考虑卫星质量的变化,则变轨前后卫星的()4A .向心加速度大小之比为4:1B.角速度大小之比为2:1C.周期之比为 1:8D.轨道半径之比为1:27、 2011 年 4 月 10 日,我国成功发射第8 颗北斗导航卫星,建成以后北斗导航卫星系统将包含多可地球同步卫星,这有助于减少我国对GPS导航系统的依赖,GPS由运行周期为 12 小时的卫星群组成,设北斗星的同步卫星和GPS导航的轨道半径分别为R1和 R2,向心加速度分别为 a1和 a2,R1 : R2=_____。
a1 : a2=_____(可用根式表示)48 级高三物理一轮复习学案—— 预习案及课堂案§6.2万有引力定律与天体运动【预习检测】1、 宇宙飞船正在离地面高h R 地 的轨道上做匀速圆周运动, 飞船内一弹簧秤下悬挂一质量为m 的重物, g 为地面处重力加速度,则弹簧秤的读数为 ()A.mg11D.0B.mgC. mg242、宇宙中两颗相距较近的天体称为“双星”, 它们以二者连线上的某一点为圆心做匀速圆周运动而不至因万有引力的作用吸引到一起.试证明它们的轨道半径之比、线速度之比都等于质量的反比. 【典型例题】一、关于重力加速度例 1、假设地球是一半径为 R 、质量分布均匀的球体。
一矿井深度为 d 。
已知质量分布均匀的球壳对壳内物体的引力为零。
矿井底部和地面处的重力加速度大小之比为dB. 1dA. 1RRC. (R d) 2D. ( R ) 2RR d二、双星模型例 2、冥王星与其附近的星体卡戎可视为双星系统,质量比约为 7: 1,同时绕它们连线上某点O 做匀速圆周运动。
由此可知冥王星绕O 点运动的A . 轨道半径约为卡戎的 1/7B . 角速度大小约为卡戎的 1/7C .线度大小约为卡戎的 7 倍 D .向心力小约为卡戎的7 倍三、相关联的独立环绕模型例 3、如图 3,甲、乙两颗卫星以相同的轨道半径分别绕质量为M 和 2M 的行星做匀速圆周运动,下列说法正确的是 ( )A. 甲的向心加速度比乙的小B. 甲的运行周期比乙的小C. 甲的角速度比乙大D. 甲的线速度比乙大【变式训练】类 1、一物体在地球表面重16N ,它在以 5m/s 2的加速度加速上升的火箭中的视重为9N ,则此火箭离开地球表面的距离是地球半径的 ()A .1倍B .2倍C.3倍D .4倍类 2、双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相若某双星系统中两星做圆周运动的周期为 T, ,经过一段时间演化后,两星总质量变为原来的k 倍,两星之间的距离变为原来的n 倍,则此时圆周运动的周期为A .n 3 T B . n 3T C .n 2 T D .n T k 2kkk类 3、火星探测项目是我国继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目。
