矢量数据压缩的Douglas_Peucker算法的实现与改进

Douglas-Peucker算法在无拓扑矢量数据压缩中的新改进

Douglas-Peucker算法在无拓扑矢量数据压缩中的新改进谢亦才;林渝淇;李岩【期刊名称】《计算机应用与软件》【年(卷),期】2010(027)001【摘要】分析常规Douglas-Peucker算法压缩无拓扑矢量数据时产生公共边"裂缝"现象的原因--公共边被两次或可能更多次压缩,而每次运用Douglas-Peucker 算法压缩时所选择的初始点和终点不同造成的.为此,提出公共边对象化Douglas-Peucker改进算法.为实现此算法,首先设计了新的公共边提取算法来提取公共边,然后使用OOP技术,把公共边的相关信息封装成类,最后根据公共边对象提供的信息对多边形的公共边和非公共边分别进行Douglas-Peucker压缩.以广东省行政界线的SVG矢量图为实验对象验证了此算法的有效性,分析了本算法相对于其它Douglas-Peucker改进算法在所需辅助空间和时间效率上的优势.【总页数】4页(P141-144)【作者】谢亦才;林渝淇;李岩【作者单位】华南师范大学计算机学院,广东,广州,510631;四川大学软件学院,四川,成都,610207;华南师范大学计算机学院,广东,广州,510631;华南师范大学空间信息研究中心,广东,广州,510631【正文语种】中文【相关文献】1.Douglas-Peucker算法在无拓扑矢量数据压缩中的改进 [J], 谢亦才;李岩2.时空数据压缩的基于Douglas-Peucker算法的改进与实现 [J], 杨家骏;郭远晴;魏诗云3.基于Douglas-Peucker的面状矢量数据压缩算法 [J], 赵真;沈敬伟;谭诗腾4.基于Douglas-Peucker的矢量数据压缩算法 [J], 尹路;周初阳5.矢量数据压缩的Douglas-Peucker算法的实现与改进 [J], 杨得志;王杰臣;闾国年因版权原因，仅展示原文概要，查看原文内容请购买。

道格拉斯—普克法(Douglas—Peucker)简化线算法报告

线简化算法程序设计报告矢量数据是GIS中，使用非常普遍的一种数据类型。

在使用中，有时需要对矢量数据进行压缩，矢量数据压缩的目的是删除冗余数据，减少数据的存贮量，节省存贮空间，加快后继处理的速度。

矢量数据的压缩方法常用的有道格拉斯—普克法、垂距法、光栏法。

本文主要讨论道格拉斯—普克法，运用该算法的思想，用C语言于TC20中编写一个小程序，实现对既有线的简化。

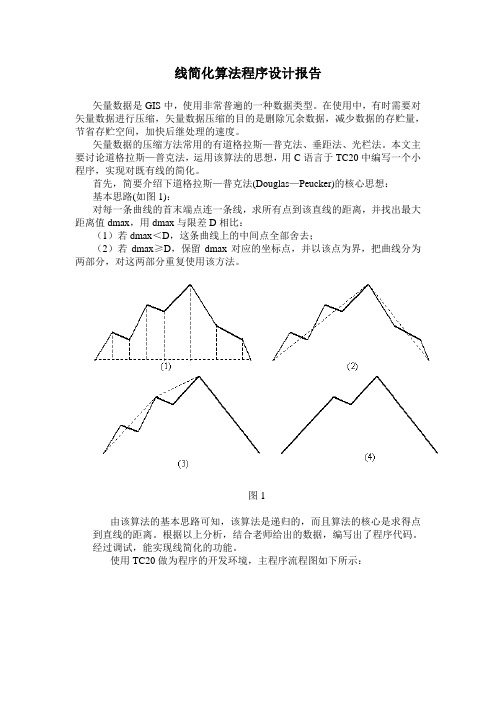
首先，简要介绍下道格拉斯—普克法(Douglas—Peucker)的核心思想：基本思路(如图1)：对每一条曲线的首末端点连一条线，求所有点到该直线的距离，并找出最大距离值dmax，用dmax与限差D相比：（1）若dmax＜D，这条曲线上的中间点全部舍去；（2）若dmax≥D，保留dmax对应的坐标点，并以该点为界，把曲线分为两部分，对这两部分重复使用该方法。

图1由该算法的基本思路可知，该算法是递归的，而且算法的核心是求得点到直线的距离。

根据以上分析，结合老师给出的数据，编写出了程序代码。

经过调试，能实现线简化的功能。

使用TC20做为程序的开发环境，主程序流程图如下所示：该算法的主要功能函数是Simp()，该函数的功能是根据输入的限差LimitDis 确定线上的点是保留还是去除。

Simp()函数的实现思想是，将曲线上的各点与曲线的端点连接，组成一个三角形，如下：先根据点到点的距离公式，求出a,b,c 的值。

然后再应用余弦公式cosA=(b*b+c*c-a*a)/(2*b*c);cosB=(a*a+c*c-b*b)/(2*a*c);sinA=(float)sqrt(1-co sA*cosA);再根据cosA ，cosB ，sinA 的值，算出距离。

对每个点进行上述的计算，求出每个点到AB 的距离，取最大值和LimitDis 比较，如果大于限差，那么从C 点将曲线分为二段，重复第一步。

如果小于，则去除AB 间的所有点。

该函数的流程图如下：CA Bb c a算法源代码：#include "stdio.h"#include "math.h"#include "graphics.h"/*---------------------------------------------------------*//*----------------define the points struct-----------------*//*---------------------------------------------------------*/ typedef struct Point{float x,y;char Res;};FILE *fp;int iNum;float LimitDis;struct Point Pt[30];/*-------------------------------------------------------*//*----------save the points to the structtype------------*//*-------------------------------------------------------*/void Savetostruct(){float px,py;int j=0;if((fp=fopen("C:\\data.txt","r"))==NULL){printf("Can't Open the File\n");exit(0);}while(!feof(fp)){fscanf(fp,"%f %f",&px,&py);Pt[iNum].x=px;Pt[iNum].y=py;Pt[iNum].Res='T';iNum++;}printf("These are the Original Points before Simplized :");for(j=0;j<=iNum-1;j++){printf("\nOriginalPt-%d x=%f y=%f \n",j,Pt[j].x,Pt[j].y);}printf("\n Toatal points: %d \n",j);};/*-------------------------------------------------------*//*--------------------Simplize the line------------------*/ /*-------------------------------------------------------*/ void Simp(p1,p2){float a,b,c,cosA,cosB,sinA,maxdis,curdis;int i=0,maxNO=0;float p2pdis();if((p2-p1)>=2){maxdis=0.00;c=p2pdis(p1,p2);i=p1+1;while(i<p2){curdis=0.00;b=p2pdis(p1,i);a=p2pdis(p2,i);cosA=(b*b+c*c-a*a)/(2*b*c);cosB=(a*a+c*c-b*b)/(2*a*c);sinA=(float)sqrt(1-cosA*cosA);if((cosA==0) || (cosB==0)){if(cosA==0){curdis=b;}else{curdis=a;}}else{curdis=b*sinA;}if(maxdis<=curdis){maxdis=curdis;maxNO=i;}i++;}/*end while*/if(maxdis>=LimitDis){Simp(p1,maxNO);Simp(maxNO,p2);}else{Delpt(p1,p2);}}/*end if*/}/*end Simp()*//*-------------------------------------------------------*//*------------------Distance of 2 pts--------------------*//*-------------------------------------------------------*/float p2pdis(pa,pb){ float d;d=(float)sqrt((Pt[pa].x-Pt[pb].x)*(Pt[pa].x-Pt[pb].x)+(Pt[pa].y-Pt[pb].y)*(Pt[ pa].y-Pt[pb].y));return d;}/*-------------------------------------------------------*//*-----------------Del point-----------------------------*//*-------------------------------------------------------*/Delpt(a,b){int c=a+1;while(c<b){Pt[c].Res='F';c++;}}/*-------------------------------------------------------*//*-----------------Draw Line-----------------------------*//*-------------------------------------------------------*/DrawLine(){int driver,mode,j,iSum=0,lastx,lasty;driver=DETECT;mode=0;initgraph(&driver,&mode,"");setcolor(15);for(j=0;j<=iNum;j++){if(Pt[j].Res=='T'){iSum++;if(iSum<2){lastx=Pt[j].x;lasty=Pt[j].y;}else{line(lastx,lasty,Pt[j].x,Pt[j].y);lastx=Pt[j].x;lasty=Pt[j].y;}putpixel(Pt[j].x,Pt[j].y,RED);}}getch();restorecrtmode();}/*-------------------------------------------------------*//*---------------------Main Function---------------------*//*-------------------------------------------------------*/main(){ int k;clrscr();Savetostruct();printf("\n Press anykey to see the Orignal Line in graphics mode: \n");getch();DrawLine();printf("Pls input a number as the limitdistance: \n");scanf("%f",&LimitDis);Simp(0,(iNum-1));printf("These are the Points after Simplized: \n");for(k=0;k<=iNum-1;k++){if(Pt[k].Res=='T')printf("ResultPt-%d x=%f y=%f \n",k,Pt[k].x,Pt[k].y);}printf("\n Press anykey to see the simplized result in graphics mode: \n");getch();DrawLine();。

矢量曲线压缩算法与实现

矢量曲线压缩算法与实现贾利峰;齐华【摘要】介绍了矢量曲线数据压缩算法--Douglas-Peucker法,提出了该算法的一种有效实现方法:利用队和栈的数据结构,保留距离最大的中间点,减少重复计算和判断偏差的操作,提高了算法的效率.【期刊名称】《铁道勘察》【年(卷),期】2005(031)002【总页数】2页(P20-21)【关键词】矢量曲线数据压缩 Douglas-Peucker算法实现【作者】贾利峰;齐华【作者单位】西南交通大学计算机与通信工程学院,四川成都,610031;西南交通大学计算机与通信工程学院,四川成都,610031;武汉大学测绘遥感信息工程国家重点实验室,湖北武昌,430079【正文语种】中文【中图分类】TP301.6曲线压缩也称为特征点提取，或者线状要素的抽样，经常用于扫描矢量化、地图综合和多比例尺空间数据库中。

随着地理信息系统(GIS)和地图综合技术的不断发展，曲线矢量数据压缩的重要性逐渐显现。

从信息论上讲，曲线矢量数据压缩是从组成曲线的数据集合A中抽取一个子集A′，用这个子集作为一个新的信息源，在规定的精度范围内，该子集能够从内容上尽可能近似反映原集合A，从数据量上则尽可能大的压缩。

数据压缩的目的主要是删除冗余数据、减少数据的存贮量、节省存储空间、加快后继处理速度。

对于矢量数据的压缩问题，目前为止，大家的重点都放在曲线的简化和压缩算法上，如垂足法、角度限制法[1]、基于自然规律的宏观综合法[2]、具有预测功能的压缩方法[3]以及纯几何的渐进式算法[4]等，其中最为经典的是Douglas-Peucker(简称D-P)法。

即使对于D-P算法，人们研究最多的也是该算法的改进，而忽略了算法本身的实现问题，本文主要介绍D-P算法一种新的实现方法，希望能对GIS的数据压缩和地图综合有所帮助。

1 Douglas-Peucker算法在矢量数据中，曲线是由离散的点列组成，曲线数据实际上是一些表示点的数据集。

时空数据压缩的基于Douglas-Peucker算法的改进与实现

间，但是却极大提高了精度。三、改进的ＤｕｓＰｕｋｒｏｇ — ｅｃｅ算法的非递归实现Ｉａ本文提出的基于改进的特征点提取的ＤｕｌｓＰｕｋｒｏｇａ — ｅｃｅ
算法非递归实现过程中用一个数组Ｄ来存放曲线的样点列Ｐ，１０Ｐ，…，１，用数组ｓ来存放特征点集。用数组的位置索Ｐ１引来指示样点，同时采用了一个与之相配合的队和一个栈，记队尾元素为ａ栈顶元素为ｂ，。具体步骤如下：（）采用本文上述基于角度的改进的特征点提取方法提１取特征点，得到特征点集ｓ。（）曲线起点Ｏ０和终点Ｄｎ的下标分别压入队列和２将［］［］栈中。然后将特征点集Ｓ中的元素按下标从大到小的顺序依次压入队列。此时ａＯ＝［］＝，ｂＳ０。（）连接Ｄａ和Ｄｂ，在Ｄａ和Ｄｂ之间的点列中寻３［］［］［］［］（下转第１５页）７
计算机光盘软件与应用
２１第７期０２年
ＣｍｕｅＤＳｆｗｒｎｐｌｃｔｏｓｏｐｔｒＣｏｔａｅａｄＡｐｉａｉｎ
软件开发设计
时空数据压缩的基于Ｄｕｌ — ｅｃｅ算法的改进与实现ｏｇ Fra bibliotekＰｕｋｒａ
杨家骏，郭远晴，魏诗云（四川大学软件学院，成都６００１２７）摘要：针对传统Ｄ０ａ— ｅｕｅ法中以点到基线的垂直距离为化简指标的不足，出现的导致某些具有代表ｕｓＰｃｋｒ算性的节点被删除的情况，在分段道格拉斯算法基础上提出了几点改进，采取优化的提取特征点的方式代替单纯的角度限制方式来实现分段Ｄｕｌ－ｅｕｅ算法。即在传统Ｄｕｌ－ｅｕｅ算法的基础上以基于提取特殊点的方式保ｏｇｓＰｃｋｒａｏｇｓＰｃｋｒａ留具有反应曲线走向的点，然后用非递归方法实现分段压缩。然后进行了曲线化简实验和方法的比较，验证了改进算法在保持线要素形态特征上的合理性。

基于Douglas-Peucker的面状矢量数据压缩算法

计算曲线内点Ｐ（ｉ＝２，３，… ，ｎ一１）到直线ＰｉＰ的距离Ｄ，通过比较距离的大小得到距离最大对应的点Ｐ，判断Ｄ的值与预先给定的阈值之间的大小关系。若小于阈值，则舍去曲线上的全部中间顶点；反之，若大于阂值，则保留点Ｐ，并以该点为界限，将首尾两点
缩，最后将压缩后的结果按原格式重建数据。刘兴科
Ｄｏｕｇｌａｓ — Ｐｅｕｃｋｅｒ算法将整个曲线考虑在内，而不是每次只考虑相邻的三个点。算法的基本思想。如下：假设组成曲线的顶点集合为Ｐ、Ｐｚ、…Ｐ，假设Ｐ、Ｐ为曲线的起始点和终止点，将其虚连成一条直线，
［关键词］Ｄｏｕｇｌａｓ — Ｐｅｕｃｋｅｒ算法；面状矢量数据；拓扑关系；数据压缩［中图分类号］Ｐ２０８［文献标识码］Ａ［文章编号］１６７４－５０１９（２０１７）０３ — ００９９ — ０４
ＳｕｒｆａｃｅＶｅｃｔｏｒＤａｔａＣｏｍｐｒｅｓｓｉｏｎＡｌｇｏｒｉｔｈｍＢａｓｅｄｏｎＤｏｕｇｌａｓ — Ｐｅｕｃｋｅｒ
些学者对矢量数据压缩进行了深入研究，提出了相
关的算法。王净等提出先采用深度搜索匹配法查找公共边并单独提取出来，按照一定的逻辑结构生成等效数据，然后利行压
［摘要］Ｄｏｕｇｌａｓ — Ｐｅｕｃｋｅｒ算法通常用于线状矢量数据压缩，但是该算法未考虑空间对象之间的拓扑关系。矢量

矢量曲线抽稀的实用算法和实现

矢量曲线抽稀的实用算法和实现吴铭杰*摘要：本文主要介绍对于AutoCAD的图形曲线进行抽稀处理的一种方法，并详细阐述了适用于程序代码快捷实现的有效算法。

关键词：Douglas-Peucker算法曲线矢量压缩堆栈 AutoLisp一．引言曲线压缩，即曲线特征点的提取，要求通过计算，将组成曲线的点数据集合按照规定的精度要求提取子集，使子集所表现出来的曲线在表现上近似于原始曲线，并使子集相对于原集合尽量的小，亦即在数据量上尽可能的少。

随着地理信息系统（GIS）的不断发展，其在各个领域应用的不断深入，各种形式的地图数据需要发布与传输，此时，作为图形主要表现形式的曲线有着不可替代的重要地位，即使是面域实体，其范围边界也由特定的曲线构成。

所以曲线矢量压缩也日益显现其重要的作用。

因为较少的数据量就意味着较快的传输效率，也就意味着更加流畅的应用效果。

在测绘工作中，无论是使用矢量采集还是数字测图，还是缩编的方式生产图形产品，都会遇到曲线节点过于密集而导致数据量偏大的问题。

这时，就要求生产单位对现有的曲线进行必要的抽稀处理，以减少数据冗余造成的对后续数据处理的不良影响。

同时，也由于不同的用户对于测绘产品有着不同的精度要求，生产部门对地形图表现区域客观地物进行恰当的简化和取舍，使经过概括表达的地物可以显示出用户所期待表现的事物本质与特征。

基于以上两点认知，研究将矢量压缩的理论算法转换为计算机实现算法有着迫切而且现实的需求。

AutoCAD图形文件（包含DWG、DXF）是当前国内测绘产品所采用的一种通用的文件格式，也是大多数用户认可的实际产品标准，它或作为测绘的最终产品提交用户，或作为中间交换数据提供后续处理，研究并提出针对AutoCAD数据格式的矢量曲线抽稀的算法及其实现对于测绘生产有着其现实的意义。

同时，由于算法自身所具有的普遍性和通用性，通过对AutoCAD 矢量数据的测试以及对于实验结果的分析，不难将之改写为不同程序选用的代码而适用于各异的环境以及可读写的格式。

物流跟踪系统中的轨迹压缩技术使用方法

物流跟踪系统中的轨迹压缩技术使用方法随着物流行业的不断发展，物流跟踪系统在物流管理中扮演着至关重要的角色。

为了提高物流运输效率并减少成本，轨迹压缩技术成为了物流跟踪系统中的一项关键技术。

本文将介绍物流跟踪系统中轨迹压缩技术的使用方法。

一、轨迹压缩技术的概念和作用轨迹压缩技术是指通过对物流跟踪系统中的移动物体轨迹数据进行简化和压缩处理，以减少存储空间和传输带宽，同时保持数据的重要特征。

通过轨迹压缩技术，可以大大降低物流数据的存储和传输成本，并提高系统的整体性能。

二、轨迹压缩技术的常用方法1. Douglas-Peucker算法Douglas-Peucker算法是一种常用的轨迹压缩方法，它通过逐步删除轨迹上的冗余点来实现数据的压缩。

该算法的基本思想是，选择轨迹上的两个端点，然后计算轨迹上的所有点到这条直线的距离，将距离最大的点作为关键点，通过不断迭代逼近原始轨迹。

2. Line Simplification算法Line Simplification算法也是一种常用的轨迹压缩方法，其核心思想是通过删除一些轨迹上的冗余线段来实现数据的压缩。

该算法通过选择与轨迹上的直线段误差最小的点，然后用直线段来逼近原始曲线，实现轨迹的压缩。

3. 网格压缩法网格压缩法是一种基于网格的轨迹压缩方法，它将轨迹数据分成等距的网格，然后在每个网格中选择代表点作为关键点，从而实现数据的压缩。

该方法可以很好地保持原始轨迹的形状特征，并有效减少数据量。

三、轨迹压缩技术的使用步骤1. 数据预处理在使用轨迹压缩技术之前，需要对原始轨迹数据进行预处理。

首先，对轨迹数据进行采样，使其采样点的数量减少到一定程度，避免数据冗余。

其次，对采样后的轨迹数据进行噪声过滤，排除那些不符合要求的数据点。

2. 选择合适的压缩方法根据实际需求和系统性能要求，选择适合的轨迹压缩方法。

不同的压缩方法适用于不同的场景和数据类型，因此需要根据具体情况进行选择。

3. 实施轨迹压缩根据选择的方法，对预处理后的轨迹数据进行压缩处理。

矢量数据压缩方法

矢量数据压缩方法
1. 矢量数据压缩方法之一是矢量数据简化。

在矢量数据中，点、线和面都可以通过简化算法进行压缩。

简化算法通过删除或合并冗余的几何信息来减少数据量，同时保持数据的整体形状和拓扑关系。

2. 矢量数据的压缩还可以使用线段压缩算法。

该方法通过将连续的线段近似为较短的线段，从而减少数据量。

常用的线段压缩算法包括Douglas-Peucker算法和Ramer-Douglas-Peucker算法。

3. 矢量数据的压缩方法还可以使用拓扑压缩。

拓扑压缩算法通过识别和编码拓扑关系来减少矢量数据的存储空间。

其中，常用的拓扑压缩算法包括基于格状编码的Quad-edge压缩算法和基于节点编码的Arc-node压缩算法。

4. 另外，矢量数据的压缩还可以采用编码压缩的方法。

编码压缩将矢量数据的几何信息和属性信息进行编码，从而减少数据的存储空间。

常见的编码压缩方法包括Huffman编码、Delta编码和LZW压缩算法。

总的来说，矢量数据的压缩方法可以通过简化、线段压缩、拓扑压缩和编码压缩等多种方法实现，根据不同的数据特点和压缩需求选择合适的方法。

基于Douglas-Peucker的矢量数据压缩算法

学术论坛科技创新导报 Science and Technology Innovation Herald248随着GIS技术的不断发展和应用，GIS 中大数据量的空间数据传输与无线通信网络带宽窄、以及移动终端设备硬件条件有限的矛盾日益凸现出来。

数据压缩就成为解决该矛盾的有效方法之一。

矢量数据压缩主要分为无损压缩和有损压缩两大类，对于有损压缩算法研究内容较多，如角度限值法[1]、D o u g la s -Peucker算法；如Zhilin Li等提出的基于“客观综合的自然规律”的线状要素的化简算法[2]；S.T.W u 等提出的一种基于星形的D o u gla s-Pe u cker算法[3]；郭庆胜提出的纯几何的基于面积的渐进式化简算法和基于弯曲以及三角形单元的渐进式化简算法。

这些算法从不同侧面提高的压缩效率及精度。

该文拟考虑压缩对象间拓扑关系，该文提出了D o u g l a s -P e u c k e r 一种改进算法，通过实验验证，改进的算法不仅能较好地保留图形特征，而且提高了压缩精度。

1 传统的Douglas-Peucker算法矢量数据压缩算法中比较经典的是D o u g l a s -P e u c k e r 算法，其基本思路如下：Ste p1：设定限差D ，将任一曲线的首末点相连，求除首位点之外的中间点到首位连线的距离，并得到最大距离值max D ，用max D 与限差D 进行比较；St e p 2：若D D <max ，这条曲线上的中间点全部舍去；St e p 3：若D D ≥max ，保留max D 对应的中间点，将首尾两点与改点连接，形成新的两条直线段，对新形成的直线段，重复step1和step2；Ste p 4：如此循环判断，直到没有满足条件为止。

D o u gla s-Pe u cker算法简单，实现容易。

具有较强的压缩效率，但D o u g l a s -Pe u c k e r算法同时也具有一些缺点，表现如下：(1）从首或尾任意端点开始执行D o u gla s-Pe u cker算法，得到的保留点结果可能不一样，对于面状地物压缩，易出现相邻两个多边形的边界压缩不一致；(2）D ou gla s-Peucker算法压缩结构受D 的取值影响较大，不同的取值结果偏差较大，局部地方易出现是真现象。

道格拉斯-普克算法的改进及其在管线制图中的应用

道格拉斯-普克算法的改进及其在管线制图中的应用文章摘要:首先对Douglas-Poiker经典算法进行了阐述，提出了对原有算法的一种改进方法，并对Douglas-Poiker和改进算法进行了分析比较；然后以Geomedia平台为基础，利用改进的算法对管线图的矢量曲线进行了压缩，对管线图进行制图综合，并对综合后的管线图进行精度分析，有效地提高了管线制图的工作效率。

(共3页)文章关键词:Douglas-Poiker算法制图综合管线图文章快照:glas—Poiker算法计算得出：这条曲线保留第4、c、F、G点，和Douglas—Poiker算法得到的结果一样。

通过比较可以看出：规定了一定的阈值之后，利用两种算法计算的结果是一样的。

本文利用改进的Douglas—Poiker算法进行计算机编程，对管线图进行制图综合。

28铁道勘察2008年第4期2改进的Douglas—Poiker算法在制图综合中的应用作为专题地图，且重要地物是线状地物，需要把管辖范围内所有油气管线绘制出来。

经过多方面的分析比较，选择GeoMedia平台来进行管线图的绘制和管理分析。

GeoMedia是美国Intergraph公司推出的新一代组件式GIS平台。

其内嵌关系数据库引擎，可直接对Access，Oracle，SQLServer进行数据读写，不需要中间件。

GeoMedia把空间数据和属性数据放在数据库的同一记录，进行统一管理，空间数据以二进制的形式存储在GEOMETRY字段，其他字段为属性数据。

这个特点为建库和数据更新等提供了最可靠的、高效率的数据管理措施，尤其适合数据量大的系统。

油气管线埋设于地下，不能直接利用GPS测量管线，而是根据管线在地面的标记(如标识桩、测试桩、转角桩)，和其附属设施(如阀室、中间站)的位置来确定管线位置的。

根据现场情况来看：首先，铺埋的管线有一定的宽度；且埋设的地面标记比铺埋的管线宽度小很多；其次，工人是通过目测管线位置来埋设标记的，并没有经过精确的测量，所以它们的相对位置就会有一定的误差。

矢量曲线压缩算法 c语言

矢量曲线压缩算法C语言矢量曲线压缩算法主要用于减少矢量曲线数据点的数量，同时尽量保持曲线的形状。

这样的算法在图形处理、数据传输、存储等方面都有广泛应用。

下面是一个简单的矢量曲线压缩算法的C语言实现，这个算法基于Douglas-Peucker算法。

该算法是一个迭代过程，每次迭代都找出曲线中最远的点，如果该点的距离超过一个预设的阈值，那么保留该点，并递归地对该点两侧的曲线段进行同样的处理。

c#include <stdio.h>#include <stdlib.h>#include <math.h>#include <float.h>typedef struct {double x, y;} Point;double distance(Point p1, Point p2) {return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));}double perpendicular_distance(Point P, Point A, Point B) {double AB2 = (B.x - A.x) * (B.x - A.x) + (B.y - A.y) * (B.y - A.y);if (AB2 == 0.0) return DBL_MAX;double t = ((P.x - A.x) * (B.x - A.x) + (P.y - A.y) * (B.y - A.y)) / AB2;if (t < 0.0) t = 0.0;else if (t > 1.0) t = 1.0;Point projection = {A.x + t * (B.x - A.x), A.y + t * (B.y - A.y)};return distance(P, projection);}void douglas_peucker(Point *points, int n, double epsilon, Point **result, int *m) {if (n <= 2) {*m = n;*result = (Point *)malloc(n * sizeof(Point));for (int i = 0; i < n; i++) {(*result)[i] = points[i];}return;}int index[2];double max_dist = 0.0;Point P[2];for (int i = 1; i < n - 1; i++) {double d = perpendicular_distance(points[i], points[0], points[n - 1]);if (d > max_dist) {index[0] = i;max_dist = d;P[0] = points[i];}}if (max_dist > epsilon) {Point *Lresult, *Rresult;int Lm, Rm;douglas_peucker(points, index[0] + 1, epsilon, &Lresult, &Lm);douglas_peucker(points + index[0], n - index[0], epsilon, &Rresult, &Rm);*m = Lm + Rm + 1;*result = (Point *)malloc(*m * sizeof(Point));for (int i = 0; i < Lm; i++) {(*result)[i] = Lresult[i];}(*result)[Lm] = P[0];for (int i = 0; i < Rm; i++) {(*result)[Lm + 1 + i] = Rresult[i];}free(Lresult);free(Rresult);} else {*m = 2;*result = (Point *)malloc(2 * sizeof(Point));(*result)[0] = points[0];(*result)[1] = points[n - 1];}}int main() {Point points[] = {{1, 1}, {2, 2}, {3, 4}, {4, 5}, {5, 4}, {6, 3}, {7, 2}, {8, 1}};int n = sizeof(points) / sizeof(points[0]);Point *result;int m;double epsilon = 1.0;douglas。

Douglas—Peucker和LZW算法在矢量数据压缩中的应用

ｐｒｓｉｎａｅｉｂｔｉｄｅｓｏｒｔｓｏａｎｅ．
Ｋｅｒｓａｏｉｍｆｕａ —ｅｃｅ；ｅｔｒｔｃｍｐｅｉ；ｌｏｔｆＺｙｗｏｄ：ｌｒｈｏｇｓＰｕｋｒｖｃａｏｒｓｎａｒｈｏＷｇｔＤｏｌ — ｏｄａｓｏｇｉｍＬ
随着ＷｅＧＳ的迅速发展，量空间数据在目前带宽有限的网络上的传输速度慢的问题越来越突出，此有必要对空间数据进ｂＩ海因
行压缩。பைடு நூலகம்
对空间数据的压缩技术可分为无损压缩和有损压缩。损压缩算法已经很成熟，常用的有ＬＷ算法。有损压缩，无最Ｚ而特别是对矢量图形（：ｐｎｏ的ＭＩ如ＭａｉｆＤ和基于ＸＭＬ的ＳＧ矢量数据）Ｖ的有损压缩，年来引起了不少学者的关注。本文提出综合应用Ｄｕ近ｏ— ｇｓＰｕｋｒＬＷ算法对矢量数据进行压缩的方法．大提高了压缩比。ｌ — ｅｃｅ和Ｚａ大
共弧段，个系统分别维护各自数据的结点表、段表和多边形表。第二种是简单数据结构（称无拓扑数据结构）如Ｍａｌｆ整弧俗，ｐｎｏ的
ＭＩＤ格式、ＶＳＧ。在简单数据结构中，理实体仅被抽象为点、、三种基本类型，个空间对象只记录、护自己所有的图形信息地线面每维和属性，每个对象都是自包含或独立对象，且没有相邻等拓扑信息＿弧段 ” １１。“ 和点、、线面都是由一系列坐标点的连线构成的。

道格拉斯普克算法代码

道格拉斯普克算法代码道格拉斯-普克（Douglas-Peucker）算法是一种用于曲线简化的算法，常用于GIS（地理信息系统）数据压缩。

这个算法的主要思想是在曲线上选择一个点，使得以该点为分割点的两段曲线的误差最小。

以下是一个简单的Python实现：```pythonimport numpy as npdef douglas_peucker(points, epsilon):# 获取点的数量n = len(points)# 如果只包含一个点，直接返回该点if n <= 1:return points# 初始化最大距离为无穷大max_dist = float('inf')# 初始化最大距离点为第一个点max_point = points[0]# 遍历所有点，计算与第一个点的距离for i in range(1, n):x = points[i] - points[0]dist = np.sqrt(x[0]**2 + x[1]**2)if dist > max_dist:max_dist = distmax_point = points[i]# 如果最大距离小于epsilon，直接返回第一个点if max_dist < epsilon:return [points[0]]else:# 使用递归对第一段曲线和第二段曲线进行道格拉斯-普克算法处理first_segment = douglas_peucker(points[:max_point+1], epsilon)second_segment =douglas_peucker(points[max_point+1:], epsilon)return first_segment + second_segment[1:] # 忽略最后一个点，因为它与第一段曲线最后一个点重合```在这个代码中，`points`是一个二维numpy数组，表示一系列的点。

道格拉斯—普客算法在动作捕捉数据优化中的应用

道格拉斯—普客算法在动作捕捉数据优化中的应用作者：孙浩鹏李杨来源：《科技创新与应用》2013年第36期摘要：数据手套因为其逼真的人机交互方式，在虚拟现实中越来越广泛地得到应用，尤其在工业装配、仿真手术、控制及手势识别等多个领域。

通过分析数据手套的数据特征，运用道格拉斯普客算法，解决了大数据量下的数据手套交互时间延迟问题。

通过改进优化数据方法，实现了数据在输入设备采集时大量数据的优化，将数据手套的数据进行优化在数据平滑上进行了处理，得到逼真的虚拟空间虚拟手或者机械手的交互效果，改善了虚拟手在仿真时的颤抖错误，实现了稳定的虚拟手交互效果。

关键词：虚拟现实；数据手套；道格拉斯-普客1 数据手套的工作方式数据手套在虚拟现实系统中占据重要位置，是一种非常昂贵的人机接口设备，其功能可以实时在虚拟系统中获取人手的各个关节空间坐标，以便在虚拟环境中再现人手动作，达到仿真的人机交互目的。

数据手套有很多种类，以cyber数据手套为例，可以对手部主要骨骼部位的关节运动进行实时测量。

系统可根据反向运动学原理测算出手指关节的位置，并将数据施加到相应的骨骼上。

由于惯性传感器主要依赖无处不在的地球重力和磁场，所以捕捉服在任何地点都可以正常使用，无需事先作任何准备工作。

每个传感器将即时数据通过发射盒以蓝牙或红外方式发射，执行标准为802.15.4 915兆赫。

在计算机中，利用蓝牙驱动即可直接读取蓝牙传输的数据。

采用惯性传感器无需铺设特殊装置，无需进行长时间校准。

相对其它光学动作捕捉系统，不会出现由标记物闭塞而造成的数据损失。

数据手套实现的关键在于各个生物器官如手指各关节的各个有效部位的弯曲、外展等测量。

并形成在此基础上的手势的表现。

完成表现不取决于人体手部姿态的建模，而是取决于确定传感器测量数据和手指各关节运动姿态的对应关系。

对一个具体的数据手套应用过程，可设由手部各弯角组成的向量f=（f1，f2，…，fn）与对应传感器示数组成的向量d=（d1，d2，…，dn）。

Douglas-Peucker算法

V3离线段 V0V7最远 V5 V1
V7

V0
V2
V6 V4

处理前的点的连线第一次计算的基准线第二次计算的基准线
Step 1
Step 2
5
Step 3
Last Step 处理前的点的连线当前基准线到基准线最远且距离大于glas-Peucker算法的问题
1、DOUGLASPEUCKER算法
曲线数据压缩算法(DouglasPeucker算法)

步骤一：确定阀值ε。
步骤二：先连接第一个和最后一个边界网格顶点，计算这对基准顶点对之间的点到基准线的距离。如果有一个及一个以上的点到基准线的距离大于ε，将距离基准线最远的点记为第n个点，删除基准线，并将第一个点和第n个点记为基准顶点对，将第n 个点和最后一个点记为基准顶点对；如果所有点到基准线的距离都小于等于ε，删除基准顶点之间的所有点，只保留基准顶点对作为基准顶点对之间曲线的控制顶点。步骤三：重复将步骤二中得到的基准顶点对进行步骤二的计算，直到所有点到他们的基准线的距离都小于等于ε。
公共边分裂
自相交的出现

Douglas-Peucker轨迹压缩算法

算法缺陷
对于一般路径而言，Douglas-Peucker算法是有效的，但是不难想到，当出现折返路径时，往外突出的部分很容易被压缩掉，因为偏差是以垂直距离为准的。下面的图片展示了这种情况下的压缩效果。
对于一般路径而言douglaspeucker算法是有效的但是不难想到当出现折返路径时往外突出的部分很容易被压缩掉因为偏差是以垂直距离为准的
Douglas-Peucker轨迹压缩算法
算法的基本思路是: 对每一条曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大距离值dmax ,用dmax与限差D相比: 若dmax <D,这条曲线上的中间点全部舍去; 若dmax ≥D,保留dmax 对重复使用该方法。

一种改进的基于Douglas-Peucker原理的轮廓采样算法

一种改进的基于Douglas-Peucker原理的轮廓采样算法作者：张真来源：《电脑知识与技术》2009年第25期摘要:文章首先介绍了Douglas-Peucker算法,它是一种经典的曲线简化方法,在此基础上提出了DP算法的一种非递归实现方法,该过程主要是利用队和栈的性质来实现的。

结果显示,用这种方法进行目标物体的轮廓采样,通过控制距离容差可以得到对轮廓线不同程度的逼近,不仅能够有效减少物体轮廓的冗余点,提高处理效率,又能够不失真地表征物体的形状。

关键词:Douglas-Peucker算法;非递归实现;轮廓采样中图分类号:TP391文献标识码:A文章编号:1009-3044(2009)25-7214-03An Improved Contour Sampling Algorithm Based on Douglas-Peucker TheoryZHANG Zhen(Department of Biological Science and Medical Engineering, Laboratory of Image Science and Technology, Southeast University, Nanjing 210096, China)Abstract: This paper, first analyses the theory of Douglas-Peucker algorithm, it is a classical curve simplification method, based on it, then proposes a non-recursive implementation of DP algorithm. This process mainly uses the property of data structure queue and stack. The results show that when using this method for contour sampling, it can obtain different degrees of contour line approaching by controlling the distance tolerance, it can not only reduce the number of redundant points of contour, improve the processing efficiency, also can characterize the shape of object without distortion.Key words: Douglas-Peucker algorithm; non-recursive implement; contour sampling在图像处理和计算机研究领域中,目标物体的定位一直是一个值得探讨的问题,目标的准确定位对于目标识别以及图像理解与分析起着十分重要的作用。

矢量数据压缩的Douglas—Peucker算法的实现与改进

据量急剧增大，数据管理和分析都带来困难。因对
此，曲线压缩的任务在于以尽可能少的抽样点来描述原始地物，保证在容许的误差限度内，并再现地物的形态特征。目前，曲线矢量数据压缩算法主要有：
测，以确定下一批压缩后的保留点。依此方法反复进行，至两端点之间的曲线上的离散点与两端点直
垂距限值法、度限值法、ｏｇａ．ｅｃｅ算法（角ＤｕｌＰｕｋｒｓ部
分文献称之为Ｓｌｉｇ算法）以及黄培之１９ｐｉｎｔ，９５年
合一形式，法的基本思想是：算设曲线由点序Ｐ１Ｐ２ … ，构成，Ｐ１Ｐ，，Ｐ取，
个新的信息源，规定的精度范围内该子集从内在
容上尽可能地反映原集合Ａ，于数量上则尽可能而
精简。在空间数据处理领域，曲线矢量数据压缩也
一
Ｄｕｌ．ｅｃｅ算法事实上是垂距限值法的改ｏｇＰｕｋｒｓａ
进，算法于１７该９３年前后有多人同时提出，一种是
常用的曲线矢量数据压缩方法和曲线多边形逼近算法。与垂距限值法的不同之处是，算法同时考虑该整个曲线，不是把曲线数据分配给数据点的三点而
关键词：矢量；数据压缩；归；法；递算地理信息系统

顾及曲线走向及局部面积特征的矢量数据压缩算法

顾及曲线走向及局部面积特征的矢量数据压缩算法韩晓霞;崔浩;孙钰珊【摘要】目前,矢量数据压缩算法存在曲线压缩精度与压缩效率不能共存的问题,基于此,本文以带有径向约束的Douglas-Peucker算法为基础,提出一种顾及曲线走向和局部面积特征的矢量数据压缩算法.该算法首先通过带有径向约束的Douglas-Peucker算法提取曲线的特征点;然后,提取各个局部曲线段形态特征点以判断局部曲线段走向特征;最后,根据曲线段走向对预先提取的各个特征点的位置进行局部微调,完成矢量数据的压缩.该算法创新在于通过局部微调特征点位置的方式使压缩后曲线较好地反映了原曲线的局部走向,并且减小了曲线局部面积偏差.实验表明所提算法在保证压缩效率的同时能够有效降低局部位移偏差和面积偏差,使压缩后曲线较好的反映原曲线形态特征.【期刊名称】《北京测绘》【年(卷),期】2017(000)006【总页数】4页(P6-9)【关键词】Douglas-Peucker算法;特征点;形态特征点;位移偏差;面积偏差【作者】韩晓霞;崔浩;孙钰珊【作者单位】中国测绘科学研究院,北京100830;中国测绘科学研究院,北京100830;兰州交通大学测绘与地理信息学院,甘肃兰州730070;中国测绘科学研究院,北京100830【正文语种】中文【中图分类】P208随着人类对于解决复杂空间信息问题需求的提高,地理信息系统受到了越来越多的关注。

其中,地图综合是地理信息系统中最为常见且富有挑战性的一个课题,其本质是从空间数据库中提取反映本质、主要和整体规律性的内容,舍去非本质、次要的细节的内容。

对矢量数据而言,曲线是构成图件最基本、最重要的要素,它既可描述地理要素的边界如房屋、湖泊边界,又可用于表示线状地理对象如河流、公路等。

因此,曲线的自动化简在制图综合中占有极为重要的地位。

目前单线压缩的算法已经比较成熟,主要经典算法有垂距法、角度法、Douglas-Peucker算法、逐点前进法、小波法、光栏法等[1-4],黄培之提出一种具有预测功能的曲线矢量数据压缩方法[5]。

Douglas_Peucker算法在无拓扑矢量数据压缩中的新改进

第27卷第1期计算机应用与软件Vol 127No .12010年1月 Computer App licati ons and Soft w are Jan .2010D ougl a s 2Peucker 算法在无拓扑矢量数据压缩中的新改进谢亦才1　林渝淇2　李　岩1,31(华南师范大学计算机学院　广东广州510631)2(四川大学软件学院　四川成都610207)3(华南师范大学空间信息研究中心　广东广州510631)收稿日期:2008-07-31。

广东省百项工程项目(2005B30801006)。

谢亦才,硕士生,主研领域:图形图像处理,空间信息处理。

摘　要分析常规Douglas 2Peucker 算法压缩无拓扑矢量数据时产生公共边“裂缝”现象的原因———公共边被两次或可能更多次压缩,而每次运用Douglas 2Peucker 算法压缩时所选择的初始点和终点不同造成的。

为此,提出公共边对象化Douglas 2Peucker 改进算法。

为实现此算法,首先设计了新的公共边提取算法来提取公共边,然后使用OOP 技术,把公共边的相关信息封装成类,最后根据公共边对象提供的信息对多边形的公共边和非公共边分别进行Douglas 2Peucker 压缩。

以广东省行政界线的S VG 矢量图为实验对象验证了此算法的有效性,分析了本算法相对于其它Douglas 2Peucker 改进算法在所需辅助空间和时间效率上的优势。

关键词 Douglas 2Peucker 算法　矢量数据压缩　S VG 公共边对象化Douglas 2Peucker 改进算法NE W IM PRO VE M ENT O F DO UGLAS 2PEUCKER AL GO R I TH M I N NO N 2TO POLO GYVECTO R DATA COM PRESS IO NXie Yicai 1　L in Yuqi 2　L i Yan1,31(School of Co m puter ,South China N or m al U niversity,Guangzhou 510631,Guangdong,China )2(College of Soft w are Engineering,S ichuan U niversity,Chengdu 610207,S ichuan,China )3(Spatial Infor m ation R esearch Center ,South China N or m al U niversity,Guangzhou 510631,Guangdong,China )Abstract The article analysed the reas on of crack phenomenon on common boundary of graphicswhen comp ressing the non 2t opol ogy vect or graphics by conventi onal Douglas 2Peucker algorith m 2the common boundary m ight be comp ressed t w ice or more,whiles each comp ressi on with Douglas 2Peucker algorith m selects different initial and end points .Theref ore,an i m p r oved Douglas 2Peucker algorith m t o objectify the common boundary is put for ward .To i m p le ment it,first,we design a ne w algorith m t o extract the common boundaries bet w een t w o polygons .Then we a 2dop t OOP technol ogy t o encap sulate the inf or mati on with regard t o common boundaries t o a class .And at last,on the basis of the class,we ap 2p ly conventi onal Douglas 2Peucker comp ressi on t o vect or graphics of the common boundary and non 2common boundary of the polygons res pec 2tively according t o the infor mati on p r ovided by common boundary object .The validity of the ne w comp ressing algorith m is p r oved in an experi 2ment with S VG vect or graphics of the ad m inistrative boundary of Guangdong Pr ovince .And the advantages in auxiliary s pace and ti m e efficien 2cy this algorith m possesses is analysed in contrasting with other i m p r oved Douglas 2Peucker algorith m s .Keywords Douglas 2Peucker algorith m Vect or data comp ressing Scalable vect or graphics (S VG )　I m p r oved Douglas 2Peucker algorith m for objectifying the common boundary0　引　言随着W ebGI S 的迅速发展,海量空间数据在目前带宽有限的网络上的传输速度慢的问题越来越突出,因此有必要对空间数据进行压缩。