详细版svpwm空间矢量控制原理及详细计算.ppt
SVPWM电压矢量控制ppt课件

2 3
(u
A
uBe j
uCe j2
)
13
8个基本空间矢量
PWM逆变器共有8种工作状态
当 SA SB SC 1 0 0
uA
uB
u
C
Ud 2
Ud 2
Ud 2
u1
2 Ud (1 e j e j2 ) 32
2
Ud
j 2
(1 e 3
j 4
e 3
)
32
2 Ud [(1 cos 2 cos 4 ) j(sin 2 sin 4 )]
3
2 Ud (1 j 3) 32
2U 3
d
e
j
3
依此类推,可得8个基本空间矢量 。
15
8个基本空间矢量
6个有效工作矢量
u1 u6
幅值为
2U 3
d
空间互差
3
2个零矢量 u0、u7
16
基本电压空间矢量图
图5-24 基本电压空间矢量图
17
正六边形空间旋转磁场
6个有效工作矢量 u1 u6
顺序分别作用△t时间,并使
SPWM的基波线电压最大幅值为
U' lm m ax
3U d 2
两者之比
U lm max U'
lm m ax
2 1.15 3
SVPWM方式的逆变器输出线电压基波最大 值为直流侧电压,比SPWM逆变器输出电压 最多提高了约15%。
33
SVPWM的实现
通常以开关损耗和谐波分量都较小为 原则,来安排基本矢量和零矢量的作用 顺序,一般在减少开关次数的同时,尽 量使PWM输出波型对称,以减少谐波 分量。
Ud
SVPWM的原理和法则推导和控制算法详细讲解

空间电压矢量调制SVPWM 技术SVPWM是近年发展的一种比较新颖的控制方法,是由三相功率逆变器的六个功率开关元件组成的特定开关模式产生的脉宽调制波,能够使输出电流波形尽可能接近于理想的正弦波形。
空间电压矢量PWM与传统的正弦PWM不同,它是从三相输出电压的整体效果出发,着眼于如何使电机获得理想圆形磁链轨迹。
SVPWM技术与SPWM相比较,绕组电流波形的谐波成分小,使得电机转矩脉动降低,旋转磁场更逼近圆形,而且使直流母线电压的利用率有了很大提高,且更易于实现数字化。
下面将对该算法进行详细分析阐述。
1.1SVPWM基本原理SVPWM 的理论基础是平均值等效原理,即在一个开关周期内通过对基本电压矢量加以组合,使其平均值与给定电压矢量相等。
在某个时刻,电压矢量旋转到某个区域中,可由组成这个区域的两个相邻的非零矢量和零矢量在时间上的不同组合来得到。
两个矢量的作用时间在一个采样周期内分多次施加,从而控制各个电压矢量的作用时间,使电压空间矢量接近按圆轨迹旋转,通过逆变器的不同开关状态所产生的实际磁通去逼近理想磁通圆,并由两者的比较结果来决定逆变器的开关状态,从而形成PWM 波形。
逆变电路如图1-1 示。
设直流母线侧电压为U dc,逆变器输出的三相相电压为U A、U B、U C,其分别加在空间上互差120°的三相平面静止坐标系上,可以定义三个电压空间矢量U A(t)、U B(t)、U C(t),它们的方向始终在各相的轴线上,而大小则随时间按正弦规律做变化,时间相位互差120°。
假设U m 为相电压有效值,f 为电源频率,则有:()cos()()cos(2/3)()cos(2/3)A mB m Cm U t U U t U U t U θθπθπ=⎧⎪=-⎨⎪=+⎩ (1-1)其中,2ft θπ=,则三相电压空间矢量相加的合成空间矢量U(t)就可以表示为:2/34/33()()()()2j j j A B C m U t U t U t e U t e U e ππθ=++=(1-2)可见 U(t)是一个旋转的空间矢量,它的幅值为相电压峰值的1.5倍,U m 为相电压峰值,且以角频率ω=2πf 按逆时针方向匀速旋转的空间矢量,而空间矢量 U(t)在三相坐标轴(a ,b ,c)上的投影就是对称的三相正弦量。
空间矢量SVPWM讲解

现实考虑
易于计算机实现
形成开关信号, 控制变换器
挖掘SVPWM优势
数字实现方式
扇区确定
Vγ1>0,则A=1,反之A=0;
V γ 2>0,则B=1,反之B=0;
V γ3 >0,则C=1,反之C=0。
N =A+2B+4C
当N=3时,Uref位于第Ⅰ扇区; 当N=1时,Uref位于第Ⅱ扇区; 当N=5时,Uref 位于第Ⅲ扇区; 当N=4时,Uref 位于第Ⅳ扇区; 当N=6时,Uref 位于第Ⅴ扇区; 当N=2时,Uref 位于第Ⅵ扇区。
当N=3时,Uref位于第Ⅰ扇区; 当N=1时,Uref位于第Ⅱ扇区; 当N=5时,Uref 位于第Ⅲ扇区; 当N=4时,Uref 位于第Ⅳ扇区; 当N=6时,Uref 位于第Ⅴ扇区; 当N=2时,Uref 位于第Ⅵ扇区。
Ⅱ
Ⅲ
Ⅰ
Ⅳ
Ⅵ
Ⅴ
开关矢量时间确定
表Ⅰ 矢量作用时间分配
扇区
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
N
3
1
5
4
传统PWM技术一般通过将三角载波和
调制函数波比较获得相应脉冲波形
cos(t 30 ) 0 t 60
3 cost
60 t 120
uA
a
c os (t c os (t
150 ) 210 )
120 t 180 180 t 240
3 cost
240 t 300
cos(t 30 )
旋转向量
U UA UB UC
3
U 2
m
(sin
t,
sin
t
2 3
, s in
详细版svpwm空间矢量控制原理及详细计算.ppt
( ) 采用对称规则采样法时的脉宽间为: t =
当载波幅值UC 为1
时t
= Tc
2
1
u(te) Uc
可得:
Tc 2
u
(
1+ U (te) Uc
te ) = 2t
Tc
-1
• 将tA、tB 、tC 代入上式(注: 2TI = Tc )得平均电压
• 矢量位于第一扇区时隐含调制函数为:
• uyA = Kcos (θ- 30°)
把公式中u1、u2 换成该扇区边界上的电压矢量就可以了。扇区时, 可 得三相脉宽时间为: • tA = 2 ( t1 + t2 + t7 ) • tB = 2 ( t2 + t7 ) • tC = 2 t7 • 将式7、式8 和式9 代入上式, 并考虑到t0 = t7 , • 可得: • tA = KTI『 sin (60°-θ) + sinθ』 + TI • tB = KTI 『- sin (60°-θ) + sinθ』 + TI • tc = KTI『 - sin (60°-θ) - sinθ 』+ TI
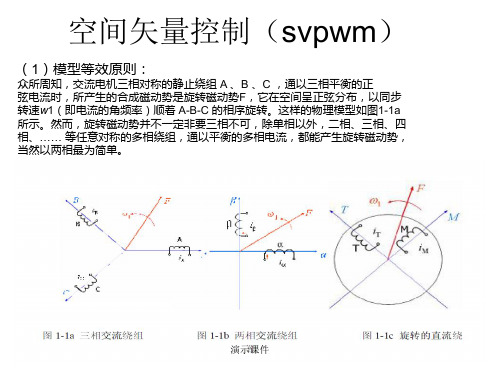
空间矢量控制(svpwm)
(1)模型等效原则:
众所周知,交流电机三相对称的静止绕组 A 、B 、C ,通以三相平衡的正 弦电流时,所产生的合成磁动势是旋转磁动势F,它在空间呈正弦分布,以同步 转速w1(即电流的角频率)顺着 A-B-C 的相序旋转。这样的物理模型如图1-1a 所示。然而,旋转磁动势并不一定非要三相不可,除单相以外,二相、三相、四 相、…… 等任意对称的多相绕组,通以平衡的多相电流,都能产生旋转磁动势, 当然以两相最为简单。
• uav TI = u0 t0 + u1 t1 + u2 t2 + u7 t7 • 式中, TI = t0 + t1 + t2 + t7 ; • t0、t1、t2、t7、为u0、u1、u2、u7 停留的时间。
SVPWM控制方法和实现ppt课件

由以上两式可得空间矢量功率表达式为 2 ' ' j j 2 j j 2 p Re U I Re k u u e u e i i e i e s s A 0B 0 C 0 A 0B 0 C 0 3 3 ' ' 2 2 p Re U I k ( u i u i u i ) k p s s A 0 A 0 B 0 B 0 C 0 C 0 2 2
LOGO
SVPWM的实现方法
要解决三个问题: 如何选择基本电压矢量,即确定电压矢量在哪个扇区 如何确定每个基本电压矢量的作用时间 如何确定每个基本电压矢量的作用顺序
LOGO
确定参考电压矢量所在扇区
已知参考电压 u ref 在两相静止坐标系下的分量为 u u
( 1 )若 u ,则 A1 ,否则 A0 0 (2 )若 3 u ,则 B1 ,否则 B0 -u 0 (3 )若 - 3 u ,则 C1 ,否则 C0 -u 0 由此得扇区号: NA2 B4 C
N Ta Tb Tc
1 Tx Ty Tz
2 Ty Tx Tz
3 Tz Tx Ty
4 Tz Ty Tx
5 Ty Tz Tx
6 Tx Tz Ty
LOGO
SVPWM控制模块
Scope3 1 Ualfa 2 Ubeta
Ubeta N Ualf a N
Scope6 Scope1 Scope
N1
T1 T1
-CConstant
PMSM
VDC/ 2
N
A
S1
B
S3
C
S5
R O
R R
svpwm空间矢量控制原理课件

03
空间矢量调制波形的生成
通过计算得到各相电压的期望值,然后利用SVPWM算法生成相应的
PWM波形。
SVPWM算法实现
SVPWM算法的基本步骤
首先计算出电压矢量的期望值,然后根据该期望 值计算出相应的扇区,再根据扇区计算出相应的 矢量时间,最后生成相应的PWM波形。
矢量时间的计算
根据扇区数和期望的电压矢量幅值,可以计算出 相应的矢量时间。
THANKS
THANK YOU FOR YOUR WATCHING
05
SVPWM控制策略优化
控制策略改进方法
引入滑模控制
通过设计滑模控制器,实 现SVPWM控制系统的快 速响应和鲁棒性。
优化死区时间
通过调整死区时间的设置 ,减小SVPWM控制过程 中的谐波分量,提高控制 精度。
引入重复控制
将重复控制算法应用于 SVPWM控制系统,减小 稳态误差,提高系统跟踪 性能。
SVPWM空间矢量控制原理课件
目录 CONTENTS
• SVPWM技术概述 • 空间矢量控制原理 • SVPWM实现方式 • SVPWM与PWM对比 • SVPWM控制策略优化 • SVPWM实验与验证
01
SVPWM技术概述
SVPWM定义
SVPWM
Space Vector Pulse Width Modulation的缩写,即空间矢量脉 宽调制技术。
波形生成的实现方式
利用SVPWM算法生成相应的PWM波形,并通 过驱动电路将PWM波形输出到逆变器中,从而 控制各相电压的大小和频率。
波形生成的优点
SVPWM波形生成具有较高的电压输出能力和较 低的谐波畸变率,能够实现精确的电压控制和较 高的功率因数。
SVPWM的原理及法则推导和控制算法详解

SVPWM的原理及法则推导和控制算法详解Space Vector Pulse Width Modulation(SVPWM)是一种用于交流电机驱动的调制技术。
它的原理是将固定电压向量分解为两个可控向量,通过改变这两个向量的占空比来控制交流电机的输出。
SVPWM利用矢量图法将三相交流电源的空间矢量变换为两相旋转矢量,从而实现对交流电机驱动电压的控制。
1.假设存在一个以0为中心的静止坐标系,其中电源相电压为Va,Vb,Vc。
我们可以将这三个电压写成以时间为函数的形式,即Va(t),Vb(t),Vc(t)。
2.将Va,Vb,Vc投影到α-β坐标系,得到α轴上的电压Vaα(t),Vbα(t),Vcα(t)和β轴上的电压Vaβ(t),Vbβ(t),Vcβ(t)。
3. 将α-β坐标系反转回静止坐标系,得到参考电压Va_ref(t), Vb_ref(t), Vc_ref(t)。
4.将参考电压投影到空间矢量图上,从而得到交流电机的输入矢量。
5.根据参考电压和输入矢量之间的关系,推导出控制算法。
1.基于所需输出电压的矢量长度和角度,计算矢量图中的两个矢量的占空比,分别为d1和d22.根据矢量长度和角度,计算三个相电压的占空比,分别为d_a,d_b,d_c。
3.根据SVPWM的特性,当d1,d2为0时,输出电压为0;当d1,d2相等时,输出电压处于峰值;当d1和d2不相等时,输出电压的大小和方向都有所改变。
因此,通过改变d1和d2的数值,可以改变输出电压的大小和方向。
4.根据d_a,d_b,d_c和d1,d2的数值,计算出PWM控制信号。
5.将PWM控制信号施加到交流电机驱动电路中,从而实现对输出电压的控制。
总结起来,SVPWM通过将固定电压向量分解为两个可控向量,通过改变这两个向量的占空比来控制交流电机的输出。
通过合理推导和计算,可以得到控制算法,从而实现对输出电压的精确控制。
SVPWM是一种高效且精确的交流电机驱动技术,被广泛应用于工业控制中。
空间矢量脉宽调制SVPWM技术原理及实现课程作业PPT课件

个整体来考虑,模型比较简单,也便于微处理器的实时控制。电机
理想的供电电压为三相对称正弦波,设线电压Vdc,相电压表示式如
下
:
根据合成电压矢量公式 由上面的式子可得
第3页/共10页
从(5)式可以看出,合成电压矢量是一个随时间变化、幅值一定 的圆形磁场,而磁场是电压的积分,因此产生的磁场也是一个圆形的 旋转磁场,图3为逆变器简化的拓扑图,定义三个开关函数sa,sb, sc,用1代表1个桥臂的上桥臂导通,用0代表1个桥臂的下桥臂导通。 则对于180°导通型逆变器来说,三相桥臂的开关有8个导通状态,包 括6个非零矢量和2个零矢量。
第2页/共10页
SVPWM控制方法简介
SVPWM的主要思想是:以三相对称正弦波电压供电时三相对称电
动机定子理想磁链圆为参考标准,以三相逆变器不同开关模式作适
当的切换,从而形成PWM波,以所形成的实际磁链矢量来追踪其准
确磁链圆。传统的SPWM方法从电源的角度出发,以生成一个可调
频调压的正弦波电源,而SVPWM方法将逆变系统和异步电机看作一
备了条件,先进的SVPWM技术在此环境下应运而生。 变频器的SVPWM算法与其拓扑结构有着密切的联系,因此必须根据变频器
拓扑结构的不同,选取相应的控制算法。 通过课堂学习和在网上查阅资料,本文对空间矢量脉宽调制(SVPWM)技
术原理及实现进行简要概述。
第1页/共10页
SVPWM原理
SVPWM将逆变器和电动机看成一个整体,建立逆变器开关模式和 电机电压空间矢量的内在联系,通过控制逆变器的开关模式,使电 机的定子电压空间矢量沿圆形轨迹运动,从而明显降低转矩脉动, 与传统的SPWM相比,其开关器件的开关次数可以减少1/3,直流电 压的利用率可提高百分之15,能获得较好的谐波抑制效果,且易于 实现数字化控制。常用的三相电压源逆变主电路结构下图所示。
SVPWM的原理讲解以及应用过程中的推导与计算

. . .一直以来对SVPWM 原理和实现方法困惑颇多,无奈现有资料或是模糊不清,或是错误百出。
经查阅众多书籍论文,长期积累总结,去伪存真,总算对其略窥门径。
未敢私藏,故公之于众。
其中难免有误,请大家指正,!1 空间电压矢量调制 SVPWM 技术SVPWM 是近年发展的一种比较新颖的控制方法,是由三相功率逆变器的六个功率开关元件组成的特定开关模式产生的脉宽调制波,能够使输出电流波形尽 可能接近于理想的正弦波形。
空间电压矢量PWM 与传统的正弦PWM 不同,它是从三相输出电压的整体效果出发,着眼于如何使电机获得理想圆形磁链轨迹。
SVPWM 技术与SPWM 相比较,绕组电流波形的谐波成分小,使得电机转矩脉动降低,旋转磁场更逼近圆形,而且使直流母线电压的利用率有了很大提高,且更易于实现数字化。
下面将对该算法进行详细分析阐述。
1.1 SVPWM 基本原理SVPWM 的理论基础是平均值等效原理,即在一个开关周期通过对基本电压矢量加以组合,使其平均值与给定电压矢量相等。
在某个时刻,电压矢量旋转到某个区域中,可由组成这个区域的两个相邻的非零矢量和零矢量在时间上的不同组合来得到。
两个矢量的作用时间在一个采样周期分多次施加,从而控制各个电压矢量的作用时间,使电压空间矢量接近按圆轨迹旋转,通过逆变器的不同开关状态所产生的实际磁通去逼近理想磁通圆,并由两者的比较结果来决定逆变器的开关状态,从而形成PWM 波形。
逆变电路如图 2-8 示。
设直流母线侧电压为Udc ,逆变器输出的三相相电压为UA 、UB 、UC ,其分别加在空间上互差120°的三相平面静止坐标系上,可以定义三个电压空间矢量 UA(t)、UB(t)、UC(t),它们的方向始终在各相的轴线上,而大小则随时间按正弦规律做变化,时间相位互差120°。
假设Um 为相电压有效值,f 为电源频率,则有:⎪⎩⎪⎨⎧+=-==)3/2cos()()3/2cos()()cos()(πθπθθm Cm B m A U t U U t U U t U (2-27) 其中,ft πθ2=,则三相电压空间矢量相加的合成空间矢量 U(t)就可以表示为:θππj m j C j B A e U e t U e t U t U t U 23)()()()(3/43/2=++= (2-28)可见 U(t)是一个旋转的空间矢量,它的幅值为相电压峰值的1.5倍,Um 为相电压峰值,且以角频率ω=2πf 按逆时针方向匀速旋转的空间矢量,而空间矢量 U(t)在三相坐标轴(a ,b ,c )上的投影就是对称的三相正弦量。
第八讲SVPWM控制

式中A=ur1,B=US,并令A( 3/2)UdM。
求解上式可得:
t1
T0M
sin
3
0
t2T0M sin0
零矢量的使用
换相周期 T0 应由旋转磁场所需的频率决定, T0 与 t1+ t2 未必相等,其间隙时间可用零矢量 u7 或 u0 来填 补。为了减少功率器件的开关次数,一般使 u7 和 u0 各 占一半时间,因此
图2-28b 电压空间矢量图
对于六脉波的逆变器,在其输出的每个周期中6 种有 效的工作状态各出现一次。逆变器每隔 /3 时刻就切换一 次工作状态(即换相),而在这 /3 时刻内则保持不变。
❖ 随着逆变器工作状态的切换,电压空间矢量的幅值不 变,而相位每次旋转 /3 ,直到一个周期结束。
这样,在一个周期中 6 个电压空间矢量共 转过 2 弧度,形成 一个封闭的正六边形, 如图所示。
设在一段换相周期时间 T0 中,可以用两个矢量之 和表示由两个矢量线性组 合后的电压矢量us = ur1 ,
新矢量的相位为 。
图2-30 电压空间矢量的线性组合
❖ 图2-30表示了由u1、u2构成新的电压空间矢量的线性组合, ❖ 设在原u1状态结束后,期望在时间T0内电压空间矢量ur1起
作用,并有ur1=u1。 ❖ 采用部分u1矢量和部分u2矢量求和得到矢量ur1, ❖ t1u1/T0和t2u2/T0分别表示部分u1和部分u2矢量,它们合成矢
t7t012(T0t1t2)≥ 0
开关状态顺序原则
❖ 在实际系统中,应该尽量减少开关状态变化时引起 的开关损耗,因此不同开关状态的顺序必须遵守下述原 则:任意一次电压矢量的变化只能有一个桥臂的开关动 作,表现在二进制矢量表示中只有一位变化,以满足最 小开关损耗。
空间电压矢量调制SVPWM 技术原理中文讲解(让初学者快速了解SVPWM控制方式)

关组合时逆变器输出的空间电压矢量,特定义开关函数 Sx ( x = a、
b、c) 为:
Sx
1上桥臂导通 0下桥臂导通
(2-30)
(Sa、Sb、Sc)的全部可能组合共有八个,包括 6 个非零矢量 Ul(001)、
U2(010) 、U3(011) 、U4(100)、U5(101) 、U6(110) 、和两个零矢量
????????????????????????66423322132tututtutudcsdcs?????????????????????????????????????段段或572333223332123212347640716264tttttttttuutututuutuuututuututututssdcsdcsdcsdcsdcsdcsdc??????浙江海得新能源有限公司第15页共23页???????????????223223321?????uuuuuuuu237同理可求得uref在其它扇区中各矢量的作用时间结果如表24所示
0
Udc
-Udc
1 3
U
dc
1 3
U
dc
2 3
U
dc
U2
-Udc Udc
0
1 3
U
dc
2 3
U
dc
1 3
U
dc
U3
-Udc
0
-Udc
2 3Байду номын сангаас
U
dc
1 3
U
dc
1 3
U
dc
第 3 页 共 23 页
浙江海得新能源有限公司
00 1
U1
0
-Udc
Udc
1 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
iM cos sin i
iT
=
sin
c os
i
演示课件
演示课件
• 可以推导出,三相逆变器输出的相电压矢量[Uu、Uv、Uw]T与开关状
态矢量[a、b、c] T的关系为:
Uu
Uv
Uw
=
Ud 3
2 1 1
1 2 1
1 a
1
b
2 c
• 将上式代入电压空间矢量公式:
•
• K = 3 Uav
Ud
演示课件
2 算法分析 SPWM生成原理采用对称规则采样Ⅱ法, 如2所示。
T2= 式中, te
为T2采c 样(1时+间M,s间inω隙1时te 间) (1为) :
1
t1 = t3 = 2 (Tc-T2) (2)
上式中, Tc 为一个载波周期时间, M =UM /UC , 是调制深度系数, UM 为调制波 幅值, UC 为载波幅值。可推广到任一演示调课制件 函数u ( t) 。
Uout=
2 3
Uu Uve j2 / 3 Uwe j4 / 3
• 得到相应逆变器工作模式与输出电压的关系,如下表
演示课件
演示课件
• 逆变器工作于开关状态, 输出电压不可能是连续变化的, 所以和逆变器 输出电压相对应的电压空间矢量也不可能连续变化在空间矢量调制中, 可以引入“一个时间间隔内的平均电压空间矢量uav ”这一概念, 并设 法使平均电压空间矢量在复数平面以不变的长度恒速旋转, 即可得到 SVPWM脉宽调制波形。为了形成这个uav , 可将每个TI 分成4 个阶段, 各个阶段中逆变器的电压空间矢量可依次为u0、u1、u2、u7 , 也可以 是u7、u2、u1、u0。因为每个TI中, uav对时间的积分应等于逆变器 输出电压空间矢量对时间的积分, 即可得出:
所需的6 路PWM。根据给定电压空间矢量在空间三
相坐标系的投影的正负可以判断该电压空间矢量位
于哪个扇区。
演示课件
• 因此记: a v , b v , c v 为其在三相坐标上的投影标量:
• aபைடு நூலகம்=U s
bv=-U s cos60°+ U s sin30° cv=- U s cos60°- U s sin30°
演示课件
图1-1b中绘出了两相静止绕组a 和 b ,它们在空间互差90°,通以时间上互差90° 的两相平衡交流电流,也产生旋转磁动势F 。。再看图1-1c中的两个互相垂 直的绕组M 和 T,通以直流电流M i 和T i ,产生合成磁动势F ,如果让包含 两个绕组在内的整个铁心以同步转速旋转,则磁动势F 自然也随之旋转起来, 成为旋转磁动势。把这个旋转磁动势的大小和转速也控制成与图 1-1a 一样, 那么这三套绕组就等效了。
( ) 采用对称规则采样法时的脉宽间为: t =
当载波幅值UC 为1
时t
= Tc
2
1
u(te) Uc
可得:
Tc 2
u
(
1+ U (te) Uc
te ) = 2t
Tc
-1
• 将tA、tB 、tC 代入上式(注: 2TI = Tc )得平均电压
• 矢量位于第一扇区时隐含调制函数为:
• uyA = Kcos (θ- 30°)
• U1= t1 Uav sin(60 )
T1
sin(120 )
• 式中, Uav为矢量uav的长度; U1 为矢量u1 的长度,U1 = 2Ud
3
由此可得出:
t1 =
Uav
3 Ud sin (60°-θ)
同理,t2 =
3
Uav Ud
TI
sin (θ)
演示课件
t0 + t7 = TI - ( t1 + t2 ) = TI - tm • 式中, tm 为有效调制时间。若uav位于其他扇区,计算公式相仿, 只要
空间矢量控制(svpwm)
(1)模型等效原则:
众所周知,交流电机三相对称的静止绕组 A 、B 、C ,通以三相平衡的正 弦电流时,所产生的合成磁动势是旋转磁动势F,它在空间呈正弦分布,以同步 转速w1(即电流的角频率)顺着 A-B-C 的相序旋转。这样的物理模型如图1-1a 所示。然而,旋转磁动势并不一定非要三相不可,除单相以外,二相、三相、四 相、…… 等任意对称的多相绕组,通以平衡的多相电流,都能产生旋转磁动势, 当然以两相最为简单。
• uav TI = u0 t0 + u1 t1 + u2 t2 + u7 t7 • 式中, TI = t0 + t1 + t2 + t7 ; • t0、t1、t2、t7、为u0、u1、u2、u7 停留的时间。
• 因为u0 = u7 = 0, 所以:uav = u1+ u2
演示课件
• 由图中的三角关系可得到:
(2)三相--两相变换(3S/2S变换) 在三相静止绕组A、B、C 和两相静止绕组a、b 之间的变换,简称3S/2S 变换。其电 流关系为
i
i
=
2 3
1 0
1 2 3
2
1 2 3 2
iA
iB
iC
(3)两相—两相旋转变换(2S/2R变换)
同步旋转坐标系中轴向电流分量与a, b, o坐标系中轴向电流分量的 转换关系为
• uyB = 3Ksin (θ- 30°)
• uyC = - Kcos (θ- 30°)
• 通过这些基本的空间矢量可以将整个空间划分成6
个扇区。考虑图中所示的空间电压矢量Uout,可以
由S U a、S U b表示其在静止坐标系中的α轴,β轴
上的分量。现以S U a、S U b作为输入信号,以直
流母线电压DC U 作参数,经过计算处理后可得到
把公式中u1、u2 换成该扇区边界上的电压矢量就可以了。扇区时, 可 得三相脉宽时间为: • tA = 2 ( t1 + t2 + t7 ) • tB = 2 ( t2 + t7 ) • tC = 2 t7 • 将式7、式8 和式9 代入上式, 并考虑到t0 = t7 , • 可得: • tA = KTI『 sin (60°-θ) + sinθ』 + TI • tB = KTI 『- sin (60°-θ) + sinθ』 + TI • tc = KTI『 - sin (60°-θ) - sinθ 』+ TI
根据以上公式,可由以下规则确定空间电压矢量所处的扇区N; N = A+ 2B + 4C (1-27)
其中,如果a v >0,那么A=1,否则A=0 如果 b v >0,那么B=1,否则B=0 如果 c v >0,那么C=1,否则C=0
