重点中学小升初数学分班考试题及详解二二

合集下载

小升初分班考试数学卷(含答案)

2
x 5 = ， x 与 y 成____比例. 3 y
【答案】正；反【解析】正比例即一边增大另一边随之增大，一边减小另一边也随之减小，反比例即一边增大另一边随之减少，一边减小另一边随之增大. 三、计算题（每小时 5 分，共 20 分） 15、 2
11
3 7 −1 4 8
16、 3.5 − 2 1 =(2 − 3) ÷ 6 = ×
四、解答题（19 小题 6 分，20－23 每小题 8 分，共 32 分） 19、【答案】46；27；26 【解析】已知： CB ＋ AD ＋ AB ＝99，A＋C＝B. 则 2B+D=19，C+2A+1=9，即 B+A=8。假设 B=5，则 A=8－5=3，C=5－3=2，D=19－2×5=9，则美国是 25 枚，英国 39 枚，中国是 35 枚，不符合题意；假设 B=6，则 A=8－6=2，C=6－2=4，D=19－2×6=7，则美国是 46 枚，英国 27 枚，中国是 26 枚，且 46+27+26=99，符合题意。
苏州石头新初一交流群：477204870
分班考试 1 时间 60 分钟，总分 100 分
一、选择题（每小题 3 分，共 24 分） 1、把一个平行四边形任意分割成两个梯形，这两个梯形中（ A、高 B、上下两底的和 C、周长 2、一个长方形长 7 厘米，宽 3 米，）总是相等. D、面积
7−3 表示（ 7
10 1
（ 2 ） (12x50x 3x4+12x50x 3x3)-1180-320=1600+600-1500=700 元 22、【答案】240 克【解析】倒完后的浓度相等,那就先求这个浓度：
2
1
400 0.2+600 0.1 =0.14 400+600 假设置换的水的重量为 x,那么：

小升初分班考试数学试卷(附答案)

小升初分班考试数学试卷2018.6.30一、填空题:(每空2分,共20分)1、一个数由8个千万，4个十万，8个千，3个百和7个十组成，这个数写作( )，四舍五入到万位约为( )万。

2、36分钟=( )小时 2.8升=( )毫升3、x=2×3×5，y=2×5×5，x和y的最小公倍数是( )，最大公因数是( )。

4、一个三位小数用四舍五入法取近似值是4.30，这个数原来最大是( )，最小是（）。

5、三角形的面积是6平方厘米，高3厘米，底是( )厘米；与它等底等高的平行四边形的面积是( )。

6、算式中的□和△各代表一个数。

已知：(△+□)×0.3=4.2，□÷0.4=12，那么,△=( ) □=( )。

7、李明骑车从家去相距5千米的图书馆借书,从所给的运行图可以看出①李明去图书馆路上停车( )分。

②返回时速度是每小时( )千米。

8、掷一枚骰子一次，掷出“1”的可能性是( )，掷出偶数的可能性是（）。

9、甲、乙两车的速度比是4:3，在同样的时间里两车所行路程比是( )；行完同样的路程，两车所用时间比是( )。

10、把一个棱长是6分米的立方体削成一个最大的圆柱体，圆柱的体积是( )；如果削成一最大的圆锥体，体积是( )。

二、选择题：(每题2分,共8分)1、9点钟时，钟面上的时针和分针所组成的角是( )。

A.锐角B.直角C.钝角D.平角2、有一个三角形的，最小的一个角是48度，这个三角形是( ) 三角形。

A.钝角三角形B.锐角三角形C.直角三角形D.不能确定3、将3克药放入100克水中，药与药水的比是( )。

A. 3:97B.3:100C.100:103D.3:1034、电影院第一排有m个座位，后面一排都比前一排多1个座位，第n排有( )个座位。

A. m+nB. m+n+I C . m+n-I D. mn三、计算题：（共40分）1、用递等式计算：（每题4分，共16分）(1)2108+540÷18×24 (2)（13+212）÷（2+323）(3)47×[0.75-(716-0.25)] (4)[118-+(0.65+)+17]×4.82、用简便方法计算：（每题3分，共9分）(1) 0.25×32×12.5 (2)(49＋512－718)×36 (3)12＋16＋112＋120＋130＋142＋156＋1723、解方程：（每题3分，共 9分）X:1.2=3:4 3.2x-4X3=52 0.4x+2x=16.84．图形计算：（每题3分，共6分）（1）求图形的周长。

2024年小升初数学重点校分班真题重组卷(二)(答案解析)

2024年小升初数学重点校分班考试全真模拟卷（二）答案解析一．填空题（满分20分，每小题2分）1．【分析】由图可知，搭1间房子用(51)+根小棒，搭2间房子用(251)×+根小棒，搭3间房子用(351)×+根小棒……，根据这个规律求出搭6间房子要用的小棒根数即可。

【解答】解：651×+301=+31=（根)答：搭6间房子要用31根小棒。

故答案为：31。

【点评】解答本题需准确分析搭成的房间数与需要的小棒根数之间的关系，灵活根据找到的规律解答。

2．【分析】根据圆锥的特征，圆锥从正面看到的图形是三角形，从上面看到的图形是圆。

所以这个立体图形是一个底面半径是3厘米，高是6厘米的圆锥。

根据圆锥的体积公式：213V r h π=，把数据代入公式求出这个圆锥的体积；要把这个圆锥用一个盒子装起来，这个盒子的底面边长等于圆锥的底面直径，盒子的高等于圆锥的高，根据正方体的体积公式：3V a =，把数据代入公式解答。

【解答】解：21 3.14363××× 1 3.14963=××× 56.52=（立方厘米）326×=（厘米）666××366=×216=（立方厘米）答：这个图形的体积是56.52立方厘米，这个盒子的容积至少是216立方厘米。

故答案为：56.52、216。

【点评】此题主要考查圆锥的体积公式、正方体的体积（容积）公式的灵活运用，关键是熟记公式。

3．【分析】根据规定的运算法则进行计算即可。

【解答】解：4◎213424=×−× 1122=−232 =故答案为：232。

【点评】解答此题的关键是，根据所给出的等式找出新的运算方法，再根据新的运算方法解决问题。

4．【分析】（1）根据正比例的意义和反比例的意义进行解答即可；（2）先根据“路程÷时间=速度”求出汽车的速度，进而根据“速度×时间=路程”进行解答即可。

2020年苏教版小升初数学重点中学分班测试题及答案.doc

2020年苏教版小升初数学重点中学分班测试题及答案1（清华附中考题）10名同学参加数学竞赛，前4名同学平均得分150分，后6名同学平均得分比10人的平均分少20分，这10名同学的平均分是________分.2（西城实验考题）某文具店用16000元购进4种练习本共6400本。

每本的单价是：甲种4元，乙种3元，丙种2元，丁种1．4元。

如果甲、丙两种本数相同，乙、丁两种本数也相同，那么丁种练习本共买了_________本。

3（人大附中考题）某商店想进饼干和巧克力共444千克，后又调整了进货量，使饼干增加了20千克，巧克力减少5%，结果总数增加了7千克。

那么实际进饼干多少千克？4（北大附中考题）六年级某班学生中有1/16的学生年龄为13岁，有3/4的学生年龄为12岁，其余学生年龄为11岁，这个班学生的平均年龄是_________岁。

5 (西城外国语考题)某个五位数加上20万并且3倍以后，其结果正好与该五位数的右端增加一个数字2的得数相等，这个五位数是__________。

6（北京二中题）某自来水公司水费计算办法如下：若每户每月用水不超过5立方米，则每立方米收费1.5元，若每户每月用水超过5立方米，则超出部分每立方米收取较高的定额费用，1月份，张家用水量是李家用水量的2/3,张家当月水费是17.5元，李家当月水费27.5元，超出5立方米的部分每立方米收费多少元？7（人大附中考题）用1～9可以组成______个不含重复数字的三位数：如果再要求这三个数字中任何两个的差不能是1，那么可以组成______个满足要求的三位数．8（首师附中考题）有甲、乙、丙三种商品，买甲3件，乙7件，丙1件，共需32元，买甲4件，乙10件，丙1件，共需43元，则甲、乙、丙各买1件需________元钱？9（三帆中学考题）某小学有一支乒乓球队，有男、女小队员各8名，在进行男女混合双打时，这16名小队员可组成＿＿对不同的阵容.10（西城实验考题）有一批长度分别为1，2，3，4，5，6，7，8，9，10和11厘米的细木条，它们的数量都足够多，从中适当选取3根木条作为三条边，可围成一个三角形;如果规定底边是11厘米，你能围成多少个不同的三角形?11（三帆中学考题）有7双白手套，8双黑手套，9双红手套放在一只袋子里。

小升初重点中学入学分班考试数学试卷含答案 (2)

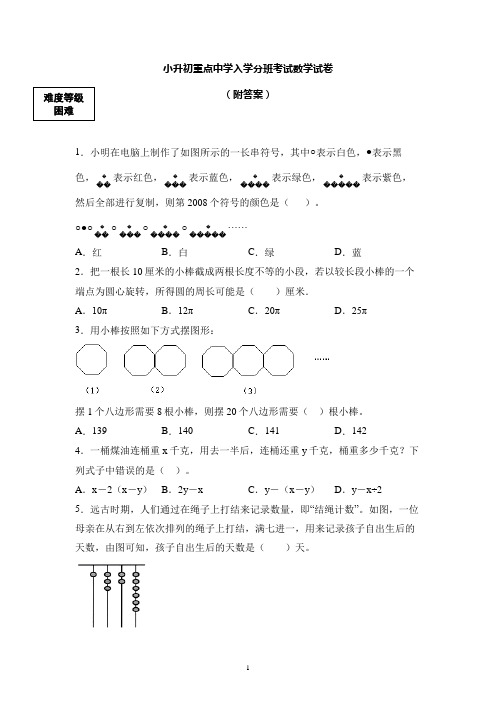
小升初重点中学入学分班考试数学试卷（附答案）1．小明在电脑上制作了如图所示的一长串符号，其中○表示白色，●表示黑色，表示红色，表示蓝色，表示绿色，表示紫色，然后全部进行复制，则第2008个符号的颜色是（）。

○●○○○○······A．红B．白C．绿D．蓝2．把一根长10厘米的小棒截成两根长度不等的小段，若以较长段小棒的一个端点为圆心旋转，所得圆的周长可能是（）厘米．A．10πB．12πC．20πD．25π3．用小棒按照如下方式摆图形：摆1个八边形需要8根小棒，则摆20个八边形需要（）根小棒。

A．139 B．140 C．141 D．1424．一桶煤油连桶重x千克，用去一半后，连桶还重y千克，桶重多少千克？下列式子中错误的是（）。

A．x－2（x－y）B．2y－x C．y－（x－y）D．y－x÷25．远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”。

如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（）天。

难度等级困难A ．84B ．336C ．510D ．1326 6．在正方形铁皮上剪下一个圆和一个扇形，恰好围成一个圆锥（如图），如果圆的直径为cm a ，扇形的半径为cm b ，那么:a b 等于（）。

A ．1:2B ．1:3C ．1:4D ．1:5 7．下边数表中的数是按规律排列的。

从上到下,依次称这些数所在的行为第1行、第2行……,从左到右,依次称这些数为第1个、第2个……,例如数表中第6行中的第3个数是10。

问数表中第102行中的第3个数是________.8．一个三角形三个内角度数的比是3 ：2：1，这是一个________三角形．9．有三根绳子，第一根用去全长的35，第二根用去全长的62.5%，第三根用去全长的一半，三根绳子剩下的长度相等。

原来的第（________）根绳子最长。

[优]2022小升初数学重点初中招生考试(分班考试)含答案

2022小升初数学重点初中招生考试（分班考试）含答案参考答案参考答案与试题解析一、填空题（每题5分）1．（5分）++++++++．【分析】通过分析式中数据发现：=+，，=+，=+=+，所以可将式中的后四个分数拆分后根据加法结合律进行巧算．【解答】解：++++++++=++++++++++++，=++++++++++++，=（++）+（+）+（++）+（++）+（），=1+1+1+1+1，=5．2．（5分）小鹏同学在一个正方体盒子的每一个面上都写上一个字，分别是：我、喜、欢、数、学、课，正方体的平面展开图如右图所示，那么在该正方体盒子中，和“我”相对的面所写的字是学．【分析】如图，根据正方形展开图的11种特征，属于“1﹣3﹣2”型，折叠成正方体后，“我”与“学”相对，“喜”与“数”相对，“欢”与“课”相对．【解答】解：如图，折叠成正方体后，“我”与“学”相对，“喜”与“数”相对，“欢”与“课”相对．故答案为：学．3．（5分）1至2008这2008个自然数中，恰好是3、5、7中两个数的倍数的数共有228 个．【分析】1到2008这2008个自然数中，3和5的倍数有个，3和7的倍数有个，5和7的倍数有个，3、5和7的倍数有个．所以，恰好是3、5、7中两个数的倍数共有133﹣19+95﹣19+57﹣19=228个．【解答】解：根据题干分析可得：1到2008这2008个自然数中，3和5的倍数有个，3和7的倍数有个，5和7的倍数有个，3、5和7的倍数有个．所以恰好是3、5、7中两个数的倍数共有133﹣19+95﹣19+57﹣19=228（个）答：恰好是3、5、7中两个数的倍数的数共有228个．故答案为：228．4．（5分）一项机械加工作业，用4台A型机床，5天可以完成；用4台A型机床和2台B型机床3天可以完成；用3台B型机床和9台C型机床，2天可以完成，若3种机床各取一台工作5天后，剩下A、C型机床继续工作，还需要 3 天可以完成作业．【分析】把这项任务看作单位“1”，根据工作量÷工作时间=工作效率，分别求出A、B、C三种机床每台每天的工作效率，再求出3种机床各取一台工作5天后，剩下的工作量，然后用剩下的工作量除以A、C两种机床的工作效率和即可．据此解答．【解答】解：：设A型机床每天能完成x，B型机床每天完成y，C型机床每天完成z，则根据题目条件有以下等式：则，若3种机床各取一台工作5天后完成：（）×5==，剩下A、C型机床继续工作，还需要的天数是：（1）===3（天）；答：还需要3天完成任务．故答案为：3．二、填空题（每题6分）5．（6分）2008年1月，我国南方普降大雪，受灾严重．李先生拿出积蓄捐给两个受灾严重的地区，随着事态的发展，李先生决定追加捐赠资金．如果两地捐赠资金分别增加10%和5%，则总捐资额增加8%；如果两地捐赠资金分别增加15%和10%，则总捐资额增加13万元．李先生第一次捐赠了100 万元．【分析】两地捐赠资金分别增加10%和5%，则总捐资额增加8%，如果再在这个基础上两地增加第一次捐资的5%，那么两地捐赠资金分别增加到15%和10%，总量增加到8%+5%=13%，所以第一次李先生捐资13÷13%=100万．【解答】解：10%﹣5%=5%15%﹣10%=5%13÷（8%+5%）=13÷13%=100（万元）答：第一次捐了100万元．故答案为：100．6．（6分）有5个连续自然数，它们的和为一个平方数，中间三数的和为立方数，则这5个数中最小数的最小值为多少？【分析】设中间数是a，则它们的和为5a，中间三数的和为3a．因为5a是平方数，所以平方数的尾数一定是5或者0；再由中间三数为立方数，所以a﹣1+a+a+1=3a，所以立方数一定是3的倍数．中间的数至少是1125，那么这五个数中最小数的最小值为1123．【解答】解：设设中间数是a，五个数分别是a﹣2，a﹣1，a，a+1，a+2；明显可以得到a﹣2+a﹣1+a+a+1+a+2=5a，由于5a是平方数，所以平方数的尾数一定是5或者0，再由3a是立方数，所以a﹣1+a+a+1=3a，所以立方数一定是3的倍数．所以这个数a一定是32×53=1125，所以最小数是1125﹣2=1123．答：这5个数中最小数的最小值为1123．7．（6分）从1，2，3，…，n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为108 ．【分析】被13除的同余序列当中，如余1的同余序列，1、14、27、40、53、66…，中只要取到两个相邻的，这两个数的差为13，如果没有两个相邻的数，则没有两个数的差为13，不同的同余序列当中不可能有两个数的差为13，对于任意一条长度为x的序列，都最多能取个数，即从第1个数起隔1个取1个基于以上，n个数分成13个序列，每条序列的长度为或，两个长度差为1的序列，能够被取得的数的个数也不会超过1，所以能使57个数任意两个数都不等于13，则这57个数被分配在13条序列中，当n取最小值时在每条序列被分配的数的个数差不会超过1，那么13个序列有8个分配了4个数，5个分配了5个数，这13个序列8个长度为8，5个长度为9，那么n=8×8+9×5=109，所以要使57个数必有两个数的差为13，那么n的最大值为108．【解答】解：基于以上分析，n个数分成13个序列，每条序列的长度为或，两个长度差为1的序列，能够被取得的数的个数也不会超过1，所以能使57个数任意两个数都不等于13，则这57个数被分配在13条序列中，当n取最小值时在每条序列被分配的数的个数差不会超过1，那么13个序列有8个分配了4个数，5个分配了5个数，这13个序列8个长度为8，5个长度为9，那么n=8×8+9×5=109，所以要使57个数必有两个数的差为13，那么n的最大值为108．故答案为：108．8．（6分）如图边长为10cm的正方形，则阴影表示的四边形面积为48 平方厘米．【分析】图中阴影部分的面积是正方形的面积减去4个空白三角形的面积，据此解答．【解答】解：如图所示，设左上角小长方形的长为a，右下角小长方形的长为b，四个空白三角形的面积是：[（10﹣b）（10﹣a）+（6﹣a）b+（a+4）（b+1）+（9﹣b）a]÷2=[100﹣10a﹣10b+ab+6b﹣ab+ab+a+4b+4+9a﹣ab]÷2=104÷2=52（平方厘米）阴影部分的面积是10×10﹣52=100﹣52=48（平方厘米）答：阴影部分的面积是48平方厘米．故答案为：48．9．（6分）新年联欢会上，共有90人参加了跳舞、合唱、演奏三种节目的演出．如果只参加跳舞的人数三倍于只参加合唱的人数；同时参加三种节目的人比只参加合唱的人少7人；只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人；50人没有参加演奏；10人同时参加了跳舞和合唱但没有参加演奏；40人参加了合唱；那么，同时参加了演奏、合唱但没有参加跳舞的有17 人．【分析】用韦恩图可以清晰的呈现各个集合之间的数量关系：设只参加合唱的有x人，那么只参加跳舞的人数为3x，由50人没有参加演奏，10人同时参加了跳舞和合唱但没有参加演奏，得到只参加合唱的和只参加跳舞的人数和为50﹣10=40，所以只参加合唱的有10人，那么只参加跳舞的人数为30人，又由“同时参加三种节目的人比只参加合唱的人少7人”，得到同时参加三项的有3人，所以参加了合唱的人中同时参加了演奏、合唱但没有参加跳舞的有：40﹣10﹣10﹣3=17人．【解答】解：只参加合唱的和只参加跳舞的人数和为：50﹣10=40（人），所以只参加合唱的有10人，那么只参加跳舞的人数为30人，所以参加了合唱的人中同时参加了演奏、合唱但没有参加跳舞的有：40﹣10﹣10﹣3=17（人），答：同时参加了演奏、合唱但没有参加跳舞的有17人．故答案为：17．三、填空题（每题6分）10．（6分）皮皮以每小时3千米的速度登山，走到途中A点，他将速度降为每小时2千米．在接下来的1小时中，他走到山顶，又立即下山，并走到A点上方200米的地方．如果他下山的速度是每小时4千米，下山比上山少用了42分钟．那么，他往返共走了11.2 千米．【分析】首先关注“在接下来的1小时中”，这一小时中，下山比上山少200米，设上山时间为x小时，则下山的时间为1﹣x小时；然后根据下山比上山少200米，可得2x﹣4（1﹣x）=0.2，解得x=0.7小时，即42分钟，这42分钟，行程1.4公里；最后根据“下山比上山少用了42分钟”，可得以每小时4千米的速度下山的时间和以每小时3千米的速度登山时间相等，所以下山距离与A点以下路程之比为3：4，所以A点以上距离是下山距离的，所以往返一共走了千米，据此解答即可．【解答】解：设速度降为每小时2千米后的1小时中，上山时间为x 小时，下山为1﹣x小时，所以2x﹣4（1﹣x）=0.2，6x﹣4=0.26x﹣4+4=0.2+46x=4.26x÷6=4.2÷6x=0.70.7小时=42分钟，因为“下山比上山少用了42分钟”，所以以每小时4千米的速度下山的时间和以每小时3千米的速度登山时间相等，所以下山距离与A点以下路程之比为3：4，所以A点以上距离是下山距离的，所以往返一共走了：0.7×2÷×2=1.4=5.6×2=11.2（千米）答：他往返共走了11.2千米．故答案为：11.2．11．在一个3×3的方格表中填有1，2，3，4，5，6，7，8，9九个数，每格中只填一个数，现将每行中放有最大数的格子染成红色，最小数的格子染成绿色．设M是红格中的最小数，m是绿格中的最大数，则M﹣m可以取到8 个不同的值．【分析】共有三行，三个红色方格中所填的数都是它们所在行中最大的数，因此它们不可能是1和2．又因为M是红格中的最小数，所以它们不可能是8和9，即M不可能是1、2、8、9．同理，m也不可能是1、2、8、9．这样M与m都介于3与7之间．因此M﹣m的差就介于3﹣7与7﹣3之间（包括﹣4与4）．据此解答即可．【解答】解：三个红色方格中所填的数都是它们所在行中最大的数，因此它们不可能是1和2．又因为M是红格中的最小数，所以它们不可能是8和9，即M不可能是1、2、8、9．同理，m也不可能是1、2、8、9．这样M与m都介于3与7之间．因此M﹣m的差就介于3﹣7与7﹣3之间（包括﹣4与4）．因此，考虑正负可以取到：﹣4、﹣3、﹣2、﹣1、1、2、3、4．所以，共有8种不同的值．答：M﹣m可以取到8个不同的值．故答案为：8．12．在1，2，3，…，7，8的任意排列中，使得相邻两数互质的排列方式共有1728 种．【分析】这8个数之间如果有公因数，那么无非是2或3．8个数中的4个偶数一定不能相邻，对于这类多个元素不相邻的排列问题，考虑使用“插入法”，即首先忽略偶数的存在，对奇数进行排列，然后将偶数插入，但在偶数插入时，还要考虑3和6相邻的情况．奇数的排列一共有4！=24种，对任意一种排列4个数形成5个空位，将6插入，可以有符合条件的3个位置可以插，再在剩下的四个位置中插入2、4、8，一共有4×3×2=24种，一共有24×3×24=1728种．【解答】解：这8个数之间如果有公因数，那么无非是2或3．8个数中的4个偶数一定不能相邻，考虑使用“插入法”，即首先忽略偶数的存在，对奇数进行排列，然后将偶数插入，但在偶数插入时，还要考虑3和6相邻的情况．奇数的排列一共有：4！=24（种），对任意一种排列4个数形成5个空位，将6插入，可以有符合条件的3个位置可以插，再在剩下的四个位置中插入2、4、8，一共有4×3×2=24（种），综上所述，一共有：24×3×24=1728（种）．答：使得相邻两数互质的排列方式共有1728种．故答案为：1728．13．如果自然数a的各位数字之和等于10，则a称为“和谐数”．将所有的“和谐数”从小到大排成一列，则2008排在第119 个．【分析】本题根据自然数的排列规律及数位知识进行分析即可．一位数的和谐数个数为0，二位数的和谐数有：19、28、…91，共9个．三位数的和谐数有：（以1开头，以0、1、2…9作十位的，分别有且仅有一个和谐数，共10个）以1开头的有109、118、127、136、…、190，共10个．同理，以2开头的9个：208，217，…271．…以9开头的2个．则三位数和谐数共有：10+9+8+…+2=54个．四位和谐数：同理，以1为千位：分别讨论，对以0、1…9为百位的有10+9+8…+1=55个．综上共9+54+55=118个．2008是2开头的第一个，因此是第119个．【解答】解：一位数的和谐数个数为0，三位数和谐数共有：10+9+8+…+2=54个．1000至2000，和谐数共有10+9+8…+1=55个．综上共9+54+55=118个．2008是2开头的第一个，因此是第119个．故答案为：119．14．由0，0，1，2，3五个数码可以组成许多不同的五位数，所有这些五位数的平均数为21111 ．【分析】以1为开头的5位数，后4位数一共有4×3=12种方法，其中在每一位上，2和3各出现3次，所以1为开头的5位数的和为10000×12+（2+3）×3333=136665，同样的，以2为开头的5位数的和为20000×12+（1+3）×3333=253332，以3为开头的5位数的和为30000×12+（2+1）×3333=369999，它们的和为759996，进而求出平均数．【解答】解：以1为开头的5位数，后4位数一共有4×3=12种方法，其中在每一位上，2和3各出现3次，所以1为开头的5位数的和为10000×12+（2+3）×3333=136665，同样的，以2为开头的5位数的和为20000×12+（1+3）×3333=253332，以3为开头的5位数的和为30000×12+（2+1）×3333=369999，（136665+253332+369999）÷（4×3×3）=759996÷36=21111．答：所有这些五位数的平均数为21111；故答案为：21111．四、填空题（每题10分）15．一场数学游戏在小聪和小明间展开：黑板上写着自然数2，3，4，…，2007，2008，一名裁判现在随意擦去其中的一个数，然后由小聪和小明轮流擦去其中的一个数（即小明先擦去一个数，小聪再擦去一个数，如此下去），若到最后剩下的两个数互质，则判小聪胜；否则判小明胜．问：小聪和小明谁有必胜策略？说明理由．【分析】（1）小聪采用如下策略：先擦去2008，然后将剩下的2006个自然数分为1003组，（2，3）（4，5），…（2006，2007），小明擦去哪个组的一个数，小聪接着就擦去同一组的另个数，这样最后剩下的两个数是相邻的两个数，而相邻的两个数是互质的，所以小聪必胜；（2）小明必胜的策略：①当小聪始终擦去偶数时，小明留下一对不互质的奇数，例如，3和9，而擦去其余的奇数；②当小聪从某一步开始擦去奇数时，乙可以跟着擦去奇数，这样最后给乙留下的三个数有两种情况，一种是剩下一个偶数和两个奇数3和9，此时乙擦掉那个偶数，另一种是至少两个偶数，此时已留下两个偶数就可以了．【解答】解：（1）小聪采用如下策略：先擦去2008，然后将剩下的2006个自然数分为1003组，（2，3）（4，5），…（2006，2007），小明擦去哪个组的一个数，小聪接着就擦去同一组的另个数，这样最后剩下的两个数是相邻的两个数，而相邻的两个数是互质的，所以小聪必胜；（2）小明必胜的策略：①当小聪始终擦去偶数时，小明留下一对不互质的奇数，例如，3和9，而擦去其余的奇数；②当小聪从某一步开始擦去奇数时，小明可以跟着擦去奇数，这样最后给小明留下的三个数有两种情况，一种是剩下一个偶数和两个奇数3和9，此时小明擦掉那个偶数，另一种是至少两个偶数，此时小明留下两个偶数就可以了．16．将一张正方形纸片，横着剪4刀，竖着剪6刀，裁成尽可能大的形状大小一样的35张长方形纸片．再把这样的一张长方形纸片裁成尽可能大的面积相等的小正方形纸片．如果小正方形边长为2厘米，那么长方形纸片的面积应为多少平方厘米？说明理由．【分析】大正方形纸片被横着剪四刀，坚着剪六刀，所以横着裁成5份，坚着裁成7份，所以裁成的长方形纸片的长宽比为7：5，把这样的一张长方形纸片裁成尽可能大的面积相等的小正方形纸块，则正方形纸块的边长应该为长、宽的公约数，而5，7的公约数是1，所以长方形纸片的宽是小正方形纸块的边长的5倍，2×5=10厘米，所以长方形纸片的宽是10厘米，依此可求长方形纸片的长，再根据长方形的面积公式：s=长×宽，即可求出长方形纸片的面积．【解答】解：根据题意可知：裁成的长方形纸片的长宽比为7：5，则正方形纸块的边长应该为长、宽的公约数，而5，7的公约数是1，所以长方形纸片的宽是小正方形纸块的边长的5倍，则长方形纸片的宽为：2×5=10（厘米）又因为长方形纸片的长宽比为7：5，所以长方形纸片的长是：10×7÷5=14（厘米）所以长方形纸片的面积是14×10=140（平方厘米）答：长方形纸片的面积应是140平方厘米．。

小升初重点中学分班考试数学试卷 (2)

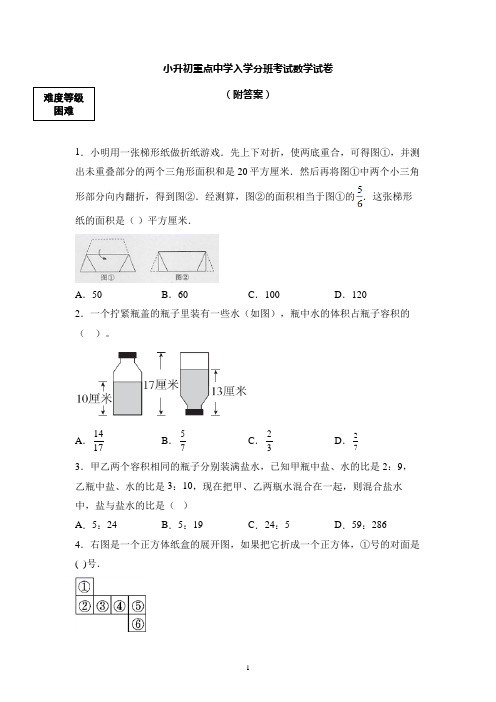
小升初重点中学入学分班考试数学试卷（附答案）1．小明用一张梯形纸做折纸游戏．先上下对折，使两底重合，可得图①，并测出未重叠部分的两个三角形面积和是20平方厘米．然后再将图①中两个小三角形部分向内翻折，得到图②．经测算，图②的面积相当于图①的．这张梯形纸的面积是（）平方厘米．A．50 B．60 C．100 D．1202．一个拧紧瓶盖的瓶子里装有一些水（如图），瓶中水的体积占瓶子容积的（）。

A．1417B．57C．23D．27 3．甲乙两个容积相同的瓶子分别装满盐水，已知甲瓶中盐、水的比是2：9，乙瓶中盐、水的比是3：10，现在把甲、乙两瓶水混合在一起，则混合盐水中，盐与盐水的比是（）A．5：24 B．5：19 C．24：5 D．59：2864．右图是一个正方体纸盒的展开图，如果把它折成一个正方体，①号的对面是( )号．难度等级困难A．③B．⑤C．④D．⑥5．聪聪和明明一起到新华书店买书，已知聪聪比明明多带48元钱，两人分别购买了一本12元的图书后，聪聪剩下钱数的314和明明剩下钱数的30%相等。

根据以上信息，下列说法中不正确的是（）。

①两人分别购买了这本12元的图书后，聪聪剩下的钱比明明剩下的钱多36元。

②聪聪原来所带钱数与明明原来所带钱数的最简单的整数比是7:5。

③聪聪和明明原来一共带了288元去买书。

A．①②B．①③C．②③D．①②③6．若b=2a（a为大于0的整数），那么b一定是（）。

A．质数B．合数C．奇数D．偶数7．×+的末尾共有零的个数是______.8．要使算式12＋16＋112＋120＋130＋142＋156＋172＋190＋□＝1成立，则□中的数等于________。

9．如图是实验小学六年级男生喜欢的球类运动统计图，已知喜欢乒乓球的有80人，那么喜欢足球的有________人。

10．伍角人民币与贰角人民币的张数比为12∶35，那么伍角与贰角总钱数的最简单整数比为（________）。

小升初重点初中分班考试数学试卷及详细答案

小升初重点初中分班考试数学试卷及详细答案一、填空题（每题5分）1．++++++++．2．小鹏同学在一个正方体盒子的每一个面上都写上一个字,分别是：我、喜、欢、数、学、课,正方体的平面展开图如右图所示,那么在该正方体盒子中,和“我”相对的面所写的字是．3．1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有个．4．一项机械加工作业,用4台A型机床,5天可以完成;用4台A型机床和2台B型机床3天可以完成;用3台B型机床和9台C型机床,2天可以完成,若3种机床各取一台工作5天后,剩下A、C型机床继续工作,还需要天可以完成作业．二、填空题（每题6分）5．2008年1月,我国南方普降大雪,受灾严重．李先生拿出积蓄捐给两个受灾严重的地区,随着事态的发展,李先生决定追加捐赠资金．如果两地捐赠资金分别增加10%和5%,则总捐资额增加8%;如果两地捐赠资金分别增加15%和10%,则总捐资额增加13万元．李先生第一次捐赠了万元．6．有5个连续自然数,它们的和为一个平方数,中间三数的和为立方数,则这5个数中最小数的最小值为多少？7．从1,2,3,…,n中,任取57个数,使这57个数必有两个数的差为13,则n的最大值为．8．如图边长为10cm的正方形,则阴影表示的四边形面积为平方厘米．9．新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出．如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有人．三、填空题（每题6分）10．皮皮以每小时3千米的速度登山,走到途中A点,他将速度降为每小时2千米．在接下来的1小时中,他走到山顶,又立即下山,并走到A点上方200米的地方．如果他下山的速度是每小时4千米,下山比上山少用了42分钟．那么,他往返共走了千米．11．在一个3×3的方格表中填有1,2,3,4,5,6,7,8,9九个数,每格中只填一个数,现将每行中放有最大数的格子染成红色,最小数的格子染成绿色．设M是红格中的最小数,m是绿格中的最大数,则M﹣m可以取到个不同的值．12．在1,2,3,…,7,8的任意排列中,使得相邻两数互质的排列方式共有种．13．如果自然数a的各位数字之和等于10,则a称为“和谐数”．将所有的“和谐数”从小到大排成一列,则2008排在第个．14．由0,0,1,2,3五个数码可以组成许多不同的五位数,所有这些五位数的平均数为．四、解答题（每题10分）15．一场数学游戏在小聪和小明间展开：黑板上写着自然数2,3,4,…,2007,2008,一名裁判现在随意擦去其中的一个数,然后由小聪和小明轮流擦去其中的一个数（即小明先擦去一个数,小聪再擦去一个数,如此下去）,若到最后剩下的两个数互质,则判小聪胜;否则判小明胜．问：小聪和小明谁有必胜策略？说明理由．16．将一张正方形纸片,横着剪4刀,竖着剪6刀,裁成尽可能大的形状大小一样的35张长方形纸片．再把这样的一张长方形纸片裁成尽可能大的面积相等的小正方形纸片．如果小正方形边长为2厘米,那么长方形纸片的面积应为多少平方厘米？说明理由．参考答案一、填空题（每题5分）1．++++++++．【分析】通过分析式中数据发现：=+,,=+,=+=+,所以可将式中的后四个分数拆分后根据加法结合律进行巧算．解：++++++++=++++++++++++,=++++++++++++,=（++）+（+）+（++）+（++）+（）,=1+1+1+1+1,=5．2．小鹏同学在一个正方体盒子的每一个面上都写上一个字,分别是：我、喜、欢、数、学、课,正方体的平面展开图如右图所示,那么在该正方体盒子中,和“我”相对的面所写的字是学．解：如图,折叠成正方体后,“我”与“学”相对,“喜”与“数”相对,“欢”与“课”相对．故答案为：学．3．1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有228个．解：根据题干分析可得：1到2008这2008个自然数中,3和5的倍数有个,3和7的倍数有个,5和7的倍数有个,3、5和7的倍数有个．所以恰好是3、5、7中两个数的倍数共有133﹣19+95﹣19+57﹣19=228（个）答：恰好是3、5、7中两个数的倍数的数共有228个．故答案为：228．4．一项机械加工作业,用4台A型机床,5天可以完成;用4台A型机床和2台B型机床3天可以完成;用3台B型机床和9台C型机床,2天可以完成,若3种机床各取一台工作5天后,剩下A、C型机床继续工作,还需要3天可以完成作业．解：：设A型机床每天能完成x,B型机床每天完成y,C型机床每天完成z,则根据题目条件有以下等式：则,若3种机床各取一台工作5天后完成：（）×5==,剩下A、C型机床继续工作,还需要的天数是：（1）===3（天）;答：还需要3天完成任务．二、填空题（每题6分）5．2008年1月,我国南方普降大雪,受灾严重．李先生拿出积蓄捐给两个受灾严重的地区,随着事态的发展,李先生决定追加捐赠资金．如果两地捐赠资金分别增加10%和5%,则总捐资额增加8%;如果两地捐赠资金分别增加15%和10%,则总捐资额增加13万元．李先生第一次捐赠了100万元．解：10%﹣5%=5%15%﹣10%=5%13÷（8%+5%）=13÷13%=100（万元）答：第一次捐了100万元．故答案为：100．6．有5个连续自然数,它们的和为一个平方数,中间三数的和为立方数,则这5个数中最小数的最小值为多少？解：设设中间数是a,五个数分别是a﹣2,a﹣1,a,a+1,a+2;明显可以得到a﹣2+a﹣1+a+a+1+a+2=5a,由于5a是平方数,所以平方数的尾数一定是5或者0,再由3a是立方数,所以a﹣1+a+a+1=3a,所以立方数一定是3的倍数．所以这个数a一定是32×53=1125,所以最小数是1125﹣2=1123．答：这5个数中最小数的最小值为1123．7．从1,2,3,…,n中,任取57个数,使这57个数必有两个数的差为13,则n的最大值为108．解：基于以上分析,n个数分成13个序列,每条序列的长度为或,两个长度差为1的序列,能够被取得的数的个数也不会超过1,所以能使57个数任意两个数都不等于13,则这57个数被分配在13条序列中,当n取最小值时在每条序列被分配的数的个数差不会超过1,那么13个序列有8个分配了4个数,5个分配了5个数,这13个序列8个长度为8,5个长度为9,那么n=8×8+9×5=109,所以要使57个数必有两个数的差为13,那么n的最大值为108．故答案为：108．8．如图边长为10cm的正方形,则阴影表示的四边形面积为48平方厘米．解：如图所示,设左上角小长方形的长为a,右下角小长方形的长为b,四个空白三角形的面积是：[（10﹣b）（10﹣a）+（6﹣a）b+（a+4）（b+1）+（9﹣b）a]÷2=[100﹣10a﹣10b+ab+6b﹣ab+ab+a+4b+4+9a﹣ab]÷2=104÷2=52（平方厘米）阴影部分的面积是10×10﹣52=100﹣52=48（平方厘米）答：阴影部分的面积是48平方厘米．故答案为：48．9．新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出．如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有17人．解：只参加合唱的和只参加跳舞的人数和为：50﹣10=40（人）,所以只参加合唱的有10人,那么只参加跳舞的人数为30人,所以参加了合唱的人中同时参加了演奏、合唱但没有参加跳舞的有：40﹣10﹣10﹣3=17（人）,答：同时参加了演奏、合唱但没有参加跳舞的有17人．故答案为：17．三、填空题（每题6分）10．皮皮以每小时3千米的速度登山,走到途中A点,他将速度降为每小时2千米．在接下来的1小时中,他走到山顶,又立即下山,并走到A点上方200米的地方．如果他下山的速度是每小时4千米,下山比上山少用了42分钟．那么,他往返共走了11.2千米．解：设速度降为每小时2千米后的1小时中,上山时间为x小时,下山为1﹣x小时,所以2x﹣4（1﹣x）=0.2,6x﹣4=0.26x﹣4+4=0.2+46x=4.26x÷6=4.2÷6x=0.70.7小时=42分钟,因为“下山比上山少用了42分钟”,所以以每小时4千米的速度下山的时间和以每小时3千米的速度登山时间相等,所以下山距离与A点以下路程之比为3：4,所以A点以上距离是下山距离的,所以往返一共走了：0.7×2÷×2=1.4=5.6×2=11.2（千米）答：他往返共走了11.2千米．故答案为：11.2．11．在一个3×3的方格表中填有1,2,3,4,5,6,7,8,9九个数,每格中只填一个数,现将每行中放有最大数的格子染成红色,最小数的格子染成绿色．设M是红格中的最小数,m是绿格中的最大数,则M﹣m可以取到8个不同的值．解：三个红色方格中所填的数都是它们所在行中最大的数,因此它们不可能是1和2．又因为M是红格中的最小数,所以它们不可能是8和9,即M不可能是1、2、8、9．同理,m也不可能是1、2、8、9．这样M与m都介于3与7之间．因此M﹣m的差就介于3﹣7与7﹣3之间（包括﹣4与4）．因此,考虑正负可以取到：﹣4、﹣3、﹣2、﹣1、1、2、3、4．所以,共有8种不同的值．答：M﹣m可以取到8个不同的值．故答案为：8．12．在1,2,3,…,7,8的任意排列中,使得相邻两数互质的排列方式共有1728种．解：这8个数之间如果有公因数,那么无非是2或3．8个数中的4个偶数一定不能相邻,考虑使用“插入法”,即首先忽略偶数的存在,对奇数进行排列,然后将偶数插入,但在偶数插入时,还要考虑3和6相邻的情况．奇数的排列一共有：4！=24（种）,对任意一种排列4个数形成5个空位,将6插入,可以有符合条件的3个位置可以插,再在剩下的四个位置中插入2、4、8,一共有4×3×2=24（种）,综上所述,一共有：24×3×24=1728（种）．答：使得相邻两数互质的排列方式共有1728种．故答案为：1728．13．如果自然数a的各位数字之和等于10,则a称为“和谐数”．将所有的“和谐数”从小到大排成一列,则2008排在第119个．解：一位数的和谐数个数为0,三位数和谐数共有：10+9+8+…+2=54个．1000至2000,和谐数共有10+9+8…+1=55个．综上共9+54+55=118个．2008是2开头的第一个,因此是第119个．故答案为：119．14．由0,0,1,2,3五个数码可以组成许多不同的五位数,所有这些五位数的平均数为21111．解：以1为开头的5位数,后4位数一共有4×3=12种方法,其中在每一位上,2和3各出现3次,所以1为开头的5位数的和为10000×12+（2+3）×3333=136665,同样的,以2为开头的5位数的和为20000×12+（1+3）×3333=253332,以3为开头的5位数的和为30000×12+（2+1）×3333=369999,（136665+253332+369999）÷（4×3×3）=759996÷36=21111．答：所有这些五位数的平均数为21111;故答案为：21111．四、填空题（每题10分）15．一场数学游戏在小聪和小明间展开：黑板上写着自然数2,3,4,…,2007,2008,一名裁判现在随意擦去其中的一个数,然后由小聪和小明轮流擦去其中的一个数（即小明先擦去一个数,小聪再擦去一个数,如此下去）,若到最后剩下的两个数互质,则判小聪胜;否则判小明胜．问：小聪和小明谁有必胜策略？说明理由．解：（1）小聪采用如下策略：先擦去2008,然后将剩下的2006个自然数分为1003组,（2,3）（4,5）,…（2006,2007）,小明擦去哪个组的一个数,小聪接着就擦去同一组的另个数,这样最后剩下的两个数是相邻的两个数,而相邻的两个数是互质的,所以小聪必胜;（2）小明必胜的策略：①当小聪始终擦去偶数时,小明留下一对不互质的奇数,例如,3和9,而擦去其余的奇数;②当小聪从某一步开始擦去奇数时,小明可以跟着擦去奇数,这样最后给小明留下的三个数有两种情况,一种是剩下一个偶数和两个奇数3和9,此时小明擦掉那个偶数,另一种是至少两个偶数,此时小明留下两个偶数就可以了．16．将一张正方形纸片,横着剪4刀,竖着剪6刀,裁成尽可能大的形状大小一样的35张长方形纸片．再把这样的一张长方形纸片裁成尽可能大的面积相等的小正方形纸片．如果小正方形边长为2厘米,那么长方形纸片的面积应为多少平方厘米？说明理由．解：根据题意可知：裁成的长方形纸片的长宽比为7：5,则正方形纸块的边长应该为长、宽的公约数,而5,7的公约数是1,所以长方形纸片的宽是小正方形纸块的边长的5倍,则长方形纸片的宽为：2×5=10（厘米）又因为长方形纸片的长宽比为7：5,所以长方形纸片的长是：10×7÷5=14（厘米）所以长方形纸片的面积是14×10=140（平方厘米）答：长方形纸片的面积应是140平方厘米．。

小升初分班考试题数学及答案

小升初分班考试题数学及答案一、选择题（每题2分，共10分）1. 下列哪个数是最小的质数？A. 0B. 1C. 2D. 3答案：C2. 如果一个长方形的长是10厘米，宽是5厘米，那么它的面积是多少平方厘米？A. 25B. 30C. 40D. 50答案：C3. 下列哪个分数是最接近1的？A. 1/2B. 3/4C. 4/5D. 5/6答案：B4. 一个数的5倍是25，这个数是多少？A. 4B. 5C. 6D. 7答案：B5. 下列哪个图形的周长最长？A. 正方形B. 长方形C. 圆形D. 三角形答案：C（注：在没有具体数值的情况下，无法确定哪个图形的周长最长，此题需要具体数值才能解答。

）二、填空题（每题2分，共10分）6. 一个数的平方是36，这个数是________。

答案：6或-67. 一个数除以5的商是8，这个数是________。

答案：408. 一个数的1/4加上5等于10，这个数是________。

答案：289. 一个数的3倍减去7等于23，这个数是________。

答案：1010. 一个数的2/3等于8，这个数是________。

答案：12三、计算题（每题5分，共20分）11. 计算下列表达式的值：(1) 36 ÷ 6 + 4 × 2(2) (15 - 9) × 4 ÷ 2答案：(1) 36 ÷ 6 = 6，4 × 2 = 8，6 + 8 = 14(2) 15 - 9 = 6，6 × 4 = 24，24 ÷ 2 = 1212. 解下列方程：(1) 2x + 5 = 13(2) 3x - 7 = 8答案：(1) 2x = 13 - 5，2x = 8，x = 8 ÷ 2，x = 4(2) 3x = 8 + 7，3x = 15，x = 15 ÷ 3，x = 513. 一个长方形的长是15厘米，宽是10厘米，求它的周长和面积。

小升初分班考试数学试卷(附答案)

小升初分班考试数学试卷一、填空题:(每空2分,共20分)1、一个数由8个千万，4个十万，8个千，3个百和7个十组成，这个数写作( )，四舍五入到万位约为( )万。

2、36分钟=( )小时 2.8升=( )毫升3、x=2×3×5，y=2×5×5，x和y的最小公倍数是( )，最大公因数是( )。

4、一个三位小数用四舍五入法取近似值是4.30，这个数原来最大是( )，最小是（）。

5、三角形的面积是6平方厘米，高3厘米，底是( )厘米；与它等底等高的平行四边形的面积是( )。

6、算式中的□和△各代表一个数。

已知：(△+□)×0.3=4.2，□÷0.4=12，那么,△=( ) □=( )。

7、李明骑车从家去相距5千米的图书馆借书,从所给的运行图可以看出①李明去图书馆路上停车( )分。

②返回时速度是每小时( )千米。

8、掷一枚骰子一次，掷出“1”的可能性是( )，掷出偶数的可能性是（）。

9、甲、乙两车的速度比是4:3，在同样的时间里两车所行路程比是( )；行完同样的路程，两车所用时间比是( )。

10、把一个棱长是6分米的立方体削成一个最大的圆柱体，圆柱的体积是( )；如果削成一最大的圆锥体，体积是( )。

二、选择题：(每题2分,共8分)1、9点钟时，钟面上的时针和分针所组成的角是( )。

A.锐角B.直角C.钝角D.平角2、有一个三角形的，最小的一个角是48度，这个三角形是( ) 三角形。

A.钝角三角形B.锐角三角形C.直角三角形D.不能确定3、将3克药放入100克水中，药与药水的比是( )。

A. 3:97B.3:100C.100:103D.3:1034、电影院第一排有m个座位，后面一排都比前一排多1个座位，第n排有( )个座位。

小升初分班考试数学试卷(附答案)

2、36分钟=( )小时 2.8升=( )毫升3、x=2×3×5，y=2×5×5，x和y的最小公倍数是( )，最大公因数是( )。

4、一个三位小数用四舍五入法取近似值是4.30，这个数原来最大是( )，最小是（）。

5、三角形的面积是6平方厘米，高3厘米，底是( )厘米；与它等底等高的平行四边形的面积是( )。

6、算式中的□和△各代表一个数。

已知：(△+□)×0.3=4.2，□÷0.4=12，那么,△=( ) □=( )。

7、李明骑车从家去相距5千米的图书馆借书,从所给的运行图可以看出①李明去图书馆路上停车( )分。

②返回时速度是每小时( )千米。

8、掷一枚骰子一次，掷出“1”的可能性是( )，掷出偶数的可能性是（）。

9、甲、乙两车的速度比是4:3，在同样的时间里两车所行路程比是( )；行完同样的路程，两车所用时间比是( )。

10、把一个棱长是6分米的立方体削成一个最大的圆柱体，圆柱的体积是( )；如果削成一最大的圆锥体，体积是( )。

二、选择题：(每题2分,共8分)1、9点钟时，钟面上的时针和分针所组成的角是( )。

A.锐角B.直角C.钝角D.平角2、有一个三角形的，最小的一个角是48度，这个三角形是( ) 三角形。

A.钝角三角形B.锐角三角形C.直角三角形D.不能确定3、将3克药放入100克水中，药与药水的比是( )。

A. 3:97B.3:100C.100:103D.3:1034、电影院第一排有m个座位，后面一排都比前一排多1个座位，第n排有( )个座位。

重点中学小升初数学分班考试模拟试题及分析

重点中学小升初数学分班考试模拟试题及分析部门： xxx时间： xxx制作人：xxx整理范文，仅供参考，可下载自行修改重点中学小升初数学分班考试模拟试题及分析1、试求1×2+23+34+45+56+…+99100的结果。

解：333300原式＝＝333300注：如果学生不明白，可以讲解1×2+23+34+45+56+…+99100＝12＋22＋……＋992＋<1＋2＋……＋99），根据连续自然数的平方和，及等差数列求和来计算。

这样也可以让学生明白实际的道理可以如题解那样，运算更为简单。

MGEDHCOdln2、甲、乙、丙三人都在银行有存款，乙的存款数比甲的2倍少100元，丙的存款数比甲、乙两人的存款和少300元，甲的存款是丙的，那么甲、乙、丙共有存款多少元?MGEDHCOdln 解：甲800、乙1500、丙2000设甲为x元，乙即为<2x-100）元，丙即为<3x-400）元。

列方程：<3x-400）=x解得：x=8003、华校给思维训练课老师发洗衣粉.如果给男老师每人3包,女老师每人4包，那么就会多出8包；如果给男老师每人4包，女老师每人5包，那么就会少7包。

已知男老师比女老师多1人，那么共有多少包洗衣粉？MGEDHCOdln解：60提示：由"男老师每人3包,女老师每人4包"到"男老师每人4包，女老师每人5包"每位老师增加1包，共用去8+7=15包，说明有15位老师，其中男老师8位，女老师7位。

MGEDHCOdln3×8＋4×7＋8=60包。

4、商店购进了一批钢笔，决定以每支9.5元的价格出售．第一个星期卖出了60％，这时还差84元收回全部成本．又过了一个星期后全部售出，总共获得利润372元．那么商店购进这批钢笔的价格是每支多少元？MGEDHCOdln解：6.4元先求出这笔钢笔的总数量：<372＋84）÷9.5=4848÷<1－60％）=120支。

小升初数学：重点学校分班考试真题及参考答案(二)

小升初数学：重点学校分班考试真题及参考答案(二)编者导语：对于六年级的学生来说,你们已经步入了小学的最后阶段了 ,在备考复习中 ,我们要务必保证各类根底题型逢做必对 ,为了到达这个目标 ,数学网整理了小升初数学：分班考试题及参考答案(二) ,助同学们考试复习一臂之力 ,同时祝愿同学们顺利考入理想学校。

一、填空题：8.直角三角形ABC的三边分别为AC=3 ,AB=1.8 ,BC=2.4 ,ED垂直于AC ,且ED=1 ,正方形的BFEG边长是______.9.有两个容器 ,一个容器中的水是另一个容器中水的2倍 ,如果从每个容器中都倒出8升水 ,那么一个容器中的水是另一个容器中水的3倍.有较少水的容器原有水______升.10.100名学生要到离校33千米处的少年宫活动.只有一辆能载25人的汽车 ,为了使全体学生尽快地到达目的地 ,他们决定采取步行与乘车相结合的方法.学生步行速度为每小时5千米 ,汽车速度为每小时55千米.要保证全体学生都尽快到达目的地 ,所需时间是______(上、下车所用的时间不计).二、解答题：1.一个四边形的广场 ,它的四边长分别是60米 ,72米 ,96米 ,84米.现在要在四边上植树 ,如果四边上每两树的间隔距离都相等 ,那么至少要种多少棵树?2.一列火车通过一条长1140米的桥梁(车头上桥直至车尾离开桥)用了50秒 ,火车穿越长1980米的隧道用了80秒 ,问这列火车的车速和车身长?3.能否把1 ,1 ,2 ,2 ,3 ,3 , ,50 ,50这100个数排成一行 ,使得两个1之间夹着这100个数中的一个数 ,两个2之间夹着这100个数中的两个数 ,两个50之间夹着这100个数中的50个数?并证明你的结论.4.两辆汽车运送每包价值相同的货物通过收税处.押送人没有带足够的税款 ,就用局部货物充当税款.第一辆车载货120包 ,交出了10包货物另加240元作为税金;第二辆车载货40包 ,交给收税处5包货 ,收到退还款80元 ,这样也正好付清税金.问每包货物销售价是多少元?。

新编重点中学小升初数学分班考试题及详解二

要点中学小升初入学模拟试题及剖析二一.选择，把正确答案的序号填在括号内。

1）有写着数字2、51、算式的结果等于自然数__________的平方．解：答案88888888原式=111111112828888888821b11a211213311......1 9999 2、，100解：答案a ＜b.试比较a 与b 的大小。

111 1 1199 100，98＋99＞98＋9999＞100，1111 9898199＜99∴100，找规律可得：a ＜b.3、甲、乙两数的最大条约数是 75，最小公倍数是 450．若它们的差最小，则两个数为 ______和______．解：．（225，150）因450÷75=6，所以最大条约数为75，最小公倍数450的两整数有75×6，75×1和75×3，75×2两组，经比较后一种差较小，即 225和150为所求．4、小虎在计算算式399+(3417－口)17时，因为没有注意到括号，所以计算出来的结果是3737,那么这个算式的正确结果应当是___________.解：答案521399+3417－口17=3737由倒推法获得口 =1343；再代入正确的算式获得 399+(3417-1343)17=5215、已知小强比小刚早出生 6年，今年小强的年纪是小刚年纪的 2倍少3岁，那么两人今年的年龄之和是________岁。

解：答案24专心爱心专心1依据年纪差不变，易知小刚年纪的1倍少3岁等于6，1倍的数就是9；二人的年纪和等于3倍的数少3，也就等于9×3－3=24.236、某班有49名同学，此中男同学的5和女同学的8参加了数学小组，那么这个班中没有参加数学小组的同学有_______名。

解：答案30由题意知男同学的人数应当是5的倍数，女同学的人数是8的倍数，简单获得男生25人，女生24人（总人数49人）；没有参加数学小组的同学人数为25×3/5＋24×3/8=30人。

2022年小学数学重点中学小升初分班考试题及详解二二

9、甲乙两瓶盐水，甲瓶盐水旳浓度是乙瓶盐水旳3倍．将100克甲瓶盐水与300克乙瓶盐水混合后得到浓度为15％旳新盐水，那么甲瓶盐水旳浓度是______．
解：提醒：甲乙重量比是1：3因此浓度差之比是3：1
设乙旳浓度是x%，那么甲就是3x%
3x-15=3(15-x) x=10
因此甲瓶盐水旳浓度是30%
10.有三个不一样旳数字，其中最大旳数字是此外两个和旳两倍，用这三个数组6个不一样旳三位数，把6个三位数相加得1998，这三个数是？
重点中学入学模拟试题及分析二十二
一填空题
1、甲、乙、丙代表互不相似旳3个正整数，并且满足：甲甲=乙+乙=丙135．那么甲最小是______．
答：90
2、已知x、y满足方程组，则x-y旳值是______．
答：8
3、大小两个圆旳周长之比是4：1，那么这两个圆旳面积之比是______．
答：16：1
4、一种正方体旳棱长由5厘米变成8厘米，表面积增长了______平方厘米．
5、如下图，边长分别为5 7、10旳三个正方形放在一起，则其中四边形ABCD旳面积是______。
解答：
延长AB交CD于E
用三角形AED-三角形BCE
15*12/2-5*7/2=72.5
6、用1～9可以构成__504___个不含反复数字旳三位数：假如再规定这三个数字中任何两个旳差不能是1，那么可以构成__210____个满足规定旳三位数．
1+3+5+7+9=25
要留下4个加起来是3旳倍数，只能去掉1或7
但取掉1旳话数字和为24不能被9整除，因此只能去掉7，留下旳4个奇数是1，3，5，9
显然只要5放在个位即可，前3位有6种不一样旳排法

重点中学小升初数学分班考试题及详解二二

小升初分班考试数学卷(含答案)

小升初分班考试数学试卷(附答案)

2024年小升初数学重点校分班真题重组卷(二)(答案解析)

2020年苏教版小升初数学重点中学分班测试题及答案.doc

小升初重点中学入学分班考试数学试卷含答案 (2)

[优]2022小升初数学 重点初中招生考试(分班考试)含答案

小升初重点中学分班考试数学试卷 (2)

小升初重点初中分班考试数学试卷及详细答案

小升初分班考试题数学及答案

小升初分班考试数学试卷(附答案)

小升初分班考试数学试卷(附答案)

重点中学小升初数学分班考试模拟试题及分析

小升初数学：重点学校分班考试真题及参考答案(二)

新编重点中学小升初数学分班考试题及详解二

2022年小学数学重点中学小升初分班考试题及详解二二

[优]2022小升初数学重点初中招生考试(分班考试)含答案