专题2-3 以函数零点为背景的解答题-2018年高考数学备考优生百日闯关系列江苏专版含解析精品

合集下载

专题突破卷02 函数零点分布问题 (学生版) 2025年高考数学一轮复习考点通关卷(新高考通用)

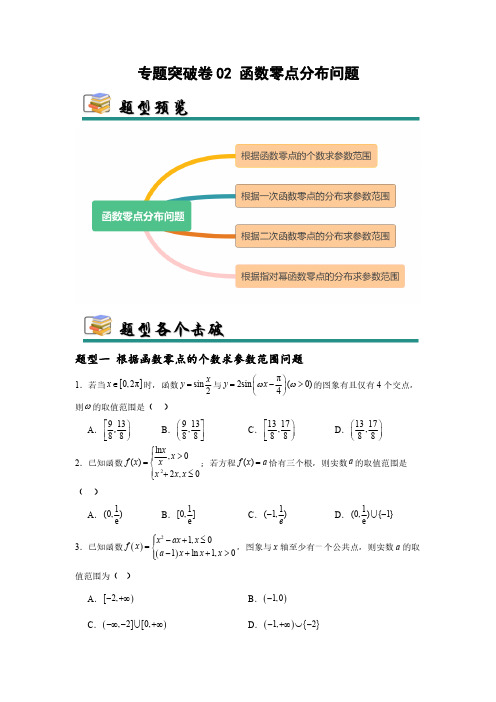
专题突破卷02 函数零点分布问题题型一根据函数零点的个数求参数范围问题1．若当[]0,2πx Î时，函数sin 2x y =与π2sin (0)4y x w w æö=->ç÷èø的图象有且仅有4个交点，则w 的取值范围是（）A ．91388éö÷êëø,B ．913,88æùçúèûC ．1317,88éö÷êëøD ．1317,88æöç÷èø2．已知函数2ln ,0()2,0xx f x x x x x ì>ï=íï+£î；若方程()f x a =恰有三个根，则实数a 的取值范围是（）A ．1(0,)e B ．1[0,e C ．1(1,)e -D ．1(0,{1}e-U 3．已知函数()()21,01ln 1,0x ax x f x a x x x ì-+£ï=í-++>ïî，图象与x 轴至少有一个公共点，则实数a 的取值范围为（）A ．[)2,-+¥B ．()1,0-C ．(][),20,-¥-+¥U D ．(){}1,2-+¥È-4．()2ln x f x x=，()()()21g x f x mf x éù=--ëû，若()g x 在其定义域上有且仅有两个零点，则m 的取值范围是（）A ．21,e æö++¥ç÷èøB ．2e e 2,e 22e æö--ç÷èøC ．2e ,e 2æö-¥-ç÷èøD ．ee 1,122æö-+ç÷èø5．已知函数()432,0,ln ,0,x x x x f x x x x ì+-<=í>î若关于x 的方程()0f x m x -=有两个不同的实根，则实数m 的取值范围是（）A ．(],0-¥B ．[]0,1C ．(){},01¥-ÈD ．(]{},01-¥U 6．已知函数()223sin 1,sin 0sin 1,sin 0x x f x x x ì-³=í-<î且()0,2πx Î，若方程()1f x a =+与方程()1f x a =-共有6个不同的实数根，则实数a 的取值范围为（）A ．12,63æöç÷èøB ．12,33æöç÷èøC ．()0,1D ．1,16æöç÷èø7．定义在R 上的偶函数()f x 满足()()11f x f x +=-，且当[]0,1x Î时，()1e xf x =-，若关于x 的方程()()()10f x m x m =+<恰有5个实数解，则实数m 的取值范围为（）A ．()0,e 1-B ．1e 1e ,56--æöç÷èøC ．e 1e 1,86--æöç÷èøD ．1e 1e ,46--æöç÷èø8．已知函数()2()3e xf x x =-，若方程()f x a =有三个实数解，则实数a 的取值范围为（）A ．360,e æöç÷èøB ．(2e,0)-C ．362e,e æö-ç÷èøD ．32,6e e æö-ç÷èø9．已知函数()ln f x a x x =-有两个零点，则（）A ．0a £B ．0ea <<C ．ea ³D ．ea >10．若不等式ln 0a x x -³有且仅有三个整数解，则实数a 的取值范围是（）A ．25,ln 2ln5éö÷êëøB ．25,ln 2ln5æùçúèûC ．35,ln 3ln5éö÷êëøD ．35,ln 3ln 5æùçúèû11．设()321f x x ax bx =++-.函数()y f x =在1x =处取得极大值3，则以下说法中正确的数量为（）个.①320a b +=；②对任意的1m <，曲线()y f x =在点()(),m f m 处的切线一定与曲线()y f x =有两个公共点；③若关于x 的方程()f x k =有三个不同的根123,,x x x ，且这三个根构成等差数列，则1k =.A ．0B ．1C ．2D ．312．设函数()()2e1ln 2ax f x a x x -=+---有2个零点，则实数a 的取值范围是（）A ．(),e ¥-B ．10,e æöç÷èøC ．1,e e æöç÷èøD ．()0,e 13．若函数()()22e e 4e e 2x x x xf x b --=+-++（b 是常数）有且只有一个零点，则b 的值为（）A ．2B ．3C ．4D ．514．若函数121,02()πsin(π6xx x f x x x w ìæö--£ïç÷ïèø=íï-<<ïî有4个零点，则正数w 的取值范围是（）A ．1319,66éö÷êëøB ．1319,66æùçúèûC ．1925,66éö÷êëøD ．1925,66æùçúèû15．若函数()2341f x ax x =-+-在区间()1,1-内恰有一个零点，则实数a 的取值范围为（）A ．5,13æö-ç÷èøB ．54,33éù-êúëûC ．54,133éùìü-íýêúëûîþU D ．24,133éùìü-íýêúëûîþU 题型二根据一次函数零点的分布求参数范围问题16．若函数f （x ）＝3ax ＋1－2a 在区间（－1，1）内存在一个零点，则a 的取值范围是（）A ．1,5æö+¥ç÷èøB ．11,5æö-ç÷èøC ．（－∞，－1）D ．（－∞，－1）∪1,5æö+¥ç÷èø17．若方程2222|1|0x ax a x -+++-=在区间()0,3内有两个不等实根，则实数a 的取值范围为（）A ．192,5æöç÷èøB．19(,3)15æö-¥-ç÷èøUC ．19(,115æö-¥+ç÷èøU D ．1915æöç÷èø18．当||1x £时，函数21y ax a =++的值有正也有负，则实数a 的取值范围是（）A ．1,3éö-+¥÷êëøB ．(,1]-¥-C ．11,3æö--ç÷èøD ．11,3æù--çúèû19．已知函数()312f x ax a =--在区间(1,1)-上存在零点，则（）A ．115a <C ．15a <-或1a >D ．15a <-20．已知函数f （x ）=3ax -1-2a 在区间（-1，1）上存在零点，则（）A ．1a <或15a >B ．15a >C ．15a <-或1a >D ．15a <-21．若函数1y ax =+在(0,1)内恰有一解，则实数a 的取值范围是（）A ．1a >-B ．1a <-C ．1a >D ．1a <22．已知函数()312f x ax a =--在区间()1,1-上存在零点，则实数a 的取值范围是A ．1(,1),5æö-¥-È+¥ç÷èøB ．1,5æö+¥ç÷èøC ．1,(1,)5æö-¥-È+¥ç÷èøD ．1,5æö-¥-ç÷èø23．已知直线:3l y x =与函数3,1,(), 1.x x x f x ax a x ì-£=í->î的图像交于三点，其横坐标分别是1x ，2x ，3x .若1230x x x ++<恒成立，则实数a 的取值范围是A ．3a >B ．04a <£C ．36a <£D ．6a >24．已知函数2|log ,0(),21,0x x f x x x ìï=í+-£ïî若函数()1y f x m =-+有四个零点,零点从小到大依次为,,,,a b c d 则a b cd ++的值为( )A ．2B ．2-C ．3-D ．325．已知函数2()21f x mx x =--在区间(2,2)-恰有一个零点，则m 的取值范围是( )A ．31,88éù-êúëûB ．31,88æö-ç÷èøC ．31,88éö-÷êëøD ．13,88æù-çúèû26．已知()213,(0)(1)f x ax a f f =-+<且在()1,2内存在零点，则实数a 的取值范围是( )A ．(11,53)B ． 11(,64C ．11(,75D ．11(,)8627．已知函数()()221,03,(0)ax x x f x ax x ì++£=í->î有3个零点，则实数a 的取值范围是（）A ．1a 28．“4a <-”是“函数()3f x ax =+在区间[]1,1-上存在零点”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件29．设函数2()3f x x ax a =-++，()2g x ax a =-，若0R x $Î，使得0()0f x <和0()0g x <同时成立，则a 的取值范围为A ．(7,)+¥B ．(6,)(,2)+¥È-¥-C ．(,2)-¥-D ．(7,)(,2)+¥È-¥-30．“函数在区间上存在零点”是“”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件题型三根据二次函数零点的分布求参数范围问题31．若函数()()2ln 0b cf x a x ac x x =++¹有且仅有极大值，则（）A ．0a >B ．0ab >C ．280b ac +>D ．0c <32．二次函数2,(,y ax bx c a b c =++是常数，且0)a ¹的自变量x 与函数值y 的部分对应值如下表：x…-1012…y…m 22n…且当32x =时，对应的函数值0y <．下列说法正确的有（）A ．0abc >B ．1009mn >C ．关于x 的方程20ax bx c ++=一定有一正、一负两个实数根，且负实数根在12-和0之间D ．()112,P t y +和()222,P t y -在该二次函数的图象上，则当实数12t <时，12y y >33．已知函数()()ln 1f x a x ax a =-+ÎR ，()()2312g x f x x =+-，则下列说法正确的是（）A ．当1a =时，()0f x £在定义域上恒成立B ．若经过原点的直线与函数()f x 的图像相切于点()()3,3f ，则1ln31a =-C ．若函数()g x 在区间3,42éùêúëû单调递减时，则a 的取值范围为[)16,¥+D ．若函数()g x 有两个极值点为()1212,x x x x ¹，则a 的取值范围为(),12¥-34．已知1x ，2x 是关于x 的方程2220()x ax a -+=ÎR 的两个不相等的实数根，则下列说法正确的有（）A ．若12112+=x x ，则2a =B ．若121x x <<，则32a >C ．若π02a b <<<，且1tan x a =，2tan x b =，则a b +为锐角D ．若1x ，2x 均小于2，则(3,2a öÎ-¥÷øU 35．已知函数()23,021,0x x x x f x x -ì-£=í->î，若关于x 的方程()()()221630f x a f x a +-×-=有4个不同的实根，则实数a 可能的取值有（）A ．112-B ．38-C ．14-D ．18-36．已知函数()222,0log ,0x x x f x x x ì--£ï=í>ïî，且()()234230f x af x a -++=有5个零点，则a 的可能取值有（）A ．1B ．32-C ．3-D ．5-37．已知函数()()2222,41log 1,14x x f x x x +ì--££-ï=í+-<£ïî，若函数()()21f x mf x --恰有5个零点，则m的值可以是（）A ．0B ．1C ．32D ．238．已知函数()()()()2221,0,22log ,0x x f x g x f x mf x x x ì+£ï==-+í>ïî，下列说法正确的是（）A ．若()y f x a =-有两个零点，则2a >B ．()y f x =只有一个零点1x =C ．若()y f x a =-有两个零点()1212,x x x x ¹，则121=x x D ．若()g x 有四个零点，则32m >.39．已知函数()e xxf x =，且关于x 的方程()()20f x mf x m ++=éùëû有3个不等实数根，则下列说法正确的是（）A ．当0x >时，()0f x >B ．()f x 在()1,+¥上单调递减C ．m 的取值范围是1,02æö-ç÷èøD ．m 的取值范围是21,0e e æö-ç÷+èø40．设函数()2e ,0313,022x x f x x x x ì£ï=í-++>ïî，函数()()()222g x f x bf x b =-+-，则下列说法正确的是（）A ．当1b =时，函数()g x 有3个零点B ．当4140b =时，函数()g x 有5个零点C ．若函数()g x 有2个零点，则2b <-或625b <<D ．若函数()g x 有6个零点，则112b <<41．已知函数()224,021,0x x x x f x x -ì+<=í-³î，若关于x 的方程()()244230f x a f x a -×++=有5个不同的实根，则实数a 的取值可以为（）A ．32-B ．43-C ．54-D ．76-42．已知函数()()21,0,0x ax x f x f x x ì++³ï=í--<ïî，有4个零点()12341234,,,x x x x x x x x <<<，则（）A ．实数a 的取值范围是(),2¥--B ．函数()f x 的图象关于原点对称C ．12342x x x x =D ．1234357x x x x +++的取值范围是()8,¥+43．已知函数()21243,0log ,0x x x f x x x ì---£ï=í>ïî，若方程()()2[]10f x mf x ++=恰有6个不相等的实数根，则实数m 的值可能是（）A ．53B ．73C ．103D ．11344．在下列命题中，正确的是（）A ．已知命题p ：“0x "³，都有tan x x ³，则命题p 的否定：“0x $<，都有tan x x <”B ．若函数()f x 满足()()2sin f x f x x +-=，则π162f æö=ç÷èøC ．“方程210x ax -+=有两个不相等的正实数根”的充要条件是“2a >”D ．若函数()1e 1x af x =-+是定义在区间[]2,a b -上的奇函数，则2b =45．已知函数()f x 的定义域为D ，且[,]a b D Í，若函数()f x 在[],x a b Î的值域为[],ka kb ，则称[],a b 为()f x 的“k 倍美好区间”.特别地，当1k =时，称[],a b 为()f x 的“完美区间”，则（）A ．函数21()2f x x x =-+存在“3倍美好区间”B ．函数1()3f x x=-+不存在“完美区间”C．若函数()f x m =-“完美区间”，则1,04m æùÎ-çúèûD ．若函数||1()||m x f x x -=存在“完美区间”，则(2,)m Î+¥题型四根据指对幂函数零点的分布求参数范围问题46．已知函数()f x 的定义域为R ，且()10f ¹，若()()()f x y f x f y xy +-=-，则（）A ．()01f =B ．()23log 32f f æö>ç÷èøC ．方程()21xf x =-有唯一的实数解D ．函数()y xf x =有最小值47．已知函数()()ln ,12,1x a x x f x f x x +³ì=í-<î存在n 个零点12,,,,N n x x x n *×××Î，则（）A ．n 为偶数B ．e 1a -££-C ．122n x x x +++=L D ．1224n x x x ×××<L 48．已知实数,,x y z满足：22log xz ==，则下列不等式中可能成立的是（）A ．y x z <-ïî，若函数()y f x m =-有三个零点1x 、2x 、3x ，且123x x x <<，则（）A ．14m <£B ．3151162x -<£-C ．函数()1f x +的增区间为[]2,1--D．2212log x x ++8+50．已知函数()14,0lg 1,0x x f x xx x ì++<ï=íï+>î，若方程()f x a =有4个不同实根()12341234,,,x x x x x x x x <<<，则（）A ．2a >B ．411110x x ->C ．341100x x =D ．221211214x x <+<51．已知1x ，2x 为函数()()32024log 3xf x x -=--的两个零点，则下列结论中正确的有（）A ．()()12440x x --D ．若12x x <，则1213320242024x x --<52．已知函数221,0()log ,0x kx x f x x x ì-+£=í>î，下列关于函数[()]1y f f x =+的零点个数的说法中，正确的是（）A ．当1k >，有1个零点B ．当1k >时，有3个零点C ．当0k <时，有9个零点D ．当4k =-时，有7个零点53．记函数1,0()lg ,0x x f x x x ì+£=í>î，若123()()()f x f x f x ==（1x ，2x ，3x 互不相等），则123x x x ++的值可以是（）A ．2-B ．6C ．8D ．954．已知函数()1231,0,log ,0,x x f x x x +ì-£ï=í>ïî1x ，2x ，3x ，4x 是函数()()g x f x m =-的4个零点，且1234x x x x <<<，则（）A ．m 的取值范围是(]0,2B ．122333x x+=C ．344x x +的最小值是4D ．1234332x x x x ++55．已知函数()121x f x -=-，若关于x 的方程()()f f x m =有6个不相等的实根，则实数m的值可能为（）A ．14B ．13C ．12D56．已知函数()()()1101xf x x x x =--×>，()()()1lg 1g x x x x x =--×>的零点分别为12,x x ，则（）A ．1210x x ×57．已知函数()222,0log ,0x x x f x x x ì--£ï=í>ïî，若1234x x x x <<<，且()()()()1234f x f x f x f x k ====，则下列结论正确的是（）A ．121x x +=-B ．341x x =C ．412x <<D ．01k <<58．已知函数()21,144,1x x f x x x x ì-<ï=í+-³ïî，若存在实数m 使得方程()f x m =有四个互不相等的实数根()12343124,,,x x x x x x x x >>>，则下列叙述中正确的有（）A ．140x x +=í--+£î，若关于x 的方程()()22210f x af x a -+-=有()k k ÎN 个不等的实根1x 、2x 、L 、k x 且12k x x x <<<L ，则下列判断正确的是（）A ．当0a =时，5k =B ．当2k =时，a 的范围为(),1-¥-C ．当8k =时，14673x x x x ++=-D ．当7k =时，a 的范围为()1,260．已知函数()()()lg2lg512xf x =+-，实数a 、()b a b <是函数()y f x m =-的两个零点，则下列结论正确的有（）A ．1m >B ．01m <<C ．222a b +=D．0a b +<1．函数()ln 1f x x =-的零点是（）A ．eB ．1eC ．10D ．1102．已知函数()()()()221,log 111x x xf x xg x x x x x =->=->--的零点分别为,a b ，则11a b +的值是（）A ．1B ．2C ．3D ．43．已知正数a b c ，，满足e ln e ln 1a c a b b c ===，则a b c ，，的大小关系为（）A ．c<a<bB ．c b a<<C ．a b c<<D ．a c b<<4．已知a 是方程e 40x x +-=的实根，则下列各数为正数的是（）A ．22a a -B ．e 2a -C ．ln aD ．23a a -5．下列命题为真命题的是（）A ．若22ac bc >，则a b>B ．函数()1f x +的定义域为[]0,1，则()3xf 的定义域为[]3,9C ．若幂函数()f x 的图像过点13,27A æöç÷èø，则()3f x x-=D ．函数()3ln f x x x=-的零点所在区间可以是()1,26．关于函数()π2sin 213f x x æö=-+ç÷èø，下列结论正确的是（）A ．π,06æöç÷èø是()f x 的一个对称中心B ．函数()f x 在π0,6æöç÷èø上单调递增C ．函数()f x 图像可由函数()2cos21g x x =+的图像向右平移5π12个单位得到D ．若方程()20f x m -=在区间π12π,2éùêúëû上有两个不相等的实根，则2,6m éùÎëû7．对于函数()3e x xf x =，下列说法正确的是（）A ．()f x 有最小值但没有最大值B ．对于任意的(),0x Î-¥，恒有()0f x <C ．()f x 仅有一个零点D ．()f x 有两个极值点8．已知函数224,0()log ,0x x x f x x x ì--£ï=í>ïî，若1234x x x x <<<，且()()()()1234f x f x f x f x ===，则下列结论正确的是（） A ．124x x +=-B ．341x x ×=C ．414x <<D ．123402x x x x <£9．（多选）已知函数()()22,02ln 11,0x x t x f x x x ì-+£ï=í+->ïî，若函数(())y f f x =恰好有4个不同的零点，则实数t 的取值可以是（）A ．-3B ．-2C ．0D ．210．已知函数3()34,[0,2]f x x x x =-+Î，则下列选项中正确的是（）A ．()f x 的值域为[]2,6B ．()f x 在1x =处取得极小值为2C ．()f x 在[]0,2上是增函数D ．若方程()f x a =有2个不同的根，则[2,4]a Î11．已知函数()1e ,01ln ,04x x x f x x x +ì-£ï=í->ïî，下列选项中正确的是（）A ．()f x 在(),1-¥-上单调递增，在()1,0-上单调递减B ．()f x 有极大值C ．()f x 无最小值D ．若函数()()()()2[]24h x f x af x a =-+ÎR 恰有6个零点，则实数a 的取值范围是5,2æö+¥ç÷èø12．方程()230x m x m +-+=有两个实根，则实数m 的取值范围是．13．若函数()cos2sin f x x m x =-在π,π6æöç÷èø上有2个零点，则m 的取值范围是.14．若关于x 的方程sin cos x x k -=无解，则实数k 的取值范围是.15．已知函数()22x f x x =+-，()2log 2g x x x =+-，()32h x x x =+-的零点分别为a ，b ，c ，则a b c ++=．若1x 满足22=5x x +，2x 满足222log (1)5x x +-=，则12=x x + .16．设函数 22,0()lg ,0x x x f x x x ì+£ï=í>ïî若关于x 的方程22()(12)()0f x m f x m m +-+-=有5个不的取值范围是．17．已知函数()44,4x f x f x x £<=-³ïî，若对于正数()*n k n ÎN ，直线n y k x =与函数()f x 的图像恰好有21n +个不同的交点，则22212n k k k +++=L．18．若函数 ()22ln 1f x ax x =--有两个零点，则a 的取值范围为 .19．已知函数()|ln |f x x b =+，关于以下四个结论：①函数()f x 的值域为[,)b +¥；②当a b >时，方程()f x a =有两个不等实根；③当0b =，0a >时，设方程()f x a =的两个根为1x ，2x ，则12x x +为定值；④当0b =，0a >时，设方程(1)f x a +=的两个根为1x ，2x ，则12120x x x x ++=．则所有正确结论的序号为．20．已知函数2)()(e x f x x ax =-.(1)若曲线()y f x =在=1x -处的切线与y 轴垂直，求()y f x =的极值.(2)若()f x 在(0,)+¥只有一个零点，求a .。

专题3.1 第01关-2018年高考数学备考优生百日闯关系列(江苏专版)(解析版)

新题原创强化训练第一关一、填空题1．已知F 是抛物线C ：28y x =的焦点，M 是C 上一点，FM 的延长线交y 轴于点N ．若M 是FN 的中点，则FN 的长度为 ▲ ．【答案】6【解析】如图，过点M 作准线的垂线，垂足为T ，交y 轴于点P ，所以112MP OF ==，3MF MT ==，所以26FN MF ==．2．若函数()f x 为定义在R 上的奇函数，当0x >时，()ln f x x x =，则不等式()e f x <-的解集为 ▲ ．【答案】 (,e)-∞-3．钢材市场上通常将相同的圆钢捆扎为正六边形垛（如图）．现将99根相同的圆钢捆扎为1个尽可能大的正六边形垛，则剩余的圆钢根数为 ▲ ．【答案】 8【解析】设99根相同的圆钢捆扎成的尽可能大的1个正六边形垛的边长为n 根，则这个正六边形垛的层数是21n -，每一层的根数从上往下依次为：则圆钢的总根数为：()222(1)2(21)33 1.2n n n n n n +--⨯+-=-+由题意2331n n -+≤99即2993n n --≤0，设函数299()3f x x x =--，则299()3f x x x =--在[)1+∞，上单调递增．因为(6)0(7)0f f <>，，所以6n =．此时剩余的圆钢根数为299(36361)8-⨯-⨯+=．4．如图，在△ABC 中，点M 为边BC 的中点，且2AM =，点N 为线段AM 的中点，若74AB AC ⋅=，则NB NC ⋅的值为 ▲ ．A BCMN【答案】 54-5．已知正数x y ，满足11910x y x y +++=，则1x y+的最小值是 ▲ ．【答案】2【解析】设1a x y=+，19b y x =+，则10a b +=．因为ab =()1x y+⋅()1191091016y xy +=+++≥ （当且仅当19xy =时取“=”），所以()1016a a -≥，解得28a ≤≤，所以1x +的最小值是2．6．设等比数列{a n }满足：1cos n n n a a θθ==+，其中π02n θ⎛⎫∈ ⎪⎝⎭，，*n ∈N ．则数列{}n θ的前2 018项之和是 ▲ ．【答案】 1009π【解析】因为()π02n θ∈，，所以()(]πcos 2sin 126n n n n a θθθ=+=+∈，，所以等比数列{a n }的公比0q >．若1q >，由1a n 充分大，则2n a >，矛盾；若01q <<，由1a =n 充分大，则1n a <，矛盾，所以1q =，从而1n a a ==π12n θ=．则数列{}n θ的前2 018项之和是1009π6．二、解答题1．在平面直角坐标系xOy 中，已知椭圆C ：222210x y a b a b +=>>()过点12⎛⎝⎭，．设P 为椭圆C 在第一象限上的点，A ，B 分别为椭圆C 的左顶点和下顶点，且PA 交y 轴于点E ，PB 交x 轴于点F ．（1）求a b ，的值；（2）若F 为椭圆C 的右焦点，求点E 的坐标；（3）求证：四边形ABFE 的面积为定值．（2）由（1）知，椭圆C 的右焦点为)0F，椭圆C 的方程为2214x y +=，①所以()()2001A B --，，，．从而直线BF1y -=． ②由①②得，)17P ，．从而直线AP的方程为：2)y x +．令0x =，得7y =-E的坐标为(07-，．（3）设()00P x y ，（0000x y >>，），且220014x y +=，即220044x y +=．则直线AP 的方程为：00(2)2y y x x =++，令0x =，得0022y y x =+．学科#网直线BP 的方程为：0011y y x ++=，令0y =，得00xx =．所以四边形ABFE 的面积S =()()00002121x y ++00000022221x y x y ++++=⋅⋅()2200000000004222441222x y x y x y x y x y +++++=⋅+++00000000224422x y x y x y x y +++=+++ 2=． 2．设数列{a n }的前n 项和为n S ，且满足：()()2*0n n n a S a p n p >=+∈∈N R ，，．（1）若29p =，求a 1的值；（2）若123a a a ，，成等差数列，求数列{a n }的通项公式．所以()211a a p =+， ①()2122a a a p +=+， ② ()21233a a a a p ++=+． ③②-①，得()()22221a a p a p =+-+，即()2122a d a a p =++， ④③-②，得()()22332a a p a p =+-+，即()3232a d a a p =++， ⑤ ⑤-④，得()()32231222a a d a a p a a p ⎡⎤-=++-++⎣⎦，即22d d =．若0d =，则230a a ==，与0n a >矛盾，故12d =．代入④得()1111112222a a a p +=+++，于是14p =．因为()()2*14n n S a n =+∈N ，所以()21114n n S a ++=+，所以()()221111144n n nn na S S a a +++=-=+-+，即()()221111044n n n a a a +++--+=，整理得()()22111044n na a +--+=，于是()()11102n n n n a a a a +++--=．因为0n a >，所以1102n n a a +--=，即112n n a a +-=．因为()21114a a =+，所以114a =．所以数列{a n }是首项为14，公差为12的等差数列．因此，*1121(1)()424n n a n n -=+-=∈N ．3．已知函数()e (1)x f x a x =-+，其中e 为自然对数的底数，a ∈R ．（1）讨论函数()f x 的单调性，并写出相应的单调区间；（2）已知0a >，b ∈R ，若()f x b ≥对任意x ∈R 都成立，求ab 的最大值；（3）设()(e)g x a x =+，若存在0x ∈R ，使得00()()f x g x =成立，求a 的取值范围．（2）由（1）知，当0a >时，min ()(ln )ln f x f a a a ==-．因为()f x b ≥对任意x ∈R 都成立，所以ln b a a -≤，所以2ln ab a a -≤．设2()ln t a a a =-，（0a >），由21()(2ln )(2ln 1)t a a a a a a a '=-+⋅=-+，令()0t a '=，得12e a -=，当10e a -<<时，()0t a '>，所以()t a 在()120e-，上单调递增；当12e a ->时，()0t a '<，所以()t a 在()12e -∞，+上单调递减，所以()t a 在12e a -=处取最大值，且最大值为12e．所以21ln 2e ab a a -≤≤，当且仅当12e a -=，11e 2b -=时，ab 取得最大值为12e ．（3）设()()()F x f x g x =-，即()e e 2x F x x ax a =--- 题设等价于函数()F x 有零点时的a 的取值范围．① 当0a ≥时，由(1)30F a =-≤，1(1)e e 0F a --=++>，所以()F x 有零点． ② 当e 02a -<≤时，若0x ≤，由e 20a +≥，得()e (e 2)0x F x a x a =-+->；若0x >，由（1）知，()(21)0F x a x =-+>，所以()F x 无零点． ③ 当e 2a <-时，(0)10F a =->，又存在010e 2a x a -=<+，00()1(e 2)0F x a x a <-+-=，所以()F x 有零点．综上，a 的取值范围是e 2a <-或0a ≥．学科&网。

2018高考数学专题大讲堂-第六讲-压轴小题中的函数零点问题(PDF 含答案)

答案：
解析：分别画出函数
和
的图象.
由图象可知,函数
关于对称, 又也是函数
的对称轴,
所以函数和的交点也关于对称，且两函数共有个交点,所以所有零点之和为 .
变式：( ·全国Ⅱ)已知函数
满足
，若函数
与
图象的交点为
，则
()
答案：变式：(2016·全国Ⅱ)已知函数
点为
，则
满足 ()
，若函数
与
图象的交
数形结合法：转化为两个函数的图象的交点个数问题．先画出两个函数的图象，看其交点的个数，其
中交点的横坐标有几个不同的值，就有几个不同的零点．
直接计算或判断零点
例 ( ·南通三模)设函数
内的所有零点的和为________．答案：
解析：当
时，
，
当
时，
，
，则函数
在区间
，此时当
时，
；由此可得
；时，
.
下面考虑
且时，的最大值的情况．
当
时，由函数的定义知
，
因为
，所以
，此时当
时，
；
当
时，同理可知，
.
由此可得
且时，
.
综上，对于一切的
，函数在区间
上有个零点，从而在区间
上有个零
点，且这些零点为
，所以当
时，所有这些零点的和为
．
变式：( ·天津二模)已知函数
在定义域
上单调递增，且对任意
，方程和为( )
压轴小题中的函数零点问题
函数的零点问题是高考的重点和难点内容，由于其和函数、方程有着密切的联系，近几年在全国各地高考

零点嵌套问题(解析版)--新高考数学函数压轴小题专题突破

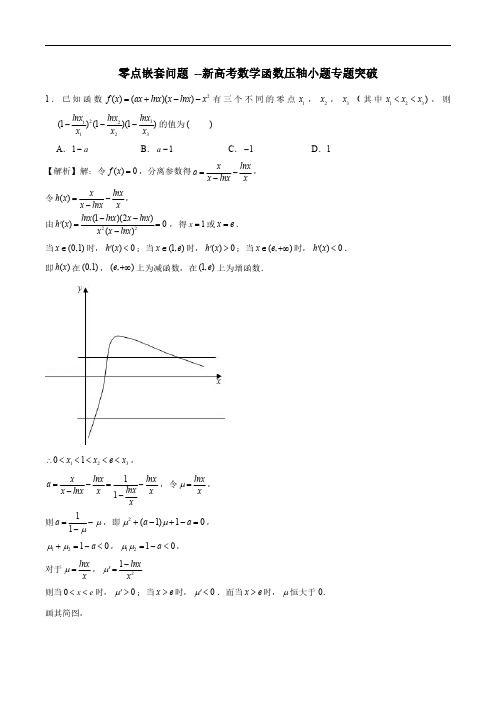
零点嵌套问题--新高考数学函数压轴小题专题突破1．已知函数2()()()f x ax lnx x lnx x =+--有三个不同的零点1x ，2x ，3x （其中123)x x x <<，则2312123(1)(1)(1)lnx lnx lnxx x x ---的值为()A ．1a -B ．1a -C ．1-D ．1【解析】解：令()0f x =，分离参数得x lnxa x lnx x=--，令()x lnxh x x lnx x=--，由22(1)(2)()0()lnx lnx x lnx h x x x lnx --'==-，得1x =或x e =．当(0,1)x ∈时，()0h x '<；当(1,)x e ∈时，()0h x '>；当(,)x e ∈+∞时，()0h x '<．即()h x 在(0,1)，(,)e +∞上为减函数，在(1,)e 上为增函数．12301x x e x ∴<<<<<，11x lnx lnx a lnx x lnx x xx =-=---，令lnxx μ=，则11a μμ=--，即2(1)10a a μμ+-+-=，1210a μμ+=-<，1210a μμ=-<，对于lnx x μ=，21lnxx μ-'=则当0x e <<时，0μ'>；当x e >时，0μ'<．而当x e >时，μ恒大于0．画其简图，不妨设12μμ<，则111lnx x μ=，322323lnx lnx x x μμ===，22312123123(1)(1)(1)(1)(1)(1)lnx lnx lnxx x x μμμ---=---2212[(1)(1)][1(1)(1)]1a a μμ=--=--+-=．故选：D ．2．已知1x ，2x ，3x 是函数2()x f x ax lnx x lnx =+--三个不同的零点，且123x x x <<，设1(1i i i lnx M i x =-=，2，3)，则2123(M M M =)A ．1B ．1-C ．e D ．1e【解析】解：令()0f x =得x lnx a x lnx x=--，令lnx t x =，则11x t x lnx t =---，11a t t∴=--．即2(1)10t a t a +-+-=．令()lnx g x x =，则21()lnxg x x -'=，()g x ∴在(0,)e 上单调递增，在(,)e +∞上单调递减，且当01x <<时，()0g x <，当x e >时，()0g x >，()g x g ∴（e ）1e=，∴当10t e<<时，关于x 的方程()g x t =有两大于1的解，当0t 时，关于x 的方程()g x t =只有一小于1的解．当1t e=时，关于x 的方程()g x t =有唯一解x e =．()f x 有三个不同的零点，∴关于t 的方程2(1)10t a t a +-+-=在(-∞，10]{}e 和1(0,e上各有1个解．不妨设两解为1t ，2t ，则121t t a +=-，121t t a =-，若1t e =，则11e a e e =--，此时方程的另一解为1101et a e e =--=-<-，∴原方程只有两解，不符合题意；同理0t =也不符合题意；设120t t <<，则111M t =-，2321M M t ==-，∴2222123121212(1)(1)(1)1M M M t t t t t t =--=--+=．故选：A ．3．已知函数2()()(1)()1x x f x xe a xe a =+-+-有三个不同的零点1x ，2x ，3x ．其中123x x x <<，则3122123(1)(1)(1)x x x x e x e x e ---的值为()A ．1B ．2(1)a -C ．1-D ．1a-【解析】解：令x t xe =，则(1)x t x e '=+，故当(1,)x ∈-+∞时，0t '>，x t xe =是增函数，当(,1)x ∈-∞-时，0t '<，x t xe =是减函数，可得1x =-处x t xe =取得最小值1e -，x →-∞，0t →，画出x t xe =的图象，由()0f x =可化为2(1)10t a t a +-+-=，故结合题意可知，2(1)10t a t a +-+-=有两个不同的根，故△2(1)4(1)0a a =--->，故3a <-或1a >，不妨设方程的两个根分别为1t ，2t ，①若3a <-，1214t t a +=->，与1220t t e-<+<相矛盾，故不成立；②若1a >，则方程的两个根1t ，2t 一正一负；不妨设120t t <<，结合x t xe =的性质可得，_111x x e t =，_221x x e t =，_332x x e t =，故3122123(1)(1)(1)x x x x e x e x e ---2112(1)(1)(1)t t t =---21212(1())t t t t =-++又121t t a =- ，121t t a +=-，31222123(1)(1)(1)(111)1x x x x e x e x e a a ∴---=-++-=．故选：A ．4．已知函数2()()xx x axf x a e e =+-有三个不同的零点1x ，2x ，3x （其中123)x x x <<，则1232312(1)(1)x x x x x x e e e---的值为()A ．1B ．1-C ．aD ．a-【解析】解：令()x x t x e =，则1x xt e-'=，∴当1x <时，()0t x '>，函数()t x 在(,1)-∞单调递增，当1x >时，()0t x '<，在(1,)+∞单调递减，且()1()1t x t e==极大值，由题意，2()g t t at a =+-必有两个根10t <，且210t e<<，由根与系数的关系有，12t t a +=-，12t t a =-，由图可知，1x x t e =有一解10x <，2xx t e =有两解2x ，3x ，且2301x x <<<，故12322222312122121212(1)(1)(1)(1)(1)[(1)(1)][1()](1)1x x x x x x t t t t t t t t t a a e e e ---=---=--=-++=+-=．故选：A ．5．若关于x 的方程0xx xx e m e x e ++=+有三个不相等的实数解1x ，2x ，3x ，且1230x x x <<<，其中m R ∈，e 为自然对数的底数，则1232312(1)(1)(1)x x x x x xe e e+++的值为()A ．1m +B ．eC ．1m -D ．1【解析】解：由方程0xx xx e m e x e ++=+⇒101xxx m x e e ++=+，令x x t e =，则有101t m t ++=+．2(1)10t m t m ⇒++++=，令函数()x x g x e =，1()x xg x e-'=，()g x ∴在(,1)-∞递增，在(1,)+∞递减，其图象如下，要使关于x 的方程0xx xx e m e x e ++=+有三个不相等的实数解1x ，2x ，3x ，且1230x x x <<<结合图象可得关于t 的方程2(1)10t m t m ++++=一定有两个实根1t ，2t ，12(0)t t <<且111x x t e =，23322x x x x t e e ==，1232312(1)(1)(1)x x x x x x e e e ∴+++212[(1)(1)]t t =++．121212(1)(1)()1(1)(1)11t t t t t t m m ++=+++=+-++=．1232231212(1)(1)(1)[(1)(1)]1x x x x x x t t e e e ∴+++=++=．故选：D ．6．若关于x 的方程0xx xx e m e x e ++=-有三个不相等的实数解1x ，2x ，3x ，且1230x x x <<<，其中m R ∈，2.718e =为自然对数的底数，则1232312(1)(1)(1)x x x x x xe e e---的值为()A ．eB ．1m -C ．1m +D ．1【解析】解：由方程0x x x x e m e x e ++=-⇒101xxx m x e e ++=-，令x x t e =，则有101t m t ++=-．2(1)10t m t m ⇒+-+'-=，令函数()x x g x e =，1()xxg x e -'=，()g x ∴在(,1)-∞递增，在(1,)+∞递减，其图象如下，要使关于x 的方程0xx xx e m e x e ++=-有3个不相等的实数解1x ，2x ，3x ，且1230x x x <<<结合图象可得关于t 的方程2(1)10t m t m +-+'-=一定有两个实根1t ，2t ，12(0)t t <<且111x x t e =，23223x x x x t e e ==∴1232231212(1)(1)(1)[(1)(1)]x x x x x x t t e e e---=--．121212(1)(1)()1(1)(1)11t t t t t t m m --=-++=---+=．∴1232231212(1)(1)(1)[(1)(1)]1x x x x x x t t e e e---=--=．故选：D ．7．若关于x 的方程2|1|0|1|1x x e m e -++=-+有三个不相等的实数解1x 、2x 、3x ，123(0)x x x <<<其中m R ∈，2.71828e =⋯，则3122(|1|1)(|1|1)(|1|1)x x x e e e -+-+-+ 的值为()A ．eB ．4C ．1m -D ．1m +【解析】解：令|1|x t e =-，函数|1|x y e =-的图象如下：方程22|1|00|1|11x xe m t m e t -++=⇒++=-++．即2(1)20t m t m ++++=，要使方程2|1|0|1|1x x e m e -++=-+有三个不相等的实数解1x 、2x 、3x ，123(0)x x x <<<，则方程2(1)20t m t m ++++=一定有两个实根1t ，2t ，可验证0t =或1不符合题意，所以方程2(1)20t m t m ++++=一定有两个实根1t ，2t ，且1201t t <<<．且_1_21|1||1|x x e e t -=-=，_32|1|x e t -=，则3122212(|1|1)(|1|1)(|1|1)[(1)(1)]x x x e e e t t -+-+-+=++ ．121212(1)(1)()1(2)(1)12t t t t t t m m ++=+++=+-++=．则3122212(|1|1)(|1|1)(|1|1)[(1)(1)]4x x x e e e t t -+-+-+=++= ，故选：B ．8．若存在正实数m ，使得关于x 的方程(224)[()]0x a x m ex ln x m lnx ++-+-=有两个不同的根，其中e 为自然对数的底数，则实数a 的取值范围是()A ．(,0)-∞B ．1(0,)2eC ．(-∞，10)(2e⋃，)+∞D ．1(2e，)+∞【解析】解：由题意得1(12)(1)(2)2m m e ln t e lnt a x x -=+-+=-，(11)mt x=+>，令()(2)f t t e lnt =-，(1)t >，则2()1e f t lnt t '=+-，212()0ef t t t''=+>，当t e >时，()f t f '>'（e ）0=，当1t e <<时，()f t f '<'（e ）0=，()f t f ∴（e ）e =-，12e a∴->-，而1t →时，()0f t →，则要满足102e a-<-<，解得：12a e>，故选：D ．9．若存在正实数m ，使得关于x 的方程(224)[()]0x a x m ex ln x m lnx ++-+-=成立，其中e 为自然对数的底数，则实数a 的取值范围是()A ．(,0)-∞B ．1(0,)2eC ．1(,0)[,)2e-∞+∞ D ．1[,)2e+∞【解析】解：由(224)[()]0x a x m ex ln x m lnx ++-+-=得2(2)0x mx a x m ex lnx+++-=，即12(2)0x m x ma e ln x x+++-=，即设x mt x+=，则0t >，则条件等价为12(2)0a t e lnt +-=，即1(2)2t e lnt a-=-有解，设()(2)g t t e lnt =-，2()1eg t lnt t'=+-为增函数，g ' （e ）211120elne e=+-=+-=，∴当t e >时，()0g t '>，当0t e <<时，()0g t '<，即当t e =时，函数()g t 取得极小值为：g （e ）(2)e e lne e =-=-，即()g t g （e ）e =-，若1(2)2t e lnt a -=-有解，则12e a--，即12e a，则0a <或12ae，∴实数a 的取值范围是1(,0)[2e-∞ ，)+∞．故选：C ．10．已知函数()(21)u x e x m =--，()()x ln x m lnx υ=+-若存在m ，使得关于x 的方程2()()a u x x x υ= 有解，其中e 为自然对数的底数则实数a 的取值范围是()A ．1(,0)(,)2e-∞+∞ B ．(,0)-∞C ．1(0,2eD ．1(,0)[,)2e-∞+∞ 【解析】解：由2()()a u x x x υ= 可得[2(21)2]0x ma e x am ln x x+---= ，即2[(21)]10m x m a e ln x x +---= ，即2(2)10x m x m a e ln x x++--= ，令x m t x +=，则方程1(2)2e t lnt a-=有解．设()(2)f t e t lnt =-，则22()1e t ef t lnt lnt t t-'=-+=-+-，显然()f t '为减函数，又f '（e ）0=，∴当0t e <<时，()0f t '>，当t e >时，()0f t '<，()f t ∴在(0,)e 上单调递增，在(,)e +∞上单调递减，()f t ∴的最大值为f （e ）e =，∴12e a ，解得0a <或12ae．故选：D ．11．已知2()()()f x ax lnx x lnx x =+--恰有三个不同零点，则a 的取值范围为(1，11)(1)e e +-．【解析】解：令()0f x =，分离参数得x lnxa x lnx x=--，令()x lnxh x x lnx x=--，由22(1)(2)()0()lnx lnx x lnx h x x x lnx --'==-，得1x =或x e =．当(0,1)x ∈时，()0h x '<；当(1,)x e ∈时，()0h x '>；当(,)x e ∈+∞时，()0h x '<．即()h x 在(0,1)，(,)e +∞上为减函数，在(1,)e 上为增函数．1x ∴=时，()h x 有极小值h （1）1=；x e =时，()h x 有极大值h （e ）11(1)e e =+-；设lnxxμ=，则1μ<；这是因为对于函数y lnx x =-，0x >，有1xy x-'=，当01x <<时，0y '>，函数单调递增；当1x >时，0y '<，函数单调递减；即1x =时函数有极大值，也是最大值1-，故0x ∀>，0lnx x -<，lnx x <，即得1lnxx<；11()(1)121111h x μμμμ=-=+---=--；∴当2()()()f x ax lnx x lnx x =+--恰有三个不同零点，即y a =与()y h x =有三个不同的交点；111(1)a e e ∴<<+-．故答案为：(1，11)(1)e e +-．12．已知函数2()x f x ax lnx x lnx=+--有三个不同的零点1x ，2x ，3x （其中123)x x x <<，则2312123(1)(1)(1)lnx lnx lnxx x x ---的值为1．【解析】解：由2()0x f x ax lnx x lnx =+-=-分离参数得x lnxa x lnx x=--，令()x lnxh x x lnx x=--，由222211(1)(2)()0()()lnx lnx lnx lnx x lnx h x x lnx x x x lnx ----'=-==--，得1x =或x e =．当(0,1)x ∈时，()0h x '<；当(1,)x e ∈时，()0h x '>；当(,)x e ∈+∞时，()0h x '<．即()h x 在(0,1)，(,)e +∞上为减函数，在(1,)e 上为增函数．而当0x →，()h x →+∞，当x →+∞，()1h x →，又h （1）1=，h （e ）11(1)e e =+-；结合函数的单调性可得，实数a 的取值范围为(1，11)(1)e e +-．则12301x x e x <<<<<，11x lnx lnx a lnx x lnx x x x=-=---，令lnx x μ=，则11a μμ=--，即2(1)10a a μμ+-+-=，1210a μμ+=-<，1210a μμ=-<，对于lnx x μ=，21lnx x μ-'=则当0x e <<时，0μ'>；当x e >时，0μ'<．而当x e >时，μ恒大于0．画其简图，不妨设12μμ<，则31212123,lnx lnx lnx x x x μμ===，∴22231212212123(1)(1)(1)(1)(1)(1)[(1)(1)]lnx lnx lnx x x x μμμμμ---=---=--221212[1()][1(1)(1)]1a a μμμμ=-++=--+-=故答案为：1。

2018年高考数学二轮复习特色专题训练专题03直击函数压轴题中零点问题理 Word版含答案

专题03 直击函数压轴题中零点问题一、解答题1．已知函数()()()2ln 10f x x a x a =+->.（1）讨论()f x 的单调性；（2）若()f x 在区间()0,1内有唯一的零点0x ，证明： 3120e x e --<<.【答案】(1)答案见解析；(2)证明见解析.【解析】试题分析：（1）求出函数的导数，通过讨论a 的范围，求出函数的单调区间即可；（2）依题可知()10f =，若()f x 在区间()0,1内有唯一的零点0x ，由（1）可知2a >，且0110,2x x ⎛⎫=∈ ⎪⎝⎭，于是： ()20010lnx a x +-= ①，2002210ax ax -+= ② 由①②得0001ln 02x x x --=，设g (x )＝lnx −12x x -，(x ∈(0，1))，求出函数的导数，根据函数的单调性证明即可．（2）依题可知()10f =，若()f x 在区间()0,1内有唯一的零点0x ，由（1）可知2a >，且0110,2x x ⎛⎫=∈ ⎪⎝⎭. 于是： ()20010lnx a x +-= ①2002210ax ax -+= ②由①②得0001ln 02x x x --=，设()()()1ln ,0,12x g x x x x -=-∈，则()2212x g x x '-=，因此()g x 在10,2⎛⎫⎪⎝⎭上单调递减，又3322402e g e -⎛⎫-=> ⎪⎝⎭， ()11302e g e ---=< 根据零点存在定理，故3120ex e --<<.点睛：本题考查了函数的单调性,零点问题，考查导数的应用以及不等式的证明，零点存在性定理，考查分类讨论思想，转化思想，构造函数的解题方法. 2．设函数f (x )＝x 2＋bx －1(b ∈R )． (1)当b ＝1时证明：函数f (x )在区间1,12⎛⎫⎪⎝⎭内存在唯一零点； (2)若当x ∈[1,2]，不等式f (x )<1有解．求实数b 的取值范围．【答案】（1）见解析；（2）(),1-∞【解析】试题分析：（1）先根据对称轴与定义区间位置关系确定函数f (x )在区间1,12⎛⎫⎪⎝⎭单调性，再根据区间端点函数值异号，结合零点存在定理确定零点个数（2）先分离变量化为对应函数最值问题： 2b x x<- ，再根据函数单调性确定函数最小值，即得实数b 的取值范围．(2)由题意可知x2＋bx－1<1在区间[1,2]上有解，所以b<＝－x在区间[1,2]上有解．令g(x)＝－x，可得g(x)在区间[1,2]上递减，所以b<g(x)max＝g(1)＝2－1＝1 ，从而实数b的取值范围为(－∞，1)．点睛：利用零点存在性定理不仅要求函数的图象在区间[a，b]上是连续不断的曲线，且f(a)·f(b)<0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点3．已知函数()()210f x ax mx m a =++-≠.（1）若()10f -=，判断函数()f x 的零点个数；（2）若对任意实数m ，函数()f x 恒有两个相异的零点，求实数a 的取值范围；（3）已知12,x x R ∈R 且12x x <， ()()12f x f x ≠，求证：方程()()()1212f x f x f x ⎡⎤=+⎣⎦ 在区间()12,x x 上有实数根.【答案】⑴见解析;⑵01a <<;⑶见解析.【解析】试题分析：（1）利用判别式定二次函数的零点个数：（2）零点个数问题转化为图象交点个数问题，利用判别式处理即可；（3）方程()()()1212f x f x f x ⎡⎤=+⎣⎦在区间()12,x x 上有实数根，即()()()()1212g x f x f x f x ⎡⎤=-+⎣⎦有零点，结合零点存在定理可以证明. 试题解析：⑴()10,10,1f a m m a -=∴-+-=∴=()21f x x mx m ∴=++-()()22412m m m ∆=--=-,当2m =时， 0∆=，函数()f x 有一个零点；当2m ≠时， 0∆> ，函数()f x 有两个零点⑶设()()()()1212g x f x f x f x ⎡⎤=-+⎣⎦，则()()()()()()1112121122g x f x f x f x f x f x ⎡⎤⎡⎤=-+=-⎣⎦⎣⎦ ()()()()()()2212211122g x f x f x f x f x f x ⎡⎤⎡⎤=-+=-⎣⎦⎣⎦ ()()12f x f x ≠()()()()21212104g x g x f x f x ⎡⎤∴⋅=--<⎣⎦,()0g x ∴=在区间()12,x x 上有实数根，即方程()()()1212f x f x f x ⎡⎤=+⎣⎦在区间()12,x x 上有实数根. 点睛：已知函数有零点求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； (2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．4．已知函数()2ln f x a x bx =-图象上一点()()2,2P f 处的切线方程为32ln22y x =-++.(1)求,a b 的值;(2)若方程()0f x m +=在1,e e⎡⎤⎢⎥⎣⎦内有两个不等实根,求m 的取值范围(其中e 2.71828= 为自然对数的底).【答案】(1)a =2,b =1.(2) 2112em <≤+. 【解析】试题分析：本题考查函数与方程，函数与导数的综合应用．(1)根据导数的几何意义，得出两个方程，然后求解．(2)先利用导数研究函数h (x )=f (x )+m =2lnx ﹣x 2+m 的单调性，根据单调性与极值点确定关系然后求解．。

2018高考数学备考百日闯关江苏专版专题2.1以解析几何中定点、定值为背景的解答题附解析

2018高考数学备考百日闯关江苏专版专题2.1以解析几何中定点、定值为背景的解答题附解析专题二压轴解答题第一讲以解析几何中定点、定值为背景的解答题【名师综述】解析几何中的定值、定点、定线问题仍是高考考试的重点与难点，都是探求"变中有不变的量".一般运用函数与方程、转化与化归、数形结合、分类讨论、特殊到一般、相关点法、设而不求、换元、消元等基本思想方法. 类型一定值问题典例 1 如图，在平面直角坐标系xOy 中，已知椭圆2222:1(0)x y E a b a b +=>>的离心率为2，左焦点()2,0F -，直线:l y t =与椭圆交于,A B 两点， M 为椭圆上异于,A B 的点.（1）求椭圆E 的方程；（2）若()1M -，以AB 为直径的圆P 过M 点，求圆P 的标准方程；（3）设直线,MA MB 与y 轴分别交于,C D ，证明： OC OD ⋅为定值.【答案】（1）22184x y +=（2）2217039x y ⎛⎫+-= ⎪⎝⎭（3）见解析【解析】（2）设(),A s t ，则(),B s t -，且2228s t +=.① ∵以AB 为直径的圆P 过M 点 ∴MA MB ⊥ ∴0MA MB ⋅=，又∵()1MA s t =++，()1MB s t =-+∴()22610s t -++=.②由①②解得： 13t =，或1t =-（舍） ∴2709s =. 又∵圆P 的圆心为AB 的中点()0,t ，半径为2ABs =， ∴圆P 的标准方程为2217039x y ⎛⎫+-= ⎪⎝⎭.（3）设()00,M x y ，则MA l 的方程为()0000t y y y x x s x --=--，若k 不存在，显然不符合条件. 令0x =得000C tx sy y s x --=-；同理00D tx sy y s x --=--，∴OC OD⋅000000C D tx sy tx sy y y s x s x -+--=⋅=⋅---222222220000222200t x s y t x s y x x x s--==-- ()()()2222002282828282t y t y y t ---=--- 2202288422t y t y -==-为定值. 【名师指点】对于定值问题，可以通过特殊位置、特殊图形、特殊数学来寻求定值再证明，或者可以直接通过运算求解求得；而范围问题需将所求量用变量表示，利用函数与方程思想求解．【举一反三】如图，在平面直角坐标系xOy 中，已知椭圆22221(0)x y a b a b +=>>的离心率为12，且过点312⎛⎫⎪⎝⎭，.F 为椭圆的右焦点， ,A B 为椭圆上关于原点对称的两点，连接,AF BF 分别交椭圆于,C D 两点.⑴求椭圆的标准方程； ⑵若AF FC =，求BFFD的值； ⑶设直线AB ， CD 的斜率分别为1k ， 2k ，是否存在实数m ，使得21k mk =，若存在，求出m 的值；若不存在，请说明理由.【答案】（1）22143x y +=（2）73 （3）53m = 【解析】（2）若AF FC =，由椭圆对称性，知31,2A ⎛⎫ ⎪⎝⎭，所以31,2B ⎛⎫-- ⎪⎝⎭，此时直线BF 方程为3430x y --=，由223430,{ 1,43x y x y--=+=，得276130x x --=，解得137x =（1x =-舍去），故()11713317BF FD --==-．（3）设00,)A x y （，则()00,B x y --，直线AF 的方程为()0011y y x x =--，代入椭圆方程22143x y +=，得()2220000156815240x x y x x ---+=，因为0x x =是该方程的一个解，所以C 点的横坐标08552C x x x -=-，又(),c C C x y 在直线()0011y y x x =--上，所以()000031152Cc y y y x x x -=-=--，同理， D 点坐标为0085(52x x ++， 03)52y x +，所以000002100000335252558585335252y y x x y k k x x x x x --+-===+--+-，即存在53m =，使得2153k k =．类型二定点问题典例2 已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ， 2F ，B 为椭圆的上顶点， 12BF F ∆A 为椭圆的右顶点.（Ⅰ）求椭圆C 的方程；（Ⅱ）若直线:l y kx m =+与椭圆C 相交于,M N 两点（,M N 不是左、右顶点），且满足MA NA ⊥，试问：直线l 是否过定点？若过定点，求出该定点的坐标，否则说明理由.【答案】(Ⅰ) 22143x y +=；（Ⅱ）直线l 过定点，定点坐标为207⎛⎫⎪⎝⎭，. 【解析】（Ⅱ）设()11M x y ，， ()22N x y ，，联立22{ 1.43y kx m x y =++=，得()()222348430k x mkx m +++-=， ()()22222264163430340m k k mk m ∆=-+->+->，即()1222122834{ 43·.34mkx x km x x k +=-+-=+，又()()()()22221212121223434m k y y kx m kx m k x x mk x x m k -=++=+++=+，因为椭圆的右顶点为()20A ，， ∴1MA NA k k =-，即1212·122y yx x =---， ∴()121212240y y x x x x +-++=，∴()()22222234431640343434m k mmkkkk--+++=+++，∴2271640m mk k ++=．解得： 12m k =-， 227km =-，且均满足22340k m +->，当12m k =-时， l 的方程为()2y k x =-，直线过定点()20，，与已知矛盾；当227k m =-时， l 的方程为27y k x ⎛⎫=- ⎪⎝⎭，直线过定点207⎛⎫⎪⎝⎭，．所以，直线l 过定点，定点坐标为207⎛⎫ ⎪⎝⎭，【名师指点】解析几何中有关定点问题等综合性问题，它涉及到解析几何中的定义、几何性质、直线与圆锥曲线位置关系，同时又与三角函数、函数、不等式、方程、平面向量等代数知识紧密联系，解这类问题时，需要有较强的代数运算能力和图形识别能力，要能准确地进行数与形的语言转换和运算、推理转换，并在运算过程中注意思维的严密性，以保证结果的完整性．【举一反三】已知定点()3,0A -、()3,0B ，直线AM 、BM 相交于点M ，且它们的斜率之积为19-，记动点M 的轨迹为曲线C . （Ⅰ）求曲线C 的方程；（Ⅱ）过点()1,0T 的直线l 与曲线C 交于P 、Q 两点，是否存在定点(),0S s ，使得直线SP 与SQ 斜率之积为定值，若存在求出S 坐标；若不存在请说明理由.【答案】(1) 曲线C 的方程为2219x y += ()3x ≠±;(2)见解析. 【解析】（Ⅱ）由已知直线l 过点()1,0T ，设l 的方程为1x my =+，则联立方程组221{99x my x y =++=，消去x 得 ()229280m y my ++-=,设()()1122,,,P x y Q x y ，则12212229{89m y y m y y m +=-+-=+，直线SP 与SQ 斜率分别为11111SP y y k x s my s ==-+- ， 22221SQ y y k x s my s==-+-， ()()121111SP SP y y k k my s my s =+-+-()()()1222121211y y m y y m s y y s =+-++-()()2228991sm s -=-+-.当3s =时， ()282991SP SP k k s -==--；当3s =-时， ()2811891SP SP k k s -==--. 所以存在定点()3,0S ±，使得直线SP 与SQ 斜率之积为定值. 类型三定线问题典例3 已知抛物线C ： 22y px =（0p >）的焦点是椭圆M ： 22221x y a b+=（0a b >>）的右焦点，且两曲线有公共点23⎛ ⎝⎭（1）求椭圆M 的方程；（2）椭圆M 的左、右顶点分别为1A ， 2A ，若过点()40B ，且斜率不为零的直线l 与椭圆M 交于P ， Q 两点，已知直线1A P 与2A Q 相较于点G ，试判断点G 是否在一定直线上？若在，请求出定直线的方程；若不在，请说明理由.【答案】(1) 22143x y += (2) 点G 在定直线1x =上【解析】∴22221{ 424199a b a b-=+=，解得224,3a b ==，椭圆M 的方程为22143x y += （2）方法一当点P 为椭圆的上顶点时，直线l40y +-=，此时点(P ，85Q ⎛ ⎝⎭，则直线120A P l y -+=和直线2:20A Q l y +-=，联立20 20y y -+=+-=，解得G ⎛ ⎝⎭，当点P 为椭圆的下顶点时，由对称性知：1,2G ⎛⎫- ⎪ ⎪⎝⎭. 猜想点G 在直线1x =上，证明如下：由条件可得直线PQ 的斜率存在，设直线()():40PQ y k x k =-≠，联立方程()224{34120y k x x y =-+-=，消y 得： ()2222343264120k x k x k +-+-=有两个不等的实根，()()()24222324434163169140k k k k ∆=-⋅+-=⋅->， 2104k ∴<<设()()1122,,,P x y Q x y ，则21223234k x x k +=+， ()21226412*34k x x k -⋅=+则直线()111:22A P y l y x x =++与直线()222:22A Q yl y x x =-- 联立两直线方程得()()12122222y yx x x x +=-+-（其中x 为G 点横坐标）将1x =代入上述方程中可得1212322y y x x -=+-，即()()()()122134242k x x k x x --=--+，即证()1212410160x x x x -++= 将()*代入上式可得()2222464121032163434k kk k ⨯-⨯-+++()2222161632034034k k k k --++==+，此式成立∴点G 在定直线1x =上. 方法二由条件可得直线PQ 的斜率存在，设直线()():40PQ y k x k =-≠ 联立方程()224{34120y k x x y =-+-=，消y 得： ()2222343264120k x k x k +-+-=有两个不等的实根，()()()24222324434163169140k k k k ∆=-⋅+-=⋅->， 2104k ∴<<设()()()112233,,,,,P x y Q x y G x y ，则21223234k x x k+=+， 2122641234k x x k -⋅=+12x x ∴-==由1A ，P ， G 三点共线，有： 311322y y x x =++ 由2A ， Q ， G 三点共线，有：323222y y x x =-- 上两式相比得()()()()()()212133121224222242y x k x x x x y x k x x +-++==---- ()()()()12122112121238338x x x x x x x x x x x x -++--==--++-+，解得31x =∴点G 在定直线1x =上．【名师指点】设而不求方法、整体思想和消元的思想的运用可有效地简化运算.【举一反三】如图，设椭圆22221(0)x y a b a b +=>>的左、右焦点分别为12,F F ，点D 在椭圆上，112DF F F ⊥，121||||F F DF =12DF F ∆的面积为2. （1）求该椭圆的标准方程；（2）是否存在圆心在y 轴上的圆，使圆在x 轴的上方与椭圆两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点？若存在，求圆的方程，若不存在，请说明理由.【答案】（1）2212x y +=；（2）存在满足条件的圆，其方程为2253239x y ⎛⎫+-= ⎪⎝⎭. 【解析】从而1DF =112DF F F ⊥得222211292DF DF F F =+=，因此2DF =所以122a DF DF =+=2221a b a c ==-=因此，所求椭圆的标准方程为：2212x y +=【精选名校模拟】1．在平面直角坐标系xOy 中，已知直线y x =与椭圆22221(0)x y a b a b+=>>交于点A ， B （A 在x 轴上方），且AB =.设点A 在x 轴上的射影为N ，三角形ABN 的面积为2（如图1）. （1）求椭圆的方程；（2）设平行于AB 的直线与椭圆相交，其弦的中点为Q . ①求证：直线OQ 的斜率为定值；②设直线OQ 与椭圆相交于两点C ， D （D 在x 轴上方），点P 为椭圆上异于A ， B ， C ， D 一点，直线PA 交CD 于点E ， PC 交AB 于点F ，如图2，求证： AF CE ⋅为定值.【答案】（1）22163x y += (2) ①12-②【解析】(2)设平行AB 的直线的方程为y x m =+，且0m ≠，① 联立22{ 163y x mx y =++=，得到2234260x mx m ++-=，所以12223Q x x m x +==-， 3Q Q my x m =+=；故，直线OQ 的斜率为13=223Q OQ Q m y k m x ==--（定值）②由题意可知1,:,:2A AB y x OQ y x ==-，联立方程组221,2{1,63y x x y =-+=得()()2,1,2,1,C D --设()00,P x y ，先考虑直线斜率都存在的情形：直线:AP y x =，联立方程组：{12y x y x==-得x y y x E ⎛⎫--,直线()001:122y PC y x x ++=--, 联立方程组： ()001122{y y x x y x++=--=得0000000022,33x y x y F y x y x ⎛⎫++ ⎪+-+-⎝⎭,则000023x y AF y x +==+-CE ==，所以AF CE ⋅==当直线斜率不存在时结果仍然成立.2．如图，在平面直角坐标系xOy 中，过椭圆C ： 2214x y +=的左顶点A 作直线l ，与椭圆C 和y 轴正半轴分别交于点P ， Q ．（1）若AP PQ =，求直线l 的斜率；（2）过原点O 作直线l 的平行线，与椭圆C 交于点M N ，，求证：2AP AQMN ⋅为定值．【答案】（1）k =2）见解析。

2018届高考数学二轮复习函数的零点与方程专项练 ppt课件(全国通用)

�� =1 ��
于( B ) A.4n B.2n
C.n
D.0
-10一、选择题二、填空题
解析: 由题意,得f(x)的图象关于点(2,0)对称;
�� 2 -4�� + 4,�� > 2, 由 g(x)= 2 可得图象如下: -�� + 4��-4,�� < 2, g(x)的图象也关于点(2,0)对称,即有f(x)与g(x)的交点关于点(2,0)对称,
解析: 函数f(x)=2ax-a+3,由∃x0∈(-1,1),f(x0)=0,可得(-3a+3)(a+3)<0, 解得a∈(-∞,-3)∪(1,+∞). 5.已知函数f(x)=ex+x,g(x)=ln x+x,h(x)=ln x-1的零点依次为a,b,c,则 ( A ) A.a<b<c B.c<b<a C.c<a<b D.b<a<c 解析: 由f(a)=ea+a=0,得a=-ea<0;b是函数y=ln x和y=-x图象交点的横坐标,画图(图略)可知0<b<1;由h(c)=ln c-1=0知c=e,所以a<b<c.
解析: 设sin x=t,则0<t≤1,则方程等价于f(t)=4t2-mt+1在(0,1]内有惟
�� = ��2 -16 = 0, �� 一解,即或f(1)=5-m<0(f(0)=1).解得m=4或m>5. 0 < < 1, 8
-7一、选择题二、填空题
4.(2017湖北武昌1月调研,理5)已知函数f(x)=2ax-a+3,若∃x0∈(1,1),f(x0)=0,则实数a的取值范围是( A ) A.(-∞,-3)∪(1,+∞) B.(-∞,-3) C.(-3,1) D.(1,+∞)

专题3.6+以函数、不等式与导数相结合的综合问题为解答题-2018年高考数学备考优生百日闯关系列+word版含解析

专题三压轴解答题第五关以函数、不等式与导数相结合的综合问题为解答题【名师综述】1.本专题在高考中的地位导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出 2．本专题在高考中的命题方向及命题角度从高考来看，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，往往与解析几何、微积分相联系． (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数． (3)利用导数求函数的最值(极值)，解决生活中的优化问题． (4)考查数形结合思想的应用类型一用导数研究函数的性质典例1 【安徽省滁州市2018届高三上学期期末考试】已知函数()2ln f x x x x =--.（1）求函数()f x 的极值；（2）若1x ， 2x 是方程()2ax f x x x +=-（0a >）的两个不同的实数根，求证： 12ln ln 2ln 0x x a ++<.【解析】（1）依题意， ()212121x x f x x x x ='--=-- ()()211x x x+-=故当()01x ∈，时， ()0f x '<，当()1x ∈+∞，时， ()0f x '> 故当1x =时，函数()f x 有极小值()10f =，无极大值.（2）因为1x ， 2x 是方程()2ax f x x x +=-的两个不同的实数根.∴()()112201{ 02ax lnx ax lnx -=-=两式相减得()2121ln 0x a x x x -+=，解得2121lnx x a x x =-要证： 12ln ln 2ln 0x x a ++<，即证： 1221x x a <，即证： ()2211221ln x x x x x x -<⎛⎫⎪⎝⎭，即证()222122111212ln 2x x x x xx x x x x -⎛⎫<=-+ ⎪⎝⎭，不妨设12x x <，令211x t x =>.只需证21ln 2t t t <-+.设()21ln 2g t t t t=--+，∴()22111ln 12ln g t t t t t t t t ⎛⎫=-+=-+ ⎝'⎪⎭；令()12ln h t t t t =-+，∴()22211110h t t t t ⎛⎫=--=--< ⎪⎝⎭'，∴()h t 在()1+∞，上单调递减，∴()()1h t h < 0=，∴()0g t '<，∴()g t 在()1+∞，为减函数，∴()()10g t g <=.即21ln 2t t t<-+在()1+∞，恒成立，∴原不等式成立，即12ln ln 2ln 0x x a ++<.【名师指点】利用导数可以研究函数的单调性、函数图像、极值点、最值、零点等性质，常用的到的方法为：1、利用对于确定函数求单调区间问题，先求定义域，然后解不等式'()0f x >和定义域求交集得单调递增区间；解不等式'()0f x <和定义域求交集得单调递减区间.2、对于含参数的函数求单调区间问题，转化为判断导函数符号，可结合函数图象判断.3、求函数的极值，先求'()0f x =的根0x ，再和函数定义域比较，如果落在定义域外或者落在定义域端点，此时函数单调，无极值；当落在定义域内时，将定义域分段，分别考虑0x 两侧导数是否异号，从而判断是否有极值.4、求函数的最值和求极值类似，先求'()0f x =的根0x ，如果落在定义域外或者落在定义域端点，此时函数单调，利用单调性求最值；当落在定义域内时，将定义域分段，分别考虑0x 两侧导数是否异号，从而判断函数大致图象，从而求最值.【举一反三】【天津市部分区2018届高三上学期期末考试】已知函数()()ln 1f x x a x =+-， a R ∈. （1）讨论()f x 的单调性；（2）当12a =-时，令()()212g x x f x =--，其导函数为()'g x ，设12,x x 是函数()g x 的两个零点，判断122x x +是否为()'g x 的零点？并说明理由.（2）122x x +不是导函数()g x '的零点. 证明如下：由（Ⅰ）知函数()22ln g x x x x =--. ∵1x ， 2x 是函数()g x 的两个零点，不妨设120x x <<，∴22111111222222222ln 02ln { { 2ln 02ln x x x x x x x x x x x x --=-=⇒--=-=，两式相减得： ()()()12121212ln ln x x x x x x -+-=-即： ()1212122ln ln 1x x x x x x -+-=-又()221g x x x-'=-. 则()1212121212122ln ln 4412x x x x g x x x x x x x x -+⎛⎫=+--=-⎪+-+⎝⎭' ()()1212121222ln ln x x x x x x x x ⎡⎤-=--⎢⎥-+⎣⎦. 设12x t x =，∵120x x <<，∴01t <<，令()()21ln 1t t t t ϕ-=-+， ()()()()22211411t t t t t t ϕ-=-=+'+.又01t <<，∴()0t ϕ'>，∴()t ϕ在()0,1上是増函数，则()()10t ϕϕ<=，即当01t <<时， ()21ln 01t t t --<+，从而()()1212122ln ln 0x x x x x x ---<+，又121200x x x x <<⇒-<所以()()1212121222ln ln 0x x x x x x x x ⎡⎤--->⎢⎥-+⎣⎦，故1202x x g +⎛⎫>⎪⎝⎭'，所以122x x +不是导函数()g x '的零点. 类型2 导数、函数与不等式典例2 已知函数()2ln ,f x x ax x a R =+-∈．（1）若函数()f x 在[]1,2上是减函数，求实数a 的取值范围；（2）令()()2g x f x x =-，是否存在实数a ，当(]0,x e ∈（e 是自然常数）时，函数()g x 的最小值是3，若存在，求出a 的值；若不存在，说明理由；（3）当(]0,x e ∈时，证明：()2251ln 2e x xx x ->+．【答案】（1（2）存在实数2a e =，使得当(]0,x e ∈时()g x 有最小值3；（3）详见解析．综上，存在实数2a e =，使得当(]0,x e ∈时()g x 有最小值3．【名师指点】证明不等式()()f x g x ≥成立，可以构造函数()()()H x f x g x =-，通过证明函数()H x 的最小值大于等于零即可，可是有时候利用导数求函数()H x 最小值不易，可以通过特例法，即证明()f x 的最小值大于等于()g x 的最大值即可．【举一反三】【湖南省郴州市一中2018届高三十二月月考理科】设函数()()1ln 2f x a x x a R x=+-∈. （1）当3a =时，求()f x 的极值；（2）当1a =时，证明： ()122x ef x x e->-+. 【解析】（1）当3a =时， ()13ln 2f x x x x=+-， ()231'2f x x x =--= ()()222211231(0)x x x x x x x ---+-=->，当10,2x ⎛⎫∈ ⎪⎝⎭时， ()'0f x <， ()f x 在10,2⎛⎫ ⎪⎝⎭上单调递减；当1,12x ⎛⎫∈⎪⎝⎭时， ()'0f x >， ()f x 在1,12⎛⎫⎪⎝⎭上单调递增；当()1,x ∈+∞时， ()'0f x <， ()f x 在()1,+∞上单调递减.所以，当12x =， ()f x 取得极小值113ln22f ⎛⎫=- ⎪⎝⎭；当1x =时， ()f x 取得极大值()11f =-.所以()1111g x g e e⎛⎫≥+=-⎪⎝⎭. 令()()1xe x h x e -=，则()()2'xe x h x e -=，在()1,2上， ()'0h x >， ()h x 是增函数；在()2,+∞上， ()'0h x <， ()h x 是减函数，所以()()1121h x h e e≤=<-，所以()()h x g x <，即()()()11ln 11xe x x x e -<--+，即()()()11ln 11xe x x x e ---+>，由此可知()122xef x x e ->-+. 类型三、恒成立及求参数范围问题典例3 【安徽省蚌埠市2018届高三上学期第一次教学质量检查】已知函数()ln f x x =，()()2g x a e x b =-+（其中e 为自然对数的底数， ()f x ）.（1）若函数()f x 的图象与函数()g x 的图象相切于1x e=处，求,a b 的值；（2）当2b e a =-时，若不等式()()f x g x ≤恒成立，求a 的最小值.【解析】（1）2a e =， 1b =-．（过程略）（2）令()()()()()ln h x f x g x x e a x e a =-=+---，则()()1h x e a x+'=-，当a e ≤时， ()h x 单调递增，而()10h =， ∴()1,x ∈+∞时， ()0h x >不合题意当a e >时，令()0h x '=，则1x a e=-， ∵()h x '为减函数， ∴10,x a e ⎛⎫∈ ⎪-⎝⎭时， ()0h x '>， ()h x 单调递增， 1,x a e ⎛⎫∈+∞ ⎪-⎝⎭时， ()0h x '<， ()h x 单调递减，∴()max 1h x h a e ⎛⎫==⎪-⎝⎭()()ln 10a e e a -----≤，即()()ln 1a e a e -≥--．（△）但0,ln 1x x x ∀>≤-，等号成立当且仅当且1x =．故（△）式成立只能1a e -= 即1a e =-．【名师指点】将已知恒成立的不等式由等价原理把参数和变量分离开，转化为一个已知函数的最值问题处理，关键是搞清楚哪个是变量哪个是参数，一般遵循“知道谁的范围，谁是变量；求谁的范围，谁是参数”的原则．常用方法有参变分离法和构造函数法．【举一反三】已知函数1ln )1(21)(2>-+-=a x a ax x x f ，． (1)求()f x 的单调区间；(2)若x x a x g ln )2()(--=,)()(x g x f ≥在区间),[+∞e 恒成立,求a 的取值范围．解析：(1)()f x 的定义域为(0,)+∞.2'11(1)(1)()a x ax a x x a f x x a x x x --+--+-=-+== ，（i ）若11a -=即2a =,则2'(1)()x f x x-=故()f x 在(0,)+∞单调增加. (ii)若11a -<,而1a >,故12a <<,则当(1,1)x a ∈-时，'()0f x <;当(0,1)x a ∈-或(1,)x ∈+∞时，'()0f x >；故()f x 在(1,1)a -单调减少，在(0,1),(1,)a -+∞单调增加.【精选名校模拟】1．【山东省济南市2018届高三上学期期末考试数学】已知函数()()ln R f x ax x a =-∈. （1）求函数()f x 的单调区间；（2）若函数()f x 有两个零点12,x x ，证明12112ln ln x x +>. 【解析】1）()()110ax f x a x x x-=-=>' 当0a ≤时， ()0f x '<，所以()f x 在()0,+∞上单调递减；当0a >时， ()0f x '=，得1x a=10,x a ⎛⎫∀∈ ⎪⎝⎭都有()0f x '<， ()f x 在10,a ⎛⎫⎪⎝⎭上单调递减；1,x a ⎛⎫∀∈+∞ ⎪⎝⎭都有()0f x '>， ()f x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递增.综上：当0a ≤时， ()f x 在()0,+∞上单调递减，无单调递增区间；当0a >时， ()f x 在10,a ⎛⎫ ⎪⎝⎭单调递减， ()f x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递增. （2）函数()f x 有两个零点分别为12,x x ，不妨设12x x <则11ln 0x ax -=， 22ln 0x ax -=()2121ln ln x x a x x -=-要证：12112ln ln x x +> 只需证：12112a x x +>只需证： 12122x x a x x +> 只需证：12211221ln ln 2x x x x x x x x +->- 只需证： 22212121ln 2x x xx x x ->只需证： 2211121ln2x x x x x x ⎛⎫<- ⎪⎝⎭令211x t x =>，即证11ln 2t t t ⎛⎫<- ⎪⎝⎭设()11ln 2t t t t φ⎛⎫=-- ⎪⎝⎭，则()222102t t t t φ'--=<，即函数()t φ在()1,+∞单调递减则()()10t φφ<= 即得12112ln ln x x +> 2．【河南省周口市2018届高三上学期期末抽测调研】已知函数()()28ln f x x x a x a R =-+∈ （Ⅰ）当1x =时， ()f x 取得极值，求a 的值；（Ⅱ）当函数()f x 有两个极值点1212,()x x x x <，且11x ≠时，总有()11ln 21a x m x >-- ()21143x x +-成立，求m 的取值范围.（Ⅱ）()f x 定义域为()0,+∞，有两个极值点1212,()x x x x <，则()2280t x x x a =-+=在()0,+∞上有两个不等正根所以()6480{00 20a t a x ∆=->=>=>，所以08a <<1212124{ 20x x ax x x x +==<<.所以()211211124{224 0x x a x x x x x x =-==-<<，所以102x <<这样原问题即102x <<且11x ≠时，()()21111ln 2431a x m x x x >-+--成立即()()()()11111124ln 2411x x x m x x x ->--+-即()()11112ln 211x x m x x >-+-即()()11112ln 2101x x m x x --+>-，即()()211111212ln 01m x x x x x ⎡⎤--⎢⎥+>-⎢⎥⎣⎦且1111110101{1201x x x x x x <-<<<-时时设()()()2212ln (02)m x h x x x x--=+<<()()()22222'(02)m x x m h x x x -++-=<<①2m =时， ()2'0h x x=>，所以()h x 在()0,2上为增函数且()10h =，所以， ()1,2x ∈时， ()0h x >不合题意舍去. ②2m >时， ()'0h x >同①舍去 ③2m <时（ⅰ）0∆≤，即1m ≤时可知()'0h x ≤，在()0,2上()h x 为减函数且()10h =，这样01x <<时， ()0h x >， 12x <<时()0h x <，这样()()2212ln 01m x x x x x⎡⎤--⎢⎥+>-⎢⎥⎣⎦成立（ⅱ）0∆>，即2l m <<时()'h x 分子中的一元二次函数的对称轴112x m=>-开口向下，且1的函数值为()210m -> 令1min ,22a m ⎧⎫=⎨⎬-⎩⎭，则()1,x a ∈时， ()'0h x >， ()h x 为增函数， ()10h =所以， ()0h x >故舍去综上可知： 1m ≤3．【广西南宁市第二中学2018届高三1月月考（期末）】已知函数()ln 1af x x x=+-， a R ∈. （1）若关于x 的不等式()112f x x ≤-在[)1,+∞上恒成立，求a 的取值范围；（2）设函数()()f xg x x=，若()g x 在21,e ⎡⎤⎣⎦上存在极值，求a 的取值范围，并判断极值的正负.【解析】（Ⅰ）由()112f x x ≤-，得11112a nx x x +-≤-．即2112a x nx x ≤-+在[)1,+∞上恒成立设函数()2112m x x nx x =-+， 1x ≥．则()'11m x nx x =-+-．设()11n x nx x =-+-．则()1'1n x x=-+．易知当1x ≥时， ()'0n x ≥． ∴()n x 在[)1,+∞上单调递增，且()()10n x n ≥=．即()()''10m x m ≥=对[)1,x ∈+∞恒成立． ∴()m x 在[)1,+∞上单调递增． ∴当[)1,x ∈+∞时， ()()()min 112m x m x m >==． ∴12a ≤，即a 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦．结合函数图象可知，若()g x 在21,e ⎡⎤⎣⎦上存在极值，则()()0{10h e h ><或()()210{h h e ≥<．（ⅰ）当()()0{10h e h ><，即12ea <<时，则必定212,1,x x e ⎡⎤∃∈⎣⎦，使得()()120h x h x ==，且2121x e x e <<<<．当x 变化时， ()h x ， ()'g x ， ()g x 的变化情况如下表：∴当12e a <<时， ()g x 在21,e ⎡⎤⎣⎦上的极值为()()12,g x g x ，且()()12g x g x <． ∵()11211111nx a g x x x x =+- 111211x nx x ax -+=．设()1x x nx x a ϕ=-+，其中12ea <<， 1x e ≤<． ∵()'10x nx ϕ=>，∴()x ϕ在()1,e 上单调递增， ()()110x a ϕϕ≥=->，当且仅当1x =时取等号． ∵11x e <<，∴()10g x >． ∴当12e a <<时， ()g x 在21,e ⎡⎤⎣⎦上的极值()()210g x g x >>．综上所述：当02e a <<时， ()g x 在21,e ⎡⎤⎣⎦上存在极值，且极值都为正数．注：也可由()'0g x =，得221a x x nx =-．令()21h x x x nx =-后再研究()g x 在21,e ⎡⎤⎣⎦上的极值问题．4．【衡水金卷2018年普通高等学校招生全国统一考试模拟试卷】已知函数()()21ln f x a x x =-+， a R ∈. （1）当2a =时，求函数()y f x =在点()()1,1P f 处的切线方程；（2）当1a =-时，令函数()()ln 21g x f x x x m =+-++，若函数()g x 在区间1,e e ⎡⎤⎢⎥⎣⎦上有两个零点，求实数m 的取值范围.【解析】（1）当2a =时， ()()221ln f x x x =-+ 224ln 2x x x =-++.当1x =时， ()10f =，所以点()()1,1P f 为()1,0P ，又()1'44f x x x=-+，因此()'11k f ==. 因此所求切线方程为()0111y x y x -=⨯-⇒=-. （2）当1a =-时， ()22ln g x x x m =-+，则()()()2112'2x x g x x x x -+-=-=. 因为1,x e e ⎡⎤∈⎢⎥⎣⎦，所以当()'0g x =时， 1x =，且当11x e<<时， ()'0g x >；当1x e <<时， ()'0g x <；故()g x 在1x =处取得极大值也即最大值()11g m =-. 又2112g m e e⎛⎫=--⎪⎝⎭， ()22g e m e =+-， ()221122g e g m e m e e ⎛⎫-=+--++ ⎪⎝⎭24e =-+ 210e <，则()1g e g e ⎛⎫< ⎪⎝⎭，所以()g x 在区间1,e e⎡⎤⎢⎥⎣⎦上的最小值为()g e ，故()g x 在区间1,e e⎡⎤⎢⎥⎣⎦上有两个零点的条件是()2110{ 1120g m g m e e =->⎛⎫=--≤ ⎪⎝⎭2112m e ⇒<≤+，所以实数m 的取值范围是211,2e ⎛⎤+⎥⎝⎦. 5．【湖北省武昌2018届元月调研考试数学】已知a 的实常数，函数()2x f x e ax -=-.（1）讨论函数()f x 的单调性；（2）若函数()f x 有两个不同的零点1212,()x x x x <，（ⅰ）求实数a 的取值范围；（ⅱ）证明： 122x x +>.（2）（ⅰ）由（1）知，当0a ≤时， ()f x 单调递增，没有两个不同的零点. 当0a >时， ()f x 在2ln x a =+处取得极小值. 由()()ln 2ln e2ln 0af a a a +=-+<，得1a e>.所以a 的取值范围为1,e⎛⎫+∞ ⎪⎝⎭. （ⅱ）由2e0x ax --=，得()2ln ln ln x ax a x -==+，即2ln ln x x a --=.所以11222ln 2ln ln x x x x a --=--=. 令()2ln g x x x =--，则()11g x x'=-. 当1x >时， ()0g x '>；当01x <<时， ()0g x '<. 所以()g x 在()0,1递减，在()1,+∞递增，所以1201x x <<<. 要证122x x +>，只需证2121x x >->.因为()g x 在()1,+∞递增，所以只需证()()212g x g x >-.因为()()12g x g x =，只需证()()112g x g x >-，即证()()1120g x g x -->. 令()()()2h x g x g x =--， 01x <<，则()()()11222h x g x g x x x ⎛⎫=--=-+-''⎝'⎪⎭. 因为()1111122222x x x x x x ⎛⎫⎡⎤+=+-+≥ ⎪⎣⎦--⎝⎭，所以()0h x '≤，即()h x 在()0,1上单调递减. 所以()()10h x h >=，即()()1120g x g x -->，所以122x x +>成立.6．【山西省吕梁市2018届高三上学期第一次模拟考试】已知函数()()ln xe f x a x x x=--. （1）当0a ≤时，试求()f x 的单调区间；（2）若()f x 在()0,1内有极值，试求a 的取值范围. 【解析】（Ⅰ）()()2e 111x xf x a x x -⎛⎫=-- ⎝'⎪⎭()()2e 11x x ax x x ---=， ()()2e 1xax x x--=．当0a ≤时，对于()0,x ∀∈+∞， e 0xax ->恒成立，所以 ()0f x '> 1x >； ()0f x '< 01x <<0. 所以单调增区间为()1,+∞，单调减区间为()0,1 ．（Ⅱ）若()f x 在()0,1内有极值，则()f x '在()0,1x ∈内有解．令()()()2e10xax x f x x --==' e 0xax -= e xa x= .设()e xg x x= ()0,1x ∈,所以 ()()e 1x x g x x='-, 当()0,1x ∈时， ()0g x '<恒成立，所以()g x 单调递减.又因为()1e g =，又当0x →时， ()g x →+∞, 即()g x 在()0,1x ∈上的值域为()e,+∞,所以当e a >时， ()()()2e 10xax x f x x --==' 有解.设()e xH x ax =-，则 ()e 0xH x a ='-< ()0,1x ∈，所以()H x 在()0,1x ∈单调递减. 因为()010H =>， ()1e 0H a =-<,所以()e xH x ax =-在()0,1x ∈有唯一解0x .所以有：所以当e a >时， ()f x 在()0,1内有极值且唯一.当e a ≤时，当()0,1x ∈时， ()0f x '≥恒成立， ()f x 单调递增，不成立．综上， a 的取值范围为()e,+∞．7．【四川省2017-2018年度高三“联测促改”活动理科数学试题】已知函数()ln xf x e x =+.（1）求函数()'y f x =在[)1,x ∈+∞上的最小值；（2）若对任意[)1,x ∈+∞恒有()()1f x e m x ≥+-，求实数m 的取值范围. 【解析】（1）由于()()1'x y h x f x e x ===+，则()21'xh x e x=-，则当()1,x ∈+∞时， 21,1xe e x ><，所以()'0h x >，即()h x 在()1,+∞上是增函数，于是y 在[)1,+∞上的最小值为()11h e =+．（2）考虑函数()()()1g x f x e m x =---，即为()0g x ≥对任意[)1,x ∈+∞恒成立，且发现()10g =，于是()1'x g x e m x=+-，由(1)知：当1m e ≤+时， ()'0g x ≥，此时()g x 单调增，于是()()10g x g ≥=，成立；若1m e >+，则存在()1,t ∈+∞使得：当()1,x t ∈时()'0g x <，当(),x t ∈+∞时()'0g x >，此时()0min g g t ≥<，矛盾，综上， 1m e ≤+．8．【2018广西贺州桂梧高中联考】已知函数()()2232ln 42f x x x x x x =--+. （1）若()f x 在(),1a a +上递增，求a 的取值范围；（2）证明： ()'24f x x >-.【答案】（1）0a =或a e ≥（2）详见解析试题解析：（1）()()()()()()21'22ln 23422ln 2222ln 1f x x x x xx x x x x x x=-+--+=-+-=--，令()'0f x =，得11x =， 2x e =，令()'0f x >，得01x <<，或x e >，∴()f x 在()0,1， (),e +∞上递增，()f x 在(),1a a +上递增，∴0a =或a e ≥.（2）证明：当12x >时， 240x -<， ()'24f x x >-显然成立. 当102x <≤时， ()()()()()'2422ln 124g x f x x x x x =--=---+， ()2'2ln +4g x x x =-在102⎛⎤ ⎥⎝⎦，上递增，且11'2ln 442ln2022g ⎛⎫=-+=-< ⎪⎝⎭， ∴()'0g x <，从而()g x 在10,2⎛⎤ ⎥⎝⎦上递减，∴()min 11ln202g x g ⎛⎫==+> ⎪⎝⎭，∴()0g x >，即()'24f x x >-. 综上， ()'24f x x >-.9．【2018安徽马鞍山联考】已知函数()22ln ax bf x x x-=-的图象在1x =处的切线过点()0,22,,a a b R -∈.（1）若85a b +=，求函数()f x 的极值点；（2）设()1212,x x x x ≠是函数()f x 的两个极值点，若111x e<<，证明： ()()211f x f x -<.（提示27.40e ≈）【答案】(1)12或2；(2)证明见解析. 【解析】试题分析：由题意结合导函数与原函数切线的关系可得a b =. (1)由题意可得45a b ==，利用导函数研究函数的极值可得()f x 的极值点为12或2. (2)由导函数的性质可得()1f x 是函数()f x 的极大值， ()2f x 是函数()f x 的极小值，据此构造函数()112111212t h t lnt lnt t t -=-=--++，据此可知()()()221021t h t t t '-=-<+，则函数()h t 在21,1e ⎛⎫⎪⎝⎭上单调递减，据此可得()()122218411f x f x h e e ⎛⎫-<=< ⎪+⎝⎭. 试题解析：()()222,12ax x bf x f a b x-+=∴='+'- ，又()1f a b =-，曲线()y f x =在1x =处的切线过点()0,22a -，()22210a b a a b ---∴=+--，得a b =.（1）84,55a b a b +=∴== ，令()0f x '=，得22520x x -+=，解得12x =或()2,f x ∴的极值点为12或2. （2）12,x x 是方程()2220ax x af x x '-+==的两个根， 1122121221,1x x x a x x x ∴===++，121111,1,0x x a e x ∴∴=， ()1f x ∴是函数()f x 的极大值， ()2f x 是函数()f x 的极小值，∴要证()()211f x f x -<，只需()()121f x f x -<，()()121122*********a a af x f x ax lnx ax lnx ax lnx x x x ⎛⎫⎛⎫-=-----=-- ⎪ ⎪⎝⎭⎝⎭2221111221111144112x x lnx lnx x x ⎛⎫⎛⎫--=-=- ⎪ ⎪++⎝⎭⎝⎭，令21t x =，则211t e<<，设()112111212t h t lnt lnt t t -=-=--++，则()()()221021t h t t t '-=-<+，函数()h t 在21,1e ⎛⎫⎪⎝⎭上单调递减， ()22121h t h e e ⎛⎫∴<= ⎪+⎝⎭， ()()122218411f x f x h e e ⎛⎫∴-<=< ⎪+⎝⎭.10．【2018安徽马鞍山联考】已知函数()()21xf x x e =-.（1）若函数()f x 在区间(),a +∞上单调递增，求()f a 的取值范围；（2）设函数()xg x e x p =-+，若存在[]01,x e ∈，使不等式()()000g x f x x ≥-成立，求实数p 的取值范围.【答案】(1) [)2,-+∞；(2) [),e -+∞. 【解析】试题分析：(1)由函数的解析式可得()f x 在()0,+∞上单调递增，则()f a 的取值范围是[)2,-+∞；(2)原问题等价于存在[]01,x e ∈，使不等式()0023xp x e ≥-成立.构造新函数()()23xh x x e =-，结合函数()h x 的性质可得实数p 的取值范围为[),e -+∞. 试题解析：（1）由()20xf x xe '=>得0x >，()f x ∴在()0,+∞上单调递增， ()()0,02a f a f ∴≥∴≥=-， ()f a ∴的取值范围是[)2,-+∞.（2）存在[]01,x e ∈，使不等式()()000021xg x x e x ≥--成立，∴存在[]01,x e ∈，使不等式()0023x p x e ≥-成立.令()()23xh x x e =-，从而()[]()1,min p h x x e ≥∈， ()()21x h x x e -'=，()1,211,0,0x x x e h x ≥∴-≥>'∴> ，()()21x h x x e ∴=-在[]1,e 上单调递增， ()()1,min h x h e ∴==- p e ∴≥-.∴实数p 的取值范围为[),e -+∞.11．【山东省泰安市2018届学年高三上学期期末考试】已知函数()2ln f x a x =， ()()1g x f x x x=+-. （1）当1a =时，求函数()f x 的曲线上点()(),e f e 处的切线方程；（2）当1a ≤时，求()g x 的单调区间；（3）若()g x 有两个极值点1x ， 2x ，其中110,3x ⎛⎤∈ ⎥⎝⎦，求()()12g x g x -的最小值.（2）由题意得： ()12ln g x a x x x=+-， 0x > ()221'1a g x x x ∴=++ 2221x ax x++=令244a ∆=-当11a -≤≤时， ()'0g x ≥， ()g x 在()0,∞上单调递增.②当1a <-时，令()'0g x >，解得：0x a <<-或x a >-令()'0g x <，解得：a x a -<-综上，当11a -≤≤时， ()g x 的单调增区间为()0,+∞，当1a <-时，单调增区间为(0,a -，()a -+∞单调减区间为(a a --（3）由（2）知， ()2221'x ax g x x++=， 0x > 由题意知， 1x ， 2x 是方程210x ax ++=的两根121x x ∴⋅=， 122x x a +=-， 211x x ∴=1112a x x ∴=--， ()()()12111g x g x g x g x ⎛⎫∴-=- ⎪⎝⎭， 11111112ln x x x x x ⎡⎤⎛⎫=--+⎢⎥ ⎪⎝⎭⎣⎦令()()()()222111112ln '21ln ln x x H x x x x H x x x x x x x +-⎡⎤⎛⎫⎛⎫=--+∴=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 当10,3x ⎛⎤∈ ⎥⎝⎦时， ()'0H x <∴ ()H x 在10,3⎛⎤ ⎥⎝⎦上单调递减， ()min 120ln31633H x H -⎛⎫∴==⎪⎝⎭即()()12g x g x -的最小值为20ln3163-. 12．【2018河南漯河三模】已知函数()1(xf x e ax a =--为常数），曲线()y f x =在与y 轴的交点A 处的切线斜率为1-.（1）求a 的值及函数()y f x =的单调区间；（2）若12ln2,ln2x x ，且()()12f x f x =，试证明： 122ln2x x +<.【答案】（1）2a =，单调递减区间为(),ln2-∞，单调递增区间为()ln2,+∞.（2）见解析【解析】试题分析：（1）求出函数的， 'x f x e a =-（），由曲线()y f x =在与y 轴的焦点A 处的切线斜率为1-，解得2a =．通过'20x f x e =-（）＞，即可求解函数f x （）在区间2ln -∞（，）上单调递减，在2ln +∞（，）上单调递增．（2）设2x ln ＞，构造函数22g x f x f ln x =--（）（）（），分别根据函数的单调性，以及1222x ln x ln ＜，＞，且12f x f x =（）（）即可证明．试题解析：（1）由()1xf x e ax =--，得()xf x e a '=-，因为曲线()y f x =在与y 轴的焦点A 处的切线斜率为1-，所以()011f a =-=-'，所以2a =，所以()()212x xf x e x f x e =--⇒=-'，由()20xf x e ='->，得ln2x >，由()20xf x e ='-<，得ln2x <，所以函数()y f x =的单调递减区间为(),ln2-∞，单调递增区间为()ln2,+∞. （2）证明:设ln2x >，所以2ln2ln2x -<，()()2ln242ln222ln21204ln21x x f x e x x e--=---=+-，令()()()42ln244ln2(ln2)xx g x f x f x e x x e=--=--+> 所以()440xxg x e e-'=+-≥，当且仅当ln2x =时，等号成立，所以()()()2ln2g x f x f x =--在()ln2,+∞上单调递增，又()ln20g =，所以当ln2x >时， ()()()()2ln2ln20g x f x f x g =-->=，即()()2ln2f x g x >-，所以()()222ln2f x g x >-，又因为()()12f x f x =，所以()()122ln2f x f x >-，由于2ln2x >，所以22ln2ln2x -<，因为1ln2x <，由（1）知函数()y f x =在区间(),ln2-∞上单调递增，所以122ln2x x <-，即122ln2x x +<.13．【北京市东城二十二中2018届高三上学期期中试卷】已知函数()()2224ln (0)f x x ax x x a =-+>．（1）当1a =时，求此函数对应的曲线在()()1,1f 处的切线方程．（2）求函数()f x 的单调区间．（3）对[)1,x ∀∈+∞，不等式()24ln x a x x ->-恒成立，求a 的取值范围．【解析】（1）当1a =时， ()()2224ln (0)f x x x x x x =-+>，∴()11f =， ()()22444ln 2x xf x x x x x-=-++'， ()10f '=，∴切线方程1y =．（2）()()22444ln 2x axf x x a x x x-=-++' ()44ln 44x a x x a =-+- ()()44ln 1x a x =-+．令()0f x '=，则1e x -=或x a =，当10e a <<时， ()f x 在()0,a ， 1,e ⎛⎫+∞ ⎪⎝⎭上为增函数．在1,e a ⎛⎫ ⎪⎝⎭上为减函数，当1ea =时， ()f x 在()0,+∞上为增函数，当1e a >时， ()f x 在10,e ⎛⎫⎪⎝⎭， (),a +∞上为单调递增，在1,e a ⎛⎫ ⎪⎝⎭上单调递减．（3）当1x =时， a R ∈，当x n >时，由()24ln x a x x ->-得42ln xa x x<+，对[)1,x ∀∈+∞恒成立．设()2ln xg x x x =+，则()()()()()()22222ln 1ln 1ln 12ln ln 12ln ln ln x x x x x g x x x x -+--=+=='+，令()0g x '=得x =1x =，()min g x g==4a <， 0a <<14．【2018北京大兴联考】已知函数()22m xf x x m=-，且0m ≠．（Ⅰ）当1m =时，求曲线()y f x =在点()00，处的切线方程；（Ⅱ）求函数()f x 的单调区间；（Ⅲ）若函数()f x 有最值，写出m 的取值范围．（只需写出结论）【答案】(1) 0x y += ;(2)详见解析;(3) 0m <（Ⅱ）因为()22m x f x x m =-，所以()()2222x m f x m x m'+=-- . 当0m >时，定义域为((),-∞⋃⋃+∞ .且()()22220x mf x mxm+-'=-<故()f x的单调递减区间为((),,,-∞+∞ ……5分当0m <时，定义域为R . 当x 变化时， ()f x '， ()f x 的变化情况如下表：故()f x 的单调递减区间为(,-∞，)+∞，单调递增区间为(．综上所述，当0m >时， ()f x 的单调递减区间为((),,,-∞+∞；当0m <时，故()f x 的单调递减区间为(,-∞， )+∞，单调递增区间为(．（Ⅲ）0m <15．【2018湖南株洲两校联考】设函数()ln xf x ax x=-．（1）若函数()f x 在()1,+∞上为减函数，求实数a 的最小值；（2）若存在212,,x x e e ⎡⎤∈⎣⎦，使()()12f x f x a '≤+成立，求实数a 的取值范围．【答案】（Ⅰ）最小值为14；（II ）21124a e≥- 【解析】试题分析： ()()1f x 在()1,+∞上为减函数，等价于()0f x '≤在()1,+∞上恒成立，进而转化为()0max f x '≤，根据二次函数的性质可得()max f x '()2命题“若存在1x ,2x 2,e e ⎡⎤∈⎣⎦，使()()12f x f x a '≤+成立”等价于“当2,x e e ⎡⎤∈⎣⎦时，有 ()()min max f x f x a '≤+”，由()1易求()max f x a '+，从而问题等价于“当2,x e e ⎡⎤∈⎣⎦时，有()min 14f x '≤”，分 14a ≥, 14a <两种情况讨论: 当14a ≥是易求()min f x ，当14a <时可求得()f x '的值域为1,4a a ⎡⎤--⎢⎥⎣⎦，再按()0i a -≥（2）命题“若存在1x ,2x 2,e e ⎡⎤∈⎣⎦，使()()12f x f x a '≤+成立”等价于 “当2,x e e ⎡⎤∈⎣⎦时，” ()()min max f x f x a '≤+”，由（1），当2,x e e ⎡⎤∈⎣⎦时， ()max 14f x a '=-， ∴ ()max 14f x a '+=. 问题等价于：“当2,x e e ⎡⎤∈⎣⎦时，有()min14f x '≤”. 当14a ≥，由（1），()f x 在2,e e ⎡⎤⎣⎦为减函数，则()()222min 1==24e f x f e ae -≤，故21124a e ≥-. 当14a <时，由于()2111=ln 24f x a x ⎛⎫--+ ⎝'-⎪⎭在2,e e ⎡⎤⎣⎦上的值域为1,4a a ⎡⎤--⎢⎥⎣⎦ （i ）0a -≥，即0a ≤， ()0f x '≥在2,e e ⎡⎤⎣⎦恒成立，故()f x 在2,e e ⎡⎤⎣⎦上为增函数，于是， ()()min 1==4f x f e e ae e -≥>，矛盾。

专题2-1 以零点个数为背景的填空题-2018年高考数学备

专题二压轴填空题第一关以零点个数为背景的填空题【名师综述】本类压轴题常以超越方程、分段函数、抽象函数等为载体，达到考查函数性质、函数零点的个数、参数的范围和通过函数性质求解不等式问题等目的。

要注意函数零点、方程的根、不等式解集三者之间的关系，进行彼此之间的转化是解决该类题的关键，等价转化是这类问题的难点．解决该类问题的途径往往是根据函数的性质作出示意图，利用数形结合研究分界位置，结合函数、方程、不等式刻画边界位置，其间要注意导数的应用. 【典例解剖】类型一周期函数零点个数问题典例1设)(x f 是定义在R 上的偶函数，对R x ∈，都有)2()2(+=-x f x f ，且当[]02，-∈x 时，1)21()(-=x x f ，若在区间]62(，-内关于x 的方程)1(0)2(log )(>=+-a x x f a 恰有3个不同的实数根，则a 的取值范围是_____.【答案】)2,4(3【名师指点】将给定区间的根的个数问题转换为熟悉函数图像在给定区间的交点个数问题,利用周期性和偶函数正确作图以及判断端点函数值的大小是解题关键．求解零点问题时，往往转化为()0f x =的根求解，若该方程不易解出，可考虑数形结合转化为两熟悉图像的交点问题求解．【举一反三】已知()f x 是以2为周期的偶函数，当[0,1]x ∈时，()f x =(1,3)-内，关于x 的方程()()f x kx k k R =+∈有4个根，则k 的取值范围是_____.【答案】B. 104k <≤【解析】∵直线()f x kx k =+过定点(1,0)-，画出函数()f x 在区间(1,3)-的图象，要使方程()()f x k x k k R =+∈有4个根，即直线y kx k =+和函数()f x 在区间(1,3)-的图象有4个交点，显然当104k <≤时满足条件，假若当直线y kx k =+和函数()f x 的图象在区间(2,3)上相切时也满足条件，但是这是不可能的，联立y y kx k⎧⎪⎨⎪⎩＝＋得230ky y k -+=，令0∆=得k =k = (舍去)，当k =时，解得5(2,3)x =∉，∴104k <≤. 类型二复合函数的零点个数问题典例2 【2018安徽阜阳一中二模】已知，若关于的方程恰好有个不相等的实数根，则实数的取值范围是______________. 【答案】【解析】∵∴∴∴当或时，，当时，∴在上单调递增，在上单调递减，在上单调递增可作出大致函数图象如图所示：令，则当时，方程有一解；当时，方程有两解；时，方程有三解 ∵关于的方程，恰好有4个不相等实数根 ∴关于的方程在和上各有一解∴，解得，故答案为【名师指点】求解复合方程问题时，往往把方程[()]0f g x =分解为()0f t =和()g x t =处理，先从方程()0f t =中求t ，再带入方程()g x t =中求x 的值．【举一反三】【湖南省常德市2018届高三上学期检测考试】设函数()2f x x =，若函数()()()23g x f x mf x m =+++有四个零点，则实数m 的取值范围为__________．【答案】()3,2--【解析】由题意得方程230t mt m +++= 有两个不等正根所以()243062{0 {0 32303m m m m m m m m m ∆=-+>><-->⇒<⇒-<<-+>>-或类型三分段函数（或含绝对值函数）的零点个数问题典例3 【江苏省镇江市2018届高三上学期期末统考】已知k 为常数，函数()2,0{ 1,0x x f x x lnx x +≤=->，若关于x 的方程()2f x kx =+有且只有4个不同解，则实数k 的取值集合为__________．【答案】()31,1e e ⎧⎫⋃--⎨⎬⎩⎭【解析】画出函数()2,0{ 1,0x x f x x lnx x +≤=->的图象如图所示：∵2y kx =+过点()0,2∴当0k ≤时，显然不满足题意，故0k > ∵2y kx =+在(],0-∞上与函数()f x 有一个交点∴2y kx =+在()0,+∞上与函数()f x 有三个交点，且由图所示2y kx =+在()0,1上与函数()f x 有一个交点设直线2y kx =+与()()()1,y f x x =∈+∞的图象在相切的切点坐标为(),m n ，则ln n m =， 2n km =+ ∵()1f x x'= ∴1k m=∴3n =， 3m e =， 3k e -= ∴实数k 的取值范围是()30,e -【名师指点】分段函数与含绝对值函数典型特征为各段解析式不一致，不仅要考虑对应性，而且需考虑自变量在结合点情况及值域包含关系．【举一反三】定义在R 上的奇函数()f x ，当0x ≥时，2,[0,1),()11|3|,[1,),xx f x x x x -⎧∈⎪=+⎨⎪--∈+∞⎩则函数1()()F x f x π=-的所有零点之和为．【答案】112π-【解析】由图知，共五个零点，从左到右交点横坐标依次为12345,,x x x x x ，，，满足1234516,,612x x x x x π+=-=+=-，因此所有零点之和为112π-【精选名校模拟】1. 【江苏省南通市2018届高三上学期第一次调研测试】已知函数()()221,0,{ ,0,x ax a x f x ln x x --+≥=-<()212g x x a =+-.若函数()()y f g x =有4个零点，则实数a 的取值范围是________.【答案】()1,⎫⋃+∞⎪⎪⎝⎭【解析】令()()0,f t t g x ==当10a -<时()f t 有两个零点121,1t t =->，需1211a a --∴当1=0a -时()f x 有三个零点， 1231,0,=2t t t =-=， 121a -=- 所以函数()()y f g x =有5个零点，舍；当10a ->时，由于121a ->-所以24440a a ∆=+-> ，且12a a >- ，所以12a <<综上实数a的取值范围是()1,⎫⋃+∞⎪⎪⎝⎭2. 【天津河西2017-2018学年高三上期中】已知函数()3 log ,x a f x x x a≤≤=>，其中0a >，若函数()2y f x =-有两个零点，则a 的取值范围是__________．【答案】[)4,93.设定义域为R 的函数|1|25 1 0()4 4 0x x f x x x x -⎧-≥⎪=⎨++<⎪⎩，若关于x 的方程22()(21)()0f x m f x m -++=有7个不同的实数解，则m=_____. 【答案】2【解析】∵题中原方程22()(21)()0f x m f x m -++=有7个不同的实数根，∴即要求对应于()f x 等于某个常数有3个不同实数解和4个不同的实数解，∴故先根据题意作出()x f 的简图：由图可知，只有当()4f x =时，它有三个根，故关于x 的方程22()(21)()0f x m f x m -++=有一个实数根4，∴()2244-4210m m ⋅++=，∴2m =或6=m ，6=m 时，方程22()(21)()0f x m f x m -++=()()()4036132=⇔=+-⇔x f x f x f 或()9=x f ,有5个不同的实数根，∴2=m ．4．已知函数()f x 是定义域为R 的偶函数，当0x ≤时， ()[]f x x x =-（符号[]x 表示不超过x 的最大整数），若方程()log (0,1)a f x x a a =>≠有6个不同的实数解，则a 的取值范围是__________．【答案】(]2,3【解析】作出函数()[]f x x x =-的图像，如图所示：()log (0,1)a f x x a a =>≠有6个不同的实数解，即为()[]f x x x =-与log (0,1)a y x a a =>≠有六个交点.当01a <<时，显然不成立；当1a >时，只需21{31a a log log <≥解得23a <≤.故答案为： (]2,3.5．【2018江西宜春六校联考】已知函数()ln 1||f x x =-， ()f x m -的四个零点1x ， 2x ， 3x ， 4x ，且12341111k x x x x =+++，则()k f k e -的值是__________．【答案】2e -【解析】分类讨论求解方程的零点：(1) 12ln 1,1,1,1m m mx m x e x e x e -=-==+=-； (2) 34ln 1,1,1,1m m mx m x e x e x e ----=--==+=-；从而12341111k x x x x =+++=2，据此计算有： ()kf k e -的值是2e -. 6．【2018辽宁庄河两校联考】函数，，若使得，则__________.【答案】7．【2018东北名校联考】函数()f x 满足对任意x R ∈，都有()()2f x f x +=--，且()()211,10{ 2log 1,01x x f x x x --<<=+≤<， ()1144g x x =-+，则函数()()()h x f x g x =-在()1,3-上的零点之和是__________．【答案】5【解析】根据题干条件()()2f x f x +=--，当x=-1,得到()10f =，根据图像得到函数是关于点()10，中心对称的，直线()1144g x x =-+和曲线的交点有四个，根据点的对称性得到每对的根之和为4，故得到和为5. 故答案为：5.8．已知定义在R 上的偶函数()f x 满足(4)()f x f x -=，且当(1,3]x ∈-时，2,(1,1]()1cos ,(1,3]2x x f x x x π⎧∈-⎪=⎨+∈⎪⎩，则函数()()|lg |g x f x x =-的零点个数是_____.【答案】109. 【2018东北名校联考】已知函数()f x 满足()()2f x f x =，且当[)1,2x ∈时()ln f x x =.若在区间[)14，内，函数()()2g x f x ax =-有三个不同零点，则a 的范围为__________．【答案】ln208⎡⎫⎪⎢⎣⎭，【解析】22x f x f x f x f =∴=（）（），（）（），当[24x ∈，）时， [122x ∈，）； 222x xf x f ln lnx ln ===-（）（），故函数[)[)12{224lnx x f x lnx ln x ∈=-∈，，（），，，作函数f x （）与2y ax = 的图象如下，，过点42ln （，）时， 222,48ln ln a a =∴== ， 12'y lnx ln y x =-=，；故21lnx ln x x -= ，故2x e =，故112,24a a e e=∴= ，故实数a 的取值范围是ln2184e ⎛⎫⎪⎝⎭，，10. 若函数2,0ln ,0x a x y x a x x ⎧-≤=⎨-+>⎩，在区间()2,2-上有两个零点，则实数a 的取值范围为__________．【答案】[)0,2ln 2+11. 【2018湖北名校联考】奇函数()f x 是R 上单调函数， ()()()313g x f ax f x =+-有唯一零点，则a的取值集合为____________．【答案】{}|0 4 a a a ≤>或【解析】由题意得()()()33133131f ax f x f x ax x =--=-∴=-有唯一零点，23310x a x x ≠∴=- 3463102a x x x '=-+=∴= 当12x ≥时, (]0,0,4a a ∈'≤ ; 当102x x <≠，时, ()()0,,40,a a >∈-∞⋃'+∞ ; 所以要有唯一零点， a 的取值集合为{}|0 4 a a a ≤>或12. 【2018湖北省部分重点中学联考】已知函数()xf x xe =，若关于x 的方程()()()2230f x tf x t R -+=∈有两个不等实数根，则t 的取值范围为__________．【答案】1322e e ⎫+⎪⎭【解析】xy xe =，易知()x f x xe =的图象如下：()11f e-=，令()f x k =，则2230k tk -+=，得32,0t k k k=+>，当()f x k =有两个不等实根是，则1k e >，所以123t e e <+，即t 的取值范围是1322e e ⎫+⎪⎭。

高考常考题-函数的零点问题(含解析)

函数的零点问题一、题型选讲题型一、运用函数图像判断函数零点个数可将零点个数问题转化成方程，进而通过构造函数将方程转化为两个图像交点问题，并作出函数图像。

作图与根分布综合的题目，英中作图是通过分析函数的单调性和关键点来进行作图，在作图的过程中还要注意渐近线的细节，从而保证图像的准确。

例1、(2019苏州三市、苏北四市二调)立义在R 上的奇函数金)满足Λx+4)=Λx),且在区间[2, 4)上例3、【2018年高考全国III 卷理数】函数/(x) = COS^3Λ + ^ ∣^[0,π]的零点个数为 ______ 题型二、函数零点问题中参数的范围已知函数零点的个数，确定参数的取值范围，常用的方法和思路：(1) 直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范囤.(2) 分离参数法：先将参数分离，转化成求函数值域问题加以解决，解法2就是此法.它的本质就是将函数转化为一个静函数与一个动函数的图像的交点问题来加以处理，这样就可以通过这种动静结合来方便地研究问题.(3) 数形结合法：先对解析式变形，在同一平面直角坐标系中，画岀函数的图像，然后数形结合求解.1∏Λ∖X≥ 1例4. (2020届山东省枣庄.滕州市髙三上期末)已知/(X) = {…、f ,若函数y = ∕(x)-l 恰有f(2-x) + k,x<∖一个零点，则实数A ∙的取值范围是( )A. (l,4∙s) B ・ ILC. (YU)D ・(Y M]Z、21og^ x,x≥∖. Z 、例5、(2020全国高三专题练习(文))函数/(M = [f(w]) JI yl ，若方程f(x) = ~2x + m 有且只有两个不相等的实数根，则实数加的取值范围是()A. (-oo,4)B. (Y ,4]C. (-2,4)D. (-2,4]2-x,2≤x<3x-4,3≤x<4则函数y=∕ω-iog s H 的零点的个数为 ____________x<b例2、(2017苏锡常镇调研)若函数Λx)=≤ IInx<x>l, )则函数y=^χ)∣~∣的零点个数为 ______若函数F(X) =/(x)-g(x)在［0,2)上只有两个零点，则实数R 的值不可能为A.丄 3 3 C.——4例6、［2020年高考天津】已知函数f(x) = < Λ j'0,若函数g(γ) =γ,(j).∣AΛ^2点，则k 的取值范围是A. (→>,-∣)U(2√2,+oo)B ∙ U(0,2√Σ)c ・(Y,0)U(0,2√Σ) D ・ YO)U(2√Σ,S例7. ［2019年髙考浙江】已知t 函数f(x) = < 1x,x < O1 c ・若函数一F --(α + l)f +ax.x≥O 13 2y = f(x)-cιx -b 恰有3个零点，则A. Λ<-L b<0B. αv -l, b>0C. α>-l, XoD ・ α>-l, b>Q例8. (2020浙江学军中学髙三3月月考)已知函数/(X)=(A -÷4)V5≤X <-3J 若函数 /(x-2),x≥-3g(x) = ∕α)-W(X+ 1)1有9个零点，则实数M 的取值范围是()A.［科丿B.1 1)匕'FD.1 1 <55例9.(2020届浙江省杭州市第二中学髙三3月月考)已知函数/(X)=2/V 『心2'B- 4D ・-1-2彳伙WR)恰有4个零二、达标训练1、(2019 IlJ 东师范大学附中高三月考)函数/(x) = √-W 的零点所在区间为()A- (一 1'O)B- [θ,^j C - (Al D- (1'2)e 丫 X V 02、【2018年髙考全国I 卷理数】已知函数/(X)=g(χ) = f(χ) + x + a •若g(x)存在2个lnx, x>O,零点，则α的取值范用是A. [一 1, 0)B. [0, +∞)C. [-1, +oo)D. [1, +∞)3、 (2020届浙江省“山水联盟"髙三下学期开学)已知αbwR,函数f(x) = <(A+(l)e +αr "≤°,若函x,x>0数y = f{x)-ax-b 恰有3个零点，则()A. a>∖J)>OB. d>l,D<0C. a<tb>OD. a<^b<O4. (2020届山东实验中学髙三上期中)设定义在/?上的函数/(X)满足/(→) + /(X) = X 2,K 当X WO 时,__________ ・若函数沧)恰有2个零点，则2的取值范圉是 _____________≥∕(1~x ))2}且★为函数 g(x) = e λ-y[ex-aZR 疋为自然对数的底数)的一个零点，则实数α的取值可能是()A. 1√E 2D ・√72√7(0<x≤l)5、(2020届山东师范大学附中髙三月考)已知函数fW = ∖2—(X > DIX若方程/(兀)=一力+ α有三个不同的实根，则实数α的取值范围是 _______6、［2018年髙考浙江】已知z∈R.函数沧)=<X - 4, % ≥ Λ X 2-4x + 3,x<2,当z=2时，不等式√(x)vθ的解集是广(X)Vx .己知存在如Λ 2+2ax + a,x ≤ O 74202O届江苏省南通市如皋市高三下学期二模】已知函数f(x) = \e x_ex I ,,若存在实数+-a2,x>O X 3使得函数y = f(χ)-k有6个零点，则实数。

专题02函数零点问题-2024高考数学尖子生辅导专题

专题02函数零点问题-2024高考数学尖子生辅导专题函数的零点问题在数学中是一个非常重要的概念和问题。

而在2024高考的数学尖子生辅导专题中，函数的零点问题无疑是一个重点内容。

下面，我们来详细探讨一下这个问题。

函数的零点问题即是求解函数的解析式方程$f(x)=0$的解$x$。

在实际问题中，函数的零点往往表示了其中一种特定情况下的平衡点或者特殊点，因此求解函数的零点问题是非常实用和重要的。

那么，如何求解函数的零点问题呢？下面，我们将从三个方面进行讨论。

首先，我们可以通过图像来求解函数的零点问题。

对于一般的函数，我们可以通过画出函数的图像来判断函数的零点。

函数的零点为函数与$x$轴相交的点，在图像上表现为函数曲线与$x$轴的交点。

通过观察函数图像上哪些点与$x$轴相交，我们可以找到函数的零点。

对于简单的函数，我们可以手工画出函数图像，对于复杂的函数，我们可以借助计算机软件进行绘图。

其次，我们可以通过函数的解析式来求解函数的零点问题。

对于一般的函数，我们可以通过解方程$f(x)=0$来求解函数的零点。

通过将方程变形化简，最终得到$x$的解析表达式。

这种方法适用于存在解析解的函数，对于一些特殊函数，解析解并不存在，我们需要采用其他方法进行求解。

最后，我们可以通过数值计算方法来求解函数的零点问题。

对于一些无法通过解析式求解的函数，我们可以采用数值计算方法进行求解。

数值计算方法包括二分法、不动点迭代法、牛顿迭代法等。

这些方法通过迭代计算，逐渐接近函数的零点。

在实际计算中，我们可以通过计算机软件来进行数值计算，以提高计算的精度和效率。

综上所述，函数的零点问题在数学中具有重要的意义，我们可以通过图像、解析式和数值计算方法等多种途径来求解函数的零点。

在2024高考的数学尖子生辅导专题中，函数的零点问题无疑是一个关键的内容，掌握这个问题对于学生的数学能力提高和应试能力提升都具有重要作用。

因此，我们应该重视并加以学习和实践。

专题2-4 以极值为背景的解答题-2018年高考数学备考优

专题二压轴解答题第四关以极值为背景的解答题【名师综述】极值点不同于零点，极值点不仅导数值为零（中学只研究可导函数），而且在其附近导数值要变号.因此以极值为背景的解答题，不仅要考虑等量关系，更要注意不等量关系，这也是考查分类讨论思想的一个常见的载体.类型一求函数极值或单调区间或最值问题典例1 已知函数()()2ln xf x x a =+，其中a 为常数.（1）若0a =，求函数()f x 的极值；（2）若函数()f x 在()0,a -上单调递增，求实数a 的取值范围；（3）若1a =-，设函数()f x 在()0,1上的极值点为0x ，求证： ()02f x <-.【答案】(1)当x = ()f x 的极大值为12e，无极小值；(2) 122a e -≤-；(3)证明见解析.【解析】∴当x = ()f x 的极大值为12e，无极小值. （2）()()312ln 'ax x f x x a +-=+，由题意()'0f x ≥对()0,x a ∈-恒成立.()0,x a ∈-， ()30x a ∴+<，∴ 12ln 0ax x+-≤对()0,x a ∈-恒成立， ∴ 2ln a x x x ≤-对()0,x a ∈-恒成立.令()2ln g x x x x =-， ()0,x a ∈-，则()'2ln 1g x x =+， ①若120a e-<-≤，即120a e->≥-，则()'2ln 10g x x =+<对()0,x a ∈-恒成立，∴ ()2ln g x x x x =-在()0,a -上单调递减，则()()()2ln a a a a ≤----， ()0ln a ∴≤-， 1a ∴≤-与12a e -≥-矛盾，舍去；②若12a e -->，即12a e-<-，令()'2ln 10g x x =+=，得12x e-=，当120x e -<<时， ()'2ln 10g x x =+>， ()2ln g x x x x ∴=-单调递减，当12ex a -<<-时， ()'2ln 10g x x =+>， ()2ln g x x x x ∴=-单调递增，∴当12x e -=时， ()12ming x g e -⎛⎫⎡⎤= ⎪⎣⎦⎝⎭ 111122222ln 2e e e e ----⎛⎫=⋅-=- ⎪⎝⎭，122a e -∴≤-.综上122a e -≤-.（3）当1a =-时， ()()2ln 1xf x x =-， ()()312ln '1x x x f x x x --=-，令()12ln h x x x x =--， ()0,1x ∈，则()()'12ln 1h x x =-+ 2ln 1x =--，令()'0h x =，得12x e -=，①当121ex -≤<时， ()'0h x ≤， ()12ln h x x x x ∴=--单调递减， ()120,21h x e -⎛⎤∈- ⎥⎝⎦，()()312ln '01x x x f x x x --∴=<-恒成立， ()()2ln 1xf x x ∴=-单调递减，且()12f x f e -⎛⎫≤ ⎪⎝⎭. ②当120x e-<≤时， ()'0h x ≥， ()12ln h x x x x ∴=--单调递增，1111222212ln h e e e e ----⎛⎫⎛⎫∴=--⋅ ⎪ ⎪⎝⎭⎝⎭12210e -=->又()()222212ln h ee e e ----=--⋅ 2510e=-<， ∴存在唯一1200,x e -⎛⎫∈ ⎪⎝⎭，使得()00h x =， ()0'0f x ∴=，当00x x <<时， ()0'0f x >， ()()2ln 1xf x x ∴=-单调递增，当120x x e -<≤时， ()0'0f x <， ()()2ln 1xf x x ∴=-单调递减，且()12f x f e -⎛⎫≥ ⎪⎝⎭，由①和②可知， ()()2ln 1xf x x =-在()00,x 单调递增，在()0,1x 上单调递减，∴当0x x =时， ()()2ln 1xf x x =-取极大值.()000012ln 0h x x x x =--=， 0001ln 2x x x -∴=， ()()020ln 1x f x x ∴=- ()2000112111222x x x ==-⎛⎫--⎪⎝⎭，又1200,2x e -⎛⎫∈ ⎪⎝⎭， 201112,0222x ⎛⎫⎛⎫∴--∈- ⎪ ⎪⎝⎭⎝⎭， ()0201211222f x x ∴=<-⎛⎫--⎪⎝⎭. 【名师指点】以导函数为研究对象，实质讨论研究方程的根与系数的关系. 【举一反三】已知函数()()()21ln f x x ax g x x a a R =++=-∈，．⑴当1a =时，求函数()()()h x f x g x =-的极值；⑵若存在与函数()f x ， ()g x 的图象都相切的直线，求实数a 的取值范围．【答案】（1）当12x =时，函数()h x 取得极小值为11+ln24，无极大值；（2）[)1,-+∞ 【解析】所以()()()211121x x h x x x x='-+=+- 所以当102x <<时， ()0h x '<，当12x >时， ()0h x '>，所以函数()h x 在区间10,2⎛⎫ ⎪⎝⎭单调递减，在区间1,2⎛⎫+∞ ⎪⎝⎭单调递增，所以当12x =时，函数()h x 取得极小值为11+ln24，无极大值；（2）设函数()f x 上点()()11,x f x 与函数()g x 上点()()22,x g x 处切线相同，则()()()()121212f xg x f x g x x x -==-''所以()211212121ln 12x ax x a x a x x x ++--+==- 所以12122ax x =-，代入()21211221ln x x x ax x a x -=++--得： ()222221ln 20*424a a x a x x -++--= 设()221ln 2424a a F x x a x x =-++--，则()23231121222a x ax F x x x x x +-=-++=' 不妨设2000210(0)x ax x +-=>则当00x x <<时， ()0F x '<，当0x x >时， ()0F x '> 所以()F x 在区间()00,x 上单调递减，在区间()0,x +∞上单调递增，代入20000121=2x a x x x -=-可得： ()()20000min 012ln 2F x F x x x x x ==+-+-设()212ln 2G x x x x x =+-+-，则()211220G x x x x=+++>'对0x >恒成立，所以()G x 在区间()0,+∞上单调递增，又()1=0G所以当01x <≤时()0G x ≤，即当001x <≤时()00F x ≤, 又当2a x e+=时()222421ln 2424a a a a a F x e a e e +++=-++--221104a a e +⎛⎫=-≥ ⎪⎝⎭因此当001x <≤时，函数()F x 必有零点；即当001x <≤时，必存在2x 使得()*成立；即存在12,x x 使得函数()f x 上点()()11,x f x 与函数()g x 上点()()22,x g x 处切线相同．又由12y x x =-得： 2120y x'=--< 所以()120,1y x x =-在单调递减，因此[)20000121=21+x a x x x -=-∈-∞，所以实数a 的取值范围是[)1,-+∞．类型二由极值确定参数取值范围问题典例2 已知函数()()ln ,,f x x ax g x ex a R =-=∈（e 是自然对数的底数）（1）若直线y ex =为曲线()y f x =的一条切线，求实数a 的值；（2）若函数()()y f x g x =-在区间()1,+∞上为单调函数，求实数a 的取值范围；（3）设()()()[],1,H x f x g x x e =⋅∈，若()H x 在定义域上有极值点（极值点是指函数取得极值时对应的自变量的值），求实数a 的取值范围. 【答案】（1）1e e -；（2）][(),1,e e -∞-⋃-+∞；（3）10a e <<或112a e <<. 【解析】（2）设()()()()()ln 1h x f x g x x a e x x =-=-+≥，当()h x 单调递增时，则()()10h x a e x=-+≥'在()1,+∞上恒成立， ∴()1a e x ≥+ 在()1,+∞上恒成立，又()10,1,x ∈ 0,a e ∴+≤解得a e ≤-．当()h x 单调递减时，则()()10h x a e x=-+≤'在()1,+∞上恒成立， ∴()1a e x≤+在()1,+∞上恒成立， 1,a e ∴+≤1a e ∴≤-综上()h x 单调时a 的取值范围为][(),1,e e -∞-⋃-+∞．（3）()2ln ln xH x x ax ex ex a x=-⋅=-，令()[]ln ,1,,x t x a x e x =-∈则()21ln xt x x-'=，当[]1,x e ∈时， ()0t x '≥， ()t x 单调递增， ∴()()()1t t x t e ≤≤，即()1a t x a e-≤≤-. 1）当0a -≥，即0a ≤时， ()0,t x ≥∴()()[]2ln ,1,H x e x x ax x e =-∈，则()()()ln 120,?H x e x ax H x =+->'单调递增，()H x ∴在[]1,x e ∈上无极值点．2）当10a e -<即1a e>时， ()0,t x < ()()[]2ln ,1,H x e x x ax x e ∴=-∈∴()()()1112ln 1,2,,1H x e ax x H x e a x x e ⎛⎫⎡⎤=--=-'''∈ ⎪⎢⎥⎝⎭⎣⎦I ）当21a ≥，即12a ≥时， ()0H x ''≥， ()H x ∴'在[]1,e 递增， ()()1210H e a '=-≥， ()H x ∴在[]1,e 上递增， ()H x ∴在[]1,e 上无极值点．II ）当112a e <<时，由()1120,2H x a x e x a=≥''-≤≤可得 ()H x ∴'在11,2a ⎡⎤⎢⎥⎣⎦递减， 1,2e a ⎡⎤⎢⎥⎣⎦递增，又()()()()()1210,22210H e a H e e ae e ae =-=-=-''()01,x e ∴∃∈使得()00,H x '=()H x ∴在()01,x 上单调递减，在(]0,x e 上单调递增， ()H x ∴在[]1,e 上有一个极小值点．3）当1a e =时， ()()221ln 1,02e H x e x x H x e x e e x "⎛⎫⎛⎫=--=->> ⎪ ⎪⎝⎭⎝⎭'由得， ()H x ∴'在1,2e ⎡⎤⎢⎥⎣⎦上单调递减，在,2e e ⎡⎤⎢⎥⎣⎦上单调递增，又()()2110,0H e H e e ⎛⎫=-<='⎪⎭'⎝， ()0H x ∴'≤在[]1,e 上恒成立， ()H x ∴无极值点．4）当10a e<<时， ()t x 在[]1,e 递增， ()01,x e ∴∃∈使得ln x a x =， ∴当[]01,x x ∈时， ()0,t x ≤当[]0,x x e ∈时， ()0t x ≥，()()()202ln ,1{ln ,e ax x x x x H x e x x ax xx e-≤≤∴=-≤≤，()()()00,1{12,e ax lnx x x H x e lnx ax x x e-≤<∴+-<≤'=，令()[]()2ln ,1,,2ln 1ax x x k x x e k x ax x '-=∈=--，下面证明()0k x '≤，即证ln 12ln 1,2x ax x a x+≤+≤，又'2ln 1ln ()0x xx x+=-< minln 12x x e +⎛⎫∴= ⎪⎝⎭，即证1a e≤，所以结论成立，即()0k x '≤， ()[]()01,1,,x e H x ⊂∴在[)01,x 递减， (]0,x e 递增，0x ∴为()H x 的极小值.综上当10a e <<或112a e <<时， ()H x 在[]1,e 上有极值点．【名师指点】由极值的情况，探讨导函数零点的情况，进而研究方程根的分布情况. 【举一反三】已知函数()()()2ln 1f x ax x x a R =--∈恰有两个极值点12,x x ，且12x x <.（1）求实数a 的取值范围；（2）若不等式12ln ln 1x x λλ+>+恒成立，求实数λ的取值范围. 【答案】（1）()2,e +∞；（2）[)1,+∞. 【解析】当()0,x e ∈时， ()0g x '>；当(),x e ∈+∞时， ()0g x '<，所以()g x 在()0,e 上单调递增，在(),e +∞上单调递减， ()10g =，当x e >时， ()0g x >，所以()20g e a << ∴()210g e a e<<=解得2a e >，故实数a 的取值范围是()2,e +∞.（2）由（1）得， 11ln 2a x x =， 22ln 2a x x =，两式相加得()()1212ln ln 2a x x x x λ+=+，故()12122ln ln x x x x aλλ++=两式相减可得()()1212ln ln 2a x x x x -=-，故12122ln ln x x a x x -=⋅-所以12ln ln 1x x λλ+>+等价于()1221x x aλλ+>+，所以()()1221x x a λλ+>+ 所以()()121212221ln ln x x x x x x λλ-+>+-，即()()121212ln ln 1x x x x x x λλ+->+-，所以112212ln 11x x x x x x λλ⎛⎫+ ⎪⎝⎭>+-，因为120x x <<，令()120,1x t x =∈，所以()ln 11t t t λλ+>+- 即()()()ln 110t t t λλ+-+-<，令()()()()ln 11h t t t t λλ=+-+-，则()0h t <在()0,1上恒成立， ()ln h t t tλλ='+-，令()ln I t t t λλ=+-， ()()()2210,1t I t t t t tλλ-=-=∈' ①当1λ≥时， ()0I t '<所以()h t '在()0,1上单调递减，()()10h t h ''>=所以()h t 在()0,1上单调递增，所以()()10h t h <=符合题意②当0λ≤时， ()0I t '>所以()h t '在()0,1上单调递增()()10h t h ''<=故()h t 在()0,1上单调递减，所以()()10h t h >=不符合题意； ③当01λ<<时， ()01I t t λ>⇔<<' 所以()h t '在(),1λ上单调递增，所以()()10h t h ''<=所以()h t 在(),1λ上单调递减，故()()10h t h >=不符合题意综上所述，实数λ的取值范围是[)1,+∞. 类型三利用极值证明不等式问题典例3 已知函数()()2ln 1.f x x mx m R =--∈ （1）当1m =时，求()f x 的单调区间；（2）令()()g x xf x =，区间1522,D e e -⎛⎫= ⎪⎝⎭， e 为自然对数的底数。

2018年高考数学黄金100题系列第21题函数零点的性质问题理

第21题函数零点的性质问题I ．题源探究·黄金母题【例1】求函数()ln 26f x x x =+-的零点的个数．【答案】1．【解析】()f x 的定义域为()0,+∞．()(),,2ln24603ln3660f f =+-<=+->由零点存在性定理知()f x 有零点．又()()120,f x f x x'=+>∴在()0,+∞上是单调递增函数，()f x ∴只有一个零点．精彩解读【试题来源】人教版A 版必修1P 88例1．【母题评析】本题考查了零点存在性定理、函数零点个数的判断．【思路方法】判断函数是否存在零点可用零点存在性定理或利用数形结合法．而要判断函数有几个零点，还需要借助函数的单调性．II ．考场精彩·真题回放【例2】【2017高考山东卷】已知当[]0,1x ∈时，函数()21y mx =-的图象与y m =的图象有且只有一个交点，则正实数m 的取值范围是（） A ．(])0,123,⎡+∞⎣B ．(][)0,13,+∞ C．()23,⎡+∞⎣D ．([)3,+∞【答案】B【解析】当01m <≤时，11m≥，2(1)y mx =-单调递减，且22(1)[(1),1]y mx m =-∈-，ym =单调递增，且[,1]y m m m =∈+，此时有且仅有一个交点；当1m >时，101m <<，2(1)y mx =-在1[,1]m 上单调递增，所以要有且仅有一个交点，需2(1)13m m m -≥+⇒≥，故选B ．【例3】【2016高考天津卷】已知函数f （x ）=2(4,0,log (1)13,03)a x a x a x x x ⎧+<⎨++≥-+⎩（a >0，且a ≠1）在R 上单调递减，且关于x 的方程|()|2f x x =-恰好有两个不相等的实数解，则a 的取值范围是（） A ．20,3⎛⎤ ⎥⎝⎦B ．23,34⎡⎤⎢⎥⎣⎦【命题意图】本题主要考查分段函数的零点问题．本题能较好的考查考生分析问题、解决问题的能力，以及数形结合、转化与化归能力等．【考试方向】这类试题在考查题型上，通常基本以选择题或填空题的形式出现，难度较大．【难点中心】已知函数有零点求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； (2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．C ．123,334⎧⎫⎡⎤⎨⎬⎢⎥⎩⎭⎣⎦ D ．123,334⎧⎫⎡⎫⎨⎬⎪⎢⎩⎭⎣⎭ 【答案】C ．【解析】由()f x 在R 上递减可知340,1331,01,34a a a a -≥⎧∴≤≤⎨≥<<⎩，由方程|()|2f x x =-恰好有两个不相等的实数解，可知132,12a a ≤-≤，1233a ≤≤，又∵34a =时，抛物线2(43)3y x a x a =+-+与直线2y x =-相切，也符合题意，∴实数a 的去范围是123,334⎧⎫⎡⎤⎨⎬⎢⎥⎩⎭⎣⎦，故选C ．【例4】【2016高考山东卷】已知函数()2,,24,,x x m f x x mx m x m ⎧≤⎪=⎨-+>⎪⎩其中0m >，若存在实数b ，使得关于x 的方程f （x）=b 有三个不同的根，则m 的取值范围是________________．【答案】()3,+∞【解析】画出函数图象如下图所示：由图所示，要()f x b =有三个不同的根，需要红色部分图象在深蓝色图象的下方，即22224,30m m m m m m >-+∴->，解得3m >．【命题意图】本题主要考查二次函数函数的图象与性质、函数与方程、分段函数的概念，考查学生分析问题与解决问题的能力．【考试方向】这类试题在考查题型上，通常基本以选择题或填空题的形式出现，难度较大，往往是高中数学主要知识的交汇题．【难点中心】解答这类问题的关键在于能利用数形结合思想，通过对函数图象的分析，转化得到代数不等式．本题能较好的考查考生数形结合思想、转化与化归思想、基本运算求解能力等．III ．理论基础·解题原理函数零点、方程的根、函数图象交点的相互转化：有关零点个数及性质的问题会用到这三者的转化，且这三者各具特点：3（1）函数的零点：有“零点存在性定理”作为理论基础，可通过区间端点值的符号和函数的单调性确定是否存在零点；（2）方程的根：方程的特点在于能够进行灵活的变形，从而可将等号两边的表达式分别构造为两个可分析的函数，为作图做好铺垫；（3）函数图象的交点：通过作图可直观的观察到交点的个数，并能初步判断交点所在区间．三者转化：函数()f x 的零点⇒方程()0f x =的根−−−−→方程变形方程()()g x h x =的根⇒函数()g x 与()h x 的交点．IV ．题型攻略·深度挖掘【考试方向】这类试题在考查题型上，通常基本以选择题或填空题的形式出现，一般综合性较强，难度较大．【技能方法】1．已知函数有零点求参数取值范围常用的方法：（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数值域问题加以解决；（3）数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解． 2．此类问题的处理步骤：（1）作图：可将零点问题转化成方程，进而通过构造函数将方程转化为两个图象交点问题，并作出函数图象；（2）确定变量范围：通过图象与交点位置确定参数和零点的取值范围；（3）观察交点的特点（比如对称性等）并选择合适的方法处理表达式的值．【易错指导】对函数零点存在的判断需要注意以下两点：（1）函数()f x 在[],a b 上连续；（2）满足()()0f a f b ⋅<．上述方法只能求变号零点，对于非变号零点不能用上述方法求解．另外需要注意的是：（1）若函数()f x 的图象在0x x =与x 轴相切，则零点0x 通常称为不变号零点；（2）函数的零点不是点，它是函()y f x =数与x 轴的交点的横坐标，是方程()0f x =的根． V ．举一反三·触类旁通考向1 函数零点所在区间的判断【例1】【2018豫西南部分示范高中高三第一学期联考】函数()22ln f x x x=-的零点所在的区间为（） A ．()0,1 B ．()1,2 C ．()2,3 D ．()3,4 【答案】B【解析】由题干知道原函数是增函数，故可以根据零点存在定理得到：()1,2上，故选B ．【例2】【2018齐鲁名校教科研协作体山东、湖北部分重点中学第一次调研】已知函数()()()0),,ln x f x x x g x x e h x x x =>=+=+ 的零点分别为123,,x x x ，则A ．123x x x <<B ．213x x x <<C ．231x x x <<D ．312x x x << 【答案】C【解析】根据函数y x = 分别与,ln x y y e y x ==-=- 图像交点，可知选C ．【跟踪练习】1．【2018河南省天一大联考】函数的零点位于区间（）A ．B ．C ．D ．【答案】C 【解析】，所以由零点存在定理得零点位于区间，选C ．2．【2018湖北部分重点中学上学期第一次联考】函数()e 43xf x x =+-的零点所在的区间为（） A ．1,04⎛⎫-⎪⎝⎭ B ．10,4⎛⎫ ⎪⎝⎭ C ．11,42⎛⎫ ⎪⎝⎭ D ．13,24⎛⎫⎪⎝⎭【答案】C考向2 由函数零点的存在情况求参数的值或取值范围【例3】【2018四川绵阳高三第一次诊断性考试】已知是函数的零点，是函数的零点，且满足，则实数的最小值是（）A ．B ．C ．D ．【答案】A【名师点睛】解题的关键是得到后，得到，然后将问题转化成方程在上有解的问题处理．在解题的过程中分离参数的方法，转化为求函数在闭区间的最值问题处理，求最值时可用导数或基本不等式处理，具体求解中要注意合理的变形．【例4】【2018南宁高三毕业班摸底联考】设函数是定义在上的偶函数，且，当时，，若在区间内关于的方程（且）有且只有4个不同的根，则实数的取值范围是（）A ．B ．C ．D ．【答案】D【解析】由题意可得函数f(x)的对称轴为x=2，周期为T=4，原方程变形为，，所以只需画出，两个函数在区间(-2，6)的图像，根据图像求a的范围，图像如下，一定过（-1，0）点，当时，显然只有一个交点，所以，只需要对数从点B，点C下面穿过就有4个零点，所以解得，选D．【名师点睛】对于求不同类的两个函数构成的方程，我们常把方程变形为f(x)=g(x)，然后根据y=f(x)与y=g(x)的两个图像交点个数来判断原方程根的个数．如本题把方程变形为，再画出两个函数的图像，根据两个图像有4个交点，求出参数a的范围．5【例5】【2018河南省天一大联考】已知函数若关于的方程有3个实数根，则实数的取值范围是（） A ．B ．C ．D ．【答案】D【解析】作图如下：因此要使方程有3个，实数的取值范围是，选D ．【名师点睛】对于方程解的个数(或函数零点个数)问题，可利用函数的值域或最值，结合函数的单调性、草图确定其中参数范围．从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等．【例6】【2018山西45校高三第一次联考】函数在区间和区间上分别存在一个零点，则实数的取值范围是（）A ．B ．C ．D ．或【答案】B【例7】【2017江西上饶一模】已知()f x 是定义域为()0,+∞的单调函数，若对任意的()0,x ∈+∞，都有()13log 4f f x x ⎡⎤+=⎢⎥⎣⎦，且方程()323694f x x x x a -=-+-+在区间(]0,3上有两解，则实数a 的取值范围是（）A ．05a <≤B ．5a <C ．05a <<D ．5a ≥ 【答案】A【解析】由题意知必存在唯一的正实数a ，满足()13log f x x a +=， ()4f a = ①，∴()13log f a a a +=7②，由①②得： 13log 4a a =-，∴413a a -⎛⎫= ⎪⎝⎭，解得3a =．故()133log f x x =-，由方程()323694f x x x x a -=-+-+在区间(]0,3上有两解，即有3213log 694x x x x a =-+-+在区间(]0,3上有两解，由()32694g x x x x a =-+-+，可得()23129g x x x =-+'，当13x <<时， ()0g x '<， ()g x 递减；当01x <<时， ()0g x '>， ()g x 递增． ()g x 在1x =处取得最大值a ， ()04g a =-， ()34g a =-，分别作出13log y x =，和32694y x x x =-+-的图象，可得两图象只有一个交点()1,0，将32694y x x x =-+-的图象向上平移，至经过点()3,1，有两个交点，由()31g =，即41a -=，解得5a =，当05a <≤时，两图象有两个交点，即方程两解．故选A ．【例8】【2018河南郑州一中模拟】已知函数()f x 满足()()22f x f x +-=，当(]0,1x ∈时，()2f x x = ，当(]1,0x ∈-时，()2f x +=若定义在()1,3-上的函数()()()1g x f x t x =-+有三个不同的零点，则实数t 的取值范围是__________．【答案】(0,6-()2,3031x x ∈⇒<-<，所以3fx =-，则()224433f x x x =-=+--．所以()222+1{ 2(243xx x f x x -=-+-， (](](](),1,0,0,1,1,2,2,3x x x x ∈-∈∈∈，画出函数()y f x =在区间()1,3-上的图像与函数()1y t x =+的图像，由于直线()1y t x =+是过定点()1,0-斜率是t 的动直线，数形结合可知：当()1y t x =+与()222y x =--相切时，即方程()()()2212242=0t x x x t x t +=--⇒+-++有唯一解，可求得6t =-故结合图像可知：当06t <<-时，函数()y f x =在区间()1,3-上的图像与直线()1y t x =+的图像有且只有三个不同的交点，即定义在()1,3-上的函数()()()1g x f x t x =-+有三个不同的零点，应填答案(0,6-．【名师点睛】解答本题的关键是充分运用题设条件先将函数()y f x =在区间()1,3-上的解析表达式求出来，再画出其图像数形结合，从而将问题转化为方程()()()2212242=0t x x x t x t +=--⇒+-++有唯一解，可求得6t =-06t <<-()y f x =在区间()1,3-上的9图像与直线()1y t x =+的图像有且只有三个不同的交点，即定义在()1,3-上的函数()()()1g x f x t x =-+有三个不同的零点．【例9】【2017江苏南师大附中模拟】函数()()()({ 4x x x t f x x x t ≤=>其中0t >，若函数()()1g x f f x ⎡⎤=-⎣⎦有6个不同的零点，则实数t 的取值范围是__________．【答案】()3,4()()()22343f x x tx t x t x t =-+=--'，则,3tx x t ==是两个极值点，且极大值为327t ，极小值为0．画出函数()()()({ 4x x x t f x xx t ≤=>的图像，和直线1,1y t y =+=的图像，结合函数的图像可知：当314{ 34127t t t<⇒<<>时，两直线1,1y t y =+=与函数()y f x =共有六个不同交点，应填答案()3,4．【名师点睛】解答本题的关键关节有两个：其一是将函数的零点问题进行等价转化；其二是要巧妙运用数形结合思想建立不等式组．求解时还要综合运用导数知识确定函数的极值点和极值．灵活运用所学知识和重要是数学思想进行分析问题和解决问题是本题一大特征，体现了数学思想在解决数学问题中四两拨千斤的功能．【跟踪练习】1．【2018届山西45校高三第一次联考】函数()221f x ax x =-+在区间（-1，1）和区间（1，2）上分别存在一个零点，则实数a 的取值范围是（） A ．31a -< 【答案】B2．【2018四川绵阳高三第一次诊断性考试】函数满足，且当时，．若函数的图象与函数（，且）的图象有且仅有4个交点，则的取值集合为（）A ．B ．C ．D ．【答案】C 【解析】因为函数满足，所以函数的周期为又在一个周期内，函数解析式为，所以可作出函数图象，在同一坐标系内作函数的图象，要使两个函数图象有且仅有四个交点，只需，所以，故选C ．3．【2018贵州黔东南州上学期第一次联考】已知函数()29,0{ 42,0x x x f x x x +-≤=->，若方程()f x a =有两个不相等的实数根，则实数a 的取值范围是（） A ．[)59,2,24⎡⎫--⋃-+∞⎪⎢⎣⎭B ．()2,-+∞C ．()59,2,24⎛⎤--⋃-+∞ ⎥⎝⎦D ．()59,2,24⎡⎫--⋃-+∞⎪⎢⎣⎭【答案】C【解析】作出函数()29,0{ 42,0x x x f x x x +-≤=->的图象如下：方程()f x a =有两个不相等的实数根等价于函数()y f x =与y a =的图象有两个不同的交点，有图可知，11()59,2,24a ⎛⎤∈--⋃-+∞ ⎥⎝⎦．故选C ．【名师点睛】方程的根或函数有零点求参数范围常用方法和思路（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数值域问题加以解决；（3）数形结合法：先对解析式变形，在同一直角坐标系中，画出函数的图象，然后数形结合求解． 4．【2018四川达州模拟】已知()2sin 26f x x m π⎛⎫=-- ⎪⎝⎭在0,2x π⎡⎤∈⎢⎥⎣⎦上有两个零点，则m 的取值范围为( )A ．（1，2）B ．[1，2]C ．[1，2)D ．（1，2] 【答案】C【名师点睛】本题考查正弦函数的图象，解答本题关键是将函数有两个零点的问题转化为两个函数有两个交点的问题，作出两函数的图象，判断出参数的取值范围，本题以形助数，是解此类题常用的方法，熟练作出相应函数的图象对解答本题很重要5．【2018江西横峰中学第一次月考】设()f x 满足()()-=f x f x -，且在[]1,1-上是增函数，且()11f -=-，若函数()221f x t at ≤-+对所有的[]1,1x ∈-，当[]1,1a ∈-时都成立，则t 的取值范围是（）A ．1122t -≤≤ B ．2t ≥或2t ≤-或0t = C ．12t ≥或12t ≤-或0t = D ．22t -≤≤ 【答案】B【解析】若函数()221f x t at ≤-+对所有的[]1,1x ∈-都成立，由已知易得()f x 的最大值是1，∴2212120t at at t ≤-+⇔-≤，设()22g a at t =- ()11a -≤≤，欲使220at t -≤恒成立，则 ()()10{210g t g -≤⇒≥≤或2t ≤-或0t =，故选B ．6．【2018湖北七校联考】已知)(x f 是奇函数并且是R 上的单调函数，若函数)()12(2x f x f y -++=λ只有一个零点，则实数λ的值是（） A ．41 B ．81 C ．87- D ．83-【答案】C ．【解析】令0)()12(2=-++=x f x f y λ，且)(x f 是奇函数，则)()()12(2λλ-=--=+x f x f x f ，又因为)(x f 是R 上的单调函数，所以λ-=+x x 122只有一个零点，即0122=-+-λx x 只有一个零点，则0)1(81=--=∆λ，解得87-=λ，故选C ． 7．已知函数()lg f x x =，若0a b <<，且()()f a f b =，则2a b +的取值范围是（）A ．()+∞ B ． )⎡+∞⎣C ．()3,+∞D ．[)3,+∞【答案】C ．【评注】（1）此类问题如果()f x 图象易于作出，可先作图以便于观察函数特点；（2）本题有两个关键点，一个是引入辅助变量t ，从而用t 表示出,a b ，达到消元效果，但是要注意t 是有范围的（通过数形结合y t =需与()y f x =有两交点）；一个是通过图象判断出,a b 的范围，从而去掉绝对值．138．已知函数()111,0,2212,,22x x x f x x -⎧⎡⎫+∈⎪⎪⎢⎪⎣⎭=⎨⎛⎤⎪∈ ⎥⎪⎝⎦⎩，若存在12,x x ，当1202x x ≤<<时，()()12f x f x =，则()()122x f x f x -的取值范围为（）A ．20,4⎛- ⎝⎭ B ．92,164⎡--⎢⎣⎭ C ． 91,162⎡⎫--⎪⎢⎣⎭ D ．2142⎡⎫--⎪⎢⎪⎣⎭ 【答案】C ．9．【2018江西新余一中二模】已知函数()y f x =的周期为2，当[]0,2x ∈时， ()()21f x x =-，如果()()5log 1g x f x x =--，则函数()y g x =的所有零点之和为（）A ．2B ．4C ．6D ．8 【答案】D【解析】由题意可得()()5log 1g x f x x =--，根据周期性画出函数()()21f x x =-的图象，以及5log 1y x =-的图象，根据5log 1y x =-在()1,+∞上单调增函数，当6x =时， 5log 11y x =-=， ∴当6x >时， 5log 11y x =->，此时与函数()y f x =无交点，再根据5log 1y x =-的图象和()f x 的图象都关于直线1x =对称，结合图象可知有8个交点，则函数()()5log 1g x f x x =--的零点个数为8，故选D ．【方法点睛】判断函数()y f x =零点个数的常用方法：(1) 直接法：令()0,f x =则方程实根的个数就是函数零点的个；(2) 零点存在性定理法：判断函数在区间[],a b 上是连续不断的曲线，且()()0,f a f b ⋅<再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数；(3) 数形结合法：转化为两个函数的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，在一个区间上单调的函数在该区间内至多只有一个零点，在确定函数零点的唯一性时往往要利用函数的单调性，确定函数零点所在区间主要利用函数零点存在定理，有时可结合函数的图象辅助解题．10．【2018河北石家庄二中八月高三模拟】已知()22,{ 2,x x a f x x x a -≥=+<，若函数()1ln g x f x a x ⎛⎫=+- ⎪⎝⎭有零点，则实数a 的取值范围是__________．【答案】[][)1,23,-⋃+∞【名师点睛】已知函数有零点求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； (2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解． 11．【2018广东茂名高三五大联盟学校9月联考】若函数至少有3个零点，则实数的取值范围是__________．【答案】15【名师点睛】本题的求解过程体现了数形结合的数学思想的巧妙运用，求解时先在同一平面直角坐标系中画出两个函数的图像，进而借助图像的直观建立不等式，进而通过解不等式求出参数的取值范围．。

专题2.1 以零点个数为背景的填空题-2020年高考数学备考优生百日闯关系列(解析版)

要注意函数零点、方程的根、不等式解集三者之间的关系，进行彼此之间的转化是解决该类题的关键，等价转化是这类问题的难点．解决该类问题的途径往往是根据函数的性质作出示意图，利用数形结合研究分界位置，结合函数、方程、不等式刻画边界位置，其间要注意导数的应用.【典例解剖】类型一周期函数零点个数问题典例1[山东省夏津一中2019届高三上学期12月月考]定义在上的函数，满足，且.若，则函数在内的零点的个数有______个【答案】2【解析】由于，故是周期为点的周期函数，画出的图像以及的图像如下图所示，由图可知，两个函数有个交点，故函数有个零点。

【名师指点】将给定区间的根的个数问题转换为熟悉函数图像在给定区间的交点个数问题,利用周期性和偶f x 的根求解，函数正确作图以及判断端点函数值的大小是解题关键．求解零点问题时，往往转化为()0若该方程不易解出，可考虑数形结合转化为两熟悉图像的交点问题求解．【举一反三】已知函数满足，且是偶函数，当时，，若在区间内，函数有4 个零点，则实数的取值范围是_____【答案】【解析】由题意可知函数是周期为的偶函数，结合当时，，绘制函数图象如图所示，函数有4个零点，则函数与函数的图象在区间内有4个交点，结合函数图象可得：当时：，求解对数不等式可得：，即实数的取值范围是.本题选择D选项.类型二复合函数的零点个数问题典例2 【2018安徽阜阳一中二模】已知，若关于的方程恰好有个不相等的实数根，则实数的取值范围是______________. 【答案】【解析】∵∴∴∴当或时，，当时，∴在上单调递增，在上单调递减，在上单调递增可作出大致函数图象如图所示：令，则当时，方程有一解；当时，方程有两解；时，方程有三解∵关于的方程，恰好有4个不相等实数根 ∴关于的方程在和上各有一解∴，解得，故答案为【名师指点】求解复合方程问题时，往往把方程[()]0f g x =分解为()0f t =和()g x t =处理，先从方程()0f t =中求t ，再带入方程()g x t =中求x 的值．【举一反三】[山东省泰安市2019届高三上学期期中考试]已知是R 上的偶函数且，若关于的方程有三个不相等的实数根，则的取值范围是_____．【答案】【解析】作出函数的图象如下图所示．由可得或．由图象可得有唯一解．∵关于的方程有三个不相等的实数根，∴方程有两个不相等的实数根，即函数的图象与函数的图象有两个不同的交点，结合图象可得或． ∴实数的取值范围是．故答案为．类型三分段函数（或含绝对值函数）的零点个数问题典例3 【江苏省镇江市2018届高三上学期期末统考】已知k 为常数，函数()2,0{ 1,0x x f x x lnx x +≤=->，若关于x 的方程()2f x kx =+有且只有4个不同解，则实数k 的取值集合为__________．【答案】()31,1e e ⎧⎫⋃--⎨⎬⎩⎭【解析】画出函数()2,0{ 1,0x x f x x lnx x +≤=->的图象如图所示：∵2y kx =+过点()0,2∴当0k ≤时，显然不满足题意，故0k > ∵2y kx =+在(],0-∞上与函数()f x 有一个交点∴2y kx =+在()0,+∞上与函数()f x 有三个交点，且由图所示2y kx =+在()0,1上与函数()f x 有一个交点设直线2y kx =+与()()()1,y f x x =∈+∞的图象在相切的切点坐标为(),m n ，则ln n m =， 2n km =+ ∵()1f x x'= ∴1k m=∴3n =， 3m e =， 3k e -=∴实数k 的取值范围是()30,e -【名师指点】分段函数与含绝对值函数典型特征为各段解析式不一致，不仅要考虑对应性，而且需考虑自变量在结合点情况及值域包含关系．【举一反三】．【安徽省2019届高三皖南八校第一次联考】已知高数的周期为4，且时，,，若方程恰有5个实数解（其中m ＞0），则m 的取值范围为_____________。

专题3.3 第03关-2018年高考数学备考优生百日闯关系列(江苏专版)(原卷版)

新题原创强化训练第三关一、填空题1．已知实数x ，y 满足条件⎩⎪⎨⎪⎧2≤x ≤4，y ≥3，x ＋y ≤8，则y z x =的最大值与最小值之和为． 2．已知函数2()||2x f x x +=+，x ∈R ，则2(2)(2)f x x f x -<-的解集是．3．将函数()π4y x =的图象向左平移3个单位，得函数()π4y x ϕ=+（πϕ<）的图象（如图），点,M N 分别是函数()f x 图象上y 轴两侧相邻的最高点和最低点，设MON θ∠=，则()tan ϕθ-的值为．4．已知正实数,x y 满足111x y +=，则3411x y x y +--的最小值为． 5．已知AB 是圆C :222x y r +=的直径,O 为坐标原点,直线l :2r x c=与x 轴垂直,过圆C 上任意一点P (不同于,A B )作直线PA 与PB 分别交直线l 于,M N 两点, 则2OM ON r ⋅的值为 . 6.若方程2|21|0x x t ---=有四个不同的实数根123,,,x x x x，且123x x x x <<<，则41322()()x x x x -+-的取值范围是 . 二、解答题1.中国古建筑中的窗饰是艺术和技术的统一体，给人于美的享受．如图（1）为一花窗；图（2）所示是一扇窗中的一格，呈长方形，长30 cm ，宽26 cm ，其内部窗芯（不含长方形边框）用一种条形木料做成，由两个菱形和六根支条构成，整个窗芯关于长方形边框的两条对称轴成轴对称．设菱形的两条对角线长分别为x cm 和y cm ，窗芯所需条形木料的长度之和为L ．（1）试用x ，y 表示L ；（2）如果要求六根支条的长度均不小于2 cm ，每个菱形的面积为130 cm 2，那么做这样一个窗芯至少需要多长的条形木料（不计榫卯及其它损耗）？2.已知函数32()3(2)f x x x a x =-+-，a ∈R ．（1）求函数()f x 的单调增区间；（2）若函数()f x 有三个互不相同的零点0，1t ，2t ，其中12t t <．（ⅰ）若213t t =，求a 的值；（ⅱ）若对任意的12[]x t t ∈，，都有()16f x a -≤成立，求a 的取值范围．3.在数列{}n a 中，11a =，28a =，111(1)n n nn a a n λ++=++，λ为常数，*n ∈N ．（1）求λ的值；（2）设n n a b n=，求数列{}n b 的通项公式；（3）是否存在正整数r s t ，，（r s t <<），使得r s t ，，与r s t a a a ，，都为等差数列？若存在，求r s t ，，的值；若不存在，请说明理由．。