旋转类几何变换
几何变换的认识和基本原理

几何变换的认识和基本原理几何变换是指通过对平面上的点、线、面进行位置、形状或尺寸上的改变,从而得到一个新的图形。
在计算机图形学和计算机视觉等领域,几何变换是非常重要的基础知识。
本文将介绍几何变换的认识和基本原理。
一、平移变换平移变换是指将一个图形沿着某个方向平行移动一定的距离。
平移变换可以用以下公式表示:[x', y'] = [x + dx, y + dy]其中,(x, y)是原始图形上的一个点,(dx, dy)是平移的距离,(x', y')是平移后得到的新点的坐标。
二、旋转变换旋转变换是指将一个图形绕着某个中心点按照一定的角度旋转。
旋转变换可以用以下公式表示:[x', y'] = [x*cosθ - y*sinθ, x*sinθ + y*cosθ]其中,(x, y)是原始图形上的一个点,θ是旋转的角度,(x', y')是旋转后得到的新点的坐标。
三、缩放变换缩放变换是指将一个图形按照一定的比例因子放大或缩小。
缩放变换可以用以下公式表示:[x', y'] = [s*x, s*y]其中,(x, y)是原始图形上的一个点,s是缩放的比例因子,(x', y')是缩放后得到的新点的坐标。
四、对称变换对称变换是指将一个图形关于某一直线或某一点进行对称。
对称变换可以分为关于x轴对称、关于y轴对称、关于原点对称等。
不同类型的对称变换具体的公式略有不同,但原理都是将图形上的点映射到其关于对称轴的对称位置。
五、仿射变换仿射变换是指将一个图形通过平移、旋转和缩放等基本变换来进行综合变换。
仿射变换可以用以下矩阵表示:[x', y'] = [a*x + b*y + c, d*x + e*y + f]其中,a、b、c、d、e、f为变换矩阵中的参数,(x, y)是原始图形上的一个点,(x', y')是变换后得到的新点的坐标。
中考数学专题复习旋转类几何变换
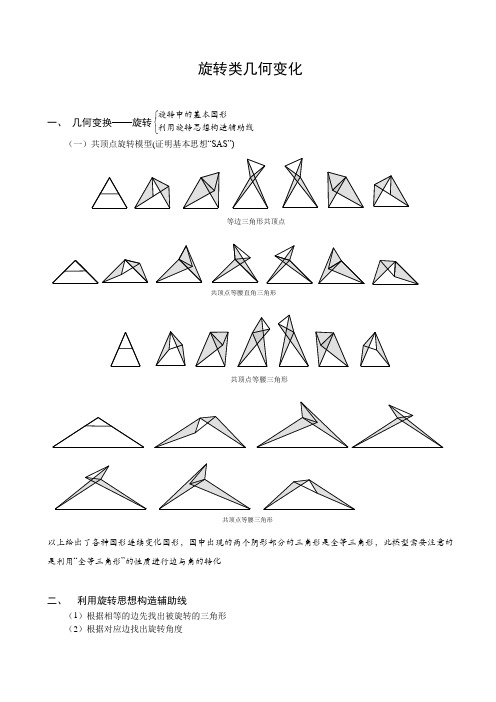
旋转类几何变化一、几何变换——旋转旋转中的基本图形利用旋转思想构造辅助线⎧⎨⎩(一)共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二、利用旋转思想构造辅助线(1)根据相等的边先找出被旋转的三角形(2)根据对应边找出旋转角度(3)根据旋转角度画出对应的旋转的三角形三 、 旋转变换前后具有以下性质:(1)对应线段相等,对应角相等 (2)对应点位置的排列次序相同(3)任意两条对应线段所在直线的夹角都等于旋转角θ.考点一 旋转与最短路程☞考点说明:旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题,同时与旋转有关路程最短的问题,比较重要的就是费马点问题,涉及费马点问题,视学生程度进行选择性讲解。
【例1】 如图,四边形ABCD 是正方形,ABE ∆是等边三角形,M 为对角线BD 上任意一点,将BM 绕点B逆时针旋转60︒得到BN ,连接AM 、CM 、EN . ⑴求证:AMB ENB ∆∆≌⑵①当M 点在何处时,AM CM +的值最小;②当M 点在何处时,AM BM CM ++的值最小,并说明理由; ⑶当AM BM CM ++的最小值为31+时,求正方形的边长.ENMDCB A【例2】 阅读下列材料对于任意的ABC ∆,若三角形内或三角形上有一点P ,若PA PB PC ++有最小值,则取到最小值时,点P 为该三角形的费马点。
①若三角形内有一个内角大于或等于120︒,这个内角的顶点就是费马点②若三角形内角均小于120︒,则满足条件120APB BPC APC ∠=∠=∠=︒时,点P 既为费马点 解决问题:⑴如图,ABC ∆中,三个内角均小于120︒,分别以AB 、AC 为边向外作等边ABD ∆、ACE ∆,连接CD 、BE 交于点P ,证明:点P 为ABC ∆的费马点。
几何形的旋转和对称变换

几何形的旋转和对称变换几何形的旋转和对称变换是数学中常见的概念和技巧。
通过旋转和对称变换,我们可以改变几何形的位置和形状,展现出不同的视觉效果和特性。
本文将介绍旋转和对称变换的定义、性质以及在实际问题中的应用。
一、旋转变换旋转变换是指将几何形绕某个点或某条直线旋转一定角度,从而改变形状和位置。
1. 定义设点A(x, y)绕点O(a, b)逆时针旋转θ度,则旋转后点A的坐标为A’(x', y')。
根据旋转变换的定义,有以下公式:x' = a + (x-a)cosθ - (y-b)sinθy' = b + (x-a)sinθ + (y-b)cosθ2. 性质- 旋转变换不改变几何形的大小。
- 旋转变换保持直线上的点的相对位置关系。
- 旋转角度可以是正数或负数,正数表示逆时针旋转,负数表示顺时针旋转。
3. 应用旋转变换在计算机图形学、机器人学和物理学等领域有广泛的应用。
在设计制图中,旋转变换可以用于生成各种艺术效果、模拟物体的运动轨迹等。
在机器人学中,旋转变换可以应用于机器人的路径规划和姿态控制。
在物理学中,旋转变换可以用于分析刚体的运动和转动。
二、对称变换对称变换是指将几何形围绕着某个轴线或中心对称,从而保持形状不变或形状镜像对称。
1. 定义- 轴对称:如果一个几何形上的任意一点到轴的距离和该点的镜像到轴的距离相等,那么这个几何形关于该轴对称。
常见的轴对称有水平轴对称、垂直轴对称和斜对称。
- 中心对称:如果一个几何形上的任意一点关于某个点对称后仍然位于几何形上,那么这个几何形关于该点中心对称。
中心对称即是以某个点为中心,投影方向相反的对称。
2. 性质- 对称变换保持几何形的面积和周长不变。
- 轴对称保持几何形的形状相同,而中心对称保持几何形的形状镜像对称。
- 轴对称和中心对称可以叠加使用,得到更复杂的变换效果。
3. 应用对称变换在几何学、物理学和图像处理等领域具有重要的应用。
几何形的旋转反射与平移

几何形的旋转反射与平移几何形的旋转、反射与平移是数学中常见的几何变换方式。
通过这些变换,可以改变图形的位置、角度和方向,从而创造出各种不同的几何形。
本文将从旋转、反射和平移三个方面探讨几何形的变换特性,展示它们的应用及相关的数学原理。
一、旋转变换旋转变换是指围绕某个中心点旋转图形的操作。
旋转变换通过改变角度,使得图形绕中心点旋转一周或某一角度。
旋转变换可以按照顺时针或逆时针方向进行,旋转的角度可以是任意值。
旋转变换的数学原理基于坐标系的旋转公式。
对于平面上的点P(x, y),以原点O为中心点,逆时针旋转θ角度后的新坐标为P'(x', y'),则旋转公式如下:x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ通过旋转变换,可以产生各种规则的几何形状,如正多边形、圆等。
旋转变换也常用于设计和计算机图形学等领域,用于创建绚丽的图形效果。
二、反射变换反射变换是指将图形围绕某个轴线进行对称操作,即将图形镜像翻转。
反射变换可以分为水平反射和垂直反射两种情况,分别以水平轴和垂直轴为对称轴进行反射。
反射变换的数学原理与对称性相关。
对于平面上的点P(x, y),以水平轴为对称轴进行水平反射后的新坐标为P'(x, -y),以垂直轴为对称轴进行垂直反射后的新坐标为P'(-x, y)。
反射变换常用于镜像对称的设计和构造问题,如设计平面图案、制作对称的艺术品等。
反射变换也可以用于解决实际问题,如建筑设计中的对称性考虑等。
三、平移变换平移变换是指将图形沿着横轴和纵轴进行平行移动的操作。
平移变换通过改变图形的位置,将图形移动到另一个位置上,而不改变其形状和大小。
平移变换的数学原理是将图形的每个点都沿着横坐标和纵坐标方向移动同一个距离。
对于平面上的点P(x, y),平移变换后的新坐标为P'(x+a, y+b),其中(a, b)为平移的距离。
几何形的旋转平移和对称变换

几何形的旋转平移和对称变换几何形的旋转、平移和对称变换几何形的旋转、平移和对称变换是几何学中的基础概念和操作,它们在数学和实际应用中都扮演着重要的角色。
通过这些变换,我们可以改变和调整图形的位置、方向和形状,使得几何问题的解决变得更加灵活和方便。
本文将对几何形的旋转、平移和对称变换进行详细介绍。
1. 旋转变换旋转变换是指沿着一个固定点旋转图形一定的角度。
在平面几何中,我们通常以原点为中心,按照逆时针方向旋转来描述旋转变换。
旋转变换可以保持图形的大小和形状不变,只改变其方向和位置。
常见的旋转角度有90度、180度和360度。
旋转变换的数学表示式为:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,(x, y)是旋转前的点的坐标,(x', y')是旋转后的点的坐标,θ是旋转的角度。
2. 平移变换平移变换是指将图形沿着平行于坐标轴的方向移动一定的距离。
平移变换只改变图形的位置,保持其大小、形状和方向不变。
平移变换可以用向量来表示,其中向量的分量表示图形在x轴和y轴上的位移。
平移变换的数学表示式为:x' = x + dxy' = y + dy其中,(x, y)是平移前的点的坐标,(x', y')是平移后的点的坐标,(dx, dy)是平移的距离。
3. 对称变换对称变换是指将图形绕着某个轴线或某个点进行翻转,使得图形在变换前后保持镜像对称关系。
常见的对称变换有关于x轴、y轴和原点的对称。
对称变换的数学表示式为:关于x轴对称:(x, y) -> (x, -y)关于y轴对称:(x, y) -> (-x, y)关于原点对称:(x, y) -> (-x, -y)4. 综合应用几何形的旋转、平移和对称变换在许多领域有着广泛的应用,如建筑设计、计算机图形学、机器人学等等。
通过这些变换,我们可以灵活地处理图形的位置和形状,满足不同需求的设计和计算要求。
初中数学旋转的六大模型

初中数学旋转的六大模型初中数学中,旋转是一个重要的几何变换方法。
通过旋转,可以将一个图形围绕某个点或轴进行转动,从而得到新的图形。
旋转不仅在几何学中有广泛应用,在实际生活中也有很多旋转的例子,比如地球自转、风车转动等。
本文将介绍初中数学中常用的六大旋转模型,分别是点的旋转、线段的旋转、直线的旋转、射线的旋转、多边形的旋转和圆的旋转。
1.点的旋转:点的旋转是指将一个点围绕某个点或轴进行转动,得到新的位置。
旋转时,需要确定旋转中心和旋转角度。
旋转角度可以用角度制或弧度制表示。
当旋转角度为正时,点按逆时针方向旋转;当旋转角度为负时,点按顺时针方向旋转。
点的旋转模型可以用来解决一些几何问题,比如求解旋转后的坐标、判断点是否在某个旋转图形内等。
2.线段的旋转:线段的旋转是指将一条线段围绕某个点或轴进行转动,得到新的线段。
旋转时,需要确定旋转中心和旋转角度。
线段的旋转模型可以用来解决一些几何问题,比如求解旋转后的线段长度、判断两条线段是否相交等。
3.直线的旋转:直线的旋转是指将一条直线围绕某个点或轴进行转动,得到新的直线。
旋转时,需要确定旋转中心和旋转角度。
直线的旋转模型可以用来解决一些几何问题,比如求解旋转后的直线方程、求解旋转后的直线与其他直线的交点等。
4.射线的旋转:射线的旋转是指将一条射线围绕某个点或轴进行转动,得到新的射线。
旋转时,需要确定旋转中心和旋转角度。
射线的旋转模型可以用来解决一些几何问题,比如求解旋转后的射线方程、判断射线是否与其他几何图形相交等。
5.多边形的旋转:多边形的旋转是指将一个多边形围绕某个点或轴进行转动,得到新的多边形。
旋转时,需要确定旋转中心和旋转角度。
多边形的旋转模型可以用来解决一些几何问题,比如求解旋转后的多边形的面积、判断多边形是否相似等。
6.圆的旋转:圆的旋转是指将一个圆围绕某个点或轴进行转动,得到新的圆。
旋转时,需要确定旋转中心和旋转角度。
圆的旋转模型可以用来解决一些几何问题,比如求解旋转后的圆的面积、判断两个圆是否相交等。
几何形的旋转和切变变换

几何形的旋转和切变变换几何形的旋转和切变变换是数学中常见的几何操作,它们在许多领域中都有广泛的应用,包括计算机图形学、物理学、工程学等。
在本文中,我们将探讨旋转和切变的基本概念、公式以及其在实际应用中的意义。
旋转变换是将一个几何形体绕着某个中心点旋转一定角度的操作。
我们常用极坐标系来描述旋转变换,其中原点代表旋转中心,角度表示旋转的程度。
假设我们有一个点P(x,y),要将它绕着中心点O旋转θ角度后的新坐标为P'(x',y'),那么有以下公式:x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ这些公式通过三角函数来描述坐标的变化。
通过改变θ的值,我们可以实现对几何形体的不同旋转效果。
切变变换是将一个几何形体沿着某个方向进行平移的操作。
它可以分为水平切变和垂直切变两种。
水平切变是将几何形体的每个点在水平方向上进行平移,而垂直切变则是在垂直方向上进行平移。
具体的切变公式如下:水平切变:x' = x + shx * yy' = y垂直切变:x' = xy' = y + shy * x其中shx和shy分别表示水平和垂直方向的切变系数。
通过改变切变系数的大小,我们可以实现对几何形体在平移方向上的不同变换效果。
旋转和切变变换在计算机图形学中有着广泛的应用。
比如,在计算机游戏中,我们经常需要对角色的模型进行旋转和切变,以实现动画效果。
同时,在CAD软件中,旋转和切变变换也被用于设计和编辑图形对象,使其具有更好的可视化效果。
除了计算机图形学,旋转和切变变换还在物理学和工程学等领域中发挥着重要作用。
在物理学中,我们可以通过旋转和切变变换来描述刚体在空间中的运动轨迹,从而研究其力学行为。
在工程学中,旋转和切变变换可以应用于材料力学、流体力学等领域,来研究材料的变形和流体的运动。
综上所述,几何形的旋转和切变变换在数学中具有重要的地位和广泛的应用。
几何形的旋转了解形的旋转变换及其性质

几何形的旋转了解形的旋转变换及其性质几何形的旋转:了解形的旋转变换及其性质几何学是一门研究形状、大小和相对位置关系的学科。
其中,形的旋转变换是一种常见的变换方式,通过对几何形进行旋转来达到不同的目的。
本文将介绍形的旋转变换以及它的性质。
1. 形的旋转变换概述形的旋转变换是指将一个几何形绕着一个点作圆周运动,保持其大小、形状和方向不变。
旋转变换可以分为顺时针旋转和逆时针旋转两种情况。
旋转中心可以是任意点,被旋转的几何形叫做原形,旋转后的几何形称为像形。
2. 旋转的基本性质(1)保角性质:旋转变换不改变角的大小。
(2)保持距离性质:旋转变换保持原始形与新形之间的线段长度不变。
(3)保直线性质:旋转变换保持原始形与新形之间的直线仍然是直线。
3. 旋转的角度与方向几何形的旋转可以通过角度来衡量。
顺时针旋转的角度为正,逆时针旋转的角度为负。
旋转角度可以是任意实数,也可以是特定的角度如90°、180°等。
不同的旋转角度会带来不同的效果和形状变化。
4. 旋转的中心旋转的中心可以是形状自身的一个点,也可以是外部指定的一点。
对于正多边形,旋转中心通常是形状的中心点,而对于任意多边形,则可以选择不同的旋转中心,从而得到不同的旋转变换。
5. 旋转的应用旋转变换在现实生活中有许多应用。
比如,地球绕着自转轴旋转,产生白昼和黑夜交替;风车的叶片沿着中心旋转,产生动力;艺术家可以运用旋转变换创作出绚丽多彩的图案等等。
6. 旋转的组合变换旋转变换可以与其他几何变换如平移、缩放和镜像等进行组合,得到更加复杂的变换效果。
通过适当选择变换的顺序和参数,可以实现多样化的几何形变。
7. 旋转的数学表示旋转变换可以通过矩阵乘法来表示。
对于二维空间中以原点为中心旋转的变换,可以使用如下的矩阵表示:[cosθ -sinθ][sinθ cosθ]其中θ表示旋转的角度,cosθ和sinθ分别为旋转角度θ的余弦和正弦值。
通过矩阵乘法,可以将原始形的坐标与旋转矩阵相乘,得到旋转后形的坐标。
几何形的旋转变换

几何形的旋转变换旋转是几何学中一种重要的变换方式,它可以通过围绕某个中心点旋转图形,使其发生位置和形态上的变化。
在几何学中,旋转变换是一种基本的刚性变换,可以通过旋转角度和中心点来描述。
旋转变换通常使用旋转矩阵来表示,其中旋转角度以逆时针方向计算。
通过旋转变换,我们可以改变图形的方向、角度和位置,从而产生不同的几何形。
在本文中,我将介绍几种常见的几何形旋转变换,以及它们的应用。
1. 点的旋转变换点的旋转变换是最基本的旋转变换方式,它将一个点绕着中心点旋转一定角度后得到一个新的点。
旋转变换可以使用坐标变换公式来描述,即给定一个点P(x, y),以原点为中心点,逆时针旋转θ度后,新的坐标为P'(x', y'),其中:x' = x * cos(θ) - y * sin(θ)y' = x * sin(θ) + y * cos(θ)这个公式描述了点P在平面上绕原点旋转θ度后得到点P'的坐标变换关系。
2. 图形的旋转变换除了点的旋转变换,我们还可以将整个图形绕着中心点进行旋转变换。
对于任意的图形,可以通过对每个顶点进行点的旋转变换来实现整个图形的旋转。
例如,对于一个三角形ABC,如果我们要将其逆时针旋转θ度,则可以分别对顶点A、B、C进行点的旋转变换,得到新的顶点A'、B'、C',连接它们即可得到旋转后的三角形A'B'C'。
同样,对于其他几何形状,也可以使用类似的方式进行旋转变换。
3. 平行四边形旋转变换在平面几何中,平行四边形是一个常见的几何形状,它由四个平行的边组成。
在进行平行四边形的旋转变换时,我们需要确定旋转的中心点和旋转角度。
假设有一个平行四边形ABCD,我们要将其绕点O旋转θ度。
首先,我们需要确定点O的坐标,然后对点A、B、C、D分别进行点的旋转变换,得到新的顶点A'、B'、C'、D'。
旋转变换与几何关系解析

旋转变换与几何关系解析旋转变换是几何学中常用的一种变换方式,通过旋转一个图形或物体,可以得到不同的几何关系。
本文将从几何关系的角度对旋转变换进行解析,并探讨其应用和实际意义。
一、旋转变换的基本概念旋转变换是指通过旋转将一个图形或物体转换为另一个图形或物体的变换方式。
在几何学中,旋转变换通常以一个点为轴心,将其他点绕轴心旋转一定角度后得到新的点。
旋转变换可以在平面内进行,也可以在三维空间中进行。
二、旋转变换与几何关系的解析1. 平面旋转变换在平面旋转变换中,我们以一个点为轴心,将其他点绕轴心旋转一定角度。
这种旋转变换可以改变图形的位置、形状和方向。
几何关系的解析包括以下几个方面:(1) 位置关系:旋转后的图形相对于原图形的位置关系可以通过坐标变换来解析。
设原图形中的点A(x, y)经过旋转变换后得到点A'(x', y'),则有以下关系:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,θ表示旋转角度。
(2) 形状关系:旋转变换可以改变图形的形状,例如,一个矩形绕一个点旋转后可以变成一个椭圆。
通过解析旋转变换的坐标变换公式,可以得到旋转后的图形的形状关系。
(3) 方向关系:旋转变换也可以改变图形的方向。
通过解析旋转变换的角度变换公式,可以得到旋转后的图形的方向关系。
2. 空间旋转变换在三维空间中,旋转变换与平面旋转变换类似,都是以一个点为轴心将其他点绕轴心旋转一定角度。
不同之处在于,旋转变换同时涉及到三个坐标轴的旋转。
几何关系的解析主要包括以下几个方面:(1) 位置关系:类似于平面旋转变换,位置关系可以通过坐标变换来解析。
设原空间中的点A(x, y, z)经过旋转变换后得到点A'(x', y', z'),则有以下关系:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθz' = z其中,θ表示旋转角度。
几何变换之旋转的性质

旋转那些事儿旋转,是三大几何变换中考察最多、难度最大的那个,平移、对称从图像观察角度来说直接显然,对应的结论也很容易用到.而旋转,变换得到的图形相对复杂些,有时候解题的突破口隐藏得更深,导致无从下手.本篇将从基本的性质开始,到一些常见的模型,最后说说关于构造旋转能给我们带来什么,全方位了解旋转在中考题中的考察.一、旋转的基本性质如下图,将△ABC 绕点A 旋转一定角度得到△ADE .性质一:对应边相等 结论:AB =AD ,AC =AE .补充:当然还可以得到BC =DE ,但这并没有什么用,因为BC 与DE 并没有特殊位置关系.性质二:对应角相等结论:∠B =∠D ,∠C =∠E ,∠BAC =∠DAE .补充:如果不是特殊角,此性质并没有什么用,但由性质二可以推性质三.性质三:旋转角都相等 结论:∠BAD =∠CAE =∠BFD . 补充:∠BAD =∠CAE 易证,∠BAD =∠BFD 可用“8字”模型证明: ∵∠BAD +∠B =∠BFD +∠D ,且∠B =∠D , ∴∠BAD =∠BFD .且第三组对应边往往用得最多.ABCDEFαααE DCBA【中考真题-关于三角形的旋转】1.(2019·眉山)如图,在Rt ABC ∆中,90B ∠=︒,5AB =,12BC =,将ABC ∆绕点A 逆时针旋转得到ADE ∆,使得点D 落在AC 上,则tan ECD ∠的值为 .【分析】对应边相等求线段长,即可得所求角的正切值. 由题意得:AD =AB =5,EN =CB =12, ∴CD =AC -AD =13-5=8, ∴123tan 82ECD ∠==.2.(2019·内江)如图,在△ABC 中,AB =2,BC =3.6,∠B =60°,将△ABC 绕点A 顺时针旋转得到△ADE ,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为( )A .1.6B .1.8C .2D .2.6【分析】利用对应边相等、对应角相等可得特殊图形. 由题意得:△ABC ≌△ADE ,∴AB =AD , 又∠B =60°,∴△ABD 是等边三角形, ∴BD =AB =2,又BC =3.6, ∴CD =1.6.故选A .ABCDEABCE3.(2019·阜新)如图,在ABC ∆中,AC BC =,将ABC ∆绕点A 逆时针旋转60︒,得到ADE ∆.若2AB =,30ACB ∠=︒,则线段CD 的长度为 .【分析】连接EC ,由题意可得△ACE 是等边三角形,∴EC =AC =BC =ED ,易证△ECD ≌△EAD ,∴CD =AD =AB =2, 故CD 的长为2.4.(2019·包头)如图,在ABC ∆中,55CAB ∠=︒,25ABC ∠=︒,在同一平面内,将ABC∆绕A 点逆时针旋转70︒得到ADE ∆,连接EC ,则tan DEC ∠的值是 .【分析】已知角度,必可求出∠DEC 的度数,且应该是个特殊角. 由题意得:∠EAC =70°,∴∠AEC =∠ACE =55°, 又∠EAD =∠CAB =55°,∴∠CAD =15°,∵∠ACE +∠CAD =∠ADE +∠DEC ,∴∠DEC =45°, ∴tan ∠DEC =1.ABCDEABCDEABCDE5.(2018·镇江)如图,ABC ∆中,90BAC ∠>︒,5BC =,将ABC ∆绕点C 按顺时针方向旋转90︒,点B 对应点B '落在BA 的延长线上.若9sin 10B AC ∠'=,则AC = .【分析】题目给出'B AC ∠的正切值,故构造包含'B AC ∠的直角三角形. 过点C 作CH ⊥'BB 交'BB 于点H,则5CH ==,根据9sin 10B AC '∠=,即910CH AC =,可得:101099AC CH ===6.(2019·山西)如图,在ABC ∆中,90BAC ∠=︒,10AB AC cm ==,点D 为ABC ∆内一点,15BAD ∠=︒,6AD cm =,连接BD ,将ABD ∆绕点A 按逆时针方向旋转,使AB 与AC 重合,点D 的对应点为点E ,连接DE ,DE 交AC 于点F ,则CF 的长为 cm .【分析】特殊特殊度数必然有特殊图形. ∵15BAD ∠=︒,∴15CAE ∠=︒,∴60AFH ∠=︒ 过点A 作AH ⊥DE 交DE 于H 点,∵AD =6cm,∴AH =cm,HF =cm ,∴AF =cm,10CF =-,故CF的长为10-.B'A'ABH B'A'A BCABC DE FHFEDCBA【中考真题-关于四边形的旋转】7.(2017·吉林)如图,在矩形ABCD中,5AB=,3AD=.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB C D'''.若点B的对应点B'落在边CD上,则B C'的长为.【分析】无论图形是什么,抓住旋转的重点来分析.过点B'作B H'⊥AB交AB于H点,则AH=4,BH=1,∴1B C'=.8.(2019·梧州)如图,在菱形ABCD中,2AB=,60BAD∠=︒,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是.【分析】特殊的菱形旋转特殊的角度必然得到其他特殊的图形.连接DE,易证△PDE是等腰直角三角形,∵AB=2,∴AC=∵2 AE AB==,∴2CE=,∴1PE=,∴1PD.D'C'B'BCDHD'C'B'A BCDA BCDEFG PA BCDEFG P9.(2018·陇南)如图,点E 是正方形ABCD 的边DC 上一点,把ADE ∆绕点A 顺时针旋转90︒到ABF ∆的位置,若四边形AECF 的面积为25,2DE =,则AE 的长为( )A .5 BC .7D【分析】旋转可以改变图形位置,或许会形成新的特殊图形. 易证△ADE ≌△ABF ,∴正方形ABCD 面积为25,所以边长AD =5, 又DE =2,∴AE D .10.(2019·贺州)如图,正方形ABCD 的边长为4,点E 是CD 的中点,AF 平分BAE∠交BC 于点F ,将ADE ∆绕点A 顺时针旋转90︒得ABG ∆,则CF 的长为 .【分析】方法较多,举一种与旋转相关的做法. 设EAF BAF α∠=∠=,DAE BAG β∠=∠=,则GAF GFA αβ∠=+=∠,∴GF =GA =EA=∴6CF CG GF =-=-,∴CF的长为6-AB CDEFGAB CDEF α+ββαβαGA BCDEF11.(2019·营口)如图,ABC ∆是等边三角形,点D 为BC 边上一点,122BD DC ==,以点D 为顶点作正方形DEFG ,且DE BC =,连接AE ,AG .若将正方形DEFG 绕点D 旋转一周,当AE 取最小值时,AG 的长为 .【分析】如图,当D 、A 、E 三点共线时,AE 最小, 过点A 作AM ⊥BC 交BC 于M 点,∵DM =1,AM =∴AD ==此时8AG ==,故AG 的长为8.ABCDEFGMABCE FG。
中考数学旋转知识点总结

中考数学旋转知识点总结一、旋转的基本概念1. 旋转的定义旋转是几何变换的一种,它将图形绕某一定点进行旋转,使得原图形经过旋转后仍符合原图形的性质。
在平面几何中,这一定点通常被称为旋转中心,而旋转的角度则是旋转的重要参数。
2. 旋转的表示在数学中,旋转可以通过不同的表示方法来描述。
最常见的是使用坐标系中的点和向量表示旋转,也可以使用矩阵来进行描述。
3. 旋转的性质旋转具有许多重要的性质,比如旋转是等距变换,旋转后的图形与原图形的关系等。
这些性质对于理解旋转的本质和应用都具有重要的意义。
二、旋转的基本公式1. 二维平面的旋转公式在平面几何中,二维平面上的点可以通过旋转变换而成。
对于坐标系中的点(x, y),绕原点逆时针旋转θ度后的新坐标可以根据公式进行计算。
2. 三维空间的旋转公式在三维空间中,点的旋转也是常见的几何变换。
旋转的角度可以沿着不同轴进行,因此三维空间中的旋转公式相对复杂一些,但也是可以通过矩阵等方式进行描述的。
三、旋转的应用1. 图形的旋转在几何中,通过旋转可以使得图形的位置和方向发生变化。
通过学习旋转的原理和公式,可以对图形的旋转进行分析和计算,从而更好地理解和掌握图形的性质和特点。
2. 向量的旋转在向量几何中,旋转是常见的几何变换。
向量的旋转不仅可以通过公式进行计算,还可以通过向量的性质和几何特点进行分析,从而更深入地理解向量的旋转。
3. 坐标系的旋转在空间几何和三维几何中,经常需要对坐标系进行旋转变换。
通过学习旋转的原理和方法,可以更清晰地理解坐标系的旋转规律,从而更好地应用于实际问题的解决中。
四、旋转的相关定理1. 旋转对称性质在平面几何中,旋转对称是一种重要的对称方式。
通过学习旋转对称的定理和性质,可以更好地理解和应用旋转对称在几何图形中的作用。
2. 旋转角度的性质旋转角度的性质是旋转的重要定理和性质之一。
通过学习旋转角度的性质,可以更深入地理解和应用旋转的基本特点。
3. 旋转的复合变换旋转可以与其他几何变换进行复合,比如平移、翻转等。
小专题(四):平面直角坐标系中图形旋转的变换规则

小专题(四):平面直角坐标系中图形旋转的变换规则1. 引言平面直角坐标系中,图形的旋转是一种常见的几何变换。
本文介绍了图形旋转的变换规则。
2. 图形旋转的基本概念图形旋转是指将一个图形绕一个中心点旋转一定角度后得到新的图形。
旋转的中心点可以位于坐标原点或任意其他点。
3. 旋转变换的规则根据旋转变换的规则,对于同一图形的旋转变换,可以得到以下规律:- 旋转360度(或2π弧度)等于恢复原状,即旋转后的图形与原图形完全相同。
- 旋转180度(或π弧度)等于将图形沿旋转中心点对称。
- 旋转90度(或π/2弧度)等于将图形逆时针旋转90度。
- 旋转270度(或3π/2弧度)等于将图形顺时针旋转90度。
4. 旋转的计算方法为了进行图形的旋转变换,可以利用旋转矩阵进行计算。
旋转矩阵是一个二维的矩阵,在平面直角坐标系中描述了图形的旋转变换。
旋转矩阵的公式如下:R = | cosθ -sinθ || sinθ cosθ |其中,θ表示旋转的角度。
5. 应用举例以矩形图形为例,假设原始矩形的坐标为A(x₁, y₁), B(x₂,y₁), C(x₂, y₂), D(x₁, y₂)。
若要将该矩形逆时针旋转90度得到新的矩形A'(x₁', y₁'), B'(x₂', y₁'), C'(x₂', y₂'), D'(x₁', y₂'),可以通过旋转矩阵计算得出新的坐标。
新的坐标计算公式如下:x₁' = x₁ * cos90 - y₁ * sin90y₁' = x₁ * sin90 + y₁ * cos90x₂' = x₂ * cos90 - y₁ * sin90y₂' = x₂ * sin90 + y₁ * cos906. 结论图形在平面直角坐标系中的旋转变换遵循一定的规则和计算方法。
通过理解和应用这些规则和计算方法,我们可以对图形进行准确的旋转变换。
七年级数学旋转的知识点

七年级数学旋转的知识点旋转是二维平面几何中的常见变换方式,它涉及到很多数学知识点,对于初学者来说可能会感到有些困难,接下来我们将系统地介绍七年级数学旋转的知识点。
一、概念旋转是将一个图形绕着定点旋转一定角度后得到的新图形。
如下图所示,将图形ABC绕着点O旋转180度,得到的新图形为A'B'C'。
(这里插入对应图片)二、旋转的性质旋转有很多有趣的性质,接下来我们重点介绍以下几个:1.旋转是一个可逆的变换,即一个图形绕着一个点旋转一定角度后,再绕着同一点旋转相反角度可以回到原来的位置。
2.旋转的图像和原图形具有相同的大小和形状。
3.不同的旋转角度和旋转中心可以得到不同的图像。
三、旋转的角度旋转的角度是计算旋转量的重要参数,下面我们对角度有以下几点介绍:1.角度可以用度数来表示,1个完整的旋转为360度。
2.对于小于360度的旋转角度,可以使用角度制和弧度制来表示。
3.在平面直角坐标系中,正的角度方向是顺时针方向,负的角度方向是逆时针方向。
四、旋转的公式旋转的公式是表示旋转变换的一种方式,在七年级数学中,通常我们只需要掌握简单的旋转公式即可。
1.围绕原点旋转时,旋转公式为:(这里插入公式图片)其中,(x,y)表示变换前的点坐标,(x',y')表示变换后的点坐标,θ表示旋转的角度。
2.围绕点P(x0,y0)旋转时,旋转公式为:(这里插入公式图片)其中,(x,y)表示变换前的点坐标,(x',y')表示变换后的点坐标,θ表示旋转的角度,P(x0,y0)表示旋转的中心点坐标。
五、旋转的应用旋转在学术研究和实际应用中都具有重要的价值,接下来我们简单举例说明一些常见的旋转应用。
1.旋转应用于计算机图形学和动画制作中,如电影特效中常出现的旋转、缩放和平移效果。
2.旋转应用于地球上某些景点的管理和规划中,如开发一个海滩公园时需要考虑观众与太阳之间的角度关系以及初日和末日的角度。
数学旋转知识点总结

数学旋转知识点总结1. 旋转的定义旋转是指物体绕某一点或某一轴进行旋转运动的几何变换。
在数学中,我们通常将旋转运动描述为一个平面上的点绕着另一个点进行旋转,或者一个图形绕着平面上的某一点进行旋转。
旋转可以分为顺时针旋转和逆时针旋转两种方向。
2. 旋转的表示方法旋转可以通过不同的表示方法来描述,其中最常见的是使用坐标变换的方式来表示。
假设我们要对一个点P(x, y)进行旋转,旋转角度为θ,则旋转后的点P'(x', y')的坐标可以表示为:x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ这个公式称为旋转矩阵,通过它我们可以计算出旋转后的点的坐标。
另外,我们也可以使用复数来表示旋转。
假设我们有一个复数z = a + bi,表示平面上的一个点,我们将z乘以一个复数e^(iθ)就可以得到z关于原点旋转θ角度后的新坐标。
3. 旋转的性质旋转具有一些重要的性质,包括保持向量长度不变、保持向量夹角不变、满足结合律和分配律等。
这些性质使得旋转在几何变换中具有重要的作用,它可以帮助我们理解和分析各种几何关系,也为我们解决问题提供了便利。
另外,旋转还具有周期性,即当一个点或一个图形进行多次旋转后,最终还会回到它原来的位置和形状,这对于解决一些周期性问题非常有用。
4. 旋转的应用旋转在各个领域都有重要的应用,特别是在几何学和物理学中。
在几何学中,旋转可以帮助我们解决各种几何问题,如图形的对称性、旋转体的体积和表面积等;在物理学中,旋转则可以用来描述物体的旋转运动、角动量的变化等。
另外,在计算机图形学中,旋转也是一个重要的概念,它可以帮助我们实现各种图形变换和动画效果。
通过旋转,我们可以实现物体的三维旋转、平面上的图形变换等操作,这对于计算机图形的渲染和建模有着很大的意义。
5. 旋转的扩展除了在平面上旋转,我们还可以将旋转的概念扩展到更高维度的空间中。
旋转变换和放缩变换

旋转变换和放缩变换旋转变换和放缩变换是计算机图形学中常用的几何变换方法,可以通过改变图形的位置、角度和尺寸来实现图形的变形效果。
本文将深入探讨旋转变换和放缩变换的原理和应用。
一、旋转变换旋转变换是指改变一个图形的角度或方向,使其相对于原始位置发生旋转。
在计算机图形学中,旋转变换通常使用矩阵变换的方式来实现。
具体来说,我们可以通过以下公式进行旋转变换:[x′ y′ 1] = [x y 1] ⨀[cosθ -sinθ 0sinθ cosθ 00 0 1]其中[x y 1]表示原始点的坐标,[x′ y′ 1]表示旋转后的点的坐标,θ表示旋转角度,⨀表示矩阵相乘。
二、放缩变换放缩变换也被称为缩放变换或伸缩变换,是指改变一个图形的尺寸,使其相对于原始大小发生放大或缩小。
放缩变换也可以使用矩阵变换的方式来实现。
具体来说,我们可以通过以下公式进行放缩变换:[x′ y′ 1] = [x y 1] ⨀ [Sx 0 00 Sy 00 0 1]其中[x y 1]表示原始点的坐标,[x′ y′ 1]表示放缩后的点的坐标,Sx和Sy分别表示在x轴和y轴方向上的放缩比例。
三、旋转变换和放缩变换的应用1. 图形变形旋转变换和放缩变换可以应用于各种图形的变形效果,例如将一个矩形图形旋转一定角度,或者将一个圆形图形缩放到指定尺寸。
通过调整旋转角度和放缩比例,我们可以实现各种各样的图形变形效果,从而满足不同的设计需求。
2. 图像处理旋转变换和放缩变换在图像处理领域也有广泛的应用。
例如,在图像拼接中,我们可以通过旋转和放缩变换将多个图像拼接成一个全景图像;在图像缩放中,我们可以通过放缩变换改变图像的尺寸,使其适应不同的显示设备。
3. 三维建模在三维建模中,旋转变换和放缩变换是非常重要的操作。
通过旋转变换,我们可以改变三维模型的角度和方向,使其呈现出不同的视角;通过放缩变换,我们可以改变三维模型的大小,使其适应不同的场景需求。
旋转变换和放缩变换在三维建模软件中扮演着重要的角色,帮助设计师实现复杂的模型效果。
几何形的旋转与相似

几何形的旋转与相似几何形的旋转与相似是几何学中的基本概念,它们在许多数学问题和实际应用中都起着重要的作用。
本文将介绍几何形的旋转和相似的定义、性质以及常见的应用。
1. 旋转旋转是指围绕某一点进行旋转操作,使得原有的图形按照一定的角度和方向进行移动。
我们可以通过几何运算的方式来描述旋转变换。
设有一点O为旋转中心,角度为θ,若点P相对于点O的旋转变换后的位置为P',则P'可以通过以下公式计算得到:x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ其中(x, y)为点P的坐标,(x', y')为点P'的坐标。
旋转变换可以将图形绕某一中心进行旋转,保持图形的形状和大小不变。
在实际应用中,旋转变换常被用于计算机图像处理、航空航天等领域。
2. 相似相似是指两个图形在形状上相似,但大小可以不同。
具体而言,若两个图形的对应角度相等,则称它们为相似图形。
对于平面图形,我们可以通过比较它们的对应边长的比值来判断是否相似。
设有两个相似图形A和B,分别具有对应边长a和b,若它们的对应边长比值为k,则可以得到以下公式:k = a / b根据相似的定义,我们可以推导出相似图形之间的性质。
例如,相似三角形的对应角度相等,对应边长成比例,面积成比例等。
相似性是几何形变换中的重要概念,它在图像压缩、模型放大缩小等领域有着广泛的应用。
3. 应用案例几何形的旋转与相似在实际应用中有着广泛的应用。
以下是其中一些常见的应用案例:3.1 建筑设计在建筑设计中,旋转和相似变换被广泛运用于建筑物的设计和布局。
设计师可以利用旋转变换来调整建筑物的方向、空间布局等,以实现更好的设计效果。
同时,相似变换也被用于模型的缩放和变形,帮助设计师更好地进行建筑规划。
3.2 机器人技术在机器人技术中,旋转变换被用于控制和定位机器人的运动。
通过旋转变换,机器人可以精确地调整自身的方向和位置,实现更准确的目标定位和路径规划。
简单的几何变换(如平移、旋转、翻转)

游戏开发:在游戏 开发中,平移变换 可以用来实现角色 的移动和场景的变 换。
数学教学:在数学 教学中,平移变换 可以用来帮助学生 义
旋转变换是一种几何变换,它将一个图形绕着某个点旋转一定的角度。 旋转变换不改变图形的大小和形状,只改变图形的位置。 旋转变换可以用矩阵来表示,其中旋转矩阵是一个正交矩阵。 旋转变换可以用极坐标来表示,其中极坐标是一个二维向量。
旋转变换的性质
旋转变换是保持 图形形状不变的 变换
旋转变换不改变 图形的大小和位 置
旋转变换不改变 图形的周长和面 积
旋转变换不改变 图形的对称性和 中心对称性
旋转变换的应用
图像处理:旋转图像,调整角度 设计软件:旋转图形,调整布局 工程设计:旋转零件,调整位置 数学研究:旋转向量,研究几何性质
感谢观看
汇报人:XXX
封闭性:组合变 换在变换空间中 是封闭的,即变 换空间中的任意 两个变换的组合 仍然是变换空间 中的变换
交换性:组合变 换具有交换性, 即两个变换的组 合顺序不影响结 果
结合性:组合变 换具有结合性, 即两个变换的组 合可以分解为两 个独立的变换
组合变换的应用
图像处理:图像的缩放、旋转、平移等操作 计算机图形学:三维模型的创建、渲染等 机器人控制:机器人的运动控制、路径规划等 虚拟现实:虚拟环境的构建、交互等
保持图形的面积不变 保持图形的对称性不变 保持图形的旋转不变
翻转变换的应用
图像处理:用于 图像的翻转、旋 转和缩放等操作
动画制作:用于 制作动画中的翻 转、旋转等效果
游戏开发:用于 游戏中的角色、 场景等元素的翻 转、旋转等操作
建筑设计:用于 建筑设计中的翻 转、旋转等操作 ,如楼梯、屋顶 等元素的设计
旋转的认识与旋转变换

旋转的认识与旋转变换旋转是我们生活中常见的一种运动形式,它可以描述物体在空间中围绕某个中心点旋转的情况。
在几何学和数学中,旋转不仅有着重要的理论意义,还被广泛应用于各个领域,如计算机图形学、物理学和工程学等。
本文将探讨旋转的认识以及旋转变换的相关内容。
一、旋转的认识1. 旋转的定义和特点在几何学中,旋转是指物体绕其自身或者其他某个中心点旋转的运动。
根据旋转轴的不同,我们可以将旋转分为二维旋转和三维旋转。
二维旋转通常是围绕平面上的某个点旋转,而三维旋转则涉及到绕一条指定轴旋转。
旋转的特点有以下几个方面:- 旋转是一种刚体运动,旋转后物体的内部结构保持不变;- 旋转是一种连续运动,物体在旋转过程中每一时刻都处于不同的位置和姿态;- 旋转可以是顺时针或逆时针方向的,根据旋转角度的正负确定。
2. 旋转的数学描述为了描述旋转,我们需要使用一些数学工具和概念。
在二维情况下,我们常用的是极坐标系。
极坐标系由中心点和极径组成,我们可以使用极坐标系中的角度来描述旋转的方向和角度。
在三维情况下,我们通常使用旋转矩阵或四元数来描述旋转。
旋转矩阵是一个3×3的矩阵,通过乘以旋转向量来实现旋转变换。
而四元数则是一种复数的扩展,可以用来表示旋转角度和旋转轴。
二、旋转变换1. 旋转变换的定义和应用旋转变换是指在空间中对物体进行旋转的变换操作。
它可以将一个初始位置的物体通过旋转操作转变为目标位置。
在计算机图形学中,旋转变换被广泛应用于三维模型的变换和动画效果的实现。
旋转变换的实现通常需要指定旋转角度和旋转轴。
通过将旋转矩阵或四元数应用于初始位置的顶点集合,我们可以得到旋转后的目标位置。
旋转变换可以用来实现物体的旋转、镜像效果的生成和动画的呈现等。
2. 旋转变换的数学表示旋转变换可以使用矩阵或四元数来表示。
以二维旋转变换为例,假设我们希望绕原点逆时针旋转一个角度θ,我们可以使用下面的旋转矩阵表示:[cos(θ) -sin(θ)][sin(θ) cos(θ)]对于三维情况,旋转矩阵为一个3×3的矩阵,具体表示方法较为复杂。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
旋转类几何变换一几何变换——旋转旋转中的基本图形利用旋转思想构造辅助线⎧⎨⎩ (一)共顶点旋转模型(证明基本思想“SAS ”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形自检自查必考点以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二 利用旋转思想构造辅助线(1)根据相等的边先找出被旋转的三角形 (2)根据对应边找出旋转角度(3)根据旋转角度画出对应的旋转的三角形 三 旋转变换前后具有以下性质: (1)对应线段相等,对应角相等 (2)对应点位置的排列次序相同(3)任意两条对应线段所在直线的夹角都等于旋转角θ.考点一 旋转与最短路程☞考点说明:旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题,同时与旋转有关路程最短的问题,比较重要的就是费马点问题,涉及费马点问题,视学生程度进行选择性讲解。
【例1】 如图,四边形ABCD 是正方形,ABE ∆是等边三角形,M 为对角线BD上任意一点,将BM 绕点B 逆时针旋转60︒得到BN ,连接AM 、CM 、中考满分必做题EN MDCBAEN.⑴求证:AMB ENB≌∆∆⑵①当M点在何处时,AM CM+的值最小;②当M点在何处时,AM BM CM++的值最小,并说明理由;⑶当AM BM CM++1时,求正方形的边长.【例2】 阅读下列材料对于任意的ABC ∆,若三角形内或三角形上有一点P ,若PA PB PC ++有最小值,则取到最小值时,点P 为该三角形的费马点。
①若三角形内有一个内角大于或等于120︒,这个内角的顶点就是费马点②若三角形内角均小于120︒,则满足条件120APB BPC APC ∠=∠=∠=︒时,点P 既为费马点 解决问题:⑴如图,ABC ∆中,三个内角均小于120︒,分别以AB 、AC 为边向外作等边ABD ∆、ACE ∆,连接CD 、BE 交于点P ,证明:点P 为ABC ∆的费马点。
(即证明120APB BPC APC ∠=∠=∠=︒)且PA PB PC CD ++=PEDCBA QA BCDEP⑵如图,点Q 为三角形内部异于点P的一点,证明:QA QC QB PA PB PC ++>++⑶若30ABC ∠=︒,3AB =,4BC =,直接写出PA PB PC ++的最小值考点二 利用旋转求点的坐标☞考点说明:利用全等三角形的性质进行边与角的转化。
【例3】 正方形ABCD绕D 点顺时针方向旋转90︒后,B 点的坐标为( A.(22)-, B.(41), C.(31), D.(40),【例4】 如图,在平面直角坐标系中,Rt OAB ∆的顶点A ,若将OAB ∆绕点O 逆时针旋转60︒后,B 点到达'B ________考点三 旋转与勾股定理☞考点说明:在等边三角形与正方形中,常见的一种题型,应重点掌握【例5】 如图,P 是等边ABC ∆中的一个点,2,4PA PB PC ===,则ABC ∆的边长是________【例6】 如图,在ABC∆中,90ACB ∠=︒,AC BC =,P 是ABC ∆内的一点,且123PB PC PA ===,,,求BPC ∠的度数.PCBAPBAC【例7】 如图点P是正方形ABCD内部一点,1PA =2PB =3PC =,则APB ∠= .考点四 利用旋转的性质解决几何有关的计算☞考点说明:此类问题多以选择填空的形式出现,较为简单,有的时候也会再综合题中出现。
【例8】 如图,将ABC ∆绕点A 顺时针旋转45︒得到ADE ∆,点E 落在边BC 上,则_______BED ∠=【例9】 如图,将直径为4的半圆AB ,绕点A 逆时针旋转60︒的面积为ABCDPEDCB ABA【例10】 如图,将ABC ∆绕点A 逆时针旋转80︒得到AB C ''∆.若50BAC ∠=︒,则CAB '∠的度数为( ) A .30︒ B .40︒ C .50︒D .80︒【例11】 如图,将矩形ABCD 绕点A 顺时针旋转90︒后,得到矩形'''AB C D ,如果22CD DA ==,那么'CC =_________.【例12】 把边长分别为4和6的矩形ABCO 如图放在平面直角坐标系中,将它绕点C 顺时针旋转α角,旋转后的矩形记为矩形EDCF .在旋转过程中,⑴如图①,当点E 在射线CB 上时,E 点坐标为___________;ABCB'C'D'C'B'DCBA⑵当CBD ∆是等边三角形时,旋转角α的度数是____________(α为锐角时);⑶如图②,设EF 与BC 交于点G ,当考点五 利用旋转的性质解决几何有关的证明☞考点说明:旋转有关的几何变换是中考的热点问题,同时也是中考试题中的重难点所在。
【例13】 E 、F 分别是正方形ABCD 的边BC 、CD 上的点,且45EAF =︒∠,AH EF ⊥,H 为垂足,求证:AH AB =.图①图②CHF E D B A【例14】 已知ABC ∆,分别以AB 、BC 、CA 为边向形外作等边三角形ABD ,等边三角形BCE ,等边三角形ACF⑴如图1,当ABC ∆是等边三角形时,请你写出满足图中条件,四个成立的结论。
FED CBAFEDCBA⑵如图2,当ABC ∆中只有60ACB ∠=︒时,请你证明ABCS∆与ABDS∆的和等于BCE S ∆与ACFS ∆的和【例15】 如图①,在ABC ∆中,D 、E 分别是AB 、AC 上的点,且DE BC ∥,将ADE∆绕A 点顺时针旋转一定角度,连结BD 、CE ,得到图②,然后将BD 、CE 分别延长至M 、N ,使12DM BD =,12EN CE =,连结AM、AN 、MN ,得到图③,请解答下列问题: ⑴若AB AC =,请探究下列数量关系:①在图②中,BD 与CE 的数量关系是________________; ②在图③中,猜想AM 与AN 的数量关系、MAN ∠与BAC ∠的数量关系,并证明你的猜想;⑵若AB k AC =⋅(1k >),按上述操作方法,得到图④,请继续探究:AM与AN 的数量关系、MAN ∠与BAC ∠的数量关系,直接写出你的猜想,不必证明.CAE图①DBCA图②EDBCA图③EMNDBC图④EMN【例16】 已知:在ABC ∆中,AB AC =,点D 为BC 边的中点,点F是AB 边上一点,点E 在线段DF 的延长线上,BAE BDF ∠=∠,点M 在线段DF 上,ABE DBM ∠=∠.⑴如图1,当45ABC ∠=︒时,求证:AE =;⑵如图2,当60ABC ∠=︒时,则线段AE 、MD 之间的数量关系为________ ⑶在⑵的条件下,延长BM 到P ,使MP BM =,连接CP ,若7AB =,的值.【例17】 ⑴如图所示,在四边形ABCD 中,AB AD =,60BAD ∠=,120BCD ∠=,证明:BC +DC AC =.⑵ 如图所示,在四边形ABCD 中,AB BC =,60ABC ∠=,P 为四边形ABCDC(图1)(图2)MBACDEF内部一点,120APD ∠=,证明:PA PD PC BD ++≥.DCBAPDCBA【例18】 如图1,若△ABC 和△ADE 为等边三角形,M ,N 分别EB ,CD的中点,易证:CD =BE ,△AMN 是等边三角形.(1)把△ADE 绕A 点旋转到图2的位置时,CD =BE 是否仍然成立?若成立请证明,若不成立请说明理由;(2)当△ADE 绕A 点旋转到图3的位置时,△AMN 是否还是等边三角形?若是,请给出证明,并求出当AB =2AD 时,△ADE 与△ABC 及△AMN 的面积之比;若不是,请说明理由.【例19】 如图1,Rt △ABC ≌Rt △EDF ,∠ACB =∠F =90°,∠A =∠E =30°.△EDF 绕着边AB 的中点D 旋转,DE ,DF 分别交线段AC 于点M ,K .图1 图2 图3(1)观察:①如图2、图3,当∠CDF =0°或60°时,AM +CK _______MK (填“>”,“<”或“=”).②如图4,当∠CDF =30°时,AM +CK _______MK (只填“>”或“<”).(2)猜想:如图1,当0°<∠CDF <60°时,AM +CK _______MK ,证明你所得到的结论. (3)如果MK2+CK2=AM2,请直接写出∠CDF的度数和AMMK的值.DBCAF EM K 图1DBC A(F ,K )EM 图2DBCA FEK图3(M )DBCAF EM K 图4【例20】 在等边ABC ∆的两边AB ,AC 所在直线上分别有两点M N D ,,为ABC ∆外一点,且60MDN ∠=︒,120BDC ∠=︒,BD CD =,探究:当点M N ,分别爱直线AB AC ,上移动时,BM BN MN ,,之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.图①M NDCBA图②M ND CBA N图③MD CBA(1)如图①,当点M N ,在边AB AC ,上,且DM DN =时,BM NC MN ,,之间的数量关系式_________;此时QL =__________(2)如图②,当点M N ,在边AB AC ,上,且DM DN ≠时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;⑶如图③,当点M N ,分别在边AB CA ,的延长线上时,若AN x =,则Q =_________(用x L ,表示)【例21】 在Rt △ABC 中,∠ACB =90°,tan ∠BAC =12. 点D 在边AC 上(不与A ,C 重合),连结BD ,F 为BD 中点.若将图1中的△ADE 绕点A 旋转,使得D 、E 、B 三点共线,点F 仍为BD 中点,如图2所示.求证:BE -DE =2CF ;B CADE FB DEA FCBAC1图2图备图。
