材料力学习题册答案-第9章-压杆稳定
材料力学简明教程(景荣春)课后答案第九章

解 设各杆与铅垂线夹角为 θ ,则由平衡的各杆的受力
130
3FN cosθ = F , FN =
设钢管材料为 Q235,则
F F 2 .5 5 F = ⋅ = = 0.417 F 3 cos θ 3 2 12
= 269 > λp D2 + d 2 30 2 + 22 2 × 10 −3 π 2 EI π 3 E (D 4 − d 4 ) π 3 × 210 × 10 9 × (30 2 − 22 2 )× 10 −12 Fcr = = = = 9.37 kN 2 64 × 2.5 2 (μl )2 64(μl ) Fcr F 1 1 9.37 × 10 3 [F ] = = × = × = 7.49 kN 0.417 0.417 [n]st 0.417 3 i = =
2
127
比值差不多时较有利。 9-8 从稳定性的角度考虑,一般压杆截面的周边取圆形较为合理,但可以是空心或实 心的。如规定压杆横截面面积相同,则: (1) 从强度方面看,它们有无区别?为什么? (2) 从稳定性方面看,哪一种截面形式较为合理?为什么? (3) 如果空心圆形截面较合理的话,是否其内、外半径越大越好? 答 (1) 从强度方面看,它们无区别。因为 σ = F / A 。 (2) 从稳定性方面看,空心截面形式较为合理,因空心截面惯性矩较大。 (3) 如果空心圆形截面较合理的话,其内、外半径不是越大越好,因为在面积一定的情 况下,内、外半径太大了会造成薄壁失稳。 9-9 如何进行压杆的合理设计? 答 (1) 选择合理的截面形状; (2) 改变压杆的约束条件; (3)合理选择材料。 9-10 满足强度条件的等截面压杆是否满足稳定性条件?满足稳定性条件的压杆是否 满足强度条件?为什么? 答 (1) 因为强度条件是 σ < [σ ] =
材料力学答案- 压杆稳定
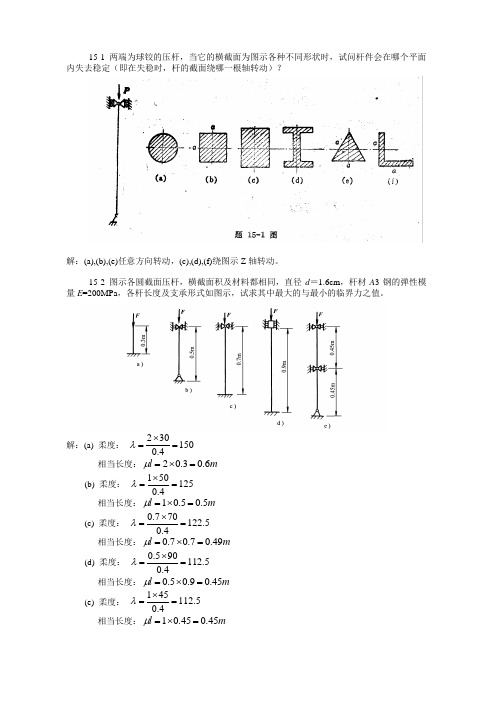
15-1 两端为球铰的压杆,当它的横截面为图示各种不同形状时,试问杆件会在哪个平面内失去稳定(即在失稳时,杆的截面绕哪一根轴转动)?解:(a),(b),(e)任意方向转动,(c),(d),(f)绕图示Z 轴转动。
15-2 图示各圆截面压杆,横截面积及材料都相同,直径d =1.6cm ,杆材A 3钢的弹性模量E =200MPa ,各杆长度及支承形式如图示,试求其中最大的与最小的临界力之值。
解:(a) 柔度: 2301500.4λ⨯== 相当长度:20.30.6l m μ=⨯=(b) 柔度: 1501250.4λ⨯== 相当长度:10.50.5l m μ=⨯=(c) 柔度: 0.770122.50.4λ⨯== 相当长度:0.70.70.49l m μ=⨯=(d) 柔度: 0.590112.50.4λ⨯== 相当长度:0.50.90.45l m μ=⨯=(e) 柔度: 145112.50.4λ⨯== 相当长度:10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出:各压杆的临界力可用欧拉公式计算。
即:()22cr EIF l πμ=各压杆的EJ 均相同,故相当长度最大的压杆(a)临界力最小,压杆(d)与(e)的临界力最大,分别为:()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ,s σ=274MPa ,E =200GPa ,直线公式λσ22.1338-=cr ,试计算该材料压杆的P λ及S λ值,并绘制1500≤≤λ范围内的临界应力总图。
解:92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆,其外径和内径分别为,12mm 和10mm ,杆长为383mm ,两端为铰支座,材料的E =210GPa ,P σ=288MPa ,试求此挺杆的临界力cr F 。
华科材料力学教材课后习题答案第九章
即:
9-6 在图示结构中,横梁AD为刚性杆,杆(1)与杆(2)均为直径d=10cm的圆杆,材料均为Q235钢,规定的稳定安
全系数 n st 6.5 。试由杆(1)的稳定性确定许可F。
2m 2m
E
(2) F
A
B
C
D
(1)
F
2m
2m
2m
9-7 图示桁架由两根材料、截面均相同的细长杆组成,试由稳定性要求确定F为最大时的 角( π / 2)。
10KN/m
A
C
B
D
1m
1m
9-10 压杆的一端固定,另一端自由(图a),为提高其稳定性,在杆的中点增加铰支座(图b)。试求加强后 压杆的欧拉临界力公式,并与加强前作比较。
Fcr
Fcr
B
B
l l/2
A
A
(a)
(b)
9-11 图示立柱,由两根槽钢焊接而成,在其中点横截面C处,开有一直径 d 6ቤተ መጻሕፍቲ ባይዱmm
度时杆将失去稳定?已知材料的热膨胀系数 12.5106 / C,E=210GPa, p =200MPa。
5m
9-5 9-5 图示正方形桁架,各杆EI相同且均为细长杆。试求当F为何值时结构将失稳?如果F力改为方向向外, 结果又如何? 解:杆AB、BC、CD、AD为压杆,所受压力相等为F`。 失稳时有:
n st 2.5,试校核该顶杆的稳定性。
9-3 简易起重机如图所示,其压杆BD为20号槽钢,材料为Q235钢,最大起重量为F=40kN, n st 5 ,试校核BD杆的稳定性。
1.5m
0.5m
A
30
B
2020年材料力学习题册答案-第9章 压杆稳定

作者:非成败作品编号:92032155GZ5702241547853215475102时间:2020.12.13第九章压杆稳定一、选择题1、一理想均匀直杆受轴向压力P=P Q时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( A )。
A、弯曲变形消失,恢复直线形状;B、弯曲变形减少,不能恢复直线形状;C、微弯状态不变;D、弯曲变形继续增大。
2、一细长压杆当轴向力P=P Q时发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形( C )A、完全消失B、有所缓和C、保持不变D、继续增大3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( D )来判断的。
A、长度B、横截面尺寸C、临界应力D、柔度4、压杆的柔度集中地反映了压杆的( A )对临界应力的影响。
A、长度,约束条件,截面尺寸和形状;B、材料,长度和约束条件;C、材料,约束条件,截面尺寸和形状;D、材料,长度,截面尺寸和形状;5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( C )A.60;B.66.7;C.80;D.507、在横截面积等其它条件均相同的条件下,压杆采用图( D )所示截面形状,其稳定性最好。
8、细长压杆的( A ),则其临界应力σ越大。
A 、弹性模量E 越大或柔度λ越小;B 、弹性模量E 越大或柔度λ越大;C 、弹性模量E 越小或柔度λ越大;D 、弹性模量E 越小或柔度λ越小; 9、欧拉公式适用的条件是,压杆的柔度( C )A 、λ≤、λ≤C 、λ≥π D、λ≥10、在材料相同的条件下,随着柔度的增大( C )A 、细长杆的临界应力是减小的,中长杆不是;B 、中长杆的临界应力是减小的,细长杆不是;C 、细长杆和中长杆的临界应力均是减小的;D 、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( A )A. 临界应力一定相等,临界压力不一定相等;B. 临界应力不一定相等,临界压力一定相等;C. 临界应力和临界压力一定相等;D. 临界应力和临界压力不一定相等;12、在下列有关压杆临界应力σe 的结论中,( D )是正确的。
材料力学 压杆稳定答案共5页

9-1(9-2)图示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(图f所示杆在中间支承处不能转动)?解:对于材料和截面相同的压杆,它们能承受的压力与成反比,此处,为与约束情况有关的长度系数。
(a)=1×5=5m(b)=0.7×7=4.9m(c)=0.5×9=4.5m(d)=2×2=4m(e)=1×8=8m(f)=0.7×5=3.5m故图e所示杆最小,图f所示杆最大。
返回9-2(9-5) 长5m的10号工字钢,在温度为时安装在两个固定支座之间,这时杆不受力。
已知钢的线膨胀系数。
试问当温度升高至多少度时,杆将丧失稳定?解:返回9-3(9-6) 两根直径为d的立柱,上、下端分别与强劲的顶、底块刚性连接,如图所示。
试根据杆端的约束条件,分析在总压力F作用下,立柱可能产生的几种失稳形态下的挠曲线形状,分别写出对应的总压力F之临界值的算式(按细长杆考虑),确定最小临界力的算式。
解:在总压力F作用下,立柱微弯时可能有下列三种情况:(a)每根立柱作为两端固定的压杆分别失稳:(b)两根立柱一起作为下端固定而上端自由的体系在自身平面内失稳失稳时整体在面内弯曲,则1,2两杆组成一组合截面。
(c)两根立柱一起作为下端固定而上端自由的体系在面外失稳故面外失稳时最小返回9-4(9-7)图示结构ABCD由三根直径均为d的圆截面钢杆组成,在点B铰支,而在点A和点C固定,D为铰接点,。
若结构由于杆件在平面ABCD内弹性失稳而丧失承载能力,试确定作用于结点D处的荷载F的临界值。
解:杆DB为两端铰支,杆DA及DC为一端铰支一端固定,选取。
此结构为超静定结构,当杆DB失稳时结构仍能继续承载,直到杆AD及DC也失稳时整个结构才丧失承载能力,故返回9-5(9-9) 下端固定、上端铰支、长m的压杆,由两根10号槽钢焊接而成,如图所示,并符合钢结构设计规范中实腹式b类截面中心受压杆的要求。
《材料力学》第9章压杆稳定习题解
v
MM
e'kkx
esin
(1coskx)
v
PP
crcr
M
e
边界条件:③xL;v0:0(1coskL)
P
cr
,1coskL0
Mቤተ መጻሕፍቲ ባይዱ
'esin
④x0v0:0kkLsinkL0
P
cr
以上两式均要求:kL2n,(n0,1,3,......)
5
2
L
。故有:
k
2
2
(0.5L)
2
P
cr
EI
其最小解是:kL2,或
Pcr
2
EI
min
2
(2.l)
?为什么?并由此判断压杆长因数是否可能大于2。
2
螺旋千斤顶(图c)的底座对丝杆(起顶杆)的稳定性有无影响?校核丝杆稳定性时,
把它看作下端固定(固定于底座上)、上端自由、长度为l的压杆是否偏于安全?
解:临界力与压杆两端的支承情况有关。因为(a)的下支座不同于(b)的下支座,所以它们的
度系数。
(a)l155m
(b)l0.774.9m
(c)l0.594.5m
(d)l224m
(e)l188m
(f)l0.753.5m(下段);l0.552.5m(上段)
故图e所示杆
F最小,图f所示杆Fcr最大。
cr
[习题9-3]图a,b所示的两细长杆均与基础刚性连接,但第一根杆(图a)的基础放在弹性
地基上,第二根杆(图b)的基础放在刚性地基上。试问两杆的临界力是否均为
失稳时整体在面内弯曲,则1,2两杆组成一组合截面。
(c)两根立柱一起作为下端固定而上端自由的体系在面外失稳
材料力学孙训芳版解答第9章 压杆稳定

&'
O
PO L
u
u
! OS
)FU
(, O
( G O u
u u u u u
u 1
N1
) )&' )FU
>) @VW
)
u
N1
V S 03D 03D ( *3D 03D ( *3D
( *3D
Ot
( VS
u u u
琥珀资源网 O t
( VS
Ot
( VS
u u u
u u u
03D >V FU @
& ]& ]
\& \
琥珀资源网
L] u P
O
PO L
u u
M
>) @ M>V @$ u u u u
uu
N1
E
\ \
]
uu
%&
G PP $&
D PP
$
%&
4
QVW
$&
O
PO L
u
u
u
! OS
)FU
(, PO
u u u u u u u
u 1
%&
L
, $
D D
H
D O '7 O
D O '7
(, PLQ
压杆稳定习题及答案

压杆稳定习题及答案【篇一:材料力学习题册答案-第9章压杆稳定】xt>一、选择题1、一理想均匀直杆受轴向压力p=pq时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( a )。
a、弯曲变形消失,恢复直线形状;b、弯曲变形减少,不能恢复直线形状; c、微弯状态不变; d、弯曲变形继续增大。
2、一细长压杆当轴向力p=pq时发生失稳而处于微弯平衡状态,此时若解除压力p,则压杆的微弯变形( c )a、完全消失b、有所缓和c、保持不变d、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( d)来判断的。
a、长度b、横截面尺寸c、临界应力d、柔度 4、压杆的柔度集中地反映了压杆的( a)对临界应力的影响。
a、长度,约束条件,截面尺寸和形状;b、材料,长度和约束条件;c、材料,约束条件,截面尺寸和形状;d、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( c )a.60;b.66.7;c.80;d.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( d )所示截面形状,其稳定性最好。
≤?≥?- 1 -10、在材料相同的条件下,随着柔度的增大( c)a、细长杆的临界应力是减小的,中长杆不是;b、中长杆的临界应力是减小的,细长杆不是; c、细长杆和中长杆的临界应力均是减小的; d、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( a )a. 临界应力一定相等,临界压力不一定相等;b. 临界应力不一定相等,临界压力一定相等;c. 临界应力和临界压力一定相等;d. 临界应力和临界压力不一定相等;a、杆的材质b、杆的长度c、杆承受压力的大小d、杆的横截面形状和尺寸二、计算题1、有一长l=300 mm,截面宽b=6 mm、高h=10 mm的压杆。
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-压杆稳定(圣才出品)

2.压杆分类(见表 9-1-4) 表 9-1-4 压杆分类
3.折减弹性模量理论(见表 9-1-5)
3 / 40
圣才电子书 十万种考研考证电子书、题库视频学习平台
表 9-1-5 折减弹性模量理论
4.压杆的临界应力总图 压杆临界应力 σcr 与柔度 λ 的关系曲线称为压杆的临界应力总图。当压杆的柔度很小时, 以屈服界限 σs 作为临界应力。临界应力总图的绘制如图 9-1-1 所示。
图 9-1-1 临界应力总图
4 / 40
圣才电子书 十万种考研考证电子书、题库视频学习平台
四、实际压杆的稳定因数 实际压杆的稳定许用应力与稳定因数的确定见表 9-1-6。
表 9-1-6 稳定许用应力与稳定因数
五、压杆的稳定计算·压杆的合理截面 1.压杆的稳定计算(见表 9-1-7)
6 / 40
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 9-2-1 令 k2=Fcr/EI,可得:w″+k2w=k2Me/Fcr。则该微分方程的通解:w=Asinkx+ Bcoskx+Me/Fcr。 其一阶导为:w′=Akcoskx-Bksinkx,由边界条件 x=0,w=0,w′=0 可确定积分 常数:A=0,B=-Me/Fcr。故方程的通解:w=-Mecoskx/Fcr+Me/Fcr。 又由 x=l,w=0 得:-Mecoskx/Fcr+Me/Fcr=0,即 coskl=1,kl=2nπ(n=1, 2,3…),取其最小解 kl=2π,则压杆的临界力 Fcr 的欧拉公式 Fcr=4π2EI/l2=π2EI/ (0.5l)2。 9-2 长 5m 的 10 号工字钢,在温度为 0℃时安装在两个固定支座之间,这时杆不受 力。已知钢的线膨胀系数 αl=125×10-7(℃)-1,E=210GPa。试问当温度升高至多少 度时,杆将丧失稳定? 解:设温度升高 Δt 时,杆件失稳。
第九章_压杆稳定

第 1 页/共 2 页9-5 未失稳失,轴向压缩 T F L L ∆=∆TEA F TL L EAFL L l l T F αα=⇒=∆=∆, 临界状态 kN 3.109)5.0(22cr ==L EIF π由cr F F =得,温升C EALEI T l ︒==2.29422απ 9-8 由铰B 平衡,22BC AB F F F +=,ABBC F F =θtan F 最大时,AB F 与BC F 均达到临界值2222)sin ()cos (βπβπAC EI F AC EI F BC AB ==, )arctan(cot cot tan 22βθβθ==⇒, 9-10 柔度临界值 p2p σπλE = (1)5.72p =λ,(2)8.65p =λ,(3)6.73p =λ 9-12 AB 与BC 均为两力杆,由铰B 平衡可得 F F BC 75=(压) 柔度 m m 320m 5.215.216=====i l i l,,,其中μμλ 稳定因素 06.028002==λϕ稳定许用应力 MPa 6.0][][st ==σϕσ st ][MPa 58.0σσ<==AF BC ,满意稳定性条件。
9-15 组合压杆的临界力cr F 为杆BC 与AB 临界力的最小值柔度临界值 1002==PP E σπλ P ACAC P BC BC i AC i BC λλλλ>=====1047.0100,大柔度杆,由欧拉公式N 1094.0)7.0(N 1004.1622622⨯==⨯==AC EIF BC EIF AC BC ππ,N 1094.06cr ⨯==⇒AC F F许用压力 kN 376][stcr ==n F F ⎪⎪⎭⎫ ⎝⎛======kN 416MPa 8.82][MPa 1.207BC kN 376MPa 6.76][MPa 4.191AC st cr st cr F F ,,:,,:σσσσ 9-17 杆AC ,强度许用应力 MPa 118][st ==n σσ 最大弯矩 26132bh W F M B ==, 最大应力 kN 6.95][41][2max =≤⇒≤=bh F W M B σσσ 杆CD ,柔度P iCD λλ>==200,大柔度杆 由欧拉公式 MPa 3.4922cr ==λπσE 稳定许用应力 MPa 4.16][st cr st ==n σσ 压力 F F CD 31=应力 kN 5.15][3][st st =≤⇒≤=A F AF CD σσσ 结构的许可荷载 kN 5.15][=F。
材料力学孙训芳版解答第9章_压杆稳定

Q
&
VLQ
NO
&
FRV NO
0 )
0 )
FRV NO
0 )
FRV NO
NO Q
NO
N
O
N
O
) (, O
)
(, O
)FU
(,
O
P
D O u ( *3D
H
D O '7 O
, $L $L u u u u P
,
>,
$
D
u @
D
>
,
, $
u
@
u u
u
G PP E PP Q
&'
%& %&
)&'
)
0%
)
P ) P
$
&
%
G' E
V
0% :
) u u EK
) EK
d
VV Q
)
d
V VEK Q
u u u u u
1 N1
N1
N1
$% $%
7&
>V @ 03D
,,
¦0&
)$% VLQ $ u
u
&
)$% N1
M >V FU @ u >V @ 03D
$
V $%
材料力学第9章 压杆稳定(土木)

2.1922年冬天下大雪,美国华盛 . 年冬天下大雪, 年冬天下大雪 顿尼克尔卜克尔剧院由于屋顶结 构中的一根压杆超载失稳,造成 构中的一根压杆超载失稳, 一根压杆超载失稳 剧院倒塌, 余人。 剧院倒塌,死98人,伤100余人。 人 余人
3.2000年10月25日 . 年 月 日 上午10时 分 上午 时30分,在南京 电视台演播中心演播厅 屋顶的浇筑混凝土施工 顶的浇筑混凝土施工 中,因脚手架失稳,造 脚手架失稳, 成演播厅屋顶模板倒塌, 成演播厅屋顶模板倒塌, 死5人,伤35人。 人 人
欧拉公式与精确解曲线 精确解曲线
F =1.152F 时,
cr
δ ≈ 0.3l
理想受压直杆 非理想受压直杆
y
适用条件: 适用条件: •理想压杆(轴线为直线,压力与 理想压杆(轴线为直线, 理想压杆 轴线重合,材料均匀) 轴线重合,材料均匀) •线弹性,小变形 线弹性, 线弹性 •两端为铰支座 两端为铰支座
hb3 Iz = = 32cm 4 12
µl
iz =
Iz 32 = = 1.155cm A 4× 6
x
h
µ z = 0.5,
0.5 × 2 λz = = = 86.6 −2 iz 1.155 ×10
A3钢的λs= 61.6, λs<λ< λp,属于中 钢的 , 长压杆稳定问题。 长压杆稳定问题。 由表9-2查得 由表 查得: 查得
挠曲线的近似微分方程 挠曲线的近似微分方程
d w M =− dx EI
2
2
d w Fw =− 2 dx EI
引入记号
2
F w′′ + w = 0 EI
F k = EI
2
w′′ + k w = 0
《材料力学》第9章压杆稳定习题解
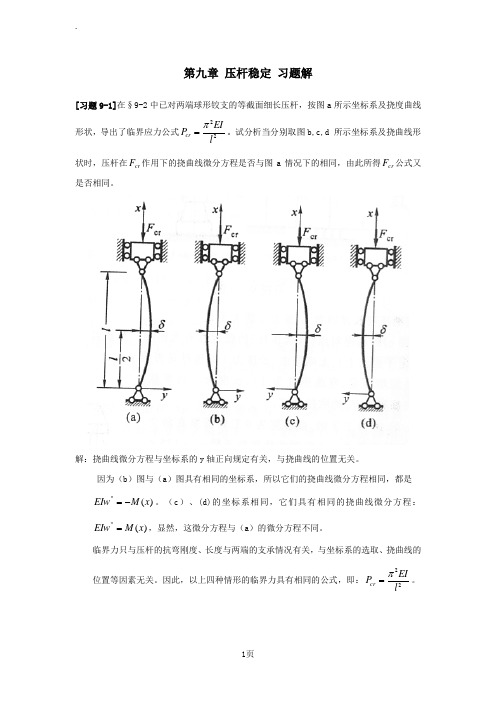
第九章 压杆稳定 习题解[习题9-1]在§9-2中已对两端球形铰支的等截面细长压杆,按图a 所示坐标系及挠度曲线形状,导出了临界应力公式22lEIP cr π=。
试分析当分别取图b,c,d 所示坐标系及挠曲线形状时,压杆在cr F 作用下的挠曲线微分方程是否与图a 情况下的相同,由此所得cr F 公式又是否相同。
解:挠曲线微分方程与坐标系的y 轴正向规定有关,与挠曲线的位置无关。
因为(b )图与(a )图具有相同的坐标系,所以它们的挠曲线微分方程相同,都是)("x M EIw -=。
(c )、(d)的坐标系相同,它们具有相同的挠曲线微分方程:)("x M EIw =,显然,这微分方程与(a )的微分方程不同。
临界力只与压杆的抗弯刚度、长度与两端的支承情况有关,与坐标系的选取、挠曲线的位置等因素无关。
因此,以上四种情形的临界力具有相同的公式,即:22lEIP cr π=。
[习题9-2] 图示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(图f 所示杆在中间支承处不能转动)?解:压杆能承受的临界压力为:22).(l EIP cr μπ=。
由这公式可知,对于材料和截面相同的压杆,它们能承受的压力与原压相的相当长度l μ的平方成反比,其中,μ为与约束情况有关的长度系数。
(a )m l 551=⨯=μ (b )m l 9.477.0=⨯=μ (c )m l 5.495.0=⨯=μ (d )m l 422=⨯=μ (e )m l 881=⨯=μ(f )m l 5.357.0=⨯=μ(下段);m l 5.255.0=⨯=μ(上段) 故图e 所示杆cr F 最小,图f 所示杆cr F 最大。
[习题9-3] 图a,b 所示的两细长杆均与基础刚性连接,但第一根杆(图a )的基础放在弹性地基上,第二根杆(图b )的基础放在刚性地基上。
试问两杆的临界力是否均为2min2).2(l EI P cr π=?为什么?并由此判断压杆长因数μ是否可能大于2。
刘鸿文《材料力学》(第5版)课后习题(压杆稳定)【圣才出品】

解:根据公式计算得: 挺杆横截面面积: 截面的惯性半径:
1 / 28
圣才电子书
十万种考研考证电子书、题库视频学习平 台
则挺杆柔度:
因此,使用欧拉公式计算挺杆的临界压力
压杆的工作安全因数:
规定的稳定安全因数为 nst 3 ~ 5 ,所以挺杆满足稳定要求。
9.3 图 9-1 所示蒸汽机的活塞杆 AB,所受的压力 F=120 kN,l=180 cm,横截面 为圆形,直径 d=7.5 cm。材料为 Q255 钢,E=210 GPa,σP=240 MPa。规定 nst=8,试校核活塞杆的稳定性。
圣才电子书
十万种考研考证电子书、题库视频学习平 台
第 9 章 压杆稳定
9.1 某型柴油机的挺杆长度 l=25.7 cm,圆形横截面的直径 d=8 mm,钢材的 E=210 GPa,σP=240 MPa。挺杆所受最大压力 F=1.76 kN。规定的稳定安全因数 nst=2~5。试校核挺杆的稳定性。
6 / 28
圣才电子书
nst=3,试求许可载荷 F。
十万种考研考证电子书、题库视频学习平 台
图 9-6 解:由于支架的对称性,三根杆所承受的压力相等,即当三根杆同时达到临界值时,
支架开始失稳。任取一根杆进行研究,设其受力为 F ' 。
又该杆的惯性半径:
则其柔度: 由此可知其为大柔度杆,故由欧拉公式计算其临界压力:
其稳定性。
图 9-3
解:对于 Q235 钢, E 200GPa, s 240MPa, p 200MPa ,则有:
4 / 28
圣才电子书
十万种考研考证电子书、题库视频学习平 台
。
又查表得 a 304MPa,b 1.12MPa ,则
第九章压杆稳定习题_材料力学

1. 一倾斜矩形截面梁AB 如图,在其中点C 处作用有铅垂力F =25kN ,试求梁AB 中的最大拉应力和最大压应力。
解:(1)受力分析力F 可分解为 30cos 1F F =和 30sin 2F F =,梁发生弯曲和压缩的组合变形。
最大弯矩发生在C 截面max cos30cos3018750N m 44l F Fl M ⋅=== AC 段轴力为 30sin F F N -=(2)应力计算m a x 2918750P a 7.81M P a 160300106w z M W σ-===⨯⨯ 36s i n 30250.510P a 0.26M P a 16030010N F A σ-⨯⨯===⨯⨯ 故 m a x 7.81M P al σ= max 0.267.818.07MPa y σ=+=2. 悬臂吊车如图,横梁用25a 号工字钢制成(工字钢的截面积和抗弯截面模量分别为:A =48.5cm 2,W z =402cm 3),梁长l =4m , F =24kN ,梁材料的许用应力〔σ〕=100MPa 。
试校核梁的强度。
解 (1)外力计算取横梁AB 为研究对象,当载荷移动到梁的中点时,可近似地认为梁处于危险状态。
此时,由平衡条件得F By =12kN , F Bx =20.8kN又由平衡条件ΣF x =0和ΣF y =0得F Ax =20.8kN , F Ay =12kN(2)内力和应力计算在梁中点截面上的弯矩最大,其值为M max =Fl /4=24000N·m所以最大弯曲应力为σW max =M max /W z =60MPa梁危险截面的上边缘处受最大压应力、下边缘处受最大拉应力作用。
轴力产生的压应力为σy =F N /A =-4.3MPa(3)强度校核数值最大的正应力发生在跨度中央截面的上边缘,是压应力|σ|max =|σy -σW max |=64.3MPa <〔σ〕悬臂吊车的横梁是安全的。
材料力学压杆稳定参考答案
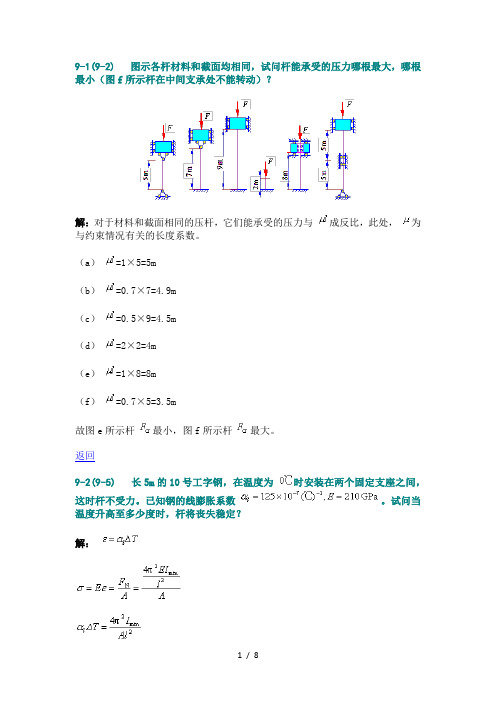
9-1(9-2)图示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(图f所示杆在中间支承处不能转动)?解:对于材料和截面相同的压杆,它们能承受的压力与成反比,此处,为与约束情况有关的长度系数。
(a)=1×5=5m(b)=0.7×7=4.9m(c)=0.5×9=4.5m(d)=2×2=4m(e)=1×8=8m(f)=0.7×5=3.5m故图e所示杆最小,图f所示杆最大。
返回9-2(9-5) 长5m的10号工字钢,在温度为时安装在两个固定支座之间,这时杆不受力。
已知钢的线膨胀系数。
试问当温度升高至多少度时,杆将丧失稳定?解:返回9-3(9-6) 两根直径为d的立柱,上、下端分别与强劲的顶、底块刚性连接,如图所示。
试根据杆端的约束条件,分析在总压力F作用下,立柱可能产生的几种失稳形态下的挠曲线形状,分别写出对应的总压力F之临界值的算式(按细长杆考虑),确定最小临界力的算式。
解:在总压力F作用下,立柱微弯时可能有下列三种情况:(a)每根立柱作为两端固定的压杆分别失稳:(b)两根立柱一起作为下端固定而上端自由的体系在自身平面内失稳失稳时整体在面内弯曲,则1,2两杆组成一组合截面。
(c)两根立柱一起作为下端固定而上端自由的体系在面外失稳故面外失稳时最小=。
返回9-4(9-7)图示结构ABCD由三根直径均为d的圆截面钢杆组成,在点B铰支,而在点A和点C固定,D为铰接点,。
若结构由于杆件在平面ABCD内弹性失稳而丧失承载能力,试确定作用于结点D处的荷载F的临界值。
解:杆DB为两端铰支,杆DA及DC为一端铰支一端固定,选取。
此结构为超静定结构,当杆DB失稳时结构仍能继续承载,直到杆AD及DC也失稳时整个结构才丧失承载能力,故返回9-5(9-9) 下端固定、上端铰支、长m的压杆,由两根10号槽钢焊接而成,如图所示,并符合钢结构设计规范中实腹式b类截面中心受压杆的要求。
材料力学习题册答案-第9章-压杆稳定
第 九 章 压 杆 稳 定一、选择题1、一理想均匀直杆受轴向压力P=P Q 时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( A )。
A 、弯曲变形消失,恢复直线形状;B 、弯曲变形减少,不能恢复直线形状;C 、微弯状态不变;D 、弯曲变形继续增大。
2、一细长压杆当轴向力P=P Q 时发生失稳而处于微弯平衡状态,此时若解除压力P ,则压杆的微弯变形( C )A 、完全消失B 、有所缓和C 、保持不变D 、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( D )来判断的。
A 、长度B 、横截面尺寸C 、临界应力D 、柔度 4、压杆的柔度集中地反映了压杆的( A )对临界应力的影响。
A 、长度,约束条件,截面尺寸和形状;B 、材料,长度和约束条件;C 、材料,约束条件,截面尺寸和形状;D 、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同, 试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m ,直径50mm 。
其柔度为 ( C )A.60;B.66.7; C .80; D.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( D )所示截面形状,其稳定性最好。
8、细长压杆的( A ),则其临界应力σ越大。
A 、弹性模量E 越大或柔度λ越小;B 、弹性模量E 越大或柔度λ越大;C 、弹性模量E 越小或柔度λ越大;D 、弹性模量E 越小或柔度λ越小; 9、欧拉公式适用的条件是,压杆的柔度( C )A 、λ≤ P E πσB 、λ≤s EπσC 、λ≥ PEπσ D 、λ≥sEπσ10、在材料相同的条件下,随着柔度的增大( C )A 、细长杆的临界应力是减小的,中长杆不是;B 、中长杆的临界应力是减小的,细长杆不是;C 、细长杆和中长杆的临界应力均是减小的;D 、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( A )A. 临界应力一定相等,临界压力不一定相等;B. 临界应力不一定相等,临界压力一定相等;C. 临界应力和临界压力一定相等;D. 临界应力和临界压力不一定相等;12、在下列有关压杆临界应力σe 的结论中,( D )是正确的。
材料力学习题压杆稳定
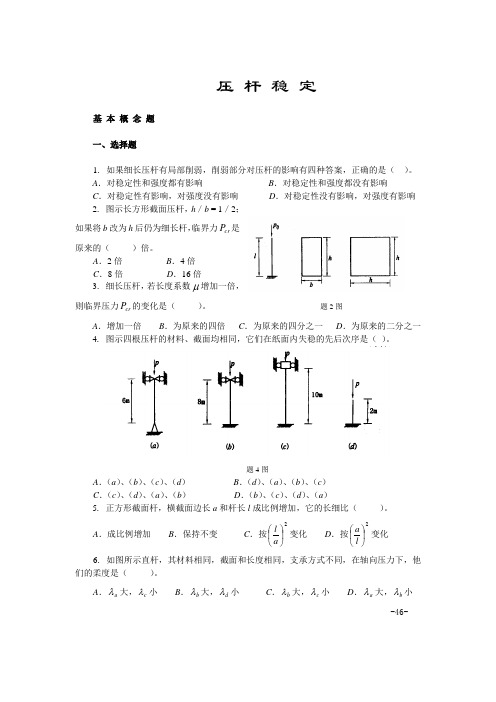
压 杆 稳 定基 本 概 念 题一、选择题1. 如果细长压杆有局部削弱,削弱部分对压杆的影响有四种答案,正确的是( )。
A .对稳定性和强度都有影响B .对稳定性和强度都没有影响C .对稳定性有影响,对强度没有影响D .对稳定性没有影响,对强度有影响2. 图示长方形截面压杆,h /b = 1/2;如果将b 改为h 后仍为细长杆,临界力cr P 是原来的( )倍。
A .2倍B .4倍C .8倍D .16倍3. 细长压杆,若长度系数μ增加一倍,则临界压力cr P 的变化是( )。
题2图A .增加一倍B .为原来的四倍C .为原来的四分之一D .为原来的二分之一4. 图示四根压杆的材料、截面均相同,它们在纸面内失稳的先后次序是( )。
题4图A .(a )、(b )、(c )、(d )B .(d )、(a )、(b )、(c )C .(c )、(d )、(a )、(b )D .(b )、(c )、(d )、(a )5. 正方形截面杆,横截面边长a 和杆长l 成比例增加,它的长细比( )。
A .成比例增加B .保持不变C .按2⎪⎭⎫ ⎝⎛a l 变化D .按2⎪⎭⎫ ⎝⎛l a 变化 6. 如图所示直杆,其材料相同,截面和长度相同,支承方式不同,在轴向压力下,他们的柔度是( )。
A .a λ大,c λ小B .b λ大,d λ小C .b λ大,c λ小D .a λ大,b λ小 -46-7. 若压杆在两个方向上的约束情况不同,且y μ>z μ。
那么该压杆的合理截面应满足的条件是( )。
A .z y I I =B .y I <z IC .y I >z ID .y z λλ=题6图8. 两压杆为管状薄壁容器式的细长杆,管两端封闭,且为铰支承。
(a )杆无内压,(b ) 杆有内压,其它条件相同。
则两杆临界应力的关系是( )。
A .()()b cr a cr σσ=B .()a cr σ>()b cr σC .()a cr σ<()b cr σD .无法比较9. 两根细长杆,直径、约束均相同,但材料不同,且212E E =,则两杆临界应力的关系是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 九 章 压 杆 稳 定一、选择题1、一理想均匀直杆受轴向压力P=P Q 时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( A )。
A 、弯曲变形消失,恢复直线形状;B 、弯曲变形减少,不能恢复直线形状;C 、微弯状态不变;D 、弯曲变形继续增大。
2、一细长压杆当轴向力P=P Q 时发生失稳而处于微弯平衡状态,此时若解除压力P ,则压杆的微弯变形( C )A 、完全消失B 、有所缓和C 、保持不变D 、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( D )来判断的。
A 、长度B 、横截面尺寸C 、临界应力D 、柔度 4、压杆的柔度集中地反映了压杆的( A )对临界应力的影响。
A 、长度,约束条件,截面尺寸和形状;B 、材料,长度和约束条件;C 、材料,约束条件,截面尺寸和形状;D 、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同, 试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m ,直径50mm 。
其柔度为 ( C )A.60;B.66.7; C .80; D.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( D )所示截面形状,其稳定性最好。
8、细长压杆的( A ),则其临界应力σ越大。
A 、弹性模量E 越大或柔度λ越小;B 、弹性模量E 越大或柔度λ越大;C 、弹性模量E 越小或柔度λ越大;D 、弹性模量E 越小或柔度λ越小; 9、欧拉公式适用的条件是,压杆的柔度( C )A 、λ≤ PEπσ B 、λ≤sEπσC 、λ≥ P Eπσ D 、λ≥sEπσ10、在材料相同的条件下,随着柔度的增大( C )A 、细长杆的临界应力是减小的,中长杆不是;B 、中长杆的临界应力是减小的,细长杆不是;C 、细长杆和中长杆的临界应力均是减小的;D 、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( A )A. 临界应力一定相等,临界压力不一定相等;B. 临界应力不一定相等,临界压力一定相等;C. 临界应力和临界压力一定相等;D. 临界应力和临界压力不一定相等;12、在下列有关压杆临界应力σe 的结论中,( D )是正确的。
A 、细长杆的σe 值与杆的材料无关;B 、中长杆的σe 值与杆的柔度无关;C 、中长杆的σe 值与杆的材料无关;D 、粗短杆的σe 值与杆的柔度无关; 13、细长杆承受轴向压力P 的作用,其临界压力与( C )无关。
A 、杆的材质B 、杆的长度C 、杆承受压力的大小D 、杆的横截面形状和尺寸二、计算题1、 有一长l =300 mm ,截面宽b =6 mm 、高h =10 mm 的压杆。
两端铰接,压杆材料为Q235钢,E =200 GPa ,试计算压杆的临界应力和临界力。
解:(1)求惯性半径i对于矩形截面,如果失稳必在刚度较小的平面内产生,故应求最小惯性半径mm 732.1126121123minmin ===⨯==b bhhb AI i(2)求柔度λλ=μl /i ,μ=1,故 λ=1×300/1.732=519>λp =100 (3)用欧拉公式计算临界应力()MPa 8.652.1731020ππ24222cr =⨯==λσE(4)计算临界力F cr =σcr ×A =65.8×6×10=3948 N=3.95 kN2、一根两端铰支钢杆,所受最大压力KN P 8.47=。
其直径mm d 45=,长度mm l 703=。
钢材的E =210GPa ,p σ=280MPa ,2.432=λ。
计算临界压力的公式有:(a) 欧拉公式;(b) 直线公式cr σ=461-2.568λ(MPa)。
试 (1)判断此压杆的类型;(2)求此杆的临界压力;解:(1) 1=μ 8621==PE σπλ 5.624===d li l μμλ由于12λλλ<<,是中柔度杆。
(2)cr σ =461-2.568λMPaKN A P cr cr 478==σ3、活塞杆(可看成是一端固定、一端自由),用硅钢制成,其直径d=40mm ,外伸部分的最大长度l=1m ,弹性模量E=210Gpa,1001=λ。
试(1)判断此压杆的类型;(2)确定活塞杆的临界载荷。
解:看成是一端固定、一端自由。
此时2=μ,而,所以,。
故属于大柔度杆-用大柔度杆临界应力公式计算。
4、托架如图所示,在横杆端点D 处受到P=30kN 的力作用。
已知斜撑杆AB 两端柱形约束(柱形较销钉垂直于托架平面),为空心圆截面,外径D=50mm 、内径d=36mm ,材料为A3钢,E=210GPa 、p σ=200MPa 、s σ=235MPa 、a=304MPa 、b=1.12MPa 。
若稳定安全系数n w =2,试校杆AB 的稳定性。
1.5m0.5mC ABD30o解 应用平衡条件可有∑=0A M ,107N 5.05.11040230sin 5.123=⨯⨯⨯==οP N BD kN 2cm 837.32=A ,4cm 144=y I ,cm 04.2=y i ,4cm 1910=x Icm 64.7=x iA3钢的4.99=P λ,1.57=S λ压杆BA 的柔度S x x i l λμλ<=⨯==7.220764.030cos 5.11οPyy i lλμλ<=⨯==9.820209.030cos 5.11ο因x λ、y λ均小于P λ,所以应当用经验公式计算临界载荷()[]N 109.8212.130400329.0)(6⨯⨯-⨯=-==y cr cr b a A A P λσ695=kN压杆的工作安全系数55.6107695=>==st n n BA 压杆的工作安全系数小于规定的稳定安全系数,故可以安全工作。
5、 如图所示的结构中,梁AB 为No.14普通热轧工字钢,CD 为圆截面直杆,其直径为d =20mm ,二者材料均为Q235钢。
结构受力如图所示,A 、C 、D 三处均为球铰约束。
若已知p F =25kN ,1l =1.25m ,2l =0.55m ,s σ=235MPa 。
强度安全因数s n =1.45,稳定安全因数st []n =1.8。
试校核此结构是否安全。
解:在给定的结构中共有两个构件:梁AB ,承受拉伸与弯曲的组合作用,属于强度问题;杆CD ,承受压缩荷载,属稳定问题。
现分别校核如下。
(1) 大梁AB 的强度校核。
大梁AB 在截面C 处的弯矩最大,该处横截面为危险截面,其上的弯矩和轴力分别为3max p 1(sin 30)(25100.5) 1.25M F l ==⨯⨯⨯° 315.6310(N m)15.63(kN m)=⨯⋅=⋅3N p cos302510cos30F F ==⨯⨯°°321.6510(N)21.65(kN)=⨯=由型钢表查得14号普通热轧工字钢的333222102cm 10210mm 21.5cm 21.510mmz W A ==⨯==⨯由此得到33max N max392415.631021.6510102101021.51010z M F W A σ--⨯⨯=+=+⨯⨯⨯⨯ 6163.210(Pa)163.2(MPa)=⨯= Q235钢的许用应力为 ss235[]162(MPa)1.45n σσ=== max σ略大于[]σ,但max ([])100%[]0.7%5%σσσ-⨯=<,工程上仍认为是安全的。
(2) 校核压杆CD 的稳定性。
由平衡方程求得压杆CD 的轴向压力为N p p 2sin 3025(kN)CD F F F ===° 因为是圆截面杆,故惯性半径为 5(mm)4I di A === 又因为两端为球铰约束 1.0μ=,所以p 31.00.55110101510li μλλ-⨯===>=⨯这表明,压杆CD 为细长杆,故需采用式(9-7)计算其临界应力,有 222932Pcrcr 2220610(2010)41104Ed F A σλ-πππ⨯⨯π⨯⨯==⨯=⨯352.810(N)52.8(kN)=⨯=于是,压杆的工作安全因数为cr Pcr w st w N 52.82.11[] 1.825CD F n n F σσ====>=这一结果说明,压杆的稳定性是安全的。
上述两项计算结果表明,整个结构的强度和稳定性都是安全的。
6、一强度等级为TC13的圆松木,长6m ,中径为300mm ,其强度许用应力为10MPa 。
现将圆木用来当作起重机用的扒杆,试计算圆木所能承受的许可压力值。
解:在图示平面内,若扒杆在轴向压力的作用下失稳,则杆的轴线将弯成半个正弦波,长度系数可取为1μ=。
于是,其柔度为168010.34liμλ⨯===⨯ 根据80λ=,求得木压杆的稳定因数为22110.39880116565ϕλ===⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭从而可得圆木所能承受的许可压力为62[][]0.398(1010)(0.3)281.34F A ϕσπ==⨯⨯⨯⨯=(kN)如果扒杆的上端在垂直于纸面的方向并无任何约束,则杆在垂直于纸面的平面内失稳时,只能视为下端固定而上端自由,即2μ=。
于是有2616010.34liμλ⨯===⨯ 求得22280028000.109160ϕλ=== 62[][]0.109(1010)(0.3)774F A ϕσπ==⨯⨯⨯⨯=(kN)显然,圆木作为扒杆使用时,所能承受的许可压力应为77 kN ,而不是281.3 kN 。
7、 如图所示,一端固定另一端自由的细长压杆,其杆长l = 2m ,截面形状为矩形,b = 20 mm 、h = 45 mm ,材料的弹性模量E = 200GPa 。
试计算该压杆的临界力。
若把截面改为b = h =30 mm ,而保持长度不变,则该压杆的临界力又为多大? 解:(一)、当b=20mm 、h=45mm 时 (1)计算压杆的柔度692.82012liμλ===>123c λ=(所以是大柔度杆,可应用欧拉公式)(2)计算截面的惯性矩由前述可知,该压杆必在xy 平面内失稳,故计算惯性矩4433100.312204512mm hb I y ⨯=⨯== (3)计算临界力μ = 2,因此临界力为 ()()kN N l EI Fcr 70.337012210310200289222==⨯⨯⨯⨯⨯==-πμπ(二)、当截面改为b = h = 30mm 时 (1)计算压杆的柔度461.93012liμλ===>123c λ=(所以是大柔度杆,可应用欧拉公式)(2)计算截面的惯性矩44431075.6123012mm bh I I z y ⨯====代入欧拉公式,可得()()N l EI F cr 8330221075.610200289222=⨯⨯⨯⨯⨯==-πμπ 从以上两种情况分析,其横截面面积相等,支承条件也相同,但是,计算得到的临界力后者大于前者。
