相交线与平行线常考题目及答案绝对经典
相交线与平行线经典测试题及解析
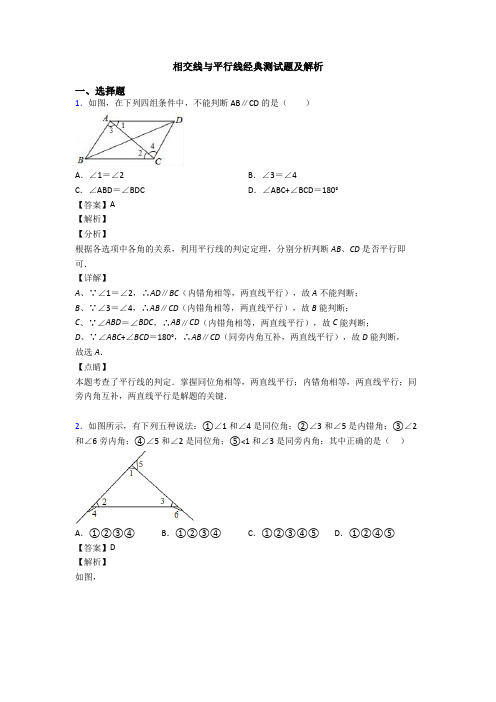
解:∵
∴∠ABE+∠CEB=180°,∠BED=
∴∠CEB=130°
∵
∴
设 =k,则∠CEF=6k,∠FEB=7k,
∴6k+7k=130°
∴∠FEB=7k=70°
∴∠DEF=∠FEB+∠BED=120°
∵
∴ =∠DEF=120°
故答案为B.
【点睛】
本题考查的是平行线的性质以及比例的应用,.熟练掌握平行线的性质是解答本题的关键.
对于C,∠3=∠4这两个角是AC与DE被EC所截得到的内错角,据此进行判断.
【详解】
∠EDC=∠EFC不是两直线被第三条直线所截得到的,因而不能判定两直线平行;
∠AFE=∠ACD,∠1=∠2是EF和BC被AC所截得到的同位角和内错角,因而可以判定EF∥BC,但不能判定DE∥AC;
∠3=∠4这两个角是AC与DE被EC所截得到的内错角,可以判定DE∥AC.
B、过直线外一点有且只有一条直线与已知直线平行,故B选项错误;
C、从直线外一点作这条直线的垂线段叫做点到这条直线的距离,应为垂线段的长度,故C选项错误;
D、在同一平面内,一条直线与两条平行线中的一条垂直,则与另一条也垂直,故D选项正确.
故选:D.
【点睛】
本题主要考查了平行线,垂线的定义,点到直线的距离及平行公理及推论,解题的关键是熟记定义与性质.
19.下列图形中线段PQ的长度表示点P到直线a的距离的是( )
A. B.
C. Байду номын сангаас.
【答案】C
【解析】
【分析】
根据点到直线的距离的定义,可得答案.
【详解】
A.左转80°B.右转80°C.左转100°D.右转100°
相交线与平行线常考题目及答案绝对经典

10.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD得度数.
(2)若∠EOC:∠EOD=4:5,求∠BOD得度数.
相交线与平行线
一.选择题(共3小题)
1.在同一平面内,有8条互不重合得直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1与l8得位置关系就是( )
A.平行B.垂直C.平行或垂直D.无法确定
2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角得有( )
26.几何推理,瞧图填空:
(1)∵∠3=∠4(已知)
∴∥()
(2)∵∠DBE=∠CAB(已知)
∴∥()
(3)∵∠ADF+=180°(已知)
∴AD∥BF()
14.如图,已知直线l1∥l2,l3、l4与l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间得关系;
(1)求∠BOD得度数;
(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE∥GH.
25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.
(1)若∠BOE=70°,求∠AOF得度数;
(2)若∠BOD:∠BOE=1:2,求∠AOF得度数.
相交线与平行线常考题目及问题详解(绝对经典)

(2)AB∥ND.
45.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.
求证:DF∥AB.
46.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.
(1)如图①,若∠A=30°,∠C=40°,则∠AEC=.
(2)如图②,若∠A=100°,∠C=120°,则∠AEC=.
28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.
(1)求证:CF∥AB.
(2)求∠DFC的度数.
29.看图填空,并在括号内注明说理依据.
如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:因为∠1=35°,∠2=35°(已知),
43.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
(1)说明:∠O=∠BEO+∠DFO.
(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.
(3)若将折线继续折下去,折三次,折四次…折n次,又会得到怎样的结论?请写出你的结论.
44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG平分∠AEC,∠NCE=75°.求证:
11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.
相交线的与平行线常考的题目及答案(绝对经典)

相交线与平行线一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个3.如图所示,同位角共有()A.6对B.8对C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B 点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= .7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.评卷人得分三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D 在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH ﹣∠BOD=90°,求证:OE∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+ =180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE 与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2= °.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,实用标准文案 精彩文档 求∠N的度数.33.阅读下面的推理过程,在括号内填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,( )所以a ∥c .( )又因为∠2+∠3=180°(已知)∠3=∠6( )所以∠2+∠6=180°,( )所以a ∥b .( )所以b ∥c .( )34.已知:如图,AB ∥CD ,FG ∥HD ,∠B=100°,FE 为∠CEB 的平分线,求∠EDH 的度数.实用标准文案精彩文档35.已知:如图,AB ∥CD ,FE ⊥AB 于G ,∠EMD=134°,求∠GEM 的度数.36.如图,∠B 和∠D 的两边分别平行.(1)在图1 中,∠B 和∠D 的数量关系是 ,在图2中,∠B 和∠D 的数量关系是 ;(2)用一句话归纳的命题为: ;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.37.已知AD ∥BC ,AB ∥CD ,E 为射线BC 上一点,AE 平分∠BAD .(1)如图1,当点E 在线段BC 上时,求证:∠BAE=∠BEA .(2)如图2,当点E 在线段BC 延长线上时,连接DE ,若∠ADE=3∠CDE ,∠AED=60°.①求证:∠ABC=∠ADC ;②求∠CED 的度数.实用标准文案38.如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.39.如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?40.已知直线AB∥CD,(1)如图1,点E在直线BD上的左侧,直接写出∠ABE,∠CDE和∠BED 之间的数量关系是.(2)如图2,点E在直线BD的左侧,BF,DF分别平分∠ABE,∠CDE,直接写出∠BFD和∠BED的数量关系是.(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.41.(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF的度数.精彩文档实用标准文案 精彩文档42.如图,已知CD ⊥DA ,DA ⊥AB ,∠1=∠2.试说明DF ∥AE .请你完成下列填空,把解答过程补充完整.解:∵CD ⊥DA ,DA ⊥AB ,∴∠CDA=90°,∠DAB=90°.( )∴∠CDA=∠DAB .(等量代换)又∠1=∠2,从而∠CDA ﹣∠1=∠DAB ﹣ .(等式的性质)即∠3= .∴DF ∥AE .( ).43.如图1,AB ∥CD ,EOF 是直线AB 、CD 间的一条折线.(1)说明:∠O=∠BEO+∠DFO .(2)如果将折一次改为折二次,如图2,则∠BEO 、∠O 、∠P 、∠PFC 会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n 次,又会得到怎样的结实用标准文案论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG平分∠AEC,∠NCE=75°.求证:(1)AB∥EF.(2)AB∥ND.45.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB.46.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.(1)如图①,若∠A=30°,∠C=40°,则∠AEC= .(2)如图②,若∠A=100°,∠C=120°,则∠AEC= .(3)如图③,请直接写出∠A,∠C与∠AEC之间关系是.47.如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.精彩文档实用标准文案精彩文档48.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC 的度数.(2)图2中AE ∥BC ,请你计算出∠AFD 的度数.49.如图,将一张矩形纸片ABCD 沿EF 对折,延长DE 交BF 于点G ,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB 平行的线段有哪些?(2)图中和AB 垂直的直线有哪些?实用标准文案精彩文档实用标准文案参考答案及解析一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定【分析】如果一条直线垂直于两平行线中的一条,那么它与另一条一定也垂直.再根据“垂直于同一条直线的两直线平行”,可知L1与L8的位置关系是平行.【解答】解:∵l2∥l3,l3⊥l4,l4∥l5,l5⊥l6,l6∥l7,l7⊥l8,∴l2⊥l4,l4⊥l6,l6⊥l8,∴l2⊥l8.∵l1⊥l2,∴l1∥l8.故选A【点评】灵活运用“垂直于同一条直线的两直线平行”是解决此类问题的关键.2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个【分析】由OE⊥AB,OF⊥CD可知:∠AOE=∠DOF=90°,而∠1、∠AOF 精彩文档实用标准文案都与∠EOF互余,可知∠1=∠AOF,因而可以转化为求∠1和∠AOF的余角共有多少个.【解答】解:∵OE⊥AB,OF⊥CD,∴∠AOE=∠DOF=90°,即∠AOF+∠EOF=∠EOF+∠1,∴∠1=∠AOF,∴∠COA+∠1=∠1+∠EOF=∠1+∠BOD=90°.∴与∠1互为余角的有∠COA、∠EOF、∠BOD三个.故选A.【点评】本题解决的关键是由已知联想到可以转化为求∠1和∠AOF的余角.3.如图所示,同位角共有()A.6对B.8对C.10对D.12对【分析】在基本图形“三线八角”中有四对同位角,再看增加射线GM、HN 后,增加了多少对同位角,求总和.【解答】解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,射线GM和直线CD被直线EF所截,形成2对同位角;射线GM和直线HN被直线EF所截,形成2对同位角;射线HN和直线AB被直线EF所截,形成2对同位角.则总共10对.故选C.精彩文档【点评】本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成8 块.【分析】一块长方体橡皮被刀切了3次,最多能被分成23=8块.【解答】解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.【点评】本题考查了学生的空间想象能力,分清如何分得到的块数最多是解决本题的关键.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B 点,则四边形OAPB的面积为9 .【分析】过P分别作x轴和y轴的垂线,交x轴和y轴与C和D.构造全等三角形△PDB≌△PCA(ASA)、正方形CODP;所以S四边形OAPB=S正方形ODPC=3×3=9.【解答】解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.∵P点坐标为(3,3),∴PC=PD;又∵l1⊥l2,∴∠BPA=90°;又∵∠DPC=90°,∴∠DPB=∠CPA,在△PDB和△PCA中∴△PDB≌△PCA(ASA),∴S△DPB=S△PCA,S四边形OAPB=S正方形ODPC+S△PCA﹣S△DPB,即S四边形OAPB=S正方形ODPC=3×3=9.故答案是:9.【点评】本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB的面积.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= 200°.【分析】过∠2的顶点作l2的平行线l,则l∥l1∥l2,由平行线的性质得出∠4=∠1=20°,∠BAC+∠3=180°,即可得出∠2+∠3=200°.【解答】解:过∠2的顶点作l2的平行线l,如图所示:则l∥l1∥l2,∴∠4=∠1=20°,∠BAC+∠3=180°,∴∠2+∠3=180°+20°=200°;故答案为:200°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是75°.【分析】根据平行线的性质得到∠EDC=∠E=45°,根据三角形的外角性质得到∠AFD=∠C+∠EDC,代入即可求出答案.【解答】解:∵∠EAD=∠E=45°,∵AE∥BC,∴∠EDC=∠E=45°,∵∠C=30°,∴∠AFD=∠C+∠EDC=75°,故答案为:75°.【点评】本题主要考查对平行线的性质,三角形的外角性质等知识点的理解和掌握,能利用性质进行推理是解此题的关键,题型较好,难度适中.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.【分析】(1)首先作MQ∥AB,根据平行线的性质,推得∠M=(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.(2)①首先判断出∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.②首先判断出∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=180°﹣2∠ENQ即可.【解答】解:(1)如图1,作MQ∥AB,,∵AB∥CD,MQ∥AB,∴MQ∥CD,∴∠1=∠FHM,∠2=∠DEM,∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),∵HP⊥EF,∴∠HPF=90°,∴∠FHP+∠HFP=180°﹣90°=90°,∵∠1+∠2=∠M,∴∠M=.(2)①如图2,,∠FHE=2∠ENQ,理由如下:∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=∠CEH=2∠ENQ.②如图3,,∠FHE=180°﹣2∠ENQ,理由如下:∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.【解答】解:如图:2条直线相交有1个交点;3条直线相交有1+2个交点;4条直线相交有1+2+3个交点;5条直线相交有1+2+3+4个交点;6条直线相交有1+2+3+4+5个交点;…n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.【点评】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交有个交点.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.【分析】(1)根据角平分线的定义求出∠AOC的度数,根据对顶角相等得到答案;(2)设∠EOC=4x,根据邻补角的概念列出方程,解方程求出∠EOC=80°,根据角平分线的定义和对顶角相等计算即可得到答案.【解答】解:(1)∵∠EOC=70°,OA平分∠EOC,∴∠AOC=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=4x,则∠EOD=5x,∴5x+4x=180°,解得x=20°,则∠EOC=80°,又∵OA平分∠EOC,∴∠AOC=40°,∴∠BOD=∠AOC=40°.【点评】本题考查的是对顶角、邻补角的概念和性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?【分析】(1)、(2)根据平角的性质求得∠AOF,又有角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;(3)由(1)、(2)的结果找出它们之间的倍数关系.【解答】解:(1)∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,∴∠AOF=140°;又∵OC平分∠AOF,∴∠FOC=∠AOF=70°,∴∠EOD=∠FOC=70°(对顶角相等);而∠BOE=∠AOB﹣∠AOE=50°,∴∠BOD=∠EOD﹣∠BOE=20°;(2)∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,∴∠AOF=180°﹣α;又∵OC平分∠AOF,∴∠FOC=∠AOF=90°﹣α,∴∠EOD=∠FOC=90°﹣α(对顶角相等);而∠BOE=∠AOB﹣∠AOE=90°﹣α,∴∠BOD=∠EOD﹣∠BOE=α;(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.【点评】本题利用垂直的定义,对顶角和互补的性质计算,要注意领会由垂直得直角这一要点.12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D 在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).【分析】(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,【解答】解:(1)如图1,过点E作EF∥PQ,∵∠CBN=100°,∠ADQ=130°,∴∠CBM=80°,∠ADP=50°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDP=∠ADP=25°,∵EF∥PQ,∴∠DEF=∠EDP=25°,∵EF∥PQ,MN∥PQ,∴EF∥MN.∴∠FEB=∠EBM=40°∴∠BED=25°+40°=65°;(2)如图2,过点E作EF∥PQ,∵∠CBN=100°,∴∠CBM=80°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDQ=∠ADQ=n°,∵EF∥PQ,∴∠DEF=180°﹣∠EDQ=180°﹣n°,∵EF∥PQ,MN∥PQ,∴EF∥MN,∴∠FEB=∠EBM=40°,∴∠BED=180°﹣n°+40°=220°﹣n°.【点评】本题主要考查了平行线的性质,运用角平分线与平行线的性质相结合来求∠BED解题的关键.13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.【分析】(1)根据平角等于180°,列式计算即可得解;(2)根据三角形的外角性质求出∠4,然后根据同位角相等,两直线平行解答.【解答】解:(1)∵∠ACB=90°,∠1=26°,∴∠2=180°﹣∠1﹣∠ACB,=180°﹣90°﹣26°,=64°;(2)结论:n∥m.理由如下:∵∠3=19°,∠A=45°,∴∠4=45°+19°=64°,∵∠2=64°,∴∠2=∠4,∴n∥m.【点评】本题考查了平行线的判定与性质,三角形外角性质的运用,熟练掌握平行线的判定方法与性质是解题的关键.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.【分析】此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.【解答】证明:(1)过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)关系:∠3=∠2﹣∠1;过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPF﹣∠QPE,∴∠3=∠2﹣∠1.(3)关系:∠3=360°﹣∠1﹣∠2.过P作PQ∥l1∥l2;同(1)可证得:∠3=∠CEP+∠DFP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP+∠1+∠2=360°,即∠3=360°﹣∠1﹣∠2.【点评】此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.【分析】(1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;(2)由(1)的结论代入计算即可.【解答】解:(1)∠ABC﹣∠BCP+∠CPN=180°;理由如下:延长NP交BC于M,如图所示:∵AB∥PN∥CD,∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,∵∠PCD=∠BCD﹣∠BCP=∠ABC﹣∠BCP,∴∠ABC﹣∠BCP+∠CPN=180°.(2)由(1)得:∠ABC﹣∠BCP+∠CPN=180°,则∠BCP=∠ABC+∠CPN﹣180°=155°+42°﹣180°=17°.【点评】本题考查了平行线的性质;熟记平行线的性质是解决问题的关键.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.【分析】(1)根据平行线的性质和等量关系可得∠EAD+∠D=180°,根据同旁内角互补,两直线平行即可证明;(2)根据平行线的性质可得∠AEB=∠C,根据三角形内角和定理和等量关系即可得到∠B的度数.【解答】(1)证明:∵AD∥BC,∴∠D+∠C=180°,∵∠EAD=∠C,∴∠EAD+∠D=180°,∴AE∥CD;(2)∵AE∥CD,∴∠AEB=∠C,∵∠FEC=∠BAE,∴∠B=∠EFC=50°.【点评】考查了平行线的判定和性质,三角形内角和定理,解题的关键是证明AE∥CD.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.【分析】(1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.(4)首先根据AB∥CD,可得∠B=∠BFD;然后根据∠D+∠E=∠BFD,可得∠D+∠E=∠B,据此解答即可.(5)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.【解答】解:(1)如图1,作EF∥AB,,∵AB∥CD,∴∠B=∠1,∵AB∥CD,EF∥AB,∴EF∥CD,∴∠D=∠2,∴∠B+∠D=∠1+∠2,又∵∠1+∠2=∠E,∴∠B+∠D=∠E.(2)如图2,作EF∥AB,,∵EF∥AB,∴∠B=∠1,∵∠E=∠1+∠2=∠B+∠D,∴∠D=∠2,∴EF∥CD,又∵EF∥AB,∴AB∥CD.(3)如图3,过E作EF∥AB,,∵EF∥AB,∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,∵∠BEF+∠DEF=∠E,∴∠E+∠B+∠D=180°+180°=360°.(4)如图4,,∵AB∥CD,∴∠B=∠BFD,∵∠D+∠E=∠BFD,∴∠D+∠E=∠B.(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,又∵AB∥CD,∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,∴∠E+∠G=∠B+∠F+∠D.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为∠P+n ∠Q=360°.(直接写结论)【分析】(1)首先过点P作PG∥AB,然后根据AB∥CD,PG∥CD,可得∠AEP=∠1,∠CFP=∠2,据此判断出∠AEP+∠CFP=∠EPF即可.(2)首先由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ;然后根据∠BEP的平分线与∠DFP的平分线相交于点Q,推得∠EQF=,即可判断出∠EPF+2∠EQF=360°.(3)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+3∠Q=360°.(4)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+n∠Q=360°.【解答】(1)证明:如图1,过点P作PG∥AB,,∵AB∥CD,∴PG∥CD,∴∠AEP=∠1,∠CFP=∠2,又∵∠1+∠2=∠EPF,∴∠AEP+∠CFP=∠EPF.(2)如图2,,由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,∵∠BEP的平分线与∠DFP的平分线相交于点Q,∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)==,∴∠EPF+2∠EQF=360°.(3)如图3,,由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+3∠Q=360°.(4)由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+n∠Q=360°.故答案为:∠P+n∠Q=360°.【点评】此题主要考查了平行线的性质的应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.【分析】设∠1=x,根据题意表示出∠2,再表示出∠3,然后根据邻补角的和等于180°列式求出x,再根据对顶角相等求出∠4即可.【解答】解:设∠1=x,则∠2=x,∠3=8x,依题意有x+x+8x=180°,解得x=18°,则∠4=18°+18°=36°.故∠4的度数是36°.【点评】本题考查了对顶角、邻补角的定义,准确识图,设出未知数并列出方程是解题的关键.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【分析】根据同位角相等,两直线平行证明OB∥AC,根据同旁内角互补,两直线平行证明OA∥BC.【解答】解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.【点评】本题考查的是平行线的判定,掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.【分析】(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=;②∠BOE=∠FOE﹣∠FOB可知∠BOE=x﹣15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.【解答】解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,∴∠EOF=∠FOB+∠BOE=35°+20°=55°,(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,∵OF平分∠COE,∴∠FOE=x,故答案为:;②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=x﹣15°,∵∠BOE+∠AOE=180°,∴x﹣15°+x=180°,解得:x=130°,∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.【点评】本题考查了对顶角,角平分线定义,角的有关定义的应用,主要考查学生的计算能力.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.【分析】(1)根据对顶角相等求出∠BOD的度数,设∠BOE=2x,根据题意列出方程,解方程即可;(2)根据角平分线的定义求出∠AOF的度数即可.【解答】解:(1)设∠BOE=2x,则∠EOD=3x,∠BOD=∠AOC=75°,∴2x+3x=75°,解得,x=15°,则2x=30°,3x=45°,∴∠BOE=30°;(2)∵∠BOE=30°,∴∠AOE=150°,∵OF平分∠AOE,∴∠AOF=75°,∴∠COF=∠AOC,∴OA是∠COF的角平分线.【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.【分析】(1)设∠BOE=x,根据题意列出方程,解方程即可;(2)分射线OF在∠AOD的内部和射线OF在∠BOC的内部两种情况,根据垂直的定义计算即可.【解答】解:(1)∵∠AOC=72°,∴∠BOD=72°,∠AOD=108°,设∠BOE=x,则∠DOE=2x,由题意得,x+2x=72°,解得,x=24°,∴∠BOE=24°,∠DOE=48°,∴∠AOE=156°;(2)若射线OF在∠BOC的内部,∠DOF=90°+48°=138°,若射线OF在∠AOD的内部,∠DOF=90°﹣48°=42°,∴∠DOF的度数是138°或42°.【点评】本题考查的是对顶角和邻补角的概念和性质以及垂直的定义,掌握对顶角相等、邻补角的和是180°是解题的关键.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH ﹣∠BOD=90°,求证:OE∥GH.【分析】(1)根据邻补角的定义求出∠EOC,再根据角平分线的定义求出∠AOC,然后根据对顶角相等解答.(2)由已知条件和对顶角相等得出∠MFC=∠MFH=∠BOD+90°=126°,得出∠ONF=90°,求出∠OFM=54°,延长∠OFG=2∠OFM=108°,证出∠OFG+∠EOC=180°,即可得出结论.【解答】解:∵∠EOC:∠EOD=2:3,∴∠EOC=180°×=72°,∵OA平分∠EOC,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.(2)延长FM交AB于N,如图所示:∵∠MFH﹣∠BOD=90°,FM平分∠OFG,∴∠MFC=∠MFH=∠BOD+90°=126°,∴∠ONF=126°﹣36°=90°,∴∠OFM=90°﹣36°=54°,∴∠OFG=2∠OFM=108°,∴∠OFG+∠EOC=180°,∴OE∥GH.【点评】本题考查了平行线的判定、角平分线定义、角的互余关系等知识;熟练掌握平行线的判定、角平分线定义是解决问题的关键,(2)有一定难度.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.【分析】(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;(2)根据角平分线的定义和邻补角的性质计算即可.【解答】解:(1)∵OE平分∠BOC,∠BOE=70°,∴∠BOC=2∠BOE=140°,∴∠AOC=180°﹣140°=40°,又∠COF=90°,∴∠AOF=90°﹣40°=50°;(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,∴∠BOD:∠BOE:∠EOC=1:2:2,∴∠BOD=36°,∴∠AOC=36°,又∵∠COF=90°,∴∠AOF=90°﹣36°=54°.【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴CD ∥AB (内错角相等,两直线平行)(2)∵∠DBE=∠CAB(已知)∴AC ∥BD (同位角相等,两直线平行)(3)∵∠ADF+ ∠5 =180°(已知)∴AD∥BF(同旁内角互补,两直线平行)【分析】(1)由∠3=∠4根据平行线的判定推出CD∥AB;(2)由∠DBE=∠CAB,根据同位角相等,两直线平行得出答案;(3)根据同旁内角互补,两直线平行即可得到答案.。
(完整版)相交线与平行线常考题目及答案(绝对经典)

一.选择题(共3小题)
1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是( )
A.平行B.垂直C.平行或垂直D.无法确定
2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有( )
26.几何推理,看图填空:
(1)∵∠3=∠4(已知)
∴∥()
(2)∵∠DBE=∠CAB(已知)
∴∥()
(3)∵∠ADF+=180°(已知)
∴AD∥BF()
27.如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.
(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.
7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.
评卷人
得分
三.解答题(共43小题)
8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
15.如图,已知AB∥PN∥CD.
(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
相交线与平行线测试题及答案

相交线与平行线测试题及答案1. 单选题:在平面上,两条互相垂直的直线称为()。
A. 平行线B. 垂直线C. 相交线D. 对称线答案:B. 垂直线2. 单选题:下面哪种说法是正确的?A. 平行线永远不会相交B. 相交线永远不会平行C. 平行线和相交线可以同时存在D. 平行线和相交线不能同时存在答案:C. 平行线和相交线可以同时存在3. 多选题:判断下列述句是否正确。
1) 平行线没有交点。
2) 相交线可以有无数个交点。
3) 两条垂直线的交点一定是直角。
A. 正确的有1)、2)、3)B. 正确的有1)、3)C. 正确的有2)、3)D. 正确的只有3)答案:B. 正确的有1)、3)4. 填空题:两条互相垂直的直线所成的角度为()度。
答案:90度5. 判断题:两条平行线的夹角为180度。
答案:错误6. 判断题:两条相交直线一定不平行。
答案:正确7. 计算题:已知直线L1与直线L2互相垂直,L1的斜率为2,过点(1,3)的直线L2的斜率为()。
答案:-1/28. 计算题:已知直线L1过点(1,2)且斜率为3/4,直线L2与L1平行且过点(3,5),求直线L2的斜率。
答案:3/49. 解答题:请解释什么是相交线和平行线,并举例说明。
答案:相交线是指两条直线或线段在平面上有唯一一点相交。
例如,在平面上有两条直线,一条通过点A和点B,另一条通过点C和点D,如果点A与点C不重合并且点B与点D不重合,则这两条直线相交于点E。
平行线是指在平面上没有任何交点的两条直线。
例如,在平面上有一条直线通过点A和点B,另一条直线通过点C和点D,如果两条直线没有任何一点相交,则这两条直线是平行线。
10. 解答题:如何通过直线的斜率来判断两条直线是否平行或垂直?答案:两条直线平行的充要条件是它们的斜率相等,即斜率相同的两条直线是平行线。
两条直线垂直的充要条件是它们的斜率的乘积为-1,即斜率之积为-1的两条直线是垂直线。
总结:在平面几何中,相交线是指两条直线或线段在平面上有唯一一点相交,平行线是指在平面上没有任何交点的两条直线。
相交线与平行线经典测试题及答案

相交线与平行线经典测试题及答案一、选择题1.下列命题错误的是( )A .平行四边形的对角线互相平分B .两直线平行,内错角相等C .等腰三角形的两个底角相等D .若两实数的平方相等,则这两个实数相等【答案】D【解析】【分析】根据平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,分别进行判断,即可得到答案.【详解】解:A 、平行四边形的对角线互相平分,正确;B 、两直线平行,内错角相等,正确;C 、等腰三角形的两个底角相等,正确;D 、若两实数的平方相等,则这两个实数相等或互为相反数,故D 错误;故选:D.【点睛】本题考查了判断命题的真假,以及平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,解题的关键是熟练掌握所学的性质进行解题.2.如图,下列能判定AB ∥CD 的条件有几个( )(1)12∠=∠ (2)34∠=∠(3)5B ∠=∠ (4)180B BCD ∠+∠=︒.A .4B .3C .2D .1【答案】B【解析】【分析】 根据平行线的判定逐一判定即可.【详解】因为12∠=∠,所有AD ∥BC ,故(1)错误.因为34∠=∠,所以AB ∥CD ,故(2)正确.因为5B ∠=∠,所以AB ∥CD ,故(3)正确.因为180B BCD ∠+∠=︒,所以AB ∥CD ,故(4)正确.所以共有3个正确条件.故选B【点睛】本题考查的是平行线的判定,找准两个角是哪两条直线被哪条直线所截形成的同位角、同旁内角、内错角是关键.3.如图,将一张矩形纸片折叠,若170∠=︒,则2∠的度数是( )A .65︒B .55︒C .70︒D .40︒【答案】B【解析】【分析】根据平行线的性质求出∠3=170∠=︒,得到∠2+∠4=110°,由折叠得到∠2=∠4即可得到∠2的度数.【详解】∵a ∥b ,∴∠3=170∠=︒,∴∠2+∠4=110°,由折叠得∠2=∠4,∴∠2=55︒,故选:B.【点睛】此题考查平行线的性质,折叠的性质.4.如图,已知AB ∥DC ,BF 平分∠ABE ,且BF ∥DE ,则∠ABE 与∠CDE 的关系是( )A .∠ABE =2∠CDEB .∠ABE =3∠CDEC .∠ABE =∠CDE +90°D .∠ABE +∠CDE =180°【解析】【分析】延长BF与CD相交于M,根据两直线平行,同位角相等可得∠M=∠CDE,再根据两直线平行,内错角相等可得∠M=∠ABF,从而求出∠CDE=∠ABF,再根据角平分线的定义解答.【详解】解:延长BF与CD相交于M,∵BF∥DE,∴∠M=∠CDE,∵AB∥CD,∴∠M=∠ABF,∴∠CDE=∠ABF,∵BF平分∠ABE,∴∠ABE=2∠ABF,∴∠ABE=2∠CDE.故选:A.【点睛】本题考查了平行线的性质和角平分线的定义,作辅助线,是利用平行线的性质的关键,也是本题的难点.5.如图,将一张含有30角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠的大小为()244∠=,则1α-A.14B.16C.90α-D.44【答案】A【解析】分析:依据平行线的性质,即可得到∠2=∠3=44°,再根据三角形外角性质,可得∠3=∠1+30°,进而得出结论.详解:如图,∵矩形的对边平行,∴∠2=∠3=44°,根据三角形外角性质,可得:∠3=∠1+30°,∴∠1=44°﹣30°=14°.点睛:本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,同位角相等.6.如图,四边形ABCD 中,//,,AB CD AD CD E F =、分别是AB BC 、的中点,若140,∠=︒则D ∠=( )A .40︒B .100︒C .80︒D .110︒【答案】B【解析】【分析】 利用E 、F 分别是线段BC 、BA 的中点得到EF 是△BAC 的中位线,得出∠CAB 的大小,再利用CD ∥AB 得到∠DCA 的大小,最后在等腰△DCA 中推导得到∠D.【详解】∵点E 、F 分别是线段CB 、AB 的中点,∴EF 是△BAC 的中位线∴EF ∥AC∵∠1=40°,∴∠CAB=40°∵CD ∥BA∴∠DCA=∠CAB=40°∵CD=DA∴∠DAC=∠DCA=40°∴在△DCA 中,∠D=100°故选:B【点睛】本题考查中位线的性质和平行线的性质,解题关键是推导得出EF 是△ABC 的中位线.7.如图,一副三角板按如图所示的位置摆放,其中//AB CD ,45A ∠=︒,60C ∠=°,90AEB CED ∠=∠=︒,则AEC ∠的度数为( )A.75°B.90°C.105°D.120°【答案】C【解析】【分析】延长CE交AB于点F,根据两直线平行,内错角相等可得∠AFE=∠C,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】解:如图,延长CE交AB于点F,∵AB∥CD,∴∠AFE=∠C=60°,在△AEF中,由三角形的外角性质得,∠AEC=∠A+∠AFE=45°+60°=105°.故选:C.【点睛】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记相关性质并作出正确的辅助线是解题的关键.8.如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )A.75°B.72°C.70°D.65°【答案】B【解析】【分析】如图,由折叠的性质可知∠3=∠4,已知AB∥CD,根据两直线平行,内错角相等可得∠3=∠1,再由∠1=2∠2,∠3+∠4+∠2=180°,可得5∠2=180°,即可求得∠2=36°,所以∠AEF=∠3=∠1=72°【详解】如图,由折叠的性质可知∠3=∠4,∵AB ∥CD ,∴∠3=∠1,∵∠1=2∠2,∠3+∠4+∠2=180°,∴5∠2=180°,即∠2=36°,∴∠AEF=∠3=∠1=72°故选B .【点睛】本题考查的是图形翻折变换的性质及平行线的性质,熟知折叠的性质及平行线的性质是解决问题的关键.9.如图,下列条件中能判定//DE AC 的是( )A .EDC EFC ∠=∠B .AEF ACD ∠=∠C .34∠=∠D .12∠=∠【答案】C【解析】【分析】 对于A ,∠EDC=∠EFC 不是两直线被第三条直线所截得到的,据此进行判断;对于B 、D ,∠AFE=∠ACD ,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,据此进行判断;对于C ,∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,据此进行判断.【详解】∠EDC=∠EFC 不是两直线被第三条直线所截得到的,因而不能判定两直线平行;∠AFE=∠ACD,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,因而可以判定EF ∥BC,但不能判定DE ∥AC ;∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,可以判定DE ∥AC.故选C.【点睛】本题考查平行线的判定,掌握相关判定定理是解题的关键.10.如图所示,某同学的家在P 处,他想尽快赶到附近公路边搭公交车,他选择P→C 路线,用几何知识解释其道理正确的是( )A .两点确定一条直线B .垂直线段最短C .两点之间线段最短D .三角形两边之和大于第三边 【答案】B【解析】【分析】根据垂线段的定义判断即可.【详解】 解: 直线外一点与直线上各点连接的所有线段中,垂线段最短,∴ 选:B.【点睛】直线外任意一点到这条直线的垂线段的长度,叫做点到这条直线的距离.直线外一点与直线上各点连接的所有线段中,垂线段最短.简称“垂线段最短”.11.在下图中,∠1,∠2是对顶角的图形是( )A .B .C .D .【答案】B【解析】略12.如图,//AB CD ,点E 在CD 上,点F 在AB 上,如果:6:7CEF BEF ∠∠=,50ABE ∠=︒,那么AFE ∠的度数为( )A .110︒B .120︒C .130︒D .140︒【答案】B【解析】【分析】由//AB CD 可得∠ABE+∠CEB=180°,∠BED=50ABE ∠=︒,即∠CEB=130°,由:6:7CEF BEF ∠∠=可得=67CEF BEF ∠∠,设=67CEF BEF ∠∠=k,则∠CEF=6k,∠FEB=7k,可得∠FEB=70°,可得∠DEF=∠FEB+∠BED=120°;又由//AB CD 可得AFE ∠=∠DEF 即可解答.【详解】解:∵//AB CD∴∠ABE+∠CEB=180°,∠BED=50ABE ∠=︒∴∠CEB=130°∵:6:7CEF BEF ∠∠=∴=67CEF BEF ∠∠ 设=67CEF BEF ∠∠=k ,则∠CEF=6k,∠FEB=7k, ∴6k+7k=130°∴∠FEB=7k=70°∴∠DEF=∠FEB+∠BED=120°∵//AB CD∴AFE ∠=∠DEF=120°故答案为B .【点睛】本题考查的是平行线的性质以及比例的应用,.熟练掌握平行线的性质是解答本题的关键.13.如图,在△ABC 中,AB =AC ,∠A =36°,D 、E 两点分别在边AC 、BC 上,BD 平分∠ABC ,DE ∥AB .图中的等腰三角形共有( )A .3个B .4个C .5个D .6个【答案】C【解析】【分析】 已知条件,根据三角形内角和等于180,角的平分线的性质求得各个角的度数,然后利用等腰三角形的判定进行判断即可.【详解】解:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠DBC=36°,∴∠BDC=180°﹣36°﹣72°=72°,∵DE∥AB,∴∠EDB=∠ABD=36°,∴∠EDC=72°﹣36°=36°,∴∠DEC=180°﹣72°﹣36°=72°,∴∠A=∠ABD,∠DBE=∠BDE,∠DEC=∠C,∠BDC=∠C,∠ABC=∠C,∴△ABC、△ABD、△DEB、△BDC、△DEC都是等腰三角形,共5个,故选C.【点睛】本题考查了等腰三角形判定和性质、角平分线的性质、平行线的性质,由已知条件利用相关的性质求得各个角相等是解题的关键.14.下列说法中不正确的是()①过两点有且只有一条直线②连接两点的线段叫两点的距离③两点之间线段最短④点B在线段AC上,如果AB=BC,则点B是线段AC的中点A.①B.②C.③D.④【答案】B【解析】【分析】依据直线的性质、两点间的距离、线段的性质以及中点的定义进行判断即可.【详解】①过两点有且只有一条直线,正确;②连接两点的线段的长度叫两点间的距离,错误③两点之间线段最短,正确;④点B在线段AC上,如果AB=BC,则点B是线段AC的中点,正确;故选B.15.如图,直线,a b 被直线c 所截,则图中的1∠与2∠是( )A .同位角B .内错角C .同旁内角D .邻补角【答案】B【解析】【分析】 根据1∠与2∠的位置关系,由内错角的定义即可得到答案.【详解】解:∵1∠与2∠在截线,a b 之内,并且在直线c 的两侧,∴由内错角的定义得到1∠与2∠是内错角,故B 为答案.【点睛】本题主要考查了内错角、同位角、同旁内角、邻补角的定义,理解内错角、同位角、同旁内角、邻补角是解题的关键.16.如图,直线//,175a b ︒∠=,则2∠的大小是( )A .75︒B .85︒C .95︒D .105︒【答案】D【解析】【分析】 把2∠的对顶角标记为3∠,根据对顶角的性质得到2∠与3∠得关系,再根据直线平行的性质得到1∠与3∠得关系,最后由等量替换得到2∠得度数.【详解】解:如图,把2∠的对顶角标记为3∠,∵2∠与3∠互为对顶角,∴23∠∠=,又∵//a b ,175︒∠=,∴13180∠+∠=︒(两直线平行,同旁内角互补),∴12180∠+∠=︒(等量替换),∴2180118075105∠=︒-∠=︒-︒=︒故D 为答案.【点睛】本题主要考查了对顶角的性质(对顶角相等)、直线平行的性质(两直线平行,同旁内角互补),学会运用等量替换原则是解题的关键.17.如图,直线,AB CD 相交于点,50,O AOC OE AB ︒∠=⊥,则DOE ∠的大小是( )A .40︒B .50︒C .70︒D .90︒【答案】A【解析】【分析】 根据对顶角的性质,把BOD ∠的度数计算出来,再结合OE AB ⊥,即可得到答案.【详解】解:∵50AOC ∠=︒,∴50BOD ∠=︒(对顶角相等),又∵OE AB ⊥,∴90EOB ∠=︒,∴905040DOE BOE DOB ∠=∠-∠=︒-︒=︒,故A 为答案.【点睛】本题主要考查了对顶角的性质(对顶角相等),判断,BOD AOC ∠∠是对顶角是解题的关键.18.如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为()A.34°B.56°C.66°D.54°【答案】B【解析】试题分析:∵AB∥CD,∴∠D=∠1=34°,∵DE⊥CE,∴∠DEC=90°,∴∠DCE=180°﹣90°﹣34°=56°.故选B.考点:平行线的性质.19.如图,小慧从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C 处,此时需要将方向调整到与出发时一致,则方向的调整应为()A.左转80°B.右转80°C.左转100°D.右转100°【答案】B【解析】【分析】如图,延长AB到D,过C作CE//AD,由题意可得∠A=60°,∠1=20°,根据平行线的性质可得∠A=∠2,∠3=∠1+∠2,进而可得答案.【详解】如图,延长AB到D,过C作CE//AD,∵此时需要将方向调整到与出发时一致,∴此时沿CE方向行走,∵从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,∴∠A=60°,∠1=20°,AM∥BN,CE∥AB,∴∠A=∠2=60°,∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°,∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质,解答时要注意以北方为参照方向,进行角度调整.20.如图,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠DAE=56°,则∠E的度数为()A.56°B.36°C.26°D.28°【答案】D【解析】分析:根据平行线的性质,可得∠DBC=56°,∠E=∠EBC,根据角平分线的定义,可得∠EBC=12∠DBC=28°,进而得到∠E=28°.详解:∵AE∥BC,∠DAE=56°,∴∠DBC=56°,∠E=∠EBC,∵BE平分∠DBC,∴∠EBC=12∠DBC=28°,∴∠E=28°,故选D.点睛:本题主要考查了角平分线的定义和平行线的性质,熟练掌握角平分线的定义和平行线的性质是解题的关键.。
相交线与平行线典型考题(附答案及解析)

A BDC第5题图 平行线相交线常见题型过关练习一、选择题一、如图,l 1∥l 2,∠1=120°,那么∠2= . (第1题图)二、如图,AB ∥CD ,∠DCE=80°,那么∠BEF=3、如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E 的大小为 (第2题图) (第3题图) (第4题图)4、如图,AB ∥CD ,AD 和BC 相交于点O ,∠A =40°,∠AOB =75°.那么∠C 等于 五、如图,AB ∥CD ,∠C =80°,∠CAD =60°,那么∠BAD 等于 六、如图,AB ∥EF ∥CD ,∠ABC =46°,∠CEF =154°,那么∠BCE 等于(第6题图) (第7题图) (第8题图) (第9题图)7、如图,AB∥CD,AC 与BD 相交于点O ,∠A=30°,∠COD=105°.那么∠D 的大小是 八、如图,直线l 1∥l 2,∠1=40°,∠2=75°,那么∠3等于九、如图,己知AB∥CD,BE 平分∠ABC,∠CDE=150°,那么∠C 的度数是 10、如图,已知AB ∥CD ,那么图中与∠1互补的角有 个。
1一、如图,CD ∥AB ,∠1=120°,∠2=80°,那么∠E 的度数是(第10题图)(第11题图) (第12题图) (第13题图)1二、如图,已知直线a ∥b ,∠1=40°,∠2=60°.那么∠3等于13、如图,已知AB∥CD,∠E=︒28,∠C=︒52,那么∠EAB 的度数是 14、如图,AB ∥EF ∥CD ,∠ABC = 46,∠CEF = 154,那么∠BCE 等于 1五、如下图,AB ∥CD ,∠E =37°,∠C =20°,那么∠EAB 的度数为1六、如图,已知AB ∥CD ,∠A =60°,∠C =25°,那么∠E 等于 (第15题图)B AD CEF 15446 (第14题图)(第16题图)(第17题图)(第18题图)17、如下图,直线a∥b.直线c与直线a,b别离相交于点A、点B,AM b⊥,垂足为点M,假设158∠=︒,那么2∠=_________1八、如图:CD平分∠ACB,DE∥AC且∠1=30°,那么∠2=度.1九、如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.(辅助线已画)(第19题图)答案及解析一、分析:由邻补角的概念,即可求得∠3的度数,又由l1∥l2,依照两直线平行,同位角相等,即可求得∠2的度数.解答:∵∠1=120°,∴∠3=180°﹣∠1=60°,∵l1∥l2,∴∠2=∠3=60°.点评:此题考查了平行线的性质与邻补角的概念.注意两直线平行,同位角相等.二、分析:依照平行线的性质推出∠DCE+∠BEF=180°,代入求出即可.解答:∵AB∥CD,∴∠DCE+∠BEF=180°,∵∠DCE=80°,∴∠BEF=180°﹣80°=100°.点评:此题要紧考查对平行线的性质,邻补角的概念等知识点的明白得和把握,依照平行线的性质推出∠DCE+∠BEF=180°是解此题的关键.3、分析:依照两直线平行,同位角相等,求得∠EFA=55°,再利用三角形内角和定理即可求得∠E的度数.解答:∵AB∥CD,∠C=125°,∴∠EFB=125°,∴∠EFA=180﹣125=55°,∵∠A=45°,∴∠E=180°﹣∠A﹣∠EFA=180°﹣45°﹣55°=80°.4、分析:由∠A=40°,∠AOB=75°,依照三角形内角和定理,即可求得∠B的度数,又由AB∥CD,依照两直线平行,内错角相等,即可求得∠C的值.解答:∵∠A=40°,∠AOB=75°.∴∠B=180°﹣∠A﹣∠AOB=180°﹣40°﹣75°=65°,∵AB∥CD,∴∠C=∠B=65°.五、分析:依照三角形的内角和为180°,即可求出∠D的度数,再依照两直线平行,内错角相等即可明白∠BAD的度数.解答:∵∠C=80°,∠CAD=60°,∴∠D=180°﹣80°﹣60°=40°,∵AB∥CD,∴∠BAD=∠D=40°。
相交线与平行线常考题目及答案(绝对经典)

相交线与平行线一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个3.如图所示,同位角共有()A.6对B.8对C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= .7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB 和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?112.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.试卷第2页,总6页20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE ∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+=180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.3(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2= °.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN 交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.33.阅读下面的推理过程,在括号内填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,()所以a∥c.()又因为∠2+∠3=180°(已知)∠3=∠6()所以∠2+∠6=180°,()所以a∥b.()所以b∥c.()试卷第4页,总6页34.已知:如图,AB∥CD,FG∥HD,∠B=100°,FE为∠CEB的平分线,求∠EDH的度数.35.已知:如图,AB∥CD,FE⊥AB于G,∠EMD=134°,求∠GEM的度数.36.如图,∠B和∠D的两边分别平行.(1)在图1 中,∠B和∠D的数量关系是,在图2中,∠B和∠D的数量关系是;(2)用一句话归纳的命题为:;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.37.已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.①求证:∠ABC=∠ADC;②求∠CED的度数.38.如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.39.如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?40.已知直线AB∥CD,(1)如图1,点E在直线BD上的左侧,直接写出∠ABE,∠CDE和∠BED之间的数量关系是.(2)如图2,点E在直线BD的左侧,BF,DF分别平分∠ABE,∠CDE,直接写出∠BFD和∠BED的数量关系是.(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.41.(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF 的度数.42.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把解答过程补充完整.解:∵CD⊥DA,DA⊥AB,∴∠CDA=90°,∠DAB=90°.()∴∠CDA=∠DAB.(等量代换)又∠1=∠2,从而∠CDA﹣∠1=∠DAB﹣.(等式的性质)即∠3= .5∴DF∥AE.().43.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)说明:∠O=∠BEO+∠DFO.(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n次,又会得到怎样的结论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG平分∠AEC,∠NCE=75°.求证:(1)AB∥EF.(2)AB∥ND.45.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB.46.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.(1)如图①,若∠A=30°,∠C=40°,则∠AEC= .(2)如图②,若∠A=100°,∠C=120°,则∠AEC= .(3)如图③,请直接写出∠A,∠C与∠AEC之间关系是.47.如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.48.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC的度数.(2)图2中AE∥BC,请你计算出∠AFD的度数.49.如图,将一张矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB平行的线段有哪些?(2)图中和AB垂直的直线有哪些?试卷第6页,总6页本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
相交线与平行线常考题目及问题详解(绝对经典)

相交线与平行线一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个 C.1个 D.0个3.如图所示,同位角共有()A.6对B.8对 C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B 点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3=.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.评卷人得分三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB ∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF=.(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH ﹣∠BOD=90°,求证:OE∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+=180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2=°.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.33.阅读下面的推理过程,在括号内填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,()所以a∥c.()又因为∠2+∠3=180°(已知)∠3=∠6()所以∠2+∠6=180°,()所以a∥b.()所以b∥c.()34.已知:如图,AB∥CD,FG∥HD,∠B=100°,FE为∠CEB的平分线,求∠EDH的度数.35.已知:如图,AB∥CD,FE⊥AB于G,∠EMD=134°,求∠GEM的度数.36.如图,∠B和∠D的两边分别平行.(1)在图1 中,∠B和∠D的数量关系是,在图2中,∠B和∠D的数量关系是;(2)用一句话归纳的命题为:;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.页眉内容页脚内容5137.已知AD ∥BC ,AB ∥CD ,E 为射线BC 上一点,AE 平分∠BAD .(1)如图1,当点E 在线段BC 上时,求证:∠BAE=∠BEA .(2)如图2,当点E 在线段BC 延长线上时,连接DE ,若∠ADE=3∠CDE ,∠AED=60°.①求证:∠ABC=∠ADC ;②求∠CED 的度数.38.如图,已知a ∥b ,ABCDE 是夹在直线a ,b 之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.39.如图,AB ∥DC ,增加折线条数,相应角的个数也会增多,∠B ,∠E ,∠F,∠G ,∠D 之间又会有何关系?40.已知直线AB ∥CD ,(1)如图1,点E 在直线BD 上的左侧,直接写出∠ABE ,∠CDE 和∠BED 之间的数量关系是 .(2)如图2,点E 在直线BD 的左侧,BF ,DF 分别平分∠ABE ,∠CDE ,直接写出∠BFD 和∠BED 的数量关系是 .页眉内容 页脚内容51(3)如图3,点E 在直线BD 的右侧BF ,DF 仍平分∠ABE ,∠CDE,那么∠BFD 和∠BED 有怎样的数量关系?请说明理由.41.(1)如图,直线a ,b ,c 两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ,OF 平分∠COE ,∠AOD :∠BOE=4:1,求∠AOF 的度数.42.如图,已知CD ⊥DA ,DA ⊥AB ,∠1=∠2.试说明DF ∥AE .请你完成下列填空,把解答过程补充完整.解:∵CD ⊥DA ,DA ⊥AB ,∴∠CDA=90°,∠DAB=90°.( )∴∠CDA=∠DAB .(等量代换)又∠1=∠2,从而∠CDA ﹣∠1=∠DAB ﹣ .(等式的性质)即∠3= .∴DF ∥AE .( ).43.如图1,AB ∥CD ,EOF 是直线AB 、CD 间的一条折线.页眉内容 页脚内容51(1)说明:∠O=∠BEO+∠DFO .(2)如果将折一次改为折二次,如图2,则∠BEO 、∠O 、∠P 、∠PFC 会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n 次,又会得到怎样的结论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG 平分∠AEC ,∠NCE=75°.求证:(1)AB ∥EF .(2)AB ∥ND .45.如图,∠E=∠1,∠3+∠ABC=180°,BE 是∠ABC 的角平分线. 求证:DF ∥AB .46.已知,直线AB ∥CD ,E 为AB 、CD 间的一点,连结EA 、EC .(1)如图①,若∠A=30°,∠C=40°,则∠AEC= .(2)如图②,若∠A=100°,∠C=120°,则∠AEC= .(3)如图③,请直接写出∠A ,∠C 与∠AEC 之间关系是 .47.如图,已知AB ∥CD ,EF ⊥AB 于点G ,若∠1=30°,试求∠F 的度数.页眉内容页脚内容5148.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC 的度数.(2)图2中AE ∥BC ,请你计算出∠AFD 的度数.49.如图,将一张矩形纸片ABCD 沿EF 对折,延长DE 交BF 于点G ,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB 平行的线段有哪些?(2)图中和AB 垂直的直线有哪些?页眉内容页脚内容51页眉内容参考答案及解析一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定【分析】如果一条直线垂直于两平行线中的一条,那么它与另一条一定也垂直.再根据“垂直于同一条直线的两直线平行”,可知L1与L8的位置关系是平行.【解答】解:∵l2∥l3,l3⊥l4,l4∥l5,l5⊥l6,l6∥l7,l7⊥l8,∴l2⊥l4,l4⊥l6,l6⊥l8,∴l2⊥l8.∵l1⊥l2,∴l1∥l8.故选A【点评】灵活运用“垂直于同一条直线的两直线平行”是解决此类问题的关键.2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个 C.1个 D.0个【分析】由OE⊥AB,OF⊥CD可知:∠AOE=∠DOF=90°,而∠1、∠AOF 都与∠EOF互余,可知∠1=∠AOF,因而可以转化为求∠1和∠AOF的余角共有多少个.【解答】解:∵OE⊥AB,OF⊥CD,∴∠AOE=∠DOF=90°,即∠AOF+∠EOF=∠EOF+∠1,∴∠1=∠AOF,∴∠COA+∠1=∠1+∠EOF=∠1+∠BOD=90°.页脚内容51页眉内容∴与∠1互为余角的有∠COA、∠EOF、∠BOD三个.故选A.【点评】本题解决的关键是由已知联想到可以转化为求∠1和∠AOF的余角.3.如图所示,同位角共有()A.6对B.8对C.10对D.12对【分析】在基本图形“三线八角”中有四对同位角,再看增加射线GM、HN 后,增加了多少对同位角,求总和.【解答】解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,射线GM和直线CD被直线EF所截,形成2对同位角;射线GM和直线HN被直线EF所截,形成2对同位角;射线HN和直线AB被直线EF所截,形成2对同位角.则总共10对.故选C.【点评】本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成8块.【分析】一块长方体橡皮被刀切了3次,最多能被分成23=8块.【解答】解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.【点评】本题考查了学生的空间想象能力,分清如何分得到的块数最多是解决本题的关键.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B 点,则四边形OAPB的面积为9.页脚内容51页眉内容页脚内容51【分析】过P 分别作x 轴和y 轴的垂线,交x 轴和y 轴与C 和D .构造全等三角形△PDB ≌△PCA (ASA )、正方形CODP ;所以S 四边形OAPB =S 正方形ODPC =3×3=9.【解答】解:过P 分别作x 轴和y 轴的垂线,交x 轴和y 轴于点C 和D . ∵P 点坐标为(3,3),∴PC=PD ;又∵l 1⊥l 2,∴∠BPA=90°;又∵∠DPC=90°,∴∠DPB=∠CPA ,在△PDB 和△PCA 中∴△PDB ≌△PCA (ASA ),∴S △DPB =S △PCA ,S 四边形OAPB =S 正方形ODPC +S △PCA ﹣S △DPB ,即S 四边形OAPB =S 正方形ODPC =3×3=9.故答案是:9.【点评】本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB 的面积.6.如图,直线l 1∥l 2,∠1=20°,则∠2+∠3= 200° .页眉内容【分析】过∠2的顶点作l2的平行线l,则l∥l1∥l2,由平行线的性质得出∠4=∠1=20°,∠BAC+∠3=180°,即可得出∠2+∠3=200°.【解答】解:过∠2的顶点作l2的平行线l,如图所示:则l∥l1∥l2,∴∠4=∠1=20°,∠BAC+∠3=180°,∴∠2+∠3=180°+20°=200°;故答案为:200°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是75°.【分析】根据平行线的性质得到∠EDC=∠E=45°,根据三角形的外角性质得到∠AFD=∠C+∠EDC,代入即可求出答案.【解答】解:∵∠EAD=∠E=45°,∵AE∥BC,∴∠EDC=∠E=45°,∵∠C=30°,∴∠AFD=∠C+∠EDC=75°,故答案为:75°.【点评】本题主要考查对平行线的性质,三角形的外角性质等知识点的理解和掌握,能利用性质进行推理是解此题的关键,题型较好,难度适中.页脚内容51三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB ∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.【分析】(1)首先作MQ∥AB,根据平行线的性质,推得∠M=(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.(2)①首先判断出∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.②首先判断出∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=180°﹣2∠ENQ即可.【解答】解:(1)如图1,作MQ∥AB,,∵AB∥CD,MQ∥AB,∴MQ∥CD,∴∠1=∠FHM,∠2=∠DEM,∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),∵HP⊥EF,∴∠HPF=90°,∴∠FHP+∠HFP=180°﹣90°=90°,∵∠1+∠2=∠M,∴∠M=.(2)①如图2,,∠FHE=2∠ENQ,理由如下:∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=∠CEH=2∠ENQ.②如图3,,∠FHE=180°﹣2∠ENQ,理由如下:∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.【解答】解:如图:2条直线相交有1个交点;3条直线相交有1+2个交点;4条直线相交有1+2+3个交点;5条直线相交有1+2+3+4个交点;6条直线相交有1+2+3+4+5个交点;…n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.【点评】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交有个交点.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.【分析】(1)根据角平分线的定义求出∠AOC的度数,根据对顶角相等得到答案;(2)设∠EOC=4x,根据邻补角的概念列出方程,解方程求出∠EOC=80°,根据角平分线的定义和对顶角相等计算即可得到答案.【解答】解:(1)∵∠EOC=70°,OA平分∠EOC,∴∠AOC=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=4x,则∠EOD=5x,∴5x+4x=180°,解得x=20°,则∠EOC=80°,又∵OA平分∠EOC,∴∠AOC=40°,∴∠BOD=∠AOC=40°.【点评】本题考查的是对顶角、邻补角的概念和性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?【分析】(1)、(2)根据平角的性质求得∠AOF,又有角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;(3)由(1)、(2)的结果找出它们之间的倍数关系.【解答】解:(1)∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,∴∠AOF=140°;又∵OC平分∠AOF,∴∠FOC=∠AOF=70°,∴∠EOD=∠FOC=70°(对顶角相等);而∠BOE=∠AOB﹣∠AOE=50°,∴∠BOD=∠EOD﹣∠BOE=20°;(2)∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,∴∠AOF=180°﹣α;又∵OC平分∠AOF,∴∠FOC=∠AOF=90°﹣α,∴∠EOD=∠FOC=90°﹣α(对顶角相等);而∠BOE=∠AOB﹣∠AOE=90°﹣α,∴∠BOD=∠EOD﹣∠BOE=α;(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.【点评】本题利用垂直的定义,对顶角和互补的性质计算,要注意领会由垂直得直角这一要点.12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).【分析】(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,【解答】解:(1)如图1,过点E作EF∥PQ,∵∠CBN=100°,∠ADQ=130°,∴∠CBM=80°,∠ADP=50°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDP=∠ADP=25°,∵EF∥PQ,∴∠DEF=∠EDP=25°,∵EF∥PQ,MN∥PQ,∴EF∥MN.∴∠FEB=∠EBM=40°∴∠BED=25°+40°=65°;(2)如图2,过点E作EF∥PQ,∵∠CBN=100°,∴∠CBM=80°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDQ=∠ADQ=n°,∵EF∥PQ,∴∠DEF=180°﹣∠EDQ=180°﹣n°,∵EF∥PQ,MN∥PQ,∴EF∥MN,∴∠FEB=∠EBM=40°,∴∠BED=180°﹣n°+40°=220°﹣n°.【点评】本题主要考查了平行线的性质,运用角平分线与平行线的性质相结合来求∠BED解题的关键.13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.【分析】(1)根据平角等于180°,列式计算即可得解;(2)根据三角形的外角性质求出∠4,然后根据同位角相等,两直线平行解答.【解答】解:(1)∵∠ACB=90°,∠1=26°,∴∠2=180°﹣∠1﹣∠ACB,=180°﹣90°﹣26°,=64°;(2)结论:n∥m.理由如下:∵∠3=19°,∠A=45°,∴∠4=45°+19°=64°,∵∠2=64°,∴∠2=∠4,∴n∥m.【点评】本题考查了平行线的判定与性质,三角形外角性质的运用,熟练掌握平行线的判定方法与性质是解题的关键.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.【分析】此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.【解答】证明:(1)过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)关系:∠3=∠2﹣∠1;过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPF﹣∠QPE,∴∠3=∠2﹣∠1.(3)关系:∠3=360°﹣∠1﹣∠2.过P作PQ∥l1∥l2;同(1)可证得:∠3=∠CEP+∠DFP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP+∠1+∠2=360°,即∠3=360°﹣∠1﹣∠2.【点评】此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.【分析】(1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;(2)由(1)的结论代入计算即可.【解答】解:(1)∠ABC﹣∠BCP+∠CPN=180°;理由如下:延长NP交BC于M,如图所示:∵AB∥PN∥CD,∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,∵∠PCD=∠BCD﹣∠BCP=∠ABC﹣∠BCP,∴∠ABC﹣∠BCP+∠CPN=180°.(2)由(1)得:∠ABC﹣∠BCP+∠CPN=180°,则∠BCP=∠ABC+∠CPN﹣180°=155°+42°﹣180°=17°.【点评】本题考查了平行线的性质;熟记平行线的性质是解决问题的关键.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.【分析】(1)根据平行线的性质和等量关系可得∠EAD+∠D=180°,根据同旁内角互补,两直线平行即可证明;(2)根据平行线的性质可得∠AEB=∠C,根据三角形内角和定理和等量关系即可得到∠B的度数.【解答】(1)证明:∵AD∥BC,∴∠D+∠C=180°,∵∠EAD=∠C,∴∠EAD+∠D=180°,∴AE∥CD;(2)∵AE∥CD,∴∠AEB=∠C,∵∠FEC=∠BAE,∴∠B=∠EFC=50°.【点评】考查了平行线的判定和性质,三角形内角和定理,解题的关键是证明AE∥CD.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.【分析】(1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.(4)首先根据AB∥CD,可得∠B=∠BFD;然后根据∠D+∠E=∠BFD,可得∠D+∠E=∠B,据此解答即可.(5)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.【解答】解:(1)如图1,作EF∥AB,,∵AB∥CD,∴∠B=∠1,∵AB∥CD,EF∥AB,∴EF∥CD,∴∠D=∠2,∴∠B+∠D=∠1+∠2,又∵∠1+∠2=∠E,∴∠B+∠D=∠E.(2)如图2,作EF∥AB,,∵EF∥AB,∴∠B=∠1,∵∠E=∠1+∠2=∠B+∠D,∴∠D=∠2,∴EF∥CD,又∵EF∥AB,∴AB∥CD.(3)如图3,过E作EF∥AB,,∵EF∥AB,∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,∵∠BEF+∠DEF=∠E,∴∠E+∠B+∠D=180°+180°=360°.(4)如图4,,∵AB∥CD,∴∠B=∠BFD,∵∠D+∠E=∠BFD,∴∠D+∠E=∠B.(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,又∵AB∥CD,∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,∴∠E+∠G=∠B+∠F+∠D.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为∠P+n∠Q=360°.(直接写结论)【分析】(1)首先过点P作PG∥AB,然后根据AB∥CD,PG∥CD,可得∠AEP=∠1,∠CFP=∠2,据此判断出∠AEP+∠CFP=∠EPF即可.(2)首先由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ;然后根据∠BEP的平分线与∠DFP的平分线相交于点Q,推得∠EQF=,即可判断出∠EPF+2∠EQF=360°.(3)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+3∠Q=360°.(4)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+n∠Q=360°.【解答】(1)证明:如图1,过点P作PG∥AB,,∵AB∥CD,∴PG∥CD,∴∠AEP=∠1,∠CFP=∠2,又∵∠1+∠2=∠EPF,∴∠AEP+∠CFP=∠EPF.(2)如图2,,由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,∵∠BEP的平分线与∠DFP的平分线相交于点Q,∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)==,∴∠EPF+2∠EQF=360°.(3)如图3,,由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+3∠Q=360°.(4)由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+n∠Q=360°.故答案为:∠P+n∠Q=360°.【点评】此题主要考查了平行线的性质的应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.【分析】设∠1=x,根据题意表示出∠2,再表示出∠3,然后根据邻补角的和等于180°列式求出x,再根据对顶角相等求出∠4即可.【解答】解:设∠1=x,则∠2=x,∠3=8x,依题意有x+x+8x=180°,解得x=18°,则∠4=18°+18°=36°.故∠4的度数是36°.【点评】本题考查了对顶角、邻补角的定义,准确识图,设出未知数并列出方程是解题的关键.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【分析】根据同位角相等,两直线平行证明OB∥AC,根据同旁内角互补,两直线平行证明OA∥BC.【解答】解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.【点评】本题考查的是平行线的判定,掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF=.(用含x的代数式表示)②求∠AOC的度数.【分析】(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=∠BOD,最后根据∠EOF=∠BOE+∠FOB 求解即可;(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=;②∠BOE=∠FOE﹣∠FOB可知∠BOE=x﹣15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.【解答】解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,∴∠EOF=∠FOB+∠BOE=35°+20°=55°,(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,∵OF平分∠COE,∴∠FOE=x,故答案为:;②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=x﹣15°,∵∠BOE+∠AOE=180°,∴x﹣15°+x=180°,解得:x=130°,∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.【点评】本题考查了对顶角,角平分线定义,角的有关定义的应用,主要考查学生的计算能力.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.【分析】(1)根据对顶角相等求出∠BOD的度数,设∠BOE=2x,根据题意列出方程,解方程即可;(2)根据角平分线的定义求出∠AOF的度数即可.【解答】解:(1)设∠BOE=2x,则∠EOD=3x,∠BOD=∠AOC=75°,∴2x+3x=75°,解得,x=15°,则2x=30°,3x=45°,∴∠BOE=30°;(2)∵∠BOE=30°,∴∠AOE=150°,∵OF平分∠AOE,∴∠AOF=75°,∴∠COF=∠AOC,∴OA是∠COF的角平分线.【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.【分析】(1)设∠BOE=x,根据题意列出方程,解方程即可;(2)分射线OF在∠AOD的内部和射线OF在∠BOC的内部两种情况,根据垂直的定义计算即可.【解答】解:(1)∵∠AOC=72°,∴∠BOD=72°,∠AOD=108°,设∠BOE=x,则∠DOE=2x,由题意得,x+2x=72°,解得,x=24°,∴∠BOE=24°,∠DOE=48°,∴∠AOE=156°;(2)若射线OF在∠BOC的内部,∠DOF=90°+48°=138°,若射线OF在∠AOD的内部,∠DOF=90°﹣48°=42°,∴∠DOF的度数是138°或42°.【点评】本题考查的是对顶角和邻补角的概念和性质以及垂直的定义,掌握对顶角相等、邻补角的和是180°是解题的关键.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH ﹣∠BOD=90°,求证:OE∥GH.【分析】(1)根据邻补角的定义求出∠EOC,再根据角平分线的定义求出∠AOC,然后根据对顶角相等解答.(2)由已知条件和对顶角相等得出∠MFC=∠MFH=∠BOD+90°=126°,得出∠ONF=90°,求出∠OFM=54°,延长∠OFG=2∠OFM=108°,证出∠OFG+∠EOC=180°,即可得出结论.【解答】解:∵∠EOC:∠EOD=2:3,∴∠EOC=180°×=72°,∵OA平分∠EOC,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.(2)延长FM交AB于N,如图所示:∵∠MFH﹣∠BOD=90°,FM平分∠OFG,∴∠MFC=∠MFH=∠BOD+90°=126°,∴∠ONF=126°﹣36°=90°,∴∠OFM=90°﹣36°=54°,∴∠OFG=2∠OFM=108°,∴∠OFG+∠EOC=180°,∴OE∥GH.【点评】本题考查了平行线的判定、角平分线定义、角的互余关系等知识;熟练掌握平行线的判定、角平分线定义是解决问题的关键,(2)有一定难度.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.【分析】(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;(2)根据角平分线的定义和邻补角的性质计算即可.【解答】解:(1)∵OE平分∠BOC,∠BOE=70°,∴∠BOC=2∠BOE=140°,∴∠AOC=180°﹣140°=40°,又∠COF=90°,∴∠AOF=90°﹣40°=50°;(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,∴∠BOD:∠BOE:∠EOC=1:2:2,∴∠BOD=36°,∴∠AOC=36°,又∵∠COF=90°,∴∠AOF=90°﹣36°=54°.【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴CD∥AB(内错角相等,两直线平行)(2)∵∠DBE=∠CAB(已知)∴AC∥BD(同位角相等,两直线平行)(3)∵∠ADF+∠5=180°(已知)∴AD∥BF(同旁内角互补,两直线平行)【分析】(1)由∠3=∠4根据平行线的判定推出CD∥AB;(2)由∠DBE=∠CAB,根据同位角相等,两直线平行得出答案;(3)根据同旁内角互补,两直线平行即可得到答案.【解答】解:(1)∵∠3=∠4(已知),∴CD∥AB(内错角相等,两直线平行),(2)∵∠DBE=∠CAB(已知),∴AC∥BD(同位角相等,两直线平行),(3)∵∠ADF+∠5=180°(已知),。
相交线与平行线常考题目及答案(绝对经典)(教学课资)
教学资源# 相交线与平行线
一.选择题(共3小题)
1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1
⊥l2,l2∥l3,
l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()
A.平行B.垂直C.平行或垂直D.无法确定
2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()
A.3个 B.2个 C.1个 D.0个
3.如图所示,同位角共有()
A.6对 B.8对 C.10对D.12对
二.填空题(共4小题)
4.一块长方体橡皮被刀切了3次,最多能被分成块.
5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为.
6.如图,直线l1∥l2,∠1=20°,则∠2+∠3=.
7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.
评卷人得分
三.解答题(共43小题)
8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB 教学资源#。
相交线与平行线常考题目及问题详解(绝对经典)

(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.
23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.
(1)求∠BOE和∠AOE的度数;
(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.
24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.
11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AO
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.
相交线与平行线
一.选择题(共3小题)
1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是( )
A.平行B.垂直C.平行或垂直D.无法确定
2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有( )
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
15.如图,已知AB∥PN∥CD.
(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.
相交线与平行线常考题目及答案(绝对经典)

相交线与平行线•选择题(共3小题)1在同一平面内,有8条互不重合的直线,11, 12, 13…l若11丄12, 12〃13 , 13丄14, 14// 15••以此类推,则11和18的位置关系是()A.平行B.垂直C.平行或垂直D.无法确定2.如图,直线AB CD相交于O, 0E± AB, OF丄CD,则与/ 1互为余角的有()A. 3 个B. 2 个C. 1 个D.3.如图所示,同位角共有()•填空题(共4小题)4•一块长方体橡皮被刀切了3次,最多能被分成 ________ 块.5•如图,P点坐标为(3,3), l i丄12, 11、12分别交x轴和y轴于A点和B点, 则四边形OAPB的面积为_______ .6•如图,直线I1//I2,/ 仁20° 则/2+Z 3= ________7•将一副学生用三角板按如图所示的方式放置•若AE// BC,则/ AFD的度数是_______ .评卷人得分三•解答题(共43小题)8. 已知:直线EF分别与直线AB, CD相交于点F, E, EM平/ FED, AB// CD, H, P分别为直线AB和线段EF上的点.七 B A H N/59(1)如图1, HM平分/ BHP,若HP丄EF,求/ M的度数.(2)如图2, EN平分/ HEF交AB于点N, NQ丄EM于点Q,当H在直线AB 上运动(不与点F重合)时,探究/ FHE与/ ENQ的关系,并证明你的结论.9 •我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10•如图,直线AB, CD相交于点O, OA平分/ EOC(1)若/ EOC=70,求/ BOD的度数.(2)若/ EOC / EOD=4 5,求/ BOD的度数.C11. 如图,直线EF, CD相交于点0, OA丄OB,且OC平分/ AOF,(1)若/ AOE=40,求/ BOD的度数;(2)若/ AOE a,求/ BOD的度数;(用含a的代数式表示)(3)从(1) (2)的结果中能看出/ AOE和/BOD有何关系?C12. 如图1,已知MN // PQ, B在MN上,C在PQ上, A在B的左侧,D在C 的右侧,DE平分/ ADC, BE平分/ ABC,直线DE、BE交于点E, / CBN=100.(1)若/ ADQ=130,求/ BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若/ADQ=n,求/ BED的度数(用含n的代数式表示).13. 如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若/仁26 (1)求/ 2的度数(2)若/ 3=19。
相交线与平行线常考题目及答案绝对

相交线与平行线一•选择题(共3小题)1 .在同一平面内,有8条互不重合的直线,丨1,丨2,丨3…1,若丨1丄12,丨2〃丨3 ,丨3丄丨4,丨4// 15…以此类推,贝U I 1和I 8的位置关系是()A.平行B.垂直C.平行或垂直D .无法确定2 .如图,直线AB CD相交于0, OEL AB, OH CD,则与/ 1互为余角的有()A. 3个B. 2个C. 1个D. 0个3. 如图所示,同位角共有()A. 6 对B. 8 对C. 10 对D. 12 对二.填空题(共4小题)4. _____________________________________________ 一块长方体橡皮被刀切了3次,最多能被分成_________________________________________ 块.5. 如图,P点坐标为(3, 3),丨1丄l2, |1> 12分别交x轴和y轴于A点和B点,则四边形0APB勺面积为______ .6. 如图,直线I 1/ 12,7 1=20°,则/ 2+Z 3= __________ .7. _______________________________________________________________________ 将一副学生用三角板按如图所示的方式放置.若AE// BQ则7 AFD的度数是 ________________ .评卷人得分三.解答题(共43 小题)8 •已知:直线EF分别与直线AB CD相交于点F, E, EM平/ FED AB// CD H, P分别为直线AB和线段EF上的点.(1)如图1, HM平分/ BHP若HP! EF,求/ M的度数.(2)如图2, EN平分/ HEF交AB于点N, NQLEM于点Q,当H在直线AB上运动(不与点F 重合)时,探究/ FHE与/ ENQ勺关系,并证明你的结论.9. 我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n 条直线最多有多少个交点?说明理由.10. 如图,直线AB CD相交于点O, OA平分/ EOC(1)若/ EOC=70 ,求/ BOM度数.(2)若/ EOC / EOD=4 5,求/ BOD的度数.11. 如图,直线EF, CD相交于点0 , OALOB且OC平分/ AOF(1) 若/ AOE=40 ,求/ BOM度数;(2) 若/ AOE a,求/ BOD勺度数;(用含a的代数式表示)(3) 从(1) (2)的结果中能看出/ AOE和/BOD有何关系?12. 如图1,已知MN PQ B在MN±, C在PQ上,A在B的左侧,D在C的右侧,DE平分 / ADC BE平分/ ABC 直线DE BE交于点E,Z CBN=100 .(1)若/ ADQ=130,求/ BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若/ ADQ=n,求/ BED的度数(用含n的代数式表示).13. 如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若/ 1=26(1)求/ 2的度数(2)若/ 3=19。
相交线与平行线常考题目及问题详解(绝对经典)

相交线与平行线一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个3.如图所示,同位角共有()A.6对B.8对C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B 点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= .7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.评卷人得分三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB ∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D 在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD 分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD 的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+ =180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2= °.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数..Word 资料33.阅读下面的推理过程,在括号内填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,( )所以a ∥c .( )又因为∠2+∠3=180°(已知)∠3=∠6( )所以∠2+∠6=180°,( )所以a ∥b .( )所以b ∥c .( )34.已知:如图,AB ∥CD ,FG ∥HD ,∠B=100°,FE 为∠CEB 的平分线,求∠EDH 的度数.35.已知:如图,AB ∥CD ,FE ⊥AB 于G ,∠EMD=134°,求∠GEM 的.Word 资料度数.36.如图,∠B 和∠D 的两边分别平行.(1)在图1 中,∠B 和∠D 的数量关系是 ,在图2中,∠B 和∠D 的数量关系是 ;(2)用一句话归纳的命题为: ;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.37.已知AD ∥BC ,AB ∥CD ,E 为射线BC 上一点,AE 平分∠BAD .(1)如图1,当点E 在线段BC 上时,求证:∠BAE=∠BEA .(2)如图2,当点E 在线段BC 延长线上时,连接DE ,若∠ADE=3∠CDE ,∠AED=60°.①求证:∠ABC=∠ADC ;②求∠CED 的度数..38.如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.39.如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?40.已知直线AB∥CD,(1)如图1,点E在直线BD上的左侧,直接写出∠ABE,∠CDE和∠BED 之间的数量关系是.(2)如图2,点E在直线BD的左侧,BF,DF分别平分∠ABE,∠CDE,直接写出∠BFD和∠BED的数量关系是.(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.41.(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF的度数.Word 资料.42.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把解答过程补充完整.解:∵CD⊥DA,DA⊥AB,∴∠CDA=90°,∠DAB=90°.()∴∠CDA=∠DAB.(等量代换)又∠1=∠2,从而∠CDA﹣∠1=∠DAB﹣.(等式的性质)即∠3= .∴DF∥AE.().43.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)说明:∠O=∠BEO+∠DFO.(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n次,又会得到怎样的结Word 资料.论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG 平分∠AEC,∠NCE=75°.求证:(1)AB∥EF.(2)AB∥ND.45.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB.46.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.(1)如图①,若∠A=30°,∠C=40°,则∠AEC= .(2)如图②,若∠A=100°,∠C=120°,则∠AEC= .(3)如图③,请直接写出∠A,∠C与∠AEC之间关系是.47.如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.Word 资料.Word 资料48.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC 的度数.(2)图2中AE ∥BC ,请你计算出∠AFD 的度数.49.如图,将一张矩形纸片ABCD 沿EF 对折,延长DE 交BF 于点G ,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB 平行的线段有哪些?(2)图中和AB 垂直的直线有哪些?. Word 资料.参考答案及解析一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定【分析】如果一条直线垂直于两平行线中的一条,那么它与另一条一定也垂直.再根据“垂直于同一条直线的两直线平行”,可知L1与L8的位置关系是平行.【解答】解:∵l2∥l3,l3⊥l4,l4∥l5,l5⊥l6,l6∥l7,l7⊥l8,∴l2⊥l4,l4⊥l6,l6⊥l8,∴l2⊥l8.∵l1⊥l2,∴l1∥l8.故选A【点评】灵活运用“垂直于同一条直线的两直线平行”是解决此类问题的关键.2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个【分析】由OE⊥AB,OF⊥CD可知:∠AOE=∠DOF=90°,而∠1、∠Word 资料.AOF都与∠EOF互余,可知∠1=∠AOF,因而可以转化为求∠1和∠AOF 的余角共有多少个.【解答】解:∵OE⊥AB,OF⊥CD,∴∠AOE=∠DOF=90°,即∠AOF+∠EOF=∠EOF+∠1,∴∠1=∠AOF,∴∠COA+∠1=∠1+∠EOF=∠1+∠BOD=90°.∴与∠1互为余角的有∠COA、∠EOF、∠BOD三个.故选A.【点评】本题解决的关键是由已知联想到可以转化为求∠1和∠AOF的余角.3.如图所示,同位角共有()A.6对B.8对C.10对D.12对【分析】在基本图形“三线八角”中有四对同位角,再看增加射线GM、HN 后,增加了多少对同位角,求总和.【解答】解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,射线GM和直线CD被直线EF所截,形成2对同位角;射线GM和直线HN被直线EF所截,形成2对同位角;射线HN和直线AB被直线EF所截,形成2对同位角.则总共10对.故选C.Word 资料【点评】本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成8 块.【分析】一块长方体橡皮被刀切了3次,最多能被分成23=8块.【解答】解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.【点评】本题考查了学生的空间想象能力,分清如何分得到的块数最多是解决本题的关键.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B 点,则四边形OAPB的面积为9 .【分析】过P分别作x轴和y轴的垂线,交x轴和y轴与C和D.构造全等三角形△PDB≌△PCA(ASA)、正方形CODP;所以S四边形OAPB=S正方形ODPC=3×3=9.【解答】解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.∵P点坐标为(3,3),∴PC=PD;又∵l1⊥l2,∴∠BPA=90°;又∵∠DPC=90°,∴∠DPB=∠CPA,在△PDB和△PCA中∴△PDB≌△PCA(ASA),∴S△DPB=S△PCA,S四边形OAPB=S正方形ODPC+S△PCA﹣S△DPB,即S四边形OAPB=S正方形ODPC=3×3=9.故答案是:9.【点评】本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB的面积.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= 200°.【分析】过∠2的顶点作l2的平行线l,则l∥l1∥l2,由平行线的性质得出∠4=∠1=20°,∠BAC+∠3=180°,即可得出∠2+∠3=200°.【解答】解:过∠2的顶点作l2的平行线l,如图所示:则l∥l1∥l2,∴∠4=∠1=20°,∠BAC+∠3=180°,∴∠2+∠3=180°+20°=200°;故答案为:200°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是75°.【分析】根据平行线的性质得到∠EDC=∠E=45°,根据三角形的外角性质得到∠AFD=∠C+∠EDC,代入即可求出答案.【解答】解:∵∠EAD=∠E=45°,∵AE∥BC,∴∠EDC=∠E=45°,∵∠C=30°,∴∠AFD=∠C+∠EDC=75°,故答案为:75°.【点评】本题主要考查对平行线的性质,三角形的外角性质等知识点的理解和掌握,能利用性质进行推理是解此题的关键,题型较好,难度适中.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB ∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.【分析】(1)首先作MQ∥AB,根据平行线的性质,推得∠M=(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.(2)①首先判断出∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.②首先判断出∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=180°﹣2∠ENQ即可.【解答】解:(1)如图1,作MQ∥AB,,∵AB∥CD,MQ∥AB,∴MQ∥CD,∴∠1=∠FHM,∠2=∠DEM,∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),∵HP⊥EF,∴∠HPF=90°,∴∠FHP+∠HFP=180°﹣90°=90°,∵∠1+∠2=∠M,∴∠M=.(2)①如图2,,∠FHE=2∠ENQ,理由如下:∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=∠CEH=2∠ENQ.②如图3,,∠FHE=180°﹣2∠ENQ,理由如下:∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.【解答】解:如图:2条直线相交有1个交点;3条直线相交有1+2个交点;4条直线相交有1+2+3个交点;5条直线相交有1+2+3+4个交点;6条直线相交有1+2+3+4+5个交点;…n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.【点评】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交有个交点.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.【分析】(1)根据角平分线的定义求出∠AOC的度数,根据对顶角相等得到答案;(2)设∠EOC=4x,根据邻补角的概念列出方程,解方程求出∠EOC=80°,根据角平分线的定义和对顶角相等计算即可得到答案.【解答】解:(1)∵∠EOC=70°,OA平分∠EOC,∴∠AOC=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=4x,则∠EOD=5x,∴5x+4x=180°,解得x=20°,则∠EOC=80°,又∵OA平分∠EOC,∴∠AOC=40°,∴∠BOD=∠AOC=40°.【点评】本题考查的是对顶角、邻补角的概念和性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?【分析】(1)、(2)根据平角的性质求得∠AOF,又有角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;(3)由(1)、(2)的结果找出它们之间的倍数关系.【解答】解:(1)∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,∴∠AOF=140°;又∵OC平分∠AOF,∴∠FOC=∠AOF=70°,∴∠EOD=∠FOC=70°(对顶角相等);而∠BOE=∠AOB﹣∠AOE=50°,∴∠BOD=∠EOD﹣∠BOE=20°;(2)∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,∴∠AOF=180°﹣α;又∵OC平分∠AOF,∴∠FOC=∠AOF=90°﹣α,∴∠EOD=∠FOC=90°﹣α(对顶角相等);而∠BOE=∠AOB﹣∠AOE=90°﹣α,∴∠BOD=∠EOD﹣∠BOE=α;(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.【点评】本题利用垂直的定义,对顶角和互补的性质计算,要注意领会由垂直得直角这一要点.12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D 在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).【分析】(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,【解答】解:(1)如图1,过点E作EF∥PQ,∵∠CBN=100°,∠ADQ=130°,∴∠CBM=80°,∠ADP=50°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDP=∠ADP=25°,∵EF∥PQ,∴∠DEF=∠EDP=25°,∵EF∥PQ,MN∥PQ,∴EF∥MN.∴∠FEB=∠EBM=40°∴∠BED=25°+40°=65°;(2)如图2,过点E作EF∥PQ,∵∠CBN=100°,∴∠CBM=80°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDQ=∠ADQ=n°,∵EF∥PQ,∴∠DEF=180°﹣∠EDQ=180°﹣n°,∵EF∥PQ,MN∥PQ,∴EF∥MN,∴∠FEB=∠EBM=40°,∴∠BED=180°﹣n°+40°=220°﹣n°.【点评】本题主要考查了平行线的性质,运用角平分线与平行线的性质相结合来求∠BED解题的关键.13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.【分析】(1)根据平角等于180°,列式计算即可得解;(2)根据三角形的外角性质求出∠4,然后根据同位角相等,两直线平行解答.【解答】解:(1)∵∠ACB=90°,∠1=26°,∴∠2=180°﹣∠1﹣∠ACB,=180°﹣90°﹣26°,=64°;(2)结论:n∥m.理由如下:∵∠3=19°,∠A=45°,∴∠4=45°+19°=64°,∵∠2=64°,∴∠2=∠4,∴n∥m.【点评】本题考查了平行线的判定与性质,三角形外角性质的运用,熟练掌握平行线的判定方法与性质是解题的关键.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.【分析】此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.【解答】证明:(1)过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)关系:∠3=∠2﹣∠1;过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPF﹣∠QPE,∴∠3=∠2﹣∠1.(3)关系:∠3=360°﹣∠1﹣∠2.过P作PQ∥l1∥l2;同(1)可证得:∠3=∠CEP+∠DFP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP+∠1+∠2=360°,即∠3=360°﹣∠1﹣∠2.【点评】此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.【分析】(1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;(2)由(1)的结论代入计算即可.【解答】解:(1)∠ABC﹣∠BCP+∠CPN=180°;理由如下:延长NP交BC于M,如图所示:∵AB∥PN∥CD,∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,∵∠PCD=∠BCD﹣∠BCP=∠ABC﹣∠BCP,∴∠ABC﹣∠BCP+∠CPN=180°.(2)由(1)得:∠ABC﹣∠BCP+∠CPN=180°,则∠BCP=∠ABC+∠CPN﹣180°=155°+42°﹣180°=17°.【点评】本题考查了平行线的性质;熟记平行线的性质是解决问题的关键.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.【分析】(1)根据平行线的性质和等量关系可得∠EAD+∠D=180°,根据同旁内角互补,两直线平行即可证明;(2)根据平行线的性质可得∠AEB=∠C,根据三角形内角和定理和等量关系即可得到∠B的度数.【解答】(1)证明:∵AD∥BC,∴∠D+∠C=180°,∵∠EAD=∠C,∴∠EAD+∠D=180°,∴AE∥CD;(2)∵AE∥CD,∴∠AEB=∠C,∵∠FEC=∠BAE,∴∠B=∠EFC=50°.【点评】考查了平行线的判定和性质,三角形内角和定理,解题的关键是证明AE∥CD.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.【分析】(1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.(4)首先根据AB∥CD,可得∠B=∠BFD;然后根据∠D+∠E=∠BFD,可得∠D+∠E=∠B,据此解答即可.(5)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.【解答】解:(1)如图1,作EF∥AB,,∵AB∥CD,∴∠B=∠1,∵AB∥CD,EF∥AB,∴EF∥CD,∴∠D=∠2,∴∠B+∠D=∠1+∠2,又∵∠1+∠2=∠E,∴∠B+∠D=∠E.(2)如图2,作EF∥AB,,∵EF∥AB,∴∠B=∠1,∵∠E=∠1+∠2=∠B+∠D,∴∠D=∠2,∴EF∥CD,又∵EF∥AB,∴AB∥CD.(3)如图3,过E作EF∥AB,,∵EF∥AB,∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,∵∠BEF+∠DEF=∠E,∴∠E+∠B+∠D=180°+180°=360°.(4)如图4,,∵AB∥CD,∴∠B=∠BFD,∵∠D+∠E=∠BFD,∴∠D+∠E=∠B.(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,又∵AB∥CD,∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,∴∠E+∠G=∠B+∠F+∠D.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为∠P+n∠Q=360°.(直接写结论)【分析】(1)首先过点P作PG∥AB,然后根据AB∥CD,PG∥CD,可得∠AEP=∠1,∠CFP=∠2,据此判断出∠AEP+∠CFP=∠EPF即可.(2)首先由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ;然后根据∠BEP的平分线与∠DFP的平分线相交于点Q,推得∠EQF=,即可判断出∠EPF+2∠EQF=360°.(3)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+3∠Q=360°.(4)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+n∠Q=360°.【解答】(1)证明:如图1,过点P作PG∥AB,,∵AB∥CD,∴PG∥CD,∴∠AEP=∠1,∠CFP=∠2,又∵∠1+∠2=∠EPF,∴∠AEP+∠CFP=∠EPF.(2)如图2,,由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ ,∵∠BEP的平分线与∠DFP的平分线相交于点Q,∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)==,∴∠EPF+2∠EQF=360°.(3)如图3,,由(1),可得∠P=∠AEP+CFP ,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+3∠Q=360°.(4)由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,Word 资料∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+n∠Q=360°.故答案为:∠P+n∠Q=360°.【点评】此题主要考查了平行线的性质的应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.【分析】设∠1=x,根据题意表示出∠2,再表示出∠3,然后根据邻补角的和等于180°列式求出x,再根据对顶角相等求出∠4即可.【解答】解:设∠1=x,则∠2=x,∠3=8x,依题意有x+x+8x=180°,解得x=18°,则∠4=18°+18°=36°.故∠4的度数是36°.【点评】本题考查了对顶角、邻补角的定义,准确识图,设出未知数并列出Word 资料方程是解题的关键.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【分析】根据同位角相等,两直线平行证明OB∥AC,根据同旁内角互补,两直线平行证明OA∥BC.【解答】解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.【点评】本题考查的是平行线的判定,掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)Word 资料②求∠AOC的度数.【分析】(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=∠BOD,最后根据∠EOF=∠BOE+∠FOB 求解即可;(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=;②∠BOE=∠FOE﹣∠FOB可知∠BOE=x﹣15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.【解答】解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,∴∠EOF=∠FOB+∠BOE=35°+20°=55°,(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,∵OF平分∠COE,∴∠FOE=x,故答案为:;Word 资料②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=x﹣15°,∵∠BOE+∠AOE=180°,∴x﹣15°+x=180°,解得:x=130°,∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.【点评】本题考查了对顶角,角平分线定义,角的有关定义的应用,主要考查学生的计算能力.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD 分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.【分析】(1)根据对顶角相等求出∠BOD的度数,设∠BOE=2x,根据题意列出方程,解方程即可;(2)根据角平分线的定义求出∠AOF的度数即可.Word 资料【解答】解:(1)设∠BOE=2x,则∠EOD=3x,∠BOD=∠AOC=75°,∴2x+3x=75°,解得,x=15°,则2x=30°,3x=45°,∴∠BOE=30°;(2)∵∠BOE=30°,∴∠AOE=150°,∵OF平分∠AOE,∴∠AOF=75°,∴∠COF=∠AOC,∴OA是∠COF的角平分线.【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD 的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.【分析】(1)设∠BOE=x,根据题意列出方程,解方程即可;(2)分射线OF在∠AOD的内部和射线OF在∠BOC的内部两种情况,根Word 资料据垂直的定义计算即可.【解答】解:(1)∵∠AOC=72°,∴∠BOD=72°,∠AOD=108°,设∠BOE=x,则∠DOE=2x,由题意得,x+2x=72°,解得,x=24°,∴∠BOE=24°,∠DOE=48°,∴∠AOE=156°;(2)若射线OF在∠BOC的内部,∠DOF=90°+48°=138°,若射线OF在∠AOD的内部,∠DOF=90°﹣48°=42°,∴∠DOF的度数是138°或42°.【点评】本题考查的是对顶角和邻补角的概念和性质以及垂直的定义,掌握对顶角相等、邻补角的和是180°是解题的关键.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE∥GH.Word 资料【分析】(1)根据邻补角的定义求出∠EOC,再根据角平分线的定义求出∠AOC,然后根据对顶角相等解答.(2)由已知条件和对顶角相等得出∠MFC=∠MFH=∠BOD+90°=126°,得出∠ONF=90°,求出∠OFM=54°,延长∠OFG=2∠OFM=108°,证出∠OFG+∠EOC=180°,即可得出结论.【解答】解:∵∠EOC:∠EOD=2:3,∴∠EOC=180°×=72°,∵OA平分∠EOC,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.(2)延长FM交AB于N,如图所示:∵∠MFH﹣∠BOD=90°,FM平分∠OFG,∴∠MFC=∠MFH=∠BOD+90°=126°,∴∠ONF=126°﹣36°=90°,∴∠OFM=90°﹣36°=54°,∴∠OFG=2∠OFM=108°,∴∠OFG+∠EOC=180°,∴OE∥GH.【点评】本题考查了平行线的判定、角平分线定义、角的互余关系等知识;熟练掌握平行线的判定、角平分线定义是解决问题的关键,(2)有一定难度.Word 资料25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.【分析】(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;(2)根据角平分线的定义和邻补角的性质计算即可.【解答】解:(1)∵OE平分∠BOC,∠BOE=70°,∴∠BOC=2∠BOE=140°,∴∠AOC=180°﹣140°=40°,又∠COF=90°,∴∠AOF=90°﹣40°=50°;(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,∴∠BOD:∠BOE:∠EOC=1:2:2,∴∠BOD=36°,∴∠AOC=36°,又∵∠COF=90°,∴∠AOF=90°﹣36°=54°.【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.26.几何推理,看图填空:(1)∵∠3=∠4(已知)Word 资料∴CD ∥AB (内错角相等,两直线平行)(2)∵∠DBE=∠CAB(已知)∴AC ∥BD (同位角相等,两直线平行)(3)∵∠ADF+ ∠5 =180°(已知)∴AD∥BF(同旁内角互补,两直线平行)【分析】(1)由∠3=∠4根据平行线的判定推出CD∥AB;(2)由∠DBE=∠CAB,根据同位角相等,两直线平行得出答案;(3)根据同旁内角互补,两直线平行即可得到答案.【解答】解:(1)∵∠3=∠4(已知),∴CD∥AB(内错角相等,两直线平行),(2)∵∠DBE=∠CAB(已知),∴AC∥BD(同位角相等,两直线平行),(3)∵∠ADF+∠5=180°(已知),∴AD∥BF(同旁内角互补,两直线平行).故答案为:(1)AB∥CD,内错角相等,两直线平行,(2)AC∥BD,同位角相等,两直线平行,(3)∠5,同旁内角互补,两直线平行.【点评】本题主要考查对同位角,内错角,同旁内角,平行线的判定等知识点的理解和掌握,能识别同位角,内错角,同旁内角和利用平行线的判定进行证明是解此题的关键.27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.Word 资料。
相交线与平行线常考题目及问题详解(绝对经典)

相交线与平行线一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个 C.1个D.0个3.如图所示,同位角共有()A.6对B.8对 C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= .7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.评卷人得分三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH ﹣∠BOD=90°,求证:OE∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+ =180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE 与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2= °.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.. '. 33.阅读下面的推理过程,在括号内填上推理的依据,如图: 因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,( )所以a ∥c .( )又因为∠2+∠3=180°(已知)∠3=∠6( )所以∠2+∠6=180°,( )所以a ∥b .( )所以b ∥c .( )34.已知:如图,AB ∥CD ,FG ∥HD ,∠B=100°,FE 为∠CEB 的平分线,求∠EDH 的度数.35.已知:如图,AB ∥CD ,FE ⊥AB 于G ,∠EMD=134°,求∠GEM 的度数.36.如图,∠B 和∠D 的两边分别平行.. '. (1)在图1 中,∠B 和∠D 的数量关系是 ,在图2中,∠B 和∠D 的数量关系是 ;(2)用一句话归纳的命题为: ;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.37.已知AD ∥BC ,AB∥CD ,E 为射线BC 上一点,AE 平分∠BAD .(1)如图1,当点E 在线段BC 上时,求证:∠BAE=∠BEA.(2)如图2,当点E 在线段BC 延长线上时,连接DE ,若∠ADE=3∠CDE ,∠AED=60°.①求证:∠ABC=∠ADC ;②求∠CED 的度数.38.如图,已知a ∥b ,ABCDE 是夹在直线a ,b 之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由..39.如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?40.已知直线AB∥CD,(1)如图1,点E在直线BD上的左侧,直接写出∠ABE,∠CDE和∠BED 之间的数量关系是.(2)如图2,点E在直线BD的左侧,BF,DF分别平分∠ABE,∠CDE,直接写出∠BFD和∠BED的数量关系是.(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.41.(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF的度数.42.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成'.. '. 下列填空,把解答过程补充完整.解:∵CD ⊥DA ,DA ⊥AB ,∴∠CDA=90°,∠DAB=90°.()∴∠CDA=∠DAB .(等量代换)又∠1=∠2,从而∠CDA ﹣∠1=∠DAB ﹣ .(等式的性质)即∠3= .∴DF ∥AE .( ).43.如图1,AB ∥CD ,EOF 是直线AB 、CD 间的一条折线.(1)说明:∠O=∠BEO+∠DFO .(2)如果将折一次改为折二次,如图2,则∠BEO 、∠O 、∠P 、∠PFC 会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n 次,又会得到怎样的结论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG 平分∠AEC ,∠NCE=75°.求证:(1)AB ∥EF .(2)AB ∥ND ..'.45.如图,∠E=∠1,∠3+∠ABC=180°,BE 是∠ABC 的角平分线. 求证:DF∥AB .46.已知,直线AB ∥CD ,E 为AB 、CD 间的一点,连结EA 、EC .(1)如图①,若∠A=30°,∠C=40°,则∠AEC= .(2)如图②,若∠A=100°,∠C=120°,则∠AEC= .(3)如图③,请直接写出∠A ,∠C 与∠AEC 之间关系是 .47.如图,已知AB ∥CD ,EF ⊥AB 于点G ,若∠1=30°,试求∠F 的度数.48.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC 的度数.. '.(2)图2中AE ∥BC ,请你计算出∠AFD 的度数.49.如图,将一张矩形纸片ABCD 沿EF 对折,延长DE 交BF 于点G ,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB 平行的线段有哪些?(2)图中和AB 垂直的直线有哪些?. '..参考答案及解析一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定【分析】如果一条直线垂直于两平行线中的一条,那么它与另一条一定也垂直.再根据“垂直于同一条直线的两直线平行”,可知L1与L8的位置关系是平行.【解答】解:∵l2∥l3,l3⊥l4,l4∥l5,l5⊥l6,l6∥l7,l7⊥l8,∴l2⊥l4,l4⊥l6,l6⊥l8,∴l2⊥l8.∵l1⊥l2,∴l1∥l8.故选A【点评】灵活运用“垂直于同一条直线的两直线平行”是解决此类问题的关键.2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个 C.1个D.0个【分析】由OE⊥AB,OF⊥CD可知:∠AOE=∠DOF=90°,而∠1、∠AOF 都与∠EOF互余,可知∠1=∠AOF,因而可以转化为求∠1和∠AOF的余角'..共有多少个.【解答】解:∵OE⊥AB,OF⊥CD,∴∠AOE=∠DOF=90°,即∠AOF+∠EOF=∠EOF+∠1,∴∠1=∠AOF,∴∠COA+∠1=∠1+∠EOF=∠1+∠BOD=90°.∴与∠1互为余角的有∠COA、∠EOF、∠BOD三个.故选A.【点评】本题解决的关键是由已知联想到可以转化为求∠1和∠AOF的余角.3.如图所示,同位角共有()A.6对B.8对 C.10对D.12对【分析】在基本图形“三线八角”中有四对同位角,再看增加射线GM、HN后,增加了多少对同位角,求总和.【解答】解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,射线GM和直线CD被直线EF所截,形成2对同位角;射线GM和直线HN被直线EF所截,形成2对同位角;射线HN和直线AB被直线EF所截,形成2对同位角.则总共10对.故选C.【点评】本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在'.被截的两条直线同侧的位置的角叫做同位角.二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成8 块.【分析】一块长方体橡皮被刀切了3次,最多能被分成23=8块.【解答】解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.【点评】本题考查了学生的空间想象能力,分清如何分得到的块数最多是解决本题的关键.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为9 .【分析】过P分别作x轴和y轴的垂线,交x轴和y轴与C和D.构造全等三角形△PDB≌△PCA(ASA)、正方形CODP;所以S四边形OAPB=S正方形ODPC=3×3=9.【解答】解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.∵P点坐标为(3,3),∴PC=PD;又∵l1⊥l2,∴∠BPA=90°;又∵∠DPC=90°,∴∠DPB=∠CPA,在△PDB和△PCA中∴△PDB≌△PCA(ASA),∴S△DPB=S△PCA,S四边形OAPB=S正方形ODPC+S△PCA﹣S△DPB,即S四边形OAPB=S正方形ODPC=3×3=9.故答案是:9.【点评】本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB的面积.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= 200°.【分析】过∠2的顶点作l2的平行线l,则l∥l1∥l2,由平行线的性质得出∠4=∠1=20°,∠BAC+∠3=180°,即可得出∠2+∠3=200°.【解答】解:过∠2的顶点作l2的平行线l,如图所示:则l∥l1∥l2,∴∠4=∠1=20°,∠BAC+∠3=180°,∴∠2+∠3=180°+20°=200°;故答案为:200°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是75°.【分析】根据平行线的性质得到∠EDC=∠E=45°,根据三角形的外角性质得到∠AFD=∠C+∠EDC,代入即可求出答案.【解答】解:∵∠EAD=∠E=45°,∵AE∥BC,∴∠EDC=∠E=45°,∵∠C=30°,∴∠AFD=∠C+∠EDC=75°,故答案为:75°.【点评】本题主要考查对平行线的性质,三角形的外角性质等知识点的理解和掌握,能利用性质进行推理是解此题的关键,题型较好,难度适中.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.【分析】(1)首先作MQ∥AB,根据平行线的性质,推得∠M=(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.(2)①首先判断出∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.②首先判断出∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=180°﹣2∠ENQ即可.【解答】解:(1)如图1,作MQ∥AB,,∵AB∥CD,MQ∥AB,∴MQ∥CD,∴∠1=∠FHM,∠2=∠DEM,∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),∵HP⊥EF,∴∠HPF=90°,∴∠FHP+∠HFP=180°﹣90°=90°,∵∠1+∠2=∠M,∴∠M=.(2)①如图2,,∠FHE=2∠ENQ,理由如下:∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=∠CEH=2∠ENQ.②如图3,,∠FHE=180°﹣2∠ENQ,理由如下:∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.【解答】解:如图:2条直线相交有1个交点;3条直线相交有1+2个交点;4条直线相交有1+2+3个交点;5条直线相交有1+2+3+4个交点;6条直线相交有1+2+3+4+5个交点;…n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.【点评】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交有个交点.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.【分析】(1)根据角平分线的定义求出∠AOC的度数,根据对顶角相等得到答案;(2)设∠EOC=4x,根据邻补角的概念列出方程,解方程求出∠EOC=80°,根据角平分线的定义和对顶角相等计算即可得到答案.【解答】解:(1)∵∠EOC=70°,OA平分∠EOC,∴∠AOC=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=4x,则∠EOD=5x,∴5x+4x=180°,解得x=20°,则∠EOC=80°,又∵OA平分∠EOC,∴∠AOC=40°,∴∠BOD=∠AOC=40°.【点评】本题考查的是对顶角、邻补角的概念和性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?【分析】(1)、(2)根据平角的性质求得∠AOF,又有角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;(3)由(1)、(2)的结果找出它们之间的倍数关系.【解答】解:(1)∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,∴∠AOF=140°;又∵OC平分∠AOF,∴∠FOC=∠AOF=70°,∴∠EOD=∠FOC=70°(对顶角相等);而∠BOE=∠AOB﹣∠AOE=50°,∴∠BOD=∠EOD﹣∠BOE=20°;(2)∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,∴∠AOF=180°﹣α;又∵OC平分∠AOF,∴∠FOC=∠AOF=90°﹣α,∴∠EOD=∠FOC=90°﹣α(对顶角相等);而∠BOE=∠AOB﹣∠AOE=90°﹣α,∴∠BOD=∠EOD﹣∠BOE=α;(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.【点评】本题利用垂直的定义,对顶角和互补的性质计算,要注意领会由垂直得直角这一要点.12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).【分析】(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,【解答】解:(1)如图1,过点E作EF∥PQ,∵∠CBN=100°,∠ADQ=130°,∴∠CBM=80°,∠ADP=50°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDP=∠ADP=25°,∵EF∥PQ,∴∠DEF=∠EDP=25°,∵EF∥PQ,MN∥PQ,∴EF∥MN.∴∠FEB=∠EBM=40°∴∠BED=25°+40°=65°;(2)如图2,过点E作EF∥PQ,∵∠CBN=100°,∴∠CBM=80°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDQ=∠ADQ=n°,∵EF∥PQ,∴∠DEF=180°﹣∠EDQ=180°﹣n°,∵EF∥PQ,MN∥PQ,∴EF∥MN,∴∠FEB=∠EBM=40°,∴∠BED=180°﹣n°+40°=220°﹣n°.【点评】本题主要考查了平行线的性质,运用角平分线与平行线的性质相结合来求∠BED解题的关键.13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.【分析】(1)根据平角等于180°,列式计算即可得解;(2)根据三角形的外角性质求出∠4,然后根据同位角相等,两直线平行解答.【解答】解:(1)∵∠ACB=90°,∠1=26°,∴∠2=180°﹣∠1﹣∠ACB,=180°﹣90°﹣26°,=64°;(2)结论:n∥m.理由如下:∵∠3=19°,∠A=45°,∴∠4=45°+19°=64°,∵∠2=64°,∴∠2=∠4,∴n∥m.【点评】本题考查了平行线的判定与性质,三角形外角性质的运用,熟练掌握平行线的判定方法与性质是解题的关键.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.【分析】此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.【解答】证明:(1)过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)关系:∠3=∠2﹣∠1;过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPF﹣∠QPE,∴∠3=∠2﹣∠1.(3)关系:∠3=360°﹣∠1﹣∠2.过P作PQ∥l1∥l2;同(1)可证得:∠3=∠CEP+∠DFP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP+∠1+∠2=360°,即∠3=360°﹣∠1﹣∠2.【点评】此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.【分析】(1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;(2)由(1)的结论代入计算即可.【解答】解:(1)∠ABC﹣∠BCP+∠CPN=180°;理由如下:延长NP交BC于M,如图所示:∵AB∥PN∥CD,∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,∵∠PCD=∠BCD﹣∠BCP=∠ABC﹣∠BCP,∴∠ABC﹣∠BCP+∠CPN=180°.(2)由(1)得:∠ABC﹣∠BCP+∠CPN=180°,则∠BCP=∠ABC+∠CPN﹣180°=155°+42°﹣180°=17°.【点评】本题考查了平行线的性质;熟记平行线的性质是解决问题的关键.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.【分析】(1)根据平行线的性质和等量关系可得∠EAD+∠D=180°,根据同旁内角互补,两直线平行即可证明;(2)根据平行线的性质可得∠AEB=∠C,根据三角形内角和定理和等量关系即可得到∠B的度数.【解答】(1)证明:∵AD∥BC,∴∠D+∠C=180°,∵∠EAD=∠C,∴∠EAD+∠D=180°,∴AE∥CD;(2)∵AE∥CD,∴∠AEB=∠C,∵∠FEC=∠BAE,∴∠B=∠EFC=50°.【点评】考查了平行线的判定和性质,三角形内角和定理,解题的关键是证明AE∥CD.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.【分析】(1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.(4)首先根据AB∥CD,可得∠B=∠BFD;然后根据∠D+∠E=∠BFD,可得∠D+∠E=∠B,据此解答即可.(5)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.【解答】解:(1)如图1,作EF∥AB,,∵AB∥CD,∴∠B=∠1,∵AB∥CD,EF∥AB,∴EF∥CD,∴∠D=∠2,∴∠B+∠D=∠1+∠2,又∵∠1+∠2=∠E,∴∠B+∠D=∠E.(2)如图2,作EF∥AB,,∵EF∥AB,∴∠B=∠1,∵∠E=∠1+∠2=∠B+∠D,∴∠D=∠2,∴EF∥CD,又∵EF∥AB,∴AB∥CD.(3)如图3,过E作EF∥AB,,∵EF∥AB,∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,∵∠BEF+∠DEF=∠E,∴∠E+∠B+∠D=180°+180°=360°.(4)如图4,,∵AB∥CD,∴∠B=∠BFD,∵∠D+∠E=∠BFD,∴∠D+∠E=∠B.(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,又∵AB∥CD,∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,∴∠E+∠G=∠B+∠F+∠D.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为∠P+n ∠Q=360°.(直接写结论)【分析】(1)首先过点P作PG∥AB,然后根据AB∥CD,PG∥CD,可得∠AEP=∠1,∠CFP=∠2,据此判断出∠AEP+∠CFP=∠EPF即可.(2)首先由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ;然后根据∠BEP的平分线与∠DFP的平分线相交于点Q,推得∠EQF=,即可判断出∠EPF+2∠EQF=360°.(3)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+3∠Q=360°.(4)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+n∠Q=360°.【解答】(1)证明:如图1,过点P作PG∥AB,,∵AB∥CD,∴PG∥CD,∴∠AEP=∠1,∠CFP=∠2,又∵∠1+∠2=∠EPF,∴∠AEP+∠CFP=∠EPF.(2)如图2,,由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,∵∠BEP的平分线与∠DFP的平分线相交于点Q,∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)==,∴∠EPF+2∠EQF=360°.(3)如图3,,由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+3∠Q=360°.(4)由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+n∠Q=360°.故答案为:∠P+n∠Q=360°.【点评】此题主要考查了平行线的性质的应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.【分析】设∠1=x,根据题意表示出∠2,再表示出∠3,然后根据邻补角的和等于180°列式求出x,再根据对顶角相等求出∠4即可.【解答】解:设∠1=x,则∠2=x,∠3=8x,依题意有x+x+8x=180°,解得x=18°,则∠4=18°+18°=36°.故∠4的度数是36°.【点评】本题考查了对顶角、邻补角的定义,准确识图,设出未知数并列出方程是解题的关键.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【分析】根据同位角相等,两直线平行证明OB∥AC,根据同旁内角互补,两直线平行证明OA∥BC.【解答】解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.【点评】本题考查的是平行线的判定,掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.【分析】(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=;②∠BOE=∠FOE﹣∠FOB可知∠BOE=x﹣15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.【解答】解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,∴∠EOF=∠FOB+∠BOE=35°+20°=55°,(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,∵OF平分∠COE,∴∠FOE=x,故答案为:;②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=x﹣15°,∵∠BOE+∠AOE=180°,∴x﹣15°+x=180°,解得:x=130°,∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.【点评】本题考查了对顶角,角平分线定义,角的有关定义的应用,主要考查学生的计算能力.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.【分析】(1)根据对顶角相等求出∠BOD的度数,设∠BOE=2x,根据题意列出方程,解方程即可;(2)根据角平分线的定义求出∠AOF的度数即可.【解答】解:(1)设∠BOE=2x,则∠EOD=3x,∠BOD=∠AOC=75°,∴2x+3x=75°,解得,x=15°,则2x=30°,3x=45°,∴∠BOE=30°;(2)∵∠BOE=30°,∴∠AOE=150°,∵OF平分∠AOE,∴∠AOF=75°,∴∠COF=∠AOC,∴OA是∠COF的角平分线.【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.【分析】(1)设∠BOE=x,根据题意列出方程,解方程即可;(2)分射线OF在∠AOD的内部和射线OF在∠BOC的内部两种情况,根据垂直的定义计算即可.【解答】解:(1)∵∠AOC=72°,∴∠BOD=72°,∠AOD=108°,设∠BOE=x,则∠DOE=2x,由题意得,x+2x=72°,解得,x=24°,∴∠BOE=24°,∠DOE=48°,∴∠AOE=156°;(2)若射线OF在∠BOC的内部,∠DOF=90°+48°=138°,若射线OF在∠AOD的内部,∠DOF=90°﹣48°=42°,∴∠DOF的度数是138°或42°.【点评】本题考查的是对顶角和邻补角的概念和性质以及垂直的定义,掌握对顶角相等、邻补角的和是180°是解题的关键.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH ﹣∠BOD=90°,求证:OE∥GH.【分析】(1)根据邻补角的定义求出∠EOC,再根据角平分线的定义求出∠AOC,然后根据对顶角相等解答.(2)由已知条件和对顶角相等得出∠MFC=∠MFH=∠BOD+90°=126°,得出∠ONF=90°,求出∠OFM=54°,延长∠OFG=2∠OFM=108°,证出∠OFG+∠EOC=180°,即可得出结论.【解答】解:∵∠EOC:∠EOD=2:3,∴∠EOC=180°×=72°,∵OA平分∠EOC,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.(2)延长FM交AB于N,如图所示:∵∠MFH﹣∠BOD=90°,FM平分∠OFG,∴∠MFC=∠MFH=∠BOD+90°=126°,∴∠ONF=126°﹣36°=90°,∴∠OFM=90°﹣36°=54°,∴∠OFG=2∠OFM=108°,∴∠OFG+∠EOC=180°,∴OE∥GH.【点评】本题考查了平行线的判定、角平分线定义、角的互余关系等知识;熟练掌握平行线的判定、角平分线定义是解决问题的关键,(2)有一定难度.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.【分析】(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;(2)根据角平分线的定义和邻补角的性质计算即可.【解答】解:(1)∵OE平分∠BOC,∠BOE=70°,∴∠BOC=2∠BOE=140°,∴∠AOC=180°﹣140°=40°,又∠COF=90°,∴∠AOF=90°﹣40°=50°;(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,∴∠BOD:∠BOE:∠EOC=1:2:2,∴∠BOD=36°,∴∠AOC=36°,又∵∠COF=90°,∴∠AOF=90°﹣36°=54°.【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴CD ∥AB (内错角相等,两直线平行)(2)∵∠DBE=∠CAB(已知)∴AC ∥BD (同位角相等,两直线平行)(3)∵∠ADF+ ∠5 =180°(已知)∴AD∥BF(同旁内角互补,两直线平行)【分析】(1)由∠3=∠4根据平行线的判定推出CD∥AB;(2)由∠DBE=∠CAB,根据同位角相等,两直线平行得出答案;(3)根据同旁内角互补,两直线平行即可得到答案.【解答】解:(1)∵∠3=∠4(已知),∴CD∥AB(内错角相等,两直线平行),(2)∵∠DBE=∠CAB(已知),∴AC∥BD(同位角相等,两直线平行),(3)∵∠ADF+∠5=180°(已知),∴AD∥BF(同旁内角互补,两直线平行).故答案为:(1)AB∥CD,内错角相等,两直线平行,(2)AC∥BD,同位角相等,两直线平行,(3)∠5,同旁内角互补,两直线平行.【点评】本题主要考查对同位角,内错角,同旁内角,平行线的判定等知识点的理解和掌握,能识别同位角,内错角,同旁内角和利用平行线的判定进行证明是解此题的关键.27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.【分析】(1)根据对顶角相等和角平分线的定义计算即可;。
相交线与平行线常考题目及答案(绝对经典)之欧阳数创编

相交线与平行线一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个3.如图所示,同位角共有()A.6对B.8对C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3=.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM 平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B 的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D 重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P 与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF=.(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE 把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE 在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+=180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2=°.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F (1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM 的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠D ON=30°,∠PEB=15°,求∠N的度数.33.阅读下面的推理过程,在括号内填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,()所以a∥c.()又因为∠2+∠3=180°(已知)∠3=∠6()所以∠2+∠6=180°,()所以a∥b.()所以b∥c.()34.已知:如图,AB∥CD,FG∥HD,∠B=100°,FE为∠CEB的平分线,求∠EDH的度数.35.已知:如图,AB∥CD,FE⊥AB于G,∠EMD=134°,求∠GEM的度数.36.如图,∠B和∠D的两边分别平行.(1)在图1 中,∠B和∠D的数量关系是,在图2中,∠B和∠D的数量关系是;(2)用一句话归纳的命题为:;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.37.已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.①求证:∠ABC=∠ADC;②求∠CED的度数.38.如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.39.如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?40.已知直线AB∥CD,(1)如图1,点E在直线BD上的左侧,直接写出∠ABE,∠CDE和∠BED之间的数量关系是.(2)如图2,点E在直线BD的左侧,BF,DF分别平分∠ABE,∠CDE,直接写出∠BFD和∠BED的数量关系是.(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.41.(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF 平分∠COE,∠AOD:∠BOE=4:1,求∠AOF的度数.42.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把解答过程补充完整.解:∵CD⊥DA,DA⊥AB,∴∠CDA=90°,∠DAB=90°.()∴∠CDA=∠DAB.(等量代换)又∠1=∠2,从而∠CDA﹣∠1=∠DAB﹣.(等式的性质)即∠3=.∴DF∥AE.().43.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)说明:∠O=∠BEO+∠DFO.(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n次,又会得到怎样的结论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MA E=45°,∠FEG=15°,EG平分∠AEC,∠NCE=75°.求证:(1)AB∥EF.(2)AB∥ND.45.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB.46.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.(1)如图①,若∠A=30°,∠C=40°,则∠AEC=.(2)如图②,若∠A=100°,∠C=120°,则∠AEC=.(3)如图③,请直接写出∠A,∠C与∠AEC之间关系是.47.如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.48.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC的度数.(2)图2中AE∥BC,请你计算出∠AFD的度数.49.如图,将一张矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB平行的线段有哪些?(2)图中和AB垂直的直线有哪些?参考答案及解析一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直D.无法确定【分析】如果一条直线垂直于两平行线中的一条,那么它与另一条一定也垂直.再根据“垂直于同一条直线的两直线平行”,可知L1与L8的位置关系是平行.【解答】解:∵l2∥l3,l3⊥l4,l4∥l5,l5⊥l6,l6∥l7,l7⊥l8,∴l2⊥l4,l4⊥l6,l6⊥l8,∴l2⊥l8.∵l1⊥l2,∴l1∥l8.故选A【点评】灵活运用“垂直于同一条直线的两直线平行”是解决此类问题的关键.2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个【分析】由OE⊥AB,OF⊥CD可知:∠AOE=∠DOF=90°,而∠1、∠AOF 都与∠EOF互余,可知∠1=∠AOF,因而可以转化为求∠1和∠AOF的余角共有多少个.【解答】解:∵OE⊥AB,OF⊥CD,∴∠AOE=∠DOF=90°,即∠AOF+∠EOF=∠EOF+∠1,∴∠1=∠AOF,∴∠COA+∠1=∠1+∠EOF=∠1+∠BOD=90°.∴与∠1互为余角的有∠COA、∠EOF、∠BOD三个.故选A.【点评】本题解决的关键是由已知联想到可以转化为求∠1和∠AOF的余角.3.如图所示,同位角共有()A.6对B.8对C.10对D.12对【分析】在基本图形“三线八角”中有四对同位角,再看增加射线GM、HN 后,增加了多少对同位角,求总和.【解答】解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,射线GM和直线CD被直线EF所截,形成2对同位角;射线GM和直线HN被直线EF所截,形成2对同位角;射线HN和直线AB被直线EF所截,形成2对同位角.则总共10对.故选C.【点评】本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成8块.【分析】一块长方体橡皮被刀切了3次,最多能被分成23=8块.【解答】解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.【点评】本题考查了学生的空间想象能力,分清如何分得到的块数最多是解决本题的关键.5.如图,P 点坐标为(3,3),l 1⊥l 2,l 1、l 2分别交x 轴和y 轴于A 点和B 点,则四边形OAPB 的面积为 9 .【分析】过P 分别作x 轴和y 轴的垂线,交x 轴和y 轴与C 和D .构造全等三角形△PDB ≌△PCA (ASA )、正方形CODP ;所以S四边形OAPB =S 正方形ODPC =3×3=9. 【解答】解:过P 分别作x 轴和y 轴的垂线,交x 轴和y 轴于点C 和D . ∵P 点坐标为(3,3),∴PC=PD ;又∵l 1⊥l 2,∴∠BPA=90°;又∵∠DPC=90°,∴∠DPB=∠CPA ,在△PDB 和△PCA 中∴△PDB ≌△PCA (ASA ),∴S △DPB =S △PCA ,S 四边形OAPB =S 正方形ODPC +S △PCA ﹣S △DPB ,即S 四边形OAPB =S 正方形ODPC =3×3=9.故答案是:9.【点评】本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB的面积.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3=200°.【分析】过∠2的顶点作l2的平行线l,则l∥l1∥l2,由平行线的性质得出∠4=∠1=20°,∠BAC+∠3=180°,即可得出∠2+∠3=200°.【解答】解:过∠2的顶点作l2的平行线l,如图所示:则l∥l1∥l2,∴∠4=∠1=20°,∠BAC+∠3=180°,∴∠2+∠3=180°+20°=200°;故答案为:200°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是75°.【分析】根据平行线的性质得到∠EDC=∠E=45°,根据三角形的外角性质得到∠AFD=∠C+∠EDC,代入即可求出答案.【解答】解:∵∠EAD=∠E=45°,∵AE∥BC,∴∠EDC=∠E=45°,∵∠C=30°,∴∠AFD=∠C+∠EDC=75°,故答案为:75°.【点评】本题主要考查对平行线的性质,三角形的外角性质等知识点的理解和掌握,能利用性质进行推理是解此题的关键,题型较好,难度适中.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB ∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.【分析】(1)首先作MQ∥AB,根据平行线的性质,推得∠M=(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M 的度数即可.(2)①首先判断出∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.②首先判断出∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=180°﹣2∠ENQ即可.【解答】解:(1)如图1,作MQ∥AB,,∵AB∥CD,MQ∥AB,∴MQ∥CD,∴∠1=∠FHM,∠2=∠DEM,∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),∵HP⊥EF,∴∠HPF=90°,∴∠FHP+∠HFP=180°﹣90°=90°,∵∠1+∠2=∠M,∴∠M=.(2)①如图2,,∠FHE=2∠ENQ,理由如下:∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=∠CEH=2∠ENQ.②如图3,,∠FHE=180°﹣2∠ENQ,理由如下:∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.【解答】解:如图:2条直线相交有1个交点;3条直线相交有1+2个交点;4条直线相交有1+2+3个交点;5条直线相交有1+2+3+4个交点;6条直线相交有1+2+3+4+5个交点;…n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.【点评】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交有个交点.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.【分析】(1)根据角平分线的定义求出∠AOC的度数,根据对顶角相等得到答案;(2)设∠EOC=4x,根据邻补角的概念列出方程,解方程求出∠EOC=80°,根据角平分线的定义和对顶角相等计算即可得到答案.【解答】解:(1)∵∠EOC=70°,OA平分∠EOC,∴∠AOC=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=4x,则∠EOD=5x,∴5x+4x=180°,解得x=20°,则∠EOC=80°,又∵OA平分∠EOC,∴∠AOC=40°,∴∠BOD=∠AOC=40°.【点评】本题考查的是对顶角、邻补角的概念和性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?【分析】(1)、(2)根据平角的性质求得∠AOF,又有角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;(3)由(1)、(2)的结果找出它们之间的倍数关系.【解答】解:(1)∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,∴∠AOF=140°;又∵OC平分∠AOF,∴∠FOC=∠AOF=70°,∴∠EOD=∠FOC=70°(对顶角相等);而∠BOE=∠AOB﹣∠AOE=50°,∴∠BOD=∠EOD﹣∠BOE=20°;(2)∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,∴∠AOF=180°﹣α;又∵OC平分∠AOF,∴∠FOC=∠AOF=90°﹣α,∴∠EOD=∠FOC=90°﹣α(对顶角相等);而∠BOE=∠AOB﹣∠AOE=90°﹣α,∴∠BOD=∠EOD﹣∠BOE=α;(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.【点评】本题利用垂直的定义,对顶角和互补的性质计算,要注意领会由垂直得直角这一要点.12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D 在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).【分析】(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF 和∠FEB,即可求出∠BED的度数,(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,【解答】解:(1)如图1,过点E作EF∥PQ,∵∠CBN=100°,∠ADQ=130°,∴∠CBM=80°,∠ADP=50°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDP=∠ADP=25°,∵EF∥PQ,∴∠DEF=∠EDP=25°,∵EF∥PQ,MN∥PQ,∴EF∥MN.∴∠FEB=∠EBM=40°∴∠BED=25°+40°=65°;(2)如图2,过点E作EF∥PQ,∵∠CBN=100°,∴∠CBM=80°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDQ=∠ADQ=n°,∵EF∥PQ,∴∠DEF=180°﹣∠EDQ=180°﹣n°,∵EF∥PQ,MN∥PQ,∴EF∥MN,∴∠FEB=∠EBM=40°,∴∠BED=180°﹣n°+40°=220°﹣n°.【点评】本题主要考查了平行线的性质,运用角平分线与平行线的性质相结合来求∠BED解题的关键.13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.【分析】(1)根据平角等于180°,列式计算即可得解;(2)根据三角形的外角性质求出∠4,然后根据同位角相等,两直线平行解答.【解答】解:(1)∵∠ACB=90°,∠1=26°,∴∠2=180°﹣∠1﹣∠ACB,=180°﹣90°﹣26°,=64°;(2)结论:n∥m.理由如下:∵∠3=19°,∠A=45°,∴∠4=45°+19°=64°,∵∠2=64°,∴∠2=∠4,∴n∥m.【点评】本题考查了平行线的判定与性质,三角形外角性质的运用,熟练掌握平行线的判定方法与性质是解题的关键.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.【分析】此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.【解答】证明:(1)过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)关系:∠3=∠2﹣∠1;过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPF﹣∠QPE,∴∠3=∠2﹣∠1.(3)关系:∠3=360°﹣∠1﹣∠2.过P作PQ∥l1∥l2;同(1)可证得:∠3=∠CEP+∠DFP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP+∠1+∠2=360°,即∠3=360°﹣∠1﹣∠2.【点评】此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.【分析】(1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;(2)由(1)的结论代入计算即可.【解答】解:(1)∠ABC﹣∠BCP+∠CPN=180°;理由如下:延长NP交BC于M,如图所示:∵AB∥PN∥CD,∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,∵∠PCD=∠BCD﹣∠BCP=∠ABC﹣∠BCP,∴∠ABC﹣∠BCP+∠CPN=180°.(2)由(1)得:∠ABC﹣∠BCP+∠CPN=180°,则∠BCP=∠ABC+∠CPN﹣180°=155°+42°﹣180°=17°.【点评】本题考查了平行线的性质;熟记平行线的性质是解决问题的关键.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.【分析】(1)根据平行线的性质和等量关系可得∠EAD+∠D=180°,根据同旁内角互补,两直线平行即可证明;(2)根据平行线的性质可得∠AEB=∠C,根据三角形内角和定理和等量关系即可得到∠B的度数.【解答】(1)证明:∵AD∥BC,∴∠D+∠C=180°,∵∠EAD=∠C,∴∠EAD+∠D=180°,∴AE∥CD;(2)∵AE∥CD,∴∠AEB=∠C,∵∠FEC=∠BAE,∴∠B=∠EFC=50°.【点评】考查了平行线的判定和性质,三角形内角和定理,解题的关键是证明AE∥CD.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.【分析】(1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.(4)首先根据AB∥CD,可得∠B=∠BFD;然后根据∠D+∠E=∠BFD,可得∠D+∠E=∠B,据此解答即可.(5)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.【解答】解:(1)如图1,作EF∥AB,,∵AB∥CD,∴∠B=∠1,∵AB∥CD,EF∥AB,∴EF∥CD,∴∠D=∠2,∴∠B+∠D=∠1+∠2,又∵∠1+∠2=∠E,∴∠B+∠D=∠E.(2)如图2,作EF∥AB,,∵EF∥AB,∴∠B=∠1,∵∠E=∠1+∠2=∠B+∠D,∴∠D=∠2,∴EF∥CD,又∵EF∥AB,∴AB∥CD.(3)如图3,过E作EF∥AB,,∵EF∥AB,∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,∵∠BEF+∠DEF=∠E,∴∠E+∠B+∠D=180°+180°=360°.(4)如图4,,∵AB∥CD,∴∠B=∠BFD,∵∠D+∠E=∠BFD,∴∠D+∠E=∠B.(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,又∵AB∥CD,∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,∴∠E+∠G=∠B+∠F+∠D.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为∠P+n ∠Q=360°.(直接写结论)【分析】(1)首先过点P作PG∥AB,然后根据AB∥CD,PG∥CD,可得∠AEP=∠1,∠CFP=∠2,据此判断出∠AEP+∠CFP=∠EPF即可.(2)首先由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ;然后根据∠BEP的平分线与∠DFP的平分线相交于点Q,推得∠EQF=,即可判断出∠EPF+2∠EQF=360°.(3)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+3∠Q=360°.(4)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+n∠Q=360°.【解答】(1)证明:如图1,过点P作PG∥AB,,∵AB∥CD,∴PG∥CD,∴∠AEP=∠1,∠CFP=∠2,又∵∠1+∠2=∠EPF,∴∠AEP+∠CFP=∠EPF.(2)如图2,,由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,∵∠BEP的平分线与∠DFP的平分线相交于点Q,∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)==,∴∠EPF+2∠EQF=360°.(3)如图3,,由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+3∠Q=360°.(4)由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+n∠Q=360°.故答案为:∠P+n∠Q=360°.【点评】此题主要考查了平行线的性质的应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.【分析】设∠1=x,根据题意表示出∠2,再表示出∠3,然后根据邻补角的和等于180°列式求出x,再根据对顶角相等求出∠4即可.【解答】解:设∠1=x,则∠2=x,∠3=8x,依题意有x+x+8x=180°,解得x=18°,则∠4=18°+18°=36°.故∠4的度数是36°.【点评】本题考查了对顶角、邻补角的定义,准确识图,设出未知数并列出方程是解题的关键.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【分析】根据同位角相等,两直线平行证明OB∥AC,根据同旁内角互补,两直线平行证明OA∥BC.【解答】解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.【点评】本题考查的是平行线的判定,掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解题的关键.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF=.(用含x的代数式表示)②求∠AOC的度数.【分析】(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=;②∠BOE=∠FOE﹣∠FOB可知∠BOE=x﹣15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.【解答】解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,∴∠EOF=∠FOB+∠BOE=35°+20°=55°,(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,∵OF平分∠COE,∴∠FOE=x,故答案为:;②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=x﹣15°,∵∠BOE+∠AOE=180°,∴x﹣15°+x=180°,解得:x=130°,∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.【点评】本题考查了对顶角,角平分线定义,角的有关定义的应用,主要考查学生的计算能力.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.【分析】(1)根据对顶角相等求出∠BOD的度数,设∠BOE=2x,根据题意列出方程,解方程即可;(2)根据角平分线的定义求出∠AOF的度数即可.【解答】解:(1)设∠BOE=2x,则∠EOD=3x,∠BOD=∠AOC=75°,∴2x+3x=75°,解得,x=15°,则2x=30°,3x=45°,∴∠BOE=30°;(2)∵∠BOE=30°,∴∠AOE=150°,∵OF平分∠AOE,∴∠AOF=75°,∴∠COF=∠AOC,∴OA是∠COF的角平分线.【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.【分析】(1)设∠BOE=x,根据题意列出方程,解方程即可;(2)分射线OF在∠AOD的内部和射线OF在∠BOC的内部两种情况,根据垂直的定义计算即可.【解答】解:(1)∵∠AOC=72°,∴∠BOD=72°,∠AOD=108°,设∠BOE=x,则∠DOE=2x,由题意得,x+2x=72°,解得,x=24°,∴∠BOE=24°,∠DOE=48°,∴∠AOE=156°;(2)若射线OF在∠BOC的内部,∠DOF=90°+48°=138°,若射线OF在∠AOD的内部,∠DOF=90°﹣48°=42°,∴∠DOF的度数是138°或42°.【点评】本题考查的是对顶角和邻补角的概念和性质以及垂直的定义,掌握对顶角相等、邻补角的和是180°是解题的关键.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE∥GH.【分析】(1)根据邻补角的定义求出∠EOC,再根据角平分线的定义求出∠AOC,然后根据对顶角相等解答.(2)由已知条件和对顶角相等得出∠MFC=∠MFH=∠BOD+90°=126°,得出∠ONF=90°,求出∠OFM=54°,延长∠OFG=2∠OFM=108°,证出∠OFG+∠EOC=180°,即可得出结论.【解答】解:∵∠EOC:∠EOD=2:3,∴∠EOC=180°×=72°,∵OA平分∠EOC,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.(2)延长FM交AB于N,如图所示:∵∠MFH﹣∠BOD=90°,FM平分∠OFG,∴∠MFC=∠MFH=∠BOD+90°=126°,∴∠ONF=126°﹣36°=90°,∴∠OFM=90°﹣36°=54°,∴∠OFG=2∠OFM=108°,∴∠OFG+∠EOC=180°,∴OE∥GH.【点评】本题考查了平行线的判定、角平分线定义、角的互余关系等知识;熟练掌握平行线的判定、角平分线定义是解决问题的关键,(2)有一定难度.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.【分析】(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;(2)根据角平分线的定义和邻补角的性质计算即可.【解答】解:(1)∵OE平分∠BOC,∠BOE=70°,∴∠BOC=2∠BOE=140°,∴∠AOC=180°﹣140°=40°,又∠COF=90°,∴∠AOF=90°﹣40°=50°;(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,∴∠BOD:∠BOE:∠EOC=1:2:2,∴∠BOD=36°,∴∠AOC=36°,又∵∠COF=90°,∴∠AOF=90°﹣36°=54°.【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴CD∥AB(内错角相等,两直线平行)(2)∵∠DBE=∠CAB(已知)∴AC∥BD(同位角相等,两直线平行)(3)∵∠ADF+∠5=180°(已知)∴AD∥BF(同旁内角互补,两直线平行)【分析】(1)由∠3=∠4根据平行线的判定推出CD∥AB;(2)由∠DBE=∠CAB,根据同位角相等,两直线平行得出答案;(3)根据同旁内角互补,两直线平行即可得到答案.【解答】解:(1)∵∠3=∠4(已知),∴CD∥AB(内错角相等,两直线平行),(2)∵∠DBE=∠CAB(已知),∴AC∥BD(同位角相等,两直线平行),(3)∵∠ADF+∠5=180°(已知),∴AD∥BF(同旁内角互补,两直线平行).故答案为:(1)AB∥CD,内错角相等,两直线平行,(2)AC∥BD,同位角相等,两直线平行,(3)∠5,同旁内角互补,两直线平行.【点评】本题主要考查对同位角,内错角,同旁内角,平行线的判定等知识点的理解和掌握,能识别同位角,内错角,同旁内角和利用平行线的判定进行证明是解此题的关键.时间:2021.03.02 创作:欧阳数。
相交线与平行线经典测试题及答案解析

相交线与平行线经典测试题及答案解析一、选择题1.如图,12180∠+∠=︒,3100∠=︒,则4∠=( )A .60︒B .70︒C .80︒D .100︒【答案】C【解析】【分析】 首先证明a ∥b ,再根据两直线平行同位角相等可得∠3=∠6,再根据对顶角相等可得∠4.【详解】解:∵∠1+∠5=180°,∠1+∠2=180°,∴∠2=∠5,a ∥b ,∴∠3=∠6=100°,∴∠4=180°-100°=80°.故选:C .【点睛】此题考查平行线的判定与性质,解题关键是掌握两直线平行同位角相等.2.如图,若AB ∥CD ,则∠α、∠β、∠γ之间关系是( )A .∠α+∠β+∠γ=180°B .∠α+∠β﹣∠γ=360°C .∠α﹣∠β+∠γ=180°D .∠α+∠β﹣∠γ=180°【答案】D试题解析:如图,作EF∥AB,∵AB∥CD,∴EF∥CD,∵EF∥AB,∴∠α+∠AEF=180°,∵EF∥CD,∴∠γ=∠DEF,而∠AEF+∠DEF=∠β,∴∠α+∠β=180°+∠γ,即∠α+∠β-∠γ=180°.故选:D.3.如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,如果∠1=32°,那么∠2的度数是()A.64°B.68°C.58°D.60°【答案】A【解析】【分析】首先根据平行线性质得出∠1=∠AEG,再进一步利用角平分线性质可得∠AEF的度数,最后再利用平行线性质进一步求解即可.【详解】∵AB∥CD,∴∠1=∠AEG.∵EG平分∠AEF,∴∠AEF=2∠AEG,∴∠AEF=2∠1=64°,∴∠2=64°.故选:A.【点睛】本题主要考查了角平分线性质以及平行线的性质,熟练掌握相关概念是解题关键.4.如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G,则图中与∠ECB相等的角有( )A.6个B.5个C.4个D.3个【答案】B【解析】【分析】由对顶角关系可得∠EOD=∠COB,则由∠COB+∠OBF=180°可知EC∥BF,再结合CE是角平分线即可判断.【详解】解:由∠EOD+∠OBF=∠COB+∠OBF=180°可知EC∥BF,结合CE是角平分线可得∠ECB=∠ACE=∠CBF,再由EC∥BF可得∠ACE=∠F=∠G,则由三角形内角和定理可得∠GDC=∠CBF.综上所得,∠ECB=∠ACE=∠CBF=∠F=∠G=∠GDC,共有5个与∠ECB相等的角,故选择B.【点睛】本题综合考查了平行线的判定及性质.5.已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是()A.2 B.4 C.5 D.7【答案】A【解析】试题分析:如图,根据垂线段最短可知:PC<3,∴CP的长可能是2,故选A.考点:垂线段最短.6.如图所示,点E 在AC 的延长线上,下列条件中不能判断BD ∥AE 的是( )A .∠D =∠DCEB .∠D +∠ACD =180°C .∠1=∠2D .∠3=∠4【答案】C【解析】【分析】 根据平行线的判定方法逐项进行分析即可得.【详解】A.由 ∠D =∠DCE ,根据内错角相等,两直线平行可得BD//AE ,故不符合题意;B. 由∠D +∠ACD =180°,根据同旁内角互补,两直线平行可得BD//AE ,故不符合题意;C.由∠1=∠2可判定AB//CD ,不能得到BD//AE ,故符合题意;D.由 ∠3=∠4,根据内错角相等,两直线平行可得BD//AE ,故不符合题意,故选C.【点睛】本题考查了平行线的判定,熟练掌握平行线的判定方法是解题的关键.7.如图,一副三角板按如图所示的位置摆放,其中//AB CD ,45A ∠=︒,60C ∠=°,90AEB CED ∠=∠=︒,则AEC ∠的度数为( )A .75°B .90°C .105°D .120°【答案】C【解析】【分析】 延长CE 交AB 于点F ,根据两直线平行,内错角相等可得∠AFE =∠C ,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】解:如图,延长CE 交AB 于点F ,∵AB ∥CD ,∴∠AFE =∠C =60°,在△AEF 中,由三角形的外角性质得,∠AEC =∠A +∠AFE =45°+60°=105°.故选:C .【点睛】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记相关性质并作出正确的辅助线是解题的关键.8.如图,已知//AB CD ,直线EF 分别交AB ,CD 于M ,N 两点,将一个含有30°角的直角三角尺按如图所示的方式放置(30PNG ∠=︒),若75EMB ∠=︒,则PNM ∠的度数是()A .30°B .45︒C .60︒D .75︒【答案】B【解析】【分析】 根据75EMB ∠=︒,可以计算75END ∠=︒(两直线平行,同位角相等),又由75END PNM PNG ∠=∠+∠=︒,30PNG ∠=︒从而得到PNM ∠的度数.【详解】解:∵//AB CD ,∴75EMB EFD ∠=∠=︒(两直线平行,同位角相等),又∵30PNG ∠=︒,75END PNM PNG ∠=∠+∠=︒,∴753045PNM END PNG ∠=∠-∠=︒-︒=︒,故答案为B.【点睛】本题主要考查了两直线平行的性质. 牢记知识点: 两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;9.如图,下列条件中能判定//DE AC 的是( )A .EDC EFC ∠=∠B .AEF ACD ∠=∠C .34∠=∠D .12∠=∠【答案】C【解析】【分析】 对于A ,∠EDC=∠EFC 不是两直线被第三条直线所截得到的,据此进行判断;对于B 、D ,∠AFE=∠ACD ,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,据此进行判断;对于C ,∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,据此进行判断.【详解】∠EDC=∠EFC 不是两直线被第三条直线所截得到的,因而不能判定两直线平行;∠AFE=∠ACD,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,因而可以判定EF ∥BC,但不能判定DE ∥AC ;∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,可以判定DE ∥AC.故选C.【点睛】本题考查平行线的判定,掌握相关判定定理是解题的关键.10.如图,现将一块含有60︒角的三角板的顶点放在直尺的一边上,若12∠=∠,那么1∠的度数为( )A .50︒B .60︒C .70︒D .80︒【答案】B【解析】【分析】先根据两直线平行的性质得到∠3=∠2,再根据平角的定义列方程即可得解.【详解】∵AB ∥CD ,∴∠3=∠2,∠1=∠2,∴∠1=∠3,∴2∠3+60°=180°,∴∠3=60°,∴∠1=60°,故选:B.【点睛】此题考查平行线的性质,三角板的知识,熟记性质是解题的关键.11.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为()A.北偏东30°B.北偏东80°C.北偏西30°D.北偏西50°【答案】A【解析】【分析】根据平行线的性质,可得∠2,根据角的和差,可得答案.【详解】如图,AP∥BC,∴∠2=∠1=50°,∵∠EBF=80°=∠2+∠3,∴∠3=∠EBF﹣∠2=80°﹣50°=30°,∴此时的航行方向为北偏东30°,故选A.【点睛】本题考查了方向角,利用平行线的性质得出∠2是解题关键.12.如图,直线AD BC ∥,30C ∠=︒,:1:3ADB BDC ∠∠=,则DBC ∠的度数是( )A .35°B .37.5°C .45°D .40° 【答案】B【解析】【分析】根据两直线平行,同旁内角互补,可得出18030015ADC ∠=︒-︒=︒,再结合:1:3ADB BDC ∠∠=即可得出ADB ∠的度数,最后,根据两直线平行,内错角相等即可得出答案.【详解】解:∵//AD BC ,30C ∠=︒∴18030015ADC ∠=︒-︒=︒∵:1:3ADB BDC ∠∠= ∴115037.513ADB ∠=︒⨯=︒+ ∴37.5DBC ADB ∠=∠=︒故选:B .【点睛】本题考查的知识点是平行线的性质,难度不大,熟记平行线性质的内容是解此题的关键.13.下列命题错误的是( )A .平行四边形的对角线互相平分B .两直线平行,内错角相等C .等腰三角形的两个底角相等D .若两实数的平方相等,则这两个实数相等【答案】D【解析】【分析】根据平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,分别进行判断,即可得到答案.【详解】解:A、平行四边形的对角线互相平分,正确;B、两直线平行,内错角相等,正确;C、等腰三角形的两个底角相等,正确;D、若两实数的平方相等,则这两个实数相等或互为相反数,故D错误;故选:D.【点睛】本题考查了判断命题的真假,以及平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,解题的关键是熟练掌握所学的性质进行解题.14.如图,△ABC中,∠C=90°,则点B到直线AC的距离是 ( )A.线段AB B.线段AC C.线段BC D.无法确定【答案】C【解析】【分析】直接利用点到直线的距离定义得出答案.【详解】解:如图,三角形ABC中,∠C=90°,则点B到直线AC的距离是:线段BC.故选:C.【点睛】本题考查点到之间的距离,正确把握相关定义是解题关键.15.如图所示,下列条件中,能判定直线a∥b的是()A.∠1=∠4 B.∠4=∠5 C.∠3+∠5=180°D.∠2=∠4【答案】B【解析】【分析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.【详解】A 、∠1=∠4,错误,因为∠1、∠4不是直线a 、b 被其它直线所截形成的同旁内角或内错角;B 、∵∠4=∠5,∴a ∥b (同位角相等,两直线平行).C 、∠3+∠5=180°,错误,因为∠3与∠5不是直线a 、b 被其它直线所截形成的同旁内角;D 、∠2=∠4,错误,因为∠2、∠4不是直线a 、b 被其它直线所截形成的同位角. 故选:B .【点睛】本题考查平行线的性质,解题关键是区分同位角、内错角和同旁内角16.如图,直线,a b 被直线,c d 所截,1110,270,360︒︒︒∠=∠=∠=,则4∠的大小是( )A .60︒B .70︒C .110︒D .120︒【答案】A【解析】【分析】 先根据对顶角相等得到15∠=∠,再根据平行线的判定得到a ∥b ,再根据平行线的性质得到34∠=∠即可得到答案.【详解】解:5∠标记为如下图所示,∵1,5∠∠是对顶角,∴15∠=∠(对顶角相等),又∵1110,270︒︒∠=∠=,∴1251107800︒︒+∠=∠=+︒,∴a ∥b (同旁内角互补,两直线平行),∴34∠=∠(两直线平行,内错角相等),∴4360∠=∠=︒,故A 为答案.【点睛】本题主要考查了对顶角的性质(对顶角相等)、直线平行的判定(同旁内角互补,两直线平行)、直线平行的性质(两直线平行,内错角相等),能灵活运用所学知识是解题的关键..17.如图,在ABC V 中,AB AC =,30A ∠=︒,直线a b ∥,顶点C 在直线b 上,直线a 交AB 于点D ,交AC 与点E ,若1145∠=︒,则2∠的度数是( )A .30°B .35°C .40°D .45°【答案】C【解析】【分析】 先根据等腰三角形的性质和三角形内角和可得ACB ∠度数,由三角形外角的性质可得AED ∠的度数,再根据平行线的性质得同位角相等,即可求得2∠.【详解】∵AB AC =,且30A ∠=︒, ∴18030752ACB ∠︒-︒==︒, 在ADE ∆中,∵1145A AED ∠∠∠=+=︒,∴14514530115AED A ∠∠=︒-=︒-︒=︒,∵//a b ,∴2AED ACB ∠∠∠=+,即21157540∠=︒-︒=︒,故选:C .【点睛】 本题考查综合等腰三角形的性质、三角形内角和定理、三角形外角的性质以及平行直线的性质等知识内容.等腰三角形的性质定理:等腰三角形两底角相等;三角形内角和定理:三角形三个内角的和等于180︒;三角形外角的性质:三角形的外角等于与它不相邻的两个内角之和;两直线平行,同位角相等.18.如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为()A.34°B.56°C.66°D.54°【答案】B【解析】试题分析:∵AB∥CD,∴∠D=∠1=34°,∵DE⊥CE,∴∠DEC=90°,∴∠DCE=180°﹣90°﹣34°=56°.故选B.考点:平行线的性质.19.下列图形中线段PQ的长度表示点P到直线a的距离的是()A.B.C.D.【答案】C【解析】【分析】根据点到直线的距离的定义,可得答案.【详解】由题意得PQ⊥a,P到a的距离是PQ垂线段的长,故选C.【点睛】本题考查了点到直线的距离,点到直线的距离是解题关键.20.如图所示,b∥c,a⊥b,∠1=130°,则∠2=().A.30°B.40°C.50°D.60°【答案】B【解析】【分析】证明∠3=90°,利用三角形的外角的性质求出∠4即可解决问题.【详解】如图,反向延长射线a交c于点M,∵b∥c,a⊥b,∴a⊥c,∴∠3=90°,∵∠1=90°+∠4,∴130°=90°+∠4,∴∠4=40°,∴∠2=∠4=40°,故选B.【点睛】本题考查平行线的性质,垂线的性质,三角形的外角的性质等知识,解题的关键是熟练掌握基本知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交线与平行线一.选择题(共3小题)1.在同一平面,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l 3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个3.如图所示,同位角共有()A.6对B.8对C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= .7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.评卷人得分三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+ =180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2= °.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.33.阅读下面的推理过程,在括号填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,()所以a∥c.()又因为∠2+∠3=180°(已知)∠3=∠6()所以∠2+∠6=180°,()所以a∥b.()所以b∥c.()34.已知:如图,AB∥CD,FG∥HD,∠B=100°,FE为∠CEB的平分线,求∠EDH的度数.35.已知:如图,AB∥CD,FE⊥AB于G,∠EMD=134°,求∠GEM的度数.36.如图,∠B和∠D的两边分别平行.(1)在图1 中,∠B和∠D的数量关系是,在图2中,∠B和∠D的数量关系是;(2)用一句话归纳的命题为:;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.37.已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.①求证:∠ABC=∠ADC;②求∠CED的度数.38.如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.39.如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?40.已知直线AB∥CD,(1)如图1,点E在直线BD上的左侧,直接写出∠ABE,∠CDE和∠BED之间的数量关系是.(2)如图2,点E在直线BD的左侧,BF,DF分别平分∠ABE,∠CDE,直接写出∠BFD和∠BED的数量关系是.(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,那么∠BFD 和∠BED有怎样的数量关系?请说明理由.41.(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF的度数.42.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把解答过程补充完整.解:∵CD⊥DA,DA⊥AB,∴∠CDA=90°,∠DA B=90°.()∴∠CDA=∠DAB.(等量代换)又∠1=∠2,从而∠CDA﹣∠1=∠DAB﹣.(等式的性质)即∠3= .∴DF∥AE.().43.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)说明:∠O=∠BEO+∠DFO.(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n次,又会得到怎样的结论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG平分∠AEC,∠NCE=75°.求证:(1)AB∥EF.(2)AB∥ND.45.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB.46.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.(1)如图①,若∠A=30°,∠C=40°,则∠AEC= .(2)如图②,若∠A=100°,∠C=120°,则∠AEC= .(3)如图③,请直接写出∠A,∠C与∠AEC之间关系是.47.如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.48.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC的度数.(2)图2中AE∥BC,请你计算出∠AFD的度数.49.如图,将一矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB平行的线段有哪些?(2)图中和AB垂直的直线有哪些?参考答案及解析一.选择题(共3小题)1.在同一平面,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l 3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定【分析】如果一条直线垂直于两平行线中的一条,那么它与另一条一定也垂直.再根据“垂直于同一条直线的两直线平行”,可知L1与L8的位置关系是平行.【解答】解:∵l2∥l3,l3⊥l4,l4∥l5,l5⊥l6,l6∥l7,l7⊥l8,∴l2⊥l4,l4⊥l6,l6⊥l8,∴l2⊥l8.∵l1⊥l2,∴l1∥l8.故选A【点评】灵活运用“垂直于同一条直线的两直线平行”是解决此类问题的关键.2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个【分析】由OE⊥AB,OF⊥CD可知:∠AOE=∠DOF=90°,而∠1、∠AOF都与∠EOF互余,可知∠1=∠AOF,因而可以转化为求∠1和∠AOF的余角共有多少个.【解答】解:∵OE⊥AB,OF⊥CD,∴∠AOE=∠DOF=90°,即∠AOF+∠EOF=∠EOF+∠1,∴∠1=∠AOF,∴∠COA+∠1=∠1+∠EOF=∠1+∠BOD=90°.∴与∠1互为余角的有∠COA、∠EOF、∠BOD三个.故选A.【点评】本题解决的关键是由已知联想到可以转化为求∠1和∠AOF的余角.3.如图所示,同位角共有()A.6对B.8对C.10对D.12对【分析】在基本图形“三线八角”中有四对同位角,再看增加射线GM、HN 后,增加了多少对同位角,求总和.【解答】解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,射线GM和直线CD被直线EF所截,形成2对同位角;射线GM和直线HN被直线EF所截,形成2对同位角;射线HN和直线AB被直线EF所截,形成2对同位角.则总共10对.故选C.【点评】本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成8 块.【分析】一块长方体橡皮被刀切了3次,最多能被分成23=8块.【解答】解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.【点评】本题考查了学生的空间想象能力,分清如何分得到的块数最多是解决本题的关键.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为9 .【分析】过P分别作x轴和y轴的垂线,交x轴和y轴与C和D.构造全等三角形△PDB≌△PCA(ASA)、正方形CODP;所以S四边形OAPB =S正方形ODPC=3×3=9.【解答】解:过P分别作x轴和y轴的垂线,交x轴和y轴于点C和D.∵P点坐标为(3,3),∴PC=PD;又∵l1⊥l2,∴∠BPA=90°;又∵∠DPC=90°,∴∠DPB=∠CPA,在△PDB和△PCA中∴△PDB≌△PCA(ASA),∴S△DPB =S△PCA,S四边形OAPB =S正方形ODPC+S△PCA﹣S△DPB,即S四边形OAPB =S正方形ODPC=3×3=9.故答案是:9.【点评】本题综合考查了垂线、坐标与图形性质、三角形的面积.解答此题时,利用了“割补法”求四边形OAPB的面积.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= 200°.【分析】过∠2的顶点作l2的平行线l,则l∥l1∥l2,由平行线的性质得出∠4=∠1=20°,∠BAC+∠3=180°,即可得出∠2+∠3=200°.【解答】解:过∠2的顶点作l2的平行线l,如图所示:则l∥l1∥l2,∴∠4=∠1=20°,∠BAC+∠3=180°,∴∠2+∠3=180°+20°=200°;故答案为:200°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁角互补;两直线平行,错角相等.7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是75°.【分析】根据平行线的性质得到∠EDC=∠E=45°,根据三角形的外角性质得到∠AFD=∠C+∠EDC,代入即可求出答案.【解答】解:∵∠EAD=∠E=45°,∵AE∥BC,∴∠EDC=∠E=45°,∵∠C=30°,∴∠AFD=∠C+∠EDC=75°,故答案为:75°.【点评】本题主要考查对平行线的性质,三角形的外角性质等知识点的理解和掌握,能利用性质进行推理是解此题的关键,题型较好,难度适中.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.【分析】(1)首先作MQ∥AB,根据平行线的性质,推得∠M=(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.(2)①首先判断出∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.②首先判断出∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=(180°﹣∠HED)=∠CEH,再根据AB∥CD,推得∠FHE=180°﹣2∠ENQ即可.【解答】解:(1)如图1,作MQ∥AB,,∵AB∥CD,MQ∥AB,∴MQ∥CD,∴∠1=∠FHM,∠2=∠DEM,∴∠1+∠2=∠FHM+∠DEM=(∠FHP+∠FED)=(∠FHP+∠HFP),∵HP⊥EF,∴∠HPF=90°,∴∠FHP+∠HFP=180°﹣90°=90°,∵∠1+∠2=∠M,∴∠M=.(2)①如图2,,∠FHE=2∠ENQ,理由如下:∠NEQ=∠NEF+∠QEF=(∠HEF+∠DEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=∠CEH=2∠ENQ.②如图3,,∠FHE=180°﹣2∠ENQ,理由如下:∠NEQ=∠QEF﹣∠NEF=(∠DEF﹣∠HEF)=∠HED,∵NQ⊥EM,∴∠NEQ+∠ENQ=90°,∴∠ENQ=(180°﹣∠HED)=∠CEH,∵AB∥CD,∴∠FHE=180°﹣∠CEH=180°﹣2∠ENQ.综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°﹣2∠ENQ.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁角互补.简单说成:两直线平行,同旁角互补.③定理3:两条平行线被第三条直线所截,错角相等.简单说成:两直线平行,错角相等.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.【解答】解:如图:2条直线相交有1个交点;3条直线相交有1+2个交点;4条直线相交有1+2+3个交点;5条直线相交有1+2+3+4个交点;6条直线相交有1+2+3+4+5个交点;…n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.【点评】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交有个交点.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.【分析】(1)根据角平分线的定义求出∠AOC的度数,根据对顶角相等得到答案;(2)设∠EOC=4x,根据邻补角的概念列出方程,解方程求出∠EOC=80°,根据角平分线的定义和对顶角相等计算即可得到答案.【解答】解:(1)∵∠EOC=70°,OA平分∠EOC,∴∠AOC=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=4x,则∠EOD=5x,∴5x+4x=180°,解得x=20°,则∠EOC=80°,又∵OA平分∠EOC,∴∠AOC=40°,∴∠BOD=∠AOC=40°.【点评】本题考查的是对顶角、邻补角的概念和性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?【分析】(1)、(2)根据平角的性质求得∠AOF,又有角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;(3)由(1)、(2)的结果找出它们之间的倍数关系.【解答】解:(1)∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,∴∠AOF=140°;又∵OC平分∠AOF,∴∠FOC=∠AOF=70°,∴∠EOD=∠FOC=70°(对顶角相等);而∠BOE=∠AOB﹣∠AOE=50°,∴∠BOD=∠EOD﹣∠BOE=20°;(2)∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,∴∠AOF=180°﹣α;又∵OC平分∠AOF,∴∠FOC=∠AOF=90°﹣α,∴∠EOD=∠FOC=90°﹣α(对顶角相等);而∠BOE=∠AOB﹣∠AOE=90°﹣α,∴∠BOD=∠EOD﹣∠BOE=α;(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.【点评】本题利用垂直的定义,对顶角和互补的性质计算,要注意领会由垂直得直角这一要点.12.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).【分析】(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数,【解答】解:(1)如图1,过点E作EF∥PQ,∵∠CBN=100°,∠ADQ=130°,∴∠CBM=80°,∠ADP=50°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDP=∠ADP=25°,∵EF∥PQ,∴∠DEF=∠EDP=25°,∵EF∥PQ,MN∥PQ,∴EF∥MN.∴∠FEB=∠EBM=40°∴∠BED=25°+40°=65°;(2)如图2,过点E作EF∥PQ,∵∠CBN=100°,∴∠CBM=80°,∵DE平分∠ADC,BE平分∠ABC,∴∠EBM=∠CBM=40°,∠EDQ=∠ADQ=n°,∵EF∥PQ,∴∠DEF=180°﹣∠EDQ=180°﹣n°,∵EF∥PQ,MN∥PQ,∴EF∥MN,∴∠FEB=∠EBM=40°,∴∠BED=180°﹣n°+40°=220°﹣n°.【点评】本题主要考查了平行线的性质,运用角平分线与平行线的性质相结合来求∠BED解题的关键.13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.【分析】(1)根据平角等于180°,列式计算即可得解;(2)根据三角形的外角性质求出∠4,然后根据同位角相等,两直线平行解答.【解答】解:(1)∵∠ACB=90°,∠1=26°,∴∠2=180°﹣∠1﹣∠ACB,=180°﹣90°﹣26°,=64°;(2)结论:n∥m.理由如下:∵∠3=19°,∠A=45°,∴∠4=45°+19°=64°,∵∠2=64°,∴∠2=∠4,∴n∥m.【点评】本题考查了平行线的判定与性质,三角形外角性质的运用,熟练掌握平行线的判定方法与性质是解题的关键.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.【分析】此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.【解答】证明:(1)过P作PQ∥l1∥l2,由两直线平行,错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPE+∠QPF,∴∠3=∠1+∠2.(2)关系:∠3=∠2﹣∠1;过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠3=∠QPF﹣∠QPE,∴∠3=∠2﹣∠1.(3)关系:∠3=360°﹣∠1﹣∠2.过P作PQ∥l1∥l2;同(1)可证得:∠3=∠CEP+∠DFP;∵∠CEP+∠1=180°,∠DFP+∠2=180°,∴∠CEP+∠DFP+∠1+∠2=360°,即∠3=360°﹣∠1﹣∠2.【点评】此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.【分析】(1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;(2)由(1)的结论代入计算即可.【解答】解:(1)∠ABC﹣∠BCP+∠CPN=180°;理由如下:延长NP交BC于M,如图所示:∵AB∥PN∥CD,∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,∵∠PCD=∠BCD﹣∠BCP=∠ABC﹣∠BCP,∴∠ABC﹣∠BCP+∠CPN=180°.(2)由(1)得:∠ABC﹣∠BCP+∠CPN=180°,则∠BCP=∠ABC+∠CPN﹣180°=155°+42°﹣180°=17°.【点评】本题考查了平行线的性质;熟记平行线的性质是解决问题的关键.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.【分析】(1)根据平行线的性质和等量关系可得∠EAD+∠D=180°,根据同旁角互补,两直线平行即可证明;(2)根据平行线的性质可得∠AEB=∠C,根据三角形角和定理和等量关系即可得到∠B的度数.【解答】(1)证明:∵AD∥BC,∴∠D+∠C=180°,∵∠EAD=∠C,∴∠EAD+∠D=180°,∴AE∥CD;(2)∵AE∥CD,∴∠AEB=∠C,∵∠FEC=∠BAE,∴∠B=∠EFC=50°.【点评】考查了平行线的判定和性质,三角形角和定理,解题的关键是证明AE∥CD.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.【分析】(1)首先作EF∥AB,根据AB∥CD,可得EF∥CD,据此分别判断出∠B=∠1,∠D=∠2,即可判断出∠B+∠D=∠E,据此解答即可.(2)首先作EF∥AB,即可判断出∠B=∠1;然后根据∠E=∠1+∠2=∠B+∠D,可得∠D=∠2,据此判断出EF∥CD,再根据EF∥AB,可得AB∥CD,据此判断即可.(3)首先过E作EF∥AB,即可判断出∠BEF+∠B=180°,然后根据EF∥CD,可得∠D+∠DEF=180°,据此判断出∠E+∠B+∠D=360°即可.(4)首先根据AB∥CD,可得∠B=∠BFD;然后根据∠D+∠E=∠BFD,可得∠D+∠E=∠B,据此解答即可.(5)首先作EM∥AB,FN∥AB,GP∥AB,根据AB∥CD,可得∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,所以∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;然后根据∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,可得∠E+∠G=∠B+∠F+∠D,据此判断即可.【解答】解:(1)如图1,作EF∥AB,,∵AB∥CD,∴∠B=∠1,∵AB∥CD,EF∥AB,∴EF∥CD,∴∠D=∠2,∴∠B+∠D=∠1+∠2,又∵∠1+∠2=∠E,∴∠B+∠D=∠E.(2)如图2,作EF∥AB,,∵EF∥AB,∴∠B=∠1,∵∠E=∠1+∠2=∠B+∠D,∴∠D=∠2,∴EF∥CD,又∵EF∥AB,∴AB∥CD.(3)如图3,过E作EF∥AB,,∵EF∥AB,∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,∵∠BEF+∠DEF=∠E,∴∠E+∠B+∠D=180°+180°=360°.(4)如图4,,∵AB∥CD,∴∠B=∠BFD,∵∠D+∠E=∠BFD,∴∠D+∠E=∠B.(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,又∵AB∥CD,∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,∴∠E+∠G=∠B+∠F+∠D.【点评】此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁角互补.简单说成:两直线平行,同旁角互补.(3)定理3:两条平行线被第三条直线所截,错角相等.简单说成:两直线平行,错角相等.18.如图1,AB∥CD,在AB、CD有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为∠P+n∠Q=360°.(直接写结论)【分析】(1)首先过点P作PG∥AB,然后根据AB∥CD,PG∥CD,可得∠AEP=∠1,∠CFP=∠2,据此判断出∠AEP+∠CFP=∠EPF即可.(2)首先由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ;然后根据∠BEP的平分线与∠DFP的平分线相交于点Q,推得∠EQF=,即可判断出∠EPF+2∠EQF=360°.(3)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+3∠Q=360°.(4)首先由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ;然后根据∠BEQ=∠BEP,∠DFQ=∠DFP,推得∠Q=×(360°﹣∠P),即可判断出∠P+n∠Q=360°.【解答】(1)证明:如图1,过点P作PG∥AB,,∵AB∥CD,∴PG∥CD,∴∠AEP=∠1,∠CFP=∠2,又∵∠1+∠2=∠EPF,∴∠AEP+∠CFP=∠EPF.(2)如图2,,由(1),可得∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,∵∠BEP的平分线与∠DFP的平分线相交于点Q,∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)==,∴∠EPF+2∠EQF=360°.(3)如图3,,由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+3∠Q=360°.(4)由(1),可得∠P=∠AEP+CFP,∠Q=∠BEQ+∠DFQ,∵∠BEQ=∠BEP,∠DFQ=∠DFP,∴∠Q=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=×(360°﹣∠P),∴∠P+n∠Q=360°.故答案为:∠P+n∠Q=360°.【点评】此题主要考查了平行线的性质的应用,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁角互补.简单说成:两直线平行,同旁角互补.(3)定理3:两条平行线被第三条直线所截,错角相等.简单说成:两直线平行,错角相等.19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.【分析】设∠1=x,根据题意表示出∠2,再表示出∠3,然后根据邻补角的和等于180°列式求出x,再根据对顶角相等求出∠4即可.【解答】解:设∠1=x,则∠2=x,∠3=8x,依题意有x+x+8x=180°,解得x=18°,则∠4=18°+18°=36°.故∠4的度数是36°.【点评】本题考查了对顶角、邻补角的定义,准确识图,设出未知数并列出方程是解题的关键.20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【分析】根据同位角相等,两直线平行证明OB∥AC,根据同旁角互补,两直线平行证明OA∥BC.【解答】解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC.【点评】本题考查的是平行线的判定,掌握平行线的判定定理:同位角相等,两直线平行;错角相等,两直线平行;同旁角互补,两直线平行是解题的关键.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.【分析】(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=;②∠BOE=∠FOE﹣∠FOB可知∠BOE=x﹣15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.【解答】解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,∴∠EOF=∠FOB+∠BOE=35°+20°=55°,(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,∵OF平分∠COE,∴∠FOE=x,故答案为:;②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=x﹣15°,∵∠BOE+∠AOE=180°,∴x﹣15°+x=180°,解得:x=130°,∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.【点评】本题考查了对顶角,角平分线定义,角的有关定义的应用,主要考查学生的计算能力.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.【分析】(1)根据对顶角相等求出∠BOD的度数,设∠BOE=2x,根据题意列出方程,解方程即可;(2)根据角平分线的定义求出∠AOF的度数即可.【解答】解:(1)设∠BOE=2x,则∠EOD=3x,∠BOD=∠AOC=75°,∴2x+3x=75°,解得,x=15°,则2x=30°,3x=45°,∴∠BOE=30°;(2)∵∠BOE=30°,∴∠AOE=150°,∵OF平分∠AOE,∴∠AOF=75°,∴∠COF=∠AOC,∴OA是∠COF的角平分线.【点评】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.【分析】(1)设∠BOE=x,根据题意列出方程,解方程即可;(2)分射线OF在∠AOD的部和射线OF在∠BOC的部两种情况,根据垂直的定义计算即可.【解答】解:(1)∵∠AOC=72°,∴∠BOD=72°,∠AOD=108°,设∠BOE=x,则∠DOE=2x,由题意得,x+2x=72°,解得,x=24°,∴∠BOE=24°,∠DOE=48°,∴∠AOE=156°;(2)若射线OF在∠BOC的部,∠DOF=90°+48°=138°,若射线OF在∠AOD的部,∠DOF=90°﹣48°=42°,∴∠DOF的度数是138°或42°.【点评】本题考查的是对顶角和邻补角的概念和性质以及垂直的定义,掌握对顶角相等、邻补角的和是180°是解题的关键.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE∥GH.【分析】(1)根据邻补角的定义求出∠EOC,再根据角平分线的定义求出∠AOC,然后根据对顶角相等解答.(2)由已知条件和对顶角相等得出∠MFC=∠MFH=∠BOD+90°=126°,得出∠ONF=90°,求出∠OFM=54°,延长∠OFG=2∠OFM=108°,证出∠OFG+∠EOC=180°,即可得出结论.【解答】解:∵∠EOC:∠EOD=2:3,∴∠EOC=180°×=72°,∵OA平分∠EOC,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.(2)延长FM交AB于N,如图所示:∵∠MFH﹣∠BOD=90°,FM平分∠OFG,∴∠MFC=∠MFH=∠BOD+90°=126°,∴∠ONF=126°﹣36°=90°,∴∠OFM=90°﹣36°=54°,∴∠OFG=2∠OFM=108°,∴∠OFG+∠EOC=180°,∴OE∥GH.【点评】本题考查了平行线的判定、角平分线定义、角的互余关系等知识;熟练掌握平行线的判定、角平分线定义是解决问题的关键,(2)有一定难度.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.【分析】(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;(2)根据角平分线的定义和邻补角的性质计算即可.【解答】解:(1)∵OE平分∠BOC,∠BOE=70°,∴∠BOC=2∠BOE=140°,∴∠AOC=180°﹣140°=40°,又∠COF=90°,∴∠AOF=90°﹣40°=50°;(2)∵∠BOD:∠BOE=1:2,OE平分∠BOC,∴∠BOD:∠BOE:∠EOC=1:2:2,∴∠BOD=36°,∴∠AOC=36°,又∵∠COF=90°,∴∠AOF=90°﹣36°=54°.【点评】本题考查的是对顶角、邻补角的性质以及角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴CD ∥AB (错角相等,两直线平行)(2)∵∠DBE=∠CAB(已知)∴AC ∥BD (同位角相等,两直线平行)(3)∵∠ADF+ ∠5 =180°(已知)∴AD∥BF(同旁角互补,两直线平行)【分析】(1)由∠3=∠4根据平行线的判定推出CD∥AB;(2)由∠DBE=∠CAB,根据同位角相等,两直线平行得出答案;(3)根据同旁角互补,两直线平行即可得到答案.【解答】解:(1)∵∠3=∠4(已知),∴CD∥AB(错角相等,两直线平行),(2)∵∠DBE=∠CAB(已知),∴AC∥BD(同位角相等,两直线平行),(3)∵∠ADF+∠5=180°(已知),∴AD∥BF(同旁角互补,两直线平行).。
