2013-2014学年洞头县六校联考九年级上期中数学试卷及答案
2013-2014学年人教版九年级上期中测试数学试题(含答案)

湖北省宜城市2013-2014学年第一学期期中测试一、选择题 (本大题有12个小题,每小题3分,共36分.)1.下列二次根式中,的取值范围是3x≥的是()B. C.2. 下列二次根式中,是最简二次根式的是()A. C.3. 下列各式计算正确的是()A.63238=- B. 5102535=+C. 222224=÷ D. 682234=⨯4. 下列方程中,一元二次方程共有().①432=-xx②04322=+-xyx③412=-xx④42=x⑤0332=+-xxA. 2个 B.3个 C.4个 D. 5个5. 关于关于x的一元二次方程1352+=-xxx的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法判断6. 某种商品零售价经过两次降价后的价格为降价前的81%,则平均每次降价()A.19% B.10% C.9.5% D.20%7.下列命题中是真命题的是( )A.经过两点不一定能作一个圆B.经过三点不一定能作一个圆C.经过四点一定不能作一个圆D.一个三角形有无数个外接圆8.四边形ABCD的对角线相交于点O,且AO=BO=CO=DO,则这个四边形()A.仅是轴对称图形B.仅是中心对称图形C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形,又不是中心对称图形 9.如图所示,在正方形ABCD 中,AB=4,点O 在AB 上,且OB=1,点P 是BC 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转90°得到线段OQ.要使点Q 恰好落在AD 上,则BP 的长是( )A .3B .2C .1D .无法确定10. 如图所示,如果AB 为⊙O 的直径,弦CD ⊥AB ,垂足为E ,那么下列结论中,错误的是( )A.CE=DEB.弧BC=弧BDC.∠BAC=∠BADD.AC ﹥AD11.下列四个命题:①顶点在圆心的角是圆心角;②两个圆心角相等, 它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中正确的有( ) A.0个 B.1个 C.2个 D.3个12. 已知⊙O 的半径为5cm ,点P 到⊙O 的最近距离是2,那么点P 到⊙O 的最远距离是( ) A.7cm B.8cm C. 7cm 或12cm D.8cm 或12cm二、填空题 (本大题有5个小题,每小题3分,共15分.)13.计算(236)(236)+-=14. 已知方程x 2-x -1=0有一根为m ,则m 2-m +2013的值为____.15.如图,已知正方形ABCD 的边长为3,E 为CD 边上一点,DE=1.以点A 为中心,把△ADE 顺时针旋转90︒,得△ABF ,连接EF ,则EF 的长等于 .16. 如图,AB 为⊙O 的直径,弦CD ⊥AB ,E 为弧BC 上一点,若∠CEA=28o,则∠ABD=°.ABCDE O · 第10题图A第16题图 17.已知等腰△的三个顶点都在半径为5cm 的⊙上,如果底边的长为8cm ,则边上的高为 .三、解答题(本大题共9个小题,计69分.)18.(本题满分5分)计算:4832426-÷+⨯.19.(本题满分7分)先化简,再求值:(a -1+12+a )÷(212+a ),其中a =2-1.20.(本题满分6分)已知方程2(1)140x m x m +-+-=的一个根是3,求m 的值及方程的另一个根.21.(本题满分7分)已知关于x 的一元二次方程04222=-++k x x 有两个不相等的实数根(1)求k 的取值范围;(2)若k 为正整数,且该方程的根都是整数,求k 的值。
2013-2014学年九年级上期中数学试题及参考答案

2013~2014学年上学期九年级期中考试数 学 试 题一、选择题(每小题3分,共计30分)1.如果01)3(2=+-+mx x m 是一元二次方程,则 ( )A 、3-≠mB 、3≠mC 、0≠mD 、03≠-≠m m 且 2. 方程032=-x x 的解是( )A .x=3B .x 1=0,x 2=3C .x 1=0,x 2=-3D .x 1=1,x 2=3 3. 对于反比例函数y = 1x,下列说法正确的是( )A .图象经过点(1,-1)B .图象位于第二、四象限C .图象是中心对称图形D .当x <0时,y 随x 的增大而增大4. 在函数131y x =-中,自变量x 的取值范围是( )(A)13x < (B) 13x ≠- (C) 13x ≠ (D) 13x >5. 用配方法解一元二次方程0782=++x x ,则方程可化为( )A 、942=+)(xB 、942=-)(xC 、23)8(2=+xD 、9)8(2=-x6.如果矩形的面积为6cm 2,那么它的长y cm 与宽x cm 之间的函数关系用图象表示大致是( )A B C D7.我地为执行“两免一补”政策, 2011年投入教育经费2500万元,预计2013年投入3600万元.设这两年投入教育经费的年平均增长率为x ,则下列方程正确的是( ). A .225003600x =B .22500(1)3600x +=C .22500(1%)3600x +=D .22500(1)2500(1)3600x x +++=8. 点(-2,3)在函数xk y =图象上,则下列点中,不在该函数图象上的是( )A. (-6, 1)B. (23,-4)C. (3, 2)D. (1, -6)9. 菱形ABCD 中,对角线AC ,BD 交于点O ,下列说法错误..的是( ) A .AB ∥DC B .AC=BD C .AC ⊥BD D .OA=OC10.函数1ky x-=的图象与直线y x =没有交点,那么k 的取值范围是( )A .1k >B .1k <C .1k >-D .1k <- 二、填空题(每小题3分,共15分)11、已知x = 1是关于x 的一元二次方程2x 2 + kx –1 =0的一个根,则实数k 的值是 。
浙江省洞头县2013-2014学年第一学期期中“六校联考”

绝密★启用前浙江省洞头县2013-2014学年第一学期期中“六校联考”题号一二三四得分注意事项:1.本试卷共XX页,四个大题,满分187分,考试时间为1分钟。
请用钢笔或圆珠笔直接答在试卷上。
2.答卷前将密封线内的项目填写清楚。
一、单选题(共40分)评卷人得分1.下列不是描述洞头天气是( ▲)(2分)A. 今天阴转多云,明天多云B. 明天气温:18℃—21℃C. 夏季温暖潮湿多雨D. 今天东北风5—6级,阵风8级2.下列自然灾害中,不属于气象灾害的是( ▲)(2分)A. 寒潮B. 台风C. 洪水D. 地震3.洞头县大门观音礁水库建成,解决了大门镇2//3人口饮水问题。
根据右图水循环示意图,水库建立主要是改变了水循环的哪一个环节( ▲)A、地下径流B、地表径流C、水汽运输D、降水(2分)试卷第2页,总13页…………外………………订…订※※线※※内※※答…………内………………订…4.规范的实验操作是科学探究成功的基础。
如图实验操作规范的是( ▲ )(2分)5.将下列四种家庭常用的调味品分别放入水中,不能形成溶液的是( ▲ )(2分) A. 镇江白醋 B. 快鹿味精 C. 食盐 D. 大门菜油6.下列现象不是用来证明大气压存在的是( ▲ )(2分)7.你是否有这样的经历:撑一把雨伞行走在雨中,如图所示,一阵大风吹来,伞面可能被“吸”,严重变形。
下列有关这一现象及其解释,正确的是( ▲ )(2分)A. 伞面被向下“吸”B. 伞上方的空气流速大于下方C. 伞上方的空气流速等于下方D. 伞上方的空气流速小于下方8.如图所示的大气对流图,其中正确的是( ▲ )(2分)9.如图所示能够说明流体压强与流速关系的是( ▲ )………○……………○……(2分)10.温瑞塘河的水经过下列哪种方法处理后,你会放心地饮用?( ▲ )(2分)A. 过滤法B. 蒸馏法C. 沉淀法D. 煮到沸腾11.以下为风向、风速的图示,一个小三角旗表示 8级,一长横线表示2级,一短横线表示1级,风向是画有风旗的一边。
2013-2014学年人教版九年级上期中考试数学试卷(含答案)

云南省大理州拥翠乡中学2013—2014学年第一学期期中考试九年级数学试卷考生注意:本试卷共三大题,23小题,总分100分,考试时间120分钟。
一、选择题(本题包括8小题,每小题3分,共24分,每小题只有一个正确答案)1.下列方程,是一元二次方程的是()①3x2+x=20,②2x2-3xy+4=0,③x2-1x=4,④x2=0,⑤x2-3x+3=0A.①②B.①②④⑤C.①③④D.①④⑤2、下图中是中心对称图形的是()A B. C. D.3、方程x2 = 3x的根是()A.x=3 B.x= -3 C.0或3 D.无解4、方程3x2-4x+1=0 ()A.有两个不相等的实数根 B.只有一个实数根C.有两个相等的实数根 D.没有实数根5、下列计算正确的是()A.20=210B.2·3= 6C.4-2= 2D.(-3)2=-36、下列二次根式中,与3是同类二次根式的是()A.18B.27C.23 D.327、一元二次方程x2-5x+6=0的两根分别是x1、x2,则x1+x2等于()A.5 B.6 C.-5 D.-68、已知如图①所示的四张牌,若将其中一张牌旋转180°后得到图②,则旋转的牌是()二、填空题(共7个小题,每小题3分,共21分) 9、二次根式 3-x 有意义的条件是10、当x 为 时,代数式3x 2的值与4x 的值相等。
11、21= , (10)2= , 2)1(-= 12、已知A (a-1,3),B(-2012,b+2)两点关于原点对称,则a= ,b= . 13、若︳x+2 ︳+ y -3=0,则x y的值为14、在平行四边形、矩形、菱形、正方形、等腰梯形的五种图形中,既是轴对称又是中心对称的图形是 。
15.已知方程x 2-7x+12=0的两根恰好是Rt △ABC 的两条边的长,则Rt △ABC•的第三边长为________.三、解答题(本题共8小题,共55分)16、计算: (5分) 4+(3.14-π)0-|-2|+108-236⨯17.(5分)先化简,再求值.a 2a 2+2a -a 2-2a +1a +2÷a 2-1a +1,其中a =2-2.18、(8分)解方程:(每小题4分) (1) 9(x-3)2- 49=0(2)若a 、b 为实数,且a 、b 是方程x 2+5x+6=0的两根,则p(a,b)关于原点对称点Q 的坐标是什么?19、(6分 )三角形两边的长分别是8和6,第三边的长是一元二次方程060162=+-x x 的一个实数根,求该三角形的面积。
2013-2014初三上学期学业水平考试初三数学(含答案)

2013-2014初三上学期学业水平考试数学试题注意事项:1.本试题分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷共3页,满45分;第Ⅱ卷共7页,满分75分.本试题共10页,满分120分,考试时间为120分钟.2.答卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上,并同时将考点、姓名、准考证号、座号填写在试卷的密封线内.3.第Ⅰ卷为选择题,每小题选出答案后,用2B 铅笔把答题卡上对应题目的正确答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,答案写在试卷上无效. 4.考试期间,一律不得使用计算器;考试结束,应将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.一个等腰三角形的顶角是40°,则它的底角是( )A .40°B .50°C .60°D .70° 2.方程 x (x +3)= 0的根是( ) A .x =0B .x =-3C .x 1=0,x 2 =3D .x 1=0,x 2 =-33.下列函数中,属于反比例函数的是( ) A .2xy =B .12y x=C .23y x =+D .223y x =+4.下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序正确的是( )A. A →B →C →DB. D →B →C →AC. C →D →A →BD. A →C →B →D北 东5.在Rt △ABC 中,∠C=90°,a =4,b =3,则cosA 的值是( ) A .54 B .35C .43 D .456.二次函数223y x x =-+顶点坐标是( )A .(-1,-2)B .(1,2)C .(-1,2)D .(0,2)7.如图,一飞镖游戏板,其中每个小正方形的大小相等,则随意投掷一个飞镖,击中黑色区域的概率是( )A .38 B .12 C .14 D .138. 与如图所示的三视图对应的几何体是( )9.下列命题中,不正确...的是( ) A .对角线相等的平行四边形是矩形.B .有一个角为60°的等腰三角形是等边三角形.C .直角三角形斜边上的高等于斜边的一半.D .正方形的两条对角线相等且互相垂直平分.10. 已知点A( -2 ,y 1 ) , ( -1 ,y 2 ) , ( 3 ,y 3 )都在反比例函数xy 4=的图象上,则 ( )A. y 1<y 2<y 3B. y 3<y 2<y 1C. y 3 <y 1<y 2D. y 2<y 1<y 311.若关于x 的一元二次方程0962=+-x kx 有两个不相等的实数根,则k 的取值范围是( )A. 1k <B. 0k =/C. 10k k <=/且D. 1k >12. 如右图,在□ABCD 中,EF ∥AB,GH ∥AD,EF 与GH 交于点O,则图中的平行四边形的个数共有 ( )A. 7个B. 8个C. 9个D. 10个13.如图,在△ABC 中,AB=a ,AC=b ,BC 边上的垂直平分线DE 交BC ,BA 分别于点D ,E ,则△AEC 的周长等于( )A. a+bB.a-bC.2a+bD.a+2b14.图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),……,则第n 个图形的周长是( )A.2nB.4nC.12n + D.22n +15.已知x y z ,,为实数,且满足253x y z +-=,25x y z --=-,则222x y z ++的最小值为( ).A.111 B. 0 C. 5 D. 5411OGHFEC BAD图1图2图3……F EDC A2011年初三上学期学业水平考试数学试题第Ⅱ卷(非选择题 共75分)注意事项:1.第Ⅱ卷共6页.用蓝、黑钢笔或圆珠笔直接答在考试卷上.二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中横线上) 16.已知反比例函数xky =的图象经过点P(一l ,2),则这个函数的图象位于_____________17.甲、乙两楼相距20m ,甲楼高20 m ,自甲楼顶看乙楼楼顶,仰角为60º,则乙楼的高为 。
2013-2014学年人教版九年级上期中考试数学试题(含答案)

海淀区九年级第一学期期中测评数学试卷(分数:120分时间:120分钟) 2013.11班级姓名学号 成绩试题答案一律填涂或书写在答题卡上,在试卷上做答无效. 一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.一元二次方程2230x x --=的二次项系数、一次项系数、常数项分别是A. 1,2,3--B. 1,-2,3C. 1,2,3D. 1,2,3- 2.在角、等边三角形、平行四边形、圆中,既是中心对称图形又是轴对称图形的是 A .角B .等边三角形 C .平行四边形 D .圆 3.函数2y x =-中,自变量x 的取值范围是A .2≠xB .2≤xC .2>xD .2≥x4.如图,点A 、B 、C 在O ⊙上,若110AOB ∠=o ,则ACB ∠的大小是 A .35o B .ο45 C .55o D .110o5.用配方法解方程09102=++x x ,配方正确的是 A .16)5(2=+x B .34)5(2=+x C .16)5(2=-x D .25)5(2=+x6.如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是 A .ο60B .ο72 C .90oD .120o7.若230a b ++-=,则a b +的值为A .-1B .1C .5D .6OCBA8.如图,⊙O 的半径为5,点P 到圆心O 的距离为10,如果过点P 作弦,那么长度为整数值的弦的条数为 A .3 B .4C .5D .6二、填空题(本题共16分,每小题4分)9.如图,将ABC △绕点C 顺时针旋转至''A B C △的位置,若 15ACB ∠=o ,120B ∠=o ,则'A ∠的大小为________.10.已知一元二次方程有一个根是0,那么这个方程可以是(填上你认为正确的一个方程即可).11.如图,AB 是⊙O 的直径,点C 、D 为⊙O 上的两点,若 ο40=∠ABD ,则BCD ∠的大小为.12.下面是一个按某种规律排列的数阵:1第1行 2 3 2第2行 5 6 7 22 3第3行 1011 2313 1415 4第4行 L L L L根据数阵排列的规律,则第5行从左向右数第5个数为,第n (3≥n ,且n 是整数)行从左向右数第5个数是(用含n 的代数式表示). 三、解答题(本题共30分,每小题5分) 13.计算:36324⨯+÷.14.用公式法解一元二次方程:241x x +=.15.如图,ABC △与AED △均是等边三角形,连接BE 、CD .请在图中找出一条与CD 长度相等的线段,并证明你的结论.结论:CD =. 证明:ODCBAPO ED CBA16.当15-=x 时,求代数式522-+x x 的值.17.如图,两个圆都以点O 为圆心,大圆的弦AB 交小圆于C 、D 两点.求证:AC =BD . 证明:18.列方程(组)解应用题:如图,有一块长20米,宽12米的矩形草坪,计划沿水平和竖直方向各修一条宽度相同的小路,剩余的草坪面积是原来的34,求小路的宽度.解:四、解答题(每小题5分,共20分)19.已知关于x 的一元二次方程210x mx m -++=的一个根为2. (1) 求m 的值及另一根;(2)若该方程的两个根分别是等腰三角形的两条边的长,求此等腰三角形的周长.20.如图,DE 为半圆的直径,O 为圆心,DE =10,延长DE 到A ,使得EA =1,直线AC 与半圆交于B 、C 两点,且ο30=∠DAC .(1)求弦BC 的长; (2)求AOC △的面积.21.已知关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根. (1)求k 的取值范围;(2)求证:1-=x 不可能是此方程的实数根.DCBA O ECADBO22.阅读下面的材料:小明在研究中心对称问题时发现:如图1,当点1A 为旋转中心时,点P 绕着点1A 旋转180°得到1P 点,点1P 再绕着点1A 旋转180°得到2P 点,这时点P 与点2P 重合.如图2,当点1A 、2A 为旋转中心时,点P 绕着点1A 旋转180°得到1P 点,点1P 绕着点2A 旋转180°得到2P 点,点2P 绕着点1A 旋转180°得到3P 点,点3P 绕着点2A 旋转180°得到4P 点,小明发现P 、4P 两点关于点2P 中心对称.(1)请在图2中画出点3P 、4P , 小明在证明P 、4P 两点关于点2P 中心对称时,除了说明P 、2P 、4P 三点共线之外,还需证明;(2)如图3,在平面直角坐标系xOy 中,当)3,0(1A 、)0,2(2 A 、)0,2(3A 为旋转中心时,点)4,0(P 绕着点1A 旋转180°得到1P 点;点1P 绕着点2A 旋转180°得到2P 点;点2P 绕着点3A 旋转180°得到3P 点;点3P 绕着点1A 旋转180°得到点4P L 点. 继续如此操作若干次得到点56P P L 、、,则点2P 的坐标为,点2017P 的坐为.图3图2图1五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知关于x 的一元二次方程02)12(2=++-x m mx . (1)求证:此方程总有两个实数根;(2)若此方程的两个实数根都是整数,求m 的整数值; (3)若此方程的两个实数根分别为1x 、2x ,求代数式5)(2))(12()(2122213231+++++-+x x x x m x x m 的值.24.已知在ABC △中,ο90=∠ACB ,26==CB CA ,AB CD ⊥于D ,点E 在直线CD 上,CD DE 21=,点F 在线段AB 上,M 是DB 的中点,直线AE 与直线CF 交于N 点. (1)如图1,若点E 在线段CD 上,请分别写出线段AE 和CM 之间的位置关系和数量关系:___________,___________;(2)在(1)的条件下,当点F 在线段AD 上,且2AF FD =时,求证:ο45=∠CNE ; (3)当点E 在线段CD 的延长线上时,在线段AB 上是否存在点F ,使得ο45=∠CNE .若存在,请直接写出AF 的长度;若不存在,请说明理由.DCBANM FED CBA 图1备用图25.在平面直角坐标系xOy 中,点A 、B 分别在x 轴、y 轴的正半轴上,且10=AB ,点M 为线段AB 的中点.(1)如图1,线段OM 的长度为________________;(2)如图2,以AB 为斜边作等腰直角三角形ACB ,当点C 在第一象限时,求直线OC 所对应的函数的解析式; (3)如图3,设点D 、E 分别在x 轴、y 轴的负半轴上,且10=DE ,以DE 为边在第三象限内作正方形DGFE ,请求出线段MG 长度的最大值,并直接写出此时直线MG 所对应的函数的解析式.GFEDxy O ABM图1图2CxyOABM BAOyx图3海淀区九年级第一学期期中练习2013.11数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3.评分参考中所注分数,表示考生正确做到此步应得的累加分数. 一、选择题(本题共32分,每小题4分) 题号 12345 6 7 8 答案A D D CABBC二、填空题(本题共16分,每小题4分)9.45°;10.20x x -=(二次项系数不为0,且常数项为0均正确);11.50°;12.21,622+-n n (每空2分).三、解答题(本题共30分,每小题5分) 13.(本小题满分5分)解:36324⨯+÷818=+………………………………………………………………………2分2322+=…………………………………………………………………4分 25=.……………………………………………………………………………5分14.(本小题满分5分)解:原方程可化为2+410x x -=,……………………………………………………1分141a ,b ,c ===-,2441(1)=20>0,∆=-⨯⨯-…………………………………………………………2分方程有两个不相等的实数根,244202522b b ac x a -±--±===-±,……………………………………4分即122525x ,x =-+=--.……………………………………………………5分15.(本小题满分5分)结论:CD BE =.……………………………………………………………………1分 证明:Θ△ABC 与△AED 是等边三角形,∴AE AD =,AB AC =,60CAB DAE ∠=∠=o.…2分 ∴CAB DAB DAE DAB ∠-∠=∠-∠,即CAD BAE ∠=∠.………………………………3分 在△CAD 和△BAE 中,EDCBAAC AB,CAD BAE,AD AE,=⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△BAE .…………………………………………………………4分 ∴CD =BE .…………………………………………………………………5分16.(本小题满分5分)解:Θ15-=x ,∴15x +=.∴5)1(2=+x .………………………………………………………………1分∴2215x x ++=.………………………………………………………………2分∴224x x +=.…………………………………………………………………3分 ∴225451x x +-=-=-.……………………………………………………5分17.(本小题满分5分)证明:过点O 作AB OM ⊥于M ,…………………………1分由垂径定理可得DM CM BM AM ==,.……………3分∴DM BM CM AM -=-.…………………………4分 即BD AC =.…………………………………………5分18.(本小题满分5分)解:设小路的宽度是x 米.………………………………………………………1分由题意可列方程,3(20)(12)20124x x --=⨯⨯.……………………………2分化简得, 232600x x -+=.解得, 12302x ,x ==.………………………………………………………3分由题意可知3020x =>不合题意舍去,2x =符合题意.…………………4分 答:小路的宽度是2米.……………………………………………………5分四、解答题(本题共20分,每小题5分) 19.(本小题满分5分)解:(1)∵关于x 的一元二次方程210x mx m -++=的一个根为2,∴22210m m -++=.……………………………………………………1分 ∴5m =.……………………………………………………………………2分∴一元二次方程为2560x x -+=.解得1223x ,x ==.…………………………………………………………3分∴5m =,方程另一根为3.(2)当长度为2的线段为等腰三角形底边时,则腰长为3,此时三角形的周长为2+3+3=8;………………………………………………………………4分当长度为3的线段为等腰三角形底边时,则腰长为2,此时三角形的周长为2+2+3=7. ………………………………………………………………5分MODCBA20.(本小题满分5分)解:(1)过点O 作OM ⊥BC 于M .由垂径定理可得:BM=CM .…1分∵30DAC ∠=o , ∴12OM OA =.∵直径DE =10, EA =1,∴=5OD OC OE ==.∴516OA OE EA =+=+=. ∴3OM =.…………………2分在R t △COM 中,222225316CM OC OM =-=-=. ∴4CM =. ∴4BM =.∴+8BC BM CM ==.……………………………………………………3分 (2)在R t △AOM 中,222226327AM OA OM =-=-=.∴33AM =.……………………………………………………………………4分 ∴+334AC AM CM ==+. ∵OM ⊥AC , ∴119(334)336222AOC S AC OM =⋅=⨯+⨯=+V .……………………………5分21.(本小题满分5分)解:(1)∵关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根,∴224(1)4=8+4>0k k k ∆=+-.………………………………………………2分 ∴1>2k -.…………………………………………………………………3分 (2)∵当1-=x 时,左边=222(1)x k x k -++22(1)2(1)(1)k k =--+⨯-+223k k =++…………………………………………4分 2(+1)20k =+>.而右边=0,∴左边≠右边.∴1-=x 不可能是此方程的实数根.……………………………………5分22.(本小题满分5分)(1)正确画出34P P 、点(图略).………………………………………………1分224=P P P P .……………………………………………………………………2分(2)(-4,-2).…………………………………………………………………3分(0,2).……………………………………………………………………5分MECA DB O五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.(本小题满分7分)解:(1)由题意可知0m ≠.2(21)42m m ∆=+-⨯⨯22=441(21)0m m m -+=-≥.……………………………………………2分∴此方程总有两个实数根.(2)方程的两个实数根为2(21)(21)2m m x m+±-=,∴1212x ,x m==.…………………………………………………………4分 ∵方程的两个实数根都是整数,且m 为整数,∴1m =±.…………………………………………………………………5分(3)∵原方程的两个实数根分别为1x 、2x ,∴211(21)20mx m x -++= 222(21)20mx m x -++=.……………………………………………………6分∴5)(2))(12()(2122213231+++++-+x x x x m x x m=1323211222[(21)2]+[(21)2]+5mx m x x mx m x x -++-++=12211222[(21)2]+[(21)2]+5x mx m x x mx m x -++-++=12005x x ⨯+⨯+=5.…………………………………………………………………………7分24.(本小题满分8分)(1)AE ⊥CM ,AE =CM .……………………………………………………2分(2)如图,过点A 作AG ⊥AB ,且AG =BM,,连接CG 、FG ,延长AE 交CM 于H .∵ο90=∠ACB ,26==CB CA ,∴∠CAB =∠CBA =45°,AB=2212CA CB +=. ∴∠GAC =∠MBC =45°. ∵AB CD ⊥,∴CD=AD=BD =162AB =. ∵M 是DB 的中点, ∴3BM DM ==. ∴3AG =. ∵2AF FD =,∴4 2.AF DF ==,∴+2+3=5.FM FD DM == ∵AG ⊥AF , ∴2222+3+4=5.FG AG AF ==FHNGM EDCBA∴.FG FM =……………………………………………………………………3分 在△CAG 和△CBM 中, CA CB CAG CBM AG BM =⎧⎪∠=∠⎨⎪=⎩,,, ∴△CAG ≌△CBM .∴CG =CM ,ACG BCM ∠=∠.∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠=o .………………………4分 在△FCG 和△FCM 中, CG CM FG FM CF CF =⎧⎪=⎨⎪=⎩,,, ∴△FCG ≌△FCM .∴FCG FCM ∠=∠.………………………………………………………5分 ∴45FCH ∠=o .由(1)知AE ⊥CM , ∴90CHN ∠=o∴ο45=∠CNE .………………………………………………………………6分 (3)存在.AF =8.…………………………………………………………………………8分25.(本小题满分7分)(1)5;…………………………………………………………………………………1分 (2)如图1, 过点C 分别作CP ⊥x 轴于P ,CQ ⊥y 轴于Q .∴∠CQB =∠CPA =90°,∵∠QOP =90°,∴∠QCP =90°. ∵∠BCA =90°,∴∠BCQ =∠ACP . ∵BC=AC ,∴△BCQ ≌△ACP .∴CQ=CP .………………………………3分 ∵点C 在第一象限,∴不妨设C 点的坐标为(a ,a )(其中0a ≠).设直线OC 所对应的函数解析式为kx y =,∴a ka =,解得k =1,∴直线OC 所对应的函数解析式为x y =.…………………………………4分 (3)取DE 的中点N ,连结ON 、NG 、OM .∵∠AOB=90°,∴OM =152AB =.同理ON =5.Fy OBDGNEAMx图2Q C xy O A BP 图1∵正方形DGFE ,N 为DE 中点,DE=10, ∴NG =2222=+10555DN DG =+=.在点M 与G 之间总有MG ≤MO +ON +NG (如图2),由于∠DNG 的大小为定值,只要12DON DNG ∠=∠,且M 、N 关于点O 中心对称时,M 、O 、N 、G 四点共线,此时等号成立(如图3).………………………5分∴线段MG 取最大值10+55.………………6分此时直线MG 的解析式x y 251+-=.……………………………………7分NM BAOyxDEG图3。
人教版2013-2014学年九年级上期中测试数学试题及答案

河北省邯郸市2013——2014学年上学期期中测试九年级数学试题一、填空题(每题3分,共30分) 1=____ ____. 2=x 的取值范围是 . 32==,且ab <0,则a b -=___ ____.4.若数字串“000”和数字串“101”既是轴对称图形,又是中心对称图形,那么数字串“110”是 .5.如图,△ABC 、△ACD 、△ADE 是三个全等的等边三角形,那么△ABC 绕着顶点A 沿着逆时针方向至少旋转度,才能与△ADE 完全重合.6.一个正边形绕它的中心至少要旋转 度,才能和原来五边形重合.7.已知方程x 2-7x +12=0的两根恰好是Rt△ABC 的两条边的长,则Rt△ABC •的第三边长为________.8.餐桌桌面是长160cm ,宽为100cm 的长方形,妈妈准备设计一块桌布,面积是桌面的2倍,且使四周垂下的边等宽.小明设四周垂下的边宽为x cm ,则应列方程为 . 9.如图,矩形ABCD 的边长1,AB AD ==ABCD 以B 为中心,按顺时针方向旋转到''''A B C D 的位置(点'A 落在对角线BD 上),则△'BDD 的形状为 . 10.某超市从我国西部某城市运进两种糖果,甲种a 千克,每千克x元,乙种b 千克,每千克y 元,如果把这两种糖果混合后销售,保本价是_________元/千克. 二、选择题(每题3分,共18分)11.若=-2)2(a 2-a ,则a 的取值范围是( )A .a =2B .a >2C .a ≥2D .a ≤2 12.在下面4个图案中,中心对称图形为( )ABC DE(第5题) ABCDD'C'(第9题)13.下列二次根式中,最简二次根式是( ) A .12 B .32+x C .23D .b a 2 14.如图,下列图形经过旋转后,与图(1)相同的是( )(第14题)图(1) A . B . C . D . 15.如果代数式4y 2-2y+5的值为7,那么代数式221y y -+的值等于( )A .2B .3C .-2D .-316.已知1x =-是关于x 的方程2220x ax a +-=的一个根,则a 为( )A .1B .-2C .1或-2D .2 三、解答题(共72分)17.(8分)计算(1)(3248)(1843);(2)2(13)(3131++-.18.(8分)解方程(1)2220x x --=; (2)22(38)(23)0x x +--=.19.(4分)先化简,再求值33(6)(436)y xxxy x xy x y y-,其中3,272x y ==.20.(4分)已知方程2(1)100x m x m +-+-=的一个根是3,求m 的值及方程的另一个根.21.(4分)如图,若将△ABC 的绕点C 顺时针旋转90°后得到△DEC ,则A 点的对应点D 的坐标是 ,B 点的对应点E 的坐标是 ,请画出旋转后的△DEC .(不要求写画法)22.(4分)如果关于x 的一元二次方程2(1)210m x x ---=有两个不相等的实数根,当m在它的取值范围内取最大整数时,求1014m m-的值.23.(6分)已知x 1,x 2是一元二次方程2x 2-2x +m +1=0的两个实数根. (1)求实数m 的取值范围;(2)如果x 1,x 2满足不等式7+4x 1x 2>x 12+x 22,且m 为整数,求m 的值.24.(6分)如图,正方形ABCD 的对角线相交于点O ,点O 是正方形'''A B C O 的一个顶点.如果两个正方形的边长都等于2,那么正方形'''A B C O 绕O 点无论怎样转动,两个正方形重叠的部分的面积是一个定值,请你写出这定值,并证明你的结论.25.(6分)观察下列分母有理化的计算:, (454)51,34341,23231,12121-=+-=--=+-=+在计算结果中找出规律,用含字母n (n 表示大于0的自然数)表示; 再利用这一规律计算下列式子的值:1)++L 1)的值.ODBFEAA‘B’C‘26.(7分)有100•米长的篱笆材料,•想围成一个矩形露天仓库,•要求面积不小于600平方米,在场地的北面有一堵长为50米的旧墙,有人用这个篱笆围成一个长40米,宽10米的矩形仓库,但面积只有400平方米,不合要求,•现请你设计矩形仓库的长和宽,使它符合要求.27.(7分)南通百货大搂服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元.元旦将至,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装因应降价多少元?28.(8分)等边△ABC边长为6,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转.(1)如图1,当P为BC的三等分点,且PE⊥AB时,判断△EPF的形状.(2)在(1)问的条件下,FE、PB的延长线交于点G,如图2,求△EGB的面积.(3)在三角板旋转过程中,若CF=AE=2,(CF≠BP),如图3,求PE的长.参考答案一、填空题1.23- 2.x ≥5 3.7- 4.轴对称 5.120 6.72 7.5或78.(1602)(1002)1601002x x ++=⨯⨯ 9.等边三角形 10.ax bya b++ 二、选择题11.D 12.B 13.B 14.D 15.A 16.C 三、解答题17.(1)30-;(2)633- 18.(1)1213,13x x ==(2)121,11x x =-=- 19.92,2xy 20.1,m =另一根为3- 21.(3,0),(2,2)D E 22.3 23.(1)m ≤12-;(2) 2-或1 24.14 25.2013 26. 27.减少库存,降价20元 28.(1)等边三角形;(23;(3)4.。
浙江省洞头县2013-2014学年九年级第一学期期中“六校联考”数学试卷

浙江省洞头县2013-2014学年九年级第一学期期中“六校联考”数学试卷(本卷满分150分 答题时间120分钟 )卷 Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选均不给分) 1.反比例函数xky =的图象经过点P(-2,3),则这个函数的图象位于( ) A .第二、三象限 B .第一、三象限 C .第二、四象限 D .第三、四象限 2. 如图,已知圆心角78BOC ∠=,则圆周角BAC ∠的度数是( ) A .156 B .39 C .78 D .123. 二次函数y=-2(x -1)2-3的图象顶点坐标是 ( )A . (-1,3)B . (-1,-3)C . (1,3)D . (1,-3) 4.抛物线232+=x y 是由抛物线23x y =经怎样平移得到?( ) A 、向左平移2个单位 B 、向右平移2个单位 C 、向上平移2个单位 D 、向下平移2个单位5. 已知一个扇形的弧长为10πcm ,圆心角是150º,则它的半径长为( )A .12cm B. 10cm C. 8cm D.6cm6. 圆锥的母线长为5cm ,底面半径为3cm ,那么圆锥的表面积为 ( )A. 15π cm 2B. 24πcm 2C. 30πcm 2D. 39πcm 27.若A (-4,y 1),B (-3,y 2),C (1,y 3)为二次函数y=x 2+4x -k 的图象上的三点,则 y 1,y 2,y 3的大小关系是( )A.y 1<y 2<y 3B.y 2<y 1<y 3C.y 3<y 1<y 2D.y 1<y 3<y 2 8. 小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数23.54.9h t t =-(t 的单位:s ,h 的单位:m)可以描述他 跳跃时重心高度的变化,则他起跳后到重心最高时所用 的时间(精确到0.01)是( )A.0.71sB.0.70sC.0.63sD.0.36s9.反比例函数xky =的图象如图所示,点A 是该 函数图象上一点,AM ⊥x 轴,垂足是点M ,如果 S △MOA =2, 则k 的值为( )A 2B -2C 4D -410.如图,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE ,BD 的延长线交于点C 。
2014九年级初三第一学期数学期中试卷(A) 及答案

九年级数学(A ) 第1页(共10页) 九年级数学(A ) 第2页(共10页)(第4题)(第10题)2013—2014学年度第一学期期中考试试卷九年级数学(A)一、精心选一选(本大题共10小题,每小题3分,共30分.每小题给出四个答案,其中只有一个正确的).1.如图所示的几何体的俯视图是( )正面A .B .C .D .2.如图.在菱形ABCD 中,对角线AC ,BD 交于点O ,下列说法错误..的是( ) A .AB ∥DC B .AC=BD C .AC ⊥BD D .OA=OC3.已知关于x 的方程062=--kx x 的一个根为x =3,则实数k 的值为( ) A .1 B .-1 C .2 D .-24.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向远移时,圆形阴影的大小的变化情 况是( )A .越来越小B .越来越大C .大小不变D .不能确定 5.已知直线y =ax (a ≠0)与双曲线的一个交点坐标为(2,6),则它们的另一个交点坐标是( )A . (﹣2,6)B .(﹣6,﹣2)C .(﹣2,﹣6)D .(6,2) 6.如图,点A 是反比例函数6y x=-(x < 0)的图象上的一点,过点 A 作平行四边形ABCD ,使点B 、C 在x 轴上,点D 在y 轴上,则平行四边形ABCD 的面积为( )A .12B .6C .3D .17.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,则参赛球队的个数是( ) A .5个B .6个C .7个D .8个8.如图,在矩形ABCD 中,AB=2,BC=4,对角线AC 的垂直平分线分别交AD 、AC 于点E 、O ,连接CE ,则CE 的长 为( )A. 3B.3.5C.2.5D.2.89.已知m ,n 是关于x 的一元二次方程x 2﹣3x +a =0的两个解,若(m ﹣1)(n ﹣1)=﹣6,则a的值为( ) A .﹣10 B . 4C . ﹣4D . 1010.如图,E 、F 分别是正方形ABCD 的边CD 、AD 上的点,且CE =DF ,AE 、BF 相交于点O ,下列结论:(1)AE =BF ;(2)AE ⊥BF ;(3)AO =OE ; (4)AOB DEOF S S ∆=四边形中正确的有( ) A. 4个B. 3个C. 2个D. 1个二、耐心填一填(本大题共5小题,每小题3分,共15分,请把答案填在答题卷相应的横线上方)11.如图,在△ABC 中,点D 、E 分别是AB 、AC 的中点. 若DE=3,则BC= . 12.已知反比例函数y=2x的图像经过点A (m ,1),则m 的值为。
2013-2014年九年级上期中考试数学试卷
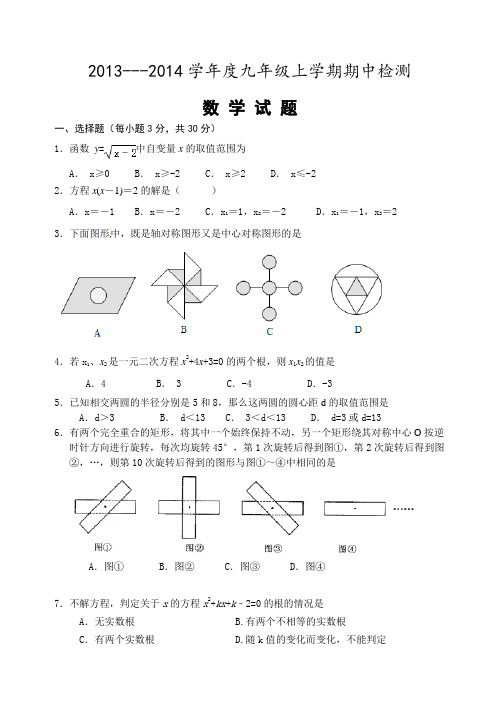
2013---2014学年度九年级上学期期中检测数学试题一、选择题(每小题3分,共30分)1.函数y=中自变量x的取值范围为A. x≥0 B. x≥-2 C. x≥2 D. x≤-22.方程x(x-1)=2的解是()A.x=-1 B.x=-2 C.x1=1,x2=-2 D.x1=-1,x2=23.下面图形中,既是轴对称图形又是中心对称图形的是4.若x1、x2是一元二次方程x2+4x+3=0的两个根,则x1x2的值是A.4 B. 3 C.-4 D.-35.已知相交两圆的半径分别是5和8,那么这两圆的圆心距d的取值范围是 A.d>3 B. d<13 C. 3<d<13 D. d=3或d=136.有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~④中相同的是A.图① B.图②C.图③D.图④7.不解方程,判定关于x的方程x2+kx+k﹣2=0的根的情况是A.无实数根 B.有两个不相等的实数根C.有两个实数根 D.随k值的变化而变化,不能判定8.某品牌电脑2009年的销售单价为7200元,由于科技进步和新型电子原材料的开发运用,该品牌电脑成本不断下降,销售单价也逐年下降.至2011年该品牌电脑的销售单价为4900元,设2009年至2010年,2010年至2011年这两年该品牌电脑的销售单价年平均降低率均为x,则可列出的正确的方程为A.4900(1+x)2=7200B.7200(1-2x)=4900C.7200(1-x)=4900(1+x)D.7200(1-x)2=49009.如图,⊙O是△ABC的外接圆,∠OBC=30°,则∠BAC的度数为A.30°B.45°C.60°D.70°10.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,公路PQ上A处距离O点240米,如果火车行驶时,周围200米以内会受到噪音的影响,那么火车在铁路MN上沿MN方向以72千米/小时的速度行驶时,A处受到噪音影响的时间为A.12秒B.16秒C.20秒 D.24秒二、填空题(每小题3分,共18分)11.计算:= ;(-)2= ;- = .12.已知点A(3,2),则点A绕原点O顺时针旋转180°后的对应点A1的坐标为.13.关于的一元二次方程的一个根为,则实数的值是 .14.两个数的差为8,积为48,则这两个数是.15.国庆期间某单位排练节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为 cm2(π取3)16.如图,在平面直角坐标系中,⊙O的半径为5,点P为直线y=-x+4上的一点,过点P作⊙O的切线PC、PD,切点分别为C、D,若PC⊥PD,则点P的坐标为.三、解答题(共9小题,共72分)17.(本题6分)解方程:x2+3x+1=018.(本题6分)计算:2738141222-++19.(本题6分)如图,在⊙O 中, 弦AB 与CD 相交于E ,且AB =CD . 求证:△AEC ≌△DEB20.(本题6分)如图所示,正方形网格中,△ABC 为格点三角形(即三角形的顶点都在格点上).(1)把△ABC 沿BA 方向平移后,点A 移到点A 1,在网格中画出平移后得到的△A 1B 1C 1; (2)把△A 1B 1C 1绕点A 1按逆时针方向旋转90°,在网格中画出旋转后的△A 1B 2C 2; (3)如果网格中小正方形的边长为1,求点B 经过(1)、(2)变换后的路径总长.EOACB D21.(本题8分)已知:关于x的方程kx2-(3k-1)x+2(k-1)=0.(1)求证:无论k为何实数,方程总有实数根;(2)若此方程有两个实数根x1,x2,且│x1-x2│=2,求k的值.22.(本题8分)如图,⊙O是Rt△ABC中以直角边AB为直径的圆,⊙O与斜边AC交于D,过D作DH⊥AB于H,又过D作直线DE交BC于点E,使∠HDE=2∠A.求证:(1)DE是⊙O的切线;(2)OE是Rt△ABC的中位线.23.(本题10分)某超市经销一种成本为每千克20元的水产品,据市场分析,若按每千克30元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg.(1)当销售单价定为每千克35元时,计算销售量和月销售利润;(2)设销售单价为x元,月销售利润为y元,请求出y与x的函数关系;(3)超市想在月销售成本不超过6000元的情况下,使得月销售利润达到8000元,销售单价应为多少?24.(本题10分)如图1,在△ABC中,∠ABC=90°,AB=BC,BD为斜边AC上的中线,将△ABD绕点D顺时针旋转α(0°<α<180°)角得到△EFD,点A的对应点为点E,点B的对应点为点F,连接BE、CF.(1)判断BE与CF的位置、数量关系,并说明理由;(2)若连接BF、CE,请直接写出在旋转过程中四边形BCEF能形成哪些特殊四边形;(3)如图2,将△ABC中AB=BC改成AB≠BC时,其他条件不变,直接写出α为多少度时(1)中的两个结论同时成立.25.(本题12分)如图1,在平面直角坐标系中,⊙O1与x轴切于A(-3,0)与y轴交于B、C两点,BC=8,连接AB.(1)求证:∠ABO1=∠ABO;(2)求AB的长;(3)如图2,过A、B两点作⊙O2与y轴的正半轴交于M,与O1B的延长线交于N,当⊙O2的大小变化时,得出下列两个结论:①BM-BN的值不变;②BM+BN的值不变.其中有且只有一个结论正确,请判断出正确结论并证明.。
2013—2014学年度第一学期九年级数学期中考试

2013—2014 学年度第一学期九年级期中考试
7.把方程 x 2 6 x 5 0 的左边配成一个完全平方式得 A. x 3 9
2
B. x 3 9
2
C. x 3 4
2
D. x 3 4
2
数
学
说明:1.全卷共 4 页,考试用时 100 分钟,满分为 120 分. 2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的班别、姓名、 学号. 3.选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂 黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试题上. 4.非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区 域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和 涂改液.不按以上要求作答的答案无效. 5.考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交回. 一、选择题(本大题 10 小题,每小题 3 分,共 30 分)在每小题列出的四个选项中,只有 一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1.化简 8 的结果是 A. 2 3 B. 3 2 C. 2 2 D. 4
一、选择题(本大题 10 小题,每小题 3 分,共 30 分) 题号 1 2 3 4 5 6 答案 C D D C A C
4 3 4
二、填空题(本大题 6 小题,每小题 4 分,共 24 分) 9 9 3 11. x1 , x2 (答对一个给 2 分) ;12. ;13.135;14. 80 ;15. 20 ;16.30. 2 2 4 三、解答题(一) (本大题 3 小题,每小题 5 分,共 15 分.本解答题参考答案只提供一种解 法,考生选择其它解法只要解答正确,相应给分.) 17.解:原式= 4 2 4
2013~2014年上学期九年级期中考试数学试题卷(附答题卷)

九年级数学试卷一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母代号填写在答题卡相应位置.......上.) 1.函数2(1)2y x =+-的最小值是 ( ▲ ) A .1 B .-1 C .2 D .-23.如果⊙A 的半径是4cm ,⊙B 的半径是10cm ,圆心距AB =8cm ,那么这两个圆的位置关系是 ( ▲ ) A .外离 B .外切 C .相交 D .内切 4.如果圆锥的底面半径为3cm ,母线长为4cm ,那么它的侧面积等于( ▲ )A .24π2cmB .12π2cmC .122cmD .6π2cm5.将抛物线23y x =先向上平移3个单位,再向左平移2个单位后得到的抛物线解析式为( ▲ )A .23(2)3y x =++B .23(2)3y x =-+C .23(2)3y x =+- D .23(2)3y x =--7.某种型号的电视机经过连续两次降价,每台售价由原来的1500元,降到了980元,设平均每次降价的百分率为x ,则下列方程中正确的是 ( ▲ ) A .215001)980x -=( B .21500(1)980x += C .2980(1)1500x -= D .2980(1)1500x +=8.如图,抛物线2(0)y ax bx c a =++≠经过点(-1,0),对称轴为:直线1x =,则下列结论中正确..的是 ( ▲ ) A .a >0 B .当1>x 时,y 随x 的增大而增大 C .c <0D .3x =是一元二次方程20(0)ax bx c a ++=≠的一个根二、填空题(本大题共10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置.......上.) 12.如图,A 、B 、C 是⊙O 上的三个点,∠ABC =25°,则∠AOC 的度数是 ▲ °.xOy -1 113.如图,PA 、PB 分别切⊙O于A 、B 两点,∠APB =50°,则∠AOP = ▲ °.14.如图所示,抛物线2y ax bx c =++(0a ≠)与x 轴的两个交点分别为(20)A -,和(60)B ,,当0y <时,x 的取值范围是 ▲ . 15.当m = ▲ 时,一元二次方程240x x m -+=(m 为常数)有两个相等的实数根. 16.已知抛物线2y ax bx c =++(a >0)的对称轴为直线12x =,且经过点(-3,1y ),(4,2y ),试比较1y 和2y 的大小:1y ▲ 2y (填“>”,“<”或“=”). 17. 已知实数m 是关于x 的方程2310x x --=的一根,则代数式2262m m -+值为 ▲ . 18.如图,依次以三角形,四边形,…,n 边形的各顶点为圆心画半径为1的圆,且任意两圆均不相交.把三角形与各圆重叠部分面积之和记为3S ,四边形与各圆重叠部分面积之和记为4S ,…,n 边形与各圆重叠部分面积之和记为n S ,则100S 的值为 ▲ .(结果保留π)……三、解答题(本大题共10小题,共96分.请在答题卡指定区域.......内作答,解答时应写出文 字说明、证明过程或演算步骤.)20.(本题满分8分)解方程:2(3)2(3)0x x x -+-=22.(本题满分8分)如图,已知CD 是⊙O 的直径,弦AB CD ⊥,垂足为点M ,点P 是AB 上一点,且60BPC ∠=︒.试判断ABC ∆的形状,并说明你的理由.24.(本题满分10分)如图,抛物线232(0) 2y ax x a=--≠的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).(1)求抛物线的解析式;(2)判断△ABC的形状,说出△ABC外接圆的圆心位置,并求出圆心的坐标.26.(本题满分10分)如图,AB是⊙O的直径,直线EF切⊙O于点C,AD⊥EF于点D.(1)求证:AC平分∠BAD;(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.(结果保留π)27.(本题满分12分)在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:(1)观察图象判断y与x之间的函数关系,并求出函数关系式;(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润W(元)与销售单价x(元/个)之间的函数关系式;(3)若许愿瓶的进货成本不超过900元,要想获得最大的利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.28.(本题满分12分)如图,抛物线2(0)y ax bx c a=++≠与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).(1)求抛物线的解析式及顶点D的坐标;(2)若P为线段BD上的一个动点,点P的横坐标为m,试用含m的代数式表示点P的纵坐标;(3)过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标;(4)若点F是第一象限抛物线上的一个动点,过点F作FQ∥AC交x轴于点Q.当点F 的坐标为时,四边形FQAC是平行四边形;当点F的坐标为时,四边形FQAC是等腰梯形(直接写出结果,不写求解过程).2013年秋学期期末教研片教学调研九年级数学参考答案及评分标准一、选择题(本大题共8小题,每题3分,计24分)题号 1 2 3 4 5 6 7 8 答案DACBADAD二、填空题(本大题共10小题,每题3分,计30分)9.4 10.3a - 11.5 12.50 13.65 14.x <-2或x >6 15.4 16.= 17.4 18.49π 三、解答题(本大题共9小题,计96分)19.解:原式=2218122+-- ………………………………………………4分 =17 ………………………………………………8分20.解:0)23)(3(=+--x x x ………………………………………………4分 0)33)(3(=--x x03=-x 或033=-x ………………………………………………6分∴31=x ,12=x ………………………………………………8分 21.解:(1)统计量 平均数 极差 方差 立定跳远 8 4 2 一分钟跳绳820.4………………………………………………6分 (说明:每空2分)(2)选一分钟跳绳 ………………………………………………7分因为平均分数相同,但一分钟跳绳成绩的极差和方差均小于立定跳远的极差和方差,说明一分钟跳绳的成绩较稳定,所以选一分钟跳绳.(答案基本正确,不扣分)………………………………………………8分22.解:方法一:ABC ∆为等边三角形 ……………………………………1分 ∵AB ⊥CD ,CD 为⊙O 的直径∴AC BC = ……………………………………3分 ∴AC =BC ……………………………………4分 又∵在⊙O 中,∠BPC =∠A ……………………………………5分 ∵∠BPC =60°∴∠A =60° ……………………………………7分 ∴ABC ∆为等边三角形 ……………………………………8分 方法二:ABC ∆为等边三角形 ……………………………………1分∵AB ⊥CD ,CD 为⊙O 的直径∴AM =BM ……………………………………3分 即CD 垂直平分AB∴AC =BC ……………………………………4分 又∵在⊙O 中,∠BPC =∠A ……………………………………5分 ∵∠BPC =60°∴∠A =60° ……………………………………7分 ∴ABC ∆为等边三角形 ……………………………………8分23.(1)证明:∵四边形ABCD 是矩形∴AC =BD , AB ∥CD又∵BE ∥AC∴四边形ABEC 是平行四边形 ……………………………………3分 ∴BE = AC∴BD =BE ……………………………………5分(2)解:∵四边形ABCD 是矩形∴∠DCB =90° ∵∠DBC =30︒,CD =4∴BD =8,BC =43 ……………………………………7分 ∴AB =DC =CE =4,DE =8 ……………………………………8分 ∵AB ∥DE ,AD 与BE 不平行∴四边形ABED 是梯形,且BC 为梯形的高∴四边形ABED 的面积=1()2AB DE BC +⨯=1(48)432+⨯=243∴四边形ABED 的面积为243 ……………………………………10分(若不说明四边形ABED 是梯形,直接按梯形面积公式计算不扣分,其它方法,参照给分)24.解:(1)∵点B (4,0)在抛物线232(0)2y ax x a =--≠的图象上 ∴3016422a =-⨯- ……………………………………2分 ∴12a =∴抛物线的解析式为:213222y x x =--………………………………4分 (2)△ABC 为直角三角形 ……………………………………5分令0x =,得:2y =- ∴C (0,-2) 令0y =,得2132022x x --=∴11x =-,24x =∴A (-1,0),B (4,0) ……………………………………7分 ∴AB =5,AC =5,BC =20 ∴222AC BC AB +=∴△ABC 为直角三角形 ……………………………………8分 ∴AB 为△ABC 外接圆的直径∴该外接圆的圆心为AB 的中点,且坐标为:(32,0)…………………10分 25.解:(1)若四边形ABCD 是菱形则AB =AD又∵AB 、AD 的长是方程的两个实数根∴240b ac -= ……………………………………1分即21()4()024m m --⨯-= ∴2210m m -+=∴121m m == ……………………………………3分此时方程可化为:2104x x -+=∴1212x x == ……………………………………4分∴当1m =时,四边形ABCD 是菱形,菱形的边长为12……………………5分(2)∵AB =2即此时方程的一个根为2 ……………………………………6分∴把2x =代入04122=-+-m mx x 得: 52m =……………………………………7分 ∴2515102224x x -+⨯-=∴1212,2x x == ……………………………………9分即此时平行四边形相邻的两边长分别为:2,12∴平行四边形的周长为5 ……………………………………10分26.解:(1)证明:连接OC∵直线EF 切⊙O 于点C ∴OC ⊥EF ∵AD ⊥EF∴OC ∥AD ……………………………………2分 ∴∠OCA =∠DAC ∵ OA =OC∴∠BAC =∠OCA ……………………………………4分 ∴∠DAC =∠BAC即AC 平分∠BAD ……………………………………5分(2)∵∠ACD =30°,∠OCD =90°∴∠OCA =60°. ∵OC =OA∴△OAC 是等边三角形 ∵⊙O 的半径为2∴AC =OA =OC =2,∠AOC =60° ……………………………………7分 ∵在R t △ACD 中,AD =12AC =1 由勾股定理得:DC =3 ……………………………………8分 ∴阴影部分的面积=S 梯形OCDA ﹣S 扇形OCA=12×(2+1)×3﹣2602360π⋅⋅33223π=- ∴阴影部分的面积为:33223π- ……………………………………10分 27.解:(1)由图象知:y 是x 的一次函数设y kx b =+ ……………………………………1分∵图象过点(10,300),(12,240)∴1030012240k b k b +=⎧⎨+=⎩ ……………………………………2分∴30600k b =-⎧⎨=⎩……………………………………3分∴30600y x =-+当14x =时,180y =;当16x =时,120y =即点(14,180),(16,120)均在函数30600y x =-+的图象上∴y 与x 之间的函数关系式为:30600y x =-+…………………………4分 (不把另两对点代入验证不扣分)(2)(6)(30600)W x x =--+ ……………………………………6分2307803600W x x =-+-即W 与x 之间的函数关系式为:2307803600W x x =-+-……………………………………8分(3)由题意得6(-30x +600)≤900解之得:x ≥15 ……………………………………9分而2307803600W x x =-+-230(13)1470W x =--+ ……………………………………10分 ∵-30<0∴当x >13时,W 随x 的增大而减小又∵x ≥15∴当x =15时,W 最大=1350即以15元/个的价格销售这批许愿瓶可获得最大利润,最大利润是1350元 ……………………………………12分28.解:(1)∵抛物线2(0)y ax bx c a =++≠与x 轴交于点A (-1,0)、B (3,0), ∴可设抛物线的解析式为:(1)(3)y a x x =+- ……………………1分 又∵抛物线 与y 轴交于点C (0,3), ∴3(01)(03)a =+-∴1a =-∴(1)(3)y x x =-+-即抛物线的解析式为:223y x x =-++ ……………………2分 ∴2(1)4y x =--+∴抛物线顶点D 的坐标为(1,4) ……………………3分(2)设直线BD 的解析式为:y kx b =+由B (3,0),D (1,4)得304k b k b +=⎧⎨+=⎩解得26k b =-⎧⎨=⎩∴直线BD 的解析式为26y x =-+ ……………………5分 ∵点P 在直线PD 上,点P 的横坐标为m∴点P 的纵坐标为:26m -+ ……………………6分 (3)由(1),(2)知:OA =1,OC =3,OM = m ,PM =26m -+ ∴OAC PMAC OMPC S S S ∆=+四边形梯形()111332622m m =⨯⨯+⨯-+⨯29322m m =-++ ……………………………………8分29105416m ⎛⎫=--+ ⎪⎝⎭∵9134<<,∴当94m =时,四边形PMAC 的面积取得最大值为10516…9分此时点P的坐标为(9342,)……………………10分(4)(2,3);(1115416,)(每空1分)……………………12分。
初中数学 浙江省洞头县第一学期期中“六校联考”九年级数学考试卷

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:反比例函数的图象经过点P(-2,3),则这个函数的图象位于()A.第二、三象限 B.第一、三象限 C.第二、四象限 D.第三、四象限试题2:如图,已知圆心角,则圆周角的度数是()A. B.C. D.试题3:二次函数y=-2(x-1)2-3的图象顶点坐标是()A. (-1,3) B. (-1,-3) C. (1,3) D. (1,-3)试题4:抛物线是由抛物线经怎样平移得到?()评卷人得分A、向左平移2个单位B、向右平移2个单位C、向上平移2个单位D、向下平移2个单位试题5:已知一个扇形的弧长为10πcm,圆心角是150º,则它的半径长为()A.12cm B. 10cm C. 8cm D.6cm试题6:圆锥的母线长为5cm ,底面半径为3cm,那么圆锥的表面积为()A. 15 cm2B. 24cm2C. 30cm2D. 39cm2试题7:若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-k的图象上的三点,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y2试题8:小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间(精确到0.01)是( )A.0.71sB.0.70sC.0.63sD.0.36s试题9:反比例函数的图象如图所示,点A是该函数图象上一点,AM⊥x轴,垂足是点M,如果△MOA=2,则k的值为()A 2 B -2 C 4 D -4试题10:如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE,BD的延长线交于点C。
2013--2014学年第一学期初三年级数学期中考试卷

第 1 页,共 4 页学 ◆校 班级 学号 姓名__________________________◆◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆2013--2014学年第一学期初三年级数学期中考试卷一、选择题:本题共8题,每题4分,共32分。
1.已知4x=7y(y ≠0),则下列比例式成立的是( )A 、x 4 = y 7B 、x 7 = y4C 、x y = 47D 、x 4 = 7y2在Rt △ABC 中,∠ C =90°,若BC =1,ABtan A 的值为( ) ABC .12D .23.若两个相似三角形的相似比为1∶2,则它们面积的比为( )A .2∶1B .1∶2C .1∶4D .1∶54. 抛物线y =-(x +2)2-3的顶点坐标是( ).(A) (2,-3); (B) (-2,3); (C) (2,3); (D) (-2,-3) 5、下列命题中,正确的是( ) A 、相似三角形是全等的三角形 B 、一个角为30°的两个等腰三角形相似 C 、全等三角形都是相似三角形 D 、所有等腰直角三角形不一定相似 6、如图所示,河堤横断面迎水坡BC:AC =1BC =5m ,则坡面AB 的长度是( )A .10mB .C .15mD .7、要从函数2x y =的图像得到函数32+=x y 的图像,则抛物线2x y =必须A 、向上平移3个单位B 、向下平移3个单位C 、向左平移3个单位D 、向右平移3个单位8.给出下列命题及函数x y =,2x y =和xy 1=的图象 ①如果21a a a >>,那么10<<a ;②如果a a a 12>>,那么1>a ; ③如果a a a >>21,那么01<<-a ;④如果a aa >>12时,那么1-<a .则(A )正确的命题是①④ (B )错误..的命题是②③④ (C )正确的命题是①② (D )错误..的命题只有③二、填空题:本题共4题,每题4分,共16分。
2013-2014上期中初三数学试题

2013-2014学年第一学期期中考试初三数学试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共5页.满分120分.考试时间120分钟.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将区(县)、毕业学校、姓名、考试号、座号填写在答题卡和试卷的相应位置.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号.答案不能答在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答(作图时可用2B 铅笔),答案必须写在答题卡各题目指定区域内相应的位置,要求字体工整、笔迹清晰;如需改动,先划掉原来的答案,然后再写上新的答案.答案不能写在试卷上.4.答案不能使用涂改液、胶带纸、修正带修改.不按以上要求作答的答案无效.第Ⅰ卷(选择题 共45分)一、选择题:本题共15小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项涂在答题卡的相应位置上.每小题3分,错选、不选或选出的答案超过一个,均记零分. 1、计算2a 2·a 3的结果是( )A .2a 6B .2a 5C .4a 5D .4a 6 2、使分式2+x x有意义的x 的取值范围为( ) A .2≠x B .2-≠x C .2->x D .2<x 3、点A (1,m )在y =2x 的图象上,则m 的值是( ) A .1 B .2 C .21D .0 4、化简aa 3,正确的结果为( )A .aB .2aC .1-aD .2-a 5、下列运算错误的是( )A .22)()(a b b a --=1 B .1-=+--ba b a C .b a b a b a b a 321053.02.05.0-+=-+ D .a b ab b a b a +-=+- 6、下列各式计算正确的是( )A .224()a a =B .2a a a +=C .22232a a a ÷=D .a 4·a 2=a 87、小芳的爷爷每天坚持体育锻炼,某天他慢步行走....到离家较远的公园,打了一会儿太极拳,然后沿原路跑步..到家里,下面能够反映当天小芳爷爷离家的距离.....y (米)与时间x (分钟)之间的关系的大致图象是()8、一次函数)0(≠+=k b kx y 的图象如图所示,当y >0时,x 的取值范围是 ( )A .x <0B .x >0C .x <2D .x >29、如图,一次函数y =(m -2)x -1的图象经过二、三、四象限,则m 的取值范围是( ) A .m >0 B .m <0 C .m >2 D .m <210、下列等式从左到右的变形,属于因式分解的是( ) A .a (x -y )=ax -ay B .x 2+2x +1=x (x +2)+1 C .(x +1)(x +3)=x 2+4x +3D .x 3-x =x (x +1)(x -1)11、图(1)是一个长为2a ,宽为2b (a >b )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )(第9题图)A .2abB .(a +b )2C .(a -b )2D .a 2-b 2 12、下列各式计算正确的是 ( )A .x x x x x x 4128)132(4232---=-+-B .3322))((y x y x y x +=++C .2161)14)(14(x x x -=---D .22242)2(y xy x y x +-=-13、若m -n = -1,则(m -n )2-2m +2n 的值是( )A .3B .2C .1D .-1 14、根据下表中一次函数的自变量x 与函数y 的对应值,可得p 的值为( )A .1B .-1C .3D .-315、如图,函数y =2x 和y =ax +4的图象相交于点A (m ,3),则不等式2x < ax + 4的解集为( )A .23<x B .3<x C .23>x D .3>x第Ⅱ卷(非选择题 共75分)二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果. 16、(-a 2b 2)2·a =___________. 17、使分式121x x +-的值为零的条件是x = .18、已知942++my y 是完全平方式,则m 的值是__________.19、已知实数a 、b 满足:a +b =2,a -b =5,则(a +b )3·(a -b )3的值是___________. 20、在平面直角坐标系中,点O 是坐标原点,过点A (1,2)的直线y=kx+b 与x 轴交于点B ,且 S △AOB =4,则k 的值为 .三、解答题:本大题共7小题,共55分.解答要写出必要的文字说明、推理过程或演算步骤. 21、计算(每题3分,共9分) (1) 计算2()()2a b a b b +-+(2) 化简:2(3)(2)a a a ++-(3)约分:yx y xy x +++3692222、(每题3分,共6分) 分解因式:x 2y -2xy +y分解因式:39a a -23、(本题满分7分)已知25)(2=+b a ,9)(2=-b a ,求ab 与22b a +的值.24、(本题满分7分)已知一次函数的图象经过点(3,6)与点(21,21-),求这个函数的解析式.25、(本题满分8分)点P (x ,y )在第一象限,且y x +=8,点A 的坐标为(6,0),设△OP A 的面积为S .(1)求S 关于x 的函数解析式,并求出x 的取值范围; (2)求S =12时P 点坐标.26、(本题满分9分)小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
秋季学期初三上期期中联考数学试卷附答案

2013年秋季学期初三上期期中联考数学试卷(附答案)安庆市2013~2014学年度第一学期期中十六校联考九年级数学试题命题:长风中学审题:长风中学(考试时间:120分钟满分:150分)题号一二三四五六七总分得分得分评卷人一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出代号为A、B、C、D的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分.1.下列函数是二次函数的是()A.B.C.D.2.与抛物线的图象形状相同的抛物线为()A.B.C.D.3.对于反比例函数,下列说法不正确的是()A.它的图象分布在第一、三象限B.点在它的图象上C.它的图象是中心对称图形D.随的增大而增大4.如图,直线与反比例函数和的图象分别交于A、B两点,点C是轴上任意一点,则△ABC的面积为()A.1B.3C.4D.85.已知抛物线与轴没有交点,那么该抛物线的顶点所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限6.已知,下列各式一定成立的是()A.B.C.D.7.如图,在△中,∥,分别与、相交于点、,若,则︰的值为()A.B.C.D.8.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是()9.如图所示,顶角为36°的等腰三角形,其底边与腰之比等于,这样的三角形叫做黄金三角形。
已知,为第一个黄金三角形,为第二个黄金三角形,为第三个黄金三角形,以此类推,第2014个黄金三角形的周长为()A.B.C.D.10.给出下列命题及函数,和的图象①如果,那么;②如果,那么;③如果,那么;④如果时,那么。
则()A.正确的命题是①④B.错误的命题是②③④C.正确的命题是①②D.错误的命题只有③题号12345678910答案得分评卷人二、填空题(本大题共4小题,每小题5分,满分20分)11.二次函数的顶点坐标是.12.若线段.13.如图,已知函数与(a0,b0)的图象交于点P,点P的纵坐标为1,则关于x的方程=0的解为.14.如图,过内一点分别作三边的平行线,形成三个小三角形①、②、③,如果这三个小三角形面积分别为1、4、9,则的面积为。
洞头县2013学年第一学期期中“六校联考”九年级(上)科学试卷(到
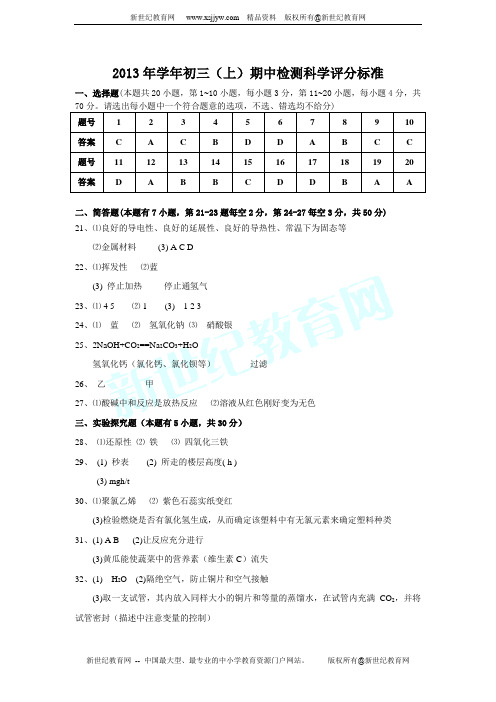
2013年学年初三(上)期中检测科学评分标准一、选择题(本题共20小题,第1~10小题,每小题3分,第11~20小题,每小题4分,共70分。
请选出每小题中一个符合题意的选项,不选、错选均不给分)题号 1 2 3 4 5 6 7 8 9 10 答案 C A C B D D A B C C 题号11 12 13 14 15 16 17 18 19 20 答案 D A B B C D D B A A二、简答题(本题有7小题,第21-23题每空2分,第24-27每空3分,共50分)21、⑴良好的导电性、良好的延展性、良好的导热性、常温下为固态等⑵金属材料(3) A C D22、⑴挥发性⑵蓝(3) 停止加热停止通氢气23、⑴ 4 5 ⑵ 1 (3) 1 2 324、⑴蓝⑵氢氧化钠⑶硝酸银25、2NaOH+CO2==Na2CO3+H2O氢氧化钙(氯化钙、氯化钡等)过滤26、乙甲27、⑴酸碱中和反应是放热反应⑵溶液从红色刚好变为无色三、实验探究题(本题有5小题,共30分)28、⑴还原性⑵铁⑶四氧化三铁29、(1) 秒表(2) 所走的楼层高度( h )(3) mgh/t30、⑴聚氯乙烯⑵紫色石蕊实纸变红(3)检验燃烧是否有氯化氢生成,从而确定该塑料中有无氯元素来确定塑料种类31、(1) A B (2)让反应充分进行(3)黄瓜能使蔬菜中的营养素(维生素C)流失32、(1) H2O (2)隔绝空气,防止铜片和空气接触(3)取一支试管,其内放入同样大小的铜片和等量的蒸馏水,在试管内充满CO2,并将试管密封(描述中注意变量的控制)四、分析计算题(本题共4小题,第33题4分,第34题8分,第35题8分。
第36题10分)33、⑴CH4⑵混合物34、(1)稀盐酸(2)(3) 氯化钠氢氧化钠35、(1)机械能36、(1) C (2)22(3)(4)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省洞头县2013-2014学年第一学期期中“六校联考”九年级数学试卷(本卷满分150分 答题时间120分钟 )卷 Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选均不给分) 1.反比例函数xky =的图象经过点P(-2,3),则这个函数的图象位于( ▲ ) A .第二、三象限 B .第一、三象限 C .第二、四象限 D .第三、四象限 2. 如图,已知圆心角78BOC ∠= ,则圆周角BAC ∠的度数是( ▲ )A .156B .39C .78D .123. 二次函数y=-2(x -1)2-3的图象顶点坐标是 ( ▲ ) A . (-1,3) B . (-1,-3) C . (1,3) D . (1,-3) 4.抛物线232+=x y 是由抛物线23x y=经怎样平移得到?( ▲ )A 、向左平移2个单位B 、向右平移2个单位C 、向上平移2个单位D 、向下平移2个单位5. 已知一个扇形的弧长为10πcm ,圆心角是150º,则它的半径长为(▲ )A .12cm B. 10cm C. 8cm D.6cm6. 圆锥的母线长为5cm ,底面半径为3cm ,那么圆锥的表面积为 ( ▲ )A. 15π cm 2B. 24πcm 2C. 30πcm 2D. 39πcm 27.若A (-4,y 1),B (-3,y 2),C (1,y 3)为二次函数y=x 2+4x -k 的图象上的三点,则 y 1,y 2,y 3的大小关系是( ▲ )A.y 1<y 2<y 3B.y 2<y 1<y 3C.y 3<y 1<y 2D.y 1<y 3<y 2 8. 小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数23.5 4.9h t t =-(t 的单位:s ,h 的单位:m)可以描述他 跳跃时重心高度的变化,则他起跳后到重心最高时所用 的时间(精确到0.01)是( ▲ )A.0.71sB.0.70sC.0.63sD.0.36s9.反比例函数xky =的图象如图所示,点A 是该 函数图象上一点,AM ⊥x 轴,垂足是点M ,如果 S △MOA =2, 则k 的值为( ▲ )A 2B -2C 4 D-410.如图,AB 是⊙O 的直径,点D 、E 是半圆的三等分点,AE ,BD 的延长线交于点C 。
若CE=2,则图中阴影部分的面积是( ▲ )A .334-πB .π32—23 C .332-π D .π31—23卷 Ⅱ二、填空题(本题有6小题,每小题5分.共30分)11. 已知直角三角形的两条直角边长分别为6 cm 和8 cm,则这个直角三角形的外接圆的半径为 ▲ cm.12. 已知⊙O 的半径为5,弦AB ∥CD ,且AB=6,CD=8,则弦AB 与CD 之间的距离是 ▲ . 13.如图在Rt △ABC 中,∠C =90°,CA =CB =2,分别以A 、B 、C 为圆心,以1 为半径画弧,三条弧与边 AB 所围成的阴影部分的面积是 ▲ 。
14.如图,在Rt △ABC 中,∠C=90°,∠A=60°,AB=2㎝,将△ABC 绕点B 旋转至△A 1BC 1的位置, 且使A 、B 、C 1三点在同一直线上,则点A 经过 的路线的长度是 ▲ cm.15.如图,在Rt △ABC 中,∠C=90°,AC=3cm ,BC=4cm ,以C 为圆心,CA 为半径的圆交斜边于D ,则BD 的长 为 ▲ cm .16.如图,△P 1OA 1 、△P 2A 1A 2 、△P 3A 2A 3 、…△P 100A 99A 100是等腰直角三角形 ,点P 1 、P 2 、 P 3 、……、P 100在反比列函数4y x=的图象上,斜边OA 1 、A 1A 2 、A 2A 3 、……、A 99A 100都在x 轴上, 则点A 100的坐标是 ▲ .B A17.(本题8分)利用尺规作图,找出右图残破圆轮的圆心,并保留作图痕迹. 18.(本题8分)已知:如图,AD 、BC 是⊙O 的两条弦, 且BC AD =.求证:CD AB =。
19.(本题10分)已知二次函数的图象经过点(0,3),顶点坐标为(1,4), (1)求这个二次函数的解析式(2)求图象与x 轴交点A 、B 两点的坐标. (3)图象与y 轴交点为点C ,求三角形ABC 的面积. 20. (本题8分)在直径是52cm 的圆柱形油槽内装入一些油后,截面如图 所示,如果油的最大深度CD 为16cm ,求油面宽度AB 的长. 21. (本题9分)某气球内充满了一定质量的气体,当温度不变时,气球内气球的气压p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)(1)写出这个函数的解析式;(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕?(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米? 22.(本题12分)温州康盛水果市场某批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)现要保证每天盈利6000元,同时又要让顾客得到实惠,那么每千克应涨价多少元? (2)若该批发商单纯从经济角度看,那么每千克应涨价多少元,能使商场获利最多.(允许涨0.5元) 23.(本题11分)如图, 直线与x 轴、y 轴分别交于点) 0,8 ( M ,点) 6,0 ( N .点P 从点N 出发, 以每秒1个单位长度的速度沿N →O 方向运动,点Q从点O 出发,以每秒2个单位长度的速度沿O →M 的方向运动.已知点QP 、同时出发,当点Q到达点M 时,QP 、两点同时停止运动, 设运动时间为秒.设四边形...MNPQ 的面积为S . (1)求S 关于的函数关系式,并写出自变量的取值范围;(2)问t 几秒时四边形面积S 有最值,请求出相应的面积。
24.(14分)如图,直线3y x =-+与x 轴,y 轴分别交于B ,C 两点,抛物线2y x bx c =-++经过B ,C 两点,点A 是抛物线与x 轴的另一个交点。
(1)求B 、C 两点坐标; (2)求此抛物线的函数解析式;(3)在抛物线上是否存在点P ,使C A B =S PAB S △△,若存在,求出P 点坐标,若不存在,请说明理由。
数学答题卷卷Ⅰ一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分) 卷Ⅱ二、填空题(本题有6小题,每小题5分,共30分) 11. ;12. ; 13. ;14. ;15. ; 16. 。
三、解答题(本大题有8小题,第17题8分,第18题8分,第19题10分、20题8分,第21题9分,第22题12分,第23题11分,第24题14分,解答需写出必要的文字说明、演算步骤或证明过程). 17.(8分) xy CABO18.(8分)19.(10分)(1)(2)(3)20.(8分)21.(9分)(1)(2)(3)22. (12分)(1)(2)23.(11分) (1)(2)24. (14分)(1)(2)xyCABO(3)参考答案及评分标准卷I一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确三、解答题(本题有8小题,共80分) 17.(本题8分)(作出1条中垂线给3分,没有利用中垂线来作图而且没有弧痕迹的不给分,并且要写出作图的正确结论,其中结论1分)18.(本题8分) AD =BC(1分)∴⌒AD 错误!未找到引用源。
错误!未指定书签。
=⌒BC (2分) ∴⌒AD +⌒BD =⌒BC +⌒BD (2分) ∴ ⌒AB =⌒CD(2分) ∴AB=CD(1分)19.(本题10分)(1)求出解析式4)1(2+--=x y .(3分其他方法也可以) (2)求出A(-1,0) 和 B (3,0) ( 2分+2分)(3)求出三角形ABC 的面积是6 (3分需要书写过程,没有过程只得1分)20.(本题8分)求出半径26cm (1分) 求出OD=10cm (1分)求出DB=24cm (4分需要书写过程,没有过程只有答案得2分) 求出AB =48cm (2分)21.(本题9分)(1)求出k=96(正确得2分,没有书写过程得1分)(写出解析式 vp 96= , 1分) (2)求出p=120 (3分) (3)求出V ≥32(3分,如果利用方程来解题正确也给3分,使用近似值得2分) 22.(本题12分)(1)(设1分,对解题有意义才行,否则不能得分)(列出正确方程(10+x )(500—20x)=6000 得2分) (解出方程1x =5或2x =10 , 共2分,写出一个得1分) 经检验x=10舍去(1分)(2)列出函数y=(10+x)(500—20x) 或5000300202++-=x x y ,正确得3分 求出应该涨价7.5元,正确得1分 求出获利最多6125元,正确得2分23.(本题满分11分)(1) 用代数式表示出 NP=t(1分) OQ=2t(1分) 表示出)6(21t t s OPQ -=∆(2分) 求出2462+-=t t s (2分)写出自变量范围0<t <4得1分,边界值可以不考虑(2) 求出当t=3时(2分,需要过程,只有答案得1分) 说出有最小值得1分,求出s=15得1分 24.(本题满分14分)解:(1) 写出B 点坐标(3,0)C 坐标(0,3) (写正确1个2分,共4分) (2) 求出b=2,c=3(写正确1个1分,共2分) 求出解析式为322++-=x x y (1分) (3)求出A 点坐标(—1,0)(1分)求出1p 点的坐标(2,3) (2分需要过程说明,没有过程得1分)求出2p 点的坐标(71-,—3)(2分需要过程说明,没有过程得1分) 求出3p 点的坐标(71 ,—3)(2分需要过程说明,没有过程得1分)。
