基于MATLAB的FIR滤波器设计
matlabfir滤波器设计

matlabfir滤波器设计MATLAB是一个高级编程语言和交互式环境,被广泛应用于各种科学和工程问题的数值分析、数据可视化和编程开发等领域。
FIR滤波器是数字信号处理中经常使用的一种滤波器,它是基于有限长冲激响应的滤波器。
在MATLAB平台上,我们可以使用fir1函数来设计FIR滤波器。
一、FIR滤波器设计基础1.1 什么是FIR滤波器FIR滤波器是有限长冲激响应滤波器,由于其具有线性相位特性和可控阶数等优点,在数字信号处理中得到了广泛的应用。
一般来说,FIR滤波器的频率响应特性由滤波器的系数函数确定。
FIR滤波器的设计一般采用窗函数法、最小二乘法、频率抽取法等方法。
窗函数法是最常见的一种方法,大部分情况下选择的是矩形窗、汉宁窗、布莱克曼窗等。
1.3 fir1函数介绍fir1函数是MATLAB中用于FIR滤波器设计的函数,用法为:h = fir1(N, Wn, type)N为滤波器的阶数,Wn是用于指定滤波器截止频率的参数,type指定滤波器类型,可以是低通、高通、带通、带阻等。
二、使用fir1函数设计FIR滤波器2.1 设计要求采样率为300Hz;滤波器阶数为50;截止频率为50Hz。
2.2 实现步骤(1)计算规范化截止频率规范化截止频率是指在数字滤波器设计中使用的无单位量,通常范围为0到1。
在本例中,我们需要将50Hz的截止频率转化为规范化截止频率。
Wn = 2*50/300 = 1/3根据计算出的规范化截止频率和滤波器阶数,我们可以使用fir1函数来进行滤波器设计。
此处滤波器的阶数为50,规范化截止频率为1/3,类型为低通。
(3)绘制滤波器的幅频响应图为了验证设计的低通FIR滤波器是否符合要求,我们需要绘制其幅频响应图。
freqz(h,1,1024,300)经过上述步骤后,我们就得到了一张低通FIR滤波器的幅频响应图,如下图所示:图1.低通FIR滤波器的幅频响应图三、总结通过上述例子,我们可以看出在MATLAB中与fir1函数可以非常方便的进行FIR滤波器的设计。
使用MATLAB设计FIR滤波器

使⽤MATLAB设计FIR滤波器1. 采⽤fir1函数设计,fir1函数可以设计低通、带通、⾼通、带阻等多种类型的具有严格线性相位特性的FIR滤波器。
语法形式:b = fir1(n, wn)b = fir1(n, wn, ‘ftype’)b = fir1(n, wn, ‘ftype’, window)b = fir1(n, wn, ‘ftype’, window, ‘noscale’)参数的意义及作⽤:b:返回的FIR滤波器单位脉冲响应,脉冲响应为偶对称,长度为n+1;n:滤波器的介数;wn:滤波器的截⽌频率,取值范围为0<wn<1,1对应信号采样频率⼀半。
如果wn是单个数值,且ftype参数为low,则表⽰设计截⽌频率为wn的低通滤波器,如果ftype参数为high,则表⽰设计截⽌频率为wn的⾼通滤波器;如果wn是有两个数组成的向量[wn1wn2],ftype为stop,则表⽰设计带阻滤波器,ftype为bandpass,则表⽰设计带通滤波器;如果wn是由多个数组成的向量,则根据ftype的值设计多个通带或阻带范围的滤波器,ftype为DC-1,表⽰设计的第⼀个频带为通带,ftype为DC-0,表⽰设计的第⼀个频带为阻带;window:指定使⽤的窗函数,默认为海明窗;noscale:指定是否归⼀化滤波器的幅度。
⽰例:N=41; %滤波器长度fs=2000; %采样频率%各种滤波器的特征频率fc_lpf=200;fc_hpf=200;fp_bandpass=[200 400];fc_stop=[200 400];%以采样频率的⼀半,对频率进⾏归⼀化处理wn_lpf=fc_lpf*2/fs;wn_hpf=fc_hpf*2/fs;wn_bandpass=fp_bandpass*2/fs;wn_stop=fc_stop*2/fs;%采⽤fir1函数设计FIR滤波器b_lpf=fir1(N-1,wn_lpf);b_hpf=fir1(N-1,wn_hpf,'high');b_bandpass=fir1(N-1,wn_bandpass,'bandpass');b_stop=fir1(N-1,wn_stop,'stop');%求滤波器的幅频响应m_lpf=20*log(abs(fft(b_lpf)))/log(10);m_hpf=20*log(abs(fft(b_hpf)))/log(10);m_bandpass=20*log(abs(fft(b_bandpass)))/log(10);m_stop=20*log(abs(fft(b_stop)))/log(10);%设置幅频响应的横坐标单位为Hzx_f=0:(fs/length(m_lpf)):fs/2;%绘制单位脉冲响应%绘制单位脉冲响应subplot(421);stem(b_lpf);xlabel('n');ylabel('h(n)');subplot(423);stem(b_hpf);xlabel('n');ylabel('h(n)');subplot(425);stem(b_bandpass);xlabel('n');ylabel('h(n)');subplot(427);stem(b_stop);xlabel('n');ylabel('h(n)');%绘制幅频响应曲线subplot(422);plot(x_f,m_lpf(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);subplot(424);plot(x_f,m_hpf(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);subplot(426);plot(x_f,m_bandpass(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);subplot(428);plot(x_f,m_stop(1:length(x_f)));xlabel('频率(Hz)','fontsize',8);ylabel('幅度(dB)','fontsize',8);2. 采⽤fir2函数设计,函数算法是:⾸先根据要求的幅频响应向量形式进⾏插值,然后进⾏傅⾥叶变换得到理想滤波器的单位脉冲响应,最后利⽤窗函数对理想滤波器的单位脉冲响应激进型截断处理,由此得到FIR滤波器系数。
基于Matlab的FIR滤波器设计与实现

二、实验平台Matlab7.1三、实验原理以低通滤波器为例,其常用的设计指标有:1.通带边缘频率f p(数字频率为Ωp)2.阻带边缘频率f st (数字频率为Ωst)3.通带内最大纹波衰减δp=-20log10(1-αp),单位为dB4.阻带最小衰减αs=-20log10(αs),单位为dB5.阻带起伏αs6.通带峰值起伏αp其中,以1、2、3、4条最为常用。
5、6条在程序中估算滤波器阶数等参数时会用到。
数字频率= 模拟频率/采样频率四、实例分析例1 用凯塞窗设计一FIR低通滤波器,通带边界频率Ωp=0.3pi,阻带边界频率Ωs=0.5pi,阻带衰减δs不小于50dB。
方法一:手动计算滤波器阶数N和β值,之后在通过程序设计出滤波器。
第一步:通过过渡带宽度和阻带衰减,计算滤波器的阶数B和β值。
第二步:通过程序设计滤波器。
程序如下:b = fir1(29,0.4,kaiser(30,4.55));[h1,w1]=freqz(b,1);figure (1)plot(w1/pi, abs(h1));grid;xlabel('归一化频率/p') ;ylabel('幅度/dB') ;figure (2)plot(w1/pi,angle(h1));grid;xlabel('归一化频率/p') ;ylabel('相位') ;波形如下:例2 利用雷米兹交替算法设计等波纹滤波器,设计一个线性相位低通FIR数字滤波器,其指标为:通带边界频率fc=800Hz,阻带边界fr=1000Hz,通带波动阻带最小衰减At=40dB,采样频率fs=4000Hz。
一般调用MATLAB信号处理工具箱函数remezord来计算等波纹滤波器阶数N和加权函数W (ω),调用函数remez可进行等波纹滤波器的设计,直接求出滤波器系数。
函数remezord中的数组fedge为通带和阻带边界频率,数组mval是两个边界处的幅值,而数组dev是通带和阻带的波动,fs是采样频率单位为Hz。
基于MATLAB设计FIR滤波器

基于MATLAB设计FIR滤波器FIR(Finite Impulse Response)滤波器是一种数字滤波器,它具有有限的冲激响应长度。
基于MATLAB设计FIR滤波器可以使用signal工具箱中的fir1函数。
fir1函数的语法如下:b = fir1(N, Wn, window)其中,N是滤波器的阶数,Wn是截止频率,window是窗函数。
要设计一个FIR低通滤波器,可以按照以下步骤进行:步骤1:确定滤波器的阶数。
阶数决定了滤波器的截止频率的陡峭程度。
一般情况下,阶数越高,滤波器的陡峭度越高,但计算复杂度也会增加。
步骤2:确定滤波器的截止频率。
截止频率是指在滤波器中将信号的频率限制在一定范围内的频率。
根据应用的需求,可以选择适当的截止频率。
步骤3:选择窗函数。
窗函数是为了在时域上窗口函数中心增加频率衰减因子而使用的函数。
常用的窗函数有Hamming、Hanning等。
窗函数可以用来控制滤波器的幅度响应特性,使得它更平滑。
步骤4:使用fir1函数设计滤波器。
根据以上步骤确定滤波器的阶数、截止频率和窗函数,可以使用fir1函数设计FIR滤波器。
具体代码如下:N=50;%设定阶数Wn=0.5;%设定截止频率window = hanning(N + 1); % 使用Hanning窗函数步骤5:使用filter函数对信号进行滤波。
设计好FIR滤波器后,可以使用filter函数对信号进行滤波。
具体代码如下:filtered_signal = filter(b, 1, input_signal);其中,input_signal是输入信号,filtered_signal是滤波后的信号。
以上,便是基于MATLAB设计FIR滤波器的简要步骤和代码示例。
根据具体需求和信号特性,可以进行相应的调整和优化。
基于MATLAB的FIR和IIR数字滤波器的设计

基于MATLAB的FIR和IIR数字滤波器的设计一、本文概述随着数字信号处理技术的飞速发展,数字滤波器作为其中的核心组件,已经广泛应用于通信、音频处理、图像处理、生物医学工程等诸多领域。
在数字滤波器中,有限脉冲响应(FIR)滤波器和无限脉冲响应(IIR)滤波器是最常见的两种类型。
它们各自具有独特的优点和适用场景,因此,对这两种滤波器的深入理解和设计掌握是工程师和研究人员必备的技能。
本文旨在通过MATLAB这一强大的工程计算工具,详细介绍FIR 和IIR数字滤波器的设计原理、实现方法以及对比分析。
我们将简要回顾数字滤波器的基本概念和分类,然后重点阐述FIR和IIR滤波器的设计理论,包括窗函数法、频率采样法、最小均方误差法等多种设计方法。
接下来,我们将通过MATLAB编程实现这些设计方法,并展示如何根据实际应用需求调整滤波器参数以达到最佳性能。
本文还将对FIR和IIR滤波器进行性能对比,分析它们在不同应用场景下的优缺点,并提供一些实用的设计建议。
我们将通过几个典型的应用案例,展示如何在MATLAB中灵活应用FIR和IIR滤波器解决实际问题。
通过阅读本文,读者将能够深入理解FIR和IIR数字滤波器的设计原理和实现方法,掌握MATLAB在数字滤波器设计中的应用技巧,为未来的工程实践和研究工作打下坚实的基础。
二、FIR滤波器设计有限脉冲响应(FIR)滤波器是一种数字滤波器,其特点是其脉冲响应在有限的时间后为零。
因此,FIR滤波器是非递归的,没有反馈路径,从而保证了系统的稳定性。
在设计FIR滤波器时,我们主要关注的是滤波器的阶数、截止频率和窗函数的选择。
在MATLAB中,有多种方法可以用来设计FIR滤波器。
其中,最常用的方法是使用fir1函数,该函数可以设计一个线性相位FIR滤波器。
该函数的基本语法是b = fir1(n, Wn),其中n是滤波器的阶数,Wn是归一化截止频率,以π为单位。
该函数返回一个长度为n+1的滤波器系数向量b。
基于matlab的FIR滤波器设计(处理加噪音频-窗函数法)

基于matlab的FIR滤波器设计(处理加噪音频,窗函数法) 一、录制音频二、利用窗函数法设计的低通滤波器处理加有噪声的音频波形f3=7000;%所加噪声正弦函数的频率[Y,fs,bits]=wavread('D:\yinpin\nihao01.wav');%利用wavread产生音频的函数及采样频率L=length(Y);t=0:1/fs:(L-1)/fs;%定义时间的范围及步长y=0.005*sin(2*pi*f3*t); n1=floor(L/2);%所加噪声f1=(0:n1)*fs/L;Y=Y(:,1);sound(Y,fs);%输出加噪前音频Y1=y+Y';%给音频加噪声FY1=abs(fft(Y1,L));FY=abs(fft(Y,L));sound(Y1,fs);%输出加噪后的音频figure(1)subplot(211)plot(t(1:1000),Y(1:1000)); grid on;%加噪前音频的时域图xlabel('时间(t)');ylabel('幅度(Y)');title('加噪前录音波形的时域图');subplot(212)plot(f1,FY(1:n1+1)); grid on;%加噪前音频的频域图xlabel('频率(f)');ylabel('幅度(FY)');title('加噪前录音波形的频域图');figure(2)subplot(211)plot(t(1:1000),Y1(1:1000)); grid on;%加噪后音频的时域图xlabel('时间(t)');ylabel('幅度(Y1)');title('加噪声后录音波形的时域图');subplot(212)plot(f1,FY1(1:n1+1)); grid on;%加噪后音频的频域图xlabel('频率(f)');ylabel('幅度(FY1)');title('加噪声后录音波形的频域图');m=0.03; M=round(8/m);N=M-1;%定义滤波器的阶数b=fir1(N,0.6);figure(3)[h,f]=freqz(b,1,512);%滤波器的幅频特性图plot(f*fs/(2*pi),20*log10(abs(h)))%参数分别是频率与幅值xlabel('频率/赫兹');ylabel('增益/分贝');title('滤波器的增益响应');figure(4)sf=filter(b,1,Y1);%使用filter函数对信号进行滤波Fsf=abs(fft(sf,L));subplot(211)plot(t(1:1000),sf(1:1000)); grid on;%滤波后音频的时域图xlabel('时间(t)');ylabel('幅度(sf)');title('滤波后录音波形的时域图');axis([0.01 0.05 -0.002 0.002])subplot(212)plot(f1,Fsf(1:n1+1)); grid on;%滤波后音频的频域图xlabel('频率(f)');ylabel('幅度(Fsf)');title('滤波后录音波形的频域图');sound(sf,fs);三、运行结果加噪前录音波形的时域图和频域图加噪后录音波形的时域图和频域图窗函数法设计低通滤波器的增益响应滤波后录音波形的时域图和频域图。
基于MATLAB的FIR数字低通滤波器设计综述

陕西理工学院课程设计基于MATLAB的FIR数字低通滤波器设计作者:周龙刚(陕西理工学院物理与电信工程学院通信工程专业 2011级4班,陕西汉中 723003)指导老师:井敏英[摘要]FIR数字滤波器是数字信号处理的一个重要组成部分,由于FIR数字滤波器具有严格的线性相位,因此在信息的采集和处理过程中得到了广泛的应用。
本文介绍了FIR数字滤波器的概念和线性相位的条件,分析了窗函数法、频率采样法和等波纹逼近法设计FIR滤波器的思路和流程。
在分析三种设计方法原理的基础上,借助Matlab仿真软件工具箱中的fir1实现窗函数法中的哈明窗设计FIR低通滤波器。
[关键词]FIR数字滤波器;线性相位窗函数;法哈明窗;MatlabDesigning FIR low-pass digital filter based on VHDLZhoulonggang(Grade11,Class4,Major of Communication Engineering,School of Physics and Telecommunication Engineering , Shaanxi University of Technology,Hanzhong 723003,Shaanxi)Tutor:JingYingMinAbstract:FIR digital filter is an important part of digital signal processing,the FIR digitalfilter with linear phase, so it has been widely applied in the collection and processing of information in the course of. This paper introduces the concept of FIR digital filter with linear phase conditions, analysis of the window functionmethod and frequency sampling method and the ripple approximation method ofFIR filter design ideas and processes. Based on analyzing the principle of three kinds of design method, using Matlab simulation software fir1 toolbox in design and implementation of FIR Hamming window window function method in the low pass filter.Keywords:FIR digital filter, linear phase,the window function method,Hamming window,Matlab目录引言 (1)1. 基本原理 ............................................................................................................................................... - 1 -1.1 FIR数字滤波器概述 ................................................................................................................... - 1 -1.2 FIR数字滤波器线性相位定义 ................................................................................................... - 2 -1.3 FIR数字滤波器线性相位时域条件 ........................................................................................... - 2 -2. 系统设计 ............................................................................................................................................... - 3 -2.1 FIR数字滤波器的窗函数设计方法 ........................................................................................... - 3 -2.1.1 窗函数法的设计思路....................................................................................................... - 3 -2.1.2 常见窗函数介绍............................................................................................................... - 3 -2.1.3 吉布斯效应....................................................................................................................... - 5 -2.2 FIR数字滤波器频率采样设计法 ............................................................................................ - 5 -2.3 FIR数字滤波器等波纹逼近设计法 ........................................................................................... - 6 -3 详细设计 ................................................................................................................................................ - 7 -3.1 程序设计流程.............................................................................................................................. - 7 -3.2 Matlab简介 .................................................................................................................................. - 7 -3.3窗函数法的Matlab实现 ............................................................................................................. - 8 -3.3.1 fir1函数介绍..................................................................................................................... - 8 -3.3.2基于fir1函数的窗函数法FIR滤波器设计.................................................................... - 8 -4 总结 .................................................................................................................................................. - 11 - 致谢 ...................................................................................................................................................... - 11 - 参考文献 .................................................................................................................................................. - 11 - 附录A . (14)引言随着信息科学和计算机技术的不断发展,数字信号处理(DSP ,Digital Signal Processing)的理论和技术也得到了飞速的发展,并逐渐成为一门重要的学科,它的重要性在日常通信、图像处理、遥感、声纳、生物医学、地震、消费电子、国防军事、医疗方面等显得尤为突出。
基于matlab的FIR低通,高通,带通,带阻滤波器设计

北京师范大学课程设计报告课程名称: DSP设计名称:FIR 低通、高通带通和带阻数字滤波器的设计姓名:学号:班级:指导教师:起止日期:课程设计任务书学生班级: 学生姓名: 学号:设计名称: FIR 低通、高通带通和带阻数字滤波器的设计 起止日期: 指导教师:设计目标:1、采用Kaiser 窗设计一个低通FIR 滤波器 要求:采样频率为8kHz ;通带:0Hz~1kHz ,带内波动小于5%; 阻带:1.5kHz ,带内最小衰减:Rs=40dB 。
2、采用hamming 窗设计一个高通FIR 滤波器 要求:通带截至频率wp=rad π6.0, 阻带截止频率ws=rad π4.0,通带最大衰减dB p 25.0=α,阻带最小衰减dB s 50=α3、采用hamming 设计一个带通滤波器低端阻带截止频率 wls = 0.2*pi ;低端通带截止频率 wlp = 0.35*pi ; 高端通带截止频率 whp = 0.65*pi ; 高端阻带截止频率 whs = 0.8*pi ;4、采用Hamming 窗设计一个带阻FIR 滤波器 要求:通带:0.35pi~0.65pi ,带内最小衰减Rs=50dB ; 阻带:0~0.2pi 和0.8pi~pi ,带内最大衰减:Rp=1dB 。
FIR 低通、高通带通和带阻数字滤波器的设计 一、 设计目的和意义1、熟练掌握使用窗函数的设计滤波器的方法,学会设计低通、带通、带阻滤波器。
2、通过对滤波器的设计,了解几种窗函数的性能,学会针对不同的指标选择不同的窗函数。
二、 设计原理一般,设计线性相位FIR 数字滤波器采用窗函数法或频率抽样法,本设计采用窗函数法,分别采用海明窗和凯泽窗设计带通、带阻和低通。
如果所希望的滤波器的理想频率响应函数为)(jw d e H ,如理想的低通,由信号系统的知识知道,在时域系统的冲击响应h d (n)将是无限长的,如图2、图3所示。
H d (w)-w c w c图2图3若时域响应是无限长的,则不可能实现,因此需要对其截断,即设计一个FIR 滤波器频率响应∑-=-=10)()(N n jwn jwe n h e H 来逼近)(jw d e H ,即用一个窗函数w(n)来截断h d (n),如式3所示:)()()(n w n h n h d =(式1)。
FIR滤波器的MATLAB设计与实现

时钟 输入模拟信号 输出模拟信号
DSP (TMS32 0C5410)
同步 FIFO
同步 FIFO
D/A 转换
A/D 转换
JTAG 接口
FLASE
RS232 接口 图3 系统总体框图
6
SRAM
JTAG(Joint Test Action Group) 联合测试行动小组)是一种国际标准测试协议 (IEEE 1149.1 兼容) ,主要用于芯片内部测试。基本原理是在器件内部定义一个 TAP(Test Access Port�测试访问口)通过专用的 JTAG 测试工具对内部节点进 行测试。JTAG 测试允许多个器件通过 JTAG 接口串联在一起,形成一个 JTAG 链, 能实现对各个器件分别测试。 FLASE 存储器具有性价比高,体积小,功耗低,可电擦写,使用方便等优点。 在 DSP 应用系统中采用 Flash 存储器和固定数据是一种比较好的选择。 SRAM 静态存储器,读写速度快,但价格较高。适合于外部存放需要经常访问 或更新的临时数据。 RS232 电平转换模块,将外部电平转换为适合 DSP 芯片内部要求的电平。 图3是系统的总体框图。主要包括输入信号缓冲及调理电路、A/D 变换器、输 入缓冲 FIFO、DSP及外围电路、输出缓冲FIFO、D/A变换器等几部分。其中DSP及 外围电路包括程序存储器、串行口、显示及键盘接口等。串行口用于实现和PC机 的通信,可以通过PC机对滤波器的控制。 假定输入模拟信号为带限信号。该信号经缓冲和调理后经A/D变换进入输入缓 冲FIFO,当 FIFO中的数据达到一定数量时产生中断,DSP将数据读入内存中并进 行计算和处理,这里DSP主要实现FIR滤波运算。处理后的数据写入输出FIFO中, 之后通过D/A变换后输出模拟信号。输出的信号是低通滤波后的结果。 4.3 用DSP实现FIR滤波器的关键问题 4.3.1 定点数的定标 在滤波器的实现过程中,DSP所要处理的数可能是整数,也可能是小数或混合 小数;然而,DSP在执行算术运算指令时,并不知道当前所处理的数据是整数还是 小数,更不能指出小数点的位置在哪里。因此,在编程时必须指定一个数的小数 点处于哪一位,这就是定标。通过定标,可以在16位数的不同位置上确定小数点, 从而表示出一个范围大小不同且精度也不同的小数。 4.3.2 误差问题 因为在用定点DSP实现时,所有的数据都是定长的,运算也都是定点运算,因 而会产生有限字长效应。所产生的误差主要包括:数模转换引起的量化误差、系 数量化引起的误差以及运算过程中的舍入误差。在用定点DSP时,产生误差是不能 避免的。
基于MATLAB的FIR数字滤波器设计
基于MATLAB 的FIR 数字滤波器设计摘自:张登奇,李望移.基于MATLAB 的FIR 数字滤波器设计[J]. 计算机时代,2007,(11)摘 要:数字滤波是数字信号处理的重要内容,数字滤波器可分为FIR 和IIR 两大类。
文章根据FIR 滤波器的设计原理,详细介绍了MATLAB 环境下FIR 数字滤波器的设计方法和操作步骤,并列出了设计实例程序及运行结果。
关键词:MATLAB ;数字信号处理;数字滤波器;有限脉冲响应2 FIR 数字滤波器的窗口设计法窗口设计法是从时域出发,将理想滤波器的单位脉冲响应截取一段作为传输函数的系数。
通常情况下,滤波器指标往往在频域给出,算出的理想单位脉冲响应一般是非因果、无限长、物理上不可实现的,需先截短再右移使之成为有限长因果序列,只要截取的长度和方法合理,总能满足频域指标要求。
截短就是加窗,矩形窗最简单,在频域属最小平方逼近,但峰肩和波纹不太理想。
一般希望窗函数的频谱主瓣尽可能地窄,以获得较陡的过渡带,同时能量又要尽量集中在主瓣,以减小峰肩和波纹,进而增加阻带衰减。
实际工程中常用窗的特性及MATLAB 函数比较如表1所示。
表1 常用窗函数性能比较利用窗口设计法设计FIR 数字滤波器的过程:)()()()()(ωωj D TFT n w d ID TFT j d e H n h n h e H −−→−−−→−−−→−⨯具体操作步骤如下:1、对设计指标进行归一化处理。
数字滤波器传输函数只与频域的相对值有关,故在设计时可先将滤波器设计指标对采样频率进行归一化处理,归一化公式为:2、根据阻带衰减要求和过渡带宽,由表1选择窗函数的类型并估计窗口长度M ,此时滤波器的阶数为M-1(注意窗口长度与滤波器类型的关系)。
3、根据滤波器的理想频响求出理想单位脉冲响应)(n h d 。
4、将理想单位脉冲响应与窗函数相乘,得系统单位脉冲响应。
5、用freqz 函数验算技术指标是否满足要求。
基于MATLAB的希尔伯特fir滤波器设计

本科毕业设计(论文)题目基于MATLAB的希尔伯特FIR滤波器设计_姓名专业电子科学与技术学号指导教师张庆辉郑州科技学院电气工程学院二○一四年五月目录摘要 (I)ABSTRACT (II)前言 (IV)1 设计的目的与意义 (1)2 Matlab概述 (3)2.1 MATLAB语言的发展 (3)2.2 MATLAB的主要功能 (3)2.3 matlab的程序结构 (4)3 希尔伯特变换的基本原理 (5)3.1希尔伯特变换的定义 (6)3.1.1 卷积积分 (6)相位 (6)3.1.2 23.1.3 解析信号的虚部 (7)3.2 希尔伯特变换的性质 (8)3.2.1 线性性质 (8)3.2.2 移位性质 (8)3.2.3 希尔伯特变换的希尔伯特变换 (8)3.2.4 逆希尔伯特变换 (8)3.2.5 奇偶特性 (9)3.2.6 能量守恒 (9)3.2.7 正交性质 (9)3.2.8 调制性质 (9)3.2.9 卷积性质 (10)4 Fir滤波器的基本原理及设计方法 (11)4.1 Fir滤波器的基本原理及其特点 (12)4.1.1 FIR数字滤波器的基本原理 (12)4.1.2 FIR滤波器的基本特点 (12)4.2 FIR数字滤波器的设计 (13)5 希尔伯特fir滤波器 (14)6 希尔伯特变换的应用 (18)6.1 希尔伯特变换在探地雷达数据处理中的应用 (18)6.1.1 公式 (18)6.1.2 算法 (19)6.2 数字I-Q下变频器 (20)6.2.1 希尔伯特变换 (21)6.2.2 基于希尔伯特变换的数字I-Q下变频器 (22)6.3 希尔伯特变换在解调中的应用 (22)6.3.1 希尔伯特变换 (22)6.3.2 在解调中的应用 (23)6.3.3 解调性能分析 (24)7 希尔伯特变换器的Matlab设计 (26)7.1 直接程序法 (26)7.2 利用FDATool工具设计法 (27)7.3 希尔伯特变换器的效果验证 (31)结论 (33)前景展望 (34)致谢 (35)参考文献 (36)附录 (37)基于MATLAB的希尔伯特FIR滤波器设计摘要在通信系统中,经常需要对一个信号进行正交分解,即分解为同相分量和正交分量,并能有效地提取复杂信号的瞬时参数——瞬时振幅、瞬时相位和瞬时频率。
matlab fir2的设计方法

matlab fir2的设计方法
MATLAB中的fir2函数用于设计滤波器的频率响应,采用基于FIR (有限脉冲响应)的方法。
fir2函数的使用方法如下:
1. 定义频率向量:在设计FIR滤波器之前,首先需要定义一个频率向量,指定所需的频率响应。
>> f = [0, 0.1, 0.2, 0.5, 0.6, 1]; % 频率向量,范围为[0, 1],其中1对应采样频率的一半
2. 定义幅度向量:在频率向量上对应的每个点上定义一个幅度值,用于指定所需的频率响应。
>> a = [1, 1, 0, 0, 0, 0]; % 幅度向量,与频率向量对应,表示在每个频率点上的幅度值
3. 定义滤波器的阶数:根据所需的频率响应,确定滤波器的阶数。
>> n = 30; % 滤波器的阶数,通常选择一个偶数值
4. 使用fir2函数设计滤波器:根据以上定义的频率向量、幅度向量和滤波器阶数,调用fir2函数设计滤波器。
>> b = fir2(n, f, a); % 调用fir2函数设计滤波器,得到系数向量b
设计完成后,可以使用filter函数将滤波器应用于信号,或使用freqz 函数查看滤波器的频率响应。
matlab滤波器设计命令

matlab滤波器设计命令Matlab滤波器设计命令滤波器是数字信号处理中常用的工具,用于去除信号中的噪声、频率干扰或其他不需要的成分。
Matlab提供了一系列有用的滤波器设计命令,使用户能够轻松设计并应用各种类型的滤波器。
在本文中,我们将详细介绍Matlab中常用的滤波器设计命令,包括滤波器设计函数、滤波器类型和设计过程。
I. Matlab中常用的滤波器设计函数在Matlab中,有几种函数可用于设计滤波器,其中最常用的函数是`designfilt`函数和`fir1`函数。
1. designfilt函数`designfilt`函数是Matlab中最灵活和功能强大的滤波器设计函数之一,可用于设计各种类型的IIR和FIR滤波器。
它的基本语法如下:`filt = designfilt(FilterType, 'PropertyName', PropertyValue, ...)`其中,`FilterType`代表滤波器类型,包括低通滤波器(Lowpass)、高通滤波器(Highpass)、带通滤波器(Bandpass)、带阻滤波器(Bandstop)等。
`PropertyName`和`PropertyValue`是可选的参数,用于设置滤波器的各种属性,如阶数(Order)、截止频率(CutoffFrequency)、通带和阻带的最大衰减(MaximumAttenuation)等。
下面是一个使用`designfilt`函数设计低通滤波器的例子:Fs = 1000; 采样频率Fpass = 20; 通带截止频率Fstop = 30; 阻带截止频率designfilt('lowpassiir', 'FilterOrder', 4, 'PassbandFrequency', Fpass, 'StopbandFrequency', Fstop, 'SampleRate', Fs)该命令将设计一个4阶的低通IIR滤波器,其通带截止频率为20Hz,阻带截止频率为30Hz,采样频率为1000Hz。
基于MATLAB的FIR滤波器的设计

用F T o设计和分析模块 电路 ,经过S h k DA o l i n 仿真 ,对其进行时域 、频域 分析和滤波 。实验结果表明, 计 mu 本设
方法能够 有效 的滤除 无用信号 , 直观 简便 , 高了信号的提取效果 。 提
【] 王蔚 . 4 MAT A L B环境 下 的数字 滤波 器设 计及其 应用 【 . 州 : 州大学 ,0 23 — 8 D1 苏 苏 20 : 3 . 6
图 3滤 波 前 信 号 源 波 形
【] CO 1 E J G a b u M , n J H . 9 , r m s Y e , b O j Li 1 91 F O
2 1 年 8月 01 第 8期
电 子 测 试
EL EC T RON I C T EST
Aug. 2011 No8 .
基 于 MAT A L B的F R滤 波 器 的设 计 ★ I
段佳佳 ,樊龙龙 ,张波涛
( 中北大学 信息探测与处理技术研 究所 太原 0 0 5 ) 3 0 1 摘要 :基于MA L B信号处理工具 箱 ,设计一种 滤波器 ,针对 信号的分离和 滤除 ,要求有 良好的幅频特 和 TA
幅频特性为 l e I 1 且无相移的理想带通滤波器 H( ) , =
图2滤 波器 幅频特性
的 响应 HaP 表 频率 ( ) 达式为 :
, 『 、 w
从图 2中来看,对于 0 z 10 H , 1H 到 40 H H 到 00 z 40 z 2 00 z
I P , ll 一 1 , ≤W≤ ×
[】 M o a d M o h a i i h lM a i .M AT AB 与 3 h n k t r, c e M re L
基于MATLAB的FIR滤波器设计

end
wnl=boxcar(N);
hnl=hdn.*wnl ;
wn2=hamming(N);
hn2=hdn.*wn2 ;
subplot(2,2,1) stem(n,hnl, .’) line(10,201,10,o1 ); t itle( 矩 形 窗 设 计 的h(n) ); xlabel( n );ytat ̄( h(n) ); subplot(223) g6em(n,hn2, . ) line(10,201,10,o]); title( hamming窗 设 计 的h(n) ); xlabel( n );yla ̄l( h(n) ); hnll=ft(hnl,512); w=2}【0:5111/512; subplot(222) plot(w ,20*logl0(abs(hnl1)))
N — l , 则其系统 函数为
划
∑ 日 (z ) =
h (n )z ”
(2 )
2 、
数字滤波器 的设计
2 . 1 窗函数的设计思想
如果希望得到的滤波 器 的理 想特性 为
以 (P 脚 ) , 那 么 F I R 滤波 器 设 计 就是 寻 求
一 个 系统 函数 H (Z ) , 用其频率响应
∑ 想 H (e 脚 ) :
gr id;
ax ̄[0,2,一80,51); t itle( 幅度特性 ’); xlabel(’w/pi );ylabel( 幅 度((1B) );
矩 形 窗 设计 的 h(n)
hn22=fft(hn2,512);
点之一 。 其中 F IR 滤波器具有严格的相位
特性 , 同时 系统 函数的极点加 固定在原
用MATLAB设计数字FIR低通滤波器(哈明窗)
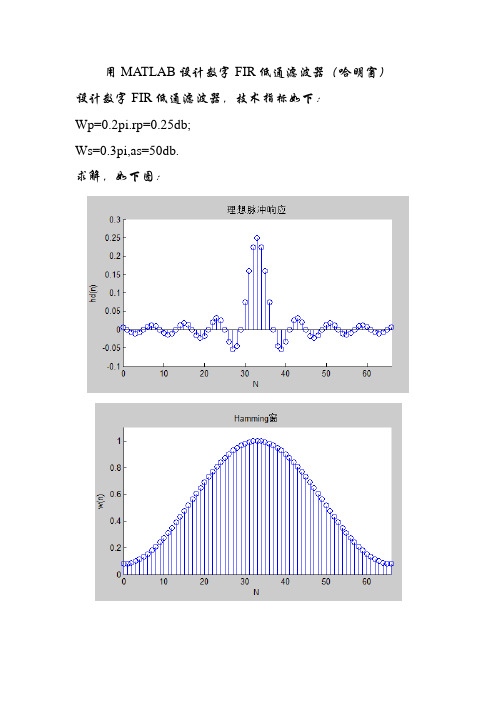
用MATLAB设计数字FIR低通滤波器(哈明窗)设计数字FIR低通滤波器,技术指标如下:Wp=0.2pi.rp=0.25db;Ws=0.3pi,as=50db.求解,如下图:程序:wp=0.2*pi;ws=0.3*pi;trwidth=ws-wp;M=ceil(6.6*pi/trwidth)+1;%朝正无穷方向取整n=[0:1:M-1];wc=(ws+wp)/2%求的截止频率(弧度)hd=ideal_lp(wc,M) %调用计算理想低通滤波器的单位取样响应wham=(hamming(M))';%哈明窗函数h=hd.*wham;[H,w]=freqz(h,1,1000,'whole'); %求Z变换频率响应函数H=(H(1:1:501))';w=(w(1:1:501))'mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);grd=grpdelay(h,1,w);deltaw=2*pi/1000;Rp=-(min(db(1:1:wp/deltaw+1)))As=-round(max(db(ws/deltaw+1:1:501)))subplot(1,1,1)subplot(2,2,1),stem(n,hd);title('理想脉冲响应')axis([0 M-1 -0.1 0.3]);xlabel('N');ylabel('hd(n)');subplot(2,2,2),stem(n,wham);title('Hamming窗')axis([0 M-1 -0 1.1]);xlabel('N');ylabel('w(n)');subplot(2,2,3),stem(n,h);title('实际脉冲响应')axis([0 M-1 -0.1 0.3]);xlabel('N');ylabel('h(n)');subplot(2,2,4),plot(w/pi,db);title('相对标尺的幅度响应');grid on;axis([0 1 -100 10]);xlabel('frequency in pi units');ylabel('decibels');set(gca,'XTickMode','manual','XTick',[0,0.2,0.3,1])%设置或修改LTI对象的属性值set(gca,'XTickMode','manual','XTick',[-50,0])set(gca,'XTickLabelMode','manual','XTickLabels',['50';'0'])子程序:function hd=ideal_lp(wc,N);a=(N-1)/2;n=[0:1:(N-1)];m=n-a+eps;hd=sin(wc*m)./(pi*m);。
基于MATLAB与CCS的FIR滤波器的C语言实现

基于MATLAB与CCS的FIR滤波器的C语言实现FIR(Finite Impulse Response)滤波器是一种数字滤波器,其输出仅取决于有限长度的输入序列。
MATLAB和CCS都提供了强大的工具和函数来设计和实现FIR滤波器。
下面将以一个具体的例子来介绍如何使用MATLAB和CCS来实现FIR滤波器的C语言实现。
首先,在MATLAB中使用fir1函数进行FIR滤波器的设计:```matlabfs = 1000; % 采样频率fpass = 200; % 通带截止频率fstop = 250; % 阻带起始频率Rp=1;%通带最大纹波(dB)Rs=60;%阻带最小衰减(dB)%计算通带和阻带频率f1 = fpass / (fs / 2);f2 = fstop / (fs / 2);% 使用fir1函数设计FIR滤波器b = fir1(30, [f1 f2], 'stop', kaiser(31, 3));%输出滤波器系数```然后,使用MATLAB中的codegen函数将FIR滤波器系数转换为C代码:```matlabcodegen -config:dll FIRFilter -args {b} -report```这将生成一个名为FIRFilter.c的文件,在该文件中包含了FIR滤波器的C语言实现。
接下来,在CCS中创建一个新的project,并将FIRFilter.c文件添加到该project中。
在Source Files文件夹中右键单击,并选择“Add Existing Files to Project”,然后选择FIRFilter.c文件。
接着,点击Build按钮来编译并生成可执行文件。
最后,在CCS中使用FIR滤波器的C语言实现进行信号处理。
可以通过以下代码示例来实现:```c#include <stdint.h>#include "FIRFilter.h"#define BUFFER_SIZE 1000//输入信号int16_t inputSignal[BUFFER_SIZE];//输出信号int16_t outputSignal[BUFFER_SIZE];int main(void)//初始化输入信号//...//调用FIR滤波器实现函数FIRFilter(inputSignal, outputSignal, BUFFER_SIZE);//处理输出信号//...return 0;```上述代码中,首先定义了输入和输出信号的数组,然后在main函数中调用FIR滤波器实现函数,并传入输入和输出信号的数组以及信号的长度。
基于matlab的数字滤波器设计及仿真

滤波器的指标
■ 滤波器的指标常在频域给出 ■ 数字滤波器的频率响应特性曲线:
H(ejw)= |H(ejw)|ej (w) |H(ejw)|为幅频特性函数,表示信号通过该 滤波器后各频率的衰减情况。
(w)为相频特性函数,表示信号通过滤波器 后在时间上的延时情况。
二、MATLAB环境下IIR数字滤波器的设计
四、两个有趣的实验
1、利用MATLAB进行声音滤波: 利用MATLAB读取wav格式的声音文件,对
信号进行离散傅里叶变换,得到其频谱图,给 信号加杂音,然后设计一个数字滤波器将杂音 滤除,得到原音,最后比较滤波器的滤波效果。
语音读取和加噪
■ clear;close all; ■ [Y,Fs,NBITS]=WAVREAD("WindowsXP.wav"); ■ n=length(Y); ■ f=0:Fs/n:Fs*(n-1)/n; ■ K=0:1/(n-1):1; ■ subplot(2,3,1);plot(K,Y);title("语音信号的时域波形"); ■ Y1=fft(Y,n); ■ subplot(2,3,3);plot(f,abs(Y1));title("语音信号的频谱"); ■ noise=0.02*sin(2*pi*4000*K); ■ subplot(2,3,2);plot(K(1:50),noise(1:50));title("噪声的时域波形"); ■ s=length(noise); ■ noise1=fft(noise,s); ■ subplot(2,3,5);plot(f,abs(noise1));title("噪声的频谱"); ■ A=Y"+noise; ■ subplot(2,3,4);plot(K,A);title("含噪语音的时域波形"); ■ A1=fft(A,s); ■ subplot(2,3,6);plot(f,abs(A1));title("含噪语音的频谱");
基于MATLAB的希尔伯特fir滤波器设计

本科毕业设计(论文)题目基于MATLAB的希尔伯特FIR滤波器设计_姓名专业电子科学与技术学号指导教师张庆辉郑州科技学院电气工程学院二○一四年五月目录摘要.............................................................................................................................. ABSTRACT . (I)前言..................................................................................................................................1 设计的目的与意义 02 Matlab概述 (2)2.1 MATLAB语言的发展 (2)2.2 MATLAB的主要功能 (2)2.3 matlab的程序结构 (3)3 希尔伯特变换的基本原理 (4)3.1希尔伯特变换的定义 (5)3.1.1 卷积积分 (5)相位 (5)3.1.2 23.1.3 解析信号的虚部 (6)3.2 希尔伯特变换的性质 (7)3.2.1 线性性质 (7)3.2.2 移位性质 (7)3.2.3 希尔伯特变换的希尔伯特变换 (7)3.2.4 逆希尔伯特变换 (7)3.2.5 奇偶特性 (8)3.2.6 能量守恒 (8)3.2.7 正交性质 (8)3.2.8 调制性质 (8)3.2.9 卷积性质 (9)4 Fir滤波器的基本原理及设计方法 (10)4.1 Fir滤波器的基本原理及其特点 (11)4.1.1 FIR数字滤波器的基本原理 (11)4.1.2 FIR滤波器的基本特点 (11)4.2 FIR数字滤波器的设计 (12)5 希尔伯特fir滤波器 (13)6 希尔伯特变换的应用 (17)6.1 希尔伯特变换在探地雷达数据处理中的应用 (17)6.1.1 公式 (17)6.1.2 算法 (18)6.2 数字I-Q下变频器 (19)6.2.1 希尔伯特变换 (20)6.2.2 基于希尔伯特变换的数字I-Q下变频器 (21)6.3 希尔伯特变换在解调中的应用 (21)6.3.1 希尔伯特变换 (21)6.3.2 在解调中的应用 (22)6.3.3 解调性能分析 (23)7 希尔伯特变换器的Matlab设计 (25)7.1 直接程序法 (25)7.2 利用FDATool工具设计法 (26)7.3 希尔伯特变换器的效果验证 (30)结论 0前景展望 (1)致谢 (2)参考文献 (3)附录 (4)基于MATLAB的希尔伯特FIR滤波器设计摘要在通信系统中,经常需要对一个信号进行正交分解,即分解为同相分量和正交分量,并能有效地提取复杂信号的瞬时参数——瞬时振幅、瞬时相位和瞬时频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
EDA 课程设计报告滤波器设计参数:根据要求,要设计一个输入8位,输出8位的17阶线性相位FIR 滤波器,所以采用图2(a)的方式,其中输入信号范围为:[±99,0,0,0, ±70,0,0,0, ±99,0,0,0, ±70,…],此滤波器 Fs 为44kHz,Fc 为10.4kHz 。
(一)FIR 数字滤波器理论简述有限冲激响应(FIR )数字滤波器和无限冲激响应(IIR )数字滤波器广泛应用于数字信号处理系统中。
IIR 数字滤波器方便简单,但它相位的非线性,要求采用全通网络进行相位校正,且稳定性难以保障。
FIR 滤波器具有很好的线性相位特性,使得它越来越受到广泛的重视。
有限冲击响应(FIR )滤波器的特点:1 既具有严格的线性相位,又具有任意的幅度;2 FIR 滤波器的单位抽样响应是有限长的,因而滤波器性能稳定;3只要经过一定的延时,任何非因果有限长序列都能变成因果的有限长序列,因而能用因果系统来实现;4 FIR 滤波器由于单位冲击响应是有限长的,因而可用快速傅里叶变换(FFT)算法来实现过滤信号,可大大提高运算效率。
5 FIR 也有利于对数字信号的处理,便于编程,用于计算的时延也小,这对实时的信号处理很重要。
6 FIR 滤波器比较大的缺点就是阶次相对于IIR 滤波器来说要大很多。
FIR 数字滤波器是一个线性时不变系统(LTI ),N 阶因果有限冲激响应滤波器可以用传输函数H (z )来描述,0()()N k k H z h k z -==∑(0.1)在时域中,上述有限冲激响应滤波器的输入输出关系如下:0[][][][][]N k y n x n h n x k h n k ==*=-∑(0.2)其中,x [n ]和y [n ]分别是输入和输出序列。
N 阶有限冲激响应滤波器要用N +1个系数描述,通常要用N+1个乘法器和N 个两输入加法器来实现。
乘法器的系数正好是传递函数的系数,因此这种结构称为直接型结构,可通过式(1.2)来实现,如图1。
2图1当冲击响应满足下列条件时, FIR 滤波器具有对称结构,为线性相位滤波器:。
(1.3) 这种对称性,可使得乘法器数量减半:对n 价滤波器,当n 为偶数时,乘法器的个数为n/2个;当n 为奇数时,乘法器的个数为(n+1)/2个。
在电路实现中,乘法器占用的逻辑单元数较多。
乘法器的增加,意味着电路成本增加,另外对电路的工作速度也有影响。
N 阶线性相位的因果FIR 系统的单位冲激响应滤波器可用对称冲激响应 [][]h n h N n =-[][]h n h N n =- (0.3) 或者反对称冲激响应[][]h n h N n =--[][]h n h N n =-- (0.4) 来描述。
具有对称冲激响应的FIR 传输函数的冲激响应可写成如下形式:当N 为偶数时 12()200()[][]()()2N N N n n N n n n N H z h n zh n z z h z ------====++∑∑ (0.5) 当N 为奇数时 112()00()[][]()N N n n N n n n H z h n z h n z z +-----====+∑∑ (0.6)则FIR 线性相位系统的结构可转化成如图2(a )和图2(b )所示。
)1()(n N h n h --=图2(a)N为奇数图2(b)N为偶数(二)设计方案随着数字技术日益广泛的应用,以现场可编程门阵列(FPGA)为代表的ASIC 器件得到了迅速普及和发展,器件集成度和速度都在高速增长。
FPGA既具有门阵列的高逻辑密度和高可靠性,又具有可编码逻辑器件的用户可编程特性,可以减少系统设计和维护的风险,降低产品成本,缩短设计周期。
分布式算法是一种以实现乘加运算为目的的运算方法。
它与传统算法实现乘加运算的不同在于执行部分积运算的先后顺序不同。
简单地说,分布式算法在完成乘加功能时是通过将各输入数据每一对应位产生的部分积预先进相加形成相应部分积,然后在对各部门积进行累加形成最终结果,而传统算法是等到所有乘积产生之后再进行相加来完成乘加运算的。
与传统算法相比,分布式算法可极大地减少硬件电路规模,很容易实现流水线处理,提高电路的执行速度。
FPGA有着规整的内部逻辑块阵列和丰富的连线资源,特别适合细粒度和高并行度结构特点的数字信号处理任务,如FIR、FFT等。
利用FPGA实现FIR滤波器的设计过程,并且对设计中的关键技术——分布式算法进行详细描述。
3一、FIR滤波器的结构FIR滤波器的结构主要是非递归结构,没有输出到输入的反馈。
并且FIR滤波器很容易获得严格的线性相位特性,避免被处理信号产生相位失真。
而线性相位体现在时域中仅仅是h(n)在时间上的延迟,这个特点在图像信号处理、数据传输等波形传递系统中是非常重要的。
此外,他不会发生阻塞现象,能避免强信号淹没弱信号,因此特别适合信号强弱相差悬殊的情况。
二、FIR数字滤波器的设计方案:通常采用窗函数设计FIR滤波器方法简单,但是这些滤波器的设计还不是最优的。
首先通带和阻带的波动基本上相等,另外对于大部分窗函数来说,通带内或阻带内的波动不是均匀的,通常离开过渡带时会减小。
若允许波动在整个通带内均匀分布,就会产生较小的峰值波动。
因此考虑通过某种方法,对滤波器的结构进行优化。
对于线性相位因果FIR滤波器,它的系列具有中心对称特性,即h(i)=±h(N-1-i)。
令s(i)=x(i) ±x(N-1-i),对于偶对称,代入式(1)可得:根据要求,要设计一个输入8位,输出8位的17阶线性相位FIR滤波器,所以采用图2(a)的方式,其中输入信号范围为:[±99,0,0,0,±70,0,0,0,±99,0,0,0,±70,…],此滤波器Fs为44kHz,Fc为10.4kHz。
MATLAB 设计计算滤波器系数过程如下:FIR滤波器参数设置,因为是17阶,所以Specify order处填16,h(0)=0.4FIR滤波器的相频响应FIR滤波器的冲激响应FIR滤波器系数56Matable 仿真图仿真结果:7仿真结果:89对FIR 滤波器的系数进行调整,整数化可得FIR 滤波器的参数为[-12 -19 13 30 -14 -54 14 170 255 170 14 -54 -14 30 13 -19 -12]根据以上所说的该思路,可以将FIR 滤波器的原理图设计如下:下面对各加法器乘法器的输出位数进行分析,对第一级加法器,输入全为8位,输出统一为9位。
对各个乘法器进行分析,12=8+4,8为2的3次方,向左移了3位,输出为12位;18=16+2,16为2的4次方,向左移了4位,输出为13位;以此类推,13乘法器输出为12位,29输出为13位,52输出为14位,162输出为16位,242输出为16位。
对剩余加法器进行分析,对输入序列进行分析,[±99,0,0,0,±70,0,0,0,±99,0,0,0,±70,…],周期为8,经分析当总值最大时,总输出应为99*18+70*29+50*70+99*162=1782+2030+3640+16038=23490,2的15次方为32768,再加上一位符号位,所以输出应为16位,由此类推,12、18乘法器输出之和为13位,13、19乘法器输出之和应为13位,总输出为14位。
另一支路上,13、52乘法器输出之和为14位,14、162乘法器输出之和为16位,其总输出之和为16位,最后这两路输出之和为16位。
将后8位舍去,加上由乘法器242输出舍取得倒的8位,总输出为8位。
至此,所有器件的输入输出都可判定。
下面进入模块设计阶段。
(三)模块电路设计设计的FIR滤波器由19个小VHD文件和一个总体BDF文件组成,VHD文件可以分为以下四种模块:寄存器、加法器、减法器、乘法器。
3.1 寄存器3.1.1 寄存器原理寄存器用于寄存一组二值代码,对寄存器的触发器只要求它们具有置1、置0的功能即可,因而本设计中用D触发器组成寄存器,实现寄存功能。
3.1.2 寄存器要求实现的功能在CP正跳沿前接受输入信号,正跳沿时触发翻转,正跳沿后输入即被封锁。
3.1.3寄存器的VHDL语言实现(8位)LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY dff8 ISPORT( clk : IN STD_LOGIC;clear : IN STD_LOGIC;Din : IN STD_LOGIC_VECTOR(7 DOWNTO 0);Dout : OUT STD_LOGIC_VECTOR(7 DOWNTO 0) );END dff8;ARCHITECTURE a OF dff8 ISBEGINPROCESS(clk,clear)BEGIN10IF clear='1' THENDout<="";ELSIF clear='0' THENIF(clk'EVENT AND clk='1') THENDout <= Din;END IF;END IF;END PROCESS;END a;其中,clear为复位信号。
3.1.4寄存器的模块图3.1.5寄存器的波形仿真完全符合设计要求。
3.2 加法器3.2.1 加法器的原理在将两个多位二进制数相加时,除了最低位以外,每一位都应该考虑来自低位的进位,即将两个对应位的加数和来自低位的进位3个数相加。
这种运算称为全加,所用的电路称为全加器。
多位加法器的构成有两种方式:并行进位和串行进位。
并行进位加法器设有进位产生逻辑,预算速度较快;串行进位方式是将全加器级联构成多位加法器。
并行进位加法器通常比串行级联加法器占用更多的资源。
随着为数的增加,相同位数的并行加法器与串行加法器的资源占用差距也越来越大,因此,在工程中使用加法器时,要在速度和容量之间寻找平衡点。
本次设计采用的是并行加法器方式。
3.2.2 加法器要求实现的功能实现两个二进制数字的相加运算。
当到达时钟上升沿时,将两数输入,运算,输出结果。
3.2.3 加法器的VHDL语言实现(以下以12位数加16位数生成16位数的加法器为例)LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_arith.ALL;ENTITY add isPORT(clk : in STD_LOGIC;Din1 :in signed (11 downto 0);Din2 :in signed (15 downto 0);Dout:out signed (15 downto 0));END add;ARCHITECTURE a of add isSIGNAL s1: signed(15 downto 0);BEGINs1<=(Din1(11)&Din1(11)&Din1(11)&Din1(11)&Din1); PROCESS(Din1,Din2,clk)BEGINif clk'event and clk='1' thenDout<=s1+Din2;end if;end process;end a;3.2.4 加法器的模块图3.2.5 加法器的波形仿真完全符合设计要求。
