七年级数学勾股定理
七年级数学勾股定理

5
4.如图,在△ABC中,D 是BC上一点, 若AB=10,BD=6,AD=8,AC=17, 求△ABC的面积.
A
B
DC
5.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm, 一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?5B Cຫໍສະໝຸດ 即b=,c= 说一说
1.如图,两个正方形的面积分别为64,49,
则AC=( )
A
64 D
49 C
2.由四根木棒,长度分别为3,4,5,6
若去其中三根木棒组呈三角形,有( )
中取法,其中,能构成直角三角形的是
()
3.直角三角形的两条直角边分别是5cm, 12cm,其斜边上的高是( )
4.以直角三角形的两直角边所作正方形的 面积分别是25和144,则斜边长是( )
15
A
6.△ABC中,周长是24, ∠C=90°,且C=9,则三角形 的面积是多少?
A
C
B
7.如图,有一块地,已知,AD=4m, CD=3m,∠ADE=90°,AB=13m, BC=12m。求这块地的面积。
C
D B
A
8.如图,四边形ABCD中,∠B=∠D=90°, ∠C=45°,AD=1,BC=2,求CD的长.
由。
A
E D
B
C
2.假期中,王强和同学到某海岛上去玩探宝游 戏,按照探宝图,他们登陆后先往东走8千米,又 往北走2千米,遇到障碍后又往西走3千米,
在折向北走到6千米处往东一拐, 仅走1千米就找到宝藏,问登陆点A
B 1 6
到宝藏埋藏点B的距离是多少千米?
3
2
初中数学-勾股定理16种证明方法
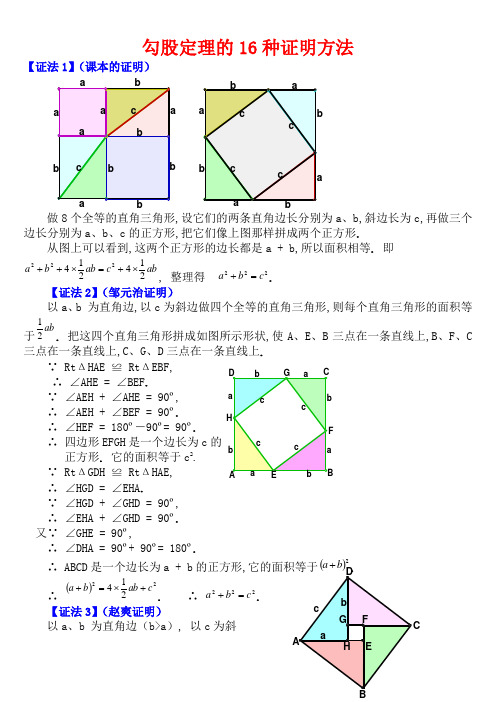
勾股定理的16种证明方法【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b,斜边长为c,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +. ∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜D 边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P . ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED,C∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC,交AC 于点P . 过点B 作BM ⊥PQ,垂足为M;再过点F 作FN ⊥PQ,垂足为N .∵ ∠BCA = 90º,QP ∥BC, ∴ ∠MPC = 90º, ∵ BM ⊥PQ, ∴ ∠BMP = 90º,∴ BCPM 是一个矩形,即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c, ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE,交AB 于点M,交DE 于点L . ∵ AF = AC,AB = AD,∠FAB = ∠GAD, ∴ ΔFAB ≌ ΔGAD,∵ ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b,斜边AB 的长为c,过点C 作CD ⊥AB,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC, ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB, 即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB,从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+. 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC,AF 交GT 于F,AF 交DT 于R . 过B 作BP ⊥AF,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c,∴ Rt ΔDHA ≌ Rt ΔBCA .K∴ DH = BC = a,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b,AP= a,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a,下底BP= b,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 = ab b 212-, 985S S S +=,∴824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º,∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º,BT = BE = b, ∴ Rt ΔHBT ≌ Rt ΔABE .∴ HT = AE = a . ∴ GH = GT ―HT = b ―a . 又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º,∴ ∠GHF = ∠DBC.R∵ DB = EB ―ED = b ―a, ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM,而AB = AQ = c,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM,又得QM = AE = a,∠AQM = ∠BAE . ∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE, ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -,即222a cb -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c (如图). 过点A 作AD ∥CB,过点B 作BD ∥CA,则ACBD为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•, ∵ AB = DC = c,AD = BC = a, AC = BD = b,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c . 作Rt ΔABC 的内切圆⊙O,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF,BF = BD,CD = CE,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AO C BO CAO B ABC S S S S ∆∆∆∆++= = brar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b,斜边AB 的长为c,过点C 作CD ⊥AB,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A,∴ 若 AD :AC ≠AC :AB,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B, ∴ 若BD :BC ≠BC :AB,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a,连结DA 、DC,则 AD = c .∵ EM = EH + HM = b + a , ED = a, ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a, ∠AED = 90º, AE = b, ∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC,DC = AD = c .∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC,CB ∥DA,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º,D D∴ ∠BAF=∠DAE .连结FB,在ΔABF 和ΔADE 中,∵ AB =AD = c,AE = AF = b,∠BAF=∠DAE, ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中, ∵ AB = BC = c,BF = CG = a, ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
数学(勾股定理规律)

勾股定理探究报告
为什么勾股数中一定会有偶数?
假设三边a、b、c(a<b<c)都为奇数,则a2 为奇数b2和c2都为奇数,奇数与奇数相加会得偶数,这不符合a2+b2=c2.我们再设a和b为奇数,c为偶数,则a2 为奇数,b2为奇数,c2为偶数,奇数与奇数相加等于偶数,这符合a2+b2=c2.以此类推再设a、b、c都为偶数,则a2b2c2都为偶数,两个偶数相加一定会等于偶数,也符合a2+b2=c2。
所以勾股数中一定会有偶数。
三个勾股数的规律
设a、b、c为一组勾股数
当a为偶数时,如6、8、10;8、15、17;12、35、37;20、99、101... ...我们发现,除a外的b、c为两个连续的偶数或奇数。
我们知道a为偶数,我们就可以用2m(m>1)来表示它,则b=m2-1,c=m2+1.我们将b和c相加等于2m2,这是发现a2/2也等于2m2,所以我们得出a2/2=b+c且b和c是两个连续的奇数或偶数。
初中数学最难的部分是什么需要怎么学习

初中数学最难的部分是什么需要怎么学习初中数学最难的部分:勾股定理指的是直角三角形直角边的平方和等于斜边的平方。
在圆中最重要的概念是圆周率π,指的是圆的周长和直径的比值,大约等于3.14159......(3到4之间的无限不循环小数),圆的面积公式是πr2(r为半径)。
初中数学最难的部分是什么1、勾股定理。
勾股定理指的是直角三角形直角边的平方和等于斜边的平方。
2、圆的难点。
在圆中最重要的概念是圆周率π,指的是圆的周长和直径的比值,大约等于3.14159......(3到4之间的无限不循环小数),圆的面积公式是πr2(r为半径)。
3、三角形的内角和和外角。
三角形的内角和是180°,三角形的外角和是360°,这是死记硬背的知识。
不只是三角形,任意四边形的外角和都等于360°。
4、分割法解题。
分割法是数学里面重要的解题方法。
恰到好处的分割,可以对解题起到至关重要的作用。
初中数学最难的部分有哪些学习方法一、主动预习预习的目的是主动获取新知识的过程,有助于调动学习积极主动性,新知识在未讲解之前,认真阅读教材,养成主动预习的习惯,是获得数学知识的重要手段。
因此,培养自学能力,在老师的引导下学会看书,带着老师精心设计的思考题去预习。
如自学例题时,要弄清例题讲的什么内容,告诉了哪些条件,求什么,书上怎么解答的,为什么要这样解答,还有没有新的解法,解题步骤是怎样的。
抓住这些重要问题,动脑思考,步步深入,学会运用已有的知识去独立探究新的知识。
二、主动思考很多同学在听课的过程中,只是简简单单的听,不能主动思考,这样遇到实际问题时,会无从下手,不知如何应用所学的知识去解答问题。
主要原因还是听课过程中不思考惹的祸。
除了我们跟着老师的思路走,还要多想想为什么要这么定义,这样解题的好处是什么,这样主动去想,不仅能让我们更加认真的听课,也能激发对某些知识的兴趣,更有助于学习。
靠着老师的引导,去思考解题的思路;答案真的不重要;重要的是方法!三、善于总结规律解答数学问题总的讲是有规律可循的。
鲁教版七年级数学上册第三章勾股定理复习

【变式 1-2】如图 2:在一个高 6 米,长 10 米的楼梯表面铺地毯,则该地毯的长
度至少是 14cm 米.
【变式 1-3】一根旗杆在离地面 9 m 处断裂,旗杆顶部落在离旗杆底部 12 m 的
地面上,旗杆在折断之前高度为 24m . 【变式 1-4】一直角三角形两条边长分别是 12 和 5,则第三边平方为 169或11. 9
4、要注意防止漏解 例 4 在 Rt△ABC 中,a=3,b=4,求 c.
当c为斜边时,c a2 b2 32 42 5 当b为斜边时,c b2 a2 42 32 7 c的值为5或 7
5、要注意正逆合用 在解题中,我们常将勾股定理及其逆定理结合起来使用,一个是性质,一个是判
定,真所谓珠联壁合.当然在具体运用时,到底是先用性质,还是先用判定,要
学习目标
XUE XI MU BIAO
1.理解勾股定理的内容,已知直角三角形的两边,会运用勾股定理求第三边. 2.勾股定理的应用. 3.会运用勾股定理的逆定理,判断直角三角形. 重点:掌握勾股定理及其逆定理. 难点:理解勾股定理及其逆定理的应用.
1 巩固新知
PART THREE
标题
一、勾股定理:_直__角__三__角__形__两__直 ___角__边__的__平__方__和__等__于 ___斜__边的平方
3 2x 4 3x, 解得x 1
BC 3x 2x 5x 5
又 32 +42 =52,即AC2 AB2 BC2
ABC是直角三角形,A=90,
SABC
1 2
AB •
AC
1 2
43
6
18.如图等腰△ABC 的底边长为 8cm,腰长为 5cm,一个动点 P 在底边上从 B 向 C 以 0.25cm/s
初中数学勾股定理教案 初中数学勾股定理教案优秀3篇

初中数学勾股定理教案初中数学勾股定理教案优秀3篇初中数学勾股定理教案优秀3篇由作者为您收集整理,希望可以在初中数学勾股定理教案方面对您有所帮助。
初中数学勾股定理教案篇一一、教案背景概述:教材分析:勾股定理是直角三角形的重要性质,它把三角形有一个直角的形的特点,转化为三边之间的数的关系,它是数形结合的榜样。
它可以解决许多直角三角形中的计算问题,它是直角三角形特有的性质,是初中数学教学内容重点之一。
本节课的重点是发现勾股定理,难点是说明勾股定理的正确性。
学生分析:1、考虑到三角尺学生天天在用,较为熟悉,但真正能仔细研究过三角尺的同学并不多,通过这样的情景设计,能非常简单地将学生的注意力引向本节课的本质。
2、以与勾股定理有关的人文历史知识为背景展开对直角三角形三边关系的讨论,能激发学生的学习兴趣。
设计理念:本教案以学生手中舞动的三角尺为知识背景展开,以勾股定理在古今中外的发展史为主线贯穿课堂始终,让学生对勾股定理的发展过程有所了解,让他们感受勾股定理的丰富文化内涵,体验勾股定理的探索和运用过程,激发学生学习数学的兴趣,特别是通过向学生介绍我国古代在勾股定理研究和运用方面的成就,激发学生热爱祖国,热爱祖国悠久文化的思想感情,培养他们的民族自豪感和探究创新的精神。
教学目标:1、经历用面积割、补法探索勾股定理的过程,培养学生主动探究意识,发展合理推理能力,体现数形结合思想。
2、经历用多种割、补图形的方法验证勾股定理的过程,发展用数学的眼光观察现实世界和有条理地思考能力以及语言表达能力等,感受勾股定理的文化价值。
3、培养学生学习数学的兴趣和爱国热情。
4、欣赏设计图形美。
二、教案运行描述:教学准备阶段:学生准备:正方形网格纸若干,全等的直角三角形纸片若干,彩笔、直角三角尺、铅笔等。
老师准备:毕达哥拉斯、赵爽、刘徽等证明勾股定理的图片以及其它有关人物历史资料等投影图片。
三、教学流程:(一)引入同学们,当你每天手握三角尺绘制自己的宏伟蓝图时,你是否想过:他们的边有什么关系呢?今天我们来探索这一小秘密。
七年级数学勾股定理

七年级数学勾股定理
勾股定理是指直角三角形中,直角边的平方和等于斜边的平方。
具体表示为:在直角三角形ABC中,设AB为直角边,BC为直角边,AC为斜边,则有AB² + BC² = AC²。
勾股定理可以用于求解直角三角形的边长、判断是否为直角三角形等。
在数学中,经常会用到勾股定理来解决与直角三角形相关的问题。
例如,已知直角三角形的两个直角边分别是3和4,求斜边的长。
根据勾股定理,可得3² + 4² = 斜边²,即9 + 16 = 斜边²,解得斜边的平方为25,再开根号可得斜边的长为5。
总结一下,勾股定理是数学中常用的重要定理,用于解决直角三角形相关的问题。
通过勾股定理,我们可以求解直角三角形的边长、判断是否为直角三角形等。
初中数学 如何证明勾股定理在平面直角坐标系中的几何意义

初中数学如何证明勾股定理在平面直角坐标系中的几何意义。
在平面直角坐标系中,我们可以使用几何方法证明勾股定理的几何意义。
以下是证明过程:假设我们有一个直角三角形ABC,其中∠C为直角,点A的坐标为(x₁, y₁),点B的坐标为(x₂, y₂),点C的坐标为(x₃, y₃)。
根据直角三角形的性质,我们可以知道点A到点B的距离为AB,点B到点C的距离为BC,点A到点C的距离为AC。
根据平面直角坐标系中两点之间的距离公式,我们可以得到:AB = √((x₂ - x₁)² + (y₂ - y₁)²)BC = √((x₃ - x₂)² + (y₃ - y₂)²)AC = √((x₃ - x₁)² + (y₃ - y₁)²)我们要证明的是:AB² + BC² = AC²。
将上述三个式子代入上式,得到:(√((x₂ - x₁)² + (y₂ - y₁)²))² + (√((x₃ - x₂)² + (y₃ - y₂)²))² = (√((x₃ - x₁)² + (y₃ - y₁)²))²化简得到:(x₂ - x₁)² + (y₂ - y₁)² + (x₃ - x₂)² + (y₃ - y₂)² = (x₃ - x₁)² + (y₃ - y₁)²进一步化简得到:(x₂ - x₁)² + (y₂ - y₁)² + (x₃ - x₂)² + (y₃ - y₂)² - (x₃ - x₁)² - (y₃ - y₁)² = 0我们可以将上式分成两部分进行证明:第一部分:(x₂ - x₁)² + (y₂ - y₁)² - (x₃ - x₁)² - (y₃ - y₁)² = 0将(x₂ - x₁)² + (y₂ - y₁)²展开得到:(x₂² - 2x₁x₂ + x₁²) + (y₂² - 2y₁y₂ + y₁²) - (x₃² - 2x₁x₃ + x₁²) - (y₃² - 2y₁y₃ + y₁²) = 0化简得到:x₂² + y₂² - x₃² - y₃² = 2x₁(x₃ - x₂) + 2y₁(y₃ - y₂)我们知道∠C为直角,所以直角三角形ABC中AB和BC垂直,即斜率之积为-1。
初一几何数学教案二:直角三角形的勾股定理与运用

初一几何数学教案二:直角三角形的勾股定理与运用
一、教学目标
1.了解直角三角形及其特点,学会画出直角三角形的各个边,学会有方向地标出直角。
2.掌握勾股定理的定义和推导过程,能够正确地使用勾股定理进行计算和验证。
3.了解勾股定理的实际应用,掌握解决勾股问题的方法。
二、教学重点
1.直角三角形及其特点
2.勾股定理的定义和推导过程
3.勾股定理的实际应用
三、教学难点
1.学生对勾股定理的理解和应用
2.学生解决勾股问题的能力
四、教学过程
1.引入
老师通过一个问题引入,如:小明爬山,发现他行进了3公里之后到了一座山脚下,他想知道山的高度,应该怎么做?
2.学生自主探究
老师教授有关直角三角形的定义和特点,学生分组自行开展探究,画出直角三角形的各个边,并标出直角和边的名称。
3.正式讲授勾股定理
老师讲解勾股定理的概念和推导过程,并通过例题进行讲解,强调勾股定理的应用。
4.例题练习
让学生分组自行练习解答勾股问题,老师进行指导和辅导。
5.课堂练习
整个课堂进行统一的练习,让学生掌握勾股定理的应用和解决勾股问题的方法。
6.归纳总结
老师归纳总结勾股定理的应用和解决勾股问题的方法,并对本节课的教学进行总结和评价。
五、教学评价
通过上述教学过程,学生能够理解直角三角形的特征及其边长关系,掌握了勾股定理的定义和推导过程,能够应用勾股定理解决勾股问题。
同时,老师还能够通过课堂练习来全面评估学生的学习效果。
(完整版)初中数学竞赛——勾股定理及其应用

(完整版)初中数学竞赛——勾股定理及其应用初中数学竞赛勾股定理与应用勾股定理直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2.勾股定理逆定理如果三角形三边长a,b,c有下面关系:a2+b2=c2那么这个三角形是直角三角形.早在3000年前,我国已有“勾广三,股修四,径阳五”的说法.关于勾股定理,有很多证法,在我国它们都是用拼图形面积方法来证明的.下面的证法1是欧几里得证法.证法1 如图2—16所示.在Rt△ABC的外侧,以各边为边长分别作正方形ABDE,BCHK,ACFG,它们的面积分别是c2,a2,b2.下面证明,大正方形的面积等于两个小正方形的面积之和.过C引CM∥BD,交AB于L,连接BG,CE.因为AB=AE,AC=AG,∠CAE=∠BAG,所以△ACE≌△AGB(SAS).而所以 S AEML=b2.①同理可证 S BLMD=a2.②①+②得S ABDE=S AEML+S BLMD=b2+a2,即 c2=a2+b2.证法2 如图2—17所示.将Rt△ABC的两条直角边CA,CB 分别延长到D,F,使AD=a,BF=b.完成正方形CDEF(它的边长为a+b),又在DE上截取DG=b,在EF上截取EH=b,连接AG,GH,HB.由作图易知△ADG≌△GEH≌△HFB≌△ABC,所以AG=GH=HB=AB=c,∠BAG=∠AGH=∠GHB=∠HBA=90°,因此,AGHB为边长是c的正方形.显然,正方形CDEF 的面积等于正方形AGHB的面积与四个全等的直角三角形(△ABC,△ADG,△GEH,△HFB)的面积和,即化简得 a2+b2=c2.证法3 如图2—18.在直角三角形ABC的斜边AB上向外作正方形ABDE,延长CB,自E作EG⊥CB延长线于G,自D 作DK⊥CB延长线于K,又作AF, DH分别垂直EG于F,H.由作图不难证明,下述各直角三角形均与Rt△ABC全等:△AFE≌△EHD≌△BKD≌△ACB.设五边形ACKDE的面积为S,一方面S=S ABDE+2S△ABC,①另一方面S=S ACGF+S HGKD+2S△ABC.②由①,②所以 c2=a2+b2.关于勾股定理,在我国古代还有很多类似上述拼图求积的证明方法,我们将在习题中展示其中一小部分,它们都以中国古代数学家的名字命名.利用勾股定理,在一般三角形中,可以得到一个更一般的结论.定理在三角形中,锐角(或钝角)所对的边的平方等于另外两边的平方和,减去(或加上)这两边中的一边与另一边在这边(或其延长线)上的射影的乘积的2倍.(完整版)初中数学竞赛——勾股定理及其应用因此,我们常又称此定理为广勾股定理(意思是勾股定理在一般三角形中的推广).由广勾股定理我们可以自然地推导出三角形三边关系对于角的影响.在△ABC中,(1)若c2=a2+b2,则∠C=90°;(2)若c2<a2+b2,则∠C<90°;(3)若c2>a2+b2,则∠C>90°.勾股定理及广勾股定理深刻地揭示了三角形内部的边角关系,因此在解决三角形(及多边形)的问题中有着广泛的应用.例1 如图2-21所示.已知:在正方形ABCD中,∠BAC 的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.求证:AB2=2FG2.分析注意到正方形的特性∠CAB=45°,所以△AGF是等腰直角三角形,从而有AF2=2FG2,因而应有AF=AB,这启发我们去证明△ABE≌△AFE.说明事实上,在审题中,条件“AE平分∠BAC”及“EF ⊥AC于F”应使我们意识到两个直角三角形△AFE与△ABE全等,从而将AB“过渡"到AF,使AF(即AB)与FG处于同一个直角三角形中,可以利用勾股定理进行证明了.例2 如图2-22所示.AM是△ABC的BC边上的中线,求证:AB2+AC2=2(AM2+BM2).推论△ABC的中线长公式:说明三角形的中线将三角形分为两个三角形,其中一个是锐角三角形,另一个是钝角三角形(除等腰三角形外).利用广勾股定理恰好消去相反项,获得中线公式.①′,②′,③′中的m a,m b,m c分别表示a,b,c边上的中线长.例3 如图2-23所示.求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍.分析如图2-23所示.对角线中点连线PQ,可看作△BDQ 的中线,利用例2的结论,不难证明本题.说明本题是例2的应用.善于将要解决的问题转化为已解决的问题,是人们解决问题的一种基本方法,即化未知为已知的方法.下面,我们再看两个例题,说明这种转化方法的应用.例4 如图2-24所示.已知△ABC中,∠C=90°,D,E分别是BC,AC上的任意一点.求证:AD2+BE2=AB2+DE2.分析求证中所述的4条线段分别是4个直角三角形的斜边,因此考虑从勾股定理入手.(完整版)初中数学竞赛——勾股定理及其应用例5 如图2-25所示.设直角三角形ABC中,∠C=90°,AM,BN分别是BC,AC边上的中线.求证:4(AM2+BN2)=5AB2.分析由于AM,BN,AB均可看作某个直角三角形的斜边,因此,仿例4的方法可从勾股定理入手,但如果我们能将本题看成例4的特殊情况——即M,N分别是所在边的中点,那么可直接利用例4的结论,使证明过程十分简洁.练习十一1.用下面各图验证勾股定理(虚线代表辅助线):(1)赵君卿图(图2-27);(2)项名达图(2—28);(3)杨作枚图(图2-29).2.已知矩形ABCD,P为矩形所在平面内的任意一点,求证:PA2+PC2=PB2+PD2.(提示:应分三种情形加以讨论,P在矩形内、P在矩形上、P在矩形外,均有这个结论.)3.由△ABC内任意一点O向三边BC,CA,AB分别作垂线,垂足分别是D,E,F.求证:AF2+BD2+CE2=FB2+DC2+EA2.4.如图2-30所示.在四边形ADBC中,对角线AB⊥CD.求证:AC2+BD2=AD2+BC2.它的逆定理是否成立?证明你的结论.5.如图2—31所示.从锐角三角形ABC的顶点B,C分别向对边作垂线BE,CF.求证:BC2=AB·BF+AC·CE.。
鲁教版五四制七年级数学上册第三章勾股定理1探索勾股定理

勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 b2 c2
直角三角形两直角边的平方和等于斜边的平方.
a
c
b
勾
弦
股
我们用另外一种方法来说明勾股定理是正确的
c
c
c
c
•
13、生气是拿别人做错的事来惩罚自 己。22.3.2322.3.2317:59:0317:59:03March 23, 2022
•
14、抱最大的希望,作最大的努力。2022年3月23日 星期三 下午5时59分3秒17:59:0322.3.23
•
15、一个人炫耀什么,说明他内心缺 少什么 。。2022年3月 下午5时59分22.3.2317:59M arch 23, 2022
9
16
?
怎么求SR的大小? 有几种方案?
P
Q CR
用“补”的方法
SR
49 4 ( 1 4 3) 2
25.
P
Q CR
用“割”的方法
SR
4
1 2
4
3
1
25.
探究勾股定理
(1)在图中,正方形A中含
C A
B
有 9 个小方格,即A的面积 是 9 个单位面积.
正方形B的面积是__9__ 个单位面积.
(图中每个小方格代表1个单位面积)
C A
(2)在图2中,正方形A, B,C中各含有多少个小方 格?它们的面积各是多少?
B
图1
C A
B
图2
(3)你能发现图1中三个 正方形A,B,C的面积之 间有什么关系吗?图2呢?
初中数学之勾股定理知识点

初中数学之勾股定理知识点勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a,b,斜边为c,那么.勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为大正方形面积为所以.方法三:,,化简得证.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形勾股定理的应用①已知直角三角形的任意两边长,求第三边在中,,则,,②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题勾股定理的逆定理如果三角形三边长a,b,c满足,那么这个三角形是直角三角形,其中c为斜边.①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和与较长边的平方作比较,若它们相等时,以a,b,c 为三边的三角形是直角三角形;若,时,以a,b,c 为三边的三角形是钝角三角形;若,时,以a,b,c 为三边的三角形是锐角三角形;②定理中a,b,c 及只是一种表现形式,不可认为是唯一的,如若三角形三边长a,b,c 满足,那么以a,b,c 为三边的三角形是直角三角形,但是b为斜边.③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即中,a,b,c 为正整数时,称a,b,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3、4、5;6、8、10;5、12、13;7、24、25等。
初中数学《勾股定理》说课稿5篇

初中数学《勾股定理》说课稿5篇初中数学《勾股定理》说课稿1一、教材分析^p :〔一〕、本节课在教材中的地位作用“勾股定理的逆定理”一节,是在上节“勾股定理”之后,继续学习的一个直角三角形的判断定理,它是前面知识的继续和深化,勾股定理的逆定理是初中几何学习中的重要内容之一,是今后判断某三角形是直角三角形的重要方法之一,在以后的解题中,将有非常广泛的应用,同时在应用中浸透了利用代数计算的方法证明几何问题的思想,为将来学习解析几何埋下了伏笔,所以本节也是本章的重要内容之一。
课标要求学生必须掌握。
〔二〕、教学目的:根据数学课标的要求和教材的详细内容,结合学生实际我确定了本节课的教学目的。
知识技能:1、理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理。
2、掌握勾股定理的逆定理,并能利用勾股定理的逆定理断定一个三角形是不是直角三角形过程与方法:1、通过对勾股定理的逆定理的探究,经历知识的发生、开展与形成的过程2、通过用三角形三边的数量关系来判断三角形的形状,体验数与形结合方法的应用3、通过勾股定理的逆定理的证明,体会数与形结合方法在问题解决中的作用,并能运用勾股定理的逆定理解决相关问题。
情感态度:1、通过用三角形三边的数量关系来判断三角形的形状,体验数与形的内在联络,感受定理与逆定理之间的和谐及辩证统一的关系2、在探究勾股定理的逆定理的活动中,通过一系列富有探究性的问题,浸透与别人交流、合作的意识和探究精神〔三〕、学情分析^p :尽管已到初二下学期学生知识增多,才能增强,但思维的局限性还很大,才能也有差距,而勾股定理的逆定理的证明方法学生第一次见到,它要求根据条件构造一个直角三角形,根据学生的智能状况,学生不容易想到,因此勾股定理的逆定理的证明又是本节的难点,这样如何添辅助线就是解决它的关键,这样就确定了本节课的重点、难点和关键。
重点:勾股定理逆定理的应用难点:勾股定理逆定理的证明关键:辅助线的添法探究二、教学过程:本节课的设计原那么是:使学生在动手操作的根底上和合作交流的良好气氛中,通过巧妙而自然地在学生的认识构造与几何知识构造之间筑了一个信息流通渠道,进而到达完善学生的数学认识构造的目的。
人教版初中数学公式大全

人教版初中数学公式大全初中数学公式一:勾股定理1勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^22勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形初中数学公式二:四边形基本性质3定理四边形的内角和等于360° 49四边形的外角和等于360°4多边形内角和定理n边形的内角的和等于(n-2)×180°5推论任意多边的外角和等于360°初中数学公式三:平行四边形6平行四边形性质定理1 平行四边形的对角相等7平行四边形性质定理2 平行四边形的对边相等8推论夹在两条平行线间的平行线段相等9平行四边形性质定理3 平行四边形的对角线互相平分10平行四边形判定定理1 两组对角分别相等的四边形是平行四边形11平行四边形判定定理2 两组对边分别相等的四边形是平行四边形12平行四边形判定定理3 对角线互相平分的四边形是平行四边形13平行四边形判定定理4 一组对边平行相等的四边形是平行四边形初中数学公式四:矩形14矩形性质定理1 矩形的四个角都是直角15矩形性质定理2 矩形的对角线相等16矩形判定定理1 有三个角是直角的四边形是矩形17矩形判定定理2 对角线相等的平行四边形是矩形初中数学公式五:菱形18菱形性质定理1 菱形的四条边都相等19菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角20菱形面积=对角线乘积的一半,即S=(a×b)÷221菱形判定定理1 四边都相等的四边形是菱形22菱形判定定理2 对角线互相垂直的平行四边形是菱形初中数学公式六:正方形23正方形性质定理1 正方形的四个角都是直角,四条边都相等24正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角初中数学公式七:梯形25定理1 关于中心对称的两个图形是全等的26定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分27逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称28等腰梯形性质定理等腰梯形在同一底上的两个角相等29等腰梯形的两条对角线相等30等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形31对角线相等的梯形是等腰梯形32平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等33推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰34推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边35 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半36 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h这是一部分初中数学公式的总结归纳,还会有继续的归纳,大家可以继续关注更新。
初中数学勾股定理

勾股定理:如果直角三角形两直角边长分别为a,b,斜边长为 c , 那么a2+b2=c2
勾股定理的应用:已知直角三角形的任意两边,求第三边;已知 直角三角形的一边,确定另两边的关系;证明含有平方(算术平 方根)关系的几何问题;构造方程(或方程组)计算有关线段的 长度解决生活、生产中的实际问题.
所以另一直角边长为8 cm,
故直角三角形的面积是:
(cm2).
9 如图,为了测得湖边上点A和点C间的距离,一观测者在点
B设立了一根标杆,使∠ACB=90°.测得AB=200m,
BC=160m.根据测量结果,求点A和点C间的距离.
解:在△ABC中,∵∠ACB=90°.
C
∴AC2+BC2=AB2(勾股定理).
C ∵AC=50-40-26=9(mm),
BC=40-18-10=12(mm),
AB AC 2 BC 2 10
B
26 A
92 122 15(mm)
15
答:A和B间的距离是15mm.
11.有一个高为1.5 m,半径是1 m的圆柱形油桶,在靠近 边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶 外的部分为0.5 m,问这根铁棒有多长?
图中有几个直角三角形,你是如何判断的?
与你的同伴交流. A 2E 2
4
解:△ABE,△DEF,△FCB均为
D 直角三角形. 1 F 由勾股定理知
BE2=22+42=20,EF2=22+12=5, 3
BF2=32+42=25,
B
4
C ∴BE2+EF2=BF2, ∴ △BEF是直角三角形.
15.一个零件的形状如图1所示,按规定这个零件中∠A和 ∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2 所示,这个零件符合要求吗?
初中数学重点梳理:勾股定理与应用

勾股定理与应用知识定位三解形是平面几何中最重要的图形,它的有关知识是今后我们学习四边形、多边形乃至立体几何的重要基础,而其中的勾股定理在初中竞赛三角形中占据非常大的地位。
必须熟练掌握勾股定理及逆定理的应用、勾股数的推算公式和判定直角三角形。
本节我们通过一些实例的求解,旨在介绍数学竞赛中勾股定理中相关问题的常见题型及其求解方法本讲将通过例题来说明这些方法的运用。
知识梳理1、勾股定理及逆定理:△ABC 中 ∠C =Rt ∠⇔a 2+b 2=c 22、勾股定理及逆定理的应用① 作已知线段a 的2,3, 5……倍② 计算图形的长度,面积,并用计算方法解几何题③ 证明线段的平方关系等。
3、勾股数的定义:如果三个正整数a,b,c 满足等式a 2+b 2=c 2,那么这三个正整数a,b,c 叫做一组勾股数.4、勾股数的推算公式④ 罗士琳法则任取两个正整数m 和n(m>n),那么m 2-n 2,2mn, m 2+n 2是一组勾股数。
⑤ 如果k 是大于1的奇数,那么k, 212-k ,212+k 是一组勾股数。
⑥ 如果k 是大于2的偶数,那么k, 122-⎪⎭⎫ ⎝⎛K ,122+⎪⎭⎫ ⎝⎛K 是一组勾股数。
⑦ 如果a,b,c 是勾股数,那么na, nb, nc (n 是正整数)也是勾股数。
5、 熟悉勾股数可提高计算速度,顺利地判定直角三角形简单的勾股数有:3,4,5; 5,12,13; 7,24,25; 8,15,17; 9,40,41。
常见勾股数3,4,5 : 勾三股四弦五5,12,13 : 5·12记一生6,8,10: 连续的偶数7,24,25 : 企鹅是二百五8,15,17 : 八月十五在一起特殊勾股数连续的勾股数只有3,4,5连续的偶数勾股数只有6,8,102.100以内的勾股数开头数字为20以内3 4 5;5 12 13; 6 8 10;7 24 25;8 15 17;9 12 15;9 40 41;10 24 26;11 60 61;12 16 20;12 35 37;13 84 85;14 48 50;15 20 25;15 36 39;16 30 34;16 63 65;18 24 30;18 80 82例题精讲【试题来源】【题目】△ABC 周长是24,M 是AB 的中点MC=MA=5,则△ABC 的面积是多少【答案】24【解析】 解:∵MA=MB=MC=5,∴∠ACB=90°知周长是24,则AC+BC=14,AC 2+BC 2=102,∴2AC ·BC=(AC+BC)2-(AC 2+BC 2)= 142-102=4×24∴2421=⋅=∆BC AC S ABC 【知识点】勾股定理与应用【适用场合】当堂例题【难度系数】2【试题来源】【题目】如图1,在正方形ABCD 中,N 是CD 的中点,M 是AD 上异于D 的点,且∠NMB=∠MBC ,则AM :AB=( )A .31;B .33;C .21;D .63【答案】A【解析】 解: 如图,延长MN 交BC 的延长线于T ,设MB 的中点为O ,连TO ,则△BAM ∽△TOB∴AM :MB=OB :BT∴MB 2=2AM ·BT (1)令DN=1,CT=MD=k ,则AM=2 – k所以BM=222)2(4k AM AB -+=+BT= 2 + k 代入(1),得4 + (2 – k )2= 2 (2 – k ) (2 + k )所以 k =34 所以AM :AB=32:2 = 31 【知识点】勾股定理与应用【适用场合】当堂练习【难度系数】4【试题来源】【题目】如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到CD 边的距离也等于10,那么,正方形ABCD 的面积是( )【答案】256【解析】 解:如图,过P 作EF ⊥AB 于E ,交CD 于F ,则PF ⊥CD所以PF=PA=PB=10,E 为AB 中点设PE = x ,则AB=AD=10 + x所以AE=21AB=21(10 + x) 在Rt △PAE 中,PA 2=PE 2+AE 2所以102= x 2+ [21(10 + x )]2 所以x = 6所以正方形ABCD 面积=AB 2=(10 + 6)2 = 256【知识点】勾股定理与应用【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,矩形ABCD 中,AB=20,BC=10,若在AB 、AC 上各取一点N 、M ,使得BM+MN 的值最小,这个最小值为( )A .12;B .102;C .16;D .20【答案】C【解析】 解:如图,作B 关于AC 的对称点B ',连A B ',则N 点关于AC 的对称点N '在A B '上,这时,B 到M 到N 的最小值等于B →M →N '的最小值,等于B 到A B '的距离BH ',连B 与A B '和DC 的交点P ,则ABP S ∆=21×20×10=100, 由对称知识,∠PAC=∠BAC=∠PCA所以PA=PC ,令PA=x ,则PC=x ,PD=20 – x ,在Rt △ADP 中,PA 2=PD 2+AD 2所以 x 2 = (20 – x )2 + 102所以 x = 12.5因为ABP S ∆=21PA ·BH ' 所以BH '=165.1221002=⨯=∆PA S ABP【知识点】勾股定理与应用【适用场合】当堂练习题【难度系数】5【试题来源】【题目】如图,△ABC 中,AB=AC=2,BC 边上有10个不同的点1021,,P P P ,记C P B P AP M i i i i ⋅+=2(i = 1,2,……,10), 那么1021M M M +++ =_________。
中考数学-勾股定理知识点与常见题型总结

勾股定理复习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证. c ba HG FEDCB A方法二:b ac b a cca b c a b四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证a b ccb a E DCB A3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,b =,a②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 常见图形:A B C 30°D CB A AD B CCB D A题型一:直接考查勾股定理例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长分析:直接应用勾股定理222a b c +=解:⑴10AB⑵8BC ==题型二:应用勾股定理建立方程例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解解:⑴4AC , 2.4AC BC CD AB⋅== DB A C⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm 例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21E DCBA分析:此题将勾股定理与全等三角形的知识结合起来解:作DE AB ⊥于E ,12∠=∠,90C ∠=︒∴ 1.5DE CD ==在BDE ∆中90,2BED BE ∠=︒=Rt ACD Rt AED ∆≅∆AC AE ∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积答案:6题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mAB CD E分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD ==答案:10m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c = 解:①22221.52 6.25a b +=+=,222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒ ②22139b c +=,22516a =,222bc a +≠ABC ∴∆不是直角三角形 例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状? 解:此三角形是直角三角形 理由:222()264a b a b ab +=+-=,且264c =222a b c ∴+= 所以此三角形是直角三角形。
初中数学几何培优第十一讲:勾股定理的应用

初中数学几何培优第十一讲:勾股定理的应用知识解读无论是解决实际问题,还是解决一些数学问题,勾股定理都有着广泛的应用。
典列示范一、在数轴上作出表示的点例1如图3-11-1,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是________【提示】这个点到原点的距离等于线段OB的长,OB是Rt△AOB 的斜边,根据勾股定理可得OB的长,就是这个点表示的实数。
【技巧点评】实数与数轴上的点是一一对应的,有理数在数轴上较易找到它对应的点,若要在数轴上直接标出无理数对应的点较难.由此我们借助勾股定理,将在数轴上表示无理数的问题转化为化长为无理数的线段长问题。
第一步:利用勾股定理拆分出哪两条线段长的平方和等于所画线段(斜边)长的平方,注意一般其中一条线段的长是整数;第二步:以数轴原点为直角三角形斜边的顶点,构造直角三角形;第三步:以数轴原点圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点。
二、在网格中作长度为无理数的线段例2如图3-11-3,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画三角形。
(1)使三角形的三边长分别为3,(在图①中画一个即可)(2)使三角形为钝角三角形且面积为4.(在图②中画一个即可)【提示】(1)长度为3的线段很好作,主要考虑如何作出长度为,的线段和把三条线段组合成一个三角形。
由于=8=22+22,因此可以构造一个两直角边分别为2和2的直角三角形,这个直角三角形的斜边长就是.同理要构造一个长度为的线段,可构造一个直角边分别为2和1的直角三角形。
(2)确定三角形的底和高分别为1和8或2和4,然后设法使三角形称为钝角三角形。
【解答】【技巧点评】在网格中作出长的线段的步骤,第一步设法将n表示成两个整数的平方和;第二步构造直角三角形,使得两条直角边等于第一步得出的两个整数的值.三、梯子下滑问题例3如图3-11-5,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时,梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足也将向外移0.4米吗?【提示】本题中出现两个直角三角形,考虑应用勾股定理,在Rt△ABC中,由AB和BC可求出AC,则A1C=AC-AA1,而A1B1与AB均为梯子之长,在Rt△A1B1C中,再次运用勾股定理求出B1C,由此便可求出梯子向外移动的距离BB1.【解答】【技巧点评】梯子下滑问题,实际上是两个直角三角形问题,比如在本题中,两个直角三角形之间的联系是,AC=A1C+0.4,分别在两个直角三角形中应用勾股定理求出AC,A1C,即可解决问题.四、长方体的对角线例4有一根长170cm的木棒,放在长、宽、高分别是40cm,30cm,120cm的木箱中,露在木箱外边的长度至少为cm.【提示】如图3-11-7,和△是直角三角形,先在中应用勾股定理求出A′C′的长,然后在△AA′C′中应用勾股定理求出AC′的长.【技巧点评】长宽高分别为a,b,c的长方体的对角线长.五、立体图形表明的最短路径例5如图3-11-8,正四棱柱的底面边长为1.5cm,侧棱长为4cm,求一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处的最短路程的长.【提示】要求最短路程,需要将正四棱柱展开成平面图形,再利用勾股定理求解,由于从A点到点C1的面上有两种情况,故需分类讨论。
初中数学勾股定理(精选课件)
初中数学勾股定理聚智堂学科教师辅导讲义年级:课时数:学科教师:学员姓名:辅导科目:数学辅导时间:课题勾股定理教学目的1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。
(即:a2+b2=c2)2、勾股定理的逆定理:如果三角形的三边长:a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形。
3、满足的三个正整数,称为勾股数。
教学内容一、日校回顾二、知识回顾1。
勾股定理如图所示,在正方形网络里有一个直角三角形和三个分别以它的三条边为边的正方形,通过观察、探索、发现正方形面积之间存在这样的关系:即C的面积=B的面积+A的面积,现将面积问题转化为直角三角形边的问题,于是得到直角三角形三边之间的重要关系,即勾股定理。
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么即直角三角形两直角边的平方和等于斜边的平方。
说明:(1)勾股定理只有在直角三角形中才适用,如果不是直角三角形,那么三条边之间就没有这种关系了。
(2)我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。
在没有特殊说明的情况下,直角三角形中,a,b是直角边,c是斜边,但有时也要考虑特殊情况。
(3)除了利用a,b,c表示三边的关系外,还应会利用AB,BC,CA表示三边的关系,在△ABC中,∠B=90°,利用勾股定理有。
2. 利用勾股定理的变式进行计算ﻩ由,可推出如下变形公式:(1);(2)(3)(4)(5)(平方根将在下一章学到)说明:上述几个公式用哪一个,取决于已知条件给了哪些边,求哪条边,要判断准确。
三、知识梳理1、勾股定理的应用勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用有:(1)已知直角三角形的两边求第三边(2)已知直角三角形的一边与另两边的关系。
求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题2、如何判定一个三角形是直角三角形(1)先确定最大边(如c)(2)验证与是否具有相等关系(3)若=,则△ABC是以∠C为直角的直角三角形;若≠则△ABC不是直角三角形。
勾股定理的背景和故事

勾股定理的背景和故事说到勾股定理,哎呀,那可真是个让人又爱又恨的话题。
很多人都知道它跟直角三角形有关,是不是?不过你知道它背后的故事吗?别着急,我给你慢慢道来。
说实话,勾股定理一开始看起来似乎没什么特别的,毕竟也就那么一个公式:“直角三角形的两个直角边的平方和,等于斜边的平方。
”乍一看就像是个简单的数学公式,谁知道,这个看似普通的定理,背后可是有一段跌宕起伏的历史哩。
故事得从古希腊说起。
你知道的,那个时候的科学家们可都是非常有头脑的,全世界都在争着怎么更好地理解这个宇宙的奥秘。
话说,在公元前6世纪左右,有个叫毕达哥拉斯的家伙,他是个数学天才,还是个哲学家。
他不仅自己研究数学,还教了很多学生。
毕达哥拉斯发现了一个看似简单但却极其重要的规律,就是我们今天所说的勾股定理。
别看他那个年代,科技和知识水平还很原始,但他却能通过巧妙的观察和推理,得出这么一个精确的结论。
要说那个时候,能有这种思维方式,真的是不得了啊。
你可能会想:“嘿,那个毕达哥拉斯,是不是啥数学天才?”是的没错,可你知道他的人生可不单单是做数学的哦。
他还是个很有哲学思想的人,甚至在他的教团里,大家一度认为数字本身就是宇宙的核心。
想象一下,他那个时候的人把数字当成了神秘的力量,仿佛一切都能通过数字来解释,甚至连音乐、天体运行,都会挂钩。
你听起来可能觉得有点疯狂,但是想一想,今天我们不也一直在用数学公式来解释宇宙万象吗?嗯,似乎也没什么不对。
不过,咱们再说回正题。
毕达哥拉斯发现的这个定理,也不是突然冒出来的。
他的想法其实很简单,就是通过测量直角三角形的边长,发现了一个规律:直角三角形的两条直角边,分别平方之后加起来,正好等于斜边的平方。
这也太神奇了吧!有点像是捉到了一个数学“鬼怪”,一旦抓住了,就能让无数的问题迎刃而解。
说实话,这个定理对于古希腊人来说,简直就是个“数学奇迹”。
但你知道吗,这个定理刚开始也不是那么被人接受的。
那个年代的人,不像我们现在有那么多的科技工具,很多事情都是通过经验和直觉来判断的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等级森严,对市场反应迟钝,韦尔奇的举措是改革内部管理体制,减少管理层次和冗员,并撤换了部分高层管理人员。最终,他成功了。 韦尔奇之所以能重振“通用”,并且自己不被人际关系所伤,无非是因为主动回避不必要的复杂关系,以自己扎实的工作和明确的目标告诉员工,他所做的 一切绝无私心。这让人想起一个故事,一位老船长长年在河上驾船,从未发生过事故。有人问他是不是对河中的暗礁险滩全部了然于心。老船长说:“不是,我只要把船开进深水区就行了,暗礁险滩就会与我无关。” 人的一生有太多的暗礁和险滩,你根本无法一一了解,也根本不必去记住。 你所要做的,只是把船开进深水区就行了。 39、留住幸福的种子 从前有个孤儿,过着贫穷的日子。这年刚刚进入初冬,他的全部口粮就只剩下父母生前为他留下的一小袋豆子了。他强忍饥饿,把那一小袋豆子藏了起来。之后,他全靠拾破烂勉强糊口。尽管如此,在他心中总有一株株绿油 油的诱人豆苗在旺盛地生长,他在梦中也似乎真的看见了来年那些可爱的豆荚。因此,在那个漫长而寒冷的冬季里,他虽然多次险些饿昏过去,却一直不愿去触摸那一袋豆子,因为他知道,那是希望的种子、生命的种子啊! 苦日子就这样过了一冬。第二年春天来了,孤儿把那一小袋豆子播种 到地里,再经过一个夏天的辛勤耕耘,到了秋天,他果然收获了数十倍的种子。孤儿并没有就此满足,他还想获得更多的豆子、更多的幸福。于是,他把收获的豆子又留下来,继续播种、耕耘、收获……后来,孤儿告别了贫困,并成为远近闻名的富裕户。不久,他娶妻生子,过上了人人羡慕的幸福 生活。再后来,他和妻子一面继续种豆,一面学做豆制品,不到40岁,他成了声名显赫的大富豪。 人生有了幸福还需要什么?还需要留住幸福;人生没有了幸福还需要什么?还需要留住幸福的种子。 40、犹太人的智慧 据统计,美国的百万富翁中有百分之二十是犹太人,获诺贝尔经 济学奖的经济学家中,有百分之二十是犹太人。因而历来犹太人被公认为是最会赚钱的民族,被誉为“世界第一商人”。 然而,犹太人并不以赚钱为人生目的,他们认为人生的目的就在于热情地享受生活。要是你继续问:“那么,人为什么而工作吗?”他们会这样回答你:“你还不是为了随 心所欲吃到美味可口的食物而工作呀!并不是为了工作而吃呀!” 犹太人活着的目的———就是为了享受和“吃”。说到吃,不能不赞叹犹太人的健康教育。他们珍惜生命,保护自然。犹太人为使最神圣的耶路撒冷清洁、美丽,实行十个特殊的规定。其中包括:在城里不得堆粪堆;不得建砖 窑;除了早期先知们留下来的玫瑰园以外,不得耕种其他花园或果园;不得养鸡;死人不能在城里过夜。 此外,犹太人特别注重卫生,保持身体的清洁被称之为一种宗教责任。值得一提的是,犹太人把饮食的节制,作为健康体格的先决条件。犹太人有一个“饮食基本法”:吃(胃的容量)三分之 一,喝三分之一,留下三分之一的空。这其实颇有科学根据,吃得太饱,非长寿之道。 ? 41、学学乔丹的爱国 篮球上帝乔丹在日前的中国之行中,拒绝乘坐主办方为他提供的奔驰、宝马,而是点名要了美国的道奇山羊。原来乔丹有一条重要的商业原则,那就是“做广告从来只做美国货”,所 以,座驾事件与“爱国精神”息息相关。 从某种意义上说,球场外的乔丹给崇拜他的那些青少年们上着很好的思想品德教育课,这才是一个“星”真正的道德良知和社会责任。相反,我们的各种“星”们,同样作为青少年们顶礼膜拜的偶像,他们的表现又如何呢?我们知道有的歌星歌唱得不 怎么样,却热衷于把奇形怪态遁入极端;有些影星表演够差,却总走不出绯闻缠身的怪圈;还有那些所谓的足球明星,球踢得极烂,可酗酒、打架等丑闻从来不绝于耳。在未成年人思想道德建设方面,我们的“星”们有着不可推卸的社会责任,从这个角度来说,是不是应该好好学学人家乔丹呢? 42、鲁迅自喻“小白象” 鲁迅先生以象自喻,鲜为人知。 在他和许广平的通信中,经常署名“小白象”,或是“你的小白象”。比如1925年5月鲁迅在北平写给在的许广平的第二封信(5月15日夜),署名的地方赫然画着一只高高举起鼻子的小象。(《鲁迅手稿全集?书信?第三册》第105页) 而《两地书》在公开出版时,署名“EL”,就是Elephant(象)的缩写。 鲁迅先生为什么要以象自喻呢?从《柔石日记》中,我们可以看到这样的记述:“鲁迅先生说,人应该学一只象。第一,皮要厚,流点血,刺激一下了,也不要紧。第二,我们强韧地慢慢地走去。我很感谢他的话,因为我 的神经末梢是太灵动得像一条金鱼了。”这给我们解开谜底提供了一些线索。鲁迅先生欣赏的正是象的宽厚和强韧的精神。 43、名人教子 家教:包拯为官公正清廉,被老百姓尊称为包青天。他担心家人子弟利用权势贪污腐化,因而自述家训:“后世子孙仕宦,有犯赃者,不得放归本家; 亡疫之后,不得葬与大茔之中。不从吾志,非吾子孙。” 铭教:宋代诗人苏东坡的长子苏迈赴任县太尉时,苏东坡送给他一个砚台,上有他亲手所刻的砚铭:“以此进道常若渴,以此求进常若惊;以此治财常若予,以此书狱常思生。” 鞭教:岳云12岁参军作战,一次骑马下坡,没注意地 形,人也栽进沟里。岳飞喝令按军法鞭打岳云,众将求情不允,责打百鞭。此后岳云刻苦训练,勇猛作战。1134年攻打随州时,挥舞80斤重的铁锤,首当其冲第一个登城。岳飞教子的原则是:受罪重于士卒,作战先于士卒,受功后于士卒。 名教:1945年,革命老前辈林伯渠6岁的小儿子要读书 上小学了。林老对儿子说:“上学,该有个地道的名字,我看你就叫‘用三吧!”儿子疑惑不解,林老解释说:“用三者,三用也,即用脑想问题,用手造机器,用足踏实地!” 联教:无产阶级革命家吴玉章曾撰写一幅对联挂在堂前。上联“创业难,守业亦难,明知物力维艰,事事莫争虚体 面”,教育子孙后辈要艰苦创业,勤俭持家,切不可铺张浪费,追求虚荣;下联:“居家易,治家不易,欲自我以身作则,行行当立好楷模”,指出做长辈的要时时刻刻以身作则,身教重于言教,处处做出好样子,成为后辈们效仿的楷模。 章程教:老舍先生的教子章程:一是不必非考一百分 不可;二是不必非上大学不可;三是应多玩,不失儿童的天真烂漫;四是要有健全的体魄。总之,老舍先生认为,孩子不必争做“人上人”,虚荣心绝对不可有。 44、感悟“国际一流大学” 日前看到一个发生在英国牛津大学的故事:苏格兰北部边远地区一个教育相对不发达的郡,有一位 女学生的毕业考试成绩达到了全A,符合牛津大学的录取标准。这是近百年来当地第一个达到牛津录取线的毕业生,当地政府对此极为重视。但牛津大学录取学生必须经过面试,教授在面试后认为该学生不具备牛津大学要求的创造潜质,拒绝了她的入学申请。当地议会将此事反映给英国中央议会, 议员们就找到教育大臣,请他出面说情,希望给予破格录取。在被牛津大学婉言拒绝之后,教育大臣又找到副首相前去求情,还是遭到拒绝。无奈之下,副首相只得请布莱尔首相出面疏通。虽然首相动之以情,晓之以理,但牛津大学仍然表示不能接收,理由就是一个:在招生问题上,任何人无权更 改学院教授的面试结论,这是牛津大学几百年来的传统。布莱尔当然觉得很没有面子,在此后的一个私人场合,当提到牛津大学的时候,他不自觉地说了一句牢骚话:牛津大学真是太古板了,要与时俱进,必须进行改革。牛津大学的师生得知后,极为愤慨,学校立即取消了授予布莱尔荣誉博士学位 的原定计划,并对政府行政干预学校事务的这一严重事件提出抗议。 这个故事实在耐人寻味。 据说,在牛津的学子中,先后出现了46位诺贝尔奖获得者。此外,英国历史上的41位首相中,有30位毕业于牛津大学。真不愧是“国际一流大学”! 我们国家也提出了创建××所“国际一 流大学”的目标,一些名牌大学也跃跃欲试,试图在短时间内跻身于“国际一流大学”之列。姑且不论我国的高水平大学在办学理念、管理体制、师资队伍、学科水平、办学条件、资金投入等方面仍有相当大的差距,仅就招收有“创造潜力”的优秀生和捍卫“独立精神”这两点上,其差距简直就是 无法比拟的。 我们的高水平大学也想招收最有创造潜力的优秀生,但目前的“应试教育”已经将学生与生俱来的个性和“创造潜质”扼杀殆尽。 我们在很大程度上还处于“人情社会”、“熟人社会”、“权力社会”之中,即使名牌大学恐怕也不能幸免,招生、考试中的不正之风、种种违 规现象屡禁不止。不要说高级别领导人出面说话,就是某级教育行政部门、招生部门,乃至其它可以制约大学的部门和权势者,都会让学校难于捍卫自己的“独立精神”。 我们都很羡慕像哈佛、牛津、斯坦福、耶鲁等“国际一流大学”,也很想创建几所这样的“国际一流大学”。但我觉得, 仅在“寻求超常规的发展和跨越”上下功夫是远远不够的。发生在牛津大学的故事,实在是有着深刻的启示意义,值得我们好好思索和玩味。 45、 不留退路才有出路 古希腊著名演说家戴摩西尼年轻的时候为了提高自己的演说能力,躲在一个地下室练习口才。由于耐不住寂寞,他时不时 就想出去遛达遛达,心总也静不下来,练习的效果很差。无奈之下,他横下心,挥动剪刀把自己的头发剃去了一半,变成了一个怪模怪样的“阴阳头”。这样一来,因为羞于见人,他只得彻底打消了出去玩的念头,一心一意地练口才,一连数月足不出室,演讲水平突飞猛进。经过一番顽强的努力, 戴摩西尼最终成为了世界闻名的大演说家。 一个人要想成功,就必须心无旁骛、全神贯注地扑下身去,持之以恒、锲而不舍地追逐既定的目标。但人都是有不小惰性、有太多欲望的动物,要做到这一点实在不易,常常就难免战胜不了身心的倦怠,抵御不住世俗的诱惑,割舍不下寻常的享乐。 一些人因此半途而废,功亏一篑。那么,当惰性膨胀、欲望汹涌,追求的脚步踯躅不前时,应该怎么办呢?不妨学学戴摩西尼,他的办法固然有些极端,但唯其如此,才能管用。他剃掉了一半头发,就彻底斩断了向惰性和欲望妥协的退路。而一旦没有退路可逃,就只能一门心思地朝前奔了。
B 1 6
到宝藏埋藏点B的距离是多少千米?
3
2
A
8
C
3.一个无盖的长方体盒子,长、 宽、高分别为5厘米, 4厘米,3 厘米,则盒内所能容下的最长小 棒能有多长?
3 4
5
4.如图,在△ABC中,D 是BC上一点, 若AB=10,BD=6,AD=8,AC=17, 求△ABC的面积.
A
B
DC
5.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm, 一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少?
1.如图,∠A=∠D=90O,
