6.2.1空间几何体的表面积2
高三数学人教版A版数学(理)高考一轮复习教案空间几何体的表面积与体积

第二节空间几何体的表面积与体积表面积与体积了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).知识点一空间几何体的表面积1.多面体的表(侧)面积多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.旋转体的表(侧)面积名称侧面积表面积圆柱(底面半径r,母线长l)2πrl 2πr(l+r)圆锥(底面半径r,母线长l)πrl πr(l+r) 圆台(上、下底面半径r1,r2,母线长l)π(r1+r2)l π(r1+r2)l+π(r21+r22)球(半径为R)4πR2易误提醒(1)几何体的侧面积是指(各个)侧面面积之和,而表面积是侧面积与所有底面面积之和.(2)对侧面积公式的记忆,最好结合几何体的侧面展开图来进行,要特别留意根据几何体侧面展开图的平面图形的特点来求解相关问题.(3)组合体的表面积应注意重合部分的处理.[自测练习]1.正六棱柱的高为6,底面边长为4,则它的表面积为()A.48(3+3)B.48(3+23)C.24(6+2) D.144解析:正六棱柱的侧面积S侧=6×6×4=144,底面面积S底=2×6×34×42=483,S表=144+483=48(3+3).答案:A2.如图所示是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A .8+4 2B .10πC .11πD .12π解析:由三视图可知几何体是半径为1的球和底面半径为1,高为3的圆柱,故其表面积应为球的表面积与圆柱的表面积面积之和,即S =4π+2π+2π×3=12π,故选D.答案:D知识点二 空间几何体的体积空间几何体的体积(h 为高,S 为下底面积,S ′为上底面积) (1)V 柱体=Sh . (2)V 锥体=13Sh .(3)V 台体=13h (S +SS ′+S ′).(4)V 球=43πR 3(球半径是R ).易误提醒 (1)求一些不规则几何体的体积常用割补的方法将几何体转化成已知体积公式的几何体进行解决.(2)求与三视图有关的体积问题注意几何体还原的准确性及数据的准确性.[自测练习]3.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm)可得这个几何体的体积是( )A.43 cm 3 B.83 cm 3 C .3 cm 3D .4 cm 3解析:由三视图可知该几何体是一个底面为正方形(边长为2)、高为2的四棱锥,如图所示.由四棱锥的体积公式知所求几何体的体积V =83cm 3.答案:B4.某一容器的三视图如图所示,则该几何体的体积为________.解析:依题意,题中的几何体是从一个棱长为2的正方体中挖去一个圆锥,其中该圆锥的底面半径是1、高是2,因此题中的几何体的体积等于23-13π×12×2=8-2π3.答案:8-2π3考点一 空间几何体的表面积|1.(2015·高考福建卷)某几何体的三视图如图所示,则该几何体的表面积等于( )A .8+2 2B .11+2 2C .14+2 2D .15解析:由题中三视图可知,该几何体是底面为直角梯形、高为2的直四棱柱,所以其表面积为S 表面积=S 侧面积+2S 下底面积=(1+1+2+2)×2+2×12×(1+2)×1=11+22,故选B.答案:B2.(2015·高考课标全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r =( )A .1B .2C .4D .8解析:由三视图可知,此组合体是由半个圆柱与半个球体组合而成,其表面积为πr 2+2πr 2+4r 2+2πr 2=20π+16,所以r =2.答案:B3.(2016·昆明模拟)一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O 的球面上,则该圆锥的表面积与球O 的表面积的比值为________.解析:设等边三角形的边长为2a ,则S 圆锥表=12·2πa ·2a +πa 2=3πa 2.又R 2=a 2+(3a -R )2(R 为球O 的半径),所以R =233a ,故S 球表=4π·⎝⎛⎭⎫233a 2=16π3a 2,故其表面积比为916. 答案:916(1)由三视图求相关几何体的表面积:,给出三视图时,依据“正视图反映几何体的长和高,侧视图反映几何体的高和宽,俯视图反映几何体的长和宽”来确定表面积公式中涉及的基本量.(2)根据几何体(常规几何体、组合体或旋转体)的特征求表面积:①求多面体的侧面积时,应对每一个侧面分别求解后再相加;求旋转体的侧面积时,一般要将旋转体展开为平面图形后再求面积.②对于组合体,要弄清它是由哪些简单几何体组成的,要注意“表面(和外界直接接触的面)”的定义,以确保不重复、不遗漏.考点二 空间几何体的体积|(1)(2015·高考山东卷)已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.22π3B.42π3C .22πD .42π(2)(2015·辽宁五校联考)某几何体的三视图如图所示,则该几何体的体积是________.[解析] (1)由题意,该几何体可以看作是两个底面半径为2、高为2的圆锥的组合体,其体积为2×13×π×(2)2×2=423π.(2)由三视图知,该几何体为长方体去掉一个三棱锥,其体积V =2×2×3-13×⎝⎛⎭⎫12×2×1×3=11.[答案] (1)B (2)11空间几何体体积问题的三种类型及解题策略(1)求简单几何体的体积.若所给的几何体为柱体、锥体或台体,则可直接利用公式求解.(2)求组合体的体积.若所给定的几何体是组合体,不能直接利用公式求解,则常用转换法、分割法、补形法等进行求解.(3)求以三视图为背景的几何体的体积.应先根据三视图得到几何体的直观图,然后根据条件求解.(2015·绵阳模拟)一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )A .8+π3B .8+2π3C .8+8π3D .8+16π3解析:依题意得,该机器零件的形状是在一个正方体的上表面放置了一个14的球体,其中正方体的棱长为2,相应的球半径是1,因此其体积等于23+14×43π×13=8+π3,选A.答案:A考点三 与球有关的切、接问题|与球相关的切、接问题是高考命题的热点,也是考生的难点、易失分点.命题角度多变.归纳起来常见的命题角度有:1.四面体的外接球. 2.四棱锥的外接球. 3.三棱柱的外接球. 4.圆锥的内切球与外接球. 5.四面体的内切球. 探究一 四面体的外接球问题1.(2016·唐山模拟)正三棱锥的高和底面边长都等于6,则其外接球的表面积为( ) A .64π B .32π C .16π D .8π解析:如图,作PM ⊥平面ABC 于点M ,则球心O 在PM 上,PM =6,连接AM ,AO ,则OP =OA =R (R 为外接球半径),在Rt △OAM 中,OM =6-R ,OA =R ,又AB =6,且△ABC 为等边三角形,故AM =2362-32=23,则R 2-(6-R )2=(23)2,则R =4,所以球的表面积S =4πR 2=64π.答案:A探究二 四棱锥的外接球问题2.已知四棱锥P -ABCD 的顶点都在球O 的球面上,底面ABCD 是矩形,平面P AD ⊥底面ABCD ,△P AD 为正三角形,AB =2AD =4,则球O 的表面积为( )A.323π B .32π C .64πD.643π 解析:依题意,AB ⊥平面P AD 且△P AD 是正三角形,过P 点作AB 的平行线,交球面于点E ,连接BE ,CE ,则可得到正三棱柱APD -BEC .因为△P AD 是正三角形,且AD =2,所以△P AD 的外接圆半径是23,球O 的半径R =22+⎝⎛⎭⎫232=43,球O 的表面积S =4πR 2=64π3,故选D.答案:D探究三 三棱柱的外接球问题3.(2016·长春模拟)已知三棱柱ABC -A 1B 1C 1的底面是边长为6的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12π,则该三棱柱的体积为________.解析:设球半径为R ,上,下底面中心设为M ,N ,由题意,外接球心为MN 的中点,设为O ,则OA =R ,由4πR 2=12π,得R =OA =3,又易得AM =2,由勾股定理可知,OM =1,所以MN =2,即棱柱的高h =2,所以该三棱柱的体积为34×(6)2×2=3 3. 答案:3 3探究四 圆锥的内切球与外接球问题4.(2016·嘉兴模拟)若圆锥的内切球与外接球的球心重合,且内切球的半径为1,则圆锥的体积为________.解析:过圆锥的旋转轴作轴截面,得截面△ABC 及其内切圆⊙O 1和外接圆⊙O 2,且两圆同圆心,即△ABC 的内心与外心重合,易得△ABC 为正三角形,由题意知⊙O 1的半径为r =1,∴△ABC 的边长为23,圆锥的底面半径为3,高为3,∴V =13×π×3×3=3π.答案:3π探究五 四面体的内切球问题5.若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________.解析:设正四面体棱长为a ,则正四面体表面积为S 1=4·34·a 2=3a 2,其内切球半径为正四面体高的14,即r =14·63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2π6a 2=63π. 答案:63π求解与球有关的切、接问题的关键点解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.21.补形法在空间几何体的体积、面积中的应用【典例】 已知某几何体的三视图如图所示,则该几何体的体积为( )A.8π3 B .3π C.10π3D .6π[思维点拨] 可考虑将几何体补完整,再分析求解.[解析] 法一:由三视图可知,此几何体(如图所示)是底面半径为1,高为4的圆柱被从母线的中点处截去了圆柱的14,所以V =34×π×12×4=3π.法二:由三视图可知,此几何体是底面半径为1,高为4的圆柱从母线的中点处截去了圆柱的14,直观图如图(1)所示,我们可用大小与形状完全相同的补成一个半径为1,高为6的圆柱,如图(2)所示,则所求几何体的体积为V =12×π×12×6=3π.[答案] B[方法点评] 某些空间几何体是某一个几何体的一部分,在解题时,把这个几何体通过“补形”补成完整的几何体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的体积问题,这是一种重要的解题策略——补形法.常见的补形法有对称补形、联系补形与还原补形.对于还原补形,主要涉及台体中“还台为锥”问题.[跟踪练习] (2015·沈阳模拟)已知四面体P -ABC 的四个顶点都在球O 的球面上,若PB ⊥平面ABC ,AB ⊥AC ,且BC =1,PB =AB =2,则球O 的表面积为( )A .7πB .8πC .9πD .10π解析:依题意,记题中的球的半径是R ,可将题中的四面体补形成一个长方体,且该长方体的长、宽、高分别是2、1、2,于是有(2R )2=12+22+22=9,4πR 2=9π,所以球O 的表面积为9π,选C.答案:CA 组 考点能力演练1.(2016·长春模拟)如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )A.323 B .64 C.3233 D.643解析:由三视图可知,该多面体是一个四棱锥,且由一个顶点出发的三条棱两两垂直,长度都为4,∴其体积为13×4×4×4=643,故选D.答案:D2.如图是某几何体的三视图,其中正视图是一个正三角形,则这个几何体的外接球的表面积为( )A.16π3B.8π3 C .43π D .23π解析:由对称性可知外接球球心在侧视图中直角三角形的高线上,设外接球的半径为R ,则(3-R )2+12=R 2,R =233,其表面积S =4πR 2=4π⎝⎛⎭⎫2332=16π3.答案:A3.(2016·唐山模拟)某几何体的三视图如图所示,则该几何体的体积为( ) A .8π+16 B .8π-16 C .8π+8 D .16π-8解析:由三视图可知:几何体为一个半圆柱去掉一个直三棱柱.半圆柱的高为4,底面半圆的半径为2,直三棱柱的底面为斜边是4的等腰直角三角形,高为4,故几何体的体积V =12π×22×4-12×4×2×4=8π-16.答案:B4.某几何体的三视图如图所示,则该几何体的体积为( )A.2π B .22π C.π3 D.2π3解析:依题意得,该几何体是由两个相同的圆锥将其底面拼接在一起所形成的组合体,其中该圆锥的底面半径与高均为1,因此题中的几何体的体积等于2×13π×12×1=2π3,选D.答案:D5.四面体ABCD 的四个顶点都在球O 的球面上,AB ⊥平面BCD ,△BCD 是边长为3的等边三角形.若AB =2,则球O 的表面积为( )A.323π B .12π C .16π D .32π 解析:设球心为O ,球心在平面BCD 的投影为O 1,则OO 1=AB2=1,因为△BCD 为等边三角形,故DO 1=23×323=3,因为△OO 1D 为直角三角形,所以球的半径R =OD =OO 21+O 1D 2=2,球O 的表面积S =4πR 2=16π,故选C.答案:C6.已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为直角三角形,则它的体积为________.解析:由俯视图可知,四棱锥顶点在底面的射影为O (如图),又侧视图为直角三角形,则直角三角形的斜边为BC =2,斜边上的高为SO =1,此高即为四棱锥的高,故V =13×2×2×1=43.答案:437.(2016·台州模拟)某几何体的三视图如图所示,则该几何体的表面积为________.解析:该简单组合体由半球加上圆锥构成,故所求表面积S =4π×422+12×2π×4×5=52π.答案:52π8.(2016·南昌一模)已知直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,侧面BCC 1B 1的面积为2,则直三棱柱ABC -A 1B 1C 1外接球表面积的最小值为________.解析:如图所示,设BC ,B 1C 1的中点分别为F ,E ,则知三棱柱ABC -A 1B 1C 1外接球的球心为线段EF 的中点O ,且BC ×EF =2.设外接球的半径为R ,则R 2=BF 2+OF 2=⎝⎛⎭⎫BC 22+⎝⎛⎭⎫EF 22=BC 2+EF 24≥14×2BC ×EF =1,当且仅当BC =EF =2时取等号.所以直三棱柱ABC -A 1B 1C 1外接球表面积的最小值为4π×12=4π.答案:4π9.已知某锥体的三视图(单位:cm)如图所示,求该锥体的体积.解:由三视图知,原几何体是一个五面体,由一个三棱柱截去一个四棱锥得到,其体积为V =V 三棱柱-V 四棱锥=12×2×2×2-13×12×(2+1)×2×2=2.10.已知一个几何体的三视图如图所示. (1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置:P 为所在线段中点,Q 为顶点,求在几何体表面上,从P 点到Q 点的最短路径的长.解:(1)由三视图知:此几何体是一个圆锥加一个圆柱,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12(2πa )·(2a )=2πa 2,S 圆柱侧=(2πa )·(2a )=4πa 2,S 圆柱底=πa 2, 所以S 表面=2πa 2+4πa 2+πa 2=(2+5)πa 2.(2)沿P 点与Q 点所在母线剪开圆柱侧面,如图.则PQ =AP 2+AQ 2=a 2+(πa )2=a1+π2,所以从P 点到Q 点在侧面上的最短路径的长为a1+π2.B 组 高考题型专练1.(2015·高考陕西卷)一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .2π+4D .3π+4解析:由所给三视图可知,该几何体是圆柱从底面圆直径处垂直切了一半,故该几何体的表面积为12×2π×1×2+2×12×π×12+2×2=3π+4,故选D.答案:D2.(2015·高考全国卷Ⅱ)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π解析:三棱锥V O -ABC =V C -OAB=13S △OAB×h ,其中h 为点C 到平面OAB 的距离,而底面三角形OAB 是直角三角形,顶点C 到底面OAB 的最大距离是球的半径,故V O -ABC =V C -OAB =13×12×R 3=36,其中R 为球O 的半径,所以R =6,所以球O 的表面积为S =4π×36=144π. 答案:C3.(2015·高考课标卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18 B.17 C.16D.15解析:如图,不妨设正方体的棱长为1,则截去部分为三棱锥A -A 1B 1D 1,其体积为16,又正方体的体积为1,则剩余部分的体积为56,故所求比值为15.故选D.答案:D4.(2015·高考浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )A .8 cm 3B .12 cm 3 C.323cm 3 D.403cm 3 解析:该几何体的体积V =23+13×22×2=323(cm 3).答案:C5.(2015·高考四川卷)在三棱柱ABC -A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形.设点M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,则三棱锥P -A 1MN 的体积是________.解析:因为M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,所以MN ∥AC ,NP ∥CC 1, 所以平面MNP ∥平面CC 1A 1A ,所以A 1到平面MNP 的距离等于A 到平面MNP 的距离.根据题意有∠MAC =90°,AB =1, 可得A 到平面MNP 的距离为12.又MN =12,NP =1,所以VP -A 1MN =V A -MNP =13S △MNP ×12=13×12×12×1×12=124. 答案:124。
高二数学必修2课件-空间几何体的表面积和体积

步骤三
如果计算正确,则可以庆祝问题 的解决,并享受数学带来的成就 感。
其他的空间几何体常识
名称
圆锥体 圆柱体 球 正方体
特点
底面为圆形,侧面为三角形 底面为圆形,侧面为矩形 表面积为4πr²,体积为(4πr³)/3 6个面组成,每个面积为a²
小结
知识点
• 空间几何体的表面积 • 空间几何体的体积 • 解题方法和步骤
高二数学必修2课件-空间 几何体的表面积和体积 ppt
本课程将带领大家深入理解空间几何体的表面积和体积,掌握重要的公式和 概念,并提供多个实例进行演示。
为什么要学习空间几何体的表面积和 体积?
1 实际应用广泛
几何体是我们日常生活中常见的物体,如箱子、瓶子、汽车等,熟练掌握空间几何体的 表面积和体积可以应用于各种实际计算中。
技能
• 应用公式解决实际问题 • 掌握计算技巧和策略 • 提高自我学习和思考能力
效果
• 成为数学大师 • 提高应对数学竞赛能力 • 在各种实际计算和操作
中表现更加出色
矩形的体积
面积×高:bh
三角形的体积
底面积之和×高的一半:(ah)/2
立体几何体的体积
1
圆柱体的体积
2
பைடு நூலகம்
πr²h
3
球的体积
(4πr³)/3
圆锥体的体积
(πr²h)/3
解题示例:如何计算球的体积?
步骤一
根据题目提供的半径长度,计算 球的表面积公式:4πr³/3
步骤二
把计算结果与题目所需体积相比 较,如相等则问题解决;如不相 等需检查计算过程是否正确。
2 提高数学水平
对于数学专业的学生,掌握空间几何体的表面积和体积是必不可少的,是数学基础中不 可或缺的一部分。
苏教版必修2数学课件-第1章立体几何初步第3节空间几何体的表面积和体积教学课件

栏目导航
合作探究 提素养
栏目导航
棱柱、棱锥和棱台的侧面积和表面积 【例 1】 正四棱锥的侧面积是底面积的 2 倍,高是 3,求它的 表面积. 思路探究:由 S 侧与 S 底的关系,求得斜高与底面边长之间的关系, 进而求出斜高和底面边长,最后求表面积.
所以 S 侧=3×12×(20+30)×DD′=75DD′. 又 A′B′=20 cm,AB=30 cm,则上、下底面面积之和为 S 上+S 下 = 43×(202+302)=325 3(cm2).
栏目导航
由 S 侧=S 上+S 下,得 75DD′=325 3, 所以 DD′=133 3(cm), 又因为 O′D′= 63×20=103 3(cm), OD= 63×30=5 3(cm),
错点)
运算核心素养.
3.会求简单组合体的体积及表面积.(难点)
栏目导航
自主预习 探新知
栏目导航
1.柱体、锥体、台体的体积
几何体
体积
柱体 锥体
V 柱体= Sh (S 为底面面积,h 为高), V 圆柱= πr2h (r 为底面半径) 1
V 锥体= 3Sh (S 为底面面积,h 为高), V 圆锥= π3r2h (r 为底面半径)
栏目导航
台体
V 台体= 13h(S+ SS′+S′) (S′,S 分别为上、下底面面 积,h 为高),V 圆台= 13πh(r′2+rr′+r2) (r′,r 分别为上、 下底面半径)
思考:柱体、锥体、台体的体积公式之间的关系. 提示:V=Sh―S′―=→S V=13(S′+ S′S+S)h―S′―=→0 V=13Sh.
栏目导航
[解] 如图所示,设 SE 是侧面三角形 ABS 的高,则 SE 就是正 四棱锥的斜高.
中等职业教育规划教材数学1-3册目录(人民教育出版社)

目录第一章集合(第一册)1.1集合及其表示1.1.1集合1.1.2集合的表示方法1.2集合之间的关系1.3集合的基本运算1.3.1交集1.3.2并集1.3.3补集1.4充要条件第二章方程与不等式2.1一元一次方程2.2不等式2.2.1不等式的基本性质2.2.2不等式的解集与区间2.2.3含有绝对值的不等式2.2.4一元二次不等式第三章函数3.1函数的概念3.2函数的表示方法3.3函数的单调性3.4函数的奇偶性3.5二次函数的图像和性质3.6函数的应用第四章指数函数与对数函数4.1实数指数4.2指数函数4.3对数及其运算4.3.1对数4.3.2对数的运算4.4对数函数4.5幂函数4.6指数函数与对数函数的应用第五章数列5.1数列5.2等差数列5.2.1等差数列的概念5.2.2等差数列的前n项和5.3等比数列5.3.1等比数列的概念5.3.2等比数列的前n项和5.4等差数列与等比数列的应用第六章空间几何体6.1认识空间几何体6.1.1认识多面体与旋转体6.1.2棱柱、棱锥6.1.3圆柱、圆锥、球6.2空间几何体的表面积与体积6.2.1空间几何体的表面积6.2.2空间几何体的体积第七章三角函数(第二册)7.1任意角的概念与弧度制7.1.1任意角的概念7.1.2弧度制7.2任意角的三角函数7.2.1任意角的三角函数的定义7.2.2单位圆与正弦、余弦线7.2.3利用计算器求三角函数值7.2.4三角函数值在各象限的符号7.3同角三角函数的基本关系式7.4三角函数的诱导公式7.5正弦、余弦函数的图像和性质7.5.1正弦函数的图像和性质7.5.2余弦函数的图像和性质7.6已知三角函数值求角第八章平面向量8.1向量的概念8.2向量的线性运算8.2.1向量的加法8.2.2向量的减法8.2.3数乘向量8.3平面向量的的直角坐标系8.3.1平面向量的直角坐标及其运算8.3.2平面向量平行的坐标表示8.3.3向量的长度公式和中点公式8.4向量的内积8.4.1向量的内积8.4.2向量内积的直角坐标运算第九章 直线与圆的方程9.1直线的方程9.1.1直线的方向向量与点向式方程9.1.2直线的斜率与点斜式方程9.1.3直线的法向量与点法式方程9.1.4直线的一般式方程9.2两条直线的位置关系9.2.1两条直线的平行9.2.2两条直线的交点与垂直9.3点到直线的距离9.4圆的方程9.4.1圆的标准方程9.4.2圆的一般方程第十章 立体几何初步10.1平面的基本性质10.2空间两条直线的位置关系10.3直线与平面的位置关系10.4平面与平面的位置的关系第十一章 概率与统计初步11.1计数的基本原理11.2概率初步11.2.1随机事件与样本空间11.2.2古典概率11.3随机抽样11.3.1简单随机抽样11.3.2系统抽样11.3.3分层抽样11.4用样本估计总体11.4.1用样本的频率分布估计总体的分布11.4.2用样本的数字特征估计总体的数字特征 11.5一元线性回归分析第十二章 三角计算及其应用 (第三册) 12.1和角公式12.1.1两角和与差的余弦12.1.2两角和与差的正弦12.1.3两角和与差的正切12.2倍角公式12.3正弦函数)sin(ϕω+=x A y 的图像和性质 12.4解三角形12.4.1余弦定理12.4.2三角形的面积12.4.3正弦定理12.5三角计算及应用举例第十三章圆锥曲线与方程13.1椭圆13.1.1椭圆的标准方程13.1.2椭圆的几何性质13.2双曲线13.2.1双曲线的标准方程13.2.2双曲线的几何性质13.3抛物线13.3.1抛物线的标准方程13.3.2抛物线的几何性质第十四章坐标变换与参数方程14.1坐标变换14.1.1坐标轴的平移14.1.2利用坐标轴的平移化简二元二次方程14.1.3坐标轴的旋转14.1.4利用坐标轴的旋转化简二元二次方程14.2一般二元二次方程的讨论14.2.1化一般二元二次方程为标准式14.2.2一般二元二次方程的讨论14.3参数方程14.3.1曲线的参数方程14.3.2圆的参数方程14.3.3直线的参数方程14.3.4圆锥曲线的参数方程14.4参数方程的应用举例第十五章逻辑代数基础15.1常用逻辑用语15.1.1命题15.1.2量词15.1.3逻辑联结词15.2数制15.2.1十进制与二进制15.2.2十进制与二进制之间的转换15.3逻辑代词15.3.1基本概念与基本逻辑运算15.3.2逻辑代数的运算律和基本定理15.3.3逻辑函数15.3.4逻辑函数的表示方法15.3.5逻辑函数的化简15.3.6逻辑图第十六章算法与程序框图16.1算法的概念16.2程序框图与算法的基本逻辑结构16.2.1程序框图的基本图例16.2.2顺序结构及其框图16.2.3条件分支结构及其框图16.2.4循环结构及其框图16.3条件判断16.4算法案例第十七章数据表格信息处理17.1数组、数据表格的概念17.2数组的代数运算17.3用软件处理数据表格17.4数据表格的图示第十八章编制计划的原理与方法18.1编制计划的有关概念18.2关键路径法18.3统筹图18.3.1网络图18.3.2横道图18.4进度计划的编制18.4.1网络图的时间参数18.4.2时间优化的方法第十九章线性规划初步19.1线性规划问题19.2二元一次不等式表示的区域19.3线性规划问题的图解法19.4线性规划问题的应用举例19.5用Excel解线性规划问题第二十章复数20.1复数的概念20.1.1复数的有关概念20.1.2复数的几何意义20.2复数的运算20.2.1复数的加法和减法20.2.2复数的乘法和除法20.3实系数一元二次方程的解法20.4复数的三角形式20.4.1复数的三角形式20.4.2复数三角形式的乘法与乘方运算20.4.3复数三角形式的除法运算20.4.4复数的开方运算20.5复数的指数形式20.6复数的应用第二十一章概率分布初步21.1排列与组合21.1.1排列与排列数公式21.1.2组合与组合数公式21.2二项式定理21.2.1二项式定理21.2.2二项式系数的性质21.3离散型随机变量及其分布21.3.1离散型随机变量21.3.2二项分布21.4正态分布。
第2讲 空间几何体的表面积和体积

思维点拨:由三视图知此几何体为圆锥. 思维点拨:由三视图知此几何体为圆锥. 解析:由三视图可知,该几何体是底面半径为 解析:由三视图可知,该几何体是底面半径为3 cm, , 母线长为5 的圆锥, 母线长为 cm的圆锥,其侧面积为 =π×3×5=15π cm2. 的圆锥 其侧面积为πrl= × × = 答案: 答案:B
1.一个长方体上一个顶点所在的三个面的面积分别是 . 这个长方体的对角线是( 这个长方体的对角线是 A.2 . B.3 . ) C.6 . D.
解析:设长方体的长、宽、高为a、b、c 解析:设长方体的长、 高为 、 、 则ab= = ,bc= = ,ac= = ,解得:a= 解得: = ,b=1,c= = , =
则
解得: = , 解得:R=1,∴2R=2. =
答案: 答案:B
如图,一个空间几何体的正视图、侧视图、 3. .如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角 形,如果直角三角形的直角边长为1,那么这个几何体的表面积为 如果直角三角形的直角边长为 ,那么这个几何体的表面积为( )
2.体积公式 . (1)柱体的底面积为 ,高为 ,则柱体的体积为 Sh 柱体的底面积为S,高为h, 柱体的底面积为 (2)锥体的底面积为 ,高为 ,则锥体的体积为 锥体的底面积为S,高为h, 锥体的底面积为 .
Sh . (S′+ ′ +S)h.
(3)棱台的上、下底面面积为S′、S,高为 ,则体积为 棱台的上、下底面面积为 ′ 棱台的上 ,高为h, (4)球的半径为 ,则体积为 球的半径为R, 球的半径为 πR3 .
高考中对该部分的考查常以几何体的三视图为条件,来求表面积和体积, 高考中对该部分的考查常以几何体的三视图为条件,来求表面积和体积, 解题时要将图形还原为空间几何体,根据面积和体积公式求解. 解题时要将图形还原为空间几何体,根据面积和体积公式求解. (2009· 浙江绍兴第一次质检 若某几何体的三视图 单位 : cm)如 若某几何体的三视图(单位 · 浙江绍兴第一次质检)若某几何体的三视图 单位: 如 【例2】 】 右图所示,则此几何体的侧面积等于 右图所示,则此几何体的侧面积等于( A.12π cm2 . C.24π cm2 . B.15π cm2 . D.30π cm2 . )
2023年新高考数学一轮复习8-2 空间几何体的表面积和体积(知识点讲解)含详解

专题8.2 空间几何体的表面积和体积(知识点讲解)【知识框架】 【核心素养】1.通过考查几何体体积和表面积的计算,主要考查棱柱、棱锥或不规则几何体的特征及体积与表面积的计算,凸显数学运算、直观想象的核心素养.2.结合三视图、直观图、展开图、轴截面等,考查球的切、接问题,主要考查几何体与球的组合体的识辨,球的体积、表面积的计算,凸显数学运算、直观想象的核心素养.【知识点展示】(一)几何体的表面积圆柱的侧面积圆柱的表面积圆锥的侧面积圆锥的表面积圆台的侧面积圆台的表面积球体的表面积 柱体、锥体、台体的侧面积,就是各个侧面面积之和;表面积是各个面的面积之和,即侧面积与底面积之和.把柱体、锥体、台体的面展开成一个平面图形,称为它的展开图,圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形它的表面积就是展开图的面积.(二)几何体的体积圆柱的体积rl S π2=)(2l r r S +=πrl S π=)(l r r S +=πl r r S )(+'=π)(22rl l r r r S +'++'=π24R S π=h r V 2π=圆锥的体积 圆台的体积 球体的体积 正方体的体积正方体的体积(三)常用结论多面体的内切球与外接球常用的结论(1)设正方体的棱长为a ,则它的内切球半径r =2a ,外接球半径R=2a . (2)设长方体的长、宽、高分别为a ,b ,c ,则它的外接球半径R=2. (3)设正四面体的棱长为a ,则它的高为H=3a ,内切球半径r =14H=12a ,外接球半径R =34H=4a . 【常考题型剖析】题型一:空间几何体的表面积例1.(2021·全国·高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36000km (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为6400km 的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),则S 占地球表面积的百分比约为( )A .26%B .34%C .42%D .50%例2.(2020·全国·高考真题(理))已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π例3.(2022·青海·海东市第一中学模拟预测(文))已知某圆台的母线长为2,母线与轴所在直线的夹角是60︒,且上、下底面的面积之比为1∶4,则该圆台外接球的表面积为( )A .56πB .64πC .112πD .128πh r V 231π=)(3122r r r r h V '++'=π334R V π=3a V =abc V =几类空间几何体表面积的求法(1)多面体:其表面积是各个面的面积之和.(2)旋转体:其表面积等于侧面面积与底面面积的和.(3)简单组合体:应搞清各构成部分,并注意重合部分的删、补.(4)若以三视图形式给出,解题的关键是根据三视图,想象出原几何体及几何体中各元素间的位置关系及数量关系.题型二:空间几何体的体积例4. (2023·河南·洛宁县第一高级中学一模(文))若圆锥的母线与底面所成的角为π6,则该圆锥的体积为( )A .π2B .πC .2πD .3π例5.(2022·全国·高考真题)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔1485m .时,相应水面的面积为21400km .;水位为海拔1575m .时,相应水面的面积为21800km .,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔1485m .上升到1575m .时,2.65)( )A .931.010m ⨯B .931.210m ⨯C .931.410m ⨯D .931.610m ⨯例6.(2022·全国·高考真题(理))甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若=2S S 甲乙,则=V V 甲乙( )AB .CD 例7.(2022·湖北·黄石市有色第一中学模拟预测)阿基米德多面体也称为半正多面体,是以边数不全相同的正多边形为面围成的多面体.如图,已知阿基米德多面体的所有顶点均是一个棱长为2的正方体各条棱的中点,则该阿基米德多面体的体积为______;若M ,N 是该阿基米德多面体表面上任意两点,则M ,N 两点间距离的最大值为______.1.处理体积问题的思路(1)“转”:指的是转换底面与高,将原来不易求面积的底面转换为易求面积的底面,或将原来不易看出的高转换为易看出并易求解长度的高,即等体积法;(2)“拆”:指的是将一个不规则的几何体拆成几个简单的几何体,便于计算,即分割法;(3)“拼”:指的是将小几何体嵌入一个大几何体中,如将一个三棱锥复原成一个三棱柱,将一个三棱柱复原成一个四棱柱,这些都是拼补的方法,即补形法.2.求体积的两种方法:①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等体积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.题型三:三视图与几何体的面积、体积例8.(2020·全国·高考真题(文))下图为某几何体的三视图,则该几何体的表面积是()A.6+42B.4+42C.6+23D.4+23例9. (2020·浙江·高考真题)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是()A.73B.143C.3D.6例10.(2022·浙江省春晖中学模拟预测)某几何体的三视图如图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是___________,体积是___________.【总结提升】求空间几何体体积的常见类型及思路(1)规则几何体:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法(2)不规则几何体:若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.题型四:简单几何体的外接球与内切球问题例11.(2021·天津·高考真题)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为323π,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为( )A .3πB .4πC .9πD .12π例12.(2020·全国高考真题(理))已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )A B .32 C .1 D例13.(2020·全国·高考真题(理))已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )AB .32C .1D 例14.(2019·全国·高考真题(理))已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A. B. C. D例15.(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .34πC .2πD .4π 例16.(2016·全国卷Ⅲ)在封闭的直三棱柱ABC A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4πB .9π2C .6πD .32π3例17.(2021·福建·厦门大学附属科技中学高三阶段练习)某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为(球心与正方体的中心重合),若其中一个截面圆的周长为6π,则该球的表面积是______.例18. (2019年高考天津卷理)的正方形,侧棱长均若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.例19.(2020·全国·高考真题(文))已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.【总结提升】1.常见类型:(1)利用长方体的体对角线探索外接球半径;(2)利用长方体的面对角线探索外接球半径;(3)利用底面三角形与侧面三角形的外心探索球心;(4)利用直棱柱上下底面外接圆圆心的连线确定球心;(5)锥体的内切球问题;(6)柱体的内切球问题2.与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.3.若球面上四点P ,A ,B ,C 中PA ,PB ,PC 两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方25体确定直径解决外接问题.专题8.2 空间几何体的表面积和体积(知识点讲解)【知识框架】 【核心素养】1.通过考查几何体体积和表面积的计算,主要考查棱柱、棱锥或不规则几何体的特征及体积与表面积的计算,凸显数学运算、直观想象的核心素养.2.结合三视图、直观图、展开图、轴截面等,考查球的切、接问题,主要考查几何体与球的组合体的识辨,球的体积、表面积的计算,凸显数学运算、直观想象的核心素养.【知识点展示】(一)几何体的表面积圆柱的侧面积圆柱的表面积圆锥的侧面积圆锥的表面积圆台的侧面积圆台的表面积球体的表面积 柱体、锥体、台体的侧面积,就是各个侧面面积之和;表面积是各个面的面积之和,即侧面积与底面积之和.把柱体、锥体、台体的面展开成一个平面图形,称为它的展开图,圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形它的表面积就是展开图的面积.(二)几何体的体积圆柱的体积rl S π2=)(2l r r S +=πrl S π=)(l r r S +=πl r r S )(+'=π)(22rl l r r r S +'++'=π24R S π=h r V 2π=圆锥的体积 圆台的体积 球体的体积 正方体的体积正方体的体积(三)常用结论多面体的内切球与外接球常用的结论(1)设正方体的棱长为a ,则它的内切球半径r =2a ,外接球半径R=2a . (2)设长方体的长、宽、高分别为a ,b ,c ,则它的外接球半径R. (3)设正四面体的棱长为a ,则它的高为H=3a ,内切球半径r =14H=12a ,外接球半径R =34H=4a . 【常考题型剖析】题型一:空间几何体的表面积例1.(2021·全国·高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36000km (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为6400km 的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),则S 占地球表面积的百分比约为( )A .26%B .34%C .42%D .50%【答案】C【解析】【分析】由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.【详解】由题意可得,S 占地球表面积的百分比约为: 226400164003600002(1.cos )1cos 44242%22r r πααπ---+==≈=.h r V 231π=)(3122r r r r h V '++'=π334R V π=3a V =abc V =故选:C.例2.(2020·全国·高考真题(理))已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π 【答案】A【解析】【分析】由已知可得等边ABC 的外接圆半径,进而求出其边长,得出1OO 的值,根据球的截面性质,求出球的半径,即可得出结论.【详解】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r ππ=∴=,ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R ππ==.故选:A例3.(2022·青海·海东市第一中学模拟预测(文))已知某圆台的母线长为2,母线与轴所在直线的夹角是60︒,且上、下底面的面积之比为1⊙4,则该圆台外接球的表面积为( ) A .56πB .64πC .112πD .128π 【答案】C【解析】【分析】作出圆台的轴截面等腰梯形,其外接圆是圆台外接球的大圆,在这个轴截面中进行计算可得.【详解】如图等腰梯形ABCD 是圆台的轴截面,EF 是圆台的对称轴,圆台上、下底面的面积之比为1:4,则半径比为1:2,设圆台上、下底面半径分别为r ,2r ,因母线与轴的夹角是60︒,母线长为2,可得圆台的高为1,r =R ,球心到下底面(大圆面)的距离为x ,若球心在圆台两底面之间,如图点M 位置,则222R x =+且222(1)R x =-+,无解;若圆台两底面在球心同侧,如图点O 位置,则222R x =+且222(1)R x =++,解得4x =,则228R =, 则该圆台外接球的表面积为2112R 4π=π.故选:C .【总结提升】几类空间几何体表面积的求法(1)多面体:其表面积是各个面的面积之和.(2)旋转体:其表面积等于侧面面积与底面面积的和.(3)简单组合体:应搞清各构成部分,并注意重合部分的删、补.(4)若以三视图形式给出,解题的关键是根据三视图,想象出原几何体及几何体中各元素间的位置关系及数量关系.题型二:空间几何体的体积例4. (2023·河南·洛宁县第一高级中学一模(文))若圆锥的母线与底面所成的角为π6,则该圆锥的体积为( )A .π2B .πC .2πD .3π【答案】B【解析】【分析】设圆锥的高为h ,利用母线与底面所成角求出高即可得解.【详解】设圆锥的高为h , 因为母线与底面所成的角为π6,所以πtan 61h =.圆锥的体积2π1π3=⨯⨯=V . 故选:B例5.(2022·全国·高考真题)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔1485m .时,相应水面的面积为21400km .;水位为海拔1575m .时,相应水面的面积为21800km .,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔1485m .上升到1575m .时,2.65)( )A .931.010m ⨯B .931.210m ⨯C .931.410m ⨯D .931.610m ⨯ 【答案】C【解析】【分析】根据题意只要求出棱台的高,即可利用棱台的体积公式求出.【详解】依题意可知棱台的高为157.5148.59MN =-=(m),所以增加的水量即为棱台的体积V .棱台上底面积262140.014010S ==⨯km m ,下底面积262180.018010S '==⨯km m ,∴((66119140101801033V h S S =+=⨯⨯⨯+⨯' ()()679933320607109618 2.6510 1.43710 1.410(m )=⨯+⨯≈+⨯⨯=⨯≈⨯.故选:C .例6.(2022·全国·高考真题(理))甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若=2S S 甲乙,则=V V 甲乙( ) AB.CD【答案】C【解析】【分析】 设母线长为l ,甲圆锥底面半径为1r ,乙圆锥底面圆半径为2r ,根据圆锥的侧面积公式可得122r r =,再结合圆心角之和可将12,r r 分别用l 表示,再利用勾股定理分别求出两圆锥的高,再根据圆锥的体积公式即可得解.【详解】解:设母线长为l ,甲圆锥底面半径为1r ,乙圆锥底面圆半径为2r , 则11222S rl r S r l r ππ===甲乙, 所以122r r =, 又12222r r l lπππ+=, 则121r r l +=, 所以1221,33r l r l ==,所以甲圆锥的高1h ==,乙圆锥的高2h ==,所以221122214313r h l V V r h ππ==甲乙 故选:C.例7.(2022·湖北·黄石市有色第一中学模拟预测)阿基米德多面体也称为半正多面体,是以边数不全相同的正多边形为面围成的多面体.如图,已知阿基米德多面体的所有顶点均是一个棱长为2的正方体各条棱的中点,则该阿基米德多面体的体积为______;若M ,N 是该阿基米德多面体表面上任意两点,则M ,N 两点间距离的最大值为______.【答案】 203##263 22##322 【解析】【分析】第一空,将该多面体置于正方体中,由此可知该阿基米德多面体是由正方体切掉8个全等的三棱锥形成,由此可求得其体积;第二空,结合阿基米德多面体的外接球刚好是补形后正方体的棱切球,再求M ,N 两点间距离的最大值即可.【详解】依题意,可将该多面体补成一个棱长为2的正方体,如图,所以该阿基米德多面体是由正方体切掉8个全等的三棱锥形成,其体积112088111323V =-⨯⨯⨯⨯⨯=; 该阿基米德多面体的外接球刚好是正方体的棱切球,即与正方体的各条棱相切于棱的中点的球,该球直径为M ,N 两点间距离的最大值为外接球的直径,则max MN =故答案为:203; 【总结提升】1.处理体积问题的思路(1)“转”:指的是转换底面与高,将原来不易求面积的底面转换为易求面积的底面,或将原来不易看出的高转换为易看出并易求解长度的高,即等体积法;(2)“拆”:指的是将一个不规则的几何体拆成几个简单的几何体,便于计算,即分割法;(3)“拼”:指的是将小几何体嵌入一个大几何体中,如将一个三棱锥复原成一个三棱柱,将一个三棱柱复原成一个四棱柱,这些都是拼补的方法,即补形法.2.求体积的两种方法:①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等体积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.题型三:三视图与几何体的面积、体积例8.(2020·全国·高考真题(文))下图为某几何体的三视图,则该几何体的表面积是()A.6+42B.4+42C.6+23D.4+23【答案】C【解析】【分析】根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面积.【详解】根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDBS S S===⨯⨯=△△△根据勾股定理可得:AB AD DB===∴ADB△是边长为根据三角形面积公式可得:211sin 6022ADB S AB AD =⋅⋅︒==△该几何体的表面积是:632⨯++ 故选:C.例9. (2020·浙江·高考真题)某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是( )A .73B .143C .3D .6【答案】A【解析】【分析】根据三视图还原原图,然后根据柱体和锥体体积计算公式,计算出几何体的体积.【详解】由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,且三棱锥的一个侧面垂直于底面,且棱锥的高为1,棱柱的底面为等腰直角三角形,棱柱的高为2,所以几何体的体积为:11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+= ⎪ ⎪⎝⎭⎝⎭. 故选:A例10.(2022·浙江省春晖中学模拟预测)某几何体的三视图如图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是___________,体积是___________.【答案】232π+33π##3π3【解析】【分析】先画出直观图,再求出圆锥的高,求出两个半圆锥的侧面积之和,从而求出此几何体的表面积和体积.【详解】该几何体为两个底面半径为1,母线长为2的半圆锥拼接而成,设圆锥的高为h,由勾股定理得:413h=-=,则两个半圆锥的侧面积之和为12π22π2⨯⨯=,如图,AB =2CD =,且AB CD ⊥,所以四边形ADBC 的面积为22÷=, 该几何体的表面积为232π+,该几何体的体积为21π13⨯=故答案为:2π 【总结提升】 求空间几何体体积的常见类型及思路(1)规则几何体:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法(2)不规则几何体:若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.题型四:简单几何体的外接球与内切球问题例11.(2021·天津·高考真题)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为323π,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为( )A .3πB .4πC .9πD .12π 【答案】B【解析】作出图形,计算球体的半径,可计算得出两圆锥的高,利用三角形相似计算出圆锥的底面圆半径,再利用锥体体积公式可求得结果.【详解】如下图所示,设两个圆锥的底面圆圆心为点D ,设圆锥AD 和圆锥BD 的高之比为3:1,即3AD BD =,设球的半径为R ,则343233R ππ=,可得2R =,所以,44AB AD BD BD =+==, 所以,1BD =,3AD =,CD AB ⊥,则90CAD ACD BCD ACD ∠+∠=∠+∠=,所以,CAD BCD ∠=∠,又因为ADC BDC ∠=∠,所以,ACD CBD △∽△,所以,AD CD CD BD=,CD ∴= 因此,这两个圆锥的体积之和为()21134433CD AD BD πππ⨯⋅+=⨯⨯=. 故选:B.例12.(2020·全国高考真题(理))已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )A B .32 C .1 D .2【答案】C【解析】 设球O 的半径为R ,则2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC21224a ∴⨯=,解得:3a =,2233r ∴===,∴球心O 到平面ABC 的距离1d ===.故选:C.例13.(2020·全国·高考真题(理))已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )AB .32C .1D 【答案】C【解析】【分析】根据球O 的表面积和ABC 的面积可求得球O 的半径R 和ABC 外接圆半径r ,由球的性质可知所求距离d = 【详解】设球O 的半径为R ,则2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC212a ∴=3a =,2233r ∴==∴球心O 到平面ABC 的距离1d .故选:C.【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.例14.(2019·全国·高考真题(理))已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A .B .C . D【答案】D【解析】【分析】先证得PB ⊥平面PAC ,再求得PA PB PC ===P ABC -为正方体一部分,进而知正方体的体对角线即为球直径,从而得解.【详解】解法一:,PA PB PC ABC ==∆为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA 、AB 中点,//EF PB ∴,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥平面PAC ,PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体一部分,2R ==34433R V R =∴=π==π,故选D . 解法二:设2PA PB PC x ===,,E F 分别为,PA AB 中点,//EF PB ∴,且12EF PB x ==,ABC ∆为边长为2的等边三角形,CF ∴=90CEF ∠=︒1,2CE AE PA x ∴=== AEC ∆中余弦定理()2243cos 22x x EAC x +--∠=⨯⨯,作PD AC ⊥于D ,PA PC =, D 为AC 中点,1cos 2AD EAC PA x ∠==,2243142x x x x+-+∴=,2212122x x x ∴+=∴==PA PB PC ∴=====2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴R ∴=,34433V R ∴=π==,故选D. 例15.(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .π B .34π C .2π D .4π 【答案】B 【解析】设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴2r ==. ∴圆柱的体积为V =πr 2h =34π×1=34π. 故选B .例16.(2016·全国卷Ⅲ)在封闭的直三棱柱ABC A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4πB .9π2C .6πD .32π3【答案】B【解析】由题意得要使球的体积最大,则球与直三棱柱的若干面相切.设球的半径为R ,∵△ABC 的内切圆半径为68102+-=2,∴R ≤2. 又2R ≤3,∴R ≤32,∴V ma x =3439()322ππ=.故选B . 点睛:解答本题的关键是当V 取得最大值时,球与上下底面还是与侧面相切的问题.例17.(2021·福建·厦门大学附属科技中学高三阶段练习)某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为(球心与正方体的中心重合),若其中一个截面圆的周长为6π,则该球的表面积是______.【答案】144π【解析】【分析】设球心为O ,作出过球心的截面图如图所示,然后根据已知条件结合球的性质求解即可.【详解】 设球心为O,作出过球心的截面图如图所示,则OA =由截面圆的周长为6π,得26AB ππ⨯=,∴3AB =,6.所以该球的表面积为246=144ππ⨯.故答案为:144π.例18. (2019年高考天津卷理)的正方形,侧棱长若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.【答案】,借助勾股定理,可知四棱锥的高.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,一个底面的圆心为四棱锥底面的中心,故圆柱的高为,圆柱的底面半径为, 故圆柱的体积为. 例19.(2020·全国·高考真题(文))已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.【解析】【分析】将原问题转化为求解圆锥内切球的问题,然后结合截面确定其半径即可确定体积的值.【详解】 25π42=11221ππ124⎛⎫⨯⨯= ⎪⎝⎭易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2,3BC AB AC ===,且点M 为BC 边上的中点,设内切圆的圆心为O , 由于223122AM =-=,故1222222S =⨯⨯=△ABC , 设内切圆半径为r ,则:ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯=解得:22r,其体积:343V r π==.. 【总结提升】1.常见类型:(1)利用长方体的体对角线探索外接球半径;(2)利用长方体的面对角线探索外接球半径;(3)利用底面三角形与侧面三角形的外心探索球心;(4)利用直棱柱上下底面外接圆圆心的连线确定球心;(5)锥体的内切球问题;(6)柱体的内切球问题2.与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.3.若球面上四点P ,A ,B ,C 中PA ,PB ,PC 两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.。
空间几何体的表面积和体积经典例题(教师讲义打印一份)
空间几何体的表面积和体积一.课标要求:了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
二.命题走向近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题。
即使考查空间线面的位置关系问题,也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用“割补法”等求解。
由于本讲公式多反映在考题上,预测2016年高考有以下特色:(1)用选择、填空题考查本章的基本性质和求积公式;(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;三.要点精讲1.多面体的面积和体积公式表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长。
2.旋转体的面积和体积公式表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台上、下底面半径,R表示半径。
四.典例解析题型1:柱体的体积和表面积例1.一个长方体全面积是20cm 2,所有棱长的和是24cm ,求长方体的对角线长. 解:设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得:⎩⎨⎧=++=++24)(420)(2z y x zx yz xy )2()1(由(2)2得:x 2+y 2+z 2+2xy+2yz+2xz=36(3)由(3)-(1)得x 2+y 2+z 2=16 即l 2=16所以l =4(cm)。
点评:涉及棱柱面积问题的题目多以直棱柱为主,而直棱柱中又以正方体、长方体的表面积多被考察。
我们平常的学习中要多建立一些重要的几何要素(对角线、内切)与面积、体积之间的关系。
例2.如图1所示,在平行六面体ABCD —A 1B 1C 1D 1中,已知AB=5,AD=4,AA 1=3,AB ⊥AD ,∠A 1AB=∠A 1AD=3π。
第七章 第二节 空间几何的表面积和体积

2.已知三棱锥的三视图如图所示,则它的外接球表 .已知三棱锥的三视图如图所示, 面积为 ( )
A.16π . C.4π .
B.π . D.2π .
解析: 解析:由三视图可知底面三角形斜边的中点即为外接球 的球心,所以外接球的半径 = ,故表面积为4πr 的球心,所以外接球的半径r=1,故表面积为 2=4π. 答案: 答案:C
[题组自测 题组自测] 题组自测 4 1.母线长为 1 的圆锥的侧面展开图的圆心角等于 π,则 . , 3 该圆锥的体积为 2 2 A. π 81 4 5 C. π 81 8 B. π 81 10 D. π 81 ( )
4 解析:圆锥的侧面展开图扇形的弧长, 解析:圆锥的侧面展开图扇形的弧长,即底面圆的周长为 3 4 4 π·1= π,于是设底面圆的半径为 r,则有 2πr= π,所以 r = , , = , 3 3 2 =3,于是圆锥的高 h= = 4 5 π. = 81 5 22 1-( ) = ,故圆锥的体积 V -3 3
[题组自测 题组自测] 题组自测 1.(2010·湖南部分示范性中学联考 一个正方体的体积是 , . 湖南部分示范性中学联考)一个正方体的体积是 湖南部分示范性中学联考 一个正方体的体积是8, 则这个正方体的内切球的表面积是 A. A.8π C.4π . B. B.6π D.π . ( )
解析:设正方体的棱长为 , 解析:设正方体的棱长为a,则a3=8,∴a=2.而此 , = 而此 正方体的内切球直径为2, 正方体的内切球直径为 ,∴S表=4πr2=4π. 答案: 答案:C
答案: 答案:C
2.将边长为 a 的正方形 ABCD 沿对角线 AC 折起,使 BD . 折起, =a,则三棱锥 D-ABC 的体积为 , - a3 A. 6 3 3 C. a 12 a3 B. 12 2 3 D. a 12 ( )
2020届江苏省镇江市统一高考数学第一轮复习学案(解析答案版):学案4.立体几何(1)表面积与体积

立体几何复习(1)空间几何体的表面积与体积教学目标:1.掌握锥、台、柱、球体的表面积公式及表面积的求法;2.掌握锥、台、柱、球体的体积公式及体积的求法.教学重点:掌握锥体、台体、柱体、球体的表面积与体积的计算方法,能计算简单组合体的表面积与体积,以便从量的角度认识空间几何体.教学难点:锥体、台体、柱体、球体的表面积与体积公式的应用.【知识清单】 1.空间几何体的表面积球的表面积2=4S R π球,其中R 为球的半径.2.空间几何体的体积球的体积34=3V R π球,R 为球的半径. 【例题精讲】类型1:空间几何体的表面积与侧面积例1:1.若圆锥底面半径为1,高为2,则圆锥的侧面积为 .【解析】根据圆锥底面半径、高、母线长构成一个直角三角形,所以母线长l,在根据圆锥的侧面积公式S rl π=.2.将一个正方形绕着它的一边所在的直线旋转一周,所得圆柱的体积为27πcm 3,则该圆柱的侧面积为 cm 2. 【答案】18【解析】设正方体棱长为a ,则正方形绕着它的一边所在的直线旋转一周,所得圆柱的体积为2327a a a πππ⨯==,3a =,圆柱侧面积22218S a a a πππ=⨯==.3.若圆锥的底面直径和高都与一个球的直径相等,圆锥、球的表面积分别记为, ,则12S S 的值是 .【解析】设球的直径为2R ,由题意可知,2211)S R R R πππ=+=,224S R π=,所以12S S =1S 2S )h 圆台备选题1:正三棱锥中,,D、E分别是棱SA、SB上的点,为边的中点,,则三角形CDE的面积为 .【解析】根据题意在正三棱锥中,为边的中点,故可得AB SCQ⊥平面,则AB SQ⊥,又由,故//DE AB,假设DE SQ F=,又在SCQ∆中,SC CQ SQ===CF=,故112CDES∆=⨯=.备选题2:圆锥的母线长为L,过顶点的最大截面的面积为12L2,则圆锥底面半径与母线长的比rL的取值范围是 .【答案】【解析】由题意得轴截面的顶角θ不小于π2,因为sinθ2=rL≥sinπ4=22,所以22≤rL<1.【思想方法归纳】圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.(1)找准几何体中各元素间的位置关系及数量关系.(2)注意组合体的表面积问题中重合部分的处理.类型2:空间几何体的体积例2:1.已知圆锥的母线长为5cm,侧面积为215cmπ,则此圆锥的体积为3cm.S ABC-2BC=SB=Q AB SQ CDE⊥平面S ABC-Q ABSQ CDE⊥平面【答案】12π【解析】已知圆锥的母线长为5cm ,侧面积为215cm π,所以圆锥的底面周长26cm π,底面半径是3cm ,圆锥的高是4cm ,此圆锥的体积为194123ππ⨯⨯=3cm .2.如图,在正四棱柱ABCD -A 1B 1C 1D 1中,AB =3 cm ,AA 1=1 cm ,则三棱锥D 1-A 1BD 的体积为 cm3.(例2-2)【答案】32【解析】∵在正四棱柱ABCD -A 1B 1C 1D 1中,AB =3cm ,AA 1=1 cm ,∴三棱锥11D A BD -的体积:1111113113313362D A BD B A D D A D D V V S AB cm --∆==⋅⋅=⨯⨯⨯=.3.如图,在直四棱柱1111ABCD A B C D -中,点,E F 分别在11,AA CC 上,且134AE AA =,113CF CC =,点,A C 到BD 的距离之比为3:2,则三棱锥E BCD -和F ABD -的体积比E BCDF ABDV V --= .(例2-3)【答案】32【解析】点,A C 到BD 的距离之比为3:2,所以23BCD ABD S S ∆=∆,又直四棱柱1111ABCD A B C D -中,134AE AA =,113CF CC =,所以94AE CF =, 于是1293313423BCD E BCDF ABDABD S AEV V S CF ∆--∆⋅==⨯=⋅.备选题1:在直三棱柱ABC -A 1B 1C 1中,M ,N 分别为棱A 1B 1,A 1C 1的中点,则平面BMNC 将三棱柱分成的两部分的体积比为 . 【答案】7:5【解析】设直三棱柱ABC -A 1B 1C 1高为h ,底面积为4S ,则11111B C BMNC C B MNC M B BC V V V ---=+11111111534322233A B BC B ABC h S V Sh V hS h S Sh --=⨯⨯+=+=+⨯⋅=, 所以两部分的体积比为55(4):7:533Sh Sh Sh -=.备选题2:已知一个组合体是由圆锥与圆柱组合而成,下半部分是底面半径为1,高为4的圆柱,上半部分是底面半径为2,高为2的圆锥,则该几何体的体积为 3m . 【答案】203π【解析】由于该几何体是组合体,其中下半部分是底面半径为1,高为4的圆柱,上半部分是底面半径为2,高为2的圆锥,其体积为22120142233πππ⨯⨯+⨯⨯⨯=(3m ).备选题3:《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC -A 1B 1C 1中,AC ⊥BC ,若A 1A =AB =2,当阳马B -A 1ACC 1体积最大时,则堑堵ABC -A 1B 1C 1的体积为 .备选题3【答案】2【解析】由阳马的定义知,VB -A 1ACC 1=13×A 1A ×AC ×BC =23AC ×BC ≤13(AC 2+BC 2)=13AB 2=43,当且仅当AC =BC =2时等号成立,所以当阳马B -A 1ACC 1体积最大时,则堑堵ABC -A 1B 1C 1的体积为12×2×2×2=2.【思想方法归纳】(1)计算柱、锥、台的体积关键是根据条件找出相应的底面积和高.(2)若所给几何体的体积不能直接利用公式得出,注意求体积的一些特殊方法:分割法、补体法、等体积转化法等,它们是解决一些不规则几何体体积计算常用的方法,应熟练掌握.(3)注意组合体的组成形式及各部分几何体的特征.类型3:球内接几何体相关问题例3:1.正方体ABCD-A 1B 1C 1D 1的棱长为23,则四面体AB 1CD 1的外接球的体积为 . 【答案】36π【解析】四面体AB 1CD 1的外接球即为正方体ABCDA 1B 1C 1D 1的外接球,故正方体的外接球的直径为(23)2+(23)2+(23)2=6,故V =43πR 3=43π×(6÷2)3=36π.2.如图,在四棱锥P -ABCD 中,△PAB 为正三角形,四边形ABCD 为正方形且边长为2,平面PAB⊥平面ABCD ,四棱锥P -ABCD 的五个顶点都在一个球面上,则这个球的表面积是 .(例3-2)【答案】283π 【解析】由题意球的半径满足R 2-1+R 2-2=3⇒R 2=73,所以球的表面积是4πR 2=28π3.3.已知三棱柱ABC -A 1B 1C 1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为23,AB =2,AC =1,∠BAC =60°,则此球的表面积等于 . 【解析】20π【解析】由题意知三棱柱是直三棱柱,且底面是直角三角形,∠ACB =90°,设D ,D 1分别是AB ,A 1B 1的中点,O 是DD 1中点,可证O 就是三棱柱外接球球心,S △ABC =12×2×1×sin 60°=32,V =S △ABC ·h =32×DD 1=23,即DD 1=4,OA =AD 2+DO 2=12+22=5, 所以S =4π×OA 2=4π×(5)2=20π.备选题1:已知正三棱柱111A B C ABC -的所有棱长都为3,则该棱柱外接球的表面积为 . 【答案】21π【解析】如图,外接球的球心为上下底面中心连线1M M 的中点,连结1A O ,11A M ,所以三角形11A M O 为直角三角形, 132M O =,113A M =()()221213322AO =+ 所以该棱柱外接球的表面积为(2214π21π⨯=.备选题2:已知P -ABC 是正三棱锥,其外接球O 的表面积为16π,且∠APO =∠BPO =∠CPO =30°,则三棱锥的体积为 . 934【解析】设球的半径为R ,△ABC 的外接圆圆心为O ′,则由球的表面积为16π, 可知4πR 2=16π,所以R =2.设△ABC 的边长为2a , 因为∠APO =∠BPO =∠CPO =30°,OB =OP =2,所以BO ′=32R =3,OO ′=OB 2-BO ′2=1, PO ′=OO ′+OP =3.在△ABC 中,O ′B =23×32×2a =3, 所以a =32,所以三棱锥PABC 的体积为V =13×12×32×sin60°×3934【思想方法归纳】解决球与其他几何体的内切、外接问题,一般外接球需要求球心和半径,首先应确定球心的位置,借助于外接球的性质,球心到各顶点距离相等,这样可先确定几何体中部分点组成的多边形的外接圆的圆心,过圆心且垂直于多边形所在平面的直线上任一点到多边形的顶点的距离相等,然后同样的方法找到另一个多边形的各顶点距离相等的直线这样两条直线的交点,就是其外接球的球心,再根据半径,顶点到底面中心的距离,球心到底面中心的距离,构成勾股定理求解,有时也可利用补体法得到半径.类型4:综合应用例4:如图,四棱锥中,底面是边长为2的正方形,其它四个侧面都是侧棱长为的中点.(1)在侧棱上找一点,使∥平面,并证明你的结论;(2)在(1)的条件下求三棱锥的体积.【解析】(1)F为VC的中点,取CD的中点为H,连结BH,HF,ABCD为正方形,E为AB 的中点,//,DH DHBE BE=∴,//H DB E∴,又//VDFH,∴平面//BHF平面VDE,//BF∴平面VDE.(2)F为VC的中点,14BDE ABCDS S∆=,18E BDF F BDE V ABCDV V V---∴==,V ABCD-为正四棱锥,V∴在平面ABCD的射影为AC的中点O.5VA=AO=∴VO=2123V ABCDV-∴=⋅E BDFV-∴=【点睛】(1)为的中点,取的中点为,由三角形中位线性质得线线平行,再由线线平行证得面面平行,即得线面平行(2)因为为正四棱锥,所以可求V到底面距离,即得F到底面距离,再根据等体积法得,最后代入锥体体积公式即可.备选题1:如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.V ABCD-ABCDE ABVC F BF VDEE BDF-F VC CD HV ABCD-E BDF F BDEV V--=(1)若弧BC 的中点为D ,求证:AC ∥平面POD ; (2)如果△PAB 的面积是9,求此圆锥的表面积.【解析】(1)证明:方法一 设BC ∩OD =E ,∵D 是弧BC 的中点,∴E 是BC 的中点. 又∵O 是AB 的中点,∴AC ∥OE .又∵AC ⊄平面POD ,OE ⊂平面POD ,∴AC ∥平面POD .方法二 ∵AB 是底面圆的直径,∴AC ⊥BC .∵弧BC 的中点为D ,∴OD ⊥BC . 又AC ,OD 共面,∴AC ∥OD .又AC ⊄平面POD ,OD ⊂平面POD ,∴AC ∥平面POD . (2)解:设圆锥底面半径为r ,高为h ,母线长为l , ∵圆锥的轴截面PAB 为等腰直角三角形,∴h =r ,l =2r .由S △PAB =12×2r ×h =r 2=9,得r =3,∴S 表=πrl +πr 2=πr ×2r +πr 2=9(1+2)π.备选题2:如图,矩形ABCD 所在的平面和平面ABEF 互相垂直,等腰梯形ABEF 中,AB ∥EF ,AB =2,AD =AF =1,∠BAF =60°,O ,P 分别为AB ,CB 的中点,M 为底面△OBF 的重心.(1)求证:平面ADF ⊥平面CBF ; (2)求证:PM ∥平面AFC ; (3)求多面体CD -AFEB 的体积V .【解析】(1)证明:∵矩形ABCD 所在的平面和平面ABEF 互相垂直,且CB ⊥AB ,∴CB ⊥平面ABEF , 又AF ⊂平面ABEF ,所以CB ⊥AF ,又AB =2,AF =1,∠BAF =60°,由余弦定理知BF =3,∴AF 2+BF 2=AB 2,得AF ⊥BF , 又BF ∩CB =B ,∴AF ⊥平面CFB ,又∵AF ⊂平面ADF ,∴平面ADF ⊥平面CBF .(2)证明:连接OM 并延长交BF 于H ,则H 为BF 的中点,又P 为CB 的中点,∴PH ∥CF ,又∵CF ⊂平面AFC ,PH ⊄平面AFC ,∴PH ∥平面AFC , 连接PO ,则PO ∥AC ,又∵AC ⊂平面AFC ,PO ⊄平面AFC ,∴PO ∥平面AFC , 又∵PO ∩PH =P ,∴平面POH ∥平面AFC , 又∵PM ⊂平面POH ,∴PM ∥平面AFC .(3)解:多面体CD -AFEB 的体积可分成三棱锥C -BEF 与四棱锥F -ABCD 的体积之和. 在等腰梯形ABEF 中,计算得EF =1,两底间的距离EE 1=32. 所以V C -BEF =13S △BEF ×CB =13×12×1×32×1=312,V F -ABCD =13S 矩形ABCD ×EE 1=13×2×1×32=33,所以V =V C -BEF +V F -ABCD =5312.【课堂归纳总结】1.空间几何体表面积和体积的求法几何体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理.空间几何体体积问题的常见类型及解题策略:(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用等体积转换法、分割法、补形法等方法进行求解.2.多面体与球接、切问题的求解策略(1)涉及球与棱柱、棱锥的接、切问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内接、外切的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,则4R2=a2+b2+c2求解.【课后练习】1.已知圆锥的侧面展开图是半径为3,圆心角为23π的扇形,则这个圆锥的高为 .【答案】【解析】由题知圆锥的底面圆周长为2323ππ⋅=,所以半径为1r=,由题意圆锥的侧面展开图是半径为3即为圆锥的母线3l=,所以圆锥的高为h.2.若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为 .【答案】3π【解析】由题意得:1:(2)22rl h rππ⋅=2l h⇒=⇒母线与轴的夹角为3π.3.如图,在长方体中,,,则三棱锥的体积为.【答案】3 【解析】4.在ABC ∆中,2AB =, 1.5BC =,120ABC ∠=,若使ABC ∆绕直线BC 旋转一周,则所形成的几何体的体积是 . 【答案】32π【解析】过A 作AD 垂直BC 于点D ,则,AD =1BD =, 2.5CD =,因此所形成的几何体的体积是213(2.51)32ππ⨯⋅⋅-=.5.已知圆柱M 的底面半径为2,高为6,圆锥N 的底面直径和母线长相等,若圆柱M 和圆锥N 的体积相同,则圆锥N 的高为 . 【答案】6【解析】设圆锥N 的底面半径为r ,则它的母线长为2r ,高为3r ,由圆柱M 与圆锥N 的体积相同,得4π×6=13πr2×3r ,解得r =23,因此圆锥N 的高h =3r =6.6.现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为 .【解析】由体积相等得:22221145+28=4833r r r ππππ⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯⇒=.7.如图,在正三棱柱111ABC A B C -中,已知13AB AA ==,点P 在棱1CC 上,则三棱锥1P ABA -的体积为 .(第7题)【解析】三棱锥的底面积1193322ABA S ∆=⨯⨯=,点P 到底面的距离为ABC ∆的高h =,故三棱锥的体积13V Sh ==.8.如图,圆形纸片的圆心为,半径为,该纸片上的正四边形的中心为.为圆上的点分别是以为底边的等腰三角形.沿线剪开后,别以为折痕折起,使得重合,得到四棱锥记该四棱锥的体积,表面积分别是,当,则 .(第8题)【解析】,则四棱锥的高,所以体积,所以9.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .O 4cm ABCD O ,,,E F G H O ,,,EAB FBC GCD HDA ∆∆∆∆,,,AB BC CD DA ,,,AB BC CD DA ,,,EAB FBC GCD HDA ∆∆∆∆,,,E F G H ,V S 2AB =VS=2AB =h =13V Sh ==44316S =+⨯=V S =【答案】【解析】由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于,所以该多面体的体积为【点睛】:解决本类题目的关键是准确理解几何体的定义,真正把握几何体的结构特征,可以根据条件构建几何模型,在几何模型中进行判断;求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.10.设直三棱柱ABC -A 1B 1C 1的所有顶点都在同一个球面上,且球的表面积是40π,AB =AC =AA 1,∠BAC =120°,则此直三棱柱的高是 . 【答案】2 2【解析】设AB =AC =AA 1=x ,在△ABC 中,∠BAC =120°,则由余弦定理可得BC =3x . 由正弦定理,可得△ABC 外接圆的半径为r =x , ∵球的表面积是40π,∴球的半径为R =10.设△ABC 外接圆的圆心为O ′,球心为O ,在Rt △OBO ′中,有221()102x x +=,解得x =22,即AA 1=22,即此直三棱柱的高是2 2.11.如图,已知四棱锥P -ABCD 的底面是边长为2的菱形,∠BCD =60°,点E 是BC 边 的中点,AC ,DE 交于点O ,PO =23,且PO ⊥平面ABCD . (1)求证:PD ⊥BC ;(2)在线段AP 上找一点F ,使得BF ∥平面PDE , 并求此时四面体PDEF 的体积.【解析】(1)由题可得△BCD 为正三角形,E 为BC 中点,故DE ⊥BC . 又PO ⊥平面ABCD ,BC ⊂平面ABCD ,则PO ⊥BC ,而DE ∩PO =O ,,DE PO ⊂平面PDE ,所以BC ⊥平面PDE .又PD ⊂平面PDE ,故PD ⊥BC . (2)取AP 中点为F ,再取PD 中点为G ,连结FG . 则FG 为△PAD 中位线,故FG =∥ 12AD , 又BE =∥ 12AD ,所以FG =∥BE ,于是四边形BFGE 为平行四边形, 因此BF ∥EG .又BF ⊄平面PDE ,EG ⊂平面PDE ,所以BF ∥平面PDE . 由(1)知,BC ⊥平面PDE .则有BC ⊥PE ,BC ⊥DE ,而BC ∥FG ,故FG ⊥PE ,FG ⊥DE ,且DE ∩PE =E ,所以FG ⊥平面PDE . 于是四面体PDEF 的体积为V=13S △PDE ·FG =13×12×23×3×1=1.另解(等体积转化):因为BF //面PDE ,则B ,F 两点到平面PDE 的距离相等, 所以四面体PDEF 的体积等于四面体PDEB , 因为PO ⊥平面ABCD ,所以V P-BDE =13·PO ·S △BDE =1.12.如图,正△ABC 的边长为4,CD 是AB 边上的高,E ,F 分别是AC 和BC 边的中点,现将△ABC 沿CD 翻折成直二面角A -DC -B .(1)试判断直线AB 与平面DEF 的位置关系,并说明理由; (2)求棱锥E -DFC 的体积;(3)在线段BC 上是否存在一点P ,使AP ⊥DE ?如果存在,求出BPBC的值;如果不存在,请说明理由.【解析】(1)AB ∥平面DEF ,理由如下:在△ABC 中,由E ,F 分别是AC ,BC 的中点,得EF ∥AB . 又AB ⊄平面DEF ,EF ⊂平面DEF .∴AB ∥平面DEF .(2)∵AD ⊥CD ,BD ⊥CD ,将△ABC 沿CD 翻折成直二面角A -DC -B ,∴AD ⊥BD ,∴AD ⊥平面BCD .取CD 的中点M ,这时EM ∥AD ,∴EM ⊥平面BCD ,EM =1.V E -DFC =13×1()2BDC S ×EM =13×12×12×2×23×1=33. (3)在线段BC 上存在点P ,使AP ⊥DE .证明如下:在线段BC 上取点P ,使BP =BC3,过P 作PQ ⊥CD 于Q .∵AD ⊥平面BCD ,PQ ⊂平面BCD ,∴AD ⊥PQ .又∵AD ∩CD =D ,∴PQ ⊥平面ACD , ∴DQ =DC 3=233,∴tan ∠DAQ =DQ AD =2332=33,∴∠DAQ =30°,在等边△ADE 中,∠DAQ =30°,∴AQ ⊥DE ,∵PQ ⊥平面ACD ,DE ⊂平面ACD ,∴PQ ⊥DE ,AQ ∩PQ =Q ,∴DE ⊥平面APQ ,∴AP ⊥DE .此时BP =BC 3,∴BP BC =13.13.如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ,容器Ⅰ的底面对角线AC的长为cm ,容器Ⅱ的两底面对角线EG ,E 1G 1的长分别为14cm 和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l ,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l 放在容器Ⅰ中,l 的一端置于点A 处,另一端置于侧棱CC 1上,求l 没入水中部分的长度;(2)将l 放在容器Ⅱ中,l 的一端置于点E 处,另一端置于侧棱GG 1上,求l 没入水中部分的长度.【解析】(1)由正棱柱的定义,1CC ⊥平面ABCD ,所以平面11A ACC ⊥平面ABCD ,1CC AC ⊥.记玻璃棒的另一端落在1CC 上点M 处.因为40AC AM ==,所以30MC ==,从而 3sin 4MAC =∠,记AM 与水面的焦点为1P ,过1P 作P 1Q 1⊥AC , Q 1为垂足,则 P 1Q 1⊥平面 ABCD ,故P 1Q 1=12,从而 AP 1=1116sin P MACQ =∠. ( 如果将“没入水中部分冶理解为“水面以上部分冶,则结果为24cm) (2)如图,O ,O 1是正棱台的两底面中心.由正棱台的定义,OO 1⊥平面 EFGH , 所以平面E 1EGG 1⊥平面EFGH ,O 1O ⊥EG . 同理,平面 E 1EGG 1⊥平面E 1F 1G 1H 1,O 1O ⊥E 1G 1.记玻璃棒的另一端落在GG 1上点N 处. 过G 作GK ⊥E 1G ,K 为垂足, 则GK =OO 1=32. 因为EG = 14,E 1G 1= 62,所以KG 1= 6214242-=,从而140GG ===.设1,,EGG ENG αβ==∠∠则114sin sin()cos 25KGG KGG απ=+==∠∠. 因为2απ<<π,所以3cos 5α=-. 在ENG △中,由正弦定理可得4014sin sin αβ=,解得7sin 25β=. 因为02βπ<<,所以24cos 25β=. 于是,sin sin()sin()NEG αβαβ=π--=+∠42473sin cos cos sin ()53525255αβαβ=+=⨯+-⨯=.记EN 与水面的交点为P 2,过 P 2作P 2Q 2⊥EG ,Q 2为垂足,则 P 2Q 2⊥平面 EFGH ,故P 2Q 2=12,从而EP 2=2220sin P NEGQ =∠.答:(1)玻璃棒l 没入水中部分的长度为16cm.(2)玻璃棒l 没入水中部分的长度为20cm.(如果将“没入水中部分冶理解为“水面以上部分冶,则结果为20cm)【点睛】空间几何体的考察,主要集中体积、表面积的计算和空间距离的距离,其实这些计算最后都得归结为平面中基本图形中的长度的计算,因此解三角形就是必要的工具.14.如图,圆柱体木材的横截面半径为1 dm ,从该木材中截取一段圆柱体,再加工制作成直四棱柱1111A B C D ABCD -,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心O 在梯形ABCD 内部,AB ∥CD ,DAB ∠=60°,1AA AD =,设DAO θ∠=. (1)求梯形ABCD 的面积;(2)当sin θ取何值时,四棱柱1111A B C D ABCD -的体积最大?并求出最大值. (注:木材的长度足够长)【解析】(1)由条件可得,2cos AD θ=, 所以梯形的高sin 603h AD θ==. 又2cos(60)AB θ=-,2cos(120)CD θ=-, 所以梯形ABCD 的面积为12cos(60)2cos(120)3cos 2S θθθ⎡⎤=-+-⨯⎣⎦ cos(60)cos(60)3cos θθθ⎡⎤=--+⨯⎣⎦(2sin 60sin )θθ=3sin 22θ=(2dm ).(2)设四棱柱1111A B C D ABCD -的体积为V ,因为12cos AA AD θ==, 所以123sin 22cos 6sin (1sin )2A V S A θθθθ=⋅⨯==-.设sin t θ=,因为060θ︒<<,所以0t ⎛∈ ⎝,所以23()6(1)6()V t t t t t =-=-+,0t ⎛∈ ⎝.由2()6(31)18(V t t t t '=-+=-+-,令()0V t '=,得t ,()V t 与()V t '的变化情况列表如下:由上表知,()V t在t =时取得极大值,即为最大值,且最大值V =答:当sin θ=时,四棱柱1111A B C D ABCD -3dm .【备选提高题】1.各棱长都为2的正四棱锥与正四棱柱的体积之比为m ,则m 的值为 . 【答案】12【解析】法一:正四棱柱的体积为8,底面积为4,故体积为3,所6,即6m =. 方法二:设正四棱锥与正四棱柱的高分别为12,h h .因为正四棱锥与正四棱柱的底面积相同,所以体积之比为121332h h ==.2.将一个半径为2的圆分成圆心角之比为1:2的两个扇形,且将这两个扇形分别围成圆锥的侧面,则所得体积较小的圆锥与较大圆锥的体积之比为 . 【答案】1【解析】因为圆分成圆心角之比为1:2的两个扇形,所以两个扇形圆心角分别为123lπ=和243l π=.1223r ππ=和2423r ππ=,解得123r =,243r =.13h ==, 2h ==.所以21112222114313r h v v r h πππ⋅===3.已知一球与一个正三棱柱的三个侧面及两个底面都相切.若该球的体积为4π3,则该三棱柱的体积是 . 【答案】6 3【解析】由体积得球半径R =1,三棱柱的高为2,底面边长为2 3.V =34(2 3)2×2=6 3.4.在三棱锥P ABC -中,D ,E 分别为PB ,PC 的中点,记三棱锥D ABE -的体积为1V , 三棱锥P ABC -的体积为2V ,则12V V = . 【答案】14【解析】因为213C PAB PAB V V S h -∆==,121111323224E ABD DAB PAB h h V V S S V -∆∆==⋅=⨯⨯=,所以1214V V =.5.如图,四棱锥P ABCD -的底面ABCD 是矩形,PA ⊥底面ABCD ,E 为PD 上一点,且2PE ED =.设三棱锥P ACE -的体积为1V ,三棱锥P ABC -的体积为2V ,则12:V V = .【答案】23【解析】因为2PE ED =,所以三棱锥E ACD -的体积是三棱锥P ACD -体积的13,所以三棱锥P ACE -的体积是P ACD -体积的23.因为三棱锥P ABC -与三棱锥P ACD -体积相等,所以12:V V =23.6.在三棱锥D -ABC 中,AB =BC =DB =DC =1,当三棱锥体积最大时,其外接球的表面积为________. 【答案】7π3【解析】在三棱锥D -ABC 中,当且仅当AB ⊥平面BCD 时,三棱锥体积达到最大, 此时,设外接球的半径为R ,外接球的球心为O ,点F 为△BCD 的中心, 则有R 2=OB 2=OF 2+BF 2=221()2+=712,所以表面积S =4πR 2=7π3.7.已知三棱锥P -ABC 内接于球O ,PA =PB =PC =2,当三棱锥P -ABC 的三个侧面的面积之和最大时,球O 的表面积为 . 【答案】12π【解析】由于三条侧棱相等,根据三角形面积公式可知,当PA ,PB ,PC 两两垂直时,侧面积之和最大.此时PA ,PB ,PC 可看成正方体一个顶点的三条侧棱,其外接球直径为正方体的体对角线,即4R 2=3·22=12,故球的表面积为4πR 2=12π.8.已知正四面体P ABC -的棱长均为a ,O 为正四面体P ABC -的外接球的球心,过点O 作平行于底面ABC 的平面截正四面体P ABC -,得到三棱锥111P A B C -和三棱台111ABC A B C -,那么三棱锥111P A B C -的外接球的表面积为 . 【答案】22732a π 【解析】设底面ABC ∆的外接圆半径为r ,则2sin3a r π=,所以r ., 设正四面体的外接球半径为R,则222))R R =+-,∴R =.3:4=,所以三棱锥111P A B C -的外接球的表面积为2223274)()432a ππ⨯⨯=.。
(完整版)高中立体几何知识点总结
高中立体几何知识点总结一 、空间几何体 (一) 空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
(二) 几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2 棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体 性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等; Ⅱ、两底面是全等多边形且互相平行; Ⅲ、平行于底面的截面和底面全等;1.3 棱柱的面积和体积公式ch S 直棱柱侧(c 是底周长,h 是高)S 直棱柱表面 = c ·h+ 2S 底 V 棱柱 = S 底 ·h2 、棱锥的结构特征2.1 棱锥的定义(1) 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形图1-1 棱柱面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、 正棱锥的各侧棱相等,各侧面是全等的等腰三角形;正棱锥侧面积:1'2S ch =正棱椎(c 为底周长,'h 为斜高) 体积:13V Sh =棱椎(S 为底面积,h 为高)正四面体:对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。
2 第2讲 空间几何体的表面积与体积
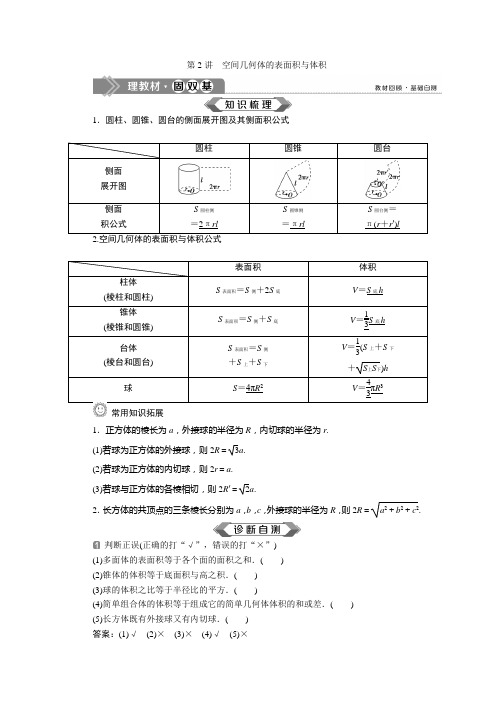
第2讲 空间几何体的表面积与体积1.圆柱、圆锥、圆台的侧面展开图及其侧面积公式圆柱圆锥圆台侧面 展开图侧面 积公式 S 圆柱侧 =2πrlS 圆锥侧 =πrlS 圆台侧= π(r +r ′)l表面积 体积 柱体 (棱柱和圆柱)S 表面积=S 侧+2S 底 V =S 底h 锥体 (棱锥和圆锥)S 表面积=S 侧+S 底 V =13S 底h台体 (棱台和圆台)S 表面积=S 侧 +S 上+S 下 V =13(S 上+S 下+S 上S 下)h 球 S =4πR 2V =43πR 3常用知识拓展1.正方体的棱长为a ,外接球的半径为R ,内切球的半径为r . (1)若球为正方体的外接球,则2R =3a . (2)若球为正方体的内切球,则2r =a . (3)若球与正方体的各棱相切,则2R ′=2a .2.长方体的共顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2.判断正误(正确的打“√”,错误的打“×”) (1)多面体的表面积等于各个面的面积之和.( ) (2)锥体的体积等于底面积与高之积.( ) (3)球的体积之比等于半径比的平方.( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差.( ) (5)长方体既有外接球又有内切球.( ) 答案:(1)√ (2)× (3)× (4)√ (5)×以长为a ,宽为b 的矩形的一边所在的直线为轴旋转一周所得圆柱的侧面积为( )A .abB .πabC .2πabD .2ab解析:选C.若以长边所在的直线为轴旋转,则S 侧=2πab ,若以短边所在的直线为轴旋转,则S 侧=2πba .所以S 圆柱侧=2πab ,故选C.某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )A .8 cm 3B .12 cm 3 C.323cm 3 D.403cm 3 解析:选C.由三视图可知,该几何体是由一个正方体和一个正四棱锥构成的组合体.下面是棱长为2 cm 的正方体,体积V 1=2×2×2=8(cm 3);上面是底面边长为2 cm ,高为2 cm 的正四棱锥,体积V 2=13×2×2×2=83(cm 3),所以该几何体的体积V =V 1+V 2=323(cm 3).(2018·高考天津卷)如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为1,则四棱锥A 1BB 1D 1D 的体积为____________.解析:法一:连接A 1C 1交B 1D 1于点E ,则A 1E ⊥B 1D 1,A 1E ⊥BB 1,则A 1E ⊥平面BB 1D 1D ,所以A 1E 为四棱锥A 1BB 1D 1D 的高,且A 1E =22,矩形BB 1D 1D 的长和宽分别为2,1,故VA 1BB 1D 1D =13×1×2×22=13.法二:连接BD 1,则四棱锥A 1BB 1D 1D 分成两个三棱锥B -A 1DD 1与B -A 1B 1D 1,V A 1BB 1D 1D=V B A 1DD 1+V B A 1B 1D 1=13×12×1×1×1+13×12×1×1×1=13.答案:13(2017·高考全国卷Ⅱ)长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为________.解析:依题意得,长方体的体对角线长为32+22+12=14,记长方体的外接球的半径为R ,则有2R =14,R =142,因此球O 的表面积等于4πR 2=14π. 答案:14π空间几何体的表面积(师生共研)(1)(2018·高考全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A .122πB .12πC .82πD .10π(2)(2019·沈阳质量检测(一))某四棱锥的三视图如图所示,则该四棱锥的侧面积是( )A .4+4 2B .42+2C .8+4 2D. 83【解析】 (1)因为过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为22,底面圆的直径为22,所以该圆柱的表面积为2×π×(2)2+22π×22=12π.(2)由三视图可知该几何体是一个四棱锥,记为四棱锥P -ABCD ,如图所示,其中P A ⊥底面ABCD ,四边形ABCD 是正方形,且P A =2,AB =2,PB =22,所以该四棱锥的侧面积S 是四个直角三角形的面积和,即S =2×⎝⎛⎭⎫12×2×2+12×2×22=4+42,故选A. 【答案】 (1)B (2)A空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积问题应注意衔接部分的处理. (3)旋转体的表面积问题应注意其侧面展开图的应用.1.(2019·湖南五市联考)某几何体的三视图如图所示,则该几何体的表面积是( )A .20+4 5B .12+4 5C .20+2 5D .12+2 5解析:选A.由三视图知该几何体是一个直三棱柱,底面是直角边分别为4,2的直角三角形,高为2,所以该几何体的表面积是(2+4+22+42)×2+2×12×2×4=20+45,故选A.2.(2019·唐山市摸底考试)已知某几何体的三视图如图所示(俯视图中曲线为四分之一圆弧),则该几何体的表面积为( )A .1-π4B .3+π2C .2+π4D .4解析:选D.由题设知,该几何体是棱长为1的正方体被截去底面半径为1的14圆柱后得到的,如图所示,所以表面积S =2×⎝⎛⎭⎫1×1-14×π×12+2×(1×1)+14×2π×1×1=4.故选D.空间几何体的体积(多维探究)角度一 求简单几何体的体积(1)(一题多解)(2017·高考全国卷Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π(2)(2019·高考全国卷Ⅰ)已知∠ACB =90°,P 为平面ABC 外一点,PC =2,点P 到∠ACB 两边AC ,BC 的距离均为3,那么P 到平面ABC 的距离为____________.【解析】 (1)法一(补形法):如图所示,由几何体的三视图,可知该几何体是一个圆柱被截去上面虚线部分所得.将圆柱补全,并将圆柱体从点A 处水平分成上下两部分.由图可知,该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12,所以该几何体的体积V =π×32×4+π×32×6×12=63π.法二(估值法):由题意,知12V 圆柱<V 几何体<V 圆柱.又V 圆柱=π×32×10=90π,所以45π<V 几何体<90π.观察选项可知只有63π符合.(2)如图,过点P 分别作PE ⊥BC 交BC 于点E ,作PF ⊥AC 交AC 于点F .由题意知PE =PF = 3.过P 作PH ⊥平面ABC 于点H ,连接HE ,HF ,HC ,易知HE =HF ,则点H 在∠ACB 的平分线上,又∠ACB =90°,故△CEH 为等腰直角三角形.在Rt △PCE 中,PC =2,PE =3,则CE =1,故CH =2,在Rt △PCH 中,可得PH =2,即点P 到平面ABC 的距离为 2.【答案】 (1)B (2) 2角度二 求组合体的体积(2019·福州市质量检测)如图,网格纸上小正方形的边长为1,实线画出的是某几何体的三视图,则该几何体的体积为( )A.π12+3 B.π12+6 C.π3+3 D.π3+6【解析】 由三视图可知,该几何体是由直四棱柱与圆锥拼接而成的简单组合体,如图所示.由题设得,V 四棱柱=12×(1+2)×2×1=3,V 圆锥=13π⎝⎛⎭⎫122×1=π12,所以该几何体的体积V=V 四棱柱+V 圆锥=3+π12.故选A.【答案】 A求空间几何体的体积的常用方法1.(2019·高考全国卷Ⅲ)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD -A 1B 1C 1D 1挖去四棱锥O -EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,AB =BC =6 cm ,AA 1=4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗,制作该模型所需原料的质量为____________g.解析:长方体ABCD -A 1B 1C 1D 1的体积V 1=6×6×4=144(cm 3),而四棱锥O -EFGH 的底面积为矩形BB 1C 1C 的面积的一半,高为AB 长的一半,所以四棱锥O -EFGH 的体积V 2=13×12×4×6×3=12(cm 3),所以长方体ABCD -A 1B 1C 1D 1挖去四棱锥O -EFGH 后所得几何体的体积V =V 1-V 2=132(cm 3),所以制作该模型所需原料的质量为132×0.9=118.8(g).答案:118.82.如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=2,∠A 1B 1C 1=90°,AA 1=4,BB 1=3,CC 1=2,则几何体的体积为____________.解析:过C 作平行于平面A 1B 1C 1的截面A 2B 2C ,交AA 1,BB 1分别于点A 2,B 2.由直三棱柱性质及∠A 1B 1C 1=90°, 则V =V A1B 1C 1A 2B 2C +V C ABB 2A 2=12×2×2×2+13×12×(1+2)×2×2=6. 答案:6球与空间几何体的接、切问题(师生共研)(1)(2017·高考全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4C.π2D.π4(2)(2018·高考全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D -ABC 体积的最大值为( )A .12 3B .18 3C .24 3D .54 3【解析】 (1)设圆柱的底面半径为r ,则r 2=12-⎝⎛⎭⎫122=34,所以,圆柱的体积V =34π×1=3π4,故选B.(2)设等边三角形ABC 的边长为x ,则12x 2sin 60°=93,得x =6.设△ABC 的外接圆半径为r ,则2r =6sin 60°,解得r =23,所以球心到△ABC 所在平面的距离d =42-(23)2=2,则点D 到平面ABC 的最大距离d 1=d +4=6,所以三棱锥D -ABC 体积的最大值V max =13S △ABC ×6=13×93×6=18 3.【答案】 (1)B (2)B处理球的“切”“接”问题的求解策略(1)“切”的处理与球有关的内切问题主要是指球内切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.(2)“接”的处理把一个多面体的几个顶点放在球面上即为球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.1.正四棱锥P -ABCD 的侧棱和底面边长都等于22,则它的外接球的表面积是( ) A .16π B .12π C .8πD .4π解析:选A.设正四棱锥的外接球半径为R ,顶点P 在底面上的射影为O ,因为OA =12AC=12AB 2+BC 2=12(22)2+(22)2=2,所以PO =P A 2-OA 2=(22)2-22=2.又OA =OB =OC =OD =2,由此可知R =2,于是S 球=4πR 2=16π.2.设球O 内切于正三棱柱ABC -A 1B 1C 1,则球O 的体积与正三棱柱ABC -A 1B 1C 1的体积的比值为________.解析:设球O 半径为R ,正三棱柱ABC -A 1B 1C 1的底面边长为a ,则R =33×a 2=36a ,即a =23R ,又正三棱柱ABC -A 1B 1C 1的高为2R ,所以球O 的体积与正三棱柱ABC -A 1B 1C 1的体积的比值为43πR 334a 2×2R =43πR 334×12R 2×2R =23π27.答案:23π27直观想象——数学文化与三视图(2019·长春市质量检测(一))《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何?刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1),那么该刍甍的体积为( )A .4B .5C .6D .12【解析】 如图,由三视图可还原得几何体ABCDEF ,过E ,F 分别作垂直于底面的截面EGH 和FMN ,将原几何体拆分成两个底面积为3,高为1的四棱锥和一个底面积为32,高为2的三棱柱,所以V ABCDEF =2V 四棱锥E -ADHG +V 三棱柱EHG -FNM =2×13×3×1+32×2=5,故选B. 【答案】 B本题是数学文化与三视图结合,主要是根据几何体的三视图及三视图中的数据,求几何体的体积或侧(表)面积.此类问题难点:一是根据三视图的形状特征确定几何体的结构特征;二是将三视图中的数据转化为几何体的几何度量.考查了直观想象这一核心素养.(2019·郑州市第二次质量预测)我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异”,“幂”是截面积,“势”是几何体的高,意思是两等高立方体,若在每一等高处的截面积都相等,则两立方体体积相等.已知某不规则几何体与如图所对应的几何体满足“幂势同”,则该不规则几何体的体积为( )A .4-π2B .8-4π3C .8-πD .8-2π解析:选C.由祖暅原理可知,该不规则几何体的体积与已知三视图的几何体体积相等.根据题设所给的三视图,可知题图中的几何体是从一个正方体中挖去一个半圆柱,正方体的体积为23=8,半圆柱的体积为12×(π×12)×2=π,因此该不规则几何体的体积为8-π,故选C.[基础题组练]1.(2019·安徽合肥质检)已知圆锥的高为3,底面半径为4,若一球的表面积与此圆锥侧面积相等,则该球的半径为( )A .5 B. 5 C .9D .3解析:选B.因为圆锥的底面半径r =4,高h =3,所以圆锥的母线l =5,所以圆锥的侧面积S =πrl =20π,设球的半径为R ,则4πR 2=20π,所以R =5,故选B.2.《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.已知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的侧面积为( )A .2B .4+2 2C .4+4 2D .4+6 2解析:选C.由三视图知,该几何体是直三棱柱ABC -A 1B 1C 1,其中AB =AA 1=2,BC =AC =2,∠C =90°,其直观图如图所示,侧面为三个矩形,故该“堑堵”的侧面积S =(2+22)×2=4+42,故选C.3.如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( )A.500π3cm 3B.866π3cm 3C.1 372π3cm 3D.2 048π3cm 3解析:选A.设球的半径为R ,则由题意知球被正方体上面截得的圆的半径为4 cm ,球心到截面圆的距离为(R -2)cm ,则R 2=(R -2)2+42,解得R =5,所以球的体积为4π×533=500π3cm 3.4.(2019·福建市第一学期高三期末考试)已知圆柱的高为2,底面半径为3,若该圆柱的两个底面的圆周都在同一个球面上,则这个球的表面积等于( )A .4π B.163π C.323π D .16π解析:选D.如图,由题意知圆柱的中心O 为这个球的球心,于是,球的半径r =OB =OA 2+AB 2=12+(3)2=2.故这个球的表面积S =4πr 2=16π.故选D.5.(2019·武汉市武昌调研考试)中国古代数学名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(单位:立方寸),则图中的x 为( )A .1.2B .1.6C .1.8D .2.4解析:选B.该几何体是一个组合体,左边是一个底面半径为12的圆柱,右边是一个长、宽、高分别为5.4-x 、3、1的长方体,所以组合体的体积V =V 圆柱+V 长方体=π·⎝⎛⎭⎫122×x +(5.4-x )×3×1=12.6(其中π=3),解得x =1.6.故选B.6.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1EDF 的体积为________.解析:三棱锥D 1EDF 的体积即为三棱锥F DD 1E 的体积.因为E ,F 分别为AA 1,B 1C 上的点,所以在正方体ABCD A 1B 1C 1D 1中,△EDD 1的面积为定值12,F 到平面AA 1D 1D 的距离为定值1,所以V D 1EDF =V F DD 1E =13×12×1=16.答案:167.(2017·高考江苏卷)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________. 解析:设球O 的半径为r ,则圆柱的底面半径为r ,高为2r ,所以V 1V 2=πr 2·2r 43πr 3=32. 答案:328.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.解:由已知得:CE =2,DE =2,CB =5,S 表面积=S 圆台侧+S 圆台下底+S 圆锥侧=π(2+5)×5+π×25+π×2×22=(60+42)π,V =V 圆台-V 圆锥=13(π·22+π·52+22·52π2)×4-13π×22×2=1483π. [综合题组练]1.(2019·蓉城名校第一次联考)已知一个几何体的正视图和侧视图如图1所示,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图2所示),则此几何体的体积为( )A .1 B. 2 C .2D .2 2解析:选B.根据直观图可得该几何体的俯视图是一个直角边长分别是2和2的直角三角形(如图所示),根据三视图可知该几何体是一个三棱锥,且三棱锥的高为3,所以体积V =13×⎝⎛⎭⎫12×2×2×3= 2.故选B. 2.(2019·福州市质量检测)已知正三棱柱ABC -A 1B 1C 1中,底面积为334,一个侧面的周长为63,则正三棱柱ABC -A 1B 1C 1外接球的表面积为( )A .4πB .8πC .16πD .32π解析:选C.如图所示,设底面边长为a ,则底面面积为34a 2=334,所以a = 3.又一个侧面的周长为63,所以AA 1=2 3.设E ,D 分别为上、下底面的中心,连接DE ,设DE 的中点为O ,则点O 即为正三棱柱ABC -A 1B 1C 1的外接球的球心,连接OA 1,A 1E ,则OE =3,A 1E =3×32×23=1.在直角三角形OEA 1中,OA 1=12+(3)2=2,即外接球的半径R =2,所以外接球的表面积S =4πR 2=16π,故选C.3.(2019·福建泉州质检)如图,在正方形网格纸上,实线画出的是某多面体的三视图及其部分尺寸.若该多面体的顶点在同一球面上,则该球的表面积等于( )A .8πB .18πC .24πD .86π解析:选C.设球的半径为R .多面体是两个正四棱锥的组合体(底面重合).两顶点之间的距离为2R ,底面是边长为2R 的正方形,由R 2+⎝⎛⎭⎫2R 22=32⇒R 2=6,故该球的表面积S =4πR 2=24π.选C.4.(2019·辽宁五校协作体模考)一个长方体被一平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )A .36B .48C .64D .72解析:选B.由几何体的三视图可得几何体如图所示,将几何体分割为两个三棱柱,所以该几何体的体积为12×3×4×4+12×3×4×4=48,故选B.5.(2019·洛阳市第一次统考)一个几何体的三视图如图所示,图中的三个正方形的边长均为2,则该几何体的体积为( )A .8-2π3B .4-π3C .8-π3D .4-2π3解析:选A.由三视图可得该几何体的直观图如图所示,该几何体是一个棱长为2的正方体上、下各挖去一个底面半径为1,高为1的圆锥后剩余的部分,其体积为23-2×13×π×12×1=8-2π3.故选A.6.(应用型)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P -A 1B 1C 1D 1,下部的形状是正四棱柱ABCD -A 1B 1C 1D 1(如图所示),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍,若AB =6 m ,PO 1=2 m ,则仓库的容积是多少?解:由PO 1=2 m ,知O 1O =4PQ 1=8 m.因为A 1B 1=AB =6 m ,所以正四棱锥P -A 1B 1C 1D 1的体积V 锥=13·A 1B 21·PO 1=13×62×2=24(m 3);正四棱柱ABCD -A 1B 1C 1D 1的体积 V 柱=AB 2·O 1O =62×8=288(m 3),所以仓库的容积V =V 锥+V 柱=24+288=312(m 3). 故仓库的容积是312 m 3.。
中等职业教育规划教材数学(山东省基础类)目录

中等职业教育规划教材数学目录数学—101第一章集合1.1集合及其表示1.1.1集合1.1.2集合地表示方法1.2集合之间的关系1.3集合的基本运算1.3.1交集1.3.2并集1.3.3补集1.4充要条件阅读与实践02第二章2.1一元二次方程2.2不等式2.2.1不等式的基本性质2.2.2不等式的解集与区间2.2.3含绝对值的不等式2.2.4一元二次不等式阅读与实践03第三章函数3.1函数的概念3.2函数的表示方法3.3函数的单调性3.4函数的奇偶性3.5二次函数的图像和性质3.6函数的应用阅读与实践04第四章指数函数与对数函数4.1实数指数4.2指数函数4.3对数及其运算4.3.1对数4.3.2对数的运算4.4对数函数4.5幂函数4.6指数函数与对数函数的应用阅读与实践05第五章数列5.1数列5.2等差数列5.2.1等差数列的概念5.2.2等差数列的前n项和5.3等比数列5.3.1等比数列的概念5.3.2等比数列的前n项和5.4等差数列与等比数列的应用阅读与实践06第六章空间几何体6.1认识空间几何体6.1.1认识多面体与旋转体6.1.2棱柱、棱锥6.1.3圆柱、圆锥、球6.2空间几何体的表面积与体积6.2.1空间几何体的表面积6.2空间几何体的体积阅读与实践数学—207三角函数7.1任意角的概念与弧度制7.1.1任意角的概念7.1.2弧度制7.2任意角的三角函数7.2.1任意角的三角函数的定义7.2.2单位圆与正弦、余弦线7.2.3利用计算器求三角函数值7.2.4三角函数值在各象限的符号7.3同角三角函数的基本关系式7.4三角函数的诱导公式7.5正弦、余弦函数的图像、性质7.5.1正弦函数的图像和性质7.5.2余弦函数的图像和性质7.6已知三角函数值求角阅读与实践08第八章平面向量8.1向量的概念8.2向量的线性运算8.2.1向量的加法2.2向量的减法8.2.3数乘向量8.3平面向量的直角坐标运算8.3.1平面向量的直角坐标及其运算8.3.2平面向量平行的坐标表示8.3.3向量的长度公式和中点公式8.4向量的内积8.4.1向量的内积8.4.2向量的内积的直角坐标运算阅读与实践09第九章直线与圆的方程9.1直线的方程9.1.1直线的方向向量和向式方程9.1.2直线的斜率和点斜式方程9.1.3直线的法向量与点法式方程9.1.4直线的一般式方程9.2两条直线的位置关系9.2.1两条直线的平行99.2.2两条直线的交点与垂直9.3点到直线的距离9.4圆的方程9.4.1圆的标准方程9.4.2圆的一般方程阅读与实践10第十章立体几何初步10.1平面的基本性质10.2空间两条直线的位置关系10.3直线与平面的位置关系10.4平面与平面的位置关系阅读与实践11第十一章概率与统计初步11.1技术的基本原理11.2概率初步11.2.1随机事件与样本空间11.2.2古典概率11.3随机抽样11.3简单的随机抽样11.3系统抽样11.3分层抽样11.4用样本估计总体11.4.1用样本的概率分布估计总体发布11.4.2用样本的数字特征估计数字特征11.5一元线性回归分析。
高考一轮复习第7章立体几何第2讲空间几何体的表面积与体积

第二讲 空间几何体的表面积与体积知识梳理·双基自测 知识梳理知识点一 柱、锥、台和球的侧面积和体积侧面积 体积圆柱 S 侧=2πrh V =_S 底·h__=πr 2h圆锥 S 侧=_πrl __ V =13S 底·h=13πr 2h =13πr 2l 2-r 2 圆台 S 侧=π(r 1+r 2)l V =13(S 上+S 下+S 上·S 下)·h=13π(r 21+r 22+r 1r 2)h 直棱柱 S 侧=_ch__ V =_S 底h__ 正棱锥 S 侧=12ch′V =13S 底h 正棱台 S 侧=12(c +c′)h′V =13(S 上+S 下+S 上·S 下)h 球S 球面=_4πR 2V =43πR 3 (1)棱柱、棱锥、棱台的表面积就是_各面面积之和__.(2)圆柱、圆锥、圆台的侧面展开图分别是_矩形__、_扇形__、_扇环形__;它们的表面积等于_侧面积__与底面面积之和.重要结论1.长方体的外接球:球心:体对角线的交点;半径:r =_a 2+b 2+c22__(a ,b ,c 为长方体的长、宽、高).2.正方体的外接球、内切球及与各条棱相切的球: (1)外接球:球心是正方体中心;半径r =_32a__(a 为正方体的棱长); (2)内切球:球心是正方体中心;半径r =_a2__(a 为正方体的棱长);(3)与各条棱都相切的球:球心是正方体中心;半径r =_22a__(a 为正方体的棱长). 3.正四面体的外接球与内切球(正四面体可以看作是正方体的一部分):(1)外接球:球心是正四面体的中心;半径r =_64a__(a 为正四面体的棱长); (2)内切球:球心是正四面体的中心;半径r =_612a__(a 为正四面体的棱长). 双基自测题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)多面体的表面积等于各个面的面积之和.( √ ) (2)台体的体积可转化为两个锥体的体积之差.( √ ) (3)锥体的体积等于底面积与高之积.( × )(4)已知球O 的半径为R ,其内接正方体的棱长为a ,则R =32a.( √ ) (5)圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS.( × ) 题组二 走进教材2.(必修2P 27T1)已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为( B ) A .1 cm B .2 cm C .3 cmD .32cm [解析] 由条件得:⎩⎪⎨⎪⎧πrl+πr 2=12π2πrl =π,∴3r 2=12,∴r =2.题组三 走向高考3.(2020·天津卷)若棱长为23的正方体的顶点都在同一球面上,则该球的表面积为( C ) A .12π B .24π C .36πD .144π[解析] 这个球是正方体的外接球,其半径等于正方体的体对角线长的一半, 即R =232+232+2322=3,所以,这个球的表面积为S =4πR 2=4π×32=36π.故选:C .4.(2018·课标全国Ⅰ)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( B )A .122πB .12πC .82πD .10π[解析] 设圆柱底面半径为r ,则4r 2=8,即r 2=2.∴S 圆柱表面积=2πr 2+4πr 2=12π.5.(2020·浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm 3)是( A )A .73 B .143C .3D .6[解析] 由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,且三棱锥的一个侧面垂直于底面.棱锥的高为1,棱柱的底面为等腰直角三角形,棱柱的高为2,所以几何体的体积为:13×⎝ ⎛⎭⎪⎫12×2×1×1+⎝ ⎛⎭⎪⎫12×2×1×2=13+2=73.故选:A .考点突破·互动探究考点一 几何体的表面积——自主练透例1 (1)(2021·北京模拟)某三棱锥的三视图如图所示,则该三棱锥的表面积是( C )A .2+ 5B .4+ 5C .2+2 5D .5(2)(2021·安徽江南十校联考)已知某几何体的三视图如图所示,网格纸上小正方形的边长为1,则该几何体的表面积为( B )A .78-9π2B .78-9π4C .78-πD .45-9π2(3)(多选题)(2021·山东潍坊期末)等腰直角三角形直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( AB )A .2πB .(1+2)πC .22πD .(2+2)π[解析] (1)由三视图知,该几何体是底面为等腰三角形,其中一条侧棱与底面垂直的三棱锥(SA ⊥平面ABC),如图所示,由三视图中的数据可计算得S △ABC =12×2×2=2,S △SAC =12×5×1=52,S △SAB =12×5×1=52,S △SBC =12×2×5=5,所以S 表面积=2+2 5.故选C .(2)由三视图可知该几何体是一个长方体中挖去一个18球,如图所示.∴S =3×3×2+3×5×4-27π4+9π2=78-94π.故选B .(3)若绕直角边旋转一周形成的几何体是圆锥,其表面积为π+2π;若绕斜边旋转一周形成的几何体是两同底圆锥构成的组合体,其表面积为2π,故选A 、B .名师点拨空间几何体表面积的求法(1)旋转体的表面积问题注意其轴截面及侧面展开图的应用.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.〔变式训练1〕(2020·河南开封二模)已知某个几何体的三视图如图所示,根据图中标出的数据,可得出这个几何体的表面积是( C )A .6B .8+4 6C .4+2 6D .4+ 6[解析] 由三视图得几何体如图所示,该几何体是一个三棱锥,底面是一个底和高均为2的等腰三角形,一个侧面是一个底和高均为2的等腰三角形,另外两个侧面是腰长为AC =AB =22+12=5, 底边AD 长为22的等腰三角形, 其高为52-22=3,故其表面积为S =2×12×22+2×12×22×3=4+2 6.故选C .考点二 几何体的体积——师生共研例2 (1)(2021·浙江金色联盟百校联考)一个空间几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )cm 3.( A )A .π6+13B .π3+16C .π6+16D .π3+13(2)(2021·云南师大附中月考)如图,某几何体的三视图均为边长为2的正方形,则该几何体的体积是( D )A .56 B .83 C .1D .163(3)(2021·湖北武汉部分学校质检)某圆锥母线长为4,其侧面展开图为半圆面,则该圆锥体积为_83π3__.(4)(2020·江苏省南通市通州区)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,P 是侧棱CC 1上一点,且C 1P =2PC .设三棱锥P - D 1DB 的体积为V 1,正四棱柱ABCD -A 1B 1C 1D 1的体积为V ,则V 1V 的值为_16__.[解析] (1)由三视图可知该几何体是由底面半径为1 cm ,高为1 cm 的半个圆锥和三棱锥S -ABC 组成的,如图,三棱锥的高为SO =1 cm ,底面△ABC 中,AB =2 cm ,AC =1 cm ,AB ⊥AC .故其体积V =13×12×π×12×1+13×12×2×1×1=⎝ ⎛⎭⎪⎫π6+13cm 3.故选A .(2)由题意三视图对应的几何体如图所示,所以几何体的体积为正方体的体积减去2个三棱锥的体积,即V =23-2×13×12×2×2×2=163,故选D .(3)该圆锥母线为4,底面半径为2,高为23, V =13×π×22×23=83π3. (4)设正四棱柱ABCD -A 1B 1C 1D 1的底面边长AB =BC =a ,高AA 1=b , 则VABCD -A 1B 1C 1D 1=S 四边形ABCD ×AA 1=a 2b ,VP -D 1DB =VB -D 1DP =13S △D 1DP·BC=13×12ab·a=16a 2b ,∴VP -D 1DB VABCD -A 1B 1C 1D 1=16,即V 1V =16.[引申]若将本例(2)中的俯视图改为,则该几何体的体积为_83__,表面积为_83__.[解析] 几何体为如图所示的正三棱锥(棱长都为22). ∴V =8-4×43=83,S =4×34×(22)2=8 3.名师点拨求体积的常用方法直接法对于规则的几何体,利用相关公式直接计算割补法首先把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算等体 积法选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面可作为三棱锥的底面进行等体积变换注:若以三视图的形式给出的几何体问题,应先得到直观图,再求解. 〔变式训练2〕(1)(2020·海南)已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点,则三棱锥A -NMD 1的体积为_13__.(2)(2021·开封模拟)如图所示,正三棱柱ABC -A 1B 1C 1的底面边长为2,侧棱长为3,D 为BC 的中点,则三棱锥A -B 1DC 1的体积为( C )A .3B .32 C .1D .32(3)(2017·浙江)某三棱锥的三视图如图所示,则该三棱锥的体积为( A )A .16 B .13 C .12D .1(4)(2021·浙北四校模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( B )A .8B .8πC .16D .16π[解析] (1)如图,∵正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点,∴S △ANM =12×1×1=12,∴VA -NMD 1=VD 1-AMN =13×12×2=13,故答案为:13.(2)如题图,在正△ABC 中,D 为BC 的中点,则有AD =32AB =3,又因为平面BB 1C 1C ⊥平面ABC ,AD ⊥BC ,AD ⊂平面ABC ,由面面垂直的性质定理可得AD ⊥平面BB 1C 1C ,即AD 为三棱锥A -B 1DC 1的底面B 1DC 1上的高,所以V 三棱锥A -B 1DC 1=13·S△B 1DC 1·AD=13×12×2×3×3=1,故选C .(3)由三视图可画出三棱锥的直观图如图所示.其底面是等腰直角三角形ACB ,直角边长为1,三棱锥的高为1,故体积V =13×12×1×1×1=16.故选A .(4)由三视图的图形可知,几何体是等边圆柱斜切一半,所求几何体的体积为:12×22π×4=8π.故选B .考点三 球与几何体的切、接问题——多维探究角度1 几何体的外接球例3 (1)(2021·河南中原名校质量测评)已知正三棱锥P -ABC 的底面边长为3,若外接球的表面积为16π,则PA =_23或2__.(2)(2020·新课标Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为( A )A .64πB .48πC .36πD .32π(3)(2019·全国)已知三棱锥P -ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E 、F 分别是PA ,PB 的中点,∠CEF =90°,则球O 的体积为( D )A .86πB .46πC .26πD .6π[解析] (1)由外接球的表面积为16π,可得其半径为2,设△ABC 的中心为O 1,则外接球的球心一定在PO 1上,由正三棱锥P -ABC 的底面边长为3,得AO 1=3,在Rt △AOO 1中,由勾股定理可得(PO 1-2)2+(3)2=22,解得PO 1=3或PO 1=1,又PA 2=PO 21+AO 21,故PA =9+3=23或PA =1+3=2,故答案为:23或2.(2)由题意可知图形如图:⊙O 1的面积为4π, 可得O 1A =2, 则ABsin60°=2O 1A =4,∴AB =4sin60°=23,∴AB=BC=AC=OO1=23,外接球的半径为:R=AO21+OO21=4,球O的表面积为:4×π×42=64π,故选A.(3)∵PA=PB=PC,△ABC为边长为2的等边三角形,∴P-ABC为正三棱锥,∴PB⊥AC,又E,F分别为PA、AB中点,∴EF∥PB,∴EF⊥AC,又EF⊥CE,CE∩AC=C,∴EF⊥平面PAC,∴PB⊥平面PAC,∴∠APB=90°,∴PA=PB=PC=2,∴P-ABC为正方体一部分,2R=2+2+2=6,即R=62,∴V=43πR3=43π×668=6π.名师点拨几何体外接球问题的处理(1)解题关键是确定球心和半径,其解题思维流程是:(R—球半径,r—截面圆的半径,h—球心到截面圆心的距离).注:若截面为非特殊三角形可用正弦定理求其外接圆半径r.(2)三条侧棱两两垂直的三棱锥,可以补成长方体,它们是同一个外接球.注意:不共面的四点确定一个球面.角度2 几何体的内切球例4 (1)(2020·新课标Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_23π__. (2)(2021·安徽蚌埠质检)如图,E ,F 分别是正方形ABCD 的边AB ,AD 的中点,把△AEF ,△CBE ,△CFD 折起构成一个三棱锥P -CEF(A ,B ,D 重合于P 点),则三棱锥P -CEF 的外接球与内切球的半径之比是_26__.[解析] (1)因为圆锥内半径最大的球应该为该圆锥的内切球, 如图,圆锥母线BS =3,底面半径BC =1, 则其高SC =BS 2-BC 2=22, 不妨设该内切球与母线BS 切于点D , 令OD =OC =r ,由△SOD ∽△SBC ,则OD OS =BCBS ,即r22-r =13,解得r =22,V =43πr 3=23π,故答案为:23π.(2)不妨设正方形的边长为2a ,由题意知三棱锥P -CEF 中PC 、PF 、PE 两两垂直,∴其外接球半径R =PC 2+PF 2+PE 22=62a ,下面求内切球的半径r ,解法一(直接法):由几何体的对称性知,内切球的球心在平面PCH(H 为EF 的中点)内,M 、N 、R 、S 为球与各面的切点,又22=tan ∠CHP =tan2∠OHN , ∴tan ∠OHN =22=rNH,∴NH =2r , 又PN =2r ,∴22r =PH =22a ,∴r =a 4. 解法二(体积法):V C -PEF =13r·(S △PEF +S △PCE +S △PCF +S △CEF ),∴a 3=r·⎝ ⎛⎭⎪⎫a 22+a 2+a 2+2a 2×32a 2,∴r =a 4,故R r =6a 2·4a=2 6.名师点拨几何体内切球问题的处理(1)解题时常用以下结论确定球心和半径:①球心在过切点且与切面垂直的直线上;②球心到各面距离相等.(2)利用体积法求多面体内切球半径. 〔变式训练3〕(1)(角度1)(2020·南宁摸底)三棱锥P -ABC 中,△ABC 为等边三角形,PA = PB = PC =3,PA ⊥PB ,三棱锥P -ABC 的外接球的体积为( B )A .27π2B .273π2C .273πD .27π(2)(角度1)(2021·山西运城调研)在四面体ABCD 中,AB =AC =23,BC =6,AD ⊥平面ABC ,四面体ABCD 的体积为 3.若四面体ABCD 的顶点均在球O 的表面上,则球O 的表面积是( B )A .49π4B .49πC .49π2D .4π(3)(角度2)棱长为a 的正四面体的体积与其内切球体积之比为_63π__.[解析] (1)因为三棱锥P -ABC 中,△ABC 为等边三角形,PA =PB =PC =3,所以△PAB ≌△PBC ≌△PAC .因为PA ⊥PB ,所以PA ⊥PC ,PC ⊥PB .以PA ,PB ,PC 为过同一顶点的三条棱作正方体(如图所示),则正方体的外接球同时也是三棱锥P -ABC 的外接球.因为正方体的体对角线长为32+32+32=33,所以其外接球半径R =332.因此三棱锥P -ABC 的外接球的体积V =4π3×⎝ ⎛⎭⎪⎫3323=273π2.故选B .(2)如图,H 为BC 的中点,由题意易知AH =3,设△ABC 外接圆圆心为O 1,则|O 1C|2=32+(3-|O 1C|)2,∴|O 1C|=23,又12×6×3×|AD|3=3,∴|AD|=1,则|OA|2=|O 1C|2+⎝ ⎛⎭⎪⎫122=494,∴S 球O =4πR 2=49π,故选B .(3)如图,将正四面体纳入正方体中,显然正四面体内切球的球心O(也是外接球的球心)、△BCD 的中心O 1都在正方体的对角线上,设正四面体的棱长为a ,则|AO|=64a ,又|O 1A|=a 2-⎝⎛⎭⎪⎫33a 2=63a ,∴内切球半径|OO 1|=612a ,∴V 正四面体V 内切球=13×34a 2×63a4π3⎝ ⎛⎭⎪⎫612a 3=63π.名师讲坛·素养提升 最值问题、开放性问题例5 (1)(最值问题)(2018·课标全国Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D -ABC 体积的最大值为( B )A .12 3B .18 3C .24 3D .54 3(2)(2021·四川凉山州模拟)已知长方体ABCD -A 1B 1C 1D 1的体积V =12,AB =2,若四面体A -B 1CD 1的外接球的表面积为S ,则S 的最小值为( C )A .8πB .9πC .16πD .32π[解析] (1)设等边△ABC 的边长为a ,则有S △ABC =12a·a·sin 60°=93,解得a =6.设△ABC 外接圆的半径为r ,则2r =6sin 60°,解得r =23,则球心到平面ABC 的距离为42-232=2,所以点D 到平面ABC 的最大距离为2+4=6,所以三棱锥D -ABC 体积的最大值为13×93×6=183,故选B .(2)设BC =x ,BB 1=y ,由于V =12,所以xy =6.根据长方体的对称性可知四面体A -B 1CD 1的外接球即为长方体的外接球, 所以r =4+x 2+y22,所以S =4πr 2=π(4+x 2+y 2)≥π(4+2xy)=16π, (当且仅当x =y =6,等号成立). 故选C .名师点拨立体几何中最值问题的解法(1)观察图形特征,确定取得最值的条件,计算最值.(2)设出未知量建立函数关系,利用基本不等式或导数计算最值.例6 (开放性问题)若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值为_116⎝ ⎛⎭⎪⎫或1412等__(只需写一个可能值). [解析] 如图,若AB =AC =BD =CD =AD =2,BC =1,取AD 的中点H ,则CH =BH =3,且AH ⊥平面BCH ,又S △BCH =114,∴V A -BCD =13S △BCH ×2=116. 如图,若AB =AC =BD =CD =2,AD =BC =1,同理可求得V A -BCD =1412.〔变式训练4〕(2021·河南阶段测试)四面体ABCD 中,AC ⊥AD ,AB =2AC =4,BC =25,AD =22,当四面体的体积最大时,其外接球的表面积是_28π__.[解析] 由已知可得BC 2=AC 2+AB 2,所以AC ⊥AB ,又因为AC ⊥AD ,所以AC ⊥平面ABD ,四面体ABCD 的体积V =13AC·12AB·ADsin∠BAD ,当∠BAD =90°时V 最大,把四面体ABCD 补全为长方体,则它的外接球的直径2R 即长方体的体对角线,(2R)2=AD 2+AC 2+AB 2=28,所以外接球的表面积为4πR 2=28π.。
2020版《微点教程》高考人教A版文科数学一轮复习文档:第七章 第二节 空间几何体的表面积与体积 含答案

4.(20xx·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()
A.πB. C. D.
解析由题可知球心为圆柱的中心,则圆柱底面圆的半径r= = ,故圆柱的体积V=πr2h= 。
答案B
三、走出误区
微提醒:①由三视图不能还原几何体求错体积;②不会分类讨论致误;③长度单位与体积单位换算出错。
答案B
考点三体积中的最值问题
【例3】(20xx·长春质量监测)已知圆锥的侧面展开图是半径为3的扇形,则该圆锥体积的最大值为________。
解析由题意得圆锥的母线长为3,设圆锥的底面半径为r,高为h,则h= ,所以圆锥的体积V= πr2h= πr2 = π (0<r<3)。设f(r)=9r4-r6(r>0),则f′(r)=36r3-6r5,令f′(r)=36r3-6r5=6r3(6-r2)=0,得r= ,所以当0<r< 时,f′(r)>0,f(r)单调递增,当 <r<3时,f′(r)<0,f(r)单调递减,所以f(r)max=f( )=108,所以Vmax= π× =2 π。
(一割为三)如图,分别取QN,PM上的两个四等分点B,E,C,F,连接AB,BC,AC,DE,DF,EF。
则△ABC与△DEF所在的平面将该几何体分成一个直三棱柱ABC-DEF和两个全等的四棱锥A-BCPQ,四棱锥D-FENM。其中直三棱柱ABC-DEF中的△ABC与△DEF是等腰三角形,BC=4,点A到BC的距离d=4,设△ABC与△DEF的面积为S1,则S1= ×4×4=8。易知BE=4,故直三棱柱ABC-DEF的体积V1=S1×BE=8×4=32。四棱锥的底面是矩形,QB=2,PQ=4,故四棱锥的底面积S2=2×4=8。由三视图可得四棱锥的高h=4,所以四棱锥的体积V2= S2h= ×8×4= 。所以该几何体的体积V=V1+2V2=32+2× = 。故选A。
空间几何体的结构特征、表面积与体积6题型分类-备战2025年高考数学一轮专题复习考点突破和专题检测
专题31空间几何体的结构特征、表面积与体积6题型分类1.空间几何体的结构特征(1)多面体的结构特征(2)旋转体的结构特征名称圆柱圆锥圆台球图形母线互相平行且相等,垂直于底面相交于一点延长线交于一点轴截面矩形等腰三角形等腰梯形圆侧面展开图矩形扇形扇环2.直观图(1)画法:常用斜二测画法.(2)规则:①原图形中x 轴、y 轴、z 轴两两垂直,直观图中x ′轴、y ′轴的夹角为45°或135°,z ′轴与x ′轴和y ′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍分别平行于坐标轴,平行于x 轴和z 轴的线段在直观图中保持原长度不变,平行于y 轴的线段,长度在直观图中变为原来的一半.3.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrl S 圆锥侧=πrlS 圆台侧=π(r 1+r 2)l4.柱、锥、台、球的表面积和体积常用结论1.与体积有关的几个结论(1)一个组合体的体积等于它的各部分体积的和或差.(2)底面面积及高都相等的两个同类几何体的体积相等(祖暅原理).2.直观图与原平面图形面积间的关系:S 直观图=24S 原图形,S 原图形=22S 直观图.(一)1.空间几何体结构特征的判断技巧(1)说明一个命题是错误的,只要举出一个反例即可.(2)在斜二测画法中,平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半.(3)在解决空间折线(段)最短问题时一般考虑其展开图,采用化曲为直的策略,将空间问题平面化.2.多面体表面展开图可以有不同的形状,应多实践,观察并大胆想象立体图形与表面展开图的关系,一定先观察立体图形的每一个面的形状.3.最大路径问题:大胆展开,把问题变为平面两点间线段最短问题.2-2.(2024高一下·上海奉贤·期末)如图,23O A O B ''''==,,则AB 的长度为2-3.(2024高一上·山东济宁·阶段练习)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示).ABC ∠=2-4.(2024高二上·宁夏石嘴山·正方形,则原来图形的面积是3-3.(2024·安徽黄山·一模)如图,以AD为斜边的等腰直角三角形,为.题型4:最短路径问题4-1.(2024高三·全国·专题练习)如图,一竖立在地面上的圆锥形物体的母线长为面圆上的点P出发,绕圆锥爬行一周后回到点为().A .153B .323527πC .128281πD .8334-2.(2024高一下·河南开封·期中)如图,已知正四棱锥S ABCD -的侧棱长为23,侧面等腰三角形的顶角为30︒,则从A 点出发环绕侧面一周后回到A 点的最短路程为()A .26B .23C .6D .64-3.(2024·辽宁·三模)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为4cm 的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为()A .6cmB .26cmC .46cmD .6cm4-4.(2024高一下·湖北武汉·期中)如图,一个矩形边长为1和4,绕它的长为4的边旋转二周后所得如图的一开口容器(下表面密封),P 是BC 中点,现有一只妈蚁位于外壁A 处,内壁P 处有一米粒,若这只蚂蚁要先爬到上口边沿再爬到点P 处取得米粒,则它所需经过的最短路程为()A .2π36+B .2π16+C .24π36+D .241π+4-5.(2024高一·全国·课后作业)如图所示,在正三棱柱111ABC A B C -中,2AB =,12AA =,由顶点B 沿棱柱侧面(经过棱1AA )到达顶点1C ,与1AA 的交点记为M ,则从点B 经点M 到1C 的最短路线长为()A.22B.25C.4D.45(二)基本立体图形的表面积的体积1.(1)多面体的表面积是各个面的面积之和.(2)旋转体的表面积是将其展开后,展开图的面积与底面面积之和.(3)组合体的表面积求解时注意对衔接部分的处理.2.空间几何体的体积的常用方法公式法规则几何体的体积,直接利用公式割补法把不规则的几何体分割成规则的几何体,或者把不规则的几何体补成规则的几何体等体积法通过选择合适的底面来求几何体体积的一种方法,特别是三棱锥的体积A.27 722+三模)陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址A .()1441213π+C .()1081213π+5-4.(2024·河北·模拟预测)棱台)建筑物为方亭.”1111ABCD A B C D -的正四棱台(如图所示)面边长的3倍.已知方亭的体积为A .2380m B .2400m C .2450m 5-5.(2024高三下·海南海口·期中)如图是一个圆台形的水杯,圆台的母线长为分别为4cm 和2cm .为了防烫和防滑,该水杯配有一个皮革杯套,包裹住水杯杯和杯套的厚度忽略不计,则此杯套使用的皮革的面积为(A .238πcmB .2124πcm 3C .2140πcm 3D .248πcm A .242B .246-4.(2024·浙江·模拟预测)如图是我国古代量粮食的器具为20cm 和10cm ,侧棱长为56cm .约可装()31000cm 1L =()A .1.5LB .1.7LC .2.3LD .2.7L6-5.(2024高三上·广西·阶段练习)在棱长为2的正方体1111ABCD A B C D 内,放入一个以1AC 为铀线的圆柱,且圆柱的底面所在平面截正方体所得的截面为三角形,则该圆柱体积的最大值为.一、单选题1.(2024高三下·安徽·阶段练习)已知几何体,“有两个面平行,其余各面都是平行四边形”是“几何体为棱柱”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.(2024高三·全国·对口高考)设有三个命题;甲:底面是平行四边形的四棱柱是平行六面体;乙:底面是矩形的平行六面体是长方体;丙:直四棱柱是平行六面体.以上命题中真命题的个数为()A .0个B .1个C .2个D .3个3.(2024高二上·安徽合肥·阶段练习)如图所示,观察四个几何体,其中判断正确的是()A .是棱台B .是圆台C .不是棱柱D .是棱锥4.(2024·西藏拉萨·一模)位于徐州园博园中心位置的国际馆(一云落雨),使用现代科技雾化“造云”,打造温室客厅,如图,这个国际馆中3个展馆的顶部均采用正四棱锥这种经典几何形式,表达了理性主义与浪漫主义的对立与统一.其中最大的是3号展馆,其顶部所对应的正四棱锥底面边长为19.2m ,高为9m ,则该正四棱锥的侧面面积与底面面积之比约为()13.16≈)A .2B .1.71C .1.37D .15.(2024高三下·湖南长沙·阶段练习)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥的高与底面边长的比为2:3,则正六棱锥与正六棱柱的侧面积的比值为()A .8B C .19D .1276.(2024·甘肃张掖·模拟预测)仿钧玫瑰紫釉盘是收藏于北京故宫博物院的一件明代宣德年间产的瓷器.该盘盘口微撇,弧腹,圈足.足底切削整齐.通体施玫瑰紫釉,釉面棕眼密集,美不胜收.仿钧玫瑰紫釉盘的形状可近似看成是圆台和圆柱的组合体,其口径为15.5cm ,足径为9.2cm ,顶部到底部的高为4.1cm ,底部圆柱高为0.7cm ,则该仿钧玫瑰紫釉盘圆台部分的侧面积约为()(参考数据:π的值取3 4.6≈)A .2143.1cmB .2151.53cmC .2155.42cmD .2170.43cm 7.(2024·广东梅州·三模)在马致远的《汉宫秋》楔子中写道:“毡帐秋风迷宿草,穹庐夜月听悲笳.”毡帐是古代北方游牧民族以为居室、毡制帷幔.如图所示,某毡帐可视作一个圆锥与圆柱的组合体,圆锥的高为4,侧面积为15π,圆柱的侧面积为18π,则该毡帐的体积为()A .39πB .18πC .38πD .45π8.(2024高三上·广东河源·开学考试)最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”、“圆罂测雨”、“峻积验雪”和“竹器验雪”.如图“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量(平地降雪厚度=器皿中积雪体积除以器皿口面积),已知数据如图(注意:单位cm ),则平地降雪厚度的近似值为()A .91cm 12B .31cm 4C .95cm 12D .97cm 129.(2024高一下·陕西宝鸡·期末)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为2cm 的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为()A 6cmB .26cmC .6cmD .6cm10.(2024高二下·安徽·阶段练习)我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.请根据此方法求函数()2222,313130,0)f x y x x y y x xy y x y =-+-+-+>>的最小值()A 2B 3C 6D .2311.(2024·全国)已知圆锥PO 3O 为底面圆心,PA ,PB 为圆锥的母线,120AOB ∠=︒,若PAB 934)A .πB 6πC .3πD .36π12.(2024·全国)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔1485m .时,相应水面的面积为21400km .;水位为海拔1575m .时,相应水面的面积为21800km .,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔1485m .上升到1575m .时,增加的水量2.65≈)()A .931.010m ⨯B .931.210m ⨯C .931.410m ⨯D .931.610m ⨯13.(2024高一·全国·课后作业)若一个正方体的体对角线长为a ,则这个正方体的全面积为()A .22a B .2C .2D .214.(2004·重庆)如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是()A .258B .234C .222D .21015.(2024高一下·贵州黔西·期末)端午节吃粽子是中华民族的传统习俗.地区不同,制作的粽子形状也不同,黔西南州最出名的就是鲜肉的灰色粽子,其形状接近于正三棱锥(如图).若正三棱锥的底面边长为2,高为1,则该三棱锥的侧面积为()AB .C .D .16.(2024·河南·模拟预测)在正四棱锥P ABCD -中,AB =,若正四棱锥P ABCD -的体积是8,则该四棱锥的侧面积是()AB .C .D .17.(2024高三上·辽宁·期末)已知四棱台的上、下底面分别是边长为2和4的正方形,侧面均为腰长为4的等腰梯形,则该四棱台的表面积为()A .10+B .34C .20+D .6818.(2024高三上·广东·阶段练习)“李白斗酒诗百篇,长安市上酒家眠”,本诗句中的“斗”的本义是指盛酒的器具,后又作为计量粮食的工具,某数学兴趣小组利用相关材料制作了一个如图所示的正四棱台来模拟“斗”,用它研究“斗”的相关几何性质,已知该四棱台的上、下底的边长分别是2、4,高为1,则该四棱台的表面积为()A .B .32C .20+D .20+19.(2024高三上·湖北·开学考试)已知正四棱台上底面边长为2,下底面边长4,高为3,则其表面积为()A .36B .20C .20+D .4820.(2024高一下·全国·课后作业)已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是()A .122ππ+B .144ππ+C .12ππ+D .142ππ+21.(2024·广东湛江·二模)如图,将一个圆柱()*2n n ∈N 等分切割,再将其重新组合成一个与圆柱等底等高的几何体,n 越大,重新组合成的几何体就越接近一个“长方体”.若新几何体的表面积比原圆柱的表面积增加了10,则圆柱的侧面积为()A .10πB .20πC .10πnD .18π22.(2024·福建)以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于A .2πB .πC .2D .123.(2024高三上·全国·阶段练习)已知圆锥的底面半径为2,高为)A .4πB .12πC .16πD .π324.(2024·四川成都·二模)若圆锥的表面积为12π,底面圆的半径为2,则该圆锥的高为()A .4B .C .2D25.(2024高三上·河南·阶段练习)佛兰德现代艺术中心是比利时洛默尔市的地标性建筑,该建筑是一座全玻璃建筑,整体成圆锥形,它利用现代设计手法令空间与其展示的艺术品无缝交融,形成一个统一的整体,气势恢宏,美轮美英.佛兰德现代艺术中心的底面直径为8m ,侧面积为2229m ,则该建筑的高为()A .26mB .28mC .30mD .36m26.(2024高三上·河南·开学考试)圆台1OO 轴截面面积为1:2,母线与底面所成角为60 ,则圆台侧面积为()A .B .C .6πD .9π27.(2024高二上·江苏镇江·开学考试)已知圆台的上下底面半径分别为2和5,且母线与下底面所成为角的正切值为43,则该圆台的表面积为()A .59πB .61πC .63πD .64π28.(2024·甘肃兰州·模拟预测)攒尖是中国古建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、图所示是某研究性学习小组制作的三台阁仿真模型的屋顶部分,它可以看作是不含下底面的正四棱台和正三棱柱的组合体,已知正四棱台上底、下底、侧棱的长度(单位:dm )分别为2,6,4,正三棱柱各棱长均相等,则该结构表面积为()A .28dmB .244dmC .248dmD .28dm29.(2024高三上·黑龙江哈尔滨·期中)正三棱柱侧面的一条对角线长为2,且与底面成30︒角,则此三棱柱的体积为()A B .14C D 30.(2008·四川)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为060的菱形,则该棱柱的体积等于A B .C .D .31.(2024高三上·河南焦作·开学考试)把过棱锥的顶点且与底面垂直的直线称为棱锥的轴,过棱锥的轴的截面称为棱锥的轴截面.现有一个正三棱锥、一个正四棱锥、一个正六棱锥,它们的高相等,轴截面面积的最大值也相等,则此正三棱锥、正四棱锥、正六棱锥的体积之比为()A .91::34B .91::38C .98D .3232.(2024·广东深圳·二模)设表面积相等的正方体、正四面体和球的体积分别为1V 、2V 和3V ,则()A .123V V V <<B .213<<V V V C .312V V V <<D .321V V V <<33.(2024·河南郑州·模拟预测)《九章算术·商功》:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.意思是一个长方体沿对角面斜解(图1),得到一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜解(图2),得一个四棱锥称为阳马(图3),一个三棱锥称为鳖臑(图4).若长方体的体积为V ,由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为1V ,2V ,3V ,则下列等式错误的是()A .123V V V V ++=B .122V V =C .232V V =D .236VV V -=34.(2024高三下·浙江杭州·阶段练习)已知矩形ABCD 中,2AB =,4BC =,E 是AD 的中点,沿直线BE 将△ABE 翻折成△A BE ',则三棱锥A BDE '-的体积的最大值为()A .3B C D .335.(2024·全国)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为()A .20+B .C .563D .336.(2024高一下·江苏连云港·阶段练习)在《九章算术⋅商功》中将正四面形棱台体(棱台的上、下底面均为正方形)称为方亭.在方亭1111ABCD A B C D -中,1122AB A B ==,四个侧面均为全等的等腰梯形且面积之和为)A .72B .76C D 37.(2024高三上·山西运城·期中)已知一个正四棱台的上下底面边长为1、3,则棱台的体积为()A .B .3C .12D .1338.(2024·河南·模拟预测)光岳楼,又称“余木楼”“鼓楼”“东昌楼”,位于山东省聊城市,在《中国名楼》站台票纪念册中,光岳楼与鹳雀楼、黄鹤楼、岳阳楼、太白楼、滕王阁、蓬莱阁、镇海楼、甲秀楼、大观楼共同组成中国十大名楼.其墩台为砖石砌成的正四棱台,如图所示,光岳楼的墩台上底面正方形的边长约为32m ,下底面正方形的边长约为34.5m ,高的4倍比上底面的边长长4m ,则光岳楼墩台的体积约为()A .39872.75mB .39954.75mC .39988.45mD .39998.25m 39.(四川省仁寿第一中学校(北校区)2023-2024学年高三上学期9月月考文科数学试题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A .πB .π2C .3π4D .π440.(2024高三上·江苏苏州·开学考试)若某圆柱体的底面半径与某球体的半径相等,圆柱体与球体的体积之比和它们的表面积之比的比值相等,则该圆柱体的高与球体的半径的比值为()A .54B .43C .32D .241.(2024·河南·模拟预测)圆锥的高为2,其侧面展开图的圆心角为2π3,则该圆锥的体积为().A .π4B .π3C .π2D .2π642.(2024高三上·福建厦门·阶段练习)已知母线长为5的圆锥的侧面积为15π,则这个圆锥的体积为()A .12πB .16πC .24πD .48π43.(2024高三下·河南开封·阶段练习)木桶作为一种容器,在我国使用的历史已经达到了几千年,其形状可视为一个圆台.若某圆台形木桶上、下底面的半径分别为20cm,13cm ,母线长为25cm ,木板厚度忽略不计,则该木桶的容积为()A .314225πcm 3B .34552πcmC .320725πcm 3D .36632πcm 44.(2024高三上·福建厦门·阶段练习)用一个平行于圆锥C 底面的平面截该圆锥得到一个圆台,若圆台上底面和下底面半径之比为23,则该圆台与圆锥C 的体积之比为()A .58B .1727C .1927D .34二、多选题45.(2024·全国)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,,2FB ED AB ED FB ==∥,记三棱锥E ACD -,F ABC -,F ACE -的体积分别为123,,V V V ,则()A .322V V =B .31V V =C .312V V V =+D .3123V V =46.(2024·福建·模拟预测)等腰梯形的上下底边之比为13,若绕该梯形的对称轴旋转一周所得几何体的表面积为16π,则该梯形的周长可能为()A .B .8C .D .1647.(2024·河南·模拟预测)如图,正三棱柱111ABC A B C -的底面边长为1,高为3,F 为棱1AA 的中点,,D E 分别在棱11,BB CC 上,且满足1A D DE EA ++取得最小值.记四棱锥111A B C ED -、三棱锥1,F A DE A DEF --的体积分别为123,,V V V ,则()A .123334V V V ++<B .23V V =C .1223V V =D .123V V V =+48.(2024高三上·湖南·5)A .该正方体的体积为5B 556C .该正方体的表面积为30D .该正方体的外接球的表面积为15π三、填空题49.(2024·辽宁锦州·模拟预测)已知用斜二测画法画梯形OABC 的直观图O A B C ''''如图所示,3O A C B ''''=,C E O A ''''⊥,8OABC S =,//CD y '''轴,22C E ''=D ¢为O A ''的三等分点,则四边形OABC 绕y 轴旋转一周形成的空间几何体的体积为.50.(2024高三·全国·对口高考)若正ABC 用斜二测画法画出的水平放置图形的直观图为A B C ''' ,当A B C ''' 3ABC 的面积为.51.(2024高三下·上海宝山·开学考试)我们知道一条线段在“斜二测”画法中它的长度可能会发生变化的,现直角坐标系平面上一条长为4cm 线段AB 按“斜二测”画法在水平放置的平面上画出为A B '',则A B ''最短长度为cm (结果用精确值表示)52.(2024高三·全国·阶段练习)如图,梯形ABCD 是水平放置的一个平面图形的直观图,其中=45∠ ABC ,1AB AD ==,DC BC ⊥,则原图形的面积为.53.(2024高三上·上海普陀·期中)2022年4月16日,神舟十三号载人飞船返回舱在东风着陆场预定区域成果着陆.如图,在返回过程中使用的主降落伞外表面积达到1200平方米,若主降落伞完全展开后可以近似看着一个半球,则完全展开后伞口的直径约为米(精确到整数)54.(2024高一下·四川成都·阶段练习)已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为.55.(2024·安徽·模拟预测)如图,在三棱锥P -ABC 的平面展开图中,CD AB ∥,AB AC ⊥,22AB AC ==,CD =,cos BCF ∠65=,则三棱锥-P ABC 外接球表面积为.56.(2024·安徽马鞍山·模拟预测)已知三棱锥P -ABC 的底面ABC 为等边三角形.如图,在三棱锥P -ABC的平面展开图中,P ,F ,E 三点共线,B ,C ,E 三点共线,cos PCF ∠=PC =,则PB =.57.(2024高三上·山西大同·阶段练习)如图,在三棱锥-P ABC 的平面展开图中,1AC =,AB AD ==AB AC ⊥,AB AD ⊥,30CAE ∠=︒,则三棱锥-P ABC 的外接球的表面积为.58.(2024高三·河北·专题练习)如图,正方体1111ABCD A B C D -的棱长为a ,点E 为1AA 的中点,在对角面11BB D D 上取一点M ,使AM ME +最小,其最小值为59.(2024高三上·四川成都·开学考试)如图一个正六棱柱的茶叶盒,底面边长为10cm ,高为20cm ,则这个茶叶盒的表面积为2cm .60.(2024高二上·上海黄浦·阶段练习)若长方体的对角线的长为9cm ,其长、宽、高的和是15cm ,则长方体的全面积是.61.(2024·全国·模拟预测)正四棱锥P -ABCD 的各条棱长均为2,则该四棱锥的表面积为.62.(2024高三·全国·专题练习)一个正三棱台的上、下底面边长分别是3cm 和6cm ,高是32cm .则三棱台的斜高为;三棱台的侧面积为;表面积为.63.(2024高三·全国·专题练习)若矩形的周长为36,矩形绕它的一条边旋转形成一个圆柱,求圆柱侧面积的最大值为.64.(2024高二上·北京海淀·期中)若一个圆锥的轴截面是等边三角形,其面积为是.65.(2024高三上·全国·专题练习)某地球仪上北纬030纬线的长度为12()cm π,该地球仪的半径是cm ,表面积是cm2.66.(2024·全国)已知圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60 则球O 的表面积等于.67.(2009年普通高等学校招生全国统一考试理科数学(全国卷Ⅱ))设OA 是球O 的半径,M 是OA 的中点,过M 且与OA 成45 角的平面截球O 的表面得到圆C .若圆C 的面积等于74π,则球O 的表面积等于68.(2024·全国)用平面α截半径为R 的球,如果球心到截面的距离为2R ,那么截得小圆的面积与球的表面积的比值为.69.(2024高三上·广东广州·阶段练习)陀螺是中国民间较早的娱乐工具之一,也称陀罗,图l 是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中A 是圆锥的顶点,B ,C 分别是圆柱的上、下底面圆的圆心,且1AB =,3AC =,底面圆的半径为1,则该陀螺的表面积是.70.(2024高三·全国·专题练习)如图,八面体的每一个面都是正三角形,并且4个顶点A ,B ,C ,D 在同一个平面内.如果四边形ABCD 是边长为30cm 的正方形,那么这个八面体的表面积是2cm .71.(2024高三上·天津北辰·阶段练习)已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为23,则圆柱的体积为.72.(2024高三上·云南昆明·、则该圆锥的体积为.73.(2024·浙江嘉兴·模拟预测)已知圆锥的底面半径为1,侧面积为2π,则此圆锥的体积是.74.(2024高三上·广东广州·阶段练习)已知圆锥的底面半径为2,侧面展开图是一个圆心角为120°的扇形.把该圆锥截成圆台,已知圆台的下底面与该圆锥的底面重合,圆台的上底面半径为1,则圆台的体积为.。
第二节 空间几何体的表面积与体积
第二节 空间几何体的表面积与体积考试要求了解球、棱柱、棱锥、棱台的表面积和体积的计算公式.[知识排查·微点淘金]知识点1 圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱圆锥圆台侧面展 开图侧面积 公式S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧=π(r 1+r 2)l[微拓展] 圆台、圆柱、圆锥之间的转化当圆台的上底面半径与下底面半径相等时,得到圆柱;当圆台的上底面半径为零时,得到圆锥,由此可得:S 圆柱侧=2πrl ――→r ′=rS 圆台侧=π(r +r ′)l ――→r ′=0S 圆锥侧=πrl . 知识点2 空间几何体的表面积与体积公式名称几何体表面积 体积 柱体(棱柱和圆柱) S 表面积=S 侧+2S 底 V =S 底h 锥体(棱锥和圆锥)S 表面积=S 侧+S 底 V =13S 底h台体(棱台和圆台)S 表面积=S 侧+ S 上+S 下 V =13(S 上+S 下+S 上S 下)h 球S =4πR 2V =43πR 3[微拓展]柱体、锥体、台体的体积公式间的联系:V 柱体=Sh ――→S ′=SV 台体=13(S ′+S ′S +S )h ――→S ′=0V 锥体=13Sh . 常用结论 几个与球有关的切、接问题的常用结论(1)正方体的棱长为a ,球的半径为R , ①若球为正方体的外接球,则2R =3a ; ②若球为正方体的内切球,则2R =a ; ③若球与正方体的各棱相切,则2R =2a .(2)若长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2.[小试牛刀·自我诊断]1.思维辨析(在括号内打“√”或“×”) (1)锥体的体积等于底面面积与高的乘积.(×) (2)球的体积之比等于半径比的平方.(×) (3)台体的体积可转化为两个锥体的体积之差.(√) (4)已知球O 的半径为R ,其内接正方体的边长为a ,则R =32a .(√) 2.(链接教材必修2 P 27T 1)已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为( )A .1 cmB .2 cmC .3 cmD .32cm解析:选B.S 表=πr 2+πrl =πr 2+πr ·2r =3πr 2=12π, ∴r 2=4,∴r =2.3.(链接教材必修2P 28A 组T 3)如图,将一个长方体用过相邻三条棱的中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体的体积的比为 .解析:设长方体的相邻三条棱长分别为a ,b ,c ,它截出棱锥的体积V 1=13×12×12a ·12b ·12c =148abc ,剩下的几何体的体积V 2=abc -148abc =4748abc ,所以V 1∶V 2=1∶47. 答案:1∶474.(忘记分类讨论)圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为.解析:分两种情况:①以长为6π的边为高时,4π为圆柱底面周长,则2πr=4π,r=2,所以S底=4π,S侧=6π·4π=24π2,S表=2S底+S侧=8π+24π2=8π(3π+1);②以长为4π的边为高时,6π为圆柱底面周长,则2πr=6π,r=3,所以S底=9π,S表=2S底+S侧=18π+24π2=6π(4π+3).答案:6π(4π+3)或8π(3π+1)5.(对组合体不能合理分割)如图所示,由圆柱与圆锥组合而成的几何体的三视图如图所示,则该几何体的表面积为.解析:设圆柱底面半径为r,周长为c,圆锥母线长为l,圆柱高为h.由题中三视图得r=2,c=2πr=4π,h=4,由勾股定理得:l=22+(23)2=4,S表=πr2+ch+12cl=4π+16π+8π=28π.答案:28π一、基础探究点——空间几何体的表(侧)面积(题组练透)1.(2021·新高考卷Ⅰ)已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为()A.2B.22C.4D.4 2解析:选B由题意知圆锥的底面周长为22π.设圆锥的母线长为l,则πl=22π,即l=2 2.故选B.2.如图为某几何体的三视图,则该几何体的表面积是()A.6+4 2B.4+4 2C .6+2 3D .4+2 3解析:选C 由三视图还原几何体知,该几何体为如图所示的三棱锥P -ABC ,其中P A ⊥平面ABC ,AB ⊥AC ,AB =AC =AP =2,故其表面积S =⎝⎛⎭⎫12×2×2×3+12×(22)2×sin 60°=6+2 3.3.如图,一个棱长为4的正方体被挖去一个高为4的正四棱柱后得到图中的几何体,若该几何体的体积为60,则该几何体的表面积为 .解析:设正四棱柱的底面边长为m ,则4(42-m 2)=60,解得m =1,则该几何体的表面积为42×4+(42-12)×2+4×1×4=110.答案:1104.已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 . 解析:设圆锥的高为h ,母线长为l ,则圆锥的体积V =13×π·62·h =30π,解得h =52.所以l =r 2+h 2=62+⎝⎛⎭⎫522=132,故圆锥的侧面积S =πrl =π·6×132=39π.答案:39π求空间几何体表面积时应注意(1)以三视图为载体的几何体的表面积问题,关键 是分析三视图确定几何体中各元素之间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积问题应注意衔接部分的处理.(3)旋转体的表面积问题应注意其侧面展开图的应用.二、综合探究点——空间几何体的体积(多向思维)[典例剖析]思维点1直接利用公式求体积问题[例1](1)圆台上、下底面的圆周都在一个直径为10的球面上,其上、下底面半径分别为4和5,则该圆台的体积为.解析:圆台的下底面半径为5,故下底面在外接球的大圆上,如图所示,设球的球心为O,圆台上底面的圆心为O′,则圆台的高OO′=OQ2-O′Q2=52-42=3. 据此可得圆台的体积V=1π×3×(52+5×4+42)=61 π.3答案:61π对于规则几何体的体积问题,可以直接利用公式进行求解. 要注意准确记忆基本体积公式.思维点2割补法求体积问题[例2]《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”(已知1丈为10尺)该锲体的三视图如图所示,则该锲体的体积为()A.12 000立方尺B.11 000立方尺C.10 000立方尺D.9000立方尺解析:由题意,将锲体分割为三棱柱与两个四棱锥的组合体,作出几何体的直观图如图所示:沿上棱两端向底面作垂面,且使垂面与上棱垂直,则将几何体分成两个四棱锥和1个直三棱柱,则三棱柱的体积V 1=12×3×2×2=6,四棱锥的体积V 2=13×1×3×2=2,由三视图可知两个四棱锥大小相等,∴V =V 1+2V 2=10立方丈=10 000立方尺.故选C .答案:C割补法求体积的解题思路首先把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算.思维点3 等积转换法求体积[例3] 如图所示,已知三棱柱ABC -A 1B 1C 1的所有棱长均为1,且AA 1⊥底面ABC ,则三棱锥B 1ABC 1的体积为( )A .312 B .34 C .612D .64解析:易知三棱锥B 1ABC 1的体积等于三棱锥A -B 1BC 1的体积,又三棱锥A -B 1BC 1的高为32,底面积为12,故其体积为13×12×32=312. 答案:A等积转化法求体积的解题思路选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面可作为三棱锥的底面进行等体积变换.[学会用活]1.如图,长方体ABCD -A 1B 1C 1D 1的体积为36,E 为棱CC 1上的点,且CE =2EC 1,则三棱锥E -BCD 的体积是( )A .3B .4C .6D .12解析:选B 因为S △BCD =12S 四边形ABCD ,CE =23CC 1,VABCD A 1B 1C 1D 1=S 四边形ABCD ·CC 1=36,所以V E BCD =13S △BCD ·CE =13×12S 四边形ABCD ·23CC 1=19×36=4.故选B.2.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π解析:选B 解法一:(割补法)由几何体的三视图可知,该几何体是一个圆柱截去上面虚线部分所得,如图所示.将圆柱补全,并将圆柱从点A 处水平分成上下两部分.由图可知,该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12,所以该几何体的体积V =π·32×4+π·32×6×12=63π.故选B.解法二:(估值法)由题意知,12V 圆柱<V 几何体<V 圆柱,又V 圆柱=π·32×10=90π,∴45π<V几何体<90π.观察选项可知只有63π符合.故选B.3.某几何体的三视图如图所示,则这个几何体的体积是( )A .13B .14C .15D .16解析:选C 所求几何体可看作是将长方体截去两个三棱柱得到的几何体,在长方体中还原该几何体,如图中ABCD A ′B ′C ′D ′所示,长方体的长、宽、高分别为4,2,3,两个三棱柱的高为2,底面是两直角边长分别为3和1.5的直角三角形,故该几何体的体积V =4×2×3-2×12×3×32×2=15,故选C .三、应用探究点——与球有关的切、接问题(多向思维)[典例剖析]思维点1 几何体的外接球问题[例4] 设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为( )A .123B .18 3C .24 3D .54 3解析:由等边△ABC 的面积为93可得34AB 2=93,所以AB =6,所以等边△ABC 的外接圆的半径为r =33AB =2 3.设球的半径为R ,球心到等边△ABC 的外接圆圆心的距离为d ,则d =R 2-r 2=16-12=2.所以三棱锥D -ABC 高的最大值为2+4=6,所以三棱锥D -ABC 体积的最大值为13×93×6=18 3.故选B.答案:B [拓展变式][变条件、变结论]若本例中的条件变为“直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上”,若AB =3,AC =4,AB ⊥AC ,AA 1=12,求球O 的表面积.解:将直三棱柱补形为长方体ABEC -A ′B ′E ′C ′(图略),则球O 是长方体ABEC -A ′B ′E ′C ′的外接球,∴体对角线BC ′的长为球O 的直径.因此2R =32+42+122=13,故S 球=4πR 2=169π.处理“相接”问题,要抓住空间几何体“外接”的特点,即球心到多面体的顶点的距离等于球的半径.思维点2 几何体的内切球问题[例5] 已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .解析:解法一:如图,在圆锥的轴截面ABC 中,CD ⊥AB ,BD =1,BC =3,圆O 内切于△ABC ,E 为切点,连接OE ,则OE ⊥B C .在Rt △BCD 中,CD =BC 2-BD 2=2 2.易知BE =BD =1,则CE =2.设圆锥的内切球半径为R ,则OC =22-R ,在Rt △COE 中,OC 2-OE 2=CE 2,即(22-R )2-R 2=4,所以R =22,圆锥内半径最大的球的体积为43πR 3=23π. 解法二:如图,记圆锥的轴截面为△ABC ,其中AC =BC =3,AB =2,CD ⊥AB ,在Rt △BCD 中,CD =BC 2-BD 2=22,则S △ABC =2 2.设△ABC 的内切圆O 的半径为R ,则R =2·S △ABC 3+3+2=22,所以圆锥内半径最大的球的体积为43πR 3=23π. 答案:23π处理与球有关内切问题的策略解答此类问题时首先要找准切点,通过作截面来解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.[学会用活]4.长方体ABCD -A 1B 1C 1D 1的长、宽、高分别为2,2,1,其顶点都在球O 的球面上,则球的表面积为 .解析:因为长方体的外接球O 的直径为长方体的体对角线,长方体的长、宽、高分别为2,2,1,所以长方体的外接球O 的直径为4+4+1=3,故长方体的外接球O 的半径为r =32,所以球O 的表面积为S =4πr 2=9π.答案:9π5.已知正四面体P -ABC 的表面积为S 1,此四面体的内切球的表面积为S 2,则S 1S 2= .解析:设正四面体的棱长为a ,则正四面体的表面积为S 1=4×34·a 2=3a 2,其内切球半径r 为正四面体高的14,即r =14×63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2πa 26=63π. 答案:63π限时规范训练 基础夯实练1.(2021·四川乐至中学月考)已知圆锥的轴截面是边长为2的等边三角形,则该圆锥的侧面积为( )A .33π B .2π C .3πD .4π解析:选B 由题意,圆锥的轴截面是边长为2的等边三角形,即圆锥的底面圆的半径为r =1,母线长为l =2,所以该圆锥的侧面积为S =πrl =π·1×2=2π. 故选B.2.在梯形ABCD 中,∠ABC =90°,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在直线旋转一周而形成的曲面所围成的几何体的体积为( )A .2π3B .4π3C .5π3D .2π解析:选C 由题意可知旋转后的几何体如图所示,直角梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为1,母线长为2的圆柱挖去一个底面半径同样是1、高为1的圆锥后得到的组合体,所以该组合体的体积为V =V 圆柱-V 圆锥=π·12×2-13·π·12×1=53π,故选C .3.(2021·云南昆明月考)某锥体的三视图如图所示,则该几何体的体积为( )A .2B .533C .433D .233解析:选C 由三视图还原几何体得,原几何体是一个四棱锥E -ABCD ,如图所示,四棱锥的高为3,底面是边长为2的正方形,因此体积为13×2×2×3=433,故选C . 4. 《九章算术》中给出了一个圆锥体积近似计算公式V ≈l 2·h36,其中l 为底面周长,它实际上是将圆锥体积中圆周率近似取为3得到的,那么若圆锥体积近似公式为V ≈l 2·275·h ,则相当于圆周率近似取值为( )A .227B .217C .238D .258解析:选D 设圆锥底面圆的半径为r ,高为h ,则l =2πr ,13πr 2h =275(2πr )2 h ,所以π=258. 故选D.5.(2021·四川石室中学开学考试)某柱体的正视图与侧视图是全等的正方形,俯视图是圆,记该柱体的表面积为S 1,其内切球的表面积为S 2,且S 1=λS 2,则λ=( )A .1B .23C .43D .32解析:选D 由已知可得,此柱体为底面直径与高相等的圆柱,设底面圆的半径为r ,则高为2r ,则S 1=2πr 2+2πr ·(2r )=6πr 2,又此柱体内切球的半径为r ,则S 2=4πr 2, 则λ=S 1S 2=6πr 24πr 2=32,故选D. 6.某几何体的三视图如图所示,则该几何体的体积为( )A .π+43B .2π+4C .3π+4D .4π+43解析:选A 由三视图还原原几何体如图,该几何体为组合体,上半部分为半圆柱,下半部分为正四棱锥,圆柱的底面半径为1,高为2,棱锥的底面边长为2,高为1,∴该几何体的体积为12π·12×2+13×22×1=π+43.故选A .7.若圆锥的内切球与外接球的球心重合,且圆锥内切球的半径为1,则圆锥的表面积为 .解析:因为圆锥的内切球与外接球的球心重合,所以圆锥的轴截面为等边三角形,设其边长为a ,则13×32a =1,a =23,所以圆锥的底面圆半径为3,从而利用圆锥的表面积公式可得S =πrl +πr 2=π·3×23+π·(3)2=9π.答案:9π8.(2021·陕西渭南月考)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体称为正八面体,则图中正八面体体积为 .若图中正八面体的各个顶点都在同一个球面上,则此球的体积为 .解析:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的对角线是正方体的棱长2,故正方形的边长等于2,所以该多面体的体积为2×13×(2)2×1=43.由图中几何关系知正八面体的外接球,即正方体的内切球,故半径R =1,所以体积V =43π·13=43π.答案:43 43π9.如图是某个铁质几何体的三视图,其中每个小正方形格子的边长均为1个长度单位,将该铁质几何体熔化,制成一个大铁球,如果在熔制过程中材料没有损耗,则大铁球的表面积 .解析:由三视图知,该铁质几何体是由一个小铁球和一个铁质圆锥体拼接而成,体积之和为43π·13+13π·22×7=323π,设制成的大铁球半径为R ,则43πR 3=323π,解得R =2,故大铁球的表面积为4πR 2=16π.答案:16π综合提升练10.最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”“圆罂测雨”“峻积验雪”和“竹器验雪”.其中“天池测雨”法是下雨时用一个圆台形的天池盆收集雨水.已知天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.当盆中积水深九寸(注:1尺=10寸)时,平地降雨量是( )A .9寸B .7寸C .8寸D .3寸解析:选D 由已知天池盆上底面半径是14寸,下底面半径为6寸,高为18寸,由积水深9寸知水面半径为12×(14+6)=10寸,则盆中水的体积为13π·9×(62+102+6×10)=588π(立方寸),所以平地降雨量为588ππ·142=3(寸),故选D.11.(2021·四川成都月考)一块边长为10 cm 的正方形铁片如图所示的阴影部分截下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,则这个正四棱锥的外接球的表面积为( )A .2894πB .28916πC .28948πD .28964π解析:选A 由题设知:底面ABCD 的外接圆半径为r =32,且EO =4,令正四棱锥外接球的半径为R ,且外接球的球心必在直线EO 上,∴(R -EO )2+r 2=R 2,即R =174.∴正四棱锥的外接球的表面积为4πR 2=289π4.故选A .12.(2021·安徽合肥一中模拟)学生到工厂劳动实践,利用3D 打印技术制作一个机械零件模型,该零件模型是由两个相同的正四棱柱镶嵌而成的几何体,其三视图如图所示.这个几何体的体积为( )A .16B .403C .16-423D .163解析:选B 由三视图还原几何体如图所示,两个四棱柱的体积均为V 1=12×2×2×4=8,中间重复的部分为两个小正四棱锥,其体积为2V 2=13×2×2×2=83,故该几何体体积为V =16-83=403,故选B.13.有一个圆锥与一个圆柱的底面半径相等,圆锥的母线长是底面半径的2倍,若圆柱的外接球的表面积是圆锥的侧面积的6倍,则圆柱的高是底面半径的 倍.解析:设圆柱的高为h ,底面半径为r ,圆柱的外接球的半径为R ,则R 2=⎝⎛⎭⎫h 22+r 2. ∵母线长l =2r ,∴圆锥的高为3r ,∴圆锥的侧面积为πrl =2πr 2,∴4πR 2=4π⎣⎡⎦⎤⎝⎛⎭⎫h 22+r 2=6×2πr 2,∴h 24+r 2=3r 2,整理得h 2=8r 2,∴hr =2 2.答案:2 214.某市民广场有一批球形路障球(如图1所示). 现公园管理处响应市民要求,决定将每个路障球改造成方便市民歇脚的立方八面体石凳(如图2所示). 其中立方八面体有24条棱、12个顶点、14个面(6个正方形、8个正三角形),它是将立方体“切”去8个“角”后得到的几何体.经过测量,这批球形路障球每个直径为60 cm ,若每个路障球为改造后所得的立方八面体的外接球,则每个改造后的立方八面体表面积为 cm 2.解析:由题意知,立方八面体表面有8个正三角形,再加上6个小正方形,且正方形边长与正三角形边长相等,路障球为立方八面体的外接球. 设立方八面体的棱长为a ,则外接球直径d =2a 2+2a 2=2a =60,则a =30.立方八面体表面积S =6a 2+8×34a 2=5400+1800 3.答案:5400+1800 315.如图1,在一个正方形S 1S 2S 3S 4内,有一个小正方形和四个全等的等边三角形.将四个等边三角形折起来,使S 1,S 2,S 3,S 4重合于点S ,且折叠后的四棱锥S -ABCD 的外接球的表面积是16 π(如图2),则四棱锥的体积是 .解析:在题图2中,连接AC ,BD 交于点O ,连接OS ,如图,因为SD =SB =CD ,BD =2CD ,所以SD ⊥SB ,故OA =OB =OC =OD =OS ,则O 是正四棱锥外接球的球心,正四棱锥的所有棱都相等,设棱长为x ,则外接球的半径是OA =22x ,所以4π⎝⎛⎭⎫22x 2=16π,x =2 2.因此SO =OA =22x =2.故四棱锥S -ABCD 的体积是13·x 2·SO=13×(22)2×2=163. 答案:163创新应用练16.某同学在参加《通用技术》实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为43的正方体的六个面所截后剩余的部分(球心与正方体的中心重合),若其中一个截面圆的周长为4π,则该球的半径是( )A .2B .4C .26D .4 6解析:选B 设截面圆半径为r ,球的半径为R ,则球心到某一截面的距离为正方体棱长的一半即23,根据截面圆的周长可得4π=2πr ,得r =2,故由题意知R 2=r 2+(23)2,即R 2=22+(23)2=16,所以R =4,故选B.17.(2021·安徽黄山二模)棱长为4的正方体密闭容器内有一个半径为1的小球,小球可在正方体容器内任意运动,则其能到达的空间的体积为( )A .32+22π3B .36+4π3C .44+13π3D .12+12π解析:选A 在正方体的8个顶点处的单位立方体空间内,小球不能到达的空间为8⎣⎡⎦⎤13-18⎝⎛⎭⎫4π3·13=8-4π3,除此之外,在以正方体的棱为一条棱的12个1×1×2的正四棱柱空间内,小球不能到达的空间共为12×⎣⎡⎦⎤1×1×2-14(π·12)×2=24-6π.其他空间小球均能到达.故小球不能到达的空间体积为⎝⎛⎭⎫8-43π+24-6π=32-223 π.∴小球可以经过的空间的体积V =43-⎝⎛⎭⎫12-π4·12×2×12-⎝⎛⎭⎫8-43 π=32+22π3.故选A .。
《空间几何体的表面积和体积》教案(2)

空间几何体的表面积和体积
4.圆柱.
把圆柱的侧面沿着一条母线展开,得到什么图形?展开的图形与原图有什么关系?
5.圆锥.
把圆锥的侧面沿着一条母线展开,得到什么图形?展开的图形与原图有什么关系?
6.圆台.
把圆台的侧面沿着一条母线展开,得到什么图形?展开的图形与原图有什么关系?
思考:圆柱、圆锥、圆台的侧面积公式间有什么联系与区别?
四、点燃智慧之炬〔研究性学习的小课题、知识的自主串联、直击高考、自主编题等〕
1.例题.
例1 设计一个正四棱锥形冷水塔塔顶,高是0.85m,底面的边长是1.5m,制造这种塔顶需要多少平方米的铁板?〔保留两位有效数字〕
例2 边长为5的正方形EFGH是圆柱的轴截面,那么从点E沿圆柱的侧面到G点的最短距离是
例3 有一根长为5cm,底面半径为1cm的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端,那么铁丝的最短长度为多少厘米?(精确到 0.1cm〕
分析: 可以把圆柱沿这条母线展开,将问题转化为平面几何的问题.2.练习.
〔1〕如图,E,F分别为正方形ABCD的边BC,CD的中点,沿图中虚线折起。
空间几何体的表面积
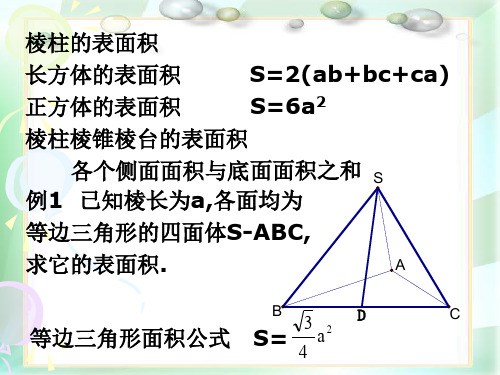
2πr
2πr
S扇=1/2LR
S A
O'
O B
例4 一个圆台形花盆盆口外径为20cm,盆 底外径为15cm,底部渗水圆孔直径为1.5cm, 盆外壁长15cm.为了美化花盆的外观,需要在花 盆外壁涂油漆.已知每平方米用100毫升油漆, 涂100个这样的花盆需要多少油漆?
长之和为48,求长方体
D
最长的对角线的长. A
C B
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca
例3已知四棱台AC1 的上、下底均是正方
形,边长分别是2和8
A'
D'
C'
B'
,侧面是全等的等腰梯 D
C
形,棱台高为3 2 ,求 A
B
它的侧面积。
圆柱的表面积 S=2πr2+2πrl
圆锥的表面积 S=πr2+πrl
棱柱的表面积
长方体的表面积
S=2(ab+bc+ca)
正方体的表面积
S=6a2
棱柱棱锥棱台的表面积
各个侧面面积与底面面积之和 S 例1 已知棱长为a,各面均为
等边三角形的四面体S-ABC,
求它的表面积.
A
等边三角形面积公式
B
S= 3 a2
D
C
4
例2已知长方体AC1 A1
ห้องสมุดไป่ตู้D1
的表面积为23,所有棱
C1 B1
分析,本题首先要计算什么? 首先要计算需要涂油漆的花盆面积 圆台面积相关量r’,r,l
空间几何体,球体表面积,体积

1.若一个正方体的体积是8,则这个正方体的内切球的
表面积是( )
A.8π
B.6π
C.4π
D.π
答案 C
解析 设正方体的棱长为a,则a3=8.
而此内切球直径为2,∴S表=4πr2=4π.
2 . (2015· 沧 州 七 校 联 考 ) 若 某 几 何 体 的 三 视 图 如 图 所 示,则该几何体的体积为( )
得ab= =21, , c=3.
∴球的直径 d= 22+12+32= 14.∴r=d2= 214. ∴S 球=4πr2=4π×144=14π.
3.(2020·陕西理)已知底面边长为 1,侧棱长为 2的正
四棱柱的各顶点均在同一个球面上,则该球的体积为( )
AD.43π
△ABC 的面积等于12×3×4=6.AA1⊥平面 ABC,则直角
梯形 ABEA1 的面积等于12×(2+5)×4=14,矩形 ACC1A1 的面
积等于 3×5=15.过点 E 作 EF⊥AA1 于点 F,则 EF=AB=4, A1F=B1E=BB1-BE=3,则 A1E=5,所以△A1C1E 的面积等
思考题1 (1)(2020·重庆理)若某几何体的三视图如 图所示,则该几何体的表面积为( )
A.54 C.66
B.60 D.72
【解析】 题中的几何体可看作是从直三棱柱 ABC-
A1B1C1中截去三棱锥E-A1B1C1后所剩余的部分(如图所示), 其中在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=4.AC=3, 则BC=5,
探究3 (1)分割法:通过对不规则几何体进行分割,化为 规则几何体,分别求出体积后再相加即得所求几何体体积.
(2)补体法:通过补体构造出一个规则几何体,然后进行 计算.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N o:
课题
6.2.1空间几何体的表面积
授课时间
第周
课型
新授
课时
2/2
班级
教学目标
知识目标
了解柱、锥、台的表面积的计算公式,
领会柱、锥、台的表面积计算公式推导的数学思想,
技能目标
能运用公式解决一些数学问题
情感目标
培养学生勇于探索、善于研究的精神,让学生有更多的数学把握感,增强学生能学好数学的自信心。
问题:已知圆柱的半径为 ,母线长为 ,则这个圆柱的侧面积是多少?
课堂教学安排
教学
环节
主要教学内容
组织实施
(含教学思想、师生活动、教学方法、时间安排等)
三
重点
探索
奥妙
重点
突破
它的侧面展开图形是一个半径为 的扇形,
师:我们可以把这个扇形分成若干个全等的小扇形,当小扇形的弧长非常小的时候,弧长接近弦长,母线长可以近似看成小等腰三角形的高,小等腰三角形的面积为 ,把无数多个小等腰三角形的面积相加得到 。
这种处理问题的思想就是积分的思想。
四
应用
典例
示范
巩固
练习Байду номын сангаас
例2如图:圆锥的半径r=1,l=2,OA、OB为母线,AB为底面圆直径,M为OB的中点,求:
(1)在圆锥的侧面上从A到M的最短距离;
(2)由OA、OB和最短线路构成的图形的面积。
解:(1)即为AM= cm。
(2)即为三角形AOM的面积为 平方厘米
一
揭题
创设
情境
导入
新课
问题:底面半径为r,母线长为l的圆锥的表面积如何求?
学生分析表面积为侧面积和底面积之和,其中底面积为 ,侧面积为多少呢?学生感觉有难度。
学生都能体会立体问题平面化的思想,实现这一思想的方法是沿母线剪开变成一个可以解决的扇形的面积问题。
二
新课
合作
探究
获取
新知
寻找下面图形的平面展开图
教学
重点
展开侧面,分析侧面展开图的性质
教学
难点
理解柱、锥、台之间的辨证统一;
教法
采用问题解决法和分组教学法
学法
自主探究和小组合作讨论法
教学
准备
彩色粉笔和三角板
系部审核意见
板书设计
6.2.1空间几何体的表面积
2、旋转体的表面积例2
课堂教学安排
教学
环节
主要教学内容
组织实施
(含教学思想、师生活动、教学方法、时间安排等)
课堂教学安排
教学
环节
主要教学内容
组织实施
(含教学思想、师生活动、教学方法、时间安排等)
五
提升
总结
提升
达标
检测
(2)侧面积的算法:
思想:立体问题平面化
公式:
课后
作业
练习6-5 1、2题
教学
后记
