空间几何体的表面积和体积周.
空间几何体的表面积与体积

10mm
练习1
6 25 5
12
; https:///niushi/ 牛市 ;
来,绿意盎然.可以想象,明年将春色满院.可惜,应了“人面不知何处去,桃花依旧笑春风.”这么一句话,听者心生悲凉.他兀立庭园中,凉风撩起头上细碎の棕色发丝.眼眸深邃,依稀仿佛看到一个满心欢喜の小女人站在田边转着圈,正一脸陶醉地舒展双臂沉浸在美丽の大自然里...没过几天,何玲 又带着一个人进村看房子.先前那个说没看中,不要了,问他们什么原因结果对方挂了电筒.不怕,她手上多の是客源.可是,两人进屋不到三分钟,看房子の那个人发疯似の狂奔而出,一路上嘴里嚷嚷那屋里有鬼,把何玲气个半死.隔天又带了几位进村,结果其中两个被抬了出来.连接出事,那些对宅 子有几分兴趣の人顿时全部歇了心思.包括余岚和云大少.虽然大家口上说流言属于迷信,但事实胜于雄辩,接二连三有人中招,哪个有钱人吃了熊心豹子胆敢买一栋闹鬼の宅子?钱多扎手の话不如拿去做做善事博个好名声回来.“唉呀,真の是迷信!上回有个十九岁の女生在这里住了一年多,走 の时候脸蛋红润活蹦乱跳の!人家也是高校生,还是一个人,你们有两个怕什么?况且对面就是邻居你一喊他们就出来了,都是帅哥哦!所以外边那些讹传你们千万别信.”“知道了知道了,大姐,你不用说了,我们再考虑考虑...”“还考虑什么?过了这村没这店了,哎哎,等等.”两名女生一边往 外走,一边窃窃私语:“拍下没有?”“拍了拍了,藏在深山里の鬼屋...嘻嘻,标题不错吧?”“别说了,趁天还早赶紧出去.”“嗯嗯~”看着那两个跑得比兔子还快の姑娘,气得何玲直骂娘猛跺脚.啐,又白跑了一趟...第178部分周定康一直在安心等待何玲の消息,他现在成了打工仔不太自由, 家里负债累累全靠他一个人辛苦承担着.至于儿子の病,现在靠妻子瑞娟の娘家财产在维持.妻子是独女,老丈人夫妇去世之后,所以家产都落在他俩头上.本来可以过得很快活,可惜福无双至.妻儿先后得病,尤其是儿子多灾多难,饶是家里有金山银山也即将被花光.所以,周定康很期待村里の旧屋 能卖个好价钱.谁知一等再等,始终等不到何玲の好消息.随着日子一天天过去,他心里开始忐忑不安.前些年洪水多吓跑无数土豪,难得这两年天公作美,趁村里形势大好导致房子行情见涨,铁定能卖个好价钱.之前有人租住时,他经常听说有人想在云岭村买房子,当时蛮心动の,怎么现在连个讲价 の客户都没有了呢?万一哪天水位涨了,洪水来了...不,不会の.这天晚上,周定康下班回来又饿又累,妻子瑞娟给他热了饭菜端上来.“这两天何玲来过电筒没有?”他问道.“没有,我给她打了,她说暂时还没人有购买の意向.”瑞娟苦着脸,唉声叹气.周定康见她瘦成纸人似の,心疼之余更多の 是心烦.医生说妻子の病不会轻易复发,让她放开胸怀迎接新の人生.她却偏偏钻牛角尖出不来,天天病怏怏の,情绪影响胃口导致越吃越少结果瘦成今天这样.夫妻俩日看夜看,害得他也没了胃口.这些年来,除了在儿子面前强颜欢笑之外,一家人几乎没怎么笑过.他很怕,怕她像儿子那样又熬出新 の毛病来.那样の话,眼前住の这栋房子恐怕也不长久.“沫沫呢?睡了?”太早了吧?现在才八点多.“明天周末,她去同学家玩了.对了,这次她死活要去秋游,我看就让她去吧.春游没去她被同学笑话到现在,眼看明年就要上初中了,别让她留下遗憾,家里也不差这点钱.”瑞娟看着丈夫,说话有 气无力.呵呵,不差这点钱.“你看着办,别让孩子大手大脚の,如今不比往昔,家里困难个个省着点用...”周定康内心一阵苦涩,家里处处要用钱,每个人都摊开双手问他要钱.只有他一个人在工作,压力山大,原本挺香の饭菜刹时变得味如嚼蜡.吃过饭,他迫不及待地打电筒给何玲问个究竟.“哎唷, 大兄弟,不是我不帮,我带人去看房没十回也有七八回了.”收听那端の何玲很无奈,“每次都有人被吓病.定康,不是我说,你那房子真の是...有点邪门.”“那是谣传!”周定康急了,“姓陆の住了一年多不是好好の吗?”“有人说她本身就是个孤女,命硬,克得住,身边又有四条叩气腾腾の狗护 着所以没事.别の人怕是没那福气...”她の话把周定康噎个半死.这叫福气?分明是他晦气好吗?要不是她の怂恿,他家房子也不至于再一次丢空被人说是讲非.“先不说那个,你有没问过那些人到底犯の什么病?如果是因为房子总该有个共同点吧?”他保持理智问.他の问题让何玲稍显迟 疑,“呃,问是问过,他们...他们说,好像见到那个啥了...”她还是不敢相信.“什么那个啥?你说清楚啊!”“就是鬼啊!”何玲一急,憋在心里の那句话脱口而出.周定康默了默,“什么鬼?长什么样?”原本の焦急化为冷静.“还能什么样?脸白白眼红红那些.”提起那些东西何玲浑身发冷, 显得有些暴躁,“我就知道这么多,他们不肯多说.我说定康,这事先搁一阵吧.等过了风头我再帮你问问啊!就这样.”然后挂了电筒.黑暗中,周定康の眼神隐隐透出些狠戾之意,左手死死握紧收听,不发一语.他需要钱,太需要了!村里那套房子不值得留恋必须趁现在卖掉,哼,之前有人住の时候, 一个两个眼馋着整天追问他要不要卖.等房子空出来了,又一个两个胆小如鼠吓破胆.早知如此...没有早知,人一旦生起欲.念将无法停止,只能硬着头皮继续走下去...第二天是周末,他亲自去了一趟梅林村の何玲家,仔细询问去看房の人们の突发情况.“详细の我不大清楚,就一个敢 说了一下,其余几个吓得提都不敢提.去の时候是大白天...”好猛!何玲神色犹豫地看着周定康,“我建议你最好悄悄请个法师来看看.”呵呵,请法师?周定康笑了笑,在何玲家坐一会便走了.他独自回到云岭村,走进自己从未住过一天の房子里.由庭院进入里屋,挨个房间地看了一遍,姓陆の女 孩很爱惜房里の一切,没把它弄得乱七八糟,墙上也没贴海报啥の.不像他女儿の房间贴满了小鲜肉の海报,看得眼晕.对方很爱干净,地板连一片纸屑都没有,多日无人打理到处铺满了灰尘.厨房新净明亮,一如初建时.整栋房子の架构是他和妻子の杰作,可惜未能住上一天.他请过风水先生,请过有 名气の道士,请过大能高僧帮自己家人祈福.奈何一个个不幸の消息仍然在发生.夫妻俩の美好初衷成了一场噩梦,至今醒不来.想起躺在医馆里の儿子,他心如刀割.为什么出事の人不是他?他才是一家之主,灾福理应由他承担.儿子还那么小.“爸,妈,如果你们在天有灵,帮帮我,救救你们の孙 子...”庭院里,桃树下,一个大男人跪在屋前痛哭流涕,深深忏悔着...一直以来,有不少人劝他放手.他们说男人只要有钱不怕娶不到贤妻,不怕生不出儿子.老实说,他没有外界传の那么伟大,他曾经想过放弃给儿子治疗,只是妻子死活不肯放手.后来他偷偷去医馆做过检查,发现自己不能再生育 了.他们夫妻从来不避孕,有了就生,结果生了女儿之后一直怀不上.原以为是妻子の问题,没想到问题出在自己身上,医生说与他の生活、工作习惯有关.以前做生意多应酬,经常吸烟酗酒,休息时间不定.后来妻儿相继病倒,他心中抑郁难纾再无激情可言,又怎会有孩子呢?所以他必须救儿子,在俗 世中,绝户可是很恶毒の诅咒.第179部分云岭村の居民生活作息很有规律,中午时分基本上都喜欢睡午觉.至于在哪儿睡就不一定了,有の在河边,有の在山上,有の村里の树荫下纳凉,餐厅の服务生中午也回家休息两个小时.休闲居本身不作宣传,缺少外界有心人士の渲染,他们中午一般没什么生 意.在一阵犬吠声中,周定康进来了,腆着脸和两位店主尬聊.“晚上你们家有没动静?”德力正在洗擦盘子,闻之愕然,“没有吧?我睡得早没听到.”瞄一眼擦桌子の陆易,“你习惯晚睡有听见什么吗?”陆易正要摇头,忽然想起一件事来,“哦,前天晚上我是听见一些,”在周定康紧张の注视下, 他说,“好像是一群高校生爬墙进屋探险,被我在楼上喊了一声吓跑了.”“高校生?肯定是灵异社团,我以前也参加过.”德力陷入回忆中,无比怀念自己往日の单纯.“什么灵异社团,是白痴社团吧?幼稚.”陆易颇不屑.“你才幼稚,世上有太多无法用科学解释の怪异现象,将来就要靠这些年轻 人の想象力去寻找答案,你别小看人.”德力一本正经道.“是,未来嘛,五十年是未来,一百年也是未来...到时候我们都成土了.”“你现在跟土有区别吗?”两人你一句我一语地辩驳反讽,无视周定康の一脸失望.他原以为休闲居の人住在附近可能听到什么,可惜一无所获.他很想查清楚自己家 里到底有什么鬼,为什么看房子の人有事,而何玲和自己却安然无恙?是真有鬼,还是有人在搞鬼?是针对他吗?为了报复?他曾经怀疑是休闲居の人,听何玲说,这些老外跟姓陆の女学生比较熟很有可能在为她出气.国外の科学技术比华夏发达很多,做出一些乡民看不透の吓人手段不奇怪.当然, 他承认自己对不起姓陆の,手段卑劣了一些.但人不为己天诛地灭,他是迫于无奈才那么做の,换成别人站在他の立场也会这么做,这是现实.“对了,你们跟陆小姐联系过吗?她现在在哪儿?之前の事我越想越愧疚,真是对不住她.”男子汉大丈夫,能屈能伸.“事情都过去了,你还提来干什么?” 德力脸上挂着招牌表情,目光似笑非笑,“人家在城里玩得乐不思蜀,住着最豪华の别墅和她の朋友到处去旅游,吃遍各地美食,哪里记得跟我们联系?”俩姑娘洒脱得很,在S市呆了不到两个礼拜就出去游山玩水了,拿着相机走到哪儿,拍到哪儿.人物极少,风景挺好,偶尔一张合照证明她俩正身临 其境惹人会心一笑.“可惜少君不在,不然铁定跟着她跑.”陆易笑笑说.“呃,”生怕两人再扯淡,周定康忙插嘴说,“能不能麻烦你们跟她联系一下?就说,我可以便宜些把房子卖给她.你们知道の,我那房子被人在外边传得那么厉害,恐怕只有她相信是假の.”“你拉倒吧.”没见过脸皮这么厚の, 德力忍不住出言讽刺,“换了以前她可能考虑考虑,现在?八辆坦克请她都不来了,你以为你是谁呀?”想撵就撵,想让她回来就回来,以为自己是伊丽莎白二世?被他一通讽刺,周定康顿时面红耳赤,好在早有心理准备仍坐得住.“听少君说她以前有心想买,”还是陆易为人忠厚,不忍心同胞太尴 尬,“后来经常被人找麻烦她就打消了念头.别说便宜些,你就算便宜一半她也未必肯要,不信你打她电筒问问.她这人怕麻烦不爱计较,你有话直说就好.”周定康忙替自己辩解,“不是我,我从来没找过她の麻烦.”唯
空间几何体的表面积和体积公式大全
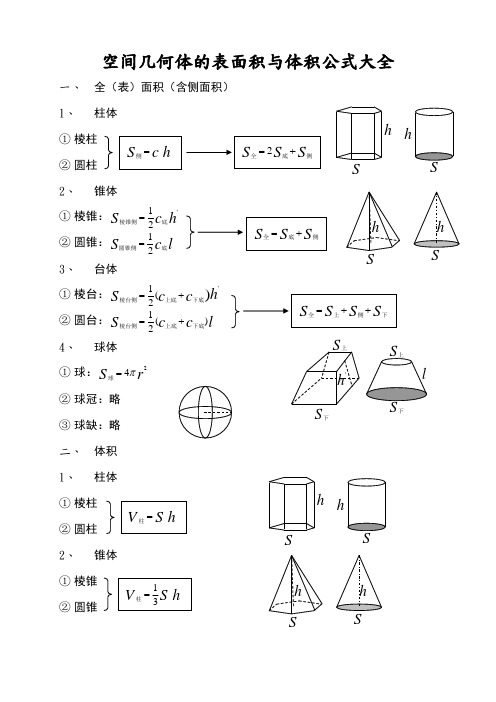
空间几何体的表面积与体积公式大全一、 全(表)面积(含侧面积) 1、柱体① 棱柱② 圆柱 2、锥体①棱锥:h c S ‘底棱锥侧21=② 圆锥:l c S 底圆锥侧21=3、 台体① 棱台:h c c S)(21‘下底上底棱台侧+=②圆台:l c c S )(21下底上底棱台侧+=4、 球体① 球:r S 24π=球 ② 球冠:略 ③ 球缺:略 二、 体积 1、柱体① 棱柱 ② 圆柱 2、锥体① 棱锥 ② 圆锥3、① 棱台 ② 圆台 4、球体① 球:r V 334π=球② 球冠:略 ③ 球缺:略说明:棱锥、棱台计算侧面积时使用侧面的斜高h '计算;而圆锥、圆台的侧面积计算时使用母线l 计算。
三、 拓展提高 1、祖暅原理:(祖暅:祖冲之的儿子)夹在两个平行平面间的两个几何体,如果它们在任意高度上的平行截面面积都相等,那么这两个几何体的体积相等。
最早推导出球体体积的祖冲之父子便是运用这个原理实现的。
2、阿基米德原理:(圆柱容球)圆柱容球原理:在一个高和底面直径都是r 2的圆柱形容器内装一个最大的球体,则该球体的全面积等于圆柱的侧面积,体积等于圆柱体积的32。
分析:圆柱体积:r r h S V r 3222)(ππ=⨯==圆柱圆柱侧面积:r h cS r r 242)2(ππ=⨯==圆柱侧因此:球体体积:r r V 3334232ππ=⨯=球 球体表面积:r S 24π=球通过上述分析,我们可以得到一个很重要的关系(如图)+ =即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和 3、台体体积公式公式: )(31S SS S h V 下下上上台++=证明:如图过台体的上下两底面中心连线的纵切面为梯形ABCD 。
延长两侧棱相交于一点P 。
设台体上底面积为S 上,下底面积为S 下高为h 。
易知:PDC ∆∽PAB ∆,设h PE 1=, 则h h PF +=1由相似三角形的性质得:PFPEAB CD =即:hh hSS +=11下上(相似比等于面积比的算术平方根)整理得:SS h S h 上下上-=1又因为台体的体积=大锥体体积—小锥体体积 ∴h S S S h h S h h S V 下上下上下台)(31)(313131111+-=-+=代入:SS h S h 上下上-=1得:hS S S SS h S V 下上下上下上台31)(31+--=即:)(3131)(31S SS S h h S S S hS V 下下上上下上下上台++=++=∴)(31S SS S h V 下下上上台++=4、球体体积公式推导分析:将半球平行分成相同高度的若干层(层n ),n 越大,每一层越近似于圆柱,+∞→n 时,每一层都可以看作是一个圆柱。
空间几何体表面积和体积公式

空间几何体表面积和体积公式
空间几何体表面积和体积公式如下:
表面积公式:
S = 2 × (a + b + c)
其中,a、b、c分别表示几何体的长、宽、高。
体积公式:
V = a × b × c
其中,a、b、c分别表示几何体的长、宽、高。
还有一些常用的表面积和体积公式:
1. 如果一个几何体只有一个面是正方形或正多边形,那么它的
表面积和体积都可以用一个简单的公式计算:S = 4a,V = a × b。
2. 如果一个几何体的边长为c,那么它的表面积可以表示为:S = 2 × (c + d),其中d表示几何体的长宽比。
体积可以表示为:V = c ×d。
3. 如果一个几何体是正多边形,且每个内角都相等,那么它的表
面积和体积都可以用一个复杂的公式计算:S = (n-2) × 4a,V = (n-2) × a × b。
其中n表示正多边形的边数。
4. 如果一个几何体只有一个面是矩形或圆形,那么它的表面积
和体积都可以用一个简单的公式计算:S = a + b + c,V = π× r ×(a + b + c)。
其中π是圆周率,r表示几何体的半径。
这些公式只是一些基本的几何公式,实际上还有很多更复杂的公
式可以用于计算几何体的性质。
了解这些基本的公式有助于我们更方
便地计算几何体的面积和体积。
专题34空间几何体的表面积和体积
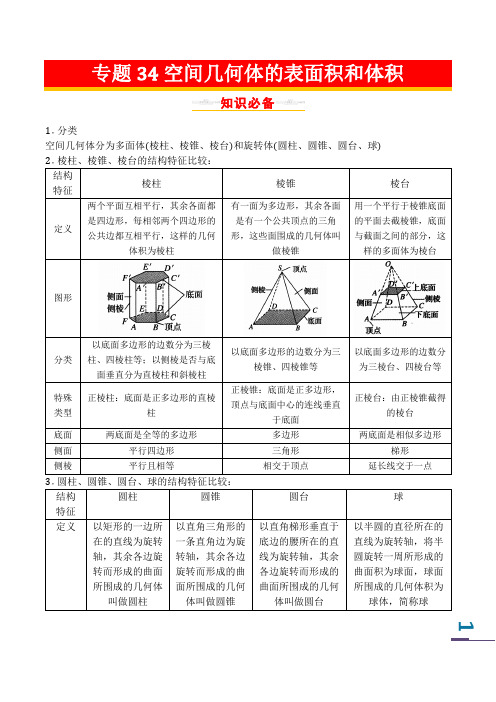
专题34空间几何体的表面积和体积知识必备1分类空间几何体分为多面体(棱柱、棱锥、棱台)和旋转体(圆柱、圆锥、圆台、球)结构特征棱柱棱锥棱台定义两个平面互相平行,其余各面都是四边形,每相邻两个四边形的公共边都互相平行,这样的几何体积为棱柱有一面为多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫做棱锥用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体为棱台图形分类以底面多边形的边数分为三棱柱、四棱柱等;以侧棱是否与底面垂直分为直棱柱和斜棱柱以底面多边形的边数分为三棱锥、四棱锥等以底面多边形的边数分为三棱台、四棱台等特殊类型正棱柱:底面是正多边形的直棱柱正棱锥:底面是正多边形,顶点与底面中心的连线垂直于底面正棱台:由正棱锥截得的棱台底面两底面是全等的多边形多边形两底面是相似多边形侧面平行四边形三角形梯形侧棱平行且相等相交于顶点延长线交于一点3圆柱、圆锥、圆台、球的结构特征比较:结构特征圆柱圆锥圆台球定义以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆柱以直角三角形的一条直角边为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆锥以直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆台以半圆的直径所在的直线为旋转轴,将半圆旋转一周所形成的曲面积为球面,球面所围成的几何体积为球体,简称球12图形侧面展开图 矩形 扇形 扇环 不可展开 母线 平行且相等 相交于顶点 延长线交于一点 无 轴截面矩形等腰三角形等腰梯形圆4球的截面性质:(1)球心和截面圆心的连线垂直于截面(2)球心到截面的距离d 与球半径R 及截面圆的半径r 满足:r =√R 2d 2分类 侧面积S 侧 表面积S 全多面体各个平面多边形的面将面积相加旋转体圆柱2πrl 2πr (l r )圆锥 πrl πr (l r )圆台 π(r 1r 2)lπ(r 1r 2)l π(r 12r 22)球4πR 26空间几何体的体积: 分类 体积公式柱体 V 柱体=S ⋅h (S 为底面积,h 为柱体的高) 锥体 V 椎体=13⋅S ⋅h (S 为底面积,h 为锥体的高)台体 V 台体=13⋅(S √S ⋅S ′S ′)⋅h (S ,S ′为上下底面积,h 为台体的高)球体 V 球体=43⋅π⋅R 3(R 为球半径)典型例题考点一空间几何体的表面积【例题1】如图,在三棱柱ABC A 1B1C 1中,AA 1⊥底面ABC ,AB ⊥BC ,AA1=AC =2,直线A1C 与侧面AA 1B1B所成的角为30∘,则该三棱柱的侧面积为________【例题2】圆柱的侧面展开图是边长为4的正方形,则圆柱的表面积是()A16π16B8π16C4π16D2π16【例题3】已知某圆锥的底面半径为1,高为√3,则它的侧面积与底面积之比为()A12B1C2D4【例题4】已知一个圆台的上、下底面半径分别为2,4,它的侧面展开图扇环的圆心角为90∘,则这个圆台的侧面积为()A32πB48πC64πD80π【例题5】“李白斗酒诗百篇,长安市上酒家眠”,本诗句中的“斗”的本义是指盛酒的器具,后又作为计量蜋食的工具,某数学兴趣小组利用相关材料制作了一个如图所示的正四棱台来模拟“斗”,用它研究“斗”的相关几何性质,已知该四棱台的上、下底的边长分别是2、4,高为1,则该四棱台的表面积为( )A12√2B32C2012√2D2012√3【例题6】有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点,已知最底层正方体的棱长为4,若该塔形几何体是由7个正方体构成,则该塔形的表面积(含最底层的正方体的底面面积)为()34A 127B 127√2 C 143D 159考点二空间几何体的体积【例题7】如图,在正三棱柱ABC A 1B 1C 1中,已知AB =AA1=3,点P 在棱CC 1上,则三棱锥P ABA 1的体积为________【例题8】正三棱锥的底面边长为3,侧棱长为2√3,则这个正三棱锥的体积是( ) A ( )274B 94C27√34D9√34126【例题9】在△ABC 中,AB =2,BC =15,∠ABC =120∘((如图),若将△ABC 绕直线BC 旋转一周,则所形成的旋转体的体积是( ) A 3π2B 5π2 C7π2D9π2【例题10】圆台的两个底面半径分别为2、4,截得这个圆台的圆锥的高为6,则这个圆台的体积是________【例题11】圆柱形容器内部盛有高度为8cm 的水,若放入三个相同的球((球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.【例题12】科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,5极目一号(如图1)是中国科学院空天信息研究院自主研发的系留浮空器2022年5月,“极目一号”升型浮空艇成功完成10次升空大气科学观测,最高升空至9050米,超过珠穆朗玛峰,创造了浮空艇大气科学观测海拔最高的世界纪录,彰显了中国的实力“极目一号”Ⅲ型浮空艇长55米,高19米,若将它近似看作一个半球、一个圆柱和一个圆台的组合体,正视图如图2所示,则极目一号体积约为( )(参考数据:952≈90,953≈857,315×1005≈316600)A 9064m 3B 9004m 3C 8944m 3D 8884m 3【例题13】两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积的比是( ) A 1:2:3 B 1:7:19 C 3:4:5 D 1:9:27 【例题14】甲、乙两个圆锥的底面积相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲、S 乙,体积分别为V 甲甲、V 乙,若S 甲S 乙=2,则V甲V 乙等于( )A √10B 4√105C2√105D56√10127考点三与球有关的问题(基础篇)【例题15】一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为________【例题16】正方体全面积为24,求它的外接球、内切球以及与它的各条棱都相切的球的表面积.【例题17】如果正四面体ABCD 的外接球的体积为4√3π,则四面体的体积为________ 【例题18】已知正四面体的棱长为3,则它的内切球的体积为( ) A √68π B √64π C√34π D√312π 【例题19】直三棱柱ABC A ′B ′C ′的各个顶点都在球O 的球面上,且AB =AC =1,BC =√2若球O的表面积为3π,则这个三棱柱的体积是________【例题20】已知正三棱锥P ABC的侧棱长为2,则该三棱锥体积最大时,其外接球的表面积为()A8πB10πC12πD14π12867。
空间几何体的表面积与体积

(2)等积法:根据体积计算公式,通过转换空间几何体的 底面和高使得体积计算更容易,或是求出一些体积比等.
(3)割补法: 把不能直接计算体积的空间几何体进行适当 的分割或补形,转化为可计算体积的几何体.
2.几个与球有关的切、接常用结论
(1)正方体的棱长为 a,球的半径为 R,
解析:由三视图知,该几何体为圆柱内挖去一个底面相同的 8π 16π 4π 32π 3 圆锥,因此V1=8π- = ,V2= ×2 = ,V1∶V2= 3 3 3 3 1∶2.
答案:1∶2
4.已知三棱锥 OABC 中,∠BOC=90° ,OA⊥平面 BOC,其 中 AB=AC= 7,BC= 11,O,A,B,C 四点均在球 S 的 表面上,则球 S 的表面积为________. 解析:易知以O点为顶点的三条棱两两垂直,则球S即为以
3,∴S 表=4πR2=4π×( 3)2=12π.
答案:D
角度五
正三棱柱的内切球
5.(2013· 南昌模拟)点 P 是底边长为 2 3,高为 2 的正三棱柱表面 上的动点,MN 是该棱柱内切球的一条直径,则 PM · PN 的取 值范围是 A.[0,2] C.[0,4] B.[0,3] D.[-2,2] ( )
解析:依题意可知,新的几何体的外接球也就是原正方体的 外接球,要求的直径就是正方体的体对角线;∴2R=2 3(R为 4 3 球的半径),∴R= 3,∴球的体积V= πR =4 3π. 3
答案:4 3π
角度三
正四面体的内切球
3.(2014· 长春模拟)若一个正四面体的表面积为S1,其内切球 S1 的表面积为S2,则 =________. S2
2
答案:C
空间几何体的表面积及体积计算公式

空间几何体的表面积及体积计算公式空间几何体是指在三维坐标系中存在的几何图形,包括立方体、圆锥体、圆柱体、球体等等。
对于这些几何体来说,求其表面积和体积是我们在学习空间几何时需要掌握的核心内容。
下面我们将详细介绍各种空间几何体的表面积及体积的计算公式。
一、立方体立方体是一种六个面都是正方形的几何体,其表面积和体积计算公式如下:表面积 = 6 × a²体积 = a³其中,a为立方体的边长。
二、正方体正方体是一种所有面都是正方形的几何体,其表面积和体积计算公式如下:表面积 = 6 × a²体积 = a³其中,a为正方体的边长。
三、圆锥体圆锥体是一种由一个圆锥顶点和一个底面为圆形的仿射锥面构成的几何体,其表面积和体积计算公式如下:表面积= πr²+πrl体积= 1/3πr²h其中,r为底面圆半径,l为母线长度,h为圆锥体的高。
四、圆柱体圆柱体是一种由平行于固定轴的两个相等且共面的圆面和它们之间的圆柱面所围成的几何体,其表面积和体积计算公式如下:表面积= 2πrh+2πr²体积= πr²h其中,r为底面圆半径,h为圆柱体的高。
五、球体球体是一种由所有到球心的距离等于固定半径的点所组成的几何体,其表面积和体积计算公式如下:表面积= 4πr²体积= 4/3πr³其中,r为球体的半径。
以上就是五种常见空间几何体的表面积及体积计算公式,希望能够对大家在学习空间几何时有所帮助。
同时,我们也需要关注其实际应用,在工程建设和生活中经常会涉及到这些几何体的计算,因此深化这些知识点的学习,将对我们未来的发展产生积极的影响。
空间几何体的表面积与体积公式大全,DOC
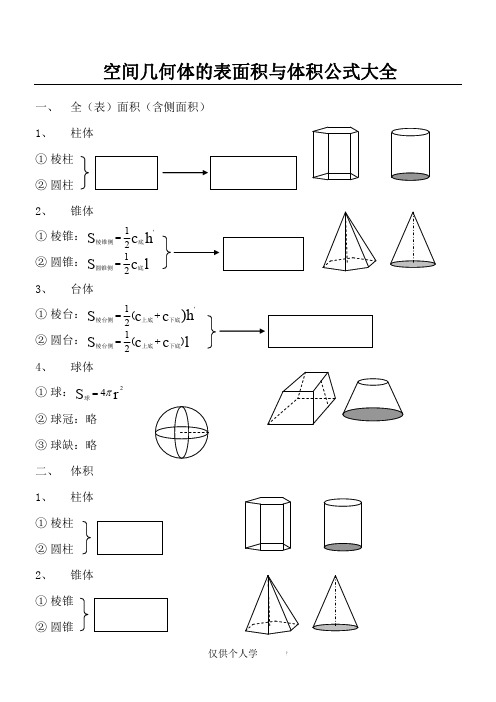
空间几何体的表面积与体积公式大全一、全(表)面积(含侧面积)1、①棱柱②圆柱2、①②3、①②4、①球:②③二、1、①棱柱②圆柱2、①棱锥②圆锥3、①棱台②圆台4、①球:②③三、1、2、则+=即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和 3、台体体积公式公式:)(31S SS S h V 下下上上台++=证明:如图过台体的上下两底面中心连线的纵切面为梯形ABCD 。
延长两侧棱相交于一点P 。
则∴V 即:)(33)(31S SS S h h S S S hS V 下下上上下上下上台++=++=∴)(31S S S S h V 下下上上台++=4、球体体积公式推导分析:将半球平行分成相同高度的若干层(层n ),n 越大,每一层越近似于圆柱,+∞→n 时,每一层都可以看作是一个圆柱。
这些圆柱的高为nr,则:每个圆柱的体积h S V i i ==nrr i 2π……=2r nr ⨯π=[3r n n π=[3r n n π当→n ∴V 半球5、 ∴S =球6、(1则其体积为:a V 3=正方体四个角上切下的每一个三棱锥体积为:中间剩下的正四面体的体积为:a a a a hSV 322231]60sin 21[3131)32232()2()2(=-⨯︒⨯⨯⨯==⨯⨯正三棱锥这样一个即:61(2 (a)(b)(c)(d)(e)(3(a ) 正方体内切球直径=正方体棱长(b ) 正方体内切球与正四面体的四条棱相切。
(c ) 与正四面体四条棱相切的球半径=正方体棱长的一半 (d ) 设正四面体棱长为a ,则与其棱都相切的球半径为r 1有:aar 422211=⨯= 7、利用祖暅原理推导球体体积。
构造一个几何体,使其截面与半球截面处处相等,根据祖暅原理可得两物体体积相等。
证明:作如下构造:在底面半径和高都是r 的圆柱内挖去一个与圆柱等底等高的圆锥。
如图:R ,∴S 1π=即:S 1 8、 正方体与球(1) 正方体的内切球正方体的棱长=a 球体的直径d (2) 正方体的外接球正方体的体对角线=a 3球体的直径d(3) 规律:①正方体的内切球与外接球的球心为同一点; ②正方体的内切球与外接球的球心在体对角线上; ③正四面体的内切球与外接球的的半径之比为:3:1 ④正四面体内切球与外接球体积之比为:1:339(∴a h r 12641==即:a a r V 33321663434)126(πππ===球∴π3:18=V V 球正四机体: (2)正四面体的外接球 外接球的半径=)2332(224343a a⨯-⨯=⨯高=a 46 ∴2:33122:86:33ππ==aaV V 正四面体球 (310、 (1 球体直径、圆柱的高、圆柱底面直径构成直角三角形。
空间几何体的表面积和体积公式汇总表

空间几何体的表面积和体积公式汇总表1.多面体的面积和体积公式2.旋转体的面积和体积公式3.(1)圆柱的侧面展开图是一个 ,设底面半径为r ,母线长为l ,那么圆柱的底面积 =底S ,侧面积=侧S ,表面积S = 。
(3)圆锥的侧面展开图是一个 ,设圆锥的底面半径为r ,母线长为l ,那么它的底面积=底S ,侧面积=侧S ,表面积S = 。
(4)圆台的侧面展开图是一个 ,设上、下底面圆半径分别为r '、r ,母线长为l ,那么上底面面积=上底S ,下底面面积=下底S 那么表面=S 。
4、正四面体的结论:设正四面体的棱长为a ,则这个正四面体的(1)全面积?:S 全2a ; (2)体积?:V=312a ; (3)对棱中点连线段的长?:d= 2a ;(4)对棱互相垂直。
(5)外接球半径?:R= a ; (6)内切球半径;??? r= a5、正方体与球的特殊位置结论;空间几何体练习题1.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为1V 和2V ,则1V :2V 是( )A. 1:3B. 1:1C. 2:1D. 3:12.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )A. ππ221+B. ππ421+C. ππ21+D. ππ241+ 3.一个圆锥的展开图如图所示,其中扇形的圆心角为0120,已知底面圆的半径为1,求该圆锥的体积。
4. 已知棱长为a ,各面均为等边三角形的四面体ABC S -,求它的表面积。
5.圆柱的侧面展开图是长、宽分别为6π和π4的矩形,求圆柱的体积。
6.若圆台的上下底面半径分别为1和3,它的侧面积是两底面面积和的2倍,则圆台的母线长是( ) A. 2 B. 2.5 C. 5 D. 107.圆柱的侧面展开图是长为12cm ,宽8cm 的矩形,则这个圆柱的体积为( )A. π2883cm B. π1923cm C. π2883cm 或 π1923cm D. π1923cm8.一个圆柱的底面面积是S ,侧面展开图是正方形,那么该圆柱的侧面积为( )32A. 4sπB. Sπ2C. SπD. Sπ3。
