14届数学教学交流

2024参加全市高三数学教学研讨会的心得体会

2024参加全市高三数学教学研讨会的心得体会2024参加全市高三数学教学研讨会的心得体会 1通过参加10月14日省举办的送教下乡活动，我不但从知识应讲授的深浅上有很大的收获，还从课程的讲授方法上学到了很多。

自从参加工作，我已送过几届高三，每次上高三课时都有不同的收获，可是很少注意总结，有时由于理解的不到位，或者掌握的知识或理论不够，即便总结也不全面。

这次王老师的“如何人认识新课标对高考的影响”报告，使我对高三课程的讲授有了全面的把握，还对某些重要的知识点有了更深的理解。

以前上课，很多问题都是我讲他们听，我讲得多学生做得少。

再加上学生对基础知识掌握的不够好，做起题来很费时间，使得平时练习少，到考试时好多同学都做不完题。

王老师在这次讲座中把每种题型都分析了一遍，同时还举了很多高考例题。

通过例题的讲解，我知道每种题型都给学生们讲解到什么程度，有多少种方法对付它们。

例如圆锥曲线问题，我就可以要求我的学生只做第一问，第二问可以尝试方程联立，不行就放弃。

这是我以前没有认识到的。

14号下午王老师上了一节《椭圆的标准方程》观摩课。

王老师的这节课有很多地方是我以前没有想到的，例如一开始用实际生活中的剪纸、卫星轨道、树叶等让学生初步认识椭圆。

以前我都是一开始就叫学生们准备一根绳子，叫两个学生到黑板上画椭圆，这样他们可能觉得学完椭圆后和现实生活没有关系，从而没有学习的兴趣。

通过这次观摩，我打算在以后的讲课中一定要充分利用网络资源和身边的资源，丰富我的教学，使我的课堂生动起来，让学生们乐学，解决上课听课效果不好的问题。

让我的学生把基础打好，使学生们在做题时有收获的喜悦，只要让他们每天都体验到一点点的成功，就会像滚雪球一样慢慢形成更大的成功感。

新鲜的理论给了我新的想法，我想从以下方面，重新规划我的高三教学：高三复习注意低起点、重探究、求能力的同时，还注重抓住分析问题、解决问题中的信息点、易错点、得分点，培养良好的审题、解题习惯，养成规范作答、不容失分的习惯。

中南林业科技大学第十四次教学经验交流暨教学优秀表彰...

中南林业科技大学第十四次教学经验交流暨教学优秀表彰大会先进集体和优秀个人表彰名单(所有奖项和获奖者排名不分先后)一、教学工作先进单位（9个）土木工程与力学学院外国语学院生命科学与技术学院机电工程学院材料科学与工程学院林学院食品科学与工程学院旅游学院商学院二、服务教学先进单位（5个）后勤集团图书馆学生工作部实验室建设与资产管理处教务处三、质量工程组织奖（3个）材料科学与工程学院林学院食品科学与工程学院四、优秀教研室、实验室（23个）力学教研室大学英语教研室木材科学与技术教研室市场营销教研室汉语言教研室生态学教研室自动化教研室材料成型及控制工程教研室饭店管理教研室物流工程教研室物理教研室环境科学教研室金融学教研室美术基础教研室食品科学与工程教研室力学实验中心大学物理实验室生物技术与工程实验室电工电子实验室机械基础实验中心林业技术实验室现代物流实验中心高分子材料与工程实验室五、优秀课程奖（12个）大学体育大学物理大学英语木材学市场营销学电路分析基础机械制图材料力学供应链管理树木学食品原料学基础英语六、专业建设优秀奖（7个）市场营销专业生物技术专业园林专业林产化工专业林学专业物流工程专业食品科学与工程专业七、优秀教材奖（12个）一等奖：《环境法学》《桥梁工程》《植物群体遗传学》二等奖：《Web数据库编程与应用》《林业生物技术》《森林旅游学》三等奖：《会计学原理与实务模拟实验教程》《机械设计基础》《供应链管理》《非木材植物人造板》《营销策划学》《管理技能开发》八、校级教学成果奖（12个）一等奖：1、林科教相结合，林业创新型人才培养模式的研究与实践完成人：章怀云吴晓芙曹福祥文仕知向春阶2、改革传统教学内容和方法，全面推进基础力学的数字化、网络化和立体化建设完成人：罗迎社唐小弟陈自力贺国京3、工商管理类本科专业实践教学模式完成人：邓德胜祝海波何志祥尹少华方威二等奖：1、普通高等学校物流管理本科专业课程体系优化研究完成人：庞燕王忠伟李义华李翔晟刘雯雯2、精品课程建设的研究与实践完成人：汤小红曹福祥向春阶邓联健柳伟3、提高英语习得者交际能力的校本课程研究与开发完成人：张沉香邓天文王小宁三等奖：1、森林工程学科专业改造与提升研究完成人：王忠伟庞燕汤小红肖玉桃刘雯雯2、森林培育博士研究生教育培养方法改革系列研究完成人：李志辉张日清王承南杨模华何方3、跨校区大学生英语演讲选手培训经验总结——大学生英语听说能力培养的实践完成人：肖旭华邓联健王琼张广酃翟红4、设计类课程实践教学的改革与探索完成人：胡希军戴向东陈友存沈守云肖瑞龙5、高校图书馆隐性文化建设的研究完成人：崔红娟章怀云孙凤英刘振西曹志希6、艺术设计专业创新人才培养模式的研究与实践完成人：戴向东李克忠曾献陈杰张秋梅九、教学名师奖（3人）吴义强钟永德谭晓风十、优秀教师一等奖（24人）王慧英车生兵邓集钢甘瑁琴邝祝芳刘破浪朱月娥朱玉林阳永恒吴章文张卉李闽杨光辉汪斌庞燕罗攀柱段祝庚项文化唐丽唐小弟陶涛黄亮谢洁飞戴向东十一、优秀教师二等奖（33人）于杰文东新王森王名学王润琪邓莉文刘亦刘俊月刘晓艳孙吉康何敏张清张亚连张响三张锡滨旷春桃李义志李志奇杨仕若陈永华陈永红周慧英欧阳勤罗卫华段志强钟芸香夏岚徐卓农晏密英晏毓晨盛忠志彭桂芬雷军十二、优秀实验教师奖（6人）文瑞芝邓凌峰邓瑞基张永忠杨清遗董旭杰十三、优秀青年教师奖（15人）马芳王传立王浩波刘红刘瑛张楠张党权李双艳邹雨真陈飞罗洁宿燕曾超珍熊丽娟谭丹十四、教学优秀奖（27人）占鸣春卢艳红刘发林朱凡张仲凤张继娟李水芳李新功肖建武陈楠周灿周健周禧玲罗俊美郑贵军柳建安徐邦俊崔敏曹兰田曹时军黄跃如黄慧华彭姣飞曾敏蒋兰香谢忠球谢禄山十五、教学管理优秀奖（25人）王蓉王碧王解军邓天文刘雯雯向春阶朱罗敬汤小红张红张阳春张晓蕾李应洪李翔晟陈自勇武燕萍钟海雁徐刚标黄宁廷蒋米卡谢丽谢冽韩健熊奇志蔡珍贵戴秀珍十六、服务教学优秀奖（51人）丁科马恕风毛纺成王仲王玉萍王劲松邓和平龙成良伍谦全彩英刘洋刘艳刘志娟刘金伟刘新民吕伟军朱婧纯汤满意严永林何志祥吴敬东张江张玫张银全李健李波涛李容贵李雄光陈名虎陈春艳陈贵云周雯周静周预分欧阳娜娜段小平洪梅夏书夏松林徐庆军栗彬袁红梅高跃军屠益萍黄海军龚铮午靖磊廖乐平管贵秋虢臻戴瑜2008-2009年度获市级以上奖励名单一、2009年全国五一劳动奖田大伦二、2009年全国优秀教师吴义强三、2009年湖南省先进工作者田大伦四、2009年湖南省优秀教师王忠伟五、2008年湖南省优秀教学成果奖二等奖1．林科教相结合，林业创新型人才培养模式的研究与实践完成人：章怀云吴晓芙曹福祥文仕知向春阶2．改革传统教学内容和方法，全面推进基础力学的数字化、网络化和立体化建设完成人：罗迎社唐小弟陈自力贺国京3．工商管理类本科专业实践教学模式完成人：邓德胜祝海波何志祥尹少华方威三等奖1．普通高等学校物流管理本科专业课程体系优化研究完成人：庞燕王忠伟李义华陈德良符瑛2．精品课程建设的研究与实践完成人：汤小红曹福祥向春阶邓联健柳伟3．提高英语习得者交际能力的校本课程研究与开发完成人：张沉香邓天文王小宁六、湖南省全国大学英语四六级考试优秀考点中南林业科技大学教务处七、2008年度全国计算机等级考试优秀考点中南林业科技大学教务处八、霍英东教育会青年教师奖三等奖方威九、湖南省普通高校思想政治理论课“优秀教师”李道志十、湖南省高等学校成人教育工作先进个人冯革非黄礼云十一、全国大学英语四六级考试先进工作者彭金波十二、全国计算机等级考试先进工作者彭金波十三、湖南省第二届高等学校专职军事教师授课比赛一等奖龙双喜十四、湖南省第三届高等学校专职军事教师授课比赛二等奖龙双喜十五、2008年度湖南省普通高校思想政治理论课“精彩一课”评选活动刘红（二等奖）陈石明（二等奖）白雪霜（三等奖）十六、湖南省高等学校第八届“中南杯”多媒体教育软件大赛陈敏（三等奖）十七、湖南省高等学校第九届“中南杯”多媒体教育软件大赛陈敏（二等奖）庞燕（三等奖）唐小弟（三等奖）十八、指导学生参加省级（含省级）以上竞赛奖1．湖南省第14届大学生英语演讲比赛本科一组团体二等奖指导老师：肖旭华王琼2．湖南省第14届大学生英语演讲比赛个人二等奖2项指导老师：肖旭华王琼3．湖南省第15届大学生英语演讲比赛本科一组团体三等奖指导老师：肖旭华王琼4．湖南省第15届大学生英语演讲比赛个人二等奖指导老师：肖旭华王琼5．湖南省第15届大学生英语演讲比赛个人三等奖2项指导教师：肖旭华王琼6．第二届全国大学生物流设计大赛一等奖指导老师：庞燕7．第三届湖南省大学生机械创新设计大赛一等奖指导老师：杨蹈宇马庆勇8．第三届湖南省大学生机械创新设计大赛三等奖指导老师：柳建安陈飞9．第三届湖南省大学生机械创新设计大赛三等奖指导老师：谢洁飞丁敬平10．第四届湖南省力学竞赛综合组一等奖指导老师：王荣海苏淑兰11．第四届湖南省力学竞赛材料力学组二等奖指导老师：王荣海12．第四届湖南省力学竞赛材料力学组三等奖2项指导老师：王荣海13．第四届湖南省力学竞赛理论力学组二等奖2项指导老师：苏淑兰14．第四届湖南省力学竞赛理论力学组三等奖4项指导老师：苏淑兰15．第五届湖南省力学竞赛综合组三等奖2项指导老师：丁科黄伟王荣海陈胜铭16．第五届湖南省力学竞赛理论力学组三等奖3项指导老师：丁科黄伟王荣海陈胜铭17．第五届湖南省力学竞赛材料力学组二等奖指导老师：丁科黄伟王荣海陈胜铭18．第五届湖南省力学竞赛材料力学组三等奖2项指导老师：丁科黄伟王荣海陈胜铭19．2009年全国大学生数学建模竞赛三等奖2项指导老师：刘勉声黄政龙石龙陈芳芳李淑花唐玲20．湖南省第四届大学生程序设计竞赛团体第四名指导老师：谭骏珊，邝祝芳、杨卫民21．湖南省第四届大学生计算机程序设计竞赛获三等奖2项指导老师：邝祝芳22．湖南省第四届大学生计算机程序设计竞赛获三等奖指导老师：杨卫民23．湖南省第五届大学生程序设计竞赛团体第四名指导老师：余绍军，邝祝芳、杨卫民24．湖南省第五届大学生计算机程序设计竞赛获二等奖2项指导老师：邝祝芳25．湖南省第五届大学生计算机程序设计竞赛获三等奖指导老师：杨卫民26．2009年全国大学生电子设计竞赛湖南省一等奖指导老师：张永忠朱俊杰任嘉27．2009年全国大学生电子设计竞赛湖南省二等奖指导老师：赵伟志周凯李颖28．2009年全国大学生电子设计竞赛湖南省三等奖指导老师：鄢永明马振燕周国雄29．2009年全国大学生电子设计竞赛湖南省三等奖指导老师：王湘中姚晔杨菊秋30．第三届全国大学生广告艺术大赛湖南分赛区一等奖1项指导老师：肖锋刚31．第三届全国大学生广告艺术大赛湖南分赛区二等奖1项指导老师：邓敏32．第三届全国大学生广告艺术大赛湖南分赛区三等奖1项指导老师：曹阳33．第三届全国大学生广告艺术大赛湖南分赛区三等奖1项指导老师：曹阳肖德荣质量工程项目获奖一、国家级特色专业资源环境与城乡规划管理食品科学与工程工业设计森林资源保护与游憩二、国家级精品课程木材学大学英语三、湖南省精品课程材料力学电路分析基础供应链管理食品原料学基础英语四、湖南省特色专业木材科学与工程农林经济管理环境科学土地资源管理林产化学加工旅游管理市场营销林学园林五、湖南省实践教学中心林业生物质资源加工工程实验中心林业技术实验中心力学实验中心现代物流实验中心六、湖南省教学团队食品科学与工程专业教学团队林学专业教学团队七、湖南省普通高等学校优秀教材电子商务概论电工与电子技术（上下）林业系统工程基础八、湖南省优秀实习基地湖南亚华乳业有限公司攸县林科所长沙金霞经济开发区物流实习教学基地张家界奥威科技有限公司实习教学基地长沙华天大酒店实习教学基地九、湖南省优秀教研室大学英语二教研室生态学教研室食品科学与工程教研室力学教研室十、湖南省普通高校教学名师罗迎社十一、2008年湖南省普通高校青年教师教学能手张锡滨熊玲君王浩波十二、2009年湖南省普通高校青年教师教学能手马芳陈飞彭湘莲2008-2009年度指导学生参加各类学会、协会获奖1．2008年湖南省第五届日语竞赛演讲比赛特等奖一项指导教师：张静懿夏丽蓉2．2008年湖南省第五届日语竞赛演讲比赛四年级组一等奖一项指导教师：张静懿夏丽蓉3．2008年湖南省第五届日语竞赛演讲比赛三年级组三等奖一项指导教师：张静懿夏丽蓉4．2008年湖南省第五届日语竞赛演讲比赛二年级组优胜奖一项指导教师：张静懿夏丽蓉5．2008年湖南省第五届日语竞赛作文比赛四年级组一等奖一项指导教师：蒋丽华任霞6．2008年湖南省第五届日语竞赛作文比赛二年级组二等奖一项指导教师：蒋丽华任霞7．2009年湖南省高校大学生数学竞赛非数学专业类二等奖指导老师：王松然柏超陈宏斌8．2009年湖南省高校大学生数学竞赛非数学专业类三等奖3项指导老师：王松然柏超陈宏斌9．2009年湖南省第二届大学生物理竞赛二等奖指导老师：李水盛忠志王新军10．2009年ACM国际大学生程序设计竞赛亚洲区哈尔滨赛区竞赛银牌指导老师：邝祝芳11．2009年ACM国际大学生程序设计竞赛亚洲区宁波赛区竞赛铜牌指导老师：邝祝芳12．2009年ACM国际大学生程序设计竞赛亚洲区上海赛区竞赛铜牌指导老师：邝祝芳13．2009年ACM国际大学生程序设计竞赛华中南区竞赛获铜牌指导老师：邝祝芳14．第六届“挑战杯”瓮福中国大学生创业计划竞赛铜奖1项指导老师：胡景初戴向东刘文金祝海波贺一姣王才喜王天翼15．第十一届“挑战杯”全国大学生课外学术科技作品竞赛一等奖指导老师：周慧宾尹少华左旦平16．第三届“挑战杯”湖南省大学生创业计划竞赛银奖1项指导老师：王才喜王天翼17．第三届“挑战杯”湖南省大学生创业计划竞赛铜奖4项指导老师：王才喜王天翼沈学杰王才喜王天翼周凯18．第八届“挑战杯”湖南省大学生课外学术科技作品竞赛三等奖6项指导老师：周先雁喻勋林周国英文仕知周慧滨尹少华19．第八届“挑战杯”湖南省大学生课外学术科技作品竞赛二等奖5项指导老师：谭晓风郑哲文徐剑莹钟永德罗明春邓德胜。

福建参观见学心得体会（精选3篇）

福建参观见学心得体会福建参观见学心得体会（精选3篇）心中有不少心得体会时，就十分有必须要写一篇心得体会，这样可以不断更新自己的想法。

应该怎么写才合适呢？下面是小编帮大家整理的福建参观见学心得体会（精选3篇），仅供参考，欢迎大家阅读。

福建参观见学心得体会1参加“现代与经典”全国数学教学观摩研讨会回来已有一段时间了，今天终于静下心来，再次细细地回味、品读名师们的精彩课堂。

曾经的我很是纳闷，如何在简约的课堂呈现教师的智慧，体现课堂的精彩。

当我有幸听了福建省福安市实验小学阳泉校区罗鸣亮校长的一节观摩课四年级《认识整万数》，课后提出交流如何做教育的有心人，终于我有了自己的理解：简约课堂，精彩无限。

当然，我无法复制罗校长的精彩，但他的课堂却留给我更多的思考和迫切想要与大家分享的几点心得。

一、留心生活，寻找现实生活中的数学素材，灵动设计教学环节。

这是罗校长上课后，与我们共同探讨如何设计教学时的一句原话。

正是因为这句话，才出现了开课时罗校长精心准备的课件赵本山表演的春晚小品《捐款》，以及与此相呼应的最后一个教学环节听计算器的响声，报出各大牌明星为汶川灾后重建家园的爱心捐款数额。

我佩服罗校长的用心，为了自己的课堂充满生活气息，为了让学生体会生活处处有数学，他从生活中给儿子买计算器放车上不小心碰到发出响声的小事，就灵机一动设计了听声音报数据的捐款游戏，既巩固了整万数的读法、突出了分级读数的重要性，又达到教育学生奉献自己爱心的深远意义；从全国观众都喜欢收看的春晚节目中找到《捐款》，引出三百万，从放出一叠1万元人民币的实际图像课件，到10万、100万、300万的展示过程让学生初步体会整万数的概念，学生在感叹三百万有这么多钱啊的时候，教师适时提出如何在已学过的只有个级的计数器上表示出来？并选出代表上来通过拨数，遇到拨不出三百万的困惑，使学生陷入迫切需要帮助的氛围中，激发学生的学习积极性，让学生因需而学，从而水到渠成地进入新知识的学习。

大家一定要珍惜此次学习机会。相信每一次与专家对话,与

大家一定要珍惜此次学习机会。

相信每一次与专家对话，与同行研讨，都会让我们的生命更加丰盈，更加充实，更加完美！培训不仅是知识的扩充、理念的提高，更是对我们心灵的一次洗涤、净化和升华！作为辅导教师，我会认真履行各项职责，做好各项研修活动，及时收集老师们的困惑与热点与指导团队沟通交流，我更愿成为大家的朋友。

虽然我没有专家学者的渊博知识，没有深邃的学术思考，但是我拥有一颗热忱真挚的心。

我会用心组织，用心指导，用心参与，愿为大家的学习贡献自己的微薄之力，愿和大家一起启迪智慧，共同成长！注重学思结合，高效完成作业学用结合，学、研、思、行集成。

课程学习丰富学识，提高理论素养：研修活动集思广益，拓展解决问题的思路；反思自己的教学，围绕问题解决重构知识与能力体系；行动指向实践，通过生成创新方案物化培训结果。

借助群体智慧突破个人认知局限创新成果酝酿：伴随培训过程，酝酿并形成一份创新性培训成果（问题解决预案）。

成果可以是解决教学问题的“教学设计方案”；可以是解决班级或学生管理问题的工作计划；也可以是解决自身专业发展问题的“专业发展规划”。

创新性培训成果作为终结性考核依据，在培训活动结束时提交。

最终的落脚点在创新性成果上。

专家视频答疑和在线指导时间安排日期时间学科会议名称密码专家（所在地）10月25日（星期四）14:30—16:30初中物理2012年山西全员培训初中物理视频答疑25032黎红(北京)10月25日（星期四）19:00—21:30师德2012年国培师德第一次专家视频答疑10250310月26日（星期五）19:00—21:30小学初中美术2012年示范性项目小学初中美术第四次专家在线指导26163侯令（北京）10月26日（星期五）9:00—11:00初中英语2012年山西全员培训初中英语视频答疑26041袁昌寰(北京)10月27日（星期六）9:30—11:30初中地理2012年山西全员培训初中地理视频答疑27061吉小梅(北京)10月27日（星期六）14:30—17:00初中历史2012年示范性项目初中历史第四次专家在线指导27152闫璟等（北京）10月29日（星期一）14:30—16:30初中化学2012年山西全员培训初中化学视频答疑29082黄燕宁(北京)10月29日（星期一）19：00-21：30初中历史2012年示范性项目初中历史第五次专家在线指导29203张静、颜世佳等（北京）10月30日（星期二）9：00--11：30幼儿教育2012年示范性项目幼儿教育第四次专家在线指导30171刘洪霞专家团队（北京）10月30日（星期二）14:00—16:30小学品德与社会2012年示范性项目小学品德与社会第四次专家在线指导30182赵亚夫10月30日（星期二）19:00—21:00初中体育2012年山西全员培训初中体育视频答疑28071毛振明(北京)10月31日（星期三）9：00--11：30初中思想品德2012年示范性项目初中思想品德第四次专家在线指导31191朱小蔓专家团队（北京）10月31日（星期三）14:30—16:30初中语文2012年山西全员培训初中语文视频答疑31092李镗(北京)11月1日（星期四）9:00—11:00初中美术2012年山西全员培训初中美术视频答疑等待更新陈卫和(北京) 14:30—16:30初中音乐2012年山西全员培训初中音乐视频答疑等待更新陈文明(北京)11月2日（星期五）9:00—11:00初中数学2012年山西全员培训初中数学视频答疑等待更新王瑞霖(北京)11月2日（星期五）19:00—21:30小学初中美术2012年示范性项目小学初中美术第五次专家在线指导等待更新魏瑞江（天津）11月3日（星期六）14:30—16:30初中综合实践2012年山西全员培训初中综合实践视频答疑等待更新郭元祥(北京)11月6日（星期二）9：00--11：30幼儿教育2012年示范性项目幼儿教育第五次专家在线指导等待更新刘洪霞专家团队（北京）11月6日（星期二）14:00—16:30小学品德与社会2012年示范性项目小学品德与社会第五次专家在线指导等待更新高峡11月7日（星期三）9：00--11：30初中思想品德2012年示范性项目初中思想品德第五次专家在线指导等待更新朱小蔓专家团队（北京）关于“我的教学故事”，尽管在考核里没有体现，但能增加自己的学习力，加分多。

国际小学数学教育研究探析--基于ICME-14小学数学教育研究专题的分析

教学月刊·小学版2021/6数学JIAOXUEYUEKANXIAOXUEBAN国际小学数学教育研究探析——基于ICME-14小学数学教育研究专题的分析□裴亦汝1曹阳2张侨平12021年7月11日至18日，第14届国际数学教育大会将在中国上海召开。

国际数学教育大会（International Congress on Mathematical Education,简称ICME ）是在国际数学教育委员会指导下每四年召开一次的国际性学术会议，是目前国际数学教育界水平最高、规模最大的学术盛会。

其宗旨为展示全球数学教育的最新进展，交流全球数学教育问题的相关信息，探讨数学学科最新进展对数学教育发展的启示。

同时，ICME-14也为世界各地数学教育研究者及爱好者提供交流与学习的平台。

作为国际性学术会议，ICME-14所展现的最新研究成果将指引今后数学教育界的发展。

小学数学教育作为数学教育中最基础的组成部分，其在ICME-14中的研究领域及热点值得探讨。

据此，本文将梳理ICME-14中有关小学数学教育和数学教学研究的专题，管中窥豹，希望能为小学数学教育工作者及爱好者略要描绘国际小学数学教育的关注点，并为其今后的研究及教学提供相应的启示。

一、ICME-14会议报告概览本届大会包括大会全体活动和非全体活动两种形式。

其中，全体活动包含4场大会个人报告和3场大会团体辩论报告。

非全体活动形式多样，包括4场专题调查、71场邀请报告、62场专题研究（Topic Study Group ，简称TSG ）以及国家展示、讨论组、工作坊和一些与数学相关的主题活动等。

本次大会在主题的分类和设计上尽可能涵盖数学教育研究中各个不同的研究领域。

已有文献将此次大会62场TSG 划分为8个主题[1]，根据按学段分类的需要，我们将学段作为独立的主题，进一步将TSG细分为9个主题（如图1）。

与ICME-13相比，本届大会新设如下几个专题：（1）编程与算法的教与学；（2）作为服务科目的数学；（3）少数民族数学教育；（4）教师教育者的知识与实践；（5）数学问题解决与提出；（6）数学教育中的国际合作。

江苏省苏锡常镇2024届高三下学期教学情况调研(一模)数学试卷及答案

2023~2024学年度苏锡常镇四市高三教学情况调研（一）数学2024.3注意事项：1.答卷前，考生务必将自己的姓名､准考证号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将答题卡交回.一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}2320A xx x =++>∣，集合{}04B x x =∣ ，则（）A.A B ⋂=∅ B.A B ⋃=R C.A B ⊆ D.B A⊆2.设5250125(12)x a a x a x a x +=++++ ，则125a a a +++= （）A.-2 B.-1 C.242 D.2433.已知平面向量,,a b c 满足0,||||1,||3a b c a b c ++====，则a 与b 的夹角为（）A.π4 B.π3 C.2π3 D.3π44.青少年的身高一直是家长和社会关注的重点，它不仅关乎个体成长，也是社会健康素养发展水平的体现.某市教育部门为了解本市高三学生的身高状况，从本市全体高三学生中随机抽查了1200人，经统计后发现样本的身高（单位：cm ）近似服从正态分布()2172,N σ，且身高在168cm 到176cm 之间的人数占样本量的75%，则样本中身高不低于176cm 的约有（）A.150人 B.300人 C.600人 D.900人5.函数()πsin 23f x x ⎛⎫=+⎪⎝⎭在区间()0,2π内的零点个数为（）A.2 B.3 C.4 D.56.在平面直角坐标系xOy 中，已知A 为双曲线2222:1(0,0)x y C a b a b-=>>的右顶点，以OA 为直径的圆与C 的一条渐近线交于另一点M ，若12AM b =，则C 的离心率为（）2 B.2 C.2 D.47.莱莫恩（Lemoine ）定理指出：过ABC 的三个顶点,,A B C 作它的外接圆的切线，分别和,,BC CA AB 所在直线交于点,,P Q R ，则,,P Q R 三点在同一条直线上，这条直线被称为三角形的Lemoine 线.在平面直角坐标系xOy 中，若三角形的三个顶点坐标分别为()()()0,1,2,0,0,4-，则该三角形的Lemoine 线的方程为（）A.2320x y --= B.2380x y +-=C.32220x y +-= D.23320x y --=8.已知正项数列{}n a 满足()*1223111121n n n n a a a a a a n ++++=∈+N ，若5627a a -=，则1a =（）A.13 B.1 C.32D.2二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知复数123,,z z z ，下列说法正确的有（）A.若1122z z z z =，则12z z = B.若22120z z +=，则120z z ==C.若1213z z z z =，则10z =或23z z = D.若1212z z z z -=+，则120z z =10.已知函数()sin 2cos2x f x x=-，则（）A.()f x 的最小正周期为πB.()f x 的图象关于点()π,0对称C.不等式()f x x >无解D.()f x 的最大值为2411.如图，在棱长为2的正方体1111ABCD A B C D -中，E 为1AA 的中点，点F 满足()11101A F A B λλ= ，则（）A.当0λ=时，1AC ⊥平面BDFB.任意[]0,1λ∈，三棱锥F BDE -的体积是定值C.存在[]0,1λ∈，使得AC 与平面BDF 所成的角为π3D.当23λ=时，平面BDF 截该正方体的外接球所得截面的面积为56π19三､填空题：本题共3小题，每小题5分，共15分.12.已知变量,x y 的统计数据如下表，对表中数据作分析，发现y 与x 之间具有线性相关关系，利用最小二乘法，计算得到经验回归直线方程为8ˆˆ0.yx a =+，据此模型预测当10x =时ˆy 的值为__________.x56789ˆy 3.5456 6.513.已知()(),0,11,,4log log 4a b a b b a ∞∈⋃++=，则2ln a b b+的最小值为__________.14.在平面直角坐标系xOy 中，已知点()1,1P -和抛物线2:4C y x =，过C 的焦点F 且斜率为(0)k k >的直线与C 交于,A B 两点.记线段AB 的中点为M ，若线段MP 的中点在C 上，则k 的值为__________；AF BF ⋅的值为__________.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）记ABC 的内角,,A B C 的对边分别为,,a b c ，已知2cos 1c B a +=.（1）证明：2B A =；（2）若2sin ,144A b ==，求ABC 的周长.16.（15分）如图，在四棱锥E ABCD -中，EC ⊥平面,,ABCD DC BC AB ⊥∥,22DC DC AB ==，CB CE =，点F 在棱BE 上，且12BF FE =.（1）证明：DE ∥平面AFC ；（2）当二面角F AC D --为135 时，求CE .17.（15分）我国无人机发展迅猛，在全球具有领先优势，已经成为“中国制造”一张靓丽的新名片，并广泛用于森林消防､抢险救灾､环境监测等领域.某森林消防支队在一次消防演练中利用无人机进行投弹灭火试验，消防员甲操控无人机对同一目标起火点进行了三次投弹试验，已知无人机每次投弹时击中目标的概率都为45，每次投弹是否击中目标相互独立.无人机击中目标一次起火点被扑灭的概率为12，击中目标两次起火点被扑灭的概率为23，击中目标三次起火点必定被扑灭.（1）求起火点被无人机击中次数的分布列及数学期望；（2）求起火点被无人机击中且被扑灭的概率.18.（17分）在平面直角坐标系xOy 中，已知点50,3P ⎛⎫- ⎪⎝⎭，过椭圆222:1(1)x C y a a+=>的上项点A 作两条动直线()112212:1,:10l y k x l y k x k k =+=+<<分别与C 交于另外两点,M N .当1k 22=时，AM PM =.（1）求a 的值；（2）若1291,8MN k k NP ==，求1k 和2k 的值.19.（17分）已知函数()24e 2(0)x f x x x x-=->，函数()()2233g x x ax a a a =-+--∈R .（1）若过点()0,0O 的直线l 与曲线()y f x =相切于点P ，与曲线()y g x =相切于点Q .①求a 的值；②当,P Q 两点不重合时，求线段PQ 的长；（2）若01x ∃>，使得不等式()()00f x g x 成立，求a 的最小值.2023~2024学年度苏锡常镇四市高三教学情况调研（一）数学参考答案1.【答案】D【解析】{2A x x =<-∣或{}1},04x B xx >-=≤≤∣，则B A ⊆，选D.2.【答案】C【解析】0x =时，55000123451,1;1,3,a a x a a a a a a =∴===+++++51234531242a a a a a ∴++++=-=，选C.3.【答案】B【解析】a b c +=- ，所以22()a b c += ，所以2223a a b b +⋅+= ，所以12a b ⋅= ，1πcos ,,,23a b a b a b a b ⋅==∴= ，选B.4.【答案】A【解析】()2172,,(168176)0.75,(172176)0.375X N P X P X σ~<<=∴<<=，(176)0.50.3750.125,0.1251200150P X ∴>=-=⨯=，选A.5.【答案】C 【解析】π2π3x k +=，则πππ5,.1,2,π6236k x k k x k x =-+∈====Z ；()4113,π;4,π,36k x k x f x ====在()0,2π选C.6.【答案】B 【解析】tan b AOM a ∠=，则112sin ,22b b AM a AOM ec OA a c ∠===∴==，选故答案选B.7.【答案】B【解析】ABC 的外接圆设为22100,4201640E F x y Dx Ey F D F E F ++=⎧⎪++++=∴++=⎨⎪-+=⎩，034D E F =⎧⎪=⎨⎪=-⎩∴外接圆：22340x y y ++-=，即2232524x y ⎛⎫++= ⎪⎝⎭，在A 处切线：31,:1,,1,C,D 242x y y BC P ⎛⎫=+=∴ ⎪-⎝⎭排除.在C 处切线()4,:1,10,42x y AB y R =-+=∴-，选B.8.【答案】D【解析】1n =时，1211;23n a a =≥时，21111212141n n n n a a n n n +-=-=+--()5666654545611117,99,2799,,18,63,9922a a a a a a a a a a a =∴=∴+=∴===∴=，343232121335,10,15,,3,22a a a a a a a a a =∴==∴==∴= ，选D.二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.【答案】AC 【解析】1122z z z z ⋅=，则221212,z z z z =∴=，A 对.2212z z =，则12i,i z z ==-满足条件，10z ≠，B 错.()12131231,0,0z z z z z z z z =∴-=∴=或230,z z C -=对.令()221212i,i,i ()()z a b z c d z z a c b d a c b d =+=+-=-+-=-+-，()22121212i ()(),z z a c b d a c b d z z z z +=+++=+++-=+，则220ac bd +=，()()()12i i i z z a b c d ac bd ad bc =++=-++不一定为0,D 错，选AC .10.【答案】BD【解析】()()()()sin πsin π,π2cos2π2cos2x x f x f x x x+-+==≠∴-+-不是()f x 的周期，A 错.()()()()()sin 2πsin 2π,2cos22π2cos2x x f x f x f x x x---===-∴---关于()π,0对称，B 对.()()π0π,f f x x -=>-∴>有解，C 错，选B D.()()22sin sin 2sin 1212sin x x f x x x ==+--，求()f x 的最小值.令()112sin 0,12222sin sin x f x x x >=≤=+，当且仅当12sin sin x x =，即2sin 2x =时取"="，D 对，选BD.11.【答案】ACD【解析】0λ=时，F 与1A 重合，平面BDF 为平面11,BDC AC ⊥ 面1BDA ，1AC ∴⊥平面,A BDF 对.11A B 不与平面BDE 平行，F ∴到面BDE 的距离不为定值，∴三棱锥F BDE -的体积不为定值，B 错.当F 在1A 时，AC 与平面BDF 所成角的正弦值为6332<，此时AC 与平面BDF 所成角小于π3，当F 在1B 时，AC 与平面BDF 所成角为ππ,23>∴存在[]0,1λ∈使AC 与平面BDF 所成角为π,C 3正确.如图所示建系，()()()0,0,0,2,2,0,2,2,2D B F λ，设平面BDF 的法向量为()0220,,,,22200n DB x y n x y z x y z n DF λ⎧⋅=+=⎧⎪=∴⎨⎨++=⋅=⎩⎪⎩ 不妨设1x =，则()()1,1,1,1,1,2,2,0y z n AC λλ=-=-=--=- .23λ=，则42,,23F ⎛⎫ ⎪⎝⎭，平面BDF 的法向量11,1,3n ⎛⎫=-- ⎪⎝⎭ ，球心()1,1,1O ，O 到面BDF 的距离19OD n d n ⋅== 44432R ++==，∴截面圆半径2225656,ππ,D 1919r R d S r =-===对，选ACD.三､填空题：本题共3小题，每小题5分，共15分.12.【答案】7.4【解析】7,5,50.87,0.6,0.80.6,ˆ0ˆˆ1x y aa y x x ==∴=⨯+∴=-=-=ˆ7.4.y=13.【答案】ln21+【解析】114log log 4,4log 4,log ,log 2a b a a a b a b b b a b +=∴+=∴=∴=，即22222,ln ln ln a b a b b b b b b b =+=+=+，令()2ln f x x x =+，()221220,2x f x x x x x'-=-===.()f x 在()()()min 0,2,2,,()2ln21,f x f ∞+==+ 此时2,2b a ==14.【答案】2；5【解析】AB 为过焦点的弦，AB 中点为M ，过M 作准线的垂线，垂足为N ，则MN 的中点在抛物线上.PM 的中点在抛物线上，,N P ∴重合.令()()()1122,,,,:1A x y B x y AB y k x =-.()214y k x y x ⎧=-⎨=⎩，消x 可得2121244240,,1,22y y y y y y k k k k +--=+===∴=.()()()22222121212121221111144164y y y y y y y y AF BF x x +-⎛⎫⎛⎫⋅=++=++=++ ⎪⎪⎝⎭⎝⎭164815164+=++=.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.【解析】（1）证明：()2cos 1sin sin sin cos cos sin B A C A B A B+==+()sin sin cos cos sin sin A B A B A B A ⇒=-=-A B A ∴=-或()πA B A +-=（舍），2B A ∴=.（2）2147sin sin22444B A ==⨯⨯=，21314cos 12sin 12,cos 844B A A =-=-⨯==，()2314710252sin sin 4444168C A B ∴=+=⨯+⨯==，由正弦定理21452752448a c =⎧⇒==⇒⎨=⎩ABC ∴ 的周长为714+16.【解析】（1）设BC m =，如图建系.()()()()21,0,1,0,0,0,0,0,2,0,,0,,,033A m C D E m F m m ⎛⎫∴ ⎪⎝⎭，()()21,0,1,,,0,0,,2,33CA m CF m m DE m ⎛⎫===- ⎪⎝⎭设平面AFC 的：一个法向量为()1,,n x y z = ，()101,2,21033mx z n m mx my +=⎧⎪∴⇒=--⎨+=⎪⎩ 1220,DE n m m DE ∴⋅=-+=∴ ∥平面AFC .（2）平面ACD 的一个法向量()20,1,0n =，122122cos1353,3251n n m CE n n m ⋅∴=-=--==+⋅ 17.【解析】（1）起火点被无人机击中次数X 的所有可能取值为0,1,2,3()()32131141120,1C 512555125P X P X ⎛⎫⎛⎫=====⋅⋅= ⎪ ⎪⎝⎭⎝⎭，()()232341484642C ,3551255125P X P X ⎛⎫⎛⎫==⋅⨯==== ⎪ ⎪⎝⎭⎝⎭.X ∴的分布列如下：X 0123P 1125121254812564125()44123,,3555X B E X ⎛⎫~∴=⨯= ⎪⎝⎭.（2）击中一次被扑灭的概率为121134116C 552125P ⎛⎫⎛⎫=⨯= ⎪ ⎪⎝⎭⎝⎭击中两次被火扑灭的概率为222341232C 553125P ⎛⎫=⋅⨯⨯= ⎪⎝⎭击中三次被火扑灭的概率为334645125P ⎛⎫== ⎪⎝⎭∴所求概率63264102125125125125P =++=.18.【解析】（1）22222222112022a y x x a x x a y a ⎧⎛⎫=+⎪⇒++=⎨ ⎪⎝⎭⎪+=⎩()22222225,,0,1,0,223a a M A P a a ⎛⎫--⎛⎫∴- ⎪ ⎪ ⎪++⎝⎭⎝⎭由22222222222221222a a a AM PM a a a ⎛⎫⎛⎫⎛⎫-=⇒+-=+ ⎪ ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭2222523a a ⎛⎫-+ ⎪+⎝⎭，解得24,2a a =∴=.（2）设()()()1122,,,,0,1M x y N x y A ，则()()121221122121211114153011141y x x y x x x y x y y x x y ⎧⎛⎫--⋅=⎪ ⎪+⎪⎝⎭⇒---=⎨⎛⎫-⎪⋅-⋅= ⎪⎪+⎝⎭⎩.()()211221503x x x y x y ⇒--+-=对比,M N 两点方程知MN 过50,3⎛⎫ ⎪⎝⎭与P 重合.1212178171588x x y y ⎧=⎪⎪⎨⎪=+⎪⎩，解得112121,202x k k y =-⎧⇒==⎨=⎩.19.【解析】（1）①()222e e 42x x x f x x --⋅-=⋅-'，设020004e ,2x P x x x -⎛⎫- ⎪⎝⎭()()0022000002004e 2e 1422,x x OPx x x k f x x x x ----∴===⋅-⇒='∴切点()2,2,1P k -=-.l ∴方程：()22y x +=--，即y x=-()2222133033y x x a x a a y x ax a a=-⎧⇒-+++=⎨=-+--⎩()()()22Δ(13)4305110a a a a a =+-+=⇒--=15a ∴=或1②当1a =时，2Q x =，此时()2,2,,Q P Q -重合，舍去.当15a =时，45Q x =，此时44,55Q ⎛⎫- ⎪⎝⎭此时22446222555PQ ⎛⎫⎛⎫=-+-+= ⎪ ⎪⎝⎭⎝⎭.（2）令()()()2224e 233x F x f x g x x x ax a a x-=-=-+-++()()()()22223e 224e 1223,420x x x x x F x x a F x x x --''-+-=-+-'=⋅+>()F x '在()1,∞+上取补集，对1x ∀>，均有()()0f x g x ->成立，即()0F x >恒成立()2222446303201F a a a a a a ∴=-+-++>⇒-+>⇒<或2a >而对1,1x a ∀><经检验均有()0F x >成立，∴原命题中1a ≥而1a =时，()()()224e 1223,x x F x x F x x -'-+-'-= ，注意到()20F '=()F x ∴在()1,2上()()min 2,,()200F x F ∞+∴==≤ 成立，符合.综上：a 的最小值为1.。

福建省福安市第一中学2024届高三3月教学情况调研(一)数学试题

福建省福安市第一中学2024届高三3月教学情况调研（一）数学试题注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B 铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设m ，n 是两条不同的直线，α，β是两个不同的平面，给出下列四个命题：①若//m n ，m β⊥，则n β⊥；②若//m α，//m β，则//αβ；③若m α⊥，//n α，则m n ⊥；④若//m α，m β⊥，则αβ⊥；其中真命题的个数为（）A ．1B ．2C ．3D ．42．已知双曲线()222210,0x y a b a b-=>>的焦距是虚轴长的2倍，则双曲线的渐近线方程为（） A ．33y x =± B ．3y x =± C ．12y x =± D ．2y x =±3．对于正在培育的一颗种子，它可能1天后发芽，也可能2天后发芽，….下表是20颗不同种子发芽前所需培育的天数统计表，则这组种子发芽所需培育的天数的中位数是( )发芽所需天数1 2 3 4 5 6 7 8≥ 种子数4 3 35 2 2 1 0 A ．2 B ．3 C ．3.5 D ．44．已知集合{}2|2150A x x x =-->，{}|07B x x =<<，则()R A B 等于( ) A ．[)5,7- B ．[)3,7- C ．()3,7- D ．()5,7-5．如图是二次函数2()f x x bx a =-+的部分图象，则函数()ln ()g x a x f x '=+的零点所在的区间是（）A ．11,42⎛⎫ ⎪⎝⎭B ．1,12⎛⎫ ⎪⎝⎭C ．(1,2)D ．(2,3)6．点,,A B C 是单位圆O 上不同的三点，线段OC 与线段AB 交于圆内一点M ，若,(0,0),2OC mOA nOB m n m n =+>>+=，则AOB ∠的最小值为（）A ．6πB ．3πC ．2πD ．23π 7．设全集为R ，集合{}02A x x =<<，{}1B x x =≥，则()AB =R A ．{}01x x <≤ B ．{}01x x <<C ．{}12x x ≤<D ．{}02x x << 8．正项等比数列{}n a 中，153759216a a a a a a ++=，且5a 与9a 的等差中项为4，则{}n a 的公比是 ( )A ．1B ．2C ．22D ．29．如图，2AB =是圆O 的一条直径，,C D 为半圆弧的两个三等分点，则()AB AC AD ⋅+=（）A ．52B ．4C ．2D ．13+10．已知函数()f x 满足当0x ≤时，2(2)()f x f x -=，且当(2,0]x ∈-时，()|1|1f x x =+-；当0x >时，()log (0a f x x a =>且1a ≠).若函数()f x 的图象上关于原点对称的点恰好有3对，则a 的取值范围是（） A ．(625,)+∞ B ．(4,64) C ．(9,625) D ．(9,64)11．已知等比数列{}n a 的各项均为正数，设其前n 项和n S ，若14+=n n n a a （n *∈N ），则5S =（）A ．30B ．312C ．2D ．62 12．函数||1()e sin 28x f x x =的部分图象大致是（）A ．B ．C ．D ．二、填空题：本题共4小题，每小题5分，共20分。

数学老师听课心得感悟

数学老师听课心得感悟•相关推荐数学老师听课心得感悟精选范文6篇在日常的学习、工作、生活中，我们心中时常会积累了不少感悟和见解，为了记录自己的所思所想，我们可以写一篇感悟的文章。

不过，你知道要怎么写感悟吗？下面是小编为大家收集的数学老师听课心得感悟精选范文6篇，欢迎阅读与收藏。

数学老师听课心得感悟精选范文6篇1听了这五堂数学课，让我感受颇深，有年龄大的老师，也有刚参加工作的年轻教师，他们的课有太多值得我学习和思考的地方，下面我就谈一下听了这几课以后给我的启发一、一名优秀的教师要具有语言魅力，作为一名数学教师，语言要做到严谨简练，并且要具有亲和力,对孩子要多表扬，多鼓励。

王老师虽然是一名男教师，但语言很轻柔，很具有亲和力，他儿童化的语言一直吸引着孩子的注意力，并且能够及时的表扬孩子，这是值得我学习的地方。

刘老师作为刚参加工作的年轻教师其语言已经做到了严谨简练。

这是我以后的教学中应时刻注意的一点。

二、数学源于生活，最后必须要回到生活当中。

学习知识是为了运用，如果脱离实际来学知识的话，其学习的意义不大。

所以在数学课上，必须让学生知道在现实中的应用。

这几位老师在讲课的最后，都会把今天学习的知识与生活实际相联系，这也是我以后课堂上应该做的。

三、教师灵活的教育机智，在巩固练习环节，翟丽华老师反馈纠正及时，分解了题的难度。

课堂上充分发挥学生的主动性和能动性，合作探究，充分发挥小组合作学习功能。

总之，这几位老师的课基本功过硬，充分展示了教师的综合魅力，很值得我学习。

今后一定多向其他教师学习，总结自己的经验教训，在教学上取得更好的成绩。

数学老师听课心得感悟精选范文6篇210月13日和10月14日我有幸参加了在山东潍坊举办的“育师启智”小学数学课堂教学观摩活动，此次一共听了8节课，对于我来讲真的是开阔了眼界，收获颇丰。

通过听课，让我学到了很多新的教学方法和新的教学理念。

每节课后上课教师都会对自己所上的课进行课前构思与课后反思的阐述，老师们的个人素质都很高，语言丰富，点评到位，教学设计新颖独特，将课标理论和实践很好的结合起来，下面是我的几点收获：一、实施差异教学，构建和谐课堂。

浙江省台州市2024届高三上学期第一次教学质量评估数学试题(含答案解析)

x 1
A． f 2 1 B． f 3 1 （ e 为自然对数的底数， e 2.71828 ）
e
C．存在 x0 R ， f x0 0
D．若 x0 0,1 ，则 f x0 0,1
三、填空题
13．若 z 1 2
2i （ i 为虚数单位），则 z
．
14．浙江省高考实行“七选三”选科模式，赋予了学生充分的自由选择权．甲、乙、丙三
19．如图，已知四边形 ABCD 为平行四边形，E 为 CD 的中点，AB 4 ，AD AE 2 ．将 V ADE 沿 AE 折起，使点 D 到达点 P 的位置．
(1)若平面 APE 平面 ABCE ，求证： AP BE ； (2)若点 A 到直线 PC 的距离为 33 ，求二面角 P AE B 的平面角的余弦值．
x x
'
1
sin 2 x cos 2 x cos 2 x
1
1 cos 2 x
1
，
当
x
0,
π 2
时，因为 cos2
x
1,即
时， y 0 ，
对于 C，当 x 0 时， y f (4) 0 ，C 不可能；
对于 D，当 x 0 时， y f (4) 0 ，D 不可能；
对于 A，当 x 0 时， y f (1) 0 ，而当 x 0 时，1 1 x 1，则 f (1 1 x) 0 ，A 可能；
2
2
对于 B，当 x 0 时， y f (1) 0 ，而当 x 0 时，1 1 x 1，则 f (1 1 x) 0 ，B 不可能.
5
5
为 100 分钟时的数学成绩：（参考数据： xi yi 22820 ， yi 435 ，xi 的方差为 200）

中南林业科技大学第十四次教学经验交流暨教学优秀表彰大会先进.

中南林业科技大学第十四次教学经验交流暨教学优秀表彰大会先进集体和优秀个人表彰名单(所有奖项和获奖者排名不分先后)一、教学工作先进单位（9个）土木工程与力学学院外国语学院生命科学与技术学院机电工程学院材料科学与工程学院林学院食品科学与工程学院旅游学院商学院二、服务教学先进单位（5个）后勤集团图书馆学生工作部实验室建设与资产管理处教务处三、质量工程组织奖（3个）材料科学与工程学院林学院食品科学与工程学院四、优秀教研室、实验室（23个）力学教研室大学英语教研室木材科学与技术教研室市场营销教研室汉语言教研室生态学教研室自动化教研室材料成型及控制工程教研室饭店管理教研室物流工程教研室物理教研室环境科学教研室金融学教研室美术基础教研室食品科学与工程教研室力学实验中心大学物理实验室生物技术与工程实验室电工电子实验室机械基础实验中心林业技术实验室现代物流实验中心高分子材料与工程实验室五、优秀课程奖（12个）大学体育大学物理大学英语木材学市场营销学电路分析基础机械制图材料力学供应链管理树木学食品原料学基础英语六、专业建设优秀奖（7个）市场营销专业生物技术专业园林专业林产化工专业林学专业物流工程专业食品科学与工程专业七、优秀教材奖（12个）一等奖：《环境法学》《桥梁工程》《植物群体遗传学》二等奖：《Web数据库编程与应用》《林业生物技术》《森林旅游学》三等奖：《会计学原理与实务模拟实验教程》《机械设计基础》《供应链管理》《非木材植物人造板》《营销策划学》《管理技能开发》八、校级教学成果奖（12个）一等奖：1、林科教相结合，林业创新型人才培养模式的研究与实践完成人：章怀云吴晓芙曹福祥文仕知向春阶2、改革传统教学内容和方法，全面推进基础力学的数字化、网络化和立体化建设完成人：罗迎社唐小弟陈自力贺国京3、工商管理类本科专业实践教学模式完成人：邓德胜祝海波何志祥尹少华方威二等奖：1、普通高等学校物流管理本科专业课程体系优化研究完成人：庞燕王忠伟李义华李翔晟刘雯雯2、精品课程建设的研究与实践完成人：汤小红曹福祥向春阶邓联健柳伟3、提高英语习得者交际能力的校本课程研究与开发完成人：张沉香邓天文王小宁三等奖：1、森林工程学科专业改造与提升研究完成人：王忠伟庞燕汤小红肖玉桃刘雯雯2、森林培育博士研究生教育培养方法改革系列研究完成人：李志辉张日清王承南杨模华何方3、跨校区大学生英语演讲选手培训经验总结——大学生英语听说能力培养的实践完成人：肖旭华邓联健王琼张广酃翟红4、设计类课程实践教学的改革与探索完成人：胡希军戴向东陈友存沈守云肖瑞龙5、高校图书馆隐性文化建设的研究完成人：崔红娟章怀云孙凤英刘振西曹志希6、艺术设计专业创新人才培养模式的研究与实践完成人：戴向东李克忠曾献陈杰张秋梅九、教学名师奖（3人）吴义强钟永德谭晓风十、优秀教师一等奖（24人）王慧英车生兵邓集钢甘瑁琴邝祝芳刘破浪朱月娥朱玉林阳永恒吴章文张卉李闽杨光辉汪斌庞燕罗攀柱段祝庚项文化唐丽唐小弟陶涛黄亮谢洁飞戴向东十一、优秀教师二等奖（33人）于杰文东新王森王名学王润琪邓莉文刘亦刘俊月刘晓艳孙吉康何敏张清张亚连张响三张锡滨旷春桃李义志李志奇杨仕若陈永华陈永红周慧英欧阳勤罗卫华段志强钟芸香夏岚徐卓农晏密英晏毓晨盛忠志彭桂芬雷军十二、优秀实验教师奖（6人）文瑞芝邓凌峰邓瑞基张永忠杨清遗董旭杰十三、优秀青年教师奖（15人）马芳王传立王浩波刘红刘瑛张楠张党权李双艳邹雨真陈飞罗洁宿燕曾超珍熊丽娟谭丹十四、教学优秀奖（27人）占鸣春卢艳红刘发林朱凡张仲凤张继娟李水芳李新功肖建武陈楠周灿周健周禧玲罗俊美郑贵军柳建安徐邦俊崔敏曹兰田曹时军黄跃如黄慧华彭姣飞曾敏蒋兰香谢忠球谢禄山十五、教学管理优秀奖（25人）王蓉王碧王解军邓天文刘雯雯向春阶朱罗敬汤小红张红张阳春张晓蕾李应洪李翔晟陈自勇武燕萍钟海雁徐刚标黄宁廷蒋米卡谢丽谢冽韩健熊奇志蔡珍贵戴秀珍十六、服务教学优秀奖（51人）丁科马恕风毛纺成王仲王玉萍王劲松邓和平龙成良伍谦全彩英刘洋刘艳刘志娟刘金伟刘新民吕伟军朱婧纯汤满意严永林何志祥吴敬东张江张玫张银全李健李波涛李容贵李雄光陈名虎陈春艳陈贵云周雯周静周预分欧阳娜娜段小平洪梅夏书夏松林徐庆军栗彬袁红梅高跃军屠益萍黄海军龚铮午靖磊廖乐平管贵秋虢臻戴瑜2008-2009年度获市级以上奖励名单一、2009年全国五一劳动奖田大伦二、2009年全国优秀教师吴义强三、2009年湖南省先进工作者田大伦四、2009年湖南省优秀教师王忠伟五、2008年湖南省优秀教学成果奖二等奖1．林科教相结合，林业创新型人才培养模式的研究与实践完成人：章怀云吴晓芙曹福祥文仕知向春阶2．改革传统教学内容和方法，全面推进基础力学的数字化、网络化和立体化建设完成人：罗迎社唐小弟陈自力贺国京3．工商管理类本科专业实践教学模式完成人：邓德胜祝海波何志祥尹少华方威三等奖1．普通高等学校物流管理本科专业课程体系优化研究完成人：庞燕王忠伟李义华陈德良符瑛2．精品课程建设的研究与实践完成人：汤小红曹福祥向春阶邓联健柳伟3．提高英语习得者交际能力的校本课程研究与开发完成人：张沉香邓天文王小宁六、湖南省全国大学英语四六级考试优秀考点中南林业科技大学教务处七、2008年度全国计算机等级考试优秀考点中南林业科技大学教务处八、霍英东教育会青年教师奖三等奖方威九、湖南省普通高校思想政治理论课“优秀教师”李道志十、湖南省高等学校成人教育工作先进个人冯革非黄礼云十一、全国大学英语四六级考试先进工作者彭金波十二、全国计算机等级考试先进工作者彭金波十三、湖南省第二届高等学校专职军事教师授课比赛一等奖龙双喜十四、湖南省第三届高等学校专职军事教师授课比赛二等奖龙双喜十五、2008年度湖南省普通高校思想政治理论课“精彩一课”评选活动刘红（二等奖）陈石明（二等奖）白雪霜（三等奖）十六、湖南省高等学校第八届“中南杯”多媒体教育软件大赛陈敏（三等奖）十七、湖南省高等学校第九届“中南杯”多媒体教育软件大赛陈敏（二等奖）庞燕（三等奖）唐小弟（三等奖）十八、指导学生参加省级（含省级）以上竞赛奖1．湖南省第14届大学生英语演讲比赛本科一组团体二等奖指导老师：肖旭华王琼2．湖南省第14届大学生英语演讲比赛个人二等奖2项指导老师：肖旭华王琼3．湖南省第15届大学生英语演讲比赛本科一组团体三等奖指导老师：肖旭华王琼4．湖南省第15届大学生英语演讲比赛个人二等奖指导老师：肖旭华王琼5．湖南省第15届大学生英语演讲比赛个人三等奖2项指导教师：肖旭华王琼6．第二届全国大学生物流设计大赛一等奖指导老师：庞燕7．第三届湖南省大学生机械创新设计大赛一等奖指导老师：杨蹈宇马庆勇8．第三届湖南省大学生机械创新设计大赛三等奖指导老师：柳建安陈飞9．第三届湖南省大学生机械创新设计大赛三等奖指导老师：谢洁飞丁敬平10．第四届湖南省力学竞赛综合组一等奖指导老师：王荣海苏淑兰11．第四届湖南省力学竞赛材料力学组二等奖指导老师：王荣海12．第四届湖南省力学竞赛材料力学组三等奖2项指导老师：王荣海13．第四届湖南省力学竞赛理论力学组二等奖2项指导老师：苏淑兰14．第四届湖南省力学竞赛理论力学组三等奖4项指导老师：苏淑兰15．第五届湖南省力学竞赛综合组三等奖2项指导老师：丁科黄伟王荣海陈胜铭16．第五届湖南省力学竞赛理论力学组三等奖3项指导老师：丁科黄伟王荣海陈胜铭17．第五届湖南省力学竞赛材料力学组二等奖指导老师：丁科黄伟王荣海陈胜铭18．第五届湖南省力学竞赛材料力学组三等奖2项指导老师：丁科黄伟王荣海陈胜铭19．2009年全国大学生数学建模竞赛三等奖2项指导老师：刘勉声黄政龙石龙陈芳芳李淑花唐玲20．湖南省第四届大学生程序设计竞赛团体第四名指导老师：谭骏珊，邝祝芳、杨卫民21．湖南省第四届大学生计算机程序设计竞赛获三等奖2项指导老师：邝祝芳22．湖南省第四届大学生计算机程序设计竞赛获三等奖指导老师：杨卫民23．湖南省第五届大学生程序设计竞赛团体第四名指导老师：余绍军，邝祝芳、杨卫民24．湖南省第五届大学生计算机程序设计竞赛获二等奖2项指导老师：邝祝芳25．湖南省第五届大学生计算机程序设计竞赛获三等奖指导老师：杨卫民26．2009年全国大学生电子设计竞赛湖南省一等奖指导老师：张永忠朱俊杰任嘉27．2009年全国大学生电子设计竞赛湖南省二等奖指导老师：赵伟志周凯李颖28．2009年全国大学生电子设计竞赛湖南省三等奖指导老师：鄢永明马振燕周国雄29．2009年全国大学生电子设计竞赛湖南省三等奖指导老师：王湘中姚晔杨菊秋30．第三届全国大学生广告艺术大赛湖南分赛区一等奖1项指导老师：肖锋刚31．第三届全国大学生广告艺术大赛湖南分赛区二等奖1项指导老师：邓敏32．第三届全国大学生广告艺术大赛湖南分赛区三等奖1项指导老师：曹阳33．第三届全国大学生广告艺术大赛湖南分赛区三等奖1项指导老师：曹阳肖德荣质量工程项目获奖一、国家级特色专业资源环境与城乡规划管理食品科学与工程工业设计森林资源保护与游憩二、国家级精品课程木材学大学英语三、湖南省精品课程材料力学电路分析基础供应链管理食品原料学基础英语四、湖南省特色专业木材科学与工程农林经济管理环境科学土地资源管理林产化学加工旅游管理市场营销林学园林五、湖南省实践教学中心林业生物质资源加工工程实验中心林业技术实验中心力学实验中心现代物流实验中心六、湖南省教学团队食品科学与工程专业教学团队林学专业教学团队七、湖南省普通高等学校优秀教材电子商务概论电工与电子技术（上下）林业系统工程基础八、湖南省优秀实习基地湖南亚华乳业有限公司攸县林科所长沙金霞经济开发区物流实习教学基地张家界奥威科技有限公司实习教学基地长沙华天大酒店实习教学基地九、湖南省优秀教研室大学英语二教研室生态学教研室食品科学与工程教研室力学教研室十、湖南省普通高校教学名师罗迎社十一、2008年湖南省普通高校青年教师教学能手张锡滨熊玲君王浩波十二、2009年湖南省普通高校青年教师教学能手马芳陈飞彭湘莲2008-2009年度指导学生参加各类学会、协会获奖1．2008年湖南省第五届日语竞赛演讲比赛特等奖一项指导教师：张静懿夏丽蓉2．2008年湖南省第五届日语竞赛演讲比赛四年级组一等奖一项指导教师：张静懿夏丽蓉3．2008年湖南省第五届日语竞赛演讲比赛三年级组三等奖一项指导教师：张静懿夏丽蓉4．2008年湖南省第五届日语竞赛演讲比赛二年级组优胜奖一项指导教师：张静懿夏丽蓉5．2008年湖南省第五届日语竞赛作文比赛四年级组一等奖一项指导教师：蒋丽华任霞6．2008年湖南省第五届日语竞赛作文比赛二年级组二等奖一项指导教师：蒋丽华任霞7．2009年湖南省高校大学生数学竞赛非数学专业类二等奖指导老师：王松然柏超陈宏斌8．2009年湖南省高校大学生数学竞赛非数学专业类三等奖3项指导老师：王松然柏超陈宏斌9．2009年湖南省第二届大学生物理竞赛二等奖指导老师：李水盛忠志王新军10．2009年ACM国际大学生程序设计竞赛亚洲区哈尔滨赛区竞赛银牌指导老师：邝祝芳11．2009年ACM国际大学生程序设计竞赛亚洲区宁波赛区竞赛铜牌指导老师：邝祝芳12．2009年ACM国际大学生程序设计竞赛亚洲区上海赛区竞赛铜牌指导老师：邝祝芳13．2009年ACM国际大学生程序设计竞赛华中南区竞赛获铜牌指导老师：邝祝芳14．第六届“挑战杯”瓮福中国大学生创业计划竞赛铜奖1项指导老师：胡景初戴向东刘文金祝海波贺一姣王才喜王天翼15．第十一届“挑战杯”全国大学生课外学术科技作品竞赛一等奖指导老师：周慧宾尹少华左旦平16．第三届“挑战杯”湖南省大学生创业计划竞赛银奖1项指导老师：王才喜王天翼17．第三届“挑战杯”湖南省大学生创业计划竞赛铜奖4项指导老师：王才喜王天翼沈学杰王才喜王天翼周凯18．第八届“挑战杯”湖南省大学生课外学术科技作品竞赛三等奖6项指导老师：周先雁喻勋林周国英文仕知周慧滨尹少华19．第八届“挑战杯”湖南省大学生课外学术科技作品竞赛二等奖5项指导老师：谭晓风郑哲文徐剑莹钟永德罗明春邓德胜。

分享成果,交流经验,展望未来——第十四届国际数学教育大会综述

第十四届国际数学教育大会（ICME-14）于2021年7月11日—18日在上海华东师范大学召开。

这是国际数学教育大会（International Con⁃gress on Mathematical Education,简称ICME ）自1969年召开以来首次在中国举办。

受全球新冠肺炎疫情的影响，本届大会推迟了一年，并最终以线上、线下相结合的方式举行。

（ICMI ）指导下举办的全球数学教育界水平最高、规模最大的学术会议，每4年举办一次，被誉为国际数学教育界的“奥林匹克”。

（本刊对ICME-12、ICME-13都做了专题报道，详见本刊2012年和2016年的第11、12期）作为国际性学术会议，其宗旨是：1.展示世界各地数学教育的最新研究成果；2.分享世界数学教育问题的相关信息；3.探讨数学研究最新进展对数学教育发展的启示。

同时，为世界各地数学教育研究者及爱好者提供学习和交流的平台。

本届大会，有129个国家和地区的3100多名数学家和数学教育工作者注册并参会，国际覆盖面为历届之最。

其中中国代表达1641人，超过了历届大会中国参会者总和的两倍之多。

在开幕式上，上海市委书记李强、教育部副部长翁铁慧、国际数学联盟主席卡洛斯·肯尼格（线上）、ICMI 主席梁贯成等领导出席大会并致辞。

随后，在梁贯成主席的主持下，举行了ICMI 颁奖仪式：宣布2017年克莱因奖（数学教育终身成就奖）、弗赖登塔尔奖（数学教育杰出贡献奖）和2019年克莱因奖、弗赖登塔尔奖以及卡斯泰尔诺奖（数学教育优秀实践奖）获奖者名单，并进行了颁奖。

在上述三个国际数学教育最高奖项中，卡斯泰尔诺奖是从2013年开始设立的，每4年颁发一次，旨在奖励那些在数学教育实践领域有突出贡献的个人、团体、项目、机构或组织，其成果需要在课堂教学、课程开发、教学设计、教师培养等方面对学校、地区或国家有重大影响，并在实践中具有较强的可实施性和借鉴性。

本届卡斯泰尔诺奖颁发给了美国数学教师协会（NCTM ）。

【三维设计】2014届高考数学一轮复习 (基础知识+高频考点+解题训练)数列求和教学案

第四节数_列_求_和[知识能否忆起]一、公式法1．如果一个数列是等差数列或等比数列，则求和时直接利用等差、等比数列的前n 项和公式，注意等比数列公比q 的取值情况要分q ＝1或q ≠1.2．一些常见数列的前n 项和公式： (1)1＋2＋3＋4＋…＋n ＝n n ＋12；(2)1＋3＋5＋7＋…＋2n －1＝n 2； (3)2＋4＋6＋8＋…＋2n ＝n 2＋n . 二、非等差、等比数列求和的常用方法 1．倒序相加法如果一个数列{a n }，首末两端等“距离”的两项的和相等或等于同一常数，那么求这个数列的前n 项和即可用倒序相加法，等差数列的前n 项和即是用此法推导的．2．分组转化求和法若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组转化法，分别求和而后相加减．3．错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n 项和即可用此法来求，等比数列的前n 项和就是用此法推导的．4．裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和．[小题能否全取]1．(2012·某某六校联考)设数列{(－1)n}的前n 项和为S n ，则对任意正整数n ，S n ＝( )A.n [－1n－1]2B.－1n －1＋12C.－1n＋12 D.－1n－12解析：选 D 因为数列{(－1)n}是首项与公比均为－1的等比数列，所以S n ＝－1－－1n×－11－－1＝－1n－12. 2．等差数列{a n }的通项公式为a n ＝2n ＋1，其前n 项的和为S n ，则数列⎩⎨⎧⎭⎬⎫S n n 的前10项的和为( )A ．120B ．70C ．75D ．100 解析：选C ∵S n ＝n a 1＋a n2＝n (n ＋2)，∴S n n ＝n ＋2.故S 11＋S 22＋…＋S 1010＝75. 3．数列a 1＋2，…，a k ＋2k ，…，a 10＋20共有十项，且其和为240，则a 1＋…＋a k ＋…＋a 10的值为( )A ．31B ．120C ．130D ．185解析：选C a 1＋…＋a k ＋…＋a 10＝240－(2＋…＋2k ＋…＋20)＝240－2＋20×102＝240－110＝130.4．若数列{a n }的通项公式为a n ＝2n＋2n －1，则数列{a n }的前n 项和为________．解析：S n ＝21－2n1－2＋n 1＋2n －12＝2n ＋1－2＋n 2.答案：2n ＋1＋n 2－25．数列12×4，14×6，16×8，…，12n 2n ＋2，…的前n 项和为________．解析：因a n ＝12n2n ＋2＝14⎝ ⎛⎭⎪⎫1n －1n ＋1则S n ＝14⎝ ⎛⎭⎪⎫1－12＋12－13＋…＋1n －1n ＋1＝14⎝ ⎛⎭⎪⎫1－1n ＋1＝n4n ＋1. 答案：n4n ＋1数列求和的方法(1)一般的数列求和，应从通项入手，若无通项，先求通项，然后通过对通项变形，转化为与特殊数列有关或具备某种方法适用特点的形式，从而选择合适的方法求和．(2)解决非等差、等比数列的求和，主要有两种思路：①转化的思想，即将一般数列设法转化为等差或等比数列，这一思想方法往往通过通项分解或错位相减来完成．②不能转化为等差或等比数列的数列，往往通过裂项相消法、错位相减法、倒序相加法等来求和．分组转化法求和典题导入[例1] (2011·某某高考)等比数列{a n }中，a 1，a 2，a 3分别是下表第一、二、三行中的某一个数，且a 1，a 2，a 3中的任何两个数不在下表的同一列.第一列第二列第三列第一行 3 2 10 第二行 6 4 14 第三行9818(1)求数列{a n }的通项公式；(2)若数列{b n }满足：b n ＝a n ＋(－1)nln a n ，求数列{b n }的前2n 项和S 2n . [自主解答] (1)当a 1＝3时，不合题意；当a 1＝2时，当且仅当a 2＝6，a 3＝18时，符合题意；当a 1＝10时，不合题意．因此a 1＝2，a 2＝6，a 3＝18.所以公比q ＝3，故a n ＝2·3n －1.(2)因为b n ＝a n ＋(－1)n ln a n ＝2·3n －1＋(－1)n ln(2·3n －1)＝2·3n －1＋(－1)n(ln 2－ln3)＋(－1)nn ln 3，所以S 2n ＝b 1＋b 2＋…＋b 2n ＝2(1＋3＋…＋32n －1)＋[－1＋1－1＋…＋(－1)2n](ln 2－ln 3)＋[－1＋2－3＋…＋(－1)2n2n ]ln 3＝2×1－32n1－3＋n ln 3＝32n＋n ln 3－1.由题悟法分组转化法求和的常见类型(1)若a n ＝b n ±，且{b n }，{}为等差或等比数列，可采用分组求和法求{a n }的前n 项和．(2)通项公式为a n ＝⎩⎪⎨⎪⎧b n ，n 为奇数，，n 为偶数的数列，其中数列{b n }，{}是等比数列或等差数列，可采用分组求和法求和.以题试法1．已知数列{x n }的首项x 1＝3，通项x n ＝2n p ＋nq (n ∈N *，p ，q 为常数)，且x 1，x 4，x 5成等差数列．求：(1)p ，q 的值；(2)数列{x n }前n 项和S n 的公式．解：(1)由x 1＝3，得2p ＋q ＝3，又因为x 4＝24p ＋4q ，x 5＝25p ＋5q ，且x 1＋x 5＝2x 4，得3＋25p ＋5q ＝25p ＋8q ，解得p ＝1，q ＝1.(2)由(1)，知x n ＝2n＋n ，所以S n ＝(2＋22＋…＋2n )＋(1＋2＋…＋n )＝2n ＋1－2＋n n ＋12.错位相减法求和典题导入[例2] (2012·某某高考)已知数列{a n }的前n 项和S n ＝k －k (其中c ，k 为常数)，且a 2＝4，a 6＝8a 3.(1)求a n ；(2)求数列{na n }的前n 项和T n .[自主解答] (1)由S n ＝k －k ，得a n ＝S n －S n －1＝k －k －1(n ≥2)．由a 2＝4，a 6＝8a 3 ，得kc (c －1)＝4，kc 5(c －1)＝8kc 2(c －1)，解得⎩⎪⎨⎪⎧c ＝2，k ＝2，所以a 1＝S 1＝2，a n ＝k －k －1＝2n(n ≥2)，于是a n ＝2n.(2)T n ＝∑i ＝1nia i ＝∑i ＝1ni ·2i，即T n ＝2＋2·22＋3·23＋4·24＋…＋n ·2n.T n ＝2T n －T n ＝－2－22－23－24－…－2n ＋n ·2n ＋1＝－2n ＋1＋2＋n ·2n ＋1＝(n －1)2n ＋1＋2.由题悟法用错位相减法求和应注意：(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n －qS n ”的表达式．(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解．以题试法2．(2012·某某模拟)已知等比数列{a n }的前n 项和为S n ，且满足S n ＝3n＋k . (1)求k 的值及数列{a n }的通项公式； (2)若数列{b n }满足a n ＋12＝(4＋k )a n b n ，求数列{b n }的前n 项和T n .解：(1)当n ≥2时，由a n ＝S n －S n －1＝3n＋k －3n －1－k ＝2·3n －1，得等比数列{a n }的公比q ＝3，首项为2.∴a 1＝S 1＝3＋k ＝2，∴k ＝－1，∴数列{a n }的通项公式为a n ＝2·3n －1.(2)由a n ＋12＝(4＋k )a n b n ，可得b n ＝n2·3n －1，即b n ＝32·n 3n .∵T n ＝32⎝ ⎛⎭⎪⎫13＋232＋333＋…＋n 3n ，∴13T n ＝32⎝ ⎛⎭⎪⎫132＋233＋334＋…＋n 3n ＋1，∴23T n ＝32⎝ ⎛⎭⎪⎫13＋132＋133＋…＋13n －n 3n ＋1，∴T n ＝94⎝ ⎛⎭⎪⎫12－12·3n －n 3n ＋1.裂项相消法求和典题导入[例3] 已知数列{a n }的前n 项和为S n ，a 1＝1，S n ＝na n －n (n －1)(n ∈N *)． (1)求数列{a n }的通项公式； (2)设b n ＝2a n a n ＋1，求数列{b n }的前n 项和T n .[自主解答] (1)∵S n ＝na n －n (n －1)，当n ≥2时，S n －1＝(n －1)·a n －1－(n －1)(n －2)，∴a n ＝S n －S n －1＝na n －n (n －1)－(n －1)a n －1＋(n －1)·(n －2)，即a n －a n －1＝2.∴数列{a n }是首项a 1＝1，公差d ＝2的等差数列，故a n ＝1＋(n －1)·2＝2n －1，n ∈N *.(2)由(1)知b n ＝2a n a n ＋1＝22n －12n ＋1＝12n －1－12n ＋1，故T n ＝b 1＋b 2＋…＋b n ＝⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫13－15＋⎝ ⎛⎭⎪⎫15－17＋…＋⎝ ⎛⎭⎪⎫12n －1－12n ＋1＝1－12n ＋1＝2n 2n ＋1.本例条件不变，若数列{b n }满足b n ＝1S n ＋n，求数列{b n }的前n 项和T n . 解：S n ＝na n －n (n －1)＝n (2n －1)－n (n －1)＝n 2.b n ＝1S n ＋n ＝1n 2＋n ＝1n n ＋1＝1n －1n ＋1，T n ＝⎝⎛⎭⎪⎫11－12＋⎝⎛⎭⎪⎫12－13＋⎝⎛⎭⎪⎫13－14＋…＋⎝⎛⎭⎪⎫1n －1n ＋1＝1－1n ＋1＝nn ＋1.由题悟法利用裂项相消法求和应注意(1)抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项； (2)将通项裂项后，有时需要调整前面的系数，使裂开的两项之差和系数之积与原通项相等．如：若{a n }是等差数列，则1a n a n ＋1＝1d ⎝ ⎛⎭⎪⎫1a n －1a n ＋1，1a n a n ＋2＝12d ⎝ ⎛⎭⎪⎫1a n －1a n ＋2. 以题试法3．(2012·“江南十校”联考)在等比数列{a n }中，a 1>0，n ∈N *，且a 3－a 2＝8，又a 1、a 5的等比中项为16.(1)求数列{a n }的通项公式；(2)设b n ＝log 4a n ，数列{b n }的前n 项和为S n ，是否存在正整数k ，使得1S 1＋1S 2＋1S 3＋…＋1S n<k 对任意n ∈N *恒成立．若存在，求出正整数k 的最小值；不存在，请说明理由．解：(1)设数列{a n }的公比为q ，由题意可得a 3＝16， ∵a 3－a 2＝8，则a 2＝8，∴q ＝2. ∴a n ＝2n ＋1.(2)∵b n ＝log 42n ＋1＝n ＋12，∴S n ＝b 1＋b 2＋…＋b n ＝n n ＋34.∵1S n ＝4nn ＋3＝43⎝ ⎛⎭⎪⎫1n －1n ＋3， ∴1S 1＋1S 2＋1S 3＋…＋1S n＝43⎝ ⎛⎭⎪⎫11－14＋12－15＋13－16＋…＋1n －1n ＋3＝43⎝⎛⎭⎪⎫1＋12＋13－1n ＋1－1n ＋2－1n ＋3<229，∴存在正整数k 的最小值为3.1．已知{a n }是首项为1的等比数列，S n 是{a n }的前n 项和，且9S 3＝S 6，则数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为( )A.158或5B.3116或5 C.3116D.158解析：选C 设数列{a n }的公比为q .由题意可知q ≠1，且91－q 31－q＝1－q 61－q，解得q ＝2，所以数列⎩⎨⎧⎭⎬⎫1a n 是以1为首项，12为公比的等比数列，由求和公式可得S 5＝3116.2．已知数列{a n }的前n 项和S n ＝an 2＋bn (a 、b ∈R )，且S 25＝100，则a 12＋a 14等于( ) A ．16 B ．8 C ．4 D ．不确定解析：选B 由数列{a n }的前n 项和S n ＝an 2＋bn (a 、b ∈R )，可知数列{a n }是等差数列，由S 25＝a 1＋a 25×252＝100，解得a 1＋a 25＝8，所以a 1＋a 25＝a 12＋a 14＝8.3．数列112，314，518，7116，…，(2n －1)＋12n ，…的前n 项和S n 的值等于( )A ．n 2＋1－12nB ．2n 2－n ＋1－12nC ．n 2＋1－12n －1D ．n 2－n ＋1－12n解析：选A 该数列的通项公式为a n ＝(2n －1)＋12n ，则S n ＝[1＋3＋5＋…＋(2n －1)]＋⎝ ⎛⎭⎪⎫12＋122＋…＋12n ＝n 2＋1－12n .4．(2012·“江南十校”联考)若数列{a n }为等比数列，且a 1＝1，q ＝2，则T n ＝1a 1a 2＋1a 2a 3＋…＋1a n a n ＋1的结果可化为( )A ．1－14nB ．1－12nC.23⎝⎛⎭⎪⎫1－14n D.23⎝ ⎛⎭⎪⎫1－12n解析：选C a n ＝2n －1，设b n ＝1a n a n ＋1＝⎝ ⎛⎭⎪⎫122n －1，则T n ＝b 1＋b 2＋…＋b n ＝12＋⎝ ⎛⎭⎪⎫123＋…＋⎝ ⎛⎭⎪⎫122n －1＝12⎝ ⎛⎭⎪⎫1－14n 1－14＝23⎝ ⎛⎭⎪⎫1－14n .5．已知等差数列{a n }的前n 项和为S n ，a 5＝5，S 5＝15，则数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前100项和为( )A.100101B.99101C.99100D.101100解析：选A 设等差数列{a n }的首项为a 1，公差为d .∵a 5＝5，S 5＝15，∴⎩⎪⎨⎪⎧a 1＋4d ＝5，5a 1＋5×5－12d ＝15，∴⎩⎪⎨⎪⎧a 1＝1，d ＝1，∴a n ＝a 1＋(n －1)d ＝n .∴1a n a n ＋1＝1nn ＋1＝1n －1n ＋1，∴数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前100项和为1－12＋12－13＋…＋1100－1101＝1－1101＝100101.6．已知函数f (n )＝⎩⎪⎨⎪⎧n 2当n 为奇数时，－n 2当n 为偶数时，且a n ＝f (n )＋f (n ＋1)，则a 1＋a 2＋a 3＋…＋a 100等于( )A ．0B ．100C ．－100D ．10 200解析：选B 由题意，a 1＋a 2＋a 3＋…＋a 100＝12－22－22＋32＋32－42－42＋52＋…＋992－1002－1002＋1012＝－(1＋2)＋(3＋2)＋…－(99＋100)＋(101＋100)＝－(1＋2＋…＋99＋100)＋(2＋3＋…＋100＋101)＝－1＋101＝100.7．在等差数列{a n }中，S n 表示前n 项和，a 2＋a 8＝18－a 5，则S 9＝________. 解析：由等差数列的性质及a 2＋a 8＝18－a 5，得2a 5＝18－a 5，则a 5＝6，故S 9＝a 1＋a 9×92＝9a 5＝54.答案：548．对于数列{a n }，定义数列{a n ＋1－a n }为数列{a n }的“差数列”，若a 1＝2，{a n }的“差数列”的通项公式为2n，则数列{a n }的前n 项和S n ＝________.解析：∵a n ＋1－a n ＝2n ，∴a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1 ＝2n －1＋2n －2＋…＋22＋2＋2＝2－2n1－2＋2＝2n －2＋2＝2n.∴S n ＝2－2n ＋11－2＝2n ＋1－2.答案：2n ＋1－29．已知等比数列{a n }中，a 1＝3，a 4＝81，若数列{b n }满足b n ＝log 3a n ，则数列⎩⎨⎧⎭⎬⎫1b n b n ＋1的前n 项和S n ＝________.解析：设等比数列{a n }的公比为q ，则a 4a 1＝q 3＝27，解得q ＝3.所以a n ＝a 1q n －1＝3×3n －1＝3n，故b n ＝log 3a n ＝n ，所以1b n b n ＋1＝1nn ＋1＝1n －1n ＋1. 则数列⎩⎨⎧⎭⎬⎫1b n b n ＋1的前n 项和为1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1.答案：nn ＋110．(2013·某某统考)在等比数列{a n }中，a 2a 3＝32，a 5＝32.(1)求数列{a n }的通项公式；(2)设数列{a n }的前n 项和为S n ，求S 1＋2S 2＋…＋nS n . 解：(1)设等比数列{a n }的公比为q ，依题意得⎩⎪⎨⎪⎧a 1q ·a 1q 2＝32，a 1q 4＝32，解得a 1＝2，q ＝2，故a n ＝2·2n －1＝2n.(2)∵S n 表示数列{a n }的前n 项和， ∴S n ＝21－2n1－2＝2(2n－1)，∴S 1＋2S 2＋…＋nS n ＝2[(2＋2·22＋…＋n ·2n )－(1＋2＋…＋n )]＝2(2＋2·22＋…＋n ·2n )－n (n ＋1)，设T n ＝2＋2·22＋…＋n ·2n，① 则2T n ＝22＋2·23＋…＋n ·2n ＋1，②①－②，得－T n ＝2＋22＋…＋2n －n ·2n ＋1＝21－2n1－2－n ·2n ＋1＝(1－n )2n ＋1－2，∴T n ＝(n －1)2n ＋1＋2，∴S 1＋2S 2＋…＋nS n ＝2[(n －1)2n ＋1＋2]－n (n ＋1)＝(n －1)2n ＋2＋4－n (n ＋1)．11．(2012·某某调研)已知等差数列{a n }满足：a 5＝9，a 2＋a 6＝14. (1)求{a n }的通项公式；(2)若b n ＝a n ＋qa n (q >0)，求数列{b n }的前n 项和S n .解：(1)设数列{a n }的首项为a 1，公差为d ，则由a 5＝9，a 2＋a 6＝14，得⎩⎪⎨⎪⎧a 1＋4d ＝9，2a 1＋6d ＝14，解得⎩⎪⎨⎪⎧a 1＝1，d ＝2，所以{a n }的通项a n ＝2n －1.(2)由a n ＝2n －1得b n ＝2n －1＋q 2n －1.当q >0且q ≠1时，S n ＝[1＋3＋5＋…＋(2n －1)]＋(q 1＋q 3＋q 5＋…＋q 2n －1)＝n 2＋q 1－q 2n1－q2；当q ＝1时，b n ＝2n ，则S n ＝n (n ＋1)．所以数列{b n }的前n 项和S n ＝⎩⎪⎨⎪⎧n n ＋1，q ＝1，n 2＋q 1－q 2n1－q 2，q >0，q ≠1.12．(2012·“江南十校”联考)若数列{a n }满足：a 1＝23，a 2＝2,3(a n ＋1－2a n ＋a n －1)＝2.(1)证明：数列{a n ＋1－a n }是等差数列；(2)求使1a 1＋1a 2＋1a 3＋…＋1a n >52成立的最小的正整数n .解：(1)由3(a n ＋1－2a n ＋a n －1)＝2可得：a n ＋1－2a n ＋a n －1＝23，即(a n ＋1－a n )－(a n －a n －1)＝23，故数列{a n ＋1－a n }是以a 2－a 1＝43为首项，23为公差的等差数列．(2)由(1)知a n ＋1－a n ＝43＋23(n －1)＝23(n ＋1)，于是累加求和得a n ＝a 1＋23(2＋3＋…＋n )＝13n (n ＋1)，∴1a n ＝3⎝ ⎛⎭⎪⎫1n －1n ＋1， ∴1a 1＋1a 2＋1a 3＋…＋1a n ＝3－3n ＋1>52，∴n >5， ∴最小的正整数n 为6.1．已知数列{a n }的前n 项和S n ＝n 2－6n ，则{|a n |}的前n 项和T n ＝( ) A ．6n －n 2B ．n 2－6n ＋18C.⎩⎪⎨⎪⎧6n －n 21≤n ≤3n 2－6n ＋18n >3 D.⎩⎪⎨⎪⎧6n －n 21≤n ≤3n 2－6n n >3解析：选C ∵由S n ＝n 2－6n 得{a n }是等差数列，且首项为－5，公差为2. ∴a n ＝－5＋(n －1)×2＝2n －7， ∴n ≤3时，a n <0，n >3时，a n >0，∴T n ＝⎩⎪⎨⎪⎧6n －n 21≤n ≤3，n 2－6n ＋18n >3.2．(2012·某某二模)若数列{a n }满足a 1＝2且a n ＋a n －1＝2n＋2n －1，S n 为数列{a n }的前n项和，则log 2(S 2 012＋2)＝________.解析：因为a 1＋a 2＝22＋2，a 3＋a 4＝24＋23，a 5＋a 6＝26＋25，….所以S 2 012＝a 1＋a 2＋a 3＋a 4＋…＋a 2 011＋a 2 012＝21＋22＋23＋24＋…＋22 011＋22 012＝21－22 0121－2＝22 013－2.故log 2(S 2 012＋2)＝log 222 013＝2 013.答案：2 0133．已知递增的等比数列{a n }满足：a 2＋a 3＋a 4＝28，且a 3＋2是a 2，a 4的等差中项． (1)求数列{a n }的通项公式；(2)若b n ＝a n log 12a n ，S n ＝b 1＋b 2＋…＋b n ，求S n .解：(1)设等比数列{a n }的首项为a 1，公比为q . 依题意，有2(a 3＋2)＝a 2＋a 4，代入a 2＋a 3＋a 4＝28，得a 3＝8. ∴a 2＋a 4＝20.∴⎩⎪⎨⎪⎧a 1q ＋a 1q 3＝20，a 3＝a 1q 2＝8，解得⎩⎪⎨⎪⎧q ＝2，a 1＝2，或⎩⎪⎨⎪⎧q ＝12，a 1＝32.又{a n }为递增数列， ∴⎩⎪⎨⎪⎧q ＝2，a 1＝2.∴a n ＝2n.(2)∵b n ＝2n ·log 122n ＝－n ·2n，∴－S n ＝1×2＋2×22＋3×23＋…＋n ×2n.①∴－2S n ＝1×22＋2×23＋3×24＋…＋(n －1)×2n ＋n ×2n ＋1.②①－②得S n ＝2＋22＋23＋…＋2n －n ·2n ＋1＝21－2n1－2－n ·2n ＋1＝2n ＋1－n ·2n ＋1－2.∴S n ＝2n ＋1－n ·2n ＋1－2.1．已知{a n }是公差不为零的等差数列，a 1＝1，且a 1，a 3，a 9成等比数列． (1)求数列{a n }的通项； (2)求数列{2a n }的前n 项和S n .解：(1)由题设知公差d ≠0，由a 1＝1，a 1，a 3，a 9成等比数列得1＋2d 1＝1＋8d1＋2d ，解得d ＝1或d ＝0(舍去)，故{a n }的通项a n ＝1＋(n －1)×1＝n . (2)由(1)知2a n ＝2n，由等比数列前n 项和公式得S n ＝2＋22＋23＋ (2)＝21－2n1－2＝2n ＋1－2.2．设函数f (x )＝x 3，在等差数列{a n }中，a 3＝7，a 1＋a 2＋a 3＝12，记S n ＝f (3a n ＋1)，令b n ＝a n S n ，数列⎩⎨⎧⎭⎬⎫1b n 的前n 项和为T n .(1)求{a n }的通项公式和S n ； (2)求证：T n <13.解：(1)设数列{a n }的公差为d ，由a 3＝a 1＋2d ＝7，a 1＋a 2＋a 3＝3a 1＋3d ＝12，解得a 1＝1，d ＝3，则a n ＝3n －2.∵f (x )＝x 3，∴S n ＝f (3a n ＋1)＝a n ＋1＝3n ＋1. (2)证明：∵b n ＝a n S n ＝(3n －2)(3n ＋1)， ∴1b n＝13n －23n ＋1＝13⎝ ⎛⎭⎪⎫13n －2－13n ＋1.∴T n ＝1b 1＋1b 2＋…＋1b n＝13⎝ ⎛⎭⎪⎫1－14＋14－17＋…＋13n －2－13n ＋1＝13⎝ ⎛⎭⎪⎫1－13n ＋1.∴T n <13. 3．已知二次函数f (x )＝x 2－5x ＋10，当x ∈(n ，n ＋1](n ∈N *)时，把f (x )在此区间内的整数值的个数表示为a n .(1)求a 1和a 2的值； (2)求n ≥3时a n 的表达式； (3)令b n ＝4a n a n ＋1，求数列{b n }的前n 项和S n (n ≥3)．解：(1)f (x )＝x 2－5x ＋10，又x ∈(n ，n ＋1](n ∈N *)时，f (x )的整数个数为a n ，所以f (x )在(1,2]上的值域为[4,6)⇒a 1＝2；f (x )在(2,3]上的值域为⎣⎢⎡⎦⎥⎤154，4⇒a 2＝1.(2)当n ≥3时，f (x )是增函数，故a n ＝f (n ＋1)－f (n )＝2n －4.(3)由(1)和(2)可知，b 1＝42×1＝2，b 2＝41×2＝2.而当n ≥3时，b n ＝42n －42n －2＝2⎝⎛⎭⎪⎫12n －4－12n －2.所以当n ≥3时，S n ＝b 1＋b 2＋b 3＋b 4＋…＋b n＝2＋2＋2⎝ ⎛⎭⎪⎫12－14＋14－16＋…＋12n －4－12n －2 ＝4＋2⎝ ⎛⎭⎪⎫12－12n －2＝5－1n －1.。

横看成林侧成峰远近高低各不同

横看成林侧成峰远近高低各不同2012年年末，在张家港市第14届课改经验交流会上，笔者和全市部分数学教师有幸先后观摩了市沙洲小学副校长陶月娟和市实验小学副校长许华红的两节精彩展示课。

陶校长执教的是四年级《探索事物搭配的规律》，许校长执教的是五年级《复式统计表》。

点评会上，笔者对听课的老师们谈了体会，特别有三点非常值得赏析。

1.知识的生成过程到结论的归纳演绎水到渠成知识的生成过程被充分演绎展示，用“一览无余”来描述一点不为过。

听课老师都欣喜地看到，寻找事物搭配的规律和复式统计表样式的形成过程，都作为重点笔墨加以突出，精心勾勒，不仅化时多，而且思维性强，数学味浓。

只有知其然，并且知其所以然，获得的知识才是完整的、深刻的。

菜谱中的搭配问题看似简单，学问却很多。

陶校长首先提供“3个木偶娃娃和2顶帽子”搭配的例题材料，让学生通过语言描述、图形替代、字母抽象等多种手段，让学生体会到语言描述的“繁”、图形字母连线的“简”；前者凭观察语言描述的“无序”、后者手脑并用其思维的“有序”；前者的“抽象”、后者的“直观”。

当初步领略“6种”搭配方法后，又进一步改变条件：一是帽子变，木偶不变，即其中的帽子变成”3顶帽子”；二是帽子变，木偶也变，即“6顶帽子，5个木偶”，逐步丰富材料，深入探究，从而揭示出规律“帽子顶数乘以木偶个数等于搭配的种数”。

单式统计表是学生的原认知，也是旧知引出新知的生长点，许校长通过提供四张单式统计表，巧妙设计提问，从学生问题回答的突然性减慢，激发学生的探究欲望，围绕“这四个班级一共有多少个男生？一共有多少个女生？一共有多少个学生？”，这些数据怎样能在统计表中体现（一看便知）？将学生带入到利用旧表、创制新表的求索活动。

许校长放手让学生自己独立尝试或者小组合作，练习纸上修修改改、涂涂画画，“半成品”慢慢从学生当中产生出来。

也就是把四张单式统计表合并到一张表上，再添上“合计”一栏。

半成品到成品的炼制过程关键在于表头设计，相信学生定有收获，课堂上不少学生设计出了像样的表头，教师引领学生稍加完善加工美化边成为标准的“复式统计表”。

2014届高考数学一轮复习教学案(基础知识+高频考点+解题训练)两直线的位置关系(含解析)2014届

两直线的位置关系[知识能否忆起]一、两条直线的位置关系斜截式一般式方程 y ＝k 1x ＋b 1 y ＝k 2x ＋b 2 A 1x ＋B 1y ＋C 1＝0(A 21＋B 21≠0) A 2x ＋B 2y ＋C 2＝0(A 22＋B 22≠0)相交 k 1≠k 2 A 1B 2－A 2B 1≠0⎝⎛⎭⎫当A 2B 2≠0时，记为A 1A 2≠B 1B 2垂直k 1＝－1k 2或k 1k 2＝－1A 1A 2＋B 1B 2＝0⎝⎛⎭⎫当B 1B 2≠0时，记为A 1B 1·A 2B 2＝－1平行k 1＝k 2 且b 1≠b 2{ A 1B 2－A 2B 1＝0，B 2C 1－B 1C 2≠0或{ A 1B 2－A 2B 1＝0，A 1C 2－A 2C 1≠0⎝⎛⎭⎫当A 2B 2C 2≠0时，记为A 1A 2＝B 1B 2≠C 1C 2 重合 k 1＝k 2 且b 1＝b 2A 1＝λA 2，B 1＝λB 2，C 1＝λC 2(λ≠0)⎝⎛⎭⎫当A 2B 2C 2≠0时，记为A 1A 2＝B 1B 2＝C 1C 2二、两条直线的交点设两条直线的方程是l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0，两条直线的交点坐标就是方程组{ A 1x ＋B 1y ＋C 1＝0，A 2x ＋B 2y ＋C 2＝0的解，若方程组有唯一解，则两条直线相交，此解就是交点坐标；若方程组无解，则两条直线无公共点，此时两条直线平行；反之，亦成立．三、几种距离 1．两点间的距离平面上的两点A (x 1，y 1)，B (x 2，y 2)间的距离公式：d (A ，B )＝|AB |＝(x 1－x 2)2＋(y 1－y 2)2.2．点到直线的距离点P (x 1，y 1)到直线l ：Ax ＋By ＋C ＝0的距离d ＝|Ax 1＋By 1＋C |A 2＋B 2.3．两条平行线间的距离两条平行线Ax ＋By ＋C 1＝0与Ax ＋By ＋C 2＝0间的距离d ＝|C 1－C 2|A 2＋B 2.(4)[小题能否全取]1．(教材习题改编)已知l 1的倾斜角为45°，l 2经过点P (－2，－1)，Q (3，m )．若l 1⊥l 2，则实数m 为( )A ．6 B ．－6 C ．5D ．－5解析：选B 由已知得k 1＝1，k 2＝m ＋15.暑期报名海外游学的人数增长达到∵l 1⊥l 2，∴k 1k 2＝－1， ∴1×m ＋15＝－1，即m ＝－6.2．(教材习题改编)点(0，－1)到直线x ＋2y ＝3的距离为( )A.55B.5教案目的是用更严格的监管、更严厉的处罚、更严肃的问责化学教案切实保障“舌尖上的安全C ．5D.15解析：选B d ＝|0＋2×(－1)－3|5＝ 5.3．点(a ，b )关于直线x ＋y ＋1＝0的对称点是( ) A ．(－a －1，－b －1)B ．(－b －1，－a －1)C ．(－a ，－b )D ．(－b ，－a )解析：选B 设对称点为(x ′，y ′)，则⎩⎨⎧y ′－b x ′－a×(－1)＝－1，x ′＋a 2＋y ′＋b2＋1＝0，解得x ′＝－b －1，y ′＝－a －1.4．l 1：x －y ＝0与l 2：2x －3y ＋1＝0的交点在直线mx ＋3y ＋5＝0上，则m 的值为( )A ．3B ．5C ．－5D ．－8解析：选D 由{x －y ＝0，2x －3y ＋1＝0，得l 1与l 2的交点坐标为(1,1)．所以m＋3＋5＝0，m＝－8.5．与直线4x＋3y－5＝0平行，并且到它的距离等于3的直线方程是______________________．|m＋5|，得m＝10或－20.解析：设所求直线方程为4x＋3y＋m＝0，由3＝42＋32答案：4x＋3y＋10＝0或4x＋3y－20＝01.在判断两条直线的位置关系时，首先应分析直线的斜率是否存在，两条直线都有斜率时，可根据斜率的关系作出判断，无斜率时，要单独考虑．2．在使用点到直线的距离公式或两平行线间的距离公式时，直线方程必须先化为Ax ＋By＋C＝0的形式，否则会出错．两直线的平行与垂直典题导入[例1](2012·浙江高考)设a∈R，则“a＝1”是“直线l1：ax＋2y－1＝0与直线l2：x ＋(a＋1)y＋4＝0平行”的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件[自主解答]由a＝1，可得l1∥l2；反之，由l1∥l2，可得a＝1或a＝－2.[答案] A在本例中若l1⊥l2，试求a.解：∵l1⊥l2，∴a×1＋2×(a＋1)＝0，∴a＝－23.由题悟法1．充分掌握两直线平行与垂直的条件是解决本题的关键，对于斜率都存在且不重合的两条直线l 1和l 2，l 1∥l 2⇔k 1＝k 2，l 1⊥l 2⇔k 1·k 2＝－1.若有一条直线的斜率不存在，那么另一条直线的斜率是多少一定要特别注意．2．(1)若直线l 1和l 2有斜截式方程l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2，则直线l 1⊥l 2的充要条件是k 1·k 2＝－1.(2)设l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0.则l 1⊥l 2⇔A 1A 2＋B 1B 2＝0.以题试法1．(2012·大同模拟)设a ，b ，c 分别是△ABC 中角A ，B ，C 所对的边，则直线x sin A ＋ay ＋c ＝0与bx －y sin B ＋sin C ＝0的位置关系是( )A ．平行 B ．重合C ．垂直D ．相交但不垂直解析：选C 由已知得a ≠0，sin B ≠0，所以两直线的斜率分别为k 1＝－sin A a ，k 2＝bsin B ，由正弦定理得k 1·k 2＝－sin A a ·bsin B＝－1，所以两条直线垂直．两直线的交点与距离问题典题导入[例2] (2012·浙江高考)定义：曲线C 上的点到直线l 的距离的最小值称为曲线C 到直线l 的距离．已知曲线C 1：y ＝x 2＋a 到直线l ：y ＝x 的距离等于曲线C 2：x 2＋(y ＋4)2＝2到直线l ：y ＝x 的距离，则实数a ＝________.[自主解答] 因曲线C 2：x 2＋(y ＋4)2＝2到直线l ：y ＝x 的距离为0－(－4)2－2＝22－2＝2，所以曲线C 1与直线l 不能相交，故x 2＋a ＞x ，即x 2＋a －x ＞0.设C 1：y ＝x 2＋a上一点为(x 0，y 0)，则点(x 0，y 0)到直线l 的距离d ＝|x 0－y 0|2＝－x 0＋x 20＋a2＝⎝⎛⎭⎫x 0－122＋a －142≥4a －142＝2，所以a ＝94.”化学教案结合全文化学教案概述作者这样认为的依据试卷试题[答案] 94由题悟法1．点到直线的距离问题可直接代入距离公式去求．注意直线方程为一般式．2．点到与坐标轴垂直的直线的距离，可用距离公式求解．也可用如下方法去求解：(1)点P (x 0，y 0)到与y 轴垂直的直线y ＝a 的距离d ＝|y 0－a |.(2)点P (x 0，y 0)到与x 轴垂直的直线x ＝b 的距离d ＝|x 0－b |.以题试法2．(2012·通化模拟)若两平行直线3x －2y －1＝0,6x ＋ay ＋c ＝0之间的距离为21313，则c的值是________．解析：由题意得63＝a －2≠c－1，得a ＝－4，c ≠－2，则6x ＋ay ＋c ＝0可化为3x －2y ＋c2＝0，则⎪⎪⎪⎪c 2＋113＝21313，解得c ＝2或－6.答案：2或－6对称问题典题导入[例3] (2012·成都模拟)在直角坐标系中，A (4,0)，B (0，4)，从点P (2,0)射出的光线经直线AB 反射后，再射到直线OB 上，最后经直线OB 反射后又回到P 点，则光线所经过的路程是( )A ．210 B ．6C ．3 3D ．25②________试卷试题它们使用着同样的文字化学教案③__________________化学[自主解答] 如图，设点P 关于直线AB ，y 轴的对称点分别为D ，C ，易求得D (4,2)，C (－2,0)，由对称性知，D ，M ，N ，C 共线，则△PMN 的周长＝|PM |＋|MN |＋|PN |＝|DM |＋|MN |＋|NC |＝|CD |＝40＝210即为光线所经过的路程．[答案] A由题悟法对称问题主要包括中心对称和轴对称 (1)中心对称①点P (x ，y )关于O (a ，b )的对称点P ′(x ′，y ′)满足{ x ′＝2a －x ，y ′＝2b －y .②直线关于点的对称可转化为点关于点的对称问题来解决． (2)轴对称①点A (a ，b )关于直线Ax ＋By ＋C ＝0(B ≠0)的对称点A ′(m ，n )，则有⎩⎨⎧n －b m －a ×⎝⎛⎭⎫－A B ＝－1，A ·a ＋m 2＋B ·b ＋n 2＋C ＝0.②直线关于直线的对称可转化为点关于直线的对称问题来解决．以题试法3．(2012·南京调研)与直线3x －4y ＋5＝0关于x 轴对称的直线方程为( )A ．3x ＋4y ＋5＝0 B ．3x ＋4y －5＝0 C ．－3x ＋4y －5＝0 D ．－3x ＋4y ＋5＝0解析：选A 与直线3x －4y ＋5＝0关于x 轴对称的直线方程是3x －4(－y )＋5＝0，即3x ＋4y ＋5＝0.1．(2012·海淀区期末)已知直线l 1：k 1x ＋y ＋1＝0与直线l 2：k 2x ＋y －1＝0，那么“k 1＝k 2”是“l 1∥l 2”的( )A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：选C 由k 1＝k 2,1≠－1，得l 1∥l 2；由l 1∥l 2知k 1×1－k 2×1＝0，所以k 1＝k 2.故“k 1＝k 2”是“l 1∥l 2”的充要条件．2．当0＜k ＜12时，直线l 1：kx －y ＝k －1与直线l 2：ky －x ＝2k 的交点在( )A ．第一象限 B ．第二象限C ．第三象限D ．第四象限解析：选B 解方程组{ kx －y ＝k －1，ky －x ＝2k ，得两直线的交点坐标为⎝ ⎛⎭⎪⎫k k －1，2k －1k －1，因为0＜k ＜12，所以k k －1＜0，2k －1k －1＞0，故交点在第二象限．3．(2012·长沙检测)已知直线l 1的方程为3x ＋4y －7＝0，直线l 2的方程为6x ＋8y ＋1＝0，则直线l 1与l 2的距离为( )A.85B.32（C ．4D ．8解析：选B ∵直线l 1的方程为3x ＋4y －7＝0，直线l 2的方程为6x ＋8y ＋1＝0，即为3x ＋4y ＋12＝0，∴直线l 1与直线l 2的距离为⎪⎪⎪⎪12＋732＋42＝32.4．若直线l 1：y ＝k (x －4)与直线l 2关于点(2,1)对称，则直线l 2恒过定点( )A ．(0,4) B ．(0,2) C ．(－2,4)D ．(4，－2)解析：选B 由于直线l 1：y ＝k (x －4)恒过定点(4,0)，其关于点(2,1)对称的点为(0,2)．又由于直线l 1：y ＝k (x －4)与直线l 2关于点(2,1)对称，故直线l 2恒过定点(0,2)．5．已知直线l 1：y ＝2x ＋3，若直线l 2与l 1关于直线x ＋y ＝0对称，又直线l 3⊥l 2，则l 3的斜率为( )A ．－2 B ．－12C.12D ．2解析：选A 依题意得，直线l 2的方程是－x ＝2(－y )＋3，即y ＝12x ＋32，其斜率是12，由l 3⊥l 2，得l 3的斜率等于－2.6．(2012·岳阳模拟)直线l 经过两直线7x ＋5y －24＝0和x －y ＝0的交点，且过点(5,1)．则l 的方程是( )A ．3x ＋y ＋4＝0 B ．3x －y ＋4＝0 C ．x ＋3y －8＝0D ．x －3y －4＝0解析：选C 设l 的方程为7x ＋5y －24＋λ(x －y )＝0，即(7＋λ)x ＋(5－λ)y －24＝0，则(7＋λ)×5＋5－λ－24＝0.解得λ＝－4.l 的方程为x ＋3y －8＝0.7．(2012·郑州模拟)若直线l 1：ax ＋2y ＝0和直线l 2：2x ＋(a ＋1)y ＋1＝0垂直，则实数a 的值为________．解析：由2a ＋2(a ＋1)＝0得a ＝－12.答案：－128．已知平面上三条直线x ＋2y －1＝0，x ＋1＝0，x ＋ky ＝0，如果这三条直线将平面划分为六部分，则实数k 的所有取值为________．解析：若三条直线有两条平行，另外一条与这两条直线相交，则符合要求，此时k ＝0或2；若三条直线交于一点，也符合要求，此时k ＝1，故实数k 的所有取值为0,1,2.答案：0,1,29．(2013·临沂模拟)已知点P (4，a )到直线4x －3y －1＝0的距离不大于3，则a 的取值范围是________．解析：由题意得，点到直线的距离为|4×4－3×a －1|5＝|15－3a |5.又|15－3a |5≤3，即|15－3a |≤15，解得，0≤a ≤10，所以a ∈[0,10]．答案：[0,10]10．(2013·舟山模拟)已知1a ＋1b ＝1(a ＞0，b ＞0)，求点(0，b )到直线x －2y －a ＝0的距离的最小值．解：点(0，b )到直线x －2y －a ＝0的距离为d ＝a ＋2b 5＝15(a ＋2b )⎝⎛⎭⎫1a ＋1b ＝15⎝⎛⎭⎫3＋2b a ＋a b ≥15(3＋22)＝35＋2105，当且仅当a 2＝2b 2，a ＋b ＝ab ，即a ＝1＋2，b ＝2＋22时取等号．所以点(0，b )到直线x －2y －a ＝0的距离的最小值为35＋2105.11．(2012·荆州二检)过点P (1,2)的直线l 被两平行线l 1：4x ＋3y ＋1＝0与l 2：4x ＋3y ＋6＝0截得的线段长|AB |＝2，求直线l 的方程．解：设直线l 的方程为y －2＝k (x －1)，由{y ＝kx ＋2－k ，4x ＋3y ＋1＝0，解得A ⎝ ⎛⎭⎪⎫3k －73k ＋4，－5k ＋83k ＋4；由{y ＝kx ＋2－k ，4x ＋3y ＋6＝0，解得B ⎝⎛⎭⎪⎫3k －123k ＋4，8－10k 3k ＋4.∵|AB |＝2， ∴⎝ ⎛⎭⎪⎫53k ＋42＋⎝ ⎛⎭⎪⎫5k 3k ＋42＝2，整理，得7k 2－48k －7＝0，解得k 1＝7或k 2＝－17.因此，所求直线l 的方程为x ＋7y －15＝0或7x －y －5＝0.12．已知直线l ：3x －y ＋3＝0，求： (1)点P (4,5)关于l 的对称点；(2)直线x －y －2＝0关于直线l 对称的直线方程．解：设P (x ，y )关于直线l ：3x －y ＋3＝0的对称点为P ′(x ′，y ′)．∵k PP ′·k l ＝－1，即y ′－yx ′－x ×3＝－1.①又PP ′的中点在直线3x －y ＋3＝0上，∴3×x ′＋x 2－y ′＋y 2＋3＝0.②由①②得⎩⎪⎨⎪⎧x ′＝－4x ＋3y －95， ③ y ′＝3x ＋4y ＋35. ④ (1)把x ＝4，y ＝5代入③④得x ′＝－2，y ′＝7， ∴P (4,5)关于直线l 的对称点P ′的坐标为(－2,7)．(2)用③④分别代换x －y －2＝0中的x ，y ，得关于l 的对称直线方程为－4x ＋3y －95－3x ＋4y ＋35－2＝0，化简得7x ＋y ＋22＝0.1．点P 到点A (1,0)和直线x ＝－1的距离相等，且点P 到直线y ＝x 的距离为22，这样的点P 的个数是( )A ．1 B ．2 C ．3D ．4解析：选C ∵点P 到点A 和定直线距离相等， ∴P 点轨迹为抛物线，方程为y 2＝4x . 设P (t 2,2t )，则22＝|t 2－2t |2，解得t 1＝1，t 2＝1＋2，t 3＝1－2，故P 点有三个．2．(2012·福建模拟)若点(m ，n )在直线4x ＋3y －10＝0上，则m 2＋n 2的最小值是( )A ．2B ．2 2C ．4D ．2 3解析：选C 设原点到点(m ，n )的距离为d ，所以d 2＝m 2＋n 2，又因为(m ，n )在直线4x ＋3y －10＝0上，所以原点到直线4x ＋3y －10＝0的距离为d 的最小值，此时d ＝|－10|42＋32＝2，所以m 2＋n 2的最小值为4.3．在直线l ：3x －y －1＝0上求一点P ，使得P 到A (4,1)和B (0，4)的距离之差最大．解：如图所示，设点B 关于l 的对称点为B ′，连接AB ′并延长交l 于P ，此时的P 满足|P A |－|PB |的值最大．设B ′的坐标为(a ，b )，则k BB ′·k l ＝－1，即3·b －4a ＝－1. 则a ＋3b －12＝0.①又由于线段BB ′的中点坐标为⎝ ⎛⎭⎪⎫a 2，b ＋42，且在直线l 上，则3×a 2－b ＋42－1＝0，即3a －b －6＝0.②解①②，得a ＝3，b ＝3，即B ′(3,3)．于是AB ′的方程为y －13－1＝x －43－4，即2x ＋y －9＝0.解{ 3x －y －1＝0，2x ＋y －9＝0，得{ x ＝2，y ＝5，即l 与AB ′的交点坐标为P (2,5)．1．点(1，cos θ)(其中0≤θ≤π)到直线x sin θ＋y cos θ－1＝0的距离是14，那么θ等于( )A.5π6B.π6或5π6mLC.π6D.π6或7π6图①可判断可逆反应“A2(g)+3B2(g)2AB3(g)”的解析：选B 由已知得|sin θ＋cos 2θ－1|sin 2θ＋cos 2θ＝14，即|sin θ－sin 2θ|＝14， ∴4sin 2θ－4sin θ－1＝0或4sin 2θ－4sin θ＋1＝0，∴sin θ＝1±22或sin θ＝12.∵0≤θ≤π，∴0≤sin θ≤1，∴sin θ＝12，即θ＝π6或5π6.2．已知直线l ：x －y －1＝0，l 1：2x －y －2＝0.若直线l 2与l 1关于l 对称，则l 2的方程是( )A ．x －2y ＋1＝0B ．x －2y －1＝0C ．x ＋y －1＝0D ．x ＋2y －1＝0解析：选B l 1与l 2关于l 对称，则l 1上任一点关于l 的对称点都在l 2上，故l 与l 1的交点(1,0)在l 2上．又易知(0，－2)为l 1上一点，设其关于l 的对称点(x ，y )，则⎩⎨⎧ x ＋02－y －22－1＝0，y ＋2x ×1＝－1，得{ x ＝－1，y ＝－1.即(1,0)，(－1，－1)为l 2上两点，可得l 2方程为x －2y －1＝0.3．光线沿直线l 1：x －2y ＋5＝0射入，遇直线l ：3x －2y ＋7＝0后反射，求反射光线所在的直线方程．解：法一：由{ x －2y ＋5＝0，3x －2y ＋7＝0，得{ x ＝－1，y ＝2.即反射点M 的坐标为(－1,2)．又取直线x －2y ＋5＝0上一点P (－5,0)，设P 关于直线l 的对称点P ′(x 0，y 0)，由PP ′⊥l 可知，k PP ′＝－23＝y 0x 0＋5.充其量只算得小河沟罢了试卷试题然而毕竟有水化学教案便是理直气壮的河了试卷试题有水化而PP ′的中点Q 的坐标为⎝ ⎛⎭⎪⎫x 0－52，y 02，Q 点在l 上，即3·x 0－52－2·y 02＋7＝0.由⎩⎪⎨⎪⎧ y 0x 0＋5＝－23，32(x 0－5)－y 0＋7＝0.得⎩⎨⎧ x 0＝－1713，y 0＝－3213.根据直线的两点式方程可得所求反射光线所在直线的方程为29x －2y ＋33＝0.法二：设直线x －2y ＋5＝0上任意一点P (x 0，y 0)关于直线l 的对称点为P ′(x ，y )，则y 0－y x 0－x ＝－23，又PP ′的中点Q ⎝ ⎛⎭⎪⎫x ＋x 02，y ＋y 02在l 上，即3×x ＋x 02－2×y ＋y 02＋7＝0，由⎩⎨⎧ y 0－y x 0－x ＝－23，3×x ＋x 02－(y ＋y 0)＋7＝0.可得P 点的坐标为x 0＝－5x ＋12y －4213，y 0＝12x ＋5y ＋2813，代入方程x －2y ＋5＝0中，化简得29x －2y ＋33＝0，故所求反射光线所在的直线方程为29x －2y ＋33＝0.。

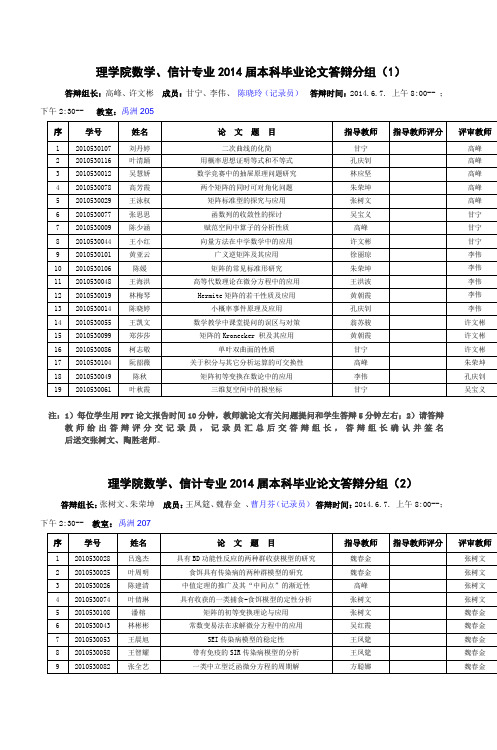
理学院数学信计专业2014届本科毕业论文答辩

理学院数学、信计专业2014届本科毕业论文答辩分组（1）答辩组长：高峰、许文彬成员：甘宁、李伟、陈晓玲（记录员）答辩时间：2014.6.7. 上午8:00-- ；下午2:30-- 教室：禹洲205注：1）每位学生用PPT论文报告时间10分钟，教师就论文有关问题提问和学生答辩5分钟左右；2）请答辩教师给出答辩评分交记录员，记录员汇总后交答辩组长，答辩组长确认并签名后送交张树文、陶胜老师。

理学院数学、信计专业2014届本科毕业论文答辩分组（2）答辩组长：张树文、朱荣坤成员：王凤筵、魏春金、曹月芬（记录员）答辩时间：2014.6.7. 上午8:00--；下午2:30-- 教室：禹洲207注：1）每位学生用PPT论文报告时间10分钟，教师就论文有关问题提问和学生答辩5分钟左右；2）请答辩教师给出答辩评分交记录员，记录员汇总后交答辩组长，答辩组长确认并签名后送交张树文、陶胜老师。

理学院数学、信计专业2014届本科毕业论文答辩分组（3）答辩组长：储理才、辛云冰成员：徐丽琼、林丽双、靳珊（记录员）答辩时间：2014.6.7. 上午8:00--；下午2:30--教室：禹洲209注：1）每位学生用PPT论文报告时间10分钟，教师就论文有关问题提问和学生答辩5分钟左右；2）请答辩教师给出答辩评分交记录员，记录员汇总后交答辩组长，答辩组长确认并签名后送交张树文、陶胜老师。

理学院数学、信计专业2014届本科毕业论文答辩分组（4）答辩组长：翁苏骏、刘小辉成员：朱福胜、刘登衍、王翠玲（记录员）答辩时间：2014.6.7. 上午8:00--；下午2:30--教室：禹洲213注：1）每位学生用PPT论文报告时间10分钟，教师就论文有关问题提问和学生答辩5分钟左右；2）请答辩教师给出答辩评分交记录员，记录员汇总后交答辩组长，答辩组长确认并签名后送交张树文、陶胜老师。

理学院数学、信计专业2014届本科毕业论文答辩分组（5）答辩组长：梁宗旗蔡南莲成员：林婉霞、王昌金、曾羽群（记录员）答辩时间：2014.6.7. 上午8:00--；下午2:30-- 教室：禹洲215注：1）每位学生用PPT论文报告时间10分钟，教师就论文有关问题提问和学生答辩5分钟左右；2）请答辩教师给出答辩评分交记录员，记录员汇总后交答辩组长，答辩组长确认并签名后送交张树文、陶胜老师。

数学教育“大先生”顾泠沅青浦实验的行与思——ICME-14报告“45年一项数学教改实验”综述

在第十四届国际数学教育大会（ICME-14）上，华东师范大学数学科学学院教授、博士生导师顾泠沅先生，做了1小时的大会报告“45年：一项数学教改实验”，成为第二位在国际数学教育大会上做大会个人报告的中国人（第一位是华罗庚先生）。

作为一名学习者、聆听者，我想结合报告内容阐述青浦实验的过程与方法，供大家学习、参考和借鉴。

（一）青浦实验的历程。

青浦实验是上海西部城乡接合地区的一个数学教改实验，从1977年至今，根据不同阶段改革的重点目标，将整个实验分为三个阶段。

1.大面积质量提高阶段。

20世纪70年代，处于上海远郊的青浦县，面临教育基础差、师资力量弱和学生起点低的问题。

1977年，时任青浦县教研员的顾泠沅在相关领导的支持下，为大面积提高教学质量，组建了一个由一线教师和教研员组成的研究小组。

为探寻教学的规律，形成了“15年磨一剑”的研究设计：3年的教学调查、1年半的经验筛选、3年的对比实验和8年的推广与深化。

从大数据宏观着眼，教学调查突出教师教与学生学的问题与症结所在，在50余次课堂循环中筛选课堂改进的关键教学行为；从精致化微观入手，在作业抽查中归纳低分学生的形成过程，在配对比较中提出针对思维水平较低学生的“变式体验”和“出声想”策略。

该阶段在最常见教育条件下发掘出了一条普遍提高教学质量的可行路径。

2.突破高认知瓶颈阶段。

在第一阶段的基础上，进一步优化提升。

面对学生成绩虽提高但认知水平提升不尽如人意的情况，注重学生认知能力的考察。

结合1990年的学生测验框架和结果，2007年再次启动八年级学生数学学习目标的大样本测验，再次评估学生计算、概念、领会、运用和分析这五种认知水平，确定记忆、理解这两个最基本的内隐主因子。

在记忆-理解两维框架下，归并和简化出操作、了解、领会和探究四层次认知目标架构，以此推进有深度的学习与教学。

此外，注重优秀经验的挖掘与深化，重温“启发尝试+及时反馈”的教学方法，凝练中国特色的变式教学经验。

由“英语不好”想到“言语互动”的三个问题——ICME-14参会随感

2021年7月11—17日，笔者有幸参加了第十四届国际数学教育大会（ICME-14），遇见几位熟识的小学数学老师，大家无不喟叹“英语水平有限，听不大懂全程英文的内容”。

虽然，笔者下载使用了同声翻译软件，但囿于机器翻译的准确度不高，只能了解大概意思，像一个饥饿的渔人眼睁睁看着一条条大鱼从脚下游走！参会时的语言障碍一直困扰着笔者，也引发关于“言语互动”的思考。

问题一：草根教师与学院派专家——专业互动，出路何方？由语言障碍引起的“言语互动”上的困难，并非仅仅发生于不同语种之间；同样使用中文的一线教师往往听不懂学术专家的报告。

后一种现象的原因是什么？该如何解决？如果说以高校教授领衔的学术专家代表着教育领域被普遍认为正统和“高大上”的“学院派”，那么一线教师则意味着教育领域的草根阶层，就现状而言，两者似乎位于一条线段的两端，一个趋向理论高空，一个深植实践大地，他们习惯于使用不同的话语体系，隔阂与断层在所难免[1]。

在ICME-14上，有专家呼吁和敦促数学家与数学教育家联手研究、协同发展；而在数学教育内部，草根教师与学院派专家也应该融汇、协同、对话与合作。

怎样才能使草根教师和学院派专家之间的专业互动有效发生呢？显然，需要打破两者“各执一端”的状态，促使他们彼此走近，这也正是中国传统的“中庸之道”。

简单地说，就是“双方努力”：学院派专家努力联系实际地做研究、深入浅出地讲道理；草根教师努力提升基于实践的反思能力和理论素养。

作为一线教师，笔者深感后一种“努力”之重要，也深感愿意做前一种“努力”的专家学者之难得。

如果一定要举例，笔者首先想到的是温州大学教育学院的章勤琼教授和杭州市上城区特级教师朱乐平老师，两位老师在笔者心中正是两种“努力”的杰出代表：章教授指导着一批一线教师正在做包括“基于学习路径分析的小学数学教学研究”在内的诸多探索，朱老师则长期坚持引领老师们做“一课研究”……非常荣幸笔者是两个优秀团队的一分子，亲身体验着两种“努力”下专业互动的美好，并且深切地感受到他们所做工作正是“跨越断层”而力求“知行合一”[2]。

2016年第十四届小学“希望杯”全国数学邀请赛试卷(五年级第1试)

2016年第十四届小学“希望杯”全国数学邀请赛试卷（五年级第1试）一、填空题（共20小题，每小题3分，满分60分）1．（3分）20.16×32+2.016×680=．2．（3分）小猫咪A、B、C、D、E、F排队依次从猫妈妈手中领鱼干，每只小猫咪每次领一条，领完后在道队尾继续排队领，直到鱼干发完．若猫妈妈有278条鱼干，则最后一个领到鱼干的小猫咪是．3．（3分）某房间内的一堵墙上挂有一面镜子，且这堵墙的对面有一块电子表，李明聪镜中看到电子表显示的时间如图所示，则此时的实际时间是．4．（3分）如果自然数a、b、c、d除以6都余4，则a+b+c+d除以3，所得的余数是．5．（3分）三位偶数A、B、C、D、E满足A＜B＜C＜D＜E，若A+B+C+D+E=4306，则A最小．6．（3分）将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是．（1步指每“加”或“减”一个数）7．（3分）如图，若每个小正方形的边长是2，则图中阴影部分的面积是．8．（3分）某商店的同种点心有大小两种包装礼盒，大盒85.6元一盒，内有点心32块，小盒46.8元一盒，内有点心15块，若王雷用654元买了9盒点心，则他可得点心块．9．（3分）如图，在梯形ABCD中，若AB=8，DC=10，S△AMD=10，S△BCM=15，则梯形ABCD的面积是．10．（3分）两个数的最大公约数和最小公倍数分别是3和135，求这两个数的差最小是．11．（3分）14袋糖果每袋的平均重量经四舍五入到小数点后第一位等于90.2克，已知每袋糖果的重量都是整数，则这14袋糖果的总重量是．12．（3分）从数字1，2，3，4，5中任意取4个组成四位数，则这些四位数的平均数是．13．（3分）某数学竞赛有10道题，规定每答对一题得5分，答错或不答扣2分．A、B两人各自答题，得分之和是58分，A比B多得14分，则A答对道题．14．（3分）如图，若长方形S长方形ABCD=60平方米，S长方形XYZR=4平方米，则四边形S四边形EFGH=平方米．15．（3分）有一个三位数A，在它的某位数字的前面添上小数点后得数B，若A ﹣B=478.8，则A=．16．（3分）商店里有若干个柚子和西瓜，其中西瓜个数是柚子个数的3倍．如果每天卖出30个西瓜和20个柚子，3天后，西瓜个数比柚子个数的4倍少26．则商店里原有个柚子．17．（3分）已知a、b、c是3个彼此不同的质数，若a+b×c=37，则a+b﹣c最大是．18．（3分）李双骑车以320米分钟的速度从A地驶向B地，途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车，15分钟后以原来骑车速度的1.5倍继续向前驶向B地，到达B地时，比预计时间多用17分钟，则李双推车步行的速度是米/分钟．19．（3分）如图，将一个等腰三角形ABC沿EF对折，顶点A与底边的中点D 重合，若△ABC的周长是16厘米，四边形BCEF的周长是10厘米，则BC=厘米．20．（3分）解放军战士在洪水不断冲毁大坝的过程中要修好大坝，若10人需45分钟，20人需要20分钟，则14人修好大坝需分钟．2016年第十四届小学“希望杯”全国数学邀请赛试卷（五年级第1试）参考答案与试题解析一、填空题（共20小题，每小题3分，满分60分）1．（3分）20.16×32+2.016×680=2016．【分析】把2.016×680变形为20.16×68，然后根据乘法的分配律简算即可．【解答】解：20.16×32+2.016×680=20.16×32+20.16×68=20.16×（32+68）=20.16×100=2016故答案为：2016．【点评】本题利用具体的算式考查了学生对于乘法分配律的理解．2．（3分）小猫咪A、B、C、D、E、F排队依次从猫妈妈手中领鱼干，每只小猫咪每次领一条，领完后在道队尾继续排队领，直到鱼干发完．若猫妈妈有278条鱼干，则最后一个领到鱼干的小猫咪是B．【分析】共有6只小猫咪，278÷6=46…2，容易得出答案．【解答】解：共有6只小猫咪，每发6条鱼重复出现，而278÷6=46…2，余数是2，则最后一个领到鱼干的小猫咪是B．故答案为：B．【点评】关键是找出周期，本题周期=6．3．（3分）某房间内的一堵墙上挂有一面镜子，且这堵墙的对面有一块电子表，李明聪镜中看到电子表显示的时间如图所示，则此时的实际时间是02：55．【分析】根据镜面对称的性质求解，在平面镜中的像与实际的实物，恰好左右或上下颠倒，关于镜面对称；据此解答即可．【解答】解：画图如下：所以，此时的实际时间是02：55．故答案为：02：55．【点评】本题考查了镜面对称知识，得到相应的对称轴是解答本题的关键，难点是作出相应的对称图形；注意2、5的关于竖直的一条直线的轴对称图形是5、2．4．（3分）如果自然数a、b、c、d除以6都余4，则a+b+c+d除以3，所得的余数是1．【分析】自然数a、b、c、d除以6都余4，则a、b、c、d都可以表示为6×整数+4，后面分析就简单了．【解答】解：因为自然数a、b、c、d除以6都余4，所以a、b、c、d都可以表示为：6×整数+4，四个这样的数的和是：6×整数+16，除以3余1，所得的余数是1．答案是1．【点评】能被6整除，一定能被3整除，只需要把四个余数加起来，看除以3余几，就是答案．5．（3分）三位偶数A、B、C、D、E满足A＜B＜C＜D＜E，若A+B+C+D+E=4306，则A最小326．【分析】最大的三位偶数是998，要使A最小，则要让其他的4个数（B、C、D、E）尽量最大，由于三位偶数A、B、C、D、E满足A＜B＜C＜D＜E，所以E 最大是998，D最大是996，C最大是994，B最大是992，用5个数的和4306减去B、C、D、E这4个数的和就是A的值；据此解答．【解答】解：最大的三位偶数是998，要满足A最小且A＜B＜C＜D＜E，则E最大是998，D最大是996，C最大是994，B最大是992，4306﹣（998+996+994+992）=4306﹣3980=326，所以此时A最小是326．故答案为：326．【点评】解答此题关键是明确最大的三位偶数是998，要使A最小，则要让其他的4个数（B、C、D、E）尽量最大．6．（3分）将100按“加15，减12，加3，加15，减12，加3，…”的顺序不断重复运算，运算26步后，得到的结果是151．（1步指每“加”或“减”一个数）【分析】加15，减12，加3，…，就相当于每一个计算周期运算3步，增加：15﹣12+3=6，则26÷3=8…2，即运算26步经过了8的计算周期，再加15，减12各一次，然后用100加上6×8，再加上15，再减去12即可．【解答】解：每一个计算周期运算3步，增加：15﹣12+3=6，则26÷3=8…2，所以，100+6×8+15﹣12=100+48+3=151答：得到的结果是151．故答案为：151．【点评】这一类问题一般要利用余数的知识来解答．这就要求我们对题目要仔细审题，判断其不断重复出现的规律，也就是找出循环的固定数，然后利用除法算式求出余数，最后根据余数得出正确的结果．7．（3分）如图，若每个小正方形的边长是2，则图中阴影部分的面积是72．【分析】可以将图中阴影部分的三角形进行剪切和拼接，变成都是小正方形组成的图形，最后再数出正方形的个数，即可求得阴影部分的面积．【解答】解：根据分析，如图，将阴影部分进行剪切和拼接后得：此时，图中阴影部分的小正方形个数为：18个，每个小正方形的面积为：2×2=4，故阴影部分的面积=18×4=72．故答案是：72．【点评】本题考查了剪切和拼接，突破点是：将阴影部分进行剪切和拼接，数出小正方形的个数，从而求得阴影部分的面积．8．（3分）某商店的同种点心有大小两种包装礼盒，大盒85.6元一盒，内有点心32块，小盒46.8元一盒，内有点心15块，若王雷用654元买了9盒点心，则他可得点心237块．【分析】设大合x 盒，小盒y 盒，依题意有方程：85.6x +46.8（9﹣x ）=654解方程可知大小各多少盒，进而可求出块数．【解答】设大合x 盒，小盒y 盒，依题意有方程：85.6x +46.8（9﹣x ）=654解方程得x=6，9﹣6=3．所以大合6盒，小盒3盒，共有32×6+15×3=237块．答：可得点心237块．【点评】本题如果用算术法求解，要用假设法．可先假设9盒全是15块一盒的，应花钱46.8×9=437.4元，比实际少232.8元，这是把其中的大合看成了小盒， 1大合看成了1小盒少算85.6﹣46.8=38.8元，大合有232.8÷38.8=6盒，小盒9﹣6=3盒．9．（3分）如图，在梯形ABCD 中，若AB=8，DC=10，S △AMD =10，S △BCM =15，则梯形ABCD 的面积是 45 ．【分析】△ADM 、△BCM 、△ABM 都等高，所以S △ABM ：（S △ADM +S △BCM ）=8：10=4：5，已知S △AMD =10，S △BCM =15，即可求出S △ABM 的面积，进而求出梯形ABCD 的面积．【解答】解：△ADM 、△BCM 、△ABM 都等高，所以S △ABM ：（S △ADM +S △BCM ）=8：10=4：5，已知S △AMD =10，S △BCM =15，所以S △ABM 的面积是：（10+15）×=20，梯形ABCD 的面积是：10+15+20=45；答：梯形ABCD 的面积是45．故答案为：45．【点评】本题关键是明确等高的三角形，面积比等于对应底的比．突破口是得到S△ABM：（S△ADM+S△BCM）=8：10．10．（3分）两个数的最大公约数和最小公倍数分别是3和135，求这两个数的差最小是12．【分析】首先要知道最大公约数和最小公倍数是如何求得的，最大公约数是两个数的公有质因数的积，最小公倍数是两个数的公有质因数和独有因数的积，所以用最小公倍数除以最大公约数就得到了两个数的独有因数的积，并且两个数的独有因数应该是互质的，然后根据质因数求出差最小的两个数即可．【解答】解：因为135÷3=45，45分解成两个互质的数有两种情况即1和45、9与5，所以差最小的是：9和5，所以这两个数分别是：9×3=275×3=1527﹣15=12答：这两个数的差最小是12．故答案为：12．【点评】本题考查了最大公因数和最小公倍数，解题关键是：最小公倍数除以最大公因数就得到了两个数的独有因数的积，并且两个数的独有因数应该是互质的．11．（3分）14袋糖果每袋的平均重量经四舍五入到小数点后第一位等于90.2克，已知每袋糖果的重量都是整数，则这14袋糖果的总重量是1263克．【分析】首先判断出这14袋糖果每袋的平均重量大于等于90.15和小于90.25之间，这14袋糖果的总重量大于或等于90.15×14=1262.1克和小于90.25×14=1263.5之间，然后求出这14袋糖果的总重量即可．【解答】解：用四舍五入取近似值的方法精确到一位小数能得到90.2的数值范围是：（大于等于90.15和小于90.25之间）所以这14袋糖果的总重量大于或等于90.15×14=1262.1克和小于90.25×14=1263.5之间，因为每袋糖果的重量都是整数，所以糖果的总重量也是整数，在1262.1和1263.5之间只有1263是整数，所以这14袋糖果的总重量是1263克．答：这14袋糖果的总重量是1263克．故答案为：1263克．【点评】解答此题的关键是判断出这14袋糖果每袋的平均重量大于等于90.15和小于90.25之间．12．（3分）从数字1，2，3，4，5中任意取4个组成四位数，则这些四位数的平均数是3333．【分析】千位上从5个数字有选择一个，就有5种选择的方法，百位上从剩下的4个数字中选择一个有4种不同的选择方法，十位上从剩下的3个数字中选择一个有3种选法，个位上从剩下的2个数字中选择一个有2种选法，它们的积就是全部的选择方法；5×4×3×2=120（种）；组成的四位数中，千位上是1的有24个数字，同理百位上是2，3，4，5的各有24个数字，十、个位上是1，2，3，4，5的也各有24个数字，即1，2，3，4，5在每个数位上各出现的24次，出现的次数相同，所以所有四位数的平均数的个位、十位、百位、千位都是1，2，3，4，5这5个数字的平均数．【解答】解：5×4×3×2=120（个），1×4×3×2=24（个），即1，2，3，4，5在每个数位上各出现的24次，可以组成120个不同的四位数；（1+2+3+4+5）÷5=3；那么平均数的各个位上的数字都是3，这个平均数就是3333．答：这些四位数的平均数是3333．故答案为：3333．【点评】根据乘法原理求出可以组成四位数的个数，再根据这些四位数的特点，找出它们的平均数．13．（3分）某数学竞赛有10道题，规定每答对一题得5分，答错或不答扣2分．A、B两人各自答题，得分之和是58分，A比B多得14分，则A答对8道题．【分析】因为得分之和是58分，A比B多得14分，根据和差公式可得A得了（58+14）÷2=36分，假设全部答对，则应得分为10×5=50分，则共相差50﹣36=14分，因为答错一道或不答和答对一道相差2+5=7分，所以答错14÷7=2道题．【解答】解：（58+14）÷2=72÷2=36（分）答错：（5×10﹣36）÷（2+5）=14÷7=2（道）答对：10﹣2=8道．故答案为：8．【点评】本题考查了和差问题与鸡兔同笼问题的综合应用，解答此类题的关键是用假设法，也可以用方程进行解答．14．（3分）如图，若长方形S长方形ABCD=60平方米，S长方形XYZR=4平方米，则四边形S四边形EFGH=32平方米．减去S 【分析】将图中面积相等的图形标出来，即等积变形，即长方形S长方形ABCD四边形后剩的八个三角形的面积可分成两半，一半再四边形EFGH中，长方形XYZR从而由此可以求得S．四边形EFGH【解答】解：根据分析，如下图所示：长方形S=S长方形XYZR+△AEF+△EFR+△FBG+△FGX+△HCG+△HGY+△DHE+△长方形ABCDHEZ=S长方形XYZR+2×（a+b+c+d）⇒60=4+2×（a+b+c+d）⇒a+b+c+d=28=△EFR+△FGX+△HGY+△HEZ+S长方形XYZR四边形S四边形EFGH=a+b+c+d+S长方形XYZR=28+4=32（平方米）．故答案是：32．【点评】本题考查了等积变形，本题突破点是：利用等积变形，将四边形的面积分割成四个三角和一个长方形，最后求和．15．（3分）有一个三位数A，在它的某位数字的前面添上小数点后得数B，若A ﹣B=478.8，则A=532．【分析】A﹣B=478.8，差是一位小数，说明B也是一位小数，原来的三位数A 变成一位小数就缩小了10倍，也就是A﹣B的差是B的9倍，用478.8除以9即可求出B，再把B的小数点向右移动一位就是A．【解答】解：A﹣B=478.8，则：B是A缩小10倍得到的478.8÷（10﹣1）=478.8÷9=53.2那么A=53.2×10=532．故答案为：532．【点评】此题应认真分析，通过观察数字得出：小数点，必在十位和个位之间，再根据差倍公式求解即可．16．（3分）商店里有若干个柚子和西瓜，其中西瓜个数是柚子个数的3倍．如果每天卖出30个西瓜和20个柚子，3天后，西瓜个数比柚子个数的4倍少26．则商店里原有176个柚子．【分析】首先找到题中的等量关系，表示出所有的数量列方程即可．【解答】解：依题意可知：3天后卖出90个西瓜和60个柚子．数量差为30个．设后来柚子是x个，西瓜是4x﹣26个．那么原来柚子是x+60个，原来西瓜是4x ﹣26+90；4x+90﹣26=3（x+60），x=116．故答案为：176【点评】本题的考查差倍问题的理解和运用，方程比较简单容易理解，问题解决．17．（3分）已知a、b、c是3个彼此不同的质数，若a+b×c=37，则a+b﹣c最大是32．【分析】要使a+b﹣c的值最大，就要使c的值最小，最小的质数是2，所以c=2；则可得：a=37﹣b×c=37﹣2b，然后再使b最小即可．当b=3时，a+3×2=37，a=31正好a、b、c都是质数将其分别代入a+b﹣c，得32【解答】解：要使a+b﹣c的值最大，就要使c的值最小，最小的质数是2，所以c=2；则可得：a=37﹣b×c=37﹣2b，要使a最大，则使b最小，b最小是3，所以，a最大是：a=37﹣2×3=31，所以，a+b﹣c最大是：a+b﹣c=31+3﹣2=32；答：a+b﹣c最大是32．故答案为：32．【点评】本题解答的突破口是先确定减数c=2，然后根据：因为b在与c的乘积中，所以只有使b尽量的小，才能保证a尽量的大解答即可．18．（3分）李双骑车以320米分钟的速度从A地驶向B地，途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车，15分钟后以原来骑车速度的1.5倍继续向前驶向B地，到达B地时，比预计时间多用17分钟，则李双推车步行的速度是72米/分钟．【分析】首先把李双原来骑车的速度看作单位“1”，用李双原来骑车的速度乘1.5，求出修完车后李双骑车的速度是多少；然后根据路程÷速度=时间，分别用1800除以修车前后李双骑车的速度，求出修车前后李双骑1800米用的时间各是多少，再用修车前李双骑1800米用的时间减去修车后李双骑1800米用的时间，求出修车后李双骑1800米少用多少分钟；最后用李双到达B地比预计多用的时间减去15，再加上修车后李双骑1800米少用的时间，求出李双步行5分钟的路程比同样的路程骑车用的时间多几分钟，再用李双骑车的速度乘李双步行5分钟的路程，骑车需要的时间，求出李双步行的路程是多少，再用它除以5，求出李双推车步行的速度是多少即可．【解答】解：1800÷320﹣1800÷（320×1.5）=5.625﹣3.75=1.875（分钟）320×[5﹣（17﹣15+1.875）]÷5=320×[5﹣3.875]÷5=320×1.125÷5=360÷5=72（米/分钟）答：李双推车步行的速度是72米/分钟．故答案为：72．【点评】此题主要考查了行程问题中速度、时间和路程的关系：速度×时间=路程，路程÷时间=速度，路程÷速度=时间，要熟练掌握，解答此题的关键是求出李双步行5分钟的路程比同样的路程骑车用的时间多几分钟．19．（3分）如图，将一个等腰三角形ABC沿EF对折，顶点A与底边的中点D 重合，若△ABC的周长是16厘米，四边形BCEF的周长是10厘米，则BC=2厘米．【分析】△ABC 的周长是16 厘米，因为△ABC 是等腰三角形，且顶点A与底边的中点D重合，所以△AEF 的周长等于△ABC 的周长的一半；可得△AEF 的周长为16÷2=8 （厘米），△AEF 和四边形BCEF周长和为8+10=18（厘米），18厘米正好比△ABC的周长是16厘米多了两条EF的长度，所以EF=（18﹣16）÷2=1 （厘米），又因为EF是中位线；则BC=2 EF=2（厘米）．【解答】解：△ABC的周长是16厘米，可得△AEF的周长为：16÷2=8 （厘米），△AEF 和四边形BCEF周长和为：8+10=18（厘米），所以BC=18﹣16=2（厘米），答：BC=2厘米．故答案为：2．【点评】本题关键是根据和差公式以及中位线的性质求出EF的长度，再进一步求出BC的长度．20．（3分）解放军战士在洪水不断冲毁大坝的过程中要修好大坝，若10人需45分钟，20人需要20分钟，则14人修好大坝需30分钟．【分析】假设每人每分钟修大坝1份，先求出洪水冲毁大坝速度：（10×45﹣20×20）÷（45﹣20）=2（份）；然后求出大坝原有的份数45×10﹣2×45=360（份）；再让14人中的2人修冲毁大坝的份数，剩下的14﹣2=12人修原有的360份，可求出需要的时间，据此解答．【解答】解：假设每人每分钟修大坝1份洪水冲毁大坝速度：（10×45﹣20×20）÷（45﹣20）=（450﹣400）÷25=50÷25=2（份）大坝原有的份数45×10﹣2×45=450﹣90=360（份）14人修好大坝需要的时间360÷（14﹣2）=360÷12=30（分钟）答：14人修好大坝需30分钟．故答案为：30．【点评】牛吃草的问题关键的是求出青草的生长速度和草地原有的草的份数．。