MATLAB遗传算法程序
用MATLAB实现遗传算法程序

用MATLAB实现遗传算法程序一、本文概述遗传算法(Genetic Algorithms,GA)是一种模拟自然界生物进化过程的优化搜索算法,它通过模拟自然选择和遗传学机制,如选择、交叉、变异等,来寻找问题的最优解。
由于其全局搜索能力强、鲁棒性好以及易于实现并行化等优点,遗传算法在多个领域得到了广泛的应用,包括函数优化、机器学习、神经网络训练、组合优化等。
本文旨在介绍如何使用MATLAB实现遗传算法程序。
MATLAB作为一种强大的数学计算和编程工具,具有直观易用的图形界面和丰富的函数库,非常适合用于遗传算法的实现。
我们将从基本的遗传算法原理出发,逐步介绍如何在MATLAB中编写遗传算法程序,包括如何定义问题、编码、初始化种群、选择操作、交叉操作和变异操作等。
通过本文的学习,读者将能够掌握遗传算法的基本原理和MATLAB编程技巧,学会如何使用MATLAB实现遗传算法程序,并能够在实际问题中应用遗传算法求解最优解。
二、遗传算法基础遗传算法(Genetic Algorithm,GA)是一种模拟自然选择和遗传学机制的优化搜索算法。
它借鉴了生物进化中的遗传、交叉、变异等机制,通过模拟这些自然过程来寻找问题的最优解。
遗传算法的核心思想是将问题的解表示为“染色体”,即一组编码,然后通过模拟自然选择、交叉和变异等过程,逐步迭代搜索出最优解。
在遗传算法中,通常将问题的解表示为一个二进制字符串,每个字符串代表一个个体(Individual)。
每个个体都有一定的适应度(Fitness),适应度越高的个体在下一代中生存下来的概率越大。
通过选择(Selection)、交叉(Crossover)和变异(Mutation)等操作,生成新一代的个体,并重复这一过程,直到找到满足条件的最优解或达到预定的迭代次数。
选择操作是根据个体的适应度,选择出适应度较高的个体作为父母,参与下一代的生成。
常见的选择算法有轮盘赌选择(Roulette Wheel Selection)、锦标赛选择(Tournament Selection)等。
matlab遗传算法工具箱导出数据的方法 -回复

matlab遗传算法工具箱导出数据的方法-回复如何使用MATLAB遗传算法工具箱导出数据MATLAB是一种广泛使用的数值计算和数据可视化软件,其遗传算法工具箱(Genetic Algorithm Toolbox)是一款强大的用于解决优化问题的工具。
在使用遗传算法工具箱时,可能会遇到需要导出数据的情况。
本文将详细介绍如何使用MATLAB遗传算法工具箱导出数据,并提供一步一步的操作指南。
第一步:加载遗传算法工具箱首先,打开MATLAB软件并加载遗传算法工具箱。
在命令窗口输入"ga"命令,即可加载遗传算法工具箱。
第二步:定义适应度函数在使用遗传算法工具箱前,需要定义一个适应度函数。
适应度函数用于度量个体对问题的适应程度,其中最佳适应程度对应最优解。
在定义适应度函数时,可以根据特定问题的要求进行自定义。
第三步:设置遗传算法参数在使用遗传算法工具箱之前,还需要设置一些遗传算法的参数。
这些参数包括种群数量、迭代次数、交叉概率、变异概率等。
根据具体问题的要求,选择合适的参数值。
第四步:运行遗传算法在完成适应度函数和参数设置后,就可以运行遗传算法了。
在命令窗口输入"ga"命令,并将适应度函数和参数作为输入参数传递给该命令。
第五步:导出数据使用遗传算法工具箱进行优化后,可能需要将优化结果导出。
下面介绍几种常用的导出数据的方法。
方法一:使用内置函数MATLAB提供了一些内置函数用于导出数据,其中比较常用的是"save"和"xlswrite"函数。
1. 使用"save"函数"save"函数用于保存变量和工作空间中的数据。
通过在命令窗口输入"save"命令,再将需要保存的变量名作为参数传递给该命令,即可将变量保存为.mat文件。
例如,要将名为"result"的变量保存为.mat文件,可以使用以下命令:save('result.mat', 'result')2. 使用"xlswrite"函数"xlswrite"函数用于将数据写入Excel文件。
Matlab中的遗传算法与优化问题求解方法介绍

Matlab中的遗传算法与优化问题求解方法介绍引言随着科技的不断进步,优化问题在各个领域中的应用越来越广泛。
在实际问题中,我们往往需要找到一个最优解或者接近最优解的近似解。
为了解决这类问题,遗传算法作为一种自适应的搜索算法,被广泛应用于各个领域。
而Matlab作为一种功能强大的数学软件,提供了丰富的遗传算法工具箱,为优化问题的求解提供了便利。
本文将介绍Matlab中的遗传算法和一些常用的优化问题求解方法。
一、遗传算法概述遗传算法是源于达尔文的进化论思想的一种优化算法。
它是通过模拟自然选择、交叉、变异等生物遗传的过程来搜索最优解的方法。
遗传算法由编码、适应度评估、选择、交叉和变异等基本操作组成。
1. 编码:遗传算法使用二进制编码或者其他离散编码,将问题的解表示为一串二进制码或离散码。
2. 适应度评估:将编码得到的解转化为问题的实际解,并计算该解的适应度,即问题的目标函数值。
3. 选择:根据适应度对解进行选择,适应度越大的解,被选中的概率越大。
4. 交叉:从父代中选择两个个体,通过某种交叉方式生成子代。
5. 变异:对子代进行变异操作,以增加解的多样性。
二、Matlab中的遗传算法函数在Matlab的遗传算法工具箱中,包含了一系列的遗传算法函数,可以快速实现遗传算法优化问题的求解。
1. ga函数:这是Matlab中最基本的遗传算法函数,用于求解普通的优化问题。
它可以通过改变种群大小、交叉概率、变异概率等参数来调整算法的性能。
2. gamultiobj函数:这个函数是用于解决多目标优化问题的。
它使用了帕累托前沿的概念,可以得到一系列的非支配解,以帮助决策者选择最优解。
3. gaplotbestf函数:这个函数可以绘制遗传算法的收敛曲线,直观地展示算法求解的过程。
三、优化问题求解方法除了遗传算法外,Matlab还提供了其他一些常用的优化问题求解方法。
1. 粒子群算法(PSO):这是一种群体智能算法,通过模拟鸟群或鱼群的行为,寻找最优解。
遗传算法及其MATLAB程序

遗传算法及其MATLAB实现主要内容遗传算法简介遗传算法的MATLAB实现应用举例一、遗传算法简介遗传算法(Genetic Algorithm,GA)最先是由美国Mic-hgan大学的John Holland于1975年提出的。
遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。
它的思想源于生物遗传学和适者生存的自然规律,是具有“生存+检测”的迭代过程的搜索算法。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。
其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定等5个要素组成了遗传算法的核心内容。
遗传算法的基本步骤:遗传算法是一种基于生物自然选择与遗传机理的随机搜索算法,与传统搜索算法不同,遗传算法从一组随机产生的称为“种群(Population)”的初始解开始搜索过程。
种群中的每个个体是问题的一个解,称为“染色体(chromos ome)”。
染色体是一串符号,比如一个二进制字符串。
这些染色体在后续迭代中不断进化,称为遗传。
在每一代中用“适值(fitness)”来测量染色体的好坏,生成的下一代染色体称为后代(offspring)。
后代是由前一代染色体通过交叉(crossover)或者变异(mutation)运算形成的。
在新一代形成过程中,根据适度的大小选择部分后代,淘汰部分后代。
从而保持种群大小是常数。
适值高的染色体被选中的概率较高,这样经过若干代之后,算法收敛于最好的染色体,它很可能就是问题的最优解或次优解。
主要步骤如下所示:(1)编码:GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合便构成了不同的点。
(2)初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了—个群体。
GA以这N个串结构数据作为初始点开始迭代。
2020年遗传算法matlab程序实例精编版

%-----------------------------------------------%---------------------------------------------------遗传算法程序(一):说明: fga.m 为遗传算法的主程序; 采用二进制Gray编码,采用基于轮盘赌法的非线性排名选择, 均匀交叉,变异操作,而且还引入了倒位操作!function [BestPop,Trace]=fga(FUN,LB,UB,eranum,popsize,pCross,pMutation,pInversion,options) % [BestPop,Trace]=fmaxga(FUN,LB,UB,eranum,popsize,pcross,pmutation)% Finds a maximum of a function of several variables.% fmaxga solves problems of the form:% max F(X) subject to: LB <= X <= UB% BestPop - 最优的群体即为最优的染色体群% Trace - 最佳染色体所对应的目标函数值% FUN - 目标函数% LB - 自变量下限% UB - 自变量上限% eranum - 种群的代数,取100--1000(默认200)% popsize - 每一代种群的规模;此可取50--200(默认100)% pcross - 交叉概率,一般取0.5--0.85之间较好(默认0.8)% pmutation - 初始变异概率,一般取0.05-0.2之间较好(默认0.1)% pInversion - 倒位概率,一般取0.05-0.3之间较好(默认0.2)% options - 1*2矩阵,options(1)=0二进制编码(默认0),option(1)~=0十进制编%码,option(2)设定求解精度(默认1e-4)%% ------------------------------------------------------------------------T1=clock;if nargin<3, error('FMAXGA requires at least three input arguments'); endif nargin==3, eranum=200;popsize=100;pCross=0.8;pMutation=0.1;pInversion=0.15;options=[0 1e-4];endif nargin==4, popsize=100;pCross=0.8;pMutation=0.1;pInversion=0.15;options=[0 1e-4];endif nargin==5, pCross=0.8;pMutation=0.1;pInversion=0.15;options=[0 1e-4];endif nargin==6, pMutation=0.1;pInversion=0.15;options=[0 1e-4];endif nargin==7, pInversion=0.15;options=[0 1e-4];endif find((LB-UB)>0)error('数据输入错误,请重新输入(LB<UB):');ends=sprintf('程序运行需要约%.4f 秒钟时间,请稍等......',(eranum*popsize/1000));disp(s);global m n NewPop children1 children2 VarNumbounds=[LB;UB]';bits=[];VarNum=size(bounds,1);precision=options(2);%由求解精度确定二进制编码长度bits=ceil(log2((bounds(:,2)-bounds(:,1))' ./ precision));%由设定精度划分区间[Pop]=InitPopGray(popsize,bits);%初始化种群[m,n]=size(Pop);NewPop=zeros(m,n);children1=zeros(1,n);children2=zeros(1,n);pm0=pMutation;BestPop=zeros(eranum,n);%分配初始解空间BestPop,TraceTrace=zeros(eranum,length(bits)+1);i=1;while i<=eranumfor j=1:mvalue(j)=feval(FUN(1,:),(b2f(Pop(j,:),bounds,bits)));%计算适应度end[MaxValue,Index]=max(value);BestPop(i,:)=Pop(Index,:);Trace(i,1)=MaxValue;Trace(i,(2:length(bits)+1))=b2f(BestPop(i,:),bounds,bits);[selectpop]=NonlinearRankSelect(FUN,Pop,bounds,bits);%非线性排名选择[CrossOverPop]=CrossOver(selectpop,pCross,round(unidrnd(eranum-i)/eranum));%采用多点交叉和均匀交叉,且逐步增大均匀交叉的概率%round(unidrnd(eranum-i)/eranum)[MutationPop]=Mutation(CrossOverPop,pMutation,VarNum);%变异[InversionPop]=Inversion(MutationPop,pInversion);%倒位Pop=InversionPop;%更新pMutation=pm0+(i^4)*(pCross/3-pm0)/(eranum^4);%随着种群向前进化,逐步增大变异率至1/2交叉率p(i)=pMutation;i=i+1;endt=1:eranum;plot(t,Trace(:,1)');title('函数优化的遗传算法');xlabel('进化世代数(eranum)');ylabel('每一代最优适应度(maxfitness)');[MaxFval,I]=max(Trace(:,1));X=Trace(I,(2:length(bits)+1));hold on; plot(I,MaxFval,'*');text(I+5,MaxFval,['FMAX=' num2str(MaxFval)]);str1=sprintf ('进化到%d 代,自变量为%s 时,得本次求解的最优值%f\n对应染色体是:%s',I,num2str(X),MaxFval,num2str(BestPop(I,:)));disp(str1);%figure(2);plot(t,p);%绘制变异值增大过程T2=clock;elapsed_time=T2-T1;if elapsed_time(6)<0elapsed_time(6)=elapsed_time(6)+60; elapsed_time(5)=elapsed_time(5)-1;endif elapsed_time(5)<0elapsed_time(5)=elapsed_time(5)+60;elapsed_time(4)=elapsed_time(4)-1;end %像这种程序当然不考虑运行上小时啦str2=sprintf('程序运行耗时%d 小时%d 分钟%.4f 秒',elapsed_time(4),elapsed_time(5),elapsed_time(6));disp(str2);%初始化种群%采用二进制Gray编码,其目的是为了克服二进制编码的Hamming悬崖缺点function [initpop]=InitPopGray(popsize,bits)len=sum(bits);initpop=zeros(popsize,len);%The whole zero encoding individualfor i=2:popsize-1pop=round(rand(1,len));pop=mod(([0 pop]+[pop 0]),2);%i=1时,b(1)=a(1);i>1时,b(i)=mod(a(i-1)+a(i),2)%其中原二进制串:a(1)a(2)...a(n),Gray串:b(1)b(2)...b(n)initpop(i,:)=pop(1:end-1);endinitpop(popsize,:)=ones(1,len);%The whole one encoding individual%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%解码function [fval] = b2f(bval,bounds,bits)% fval - 表征各变量的十进制数% bval - 表征各变量的二进制编码串% bounds - 各变量的取值范围% bits - 各变量的二进制编码长度scale=(bounds(:,2)-bounds(:,1))'./(2.^bits-1); %The range of the variablesnumV=size(bounds,1);cs=[0 cumsum(bits)];for i=1:numVa=bval((cs(i)+1):cs(i+1));fval(i)=sum(2.^(size(a,2)-1:-1:0).*a)*scale(i)+bounds(i,1);end%选择操作%采用基于轮盘赌法的非线性排名选择%各个体成员按适应值从大到小分配选择概率:%P(i)=(q/1-(1-q)^n)*(1-q)^i, 其中P(0)>P(1)>...>P(n), sum(P(i))=1function [selectpop]=NonlinearRankSelect(FUN,pop,bounds,bits)global m nselectpop=zeros(m,n);fit=zeros(m,1);for i=1:mfit(i)=feval(FUN(1,:),(b2f(pop(i,:),bounds,bits)));%以函数值为适应值做排名依据endselectprob=fit/sum(fit);%计算各个体相对适应度(0,1)q=max(selectprob);%选择最优的概率x=zeros(m,2);x(:,1)=[m:-1:1]';[y x(:,2)]=sort(selectprob);r=q/(1-(1-q)^m);%标准分布基值newfit(x(:,2))=r*(1-q).^(x(:,1)-1);%生成选择概率newfit=cumsum(newfit);%计算各选择概率之和rNums=sort(rand(m,1));fitIn=1;newIn=1;while newIn<=mif rNums(newIn)<newfit(fitIn)selectpop(newIn,:)=pop(fitIn,:);newIn=newIn+1;elsefitIn=fitIn+1;endend%交叉操作function [NewPop]=CrossOver(OldPop,pCross,opts)%OldPop为父代种群,pcross为交叉概率global m n NewPopr=rand(1,m);y1=find(r<pCross);y2=find(r>=pCross);len=length(y1);if len>2&mod(len,2)==1%如果用来进行交叉的染色体的条数为奇数,将其调整为偶数y2(length(y2)+1)=y1(len);y1(len)=[];endif length(y1)>=2for i=0:2:length(y1)-2if opts==0[NewPop(y1(i+1),:),NewPop(y1(i+2),:)]=EqualCrossOver(OldPop(y1(i+1),:),OldPop(y1(i+2),:));else[NewPop(y1(i+1),:),NewPop(y1(i+2),:)]=MultiPointCross(OldPop(y1(i+1),:),OldPop(y1(i+2),:));endendendNewPop(y2,:)=OldPop(y2,:);%采用均匀交叉function [children1,children2]=EqualCrossOver(parent1,parent2)global n children1 children2hidecode=round(rand(1,n));%随机生成掩码crossposition=find(hidecode==1);holdposition=find(hidecode==0);children1(crossposition)=parent1(crossposition);%掩码为1,父1为子1提供基因children1(holdposition)=parent2(holdposition);%掩码为0,父2为子1提供基因children2(crossposition)=parent2(crossposition);%掩码为1,父2为子2提供基因children2(holdposition)=parent1(holdposition);%掩码为0,父1为子2提供基因%采用多点交叉,交叉点数由变量数决定function [Children1,Children2]=MultiPointCross(Parent1,Parent2)global n Children1 Children2 VarNumChildren1=Parent1;Children2=Parent2;Points=sort(unidrnd(n,1,2*VarNum));for i=1:VarNumChildren1(Points(2*i-1):Points(2*i))=Parent2(Points(2*i-1):Points(2*i));Children2(Points(2*i-1):Points(2*i))=Parent1(Points(2*i-1):Points(2*i));end%变异操作function [NewPop]=Mutation(OldPop,pMutation,VarNum)global m n NewPopr=rand(1,m);position=find(r<=pMutation);len=length(position);if len>=1for i=1:lenk=unidrnd(n,1,VarNum); %设置变异点数,一般设置1点for j=1:length(k)if OldPop(position(i),k(j))==1OldPop(position(i),k(j))=0;elseOldPop(position(i),k(j))=1;endendendendNewPop=OldPop;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%倒位操作function [NewPop]=Inversion(OldPop,pInversion)global m n NewPopNewPop=OldPop;r=rand(1,m);PopIn=find(r<=pInversion);len=length(PopIn);if len>=1for i=1:lend=sort(unidrnd(n,1,2));if d(1)~=1&d(2)~=nNewPop(PopIn(i),1:d(1)-1)=OldPop(PopIn(i),1:d(1)-1);NewPop(PopIn(i),d(1):d(2))=OldPop(PopIn(i),d(2):-1:d(1));NewPop(PopIn(i),d(2)+1:n)=OldPop(PopIn(i),d(2)+1:n);endendend遗传算法程序(二):function youhuafunD=code;N=50; % Tunablemaxgen=50; % Tunablecrossrate=0.5; %Tunablemuterate=0.08; %Tunablegeneration=1;num = length(D);fatherrand=randint(num,N,3);score = zeros(maxgen,N);while generation<=maxgenind=randperm(N-2)+2; % 随机配对交叉A=fatherrand(:,ind(1:(N-2)/2));B=fatherrand(:,ind((N-2)/2+1:end));% 多点交叉rnd=rand(num,(N-2)/2);ind=rnd tmp=A(ind);A(ind)=B(ind);B(ind)=tmp;% % 两点交叉% for kk=1:(N-2)/2% rndtmp=randint(1,1,num)+1;% tmp=A(1:rndtmp,kk);% A(1:rndtmp,kk)=B(1:rndtmp,kk);% B(1:rndtmp,kk)=tmp;% endfatherrand=[fatherrand(:,1:2),A,B];% 变异rnd=rand(num,N);ind=rnd [m,n]=size(ind);tmp=randint(m,n,2)+1;tmp(:,1:2)=0;fatherrand=tmp+fatherrand;fatherrand=mod(fatherrand,3);% fatherrand(ind)=tmp;%评价、选择scoreN=scorefun(fatherrand,D);% 求得N个个体的评价函数score(generation,:)=scoreN;[scoreSort,scoreind]=sort(scoreN);sumscore=cumsum(scoreSort);sumscore=sumscore./sumscore(end);childind(1:2)=scoreind(end-1:end);for k=3:Ntmprnd=rand;tmpind=tmprnd difind=[0,diff(tmpind)];if ~any(difind)difind(1)=1;endchildind(k)=scoreind(logical(difind));endfatherrand=fatherrand(:,childind);generation=generation+1;end% scoremaxV=max(score,[],2);minV=11*300-maxV;plot(minV,'*');title('各代的目标函数值');F4=D(:,4);FF4=F4-fatherrand(:,1);FF4=max(FF4,1);D(:,5)=FF4;save DData Dfunction D=codeload youhua.mat% properties F2 and F3F1=A(:,1);F2=A(:,2);F3=A(:,3);if (max(F2)>1450)||(min(F2)<=900)error('DATA property F2 exceed it''s range (900,1450]')end% get group property F1 of data, according to F2 valueF4=zeros(size(F1));for ite=11:-1:1index=find(F2<=900+ite*50);F4(index)=ite;endD=[F1,F2,F3,F4];function ScoreN=scorefun(fatherrand,D)F3=D(:,3);F4=D(:,4);N=size(fatherrand,2);FF4=F4*ones(1,N);FF4rnd=FF4-fatherrand;FF4rnd=max(FF4rnd,1);ScoreN=ones(1,N)*300*11;% 这里有待优化for k=1:NFF4k=FF4rnd(:,k);for ite=1:11F0index=find(FF4k==ite);if ~isempty(F0index)tmpMat=F3(F0index);tmpSco=sum(tmpMat);ScoreBin(ite)=mod(tmpSco,300);endendScorek(k)=sum(ScoreBin);endScoreN=ScoreN-Scorek;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%遗传算法程序(三):%IAGAfunction best=gaclearMAX_gen=200; %最大迭代步数best.max_f=0; %当前最大的适应度STOP_f=14.5; %停止循环的适应度RANGE=[0 255]; %初始取值范围[0 255]SPEEDUP_INTER=5; %进入加速迭代的间隔advance_k=0; %优化的次数popus=init; %初始化for gen=1:MAX_genfitness=fit(popus,RANGE); %求适应度f=fitness.f;picked=choose(popus,fitness); %选择popus=intercross(popus,picked); %杂交popus=aberrance(popus,picked); %变异if max(f)>best.max_fadvance_k=advance_k+1;x_better(advance_k)=fitness.x;best.max_f=max(f);best.popus=popus;best.x=fitness.x;endif mod(advance_k,SPEEDUP_INTER)==0RANGE=minmax(x_better);RANGEadvance=0;endendreturn;function popus=init%初始化M=50;%种群个体数目N=30;%编码长度popus=round(rand(M,N));return;function fitness=fit(popus,RANGE)%求适应度[M,N]=size(popus);fitness=zeros(M,1);%适应度f=zeros(M,1);%函数值A=RANGE(1);B=RANGE(2);%初始取值范围[0 255]for m=1:Mx=0;for n=1:Nx=x+popus(m,n)*(2^(n-1));endx=x*((B-A)/(2^N))+A;for k=1:5f(m,1)=f(m,1)-(k*sin((k+1)*x+k));endendf_std=(f-min(f))./(max(f)-min(f));%函数值标准化fitness.f=f;fitness.f_std=f_std;fitness.x=x;return;function picked=choose(popus,fitness)%选择f=fitness.f;f_std=fitness.f_std;[M,N]=size(popus);choose_N=3; %选择choose_N对双亲picked=zeros(choose_N,2); %记录选择好的双亲p=zeros(M,1); %选择概率d_order=zeros(M,1);%把父代个体按适应度从大到小排序f_t=sort(f,'descend');%将适应度按降序排列for k=1:Mx=find(f==f_t(k));%降序排列的个体序号d_order(k)=x(1);endfor m=1:Mpopus_t(m,:)=popus(d_order(m),:);endpopus=popus_t;f=f_t;p=f_std./sum(f_std); %选择概率c_p=cumsum(p)'; %累积概率for cn=1:choose_Npicked(cn,1)=roulette(c_p); %轮盘赌picked(cn,2)=roulette(c_p); %轮盘赌popus=intercross(popus,picked(cn,:));%杂交endpopus=aberrance(popus,picked);%变异return;function popus=intercross(popus,picked) %杂交[M_p,N_p]=size(picked);[M,N]=size(popus);for cn=1:M_pp(1)=ceil(rand*N);%生成杂交位置p(2)=ceil(rand*N);p=sort(p);t=popus(picked(cn,1),p(1):p(2));popus(picked(cn,1),p(1):p(2))=popus(picked(cn,2),p(1):p(2));popus(picked(cn,2),p(1):p(2))=t;endreturn;function popus=aberrance(popus,picked) %变异P_a=0.05;%变异概率[M,N]=size(popus);[M_p,N_p]=size(picked);U=rand(1,2);for kp=1:M_pif U(2)>=P_a %如果大于变异概率,就不变异continue;endif U(1)>=0.5a=picked(kp,1);elsea=picked(kp,2);endp(1)=ceil(rand*N);%生成变异位置p(2)=ceil(rand*N);if popus(a,p(1))==1%0 1变换popus(a,p(1))=0;elsepopus(a,p(1))=1;endif popus(a,p(2))==1popus(a,p(2))=0;elsepopus(a,p(2))=1;endendreturn;function picked=roulette(c_p) %轮盘赌[M,N]=size(c_p);M=max([M N]);U=rand;if U<c_p(1)picked=1;return;endfor m=1:(M-1)if U>c_p(m) & U<c_p(m+1)picked=m+1;break;endend全方位的两点杂交、两点变异的改进的加速遗传算法(IAGA)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%。
遗传算法应用实例及matlab程序

遗传算法应用实例及matlab程序遗传算法是一种模拟自然进化过程的优化算法,在多个领域都有广泛的应用。
下面将以一个经典的实例,车间调度问题,来说明遗传算法在实际问题中的应用,并给出一个基于MATLAB的实现。
车间调度问题是一个经典的组合优化问题,它是指在给定一系列任务和一台机器的情况下,如何安排任务的执行顺序,以便最小化任务的完成时间或最大化任务的完成效率。
这个问题通常是NP困难问题,因此传统的优化算法往往难以找到全局最优解。
遗传算法能够解决车间调度问题,其基本思想是通过模拟生物进化的过程,不断演化和改进任务的调度顺序,以找到最优解。
具体步骤如下:1. 初始种群的生成:生成一批初始调度方案,每个方案都表示为一个染色体,一般采用随机生成的方式。
2. 个体适应度的计算:根据染色体中任务的执行顺序,计算每个调度方案的适应度值,一般使用任务完成时间作为适应度度量。
3. 选择操作:根据个体的适应度,采用选择策略选择一部分优秀个体作为父代。
4. 交叉操作:对选中的个体进行交叉操作,生成新的子代个体。
5. 变异操作:对子代个体进行变异操作,引入随机性,增加搜索空间的广度。
6. 替换操作:用新的个体替换原来的个体,形成新一代的种群。
7. 迭代过程:重复执行选择、交叉、变异和替换操作,直到达到预定的终止条件。
下面给出基于MATLAB的实现示例:matlabfunction [best_solution, best_fitness] =genetic_algorithm(num_generations, population_size) % 初始化种群population = generate_population(population_size);for generation = 1:num_generations% 计算适应度fitness = calculate_fitness(population);% 选择操作selected_population = selection(population, fitness);% 交叉操作crossed_population = crossover(selected_population);% 变异操作mutated_population = mutation(crossed_population);% 替换操作population = replace(population, selected_population, mutated_population);end% 找到最优解[~, index] = max(fitness);best_solution = population(index,:);best_fitness = fitness(index);endfunction population = generate_population(population_size) % 根据问题的具体要求,生成初始种群population = randi([1, num_tasks], [population_size, num_tasks]); endfunction fitness = calculate_fitness(population)% 根据任务执行顺序,计算每个调度方案的适应度% 这里以任务完成时间作为适应度度量fitness = zeros(size(population, 1), 1);for i = 1:size(population, 1)solution = population(i,:);% 计算任务完成时间completion_time = calculate_completion_time(solution);% 适应度为任务完成时间的倒数fitness(i) = 1 / completion_time;endendfunction selected_population = selection(population, fitness) % 根据适应度值选择父代个体% 这里采用轮盘赌选择策略selected_population = zeros(size(population));for i = 1:size(population, 1)% 计算选择概率prob = fitness / sum(fitness);% 轮盘赌选择selected_population(i,:) = population(find(rand <= cumsum(prob), 1),:);endendfunction crossed_population = crossover(selected_population) % 对选中的个体进行交叉操作% 这里采用单点交叉crossed_population = zeros(size(selected_population));for i = 1:size(selected_population, 1) / 2parent1 = selected_population(2*i-1,:);parent2 = selected_population(2*i,:);% 随机选择交叉点crossover_point = randi([1, size(parent1,2)]);% 交叉操作crossed_population(2*i-1,:) = [parent1(1:crossover_point), parent2(crossover_point+1:end)];crossed_population(2*i,:) = [parent2(1:crossover_point), parent1(crossover_point+1:end)];endendfunction mutated_population = mutation(crossed_population) % 对子代个体进行变异操作% 这里采用单点变异mutated_population = crossed_population;for i = 1:size(mutated_population, 1)individual = mutated_population(i,:);% 随机选择变异点mutation_point = randi([1, size(individual,2)]);% 变异操作mutated_population(i,mutation_point) = randi([1, num_tasks]);endendfunction new_population = replace(population, selected_population, mutated_population)% 根据选择、交叉和变异得到的个体替换原来的个体new_population = mutated_population;for i = 1:size(population, 1)if ismember(population(i,:), selected_population, 'rows')% 保留选择得到的个体continue;else% 随机选择一个父代个体进行替换index = randi([1, size(selected_population,1)]);new_population(i,:) = selected_population(index,:);endendend该示例代码实现了车间调度问题的遗传算法求解过程,具体实现了种群的初始化、适应度计算、选择、交叉、变异和替换等操作。
遗传算法MATLAB完整代码(不用工具箱)

遗传算法MATLAB完整代码(不用工具箱)遗传算法解决简单问题%主程序:用遗传算法求解y=200*exp(-0.05*x).*sin(x)在区间[-2,2]上的最大值clc;clear all;close all;global BitLengthglobal boundsbeginglobal boundsendbounds=[-2,2];precision=0.0001;boundsbegin=bounds(:,1);boundsend=bounds(:,2);%计算如果满足求解精度至少需要多长的染色体BitLength=ceil(log2((boundsend-boundsbegin)'./precision));popsize=50; %初始种群大小Generationmax=12; %最大代数pcrossover=0.90; %交配概率pmutation=0.09; %变异概率%产生初始种群population=round(rand(popsize,BitLength));%计算适应度,返回适应度Fitvalue和累计概率cumsump[Fitvalue,cumsump]=fitnessfun(population);Generation=1;while Generation<generationmax+1< p="">for j=1:2:popsize%选择操作seln=selection(population,cumsump);%交叉操作scro=crossover(population,seln,pcrossover);scnew(j,:)=scro(1,:);scnew(j+1,:)=scro(2,:);%变异操作smnew(j,:)=mutation(scnew(j,:),pmutation);smnew(j+1,:)=mutation(scnew(j+1,:),pmutation);endpopulation=scnew; %产生了新的种群%计算新种群的适应度[Fitvalue,cumsump]=fitnessfun(population);%记录当前代最好的适应度和平均适应度[fmax,nmax]=max(Fitvalue);fmean=mean(Fitvalue);ymax(Generation)=fmax;ymean(Generation)=fmean;%记录当前代的最佳染色体个体x=transform2to10(population(nmax,:));%自变量取值范围是[-2,2],需要把经过遗传运算的最佳染色体整合到[-2,2]区间xx=boundsbegin+x*(boundsend-boundsbegin)/(power((boundsend),BitLength)-1);xmax(Generation)=xx;Generation=Generation+1;endGeneration=Generation-1;Bestpopulation=xx;Besttargetfunvalue=targetfun(xx);%绘制经过遗传运算后的适应度曲线。
遗传算法matlab函数的源程序

end
end
end
%确定下一代父代个体
%确定实际子代个体数值
chi_fact=zeros(x_num,chi_num*3);
for j=1:x_num
chi_fact(j,:)=x_range(j,1)+(x_range(j,2)-x_range(j,1))*chi(j,:);
par=chi(:,chi_ada_no(1:par_num));
end ');
par_fac_exc(:,1)=x_range(:,1)+(x_range(:,2)-x_range(:,1)).*par(:,1);%父代个体最优函数值
par_fun_exc=fun(par_fac_exc);
%输出父代样本实际值
par_fact=zeros(x_num,par_num);
for i=1:x_num
par_fact(i,:)=x_range(i,1)+(x_range(i,2)-x_range(i,1))*par(i,:);
if chi_ran(3)<0.5
chi(j,i)=chi_ran(1)*par(j,chi_sel1)+(1-chi_ran(1))*par(j,chi_sel2);
else
chi(j,i)=chi_ran(2)*par(j,chi_sel1)+(1-chi_ran(2))*par(j,chi_sel2);
%例子2:
%fun=@(x) sum(x.*x-cos(18*x))+5;
%x_range=[-1,1;-1,1;-1,1;-1,1;-1,1];
遗传算法 matlab

遗传算法 Matlab什么是遗传算法?遗传算法是一种模拟生物进化过程的优化算法。
它模拟了自然界中的遗传、突变和选择等过程,利用这些操作来搜索和优化问题的解空间。
遗传算法具有以下几个关键步骤:1.初始化种群:通过生成一组随机解来初始化初始种群。
每个解被编码为一个染色体,染色体通常由二进制字符串表示。
2.评价适应度:使用适应度函数评估每个个体的适应度。
适应度函数通常通过衡量个体在解空间中的性能来定义。
3.选择操作:选择操作基于个体的适应度进行,通过概率选择操作来确定哪些个体应该参与繁殖下一代。
适应度较高的个体有更大的概率被选中。
4.交叉操作:选择的个体进行交叉操作,生成下一代的染色体。
交叉操作通过交换个体染色体中的信息来生成新的个体。
5.变异操作:为了保持种群的多样性,变异操作在染色体中进行随机的变异。
这个过程通过随机改变染色体中的部分基因来进行。
6.替换操作:根据新生成的染色体替换当前种群中某些个体,以此来形成新的种群。
7.重复上述步骤:重复执行上述步骤直到满足终止条件(例如达到最大迭代次数或找到满意的解)。
如何在 Matlab 中实现遗传算法?在 Matlab 中,可以使用遗传算法和优化工具箱来实现遗传算法。
以下是实现遗传算法的一般步骤:1.定义适应度函数:根据具体问题定义适应度函数,该函数衡量每个个体在解空间中的性能。
适应度函数的设计将影响到最终结果。
2.初始化种群:使用内置函数或自定义函数来生成初始种群。
每个个体都应该表示为染色体形式的解。
3.设置遗传算法参数:根据具体问题设置遗传算法的参数,如种群大小、迭代次数、选择操作和交叉操作的概率等。
4.编写遗传算法主循环:在主循环中,使用选择操作、交叉操作和变异操作来生成新的染色体,并计算每个个体的适应度。
5.选择操作:使用选择函数根据适应度值选择染色体。
具体的选择函数可以根据问题的特点进行调整。
6.交叉操作:使用交叉函数对染色体进行交叉操作,生成下一代的染色体。
使用MATLAB遗传算法工具实例

使用MATLAB遗传算法工具实例MATLAB中提供了一种用于优化问题的遗传算法工具箱,可以帮助用户通过遗传算法来寻找最优解。
下面是一个示例,展示了如何使用MATLAB遗传算法工具箱解决一个简单的优化问题。
假设我们要求解以下函数的最大值:f(x)=x^2,其中x的取值范围在[-10,10]之间。
首先,我们需要定义适应度函数,即用来评估个体适应度的函数。
在本例中,适应度函数可以直接使用目标函数,即f(x)=x^2、在MATLAB中,我们可以使用函数句柄来定义适应度函数:```matlabfunction fitness = fitnessFunction(x)fitness = x^2;end```接下来,我们需要配置遗传算法的参数。
我们可以使用`gaoptimset`函数来创建一个参数结构体,并设置算法的各个参数:```matlaboptions = gaoptimset('PopulationSize', 50, 'Generations', 100, 'FitnessLimit', 1e-6, 'StallGenLimit', 10);```上述代码将设置种群大小为50,迭代次数为100,适应度极限为1e-6(即当适应度较小时停止迭代),最大迭代代数为10(即如果连续10代迭代没有改进,则停止迭代)。
接下来,我们需要调用`ga`函数来运行遗传算法并求解最优解。
我们可以使用以下代码来实现:```matlab```最后,我们可以打印出最优解及其目标函数值:```matlabdisp(['Optimal solution: x = ' num2str(x) ', f(x) = 'num2str(fval)]);```上述代码中,`num2str`函数用于将数字转换为字符串,然后使用`disp`函数打印出最优解和目标函数值。
遗传算法在matlab中的实现

遗传算法是一种模拟自然选择与遗传机制的优化算法,它模拟了生物进化的过程,通过优化个体的基因型来达到解决问题的目的。
在工程和科学领域,遗传算法被广泛应用于求解优化问题、寻找最优解、参数优化等领域。
而MATLAB作为一款强大的科学计算软件,拥有丰富的工具箱和编程接口,为实现遗传算法提供了便利。
下面将通过以下步骤介绍如何在MATLAB中实现遗传算法:1. 引入遗传算法工具箱需要在MATLAB环境中引入遗传算法工具箱。
在MATLAB命令窗口输入"ver",可以查看当前已安装的工具箱。
如果遗传算法工具箱未安装,可以使用MATLAB提供的工具箱管理界面进行安装。
2. 定义优化问题在实现遗传算法前,需要清楚地定义优化问题:包括问题的目标函数、约束条件等。
在MATLAB中,可以通过定义一个函数来表示目标函数,并且可以采用匿名函数的形式来灵活定义。
对于约束条件,也需要进行明确定义,以便在遗传算法中进行约束处理。
3. 设置遗传算法参数在实现遗传算法时,需要对遗传算法的参数进行设置,包括种群大小、交叉概率、变异概率、迭代次数等。
这些参数的设置将会直接影响遗传算法的收敛速度和优化效果。
在MATLAB中,可以通过设置遗传算法工具箱中的相关函数来完成参数的设置。
4. 编写遗传算法主程序编写遗传算法的主程序,主要包括对适应度函数的计算、选择、交叉、变异等操作。
在MATLAB中,可以利用遗传算法工具箱提供的相关函数来实现这些操作,简化了遗传算法的实现过程。
5. 运行遗传算法将编写好的遗传算法主程序在MATLAB环境中运行,并观察优化结果。
在运行过程中,可以对结果进行实时监测和分析,以便对遗传算法的参数进行调整和优化。
通过以上步骤,可以在MATLAB中实现遗传算法,并应用于实际的优化问题与工程应用中。
遗传算法的实现将大大提高问题的求解效率与精度,为工程领域带来更多的便利与可能性。
总结:遗传算法在MATLAB中的实现涉及到了引入遗传算法工具箱、定义优化问题、设置算法参数、编写主程序和运行算法等步骤。
matlab 并行多种群遗传算法

《使用MATLAB实现并行多种群遗传算法》1. 引言在当今信息时代,计算机科学和人工智能技术的迅猛发展,为解决复杂问题和优化算法提供了无限可能。
而遗传算法作为一种基于自然选择和遗传机制的优化算法,被广泛应用于工程、经济、生物等领域。
而在现实中,我们面对的问题往往是复杂多样的,传统的遗传算法可能无法满足需求,本文将探讨如何利用MATLAB实现并行多种群遗传算法,来解决这类问题。
2. 并行多种群遗传算法介绍并行多种群遗传算法是将多个遗传算法进行并行化处理的一种优化方法。
它通过将种群划分为多个子种群,每个子种群独立运行遗传算法进化过程,最终融合各子种群的结果,以达到更好的全局搜索能力和更快的优化速度。
与传统的遗传算法相比,这种并行化设计可以显著提高算法的收敛性和全局搜索能力。
3. MATLAB实现并行多种群遗传算法的步骤在MATLAB中实现并行多种群遗传算法,主要包括以下步骤:(1)初始化参数:包括种群数量、染色体长度、遗传代数等;(2)初始化种群:生成多个子种群,并对每个子种群进行初始化;(3)并行遗传算法进化:对每个子种群分别进行遗传算法的选择、交叉和变异操作;(4)合并结果:将每个子种群得到的优化结果进行合并,得到最终的全局最优解。
4. 并行多种群遗传算法的优势和应用相对于传统的遗传算法,使用MATLAB实现并行多种群遗传算法具有以下优势:(1)加速算法收敛速度:并行处理多个子种群可以大大加快整体算法的求解速度;(2)增强全局搜索能力:多个独立的子种群有助于更好地探索搜索空间;(3)解决复杂问题:对于复杂多样的实际问题,通过并行多种群设计可以更好地适应问题的特性。
具体应用上,MATLAB实现的并行多种群遗传算法可应用于工程领域的优化设计、机器学习中的参数优化、生物统计学的模型拟合等多个领域,帮助用户更高效地实现优化目标。
5. 个人观点和总结笔者认为,MATLAB实现并行多种群遗传算法作为一种先进的优化算法设计,具有很大的应用潜力。
遗传算法matlab程序

遗传算法matlab程序
遗传算法(Genetic Algorithm,GA)是一种基于自然进化原理的模拟退火算法,它以一种类似生物进化的方式来搜索最优解,它可以用来解决组合优化问题。
MATLAB中的遗传算法可以帮助用户构建复杂的遗传算法,以解决各种组合优化问题。
MATLAB中的遗传算法使用一个用户定义的函数,允许用户定义要优化的目标函数,以及要优化的参数空间。
遗传算法使用种群,以随机的方式初始化参数空间,并在每一代(仿真步骤)中进行参数更新,以最小化或最大化用户定义的目标函数。
MATLAB中的遗传算法程序包括三个基本步骤:
1. 初始化算法:确定种群大小、编码类型、进化操作(例如交叉、突变、选择)、适应度函数等;
2. 进行优化:执行进化操作,通过不断迭代来获得最优解;
3. 结果分析:根据最优解的性能,进行可视化分析,以评估算法的性能。
遗传算法matlab代码

遗传算法matlab代码以下是一个简单的遗传算法的MATLAB 代码示例:matlab复制代码% 遗传算法参数设置pop_size = 50; % 种群大小num_vars = 10; % 变量数目num_generations = 100; % 进化的代数mutation_rate = 0.01; % 变异率crossover_rate = 0.8; % 交叉率% 初始化种群population = rand(pop_size, num_vars);% 开始进化for i = 1:num_generations% 计算适应度fitness = evaluate_fitness(population);% 选择操作selected_population = selection(population, fitness);% 交叉操作offspring_population = crossover(selected_population,crossover_rate);% 变异操作mutated_population = mutation(offspring_population,mutation_rate);% 生成新种群population = [selected_population; mutated_population];end% 选择最优解best_solution = population(find(fitness == max(fitness)), :);% 适应度函数function f = evaluate_fitness(population)f = zeros(size(population));for i = 1:size(population, 1)f(i) = sum(population(i, :));endend% 选择函数function selected_population = selection(population, fitness)% 轮盘赌选择total_fitness = sum(fitness);probabilities = fitness / total_fitness;selected_indices = zeros(pop_size, 1);for i = 1:pop_sizer = rand();cumulative_probabilities = cumsum(probabilities);for j = 1:pop_sizeif r <= cumulative_probabilities(j)selected_indices(i) = j;break;endendendselected_population = population(selected_indices, :);end% 交叉函数function offspring_population = crossover(parental_population, crossover_rate)offspring_population = zeros(size(parental_population));num_crossovers = ceil(size(parental_population, 1) *crossover_rate);crossover_indices = randperm(size(parental_population, 1),num_crossovers);以下是另一个一个简单的遗传算法的MATLAB 代码示例:matlab复制代码% 初始化种群population = rand(nPopulation, nGenes);% 进化迭代for iGeneration = 1:nGeneration% 计算适应度fitness = evaluateFitness(population);% 选择父代parentIdx = selection(fitness);parent = population(parentIdx, :);% 交叉产生子代child = crossover(parent);% 变异子代child = mutation(child);% 更新种群population = [parent; child];end% 评估最优解bestFitness = -Inf;for i = 1:nPopulationf = evaluateFitness(population(i, :));if f > bestFitnessbestFitness = f;bestIndividual = population(i, :);endend% 可视化结果plotFitness(fitness);其中,nPopulation和nGenes分别是种群大小和基因数;nGeneration是迭代次数;evaluateFitness函数用于计算个体的适应度;selection函数用于选择父代;crossover函数用于交叉产生子代;mutation函数用于变异子代。
(完整版)遗传算法matlab实现源程序
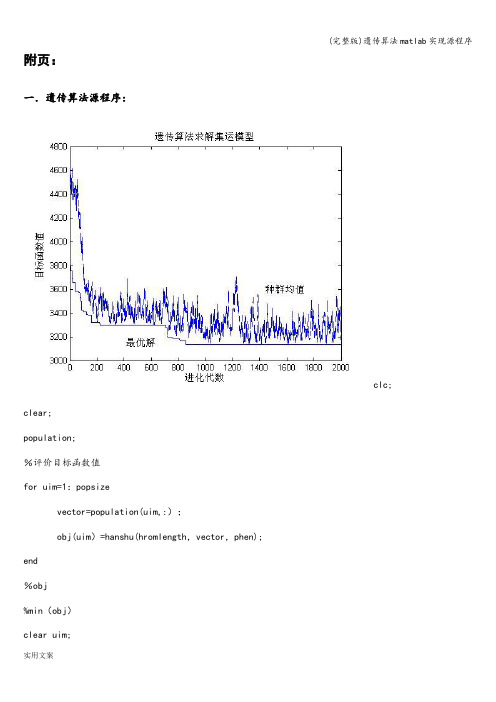
附页:一.遗传算法源程序:clc; clear;population;%评价目标函数值for uim=1:popsizevector=population(uim,:);obj(uim)=hanshu(hromlength,vector,phen);end%obj%min(obj)clear uim;objmin=min(obj);for sequ=1:popsizeif obj(sequ)==objminopti=population(sequ,:);endendclear sequ;fmax=22000;%==for gen=1:maxgen%选择操作%将求最小值的函数转化为适应度函数for indivi=1:popsizeobj1(indivi)=1/obj(indivi);endclear indivi;%适应度函数累加总合total=0;for indivi=1:popsizetotal=total+obj1(indivi);endclear indivi;%每条染色体被选中的几率for indivi=1:popsizefitness1(indivi)=obj1(indivi)/total;endclear indivi;%各条染色体被选中的范围for indivi=1:popsizefitness(indivi)=0;for j=1:indivifitness(indivi)=fitness(indivi)+fitness1(j);endendclear j;fitness;%选择适应度高的个体for ranseti=1:popsizeran=rand;while (ran>1||ran<0)ran=rand;endran;if ran〈=fitness(1)newpopulation(ranseti,:)=population(1,:);elsefor fet=2:popsizeif (ran〉fitness(fet—1))&&(ran<=fitness(fet))newpopulation(ranseti,:)=population(fet,:);endendendendclear ran;newpopulation;%交叉for int=1:2:popsize-1popmoth=newpopulation(int,:);popfath=newpopulation(int+1,:);popcross(int,:)=popmoth;popcross(int+1,:)=popfath;randnum=rand;if(randnum〈 P>cpoint1=round(rand*hromlength);cpoint2=round(rand*hromlength);while (cpoint2==cpoint1)cpoint2=round(rand*hromlength);endif cpoint1>cpoint2tem=cpoint1;cpoint1=cpoint2;cpoint2=tem;endcpoint1;cpoint2;for term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int,ss)==popfath(term)tem1=popcross(int,ss);popcross(int,ss)=popcross(int,term);popcross(int,term)=tem1;endendclear tem1;endfor term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int+1,ss)==popmoth(term)tem1=popcross(int+1,ss);popcross(int+1,ss)=popcross(int+1,term);popcross(int+1,term)=tem1;endendclear tem1;endendclear term;endclear randnum;popcross;%变异操作newpop=popcross;for int=1:popsizerandnum=rand;if randnumcpoint12=round(rand*hromlength);cpoint22=round(rand*hromlength);if (cpoint12==0)cpoint12=1;endif (cpoint22==0)cpoint22=1;endwhile (cpoint22==cpoint12)cpoint22=round(rand*hromlength);if cpoint22==0;cpoint22=1;endendtemp=newpop(int,cpoint12);newpop(int,cpoint12)=newpop(int,cpoint22);newpop(int,cpoint22)=temp;。
matlab遗传算法实例

matlab遗传算法实例Matlab遗传算法实例引言:遗传算法是一种模拟自然进化过程的优化算法,它通过模拟优胜劣汰、基因交叉和变异等自然选择机制,来寻找问题的最优解。
在Matlab中,我们可以利用遗传算法工具箱来快速实现遗传算法,并解决各种实际问题。
本文将介绍一个基于Matlab的遗传算法实例,以帮助读者更好地理解和应用遗传算法。
一、问题描述假设我们要在一个由0和1组成的二进制串中寻找最优解。
具体而言,我们定义了一个目标函数,目标函数的输入是一个二进制串,输出是一个实数值。
我们的目标是找到一个二进制串,使得目标函数的输出值最大化。
二、遗传算法的基本原理遗传算法是基于自然进化过程的优化算法,它的基本原理如下:1. 初始化种群:随机生成一组二进制串作为初始种群。
2. 评估适应度:根据目标函数计算每个个体的适应度值。
3. 选择操作:根据适应度值选择优秀个体作为父代,进行繁殖。
4. 交叉操作:对选出的父代个体进行基因交叉,生成新的子代个体。
5. 变异操作:对子代个体进行基因变异,引入新的基因信息。
6. 更新种群:用子代替换父代,生成新的种群。
7. 终止条件判断:判断是否满足终止条件,若满足则输出最优解,否则返回第3步。
三、Matlab代码实现以下是一个简单的Matlab代码实例,用于求解上述问题:```matlab% 目标函数定义function y = fitnessFunc(x)y = sum(x);end% 遗传算法主函数function [bestSolution, bestFitness] = geneticAlgorithm(popSize, numGen, pc, pm)% 初始化种群population = round(rand(popSize, numGen));% 迭代进化for t = 1:numGen% 评估适应度fitness = arrayfun(@fitnessFunc, population);% 选择操作[~, sortedIdx] = sort(fitness, 'descend');eliteIdx = sortedIdx(1:round(popSize/2));elite = population(eliteIdx, :);% 交叉操作crossIdx = rand(popSize, 1) < pc;crossPairs = reshape(population(crossIdx, :), [], 2);crossPoints = randi(numGen-1, size(crossPairs, 1), 1) + 1;offsprings = [elite; arrayfun(@(i) [crossPairs(i, 1:crossPoints(i)), crossPairs(i, crossPoints(i)+1:end)], 1:size(crossPairs, 1), 'UniformOutput', false)];population = vertcat(offsprings{:});% 变异操作mutateIdx = rand(popSize, numGen) < pm;population(mutateIdx) = 1 - population(mutateIdx);end% 输出结果fitness = arrayfun(@fitnessFunc, population);[bestFitness, bestIdx] = max(fitness);bestSolution = population(bestIdx, :);end% 调用遗传算法求解最优解popSize = 100; % 种群大小numGen = 100; % 进化代数pc = 0.8; % 交叉概率pm = 0.01; % 变异概率[bestSolution, bestFitness] = geneticAlgorithm(popSize, numGen, pc, pm);```四、实验结果与讨论根据上述Matlab代码实例,我们可以得到一个最优解,即一个二进制串。
Matlab技术在遗传算法优化中的应用指南

Matlab技术在遗传算法优化中的应用指南遗传算法是一种模拟生物进化的优化算法,它通过模拟进化的过程来寻找问题的最优解。
近年来,随着计算机技术的不断发展和Matlab软件的广泛应用,遗传算法在工程和科学领域的应用越来越广泛。
本文将介绍如何利用Matlab技术在遗传算法优化中取得更好的效果。
一、遗传算法概述遗传算法是一种模拟自然界进化过程的优化算法。
其基本思想是通过模拟生物遗传、突变和选择等过程,不断改进解的质量,逐步逼近最优解。
在遗传算法中,解被表示为染色体,染色体由若干个基因组成。
每个基因代表问题的一个自变量或参数。
遗传算法通过种群中个体间的交叉、突变和选择等操作,模拟出基因在自然界中的交换和变异,最终得到能够适应环境的个体。
二、Matlab中的遗传算法工具箱Matlab提供了全面的遗传算法工具箱,包含了丰富的函数和算法,使得用户能够方便地使用和实现遗传算法。
下面将介绍Matlab中一些常用的遗传算法函数和工具。
1. ga函数ga函数是Matlab中最基本的遗传算法函数,它实现了标准的遗传算法框架。
用户可以通过设置参数,如目标函数、变量范围、种群大小、迭代次数等来调用ga函数进行优化。
2. Genome类Genome类是Matlab中用于描述染色体的一个重要类。
通过设置基因和适应度函数等属性,可以方便地定义问题的解空间和优化目标。
3. 优化工具Matlab的优化工具箱中提供了多种遗传算法优化函数,如gamultiobj、paretosearch等。
这些函数用于多目标优化问题,能够得到问题的各种最优解。
三、遗传算法的应用遗传算法在各个领域的应用越来越广泛,包括机器学习、控制算法设计、电力系统优化等。
下面将举几个具体的例子来说明遗传算法在工程领域的应用。
1. 机器学习遗传算法可以用于优化神经网络的结构和权重。
通过调整网络的连接和节点数,以及不同的激活函数和损失函数,可以得到更好的机器学习模型。
2. 控制算法设计在控制系统设计中,遗传算法可以用于调整控制器的参数,使得系统的性能指标达到最优。
matlab中遗传算法验证算例

matlab中遗传算法验证算例
1. 问题描述:
假设有一个旅行商问题(TSP)的问题实例,即有n个城市,
需要找到一条路径,使得从起始城市出发,途经每个城市一次且仅一次,最后回到起始城市,并使得路径长度最短。
2. 遗传算法设计:
- 编码方式:使用一个长度为n的序列来表示路径,每个元素
代表对应的城市。
- 初始化种群:随机生成一定数量的路径序列,并将其作为初
始种群。
3. 适应度函数设计:
路径的适应度函数即为路径的长度,长度越短,适应度越高。
4. 选择操作:
使用轮盘赌选择算子,按照路径长度的适应度比例选择父代个体。
5. 交叉操作:
采用顺序交叉(Order Crossover)算子,从父代选取两个路径,随机选择一个交叉点,然后将其中一个路径的交叉点之后的部分插入到另一个路径中。
6. 变异操作:
随机选择一个父代路径,然后随机选择两个位置,交换这两个位置上的城市。
7. 更新种群:
使用选择、交叉和变异操作得到的新个体替代原来的个体,得到新的种群。
8. 终止条件:
设置迭代次数或达到一定的停止条件。
将上述算法设计写成Matlab代码,定义问题实例,运行并验证算法正确性。
matlab遗传算法设计

matlab遗传算法设计在MATLAB中设计遗传算法需要遵循以下步骤:1.定义问题参数:首先,你需要定义问题的参数,包括适应度函数、种群大小、交叉概率、变异概率和迭代次数等。
2.初始化种群:根据问题的参数,初始化一个种群,通常可以使用随机数生成器来生成初始解。
3.评估适应度:对于每个个体,计算其适应度值,这通常是通过将个体作为输入参数传递给适应度函数来完成的。
4.选择操作:根据适应度值,选择出适应度较高的个体,用于下一代种群的生成。
5.交叉操作:随机选择两个个体进行交叉操作,生成新的个体。
6.变异操作:对新的个体进行变异操作,以增加种群的多样性。
7.迭代更新:重复上述步骤,直到达到预设的迭代次数或满足终止条件。
8.输出结果:输出最终的种群中最优的个体作为问题的解。
下面是一个简单的MATLAB遗传算法示例代码:matlab复制代码% 遗传算法参数设置popSize = 100; % 种群大小crossoverRate = 0.8; % 交叉概率mutationRate = 0.01; % 变异概率maxGeneration = 100; % 最大迭代次数% 初始化种群pop = round(rand(popSize,1)); % 生成初始种群% 适应度函数(这里假设我们要最小化的目标函数是 x^2)fitnessFunction = @(x) x.^2;% 迭代更新种群for generation = 1:maxGeneration% 评估适应度fitness = fitnessFunction(pop);% 选择操作[newPop,~] = rouletteWheelSelection(pop,fitness);% 交叉操作newPop = crossover(newPop, crossoverRate);% 变异操作newPop = mutation(newPop, mutationRate);% 更新种群pop = newPop;end% 输出最优解[~, bestIndex] = min(fitness);bestSolution = pop(bestIndex);fprintf('最优解:%d\n', bestSolution);在这个示例中,我们使用了轮盘赌选择、均匀交叉和均匀变异等遗传算法的操作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
function [bestsole,bestpop]=ga_scomplex(num,bounds,ps,pc,pm,b,dtc)% GA_scomple是基于浮点编码的单纯形遗传算法主程序% num定义种群数量%bounds定义参数取值范围,格式为[Var1min,Var1max;Var2min,Var2max;…….]; %ps选择概率%pc交叉概率%pm变异概率%b变异程度系数%dtc迭代次数% $Date: 2005/5/25 $%%email:damao_pq@numvars=size(bounds,1);xzomelength=numvars+1;flag=1;n=1;[pop]=initializega(num,bounds);while (n<=dtc&flag>0.00001)[newpop]=select(pop,ps);[crosspop]=crossover(bounds,newpop,pc);[mupop]=mutation(crosspop,bounds,pm,[b,n,dtc]);spop=[newpop;crosspop;mupop];[y,x]=sort(spop(:,xzomelength));spop=spop(x,:);n_spop=size(spop,1);bestpop=spop(n_spop:-1:n_spop-num+1,:);[scopop]=scomplex(bounds,bestpop(1,1:numvars), 100); %加入单纯形算法bestpop(num,:)=scopop;bestpop(num,xzomelength)=-scopop(xzomelength);trace1(n)=mean(bestpop(:,xzomelength));bestsole=bestpop(1,1:numvars);trace2(n)=bestpop(1,xzomelength);flag=abs(trace2(n)-trace1(n));bmax=max(bestpop(:,1:numvars));bmin=min(bestpop(:,1:numvars));bounds=[bmin',bmax'];pop=bestpop;n=n+1;endt=1:n-1;plot(t,trace1,'r-',t,trace2,'g-');legend('均值','最优解');toc%%初始种群值生成子程序%%%%%%%%%%%%%%%%%%%%%%%%% function [pop]=initializega(num,bounds)numvars=size(bounds,1);rng=(bounds(:,2)-bounds(:,1))';xzomelength=numvars+1;pop=zeros(num,xzomelength);pop(:,1:numvars)=(ones(num,1)*rng).*(rand(num,numvars))+(ones(num,1)*bounds(:,1)'); pop(:,xzomelength)=fitness(pop(:,1:numvars));%%选择子程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5function [newpop]=select(oldpop,options)q=options;e=size(oldpop,2);n=size(oldpop,1);fit=zeros(n,1);x=zeros(n,2);x(:,1)=[n:-1:1]';[y,x(:,2)]=sort(oldpop(:,e));r=q/(1-(1-q).^n);fit(x(:,2))=r*(1-q).^(x(:,1)-1);fit=cumsum(fit);rnums=sort(rand(n,1));fitin=1;newin=1;while newin<=nif(rnums(newin)<fit(fitin))newpop(newin,:)=oldpop(fitin,:);newin=newin+1;elsefitin=fitin+1;endend%%%交叉子程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [crosspop]=crossover(bounds,newpop,ops)pc=ops;sn=size(newpop,1);sz=size(newpop,2)-1;nc=pc*sn*sz;cs=1;while cs<=ncnsite=round(rand(2,1).*sn+0.5);zsite=round(rand*sz+0.5);r=rand;newpop(nsite,zsite)=[r,1-r;1-r,r]*newpop(nsite,zsite);cs=1+cs;endxzomelength=sz+1;newpop(:,xzomelength)=fitness(newpop(:,1:sz));crosspop=newpop;%变异子程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [mupop]=mutation(crosspop,bounds,pm,ops);b=ops(1);gc=ops(2);gm=ops(3);sn=size(crosspop,1);sz=size(crosspop,2)-1;xzomelength=sz+1;nm=round(pm*sn*sz);t=gc/gm;if t>1t=0.99;disp(sprintf('max gen %d < current gen %d setting ratio = 1',gm,gc));endn=1;while n<=nmnsite=round(rand*sn+0.5);zsite=round(rand*sz+0.5);md=round(rand);if mdy=bounds(zsite,2)-crosspop(nsite,zsite);dvl=y.*(rand.*(1-t)).^b;newvalue=crosspop(nsite,zsite)+dvl;elsey=crosspop(nsite,zsite)-bounds(zsite,1);dvl=y.*(rand.*(1-t)).^b;newvalue=crosspop(nsite,zsite)-dvl;endcrosspop(nsite,zsite)=newvalue;crosspop(nsite,xzomelength)=fitness(crosspop(nsite,1:sz));mupop(n,:)=crosspop(nsite,:);n=n+1;end%%单纯形子程序%%%%%%%%%%%%%%%%%%%%%%%%function [out]=scomplex(bounds,x, maxiter)%% step 1alf=1.3 ; %反映系数>=1belt=0.5; % 收缩系数(0,1)glm=2.0; %延伸,扩展系数>1ct=0.5; %紧缩(压缩)系数(0,1)cgm= 0.01; %允许误差>0n=size(bounds,1);% 转换区间bs=bounds(:,2)-bounds(:,1);xx=[x'-bounds(:,1)]./bs;%求各参数值a=0.2;q=a.*((sqrt(n+1)-1)./(n.*sqrt(2)));p=a.*((sqrt(n+1)+n-1)./(n.*sqrt(2)));% 定义n+1个点dx0=xx;dx=ones(n,1)*xx';dx=dx+q;for i=1:ndx(i,i)=dx0(i)+p-q;enddx=[dx0';dx];%区间转回px=ones(n+1,1)*bs'.*dx+ones(n+1,1)*bounds(:,1)';px(:,n+1)=-fitness(px(:,1:n)); % 求值注意此处加了负号是为求出最小值px(n+2,:)=(sum(px(1:n,:)))./n; % 重心px(n+2,n+1)=-fitness(px(n+2,1:n));itercount=1;how='step2';while itercount < maxiter%% step2if strcmp(how,'step2')%排序[y,t]=sort(px(:,n+1));px=px(t,:);how='step3';end%% step3if strcmp(how,'step3')px(n+2,:)=(sum(px(1:n,:)))./n; % 重心px(n+2,n+1)=-fitness(px(n+2,1:n));flg=1./(n+1).*sqrt(sum((px(1:n+1,n+1)-px(n+2,n+1).*ones(n+1,1)).^2));if flg<=cgmbreak;else% goto step4how='step4';endend%% step4if strcmp(how,'step4');px(n+3,:)=px(n+2,:)+alf.*(px(n+2,:)-px(n+1,:));xs=10;r1=1while any(px(n+3,1:n)>bounds(:,2)') | any(px(n+3,1:n)<bounds(:,1)') xs=xs-.01;px(n+3,:)=px(n+2,:)+xs.*alf.*(px(n+2,:)-px(n+1,:));r1=r1+1endpx(n+3,n+1)=-fitness(px(n+3,1:n));if px(n+3,n+1)<px(1,n+1)% goto step5how='step5';elseif px(n+3,n+1)<px(n,n+1)% goto step6how='step6';else% goto step7how='step7';endendend%% step 5if strcmp(how,'step5')px(n+4,:)=px(n+2,:)+glm.*(px(n+3,:)-px(n+2,:));r2=1;xs=1;while any(px(n+4,1:n)>bounds(:,2)')| any(px(n+4,1:n)<bounds(:,1)') xs=xs-0.01;px(n+4,:)=px(n+2,:)+xs.*glm.*(px(n+3,:)-px(n+2,:));r2=r2+1endpx(n+4,n+1)=-fitness(px(n+4,1:n));if px(n+4,n+1)<px(1,n+1)px(n+1,:)=px(n+4,:);% goto step2how='step2';else% goto step6how='step6';endend%% step6if strcmp(how,'step6')px(n+1,:)=px(n+3,:);% goto step2how='step2';end%% step 7if strcmp(how,'step7')gx=px(n+1:n+3,:);[l,g]=sort(gx(1:3,n+1));gx=px(g,:);px(n+1,:)=gx(1,:);px(n+5,:)=px(n+2,:)+belt.*(px(n+1,:)-px(n+2,:));r3=1;xs=1;while any(px(n+5,1:n)>bounds(:,2)') | any(px(n+5,1:n)<bounds(:,1)')xs=xs-.01;px(n+5,:)=px(n+2,:)+0.9*belt.*(px(n+1,:)-px(n+2,:));r3=r3+1endpx(n+5,n+1)=-fitness(px(n+5,1:n));if px(n+5,n+1)<px(n+1,n+1)px(n+1,:)=px(n+5,:);% goto step2how='step2';else% goto step8how='step8';endend%% step 8if strcmp(how,'step8')px(1:n+1,:)=ones(n+1,1)*px(1,:)+ct.*(px(1:n+1,:)-ones(n+1,1)*px(1,:));xs=1;whileany(px(1:n+1,1:n)>ones(n+1,1)*bounds(:,2)') any(px(1:n+1,1:n)<ones(n+1,1)*bounds(:,1)') xs=xs-0.01;px(1:n+1,:)=ones(n+1,1)*px(1,:)+xs.*ct.*(px(1:n+1,:)-ones(n+1,1)*px(1,:))endpx(:,n+1)=-fitness(px(:,1:n));% goto step2how='step2';enditercount=itercount+1;end %whileout=px(1,:);。
