重要三角公式汇总
三角函数公式大全

三角函数公式大全三角函数是数学中非常重要的概念,它们在几何、三角学、物理学等领域都有着广泛的应用。
在学习三角函数的过程中,掌握三角函数的基本公式是非常重要的。
本文将为大家详细介绍三角函数的公式大全,帮助大家更好地理解和掌握三角函数的知识。
1. 正弦函数的公式。
正弦函数是最基本的三角函数之一,其公式为,sinθ = 对边/斜边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,斜边为直角三角形的斜边。
正弦函数的图像是一条连续的曲线,其周期为2π,在0到2π之间有一个完整的周期。
2. 余弦函数的公式。
余弦函数也是常见的三角函数,其公式为,cosθ = 邻边/斜边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,斜边为直角三角形的斜边。
余弦函数的图像也是一条连续的曲线,其周期也为2π,与正弦函数的图像相似。
3. 正切函数的公式。
正切函数是另外一个常见的三角函数,其公式为,tanθ = 对边/邻边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,邻边为与角度θ相邻的直角三角形的斜边。
正切函数的图像在一些特定的角度上会出现无穷大的情况,因此在使用时需要注意。
4. 余切函数的公式。
余切函数是正切函数的倒数,其公式为,cotθ= 邻边/对边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,对边为与角度θ相对的直角三角形的斜边。
余切函数的图像也会在一些特定的角度上出现无穷大的情况。
5. 正割函数的公式。
正割函数是余弦函数的倒数,其公式为,secθ= 斜边/邻边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,斜边为直角三角形的斜边。
正割函数的图像是一条连续的曲线,其周期也为2π。
6. 余割函数的公式。
余割函数是正弦函数的倒数,其公式为,cscθ= 斜边/对边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,斜边为直角三角形的斜边。
余割函数的图像也是一条连续的曲线,其周期也为2π。
各种三角函数公式汇总

各种三角函数公式汇总三角函数是数学中的一门重要分支,它研究三角形的边长与角度之间的关系。
在应用数学、物理学、工程学等领域中,三角函数有广泛的应用。
本文将汇总各种常见的三角函数公式,供读者参考。
一、正弦函数(sin)的公式:1.单位圆上的正弦公式:性质:单位圆上一点的坐标恰为该点的角度对应的正弦值。
公式:对于角度θ,有sinθ = y,其中(x, y)为单位圆上的点坐标。
2.正弦函数的周期性:性质:正弦函数的最小正周期为2π(或360°)。
公式:sin(θ + 2nπ) = sinθ,其中n为整数。
3.正弦函数的奇偶性:性质:正弦函数是奇函数,即满足sin(-θ) = -sinθ。
公式:sin(-θ) = -sinθ。
4.正弦函数的反正弦函数:性质:反正弦函数是正弦函数的反函数,记为sin⁻¹。
公式:若y = sinθ,则θ = sin⁻¹(y),其中-π/2 ≤ θ ≤ π/2二、余弦函数(cos)的公式:1.单位圆上的余弦公式:性质:单位圆上一点的横坐标恰为该点的角度对应的余弦值。
公式:对于角度θ,有cosθ = x,其中(x, y)为单位圆上的点坐标。
2.余弦函数的周期性:性质:余弦函数的最小正周期为2π(或360°)。
公式:cos(θ + 2nπ) = cosθ,其中n为整数。
3.余弦函数的奇偶性:性质:余弦函数是偶函数,即满足cos(-θ) = cosθ。
公式:cos(-θ) = cosθ。
4.余弦函数的反余弦函数:性质:反余弦函数是余弦函数的反函数,记为cos⁻¹。
公式:若x = cosθ,则θ = cos⁻¹(x),其中0 ≤ θ ≤ π。
三、正切函数(tan)的公式:1.正切函数的定义公式:性质:正切值等于对边与临边的比值。
公式:对于角度θ,有tanθ = y/x。
2.正切函数的周期性:性质:正切函数的最小正周期为π(或180°)。
三角函数公式大全及记忆口诀

三角函数公式大全及记忆口诀
在数学中,三角函数是一类重要的函数,它们在几何、物理、
工程等领域中都有着广泛的应用。
为了更好地掌握三角函数,我们
需要熟练掌握它们的公式,同时也需要一些记忆口诀来帮助我们记忆。
首先,我们来看一下三角函数的公式大全:
1. 正弦函数(sine function),sin(θ) = 对边/斜边。
2. 余弦函数(cosine function),cos(θ) = 邻边/斜边。
3. 正切函数(tangent function),tan(θ) = 对边/邻边。
4. 余切函数(cotangent function),cot(θ) = 邻边/对边。
5. 正割函数(secant function),sec(θ) = 斜边/邻边。
6. 余割函数(cosecant function),csc(θ) = 斜边/对边。
这些公式是我们在解决三角函数相关问题时经常会用到的,熟练掌握它们对我们的学习至关重要。
除了公式外,记忆口诀也是我们学习三角函数的好帮手。
下面是一个简单的记忆口诀:
正弦对,余弦邻,正切比,余切颠,正割斜,余割对。
这个口诀可以帮助我们记忆三角函数的定义和关系,使我们更容易在解题时迅速找到正确的公式和方法。
总之,三角函数是数学中的重要内容,掌握好三角函数的公式和记忆口诀,对我们的学习和工作都有着重要的帮助。
希望大家能够通过不断的练习和记忆,熟练掌握三角函数,为自己的数学学习打下坚实的基础。
数学常用三角函数公式全集

数学常用三角函数公式全集三角函数是数学中的一类重要函数,求解各种三角形和角度问题时经常用到。
下面是一些常用的三角函数公式:1. 正弦函数 (sine function):正弦函数是由一个角的对边和斜边的比值定义的。
在直角三角形中,正弦函数可以表示为:sinθ = opposite / hypotenuse。
注意,θ 是角的度数。
2. 余弦函数 (cosine function):余弦函数是由一个角的邻边和斜边的比值定义的。
在直角三角形中,余弦函数可以表示为:cosθ = adjacent / hypotenuse。
3. 正切函数 (tangent function):正切函数是由一个角的对边和邻边的比值定义的。
在直角三角形中,正切函数可以表示为:tanθ = opposite / adjacent。
这些是最基本的三角函数,我们还可以通过它们来推导出其他与其相关的函数。
4. 余割函数 (cosecant function):余割函数是正弦函数的倒数:cscθ = 1 / sinθ。
5. 余切函数 (cotangent function):余切函数是正切函数的倒数:cotθ = 1 /tanθ。
6. 余举函数 (secant function):余举函数是余弦函数的倒数:secθ = 1 / cosθ。
这些函数可以帮助我们求解各种三角形和角度问题。
此外,它们还有一些性质和公式,可以进一步扩展我们的计算范围。
7.三角函数的周期性:正弦函数、余弦函数、正切函数都具有周期性,周期为360度或2π弧度。
即sin(θ+360n) = sinθ,cos(θ+360n) = cosθ,tan(θ+πn) = tanθ,其中 n 为整数。
8.三角函数的正负关系:正弦函数在0到180度范围内是正数,在180到360度范围内是负数;余弦函数在90到270度范围内是负数,在其他角度范围内是正数;正切函数在0到90度和180到270度范围内是正数,在90到180度和270到360度范围内是负数。
初中数学必背三角函数公式大全

初中数学必背三角函数公式大全初中数学必背的知识点,三角函数公式大全同学们总结归纳过吗?如果没有快来小编这里瞧瞧。
下面是由小编为大家整理的“初中数学必背三角函数公式大全”,仅供参考,欢迎大家阅读。
初中数学必背三角函数公式大全常用三角函数公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB- ctgA+ctgBsin(A+B)/sinAsinB拓展阅读:三角函数导数公式大全(sinx)' = cosx(cosx)' = - sinx(tanx)'=1/(cosx)^2=(secx)^2=1+(tanx)^2 -(cotx)'=1/(sinx)^2=(cscx)^2=1+(cotx)^2 (secx)'=tanx·secx(cscx)'=-cotx·cscx(arcsinx)'=1/(1-x^2)^1/2(arccosx)'=-1/(1-x^2)^1/2(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)(arcsecx)'=1/(|x|(x^2-1)^1/2)(arccscx)'=-1/(|x|(x^2-1)^1/2)(sinhx)'=coshx(coshx)'=sinhx(tanhx)'=1/(coshx)^2=(sechx)^2(coth)'=-1/(sinhx)^2=-(cschx)^2(sechx)'=-tanhx·sechx(cschx)'=-cothx·cschx。
三角公式大全

三角公式总表⒈L 弧长=αR=nπR 180 S 扇=21L R=21R 2α=3602R n ⋅π⒉正弦定理:A asin =B b sin =Cc sin = 2R (R 为三角形外接圆半径) ⒊余弦定理:a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cosbca cb A 2cos 222-+=⒋S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin =A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=CB A c sin 2sin sin 2=pr=))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径) ⒌同角关系: ⑴商的关系:①θtg =x y =θθcos sin =θθsec sin ⋅ ②θθθθθcsc cos sin cos ⋅===y x ctg ③θθθtg ry⋅==cos sin ④θθθθcsc cos 1sec ⋅===tg x r ⑤θθθctg rx⋅==sin cos⑥θθθθsec sin 1csc ⋅===ctg y r ⑵倒数关系:1sec cos csc sin =⋅=⋅=⋅θθθθθθctg tg⑶平方关系:1csc sec cos sin 222222=-=-=+θθθθθθctg tg ⑷)sin(cos sin 22ϕθθθ++=+b a b a (其中辅助角ϕ与点(a,b )在同一象限,且abtg =ϕ) ⒍函数y=++⋅)sin(ϕωx A k 的图象及性质:(0,0>>A ω)振幅A ,周期T=ωπ2, 频率f=T1, 相位ϕω+⋅x ,初相ϕ⒎五点作图法:令ϕω+x 依次为ππππ2,23,,20 求出x 与y , 依点()y x ,作图⒏诱导公试α的同名三角函数α看作锐角时,三角函数值的符号;即:函数名不三角函数值等于α的异名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名改变,符号看象限 ⒐和差角公式 ①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos(μ=± ③βαβαβαtg tg tg tg tg ⋅±=±μ1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±μ⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ⋅-⋅-⋅-⋅⋅-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ⋅⋅=++ ii).1222222=++C tg B tg C tg A tg B tg A tg ⒑二倍角公式:(含万能公式)①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-=③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=⒒三倍角公式:①)60sin()60sin(sin 4sin 4sin 33sin 3θθθθθθ+︒-︒=-= ②)60cos()60cos(cos 4cos 4cos 33cos 3θθθθθθ+︒-︒=+-=③)60()60(313323θθθθθθθ+⋅-⋅=--=tg tg tg tg tg tg tg ⒓半角公式:(符号的选择由2θ所在的象限确定) ①2cos 12sinθθ-±= ②2cos 12sin 2θθ-=③2cos 12cos θθ+±= ④2cos 12cos2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=± ⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg⒔积化和差公式:[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++=()[]βαβαβα--+-=cos )cos(21sin sin ⒕和差化积公式: ①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos2cos 2cos cos βαβαβα-+=+ ④2sin2sin2cos cos βαβαβα-+-=-⒖反三角函数: ⒗最简单的三角方程高等数学最难的包括积分和证明。
三角形所有基本公式汇总

三角形所有基本公式汇总三角形是平面几何中最简单的多边形之一,有许多重要的基本公式和性质。
下面是三角形的一些基本公式的总结:1.三角形的面积公式:三角形的面积可以通过三边长度或高和底边长度来计算。
以下是一些常见的面积公式:-海伦公式:已知三边长a、b、c的三角形的面积可以通过海伦公式计算:面积=√(s*(s-a)*(s-b)*(s-c))其中s是三边长的半周长,s=(a+b+c)/2-高和底边:已知三角形的底边长度b和对应的高h,三角形的面积可以通过以下公式计算:面积=0.5*b*h。
2.三角形的重心:三角形的重心是连接三条中线的交点,每条中线连接一个顶点和对边中点。
重心到三个顶点的距离相等,即将三个重心连接成一个等边三角形。
3.三角形的外心和外接圆:三角形的外心是指圆心位于三个顶点外部,且与三条边都相切的圆心。
外心到三个顶点的距离相等,即将三个外心连接成一个等腰三角形。
外接圆是围绕三角形的外接圆,该圆经过三个顶点。
4.三角形的内心和内切圆:三角形的内心是指围绕三个角的圆心,且与三条边都相切的圆心。
内心到三个边的距离相等,即将三个内心连接成一个等腰三角形。
内切圆是三角形的固定在内部相切的圆。
5.三角形的中心:三角形的中心包括重心、外心和内心。
重心、外心和内心构成的三点连线有许多特殊的性质和关系。
6.三角形的角度和边长关系:三角形的三个角度之和为180度,即A+B+C=180度。
另外,三角形的两边之和大于第三边,即a+b>c,b+c>a,c+a>b。
7.三角形的角平分线:三角形的角平分线是从一个顶点出发,将对应的角平分为两个相等的角的线段。
三角形的三条角平分线交于一个点,该点叫做三角形的内心。
8.三角形的边比公式:如果两个三角形的相应边的比例相等,则这两个三角形是相似的。
根据相似三角形的性质,可以得到以下比例关系:a/a'=b/b'=c/c',其中a、b、c是两个相似三角形对应边的长度。
三角函数公式大全

三角函数公式大全三角函数是数学中重要的概念,它们在几何、物理、工程等领域都有广泛的应用。
下面将详细介绍一些常用的三角函数公式。
1. 正弦函数(sine function):正弦函数是一个周期函数,它表示角度为x的点在单位圆上的y坐标。
正弦函数的公式如下:sin(x) = y,其中-1≤y≤12. 余弦函数(cosine function):余弦函数也是一个周期函数,它表示角度为x的点在单位圆上的x坐标。
余弦函数的公式如下:cos(x) = x,其中-1≤x≤13. 正切函数(tangent function):正切函数表示角度为x的点在单位圆上的斜率。
正切函数的公式如下:tan(x) = sin(x)/cos(x)。
4. 余切函数(cotangent function):余切函数表示角度为x的点在单位圆上斜率的倒数。
余切函数的公式如下:cot(x) = 1/tan(x) = cos(x)/sin(x)。
5. 正割函数(secant function):正割函数表示角度为x的点在单位圆上的x坐标的倒数。
正割函数的公式如下:sec(x) = 1/cos(x)。
6. 余割函数(cosecant function):余割函数表示角度为x的点在单位圆上的y坐标的倒数。
余割函数的公式如下:csc(x) = 1/sin(x)。
7. 和差公式(sum and difference formulas):和差公式用于计算两个角的正弦、余弦和正切的和或差。
具体公式如下:sin(A±B) = sin(A)cos(B) ± cos(A)sin(B)cos(A±B) = cos(A)cos(B) ∓ sin(A)sin(B)tan(A±B) = (tan(A) ± tan(B))/(1∓tan(A)tan(B))8. 倍角公式(double angle formulas):倍角公式用于计算一个角的正弦、余弦和正切的两倍。
高中三角函数公式归纳总结

高中三角函数公式归纳总结1500字高中三角函数是数学中的一个重要分支,它是描述角度与直角三角形各边之间关系的数学函数。
在学习三角函数的过程中,我们会经常使用到一些公式来简化问题和推导关系。
下面,我将对高中三角函数公式进行归纳总结。
一、正弦函数公式1. 任意角的正弦定义公式:sinA = a / c其中,A是角A的度数,a是角A的对边的长度,c是斜边的长度。
2. 正弦函数的基本关系式:sinA = cos(90° - A)sin(90° + A) = cosA3. 正弦函数的和差化积公式:sin(A ± B) = sinA·cosB ± cosA·sinB4. 二倍角公式:sin2A = 2sinA·cosA5. 半角公式:sin(A/2) = ±√((1 - cosA) / 2)二、余弦函数公式1. 任意角的余弦定义公式:cosA = b / c其中,A是角A的度数,b是角A的邻边的长度,c是斜边的长度。
2. 余弦函数的基本关系式:cosA = sin(90° - A)cos(90° + A) = -sinA3. 余弦函数的和差化积公式:cos(A ± B) = cosA·cosB ∓ sinA·sinB4. 平方差公式:cos2A = cos^2(A) - sin^2(A)5. 半角公式:cos(A/2) = ±√((1 + cosA) / 2)三、正切函数公式1. 任意角的正切定义公式:tanA = a / b其中,A是角A的度数,a是角A的对边的长度,b是角A的邻边的长度。
2. 正切函数的基本关系式:tanA = 1 / cotAtan(90° + A) = -tanA3. 正切函数的和差化积公式:tan(A ± B) = (tanA ± tanB) / (1 ∓ tanA·tanB)4. 二倍角公式:tan2A = (2tanA) / (1 - tan^2(A))5. 半角公式:tan(A/2) = ±√((1 - cosA) / (1 + cosA))四、余切函数公式1. 任意角的余切定义公式:cotA = b / a其中,A是角A的度数,a是角A的对边的长度,b是角A的邻边的长度。
三角函数和角公式有哪些

三角函数和角公式有哪些三角函数是数学中的一种特殊函数类型,其定义基于数学中的三角形概念。
三角函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)、余切函数(cot)、正割函数(sec)和余割函数(csc)等。
角公式指的是在三角函数中,根据不同角的关系而得出的一系列重要公式。
下面将逐一介绍常见的三角函数和角公式。
1.周期性:所有的三角函数都具有周期性。
对于常用角度的三角函数,它们的周期为360°,或2π弧度。
2. 正弦函数(sin):正弦函数以角度或弧度为自变量,在-1到1之间取值。
一些重要的角公式如下:- 正弦函数的正交性:sin(θ) = sin(180°-θ)- 余弦函数的补角关系:sin(90°-θ) = cos(θ)3. 余弦函数(cos):余弦函数以角度或弧度为自变量,在-1到1之间取值。
一些重要的角公式如下:- 余弦函数的正交性:cos(θ) = cos(180°-θ)- 正弦函数的补角关系:cos(90°-θ) = sin(θ)- 余弦函数的和差公式:cos(α±β) = cosαcosβ± sinαsinβ4. 正切函数(tan):正切函数以角度或弧度为自变量,没有界限和特殊值。
一些重要的角公式如下:- 正切函数的周期性:tan(θ) = tan(θ + nπ),其中n为整数- 正切函数的倒数与角度的关系:cot(θ) = 1/tan(θ)- 正切函数的和差公式:tan(α±β) =(tanα±tanβ)/(1∓tanαtanβ)5. 余切函数(cot):余切函数以角度或弧度为自变量,没有界限和特殊值。
一些重要的角公式如下:- 余切函数的周期性:cot(θ) = cot(θ+ nπ),其中n为整数- 余切函数的倒数与角度的关系:tan(θ) = 1/cot(θ)6. 正割函数(sec):正割函数以角度或弧度为自变量,在正弦函数定义域之外取值。
任意三角形三角函数公式

任意三角形三角函数公式一、正弦定理正弦定理是三角形中的重要定理之一,它描述了三角形的边长和角度之间的关系。
在任意三角形ABC中,我们可以用正弦定理来表示三角形的边长和角度之间的关系。
正弦定理的数学表达式为:a/sinA = b/sinB = c/sinC其中a、b、c分别表示三角形ABC的三边的长度,A、B、C表示对应的角度。
通过正弦定理,我们可以计算出三角形中任意一个角的正弦值,从而进一步计算出三角形的边长。
二、余弦定理余弦定理是三角形中的另一个重要定理,它描述了三角形的边长和角度之间的关系。
在任意三角形ABC中,我们可以用余弦定理来表示三角形的边长和角度之间的关系。
余弦定理的数学表达式为:c^2 = a^2 + b^2 - 2abcosC其中a、b、c分别表示三角形ABC的三边的长度,C表示对应的角度。
通过余弦定理,我们可以计算出三角形中任意一个角的余弦值,从而进一步计算出三角形的边长。
三、正切定理正切定理是三角形中的另一个重要定理,它描述了三角形的边长和角度之间的关系。
在任意三角形ABC中,我们可以用正切定理来表示三角形的边长和角度之间的关系。
正切定理的数学表达式为:tanA = a/b其中a、b分别表示三角形ABC的两边的长度,A表示对应的角度。
通过正切定理,我们可以计算出三角形中任意一个角的正切值,从而进一步计算出三角形的边长。
正弦定理、余弦定理和正切定理是三角形中常用的三角函数公式。
它们描述了三角形中边长和角度之间的关系,可以方便地计算三角形的边长和角度。
在实际应用中,这些三角函数公式被广泛运用于测量、导航、建筑等领域。
通过测量三角形的边长和角度,我们可以确定物体的位置、测量距离、计算高度等。
这些三角函数公式为我们提供了一个强大的工具,帮助我们解决实际问题。
正弦定理、余弦定理和正切定理是解决三角形问题的重要工具。
它们通过三角函数的关系,将三角形的边长和角度联系起来,为我们提供了便捷的计算方法。
(完整版)三角函数常用公式表
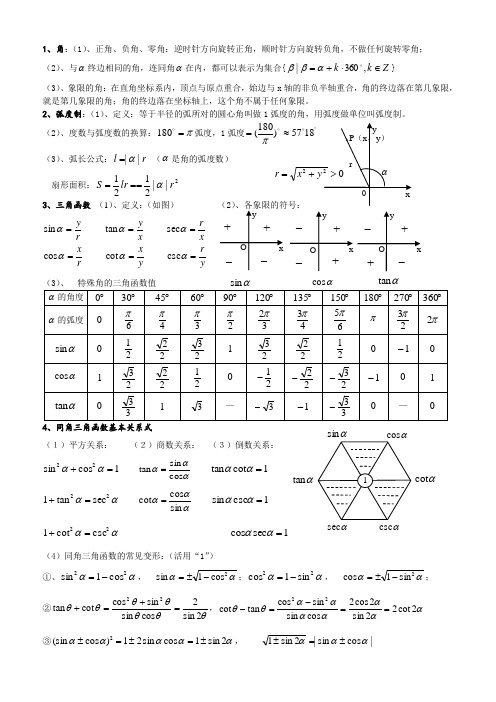
1、角:(1)、正角、负角、零角:逆时针方向旋转正角,顺时针方向旋转负角,不做任何旋转零角; (2)、与α终边相同的角,连同角α在内,都可以表示为集合{Z k k ∈⋅+=,360|αββ}(3)、象限的角:在直角坐标系内,顶点与原点重合,始边与x 轴的非负半轴重合,角的终边落在第几象限,就是第几象限的角;角的终边落在坐标轴上,这个角不属于任何象限。
2、弧度制:(1)、定义:等于半径的弧所对的圆心角叫做1弧度的角,用弧度做单位叫弧度制。
(2)、度数与弧度数的换算:π=180弧度,1弧度)180( =π(3)、弧长公式:r l ||α= (α是角的弧度数)扇形面积:2||2121r lr S α===3、三角函数 (1)、定义:(如图) (2)yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin 4、同角三角函数基本关系式(1)平方关系: (2)商数关系: (3)倒数关系:1cos sin 22=+αα αααcos sin tan = 1cot tan =αα αα22sec tan 1=+ αααsin cos cot =1csc sin =αα αα22csc cot 1=+ 1sec cos =αα(4)同角三角函数的常见变形:(活用“1”) ①、αα22cos 1sin-=, αα2cos 1sin -±=;αα22sin 1cos -=, αα2sin 1cos -±=;②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+,αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±, |cos sin |2sin 1ααα±=±xy+ +_ _O xy++__ Oαtanxy+ +__O=r αsec αsinαtan αcotcsc5、诱导公式:(奇变偶不变,符号看象限)公式一: ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k公式二: 公式三: 公式四: 公式五:ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充:ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切 7 .辅角公式 ⎪⎪⎭⎫ ⎝⎛++++=+x b a b x b a a b a xb x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a(其中ϕ称为辅助角,ϕ的终边过点),(b a ,ab =ϕtan ) (多用于研究性质) 8、二倍角公式:(1)、α2S : αααcos sin 22sin = (2)、降次公式:(多用于研究性质) α2C : ααα22sin cos 2cos -= ααα2sin 21cos sin =1cos 2sin 2122-=-=αα 212cos 2122cos 1sin 2+-=-=αααα2T : ααα2tan 1tan 22tan -= 212cos 2122cos 1cos 2+=+=ααα (3)、二倍角公式的常用变形:①、|sin |22cos 1αα=-, |cos |22cos 1αα=+;②、|sin |2cos 2121αα=-, |cos |2cos 2121αα=+③22sin 1cos sin 21cos sin 22244ααααα-=-=+; ααα2cos sin cos 44=-;④半角:2cos 12sin αα-±=,2cos 12cos αα+±=,αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-=9、三角函数的图象性质 (1)、函数的周期性:①、定义:对于函数f (x ),若存在一个非零常数T ,当x 取定义域内的每一个值时,都有:f (x +T )= f (x ),那么函数f (x )叫周期函数,非零常数T 叫这个函数的周期;②、如果函数f (x )的所有周期中存在一个最小的正数,这个最小的正数叫f (x )的最小正周期。
中考生常用三角函数公式

中考生常用三角函数公式1、同角三角函数的差不多关系倒数关系: tan cot=1 sin csc=1 cos sec=1商的关系:sin/cos=tan=sec/csc cos/sin=cot=csc/sec平方关系:sin^2()+cos^2()=1 1+tan^2()=sec^2() 1+cot^2()=csc^2()平常针对不同条件的常用的两个公式sin +cos =1tan *cot =1一个专门公式(sina+sin)*(sina+sin)=sin(a+)*sin(a-)2、锐角三角函数公式正弦:sin =的对边/ 的斜边余弦:cos =的邻边/的斜边正切:tan =的对边/的邻边余切:cot =的邻边/的对边3、二倍角公式正弦sin2A=2sinAcosA余弦1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1正切tan2A=(2tanA)/(1-tan^2(A))4、三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a = tan a tan(/3+a) tan(/3-a)5、n倍角公式sin(n a)=Rsina sin(a+/n)……sin(a+(n-1)/n)。
其中R=2^(n-1)6、半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cos A)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/s in(a)=sin(a)/(1+cos(a))7、和差化积sin+sin = 2 sin[(+)/2] cos[(-)/2]sin-sin = 2 cos[(+)/2] sin[(-)/2]cos+cos = 2 cos[(+)/2] cos[(-)/2]cos-cos = -2 sin[(+)/2] sin[(-)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)8、两角和公式cos(+)=coscos-sinsincos(-)=coscos+sinsinsin(+)=sincos+cossinsin(-)=sincos -cossin9、积化和差sinsin = [cos(-)-cos(+)] /2 coscos = [cos(+)+cos(-)]/2 sincos = [sin(+) +sin(-)]/2 cossin = [sin(+)-sin(-)]/210、双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a)公式一:设为任意角,终边相同的角的同一三角函数的值相等:sin(2 k+)= sin cos(2k+)= cos tan(2k+)= tan cot(2k+)= cot 公式二:设为任意角,的三角函数值与的三角函数值之间的关系:sin (+)= -sin cos(+)= -cos tan(+)= tan cot(+)= cot 公式三:任意角与-的三角函数值之间的关系:sin(-)= -sin cos(-)= cos tan(-)= -tan cot(-)= -cot公式四:利用公式二和公式三能够得到与的三角函数值之间的关系:s in()= sin cos()= -cos tan()= -tan cot()= -cot公式五:利用公式-和公式三能够得到2与的三角函数值之间的关系:s in(2)= -sin cos(2)= cos tan(2)= -tan cot(2)= -cot公式六:/2及3/2与的三角函数值之间的关系:sin(/2+)= cos cos(/ 2+)= -sin tan(/2+)= -cot cot(/2+)= -tan sin(/2-)= cos cos(/2-)=sin tan(/2-)= cot cot(/2-)= tan sin(3/2+)= -cos cos(3/2+)= sin tan(3/2+)= -cot cot(3/2+)= -tan sin(3/2-)= -cos cos(3/2-)= -sin tan(3/2-)= cot cot(3/2-)= tan (以上kZ) Asin(t+)+ Bsin(t+) = {(A +B +2ABcos(-)} sin{ t + arcsin[ (Asin+Bsin) / {A^2 +B^2; +2ABcos(-)} } 表示根号,包括{……}中的内容11、诱导公式sin(-) = -sin cos(-) = cos tan (-)=-tan sin(/2-) = cos cos(/2-) = sin si n(/2+) = cos cos(/2+) = -sin sin() = sin cos() = -cos sin() = -sin cos() = -cos tanA= sinA/cosA tan(/2+)=-cot tan(/2-)=cot tan(-)=-tan tan(+)=tan 诱导公式记背诀窍:奇变偶不变,符号12、万能公式sin=2tan(/2)/[1+(tan(/2))] cos=[1-(tan(/2))]/[1+(tan(/2))] tan=2tan(/2)/[1-(t an(/2))]13、其它公式(1) (sin)+(cos)=1(2)1+(tan)=(sec)(3)1+(cot)=(csc)(4)关于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC (5)cotA cotB+cotAcotC+cotBcotC=1 (6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)c ot(C/2)(7)(cosA)+(cosB)+(cosC)=1-2cosAcosBcosC(8)(sinA)+(sinB)+(sinC)=2+2cosAcosBcosC家庭是幼儿语言活动的重要环境,为了与家长配合做好幼儿阅读训练工作,小孩一入园就召开家长会,给家长提出早期抓好幼儿阅读的要求。
三角函数运算公式归纳整理

三角函数运算公式归纳整理三角函数是数学中重要的概念,它们在几何学、物理学和工程学等领域中起着非常重要的作用。
在进行三角函数运算时,我们可以利用一系列公式来简化计算过程,提高效率。
在本文中,我将对常用的三角函数运算公式进行归纳整理。
1. 正弦函数(sin):(1) 基本关系式:sin^2θ + cos^2θ = 1 (θ为任意角度)(2)正弦的和差公式:sin(α ± β) = sinαcosβ ± cosαsinβ(3)正弦的倍角公式:sin2θ = 2sinθcosθ(4)正弦的半角公式:sin(θ/2) = ±√((1 - cosθ) / 2)(5)正弦的积化和差公式:sinαsinβ = (cos(α - β) - cos(α + β)) / 22. 余弦函数(cos):(1) 基本关系式:sin^2θ + cos^2θ = 1 (θ为任意角度)(2)余弦的和差公式:cos(α ± β) = cosαcosβ ∓ sinαsinβ(3)余弦的倍角公式:cos2θ = cos^2θ - sin^2θ = 2cos^2θ - 1 = 1 - 2sin^2θ(4)余弦的半角公式:cos(θ/2) = ±√((1 + cosθ) / 2)(5)余弦的积化和差公式:cosαcosβ = (cos(α + β) + cos(α - β)) / 23. 正切函数(tan):(1) 基本关系式:tanθ = sinθ / cosθ(2)正切的和差公式:tan(α ± β) = (tanα ± tanβ) / (1 ∓ tanαtanβ) (3)正切的倍角公式:tan2θ = (2tanθ) / (1 - tan^2θ)4. 余切函数(cot):(1) 基本关系式:cotθ = 1 / tanθ = cosθ / sinθ(2)余切的和差公式:cot(α ± β) = (cotαcotβ ∓ 1) / (cotβ ± cotα) (3)余切的倍角公式:cot2θ = (cot^2θ - 1) / (2cotθ)5. 正割函数(sec):(1) 基本关系式:secθ = 1 / cosθ(2)正割的和差公式:sec(α ± β) = (secαsecβ ± tanαtanβ) / (secβ ± secα) (3)正割的倍角公式:se c2θ = (2sec^2θ - 1) / (sec^2θ)6. 余割函数(csc):(1) 基本关系式:cscθ = 1 / sinθ(2)余割的和差公式:csc(α ± β) = (cscαcscβ ∓ cotαcotβ) / (cscβ ± cscα) (3)余割的倍角公式:csc2θ = (2csc^2θ - 1) / (csc^2θ)以上是常见的三角函数运算公式的归纳整理,可以帮助我们在进行三角函数的计算时快速、准确地得到结果。
三角函数相关公式

三角函数相关公式三角函数属于数学中的一类特殊函数,它们是描述角度和三角形边长之间关系的重要工具。
在解决几何问题、物理问题和工程问题中广泛应用。
下面将介绍三角函数的相关公式。
1. 正弦函数(sin)公式:正弦函数表示一个角的对边与斜边的比值。
常用的公式有:(1) 正弦函数的正值范围:-1 ≤ sinθ ≤ 1(2) 周期性:sin(θ + 2πn) = sinθ (其中n为整数)(3) 奇偶性:sin(-θ) = -sinθ(4) 反函数: sin^{-1}(x) = θ( - π/2 ≤ θ≤ π/2 )(5) 三角恒等式:sin^2θ + cos^2θ = 12. 余弦函数(cos)公式:余弦函数表示一个角的邻边与斜边的比值。
常用的公式有:(1) 余弦函数的正值范围:-1 ≤ cosθ ≤ 1(2) 周期性:cos(θ + 2πn) = cosθ (其中n为整数)(3) 奇偶性:cos(-θ) = cosθ(4) 反函数:cos^{-1}(x) = θ(0 ≤ θ ≤ π )(5) 三角恒等式:sin^2θ + cos^2θ = 13. 正切函数(tan)公式:正切函数表示一个角的对边与邻边的比值。
常用的公式有:(1) 正切函数的定义域:tanθ存在的条件为θ ≠ (π/2 + nπ),其中n为整数(2) 正切函数的正值范围:tanθ > 0时,θ位于第一象限和第三象限;tanθ < 0时,θ位于第二象限和第四象限(3) 周期性:tan(θ + πn) = tanθ (其中n为整数)(4) 奇偶性:tan(-θ) = -tanθ(5) 反函数:tan^{-1}(x) = θ( - π/2 < θ < π/2 )4. cosec函数(csc)公式:与sin函数互为倒数关系,即cscθ = 1/sinθ5. sec函数公式:与cos函数互为倒数关系,即secθ = 1/cosθ6. cot函数公式:与tan函数互为倒数关系,即cotθ = 1/tanθ7.三角函数的和差公式:(1) sin(α + β) = sinαcosβ + cosαsinβ(2) cos(α + β) = cosαcosβ - sinαsinβ(3) tan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)(4) sin(α - β) = sinαcosβ - cosαsinβ(5) cos(α - β) = cosαcosβ + sinαsinβ(6) tan(α - β) = (tanα - tanβ) / (1 + tanαtanβ)8.二倍角公式:(1) sin2θ = 2sinθcosθ(2) cos2θ = cos^2θ - sin^2θ = 2cos^2θ - 1 = 1 - 2sin^2θ(3) tan2θ = (2tanθ) / (1 - tan^2θ)9.半角公式:(1) sin(θ/2) = ±√[(1 - cosθ) / 2](2) cos(θ/2) = ±√[(1 + cosθ) / 2](3) tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)]10.三角函数的和倍角公式:(1) sinα + sinβ = 2sin((α + β)/2)cos((α - β)/2)(2) sinα - sinβ = 2sin((α - β)/2)cos((α + β)/2)(3) cosα + cosβ = 2cos((α + β)/2)cos((α - β)/2)(4) cosα - cosβ = -2sin((α + β)/2)sin((α - β)/2)(5) tanα + tanβ = (sinα + sinβ) / (cosαcosβ)(6) tanα - tanβ = (sinα - sinβ) / (cosαcosβ)以上是三角函数相关的公式,它们在解决三角函数相关问题中起到了重要的作用。
三角函数重要公式

tan3a=tanatan(60°-a)tan(60°+a)
三倍角
sin3α=3sinα-4sin^3α=4sinα·sin(π/3+α)sin(π/3-α)
cos3α=4cos^3α-3cosα=4cosα·cos(π/3+α)cos(π/3-α)
tan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)=tan a·tan(π/3+a)·tan(π/3-a)
cot(-α)= -cotα
公式四:
利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:
sin(π-α)= sinα
cos(π-α)= -cosα
tan(π-α)= -tanα
cot(π-α)= -cotα
公式五:
利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:
sin(2π-α)= -sinα
tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)
九倍角
sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))
cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))
tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA-15*tanA^4+tanA^6)
三角函数运算公式

三角函数运算公式三角函数是高中数学中比较重要的一个章节,也是数学中非常基础的概念。
在三角函数的学习中,我们需要掌握许多的运算公式。
以下是几个重要的三角函数运算公式:1. 正弦函数的运算公式:sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)sin(2a) = 2sin(a)cos(a)sin(a) ± sin(b) = 2sin( (a ± b) / 2 )cos( (a ∓ b) / 2 )2. 余弦函数的运算公式:cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b)cos(2a) = cos²(a) - sin²(a) = 2cos²(a) - 1 = 1 - 2sin²(a)cos(a) ± cos(b) = -2sin( (a ± b) / 2 )sin( (a ∓ b) / 2 )3. 正切函数的运算公式:tan(a ± b) = (tan(a) ± tan(b)) / (1 ∓ tan(a)tan(b))tan(2a) = (2tan(a)) / (1 - tan²(a))tan(a) ± tan(b) = sin(a ± b) / (cos(a)cos(b))4. 余切函数的运算公式:cot(a ± b) = (cot(a)cot(b) ∓ 1) / (cot(b) ± cot(a))cot(2a) = (cot²(a) - 1) / 2cot(a) = (1 - tan²(a)) / 2tan(a)cot(a) ± cot(b) = (sin(a)sin(b) ∓ cos(a)cos(b)) / (sin(a)cos(b) ± cos(a)sin(b)) 以上是常用的几个三角函数运算公式,这些公式在高中数学以及大学高等数学中都非常重要,学好这些公式对于深入掌握数学知识有着至关重要的作用。
三角关系公式大全高数

三角关系公式大全在高等数学中,三角函数是十分重要的内容之一。
三角函数的定义涉及到三角关系,而三角关系则可以通过一系列公式来表示和计算。
下面将介绍一些常用的三角关系公式。
1. 三角函数的定义在直角三角形中,假设一条直角边的长度为 a,另一条直角边的长度为 b,斜边的长度为 c。
则定义如下三个三角函数:•正弦(sine):sine(A) = a/c•余弦(cosine):cos(A) = b/c•正切(tangent):tan(A) = a/b其中 A 为直角边 a 的对角(角度)。
2. 基本关系公式基本关系公式可以通过三角函数的定义推导得出,它们是解决三角函数相关计算的基础。
下面是几个常用的基本关系公式:•余弦定理(cosine formula):c^2 = a^2 + b^2 - 2ab * cos(C)•正弦定理(sine formula):a/sin(A) = b/sin(B) = c/sin(C)•正切定义:tan(A) = sin(A) / cos(A)这些基本关系公式能够在解决直角三角形问题中提供重要的参考。
3. 和差公式和差公式可以用于计算三角函数求和或差的情况,下面是几个常用的和差公式:•正弦的和差公式:–sin(A + B) = sin(A) * cos(B) + cos(A) * sin(B)–sin(A - B) = sin(A) * cos(B) - cos(A) * sin(B)•余弦的和差公式:–cos(A + B) = cos(A) * cos(B) - sin(A) * sin(B)–cos(A - B) = cos(A) * cos(B) + sin(A) * sin(B)•正切的和差公式:–tan(A + B) = (tan(A) + tan(B)) / (1 - tan(A) * tan(B))–tan(A - B) = (tan(A) - tan(B)) / (1 + tan(A) * tan(B)) 这些和差公式可以在解决三角函数的简化、展开和求值问题时发挥作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重要三角公式汇总
一、任意角的三角函数
在角α的终边上任取..一点),(y x P ,记:22y x r +=,
正弦:r y =αsin 余弦:r x
=αcos 正切:x y =αtan 余切:y x =αcot 正割:x
r =
αsec 余割:y
r =
αcsc 二、同角三角函数的基本关系式
倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα。
商数关系:αααcos sin tan =
,α
α
αsin cos cot =。
平方关系:1cos sin 22=+αα,αα22sec tan 1=+,αα22csc cot 1=+。
三、诱导公式
⑴sin(2)sin cos(2)=cos tan()tan x k x
x k x x k x πππ+=++=( ⑵cos()cos sin()sin tan()tan x x
x x x x
-=-=--=-(奇偶性)
⑶sin()sin cos()cos tan()tan x x x x x x πππ±=-±=-±= (对称性) ⑷sin()sin cos()cos tan()tan x x x x x x
πππ-=-=--=- ⑸sin(
)cos 2
cos()sin 2
tan()cot 2
x x
x x x x
π
π
π
-=-=-= ⑹sin()cos 2
cos()sin 2tan()cot 2x x
x x x x π
π
π+=+=-+=-
四、和角公式和差角公式
βαβαβαsin cos cos sin )sin(⋅+⋅=+ βαβαβαs i n c o s c o s s i n )s i n (⋅-⋅=- βαβαβαsin sin cos cos )cos(⋅-⋅=+ βαβαβαs i n s i n c o s c o s )c o s (⋅+⋅=-
βαβαβαtan tan 1tan tan )tan(⋅-+=
+ β
αβ
αβαt a n t a n 1t a n t a n )t a n (⋅+-=
- 五、二倍角公式
αααcos sin 22sin = ααααα2
222s i n 211c o s 2s i n c o s 2c o s -=-=-=…)(*
α
α
α2
tan 1tan 22tan -=
二倍角的余弦公式)(*有以下常用变形:(规律:降幂扩角,升幂缩角)
αα2cos 22cos 1=+ αα2sin 22cos 1=-
2)cos (sin 2sin 1ααα+=+ 2)cos (sin 2sin 1ααα-=-
22cos 1cos 2αα+=
,2
2sin 1sin 2α
α+=,ααααα2cos 12sin 2sin 2cos 1tan +=-=。
六、万能公式(可以理解为二倍角公式的另一种形式)
ααα2tan 1tan 22sin +=,α
α
α22tan 1tan 12cos +-=,ααα2tan 1tan 22tan -=。
万能公式告诉我们,单角的三角函数都可以用半角的正切..
来表示。
七、和差化积公式
2
cos 2
sin 2sin sin β
αβ
αβα-+=+ 2sin
2cos
2sin sin β
αβ
αβα-+=- 2
cos
2cos
2cos cos β
αβ
αβα-+=+ 2
sin
2
sin
2cos cos β
αβ
αβα-+-=-
八、积化和差公式
[])sin()sin(21cos sin βαβαβα-++=⋅ [])s i n ()s i n (21s i n c o s βαβαβα--+=⋅ [])cos()cos(21cos cos βαβαβα-++=
⋅ [])c o s ()c o s (2
1s i n s i n βαβαβα--+-=⋅ 九、辅助角公式
)sin(cos sin 22ϕ++=+x b a x b x a
其中:角ϕ的终边所在的象限与点),(b a 所在的象限相同,由a
b
=
ϕtan 确定。
十、正弦定理 R C
c
B b A a 2sin sin sin ===(R 为AB
C ∆外接圆半径) 十一、余弦定理
A bc c b a cos 2222⋅-+=
B ac c a b cos 2222⋅-+=
C ab b a c cos 2222⋅-+=
十二、三角形的面积公式
B ca A bc
C ab S ABC sin 2
1sin 21sin 21===∆(二分之一两边积×夹角正弦值) 十四、反三角
名称 函数式
定义域
值域
性质
反正弦函数
x y arcsin = []1,1-增
⎥⎦
⎤⎢⎣⎡-2,2ππ -arcsinx arcsin(-x)= 奇 反余弦函数 x y arccos =
[]1,1-减
[]π,0
x x arccos )arccos(-=-π 反正切函数
arctgx y =
R 增
⎪⎭
⎫ ⎝⎛-2,2ππ arctgx - arctg(-x)= 奇 反余切函数
arcctgx y =
R 减
()π,0
arcctgx x arcctg -=-π)(。
