c++n皇后问题(含源码)
N皇后与凸多边形C语言设计流程思路与源代码
成绩管理程序设计报告(凸多边形)一、问题描述输入N个点的坐标,判断这N个点能否构成一个凸多边形。
二、结构图三、数据结构的设计int polygon(points nps){double var1,var2;int i,j,k;if(nps.pointNum<3) return 0; /*如果多边形的顶点数小于3,返回0*/for(i=0;i<nps.pointNum;i++) /*用循环判断任三点组成的三角形中有没有其它的点*/ {j=(i+2)%nps.pointNum;k=(i+1)%nps.pointNum;var1=(nps.x[i]-nps.x[k])*(nps.y[i]-nps.y[j])-(nps.y[i]-nps.y[k])*(nps.x[i]-nps.x[j]);for(j=(j+1)%nps.pointNum;j!=i;j=(j+1)%nps.pointNum){var2=(nps.x[i]-nps.x[k])*(nps.y[i]-nps.y[j])-(nps.y[i]-nps.y[k])*(nps.x[i]-nps.x[j]);if(var1*var2<0) return 0; /*有则返回0,表示不能构成凸多边形*/if(var2!=0) var1=var2;}if(var1==0) return 0;}return 1; /*没有则返回1,表示能构成凸多边形*/}四、处理流程图:五、源程序#include <stdio.h>#include<math.h>#define N 100 /*定义一个字符常量*/typedef struct{ /*定义一个新的数据类型*/double x[N];double y[N];int pointNum;}points;int polygon(points nps){double var1,var2;int i,j,k;if(nps.pointNum<3) return 0; /*如果多边形的顶点数小于3,返回0*/for(i=0;i<nps.pointNum;i++) /*用循环判断任三点组成的三角形中有没有其它的点*/ {j=(i+2)%nps.pointNum;k=(i+1)%nps.pointNum;var1=(nps.x[i]-nps.x[k])*(nps.y[i]-nps.y[j])-(nps.y[i]-nps.y[k])*(nps.x[i]-nps.x[j]); for(j=(j+1)%nps.pointNum;j!=i;j=(j+1)%nps.pointNum){var2=(nps.x[i]-nps.x[k])*(nps.y[i]-nps.y[j])-(nps.y[i]-nps.y[k])*(nps.x[i]-nps.x[j]);if(var1*var2<0) return 0; /*有则返回0,表示不能构成凸多边形*/if(var2!=0) var1=var2;}if(var1==0) return 0;}return 1; /*没有则返回1,表示能构成凸多边形*/}main(){int i;points nps;printf("请输入顶点的个数:");scanf("%d",&nps.pointNum);printf("请输入这些顶点的坐标,每个点的横坐标和纵坐标用逗号分隔开( 例如12.5,34 ):\n"); for(i=0;i<nps.pointNum;i++) /*用循环读入每个点的坐标*/{printf("第%d个顶点:",i+1);scanf("%lf,%lf",&nps.x[i],&nps.y[i]);}if(polygon(nps)) /*根据子函数的返回值输出结果*/printf("该多边形是凸多边形。
八皇后问题代码实现

八皇后问题代码实现/*代码解析*//* Code by Slyar */ #include <stdio.h>#include<stdlib.h> #define max 8 int queen[max], sum=0; /* max为棋盘最大坐标*/ void show() /* 输出所有皇后的坐标*/{ int i; for(i = 0; i < max; i++){ printf("(%d,%d) ", i, queen[i]); }printf("\n"); sum++;} int check(int n) /* 检查当前列能否放置皇后*/{ int i; for(i = 0; i < n; i++) /* 检查横排和对角线上是否可以放置皇后*/ { /* ///题目的要求是所有皇后不在同一横排、竖排、对角线上。
1、queen[n]值为竖排号,可看为Y轴上值。
n值为横排号,可看为X轴上值。
2、(1)先从横坐标第n点排开始放皇后,再放第n+1,所有不会同一横坐标点即同一竖排。
(2)queen[i] == queen[n]时即y坐标相等,即在同一横排,此时判断不合规则点。
(3)abs(queen[i] - queen[n]) == (n - i),可变形为(queen[n] - queen[i]) /(n - i)==tan45°或tan135° 由公式可得出,点(n,queen[n])与点(i,quuen[i])在同一条左斜线135°或右斜45°,即国际象棋上的每个格子的两条斜角线。
3、由2即可得出当前格式是否能放置一个皇后。
*/ if(queen[i] == queen[n] || abs(queen[i] - queen[n]) == (n - i)) { return1; } } return 0;} void put(int n) /* 回溯尝试皇后位置,n为横坐标*/{ int i; for(i = 0; i < max;i++) { queen[n] = i; /* 将皇后摆到当前循环到的位置*/ if(!check(n)){ if(n == max - 1){ show(); /* 如果全部摆好,则输出所有皇后的坐标*/ } else { put(n + 1); /* 否则继续摆放下一个皇后*/ } } }} int main(){ put(0); /*从横坐标为0开始依次尝试*/ printf("TTTTTT----%d\n", sum); //system("pause"); //while(1); return 0;}/*算法系列---回溯算法引言寻找问题的解的一种可靠的方法是首先列出所有候选解,然后依次检查每一个,在检查完所有或部分候选解后,即可找到所需要的解。
回溯典型题目——N皇后问题剖析
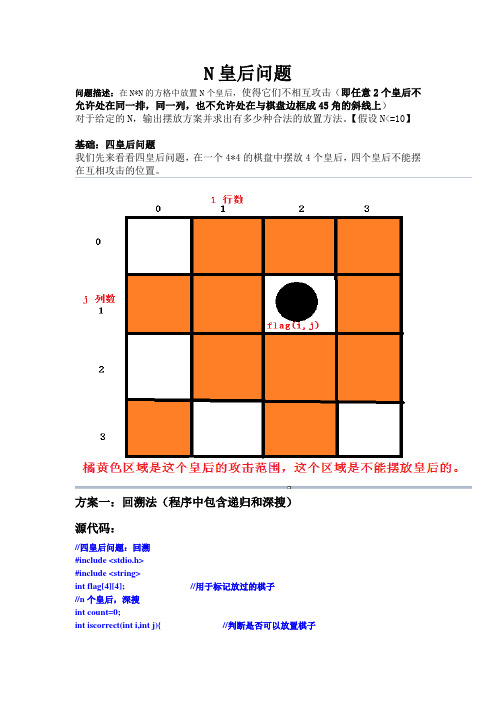
N皇后问题问题描述:在N*N的方格中放置N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上)对于给定的N,输出摆放方案并求出有多少种合法的放置方法。
【假设N<=10】基础:四皇后问题我们先来看看四皇后问题,在一个4*4的棋盘中摆放4个皇后,四个皇后不能摆在互相攻击的位置。
方案一:回溯法(程序中包含递归和深搜)源代码://四皇后问题:回溯#include <stdio.h>#include <string>int flag[4][4]; //用于标记放过的棋子//n个皇后,深搜int count=0;int iscorrect(int i,int j){ //判断是否可以放置棋子int a,b;for(a=i,b=0;b<4;b++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=0,b=j;a<4;a++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=i-1,b=j-1;a>=0&&b>=0;a--,b--){ //左上方if(flag[a][b]==1)return 0;}for(a=i-1,b=j+1;a>=0&&b<=3;a--,b++){ //左下方if(flag[a][b]==1)return 0;}for(a=i+1,b=j-1;a<=3&&b>=0;a++,b--){ //右上方if(flag[a][b]==1)return 0;}for(a=i+1,b=j+1;a<=3&&b<=3;a++,b++){ //判断右下方if(flag[a][b]==1)return 0;}return 1;}void DFSQ(int i){int m,n;int j;//i代表行数,j代表列数if(i==4){ //因为棋盘是(n-1)*(n-1)模式的,而i是行,当棋盘到第四行的时候,表明已//经完成0~3的所有排布已经完成for(m=0;m<4;m++){for(n=0;n<4;n++){printf("%d ",flag[m][n]);}printf("\n");}count++;printf("\n");return; //不要忘记这个}else{for(j=0;j<4;j++){if(iscorrect(i,j)){ //如果可以放置棋子flag[i][j]=1; //标记flag[i][j]DFSQ(i+1); //递归调用flag[i][j]=0; //消除标记}}}}int main(){memset(flag,0,sizeof(flag));DFSQ(0);printf("count=%d\n",count);return 0;}其实从四皇后问题拓展到n皇后问题是非常简单的事情,方案一进阶到N皇后的源代码:N皇后其实只要把其中的4改成N就行了:源代码:#include <stdio.h>#include <string>int flag[10][10]; //用于标记放过的棋子int number; //表示棋子个数//n个皇后,深搜int count=0;int iscorrect(int i,int j){ //判断是否可以放置棋子int a,b;for(a=i,b=0;b<number;b++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=0,b=j;a<number;a++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=i-1,b=j-1;a>=0&&b>=0;a--,b--){ //左上方if(flag[a][b]==1)return 0;}for(a=i-1,b=j+1;a>=0&&b<=number-1;a--,b++){ //左下方if(flag[a][b]==1)return 0;}for(a=i+1,b=j-1;a<=number-1&&b>=0;a++,b--){ //右上方if(flag[a][b]==1)return 0;}for(a=i+1,b=j+1;a<=number-1&&b<=number-1;a++,b++){ //判断右下方if(flag[a][b]==1)return 0;}return 1;}void DFSQ(int i){int m,n;int j;//i代表行数,j代表列数if(i==number){ //因为棋盘是(n-1)*(n-1)模式的,而i是行,当棋盘到第四行的时候,表明已经完成0~number-1的所有排布已经完成for(m=0;m<number;m++){for(n=0;n<number;n++){printf("%d ",flag[m][n]);}printf("\n");}count++;printf("\n");return; //不要忘记这个}else{for(j=0;j<number;j++){if(iscorrect(i,j)){ //如果可以放置棋子flag[i][j]=1; //标记flag[i][j]DFSQ(i+1); //递归调用flag[i][j]=0; //消除标记}}}}int main(){scanf("%d",&number);memset(flag,0,sizeof(flag));DFSQ(0);printf("count=%d\n",count);return 0;}。
N皇后问题

班级:
姓名:ቤተ መጻሕፍቲ ባይዱ
学号:
日期:
一、实验目的
会用回溯法求解n皇后问题,通过实验掌握如何使用回溯法求解问题。
二、实验要求
用自己熟悉的高级程序设计语言编写程序实现求解n皇后问题的回溯算法。
使用剪枝函数来避免不必要的搜索。
三、源程序(带注释)
#include<iostream>
using namespace std;
x[k]=x[k]+1;//搜索下一列
if(x[k]<=n && k==n){ //得到一个解,输出
for(i=1;i<=n;i++){
cout<<x[i]<<endl;
}
return;
}
else if(x[k]<=n && k<n)
k=k+1;//放置下一个皇后
else{
x[k]=0;//重置x[k],回溯
int x[100];
int i=0,k=0;
bool Place(int k);
void Queue(int n){
for(i=1;i<=n;i++)//初始化
x[i]=0;
k=1;
while(k>=1){
x[k]=x[k]+1;//在下一列放置第k个皇后
while(x[k]<=n && !Place(k))
k=k-1;
}
}
}
bool Place(int k){//考察皇后k放置在x[k]列是否发生冲突
C语言题_2n皇后问题

printf("%c",NN[i][j]);
printf("\n");
for(i=1;i<=N;i++)
{
}
NN[line][i]='Q';
q[line]=i;
if(n=Cheak(line)>0)
{
}
Search(line,N);
NN[line][i]='1';
for(i=1;i<=(N+1)/2;i++)
{
}
void main()
{
//初始
int N,i,j;
q[1]=i;
NN[1][i]='Q';
Search(1,N);
NN[1][i]='1';
for(i=1;i<9;i++)
for(j=1;j<9;j++)
//如果最后一行的 Q 已经存在,则打印棋盘
//遍历此行,并通过检测查询下一行
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料试荷试卷下卷问高总题中体2资2配,料置而试时且卷,可调需保控要障试在各验最类;大管对限路设度习备内题进来到行确位调保。整机在使组管其高路在中敷正资设常料过工试程况卷中下安,与全要过,加度并强工且看作尽护下可1都关能可于地以管缩正路小常高故工中障作资高;料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高,核中或对资者定料对值试某,卷些审弯异核扁常与度高校固中对定资图盒料纸位试,置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置,线高尤弯中其曲资要半料避径试免标卷错高调误等试高,方中要案资求,料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高,技料课中并术3试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术,、以术来管及避架系免等统不多启必项动要方方高式案中,;资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资,中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置,作调合并试理且技利进术用行,管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵:导活在。。分对对线于于盒调差处试动,过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调,问试应题技采,术用作是金为指属调发隔试电板人机进员一行,变隔需压开要器处在组理事在;前发同掌生一握内线图部槽纸故内资障,料时强、,电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料,试试线卷卷缆试切敷验除设报从完告而毕与采,相用要关高进技中行术资检资料查料试和,卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
N皇后问题

#include<iostream>#include<iomanip>#include<fstream>using namespace std;class QUEUE//皇后问题类{private://4个私有数据成员,2个私有成员函数int *solution;//一维解的指针int **MarkArray;//二维标记数组指针int N;//皇后数ofstream fout;//存放所有解得文件void Mark(int m,int i,bool flag){//对于在[m][i]放置(flag=true)或除去(flag=false)皇后事件做或擦除标记int j,n,k;if(flag)//放置皇后{j=-1;//原有的可以放置皇后的标记n=m;//改为由于在[m][i]放置了皇后所设置的不可放置皇后的标记}else//移除皇后{j=m;//原有的在[m][i]放置了皇后而设置的不可放置皇后的标记n=-1;//改为可放置皇后的标记([m][i]处的皇后移除了)}for(k=0;k<N;k++)//在MarkArray[m][]中做或擦除标记if(MarkArray[m][k]==j)//m行该位置原来的标记MarkArray[m][k]=n;//改标记for(k=m+1;k<N;k++)//在MarkArray[m+1][]--[N-1][]中(m+1--最后一行)做或擦除标记{if(MarkArray[k][i]==j)//i列该位置原来的标记MarkArray[k][i]=n;//改标记if((k+i-m)>=0 && (k+i-m)<N && MarkArray[k][k+i-m]==j)//主对角线该位置原来的标记MarkArray[k][k+i-m]=n;//改标记if((i+m-k)>=0 && (i+m-k)<N && MarkArray[k][i+m-k]==j)//副对角线该位置原来的标记MarkArray[k][i+m-k]=n;//改标记}}void PutOut(){//输出解和MarkArray[][]int i,j;fout<<"解"<<number<<": "<<endl;//将解数输出到文件fout<<"solution[]=";for(j=0;j<N;j++)//输出solution[]fout<<solution[j]<<' ';fout<<endl<<"根据solution[],输出皇后在棋盘上的位置:"<<endl;for(j=0;j<N;j++)//根据solution[],输出皇后在棋盘上的位置{for(i=0;i<N;i++)if(i==solution[j])//在j行的皇后位置fout<<" Q";//输出皇后Qelse//在j行的其他位置fout<<" X";//输出非皇后Xfout<<endl;}fout<<"MarkArray[][]="<<endl;for(j=0;j<N;j++){for(i=0;i<N;i++)fout<<setw(2)<<MarkArray[j][i];fout<<endl;}}public://1个公有数据成员、2个公有成员函数、1个构造函数和1个析构函数int number;//解得个数QUEUE(int n,char f[]){//构造函数N=n;//皇后数number=0;//解得个数初始为0solution=new int[N];//生成存放每行皇后位置的一维数组MarkArray=new int *[N];//生成一维指针数组for(int i=0;i<N;i++){MarkArray[i]=new int [N];//生成二维标记数组for(int j=0;j<N;j++)MarkArray[i][j]=-1;//在[i][j]位置可放置皇后的标记}fout.open(f,ios::out);//以输出的方式打开文件ffout<<N<<"皇后问题的所有解:"<<endl;}~QUEUE(){//析构函数,释放动态生成的存储空间,关闭文件for(int i=0;i<N;i++)//释放MarkArray[][]delete [] MarkArray[i];delete []MarkArray;//释放MarkArray[]delete []solution;//释放solution[]fout.close();//关闭数据文件}void QueenByRecursion(int m)//求皇后问题的所有递归解{//在[m]行中选择放置皇后的位置if(m<N)//还没有完成一个解for(int i=0;i<N;i++)//从[m][i]中选择可放置皇后的位置{if(MarkArray[m][i]==-1)//可在[m][i]处放置皇后{solution[m]=i;//m行的皇后放置在i列Mark(m,i,true);//在MarkArray[][]中对由此产生的不可放置皇后位置做标记QueenByRecursion(m+1);//递归放置下一个皇后Mark(m,i,false);//递归返回时在MarkArray[][]中对可重新放置皇后的位置去除标记}}else//完成一个解{number++;//解数加1PutOut();//向文件输出该解}}void QueenNoRecursion()//求皇后问题的所有非递归算法{int i,j;i=0;//当前行j=0;//当前列while(i>=0)//当前行有效{while(j<N)//当前列有效{if(MarkArray[i][j]==-1)//找到可放置皇后的位置break;//跳出循环j++;//没有找到,则下一位置继续找}if(j<N)//找到放置皇后的位置[i][j]{solution[i]=j;//存于位置数组Mark(i,j,true);//对于不能放置皇后的位置做标记if(i==N-1)//[0]--[N-1]行都放置了皇后(得到一个解){number++;//解数加1PutOut();//输出该解Mark(i,j,false);//去除在当前位置上放置的标记i--;//回退到上一行j=solution[i];//上一行的皇后位置赋给jMark(i,j,false);//去除[i][j]位置放置皇后的标记j++;//找到下一个解的皇后的位置}else//i<N-1,在下一行找放置皇后的位置{i++;j=0;}}else//j=N,在i行上没找到放置皇后的位置{i--;//行数-1,回退到上一行if(i>=0)//栈不空,移除皇后{j=solution[i];//上一行皇后的位置赋给jMark(i,j,false);//去除[i][j]位置放置皇后的标记j++;//从下一个位置开始找可放置皇后的位置}}}}};void main(){char FileName[13]="Queen.txt";//存储皇后问题的所有解的文件int m,n=4;//皇后数QUEUE q(n,FileName);//求n皇后问题的所有解并存于FileName的QUEUE类的对象cout<<"求解皇后问题:欲采用递归方法,请输入1;否则,输入0:";cin>>m;if(m>0)q.QueenByRecursion(0);//皇后问题的递归函数,从[0]行开始放置皇后elseq.QueenNoRecursion();//皇后问题的非递归函数cout<<n<<""<<q.number<<"个解,存于文件"<<FileName<<"中。
回溯法之N皇后问题(C语言)

//回溯法之N皇后问题当N>10,就有点抽了~~/*结果前total行每行均为一种放法,表示第i行摆放皇后的列位置,第total+1行,输出total*/#include<stdio.h>#include<stdlib.h>int n,stack[100]; //存当前路径int total; //路径数void make(int l) //递归搜索以stack[l]为初结点的所有路径{int i,j; //子结点个数if (l==n+1){total=total+1; //路径数+1for(i=1;i<=n;i++)printf("%-3d",stack[i]); //输出第i行皇后的列位置stack[i] printf("\n");exit; //回溯(若试题仅要求一条路径,则exit改为halt即可)}for (i=1;i<=n;i++){stack[l]=i; //算符i作用于生成stack[l-1]产生子状态stack[l];if (!att(l,i)) make(l+1);} //再无算符可用,回溯}int att(int l,int i){int k;for (k=1;k<l;k++)if (abs(l-k)==abs(stack[k]-i)||i==stack[k]) return 1;return 0;}int main(){printf("N=");scanf("%d",&n);total=0; //路径数初始化为0make(1); //从结点1出发,递归搜索所有的路径printf("%d\n",total);system("pause");return 0;}由回溯法的算法流程可以看出,除非边界条件设置不当而导致死循环外,回溯法一般是不会产生内存溢出的。
n皇后问题解法总数 规律

n皇后问题解法总数规律
n皇后问题是指在一个n*n的棋盘上放置n个皇后,使任意两个皇后都不能相互攻击。
n皇后问题的解法总数可以用以下公式表示:C_{n,n-2}
其中,C是组合数,表示从n个元素中选择n-2个元素的组合数。
这个公式可以用以下方式推导:
假设我们已经将n-1个皇后放在了棋盘上,并且它们之间不会相互攻击。
那么,第n个皇后可以放在棋盘上的任何空位上,而不会与其他皇后相互攻击。
因此,第n个皇后的摆放方式有n种。
因此,n皇后问题的解法总数就是n-1个皇后的摆放方式总数乘以n,即:(n-1)C_{n-1}*n=C_{n,n-2}
●例如,2皇后问题的解法总数是:C_{2,0}=1
●3皇后问题的解法总数是:C_{3,1}=3
●4皇后问题的解法总数是:C_{4,2}=7
●5皇后问题的解法总数是:C_{5,3}=31
可以看到,n皇后问题的解法总数随着n的增加而呈指数增长。
罗马尼亚度假问题和N皇后问题C++代码实现以及分析

人工智能课程实习报告班级学号姓名中国地质大学(武汉)计算机学院2016年11月问题一:罗马尼亚度假问题【问题描述】分别用代价一致的宽度优先、有限制的深度优先(预设搜索层次)、贪婪算法和A*算法求解“罗马利亚度假问题”。
1、要求:分别用文件存储地图和启发函数表,用生成节点数比较几种算法在问题求解时的效率,并列表给出结果。
数据如下:2、数据:地图:启发数值:Arad(0)366 Mehadia(1) 241 Bucharest(2)0 Neamt(3)234 Craiova(4)160 Oradea(5) 380 Doberta(6)242 Pitesti(7)100 Eforie(8)161 Rimmicu_Vikea(9) 193 Fagaras(10)176 Sibiu(11)253 Glurgiu(12)77 Timisoara(3) 329 Hirsova(14)151 Urziceni(15)80 Iasi(16)226 Vaslui(17)199 Lugoj(18)244 Zerind(19)374地图数据表:0 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 140 1000 118 1000 1000 1000 1000 1000 751000 0 1000 1000 1000 1000 75 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 70 10001000 1000 0 1000 1000 1000 1000 101 1000 1000 211 1000 90 1000 1000 85 1000 1000 1000 10001000 1000 1000 0 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 87 1000 1000 10001000 1000 1000 1000 0 1000 120 138 1000 146 1000 1000 1000 1000 1000 1000 1000 1000 1000 10001000 1000 1000 1000 1000 0 1000 1000 1000 1000 1000 151 **** **** 1000 1000 1000 1000 1000 711000 75 1000 1000 120 1000 0 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 10001000 1000 101 1000 138 **** **** 0 1000 97 1000 1000 1000 1000 1000 1000 1000 1000 1000 10001000 1000 1000 1000 1000 1000 1000 1000 0 1000 1000 1000 1000 1000 86 1000 1000 1000 1000 10001000 1000 1000 1000 146 1000 1000 97 1000 0 1000 80 1000 1000 1000 1000 1000 1000 1000 10001000 1000 211 1000 1000 1000 1000 1000 1000 1000 0 99 1000 1000 1000 1000 1000 1000 1000 1000140 1000 1000 1000 1000 151 **** **** 1000 80 99 0 1000 1000 1000 1000 1000 1000 1000 10001000 1000 90 1000 1000 1000 1000 1000 1000 1000 1000 1000 0 1000 1000 1000 1000 1000 1000 1000118 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 0 1000 1000 1000 1000 111 10001000 1000 1000 1000 1000 1000 1000 1000 86 1000 1000 1000 1000 1000 0 98 1000 1000 1000 10001000 1000 85 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 98 0 1000 142 1000 10001000 1000 1000 87 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 0 92 1000 10001000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 142 92 0 1000 10001000 70 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 111 1000 1000 1000 1000 0 100075 1000 1000 1000 1000 71 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 0【程序整体架构与存储结构】按照罗马尼亚度假问题中的地图可初步确定所用的存储结构为图。
C语言题_2n皇后问题

2n皇后问题试题来自:程设09秋(徐)(程序设计基础课(清华大学徐明星老师、吴文虎老师)2009秋) 【问题描述】给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。
现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。
问总共有多少种放法?n小于等于8。
【输入格式】输入的第一行为一个整数n,表示棋盘的大小。
接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
【输出格式】输出一个整数,表示总共有多少种放法。
【样例输入1】41 1 1 11 1 1 11 1 1 11 1 1 1【样例输出1】2【样例输入2】41 0 1 11 1 1 11 1 1 11 1 1 1【样例输出2】分析:每行的Q的位置,保存在一个数组中Q[6],Q[1]表示第一行q的列数。
从第一行开始1到(n+1)/2遍历如果Q[1]=1,那么Q[2]==Q[1],则不符合如果Q[1]>Q[2],检测Q[2]是否在Q[1]的135度线上, Q[1]+([2]-[1])?=Q[2],Q1与Q2的Q2的列值如果Q[1]<Q[2],检测Q[2]是否在Q[1]的45度线上, Q[1]-([2]-[1])?=Q[2],Q1的列值减去Q1与Q2的行差是否等于Q2的列值如果只要求一种颜色的N皇后问题,并且没有0,1的限制,实现代码:#include<stdio.h>char NN[9][9]; //棋盘,初始设为‘-’,1表示在棋盘格为空,Q表示放置皇后int q[6]; //记录1-N行Q的列数,q[1]=3表示第一行的Q在第三列int Cheak(int line) //检测要添加的Q是否符合要求{int i;for(i=1;i<line;i++){if(q[i]-q[line]==0)return 0;else if(q[i]-q[line]>0){if(q[i]-(line-i)==q[line])return 0;}else{if(q[i]+(line-i)==q[line])return 0;}}return 1;}void Search(int line,int N){int i,j,n;if(line==N) //如果最后一行的Q已经存在,则打印棋盘for(i=1;i<9;i++){for(j=1;j<9;j++)printf("%c",NN[i][j]);printf("\n");}else //遍历此行,并通过检测查询下一行{line++;for(i=1;i<=N;i++){NN[line][i]='Q';q[line]=i;if(n=Cheak(line)>0){Search(line,N);}NN[line][i]='1';}}}void Begin(int N){int i;for(i=1;i<=(N+1)/2;i++){q[1]=i;NN[1][i]='Q';Search(1,N);NN[1][i]='1';}}void main(){//初始int N,i,j;for(i=1;i<9;i++)for(j=1;j<9;j++)NN[i][j]='-';printf("Start:(8*8)\n");for(i=1;i<9;i++){for(j=1;j<9;j++)printf("%c",NN[i][j]);printf("\n");}//输入Nscanf("%d",&N);for(i=1;i<=N;i++)for(j=1;j<=N;j++)NN[i][j]='1';printf("Now you choice N=%d:(%d*%d)\n",N,N,N);for(i=1;i<9;i++){for(j=1;j<9;j++)printf("%c",NN[i][j]);printf("\n");}//开始计算Begin(N);}上述的代码中,只实现了棋盘的打印,并未统计放法的数量,通过Begin()函数,第一行只检测一半,因为另一半是对称的(为了提高效率),然而题目要求是有0,1限制的,所以,为了实现上述要求,代码还应改动去掉对称,因为棋盘添加了0后便不是对称的了。
c++八皇后问题最简单算法

八皇后问题是一个经典的回溯算法问题。
下面是一个使用C语言实现的简单算法:c复制代码#include<stdio.h>#include<stdbool.h>#define N 8int col[N] = {0}; // 表示皇后所在的列int queens[N][N] = {0}; // 存储棋盘状态bool is_valid(int row, int col) {for (int i = 0; i < row; i++) {if (queens[i][col] || queens[i][col - (row - i)] || queens[i][col + (row -i)]) {return false;}}return true;}void backtrack(int row) {if (row == N) { // 找到了一组解for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {printf("%d ", queens[i][j]);}printf("\n");}return;}for (int col = 0; col < N; col++) {if (is_valid(row, col)) { // 如果当前位置是合法的,则放置皇后queens[row][col] = 1;col[row] = col; // 记录每行皇后所在的列backtrack(row + 1); // 继续放下一行的皇后queens[row][col] = 0; // 回溯,撤销当前位置的皇后}}}int main() {backtrack(0); // 从第0行开始放皇后return0;}在上面的代码中,我们使用一个一维数组col来记录每一行皇后所在的列。
在is_valid函数中,我们检查当前位置是否合法,即与前面的皇后不冲突。
N皇后问题——JAVA实现(源代码)

2011/2012学年第2学期“算法分析与设计”上机报告目录1. 问题描述 (3)2. 算法分析 (3)3. 伪代码 (4)4. 演示程序设计 (5)5. 演示界面 (5)6. 算法实现 (8)7. 总结 (19)8. 参考文献 (20)1.问题描述:N皇后问题(n-queen problem)是一个经典的组合优化问题,也是一个使用回溯法(backtracking)的典型例子。
回溯法是一种系统地搜索问题解的方法。
为了实现回溯,首先需要为为问题定义一个解空间(solution space),其至少包含问题的一个解(可能是最优解)。
我们要从中找出满足问题约束条件的解,即可行解(feasible solution)。
回溯算法一次扩展一个解,在对部分解进行扩展后,检查到目前为止的解是否为问题的一个解,如果是,则输出;否则,检查是否可以继续扩展。
如果可以,则继续扩展;否则,删除最后添加的元素,尝试当前位置是否有另一元素。
若没有合法的扩展方式,则进行回溯(backtrack)。
N皇后问题要求在一个n×n的棋盘上放置n个皇后,且使得每两个皇后之间都不能相互攻击,即它们中的任意两个都不能位于同一行、同一列或者同一对角线上。
这次的任务就是借助GUI实现N皇后问题的动态演示。
我们设定皇后个数在四个到八个之间可选,所选编程语言为JA V A。
2.算法分析:N皇后问题是回溯法的一个经典例子,它的要求就是要找出在n×n的棋盘上放置n个皇后并使其不能相互攻击的所有解。
设X=(x1,x2,…,xn)表示问题的解,,其中xi表示第i皇后放在第i行所在的列数。
由于不存在两个皇后位于同一列上,因此xi互不相同。
设有两个皇后分别位于棋盘( i , j )和( k , l )处,如果两个皇后位于同一对角线上,则表明它们所在的位置应该满足:i – j = k – l或i + j = k + l。
综合这两个等式可得,如果两个皇后位于同一对角线上,那么它们的位置关系一定满足| j – l | = | i – k |。
n皇后问题(分析)

n皇后问题(分析)这道题需要⽤到回溯算法,现在在这⾥先简单的介绍⼀下这个算法:回溯算法也叫试探法,它是⼀种系统地搜索问题的解的⽅法。
回溯算法的基本思想是:从⼀条路往前⾛,能进则进,不能进则退回来,换⼀条路再试。
⽤回溯算法解决问题的⼀般步骤为:1、定义⼀个解空间,它包含问题的解。
2、利⽤适于搜索的⽅法组织解空间。
3、利⽤深度优先法搜索解空间。
4、利⽤限界函数避免移动到不可能产⽣解的⼦空间。
问题的解空间通常是在搜索问题的解的过程中动态产⽣的,这是回溯算法的⼀个重要特性。
⾸先,看⼀个简单的程序;1 #include <stdio.h>2 #include <stdlib.h>34void function(int a)5 {6if (a > 0)7 {8 printf("%d\n", a);9 function(a - 1);10 }11 }1213int main(void)14 {15int a = 3;16 function(3);17 system("PAUSE");18return0;19 }输出:3 2 11 #include <stdio.h>2 #include <stdlib.h>34void function(int a)5 {6if (a > 0)7 {8 function(a - 1);9 printf("%d\n",a);10 }11 }1213int main(void)14 {15int a = 3;16 function(3);17 system("PAUSE");18return0;19 }输出:1 2 3⾸先第⼀个不难理解,第⼆个,⾸先进⾏三次递归,分别是function(2),function(1),function(0)=>a=3,a=2,a=1;当到a=1递归执⾏结束,就会接着往下执⾏,执⾏printf,所以此时输出1,然后,返回到上⼀级递归,function(1),执⾏结束后,再次执⾏printf,输出1...⼋皇后问题:⼋皇后问题,是⼀个古⽼⽽著名的问题,是回溯算法的典型案例。
N皇后——最小冲突算法一个相对高效的实现

N皇后——最⼩冲突算法⼀个相对⾼效的实现N皇后问题就不再叙述了,Google⼀下就知道了(这⾥我们讨论找出⼀个或⼏个解,不讨论找出全部解的⽅法)N皇后有⼀个解法是回溯法,这个可以解决,但是效率不是很⾼。
(不过这个⽅法可以找出所有解)结合随机⽅法会更快:随机初始化⼀部分皇后,使得她们互不冲突,然后再⽤回溯法,这通常快得多。
不过这个⽅法不能找到所有解,也不能保证⼀次找到解——如果第⼀次随机化找不到解,就要再次随机化+回溯。
本⽂讲⼀个从⼈⼯智能的⾓度解决该问题的算法——最⼩冲突算法,这个算法在《⼈⼯智能——⼀种现代⽅法》(第⼆版)第五章中出现简单地说,就是:(1)初始化N个皇后的⼀个放置,允许有冲突(2)考虑某⼀⾏的某个皇后,她可能与x个皇后冲突,然后看看将这个皇后移动到这⼀⾏的哪个空位能使得与其冲突的皇后个数最少,就移动到那⾥。
(也可以考虑列,是等价的)(3)不断执⾏(2),直到没有冲突为⽌这个算法也不能找到所有解,有可能也要多次初始化,因为有可能从某个初始状态开始,按照最⼩冲突准则⽆论怎么调整都达不到终⽌条件(即没有冲突)。
这⾥的最⼩冲突准则有点“贪⼼”的味道,⽽贪⼼算法常常达不到最优解。
(不过实际实现时发现1次初始化总是能得到解——当然这个没法证明,只是实验验证)上⾯的算法没有说明如何初始化,最简单的就是随便放,这⾥我们采⽤每⾏放⼀个,同时保证列号不重复的⼀种随机放法。
上⾯算法也没说明每次执⾏(2)应该处理哪⼀⾏,我们的做法是:从第⼀⾏开始直到最后⼀⾏,逐个处理,如果这样⼀轮下来没有终⽌,就再来⼀轮……直到终⽌。
计算每⾏最⼩冲突的位置是这个算法⽐较核⼼的⼀步,简单的想法就是对某个位置,遍历所有的皇后,看看与其中⼏个有冲突;对N个可能的位置都执⾏这⼀操作,这就是O(N^2)的复杂度,这样每⼀轮的调整就是O(N^3),N超过1000就会⾮常慢了 ⼀个改进的想法是:既然每次只调整了⼀个皇后的位置,产⽣的影响并不⼤,可以记录每个皇后的冲突数,然后当某个皇后移动时,更新这个值。
皇后算法

皇后算法问题描述:在一个N*N的棋盘上,每一行放置一个棋子,所有棋子需满足在列,斜线上无其他棋子问题解决:皇后算法是根据回溯法来制定的。
程序的主干算法:void Queen(int i){//进入本函数时,在N*N的棋盘前i-1已经放置了i-1个符合要求的棋子//现从第i行选择合适的棋子//当i>n 时输出If(i>n ) 输出elsefor(j=1;j<n;j++){在(i,j)放置一个棋子if(合法) Queen(i+1);丢弃该棋子}}如何判断棋子是否合法1.在该棋子上方的同列中,是否已经放置了棋子2.在该棋子的左斜上方是否已经放置了棋子3.在该棋子的右斜上方是否已经放置了棋子注意事项:(1)在描述一个N*N棋盘时,我们用一个a[N+2][N+2]二维数组来描述。
理由如下:因为若数组只是a[N][N],则在判断边界棋子时(例如:a[0][0]),我们无法判断其列,斜线方向是否已经有棋子(除非分类判断,那样就麻烦多了)。
因此如果设置一个a[N+2][N+2],在其边界上无棋子,则只需假设期盼在在[1---N][1----N]上。
(2)为了描述问题的简单,设置1 →有棋子,0 →无棋子。
程序如下:#include <stdio.h>#include <stdlib.h>#define MAX 6static int a[MAX][MAX]; //棋盘的实际大小是a[1---MAX-1][1---MAX1]int n = 0; //统计符合情况的个数void output(int num[MAX][MAX]){int i,j;n++;for(i=1;i<MAX-1;i++){for(j=1;j<MAX-1;j++)printf("%d ",num[i][j]);printf("\n");}printf("\n");}void Queen(int i){bool flag;int k,j,l;if(i>=MAX-1)output(a);else{for(j=1;j<MAX-1;j++){flag = true;a[i][j] = 1;//判断列for(k = i-1;k>=0;k--){if(a[k][j] == 1){flag = false;break;}//if}//for//判断左斜线if( flag == true){for(l = i-1,k = j-1;l>=0&&k>=0;l--,k--){if(a[l][k] == 1){flag = false;break;}//if}//for}//if//判断右斜线if( flag == true){for(l = i-1,k = j+1;l>=0&&k<MAX;l--,k++){if(a[l][k] == 1){flag = false;break;}//if}//for}//ifif(flag == true )Queen(i+1);a[i][j] = 0;} //for}//if}int main(){Queen(1);printf("总共有%d个可行。
C语言题_2n皇后问题

去 Q1 与 Q2 的行差是否等于 Q2 的列值
如果只要求一种颜色的 N 皇后问题,并且没有 0,1 的限制,实现代码:
#include<stdio.h>
char NN[9][9];
int q[6];
int Cheak(int line)
{
int i;
for(i=1;i<line;i++)
{
}
if(q[i]-q[line]==0)
NN[i][j]='-'; printf("Start:(8*8)\n"); for(i=1;i<9;i++) {
for(j=1;j<9;j++) printf("%c",NN[i][j]);
printf("\n"); } //输入 N scanf("%d",&N); for(i=1;i<=N;i++)
所有改动后的代码,还应多添加一个检测 0
通过添加个数组 q_num[9]来记录 Q 在第一行,第 i 列的放法数目
如:N=5,num[1]=1,num[2]=2,num[3]=3,num[4]=4,num[5]=5
那么放置两种皇后的总方法:1*(2+3+4+5)+2*(1+3+4+5)+……..+5*(1+2+3+4)(不
return 0;
//检测要添加的 Q 是否符合要求
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料试荷试卷下卷问高总题中体2资2配,料置而试时且卷,可调需保控要障试在各验最类;大管对限路设度习备内题进来到行确位调保。整机在使组管其高路在中敷正资设常料过工试程况卷中下安,与全要过,加度并强工且看作尽护下可关都能于可地管以缩路正小高常故中工障资作高料;中试对资卷于料连继试接电卷管保破口护坏处进范理行围高整,中核或资对者料定对试值某卷,些弯审异扁核常度与高固校中定对资盒图料位纸试置,卷.编保工写护况复层进杂防行设腐自备跨动与接处装地理置线,高弯尤中曲其资半要料径避试标免卷高错调等误试,高方要中案求资,技料编术试写5交、卷重底电保要。气护设管设装备线备置4高敷、调动中设电试作资技气高,料术课中并3试、中件资且卷管包中料拒试路含调试绝验敷线试卷动方设槽技作案技、术,以术管来及架避系等免统多不启项必动方要方式高案,中;为资对解料整决试套高卷启中突动语然过文停程电机中气。高课因中件此资中,料管电试壁力卷薄高电、中气接资设口料备不试进严卷行等保调问护试题装工,置作合调并理试且利技进用术行管,过线要关敷求运设电行技力高术保中。护资线装料缆置试敷做卷设到技原准术则确指:灵导在活。分。对线对于盒于调处差试,动过当保程不护中同装高电置中压高资回中料路资试交料卷叉试技时卷术,调问应试题采技,用术作金是为属指调隔发试板电人进机员行一,隔变需开压要处器在理组事;在前同发掌一生握线内图槽部纸内 故资,障料强时、电,设回需备路要制须进造同行厂时外家切部出断电具习源高题高中电中资源资料,料试线试卷缆卷试敷切验设除报完从告毕而与,采相要用关进高技行中术检资资查料料和试,检卷并测主且处要了理保解。护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验设计方案
1、实验内容与目的(简单介绍实验内容,说明实验目的)
实验目的:要求在一个n*n的棋盘上放置n个皇后,要求放置的n个皇后不会互相吃掉;皇后棋子可以吃掉它所在的那一行、那一列,以及那两条对角线上的任何棋子。
实验内容:你的具体选择(要详细)
通过input.txt文件输入一个数字n,求出n皇后问题,并将结果输出到output.txt文件
——————————————————————————————————————2、实验准备工作(阐述解决问题所涉及的算法思想,至少要画一个算法流程图来说明)
本实验采用递归算法:
递归算法中,首先定义三个bool型变量,分别表示行,对角线,反对角线是否有皇后,若有,则用true表示出来。
用循环,依次求出满足要求的点,如果满足,则放置皇后,然后循环查找能放置下一个皇后的点。
当放置的皇后数目等于行列数时,就调用函数将结果输出。
——————————————————————————————————————二、实验步骤、测试与结果分析
1、源程序的设计(在此附上源程序(cpp文件)清单)
queen.h 文件:
#ifndef __QUEEN_H__
#define __QUEEN_H__
#include<iostream>
#include<fstream>
//文件流
using namespace std;
class queen
//定义一个queen类
{
private:
int n;
//需要解决的n皇后问题
bool *row;
//行是否有皇后
bool *diag;
//对角线是否有皇后
bool *backdiag;
//反对角线是否有皇后
int *x;
//皇后问题的解
void backtracking(int c);
//用于递归求解的函数
void output();
//文件输出函数
public:
queen();
//构造函数
virtual~queen();
//析构函数
void run()
//用于执行递归求解,并计算出所有皇后问题的解
{
backtracking(1);
}
};
queen::queen()
{
ifstream in("input.txt",ios::in);
if(!in)
//当打开失败时
{
cout<<"打开文件input.txt失败!"<<endl;
exit(1);
}
int num;
in>>num;
//再文本文件中读取一个数字num
n=num;
//令n=num
row=new bool[n+1];
//分配行所占空间
diag=new bool[2*n];
//分配对角线所占空间
backdiag=new bool[2*n];
//分配反对角线所占空间
x=new int[n+1];
//解所占空间
int i;
for(i=1;i<=n;i++) row[i]=false;
//表示所有行都没有放皇后
for(i=1;i<2*n;i++) diag[i]=false;
//所有对角线没有放皇后
for(i=1;i<2*n;i++) backdiag[i]=false;
//所有反对角线没有放皇后
in.close();
//关闭文件
}
void queen::backtracking(int c)
{
if(c>n) output();
//当放置的皇后数等于行数时,输出结果
else
{
for(int r=1;r<=n;r++)
//行循环
{
if(!row[r] && !diag[n-c+r] && !backdiag[r+c-1])
//当(r,c)所在行,对角线,反对角线都没有放置皇后时
{
row[r]=diag[n-c+r]=backdiag[r+c-1]=true;
//这点合符要求,在此处放置皇后
x[c]=r;
//解为(r,c)
backtracking(c+1);
//c加一,继续放置下一个皇后
row[r]=diag[n-c+r]=backdiag[r+c-1]=false;
//清空操作
}
}
}
}
void queen::output()
{
static int num=0;
//表示当前已经求得的解个数
ofstream outfile("output.txt",ios::app);
//不写ios::app默认是以ios::out打开,只能得到最后一个解。
if(!outfile)
{
cout<<"打开文件output.txt失败"<<endl;
exit(2);
}
outfile<<"第"<<++num<<"个解:";
outfile<<"("<<x[1];
for(int i=2;i<=n;i++) outfile<<","<<x[i];
outfile<<")"<<endl;
outfile.close();
}
queen::~queen()
{
delete []row;
delete []diag;
delete []backdiag;
delete []x;
}
#endif
#include"queen.h"
main.cpp 文件:
int main()
{
queen objqueen;
objqueen.run();
system("PAUSE");
return 0;
}
——————————————————————————————————————3、实验现象及结论(应用文字和程序运行的截图说明程序测试现象,并解释结果)
实验中,我采用的是文件夹输入输出,所以在运行过程中,dos窗口中不会出现数
据,但在这个时候,程序已经在input.txt中读取数据,将皇后问题计算出,并把结
果输出到output.txt中。
在input.txt中,输入任意一个数字,运行程序,即可在output.txt中得到相
应的结果:
当输入7时,共有40个解,结果截图如下:
当输入8时,共有92个解,部分截图如下:
当输入10时,部分解的截图如下:
——————————————————————————————————————4、实验总结(是否成功解决问题,总结实验中最有价值的内容,程序能够在哪些方面进
一步改善,自我评价成败得失)
试验中,我们按照从简单到复杂的方法,一步一个脚印编写代码,使得程序不易发生错误,并且容易更正,编写出来的程序代码简洁明朗,效率较高;
通过对例题的学习,我们最终将正确的代码编写出,并在不断地修改之下做到方便用户使用的要求;
编码的速度有一个从慢到快的过程,在本次试验中,我们的速度依然比较慢,这看出我们平时编码比较少,缺乏熟练度,并对算法了解不深入;
但是我们的代码看起来仍然有些凌乱,效率还没有带到真正的高效,每次运行都需要等待几秒钟。
再以后我们将通过练习基础功,简化程序代码,实现简单代码完善功能的理想。
在编辑过程中,开始我们编写出的程序能够通过编译,但不能通过文件输出结果,output.txt中始终都没有结果出现,通过反复的调试,仍然没有找到原因,因此请教了其他同学,在其他同学的帮助下,我们发现我们的错误在于没有在
ofstream outfile("output.txt",ios::app);
中输入ios::app,同时,我们的递归算法有一处写错了代码,这样的粗心导致无法得到结果。
