回溯法之N皇后问题(C语言)
回溯法解皇后问题

Ch1-绪论1. 回溯法解皇后问题#include "stdio.h"#include "math.h"#include "stdlib.h"void queen(int n){ int i,j,k,jt,*q;q=malloc(n*sizeof(int));for(i=0; i<n; i++) q[i]=0;i=0; jt=1;printf("\n");printf("%d queen problem\n",n);while(jt==1){ if (q[i]<n){ k=0;while((k<i)&&((q[k]-q[i])*(fabs(q[k]-q[i])-fabs(k-i)))!=0) k=k+1;if (k<i) q[i]=q[i]+1;else{ if (i==n-1){ for(j=0; j<n; j++)printf("%5d",q[j]+1);printf("\n");q[n-1]=q[n-1]+1;}else i=i+1;}}else{ q[i]=0; i=i-1;if (i<0){ printf("\n"); free(q); return; }q[i]=q[i]+1;}}}2. 简单二分法求方程实根(1)#include "stdio.h"#include "math.h"double root(a,b,eps,f)double a,b,eps,(*f)();{ double f0,f1,c;f0=(*f)(a);while (fabs(a-b)>=eps){ c=(a+b)/2; f1=(*f)(c);if (f1==0) return(c);if (f0*f1>0) a=c;else b=c;}c=(a+b)/2;return(c);}(2)#include "root.c"main(){ double a,b,eps,f();a=1; b=2; eps=0.000001;printf("x=%7.3f\n",root(a,b,eps,f));}double f(x)double x;{ double y;y=x+log(x)-2.2;return(y);}Ch2-矩阵与线性代数方程组(1)文件头:#include "math.h"#include "stdio.h"int maqr(m,n,a,q)int m,n;double a[],q[];{ int i,j,k,l,nn,p,jj;double u,alpha,w,t;if (m<n){ printf("fail\n"); return(0);}for (i=0; i<=m-1; i++)for (j=0; j<=m-1; j++){ l=i*m+j; q[l]=0.0;if (i==j) q[l]=1.0;}nn=n;if (m==n) nn=m-1;for (k=0; k<=nn-1; k++){ u=0.0; l=k*n+k;for (i=k; i<=m-1; i++){ w=fabs(a[i*n+k]);if (w>u) u=w;}alpha=0.0;for (i=k; i<=m-1; i++){ t=a[i*n+k]/u; alpha=alpha+t*t;}if (a[l]>0.0) u=-u;alpha=u*sqrt(alpha);if (fabs(alpha)+1.0==1.0){ printf("fail\n"); return(0);}u=sqrt(2.0*alpha*(alpha-a[l]));if ((u+1.0)!=1.0){ a[l]=(a[l]-alpha)/u;for (i=k+1; i<=m-1; i++){ p=i*n+k; a[p]=a[p]/u;}for (j=0; j<=m-1; j++){ t=0.0;文件尾:for (jj=k; jj<=m-1; jj++)t=t+a[jj*n+k]*q[jj*m+j];for (i=k; i<=m-1; i++){ p=i*m+j; q[p]=q[p]-2.0*t*a[i*n+k];}}for (j=k+1; j<=n-1; j++){ t=0.0;for (jj=k; jj<=m-1; jj++)t=t+a[jj*n+k]*a[jj*n+j];for (i=k; i<=m-1; i++){ p=i*n+j; a[p]=a[p]-2.0*t*a[i*n+k];}}a[l]=alpha;for (i=k+1; i<=m-1; i++)a[i*n+k]=0.0;}}for (i=0; i<=m-2; i++)for (j=i+1; j<=m-1;j++){ p=i*m+j; l=j*m+i;t=q[p]; q[p]=q[l]; q[l]=t;}return(1);}(2)#include "stdio.h"#include "maqr.c"main(){ int i,j;static double q[4][4],a[4][3]={ {1.0,1.0,-1.0}, {2.0,1.0,0.0},{1.0,-1.0,0.0},{-1.0,2.0,1.0}};i=maqr(4,3,a,q);if (i!=0){ printf("MAT Q IS:\n");for (i=0; i<=3; i++){ for (j=0; j<=3; j++)printf("%13.7e ",q[i][j]);printf("\n");}printf("\n");printf("MAT R IS:\n");for (i=0; i<=3; i++){ for (j=0; j<=2; j++)printf("%13.7e ",a[i][j]);printf("\n");}printf("\n");}}(3)文件头:#include "stdlib.h"#include "math.h"int muav(m,n,a,u,v,eps,ka)int m,n,ka;double eps,a[],u[],v[];{ int i,j,k,l,it,ll,kk,ix,iy,mm,nn,iz,m1,ks;double d,dd,t,sm,sm1,em1,sk,ek,b,c,shh,fg[2],cs[2]; double *s,*e,*w;void ppp();void sss();s=malloc(ka*sizeof(double));e=malloc(ka*sizeof(double));w=malloc(ka*sizeof(double));it=60; k=n;if (m-1<n) k=m-1;l=m;if (n-2<m) l=n-2;if (l<0) l=0;ll=k;if (l>k) ll=l;if (ll>=1){ for (kk=1; kk<=ll; kk++){ if (kk<=k){ d=0.0;for (i=kk; i<=m; i++){ ix=(i-1)*n+kk-1; d=d+a[ix]*a[ix];}s[kk-1]=sqrt(d);if (s[kk-1]!=0.0){ ix=(kk-1)*n+kk-1;if (a[ix]!=0.0){ s[kk-1]=fabs(s[kk-1]);if (a[ix]<0.0) s[kk-1]=-s[kk-1];}for (i=文件尾:{ int i,j,p,q;double d;if (m>=n) i=n;else i=m;for (j=1; j<=i-1; j++){ a[(j-1)*n+j-1]=s[j-1];a[(j-1)*n+j]=e[j-1];}a[(i-1)*n+i-1]=s[i-1];if (m<n) a[(i-1)*n+i]=e[i-1];for (i=1; i<=n-1; i++)for (j=i+1; j<=n; j++){ p=(i-1)*n+j-1; q=(j-1)*n+i-1;d=v[p]; v[p]=v[q]; v[q]=d;}return;}static void sss(fg,cs)double cs[2],fg[2];{ double r,d;if ((fabs(fg[0])+fabs(fg[1]))==0.0){ cs[0]=1.0; cs[1]=0.0; d=0.0;} else{ d=sqrt(fg[0]*fg[0]+fg[1]*fg[1]);if (fabs(fg[0])>fabs(fg[1])){ d=fabs(d);if (fg[0]<0.0) d=-d;}if (fabs(fg[1])>=fabs(fg[0])){ d=fabs(d);if (fg[1]<0.0) d=-d;}cs[0]=fg[0]/d; cs[1]=fg[1]/d;}r=1.0;if (fabs(fg[0])>fabs(fg[1])) r=cs[1];elseif (cs[0]!=0.0) r=1.0/cs[0];fg[0]=d; fg[1]=r;return;}#include "stdio.h"#include "cgauss.c"main(){ int i;static double ar[4][4]={ {1.0,3.0,2.0,13.0},{7.0,2.0,1.0,-2.0},{9.0,15.0,3.0,-2.0},{-2.0,-2.0,11.0,5.0}};static double ai[4][4]={ {3.0,-2.0,1.0,6.0},{-2.0,7.0,5.0,8.0},{9.0,-3.0,15.0,1.0},{-2.0,-2.0,7.0,6.0}}; static double br[4]={2.0,7.0,3.0,9.0};static double bi[4]={1.0,2.0,-2.0,3.0};if (cgauss(4,ar,ai,br,bi)!=0)for (i=0;i<=3;i++)printf("b(%d)=%13.7e +j %13.7e\n",i,br[i],bi[i]); }。
回溯法求解N皇后问题

① 如果xi+1= ai+1k不是集合Si+1的最后一个元素,则令xi+1= ai+ 1k+1,即选择Si+1的下一个元素作为解向量X的第i+1个分量;
② 如果xi+1= ai+1k是集合Si+1的最后一个元素,就回溯到X=(x1, x2, …, xi),选择Si的下一个元素作为解向量X的第i个分量,假 设xi= aik,如果aik不是集合Si的最后一个元素,则令xi= aik+1; 否则,就继续回溯到X=(x1, x2, …, xi-1);
global X(1:k); integer i,k;
i1
while i<k do
if X(i)=X(k) or ABS(X(i)-X(k))=ABS(i-k) then
return (false)
end if
ii+1 repeat return (true)
判断是否有其它的皇 后与之在同一列或同 一斜对角线上
HHIT
Algorithm
(1)如果X=(x1, x2, …, xi+1)是问题的最终解,则输出这个解。 如果问题只希望得到一个解,则结束搜索,否则继续搜索其
他解;
(2)如果X=(x1, x2, …, xi+1)是问题的部分解,则继续构造解 向量的下一个分量;
(3)如果X=(x1, x2, …, xi+1)既不是问题的部分解也不是问题 的最终解,则存在下面两种情况:
while k>0 do // 对所有的行,执行以下语句 //
X(k)X(k)+1 //移到下一列//
while X(k)<=n and Not PLACE(k) do //此处能放这个皇后吗//
X(k)X(k)+1 //不能放则转到下一列//
实验四回溯法求n皇后问题

return true;
}
void queue(intn)
{
inti,k;
for(i=1;i<=n;i++)
x[i]=0;
k=1;
while(k>=1)
{
x[k]=x[k]+1; //在下一列放置第k个皇后
while(x[k]<=n&&!place(k))
x[k]=x[k]+1;//搜索下一列
k=k+1;//放置下一个皇后
else
{
x[k]=0;//重置x[k],回溯
k=k-1;
}
}
}
void main()
{
intn;
printf("输入皇后个数n:\n");
scanf("%d",&n);
queue(n);
}
五、实验结果截图
六、实验总结
关于n皇后问题,看似复杂难懂,运行结果也很多,但是如果掌握了算法的要点,并且编写的准确无误,其实很简单明了的,而且在组实验的过程中会体会到很多乐趣,当然也有不懂得地方,需要请教别人,总之受益匪浅。
if(x[k]<=n&&k==n)//得到一个输出
{
for(i=1;i<=n;i++)
printf("%d ",x[i]);
printf("\n");
//return;//若return则只求出其中一种解,若不return则可以继续回溯,求出全部的可能的解
}
else if(x[k]<=n&&k<n)
n皇后问题递归算法c语言

n皇后问题递归算法c语言概述n皇后问题是一个经典的回溯算法问题,它要求在一个n×n的棋盘上放置n个皇后,使得它们互不攻击。
本文将使用递归算法来解决n皇后问题,并使用C语言进行实现。
问题描述在n×n的棋盘上放置n个皇后,使得它们不在同一行、同一列或同一斜线上。
其中,皇后的移动规则是可以横向、纵向、对角线方向上自由移动任意步数。
算法思路为了解决n皇后问题,我们可以采用递归的方式逐行放置皇后。
具体地,可以按照行优先的顺序,从第一行开始放置皇后,并逐行向下递归,直到放置了n个皇后,或者无法再放置皇后为止。
算法的关键在于如何判断当前位置是否可以放置皇后,即判断是否与已经放置的皇后位置冲突。
为了判断冲突,我们需要考虑以下几个方面:1.所有皇后不能在同一列:我们可以使用一个数组q ue en[]来记录每一行放置的皇后的列位置。
2.所有皇后不能在同一对角线上:我们可以使用两个数组up D ia g[]和d ow nD ia g[]来记录每一条对角线上是否已经存在皇后。
对于任意一个位置(i,j),它所在的主对角线上的元素满足i-j的值相等,次对角线上的元素满足i+j的值相等。
在放置皇后时,我们可以逐个尝试每一列,然后检查当前位置是否与已经放置的皇后位置冲突,如果冲突则继续尝试下一列,直到找到一个合适的位置。
然后,继续递归放置下一行的皇后,直到放置了n个皇后或者无法再放置为止。
伪代码定义一个全局整型数组q ue en[],用于记录每一行放置的皇后的列位置定义两个全局整型数组u pD ia g[]和do wn D ia g[],用于记录每一条对角线上是否已经存在皇后P r oc ed ur en Qu ee ns(r ow):i f ro w=n://找到一个解P r in tS ol ut io n()r e tu rnf o rc ol fr om0t on-1:i f Ca nP la ce Qu ee n(r o w,co l):P l ac eQ ue en(r ow,co l)n Q ue en s(ro w+1)R e mo ve Qu ee n(ro w,c o l)P r oc ed ur eC an Pl ace Q ue en(r ow,c ol):i f qu ee n[co l]!=-1:r e tu rn fa ls ei f up Di ag[r ow-c ol+n-1]!=-1o rd ow nDi a g[ro w+co l]!=-1:r e tu rn fa ls er e tu rn tr ueP r oc ed ur eP la ce Que e n(ro w,co l):q u ee n[co l]=r owu p Di ag[r ow-c ol+n-1]=1d o wn Di ag[r ow+c ol]=1q u ee n[co l]=-1u p Di ag[r ow-c ol+n-1]=-1d o wn Di ag[r ow+c ol]=-1P r oc ed u r eP ri nt Sol u ti on():f o rr ow fr om0t on-1:f o rc ol fr om0t on-1:i f qu ee n[co l]=r ow:p r in t"Q"e l se:p r in t"*"p r in tn ew li nep r in tn ew li neC语言实现下面是使用C语言实现的n皇后问题递归算法的代码示例:#i nc lu de<s td io.h>#d ef in eN8i n tq ue en[N];//记录每一行放置的皇后的列位置i n tu pD ia g[2*N-1];//记录每一条对角线上是否已经存在皇后i n td ow nD ia g[2*N-1];//记录每一条对角线上是否已经存在皇后v o id nQ ue en s(in tro w);i n tc an Pl ac eQ ue en(i nt ro w,in tc ol);v o id pl ac eQ ue en(in t ro w,in tc ol);v o id pr in tS ol ut ion();i n tm ai n(){f o r(in ti=0;i<N;i++){q u ee n[i]=-1;}f o r(in ti=0;i<2*N-1;i++){u p Di ag[i]=-1;d o wn Di ag[i]=-1;}n Q ue en s(0);r e tu rn0;}v o id nQ ue en s(in tro w){i f(r ow==N){p r in tS ol ut io n();r e tu rn;}f o r(in tc ol=0;c ol<N;c ol++){ i f(c an Pl ac eQ ue en(r ow,c ol)){ p l ac eQ ue en(r ow,co l);n Q ue en s(ro w+1);r e mo ve Qu ee n(ro w,c o l);}}}i n tc an Pl ac eQ ue en(i nt r o w,in tc ol){i f(q ue en[c ol]!=-1){r e tu rn0;}i f(u pD ia g[ro w-col+N-1]!=-1||do wnD i ag[r ow+c ol]!=-1){ r e tu rn0;}r e tu rn1;}v o id pl ac eQ ue en(in t ro w,in tc ol){q u ee n[co l]=r ow;u p Di ag[r ow-c ol+N-1]=1;d o wn Di ag[r ow+c ol]=1;}v o id re mo ve Qu ee n(i n tr ow,i nt co l){q u ee n[co l]=-1;u p Di ag[r ow-c ol+N-1]=-1;d o wn Di ag[r ow+c ol]=-1;}v o id pr in tS ol ut ion(){f o r(in tr ow=0;r ow<N;r ow++){f o r(in tc ol=0;c ol<N;c ol++){i f(q ue en[c ol]==ro w){p r in tf("Q");}e ls e{p r in tf("*");}}p r in tf("\n");}p r in tf("\n");}总结本文使用C语言实现了n皇后问题的递归算法。
回溯法求N皇后问题

Tree-回溯法求N皇后问题#include <stdio.h>#include <malloc.h>#define N 4 //N皇后typedef int Chessboard[N + 1][N + 1]; //第0号位置不用bool check(Chessboard cb, int i, int j) { //看棋盘cb是否满足合法布局int h, k;int m = i + j, n = i - j;for(h=1; h<i; h++) {if(cb[h][j] == 1 && h != i) return false; //检查第j列if(m-h<=N && cb[h][m-h] == 1 && h != i) return false; //检查斜的,m-h<=N是为了保证不越界if(h-n<=N && cb[h][h-n] == 1 && h != i) return false; //检查斜的,h-n<=N是为了保证不越界}for(k=1; k<N; k++)/*检查第i行的*/ if(cb[i][k] == 1 && k != j) return false;return true;}void printfChessboard(Chessboard cb) {//打印棋盘int i, j;for(i=1; i<=N; i++) {for(j=1; j<=N; j++) printf("%d ", cb[i][j]);printf("\n");}printf("\n");}/*进入本函数时,在n*n棋盘前n-1行已放置了互不攻击的i-1个棋子。
现从第i行起继续为后续棋子选择合适位置。
回溯典型题目——N皇后问题剖析
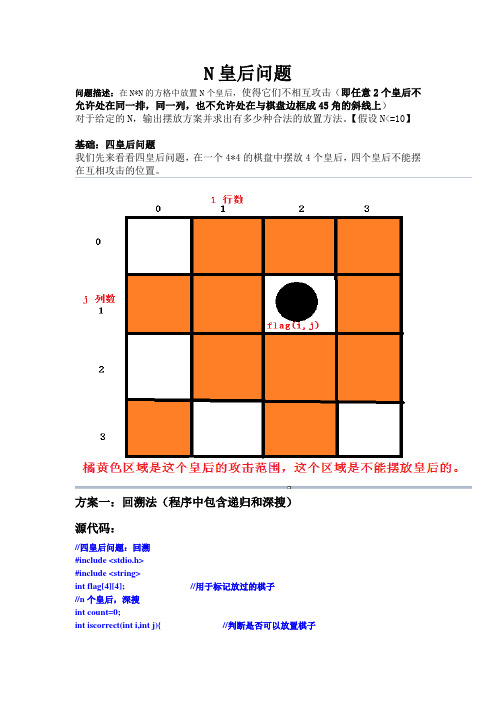
N皇后问题问题描述:在N*N的方格中放置N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上)对于给定的N,输出摆放方案并求出有多少种合法的放置方法。
【假设N<=10】基础:四皇后问题我们先来看看四皇后问题,在一个4*4的棋盘中摆放4个皇后,四个皇后不能摆在互相攻击的位置。
方案一:回溯法(程序中包含递归和深搜)源代码://四皇后问题:回溯#include <stdio.h>#include <string>int flag[4][4]; //用于标记放过的棋子//n个皇后,深搜int count=0;int iscorrect(int i,int j){ //判断是否可以放置棋子int a,b;for(a=i,b=0;b<4;b++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=0,b=j;a<4;a++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=i-1,b=j-1;a>=0&&b>=0;a--,b--){ //左上方if(flag[a][b]==1)return 0;}for(a=i-1,b=j+1;a>=0&&b<=3;a--,b++){ //左下方if(flag[a][b]==1)return 0;}for(a=i+1,b=j-1;a<=3&&b>=0;a++,b--){ //右上方if(flag[a][b]==1)return 0;}for(a=i+1,b=j+1;a<=3&&b<=3;a++,b++){ //判断右下方if(flag[a][b]==1)return 0;}return 1;}void DFSQ(int i){int m,n;int j;//i代表行数,j代表列数if(i==4){ //因为棋盘是(n-1)*(n-1)模式的,而i是行,当棋盘到第四行的时候,表明已//经完成0~3的所有排布已经完成for(m=0;m<4;m++){for(n=0;n<4;n++){printf("%d ",flag[m][n]);}printf("\n");}count++;printf("\n");return; //不要忘记这个}else{for(j=0;j<4;j++){if(iscorrect(i,j)){ //如果可以放置棋子flag[i][j]=1; //标记flag[i][j]DFSQ(i+1); //递归调用flag[i][j]=0; //消除标记}}}}int main(){memset(flag,0,sizeof(flag));DFSQ(0);printf("count=%d\n",count);return 0;}其实从四皇后问题拓展到n皇后问题是非常简单的事情,方案一进阶到N皇后的源代码:N皇后其实只要把其中的4改成N就行了:源代码:#include <stdio.h>#include <string>int flag[10][10]; //用于标记放过的棋子int number; //表示棋子个数//n个皇后,深搜int count=0;int iscorrect(int i,int j){ //判断是否可以放置棋子int a,b;for(a=i,b=0;b<number;b++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=0,b=j;a<number;a++){if(flag[a][b]==1) //说明在同一行有棋子return 0;}for(a=i-1,b=j-1;a>=0&&b>=0;a--,b--){ //左上方if(flag[a][b]==1)return 0;}for(a=i-1,b=j+1;a>=0&&b<=number-1;a--,b++){ //左下方if(flag[a][b]==1)return 0;}for(a=i+1,b=j-1;a<=number-1&&b>=0;a++,b--){ //右上方if(flag[a][b]==1)return 0;}for(a=i+1,b=j+1;a<=number-1&&b<=number-1;a++,b++){ //判断右下方if(flag[a][b]==1)return 0;}return 1;}void DFSQ(int i){int m,n;int j;//i代表行数,j代表列数if(i==number){ //因为棋盘是(n-1)*(n-1)模式的,而i是行,当棋盘到第四行的时候,表明已经完成0~number-1的所有排布已经完成for(m=0;m<number;m++){for(n=0;n<number;n++){printf("%d ",flag[m][n]);}printf("\n");}count++;printf("\n");return; //不要忘记这个}else{for(j=0;j<number;j++){if(iscorrect(i,j)){ //如果可以放置棋子flag[i][j]=1; //标记flag[i][j]DFSQ(i+1); //递归调用flag[i][j]=0; //消除标记}}}}int main(){scanf("%d",&number);memset(flag,0,sizeof(flag));DFSQ(0);printf("count=%d\n",count);return 0;}。
回溯法解决N皇后问题C语言
回溯法解决N皇后问题C语⾔问题描述:⼋皇后问题是⼀个以国际象棋为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置⼋个皇后,使得任何⼀个皇后都⽆法直接吃掉其他的皇后?为了达到此⽬的,任两个皇后都不能处于同⼀条横⾏、纵⾏或斜线上。
回溯法:回溯法⼜称试探法。
回溯法的基本做法是深度优先搜索。
即从⼀条路往前⾛,能进则进,不能进则退回来,换⼀条路再试。
源代码:#include<stdio.h>#include<math.h>int x[9]={0};bool PLACE(int k)//检测第k个皇后能否放进棋盘{int i=1;while(i<k){if(x[i]==x[k]||fabs(x[i]-x[k])==fabs(i-k))return false;i++;}return true;}void NQUEENS(int n){int i,k=1; //k为当前⾏号x[1]=0;//x[k]为第k⾏皇后所放的列号while(k>0){x[k]++;while(x[k]<=n&&!PLACE(k))//该⾏不符合,则放⼊下⼀⾏x[k]++;if(x[k]<=n){if(k==n)//输出x[]{for(i=1;i<=n;i++)printf("x[%d]:%d ",i,x[i]);printf("\n");}else//判断下⼀⾏{k++; x[k]=0;}}else k--;//没找到,则回溯}return ;}int main(){NQUEENS(8);return0;}。
C语言回溯法解八皇后问题(八皇后算法)

C语⾔回溯法解⼋皇后问题(⼋皇后算法)⼋皇后问题(N皇后问题)的回溯法求解⼀、问题描述在⼀个国际象棋棋盘上放置⼋个皇后,使得任何两个皇后之间不相互攻击,求出所有的布棋⽅法,并推⼴到N皇后情况。
⼆、参考资料啥⽂字都不⽤看,B站上有个⾮常详细的动画视频解说,上链接三、源代码#include<iostream>#include<vector>#include<string>using namespace std;void put_queen(int x, int y, vector<vector<int>>&attack){//实现在(x,y)放置皇后,对attack数组更新,xy表⽰放置皇后的坐标,attack表⽰是否可以放置皇后//⽅向数组,⽅便后⾯对8个⽅向进⾏标记static const int dx[] = { -1,-1,-1,0,0,1,1,1 };static const int dy[] = { -1,0,1,-1,1,-1,0,1 };attack[x][y] = 1;//将皇后位置标记为1//通过两层for循环,将该皇后可能攻击到的位置标记for (int i = 1; i < attack.size(); i++)//从皇后位置向1到n-1个距离延伸{for (int j = 0; j < 8; j++)//遍历8个⽅向{int nx = x + i * dx[j];//⽣成的新位置⾏int ny = y + i * dy[j];//⽣成的新位置列//在棋盘范围内if (nx >= 0 && nx < attack.size() && ny >= 0 && ny < attack.size())attack[nx][ny] = 1;//标记为1}}}//回溯算法//k表⽰当前处理的⾏//n表⽰n皇后问题//queen存储皇后的位置//attack标记皇后的攻击范围//solve存储N皇后的全部解法void backtrack(int k, int n, vector<string>& queen,vector<vector<int>>& attack,vector<vector<string>>& solve){if (k == n)//找到⼀组解{solve.push_back(queen);//将结果queen存储⾄solvereturn;}//遍历0⾄n-1列,在循环中,回溯试探皇后可放置的位置for (int i = 0; i < n; i++){if (attack[k][i] == 0)//判断当前k⾏第i列是否可以放置皇后{vector<vector<int>> tmp = attack;//备份attack数组queen[k][i] = 'Q';//标记该位置为Qput_queen(k, i, attack);//更新attack数组backtrack(k + 1, n, queen, attack, solve);//递归试探k+1⾏的皇后的位置attack = tmp;//恢复attack数组queen[k][i] = '.';//恢复queen数组}}}vector<vector<string>>solveNQueens(int n){//string存储具体的摆放位置,<vector<string>>存放⼀种解法,⼆维vector存放全部解法vector<vector<string>>solve;//存储最后结果vector<vector<int>>attack;//标记皇后的攻击位vector<string>queen;//保存皇后位置//使⽤循环初始化attack和queen数组for (int i = 0; i < n; i++){attack.push_back((vector<int>()));for (int j = 0; j < n; j++){attack[i].push_back(0);}queen.push_back("");queen[i].append(n, '.');}backtrack(0, n, queen, attack, solve);return solve;//返回结果数组}int main(){//int num;//cin >> num;//输⼊皇后数初始化attack数组//vector<vector<int>> attack(num,vector<int>(num, 0));初始化queen数组//string s;//for (int i = 0; i < num; i++)s += '.';//vector<string> queen(num, s);int n;cin >> n;vector<vector<string>>result;result = solveNQueens(n);cout << n << "皇后共有" << result.size() << "种解法" << endl;for (int i = 0; i < result.size(); i++){cout << "解法" << i + 1 << ":" << endl;for (int j = 0; j < result[i].size(); j++){cout << result[i][j] << endl;}cout << endl;}system("pause");return 0;}四、测试结果四皇后⼋皇后到此这篇关于C语⾔回溯法解⼋皇后问题的⽂章就介绍到这了。
n皇后问题 (回溯法) 原创

for (int i=1;i<=n;i++) {//搜索子结点
x[t]=i;//进入第i个子结点
பைடு நூலகம்if (Place(t)) Backtrack(t+1);}}
int nQueen(int n){Queen X;
//初始化X
X.n=n;
X.sum=0;
int *p=new int [n+1];
};
bool Queen:
:Place(int k){for (int j=1;j<k;j++)
if ((abs(k-j)==abs(x[j]-x[k]))||(x[j]==x[k])) return false;return true;}void Queen:
:Backtrack(int t){if (t>n) sum++;//达到叶结点
for(int i=0;i<=n;i++)
p[i]=0;
X.x=p;
X.Backtrack
(1);//对整个解空间回溯搜索
delete []p;
return X.sum;}运行结果:
•隐约束:
1)不同列:
xixj
2)不处于同一正、反对角线:
|i-j||xi-xj|
代码实现:
class Queen{friend int nQueen(int)
private:
bool Place(int k);
void Backtrack(int t);
int n,//皇后个数
*n;//当前解
long sum;//当前已找到的可行方案数
n
皇后问题 C语言编程

}
if(Q[i][j]==1&&i!=s)
return 0;
for(i=s-1,j=t-1;i>=0&&j>=0;i--,j--) //左上方检察
if(Q[i][j]==1)
return 0;
for(i=s+1,j=t+1;i<N&&j<N;i++,j++) //右下方检察
if(Q[i][j]==1)
{
if(j==N)
{
printf("\nthe %dth:\n",++t);
for(int k=0;k<N;k++)
{
for(int i=0;i<N;i++)
printf("%3d",Q[k][i]);
putchar('\n');
}
}
else
{
for(int n=0;n<N;n++)
if(inspect(n,j,Q))
/*回溯法解决《n皇后问题》C语言算法*/
#include<stdio.h>
#define N 4 //皇后的个数
int t=0; //表示第几种皇后放法
int inspect(int s,int t,int Q[][N]);
void Queen(int j,int Q[][N]);
void main()
{
int Q[N][N]={0};
Queen(0,Q);
}
int inspect(int s,int t,int Q[][N])//检察是否满足要求
用回溯法求解n皇后问题

c程序实现
分析问题
//求解的递归函数 void Queen(int i,int n) { if(i>n) Output(); else { for(int j=1;j<=n;++j) // j代表列值 { int k=1; x[i]=j;//重新换一个列值,这里就是体现回溯的地方 while(k<i) { if((x[k]-x[i])*(abs(x[k]-x[i])-abs(k-i))!=0)
分析问题
问题分析
如何保证任何两个皇后不再一 条斜线上?设两个皇后q1和q2放 在(i,j)和(k,l)位置上,如 果q1和q2在斜率为-1的对角线上, 那么i - j = k - l成立,如果在斜率 为1的对角线上,那么 i + j = k + l成立,由此可知只要 | i - k | ≠ | j - l |成立,q1和q2就不 再同一条斜线上。 |i-k|≠|j-l|
分析问题
2.确定解空间 用完全n叉树表示解空间,现在以n=4为例:
分析问题
问题分析
1
1
2 1 34
3 1 24
4 123
2 34
× ×× ×34 24 23 ×14 13 × 34 ×
√
24 14 12 23 13 12
√
4 3 4 2 3 2 4 3 4 1 3 1 4 2 41 21 3 2 31 2 1
回溯法的基本思想
回溯法的基本思想是在问题的解空间树上按 深度优先搜索策略,从根节点出发搜索整个解 空间。搜索过程中,每到达一个结点时,则判 断该结点为根的子树是否含有问题的解,如果 可以确定该子树中不含有问题的解,则放弃对 该子树的搜索,逐层向其祖先节点回溯。否则, 进入该子树。
回溯法之N皇后问题(C语言)

//回溯法之N皇后问题当N>10,就有点抽了~~/*结果前total行每行均为一种放法,表示第i行摆放皇后的列位置,第total+1行,输出total*/#include<stdio.h>#include<stdlib.h>int n,stack[100]; //存当前路径int total; //路径数void make(int l) //递归搜索以stack[l]为初结点的所有路径{int i,j; //子结点个数if (l==n+1){total=total+1; //路径数+1for(i=1;i<=n;i++)printf("%-3d",stack[i]); //输出第i行皇后的列位置stack[i] printf("\n");exit; //回溯(若试题仅要求一条路径,则exit改为halt即可)}for (i=1;i<=n;i++){stack[l]=i; //算符i作用于生成stack[l-1]产生子状态stack[l];if (!att(l,i)) make(l+1);} //再无算符可用,回溯}int att(int l,int i){int k;for (k=1;k<l;k++)if (abs(l-k)==abs(stack[k]-i)||i==stack[k]) return 1;return 0;}int main(){printf("N=");scanf("%d",&n);total=0; //路径数初始化为0make(1); //从结点1出发,递归搜索所有的路径printf("%d\n",total);system("pause");return 0;}由回溯法的算法流程可以看出,除非边界条件设置不当而导致死循环外,回溯法一般是不会产生内存溢出的。
回溯法解决n皇后问题

n 皇 后 问 题N 皇后问题,是一个古老而着名的问题,是回溯算法的典型例题:在N*N 格的格子上摆放N 个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法? 1、定义问题的解空间首先以八皇后为例,可以用一棵树表示8皇后问题的解空间。
由于8皇后问题的解空间为8!种排列,因此我们将要构造的这棵树实际上是一棵排列树。
2、确定解空间树的结构给棋盘上的行和列从1到8编号,同时也给皇后从1到8编号。
由于每一个皇后应放在不同的行上,不失一般性,假设皇后i 放在第i 行上,因此8皇后问题可以表示成8元组(x 1, x 2, …, x 8), 其中xi (i =1, 2, …, 8)表示皇后i 所放置的列号。
这种表示法的显式约束条件是S i ={1, 2, 3, 4, 5, 6, 7, 8},i =1, 2, …, 8。
在这种情况下, 解空间为88个8元组组成,而隐式约束条件是没有两个xi 相同(即所有皇后必须在不同列上),且满足不存在两个皇后在同一条对角线上。
加上隐式约束条件,问题的解空间可进一步减小。
此时,解空间大小为8!,因为所有解都是8元组的一个置换。
图5-7表示了8皇后问题的一个解。
图5-7 8皇后问题的一个解为了简单起见,图5-8只给出了n =4时问题的一种可能树结构。
QQQQQQQQ8765432112345678图5-8 4皇后问题解空间的树结构在实际中,并不需要生成问题的整个状态空间。
通过使用限界函数来删除那些还没有生成其所有子结点的活结点。
如果用(x1,x2,…,x i)表示到当前E结点的路径,那么xi+1就是这样的一些结点,它使得(x1,x2,…,x i,x i+1)没有两个皇后处于相互攻击的棋盘格局。
在4皇后问题中,惟一开始结点为根结点1,路径为( )。
开始结点既是一个活结点,又是一个E结点,它按照深度优先的方式生成一个新结点2,此时路径为(1),这个新结点2变成一个活结点和新的E结点,原来的E结点1仍然是一个活结点。
回溯法实验(n皇后问题)(迭代法)

算法分析与设计实验报告第三次附加实验附录:完整代码(回溯法)//回溯算法递归回溯n皇后问题#include<iostream>#include<time.h>#include<iomanip>#include"math.h"using namespace std;class Queen{friend int nQueen(int); //定义友元函数,可以访问私有数据private:bool Place(int k); //判断该位置是否可用的函数void Backtrack(int t); //定义回溯函数int n; //皇后个数int *x; //当前解long sum; //当前已找到的可行方案数};int main(){int m,n;for(int i=1;i<=1;i++){cout<<"请输入皇后的个数:"; //输入皇后个数cin>>n;cout<<"皇后问题的解为:"<<endl;clock_t start,end,over; //计算程序运行时间的算法start=clock();end=clock();over=end-start;start=clock();m=nQueen(n); //调用求解的函数cout<<n<<"皇后问题共有";cout<<m<<"个不同的解!"<<endl; //输出结果end=clock();printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间cout<<endl;}system("pause");return 0;}bool Queen::Place(int k)//传入行号{for(int j=1;j<k;j++){if((abs(k-j)==abs(x[j]-x[k]))||(x[j]==x[k]))//如果两个在同一斜线或者在同一列上,说明冲突,该位置不可用{return false;}}return true;}void Queen::Backtrack(int t){if(t>n){sum++;/*for(int i=1;i<=n;i++) //输出皇后排列的解{cout<<x[i]<<" ";}cout<<endl;*/}else{//回溯探索第i行的每一列是否有元素满足要求for(int i=1;i<=n;i++){x[t]=i;if(Place(t)){Backtrack(t+1);}}}}int nQueen(int n){Queen X; //定义Queen类的对象X//初始化XX.n=n;X.sum=0;int *p=new int[n+1]; //动态分配for(int i=0;i<=n;i++) //初始化数组{p[i]=0;}X.x=p;X.Backtrack(1);delete[] p;return X.sum;//输出解的个数}完整代码(回溯法)//回溯算法迭代回溯n皇后问题#include<iostream>#include<time.h>#include<iomanip>#include"math.h"using namespace std;class Queen{friend int nQueen(int); //定义友元函数private:bool Place(int k); //定义位置是否可用的判断函数void Backtrack(void); //定义回溯函数int n; // 皇后个数int *x; // 当前解long sum; // 当前已找到的可行方案数};int main(){int n,m;for(int i=1;i<=1;i++){cout<<"请输入皇后的个数:";cin>>n;cout<<n<<"皇后问题的解为:"<<endl;clock_t start,end,over; //计算程序运行时间的算法start=clock();end=clock();over=end-start;start=clock();m=nQueen(n); //调用求解皇后问题的函数cout<<n<<"皇后问题共有";cout<<m<<"个不同的解!"<<endl;end=clock();printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间cout<<endl;}system("pause");return 0;}bool Queen::Place(int k){for (int j=1;j<k;j++){if ((abs(k-j)==abs(x[j]-x[k]))||(x[j]==x[k])) //如果两个皇后在同一斜线或者在同一列上,说明冲突,该位置不可用{return false;}}return true;}void Queen::Backtrack() //迭代法实现回溯函数{x[1] = 0;int k = 1;while(k>0){x[k] += 1; //先将皇后放在第一列的位置上while((x[k]<=n)&&!(Place(k))) //寻找能够放置皇后的位置{x[k] += 1;}if(x[k]<=n) //找到位置{if(k == n) //如果寻找结束输出结果{/*for (int i=1;i<=n;i++){cout<<x[i]<<" ";}cout<<endl; */sum++;}else//没有结束则找下一行{k++;x[k]=0;}}else//没有找到合适的位置则回溯{ k--; }}}int nQueen(int n){Queen X; //定义Queen类的对象X//初始化XX.n=n;X.sum=0;int *p=new int[n+1];for(int i=0;i<=n;i++){p[i]=0;}X.x=p;X.Backtrack();delete []p;return X.sum; //返回不同解的个数}。
回溯法求解N皇后问题

算法的实现
• 假设回溯法要找出所有的答案结点 。 • 设(x1,x2,…,xi-1)是状态空间树中由根到一个结 点的路径,而T(x1,…xi-1)是下述所有结点xi的 集合,它使得对于每一个xi,(x1,x2,…,xi)是由 根到一个结点xi的路径;假定还存在着一些限 界函数Bi,如果路径(x1,x2,…,xi)不可能延伸到 一个答案结点,则Bi(x1,x2,…,xi)取假值,否则 取真值。 • 于是解向量X(1:n)中的第i个分量,就是那些 选自集合T (x1,x2,…,xi-1)且使Bi为真的xi
HHIT
算法8.5:n-皇后问题的解
Algorithm
Procedure NQUEENS(n) //此过程使用回溯法求出一个n*n棋盘上放置n个皇后,使其不能互相攻 击的所有可能位置// integer k,n,X(1:n) X(1)0 ; k1 // k是当前行;X(k)是当前列 // while k>0 do // 对所有的行,执行以下语句 // X(k)X(k)+1 //移到下一列// while X(k)<=n and Not PLACE(k) do //此处能放这个皇后吗// X(k)X(k)+1 //不能放则转到下一列// repeat if X(k)<=n then //找到一个位置// if k=n then print (X) //是一个完整的解则打印这个数组// else kk+1;X(k)0 //否则转到下一行// end if else kk-1 //回溯// end if repeat End NQUEENS
HHIT
Algorithm
显然,棋盘的每一行上可以而且必须摆放一个皇后, 所以,n皇后问题的可能解用一个n元向量X=(x1, x2, …, xn) 表示,其中,1≤i≤n并且1≤xi≤n,即第i个皇后放在第i行第 xi列上。 由于两个皇后不能位于同一列上,所以,解向量X必 须满足约束条件: xi≠xj (式8.1)
n皇后问题解法总数 规律

n皇后问题解法总数规律
n皇后问题是指在一个n*n的棋盘上放置n个皇后,使任意两个皇后都不能相互攻击。
n皇后问题的解法总数可以用以下公式表示:C_{n,n-2}
其中,C是组合数,表示从n个元素中选择n-2个元素的组合数。
这个公式可以用以下方式推导:
假设我们已经将n-1个皇后放在了棋盘上,并且它们之间不会相互攻击。
那么,第n个皇后可以放在棋盘上的任何空位上,而不会与其他皇后相互攻击。
因此,第n个皇后的摆放方式有n种。
因此,n皇后问题的解法总数就是n-1个皇后的摆放方式总数乘以n,即:(n-1)C_{n-1}*n=C_{n,n-2}
●例如,2皇后问题的解法总数是:C_{2,0}=1
●3皇后问题的解法总数是:C_{3,1}=3
●4皇后问题的解法总数是:C_{4,2}=7
●5皇后问题的解法总数是:C_{5,3}=31
可以看到,n皇后问题的解法总数随着n的增加而呈指数增长。
回溯算法解决N皇后问题实验及其代码

实验报告4回溯算法实验4回溯算法解决N皇后问题一、实验目的1)掌握回溯算法的实现原理,生成树的建立以及限界函数的实现;2)利用回溯算法解决N皇后问题;二、实验内容回溯算法解决N皇后问题。
三、算法设计1)编写限界函数bool PLACE(int k,int x[]),用以确定在k列上能否放置皇后;2)编写void NQUEENS(int n)函数用以摆放N个皇后;3)编写主函数,控制输入的皇后数目;4)改进和检验程序。
四、程序代码//回溯算法解决N皇后问题的c++程序#include<math.h>#include<iostream>using namespace std;int count=0; //皇后摆放的可能性bool PLACE(int k,int x[]);//限界函数void NQUEENS(int n);//摆放皇后int main(){}int queen;cout<<"先生(女士)请您输入皇后的总数,谢谢!:"<<endl;cin>>queen;NQUEENS(queen);cout<<"所有可能均摆放完毕,谢谢操作"<<endl;return 0;void NQUEENS(int n){/*此过程使用回溯算法求出在一个n*n棋盘上放置n个皇后,使其即不同行,也不同列,也不在同一斜角线上*/int k, *x=new int[n];//存放皇后所在的行与列x[0]=0;k=0;while (k>=0&&k<n){ //对所有的行执行以下语句x[k]=x[k]+1; //移到下一列while(x[k]<=n&&(!PLACE(k,x))){ //此处能放置一个皇后吗?}if( x[k]<=n ) { //找到一个位置if( k==n-1 ){ //是一个完整的解吗cout<<"第"<<++count<<"排法是:"<<endl;for(int i=0;i<n;i++)//打印皇后的排列{}cout<<"\n";for (int j=0;j<n;j++){}cout<<"\n";if (x[i] == j+1){}else{}cout<<". ";cout<<"*";x[k]=x[k]+1; //移到下一列}}}}else { k=k+1; x[k]=0;} //移向下一行else k=k-1; //回溯bool PLACE(int k,int x[]){/*如果一个皇后能放在第k行和x(k)列,返回ture;否则返回false。
n皇后问题的随机解法代码实现

n皇后问题的随机解法实验要求:运用随机算法和回溯法对皇后问题进行求解。
先用随机算法预先对一部分皇后随机出其位置,对剩余的皇后,用回溯法求才出合理的位置。
实验步骤:1.定义初始标记。
int *s=new int[n+1]; 用随机算法求出一部分皇后的位置时,用s进行标记,s[i]=1表示第i个皇后的位置已经确定。
Int *x=new int[n+1]; x[i]表示第i个皇后的位置2.验证皇后的位置是否可行函数(利用标记x),函数代码如下bool place(int x[],int k,int n){int i;for(i=1;i<=n;i++)if(x[i]!=0&&i!=k)if(x[i]==x[k]||abs(x[i]-x[k])==abs(i-k))return false;return true;}3.随机算法过程。
在用户输入皇后个数后,用户可自定义那些皇后先进行定位,也可以停止随机过程,进入到回溯过程。
4.回溯法,(这时要考虑一部分的皇后已确定位置,利用s标记)5.用print函数输出可行的皇后位置图。
代码实现:#include <iostream>#include <ctime>#include <cstdlib>#include "math.h"using namespace std;bool place(int x[],int k,int n) //判别皇后位置是否可行{int i;for(i=1;i<=n;i++)if(x[i]!=0&&i!=k)if(x[i]==x[k]||abs(x[i]-x[k])==abs(i-k))return false;return true;}void print(int x[],int n) //以矩阵的形式输出皇后的位置图{int i,j;int **xx=new int *[n+1];for(i=1;i<=n;i++)xx[i]=new int[n+1];for(i=1;i<=n;i++)for(j=1;j<=n;j++){xx[i][j]=0;if(j==x[i])xx[i][j]=1;}for(i=1;i<=n;i++){cout<<'\n';for(j=1;j<=n;j++){cout<<xx[i][j]<<" ";}}cout<<'\n';}/*****************************************************************************/ void queen(int n,int x[],int s[]) //回溯法过程{bool T=true;int i,k=1;for(i=1;i<=n;i++)if(s[i]==0) break;k=i;while(k>=i){x[k]++;while(x[k]<=n){if(place(x,k,n))if(k==n){print(x,n);T=false;break;x[k]++;}else{do{k++;}while(s[k]==1);x[k]=1;}else x[k]++;}if(T==false)break;x[k]=0;do{k--;}while(s[k]==1);}if(k<i)cout<<"回溯法后找不到可行的皇后位置";}/****************************************************************************** *********/int main(){int n,n0,i; //n0 是每次皇后定位的随机次数cout<<"请输入皇后的数目:";cin>>n;cout<<"皇后数目为"<<n<<'\n'<<'\n';int *x=new int[n+1];for(i=1;i<=n;i++)x[i]=0;int *s=new int[n+1];for(i=1;i<=n;i++)s[i]=0; //s为随机时固定的皇后标记,当其值为1时表示为改皇后已固定位置,在回溯法在要相应跳过//随机过程cout<<"随机过程:"<<'\n';int k=1;int r;bool T;while(k) //是否结束随机过程,当输入k值为0时停止随机法{cout<<"请输入随机第几个皇后:";cin>>k;n0=1;while(n0<50){srand(time(0)+n0);r=rand()%n+1; //随机产生1到n的数x[k]=r;if(place(x,k,n)) //判断随机的位置时否可行{cout<<" 找到第"<<k<<"个皇后的位置为:"<<" "<<r<<'\n';s[k]=1; //可行,讲s[i]的值设为1T=true;for(i=1;i<=n;i++)if(s[i]!=1) T=false;if(T)print(x,n); //找到可行的解break;}n0++;}if(n0==50){x[k]=0;cout<<"找不到第"<<k<<"个皇后的位置";}cout<<"是否继续随机,输入0,停止随机开始回溯过程,输入1,继续:"<<" ";cin>>k;cout<<'\n'<<'\n';if(k==0)break;}cout<<'\n';cout<<"以上为随机过程,看看现在皇后的排列情况"<<'\n';print(x,n);cout<<'\n';//以上为随机过程cout<<"回溯过程及回溯法后皇后的排列情况:"<<'\n';queen(n,x,s);//回溯法解决后面的问题delete x;return 0;}实验结果:1.一直随机法到所有皇后都定好位置,不用回溯法,取皇后个数为5.随机过程:回溯过程:无输出皇后位置图:2.随机一部分皇后。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
//回溯法之N皇后问题当N>10,就有点抽了~~
/*结果前total行每行均为一种放法,表示第i行摆放皇后的列位置,第total+1行,输出total*/
#include<stdio.h>
#include<stdlib.h>
int n,stack[100]; //存当前路径
int total; //路径数
void make(int l) //递归搜索以stack[l]为初结点的所有路径
{
int i,j; //子结点个数
if (l==n+1)
{
total=total+1; //路径数+1
for(i=1;i<=n;i++)
printf("%-3d",stack[i]); //输出第i行皇后的列位置stack[i] printf("\n");
exit; //回溯(若试题仅要求一条路径,则exit改为halt即可)}
for (i=1;i<=n;i++)
{
stack[l]=i; //算符i作用于生成stack[l-1]产生子状态stack[l];
if (!att(l,i)) make(l+1);
} //再无算符可用,回溯
}
int att(int l,int i)
{
int k;
for (k=1;k<l;k++)
if (abs(l-k)==abs(stack[k]-i)||i==stack[k]) return 1;
return 0;
}
int main()
{
printf("N=");
scanf("%d",&n);
total=0; //路径数初始化为0
make(1); //从结点1出发,递归搜索所有的路径
printf("%d\n",total);
system("pause");
return 0;
}
由回溯法的算法流程可以看出,除非边界条件设置不当而导致死循环外,回溯法一般是不会产生内存溢出的。
但是,回溯法亦有其致命的弱点——时间效率
比数学解析法低。
为了改善其时效,我们可以从下述几个方面考虑优化:
1、递归时对尚待搜索的信息进行预处理,减少搜索量;
2、尽可能减少分支(解答树的次数);
3、增加约束条件,使其在保证出解的前提下尽可能“苛刻”;
4、在约束条件中设置限定搜索层次的槛值。
