《管理运筹学》第二版习题答案(韩伯棠教授)高等教育出版社,超详细版
韩棠伯管理运筹学习题答案

韩棠伯管理运筹学习题答案韩棠伯管理运筹学习题答案韩棠伯是一位热爱学习的年轻人,对于管理运筹学这门课程也充满了兴趣。
每天晚上,他都会认真完成老师布置的学习题,以便更好地掌握这门学科的知识。
在这里,我们将为大家分享韩棠伯管理运筹学习题的答案。
第一题:线性规划韩棠伯在学习线性规划时,遇到了以下一道题目:某公司生产两种产品A和B,每个单位产品A的利润为10元,产品B的利润为15元。
产品A每个单位需要2个工时,产品B每个单位需要3个工时。
公司每天可用的总工时为60个。
问应该如何安排生产,才能获得最大利润?答案:设产品A的产量为x,产品B的产量为y。
根据题目中的条件,我们可以列出以下线性规划模型:目标函数:Maximize 10x + 15y约束条件:2x + 3y ≤ 60非负约束:x ≥ 0, y ≥ 0通过求解这个线性规划模型,我们可以得到最大利润的产量分配方案。
第二题:排队论在学习排队论时,韩棠伯碰到了以下一道题目:某家餐厅有一个服务台,平均每小时有30名顾客到达,服务员平均每小时能为25名顾客提供服务。
问在稳定状态下,平均顾客等待时间是多少?答案:根据排队论的基本原理,我们可以使用排队模型来解决这个问题。
根据题目中的条件,我们可以得到以下参数:顾客到达率(λ)= 30人/小时服务率(μ)= 25人/小时利用排队模型中的公式,我们可以计算出平均顾客等待时间(Wq):Wq = λ / (μ - λ)将具体数值代入公式,我们可以计算出平均顾客等待时间。
第三题:决策树在学习决策树时,韩棠伯遇到了以下一道题目:某公司要决定是否投资于一个新的项目。
如果投资成功,公司将获得300万元的利润;如果投资失败,公司将损失200万元。
根据市场分析,投资成功的概率为0.6,失败的概率为0.4。
问公司应该如何决策?答案:我们可以使用决策树来解决这个问题。
根据题目中的条件,我们可以绘制出以下的决策树:投资成功(0.6)/ \获得300万元损失200万元投资失败(0.4)/ \获得0万元损失200万元根据决策树,我们可以计算出投资的期望值,即投资成功的利润乘以成功的概率加上投资失败的利润乘以失败的概率。
管理运筹学课后答案-----韩伯裳

第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
《管理运筹学》(第二版)课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0b,≥i决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0bAX,的解,称为可行解。
=X≥基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124m a x x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
韩伯棠《管理运筹学(第2版)》案例题解

韩伯棠《管理运筹学(第2版)》案例题解《管理运筹学》案例题解案例1:北⽅化⼯⼚⽉⽣产计划安排解:设每⽉⽣产产品i (i=1,2,3,4,5)的数量为X i ,价格为P 1i ,Y j 为原材料j 的数量,价格为P 2i ,a ij 为产品i 中原材料j 所需的数量百分⽐,则:510.6j i ij i Y X a ==∑总成本:1521i i i TC Y P ==∑总销售收⼊为:511i i i TI X P ==∑⽬标函数为:MAX TP (总利润)=TI-TC 约束条件为:1030248002151×××≤∑=j j Y X 1+X 3=0.7∑=51i i XX 2≤50.05∑=51i i XX 3+X 4≤5X 1 Y 3≤54000 X i ≥0,i=1,2,3,4,5 应⽤计算⼯具求解得到:X 1=19639.94kg X 2=0kg X 3=7855.97kg X 4=11783.96kgX5=0kg最优解为:348286.39元案例2:⽯华建设监理⼯程师配置问题解:设X i表⽰⼯地i在标准施⼯期需要配备的监理⼯程师,Y j表⽰⼯地j在⾼峰施⼯期需要配备的监理⼯程师。
约束条件为:X1≥5X2≥4X3≥4X4≥3X5≥3X6≥2X7≥2Y1+Y2≥14Y2+Y3≥13Y3+Y4≥11Y4+Y5≥10Y5+Y6≥9Y6+Y7≥7Y7+Y1≥14Y j≥ X i (i=j,i=1,2, (7)总成本Y为:Y=∑=+71)12/353/7(ii iY X解得X1=5;X2=4;X3=4;X4=3;X5=3;X6=2;X7=2;Y1=9;Y2=5;Y3=8;Y4=3;Y5=7;Y6=2;Y7=5总成本Y=167案例3:北⽅印染公司应如何合理使⽤技术培训费解:变量的设置如下表所⽰,其中X ij为第i类培训⽅式在第j年培训的⼈数:第⼀年第⼆年第三年1.⾼中⽣升初级⼯X11X12X132.⾼中⽣升中级⼯X213.⾼中⽣升⾼级⼯X314.初级⼯升中级⼯X41X42X435.初级⼯升⾼级⼯X51X526.中级⼯升⾼级⼯X61X62X63则每年年底培养出来的初级⼯、中级⼯和⾼级⼯⼈数分别为:第⼀年底第⼆年底第三年底初级⼯X11X12X13中级⼯X41X42X21 +X43⾼级⼯X61X51 +X62X31 +X52+X63则第⼀年的成本TC1为:1000X11+3000X21+3000X31+2800X41+2000X51+3600 X61≤550000;第⼆年的成本TC2为:1000X12+3000X21+2000X31+2800X42+(3200 X51+2000X52)+3600X62≤450000;第三年的成本TC3为:1000X13+1000X21+4000X31+2800X43+3200 X52+3600X63≤500000;总成本TC= TC1 +TC2 +TC3≤1500000;其他约束条件为:X41 +X42 +X43+X51 +X52≤226;X61+X62 +X63≤560;X1j≤90 (j=1,2,3);X21 +X41≤80;X21 +X42≤80;X21 +X43≤80;X31 +X51+X61≤80;X31 +X51+X52+X62≤80;X31 +X52+X63≤80;以下计算因培训⽽增加的产值Max TO=(X11+ X12+ X13) + 4(X41 +X42 +X21 +X43) +5.5(X61 +X51 +X62 +X31 +X52+X63);利⽤计算机求解:X11=38;X41=80;X42=59;X43=77;X61=80;X62=79;X63=79;其余变量都为0;TO=2211案例4:光明制造⼚经营报告书设直径4.76、6、8、10和12的钢管的需求量分别是X1,X2,X3,X4,X5。
管理运筹学第二版习题答案

12-2《管理运筹学》课后习题详解 第2章 线性规划的图解法1. ( 1)可行域为0, 3, A ,3围成的区域。
(2) 等值线为图中虚线所示。
(3) 如图,最优解为 A 点(12/7,15/7 ),对应最 优目标函数值 Z=69/7。
2.( 1)有唯一最优解 A 点,对应最优目标函数 值 Z=3.6。
(2)无可行解。
(3)有无界解。
40.7 0-33X 1+ X2(4)无可行解。
9y -F 2.r, + 6 = 30 3x x+2X2 + s2 =13 2x{—2xi+6=9 gx”片宀宀二0max f = 一4形—— 0町—Os2(5)无可行解。
X22max最优解A点最优函数值3. (1)标准形式(2)标准形式Xj + 2X2 H-S2 = 107,v:—6.v* = 4M , .Y2 , % 出> O(3)标准形式|!_|_fifmax f = —x 1 + 2 屯—2 込—0® — 0^2—3x x * 5X 2 — 5X 2 + s x = 70 2x x — 5X 2 + 5X 2 = 50 3xj + 2X 2 — 2X 2 —=305x ;,歩1 .s 2 土 0max z = 10.^! + 5.Y 2 \ 0^t 1 0©3x 】十 4X 2 + S J = 95.巧 +2.Y 2 -b >s 2 = 8 x t ,x 2 ^s lr>s 2 > 04.解: (1)标准形式求解:3X 〔 4X 2 9 5X 〔 2X 28X , 1 X 21.5S , S 25.标准形式:x , x 2 6 x , 3.6 S 3 S 2 0 4x , 9x 2 16x 2 2.4s , 11.27. 模型: (1) X 1=150, X 2=150;最优目标函数值 Z=103000。
(2) 第2、4车间有剩余。
剩余分别为: 330、15,均为松弛变量。
《管理运筹学》(第二版)课后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
.解:标准化.列出单纯形表412b02[8]2 /80868 /641241/41/81/8]/8(1/4/(1/813/265/4/43/4(13/2/(1/4 0-1/23/21/222806-221-12-502故最优解为,即,此时最优值为.6.表1—15中给出了求极大化问题的单纯形表,问表中为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s.t.解:标准化s.t .列出单纯形表4 12b0 2 [8]2/80 8 68/64 1 241/41/8 1/8] /8(1/4/(1/813/265/4 /4 3/4(13/2/(1/4-1/23/21/22 2 80 6 -22 1-12-52故最优解为,即,此时最优值为.6.表1—15中给出了求极大化问题的单纯形表,问表中为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学课后答案-----韩伯裳
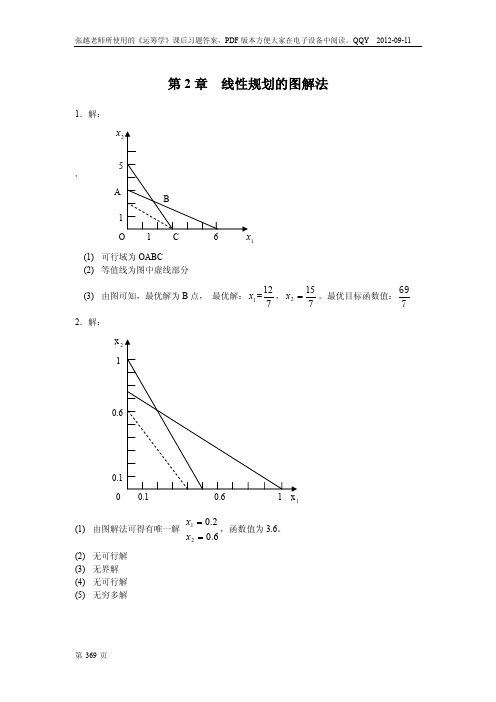
12 15 69 , x2 。最优目标函数值: 7 7 7
0.6
0.1 0 0.1 0.6 1 x1
(1) 由图解法可得有唯一解 (2) (3) (4) (5) 无可行解 无界解 无可行解 无穷多解
x1 0.2 x 2 0 .6
,函数值为 3.6。
第 369 页
张越老师所使用的《运筹学》课后习题答案,PDF 版本方便大家在电子设备中阅读。QQY 2012-09-11
从上午11时到下午10时分成11个班次设xi表示第i班次安排的临时工的人数模型如minf16x1x2x3x4x5x6x7x8x9x10x11x1x2x2x3x1x2x3x4x3x4x5x4x5x6x5x6x7x6x7x8x6x7x8x9x8x9x10x9x10x11在满足对职工需求的条件下在11时安排8个临时工13时新安排1个临时工14时新安排1个临时工16时新安排4个临时工18时新安排6个临时工可使临时工的总成本最小
' '' 3 x1 5 x 2 5x2 s1 70 ' '' 2 x1' 5 x 2 5x2 50 ' '' 3 x1' 2 x 2 2 x2 s 2 30 ' '' x1' , x 2 , x2 , s1 , s 2 0
4.解: 标准形式:
max z 10 x1 5 x2 0s1 0s 2
3 x1 4 x 2 s1 9 5 x1 2 x 2 s 2 8 x1 , x 2 , s1 , s 2 0
松弛变量(0,0) 最优解为 x1 =1,x 2 =3/2.
第 370 页
张越老师所使用的《运筹学》课后习题答案,PDF 版本方便大家在电子设备中阅读。QQY 2012-09-11
《管理运筹学》课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么就是线性规划?线性规划的三要素就是什么?答:线性规划(Linear Programming,LP)就是运筹学中最成熟的一个分支,并且就是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,就是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量就是决策问题待定的量值,取值一般为非负;约束条件就是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数就是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域就是空集。
当无界解与没有可行解时,可能就是建模时有错。
3.什么就是线性规划的标准型?松弛变量与剩余变量的管理含义就是什么? 答:线性规划的标准型就是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不就是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
管理运筹学第二版课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming, LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、LI标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;U标函数是决策者希望实现的LI标,为决策变量的线性函数表达式,有的LI标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现儿种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解:(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:LI标函数极大化,约束条件为等式,右端常数项^>0, 决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“事”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件AX=b, X>0的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使訂标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:基可行解5.用表格单纯形法求解如下线性规划。
max Z = 4Xj + x2+ 2x3 8Xj + 3X2 +x3 <26xj + x 2 + 兀3 § 8 飞°解:标准化max Z = 4x t + x2 + 2x38xj + 3X2+x3 + x4 = 2< + x2 + x3 +x5 = 8列出单纯形表故最优解为X* = (0Q2Q6V ,即M = 09x2 = 0內=2 ,此时最优值为Z(X*) = 4 •6.表1—15中给出了求极大化问题的单纯形表,问表中5<2,5心,〃为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以“代替基变量心;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学韩伯棠答案

管理运筹学韩伯棠答案【篇一:管理运筹学(第四版)第五章习题答案】时间为x2小时;产品i加班生产时间为x3小时,产品ii加班生产时间为x4小时。
minzp1d1p2d2p3d3s.t.3x1?2.5x2?d1??d1??1203x3?2.5x4?d2?d2?4010x1?8x2??10?1.5?x3??8?1?x4?d3??d3??640xj,di?,di??0,i?1,2,3;j?1,2,3,4运行结果:5.10解:设a电视机生产x1台,b电视机生产x2台,c电视机生产x3台。
minz?p1d1??p2d2?p3d3??d3??d4?d4?d5??d5s.t.500x1?650x2?900x3?d1??d1??18000??6x1?8x2?10x3?d2?d2?224x1?d3??d3??14x2?d4?d4?15x3?d5??d5??10xj,di?,di??0,i?1,2,3,4,5;j?1,2,3运行结果:5.10解:设电台a时间x1分钟,电台b时间x2分钟,电台c时间x3分钟。
minz?p1d1p22d2?d2?p3d3?s.t.400x1?600x2?80x3?24002000x1?4000x2?1000x3?d1??d1??80000 ??x1?x2?x3?d2?d2?30x3?d3??d3??0xj,di?,di??0,i?1,2,3;j?1,2,3运行结果:【篇二:《管理运筹学》第二版习题答案(韩伯棠教授)1】txt>11a.可行域为 oabc。
b.等值线为图中虚线所示。
c.由图可知,最优解为 b 点,最优解: x1 = 1215x2=69 7,7 。
2、解: a x210.60.1o1有唯一解x1= 0.2x函数值为 3.62= 0.6b 无可行解c 无界解d 无可行解e 无穷多解最优目标函数值:20 x1=3 函数值为92f 有唯一解8 3x2=33、解:a 标准形式:b 标准形式:max f = 3x1 + 2 x2+ 0s1 + 0s2+ 0s3 9 x1 + 2x2+ s1= 30 3x1 + 2 x2+ s2= 13 2 x1 + 2x2+ s3= 9 x1 , x2 , s1 , s2 , s3≥ max f = ?4 x1 ? 6x3 ? 0s1 ? 0s23x1 ? x2? s1=6x1 + 2x2+ s2= 10 7 x1 ? 6 x2= 4c 标准形式:x1 , x2 , s1 , s2≥max f = ?x1 + 2x2 ? 2 x? 0s ? 0s 2 1 23x1 + 5x2 5x2+ s1= 70 2 x 5x + 5x = 50123x1 + 2 x 2? 2x2? s2= 302x, x, x, s1 , s2≥ 04 、解:标准形式: max z = 10 x1 + 5x2+ 0s1 + 0s23x1 + 4 x2+ s1= 9 5x1 + 2 x2+ s2= 8 x1 , x2 , s1 , s2≥ 0s1 = 2, s2= 01 225 、解:标准形式: min f = 11x1 + 8x2+ 0s1 + 0s2+ 0s310 x1 + 2x2? s1= 203x1 + 3x2? s2= 18 4 x1 + 9x2? s3= 36 x1 , x2 , s1 , s2 , s3≥ 0s1 = 0, s2= 0, s3 = 136 、解:b 1 ≤ c1≤ 3 c 2 ≤ c2≤ 6 d x1= 6 x2= 4e x1 ∈ [4,8] x2= 16 ? 2x1 2f 变化。
《管理运筹学》第二课后习题答案

《管理运筹学》第⼆课后习题答案《管理运筹学》(第⼆版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming, LP)是运筹学中最成熟的⼀个分⽀,并且是应⽤最⼴泛的⼀个运筹学分⽀。
线性规划属于规划论中的静态规划,是⼀种重要的优化⼯具,能够解决有限资源的最佳分配问题。
建⽴线性规划问题要具备三要素:决策变量、约束条件、⽬标函数。
决策变量是决策问题待定的量值,取值⼀般为⾮负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策⽅案的可⾏性;⽬标函数是决策者希望实现的⽬标,为决策变量的线性函数表达式,有的⽬标要实现极⼤值,有的则要求极⼩值。
2.求解线性规划问题时可能出现⼏种结果,哪种结果说明建模时有错误?答:(1)唯⼀最优解:只有⼀个最优点;(2)多重最优解:⽆穷多个最优解;(3)⽆界解:可⾏域⽆界,⽬标值⽆限增⼤;(4)没有可⾏解:线性规划问题的可⾏域是空集。
当⽆界解和没有可⾏解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:⽬标函数极⼤化,约束条件为等式,右端常数项b i 0,决策变量满⾜⾮负性。
如果加⼊的这个⾮负变量取值为⾮零的话,则说明该约束限定没有约束⼒,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为⾮零的话,则说明型约束的左边取值⼤于右边规划值,出现剩余量。
4.试述线性规划问题的可⾏解、基础解、基可⾏解、最优解的概念及其相互关系。
答:可⾏解:满⾜约束条件AX b,X 0的解,称为可⾏解。
基可⾏解:满⾜⾮负性约束的基解,称为基可⾏解可⾏基:对应于基可⾏解的基,称为可⾏基。
最优解:使⽬标函数最优的可⾏解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所⽰:5.⽤表格单纯形法求解如下线性规划。
8x 1 3X 2 x 32s. t. 6X 1 X 2 X 3 8X i , X 2,X 3 0解:标准化max Z 4X -IX 2 2x 38X 13X 2 X 3X 42s.t.6X 1X 2X 3X 5 8X 1,X 2 ,X 3,X 4,X s列出单纯形表故最优解为X* (0,0,2,0,6)T,即X i 0,X 2 0, X 3 2,此时最优值为 Z (X*)4 .6. 表1 —15中给出了求极⼤化问题的单纯形表,问表中 a 1,a 2,c 1,c 2,d 为何值及变量属于哪⼀类型时有:(1)表中解为唯⼀最优解;(2)表中解为⽆穷多最优解之⼀;(3)下⼀步迭代将以X i 代替基变量X s ;( 4)该线性规划问题具有⽆界解;(5)该线性规划问题⽆可⾏解。
管理运筹学-韩伯棠版答案-word版

第 2 章 线性规划的图解法a.可行域为 OABC 。
b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解: x 1=1215x 2=, 最优目标函数值: 69 。
77x 1=0.2有唯一解 x 2= 0.6 函数值为 3.6b 无可行解c 无界解d 无可行解e 无穷多解f 有唯一解3、解:a 标准形式:x1x2==20383函数值为923max f= 3x1+2x2+ 0s1+ 0s2+ 0s3 x+91+ =2x s30x+31x+21222 1+ s=x22+ s=139b 标准形式:x1x23s s, x2, s1, ,2 3≥ 0max f= −x x s s41− 63− 01− 023 − x− s= 6x12 1x+ + =1 2x s2 2107 x1− 6x2= 4c 标准形式:x1, x2, , ss12= − +x'x'≥ 0' −max f 2 − 2x s s0 − 021−x+2x' −2 1' + =x s3 5 5 701 2 2 12x'− 5x'+ 5x'= 501x'+312x'−222' −=2x s30x', x2',x2',, s 2 ≥ 024、解:1s 12z = x + x + + max 10 5 s s标准形式: 1 2 0 0x + 31x + 514 2 1+ s = x 21+ s = x 229 82s 1= 2, s 2= 0x 1, x 2, , s s 12≥ 05 、解:f = x + x + ++ min118s s s 标准形式:12x + 101x +2 1− s = x 21− =220331x +413x s 2 2− =9xs1836s 1= 0, s 2= 0, s 3= 13 6 、解: b 1 ≤ c 1≤ 3c 2 ≤ c 2≤ 6x 1= 6 x123s s , x 2, s 1, ,23≥ 0 dex 2= 4 x 1∈ [ ]8x = 16 − 2x2 21f 变化。
《管理运筹学》(第二版)课后习题参考答案(2020年7月整理).pdf

max Z = 2.7x1 + 3x2 + 4.5x3 + 2.5x4 + 3x5
3x1 + 4x2 + 6x3 + 2x4 + 3x5 3600
s.t.
42xx11
+ +
3x2 3x2
+ +
5x3 3x3
+ +
6x4 4x4
+ +
4x5 3x5
3950 2800
xi 0,i = 1,2,,5
通过 LINGO 软件计算得: x1 = 0, x2 = 38, x3 = 254, x4 = 0, x5 = 642, Z = 3181 .
11.某厂生产甲、乙、丙三种产品,分别经过 A,B,C 三种设备加工。已知生产
单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表 2—10 所示。
《管理运筹学》(第二版)课后习题参考答案
第 1 章 线性规划(复习思考题)
1.什么是线性规划?线性规划的三要素是什么? 答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是 应用最广泛的一个运筹学分支。线性规划属于规划论中的静态规划,是一种重要的优化 工具,能够解决有限资源的最佳分配问题。 建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。决策变量是决 策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条 件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的 线性函数表达式,有的目标要实现极大值,有的则要求极小值。 2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。 当无界解和没有可行解时,可能是建模时有错。 3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么? 答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项 bi 0 , 决策变量满足非负性。 如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业 来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束 的左边取值大于右边规划值,出现剩余量。 4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。 答:可行解:满足约束条件 AX = b,X 0 的解,称为可行解。 基可行解:满足非负性约束的基解,称为基可行解。 可行基:对应于基可行解的基,称为可行基。 最优解:使目标函数最优的可行解,称为最优解。 最优基:最优解对应的基矩阵,称为最优基。 它们的相互关系如右图所示: 5.用表格单纯形法求解如下线性规划。
管理运筹学_韩伯堂主编_答案

、1、解:C 36 x 1a.可行域为 OABC 。
b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解: x 1=1215x 2=, 最优目标函数值: O0.1x 1=0.20.6x 1有唯一解 x 2= 0.6 函数值为 3.6b 无可行解c 无界解d 无可行解e 无穷多解f 有唯一解3、解:a 标准形式:x1x2==20383函数值为923max f= 3x1+2x2+ 0s1+ 0s2+ 0s3 x+91+ =2x s30x+31x+21222 1+ s=x22+ s=139b 标准形式:x1x23s s, x2, s1, ,2 3≥ 0max f= −x x s s41− 63− 01− 023 −x−s= 6x12 1x+ + =1 2x s2 2107 x1− 6x2= 4c 标准形式:x1, x2, , ss12= − +x'x'≥ 0' −max f 2 − 2 x s s0 − 021−x+2x' −2 1' + =x s3 5 5 701 2 2 12x'− 5x'+ 5x'= 501x'+312x'−222' −=2x s30x', x2',x2',, s 2 ≥ 024 、解:1 s12z = x+ x+ +max 10 5 s s 标准形式: 1 2 0 0x+ 31x+51 421+s=x21+ s=x22982s1= 2, s2= 0 x1, x2, , ss12≥ 05 、解:f = x + x + ++ min 11 8 s s s标准形式: 1 2 0 0 0x + 101x +2 1 − s = x 21− =2 20331x +413x s 2 2− =9xs1836s 1= 0, s 2= 0, s 3= 13 6 、解: b 1 ≤ c 1≤ 3c 2 ≤ c 2≤ 6x 1= 6 x123s s , x 2, s 1, ,23≥ 0 dex 2= 4 x 1∈ [ ]8x = 16 − 2x2 21f 变化。
管理运筹学_韩伯棠版答案_word版
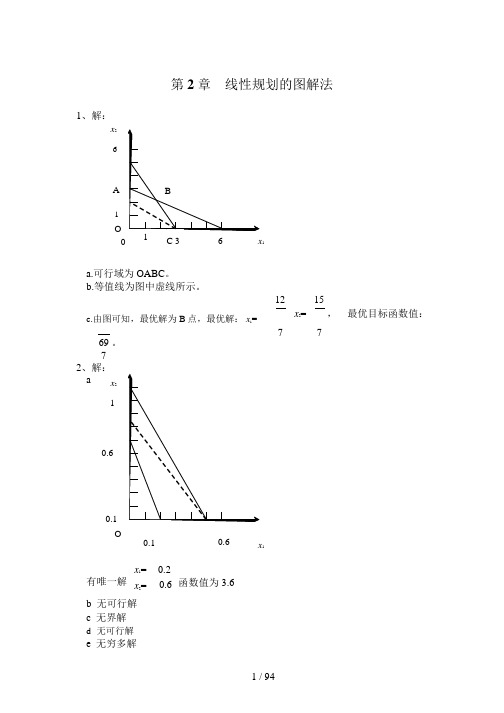
第 2 章 线性规划的图解法a.可行域为 OABC 。
b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解: x 1=1215x 2=, 最优目标函数值: 69 。
77x 1=0.2有唯一解 x 2= 0.6 函数值为 3.6b 无可行解c 无界解d 无可行解e 无穷多解f 有唯一解3、解:a 标准形式:x1x2==20383函数值为923max f= 3x1+2x2+ 0s1+ 0s2+ 0s3 x+91+ =2x s30x+31x+21222 1+ s=x22+ s=139b 标准形式:x1x23s s, x2, s1, ,2 3≥ 0max f= −x x s s41− 63− 01− 023 − x− s= 6x12 1x+ + =1 2x s2 2107 x1− 6x2= 4c 标准形式:x1, x2, , ss12= − +x'x'≥ 0' −max f 2 − 2x s s0 − 021−x+2x' −2 1' + =x s3 5 5 701 2 2 12x'− 5x'+ 5x'= 501x'+312x'−222' −=2x s30x', x2',x2',, s 2 ≥ 024、解:1s 12z = x + x + + max 10 5 s s标准形式: 1 2 0 0x + 31x + 514 2 1+ s = x 21+ s = x 229 82s 1= 2, s 2= 0x 1, x 2, , s s 12≥ 05 、解:f = x + x + ++ min118s s s 标准形式:12x + 101x +2 1− s = x 21− =220331x +413x s 2 2− =9xs1836s 1= 0, s 2= 0, s 3= 13 6 、解: b 1 ≤ c 1≤ 3c 2 ≤ c 2≤ 6x 1= 6x123s s , x 2, s 1, ,23≥ 0 de x 2= 4x 1∈ [ ]8x = 16 − 2x221f 变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《管理运筹学》第二版习题答案(韩伯棠教授)高等教育出版社第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
原斜率从 − 2变为 − 137、解: 模型:max z = 500 x 1 + 400 x 22 x 1 ≤ 300 3x 2 ≤ 540 2 x 1 + 2x 2 ≤ 440 1.2 x 1 +1.5x 2 ≤ 300 x 1 , x 2 ≥ 0a x 1 = 150x 2 = 70 即目标函数最优值是 103000b 2,4 有剩余,分别是 330,15。
均为松弛变量c 50, 0 ,200, 0 额外利润 250d 在 [0,500]变化,最优解不变。
e 在 400 到正无穷变化,最优解不变。
f 不变a 模型:min f=8xa +3xb50xa +100 xb≤12000005xa +4xb≥60000100 xb≥300000x a , xb≥0基金a,b 分别为4000,10000。
回报率:60000b 模型变为:max z = 5xa +4 xb50xa +100 xb≤1200000100 xb≥300000x a , xb≥0推导出:x1 =18000x2=3000故基金a 投资90 万,基金b 投资30 万。
第4 章线性规划在工商管理中的应用1、解:为了用最少的原材料得到10 台锅炉,需要混合使用14 种下料方案设按14 种方案下料的原材料的根数分别为x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,则可列出下面的数学模型:min f=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14s.t.2x1+x2+x3+x4 ≥80x2+3x5+2x6+2x7+x8+x9+x10 ≥350x3+x6+2x8+x9+3x11+x12+x13 ≥420x4+x7+x9+2x10+x12+2x13+3x14 ≥10x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14≥0用管理运筹学软件我们可以求得此问题的解为:x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0,x9=0,x10=0,x11=140,x12=0,x13=0,x14=3.333最优值为300。
2、解:从上午11 时到下午10 时分成11 个班次,设x i 表示第i 班次安排的临时工的人数,则可列出下面的数学模型:min f=16(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11)s.t.x1+1 ≥9x1+x2+1 ≥9x1+x2+x3+2 ≥9x1+x2+x3+x4+2 ≥ 3x2+x3+x4+x5+1≥ 3x3+x4+x5+x6+2≥ 3x4+x5+x6+x7+1≥ 6x5+x6+x7+x8+2≥12x6+x7+x8+x9+2≥12x7+x8+x9+x10+1 ≥7x8+x9+x10+x11+1 ≥7x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥0用管理运筹学软件我们可以求得此问题的解为:x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0,x10=0,x11=0最优值为320。
a、在满足对职工需求的条件下,在10 时安排8 个临时工,12 时新安排1个临时工,13 时新安排1 个临时工,15 时新安排4 个临时工,17 时新安排6 个临时工可使临时工的总成本最小。
b、这时付给临时工的工资总额为80 元,一共需要安排20 个临时工的班次。
约束松弛/剩余变量对偶价格------- ------------------ -------------1 0 -42 0 03 2 04 9 05 0 -46 5 07 0 08 0 09 0 -410 0 011 0 0根据剩余变量的数字分析可知,可以让11 时安排的8 个人工作3 小时,13 时安排的1 个人工作3 小时,可使得总成本更小。
C、设在11:00-12:00 这段时间内有x1 个班是4 小时,y1个班是3 小时;设在12:00-13:00 这段时间内有x2 个班是4 小时,y2个班是3 小时;其他时段也类似。
则:由题意可得如下式子:11 11min z =16∑x1 +12∑y1i =1i =1S.Tx 1 + y1+1≥9x 1 + y1+x2+ y2+1≥9x 1 + y1+x2+ y2+x3+ y3+1+1≥9x 1 +x2+ y2+x3+ y3+x4+ y4+1+1≥3x 2 +x3+ y3+x4+ y4+x5+ y5+1≥3x 3 +x4+ y4+x5+ y5+x6+ y6+1+1≥3x 4 +x5+ y5+x6+ y6+x7+ y7+1≥6x 5 +x6+ y6+x7+ y7+x8+ y8+1+1≥12x 6 +x7+ y7+x8+ y8+x9+ y9+1+1≥12x 7 +x8+ y8+x9+ y9+x10+ y10+1≥7x 8 +x9+ y9+x10+ y10+x11+ y11+1≥7x i ≥0, yi≥i=1,2,…,11稍微变形后,用管理运筹学软件求解可得:总成本最小为264 元。
安排如下:y1=8(即在此时间段安排8 个3 小时的班),y3=1,y5=1,y7=4,x8=6 这样能比第一问节省:320-264=56 元。
3、解:设生产A、B、C 三种产品的数量分别为x1,x2,x3,则可列出下面的数学模型:max z=10 x1+12 x2+14 x2s.t.x1+1.5x2+4x3 ≤20002x1+1.2x2+x3 ≤1000x1 ≤200x2 ≤250x3 ≤100x1,x2,x3≥0用管理运筹学软件我们可以求得此问题的解为:x1=200,x2=250,x3=100最优值为6400。
a、在资源数量及市场容量允许的条件下,生产A 200 件,B 250 件,C 100件,可使生产获利最多。
b、A、B、C 的市场容量的对偶价格分别为10 元,12 元,14 元。
材料、台时的对偶价格均为0。
说明A 的市场容量增加一件就可使总利润增加10元,B 的市场容量增加一件就可使总利润增加12 元,C 的市场容量增加一件就可使总利润增加14 元。
但增加一千克的材料或增加一个台时数都不能使总利润增加。
如果要开拓市场应当首先开拓C 产品的市场,如果要增加资源,则应在975 到正无穷上增加材料数量,在800 到正无穷上增加机器台时数。
4、解:设白天调查的有孩子的家庭的户数为x11,白天调查的无孩子的家庭的户数为x12,晚上调查的有孩子的家庭的户数为x21,晚上调查的无孩子的家庭的户数为x22,则可建立下面的数学模型:min f=25x11+20x12+30x21+24x22s.t.x11+x12+x21+x22 ≥2000x11+x12 =x21+x22x11+x21 ≥700x12+x22 ≥450x11, x12, x21, x22 ≥0用管理运筹学软件我们可以求得此问题的解为:x11=700,x12=300,x21=0,x22=1000最优值为47500。
a、白天调查的有孩子的家庭的户数为700 户,白天调查的无孩子的家庭的户数为300 户,晚上调查的有孩子的家庭的户数为0,晚上调查的无孩子的家庭的户数为1000 户,可使总调查费用最小。
b、白天调查的有孩子的家庭的费用在20-26 元之间,总调查费用不会变化;白天调查的无孩子的家庭的费用在19-25 元之间,总调查费用不会变化;晚上调查的有孩子的家庭的费用在29-无穷之间,总调查费用不会变化;晚上调查的无孩子的家庭的费用在-20-25 元之间,总调查费用不会变化。
c、调查的总户数在1400-无穷之间,总调查费用不会变化;有孩子家庭的最少调查数在0-1000 之间,总调查费用不会变化;无孩子家庭的最少调查数在负无穷-1300 之间,总调查费用不会变化。
