[09真题] 2009年青海省初中毕业升学考试数学试卷[word][评分标准]
2009年青海省中考数学试题(word版含答案)

青海省2009年初中考试数 学 试 卷(本试卷满分120分,考试时间120分钟)考生注意:1.答卷前将密封线以内的项目填写清楚. 2.用蓝黑钢笔或中性笔答题.一、填空题(本大题共12小题15空,每空2分,共30分). 1.15-的相反数是 ;立方等于8-的数是 . 2.计算:3120092-0⎛⎫+= ⎪⎝⎭;分解因式:332244x y x y xy -+= .3.三江源实业公司为治理环境污染,8年来共投入23940000元,那么23940000元用科学记数法表示为 元(保留两个有效数字). 4.如图1,PA 是O ⊙的切线,切点为30A PA APO =∠=,°,则O ⊙的半径长为 .5.已知一次函数y kx b =+的图象如图2,当0x <时,y 的取值范围是 . 6.第二象限内的点()P x y ,满足||9x =,24y =,则点P 的坐标是 .7.不等式组250112x x -<⎧⎪⎨+⎪⎩≥所有整数解的和是 .8.若2||323x x x ---的值为零,则x 的值是 . 9.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 个. 10.如图3,四边形ABCD 的对角线互相平分,要使它变为菱形, 需要添加的条件是 (只填一个你认为正确的即可). 毕业升学图1 图2A D CB 图3O11.如图4,函数y x =与4y x=的图象交于A 、B 两点, 过点A 作AC 垂直于y 轴,垂足为C ,则ABC △的面积 为 .12.观察下面的一列单项式:x ,22x -,34x ,48x -,…根据你发现的规律,第7个单项式为 ;第n 个单项式为 .二、选择题(本大题共8小题,每小题3分,共24分,每小题给出的四个选项中,只有一个选项符合要求,请把你认为正确的选项序号填入下面相应题号的表格内).13.计算3212xy ⎛⎫- ⎪⎝⎭,结果正确的是( )A .2414x yB .3618x y -C .3618x yD .3518x y -14.方程29180x x -+=的两个根是等腰三角形的底和腰,则这个三角形的周长为( ) A .12B .12或15C .15D .不能确定15.在函数2y x=中,自变量x 的取值范围是( ) A .3x -≥且0x ≠ B .3x ≤且0x ≠ C .0x ≠ D .3x -≥16.在一幅长为80cm ,宽为50cm 的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图5所示,如果要使整个挂图的面积是5400cm 2,设金色纸边的宽为x cm ,那么x 满足的方程是( )A .213014000x x +-= B .2653500x x +-= C .213014000x x --=D .2653500x x --=17.已知代数式133m xy --与52n m n x y +是同类项,那么m n 、的值分别是( )A .21m n =⎧⎨=-⎩B .21m n =-⎧⎨=-⎩C .21m n =⎧⎨=⎩D .21m n =-⎧⎨=⎩18.如图6,一根电线杆的接线柱部分AB 在阳光下的投影CD的长为 1米,太阳光线与地面的夹角60ACD ∠=°,则AB 的长为( ) A .12米BC D 60°A BC D 图619.如图7是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( )20.将三个均匀的六面分别标有1、2、3、4、5、6的正方体同时掷出,出现的数字分别为a b c 、、,则a b c 、、正好是直角三角形三边长的概率是( ) A .1216B .172C .112D .136三、(本大题共3小题,每小题7分,共21分)21.请你先化简分式2222x xy y x y x xyy x ⎛⎫-+÷- ⎪-⎝⎭,再将3x =y =22.如图8,请借助直尺按要求画图:(1)平移方格纸中左下角的图形,使点1P 平移到点2P 处. (2)将点1P 平移到点3P 处,并画出将原图放大为两倍的图形.23.如图9,梯形ABCD 中,AD BC ∥,AB DC =,P 为梯形ABCD 外一点,PA PD 、分别交线段BC 于点E F 、,且PA PD =.(1)图中除了ABE DCF △≌△外,请你再找出其余三对全等的三角形(不再添加辅助线).(2)求证:ABE DCF △≌△.1 3 21 图7 A . B . C . D .图8D CF EA B P四、(本大题共3小题,每小题8分,共24分)24.某玩具店采购人员第一次用100元去采购“企鹅牌”玩具,很快售完.第二次去采购时发现批发价上涨了0.5元,用去了150元,所购玩具数量比第一次多了10件.两批玩具的售价均为2.8元.问第二次采购玩具多少件?(说明:根据销售常识,批发价应该低于销售价)25.美国NBA 职业篮球赛的火箭队和湖人队在本赛季已进行了5场比寒.将比赛成绩进行统计后,绘制成统计图(如图10-1).请完成以下四个问题:(1)在图10-2中画出折线表示两队这5场比赛成绩的变化情况;(2)已知火箭队五场比赛的平均得分90x =火,请你计算湖人队五场比赛成绩的平均得分x 湖;(3)就这5场比赛,分别计算两队成绩的极差;(4)根据上述统计情况,试从平均得分、折线的走势、获胜场次和极差四个方面分别进行简要分析,请预测下一场比赛哪个队更能取得好成绩?26.如图11,一个圆锥的高为,侧面展开图是半圆. 求:(1)圆锥的母线长与底面半径之比; (2)求BAC ∠的度数;(3)圆锥的侧面积(结果保留π)./场 图10-2 图11场次/场 图10-1五、(本大题共2小题,第27题10分,第28题11分,共21分) 27.请阅读,完成证明和填空.九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:(1)如图12-1,正三角形ABC 中,在AB AC 、边上分别取点M N 、,使BM AN =,连接BN CM 、,发现BN CM =,且60NOC ∠=°. 请证明:60NOC ∠=°.(2)如图12-2,正方形ABCD 中,在AB BC 、边上分别取点M N 、,使AM BN =,连接AN DM 、,那么AN = ,且DON ∠= 度.(3)如图12-3,正五边形ABCDE 中,在AB BC 、边上分别取点M N 、,使A M B N =,连接AN EM 、,那么AN = ,且EON ∠= 度.(4)在正n 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现: .28.矩形OABC 在平面直角坐标系中位置如图13所示,A C 、两点的坐标分别为(60)A ,,(03)C -,,直线34y x =-与BC 边相交于D 点. (1)求点D 的坐标;(2)若抛物线294y ax x =-经过点A ,试确定此抛物线的表达式; (3)设(2)中的抛物线的对称轴与直线OD 交于点M ,点P 为对称轴上一动点,以P O M 、、为顶点的三角形与OCD △相似,求符合条件的点P 的坐标.A A AB B BC C CD D O O O MM MN N N E图12-1 图12-2 图12-3…青海省2009年初中毕业升学考试数学试卷参考答案及评分标准(普通卷)注:①全卷不给小数分;②以下各题用不同于本参考答案的解法做正确的相应给分一、填空题(本大题共12小题15空,每空2分,共30分) 1.15;2- 2.9;2(2)xy xy - 3.72.410⨯ 4.2 5.2y <- 6.(32)-,7.3 8.3- 9.24 10.AC BD ⊥或AB BC =,或BC CD =,或CD DA =,或AB AD = 11.4 12.764x ;1(2)n n x --二、选择题(本大题共8小题,每小题3分,共24分)题号13 14 15 16 17 18 19 20 选项B C A B C B A D三、本大题共3小题,每小题7分,共21分21.解:2222x xy y x y x xyy x ⎛⎫-+÷- ⎪-⎝⎭222()()x y x y x x y xy--=÷- ·························································································· (2分) ()()x y xyx x y x y -=+-· ···················································································· (4分) y x y=+ ············································································································· (5分)当3x =y =原式=········································································································ (6分)3=······················································································································· (7分) 22.本题共7分(1)从1P 平移到2P 处,若图象正确得3分;(2)放大2倍且正确,再得4分.23.本题共7分,其中第(1)小题3分,第(2)小题4分(1)ABP DCP △≌△;BEP CEP △≌△;BFP CEP △≌△. ······················ (3分) (2)∵AD BC ∥,AB DC =, ∴梯形ABCD 为等腰梯形.∴BAD CDA ABE DCF ∠=∠∠=∠,. ···································································· (4分) 又∵PA PD =,∴PAD PDA ∠=∠,∴BAD PAD CDA PDA ∠-∠=∠-∠. 即BAP CDP ∠=∠. ···································································································· (6分) 在ABE △和DCF △中,BAP CDP AB DCABE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABE DCF △≌△. ································································································· (7分) 四、本大题共3小题,每题8分,共24分.24.解法一:设第二次采购玩具x 件,则第一次采购玩具(10)x -件,由题意得 ····· (1分)1001150102x x+=- ··········································································································· (4分) 整理得 211030000x x -+=解得 150x =,260x =. ····························································································· (6分) 经检验150x =,260x =都是原方程的解.当50x =时,每件玩具的批发价为150503÷=(元),高于玩具的售价,不合题意,舍去; 当60x =时,每件玩具的批发价为15060 2.5÷=(元),低于玩具的售价,符合题意,因此第二次采购玩具60件. ····························································································· (8分) 解法二:设第一次采购玩具x 件,则第二次采购玩具(10)x +件,由题意得 ············ (1分)1001150210x x +=+ ··········································································································· (4分) 整理得 29020000x x -+=解得 140x =,250x =. ····························································································· (6分) 经检验,140x =,250x =都是原方程的解.第一次采购40件时,第二次购401050+=件,批发价为150503÷=(元)不合题意,舍去;第一次采购50件时,第二次购501060+=件,批发价为15060 2.5÷=(元)符合题意,因此第二次采购玩具60件. ························································································· (8分) 25.(1)如图. ·············································································································· (2分) (注:本小题每画对一条折线得1分.)(2)90x =湖(分); ·································· (3分) (3)火箭队成绩的极差是18分,湖人队成绩的极差是30分; ······················································· (4分) (4)从平均分看,两队的平均分相同,实力大体相当; 从折线的走势看,火箭队比赛成绩呈上升趋势,而湖人队比赛成绩呈下降趋势; 从获胜场数看,火箭队胜三场,湖人队胜两场,火箭队成绩好; 从极差看,火箭队比赛成绩比湖人队比赛成绩波动小,火箭队成绩较稳定.综上,下一场比赛火箭队更能取得好成绩. ································································ (8分) 26.(1)设此圆锥的高为h ,底面半径为r ,母线长AC l =. ∵2ππr l =,∴2lr=. ············································································· (2分) (2)∵2lr=,∴圆锥高与母线的夹角为30°,则60BAC ∠=° ··············· (4分)(3)由图可知222l h r h =+=,,∴222(2)r r =+,即22427r r =+.解得 3cm r =. ∴26cm l r ==. ·········································································································· (6分)∴圆锥的侧面积为22π18π(cm )2l =. ·········································································· (8分)/场五、本大题共2小题,第27题10分,第28题11分,共21分. 27.(1)证明:∵ABC △是正三角形,∴60A ABC AB BC ∠=∠==°,, 在ABN △和BCM △中,AB BC A ABC AN BM =⎧⎪∠=∠⎨⎪=⎩∴ABN BCM △≌△. ································································································ (2分) ∴ABN BCM ∠=∠.又∵60ABN OBC ∠+∠=°, ∴60BCM OBC ∠+∠=°, ∴60NOC ∠=°. ········································································································· (4分) 注:学生可以有其它正确的等价证明.(2)在正方形中,90AN DM DON =∠=,°. ······················································ (6分) (3)在正五边形中,108AN EM EON =∠=,°. ················································· (8分) 注:每空1分.(4)以上所求的角恰好等于正n 边形的内角(2)180n n-°. ··································· (10分)注:学生的表述只要合理或有其它等价且正确的结论,均给分.本题结论着重强调角和角的度数.28.解:(1)点D 的坐标为(43)-,. ········································································· (2分)(2)抛物线的表达式为23984y x x =-. ···································································· (4分) (3)抛物线的对称轴与x 轴的交点1P 符合条件. ∵OA CB ∥, ∴1POM CDO ∠=∠. ∵190OPM DCO ∠=∠=°, ∴1Rt Rt POM CDO △∽△. ····························· (6∵抛物线的对称轴3x =,∴点1P 的坐标为1(30)P ,. ···························································································· (7分) 过点O 作OD 的垂线交抛物线的对称轴于点2P . ∵对称轴平行于y 轴, ∴2P MO DOC ∠=∠. ∵290POM DCO ∠=∠=°,∴21Rt Rt P M O DOC △∽△. ···················································································· (8分) ∴点2P 也符合条件,2OP M ODC ∠=∠. ∴121390PO CO P PO DCO ==∠=∠=,°, ∴21Rt Rt P PO DCO △≌△. ······················································································ (9分) ∴124PP CD ==. ∵点2P 在第一象限,∴点2P 的坐标为2P (34),, ∴符合条件的点P 有两个,分别是1(30)P ,,2P (34),. ·········································· (11分)。
2009年青海省初中毕业升学考试数学试卷及答案

x y·
xy
·······································································(4 分)
x (x y)(x y)
y ···························································································(5 分) x y
11.4
12. 64x7 ; (2)n1 xn
二、选择题(本大题共 8 小题,每小题 3 分,共 24 分)
题号
13
14
15
16
17
18
19
20
选项
B
C
A
B
C
B
A
D
三、本大题共 3 小题,每小题 7 分,共 21 分
21.解:
x2 2xy y2 x y
x2 xy
y
x
(x y)2 x2 y2 ···········································································(2 分) x(x y) xy
D. 1 x3 y5 8
14.方程 x2 9x 18 0 的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
A.12
B.12 或 15
C.15
D.不能确定
15.在函数 y x 3 中,自变量 x 的取值范围是( ) 2x
A. x ≥ 3且 x 0
B. x ≤3 且 x 0
C. x 0
.
28 . 矩 形 OABC 在 平 面 直 角 坐 标 系 中 位 置 如 图 13 所 示 , A、C 两 点 的 坐 标 分 别 为
2009年青岛市中考数学试题及答案
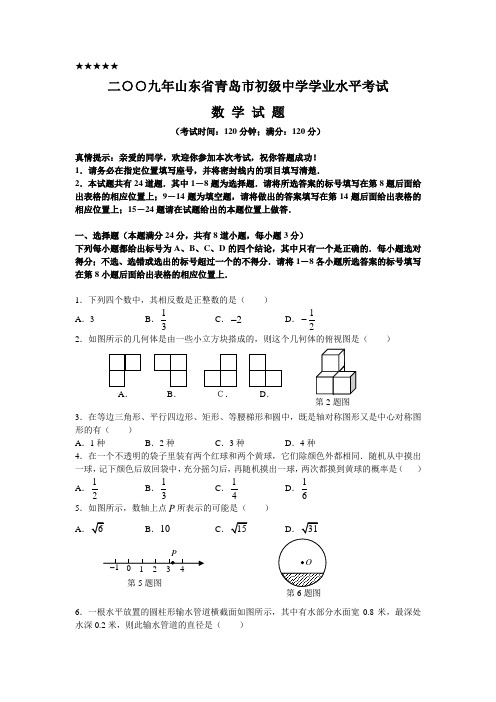
★★★★★二○○九年山东省青岛市初级中学学业水平考试数 学 试 题(考试时间:120分钟;满分:120分)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功! 1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.2.本试题共有24道题.其中1-8题为选择题.请将所选答案的标号填写在第8题后面给出表格的相应位置上;9-14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15-24题请在试题给出的本题位置上做答.一、选择题(本题满分24分,共有8道小题,每小题3分)下列每小题都给出标号为A 、B 、C 、D 的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1-8各小题所选答案的标号填写在第8小题后面给出表格的相应位置上.1.下列四个数中,其相反数是正整数的是( ) A .3B .13C .2-D .12-2.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是( )3.在等边三角形、平行四边形、矩形、等腰梯形和圆中,既是轴对称图形又是中心对称图形的有( ) A .1种 B .2种 C .3种 D .4种4.在一个不透明的袋子里装有两个红球和两个黄球,它们除颜色外都相同.随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到黄球的概率是( )A .12B .13 C .14 D .165.如图所示,数轴上点P 所表示的可能是( )AB .10CD6.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( )第2题图A .B . C. D .第5题图A .0.4米B .0.5米C .0.8米D .1米7.一块蓄电池的电压为定值,使用此蓄电池为电源时,电流I (A )与电阻R (Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A ,那么此用电器的可变电阻应( ) A .不小于4.8Ω B .不大于4.8Ω C .不小于14Ω D .不大于14Ω8.一艘轮船从港口O 出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B .若以港口O 为坐标原点,正东方向为x 轴的正方向,正北方向为y 轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B 所在位置的坐标是( )A.5030),B.(3050), C. D.(30, 二、填空题(本题满分18分,共有6道小题,每小题3分)请将9-14各小题的答案填写在第14小题后面给出表格的相应位置上9.我国首个火星探测器“萤火一号”已通过研制阶段的考核和验证,并将于今年下半年发射升空,预计历经约10个月,行程约380 000 000公里抵达火星轨道并定位.将380 000 000公里用科学记数法可表示为 公里.10.在第29届奥林匹克运动会上,青岛姑娘张娟娟为中国代表团夺得了历史上首枚奥运会射箭金牌,为祖国争得了荣誉.下表记录了她在备战奥运会期间的一次训练成绩(单位:环):根据表中的数据可得:张娟娟这次训练成绩的中位数是环,众数是 环. 11.如图,AB 为O ⊙的直径,CD为O ⊙的弦,42ACD∠=°,则BAD ∠=°. 12.某公司2006年的产值为500万元,2008年的产值为720万元,则该公司产值的年平均增长率为 .13.如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A 顺时针旋转45°,则这两个正方形重叠部分的面积是 .14.如图,长方体的底面边长分别为1cm 和3cm ,高为6cm .如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ,那么所用细线最短需要 cm ;如果从点A 开始经过4R /Ω 第7题图 x 第8题图 A 第11题图 C ' B ' 第13题图 B A 6cm 3cm 1cm第14题图个侧面缠绕n 圈到达点B ,那么所用细线最短需要 cm . 三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.15.为美化校园,学校准备在如图所示的三角形(ABC △)空地上修建一个面积最大的圆形花坛,请在图中画出这个圆形花坛. 解:结论:四、解答题(本题满分74分,共有9道小题) 16.(本小题满分8分,每题4分)(1)化简:2211x x x x +-÷ (2)解不等式组:3221317.22x x x x ->+⎧⎪⎨--⎪⎩,≤17.(本小题满分6分)某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣爱好情况,并根据调查结果制作了如下两幅统计图.根据图中提供的信息解答下列问题: (1)补全人数统计图;(2)若该校共有1500名学生,请你估计该校在课余时间喜欢阅读的人数;(3)结合上述信息,谈谈你对该校学生课余活动的意见和建议(字数不超过30字).AB C人数统计图 阅读 其他 娱乐 运动 40%分布统计图18.(本小题满分6分)在“六·一”儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得15元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算?请说明理由.19.(本小题满分6分) 在一次数学活动课上,老师带领同学们去测量一座古塔CD 的高度.他们首先从A 处安置测倾器,测得塔顶C 的仰角21CFE ∠=°,然后往塔的方向前进50米到达B 处,此时测得仰角37CGE ∠=°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD 的高度. (参考数据:3sin 375°≈,3tan 374°≈,9sin 2125°≈,3tan 218°≈)20.(本小题满分8分) 北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元. (1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率100%=⨯利润成本)CG E D B A F第19题图红 黄黄 绿绿绿 绿黄绿第18题图21.(本小题满分8分)已知:如图,在ABCD 中,AE 是BC 边上的高,将ABE △沿BC 方向平移,使点E 与点C 重合,得GFC △. (1)求证:BE DG =;(2)若60B ∠=°,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.22.(本小题满分10分)某水产品养殖企业为指导该企业某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查.调查发现这种水产品的每千克售价1y (元)与销售月份x (月)满足关系式3368y x =-+,而其每千克成本2y (元)与销售月份x (月)满足的函数关系如图所示.(1)试确定b c 、的值;(2)求出这种水产品每千克的利润y (元)与销售月份x (月)之间的函数关系式;(3)“五·一”之前,几月份出售这种水产品每千克的利润最大?最大利润是多少?23.(本小题满分10分)我们在解决数学问题时,经常采用“转化”(或“化归”)的思想方法,把待解决的问题,通过某种转化过程,归结到一类已解决或比较容易解决的问题.譬如,在学习了一元一次方程的解法以后,进一步研究二元一次方程组的解法时,我们通常采用“消元”的方法,把二元一次方程组转化为一元一次方程;再譬如,在学习了三角形内角和定理以后,进一步研究多边形的内角和问题时,我们通常借助添加辅助线,把多边形转化为三角形,从而解决问题.问题提出:如何把一个正方形分割成n (n ≥9)个小正方形?A D G CB F E 第21题图y 2为解决上面问题,我们先来研究两种简单的“基本分割法”.基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形.基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.问题解决:有了上述两种“基本分割法”后,我们就可以把一个正方形分割成n (n ≥9)个小正方形.(1)把一个正方形分割成9个小正方形.一种方法:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成459+=(个)小正方形.另一种方法:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成639+=(个)小正方形. (2)把一个正方形分割成10个小正方形.方法:如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加32⨯个小正方形,从而分割成43210+⨯=(个)小正方形.(3)请你参照上述分割方法,把图⑥给出的正方形分割成11个小正方形(用钢笔或圆珠笔画出草图即可,不用说明分割方法)(4)把一个正方形分割成n (n ≥9)个小正方形. 方法:通过“基本分割法1”、“基本分割法2”或其组合把一个正方形分割成9个、10个和11个小正方形,再在此基础上每使用1次“基本分割法1”,就可增加3个小正方形,从而把一个正方形分割成12个、13个、14个小正方形,依次类推,即可把一个正方形分割成n (n ≥9)个小正方形. 从上面的分法可以看出,解决问题的关键就是找到两种基本分割法,然后通过这两种基本分割法或其组合把正方形分割成n (n ≥9)个小正方形.类比应用:仿照上面的方法,我们可以把一个正三角形分割成n (n ≥9)个小正三角形. (1)基本分割法1:把一个正三角形分割成4个小正三角形(请你在图a 中画出草图). (2)基本分割法2:把一个正三角形分割成6个小正三角形(请你在图b 中画出草图). (3)分别把图c 、图d 和图e 中的正三角形分割成9个、10个和11个小正三角形(用钢笔或圆珠笔画出草图即可,不用说明分割方法)(4)请你写出把一个正三角形分割成n (n ≥9)个小正三角形的分割方法(只写出分割方法,不用画图).图① 图② 图③ 图④ 图⑤ 图⑥图a图b图c图d图e24.(本小题满分12分)如图,在梯形ABCD 中,AD BC ∥,6cm AD =,4cm CD =,10cm BC BD ==,点P 由B 出发沿BD 方向匀速运动,速度为1cm/s ;同时,线段EF 由DC 出发沿DA 方向匀速运动,速度为1cm/s ,交BD 于Q ,连接PE .若设运动时间为t (s )(05t <<).解答下列问题:(1)当t 为何值时,PE AB ∥?(2)设PEQ △的面积为y (cm 2),求y 与t 之间的函数关系式; (3)是否存在某一时刻t ,使225PEQ BCD S S =△△?若存在,求出此时t 的值;若不存在,说明理由.(4)连接PF ,在上述运动过程中,五边形PFCDE 的面积是否发生变化?说明理由.第24题图二○○九年山东省青岛市初级中学学业水平考试数学试题参考答案及评分标准说明:1.如果考生的解法与本解法不同,可参照本评分标准制定相应评分细则.2.当考生的解答在某一步出现错误,影响了后继部分时,如果这一步以后的解答未改变这道题的内容和难度,可视影响程度决定后面部分的给分.但不得超过后面部分应给分数的一半,如果这一步以后的解答有较严重的错误,就不给分.3.为阅卷方便,本解答中的推算步骤写得较为详细,但允许考生在解答过程中,合理省略非关键性的推算步骤.4.解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题满分24分,共有8道小题,每小题3分)15.正确画出两条角平分线,确定圆心; ···························································· 2分确定半径;······························································································ 3分 正确画出图并写出结论. ··········································································· 4分 四、解答题(本题满分74分,共有9道小题) 16.(本小题满分8分)(1)解:原式21(1)(1)x x x x x +=+-1xx =-. ·················································································· 4分 (2)322131722x x x x ->+⎧⎪⎨--⎪⎩①≤② 解:解不等式①得 2x >, 解不等式②得 4x ≤.所以原不等式组的解集为24x <≤. ·························································· 4分 17.(本小题满分6分)解:(1)正确补全统计图; ·············································································· 2分 (2)300人. ································································································ 4分 (3)合理即可. ···························································································· 6分 18.(本小题满分6分)解:13580502016.5202020⨯+⨯+⨯=(元), ···················································· 4分 ∵16.55>元元∴选择转转盘对顾客更合算. ··········································································· 6分 19.(本小题满分6分)解:由题意知CD AD ⊥,EF AD ∥,∴90CEF ∠=°,设CE x =, 在Rt CEF △中,tan CE CFE EF ∠=,则8tan tan 213CE x EF x CFE ===∠°; 在Rt CEG △中,tan CECGE GE ∠=, 则4tan tan 373CE x GE x CGE ===∠°; ················· 4分 ∵EF FG EG =+, ∴845033x x =+. 37.5x =,∴37.5 1.539CD CE ED =+=+=(米). 答:古塔的高度约是39米. ············································································· 6分 20.(本小题满分8分) 解:(1)设商场第一次购进x 套运动服,由题意得:6800032000102x x-=, ··················································································· 3分 解这个方程,得200x =.经检验,200x =是所列方程的根. 22200200600x x +=⨯+=.所以商场两次共购进这种运动服600套. ···························································· 5分 (2)设每套运动服的售价为y 元,由题意得:600320006800020%3200068000y --+≥,解这个不等式,得200y ≥,所以每套运动服的售价至少是200元. ······························································· 8分 21.(本小题满分8分) 证明:(1)∵四边形ABCD 是平行四边形, ∴AB CD =.∵AE 是BC 边上的高,且CG 是由AE 沿BC 方向平移而成. ∴CG AD ⊥.CGEDB AF 第19题图∴90AEB CGD ∠=∠=°. ∵AE CG =,∴Rt Rt ABE CDG △≌△. ∴BE DG =. ······························································································ 4分(2)当32BC AB =时,四边形ABFC 是菱形. ∵AB GF ∥,AG BF ∥, ∴四边形ABFG 是平行四边形.∵Rt ABE △中,60B ∠=°, ∴30BAE ∠=°,∴12BE AB =.∵32BE CF BC AB ==,,∴12EF AB =.∴AB BF =.∴四边形ABFG 是菱形. ················································································ 8分22.(本小题满分10分) 解:(1)由题意:22125338124448b c b c ⎧=⨯++⎪⎪⎨⎪=⨯++⎪⎩解得7181292b c ⎧=-⎪⎪⎨⎪=⎪⎩ ······························································································· 4分(2)12y y y =- 23115136298882x x x ⎛⎫=-+--+ ⎪⎝⎭ 21316822x x =-++; ············································································ 6分 (3)21316822y x x =-++2111(1236)46822x x =--+++21(6)118x =--+A DG C B FE 第21题图∵108a =-<, ∴抛物线开口向下.在对称轴6x =左侧y 随x 的增大而增大.由题意5x <,所以在4月份出售这种水产品每千克的利润最大. ···························· 9分 最大利润211(46)111082=--+=(元). ························································ 10分 23.(本小满分10分)解:把一个正方形分割成11个小正方形:·································································· 2分 把一个正三角形分割成4个小正三角形:·································································· 3分 把一个正三角形分割成6个小正三角形:······························································· 5分 把一个正三角形分割成9个、10个和11个小正三角形:·········································· 8分 把一个正三角形分割成n (9n ≥)个小正三角形的分割方法:通过“基本分割法1”、“基本分割法2”或其组合,把一个正三角形分割成9个、10个和11个小正三角形,再在此基础上每使用1次“基本分割法1”,就可增加3个小正三角形,从而把一个正三角形分割成12个、13个、14个小正三角形,依次类推,即可把一个正三角形分割成n (9n ≥)个小正三角形. ·································································································· 10分24.(本小题满分12分)解:(1)∵PE AB ∥ ∴DE DP DA DB=. 而10DE t DP t ==-,, ∴10610t t -=, ∴154t =.图⑥图a图b图c 图e图dF∴当15(s)4t PE AB =,∥. ···················· 2分 (2)∵EF 平行且等于CD ,∴四边形CDEF 是平行四边形. ∴DEQ C DQE BDC ∠=∠∠=∠,.∵10BC BD ==,∴DEQ C DQE BDC ∠=∠=∠=∠.∴DEQ BCD △∽△. ∴DE EQ BC CD=. 104t EQ =. ∴25EQ t =. 过B 作BM CD ⊥,交CD 于M ,过P 作PN EF ⊥,交EF 于N .BM ====.∵ED DQ BP t ===,∴102PQ t =-.又PNQ BMD △∽△,PQ PN BD BM=, 10210t -=,15t PN ⎫=-⎪⎭211212255255PEQ t S EQ PN t ⎫==⨯⨯-=-+⎪⎭△. ···························· 6分(3)11422BCD S CD BM ==⨯⨯=△ 若225PEQ BCD S S =△△,则有2225525-+=⨯,解得1214t t ==,. ······················································································· 9分(4)在PDE △和FBP △中,10DE BP t PD BF t PDE FBP PDE FBP ==⎫⎪==-⇒⎬⎪∠=∠⎭,,△≌△,∴PDE PFCDE PFCD S S S =+△五边形四边形FBP PFCD S S =+△四边形BCD S ==△.∴在运动过程中,五边形PFCDE 的面积不变. ················································· 12分。
2009年全国中考数学压轴题精选精析(青海)

2009年全国中考数学压轴题精选精析(青海)1.(2009年青海)28.矩形OABC 在平面直角坐标系中位置如图13所示,A C 、两点的坐标分别为(60)A ,,(03)C -,,直线34y x =-与BC 边相交于D 点. (1)求点D 的坐标;(2)若抛物线294y ax x =-经过点A ,试确定此抛物线的表达式;(3)设(2)中的抛物线的对称轴与直线OD 交于点M ,点P 为对称轴上一动点,以P O M 、、为顶点的三角形与OCD △相似,求符合条件的点P 的坐标.(2009年青海26题解析)解:(1)点D 的坐标为(43)-,. ···························· (2分)(2)抛物线的表达式为23984y x x =-. ······················································ (4分) (3)抛物线的对称轴与x 轴的交点1P 符合条件. ∵OA CB ∥, ∴1POM CDO ∠=∠. ∵190OPM DCO ∠=∠=°, ∴1Rt Rt POM CDO △∽△. ······················· (6∵抛物线的对称轴3x =,∴点1P 的坐标为1(30)P ,. ········································································· (7分) 过点O 作OD 的垂线交抛物线的对称轴于点2P . ∵对称轴平行于y 轴, ∴2P MO DOC ∠=∠. ∵290POM DCO ∠=∠=°, ∴21Rt Rt P M O DOC △∽△. ·································································· (8分) ∴点2P 也符合条件,2OP M ODC ∠=∠. ∴121390PO CO P PO DCO ==∠=∠=,°, ∴21Rt Rt P PO DCO △≌△. ···································································· (9分)∴124PP CD ==. ∵点2P 在第一象限, ∴点2P 的坐标为2P (34),, ∴符合条件的点P 有两个,分别是1(30)P ,,2P (34),. (11分)。
2009年青海省中考英语真题及答案

2009年青海省中考英语真题及答案(满分120分,考试时间120分钟)I.听力测试(共四大题,计20分)A.听句子,从A、B、 C、 D、E中,选择与所听到的1〜5题相对应的选项。
(每小题 1分,共5分)I. 2. 3. 4. 5.B. 听句子,选择最佳答语。
小题1分,共5分)6. A. No more. B. No, thanks. C. No, never.7. A. It's new. B. It's Jane Eyre. C. It's expensive.8. A. Every day. B. Three times. C. For a week.9. A. Don't worry. B. You're welcome. C. No hurry.10. A. Oh dear! How did he do thai?B. Oh dear! Why did he do that?C. Oh dear! Never mind !C. 听对活,选择正确的答案。
(每小题1分,共5分)听第1段对话,回答第11,12题。
II. What colour does the man NOT like?、A. Black.B. Red.C. White.12. How much will the man pay for the MPS?A. 5 dollars.B. 45 dollars.C. 50 dollars.听第2段对话,回答第小题。
13. What does the woman want to do?A. To sell the flat.B. To buy the flat.C. To change the flat.14. How many bedrooms are there in the flat?A. One.B. Two.C. Three.15. When will the man go lo the flat?A. At about 2 pm.B. At about 4 prn.C. At about 6 pm.Welcome to Science Museum. Your guide will be happy to answer the questions you may have throughout the day. Remember, the more you ask, the moreyou learn.1st floor:Science experiments. Try them all by 16 . You will have a lot of time to do this.2nd floor:The IT Floor. How 17 work, eel! phones, etc.The 18 of the car. We have some very 19 cars for you to see.3rd floor: How the human body 20 . and all about plants, trees and nature.II.单项选择(每小题1分,共20分)从A 、 B 、 C三个选项中选出一个可以填入空白处的最佳答案。
2009年初中毕业生学业考试(有答案)

港中数学网2009年初中毕业生学业考试数 学 试 卷说明:本试卷共 4 页,23 小题,满分 120 分.考试用时 90 分钟.注意事项:1.答题前,考生务必在答题卡上用黑色字迹的钢笔或签字笔填写准考证号、姓名、试室号、座位号,再用2B 铅笔把试室号、座位号的对应数字涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应答案选项涂黑,如需改动,用橡皮擦擦干净后,再重新选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 5.本试卷不用装订,考完后统一交县招生办(中招办)封存. 参考公式: 抛物线2y ax bx c =++的对称轴是直线2b x a=-, 顶点坐标是424b ac b a a 2⎛⎫-- ⎪⎝⎭,.一、选择题:每小题 3分,共 15 分.每小题给出四个答案,其中只有一个是正确的. 1.12-的倒数为( ) A .12B .2C .2-D .1-2.下列图案是我国几家银行的标志,其中不是..轴对称图形的是( )根据表中数据可知,全班同学答对的题数所组成的样本的中位数和众数分别是( ) A .8、8 B . 8、9 C .9、9 D .9、8 4.下列函数:①y x =-;②2y x =;③1y x=-;④2y x =.当0x <时,y 随x 的增大而减小的函数有( )A .1 个B .2 个C .3 个D .4 个 5.一个正方体的表面展开图可以是下列图形中的( )A .B .C .D . 港中数学网二、填空题:每小题 3分,共 24 分. 6.计算:2()a a -÷= .7.梅州是中国著名侨乡,祖籍在梅州的华侨华人及港澳台同胞超过360万人,360万用科学计数法表示为 .8.如图1,在O ⊙中,20ACB ∠=°,则AOB ∠=_______度.9.如图2 所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O 至少经过____________次旋转而得到, 每一次旋转_______度.10.小张和小李去练习射击,第一轮10发子弹打完后,两人的成绩如图3所示.根据图中的信息,小张和小李两人中成绩较稳定的是 .11.已知一元二次方程22310x x --=的两根为12x x ,,则12x x = ___________. 12.如图4,把一个长方形纸片沿EF 折叠后,点D C 、分别落在11 D C 、的位置.若65EFB ∠=°,则1AED ∠等于_______度.13. 如图5,每一幅图中有若干个大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第4幅图中有 个,第n 幅图中共有 个.A .B .C .D .C 图1图3 A E D C F B D 1C 1图4… … 第1幅 第2幅 第3幅 第n 幅 图5 港中数学网三、解答下列各题:本题有 10 小题,共 81 分.解答应写出文字说明、推理过程或演算步骤.14.本题满分 7 分. 如图 6,已知线段AB ,分别以A B 、为圆心,大于12AB 长为半径画弧,两弧相交于点C 、Q ,连结CQ 与AB 相交于点D ,连结AC ,BC .那么: (1)∠ ADC =________度;(2)当线段460A B A C B =∠=,°时,ACD ∠= ______度, ABC △的面积等于_________(面积单位).15.本题满分 7 分.星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y (千米)与时间t (分钟)的关系如图7所示.根据图象回答下列问题:(1)小明家离图书馆的距离是____________千米; (2)小明在图书馆看书的时间为___________小时; (3)小明去图书馆时的速度是______________千米/小时.16.本题满分 7 分.计算:112)4cos30|3-⎛⎫++- ⎪⎝⎭°.17.本题满分 7 分. 求不等式组1184 1.x x x x --⎧⎨+>-⎩≥,的整数解.C BD A 图6Q(分)图7 港中数学网18.本题满分 8 分.先化简,再求值:2224441x x xx x x x --+÷-+-,其中32x =.19.本题满分 8 分.如图 8,梯形ABCD 中,AB CD ∥,点F 在BC 上,连DF 与AB 的延长线交于点G . (1)求证:CDF BGF △∽△; (2)当点F 是BC 的中点时,过F 作EF CD ∥交AD 于点E ,若6cm 4cm AB EF ==,,求CD 的长.20.本题满分 8 分.“五·一”假期,梅河公司组织部分员工到A 、B 、C 三地旅游,公司购买前往各地的车票种类、数量绘制成条形统计图,如图9.根据统计图回答下列问题:(1)前往 A 地的车票有_____张,前往C 地的车票占全部车票的________%;(2)若公司决定采用随机抽取的方式把车票分配给 100 名员工,在看不到车票的条件下,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小王抽到去 B 地车票的概率为______;(3)若最后剩下一张车票时,员工小张、小李都想要,决定采用抛掷一枚各面分别标有数字1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小张掷得着地一面的数字比小李掷得着地一面的数字大,车票给小张,否则给小李.”试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?21.本题满分 8 分. 如图10,已知抛物线233y x x =+与x 轴的两个交点为A B 、,与y 轴交于点C . (1)求A B C ,,三点的坐标;D C FE A BG 图8图9地点 港中数学网(2)求证:ABC △是直角三角形; (3)若坐标平面内的点M ,使得以点M 和三点 A B C 、、为顶点的四边形是平行四边形,求点M 的坐标.(直接写出点的坐标,不必写求解过程)22.本题满分 10 分.如图 11,矩形ABCD 中,53AB AD ==,.点E 是CD 上的动点,以AE 为直径的O ⊙与AB 交于点F ,过点F 作FG BE ⊥于点G . (1)当E 是CD 的中点时:①tan EAB ∠的值为______________; ② 证明:FG 是O ⊙的切线;(2)试探究:BE 能否与O ⊙相切?若能,求出此时DE 的长;若不能,请说明理由.23.本题满分 11 分.(提示:为了方便答题和评卷,建议在答题卡上画出你认为必须的图形)如图 12,已知直线L 过点(01)A ,和(10)B ,,P 是x 轴正半轴上的动点,OP 的垂直平分线交L 于点Q ,交x 轴于点M . (1)直接写出直线L 的解析式;(2)设OP t =,OPQ △的面积为S ,求S 关于t 的函数关系式;并求出当02t <<时,S 的最大值;(3)直线1L 过点A 且与x 轴平行,问在1L 上是否存在点C , 使得CPQ △是以Q 为直角顶点的等腰直角三角形?若存在,求出点C 的坐标,并证明;若不存在,请说明理由.L 1xC B 图11 港中数学网2009年梅州市初中毕业生学业考试数学参考答案及评分意见一、选择题:每小题 3分,共 15 分.每小题给出四个答案,其中只有一个是正确的. 1.C 2.B 3.D 4.B 5.C 二、填空题:每小题 3分,共 24 分.6.a 7.63.610⨯ 8.40 9.4(1分),72(2分) 10.小张 11.12-12.50 13.7(1分),21n -(2分) 三、解答下列各题:本题有 10 小题,共 81 分.解答应写出文字说明、推理过程或演算步骤.14.本题满分7分. (1)90 ···································································································································· 2分 (2)30 ···································································································································· 4分······························································································································· 7分 15.本题满分 7 分. (1)3 ····································································································································· 2分 (2)1 ····································································································································· 4分 (3)15 ···································································································································· 7分 16.本题满分 7 分.解:112)4cos30|3-⎛⎫++- ⎪⎝⎭°.1342=++······································································································ 4分43=+-················································································································ 6分 4= ······································································································································ 7分17.本题满分 7 分.解:由11x x --≥得1x ≥, ······························································································ 2分 由841x x +>-,得3x <. ······························································································ 4 分 所以不等式组的解为:13x <≤, ···················································································· 6 分 所以不等式组的整数解为:1,2. ······················································································· 7 分 18.本题满分 8 分.解:2224441x x x x x x x --+÷-+-2(2)(2)(1)(2)1x x x x x x x -+-=+÷-- ············································· 3分212x x +=+- 港中数学网22xx =- ··································································································································· 6分 当32x =时,原式3226322⨯==--. ························································································ 8分 19.本题满分8 分.(1)证明:∵梯形ABCD ,AB CD ∥, ∴CDF FGB DCF GBF ∠=∠∠=∠,, ······················ 2 分∴CDF BGF △∽△. ···························· 3分(2) 由(1)CDF BGF △∽△,又F 是BC 的中点,BF FC = ∴CDF BGF △≌△, ∴DF FG CD BG ==, ················································ 6分又∵EF CD ∥,AB CD ∥,∴EF AG ∥,得2EF BG AB BG ==+. ∴22462BG EF AB =-=⨯-=, ∴2cm CD BG ==. ··········································································································· 8分 20.本题满分 8 分. 解:(1)30;20. ·············································································································· 2 分 (2)12. ···························································································································· 4 分或画树状图如下:共有 16 种可能的结果,且每种的可能性相同,其中小张获得车票的结果有6种: (2,1),(3,1),(3,2),(4,1),(4,2),(4,3), ∴小张获得车票的概率为63168P ==;则小李获得车票的概率为35188-=. ∴这个规则对小张、小李双方不公平. ························································ 8 分D C F EA BG19题图 1 2 3 4 1 1 2 3 4 2 1 2 3 4 3 1 2 3 4 4 开始 小张 小李 港中数学网21.本题满分 8 分.(1)解:令0x =,得y =(0C . ························································ 1分令0y =,得20x x ,解得1213x x =-=,, ∴(10)(30)A B -,,,. ·································································································· 3分(2)法一:证明:因为22214AC =+=,222231216BC AB =+==,, ························ 4分 ∴222AB AC BC =+, ··············································· 5分 ∴ABC △是直角三角形. ·········································· 6分法二:因为13OC OA OB ===,,∴2OC OA OB = , ··············································································································· 4分 ∴OC OB OA OC=,又AOC COB ∠=∠, ∴Rt Rt AOC COB △∽△. ································································································ 5分 ∴90ACO OBC OCB OBC ∠=∠∠+∠=,°, ∴90ACO OCB ∠+∠=°,∴90ACB ∠=°, 即ABC △是直角三角形. ····················································· 6 分(3)1(4M,2(4M -,3(2M .(只写出一个给1分,写出2个,得1.5分) ····································································· 8分22.本题满分 10 分.(1)①65····································································· 2分②法一:在矩形ABCD 中,AD BC =,ADE BCE ∠=∠,又CE DE =, ∴ADE BCE △≌△, ················································ 3分得AE BE EAB EBA =∠=∠,,连OF ,则OF OA =, ∴OAF OFA ∠=∠, OFA EBA ∠=∠, ∴OF EB ∥, ·················································································· 4 分 ∵FG BE ⊥, ∴FG OF ⊥, ∴FG 是O ⊙的切线 ································································································· 6分 (法二:提示:连EF DF ,,证四边形DFBE 是平行四边形.参照法一给分.) (2)法一:若BE 能与O ⊙相切, ∵AE 是O ⊙的直径, ∴AE BE ⊥,则90DEA BEC ∠+∠=°,又90EBC BEC ∠+∠=°, ∴DEA EBC ∠=∠,∴Rt Rt ADE ECB △∽△,22题图x21题图M 1 3 港中数学网∴AD DE EC BC =,设DE x =,则53EC x AD BC =-==,,得353xx =-, 整理得2590x x -+=. ······································································································· 8 分 ∵242536110b ac -=-=-<, ∴该方程无实数根.∴点E 不存在,BE 不能与O ⊙相切. ·········································· 10分 法二: 若BE 能与O ⊙相切,因AE 是O ⊙的直径,则90AE BE AEB ∠=⊥,°,设DE x =,则5EC x =-,由勾股定理得:222AE EB AB +=,即22(9)[(5)9]25x x ++-+=, 整理得2590x x -+=, ······································· 8分 ∵242536110b ac -=-=-<, ∴该方程无实数根.∴点E 不存在,BE 不能与O ⊙相切. ·········································· 10分 (法三:本题可以通过判断以AB 为直径的圆与DC 是否有交点来求解,参照前一解法给分) 23.本题满分 11 分.(1)1y x =- ························································································································ 2分 (2)∵OP t =,∴Q 点的横坐标为12t , ①当1012t <<,即02t <<时,112QM t =-, ∴11122OPQ S t t ⎛⎫=- ⎪⎝⎭△. ······································································································ 3分 ②当2t ≥时,111122QM t t =-=-, ∴11122OPQ S t t ⎛⎫=- ⎪⎝⎭△. ∴1110222111 2.22t t t S t t t ⎧⎛⎫-<< ⎪⎪⎪⎝⎭=⎨⎛⎫⎪- ⎪⎪⎝⎭⎩,,,≥ ······························································································ 4分当1012t <<,即02t <<时,211111(1)2244S t t t ⎛⎫=-=--+ ⎪⎝⎭, ∴当1t =时,S 有最大值14. ······························································································ 6分 (3)由1O A O B ==,所以OAB △是等腰直角三角形,若在1L 上存在点C ,使得CPQ△。
2009年初中毕业生学业考试数学调研测试卷试题卷

2009学年初三数学调研测试试题卷一、选择题(本题有10小题,每小题3分,共30分) 2的相反数是( ▲ )A .2-B 2C .2-D 2 2.下列各点在如图4×4网格区域内的是 ( ▲ )A .(3,2)B .(-3,2)C .(3,-2)D .(-3,-2)3. 已知α是等腰直角三角形的一个锐角,则sin α的值为( ▲ )A .12B .22C .32D .1 4. 计算32)(x x ⋅-所得的结果是( ▲ )A. 5xB.-5xC. 6xD. -6x5. 15 ▲ )A .点P 子B .点QC .点MD .点N6. 在平面直角坐标系中,将点A (1,2)的横坐标乘以-1,纵坐标不变,得到点A ',则点A 与点A '的关系是( ▲ )A .关于x 轴对称B .关于y 轴对称C .关于原点对称D .将点A 向x 轴负方向平移一个单位得点A '7. 若等腰三角形的一条边长等于6,另一条边长等于3,则它的周长是( ▲ )A .9B .12C .15D .12或158. “龟兔赛跑”的故事大家都非常熟悉:对兔子来说,真是“身手敏捷速度快,赛时先快后却慢,中途美梦来相伴,输了比赛留遗憾” .下列图像中,最能反映寓言故事中兔子行进的距离s (米)与行进时间t (小时)关系的是( ▲ )9. 如图是一个几何体的三视图,根据图中提供的数据(单位:cm )可求得这个几何体的体积为( ▲ )A . 83cmB .63cmC .4 3cmD .2 3cm10.在同一直角坐标系中,函数y mx m =+和222y mx x =-++(m 是常数,且0m ≠)的图象可能..是( ▲ )二、填空题 (本题有6小题,每小题4分,共24分) 11. 分解因式:=-a ax 42 ▲ .12. 0,3),和(0,1),它们的半径分别是3和5,那么这两个圆的位置关系是 ▲ .13. 一只小鸟自由自在地在空中飞行,然后随意落在图中所示某个方格中(每个方格除颜色外完全一样),那么小鸟停在深色方格中的概率是 ▲ .14. 如图,在ΔABC 中,M 、N 分别是AB 、AC 的中点,且∠A +∠B ﹦120°,则∠ANM ﹦ ▲ .15. 为了能有效地使用电力资源,我市供电部门鼓励居民使用“峰谷”电:每天8:00至21:00用电每千瓦时0.55元(“峰电”价),每天21:00至次日8:00每千瓦时0.30元(“谷电”价).王老师家使用“峰谷”电后,一月份用电量为300千瓦时,付电费115元,则王老师家该月使用“峰电” ▲ 千瓦时.16.如图,在平面直角坐标系中,矩形OABC 的两边分别在x 轴和y轴上,OA =10cm ,OC =6cm .P 是线段OA 上的动点,从O 点出发,以1cm /s 的速度沿OA 方向作匀速运动,点Q 在线段AB上. 已知A 、Q 两点间距离是O 、P 两点间距离的a 倍,若用(a ,t )表示经过时间t (s )时,△OCP 、△PAQ 和△CBQ 中有两个三角形全等.请写出(a ,t )的所有可能情况▲ .三、解答题 (本题有8小题,共66分) 17.(本题6分) (1)计算 ︒---30tan 3)14.3(270π ;(2)解方程:1321x x =+. 18.(本题6分)如图,在△ABC 中,DF ∥AB ,DE ∥BC ,连接BD .(1) 求证:△DEB ≌△BFD ;(2) 若点D 是AC 边的中点,当△ABC 满足条件▲ 时,四边形DEBF 为菱形.x y O A.x y O B. x y O C. x y O D. A M NB C第14题19.(本题6分)如图,在等腰直角三角形OAB 中,∠OAB =90°,B 点在第一象限,A 点坐标为(1,0).(1)作△OCD ,使它与△OAB 关于y 轴对称,则D 点的坐标为 ▲ ;(2)在(1)的基础上,若将△OCD 向上平移k (k >0)个单位至△D C O '''(如图乙),已知反比例函数xy 3-=的图像经过点D ',求k 的值.20.(本题8分)如图,已知AB 是⊙O 的直径,点C 在⊙O 上,且13AB =,5BC =.(1)求sin BAC ∠的值;(2)如果OD AC ⊥,垂足为D ,求AD 的长;(3)求图中阴影部分的面积(精确到0.1).21.(本题8分)如图,有一座大桥是靠抛物线型的拱形支撑的,它的桥面处于拱形中部(金华市区的双龙大桥就是这种模型).已知桥面在拱形之间的宽度CD 为40m ,桥面CD 离拱形支撑的最高点O 的距离为10m ,且在正常水位时水面宽度AB 为48m .(1)建立如图所示的直角坐标系,求此抛物线的解析式;(2)现有一辆载有救援物质的货车正以40h km /的速度必需经过此桥匀速开往乙地.当货车行驶到甲地时接到紧急通知:前方连降暴雨,造成水位以每小时0.3m 的速度持续上涨(接到通知时水位已经比正常水位高出2m 了,当水位到达桥面CD 的高度时,禁止车辆通行).已知甲地距离此桥360km (桥长忽略不计),请问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度不得低于多少h km /?22.(本题10分)2008年5月12日,四川汶川发生特大地震灾难,造成数万人遇难,数十万人受伤, 还有数万人失踪. 灾难发生后,社会各界纷纷捐款捐物支援灾区人民. 如图(1)是根据我区某中学学生捐款情况制成的条形图,图(2)是该中学学生人数分布统计表.(1) 该校共有学生 ▲ 人;(2) 该校学生平均每人捐款 ▲ 元(精确到0.01元);(3) 在得知灾区急需帐篷后,学校立即用全校师生的捐款到当地的一家帐篷厂采购了300顶小帐篷,130顶大帐篷。
2009年青岛中考数学试题及答案

二○○九年山东省青岛市初级中学学业水平考试数学试题(考试时间:120分钟;满分:120分)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.2.本试题共有24道题.其中1-8题为选择题.请将所选答案的标号填写在第8题后面给出表格的相应位置上;9-14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15-24题请在试题给出的本题位置上做答.一、选择题(本题满分24分,共有8道小题,每小题3分)下列每小题都给出标号为A 、B 、C 、D 的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1-8各小题所选答案的标号填写在第8小题后面给出表格的相应位置上.1.下列四个数中,其相反数是正整数的是()A .3B .13C .2D .122.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是()3.在等边三角形、平行四边形、矩形、等腰梯形和圆中,既是轴对称图形又是中心对称图形的有()A .1种B .2种C .3种D .4种4.在一个不透明的袋子里装有两个红球和两个黄球,它们除颜色外都相同.随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到黄球的概率是()A .12B .13C .14D .165.如图所示,数轴上点P 所表示的可能是()A .6B .10C .15D .316.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是()A .0.4米B .0.5米C .0.8米D .1米第2题图A .B .C.D .10 1 2 3 4 P第5题图O第6题图7.一块蓄电池的电压为定值,使用此蓄电池为电源时,电流I (A )与电阻R (Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A ,那么此用电器的可变电阻应()A .不小于 4.8ΩB .不大于 4.8ΩC .不小于14ΩD .不大于14Ω8.一艘轮船从港口O 出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B .若以港口O 为坐标原点,正东方向为x 轴的正方向,正北方向为y 轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B 所在位置的坐标是()A .(3035030),B .(3030350),C .(30330),D .(30303),二、填空题(本题满分18分,共有6道小题,每小题3分)请将9-14各小题的答案填写在第14小题后面给出表格的相应位置上9.我国首个火星探测器“萤火一号”已通过研制阶段的考核和验证,并将于今年下半年发射升空,预计历经约10个月,行程约380 000 000公里抵达火星轨道并定位.将380 000 000公里用科学记数法可表示为公里.10.在第29届奥林匹克运动会上,青岛姑娘张娟娟为中国代表团夺得了历史上首枚奥运会射箭金牌,为祖国争得了荣誉.下表记录了她在备战奥运会期间的一次训练成绩(单位:环):序号 1 2 3 4 5 6 7 8 9 10 11 12 成绩9910981010987109 根据表中的数据可得:张娟娟这次训练成绩的中位数是环,众数是环.11.如图,A B 为O ⊙的直径,C D 为O ⊙的弦,42A C D°,则B A D°.12.某公司2006年的产值为500万元,2008年的产值为720万元,则该公司产值的年平均增长率为.13.如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A 顺时针旋转45°,则这两个正方形重叠部分的面积是.14.如图,长方体的底面边长分别为1cm 和3cm ,高为6cm .如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ,那么所用细线最短需要cm ;如果从点A 开始经过4个侧面缠绕n 圈到达点B ,那么所用细线最短需要cm .6 OR/ΩI /A8 第7题图Oxy第8题图AO DACB第11题图ADCBCDB第13题图EB A6cm3cm 1cm第14题图三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.15.为美化校园,学校准备在如图所示的三角形(A B C △)空地上修建一个面积最大的圆形花坛,请在图中画出这个圆形花坛.解:结论:四、解答题(本题满分74分,共有9道小题)16.(本小题满分8分,每题4分)(1)化简:2211x xx x(2)解不等式组:3221317.22xxxx ,≤17.(本小题满分6分)某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣爱好情况,并根据调查结果制作了如下两幅统计图.根据图中提供的信息解答下列问题:(1)补全人数统计图;(2)若该校共有1500名学生,请你估计该校在课余时间喜欢阅读的人数;(3)结合上述信息,谈谈你对该校学生课余活动的意见和建议(字数不超过30字).ABC50 40 30 20 10 0运动娱乐阅读其他项目402515人数统计图人数/人阅读其他娱乐运动40%分布统计图在“六·一”儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得15元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算?请说明理由.19.(本小题满分6分)在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角21C F E°,然后往塔的方向前进50米到达B处,此时测得仰角37C G E°,已知测倾器高 1.5米,请你根据以上数据计算出古塔CD的高度.(参考数据:3sin375°≈,3ta n374°≈,9sin2125°≈,3ta n218°≈)20.(本小题满分8分)北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率100%利润成本)CG EDBAF第19题图红黄黄绿绿绿绿黄绿第18题图已知:如图,在A B C D 中,AE 是BC 边上的高,将A B E △沿B C 方向平移,使点E 与点C 重合,得G F C △.(1)求证:B E D G ;(2)若60B°,当AB 与BC 满足什么数量关系时,四边形A B F G 是菱形?证明你的结论.22.(本小题满分10分)某水产品养殖企业为指导该企业某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查.调查发现这种水产品的每千克售价1y (元)与销售月份x (月)满足关系式3368yx,而其每千克成本2y (元)与销售月份x (月)满足的函数关系如图所示.(1)试确定b c 、的值;(2)求出这种水产品每千克的利润y (元)与销售月份x (月)之间的函数关系式;(3)“五·一”之前,几月份出售这种水产品每千克的利润最大?最大利润是多少?23.(本小题满分10分)我们在解决数学问题时,经常采用“转化”(或“化归”)的思想方法,把待解决的问题,通过某种转化过程,归结到一类已解决或比较容易解决的问题.譬如,在学习了一元一次方程的解法以后,进一步研究二元一次方程组的解法时,我们通常采用“消元”的方法,把二元一次方程组转化为一元一次方程;再譬如,在学习了三角形内角和定理以后,进一步研究多边形的内角和问题时,我们通常借助添加辅助线,把多边形转化为三角形,从而解决问题.问题提出:如何把一个正方形分割成n (n ≥9)个小正方形?为解决上面问题,我们先来研究两种简单的“基本分割法”.ADGCBFE 第21题图2524y 2(元)x (月)1 2 3 4 5 6 7 8 910 11 12第22题图2218y xbx cO基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形.基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.图①图②图③图④图⑤图⑥问题解决:有了上述两种“基本分割法”后,我们就可以把一个正方形分割成n(n≥9)个小正方形.(1)把一个正方形分割成9个小正方形.一种方法:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成459(个)小正方形.另一种方法:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成639(个)小正方形.(2)把一个正方形分割成10个小正方形.方法:如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加32个小正方形,从而分割成43210(个)小正方形.(3)请你参照上述分割方法,把图⑥给出的正方形分割成11个小正方形(用钢笔或圆珠笔画出草图即可,不用说明分割方法)(4)把一个正方形分割成n(n≥9)个小正方形.方法:通过“基本分割法1”、“基本分割法2”或其组合把一个正方形分割成9个、10个和11个小正方形,再在此基础上每使用1次“基本分割法1”,就可增加3个小正方形,从而把一个正方形分割成12个、13个、14个小正方形,依次类推,即可把一个正方形分割成n (n≥9)个小正方形.从上面的分法可以看出,解决问题的关键就是找到两种基本分割法,然后通过这两种基本分割法或其组合把正方形分割成n(n≥9)个小正方形.类比应用:仿照上面的方法,我们可以把一个正三角形分割成n(n≥9)个小正三角形.(1)基本分割法1:把一个正三角形分割成4个小正三角形(请你在图a中画出草图).(2)基本分割法2:把一个正三角形分割成6个小正三角形(请你在图b中画出草图).(3)分别把图c、图d和图e中的正三角形分割成9个、10个和11个小正三角形(用钢笔或圆珠笔画出草图即可,不用说明分割方法)图a图b图c图d图e(4)请你写出把一个正三角形分割成n(n≥9)个小正三角形的分割方法(只写出分割方法,不用画图).24.(本小题满分12分)如图,在梯形ABCD 中,A D B C ∥,6cm A D,4cm C D,10cm B CB D,点P由B 出发沿BD 方向匀速运动,速度为1cm/s ;同时,线段EF 由DC 出发沿DA 方向匀速运动,速度为1cm/s ,交B D 于Q ,连接PE .若设运动时间为t (s )(05t).解答下列问题:(1)当t 为何值时,P E A B ∥?(2)设P E Q △的面积为y (cm 2),求y 与t 之间的函数关系式;(3)是否存在某一时刻t ,使225P E QB C DS S △△?若存在,求出此时t 的值;若不存在,说明理由.(4)连接P F ,在上述运动过程中,五边形P F C D E 的面积是否发生变化?说明理由.AE DQPBFC第24题图二○○九年山东省青岛市初级中学学业水平考试数学试题参考答案及评分标准说明:1.如果考生的解法与本解法不同,可参照本评分标准制定相应评分细则.2.当考生的解答在某一步出现错误,影响了后继部分时,如果这一步以后的解答未改变这道题的内容和难度,可视影响程度决定后面部分的给分.但不得超过后面部分应给分数的一半,如果这一步以后的解答有较严重的错误,就不给分.3.为阅卷方便,本解答中的推算步骤写得较为详细,但允许考生在解答过程中,合理省略非关键性的推算步骤.4.解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题满分24分,共有8道小题,每小题3分)题号 1 2 3 4 5 6 7 8答案 C D B C B D A A 二、填空题(本题满分18分,共有6道小题,每小题3分)题号9 10 11答案83.8109 9 48题号12 13 14答案20% 211022916n(或23664n)三、作图题(本题满分4分)15.正确画出两条角平分线,确定圆心;···········································································2分确定半径;·····················································································································3分正确画出图并写出结论.······························································································4分四、解答题(本题满分74分,共有9道小题)16.(本小题满分8分)(1)解:原式21(1)(1)x xx x x1xx.········································································································4分(2)322131722x xx x①≤②解:解不等式①得2x,解不等式②得4x≤.所以原不等式组的解集为24x≤.··········································································4分17.(本小题满分6分)解:(1)正确补全统计图; ··································································································2分(2)300人. ························································································································4分(3)合理即可. ···················································································································6分18.(本小题满分6分)解:13580502016.5202020(元),··································································4分∵16.55元元∴选择转转盘对顾客更合算. ······························································································6分19.(本小题满分6分)解:由题意知C D A D ⊥,E F A D ∥,∴90C E F°,设C Ex ,在R t C E F △中,ta nC E C F EE F,则8ta nta n 213C E x E Fx C F E°;在R t C E G △中,ta nC E C G EG E,则4ta nta n 373C E x G Ex C G E °;······················ 4分∵E F F G E G ,∴845033xx .37.5x ,∴37.51.539C DC EE D(米).答:古塔的高度约是39米. ································································································6分20.(本小题满分8分)解:(1)设商场第一次购进x 套运动服,由题意得:6800032000102xx,·········································································································3分解这个方程,得200x.经检验,200x是所列方程的根.22200200600xx.所以商场两次共购进这种运动服600套. ···········································································5分(2)设每套运动服的售价为y 元,由题意得:600320006800020%3200068000y≥,解这个不等式,得200y ≥,所以每套运动服的售价至少是200元. ···············································································8分21.(本小题满分8分)证明:(1)∵四边形A B C D 是平行四边形,∴A BC D .∵A E 是B C 边上的高,且C G 是由A E 沿B C 方向平移而成.∴C G A D ⊥.CGEDB AF第19题图∴90A E B C G D°.∵A E C G ,∴R t R t A B E C D G △≌△.∴B ED G . ······················································································································4分(2)当32B CA B 时,四边形A B F C 是菱形.∵A B G F ∥,A G B F ∥,∴四边形A B F G 是平行四边形.∵R t A B E △中,60B°,∴30B A E°,∴12B E A B .∵32B E C F B C A B ,,∴12E F A B .∴A BB F .∴四边形A B F G 是菱形. ····································································································8分22.(本小题满分10分)解:(1)由题意:22125338124448b cb c解得7181292b c························································································································4分(2)12yy y 23115136298882x xx 21316822xx ;································································································6分(3)21316822yxx2111(1236)46822xx21(6)118x ADGCBFE 第21题图08a,∴抛物线开口向下.在对称轴6x 左侧y 随x 的增大而增大.由题意5x ,所以在4月份出售这种水产品每千克的利润最大. ···································9分最大利润211(46)111082(元).········································································10分23.(本小满分10分)解:把一个正方形分割成11个小正方形:···················································································2分把一个正三角形分割成4个小正三角形:···················································································3分把一个正三角形分割成6个小正三角形:················································································5分把一个正三角形分割成9个、10个和11个小正三角形:······················································8分把一个正三角形分割成n (9n ≥)个小正三角形的分割方法:通过“基本分割法1”、“基本分割法2”或其组合,把一个正三角形分割成9个、10个和11个小正三角形,再在此基础上每使用1次“基本分割法1”,就可增加3个小正三角形,从而把一个正三角形分割成12个、13个、14个小正三角形,依次类推,即可把一个正三角形分割成n (9n ≥)个小正三角形.····························································································································10分24.(本小题满分12分)解:(1)∵P E A B ∥∴D E D P D AD B.而10D E t D P t ,,∴10610t t,∴154t.图⑥图a图b图c图e图d AE DQPBFCN M(s )4tP E A B ,∥.···························2分(2)∵E F 平行且等于C D ,∴四边形C D E F 是平行四边形.∴D E QC D Q EB DC ,.∵10B C B D,∴D E QCD Q EB DC .∴D E Q B C D △∽△.∴D E E Q B CC D.104t E Q .∴25E Qt .过B 作B M C D ⊥,交C D 于M ,过P 作P N E F ⊥,交E F 于N .2210210049646B M.∵E D D Q B Pt ,∴102P Qt .又P N Q B M D △∽△,P Q P N B D B M,1021046t P N,4615t P N 211246464612255255P E Qt S E Q P Nt tt △.····································6分(3)114468622B C DS C D B M△.若225P E QB C DS S △△,则有2464628625525tt,解得1214t t ,.···············································································································9分(4)在P D E △和F B P △中,10D E B P t P DB Ft P D E F B PP D EF B P ,,△≌△,∴P D EP F C D EP F C DS S S △五边形四边形F B PP F C DS S △四边形86B C DS △.∴在运动过程中,五边形P F C D E 的面积不变.·······························································12分。
2009中考数学题及答案

2009年大连市中考数学试题与参考答案注意事项:1.请将答案写在答题卡上,写在试卷上无效. 2.本试卷满分150分,考试时间120分钟.一、选择题(在每小题给出的四个选项中,只有一个正确答案.本大题共有8小题,每小题3分,共24分) 1.|-3|等于 ( )A .3B .-3C .31D .-31 2.下列运算正确的是 ( )A .523x x x =+ B .x x x =-23C .623x x x =⋅ D .x x x =÷233.函数2-=x y 中,自变量x 的取值范围是 ( )A .x < 2B .x ≤2C .x > 2D .x ≥24.将一张等边三角形纸片按图1-①所示的方式对折,再按图1-②所示 的虚线剪去一个小三角形,将余下纸片展开得到的图案是 ( )5.下列的调查中,选取的样本具有代表性的有 ( )A .为了解某地区居民的防火意识,对该地区的初中生进行调查B .为了解某校1200名学生的视力情况,随机抽取该校120名学生进行调查C .为了解某商场的平均晶营业额,选在周末进行调查D .为了解全校学生课外小组的活动情况,对该校的男生进行调查6.如图,等腰梯形ABCD 中,AD ∥BC ,AE ∥DC ,∠AEB =60°, AB = AD = 2cm ,则梯形ABCD 的周长为 ( ) A .6cm B .8cm C .10cm D .12cm 7.下列四个点中,有三个点在同一反比例函数xky =的图象上,则不在这个函数图象上的点是 ( ) A .(5,1) B .(-1,5) C .(35,3) D .(-3,35-)8.图3是一个几何体的三视图,其中主视图、左视图都是腰为13cm ,底为10cm 的等腰三角形,则这个几何的侧面积是 ( )A .60πcm 2B .65πcm 2C .70πcm 2D .75πcm 2图1②①DCBA 图2俯视图左视图主视图图3DC BA二、填空题(本题共有9小题,每小题3分,共27分)9.某天最低气温是-5℃,最高气温比最低气温高8℃,则这天的最高气温是_________℃. 10.计算)13)(13(-+=___________.11.如图4,直线a ∥b ,∠1 = 70°,则∠2 = __________.12.如图5,某游乐场内滑梯的滑板与地面所成的角∠A = 35°,滑梯的高度BC = 2米,则滑板AB 的长约为_________米(精确到0.1).13.在某智力竞赛中,小明对一道四选一的选择题所涉及的知识完全不懂,只能靠猜测得出结果,则他答对这道题的概率是_______________.14.若⊙O 1和⊙O 2外切,O 1O 2 = 10cm ,⊙O 1半径为3cm ,则⊙O 2半径为___________cm .15.图6是某班为贫困地区捐书情况的条形统计图,则这个班平均每名学生捐书_____________册. 16.图7是一次函数b kx y +=的图象,则关于x 的不等式0>+b kx 的解集为_________________.17.如图8,原点O 是△ABC 和△A ′B ′C ′的位似中心,点A (1,0)与点A ′(-2,0)是对应点,△ABC 的面积是23,则△A ′B ′C ′的面积是________________. 三、解答题(本题共有3小题,18题、19题、20题各12分,共36分) 18.如图9,在△ABC 和△DEF 中,AB = DE ,BE = CF ,∠B =∠1. 求证:AC = DF (要求:写出证明过程中的重要依据)21c b a 图 4CBA 图 5 491017201510554320人数册数图 6 O y x -24图 7 A C B A′123-1-2-3-4-3-2-14321O y x 图 8 1F E DCBA19.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图10所示的统计表,根据统计图提供的信息解决下列问题:⑴这种树苗成活的频率稳定在_________,成活的概率估计值为_______________. ⑵该地区已经移植这种树苗5万棵. ①估计这种树苗成活___________万棵;②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?20.甲、乙两车间生产同一种零件,乙车间比甲车间平均每小时多生产30个,甲车间生产600个零件与乙车间生产900个零件所用时间相等,设甲车间平均每小时生产x 个零件,请按要求解决下列问题: ⑴根据题意,填写下表: 车间 零件总个数平均每小时生产零件个数所用时间甲车间 600xx600乙车间900________⑵甲、乙两车间平均每小时各生产多少个零件?四、解答题(本题3小题,其中21、22题各9分,23题10分,共28分) 21.如图11,在⊙O 中,AB 是直径,AD 是弦,∠ADE = 60°, ∠C = 30°.⑴判断直线CD 是否是⊙O 的切线,并说明理由; ⑵若CD = 33 ,求BC 的长.图 10 0成活的概率移植数量/千棵10.90.8108642E DCBA O图 1122.如图12,直线2--=x y 交x 轴于点A ,交y 轴于点B ,抛物线c bx ax y ++=2的顶点为A ,且经过点B . ⑴求该抛物线的解析式; ⑵若点C(m ,29-)在抛物线上,求m 的值.23.A 、B 两地的路程为16千米,往返于两地的公交车单程运行40分钟.某日甲车比乙车早20分钟从A 地出发,到达B 地后立即返回,乙车出发20分钟后因故停车10分钟,随后按原速继续行驶,并与返回途中的甲车相遇.图13是乙车距A 地的路程y (千米)与所用时间x (分)的函数图象的一部分(假设两车都匀速行驶). ⑴请在图13中画出甲车在这次往返中,距A 地的路程y (千米)与时间x (分)的函数图象; ⑵乙车出发多长时间两车相遇?五、解答题(本题共有3小题,其中24题11分,25、26题各12分,共25分)24.如图14,矩形ABCD 中,AB = 6cm ,AD = 3cm ,点E 在边DC 上,且DE = 4cm .动点P 从点A 开始沿着A →B →C →E 的路线以2cm/s 的速度移动,动点Q 从点A 开始沿着AE 以1cm/s 的速度移动,当点Q 移动到点E 时,点P 停止移动.若点P 、Q 同时从点A 同时出发,设点Q 移动时间为t (s),P 、Q 两点运动路线与线段PQ 围成的图形面积为S (cm2),求S 与t 的函数关系式.25.如图15,在△ABC 和△PQD 中,AC = k BC ,DP = k DQ ,∠C =∠PDQ ,D 、E 分别是AB 、AC 的中点,点P 在直线BC 上,连结EQ 交PC 于点H .PQE D CB A 图 14 y/千米16O -2080604020x/分图 13 yx O B A 图 12猜想线段EH 与AC 的数量关系,并证明你的猜想.26.如图18,抛物线F :c bx ax y ++=2的顶点为P ,抛物线:与y 轴交于点A ,与直线OP 交于点B .过点P 作PD ⊥x 轴于点D ,平移抛物线F 使其经过点A 、D 得到抛物线F ′:'+'+'=c x b x a y 2,抛物线F ′与x 轴的另一个交点为C .⑴当a = 1,b =-2,c = 3时,求点C 的坐标(直接写出答案); ⑵若a 、b 、c 满足了ac b 22=①求b :b ′的值;②探究四边形OABC 的形状,并说明理由.Q(H)EDCQAB CDEPH H Q P ED CB A B(P)A图 15 图 16图 17yxO P DC BA图 18大连市2009年初中升学考试评分标准与参考答案一、选择题1. A 2.D 3.D 4.A 5.B 6.C 7.B 8.B 二、填空题9.3 10.2 11.110° 12.3.5 13.4114.7 15.3 16.2->x 17.6 三、解答题18.证明:∵BE=CF , ∴BE+EC=CF+EC ,即 B C =E F . ………………………………………………………………………………2分 在△ABC 和△DEF 中,314AB DE B BC EF =⎧⎪∠=∠⎨⎪=⎩,分,分. ∴△A B C ≌△D E F …………………………………………………………………………6分 (S A S ) . ……………………………………………………………………………………8分 ∴A C =D F …………………………………………………………………………………10分 (全等三角形对应边相等) . ……………………………………………………………12分 19.解:(1)0.9,……………………………………………………………………………2分 0.9; ………………………………………………………………………………………5分 (2) ①4.5;…………………………………………………………………………………8分 ②方法1:18÷0.9-5 …………………………………………………………………………………10分 =15.…………………………………………………………………………………………11分方法2:设还需移植这种树苗x 万棵.根据题意,得189.0)5(=⨯+x ,…………………………………………………………10分 解得15=x . ………………………………………………………………………………11分 答:该地区需移植这种树苗约15万棵. ………………………………………………12分 20. 解:(1) 30+x , ……………………………………………………………………2分 3900+x ;………………………………………………………………………………………4分 (2)根据题意,得30900600+=x x ,..................................................................7分 解得 60=x . (9)分 9030=+x . …………………………………………………………………10分 经检验60=x 是原方程的解,且都符合题意.………………………………………11分 答:甲车间每小时生产60个零件,乙车间每小时生产90个零件.…………………12分 21.(1)C D 是⊙O 的切线. …………………………………………………………………1分 证明:连接OD .∵∠A D E =60°,∠C =30°,∴∠A =30°. ............................................................2分 ∵O A =O D ,∴∠O D A =∠A =30°. (3)分∴∠O D E =∠O D A +∠A D E =30°+60°=90°,∴O D ⊥C D .…………………………………4分 ∴C D 是⊙O 的切线. ……………………………………………………………………5分 (2)解:在Rt △ODC 中,∠ODC =90°, ∠C =30°, CD =33.∵t a n C =CDOD, …………………………………………………………………………6分 ∴O D =C D ·t a n C =33×33=3. (7)分 ∴O C =2O D =6.…………………………………………………………………………8分 ∵O B =O D =3,∴B C =O C -O B =6-3=3.………………………………………………9分22. 解:(1)直线2--=x y .令2,0-==y x 则,∴点B 坐标为(0,-2).………………………………………………1分 令2,0-==x y 则 ∴点A 坐标为(-2,0). ………………………………………………2分 设抛物线解析式为k h x a y +-=2)(. ∵抛物线顶点为A ,且经过点B ,∴2)2(+=x a y ,………………………………………………………………………4分∴-2=4a ,∴21-=a .…………………………………………………………………5分 ∴抛物线解析式为2)2(21+-=x y ,…………………………………………………5分∴22212---=x x y .………………………………………………………………6分(2)方法1:∵点C (m ,29-)在抛物线2)2(21+-=x y 上,∴29)2(212-=+-m ,9)2(2=+m ,………………………………………………7分解得11=m ,52-=m .……………………………………………………………9分 方法2:∵点C (m ,29-)在抛物线22212---=x x y 上,∴22212---m m 29-=,∴,0542=-+m m (7)分解得11=m ,52-=m .……………………………………………………………9分 23.解:(1)画出点P 、M 、N (每点得1分)……………………………………3分 (2)方法1.设直线EF 的解析式为11b x k y +=. 根据题意知,E (30,8),F (50,16),⎪⎩⎪⎨⎧+=+=分分5.1150164,11308 b k b k 解得⎪⎩⎪⎨⎧-==.4,5211b k ∴452-=x y .①……………………………………………………………6分设直线MN 的解析式为22b x k y +=. 根据题意知,M (20,16),N (60,0),∴⎩⎨⎧+=+=分分8.6007,20162222 b k b k 解得⎪⎩⎪⎨⎧=-=.24,5222b k ∴2452+-=x y .②………………………………………………………9分由①、②得方程452-x 2452+-=x ,解得x =35. ……………………………………(10分) 答:乙车出发35分钟两车相遇. ………………………………………………………10分 方法2.公交车的速度为16÷40=52(千米/分). …………………………………………………4分设乙车出发x 分钟两车相遇. ……………………………………………………………5分根据题意,得32)20(52)10(52=++-x x ,………………………………………………8分解得x =35. …………………………………………………………………………………9分 答:乙车出发35分钟两车相遇. ………………………………………………………10分 方法3.公交车的速度为16÷40=52(千米/分). …………………………………………………4分设乙车出发x 分钟两车相遇. ……………………………………………………………5分根据题意,得16)20(52)10(52=-+-x x ,………………………………………………8分解得x =35. …………………………………………………………………………………9分 答:乙车出发35分钟两车相遇. ………………………………………………………10分 方法4.由题意知:M (20,16),F (50,16),C (10,0),∵△DMF ∽△DNC ,∴DHDICN MF =∴DHDH -=165030,∴DH =10; ∵△CDH ∽△CFG ,∴CGCH FG DH =,∴25164010=⨯=CH ; ∴OH =OC +CH =10+25=35.答:乙车出发35分钟两车相遇. …………………………………………………………10分24.解:在R t △A D E 中,.5432222=+=+=DE AD AE …………………………1分当0<t ≤3时,如图1. ……………………………………………………………………2分过点Q 作QM ⊥AB 于M ,连接QP . ∵AB ∥CD , ∴∠QAM =∠DEA ,又∵∠AMQ =∠D =90°, ∴△AQM ∽△EAD .∴AEAQAD QM =,∴t AE AQ AD QM 53=⋅=.……………………………………………………3分 .5353221212t t t QM AP S =⨯⨯=⋅= (4)分 当3<t ≤29时,如图2. (5)分方法1 :在Rt △ADE 中,.5432222=+=+=DE AD AE过点Q 作QM ⊥AB 于M , QN ⊥BC 于N , 连接QB . ∵AB ∥CD , ∴∠QAM =∠DEA , 又∵∠AMQ =∠ADE =90°, ∴△AQM ∽△EAD . ∴AE AQ AD QM =, AEAQ DE AM =, ∴t AE AQ AD QM 53=⋅=.………………………………………………………………………6分t AE AQ DE AM 54=⋅=,∴Q N =t AM BM 5466-=-=.…………………………………7分∴QAB S ∆,595362121t t QM AB =⨯⨯=⋅=QBP S ∆.1854254)546)(62(21212-+-=--=⋅=t t t t QN BP∴QBP QAB S S S ∆∆+=t 59=+(18542542-+-t t ).18551542-+-=t t ……………………8分方法2 :过点Q 作QM ⊥AB 于M , QN ⊥BC 于N ,连接QB . ∵AB ∥BC , ∴∠QAM =∠DEA , 又∵∠AMQ =∠ADE =90°,∴△AQM ∽△EAD . ∴AE AQ AD QM =, AEAQ DE AM =, ∴t AE AQ AD QM 53=⋅=.………………………………………………………………………6分t AE AQ DE AM 54=⋅=,∴Q N =t AM BM 5466-=-=.…………………………………7分∴.256535421212t t t QM AM S AMQ =⨯⨯=⋅=∆.185512526)546)(5362(21)(212-+-=-+-=⋅+=t t t t t BM QM BP S BPQM 梯∴BPQM AMQ S S S 梯+=∆2256t =+(1855125262-+-t t ).18551542-+-=t t ……………8分 当29<t ≤5时. 方法1 :过点Q 作QH ⊥CD 于H . 如图3.由题意得QH ∥AD ,∴△EHQ ∽△EDA ,∴,AEQEAD QH = ∴).5(53t AE QE AD QH -=⋅=…………………………………………………………………10分 ∴,123)62(21)(21=⨯+=⋅+=BC AB EC S ABCE 梯,233106353)5(53)211(21212+-=-⨯-=⋅=∆t t t t QH EP S EQP∴EQP ABCE S S S ∆-=梯12=2331063532-+-t t .291063532-+-=t t ………………………11分方法2:连接QB 、QC ,过点Q 分别作QH ⊥DC 于H ,QM ⊥AB 于M ,QN ⊥BC 于N . 如图4.由题意得QH ∥AD ,∴△EHQ ∽△EDA ,∴,AEQEAD QH =∴).5(53t AE QE AD QH -=⋅=…………………………………………………………………10分∴.595362121t t QN AB S QAB =⨯⨯=⋅=∆.569)546(32121t t QN BC S QBC -=-⨯=⋅=∆.227105753)533)(92(21212-+-=--=⋅=∆t t t t QH PC S QCP∴QCP QBC QAB S S S S ∆∆∆++=t 59=)569(t -+)227105753(2-+-+t t .291063532-+-=t t ………………………………11分 25.结论:E H =21A C . (1)分 证明:取B C 边中点F ,连接D E 、D F . ……………………………………………………2分∵D 、E 、F 分别是边AB 、AC 、BC 的中点.∴DE ∥BC 且DE =21BC ,D F ∥A C 且D F =21A C , (4)分EC =21AC ∴四边形DFCE 是平行四边形.∴∠EDF=∠C .∵∠C =∠P D Q ,∴∠P D Q =∠E D F , ∴∠P D F =∠Q D E .…………………………6分又∵AC=kBC ,∴DF=kDE . ∵D P =k D Q ,∴k DEDFDQ DP ==.……………………………………………………………7分 ∴△PDF ∽△QDE . …………………………………………………………………………8分∴∠D E Q =∠D F P . ……………………………………………………………………………9分 又∵DE ∥BC ,DF ∥AC , ∴∠DEQ=∠EHC ,∠DFP=∠C .∴∠C =∠E H C . ……………………………………………………………………………10分∴E H =E C . (11)分 ∴E H =21A C . (12)分 选图16.结论:E H =21A C . (1)分 证明:取B C 边中点F ,连接D E 、D F . ……………………………………………2分∵D 、E 、F 分别是边AB 、AC 、BC 的中点,∴D E ∥B C 且D E =21B C , D F ∥A C 且D F =21A C , (4)分EC=21AC ,∴四边形DFCE 是平行四边形.∴∠EDF=∠C .∵∠C =∠P D Q ,∴∠P D Q =∠E D F , ∴∠P D F =∠Q D E . ……………………………6分 又∵A C =B C , ∴D E =D F ,∵P D =Q D ,∴△P D F ≌△Q D E . ……………………………7分∴∠DEQ=∠DFP .∵DE ∥BC ,DF ∥AC , ∴∠DEQ=∠EHC ,∠DFP=∠C .∴∠C =∠E H C .............................................................................................8分 ∴E H =E C . (9)分 ∴E H =21A C . (10)分 选图17. 结论: E H =21A C . (1)分证明:连接A H . ………………………………………………………………………………2分 ∵D 是AB 中点,∴DA=DB .又∵DB=DQ ,∴DQ=DP=AD .∴∠DBQ=∠DQB ,.∵∠DBQ+∠DQB+∠DQA+∠DAQ ,=180°,∴∠AQB=90°,∴AH ⊥BC .……………………………………………………………………………………4分又∵E 是A C 中点,∴H E =21A C . ……………………………………………………6分 26.解:(1) C (3,0);……………………………………………………………………3分(2)①抛物线c bx ax y ++=2,令x =0,则y =c , ∴A 点坐标(0,c ).∵ac b 22=,∴ 242424442ca ac a ac ac ab ac ==-=-,∴点P 的坐标为(2,2ca b -). ……………………………………………………4分∵P D ⊥x 轴于D ,∴点D 的坐标为(0,2ab-). ……………………………………5分根据题意,得a=a ′,c= c ′,∴抛物线F ′的解析式为c x b ax y ++='2.又∵抛物线F ′经过点D (0,2a b-),∴c a b b ab a +-+⨯=)2('4022.……………6分∴ac bb b 4'202+-=.又∵ac b 22=,∴'2302bb b -=.∴b :b ′=32.…………………………………………………………………………………7分 ②由①得,抛物线F ′为c bx ax y ++=232.令y =0,则0232=++c bx ax .………………………………………………………………8分∴abx a b x -=-=21,2.∵点D 的横坐标为,2a b -∴点C 的坐标为(0,ab-). ……………………………………9分设直线OP 的解析式为kx y =.∵点P 的坐标为(2,2ca b -), ∴k a b c 22-=,∴22222b b b b ac b ac k -=-=-=-=,∴x b y 2-=.………………………10分 ∵点B 是抛物线F 与直线OP 的交点,∴x bc bx ax 22-=++.∴abx a b x -=-=21,2.∵点P 的横坐标为a b 2-,∴点B 的横坐标为ab-.把a b x -=代入x b y 2-=,得c a aca b a b b y ===--=222)(22.∴点B 的坐标为),(c ab-.…………………………………………………………………11分∴BC ∥OA ,AB ∥OC .(或BC ∥OA ,BC =OA ), ∴四边形OABC 是平行四边形. 又∵∠AOC =90°,∴四边形OABC 是矩形. ………………………………………………12分。
【青岛中考数学试题及答案】2009

二○○九年山东省青岛市初级中学学业水平考试数 学 试 题(考试时间:120分钟;满分:120分)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功! 1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.2.本试题共有24道题.其中1-8题为选择题.请将所选答案的标号填写在第8题后面给出表格的相应位置上;9-14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15-24题请在试题给出的本题位置上做答.一、选择题(本题满分24分,共有8道小题,每小题3分)下列每小题都给出标号为A 、B 、C 、D 的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1-8各小题所选答案的标号填写在第8小题后面给出表格的相应位置上.1.下列四个数中,其相反数是正整数的是( ) A .3B .13C .2-D .12-2.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是( )3.在等边三角形、平行四边形、矩形、等腰梯形和圆中,既是轴对称图形又是中心对称图形的有( ) A .1种 B .2种 C .3种 D .4种4.在一个不透明的袋子里装有两个红球和两个黄球,它们除颜色外都相同.随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到黄球的概率是( ) A .12B .13C .14D .165.如图所示,数轴上点P 所表示的可能是( ) A .6B .10C .15D .316.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是( ) A .0.4米 B .0.5米 C .0.8米 D .1米7.一块蓄电池的电压为定值,使用此蓄电池为电源时,电流I (A )与电阻R (Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A ,那么此用电器的可变电阻应( ) A .不小于4.8Ω B .不大于4.8Ω C .不小于14Ω D .不大于14Ω第2题图A .B . C. D .1- 0 1 2 3 4P第5题图 O第6题图8.一艘轮船从港口O 出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A 处,此时观测到其正西方向50海里处有一座小岛B .若以港口O 为坐标原点,正东方向为x 轴的正方向,正北方向为y 轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B 所在位置的坐标是( ) A .(3035030)-, B .(3030350)-, C .(30330),D .(30303), 二、填空题(本题满分18分,共有6道小题,每小题3分)请将9-14各小题的答案填写在第14小题后面给出表格的相应位置上9.我国首个火星探测器“萤火一号”已通过研制阶段的考核和验证,并将于今年下半年发射升空,预计历经约10个月,行程约380 000 000公里抵达火星轨道并定位.将380 000 000公里用科学记数法可表示为 公里.10.在第29届奥林匹克运动会上,青岛姑娘张娟娟为中国代表团夺得了历史上首枚奥运会射箭金牌,为祖国争得了荣誉.下表记录了她在备战奥运会期间的一次训练成绩(单位:环): 序号 123456789101112成绩9 9 10 9 8 10 10 9 8 7 10 9根据表中的数据可得:张娟娟这次训练成绩的中位数是 环,众数是 环. 11.如图,AB 为O ⊙的直径,CD 为O ⊙的弦,42ACD ∠=°,则BAD ∠= °. 12.某公司2006年的产值为500万元,2008年的产值为720万元,则该公司产值的年平均增长率为 . 13.如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A 顺时针旋转45°,则这两个正方形重叠部分的面积是 .14.如图,长方体的底面边长分别为1cm 和3cm ,高为6cm .如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ,那么所用细线最短需要 cm ;如果从点A 开始经过4个侧面缠绕n 圈到达点B ,那么所用细线最短需要 cm .三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹.15.为美化校园,学校准备在如图所示的三角形(ABC △)空地上修建一个面积最大的圆形花坛,请在图中画出这个圆形花坛. 解:6 O R /Ω I /A 8 第7题图O x y 第8题图 A OD A C B第11题图 ABA D CBC 'D ' B ' 第13题图E B A 6cm3cm 1cm第14题图结论:四、解答题(本题满分74分,共有9道小题) 16.(本小题满分8分,每题4分)(1)化简:2211x x x x +-÷ (2)解不等式组:3221317.22x x x x ->+⎧⎪⎨--⎪⎩,≤17.(本小题满分6分)某中学为了解该校学生的课余活动情况,采用抽样调查的方式,从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣爱好情况,并根据调查结果制作了如下两幅统计图.根据图中提供的信息解答下列问题: (1)补全人数统计图;(2)若该校共有1500名学生,请你估计该校在课余时间喜欢阅读的人数;(3)结合上述信息,谈谈你对该校学生课余活动的意见和建议(字数不超过30字).18.(本小题满分6分)在“六·一”儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得15元的购物券. 转转盘和直接获得购物券,你认为哪种方式对顾客更合算?请说明理由.50 40 30 20 10运动 娱乐 阅读 其他 项目40 25 15人数统计图 人数/人 阅读 其他 娱乐 运动 40% 分布统计图 红 黄黄绿绿绿绿黄 绿19.(本小题满分6分)在一次数学活动课上,老师带领同学们去测量一座古塔CD 的高度.他们首先从A 处安置测倾器,测得塔顶C 的仰角21CFE ∠=°,然后往塔的方向前进50米到达B 处,此时测得仰角37CGE ∠=°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD 的高度. (参考数据:3sin 375°≈,3tan 374°≈,9sin 2125°≈,3tan 218°≈)20.(本小题满分8分)北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套? (2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率100%=⨯利润成本)21.(本小题满分8分) 已知:如图,在ABCD中,AE 是BC 边上的高,将ABE △沿BC 方向平移,使点E 与点C 重合,得GFC △. (1)求证:BE DG =;(2)若60B ∠=°,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.CG E D B A F第19题图 ADGCBF E 第21题图22.(本小题满分10分)某水产品养殖企业为指导该企业某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查.调查发现这种水产品的每千克售价1y (元)与销售月份x (月)满足关系式3368y x =-+,而其每千克成本2y (元)与销售月份x (月)满足的函数关系如图所示. (1)试确定b c 、的值;(2)求出这种水产品每千克的利润y (元)与销售月份x (月)之间的函数关系式; (3)“五·一”之前,几月份出售这种水产品每千克的利润最大?最大利润是多少?24.(本小题满分12分)如图,在梯形ABCD 中,AD BC ∥,6cm AD =,4cm CD =,10cm BC BD ==,点P 由B 出发沿BD 方向匀速运动,速度为1cm/s ;同时,线段EF 由DC 出发沿DA 方向匀速运动,速度为1cm/s ,交BD 于Q ,连接PE .若设运动时间为t (s )(05t <<).解答下列问题: (1)当t 为何值时,PE AB ∥?(2)设PEQ △的面积为y (cm 2),求y 与t 之间的函数关系式;(3)是否存在某一时刻t ,使225PEQ BCD S S =△△?若存在,求出此时t 的值;若不存在,说明理由. (4)连接PF ,在上述运动过程中,五边形PFCDE 的面积是否发生变化?说明理由.2524y 2(元) x (月) 1 2 3 4 5 6 7 8 9 10 11 12 第22题图 2218y x bx c =++ O A E DQPBFC第24题图二○○九年山东省青岛市初级中学学业水平考试数学试题参考答案及评分标准说明:1.如果考生的解法与本解法不同,可参照本评分标准制定相应评分细则.2.当考生的解答在某一步出现错误,影响了后继部分时,如果这一步以后的解答未改变这道题的内容和难度,可视影响程度决定后面部分的给分.但不得超过后面部分应给分数的一半,如果这一步以后的解答有较严重的错误,就不给分.3.为阅卷方便,本解答中的推算步骤写得较为详细,但允许考生在解答过程中,合理省略非关键性的推算步骤. 4.解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题满分24分,共有8道小题,每小题3分) 题号 123456 7 8 答案C D B C BDAA二、填空题(本题满分18分,共有6道小题,每小题3分)题号 91011答案 83.810⨯9 948题号 12 1314答案20%21- 1022916n +(或23664n +)三、作图题(本题满分4分)15.正确画出两条角平分线,确定圆心; ············································································ 2分确定半径; ····················································································································· 3分 正确画出图并写出结论. ······························································································· 4分 四、解答题(本题满分74分,共有9道小题) 16.(本小题满分8分)(1)解:原式21(1)(1)x x x x x +=+-1xx =-. ······································································································· 4分 (2)322131722x x x x ->+⎧⎪⎨--⎪⎩①≤② 解:解不等式①得 2x >, 解不等式②得 4x ≤.所以原不等式组的解集为24x <≤. ········································································· 4分 17.(本小题满分6分)解:(1)正确补全统计图;································································································· 2分 (2)300人. ························································································································ 4分 (3)合理即可. ···················································································································· 6分 18.(本小题满分6分)解:135********.5202020⨯+⨯+⨯=(元), ······························································· 4分 ∵16.55>元元∴选择转转盘对顾客更合算. ······························································································· 6分 19.(本小题满分6分)解:由题意知CD AD ⊥,EF AD ∥,∴90CEF ∠=°,设CE x =, 在Rt CEF △中,tan CE CFE EF ∠=,则8tan tan 213CE x EF x CFE ===∠°; 在Rt CEG △中,tan CECGE GE ∠=,则4tan tan 373CE x GE x CGE ===∠°; ······················ 4分∵EF FG EG =+, ∴845033x x =+. 37.5x =,∴37.5 1.539CD CE ED =+=+=(米).答:古塔的高度约是39米.································································································· 6分 20.(本小题满分8分)解:(1)设商场第一次购进x 套运动服,由题意得:6800032000102x x-=, ········································································································ 3分 解这个方程,得200x =.经检验,200x =是所列方程的根. 22200200600x x +=⨯+=.所以商场两次共购进这种运动服600套. ············································································ 5分 (2)设每套运动服的售价为y 元,由题意得:600320006800020%3200068000y --+≥,解这个不等式,得200y ≥,所以每套运动服的售价至少是200元. ··············································································· 8分 21.(本小题满分8分)证明:(1)∵四边形ABCD 是平行四边形, ∴AB CD =.∵AE 是BC 边上的高,且CG 是由AE 沿BC 方向平移而成. ∴CG AD ⊥.∴90AEB CGD ∠=∠=°. ∵AE CG =,∴Rt Rt ABE CDG △≌△. ∴BE DG =. ······················································································································ 4分 (2)当32BC AB =时,四边形ABFC 是菱形. CGEDB AF 第19题图∵AB GF ∥,AG BF ∥, ∴四边形ABFG 是平行四边形. ∵Rt ABE △中,60B ∠=°, ∴30BAE ∠=°, ∴12BE AB =. ∵32BE CF BC AB ==,,∴12EF AB =.∴AB BF =.∴四边形ABFG 是菱形. ····································································································· 8分 22.(本小题满分10分) 解:(1)由题意:22125338124448b c b c ⎧=⨯++⎪⎪⎨⎪=⨯++⎪⎩解得7181292b c ⎧=-⎪⎪⎨⎪=⎪⎩ ······················································································································· 4分(2)12y y y =- 23115136298882x x x ⎛⎫=-+--+ ⎪⎝⎭21316822x x =-++; ······························································································· 6分 (3)21316822y x x =-++2111(1236)46822x x =--+++21(6)118x =--+ ∵108a =-<,∴抛物线开口向下.在对称轴6x =左侧y 随x 的增大而增大.由题意5x <,所以在4月份出售这种水产品每千克的利润最大. ··································· 9分 最大利润211(46)111082=--+=(元). ······································································ 10分 23.(本小满分10分)ADGC B FE 第21题图解:把一个正方形分割成11个小正方形:··················································································· 2分把一个正三角形分割成4个小正三角形:··················································································· 3分 把一个正三角形分割成6个小正三角形:··············································································· 5分 把一个正三角形分割成9个、10个和11个小正三角形:····················································· 8分把一个正三角形分割成n (9n ≥)个小正三角形的分割方法:通过“基本分割法1”、“基本分割法2”或其组合,把一个正三角形分割成9个、10个和11个小正三角形,再在此基础上每使用1次“基本分割法1”,就可增加3个小正三角形,从而把一个正三角形分割成12个、13个、14个小正三角形,依次类推,即可把一个正三角形分割成n (9n ≥)个小正三角形. ······································································· 10分 24.(本小题满分12分) 解:(1)∵PE AB ∥∴DE DPDA DB=. 而10DE t DP t ==-,, ∴10610t t -=, ∴154t =.∴当15(s)4t PE AB =,∥. ·························· 2分 (2)∵EF 平行且等于CD , ∴四边形CDEF 是平行四边形.∴DEQ C DQE BDC ∠=∠∠=∠,. ∵10BC BD ==,∴DEQ C DQE BDC ∠=∠=∠=∠. ∴DEQ BCD △∽△.图⑥图a图b图c图e图d A E D Q PBFCN M∴DE EQBC CD =. 104t EQ =. ∴25EQ t =.过B 作BM CD ⊥,交CD 于M ,过P 作PN EF ⊥,交EF 于N .2210210049646BM =-=-==.∵ED DQ BP t ===, ∴102PQ t =-. 又PNQ BMD △∽△,PQ PNBD BM=, 1021046t PN-=, 4615t PN ⎛⎫=- ⎪⎝⎭211246464612255255PEQ t S EQ PN t t t ⎛⎫==⨯⨯-=-+ ⎪⎝⎭△. ··································· 6分 (3)114468622BCD S CD BM ==⨯⨯= △. 若225PEQ BCD S S =△△, 则有2464628625525t t -+=⨯, 解得1214t t ==,. ·············································································································· 9分 (4)在PDE △和FBP △中,10DE BP t PD BF t PDE FBP PDE FBP ==⎫⎪==-⇒⎬⎪∠=∠⎭,,△≌△, ∴PDE PFCDE PFCD S S S =+△五边形四边形 FBP PFCD S S =+△四边形 86BCD S ==△.∴在运动过程中,五边形PFCDE的面积不变.·······························································12分11。
中考数学试题(word版含答案)

初中毕业生学业考试数 学 试 卷※考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个是正确的,请将正确答案的选项填在下表中相应题号下的空格内.每小题3分,共24分)1.目前国内规划中的第一高楼上海中心大厦,总投入约14 800 000 000元.14 800 000 000元用科学记数法表示为( ) A .111.4810⨯元B .90.14810⨯元C .101.4810⨯元D .914.810⨯元2.计算23(2)a -的结果为( ) A .52a -B .68a -C .58a -D .66a -3.如图所示,已知直线AB CD ∥,125C ∠=°,45A ∠=°, 则E ∠的度数为( ) A .70° B .80° C .90° D .100°4.一个圆柱体钢块,正中央被挖去了一个长方体孔,其俯视图如图所示,则此圆柱体钢块的左.视图是( )5.数据21,21,21,25,26,27的众数、中位数分别是( ) A .21,23 B .21,21 C .23,21 D .21,256.为了美化环境,某市加大对绿化的投资.2007年用于绿化投资20万元,2009年用于绿化投资25万元,求这两年绿化投资的年平均增长率.设这两年绿化投资的年平均增长率为x ,根据题意所列方程为( ) A .22025x =B .20(1)25x +=C .220(1)25x +=D .220(1)20(1)25x x +++=7.如图所示,反比例函数1y 与正比例函数2y 的图象的一个交点坐标是(21)A ,,若210y y >>,则x 的取值范围在数轴上表示为( )A .B .C .D . 俯视图第4题图 EA BCD第3题图45°125°8.将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )二、填空题(每小题3分,共24分) 9.分解因式:34a a -= . 10.函数33y x =+自变量x 的取值范围是 . 11.小丽想用一张半径为5cm 的扇形纸片围成一个底面半径为4cm 的圆锥,接缝忽略不计,则扇形纸片的面积是 cm 2.(结果用π表示)12.如图所示,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的概率是 . 13.如图所示,AB 为O ⊙的直径,P 点为其半圆上一点,40POA C ∠=°,为另一半圆上任意一点(不含A B 、),则PCB ∠= 度.14.已知抛物线()经过点,且顶点在第一象限.有下列三个结论:①0a < ②0a b c ++> ③02ba->.把正确结论的序号填在横线上 .15.如图所示,在正方形网格中,图①经过 变换(填“平移”或“旋转”或“轴对称”)可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点 (填“A ”或“B ”或“C ”). 16.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是 .A .B .C .D .y 1 2 2 1 1- (21)A , y 2 y 1 x O垂直 A . B . C . D . 第8题图 第12题图 CB A P O 40° 第13题图O y x 第14题图1- ①② ③ 第15题图A B C三、解答题(每题8分,共16分)17.计算:012|32|(2π)+-+-.18.解方程:2111x x x -=-+.四、解答题(每题10分,共20分)19.如图所示,在Rt ABC △中,9030C A ∠=∠=°,°.(1)尺规作图:作线段AB 的垂直平分线l (保留作图痕迹,不写作法);(2)在已作的图形中,若l 分别交AB AC 、及BC 的延长线于点D E F 、、,连接BE . 求证:2EF DE =.20.某市开展了党员干部“一帮一扶贫”活动.为了解贫困群众对帮扶情况的满意程度,有关部门在该市所管辖的两个区内,分别随机抽取了若干名贫困群众进行问卷调查.根据收集的信息进行了统计,并绘制了下面尚不完整的统计图.已知在甲区所调查的贫困群众中,非常满意的人数占甲区所调查的总人数的35%.根据统计图所提供的信息解答下列问题: (1)甲区参加问卷调查的贫困群众有 人; (2)请将统计图补充完整; (3)小红说:“因为甲区有30人不满意,乙区有40人不满意,所以甲区的不满意率比乙区低.”你认为这种说法正确吗?为什么?第1个图形 第2个图形 第3个图形 第4个图形第16题图A CB 第19题图 非常满意 人数 800 600 400 200 满意 比较满意 不满意 满意程度 甲 乙第20题图420 700 760500250 3040五、解答题(每题10分,共20分)21.小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选. (1)用树状图或列表法求出小明先挑选的概率; (2)你认为这个游戏公平吗?请说明理由.22.如图所示,已知AB 是半圆O 的直径,弦106CD AB AB CD ==∥,,,E 是AB 延长线上一点,103BE =.判断直线DE 与半圆O 的位置关系,并证明你的结论.六、解答题(每题10分,共20分)23.某旅游区有一个景观奇异的望天洞,D 点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A 处观看旅游区风景,最后坐缆车沿索道AB 返回山脚下的B 处.在同一平面内,若测得斜坡BD 的长为100米,坡角10DBC ∠=°,在B 处测得A 的仰角40ABC ∠=°,在D 处测得A 的仰角85ADF ∠=°,过D 点作地面BE 的垂线,垂足为C .(1)求ADB ∠的度数; (2)求索道AB 的长.(结果保留根号)O AB ED C 第22题图A C DE F B 第23题图24.为迎接国庆六十周年,某校团委组织了“歌唱祖国”有奖征文活动,并设立了一、二、三等奖.学校计划派人根据设奖情况买50件奖品,其中二等奖件数比一等奖件数的2倍还少10件,三等奖所花钱数不超过二等奖所花钱数的1.5倍.各种奖品的单价如下表所示.如果计划一等奖买x 件,买50件奖品的总钱数是w 元. (1)求w 与x 的函数关系式及自变量x 的取值范围; (2)请你计算一下,如果购买这三种奖品所花的总钱数最少?最少是多少元?一等奖 二等奖 三等奖 单价(元) 12 10 5 E图(b ) 第25题图八、解答题(本题14分)26.如图所示,已知在直角梯形OABC 中,AB OC BC x ∥,⊥轴于点(11)(31)C A B ,,、,.动点P 从O 点出发,沿x 轴正方向以每秒1个单位长度的速度移动.过P 点作PQ 垂直于直线..OA ,垂足为Q .设P 点移动的时间为t 秒(04t <<),OPQ △与直角梯形OABC 重叠部分的面积为S .(1)求经过O A B 、、三点的抛物线解析式; (2)求S 与t 的函数关系式;2009年铁岭市初中毕业生学业考试 数学试题参考答案及评分标准注:本参考答案只给出一种或几种解法(证法),若用其他方法解答并正确,可参考此评分标准相应步骤赋分.一、选择题(每小题3分,共24分) 题号 1 2 3 4 5 6 7 8 答案 C B B C A C D A∴3060EBA A AED BED ∠=∠=∠=∠=°,°,∴3060EBC EBA FEC ∠==∠∠=°,°. 又∵ED AB EC BC ⊥,⊥, ∴ED EC =. ······························································································· 8分 在Rt ECF △中,6030FEC EFC ∠=∴∠=°,°, ∴2EF EC =, ∴2EF ED =. ··························································································· 10分 第19题图(2)图形正确(甲区满意人数有500人) ··························································· 5分 (3)不正确. ······························································································· 6分 ∵甲区的不满意率是30 2.5%1200=,乙区的不满意率是402%70076050040=+++, ∴甲区的不满意率比乙区的不满意率高. ·························································· 10分五、(每题10分,共20分) 21.解:(1)根据题意可列表或树状图如下:第一次第二次1 2 3 4∵,∴2.······························· 2分 ∵1025533OE OB BE =+=+=. ····························· 3分 ∴35325553DF OD OD OE ===,, ∴DF ODOD OE=. ····························································································· 6分 ∵CD AB ∥,∴CDO DOE ∠=∠. ································································ 7分3) A第22题图∴90ODE OFD ∠=∠=°, ∴OD DE ⊥∴直线DE 与半圆O 相切. ············································································ 10分 法二:连接OD ,作OF CD ⊥于点F ,作DG OE ⊥于点G . ∵6CD =,∴132DF CD ==. 在Rt ODF △中,2222534OF OD DF =-=-= ·········································· 3分 ∵CD AB ∥,DG AB OF CD ⊥,⊥, ∴四边形OFDG 是矩形,∴43DG OF OG DF ====,. ∵1025533OE OB BE =+=+=,2516333GE OE OG =-=-=, ························ 5分 在Rt DGE △中,22221620433DE DG GE ⎛⎫=+=+= ⎪⎝⎭.∵2222025533⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭, ∴222OD DE OE += ····················································································· 8分 ∴CD DE ⊥.∴直线DE 与半圆O 相切. ············································································ 10分 六、(每题10分,共20分) 23.(1)解:∵DC CE ⊥,∴90BCD ∠=°. 又∵10DBC ∠=°, ∴80BDC ∠=°, ····················································· 1分∵85ADF ∠=°,∴360809085105ADB ∠=---=°°°°°. ·················· 2分(2)过点D 作DG AB ⊥于点G . ······························ 3分 在Rt GDB △中,401030GBD ∠=-=°°°, ∴903060BDG ∠=-=︒°° ········································ 4分 又∵100BD =, ∴111005022GD BD ==⨯=. 3cos301005032GB BD ==⨯=°. ···························································· 6分 在Rt ADG △中,1056045GDA ∠=-=︒°° ······················································ 7分 ∴50GD GA ==, ························································································ 8分 ∴50503AB AG GB =+=+(米)································································ 9分A CDEF B 第23题图G答:索道长50+ ············································································· 10分 24.解:(1)1210(210)5[50(210)]x x x x ω=+-+--- ····································· 2分17200x =+.·········································································· 3分 由02100[50(210)]05[50(210)] 1.510(210)x x x x x x x >⎧⎪->⎪⎨--->⎪⎪---⨯-⎩≤ ························································ 5分(3)当CD CB =(2BD CD =或12CD BD =或30CAD ∠=°或90BAD ∠=°或30ADC ∠=°)时,四边形BCGE 是菱形. ················ 9分 理由:法一:由①得AEB ADC △≌△, ∴BE CD = ························································· 10分 又∵CD CB =, ∴BE CB =. ······················································ 11分 由②得四边形BCGE 是平行四边形, ∴四边形BCGE 是菱形. ······································· 12分ADCBFEG 图(b ) 第25题图法二:由①得AEB ADC △≌△, ∴BE CD =. ······························································································ 9分 又∵四边形BCGE 是菱形, ∴BE CB = ································································································ 11分 ∴CD CB =. ····························································································· 12分 法三:∵四边形BCGE 是平行四边形, ∴BE CG EG BC ∥,∥, ∴6060FBE BAC F ABC ∠=∠=∠=∠=°,° ··················································· 9分 ∴60F FBE ∠=∠=°, ∴BEF △是等边三角形. ············································································· 10分220(02)1(12)a h a h ⎧=-+⎪⎨=-+⎪⎩ 解得1343a h ⎧=-⎪⎪⎨⎪=⎪⎩································································· 3分 ∴所求抛物线解析式为214(2)33y x x =--+. ···················································· 4分 (2)分三种情况:①当02t <≤,重叠部分的面积是OPQ S △,过点A 作AF x ⊥轴于点F , ∵(11)A ,,在Rt OAF △中,1AF OF ==,45AOF ∠=°在Rt OPQ △中,OP t =,45OPQ QOP ∠=∠=°,∴cos 452PQ OQ t ===°, (3)存在 11t = ······················································································ 12分 22t = ···················································································· 14分。
初中数学中考真题精编-2009年答案及评分标准

2009年来宾市初中毕业升学统一考试试题数学参考答案及评分标准一、填空题:本大题共10小题,每小题3分,共30分.1.-237; 2.10; 3.(x +2)(x -2); 4.25; 5.⎩⎨⎧==11y x ; 6.x y 2-=;7.1.30×105; 8.65; 9.2; 10.答案不唯一,只要符合题意均给分.二、选择题:本大题共8小题,每小题3分,共24分.题号 11 12 13 14 15 16 17 18 答案DBCDACCB三、解答题:本大题共8小题,满分66分. 19.解:原式=222919⨯+-+ …………4分(每对一个值给1分)=1+1=2……………………5分20.解:设该镇这两年中财政净收入的平均年增长率为x , ……………………1分依题意可得:5000(1+x )2=2×5000 ………………………………4分解得 21=+x ,或021<-=+x (舍去) ……………………5分∴%4.41414.012=≈-=x……………………………………6分答:该镇这两年中财政净收入的平均年增长率约为41.4﹪.…………7分21.解:(1)502;(2)23.71;(3)图略,值为150(图、值各1分);(4)80—99.(每小题各2分)22.证明:∵四边形ABCD 是平行四边形∴CD =AB ,AD =CB ,∠DAB =∠BCD ……2分 又∵△ADE 和△CBF 都是等边三角形 ∴DE =BF ,AE =CF∠DAE =∠BCF =60° ………………4分∵∠DCF =∠BCD -∠BCF ∠BAE =∠DAB -∠DAE ∴∠DCF =∠BAE……………………6分∴△DCF ≌△BAE (SAS ) ………………7分∴DF =BE∴四边形BEDF 是平行四边形. …………8分23.解:(1)见参考图 ……………………………3分(不用尺规作图,一律不给分。
2012年青海省数学中考真题(word版含答案)

青海省2012年初中毕业升学考试数学试卷(本试卷满分120分,考试时间120分钟)考生注意:1. 答卷前将密封线以内的项目填写清楚.2. 用蓝黑钢笔或中性笔答题.一、填空题(本大题共12小题15空,每空2分,共30分)1.12-的相反数是 ;计算23a a ⋅= . 2.分解因式:34m m -+= ;不等式组110230x x ⎧+⎪⎨⎪-⎩>≥的解集为 .3.2012年3月,青海省财政下达农牧区学生营养改善计划补助资金265 000 000元,用于改善我省农牧区义务教育阶段中小学生的营养状况,该补助资金用科学记数法表示为 元.4.函数y x 的取值范围是 . 5.如图1,直线l ∥2l ,且12l l 、被直线3l 所截,∠1=∠2=35°,∠P=90°.则∠3= . 6.若m 、n 为实数,且|21|m n +-,则2012(+)m n 的值为;分式 方程2215212141x x x +=+--的解为 . 7.随意抛一粒豆子,恰好落在图2的方格中(每个方格除颜色外完全一样),那么这粒豆子 落在黑色方格中的概率是.8.如图3,已知点E 是⊙O 上的点,B 、C 分别是劣弧AD 的三等分点,∠BOC=46°,则∠AED 的度数为 .9.如图4所示,点D 、E 分别在线段AB 、AC 上,BE 、CD 相交于点O ,AE=AD ,要使 △ABE ≌△ACD ,则需要添加的条件是(只需一个即可,图中不能再添加其他点或线).10.如图5,利用标杆BE 测量建筑物的高度,标杆BE 高1.5m ,测得AB=2m ,BC=14m ,则 楼高CD 为 m .11.观察下列一组图形:它们是按照一定规律排列的,依照此规律,第n 个图形中共有 个★.12.如图7,Rt △ABC 中,∠C=90°,AC=2,BC=4,分别以AC 、BC 为直径作半圆,则图中二、8小题,每小题3分,共24分,每小题给出的四个选项中,只有一14.A. 326211()=24x y x y B. 322=2x x x ÷ C. 246=x x x ⋅ D. 235()=x x -- 15.甲、乙两名射击运动员各进行10次射击练习,成绩均为95环,这两名运动员成绩的方差分别是20.6S =甲,20.4S =乙,则下列说法正确的是( )A.甲比乙的成绩稳定B.乙比甲的成绩稳定C.甲、乙两人的成绩一样稳定D.无法确定谁的成绩更稳定16.如图8,一次函数=3y kx -的图象与反比例函数=m y x的图象交A 、B 两点,其中A 点坐标为(2,1),则k 、m 的值为( )A. 12k m ==, B. 21k m ==, C. 22k m ==, D. 11k m ==,17.如图9,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD=5,AC=6,则tan B 的值是( ) A. 45 B. 35 C. 34 D. 4318.把抛物线2=3y x 向右平移1个单位长度后,所得的函数解析式为( )A. 2=31y x -B. 2=3(1)y x -C. 2=3+1y xD. 2=3(+1)y x19.通信市场竞争日益激烈,某通信公司的手机本地话费标准按原标准每分钟降低a 元后,再次下调了20%,现在的收费标准是每分钟b 元,则原收费标准是( )A. 5(+)4a b 元B. 5()4a b -元 C. (+5)a b 元 D. (5)a b -元20.如图10反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家.如果菜地和青稞地的距离为a 千米,小刚在青稞地除草比在菜地浇水多用了b 分钟,则a 、b 的值分别为( )A.1,8 D.0.5,8三、(本大题共3小题,第21题5分,第22题6分,第23题8分,共19分)21.计算:201|5|2cos 60+())2---︒π.22.先化简,再求值:211(1)34121x x x x -÷+---+,其中23.已知:如图11,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC. (1)求证:CD=AN;(2)若∠AMD=2∠MCD,求证:四边形ADCN是矩形.四、(本大题共3小题,第24题8分,第25题7分,第26题10分,共25分)24.夏都花卉基地出售两种花卉,其中马蹄莲每株3.5元,康乃馨每株5元,如果同一客户所购的马蹄莲数量多于1000株,那么所有的马蹄莲每株还可优惠0.5元.现某鲜花店向夏都花卉基地采购马蹄莲800~1200株、康乃馨若干株,本次采购共用了7000元,然后再以马蹄莲每株4.5元、康乃馨每株7元的价格卖出.问该鲜花店应如何采购这两种鲜花才能使获得的利润最大?(注:800~1200株表示采购株数大于或等于800株,且小于或等于1200株;利润=销售所得金额-进货所需金额)25.如图12,AB是⊙O的直径,弦CD⊥AB于点N,点M在⊙O上,∠1=∠C.(1)求证:CB∥MD;(2)若BC=4,sin M=2,求⊙O的直径.26.现代树苗培育示范园要对A、B、C、D四个品种共800株松树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知,B种松树幼苗成活率为90%,将实验数据绘制成两幅统计图,如图13-1,13-2所示(部分信息未给出).(1)实验所用的C种松树幼苗的数量为;(2)试求出B种松树的成活数,并把图13-2的统计图补充完整;(3)你认为应该选哪一种品种进行推广?试通过计算说明理由.五、(本大题共2小题,第27题10分,第28题12分,共22分)27.如图(14-*),四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.(1)探究1:小强看到图(14-*)后,很快发现AE=EF.这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个直角三角形,一个钝角三角形).考虑到点E 是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证明△AEM≌△EFC就行了.随即小强写出了如下的证明过程:证明:如图14-1,取AB的中点M,连接EM.∵∠AEF=90°,∴∠FEC+∠AEB=90°,又∵∠EAM+∠AEB=90°,∴∠EAM=∠FEC.∵点E 、M 分别为正方形的边BC 和AB 的中点,∴AM=EC .又可知△BME 是等腰直角三角形,∴∠AME=135°,又∵CF 是正方形外角的平分线,∴∠ECF=135°,∴△AEM ≌△EFC (ASA ),∴AE=EF .(2)探究2:小强继续探索,如图14-2,若把条件“点E 是边BC 的中点”改为“点E 是边BC 上的任意一点”,其余条件不变,发现AE=EF 仍然成立.请你证明这一结论.(3)探究3:小强进一步还想试试,如图14-3,若把条件“点E 是边BC 的中点”改为“点E 是边BC 延长线上的一点”,其余条件仍不变,那么结论AE=EF 是否成立呢?若成立请你完成证明过程给小强看.若不成立请你说明理由.28.如图15,在平面直角坐标系中,二次函数2=++y x bx c 的图象与x 轴交于A 、B 两点,B 点的坐标为(3,0),与y 轴交于(03)C -,点,点P 是直线BC 下方抛物线上的动点. (1)求这个二次函数表达式;(2)连接PO ,PC ,并将△POC 沿y 轴对折,得到四边形POP C ',那么是否存在点P ,使四边形POP C '为菱形?若存在,求出此时点P 的坐标;若不存在,请说明理由;(3)当点P 运动到什么位置时,四边形ABPC 的面积最大?求出此时P 点的坐标和四边形ABPC 的最大面积.青海省2012年初中毕业升学考试试卷数学(普通卷)参考答案及评分标准说明:①本解答的解证题给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考察内容比照评分标准参考制订相应的评分细则.②注意,解证题评分采用累积评分制,解答右端所注分数,表示考生正确做到这一步应得的累积分数.一、填空题(本大题共12小题15空,每空2分,共30分) 1.12;5a 2. (2)(2)23m m m x -+--<;≤3. 82.6510⨯4. 42x x -≠≥且5. 556.1;1x =7.4158. 699.开放型题,答案不唯一(参考答案:B C AEB ADC AB AC ===∠∠,∠∠,) 10.1211. 31n + 12. 542π-三、(本大题共3小题,第21题5分,第22题6分,第23题8分,共19分)21.解:20152cos 60+())2---︒π =2152212-⨯++ ·········································································································· 4分 =5141-++=9. ···································································································································· 5分22. 解:原式=2111()3411(1)x x x x x --÷+---- ························································· 2分 =221341(1)x x x x -÷+--- ····························································································· 3分 =22(1)341x x x x -∙-+-- =(2)(1)34x x x -∙-+- ······························································································· 4分 =23234x x x -++- ····································································································· 5分 =22x -.把2222 5.x -=-= ··························································· 6分23. 证明:(1)∵CN ∥AB ,∴∠DAC=∠NCA . ································································ 1分 又∵MA=MC ,∠AMD=∠CMN ,∴△AMD ≌△CMN (ASA ) ······························································································ 3分 ∴AD=CN .又∵AD ∥CN ,∴四边形ADCN 是平行四边形,∴CD=AN ············································ 4分(2)∵∠AMD=2∠MCD ,∠AMD=∠MCD +∠MDC ,∴∠ MCD=∠MDC ,∴MD=MC. ······················································································ 6分 由(1)知四边形ADCN 是平行四边形,∴MD=MN=MA=MC ,∴AC=DN ,∴四边形ADCN 是矩形. ········································· 8分四、(本大题共3小题,第24题8分,第25题7分,第26题10分,共25分)24. 解:设采购马蹄莲x 株,康乃馨y 株,利润为w 元. ············································· 1分 ①当800≤x ≤1000时,得3.5x+5y=7000,7000 3.5==14000.75x y x --, ··················································· 2分 w=(4.5-3.5)x+(7-5)y=x+2y= x+2(1400-0.7x )=2800-0.4x. ·································· 3分 ∴当x=800时,w 有最大值2480. ··············································································· 4分 ②当1000<x ≤1200时,得3x+5y=7000,70003==14000.65x y x --,·························································· 5分 w=(4.5-3)x+(7-5)y=1.5x+2y=1.5 x+2(1400-0.6x )=2800+0.3x. ····························· 6分 ∴当x=1200时,w 有最大值3160. ············································································· 7分 ③综上所述,采用后者方式进货,即采购马蹄莲花去1200×3=3600(元);采购康乃馨(7000-3600)÷5=680(株).答:采购马蹄莲1200株、康乃馨680株,利润最大,为3160元. ····························· 8分25. (1)证明:∵BD BD =,∴C M =∠∠. ················································································································ 1分又∵1C =∠∠,∴1M =∠∠. ∴CB MD ∥. ·················································································································· 3分(2)连接AC .∵AB 是⊙O 的直径,∴∠ACB=90°. ················································································· 4分 又∵CD ⊥AB ,∴BC BD =,∴∠A=∠M ,∴sin A=sin M . ··············································· 5分 在Rt △ACB 中,sin BC A AB=,∵2sin 3M =,∴23BC AB =. ···························································································· 6分 又∵BC=4,∴AB=6,即⊙O 的直径为6. ········································································ 7分26. (1)160株; ·········································································································· 2分(2)B 种松树幼苗数量为:800×20%=160(株),B 种松树幼苗的成活数为:160×90%=144(株), ························································ 4分 补充统计图如图所示:(3)说清每种松树苗成活率各得1分.A 种松树幼苗的成活率为:[238÷(238×35%)]×100%=85%,B 种松树幼苗的成活率为:90%,C 种松树幼苗的成活率为:[148÷(800×20%)]×100%=92.5%,D 种松树幼苗的成活率为:[190÷(800×25%)]×100%=95%. ··········································· 9分 所以应选择D 种松树品种进行推广. ············································································ 10分五、(本大题共2小题,第27题10分,第28题12分,共22分)27.(本题给出探究2的推理过程得5分,给出探究3的推理过程再得5分,共10分)(2)探究2:在AB 上截取AM=EC ,连接ME . ·················································································· 1分 由(1)知∠EAM=∠FEC.∵AM=EC ,AB=BC ,∴BM=BE . ····················································································· 2分 ∴∠BME=45°。
2009年青海省西宁市中考数学试卷

2009年青海省西宁市中考数学试卷一、填空题(共12小题,满分30分)1.(4分)写出一个小于﹣4的有理数;在函数y=中,自变量x 的取值范围是.2.(4分)一元二次方程x2=x的解为;二元一次方程组的解为.3.(2分)为应对2008年以来的世界金融危机,中国政府出台了多项政策以阻止我国经济继续下滑,其中一项是4万亿元经济刺激方案.将4万亿元用科学记数法可表示为元.4.(2分)如图,等腰梯形ABCD的周长为18,腰AD=4,则等腰梯形ABCD的中位线EF=.5.(2分)如图,如将飞镖投中一个被平均分成6份的靶子,则落在阴影部分的概率是.6.(2分)在正方形网格中,△ABC的位置如图所示,则cos∠B的值为.7.(2分)如图,要测量池塘两端A、B的距离,可先取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接ED,如果量出DE的长为25米,那么池塘宽AB为米.8.(2分)二次函数y=﹣x2+x﹣的图象的顶点坐标为.9.(2分)已知圆锥的底面半径为2cm,母线长是4cm,则圆锥的侧面积是cm2(结果保留π).10.(4分)如图1,矩形AOBP的面积为6,反比例函数y=的图象经过点P,那么k的值为;直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图2所示,则关于x的不等式k1x+b>k2x的解为.11.(2分)如图,在12×6的网格图中(每个小正方形的边长均为1个单位),⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B外切,那么⊙A由图示位置需向右至少平移个单位.12.(2分)如图,某建筑物直立于水平地面,BC=9米,∠B=30°,要建造楼梯,使每阶台阶高度不超过20厘米,那么此楼梯至少要建阶(最后一阶不足20厘米按一阶计算,≈1.732).二、选择题(共8小题,每小题3分,满分24分)13.(3分)下面计算正确的是()A.2﹣1=﹣2B.C.(m•n3)2=m•n6D.m6÷m2=m414.(3分)下列交通标志中既是中心对称图形,又是轴对称图形的是()A.B.C.D.15.(3分)班主任为了解学生星期六、日在家的学习情况,家访了班内的六位学生,了解到他们在家的学习时间如下表所示.那么这六位学生学习时间的众数与中位数分别是()A.4小时和4.5小时B.4.5小时和4小时C.4小时和3.5小时D.3.5小时和4小时16.(3分)用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是()A.(S.S.S.)B.(S.A.S.)C.(A.S.A.)D.(A.A.S.)17.(3分)下列事件中是必然事件的是()A.西宁一月一日刮西北风B.抛掷一枚硬币,落地后正面朝上C.当x是实数时,x2≥0D.三角形内角和是360°18.(3分)在学校开展的“为灾区儿童过六一”的活动中,晶晶把自己最喜爱的铅笔盒送给了一位灾区儿童.这个铅笔盒(如图)的左视图是()A.B.C.D.19.(3分)为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元.设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是()A.2500x2=3600B.2500(1+x)2=3600C.2500(1+x%)2=3600D.2500(1+x)+2500(1+x)2=360020.(3分)身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形纸片ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC 上,折痕EF交AD于F.则∠AFE=()A.60°B.67.5°C.72°D.75°三、解答题(共8小题,满分66分)21.(7分)计算:|﹣3|+(﹣1)0﹣2×()﹣122.(7分)请从下列三个代数式中任选两个(一个作为分子,一个作为分母)构造一个分式,并化简该分式.(a2﹣1,a2﹣a,a2﹣2a+1)然后请你自选一个合理的数代入求值.23.(7分)如图,在平行四边形ABCD中.(1)尺规作图(不写作法,保留作图痕迹):作∠ABC的平分线BE交AD于E;在线段BC上截取CF=DE;连接EF.(2)求证:四边形ABFE是菱形.24.(8分)阅读下列材料并填空:(1)探究:平面上有n个点(n≥2)且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?我们知道,两点确定一条直线.平面上有2个点时,可以画条直线,平面内有3个点时,一共可以画条直线,平面上有4个点时,一共可以画条直线,平面内有5个点时,一共可以画条直线,…平面内有n个点时,一共可以画条直线.(2)迁移:某足球比赛中有n个球队(n≥2)进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?有2个球队时,要进行场比赛,有3个球队时,要进行场比赛,有4个球队时,要进行场比赛,…那么有20个球队时,要进行场比赛.25.(8分)已知:如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC 于E.(1)请判断DE与⊙O的位置关系,并证明;(2)连接AD,若⊙O的半径为,AD=3,求DE的长.26.(8分)《西海都市报》(2009年05月21日)文章《创卫让西宁焕发出勃勃生机》报道说:“西宁创建卫生城市已到了关键阶段,西宁处处焕发出勃勃生机.”省城西宁,无论是市容环境,还是市民意识,都发生了可喜的变化.西宁市教育局对全市约11000名九年级学生就西宁创建卫生城市知识的了解情况进行了问卷调查.现随机抽取了部分学生的答卷进行统计分析,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图1)和条形统计图(如图2).请你根据图中信息回答下列问题:(1)本次问卷调查的样本容量是;(2)扇形统计图中,圆心角α=°;(3)补全条形统计图;(4)根据以上信息,请提出一条合理化的创卫建议:.27.(9分)已知一只口袋中放有x只白球和y只红球,这两种球除颜色以外没有任何区别.袋中的球已经搅匀.蒙上眼睛从袋中取一只球,取出白球的概率是.(1)试写出y与x的函数关系式;(2)当x=3时,第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表法,求两次摸到都是白球的概率.28.(12分)已知OABC是一张矩形纸片,AB=6.(1)如图1,在AB上取一点M,使得△CBM与△CB′M关于CM所在直线对称,点B′恰好在边OA上,且△OB′C的面积为24cm2,求BC的长;(2)如图2.以O为原点,OA、OC所在直线分别为x轴、y轴建立平面直角坐标系.求对称轴CM所在直线的函数关系式;(3)作B′G∥AB交CM于点G,若抛物线y=x2+m过点G,求这条抛物线所对应的函数关系式.2009年青海省西宁市中考数学试卷参考答案与试题解析一、填空题(共12小题,满分30分)1.(4分)写出一个小于﹣4的有理数﹣5,﹣6等;;在函数y=中,自变量x的取值范围是x≥3.【解答】解:小于﹣4的有理数有:﹣5,﹣6等;由x﹣3≥0,解得x≥3,即自变量x的取值范围是x≥3.2.(4分)一元二次方程x2=x的解为0,1;二元一次方程组的解为.【解答】解:(1)移项得x2﹣x=0,x(x﹣1)=0所以x=0或x=1.(2)(1)+(2)得8x=8,即x=1,代入(1)得5+y=7,y=2.3.(2分)为应对2008年以来的世界金融危机,中国政府出台了多项政策以阻止我国经济继续下滑,其中一项是4万亿元经济刺激方案.将4万亿元用科学记数法可表示为4×1012元.【解答】解:∵1万=104,1亿=108,一万亿=1012,∴4万亿元=4×1012元.4.(2分)如图,等腰梯形ABCD的周长为18,腰AD=4,则等腰梯形ABCD的中位线EF=5.【解答】解:∵等腰梯形ABCD的周长为18,腰AD=4,∴等腰梯形ABCD的中位线EF==5.5.(2分)如图,如将飞镖投中一个被平均分成6份的靶子,则落在阴影部分的概率是.【解答】解:因为阴影部分占图形靶子的,所以飞镖落在阴影部分的概率是.6.(2分)在正方形网格中,△ABC的位置如图所示,则cos∠B的值为.【解答】解:作AD⊥BC的延长线于点D.在Rt△ABD中,BD=AD,则AB=BD.故cos∠B=.故答案为:.7.(2分)如图,要测量池塘两端A、B的距离,可先取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接ED,如果量出DE的长为25米,那么池塘宽AB为50米.【解答】解:∵CD=CA,CE=CB∴CD:AC=CE:CB=1:2∵∠ACB=∠DCE∴△ACB∽△DCE∴AB:ED=AC:CD=2:1∵DE=25米∴AB=50米.8.(2分)二次函数y=﹣x2+x﹣的图象的顶点坐标为(1,﹣2).【解答】解:根据顶点坐标公式,x==1,y==﹣2,即顶点坐标为(1,﹣2).故答案为:(1,﹣2).9.(2分)已知圆锥的底面半径为2cm,母线长是4cm,则圆锥的侧面积是8πcm2(结果保留π).【解答】解:底面圆的半径为2,则底面周长=4π,侧面面积=×4π×4=8πcm2.10.(4分)如图1,矩形AOBP的面积为6,反比例函数y=的图象经过点P,那么k的值为﹣6;直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图2所示,则关于x的不等式k1x+b>k2x的解为x>﹣1.【解答】解:S=|k|=6,又图象在二、四象限,所以k=﹣6.矩形AOBP由图可知不等式k1x+b>k2x的解为:x>﹣1.故答案为:﹣6、x>﹣1.11.(2分)如图,在12×6的网格图中(每个小正方形的边长均为1个单位),⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B外切,那么⊙A由图示位置需向右至少平移2个单位.【解答】解:根据题意,得要使两圆外切,则AB=2+1=3.结合图形,知AB=5,至少要平移2个单位.故答案为2.12.(2分)如图,某建筑物直立于水平地面,BC=9米,∠B=30°,要建造楼梯,使每阶台阶高度不超过20厘米,那么此楼梯至少要建26阶(最后一阶不足20厘米按一阶计算,≈1.732).【解答】解:所有台阶高度和为AC的长.设此楼梯至少要建x阶,可得tan30°==,∴x=15≈26(阶).二、选择题(共8小题,每小题3分,满分24分)13.(3分)下面计算正确的是()A.2﹣1=﹣2B.C.(m•n3)2=m•n6D.m6÷m2=m4【解答】解:A、2﹣1=,故A错;B、=2,故B错;C、(m•n3)2=m2n6,故C错;D、m6÷m2=m4;故D对.故选:D.14.(3分)下列交通标志中既是中心对称图形,又是轴对称图形的是()A.B.C.D.【解答】解:根据轴对称图形与中心对称图形的概念,知:A:是轴对称图形,而不是中心对称图形;B、C:两者都不是;D:既是中心对称图形,又是轴对称图形.故选:D.15.(3分)班主任为了解学生星期六、日在家的学习情况,家访了班内的六位学生,了解到他们在家的学习时间如下表所示.那么这六位学生学习时间的众数与中位数分别是()A.4小时和4.5小时B.4.5小时和4小时C.4小时和3.5小时D.3.5小时和4小时【解答】解:从小到大排列此数据为:3,4,4,5,6,8,数据4出现了2次最多为众数.4,5处在第5位和6位,其平均数4.5为中位数,所以本题这组数据的中位数是4.5,众数是4.故选:A.16.(3分)用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是()A.(S.S.S.)B.(S.A.S.)C.(A.S.A.)D.(A.A.S.)【解答】解:作图的步骤:①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′;③以C′为圆心,CD长为半径画弧,交前弧于点D′;④过点D′作射线O′B′.所以∠A′O′B′就是与∠AOB相等的角;作图完毕.在△OCD与△O′C′D′,,∴△OCD≌△O′C′D′(SSS),∴∠A′O′B′=∠AOB,显然运用的判定方法是SSS.故选:A.17.(3分)下列事件中是必然事件的是()A.西宁一月一日刮西北风B.抛掷一枚硬币,落地后正面朝上C.当x是实数时,x2≥0D.三角形内角和是360°【解答】解:A、B:选项为不确定事件,即随机事件,不符合题意;C:是必然事件,符合题意;D:是不可能事件,不符合题意.故选:C.18.(3分)在学校开展的“为灾区儿童过六一”的活动中,晶晶把自己最喜爱的铅笔盒送给了一位灾区儿童.这个铅笔盒(如图)的左视图是()A.B.C.D.【解答】解:从物体左面看,是2个叠放的矩形,上面的矩形的宽较小,因为左边看到的是笔盒的宽,对比A、B选项,故选B.19.(3分)为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元.设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是()A.2500x2=3600B.2500(1+x)2=3600C.2500(1+x%)2=3600D.2500(1+x)+2500(1+x)2=3600【解答】解:依题意得2008年的投入为2500(1+x)2,∴2500(1+x)2=3600.故选:B.20.(3分)身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形纸片ABCD(矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC 上,折痕EF交AD于F.则∠AFE=()A.60°B.67.5°C.72°D.75°【解答】解:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E点,∠AEB=45°,(2)中,可得∠FEC==67.5(度)∵AF∥EC,∴∠AFE=∠FEC=67.5°.故选:B.三、解答题(共8小题,满分66分)21.(7分)计算:|﹣3|+(﹣1)0﹣2×()﹣1【解答】解:原式=|﹣3|+(﹣1)0﹣2×()﹣1=3+1﹣2×2=0.故答案为0.22.(7分)请从下列三个代数式中任选两个(一个作为分子,一个作为分母)构造一个分式,并化简该分式.(a2﹣1,a2﹣a,a2﹣2a+1)然后请你自选一个合理的数代入求值.【解答】解:答案不唯一,如:=∵a≠1,∴当a=0时,原式=0.23.(7分)如图,在平行四边形ABCD中.(1)尺规作图(不写作法,保留作图痕迹):作∠ABC的平分线BE交AD于E;在线段BC上截取CF=DE;连接EF.(2)求证:四边形ABFE是菱形.【解答】解:(1)如图所示:(2)证明:∵ABCD是平行四边形,∴AD∥BC,AD=BC又∵DE=CF∴AD﹣DE=BC﹣CF,即AE=BF∵AE∥BF∴四边形ABFE是平行四边形,又∵BE平分∠ABC∴∠ABE=∠EBF又∵AD∥BC∴∠AEB=∠EBF∴∠ABE=∠AEB∴AB=AE∴▱ABFE是菱形.24.(8分)阅读下列材料并填空:(1)探究:平面上有n个点(n≥2)且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?我们知道,两点确定一条直线.平面上有2个点时,可以画条直线,平面内有3个点时,一共可以画条直线,平面上有4个点时,一共可以画条直线,平面内有5个点时,一共可以画10条直线,…平面内有n个点时,一共可以画条直线.(2)迁移:某足球比赛中有n个球队(n≥2)进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?有2个球队时,要进行场比赛,有3个球队时,要进行场比赛,有4个球队时,要进行6场比赛,…那么有20个球队时,要进行190场比赛.【解答】解:(1)当平面上有2个点时,可以画=条直线;当平面上有3个点时,可以画==3条直线;…当平面上有n(n≥2)个点时,可以画条直线;因此当n=5时,一共可以画=10条直线.(2)同(1)可得:当比赛中有n(n≥2)个球队时,一共进行场比赛,因此当n=4时,要进行=6场比赛.当n=20时,要进行=190场比赛.25.(8分)已知:如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC 于E.(1)请判断DE与⊙O的位置关系,并证明;(2)连接AD,若⊙O的半径为,AD=3,求DE的长.【解答】(1)解:DE与⊙O相切,证明:连接AD、OD,∵AB为⊙O的直径,∴∠BDA=90°,∴AD⊥BC.又∵AB=AC,∴BD=DC,又∵OB=OA,∴OD是△ABC的中位线,∴OD∥AC.又∵DE⊥AC,∴DE⊥OD,∴DE是⊙O的切线.(2)解:若⊙O的半径为,则AB=AC=5,在Rt△ADC中,AD=3,AC=5,∴DC=,又∵AC•DE=AD•DC,∴DE=.26.(8分)《西海都市报》(2009年05月21日)文章《创卫让西宁焕发出勃勃生机》报道说:“西宁创建卫生城市已到了关键阶段,西宁处处焕发出勃勃生机.”省城西宁,无论是市容环境,还是市民意识,都发生了可喜的变化.西宁市教育局对全市约11000名九年级学生就西宁创建卫生城市知识的了解情况进行了问卷调查.现随机抽取了部分学生的答卷进行统计分析,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图1)和条形统计图(如图2).请你根据图中信息回答下列问题:(1)本次问卷调查的样本容量是200;(2)扇形统计图中,圆心角α=72°;(3)补全条形统计图;(4)根据以上信息,请提出一条合理化的创卫建议:增强市民创建卫生城市的意识,是搞好市容环境的前.【解答】解:(1)根据条形图可知本次问卷调查中“较差”的人数是10人,再观察扇形统计图“较差”的人数占5%,所以样本容量是10÷5%=200;(2)扇形统计图“一般”的人数占1﹣25%﹣50%﹣5%=20%,所以圆心角α=360°×20%=72°;(3)因为样本容量是200,由条形图可知“一般”的人数是200﹣50﹣100﹣10=40,从而可以补全条形统计图;(4)增强市民创建卫生城市的意识,是搞好市容环境的前提.答案不唯一,建议合理即可.27.(9分)已知一只口袋中放有x只白球和y只红球,这两种球除颜色以外没有任何区别.袋中的球已经搅匀.蒙上眼睛从袋中取一只球,取出白球的概率是.(1)试写出y与x的函数关系式;(2)当x=3时,第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表法,求两次摸到都是白球的概率.【解答】解:(1)由题可知:,即3x+3y=4x,所以y与x的函数关系式为y=;(2)由(1)可知,当x=3时,y=1.袋中有3只白球和1只红球.由上面列表可知:共有12种等可能的结果,其中两次都是白球的占6种,所以两次摸到都是白球的概率是.28.(12分)已知OABC是一张矩形纸片,AB=6.(1)如图1,在AB上取一点M,使得△CBM与△CB′M关于CM所在直线对称,点B′恰好在边OA上,且△OB′C的面积为24cm2,求BC的长;(2)如图2.以O为原点,OA、OC所在直线分别为x轴、y轴建立平面直角坐标系.求对称轴CM所在直线的函数关系式;(3)作B′G∥AB交CM于点G,若抛物线y=x2+m过点G,求这条抛物线所对应的函数关系式.【解答】解:(1)如图1,∵△OB′C的面积为24cm2,且OC=AB=6cm.∴OB′=2×24÷6=8cm∴B′C==10cm∴BC=B′C=10cm.(2)由(1)可知B′A=OA﹣OB′=10﹣8=2设AM=x,则BM=B′M=6﹣x由勾股定理可得方程:22+x2=(6﹣x)2解得:x=所以M(10,),C(0,6)设CM所在直线的函数关系式为y=kx+b则,解得,∴CM所在直线的函数关系式为y=﹣x+6.(3)∵B′G∥AB,OB′=8∴G点的横坐标为8,又∵点G在直线CM上,CM关系式为y=﹣x+6所以G点的纵坐标为y=即G(8,).∵抛物线y=x2+m过点G,∴∴m=﹣所求抛物线的关系式为y=x2﹣.。
2009年定西市中考数学试卷

2.图1所示的物体的左视图(从左面看得到的视图)是()图1A.B.C.D.3.计算:a b a b-⎛⎫-÷=⎪()A .12mB .10m图2 图3 图410.如图4,四边形ABCD 中,AB =BC ,∠ABC =∠CDA °,BE ⊥AD 于点E ,且四边形ABCD 的面积为8,则( ) A .2B .316.如图6,四边形ABCD 是平行四边形,使它为矩形的条件可以是图6 图7 图817.如图7,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为过点B 、C ,那么线段AO = cm .图9)是一扇半开着的办公室门的照片,门框镶嵌在墙体中间,门是向室内图10(1)图10(2)cm)存在一种换算关系,下表是几组“鞋码”与鞋长图11(1)图11(2)日,四川省汶川县发生了里氏8.0级大地震,兰州某中学师生自愿6000元,第二天捐款人数比第一天捐款人数多人,且两天人均捐款数相等,那么两天共参加捐款的人数是多少?人均捐款多少元?图12x轴交于A、B两点,与y附加题:如果你的全卷得分不足分,则本题与28题附加的分的得分将记入总分,但记入总分后全卷得分不得超过150分,超过按150分算.分)本试卷第19题为:若20072008=,20082009b=,试不用..将分数化小数的方法比较图13图14(1)图14(2)图14(3)···································2分···································3分参加足球运动项目的学生占所有运动项目学生的比例为1=. ······36072O图14(1)··························6分图14(2)。
青海昆仑中学2009年第一次中考模拟数学试题

2009年某某昆仑中学第一次中考模拟试题数 学 试 卷班级 考号 某某 总分注意:1、本试卷分试题卷和答卷两部分,其中试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷共三大题25小题,共150分.考试时间120分钟. 2、可以带计算器进考场.第Ⅰ卷(选择题 共30分)一.选择题:每小题的四个选项中有且只有一个符合题意,本题共10个小题,每小题3分,满分30分。
1.-2的相反数是( ) A .2B .-2C .22D .22-2.下列运算正确的是( )A.321x x -= B.22122xx --=-C.236()a a a -=·D.623)(a a -=-3.如图,D 是ABC ∆的重心,则下列结论正确的是 ( ) A .DE AD =2 B .DE AD 2= C .DE AD 23= D .DE AD 3= 4.下列命题中,真命题是( ) A .两条对角线相等的四边形是矩形B .两条对角线互相垂直的四边形是菱形C .两条对角线互相垂直且相等的四边形是正方形D .两条对角线互相平分的四边形是平行四边形 5.在下面的四个几何体中,它们各自的主视图、左视图与俯视图都一样的是( )6.把不等式组1020x x +⎧⎨->⎩≥的解集表示在数轴上,正确的是( )A.B.C.D.正方体 正四棱台 有正方形孔的正方体底面是长方形的四棱锥ABC D E· (第3题图)7.如图,一个小球由地面沿着坡度i =1∶2的坡面向上前进了10 m ,此时小球距离地面的高度为( ) A .5 m B .52 m C .54 m D .310m8.已知正比例函数y kx =(0k ≠)的函数值y 随x 的增大而增大,则一次函数y kx k =+的图象大致是( )9.如图,正方体''''D C B A ABCD -中,面''A ABB 上'AOA ∆的实际图形是( )10.如图,如果从半径为9cm 的圆形纸片剪去13圆周的 一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠), 那么这个圆锥的高为( ) A .6cm B .35cm C .8cmD .53cmA AA A O O O A ′ A ′ A ′ A ′ ABCD O O x y O x y O x y y x O A. B . C . D. (第7题图) O A ′ B ′ C ′ D ′ BC D A (第9题图) (第10题图)第Ⅱ卷(非选择题 共120分)二.填空题:本大题共有6个小题,每小题3分,共18分. 11.已知,0<a 化简2a =.12.函数y =x 的取值X 围是13.2008年奥运会火炬接力,火炬手达到21780人,把这个数用科学记数法表示约为人(保留两个有效数字).14.已知正三角形的外接圆的半径为R ,则此正三角形的边长为. 15.在Rt ΔABC 中,∠C=90°,AC=6,32sin =BAB 的长是16.已知二次函数的图象如图所示,则 (1)这个二次函数的解析式是; (2)当x =时,3=y ;(3)当x 的取值X 围是时,0>y .三.解答题:本大题共9小题,满分102分,其中第24A 、24B 、题是选做题,考生只需选做一题,两题全答者,只计算前一题得分. 17.(本小题满分9分)先将)11(132-⋅-+xx x x 化简,然后请自选你喜欢的一个适合的x 值代入,再求原式的值。
西宁市2009年高中招生考试数学试卷

西宁市2009年高中招生考试数 学 试 卷(试卷满分120分,考试时间120分钟)考生注意:1.答卷前将密封线以内的项目填写清楚;2.用钢笔或圆珠笔直接答在试卷上.一、细心填一填(本大题共12小题15空,每空2分,共30分.只要你理解概念,仔细运算,相信你一定会填对的!)1.写出一个小于4-的有理数;在函数y =x 的取值范围是 . 2.一元二次方程2x x =的解为 ;二元一次方程组5731x y x y +=⎧⎨-=⎩的解为 .3.为应对2008年以来的世界金融危机,中国政府出台了多项政策以阻止我国经济继续下滑,其中一项是4万亿元经济刺激方案.将4万亿元用科学记数法可表示为 元.4.如图1,等腰梯形ABCD 的周长为18,腰4AD =,则等腰梯形ABCD 的中位线EF = .5.如图2,若将飞镖投中一个被平均分成6份的圆形靶子,则落在阴影部分的概率是 .6.在正方形网格中,ABC △的位置如图3所示,则cos B ∠的值为 .7.如图4,要测量池塘两端A B 、的距离,可先取一个可以直接到达A 和B 的点C ,连结AC 交延长到D ,使12C D C A =,连结BC 并延长到E ,使12CE CB =,连结ED ,如果量出DE 的长为25米,那么池塘宽AB 为 米. 8.二次函数21522y x x =-+-的图象的顶点坐标为 . 9.已知圆锥的底面半径为2cm ,母线长是4cm ,则圆锥的侧面积是 cm 2.(结果保留π). 10.如图5,矩形AOBP 的面积为6,反比例函数k y x =的图象经过点P ,那么k 的值为 ;直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标系中的图象如图6所示,则关于x 的不等式12k x b k x +>的解为 .11.如图7,在126⨯的网格图中(每个小正方形的边长均为1个单位),A ⊙的半径为1,B ⊙的半径为2,要使A ⊙与静止的B ⊙相外切..,那么A ⊙由图示位置需向右平移 个单位. D C F E A B 图1 图2 A C B 图3 A B D C E 图4 图51k x b +图7 AC图812.如图8,某建筑物直立于水平地面,9BC =米,30B ∠=°,要建造楼梯,使每阶台阶高度不超过20厘米,那么此楼梯至少要建 阶(最后一阶不足201.732).二、精心选一选(本大题共8个小题,每小题3分,共24分.每小题给出的四个选项中,只有一个符合要求,请把你认为正确的选项序号填入下面相应题号的表格内.只要你掌握概念,认真思考,相信你一定会选对!)13.下面计算正确的是( )A .122-=- B2=± C .326()m n m n = D .624m m m ÷= 14.如图9,下列交通标志中既是中心对称图形,又是轴对称图形的是( )15.班主任为了解学生星期六、日在家的学习情况,家访了班内的六位学生,了解到他们在家的学习时间如下表所示:学生姓名 小丽 小明 小颖 小华 小乐 小恩学习时间(小时)4 6 3 45 8 那么这六位学生学习时间的众数和中位数分别是( )A .3.5小时和4小时B .4小时和4.5小时C .4小时和3.5小时D .4.5小时和4小时16.用直尺和圆规作一个角等于已知角,如图10,能得出A O B AOB '''∠=∠的依据是( )A .(S .S .S )B .(S .A .S )C .(A .S .A )D .(A .A .S )17.下列事件中是必然事件的是( )A .西宁一月一日刮西北风B .抛掷一枚硬币,落地后正面朝上C .当x 是实数时,20x ≥D .三角形内角和是360°18.在学校开展的“为灾区儿童过六一”的活动中,晶晶把自己最喜爱的钢笔盒送给了一位灾区儿童.这个铅笔盒(图11)的左视图是( )19.为执行“两免一补”政策,某地区2007年投入教育经费2500万元,预计2009年投入3600万元.设这两年投入教育经费的年平均增长百分率为x ,那么下面列出的方程正确的是( )A .225003600x =B .22500(1%)3600x +=C .22500(1)3600x +=D .22500(1)2500(1)3600x x +++= 20.当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图12,已知矩形纸片ABCD (矩形纸片要足够长),我们按如下步骤操作可以得到一个特定的角:(1)以点A 所在直线为折痕,折叠纸片,使点B 落在AD 上,折痕与BC 交于E ;(2)将纸片展平后,再一次折叠纸片,以E 所在直线为折痕,使点A 落在BC 上,折痕EF 交AD 于F .则AFE ∠=( )A .B .C .D .图9D A B C O O ' D ' A ' B ' C ' 图10 图11A . B . C . D . A BC D 图12A .60°B .67.5°C .72°D .75°三、认真答一答(本大题共8个小题,满分66分.解答须写出必要的文字说明、演算步骤或证明过程.只要你积极思考,细心运算,你一定会解答正确的!)21.(本小题满分7分)计算:101|3|1)22-⎛⎫-+-⨯ ⎪⎝⎭.22.(本小题满分7分)请从下列三个代数式中任选两个(一个作为分子,一个作为分母)构造一个分式,并化简该分式. 21a - 2a a - 221a a -+然后请你自选一个合理的数代入求值.23.(本小题满分7分)如图13,在ABCD中,(1)尺规作图(不写作法,保留作图痕迹):作ABC ∠的平分线BE 交AD 于E ;在线段BC 上截取CF DE =;连结EF .(2)求证:四边形ABFE 是菱形.24.(本小题满分8分)阅读下列材料并填空:(1)探究:平面上有n 个点(2n ≥)且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线? 我们知道,两点确定一条直线.平面上有2个点时,可以画2112⨯=条直线,平面内有3个点时,一共可以画3232⨯=条直线,平面上有4个点时,一共可以画4362⨯=条直线,平面内有5个点时,一共可以画 条直线,……平面内有n 个点时,一共可以画 条直线.(2)迁移:某足球比赛中有n 个球队(2n ≥)进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛? 有2个球队时,要进行2112⨯=场比赛,有3个球队时,要进行3232⨯=场比赛,有4个球队时,要进行 场比赛,……那么有20个球队时,要进行 场比赛.25.(本小题满分8分)已知:如图14,AB 为O ⊙的直径,AB AC =,O ⊙交BC 于D ,DE AC ⊥于E .A DBC 图13(1)请判断DE 与O ⊙的位置关系,并证明;(2)连结AD ,若O ⊙的半径为52,3AD =,求DE26.(本小题满分8分)《西海都市报》(2009年05月21日)文章《创卫让西宁焕发出勃勃生机》报道说:“西宁创建卫生城市已到了关键阶段,西宁处处焕发出勃勃生机.”省城西宁,无论是市容环境,还是市民意识,都发生了可喜的变化.西宁市教育局对全市约11000名九年级学生就西宁创建卫生城市知识的了解情况进行了问卷调查.现随机抽取了部分学生的答卷进行统计分析,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图15)和条形统计图(如图16).请你根据图中信息回答下列问题:(1)本次问卷调查的样本容量是 ;(2)扇形统计图中,圆心角α= ;(3)补全条形统计图;(4)根据以上信息,请提出一条合理化的创卫建议: .27.(本小题满分9分)已知一只口袋中放有x 只白球和y 只红球,这两种球除颜色以外没有任何区别.袋中的球已经搅匀.蒙上眼睛从袋中取一只球,取出白球的概率是34. (1)试写出y 与x 的函数关系式;(2)当3x =时,第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表法,求两次摸到都是白球的概率.28.(本小题满分12分)已知OABC 是一张矩形纸片,6AB =.(1)如图17,在AB 上取一点M ,使得CBM △与CB M '△关于CM 所在直线对称,点B '恰好在边OA 上,且OB C '△的面积为24cm 2,求BC 的长;(2)如图18.以O 为原点,OA OC 、所在直线分别为x 轴、y 轴建立平面直角坐标系.求对称轴CM 所在直线的函数关图14B 图16很好25% 一般 α 较差5% 较好50% 图15系式;(3)作B G AB '∥交CM 于点G ,若抛物线216y x m =+过点G ,求这条抛物线所对应的函数关系式.西宁市2009年高中招生考试数学试卷参考答案及评分意见一、填空题(本大题共12个小题15空,每空2分,共30分)1.5-等(答案不惟一);3x ≥. 2.x =0,x =1;12x y =⎧⎨=⎩. 3.4⨯1012. 4.5. 5.21. 6. 22. 7.50. 8.(1,-2). 9.8π. 10.6-; 1x >-. 11.2或8. 12.26.二、选择题(本大题共8个小题,每小题3分,共24分)D D BA C B C B三、解答题(本大题共66分,21、22、23小题每小题7分,24、25、26小题每小题8分,27小题9分,28小题12分)21.解:原式=3+1-2⨯2 ··············································································· 6分= 0 ····················································································· 7分22.解:构造的分式为:221a a a --、22121a a a --+、2221a a a a --+等(答案不惟一) ········· 2分 化简、求值:C B O A M B ' 图17图18例如:221a a a --=()()111a a a a +--()·········································································· 4分 =1a a + ······································································ 5分 当a =2时,原式=23 ·················································································· 7分 (答案不惟一)23.解:(1)正确作出∠ABC 的平分线BE ············································ 1分(图略) 正确作出CF =DE ······························································· 2分(图略)(2)证明:由作图可知∠ABE =∠FBE∵□ABCD ∴AD ∥BC∴∠AEB =∠EBF (两直线平行,内错角相等)∴∠AEB =∠ABE∴ AB =AE (等角对等边) ······················································ 4分 ∵□ABCD ∴AD =BC∵DE =CF ∴AE =BF∵AE ∥BF∴□ABFE (一组对边平行且相等的四边形是平行四边形) ··············· 6分∴四边形ABFE 是菱形(一组邻边相等的平行四边形是菱形) ··········· 7分24.解:10245=⨯ ······················································································· 2分 ()12n n ⨯- ························································································· 4分 6 ··································································································· 6分 19021920=⨯ ················································································· 8分 25.解:(1)DE 与⊙O 相切. ··············································································· 1分 证明:连结OD . ························································································ 2分 ∵OB =OD ∴∠B =∠1∵AB =AC ∴∠B =∠C ∴∠C =∠1∴OD ∥AC (同位角相等,两直线平行) ∵DE ⊥AC ∴∠DEC =90°∴∠ODE =∠DEC =90°(两直线平行,内错角相等)∴OD ⊥DE∵OD 为⊙O 半径∴DE 是⊙O 的切线(过半径外端且垂直于半径的直线是圆的切线) ······· 5分(2)∵AB 为⊙O 直径∴∠ADB =90°∴在Rt △BDA 中,∠ADB =90°∴BD =4∵AB =AC ∴BD =CD =4∵DE ⊥AC ∴S △ADC =AD CD ∙21 S △ADC =DE AC ∙21 ∴AD CD ∙21=DE AC ∙21∴DE ⨯=⨯534 ∴DE =512 ··················································································· 8分 26.解:(1)200%50100=(名) ········································································· 2分 (2)(1-50%-25%-5%)⨯360°=72° ··························································· 4分(3)见图. ·························································································· 6分(4)略. ····························································································· 8分27.解:(1)由题意可知:34x x y =+ ····························································· 2分 ∴所求的函数关系式是:y =13x ························································· 4分 (2)当x =3时,y =1树状图如下:(列表法略)······························································· 8分∴P (白白)=21 ···························································································· 9分 28.解:(1)∵S △OB ′C =21OB ′∙OC ∴OB ′=8cm ····················································· 2分 ∴Rt △OB ′C 中, B ′C =10cm ····························································· 3分∵△CBM 与△C B ′M 关于CM 所在直线对称∴BC = B ′C =10cm ································· 4分(2)∵∠OB ′C +∠AB ′M +∠MB ′C =180°∵∠MB ′C =90°∴∠OB ′C +∠AB ′M =90°∵∠AB ′M +∠OB ′C =90°∴∠OB ′C =∠OB ′C ∵∠COB ′=90°=∠MB ′A ∴△COB ′∽△B ′AM ∴AMOB AB OC=⋅∴AM =38∴M (10,38) ··························································· 6分 ∵C (0,6) ∴设直线CM 的解析式为:y =kx +b ∴81036k b b⎧=+⎪⎨⎪=⎩∴136k b ⎧=-⎪⎨⎪=⎩∴CM 的函数关系式为:y =-163x + ······························ 8分 (3)∵B ′G ∥AB ∴设G 点坐标为(8,n )∵点G 在CM 上∴n =310∴G 点坐标为(8,310) ··············································· 10分 ∵点G 在抛物线216y x m =+上 ∴m =223-∴抛物线的函数关系式为:212263y x =- ·········································· 12分 (注:每题只给出一种解法,如有不同解法请参照评分意见给分.)。
青海省中考真题

青海省2007年初中毕业升学考试(课改)数 学(本试卷满分120分,考试时间120分钟)一、填空题(本大题共12小题15空,每空2分,共30分)1.比较大小:23- 0.02-;35 43.2.任意选择电视的某一频道,正在播放动画片,这个事件是 事件(填“必然”“不可能”或“不确定”).3.我国自2005年在我省实施三江源保护区生态保护和建设工程以来,已累计投入资金10.26亿元,这个数据用科学记数法表示(保留两个有效数字)约为 元. 4.分解因式:324x x y -+= . 5.不等式830x -≥的最大整数解是 .6.函数0(32)y x =-的自变量的取值范围是 .7.观察规律并填空:111123248,,,…,第5个数是 ,第n 个数是 . 8.已知一个角的补角是12837' ,那么这个角的余角是 .9.已知圆的直径为10cm ,圆心到直线l 的距离为5cm ,那么l 和这个圆有 个公共点. 10.若圆锥的底面半径为4cm ,圆锥的全面积为2cm S ,母线长为x cm ,则S 与x 的函数关系式为 ,且S 随x 的减小而 .11.在一次数学活动课上,张明同学将矩形A B C D 沿直线C E 折叠,顶点B 恰好落在A D 边上F 点处,如图所示,已知8C D =cm ,5B E =cm ,则AD = cm .12.为了发展农业经济,致富奔小康,李伯伯家2006年养了4000条鲤鱼,现在准备打捞出售,为估计鱼塘中鲤鱼的总质量,从鱼塘中捕捞了三次进行统计,得到的数据如下表所示:鱼的条数 鱼的总质量(千克) 第一次捕捞 25 41 第二次捕捞 1017 第三次捕捞1527那么,估计鱼塘中鲤鱼的总质量为 千克.二、选择题(本大题共8小题,每小题3分,共24分,每小题给出的四个选项中,只有一个选项符合要求,请把你认为正确的选项序号填入题后的括号内) 13.如果双曲线m y x=经过点(32)-,,那么m 的值是( )A F DCBE第11题图A .6B .6-C .23-D .114.已知二元一次方程组2423m n m n -=⎧⎨-=⎩,,则m n +的值是( )A .1B .0C .2-D .1-15.张华的哥哥在西宁工作,今年“五 一”期间,她想让哥哥买几本科技书带回家,于是发短信给哥哥,可一时记不清哥哥手机号码后三位数的顺序,只记得是0,2,8三个数字,则张华一次发短信成功的概率是( ) A .16B .13C .19D .1216.化简:29333a a a aa ⎛⎫++÷⎪--⎝⎭的结果是( ) A .a - B .a C .2(3)a a+ D .117.第二十九届奥运会2008年将在我国北京举行,如图是国际奥林匹克运动会旗的标志图案,它由五个半径相同的圆组成,象征着五大洲体育健儿,为发扬奥林匹克精神而团结起来,携手拼搏,这个图案是( )A .既不是轴对称图形,又不是中心对称图形B .既是轴对称图形,又是中心对称图形C .中心对称图形D .轴对称图形18.在梯形A B C D 中,A DBC ∥,A BD C =,EFGH ,,,分别是A B B C C D D A ,,,的中点,则四边形E F G H 是( )A .等腰梯形B .矩形C .菱形D .正方形19.如右图是某几何体的主视图、左视图、俯视图, 它对应的几何体是下图中的()第17题图 主视图 左视图 俯视图第19题图A.B.C.D.20.如图,为了测量河的宽度,王芳同学在河岸边相距200m 的M 和N 两点分别测定对岸一棵树P 的位置,P 在M 的正北方向,在N 的北偏西30 的方向,则河的宽度是( )A .2003mB .20033m C .1003m D .100m三、(本大题共3小题,每小题7分,共21分) 21.计算:121127332cos 602-⎛⎫-⨯-+-+ ⎪⎝⎭.22.已知,如图所示,图①和图②中的每个小正方形的边长都为1个单位长度.(1)将图①中的格点A B C △(顶点都在网络线交点处的三角形叫做格点三角形)向上平移2个单位长度得到111A B C △,请你在图中画出111A B C △;(2)在图②中画一个与格点A B C △相似的格点222A B C △,且222A B C △与A B C △的相似比为2:1.PM N第20题图C B A图①CB A图②第22题图23.如图所示,在A B C D中,E F ,分别是A B C D ,上的点,且A E C F =,连接B F D E ,,试猜测AD E ∠与C B F ∠的大小关系,并加以证明.四、(本大题共3小题,每小题8分,共24分)24.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利,尽快减少库存......,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2 100元,每件衬衫应降价多少元?25.某地区就1980年以来的小麦生产情况提供了如下的统计信息,如图所示,结合图中所提供的信息回答下列问题:(1)由图①可知,该地区的小麦平均亩产量从1980年到2006年在逐年 ; 由图②可知,该地区的耕地面积从1980年到2006年在逐年 (填“增加”或“减少”);(2)根据图中所提供的信息,通过计算判断该地区的小麦总产量从1990年到2006年的变化趋势;(3)结合(2)中得到的变化趋势,谈谈自己的感想(不少于20个字).D FCBEA第23题图500 400 300 200 1001980 1990 2000 2006 2010图①平均亩产量(公斤)年份第25题图 图②350 420 70 60 50 40 30 20 101980 1990 2000 2006 2010耕地面积(万亩)年份55 6526.已知,如图,A B 是半圆O 的直径,点C 是半圆上的一点,过点C 作C D AB ⊥于D ,210AC =cm .:1:1A D D B =,求A D 的长.五、(本大题共2小题,第27题10分,第28题11分,共21分) 27.先阅读,再填空解答:方程2340x x --=的根是:11x =-,24x =,则123x x +=,124x x =-; 方程231080x x ++=的根是:12x =-,243x =-,则12103x x +=-,1283x x =.(1)方程2230x x +-=的根是:1x = ,2x = ,则12x x += ,12x x = ;(2)若12x x ,是关于x 的一元二次方程20ax bx c ++=(0a ≠,且a b c ,,为常数)的两个实数根,那么12x x +,12x x 与系数a b c ,,的关系是:12x x += ,12x x = ;(3)如果12x x ,是方程230x x +-=的两个根,根据(2)所得结论,求2212x x +的值.28.如图,抛物线2y x bx c =+-经过直线3y x =-与坐标轴的两个交点A B ,,此抛物线与x 轴的另一个交点为C ,抛物线的顶点为D . (1)求此抛物线的解析式;(2)点P 为抛物线上的一个动点,求使:5:4APC AC D S S =△△的点P 的坐标.BAO CD第26题图ABC D Oy x第28题图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
青海省2009年初中考试数 学 试 卷(本试卷满分120分,考试时间120分钟)考生注意:1.答卷前将密封线以内的项目填写清楚. 2.用蓝黑钢笔或中性笔答题.一、填空题(本大题共12小题15空,每空2分,共30分). 1.15-的相反数是 ;立方等于8-的数是 . 2.计算:3120092-0⎛⎫+= ⎪⎝⎭;分解因式:332244x y x y xy -+= .3.三江源实业公司为治理环境污染,8年来共投入23940000元,那么23940000元用科学记数法表示为 元(保留两个有效数字).4.如图1,PA 是O ⊙的切线,切点为30A PA APO =∠=,°,则O ⊙的半径长为 .5.已知一次函数y kx b =+的图象如图2,当0x <时,y 的取值范围是 . 6.第二象限内的点()P x y ,满足||9x =,24y =,则点P 的坐标是 .7.不等式组250112x x -<⎧⎪⎨+⎪⎩≥所有整数解的和是 .8.若2||323x x x ---的值为零,则x 的值是 . 9.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 个.10.如图3,四边形ABCD 的对角线互相平分,要使它变为菱形, 需要添加的条件是 (只填一个你认为正确的即可).毕业升学A 图1图2ADCBO11.如图4,函数y x =与4y x=的图象交于A 、B 两点, 过点A 作AC 垂直于y 轴,垂足为C ,则ABC △的面积 为 .12.观察下面的一列单项式:x ,22x -,34x ,48x -,…根据你发现的规律,第7个单项式为 ;第n 个单项式为 .二、选择题(本大题共8小题,每小题3分,共24分,每小题给出的四个选项中,只有一个选项符合要求,请把你认为正确的选项序号填入下面相应题号的表格内).13.计算3212xy ⎛⎫- ⎪⎝⎭,结果正确的是( )A .2414x yB .3618x y -C .3618x yD .3518x y -14.方程29180x x -+=的两个根是等腰三角形的底和腰,则这个三角形的周长为( ) A .12B .12或15C .15D .不能确定15.在函数2y x=中,自变量x 的取值范围是( ) A .3x -≥且0x ≠ B .3x ≤且0x ≠ C .0x ≠ D .3x -≥16.在一幅长为80cm ,宽为50cm 的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图5所示,如果要使整个挂图的面积是5400cm 2,设金色纸边的宽为x cm ,那么x 满足的方程是( )A .213014000x x +-= B .2653500x x +-= C .213014000x x --=D .2653500x x --=17.已知代数式133m xy --与52n m n x y +是同类项,那么m n 、的值分别是( )A .21m n =⎧⎨=-⎩B .21m n =-⎧⎨=-⎩C .21m n =⎧⎨=⎩D .21m n =-⎧⎨=⎩18.如图6,一根电线杆的接线柱部分AB 在阳光下的投影CD的长为 1米,太阳光线与地面的夹角60ACD ∠=°,则AB 的长为( ) A .12米BC 米D 米60°A BC D19.如图7是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( )20.将三个均匀的六面分别标有1、2、3、4、5、6的正方体同时掷出,出现的数字分别为a b c 、、,则a b c 、、正好是直角三角形三边长的概率是( ) A .1216B .172C .112D .136三、(本大题共3小题,每小题7分,共21分)21.请你先化简分式2222x xy y x y x xy y x ⎛⎫-+÷- ⎪-⎝⎭,再将3x =,y =代入求值.22.如图8,请借助直尺按要求画图:(1)平移方格纸中左下角的图形,使点1P 平移到点2P 处. (2)将点1P 平移到点3P 处,并画出将原图放大为两倍的图形.23.如图9,梯形ABCD 中,AD BC ∥,AB DC =,P 为梯形ABCD 外一点,PA PD 、分别交线段BC 于点E F 、,且PA PD =.(1)图中除了ABE DCF △≌△外,请你再找出其余三对全等的三角形(不再添加辅助线).(2)求证:ABE DCF △≌△.1 3 21 图7 A . B . C . D .图8D C F EAB四、(本大题共3小题,每小题8分,共24分)24.某玩具店采购人员第一次用100元去采购“企鹅牌”玩具,很快售完.第二次去采购时发现批发价上涨了0.5元,用去了150元,所购玩具数量比第一次多了10件.两批玩具的售价均为2.8元.问第二次采购玩具多少件?(说明:根据销售常识,批发价应该低于销售价)25.美国NBA 职业篮球赛的火箭队和湖人队在本赛季已进行了5场比寒.将比赛成绩进行统计后,绘制成统计图(如图10-1).请完成以下四个问题:(1)在图10-2中画出折线表示两队这5场比赛成绩的变化情况;(2)已知火箭队五场比赛的平均得分90x =火,请你计算湖人队五场比赛成绩的平均得分x 湖;(3)就这5场比赛,分别计算两队成绩的极差;(4)根据上述统计情况,试从平均得分、折线的走势、获胜场次和极差四个方面分别进行简要分析,请预测下一场比赛哪个队更能取得好成绩?26.如图11,一个圆锥的高为,侧面展开图是半圆. 求:(1)圆锥的母线长与底面半径之比; (2)求BAC ∠的度数;(3)圆锥的侧面积(结果保留π).场次/场图10-2 图11场次/场 图10-1五、(本大题共2小题,第27题10分,第28题11分,共21分) 27.请阅读,完成证明和填空.九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:(1)如图12-1,正三角形ABC 中,在AB AC 、边上分别取点M N 、,使BM AN =,连接BN CM 、,发现BN CM =,且60NOC ∠=°. 请证明:60NOC ∠=°.(2)如图12-2,正方形ABCD 中,在AB BC 、边上分别取点M N 、,使AM BN =,连接AN DM 、,那么AN = ,且DON ∠= 度.(3)如图12-3,正五边形ABCDE 中,在AB BC 、边上分别取点M N 、,使A M B N =,连接AN EM 、,那么AN = ,且EON ∠= 度.(4)在正n 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现: .28.矩形OABC 在平面直角坐标系中位置如图13所示,A C 、两点的坐标分别为(60)A ,,(03)C -,,直线34y x =-与BC 边相交于D 点.(1)求点D 的坐标;(2)若抛物线294y ax x =-经过点A ,试确定此抛物线的表达式;(3)设(2)中的抛物线的对称轴与直线OD 交于点M ,点P 为对称轴上一动点,以P O M 、、为顶点的三角形与OCD △相似,求符合条件的点P 的坐标.A A AB B BC C CD D O O O MM MN N N E图12-1 图12-2 图12-3…青海省2009年初中毕业升学考试数学试卷参考答案及评分标准(普通卷)注:①全卷不给小数分;②以下各题用不同于本参考答案的解法做正确的相应给分一、填空题(本大题共12小题15空,每空2分,共30分) 1.15;2- 2.9;2(2)xy xy - 3.72.410⨯ 4.2 5.2y <- 6.(32)-, 7.3 8.3- 9.24 10.AC BD ⊥或AB BC =,或BC CD =,或CD DA =,或AB AD = 11.4 12.764x ;1(2)n n x --三、本大题共3小题,每小题7分,共21分21.解:2222x xy y x y x xy y x ⎛⎫-+÷- ⎪-⎝⎭222()()x y x y x x y xy--=÷- ·························································································· (2分) ()()x y xyx x y x y -=+-····················································································· (4分) y x y=+ ············································································································· (5分)当3x =y =原式=········································································································ (6分)3=······················································································································· (7分) 22.本题共7分(1)从1P 平移到2P 处,若图象正确得3分; (2)放大2倍且正确,再得4分.23.本题共7分,其中第(1)小题3分,第(2)小题4分(1)ABP DCP △≌△;BEP CEP △≌△;BFP CEP △≌△. ······················ (3分) (2)∵AD BC ∥,AB DC =, ∴梯形ABCD 为等腰梯形. ∴BAD CDA ABE DCF ∠=∠∠=∠,. ···································································· (4分) 又∵PA PD =,∴PAD PDA ∠=∠,∴BAD PAD CDA PDA ∠-∠=∠-∠. 即BAP CDP ∠=∠. ···································································································· (6分) 在ABE △和DCF △中,BAP CDP AB DCABE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABE DCF △≌△. ································································································· (7分) 四、本大题共3小题,每题8分,共24分.24.解法一:设第二次采购玩具x 件,则第一次采购玩具(10)x -件,由题意得 ····· (1分)1001150102x x+=- ··········································································································· (4分) 整理得 211030000x x -+=解得 150x =,260x =. ····························································································· (6分) 经检验150x =,260x =都是原方程的解.当50x =时,每件玩具的批发价为150503÷=(元),高于玩具的售价,不合题意,舍去; 当60x =时,每件玩具的批发价为15060 2.5÷=(元),低于玩具的售价,符合题意,因此第二次采购玩具60件. ····························································································· (8分) 解法二:设第一次采购玩具x 件,则第二次采购玩具(10)x +件,由题意得 ············ (1分)1001150210x x +=+ ··········································································································· (4分) 整理得 29020000x x -+=解得 140x =,250x =. ····························································································· (6分) 经检验,140x =,250x =都是原方程的解.第一次采购40件时,第二次购401050+=件,批发价为150503÷=(元)不合题意,舍去;第一次采购50件时,第二次购501060+=件,批发价为15060 2.5÷=(元)符合题意,因此第二次采购玩具60件. ························································································· (8分)25.(1)如图. ············································································································ (2分) (注:本小题每画对一条折线得1分.)(2)90x =湖(分); ································ (3分) (3)火箭队成绩的极差是18分,湖人队成绩的极差是30分; ······················································· (4分) (4)从平均分看,两队的平均分相同,实力大体相当; 从折线的走势看,火箭队比赛成绩呈上升趋势,而湖人队比赛成绩呈下降趋势; 从获胜场数看,火箭队胜三场,湖人队胜两场,火箭队成绩好; 从极差看,火箭队比赛成绩比湖人队比赛成绩波动小,火箭队成绩较稳定.综上,下一场比赛火箭队更能取得好成绩. ································································ (8分) 26.(1)设此圆锥的高为h ,底面半径为r ,母线长AC l =. ∵2ππr l =,∴2lr=. ············································································· (2分) (2)∵2lr=,∴圆锥高与母线的夹角为30°,则60BAC ∠=° ··············· (4分)(3)由图可知222l h r h =+=,,∴222(2)r r =+,即22427r r =+.解得 3cm r =. ∴26cm l r ==. ·········································································································· (6分)∴圆锥的侧面积为22π18π(cm )2l =. ·········································································· (8分)/场五、本大题共2小题,第27题10分,第28题11分,共21分. 27.(1)证明:∵ABC △是正三角形, ∴60A ABC AB BC ∠=∠==°,, 在ABN △和BCM △中,AB BC A ABC AN BM =⎧⎪∠=∠⎨⎪=⎩∴ABN BCM △≌△. ································································································ (2分) ∴ABN BCM ∠=∠.又∵60ABN OBC ∠+∠=°, ∴60BCM OBC ∠+∠=°, ∴60NOC ∠=°. ········································································································· (4分) 注:学生可以有其它正确的等价证明.(2)在正方形中,90AN DM DON =∠=,°. ······················································ (6分) (3)在正五边形中,108AN EM EON =∠=,°. ················································· (8分) 注:每空1分.(4)以上所求的角恰好等于正n 边形的内角(2)180n n- °. ··································· (10分)注:学生的表述只要合理或有其它等价且正确的结论,均给分.本题结论着重强调角和角的度数.28.解:(1)点D 的坐标为(43)-,. ······································································· (2分) (2)抛物线的表达式为23984y x x =-. ···································································· (4分) (3)抛物线的对称轴与x 轴的交点1P 符合条件. ∵OA CB ∥,∴1POM CDO ∠=∠. ∵190OPM DCO ∠=∠=°, ∴1Rt Rt POM CDO △∽△. ····························· (6∵抛物线的对称轴3x =,∴点1P 的坐标为1(30)P,. ···························································································· (7分) 过点O 作OD 的垂线交抛物线的对称轴于点2P . ∵对称轴平行于y 轴, ∴2P MO DOC ∠=∠. ∵290P OM DCO ∠=∠=°,∴21Rt Rt P M O DOC △∽△. ···················································································· (8分) ∴点2P 也符合条件,2OP M ODC ∠=∠.∴121390PO CO P PO DCO ==∠=∠=,°, ∴21Rt Rt P PO DCO △≌△. ······················································································ (9分) ∴124PP CD ==. ∵点2P 在第一象限, ∴点2P 的坐标为2P (34),,∴符合条件的点P 有两个,分别是1(30)P ,,2P (34),. ·········································· (11分)。
