绵阳市2010—2011学年八年级(上)期末考试数学试卷(含答案)
2010-2011学年四川省绵阳市八年级(上)期末数学试卷

2010-2011学年四川省绵阳市八年级(上)期末数学试卷一、选择题(共12小题,每小题3分,满分36分)2.(3分)从实数,,0,π,4中,挑选出的两个数都是无理数的为( ) ,0 B ,4 ,π || 4.(3分)如图,正方形OABC 的边长为1,以A 为圆心,AC 为半径画弧,与数轴的一个交点是D ,则D 点表示的数为( )BB7.(3分)已知一次函数y=kx+b (k ≠0)的图象如右,则关于x 的不等式kx+b <0的解集为( )8.(3分)如图,点D、E在△ABC的BC边上,AB=AC,AD=AE,则图中全等三角形共有()9.(3分)如图是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形,这样的白色小正方形有()10.(3分)平面直角坐标系中,把点A向上平移2个单位后得点B,点B关于直线x=﹣1C12.(3分)某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)二、填空题(共6小题,每小题3分,满分18分)13.(3分)若式子有意义,则x的取值范围是_________.14.(3分)(2008•茂名)分解因式:3x2﹣27=_________.15.(3分)计算:=_________.16.(3分)如图,△ABC的三个顶点在单位正方形网格的交点上,如果△A′B′C′与△ABC关于y轴对称,那么点C的对应点C′的坐标为_________.17.(3分)已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为_________.18.(3分)如图,△ABC中,CD是AB边上的高,若2∠ACB=3∠B=6∠A,则BC:AD=_________.三、解答题(共6小题,满分46分)19.(7分)计算:.20.(7分)先化简,再求值:(3x﹣1)(3x+1)﹣9 (x﹣1)2+10,其中.21.(7分)如图,△ABC中,AB=AD=DC,设∠BAD=x,∠C=y,试求y与x的函数关系式,并写出x的取值范围.22.(7分)如图,△ABC和△ADE都是等边三角形,BD与CE相交于O.(1)求证:BD=CE;(2)OA平分∠BOE吗?说明理由.23.(8分)如图,是一个上、下两部分均为圆柱体的容器,现向其中注水,直到注满为止,容器中水的体积v(cm3)随水面高度h(cm)变化的图象如下.(1)求容器下部分圆柱体的高和底面圆的半径;(2)求水的体积v(cm3)与水面高度h(cm)的函数关系式,并写出h的取值范围.(圆柱体的体积v=πr2h,其中r是柱体底面圆的半径,h是圆柱的高)24.(10分)平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).(1)如图1,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个?(2)过A、B向直线l:y=﹣2x作垂线,垂足分别为M,N(如图2),试判断线段AM、BN、MN之间的数量关系,并说明理由.(3)过A、B向动直线l:y=kx(k>0)作垂线,垂足分别为M,N,请直接写出线段AM、BN、MN之间的数量关系.2010-2011学年四川省绵阳市八年级(上)期末数学试卷参考答案与试题解析一、选择题(共12小题,每小题3分,满分36分)1.C2.D3.D4.A5.C6.A7.A8.C9.A10.D11.B12.A二、填空题(共6小题,每小题3分,满分18分)13.x>3.14.3(x+3)(x﹣3).15.4a3.16.(﹣4,4).17.40°或100°.18.2:3.时,原式x+45。
绵阳市级上期末数学考试试题doc

绵阳市示范初中2008级第五学期末教学质量测试数 学 试 题本试卷分为试题卷和答题卷两部分,其中试题卷由第Ⅰ卷(选择题)和第Ⅱ卷组成,共4页;答题卷共4页.满分100分.考试结束后将答题卡和答题卷一并交回.第Ⅰ卷(选择题,共36分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案,不能答在试题卷上.一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的,把它选出来填涂在答题卡上.1.将方程 3x (x -1)= 5(x + 2)化为一元二次方程的一般式,正确的是( ).A .4x 2-4x + 5 = 0B .3x 2-8x -10 = 0C .4x 2 + 4x -5 = 0D .3x 2 + 8x + 10 = 02.将一元二次方程x 2-2x -2 = 0通过配方后所得的方程是( ).A .(x -2)2 = 2B .(x -1)2 = 2C .(x -1)2 = 3D .(x -2)2 = 33.下列计算正确的是( ).A .257=-B .428=÷C .2318=D .1)21)(21(=-+4.若a <0,则化简232a 得( ). A .a 32 B .a 36 C .-a 32 D .-a36 5.在一次国际乒乓球比赛中,甲、乙两名中国选手进入最后的决赛,下列事件中,必然发生的事件是( ).A .冠军属于中国选手B .冠军属于外国选手C .冠军属于中国选手甲D .冠军属于中国选手乙6.将一个各面涂有颜色的正方体,分割成同样大小的27个小正方体,从这些正方体中任取一个,恰有3个面涂有颜色的概率是( ).A .2719B .94C .32D .278 7.如图,平行四边形ABCD 的两条对角线AC 与BD 相交于直角坐标系的原点.若点A 的坐标为(-2,3),则点C 的坐标为(). A .(2,3) B .(2,-3)C .(-2,3)D .(-2,-3) 8.如图,BD 是⊙O 的直径,圆周角∠A = 30︒,则 ∠CBD 的度数是( ). A .30︒ B .45︒ C .60︒ D .80︒9.已知相切两圆的半径是一元二次方程x 2-9x + 20 = 0的两个根,则这两个圆的圆心距是( ).A .9B .1或9C .1D .4或510.如图,△DEC 是由△ABC 经过了如下的几何变换而得到的: ① 以AC 所在直线为对称轴作轴对称, 再以C 为旋转中心,顺时针旋转90︒; ② 以C 为旋转中心,顺时针旋转90︒得△A ′B ′C ′,再以A ′C ′ 所在直线为对称轴作轴对称;③ 将△ABC 向下、 向左各平移1个单位,再以AC 的中点为中心作中心对称.其中正确的变换有( ).A .①②B .①③C .②③D .①②③ 11.已知如图,圆锥的底面圆的半径为r (r >0),母线长OA 为3r ,C 为母线OB 的中点.在圆锥的侧面上, 一只蚂蚁从点A 爬行到点C 的最短线路长为( ).A .r 23B .r 233 C .r 33 D .r 33 12.若关于x 的一元二次方程 ax 2 + bx + c = 0(a ≠0)各项系数满足a + b + c =0,则此方程的根的情况:① 必有两个不相等的实数根; ② 当a = c 时,有两个相等的实数根;③ 当a 、c 同号时,方程有两个正的实数根. 其中正确结论的个数是( ).A .0B .1C .2D .3第Ⅱ卷(非选择题,共64分)A E CB D注意事项:1.用钢笔或圆珠笔答在答题卷中.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共 6个小题,每小题3分,共18分.把答案直接填在答题卷的横线上.13.若32-x 在实数范围内有意义,则x 的取值范围是 .14.如图,AB 是⊙O 的直径,C 、D 是BE⌒的两个等分点, ∠COD = 35︒,则∠AOE 的度数为 .15.若方程x 2-m = 0有非零整数根,则m 的值可以是.(只填一个)16.如图,在△ABC 中,∠A = 90︒,BC = 4 cm ,分别以点B 、C 为圆心的两个等圆相外切,则这两个阴影扇形的面积之和为 cm 2.(结果不取近似值)17.如图,AB 是⊙O 的直径,AB = AC ,BC 交⊙O 于点D ,AC 交⊙O 于点E ,∠BAC = 45︒.给出下列五个结论:①∠EBC = 22.5︒;② BD = DC ;③ AE = 2EC ;④ 劣弧AE ⌒ 是劣孤 DE ⌒ 的2倍; ⑤ AE = BC . 其中正确结论的序号是 . 18.在围棋盒中有x 颗黑色棋子和y 颗白色棋子,从盒中 随机地取出一个棋子,如果它是白色棋子的概率是72, 则y 与x 的函数关系式为 .三、解答题:本大题共6个小题,共46分.解答应写出文字说明、证明过程或演算步骤.19.(本题满分6分)计算:272)6322(+÷-.20.(本题满分6分)如图,E 为正方形ABCD 的边AB 上一点(不含A 、B 点),F 为BC 边的延长线上一点,△DAE 旋转后能与△DCF 重合.(1)旋转中心是哪一点?(2)旋转了多少度? (3)如果连结EF ,那么△DEF 是怎样的三角形?21.(本题满分8分)某电脑公司现有A 、B 、C 三种型号的甲品牌电脑和D 、E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.(1)写出所有的选购方案(利用树状图或列表法表示);(2)如果(1)中各种选购方案被选中的可能性相同,那么A 型号电脑被O A B C D ED AE B C FAB C选中的概率是多少?22.(本题满分8分)如图,△ABC中,AB = AC = 10,BC = 16.(1)试用尺规作图法作出△ABC的外接圆O(保留作图痕迹,不写作法);(2)求出⊙O的半径.23.(本题满分10分)如图甲,直线P A交⊙O于A、E两点,P A的垂线CD 切⊙O于点C,过点A作⊙O的直径AB.(1)求证:AC平分∠DAB;(2)如图乙,将直线CD向下平行移动,得到CD与⊙O相切于C,AC 还平分∠DAB吗?说明理由;(3)在将直线CD向下平行移动的过程中,如图丙、丁,试指出与∠DAC 相等的角(不要求证明).24.(本题满分8分)在一块长16 m、宽12 m的矩形荒地上,要建造一个花园,并使花园所占的面积为荒地面积的一半.小明的设计方案如图甲所示,其中花园四周小路的宽度都相等.小明通过列方程,并解方程,得到小路的宽为2 m或12 m.请解答下列问题:(1(2数学试题参考答案及评分意见一、选择题:本大题共12小题,每小题3分,共36分.BCCD ADBC BABC二、填空题:本大题共6小题,每小题3分,共18分.13.x ≥23 14.75(75︒) 15.1,4等 16.π 17.①②④ 18.x y 52=,x 是正整数,且是5的倍数 三、解答题:本大题共6小题,共46分,解答应写出文字说明、证明过程或演算步骤.19.原式=332632222⋅+÷-÷=33332+-= 2.……………………… 6分20.(1)D ……………………… 2分(2)90︒ ……………………… 4分(3)等腰直角三角形 ……………………… 6分21.(1)树状图如下:甲品牌乙品牌……………………… 2分 列表如下:有6种可能的结果(A ,D ),(A ,E ),(B ,D),(B ,E ),(C ,D ),(C ,E ). ……………………… 4分(2)因为选中A 型号电脑有2种方案,即(A ,D ),(A ,E ),所以A •型号电脑被选中的概率是3162=. ……………………… 8分 22.(1)略(有作图痕迹,圆心等). ……………………… 3分(2)连结OA 交BC 于D ,连结OC .因为 AB = AC ,所以由垂径定理,得 OA ⊥BC 于D ,BD = CD = 8. 在Rt △ADC 中,68102222=-=-=CE AC AD .设 OC = OA = R ,则OD = R -6.在Rt △OCD 中,由 OC 2 = OD 2 + CD 2,得 R 2 =(R -6)2 + 82,解得 325=R . ……… 8分23.(1)连结OC .∵ OA 、OC 是⊙O 的半径,∴ OA = OC ,得 ∠OAC =∠OCA .∵ CD 切⊙O 于点C ,∴ CD ⊥OC .又 ∵ CD ⊥P A ,∴ OC ∥P A ,于是得∠P AC =∠OCA ,故 ∠OAC =∠P AC ,表明AC 平分∠DAB . ……………………… 4分(2)AC 平分∠DAB .连结OC .∵ CD 切⊙O 于C ,∴ CD ⊥OC . 又 ∵ AD ⊥CD ,∴ OC ∥AD ,于是得∠COB =∠DAB .而 OA = OC ,所以 ∠CAO =∠ACO , 因此 ∠DAC =∠ACO =∠CAO ,表明AC 平分∠DAB……………………… 8分(3)∠DAC =∠BAF . ……………………… 10分 24.甲 乙(1)小明的设计方案:由于花园四周小路的宽度相等,设其宽为x 米.则根据题意,列出方程,得 121621)212)(216(⨯⨯=--x x ,即 x 2-14x + 24 = 0,解得x = 2 或 x = 12.由于矩形荒地的宽是12 m ,故舍去x = 12,得花园四周小路宽为2 cm ,所以小明的结果不对.……………………5分(2)小亮的设计方案:由于其中花园的四个角上均为相同的扇形,所以设扇形的半径为x 米,列方程得1216212⨯⨯=x π,所以πππ6464==x (≈5.53). ……………………8分。
高等数学期末考试试题及答案(大一考试)

五、设函数由方程确定,求.(8分)六、若有界可积函数满足关系式,求。
(8分)七、求下列各不定积分(每题6分,共12分)(1).八、设求定积分。
(6分)九、讨论函数的单调区间、极值、凹凸区间和拐点坐标.(10分)十、求方程的通解(6分)十一、求证:.(5分)第一学期高等数学(上)(A)卷分标准题3分,共15分)2。
B 3。
D 4。
B 5.D分,共18分)为任意常数),4. 2 , 5。
6。
分 (6)分解:………………3分…………….6分 (8)导 (3)数)…………6分分解:(1)。
……。
.3分 (6)分分=……………6分时有极大值2,有极小值。
在上是凸的,在上是凹的,拐点为(0,0)………10分十、解;…………………..3分设方程(1)的解为代入(1)得………5分…………………….6分十一、证明:令………………1 分又…。
3分的图形是凸的,由函数在闭区间连续知道最小值一定在区间端点取到。
,所以…………。
5分.(2010至2011学年第一学期)一、单项选择题(15分,每小题3分)1、当时,下列函数为无穷小量的是( )(A)(B) (C)(D)2.函数在点处连续是函数在该点可导的()(A)必要条件(B)充分条件(C)充要条件(D)既非充分也非必要条件3.设在内单增,则在内()(A)无驻点(B)无拐点(C)无极值点(D)4.设在内连续,且,则至少存在一点使()成立。
(A)(B)(C)(D)5.广义积分当( )时收敛。
(A) (B) (C)(D)二、填空题(15分,每小题3分)1、若当时,,则;2、设由方程所确定的隐函数,则;3、函数在区间单减;在区间单增;4、若在处取得极值,则;5、若,则;三、计算下列极限.(12分,每小题6分)1、2、四、求下列函数的导数(12分,每小题6分)1、,求2、,求五、计算下列积分(18分,每小题6分)1、2、3、设,计算六、讨论函数的连续性,若有间断点,指出其类型。
(7分)七、证明不等式:当时,(7分)八、求由曲线所围图形的面积。
绵阳市八年级数学期末考试题答案

绵阳市八年级数学期末考试题答案2012年绵阳市八年级数学期末考试题(答案)XX中学2011—2012学年度第二学期期末考试八年级数学试卷(考试时间:100分钟满分:100分)题号一二三总分2122232425得分一、选择题。
(每小题3分,共30分)题号12345678910答案1.使分式有意义的的取值范围是().(A)x≥(B)x≤(C)(D)2.如图,某反比例函数的图像过点M(,1),则此反比例函数表达式为。
A.B.C.D.3.一位经销商计划进一批“运动鞋”,他到滨州的一所学校里对初二的100名男生的鞋号进行了调查,经销商最感兴趣的是这组鞋号的()A.中位数B.平均数C.方差D.众数4.下列各数据中,不能组成直角三角形的是()(A)3,4,5;(B)1,,3;(C)1,,;(D)6,8,105、已知四边形ABCD是平行四边形,下列结论中不正确的是()A、当AB=BC时,它是菱形B、当AC⊥BD时,它是菱形C、当∠ABC=900时,它是矩形D、当AC=BD时,它是正方形6、放学以后,小丽和小宏从学校分手,分别沿东南方向和西南方向回家,若小丽和小宏行走的速度都是40米/分,小丽用15分钟到家,小宏用20分钟到家,小丽和小宏家的距离为()A.600米B.800米C.1000米D.不能确定7、反比例函数(k>0)的部分图象如图所示,A、B是图象上两点,AC⊥轴于点C,BD⊥轴于点D,若△AOC的面积为S,△BOD的面积为S,则S和S的大小关系为()A.S>SB.S=SC.S<SD.无法确定8.分式的计算结果是()A.B.C.D.9.正比例函数与反比例函数在同一坐标系中的图象不可能是()10.如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是()A、(4,1)B、(-3,1)C、(-2,1)D、(2,-1)二、填空题(每小师2分,共20分)11.x=_______时,分式的值为零.12.数据2,x,9,2,8,5的平均数为5,它的极差为。
2023-2024学年四川省绵阳市游仙区示范学校八年级(上)期末数学试卷(含解析)

2023-2024学年四川省绵阳市游仙区示范学校八年级(上)期末数学试卷一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个图形中,不是轴对称图形的是( )A. B.C. D.2.下列计算正确的是( )A. a+a=a2B. a2⋅a3=a6C. (−a3)2=−a6D. a7÷a5=a23.计算下列各式,其结果是4y2−1的是( )A. (−2y−1)(−2y+1)B. (2y−1)2C. (4y−1)2D. (2y+1)(−2y+1)4.化简(xx−2−xx+2)÷14−x2的结果是( )A. −4xB. −4C. 4xD. 45.已知(4x−2)与(3x2+mx+1)的乘积中不含x2项,则m的值是( )A. 2B. 3C. 32D. −326.如图,△ABC中,AB=6,BC=4,AC的垂直平分线交AB,AC于点D和E,则△BCD的周长为( )A. 6B. 8C. 10D. 127.将分式x2yx−y中的x,y的值同时扩大为原来的3倍,则分式的值( )A. 扩大6倍B. 扩大9倍C. 不变D. 扩大3倍8.如图,将两块相同的三角板(含30°角)按图中所示位置摆放,若BE交CF于D,AC交BE于M,AB交CF于N,则下列结论中错误的是( )A. ∠EAC=∠FABB. ∠EAF=∠EDFC. △ACN≌△ABMD. AM=AN9.某施工队挖掘一条长96米的隧道,开工后每天比原计划多挖2米,结果提前4天完成任务,原计划每天挖多少米?若设原计划每天挖x米,则依题意列出正确的方程为( )A. 96x−2−96x=4 B. 96x−96x−2=4 C. 96x−96x+2=4 D. 96x+2−96x=410.如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )A. 9cmB. 6cmC. 12cmD. 3cm11.如果4是关于x的分式方程a+2x−3−12x−7=2的解,则a等于( )A. −1B. −3C. 1D. 312.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,若AD=12,CD=5,则ED的长度是( )A. 8B. 7C. 6D. 5二、填空题:本题共6小题,每小题3分,共18分。
四川省绵阳市八年级上学期数学期末考试试卷

四川省绵阳市八年级上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题(本题有10小题,每小题3分,共30分) (共10题;共28分)1. (3分)已知三角形的两边分别为2和6,则此三角形的第三边可能是()A . 2B . 4C . 6D . 82. (3分)如图:,则∠D的度数为().A . 30ºB . 45ºC . 60ºD . 90º3. (3分)如图,下列条件中,不能判断直线ι1//ι2的是()A . ∠1=∠3B . ∠2=∠3C . ∠4=∠5D . ∠2+∠4=180°4. (2分) (2017七下·平南期末) 下列“慢行通过,注意危险,禁止行人通行,禁止非机动车通行”四个交通标志图(黑白阴影图片)中为轴对称图形的是()A .B .C .D .5. (3分) (2017八下·山西期末) 下列命题中的真命题是()A . 一组对边平行,另一组对边相等的四边形是平行四边形B . 有一组对边和一组对角分别相等的四边形是平行四边形C . 一组对边平行一组对角相等的四边形是平行四边形D . 两条对角线相等的四边形是平行四边形6. (3分)以下展示四位同学对问题“已知a<0,试比较2a和a的大小”的解法,其中正确的解法个数是()①方法一:∵2>1,a<0,∴2a<a;②方法二:∵a<0,即2a-a<0,∴2a<a;③方法三:∵a<0,∴两边都加a 得2a<a;④方法四:∵当a<0时,在数轴上表示2a的点在表示a的点的左边,∴2a<a.A . 1个B . 2个C . 3个D . 4个7. (3分) (2016八上·灌阳期中) △ABC是不规则三角形,若线段AD把△ABC分为面积相等的两部分,则线段AD应该是()A . 三角形的角平分线B . 三角形的中线C . 三角形的高D . 以上都不对8. (3分) (2017九上·乐清月考) 如图,在下列三角形中,若AB=AC ,则能被一条直线分成两个小等腰三角形的是()A . ①②③B . ①②④C . ②③④D . ①③④9. (2分)如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是()A . 180°B . 270°C . 360°D . 无法确定10. (3分)如图,点C是∠PAQ的平分线上一点,点B、B′分别在边AP、AQ上,如果再添加一个条件,即可推出AB=AB′,那么该条件不可以是()A . BB′⊥ACB . CB=CB'C . ∠ACB=∠ACB'D . ∠ABC=∠AB′C二、填空题(本题有10小题,每小题3分,共30分) (共10题;共30分)11. (3分) (2019八上·海伦期中) 把“对顶角相等”改写成“如果…那么…”的形式是:________.12. (3分)(2018·柳州模拟) 某不等式的解集在数轴上的表示如下图所示,则该不等式的解集是________.13. (3分) (2018八上·江北期末) 已知△ABC≌△DEF,若AB=5,BC=6,AC=8,则△DEF的周长是________.14. (3分)如图,AC=AD,BC=BD,则△ABC≌△________;应用的判定方法是(简写)________.15. (3分)(2016·安陆模拟) 如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为________.16. (3分) (2017七下·河东期中) 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3=________°.17. (3分)如图所示的一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,这块地的面积为________m218. (3分) (2017七上·宁城期末) 数轴上点A、B的位置如图所示,则A,B间的距离是________.19. (3分) (2017八上·中江期中) 如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB=________度.20. (3分) (2015九上·龙岗期末) 如图:是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边上摆20(即n=20)根时,需要的火柴棍总数为________根.三、解答题(本大题6小题,第21-24题每题6分,第25题、26 (共6题;共40分)21. (6分)(2018·滨湖模拟) 解答题(1)解方程:-=-1;(2)解不等式组:22. (6分)(2019·福州模拟) 已知:如图,点A、B、E在同一直线上,AC∥BD且AC=BE,∠ABC=∠D.求证:AB=BD.23. (6分)如图(1)如图1,点P是等腰三角形ABC的底边BC上的一个动点,过点P作BC的垂线,交直线AB于点Q,交CA 的延长线于点R,请观察AR与AQ,它们有何数量关系?并证明你的猜想.(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图2中完成图形,并直接写出结论.24. (6分) (2017八下·汶上期末) 我市某西瓜产地组织40辆汽车装运完A,B,C三种西瓜共200吨到外地销售.按计划,40辆汽车都要装运,每辆汽车只能装运同一种西瓜,且必须装满.根据下表提供的信息,解答以下问题:西瓜种类A B C每辆汽车运载量(吨)456每吨西瓜获利(百元)161012(1)设装运A种西瓜的车辆数为x辆,装运B种西瓜的车辆数为y辆,求y与x的函数关系式;(2)如果装运每种西瓜的车辆数都不少于10辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)若要是此次销售获利达到预期利润25万元,应采取怎样的车辆安排方案?25. (8分)长方形具有四个内角均为直角,并且两组对边分别相等的特征.如图,把一张长方形纸片ABCD 折叠,使点C与点A重合,折痕为EF.(1)如果∠DEF=130°,求∠BAF的度数;(2)判断△ABF和△AGE是否全等吗?请说明理由.26. (8分) (2019九下·十堰月考) 在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;(2)通过观察、测量、猜想: =________,并结合图2证明你的猜想;________(3)把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,求的值.(用含α的式子表示)参考答案一、选择题(本题有10小题,每小题3分,共30分) (共10题;共28分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题(本题有10小题,每小题3分,共30分) (共10题;共30分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题(本大题6小题,第21-24题每题6分,第25题、26 (共6题;共40分)21-1、21-2、22-1、23-1、23-2、24-1、24-2、24-3、25-1、25-2、26-1、26-2、26-3、。
新人教版八年级上数学期末试卷及答案详解

2010—2011学年度上学期八年级期末考试数 学 试 卷亲爱的同学:紧张而忙碌的一学期即将结束,这里是你展示本学期来学业成果的舞台;在你答题前,请认真阅读下面的注意事项:1、本试卷共3页,25小题,满分120分.用时120分钟.2、请将答案填、涂在相应的答题卡上。
预祝你取得优异成绩! 一、选择题(下面各题的四个备选答案中,有且只有一个是正确的。
12×3=36分) 1、16的算术平方根是( )A 、±4B 、4C 、±2D 、2 2、函数02(3)y x x =-+-中自变量的取值范围是( ) A 、2x ≠ B 、2x ≤ C 、23x x ≠且 D 、23x x ≥≠且3、下列运算正确的是( )A 、a+2a 2=3a 3B 、(a 3)2=a 6C 、a 3•a 2=a 6D 、a 6÷a 2=a 3 4、下列美丽的图案中,是轴对称图形的是( )5、一次函数36y x =--的图象不经过( )A 第一象限B 、第二象限C 、第三象限D 、第四象限 6、点(—2,4)关于x 轴对称的点的坐标是( )A(-2,-4) B 、(-2,4) C 、(2,—4) D 、(2,4)7、如图,∠ACB=900,AC=BC ,BE ⊥CE ,AD ⊥CE 于D ,AD=2.5cm ,DE=1.7cm ,则BE=A 、1cmB 、0.8cmC 、4.2cmD 、1.5cm 8、下列各式能用完全平方公式分解因式的是( )A 、x 2+2xy -y 2B 、x 2-xy+4y 2C 、x 2-xy+42y D 、x 2—5xy+10y 2 9、点11(,)x y 、22(,)x y 在直线y x b =-+上,若12x x <,则1y 与2y 大小关系是( )A .B .C .D .A 、12y y <B 、12y y =C 、12y y >D 、无法确定10、如图,过边长为1的等边△ABC 的边AB 上一点P ,作PE ⊥AC 于E ,Q 为BC 延长线上一点,当PA =CQ 时,连PQ 交AC 边于D ,则DE 的长为( )A .13 B .12 C .23D .不能确定11、如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。
四川省绵阳市八年级数学试卷

四川省绵阳市八年级数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共15题;共16分)1. (1分) (2020八上·江城月考) 如图,AD是△ABC的角分平线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一动点,当△BDF为直角三角形时,则∠ADF的度数为________.2. (1分) (2019八下·兰州期中) 如图,在中,,,平分,交于点,若,则 ________.3. (1分) (2019七上·静安期中) 计算(x+3)(x-5)=________.4. (1分)(2017·长春模拟) 在平面直角坐标系中,点A(1,2)关于y轴对称的点为B(a,b),则a=________.5. (1分)(2020·达县) 已知的三边a、b、c满足,则的内切圆半径=________.6. (1分)(2016·毕节) 若a2+5ab﹣b2=0,则的值为________.7. (1分) (2020八上·大新期中) 如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,则它们的和等于________度.8. (1分)(2011·成都) 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为,则图中阴影部分的面积是________.9. (1分) (2018八上·建昌期末) 如图,从边长为a的大正方形中去掉一个边长为b的小正方形,然后将剩部分剪后拼成一个长方形,这个操作过程能验证的等式是________10. (1分)(2019·甘肃) 分式方程的解为________.11. (1分)(2020·石城模拟) 如图,两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于 ________度。
绵阳市八年级上学期期末数学试卷

绵阳市八年级上学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2019七上·句容期末) 下列生活实例中,数学原理解释错误的一项是()A . 从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线B . 两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短C . 把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线D . 从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短2. (2分)已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab+2cd,则此四边形一定是()A . 任意四边形B . 对角线相等的四边形C . 对角线互相垂直且相等的四边形D . 平行四边形3. (2分) (2015八上·惠州期末) 下列运算正确的是()A . (a+b)2=a2+b2B . 2a+3b=5abC . a6÷a3=a2D . a3•a2=a54. (2分)如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A . SSSB . SASC . AASD . ASA5. (2分) (2015八上·惠州期末) 方程 = 的解为()A . x=0B . x=﹣1C . x=3D . x=46. (2分) (2015八上·惠州期末) 把分式中的分子分母的x、y都同时扩大为原来的2倍,那么分式的值将是原分式值的()A . 2倍B . 4倍C .D . 不变7. (2分) (2015八上·惠州期末) “H7N9”是一种新型禽流感,其病毒颗粒呈多形性,其汇总球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为()A . 1.2×10﹣9米B . 1.2×10﹣8米C . 1.2×10﹣7米D . 12×10﹣9米8. (2分) (2015八上·宜昌期中) 一个多边形的内角和是外角和的2倍,则这个多边形是()A . 四边形B . 五边形C . 六边形D . 八边形9. (2分) (2015八上·惠州期末) 等腰三角形的一个内角为40°,则它的底角的度数为()A . 70°B . 40°C . 40°或70°D . 无法确定10. (2分) (2015八上·惠州期末) 在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有()A . 1个B . 2个C . 3个D . 4个二、填空题 (共6题;共6分)11. (1分) (2018九上·三门期中) 如图,△ABD,△AEC 都是等边三角形中,∠BAC=90°,将△ABE 绕点 A 顺时针旋转________可以到△ADC 处.12. (1分) (2015八上·惠州期末) 分解因式:a3﹣2a2+a=________.13. (1分) (2015八上·惠州期末) 计算:(﹣3x2y)•( xy2)=________.14. (1分) (2015八上·惠州期末) 若分式的值为正数,则x的取值范围是________.15. (1分) (2015八上·惠州期末) 如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,L与M相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为________.16. (1分) (2015八上·惠州期末) 如图,△ABC三边的中线AD,BE,CF相交于点G,若S△ABC=6,则图中阴影部分面积是________.三、解答题 (共9题;共76分)17. (10分)计算:(1)(2).18. (10分) (2015八上·惠州期末) 如图,点D在△ABC的AB边上,且∠ACD=∠A.(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).19. (5分) (2015八上·惠州期末) 先化简( + )÷ ,再求值.(其中,a是满足﹣2≤a≤2的整数)20. (6分) (2017七上·西城期中) 直接写出计算结果(1)﹣8﹣8=________(2)﹣24×(﹣1 )=________(3)﹣3÷3× =________(4)5+5÷(﹣5)=________(5) 3﹣(﹣1)2=________(6) x2y﹣ x2y=________.21. (5分) (2015八上·惠州期末) 比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴而行,到相距16米的银树下参加探讨环境保护的微型动物首脑会议.蜗牛神想到“笨鸟先飞”的古训,于是给蚂蚁王留下一纸便条后,提前2小时独自先行,蚂蚁王按既定时间出发,结果它们同时到达.已知蚂蚁王的速度是蜗牛神的4倍,求它们各自的速度.22. (10分) (2015八上·惠州期末) 在平面直角坐标系中,B点坐标为(x、y),且x、y满足|x+y﹣8|+(x ﹣y)2=0.(1)求B点坐标;(2)如图,点A为y轴正半轴上一点,过点B作BC⊥AB,交x轴正半轴于点C,求证:AB=BC.23. (10分) (2016七上·江津期中) 在一次抗震救灾中,某市组织20辆汽车装运食品、药品、生活用品三种救灾物资到灾民安置区,按计划20辆汽车都要装运,每辆汽车只能装运一种救灾物资且必须装满.设装运食品的汽车为x辆,装运药品的汽车为y辆,根据表中提供的信息,解答下列问题:物资种类食品药品生活用品每辆汽车运载(吨)654每吨所需运费(元)120160100(1) 20辆汽车共装载了多少吨救灾物资?(2)装运这批救灾物资的总费用是多少元?24. (10分) (2016八上·靖江期末) 如图所示,“赵爽弦图”由4个全等的直角三角形拼成,在Rt△ABC 中,∠ACB=90°,AC=b,BC=a,请你利用这个图形解决下列问题:(1)证明勾股定理;(2)说明a2+b2≥2ab及其等号成立的条件.25. (10分) (2019八上·盐田期中) 等腰三角形的边长分别为a,b,且 +(2a+3b-19)2=0.(1)求a,b的值;(2)求这个三角形的面积。
四川省绵阳市八年级上学期数学期末考试试卷

四川省绵阳市八年级上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分)下列实数中,为无理数的是()A . 0.2B .C .D . -52. (2分) (2019八上·宜兴月考) 下列命题: (1) =a,(2) =a,(3)无限小数都是无理数,(4)有限小数都是有理数,(5)实数分为正实数和负实数两类.正确的有()A . 1个B . 2个C . 3个D . 4个3. (2分) (2018七上·青浦期末) 下列各式计算结果不为的是()A .B .C .D .4. (2分) (2019七下·光明期末) 下列运算正确的是()A . (﹣a2b3)2=a4b6B . (﹣a3)•a5=a8C . (﹣a2)3=a5D . 3a2+4a2=7a45. (2分)下列长度的三条线段,能组成三角形的是()A . 1,2,3B . 2,3,4C . 3,6,9D . 4,4,106. (2分) 2008年奥运会上要清楚地反映我国奖牌中的金、银、铜牌的分布情况,最好把奖牌榜绘制成()A . 条形统计图B . 扇形统计图C . 折线统计图D . 以上都可以7. (2分)在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,CD=2,则点D到AB的距离是()A . 1B . 2C . 3D . 48. (2分) (2019九上·罗湖期中) 《代数学》中记载,形如的方程,求正数解的几何方法是:“如图1,先构造一个面积为的正方形,再以正方形的边长为一边向外构造四个面积为的矩形,得到大正方形的面积为,则该方程的正数解为.”小聪按此方法解关于的方程时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为()A . 6B .C .D .二、填空题 (共6题;共6分)9. (1分) (2016七下·鄂城期中) 若|a|=3, =2且ab<0,则a﹣b=________.10. (1分)(2020·衢州) 定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8,则(x-1)※x的结果为________。
四川省绵阳地区-八年级(上)半期考试数学试卷 (2).doc

四川省绵阳地区2012-2013学年八年级(上)半期考试数学试卷(满分100分,考试时间90分钟)一、细心选一选(本题有10个小题,每小题3分,满分30分,下面每小题给出的四个选项中,只有一个是正确的。
)1. 下列交通标识中,是轴对称图形的是A .B .C .D .2.有6个数:4,0,0.010010001,2π,722,2,其中无理数的个数是 A .1个B .2个C .3个D .4个3.下列运算正确的是A .-︱2-︱=2B .︱2-︱=2-C .3273±=D .3273-=-4.估算234+的值 A .在5和6之间B .在6和7之间C .在7和8之间D .在8和9之间5.为了加快灾后重建的步伐,我市某镇要在三条公路围成的一块平地上修建一个砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址A .仅有一处B .有四处C .有七处D .有无数处 6.已知:△ABC ≌△DEF ,AB =DE ,∠A =70°,∠E =30°,则∠F 的度数为A .80°B .70°C .30 °D .100° 7.若a 是任意实数,则下列等式一定成立的是A .a a =2B .a a ±=2C .a a -=28.如图,点D 、E 在△ABC 的BC 边上,AB = AC ,AD = AE , 则图中全等三角形共有A .0对B .1对C .2对D .3对 9.如果一个三角形是轴对称图形,且有一个角是,那么这个三角形是A .等边三角形B .含120°角的等腰三角形(第5题)C .等腰直角三角形D .含30°角的直角三角形10.平面直角坐标系中,把点A 向上平移2个单位后得点B ,点B 关于直线x =-1对称的点为(-3,1),则点A 的坐标为 A .(1,1)B .(-1,1)C .(0,1)D .(1,-1)二、耐心填一填(本题有8个小题,每小题2分, 满分16分)11.等腰三角形的两边分别为5 cm 和8 cm ,则它的周长为 .12.已知等腰三角形的一个内角为40︒,则这个等腰三角形的一个底角为 . 13.平方根是本身的数是 ;立方根是本身的数是 。
四川省绵阳市八年级上学期期末考试数学试题
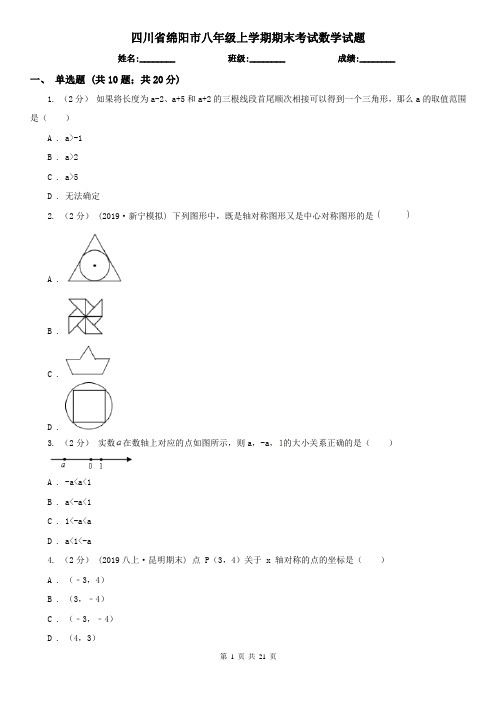
四川省绵阳市八年级上学期期末考试数学试题姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是()A . a>-1B . a>2C . a>5D . 无法确定2. (2分)(2019·新宁模拟) 下列图形中,既是轴对称图形又是中心对称图形的是A .B .C .D .3. (2分)实数在数轴上对应的点如图所示,则a,-a,的大小关系正确的是()A . -a<a<1B . a<-a<1C . 1<-a<aD . a<1<-a4. (2分) (2019八上·昆明期末) 点 P(3,4)关于 x 轴对称的点的坐标是()A . (﹣3,4)B . (3,﹣4)C . (﹣3,﹣4)D . (4,3)5. (2分)(2017·江东模拟) 下列命题中,真命题是()A . 周长相等的锐角三角形都全等B . 周长相等的等腰直角三角形都全等C . 周长相等的钝角三角形都全等D . 周长相等的直角三角形都全等6. (2分) (2015九上·淄博期中) 如图,在△ABC中,BD是角平分线,∠A=∠CBD36°,则图中有等腰三角形()A . 3个B . 2个C . 1个D . 0个7. (2分) (2019八上·南山期中) 在同一坐标系中,正比例函数y=kx与一次函数y=x-k的图象为()A .B .C .D .8. (2分) (2020九上·温州开学考) 如图,在,则的面积是()A .B .C .D .9. (2分) (2017七下·蒙阴期末) 不等式组的正整数解的个数是()A . 1B . 2C . 3D . 410. (2分) (2018八上·浏阳期中) 如图:△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB 于E,且AC=6cm,则DE+BD等于()A . 5cmB . 4cmC . 6cmD . 7cm二、填空题 (共8题;共8分)11. (1分)写出一个解为x≥1的一元一次不等式:________12. (1分) (2019七下·融安期中) 若点B(a,b)在第三象限,则点C(-a+1,3b-5)在第________象限.13. (1分) (2017八上·江阴开学考) 命题“直角三角形两锐角互余”的逆命题是:________.14. (1分)如图,D、E、F分别是△ABC三边延长线上的点,则∠D+∠E+∠F+∠1+∠2+∠3=________度.15. (1分) (2019七下·定边期末) 如图,已知,要使,只需添加一个条件是________(填一个即可).16. (1分) (2019八上·漳州月考) 有一个如图所示的长方体透明玻璃鱼缸,假设其长,高,水深为,在水面上紧贴内壁处有一鱼饵,在水面线上,且.一小虫想从鱼缸外的点沿壁爬进鱼缸内处吃鱼饵,则小虫爬行的最短路线长为________ .17. (1分) (2017八下·金华期中) 在平面直角坐标系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是________.18. (1分)(2017·丹东模拟) 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1 ,以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1 ,过点B1作直线l的垂线交y轴于点A2 ,以A2B1 . B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则Cn的坐标是________.三、解答题 (共6题;共44分)19. (5分) (2020八上·巴东期末) 如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.20. (10分) (2016八上·龙湾期中) 在如图所示的网格中,每个小正方形的边长均为1个单位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二学校教学质量监测
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.下列多项式中,能用公式法分解因式的是
A .m 2-mn
B .m 2 + mn
C .m 2-n 2
D .m 2 + n 2 2.从实数5-,3
1
-
,0,π,4中,挑选出的两个数都是无理数的为 A .3
1
-
,0 B .π,4 C .5-,4 D .5-,π 3.下列运算正确的是
A .-︱2-︱=2
B .︱2-︱=2-
C .3273±=
D .3273-=- 4.如图,正方形OABC 的边长为1,以A 为圆心,AC
与数轴的一个交点是D ,则D 点表示的数为
A
.21- B
.12-
C .21
-
D .
-5.下列计算错误..
的是 A .(π-3.14)0 = 1 B .-c 4 ÷(-c ) 2 =-c 2 C .2x 6 ÷ x 2 = 2x 3 D .3x 2 · 2x 3 = 6x 5
6.如图所示,在平面直角坐标系中,不能..
表示y 是x 的函数的曲线为 A . B . C . 7.已知一次函数y = kx + b (k ≠0)的图象如右,则关于x 的
不等式kx + b <0的解集为
A .x >-2
B .x >-1
C .x <-2
D .x <-1
8.如图,点D 、E 在△ABC 的BC 边上,AB = AC ,AD = AE ,
则图中全等三角形共有
A .0对
B .1对
C .2对
D .3对 9.如图是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,
使整个阴影部分......成为轴对称图形,这样的白色小正方形有 A .4个 B .3个 C .2个 D .1个
10.平面直角坐标系中,把点A 向上平移2个单位后得点B ,点B 关于直线x =-1对称的点
为(-3,1),则点A 的坐标为
A .(1,1)
B .(-1,1)
C .(0,1)
D .(1,-1) 11.下列各式,正确的是
A .(-2a -3)(2a -3)= 4a 2-9
B .2)2)(2(2-=-+x x x
C .(a -b )2 = a 2-b 2
D .(3x -1)2 = 3x 2-6x + 1
12.某学校计划租用甲、乙两种客车送240名师生(其中学生233名、教师7名)集体外出
活动,要求每辆客车上至少要有1名教师.甲、乙两种客车的载客量和租金如下表:
则最节省费用的租车方案是
A .租甲种车4辆,租乙种车2辆
B .租甲种车5辆,租乙种车1辆
C .租甲种车2辆,租乙种车5辆
D .租甲种车3辆,租乙种车4辆 二、填空题:本大题共6小题,每小题3分,共18分.将答案直接填写在题中横线上. 13.使
3
1
-x 有意义的x 的取值范围是 . 14.分解因式:3x 2-27 = . 15.计算:2
222
3)(6a a a ÷
-= . 16.如图,△ABC 的三个顶点在单位正方形网格的交点上,
如果△A ′B ′C ′ 与△ABC 关于y 轴对称,那么点C 的对应点C ′
的坐标为
. 17.已知等腰三角形的一个内角为40︒,则这个等腰三角形的一个底角为 . 18.如图,△ABC 中,CD 是AB 边上的高,若2∠ACB = 3∠B = 6∠
则BC :AD = .
三、解答题:本大题共6小题,共46分,解答应写出文字说明、证明过程或演算步骤. 19.(本题满分7分)计算:)13(3|23|---.
20.(本题满分7分)先化简,再求值:(3x -1)(3x + 1)-9 ( x -1) 2 + 10,其中 2
1-=x .
21.(本题满分7分)如图,△ABC 中,AB = AD = DC ,设∠BAD = x ,
∠C = y ,试求y 与x 的函数关系式,并写出x 的取值范围.
22.(本题满分7分)如图,△ABC 和△ADE 都是等边三角形,
BD 与CE 相交于O . (1)求证:BD = CE ;
O
D C
E
B
y
x
D
A
B
C
(2)OA平分∠BOE吗?说明理由.
23.(本题满分8分)如图,是一个上、下两部分均为圆柱体的容器,现向其中注水,直到注满为止,容器中水的体积v(cm3)随水面高度h(cm)变化的图象如下.
(1)求容器下部分圆柱体的高和底面圆的半径;
(2)求水的体积v(cm3)与水面高度h(cm)的函数关系式,并写出h的取值范围.(圆柱体的体积v = πr2h,其中r是柱体底面圆的半径,h是圆柱的高)
24.(本题满分10分)平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).(1)如图1,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个?
(2)过A、B向直线l:y =-2x作垂线,垂足分别为M,N(如图2),试判断线段AM、BN、MN之间的数量关系,并说明理由.
(3)过A、B向动直线l:y = kx(k>0)作垂线,垂足分别为M,N,请直接写出线段AM、BN、MN之间的数量关系.
图1 图2
初中2012级第三学期样本学校教学质量监测
数学试题参考答案(题源)及评分意见
一、选择题:本大题共12个小题,每小题3分,共36分.
1.C 2.D 3.D 4.A(8年级上册课本第83页探究)5.C(8年级上册课本第160页第3题)6.A(8年级上册课本第103页思考2)7.B(8年级上册课本第125页第2题)8.C (8年级上册课本第56页第6题)9.A(8年级上册课本第45页第3题)10.D(8年级上册课本第46页第6,8题)11.B(8年级上册课本第153、155页第1、2题)12.A(8年级上册课本第132页问题2)
二、填空题:本大题共6个小题,每小题3分,共18分.
13.x>3 14.3(x + 3)(x-3)15.4a3(8年级上册课本第175页第2(2)题)16.(-4,4)17.40︒或70︒18.2:3(8年级上册课本第64页第7题)三、解答题
19.解原式1
+
-
-
=.(8年级上册课本第86页第4题,91页第8题)
=
3
2(-
3
)3
………………………7分
20.解 原式x x x x 1810)12(91922=++---=. ………………………4分
当21-=x 时,原式9)21
(18-=-⨯=. ………………………7分
(8年级上册课本第149页第7题)
21.解 ∵ AD = DC ,∴ ∠DAC =∠C = y ,得 ∠ADB =∠DAC +∠C = 2y .
∵ AB = AD ,∴ ∠B =∠ADB = 2y . ………………………3分 于是,在△ABD 中,由∠BAD +∠B +∠ADB = 180︒, 得 x + 2y + 2y = 180︒,即︒+-
=454
1
x y ,0︒<x <180︒. ………………………7分 (8年级上册课本第51页第3题)
22.解 (1)∵ △ABC 和△ADE 都是等边三角形,
∴ AB = AC ,AD = AE ,∠BAC =∠DAE = 60︒,
∴ ∠BAC +∠CAD =∠DAE +∠CAD ,即 ∠BAD =∠CAE ,
从而 △BAD ≌△CAE ,得BD = CE . ………………………4分 (2)作AF ⊥BD ,AG ⊥CE ,垂足分别是F 、G ,则AF 、AG 恰好是两个全等三角形△BAD 与△CAE 对应边上的高,因此AF = AG ,表明点A 到∠BOE 两边的距离相等,所以A 在∠BOE 的平分线上,进而AO 平分∠BOE . ………………………7分
(8年级上册课本第58页第11题)
23.解 (1)容器下部分圆柱体的高h = 4 cm ,由 36π = πr 2 · 4 得底面圆的半径r = 3.
………………………3分
(2)当0<h ≤4时,v = 9πh ; ………………………5分 设 v = kh + b (k ≠0).当 h = 4时,v = 36π, ∴ 4k + b = 36π. ① 当h = 6时,v = 44π, ∴ 6k + b = 44π. ② 联立①、②,解得 k = 4π,b = 20π, ∴ v = 4πh + 20π.
G
F O D A C
E B
故 ⎩⎨
⎧≤<+≤<=.
64,204;
40,9h h h h v πππ ………………………8分
(8年级上册课本第129页第10题,138页第8题) 24.解 (1)4个. ……………………… 3分
(2)AM + BN = MN .
由已知可得 OA = OB ,∠AOM = 90︒-∠BON =∠OBN , ∴ Rt △AOM ≌Rt △OBN ,从而 AM = ON ,OM = BN ,
∴ AM + BN = ON + OM = MN . ……………………… 6分 (3)当k >1时,AM = BN + MN . 当k = 1时,AM = BN ,MN = 0.
当0<k <1时,BN = AM + MN . ……………………… 10分 或者表为 MN =︱AM -BN ︱. (8年级上册课本第83页数轴图示)。
