浙江工商大学 信号与系统2005
信号与系统2005年四月信号与系统自考真题与答案

2005年上半年高等教育自学考试全国统一命题考试信号与系统试卷(课程代码2354)一、单项选择题(本大题共12小题,每小题2分,共24分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
l.如题1图所示电路中∙U=10 / 0o V,则此电路谐振时电流∙I为A.2 / 0o A B.2 / 90o AC.10 / 0o A D.10/ 90o A2.积分式⎰∞∞-(-cos3t) δ (-t)dt等于【】A.1 B.0 C.-l D.-23.已知信号f (t) 如题3(a)图所示,则f ( -2t -2)为题3(b)图中的【】4.已知一线性时不变系统在题4(a)图所示信号的激励下的零状态响应如题4(b)图所示,则在如题4(c)图所示信号的激励下的零状态响应为题4(d)图中的【】5.题5图中f (t)是周期为T 的周期信号, f (t)的三角函数形式的傅里叶级数系数的特点是 【 】A .仅有正弦项B .既有正弦项和余弦项。
又有直流项C .既有正弦项又有余弦项D .仅有余弦项6.已知 则F(j ω)所对应的时间函数为 【 】A .ttπsin B .ttπ2sin C .tt sin D .tt 2sin7.题7图所示信号f (t)的傅里叶变换为 【 】A .2Sa(ω) sin 2ωB .4Sa(ω) sin2ωC .2Sa(ω) cos2ωD .4Sa(ω) cos2ω 8.的拉氏变换F(s)为 【 】9.象函数F(s)=2312+-s s (Re[s] >2)的原函数为 【 】A . )()(2t e e t t ε---B .)()(2t e e t t ε-C . )()(2t e e t t ε---D .)()(2t e e t t ε-10.若系统冲激响应为h(t),下列式中可能是系统函数H(s)的表达式为 【 】11.序列f 1 (n)和f 2 (n)的波形如题11图所示,设f (n)= f 1 (n)* f 2 (n),则f 2 (n)等于【 】A .0B .1C .3D .512.序列f (n)=)1(2--n n ε的单边Z 变换F(z)等于 【 】二、填空题(本大题共12小题,每小题2分,共24分)请在每小题的空格中填上正确答案。
浙江工商大学822信号与系统2006-2019年考研专业课真题试卷

( 6(t) , g,(t) r)lll#fr+,ftrtfiff6#. itrxrff, Sa(l) , sgn(r) rilrl*a-+,ir.Hxt+ drffi. ff++drff, s(t), u(t) VsXX.+,i",7Fi<Sff , ! r;; ! * ya#.?r4+trJAurtJil,, !ar, ! 7 jg#z\€)|tffuHN-,lrr fHt{tfH{Z.MKg}..)
2019年浙江工商大学考研专业课初试真题试卷
2019年浙江工商大学考研专业课初试真题试卷
精都教育——全国 100000 考生的选择
我们的梦想,为成就更多人的梦想
浙 江 工 商 大 学 研 究 生 入 学 考 试 试 题
原版考研真题试卷
更多考研真题、笔记、模拟、题库、讲义资料就上精都考研网 /
我们的梦想,为成就更多人的梦想
浙 江 工 商 大 学 研 究 生 入 学 考 试 试 题
原版考研真题试卷
更多考研真题、笔记、模拟、题库、讲义资料就上精都考研网 /
精都教育——全国 100000 考生的选择
我们的梦想,为成就更多人的梦想
浙 江 工 商 大 学 研 究 生 入 学 考 试 试 题
(^ - J t , , la l<6 rad/s 1 0 , latl>6 rad/s
hffi x!(ty:th 4l .or6t, &AthfuIffJi .yj (0.
t
- . ( r0t|) * LrtyE*F:r , H+ft f (t)J-jffiaft) fr\ftfr).t
y\t)= Ii, u-o'-f"(*- ZW
计算机专业基础综合计算机网络物理层历年真题试卷汇编1_真题-无答案

计算机专业基础综合计算机网络(物理层)历年真题试卷汇编1(总分88,考试时间90分钟)1. 单项选择题1. 数据传输速率是指____。
【北京科技大学2004年】A. 每秒传输的字节数B. 电磁波在传输介质上的传播速率C. 每秒传输的比特数D. 每秒传输的码元个数2. 在同一时刻,通信双方可以同时发送数据的信道通信模式是____。
【西安电子科大2005年】A. 半双工通信B. 单工通信C. 数据报D. 全双工通信3. 一个码元传输速率为300Baud的信道,如果采用4元制,则其信:道的传输速率为____。
【重庆大学2005年】A. 300bit/sB. 600bit/sC. 1200bit/sD. 2400bit/s4. 利用模拟通信信道传输数字信号的方法称为____。
【华中科技大学2001年】A. 同步传输B. 异步传输C. 基带传输D. 频带传输5. 采用8个相位的调相传输其码元,传输速率为200Baud,则数据传输率为____。
【重庆大学2004年】A. 400bit/sB. 600bit/sC. 800bit/sD. 1600bit/s6. 采用8种相位,每种相位各有两种幅度的QAM调制方法,在1200Baud的信号传输速率下能达到的数据传输速率为____。
【北京航空航天大学2006年】A. 2400bit/sB. 3600bit/sC. 9600bit/sD. 4800bit/s7. 一个信道每1/8s采样一次,传输信号共有16种变化状态,最大数据传输率是____。
【华东理工大学2006年]A. 16bit/sB. 32bit/sC. 48bit/sD. 64biUs8. 对于某带宽为4000Hz的低通信道,采用16种不同的物理状态来表示数据。
按照奈奎斯特定理,信道的最大传输速率是____。
【中央财经大学2004年】A. 4kbit/sB. 8kbit/sC. 16kbit/sD. 32kbit/s9. 电话系统的典型参数是信道带宽为3000Hz,信噪比为30dB,则该系统的最大数据传输速率为____。
浙江工商大学2017年信息与通信工程硕士招生录取名单

浙江工商大学2017年信息与通信工程硕士招生录取名单100046330106557陈龙信息与通信工程
100046330106560邓毅晨信息与通信工程
101416133014670金伟妹信息与通信工程
102486121612545汤柳君信息与通信工程
102806210006883黄肖琳信息与通信工程
102886500005388郑月燃信息与通信工程
102936210102861亓一航信息与通信工程
102936210102913张威信息与通信工程
102936210103080李鹏程信息与通信工程
102936210103264苏雪信息与通信工程
102946211304631唐悦信息与通信工程
103356000900707项火星信息与通信工程
103356000900790徐振驰信息与通信工程
103356000900796宋艳玲信息与通信工程
103356000900799叶崇强信息与通信工程
103536210000279张之阳信息与通信工程
103536210000378蔡佳琪信息与通信工程
103536210001234陈慧霖信息与通信工程
103536210001502李姣姣信息与通信工程
103576210009476张伟信息与通信工程103846213310539刘豪信息与通信工程104976450338071曹露信息与通信工程106146081006203刘冠思信息与通信工程106986330103455李秀玲信息与通信工程文章来源:文彦考研。
信号与系统(第1章)上册课后习题答案

0, 0 等幅 0, 0 增幅振荡 0, 0 衰减
第 21 页
4.抽样信号(Sampling Signal)
O
2
2
第 37 页
c.表示符号函数 符号函数:(Signum)
1 sgn( t ) 1
1 u( t ) [sgn( t ) 1] 2
sgnt
t 0 t0
O
t
sgn( t ) u( t ) u( t ) 2u( t ) 1
第 38 页
e
j t
cost j sint
第 20 页
3.复指数信号
f ( t ) Ke st
Ke t cos t jKe t sin t
为复数,称为复频率
( t )
s j
, 均为实常数
的量纲为1 /s , 的量纲为rad/s 讨论
瞬态信号:除准周期信号外的 一切可以用时间函数描述的非 周期信号。
第 10 页
3.连续信号和离散信号
连续时间信号:信号存在的 时间范围内,任意时刻都有定 义(即都可以给出确定的函数 值,可以有有限个间断点)。 用t表示连续时间变量。 离散时间信号:在时间上是 离散的,只在某些不连续的规 定瞬时给出函数值,其他时间 没有定义。 用n表示离散时间变量。
f t f at a 0 波形的压缩与扩展,尺度变换
f (t ) f t 2
f t
2
1
t f 2
2
信号与系统试题库史上内含答案

信号与系统试题库史上内含答案It was last revised on January 2, 2021信号与系统考试方式:闭卷 考试题型:1、简答题(5个小题),占30分;计算题(7个大题),占70分。
一、简答题:1.dtt df t f x e t y t )()()0()(+=-其中x(0)是初始状态,为全响应,为激励,)()(t y t f 试回答该系统是否是线性的[答案:非线性]2.)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的,是时变的还是非时变的[ 答案:线性时变的]3.已知有限频带信号)(t f 的最高频率为100Hz ,若对)3(*)2(t f t f 进行时域取样,求最小取样频率s f =[ 答案:400s f Hz =]4.简述无失真传输的理想条件。
[答案:系统的幅频特性为一常数,而相频特性为通过原点的直线]5.求[]⎰∞∞--+dt t t e t )()('2δδ的值。
[答案:3]6.已知)()(ωj F t f ↔,求信号)52(-t f 的傅立叶变换。
[答案:521(25)()22j f t e F j ωω--↔]7.已知)(t f 的波形图如图所示,画出)2()2(t t f --ε的波形。
[答案: ]8.已知线性时不变系统,当输入)()()(3t e e t x t t ε--+=时,其零状态响应为)()22()(4t e e t y t t ε--+=,求系统的频率响应。
[答案:())4)(2(52)3(++++ωωωωj j j j ] 9.求象函数2)1(32)(++=s s s F ,的初值)0(+f 和终值)(∞f 。
[答案:)0(+f =2,0)(=∞f ]10.若LTI 离散系统的阶跃响应为)(k g ,求其单位序列响应。
其中:)()21()(k k g k ε=。
[答案:1111()()(1)()()()(1)()()(1)222k k k h k g k g k k k k k εεδε-=--=--=--]11.已知()1 1 , 0,1,20 , k f k else ==⎧⎨⎩ ,()2 1 , 0,1,2,30 , k k f k else -==⎧⎨⎩设()()()12f k f k f k =*,求()3?f =。
信号与系统实验答案
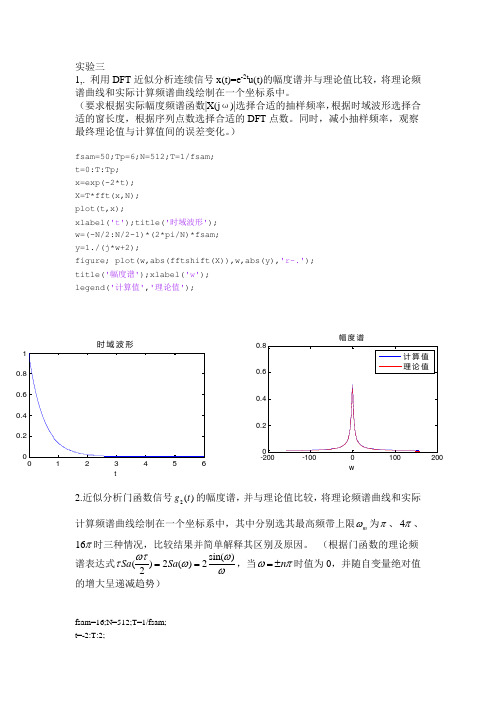
实验三1,. 利用DFT 近似分析连续信号x(t)=e -2t u(t)的幅度谱并与理论值比较,将理论频谱曲线和实际计算频谱曲线绘制在一个坐标系中。
(要求根据实际幅度频谱函数|X(j ω)|选择合适的抽样频率,根据时域波形选择合适的窗长度,根据序列点数选择合适的DFT 点数。
同时,减小抽样频率,观察最终理论值与计算值间的误差变化。
)fsam=50;Tp=6;N=512;T=1/fsam; t=0:T:Tp; x=exp(-2*t); X=T*fft(x,N); plot(t,x);xlabel('t');title('时域波形'); w=(-N/2:N/2-1)*(2*pi/N)*fsam; y=1./(j*w+2);figure; plot(w,abs(fftshift(X)),w,abs(y),'r-.'); title('幅度谱');xlabel('w'); legend('计算值','理论值');2.近似分析门函数信号2()g t 的幅度谱,并与理论值比较,将理论频谱曲线和实际计算频谱曲线绘制在一个坐标系中,其中分别选其最高频带上限m ω为π、4π、16π时三种情况,比较结果并简单解释其区别及原因。
(根据门函数的理论频谱表达式sin()()2()22Sa Sa ωτωτωω==,当n ωπ=±时值为0,并随自变量绝对值的增大呈递减趋势)fsam=16;N=512;T=1/fsam; t=-2:T:2;12345600.20.40.60.81t时域波形-200-100010020000.20.40.60.8幅度谱wx=[(t>=-1)&(t<=1)];X=T*fft(x,N);%消除1/T 因子的影响 plot(t,x);xlabel('t');title('时域波形'); w=(-N/2:N/2-1)*(2*pi/N)*fsam; y=2*sin(w)./w;%理论频谱值figure; plot(w,abs(fftshift(X)),w,abs(y),'r-.'); title('幅度谱');xlabel('w'); legend('计算值','理论值');-2-1.5-1-0.500.51 1.5200.20.40.60.81t时域波形-60-40-20020406000.511.522.5幅度谱w实验四。
信号与系统习题(陈后金版)

4-8 已知周期信号f(t)=2cos(2лt-3)+sin(6лt), 求傅立叶级数指数表示式,并画出其频谱.
0 2
f (t ) e
j ( 2t 3 )
e
j ( 2t 3 )
• 3-16
• 3-24
解:
•
3-26
3-39 计算序列卷积和。 (1)2ku[k]*u[k-4] (3)(1/2)k u[k]*u[k]
(1)
n
2 u[n] u[k n 4] 2 n u[k 4]
n n0
k 4
1 2 k 3 u[k 4] (2 k 3 1)u[k 4] 1 2
动态方程式的特征根s1,2 = -1,2, 且n>m, 故h(t)的形式为
3 8 为y(t ) (3te
2 t
e
2 t
e )u(t )
t
1 t 1 3 t 2 t 3 7 y f (t ) ( e e e )u (t ) 2 2
3-14
3-14
• (2) y"(t ) 4 y' (t ) 4 y(t ) 3 f') 2 f (t ),t 0; f (t ) et u(t ),y(0 ) 2, y' (0 ) 3 (t
动态方程式的特征根s1,2 =
2, 则零输入响应的形式为
2 t
y x (t ) K1e
动态方程式的特征根s1,2 = -1,2, 且n>m, 故h(t)的形式为
3 8 为y(t ) (3te
浙江工商大学信号系统实验考题

实验一 MATLAB 基础知识1. 矩阵的建立:方括号、逗号、冒号、分号、回车符2. 矩阵的计算:加+、减-、乘*、除(除分为左除\、右除/)例:B A B A 1,783664321,987654321-⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=求 >> A\B 3. 生成全是1的矩阵:ones(n,m)例:ones(5) 生成的是什么?5行5列的1例:若t=0:0.1:10,产生与t 同维的、元素全是1的向量:ones 、length >> t=0:0.1:10;>> ones(1,length(t))或4. 数组对应元素的加减乘运算:加+、减-、点运算“.*”、“./”、“.^”5. 建立等间隔向量:冒号表达式e1:e2:e3与linspace(a,b,n)至少要掌握一种。
e1为初始值,e2为步长,e3为终止值a 和b 是生成向量的第一个和最后一个元素,n 是元素总数(linspace(a,b,n)与a:(b-a)/(n-1):b 等价)6. 会在指定的区间画给定的函数:plot 、ezplot 、fplot 至少熟练掌握一种。
subplot 、title 、xlabel 、ylabel 要会用。
例:判断下列语句的对错plot(‘sin(x)’); 错误 plot(sin(x));或plot(x,y);ezplot(‘sin(x)’); 正确fplot(‘sin(x)’) 错误例:在0≤x ≤2区间内,绘制曲线 y=2e^(-0.5x)cos(4πx)>> x=0:0.2:2;>> y=2*exp(-0.5*x).*cos(4*pi*x);>> plot(x,y)例:画图:]2,0[,)3(sin )()3sin()(2π∈⎩⎨⎧==t t t t y t t t x >> t=0:0.2:2*pi; >> y1=t.*sin(3*t);>> y2=t.*sin(3*t).*sin(3*t);>> plot(t,y1)>> plot(t,y2)例:将当前图形窗口分成4个绘图区,分别画f1,f2,f3,f4,并且标题、横坐标、纵坐标标注为“......”.>> x=-2*pi:0.1:2*pi;>> f1=sin(x);>> f2=cos(x);>> f3=2*sin(x)+cos(x);>> f4=5*sin(x)-3*cos(x);(f 可换)>> subplot(2,2,1)>> plot(x,f1)>> xlabel('t');ylabel('f1(t)'); title('f1(t)');后几个同上-------------------------------------------------------------------小问题:① 命令行结束时后面跟“,”和“;”有什么区别?表达式后面跟分号“;”,将不显示结果; 跟…,‟或…回车‟,将显示表达式② 符号j 和pi 表示什么?j: 虚数符号 pi: π③ 指数函数xe 如何表示?exp(x)④ 如何清除Command Window 里的所有内容?clc 实验二 系统的时域分析实验7. 已知微分方程,求其冲激响应和阶跃响应,并与各种响应的理论值进行比较:定义系统函数tf 、计算冲激响应impulse 、阶跃响应step ;理论结果由试卷给出,学生不必计算(下同);比较用subplot 、figure 。
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集?解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m 和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
浙江工商大学822信号与系统2020到2004十七套考研真题

输入 f (t ) = sint 时,试求输出信号的频谱Y ( j ) ,并画出Y ( j ) 的图形。 t
四、(10 分) 已知某 LTI 系统输入 f(t) 与零状态响应 yzs(t) 分别为 f(t)=2e–4t(t),
yzs(t)= (1+e–4t)(t) ,求系统的冲激响应 h(t),并写出该系统的微分方程。
浙江工商大学 2012 年硕士研究生入学考试试卷(A)卷
招生专业:通信与信息系统,信号与信息处理, 工程硕士(电子与通信工程领域)
考试科目:822 信号与系统 总分:150 分 考试时间:3 小时
(δ(t) , g (t) 分别表示单位冲激函数、门函数, (t) , u(t ) 均表示单位阶跃函数, yzi, yx 均表示零输入响应, yzs, y f 均表示零状态响应)
4 4 3 6
4、某 LTI 连续系统, 其输入 f (t ) 与输出 yzs (t) 的关系为
yzs (t) =
t −1
e−2(t−x) f ( x − 2)dx
求该系统的冲激响应 h(t) 。
5、计算卷积和ε(k)*[δ(k–2) –δ(k–3)]。
6、求 f (t) = e−2t (t + 1) 的 Fourier 变换。
统的零状态响应不为零的点数是多少?
二、(15 分) 设 y(t) = f (t)*h(t),r(t) = f (3t)*h(3t),并且 f (t),h(t)的 Fourier 变
换分别为 F(jω),H(jω) 。试证明:
r(t) = Ay(Bt )
并求出 A 和 B 的数值。
三、(10 分) 一理想低通滤波器的频率响应 H( j) = g2 () = ( + ) − ( − ) ,当
杭州商学院信号与系统2005真题

浙江工商大学2005年研究生入学考试试卷(A 卷)招生专业:通信与信号系统,信号与信息处理考试科目:信号与系统考试时间:3小时(δ(t ),ε(t ),g (t )分别表示冲激函数、阶跃函数、门函数)一、(共75分,每小题5分)1、()dt t t t 24sin 2+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎰∞∞-δπ2、计算卷积 e -2t (t +3)* ε(t -5)=3、已知系统的激励f(k)= ε(k+3),单位序列响应h(k)= δ(k)—δ(k-3),求系统的零状态响应。
4、ε(t)- ε(t+2)的Fourier 变换。
5求f(t)=sgn(t 2-4) 的 Fourier 变换。
6、设f(t)F(jw),则 f(3-4t)的Fourier 变换。
↔7、求F(jw) = δ(w+w o )- δ(w-w o ) 的Fourier 逆变换。
8、求t 2e -2t ε(t)的单边Laplace 变换。
9、求t 2cost ε(t) 的单边Laplace 变换。
10、求F(s)= 的单边Laplace 逆变换。
235422++++s s s s 11、证明单边Z 变换的移位性质:若f(k)F(z),|z|>a,且m 为正整数,则↔f(k-m) 。
↔∑-=---+10)()(m k k m z m k f z F z 12、求序列的Z 的变换。
()k k kεπ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2cos 2113、求周期为N 的有始周期性单位序的Z 变换。
()∑∞=-0m mN k δ14、已知象函数,其收敛域为1<|Z|<2,求原()()()3212121294)(23---⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛++-=z z z z z z z z z F 序列(双边)。
15、求,|z |>|a |的逆Z 变换。
()32a z azz -+二、(15分)某LTI系统的幅频响应|H (jw )|和相频响应φ(w )如图所示若系统的激励f(t)=2+4cos(5t)+4cos(10t),求系统的零状态响应。
信号与系统

包晓敏:硕士,教授,硕士导师,女,浙江理工大学。
主要从事模式识别和计算机应用的研究和开发,曾主持与参加浙江省自然科学基金、国家自然科学基金、浙江省科技计划重点项目、杭州市科技计划项目,发表相关论文十余篇,曾多次获科技奖项,取得二项国家软件著作权登记。
教育和工作经历1982/09-1986/07 浙江理工大学(原浙江丝绸工学院)工业电气自动化专业学士1986/07至今浙江理工大学信息电子学院电子工程系2003/09-2006/04浙江理工大学纺织工程领域工程专业硕士研究领域模式识别、跟踪与估计、视频图像处理与跟踪、电子信息处理及应用等。
近期发表论文[1] 包晓敏, 彭霄, 汪亚明, 等. 基于贝叶斯决策及半监督聚类的织物图像分割. 纺织学报, 2010, 31(2): 125-128.[2] 包晓敏, 汪亚明, 郝保明.基于聚类和α-β-γ滤波的运动跟踪.测试技术学报, 2009, 23(4): 288-292.[3] Bao Xiao-Min, Peng Xiao, Wang Ya-Ming, et al. Textile Image Segmentation Based onSemi-supervised. Artificial Intelligence and Compu-tational Intelligence, The 2009 International Conference on (AICI'09), 2009. 559-561.[4]包晓敏, 汪亚明, 何杭. 基于熵方法广义关联度的织物检测. 测试技术学报, 2008,22(4):368-371.[5] 郝保明, 包晓敏, 汪亚明, 彭霄. 基于改进遗传算法的图像分割. 浙江理工大学学报, 2008,25(6) ,700-703.[6] 包晓敏,汪亚明. 基于最小错误率贝叶斯决策的水果图像分割.农业工程学报, 2006, 22(5): 122-124(EI 收录) .[7] 包晓敏, 汪亚明. 基于最小风险贝叶斯决策的织物图像分割. 纺织学报,2006, 27(2): 33-36.[8]包晓敏, 汪亚明. 基于互相关函数的织物纬档检测. 纺织学报, 2005,26(6):39-40,43.[9]包晓敏, 张云华, 汪亚明, 罗一平. 基于离散高斯滤波器的纺织品图像增强. 纺织学报, 2005,26(4):121-123.[10]包晓敏, 汪亚明, 罗一平, 许洲. 基于最大多符号信息熵的织物图像匹配. 纺织学报, 2005,26(2):69-71.近年所获知识产权情况[1]金学波,包晓敏.基于LMI方法的参数不确定多传感器集中式估计算法软件, 软件著作权登记, 授权公开号:2008SR20216, 2008.[2]彭霄,包晓敏,郝保明,曹作宝.基于贝叶斯决策及半监督聚类的织物图像分割算法软件V1.0, 软件著作权登记, 授权公开号:2009SR032616, 2009.获奖情况[1] 黄振堃,葛丰平,胡觉亮,包晓敏,朱金连,傅岳琴,周金彪,占金木.浙江省重点课题《一步法电脑数控复合捻线机》获浙江省政府科技进步三等奖,2006年.[2] 黄振堃,葛丰平,胡觉亮,包晓敏,朱金连,傅岳琴,周金彪,占金木.浙江省重点课题《一步法电脑数控复合捻线机》获浙江省教育厅颁发的浙江省高校优秀科研成果二等奖,2005年.科研项目[1]基于半监督聚类和熵方法织物组织识别系统中关键技术研究(Y107124),经费额度为7万元,经费来源为浙江省自然科学基金项目,2008.01-2009.12,主持。
期末复习资料(信号与系统)

《信号与系统》期末复习材料一、考核目标和范围通过考核使学生了解和掌握信号与系统的基本原理、概念和方法,运用数学分析的方法解决一些简单问题,使学生在分析问题和解决问题的能力上有所提高,为学生进一步学习后续课程打下坚实的基础。
课程考核的命题严格限定在教材第1—8章内,对第9、10章不做要求。
二、考核方式三、复习资源和复习方法(1)教材《信号与系统》第2版,陈后金,胡健,薛健编著,清华大学出版社,北方交通大学出版社,2003年。
结合教材习题解答参考书(陈后金,胡健,薛健,钱满义,《信号与系统学习指导与习题精解》,清华大学出版社,北京交通大学出版社,2005)进行课后习题的练习、复习。
(2)离线作业。
两次离线作业题目要熟练掌握。
(3)复习方法:掌握信号与系统的时域、变换域分析方法,理解各种变换(傅里叶变换、拉普拉斯变换、Z变换)的基本内容、性质与应用。
特别要建立信号与系统的频域分析的概念以及系统函数的概念。
结合习题进行反复练习。
四、期末复习重难点第1章信号与系统分析导论1. 掌握信号的定义及分类。
2. 掌握系统的描述、分类及特性。
3. 重点掌握确定信号及线性非时变系统的特性。
第2章信号的时域分析1.掌握典型连续信号与离散信号的定义、特性及其相互关系。
2.掌握连续信号与离散信号的基本运算。
3.掌握信号的分解,重点掌握任意连续信号分解为冲激信号的线性组合,任意离散信号分解为单位脉冲序列的线性组合。
第3章系统的时域分析1.掌握线性非时变连续时间系统时域描述。
2.掌握用卷积法计算连续时间系统的零状态响应3.掌握离散时间系统的时域描述。
4.掌握用卷积法计算离散时间系统的零状态响应。
第4章 周期信号的频域分析1.掌握连续周期信号的频域分析方法。
2.掌握离散周期信号的频域分析方法。
第5章 非周期信号的频域分析1.掌握常见连续时间信号的频谱,以及Fourier 变换的基本性质及物理含义。
2.掌握连续非周期信号的频域分析。
《信号与系统》考研试题解答第一章信号与系统

第一章信号与系统一、单项选择题X1.1 (北京航空航天大学 2000 年考研题)试确定下列信号的周期:( 1) x(t )3cos 4t3;(A ) 2( B )( C )2(D )2( 2) x(k ) 2 cosk sin8k 2 cosk642(A ) 8 ( B ) 16 ( C )2 (D ) 4X1.2 (东南大学 2000 年考研题)下列信号中属于功率信号的是。
(A ) cost (t)(B ) e t (t)(C ) te t (t )t( D ) eX1.3 (北京航空航天大学 2000 年考研题)设 f(t)=0 ,t<3,试确定下列信号为 0 的 t 值:(1) f(1- t)+ f(2- t);(A ) t>-2 或 t>-1 ( B ) t=1 和 t=2(C ) t>-1( D ) t>-2(2) f(1- t) f(2- t) ;(A ) t>-2 或 t>-1 ( B ) t=1 和 t=2(C ) t>-1 ( D ) t>-2(3) ft ;3(A ) t>3 (B ) t=0 (C ) t<9 (D ) t=3X1.4 (浙江大学 2002 年考研题)下列表达式中正确的是 。
(A ) ( 2t )(t)( B ) ( 2t)1(t)2(C ) ( 2t )2 (t )( D )2 (t)1(2 )2X1.5 (哈尔滨工业大学 2002 年考研题)某连续时间系统的输入f( t) 和输出 y(t)满足y(t) f (t ) f (t 1) ,则该系统为。
(A )因果、时变、非线性 ( B )非因果、时不变、非线性 (C )非因果、时变、线性( D )因果、时不变、非线性X1.6 (东南大学 2001 年考研题)微分方程 y (t) 3y (t) 2 y(t) f (t 10) 所描述的系统为。
(A)时不变因果系统(B)时不变非因果系统(C)时变因果系统(D)时变非因果系统X1.7 (浙江大学2003 年考研题)y(k) f ( k 1) 所描述的系统不是。
电子科大历年信号与系统考研试题

2. 试求系统的单位冲激响应 ht ;
3. 若输入 x t et , t ,试求系统的输出 y t ;
4. 该系统是否稳定,是否因果。
xt
1/ s
1/ s
yt
2
2005年信号与系统考研试题
五、(16分)某离散时间系统的差分方程为:
yn 5 yn 1 1 yn 2 f n 1
电子科技大学
2008 年攻读硕士学位研究生入学试题
考试科目:836 信号与系统和数字电路
1.(15 分)完成下列卷积和与卷积积分的运算:
⑴.已知 x1n n n 1, x2 n 2n un 1 un 2
计算 xn x1n x2 n ,并画出 xn的波形;
⑵.已知 x1 t ut u t 2 , x2 t x1 2t
2009年信号与系统考研试题
试求出 xt 并画出其波形。
2.
(15
分)已知信号
x
t
sin
t
t
2
和
g
t
x nTS
t
nTS
,TS
2 3
,其傅里
叶变换分别为 X j 和 G j 。为确保 G j 1.5X j , 0 ,求出0 的最大
值。
3. (9 分) 实基带信号 xt 具有频谱 X j 0 , 100 ,假定 y t xt e jct ,试
3. 画出系统的幅频特性曲线,说明这是一个什么类型的系统。
R
Vi
Vo
R
C
2007年信号与系统考研试题
1. (10 分)某离散时间系统的输入为 xn,输出为 yn ,其输入输出关系为
y
《信号与系统教程》教学指导书--燕庆明(可编辑)

《信号与系统教程》教学指导书--燕庆明教育科学“十五”国家规划课题研究成果《信号与系统教程》教学指导书燕庆明高等教育出版社书书书内容提要本书是与燕庆明主编《信号与系统教程》相配套的教学指导书。
书中明确了主教材各章的教学目标和教学重点,并对重点给予指导。
内容精炼,例题丰富。
书中除了对全书的习题进行解析外,还编写了!套模拟试题,为学生自学检测提供帮助。
本书适合于高等学校电子信息类专业的教师和学生作为“信号与系统”课程的教学参考书和学习指导书。
" 图书在版编目(!"#)数据"《信号与系统教程》教学指导书#燕庆明$ ?北京:高等教育出版社, %&&’ %" *+,-/&0 /&’&1 /." 信?" 燕?" 信号系统 /高等学校 /! " #教学参考资料" 2-3$4$" 中国版本图书馆 5*6数据核字(%&&’)第&331’号出版发行" 高等教育出版社" " " " " " " " 购书热线" && /40&101!!社" " 址" 北京市西城区德外大街0号免费咨询" !&& /!& /&13!邮政编码" &&& 网" " 址" 7889:# #::: 7;9 ; ?总" " 机" && /!%&%!!33 " " " " " 7889:# #::: 7;9 @A ?经" " 销" 新华书店北京发行所印" " 刷"开" " 本" .!. B34&" #4 版" " 次" " " 年" 月第版印" " 张" 3$1 印" " 次" " " 年" 月第次印刷字" " 数" .& &&& 定" " 价" % 1&元本书如有缺页、倒页、脱页等质量问题,请到所购图书销售部门联系调换。
研究生入学考试计算机网络试题

中南大学信息与通信工程专业研究生入学考试计算机网络试题2005一、填空题(每小题2分,共30分)1、世界上第一个真正的计算机网络是1969年建成的、具有_4_结点的试验网,名称为_ARPANET_。
2、ISDN为_Integrated services digital network_的缩写,中文名称为_综合业务数字网_。
3、举出6种网络拓扑结构如总线型、星形_环型、树型、网状型、无线型_等。
4、数据传输方式按信道信号分为_窄带_与宽带,按同步方式分为同步与_异步_传输。
5、位串0111110111101111110是经过位填充的,那么输出串是_011111111101111110_。
6、标准10Mb/s 802.3LAN的波特率是_20Mb/s_。
习P163-27、尼奎斯特原理适用于_同轴电缆_、_光纤_通信介质。
8、通信中的信息交换方式有_电路交换_、_报文交换_及分组交换。
9、RS-232采用_负_(正/负选一)逻辑,在控制线上,On(通)=__V~__V逻辑“0”电平。
10、在联接建建立时,可能需要协商_窗口大小_、_最大分组尺寸_和超时值。
习P212-1011、为了提供比一个同等位所给的检错更高的可靠性,一个检错代码方法用一个奇偶位检测到所有奇数位,用第二个奇偶位检测所有的偶数位,那么此代码的海明距离是_2_。
习P95-1 12、一个用于发送二进制信号的3KHz信道,其信噪比为20dB,则最大数据传输速率为_6kb/s_。
习P51-713、电视频道的带宽是6MHz,如果使用4级信号传输,每秒能发送_24M_比特。
假定为无噪声信道。
习P51-614、T1线路的开销比例为_13%_。
习P55-2515、数据链路层协议在国际上采用比较通用的有面向字符控制规程与面向_比特_控制规程,其中面向_比特_控制规程有更多的优越性而被广泛应用。
二、计算题,请明确写出计算过程或具体理由(每个6分,共48分)1、x7+x5+1被发生器多项式x3-1所除,所得的余数是多少?习P99-112、一台采用TCP协议的机器正在单向延迟为10ms的1Gb/s的线路上发送65535字节的窗口数据。
《信号与系统》陈后金第1章习题练习

f [ k ] cos ( k / 8 )
2
1 2
cos( k / 4 )
由于 0 / 4 ,
0 2
1 8
故此信号是周期的,且周期N=16
Page 3
f [ k ] cos( k / 4 ) sin( k / 8 ) 2 cos( k / 2 )
y (t ) y (0 ) x (t ) dx ( t ) dt
t
非时变系统 非时变系统 非时变系统
y ( t ) lg y ( 0 )
2
x ( ) d
0Hale Waihona Puke y [ k ] ky [ 0 ] x [ k ]
Page 8
y ( t ) sin[ x ( t )] y ( t ) sin t x ( t ) y [ k ] kx [ k ] y [ k ] x[ 2 k ]
T
2 16
8
Page 4
第一章 3、已知正弦信号f(t)=sin20t,(-∞<t<+∞) 1)对f(t)等间隔取样,求出使f[k]=f[kTs]为周期序列 的取样间隔Ts 2)如果Ts=0.15π,求出f[k]=f[kTs]的基本周期
1 ) f [ k ] f [ kT s ] sin 20 kT s , 如果 f [ k ]是周期的,则 Ts 2 m N0
2
a
2
(1 cos( 2 t ))
2
故f(t)是周期信号,周期为π
Page 2
f [k ] e
0 2
jk / 4
如果离散的虚指数和正弦信号是周期的,则有
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江工商大学2005年研究生入学考试试卷(A 卷)
招生专业:通信与信号系统,信号与信息处理
考试科目:信号与系统
考试时间:3小时
(δ(t ),ε(t ),g (t )分别表示冲激函数、阶跃函数、门函数)
一、(共75分,每小题5分)
1、()dt t t t 24sin 2+⎥⎦⎤⎢⎣
⎡⎪⎭⎫ ⎝⎛+⎰∞∞-δπ 2、计算卷积 e -2t (t +3)* ε(t -5)=
3、已知系统的激励f(k)= ε(k+3),单位序列响应h(k)= δ(k)—δ(k-3),求系统的零状态响应。
4、ε(t)- ε(t+2)的Fourier 变换。
5求f(t)=sgn(t 2-4) 的 Fourier 变换。
6、设f(t)↔F(jw),则 f(3-4t)的Fourier 变换。
7、求F(jw) = δ(w+w o )- δ(w-w o ) 的Fourier 逆变换。
8、求t 2e -2t ε(t)的单边Laplace 变换。
9、求t 2cost ε(t) 的单边Laplace 变换。
10、求F(s)=2
35422++++s s s s 的单边Laplace 逆变换。
11、证明单边Z 变换的移位性质:若f(k)↔F(z),|z|>a,且m 为正整数,则f(k-m)
↔∑-=---+1
)()(m k k m z m k f z F z 。
12、求序列()k k k
επ⎪⎭
⎫ ⎝⎛⎪⎭⎫ ⎝⎛2cos 21的Z 的变换。
13、求周期为N 的有始周期性单位序()∑∞=-0m mN k δ的Z 变换。
14、已知象函数()()()3212121294)(23---⎪⎭⎫ ⎝
⎛-⎪⎭⎫ ⎝⎛++-=z z z z z z z z z F ,其收敛域为1<|Z|<2,求原序列(双边)。
15、求()32a z az
z -+,|z |>|a |的逆Z 变换。
二、(15分)某LTI 系统的幅频响应|H (jw )|和相频响应φ(w )如图所示若系统的激励f(t)=2+4cos(5t)+4cos(10t),求系统的零状态响应。
三、(10分)已知理想低通滤波器的频率特性为H (jw )=⎩
⎨⎧01 c c ϖϖϖϖ><,输入信号为t
at t f sin 1)(π=
,(1)求a <w c 时滤波器的输出y(t)。
(2)求a >w c 时滤波器的输出y(t)。
(3)哪种情况下输出有失真?
四(15分)设某LTI 系统的初始状态一定。
已知当输入f 1(t)=δ(t)时,系统的
全响应y 1(t)= δ(t)+e -t ε(t) ;当f 2(t)= ε(t)时,系统的全响应为y 2(t)=3e -t ε(t),当输入f 3(t)=t[ε(t)- ε(t-1)]时,求系统的全响应。
五、(10分)已知某LTI 系统的阶跃响应g(t)=(1-e -2t ) ε(t),欲使系统的零状态响应y f (t)=(1-e -2t +te -2t ) ε(t),求系统的输入信号
六、(15分)如图所示系统,(1)求系统函数H(z),(2)求单位序列响应h(k),
(3)写出该系统的差分方程。
七、(10分)某离散系统的系统函数()
15.01)(22+++-=K z z z z H ,当常数K 满足什么条件时,系统是稳定的?
ϖ。
