天津市和平区2016年九年级中考数学压轴题综合训练
和平区2016-2017九年级上数学期中试卷(含答案)

和平区 2016-2017 九年级上数学期中试卷一、选择题:本大题共 12 小题,每小题 3 分,共 36 分。
在每小题给出的四个选项中,只有 一项是符合题目的要求的。
1.下列图形中,可以看作是中心对称图形的是A .B . C. D.2.已知点 A (a ,b )与点 B (2,2)是关于原点 O 的对称点,则 A .a 2,b 2 B .a 2,b 2 C . a 2,b 2 D . a 2,b 23.用配方法解一元二次方程 x 2 6x 4 0 .下列变形正确的是 A. xB.26 4 3634 9 x 3 4 92x2C. x 2D.64 361 34.方程 x 2x x 2x 的根是5 2 24 4A .11 x ,xB . 122 2 1 x xC . 122 x 1 2,x 2 2 D . 1 1x ,x124 45. 某学校准备修建一个面积为 200m 2 的矩形花圃,它的长比宽多 10m ,设花圃的宽为 xm , 则可列方程为A. x x 10 200B. 2x 2 x 10 200 C . x x 10 200D . 2x 2 x 10 2006.对抛物线 y x 2 2x 3 而言,下列结论正确的是A .与 x 轴有两个公共点B .与 y 轴的交点坐标是(0,3)C .当 x <1 时,y 随 x 的增大而增大,当 x >1 时,y 随 x 的增大而减小D .开口向上7.将抛物线 y 5x 2 向左平移 2 个单位,再向下平移 3 个单位,得到的抛物线是 A. y 5 x 2 3 B. 5 2 3 5 2 3y 5 x 2 32 y x 2 C. y xD.228.二次函数 y ax 2 bx c 图象上部分点的坐标如下表所示:x… -3 -2 -1 0 1 … y…-3-2-3-6-11…则该函数图象的顶点坐标为A. (-3,-3)B. (-2,-2)C. (-1,-3)D. (0,-6)9.如图,小华同学设计了一个圆的直径的测量器,标有刻度的两把尺子OA,OB 在O 点被钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,尺子OA 与圆交于点F,尺子OB 与圆交于点E,读得OE 为 8 个单位长度,OF 为 6 个单位长度,则圆的直径为A. 25 个单位长度B. 14 个单位长度C. 12 个单位长度D. 10 个单位长度10. 如图,AB 是⊙O 的直径,点D,点E 在⊙O 上,且AD=DE,AE 与BD 交于点C,则图中与∠BCE 相等的角有A.2 个B.3 个C.4 个D.5 个11. 已知二次函数y x2 2mx m2 3(m 是常数),把该函数的图像沿y 轴平移后,得到的函数的图像与x 轴只有一个公共点,则应把该函数的图像A. 向上平移 3 个单位B. 向下平移 3 个单位C. 向上平移 1 个单位D. 向下平移 1 个单位12. 已知二次函数y x2 x a a 0 ,当自变量x 取m 时,其对应的函数值小于 0,那么当自变量x 取m-1 时,其对应的函数值A. 小于 0B. 大于 0C. 等于 0D. 与 0 的大小关系不确定二、填空题:本大题共 6 小题,每小题 3 分,共 18 分,请将答案直接填在答题纸中对应横线上.13. 如图,AB 是⊙O 的弦,若∠A=35°,则∠AOB 的大小为(度)14. 如图,点D 为AC 上一点,点O 为AB 上一点,AD=DO,以O 为圆心,OD 长为半径作圆,交AC 于另一点E,交AB 于点F,G,连接EF,若∠BAC=22°,则∠EFG 的大小为(度)15. 抛物线y=x2+3x+2 不经过第象限116. 关于x 的一元二次方程ax2 bx 0 有两个相等的实数根,写出一组满足条件的实数4a,b 的值:a= ,b=17. 如图,P 是等腰直角△ABC 外一点,把BP 绕直角顶点B 顺时针旋转 90°到BP 已知AP B ,P A: P C 1:3 ,则PB : P A 的值为13518. 在Rt△ABC 中,∠ACB=90°,∠BAC=30°,BC=6⑴如图①,将线段CA 绕点C 顺时针旋转 30°,所得线段与AB 交于点M,则CM 的长=⑵如图②,点D 是边AC 上一点,且AD= 2 3 ,将线段AD 绕点A 旋转,得线段AD ,点F 始终为BD 的中点,则将线段AD 绕点A 逆时针旋转度时,线段CF 的长最大,最大值为D'AAFDC BC B图①图②三、解答题19.(本小题 8 分)⑴如图①,画出△ABC 绕点B 逆时针旋转 90°后的△A1BC1⑵如图②,画出△ABC 绕点B 旋转 180°后的△A1BC1B BC A C A图①图②20.(本小题 8 分)已知关于x 的一元二次方程 x x a23 2⑴求证:对于任何实数a,方程总有两个不相等的实数根⑵若方程的一个根是 1,求a 的值及方程的另一个根21.(本小题 10 分)如图,在半径为 50 的⊙O 中,弦AB 的长为 50⑴求∠AOB 的度数⑵求点O 到AB 的距离22.(本小题 10 分)某公司今年销售一种产品,1 月份获得利润 20 万元,由于产品畅销,利润逐月增加,3 月份的利润比 2 月份的利润增加 4.8 万元,假设该产品利润每月的增长率相同,求这个增长率设这个增长率为x⑴填空:(用含x 的代数式表示)①2 月份的利润为②3 月份的利润为⑵列出方程,并求出问题的解23.(本小题 10 分)某商店经营一种小商品,进价是 2.5 元,据市场调查,销售价是 13.5 元时,平均每天销售是 500 件,而销售价每降低 1 元,平均每天就可以多售出 100 件⑴假定每件商品降价x 元,商店每天销售这种小商品的利润是y 元,请写出y 与x 间的函数关系式⑵每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?24.(本小题 10 分)已知:AB,PG 是⊙O 的两条直径,连接PB,AG⑴如图①,求证:AG=BP,AG∥BP⑵如图②,过点B 做BC⊥PG 于点D,交⊙O 于点C,在DG 上取一点K,使DK=DP,求证四边形AGKC 是平行四边形PPCDA B AOBOKG G图①图②25.(本小题 10 分)已知二次函数y=ax2+bx+c 的图象经过点A(1,0)⑴当b=2,c=-3 时,求二次函数的解析式及二次函数的最小值⑵二次函数的图象经过点B(m,e),C(3-m,e)①求该二次函数图象的对称轴②若对任意实数x,函数值y 都不小于1 1,求此时二次函数的解析式4a 2参考答案一、选择题1 2 3 4 5 6A A D A C C7 8 9 10 11 12A B D D B B二、填空题13.110°14. 33°15. 四16.1:1(答案不唯一,满足b2 a ,a 0 即可)17.2 18. ⑴150;⑵6+ 3三、解答题19.⑴⑵A1A1 C1C120. 解:⑴原方程可化为x2 5x 6 a2 0△=2 2 25 2 4 16 a 25 24 4a 1 4a∵a2 0∴1 4a2∴对于任意实数a,方程总有两个不相等的实数根⑵把x=1 代入原方程,得a2 2∴a 2把a2 2 代入原方程,得x2 5x 4 0∴ 1 1, 2 4a x∴a 的值为 2 ,方程的另一根为 421.解:⑴∵OA=OB=50,AB=50∴OA=OB=AB∴△OAB 是等边三角形∴∠ABO =60°⑵过点 O 作 OC ⊥AB 于点 C则 AC =BC = 1 2AB 25在 Rt △OAC 中OC = OA 2 AC 2 502 252 25 3 ∴点 O 到 AB 的距离是 25 322. 解⑴① 20 1 x② 20 1 x (或 20 1 x 4.8 )2⑵依题意得: 20 1 x 20 1 x 4.82解得 x 1 0.2 , x (不合题意,舍去)2 1.2 0.2 20%答:这个增长率为 20%23. 解:⑴根据题意,得 y 13.5 x 2.5 500 100x 整理,得y 100x 600x 5500 0 x 112⑵当 x b 6002a 2 1003 时,y 有最大值4ac b 2 4 100 5500 60024a 4 1006400 即降价 3 元时利润最大,∴销售价为 10.5 元时,最大利润是 6400 元答:每件小商品销售价是 10.5 元时,商店每天销售这种小商品的利润的最大,最大利润是 6400 元24. 证明:⑴∵∠AOG =∠BOP ∴AG =BP ∵OP =OB ∴∠P =∠PBO又∠G=∠PBO,在△CAN 和△MCB 中,∴∠P=∠G∴AG∥PB⑵∵PG 是⊙O 的直径,BC⊥PG 于点D∴CD=BD∵∠CDK=∠BDP,DK=DP,∴△KDC≌△PDB∴CK=BP由⑴得AG=BP∴AG=CK∵△KDC≌△PDB,∴∠CKD=∠BPD.∴CK∥PB由⑴得AG∥PB∴AG∥CK∵AG=CK∴四边形AGKC 是平行四边形25. 解:⑴当b=2,c=-3 时,二次函数的解析式为y ax2 2x 3由已知,二次函数的图象经过点A(1,0)得a+2-3=0∴a=1所求二次函数的解析式为y x2 2x 3y x2 2x 3x 1 42∴当x=-1 时,二次函数取得最小值-4⑵①由二次函数的图象经过点B、C,且点B、C 的纵坐标相等知B、C 两点关于此抛物线的对称轴对称∴该抛物线的对称轴是直线x m m32即直线x 3 2②设二次函数的解析式为2y a x 32∵二次函数的图象经过点(1,0)∴14a k , 10 k a4∴2y a x 32 4∵对任意实数x,函数值y 都不小于1 14a 2a 1 1∴,且a>04 4a 2即1a 14a 4 2∴1 a2 2a 0 ,a 1 02∴a=1∴此时二次函数的解析式为2y x 32 4,即y x2 3x 2。
2016天津中考数学压轴题及答案解析

2016天津中考数学压轴题及答案解析
2016年天津中考数学压轴题及答案解析,更多2016中考真题答案、2016中考志愿填报、2016中考成绩查询、2016中考分数线等信息,请及时关注2016年中考真题及答案※中考作文※成绩查询
选择压轴题
今年的选择压轴题考查的内容沿用了2015天津中考数学试卷的最后一道大题,也就是区间最值问题,难度不大。
填空压轴题
今年的填空压轴题已经是连续第五年考察格点作图问题,同学们平日的练习以及各级各类考试中都会涉及到,难度还没有到想不出来的地步,如果用。
(完整版)九年级数学选择、填空压轴题训练(含答案),推荐文档

九年级数学综合训练一、选择题(本大题共9 小题,共27.0 分)1.如图,在平面直角坐标系中2 条直线为l1:y=-3x+3,l2:y=-3x+9,直线l1交x 轴于点A,交y 轴于点B,直线l2交x 轴于点D,过点B 作x 轴的平行线交l2于点C,点A、E 关于y 轴对称,抛物线y=ax2+bx+c 过E、B、C 三点,下列判断中:①a-b+c=0;②2a+b+c=5;③抛物线关于直线x=1 对称;④抛物线过点(b,c);⑤S 四边形ABCD=5,其中正确的个数有()A. 5B. 4C. 3D. 22.如图,10 个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如,表示a1=a2+a3,则a1的最小值为()A.32B.36C.38D.403.如图,直线y= ��x -6 分别交x 轴,y 轴于A,B,M 是反比例函数y=�(x>0)的图象上位于直线上方的一点,MC∥x 轴交AB 于C,MD⊥MC 交AB 于D,AC•BD=43,则k 的值为()A. ‒ 3B. ‒ 4C. ‒ 5D. ‒ 64.在平面直角坐标系xOy 中,将一块含有45°角的直角三角板如图放置,直角顶点C 的坐标为(1,0),顶点A 的坐标为(0,2),顶点B 恰好落在第一象限的双曲线上,现将直角三角板沿x 轴正方向平移,当顶点A 恰好落在该双曲线上时停止运动,则此时点C 的对应点C′的坐标为()(3,0) (2,0) (5,0) (3,0)A. 2B.C. 2D.5.如图,在矩形ABCD 中,AB<BC,E 为CD 边的中点,将△ADE 绕点E 顺时针旋转180°,点D 的对应点为C,点A 的对应点为F,过点E 作ME⊥AF 交BC 于点M,连接AM、BD 交于点N,现有下列结论:35 ①AM =AD +MC ;②AM =DE +BM ;③DE 2=AD •CM ;④点 N 为△ABM 的外心. 其中正确的个数为()A. 1 个B. 2 个C. 3 个D. 4 个6. 规定:如果关于 x 的一元二次方程 ax 2+bx +c =0(a ≠0)有两个实数根,且其中一个根是另一个根的 2倍,则称这样的方程为“倍根方程”.现有下列结论:①方程 x 2+2x -8=0 是倍根方程;②若关于 x 的方程 x 2+ax +2=0 是倍根方程,则 a =±3;③若关于 x 的方程 ax 2-6ax +c =0(a ≠0)是倍根方程,则抛物线 y =ax 2-6ax +c 与 x 轴的公共点的坐标是 (2,0)和(4,0); 4 ④若点(m ,n )在反比例函数 y =x 的图象上,则关于 x 的方程 mx 2+5x +n =0 是倍根方程. 上述结论中正确的有( )A. ①②B. ③④C. ②③D. ②④7. 如图,六边形 ABCDEF 的内角都相等,∠DAB =60°,AB =DE ,则下列结论成立的个数是() ①AB ∥DE ;②EF ∥AD ∥BC ;③AF =CD ;④四边形 ACDF 是平行四边形;⑤六边形 ABCDEF 既是中心对称图形,又是轴对称图形.A. 2B. 3C. 4D. 58. 如图,在 Rt △ABC 中,∠C =90°,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )A. 4B. 5C. 6D. 79. 如图,矩形 ABCD 中,AE ⊥BD 于点 E ,CF 平分∠BCD ,交 EA 的延长线于点 F ,且 BC =4,CD =2,给出下列结论:①∠BAE =∠CAD ;4②∠DBC =30°;③AE =5 5;④AF =2 ,其中正确结论的个数有( )A. 1 个B. 2 个C. 3 个D. 4 个二、填空题(本大题共 10 小题,共 30.0 分)10.如图,在Rt△ABC 中,∠BAC=30°,以直角边AB 为直径作半圆交AC 于点D,以AD 为边作等边△ADE,延长ED 交BC 于点F,BC=2 3,则图中阴影部分的面积为.(结果不取近似值)11.如图,在6×6 的网格内填入1 至6 的数字后,使每行、每列、每个小粗线宫中的数字不重复,则a×c=.12.如图,正方形ABCD 中,BE=EF=FC,CG=2GD,BG 分别交AE,AF 于M,N.下列结论:4 �M 3 1①AF⊥BG;②BN=3NF;③M G=8;④S 四边形CGNF=2S 四边形ANGD.其中正确的结论的序号是.13.已知:如图,在△AOB 中,∠AOB=90°,AO=3cm,BO=4cm.将△AOB 绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB 的交点D 恰好为AB 的中点,则线段B1D= cm.14.如图,边长为4 的正六边形ABCDEF 的中心与坐标原点O 重合,AF∥x 轴,将正六边形ABCDEF 绕原点O 顺时针旋转n 次,每次旋转60°.当n=2017 时,顶点A 的坐标为.15.如图,在Rt△ABC 中,BC=2,∠BAC=30°,斜边AB 的两个端点分别在相互垂直的射线OM、ON 上滑动,下列结论:①若C、O 两点关于AB 对称,则OA=2 3;②C、O 两点距离的最大值为4;③若AB 平分CO,则AB⊥CO;�④斜边AB 的中点D 运动路径的长为2;其中正确的是(把你认为正确结论的序号都填上).16.如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N(3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB=30°,要使PM+PN 最小,则点P 的坐标为.17.在一条笔直的公路上有A、B、C 三地,C 地位于A、B 两地之间,甲车从A地沿这条公路匀速驶向C 地,乙车从B 地沿这条公路匀速驶向A 地,在甲车出发至甲车到达C 地的过程中,甲、乙两车各自与C 地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h 时,两车相遇;②乙车出发1.5h 时,两车相距170km;③乙车出5发27h 时,两车相遇;④甲车到达C 地时,两车相距40km.其中正确的是(填写所有正确结论的序号).�18.如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=x(x>0)的图象经过A,B 两点.若点A 的坐标为(n,1),则k 的值为.19.如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-1,1),B(0,-2),C(1,0),点P(0,2)绕点A 旋转180°得到点P1,点P1绕点B 旋转180°得到点P2,点P2绕点C 旋转180°得到点P3,点P3绕点A 旋转180°得到点P4,…,按此作法进行下去,则点P2017的坐标为.答案和解析1.【答案】C【解析】解:∵直线l1:y=-3x+3 交x 轴于点A,交y 轴于点B,∴A(1,0),B(0,3),∵点A、E 关于y 轴对称,∴E(-1,0).∵直线l2:y=-3x+9 交x 轴于点D,过点B 作x 轴的平行线交l2 于点C,∴D(3,0),C 点纵坐标与B 点纵坐标相同都是3,把y=3 代入y=-3x+9,得3=-3x+9,解得x=2,∴C(2,3).∵抛物线y=ax2+bx+c 过E、B、C 三点,∴,解得,∴y=-x2+2x+3.①∵抛物线y=ax2+bx+c 过E(-1,0),∴a-b+c=0,故①正确;②∵a=-1,b=2,c=3,∴2a+b+c=-2+2+3=3≠5,故②错误;③∵抛物线过B(0,3),C(2,3)两点,∴对称轴是直线x=1,∴抛物线关于直线x=1 对称,故③正确;④∵b=2,c=3,抛物线过C(2,3)点,∴抛物线过点(b,c),故④正确;⑤∵直线l1∥l2,即AB∥CD,又BC∥AD,∴四边形ABCD 是平行四边形,∴S 四边形ABCD=BC•OB=2×3=6≠5,故⑤错误.综上可知,正确的结论有3个.故选:C.根据直线l1的解析式求出A(1,0),B(0,3),根据关于y 轴对称的两点坐标特征求出E(- 1,0).根据平行于x 轴的直线上任意两点纵坐标相同得出C 点纵坐标与B 点纵坐标相同都是3,再根据二次函数图象上点的坐标特征求出C(2,3).利用待定系数法求出抛物线的解析式为y=-x2+2x+3,进而判断各选项即可.本题考查了抛物线与x 轴的交点,一次函数、二次函数图象上点的坐标特征,关于y 轴对称的两点坐标特征,平行于x 轴的直线上任意两点坐标特征,待定系数法求抛物线的解析式,平行四边形的判定及面积公式,综合性较强,求出抛物线的解析式是解题的关键.2.【答案】D【解析】解:∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3(a8+a9)+a10,∴要使a1 取得最小值,则a8+a9 应尽可能的小,取a8=2、a9=4,∵a5=a8+a9=6,则a7、a10 中不能有6,若a7=8、a10=10,则a4=10=a10,不符合题意,舍去;若a7=10、a10=8,则a4=12、a6=4+8=12,不符合题意,舍去;若a7=10、a10=12,则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40,符合题意;综上,a1的最小值为40,故选:D.由a1=a7+3(a8+a9)+a10 知要使a1 取得最小值,则a8+a9 应尽可能的小,取a8=2、a9=4,根据a5=a8+a9=6,则a7、a10 中不能有6,据此对于a7、a8,分别取8、10、12 检验可得,从而得出答案.本题主要考查数字的变化类,根据题目要求得出a1取得最小值的切入点是解题的关键.3.【答案】A【解析】解:过点D 作DE⊥y 轴于点E,过点C 作CF⊥x 轴于点F,令x=0 代入y= x-6,∴y=-6,∴B(0,-6),∴OB=6,令y=0 代入y= x-6,∴x=2 ,∴(2 ,0),∴OA=2 ,∴勾股定理可知:AB=4 ,∴sin∠OAB= = ,cos∠OAB= =设M(x,y),∴CF=-y,ED=x,∴sin∠OAB= ,∴AC=- y,∵cos∠OAB=cos∠EDB= ,∴BD=2x,∵AC•BD=4,∴- y×2x=4 ,∴xy=-3,∵M 在反比例函数的图象上,∴k=xy=-3,故选(A)过点D 作DE⊥y 轴于点E,过点C 作CF⊥x 轴于点F,然后求出OA 与OB 的长度,即可求出∠OAB 的正弦值与余弦值,再设M(x,y),从而可表示出BD 与AC 的长度,根据AC•BD=4列出即可求出k 的值.本题考查反比例函数与一次函数的综合问题,解题的关键是根据∠OAB 的锐角三角函数值求出BD、AC,本题属于中等题型.4.【答案】C【解析】解:过点B 作BD⊥x 轴于点D,∵∠ACO+∠BCD=90°,∠OAC+∠ACO=90°,∴∠OAC=∠BCD,在△ACO 与△BCD 中,∴△ACO➴△BCD(AAS)∴OC=BD,OA=CD,∵A(0,2),C(1,0)∴OD=3,BD=1,∴B(3,1),∴设反比例函数的解析式为y= ,将B(3,1)代入y= ,∴k=3,∴y= ,∴把y=2 代入y= ,∴x= ,当顶点A 恰好落在该双曲线上时,此时点A 移动了个单位长度,∴C 也移动了个单位长度,此时点C 的对应点C′的坐标为(,0)故选:C.过点B 作BD⊥x 轴于点D,易证△ACO➴△BCD(AAS),从而可求出B 的坐标,进而可求出反比例函数的解析式,根据解析式与 A 的坐标即可得知平移的单位长度,从而求出 C 的对应点.本题考查反比例函数的综合问题,涉及全等三角形的性质与判定,反比例函数的解析式,平移的性质等知识,综合程度较高,属于中等题型.5.【答案】B【解析】解:∵E 为CD 边的中点,∴DE=CE,又∵∠D=∠ECF=90°,∠AED=∠FEC,∴△ADE➴△FCE,∴AD=CF,AE=FE,又∵ME⊥AF,∴ME 垂直平分AF,∴AM=MF=MC+CF,∴AM=MC+AD,故①正确;如图,延长CB 至G,使得∠BAG=∠DAE,由AM=MF,AD∥BF,可得∠DAE=∠F=∠EAM,可设∠BAG=∠DAE=∠EAM=α,∠BAM=β,则∠AED=∠EAB=∠GAM=α+β,由∠BAG=∠DAE,∠ABG=∠ADE=90°,可得△ABG∽△ADE,∴∠G=∠AED=α+β,∴∠G=∠GAM,∴AM=GM=BG+BM,由△ABG∽△ADE,可得= ,而AB<BC=AD,∴BG<DE,∴BG+BM<DE+BM,即AM<DE+BM,∴AM=DE+BM 不成立,故②错误;∵ME⊥FF,EC⊥MF,∴EC2=CM×CF,又∵EC=DE,AD=CF,∴DE2=AD•CM,故③正确;∵∠ABM=90°,∴AM 是△ABM 的❧➓圆的直径,∵BM<AD,∴当BM∥AD 时,= <1,∴N 不是AM 的中点,∴点N 不是△ABM 的❧心,故④错误.综上所述,正确的结论有2 个,故选:B.根据全等三角形的性质以及线段垂直平分线的性质,即可得出AM=MC+AD;根据△ABG∽△ ADE,且AB<BC,即可得出BG<DE,再根据AM=GM=BG+BM,即可得出AM=DE+BM 不成立;根据ME⊥FF,EC⊥MF,运用射影定理即可得出EC2=CM×CF,据此可得DE2=AD•CM 成立;根据N 不是AM 的中点,可得点N 不是△ABM 的❧心.本题主要考查了相似三角形的判定与性质,全等三角形的判定与性质,矩形的性质以及旋转的性质的综合应用,解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例进行推导,解题时注意:三角形❧➓圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的❧心,故❧心到三角形三个顶点的距离相等.6.【答案】C【解析】解:①由x2-2x-8=0,得(x-4)(x+2)=0,解得x1=4,x2=-2,∵x1≠2x2,或x2≠2x1,1 1 ∴方程 x 2-2x-8=0 不是倍根方程. 故①错误;②关于 x 的方程 x 2+ax+2=0 是倍根方程,∴设 x 2=2x 1,∴x 1•x 2=2x 2=2,∴x 1=±1,当 x 1=1 时 ,x 2=2,当 x 1=-1 时 ,x 2=-2,∴x 1+x 2=-a=±3,∴a=±3,故②正确;③关于 x 的方程 ax 2-6ax+c=0(a≠0)是倍根方程,∴x 2=2x 1,∵抛物线 y=ax 2-6ax+c 的对称轴是直线 x=3,∴抛物线 y=ax 2-6ax+c 与 x 轴的交点的坐标是(2,0)和(4,0),故③正确;④∵点(m ,n )在反比例函数 y= 的图象上,∴mn=4,解 mx 2+5x+n=0 得 x 1=- ,x 2=- ,∴x 2=4x 1,∴关于 x 的方程 mx 2+5x+n=0 不是倍根方程;故选:C .①通过解方程得到该方程的根,结合“倍根方程”的定义进行判断;②设 x 2=2x 1,得到 x 1•x 2=2x 2=2,得到当 x 1=1 时,x 2=2,当 x 1=-1 时,x 2=-2,于是得到结论;③根据“倍根方程”的定义即可得到结论;④若点(m,n)在反比例函数y= 的图象上,得到mn=4,然后解方程mx2+5x+n=0 即可得到正确的结论;本题考查了反比例函数图象上点的坐标特征,根与系数的关系,正确的理解倍根方程的定义是解题的关键.7.【答案】D【解析】解:∵六边形ABCDEF 的内角都相等,∴∠EFA=∠FED=∠FAB=∠ABC=120°,∵∠DAB=60°,∴∠DAF=60°,∴∠EFA+∠DAF=180°,∠DAB+∠ABC=180°,∴AD∥EF∥CB,故②正确,∴∠FED+∠EDA=180°,∴∠EDA=∠ADC=60°,∴∠EDA=∠DAB,∴AB∥DE,故①正确,∵∠FAD=∠EDA,∠CDA=∠BAD,EF∥AD∥BC,∴四边形EFAD,四边形BCDA 是等腰梯形,∴AF=DE,AB=CD,∵AB=DE,∴AF=CD,故③正确,连➓CF 与AD 交于点O,连➓DF、AC、AE、DB、BE.∵∠CDA=∠DAF,∴AF∥CD,AF=CD,∴四边形AFDC 是平行四边形,故④正确,同法可证四边形AEDB 是平行四边形,∴AD 与CF,AD 与BE 互相平分,∴OF=OC,OE=OB,OA=OD,∴六边形ABCDEF 既是中心对称图形,故⑤正确,故选D.根据六边形ABCDEF 的内角都相等,∠DAB=60°,平行线的判定,平行四边形的判定,中心对称图形的定义一一判断即可.本题考查平行四边形的判定和性质、平行线的判定和性质、轴对称图形、中心对称图形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.8.【答案】D【解析】解:如图:故选:D.①以B 为圆心,BC 长为半径画弧,交AB 于点D,△BCD 就是等腰三角形;②以A 为圆心,AC 长为半径画弧,交AB 于点E,△ACE 就是等腰三角形;③以C 为圆心,BC 长为半径画弧,交AC 于点F,△BCF 就是等腰三角形;④以C 为圆心,BC 长为半径画弧,交AB 于点K,△BCK 就是等腰三角形;⑤作AB 的垂直平分线交AC 于G,则△AGB 是等腰三角形;➅作BC 的垂直平分线交AB 于I,则△BCI 和△ACI 是等腰三角形.本题考查了等腰三角形的判定的应用,主要考查学生的理解能力和动手操作能力.9.【答案】C【解析】解:在矩形ABCD 中,∵∠BAD=90°,∵AE⊥BD,∴∠AED=90°,∴∠ADE+∠DAE=∠DAE+∠BAE=90°,∴∠BAE=∠ADB,∵∠CAD=∠ADB,∴∠BAE=∠CAD,故①正确;∵BC=4,CD=2,∴tan∠DBC= = ,∴∠DBC≠30°,故②错误;∵BD= =2 ,∵AB=CD=2,AD=BC=4,∵△ABE∽△DBA,∴,即,∴AE= ;故③正确;∵CF 平分∠BCD,∴∠BCF=45°,∴∠ACF=45°-∠ACB,∵AD∥BC,∴∠DAC=∠BAE=∠ACB,∴∠EAC=90°-2∠ACB,∴∠EAC=2∠ACF,∵∠EAC=∠ACF+∠F,∴∠ACF=∠F,∴AF=AC,∵AC=BD=2 ,∴AF=2 ,故④正确;故选C.根据余角的性质得到∠BAE=∠ADB,等量代换得到∠BAE=∠CAD,故①正确;根据三角函数的定义得到tan∠DBC= = ,于是得到∠DBC≠30°,故②错误;由勾股定理得到BD==2 ,根据相似三角形的性质得到AE= ;故③正确;根据角平分线的定义得到∠BCF=45°,求得∠ACF=45°-∠ACB,推出∠EAC=2∠ACF,根据❧角的性质得到∠EAC=∠ACF+∠F,得到∠ACF=∠F,根据等腰三角形的判定得到AF=AC,于是得到AF=2 ,故④正确.本题考查了矩形的性质,相似三角形的判定和性质,三角形的❧角的性质,角平分线的定义,熟练掌握相似三角形的判定和性质是解题的关键.10.【答案】3【解析】3 3-2π解:如图所示:设半圆的圆心为O,连➓DO,过D 作DG⊥AB 于点G,过D 作DN⊥CB 于点N,∵在Rt△ABC 中,∠BAC=30°,∴∠ACB=60°,∠ABC=90°,∵以AD 为边作等边△ADE,∴∠EAD=60°,∴∠EAB=60°+30°=90°,可得:AE∥BC,则△ADE∽△CDF,∴△CDF 是等边三角形,∵在Rt△ABC 中,∠BAC=30°,BC=2 ,∴AC=4 ,AB=6,∠DOG=60°,则AO=BO=3,故DG=DO•sin60°=,则AD=3 ,DC=AC-AD= ,故DN=DC•sin60°=×= ,则S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF= ×2 ×6- ×3×- - × ×=3 - π.故答案为:3 - π.根据题意结合等边三角形的性质分别得出AB,AC,AD,DC 的长,进而利用S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF 求出答案.此题主要考查了扇形面积求法以及等边三角形的性质和锐角三角函数关系等知识,正确分割图形是解题关键.11.【答案】2【解析】解:对各个小宫格编号如下:先看己:已经有了数字3、5、6,缺少1、2、4;观察发现:4 不能在第四列,2 不能在第五列,而2 不能在第六列;所以2 只能在第六行第四列,即a=2;则b 和c 有一个是1,有一个是4,不确定,如下:观察上图发现:第四列已经有数字2、3、4、6,缺少1 和5,由于5 不能在第二行,所以5 在第四行,那么1 在第二行;如下:再看乙部分:已经有了数字1、2、3,缺少数字4、5、6,观察上图发现:5 不能在第六列,所以5在第五列的第一行;4 和6 在第六列的第一行和第二行,不确定,分两种情况:①当4 在第一行时,6 在第二行;那么第二行第二列就是4,如下:再看甲部分:已经有了数字1、3、4、5,缺少数字2、6,观察上图发现:2 不能在第三列,所以2 在第二列,则6 在第三列的第一行,如下:观察上图可知:第三列少1 和4,4 不能在第三行,所以4 在第五行,则1 在第三行,如下:观察上图可知:第五行缺少1 和2,1 不能在第1 列,所以1 在第五列,则2 在第一列,即c=1,所以b=4,如下:观察上图可知:第六列缺少1 和2,1 不能在第三行,则在第四行,所以2 在第三行,如下:再看戊部分:已经有了数字2、3、4、5,缺少数字1、6,观察上图发现:1 不能在第一列,所以1 在第二列,则6 在第一列,如下:观察上图可知:第一列缺少3 和4,4 不能在第三行,所以4 在第四行,则3 在第三行,如下:观察上图可知:第二列缺少5 和6,5 不能在第四行,所以5 在第三行,则6 在第四行,如下:观察上图可知:第三行第五列少6,第四行第五列少3,如下:所以,a=2,c=1,ac=2;②当6 在第一行,4 在第二行时,那么第二行第二列就是6,如下:再看甲部分:已经有了数字1、3、5、6,缺少数字2、4,观察上图发现:2 不能在第三列,所以2 在第2 列,4 在第三列,如下:观察上图可知:第三列缺少数字1 和6,6 不能在第五行,所以6 在第三行,则1 在第五行,所以c=4,b=1,如下:观察上图可知:第五列缺少数字3 和6,6 不能在第三行,所以6 在第四行,则3 在第三行,如下:观察上图可知:第六列缺少数字1 和2,2 不能在第四行,所以2 在第三行,则1 在第四行,如下:观察上图可知:第三行缺少数字1 和5,1 和5 都不能在第一列,所以此种情况不成立;综上所述:a=2,c=1,a×c=2;故答案为:2.粗线把这个数独分成了6 块,为了便于解答,对各部分进行编号:甲、乙、丙、丁、戊、己,先从各部分中数字最多的己出发,找出其各个小方格里面的数,再根据每行、每列、每小宫格都不出现重复的数字进行推算.本题是六阶数独,比较复杂,关键是找出突破口,先推算出一个区域或者一行、一列,再逐步的进行推算.12.【答案】①③【解析】解:①∵四边形ABCD 为正方形,∴AB=BC=CD,∵BE=EF=FC,CG=2GD,∴BF=CG,∵在△ABF 和△BCG 中,,∴△ABF➴△BCG,∴∠BAF=∠CBG,∵∠BAF+∠BFA=90°,∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;②∵在△BNF 和△BCG 中,,∴△BNF∽△BCG,∴ = = ,∴BN= NF;②错误;③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,AF= = ,∵S△ABF= AF•BN=AB•BF,∴BN= ,NF= BN= ,∴AN=AF-NF= ,∵E 是BF 中点,∴EH 是△BFN 的中位线,∴EH= ,NH= ,BN∥EH,∴AH= , = ,解得:MN= ,∴BM=BN-MN= ,MG=BG-BM= ,∴ = ;③正确;④连➓AG,FG,根据③中结论,则NG=BG-BN= ,∵S 四边形CGNF=S△CFG+S△GNF= CG•CF+NF•NG=1+= ,S 四边形ANGD=S△ANG+S△ADG= AN•GN+AD•DG= + = ,∴S 四边形CGNF≠S 四边形ANGD,④错误;故答案为①③.①易证△ABF➴△BCG,即可解题;②易证△BNF∽△BCG,即可求得的值,即可解题;③作EH⊥AF,令AB=3,即可求得MN,BM 的值,即可解题;④连➓AG,FG,根据③中结论即可求得S 四边形CGNF 和S 四边形ANGD,即可解题.本题考查了全等三角形的判定和性质,考查了相似三角形的判定和对应边成比例的性质,本题中令AB=3 求得AN,BN,NG,NF 的值是解题的关键.13.【答案】1.5【解析】解:∵在△AOB 中,∠AOB=90°,AO=3cm,BO=4cm,∴AB= =5cm,∵点D 为AB 的中点,∴OD= AB=2.5cm.∵将△AOB 绕顶点O,按顺时针方向旋转到△A1OB1 处,∴OB1=OB=4cm,∴B1D=OB1-OD=1.5cm.故答案为1.5.先在直角△AOB 中利用勾股定理求出AB= =5cm,再利用直角三角形斜边上的中线等于斜边的一半得出OD= AB=2.5cm.然后根据旋转的性质得到OB1=OB=4cm,那么B1D=OB1-OD=1.5cm.本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了直角三角形斜边上的中线等于斜边的一半的性质以及勾股定理.14.【答案】(2,2 3)【解析】解:2017×60°÷360°=336…1,即与正六边形ABCDEF 绕原点O 顺时针旋转1 次时点A 的坐标是一样的.当点A 按顺时针旋转60°时,与原F 点重合.连➓OF,过点F 作FH⊥x 轴,垂足为H;由已知EF=4,∠FOE=60°(正六边形的性质),∴△OEF 是等边三角形,∴OF=EF=4,∴F(2,2 ),即旋转2017 后点A 的坐标是(2,2 ),故答案是:(2,2 ).将正六边形ABCDEF 绕原点O 顺时针旋转2017 次时,点A 所在的位置就是原F 点所在的位置.此题主要考查了正六边形的性质,坐标与图形的性质-旋转.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.15.【答案】①②③【解析】解:在Rt△ABC 中,∵BC=2,∠BAC=30°,∴AB=4,AC= =2 ,①若C、O 两点关于AB 对称,如图1,∴AB 是OC 的垂直平分线,则OA=AC=2 ;所以①正确;②如图1,取AB 的中点为E,连➓OE、CE,∵∠AOB=∠ACB=90°,∴OE=CE= AB=2,当OC 经过点E 时,OC 最大,则C、O 两点距离的最大值为4;所以②正确;③如图2,同理取AB 的中点E,则OE=CE,∵AB 平分CO,∴OF=CF,∴AB⊥OC,所以③正确;④如图3,斜边AB 的中点D 运动路径是:以O 为圆心,以2 为半径的圆周的,则:=π.所以④不正确;综上所述,本题正确的有:①②③;故答案为:①②③.①先根据直角三角形30°的性质和勾股定理分别求AC 和AB,由对称的性质可知:AB 是OC 的垂直平分线,所以OA=AC;②当OC 经过AB 的中点E 时,OC 最大,则C、O 两点距离的最大值为4;③如图2,根据等腰三角形三线合一可知:AB⊥OC;④如图3,半径为2,圆心角为90°,根据弧长公式进行计算即可.本题是三角形的综合题,考查了直角三角形30°的性质、直角三角形斜边中线的性质、等腰三角形的性质、轴对称的性质、线段垂直平分线的性质、动点运动路径问题、弧长公式,熟练掌握直角三角形斜边中线等于斜边一半是本题的关键,难度适中.3 316.【答案】(2, 2 )【解析】解:作N 关于OA 的对称点N′,连➓N′M 交OA 于P,则此时,PM+PN 最小,∵OA 垂直平分NN′,∴ON=ON′,∠N′ON=2∠AON=60°,∴△NON′是等边三角形,∵点M 是ON 的中点,∴N′M⊥ON,∵点N(3,0),∴ON=3,∵点M 是ON 的中点,∴OM=1.5,∴PM= ,∴P(,).故答案为:(,).作N 关于OA 的对称点N′,连➓N′M 交OA 于P,则此时,PM+PN 最小,由作图得到ON=ON′,∠N′ON=2∠AON=60°,求得△NON′是等边三角形,根据等边三角形的性质得到N′M⊥ON,解直角三角形即可得到结论.本题考查了轴对称-最短路线问题,等边三角形的判定和性质,解直角三角形,关键是确定P 的位置.17.【答案】②③④【解析】解:①观察函数图象可知,当t=2 时,两函数图象相交,∵C 地位于A、B 两地之间,∴交点代表了两车离C 地的距离相等,并不是两车相遇,结论①错误;②甲车的速度为240÷4=60(km/h),乙车的速度为200÷(3.5-1)=80(km/h),∵(240+200-60-170)÷(60+80)=1.5(h),∴乙车出发1.5h 时,两车相距170km,结论②正确;③∵(240+200-60)÷(60+80)=2 (h),∴乙车出发2 h 时,两车相遇,结论③正确;④∵80×(4-3.5)=40(km),∴甲车到达C 地时,两车相距40km,结论④正确.综上所述,正确的结论有:②③④.故答案为:②③④.①观察函数图象可知,当t=2 时,两函数图象相交,结合交点代表的意义,即可得出结论①错误;②根据速度=路程÷时间分别求出甲、乙两车的速度,再根据时间=路程÷速度和可求出乙车出发1.5h 时,两车相距170km,结论②正确;③根据时间=路程÷速度和可求出乙车出发2 h 时,两车相遇,结论③正确;④结合函数图象可知当甲到C 地时,乙车离开C 地0.5 小时,根据路程=速度×时间,即可得出结论④正确.综上即可得出结论.本题考查了一次函数的应用,根据函数图象逐一分析四条结论的正误是解题的关键.18.【答案】【解析】5 ‒ 1 2解:作AE⊥x 轴于E,BF⊥x 轴于F,过B 点作BC⊥y 轴于C,交AE 于G,如图所示:则AG⊥BC,∵∠OAB=90°,∴∠OAE+∠BAG=90°,∵∠OAE+∠AOE=90°,∴∠AOE=∠GAB ,在△AOE 和△BAG 中,,∴△AOE ➴△BAG (AAS ),∴OE=AG ,AE=BG ,∵点 A (n ,1),∴AG=OE=n ,BG=AE=1,∴B (n+1,1-n ),∴k=n×1=(n+1)(1-n ),整理得:n 2+n-1=0,解得:n= ∴n=,(负值舍去), ∴k=故答案为: ;.作 AE ⊥x 轴于 E ,BF ⊥x 轴于 F ,过 B 点作 BC ⊥y 轴于 C ,交 AE 于 G ,则 AG ⊥BC ,先求得△ AOE ➴△BAG ,得出 AG=OE=n ,BG=AE=1,从而求得 B (n+1,1-n ),根据 k=n×1=(n+1)(1-n )得出方程,解方程即可.本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识;熟练掌握反比例函数图象上点的坐标特征,证明三角形全等是解决问题的关键.19.【答案】(-2,0)【解析】解:如图所示,P 1(-2,0),P 2(2,-4),P 3(0,4),P 4(-2,-2),P 5(2,-2),P 6(0,2),发现 6 次一个循环,∵2017÷6=336…1,∴点 P 2017 的坐标与 P 1 的坐标相同,即 P 2017(-2,0),故答案为(-2,0).画出P1~P6,寻找规律后即可解决问题.本题考查坐标与图形的性质、点的坐标等知识,解题的关键是循环探究问题的方法,属于中考常考题型.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
最新整理天津市和平区中考数学压轴题综合训练及答案详解

心位置,正方形 EFGH绕点 E 顺时针方向旋转,设它们重叠部分的面积为
S,旋转的角度为 θ , S 与
θ 的函数关系的大致图象是(
)
6. 如图,D 是△ ABC的 AC边上一点, AB=AC,BD=BC,将△ BCD沿 BD折叠, 顶点 C恰好 落在 AB边的 C′
处,则∠ A′的大小是(
)
A. 40°
( 1)分别求出 y 与 x,w 与 x 的函数关系式;
( 2)在今年内该单位哪个月获得利润达到 5800 元?
15. 如图,矩形 ABCD中, AB=6cm,BC=8cm动, 点 P 从点 A 出发 , 在 AC上以每秒 5cm 的速度向点 C匀速 运动,同时动点 Q 从点 D 出发,在 DA 边上以每秒 4cm 的速度向点 A 匀速运动,运动时间为 t 秒
天津市和平区 20XX 年九年级中考数学压轴题综合训练
1. 若实数 a,b 满足 a﹣ ab+b2+2=0,则 a 的取值范围是(
)
A . a≤﹣ 2 B . a≥ 4 C. a≤﹣ 2 或 a≥ 4 D.﹣ 2≤ a≤ 4
2. 如图, A、 B是双曲线上的点, A、 B 两点的横坐标分别是 a、 2a,线段 AB 的延长线交 x 轴于点 C,
再生资源重新利用.今年 1 月份,再生资源处理量为 40 吨,从今年 1 月 1 日起,该单位每月再生资
源处理量每一个月将提高 10 吨.月处理成本(元)与月份之间的关系可近似地表示为:
2
p=50x +100x+450 ,每处理一吨再生资源得到的新产品的售价定为
100 元.若该单位每月再生资源处
理量为 y(吨),每月的利润为 w(元).
精品 天津和平区2016年中考数学二轮专题复习 最大(小)值问题及详解

天津和平区2016年中考数学二轮专题复习最大(小)值问题1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )A、1B、2C、3D、4第1题图第2题图第3题图2.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ 的最小值为( )A.错误!未找到引用源。
B.错误!未找到引用源。
C.3 D.23.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )A.30° B.45° C.60° D.90°4.如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )A.13cmB.12cmC.10cmD.8cm第4题图第5题图第6题图5.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=23BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )A.6(4)π+㎝ B.5cm C.35㎝ D.7cm6.已知⊙O的半径为1,圆心O到直线l的距离为2,过l上的点A作⊙O的切线,切点为B,则线段AB 的长度的最小值为( )A.1 B. 2 C. 3 D.27.如图,在矩形ABCD 中,AB=6,BC=8,点E 是BC 中点,点F 是边CD 上的任意一点,当△AEF 的周长最小时,则DF 的长为( )A .1B .2C .3D .4第7题图 第8题图 第9题图8.如图,在菱形ABCD 中,对角线AC=6,BD=8,点E 、F 分别是边AB 、BC 的中点,点P 在AC 上运动,在运动过程中,存在PE+PF 的最小值,则这个最小值是( )A .3B .4C .5D .69.如图,点A 的坐标为(-1,0),点B 在直线y x =上运动,当线段AB 最短时,点B 的坐标为( )A.(0,0)B.(21-,21-)C.(22,22-)D.(22-,22-) 10.如图,∠MON=900,矩形ABCD 的顶点A 、B 分别在边OM,ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1,运动过程中,点D 到点O 的最大距离为( )A .21+B .5C .1455D .52第10题图 第11题图 第12题图11.如图,四边形ABCD 中,∠BAD =1200,∠B =∠D =900,在BC 、CD 上分别找一点M 、N ,使△AMN 周长最小时,则∠AMN+∠ANM 的度数为( )A .130° B.120° C.110° D.100°12.如图,在△ABC 中,∠C=900,AC=BC=4,D 是AB 的中点,点E 、F 分别在AC 、BC 边上运动(点E 不与点A 、C 重合),且保持AE=CF ,连接DE 、DF 、EF .在此运动变化的过程中,有下列结论:①△DFE 是等腰直角三角形; ②四边形CEDF 不可能为正方形;③四边形CEDF 的面积随点E 位置的改变而发生变化;④点C 到线段EF 的最大距离为.其中正确结论的个数是( )A .1个B .2个C .3个D .4个13.如图,在四边形ABCD中,∠A=900,∠ABD=300,AB=6连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为.第13题图第14题图第15题图14.如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是.15.如图,已知点A(1,1)、B(3,2),且P为x轴上一动点,则△ABP的周长的最小值为.16.如图,在平面直角坐标系中,有A(1,2),B(3,3)两点,现另取一点C(a,1),当a= 时,AC+BC 的值最小.第16题图第17题图第18题图17.如图,正方形ABCD中,AB=4,E是BC的中点,点P是对角线AC上一动点,则PE+PB的最小值为.18.如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是 .19.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .第19题图第20题图第21题图20.如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=34x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为 .21.如图,在梯形ABCD中,AB∥CD,∠BAD=90°,AB=6,对角线AC平分∠BAD,点E在AB上,且AE=2(AE <AD),点P是AC上的动点,则PE+PB的最小值是.22.如图,MN为⊙O的直径,A、B是O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是。
2016-2017年天津市和平区九年级上学期期中考试数学试卷(精品资料).doc

【最新整理,下载后即可编辑】2016-2017年度和平区初三上学期期中考试数学试卷一 选择题(3×12=36)1.下列图形中.可以看做是中心对称图形的是( )2.已知点A(a ,b)与点B(2,2)是关于原点0的对称点,则( )A. a=-2,b=-2B.a=-2,b=2C. a=2,b=-2D.a=2,b=23.用配方法解一元二次方程x 2-6x-4=0,下列变开征确的是( )A. (x-6)2=-4+36B. (x-6)2=4+36 C (x-3)2=-4+9D. (x-3)2=4+94.方程432412522+-=--x x x x 的根是( ) A.21,2121=-=x x B.2121==x x C. 2,221=-=x x D.41,4121=-=x x 5.某学校准备食建一个面积为200m 2的矩形花圃,它的长比宽多10m ,设花圃的宽为xm.则可列方程为( )A.x (x-10)=200B. 2x+2 (x-10)=200C. x (x+10)=200D.2x+2 (x+10)=2006.对抛物线y= -x 2+2x-3而言,下列结论正确的是( )A.与x 轴由两个公共点B.与y轴的交点坐标是(0,3〕C.当x<1时y随x的增大而增大;当x>1时y随x的增大而减小D.开口向上7.将抛物线y=5x2向左平移2个单位,再向下平移3个单位,得到的抛物线是( )A. y=5 (x+2) 2-3B.y=5 (x+2)2+3C. y=5 (x-2) 2-3D.y=5 (x-2) 2+38.二次函数y=ace+bx+c图像上部分点的坐标如下表所示则该函数的顶点坐标为( )A.(-3,-3)B.(-2.-2)C.(-1,-3)D.(0,-6〕9.如图,小华同学设计了一个圆的直径的测量器,标有刻度的两把尺子OA, OB 在O点被钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,尺子OA与圆交于点F,尺子OB与圆交于点E,读得OF为8个单位长度.,OE为6个单位长度.则圆的直径为( )A. 25个单位长度B. 14个单位长度C. 12个单位长度D. 10个单位长度10.如图,AB是圆0的直径,点D,点E在圆O上,且AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( )A.2个B.3个C. 4个D. 5个11.已知二次函数y=x2-2mx+m2+3(m是常数),把该函数的图像沿y轴平移后,得到的函数图像与x轴只有一个公共点,则应把该函数的图像()A.向上平移3个单位B.向下平移3个单位C.向上平移1个单位D.向下平移1个单位12.已知二次函数y=x2-x+a(a>0),当自变量x取m时,其对应的函数值小于0,那么当自变量x取m-1时,其对应的函数值()A.小于0B.大于0C.等于0D.与0的大小关系不石龟定二填空题(3×6=18)13.如图,AB是圆O的弦,若∠A=350,则∠AOB的大小为度.14.如图,点D为AC上一点,点O为AB上一点.AD=DO,以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF,若∠BAC=220,则∠EFG的大小为(度)15.抛物线y=x2+3x+2不经过第象限.1=0有两个相等的实数根,写出一组满足条16.关于x的一元二次方程ax2+bx+4件的实数a,b的值:a= ;b= .17.如图,P是等腰直角△ABC外一点,把BP绕直角顶点BB顺时针旋转900到BP/,已知∠AP/B=1350,P/A:P/C=1:3,则PB:P/A的值为.18.在RtABC 中,∠ACB=900,BAC=300,BC=6.(I)如图①,将线段CA 绕点C 顺匡件十旋转300,所得到与AB 交于点M ,则CM 的长= ;(II)如图②,点D 是边AC 上一点D 且AD=32,将线段AD 绕点A 旋转,得线段AD /,点F 始终为BD /的中点,则将线段AD 绕点A 逆时针旋转 度时,线段CF 的长最大,最大值为 。
精品教学 天津市和平区2016年中考数学专题-图形的变换 轻松过关及详解

2016年中考数学图形的变换轻松过关1.如图,矩形OABC在平面直角坐标系中,并且OA、OC的长满足:|OA﹣2|+(OC﹣6)2=0.(1)求A、B、C三点的坐标.(2)把△ABC沿AC对折,点B落在点B1处,AB1与x轴交于点D,求直线BB1的解析式.(3)在直线AC上是否存在点P使PB1+PD的值最小?若存在,请找出点P的位置,并求出PB1+PD的最小值;若不存在,请说明理由.(4)在直线AC上是否存在点P使|PD﹣PB|的值最大?若存在,请找出点P的位置,并求出|PD﹣PB|最大值.2.如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合)(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是;(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.3.已如图,在△ABC中,已知AB=AC=6,BC=8,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于P点.(1)求证:△ABE∽△ECP;(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形,使得AP=EP,若能,求出BE的长;若不能,请说明理由;(3)当BE为何值时,AP有最小值.4.如图,已知一个三角形纸片ABC,BC边的长为8,BC边上的高为6,∠B和∠C都为锐角,M为AB一动点(点M与点A,B不重合),过点M作MN//BC,交AC于点N,在△AMN中,设MN的长为x,MN上的高为h.(1)请你用含x的代数式表示h.(2)将△AMN沿MN折叠,使△AMN落在四边形BCNM所在平面,设点A落在平面的点为A1,△A1MN与四边形BCNM重叠部分的面积为y,当x为何值时,y最大,最大值为多少?5.正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直,(1)证明:Rt Rt ABM MCN △∽△;(2)设BM x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积;(3)当M 点运动到什么位置时Rt Rt ABM AMN △∽△,求x 的值.6.在△ABC 中,∠BAC=90°,AB <AC ,∠PMQ 是直角,且直角顶点M 是BC 边的中点,MN ⊥BC 交AC 于点N .PM 边上动点P 从点B 出发沿射线BA 以每秒2cm 的速度运动,同时,MQ 边上动点Q 从点N 出发沿射线NC 运动,设运动时间为t 秒(t >0). (1)求证:△PBM ∽△QNM ;(2)探求BP 2、PQ 2、CQ 2三者之间的数量关系,并说明理由. (3)若∠ABC=60°,BC=8cm . ①求动点Q 的运动速度;②设△APQ 的面积为S (平方厘米),求S 与t 的函数关系式;7.如图(1),在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.容易证得:CE=CF;(1)在图1中,若G在AD上,且∠GCE=45°.试猜想GE、BE、GD三线段之间的数量关系,并证明你的结论.(2)运用(1)中解答所积累的经验和知识,完成下面两题:①如图(2),在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α°,∠ECG=β°,试探索当α和β满足什么关系时,图(1)中GE、BE、GD三线段之间的关系仍然成立,并说明理由.②在平面直角坐标中,边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图(3)).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.8.如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.(1)求证:AE⊥BF;(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP到BA的延长线于点Q,求sin∠BQP的值;(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.9.如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.(1)当t=秒时,则OP= ,S△ABP= ;(2)当△ABP是直角三角形时,求t的值;(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ•BP=3.10.已知:在四边形ABCD中,AD∥BC,∠BAC=∠D,点E、F分别在BC、CD上,且∠AEF=∠ACD.(1)如图1,若AB=BC=AC,求证:AE=EF;(2)如图2,若AB=BC,(1)中的结论是否仍然成立?证明你的结论;(3)如图3,若AB=kBC,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出AE与EF之间的数量关系,并证明.11.已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.(1)当三角板绕点C旋转到CD与OA垂直时(如图1),易证:OD+OE=OC;(2)当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.12.如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.(1)请判断:AF与BE的数量关系是,位置关系是;(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.13.如图1,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.(1)操作:如图2,将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).求证:BH•GD=BF2(2)操作:如图3,△ECF的顶点F在△ABD的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.探究:FD+DG= .请予证明.14.已知:如图,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.(1)求过点E、D、C的抛物线的解析式;(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.15.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.16.已知:如图①,在矩形ABCD中,AB=5,AD=,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.(1)求AE和BE的长;(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.17.矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.①求证:△OCP∽△PDA;②若△OCP与△PDA的面积比为1:4,求边AB的长.(2)如图2,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M、N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.18.已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动、DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)解答下列问题:(1)当t为何值时,点A在线段PQ的垂直平分线上?(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.19.已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系是;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.20.如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD 与y轴交于点E,连接PE.设点P运动的时间为t(s).(1)∠PBD的度数为,点D的坐标为(用t表示);(2)当t为何值时,△PBE为等腰三角形?(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.21.如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.(1)求△ABC的面积;(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.22.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长.23.已知:正方形ABCD的边长为4,点E为BC的中点,点P为AB上一动点,沿PE翻折△BPE得到△FPE,直线PF交CD边于点Q,交直线AD于点G,联接EQ.(1)如图,当BP=1.5时,求CQ的长;(2)如图,当点G在射线AD上时,BP=x,DG=y,求y关于x的函数关系式,并写出x的取值范围;(3)延长EF交直线AD于点H,若△CQE与△FHG相似,求BP的长.24.情境观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是,∠CAC′= °.问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.25.(1)操作发现:将等腰Rt△ABC与等腰Rt△ADE按如图1方式叠放,其中∠ACB=∠ADE=90°,点D,E分别在AB,AC边上,M为BE的中点,连结CM,DM.小明发现CM=DM,你认为正确吗?请说明理由.(2)思考探究:小明想:若将图1中的等腰Rt△ADE绕点A沿逆时针方向旋转一定的角度,上述结论会如何呢?为此进行以下探究:探究一:将图1中的等腰Rt△ADE绕点A沿逆时针方向旋转45°(如图2),其他条件不变,发现结论CM=DM 依然成立.请你给出证明.探究二:将图1中的等腰Rt△ADE绕点A沿逆时针方向旋转135°(如图3),其他条件不变,则结论CM=DM 还成立吗?请说明理由.26.【提出问题】(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.【类比探究】(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.27.如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB 的长分别是方程x2﹣7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q 运动的时间为t秒.(1)求A、B两点的坐标.(2)求当t为何值时,△APQ与△AOB相似,并直接写出此时点Q的坐标.(3)当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.28.如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.(1)当BC=1时,求线段OD的长;(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.29.如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.(1)求证:△ADP∽△ABQ;(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;(3)若AD=10,AB=a,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD外部时,求a的取值范围.30.在矩形ABCD中,点F在AD延长线上,且DF=DC,M为AB边上一点,N为MD的中点,点E在直线CF 上(点E、C不重合).(1)如图1,若AB=BC,点M、A重合,E为CF的中点,试探究BN与NE的位置关系及的值,并证明你的结论;(2)如图2,且若AB=BC,点M、A不重合,BN=NE,你在(1)中得到的两个结论是否成立?若成立,加以证明;若不成立,请说明理由;(3)如图3,若点M、A不重合,BN=NE,你在(1)中得到的结论两个是否成立,请直接写出你的结论.31.正方形ABCD中,将一个直角三角板的直角顶点与点A重合,一条直角边与边BC交于点E(点E不与点B和点C重合),另一条直角边与边CD的延长线交于点F.(1)如图①,求证:AE=AF;(2)如图②,此直角三角板有一个角是45°,它的斜边MN与边CD交于G,且点G是斜边MN的中点,连接EG,求证:EG=BE+DG;(3)在(2)的条件下,如果=,那么点G是否一定是边CD的中点?请说明你的理由.32..如图,在平面直角坐标系中,四边形OABC是矩形,OA=4,AB=2,直线与坐标轴交于D、E.设M是AB的中点,P是线段DE上的动点.(1)求M、D两点的坐标;(2)当P在什么位置时,PA=PB求出此时P点的坐标;(3)过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,求梯形PMBH的面积.33.如图1,在Rt△ABC中,∠CAB=90°,AC=6,AB=8,点P是边AB上一动点,过点P作PQ⊥AB交BC于点E,截取PQ=AP,连接AQ交边BC于点D.(1)若AP4,求段DQ、DE的长;(2)如图2,连接CQ,设AP=PQ=x,当△CDQ和△ADB相似时,x的值;(3)如图3,将△BCQ沿BC翻折,Q点恰好落在边AB上的M点时,直接写出线段AP的长为.34.如图在△ABC中,AB=BC=10,AC=,D为边AB上的一动点(D与A、B不重合),过D作DE∥BC交AC于E,并以DE为边向BC一侧作正方形DEFG,设AD=x,(1)当边FG落在BC边上时,求x的值;(2)当正方形的边FG在△ABC外部时,如图2,DG、EF分别交边BC于M、N,若,求x的值;(3)点D在运动过程中,若存在D、G、B三点中的两点落在以第三点为圆心的圆上的情况,请直接写出此时AD的值.35.如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.(1)点E、F中,哪个点最先到达终点?(2)求△PEC的面积S与运动时间t的函数表达式,并写出自变量t的取值范围.当t为何值时,S的值最大;(3)当△CEP为锐角三角形时,求运动时间t的取值范围.36.如图,在▱ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t≤2.5).(1)当t为何值时,PE∥CD;(2)设△PEQ的面积为y(cm2),求出y与t之间的函数关系式;(3)是否存在某一时刻t,使S△PEQ=S△ABC?若存在,求出此时t的值;若不存在,说明理由;(4)在上述运动过程中,五边形ABFPE的面积是否发生变化?说明理由.37.如图1,已知AB⊥BM,AB=2,点P为射线BM上的动点,联结AP,作BH⊥AP,垂足为H,∠APM的平分线交BH的延长线于点D,联结AD.(1)若∠BAP=30°,求∠ADP的度数;(2)若S△ADP:S△ABP=3:2,求BP的长;(3)若AD∥BM(如图2),求BP的长.38.在Rt△ABC中,AB=BC,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC上,将三角板绕点O旋转.(1)当点O为AC中点时:①如图1,三角板的两直角边分别交AB,BC于E、F两点,连接EF,猜想线段AE、CF与EF之间存在的等量关系(无需证明);②如图2,三角板的两直角边分别交AB,BC延长线于E、F两点,连接EF,判断①中的结论是否成立.若成立,请证明;若不成立,请说明理由;(2)当点O不是AC中点时,如图3,三角板的两直角边分别交AB,BC于E、F两点,若=,则= .39.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x 轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造▱PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中,设▱PCOD的面积为S.①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.40.如图1,等边三角形ABC的边长为4,直线l经过点A并与AC垂直.当点P从点A开始沿射线AM运动,连接PC,并将△ACP绕点C按逆时针方向旋转60°得到△BCQ,记点P的对应点为Q,线段PA的长为m(m ≥0),当点Q恰好落在直线l上时,点P停止运动.(1)在图1中,当∠ACP=20°,求∠BQC的值;(2)在图2中,已知BD⊥l于点D,QE⊥l于点E,ΩF⊥BD于点F,试问:∠BQF的值是否会随着点P的运动而改变?若不会,求出∠BQF的值;若会,请说明理由.(3)在图3中,连接PQ,记△PAQ的面积为S,请求出S与m的函数关系式(注明m的取值范围),并求出当m为何值时,S有最大值?最大值为多少?41.已知四边形ABCD是边长为2的正方形,在以AB为直径的正方形内作半圆O,P为半圆上的动点(不与A、B重合)连接PA、PB、PC、PD,(1)若DP与半圆O相切时,求PA的长.(2)如图,以BC边为x轴,以AB边为y轴,建立如图所示的平面直角坐标系,把△PAD、△PAB、△PBC 的面积分别记为S1、S2、S3,试求2S1S3﹣S22的最大值,并求出此时点P的坐标.(3)在(2)的条件下,E为边AD上一点,且AE=3DE,连接BE交半圆O于F.连接FP并延长至点Q,使得PQ=PB,求OQ的长.42.如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD 与y轴交于点E,连接PE.设点P运动的时间为t(s).(1)∠PBD的度数为,点D的坐标为(用t表示);(2)当t为何值时,△PBE为等腰三角形?(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.43.如图,已知在△ABC中,射线AM∥BC,P是边BC上一动点,∠APD=∠B,PD交射线AM于点D.联结CD.AB=4,BC=6,∠B=60°.(1)求证:AP2=AD•BP;(2)如果以AD为半径的圆A以与A以BP为半径的圆B相切.求线段BP的长度;(3)将△ACD绕点A旋转,如果点D恰好与点B重合,点C落在点E的位置上,求此时∠BEP的余切值.44.如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB,过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.(1)当点B与点D重合时,求t的值;(2)当t为何值时,S△BCD=?45.在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0°<θ<90°),连接AC1、BD1,AC1与BD1交于点P.(1)如图1,若四边形ABCD是正方形.①求证:△AOC1≌△BOD1.②请直接写出AC1与BD1的位置关系.(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1=kBD1.请直接写出k的值和AC12+(kDD1)2的值.46.如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s,过点P作PE∥AC交DC于点E,同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,连接PQ、QE,PQ与AC交与点F,设运动时间为t(s)(0<t<8).(1)当t为何值时,四边形PFCE是平行四边形;(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的;(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.47.问题背景:将已知△ABC绕点A逆时针旋转得到△AB′C′,顶点B、C的对应点分别为点B′,C′,连接CC′,且满足CC′∥AB.探索发现:(1)若∠BAC=40°,如图1,求旋转角∠CAC′的度数.(2)若∠BAC=70°,如图2,则旋转角∠CAC′°(3)基∠BAC=α,旋转角为β,则β= (用含α的代数式表示),其中α=取值范围是.应用提升:(1)将矩形ABCD绕其顶点A逆时针旋转得到矩形AB′C′D′,且点C′落在CD的延长线上.①当BC=1,AB=时,旋转角的度数为.②若旋转角度为β(0°<β<180°),∠BAC=α,则α= (用含β的代数式表示).48.如图1,平面直角坐标系中,已知A(0,4),B(5,0),D(3,0),点P从点A出发,沿y轴负方向在y轴上以每秒1个单位长度的速度匀速运动,过点P作PE∥x轴交直线AD于点E.(1)设点P的运动时间为t(s),DE的单位长度为y,求y关于t的函数关系式,并写出t的取值范围;(2)当t为何值时,以EP为半径的⊙E恰好与x轴相切?并求此时⊙E的半径;(3)在点P的运动过程中,当以D,E,P三点为顶点的三角形是等腰三角形时,求此时t的值;(4)如图2,将△ABD沿直线AD翻折,得到△AB′D,连结B′O,如果∠AOE=∠BOB′,求t值.(直接写出答案,不要求解答过程).49.如图,足够大的直角三角板ABP的顶点P固定在直线OM:y=x上,且点P的横坐标为,直角三角板的边AP、BP分别与y轴、x轴交于C、D两点,在图1中直角三角板的边AP与y轴垂直.(1)将图1中的直角三角板绕顶点P逆时针旋转30°,如图2,则PC= ,PD= ;若CD交OP于点E,求△PED的面积;(2)将(1)问中的三角板继续绕顶点P逆时针旋转,若PA交直线OD于点G,当△PGD与△OCD相似时,求OD的长.50.已知:点E为AB边上的一个动点.(1)如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC,连结AD.试判断AD与BC的位置关系,并说明理由;(2)如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC,∠CDE=∠CAB连结AD.试判断AD与BC的位置关系,并说明理由;(3)如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.①试说明点G一定在AD的延长线上;②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.答案详解1.1.【解答】解:(1)∵|OA ﹣2|+(OC ﹣6)2=0.∴OA=2,OC=6,∴A (0,2),C (6,0),∵四边形OABC 为矩形,∴BC=OA=2,∴B (6,2);(2)设直线AC 的解析式为y=kx+b ,把A 、C 坐标代入可得,解得,∴直线AC 的解析式为y=﹣x+2,由折叠的性质可知AC ⊥BB 1,∴可设直线BB 1的解析式为y=x+m ,把B 点坐标代入可得2=6+m ,解得m=﹣4, ∴直线BB 1的解析式为y=x ﹣4;(3)由(2)可知B 和B 1关于直线AC 对称,如图1,连接BD 交AC 于点P ,则PB=PB 1,∴PD+PB=PD+PB 1=BD ,∴此时PD+PB 1最小,由折叠的性质可知B 1C=BC=OA=2,∠AOD=∠CB 1D=90°,在△AOD 和△CB 1D 中,,∴△AOD ≌△CB 1D (AAS ),∴AD=DC ,OD=DB 1,设OD=x ,则DC=AD=6﹣x ,且OA=2,在Rt △AOD 中,由勾股定理可得AO 2+OD 2=AD 2,即(2)2+x 2=(6﹣x )2,解得x=2,∴CD=AD=6﹣2=4,在Rt △BCD 中,由勾股定理可得BD===2,综上可知存在使PB 1+PD 的值最小的点P ,PB 1+PD 的最小值为2;(4)如图2,连接PB 、PD 、BD ,当p 在点A 时|PD ﹣PB|最大,B 与B1对称,|PD ﹣PB|=|PD ﹣PB 1|,根据三角形三边关系|PD ﹣PB 1|小于或等于DB 1,故|PD ﹣PB 1|的最大值等于DB 1.∵AB 1=AB=6,AD==4,∴DB 1=2,∴在直线AC 上,存在点P 使|PD ﹣PB|的值最大,最大值为:2. 2.解答: 解:(1)正方形ABCD 的对角线AC ,BD 交于点P ,∴PA=PD ,∠PAE=∠PDF=45°,∵∠APE+∠EPD=∠DPF+∠EPD=90°,∴∠APE=∠DPF ,在△APE 和△DPF 中∴△APE ≌△DPF (ASA ),∴AE=DF ,∴DE+DF=AD ,(2)如图②,取AD 的中点M ,连接PM ,∵四边形ABCD 为∠ADC=120°的菱形,∴BD=AD ,∠DAP=30°,∠ADP=∠CDP=60°, ∴△MDP 是等边三角形,∴PM=PD ,∠PME=∠PDF=60°,∵∠PAM=30°,∴∠MPD=60°,∵∠QPN=60°,∴∠MPE=∠FPD , 在△MPE 和△FPD 中,∴△MPE ≌△FPD (ASA )∴ME=DF ,∴DE+DF=AD ,(3)如图,在整个运动变化过程中,①当点E 落在AD 上时,DE+DF=AD ,②当点E 落在AD 的延长线上时,DE+DF 逐渐增大,当点F 与点C 重合时DE+DF 最大,即AD <DE+DF ≤AD .3. (1)证明:∵AB=AC , ∴∠B=∠C , ∵△ABC ≌△DEF , ∴∠AEF=∠B ,又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE , ∴∠CEP=∠BAE , ∴△ABE ∽△ECP ;(2)解: 当AP=EP 时,则∠PAE=∠PEA , ∴∠PAE+∠BAE=∠PEA+∠CEP ,即∠CAB=∠CEA , 又∵∠C=∠C , ∴△CAE ∽△CBA , ∴CE ACAC BC= ∴226982AC CE BC ===∴97822BE =-= (3)解:设BE=x ,AP=y ∵由(1)得△ABE ∽△ECP ∴BE ABCP EC= 又∵CP=AC-AP=6-AP EC=BC-BE=8-BE ∴668BE AP BE =--即668x y x=--()2110463y x =-+∴当x=4时,y 有最小值为103∴当BE 为4时,AP 有最小值1034.解:(1)MN BC ∥AMN ABC ∴△∽△68h x ∴=34xh ∴=(2)1AMN A MN △≌△1A MN ∴△的边MN 上的高为h ,。
【名师点睛】天津市和平区2016-2017年九年级数学同步练习 相似--单元复习题及答案(WORD版)
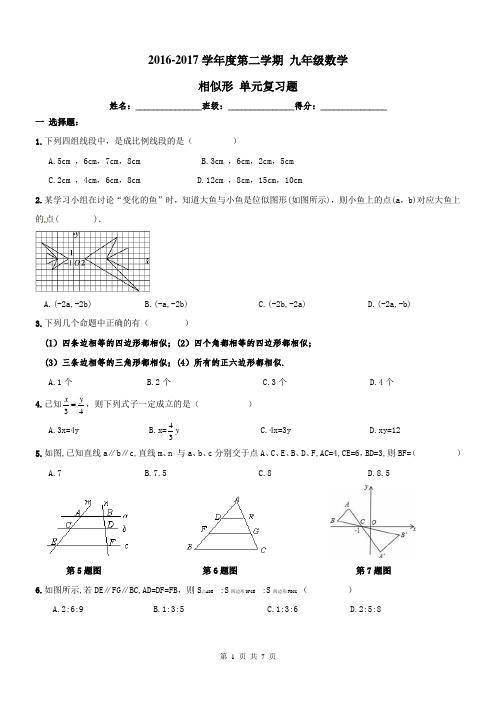
2016-2017学年度第二学期 九年级数学相似形 单元复习题姓名:_______________班级:_______________得分:_______________一 选择题:1.下列四组线段中,是成比例线段的是( )A.5cm ,6cm ,7cm ,8cmB.3cm ,6cm ,2cm ,5cmC.2cm ,4cm ,6cm ,8cmD.12cm ,8cm ,15cm ,10cm2.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),则小鱼上的点(a ,b)对应大鱼上的点( ).A.(-2a,-2b)B.(-a,-2b)C.(-2b,-2a)D.(-2a,-b)3.下列几个命题中正确的有( )(l )四条边相等的四边形都相似;(2)四个角都相等的四边形都相似;(3)三条边相等的三角形都相似;(4)所有的正六边形都相似.A.1个B.2个C.3个D.4个4.已知43y x ,则下列式子一定成立的是( ) A.3x=4y B.x=y 34 C.4x=3y D.xy=12 5.如图,已知直线a ∥b ∥c,直线m 、n 与a 、b 、c 分别交于点A 、C 、E 、B 、D 、F,AC=4,CE=6,BD=3,则BF=( )A.7B.7.5C.8D.8.5第5题图 第6题图 第7题图6.如图所示,若DE ∥FG ∥BC,AD=DF=FB ,则S △ADE :S 四边形DFGE :S 四边形FBCG ( )A.2:6:9B.1:3:5C.1:3:6D.2:5:87.如图,△ABC 中,A ,B 两个顶点在x 轴的上方,点C 的坐标是(﹣1,0).以点C 为位似中心,在x 轴的下作△ABC 的位似图形△A ′B ′C ,并把△ABC 的边长放大到原来的2倍.设点A ′的对应点A 的纵坐标是1.5,则点A 的纵坐标是( )A.3B.3C.﹣4D.48.如图,小正方形的边长均为1,关于△ABC 和△DEF 的下列说法正确的是( )A.△ABC 和△DEF 一定不相似B.△ABC 和△DEF 是位似图形C.△ABC 和△D EF 相似且相似比是1∶2;D.△ABC 和△DEF 相似且相似比是1∶4第8题图 第9题图 第10题图9.如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD 沿EF 对开后,再把矩形EFCD 沿MN 对开,依次类推,若各种开本的矩形都相似,那么AD AB 等于( ) A.0.618 B.22 C.2 D.2 10.已知矩形ABCD 中,AB=1,在BC 上取一点E ,沿AE 将△ABE 向上折叠,使B 点落在AD 上的F 点,若四边形EFDC 与矩形ABCD 相似,则AD=( ) A.215- B.215+ C.3 D 。
天津市和平区中考数学综合训练题二

天津市和平区2015-2016年九年级中考数学综合训练题 二1.下列运算:sin30°,0-2==ππ-,24.其中运算结果正确的个数为( ) A.4 B.3 C.2 D.12.顺次连接矩形ABCD 各边的中点,所得四边形必定是( )A.邻边不等的平行四边形B.矩形C.正方形D.菱形3.某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图. 依据图中信息,得出下列结论:(1)接受这次调查的家长人数为200人;(2)在扇形统计图中,“不赞同”的家长部分所对应的扇形圆心角大小为162°;(3)表示“无所谓”的家长人数为40人;(4)随机抽查一名接受调查的家长,恰好抽到“很赞同”的家长的概率是110 . 其中正确的结论个数为( )A.4B.3C.2D.14.如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AM 的长为1.2km,则M ,C 两点间的距离为( ) A.0.5km B.0.6km C.0.9km D.1.2km5.已知不等式组⎩⎨⎧<>a x x 2的解集中共有5个整数,则a 的取值范围为( ) A.7<a ≤8 B.6<a ≤7 C.7≤a <8 D.7≤a ≤86.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )B.2C.217.如图,在直角∠O 的内部有一滑动杆AB.当端点A 沿直线AO 向下滑动时,端点B 会随之自动地沿直线OB 向左滑动.如果滑动杆从图中AB 处滑动到A'B'处,那么滑动杆的中点C 所经过的路径是( )A.直线的一部分B.圆的一部分C.双曲线的一部分D.抛物线的一部分8.如图,在x 轴的上方,直角∠BOA 绕原点O 按顺时针方向旋转.若∠BOA 的两边分别与函数1y x=-、2y x =的图象交于B 、A 两点,则∠OAB 大小的变化趋势为( )A.逐渐变小B.逐渐变大C.时大时小D.保持不变9.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB ,BC ,CA ,OA ,OB ,OC 组成。
天津市和平区2015-2016年九年级中考数学综合训练题 一

天津市和平区2015-2016年九年级中考数学综合训练题 一1.已知三角形两边的长是3和4,第三边的长是方程035122=+-x x 的根,则该三角形的周长是( )A.14B.12C.12或14D.以上都不对2.在四边形ABCD 中,∠A=∠B=∠C ,点E 在边AB 上,∠AED=60°,则一定有( )A.∠ADE=20°B.∠ADE=30°C.∠ADE= 1 2∠ADCD.∠ADE= 1 3∠ADC 3.如图,□ABCD 中,点E 是边A D 的中点,EC 交对角线BD 于点F,则EF:FC 等于( )A.3:2B.3:1C.1:1D.1:24.如图,矩形ABCD 中,AB=8,BC=4,点E 在边AB 上,点F 在边CD 上,点G 、H 在对角线AC 上.若四边形EGFH 是菱形,则AE 的长( ) A.2 5 B.3 5 C.5 D.65.若一元二次方程x 2- 2x - m = 0无实数根,则一次函数y = (m+1)x + m - 1的图像不经过第( )象限。
A .四B .三C .二D .一 6.如图,点O 是矩形ABCD 的中心,E 是AB 上的点,折叠后,点B 恰好与点O 重合,若BC=3。
则折痕CE 的长为( ) A.32 B.323 C.3 D.67.如图为二次函数y=ax 2 +bx+c (a ≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确的个数为( )A .1B .2C .3D .48.若实数a 、b 、c 满足a+b+c=0,且a <b <c,则函数y=cx+a 的图象可能是( )9.如图,一次函数y 1=x 与二次函数y 2=ax 2+bx +c 图象相交于P 、Q 两点,则函数y=ax 2+(b-1)x+c 的图象可能是( )10.与4+5最接近的整数是11.不等式组⎪⎩⎪⎨⎧<->+x x x 4103160103的最小整数解是 . 12.已知12-=x ,则分式⎪⎭⎫ ⎝⎛-+-÷-+2824222x x x x x x = . 13.如图,点A 、B 、C 在半径为9的⊙O 上,AB ⌒的长为π2,则∠ACB 的大小是 .14.如图,在□ABCD 中,AD=2,AB=4,∠A=300,以点A 为圆心,AD 的长为半径画弧交AB 于点E,连接CE,则阴影部分的面积是_________(结果保留π).15.如图,正方形ABCD 的边长为4,E 为BC 上的一点,BE=1,F 为AB 上的一点,AF=2,P 为AC 上一个动点,则PF+PE 的最小值为 .16.如图,E 是边长为1的正方形ABCD 的对角线BD 上的一点,且BE=BA,P 是CE 上任意一点,PQ ⊥BC 于点Q,PR ⊥BE 于点R.则(1)DE= ;(2)PQ +PR= .17.已知实数a 、b 、c 满足a +b=ab =c ,有下列结论:①若c ≠0,则 1 a + 1 b=1;②若a=3,则b +c=9; ③若a=b=c ,则abc=0;④若a 、b 、c 中只有两个数相等,则a+b+c=8.18.如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(3=1.7).19.A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.(1)求两次传球后,球恰在B手中的概率;(2)求三次传球后,球恰在A手中的概率.20.某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图。
天津市和平区2015-2016年中考数学综合训练题(四)

天津市和平区2015-2016年九年级中考数学综合训练题 四1.如图,在△ABC 中,∠C=90°,AC=2,点D 在BC 上,∠ADC=2∠B,AD=5,则BC 的长为( ) A.3-1 B.3+1 C.5-1 D.5+12.过矩形ABCD 的对角线AC 的中点O 作EF ⊥AC ,交BC 边于点E ,交AD 边于点F ,分别连接AE 、CF ,若AB =3,∠DCF =300,则EF 的长为( )A.2B.3C.23D.3 3.一次函数3-+-=a x y (a 为常数)与反比例函数xy 4-=的图象交于A 、B 两点,当A 、B 两点关于原点对称时a 的值是( )A. 0B. -3C. 3D. 4 4.分解因式:=+-121232x x .5.若b a <+<26,且a 、b 是两个连续的整数,则=ba .6.在平面直角坐标系中,点A 、B 的坐标分别是(m,3)、(3m-1,3).若线段AB 与直线y=2x+1相交,则m 的取值范围为__________.7.如图,线段AB 是⊙O 的直径,点C 在圆上,∠AOC=80°,点P 是线段AB 延长线上的一动点,连接PC ,则∠APC 的度数是 度(写出一个即可).8.在□ABCD 中,点O 是对角线AC 、BD 的交点,AC 垂直于BC,且AB=10cm,AD=8cm ,则OB=________cm . 9.如图,在△ABC 中,∠BAC=460,E 为BC 延长线上一点,∠ABC 与∠ACE 的平分线相交于点D,则∠CAD 的度数为10.如图,从一个建筑物的A 处测得对面楼BC 的顶部B 的仰角为32°,底部C 的俯角为45°,观测点与楼的水平距离AD 为31cm ,则楼BC 的高度约为_______m(结果取整数)。
(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)11.如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△A n A n+1B n均为等边三角形,点A1、A2、A3…A n+1在x轴的正半轴上依次排列,点B1、B2、B3…B n在直线OD上依次排列,那么点B n的坐标为 .12.4个数a,b,c,d排列成,我们称之为二阶行列式.规定它的运算法则为:=ad﹣bc.若=12,则x= .13.一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y. (1)小红摸出标有数字3的小球的概率是;(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;(3)若规定:点P (x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.14.为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2013年市政府共投资3亿元人民币建设了廉租房12万平方米,2015年投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(1)求每年市政府投资的增长率;(2)若这两年内的建设成本不变,问2015年建设了多少万平方米廉租房?15.某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:(1)已知y 与x 满足一次函数关系,根据上表,求出y 与x 之间的关系式(不写出自变量x 的取值范围); (2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?(3)设该商店每天销售这种商品所获利润为w(元),求出w 与x 之间的关系式,并求出每件商品销售价定为多少元时利润最大?16.如图,在平面坐标系中,∠AOB=900,AB ∥x 轴,OB=2,双曲线y=xk经过点B.将△AOB 绕点B 逆时针旋转,使点O 的对应点D 落在X 轴的正半轴上.若AB 的对应线段CB 恰好经过点O. (1)点B 的坐标和双曲线的解析式。
天津市和平区2015-2016学年度第一学期九年级数学期中(完整资料).doc

【最新整理,下载后即可编辑】和平区2015-2016学年度第一学期九年级数学学科期中质量调查试卷本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分.第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第7页.试卷满分120分.考试时间100分钟.祝你考试顺利!第Ⅰ卷注意事项:1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点.2.本卷共12题,共36分.一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列图形中,是中心对称图形但不是轴对称图形的是(A)(B)(C)(D)2.方程23214x x+=-的两个根的和为(A)43(B)13(C)23-(D)43-3.下列方程有实数根的是(A)210x x-+=(B)210x x++=(C)(1)(2)0x x-+=(D)2(1)10x-+=4.一元二次方程210x x--=的两个实数根中较大的根是(A)1+(B(C(D5.把抛物线2y x=向上平移3个单位,再向右平移1个单位,则平移后抛物线的解析式为(A)2(3)1y x=++(B)2(3)1y x=+-(C)2(1)3y x=-+(D)2(1)3y x=++6.如图,⊙O的直径AB为10cm,弦AC为6cm,则BC=(A)6cm(B )8cm (C )10cm (D)7.如图,⊙O 中,AB AC =,C ∠=75°,则A ∠=(A )15° (B )20° (C )25° (D )30°8.如图,已知点E 是O 上的点,B 、C 分别是劣弧AD 的三等分点,BOC ∠=46°,则AED ∠=(A )46°(B )68° (C )69° (D )70°9.已知抛物线2y ax bx c =++(0a ≠)与x 轴交于A ,B 两点,若点A 的坐标为(-2,0),抛物线的对称轴为直线2x =,则线段AB 的长为 (A )2 (B )4 (C )6 (D )810.如图,在Rt △AOB 中,O ∠=90°,ABO ∠=30°,以点A 为旋转中心,把△ABO顺时针旋转得△ACD ,当旋转后满足BC ∥OA 时,旋转角的大小为(A )75° (B )60° (C )45° (D )30° 11.二次函数2y ax bx=+的图象如图所示,若一元二次方程20ax bx m ++=有实数根,则m 的取值范围是 (A )m ≤3 (B )m ≥ 3 (C )m ≤-3 (D )m ≥-312.如果关于x 的一元二次方程20ax bx c ++=有两个实数根,且BCD AO其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”. 下列说法: ①方程2280xx --=是倍根方程;②若(2)()0x mx n -+=是倍根方程,则m n =-或14m n =-;③若方程2axbx c ++=是倍根方程,且相异两点(2)M t s +,,N(4t -,s )都在抛物线2y ax bx c =++上,则方程20ax bx c ++=的一个根为2. 其中,正确说法的个数是(A )0 (B )1 (C )2 (D )3第Ⅱ卷注意事项:1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用2B 铅笔).2.本卷共13题,共84分.二、填空题(本大题共6小题,每小题3分,共18分) 13.时钟的时针在不停地旋转,从上午6时到上午9时,时针旋转的旋转角是 度.14.请写出一个开口向上,并且与y 轴交于点(0,1)的抛物线的解析式,y =__________.15.参加一次足球联赛的每两队之间都进行两次比赛,共要比赛30场,共有 个队参加比赛.16.如图,⊙A 中,弦6DE =,BAC EAD ∠+∠=180°,则点A 到弦BC的距离等于 .17.已知抛物线2(2)9y x k x =-++的顶点在坐标轴上,则k 的值为 .18.在边长为2的菱形ABCD 中,A ∠=60°,M 是AD 边的中点,若线段MA 绕点M 旋转得线段MA ',(Ⅰ)如图①,当线段MA 绕点M 逆时针旋转60°时.线段AA '的长= .(Ⅱ)如图②,连接A C',则A C'长度的最小值是 .三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程) 19.(本小题8分)(Ⅰ)如图①,画出△ABC 绕点O 逆时针旋转90°后的△111A B C ;(Ⅱ)如图②,画出△ABC 绕点O 旋转180°后的△111A B C .图① 图②A 'ABCD M'ABCDM图① 图②20.(本小题8分)已知关于x的一元二次方程220x ax+-=,(Ⅰ)若该方程的一个根为1,求a的值及该方程的另一根;(Ⅱ)求证:不论a取何实数,该方程都有两个不相等的实数根.21.(本小题10分)已知,AB是⊙O的直径,弦CD AB⊥于点E,(Ⅰ)如图①,若16CD=,4BE=,求⊙O的直径;(Ⅱ)如图②,连接DO并延长交⊙O于点M,连接MB,若M D∠=∠22.(本小题10分)图①图②要对一块长60 m、宽40 m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L,M,N为三块绿地,其余为硬化路面,L,M,N三块绿地周围的硬化路面宽都相等,并使三块绿地面积的和为矩形,M,N三块绿地周围的硬化路面的宽.23.(本小题10分)某果园有100棵枇杷树,每棵平均产量为60千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少.根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.5千克.增种多少棵枇杷树,投产后可以使果园枇杷的总产量最多?最多总产量是多少千克?24.(本小题10分)已知,AB是⊙O的直径,C、D是⊙O上的两点,且AC CD,连接BC ,BD .(Ⅰ)如图①,若CBD ∠=20°,求A ∠的大小;(Ⅱ)如图②,连接OC ,若OC BD =,求证四边形OCDB 是菱形;(Ⅲ)如图③,4AB =,1AC =,求BD 的长(直接写出结果即可).25.(本小题10分)在平面直角坐标系xOy中,抛物线22y x mx n =++经过点A(0,2-),B (3,4). (Ⅰ)求抛物线的解析式、对称轴和顶点;(Ⅱ)设点B 关于原点的对称点为C ,记抛物线在A ,B 之BBB图① 图② 图③间的部分为图象G(包含A,B两点).①点D是抛物线对称轴上一动点,若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围;②点E是图象G上一动点,动点E与点B,点C构成无数个三角形,在这些三角形中存在一个面积最大的三角形,求出这个三角形的面积,并求出此时点E的坐标.和平区2015-2016学年度第一学期九年级 数学学科期中质量调查试卷参考答案一、选择题(本大题共12小题,每小题3分,共36分)1.A 2.D 3.C 4.B 5.C 6.B 7.D 8.C 9.D 10.B 11.A 12.C 二、填空题(本大题共6小题,每小题3分,共18分)13.9014.21x +(答案不惟一.设抛物线的解析式为2y ax bx c=++(0a ≠),所写解析式满足a >0,1c =即可). 15.6 16.3 17.4,8-,2-18.(Ⅰ)11三、解答题(本大题共7小题,共66分) 19.(本小题8分)解: (Ⅰ) (Ⅱ)…………………………………8分 20.(本小题8分)解:(Ⅰ)将1x =代入方程220x ax +-=, 得120a +-=.…………………………………1分解得1a=.…………………………………2分方程为220x x+-=.…………………………………3分(1)(2)0x x-+=,10x-=或20x+=.∴11x=,22x=-.∴该方程另一根为-2.…………………………………5分(Ⅱ)证明:2241(2)80a a∆=-⨯⨯-=+>,…………………………………7分∴不论a取何实数,该方程都有两个不相等的实数根.………………………………8分21.(本小题10分)解:(Ⅰ)连接OD,…………………………………1分∵直径AB CD⊥,16CD=,∴==.……………8CE DE……………………2分设⊙O的半径为x,∵4BE=,∴4=-.OE x在Rt△OED中,222=+,OD OE DE∴222=-+.………………x x(4)8…………………3分解得x=.………………10…………………4分∴⊙O的直径是20. …………………………………5分(Ⅱ)∵12M BOD ∠=∠,M D ∠=∠, …………………………………7分∴12D BOD ∠=∠.…………………………………8分 ∵CD AB ⊥, ∴D BOD ∠+∠=90°…………………………………9分 ∴D ∠=30°.………………………………10分 22.(本小题10分) 解:设L,M,N三块绿地周围的硬化路面的宽为x m ,……………………1分根据题意,得1(604)2(402)6040x x --=⨯⨯. (5)分整理,得2351500x x -+=. 解这个方程,得12530x x ==,. ………………………………8分230x =不符合题意,舍去.只取5x =.答:L,M,N三块绿地周围的硬化路面宽为 5m . ……………………………10分 23.(本小题10分) 解:设增种x棵枇杷树,投产后果园的总产量为y千克, ………………………1分 根据题意,得(100)(600.5)y x x =+-. ………………………………4分 即20.5106000y x x =-++.………………………………6分其中0≤x ≤ 120, 将上式化为21(10)60502y x =--+.………………………………8分 因为12a =-<0,所以当10x =时,y 最大,最大值为6050.所以增种10棵枇杷树,投产后可以使果园枇杷的总产量最多,最多总产量是6050千克.………………………………10分 24.(本小题10分) 解:(Ⅰ)∵AC CD =, ∴AC CD =.………………………………1分 ∴ABC CBD ∠=∠. ∵CBD ∠=20°, ∴∠=20°.…………ABC……………………2分∵AB是⊙O的直径,∴∠=90°.…………ACB……………………3分∴∠=70°.…………A……………………4分(Ⅱ)∵OB OC=,∴∠=∠.……………OCB ABC…………………5分由(Ⅰ)知,ABC CBD∠=∠.∴OCB CBD∠=∠.∴OC∥BD.………………………………6分∵OC BD =,∴四边形OCDB 是平行四边形. ………………………………7分 ∵OC OB =,∴□OCDB 是菱形. ………………………………8分(Ⅲ)72 ………………………………10分25.(本小题10分)解:(Ⅰ)∵抛物线22y x mx n =++经过点A (0,2-),B (3,4), ∴将两点坐标代入得2,183 4.n m n =-⎧⎨++=⎩ 解这个方程组得,4,2.m n =-⎧⎨=-⎩∴抛物线的解析式为2242y x x =-- ………………………………3分22(1)4x =--.对称轴为直线1x =. ………………………………4分顶点为(1,-4). ………………………………5分(Ⅱ)①如图,由题意可知C(―3,―4). ………………………………6分 由2242y x x =--的最小值为-4,可知D 点纵坐标的最小值为-4.最大值为直线BC 与对称轴交点的纵坐标.易得直线BC 的解析式为43y x =. 当1x =时,43y =. 综上知-4≤t ≤43. ………………………………8分②如图,过点E 作x 轴的垂线交BC 与点F ,EF 把△EBC 分成两个△BEF 和△CEF .设这两个三角形的EF 边上的高分别为1h 、2h . 设E 点坐标为(x ,2242x x --),则F 点的坐标为(x ,43x ). 24(242)3EF x x x =--- 216223x x =-++. 121122EBC BEF CEF S S S EF h EF h ∆∆∆=+=+121()2EF h h =+ []22116(22)3(3)616623x x x x =-++--=-++(0≤x <3) ∵-6<0,∴当1642(6)3x =-=⨯-时, △EBC 的面积最大,最大面积为24(6)616504(6)3⨯-⨯-=⨯-. 此时点E 的坐标为(43,349-). ………………………………10分EF。
天津市和平区2015-2016学年度九年级数学一模试卷及答案

天津市和平区2015-2016学年度九年级数学一模试卷及答案温馨提示:本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分.第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第7页.试卷满分120分.考试时间100分钟.祝你考试顺利!第Ⅰ卷注意事项:1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点.2.本卷共12题,共36分.一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算3(2) 的结果等于(A)-8 (B)8(C)- 6 (D)62.tan30°的值等于(A)12(B(C(D3.下列图形中,不是中心对称图形的是(A)(B)(C)九年级数学试卷第1页(共7页)九年级数学试卷第2页(共7页)4.将1 339 000 000用科学记数法表示为(A)81.33910⨯(B)91.33910⨯(C)101.33910⨯(D)813.3910⨯5.右图是一个由5个相同的正方体组成的立体图形,它的俯视图是6.估计312-的值(A)在4和5之间(B)在3和4之间(C)在2和3之间(D)在1和2之间7.计算222xx x---的结果是(A)0 (B)1 (C)- 1 (D)x8.当0>x时,函数xy5-=的图象在(A)第一象限(B)第二象限(C)第三象限(D)第四象限(A)(B)九年级数学试卷第1页(共7页)九年级数学试卷第2页(共7页)9.如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图.则下列说法正确的是(A)甲比乙的成绩稳定(B)乙比甲的成绩稳定(C)甲、乙两人的成绩一样稳定(D)无法确定谁的成绩更稳定10.一个菱形绕它的两条对角线的交点旋转,使它和原来的菱形重合,那么旋转的角度至少是(A)360°(B)270°(C)180°(D)90°11.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地.已知甲、乙两地相距180 千米,货车的速度为60 千米/时,小汽车的速度为90 千米/时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是()()()()▲▲▲▲▲▲▲▲▲▲▲九年级数学试卷第1页(共7页)九年级数学试卷第2页(共7页)九年级数学试卷 第1页(共7页)九年级数学试卷 第2页(共7页)12.如图是抛物线21y axbx c=++(0a ≠)的一部分,抛物线的顶点为A (1,3),与x 轴的一个交点为B (4,0),直线2ymx n=+(0m ≠)与抛物线交于A ,B 两点,下列结论: ①20a b +=; ②abc >0; ③方程23axbx c ++=有两个相等的实数根;④抛物线与x 轴的另一个交点是(-1,0); ⑤当1<x <4时,有2y <1y .其中,正确结论的个数是(A )4 (B )3 (C )2 (D )1第Ⅱ卷注意事项:1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用2B 铅笔).2.本卷共13题,共84分.二、填空题(本大题共6小题,每小题3分,共18分)13.计算(1)(1)x x +-的结果等于 . 14.一次函数32y x =-与y轴的交点坐标为 .15.把一个骰子掷两次,观察向上一面的点数,它们的点数都是4的概率是 .16.如图,△ABC内接于⊙O,2AO=,BC=则BAC∠的度数为_______ .17.如图,四边形ABCD中,DAB∠=90°,AD CD=,BCD CDA∠=∠=120°,则ABD BDC S S∆∆=.AB CD九年级数学试卷第1页(共7页)九年级数学试卷第2页(共7页)九年级数学试卷 第5页(共7页) 九年级数学试卷 第6页(共7页)18.定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.(Ⅰ)如图①,已知A ,B ,C 在格点(小正方形的顶点)上,请在图①中画出一个以格点为顶点,AB ,BC 为边的对等四边形ABCD ;(Ⅱ)如图②,在Rt △PBC 中,PCB ∠=90°,11BC =,12tan 5PBC ∠=,点A 在BP 边上,且13AB =.点D 在PC边上,且四边形ABCD 为对等四边形,则CD 的长为 .三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程) 19.(本小题8分)解不等式组2662423x xx x-<-⎧⎨+>+⎩. 20.(本小题8分)物理兴趣小组20位同学在实验操作中的得分情况如下表:(Ⅰ)将此次操作得分按人数制成如图所示的扇形统计图.扇形 ①的圆心角= ;(Ⅱ)这组数据的众数是 ,中位数是 ;图① 图②A BC九年级数学试卷 第5页(共7页)九年级数学试卷 第6页(共7页)(Ⅲ)求这组数据的平均数.21.(本小题10分)如图,AB 是半圆O 的直径,CD ⊥AB 于点C ,交半圆O 于点E ,DF 切半圆O 于点F ,B ∠=45°.(Ⅰ)求D ∠的大小;(Ⅱ)若OC CE =,22BF =DE 的长.22.(本小题10分)已知B 港口位于A 观测点的东北方向,且其到A 观测点正北方向的距离BD 的长为16千米,一艘货轮从B 港口以48千米/时的速度沿如图所示的BC 方向航行,15分后到达C 处,现测得C 处位于A 观测点北偏东75°方向,求此时货轮与A 观测点之间的距离AC 的长(精确到0.1千米).(参考数据:2 1.41≈,3 1.73,5 2.24,6 2.45)23.(本小题10分)用总长为60m 的篱笆围成矩形场地.A BC D EFOB CDA(Ⅰ)根据题意,填写下表:矩形一边长/ m5 10 15 20矩形面积/㎡12 5(Ⅱ)设矩形一边长为l m,矩形面积为S ㎡,当l是多少时,矩形场地的面积S最大?并求出矩形场地的最大面积;(Ⅲ)当矩形的长为m,宽为m时,矩形场地的面积为216㎡.24.(本小题10分)在平面直角坐标系中,O是坐标原点,□ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,23),点B在x轴的正半轴上,点E为线段AD的中点.(Ⅰ)如图①,求DAO∠的大小及线段DE的长;(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF'是△OEF关于直线OE对称的图形,记直线EF'与射线DC的交点为H,△EHG的面积为33.①如图②,当点G在点H的左侧时,求GH,DG的长;②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).图①图②备用图九年级数学试卷第5页(共7页)九年级数学试卷第6页(共7页)25.(本小题10分)已知直线l:y=x,抛物线C:y=x2+bx+c.(Ⅰ)当b=4,c=1时,求直线l与抛物线C的交点坐标;(Ⅱ)当b=3,c=-4时,将直线l绕原点逆时针旋转15°后与抛物线C交于A,B两点(A点在B点的左侧),求A,B两点的坐标;(Ⅲ)若将(Ⅱ)中的条件“c=-4”去掉,其它条件不变,且2≤AB≤4,求c的取值范围.九年级数学试卷第5页(共7页)九年级数学试卷第6页(共7页)九年级数学答案 第1页(共6页)九年级数学答案 第2页(共6页)和平区2015-2016学年度第二学期九年级第一次质量调查数学学科试卷参考答案一、选择题(本大题共12小题,每小题3分,共36分)1.A 2.D 3.A 4.B 5.D 6.B7.C 8.D 9.A 10.C 11.C 12.B二、填空题(本大题共6小题,每小题3分,共18分)13.21x - 14.(0,-2)15.136 16.60°17.43 18.(Ⅰ)如图(答案不惟一):(Ⅱ)13,1212三、解答题(本大题共7小题,共66分) 19.(本小题8分)解:∵2662423x xx x-<-⎧⎨+>+⎩①②解不等式①,得3x <. …………………………3分解不等式②,得13x >. …………………………6分∴原不等式组的解集为133x <<. A BCAB C ABC DDD九年级数学答案 第1页(共6页)九年级数学答案 第2页(共6页)…………………………8分 20.(本小题8分)解:(Ⅰ)54°. …………………………2分(Ⅱ)9,9;…………………………6分(Ⅲ)这组数据的平均数是51089483720x ⨯+⨯+⨯+⨯==8.75.∴ 这组数据的平均数是8.75. …………………………8分 21.(本小题10分)解:(Ⅰ)∵DF 切半圆O 于点F , ∴DF OF ⊥. …………………………1分∴DFO ∠=90°.∵OB OF =,∴OFB B ∠=∠=45°. …………………………2分 ∴180FOB OFB B∠=-∠-∠o =180°-45°-45°=90°. ∴DFO FOB ∠=∠. …………………………3分 ∴DF ∥AB .…………………………4分 ∴D DCO ∠+∠=180°. ∵CD AB ⊥, ∴DCO ∠=90°.∴D ∠=90°. …………………………5分 (Ⅱ)连接OE , …………………………6分在Rt△OBF中,sin OFBBF=.∴sin sin452OF BF B====o.…………………………7分在Rt△ECO中,∵OC CE=,设OC CE x==,∵2OE OF==,∴2222x x+=,x∴EC=.…………………………8分∵D DFO DCO∠=∠=∠=90°,∴四边形DCOF是矩形.∴2CD OF==.…………………………9分∴2DE CD EC=-=………………………10分22.(本小题10分)解:过点B作BH AC⊥,交AC的延长线于点H,…………………………1分∵BD AD⊥,DAB∠=45°,∴DBA∠=45°.∴DAB DBA∠=∠.∴16AD BD==.…………………………2分∴AB==…………………………3分∵DAC∠=75°,DAB∠=45°,∴BAH∠=30°.在Rt△BAH中,1122BH AB==⨯BCDAH九年级数学答案第1页(共6页)九年级数学答案第2页(共6页)九年级数学答案 第1页(共6页)九年级数学答案 第2页(共6页)…………………………4分由cos AH BAH AB ∠=,得cos cosAH AB BAH =⋅∠=30°==…………………………6分在Rt △BCH 中,15481260BC =⨯=.∴4CH =.…………………………8分∴4AC AH CH =-=…………………………9分≈8×2.45-4=19.60-4≈15.6.答:AC 的长约为15.6千米.………………………10分23.(本小题10分)解:(Ⅰ)200,225,200; …………………………3分(Ⅱ)矩形场地的周长是60m ,一边长为l m ,则另一边长为60()2l -m .…4分 矩形场地的面积(30)S l l =-, 即230S ll=-+(0<l <30).…………………………6分当301522(1)b l a =-=-=⨯-时, S有最大值2243022544(1)ac b a --==⨯-.∴当l 是15m 时,矩形场地的面积S 最大,最大面积是225㎡. ………………8分(Ⅲ)18 12.………………………10分 24.(本小题10分)解:(Ⅰ)由点A 的坐标为(-2,0),点D 的坐标为(0,九年级数学答案 第1页(共6页) 九年级数学答案 第2页(共6页)得2AO =,DO = …………………………1分在Rt △AOD中,tan DO DAO AO ∠=== ∴DAO ∠=60°. …………………………2分∴ADO ∠=30°. ∴24AD AO ==. ∵E 是AD 的中点,∴2DE =. …………………………3分(Ⅱ)①过点E 作EM ⊥直线CD 于点M , …………………………4分∵四边形ABCD 是平行四边形, ∴CD ∥AB ,∴60EDM DAB ∠=∠=︒.∴sin 602EM DE =⋅︒==…………………………5分∵1122EHGSGH EM GH ∆=⋅⋅=⋅∴6GH =. …………………………6分九年级数学答案 第5页(共6页)九年级数学答案 第6页(共6页)∵CD ∥AB , ∴DGE OFE ∠=∠.∵△OEF '是△OEF 关于直线OE 对称的图形, ∴△OEF '≌△OEF . ∴OFE OF E '∠=∠. ∴DGE OF E '∠=∠.在Rt △AOD 中,∵E 是AD 的中点, ∴12OE AD AE ==. 又EAO ∠=60°,∴△EAO 是等边三角形, ∴EOA ∠=60°,AEO ∠=60°. ∵△OEF '≌△OEF , ∴EOF EOA '∠=∠=60°, ∴EOF AEO '∠=∠,∴AD ∥OF '. ∴OF E DEH '∠=∠, ∴DEH DGE ∠=∠. 又HDE EDG ∠=∠, ∴△DHE ∽△DEG .∴DE DHDG DE=即2DE DG DH=⋅.设DG x =,则6DH x =+. 由2DEDG DH=⋅得4(6)x x =+.解得13x =-+23x=-∴3DG =-…………………………8分②(5-0)………………………10分 25.(本小题10分)九年级数学答案 第5页(共6页)九年级数学答案 第6页(共6页)解:(Ⅰ)当b =4,c =1时,抛物线C 为y=x 2+4x+1,由方程x 2+4x +1=x , 得x 2+3x +1=0的两根为:x 1, x 2, 所以直线l 与抛物线C 的交点坐标为:(),). …………………………3分(Ⅱ)直线l 绕原点逆时针旋转15°后得到直线l 1,设l 1在第一象限内的一点为M (m ,n ),由已知得∠MOx =60°.∴n.设直线l 1的解析式为y =kx ,∴, k∴直线l 1的解析式为. …………………………4分当bc =-4时,抛物线C 为y = x 2-4,由方程x 2-, 得x 2=4的两个根为x 1=2, x 2=-2. …………………………5分∴A ,B 两点的坐标为(-2,-,(2,……………………6分(Ⅲ)当b =时,抛物线C 为y = x 2+c , 由方程x 2+c, 得x 2=-c 的两个根为x 1x 2=,…………………………7分∴A ,B 两点的坐标为A(,B,).九年级数学答案 第5页(共6页) 九年级数学答案 第6页(共6页)由勾股定理,得222((AB⎤⎤=+⎦⎦412c c =--16c=-.…………………………8分∵2≤AB ≤4, ∴4≤AB 2≤16. 即4≤-16c ≤16,∴-1≤c ≤14-. ………………………10分。
天津市和平区中考数学专题练习 解直角三角形50题-人教版初中九年级全册数学试题

解直角三角形50题一、选择题:1.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底端G为BC的中点,则矮建筑物的高CD为( )A.20米B.10 米C.15 米D.5 米2.若一个三角形三个内角度数的比为1:2:3,那么这个三角形最小角的正切值为()A. B. C. D.3.如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧AmB上的一点,则cos∠APB的值是()° B.1 C.4.如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A.sinA的值越大,梯子越陡B.cosA的值越大,梯子越陡∠A的函数值无关5.当锐角α>30°时,则cosα的值是()6.在Rt△ABC中,∠C=90°,∠B=60°,那么sinA+cosB的值为()A.1B.C.D.7.如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为()m C.(2﹣2)m D.(2﹣2)m8.如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里 B.(10-10)海里 C.10海里 D.(10-10)海里9.在Rt△ABC中,∠C=90°,若tanA=,则sinA=()A. B. C. D.10.一座楼梯的示意图如图,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要()A.米2B.米2C.(4+)米2D.(4+4tanθ)米211.已知∠A为锐角,且sinA≤0.5,则()°≤A≤60°°≤A <90°°<A ≤30°°≤A≤90°12.如图,已知∠α的一边在x轴上,另一边经过点A(2,4),顶点为(﹣1,0),则sinα的值是()B. C.0.6 D.0.813.如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)()B.41.6814.2sin60°的值等于()A.1B.C.D.15.在Rt△ABC中,∠ABC=90°、tanA=,则sinA的值为()A. B. C. D.16.已知tanα=,则锐角α的取值X围是()°<α<30°°<α<45°°<α<60°°<α<90°17.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端O点30米的B处,测得树顶4的仰角∠ABO为α,则树OA的高度为( )A.ααα米18.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为()A. B. C. D.19.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°°的方向,则船C离海岸线l的距离(即CD的长)为()A.kmB.kmC.kmD.km20.如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC长为()米.A. B.° D.二、填空题:21.在Rt△ABC中,∠C=90°,AB=4,BC=2,则sin=.22.如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为m(结果保留根号)23.如图所示,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为米.(保留根号)24.如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是海里(结果保留根号).25.如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD 为1m,则旗杆高BC为m(结果保留根号).26.如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为米.27.如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=5,BC=6,则sinC=.28.某同学沿坡比为1:的斜坡前进了90米,那么他上升的高度是米.29.如图,为测量某物体AB的高度,在在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为米.30.同角三角函数的基本关系为:(sinα)2+(cosα)2=1, =tanα.利用同角三角函数的基本关系求解下题:已知tanα=2,则=.31.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为32.如图,将三角板的直角顶点放置在直线AB上的点O处.使斜边CD∥AB,则∠a的余弦值为__________.33.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosC=.34. (1)如图1,如果ɑ,β都为锐角,且tanɑ=,tanβ=,则ɑ+β=;(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ=时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON,使得∠MON=ɑ-β.此时ɑ-β=度.35.如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为.36.在△ABC中,∠C=90°,若BC=5,AB=13,则sinA=.37.如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是.38.如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF.以下结论:(1)△ABF≌△CBF;②点E到AB的距离是2;③tan∠DCF=;④△ABF的面积为12.其中一定成立的是(把所有正确结论的序号都填在横线上).39.如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为.40.如图,等腰△ABC中,AB=AC,tan∠B=,BC=30,D为BC中点,射线DE⊥△ABC绕点C顺时针旋转(点A的对应点为A′,点B的对应点为B′),射线A′B′分别交射线DA、DE于M、N.当DM=DN时,DM长为.三、解答题:41.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.42.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)43.先化解,再求值:,已知,.44.如图,某建筑物BC上有一旗杆AB,小X在与BC相距24m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B 的仰角为45°,小X的观测点与地面的距离EF为.(1)求建筑物BC的高度;(2)求旗杆AB的高度.(结果精确到.参考数据:≈1.41,sin52°≈0.79,tan52°≈1.28)45.图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到).(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)46.在△ABC中,AD是BC边上的高,∠C=45°,sinB=,AD=1.求BC的长.47.如图,小明家小区空地上有两颗笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=30°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点在一条直线上,求树EF的高度.(≈1.7,≈1.4,结果保留一位小数)48.如图,某居民小区有一栋居民楼,在该楼的前面32米处要再盖一栋30米的新楼,现需了解新楼对采光的影响,当冬季正午的阳光与水平线的夹角为37°时,求新楼的影子在居民楼上有多高?(参考数值:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)49.如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10的D处.(1)求该轮船航行的速度;(2)如果该轮船不改变航向继续航行,那么该轮船能否正好行至码头AB靠岸?请说明理由.50.在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式.(2)若α为锐角,tanα=,当AE取得最小值时,求正方形OEFG的面积.(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为:1?若能,求点P的坐标;若不能,试说明理由参考答案21.答案为:0.5.22.答案为:(5+5).23.答案为:10.24.答案为:。
天津市和平区中考数学考前集训题及答案详解

2016年中考数学考前集训 50题1.若顺次连接四边形ABCD 各边的中点所得四边形是矩形,则四边形ABCD 一定是( )A.矩形B.菱形C.对角线互相垂直的四边形D.对角线相等的四边形2.在Rt △ABC 中,∠C=90°,sinA=54,则tanB 的值为( ) A.34 B.43 C.53 D.54 3.已知点(-1,y 1),(2,y 2),(3,y 3)在反比例函数xk y 12--=的图象上.下列结论中正确的是( ) A.y 1>y 2>y 3 B.y 1>y 3>y 2 C.y 3>y 1>y 2 D.y 2>y 3>y 1 4.将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )A.45°B.60°C.75°D.90°第4题图 第5题图 第7题图 5.如图,在Rt △ABC 中,AB=AC,AD ⊥BC,垂足为D,E 、F 分别是CD 、AD 上的点,且CE=AF .如果∠AED=62°,那么∠DBF=( )A.62°B.38°C.28°D.26° 6.设0<k <2,关于x 的一次函数y=kx+2(1﹣x ),当1≤x≤2时的最大值是( )A.2k ﹣2B.k ﹣1C.kD.k+1 7.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到△DEF 的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )A.48B.96C.84D.42 8.如图,在2×2的正方形网格中有9个格点,已经取定点A 和B ,在余下的7个点中任取一点C ,使△ABC 为直角三角形的概率是( )A.21 B.52 C.73 D.749.现有A 、B 两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A 立方体朝上的数字为x 小明掷B 立方体朝上的数字为y 来确定点P (x ,y ),那么它们各掷一次所确定的点P 落在已知抛物线y=﹣x 2+4x 上的概率为( )A.181 B.121 C.91 D.61 10.如图,延长RT △ABC 斜边AB 到点D,使BD=AB,连接CD,若tan ∠BCD=31,则tanA=( ) A.23 B.1 C.31 D.32第10题图 第12题图11.对于一次函数y=kx+k ﹣1(k≠0),下列叙述正确的是( )A.当0<k <1时,函数图象经过第一、二、三象限B.当k >0时,y 随x 的增大而减小C.当k <1时,函数图象一定交于y 轴的负半轴D.函数图象一定经过点(﹣1,﹣2)12.如图,若△ABC 和△DEF 的面积分别为S 1、S 2,则( )A.S 1=21S 2B.S 1=27S 2 C.S 1=S 2 D.S 1=58S 2 13.如图,△ABC 内接于⊙O ,BC=8,⊙O 半径为5,则sinA 的值为( )A.53B.54C.43 D.34第13题图 第14题图 第15题图14.太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是cm 310,则皮球的直径是( )A.35B.15C.10D.3815.如图,将放置于平面直角坐标系中的三角板AOB 绕O 点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1,则B′点的坐标为( )A.)21,23(B.)23,23(C.)23,21(D.)23,23(16.如图,已知双曲线)0(<=k xk y 经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(﹣6,4),则△AOC 的面积为( )A.12B.9C.6D.4第16题图 第17题图 第18题图 17.如图,边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1、S 2,则S 1+S 2的值为( )A.60B.64C.68D.7218.如图,扇形AOB 的半径为1,∠AOB=90°,以AB 为直径画半圆,则图中阴影部分的面积为( )A.π41B.21-π C.21 D.2141+π 19.已知实数a,b 分别满足a 2﹣6a+4=0,b 2﹣6b+4=0,且a≠b ,则b a a b +的值是( ) A.7 B.﹣7 C.11 D.﹣1120.如图,正方形PQMN 的边PQ 在x 轴上,点M 坐标为(2,1),将正方形PQMN 沿x 轴连续翻转,则经过点(2015,2)的顶点是( )A.点PB.点QC.点MD.点N第20题图 第21题图21.函数y=x 2+bx+c 与y=x 的图象如图所示,有以下结论:①b 2﹣4c >0;②b+c+1=0;③3b+c+6=0;④当1<x <3时,x 2+(b-1)x+c <0.其中正确的个数为( )A.1B.2C.3D.422.如图,在Rt △ABC 中,∠ACB=90°,AC=BC=6cm,动点P 从点A 出发,沿AB 方向以每秒2cm 的速度向终点B 运动;同时,动点Q 从点B 出发沿BC 方向以每秒1cm 的速度向终点C 运动,将△PQC 沿BC 翻折,点P 的对应点为点P′.设Q 点运动的时间为t 秒,若四边形QP′CP 为菱形,则t 的值为( )A.2B.2C.22D.3 23.已知二次函数y=x 2+bx+c 过点(0,﹣3)和(﹣1,2m ﹣2)对于该二次函数有如下说法: ①它的图象与x 轴有两个公共点;②若存在一个正数x 0,使得当x <x 0时,函数值y 随x 的增大而减小,则m >0;若存在一个负数x 0,使得当x >x 0时,函数值y 随x 的增大而增大,则m <0;③若将它的图象向左平移3个单位后过原点,则m=﹣1;④若当x=2时的函数值与x=2012时的函数值相等,则当x=20时的函数值为﹣3.其中正确的说法的个数是( )A.1B.2C.3D.424.分解因式:xy 2﹣25x= .25.若函数⎪⎩⎪⎨⎧>≤+=)2(2)2(22x x x x y ,则当函数值y=8时,自变量x 的值是 26.如图,在△ABC 中,∠B=50°,三角形的外角∠DAC 和∠ACF 的平分线交于点E ,则∠AEC= .第26题图 第27题图 第28题图 27.如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB 的长为 . 28.如图,PA 、PB 是⊙O 的切线,Q 为弧AB 上一点,过点Q 的直线MN 与⊙O 相切,已知PA=4,则△PMN 周长= .29.双曲线y 1、y 2在第一象限的图象如图,xy 41=过y 1上的任意一点A ,作x 轴的平行线交y 2于B ,交y 轴于C ,若S △AOB =1,则y 2的解析式是 .30.如图,直线l ∥x 轴,分别与函数)0(2>=x x y 和)0(<=x xk y 的图象相交于点A 、B ,交y 轴于点C ,若AC=2BC ,则k= .第30题图 第31题图 第32题图 31.如图,在正方形ABCD 内有一折线段,其中AE ⊥EF ,EF ⊥FC ,并且AE=6,EF=8,FC=10,则正方形的边长为 .32.如图,已知点A (1,1),B (3,2),且P 为x 轴上一动点,则△ABP 周长的最小值为 . 33.如图,正方形ABCD 的边长为4,∠DAC 的平分线交DC 于点E,若点P 、Q 分别是AD 和AE 上的动点,则DQ+PQ 的最小值是 .第33题图 第34题图 第35题图 34.如图,在等边三角形ABC 中,AB=6,D 是BC 上一点,且BC=3BD ,△ABD 绕点A 旋转后得到△ACE ,则AE 的长度为 .35.如图,已知在Rt △OAC 中,O 为坐标原点,直角顶点C 在x 轴的正半轴上,反比例函数xk y =(k≠0)在第一象限的图象经过OA 的中点B,交AC 于点D,连接OD.若△OCD ∽△ACO,则直线OA 的解析式为 .36.如图1,正方形ABCD中,点P从点A出发,以每秒2厘米的速度,沿A→D→C方向运动,点Q从点B出发,以每秒1厘米的速度,沿BA向点A运动,P、Q同时出发,当点P运动到点C时,两动点停止运动,若△PAQ的面积y(cm2)与运动时间x(s)之间的函数图象为图2,若线段PQ 将正方形分成面积相等的两部分,则x的值为.37.甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:(1)港口A与小岛C之间的距离;(2)甲轮船后来的速度.38.如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.求证:(1)∠AOC=2∠ACD;(2)AC2=AB•AD.39.如图,AB 是⊙O 直径,∠DAC=∠BAC,CD ⊥AD,交AB 延长线于点P ,(1)求证:PC 是⊙O 的切线;(2)若tan ∠BAC=21,PB=2,求⊙O 半径.40.如图,已知在△ABC 中,AB=AC,以AB 为直径的⊙O 与边BC 交于点D,与边AC 交于点E,过点D 作DF ⊥AC 于F .(1)求证:DF 为⊙O 的切线;(2)若DE=25,AB=25,求AE 的长.41.如图,以△ABC 的一边AB 为直径作⊙O ,⊙O 与BC 边的交点D 恰好为BC 的中点,过点D 作⊙O 的切线交AC 边于点E .(1)求证:DE ⊥AC ;(2)连结OC 交DE 于点F ,若sin ∠ABC=43,求FCOF 的值.42.谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石,某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:收费方式月使用费/元包时上网时间/h 超时费/(元/min)A 7 25 0.6B 10 50 0.8设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为y A元,y B元.(1)当x≥50时,分别求出y A,y B与x之间的函数关系式;(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?43.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:已知该运动服的进价为每件60元,设售价为x元.(1)请用含x的式子表示:①销售该运动服每件的利润是__________元;②月销量是__________件(直接写出结果)(2)若设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?44.如图,已知AB 是⊙O 的直径,点C 为圆上一点,点D 在OC 的延长线上,连接DA,交BC 的延长线于点E,使得∠DAC=∠B .(1)求证:DA 是⊙O 切线;(2)求证:△CED ∽△ACD;(3)若OA=1,sinD=31,求AE 的长.45.如图,某处有一座信号塔AB,山坡BC 的坡度为1:3,现为了测量塔高AB,测量人员选择山坡C 处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E 处,再测得∠FEA=60°.(1)求出山坡BC 的坡角∠BCD 的大小;(2)求塔顶A 到CD 的铅直高度AD .46.如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.(1)求直线AB 的解析式;(2)当t 为何值时,△APQ 与△AOB 相似?(3)当t 为何值时,△APQ 的面积为524个平方单位?47.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A 处测得广告牌底部D 的仰角为60°.沿坡面AB 向上走到B 处测得广告牌顶部C 的仰角为45°,已知山坡AB 的坡度i=1:3,AB=10米,AE=15米.(i=1:3是指坡面的铅直高度BH 与水平宽度AH 的比)(1)求点B 距水平面AE 的高度BH ;(2)求广告牌CD 的高度.48.为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.(1)求每台电冰箱与空调的进价分别是多少?(3)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.49.已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC 的面积最大?求出此时点P的坐标;(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.50.如图,抛物线y=x 2﹣2mx ﹣3m 2(m 为常数,m >0),与x 轴相交于点A 、B ,与y 轴相交于点C , (1)用m 的代数式表示:点C 坐标为 ,AB 的长度为 ;(2)过点C 作CD ∥x 轴,交抛物线于点D,将△ACD 沿x 轴翻折得到△AEM,延长AM 交抛物线于点N. ①求ANAM的值; ②若AB=4,直线x=t 交线段AN 于点P ,交抛物线于点Q ,连接AQ 、NQ ,是否存在实数t ,使△AQN 的面积最大?如果存在,求t 的值;如果不存在,请说明理由.答案详解1.【解答】解:已知:如右图,四边形EFGH 是矩形,且E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点,求证:四边形ABCD 是对角线垂直的四边形.证明:由于E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点, 根据三角形中位线定理得:EH ∥FG ∥BD ,EF ∥AC ∥HG ; ∵四边形EFGH 是矩形,即EF ⊥FG ,∴AC ⊥BD ,故选:C .2.【解答】解:由题意,设BC=4x ,则AB=5x ,AC=22BC AB -=3x ,∴tanB=4343==x x BC AC .故选B .3.【解答】解:∵k 2≥0,∴﹣k 2≤0,﹣k 2﹣1<0,∴反比例函数xk y 12--=的图象在二、四象限,∵点(﹣1,y 1)的横坐标为﹣1<0,∴此点在第二象限,y 1>0;∵(2,y 2),(3,y 3)的横坐标3>2>0,∴两点均在第四象限y 2<0,y 3<0, ∵在第四象限内y 随x 的增大而增大,∴0>y 3>y 2,∴y 1>y 3>y 2.故选:B .4.解答】解:如图,∠1=90°﹣60°=30°,所以,∠α=45°+30°=75°.故选C .5.【解答】解:∵AB=AC ,AD ⊥BC ,∴BD=CD .又∵∠BAC=90°,∴BD=AD=CD .又∵CE=AF ,∴DF=DE .∴Rt △BDF ≌Rt △ADE (SAS ).∴∠DBF=∠DAE=90°﹣62°=28°.故选C . 6.【解答】解:原式可以化为:y=(k ﹣2)x+2,∵0<k <2,∴k ﹣2<0,则函数值随x 的增大而减小.∴当x=1时,函数值最大,最大值是:(k ﹣2)+2=k .故选:C .7.【解答】解:由平移的性质知,BE=6,DE=AB=10,∴OE=DE ﹣DO=10﹣4=6, ∴S 四边形ODFC =S 梯形ABEO =21(AB+OE )•BE=21(10+6)×6=48.故选:A . 8.【解答】解:如图,C 1,C 2,C 3,C 4均可与点A 和B 组成直角三角形.P=74,故选:D .9.【解答】解:点P 的坐标共有36种可能,其中能落在抛物线y=﹣x 2+4x 上的共有(1,3)、(2,4)、(3,3)3种可能,其概率为121363=.故选B . 10.【解答】解:过B 作BE ∥AC 交CD 于E .∵AC ⊥BC ,∴BE ⊥BC ,∠CBE=90°.∴BE ∥AC . ∵AB=BD ,∴AC=2BE .又∵tan ∠BCD=31,设BE=x ,则AC=2x ,∴tanA=2323==x x AC BC ,故选A .11.【解答】解:A 、当0<k <1时,函数图象经过第一、三、四象限,所以A 选项错误; B 、当k >0时,y 随x 的增大而增大,所以B 选项错误;C 、当k <1时,函数图象一定交于y 轴的负半轴,所以C 选项正确;D 、把x=﹣1代入y=kx+k ﹣1得y=﹣k+k ﹣1=﹣1,则函数图象一定经过点(﹣1,﹣1),所以D 选项错误.故选:C .12.【解答】解:过A 点作AG ⊥BC 于G ,过D 点作DH ⊥EF 于H .在Rt △ABG 中,AG=AB •sin40°=5sin40°,∠DEH=180°﹣140°=40°,在Rt △DHE 中,DH=DE •sin40°=8sin40°,S 1=8×5sin40°÷2=20sin40°,S 2=5×8sin40°÷2=20sin40°.则S 1=S 2.故选:C .13.【解答】解:连接BO 并延长交⊙O 于D ,连接CD ,则∠BCD=90°,∠D=∠A , ∵⊙O 半径为5,∴BD=10,∴sinA=sinD=54108==BD BC ,故选B .14.解答】解:由题意得:DC=2R ,DE=103,∠CED=60°,∴可得:DC=DEsin60°=15.故选B .15.【解答】解:已知B ′A ′=BA=1,∠A ′OB ′=∠AOB=30°,OB ′=OB=3, 做B ′C ⊥x 轴于点C ,那么∠B ′OC=60°,OC=OB ′×cos60°=23,B ′C=OB ′×sin60°=3×23=23, ∴B ′点的坐标为(23,23).故选D .16【解答】解:∵OA 的中点是D ,点A 的坐标为(﹣6,4),∴D (﹣3,2), ∵双曲线y=x k经过点D ,∴k=﹣3×2=﹣6,∴△BOC 的面积=21|k|=3. 又∵△AOB 的面积=21×6×4=12,∴△AOC 的面积=△AOB 的面积﹣△BOC 的面积=12﹣3=9.故选B . 17.【解答】解:如图,设正方形S 2的边长为x ,根据等腰直角三角形的性质知,AC=2x ,x=2CD ,∴AC=2CD ,CD=4,∴EC 2=42+42,即EC=42, ∴S 2的面积为EC 2=32,∵S 1的边长为6,S 1的面积为6×6=36,∴S 1+S 2=32+36=68.故选:C .18.【解答】解:在Rt △AOB 中,AB=22OB OA +=2,S 半圆=21π×(2AB )2=41π,S △AOB =21OB ×OA=21,S 扇形OBA =436090ππ=,故S 阴影=S 半圆+S △AOB ﹣S 扇形AOB =21.故选C . 19.【解答】解:根据题意得:a 与b 为方程x 2﹣6x+4=0的两根,∴a+b=6,ab=4, 则原式=72)(2=-+abab b a .故选A20.【解答】解:第1次将正方形PQMN 沿x 轴翻转时,经过点(2,2)的点为点N , 第2次将正方形PQMN 沿x 轴翻转时,经过点(3,2)的点为点P , 第3次将正方形PQMN 沿x 轴翻转时,经过点(4,2)的点为点Q , 第4次将正方形PQMN 沿x 轴翻转时,经过点(5,2)的点为点M ,第5次将正方形PQMN 沿x 轴翻转时,经过点(6,2)的点为点N , 而2015﹣2=503×4+1,所以经过点(2015,2)的顶点是点P .故选A .21.【解答】解:∵函数y=x 2+bx+c 与x 轴无交点,∴b 2﹣4ac <0;故①错误; 当x=1时,y=1+b+c=1,故②错误;∵当x=3时,y=9+3b+c=3,∴3b+c+6=0;③正确;∵当1<x <3时,二次函数值小于一次函数值,∴x 2+bx+c <x ,∴x 2+(b ﹣1)x+c <0.故④正确. 故选B .22.【解答】解:连接PP ′交BC 于O ,∵若四边形QPCP ′为菱形,∴PP ′⊥QC ,∴∠POQ=90°, ∵∠ACB=90°,∴PO ∥AC ,∴CBCOAB AP =, ∵设点Q 运动的时间为t 秒,∴AP=2t ,QB=t ,∴QC=6﹣t ,∴CO=3﹣2t, ∵AC=CB=6,∠ACB=90°,∴AB=62,∴623262tt -=,解得:t=2,故选:B .23.【解答】解:∵二次函数y=x 2+bx+c 过点(0,﹣3)和(﹣1,2m ﹣2)∴代入可求得c=﹣3,b=﹣2m ,∴二次函数解析式为y=x 2﹣2mx ﹣3,令y=0可得x 2﹣2mx ﹣3=0,则其判别式△=4m 2+12>0,故二次函数图象与x 轴有两个公共点,∴①正确;∴二次函数的对称轴为x=m ,且二次函数图象开口向上,∴若存在一个正数x 0,使得当x <x 0时,函数值y 随x 的增大而减小,则m >0;若存在一个负数x 0,使得当x >x 0时,函数值y 随x 的增大而增大,则m <0,∴②正确;由平移可得向左平移3个单位后其函数解析式为y=(x+3)2﹣2m (x+3)﹣3,把点(0,0)代入可得m=1,∴③不正确;由当x=2时的函数值与x=2012时的函数值相等,代入可求得m=1007,∴函数解析式为y=x 2﹣2014x ﹣3,当x=20时,代入可得y=400﹣4028﹣3≠﹣3,∴④不正确;综上可知正确的有两个,故选B . 24.【解答】解:原式=x (y+5)(y ﹣5).故答案为:x (y+5)(y ﹣5)25.【解答】解:把y=8代入函数⎪⎩⎪⎨⎧>≤+=)2(2)2(22x x x x y ,先代入上边的方程得x=6±,∵x ≤2,x=6不合题意舍去,故x=﹣6;再代入下边的方程x=4, ∵x >2,故x=4,综上,x 的值为4或﹣6.26.【解答】解:∵三角形的外角∠DAC 和∠ACF 的平分线交于点E ,∴∠EAC=21∠DAC ,∠ECA=21∠ACF ;又∵∠B=47°(已知),∠B+∠1+∠2=180°(三角形内角和定理),∴21∠DAC+21∠ACF=21(∠B+∠2)+21(∠B+∠1)=21(∠B+∠B+∠1+∠2)=2805000+=115°(外角定理),∴∠AEC=180°﹣(21∠DAC+21∠ACF )=180°﹣115°=65°;故答案为:65.27.【解答】解:作OD ⊥AB 于D ,连接OA .∵OD ⊥AB ,OA=2,∴OD=21OA=1, 在Rt △OAD 中AD=322=-OD OA ,∴AB=2AD=23.故答案为:23.28.【解答】解:∵直线PA 、PB 、MN 分别与⊙O 相切于点A 、B 、Q ,∴MA=MQ ,NQ=NB , ∴△PMN 的周长=PM+PN+MQ+NQ=PM+MA+PN+NM=PA+PB=4+4=8.故答案为:8. 29.【解答】解:∵xy 41=,过y 1上的任意一点A ,作x 轴的平行线交y 2于B ,交y 轴于C ,∴S △AOC =21×4=2,∵S △AOB =1,∴△CBO 面积为3,∴k=xy=6,∴y 2的解析式是:y 2=x 6.故答案为:y 2=x6. 30.【解答】解:设B 点坐标为(x ,y ),∵BC ∥x 轴,AC=2BC ,∴C 点坐标为(﹣2x ,y ), 故xkx =-22,解得k=﹣1.故答案是:﹣1. 31.【解答】解:解:连接AC ,∵AE 丄EF ,EF 丄FC ,∴∠E=∠F=90°, ∵∠AME=∠CMF ,∴△AEM ∽△CFM ,∴FM EM CF AE =,∵AE=6,EF=8,FC=10,∴53106==FM EM ,∴EM=3,FM=5,在Rt △AEM 中,AM=22EM AE +=35,在Rt △FCM 中,CM=5522=+FM CF , ∴AC=85,在Rt △ABC 中,AB=AC •sin45°=85×22=410,故答案为:410.32.【解答】解:做点B 关于x 轴的对称点B ′,连接AB ′,当点P 运动到AB ′与x 轴的交点时,△ABP 周长的最小值.∵A (1,1),B (3,2),′∴AB 52122=+, 又∵P 为x 轴上一动点,当求△ABP 周长的最小值时,∴AB ′=133222=+, ∴△ABP 周长的最小值为:AB+AB ′=135+.故答案为:135+.33.【解答】解:作D 关于AE 的对称点D ′,再过D ′作D ′P ′⊥AD 于P ′, ∵DD ′⊥AE ,∴∠AFD=∠AFD ′,∵AF=AF ,∠DAE=∠CAE ,∴△DAF ≌△D ′AF , ∴D ′是D 关于AE 的对称点,AD ′=AD=4,∴D ′P ′即为DQ+PQ 的最小值,∵四边形ABCD 是正方形,∴∠DAD ′=45°,∴AP ′=P ′D ′,∴在Rt △AP ′D ′中,P ′D ′2+AP ′2=AD ′2,AD ′2=16,∵AP ′=P ′D',2P ′D ′2=AD ′2,即2P ′D ′2=16,∴P ′D ′=22,即DQ+PQ 的最小值为22,故答案为:22.34.【解答】解:∵在等边三角形ABC 中,AB=6,∴BC=AB=6,∵BC=3BD ,∴BD=31BC=2,∵△ABD 绕点A 旋转后得到△ACE ,∴△ABD ≌△ACE ,∴CE=BD=2.故答案为:2.35.【解答】解:设OC=a ,∵点D 在y=x k 上,∴CD=ak , ∵△OCD ∽△ACO ,∴OCACCD OC =,∴AC=k a CD OC 32=,∴点A (a ,k a 3),∵点B 是OA 的中点,∴点B 的坐标为(2a,k a 23),∵点B 在反比例函数图象上,∴k a a k223=,∴24a =2k 2,∴a 4=4k 2,解得,a 2=2k ,∴点B 的坐标为(2a ,a ),设直线OA 的解析式为y=mx ,则m •2a=a ,解得m=2,所以,直线OA 的解析式为y=2x .故答案为:y=2x . 36.【解答】解:设正方形的边长为acm ,由题意知,点P 的运动路程为2xcm ,BQ=xcm , 当0<x ≤2a 时,y=21•AQ •AP=21(a ﹣x )•2x=﹣x 2+ax=﹣(x ﹣2a )2+42a ,则当x=2a时,y 取得最大值,最大值为42a ,由题意可知,42a =9,解得:a=6或a=﹣6(舍),当y=9时,x=2a=3,故答案为:3.37.【解答】解:(1)作BD ⊥AC 于点D ,如图所示:由题意可知:AB=30×1=30海里,∠BAC=30°,∠BCA=45°,在Rt △ABD 中,∵AB=30海里,∠BAC=30°,∴BD=15海里,AD=ABcos30°=153海里, 在Rt △BCD 中,∵BD=15海里,∠BCD=45°,∴CD=15海里,BC=152海里, ∴AC=AD+CD=153+15海里,即A 、C 间的距离为(153+15)海里.(2)∵AC=153+15(海里),轮船乙从A 到C 的时间为131515315+=+,由B 到C 的时间为3+1﹣1=3,∵BC=152海里,∴轮船甲从B 到C 的速度为653215=(海里/小时).38.【解答】证明:(1)∵CD 是⊙O 的切线,∴∠OCD=90°,即∠ACD+∠ACO=90°.① ∵OC=OA ,∴∠ACO=∠CAO ,∴∠AOC=180°﹣2∠ACO ,即∠AOC+2∠ACO=180°, 两边除以2得:21∠AOC+∠ACO=90°.② 由①,②,得:∠ACD ﹣21∠AOC=0,即∠AOC=2∠ACD ; (2)如图,连接BC .∵AB 是直径,∴∠ACB=90°.在Rt △ACD 与Rt △ABC 中,∵∠AOC=2∠B ,∴∠B=∠ACD ,∴Rt △ACD ∽Rt △ABC ,∴ACAD AB AC =,即AC 2=AB •AD .39.【解答】(1)证明:∵OA=OC ,∴∠OAC=∠OCA ,又∠DAC=∠BAC ,∴∠DAC=∠OCA ,∴OC ∥AD ,又CD ⊥AD ,∴∠OCP=90°,∴PC 是⊙O 的切线; (2)解:如图,连接BC ,∵PC 是⊙O 的切线,∴∠PCB=∠PAC ,∵∠BPC=∠CPA ,∴△PBC ∽△CPA ,∴PCPBAC CB PA PC ==, ∵tan ∠BAC=AC BC =21,∴PC 2=PB •PA ,PA=2PC ,∴PC 2=2PB •PC ,PC=2PB=4, 设⊙O 半径为x ,则OP=x+2,在RT △OPC 中,OP 2=OC 2+PC 2,即(x+2)2=x 2+42,解得x=3, ∴⊙O 半径为3.40.【解答】(1)证明:连接AD ,OD ;∵AB 为⊙O 的直径,∴∠ADB=90°,即AD ⊥BC ; ∵AB=AC ,∴BD=DC .∵OA=OB ,∴OD ∥AC .∵DF ⊥AC ,∴DF ⊥OD . ∴∠ODF=∠DFA=90°,∴DF 为⊙O 的切线. (2)解:连接BE 交OD 于G ;∵AC=AB ,AD ⊥BC ,ED=BD ,∴∠EAD=∠BAD .∴弧DE=弧BD . ∴ED=BD ,OE=OB .∴OD 垂直平分EB .∴EG=BG . 又AO=BO ,∴OG=21AE .在Rt △DGB 和Rt △OGB 中, BD 2﹣DG 2=BO 2﹣OG 2∴2222)45()25(OG OB OG -=--解得:OG=43.∴AE=2OG=23.41.【解答】(1)证明:连接OD .∵DE 是⊙O 的切线,∴DE ⊥OD ,即∠ODE=90°. ∵AB 是⊙O 的直径,∴O 是AB 的中点.又∵D 是BC 的中点,.∴OD ∥AC .∴∠DEC=∠ODE=90°.∴DE ⊥AC ;(2)解:连接AD .∵OD ∥AC ,∴CEOD FC OF =.∵AB 为⊙O 的直径,∴∠ADB=∠ADC=90°. 又∵D 为BC 的中点,∴AB=AC .∵sin ∠ABC=43=AB AD ,故设AD=3x ,则AB=AC=4x ,OD=2x . ∵DE ⊥AC ,∴∠ADC=∠AED=90°.∵∠DAC=∠EAD ,∴△ADC ∽△AED .∴AD AC AE AD =. ∴AD 2=AE •AC .∴x AE 49=.∴x CE 47=.∴78==CE OD CF OF . 42.【解答】解:(1)当x ≥50时,y A 与x 之间的函数关系式为:y A =7+(x ﹣25)×0.6=0.6x ﹣8,当x ≥50时,y B 与x 之间的函数关系式为:y B =10+(x ﹣50)×0.8=0.8x ﹣30.(2)当x=60时,y A =0.6×60﹣8=28,y B =0.8×60﹣30=18,∴y A >y B .故选择B 方式上网学习合算.44.【解答】(1)证明:∵AB 为⊙O 的直径,∴∠ACB=90°,∴∠CAB+∠B=90°,∵∠DAC=∠B ,∴∠CAB+∠DAC=90°.∴AD ⊥AB .∵OA 是⊙O 半径,∴DA 为⊙O 的切线;(2)解:∵OB=OC ,∴∠OCB=∠B .∵∠DCE=∠OCB ,∴∠DCE=∠B .∵∠DAC=∠B ,∴∠DAC=∠DCE .∵∠D=∠D ,∴△CED ∽△ACD ;(3)解:在Rt △AOD 中,OA=1,sinD=31,∴OD=DOA sin =3,∴CD=OD ﹣OC=2. ∵AD 2222=-OA OD ,又∵△CED ∽△ACD ,∴DE CD CD AD =,∴DE=22=AD CD , ∴AE=AD ﹣DE=22﹣2=2.45.【解答】解:(1)依题意得:tan ∠BCD=3331=,∴∠BCD=30°; (2)方法1:作EG ⊥CD ,垂足为G .在Rt △CEG 中,CE=100,∠ECG=30°,∴EG=CE •sin30°=50, CG=CE •cos30°=503,设AD=x ,则CD=AD=x .∴AF=x ﹣50,EF=x ﹣503,在Rt △AEF 中,EF AE =tan60°,∴335050=--x x .解得:x=503+50≈136.5(米). 答:塔顶A 到CD 的铅直高度AD 约为137米.方法2:∵∠ACD=45°,∴∠ACE=15°.∵∠AEF=60°,∴∠EAF=30°.∵∠DAC=45°,∴∠EAC=∠DAC ﹣∠EAF=15°,∴∠ACE=∠EAC .∴AE=CE=100.在Rt △AEF 中,∠AEF=60°,∴AF=AE •sin60°=503(m ),在Rt △CEG 中,CE=100m ,∠ECG=30°,∴EG=CE •sin30°=50m .∴AD=AF+FD=AF+EG=503+50≈136.5(米).答:塔顶A 到CD 的铅直高度AD 约为137米.46.【解答】解:(1)设直线AB 的解析式为y=kx+b ,由题意,得⎩⎨⎧=+=086b k b ,解得⎪⎩⎪⎨⎧=-=643b k , 所以,直线AB 的解析式为y=﹣43x+6; (2)由AO=6,BO=8得AB=10,所以AP=t ,AQ=10﹣2t , ①当∠APQ=∠AOB 时,△APQ ∽△AOB .所以62106t t -=,解得t=1130(秒), ②当∠AQP=∠AOB 时,△AQP ∽△AOB .所以621010t t -=,解得t=1350(秒); ∴当t 为1350秒或1130秒时,△APQ 与△AOB 相似; (3)过点Q 作QE 垂直AO 于点E .在Rt △AOB 中,sin ∠BAO=54=AB BO , 在Rt △AEQ 中,QE=AQ •sin ∠BAO=(10﹣2t )•54=8﹣58t , S △APQ =21AP •QE=21t •(8﹣58t )=﹣54t 2+4t=524,解得t=2(秒)或t=3(秒). ∴当t 为2秒或3秒时,△APQ 的面积为524个平方单位. 47.【解答】解:(1)过B 作BG ⊥DE 于G ,Rt △ABH 中,i=tan ∠BAH=3331=,∴∠BAH=30°,∴BH=21AB=5; (2)∵BH ⊥HE ,GE ⊥HE ,BG ⊥DE ,∴四边形BHEG 是矩形.∵由(1)得:BH=5,AH=53,∴BG=AH+AE=53+15,Rt △BGC 中,∠CBG=45°,∴CG=BG=53+15.Rt △ADE 中,∠DAE=60°,AE=15,∴DE=3AE=153.∴CD=CG+GE ﹣DE=53+15+5﹣153=20﹣103≈2.7m .答:宣传牌CD 高约2.7米.48.【解答】解:(1)设每台空调的进价为m 元,则每台电冰箱的进价为(m+400)元, 根据题意得:mm 6400040080000=+,解得:m=1600经检验,m=1600是原方程的解, m+400=1600+400=2000,答:每台空调的进价为1600元,则每台电冰箱的进价为2000元.(2)设购进电冰箱x 台(x 为正整数),这100台家电的销售总利润为y 元,则y=(2100﹣2000)x+(1750﹣1600)(100﹣x )=﹣50x+15000,…根据题意得:⎩⎨⎧≤+-≤-13000150********x x x ,解得:3331≤x ≤40,∵x 为正整数, ∴x=34,35,36,37,38,39,40,∴合理的方案共有7种,即①电冰箱34台,空调66台;②电冰箱35台,空调65台;③电冰箱36台,空调64台; ④电冰箱37台,空调63台;⑤电冰箱38台,空调62台;⑥电冰箱39台,空调61台;⑦电冰箱40台,空调60台;∵y=﹣50x+15000,k=﹣50<0,∴y 随x 的增大而减小, ∴当x=34时,y 有最大值,最大值为:﹣50×34+15000=13300(元),答:当购进电冰箱34台,空调66台获利最大,最大利润为13300元.50.【解答】解:(1)令x=0,则y=﹣3m 2,即C 点的坐标为(0,﹣3m 2),∵y=x 2﹣2mx ﹣3m 2=(x ﹣3m )(x+m ),∴A (﹣m ,0),B (3m ,0),∴AB=3m ﹣(﹣m )=4m ,故答案为:(0,﹣3m 2),4m ;(2)①令y=x 2﹣2mx ﹣3m 2=﹣3m 2,则x=0(舍)或x=2m ,∴D (2m ,﹣3m 2),∵将△ACD 沿x 轴翻折得到△AEM ,∴D 、M 关于x 轴对称,∴M (2m ,3m 2),设直线AM 的解析式为y=kx+b ,将A 、M 两点的坐标代入y=kx+b 得:⎪⎩⎪⎨⎧=+=+-2320m b mk b mk ,解得:⎪⎩⎪⎨⎧==2mb m k ,∴直线AM 的解析式为:y=mx+m 2, 联立方程组:⎪⎩⎪⎨⎧--=+=22232mmx x y m mx y ,解得:⎩⎨⎧=-=0y m x (舍)或⎪⎩⎪⎨⎧==254m y m x ,∴N (4m ,5m 2),∴35==N M y y AN AM ; ②如图:∵AB=4,∴m=1,∴抛物线的解析式为y=x 2﹣2x ﹣3,直线AM 的解析式为y=x+1,∴P (t ,t+1),Q (t ,t 2﹣2t ,﹣3),N (4,5),A (﹣1,0),B (3,0)设△AQN 的面积为S ,则:8125)23(25)321)(14(21))((2122+--=++-++=--=t t t t y y x x S Q P A N ∴t=23,S 最大.。
天津市和平区2016年12月16日九年级数学上册周末练习及答案

17.如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=6,EF=8,FC=10,则正
方形与其外接圆之间形成的阴影部分的面积为
.
18.对于二次函数 y=x2-2mx-3,有下列说法:
①如果当 x≤1 时 y 随 x 的增大而减小,则 m≥1;
②如果它的图象与 x 轴的两交点的距离是 4,则 m=±1;
则 a、b、c、d 的大小关系为
.
14.如图,AD是正五边形 ABCDE的一条对角线,则∠BAD= .
15.如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1 B1C 的位置 (A、C、B1 在同一直线上), 1
∠B=90°,如果AB=1,那么AC运动到1A C 所经过的图形的面积是 . 1
16.小明把如图所示的矩形纸板ABCD挂在墙上,E为AD中点,且∠ABD=60°,并用它玩飞镖游 戏(每次飞镖均落在纸板上),击中阴影区域的概率是________.
从中任选一名学生,其身高超过 165cm的概率是(
)
A.
B.
C.
D.
3.用配方法解一元二次方程 x 4x-5=0,此方程可变形为(
)
A.(x+2)2=9
B.(x-2) 2=9
C.(x+2) 2=1
D.(x-2)2=1
4.在相同时刻太阳光线 是平行的,如果高 1.5米的测杆影长 3 米,那么此时影长 30米的旗杆高
交于点(x ,1 0),若函数 y=y +2 y 的图象与 x 轴仅有一个交点,则(
)
1
A. a(x -x )=2 d 1
B. a(x -2 x )=d 1
C. a(x -x ) 2 2=d 1
D. a(x +1 x )2=d 2
数学中考试题天津市和平区九年级压轴题综合训练

天津市和平区2019年九年级中考数学压轴题综合训练1.若实数a,b满足a﹣ab+b2+2=0,则a的取值范围是()A.a≤﹣2 B.a≥4 C.a≤﹣2或a≥4 D.﹣2≤a≤42.如图,A、B是双曲线上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=9.则k的值是()A.9 B.6 C.5 D.43.已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<;④b>1.其中正确的结论是()A.①②B.②③ C.③④ D.②④4.如图,将足够大的等腰直角三角板PCD的锐角顶点P放在另一个等腰直角三角板PAB的直角顶点处,三角板PCD绕点P在平面内转动,且∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,设AB=2,AN=x,BM=y,则能反映y与x的函数关系的图象大致是()5.如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是()6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C ′处,则∠A′的大小是()A.40°B.36°C.32°D.30°7.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为()A.3B.2C.2D.28.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN的面积是()A.B.C.D.9.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中将正确结论的序号全部选对的是()A.①②③B.①②④C.②③④D.①②③④10.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG 的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG 的面积相等;⑤若,则.以上命题,正确的有( ) A.2个B. 3个C. 4个D. 5个11.已知M 、N 两点关于y 轴对称,且点M 在双曲线上,点N 在直线y=﹣x+3上,设点M 坐标为(a ,b ),则y=﹣abx 2+(a+b )x 的顶点坐标为 .12.如图,△AEF 中,∠EAF=45°,AG ⊥EF 于点G ,现将△AEG 沿AE 折叠得到△AEB ,将△AFG 沿AF 折叠得到△AFD ,延长BE 和DF 相交于点C . (1)求证:四边形ABCD 是正方形;(2)连接BD 分别交AE 、AF 于点M 、N ,将△ABM 绕点A 逆时针旋转,使AB 与AD 重合,得到△ADH ,试判断线段MN 、ND 、DH 之间的数量关系,并说明理由.(3)若EG=4,GF=6,BM=3,求AG 、MN 的长.13.如图,AB 为⊙O 的直径,C ,D 为⊙O 上不同于A ,B 的两点,过点C 作⊙O 的切线CF 交直线AB 于点F ,直线DB ⊥CF 于点E .(1) 求证:∠ABD=2∠CAB ;(2) 若BF=5,sin ∠F=53,求BD 的长.14.为深化“携手节能低碳,共建碧水蓝天”活动,发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.今年1月份,再生资源处理量为40吨,从今年1月1日起,该单位每月再生资源处理量每一个月将提高10吨.月处理成本(元)与月份之间的关系可近似地表示为:p=50x2+100x+450,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).(1)分别求出y与x,w与x的函数关系式;(2)在今年内该单位哪个月获得利润达到5800元?15.如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒()t<<,连接PQ.02△相似,求t的值.⑴若APQ△与ADC⑵连结CQ,DP,若CQ DP⊥,求t的值.⑶连结BQ,PD,请问BQ能和PD平行吗?若能,求出t的值;若不能,说明理由.16.如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.(1)求此抛物线的解析式;(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;(3)在抛物线y=ax2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.17.如图,抛物线21:C y x bx c =++ 经过原点,与x 轴的另一个交点为()20,,将抛物线1C 向右平移()0m m >个单位得到抛物线2C ,2C 交x 轴于A ,B 两点(点A 在点B 的左边),交y 轴于点C . ⑴求抛物线1C 的解析式及顶点坐标.⑵以AC 为直角边向上作等腰Rt ACD △(CAD ∠是直角),当点D 落在抛物线2C 的对称轴上时,求抛物线2C 的解析式.⑶若抛物线2C 的对称轴上存在点P ,使PAC △为等边三角形,求m 的值.18.已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣).(1)求抛物线l2的函数表达式;(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.答案详解1.【解答】解:∵b是实数,∴关于b的一元二次方程b2﹣ab+a+2=0,△=(﹣a)2﹣4×1×(a+2)≥0解得:a≤﹣2或a≥4;∴a的取值范围是a≤﹣2或a≥4.故选C.2.【解答】解:作AD⊥x轴于D,BE⊥x轴于E,如图,设反比例函数解析式为y=(k>0),∵A、B两点的横坐标分别是a、2a,∴A、B两点的纵坐标分别是、,∵AD∥BE,∴△CEB∽△CDA,∴===,∴DE=CE,∵OD:OE=a:2a=1:2,∴OD=DE,∴OD=OC,∴S△AOD=S△AOC=×9=3,∴|k|=3,而k>0,∴k=6.故选B.3.【解答】解:①∵抛物线的开口向上,∴a>0,∵与y轴的交点为在y轴的负半轴上,∴c<0,∵对称轴为x=<0,∴a、b同号,即b>0,∴abc<0,故本选项错误;②当x=1时,函数值为2,∴a+b+c=2;故本选项正确;③∵对称轴x=>﹣1,解得:<a,∵b>1,∴a>,故本选项错误;④当x=﹣1时,函数值<0,即a﹣b+c<0,(1)又a+b+c=2,将a+c=2﹣b代入(1),2﹣2b<0,∴b>1故本选项正确;综上所述,其中正确的结论是②④;故选D.4.【解答】解:作PH⊥AB于H,如图,∵△PAB为等腰直角三角形,∴∠A=∠B=45°,AH=BH=AB=1,∴△PAH和△PBH都是等腰直角三角形,∴PA=PB=AH=,∠HPB=45°,∵∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,而∠CPD=45°,∴1≤AN≤2,即1≤x≤2,∵∠2=∠1+∠B=∠1+45°,∠BPM=∠1+∠CPD=∠1+45°,∴∠2=∠BPM,而∠A=∠B,∴△ANP∽△BPM,∴=,即=,∴y=,∴y与x的函数关系的图象为反比例函数图象,且自变量为1≤x≤2.故选:A.5.【解答】解:如右图,过点E作EM⊥BC于点M,EN⊥AB于点N,∵点E是正方形的对称中心,∴EN=EM,由旋转的性质可得∠NEK=∠MEL,在Rt△ENK和Rt△EML中,,故可得△ENK≌△EML,即阴影部分的面积始终等于正方形面积的.故选B.6.解答:解:连接C'D,∵AB=AC,BD=BC,∴∠ABC=∠ACB=∠BDC,∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,∴∠BCD=∠BC'D,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,∵四边形BCDC'的内角和为360°,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D==72°,∴∠A=180°﹣∠ABC﹣∠ACB=36°.故选B.7.解答:解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,∵∠ENG=∠BNM,∴△ENG≌△BNM(AAS),∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.故选B.8.解答:解:连接CD,交MN于E,∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,∴MN⊥CD,且CE=DE,∴CD=2CE,∵MN∥AB,∴CD⊥AB,∴△CMN∽△CAB,∴,∵在△CMN中,∠C=90°,MC=6,NC=,∴S△CMN=CM•CN=×6×2=6,∴S△CAB=4S△CMN=4×6=24,∴S四边形MABN=S△CAB﹣S△CMN=24﹣6=18.故选C.9.解答:解:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF,由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC,∵BF平分∠EBC,∴CF=MF,∴DF=CF;故①正确;∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC,∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN,∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN,故②正确;∵在△DEF和△CNF中,,∴△DEF≌△CNF(ASA),∴EF=FN,∴BE=BN,但无法求得△BEN各角的度数,∴△BEN不一定是等边三角形;故③错误;∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM,∴BE=3EM,∴S△BEF=3S△EMF=3S△DEF;故④正确.故选B.10.解答:解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;②可证△EDF∽△HCF,DF>CF,故DE≠CH,故错误;③只可证△EDF∽△BAE,无法证明BE=EF,故错误;④可证△GEB,△GEH是等腰三角形,则G是BH边的中线,∴△BEG和△HEG的面积相等,故正确;⑤过E点作EK⊥BC,垂足为K.设BK=x,AB=y,则有y2+(2y﹣2x)2=(2y﹣x)2,解得x1=y(不合题意舍去),x2=y.则,故正确.故正确的有3个.故选B.11.【解答】解:∵M、N两点关于y轴对称,∴M坐标为(a,b),N为(﹣a,b),分别代入相应的函数中得,b=①,a+3=b②,∴ab=,(a+b)2=(a﹣b)2+4ab=11,a+b=±,∴y=﹣x2±x,∴顶点坐标为(=±, =),即(±,).故答案为:(±,).12.【解答】(1)证明:∵△AEB由△AED翻折而成,∴∠ABE=∠AGE=90°,∠BAE=∠EAG,AB=AG,∵△AFD由△AFG翻折而成,∴∠ADF=∠AGF=90°,∠DAF=∠FAG,AD=AG,∵∠EAG+∠FAG=∠EAF=45°,∴∠ABE=∠AGE=∠BAD=∠ADC=90°,∴四边形ABCD是矩形,∵AB=AD,∴四边形ABCD是正方形;(2)MN2=ND2+DH2,理由:连接NH,∵△ADH由△ABM旋转而成,∴△ABM≌△ADH,∴AM=AH,BM=DH,∵由(1)∠BAD=90°,AB=AD,∴∠ADH=∠ABD=45°,∴∠NDH=90°,∵,∴△AMN≌△AHN,∴MN=NH,∴MN2=ND2+DH2;(3)设AG=BC=x,则EC=x﹣4,CF=x﹣6,在Rt△ECF中,∵CE2+CF2=EF2,即(x﹣4)2+(x﹣6)2=100,x1=12,x2=﹣2(舍去)∴AG=12,∵AG=AB=AD=12,∠BAD=90°,∴BD===12,∵BM=3,∴MD=BD﹣BM=12﹣3=9,设NH=y,在Rt△NHD中,∵NH2=ND2+DH2,即y2=(9﹣y)2+(3)2,解得y=5,即MN=5.13.(1)证明:如图,连接OC,∵OA=OC错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津市和平区2016年九年级中考数学压轴题综合训练1.若实数a,b满足a﹣ab+b2+2=0,则a的取值范围是()A.a≤﹣2 B.a≥4 C.a≤﹣2或a≥4 D.﹣2≤a≤42.如图,A、B是双曲线上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=9.则k的值是()A.9 B.6 C.5 D.43.已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<;④b>1.其中正确的结论是()A.①②B.②③ C.③④ D.②④4.如图,将足够大的等腰直角三角板PCD的锐角顶点P放在另一个等腰直角三角板PAB的直角顶点处,三角板PCD绕点P在平面内转动,且∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,设AB=2,AN=x,BM=y,则能反映y与x的函数关系的图象大致是()5.如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是()6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,则∠A′的大小是()A.40°B.36°C.32°D.30°7.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为()A.3B.2C.2D.28.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=,则四边形MABN的面积是()A.B.C.D.9.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中将正确结论的序号全部选对的是()A.①②③B.①②④C.②③④D.①②③④10.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG 的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若,则.以上命题,正确的有()A.2个B. 3个C. 4个D. 5个11.已知M、N两点关于y轴对称,且点M在双曲线上,点N在直线y=﹣x+3上,设点M坐标为(a,b),则y=﹣abx2+(a+b)x的顶点坐标为.12.如图,△AEF 中,∠EAF=45°,AG ⊥EF 于点G ,现将△AEG 沿AE 折叠得到△AEB ,将△AFG 沿AF 折叠得到△AFD ,延长BE 和DF 相交于点C .(1)求证:四边形ABCD 是正方形;(2)连接BD 分别交AE 、AF 于点M 、N ,将△ABM 绕点A 逆时针旋转,使AB 与AD 重合,得到△ADH ,试判断线段MN 、ND 、DH 之间的数量关系,并说明理由.(3)若EG=4,GF=6,BM=3,求AG 、MN 的长.13.如图,AB 为⊙O 的直径,C ,D 为⊙O 上不同于A ,B 的两点,过点C 作⊙O 的切线CF 交直线AB 于点F ,直线DB ⊥CF 于点E .(1) 求证:∠ABD=2∠CAB ;(2) 若BF=5,sin ∠F=53,求BD 的长.14.为深化“携手节能低碳,共建碧水蓝天”活动,发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.今年1月份,再生资源处理量为40吨,从今年1月1日起,该单位每月再生资源处理量每一个月将提高10吨.月处理成本(元)与月份之间的关系可近似地表示为:p=50x2+100x+450,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).(1)分别求出y与x,w与x的函数关系式;(2)在今年内该单位哪个月获得利润达到5800元?15.如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒()t<<,连接PQ.02△相似,求t的值.⑴若APQ△与ADC⑵连结CQ,DP,若CQ DP⊥,求t的值.⑶连结BQ,PD,请问BQ能和PD平行吗?若能,求出t的值;若不能,说明理由.16.如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.(1)求此抛物线的解析式;(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;(3)在抛物线y=ax2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.17.如图,抛物线21:C y x bx c =++ 经过原点,与x 轴的另一个交点为()20,,将抛物线1C 向右平移()0m m >个单位得到抛物线2C ,2C 交x 轴于A ,B 两点(点A 在点B 的左边),交y 轴于点C . ⑴求抛物线1C 的解析式及顶点坐标.⑵以AC 为直角边向上作等腰Rt ACD △(CAD ∠是直角),当点D 落在抛物线2C 的对称轴上时,求抛物线2C 的解析式.⑶若抛物线2C 的对称轴上存在点P ,使PAC △为等边三角形,求m 的值.18.已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣).(1)求抛物线l2的函数表达式;(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.答案详解1.【解答】解:∵b是实数,∴关于b的一元二次方程b2﹣ab+a+2=0,△=(﹣a)2﹣4×1×(a+2)≥0解得:a≤﹣2或a≥4;∴a的取值范围是a≤﹣2或a≥4.故选C.2.【解答】解:作AD⊥x轴于D,BE⊥x轴于E,如图,设反比例函数解析式为y=(k>0),∵A、B两点的横坐标分别是a、2a,∴A、B两点的纵坐标分别是、,∵AD∥BE,∴△CEB∽△CDA,∴===,∴DE=CE,∵OD:OE=a:2a=1:2,∴OD=DE,∴OD=OC,∴S△AOD=S△AOC=×9=3,∴|k|=3,而k>0,∴k=6.故选B.3.【解答】解:①∵抛物线的开口向上,∴a>0,∵与y轴的交点为在y轴的负半轴上,∴c<0,∵对称轴为x=<0,∴a、b同号,即b>0,∴abc<0,故本选项错误;②当x=1时,函数值为2,∴a+b+c=2;故本选项正确;③∵对称轴x=>﹣1,解得:<a,∵b>1,∴a>,故本选项错误;④当x=﹣1时,函数值<0,即a﹣b+c<0,(1)又a+b+c=2,将a+c=2﹣b代入(1),2﹣2b<0,∴b>1故本选项正确;综上所述,其中正确的结论是②④;故选D.4.【解答】解:作PH⊥AB于H,如图,∵△PAB为等腰直角三角形,∴∠A=∠B=45°,AH=BH=AB=1,∴△PAH和△PBH都是等腰直角三角形,∴PA=PB=AH=,∠HPB=45°,∵∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,而∠CPD=45°,∴1≤AN≤2,即1≤x≤2,∵∠2=∠1+∠B=∠1+45°,∠BPM=∠1+∠CPD=∠1+45°,∴∠2=∠BPM,而∠A=∠B,∴△ANP∽△BPM,∴=,即=,∴y=,∴y与x的函数关系的图象为反比例函数图象,且自变量为1≤x≤2.故选:A.5.【解答】解:如右图,过点E作EM⊥BC于点M,EN⊥AB于点N,∵点E是正方形的对称中心,∴EN=EM,由旋转的性质可得∠NEK=∠MEL,在Rt△ENK和Rt△EML中,,故可得△ENK≌△EML,即阴影部分的面积始终等于正方形面积的.故选B.6.解答:解:连接C'D,∵AB=AC,BD=BC,∴∠ABC=∠ACB=∠BDC,∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,∴∠BCD=∠BC'D,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,∵四边形BCDC'的内角和为360°,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D==72°,∴∠A=180°﹣∠ABC﹣∠ACB=36°.故选B.7.解答:解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,∵∠ENG=∠BNM,∴△ENG≌△BNM(AAS),∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.故选B.8.解答:解:连接CD,交MN于E,∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,∴MN⊥CD,且CE=DE,∴CD=2CE,∵MN∥AB,∴CD⊥AB,∴△CMN∽△CAB,∴,∵在△CMN中,∠C=90°,MC=6,NC=,∴S△CMN=CM•CN=×6×2=6,∴S△CAB=4S△CMN=4×6=24,∴S四边形MABN=S△CAB﹣S△CMN=24﹣6=18.故选C.9.解答:解:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF,由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC,∵BF平分∠EBC,∴CF=MF,∴DF=CF;故①正确;∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC,∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN,∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN,故②正确;∵在△DEF和△CNF中,,∴△DEF≌△CNF(ASA),∴EF=FN,∴BE=BN,但无法求得△BEN各角的度数,∴△BEN不一定是等边三角形;故③错误;∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM,∴BE=3EM,∴S△BEF=3S△EMF=3S△DEF;故④正确.故选B.10.解答:解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;②可证△EDF∽△HCF,DF>CF,故DE≠CH,故错误;③只可证△EDF∽△BAE,无法证明BE=EF,故错误;④可证△GEB,△GEH是等腰三角形,则G是BH边的中线,∴△BEG和△HEG的面积相等,故正确;⑤过E点作EK⊥BC,垂足为K.设BK=x,AB=y,则有y2+(2y﹣2x)2=(2y﹣x)2,解得x1=y(不合题意舍去),x2=y.则,故正确.故正确的有3个.故选B.11.【解答】解:∵M、N两点关于y轴对称,∴M坐标为(a,b),N为(﹣a,b),分别代入相应的函数中得,b=①,a+3=b②,∴ab=,(a+b)2=(a﹣b)2+4ab=11,a+b=±,∴y=﹣x2±x,∴顶点坐标为(=±, =),即(±,).故答案为:(±,).12.【解答】(1)证明:∵△AEB由△AED翻折而成,∴∠ABE=∠AGE=90°,∠BAE=∠EAG,AB=AG,∵△AFD由△AFG翻折而成,∴∠ADF=∠AGF=90°,∠DAF=∠FAG,AD=AG,∵∠EAG+∠FAG=∠EAF=45°,∴∠ABE=∠AGE=∠BAD=∠ADC=90°,∴四边形ABCD是矩形,∵AB=AD,∴四边形ABCD是正方形;(2)MN2=ND2+DH2,理由:连接NH,∵△ADH由△ABM旋转而成,∴△ABM≌△ADH,∴AM=AH,BM=DH,∵由(1)∠BAD=90°,AB=AD,∴∠ADH=∠ABD=45°,∴∠NDH=90°,∵,∴△AMN≌△AHN,∴MN=NH,∴MN2=ND2+DH2;(3)设AG=BC=x,则EC=x﹣4,CF=x﹣6,在Rt△ECF中,∵CE2+CF2=EF2,即(x﹣4)2+(x﹣6)2=100,x1=12,x2=﹣2(舍去)∴AG=12,∵AG=AB=AD=12,∠BAD=90°,∴BD===12,∵BM=3,∴MD=BD﹣BM=12﹣3=9,设NH=y,在Rt△NHD中,∵NH2=ND2+DH2,即y2=(9﹣y)2+(3)2,解得y=5,即MN=5.13.(1)证明:如图,连接OC,∵OA=OC错误!未找到引用源。
