天津中考数学压轴题全搞定
2024届天津市和平区二十一中中考数学押题卷含解析

2024学年天津市和平区二十一中中考数学押题卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(共10小题,每小题3分,共30分)1.下列图形中,是正方体表面展开图的是()A.B.C. D.2.改革开放40年以来,城乡居民生活水平持续快速提升,居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出,如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图.说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.根据上述信息,下列结论中错误的是()A.2017年第二季度环比有所提高B.2017年第三季度环比有所提高C.2018年第一季度同比有所提高D.2018年第四季度同比有所提高3.小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是().A .众数是6吨B .平均数是5吨C .中位数是5吨D .方差是4.一艘在南北航线上的测量船,于A 点处测得海岛B 在点A 的南偏东30°方向,继续向南航行30海里到达C 点时,测得海岛B 在C 点的北偏东15°方向,那么海岛B 离此航线的最近距离是( )(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)A .4.64海里B .5.49海里C .6.12海里D .6.21海里 5.函数y=ax 2+1与ay x=(a≠0)在同一平面直角坐标系中的图象可能是( ) A . B . C . D .6.四张分别画有平行四边形、菱形、等边三角形、圆的卡片,它们的背面都相同。
最新整理天津市和平区中考数学压轴题综合训练及答案详解

心位置,正方形 EFGH绕点 E 顺时针方向旋转,设它们重叠部分的面积为
S,旋转的角度为 θ , S 与
θ 的函数关系的大致图象是(
)
6. 如图,D 是△ ABC的 AC边上一点, AB=AC,BD=BC,将△ BCD沿 BD折叠, 顶点 C恰好 落在 AB边的 C′
处,则∠ A′的大小是(
)
A. 40°
( 1)分别求出 y 与 x,w 与 x 的函数关系式;
( 2)在今年内该单位哪个月获得利润达到 5800 元?
15. 如图,矩形 ABCD中, AB=6cm,BC=8cm动, 点 P 从点 A 出发 , 在 AC上以每秒 5cm 的速度向点 C匀速 运动,同时动点 Q 从点 D 出发,在 DA 边上以每秒 4cm 的速度向点 A 匀速运动,运动时间为 t 秒
天津市和平区 20XX 年九年级中考数学压轴题综合训练
1. 若实数 a,b 满足 a﹣ ab+b2+2=0,则 a 的取值范围是(
)
A . a≤﹣ 2 B . a≥ 4 C. a≤﹣ 2 或 a≥ 4 D.﹣ 2≤ a≤ 4
2. 如图, A、 B是双曲线上的点, A、 B 两点的横坐标分别是 a、 2a,线段 AB 的延长线交 x 轴于点 C,
再生资源重新利用.今年 1 月份,再生资源处理量为 40 吨,从今年 1 月 1 日起,该单位每月再生资
源处理量每一个月将提高 10 吨.月处理成本(元)与月份之间的关系可近似地表示为:
2
p=50x +100x+450 ,每处理一吨再生资源得到的新产品的售价定为
100 元.若该单位每月再生资源处
理量为 y(吨),每月的利润为 w(元).
2021年天津市中考数学压轴题总复习(附答案解析)

4.如图①,在△ABC中,∠ABC=90°,AB=4,BC=3.点P从点A出发,沿折线AB﹣BC以每秒5个单位长度的速度向点C运动,同时点D从点C出发,沿CA以每秒2个单位长度的速度向点A运动,点P到达点C时,点P、D同时停止运动.当点P不与点A、C重合时,作点P关于直线AC的对称点Q,连结PQ交AC于点E,连结DP、DQ.设点P的运动时间为t秒.
2.如图,一次函数y=kx+b和反比例函数 的图象相交于A(2,4)、B(﹣1,n)两点,一次函数的图象交x轴于点D.
(1)直接写出一次函数与反比例函数的解析式.
(2)请结合函数图象,直接写出不等式 的解集.
(3)过点A作直线AC⊥x轴,垂足为点C,过点B的直线交x轴于点E,交直线AC于点F,若△ECF∽△ACD,求点E的坐标.
③在②的条件下,若点A与A′B′的中点重合,A′B′=4,AB=2,在整个旋转过程中,当点P与点M重合时,请直接写出线段BM的长.
9.【了解概念】
有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.
【理解运用】
(1)如图①,对余四边形ABCD中,AB=5,BC=6,CD=4,连接AC.若AC=AB,求sin∠CAD的值;
(1)求二次函数y x2+bx+c的表达式;
(2)判断△ABD的形状,并说明理由;
(3)在点E的运动过程中,直线BD上存在一点G,使得四边形AFGE为矩形,请判断此时AG与BD的数量关系,并求出点E的坐标;
(4)点H是抛物线的顶点,在(3)的条件下,点P是平面内使得∠EPF=90°的点,在抛物线的对称轴上,是否存在点Q,使得△HPQ是以∠PQH为直角的等腰直角三角形,若存在,直接写出符合条件的所有点Q的坐标;若不存在,请说明理由.
近10年2005-2014天津中考数学卷压轴题详解

(25)(本小题10分)在△ABC 中,∠A 、∠B 、∠C 所对的边分别用a 、b 、c 表示。
(Ⅰ)如图,在△ABC 中,∠A=2∠B ,且∠A =60°。
求证:a 2=b (b +c )(Ⅱ)如果一个三角形的一个内角等于另一个内角的2 倍,我们称这样 的三角形为“倍角三角形”。
本题第一问中的三角形是一个特殊的倍角三 角形,那么对于任意的倍角三角形ABC ,其中∠A =2∠B ,关系式 a 2=b (b +c )是否仍然成了?并证明你的结论;(Ⅲ)试求出一个倍角三角形的三条边的长,使这三条边长恰为三个连续的正整数。
(26) (本小题10分)已知二次函数y =ax 2+bx +c .(Ⅰ)若a =2,c =-3,且二次函数的图象经过点(-1,-2),求b 的值(Ⅱ)若a =2,b +c =-2,b >c ,且二次函数的图象经过点(p ,-2),求证:b ≥0;(Ⅲ)若a +b +c =0,a >b >c ,且二次函数的图象经过点(q ,-a ),试问自变量x =q +4时,二次函数y =ax 2+bx +c 所对应的函数值y 是否大于0?并证明你的结论。
(25)(本小题10分)已知Rt △ABC 中,∠ACB =90°,AC =6,BC =8。
(Ⅰ)如图①,若半径为r 1的⊙O 1是Rt △ABC 的内切圆,求r 1;(Ⅱ)如图②,若半径为r 2的两个等圆⊙O 1、⊙O 2外切,且⊙O 1与AC 、AB 相切,⊙O 2与BC 、AB 相切,求r 2;(Ⅲ)如图③,当n 大于2的正整数时,若半径r n 的n 个等圆⊙O 1、⊙O 2、…、⊙O n依次外切,且⊙O 1与AC 、BC 相切,⊙O n 与BC 、AB 相切,⊙O 1、⊙O 2、⊙O 3、…、⊙O n -1均与AB 边相切,求r n . (26) (本小题10分)已知抛物线y =ax 2+bx +c 的定点坐标为(2,4). (Ⅰ)试用含a 的代数式分别表示b ,c ;(Ⅱ)若直线y =kx +4(k ≠0)与y 轴及该抛物线的交点依次为D 、E 、F ,且13ODEOEFS S=,其中O 为坐标原点,试用含a 的代数式表示k ;(Ⅲ)在(Ⅱ)的条件下,若线段EF 的长m 满足m ≤≤a 的取值范围。
天津市蓟州区2024届中考数学押题卷含解析

天津市蓟州区2024届中考数学押题卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1.下列天气预报中的图标,其中既是轴对称图形又是中心对称图形的是( )A .B .C .D .2.计算(﹣ab 2)3的结果是( )A .﹣3ab 2B .a 3b 6C .﹣a 3b 5D .﹣a 3b 63.如图,点A 、B 、C 是⊙O 上的三点,且四边形ABCO 是平行四边形,OF ⊥OC 交圆O 于点F ,则∠BAF 等于()A .12.5°B .15°C .20°D .22.5°4.将抛物线y =2x 2向左平移3个单位得到的抛物线的解析式是( )A .y =2x 2+3B .y =2x 2﹣3C .y =2(x+3)2D .y =2(x ﹣3)25.已知二次函数2(0)y x x a a =-+>,当自变量x 取m 时,其相应的函数值小于0,则下列结论正确的是( )A .x 取1m -时的函数值小于0B .x 取1m -时的函数值大于0C .x 取1m -时的函数值等于0D .x 取1m -时函数值与0的大小关系不确定6.下列运算中,正确的是( )A .(a 3)2=a 5B .(﹣x )2÷x=﹣xC .a 3(﹣a )2=﹣a 5D .(﹣2x 2)3=﹣8x 67.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②244b aca->;③ac-b+1=0;④OA·OB=ca-.其中正确结论的个数是()A.4 B.3 C.2 D.18.将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为()A.10°B.15°C.20°D.25°9.如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为()A.12 B.16 C.18 D.2410.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为4的正方形ABCD的边AB在x轴上,AB 的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为()A.32) B.(4,1) C.(43) D.(4,23二、填空题(共7小题,每小题3分,满分21分)11.一元二次方程x2+mx+3=0的一个根为- 1,则另一个根为.12.一个正多边形的每个内角等于150,则它的边数是____.13.已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45º.则图中阴影部分的面积是____________.14.在临桂新区建设中,需要修一段全长2400m 的道路,为了尽量减少施工对县城交通工具所造成的影响,实际工作效率比原计划提高了20%,结果提前8天完成任务,求原计划每天修路的长度.若设原计划每天修路xm ,则根据题意可得方程 .15.已知直线m ∥n ,将一块含有30°角的直角三角板ABC 按如图方式放置,其中A 、B 两点分别落在直线m 、n 上,若∠1=20°,则∠2=_____度.16.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD 为_______米(结果保留根号).17.如果点()14,A y -、()23,B y -是二次函数22(y x k k =+是常数)图象上的两点,那么1y ______2.(y 填“>”、“<”或“=”)三、解答题(共7小题,满分69分)18.(10分)如图1,图2分别是某款篮球架的实物图与示意图,已知底座BC=1.5米,底座BC 与支架AC 所成的角∠ACB=60°,支架AF 的长为2.50米,篮板顶端F 点到篮筐D 的距离FD=1.3米,篮板底部支架HE 与支架AF 所成的角∠FHE=45°,求篮筐D 到地面的距离.(精确到0.0132≈1.41)19.(5分)如图,曲线BC 是反比例函数y =k x(4≤x ≤6)的一部分,其中B (4,1﹣m ),C (6,﹣m ),抛物线y =﹣x 2+2bx 的顶点记作A .(1)求k 的值.(2)判断点A 是否可与点B 重合; (3)若抛物线与BC 有交点,求b 的取值范围.20.(8分)如图,AB 是⊙O 的直径,C 是弧AB 的中点,弦CD 与AB 相交于E .若∠AOD =45°,求证:CE =2ED ;(2)若AE =EO ,求tan ∠AOD 的值.21.(10分)如图,在平面直角坐标系中,二次函数2y x bx c =++的图象与x 轴交于A ,B 两点,与y 轴交于点()0,3C -,A 点的坐标为()1,0-.(1)求二次函数的解析式;(2)若点P 是抛物线在第四象限上的一个动点,当四边形ABPC 的面积最大时,求点P 的坐标,并求出四边形ABPC 的最大面积;(3)若Q 为抛物线对称轴上一动点,直接写出使QBC ∆为直角三角形的点Q 的坐标.22.(10分)平面直角坐标系xOy 中(如图),已知抛物线2y x bx c ++=经过点10(,)A 和30B (,),与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标;(2)点E 在抛物线的对称轴上,且EA EC =,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线上,MEQ NEB ∠∠=,求点Q 的坐标.23.(12分)如图,AB 是⊙O 的直径,点C 在⊙O 上,CE^ AB 于E , CD 平分ÐECB , 交过点B 的射线于D , 交AB 于F , 且BC=BD .(1)求证:BD 是⊙O 的切线;(2)若AE=9, CE=12, 求BF 的长.24.(14分)将二次函数2241y x x =+-的解析式化为2()y a x m k =++的形式,并指出该函数图象的开口方向、顶点坐标和对称轴.参考答案一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1、A【解题分析】根据轴对称图形与中心对称图形的概念求解.【题目详解】解:A、是轴对称图形,也是中心对称图形,符合题意;B、是轴对称图形,不是中心对称图形,不合题意;C、不是轴对称图形,也不是中心对称图形,不合题意;D、不是轴对称图形,不是中心对称图形,不合题意.故选:A.【题目点拨】此题主要考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.2、D【解题分析】根据积的乘方与幂的乘方计算可得.【题目详解】解:(﹣ab2)3=﹣a3b6,故选D.【题目点拨】本题主要考查幂的乘方与积的乘方,解题的关键是掌握积的乘方与幂的乘方的运算法则.3、B【解题分析】解:连接OB,∵四边形ABCO是平行四边形,∴OC=AB,又OA=OB=OC,∴OA=OB=AB,∴△AOB为等边三角形,∵OF⊥OC,OC∥AB,∴OF⊥AB,∴∠BOF=∠AOF=30°,由圆周角定理得∠BAF=12∠BOF=15°故选:B4、C【解题分析】按照“左加右减,上加下减”的规律,从而选出答案.【题目详解】y=2x2向左平移3个单位得到的抛物线的解析式是y=2(x+3)2,故答案选C.【题目点拨】本题主要考查了抛物线的平移以及抛物线解析式的变换规律,解本题的要点在于熟知“左加右减,上加下减”的变化规律.5、B【解题分析】画出函数图象,利用图象法解决问题即可;【题目详解】由题意,函数的图象为:∵抛物线的对称轴x=12,设抛物线与x轴交于点A、B,∴AB<1,∵x取m时,其相应的函数值小于0,∴观察图象可知,x=m-1在点A的左侧,x=m-1时,y>0,故选B.【题目点拨】本题考查二次函数图象上的点的坐标特征,解题的关键是学会利用函数图象解决问题,体现了数形结合的思想.6、D【解题分析】根据同底数幂的除法、乘法的运算方法,幂的乘方与积的乘方的运算方法,以及单项式乘单项式的方法,逐项判定即可.【题目详解】∵(a3)2=a6,∴选项A不符合题意;∵(-x)2÷x=x,∴选项B不符合题意;∵a3(-a)2=a5,∴选项C不符合题意;∵(-2x2)3=-8x6,∴选项D符合题意.故选D.【题目点拨】此题主要考查了同底数幂的除法、乘法的运算方法,幂的乘方与积的乘方的运算方法,以及单项式乘单项式的方法,要熟练掌握.7、B【解题分析】试题分析:由抛物线开口方向得a<0,由抛物线的对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,则可对①进行判断;根据抛物线与x轴的交点个数得到b2﹣4ac>0,加上a<0,则可对②进行判断;利用OA=OC可得到A(﹣c,0),再把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,两边除以c则可对③进行判断;设A(x1,0),B(x2,0),则OA=﹣x1,OB=x2,根据抛物线与x轴的交点问题得到x1和x2是方程ax2+bx+c=0(a≠0)的两根,利用根与系数的关系得到x1•x2=,于是OA•OB=﹣,则可对④进行判断.解:∵抛物线开口向下,∴a<0,∵抛物线的对称轴在y轴的右侧,∴b>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,所以①正确;∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,而a<0,∴<0,所以②错误;∵C(0,c),OA=OC,∴A(﹣c,0),把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,∴ac﹣b+1=0,所以③正确;设A(x1,0),B(x2,0),∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,∴x1•x2=,∴OA•OB=﹣,所以④正确.故选B.考点:二次函数图象与系数的关系.8、A【解题分析】先根据∠CDE=40°,得出∠CED=50°,再根据DE∥AF,即可得到∠CAF=50°,最后根据∠BAC=60°,即可得出∠BAF 的大小.【题目详解】由图可得,∠CDE=40°,∠C=90°,∴∠CED=50°,又∵DE ∥AF ,∴∠CAF=50°,∵∠BAC=60°,∴∠BAF=60°−50°=10°,故选A.【题目点拨】本题考查了平行线的性质,熟练掌握这一点是解题的关键. 9、A【解题分析】解:∵四边形ABCD 为矩形,∴AD=BC=10,AB=CD=8,∵矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上的F 处, ∴AF=AD=10,EF=DE ,在Rt △ABF 中,∵,∴CF=BC-BF=10-6=4,∴△CEF 的周长为:CE+EF+CF=CE+DE+CF=CD+CF=8+4=1. 故选A .10、D【解题分析】由已知条件得到AD′=AD=4,AO=12AB=2,根据勾股定理得到 【题目详解】解:∵AD′=AD=4, AO=12AB=1,∴∵C′D′=4,C′D′∥AB ,∴C′(4,,故选:D .【题目点拨】本题考查正方形的性质,坐标与图形的性质,勾股定理,正确的识别图形是解题关键.二、填空题(共7小题,每小题3分,满分21分)11、-1.【解题分析】因为一元二次方程的常数项是已知的,可直接利用两根之积的等式求解.【题目详解】∵一元二次方程x 2+mx+1=0的一个根为-1,设另一根为x 1,由根与系数关系:-1•x 1=1,解得x 1=-1.故答案为-1.12、十二【解题分析】首先根据内角度数计算出外角度数,再用外角和360°除以外角度数即可.【题目详解】∵一个正多边形的每个内角为150°,∴它的外角为30°,360°÷30°=12,故答案为十二.【题目点拨】此题主要考查了多边形的内角与外角,关键是掌握内角与外角互为邻补角.13、(254π-252)cm 2 【解题分析】S阴影=S 扇形-S △OBD =90360π 52-12×5×5=225504cm π-. 故答案是: 225504cm π-. 14、()240024008.120%x x -=+. 【解题分析】试题解析:∵原计划用的时间为:2400x, 实际用的时间为:()2400120%x +, ∴可列方程为:()240024008.120%x x-=+ 故答案为()240024008.120%x x -=+ 15、1【解题分析】根据平行线的性质即可得到∠2=∠ABC+∠1,据此进行计算即可.【题目详解】解:∵直线m ∥n ,∴∠2=∠ABC+∠1=30°+20°=1°,故答案为:1.【题目点拨】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.16、 4【解题分析】分析:利用特殊三角函数值,解直角三角形,AM=MD,再用正切函数,利用MB 求CM ,作差可求DC.【题目详解】因为∠MAD =45°, AM =4,所以MD =4, 因为AB =8,所以MB =12,因为∠MBC=30°,所以CM=MB tan30°.所以CD 【题目点拨】本题考查了解直角三角形的应用,熟练掌握三角函数的相关定义以及变形是解题的关键.17、>【解题分析】根据二次函数解析式可知函数图象对称轴是x=0,且开口向上,分析可知两点均在对称轴左侧的图象上;接下来,结合二次函数的性质可判断对称轴左侧图象的增减性,【题目详解】解:二次函数22y x k =+的函数图象对称轴是x=0,且开口向上,∴在对称轴的左侧y 随x 的增大而减小,∵-3>-4,∴1y >2y .故答案为>.【题目点拨】本题考查了二次函数的图像和数形结合的数学思想.三、解答题(共7小题,满分69分)18、3.05米【解题分析】延长FE 交CB 的延长线于M, 过A 作AG ⊥FM 于G , 解直角三角形即可得到正确结论.【题目详解】 解:如图:延长FE 交CB 的延长线于M ,过A 作AG ⊥FM 于G ,在Rt △ABC 中,tan ∠ACB=,∴AB=BC•tan60°=1.5×1.73=2.595,∴GM=AB=2.595,在Rt △AGF 中,∵∠FAG=∠FHE=45°,sin ∠FAG=,∴sin45°=, ∴FG=1.76,∴DM=FG+GM ﹣DF≈3.05米.答:篮框D 到地面的距离是3.05米.【题目点拨】本题主要考查直角三角形和三角函数,构造合适的辅助线是本题解题的关键.19、(1)12;(2)点A不与点B重合;(3)1919 86b≤≤【解题分析】(1)把B、C两点代入解析式,得到k=4(1﹣m)=6×(﹣m),求得m=﹣2,从而求得k的值;(2)由抛物线解析式得到顶点A(b,b2),如果点A与点B重合,则有b=4,且b2=3,显然不成立;(3)当抛物线经过点B(4,3)时,解得,b=198,抛物线右半支经过点B;当抛物线经过点C,解得,b=196,抛物线右半支经过点C;从而求得b的取值范围为198≤b≤196.【题目详解】解:(1)∵B(4,1﹣m),C(6,﹣m)在反比例函数kyx=的图象上,∴k=4(1﹣m)=6×(﹣m),∴解得m=﹣2,∴k=4×[1﹣(﹣2)]=12;(2)∵m=﹣2,∴B(4,3),∵抛物线y=﹣x2+2bx=﹣(x﹣b)2+b2,∴A(b,b2).若点A与点B重合,则有b=4,且b2=3,显然不成立,∴点A不与点B重合;(3)当抛物线经过点B(4,3)时,有3=﹣42+2b×4,解得,b=198,显然抛物线右半支经过点B;当抛物线经过点C(6,2)时,有2=﹣62+2b×6,解得,b=196,这时仍然是抛物线右半支经过点C,∴b的取值范围为198≤b≤196.【题目点拨】本题考查了二次函数的性质,二次函数图象上点的坐标特征,解题的关键是学会用讨论的思想思考问题.20、(1)见解析;(2)tan∠AOD=3 4 .【解题分析】(1)作DF⊥AB于F,连接OC,则△ODF是等腰直角三角形,得出OC=OD=2DF,由垂径定理得出∠COE=90°,证明△DEF∽△CEO得出22ED OC DFCE DF DF===,即可得出结论;(2)由题意得OE=12OA=12OC,同(1)得△DEF∽△CEO,得出12EF EODF OC==,设⊙O的半径为2a(a>0),则OD=2a,EO=a,设EF=x,则DF=2x,在Rt△ODF中,由勾股定理求出x=35a,得出DF=65a,OF=EF+EO=85a,由三角函数定义即可得出结果.【题目详解】(1)证明:作DF⊥AB于F,连接OC,如图所示:则∠DFE=90°,∵∠AOD=45°,∴△ODF是等腰直角三角形,∴OC=OD2DF,∵C是弧AB的中点,∴OC⊥AB,∴∠COE=90°,∵∠DEF=∠CEO,∴△DEF∽△CEO,∴22 ED OC DFCE DF DF===∴CE2ED;(2)如图所示:∵AE =EO ,∴OE=12OA=12OC , 同(1)得:,△DEF ∽△CEO , ∴12EF EO DF OC ==, 设⊙O 的半径为2a (a >0),则OD =2a ,EO =a ,设EF =x ,则DF =2x ,在Rt △ODF 中,由勾股定理得:(2x )2+(x+a )2=(2a )2,解得:x =35a ,或x =﹣a (舍去), ∴DF =65a ,OF =EF+EO =85a , ∴DF 3tan AOD OF 4∠==. 【题目点拨】本题考查了等腰直角三角形的判定与性质、相似三角形的判定与性质、勾股定理、垂径定理、三角函数等知识,熟练掌握相似三角形的判定与性质、勾股定理是关键.21、(1)223y x x =--;(2)P 点坐标为315,24⎛⎫- ⎪⎝⎭, 758;(3)Q 31,2⎛- ⎝⎭或31,2⎛- ⎝⎭或()1,2或()1,4-. 【解题分析】(1)根据待定系数法把A 、C 两点坐标代入2y x bx c =++可求得二次函数的解析式;(2)由抛物线解析式可求得B 点坐标,由B 、C 坐标可求得直线BC 解析式,可设出P 点坐标,用P 点坐标表示出四边形ABPC 的面积,根据二次函数的性质可求得其面积的最大值及P 点坐标;(3)首先设出Q 点的坐标,则可表示出QB 2、QC 2和BC 2,然后分∠BQC=90°、∠CBQ=90°和∠BCQ=90°三种情况,求解即可.【题目详解】解:(1)∵A(-1,0),()0,3C -在2y x bx c =++上,103b c c -+=⎧∴⎨=-⎩,解得23b c =-⎧⎨=-⎩, ∴二次函数的解析式为223y x x =--;(2)在223y x x =--中,令0y =可得2023x x -=-,解得3x =或1x =-,()3,0B ∴,且()0,3C -,∴经过B 、C 两点的直线为3y x =-,设点P 的坐标为()223x x x --,,如图,过点P 作PD x ⊥轴,垂足为D ,与直线BC 交于点E ,则(),3E x x -,ABC BCP ABPC S S S ∆∆=+四边形()211433322x x =⨯⨯+-⨯239622x x =-++23375228x ⎛⎫=-+ ⎪⎝⎭, ∴当32x =时,四边形ABPC 的面积最大,此时P 点坐标为315,24⎛⎫- ⎪⎝⎭, ∴四边形ABPC 的最大面积为758; (3)()222314y x x x =--=--,∴对称轴为1x =,∴可设Q 点坐标为()1,t ,()3,0B ,()0,3C -,()2222134BQ t t ∴=-+=+,()222213610CQ t t t =++=++,218BC =,QBC ∆为直角三角形,∴有90BQC ∠=︒、90CBQ ∠=︒和90BCQ ∠=︒三种情况,①当90BQC ∠=︒时,则有222BQ CQ BC +=,即22461018t t t ++++=,解得317t -+=或317t --=,此时Q 点坐标为3171,2⎛-+ ⎝⎭或3171,2⎛- ⎝⎭; ②当90CBQ ∠=︒时,则有222BC BQ CQ +=,即22418610t t t ++=++,解得2t =,此时Q 点坐标为()1,2; ③当90BCQ ∠=︒时,则有222BC CQ BQ +=,即22186104t t t +++=+,解得4t =-,此时Q 点坐标为()1,4-;综上可知Q 点的坐标为⎛ ⎝⎭或⎛ ⎝⎭或()1,2或()1,4-. 【题目点拨】本题考查了待定系数法、三角形的面积、二次函数的性质、勾股定理、方程思想及分类讨论思想等知识,注意分类讨论思想的应用.22、(1)243y x x +=﹣,顶点P 的坐标为21(,﹣);(2)E 点坐标为22(,);(3)Q 点的坐标为58(,). 【解题分析】(1)利用交点式写出抛物线解析式,把一般式配成顶点式得到顶点P 的坐标;(2)设2E t (,),根据两点间的距离公式,利用EA EC =得到22222123t t ++(﹣)=(﹣),然后解方程求出t 即可得到E 点坐标;(3)直线2x =交x 轴于F ,作2MH x ⊥直线=于H ,如图,利用12tan NEB ∠=得到12tan MEQ ∠=,设243Q m m m +(,﹣),则2412HE m m QH m +=﹣,=﹣,再在Rt QHE 中利用正切的定义得到H 1tan HE 2Q HEQ ∠==,即24122m m m +﹣=(﹣),然后解方程求出m 即可得到Q 点坐标.【题目详解】解:(1)抛物线解析式为13y x x =(﹣)(﹣), 即243y x x +=﹣, 221y x =(﹣)﹣,∴顶点P 的坐标为21(,﹣); (2)抛物线的对称轴为直线2x =,设2E t (,), EA EC =,22222123t t ∴++(﹣)=(﹣),解得2t =,∴E 点坐标为22(,); (3)直线2x =交x 轴于F ,作MN ⊥直线x=2于H ,如图,MEQ NEB ∠∠=, 而BF 1tan EF 2NEB ∠==, 1tan 2MEQ ∴∠=,设243Q m m m +(,﹣),则22432412HE m m m m QH m ++=﹣﹣=﹣,=﹣,在Rt QHE 中,H 1tan HE 2Q HEQ ∠==, 24122m m m ∴+﹣=(﹣),整理得2650m m +﹣=,解得11m =(舍去),25m =, ∴Q 点的坐标为58(,).【题目点拨】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和锐角三角函数的定义;会利用待定系数法求函数解析式;理解坐标与图形性质,记住两点间的距离公式.23、(1)证明见解析;(2)1.【解题分析】试题分析:(1)根据垂直的定义可得∠CEB=90°,然后根据角平分线的性质和等腰三角形的性质,判断出∠1=∠D ,从而根据平行线的判定得到CE ∥BD ,根据平行线的性质得∠DBA=∠CEB ,由此可根据切线的判定得证结果;(2)连接AC ,由射影定理可得,进而求得EB 的长,再由勾股定理求得BD=BC 的长,然后由“两角对应相等的两三角形相似”的性质证得△EFC ∽△BFD ,再由相似三角形的性质得出结果.试题解析:(1)证明:∵,∴. ∵CD 平分,BC=BD , ∴,. ∴. ∴∥. ∴. ∵AB 是⊙O 的直径,∴BD 是⊙O 的切线.(2)连接AC ,∵AB 是⊙O 直径, ∴. ∵, 可得. ∴ 在Rt △CEB 中,∠CEB=90°,由勾股定理得∴. ∵,∠EFC =∠BFD ,∴△EFC ∽△BFD . ∴. ∴.∴BF=1.考点:切线的判定,相似三角形,勾股定理24、开口方向:向上;点坐标:(-1,-3);称轴:直线1x =-.【解题分析】将二次函数一般式化为顶点式,再根据a 的值即可确定该函数图像的开口方向、顶点坐标和对称轴.【题目详解】解:()2221y x x =+-, ()222121y x x =++--,()2213y x =+-,∴开口方向:向上,顶点坐标:(-1,-3),对称轴:直线1x =-.【题目点拨】熟练掌握将一般式化为顶点式是解题关键.。
天津中考数学压轴题解析

2008年—2013年天津中考压轴题解析1. (2013·天津)已知抛物线y 1=ax 2+bx +c (a ≠0)的对称轴是直线l ,顶点为点M .若自变量x 和函数值y 1的部分对应值如下表所示: (Ⅰ)求y 1与x 之间的函数关系式;(Ⅱ)若经过点T (0,t )作垂直于y 轴的直线l ′,A 为直线l ′上的动点,线段AM 的垂直平分线交直线l 于点B ,点B 关于直线AM 的对称点为P ,记P (x ,y 2). (1)求y 2与x 之间的函数关系式;(2)当x<y 恒成立,求t 的取值范围.解:(Ⅰ)∵抛物线经过点(0,94),∴c =94.∴y 1=ax 2+bx +94,∵点(–1,0)、(3,0)在抛物线y 1=ax 2+bx +94上, ∴90499304a b a b ⎧-+=⎪⎪⎨⎪++=⎪⎩,解得,3432a b ⎧=-⎪⎪⎨⎪=⎪⎩∴y 1与x 之间的函数关系式为:y 1= –34x 2+32x +94;(II)∵y 1= –34x 2+32x +94,∴y 1= –34(x –1)2+3,∴直线l 为x =1,顶点M (1,3). ①由题意得,t ≠3,如图,记直线l 与直线l ′交于点C (1,t ),当点A 与点C 不重合时, ∵由已知得,AM 与BP 互相垂直平分, ∴四边形ANMP 为菱形, ∴P A ∥l ,又∵点P (x ,y 2), ∴点A (x ,t ) (x ≠1), ∴PM =P A =|y 2–t |,过点P 作PQ ⊥l 于点Q ,则点Q (1,y 2), ∴QM =|y 2–3|,PQ =AC =|x –1|, 在Rt △PQM 中,∵PM 2=QM 2+PQ 2,即(y 2–t )2=(y 2–3)2+(x –1)2,整理得,y 2=162t -(x –1)2+32t +, 即y 2=162t -x 2–13t -x +21062t t--,∵当点A 与点C 重合时,点B 与点P 重合, ∴P (1,32t +), ∴P 点坐标也满足上式,∴y 2与x 之间的函数关系式为y 2=162t -x 2–13t -x +21062tt-- (t ≠3); ②根据题意,借助函数图象:当抛物线y 2开口方向向上时,6–2t >0,即t <3时,抛物线y 1的顶点M (1,3),抛物线y 2的顶点(1,32t +), ∵3>32t +,∴不合题意,当抛物线y 2开口方向向下时,6–2t <0,即t >3时,y 1–y 2= –34(x –1)2+3–[162t -(x –1)2+32t +]=3114(3)t t --(x –1)2+32t -,若3t –11≠0,要使y 1<y 2恒成立, 只要抛物线y =3114(3)t t --(x –1)2+32t -开口方向向下,且顶点(1,32t -)在x 轴下方,∵3–t <0,只要3t –11>0,解得t >113,符合题意; 若3t –11=0,y 1–y 2= –13<0,即t =113也符合题意.综上,可以使y 1<y 2恒成立的t 的取值范围是t ≥113.2. (2012·天津)已知抛物线y =ax 2+bx +c (0<2a <b )的顶点为P (x 0,y 0),点A (1,y A )、B (0,y B )、 C (-1,y C )在该抛物线上.(Ⅰ)当a =1,b =4,c =10时,①求顶点P 的坐标;②求AB Cy y y -的值;(Ⅱ)当y 0≥0恒成立时,求AB Cy y y -的最小值.解:(Ⅰ)若a =1,b =4,c =10,此时抛物线的解析式为y =x 2+4x +10. ①∵y =x 2+4x +10=(x +2)2+6,∴抛物线的顶点坐标为P (-2,6). ②∵点A (1,y A )、B (0,y B )、C (-1,y C )在抛物线y =x 2+4x +10上, ∴y A =15,y B =10,y C =7.∴155107A B C y y y ==--.(Ⅱ)由0<2a <b ,得012bx a=--<. 由题意,如图过点A 作AA 1⊥x 轴于点A 1, 则AA 1=y A ,OA 1=1.连接BC ,过点C 作CD ⊥y 轴于点D , 则BD =y B -y C ,CD =1.过点A 作AF ∥BC ,交抛物线于点E (x 1,y E ), 交x 轴于点F (x 2,0).则∠F AA 1=∠CBD .∴Rt △AF A 1∽Rt △BCD .∴11AA FA BD CD = ,即22111A B C y x x y y -==--. 过点E 作EG ⊥AA 1于点G ,易得△AEG ∽△BCD . ∴AG EG BD CD =,即A EB Cy y y y --=1–x 1. ∵点A (1,y A )、B (0,y B )、C (-1,y C )、E (x 1,y E )在抛物线y =ax 2+bx +c 上, ∴y A =a +b +c ,y B =c ,y C =a -b +c ,y E =ax 12+bx 1+c ,∴2111()()1()a b c ax bx c x c a b c ++-++=---+,化简,得x 12+x 1-2=0,解得x 1=-2(x 1=1舍去).∵y 0≥0恒成立,根据题意,有x 2≤x 1<-1. 则1-x 2≥1-x 1,即1-x 2≥3.∴AB Cy y y -的最小值为3.解法2:(Ⅱ)解:设m >0,由于b >2a >0,令b =2a +m 当y 0≥0恒成立时,应有b 2–4ac ≤0 ∴(2a +m )2–4ac ≤0 ∵a >0∴c ≥2(2)4a m a +=2(2)4a m a +–2m +2m =2(2)4a m a-+2m∵2(2)4a m a-≥0∴c ≥2m∵点A (1,y A )、B (0,y B )、C (–1,y C )在抛物线y =ax 2+bx +c 上 ∴y A =a +b +c , y B =c , y C = a –b +c ∴A B C y y y -=()a b cc a b c ++--+= a b c b a ++-代入b =2a +m ,得AB Cy y y -= 22a a m c a m a ++++-= 2a m a c a m ++++= 21a c a m +++∵c ≥2m , ∴AB Cy y y -= 21a c a m +++≥221a m a m +++=3∴AB Cy y y -的最小值为3解法3:A (1,a +b +c )、B (0,c )、C (–1,a –b +c )由B (0,c )、C (–1,a –b +c )得直线BC 为y =(b –a )x +c ∵AE ∥BC ∴设直线AE 为y =(b –a )x +m将A (1,a +b +c )代入上式,得m =2a +c . ∴直线AE 为y =(b –a )x +2a +c由()2–2y b a x a c y ax bx c⎧=++⎪⎨=++⎪⎩得x 2+x –2=0. 解得E 点横坐标为x 1=–2(x 1=1舍去)∵y 0≥0恒成立,根据题意,有x 2≤x 1<-1. 则1-x 2≥1-x 1,即1-x 2≥3.∴AB Cy y y -的最小值为3.3. (2011·天津)已知抛物线1C :21112y x x =-+.点F (1,1). (Ⅰ) 求抛物线1C 的顶点坐标;(Ⅱ) ①若抛物线1C 与y 轴的交点为A .连接AF ,并延长交抛物线1C 于点B ,求证:112AF BF+= ②抛物线1C 上任意一点P (P P x y ,))(01P x <<).连接PF .并延长交抛物线1C 于点Q (Q Q x y ,),试判断112PF QF+=是否成立?请说明理由; (Ⅲ) 将抛物线1C 作适当的平移.得抛物线2C :221()2y x h =-,若2x m <≤时.2y x ≤恒成立,求m 的最大值.解 (I)∵2211111(1)222y x x x =-+=-+, ∴抛物线1C 的顶点坐标为(112, ).(II)①根据题意,可得点A (0,1), ∵F (1,1).∴AB ∥x 轴.得AF =BF =1,112AF BF+= ②112PF QF+=成立. 理由如下:如图,过点P (P P x y ,)作PM ⊥AB 于点M ,则FM =1P x -,PM =1P y -(01P x <<) ∴Rt △PMF 中,由勾股定理,得22222(1)(1)P P PF FM PM x y =+=-+-又点P (P P x y ,)在抛物线1C 上, 得211(1)22P P y x =-+,即2(1)21P P x y -=- ∴22221(1)P P P PF y y y =-+-= 即P PF y =.过点Q (Q Q x y ,)作QN ⊥A B ,与AB 的延长线交于点N , 同理可得Q QF y =.图文∠PMF =∠QNF =90°,∠MFP =∠NFQ ,∴△PMF ∽△QNF 有PF PMQF QN= 这里11P PM y PF =-=-,11Q QN y QF =-=-x∴11PF PFQF QF -=- 即112PF QF+= (Ⅲ) 令3y x =,设其图象与抛物线2C 交点的横坐标为0x ,x 0′,且0x < x 0′, ∵抛物线2C 可以看作是抛物线212y x =左右平移得到的, 观察图象.随着抛物线2C 向右不断平移,0x ,x 0′ 的值不断增大, ∴当满足2x m <≤,.2y x ≤恒成立时,m 的最大值在x 0′ 处取得. 可得当02x =时.所对应的x 0′ 即为m 的最大值.于是,将02x =带入21()2x h x -=,有21(2)22h -=解得4h =或0h =(舍) ∴221(4)2y x =-此时,23y y =,得21(4)2x x -=解得02x =,x 0′=8 ∴m 的最大值为8.4. (2010·天津)在平面直角坐标系中,已知抛物线2y x bx c =-++与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴的正半轴交于点C ,顶点为E . (Ⅰ)若2b =,3c =,求此时抛物线顶点E 的坐标;(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC 中满足S △BCE = S △ABC ,求此时直线BC 的解析式;(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC 中满足S △BCE = 2S △AOC ,且顶点E恰好落在直线43y x =-+上,求此时抛物线的解析式.解:(Ⅰ)当2b =,3c =时,抛物线的解析式为223y x x =-++,即2(1)4y x =--+.∴ 抛物线顶点E 的坐标为(1,4). .................2分(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点E 在对称轴1x =上,有2b =,∴ 抛物线的解析式为22y x x c =-++(0c >).∴ 此时,抛物线与y 轴的交点为0( )C c ,,顶点为1( 1)E c +,. ∵ 方程220x x c -++=的两个根为11x =21x = ∴ 此时,抛物线与x轴的交点为10()A,10()B . 如图,过点E 作EF ∥CB 与x 轴交于点F ,连接CF ,则S △BCE = S △BCF . ∵ S △BCE = S △ABC , ∴ S △BCF = S △ABC . ∴BF AB ==设对称轴1x =与x 轴交于点D ,则12DF AB BF =+= 由EF ∥CB ,得EFD CBO ∠=∠. ∴ Rt △EDF ∽Rt △COB .有ED CODF OB=. ∴=54c =. ∴ 点54(0 )C ,,52( 0)B ,.设直线BC 的解析式为y mx n =+,则5,450.2n m n ⎧=⎪⎪⎨⎪=+⎪⎩ 解得 1,25.4m n ⎧=-⎪⎪⎨⎪=⎪⎩ ∴ 直线BC 的解析式为1524y x =-+. .....................6分(Ⅲ)根据题意,设抛物线的顶点为( )E h k ,,(0h >,0k >) 则抛物线的解析式为2()y x h k =--+, 此时,抛物线与y 轴的交点为2(0 )C h k -+,,与x轴的交点为0()A h,0()B h0h >>) 过点E 作EF ∥CB 与x 轴交于点F ,连接CF , 则S △BCE = S △BCF . 由S △BCE = 2S △AOC ,x∴ S △BCF = 2S △AOC . 得2)BF AO h ==. 设该抛物线的对称轴与x 轴交于点D .则 122DF AB BF h =+=. 于是,由Rt △EDF ∽Rt △COB ,有ED CODF OB=.∴2=2220h k -+=.结合题意,解得 h =① ∵ 点( )E h k ,在直线43y x =-+上,有43k h =-+. ②∴ 1=. 有1k =,12h =.∴ 抛物线的解析式为234y x x =-++. ..........10分5. (2009·天津)已知函数y 1=x ,y 2=x 2+bx+c ,α,β为方程y 1–y 2=0的两个根,点M (t ,T )在函数y 2的图象上. (Ⅰ)若α=13,β=12,求函数y 2的解析式; (Ⅱ)在(Ⅰ)的条件下,若函数y 1与y 2的图象的两个交点为A ,B ,当△ABM 的面积为3112时,求t 的值; (Ⅲ)若0<α<β<1,当01t <<时,试确定T ,α,β三者之间的大小关系,并说明理由.解:(Ⅰ)212120y x y x bx c y y ==++-=,,,()210x b x c ∴+-+=.将1132αβ==,分别代入()210x b x c +-+=,得 ()()22111110103322b c b c ⎛⎫⎛⎫+-⨯+=+-⨯+= ⎪ ⎪⎝⎭⎝⎭,, 解得1166b c ==,. ∴函数2y 的解析式为2y 25166x x =-+.另解第(Ⅰ)问:比较系数法∵α=13,β=12是方程的两个根,∴11()()032x x --=,即251066x x -+=. …… ①∵120y y -=, ∴2(1)0x b x c +-+=. …… ②方程①,②相同,比较系数得 516b -=-,即16b =,16c =.∴221166y x x =++另解第(Ⅰ)问:韦达定理法 ∵α+β=56αβ=16∴α、β是一元二次方程251066x x -+=的两个根又α、β是一元二次方程2(1)0x b x c +-+=的两个根∴比较系数得 516b -=-,即16b =,16c =.∴221166y x x =++(Ⅱ)由已知,得AB ,设△ABM 的高为h ,31121212ABM S AB h h ∴===△·1144=. 根据题意,t T -=,∴t T -=1144由21166T t t =++,得251166144t t -+-=. 当251166144t t -+=-时,解得12512t t ==;当251166144t t -+=时,解得34551212t t +==. ∴t 的值为555121212+,,另解第(Ⅱ)问:方法1:过点M 作x 轴的垂线,与y x =交于点N ,111()(||)223ABM S T t ∆=--,21166T t t =++,解得 1512t =,2t =,3t =.方法2:当t α<<β时,S △ABM =S △ABC -S △ADM -S 梯形MDCB ,即311111*********()()()()[()()]()122232323323232t T T t =-------+--,解得 1512t =. 同理,当0t <<α时,3111111111111()()()()[()()]()1222223323223t T t T T T =-------+--,解得2t =. 当1t β<<时,即311111*********()()()()[()()]()122332232323232t T T t =-------+--,解得3t =. 方法3:∵11(,)33A ,11(,)22B , ∴||AB =.设在△ABM 中以AB 为底的高为h ,则h y x =向上或向下平移1144个单位,得31144y x =-,41144y x =+.解3y 与2y 的交点,得1512t =,解4y 与2y 的交点,得2t =3t =.注:第二问的每一种解法都充分利用了数形结合数学思想,特别是利用直线y =x 的本质特征,使T 、t 转化为统一级别的量再运算. (Ⅲ)由已知,得222b c b c T t bt c αααβββ=++=++=++,,.()()T t t b ααα∴-=-++, ()()T t t b βββ-=-++,()()22b c b c αβααββ-=++-++,化简得()()10b αβαβ-++-=.01αβ<<<,得0αβ-≠, 10b αβ∴++-=.有1010b b αββα+=->+=->,. 又01t <<,0t b α∴++>,0t b β++>,∴当0t a <≤时,T αβ≤≤;当t αβ<≤时,T αβ<≤; 当1t β<<时,T αβ<<.第(Ⅲ)问:图象分析法 ①当对称轴在y 轴左侧时,在0<x <1,y 随x 的增大而增大, ②当对称轴在y 轴右侧时,当α<t ≤β时,α<T ≤β; 当β<t <1时,α<β<T .6. (2008·天津)已知抛物线c bx ax y ++=232,(Ⅰ)若1==b a ,1-=c ,求该抛物线与x 轴公共点的坐标; (Ⅱ)若1==b a ,且当11<<-x 时,抛物线与x 轴有且只有一个公共点,求c 的取值范围; (Ⅲ)若0=++c b a ,且01=x 时,对应的01>y ;12=x 时,对应的02>y ,试判断当10<<x 时,抛物线与x 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.解(Ⅰ)当1==b a ,1-=c 时,抛物线为1232-+=x x y , 方程01232=-+x x 的两个根为11-=x ,312=x . ∴该抛物线与x 轴公共点的坐标是()10-,和103⎛⎫ ⎪⎝⎭,. (Ⅱ)当1==b a 时,抛物线为c x x y ++=232,且与x 轴有公共点.对于方程0232=++c x x ,判别式c 124-=∆≥0,有c ≤31.①当31=c 时,由方程031232=++x x ,解得3121-==x x . 此时抛物线为31232++=x x y 与x 轴只有一个公共点103⎛⎫- ⎪⎝⎭,. ②当31<c 时, 11-=x 时,c c y +=+-=1231, 12=x 时,c c y +=++=5232.由已知11<<-x 时,该抛物线与x 轴有且只有一个公共点,考虑其对称轴为31-=x ,应有1200.y y ⎧⎨>⎩≤, 即1050.c c +⎧⎨+>⎩≤,解得51c -<-≤. 综上,31=c 或51c -<-≤.第(Ⅱ)问解法二(图象法)或103c ∆=⇒=; 或 01010x y x y ∆>⎧⎪=-≤⇒⎨⎪=>⎩时时51c -<-≤综上,31=c 或51c -<-≤. (Ⅲ)对于二次函数c bx ax y ++=232,由已知01=x 时,01>=c y ;12=x 时,0232>++=c b a y , 又0=++c b a ,∴b a b a c b a c b a +=++++=++22)(23. 于是02>+b a .而c a b --=,∴02>--c a a ,即0>-c a .∴0>>c a .∵关于x 的一元二次方程0232=++c bx ax 的判别式0])[(412)(4124222>+-=-+=-=∆ac c a ac c a ac b ,∴抛物线c bx ax y ++=232与x 轴有两个公共点,顶点在x 轴下方. 又该抛物线的对称轴abx 3-=, 由0=++c b a ,0>c ,,c a b o ∴-=+<b a ∴<- 又02>+b a , 得a b a -<<-2,∴32331<-<a b . 又由已知01=x 时,01>y ;12=x 时,02>y ,观察图象, 可知在10<<x 范围内,该抛物线与x 轴有两个公共点. 说明:适时画出图象草图更能说明问题,体现数形结合.。
天津市中考数学压轴题大集合

解法三:(接上)求得∴ h= 5 因为抛物线的方程为 y= ax2+ bx+ c( a≠0)
abc 0
a=-5
a5
由已知得 a b c 0 解得 b 0 或 b 0
4ac b 2
5
4a
c5
∴抛物线的解析式为 y = 5x2- 5 或 y =- 5x2+ 5.
c5
3.(2004 湖北荆门 )如图,在直角坐标系中,以点 P(1,- 1)为圆心, 2 为半径作圆,交
4. ( 2004 湖北襄樊)如图,在平面直角坐标系内, Rt△ ABC 的直角顶点 C( 0, 3 ) 在 y 轴的正半轴上, A、B 是 x 轴上是两点,且 OA∶ OB= 3∶ 1,以 OA、OB 为直径
的圆分别交 AC 于点 E,交 BC 于点 F .直线 EF 交 OC 于点 Q.
( 1)求过 A、B、C 三点的抛物线的解析式;
在 Rt△ PMB 中, PB=2,PM=1,
∴∠ MPB = 60°,∴∠ APB = 120 °
⌒
120
AB 的长=
180
4 2
3
( 2)在 Rt△ PMB 中, PB=2,PM=1, 则 MB = MA = 3 .
A
B
O·
x
P( 1,- 1)
C y
又 OM=1 ,∴ A( 1- 3 , 0), B ( 1+ 3 , 0),
在△ ABM 中, AB = 2 , AM = 2 , BM = 2
AB2 AM 2 ( 2 )2 ( 2) 2 4 BM 2
∴△ ABM 是直角三角形,∠ BAM = 90° ∴ 直线 AB 是⊙ M 的切线
( 3)解法一:由⑵得∠ BAC = 90°, AB = 2 , AC = 2 2 ,
天津中考数学第24题(几何压轴题)思路分析及真题练习

天津中考数学第24题(几何压轴题)思路分析及真题练习思路分析:观察近几年的中考真题可以发现,每年倒数第二题的出题形式,都是将几何图形放在平面直角坐标系中。
但是,由于解析几何要到高中才学,所以坐标系在这里其实只能起到一个确定点的坐标的作用。
当然,如果把直线看成一次函数图像,一次函数解析式就是直线方程,也就可以将直线交点问题,转化为方程组求解问题,但在这道题中通常都不需要这样做。
题目每年都会对几何图形进行变换,近六年的变换规律是:旋转、对称、旋转、对称、旋转、平移,明年应该大概率是旋转。
因为无论是对称变换、旋转变换还是平移变换,图形的大小和形状都不会发生改变,所以每年的题目都会涉及到全等。
由于在图形变换的过程中,全等的判定通常都是比较容易的,所以本题对全等的考察又主要在全等性质的应用上。
题目设问无论是点的坐标、线段的长还是图形的面积,其核心都是求距离。
所有的距离又都可以转化为求两点间的距离或求点到直线间的距离。
任意两点之间的距离公式虽然要高中才学,但我们可以将两点之间的距离转化为求一个直角三角形的斜边长,用勾股定理求解。
因此,我们会发现每年的题目中几乎都会涉及到勾股定理。
任意点到任意直线的距离公式也要到高中才会学习,但对于一些特殊情况,我们现在就可以做了。
每年的第一问,都是送分问,用一次勾股定理基本都可以解决。
第二问和第三问,解题的关键是要抓住全等的性质和特殊三角形。
第三问通常也会和其它知识点结合,但涉及的都是一些基础知识点,基本功扎实的同学,问题都不大。
最后提醒一下,当对图形进行旋转变换时,尤其需要注意其与圆的结合。
在研究点、直线、圆和圆的位置关系时,只需要研究它们和圆心的位置关系即可。
而在旋转变换时,旋转中心自然就是圆心。
真题练习参考答案。
2024-2025学年度天津市中考数学模拟试卷 压轴4卷
2024-2025学年度天津市中考数学模拟试卷 压轴4卷一、选择题:本大题共 12 小题,每小题 3 分,共 36 分1.计算:(﹣5)+3 的结果是( )A .﹣2B .﹣8C .2D .82.tan60°的值等于()A . 12B .C .D .3.大自然中存在许多对称现象,下列植物叶子的图案中既是轴对称,又是中心对称图形的是()A .B .C .D . 4.据统计去年来国内旅游人数达到 9.98 亿人次,用科学记数法表示 9.98 亿正确的是()A .9.98×107B .0.998×109C .9.98×108D .99.8×107 5.如图是由 6 个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )A .B .C .D .6) A .2 和 3 之间B .3 和 4 之间C .4 和 5 之间D .5 和 6 之间7.化简211x xx x+--的结果是( )A .xB .x ﹣1C .﹣xD .x +18.关于 x 的一元二次方程 (a -1) x 2 + x + a 2 -1 = 0 的一个根是 0,则 a 的值为( )A .1B .﹣1C .1 或﹣1D .129.如图数轴的 A 、B 、C 三点所表示的数分别为 a 、b 、c .若|a ﹣b |=3,|b ﹣c |=5,且原点 O 与 A 、B 的距离 分别为 4、1,则关于 O 的位置,下列叙述何者正确?( )A .在 A 的左边B .介于 A 、B 之间C .介于 B 、C 之间D .在 C 的右边10.如图,把一张矩形纸片 ABCD 沿 EF 折叠后,点 A 落在 CD 边上的点 A ′处,点 B 落在点 B ′处,若∠2=40°, 则图中∠1 的度数为( ) A .115° B .120° C .130°D .140°11.已知 A (x 1,y 1),B (x 2,y 2)是反比例函数 y =kx(k ≠0)图象上的两个点,当 x 1<x 2<0 时,y 1>y 2,那 么一次函数 y =kx ﹣k 的图象不经过( )A .第一象限B .其次象限C .第三象限D .第四象限12. 二次函数 y = -( x -1)2+ 5 ,当 m ≤x ≤n 且 mn <0 时,y 的最小值为 2m ,最大值为 2n ,则 m +n 的值为 A . 52B . 3C . 32D . 12二、填空题:本大题共 6 小题,每小题 3 分,共 18 分13. 4 - (-2)2=14.计算: (5- 2)(5 + 2)= .2024202415.不透亮的袋子里装有将 10 个乒乓球,其中 5 个白色的,2 个黄色的,3 个红色的,这些乒乓球除颜色外全相同,从中随意摸出一个,则摸出白色乒乓球的概率是 .16.某盏路灯照耀的空间可以看成如图所示的圆锥,它的高 AO =8 米,母线 AB 与底面半径 OB 的夹角为 α, tan α =43,则圆锥的侧面积是 平方米(结果保留 π). 17.如图,∠AOB =30°,点 M 、N 分别是射线 OA 、OB 上的动点,OP 平分∠AOB ,且 OP =6,△PMN 的周长最 小值为.18. 如图,在每个小正方形的边长为1 的网格中,取格点A、B、C 并连接AB,BC.取格点D、E 并连接,交AB 于点F.(Ⅰ)BF 的长等于;(Ⅱ)若点G 在线段BC 上,且满意AF+CG=FG,请在如图所示的网格中,用无刻度的直尺,确定点G 的位置,并简要说明点G 的位置是如何找到的(不要求证明).(学而思原创题)三、综合题:本大题共7 小题,共66 分19.(8 分)解不等式2(2)3(1)134x xx x-≤-⎧⎪+⎨⎪⎩请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得;(Ⅱ)解不等式②,得;(Ⅲ)把不等式①和②的解集在数轴上表示出来;(Ⅳ)原不等式组的解集为.20.(8 分)为了解某中学学生对“厉行勤俭节约,反对铺张奢侈”主题活动的参加状况.大宝在全校范围内随机抽取了若干名学生并就某日午饭奢侈饭菜状况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.依据调查结果,绘制了如图所示两幅尚不完整的统计图.回答下列问题:(Ⅰ)这次被抽查的学生共有人,扇形统计图中,“B 组”所对应的圆心角的度数为;(Ⅱ)补全条形统计图;(Ⅲ)已知该中学共有学生2500 人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10 克米饭计算,这日午饭将奢侈多少千克米饭?21.(10 分)如图1,以△ABC 的边AB 为直径的⊙O 交边BC 于点E,过点E 作⊙O 的切线交AC 于点D,且ED⊥AC.(Ⅰ)试推断△ABC 的形态,并说明理由;(Ⅱ)如图2,若线段AB、DE 的延长线交于点F,∠C=75°,CD=2,求⊙O 的半径和BF 的长.22.(10 分)如图,某飞机于空中探测某座山的高度,在点A 处飞机的飞行高度是AF=3700 米,从飞机上观测山顶目标C 的俯角是45°,飞机接着以相同的高度飞行300 米到B 处,此时观测目标C 的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).23.(10 分)某工厂安排聘请A、B 两个工种的工人共120 人,A、B 两个工种的工人月工资分别为1600 元和2024 元.(Ⅰ)若某工厂每月支付的工人工资为220240 元,那么A、B 两个工种的工人各聘请多少人?设聘请A 工种的工人A 工种人数的2 倍,那么聘请A 工种的工人多少人时,可使工厂每月支付的工人工资最少?24.(10 分)如图1,点A 是x 轴正半轴上的动点,点B 坐标为(0,4),M 是线段AB 的中点,将点M 绕点A 顺时针方向旋转90°得到点C,过点C 作x 轴的垂线,垂足为F,过点B 作y 轴的垂线与直线CF 相交于点E,点D 是点A 关于直线CF 的对称点,连结AC,BC,CD,设点A 的横坐标为t.(Ⅰ)当t=2 时,求CF 的长;(Ⅱ)①当t 为何值时,点C 落在线段BD 上;②设△BCE 的面积为S,当0<t<8 时,求S 与t 之间的函数关系式;(Ⅲ)如图2,当点C 与点E 重合时,将△CDF 沿x 轴左右平移得到△C'D'F',再将A,B,C',D'为顶点的四边形沿C'F'剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请干脆写出全部符合上述条件的点C'的坐标.25.(10 分)在平面直角坐标系中,点 O 为原点,平行于 x 轴的直线与抛物线 L :y =ax 2 相交于 A ,B 两点(点 B 在第一象 限),点 D 在 AB 的延长线上. (Ⅰ)已知 a =1,点 B 的纵坐标为 2. ①如图 1,向右平移抛物线 L 使该抛物线过点 B ,与 AB 的延长线交于点 C ,求 AC 的长.②如图 2,若BD = 12AB ,过点 B ,D 的抛物线 L ,其顶点 M 在 x 轴上,求该抛物线的函数表达式.(Ⅱ)如图 3,若 BD =AB ,过 O ,B ,D 三点的抛物线 L 3,顶点为 P ,对应函数的二次项系数为 a 3,过点 P作 PE ∥x 轴,交抛物线 L 于 E ,F 两点,求32a a的值,并干脆写出AB EF 的值.。
押中考数学第25-26题(解答压轴题:函数探究)考前预测

押中考数学第25-26题(解答压轴题:函数探究)专题诠释:函数探究,历年作为中考数学的压轴题出现,难度大,综合性强。
但是这道题本身的难度跨度也比较大,一般第一问较简单,然后逐渐变难。
因此,这种题的策略就是先把基础题做对,逐渐攻克中等题和难题,尽量拿到更多的分数!知识点一:一次函数探究〖押题冲关〗1.(2023·天津西青·统考一模)在平面直角坐标系中,O为原点,△DOE是等腰直角三角形,∠ODE=90°,DO=DE=3,点D在x轴的负半轴上,点E在第二象限,矩形ABCO的顶点B(4,2),点C在x轴的正半轴上,点A在y轴的正半轴上.将△DOE沿x轴向右平移,得到△D′O′E′,点D,O,E的对应点分别为D′,O′,E′.(1)如图1,当E′O′经过点A时,求点E′的坐标;(2)设OO′=t,△D′O′E′与矩形ABCO重叠部分的面积为S;①如图②,当△D′O′E′与矩形ABCO重叠部分为五边形时,D′E′与AB相交于点M,E′O′分别与A B,BC交于点N,P,试用含有t的式子表示S,并直接写出t的取值范围;的所有t的值.②请直接写出满足S=722.(2023·陕西宝鸡·统考二模)太白山国家森林公园位于秦岭主峰太白山北麓的陕西省宝鸡市眉县境内,公园以森林景观为主体,苍山奇峰为骨架,清溪碧潭为脉络,文物古迹点缀其间,自然景观与人文景观浑然一体,是中国西部不可多得的自然风光旅游区,被誉为中国西部的一颗绿色明珠.小明一家准备去离家200千米的该景区自驾游,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.(1)他们出发半小时时,离家______千米;(2)出发1小时后,在服务区等候另一家人一同前往,然后,以匀速直达目的地.①求BC所在直线的函数解析式;②出发3小时时,他们距终点还有多少千米?3.(2023·黑龙江哈尔滨·统考三模)如图1,平面直角坐标系中,点O为坐标原点,直线y=−x+b与x轴交于点A,与y轴交于点C,过点C作直线BC⊥AC,交x轴于点B,且线段AB=8.(1)求直线BC的解析式;(2)如图2,点D是线段AC上一点,点E在BD的延长线上,连接CE,AE,若∠CED=45°,求证:AE⊥BE;(3)如图3,在(2)的条件下,点G为第四象限内一点,且点E的横坐标小于点G的横坐标,连接AG,OG,且∠AGO=150°,连接EG交x轴于点F,使EG=AE.点M为第二象限内一点,连接MG交x轴于点P,交y轴于点N,连接OM,使OM=AG,若PF=√6FG,∠AGP+∠M=180°,求点N的坐标.4.(2023·江苏徐州·统考一模)学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离y (米)与时间t(分钟)之间的函数关系如图所示.(1)甲、乙何时相遇?相遇时甲的速度为多少?(2)求乙到达目的地时,两人之间的距离;(3)求出线段AB所表示的函数关系式.5.(2023·陕西西安·统考二模)如图,已知直线l:y=kx+b与x轴、y轴分别交于A,B两点,且OA=2OB=8,x轴上一点C的坐标为(6,0),P是直线l上一点.(1)求直线l的函数表达式;(2)连接OP和CP,当点P的横坐标为2时,求△COP的面积.知识点二:二次函数探究〖押题冲关〗1.(2023·四川成都·统考二模)如图1,已知一次函数y=−x+3的图象与y轴,x轴相交于点A,B,抛物线y=−x2+bx+c与y轴交于点C,顶点M在直线AB上,设点M横坐标为m.(1)如图2,当m=3时,求此时抛物线y=−x2+bx+c的函数表达式;(2)求当m为何值时,点C的纵坐标最大;(3)如图3,当m=0时,此时的抛物线y=−x2+bx+c与直线y=kx+2相交于D,E两点,连接AD,AE并延长,分别与x轴交于P,Q两点.试探究OP⋅OQ是否为定值?若是,请求出该定值;若不是,请说明理由.2.(2023·湖北恩施·统考一模)已知直线y=x−1与x轴交于点A,过x轴上A,C两点的抛物线y=ax2+bx+3与y轴交于点B,与直线y=x−1交于D且OB=OC,(1)直接写出A,B,C三点的坐标;(2)求抛物线的解析式;(3)若点M是抛物线对称轴l上一动点,当△CDM的周长最小时,求△CDM的面积;(4)点P是抛物线上一动点(点P不与B,C重合),连接AP,DP,若△ADP的面积等于3,求点P的坐标.x+b与抛物线y=ax2交于A,B两点,3.(2023·广西崇左·统考二模)如图1,直线y=−12与y轴交于点C,其中点A的坐标为(−4,8).(1)求a,b的值.(2)将点A绕点C逆时针旋转90°得到点D.①判断点D是否在抛物线上,并说明理由.②如图2,将直线AB向下平移,交抛物线于E,F两点(点E在点F的左侧),点G在线段OC 上.若△GEF∽△DBA,求出点G的坐标.x+c(a≠0)与x轴交于A(−2,0),4.(2023·四川南充·统考一模)如图1,抛物线y=ax2+23B两点,与y轴交于点C(0,4).(1)求抛物线的解析式;(2)若点D是第一象限内抛物线上的一点,AD与BC交于点E,且AE=5DE,求点D的坐标;若(3)如图2,已知点M(0,1),抛物线上是否存在点P,使锐角∠MBP满足tan∠MBP=12存在,求出点P的坐标;若不存在,说明理由.5.(2023·四川成都·统考二模)如图,Rt△ABC的顶点A(−1,0),B(4,0),直角顶点C在y 轴的正半轴上,抛物线y=ax2+bx+c经过A、B、C三点.(1)求抛物线的解析式;(2)动点P从点A出发以2个单位/s的速度沿AB向点B运动,动点Q从点C出发以√5个单位/s的速度沿CB向点B运动,当其中一点到达终点时,另一点也停止运动,连接CP、PQ,当△CPQ的面积最大时,求点P的坐标及最大面积;(3)如图2,过原点的直线与抛物线交于点E、F(点E在点F的左侧),点G(0,4),若设直线GE的解析式为y=mx+4,直线GF的解析式为y=nx+4,试探究:m+n是否为定值?若是,请求出定值;若不是,请说明理由.x2+bx−3的6.(2023·江苏常州·统考二模)如图,在平面直角坐标系中,二次函数y=−13图像与x轴交于点A和点B(9,0),与y轴交于点C.(1)求二次函数的表达式;(2)若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;(3)若点Q在第四象限内,且cos∠AQB=3,点M在y轴正半轴,∠MBO=45°,线段MQ是5否存在最大值,如果存在,直接写出最大值;如果不存在,请说明理由.7.(2023·广东汕尾·统考二模)如图,抛物线y=−x2+3x+4与x轴交于A、B两点(点A 在点B左侧),与y轴交于点C,连接AC、BC,点E为线段BC上的一点,直线AE与抛物线交于点H.(1)直接写出A、B、C三点的坐标,并求出直线BC的表达式;(2)连接HB、HC,求△HBC面积的最大值;(3)若点P为抛物线上一动点,试判断在平面内是否存在一点Q,使得以B、C、P、Q为顶点的四边形是以BC为边的矩形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.8.(2023·辽宁本溪·统考一模)如图,抛物线y=ax2+bx+3经过点A(−1,0),B(3,0),与y轴交于点C.(1)求抛物线的解析式;(2)如图①,若点E是直线BC上方抛物线上的点,EG⊥x轴于点G,交BC于点F,当tan∠CEF=2时,求点E的坐标;(3)如图②,点P(m,0)在线段OB上,点Q线段CB上,且BQ=√2OP.以PQ为边作矩形PQNM,使点M在y轴上,直接写出当m为何值时,恰好有矩形PQNM的顶点落在抛物线上.9.(2023·四川成都·统考二模)如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A(−1,0),B(4,0),与y轴交于点C,直线BC的函数表达式为y=x+m,直线x=1与x轴交于点D,P为该直线上一动点,连接PB,将PB绕P顺时针旋转一定角度得到PQ.(1)求二次函数与直线BC的函数表达式.(2)如图1,若点Q恰好落在抛物线位于第四象限的图像上,连接AQ交BC于点E,连接AC,CQ,当△CEQ与△ACE的面积之比最大时,求点P的坐标.(3)如图2,若∠BPQ=90°,在点P运动过程中,当点Q落在抛物线上时,求点Q的坐标,连接BQ,DQ,请直接写出△BDQ周长的最小值.10.(2023·山西晋中·统考一模)综合与探究.如图1,在平面直角坐标系中,已知二次函数y=−23x2+43x+2的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;(2)点P是二次函数图象上的一个动点,请问是否存在点P使∠PCB=∠ABC?若存在,请求出点P的坐标;若不存在,请说明理由;(3)如图2,作出该二次函数图象的对称轴直线l,交x轴于点D.若点M是二次函数图象上一动点,且点M始终位于x轴上方,作直线AM,BM,分别交l于点E,F,在点M的运动过程中,DE+DF的值是否为定值?若是,请直接写出该定值;若不是,请说明理由.。
天津市中考数学压轴题大集合精品资料
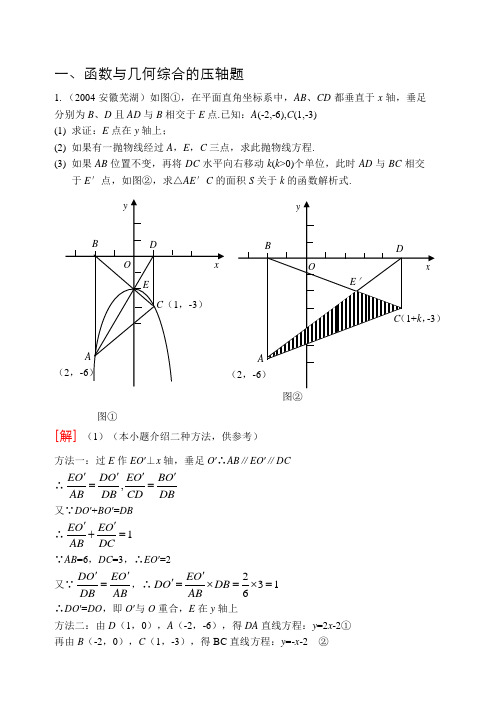
一、函数与几何综合的压轴题1.(2004安徽芜湖)如图①,在平面直角坐标系中,AB 、CD 都垂直于x 轴,垂足分别为B 、D 且AD 与B 相交于E 点.已知:A (-2,-6),C (1,-3) (1) 求证:E 点在y 轴上;(2) 如果有一抛物线经过A ,E ,C 三点,求此抛物线方程.(3) 如果AB 位置不变,再将DC 水平向右移动k (k >0)个单位,此时AD 与BC 相交于E ′点,如图②,求△AE ′C 的面积S 关于k 的函数解析式.[解] (1)(本小题介绍二种方法,供参考)方法一:过E 作EO ′⊥x 轴,垂足O ′∴AB ∥EO ′∥DC ∴,EO DO EO BO AB DB CD DB ''''==又∵DO ′+BO ′=DB ∴1EO EO AB DC''+= ∵AB =6,DC =3,∴EO ′=2又∵DO EO DB AB ''=,∴2316EO DO DB AB ''=⨯=⨯=∴DO ′=DO ,即O ′与O 重合,E 在y 轴上方法二:由D (1,0),A (-2,-6),得DA 直线方程:y =2x -2① 再由B (-2,0),C (1,-3),得BC 直线方程:y =-x -2 ②图①图②联立①②得02x y =⎧⎨=-⎩∴E 点坐标(0,-2),即E 点在y 轴上(2)设抛物线的方程y =ax 2+bx +c (a ≠0)过A (-2,-6),C (1,-3)E (0,-2)三点,得方程组42632a b c a b c c -+=-⎧⎪++=-⎨⎪=-⎩解得a =-1,b =0,c =-2 ∴抛物线方程y =-x 2-2(3)(本小题给出三种方法,供参考)由(1)当DC 水平向右平移k 后,过AD 与BC 的交点E ′作E ′F ⊥x 轴垂足为F 。
同(1)可得:1E F E FAB DC''+= 得:E ′F =2 方法一:又∵E ′F ∥AB E F DF AB DB '⇒=,∴13DF DB = S △AE ′C = S △ADC - S △E ′DC =11122223DC DB DC DF DC DB ∙-∙=∙=13DC DB ∙=DB=3+k S=3+k 为所求函数解析式方法二:∵ BA ∥DC ,∴S △BCA =S △BDA ∴S △AE ′C = S △BDE ′()1132322BD E F k k '=∙=+⨯=+ ∴S =3+k 为所求函数解析式.证法三:S △DE ′C ∶S △AE ′C =DE ′∶AE ′=DC ∶AB =1∶2同理:S △DE ′C ∶S △DE ′B =1∶2,又∵S △DE ′C ∶S △ABE ′=DC 2∶AB 2=1∶4 ∴()2213992AE C ABCD S S AB CD BD k '∆==⨯+∙=+梯形 ∴S =3+k 为所求函数解析式.2. (2004广东茂名)已知:如图,在直线坐标系中,以点M (1,0)为圆心、直径AC 为22的圆与y 轴交于A 、D 两点.(1)求点A 的坐标;(2)设过点A 的直线y =x +b 与x 轴交于点B.探究:直线AB 是否⊙M 的切线?并对你的结论加以证明;(3)连接BC ,记△ABC 的外接圆面积为S 1、⊙M 面积为S 2,若421hS S =,抛物线 y =ax 2+bx +c 经过B 、M 两点,且它的顶点到x 轴的距离为h .求这条抛物线的解析式.[解](1)解:由已知AM =2,OM =1,在Rt △AOM 中,AO =122=-OM AM ,∴点A 的坐标为A (0,1)(2)证:∵直线y =x +b 过点A (0,1)∴1=0+b 即b =1 ∴y =x +1 令y =0则x =-1 ∴B (—1,0),AB =2112222=+=+AO BO 在△ABM 中,AB =2,AM =2,BM =2222224)2()2(BM AM AB ==+=+∴△ABM 是直角三角形,∠BAM =90° ∴直线AB 是⊙M 的切线(3)解法一:由⑵得∠BAC =90°,AB =2,AC =22, ∴BC =10)22()2(2222=+=+AC AB∵∠BAC =90° ∴△ABC 的外接圆的直径为BC ,∴πππ25)210()2(221=∙=∙=BC S而πππ2)222()2(222=∙=∙=AC S421h S S = ,5,4225=∴=h h 即 ππ 设经过点B (—1,0)、M (1,0y =a (+1)(x -1),(a≠0)即y =ax 2-a ,∴-a =±5,∴a =±5 ∴抛物线的解析式为y =5x 2-5或y =-5x 2+5 解法二:(接上) 求得∴h =5由已知所求抛物线经过点B (—1,0)、M (1、0),则抛物线的对称轴是y 轴,由题意得抛物线的顶点坐标为(0,±5)∴抛物线的解析式为y =a (x -0)2±5又B (-1,0)、M (1,0)在抛物线上,∴a±5=0, a =±5∴抛物线的解析式为 y =5x 2-5或y =-5x 2+5 解法三:(接上)求得∴h =5因为抛物线的方程为y =ax 2+bx +c (a≠0)由已知得⎪⎩⎪⎨⎧-===⎪⎩⎪⎨⎧==⎪⎪⎪⎩⎪⎪⎪⎨⎧±=-=+-=++5055c 0b 5544002c b a a ab ac c b a c b a 或 =- 解得∴抛物线的解析式为 y =5x 2-5或y =-5x 2+5.3.(2004湖北荆门)如图,在直角坐标系中,以点P (1,-1)为圆心,2为半径作圆,交x 轴于A 、B 两点,抛物线)0(2>++=a c bx ax y 过点A 、B ,且顶点C 在⊙P 上. (1)求⊙P 上劣弧⌒AB 的长; (2)求抛物线的解析式;(3)在抛物线上是否存在一点D ,使线段OC 与PD若不存在,请说明理由.[解] (1)如图,连结PB ,过P 作PM ⊥x 轴,垂足为在Rt △PMB 中,PB=2,PM=1, ∴∠MPB=60°,∴∠APB =120° ⌒AB 的长=342180120ππ=⋅⋅︒︒ (2)在Rt △PMB 中,PB=2,PM=1,则MB =MA =3. 又OM=1,∴A (1-3,0),B (1+3,0), 由抛物线及圆的对称性得知点C 在直线PM 上, 则C(1,-3).点A 、B 、C 在抛物线上,则⎪⎪⎩⎪⎪⎨⎧++=-+-+-=++++=c b a c b a c b a 3)31()31(0)31()31(022 解之得⎪⎩⎪⎨⎧-=-==221c b a ∴抛物线解析式为222--=x x y(3)假设存在点D ,使OC 与PD 互相平分,则四边形OPCD 为平行四边形,且PC ∥OD.又PC ∥y 轴,∴点D 在y 轴上,∴OD =2,即D (0,-2).又点D (0,-2)在抛物线222--=x x y 上,故存在点D (0,-2), 使线段OC 与PD 互相平分.4.(2004湖北襄樊)如图,在平面直角坐标系内,Rt △ABC 的直角顶点C (0在y 轴的正半轴上,A 、B 是x 轴上是两点,且OA ∶OB =3∶1,以OA 、OB 为直径的圆分别交AC 于点E ,交BC 于点F .直线EF 交OC 于点Q . (1)求过A 、B 、C 三点的抛物线的解析式;(2)请猜想:直线EF 与两圆有怎样的位置关系?并证明你的猜想.(3)在△AOC 中,设点M 是AC 边上的一个动点,过M 作MN ∥AB 交OC 于点N .试问:在x 轴上是否存在点P ,使得△PMN 是一个以MN 为一直角边的等腰直角三角形?若存在,求出P[解] (1)在Rt △ABC 中,OC ⊥AB ,∴△AOC ≌△COB .∴OC 2=OA ·OB . ∵OA ∶OB =3∶1,C ∴23.OB OB = ∴OB =1.∴OA =3.∴A (-3,0),B (1,0).设抛物线的解析式为2.y ax bx c =++则930,0,a b c a b c c ⎧-+=⎪++=⎨⎪=⎩解之,得a b c ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩∴经过A 、B 、C三点的抛物线的解析式为23y x =-- (2)EF 与⊙O 1、⊙O 2都相切.证明:连结O 1E 、OE 、OF .∵∠ECF =∠AEO =∠BFO =90°, ∴四边形EOFC 为矩形. ∴QE =QO . ∴∠1=∠2.∵∠3=∠4,∠2+∠4=90°, ∴EF 与⊙O 1相切. 同理:EF 理⊙O 2相切.(3)作MP ⊥OA 于P ,设MN =a ,由题意可得MP =MN =a . ∵MN ∥OA ,∴△CMN ∽△CAO .∴.MN CNAO CO =∴3a =解之,得a =此时,四边形OPMN 是正方形.∴3.2MN OP ==∴3(,0).2P -考虑到四边形PMNO 此时为正方形,∴点P 在原点时仍可满足△PNN 是以MN 为一直角边的等腰直角三角形.故x 轴上存在点P 使得△PMN 是一个以MN为一直角边的等腰直角三角形且3(,0)2P -或(0,0).P 5.(2004湖北宜昌)如图,已知点A(0,1)、C(4,3)、E(415,823),P 是以AC 为对角线的矩形ABCD 内部(不在各边上)的—个动点,点D 在y 轴,抛物线y =ax 2+b x +1以P 为顶点.(1)说明点A 、C 、E 在一条条直线上;(2)能否判断抛物线y =ax 2+b x +1的开口方向?请说明理由;(3)设抛物线y =ax 2+b x +1与x 轴有交点F 、G(F 在G 的左侧),△GAO 与△FAO 的面积差为3,且这条抛物线与线段AE 有两个不同的交点.这时能确定a 、b 的值吗?若能,请求出a 、b 的值;若不能,请确定a 、b 的取值范围. (本题图形仅供分析参考用)[解] (1)由题意,A(0,1)、C(4,3)确定的解析式为:y=21x 将点E 的坐标E(415,823)代入y=21x +1中,左边=823,右边=21×415+1=823, ∵左边=右边,∴点E 在直线y=21x +1上,即点A 、C 、E 在一条直线上.(2)解法一:由于动点P 在矩形ABCD 内部,∴点P 的纵坐标大于点A 的纵坐标,而点A 与点P 都在抛物线上,且P 为顶点,∴这条抛物线有最高点,抛物线的开口向下解法二:∵抛物线y=ax 2+b x +c 的顶点P 的纵坐标为ab a 442—,且P 在矩形ABCD 内部,∴1<a b a 442—<3,由1<1—a b 42得—ab 42>0,∴a <0,∴抛物线的开口向下.(3)连接GA 、FA ,∵S △GAO —S △FAO =3 ∴21GO ·AO —21FO ·AO=3 ∵OA=1,∴GO —FO=6. 设F (x 1,0)、G (x 2,0),则x 1、x 2为方程ax 2+b x +c=0的两个根,且x 1<x 2,又∵a <0,∴x 1·x 2=a1<0,∴x 1<0<x 2, ∴GO= x 2,FO= —x 1,∴x 2—(—x 1)=6, 即x 2+x 1=6,∵x 2+x 1= —a b ∴—ab=6, ∴b= —6a ,∴抛物线解析式为:y=ax 2—6ax +1, 其顶点P 的坐标为由方程组 y=ax 2—6ax +1 y=21x +1 得:ax 2—(6a +21)x =0 (3,1—9a ), ∵顶点P 在矩形ABCD 内部, ∴1<1—9a <3, ∴—92<a <0.∴x =0或x =a a 216=6+a21. 当x =0时,即抛物线与线段AE 交于点A ,而这条抛物线与线段AE 有两个不同的交 点,则有:0<6+a 21≤415,解得:—92≤a <—121 综合得:—92<a <—121 ∵b= —6a ,∴21<b <346.(2004湖南长沙)已知两点O(0,0)、B(0,2),⊙A 过点B 且与x 轴分别相交于点O 、C ,⊙A 被y 轴分成段两圆弧,其弧长之比为3∶1,直线l 与⊙A 切于点O ,抛物线的顶点在直线l 上运动. (1)求⊙A 的半径;(2)若抛物线经过O 、C 两点,求抛物线的解析式;(3)过l 上一点P 的直线与⊙A 交于C 、E 两点,且PC =CE ,求点E 的坐标; (4)若抛物线与x 轴分别相交于C 、F 两点,其顶点P 的横坐标为m ,求△PEC 的面积关于m 的函数解析式.[解] (1)由弧长之比为3∶1,可得∠BAO =90º再由AB =AO =r ,且OB =2,得r = 2 (2)⊙A 的切线l 过原点,可设l 为y =kx任取l 上一点(b ,kb ),由l 与y 轴夹角为45º可得: b =-kb 或b =kb ,得k =-1或k =1, ∴直线l 的解析式为y =-x 或y =x又由r ,易得C(2,0)或C(-2,0)由此可设抛物线解析式为y =ax (x -2)或y =ax (x +2) 再把顶点坐标代入l 的解析式中得a =1 ∴抛物线为y =x 2-2x 或y =x 2+2x……6分(3)当l 的解析式为y =-x 时,由P 在l 上,可设P(m ,-m)(m >0) 过P 作PP′⊥x 轴于P′,∴OP′=|m|,PP′=|-m|,∴OP =2m 2,又由切割线定理可得:OP 2=PC·PE,且PC =CE ,得PC =PE =m =PP′7分∴C 与P′为同一点,即PE ⊥x 轴于C ,∴m =-2,E(-2,2)…8分 同理,当l 的解析式为y =x 时,m =-2,E(-2,2)(4)若C(2,0),此时l 为y =-x ,∵P 与点O 、点C 不重合,∴m≠0且m≠2, 当m <0时,FC =2(2-m),高为|y p |即为-m , ∴S =22(2)()22m m m m --=-同理当0<m <2时,S =-m 2+2m ;当m >2时,S =m 2-2m ;∴S =222(02)2(02)m m m m m m m ⎧-<>⎨-+<<⎩或 又若C(-2,0), 此时l 为y =x ,同理可得;S =222(20)2(20)m m m m m m m ⎧+<->⎨---<<⎩或7.(2006江苏连云港)如图,直线4+=kx y 与函数)0,0(>>=m x xmy 的图像交于A 、B 两点,且与x 、y 轴分别交于C 、D 两点.(1)若COD ∆的面积是AOB ∆的面积的2倍,求k 与m 之间的函数关系式; (2)在(1)的条件下,是否存在k 和m ,使得以AB 为直径的圆经过点)0,2(P .若存在,求出k 和m 的值;若不存在,请说明理由.[解](1)设),(11y x A ,),(22y x B (其中2121,y y x x ><),由AOB COD S S ∆∆=2,得)(2BOD AOD COD S S S ∆∆∆-= ∴21·OC ·2=OD (21·OD ·-1y 21·OD ·2y ),(21y OC =又4=OC ,∴8)(221=-y y ,即84)(21221=-+y y y y , 由xmy =可得y m x =,代入4+=kx y 可得042=--km y y ①∴421=+y y ,km y y -=⋅21,∴8416=+km ,即mk 2-=. 又方程①的判别式08416>=+=∆km ,∴所求的函数关系式为mk 2-=)0(>m . (2)假设存在k ,m ,使得以AB 为直径的圆经过点)0,2(P则BP AP ⊥,过A 、B 分别作x 轴的垂线,垂足分别为M ∵MAP ∠与BPN ∠都与APM ∠互余,∴MAP ∠ BPN ∠=. ∴Rt MAP ∆∽Rt NPB ∆,∴NBMPPN AM =. ∴212122y x x y -=-,∴0)2)(2(2121=+--y y x x , ∴0)2)(2(2121=+--y y y m y m , 即0)(4)(222121212=+++-y y y y y y m m ②由(1)知421=+y y ,221=⋅y y ,代入②得01282=+-m m ,∴2=m 或6,又m k 2-=,∴⎩⎨⎧-==12k m 或⎪⎩⎪⎨⎧-==316k m , ∴存在k ,m ,使得以AB 为直径的圆经过点)0,2(P ,且⎩⎨⎧-==12k m 或⎪⎩⎪⎨⎧-==316k m . 8.(2004江苏镇江)已知抛物线2(5)5(0)y mx m x m =--->与x 轴交于两点1(,0)A x 、2(,0)B x 12()x x <,与y 轴交于点C ,且AB =6.(1)求抛物线和直线BC 的解析式.(2)在给定的直角坐标系中,画抛物线和直线BC .(3)若P 过A 、B 、C 三点,求P 的半径.(4)抛物线上是否存在点M ,过点M 作MN x ⊥轴于点N ,使MBN ∆被直线BC分成面积比为13:的两部分?若存在,请求出点M 的坐标;若不存在,请说明理由.[解](1)由题意得:12122155,, 6.m x x x x x x m m--+=⋅=-= 221212520()436,36,m x x x x m m -⎛⎫+-=+= ⎪⎝⎭解得1251,.7m m ==-经检验m =1,∴抛物线的解析式为:24y x =+或:由2(5)50m x m x ---=得,1x =或5x m-=0,m >516, 1.m m-∴-=∴= 抛物线的解析式为24 5.y x x =+-由2450x x +-=得125, 1.x x =-=∴A (-5,0),B (1,0),C (0,-5). 设直线BC 的解析式为,y kx b =+ 则5,5,0. 5.b b k b k =-=-⎧⎧∴⎨⎨+==⎩⎩ ∴直线BC 的解析式为5 5.y x =- (2)图象略.(3)法一:在Rt AOC D 中,5,45.OA OC OAC ==∴∠=︒90BPC ∴∠=︒.又BC == ∴P的半径PB == 法二:由题意,圆心P 在AB 的中垂线上,即在抛物线245y x x =+-的对称轴直线2x =-上,设P (-2,-h )(h >0),连结PB 、PC ,则222222(12),(5)2PB h PC h =++=-+,由22PB PC =,即2222(12)(5)2h h ++=-+,解得h =2.(2,2),P P ∴--∴的半径PB ==.法三:延长CP 交P 于点F .为P 的直径,90.CAF COB ∴∠=∠=︒ 又,.ABC AFC ACF OCB ∠=∠∴D ~D,.CF AC AC BCCF BC OC OC⋅∴=∴=又AC ==5,CO BC ===∞5CF ∴==(4)设MN 交直线BC 于点E ,点M 的坐标为2(,45),t t t +-则点E 的坐标为(,55).t t -若13,MEB ENB S S =D D ::则13.ME EN =::2434,45(55).3EN MN t t t ∴=∴+-=-::解得11t =(不合题意舍去),25,3t =540,.39M ⎛⎫∴ ⎪⎝⎭若31,MEB ENB S S =D D ::则31.ME EN =::214,454(55).EN MN t t t ∴=∴+-=-::解得31t =(不合题意舍去),415,t =()15,280.M ∴∴存在点M ,点M 的坐标为540,39⎛⎫⎪⎝⎭或(15,280).9. 如图,⊙M 与x 轴交于A 、B 两点,其坐标分别为)03(,-A 、)01(,B ,直径CD ⊥x 轴于N ,直线CE 切⊙M 于点C ,直线FG 切⊙M 于点F ,交CE 于G ,已知点G 的横坐标为3.(1) 若抛物线m x x y +--=22经过A 、B 、D 三点,求m 的值及点D 的坐标. (2) 求直线DF 的解析式.(3) 是否存在过点G 的直线,使它与(1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由.[解] (1) ∵抛物线过A 、B 两点,∴11)3(-=⨯-m,m =3.∴抛物线为322+--=x x y .又抛物线过点D ,由圆的对称性知点D 为抛物线的顶点. ∴D 点坐标为)41(,-.(2) 由题意知:AB =4.∵CD ⊥x 轴,∴NA =NB =2. ∴ON =1. 由相交弦定理得:NA ·NB =ND ·NC , ∴NC ×4=2×2. ∴NC =1. ∴C 点坐标为)11(--,.设直线DF 交CE 于P ,连结CF ,则∠CFP =90°. ∴∠2+∠3=∠1+∠4=90°. ∵GC 、GF 是切线, ∴GC =GF . ∴∠3=∠4. ∴∠1=∠2. ∴GF =GP . ∴GC =GP . 可得CP =8.∴P 点坐标为)17(-,设直线DF 的解析式为b kx y +=则⎩⎨⎧-=+=+-174b k b k 解得⎪⎪⎩⎪⎪⎨⎧=-=82785b k∴直线DF 的解析式为:82785+-=x y(3) 假设存在过点G 的直线为11b x k y +=,(第9题图)则1311-=+b k ,∴1311--=k b .由方程组⎩⎨⎧+--=--=3213211x x y k x k y 得034)2(112=--++k x k x 由题意得421=--k ,∴61-=k . 当61-=k 时,040<-=∆, ∴方程无实数根,方程组无实数解. ∴满足条件的直线不存在.10.(2004山西)已知二次函数212y x bx c =++的图象经过点A (-3,6),并与x 轴交于点B (-1,0)和点C ,顶点为P.(1)求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象; (2)设D 为线段OC 上的一点,满足∠DPC =∠BAC ,求点D 的坐标; (3)在x 轴上是否存在一点M ,使以M 为圆心的圆与AC 、PC 所在的直线及y 轴都相切?如果存在,请求出点M 的坐标;若不存在,请说明理由.[解] (1)解:∵二次函数212y x bx c =++的图象过点A (-3,6),B (-1,0)得9362102b c b c ⎧-+=⎪⎪⎨⎪-+=⎪⎩ 解得132b c =-⎧⎪⎨=-⎪⎩∴这个二次函数的解析式为:21322y x x =-- 由解析式可求P (1,-2),C (3,0) 画出二次函数的图像(2)解法一:易证:∠ACB =∠PCD =45°又已知:∠DPC =∠BAC ∴△DPC ∽△BAC ∴DC PCBC AC=易求4AC PC BC === ∴43DC = ∴45333OD =-= ∴5,03D ⎛⎫⎪⎝⎭解法二:过A 作AE ⊥x 轴,垂足为E.设抛物线的对称轴交x 轴于F. 亦可证△AEB ∽△PFD 、 ∴PE EBPF FD=. 易求:AE =6,EB =2,PF =2∴23FD =∴25133OD =+= ∴5,03D ⎛⎫ ⎪⎝⎭(3)存在.(1°)过M 作MH ⊥AC ,MG ⊥PC 垂足分别为H 、G ,设AC 交y 轴于S ,CP 的延长线交y 轴于T∵△SCT 是等腰直角三角形,M 是△SCT 的内切圆圆心, ∴MG =MH =OM又∵MC =且OM +MC =OC3,3OM OM +==得∴()3,0M(2°)在x 轴的负半轴上,存在一点M ′ 同理OM′+OC =M′C,OM OC ''+=得3OM '= ∴M′()3,0- 即在x 轴上存在满足条件的两个点.11.(2004浙江绍兴)在平面直角坐标系中,A (-1,0),B (3,0).(1)若抛物线过A ,B 两点,且与y 轴交于点(0,-3),求此抛物线的顶点坐标;(2)如图,小敏发现所有过A ,B 两点的抛物线如果与y 轴负半轴交于点C ,M 为抛物线的顶点,那么△ACM 与△ACB 的面积比不变,请你求出这个比值; (3)若对称轴是AB 的中垂线l 的抛物线与x 轴交于点E ,F ,与y 轴交于点C ,过C 作CP ∥x 轴交l 于点P ,M 为此抛物线的顶点.若四边形PEMF 是有一个内角为60°的菱形,求次抛物线的解析式.[解] (1)322--=x x y ,顶点坐标为(1,-4).(2)由题意,设y =a (x +1)(x -3), 即y =ax 2-2ax -3a ,∴ A (-1,0),B (3,0),C (0,-3a ), M (1,-4a ),∴ S △ACB =21×4×a 3-=6a ,而a >0, ∴ S △ACB =6A 、 作MD ⊥x 轴于D ,又S △ACM =S △ACO +S OCMD -S △AMD =21·1·3a +21(3a +4a )-21·2·4a =a , ∴ S △ACM :S △ACB =1:6.(3)①当抛物线开口向上时,设y =a (x -1)2+k ,即y =ax 2-2ax +a +k , 有菱形可知k a +=k ,a +k >0,k <0, ∴ k =2a-, ∴ y =ax 2-2ax +2a, ∴ 2=EF . 记l 与x 轴交点为D ,若∠PEM =60°,则∠FEM =30°,MD =DE·tan30°=66, ∴ k =-66,a =36, ∴ 抛物线的解析式为666326312+-=x x y .若∠PEM =120°,则∠FEM =60°,MD =DE·tan60°=26, ∴ k =-26,a =6, ∴ 抛物线的解析式为266262+-=x x y . ②当抛物线开口向下时,同理可得666326312-+-=x x y ,266262-+-=x x y . 12.(2005北京)已知:在平面直角坐标系xOy 中,一次函数y k x k=-4的图象与x 轴交于点A ,抛物线y a xb x c =++2经过O 、A 两点。
2023天津中考数学压轴题

2023天津中考数学压轴题
一辆汽车以每小时60公里的速度行驶,行驶了4小时后,剩余的路程还有多少公里?
一个长方形花坛的长是8米,宽是5米,如果每平方米能种3株花,那么这个花坛最多能种多少株花?
一桶水有30升,小明用每分钟2升的速度倒水,需要多少分钟才能倒完?
一个正方形的边长是6厘米,求其面积和周长。
一条绳子长12米,小明每天用1.5米的速度剪断,需要多少天才能剪断整条绳子?
一个三角形的底边长是10厘米,高是8厘米,求其面积。
一辆自行车以每小时15公里的速度行驶,行驶了3小时后,剩余的路程还有多少公里?一个长方形的长是18米,宽是5米,求其面积和周长。
一桶油有40升,小明用每分钟3升的速度倒油,需要多少分钟才能倒完?
一个正方形的边长是9厘米,求其面积和周长。
天津市武清区重点名校2024届中考数学最后冲刺浓缩精华卷含解析

天津市武清区重点名校2024届中考数学最后冲刺浓缩精华卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1.图1~图4是四个基本作图的痕迹,关于四条弧①、②、③、④有四种说法:弧①是以O为圆心,任意长为半径所画的弧;弧②是以P为圆心,任意长为半径所画的弧;弧③是以A为圆心,任意长为半径所画的弧;弧④是以P为圆心,任意长为半径所画的弧;其中正确说法的个数为()A.4 B.3 C.2 D.12.“保护水资源,节约用水”应成为每个公民的自觉行为.下表是某个小区随机抽查到的10户家庭的月用水情况,则下列关于这10户家庭的月用水量说法错误的是()月用水量(吨) 4 5 6 9户数(户) 3 4 2 1A.中位数是5吨B.众数是5吨C.极差是3吨D.平均数是5.3吨3.如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数6的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正yx比例函数y=kx图象上,则k的值是()A .25-B .121-C .15-D .124-4.估计3﹣2的值应该在( ) A .﹣1﹣0之间B .0﹣1之间C .1﹣2之间D .2﹣3之间5.每个人都应怀有对水的敬畏之心,从点滴做起,节水、爱水,保护我们生活的美好世界.某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表,下列关于用水量的统计量不会发生改变的是( ) 用水量x (吨) 3 4 5 6 7 频数1254﹣xxA .平均数、中位数B .众数、中位数C .平均数、方差D .众数、方差6.二次函数2y ax bx c =++(a ≠0)的图象如图所示,则下列命题中正确的是( )A .a >b >cB .一次函数y =ax +c 的图象不经第四象限C .m (am +b )+b <a (m 是任意实数)D .3b +2c >07.如图,在平面直角坐标系中,直线y=k 1x+2(k 1≠0)与x 轴交于点A ,与y 轴交于点B ,与反比例函数y=2k x在第二象限内的图象交于点C ,连接OC ,若S △OBC =1,tan ∠BOC=13,则k 2的值是( )A .3B .﹣12C .﹣3D .﹣68.如图,等腰三角形ABC 的底边BC 长为4,面积是16,腰AC 的垂直平分线EF 分别交AC ,AB 边于E ,F 点.若点D 为BC 边的中点,点M 为线段EF 上一动点,则CDM 周长的最小值为( )A .6B .8C .10D .129.下列图形是中心对称图形的是( )A .B .C .D .10.某春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示: 成绩()m 1.50 1.60 1.65 1.70 1.75 1.80 人数124 332这些运动员跳高成绩的中位数是( ) A .1.65mB .1.675mC .1.70mD .1.75m二、填空题(共7小题,每小题3分,满分21分) 11.抛物线y=2x 2+4x ﹣2的顶点坐标是_______________.12.有一组数据:3,a ,4,6,7,它们的平均数是5,则a =_____,这组数据的方差是_____. 13.一个正四边形的内切圆半径与外接圆半径之比为:_________________14.如图,在平面直角坐标系中,点O 为坐标原点,点P 在第一象限,⊙P 与x 轴交于O ,A 两点,点A 的坐标为(6,0),⊙P 的半径为13,则点P 的坐标为_______.15.分解因式:22a 4a 2-+=_____.16.从“线段,等边三角形,圆,矩形,正六边形”这五个图形中任取一个,取到既是轴对称图形又是中心对称图形的概率是_____.17.不等式组13210x x -≤⎧⎨-<⎩的解集为_____.三、解答题(共7小题,满分69分)18.(10分)小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)19.(5分)如图二次函数的图象与x 轴交于点()30A -,和()10B ,两点,与y 轴交于点()0,3C ,点C 、D 是二次函数图象上的一对对称点,一次函数的图象经过B 、D求二次函数的解析式;写出使一次函数值大于二次函数值的x的取值范围;若直线BD 与y 轴的交点为E 点,连结AD 、AE ,求ADE ∆的面积;20.(8分)如图,在平面直角坐标系中,等边三角形ABC 的顶点B 与原点O 重合,点C 在x 轴上,点C 坐标为(6,0),等边三角形ABC 的三边上有三个动点D 、E 、F (不考虑与A 、B 、C 重合),点D 从A 向B 运动,点E 从B 向C 运动,点F 从C 向A 运动,三点同时运动,到终点结束,且速度均为1cm/s ,设运动的时间为ts ,解答下列问题: (1)求证:如图①,不论t 如何变化,△DEF 始终为等边三角形.(2)如图②过点E 作EQ ∥AB ,交AC 于点Q ,设△AEQ 的面积为S ,求S 与t 的函数关系式及t 为何值时△AEQ 的面积最大?求出这个最大值.(3)在(2)的条件下,当△AEQ 的面积最大时,平面内是否存在一点P ,使A 、D 、Q 、P 构成的四边形是菱形,若存在请直接写出P 坐标,若不存在请说明理由?21.(10分)如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB求证:DC是⊙O的切线;若AB=9,AD=6,求DC的长.,,,,五类校本课22.(10分)某中学为了了解在校学生对校本课程的喜爱情况,随机调查了部分学生对A B C D E程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个不完整统计图.请根据图中所提供的信息,完成下列问题:(1)本次被调查的学生的人数为;(2)补全条形统计图(3)扇形统计图中,C类所在扇形的圆心角的度数为;,两类校本课程的学生约共有多少名.(4)若该中学有2000名学生,请估计该校最喜爱C D23.(12分)已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.求证:AB=AF;若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.24.(14分)如图,已知AC和BD相交于点O,且AB∥DC,OA=OB.求证:OC=OD.参考答案一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1、C【解题分析】根据基本作图的方法即可得到结论.【题目详解】解:(1)弧①是以O为圆心,任意长为半径所画的弧,正确;(2)弧②是以P为圆心,大于点P到直线的距离为半径所画的弧,错误;(3)弧③是以A为圆心,大于12AB的长为半径所画的弧,错误;(4)弧④是以P为圆心,任意长为半径所画的弧,正确.故选C.【题目点拨】此题主要考查了基本作图,解决问题的关键是掌握基本作图的方法.2、C【解题分析】根据中位数、众数、极差和平均数的概念,对选项一一分析,即可选择正确答案.【题目详解】解:A、中位数=(5+5)÷2=5(吨),正确,故选项错误;B、数据5吨出现4次,次数最多,所以5吨是众数,正确,故选项错误;C、极差为9﹣4=5(吨),错误,故选项正确;D、平均数=(4×3+5×4+6×2+9×1)÷10=5.3,正确,故选项错误.故选:C.【题目点拨】此题主要考查了平均数、中位数、众数和极差的概念.要掌握这些基本概念才能熟练解题.3、B【解题分析】根据矩形的性质得到,CB∥x轴,AB∥y轴,于是得到D、E坐标,根据勾股定理得到ED,连接BB′,交ED于F,过B′作B′G⊥BC于G,根据轴对称的性质得到BF=B′F,BB′⊥ED求得BB′,设EG=x,根据勾股定理即可得到结论.【题目详解】解:∵矩形OABC,∴CB∥x轴,AB∥y轴.∵点B坐标为(6,1),∴D的横坐标为6,E的纵坐标为1.∵D,E在反比例函数6yx=的图象上,∴D(6,1),E(32,1),∴BE=6﹣32=92,BD=1﹣1=3,∴ED22BE BD+3132.连接BB′,交ED于F,过B′作B′G⊥BC于G.∵B,B′关于ED对称,∴BF=B′F,BB′⊥ED,∴BF •ED =BE •BD BF =3×92, ∴BF, ∴BB设EG =x ,则BG =92﹣x . ∵BB ′2﹣BG 2=B ′G 2=EB ′2﹣GE 2, ∴222299()()22x x --=-,∴x =4526, ∴EG =4526,∴CG =4213,∴B ′G =5413,∴B ′(4213,﹣213),∴k =121-.故选B . 【题目点拨】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,熟练掌握折叠的性质是解题的关键. 4、A 【解题分析】【题目详解】解:∵12,∴1-2﹣2<2-2,∴-1﹣2<0即3-2在-1和0之间. 故选A . 【题目点拨】此题主要考查了估算无理数大小,正确得出3的取值范围是解题关键. 5、B 【解题分析】由频数分布表可知后两组的频数和为4,即可得知频数之和,结合前两组的频数知第6、7个数据的平均数,可得答案. 【题目详解】∵6吨和7吨的频数之和为4-x+x=4, ∴频数之和为1+2+5+4=12,则这组数据的中位数为第6、7个数据的平均数,即=5,∴对于不同的正整数x ,中位数不会发生改变, ∵后两组频数和等于4,小于5,∴对于不同的正整数x ,众数不会发生改变,众数依然是5吨. 故选B . 【题目点拨】本题主要考查频数分布表及统计量的选择,由表中数据得出数据的总数是根本,熟练掌握平均数、中位数、众数的定义和计算方法是解题的关键. 6、D 【解题分析】解:A .由二次函数的图象开口向上可得a >0,由抛物线与y 轴交于x 轴下方可得c <0,由x =﹣1,得出2ba=﹣1,故b >0,b =2a ,则b >a >c ,故此选项错误;B .∵a >0,c <0,∴一次函数y =ax +c 的图象经一、三、四象限,故此选项错误;C .当x =﹣1时,y 最小,即a ﹣b ﹣c 最小,故a ﹣b ﹣c <am 2+bm +c ,即m (am +b )+b >a ,故此选项错误;D .由图象可知x =1,a +b +c >0①,∵对称轴x =﹣1,当x =1,y >0,∴当x =﹣3时,y >0,即9a ﹣3b +c >0② ①+②得10a ﹣2b +2c >0,∵b =2a ,∴得出3b +2c >0,故选项正确; 故选D .点睛:此题主要考查了图象与二次函数系数之间的关系,二次函数与方程之间的转换,会利用特殊值代入法求得特殊的式子,如:y =a +b +c ,然后根据图象判断其值. 7、C【解题分析】如图,作CH ⊥y 轴于H .通过解直角三角形求出点C 坐标即可解决问题. 【题目详解】解:如图,作CH ⊥y 轴于H .由题意B (0,2), ∵112OB CH ⋅⋅=, ∴CH=1, ∵tan ∠BOC=1,3CH OH = ∴OH=3, ∴C (﹣1,3),把点C (﹣1,3)代入2k y x=,得到k 2=﹣3, 故选C . 【题目点拨】本题考查反比例函数于一次函数的交点问题,锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型. 8、C 【解题分析】连接AD ,由于△ABC 是等腰三角形,点D 是BC 边的中点,故AD ⊥BC ,再根据三角形的面积公式求出AD 的长,再再根据EF 是线段AC 的垂直平分线可知,点C 关于直线EF 的对称点为点A ,故AD 的长为CM+MD 的最小值,由此即可得出结论. 【题目详解】 连接AD ,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=12BC•AD=12×4×AD=16,解得AD=8,∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴AD的长为CM+MD的最小值,∴△CDM的周长最短=(CM+MD)+CD=AD+12BC=8+12×4=8+2=1.故选C.【题目点拨】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.9、B【解题分析】根据中心对称图形的概念,轴对称图形与中心对称图形是图形沿对称中心旋转180度后与原图重合,即可解题.A、不是中心对称图形,故本选项错误;B、是中心对称图形,故本选项正确;C、不是中心对称图形,故本选项错误;D、不是中心对称图形,故本选项错误.故选B.考点:中心对称图形.【题目详解】请在此输入详解!10、C【解题分析】根据中位数的定义解答即可.【题目详解】解:在这15个数中,处于中间位置的第8个数是1.1,所以中位数是1.1.所以这些运动员跳高成绩的中位数是1.1.故选:C.【题目点拨】本题考查了中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.二、填空题(共7小题,每小题3分,满分21分)11、(﹣1,﹣1)【解题分析】利用顶点的公式首先求得横坐标,然后把横坐标的值代入解析式即可求得纵坐标.【题目详解】 x=-422⨯=-1, 把x=-1代入得:y=2-1-2=-1.则顶点的坐标是(-1,-1).故答案是:(-1,-1).【题目点拨】本题考查了二次函数的顶点坐标的求解方法,可以利用配方法求解,也可以利用公式法求解.12、5 1. 【解题分析】∵一组数据:3,a ,4,6,7,它们的平均数是5,∴346755a ++++=⨯,解得,5a =,∴2222221[(35)(55)(45)(65)(75)]5s =-+-+-+-+-=1. 故答案为5,1.13、【解题分析】如图,正方形ABCD 为⊙O 的内接四边形,作OH ⊥AB 于H ,利用正方形的性质得到OH 为正方形ABCD 的内切圆的半径,∠OAB =45°,然后利用等腰直角三角形的性质得OA =OH 即可解答.【题目详解】解:如图,正方形ABCD 为⊙O 的内接四边形,作OH ⊥AB 于H ,则OH 为正方形ABCD 的内切圆的半径,∵∠OAB =45°,∴OA =OH , ∴ 即一个正四边形的内切圆半径与外接圆半径之比为, 故答案为:.【题目点拨】本题考查了正多边形与圆的关系:把一个圆分成n (n 是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆.理解正多边形的有关概念.14、(3,2).【解题分析】过点P 作PD ⊥x 轴于点D ,连接OP ,先由垂径定理求出OD 的长,再根据勾股定理求出PD 的长,故可得出答案.【题目详解】过点P 作PD ⊥x 轴于点D ,连接OP ,∵A (6,0),PD ⊥OA ,∴OD=12OA=3, 在Rt △OPD 中 ∵13 OD=3,∴PD=2∴P(3,2) .故答案为(3,2).【题目点拨】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.15、()22a 1-【解题分析】分析:要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出来,之后再观察是否是完全平方公式或平方差公式,若是就考虑用公式法继续分解因式.因此,先提取公因式2后继续应用完全平方公式分解即可:()()2222a 4a 22a 2a 12a 1-+=-+=-. 16、45. 【解题分析】试题分析:在线段、等边三角形、圆、矩形、正六边形这五个图形中,既是中心对称图形又是轴对称图形的有线段、圆、矩形、正六边形,共4个,所以取到的图形既是中心对称图形又是轴对称图形的概率为45. 【题目点拨】本题考查概率公式,掌握图形特点是解题关键,难度不大.17、﹣2≤x <12【解题分析】根据解不等式的步骤从而得到答案.【题目详解】1-x 32x-10≤⎧⎨⎩①<②, 解不等式①可得:x ≥-2,解不等式②可得:x <12, 故答案为-2≤x <12. 【题目点拨】本题主要考查了解不等式,解本题的要点在于分别求解①,②不等式,从而得到答案.三、解答题(共7小题,满分69分)18、(1)13;(2)19;(3)第一题. 【解题分析】(1)由第一道单选题有3个选项,直接利用概率公式求解即可求得答案;(2)画出树状图,再由树状图求得所有等可能的结果与小明顺利通关的情况,继而利用概率公式即可求得答案; (3)由如果在第一题使用“求助”小明顺利通关的概率为:18;如果在第二题使用“求助”小明顺利通关的概率为:19;即可求得答案.【题目详解】(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率=13;故答案为13; (2)画树状图为:共有9种等可能的结果数,其中两个都正确的结果数为1,所以小明顺利通关的概率为19; (3)建议小明在第一题使用“求助”.理由如下:小明将“求助”留在第一题,画树状图为:小明将“求助”留在第一题使用,小明顺利通关的概率=18, 因为18>19, 所以建议小明在第一题使用“求助”.【题目点拨】本题考查的是概率,熟练掌握树状图法和概率公式是解题的关键.19、(1)()()31y x x =-+-;(2)2x <-或1x >;(3)1.【解题分析】(1)直接将已知点代入函数解析式求出即可;(2)利用函数图象结合交点坐标得出使一次函数值大于二次函数值的x 的取值范围;(3)分别得出EO ,AB 的长,进而得出面积.【题目详解】(1)∵二次函数与x 轴的交点为()30A -,和()10B , ∴设二次函数的解析式为:()()31y a x x =+-∵()0,3C 在抛物线上,∴3=a(0+3)(0-1),解得a=-1,所以解析式为:()()31y x x =-+-;(2)()()31y x x =-+-=−x 2−2x +3,∴二次函数的对称轴为直线1x =-;∵点C 、D 是二次函数图象上的一对对称点;()0,3C∴()2,3D -;∴使一次函数大于二次函数的x 的取值范围为2x <-或1x >;(3)设直线BD :y =mx +n ,代入B (1,0),D (−2,3)得023m n m n ⎧⎨-⎩+=+=, 解得:11m n -⎧⎨⎩==, 故直线BD 的解析式为:y =−x +1,把x =0代入()()31y x x =-+-得,y=3,所以E (0,1),∴OE =1,又∵AB =1,∴S △ADE =12×1×3−12×1×1=1. 【题目点拨】此题主要考查了待定系数法求一次函数和二次函数解析式,利用数形结合得出是解题关键.20、(1)证明见解析;(2)当t=3时,△AEQ 93cm 2;(3)(3,0)或(6,30,3 【解题分析】(1)由三角形ABC 为等边三角形,以及AD=BE=CF ,进而得出三角形ADF 与三角形CFE 与三角形BED 全等,利用全等三角形对应边相等得到BF=DF=DE ,即可得证;(2)先表示出三角形AEC 面积,根据EQ 与AB 平行,得到三角形CEQ 与三角形ABC 相似,利用相似三角形面积比等于相似比的平方表示出三角形CEQ 面积,进而表示出AEQ面积,利用二次函数的性质求出面积最大值,并求出此时Q 的坐标即可;(3)当△AEQ 的面积最大时,D 、E 、F 都是中点,分两种情形讨论即 可解决问题;【题目详解】(1)如图①中,∵C (6,0),∴BC=6在等边三角形ABC 中,AB=BC=AC=6,∠A=∠B=∠C=60°,由题意知,当0<t <6时,AD=BE=CF=t ,∴BD=CE=AF=6﹣t ,∴△ADF ≌△CFE ≌△BED (SAS ),∴EF=DF=DE ,∴△DEF 是等边三角形,∴不论t 如何变化,△DEF 始终为等边三角形;(2)如图②中,作AH ⊥BC 于H ,则AH=AB•sin60°=33,∴S △AEC =12×3(6﹣t )=33(6)2t -, ∵EQ ∥AB ,∴△CEQ ∽△ABC ,∴CEQ ABC S S =(CE CB )2=2(6)36t -,即S △CEQ =2(6)36t -S △ABC =2(6)36t -×323(6)t -,∴S△AEQ=S△AEC﹣S△CEQ=33(6)2t-﹣23(6)4t-=﹣34(t﹣3)2+934,∵a=﹣34<0,∴抛物线开口向下,有最大值,∴当t=3时,△AEQ的面积最大为934cm2,(3)如图③中,由(2)知,E点为BC的中点,线段EQ为△ABC的中位线,当AD为菱形的边时,可得P1(3,0),P3(6,3,当AD为对角线时,P2(0,3),综上所述,满足条件的点P坐标为(3,0)或(6,30,3.【题目点拨】本题考查四边形综合题、等边三角形的性质和判定、菱形的判定和性质、二次函数的性质等知识,解题的关键是学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,属于中考压轴题.21、(1)见解析;(2)25【解题分析】分析:(1)如下图,连接OD,由OA=OD可得∠DAO=∠ADO,结合∠CAD=∠DAB,可得∠CAD=∠ADO,从而可得OD∥AC,由此可得∠C+∠CDO=180°,结合∠C=90°可得∠CDO=90°即可证得CD是⊙O的切线;(2)如下图,连接BD,由AB是⊙O的直径可得∠ADB=90°=∠C,结合∠CAD=∠DAB可得△ACD∽△ADB,由此可得AD ABCD BD=,在Rt△ABD中由AD=6,AB=9易得BD=35,由此即可解得CD的长了.详解:(1)如下图,连接OD.∵OA=OD,∴∠DAB=∠ODA,∵∠CAD=∠DAB,∴∠ODA=∠CAD∴AC∥OD∴∠C+∠ODC=180°∵∠C=90°∴∠ODC=90°∴OD⊥CD,∴CD是⊙O的切线.(2)如下图,连接BD,∵AB是⊙O的直径,∴∠ADB=90°,∵AB=9,AD=6,∴BD=2296-=45=35,∵∠CAD=∠BAD,∠C=∠ADB=90°,∴△ACD∽△ADB,∴AD AB CD BD=,∴6935 CD=,∴CD=185=259.点睛:这是一道考查“圆和直线的位置关系与相似三角形的判定和性质”的几何综合题,作出如图所示的辅助线,熟悉“圆的切线的判定方法”和“相似三角形的判定和性质”是正确解答本题的关键.22、(1)300;(2)见解析;(3)108°;(4)约有840名.【解题分析】(1)根据A种类人数及其占总人数百分比可得答案;(2)用总人数乘以B的百分比得出其人数,即可补全条形图;(3)用360°乘以C类人数占总人数的比例可得;(4)总人数乘以C、D两类人数占样本的比例可得答案.【题目详解】解:(1)本次被调查的学生的人数为69÷23%=300(人),故答案为:300;(2)喜欢B类校本课程的人数为300×20%=60(人),补全条形图如下:(3)扇形统计图中,C类所在扇形的圆心角的度数为360°×90300=108°,故答案为:108°;(4)∵2000×90+36300=840,∴估计该校喜爱C,D两类校本课程的学生共有840名.【题目点拨】本题考查条形统计图、扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解题关键.条形统计图能清楚地表示出每个项目的数据.23、(1)证明见解析;(2)结论:四边形ACDF是矩形.理由见解析.【解题分析】(1)只要证明AB=CD,AF=CD即可解决问题;(2)结论:四边形ACDF是矩形.根据对角线相等的平行四边形是矩形判断即可;【题目详解】(1)证明:∵四边形ABCD是平行四边形,∴BE∥CD,AB=CD,∴∠AFC=∠DCG,∵GA=GD,∠AGF=∠CGD,∴△AGF≌△DGC,∴AF=CD,∴AB=CF.(2)解:结论:四边形ACDF是矩形.理由:∵AF=CD,AF∥CD,∴四边形ACDF是平行四边形,∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=120°,∴∠FAG=60°,∵AB=AG=AF,∴△AFG是等边三角形,∴AG=GF,∵△AGF≌△DGC,∴FG=CG,∵AG=GD,∴AD=CF,∴四边形ACDF是矩形.【题目点拨】本题考查平行四边形的判定和性质、矩形的判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.24、证明见解析.【解题分析】试题分析:首先根据等边对等角可得∠A=∠B,再由DC∥AB,可得∠D=∠A,∠C=∠B,进而得到∠C=∠D,根据等角对等边可得CO=DO.试题解析:证明:∵AB∥CD∴∠A=∠D ∠B=∠C∵OA=OB∴∠A=∠B∴∠C=∠D∴OC=OD考点:等腰三角形的性质与判定,平行线的性质。
天津中考数学压轴题全搞定

九年级数学冲刺讲义二次函数12题1. 已知关于x的函数同时满足下列三个条件:①函数的图象不经过第二象限;②当x<2时,对应的函数值y<0;③当x<2时,函数值y随x的增大而增大.你认为符合要求的函数的解析式可以是:(写出一个即可,答案不唯一).2.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0;④的最小值为3.其中,正确结论的个数为()A.1个B.2个C.3个D.4个3.已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为()A.B.C.D.4.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为()A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或35.已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m>2.其中,正确结论的个数是()A.0 B.1 C.2 D.36.若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3;②m>﹣;③二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是()A.0 B.1 C.2 D.37.已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列结论:①b 2﹣4ac >0;②abc >0;③8a+c >0;④9a+3b+c <0其中,正确结论的个数是( )A .1B .2C .3D .48.已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列5个结论:①abc >0;②b <a+c ;③4a+2b+c >0;④2c <3b ;⑤a+b >m (am+b )(m≠1的实数).其中正确的结论有( )A .2个B .3个C .4个D .5个9. 已知抛物线y=x 2-(2m-1)x+2m 不经过第三象限,且当x>2时,函数值y 随x 的增大而增大,则实数m 的取值范围是( )A.0≤m≤1.5B.m≥1.5C.0≤m≤1D.0<m≤1.5网格题18题1. 如图,在下列网格中,每个小正方形的边长都是1,点A 、B 、Q 、P 均为格点。
天津中考压轴题

(天津05)26. 已知二次函数y=ax2+bx+c.(Ⅰ)若a=2,c=-3,且二次函数的图象经过点(-1,-2),求b的值(Ⅱ)若a=2,b+c=-2,b>c,且二次函数的图象经过点(p,-2),求证:b ≥0;(Ⅲ)若a+b+c=0,a>b>c,且二次函数的图象经过点(q,-a),试问自变量x=q+4时,二次函数y=ax2+bx+c所对应的函数值y是否大于0?并证明你的结论。
27.已知:抛物线)0(2≠++=a c bx ax y 的图象经过点(1,0),一条直线b ax y +=,它们的系数之间满足如下关系:c b a >>。
(1)求证:抛物线与直线一定有两个不同的交点;(2)设抛物线与直线的两个交点为A 、B ,过A 、B 分别作x 轴的垂线,垂足分别为A 1、B 1。
令ac k =,试问:是否存在实数k ,使线段A1B1的长为24。
如果存在,求出k 的值;如果不存在,请说明理由。
(天津04)已知一次函数y 1=2x ,二次函数y 2=x 2+1.(Ⅰ)根据表中给出的x 的值,计算对应的函数值y 1、y 2,并填在表格中:(Ⅱ)观察第(Ⅰ)问表中有关的数据,证明如下结论:在实数范围内,对于x 的同一个值,这两个函数所对应的函数值y 1≤y 2均成立;(Ⅲ)试问,是否存在二次函数y 3=ax 2+bx +c ,其图象经过点(-5,2),且在实数范围内,对于x 的同一个值,这三个函数所对应的函数值y 1≤y 3≤y 2均成立,若存在,求出函数y 3的解析式;若不存在,请说明理由. (天津03)26.已知关于x 的方程())0(012≥=+++-q p x p q x 的两个实数根为α、β,且α≤β。
(1)试用含有α、β的代数式表示p 、q ;(2)求证:α≤1≤β;(3)若以α、β为坐标的点M (α、β)在△ABC 的三条边上运动,且△ABC 顶点的坐标分别为A (1,2),B (21,1),C (1,1),问是否存在点M ,使45=+q p ,若存在,求出点M 的坐标;若不存在,请说明理由。
天津市北辰区重点中学2024届中考数学押题试卷含解析

天津市北辰区重点中学2024届中考数学押题试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1.如图,在ABC ∆中,90,4,3C AC BC ︒∠===,将ABC ∆绕点A 逆时针旋转,使点C 落在线段AB 上的点E 处,点B 落在点D 处,则,B D 两点间的距离为( )A .10B .22C .3D .52.在圆锥、圆柱、球、正方体这四个几何体中,主视图不可能...是多边形的是( ) A .圆锥B .圆柱C .球D .正方体3.如果零上2℃记作+2℃,那么零下3℃记作( ) A .-3℃ B .-2℃C .+3℃D .+2℃4.反比例函数y =mx的图象如图所示,以下结论:①常数m <﹣1;②在每个象限内,y 随x 的增大而增大;③若点A(﹣1,h),B(2,k)在图象上,则h <k ;④若点P(x ,y)在上,则点P′(﹣x ,﹣y)也在图象.其中正确结论的个数是( )A .1B .2C .3D .45.点M (1,2)关于y 轴对称点的坐标为( ) A .(﹣1,2)B .(﹣1,﹣2)C .(1,﹣2)D .(2,﹣1)6.如图所示是由几个完全相同的小正方体组成的几何体的三视图.若小正方体的体积是1,则这个几何体的体积为( )A .2B .3C .4D .57.如图,不等式组1010x x +⎧⎨-≤⎩的解集在数轴上表示正确的是( )A .B .C .D .8.若关于x 、y 的方程组4xy kx y =⎧⎨+=⎩有实数解,则实数k 的取值范围是( )A .k >4B .k <4C .k≤4D .k≥49.实数6 的相反数是 ( )A .-6B .6C .16D .6-10.若不等式组的整数解共有三个,则a 的取值范围是( ) A .5<a <6B .5<a ≤6C .5≤a <6D .5≤a ≤6二、填空题(共7小题,每小题3分,满分21分)11.四边形ABCD 中,向量AB BC CD ++=_____________.12.七巧板是我们祖先的一项创造,被誉为“东方魔板”,如图所示是一副七巧板,若已知S △BIC =1,据七巧板制作过程的认识,求出平行四边形EFGH_____.13.小华到商场购买贺卡,他身上带的钱恰好能买5张3D 立体贺卡或20张普通贺卡.若小华先买了3张3D 立体贺卡,则剩下的钱恰好还能买______张普通贺卡.14.如图,AB 是⊙O 的直径,点C 在⊙O 上,AE 是⊙O 的切线,A 为切点,连接BC 并延长交AE 于点D .若AOC=80°,则ADB 的度数为( )A.40°B.50°C.60°D.20°15.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是______.16.分解因式:a3b+2a2b2+ab3=_____.17.如图,△ABC中,过重心G的直线平行于BC,且交边AB于点D,交边AC于点E,如果设AB=a,AC=b,用a,b表示GE,那么GE=___.三、解答题(共7小题,满分69分)18.(10分)在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与点B、C重合),以AD为直角边在AD右侧作等腰三角形ADE,使∠DAE=90°,连接CE.探究:如图①,当点D在线段BC上时,证明BC=CE+CD.应用:在探究的条件下,若AB=2,CD=1,则△DCE的周长为.拓展:(1)如图②,当点D在线段CB的延长线上时,BC、CD、CE之间的数量关系为.(2)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为.19.(5分)对于平面上两点A,B,给出如下定义:以点A或B为圆心,AB长为半径的圆称为点A,B的“确定圆”.如图为点A,B的“确定圆”的示意图.(1)已知点A的坐标为(-1,0),点B的坐标为(3,3),则点A,B的“确定圆”的面积为______;(2)已知点A的坐标为(0,0),若直线y=x+b上只存在一个点B,使得点A,B的“确定圆”的面积为9π,求点B 的坐标;(3)已知点A在以P(m,0)为圆心,以1为半径的圆上,点B在直线333=-+y x上,若要使所有点A,B的“确定圆”的面积都不小于9π,直接写出m的取值范围.20.(8分)为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:(1)本次抽测的男生人数为,图①中m的值为;(2)求本次抽测的这组数据的平均数、众数和中位数;(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.21.(10分)如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.求BF的长.22.(10分)如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;(2)把△A 1B 1C 1绕点A 1按逆时针方向旋转90°,在网格中画出旋转后的△A 1B 2C 2; (3)如果网格中小正方形的边长为1,求点B 经过(1)、(2)变换的路径总长.23.(12分)已知2410x x --=,求代数式22(23)()()x x y x y y --+--的值.24.(14分)某厂按用户的月需求量(件)完成一种产品的生产,其中.每件的售价为18万元,每件的成本(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量(件)成反比.经市场调研发现,月需求量与月份(为整数,)符合关系式(为常数),且得到了表中的数据.月份(月) 1 2 成本(万元/件)11 12 需求量(件/月) 120100(1)求与满足的关系式,请说明一件产品的利润能否是12万元;(2)求,并推断是否存在某个月既无盈利也不亏损; (3)在这一年12个月中,若第个月和第个月的利润相差最大,求.参考答案一、选择题(每小题只有一个正确答案,每小题3分,满分30分) 1、A 【解题分析】先利用勾股定理计算出AB,再在Rt△BDE中,求出BD即可;【题目详解】解:∵∠C=90°,AC=4,BC=3,∴AB=5,∵△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,∴AE=AC=4,DE=BC=3,∴BE=AB-AE=5-4=1,在Rt△DBE中,=故选A.【题目点拨】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.2、C【解题分析】【分析】根据各几何体的主视图可能出现的情况进行讨论即可作出判断.【题目详解】A. 圆锥的主视图可以是三角形也可能是圆,故不符合题意;B. 圆柱的主视图可能是长方形也可能是圆,故不符合题意;C. 球的主视图只能是圆,故符合题意;D. 正方体的主视图是正方形或长方形(中间有一竖),故不符合题意,故选C.【题目点拨】本题考查了简单几何体的三视图——主视图,明确主视图是从物体正面看得到的图形是关键.3、A【解题分析】一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.【题目详解】∵“正”和“负”相对,∴如果零上2℃记作+2℃,那么零下3℃记作-3℃.故选A.4、B【解题分析】根据反比例函数的图象的位置确定其比例系数的符号,利用反比例函数的性质进行判断即可.【题目详解】解:∵反比例函数的图象位于一三象限, ∴m >0 故①错误;当反比例函数的图象位于一三象限时,在每一象限内,y 随x 的增大而减小,故②错误; 将A(﹣1,h),B(2,k)代入y =xm,得到h =﹣m ,2k =m , ∵m >0 ∴h <k 故③正确; 将P(x ,y)代入y =x m 得到m =xy ,将P′(﹣x ,﹣y)代入y =xm得到m =xy , 故P(x ,y)在图象上,则P′(﹣x ,﹣y)也在图象上 故④正确, 故选:B . 【题目点拨】本题考查了反比例函数的性质,牢记反比例函数的比例系数的符号与其图象的关系是解决本题的关键. 5、A 【解题分析】关于y 轴对称的点的坐标特征是纵坐标不变,横坐标变为相反数. 【题目详解】点M (1,2)关于y 轴对称点的坐标为(-1,2) 【题目点拨】本题考查关于坐标轴对称的点的坐标特征,牢记关于坐标轴对称的点的性质是解题的关键. 6、C 【解题分析】根据左视图发现最右上角共有2个小立方体,综合以上,可以发现一共有4个立方体,主视图和左视图都是上下两行,所以这个几何体共由上下两层小正方体组成,俯视图有3个小正方形,所以下面一层共有3个小正方体,结合主视图和左视图的形状可知上面一层只有最左边有个小正方体,故这个几何体由4个小正方体组成,其体积是4. 故选C. 【题目点拨】错因分析 容易题,失分原因:未掌握通过三视图还原几何体的方法.【解题分析】首先分别解出两个不等式,再确定不等式组的解集,然后在数轴上表示即可. 【题目详解】解:解第一个不等式得:x >-1; 解第二个不等式得:x≤1, 在数轴上表示,故选B. 【题目点拨】此题主要考查了解一元一次不等式组,以及在数轴上表示解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时 “≥” ,“≤” 要用实心圆点表示; “ <“ >” 要用空心圆点表示. 8、C 【解题分析】利用根与系数的关系可以构造一个两根分别是x ,y 的一元二次方程,方程有实数根,用根的判别式≥0来确定k 的取值范围. 【题目详解】解:∵xy =k ,x +y =4,∴根据根与系数的关系可以构造一个关于m 的新方程,设x ,y 为方程240m m k -+=的实数根. 241640b ac k =-=-≥, 解不等式1640k -≥得 4k ≤. 故选:C . 【题目点拨】本题考查了一元二次方程的根的判别式的应用和根与系数的关系.解题的关键是了解方程组有实数根的意义. 9、A 【解题分析】根据相反数的定义即可判断. 【题目详解】6 的相反数是6【题目点拨】此题主要考查相反数的定义,解题的关键是熟知相反数的定义即可求解.10、C【解题分析】首先确定不等式组的解集,利用含a的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a的不等式,从而求出a的范围.【题目详解】解不等式组得:2<x≤a,∵不等式组的整数解共有3个,∴这3个是3,4,5,因而5≤a<1.故选C.【题目点拨】本题考查了一元一次不等式组的整数解,正确解出不等式组的解集,确定a的范围,是解答本题的关键.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.二、填空题(共7小题,每小题3分,满分21分)11、AD【解题分析】分析:根据“向量运算”的三角形法则进行计算即可.详解:如下图所示,由向量运算的三角形法则可得:++AB BC CD=AC CD+=AD.故答案为AD.点睛:理解向量运算的三角形法则是正确解答本题的关键.12、1【解题分析】根据七巧板的性质可得BI=IC=CH=HE,因为S△BIC=1,∠BIC=90°,可求得2,BC=1,在求得点G到EF 2sin45°,根据平行四边形的面积即可求解.【题目详解】由七巧板性质可知,BI=IC=CH=HE.又∵S△BIC=1,∠BIC=90°,∴12BI•IC=1,∴2,∴22BI IC+,∵EF=BC=1,2,∴点G到EF2 2∴平行四边形EFGH的面积2 222×22=1.故答案为1【题目点拨】本题考查了七巧板的性质、等腰直角三角形的性质及平行四边形的面积公式,熟知七巧板的性质是解决问题的关键.13、1【解题分析】根据已知他身上带的钱恰好能买5张3D立体贺卡或20张普通贺卡得:1张3D立体贺卡的单价是1张普通贺卡单价的4倍,所以设1张3D 立体贺卡x 元,剩下的钱恰好还能买y 张普通贺卡,根据3张3D 立体贺卡y +张普通贺卡5=张3D 立体贺卡,可得结论.【题目详解】解:设1张3D 立体贺卡x 元,剩下的钱恰好还能买y 张普通贺卡.则1张普通贺卡为:5x 1x 204=元, 由题意得:15x 3x x y 4-=⋅, y 8=,答:剩下的钱恰好还能买1张普通贺卡.故答案为:1.【题目点拨】本题考查了一元一次方程的应用以及列代数式,解题的关键是:根据总价=单价⨯数量列式计算.14、B .【解题分析】试题分析:根据AE 是⊙O 的切线,A 为切点,AB 是⊙O 的直径,可以先得出∠BAD 为直角.再由同弧所对的圆周角等于它所对的圆心角的一半,求出∠B ,从而得到∠ADB 的度数.由题意得:∠BAD=90°,∵∠B=∠AOC=40°,∴∠ADB=90°-∠B=50°.故选B .考点:圆的基本性质、切线的性质.15、(32,32) 【解题分析】由题意可得OA :OD =2:3,又由点A 的坐标为(1,0),即可求得OD 的长,又由正方形的性质,即可求得E 点的坐标.【题目详解】解:∵正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为2:3,∴OA :OD =2:3,∵点A 的坐标为(1,0),即OA =1,∴OD =32, ∵四边形ODEF 是正方形,∴DE =OD =32. ∴E 点的坐标为:(32,32). 故答案为:(32,32). 【题目点拨】此题考查了位似变换的性质与正方形的性质,注意理解位似变换与相似比的定义是解此题的关键.16、ab (a +b )1.【解题分析】a 3b+1a 1b 1+ab 3=ab (a 1+1ab+b 1)=ab (a+b )1.故答案为ab (a+b )1.【题目点拨】此题主要考查了提取公因式法以及公式法分解因式,熟练应用乘法公式是解题关键. 17、1133a b -+ 【解题分析】连接AG ,延长AG 交BC 于F .首先证明DG=GE ,再利用三角形法则求出DE 即可解决问题.【题目详解】连接AG ,延长AG 交BC 于F .∵G 是△ABC 的重心,DE ∥BC ,∴BF=CF ,23AD AE AG ABAC AF ===, ∵DG AD BFAB =,GE AE CF AC =, ∴DG GE BF CF=, ∵BF=CF ,∴DG=GE ,∵23AD a =,23AE b =,∴2233DE DA AE b a =+=-,∴111233 GE DE b a==-,故答案为1133b a-.【题目点拨】本题考查三角形的重心,平行线的性质,平面向量等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.三、解答题(共7小题,满分69分)18、探究:证明见解析;应用:2+;拓展:(1)BC= CD-CE,(2)BC= CE-CD【解题分析】试题分析:探究:判断出∠BAD=∠CAE,再用SAS即可得出结论;应用:先算出BC,进而算出BD,再用勾股定理求出DE,即可得出结论;拓展:(1)同探究的方法得出△ABD≌△ACE,得出BD=CE,即可得出结论;(2)同探究的方法得出△ABD≌△ACE,得出BD=CE,即可得出结论.试题解析:探究:∵∠BAC=90°,∠DAE=90°,∴∠BAC=∠DAE.∵∠BAC=∠BAD+∠DAC,∠DAE=∠CAE+∠DAC,∴∠BAD=∠CAE.∵AB=AC,AD=AE,∴△ABD≌△ACE.∴BD=CE.∵BC=BD+CD,∴BC=CE+CD.应用:在Rt△ABC中,,∴∠ABC=∠ACB=45°,BC=2,∵CD=1,∴BD=BC-CD=1,由探究知,△ABD≌△ACE,∴∠ACE=∠ABD=45°,∴∠DCE=90°,在Rt△BCE中,CD=1,CE=BD=1,根据勾股定理得,,∴△DCE 的周长为故答案为拓展:(1)同探究的方法得,△ABD ≌△ACE .∴BD=CE∴BC=CD-BD=CD-CE ,故答案为BC=CD-CE ;(2)同探究的方法得,△ABD ≌△ACE .∴BD=CE∴BC=BD-CD=CE-CD ,故答案为BC=CE-CD .19、(1)25π;(2)点B 的坐标为22⎛⎫- ⎪ ⎪⎝⎭或22⎛- ⎝⎭;(3)m ≤-5或m ≥2 【解题分析】(1)根据勾股定理,可得AB 的长,根据圆的面积公式,可得答案;(2)根据确定圆,可得l 与⊙A 相切,根据圆的面积,可得AB 的长为3,根据等腰直角三角形的性质,可得2BE AE ==,可得答案;(3)根据圆心与直线垂直时圆心到直线的距离最短,根据确定圆的面积,可得PB 的长,再根据30°的直角边等于斜边的一半,可得CA 的长.【题目详解】(1)(1)∵A 的坐标为(−1,0),B 的坐标为(3,3),∴=5,根据题意得点A ,B 的“确定圆”半径为5,∴S 圆=π×52=25π.故答案为25π;(2)∵直线y =x +b 上只存在一个点B ,使得点A ,B 的“确定圆”的面积为9π,∴⊙A 的半径AB =3且直线y =x +b 与⊙A 相切于点B ,如图,∴AB ⊥CD ,∠DCA =45°.,①当b>0时,则点B在第二象限.过点B作BE⊥x轴于点E,∵在Rt△BEA中,∠BAE=45°,AB=3,∴322BE AE==.∴3232,22B⎛⎫-⎪⎝⎭.②当b<0时,则点B'在第四象限.同理可得3232,22B⎛⎫'-⎪⎝⎭.综上所述,点B的坐标为3232,22⎛⎫-⎪⎪⎝⎭或3232,22⎛⎫-⎪⎝⎭.(3)如图2,,直线333=-y x当y=0时,x=3,即C(3,0).∵tan ∠BCP ∴∠BCP =30°,∴PC =2PB .P 到直线3=-y x 的距离最小是PB =4, ∴PC =1.3-1=-5,P 1(-5,0),3+1=2,P (2,0),当m ≤-5或m ≥2时,PD 的距离大于或等于4,点A ,B 的“确定圆”的面积都不小于9π.点A ,B 的“确定圆”的面积都不小于9π,m 的范围是m ≤-5或m ≥2.【题目点拨】本题考查了一次函数综合题,解(1)的关键是利用勾股定理得出AB 的长;解(2)的关键是等腰直角三角形的性质得出2BE AE ==;解(3)的关键是利用30°的直角边等于斜边的一半得出PC=2PB. 20、(1)50、1;(2)平均数为5.16次,众数为5次,中位数为5次;(3)估计该校350名九年级男生中有2人体能达标.【解题分析】分析:(Ⅰ)根据4次的人数及其百分比可得总人数,用6次的人数除以总人数求得m 即可;(Ⅱ)根据平均数、众数、中位数的定义求解可得;(Ⅲ)总人数乘以样本中5、6、7次人数之和占被调查人数的比例可得.详解:(Ⅰ)本次抽测的男生人数为10÷20%=50,m %=1450×100%=1%,所以m =1. 故答案为50、1; (Ⅱ)平均数为344105166147650⨯+⨯+⨯+⨯+⨯=5.16次,众数为5次,中位数为552+=5次; (Ⅲ)1614650++×350=2. 答:估计该校350名九年级男生中有2人体能达标.点睛:本题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.21、BF 的长度是1cm .【解题分析】利用“两角法”证得△BEF∽△CDF,利用相似三角形的对应边成比例来求线段CF的长度.【题目详解】解:如图,在矩形ABCD中:∠DFC=∠EFB,∠EBF=∠FCD=90°,∴△BEF∽△CDF;∴BECD=BFCF,又∵AD=BC=260cm ,AB=CD=130cm,AE=60cm∴BE=70cm,CD=130cm,BC=260cm ,CF=(260-BF)cm∴70130=260BFBF-,解得:BF=1.即:BF的长度是1cm.【题目点拨】本题主要考查相似三角形的判定和性质,关键要掌握:有两角对应相等的两三角形相似;两三角形相似,对应边的比相等.22、(1)(2)作图见解析;(3)2222π+.【解题分析】(1)利用平移的性质画图,即对应点都移动相同的距离.(2)利用旋转的性质画图,对应点都旋转相同的角度.(3)利用勾股定理和弧长公式求点B经过(1)、(2)变换的路径总长.【题目详解】解:(1)如答图,连接AA1,然后从C点作AA1的平行线且A1C1=AC,同理找到点B1,分别连接三点,△A1B1C1即为所求.(2)如答图,分别将A1B1,A1C1绕点A1按逆时针方向旋转90°,得到B2,C2,连接B2C2,△A1B2C2即为所求.(3)∵2211290222222,?1802BB B B ππ⋅⋅=+===, ∴点B 所走的路径总长=2222π+. 考点:1.网格问题;2.作图(平移和旋转变换);3.勾股定理;4.弧长的计算.23、12 【解题分析】解:∵2410x x --=,∴241x x -=. ∴()22222222(23)()()4129312934931912x x y x y y x x x y y x x x x --+--=-+-+-=-+=-+=⨯+=.将代数式应用完全平方公式和平方差公式展开后合并同类项,将241x x -=整体代入求值.24、 (1),不可能;(2)不存在;(3)1或11. 【解题分析】试题分析:(1)根据每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,结合表格,用待定系数法求y 与x 之间的函数关系式,再列方程求解,检验所得结果是还符合题意;(2)将表格中的n ,对应的x 值,代入到,求出k ,根据某个月既无盈利也不亏损,得到一个关于n 的一元二次方程,判断根的情况;(3)用含m 的代数式表示出第m 个月,第(m+1)个月的利润,再对它们的差的情况讨论. 试题解析:(1)由题意设,由表中数据,得解得∴.由题意,若,则. ∵x >0,∴. ∴不可能.(2)将n=1,x=120代入,得 120=2-2k+9k+27.解得k=13.将n=2,x=100代入也符合. ∴k=13.由题意,得18=6+,求得x=50.∴50=,即.∵,∴方程无实数根.∴不存在.(3)第m个月的利润为w==;∴第(m+1)个月的利润为W′=.若W≥W′,W-W′=48(6-m),m取最小1,W-W′=240最大.若W<W′,W′-W=48(m-6),m+1≤12,m取最大11,W′-W=240最大.∴m=1或11.考点:待定系数法,一元二次方程根的判别式,二次函数的性质,二次函数的应用.。
解答压轴题2022年天津数学中考真题汇编

解答压轴题2022年天津数学中考真题汇编1.已知点A(1,0)是抛物线y=ax2+bx+m(a,b,m为常数,a≠0,m<0)与x轴的一个交点.(1) 当a=1,m=−3时,求该抛物线的顶点坐标;(2) 若抛物线与x轴的另一个交点为M(m,0),与y轴的交点为C,过点C作直线l平行于x轴,E是直线l上的动点,F是y轴上的动点,EF=2√2.①当点E落在抛物线上(不与点C重合),且AE=EF时,求点F的坐标;②取EF的中点N,当m为何值时,MN的最小值是√222.已知抛物线y=x2−bx+c(b,c为常数,b>0)经过点A(−1,0),点M(m,0)是x轴正半轴上的动点.(1) 当b=2时,求抛物线的顶点坐标;(2) 点D(b,y D)在抛物线上,当AM=AD,m=5时,求b的值;(3) 点Q(b+12,y Q)在抛物线上,当√2AM+2QM的最小值为33√24时,求b的值.3.在平面直角坐标系中,O(0,0),A(1,0).已知抛物线y=x2+mx−2m(m是常数),顶点为P.(1) 当抛物线经过点A时,求顶点P的坐标;(2) 若点P在x轴下方,当∠AOP=45∘时,求抛物线的解析式;(3) 无论m取何值,该抛物线都经过定点H.当∠AHP=45∘时,求抛物线的解析式.4.已知抛物线y=x2+bx−3(b是常数)经过点A(−1,0).(1) 求该抛物线的解析式和顶点坐标;(2) P(m,t)为抛物线上的一个动点,P关于原点的对称点为Pʹ.①当点Pʹ落在该抛物线上时,求m的值;②当点Pʹ落在第二象限内,PʹA2取得最小值时,求m的值.5.已知抛物线C:y=x2−2x+1的顶点P,与y轴的交点为Q,点F(1,12).(1) 求点P,Q的坐标;(2) 将抛物线C向上平移得到抛物线Cʹ,点Q平移后的对应点为Qʹ,且FQʹ=OQʹ.①求抛物线Cʹ的解析式;②若点P关于直线QʹF的对称点为K,射线FK与抛物线Cʹ相交于点A,求点A的坐标.答案1. 【答案】(1) 当 a =1,m =−3 时,抛物线的解析式为 y =x 2+bx −3, ∵ 抛物线经过点 A (1,0), ∴0=1+b −3,解得 b =2, ∴ 抛物线的解析式为 y =x 2+2x −3, ∵y =x 2+2x −3=(x +1)2−4, ∴ 抛物线的顶点坐标为 (−1,−4).(2) ① ∵ 抛物线 y =ax 2+bx +m 经过点 A (1,0) 和 M (m,0),m <0, ∴0=a +b +m ,0=am 2+bm +m ,即 am +b +1=0, ∴a =1,b =−m −1,∴ 抛物线的解析式为 y =x 2−(m +1)x +m , 根据题意,得点 C (0,m ),点 E (m +1,m ), 过点 A 作 AH ⊥l 于点 H , 由点 A (1,0),得点 H (1,m ),在 Rt △EAH 中,EH =1−(m +1)=−m ,HA =0−m =−m , ∴AE =√EH 2+HA 2=−√2m , ∵AE =EF =2√2,∴−√2m =2√2,解得 m =−2,此时,点 E (−1,−2),点 C (0,−2),有 EC =1, ∵ 点 F 在 y 轴上,∴ 在 Rt △EFC 中,CF =√EF 2−EC 2=√7, ∴ 点 F 的坐标为 (0,−2−√7) 或 (0,−2+√7). ②由 N 是 EF 的中点,得 CN =12EF =√2,根据题意,点 N 在以点 C 为圆心、 √2 为半径的圆上, 由点 M (m,0),点 C (0,m ),得 MO =−m ,CO =−m , ∴ 在 Rt △MCO 中,MC =√MO 2+CO 2=−√2m ,当 MC ≥√2,即 m ≤−1 时,满足条件的点 N 落在线段 MC 上, MN 的最小值为 MC −NC =−√2m −√2=√22,解得 m =−32;当 MC <√2,即 −1<m <0 时,满足条件的点 N 落在线段 CM 的延长线上, MN 的最小值为 NC −MC =√2−(−√2m)=√22,解得 m =−12,∴ 当 m 的值为 −32或 −12时,MN 的最小值是 √22.2. 【答案】(1) ∵ 抛物线 y =x 2−bx +c 经过点 A (−1,0),∴ 1+b +c =0, 即 c =−b −1.当 b =2 时,y =x 2−2x −3=(x −1)2−4, ∴ 抛物线的顶点坐标为 (1,−4).(2) 由(1)知,抛物线的解析式为 y =x 2−bx −b −1. ∵ 点 D (b,y D ) 在抛物线 y =x 2−bx −b −1 上, ∴ y D =b 2−b ⋅b −b −1=−b −1. 由 b >0,得 b >b2>0,−b −1<0,∴ 点 D (b,−b −1) 在第四象限,且在抛物线对称轴 x =b2 的右侧. 如图,过点 D 作 DE ⊥x 轴,垂足为 E ,则点 E (b,0). ∴ AE =b +1,DE =b +1.得 AE =DE . ∴ 在 Rt △ADE 中,∠ADE =∠DAE =45∘. ∴ AD =√2AE .由已知 AM =AD ,m =5, ∴ 5−(−1)=√2(b +1). ∴ b =3√2−1.(3) ∵ 点 Q (b +12,y Q ) 在抛物线 y =x 2−bx −b −1 上,∴ y Q =(b +12)2−b (b +12)−b −1=−b 2−34.可知点 Q (b +12,−b2−34) 在第四象限,且在直线 x =b 的右侧,考虑到 √2AM +2QM =2(√22AM +QM),可取点 N (0,1),如图,过点 Q 作直线 AN 的垂线,垂足为 G ,QG 与 x 轴相交于点 M , 有 ∠GAM =45∘,得√22AM =GM ,则此时点 M 满足题意.过点 Q 作 QH ⊥x 轴于点 H ,则点 H (b +12,0), 在 Rt △MQH 中,可知 ∠QMH =∠MQH =45∘. ∴ QH =MH ,QM =√2MH .∵ 点 M (m,0),∴ 0−(−b2−34)=(b +12)−m ,解得 m =b2−14.∵ √2AM +2QM =33√24, ∴ √2[(b2−14)−(−1)]+2√2[(b +12)−(b2−14)]=33√24.∴ b =4.3. 【答案】(1) ∵ 抛物线 y =x 2+mx −2m 经过 A (1,0), ∴0=1+m −2m ,解得 m =1. ∴ 抛物线的解析式为 y =x 2+x −2. ∵y =x 2+x −2=(x +12)2−94,∴ 顶点 P 的坐标为 (−12,94). (2) 由题意可知,抛物线 y =x 2+mx −2m 的顶点 P 的坐标为 (−m 2,−m 2+8m4).由点 A (1,0) 在 x 轴正半轴上,点 P 在 x 轴下方,∠AOP =45∘,知点 P 在第四象限. 如图 1,过点 P 作 PQ ⊥x 轴于点 Q , 则 ∠POQ =∠OPQ =45∘. 可知 PQ =OQ ,即m 2+8m4=−m2,解得 m 1=0,m 2=−10.当 m =0 时,点 P 不在第四象限,舍去. ∴m =−10.∴ 抛物线解析式为 y =x 2−10x +20.(3) 由 y =x 2+mx −2m =(x −2)m +x 2 可知,当 x =2 时,无论 m 取何值,y 都等于 4,得点 H 的坐标为 (2,4).如图 2,过点 A 作 AD ⊥AH ,交射线 HP 于点 D ,分别过点 D ,H 作 x 轴的垂线,垂足分别为 E ,G ,则 ∠DEA =∠AGH =90∘. ∵∠DAH =90∘,∠AHD =45∘, ∴∠ADH =45∘. ∴AH =AD .∵∠DAE +∠HAG =∠AHG +∠HAG =90∘, ∴∠DAE =∠AHG . 在 △ADE 和 △HAG 中, {∠DEA =∠AGH =90∘,∠DAE =∠AHG,AD =HA,∴△ADE ≌△HAG .∴DE =AG =1,AE =HG =4.可得点 D 的坐标为 (−3,1) 或 (5,−1).①当点 D 的坐标为 (−3,1) 时,可得直线 DH 的解析式为 y =35x +145.∵P (−m2,−m 2+8m4) 在直线 y =35x +145上,∴−m 2+8m4=35×(−m 2)+145,解得 m 3=−4,m 4=−145. 当 m =−4 时,点 P 与点 H 重合,不符合题意, ∴m =−145.②当点 D 的坐标为 (5,−1) 时,可得直线 DH 的解析式为 y =−53x +223.∵P (−m 2,−m 2+8m4) 在直线 y =−53x +223上,∴−m 2+8m4=−53×(−m2)+223,解得 m 5=−4(舍),m 6=−223. ∴m =−223.综上,m =−145 或 m =−223. 故抛物线解析式为 y =x 2−145x +285或 y =x 2−223x +443.4. 【答案】(1) ∵ 抛物线 y =x 2+bx −3 经过点 A (−1,0), ∴ 0=1−b −3,解得 b =−2. ∴ 抛物线的解析式为 y =x 2−2x −3. ∵ y =x 2−2x −3=(x −1)2−4,∴ 顶点坐标为 (1,−4).(2) ①由点 P (m,t ) 在抛物线 y =x 2−2x −3 上,有 t =m 2−2m −3. 又点 Pʹ 和 P 关于原点对称,有 Pʹ(−m,−t ). ∵ 点 Pʹ 落在抛物线 y =x 2−2x −3 上,∴ −t =(−m )2−2(−m )−3,即 t =−m 2−2m +3. ∴ m 2−2m −3=−m 2−2m +3. 解得 m 1=√3,m 2=−√3.②由题意知,Pʹ(−m,−t ) 在第二象限, ∴ −m <0,−t >0,即 m >0,t <0.又抛物线 y =x 2−2x −3 的顶点坐标是 (1,−4),得 −4≤t <0. 过点 Pʹ 作 PʹH ⊥x 轴,H 为垂足,又 H (−m,0). 又 A (−1,0),t =m 2−2m −3,则 PʹH 2=t 2,AH 2=(−m +1)2=m 2−2m +1=t +4. 当点 A 和 H 不重合时,在 Rt △PʹAH 中,PʹA 2=PʹH 2+AH 2; 当点 A 和 H 重合时,AH =0,PʹA 2=PʹH 2,符合上式. ∴ PʹA 2=PʹH 2+AH 2,即 PʹA 2=t 2+t +4(−4≤t <0). 记 yʹ=t 2+t +4,则 yʹ=(t +12)2+154.∴ 当 t =−12 时,yʹ 取得最小值.把 t =−12代入 t =m 2−2m −3,得 −12=m 2−2m −3.解得 m 1=2−√142,m 2=2+√142.由 m >0,可知 m =2−√142不符合题意.∴ m =2+√142.5. 【答案】(1) ∵ y =x 2−2x +1=(x −1)2, ∴ 顶点 P 的坐标为(1,0). ∵ 当 x =0 时,y =1, ∴ 点 Q 的坐标为(0,1).(2) ①根据题意,设抛物线 Cʹ 的解析式为 y =x 2−2x +m , 则点 Qʹ 的坐标为 (0,m ),其中 m >1.得 OQʹ=m . ∵ 点 F (1,12),过点 F 作 FH ⊥OQʹ,垂足为 H , 则 FH =1,QʹH =m −12.在 Rt △FQʹH 中,根据勾股定理, 得 FQʹ2=QʹH 2+FH 2.∴ FQʹ2=(m −12)2+12=m 2−m +54.∵ FQʹ=OQʹ,∴ m 2−m +54=m 2,解得 m =54. ∴ 抛物线 Cʹ 的解析式为 y =x 2−2x +54.②由①有,Qʹ(0,54),F (1,12),P (1,0), ∴ 直线 FQʹ 的解析式为 y =−34x +54①,∵FQʹ⊥PK ,P (1,0),∴ 直线 PK 的解析式为 y =43x −43 ②联立①②得出,直线 FQʹ 与 PK 的交点 M 坐标为 (3125,825),∵ 点 P ,K 关于直线 FQʹ 对称, ∴K (3725,1625). ∵F (1,12),∴ 直线 FK 的解析式为 y =724x +524③,∵ 射线 FK 与抛物线 C ′:y =x 2−2x +54④相交于点 A , ∴ 联立③④得,{x =53,y =2536或 {x =58,y =2564(舍), ∴A (53,2536).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津中考数学压轴题全搞定文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]九年级数学冲刺讲义二次函数12题1. 已知关于x的函数同时满足下列三个条件:①函数的图象不经过第二象限;②当x<2时,对应的函数值y<0;③当x<2时,函数值y随x的增大而增大.你认为符合要求的函数的解析式可以是:(写出一个即可,答案不唯一).2.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0;④的最小值为3.其中,正确结论的个数为()A.1个B.2个C.3个D.4个3.已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB 的中点,则CD的长为()A.B.C.D.4.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为()A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或35.已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m>2.其中,正确结论的个数是()A.0 B.1 C.2 D.36.若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3;②m>﹣;③二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是()A.0 B.1 C.2 D.37.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0其中,正确结论的个数是()A.1 B.2 C.3 D.48.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.2个B.3个C.4个D.5个9. 已知抛物线y=x2-(2m-1)x+2m不经过第三象限,且当x>2时,函数值y随x的增大而增大,则实数m的取值范围是()≤m≤ ≥ ≤m≤1 <m≤网格题18题1. 如图,在下列网格中,每个小正方形的边长都是1,点A 、B 、Q 、P 均为格点。
(1)线段AB 的长度等于___________(2)点M 、N 是线段AB 上的两个动点,且始终满足BN+AM=10267,若点M 、N 运动到恰好使得QN+PM 的值最小时,请借助网格用无刻度直尺画出点N 的位置,并简要说明你的作图方法___________________________________________________________________2. (2015天津)在每个小正方形的边长为1的网格中.点A ,B ,C ,D 均在格点上,点E 、F 分别为线段BC 、DB 上的动点,且BE=DF .(Ⅰ)如图①,当BE=时,计算AE +AF 的值等于(Ⅱ)当AE +AF 取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段AE ,AF ,并简要说明点E 和点F 的位置如何找到的(不要求证明) .3. 如图,将△ABC 放在每个小正方形的边长为1的网格中,点A ,点B ,点C 均落在格点上.(1)边AC 的长等于 .(2)以点C 为旋转中心,把△ABC 顺时针旋转,得到△A ′B ′C ,使点B 的对应点B ′恰好落在边AC 上,请在如图所示的网格中,用无刻度的直尺,作出旋转后的图形,并简要说明画图方法(不要求证明).4. 如图,将△ABP 放在每个小正方形的边长为1的网格中,点A 、B 、P 均落在格点上.(1)△ABP 的面积等于 ;(2)若线段AB 水平移动到A ′B ′,且使PA ′+PB ′最短,请你在如图所示的网格中,用直尺画出A ′B ′,并简要说明画图的方法(不要求证明)24题(平移1-4、翻折问题5-8)1.(天津)在平面直角坐标系中,已知点A(﹣2,0),点B(0,4),点E在OB 上,且∠OAE=∠OBA.(Ⅰ)如图①,求点E的坐标;(Ⅱ)如图②,将△AEO沿x轴向右平移得到△A′E′O′,连接A′B、BE′.①设AA′=m,其中0<m<2,试用含m的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;②当A′B+BE′取得最小值时,求点E′的坐标(直接写出结果即可).2. 两个直角边为6的全等的等腰Rt△AOB和Rt△CED中,按图1所示的位置放置,A 与C重合,O与E重合.(1)求图1中A,B,D三个点的坐标.(2)Rt△AOB固定不动,Rt△CED沿x轴以每秒2个单位长度的速度向右运动,当点D运动到与B点重合时停止,设运动x秒后Rt△AOB和Rt△CED的重叠部分面积为y,求y与x之间的函数关系式.(3)当Rt△CED以(2)中的速度和方向运动,运动时间x=4秒时,Rt△CED运动到如图2所示的位置,求点G的坐标.(4)何时Rt△AOB和Rt△CED的重叠部分面积等于1,直接写出此时x的值3.如图,在平面直角坐标系中,∠OCA=90°,点A在x轴上,OC=AC=4,D、E分别是OC、AC的中点,将四边形OAED沿x轴向右平移,得四边形PQRS.设OP=m(0<m <4).(Ⅰ)在平移过程中,四边形OPSD能否成为菱形若能,求出此时m的值;若不能,说明理由.(Ⅱ)设平移过程中△OAC与四边形SPQR重叠部分的面积为S,试用含m的式子表示S.(Ⅲ)当S=3时,求点P的坐标(直接写出结果即可)4,两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上.其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).(1)当点C落在边EF上时,x=cm;(2)求y关于x的函数解析式,并写出自变量x的取值范围;(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.5.如图,在平面直角坐标系中,直角三角形OAB的顶点O在坐标原点,A(2,0),B(0,32),将△OAB沿y轴翻折,得△OCB.(1)求OCB的度数;(2)动点P在线段CA上从点C向点A运动,PD⊥BC于点D,把△PCD沿y轴翻折,得△QAE,设△ABC被△PCD和△QAE盖住部分的面积为S1,未被盖住的部分的面积为S2.①设CP=a(a>0),用含a的代数式分别表示S1,S2;②直接写出当S1=S2时点P的坐标.6. 如图,将一个矩形纸片ABCD,放置在平面直角坐标系中,A(0,0),B(4,0),D(0,3),M是边CD上一点,将△ADM沿直线AM折叠,得到△ANM.(Ⅰ)当AN平分∠MAB时,求∠DAM的度数和点M的坐标;(Ⅱ)连接BN,当DM=1时,求△ABN的面积;(Ⅲ)当射线BN交线段CD于点F时,求DF的最大值.(直接写出答案)7.(天津)将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m,折叠后的△AM′N与四边形OMNB重叠部分的面积为S.(Ⅰ)如图①,当点A′与顶点B重合时,求点M的坐标;(Ⅱ)如图②,当点A′,落在第二象限时,A′M与OB相交于点C,试用含m的式子表示S;(Ⅲ)当S=时,求点M的坐标(直接写出结果即可).8. (天津)已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0)、B(0,6),点P为BC边上的动点(点P不与点点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.(1)如图1,当∠BOP=30°时,求点P的坐标;(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;(3)在(2)的条件下,当点C′恰好落在边OA上时如图3,求点P的坐标(直接写出结果即可).25题1.已知:关于x 的方程x 2+(m-4)x-3(m-1)=0有两个不相等的实数根.(1)求m 的取值范围; (2)抛物线C :y=-x 2-(m-4)x+3(m-1)与x 轴交于A 、B 两点.若m ≤-1且直线l 1:12m y x =--经过点A ,求抛物线C 的函数解析式; (3)在(2)的条件下,直线l 1:12m y x =--绕着点A 旋转得到直线l 2:y=kx+b ,设直线l 2与y 轴交于点D ,与抛物线C 交于点M (M 不与点A 重合),当32MA AD ≤时,求k 的取值范围.2. 如图,抛物线y 1=x 2﹣1交x 轴的正半轴于点A ,交y 轴于点B ,将此抛物线向右平移4个单位得抛物线y 2,两条抛物线相交于点C .(1)请直接写出抛物线y 2的解析式;(2)若点P 是x 轴上一动点,且满足∠CPA=∠OBA ,求出所有满足条件的P 点坐标;(3)在第四象限内抛物线y 2上,是否存在点Q ,使得△QOC 中OC 边上的高h 有最大值若存在,请求出点Q 的坐标及h 的最大值;若不存在,请说明理由。
3. 如图,平面直角坐标系中,抛物线y=x 2﹣2x 与x轴交与O 、B 两点,顶点为P ,连接OP 、BP ,直线y=x ﹣4与y 轴交于点C ,与x 轴交于点D .(1)直接写出点B 坐标 ;判断△OBP 的形状 ;(2)将抛物线向下平移m 个单位长度,平移的过程中交y 轴于点A ,分别连接CP 、DP :①当S △PCD =S △POC 时,求平移后的抛物线的顶点坐标;②在向下平移的过程中,试用含m 的式子表示S △PCD 和S △POD4. 已知O点为坐标原点,抛物线y1=ax2+bx+c(a≠0)与y轴交于点C,且O,C两点间的距离为3.(1)求点C的坐标;(2)抛物线y1=ax2+bx+c(a≠0)与x轴交于点A(x1,0),B(x2,0),x1x2<0,|x1|+|x2|=4.点A,C在直线y2=-3x+t上.①求该抛物线的顶点坐标;②将抛物线y1=ax2+bx+c(a≠0)向左平移n(n>0)个单位,记平移后y随x的增大而增大的部分为P,直线y2=-3x+t向下平移n个单位,当平移后的直线与P有公共点,求2n2-5n 的最小值.5. 在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.(1)求过A,B,C三点的抛物线的解析式;(2)P为抛物线上一点,它关于原点的对称点为Q.①当四边形PBQC为菱形时,求点P的坐标;②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大并说明理由.6. 已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1,).(Ⅰ)求点P,Q的坐标;(Ⅱ)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.①求抛物线C′的解析式;②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.。
